| Issue |
A&A
Volume 648, April 2021
The LOFAR Two Meter Sky Survey
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 20 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202038828 | |
| Published online | 07 April 2021 | |
The LOFAR Two-meter Sky Survey: Deep Fields Data Release 1
II. The ELAIS-N1 LOFAR deep field★,★★
1
SUPA, Institute for Astronomy,
Royal Observatory,
Blackford Hill,
Edinburgh,
EH9 3HJ,
UK
e-mail: jsm@roe.ac.uk
2
UK Astronomy Technology Centre, Royal Observatory,
Blackford Hill,
Edinburgh,
EH9 3HJ,
UK
3
GEPI, Observatoire de Paris, CNRS, Universite Paris Diderot,
5 place Jules Janssen,
92190
Meudon,
France
4
Department of Physics & Electronics, Rhodes University,
PO Box 94,
Grahamstown,
6140,
South Africa
5
Centre for Astrophysics Research, School of Physics, Astronomy and Mathematics, University of Hertfordshire,
College Lane,
Hatfield
AL10 9AB,
UK
6
ASTRON, the Netherlands Institute for Radio Astronomy,
Postbus 2,
7990 AA
Dwingeloo,
The Netherlands
7
Ruđer Bošković Institute,
Bijenička cesta 54,
10 000
Zagreb,
Croatia
8
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
9
INAF – Istituto di Radioastronomia,
via Gobetti 101,
40129
Bologna,
Italy
10
Italian ALMA Regional Centre,
Via Gobetti 101,
40129
Bologna,
Italy
11
INAF – Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova,
Italy
12
Max Planck Institute for Astrophysics,
Karl-Schwarzschild-Str. 1,
85748
Garching, Germany
13
Harvard-Smithsonian Center for Astrophysics,
60 Garden St,
Cambridge,
MA
02138,
USA
14
Astrophysics, Department of Physics,
Keble Road,
OX1 3RH,
UK
15
University of the Western Cape,
Private Bag X17,
Bellville,
Cape Town
7535,
South Africa
16
Kapteyn Astronomical Institute, University of Groningen,
Postbus 800,
9700 AV
Groningen,
The Netherlands
17
School of Physical Sciences and Centre for Astrophysics & Relativity, Dublin City University,
Glasnevin,
D09 W6Y4,
Ireland
18
Fakultät für Physik, Universität Bielefeld,
Postfach 100131,
33501
Bielefeld,
Germany
19
SRON Netherlands Institute for Space Research,
Landleven 12
9747 AD,
Groningen,
The Netherlands
Received:
2
July
2020
Accepted:
31
July
2020
The LOFAR Two-metre Sky Survey (LoTSS) will cover the full northern sky and, additionally, aims to observe the LoTSS deep fields to a noise level of ≲10 μJy beam−1 over several tens of square degrees in areas that have the most extensive ancillary data. This paper presents the ELAIS-N1 deep field, the deepest of the LoTSS deep fields to date. With an effective observing time of 163.7 h, it reaches a root mean square noise level of ≲20 μJy beam−1 in the central region (and below 30 μJy beam−1 over 10 square degrees). The resolution is ~6 arcsecs and 84 862 radio sources were detected in the full area (68 square degrees) with 74 127 sources in the highest quality area at less than 3 degrees from the pointing centre. The observation reaches a sky density of more than 5000 sources per square degree in the central region (~5 square degrees). We present the calibration procedure, which addresses the special configuration of some observations and the extended bandwidth covered (115–177 MHz; central frequency 146.2 MHz) compared to standard LoTSS. We also describe the methods used to calibrate the flux density scale using cross-matching with sources detected by other radio surveys in the literature. We find the flux density uncertainty related to the flux density scale to be ~6.5 per cent. By studying the variations of the flux density measurements between different epochs, we show that relative flux density calibration is reliable out to about a 3 degree radius, but that additional flux density uncertainty is present for all sources at about the 3 per cent level; this is likely to be associated with residual calibration errors, and is shown to be more significant in datasets with poorer ionosphere conditions. We also provide intra-band spectral indices, which can be useful to detect sources with unusual spectral properties. The final uncertainty in the flux densities is estimated to be ~10 per cent for ELAIS-N1.
Key words: surveys / catalogs / radio continuum: general / radio continuum: galaxies
Catalogs and images are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/648/A2
The data associated with this article are released at: https://lofar-surveys.org
© ESO 2021
1 Introduction
Deep, wide-area radio surveys, especially when combined with high-quality pan-chromatic data from ultraviolet to far-infrared wavelengths, provide an unparalleled view of the evolving Universe. As radio emission is unaffected by dust absorption, the radio waveband offers an unbiased view of star-forming galaxies, which at low radio frequencies primarily emit due to non-thermal synchrotron emission associated with supernovae (e.g. Condon 1992). Radio observations also provide a unique insight into the growth of the supermassive black holes that can be found in the centres of massive galaxies. As well as providing a largely dust- and orientation-independent view of powerful active galactic nuclei (AGN), radio observations are the only way to reliably identify the low-luminosity ‘jet-mode’ AGN, hosted by massive quiescent galaxies, the feedback from which is understood to play a critical role in regulating the growth of massive galaxies (Best et al. 2005; Bower et al. 2006; Croton et al. 2006; Best & Heckman 2012; Heckman & Best 2014).
Radio surveys have been used to study the mechanisms triggering AGN jets and their feedback (e.g. Best & Heckman 2012), but deep observations are required to study their evolution through the history of the Universe (Best et al. 2014). The population of star-forming galaxies starts to dominate at lower radio luminosities and deep surveys are crucial to further understand their properties (Gürkan et al. 2019). The low-luminosity end of the far infrared to radio correlation can also be probed this way (Calistro Rivera et al. 2017). However, the deep radio observations required to study these source populations at high redshifts are usually limited to pencil beam surveys (Ciliegi et al. 2005; Bondi et al. 2007; Morrison et al. 2010; Murphy et al. 2017a; Owen 2018), and the deepest degree-scale surveys currently available only cover 2 square degrees (e.g. Schinnerer et al. 2007; Smolčić et al. 2017). Although MIGHTEE (Jarvis et al. 2016) will extend this at GHz frequencies.
The Low Frequency Array (LOFAR; van Haarlem et al. 2013) combines a wide field of view with a high sensitivity and high angular resolution; this combination of capabilities enables deep, wide-area, high-fidelityradio surveys. The LOFAR Two Metre Sky Survey (LoTSS; Shimwell et al. 2017, 2019) is generating a wide-area survey of the sky covering the Northern Hemisphere. It reaches a sensitivity of ≲ 100 μJy beam−1 with a full width at half maximum (FWHM) synthesized beam of ~6 arcsecs and its first data release (DR1) covering 424 square degrees is already public. This first data release has already enabled the study of the low-frequency sky in unprecedented ways (Croston et al. 2019; Gürkan et al. 2019; Hardcastle et al. 2019; Mahatma et al. 2019; Mingo et al. 2019; Mooney et al. 2019; Morabito et al. 2019; Sabater et al. 2019; Stacey et al. 2019; Wang et al. 2019). The LoTSS DR1 has already probed the relation between the triggering of AGN and the stellar mass (Sabater et al. 2019) showing that all the most massive galaxies present AGN-related radio emission once the observations are deep enough to detect it.
We are complementing the wide-area LoTSS survey with a series of deeper pointings, known as the LoTSS deep fields. The LoTSS deep fields ultimately aim to reach an RMS depth of ~10 μJy beam−1, which is comparable to the deepest existing pencil-beam surveys, but will achieve this over a sky area of 30–50 square degrees. This is sufficient sky area to probe all cosmic environments at z ≳ 1, as well as to build up statistically meaningful samples of the rarer objects, such as low-luminosity AGN and starburst galaxies at high redshifts. It will have the sensitivity to detect Milky Way like galaxies at z ≳ 1 or strong starburst galaxies up to z ~ 5. The fields selected for the deep survey are those with the highest-quality degree-scale multi-wavelength data at declinations above 30 degrees, where LOFAR has its highest sensitivity: Boötes (Jannuzi & Dey 1999), the Lockman Hole (Lockman et al. 1986), and the European Large-Area ISO Survey-North 1 (ELAIS-N1 Oliver et al. 2000) which is the subject of this paper. The coverage of wide areas in different lines of sight will help to minimize the effects of cosmic variance. The LoTSS deep fields will remain competitive even after the advent of the first phase of the Square Kilometre Array (SKA; Dewdney et al. 2009; Ekers 2012), as their sensitivity will reach below the expected confusion noise of SKA-low at these frequencies (Prandoni & Seymour 2015; Zwart et al. 2015). Finally, given the multi-epoch observations required by the LoTSS deep surveys, the data can be used to detect transients, source variability and stellar emission.
The calibration of the deep fields data presents several challenges. The errors in the primary beam models of a phased array like LOFAR and the direction-dependent ionospheric effects are addressed by the new calibration techniques developed by Tasse et al. (2021; hereafter Paper I). These third generation radio-interferometry calibration techniques allow us to reach depths very close to the thermal noise limit. Paper I also presents the calibration of Boötes and the Lockman Hole fields. The management of the big data volumes and computing requirements were explored and solved using new computing infrastructures like the cloud (Sabater et al. 2017) or advanced High Throughput Processing infrastructures and techniques (e.g. Mechev et al. 2017). This first LoTSS deep fields data release already covers a sky area of ≳ 30 deg2 (in Boötes, the Lockman Hole, and ELAIS-N1) to rms depths ~30 μJy beam−1. The astrometric precision achieved in the calibration is good enough to allow the cross-match with multi-wavelength counterparts to radio sources. This data enrichment has proven to be fundamental for the generation of value added science in LoTSS DR1 (Williams et al. 2019; Duncan et al. 2019). Kondapally et al. (2021; hereafter Paper III) has performed a careful compilation of the multiwavelength data available for radio source cross-identification in the deep fields. Host galaxy identifications were found for over 97 per cent of the radio sources detected in the region of excellent multiwavelength photometry.In the future, WEAVE-LOFAR (Smith et al. 2016) will obtain deep spectroscopic measurements for essentially all sources detected in the LoTSS deep fields but high quality photometric redshifts have been produced by Duncan et al. (2021; hereafter Paper IV). That study provides photometric redshifts and stellar mass estimates for millions of sources in the fields, including faint radio sources and optical sources not detected in radio.
In this paper, which is the second in the LoTSS deep fields series, we present the ELAIS-N1 deep field. In Sect. 2 we go through a description of the LOFAR observations and the additional radio data used in this study. Section 3 describes the specific calibration process followed for ELAIS-N1, which differed in some respects from the standard LoTSS approach due to the adoption of a different observing set-up. This section also contains a discussion of the techniques used to carefully calibrate the flux density scale. We describe the final data products and catalogues in Sect. 4 while in Sect. 5 a detailed study of the noise levels, flux density variability, extended sources, and spectralindex are presented. Finally, Sect. 6 summarizes the work and highlights the main conclusions.
ELAIS-N1 observations.
2 The data
The ELAIS-N1 field (Oliver et al. 2000) was chosen for its ample multi-frequency coverage. To allow deep observations, it was originally selected: (a) to be at high ecliptic latitudes to minimize the impact of zodiacal light; (b) to have low far infrared intensity to minimize the impact of galactic cirrus and; (c) to avoid bright infrared sources that can saturate infrared observations. The deep multi-wavelength (150 nm–500 μm) data are covered by Paper III and here we focus in the radio observations.
2.1 LOFAR observations
The ELAIS-N1 data presented in this paper were taken in the LOFAR observation cycles 0, 2, and 4 (proposals LC0_019, LC2_024, and, LC4_008 respectively) from May 2013 to August 2015. The different observations and datasets are summarized in Table 1. The data observed in early LOFAR cycles (0 and 2) were taken jointly with the LOFAR Epoch of Reionization Key Science Project team, as a potential field for EoR studies (Jelić et al. 2014). Hence, the observing configuration was different from the standard LoTSS configuration. The observations of the ELAIS-N1 field were taken with the LOFAR high band antennas with a frequency ranging from 114.9 to 177.4 MHz. The phase centre of the main field is located at 16:11:00 +55:00:00 (J2000). The configuration of the antennas was ‘HBA_DUAL_INNER’. In this configuration the HBA antennas of the LOFAR core stations are split into two independentstations and the HBA tiles of the LOFAR remote stations are cropped to a shape similar to that of the core stations. This provides a uniform general shape of the primary beam over the entirety of the LOFAR stations in the Netherlands.
The observations contain additional data for either 3 (Cycle 4) or 6 (cycles 0 and 2) flanking fields simultaneously observed with the ELAIS-N1 central region but with a much lower effective bandwidth (6 × 19 or 3 × 38 spectral sub-bands in comparison to 371 sub-bands in the main target field). These data were not used, except for the dataset 000 in which the bandwidth was evenly distributed between the 7 target fields (7 × 69 sub-bands each). In this case, we used the data of the flanking field whose centre was close to the calibrator source 87GB 160333.2+573543 (at 16:04:34.5 +57:28:01.7 in J2000) to assist with calibrating the flux density scale, as explained later in Sect. 3.5. The frequency limits for this dataset were similar to that of the other datasets but its frequency coverage was sparse for each of the fields.
Of the 371 spectral sub-bands observed in the central field, 320 correspond to a 62.5 MHz frequency range centred at 146 MHz which was used for the deep images presented in this paper. The rest of the sub-bands correspond to a higher frequency band ranging from 179.4 to 189.2 MHz which was not considered for this study. The reduced size of the primary beam at those high frequencies, combined with the significant modification of the calibration pipeline that would be required to take them into account, contributed to the decision to study them at a later stage. We limited the analysis to the core and remote LOFAR stations but the observations also include data from the international stations that will be used in the future for sub-arcsecond imaging in the central part of this field (Jackson et al. 2016; Morabito et al. 2016, Sweijen et al., in prep.).
All the observations were preceded by a 5 to 10-minute run on the calibrator 3C295 and succeeded by another 5 to 10-minute run on 3C380. The latter was the one selected for the calibration process because the pre-existing model for this source seemed to produce the best results. The model was in the flux density scale of Scaife & Heald (2012). The calibration and analysis of the data are presented in Sect. 3.
2.2 Additional radio surveys of ELAIS-N1
Additional radio data for the ELAIS-N1 are available from several large-area radio surveys and catalogues such as: the 87GB catalogue (Becker et al. 1991; Gregory & Condon 1991) at 4.85 GHz; the NRAO Very Large Array (VLA) Sky Survey (NVSS; Condon et al. 1998) at 1.4 GHz; the Faint Images of the Radio Sky at Twenty-Centimeters survey (FIRST; Becker et al. 1995) at 1.4 GHz; the Texas Survey of Radio Sources (Douglas et al. 1996) at 365 MHz; the Westerbork Northern Sky Survey (WENSS; Rengelink et al. 1997) at 325 MHz; the Sixth Cambridge Survey of Radio Sources (6C; Hales et al. 1990) at 151 MHz; the GMRT 150 MHz All-sky Radio Survey (TGSS; Intema et al. 2017); the VLA Low-frequency Sky Survey (VLSS; Cohen et al. 2007) at 74 MHz; the VLSS Redux (VLSSr; Lane et al. 2014) at 74 MHz; and the Eighth Cambridge Survey of Radio Sources catalogue (8C; Hales et al. 1995) at 38 MHz.
Apart from these, it has also been observed to greater depths by targeted radio surveys. Ciliegi et al. (1999) observed the ELAIS-N1 field with the VLA at 1.4 GHz and detected 867 sources. Later, Taylor et al. (2007) observed the field in polarization at the same frequency but over a wider area, finding 786 compact sources. Garn et al. (2008a) and Sirothia et al. (2009) observed the field with the Giant Metrewave Radio Telescope (GMRT) at 610 and 325 MHz respectively, detecting 2500 and 1286 sources. Croft et al. (2013) observed several fields including ELAIS-N1 with the Allen Telescope Array at 3.1 GHz detecting ≈200 sources in the area. Taylor & Jagannathan (2016) studied the orientation of extended radio sources based on new data taken by the GMRT at 612 MHz. Chakraborty et al. (2019) observed ELAIS-N1 with the upgraded GMRT at frequencies between 300 and 500 MHz resulting in a catalogue of 2528 sources. Finally, the most recent observation of ELAIS-N1 was taken by Ocran et al. (2020) with the GMRT at 610 MHz and produced a catalogue of 4290 sources. In Fig. 1 we show the parameters of these previous observations targeting ELAIS-N1 compared to our study, focusing mainly on the RMS noise achieved, the area covered, the resolution, and the public availability of the data. As shown in the figure, if we consider a canonical spectral index of α = 0.7 (for Sν ∝ν−α; Condon et al. 2002)our catalogue reaches greater depth than any of the previous catalogues as well as covering a substantially wider area than the other deeper surveys, at higher angular resolution than most.
3 Data calibration
The calibration and processing of the ELAIS-N1 data presents several challenges. The first one is the data size and computing power required. Each dataset can amount to 80 TB and its calibration requires several CPU-years which makes critical the use of a High Throughput Computing (HTC) or High Performance Computing (HPC) system for their processing (Sabater et al. 2017). The second one is the correction of the especially strong effect of the ionosphere on the signal at low frequencies (e.g. Intema et al. 2009). This correction required the development of new calibration pipelines and software which are outlined in Paper I of this series.
The volume of data is reduced as it is processed through the pipeline. The original amount of data corresponding to the observations listed in Table 1 is ≈2 PB. An individual Cycle 2 observation of 8 h amounts to ≈80 TB as outputted from the observatory in raw format. This volume was reduced to about 12 TB by pre-processing (see Sect. 3.1) and to 4 TB after the first calibration step (PREFACTOR; see Sect. 3.2). The final calibrated measurement set (MS; van Diepen 2015) for each observation occupies ≈0.9 TB which can be further compressed to about 80 GB by averaging and removing redundant data and using DYSCO compression (Offringa 2016). Finally, the deep image of the ELAIS-N1 field that corresponds to 163.7 h of observation amounts to a mere 1.5 GB. Hence, the data rates expressed as a fraction of total observing time follow this sequence as the calibration progresses: 2.7 GB s−1 → 350 MB s−1 → 88 MB s−1 → 31 MB s−1 → 2.6 MB s−1 → 2.5 kB s−1.
 |
Fig. 1 Depths and frequencies of radio surveys in the literature targeting the ELAIS-N1 field. The area of each circle is proportional to the area covered by the survey. The area of the inner dot is proportional to the resolution with smaller dots indicating better resolutions (ranging from 4.5 arcsecs up to 100 arcsecs). The data were not found to be publicly available for the observations outlined with a dashed line (those of Taylor et al. 2007; Taylor & Jagannathan 2016; Ocran et al. 2020). The solid line indicates a spectral index of 0.8 and the dashed line one of 0.7. |
3.1 Pre-processing
The calibration of data taken in different cycles was performed slightly differently. Cycle 0 and 2 data were pre-processed by the Epoch of Reionization LOFAR Key Science Project team in order to remove radio-frequency interference (RFI) and demix the contribution of bright off-axis sources (van der Tol et al. 2007). Each of the 320 sub-bands into which the frequency range was divided consisted of 64 channels. To minimize bandpass effects, the two upper and two lower channels were removed and the remaining 60 channels averaged by a factor 4 to a final 15 channels per sub-band. The scan time was averaged by a factor 2 up to 2 s.
The Cycle 4 data were observed in a configuration similar to that of the rest of LoTSS Survey data (Shimwell et al. 2017, 2019) but maintaining the extended bandwidth. In this case the channels at the edge of the sub-bands were not discarded and the data were averaged to 16 channels per sub-band and 2 s per scan.
3.2 Direction-independent calibration
The first step of the calibration for all the datasets used for the final deep image was made with the software PREFACTOR1 or earlier versions of this pipeline. The pipeline is described by de Gasperin et al. (2019) and earlier versions are outlined in van Weeren et al. (2016) and Williams et al. (2016). The observation of a calibrator source before or after the main target is used to obtain an estimation of several calibration parameters. In our case we used 3C380 as our calibrator source. The calibrator data are first flagged for RFI with AOFLAGGER (Offringa et al. 2012) and for problematic antennas or periods of time. The data are then averaged to 4 s of time resolution and 1 channel per sub-band. Then the following effects are estimated and corrected for, in order: (a) the polarization misalignment introduced by the station calibration tables; (b) the Faraday rotation; (c) the amplitude bandpass; (d) the clock offset originating mainly from the drift of the clock in the remote stations and; (e) the ionospheric direction-independent delays.
Once the calibration tables are generated, a first estimation of the effect of the ionosphere (Mevius et al. 2016) is made with RMEXTRACT2 (Mevius 2018). The data are flagged for RFI and the parts of the data that are heavily affected by A-team sources3 (data with an A-team predicted flux density contribution higher than 5 Jy) are flagged. After that, the calibration solutions obtained forthe calibration target combined with the preliminary ionospheric effect estimations are applied to the target field. The data are then concatenated in chunks of 10 sub-bands which increases their signal-to-noise ratio (S/N) for the final phase gain calibration. A model of the field is required for this step. For ELAIS-N1, the sky model was built up historically from early Cycle observations. Appendix A details the creation of that model. The final outputs of the pipeline are the corrected uv data, an estimated model of the sky and several diagnostics plots to check the accuracy of the calibration.
A primitive version of PREFACTOR was used for Cycle 0 datasets which were used as test-beds for the development of the first direction-independent attempts. As a preparation for the final deep imaging calibration combining all the datasets, the PREFACTOR calibration pipeline was applied to Cycle 2 data in the Amazon Web Services (AWS) cloud premises (see Appendix B and Sabater et al. 2017). Cycle 4 data were run through the PREFACTOR pipeline set up in SURF-Sara (Mechev et al. 2017). One technical difficulty arose from the uneven spacing between channels in Cycle 0 and 2 data after the sub-bands were combined. The frequencies for the different bands were edited to be spaced homogeneously which changed some of them by factors of a few per thousand. This modification permitted us to run the standard LOFAR software on the data without introducing significant biases into the calibration. All the pre-calibrated datasets were transferred to the compute cluster CUILLIN at the University of Edinburgh for further processing.
3.3 Direction-dependent calibration
The third generation calibration and imaging techniques for radio astronomy involve the estimation and compensation for direction-dependent effects (Paper I). The development of the solver KILLMS4 (Tasse 2014a,b; Smirnov & Tasse 2015) and the imager DDFACET5 (Tasse et al. 2018) constituted a big step forwards in the calibration effort. A pipeline that leverages these tools, named DDF-PIPELINE6, was developed. Versions 1 and 2 of the pipeline are explained in detail in Sect. 3 and 4 of Paper I respectively, and the reader is refered to that paper for full details; here a brief summary is provided.
DDF-PIPELINE works on the data that has been calibrated by PREFACTOR in a direction-independent manner. A subset of the data, composed of the central 60 sub-bands, is imaged and the field is divided in facets7 using a clustering process. This subset is calibrated and imaged to produce a preliminary direction-dependent sky model and a deconvolution mask. Due to the difficulty to obtain a true flux density calibration from LOFAR data alone, these steps also include a bootstrap process to determine the flux density scale corrections (Hardcastle et al. 2016). In DDF-PIPELINE V2, the corrections are derived by comparison with matched WENSS and NVSS sources, using an empirical mean spectral index. With the new improved and flux-corrected model and the preliminary deconvolution masks, the full bandwidth data are subsequently processed. The final steps consist of a direction-dependent calibration followed by a direction-independent calibration, an imaging step and a further set of direction-dependent calibrations (slow and fast) designed to recover as much extended emission as possible. The final step is an imaging run including the solution and correction of the astrometric errors for each individual facet.
The run combining all the datasets was prepared by running the last version of the DDF-PIPELINE on dataset 015 which had a low noise level. The output model and mask of this run was used as the final input of the pipeline run on the combined set of data. In this case, the model and mask were used as an input to do a direction-independent and direction-dependent calibration of each dataset. After that they were imaged all together with the appropriate calibration solutions applied. During the imaging step the mask was updated to ensure that faint sources which were only detected in the combined dataset were deconvolved. Cycle 0 datasets and datasets 025 and 029 were excluded from the final image due to the poor noise levels or problems with the data. The final list of datasets used is flagged ‘1’ in the column ‘Deep’ of Table 1.
3.4 Pipeline data products
The final run of the DDF-PIPELINE produced the following set of data products: (a) Solutions corresponding to each facet and dataset composed of quick and slow smoothed solutions (see Sect. 4.3 in Paper I); (b) deep high resolution (6 arcsecs) Stokes I image of the field which is shown in Fig. 2 and; (c) deep low resolution (20 arcsecs) Stokes I image and Stokes V uncleaned image of the field. The data were also divided in frequency bands for further study of the consistency of the data and the intra-band spectral indices. Three bands with a set of frequencies nearly-equivalent to the ones used in the LoTSS wide area survey were produced, additionally three different bands covering the full extended spectral range of the ELAIS-N1 data were also produced. The frequency ranges used are shown in Table 2. Bands 0, 1, and 2 correspond to the LoTSS wide-field survey configuration and bands X, Y, Z are extended. The spectral coverage of these extended bands was selected empirically in order to produce a similar median signal-to-noise level in the three bands for the sources in the central 2 degree radius region of the ELAIS-N1 field.
The solutions were later used to produce Stokes I and V images corresponding to the individual datasets. Low resolution (20 arcsecs) andvery low resolution (4.3 arcmin) Stokes QU datacubes of the individual datasets were also obtained for further processing (see Herrera Ruiz et al. 2021). Those datacubes are split in 800 or 640 frequency channels in the case of Cycle 2 or 4 datasets respectively due to their different frequency configuration.
Preliminary ELAIS-N1 catalogues were produced from the high resolution Stokes-I images of the deep field, the spectral bands, and the individual dataset images. The sources were extracted from the images using PYBDSF (Mohan & Rafferty 2015). PYBDSF extracts a catalogue of sources that can be composed of either individual or multiple Gaussians. It takes into account different scale effects by using wavelets. An rms noise distribution image is also produced by the software. The parameters used to extract the sources are detailed in Appendix C. More than 80 000 sources were extracted from the deep image (see Sect. 4 for more details).
Band frequency ranges of different datasets available in the data release.
3.5 Flux scale calibration
The preliminary version of the catalogues was compared to the initial sky model derived in Appendix A. This indicated a possible over-estimation of the flux density scale by DDF-PIPELINE. The high quality of existing multi-frequency radio data in the ELAIS-N1 field should permit a higher accuracy flux density calibration than the default DDF-PIPELINE methods which rely on cross matching to other very wide area radio surveys. We therefore used two methods to test the flux density scale of ELAIS-N1: (a) a comparison of the flux density of a calibrator source within the field, and (b) a cross-match with additional radio catalogues covering the area.
The calibrator 87GB 160333.2+573543 is observed within the main target field, and close enough to the pointing centre not to be significantly affected by primary beam correction problems (2.6 degrees). Accordingly, we compared its flux density with that estimated during the construction of the initial sky model in Appendix A. We measure a surface brightness of 5.58 Jy beam−1 and the expected flux density according to the model is 4.44 Jy as shown in Appendix A. As the source is not extended at 6 arcsec resolution this implies that the flux density is overestimated by 26 per cent and a correction factor of 0.796 should be applied. However, as this estimate is based on a single source whose properties as calibrator are not well determined we looked into more robust methods that used additional data.
The flux density of sources in common between our catalogue and additional external radio catalogues was compared as well. We compared with the VLSSr at 74 MHz, the TGSS at 150 MHz, the 6C at 151 MHz, the ELAIS-N1 GMRT survey at 325 MHz, WENSS at 350 MHz, the ELAIS-N1 GMRT survey at 610 MHz, NVSS at 1.4 GHz, and FIRST at 1.4 GHz. The external catalogues were cross-matched with the LOFAR catalogue, within the inner 3 degrees radius from the LOFAR pointing centre. The catalogues were on (or, where necessary, adjusted to) Baars et al. (1977) flux density scale for the higher frequencies and for the lower ones on Scaife & Heald (2012) flux density scale which is set to be compatible with Baars et al. (1977) but more accurate at frequencies below ~ 300 MHz. We also applied some constraints to avoid the introduction of biases produced by the different effective depths and angular resolutions of the surveys. The exact numerical parameters used are shown in Table 3. In order to ensure a fair comparison of surveys with different angular resolutions, with no contamination by neighbouring sources, only isolated LOFAR sources were considered. An offset limit to the nearest neighbour LOFAR source was empirically chosen. This offset depended on the angular resolution of the comparison survey with lower resolution surveys requiring larger values to avoid contamination from neighbours. Additionally, the maximum cross-match distance between the LOFAR and the survey source was empirically set depending on the resolution of the matched survey. Surveys with lower resolution require larger cross-match distances. To avoid resolution selection effects, only compact LOFAR sources were selected by restricting their maximum size. Higher resolution surveys require the consideration of less extended LOFAR sources (e.g. because FIRST does not have the same surface brightness sensitivity to extended structures that LOFAR has). Incompleteness effects were minimized by considering the completeness limit of each comparison survey (e.g. Nisbet 2018). A survey dependent minimum flux density threshold was applied. Setting a threshold in only one of the cross-matched surveys may introduce a bias towards sources with high absolute values of their spectral indices. Therefore, an additional constraint was introduced as a threshold in the product of flux densities of our LOFAR measurement and each comparison survey. The threshold was set to be the flux density that a source at the completeness limit of the comparison survey multiplied by the LOFAR flux density that such a source would have for a spectral index of 1.5 (except for the lower frequency survey VLSSr, where a flat spectral index was used). The two panels of Fig. 3 show this threshold as well as the completeness threshold for two of the surveys used. Most of the optimal parameters shown in Table 3 were empirically determined by Nisbet (2018). All these parameters were used to filter the LOFAR sample down to that which would produce an unbiased comparison for each comparison survey.
After the filtering was applied, the ratio between the LOFAR and the survey flux density was computed and the results are shown in Fig. 4. Some surveys like TGSS or WENSS present some region-dependent issues with the flux density scale (e.g. Murphy et al. 2017b). Hence, we took into account the flux density uncertainty associated to a survey by adding it in quadrature to the error of the median of the flux density ratios. The ratio obtained for the 87GB calibrator is also shown in the figure. An Orthogonal Distance Regression (ODR; Boggs & Rogers 1990) fit that takes into account the uncertainties in the ratioswas fitted and used to estimate the flux density scale ratio at 146 MHz. We obtained a value of 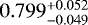 . A fit with a second order polynomial gives a value of 0.795 ± 0.024 and it is favoured using the Bayesian information criterion (BIC; Schwarz 1978) but not the Akaike information criterion (AIC; Akaike 1998). The fitted 146 MHz flux density scaling factor points lie very close to that estimated using the 87GB calibrator data, suggesting that the DDF-PIPELINE flux density scale is over-estimated by ~ 25 per cent.
. A fit with a second order polynomial gives a value of 0.795 ± 0.024 and it is favoured using the Bayesian information criterion (BIC; Schwarz 1978) but not the Akaike information criterion (AIC; Akaike 1998). The fitted 146 MHz flux density scaling factor points lie very close to that estimated using the 87GB calibrator data, suggesting that the DDF-PIPELINE flux density scale is over-estimated by ~ 25 per cent.
Finally, for practical reasons, we used the numerical value obtained from the 87GB calibrator as the final value to correct the LOFAR fluxdensity scale (0.796). This value is well within the confidence interval estimated with the linear fit with a difference ofonly 0.5 per cent in value (less than one tenth of the estimated uncertainty). We also note a likely uncertainty of around 6.5 per cent in the flux density scale. However, we note that the uncertainty in the flux density scale is not included in the final quoted flux density uncertainties for each source. Uncertainty for individual sources can be affected by several factors and some of these factors will be studied in Sect. 5.2.
The flux density scale corrections for the Lockman Hole and Boötes deep fields presented in Paper I were also estimated using the same method. The final values are 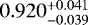 for the Lockman Hole and
for the Lockman Hole and 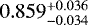 for the Boötes field. Their derivation is shown in Appendix D.
for the Boötes field. Their derivation is shown in Appendix D.
 |
Fig. 2 Final deep image of the central region of ELAIS-N1 field. Top panel: a wide-field view containing about one third of the total area. Lower panels: zoomed-in regions (each around 0.1 per cent of the full image area), showing the high image quality for extended sources and sensitivity to faint sources. All images are Stokes I, with 6 arcsecs resolution. The full-field image contains more than 85 000 sources. |
Cross-match parameters and figures.
 |
Fig. 3 Selection of sources for the cross-match for the GMRT 610 MHz (left panel) and the NVSS (right panel) samples. All the cross-matched sources are shown as blue dots and the finally selected ones are marked with an orange cross. The completeness limit of the survey is shown as a vertical dashed line. The line at which the flux densities are equal is shown as reference as a solid green line. The locus of sources with a spectral index of 1.5 is shown as a dash-dotted red line. The point at which this line and the survey completeness line cross is used as a reference for the selection threshold in the product of flux densities (see text) which is marked as a purple dotted line. |
 |
Fig. 4 Calibration of the ELAIS-N1 flux density scale using different methods. The default DDF-PIPELINE scale is set to unity and marked with a blue cross. The scaling factor obtained with the 87GB calibrator is marked with an encircled orange cross. The flux density ratios with respect to other surveys in the literature and their errors are shown in different colours and the fitting line is shown as a red dashed line. The inset shows a zoom view of the area close to the 146 MHz frequency of the observation. |
Flux scale correction factors for the individual datasets.
3.5.1 Flux scale of individual dataset images
The DDF-PIPELINE output flux density values for the individual dataset catalogues were pre-scaled by the same correction factor derived above (0.796). To investigate the magnitude of the residual corrections, we cross-matched the sources extracted from each of the individual datasets to those of the deep image catalogue and compared the relative flux densities of the matches. In Fig. 5 the distribution of flux density ratios for the cross-matched sources is shown. The medians of the distributions of flux density ratios are close to one which is expected after the pre-scaling factor was applied. Nevertheless, for many datasets, there is a non negligible deviation from this value. These medians and the final scaling factors obtained from combining these values with the pre-scaling factor are summarized in Table 4. In Fig. 6 we show the relation of these medians with the overall noiselevel of the dataset. To estimate the latter in a robust manner, we use the RMS noise level at an accumulated area of 2 square degrees using the cumulative distribution of area with respect to the noise level. This value is a proxy for the quality of the calibration and data. From the figure it is clear that the flux densities are systematically underestimated as the quality of calibration and data gets worse. This effect will be further studied in Sect. 5.2.
We also applied the method presented previously which cross-matches to the external surveys. The values obtained are also presented inTable 4. They are usually similar but differ in the datasets that are more noisy. We favour the method of cross-matching to the final deep image as the number of cross-matched sources to obtain the estimate is substantially higher.
3.5.2 Flux scale of band images
The scaling factors for the bands shown in Table 2 (0, 1, 2, X, Y, and Z) were estimated using the method of cross-matching to the external surveys. The results are shown in Table 5. These scaling factors are critical to obtain reliable intra-band spectral indices (see Sect. 5.4).
To check the robustness of the method, we selected the 19264 sources that: (a) were cross-matched between the three bands X, Y and Z within a 1 arcsec radius, (b) had an S/N of more than 15, and (c) had a major axis of less than 15 arcsecs. A fit to a simple Bayesian model can be used to estimate the additional scaling corrections that must be applied to the band scalings to get a given mean intra-band spectral index. We used PYMC3 (Salvatier 2016) to fit this model which was configured to obtain a final spectral index of α = 0.63 (Sabater et al. 2019). The corrections found were applied and this produced scaling factors that were similar within the error to those obtained using the method of fitting to external surveys (see Table 5).
 |
Fig. 5 Distribution of the flux density ratio of the sources in common between the individual datasets and the final deep image. The distributions of the datasets are symmetrical in general in flux density scale but their median is systematically different from the expected value of 1. Figure 6 shows that the offsets are correlated with the noise level of the datasets. |
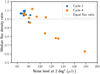 |
Fig. 6 Relation between the deviation of the flux density ratio (observed over expected flux density) from the expected value and the noise level of each individual dataset. The vertical axis represents the median value of the flux density ratio distribution.The horizontal axis shows the noise level of the noise-area cumulative distribution at 2 square degrees. This value is a proxy for the calibration and data quality. Datasets of Cycle 2 are marked as blue circles and Cycle 4 as orange squares. The flux density ratios cluster around a line with value 1 (grey horizontal line) as expected but there is a clear inverse relation between flux density ratio and noise level. |
Flux scale factors for the different bands.
4 Final data products and catalogues
To produce the final radio catalogues the image was scaled by the scaling factor determined in the previous section (0.796 for the deep image) and PYBDSF was run again using the same parameters (see Table C.1). A catalogue ofsources and a catalogue of individual Gaussians are produced. The columns of the catalogues are those of a typical PYBDSF default output including the position, integrated and peak flux density, structural parameters (raw and deconvolved) and their estimated errors (Mohan & Rafferty 2015). The radio catalogue produced in this way, and presented in this paper, is in raw state and the generation of a final source catalogue requires further processing to consider blended sources, artefacts, and the merging of some PYBDSF components into a singlesource. All of that work, and the cross-correlation with multiwavelength catalogues is presented in Paper III.
The deep radio catalogue contains 84862 sources composed of 96039 Gaussians. There are 78885 sources composed of a single Gaussian and 5951 multicomponent sources that correspond to 17128 Gaussians. The number of sources within 1, 2, and 3 degrees from the centre are 16435, 50026, and 74127 respectively. Figure 7 shows the total sky density of sources at different radii. It also compares the sky density to that obtained for previous targeted surveys of ELAIS-N1. It shows that the LOFAR data are much deeper as well as wider and at the same time it typically has a better resolution.
We also extracted catalogues for the 6 spectral bands shown in Table 2. Finally, we extracted catalogues for the individual datasets used in the deep image. All these catalogues were extracted with PYBDSF using the same parameters (see Table C.1). The spectral band and individual dataset catalogues are offered with the flux density scaling factors shown in Tables 4 and 5 applied.
 |
Fig. 7 Comparison of the sky density of radio sources in our work with those quoted by other radio ELAIS-N1 surveys. The solid blue line shows the total density of sources at each radius for our study. The points show the density of sources quoted in the literature at the corresponding radius to the area covered by those surveys. The density is extended with dashed lines to give an idea of the radius out to which a similar average source density would be achieved with our data. We also show as a comparison the estimated sky density of VLA-COSMOS-3GHz (Smolčić et al. 2017) which reaches a comparable source density in the total 2 square degree area that it covers. |
5 Discussion
5.1 Noise levels and source confusion
The rms noise level of the deep image (see Fig. 8) reaches a minimum value of 17.1 μJy beam−1. The median value in the ≈ 7 deg2 area covered by the added value datasets (Paper III) is 22.9 μJy beam−1. The cumulative distribution of area with respect to the noise level is shown in Fig. 9. The distribution is also compared with those of the Boötes and the Lockman Hole deep fields (Paper I). They present slightly higher noise levels as they were observed for a shorter period of time (~ 100 and ~ 112 h respectively) and have smaller bandwidths (48 MHz each). In the case of Boötes it is also located at a significantly lower declination (~ 34°) and additional noise produced by the projection of the station beams is added.
Factors that would limit the depth of the images as additional data are combined include confusion noise from faint sources below the flux density limit of the survey, or the growing importance of residual calibration errors. The latter leads to the reduction of the dynamic range around the brightest sources (see Fig. 8), but can have also wider effects due to correlated sidelobe structures around less bright sources.
To investigate the magnitude of these effects, we compared the noise level of the final deep image with that predicted by theoretical combination of the noise from the individual images (assuming that the noise in each image is completely uncorrelated). If there is negligible confusion noise and no errors in the calibration, the values should be similar. The comparison between the predicted and obtained noise levels are shown in Fig. 10. A histogram for the values in the inner 3 degrees region is shown in Fig. 11. There are some regions around bright sources in which the dynamic range limitations are clearly visible but for most of the area the observed noise level in the final image is less than 16 per cent higher than the ideally predicted value. This suggests that any increase in noise due to imperfect calibration is relatively small. Interestingly, there are some areas at the edge where the obtained noise level is better than that predicted from the individual images. This may arise from several factors like, for example, a reduction in the noise produced by faint sources which were not able to be properly deconvolved in the individual datasets, but may also reflect the improvement in the performance of the third generation calibration algorithms as the amount of data fed increases (Paper I).
For the increased noise in the central regions to be caused entirely by source confusion, a confusion noise of 11 μJy beam−1 would be required. For shallower LoTSS observations, Shimwell et al. (2019) estimated a confusion level for LOFAR 150 MHz observations of 14 μJy beam−1, but with a wide uncertainty range depending upon the slope of the faint number counts. Condon et al. (2012) estimated the confusion noise at higher frequencies using ultra-deep 1.4 and 3 GHz data, and provide an equation (their Eq. (27)) for conversion of these to other frequencies: 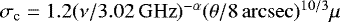 Jy beam−1, where ν is the frequency of observation and θ is the synthesized beam size. For the ELAIS-N1 data (ν = 146 MHz; θ = 6 arcsec), taking α = 0.63 as a medianspectral index (Sabater et al. 2019), this gives an estimate for the confusion noise of σc ≈ 3 μJy beam−1. However, this estimate involves a long extrapolation in frequency, which may not be appropriate.
Jy beam−1, where ν is the frequency of observation and θ is the synthesized beam size. For the ELAIS-N1 data (ν = 146 MHz; θ = 6 arcsec), taking α = 0.63 as a medianspectral index (Sabater et al. 2019), this gives an estimate for the confusion noise of σc ≈ 3 μJy beam−1. However, this estimate involves a long extrapolation in frequency, which may not be appropriate.
The confusion noise level can be directly estimated from the source count distribution (e.g. Condon et al. 2012):
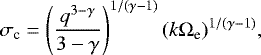
where q is the S/N threshold of the catalogue, k and γ are the normalization and slope of a power-law fit to the source counts at low flux densities, N(S) = kS−γ, and Ωe is the effective beam solid angle, given by Ωe = πθ2∕(4ln(2)(γ − 1)). The values of k and γ are very sensitive to incompleteness corrections at the faint end: analysis of these is beyond the scope of this paper, but is instead investigated in the accompanying paper of Mandal et al. (2021). In ELAIS-N1, the Euclidean-normalized source counts begin to turn down below about S150 MHz ≈ 400 μJy; both theoretical models and high-frequency observations suggest that this will turn over to a slope of γ ≈ 1.5−1.8. Normalizing to the observed counts at 200 μJy (N(S)S5∕2 ≈ 30 sr−1Jy1.5) provides an estimate for the confusion noise of ≈ 8 μJy beam−1 for γ = 1.7. The precise confusion noise, however, remains sensitive to the choice of γ, which the data do not yet constrain to sufficient accuracy. We conclude that confusion noise is likely to account for a significant fraction of the median increase in noise in the central regions compared to the predicted value, but probably does not account for all of it.
 |
Fig. 8 rms noise level in the ELAIS-N1 field. The minimum value is close to the centre at a level of 17.1 μJy beam−1. The effect of the facet division used for the calibration is only visible in areas very far from the centre. The small calibration errors around very bright sources have an adverse effect in the dynamic range of the nearby region. |
 |
Fig. 9 Area coverage with RMS noise equal to or better than a given value. The distribution for ELAIS-N1 (solid blue line) is compared to that of the other two LoTSS deep fields, the Lockman Hole (dash-dot green line) and Boötes (dashed orange line), observed using similar techniques as presented in Paper I. |
5.2 Estimation of source flux density variation
The imaging of the individual datasets allows to perform an analysis of the empirical variation between observations of the source flux density. Calibration effects should be disentangled from intrinsic variability and the first step was to bring all the datasets to the same flux density scale frame using their individual correction factors as presented in Sect. 3.5.1.
To measure the variations of the flux density and determine their origins, we studied the sources that were detected in common in all the individual images. There are 5504 sources cross-matched and detected in all the 22 individual snapshots. For all these sources, we computed the relative flux density of each individual observation with respect to the flux density estimated from the deep image. The values of these relative fluxes have a mean close to 1 and on a log scale their distribution is in general symmetrical on both sides of the zero value. We have studied the standard deviation of this distribution (log10(Si∕S0); hereafter called σ) applying different constraints to the data in order to find what the most important factors affecting it are.
We have identified four main factors that have a significant effect in the variation of the relative flux densities: the radial distance from the centre, the size of the source, the S/N of the measurement, and the overall noise level of the dataset image. The effect of these parameters in σ are shown in Fig. 12. To study the effect of the radius, size, and S/N we have partitioned the sample in sub-samples according to terciles of their distribution. The thresholds are: (a) in radius, 1.7 and 2.7 degrees from the centre; (b) in size, major axes of 6.9 and 8.9 arcsecs; and (c) in S/N, the values of 89 and 227. We studied the relation of σ with each parameter for sub-samples comprising the combination of terciles of the remaining two parameters, while dividing the studied parameter in ≈20 bins. The σ was computed for each individual bin and the result smoothed with a Savitzky-Golay filter (Savitzky & Golay 1964).
The effect of the S/N in σ is shown in the upper left panel of Fig. 12. As it would be expected, this is very pronounced at lower signal-to-noise values, decreasing rapidly as S/N increases. However, for all but extended sources, it then flattens out (rather than continuing to decrease towards zero) once an S/N of 100–300 is exceeded, at a floor value of σ ≈0.025. The effect of the radius is shown in the upper right panel of Fig. 12. The σ is independentof radius from the pointing centre until a radius of between 3 and 4 degrees is reached, after which it rises very steeply. This effect can be produced by the quality of the calibration degrading in facets far from the centre but also due to errors in the modelling of the primary beam shape. The effect of the size of the source is shown in the lower left panel of Fig. 12. In this case there is no visible relation for sources with high S/N and at low and mid radii. For the rest there is an increase in σ with the size that depends on their S/N and radius. This is likely related to the PYBDSF extraction of sources. For extended sources with low S/N the PYBDSF fitted Gaussians can be different from one dataset to the next, introducing artificial variability.
Finally, the effect of the dataset can be estimated in a sample that minimizes the effect of the remaining parameters. We select the 240 sources with an S/N above 300, a distance to the centre of less than 3 degrees, and a major axis of less than 7 arcsecs. For each of these sources, we calculate the observed distribution of σ associated with that dataset(σobserved), and also calculate the expected distribution, based on the tabulated flux densities and uncertainties for each source (σexpected). We then estimate the contribution of the dataset as the difference in quadrature between the observed and the expected σ based on the individual measurements (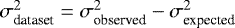 ). In the lower right panel of Fig. 12 we show the dependence of σdataset on an estimation of the noise level of the dataset. The RMS noise shown in the horizontal axis is the noise level at 2 square degrees based on the cumulative distribution for each individual dataset (see Sect. 5.1). This value is a proxy for the quality of the data and calibration. We find that the value of σdataset is clearly higher in the datasets with higher rms noise, indicative of poorer calibration solutions mainly due to bad ionospheric conditions.
). In the lower right panel of Fig. 12 we show the dependence of σdataset on an estimation of the noise level of the dataset. The RMS noise shown in the horizontal axis is the noise level at 2 square degrees based on the cumulative distribution for each individual dataset (see Sect. 5.1). This value is a proxy for the quality of the data and calibration. We find that the value of σdataset is clearly higher in the datasets with higher rms noise, indicative of poorer calibration solutions mainly due to bad ionospheric conditions.
It is worth noting that the levels of σdataset are larger now than the levels of σ found for these ‘well-behaved’ sources individually (lower lines in the upper and lower left panels of Fig. 12). This is produced by the extra variance introduced by the fact that the ratio between the flux density measurement in the deep image and the average flux density measured in the individual dataset is in general not exactly equal to unity for individual sources. If we correct by this factor the values obtained are similar. However, we kept this term because real measurements would include it as well.
We fitted a linear relation to the σdataset versus noise level data and obtained σdataset = 0.00194x + 0.00058 where x is the rms noise level at 2 square degrees. An extrapolation of this equation down to the noise level of the deep image (taking into account the confidence interval of the prediction) suggests a value of σdataset of 0.014 ± 0.004 in the deep data, which is equivalent to 3.3 ± 0.8 per cent of the flux density ratio. This indicates that, even for compact central sources with the higher S/N, there is likely to be an extra component in the flux density uncertainty of this magnitude. This possible error was not included in the final catalogues but must be taken into account if this order of precision is required.
Once the magnitude of the flux density error is determined it is possible to robustly identify the subset of sources that present significant intrinsic variability. A full investigation of variable sources in the dataset, using advanced techniques complemented by careful visual inspection, will be presented in a companion paper (Sabater et al., in prep.).
 |
Fig. 10 Noise deviation in the combined image with respect to that predicted from the combination of the individual dataset images. In the areas with high deviations from the expected value these are limited because the dynamic range of the deep image is reduced due to residual errors in the calibration around bright sources. |
 |
Fig. 11 Histogram of the noise deviation in the combined image with respect to that predicted from the individual images, assuming that the noise in each is uncorrelated. The histogram is computed in the area closer than 3 degrees to the centre. The median value of the distribution (solid grey line) is a 15.6 per cent increase in noise in the deep image. |
 |
Fig. 12 Standard deviation (σ) of the logarithmic relative flux density with respect to several parameters. Upper left panel: relation of σ with respect to the signal-to-noise level for sub-samples separated in terciles of distance from the pointing centre and major axis. The different terciles are marked with arrow symbols in the legend: up arrows for the higher tercile, left-right arrows for the middle tercile, and down arrows for the lower one. Upper right panel: relation of σ with respect to the distance to the centre for terciles of major axis and S/N. Lower left panel: relation of σ with respect to the major axis of the sources for terciles of distance to the centre and S/N. Lower right panel: contribution of the calibration effects of the dataset (σdataset, as explainedin the text) with respect to the rms noise at 2 square degrees for the individual datasets (coloured circles). The linear fit to the relation is shown as a orange line and its 95 per cent confidence interval as a shaded orange band. The extrapolated location of the final deep image is also marked in the diagram as a green cross. |
5.3 Extended sources
It is of interest to identify which sources in the radio catalogue are extended and which are point-like. A particular technique to achieve this is explained by Franzen et al. (2015) and, for this study, we propose a further improvement to this method that adds some modifications based on the work of Shimwell et al. (2019). If R is defined as R = ln(Stotal∕Speak), its distribution should be Gaussian and centred on zero for unresolved sources (Franzen et al. 2015). The rms of R can be given as a combination in quadrature of different error terms as:

where the term C accounts foradditional errors and is empirically determined for our data.
To empirically compute the parameter C, we select isolated sources as in Shimwell et al. (2019), that is, sources that are: (a) flagged as single sources by PYBDSF (code ‘S’); (b) have a major axis smaller than 15 arcsecs; and (c) have no nearest neighbours at a distance of less than 45 arcsecs. The empirical distribution of C for these sources is strongly dependent on radius as shown in Fig. 13 and as explained in Sect. 5.2. We fit the points to a modified softplus function with the following formula:
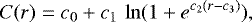
where r is the radius and (c0, c1, c2, c3) are the free parameters to be adjusted indicating respectively: the level of C at low radii, the slope of the line at high radii, a scaling factor to adjust the shape of the curve, and the position of the turnover radius. The fit is done by minimizing the square vertical distance between the points and the curve using the method of Powell (1964) which is implemented in SCIPY. The fitted line is shown in Fig. 13 and σR can be computed using
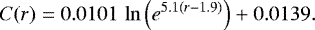
Computing the ratio R∕σR, we can estimate at which level the source is expected to be extended. In Fig. 14 we show the distribution of concentrations (R) versus S/N and theratio in different colours. Although the values of the ratio depend on the individual sources, they follow clear trends and the shape is similar to that found in Franzen et al. (2015); Shimwell et al. (2019) and Chakraborty et al. (2019). Applying a threshold of 5 sigma there are 3426 sources (4.0 per cent) classified as extended while a 3 sigma threshold gives 9630 extended sources (11.3 per cent).
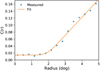 |
Fig. 13 Dependence of the additional noise term C with radius. The empirical values (blue crosses) are fitted with a modified softplus function (orange line). |
 |
Fig. 14 Diagram showing the location of extended sources. The concentration (total over peak flux density) is plotted with respectto the S/N of the total flux density. The colour scale represents the confidence level at which a source can be considered to be extended after also taking into account the radial location of the source in the field (see text for more details). |
 |
Fig. 15 Comparison of the intra-band spectral index (αLOFAR) with the NVSS to LOFAR spectral index (αLOFAR-NVSS). The colour of the dots is proportional to the deviation from the (black solid) line where the spectral indices are equal. The errors are plotted as faint grey lines and indicate the 95 per cent confidence interval. The median of the distributions for all the sources are shown as grey dash-dotted lines. The median of the distribution of αLOFAR for the sources that were matched to NVSS sources is shown as a dotted line. The orange dashed line shows the total least squares fit to the distribution (see text). Upper panel: histogram with the distribution of αLOFAR-NVSS. Right panel: histogram with the distribution of αLOFAR for the cross-matched sources (blue) and for the total sample over-plotted (green). |
5.4 Intra-band spectral index
We estimated the intra-band spectral index for the sources that were matched between the three extended band images (X, Y and Z). The estimation uses the accurate calibration of the relative flux densities presented in Sect. 3.5.2. The intra-band spectral index (αLOFAR) compared to the LOFAR to NVSS spectral index (αLOFAR-NVSS) is shown in Fig. 15. The distribution of αLOFAR has a median of 0.92 with an uncertainty on this median of 0.27. This large uncertainty on the intrinsic value arises from the combined flux density scaling uncertainties in the three bands (see Sect. 3.5.2); flux density calibration changes would systematically shift all of the measured αLOFAR in the field in the same direction. The value is in agreement with that found for the GLEAM survey (Hurley-Walker et al. 2017). The standard deviation of the αLOFAR distribution is 0.47.
To obtain αLOFAR-NVSS, the NVSS sources cross-matched were required: (a) to be at a distance of less than 3 degrees to the centre of the field; (b) be cross-matched at a distance of less than 10 arcsecs; and (c) have a major axis of less than 15 arcsecs. A final set of 799 sources were cross-matched to NVSS using these constraints. The distribution of αLOFAR-NVSS (upper panel of Fig. 15) has a median of 0.61 and a standard deviation of 0.47. The points in the main panel of Fig. 15 show strong scatter around the αLOFAR = αLOFAR-NVSS line which can be related to the relatively high errors in their measurement. In Fig. 16 we check the relation between the S/N and the deviation from this line to test for incompleteness effects. The distribution of αLOFAR − αLOFAR-NVSS below an S/N of 500 is skewed towards flatter spectral indices. This is likely to be produced primarily by the shallower depth of NVSS compared to LOFAR.
A total least squares fit that takes into account possible correlated errors in the measurements (Hogg et al. 2010) is applied to sources with S∕N > 500. We use the implementation of ASTROML (Vanderplas et al. 2012; Ivezić et al. 2014). The fitting line is αLOFAR = (0.78 ± 0.03)(αLOFAR-NVSS − 0.73) − 0.09 ± 0.13. The small shift downwards is related to the small difference in the median distribution of the αLOFAR sources thatare matched to NVSS with respect to the median of the total sample.
The intra-band spectral index is very sensitive to small variations in the flux density scale calibration. We studied the distribution of the spectral index with respect of the facet used in the calibration to check the accuracy of the flux density calibration in different facets. We used the 20 solution facets closer to the pointing centre as they cover the inner 3 degree radius where flux density calibration is more accurate as seen in Sect. 5.2. We observe an scatter of about 0.2 in the distribution of the spectral indices that can be associated to the global facet to facet calibration. We checked that this level of scatter can be produced by a variation in the flux density scale of the order of a few per cent in the band images which is compatible with the accuracy of 6.5 per cent estimated in Sect. 3.5. Hence, apart from the possible global systematic shift of αLOFAR which has a magnitude of 0.27 there is an additional uncertainty within the field of the order of 0.2 that must be taken into account. Nevertheless, despite this uncertainty, and the relatively large statistical uncertainties on the measured intra-band spectral index of individual sources, it can still be useful to detect sources with unusual spectral indices or general trends. For example, some sources in the lower right region of Fig. 15 have a steep αLOFAR-NVSS but inverted αLOFAR indicating a likely spectral peak at a few hundred MHz (Callingham et al. 2017).
 |
Fig. 16 Difference between the intra-band spectral index (αLOFAR) and the NVSS to LOFAR spectral index (αLOFAR-NVSS) compared to the S/N of the cross-matched sources. The distribution of S/N is divided in deciles and the median of the difference is computed and shown as orange lines. The spectral indices are flatter (lower values of the difference) for low S/N likely due to incompletness effects. The distribution is close to zero (marked as a horizontal grey line) for sources with S∕N > 500 (shown as a vertical green dashed line). |
5.5 Circularly polarized sources
We detectedtwo sources that present significant circularly polarized emission in the Stokes-V image. The first is the star CR Draconis which is an eruptive variable star, also detected by Callingham et al. (2021) in the wider LoTSS survey. It presents a relatively flat spectral index of − 0.8 ± 0.7 and the circularly polarized emission can be detected above the noise level in a couple of individual datasets, as will be explored in greater detail in Callingham et al. (2021). The second source is the pulsar PSR J1552+5437. This millisecond pulsar was discovered using tied-array beam LOFAR observations (Pleunis et al. 2017). The pulsar is detected with an intra-band spectral index of 3.2 ± 0.5 which is similar to the value of Pleunis et al. (2017) within the error (2.8 ± 0.4).
6 Summary and conclusions
In this paper we present the data and calibration procedure followed for the ELAIS-N1 field, the deepest of the LoTSS deep fields to date. The extended frequency coverage and configuration set-up arising from the co-observation with the EoR project of this field required a modified calibration process based on that used for the other deep fields (Paper I).
We applied to the field a careful flux density calibration method that took advantage of its good multi-frequency radio coverage. The uncertainty in the flux density derived from the flux density scale calibration method is at the level of 6.5 per cent. We provide the factors required to correct the flux density scale of the data.
We produced high resolution (6 arcsecs) Stokes-I images for the deep full dataset as well as for the individual datasets and spectral bands. Additionally low resolution (20 arcsecs) Stokes-I and V (uncleaned) images and QU datacubes were generated for the individual datasets. Source catalogues were produced for the high resolution Stokes-I images. Catalogues for the deep image, the spectral bands, and the individual datasets are provided. The final catalogue for the deep image contains 84 862 sources.
We also examined in detail some properties of the data:
-
We analysed the reduction of the noise level as more data are added. The noise decreased almost as expected theoretically but there is some additional noise contribution, which is a combination of confusion noise, and additional noise that is likely to be associated with low-level residual calibration errors. The median of this extra contribution in the final deep image is at the 16 per cent level.
-
We studied the origin of the variation of flux density measurements between the individual datasets. The signal-to-noise ratio has the biggest impact as expected but we detect a remaining effect even at the higher signal-to-noise ratios. This effect has been linked to the quality of the data and calibration of the individual dataset. The primary beam correction seems to have an effect at large radii (larger than 3–4 degrees from the centre), but within 3 degree radius the flux density calibration is independent of radius. Variability also increases for more extended sources, particularly at low S/N, where the PYBDSF extracted-source parameters may vary from dataset to dataset.
-
We find an empirical fit to the contribution of the quality of the data and calibration of a dataset to the variability of the flux density measurements. Using this relation we find that an additional error of 3.3 ± 0.7 per cent in the flux density measurement could be expected for the deep dataset. The final flux density uncertainty for ELAIS-N1, the Lockman Hole, and Boötes considering all the contributing factors is estimated to be ~10 per cent.
-
We provide an analytic formula based on that of Franzen et al. (2015) and Shimwell et al. (2019) to estimate whether a source is likely to be extended or not. The estimation is dependent on the distance of the source to the centre of the field. Using this relation, we classify 9630 sources as extended at a 3 sigma significance level.
-
We provide values and an analysis of the intra-band spectral indices. A systematic global shift of the values is expected due to the uncertainty in the flux density scale calibration. This uncertainty follows a normal distribution with a sigma of 0.27. Apart from the error propagated from the uncertainty in the measurements, an additional error of the order of 0.2 in the intra-band spectral index is estimated.
This survey of ELAIS-N1 is the deepest radio survey of the region to date. We reach a sky density of sources of more than ~ 5000 sources per square degree in the central part (up to ≈2 square degrees). The survey covers a wide area with a good spatial resolution. The number of sources detected in the central 2 square degrees is similar to that detected in total by VLA-COSMOS at 3 GHz in a similar sky area (10 973 versus 10 830 in VLA-COSMOS at 3 GHz; see Smolčić et al. 2017). However, we pick up several times more sources over more than an order of magnitude larger sky area.
These radio data have been enriched with multiwavelength information and cross identifications (Paper III) as well as photometric redshifts (Paper IV). This, combined with the quality of the radio data of ELAIS-N1, will enable a wide range of scientific studies of faint radio sources with high statistical significance and in representative environments.
At the time of publication, more data have already been taken, and additional time is allocated for observation to reach a total exposure time of 500 h by the middle of 2022. These data will allow us to approach the final depth of ~10 μJy beam−1.
Acknowledgements
The authors are indebted to Ger de Bruyn, sadly deceased, who played a critical role in the inception of the project. We acknowledge the useful comments of the anonymous referee. We acknowledge the joint SKA and AWS Astrocompute proposal call that was used to fund all the tests and calibration in the AWS infrastructure with the projects ‘Calibration of LOFAR ELAIS-N1 data in the Amazon cloud’ and ‘Amazon Cloud Processing of LOFAR Tier-1 surveys: opening up a new window on the Universe’. Cycle 0 and 2 data are available in the Registry of Open Data on AWS in: https://registry.opendata.aws/lofar-elais-n1/. This paper is based on data obtained with the International LOFAR Telescope (ILT) under project codes LC0_019, LC2_024 and LC4_008. LOFAR (van Haarlem et al. 2013) is the LOw Frequency ARray designed and constructed by ASTRON. It has observing, data processing, and data storage facilities in several countries, which are owned by various parties (each with their own funding sources) and are collectively operated by the ILT foundation under a joint scientific policy. The ILT resources have benefited from the following recent major funding sources: CNRS-INSU, Observatoire de Paris and Université d’Orléans, France; BMBF, MIWF-NRW, MPG, Germany; Science Foundation Ireland (SFI), Department of Business, Enterprise and Innovation (DBEI), Ireland; NWO, The Netherlands; The Science and Technology Facilities Council, UK. This work was carried out in part on the Dutch national e-infrastructure with the support of SURF Cooperative through e-infra grants 160022 & 160152. JS, PNB, RKC, and RK are grateful for support from the UK Science and Technology Facilities Council (STFC) via grant ST/M001229/1 and ST/R000972/1. MJH acknowledges support from the UK Science and Technology Facilities Council (ST/R000905/1) VJ acknowledges support by the Croatian Science Foundation for the project IP-2018-01-2889 (LowFreqCRO). HR acknowledges support from the ERC Advanced Investigator programme NewClusters 321271. MB acknowledges support from INAF under PRIN SKA/CTA FORECaST and from the Ministero degli Affari Esteri della Cooperazione Internazionale - Direzione Generale per la Promozione del Sistema Paese Progetto di Grande Rilevanza ZA18GR02. MJJ acknowledges support from the UK Science and Technology Facilities Council [ST/N000919/1] and the Oxford Hintze Centre for Astrophysical Surveys which is funded through generous support from the Hintze Family Charitable Foundation. RK acknowledges support from the Science and Technology Facilities Council (STFC) through an STFC studentship via grant ST/R504737/1. IP acknowledges support from INAF under the SKA/CTA PRIN ‘FORECaST’ and the PRIN MAIN STREAM ‘SAuROS’ projects. This research made use of ASTROPY, a community-developed core Python package for Astronomy (Astropy Collaboration, 2013, 2018); IPYTHON (Pérez & Granger 2007); MATPLOTLIB (Hunter 2007); NUMPY (Walt et al. 2011); PANDAS (McKinney 2010); SCIPY (Jones et al. 2001), TOPCAT (Taylor 2005), and KERN suite (Molenaar & Smirnov 2018).
Appendix A Sky model inception
The first step of the processing consisted of the generation of an initial model for the ELAIS-N1 field. An initial model of the unresolved calibrator source 87GB 160333.2+573543 was used for a direction-independent calibration of the flanking field that was centred in it.
We used data from several radio catalogues to characterize the flux, spectral index slope and curvature for the calibrator source. The data were taken from the 87GB, Texas Survey of Radio Sources, WENSS, VLSS and 8C, covering from 38 MHz to 5 GHz. The measurements were fitted with a polynomial fit of second order, to determine that the flux density of the calibrator at 146 MHz is 4.44 Jy with a spectral index of 0.72 and a curvature of − 0.22. A sky model with a single source with these parameters was the one used as an initial input for the calibration of the flanking field. Figure A.1 shows the result of the fit along the measurements and the location of the ELAIS-N1 LOFAR band. The error of the measurements was also considered in an ODR fit and the results were similar to the polynomial fit within a 0.2 per cent factor.
 |
Fig. A.1 Determination of the flux density of the calibrator 87GB 160333.2+573543 in the LOFAR band using literature data. The measurements from the literature and their respective errors are shown as blue dots. The vertical grey band represents the LOFAR bandwidth of the ELAIS-N1 data. The green dot marks the value of the flux density adopted at a frequency of 146 MHz. |
The gain solutions (amplitude and phase) for this flanking field were transferred to the ELAIS-N1 target field and a direction-independent calibration was applied to obtain a preliminary sky model of the ELAIS-N1 field. The mosaic observation with id. 000 was used because the frequency configuration for the flanking and target fields is the same and allowed a direct transfer of the solutions. The initial sky model was thereafter fed in as the input for the calibration of the dataset 003. A simple direction-independent calibration was performed, solving and correcting for the phase and amplitude gains. The calibration was executed in 8 different bands. A model was extracted from the images using PYBDSF (Mohan & Rafferty 2015). The number of sources increased by a factor 10 due to the wider bandwidth used on the target field in this dataset.
Appendix B Infrastructure
The processing of the data required a combination of high throughput and high performance computing facilities. As the calibration pipeline was developed the computing and storage requirement changed mainly in two ways: (a) the storage requirements diminished by applying optimized levels of averaging to the data and compression (Offringa 2016); (b) the memory and scratch area size requirements increased as the third generation calibration software performance was tuned. The software installation also played an important role in the selection of the infrastructure as explained in Sabater et al. (2017).
The computing cluster of the Instituto de Astrofísica de Andalucía (Consejo Superior de Investigaciones Científicas) in Granada is composed of 28 working nodes with 16 cores and 128 GB of memory. A shared filesystem between the nodes allowed the system to seamlessly access the data. The Cycle 0 datasets 000 and 003 were processed in this cluster with the first direction-independent pipelines.
The grant of a SKA-AWS astrocompute project allowed the use of the Amazon Web Services cloud infrastructure. This mainly solved the problems with the installation and management of the software that was blocking the progress of the calibration at this stage. The run of the pre-factor pipelines for the cycles 0 and 2 of the data and several direction-dependent calibration tests were performed in this infrastructure (Sabater et al. 2017).
The PRE-FACTOR pipeline was adapted to work in the SURF-Sara GRID infrastructure for the calibration of the LoTSS data (Mechev et al. 2017). The use of a custom data model for the ELAIS-N1 field and the processing of the extended bandwidth was allowed with minimal modifications to the pipeline. Hence, the pre-processing of the Cycle 4 datasets was performed in this infrastructure.
Finally, the Cuillin cluster of the Institute of Astronomy of the University of Edinburgh was adapted to the requirements of the next generation direction-dependent pipelines. The cluster contains several nodes with 32 cores and 512 GB of memory. It also provides storage for the data which is accessible from the nodes and big enough scratch data areas to hold the intermediate data. The final direction-dependent calibration was performed in Cuillin.
Appendix C PyBDSF parameters
The parameters used to extract the sources are similar to those used in LoTSS DR1 and are listed in Table C.1. The primary beam uncorrected image, which has more uniform noise properties than the corrected one, was entered as the detection image (detection_image parameter) to detect islands of emission whose characteristics were then derived from the primary beam corrected image.
PyBDSF parameters.
Appendix D Flux scale corrections for the Lockman Hole and Boötes deep fields
We applied the method presented in Sect. 3.5 to determine the flux density scale corrections to the Lockman Hole and BoötesLoTSS deep fields that are presented in Paper I. The surveys used for the Lockman Hole are the VLSSr, TGSS, 6C, the VLA survey at 325 MHz by Owen et al. (2009), WENSS, WSRT 345 MHz by Mahony et al. (2016), the GMRT survey at 610 MHz by Garn et al. (2008b), the WSRT survey at 1.4 GHz by Prandoni et al. (2018), NVSS, and FIRST.For the Boötes field the surveys used are VLSSr, TGSS, 6C, the T-RaMiSu survey at 153 MHz by Williams et al. (2013), the VLA study at 325 MHz by Coppejans et al. (2015), WENSS, the GMRT survey at 610 MHz by Coppejans et al. (2016), the WSRT survey at 1.4 GHz by de Vries et al. (2002), NVSS, and FIRST. Figure D.1 show the flux density ratios and the fit line. The linear fit gives values of 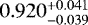 for the Lockman Hole and
for the Lockman Hole and 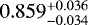 for Boötes at a nominal frequency of 144 MHz. The linear fits were favoured over higher order polynomial fits by the AIC and BIC. The final uncertainty in the flux density scale calibration for the two fields is ~10 per cent if the additional uncertainty term derived in Sect. 5.2 is included.
for Boötes at a nominal frequency of 144 MHz. The linear fits were favoured over higher order polynomial fits by the AIC and BIC. The final uncertainty in the flux density scale calibration for the two fields is ~10 per cent if the additional uncertainty term derived in Sect. 5.2 is included.
 |
Fig. D.1 Calibration of the Lockman Hole (upper panel) and Boötes (lower panel) flux density scales. The default DDF-PIPELINE scale is set to unity and marked with a blue cross. The flux density ratios with respect to other surveys in the literature and their errors are shown in different colours and the fitting line is shown as a red dashed line. The inset shows a zoom view of the area close to the 144 MHz frequency of the observation. |
References
- Akaike, H. 1998, Information Theory and an Extension of the Maximum Likelihood Principle, eds. E. Parzen, K. Tanabe, & G. Kitagawa (New York, NY: Springer New York), 199 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Baars, J. W. M., Genzel, R., Pauliny-Toth, I. I. K., & Witzel, A. 1977, A&A, 500, 135 [NASA ADS] [Google Scholar]
- Becker, R. H., White, R. L., & Edwards, A. L. 1991, ApJS, 75, 1 [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., & Heckman, T. M. 2012, MNRAS, 421, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Kauffmann, G., Heckman, T. M., et al. 2005, MNRAS, 362, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Best, P. N., Ker, L. M., Simpson, C., Rigby, E. E., & Sabater, J. 2014, MNRAS, 445, 955 [NASA ADS] [CrossRef] [Google Scholar]
- Boggs, P. T., & Rogers, J. E. 1990, Contem. Math., 112, 183 [Google Scholar]
- Bondi, M., Ciliegi, P., Venturi, T., et al. 2007, A&A, 463, 519 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Williams, W. L., Hardcastle, M. J., et al. 2017, MNRAS, 469, 3468 [NASA ADS] [CrossRef] [Google Scholar]
- Callingham, J. R., Ekers, R. D., Gaensler, B. M., et al. 2017, ApJ, 836, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Callingham, J. R., Pope, B. J. S., Feinstein, A. D., et al. 2021, A&A, 648, A13 (LoTSS SI) [EDP Sciences] [Google Scholar]
- Chakraborty, A., Roy, N., Datta, A., et al. 2019, MNRAS, 490, 243 [Google Scholar]
- Ciliegi, P., McMahon, R. G., Miley, G., et al. 1999, MNRAS, 302, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Ciliegi, P., Zamorani, G., Bondi, M., et al. 2005, A&A, 441, 879 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cohen, A. S., Lane, W. M., Cotton, W. D., et al. 2007, AJ, 134, 1245 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., & Broderick, J. J. 2002, AJ, 124, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Fomalont, E. B., et al. 2012, ApJ, 758, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Coppejans, R., Cseh, D., Williams, W. L., van Velzen, S., & Falcke, H. 2015, MNRAS, 450, 1477 [Google Scholar]
- Coppejans, R., Cseh, D., van Velzen, S., et al. 2016, MNRAS, 459, 2455 [CrossRef] [Google Scholar]
- Croft, S., Bower, G. C., & Whysong, D. 2013, ApJ, 762, 93 [Google Scholar]
- Croston, J. H., Hardcastle, M. J., Mingo, B., et al. 2019, A&A, 622, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- de Gasperin, F., Dijkema, T. J., Drabent, A., et al. 2019, A&A, 622, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Vries, W. H., Morganti, R., Röttgering, H. J. A., et al. 2002, AJ, 123, 1784 [NASA ADS] [CrossRef] [Google Scholar]
- Dewdney, P. E., Hall, P. J., Schilizzi, R. T., & Lazio, T. J. L. W. 2009, IEEE Proc., 97, 1482 [Google Scholar]
- Douglas, J. N., Bash, F. N., Bozyan, F. A., Torrence, G. W., & Wolfe, C. 1996, AJ, 111, 1945 [NASA ADS] [CrossRef] [Google Scholar]
- Duncan, K. J., Sabater, J., Röttgering, H. J. A., et al. 2019, A&A, 622, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duncan, K. J., Kondapally, R., Brown, M. J. I., et al. 2021, A&A, 648, A4 (LoTSS SI) [EDP Sciences] [Google Scholar]
- Ekers, R. 2012, PoS(RTS2012)007 [arXiv:1212.3497] [Google Scholar]
- Franzen, T. M. O., Banfield, J. K., Hales, C. A., et al. 2015, MNRAS, 453, 4020 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., Green, D. A., Riley, J. M., & Alexander P. 2008a, MNRAS, 383, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Garn, T., Green, D. A., Riley, J. M., & Alexander, P. 2008b, MNRAS, 387, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Gregory, P. C., & Condon, J. J. 1991, ApJS, 75, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Gürkan, G., Hardcastle, M. J., Best, P. N., et al. 2019, A&A, 622, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hales, S. E. G., Masson, C. R., Warner, P. J., & Baldwin, J. E. 1990, MNRAS, 246, 256 [NASA ADS] [Google Scholar]
- Hales, S. E. G., Waldram, E. M., Rees, N., & Warner, P. J. 1995, MNRAS, 274, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Gürkan, G., van Weeren, R. J., et al. 2016, MNRAS, 462, 1910 [NASA ADS] [CrossRef] [Google Scholar]
- Hardcastle, M. J., Williams, W. L., Best, P. N., et al. 2019, A&A, 622, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heckman, T. M., & Best, P. N. 2014, ARA&A, 58, 589 [Google Scholar]
- Herrera Ruiz, N., O’Sullivan, S. P., Vacca, V., et al. 2021, A&A, 648, A12 (LoTSS SI) [EDP Sciences] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, ArXiv e-prints [arXiv:1008.4686] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Callingham, J. R., Hancock, P. J., et al. 2017, MNRAS, 464, 1146 [NASA ADS] [CrossRef] [Google Scholar]
- Intema, H. T., van der Tol, S., Cotton, W. D., et al. 2009, A&A, 501, 1185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Intema, H. T., Jagannathan, P., Mooley, K. P., & Frail, D. A. 2017, A&A, 598, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivezić, Ž., Connolly, A., Vanderplas, J., & Gray, A. 2014, Statistics, Data Mining and Machine Learning in Astronomy (Princeton: Princeton University Press) [CrossRef] [Google Scholar]
- Jackson, N., Tagore, A., Deller, A., et al. 2016, A&A, 595, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jannuzi, B. T., & Dey, A. 1999, ASP Conf. Ser., 191, 111 [Google Scholar]
- Jarvis, M., Taylor, R., Agudo, I., et al. 2016, in MeerKAT Science: On the Pathway to the SKA (USA: NASA), 6 [Google Scholar]
- Jelić, V., de Bruyn, A. G., Mevius, M., et al. 2014, A&A, 568, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open source scientific tools for Python, [Online; accessed 2014-08-26] [Google Scholar]
- Kondapally, R., Best, P. N., Hardcastle, M. J., et al. 2021, A&A, 648, A3 (LoTSS SI) [EDP Sciences] [Google Scholar]
- Lane, W. M., Cotton, W. D., van Velzen, S., et al. 2014, MNRAS, 440, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J., Jahoda, K., & McCammon, D. 1986, ApJ, 302, 432 [NASA ADS] [CrossRef] [Google Scholar]
- Mahatma, V. H., Hardcastle, M. J., Williams, W. L., et al. 2019, A&A, 622, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mahony, E. K., Morganti, R., Prandoni, I., et al. 2016, MNRAS, 463, 2997 [NASA ADS] [CrossRef] [Google Scholar]
- Mandal, S., Prandoni, I., Hardcastle, M. J., et al. 2021, A&A, 648, A5 (LoTSS SI) [EDP Sciences] [Google Scholar]
- McKinney, W. 2010, Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 5 [Google Scholar]
- Mechev, A., Oonk, J. B. R., Danezi, A., et al. 2017, in Proceedings of the International Symposium on Grids and Clouds (ISGC) 2017, held 5 March, 2017 at Academia Sinica, Taipei, Taiwan (ISGC2017) Online at https://pos.sissa.it/cgi-bin/reader/conf.cgi?confid=293, id.2, 2 [Google Scholar]
- Mevius, M. 2018, RMextract: Ionospheric Faraday Rotation calculator (USA: NASA) [Google Scholar]
- Mevius, M., van der Tol, S., Pandey, V. N., et al. 2016, Rad. Sci., 51, 927 [Google Scholar]
- Mingo, B., Croston, J. H., Hardcastle, M. J., et al. 2019, MNRAS, 488, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Mohan, N., & Rafferty, D. 2015, PyBDSF: Python Blob Detection and Source Finder (USA: NASA) [Google Scholar]
- Molenaar, G., & Smirnov, O. 2018, Astron. Comput., 24, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Mooney, S., Quinn, J., Callingham, J. R., et al. 2019, A&A, 622, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morabito, L. K., Deller, A. T., Röttgering, H., et al. 2016, MNRAS, 461, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Morabito, L. K., Matthews, J. H., Best, P. N., et al. 2019, A&A, 622, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morrison, G. E., Owen, F. N., Dickinson, M., Ivison, R. J., & Ibar, E. 2010, ApJS, 188, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Momjian, E., Condon, J. J., et al. 2017a, ApJ, 839, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, T., Kaplan, D. L., Croft, S., et al. 2017b, MNRAS, 466, 1944 [Google Scholar]
- Nisbet, D. 2018, PhD thesis, The University of Edinburgh, UK [Google Scholar]
- Ocran, E. F., Taylor, A. R., Vaccari, M., Ishwara-Chandra, C. H., & Prandoni, I. 2020, MNRAS, 491, 1127 [Google Scholar]
- Offringa, A. R. 2016, A&A, 595, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Offringa, A. R., van de Gronde, J. J., & Roerdink, J. B. T. M. 2012, A&A, 539, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S., Rowan-Robinson, M., Alexander, D. M., et al. 2000, MNRAS, 316, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N. 2018, ApJS, 235, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Owen, F. N., Morrison, G. E., Klimek, M. D., & Greisen, E. W. 2009, AJ, 137, 4846 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Pleunis, Z., Bassa, C. G., Hessels, J. W. T., et al. 2017, ApJ, 846, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Powell, M. J. D. 1964, Comput. J., 7, 155 [CrossRef] [MathSciNet] [Google Scholar]
- Prandoni, I., & Seymour, N. 2015, in Advancing Astrophysics with the Square Kilometre Array (SKA: New Mexico), 67 [Google Scholar]
- Prandoni, I., Guglielmino, G., Morganti, R., et al. 2018, MNRAS, 481, 4548 [NASA ADS] [CrossRef] [Google Scholar]
- Rengelink, R. B., Tang, Y., de Bruyn, A. G., et al. 1997, A&AS, 124, 259 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sabater, J., Sánchez-Expósito, S., Best, P., et al. 2017, Astron. Comput., 19, 75 [Google Scholar]
- Sabater, J., Best, P. N., Hardcastle, M. J., et al. 2019, A&A, 622, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salvatier, J., Wiecki, T.V., F. C. 2016, Peer J Comput. Sci., 2, e55 [Google Scholar]
- Savitzky, A., & Golay, M. J. E. 1964, Anal. Chem., 36, 1627 [Google Scholar]
- Scaife, A. M. M., & Heald, G. H. 2012, MNRAS, 423, L30 [NASA ADS] [CrossRef] [Google Scholar]
- Schinnerer, E., Smolčić, V., Carilli, C. L., et al. 2007, ApJS, 172, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sirothia, S. K., Dennefeld, M., Saikia, D. J., et al. 2009, MNRAS, 395, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Smirnov, O. M., & Tasse, C. 2015, MNRAS, 449, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, D. J. B., Best, P. N., Duncan, K. J., et al. 2016, in SF2A-2016: Proceedings of the Annual meeting of the French Society of Astronomy and Astrophysics, eds. C. Reylé, J. Richard, L. Cambrésy, M. Deleuil, E. Pécontal, L. Tresse, & I. Vauglin, 271 [Google Scholar]
- Smolčić, V., Novak, M., Bondi, M., et al. 2017, A&A, 602, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stacey, H. R., McKean, J. P., Jackson, N. J., et al. 2019, A&A, 622, A18 [EDP Sciences] [Google Scholar]
- Tasse, C. 2014a, A&A, 566, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C. 2014b, ArXiv e-prints [arXiv:1410.8706] [Google Scholar]
- Tasse, C., Hugo, B., Mirmont, M., et al. 2018, A&A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Shimwell T., Hardcastle, M. J., et al. 2021, A&A, 648, A1 (LoTSS SI) [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, A. R., & Jagannathan, P. 2016, MNRAS, 459, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Taylor, A. R., Stil, J. M., Grant, J. K., et al. 2007, ApJ, 666, 201 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tol, S., Jeffs, B. D., & van der Veen, A.-J. 2007, IEEE Transac. Signal Process., 55, 4497 [Google Scholar]
- van Diepen, G. N. J. 2015, Astron. Comput., 12, 174 [NASA ADS] [CrossRef] [Google Scholar]
- van Haarlem, M. P., Wise, M. W., Gunst, A. W., et al. 2013, A&A, 556, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Weeren, R. J., Williams, W. L., Hardcastle, M. J., et al. 2016, ApJS, 223, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderplas, J., Connolly, A., Ivezić, Ž., & Gray, A. 2012, in Conference on Intelligent Data Understanding (CIDU), 47 –54 [Google Scholar]
- Walt, S. v. d., Colbert, S. C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [CrossRef] [Google Scholar]
- Wang, L., Gao, F., Duncan, K. J., et al. 2019, A&A, 631, A109 [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, W. L., Intema, H. T., & Röttgering, H. J. A. 2013, A&A, 549, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Williams, W. L., van Weeren, R. J., Röttgering, H. J. A., et al. 2016, MNRAS, 460, 2385 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, W. L., Hardcastle, M. J., Best, P. N., et al. 2019, A&A, 622, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zwart, J., Wall, J., Karim, A., et al. 2015, Advancing Astrophysics with the Square Kilometre Array (SKA: New Mexico), 172 [Google Scholar]
Development: https://github.com/lofar-astron/ prefactor; Documentation: https://www.astron.nl/citt/ prefactor/
The ‘A-team’ sources are extremely bright sky sources that can affect the observations even when they are far off-axis. They are usually designated as the name of the constellation where they are found and the suffix ‘A’. The main sources that are considered are Cygnus A, Cassiopeia A, Virgo A, and Taurus A but also Hercules A, Hydra A, and some bright 3C sources.
A facet is a sky polygon associated to a given direction (or coordinates) in the sky. The facet is associated to a set of solutions and parameters that are considered to be valid within this region of the sky. A tessellation of A big field is tessellated into smaller facets in order to consider direction-dependent effects.
All Tables
All Figures
 |
Fig. 1 Depths and frequencies of radio surveys in the literature targeting the ELAIS-N1 field. The area of each circle is proportional to the area covered by the survey. The area of the inner dot is proportional to the resolution with smaller dots indicating better resolutions (ranging from 4.5 arcsecs up to 100 arcsecs). The data were not found to be publicly available for the observations outlined with a dashed line (those of Taylor et al. 2007; Taylor & Jagannathan 2016; Ocran et al. 2020). The solid line indicates a spectral index of 0.8 and the dashed line one of 0.7. |
| In the text | |
 |
Fig. 2 Final deep image of the central region of ELAIS-N1 field. Top panel: a wide-field view containing about one third of the total area. Lower panels: zoomed-in regions (each around 0.1 per cent of the full image area), showing the high image quality for extended sources and sensitivity to faint sources. All images are Stokes I, with 6 arcsecs resolution. The full-field image contains more than 85 000 sources. |
| In the text | |
 |
Fig. 3 Selection of sources for the cross-match for the GMRT 610 MHz (left panel) and the NVSS (right panel) samples. All the cross-matched sources are shown as blue dots and the finally selected ones are marked with an orange cross. The completeness limit of the survey is shown as a vertical dashed line. The line at which the flux densities are equal is shown as reference as a solid green line. The locus of sources with a spectral index of 1.5 is shown as a dash-dotted red line. The point at which this line and the survey completeness line cross is used as a reference for the selection threshold in the product of flux densities (see text) which is marked as a purple dotted line. |
| In the text | |
 |
Fig. 4 Calibration of the ELAIS-N1 flux density scale using different methods. The default DDF-PIPELINE scale is set to unity and marked with a blue cross. The scaling factor obtained with the 87GB calibrator is marked with an encircled orange cross. The flux density ratios with respect to other surveys in the literature and their errors are shown in different colours and the fitting line is shown as a red dashed line. The inset shows a zoom view of the area close to the 146 MHz frequency of the observation. |
| In the text | |
 |
Fig. 5 Distribution of the flux density ratio of the sources in common between the individual datasets and the final deep image. The distributions of the datasets are symmetrical in general in flux density scale but their median is systematically different from the expected value of 1. Figure 6 shows that the offsets are correlated with the noise level of the datasets. |
| In the text | |
 |
Fig. 6 Relation between the deviation of the flux density ratio (observed over expected flux density) from the expected value and the noise level of each individual dataset. The vertical axis represents the median value of the flux density ratio distribution.The horizontal axis shows the noise level of the noise-area cumulative distribution at 2 square degrees. This value is a proxy for the calibration and data quality. Datasets of Cycle 2 are marked as blue circles and Cycle 4 as orange squares. The flux density ratios cluster around a line with value 1 (grey horizontal line) as expected but there is a clear inverse relation between flux density ratio and noise level. |
| In the text | |
 |
Fig. 7 Comparison of the sky density of radio sources in our work with those quoted by other radio ELAIS-N1 surveys. The solid blue line shows the total density of sources at each radius for our study. The points show the density of sources quoted in the literature at the corresponding radius to the area covered by those surveys. The density is extended with dashed lines to give an idea of the radius out to which a similar average source density would be achieved with our data. We also show as a comparison the estimated sky density of VLA-COSMOS-3GHz (Smolčić et al. 2017) which reaches a comparable source density in the total 2 square degree area that it covers. |
| In the text | |
 |
Fig. 8 rms noise level in the ELAIS-N1 field. The minimum value is close to the centre at a level of 17.1 μJy beam−1. The effect of the facet division used for the calibration is only visible in areas very far from the centre. The small calibration errors around very bright sources have an adverse effect in the dynamic range of the nearby region. |
| In the text | |
 |
Fig. 9 Area coverage with RMS noise equal to or better than a given value. The distribution for ELAIS-N1 (solid blue line) is compared to that of the other two LoTSS deep fields, the Lockman Hole (dash-dot green line) and Boötes (dashed orange line), observed using similar techniques as presented in Paper I. |
| In the text | |
 |
Fig. 10 Noise deviation in the combined image with respect to that predicted from the combination of the individual dataset images. In the areas with high deviations from the expected value these are limited because the dynamic range of the deep image is reduced due to residual errors in the calibration around bright sources. |
| In the text | |
 |
Fig. 11 Histogram of the noise deviation in the combined image with respect to that predicted from the individual images, assuming that the noise in each is uncorrelated. The histogram is computed in the area closer than 3 degrees to the centre. The median value of the distribution (solid grey line) is a 15.6 per cent increase in noise in the deep image. |
| In the text | |
 |
Fig. 12 Standard deviation (σ) of the logarithmic relative flux density with respect to several parameters. Upper left panel: relation of σ with respect to the signal-to-noise level for sub-samples separated in terciles of distance from the pointing centre and major axis. The different terciles are marked with arrow symbols in the legend: up arrows for the higher tercile, left-right arrows for the middle tercile, and down arrows for the lower one. Upper right panel: relation of σ with respect to the distance to the centre for terciles of major axis and S/N. Lower left panel: relation of σ with respect to the major axis of the sources for terciles of distance to the centre and S/N. Lower right panel: contribution of the calibration effects of the dataset (σdataset, as explainedin the text) with respect to the rms noise at 2 square degrees for the individual datasets (coloured circles). The linear fit to the relation is shown as a orange line and its 95 per cent confidence interval as a shaded orange band. The extrapolated location of the final deep image is also marked in the diagram as a green cross. |
| In the text | |
 |
Fig. 13 Dependence of the additional noise term C with radius. The empirical values (blue crosses) are fitted with a modified softplus function (orange line). |
| In the text | |
 |
Fig. 14 Diagram showing the location of extended sources. The concentration (total over peak flux density) is plotted with respectto the S/N of the total flux density. The colour scale represents the confidence level at which a source can be considered to be extended after also taking into account the radial location of the source in the field (see text for more details). |
| In the text | |
 |
Fig. 15 Comparison of the intra-band spectral index (αLOFAR) with the NVSS to LOFAR spectral index (αLOFAR-NVSS). The colour of the dots is proportional to the deviation from the (black solid) line where the spectral indices are equal. The errors are plotted as faint grey lines and indicate the 95 per cent confidence interval. The median of the distributions for all the sources are shown as grey dash-dotted lines. The median of the distribution of αLOFAR for the sources that were matched to NVSS sources is shown as a dotted line. The orange dashed line shows the total least squares fit to the distribution (see text). Upper panel: histogram with the distribution of αLOFAR-NVSS. Right panel: histogram with the distribution of αLOFAR for the cross-matched sources (blue) and for the total sample over-plotted (green). |
| In the text | |
 |
Fig. 16 Difference between the intra-band spectral index (αLOFAR) and the NVSS to LOFAR spectral index (αLOFAR-NVSS) compared to the S/N of the cross-matched sources. The distribution of S/N is divided in deciles and the median of the difference is computed and shown as orange lines. The spectral indices are flatter (lower values of the difference) for low S/N likely due to incompletness effects. The distribution is close to zero (marked as a horizontal grey line) for sources with S∕N > 500 (shown as a vertical green dashed line). |
| In the text | |
 |
Fig. A.1 Determination of the flux density of the calibrator 87GB 160333.2+573543 in the LOFAR band using literature data. The measurements from the literature and their respective errors are shown as blue dots. The vertical grey band represents the LOFAR bandwidth of the ELAIS-N1 data. The green dot marks the value of the flux density adopted at a frequency of 146 MHz. |
| In the text | |
 |
Fig. D.1 Calibration of the Lockman Hole (upper panel) and Boötes (lower panel) flux density scales. The default DDF-PIPELINE scale is set to unity and marked with a blue cross. The flux density ratios with respect to other surveys in the literature and their errors are shown in different colours and the fitting line is shown as a red dashed line. The inset shows a zoom view of the area close to the 144 MHz frequency of the observation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


