| Issue |
A&A
Volume 687, July 2024
|
|
|---|---|---|
| Article Number | A267 | |
| Number of page(s) | 18 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202349085 | |
| Published online | 23 July 2024 | |
LOFAR Deep Fields: Probing the sub-mJy regime of polarized extragalactic sources in ELAIS-N1
I. The catalog
1
Department of Space, Earth and Environment, Chalmers University of Technology,
412 96
Gothenburg,
Sweden
e-mail: sara.piras@chalmers.se
2
Department of Space, Earth and Environment, Chalmers University of Technology,
Onsala Space Observatory,
43992
Onsala,
Sweden
3
ASTRON, Netherlands Institute for Radio Astronomy,
Oude Hoogeveensedijk 4,
7991 PD,
Dwingeloo,
The Netherlands
4
Leiden Observatory, Leiden University,
PO Box 9513,
2300 RA
Leiden,
The Netherlands
5
Departamento de Física de la Tierra y Astrofísica & IPARCOS-UCM, Universidad Complutense de Madrid,
28040
Madrid,
Spain
6
INAF Istituto di Radioastronomia,
Via Gobetti 101,
40129
Bologna,
Italy
7
Ruđer Bošković Institute,
Bijenička cesta 54,
10000
Zagreb,
Croatia
8
Ruhr University Bochum, Faculty of Physics and Astronomy, Astronomical Institute,
Universitätstrasse 150,
44801
Bochum,
Germany
9
Institute for Astronomy, University of Edinburgh,
Royal Observatory, Blackford Hill,
Edinburgh,
EH9 3HJ,
UK
10
Hamburger Sternwarte, University of Hamburg,
Gojenbergsweg 112,
21029
Hamburg,
Germany
11
INAF-Osservatorio Astronomico di Cagliari,
Via della Scienza 5,
09047
Selargius (CA),
Italy
Received:
22
December
2023
Accepted:
10
May
2024
Context. Quantifying the number density and physical characteristics of extragalactic polarized sources is important for the successful planning of future studies based on Faraday rotation measure (RM) grids of polarized sources to probe foreground Galactic and intergalactic magnetic fields. However, it is proving very hard to detect polarized signal from the population of very faint (sub-mJy) polarized sources at low radio frequencies, and their properties are mostly unknown. LOFAR can play an important role in such studies thanks to its sensitivity and angular resolution, combined with the precision on the inferred RM values that can be achieved through low-frequency broad-band polarimetry.
Aims. The aim of this study is to probe the sub-mJy polarized source population with LOFAR. In this first paper, we present the method used to stack LOFAR polarization datasets, the resulting catalog of polarized sources, and the derived polarized source counts.
Methods. The European Large Area ISO Survey-North 1 (ELAIS-N1) field, one of the deepest of the LOFAR Two-Metre Sky Survey (LoTSS) Deep Fields so far, was selected for a polarimetric study at 114.9–177.4 MHz. A total area of 25 deg2 was imaged at 6″-resolution in the Stokes Q and U parameters. Alignment of polarization angles was done both in frequency and in Faraday space before stacking datasets from 19 eight-hour-long epochs taken in two different LOFAR observing cycles. A search for polarized sources was carried out in the final, stacked dataset, and the properties of the detected sources were examined. The depolarization level of sources known to be polarized at 1.4 GHz was quantified.
Results. A one-sigma noise level, σQU, of 19 µJy beam−1 was reached in the central part of the field after stacking. Twenty-five polarized sources were detected above 8σQU, five of which had not been detected in polarization at any other radio frequencies before. Seven additional polarized components were found by lowering the threshold to 6σQU at positions corresponding to sources known to be polarized at 1.4 GHz. In two radio galaxies, polarization was detected from both radio lobes, so the final number of associated radio continuum sources is 31. The detected sources are weakly polarized, with a median degree of polarization of 1.75% for the sample of sources detected in polarized emission. For the 10 polarized sources previously identified in a pilot LOFAR study of the ELAIS-N1 field at 20″-resolution, the RM values are consistent but the degrees of polarization are higher in the 6″-resolution data. The sources previously detected in polarization at 1.4 GHz are significantly depolarized at 150 MHz. The catalog is used to derive the polarized source counts at 150 MHz.
Conclusions. This is the deepest and highest-resolution polarization study at 150 MHz to date. A full characterization of the sources and an analysis of the catalog will be presented in Paper II.
Key words: magnetic fields / polarization / methods: numerical / methods: observational / techniques: polarimetric / galaxies: individual: ELAIS-N1
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The measurement of polarized radio emission from extragalactic sources provides information not only on the polarization properties of the sources themselves but also on the properties of the intervening medium, through Faraday rotation effects, which are related to the distribution of thermal electrons and magnetic fields along the line of sight (which goes through any intervening intergalactic medium (IGM), galactic and interstellar medium, including that of the Milky Way). Faraday rotation causes the polarization angle χ of the linearly polarized wave emitted by a source to rotate as it propagates through a magneto-ionic medium:
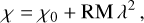 (1)
(1)
where χ is measured at the wavelength λ of the observation, χ0 is the intrinsic value of the polarization angle, and RM is the rotation measure. In the simplest possible scenario where Faraday rotation occurs in a purely thermal foreground medium, RM is equal to a physical quantity, ϕ(L), the Faraday depth of the source at distance Ľ from the observer:
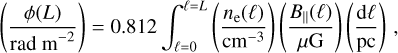 (2)
(2)
where ne is the density of thermal electrons, B‖ is the line-of-sight component of the magnetic field, B, taken to be positive if B points from the source toward the observer, and dℓ is the infinitesimal pathlength along the line of sight from the source at ℓ = 0 to the observer at distance L from the source (e.g., Burn 1966; Ferrière et al. 2021).
The detection of polarization from extragalactic sources across the sky makes it possible to obtain information on the properties of the IGM through the construction of so-called “RM grids”. The denser the grid, the finer the reconstruction of IGM polarization structures. The largest RM catalog available so far covers the entire sky north of −40° declination at 1.4 GHz (Taylor et al. 2009) and contains an average of one polarized source per square degree. It was based on the NRAO Very Large Array Sky Survey (NVSS; Condon et al. 1998). Stacking polarized intensities from NVSS sources, Stil et al. (2014) found a gradual increase in median fractional polarization toward fainter sources. Earlier studies of bright steep-spectrum NVSS sources had shown that the median fractional polarization was higher in low flux-density bins than in high flux-density bins (Mesa et al. 2002, Tucci et al. 2004). The behavior of fractional polarization vs flux density at low flux densities is still an open question and dictates the number of polarized sources that will be detected in future polarization surveys, such as with the Square Kilometre Array (SKA). Van Eck et al. (2023) recently published an RM catalog of 55 819 sources (including Galactic sources) gathered from 42 published catalogs, and proposed standards for reporting polarization and RM measurements.
Deeper polarization surveys will produce denser RM grids. The deepest extragalactic polarization studies at 1.4 GHz of the northern sky are those of ELAIS-N11 (Grant et al. 2010), of the Lockman Hole (Berger et al. 2021), and of GOODS-N (Rudnick & Owen 2014). Deep polarization surveys of the southern sky, also at 1.4 GHz, were carried out in ELAIS-S1 and CDF-S (Hales et al. 2014). Those surveys vary greatly in sky coverage (about 15 deg2 for ELAIS-N1, 6.5 deg2 for the Lockman Hole, and 0.3 deg2 for GOODS-N) and in depth, the deepest survey being that of the Lockman hole with a one-sigma sensitivity of 7 µJy beam−1, and a beam of 15″ (Berger et al. 2021). The largest number density of polarized sources (51 per square degree) was found in the small GOODS-N field that was observed at higher angular resolutions (1.6″ and 10″; Rudnick & Owen 2014).
The aim of the LOFAR Magnetism Key Science Project (MKSP)2 is to investigate the magnetized Universe using LOFAR. The search for polarized sources at low radio frequencies is particularly arduous due to the influence of the ionosphere (e.g., Sotomayor-Beltran et al. 2013) and Faraday depolarization effects which become increasingly strong towards lower frequencies because of the large amounts of Faraday rotation suffered by different regions of a synchrotron-emitting source within the telescope beam (e.g. Burn 1966; Sokoloff et al. 1998). Some of these difficulties can, however, be overcome with LOFAR thanks to the angular resolution that reduces beam depolarization, the high precision on rotation measures (approximately 1 rad m−2) that can be achieved through broadband polarimetry, and the sensitivity.
Polarization studies with LOFAR at 150 MHz in the field of nearby galaxy M51 resulted in the detection of 0.3 polarized sources per square degree at 20″ resolution and one-sigma sensitivity of 100 µJy beam−1 (Mulcahy et al. 2014, Neld et al. 2018). By analyzing the 570 deg2 region presented in the Preliminary Data Release from the LOFAR Two-Metre Sky Survey (LoTSS, Shimwell et al. 2017, 2019). Van Eck et al. (2019) found 92 polarized radio sources in images of 4.3′-resolution and 1 mJy beam−1 one-sigma sensitivity. Polarization was detected in a number of giant radio galaxies (O’Sullivan et al. 2018, 2019, Stuardi et al. 2020, Mahatma et al. 2021), an indication that radio sources located in low-density environments have a greater chance to survive depolarization at low frequencies. O’Sullivan et al. (2020) used the RM differences measured between close physical and non-physical pairs of radio sources in LoTSS data to place constraints on the magnetization of the cosmic web. A catalog of 2461 polarized sources with RM values across 5720 deg2 of the northern sky was produced by O’Sullivan et al. (2023) who used the second data release (DR2) of the LoTSS at 20″ resolution. Carretti et al. (2022, 2023) used this catalog to probe the strength and evolution of magnetic fields in cosmic filaments.
The LOFAR Deep Fields (Boötes, the Lockman Hole and ELAIS-N1; Tasse et al. 2021, Sabater et al. 2021), along with deep observations of GOODS-N (Vacca et al., in prep.), are best suited for deep polarization searches. To date, the deepest published polarization study with LOFAR was carried out on the ELAIS-N1 field by Herrera Ruiz et al. (2021), who developed a method to stack polarization data taken at different epochs. By combining six datasets, each from eight-hour-long observations, they were able to reach a one-sigma sensitivity of 26 µJy beam−1 in the central part of the final image of the field at a resolution of 20″, which enabled the detection of 10 polarized sources in an area of 16 deg2 (0.6 polarized source per square degree).
In this work, we expand on the pilot study of Herrera Ruiz et al. (2021) by improving on both the angular resolution and the sensitivity, and enlarging the analyzed field area; this was achieved by re-imaging the data at a resolution of 6 arcseconds, stacking data from 19 different epochs, and imaging a field of 25 deg2. The paper is organized as follows. After summarizing the existing polarization studies of the ELAIS-N1 field in Sect. 2, we present in Sect. 3 the observations, the imaging and calibration procedures, the datasets, and the data processing to produce Faraday cubes. The stacking method is described in Sect. 4 and the search for polarized sources in the stacked data in Sect. 5. In Sect. 6 we present and discuss the results, and conclude in Sect. 7. Further analysis of the catalog of polarized sources will be presented in a companion paper (Piras et al. 2024, Paper II).
Basic characteristics of polarization studies covering the ELAIS-N1 field.
2 Polarization searches in the ELAIS-N1 field
The ELAIS-N1 field is a region of the northern hemisphere3 observed by the ELAIS survey (Oliver et al. 2000), originally chosen for deep extragalactic observations with the Infrared Space Observatory (ISO) because of its low infrared background (Rowan-Robinson et al. 2004; Vaccari et al. 2005). The ELAIS-N1 field has been the target of a number of polarization studies. The Galactic polarized foregrounds were imaged with LOFAR by Jelić et al. (2014), and more recently by Šnidarić et al. (2023) who used 150 h of LOFAR observations at very low resolution (4.3 arcmin) to study the diffuse Galactic polarized emission. Extragalactic polarized sources were detected in different surveys, as summarized in Table 1. Deep polarization imaging has been carried out at 1.4 GHz by Taylor et al. (2007) and Grant et al. (2010) at the Dominion Radio Astronomical Observatory (DRAO). Of particular interest are the results from Grant et al. (2010) that can be used to compare the characteristics of the polarized sources at 1.4 GHz and at 150 MHz and investigate depolarization between those two frequencies in the region of overlap (about 15 square degrees). Grant et al. (2010) detected 136 polarized sources and used the catalog to construct the Euclidean-normalized polarized differential source counts down to 400 µJy. They found, at 1.4 GHz, that fainter radio sources have a higher fractional polarization than the brighter ones. This catalog, however, does not contain any information on rotation measures, and for this we rely on the RM catalog of Taylor et al. (2009) derived from data from the NRAO Very Large Array Sky Survey (NVSS; Condon et al. 1998) taken in two frequency bands centered at 1.365 and 1.435 GHz.
Figure 1 shows the central 25 deg2 area of the 6″-resolution LOFAR image of the ELAIS-N1 field (Sabater et al. 2021); highlighted in magenta is the central region of the field with ample multiwavelength coverage (see Kondapally et al. 2021 for a summary). Also overlaid on Fig. 1 are the two regions within the field where dedicated polarization searches were performed: at 1.4 GHz with DRAO (Grant et al. 2010) and at 150 MHz with LOFAR (Herrera Ruiz et al. 2021). Also shown are the locations of the polarized sources detected in those surveys, of the sources with RM values from the NVSS (Taylor et al. 2009), and the polarized sources identified in this work.
3 Data
3.1 Observations
A detailed description of the observations has been given by Sabater et al. (2021). The datasets used in this work4 consist of observations of the ELAIS-N1 field taken in full polarization with the LOFAR High Band Antenna (HBA) between May 2013 and 27 August 2015 (Cycles 0, 2, and 4; proposals LC0_019, LC2_024, and LC4_008). Defining as epoch an eight-hour LOFAR observation, 22 epochs from Cycles 2 and 4 are available for a total of 176 hours of observations. The observations are centered on RA = 16h11m00s, Dec = 55°00′00″ (J2000).
As shown in Table 2, the frequency setup of the Cycle 4 observations was different from that of Cycle 2. This meant that the stacking of data from different cycles could not be done directly in frequency space; it was done in Faraday space, as will be described in Sect. 4. Šnidarić et al. (2023) also stacked data in Faraday space to investigate the Galactic polarized emission in ELAIS-N1, but used a different approach, cross-correlating data from different epochs to determine the offsets. The last three parameters in Table 2 will be defined in Sect. 3.4.
3.2 Data imaging and calibration
The data for ELAIS-N1 were calibrated for the Sabater et al. (2021) study and reprocessed for the work presented here. For each frequency channel of the data from the 22 epochs we created primary-beam-corrected Stokes Q and U images at 6″ angular resolution. The images were created with the software DDFacet (Tasse et al. 2018), allowing us to apply the direction independent and dependent (45 directions) calibration solutions derived by Sabater et al. (2021) whilst correcting for the LOFAR beam. As described in more detail in O’Sullivan et al. (2023), the calibration solutions were derived with the assumption that Q = U = V = 0, which has the effect of suppressing instrumental polarization – although it can produce spurious polarized sources if there are genuinely bright (>10 mJy beam−1) polarized sources in the field, but this is not an issue for the ELAIS-N1 field. The images were not deconvolved as this functionality was not available in DDFacet at the time of processing. For six of the 22 datasets, some frequency channels were missing after the data processing. The reason for this is unknown to us, but we suspect that it has to do with the large data volumes and memory issues. For three datasets (L229064, L230461, L346154), we could identify the missing channels as this information was present in the original Measurement Sets and those datasets were included in the analysis. The remaining three datasets (L229387, L347512, L366792) were excluded as the missing frequency channels could not be identified and the frequency information could not be recovered.
Because of the lack of polarization calibrators at low frequencies, the inferred polarization angles are not absolute. However, this is not an issue in the work presented here that focuses on measurements of Faraday rotation of the polarization angles across the frequency band. Although the data are corrected for ionospheric Faraday rotation during the eight-hour-long integrations, some variations remain between the various datasets and the polarization angles will need to be aligned before stacking. This will be done using one of our brightest polarized sources as a polarization calibrator, as explained in Sect. 4.
 |
Fig. 1 LOFAR 150 MHz total-intensity image of the ELAIS-N1 field at 6″-resolution and of size 5 × 5 deg2 (Sabater et al. 2021), on which the coverages of various polarization surveys and the locations of polarized sources are overlaid, as indicated in the legend. |
LOFAR observing configurations for the ELAIS-N1 Deep Field and parameters of RM synthesis.
3.3 Datasets
In Table 3 we summarize the 19 observations and datasets used in this paper. Each dataset consists of Stokes Q and U frequency cubes of the imaged region of 25 deg2 area. The size of each Stokes-parameter cube is 12 005 pixels × 12 005 pixels × number of frequency channels (800 for datasets from Cycle 2 and 640 for Cycle 4 data). The pixel size in (RA, Dec) is 1.5″×1.5″. The data volume of each Stokes-parameter cube is ~400 GB, resulting in a total data volume of ~15 TB for all epochs. Because of the large size of the input data, and estimating that the output data would be about three times larger, the data processing had to be carried out on a supercomputer (Vera, at the Chalmers Centre for Computational Science and Engineering) and a strategy had to be developed to manage memory issues and optimize the processing times. In particular, the Stokes Q, U frequency cubes were divided in horizontal strips in ranges of declination (Sect. 5).
3.4 Rotation measure synthesis
The complex linear polarization is:
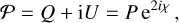 (3)
(3)
where P is the polarized intensity and χ the polarization angle. All these quantities (𝒫, Q, U, P, χ) depend on frequency, v, but it is common to express them as a function of wavelength squared, λ2, because of the nature of Faraday rotation. In this section we describe how data are transformed from frequency space to Faraday depth space using the rotation measure synthesis (Burn 1966; Brentjens & de Bruyn 2005).
The complex linear polarization can be expressed as the integral over all Faraday depths, ϕ, of the complex Faraday dispersion function 𝓕(ϕ) modulated by the Faraday rotation:
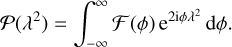 (4)
(4)
This is a Fourier-transform-like relation that can in principle be inverted to express 𝓕(ϕ):
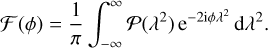 (5)
(5)
In practice, because of the limited number of channels at which the polarized intensity can be measured, the inferred Faraday dispersion function is the convolution of the true Faraday dispersion function 𝓕(ϕ) with the so-called RM Spread Function (RMSF):
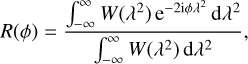 (6)
(6)
where the sampling function or weight function W(λ2) is nonzero at the measured λ2 and zero elsewhere.
Figure A.1 shows two examples of RMSFs for two LOFAR observation cycles. They are very similar despite the slightly different frequency setups during Cycle 2 and Cycle 4. Even within the same observation cycle, the RMSF may be slightly different as it depends on the locations of flagged frequency channels.
Three key parameters of RM synthesis are the resolution in Faraday space, the largest scale in Faraday depth and the maximum Faraday depth to which the technique is sensitive:
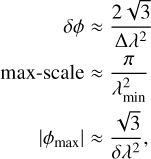 (7)
(7)
where 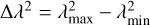 is the λ2 coverage, λmax = c/νmin is the maximum wavelength, λmin = c/νmax the minimum wavelength, vmin and νmax are the lowest and highest frequencies of the whole bandwidth, and δλ2 is the channel width in λ2 space (Brentjens & de Bruyn 2005). In Table 2 we list the values of those parameters for the LOFAR datasets from each observing cycle. The main difference between the frequency setups of Cycle 2 and Cycle 4 is the width of the frequency channels, which affects ϕmax. Because the total frequency coverage was very similar during both cycles, the resolution in ϕ space, δϕ, and the largest scale in ϕ, max-scale, are basically identical.
is the λ2 coverage, λmax = c/νmin is the maximum wavelength, λmin = c/νmax the minimum wavelength, vmin and νmax are the lowest and highest frequencies of the whole bandwidth, and δλ2 is the channel width in λ2 space (Brentjens & de Bruyn 2005). In Table 2 we list the values of those parameters for the LOFAR datasets from each observing cycle. The main difference between the frequency setups of Cycle 2 and Cycle 4 is the width of the frequency channels, which affects ϕmax. Because the total frequency coverage was very similar during both cycles, the resolution in ϕ space, δϕ, and the largest scale in ϕ, max-scale, are basically identical.
In the simplest scenario, in which the synchrotron radiation is Faraday-rotated by a foreground magneto-ionic medium, the measured RM is equal to the Faraday depth. For simplicity, ϕ and RM are used here as synonyms.
We used the Python code pyrmsynth_lite5 to perform RM synthesis (Brentjens & de Bruyn 2005), with uniform weighting and with the RMCLEAN option (Heald et al. 2009) to deconvolve the Faraday dispersion function from the RMSF. The outputs of pyrmsynth_lite are three-dimensional Faraday cubes (RA, Dec, ϕ) and two-dimensional sky maps:
The Stokes Q and U Faraday cubes (Q(ϕ), U(ϕ)) are the real and imaginary parts of the reconstructed Faraday dispersion function;
The polarized intensity cube
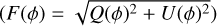 ;
;The corresponding two-dimensional maps, obtained at values of ϕ that correspond to the peaks of F(ϕ); we name these maps Fmap, Qmap, Umap, RMmap.
The Faraday cubes have a span in Faraday depth of ±450 rad m−2 and a spacing of 0.3 rad m−2. The range [−3, +1.5] rad m−2 was excluded from the analysis to avoid the leakage signal (following Herrera Ruiz et al. 2021). Additionally, noise maps were created with pixel values equal to the mean of the noise levels in Q(ϕ) and U(ϕ), calculated as the standard deviations in the [350, 450] rad m−2 range of Faraday depths, where no polarized signal is expected.
LOFAR ELAIS-N1 datasets used in this paper.
4 Stacking
The stacking procedure is summarized in Fig. 2. Although the data from each given epoch were corrected for ionospheric Faraday rotation, polarization angles from different observing runs may differ due to ionospheric correction effects, as a full polarization calibration (for the ensemble of 19 datasets) was not performed. This can lead to depolarization when data from different epochs are combined. It is therefore crucial to align the polarization angles before stacking. Because of the different frequency setups in Cycle 2 and Cycle 4, the stacking had to be done in two steps: first, data from a given cycle were stacked in frequency space, following the method used by Herrera Ruiz et al. (2021); then the two stacked datasets from both cycles were stacked in Faraday depth space.
4.1 Stacking frequency cubes from same observation cycle
4.1.1 The reference source: calculating corrections
The stacking method is based on the use of a polarized reference source in a reference epoch as polarization angle calibrator. For each epoch, angular corrections are calculated for the reference source and applied to the whole field.
As reference source we used the same polarized source as the one selected by Herrera Ruiz et al. (2021) in their LOFAR pilot polarization study of ELAIS-N1 (ILTJ160538.33+543922.6; their source 02, our source 07). This source has a peak polarized intensity of ~6 mJy beam−1 and an RM of ~6 rad m−2 in data from all epochs. It is located in the part of the ELAIS-N1 field for which value-added data are available, including a photometric redshift estimate of 0.7911 (Duncan et al. 2021). In the LOFAR 6-arcsec Stokes I image of Sabater et al. (2021), there are two radio components on either side of the host galaxy, and polarization is detected in the south-western component which is probably a radio lobe. As will be shown later, this source is the one in which we detect polarization with the highest signal-to-noise ratio (S/N). It is well detected at each epoch.
Cut-outs of 2.5 × 2.5 arcmin2 in the data cubes centered at the reference source were made for each epoch. RM synthesis was performed on each cut-out. To achieve a better precision on the RM values of the reference source, RM synthesis was performed with a sampling of 0.01 rad m−2 around the RM value of the reference source in the range of ± 10 rad m−2.
As reference epoch we used Epoch 014 from Cycle 2, which is the dataset of highest quality, with the lowest and most uniform noise. Herrera Ruiz et al. (2021) had stacked only data from Cycle 4 and used Epoch 24 as their reference epoch.
The polarization angle calibrator is the reference source at the reference epoch. Its coordinates6 are those of the pixel of the peak intensity in the polarized intensity map.
In Fig. 3 we show the polarization characteristics of the polarization angle calibrator, and the same quantities for the corresponding pixels in stacked data from Cycle 2 and from Cycle 4 for the reference source. The Q and U Stokes parameters show clear oscillations with frequency (or wavelength squared), as expected with Faraday rotation. The polarized intensity decreases with increasing λ2, which is a sign of Faraday depolarization. The polarization angle (χ, bottom right, and corresponding panels above) varies linearly with λ2. The positive slope indicates a positive RM. These graphs show clearly that stacking reduced the scatter in the data.
Each dataset has a slightly different frequency coverage, and therefore the mean frequency and the corresponding wavelength squared 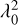 are slightly different, as listed in Table 4. This means that the polarization angles output from RM synthesis refer to a different
are slightly different, as listed in Table 4. This means that the polarization angles output from RM synthesis refer to a different 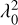 for each epoch. Therefore, the polarization angles must be corrected to take into account the Faraday rotation,
for each epoch. Therefore, the polarization angles must be corrected to take into account the Faraday rotation, 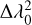 , that occurs between two different values of
, that occurs between two different values of 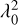 .
.
For each epoch we computed the difference 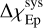 between the polarization angle at the reference epoch (the “calibrator”) and the polarization angle of the epoch to be corrected. The difference
between the polarization angle at the reference epoch (the “calibrator”) and the polarization angle of the epoch to be corrected. The difference 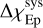 is calculated as follows:
is calculated as follows:
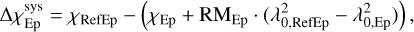 (8)
(8)
where χRefEp is the polarization angle of the reference source at the reference epoch; χEp is the polarization angle of the reference source at Epoch Ep; the term 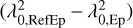 is the rotation due to the Faraday rotation between the different
is the rotation due to the Faraday rotation between the different 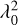 , values between the reference epoch RefEp and epoch Ep.
, values between the reference epoch RefEp and epoch Ep.
The RM values of the reference source (RMEp) are listed in the third column of Table 4; the systematic corrections, 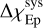 , are given in the last column, for each epoch. The errors on the corrections were computed from the standard deviations of Q(ϕ) and U(ϕ) in the outer 20% of the Faraday depth range, with sampling 0.3 rad m−2, using error propagation rules.
, are given in the last column, for each epoch. The errors on the corrections were computed from the standard deviations of Q(ϕ) and U(ϕ) in the outer 20% of the Faraday depth range, with sampling 0.3 rad m−2, using error propagation rules.
4.1.2 Weights
In the stacking process, weights were attributed to each dataset, based on the noise in each dataset. For each epoch, we selected a small (2.5 × 2.5 arcmin2) central region, centered on RA=16h11m00s and Dec = 55°00′00″, and RM synthesis was performed. The mean of the noise map, σQU,Ep, was used to calculate the weight 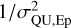 . Table 3 shows the values of σQU,Ep for each epoch.
. Table 3 shows the values of σQU,Ep for each epoch.
4.1.3 Making strips
Because of the large size of the datasets (about 400 GB for a single Stokes-parameter frequency cube), we had to divide the field into strips to perform the analysis in parallel on multiple cores of the supercomputer. We produced 80 strips of 12 005 × 150 pixels (about 5 degree width in RA and 3.75 arcmin height in Dec). The Stokes I image (Sabater et al. 2021) was divided in a similar way. All pixels below 320 µJy beam−1 in total intensity (~10 σI) were masked during RM synthesis.
4.2 Applying corrections and stacking
We applied the corrections ΔχEp calculated on the reference source to the whole field at each epoch:
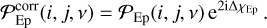 (9)
(9)
Finally, for each cycle, inverse-variance-weighted averages of Stokes Q and U parameters, QCycle and UCycle, were calculated at each pixel in the frequency cube:
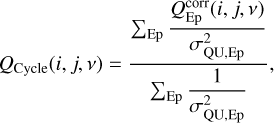 (10)
(10)
and similarly for the Stokes parameter U.
Stacked Stokes Q and U cubes of the central region were produced with the same method to compute the weights used to stack the various datasets.
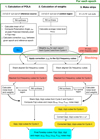 |
Fig. 2 Flowchart of the stacking process. POLA stands for Polarization Angle. |
 |
Fig. 3 Polarization characteristics of the reference source (Source 07). Stokes Q and U intensities, polarized intensity P and polarization angle χ are shown as a function of frequency and wavelength squared λ2 (bottom and top axes) for the reference epoch (in black, first two rows), and for the stacked data from Cycle 2, (in blue, third and fourth row) and from Cycle 4 (in orange, two last rows). The scatter in the data is reduced by stacking. The effect of Faraday rotation is clearly visible in the variations of Q, U and χ; the decrease of the polarized intensity with λ2 is an indication of Faraday depolarization. The final combination of Cycle 2 and Cycle 4 data is done in Faraday depth space, as described in the text. |
Values of  in datasets of different epochs, RM values of the reference source and applied polarization angle corrections.
in datasets of different epochs, RM values of the reference source and applied polarization angle corrections.
4.3 Stacking Faraday cubes from different observation cycles
Because of the different frequency setup of data taken in Cycle 2 and in Cycle 4, the data could not easily be combined in frequency space but had to be combined in Faraday depth space. We performed RM synthesis on each stacked QU frequency cube strip from Cycle 2 and from Cycle 4.
The mean wavelength squared, 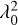 slightly differs between the two cycles:
slightly differs between the two cycles:
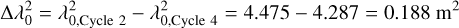 (11)
(11)
and we used this difference to correct data from Cycle 4:
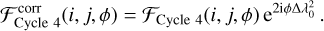 (12)
(12)
RM synthesis was performed on the stacked Stokes Q and U cubes of the central region and the means of the noise maps, σQU,Cycle, were used to weigh the two cycles. The final stacked data cubes (Cycle 2+Cycle 4) of Qst(ϕ) and Ust(ϕ) were produced by an inverse-variance weighted average of the Q(ϕ) and U(ϕ) cubes of the two cycles:
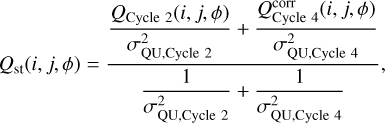 (13)
(13)
and similarly for Stokes parameter U.
The final Faraday cube Fst(ϕ) was obtained by combining Qst(ϕ) and Ust(ϕ) at each pixel and ϕ:
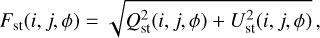 (14)
(14)
and final maps were produced from the Faraday cubes (polarized intensity map; Stokes Q and U maps; RM map; noise map).
Figure 4 shows the Faraday spectra of three sources in the reference epoch (Epoch 014), in stacked Cycle 2, stacked Cycle 4, and combining both cycles. The three sources are the reference source (source 07, left panel), source 04B (middle panel; this is the brightest source in polarized intensity, and the source with the highest RM value), and source 11 (right panel; a faint source detectable only after stacking the two cycles). These figures illustrate how noise levels in Faraday spectra are decreased by stacking, and that the leakage peak is also reduced.
4.4 Noise properties
The noise levels, σQU, were measured in the central 2.5′ × 2.5′ region, both in datasets from individual epochs (Table 3) and after stacking (Table 5). The second column of Table 3 gives the measured median noise values after stacking, while the third column gives the noise values calculated from Gaussian statistics (where 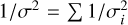 , where the index i runs from one to the number of elements in the stacked dataset). The decrease in the noise level after stacking is in agreement with expectations from Gaussian statistics.
, where the index i runs from one to the number of elements in the stacked dataset). The decrease in the noise level after stacking is in agreement with expectations from Gaussian statistics.
Figure 5 shows the improvement in the sensitivity brought by stacking: the noise level in the field is lower after stacking the datasets from both cycles. The curves also clearly show the better quality of the Cycle 2 data compared to Cycle 4 data. Up to a radius of 2.5° (which corresponds to an area of 19.6 deg2), the shape of the curves follows the profile expected from the noise increase with radius within a circular Gaussian primary beam, in which case the corresponding area with a noise lower than a given σ is given by:
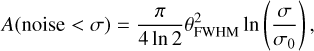 (15)
(15)
where θFWHM = 3.80° is the full-width half maximum of the primary beam of the LOFAR High Band Array at 150 MHz7 and σ0 is the value of the noise in the center of the image, as shown by the dashed black curve. The noise increases rapidly for areas greater than about 20 deg2; this is because of the contributions from pixels in the four corners of the map in the regions that are within the 5 × 5 deg2 area but outside the disk of 2.5° radius.
 |
Fig. 4 Faraday spectra of three sources: the reference source (source 07, left panel); the brightest polarized source component (04B, middle panel), and a faint source detected only after stacking data from both cycles (source 11, right panel). The displayed Faraday spectra are from the reference epoch (Epoch 014), from stacked Cycle 2, stacked Cycle 4, and combining both cycles. The gray region outlines the range in Faraday depth that was excluded from the analysis due to instrumental polarization. The horizontal lines indicate the corresponding 8σQU levels. Stacking reduces the noise levels (as shown by the magenta horizontal lines that are lowest). The data were of higher quality in Cycle 2 than in Cycle 4 (the horizontal blue lines are below the green ones). |
 |
Fig. 5 Area of the field with noise σQU equal to or lower than a given value in data from stacked individual cycles and in the final dataset. The black dashed curve is the expected profile from a Gaussian primary beam (Eq. (15)), with σ0 = 20 µJy beam−1. |
Measured noise levels in the central 2.5′ × 2.5′ region after stacking and expected values from Gaussian statistics.
5 Source finding
The analysis was performed for the whole 25 deg2 field, where a threshold of 8σQU was used. A lower threshold of 6σQU was used for the sources known to be polarized at 1.4 GHz (either from the DRAO work of Grant et al. 2010 or from the NVSS RM catalog of Taylor et al. 2009).
5.1 Whole field
As described in Sect. 4, the large data cubes were divided into strips, and datasets from all epochs were stacked. We created S/N maps by dividing the polarized intensity map of each strip by its corresponding noise map. Pixels with S/N > 8 were selected, as they represent the most reliable detections: indeed, George et al. (2012) found the false detection rate to be less than 10−4 for an 8σQU detection threshold.
A preliminary catalog was then made by cross-matching the positions of the detections with the catalog of Stokes I components in the field from Sabater et al. (2021). We used a cross-matching radius of 1 arcmin in order to include matches with extended sources. This resulted in a preliminary catalog of 84 matches. Because of the size of the cross-matching radius, some matched Stokes I components (including artifacts) referred to the same detection. We selected the Stokes I components that were counterparts of the detections, resulting in a list of 44 polarized components. We identified two regions of diffuse Stokes I emission that had been cataloged as multiple Stokes I components by Sabater et al. (2021); for these, we selected the component closer to the polarization detection.
5.2 Sources known to be polarized at 1.4 GHz
This analysis was performed on sources known to be polarized at 1.4 GHz. We selected the pixels with S /N > 6 in each strip and cross-matched this list with the DRAO ELAIS-N1 catalog of Grant et al. (2010) and the NVSS RM catalog of Taylor et al. (2009), using a conservative radius of 1.5 arcmin. This resulted in the identification of 21 components between 6 and 8σQU from the DRAO ELAIS-N1 catalog, but none from the NVSS RM catalog.
5.3 Identification of the most reliable sources
For each potentially polarized source, we visually inspected the LOFAR Stokes I image, the polarized intensity image (POLI), and the Faraday spectrum. The following criteria were used to reject candidates from the final catalog:
- 1.
only one isolated pixel in the POLI image was found above the threshold, or no Stokes I counterpart was associated with a group of pixels above the threshold in POLI;
- 2.
the POLI detection was associated with image artifacts (for instance around bright Stokes I sources);
- 3.
the Faraday spectrum showed multiple peaks close to the instrumental polarization region and/or in the outer part of the spectrum;
- 4.
the fractional polarization was greater than 100% or lower than 0.2% (this lower limit on fractional polarization was also used by Herrera Ruiz et al. 2021).
This resulted in the rejection of:
19 sources from the whole field above 8σQU (out of which 15 were in the DRAO ELAIS-N1 catalog of polarized sources and 7 in the NVSS RM catalog);
29 sources detected at 1.4 GHz by Grant et al. (2010) (14 in the 6-8σQU range and 15 above 8σQU).
6 Result and discussion
In this section we start by presenting the list of polarized sources identified in the field. We compare our results with previous works on polarization.
6.1 Catalog of polarized sources
In Table B.1 we provide a list of the detected polarized components. The results can be summarized as follows:
The first 26 entries (above the horizontal line) correspond to polarized components detected above 8σQU in the 25 deg2 field; of these, six components were detected in the reference epoch alone; 16 were also detected in the stacked Cycle 2 data, and 15 in the stacked Cycle 4 data; 13 were detected in polarization at 1.4 GHz by Grant et al. (2010).
The next seven entries below the horizontal line correspond to polarized components that were known to be polarized at 1.4 GHz from the Grant et al. (2010) study and in which we searched for polarization in the 6–8σQU range of the LOFAR data. Of these, two were detected in stacked Cycle 2 data and three in stacked Cycle 4 data. One of the entries (29) corresponds to the second lobe of Source 13.
The 33 polarized components detected by stacking Cycle 2 and Cycle 4 data are therefore associated to 31 radio continuum sources: in one radio galaxy, polarization is detected from both lobes above 8σQU (components 04A and 04B), while in another radio galaxy, one lobe is polarized above 8σQU (component 13) and the other lobe below 8σQU (component 29).
-
The polarized intensities (in Col. 5) were corrected for the polarization bias following Eq. (5) from George et al. (2012):
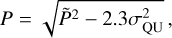 (16)
(16)where
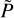 is the polarized intensity before correction, from the Fmap, and σQU is the mean of the rms noise in Q(ϕ) and U(ϕ), calculated in the outer 20% of the Faraday depth range.
is the polarized intensity before correction, from the Fmap, and σQU is the mean of the rms noise in Q(ϕ) and U(ϕ), calculated in the outer 20% of the Faraday depth range. The RM values of the sources and their corresponding uncertainties are given in column 6. A parabola was fitted to the polarized intensity peak in the Faraday spectra to improve the precision on the RM measurements. The error in the RM was calculated as the RM resolution, δϕ, divided by twice the S/N of the detection, following Brentjens & de Bruyn (2005).
6.2 Fraction of missed polarized sources
A number of polarized sources is missing from the catalog for at least two reasons: the exclusion of part of the RM range due to instrumental polarization, and the threshold that we imposed on the minimal fractional polarization, as discussed below.
Because of instrumental polarization due to leakage in the RM range [−3, 1.5] rad m−2, this range in the Faraday cubes was excluded from the search (Sect. 3.4). Assuming a uniform distribution between the lowest and highest RM values of our catalog, we estimate that about four polarized sources were missed.
The threshold we imposed on the minimal reliable fractional polarization, equal to 0.2% based on the study of Herrera Ruiz et al. (2021), may have caused us to miss the detection of real polarized sources. In the LoTSS-DR2 RM grid catalog, such a threshold was not applied and O’Sullivan et al. (2023) found that ~3% of polarized sources have a degree of polarization lower than 0.2% (and above 0.05%). We detected 25 sources above 8σQU after stacking, and may be missing ~1 polarized source because of the threshold in the minimal fractional polarization. We re-analyzed the preliminary list of 44 components detected above 8σQU removing the threshold in the minimal fractional polarization and we found one possible candidate as polarized source. We decided, however, not to include this source because the region of the Faraday spectrum close the detection, at ~5 rad m−2, showed several peaks close to the 8σQU threshold, making the detection uncertain.
We therefore estimate that about five sources were missed; taking this into account, the number of polarized sources above 8σQU would be ~30 instead of 25 in the 25 deg2 region of the LOFAR ELAIS-N1 field.
6.3 Comparison with previous polarization studies of the ELAIS-N1 LOFAR deep field
6.3.1 20″ resolution
In their pilot study of polarization in the ELAIS-N1 LOFAR deep field, Herrera Ruiz et al. (2021) detected ten polarized sources in a 16-deg2 field imaged at a resolution of 20″. All those sources are detected in the deeper, 6″-resolution data presented here. The RM values agree, as shown in the left panel of Fig. 6 and in Table 6. The peak polarized intensities at 20 and 6 are in agreement, too (right panel of Fig. 6), except for the brightest polarized sources, Source 07 (the reference source) and Source 24, where the peak polarized intensities are higher at 6″ than at 20″. The reference source is a double-lobed radio galaxy (Sect. 4.1.1), with two components separated by ~12″, and the different levels of polarization are probably due to beam depolarization within the 20″ beam. For Source 24 (a blazar), the polarized intensity at 6″ is higher than at 20″ by about 10 percent; this can be due to calibration uncertainty or to the variability of the source.
 |
Fig. 6 Comparison of RM values and peak polarized intensities measured with LOFAR at 6 resolution (this work) and at 20 resolution for the ten sources of Herrera Ruiz et al. (2021). The dashed lines are the lines of equality. |
6.3.2 4.3′ resolution
Šnidarić et al. (2023) carried out a deep polarimetric study of Galactic synchrotron emission at low radio frequencies by stacking 21 epochs of the ELAIS-N1 LOFAR Deep Field at 4.3 arcmin-resolution. They also checked how many extragalactic polarized sources from the catalog of Herrera Ruiz et al. (2021) were detected at their resolution, and found nine out of ten radio sources (our IDs: 03, 06, 07, 12, 14, 17, 18, 20, 24). By inspecting the Faraday spectra of the stacked polarized intensity cube of Šnidarić et al. (2023) at the locations of our polarized sources, we could see that five additional sources (our IDs: 04, 10, 11, 15, 25) were visible in the low-resolution polarization data, while the others were contaminated by diffuse polarized emission. The rotation measures of the detected sources are in agreement despite the very different angular resolutions of the data.
RM values from LOFAR at 6″ -resolution (this work), 20″ -resolution (Herrera Ruiz et al. 2021) and NVSS (Taylor et al. 2009).
6.4 Comparison with NVSS 1.4 GHz RM catalog
The NVSS 1.4 GHz RM catalog (Taylor et al. 2009) contains entries for 25 radio sources in the ELAIS-N1 25 deg2 field. Of these 25 sources, five are in our LOFAR catalog and three of those are the top brightest in polarization (sources 04, 07, 24). Table 6 lists the RM values from LOFAR and from NVSS for the five matches. They are in agreement within the relatively large uncertainties on the RM values from NVSS (several rad m−2). The different RM values for Source 24 may come from the fact that the source is a blazar that may be variable (Anderson et al. 2019; Herrera Ruiz et al. 2021).
6.5 Depolarization
In Fig. 7 we show the distributions of peak polarized intensities, corresponding total intensities and fractional polarizations for the polarized sources in the LoTSS-DR2 RM grid catalog (20″ resolution, O’Sullivan et al. 2023), our deep LOFAR catalog of polarized sources in ELAIS-N1 (6 resolution), and the polarized sources in the DRAO ELAIS-N1 catalog at 1.4 GHz (Grant et al. 2010). Our study reaches lower levels in polarized intensities (≤0.7 mJy beam−1) than the shallower but much larger LoTSS-DR2 RM grid. In terms of degrees of polarization, however, they do not appear to be very different from those of sources in the LoTSS-DR2 RM catalog.
Our LOFAR catalog of polarized sources and the DRAO ELAIS-N1 Source Catalog make it possible to investigate the depolarization between 150 MHz and 1.4 GHz for the sources in common. In Table 7 the names of these 20 sources are listed, along with the values of their total intensity and degree of polarization at both frequencies. In the last column we give the positional offsets of the peak polarized intensities at 1.4 GHz (Grant et al. 2010) and 150 MHz (this work). In three sources (15, 27, 05), the offsets are greater than 20″: in Source 15 (offset of 81″) and Source 05 the polarization was found in different lobes, while in Source 27 the peak polarization was from the center at 1.4 GHz but from a lobe at 150 MHz. Also in Sources 19 and 30, the polarization peaks near the center at 1.4 GHz, but in a lobe at 150 MHz. These differences are likely due to stronger depolarization at LOFAR frequencies that favors detection of polarization from outer regions of radio galaxies that are less depolarized by the magneto-ionic medium of the host galaxies.
In Fig. 8 we show the fractional polarization at 150 MHz versus that at 1.4 GHz for the eight sources whose peak polarized intensity at 1.4 GHz and at 150 MHz coincide within 6″ (the resolution of the LOFAR observations; the uncertainties given by Grant et al. 2010 on the positions of the peak polarized intensities at 1.4 GHz are of the order of 1″)· All sources show a lower fractional polarization at lower frequencies. The fractional polarization is calculated by dividing the peak polarized intensity by the value of the Stokes I intensity at the corresponding pixel. Despite the larger beam at 1.4 GHz that covers more of the extended Stokes I emission, all sources show significant depolarization at 150 MHz, an indication of Faraday depolarization across the 6″ beam.
 |
Fig. 7 Peak polarized intensity vs. total intensity (left panel) and degree of polarization vs. peak polarized intensity (right panel) for three catalogs: in gray the LoTSS-DR2 RM grid catalog of O’Sullivan et al. (2023); in black the polarized sources in ELAIS-N1 at 150 MHz (this work); in orange the values for sources in the DRAO ELAIS-N1 catalog, where both I and P have been converted from 1.4 GHz to 150 MHz using the spectral indices given by Grant et al. (2010). The diagonal lines correspond to the indicated degrees of polarization. |
Stokes I intensities (in mJy beam−1) and corresponding degrees of polarization (in %) at the pixel of peak polarized intensity for the 20 polarized sources detected both at 150 MHz (this work) and at 1.4 GHz (Grant et al. 2010).
 |
Fig. 8 Degrees of polarization at 150 MHz and 6″ resolution (this work) and 1.4 GHz and 49″ × 49″ / sin δ resolution (Grant et al. 2010) for the eight sources of ELAIS-N1 with both LOFAR and DRAO polarization data and with peak polarized intensities that coincide within 6″. |
Polarized source counts in ELAIS-N1 at 150 MHz.
6.6 Number counts
Source counts in polarization are unknown at low radio frequencies as most analyses were carried out at 1.4 GHz (Tucci et al. 2004; Beck & Gaensler 2004; Taylor et al. 2007; O’Sullivan et al. 2008; Hales et al. 2014; Berger et al. 2021). Tucci et al. (2004) investigated the distribution of fractional polarization for NVSS sources with S > 100 mJy. Beck & Gaensler (2004) modeled the distribution of fractional polarization for NVSS sources with total flux density S > 80 mJy, using two log-normal distributions. Taylor et al. (2007) studied the distribution of fractional polarization of fainter sources (S < 30 mJy) in the ELAIS-N1 field and found a constant fractional polarization for sources brighter than 0.5 mJy, where the fainter source population is more strongly polarized. Stil et al. (2014) also observed an increase of median fractional polarization for the fainter sources in the stacked NVSS polarization data, but more gradual than what was found in previous polarization studies. In the studies of their fields, Hales et al. (2014) and Berger et al. (2021) found this to be a selection effect. O’Sullivan et al. (2008) simulated the extragalactic polarized sky by using Gaussian fractional polarization distributions and a semi-empirical simulation of the extragalactic total intensity continuum sky (Wilman et al. 2008), finding a good agreement with the observational results from the NVSS.
We estimated the number counts from the catalog of polarized sources detected above 8σQU as this catalog is well defined and complete in the 25 deg2 area of the LOFAR ELAIS-N1 field, while the catalog of sources detected in the 6-to-8σQU range contains only sources that had a prior detection in the 1.4 GHz catalog of Grant et al. (2010). All our detections are point-like in polarization, so the peak polarized intensity values (in, for instance, µJy beam−1) correspond to the polarized flux densities (in µJy).
In Table 8 we present the derived polarized source counts for the LOFAR ELAIS-N1 field. The data were split into three bins of polarized flux densities. The actual numbers of sources detected in each bin are given in the third column. To calculate the effective area of the field, Ωeff, within which the polarized sources in a given bin could be detected at S/N ≥ 8 (Fig. 5), we followed Condon et al. (1982): the weighted number of sources per square degree, Nw, in each flux-density bin can be obtained from
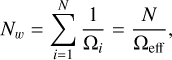 (17)
(17)
where Ωi· is the area within which the ith source in the considered bin could be detected and N is the total number of sources in that bin. The errors on the number counts were propagated from the statistical error in Nw, given by
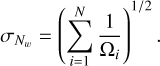 (18)
(18)
The counts were corrected to take into account the five missed sources (discussed in Sect. 6.2), by scaling the number in each bin by a factor of 1.2, equal to the ratio of the expected total number of sources over 8σQU to the number of detected sources, 30/25. The last columns give the Euclidean-normalized differential source counts before and after correction for the missed sources; the values for the corrected counts are shown as red dots in Fig. 9. Also shown on Fig. 9 are the modeled polarized source counts, which were computed as described below.
The differential polarized source counts n(P) can be obtained by convolving the sources counts in Stokes I, n(S), with the probability distribution function of the fractional polarization, 𝒫(Π) (e.g. Beck & Gaensler 2004, Tucci & Toffolatti 2012), assuming Π independent of total flux density S and for sources with S ≥ S0:
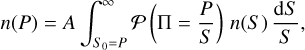 (19)
(19)
where A is a scaling factor. As for n(S), we use the empirical polynomial fit performed by Mandal et al. (2021) (their Eq. (13)) to the deepest source counts in Stokes I to date at 150 MHz: the ones based on the 6″-resolution images from the central parts of the LoTSS Deep Fields (10.3 deg2 in the Lockman Hole, 8.6 deg2 in Boötes, and 6.7 deg2 in ELAIS-N1; Tasse et al. 2021, Sabater et al. 2021).
The probability distribution function of fractional polarization is taken to be a log-normal function:
![${\cal P}(\Pi ) = {1 \over {\sigma \sqrt {2\pi } \Pi }}\exp \left( { - {{{{\left[ {\log \left( {\Pi /{\Pi _{{\rm{med}}}}} \right)} \right]}^2}} \over {2{\sigma ^2}}}} \right),$](/articles/aa/full_html/2024/07/aa49085-23/aa49085-23-eq37.png) (20)
(20)
where Πmed is the median of the distribution and σ2 = 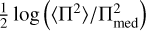 .
.
The model of polarized source counts has three parameters: Πmed, σ, and the scaling factor A in Eq. (19). The values of these parameters depend on the frequency and angular resolution of the survey. With only three flux density bins, the model is degenerate and different combinations of parameters provide a comparable match to the data. With a scaling factor A = 1 , a very low value of the median fractional polarization is required (Fig. 9). More realistically, the scaling factor A can be reduced to indicate that only a fraction of the radio sources detected in continuum have measurable polarization. Polarization measurements of a larger field or even deeper measurements in ELAIS-N1 would increase the number of bins of polarized sources, and make it possible to include several polarized source populations with different characteristics in the model.
 |
Fig. 9 Euclidean-normalized differential source counts at 150 MHz in radio continuum and in polarization. The solid line shows the fit to the source counts in Stokes I in three LOFAR deeps fields (Mandal et al. 2021). The other lines show the modeled polarized source counts in ELAIS-N1. The red dots represent our data; the horizontal bars indicate the widths of the bins. |
7 Conclusions
In this work, we developed a new method to stack LOFAR datasets taken in different observing cycles with different frequency configurations. Stacking datasets from 19 epochs allowed us to reach a noise level in polarization of 19 µJy beam−1 in the central part of the final image of 25 deg2 of the ELAIS-N1 field. To our knowledge, this is is the most sensitive polarization dataset obtained at 150 MHz so far. This allowed us to detect 33 polarized components in 31 sources in ELAIS-N1 (two of the sources are double-lobed radio galaxies in which polarization was detected from both lobes) and probe the sub-mJy population of polarized sources at low frequencies.
The number density of polarized sources found is 1.24 per square degree, which is approximately twice as high as what was found in the first LOFAR polarization survey of ELAIS-N1 by Herrera Ruiz et al. (2021), and three times more than in the LoTSS-DR2 RM grid (O’Sullivan et al. 2023). The catalog has two parts: one resulting from a search in the whole 25 deg2 field, and another resulting from a polarization search towards sources known to be polarized at 1.4 GHz from the work of Grant et al. (2010) and the RM catalog from NVSS (Taylor et al. 2009). For these sources with prior information on polarization the detection threshold was lowered to 6σQU. The catalog of 25 sources detected above 8σQU was used to construct polarized source counts down to a polarized point-source flux density of 200 µJy. The observed polarized counts were modeled using the polynomial fit to source counts in total-intensity obtained for three LOFAR Deep Fields by Mandal et al. (2021), convolved with a log-normal probability distribution function of fractional polarizations; the parameters of the model were partly taken from the statistical properties of the sample and adjusted to match the observed data points.
The methods presented here may be used in future polarization studies of LOFAR deep and ultra-Deep Fields and for polarization data taken in other radio frequency bands. Our work has shown that the polarization fraction is higher at 6″ resolution than at 20″, and that the combination of stacking with imaging at higher angular resolution leads to a higher number of detections of polarized sources. Future promising work includes searching for polarization in LOFAR data at even higher angular resolution: sub-arcsecond resolution with the international baselines.
Whereas the frequency range of LOFAR allows for precise RM determinations, Faraday depolarization is a limiting factor. The POlarisation Sky Survey of the Universe’s Magnetism (POSSUM), carried out in a band centred at ~890 MHz with the Australian Square Kilometre Array Pathfinder (e.g. Anderson et al. 2021; Vanderwoude et al. 2024), as well as future observations in Band 1 and Band 2 of SKA-Mid (350-1050 MHz; 950–1760 MHz) will provide a trade-off between depolarization and precision on the RM values and will be powerful tools to construct large RM grids (Heald et al. 2020).
In a companion paper (Piras et al. 2024; Paper II) we will characterize the detected extragalactic polarized sources in ELAIS-N1 in terms of their morphologies in radio continuum, their redshifts, linear sizes, rest-frame luminosities and environments, and present the RM grid derived from the RM values obtained with LOFAR.
Acknowledgements
We thank the referee for helpful comments. LOFAR, the Low Frequency Array designed and constructed by ASTRON, has facilities in several countries, that are owned by various parties (each with their own funding sources), and that are collectively operated by the International LOFAR Telescope (ILT) foundation under a joint scientific policy. This work was done within the LOFAR Surveys and the LOFAR Magnetism Key Science Projects. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the VizieR catalog access tool, CDS, Strasbourg, France. The original description of the VizieR service was published in Ochsenbein et al. (2000). We have also made use of the table analysis software topcat (Taylor 2005). This research made use of Astropy, a community-developed core Python package for astronomy (Astropy Collaboration 2013), of Matplotlib (Hunter 2007), and of APLpy (Robitaille & Bressert 2012), an open-source astronomical plotting package for Python. The processing of LOFAR data was enabled by resources provided by the Swedish National Infrastructure for Computing (SNIC) at Chalmers Centre for Computational Science and Engineering (C3SE) partially funded by the Swedish Research Council through grant agreement no. 2018-05973. S.P. would like to thank R. Beck, T. Carozzi and M. C. Toribio for useful comments and discussions. S.d.P. gratefully acknowledges support from the European Research Council (ERC) Advanced Grant, 789410. S.P.O. acknowledges support from the Comunidad de Madrid Atracción de Talento program via grant 2022-T1/TIC-23797. V.J. acknowledges support by the Croatian Science Foundation for a project IP-2018-01-2889 (LowFre-qCRO). A.B. was supported by funding from the German Research Foundation DFG, within the Collaborative Research Center SFB1491 “Cosmic Interacting Matters - From Source to Signal”. P.N.B. is grateful for support from the UK STFC via grant ST/V000594/1. I.P. acknowledges support from INAF under the Large Grant 2022 funding scheme (project “MeerKAT and LOFAR Team up: a Unique Radio Window on Galaxy/AGN co-Evolution”). N.H.R. acknowledges support from the BMBF through projects D-LOFAR IV (FKZ: 05A17PC1) and MeerKAT (FKZ: 05A17PC2).
Appendix A The RM spread function
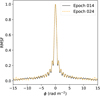 |
Fig. A.1 Amplitude of the RM Spread Function (RMSF) corresponding to data taken in Cycle 2 (Epoch 014) in black line and Cycle 4 (Epoch 024) in dashed orange line. |
Appendix B Catalog of polarized sources in the ELAIS-N1 field detected with LOFAR
Catalog of polarized sources in the ELAIS-N1 field detected with LOFAR.
References
- Anderson, C. S., O’Sullivan, S. P., Heald, G. H., et al. 2019, MNRAS, 485, 3600 [Google Scholar]
- Anderson, C. S., Heald, G. H., Eilek, J. A., et al. 2021, PASA, 38, e020 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, R., & Gaensler, B. M. 2004, New Astron. Rev., 48, 1289 [CrossRef] [Google Scholar]
- Berger, A., Adebahr, B., Herrera Ruiz, N., et al. 2021, A&A, 653, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Best, P. N., Kondapally, R., Williams, W. L., et al. 2023, MNRAS, 523, 1729 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burn, B. J. 1966, MNRAS, 133, 67 [Google Scholar]
- Carretti, E., Vacca, V., O’Sullivan, S. P., et al. 2022, MNRAS, 512, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Carretti, E., O’Sullivan, S. P., Vacca, V., et al. 2023, MNRAS, 518, 2273 [Google Scholar]
- Condon, J. J., Condon, M. A., & Hazard, C. 1982, AJ, 87, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
- Duncan, K. J., Kondapally, R., Brown, M. J. I., et al. 2021, A&A, 648, A4 [EDP Sciences] [Google Scholar]
- Ferrière, K., West, J. L., & Jaffe, T. R. 2021, MNRAS, 507, 4968 [Google Scholar]
- George, S. J., Stil, J. M., & Keller, B. W. 2012, PASA, 29, 214 [Google Scholar]
- Grant, J. K., Taylor, A. R., Stil, J. M., et al. 2010, ApJ, 714, 1689 [Google Scholar]
- Hales, C. A., Norris, R. P., Gaensler, B. M., & Middelberg, E. 2014, MNRAS, 440, 3113 [Google Scholar]
- Heald, G., Braun, R., & Edmonds, R. 2009, A&A, 503, 409 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heald, G., Mao, S. A., Vacca, V., et al. 2020, Galaxies, 8, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera Ruiz, N., O’Sullivan, S. P., Vacca, V., et al. 2021, A&A, 648, A12 [EDP Sciences] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jelić, V., de Bruyn, A. G., Mevius, M., et al. 2014, A&A, 568, A101 [Google Scholar]
- Kondapally, R., Best, P. N., Hardcastle, M. J., et al. 2021, A&A, 648, A3 [EDP Sciences] [Google Scholar]
- Mahatma, V. H., Hardcastle, M. J., Harwood, J., et al. 2021, MNRAS, 502, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Mandal, S., Prandoni, I., Hardcastle, M. J., et al. 2021, A&A, 648, A5 [EDP Sciences] [Google Scholar]
- Mesa, D., Baccigalupi, C., De Zotti, G., et al. 2002, A&A, 396, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulcahy, D. D., Horneffer, A., Beck, R., et al. 2014, A&A, 568, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neld, A., Horellou, C., Mulcahy, D. D., et al. 2018, A&A, 617, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ochsenbein, F., Bauer, P., & Marcout, J. 2000, A&AS, 143, 23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oliver, S., Rowan-Robinson, M., Alexander, D. M., et al. 2000, MNRAS, 316, 749 [Google Scholar]
- O’Sullivan, S., Stil, J., Taylor, A. R., et al. 2008, in The role of VLBI in the Golden Age for Radio Astronomy, 9, 107 [Google Scholar]
- O’Sullivan, S., Brüggen, M., Van Eck, C., et al. 2018, Galaxies, 6, 126 [Google Scholar]
- O’Sullivan, S. P., Machalski, J., Van Eck, C. L., et al. 2019, A&A, 622, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Sullivan, S. P., Brüggen, M., Vazza, F., et al. 2020, MNRAS, 495, 2607 [Google Scholar]
- O’Sullivan, S. P., Shimwell, T. W., Hardcastle, M. J., et al. 2023, MNRAS, 519, 5723 [CrossRef] [Google Scholar]
- Piras, S., Horellou, C., Conway, J. E., et al. 2024, A&A, submitted (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Rowan-Robinson, M., Lari, C., Perez-Fournon, I., et al. 2004, MNRAS, 351, 1290 [NASA ADS] [CrossRef] [Google Scholar]
- Rudnick, L., & Owen, F. N. 2014, ApJ, 785, 45 [Google Scholar]
- Sabater, J., Best, P. N., Tasse, C., et al. 2021, A&A, 648, A2 [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Röttgering, H. J. A., Best, P. N., et al. 2017, A&A, 598, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shimwell, T. W., Tasse, C., Hardcastle, M. J., et al. 2019, A&A, 622, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sokoloff, D. D., Bykov, A. A., Shukurov, A., et al. 1998, MNRAS, 299, 189 [Google Scholar]
- Sotomayor-Beltran, C., Sobey, C., Hessels, J. W. T., et al. 2013, A&A, 552, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stil, J. M., Keller, B. W., George, S. J., & Taylor, A. R. 2014, ApJ, 787, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Stuardi, C., O’Sullivan, S. P., Bonafede, A., et al. 2020, A&A, 638, A48 [EDP Sciences] [Google Scholar]
- Tasse, C., Hugo, B., Mirmont, M., et al. 2018, A&A, 611, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tasse, C., Shimwell, T., Hardcastle, M. J., et al. 2021, A&A, 648, A1 [EDP Sciences] [Google Scholar]
- Šnidarić, I., Jelic, V., Mevius, M., et al. 2023, A&A, 674, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
- Taylor, A. R., Stil, J. M., Grant, J. K., et al. 2007, ApJ, 666, 201 [Google Scholar]
- Taylor, A. R., Stil, J. M., & Sunstrum, C. 2009, ApJ, 702, 1230 [Google Scholar]
- Tucci, M., & Toffolatti, L. 2012, Adv. Astron., 2012, 624987 [Google Scholar]
- Tucci, M., Martínez-González, E., Toffolatti, L., González-Nuevo, J., & De Zotti, G. 2004, MNRAS, 349, 1267 [NASA ADS] [CrossRef] [Google Scholar]
- Vaccari, M., Lari, C., Angeretti, L., et al. 2005, MNRAS, 358, 397 [NASA ADS] [CrossRef] [Google Scholar]
- Vanderwoude, S., West, J. L., Gaensler, B. M., et al. 2024, AJ, 167, 226 [CrossRef] [Google Scholar]
- Van Eck, C. L., Haverkorn, M., Alves, M. I. R., et al. 2019, A&A, 623, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van Eck, C. L., Gaensler, B. M., Hutschenreuter, S., et al. 2023, ApJS, 267, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Wilman, R. J., Miller, L., Jarvis, M. J., et al. 2008, MNRAS, 388, 1335 [NASA ADS] [Google Scholar]
New observations were analyzed recently, as described fully in Best et al. (2023), and will be presented in Shimwell et al. (in prep.).
All Tables
LOFAR observing configurations for the ELAIS-N1 Deep Field and parameters of RM synthesis.
Values of  in datasets of different epochs, RM values of the reference source and applied polarization angle corrections.
in datasets of different epochs, RM values of the reference source and applied polarization angle corrections.
Measured noise levels in the central 2.5′ × 2.5′ region after stacking and expected values from Gaussian statistics.
RM values from LOFAR at 6″ -resolution (this work), 20″ -resolution (Herrera Ruiz et al. 2021) and NVSS (Taylor et al. 2009).
Stokes I intensities (in mJy beam−1) and corresponding degrees of polarization (in %) at the pixel of peak polarized intensity for the 20 polarized sources detected both at 150 MHz (this work) and at 1.4 GHz (Grant et al. 2010).
All Figures
 |
Fig. 1 LOFAR 150 MHz total-intensity image of the ELAIS-N1 field at 6″-resolution and of size 5 × 5 deg2 (Sabater et al. 2021), on which the coverages of various polarization surveys and the locations of polarized sources are overlaid, as indicated in the legend. |
| In the text | |
 |
Fig. 2 Flowchart of the stacking process. POLA stands for Polarization Angle. |
| In the text | |
 |
Fig. 3 Polarization characteristics of the reference source (Source 07). Stokes Q and U intensities, polarized intensity P and polarization angle χ are shown as a function of frequency and wavelength squared λ2 (bottom and top axes) for the reference epoch (in black, first two rows), and for the stacked data from Cycle 2, (in blue, third and fourth row) and from Cycle 4 (in orange, two last rows). The scatter in the data is reduced by stacking. The effect of Faraday rotation is clearly visible in the variations of Q, U and χ; the decrease of the polarized intensity with λ2 is an indication of Faraday depolarization. The final combination of Cycle 2 and Cycle 4 data is done in Faraday depth space, as described in the text. |
| In the text | |
 |
Fig. 4 Faraday spectra of three sources: the reference source (source 07, left panel); the brightest polarized source component (04B, middle panel), and a faint source detected only after stacking data from both cycles (source 11, right panel). The displayed Faraday spectra are from the reference epoch (Epoch 014), from stacked Cycle 2, stacked Cycle 4, and combining both cycles. The gray region outlines the range in Faraday depth that was excluded from the analysis due to instrumental polarization. The horizontal lines indicate the corresponding 8σQU levels. Stacking reduces the noise levels (as shown by the magenta horizontal lines that are lowest). The data were of higher quality in Cycle 2 than in Cycle 4 (the horizontal blue lines are below the green ones). |
| In the text | |
 |
Fig. 5 Area of the field with noise σQU equal to or lower than a given value in data from stacked individual cycles and in the final dataset. The black dashed curve is the expected profile from a Gaussian primary beam (Eq. (15)), with σ0 = 20 µJy beam−1. |
| In the text | |
 |
Fig. 6 Comparison of RM values and peak polarized intensities measured with LOFAR at 6 resolution (this work) and at 20 resolution for the ten sources of Herrera Ruiz et al. (2021). The dashed lines are the lines of equality. |
| In the text | |
 |
Fig. 7 Peak polarized intensity vs. total intensity (left panel) and degree of polarization vs. peak polarized intensity (right panel) for three catalogs: in gray the LoTSS-DR2 RM grid catalog of O’Sullivan et al. (2023); in black the polarized sources in ELAIS-N1 at 150 MHz (this work); in orange the values for sources in the DRAO ELAIS-N1 catalog, where both I and P have been converted from 1.4 GHz to 150 MHz using the spectral indices given by Grant et al. (2010). The diagonal lines correspond to the indicated degrees of polarization. |
| In the text | |
 |
Fig. 8 Degrees of polarization at 150 MHz and 6″ resolution (this work) and 1.4 GHz and 49″ × 49″ / sin δ resolution (Grant et al. 2010) for the eight sources of ELAIS-N1 with both LOFAR and DRAO polarization data and with peak polarized intensities that coincide within 6″. |
| In the text | |
 |
Fig. 9 Euclidean-normalized differential source counts at 150 MHz in radio continuum and in polarization. The solid line shows the fit to the source counts in Stokes I in three LOFAR deeps fields (Mandal et al. 2021). The other lines show the modeled polarized source counts in ELAIS-N1. The red dots represent our data; the horizontal bars indicate the widths of the bins. |
| In the text | |
 |
Fig. A.1 Amplitude of the RM Spread Function (RMSF) corresponding to data taken in Cycle 2 (Epoch 014) in black line and Cycle 4 (Epoch 024) in dashed orange line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


