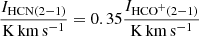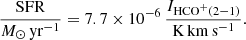EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 643 (November 2020) A&A, 643 (2020) A63 Full HTML
Open Access
Issue
A&A
Volume 643, November 2020
Article Number A63
Number of page(s) 23
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202038641
Published online 03 November 2020

© M. Galametz et al. 2020

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1. Introduction

The study of the star formation mechanisms is key to understanding the evolution of galaxies. To understand their star formation activity, it is crucial to have precise knowledge of the morphology and properties (mass, density, temperature, velocity) of their molecular gas complexes and how these are affected by the physical conditions to which they are exposed. H2 is the most abundant molecular species in the interstellar medium (ISM) but requires high temperatures to be excited, which makes it very difficult to observe in emission in cold clouds (Shull & Beckwith 1982; Wakelam et al. 2017). Cold H2 can be traced in absorption (UV radiation is absorbed by H2 through the Lyman and Werner bands) but this technique can be limited by extinction along the line of sight (Flower 2012).

CO is the most common molecule after H2 and its observation has been extensively used to probe the molecular gas, from local star-forming (Dickman 1978; Bolatto et al. 2013) to high-redshift environments (Carilli & Walter 2013). However, using CO luminosity as a tracer of H2 has its limitations, as the CO emission does not solely arise from the densest phases of the cold gas where star formation occurs (Liszt et al. 2010; Caldú-Primo & Schruba 2016) and can also be optically thick in the densest regions. Additionally, the CO molecule can be subject to widespread photo-dissociation due to strong UV radiation fields and in porous ISM such as that encountered in low-metallicity environments (Israel 1997; Cormier et al. 2014; Chevance et al. 2016, 2020). Moreover, its emission has a nonlinear relation with the H2 column density it is supposed to trace (Liszt et al. 2010).

Many molecules have now been targeted to probe higher density regions in nearby galaxies, in particular molecules such as N2H+, HCN, HNC, HCO+, CS, HC3N, H2CO (Schlingman et al. 2011; Zhang et al. 2014; Kepley et al. 2018; Gallagher et al. 2018a; Jiménez-Donaire et al. 2019) and their isotopologs (H13CN, H13NC, H13CO+; Mauersberger & Henkel 1991; Jiménez-Donaire et al. 2017). Molecules like HCO+ and HCN are commonly used to trace molecular gas that is more dense than detected in CO. In Table 1, we report the dipole moments and critical densities for optically thin emission of the HCN and HCO+ molecules for the J = 2−1 transitions analyzed in the current study (Schöier et al. 2005; Shirley 2015). While substantial fractions of the CO emission have been argued to lie in extended translucent regions (Pety et al. 2013; Leroy et al. 2017), studies toward Galactic giant molecular clouds have suggested that HCN or HCO+ emission could also arise from more extended diffuse areas (Nishimura et al. 2017; Pety et al. 2017; Shimajiri et al. 2017; Watanabe et al. 2017), especially in the lowest J transitions. Reinforcing our analysis of the HCN or HCO+ emissions in nearby environments is therefore crucial to better understanding their robustness as tracers of dense gas.

Table 1.

Lines targeted and used in this analysis.

The HCO+ and HCN luminosities have been shown to correlate over ten orders of magnitude with star formation rate (SFR) (Gao & Solomon 2004; Chen et al. 2015; Shimajiri et al. 2017; Jiménez-Donaire et al. 2019). Here again, a deeper knowledge of how the tracers evolve with the local conditions is crucial to be able to use them as star-forming reservoirs at higher redshifts and in local environments as tools to investigate whether there is a universality in the dense gas properties that lead to star formation or if the star formation efficiency (SFE = ΣSFR/Σdense, i.e., the ratio of the SFR surface density to the dense gas mass surface density) varies with the dense gas fraction or the gas physical conditions (García-Burillo et al. 2012; Usero et al. 2015; Jiménez-Donaire et al. 2019).

At a distance of ∼50–60 kpc, the Large and Small Magellanic Clouds (LMC and SMC) are among the very few extragalactic sources in which we can resolve individual Giant Molecular Clouds (GMCs) and study young stellar objects (YSOs), making them prime laboratories to compare Galactic star formation activity and efficiency with those of nearby galaxy populations. The LMC and SMC host a wide range of star formation regimes, from quiescent clouds to very active star-forming regions, allowing us to study how the local physical conditions impact the dense gas reservoirs. Their low metallicities (∼1/2 and 1/5 Z⊙, respectively; Dufour et al. 1982; Russell & Dopita 1990) enable us to extend the parameter range to more primordial physical conditions. The elemental abundance of the LMC (respectively SMC) differs from that of more metal-rich environments, with an abundance in nitrogen that is a factor of 10 (respectively 20) lower than that of the Milky Way but an abundance in oxygen only a factor of 3 (respectively 7) lower (Dufour et al. 1982). This difference in the elemental abundance ratio is one of several hypotheses suggested to explain the variation of the HCO+/HCN ratio with the galaxy host metallicity (Bayet et al. 2012; Braine et al. 2017; Johnson et al. 2018; Kepley et al. 2018).

Observations of HCO+(1−0) and HCN(1−0) have been performed in several LMC star-forming complexes to study the impact of low-metallicity ISM and more extreme star-forming conditions on the dense gas tracers (Chin et al. 1997; Heikkilä et al. 1999; Wong et al. 2006; Wang et al. 2009; Seale et al. 2012; Anderson et al. 2014; Nishimura et al. 2016), although in most cases, observations predominantly targeted very active star-forming regions. Additionally, very few positions have been targeted in the SMC in HCO+ and HCN and our knowledge of its dense molecular gas content and its local variations is still very limited. Finally, the 1−0 transition is often the only transition observed: to the best of our knowledge the 2−1 transition has never been observed in the Magellanic Clouds, despite its importance to complement the HCO+ and HCN spectral line energy distributions and constrain dense gas properties such as excitation temperature or gas density.

The aim of the Dense Gas Survey in the Magellanic Clouds (DeGaS-MC; PI: Galametz) project is to expand our knowledge of the relation between the dense gas properties and star formation activity by targeting more diverse environments, from OB complexes to star-forming clouds of lower masses and less extreme UV radiation. HCO+(2−1) and HCN(2−1) observations were obtained toward ∼30 LMC and SMC molecular clouds using the SEPIA180 instrument installed on the Atacama Pathfinder Experiment (APEX) telescope at a resolution of 35″, thus ∼8–10 pc for the Magellanic Clouds. A follow-up mapping campaign was then performed for a subset of these positions.

The goal of this first paper of the collaboration is to (i) present the survey characteristics, (ii) provide catalogs and maps of the two targeted lines, and (iii) to present the first results in order to showcase the dataset potential in terms of chemistry, dynamics, and dense gas fraction analysis. Future papers of the collaboration will present more detailed statistical analyses and modeling of the lines. We describe the sample and observations in Sect. 2. We present the detection statistics, the line properties, and the intensity maps in Sect. 3. We analyze the line characteristics (velocities, line widths, and line ratios) in Sect. 4. We discuss the relation between the dense tracers and star formation activity as well as the dense gas fraction in Sect. 5. We summarize our findings in Sect. 6.

2. The DeGaS-MC survey

The LMC is our nearest neighbor located at 50 kpc (Schaefer 2008). It has an almost face-on orientation (23–37deg, Subramanian & Subramaniam 2012) and a half-solar metallicity (Dufour et al. 1982). In this paper, we assume a systemic velocity vsys = 262.2 km s−1 for the LMC (van der Marel et al. 2002). The SMC is located at a distance of ∼60 kpc (Hilditch et al. 2005) and has a more metal-poor ISM (1/5–1/8 Z⊙ Russell & Dopita 1990). We assume a systemic velocity vsys = 158 km s−1 for the SMC (Richter et al. 1987).

The SEPIA (Swedish-European Southern Observatory PI receiver for APEX; Belitsky et al. 2018, 159–211 GHz) Band-5 instrument, now SEPIA180, is a dual polarization two-sideband receiver based on the ALMA Band-5 receivers. The central frequencies of the lower and upper sidebands (LSB and USB) are separated by 12 GHz. Each sideband is recorded by two XFFTS (eXtended bandwidth Fast Fourier Transform Spectrometer; Klein et al. 2012) units of 2.5 GHz width each, with a 1 GHz overlap. The backend provides 65536 channels for each of these 2.5 GHz sub-bands, which corresponds to a spectral resolution of 0.065 km s−1 at 177 GHz. The beam size is close to 35″ at this frequency, equivalent to ∼8–10 pc for the Magellanic Clouds. We refer to Billade et al. (2012), Immer et al. (2016), and Belitsky et al. (2018) for more details on the receivers and the offline data calibration. In order to observe both lines together, we choose a tuning frequency of 177.82 GHz in the USB, in the middle of the rest frequencies of the HCN(2−1) and HCO+(2−1) lines (177.26 and 178.38 GHz, respectively).

2.1. The DeGaS-MC single pointing campaign

2.1.1. Source selection

Wong et al. (2011) and Muller et al. (2010) provide catalogs of CO clouds in the LMC and SMC as part of the Magellanic Mopra Assessment (MAGMA) project1. We chose our pointing positions in the LMC to match the center of a selection of CO clumps provided by their catalogs, regularly ranging from CO luminosities of 8.9 × 104 down to 3.6 × 103 K km s−1 pc−2. We complemented the sample with targets from the SMC main star-forming body in order to probe a lower metallicity regime than the LMC. From the originally proposed sample, 21 sources were observed in the LMC and 8 in the SMC. The list of pointings is provided in Table A.12 and their positions are overlaid on the Herschel 500 μm emission map in Fig. 1. We note that since the SEPIA beam is small compared to the full extent of some of the CO complexes, some of our pointings might be missing the densest part of the targeted molecular complexes.

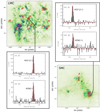thumbnail Fig. 1.

DeGaS-MC pointing campaign: the positions of our pointings are indicated by the red crosses overlaid on the LMC and the SMC Herschel 500 μm observations (FWHM = 36″). An example of the HCO+(2−1) and HCN(2−1) spectra obtained towards regions LMC #5 and SMC #5 are shown (2 km s−1 spectral resolution). The x-axis is expressed in velocity with respect to the systemic velocities (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). The catalogue of HCO+(2−1) and HCN(2−1) spectra is shown in Figs. A.1 and A.2. The yellow squares indicate the position of the sources targeted during the follow-up mapping campaign (see Sect. 2.2). Please note that the areas mapped are ∼4′ × 4′, i.e., smaller than these squares.

2.1.2. Observations

Observations were carried out in May and June 2016 (Project ID: 097.C-0758; PI: Galametz). Most of the regions were observed using the wobbler switch mode. Two LMC sources and one SMC source were observed using the total power mode. The system temperatures varied between 170 and 290 K. The precipitable water vapor was 0.9 < pwv < 2.0 mm. We selected off-positions for each pointing based on the LMC and SMC Herschel maps, typically a few degrees away from the observed region. The observations were carried out for a total time of 40h, with more than 16h on-source.

2.2. The DeGaS-MC mapping campaign

2.2.1. Source selection

Following our successful detections of HCO+(2−1) and HCN(2−1) in the LMC and SMC, we initiated a follow-up mapping campaign. The original selection of 28 sources included regions in which one or both tracers were detected during the pointing campaign. We also added regions that were not targeted during the pointing campaign, including known bright star-forming regions (i.e., N11B, N105, N113 in the LMC, N66 in the SMC) or sources with previously published HCO+(1−0) and HCN(1−0) data (i.e., N214). Regions where deep YSO analyses had been carried out (Chen et al. 2009, 2010; Carlson et al. 2012; Oliveira et al. 2013) were targeted in priority. Thirteen sources were finally mapped during the allocated time: ten in the LMC and three in the SMC. The observed sources are listed in Table B.1 and the mapping positions overlaid with yellow squares on Fig. 1.

2.2.2. Observations

The mapping campaign benefited from 6h of Director’s Discretionary Time (Project ID: E-297.C-5052A-2016; PI: Galametz) and 140 h of allocated time in Period 99 (OSO and Max-Planck APEX time; Project ID: O-099.F-9301A-2017; PIs: Galametz & Schruba). The DDT observations, carried out in August 2016, were the first to demonstrate the feasibility of mapping extragalactic dense molecular clouds with the SEPIA180 receiver using on-the-fly mode. The rest of the observations were carried out from April to June 2017, with 0.8 < pwv < 2.5 mm for most of the data (pwv ∼ 4 on May 20 2017). The size of the area covered around the sources is of about 50–70 pc.

2.3. Data reduction

Data of the pointing and mapping campaigns were reduced using CLASS/GILDAS3 (Pety 2005). For the pointing campaign data, we removed a linear baseline from each individual spectrum before averaging the data. The final spectra were smoothed to a velocity resolution of 2 km s−1. Following Belitsky et al. (2018), we assume an antenna forward efficiency ηf of 0.95, and a beam efficiency ηmb of 0.67 to convert the antenna temperature 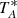T A * $ T^*_A $ into Tmb4. The rms reached during the pointing campaign ranges (in Tmb) from 7.8 to 17.6 mK for both Clouds. The exact rms value for each line of sight is indicated in Table A.1. For the mapping campaign data, two linear baseline subtractions were performed before and after a resampling of the data to a resolution of 2 km s−1. The final pixel size of the spectral cubes is half a beam size (18″). The rms reached throughout the maps (estimated with go noise in CLASS) are provided in Table B.1.

2.4. Ancillary data available

2.4.1. CO observations

A 12CO(1−0) mapping of the LMC and SMC has been performed using NANTEN (Fukui et al. 2008) (2.6′ resolution). A follow-up survey was carried out with the Mopra MAGMA project (Hughes et al. 2010; Muller et al. 2010; Wong et al. 2011), allowing us to trace the structures of GMCs at a resolution of 45″. A cloud decomposition has been performed using the CPROPS decomposition technique (Rosolowsky & Leroy 2006) and catalogs of the CO cloud properties are available on the VizieR database5. Observations of 12CO(1−0) in the SMC were conducted as part of the MAGMA-SMC program (Muller et al. 2013) but maps are not released at the time of writing. Observations of the 12CO(2−1) transition in the SMC were also performed using the SHeFI/APEX-1 receiver as part of the CO Survey of the Small Magellanic Cloud (COSSA) large programme (ESO periods P92-95) by van Kempen et al. (in prep.) at a 28″ resolution.

2.4.2. Spitzer and Herschel maps

The dust emission in the LMC and SMC has been extensively observed in the IR and submillimeter(submm) regimes. Both Magellanic Clouds were fully mapped with Spitzer as part of the Surveying the Agents of a Galaxy’s Evolution project (SAGE; Meixner et al. 2006). Observations are available at 3.6, 4.5, 5.8, and 8 μm (IRAC) and 24, 70, and 160 μm (MIPS). We refer to Meixner et al. (2006) and Gordon et al. (2014) for a detailed description of the various steps of the data reduction. Both Clouds were also observed with Herschel as part of the successor project of SAGE, the HERschel Inventory of The Agents of Galaxy’s Evolution project (HERITAGE; Meixner et al. 2010, 2013). They were mapped at 100 and 160 μm (PACS) and 250, 350, and 500 μm (SPIRE). Details of the Herschel data reduction and image treatment can be found in Meixner et al. (2013) and Gordon et al. (2014). The coarsest resolution of this IR-to-submm dataset is 36″, thus equal to the beam of our SEPIA180 observations.

We convolve all the IR-submm maps to this limiting resolution to be able to locally compare the dense gas tracers with the dust emission and the total IR luminosity LTIR, an extensively used proxy for the SFR in extragalactic studies (Kennicutt 1998; Murphy et al. 2011). To estimate LTIR, we use the 100–160–250 LTIR empirical calibration derived for nearby galaxies from the Herschel/KINGFISH project by Galametz et al. (2013). For the DeGaS-MC pointings, we produce a full LMC and SMC LTIR map and the LTIR per pointing using a photometric aperture of the size of the SEPIA beam. For the DeGaS-MC maps, the Herschel PACS 100 and 160 μm and SPIRE 250 μm maps are first cut and regridded to our intensity map pixel grids for each region, and were then combined to produce an individual LTIR map for each region targeted. Uncertainties on the LTIR are estimated using a Monte-Carlo technique, varying the Herschel fluxes and calibration coefficients 5000 times within their error bars following Gaussian distributions. These uncertainties are dominated by the calibration uncertainties of the PACS and SPIRE instruments (10% at 100 μm and 250 μm, 20% at 160 μm; Poglitsch et al. 2010; Griffin et al. 2010).

3. Detection statistics and line characteristics

3.1. Pointing campaign

The spectra obtained during the pointing campaign are provided in Figs. A.1 (HCO+ observations) and A.2 (HCN observations). We fit the spectra with Gaussian line profiles. We thus assume single-component symmetric profiles (we discuss this hypothesis in Sect. 4.2). We consider the line as detected when the peak brightness is 3-σ above the S/N of the Gaussian fit. HCO+(2−1) is detected above 3-σ in 15 out of the 21 pointings observed in the LMC, HCN(2−1) in six of them. HCO+(2−1) is detected in 5 out of the 8 regions observed in the SMC, HCN(2−1) in two of them. For both Magellanic Clouds, HCN(2−1) is only detected in the brightest HCO+ sources, namely those whose HCO+(2−1) integrated intensity is > 0.35 K km s−1. The brightest detections in the LMC are the LMC pointings #2, #5, #17, #24 and #25 located in the star-forming regions N159W, N44, N11C, N55, and N57, respectively6. All these regions are known as complexes where large numbers of stars are formed and which host large CO reservoirs (Israel et al. 2003). The brightest detections of the targeted SMC sources are found for pointings SMC #1 and #5 in the N27 and N13 star-forming regions, respectively. N27 is also the brightest CO source observed in the SMC (van Kempen et al., in prep., Israel et al. 2003).

From the Gaussian fit, we derive the velocity offset from the systemic velocity, line widths, and integrated intensities and report the line characteristics in Table A.1. Table A.2 lists the corresponding HCO+(2−1)/HCN(2−1) ratios along with the LTIR and corresponding SFR for each pointing.

3.2. Mapping campaign

From the reduced spectral cubes (mapping campaign), we derive integrated line-intensity maps by performing a Gaussian fit to each spectrum. We restrict our calculation to pixels whose peak brightness is 3-σ above the S/N of the Gaussian fit. The HCO+(2−1) and HCN(2−1) intensity maps of the LMC regions are shown in Figs. 2–5. The final pixel size is 17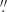 . ″ $ \overset{\prime \prime }{.} $6, thus half the beam size. The Herschel 160 μm contours (convolved at a 36″ resolution) delineate the dust reservoirs observed at similar resolution to the SEPIA observation. The 160 μm is also a good proxy of the TIR luminosity in the region, tracing the SFR pockets. We also show in the bottom panels the HCO+(2−1) and HCN(2−1) spectra associated with the peak of their respective emission. The line characteristics (position, velocity offsets, linewidths and integrated line intensities) at the peak position for both lines are provided in Table B.1 along with the corresponding SFR at this position.

thumbnail Fig. 2.

From top to bottom: HCO+(2−1) and HCN(2−1) integrated intensity maps of 30Dor, N159W, and N159E, from left to right, respectively (3-σ detections). The cold dust emission as traced by Herschel PACS 160 μm is overlaid as contours. For each map, we show the corresponding spectrum at peak position (2 km s−1 spectral resolution) and overlay in red the Gaussian fit performed to derive the peak position line characteristics of Table B.1. The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1). Candidate YSOs retrieved from different catalogs are overlaid: purple down-tridents from Whitney et al. (2008), blue crosses from Seale et al. (2012), red and salmon plus symbols from Gruendl & Chu (2009), yellow up-tridents from Chen et al. (2009, 2010), and green left-tridents from Carlson et al. (2012).

thumbnail Fig. 3.

Same as Fig. 2, but for N11B, N11C, and N44.

thumbnail Fig. 4.

Same as Fig. 2, but for N55, N105, and N113.

thumbnail Fig. 5.

Same as Fig. 2, but for N214.

Both lines are well detected in LMC 30Dor, N44, N105, N113, N159W, N159E and N214 while very few detections are obtained in N11B and N11C. For most of the sources, the location of the HCN and HCO+ emission peaks correspond to peaks in the dust emission, except for N113 whose molecular line peaks seem to be shifted 35″ south from the dust peak, as already noted in Wong et al. (2006). The HCO+ emission is more extended than the HCN emission (except in N11B), with HCN restricted to the densest regions of the targeted clouds. This more extended morphology is consistent with previous 3 mm HCO+ and HCN observations obtained in the LMC at higher resolution with the ATCA by Seale et al. (2012) in N105, N113, N159, and N44. We note that our SEPIA observations trace the larger scale emission in the clouds surrounding the individual clumps that the ATCA and now ALMA observations are able to separate. The HCN and HCO+ difference in spatial extent is also consistent with observations of Galactic GMCs (Pety et al. 2017). Part of the difference can be linked with the fact that HCN(2−1) probes higher densities (ncrit = 2.8 × 106 cm−3 at 20 K) than HCO+ (ncrit = 4.2 × 105 cm−3 at 20 K; Shirley 2015). The (sub-thermal) excitation of both lines in the lower density parts of the clouds could also contribute to the spatial difference we observe, along with a lower relative abundance of HCN in the outer part of the clouds.

We do not detect HCN toward N55. This is surprising, as recent observations with the Atacama Large Millimeter Array (ALMA) have resolved HCN clumps in the southern region of N55. The ALMA observations are centered at RA = 05h32m31.50s Dec = −66°26′22.5″, which is at the border of our map (Nayana et al. 2020). The ALMA map beam size is 4″ × 3″: the absence of detection could suggest that the emission detected with ALMA is smeared out in an APEX beam. For N11B and N55, the spectral cubes have among the highest rms values of the sample: deeper integrations toward these two regions might reveal the weak HCN emission in these clouds. We finally note that we do not obtain any detection of HCO+ or HCN in our SMC maps, here again because the mapping observations were unfortunately not sufficiently deep.

4. Analysis

4.1. Velocity gradient across the Clouds

The velocity gradients in the LMC have been studied using stellar emission (Feitzinger et al. 1977; Schommer et al. 1992) and atomic gas Kim et al. (2003). Our observations enable us to compare the line-of-sight (LOS) velocity gradient of the dense gas motions with these previous estimates. The correlation between the velocity offsets of the HCO+ and the HCN lines is extremely good (Pearson correlation coefficient R = 0.99). We therefore use the velocity offsets of the HCO+ lines for the velocity field analysis.

We derive the individual LOS velocities of the dense gas in each pointing where the line is detected. We overlay the respective velocities as colored circles on the LMC map in Fig. 6. Velocities in the LMC range from 229.7 km s−1 in the southern part of the galaxy (LMC #4) to 289.6 km s−1 in the north (LMC #24). This velocity pattern follows the LOS velocity field which was derived using 7000 carbon stars velocities by van der Marel & Kallivayalil (2014). It also corresponds to the velocity range where H I peak column densities of 7 × 1021 cm−2 are found by Kim et al. (2003) (225–310 km s−1). More quantitatively, we estimate velocity gradient via a least-square minimization, with vgrad = vsys + aΔα + bΔβ, where Δα and Δβ are the offsets with respect to the center of mass taken at 5h27.6m, −69.87° (as determined by van der Marel et al. 2002). We find a velocity gradient of 0.31 ± 0.1 km s−1 kpc−1 with a position angle of 5°. We overlay the fitted velocity gradient in Fig. 6.

thumbnail Fig. 6.

LMC and SMC LOS velocity fields as traced by the HCO+ line. The pointings are represented by circles coded by their associated velocity (in units of km s−1) according to the provided color scales. For the LMC, we derive a velocity gradient of 0.31 ± 0.1 km s−1 kpc−1 (P.A. = 5°; overlaid in rainbow).

The velocity field of the SMC is far less constrained by our pointing observations, as we only have a few detections of HCO+ mostly in the southern part of the bar, with velocities ranging from 115 to 127 km s−1. The velocity in the northern part of the bar is constrained by the detection of HCO+ in SMC #8 and is equal to 157 km s−1. The overall velocity field is consistent with that derived from the H I observations by Stanimirović et al. (2004). These latter authors find a large-scale gradient of about 70 km s−1 from the southwest to the northeast, and of about 40 km s−1 between the two large supershells 37A and 304A corresponding to our SW and NE detections, respectively.

4.2. HCO+ and HCN line widths

Previous surveys have been performed to derive HCO+(1−0)/ HCN(1−0) ratios toward six of our targeted regions. Estimates taken from the literature are summarized in Table 2 for reference, with studies performed for the 1−0 transition toward H II regions at cloud scale (for instance by Chin et al. 1997) down to clump scales (Seale et al. 2012; Anderson et al. 2014). Observations of the 4−3 transition in N159 are reported by Paron et al. (2016) (with a HCO+/HCN ratio of 8.75). To quantitatively compare the two molecular line emissions in the 2−1 transition, we show in Fig. 7a how the HCN(2−1) integrated intensity relates to HCO+(2−1) integrated intensity. We observe that both tracers scale relatively tightly with each other (Pearson correlation coefficient R = 0.79). The dashed line indicates the linear fit to the data with the intercept fixed to 0. The relation is:

I HCN ( 2 − 1 ) K km s − 1 = 0.35 I HCO + ( 2 − 1 ) K km s − 1 $$ \begin{aligned} \frac{I_{\mathrm{HCN}(2{-}1)}}{\mathrm{K\,km\,s^{-1}}} = 0.35 \frac{I_{\mathrm{HCO}^+(2-1)}}{\mathrm{K\,km\,s^{-1}}} \end{aligned} $$(1)

thumbnail Fig. 7.

Relations between the HCO+(2−1) and HCN(2−1) integrated intensities and the line widths (FWHM) of the lines. The LMC pointings appear as blue triangles and the SMC pointings as red triangles. The light and dark blue squares indicate the individual detections from the LMC spectral maps (18″ pixels) detected at a 3 and 5-σ level, respectively. Panel a: the dashed black line indicates the best linear fit to all the data. Panels a and c: the dotted gray line is the 1:1 relation.

Table 2.

HCO+(1−0)/HCN(1−0) (a) estimates from literature.

Our targets are systematically brighter in HCO+(2−1) than in HCN(2−1), with a mean HCO+/HCN integrated intensity ratio (calculated with intensities in K km s−1) of approximately 3 for the LMC pointings and 2.5 for the SMC pointings. The ratio is always above unity in both Magellanic Clouds (except one LOS in N11C) contrary to the Galaxy (Pety et al. 2017; Shimajiri et al. 2017) or more metal-rich nearby galaxies7 (Nguyen et al. 1992; Martín et al. 2015; Knudsen et al. 2007). The highest HCO+(2−1)/HCN(2−1) ratio (∼7) is found in the luminous 30Dor region. Overall, the HCO+(2−1)/HCN(2−1) observed ratios are consistent with the fact that high HCO+-to-HCN values are expected in the LMC and SMC, as the ratio is known to increase with decreasing metallicity (Braine et al. 2017; Johnson et al. 2018; Kepley et al. 2018).

The use of RADEX or LVG methods have shown that low-J HCN lines usually become thermalized at higher densities than the HCO+ lines (Muller & Dinh-V-Trung 2009; Mills et al. 2013). Therefore, variations in the HCO+/HCN ratio could be driven by local variations in density. Combining our dataset with observations of lower and higher excitation lines would be needed to properly quantify these densities. Variations in the HCO+/HCN ratio could also be driven by local variations in the species ratio itself (Nishimura et al. 2016). Finally, higher HCO+ intensities are also often attributed to the variations in the N/O abundance ratio with metallicity (Nicholls et al. 2017; Vincenzo & Kobayashi 2018; Berg et al. 2019), in particular the elemental deficiency of nitrogen leading to a deficiency in N-bearing molecules (HCN but also HNC; see Nishimura et al. 2016). The two Magellanic Clouds also have different metallicities, but unfortunately HCO+ and HCN are only detected simultaneously in two LOSs for the SMC, which does not allow us to robustly analyze metallicity effects between the two Clouds. For these two SMC LOSs, the dense gas tracer intensities follow the overall relation of Fig. 7a.

4.3. HCO+ and HCN intensities

On the scales traced by our survey, the line widths provide information on the GMC dynamics. Giant molecular clouds are known to follow scaling relations between their size, luminosity, and line width (Larson 1981), suggesting that a relation also exists between the mass of a star-forming cores and its dynamical status. These scaling relations have been studied in CO for extragalactic GMCs (e.g. by Bolatto et al. 2008; Schruba et al. 2019; Sun et al. 2020), including the LMC where line widths have been found to be narrower (Hughes et al. 2010) or wider (Indebetouw et al. 2013) than the overall size–line width relation, depending on the region probed. As far as dense gas tracers are concerned, in the Galaxy, HCO+ line widths of Galactic dense clouds in the plane or at high-latitude are in the [2–5] km s−1 range (Pirogov et al. 1995; Schlingman et al. 2011) while this value raises to 6 km s−1 toward Galactic high-mass star-forming cores (Shirley et al. 2003). Other parameters than mass alone can also affect the line width, such as inter-clump pressure or the cloud turbulence (Heyer et al. 2009; Schruba et al. 2017, 2019).

Figure 7d shows the relation between the HCO+(2−1) and HCN(2−1) (FWHM) line widths while the side panels b and c show how the line width varies as a function of the line integrated intensity. Part of the relationship between line width and its integrated intensity could be due to the definition of the line integrated intensity itself8, although three sources (LMC #4, #7 and #13) seem to be slightly above the overall positive correlation in panel c. These three regions have no HCN detection, which prevents us from confirming the deviation from this line. The HCN and HCO+ line widths and line profiles are relatively similar, both covering line width values from 2 to 10 km s−1. For the LMC pointing sample campaign (blue triangles), the mean HCO+(2−1) line width is 4.3 km s−1 (5.6 km s−1 for HCN). The mean line width in the SMC is similar for HCO+ (4.4 km s−1) but larger for HCN (7.1 km s−1) whose detection remains limited to the densest central, and therefore probably more turbulent, parts of the clouds. We observe that our pointing campaign, which targeted lower cloud masses, includes LOSs with lower HCO+ line widths < 3 km s−1 in LMC#12, #22, and #23. The largest line widths are found toward the 30Dor (9.8 km s−1), N159 (9.4 km s−1), and N44 (8.1 km s−1) star-forming regions, a signature that these regions could host more massive clumps than the other regions targeted.

We note a larger dispersion in the HCN(2−1) line widths compared to HCO+(2−1) line widths (see Fig. 7d). This dispersion might be linked with the fact that we model the HCN(2−1) line as a single component in spite of the line having a hyperfine structure of a few km s−1, which is not resolved at our working spectral resolution of 2 km s−1.

5. Discussion

5.1. Relation with the YSO populations

Most of the sources targeted during the mapping campaign benefit from intensive identification campaigns of their population of YSOs (Whitney et al. 2008; Gruendl & Chu 2009; Chen et al. 2009, 2010; Seale et al. 2012; Carlson et al. 2012). We retrieved these catalogs from the VizieR database and overlay the YSO candidates on the HCO+ and HCN maps (Fig. 2). If sources are listed in several catalogs, they only appear once in the maps and in our analysis. We note the double color-code for the Gruendl & Chu (2009) catalog: red plus symbols on our maps indicate sources classified as YSOs while salmon-colored plus symbols indicate sources that have been primarily classified as YSOs but show other characteristics that could suggest another nature (star or evolved star, diffuse source, background galaxies; classified as “CA”,“CS”,“CG” or “CD” in the catalog). From their spatial distribution, we produce maps of YSO candidates per LOS for each targeted SF region. The total number of YSOs in each mapped field is reported in Table B.1.

We plot the distribution of the number of YSO candidates per LOS as a function of the HCO+(2−1) integrated intensity in Fig. 8 (top left). The bottom panels highlight the characteristics of each distribution: the black boxes indicate the standard deviation for each distribution and the colored line their mean value. We observe a higher number of YSOs at high HCO+ or HCN intensities, which is consistent with the expectations that stars should primarily form in high-density gas (among many others Myers et al. 1987; Yun et al. 1999; Sadavoy et al. 2014). The highest number of YSOs per LOS is found toward N44 (3 YSOs/pixel) and N159W (2 YSOs/pixel). However, we note that an extensive and targeted analysis was performed for these two sources by Chen et al. (2009, 2010), which might introduce biases. Deeper analysis of YSOs on the other regions or at higher resolution (with JWST for instance) might also reveal more YSOs clustered toward the central regions, in particular in crowded environments such as 30Dor.

thumbnail Fig. 8.

Top: histograms of the HCO+(2−1) integrated intensities in K km s−1 (left) and HCO+(2−1)/HCN(2−1) integrated intensity ratios (right) of all the LOSs observed. LOSs with 0, 1, 2, and 3 YSOs are shown in green, orange, blue, and red, respectively. Bottom: characteristics of each of these distributions. The black box indicates the standard deviation, the colored line the mean value, and the dashed line indicates the minimum and maximum HCO+(2−1) intensity (left) or HCO+(2−1)/HCN(2−1) (right) for each distribution. The gray thick line indicates the standard deviation of the distribution when LOSs that have HCO+ detection and HCN upper limits are included.

Figure 8 (right) shows the distribution of the number of YSO candidates per LOS, this time as a function of the HCO+(2−1)/HCN(2−1) ratio. To reinforce the statistics, we also indicate with the gray thick line (bottom right panel) how the standard deviation of each distribution evolves if we also consider the HCN upper limits combined with the HCO+ detections. In both cases, more candidates seem to be found toward LOSs with lower HCO+/HCN ratios, which is consistent with the previous findings of Seale et al. (2012) at clump scales. However, our statistics are sparse for the > 1 YSO / LOS bins. If real, such a correlation of the YSO number with the line ratio would not be easy to interpret, as both lines can be independently affected by local conditions (temperature, radiation field, shocks). Nevertheless, one explanation could be that given the difference in thermalization of the two lines, lower HCO+/HCN ratios could be found toward LOSs containing gas at larger densities, hence where YSOs could preferentially form. Part of the correlation could also be driven by chemistry effects; for instance, HCN and HCO+ have been shown to trace different ionization conditions in YSO outflows (Tappe et al. 2012).

5.2. Scaling relations with the star formation rate

The correlation between HCO+ and HCN luminosities and SFR has been studied over ten orders of magnitude, from individual Galactic clouds to full galaxies (Gao & Solomon 2004; Chen et al. 2015; Usero et al. 2015; Jiménez-Donaire et al. 2019). Our observations help us investigate the relation on GMC scales, thus populating the bridge between these two scales in a low-metallicity environment whose ISM structure and abundance might affect the relation. Given the larger detection rate of HCO+(2−1), we selected this line for the HCO+(2−1) versus SFR comparison in panels a and c of Fig. 9. The IR luminosity LTIR, which is a proxy of the recent star formation, is derived as described in Sect. 2.4.2. The LTIR are then converted in SFR using the calibration from Murphy et al. (2011). Both LTIR and SFR are indicated on the left and right y-axes, respectively. The uncertainties on LTIR, although plotted in Fig. 9, are smaller than the symbol size. LTIR and/or SFR for the pointings and toward the peak positions of the maps are indicated in Tables A.2 and B.1.

thumbnail Fig. 9.

Panels a and b: variation of the HCO+(2−1) intensity and the HCO+(2−1)/HCN(2−1) ratio as a function of the SFR traced by LTIR for the LMC (blue upward triangles) and SMC (red downward triangles) pointings. Intensities are in units of K km s−1. The light and dark blue squares indicate the individual detections from the LMC spectral maps (18″ pixels) detected at a 3 and 5-σ level, respectively. Panel a: the dashed line indicates the linear fit to the data. The Pearson’s correlation coefficient is indicated Panels c and d: same but with colors indicating the star-forming region of each resolved element. Black triangles indicate LMC and SMC pointings shown with their corresponding DeGaS-MC numbers.

Our DeGaS-MC pointings nearly cover two orders of magnitude in terms of SFR and the HCO+(2−1) luminosity correlates well with this SFR (Pearson’s R = 0.6) throughout the LMC and the SMC (triangles). The dispersion around the relation increases when the full dataset is taken into account (Pearson’s R = 0.28). The relationship between HCO+(2-1) integrated intensity and SFR (dashed line in Fig. 9a) is as follows:

SFR M ⊙ yr − 1 = 7.7 × 10 − 6 I HCO + ( 2 − 1 ) K km s − 1 . $$ \begin{aligned} \frac{\mathrm{SFR}}{M_\odot \, \mathrm{yr}^{-1}} = 7.7 \times 10^{-6} \, \frac{I_{\mathrm{HCO}^+(2-1)}}{\mathrm{K\,km\,s^{-1}}} .\end{aligned} $$(2)

The correlation confirms that in the Magellanic Clouds, as in nearby spirals (e.g. Bigiel et al. 2015) up to high-redshifts starbursts (e.g., Oteo et al. 2017), the SFR is closely related with denser regions (we show in Sect. 5.3 that the correlation is more scattered with the total molecular gas traced by the CO(1−0) line). Similarly to what is observed in other nearby galaxies (Querejeta et al. 2019), we observe strong variations in the dense-gas-luminosity–SFR relation from one SF region to another and within the regions themselves. While N159E, N159W, N113, and N44 follow the global trend, 30Dor and N214 are diverging from the overall relation with opposite behaviors. 30Dor systematically presents SFRs larger than predictions from Eq. (2), which translates into a higher SF efficiency, while N214 has a more quiescent SFR than predicted.

Several studies have also suggested that the HCO+/HCN ratio varies with star formation activity in molecular clouds. In M31 for instance, Brouillet et al. (2005) show that the HCO+ emission is slightly stronger than the HCN emission toward GMCs with a high star formation activity (presence of an associated large H II region) compared to more quiescent clouds. Panels b and d of Fig. 9 show the relation between the HCO+(2−1)/HCN(2−1) ratio and the SFR. These results suggest that the local relation between the two parameters is actually not straightforward when probed on GMC scales. For our selection of sources, the HCO+(2−1)/HCN(2−1) ratio and the SFR are indeed only weakly correlated, with most of our LOSs having ratios of around two to three and a strong dispersion at SFR > 5 × 10−6 M⊙ yr−1. However, we note that the largest HCO+/HCN ratios are preferentially found towards more actively star-forming LOSs in N159W and 30Dor.

As will be shown in Fig. 11 (bottom), the HCO+(2−1)/ HCN(2−1) ratio does not depend strongly on the local CO intensity toward the same LOS. No correlation is found either with the local temperature (that we traced via the 100 μm/350 μm luminosity ratio). For instance, all LOSs in 30Dor are warmer than the other regions, but the majority of these LOSs cover similar HCO+(2−1)/HCN(2−1) ratios (between 2 and 4) to the other regions.

5.3. Dense gas fraction

The HCN/CO or HCO+/CO flux ratios are commonly used as tracers of the dense gas fractions (Bigiel et al. 2015; Usero et al. 2015). The HCO+(1−0)/CO(1−0) ratio has been derived toward a few LMC molecular clouds (Johansson et al. 1998; Heikkilä et al. 1999). Targeting dense clumps within 30Dor, Anderson et al. (2014) also find relatively low (10%) dense gas fractions in the region. As a comparison, Milky Way estimates of the dense gas fraction in Galactic center clouds have led to values of about 15% (Mills et al. 2018). To analyze how this ratio varies throughout the LMC, we use the CO(1−0) map from the MAGMA survey (second data release). A map is provided at a resolution of 45″, close to that of our analysis (35″). As this difference in resolution is minor and the beam profile shapes are rather uncertain, we do not attempt to convolve the data and directly regrid the CO intensity map to the pixel grids of our individual intensity maps. The CO, HCN, and HCO+ data are kept in K km s−1. We assume that the CO(1−0) line is not saturated.

Figure 10 (top) first presents the relation between the CO(1−0) intensity with the SFR (as traced by the TIR luminosity) for LOSs where HCO+(2−1) has been detected during our DeGaS-MC campaign. The shaded points complement the relation for all LOSs where CO(1−0) has been detected in our fields of view. The very weak correlation between the two parameters (whether or not we include the LOSs where HCO+ is not detected) reinforces the numerous previous claims that the HCO+ line emission is a far better tracer of the gas that forms stars than the CO(1−0) line. Part of the lack of correlation could be linked with saturation effects affecting the CO emission. Figure 10 (middle and bottom) highlights the substantial variations of the HCO+(2−1)/CO(1−0) and HCN(2−1)/CO(1−0) ratios, and thus of the dense gas fraction from one LMC region to another. The highest dense gas fractions are found in 30Dor while the lowest are found in N214. Figure 10 also provides information on how the dense gas fractions evolve as a function of LTIR: the 30Dor and N214 regions are also the two regions with respectively highest and lowest SFR on average. The positive correlation between LTIR and the HCO+(2−1)/CO(1−0) is therefore in line with the expected correlation between the SFR and the dense gas fraction, though the relation presents significant scatter (Pearson’s R = 0.37).

thumbnail Fig. 10.

Top: relation between the CO(1−0) intensity (in K km s−1) and the local LTIR for LOSs where HCO+(2−1) has been detected with DeGaS-MC (and associated Pearson correlation coefficient R). The shaded points complement the relation for all LOSs where CO(1−0) has been detected. The colors separate the various star-forming regions and the increasing size of the symbols indicates an increase in the YSO number (0, 1, 2 or 3) for each LOS. The corresponding local SFRs are indicated on the upper x-axis. Middle and bottom: variation of the HCO+(2−1)/CO(1−0) (middle), a proxy for the dense gas fraction, and of the HCN(2−1)/CO(1−0) (bottom) ratio (with intensities in K km s−1) as a function of the local LTIR.

The size of the circles in Fig. 10 is proportional to the number of YSOs per LOS. The number of YSOs does not seem to correlate with the HCO+/CO ratio, which indicates that YSOs are not preferentially found where the dense gas fraction is the highest. We note however that the lack of a strong correlation could also be linked with the complexity of detecting YSOs toward crowded regions or the lower mass YSO populations, which could lead to an underestimation of the number of YSOs toward certain LOSs.

Finally, in Gallagher et al. (2018b), a positive correlation is found between the dense gas fraction (traced by HCN(1−0)/CO(1−0)) and the cloud-scale molecular gas surface density (traced by CO(2−1)) at kiloparsec-scales. However, substantial galaxy-to-galaxy variations are observed and the authors predict that a study at cloud scales could reveal intrinsic variations from region to region (e.g., as found by Querejeta et al. 2019, for individual molecular clouds in M51). Figure 11 (top) shows how the dense gas fraction (here traced via HCO+(2−1)/CO(1−0) ratio) scales with the CO(1−0) integrated intensity in our survey. Substantial scatter is observed from one star-forming region to another. Contrary to the findings of Gallagher et al. (2018b), the two tracers seem to be anti-correlated. We note that the DeGaS-MC trend is derived for a particular cloud regime: low-Z, massive, star-forming clouds. Observations of more quiescent clouds would be necessary to construct the full LMC-scale relation as in Gallagher et al. (2018b). The scatter in Fig. 11 is mostly driven by the shifted 30Dor region. The CO emission in this region could be “underluminous" because of photo-dissociation by the strong star formation and stellar feedback, while HCO+ would be better shielded (Schruba et al. 2017). As mentioned previously, Fig. 11 (bottom) shows that the HCO+(2−1)/HCN(2−1) ratio does not depend strongly on the local CO intensity toward the same LOS.

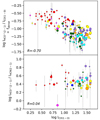thumbnail Fig. 11.

Variation of the HCO+(2−1)/CO(1−0) (top), a proxy for the dense gas fraction, and of the HCO+/HCN(2−1) (bottom) ratio as a function of CO luminosity (all intensities in K km s−1). For symbol sizes and colors: see convention in Fig. 10.

5.4. Potential impact of X-rays on the chemistry?

As agents of ionization, X-rays can lead to an enhancement of the ionization rate. High ionization rates have a direct impact on chemistry; they are suspected to decrease the HCO+ abundance (Krolik & Kallman 1983; Maloney et al. 1996) and have been found to boost the abundance of free electrons. A as electrons might be dominant for the excitation of the HCN molecule over HCO+ (Goldsmith & Kauffmann 2017), high ionization rates will also result in an enhancement of the excitation of HCN, although how these various chemical processes dominate in the studied regions remains unclear.

In our survey, the lowest HCO+(2−1)/HCN(2−1) ratio is found in the N11C region (< 1), in the southern part of the complex. This southern region is irradiated by the LH 13 massive cluster and hosts various compact stellar clusters (Sk−66°41 and HNT) as well as extremely luminous stars, such as Wo 599, which has been suggested to be the main ionizing source of N11C (Heydari-Malayeri et al. 1987, 2000). X-ray emission has been associated to LH 13 in particular (Nazé et al. 2004) and could be responsible for the lower HCO+(2−1)/HCN(2−1) observed in N11C south. The other region observed toward the N11 bubble, N11B, also contains an embedded extremely young OB association (with multiple O and other massive stars). Its associated diffuse X-ray emission exceeds that expected from the stars and could be potentially powered by stellar winds (Mac Low et al. 1998). Here again, the presence of ionization enhanced by X-rays could partly explain the very weak HCO+ detected toward N11B. X-rays probably affect the HCO+(2−1) and HCN(2−1) emission as well in 30Dor. However, most of the X-ray emission observed by ROSAT (Kennicutt & Chu 1994) or Chandra (Townsley et al. 2006) toward the sub-region targeted by our DeGaS-MC survey arises from the massive stellar cluster R136 located at RA = 5h38m42.4s Dec = −69°06′03.4″, which is in-between the two HCO+(2−1) and HCN(2−1) peaks, a region devoid of molecular emission in our survey.

5.5. Future work

This first paper of this series highlights the potential of the DeGaS-MC survey to characterize the dense molecular gas at GMC scales and show how it evolves within a low-metallicity ISM. Future papers of the collaboration will provide a more detailed analysis of the line profiles and velocity information and how it translates in terms of dense molecular gas dynamics. Combined with other transitions, we will perform a modeling of the various regions with photo-dissociation region or X-ray illuminated cloud models using the CLOUDY model by Ferland et al. (2017) or multi-structural, thermo-chemical modeling by Bisbas et al. (2019), and in prep.). This will allow us to derive constraints on the density structure or kinetic temperature of the clouds and quantify the impact of the local physical conditions (ambient gas density, turbulence, stellar population, impact of X-rays on the ionization, supernova shocks) on the dense gas content.

In this analysis, we mention that no correlation is found between the HCO+(2−1)/HCN(2−1) ratio and the local temperature traced via the 100 μm/350 μm luminosity ratio, but a more thorough dust SED modeling of the various regions using the Herschel measurements would allow us to properly quantify the dust temperature, derive dust (and gas) column densities, and compare them with the molecular intensities. The modeling would also help us to probe whether the source-to-source dispersion we observe in Figs. 10 and 11 could be partly caused by the differences in the temperature structure of the different sources. As most of the line mapping survey targets solar-metallicity environments, these analyses would allow us to extend studies of ISM chemical composition at different dust (or gas) columns to the low-metallicity ISM conditions.

We finally note that this survey provides crucial constraints on the fluxes expected for follow-up studies of larger areas and/or at higher resolution with ALMA, but could also, via stacking analysis of the diffuse emission, provide constraints for unresolved studies of high-redshift galaxies.

6. Summary

We report new observations of HCO+ and HCN molecules in the 2−1 transition obtained with the APEX SEPIA180 instrument. We performed a pointing campaign toward 30 LMC and SMC regions followed up by a mapping campaign of bright star-forming regions in the Clouds.

(i) HCO+(2−1) is detected in two thirds of the regions observed in the LMC and SMC and HCN(2−1) in about one-quarter of the 29 DeGaS-MC pointings observed, with HCN(2−1) detected only toward the brightest HCO+ sources. The three targeted SMC sources were unfortunately not detected in our mapping campaign but both lines are detected toward the LMC 30Dor, N44, N105, N113, N159W, N159E, and N214 regions. For most of the sources targeted during the mapping campaign, the HCN(2−1) and HCO+(2−1) peaks correspond to peaks in the molecular gas and dust emission. The HCN emission is generally less extended than the HCO+ emission and is restricted to the densest regions. The largest line widths are found toward 30Dor, N159, and N44 star-forming regions and could be a sign that these regions host more massive, high-column-density clumps.

(ii) The HCO+(2−1)/HCN(2−1) brightness temperature ratio is above unity in both Magellanic Clouds and can reach values up to 7. These high values are consistent with the generally high ratios observed in low-metallicity environments. The ratio does not seem to strongly correlate with the gas surface density or temperature and only moderately correlates with the SFR, with the relation showing strong source-to-source dispersion.

(iii) The highest number of YSOs per LOS is found at higher HCO+ intensities, consistent with the fact that YSOs are generally expected toward denser LOSs. More YSO candidates are preferentially found at lower HCO+/HCN flux ratios, although more statistics would be needed to confirm and interpret the trend.

(iv) The highest dense gas fractions are found in 30Dor and the lowest are found in N214. The dense gas fraction correlates with the SFR, although most of the relation is driven by these two more active or more quiescent regions. Finally, substantial region-to-region variations are observed in the dense gas fraction versus the ( LOS) molecular surface density.

2

Four additional sources were originally planned for the LMC but not observed within the allocated telescope time, hence the gaps in the source numbering of Table A.1.

3

Gildas Continuum and Line Analysis Single-dish Software, http://www.iram.fr/IRAMFR/GILDAS

6

Correspondence between the pointing number and the name can be found in Table A.1.

7

HCN intensities observed toward the center of metal-rich active galaxies should however be taken with caution as they could be enhanced via IR pumping or affected by shocks.

8

The integrated intensity directly depends on the FWHM and the peak intensity.

Acknowledgments

We would like to first thank the referee for his/her thorough reading and very helpful feedback. This publication is based on data acquired with the Atacama Pathfinder Experiment. We thank the APEX observing staff for completing this large program as well as their constant motivation and dedication to the community. APEX is a collaboration between the Max-Planck-Institut fur Radioastronomie, the European Southern Observatory (ESO), and the Onsala Space Observatory. SEPIA is a collaboration between Sweden and ESO. M. G. has received funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation programme (MagneticYSOs project, Grant agreement No 679937, PI: Maury). M. C. gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through an Emmy Noether Research Group (grant number KR4801/1-1) and the DFG Sachbeihilfe (Grant number KR4801/2-1). FLP acknowledges funding from the ANR Grant LYRICS (ANR-16-CE31-0011). This work was partly supported by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.

References

  1. Anderson, C. N., Meier, D. S., Ott, J., et al. 2014, ApJ, 793, 37 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bayet, E., Davis, T. A., Bell, T. A., & Viti, S. 2012, MNRAS, 424, 2646 [NASA ADS] [CrossRef] [Google Scholar]
  3. Belitsky, V., Lapkin, I., Fredrixon, M., et al. 2018, A&A, 612, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Berg, D. A., Erb, D. K., Henry, R. B. C., Skillman, E. D., & McQuinn, K. B. W. 2019, ApJ, 874, 93 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bigiel, F., Leroy, A. K., Blitz, L., et al. 2015, ApJ, 815, 103 [NASA ADS] [CrossRef] [Google Scholar]
  6. Billade, B., Nystrom, O., Meledin, D., et al. 2012, Terahertz Sci. Technol., 2, [Google Scholar]
  7. Bisbas, T. G., Schruba, A., & van Dishoeck, E. F. 2019, MNRAS, 485, 3097 [NASA ADS] [Google Scholar]
  8. Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
  10. Braine, J., Shimajiri, Y., André, P., et al. 2017, A&A, 597, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Brouillet, N., Muller, S., Herpin, F., Braine, J., & Jacq, T. 2005, A&A, 429, 153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Caldú-Primo, A., & Schruba, A. 2016, AJ, 151, 34 [NASA ADS] [CrossRef] [Google Scholar]
  13. Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Carlson, L. R., Sewiło, M., Meixner, M., Romita, K. A., & Lawton, B. 2012, A&A, 542, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Chen, C. H. R., Chu, Y.-H., Gruendl, R. A., Gordon, K. D., & Heitsch, F. 2009, ApJ, 695, 511 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chen, C.-H. R., Indebetouw, R., Chu, Y.-H., et al. 2010, ApJ, 721, 1206 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chen, X., Ellingsen, S. P., Baan, W. A., et al. 2015, ApJ, 800, L2 [NASA ADS] [CrossRef] [Google Scholar]
  18. Chevance, M., Madden, S. C., Lebouteiller, V., et al. 2016, A&A, 590, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Chevance, M., Madden, S. C., Fischer, C., et al. 2020, MNRAS, 494, 5279 [CrossRef] [Google Scholar]
  20. Chin, Y. N., Henkel, C., Whiteoak, J. B., et al. 1997, A&A, 317, 548 [Google Scholar]
  21. Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2014, A&A, 564, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Dickman, R. L. 1978, ApJS, 37, 407 [NASA ADS] [CrossRef] [Google Scholar]
  23. Dufour, R. J., Shields, G. A., & Talbot, R. J., Jr. 1982, ApJ, 252, 461 [NASA ADS] [CrossRef] [Google Scholar]
  24. Feitzinger, J. V., Isserstedt, J., & Schmidt-Kaler, T. 1977, A&A, 57, 265 [Google Scholar]
  25. Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
  26. Flower, D. 2012, Molecular Collisions in the Interstellar Medium (Cambridge University Press) [Google Scholar]
  27. Fukui, Y., Kawamura, A., Minamidani, T., et al. 2008, ApJS, 178, 56 [NASA ADS] [CrossRef] [Google Scholar]
  28. Galametz, M., Kennicutt, R. C., Calzetti, D., et al. 2013, MNRAS, 431, 1956 [NASA ADS] [CrossRef] [Google Scholar]
  29. Gallagher, M. J., Leroy, A. K., Bigiel, F., et al. 2018a, ApJ, 868, L38 [NASA ADS] [CrossRef] [Google Scholar]
  30. Gallagher, M. J., Leroy, A. K., Bigiel, F., et al. 2018b, ApJ, 858, 90 [NASA ADS] [CrossRef] [Google Scholar]
  31. Gao, Y., & Solomon, P. M. 2004, ApJS, 152, 63 [NASA ADS] [CrossRef] [Google Scholar]
  32. García-Burillo, S., Usero, A., Alonso-Herrero, A., et al. 2012, A&A, 539, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Goldsmith, P. F., & Kauffmann, J. 2017, ApJ, 841, 25 [NASA ADS] [CrossRef] [Google Scholar]
  34. Gordon, K. D., Roman-Duval, J., Bot, C., et al. 2014, ApJ, 797, 85 [NASA ADS] [CrossRef] [Google Scholar]
  35. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
  36. Gruendl, R. A., & Chu, Y.-H. 2009, ApJS, 184, 172 [Google Scholar]
  37. Heikkilä, A., Johansson, L. E. B., & Olofsson, H. 1999, A&A, 344, 817 [NASA ADS] [Google Scholar]
  38. Henize, K. G. 1956, ApJS, 2, 315 [NASA ADS] [CrossRef] [Google Scholar]
  39. Heydari-Malayeri, M., Niemela, V. S., & Testor, G. 1987, A&A, 184, 300 [Google Scholar]
  40. Heydari-Malayeri, M., Royer, P., Rauw, G., & Walborn, N. R. 2000, A&A, 361, 877 [NASA ADS] [Google Scholar]
  41. Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [NASA ADS] [CrossRef] [Google Scholar]
  42. Hilditch, R. W., Howarth, I. D., & Harries, T. J. 2005, MNRAS, 357, 304 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hughes, A., Wong, T., Ott, J., et al. 2010, MNRAS, 406, 2065 [NASA ADS] [Google Scholar]
  44. Immer, K., Belitsky, V., Olberg, M., et al. 2016, Messenger, 165, 13 [Google Scholar]
  45. Indebetouw, R., Brogan, C., Chen, C. H. R., et al. 2013, ApJ, 774, 73 [NASA ADS] [CrossRef] [Google Scholar]
  46. Israel, F. P. 1997, A&A, 328, 471 [NASA ADS] [Google Scholar]
  47. Israel, F. P., Johansson, L. E. B., Rubio, M., et al. 2003, A&A, 406, 817 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Jiménez-Donaire, M. J., Bigiel, F., Leroy, A. K., et al. 2017, MNRAS, 466, 49 [NASA ADS] [CrossRef] [Google Scholar]
  49. Jiménez-Donaire, M. J., Bigiel, F., Leroy, A. K., et al. 2019, ApJ, 880, 127 [NASA ADS] [CrossRef] [Google Scholar]
  50. Johansson, L. E. B., Greve, A., Booth, R. S., et al. 1998, A&A, 331, 857 [NASA ADS] [Google Scholar]
  51. Johnson, K. E., Brogan, C. L., Indebetouw, R., et al. 2018, ApJ, 853, 125 [NASA ADS] [CrossRef] [Google Scholar]
  52. Kennicutt, R. C., Jr 1998, ApJ, 498, 541 [Google Scholar]
  53. Kennicutt, R. C., & Chu, Y. H. 1994, Violent Star Formation: From 30 Doradus to QSOs, Proceedings of the first IAC-RGO meeting [Google Scholar]
  54. Kepley, A. A., Bittle, L., Leroy, A. K., et al. 2018, ApJ, 862, 120 [NASA ADS] [CrossRef] [Google Scholar]
  55. Kim, S., Staveley-Smith, L., Dopita, M. A., et al. 2003, ApJS, 148, 473 [NASA ADS] [CrossRef] [Google Scholar]
  56. Klein, B., Hochgürtel, S., Krämer, I., et al. 2012, A&A, 542, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Knudsen, K. K., Walter, F., Weiss, A., et al. 2007, ApJ, 666, 156 [NASA ADS] [CrossRef] [Google Scholar]
  58. Krolik, J. H., & Kallman, T. R. 1983, ApJ, 267, 610 [NASA ADS] [CrossRef] [Google Scholar]
  59. Larson, R. B. 1981, MNRAS, 194, 809 [CrossRef] [Google Scholar]
  60. Lequeux, J. 2005, The Interstellar Medium (Springer-Verlag) [Google Scholar]
  61. Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2017, ApJ, 846, 71 [NASA ADS] [CrossRef] [Google Scholar]
  62. Liszt, H. S., Pety, J., & Lucas, R. 2010, A&A, 518, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Mac Low, M.-M., Chang, T. H., Chu, Y.-H., et al. 1998, ApJ, 493, 260 [NASA ADS] [CrossRef] [Google Scholar]
  64. Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [NASA ADS] [CrossRef] [Google Scholar]
  65. Martín, S., Kohno, K., Izumi, T., et al. 2015, A&A, 573, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Mauersberger, R., & Henkel, C. 1991, A&A, 245, 457 [NASA ADS] [Google Scholar]
  67. Meixner, M., Gordon, K. D., Indebetouw, R., et al. 2006, AJ, 132, 2268 [NASA ADS] [CrossRef] [Google Scholar]
  68. Meixner, M., Galliano, F., Hony, S., et al. 2010, A&A, 518, L71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Meixner, M., Panuzzo, P., Roman-Duval, J., et al. 2013, AJ, 146, 62 [NASA ADS] [CrossRef] [Google Scholar]
  70. Mills, E. A. C., Güsten, R., Requena-Torres, M. A., & Morris, M. R. 2013, ApJ, 779, 47 [NASA ADS] [CrossRef] [Google Scholar]
  71. Mills, E. A. C., Ginsburg, A., Immer, K., et al. 2018, ApJ, 868, 7 [NASA ADS] [CrossRef] [Google Scholar]
  72. Muller, S., & Dinh-V-Trung, 2009, ApJ, 696, 176 [CrossRef] [Google Scholar]
  73. Muller, E., Ott, J., Hughes, A., et al. 2010, ApJ, 712, 1248 [NASA ADS] [CrossRef] [Google Scholar]
  74. Muller, E., Wong, T., Hughes, A., et al. 2013, in Molecular Gas, Dust, and Star Formation in Galaxies, eds. T. Wong, J. Ott, et al., IAU Symp., 292, 110 [Google Scholar]
  75. Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
  76. Myers, P. C., Fuller, G. A., Mathieu, R. D., et al. 1987, ApJ, 319, 340 [NASA ADS] [CrossRef] [Google Scholar]
  77. Nayana, A. J., Naslim, N., Onishi, T., et al. 2020, ApJ, 902, 140 [CrossRef] [Google Scholar]
  78. Nazé, Y., Antokhin, I. I., Rauw, G., et al. 2004, A&A, 418, 841 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Nguyen, Q. R., Jackson, J. M., Henkel, C., Truong, B., & Mauersberger, R. 1992, ApJ, 399, 521 [NASA ADS] [CrossRef] [Google Scholar]
  80. Nicholls, D. C., Sutherland, R. S., Dopita, M. A., Kewley, L. J., & Groves, B. A. 2017, MNRAS, 466, 4403 [Google Scholar]
  81. Nishimura, Y., Shimonishi, T., Watanabe, Y., et al. 2016, ApJ, 818, 161 [NASA ADS] [CrossRef] [Google Scholar]
  82. Nishimura, Y., Watanabe, Y., Harada, N., et al. 2017, ApJ, 848, 17 [NASA ADS] [CrossRef] [Google Scholar]
  83. Oliveira, J. M., van Loon, J. T., Sloan, G. C., et al. 2013, MNRAS, 428, 3001 [NASA ADS] [CrossRef] [Google Scholar]
  84. Oteo, I., Zhang, Z. Y., Yang, C., et al. 2017, ApJ, 850, 170 [NASA ADS] [CrossRef] [Google Scholar]
  85. Paron, S., Ortega, M. E., Fariña, C., et al. 2016, MNRAS, 455, 518 [NASA ADS] [CrossRef] [Google Scholar]
  86. Pety, J. 2005, in SF2A-2005: Semaine de l’Astrophysique Francaise, eds. F. Casoli, T. Contini, J. M. Hameury, & L. Pagani, 721 [Google Scholar]
  87. Pety, J., Schinnerer, E., Leroy, A. K., et al. 2013, ApJ, 779, 43 [NASA ADS] [CrossRef] [Google Scholar]
  88. Pety, J., Guzmán, V. V., Orkisz, J. H., et al. 2017, A&A, 599, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  89. Pirogov, L., Zinchenko, I., Lapinov, A., Myshenko, V., & Shul’Ga, V. 1995, A&AS, 109, 333 [Google Scholar]
  90. Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Querejeta, M., Schinnerer, E., Schruba, A., et al. 2019, A&A, 625, A19 [CrossRef] [EDP Sciences] [Google Scholar]
  92. Richter, O.-G., Tammann, G. A., & Huchtmeier, W. K. 1987, A&A, 171, 33 [NASA ADS] [Google Scholar]
  93. Rosolowsky, E., & Leroy, A. 2006, PASP, 118, 590 [NASA ADS] [CrossRef] [Google Scholar]
  94. Russell, S. C., & Dopita, M. A. 1990, ApJS, 74, 93 [NASA ADS] [CrossRef] [Google Scholar]
  95. Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
  96. Schaefer, B. E. 2008, AJ, 135, 112 [Google Scholar]
  97. Schlingman, W. M., Shirley, Y. L., Schenk, D. E., et al. 2011, ApJS, 195, 14 [NASA ADS] [CrossRef] [Google Scholar]
  98. Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Schommer, R. A., Suntzeff, N. B., Olszewski, E. W., & Harris, H. C. 1992, AJ, 103, 447 [NASA ADS] [CrossRef] [Google Scholar]
  100. Schruba, A., Leroy, A. K., Kruijssen, J. M. D., et al. 2017, ApJ, 835, 278 [NASA ADS] [CrossRef] [Google Scholar]
  101. Schruba, A., Kruijssen, J. M. D., & Leroy, A. K. 2019, ApJ, 883, 2 [CrossRef] [Google Scholar]
  102. Seale, J. P., Looney, L. W., Wong, T., et al. 2012, ApJ, 751, 42 [NASA ADS] [CrossRef] [Google Scholar]
  103. Shimajiri, Y., André, P., Braine, J., et al. 2017, A&A, 604, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  104. Shirley, Y. L. 2015, PASP, 127, 299 [NASA ADS] [CrossRef] [Google Scholar]
  105. Shirley, Y. L., Evans, N. Jr, Young, K. E., Knez, C., & Jaffe, D. T. 2003, ApJS, 149, 375 [NASA ADS] [CrossRef] [Google Scholar]
  106. Shull, J. M., & Beckwith, S. 1982, ARA&A, 20, 163 [NASA ADS] [CrossRef] [Google Scholar]
  107. Stanimirović, S., Staveley-Smith, L., & Jones, P. A. 2004, ApJ, 604, 176 [NASA ADS] [CrossRef] [Google Scholar]
  108. Subramanian, S., & Subramaniam, A. 2012, ApJ, 744, 128 [NASA ADS] [CrossRef] [Google Scholar]
  109. Sun, J., Leroy, A. K., Ostriker, E. C., et al. 2020, ApJ, 892, 148 [CrossRef] [Google Scholar]
  110. Tappe, A., Forbrich, J., Martín, S., Yuan, Y., & Lada, C. J. 2012, ApJ, 751, 9 [NASA ADS] [CrossRef] [Google Scholar]
  111. Townsley, L. K., Broos, P. S., Feigelson, E. D., Garmire, G. P., & Getman, K. V. 2006, AJ, 131, 2164 [NASA ADS] [CrossRef] [Google Scholar]
  112. Usero, A., Leroy, A. K., Walter, F., et al. 2015, AJ, 150, 115 [NASA ADS] [CrossRef] [Google Scholar]
  113. van der Marel, R. P., Alves, D. R., Hardy, E., & Suntzeff, N. B. 2002, AJ, 124, 2639 [NASA ADS] [CrossRef] [Google Scholar]
  114. van der Marel, R. P., & Kallivayalil, N. 2014, ApJ, 781, 121 [NASA ADS] [CrossRef] [Google Scholar]
  115. Vincenzo, F., & Kobayashi, C. 2018, MNRAS, 478, 155 [NASA ADS] [CrossRef] [Google Scholar]
  116. Wakelam, V., Bron, E., Cazaux, S., et al. 2017, Mol. Astrophys., 9, 1 [Google Scholar]
  117. Wang, M., Chin, Y. N., Henkel, C., Whiteoak, J. B., & Cunningham, M. 2009, ApJ, 690, 580 [NASA ADS] [CrossRef] [Google Scholar]
  118. Watanabe, Y., Nishimura, Y., Harada, N., et al. 2017, ApJ, 845, 116 [NASA ADS] [CrossRef] [Google Scholar]
  119. Whitney, B. A., Sewilo, M., Indebetouw, R., et al. 2008, AJ, 136, 18 [NASA ADS] [CrossRef] [Google Scholar]
  120. Wong, T., Whiteoak, J. B., Ott, J., Chin, Y.-N., & Cunningham, M. R. 2006, ApJ, 649, 224 [NASA ADS] [CrossRef] [Google Scholar]
  121. Wong, T., Hughes, A., Ott, J., et al. 2011, ApJS, 197, 16 [NASA ADS] [CrossRef] [Google Scholar]
  122. Yun, J. L., Moreira, M. C., Afonso, J. M., & Clemens, D. P. 1999, AJ, 118, 990 [NASA ADS] [CrossRef] [Google Scholar]
  123. Zhang, Z.-Y., Gao, Y., Henkel, C., et al. 2014, ApJ, 784, L31 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Pointing campaign

thumbnail Fig. A.1.

HCO+(2−1) observations toward the LMC and SMC (2 km s−1 spectral resolution). The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). We indicate with a red line the Gaussian fit on the lines detected at a 3-σ level.

thumbnail Fig. A.1.

continued.

thumbnail Fig. A.2.

HCN(2−1) observations toward the LMC and SMC (2 km s−1 spectral resolution). The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). We indicate with a red line the Gaussian fit on the lines detected at a 3-σ level.

thumbnail Fig. A.2.

continued.

Table A.1.

Characteristics of the pointing campaign sample.

Table A.2.

Pointing campaign: line ratios and SFR.

Appendix B: Mapping campaign

Table B.1.

Characteristics of the mapping campaign sample.

All Tables

Table 1.

Lines targeted and used in this analysis.

In the text
Table 2.

HCO+(1−0)/HCN(1−0) (a) estimates from literature.

In the text
Table A.1.

Characteristics of the pointing campaign sample.

In the text
Table A.2.

Pointing campaign: line ratios and SFR.

In the text
Table B.1.

Characteristics of the mapping campaign sample.

In the text

All Figures

thumbnail Fig. 1.

DeGaS-MC pointing campaign: the positions of our pointings are indicated by the red crosses overlaid on the LMC and the SMC Herschel 500 μm observations (FWHM = 36″). An example of the HCO+(2−1) and HCN(2−1) spectra obtained towards regions LMC #5 and SMC #5 are shown (2 km s−1 spectral resolution). The x-axis is expressed in velocity with respect to the systemic velocities (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). The catalogue of HCO+(2−1) and HCN(2−1) spectra is shown in Figs. A.1 and A.2. The yellow squares indicate the position of the sources targeted during the follow-up mapping campaign (see Sect. 2.2). Please note that the areas mapped are ∼4′ × 4′, i.e., smaller than these squares.
In the text
thumbnail Fig. 2.

From top to bottom: HCO+(2−1) and HCN(2−1) integrated intensity maps of 30Dor, N159W, and N159E, from left to right, respectively (3-σ detections). The cold dust emission as traced by Herschel PACS 160 μm is overlaid as contours. For each map, we show the corresponding spectrum at peak position (2 km s−1 spectral resolution) and overlay in red the Gaussian fit performed to derive the peak position line characteristics of Table B.1. The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1). Candidate YSOs retrieved from different catalogs are overlaid: purple down-tridents from Whitney et al. (2008), blue crosses from Seale et al. (2012), red and salmon plus symbols from Gruendl & Chu (2009), yellow up-tridents from Chen et al. (2009, 2010), and green left-tridents from Carlson et al. (2012).
In the text
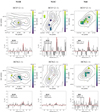thumbnail Fig. 3.

Same as Fig. 2, but for N11B, N11C, and N44.
In the text
thumbnail Fig. 4.

Same as Fig. 2, but for N55, N105, and N113.
In the text
thumbnail Fig. 5.

Same as Fig. 2, but for N214.
In the text
thumbnail Fig. 6.

LMC and SMC LOS velocity fields as traced by the HCO+ line. The pointings are represented by circles coded by their associated velocity (in units of km s−1) according to the provided color scales. For the LMC, we derive a velocity gradient of 0.31 ± 0.1 km s−1 kpc−1 (P.A. = 5°; overlaid in rainbow).
In the text
thumbnail Fig. 7.

Relations between the HCO+(2−1) and HCN(2−1) integrated intensities and the line widths (FWHM) of the lines. The LMC pointings appear as blue triangles and the SMC pointings as red triangles. The light and dark blue squares indicate the individual detections from the LMC spectral maps (18″ pixels) detected at a 3 and 5-σ level, respectively. Panel a: the dashed black line indicates the best linear fit to all the data. Panels a and c: the dotted gray line is the 1:1 relation.
In the text
thumbnail Fig. 8.

Top: histograms of the HCO+(2−1) integrated intensities in K km s−1 (left) and HCO+(2−1)/HCN(2−1) integrated intensity ratios (right) of all the LOSs observed. LOSs with 0, 1, 2, and 3 YSOs are shown in green, orange, blue, and red, respectively. Bottom: characteristics of each of these distributions. The black box indicates the standard deviation, the colored line the mean value, and the dashed line indicates the minimum and maximum HCO+(2−1) intensity (left) or HCO+(2−1)/HCN(2−1) (right) for each distribution. The gray thick line indicates the standard deviation of the distribution when LOSs that have HCO+ detection and HCN upper limits are included.
In the text
thumbnail Fig. 9.

Panels a and b: variation of the HCO+(2−1) intensity and the HCO+(2−1)/HCN(2−1) ratio as a function of the SFR traced by LTIR for the LMC (blue upward triangles) and SMC (red downward triangles) pointings. Intensities are in units of K km s−1. The light and dark blue squares indicate the individual detections from the LMC spectral maps (18″ pixels) detected at a 3 and 5-σ level, respectively. Panel a: the dashed line indicates the linear fit to the data. The Pearson’s correlation coefficient is indicated Panels c and d: same but with colors indicating the star-forming region of each resolved element. Black triangles indicate LMC and SMC pointings shown with their corresponding DeGaS-MC numbers.
In the text
thumbnail Fig. 10.

Top: relation between the CO(1−0) intensity (in K km s−1) and the local LTIR for LOSs where HCO+(2−1) has been detected with DeGaS-MC (and associated Pearson correlation coefficient R). The shaded points complement the relation for all LOSs where CO(1−0) has been detected. The colors separate the various star-forming regions and the increasing size of the symbols indicates an increase in the YSO number (0, 1, 2 or 3) for each LOS. The corresponding local SFRs are indicated on the upper x-axis. Middle and bottom: variation of the HCO+(2−1)/CO(1−0) (middle), a proxy for the dense gas fraction, and of the HCN(2−1)/CO(1−0) (bottom) ratio (with intensities in K km s−1) as a function of the local LTIR.
In the text
thumbnail Fig. 11.

Variation of the HCO+(2−1)/CO(1−0) (top), a proxy for the dense gas fraction, and of the HCO+/HCN(2−1) (bottom) ratio as a function of CO luminosity (all intensities in K km s−1). For symbol sizes and colors: see convention in Fig. 10.
In the text
thumbnail Fig. A.1.

HCO+(2−1) observations toward the LMC and SMC (2 km s−1 spectral resolution). The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). We indicate with a red line the Gaussian fit on the lines detected at a 3-σ level.
In the text
thumbnail Fig. A.1.

continued.
In the text
thumbnail Fig. A.2.

HCN(2−1) observations toward the LMC and SMC (2 km s−1 spectral resolution). The bottom x-axis is expressed in velocity with respect to the systemic velocity (v = 0 corresponding to 262.2 km s−1 for the LMC and 158 km s−1 for the SMC). We indicate with a red line the Gaussian fit on the lines detected at a 3-σ level.
In the text
thumbnail Fig. A.2.

continued.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.