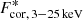| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A100 | |
| Number of page(s) | 21 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202037969 | |
| Published online | 19 June 2020 | |
Do stellar-mass and super-massive black holes have similar dining habits?
1
Max-Planck-Institut für Extraterrestrische Physik (MPE), Giessenbachstrasse 1, 85748 Garching bei München, Germany
e-mail: arcodia@mpe.mpg.de
2
INAF-Osservatorio Astronomico di Brera, Via Bianchi 46, 23807 Merate, LC, Italy
Received:
16
March
2020
Accepted:
14
April
2020
Over the years, numerous attempts have been made to connect the phenomenology and physics of mass accretion onto stellar-mass and super-massive black holes in a scale-invariant fashion. In this paper, we explore this connection at the radiatively efficient (and non-jetted) end of accretion modes by comparing the relationship between the luminosity of the accretion disc and corona in the two source classes. Motivated by the apparently tight relationship between these two quantities in active galactic nuclei (AGNs), we analyse 458 RXTE-PCA archival observations of the X-ray binary (XRB) GX 339–4, using this object as an exemplar for the properties of XRBs in general. We focus on the soft and soft-intermediate states, which have been suggested to be analogous to radiatively efficient AGNs. The observed scatter in the log Ldisc − log Lcorona relationship of GX 339–4 is high (∼0.43 dex) and significantly larger than in a representative sample of radiatively efficient, non- or weakly jetted AGNs (∼0.30 dex). At first glance, this would appear contrary to the hypothesis that the systems simply scale with mass. On the other hand, we also find that GX 339–4 and our AGN sample show different accretion rate and power-law index distributions, with the latter in particular being broader in GX 339–4 (dispersion of ∼0.16 cf. ∼0.08 for AGN). GX 339–4 also shows an overall softer slope, with a mean value of ∼2.20 as opposed to ∼2.07 for the AGN sample. Remarkably, once similarly broad Γ and ṁ distributions are selected, the AGN sample overlaps nicely with GX 339–4 observations in the mass-normalised log Ldisc − log Lcorona plane, with a scatter of ∼0.30 − 0.33 dex in both cases. This indicates that a mass-scaling of properties might hold after all, with our results being consistent with the disc-corona systems in AGNs and XRBs exhibiting the same physical processes, albeit under different conditions for instance in terms of temperature, optical depth and/or electron energy distribution in the corona, heating-cooling balance, coronal geometry and/or black hole spin.
Key words: X-rays: binaries / quasars: supermassive black holes / accretion / accretion disks / galaxies: active / X-rays: general
© R. Arcodia et al. 2020
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
An intriguing and long-standing question exists as to whether the accretion flow around black holes (BHs) is similar among masses (m = MBH/M⊙) that are orders of magnitude apart, ranging from X-ray binaries (XRBs; m ∼ 5 − 15; Casares et al. 2017) to active galactic nuclei (AGNs; m ∼ 106 − 1010; Padovani et al. 2017). There is evidence that the phenomenology of how BHs accrete matter is indeed somewhat analogous (e.g. Ruan et al. 2019a) between AGNs and XRBs, suggesting that they lack not only “hair” (Ruffini & Wheeler 1971) but also diversity in dining habits. What is yet to be established is the extent of this analogy between supermassive and stellar BHs and the impact of a different matter reservoir (i.e. density, temperature, ionisation, and consequently pressure support) and surrounding environment (i.e. a single star with respect to the centre of a galaxy) on the physical processes behind the observed phenomenology.
The description of the accretion flow structure around BHs is typically simplified with a more (e.g. Shakura & Sunyaev 1973; Pringle 1981) or less (e.g. Narayan & Yi 1994) radiatively efficient disc – which in the former case peaks in the soft X-rays for XRBs and in the UV for AGNs – with a “corona” (Galeev et al. 1979; Haardt & Maraschi 1991; Svensson & Zdziarski 1994), responsible for the X-ray emission between fractions and hundreds of keV in both systems, and, possibly, a relativistic jet (Fender 2001; Blandford et al. 2019). Similarities in a scale-invariant fashion between XRBs and AGNs have always been sought after, and they were found, for example in the break of the power spectrum, and hence in the X-ray variability amplitudes (e.g. Uttley et al. 2002; McHardy et al. 2004, 2006; Uttley & McHardy 2005), or by exploring possible correlations among observational proxies of these different spectral components (Heinz & Sunyaev 2003).
In particular, evidence of a common accretion–ejection paradigm emerged from the so-called “fundamental plane” (Merloni et al. 2003), which connects radio and X-ray luminosity with the BH mass: low-luminosity AGNs (which are found to be more radio loud1, e.g. Ho 2002; Sikora et al. 2007) were shown to be scaled-up hard-state XRBs (e.g. Belloni & Motta 2016, for a review on XRBs states) with a prominent jet component and a radiatively inefficient accretion flow (Merloni et al. 2003; Falcke et al. 2004) while moderately and high-accreting AGNs (both combined spanning λedd = L/Ledd ≃ 0.02 − 1; e.g. Noda & Done 2018; Vahdat Motlagh et al. 2019) were connected to XRBs in the soft states (SS; Maccarone et al. 2003) and soft-intermediate states (SIMS; Sobolewska et al. 2009). This picture has been confirmed and expanded by Körding et al. (2006) to include the analogy between hard-intermediate states in XRBs, where there is some disc contribution but the radio jet is present as well, and radiatively efficient radio-loud quasars; and by analysing AGNs caught in the (very slow) act of transitioning between these states (e.g. Marchesini et al. 2004; Marecki & Swoboda 2011). Further, this scale-invariant accretion-ejection scenario has been proven to hold using simultaneous UV and X-ray observations of AGNs (Svoboda et al. 2017).
Here, we aim to improve on this connection in the radiatively efficient (and non-jetted) end of accretion modes, comparing AGNs and XRBs in such regime and test whether they share the same phenomenology and physics based on their disc–corona energetic output. Regarding the phenomenology, the disc–corona connection has been studied in AGNs for decades (e.g. Arcodia et al. 2019, and references therein) via the X-ray loudness parameter αOX (Tananbaum et al. 1979) and was also tested in XRBs with an analogous proxy (e.g. Sobolewska et al. 2009). For the case of AGN, there are many indications that the physical scatter in X-ray coronae for a given disc luminosity (once excluding variability and non-simultaneous observations) is very small (⪅0.19 − 0.20 dex; Lusso & Risaliti 2016; Chiaraluce et al. 2018). However, in SSs and SIMSs of XRBs (i.e. supposedly scaled-down radiatively efficient AGN) the relative strength of the X-ray corona with respect to the disc shows large scatter in a relatively narrow range of soft X-ray monochromatic (i.e. disc) flux (Sobolewska et al. 2009). Furthermore, one should keep in mind that when a single XRB is used, any possible issue arising from non-simultaneity of the data probing the two components is circumvented and there is no additional scatter coming from a mixed bag of masses, distances, and inclinations. Then, under the assumption of a scale-invariant accretion paradigm, one would rather expect the scatter in XRBs to be smaller.
A more thorough study of the source of the scatter in the XRBs disc–corona plane may help to shed light on the putative analogy between accretion flows around stellar-mass and supermassive BHs. This highlights the importance of our work, since the αOX − Ldisc relation in AGNs revealed itself to be a powerful tool for studying the physics of accretion (Lusso & Risaliti 2017; Kubota & Done 2018; Arcodia et al. 2019) up to high redshift (Nanni et al. 2017; Vito et al. 2019; Salvestrini et al. 2020) and its scatter represents an important factor in the now rejuvenated role of quasars as cosmology probes (Risaliti & Lusso 2015, 2019; Melia 2019; Khadka & Ratra 2020; Lusso et al. 2019; Yang et al. 2019; Velten & Gomes 2020; Zheng et al. 2020).
In summary, in this study we tested the disc–corona emission in SSs and SIMSs of the X-ray binary GX 339–4 (Sect. 2), with a more quantitative focus on the phenomenology and physics hidden in the scatter of the Ldisc − Lcor relation (Sect. 4) in order to investigate how it compares to the relation that we observe in their putative scaled-up analogues, namely AGNs in their efficient accretion mode (Sects. 5 and 6).
2. Our sandbox: GX 339–4
GX 339–4 was discovered almost five decades ago (Markert et al. 1973) and is one of the most studied Galactic BH candidates (Zdziarski et al. 1998; Hynes et al. 2003). It has since undergone several X-ray outbursts, which were also simultaneously detected and monitored at almost all wavebands (e.g. Homan et al. 2005; Coriat et al. 2009; Cadolle Bel et al. 2011; Dinçer et al. 2012; Buxton et al. 2012; Corbel et al. 2013; Vincentelli et al. 2018), with particularly good coverage during the Rossi X-ray Timing Explorer (RXTE) era.
We are interested in comparing XRBs in regions of the q-plot (i.e. hardness–intensity or hardness–luminosity diagram, HID, or HLD; e.g. Fender et al. 2004) where the analogy with bright radiatively efficient quasars might hold (e.g. Maccarone et al. 2003; Körding et al. 2006; Sobolewska et al. 2009). We conservatively selected both SS and SIMS states, including spectra in which the hard component can be almost as strong as the soft component. This selection criterion was then confirmed a posteriori with our control AGN sample (Sects. 5 and 6.3.1).
We selected the 2002–2003, 2004–2005, 2006–2007, and 2010–2011 outbursts, which are the ones with the highest coverage in the RXTE archive for GX 339–4. We referred to the extensive literature on GX 339–4 to select SSs and SIMSs in the above-mentioned outbursts (hereafter SS02, SS04, SS07, and SS10, respectively), from both spectral (i.e. low hardness-ratio) and timing analysis (i.e. low fractional rms) constraints: in SS02 we included all RXTE observations between MJD = 52411.60 and 52694 (Belloni et al. 2005), 116 in total; SS04 started at MJD ∼ 53235 (Belloni et al. 2006) and ended at MJD ∼ 53456 (using colour constraints from Dunn et al. 2008), with 78 observations in total; our SS07 selection started in MJD=54147 and ended around MJD = 54230, including only observations marked as high-SSs or SIMSs from timing analysis constraints (Motta et al. 2009), 69 in total2; SS10 contains observations within MJD = 55331–55565 (Debnath et al. 2010; Nandi et al. 2012), 195 in total. This adds up to 458 observations, covering almost 10 years of RXTE data.
3. Data analysis
RXTE observations during SS02, SS04, SS07, and SS10 include data from the Proportional Counter Array (PCA, Jahoda et al. 1996). Data from the High-Energy X-ray Timing Experiment (HEXTE, Rothschild et al. 1998) were not included in the analysis, since the background of the instrument dominates over the (faint) hard spectral component in the SSs and SIMSs. In the PCA, we analysed only energies in the range 3 − 25 keV, where the effective area of the instrument is at its best.
We reduced the selected observations following the standard procedure outlined in the RXTE cookbook3. PCA spectra were extracted from the top layer of the Proportional Counter Unit (PCU) 2, which is reported to be the best calibrated. A systematic uncertainty of 0.5% was added to all channels to account for calibration uncertainties.
In this work, the spectral analysis on each individual observation was performed using v2.8 of the Bayesian X-ray Analysis software (BXA, Buchner et al. 2014)4, which connects a nested sampling algorithm (Feroz et al. 2009) with a fitting environment. For the latter, we used Sherpa v4.11.0 (Freeman et al. 2001; Doe et al. 2007) for the spectral fits and XSPEC v12.10.1 (Arnaud 1996), with its Python oriented interface5, for the flux calculations and spectral simulations (see Appendix A).
Our approach was to first model the PCA background spectrum empirically in the 3 − 25 keV band with a mixture of broken power-law and Gaussian components for each observation. Once satisfactory residuals were obtained, this background model was included as a model component in the spectral fit of source plus background spectra, leaving the power-law normalisation as the single free background parameter. This ensured a more robust statistical treatment of the counts (e.g. Loredo 1992; van Dyk et al. 2001), since all the background-subtracted spectra would have had several bins with negative counts close to the high-energy end of the adopted 3 − 25 keV range. Moreover, the free background normalisation was allowed to span along the 3σ errors of the value obtained in the background fit alone, which excludes an overestimation of our knowledge of the PCA background. Unless stated otherwise, we quote and plot median values with 16th and 84th percentiles of the BXA posterior distributions.
3.1. The spectral model
DISKBB free parameters are the temperature at the inner disc radius Tin and the normalisation, which is a function of the inner radius Rin, the distance d of the source and the inclination i of the disc. The NTHCOMP free parameters were the asymptotic photon index Γ, the normalisation, and the electron temperature kTe (see footnote 6), while we tied the temperature of the seed photons (i.e. the low-energy rollover) to the typical disc temperature as fit by DISKBB. The multi-colour black-body approximation in the DISKBB model was chosen over more rigorous accretion disc models, such as for example BHSPEC (Davis & Hubeny 2006), due to its simplicity and easier coupling with the Comptonisation emission of NTHCOMP. In Appendix C we further discussed our choice and we presented our tests with BHSPEC performed in order to verify the impact of a different disc model on our results. All the parameters in the Gaussian line model were left free to vary within the following intervals: a line with Eline = 6.4 − 6.966 keV, width σline = 0 − 1.5 keV, and free normalisation.
Each X-ray spectrum was fit with a source model consisting of an accretion disc (DISKBB; Mitsuda et al. 1984) plus a Comptonisation component (NTHCOMP; Zdziarski et al. 1996; Życki et al. 1999)6, with the complex features of the reflection spectrum approximated with a Gaussian component7. The source model was then absorbed by a Galactic column density free to vary in a ±15% uncertainty interval (see Arcodia et al. 2018, Sect. 5.7.2) around the tabulated value including the molecular component (NH = 5.18 × 1021 cm−2; Willingale et al. 2013). This source model corresponds to xstbabs*(xsdiskbb+xsnthcomp+xsGaussian) in Sherpa and tbabs*(diskbb+nthcomp+Gaussian) in XSPEC, to which a complex background spectral model was added, with only a free normalisation parameter.
In BXA, we adopted uninformative priors for all ten free parameters8. The Bayesian methodology allowed us to use this complex model for all spectra, even for the few ones in which the Gaussian component might not have been needed. In this cases, the procedure would yield a flat posterior distribution for (i.e. a correct marginalisation over) the free parameters of that component.
3.2. Results of the spectral fits
The overall behaviour of GX 339–4 in its SSs and SIMSs is studied with 458 observations. We show in Fig. 1 the HLD, in which the four complete outbursts are shown in grey (data from Dunn et al. 2010) and our data from SS02, SS04, SS07, and SS10 are represented with purple stars, blue triangles, green squares, and yellow circles, respectively. Three examples of source plus background spectra are reported in Fig. 2, selected taking the 84th percentile, median, and 16th percentile of the total 3 − 25 keV flux distribution of the total XRB sample used in Sect. 5.
 |
Fig. 1. Hardness-luminosity diagram (HLD) of GX 339–4 in its four outbursts used in this analysis (i.e. 2002–2003, 2004–2005, 2006–2007 and 2010–2011). Grey circles are archival data taken from Dunn et al. (2010), over which our own data points for SS02, SS04, SS07, and SS10 are superimposed; these are colour coded following the legend in the figure. Black symbols with red contours refer to the examples in Fig. 2. |
 |
Fig. 2. Three examples of source plus background spectra (black dots, error bars included), with related data–model ratios in the lower panels. The three observations were selected taking the 84th percentile, median, and 16th percentile of the total 3 − 25 keV flux distribution of the full XRB sample used in Sect. 5, shown from left to right respectively. These correspond to the three larger black symbols in Fig. 1, going downwards in the q-plot. All additive model components are shown and defined in the legend, with the total source plus background model shown in red. For each component, the solid lines represent the median of the model distribution computed from the posteriors of the fit parameters (with 16th–84th percentile coloured contours around them, in some cases smaller than the thickness of the line). |
In Fig. 3 we show the evolution of spectral quantities with time along the four outbursts, namely the source plus background count rate in the 3 − 25 keV, the X-ray photon index Γ, the disc temperature Tin (i.e. a proxy of the mass accretion rate), and the disc fraction DF. The latter is defined as in Dunn et al. (2010):
 |
Fig. 3. Evolution of the 3 − 25 keV count rate, of the fit photon index and disc temperature, and of the disc fraction DF (see Eq. (1)) is shown along the four different outbursts (same colour coding and symbols as in Fig. 1). Top panels: filled coloured symbols represent the total (source plus background) 3 − 25 keV count rates, the coloured empty symbols the total count rates in the 10 − 25 keV band, and the grey symbols the background count rates in the 10 − 25 keV band. Middle-top panel: a black dashed line at Γ = 2 is shown to guide the eye, whereas the red dot-dashed line highlights the median Γ = 2.20 of the whole XRB sample used in Sect. 5. |
The NTHCOMP parameter kTe was completely unconstrained as expected given the RXTE-PCA bandpass (see also footnote 6). It was left free to vary to avoid, as much as possible, systematic errors on the estimate of Γ, which, with the used nested sampling algorithm, is marginalised over the unconstrained kTe. Thus, the uncertainties on Γ should include our lack of knowledge on the corona temperature. We refer to Appendix A for our spectral simulations and posterior predictive checks that were made to investigate the robustness of our fit results.
4. The disc–corona relationship in GX 339–04
In radiatively efficient AGNs, we observe a tight correlation between monochromatic X-ray and UV luminosities. Its small physical intrinsic scatter (σphys ⪅ 0.19 − 0.20 dex; e.g. Vagnetti et al. 2013; Lusso & Risaliti 2016; Chiaraluce et al. 2018) defines the diversity in coronae emission for a given disc. Its slope, which is smaller than unity in log space, represents instead the evidence that the coronal emission increases less than the disc emission when going from fainter to brighter sources (see, e.g., Kubota & Done 2018; Arcodia et al. 2019).
A similar disc-corona regulating mechanism might also be in place in SSs and SIMSs of XRBs, although previous comparisons have only been qualitative. For example, the XRB equivalent of the AGN αOX parameter has been reported with large scatter in a relatively narrow range of soft X-ray monochromatic (i.e. disc) flux (Sobolewska et al. 2009, 2011). However, one would expect the scatter in XRBs to be smaller, since they are free from any non-simultaneity biases and the single source obviously comes with the same mass, distance, and inclination.
In this work we want to populate the log Fdisc − log Fcor plane (hereafter also simply referred to as Fdisc − Fcor), which is the XRB equivalent of the LX − LUV (or αOX − LUV) relation in AGNs (see Arcodia et al. 2019, and references therein). With respect to earlier literature, we refined the choice of the observables going in the Fdisc − Fcor. For instance, we refrained from using a monochromatic flux in the soft band obtained with the full (soft plus hard component) model (e.g. as in Sobolewska et al. 2009) as a disc emission proxy, as this would bias the estimate in a relatively unpredictable way moving along the HLD. In the bottom panels of Fig. 3 one can see the DF distribution: even conservatively selecting states above DF ∼ 0.8 (e.g., Dunn et al. 2010), there is still up to ∼20% of the total flux coming from the Comptonisation component. Instead, we computed our disc and corona emission proxies with fluxes under the single DISKBB and NTHCOMP model, respectively. Moreover, the hard component in SSs and SIMSs can fluctuate down to the background level (e.g. see white symbols with respect to the grey in the top panel of Fig. 3), and therefore we consider our approach of modelling the background emission crucial to disentangle the hard component and the background, minimising statistical problems related to the counts-subtraction process (e.g. Loredo 1992; van Dyk et al. 2001).
In the following sections, unless otherwise stated, we use the 2 − 10 keV flux under the single DISKBB and NTHCOMP model as proxy for the disc and corona components, respectively. We adopted a non-monochromatic proxy because the corona emission estimate was found to be more stable against the variations of the putative disc–corona relation due to the Γ distribution, and the 2 − 10 keV band because it is more easily comparable with AGNs (see Appendix B for differences in the Fdisc − Fcor among the different proxies).
4.1. The Fdisc − Fcor plane across the outbursts
In this section we focus on the log Fdisc − log Fcor plane across the four outbursts of GX 339–4 separately in order to see if and how they compare. We show the relations in Fig. 4 and report the related results of the linear regression performed with emcee (Foreman-Mackey et al. 2013) in Table 1. The full relation used is log Fcor − c1 = a + b (log Fdisc − c2), where c1 and c2 are the median value of log Fcor and log Fdisc, respectively (i.e. a different scaling for each regression). Uncertainties on all variables and an additional scatter term (hereafter also referred to as observed scatter) were accounted for using the likelihood provided in D’Agostini (2005).
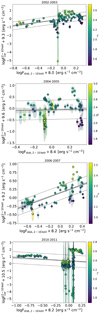 |
Fig. 4. Fdisc − Fcor plane for SS02, SS04, SS07, and SS10 (from top to bottom), with fluxes scaled with their median value. As uncertainties, we report 3σ contours of the 2D distribution of fluxes from the posterior chains, shown with ellipsoids. The solid black line is the median regression line obtained with emcee, with the corresponding 16th and 84th percentiles represented with the shaded grey area. The dashed black lines show the fit scatter around the median relation. |
Summary of slope and scatter of the log Fdisc − log Fcor plane computed in the 2 − 10 keV energy band across the four outbursts.
The main conclusion from Fig. 4 is that, at first glance, the four separate log Fdisc − log Fcor planes do not appear the same. First, the linear correlations do not show evidence of a common slope, which instead spans positive to negative values. A possible reason for this might be that the dynamic range covered by Fdisc (i.e. the horizontal axis) of one order of magnitude and even less is too small for a solid estimate of the slope. Such a range is in fact not even close to the three to four orders of magnitude spanned by UV luminosities in bright AGNs (e.g. Lusso & Risaliti 2016). This is discussed further in Sect. 5, nevertheless here we conclude that the slope in the Fdisc − Fcor plane does not appear to be a good proxy for the disc–corona physics in XRBs.
Furthermore, the path of an outburst in the HLD also somewhat reverberates on the log Fdisc − log Fcor. It is particularly evident in SS10, where both the HLD and the log Fdisc − log Fcor are populated by three clumps (e.g. see the bottom panel of Fig. 4 and the yellow points in Fig. 1). Moreover, in Fig. 4 data points seem to oscillate around the putative relation rather than sitting on it; these abrupt changes in Fcor for a narrow range of Fdisc reflect the horizontal paths in the HLD commonly observed during SSs and SIMSs, in which a source can significantly change its hardness ratio while maintaining the same total (disc-dominated) luminosity (e.g. see Fig. 1). This could be either a peculiarity of XRBs or a trend that we would observe in more massive sources if the coverage was of comparably high cadence. However, a crude mass-scaling of these relatively short timescales (i.e. days) would be around hundreds of thousands of years for AGNs.
Finally, the observed scatter, which is in general very high (between ∼0.2 and 0.8 dex), also seems to be inconsistently different across the outbursts, although it appears to be clearly proportional to the range spanned by Γ during the outburst (see colour coding in Fig. 4). Before comparing XRBs to AGNs, the data for the former need to be homogenised across the outbursts and the differences among them understood and addressed. In particular, the observed scatter seems a more promising and understandable proxy of the disc–corona relation in XRBs and will be the focus of the following section.
4.2. The observed scatter of the disc–corona relation
The scatter of the Fdisc − Fcor relation is likely due to a combination of factors and, before a comparison with AGNs is performed, a more thorough test on our whole GX 339–4 dataset is necessary since it spans rather different values across the outbursts. For instance, the scatter does not depend on the luminosity range covered by an outburst in the HLD or by the dynamic range in Fdisc (i.e. accretion rate). This is indicated by the scatter in SS04 being compatible with that in SS02, despite the former having a much lower spread in Fdisc (see Fig. 4) and in L3 − 10 keV/Ledd (see Fig. 1); and by the fact that SS02 and SS07 span roughly the same range in luminosity and disc temperature, somewhat related to accretion rate, despite the latter showing an incompatibly smaller scatter. Conversely, the scatter appears to be lower for outbursts with a narrower Γ distribution and particularly high in SS10, for which several states had hard count rates (≳10 keV) at background level (see top panel in Fig. 3).
The two quantities seem to be somewhat correlated, as Γ seems to reach the extremes of its distribution mostly in these background-contaminated states (see Fig. A.4). Nonetheless, since a simple cut in Γ is rather arbitrary and there is no physical reason to remove the flat or steep end of the corona emission a priori, it is experimentally meaningful to test the impact of the background influence on the scatter of the Fdisc − Fcor. Moreover, this test is particularly relevant for the comparison with AGNs (Sect. 5), for which the disc is observed in a different energy band, and background-dominated coronae would be either undetected, or poorly constrained and therefore excluded from any quality selection.
We show in the top panel of Fig. 5 how the scatter of the Fdisc − Fcor changes as a function of a cut performed on the ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see, e.g. white and grey symbols in the top panel of Fig. 3). In Fig. 5, grey symbols show results obtained excluding SS10, stating that the enormous scatter is mostly due to some SS10 states in which the hard component is background-contaminated. From spectral simulations (see Appendix A), we conservatively obtained a value of ∼1.3 for this count-rate ratio above which all spectral fits can be considered robust. Above this threshold, the fraction of states that did not retrieve the input Γ within the 16th–84th interquantile range in the simulations is below ∼4% and remains roughly constant. Moreover, this value is also approximately where the scatter with and without SS10 share the same trend (top panel of Fig. 5), namely where the critical states seem to be excluded.
 |
Fig. 5. Top panel: scatter of the Fdisc − Fcor relation as a function of a cut in the ratio between the total (source plus background) and background-only 10 − 25 keV count rates. Coloured points are relative to the full sample and coded with the 16th–84th interquantile range in the related Γ distributions, whereas grey points are obtained excluding SS10. Stars correspond to the starting sample with no filters. Bottom panel: scatter as a function of a cut in the fraction of time spent by GX 339–4 in a region of the outburst, including SSs and SIMSs only (see Sect. 4.2 for a detailed description). Colour coding and symbols are the same as in the top panel. |
Furthermore, an accurate comparison between XRBs and AGNs should take their different sampling and evolution timescales into account. Building the Fdisc − Fcor plane with multi-epoch observations of a single super-massive AGN requires too greater an effort, although the first test cases at the low-mass end are now being explored (e.g. Ruan et al. 2019b). Therefore, large AGN samples are typically used to trace the evolution of one (or a few) XRB(s), assuming a putative scaling between the two classes. AGNs would be preferentially found in periods of their evolution that broadly correspond to regions of the HLD where XRBs spend most of their time. Therefore, we tried to compute a rough but motivated estimate of the fraction of time spent by GX 339−4 in each portion of its SS and SIMS phases combined, for each outburst separately. We first verified that the duration and cadence of observations were fairly uniform, which is often the case with monitoring instruments like RXTE. We then computed a modified duration adding half of the unobserved time fraction, both before and after, to each observation exposure in order to sample the whole SS and SIMS duration. We then built a grid in HR (six bins) and luminosity (eight bins) in the HLD and summed this extended duration in each bin. The resulting smoothed maps obtained by normalising for the total time spent in the SS and SIMS for each outburst separately, are shown in Fig. 6.
 |
Fig. 6. Hardness-intensity diagram of the four outbursts, colour coded from white to black, with MJD values, superimposed to a smoothed map showing the fraction of time spent in each region, including only SSs and SIMSs. |
The bottom panel of Fig. 5 shows how the scatter of the Fdisc − Fcor changes as a function of a cut performed on this fraction of time T/Ttot (which colour codes Fig. 6). Because each SS-SIMS outburst did not last the same amount of time, we cut the data subsets selecting above a given percentile (e.g. from the 10th to the 80th) of T/Ttot, with the actual value then changing among the outbursts accordingly. As can be seen in Fig. 5, the scatter changes as a function of the cut in the time fraction only if SS10 is included and this is a spurious effect driven by the background contamination described above: the scatter jumps to lower values around the cut with the 50th percentile of T/Ttot simply because the low Fcor data points in SS10 are cut out of the data set; as a matter of fact, there is no evolution if SS10 is left out from the exercise (grey points in the bottom panel of Fig. 5). Hence, the scatter in XRBs is not high because of the frequent sampling and the shorter variability timescales.
Summarising, the overall conclusion to be taken from this section is that the scatter in the Fdisc − Fcor plane for XRBs is very high mostly because of a subset of spectra in which the hard band count rate (≳10 keV) is comparable to the background level (see also Appendix A). Nonetheless, even excluding the most critical states (e.g. a ratio of ≳1.3 − 1.5 in the top panel of Fig. 5) the scatter of the relation is between ∼0.30 and 0.45 dex, still higher than what is claimed to be the physical scatter of the Ldisc − Lcor in AGNs (⪅0.19 − 0.20 dex; Lusso & Risaliti 2016; Chiaraluce et al. 2018). Furthermore, we stress that in XRBs, all disc–corona data come simultaneously and from the same source, namely from constant mass, distance, and inclination, even if the estimates are uncertain in an absolute sense. Therefore, the source of this scatter cannot be due to these factors, which makes the high observed scatter even more puzzling. This result is important because a higher scatter for XRBs would either disfavour a common scale-invariant accretion paradigm, or would mean that the physical scatter in AGNs is not necessarily as low as we think.
Here, we showed that different outbursts are not intrinsically homogeneous, the main differences being both observational (a different background contamination of the hard component) and physical (different Γ distribution spanned during the outbursts). Based on the above arguments and on spectral simulations (see Appendix A), we solved the former selecting a subset of XRB states that are above a ratio between the total (source plus background) and background-only 10 − 25 keV count rates of ∼1.3. The top and bottom panels of Fig. 7 show the Fdisc − Fcor relation of the full XRB sample and the one of this subset, respectively. The related slope and scatter in the last two rows of Table 1.
 |
Fig. 7. Fdisc − Fcor plane as described in Fig. 4, but shown here for all outbursts combined (top panel) and for the subset used for the comparison with AGNs (bottom panel), as described and motivated in Sect. 4.2. Bottom panel: points with a red contour highlight three states taken as examples for Fig. 8. |
In Fig. 8 we show count spectra and the related spectral energy distributions (SEDs) of three states, selected by taking the 10th, 50th, and 90th percentile of log Fcor in a narrow range of Fdisc (namely around a ±0.05 dex of the median log Fdisc). This allows us to more clearly illustrate the scatter in the Fdisc − Fcor as a variety of observed spectra and modelled SEDs. Data and models are colour coded by the fit Γ to highlight the softer-when-brighter trend (where both softer and brighter here refer to log Lcor alone in this context) also visible from the colour coding of Fig. 4. These three states are represented by red-contour data points in the bottom panel of Fig. 7.
 |
Fig. 8. Examples of observed spectra with best-fit models (left, including background, shown with a grey-dashed line) and modelled spectral energy distributions (right, without background) of three states, selected taking the 10th, 50th, and 90th percentile of log Fcor in a narrow range of Fdisc (namely around a ±0.05 dex of the median log Fdisc). Both data and models are colour-coded with the fit Γ, highlighting a softer-when-brighter trend in log Fcor. These three states are represented by red-contour data points in the bottom panel of Fig. 7. |
5. Comparisons between XRBs and AGNs
For the rest of the AGN–XRB comparison, we adopt an Eddington-normalised (i.e. mass-normalised) monochromatic luminosity (i.e. νLdisc, ν/Ledd) as disc proxy, which is computed at 0.2 keV and 3000 Å for XRBs and AGN, respectively. The physical reason for adopting 0.2 keV is that this energy is roughly the XRB equivalent of what is 3000 Å for AGN, assuming ν ∝ m−1/4 for a given Eddington ratio (e.g. Calderone et al. 2013). We note that, from an experimental point of view, at such a soft energy the required extrapolation of the RXTE response is large and there are covariances with the Galactic column density value. For the latter, we note that we left NH free to vary within a ±15% of the tabulated value (e.g. Arcodia et al. 2018) in the spectral fits; thus this effect can be considered under control as we are marginalising over this uncertainty interval in Galactic NH. We also tested in Appendix B the impact of this change of disc emission proxy on the results discussed in the previous sections. All the scatter values remain compatible within their 16th–84th interquantile range (see Table B.2), stating that uncertainties in NH and in the RXTE response extrapolation are not significant. In addition, we added an offset to the 0.2 keV fluxes in order to correct for the known underestimation of soft fluxes in RXTE-like instruments by DISKBB (refer to the end Appendix C for a more detailed description).
Instead, the proxy for the corona is the Eddington-normalised broadband luminosity (Lcor/Ledd, also in erg cm−2 s−1) computed in the 2 − 10 keV energy band, which is easily available for both XRBs and AGN. We adopted a black hole mass m = 5.8 and a distance d = 7.8 kpc to estimate these luminosities for GX 339−4 (see Appendix C). The estimates of mass and distance for GX 339−4 are very uncertain and are debated, although the value is obviously the same for all data points and the resulting systematic error would be imprinted in the same way on both axes for all the points.
We show this mass-normalised log Ldisc − log Lcor plane in the top-right panel of Fig. 9 and we report regression results in the top section of Table 2. Data for AGNs consist of a subset of 651 XMM-XXL broad-line AGNs (BLAGNs; Liu et al. 2016; Menzel et al. 2016), which were obtained excluding some objects to minimise the contamination from extinction in the UV (selecting optical-UV continuum α′< − 0.5; see Liu et al. 2018) and obscuration in X-rays (selecting sources for which the 84th percentile of the log NH posterior is < 21.5; e.g. Merloni et al. 2014). Moreover, 44 radio-loud sources were excluded9, which are thought to be scaled-up HIMSs (Körding et al. 2006), in order to validate our comparison with SSs and SIMSs only (see also Sect. 6.1). Hereafter, when referring to our AGN sample we refer to radiatively efficient radio-quiet AGNs.
 |
Fig. 9. Left panels: Γ, ṁ and DF histograms of the full AGN and XRB samples (blue and red-dashed lines) with additional subsamples: “AGNc” (light blue) is obtained reshaping the original ṁ distribution to be as narrow as the one in XRBs (using its 16th and 84th percentiles), albeit keeping the same median as in the full “AGN” sample; the same reasoning is applied with the Γ distributions to select “XRBc” (orange) from “XRB”; instead, “AGNc2” (dark azure) is obtained by selecting sources with ṁ compatible within 0.4 dex with the 5th–95th interquantile of “XRB”, whereas “XRBc2” (dark orange) follows the same reasoning, selecting Γ compatible within errors with the “AGN” Γ distribution. The vertical dashed lines in the middle-left panel represent the location of the 1st and 99th percentile of multiple XRB ṁ distributions, obtained by converting the fit Tin spanning a* = 0 − 0.98 and m = 5 − 10, while we highlight with a red-dashed histogram the one obtained with a* = 0.5 and m = 5.8 (see text). Right panels: mass-normalised log Ldisc − log Lcor plane for the full AGN and XRB samples (top) and the above-mentioned “c” (middle) and “c2” (bottom) subsamples. In the latter case, the uncertainty in determining ṁ for XRBs (vertical dashed lines in the middle-left panel) reverberated in the dark-azure points spreading in the log Ldisc − log Lcor plane, covering the same dynamic range of the full AGN sample. The computed observed scatter of each relation is shown on the side, with the same colour coding as the data: 0.30 ± 0.01 dex and 0.43 ± 0.02 dex for the full samples of AGNs and XRBs, respectively; 0.30 ± 0.01 and 0.33 ± 0.02 in the respective “c” subsamples, 0.31 ± 0.01 and 0.36 ± 0.02 for the “c2”. |
The observed scatter for the AGN sample is ∼0.31 dex. This is higher than the putative upper-limit on the real physical scatter of the relation, tentatively estimated at ⪅0.19 − 0.20 by controlling for non-simultaneity, variability (e.g. Vagnetti et al. 2013; Lusso & Risaliti 2016; Chiaraluce et al. 2018), and potential instrumental calibration uncertainties (Lusso 2019). This is partially because no further selections (i.e. on Γ or X-ray counts) were performed in this work. Nevertheless, the observed scatter in AGNs is incompatibly lower than in the XRB data-set (∼0.43 dex). Furthermore, the dynamic range in disc luminosity is obviously larger for AGNs (top-right panel of Fig. 9) and this is related to the wider ṁ distribution (middle-left panel of Fig. 9). The accretion rate for GX 339−4 is shown with a red dashed line distribution and was estimated from the fit Tin using the standard formulae of the multi-colour black body used in DISKBB (Mitsuda et al. 1984) with the modifications of Kubota et al. (1998), taking the radiative efficiency and innermost stable circular orbit (ISCO) given a spin of 0.5 and assuming m = 5.8 (see Appendix C for these estimates). The vertical dashed lines in the middle-left panel of Fig. 9 represent the location of the 1st and 99th percentiles of the same distribution spanning from spin 0 to 0.98 and m from 5 to 10.
Also, the Γ distribution appears significantly different and is narrower and peaked to harder values in AGNs compared to XRBs (top-left panel in Fig. 9). Before thoroughly addressing the possible causes for the differences between these distributions (see Sect. 6), it is intriguing that once these distributions are made equally narrow the overlap in the log Ldisc − log Lcor plane becomes remarkable. For example, in the middle-right panel of Fig. 9, light blue points are a subset (named “AGNc”) of the parent AGN sample obtained by selecting all sources with ṁ values (taken conservatively with a ∼0.4 dex systematic uncertainty, coming from the mass measurement) compatible with an interquantile range as wide as the 16th–84th range of the ṁ distribution of the XRB sample; orange points are instead a subset (named “XRBc”) of the XRB parent sample obtained by selecting all sources with Γ values compatible with an interquantile range as wide as the 16th–84th range of the Γ distribution of the AGN sample (see also the left panels in Fig. 9). In this case, the distributions were kept at the same median values and simply narrowed according to the other source class. However, we note that a very similar result for the observed scatter is obtained if the AGN and XRB Γ and ṁ distributions are aligned in a different way (defined with “c2”, see Fig. 9), namely taking values of Γ (ṁ) for XRBs (AGNs) that are compatible within errors with the 5th–95th interquantile ranges of the analogous distribution for AGNs (XRBs). Regression results on both sets of AGN and XRB subsamples are shown in Table 2, all showing a compatible scatter within errors around ∼0.33 dex. This is the reference value we attribute to the observed scatter in the log Ldisc − log Lcor plane for XRBs, using GX 339−4 as a test case.
The AGN disc–corona connection has been studied for decades and more recently it was also tested in XRBs with an analogous proxy (Sobolewska et al. 2009). A comparison between the two BH classes was then performed using this observable, which is now more generically referred to as “corona” loudness because in XRBs both components emit in X-rays. This was shown by Sobolewska et al. (2011), who produced a set of simulated AGN spectral states scaling the luminosity (∝MBH) and the disc temperature (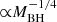 ) from a selection of the XRB GROJ1655−40 spectral fits. These latter authors predicted an inversion of the corona loudness trend with λedd to occur at low luminosity (λedd ⪅ 0.01), approximately where the accretion flow is thought to become radiatively inefficient (e.g. Maccarone 2003; Noda & Done 2018). This transition was recently confirmed by Ruan et al. (2019a) using changing-look (or state) AGNs (or quasars, here referred to as CLAGNs; e.g., LaMassa et al. 2015; MacLeod et al. 2016; Trakhtenbrot et al. 2019) in their shut-down phase.
) from a selection of the XRB GROJ1655−40 spectral fits. These latter authors predicted an inversion of the corona loudness trend with λedd to occur at low luminosity (λedd ⪅ 0.01), approximately where the accretion flow is thought to become radiatively inefficient (e.g. Maccarone 2003; Noda & Done 2018). This transition was recently confirmed by Ruan et al. (2019a) using changing-look (or state) AGNs (or quasars, here referred to as CLAGNs; e.g., LaMassa et al. 2015; MacLeod et al. 2016; Trakhtenbrot et al. 2019) in their shut-down phase.
However, with respect to the better-studied radio-to-X-ray correlations, one should be careful in testing the inefficient mode of accretion with UV-to-X-ray proxies in AGNs and with scaled-up XRB spectra (i.e. not direct flux measurements). For instance, the simulated AGN spectral states were obtained by Sobolewska et al. (2011) for the complete hard-to-soft (i.e. inefficient to efficient) outburst using mass-scaling laws that are however only suitable for efficient flows. Moreover, the monochromatic flux proxies for the putative disc–corona components were computed on the full model and not on the model components separately. Therefore, in the hard state this corresponds to measuring two fluxes of the hard power-law component and the resulting corona loudness is the photon index itself. While it is true that in XRBs, Γ shows an inversion in the trend with the Eddington ratio, going from softer-when-fainter to softer-when-brighter (e.g. Corbel et al. 2006; Wu & Gu 2008; Russell et al. 2010; Homan et al. 2013; Kalemci et al. 2013), this inversion should be tested with Γ also in AGNs (or with an X-ray hardness ratio, e.g., Ai et al. 2020) and not with the αOX slope. Furthermore, RXTE results at low fluxes should be taken with care (see, e.g. the discussion in Homan et al. 2013), as Chandra finds this putative softening at much lower fluxes and for a very narrow range in flux, below which Γ saturates in a plateau (Plotkin et al. 2013, 2017) rather than continuing in a v-shape pattern as claimed by earlier RXTE results. Finally, whatever the origin of the X-ray power law is in XRB hard states (see, e.g. Heinz & Sunyaev 2003; Markoff et al. 2003), it is not trivial to assess how this relates to what produces the UV emission in faint AGNs, as one is forced to extrapolate assuming some QSO-like continuum and to rely on very good knowledge of the host-galaxy subtraction (but see Ruan et al. 2019a, for some interpretations). Our purpose here is instead to study the disc–corona relation in AGNs and XRBs only in the bright end of (radiatively efficient) accretion states, where, despite the supposedly more secure observational proxies, there are still puzzling differences between the two source classes.
6. Discussion
Results from Sect. 5 show that AGNs and XRBs overlap considerably in the Ldisc − Lcor plane, in terms of a compatible observed scatter (∼0.30 − 0.33 dex) and dynamic range on the x-axis, but only after similarly broad Γ and ṁ distributions were selected, which represent the diversity in coronae and discs, respectively. This was merely a sanity check on the putative AGN–XRB analogy and it is indeed interesting to understand why the two distributions appear different.
6.1. Our selection of AGN and XRB accretion states
Our comparison performed in Sect. 5 relied on the key assumption that radiatively efficient AGNs not dominated by the jet emission resemble scaled up XRBs in their SS and SIMS. This association is based on the fact that for both source classes the radio emission appears to be quenched with respect to their radio-loud phases, looking both at the fundamental plane of accretion (Maccarone et al. 2003) and at the disc-fraction–luminosity diagram (Körding et al. 2006); and on the fact that the corona-loudness was already found to be broadly compatible (Sobolewska et al. 2009). It is true that the definition of XRB accretion states based on both spectral (via DF) or timing (via fractional rms) analysis is rather a continuum and the same should also be true for AGNs. However, one can obtain a fairly reliable understanding of the HIMS-SIMS and SIMS-SS transitions from timing analysis constraints (e.g. Belloni & Motta 2016, and references therein) and this is indeed the criterion on which we mostly relied to select our SS-SIMS sample (see Sect. 2).
In this section, our aim is to further elaborate on the choice of including SSs and SIMSs and excluding HIMS from our XRB sample. We note that a comparably clear accretion state separation, which is nicely obtained in XRBs with fractional rms constraints, is more elusive for AGNs where we can only more crudely rely on radio-loudness or spectral estimates. Therefore, we first tested whether the inclusion of SIMSs could also be motivated a posteriori comparing DF estimates for both our XRB and AGN samples (see the bottom left panel of Fig. 9). For AGNs, DF was computed extrapolating the 2 − 10 keV catalogue value to the bandwidth used in Eq. (1) for the corona emission and with the disc luminosity defined in the XMM-XXL AGN catalogue (Liu et al. 2016) that was approximated with standard thin-disc formulae from an optical monochromatic luminosity. The two distributions in the bottom-left panel of Fig. 9 do appear quite similar, with the only significant difference being a longer tail at low DF for AGNs, although one must bear in mind that the full-band Ldisc estimate for AGNs suffers from a much more uncertain extrapolation of the peak in the UV. From this comparison, there is no apparent reason to exclude SIMSs, which by definition sit at the lower end of the reported DF distribution of our XRBs sample (red dashed and dot-dashed histograms in Fig. 10; see also Sect. 6.3.1).
 |
Fig. 10. Top panel: same as the top-right panel of Fig. 9, with only the SSs and SIMSs of the 2002−2003 outburst (dark red circles, with SIMS highlighted by a thicker black contour) and its HIMSs (grey squares). Lines of approximately constant DF are shown with dashed lines, and the related values are shown in the figure. Bottom panel: same as the bottom left panel of Fig. 9, but with again the SS-SIMS (dark red dashed, with SIMS only highlighted by the dot-dashed line) and HIMS (grey) of the 2002−2003 outburst, plus the 44 radio-loud AGNs excluded from our AGN sample (black dotted line). |
We also tested the exclusion of HIMS from our analysis by fitting with the same disc–corona model the HIMS states of the 2002−2003 outburst (see Sect. 3.1), as defined by Belloni et al. (2005) with timing analysis constraints, which we note are independent of DF-based classifications. The top panel of Fig. 10 shows the mass-normalised Ldisc − Lcor plane (as in the top-right panel of Fig. 9) with the SS02 states (i.e. SSs plus SIMSs; dark red) plus the newly fitted HIMSs (grey squares). Soft-intermediate states are highlighted with a thicker black contour and we also show lines of approximately constant DF with related values annotated in the figure. Hard-intermediate states indeed appear as different branches in the disc–corona emission plane, similarly to HLD diagrams, perhaps confirming that they are dominated by the jet emission processes while the SS-SIMS are not. In the bottom panel of Fig. 10 we display instead the related DF distributions for SS-SIMSs (dashed red) and HIMSs (grey), which show again different properties with a small expected overlap, also visible in the top panel via the drawn DF lines. We also report the radio-loud (but radiatively efficient) AGN distribution (black-dotted line) of the 44 such sources in XMM-XXL that were excluded from our analysis, which is remarkably similar to the HIMS confirming the analogy between the two source classes (Körding et al. 2006). We therefore verified that our analysis included a relatively pure sample of radiatively efficient accreting systems which are not jet-dominated, selected among SS-SIMS in XRBs and (optical and X-ray) bright radio-weak AGNs.
6.2. The different ṁ distribution in AGNs and XRBs
The different ṁ distribution and dynamic range in log Ldisc covered by the two samples (see Fig. 9) might indicate that the two systems do not follow the same accretion regimes. However, the almost four orders of magnitude span in AGN mass can play a role in enhancing this difference. Indeed, predictions from disc–corona models do indicate that for the single mass the Ldisc − Lcor in AGNs is in place but with a much lower dynamic range in log Ldisc (slightly more than one order of magnitude for the typical m ∼ 108 − 109 spanning ṁ ∼ 0.03 − 1; e.g. Kubota & Done 2018; Arcodia et al. 2019), similarly to our XRB results (see Figs. 4 and 7). Moreover, ṁ values for both AGNs and XRBs are not a secure measurement, particularly if compared to a quantity such as Γ: ṁ values for the AGN sample were computed with a single bolometric correction (5.15; Shen et al. 2008) on the monochromatic luminosity at 3000 Å divided by a notoriously uncertain mass estimate (Shen et al. 2008) which also hampers the selection of AGNs within a narrow mass range; and ṁ for XRBs was converted from the fit Tin distributions assuming a m = 5.8 and d = 7.8 kpc and changing these values, even within some reasonable intervals around spin and mass (e.g. a* = 0 − 0.98 and m = 5 − 10), would significantly shift the ṁ distribution (see middle-left panel in Fig. 9). However, the width of this distribution would remain approximately the same and this validates our exercise in Sect. 5, where we relied on the width rather than the location of the XRB ṁ distribution (i.e. relying on the “c” subsamples; see middle-right panel of Fig. 9). We conclude that AGNs and XRBs do appear to have different ṁ distributions and dynamic range in log Ldisc, although a significant role is played by the uncertainties and systematic errors on the m and ṁ estimates. Therefore, we cannot rule out that the intrinsic ṁ distributions are instead broadly compatible.
6.3. The different Γ distribution in AGNs and XRBs
In principle, Γ is a quantity that can be more securely estimated (see Appendix A). In our work, we found evidence that XRBs have a distribution that is broader and shifted to softer values with respect to AGNs (see Fig. 9). This result is puzzling and deserves a more in-depth analysis.
The AGN sample used in this work has a Γ distribution with mean and standard deviation of Γ = 2.06 ± 0.11. This is in line with diverse large samples of bright AGNs (with either no jet or a non-jet-dominated emission) which show a fairly narrow distribution of Γ, typically centred in the range Γ = 1.9 − 2.1 up to high redshift (e.g. Vito et al. 2019, and references therein), with a dispersion spanning ≈0.10 − 0.40 which is not always corrected for uncertainties and depends on the sample selection (e.g. Zdziarski et al. 2000; Caccianiga et al. 2004; Piconcelli et al. 2005; Beckmann et al. 2009; Young et al. 2009; Mateos et al. 2010; Corral et al. 2011; de Rosa et al. 2012; Liu et al. 2016; Ricci et al. 2017; Zappacosta et al. 2018; Ananna et al. 2020). Instead, from our analysis of GX 339–4, the fitted Γ values compile a distribution that is broader and shifted to softer values, with a mean and standard deviation of Γ = 2.19 ± 0.21. This is consistent with previous results for GX 339–4 in its SSs and SIMSs obtained with RXTE alone (Zdziarski et al. 2004; Dunn et al. 2008), with XMM-Newton and INTEGRAL data (Caballero-García et al. 2009), and with simultaneous XMM-Newton and RXTE data (Aneesha et al. 2020). For instance, cross-matching our MJD with Dunn et al. (2010) we computed Γ = 2.26 ± 0.47 for 213 states, and from the SSs and SIMSs in Motta et al. (2009) we computed Γ = 2.31 ± 0.15. These distributions are peaked at even softer energies, which is also in line with what is generally observed in disc-dominated states for all XRBs (e.g. Remillard & McClintock 2006). We note that this difference persists also after accounting for uncertainties in the Γ values: we sampled for the mean and intrinsic deviation with emcee values using the likelihood defined in Maccacaro et al. (1988), obtaining 2.07 ± 0.08 (2.20 ± 0.16) for the AGN (XRB) sample. Therefore, at least for our samples, uncertainties do not play a significant role in the difference between the two source classes.
In Sect. 5 we showed that a compatible scatter (∼0.30−0.33 dex) of the log Ldisc − log Lcor between AGNs and XRBs is reached when both Γ distributions were taken with the same 16th–84th interquantile width, leaving the median values unchanged (2.04 and 2.21, respectively). This suggests that no matter where the preferred Comptonisation slope lies, a similar scatter in Γ leads to a similar diversity in X-ray coronae for a given disc (see the middle-right panel of Fig. 9). Indeed, in the above-mentioned literature of AGN samples there is relatively good agreement on where most of the observed Γ values lie, although there is a variety of dispersion estimates according to the varying sample selections (i.e. soft or hard X-rays), instruments, analysis techniques, and model degeneracies. Interestingly, in order to match the cosmic X-ray background shape, a diversity in photon indexes is needed (e.g. with a dispersion of ∼0.2; Gilli et al. 2007) with an impact also on the complex parameters space involved, part of which includes Γ, the reflection fraction, and the high-energy cutoff (e.g. Ananna et al. 2020). In particular, Ananna et al. (2020) explored the allowed regions of this very complex parameters space and showed that, independently from the luminosity function assumed, even a broad Γ distribution with a dispersion of ∼0.2 − 0.3 can reproduce the CXB. If the true intrinsic Γ distribution of AGNs followed this scenario, it would be somewhat closer to the one observed for XRBs.
However, combining several AGN samples with very different selections and characteristics to form a homogeneous picture is beyond the scope of this work. Here we focus on addressing the role of possible contaminants shaping the observed Γ distributions (Sects. 6.3.1–6.3.3) and, if these are understood, explore possible similarities and differences in the physical process producing the observed distribution (Sects. 6.3.4 and 6.3.5).
6.3.1. Possible biases: the soft-excess component
We note that only BLAGNs were included in our AGN sample, although the parent XMM-XXL sample also contains narrow-line AGNs (NLAGNs). However, the exclusion of NLAGNs does not have an impact, as their Γ distribution completely overlaps with the BLAGN one (Liu et al. 2016). An obvious objection is that we included SIMSs for XRBs, namely the brightest spectra with almost equally strong soft and hard components, although we did not include narrow-line Seyfert1 galaxies (NLS1), which might be the AGN equivalent of SIMSs (e.g. Pounds et al. 1995; Gierliński et al. 2008). This could indeed contribute to broadening the AGNs Γ distribution, as the X-ray emission in NLS1s is observed to be very soft (Boller et al. 1996). However, the overall emission is softer because an additional spectral component, broadly referred to as “soft-excess”, is present (e.g. Done et al. 2012). If this extra-component is taken into account, the emission from the hard component only would be compatible with the X-ray slopes from hot Comptonizing coronae in BLAGN: for instance, in NLS1 values around Γ ∼ 1.8 − 2.1 are obtained by analysing spectra only above 2 keV (e.g. Ai et al. 2011) or looking only at the hard photon-index when a broken power law is used (e.g. Grupe et al. 2010). Hence, the Γ distribution in BLAGNs can be considered representative of the observed (i.e. not necessarily the intrinsic) properties of hot coronae in AGN. However, since the hard X-ray emission in soft NLS1s is only matched to the one in BLAGNs when an extra-component is added to account for the soft-excess, this begs the question of whether the same should also be expected to happen in XRB SIMSs. As a matter of fact, if the different spectral states of Mrk 1018 (Noda & Done 2018) are compared to XRBs on a HLD, the brightest ones with a strong soft-excess component would broadly overlap with bright SIMSs and not with SSs (H. Noda, priv. comm.). Moreover, there has been evidence of intermediate states requiring an additional spectral component to the thermal disc and hot Comptonisation alone in XRBs (e.g. Kubota et al. 2001; Kubota & Makishima 2004; Kubota & Done 2004; Abe et al. 2005; Yamada et al. 2013; Hjalmarsdotter et al. 2016; Kawano et al. 2017; Oda et al. 2019) and in GX 339–4 itself (e.g. Kubota & Done 2016).
In order to test the impact of these states on our results, we excluded SIMSs as defined in the earlier literature (see Sect. 2) and the mean and standard deviation values change from Γ = 2.19 ± 0.21 to 2.16 ± 0.21. Thus, even including only previously defined SSs the XRB Γ distribution is still broader and peaked at softer slopes with respect to our AGN sample. Instead, the scatter in the Fdisc − Fcor plane would go from 0.43 ± 0.02 to 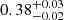 dex, thus it would be compatible within errors but slightly smaller. Moreover, we conservatively tested a different selection, excluding states below DF ∼ 0.8 (e.g. Dunn et al. 2010): the resulting mean with standard deviation is Γ = 2.18 ± 0.21, thus almost identical; the scatter in the Fdisc − Fcor plane would be 0.40 ± 0.02 dex, thus again compatible within errors but slightly smaller. Therefore, here we simply highlight that the role of SIMSs, which possibly include a soft-excess component, is not trivial and may contribute in broadening the observed Γ distribution and slightly increasing the scatter in the Fdisc − Fcor plane, although not to the extent needed to conciliate XRBs to AGN samples. Moreover, we showed in Sect. 6.1 the AGN DF distribution, for which the threshold DF = 0.8 is actually the ∼35th percentile, with a significant tail of lower DF values. This would argue against the exclusion of SIMSs from the comparison.
dex, thus it would be compatible within errors but slightly smaller. Moreover, we conservatively tested a different selection, excluding states below DF ∼ 0.8 (e.g. Dunn et al. 2010): the resulting mean with standard deviation is Γ = 2.18 ± 0.21, thus almost identical; the scatter in the Fdisc − Fcor plane would be 0.40 ± 0.02 dex, thus again compatible within errors but slightly smaller. Therefore, here we simply highlight that the role of SIMSs, which possibly include a soft-excess component, is not trivial and may contribute in broadening the observed Γ distribution and slightly increasing the scatter in the Fdisc − Fcor plane, although not to the extent needed to conciliate XRBs to AGN samples. Moreover, we showed in Sect. 6.1 the AGN DF distribution, for which the threshold DF = 0.8 is actually the ∼35th percentile, with a significant tail of lower DF values. This would argue against the exclusion of SIMSs from the comparison.
6.3.2. Possible biases: X-ray absorption and continuum models
The AGN sample used in this work was compiled from the parent XMM-XXL BLAGN sample (Liu et al. 2016; Menzel et al. 2016), minimising the extinction in the UV (selecting optical-UV continuum α′< − 0.5; see Liu et al. 2018) and obscuration in X-rays (selecting sources for which the 84th percentile of the log NH posterior is < 21.5; e.g. Merloni et al. 2014). We tested the impact of the latter selection criterion on the observed Γ distribution, since obscuration in AGNs plays an important role within a complicated mixture of orientation and evolution effects (e.g. Klindt et al. 2019, and references therein). Further, fitting for both absorption and continuum emission in X-ray spectra within the typical ∼0.5 − 10 keV energy band leads to well-known covariances between the two parameters, which enhance or hamper a possible intrinsic correlation merely for observational and/or instrumental reasons. However, we tested this and the effect of selecting very unobscured objects is minimal and the observed Γ distribution is equally narrow: for the totality of 1659 objects in the XMM-XXL BLAGN sample the mean is Γ = 2.01 ± 0.10, with respect to Γ = 2.06 ± 0.11 of the adopted subsample. We also conservatively tested the impact of leaving the Galactic absorption free to vary within ±15% of the value tabulated in Willingale et al. (2013), since this may artificially broaden the spread in Γ. We used SS02 as representative of all outburts and kept the Galactic absorption column fixed, producing an almost identical Γ distribution.
Finally, since the continuum was modelled with a simple power law for AGNs (Liu et al. 2016) and with a Comptonisation model for XRBs in this work, we verified that adopting a simple power law as well has negligible effects: we fitted states in SS02 and SS07 and obtained a compatible distribution, even shifted even more to softer values with a slightly larger width. Hence, the use of the NTHCOMP model had a minor impact.
6.3.3. Possible biases: X-ray reflection
Furthermore, X-ray reflection was included in the analysis of the AGN sample done by Liu et al. (2016). We here simply empirically tested whether excluding objects with the strongest X-ray reflection (including only sources in which the 16th percentile of log R was < − 0.2 and the 84th was < 0.5, where R is the ratio of the normalisation of the reflection component with respect to the power-law component) had an impact on the observed Γ distribution: the mean and standard deviation values become 2.07 ± 0.11, thus almost identical to Γ = 2.06 ± 0.11 of the subsample adopted here.
For XRBs, we note that the reflection contribution was approximated in all spectral states with a Gaussian line bound to be centred between 6.4 and 6.97 keV, and therefore its flux did not contaminate our Lcor estimates. Moreover, fitting in the 3 − 25 keV band avoided most of the contamination from the Compton hump, although the reflection spectrum can be quite complex and its contribution should be at least tentatively quantified. A thorough treatment is beyond the scope of this paper, although we performed a few tests to exclude that our simplified treatment of the reflection features had an impact on our main results. We fit SS02 (which is representative of the range of observational properties explored with the complete XRB sample) with a laor model (Laor 1991) and compared the newly obtained parameters (e.g. Γ, Tin) with the ones obtained with a simple Gaussian. The biggest effect resulted in a slight offset towards softer Γ obtained with the laor model, although most of the parameters are compatible within 1-sigma uncertainty intervals and almost all of them within 3σ. Hence, we consider this not to imprint a significant impact on our results and, if anything, it would enhance the difference between the observed AGN and XRB Γ distributions, strengthening our results. Moreover, Sridhar et al. (2020) recently performed a detailed characterisation of the reflection features across the hard-to-soft transition of the 2002 and 2004 outbursts in GX 339−4. With respect to the total of 14 observations they used to sample SS02 and SS04, we only shared five, namely Obs. ID 40031-03-03-04 and 70110-01-33-00 for SS02 and Obs. ID 90704-01-03-00, 60705-01-76-00, and 90118-01-10-01 for SS04. The former two in SS02 were defined as SIMSs by Belloni et al. (2005) from timing analysis constraints and were included in our selection, while the latter in SS04 were included with our selection criterion following Belloni et al. (2006). The remaining states in Sridhar et al. (2020) were instead defined either as hard or as hard-intermediate states by Belloni et al., therefore they were not analysed in this work.
In the top panel of Fig. 11 we compare our fit Γ with the values from Sridhar et al. (2020), which apart from the reflection component shared the same model configuration for DISKBB and NTHCOMP. It is evident that by including the reflection, the incident Γ becomes steeper, although our median source has Γ ∼ 2.2 and so the typical displacement would be small. This also appears from other works that included a reflection component in the fit of SSs and SIMSs (e.g. Plant et al. 2014) and it would increase the difference between the observed Γ distributions in AGNs and XRBs even more, which is also in line with the above-mentioned laor model test. Furthermore, in order to check the impact on our broadband fluxes for the corona emission, we tentatively corrected them using the reflection strength defined by Sridhar et al. (2020), namely the ratio between the observed reflected component and the incident continuum component in the 20 − 40 keV band. Our original fluxes Fcor, 20 − 40 keV were then turned into reflection-corrected 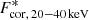 and then the reflection-corrected
and then the reflection-corrected 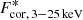 was extrapolated using the asymptotic NTHCOMP photon index computed by Sridhar et al. (2020). We show in the bottom panel of Fig. 11 how this correction affected the five observations in common in the Ldisc − Lcor plane. We want to stress that this test on five sources cannot be taken as conclusive, but since the change in flux is not dramatic we can exclude a huge impact of the reflection component on our results in the Ldisc − Lcor plane. A proper treatment of the reflection should be done directly via spectral fitting and even then, in SSs and SIMSs it is unclear to what extent the prominent disc emission contributes to the incident radiation, both self-illuminating the outer radii from the inner ones and with returning radiation due to general relativistic effects (see, e.g. Connors et al. 2020).
was extrapolated using the asymptotic NTHCOMP photon index computed by Sridhar et al. (2020). We show in the bottom panel of Fig. 11 how this correction affected the five observations in common in the Ldisc − Lcor plane. We want to stress that this test on five sources cannot be taken as conclusive, but since the change in flux is not dramatic we can exclude a huge impact of the reflection component on our results in the Ldisc − Lcor plane. A proper treatment of the reflection should be done directly via spectral fitting and even then, in SSs and SIMSs it is unclear to what extent the prominent disc emission contributes to the incident radiation, both self-illuminating the outer radii from the inner ones and with returning radiation due to general relativistic effects (see, e.g. Connors et al. 2020).
 |
Fig. 11. Top panel: comparison between our fit Γ (black circles) and the values obtained by Sridhar et al. (2020) for the five observations in common (squares, colour coded by the reflection strength as defined by Sridhar et al. 2020). The grey points with red contours refer to our whole sample. Bottom panel: similar comparison in the Ldisc − Lcor plane where we highlight the difference between our original Fcor, 3 − 25 keV (black circles) and the reflection-corrected |
6.3.4. Possible physical reasons for the different Γ distributions
In the previous sections we investigated some possible reasons for which the observed Γ distribution of the AGN and XRB samples might have been biased narrow or broad, respectively. Nonetheless, none of those reasons alone seems to play a major role and even a conspired combination of all is unlikely to explain all the differences. Thus, we can assume that the observed Γ distributions appear different for AGNs and XRBs in their radiatively efficient phase and at least some or most of the differences is likely intrinsic to the physical mechanisms of the hard component emission. The observed differences in Γ could be due to different emission mechanisms responsible for the coronal emission in the two source classes. However, and in line with almost all past observational evidence, throughout this discussion we assume that the Γ distributions arise from hot electrons (thermally and/or non-thermally distributed; Coppi 1999; Gilfanov 2010) Compton (up)scattering the seed photons emitted by the thermal disc.
In this framework, the observational evidence we present here is that XRBs produce a preferentially softer emission than AGNs. Results from MONK, a general relativistic Monte Carlo code of Comptonised spectra in the Kerr space-time (Zhang et al. 2019), indicate the opposite, namely that X-ray spectra in XRBs would appear harder if, apart from the different mass and seed photons temperature, the two source classes share the same geometry and extent of the corona, spin, inclination, and accretion rate in Eddington units (W. Zhang, priv. comm.). Regarding the inclination, the unobscured AGN sample used here is likely composed of a mixture of objects below ≈30° −40°, and although the inclination in GX 339−4 is still debated, even a large difference would have a small impact on the X-ray slope above ∼2 keV (Zhang et al. 2019). Regarding the accretion rate, we note that in Sect. 5 we test an AGN subsample (labelled “c2”) with accretion rate values compatible with the XRB distribution, for which Γ values were found to be consistent with the ones of the parent AGN sample, thus harder than in XRBs. Moreover, for both AGNs and XRBs, ṁ should not be considered a solid estimate and we cannot exclude that the two distributions are compatible within the very large uncertainties (see Sect. 6.2).
The spin is another largely unconstrained and still lively debated quantity for both AGNs and XRBs (e.g. for GX 339−4, Kolehmainen & Done 2010; Parker et al. 2016; Ludlam et al. 2015; García et al. 2015), although flux-limited AGN samples are likely biased in being preferentially populated by high spin sources from several different lines of reasoning (Brenneman et al. 2011; Vasudevan et al. 2016; Baronchelli et al. 2018; Reynolds 2019), including modelling the Ldisc − Lcor itself (Arcodia et al. 2019). Moreover, the effect of the spin on the corona luminosity is likely degenerate with its geometry and extent and a thorough treatment of these unknowns is beyond the scope of this paper. However, we tried to qualitatively discuss their effect on our results. Using a simplified but physically motivated model which couples the disc and corona energetically (Arcodia et al. 2019)10, we were able to infer that for a given accretion rate11 the mass-normalised corona luminosity increases with the spin (i.e. a factor ≈2 between 2 and 10 keV from a* = 0 to 0.998). Further, the corona luminosity also appears to increase with the radial (Zhang et al. 2019) and vertical extent of the corona (Kara et al. 2019; Alston et al. 2020). Therefore, it is remarkable that we observed a compatible normalisation in the Ldisc − Lcor plane for the AGN population and GX 339−4 (see right panels of Fig. 9). This might suggest that the spin distributions and/or the extent of the X-ray coronae, both in mass-normalised units, are not too far apart; or that obtaining a compatible normalization in the Ldisc − Lcor plane is just a combination of these multiple unknowns (i.e. one of the two source classes has lower spin but a wider corona or vice versa).
Finally, in case all the above quantities were found to be broadly compatible between the AGNs and XRBs, a remaining possibility is that the Γ distributions are different because the typical values for temperature and/or optical depth are not the same. As a matter of fact, the Comptonisation slope depends on both (e.g. Pozdnyakov et al. 1983), and neither can be constrained in this work because we are not able to constrain the high-energy cut-off with RXTE-PCA (see footnote 6), which is in general the case for SSs (e.g. Grove et al. 1998; Gierliński et al. 1999; Motta et al. 2009). Alternatively, the energy distribution of the hot scattering electrons might not be the same in the two source classes. However, in both radiatively efficient AGNs and XRBs we have a photon-rich environment and we are (relatively) far from the tails of the emitted spectrum, and therefore the underlying electron distribution is not necessarily a major concern (Coppi 1999).
Hence, despite the different environmental conditions (a single star versus a galactic centre) and characteristics of the matter reservoir (different density, temperature, ionisation, and pressure support), the phenomenology of the disc–corona energetic emission in radiatively efficient AGNs and XRBs seems indeed very similar (see Fig. 9). However, what might not be entirely understood is whether the physics of the disc–corona emission is also the same. Based on all the arguments in the discussion presented here, our results are consistent with disc–corona systems in AGNs and XRBs that undergo the same physical processes under different conditions (e.g. temperature, optical depth, and electron distribution in the corona, spin regime, and/or heating-cooling balance) and/or geometry (radial and vertical extent of the corona). However, our results are also consistent with a scenario in which the physical processes are not the same and the mass-normalised disc–corona energetics are comparable by chance, although we consider this less favourable and to be in contention with decades of past results (e.g. Merloni et al. 2003; Maccarone et al. 2003; Falcke et al. 2004; Uttley & McHardy 2005; McHardy et al. 2006; Körding et al. 2006; Sobolewska et al. 2009, 2011; Svoboda et al. 2017; Ruan et al. 2019a, and references therein).
6.3.5. Similarities between AGNs and XRBs despite the differences
In the previous section we outlined that, contrary to the observed difference in ṁ for which we cannot securely claim that the intrinsic distributions are actually compatible, Γ values seem to be intrinsically different for (radiatively efficient and not jet-dominated) AGNs and XRBs. However, we showed in Sect. 5 that when the two Γ distributions are taken with the same width, independently of where the peak lies, both AGNs and XRBs show a similar scatter of ∼0.30 − 0.33 dex in the log Ldisc − log Lcor plane. Thus, as far as the disc–corona relation is concerned, it seems to be more important how similarly diverse (i.e. σΓ) X-ray coronae are rather than how different the typical one (i.e. ⟨Γ⟩) is between the two source classes. Moreover, another similarity is that in XRBs there is a clear dependence of log Lcor from Γ (see Figs. 4 and 7) in a softer-when-brighter pattern (where both softer and brighter refer to log Lcor alone in this context; see Fig. 8). This trend is absent in our sample of BLAGNs (see also Beckmann et al. 2009; Corral et al. 2011; de Rosa et al. 2012) or is hidden among the various mass, distance, and inclination effects, although steeper Γ values for brighter sources have often been noticed in AGN samples (Sobolewska & Papadakis 2009; Mateos et al. 2010; Gibson & Brandt 2012; Serafinelli et al. 2017; Zappacosta et al. 2018), provided they lie in the radiatively efficient regime (Gu & Cao 2009; Connolly et al. 2016; Peretz & Behar 2018).
Assuming there is indeed not only a phenomenological but also a physical connection between radiatively efficient (not jet-dominated) AGNs and XRBs, we can exploit the high-cadence monitoring on single XRBs to obtain a less-biased and more comprehensive analysis of the possible co-evolution of the disc–corona spectral components. However, our results then imply that the physical scatter of the log Ldisc − log Lcor cannot be ⪅0.19 − 0.20 dex (Lusso & Risaliti 2016; Chiaraluce et al. 2018). Indeed, this estimate might be contaminated by the adopted Γ distribution, which is likely biased narrow in flux-limited AGN samples. A common procedure in AGN samples is indeed to cut the extreme Γ values as a selection criterion for more robust sources. Alternatively, a standard photon index of ∼1.8 − 1.9 is typically attributed to faint spectra that do not allow its constraint, with the obvious consequence of an artificial narrowing of the observed Γ distribution. Including all these extreme Γ values would result in a larger scatter of the log Ldisc − log Lcor and possibly an increased fraction of X-ray weak sources (e.g. Nardini et al. 2019). Hence, assuming a priori that extreme Γ values come from unreliable spectral fits, and then looking for physical correlations involving that parameter itself, is circular and might be misleading. Here, we simply selected spectra above a ratio of ∼1.3 between source-plus-background and background-only 10 − 25 keV count rates (see Sect. 4 and Appendix A). This approach was purely observational and resulted in a slight narrowing in the Γ distribution (see colour-coding in Fig. 7) only as a secondary consequence. This being said, we want to highlight that increasing the observed scatter of the log Ldisc − log Lcor relation in AGNs was shown with detailed simulations to imprint a minor effect on the cosmology, only slightly enlarging the uncertainty in the slope and, consequently, on the cosmological contours (D. Coffey, PhD Thesis and priv. comm.).
Finally, still working under the assumption that a unified prescription of radiatively efficient XRBs and AGNs is present, it is of interest to find out what the AGN counterparts of the excluded background-contaminated XRB states (i.e. with a very weak, hard component) would look like. Some AGN counterparts could be the optically bright X-ray weak quasars found at z ∼ 3.0 − 3.3 by Nardini et al. (2019; see also Martocchia et al. 2017) showing unusually flat slopes, which would be in accordance with the softer-when-brighter trend we discussed above. This could be indeed an interesting science case for the now launched extended ROentgen Survey with an Imaging Telescope Array (eROSITA; Predehl et al., in prep.).
7. Conclusions
Throughout the last two decades, several attempts have been made to connect accretion in AGNs and XRBs in a BH mass scale-invariant fashion (e.g. Merloni et al. 2003; Maccarone et al. 2003; Falcke et al. 2004; Uttley & McHardy 2005; McHardy et al. 2006; Körding et al. 2006; Sobolewska et al. 2009, 2011; Svoboda et al. 2017; Ruan et al. 2019a, and references therein). Besides the more or less understood differences in the composition of their matter reservoir (i.e. density, temperature, ionisation, and consequently pressure support) and their environmental surroundings (a single star with respect to the centre of a galaxy) their timing and spectral phenomenology have always been found to be comparable. The simplistic but commonly accepted picture that has emerged from decades of multi-wavelength efforts connects strong radio-emitting low-luminosity AGNs to hard-state XRBs, both showing a prominent jet component and a radiatively inefficient accretion flow (e.g. Merloni et al. 2003; Falcke et al. 2004), strong radio-emitting high-luminosity AGNs to hard-intermediate states in XRBs, both showing an efficient accretion flow in coexistence with a jet (e.g. Körding et al. 2006; Svoboda et al. 2017), and (very) weak radio-emitting moderately- to highly accreting AGNs (both combined spanning λedd = L/Ledd ≃ 0.0x − 1) to XRBs in the soft states and soft-intermediate states (e.g. Maccarone et al. 2003; Körding et al. 2006; Sobolewska et al. 2009).
Here, we attempt to improve on this AGN–XRB connection in the radiatively efficient (and non- or weakly jetted) end of accretion mode. Motivated by the tight relationship observed between the disc and coronal luminosities in AGNs (e.g. Lusso & Risaliti 2016, and references therein), we analysed 458 RXTE-PCA archival observations of the XRB GX 339–4, using this object as a test case for XRB properties in general (Sect. 2). We focused on soft and soft-intermediate states, which have been suggested to be analogous to radiatively efficient (and non- or weakly jetted) AGNs (e.g. Maccarone 2003; Körding et al. 2006; Sobolewska et al. 2009), modelling the emission with a thermal accretion disc and a Comptonising corona (Sect. 3). We then populated the log Ldisc − log Lcor plane with a quantitative focus on the physics hidden in the scatter, which represents the diversity of X-ray corona emission given a narrow range in accretion discs (Sect. 4).
The observed scatter in the log Ldisc − log Lcor plane of XRBs is high (∼0.43 dex) and significantly larger than in our control sample of radiatively efficient (non- or weakly jetted) broad-line AGNs (∼0.30 dex). This would appear contrary to the hypothesis that the systems simply scale with mass. However, we also find that our AGN and XRB samples appear to have very different observed ṁ and Γ distributions. In particular, while we are not able to exclude that the intrinsic ṁ distributions are compatible, Γ is arguably a more robust estimate and appears to be directly linked to the observed scatter (Fig. 7). Even after accounting for the measured uncertainties, the XRB Γ distribution was estimated to be broader (dispersion of ∼0.16 with respect to ∼0.08) and shifted to softer slopes (mean value of ∼2.20 with respect to ∼2.07).
It is nonetheless remarkable that once similarly broad Γ and ṁ distributions were selected (i.e. compatible σΓ and σṁ, regardless of ⟨Γ⟩ and ⟨ṁ⟩), AGNs and XRBs overlapped quite nicely in the mass-normalised log Ldisc − log Lcor plane, both showing an observed scatter of ∼0.30 − 0.33 dex (Sect. 5). This indicates that a mass-scaling between the properties of the two might indeed hold, with our results being consistent with the disc–corona systems in AGNs and XRBs exhibiting the same physical processes, albeit under different conditions, for instance in terms of temperature, optical depth, electron energy distribution in the corona, heating–cooling balance, coronal geometry, and/or black hole spin (see Sect. 6.3).
The amplitude of this common scatter (∼0.30 − 0.33 dex) is still significantly higher than ⪅0.19 − 0.20 dex, which is what was claimed to be the physical intrinsic (i.e. not due to variability and non-simultaneity) scatter in the LX − LUV (or αOX − LUV) relation in AGNs (e.g. Vagnetti et al. 2013; Lusso & Risaliti 2016; Chiaraluce et al. 2018). On the other hand, it is worth stressing that when a single XRB is used, as in our case, any possible issue arising from non-simultaneity of the data probing the two components is avoided and there is no additional scatter coming from a mixed bag of masses, distances, and inclinations, which is instead typical of AGNs. Hence, under the assumption of a mass-scaling paradigm, one would expect the scatter in XRBs to be lower. We conclude that, as the results of the past few decades and in this work suggest, since the two systems are similar, both in their phenomenology and physical processes, the physical scatter of the disc-corona emission in AGNs is likely not as low as we think, with important implications for both accretion physics and quasar cosmology.
See Hao et al. (2014) for a few definitions of radio loudness, usually defined as a flux or luminosity ratio between the radio with respect to another band.
Motta et al. (2009) performed the timing analysis up to MJD = 54208. We included all observations up to MJD = 54230 with a cut in HR corresponding to the value at the start of the SIMS as reported by Motta et al. (2009).
The model compps (Poutanen & Svensson 1996) is reported to be more accurate for Comptonisation (e.g. see comparison figures in Niedźwiecki et al. 2019), although the major problems of NTHCOMP lie in the estimate of the high-energy cutoff. First, our analysis is restricted in the 3 − 25 keV band; moreover, we leave the cutoff energy parameter free to vary and we are not interested in using the (likely unconstrained) fit values. We are confident that the impact on our analysis would be minor and we use NTHCOMP for its simplicity.
In a few rare cases we observed a bimodality in some of the Photon Index posterior distributions, or a posterior pegged at one of the extremes (Γ = 1 − 4). For those, a broad Gaussian prior centered at the peak of the observed distribution with a sigma of 0.3 − 0.5 was adopted. This avoids unphysical posterior distributions without strongly affecting the spectral fit, the prior being very broad.
Selected cross-matching the XMM-XXL sample with the FIRST survey (Becker et al. 1995) using both RX and Ruv, as defined in Hao et al. (2014), as radio-loudness parameter.
Code available here: https://github.com/rarcodia/DiskCoronasim
Both results refer to a SS02 subsample of 105 states above the threshold of ∼1.3 of counts ratio between source plus background and background only; see Appendix A.
Acknowledgments
We thank the referee for his/her helpful comments. RA warmly thanks the organizers and participants of the workshop “AGN Spectral States – Unification of Black Holes across the Mass Scale” held in Prague between 27th and 29th of November 2019 for stimulating discussions and conversations. RA is particularly grateful to Wenda Zhang for kindly sharing MONK calculations. We acknowledge the work done by Mickael Coriat in the data processing and we thank Robert Dunn for sharing results from Dunn et al. (2010). We thank Marat Gilfanov, Mara Salvato and Damien Coffey for useful discussions, and Efrain Gatuzz for a careful read of the manuscript. RA also thanks Johannes Buchner and J. Michael Burgess for insightful comments on the statistical side of the analysis and hopes he did not misuse tools and/or terms. We acknowledge the use of the matplotlib package (Hunter 2007).
References
- Abe, Y., Fukazawa, Y., Kubota, A., Kasama, D., & Makishima, K. 2005, PASJ, 57, 629 [NASA ADS] [Google Scholar]
- Ai, Y. L., Yuan, W., Zhou, H. Y., Wang, T. G., & Zhang, S. H. 2011, ApJ, 727, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Ai, Y., Dou, L., Yang, C., et al. 2020, ApJ, 890, L29 [CrossRef] [Google Scholar]
- Alston, W. N., Fabian, A. C., Kara, E., et al. 2020, Nat. Astron., 4, 597 [CrossRef] [Google Scholar]
- Ananna, T. T., Treister, E., Urry, C. M., et al. 2020, ApJ, 889, 17 [CrossRef] [Google Scholar]
- Aneesha, U., Mandal, S., & Sreehari, H. 2019, MNRAS, 486, 2705 [NASA ADS] [CrossRef] [Google Scholar]
- Arcodia, R., Campana, S., Salvaterra, R., & Ghisellini, G. 2018, A&A, 616, A170 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcodia, R., Merloni, A., Nandra, K., & Ponti, G. 2019, A&A, 628, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Baronchelli, L., Nandra, K., & Buchner, J. 2018, MNRAS, 480, 2377 [NASA ADS] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Beckmann, V., Soldi, S., Ricci, C., et al. 2009, A&A, 505, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, T. M., & Motta, S. E. 2016, in Transient Black Hole Binaries, ed. C. Bambi, Astrophys. Space Sci. Lib., 440, 61 [Google Scholar]
- Belloni, T., Homan, J., Casella, P., et al. 2005, A&A, 440, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloni, T., Parolin, I., Del Santo, M., et al. 2006, MNRAS, 367, 1113 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R., Meier, D., & Readhead, A. 2019, ARA&A, 57, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53 [NASA ADS] [Google Scholar]
- Brenneman, L. W., Reynolds, C. S., Nowak, M. A., et al. 2011, ApJ, 736, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buxton, M. M., Bailyn, C. D., Capelo, H. L., et al. 2012, AJ, 143, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero-García, M. D., Miller, J. M., Trigo, M. D., et al. 2009, ApJ, 692, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- Caccianiga, A., Severgnini, P., Braito, V., et al. 2004, A&A, 416, 901 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cadolle Bel, M., Rodriguez, J., D’Avanzo, P., et al. 2011, A&A, 534, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calderone, G., Ghisellini, G., Colpi, M., & Dotti, M. 2013, MNRAS, 431, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Casares, J., Jonker, P. G., & Israelian, G. 2017, X-ray Binaries (Berlin: Springer), 1499 [Google Scholar]
- Chiaraluce, E., Vagnetti, F., Tombesi, F., & Paolillo, M. 2018, A&A, 619, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Connolly, S. D., McHardy, I. M., Skipper, C. J., & Emmanoulopoulos, D. 2016, MNRAS, 459, 3963 [NASA ADS] [CrossRef] [Google Scholar]
- Connors, R. M. T., Garcia, J. A., Dauser, T., et al. 2020, ApJ, 892, 47 [CrossRef] [Google Scholar]
- Coppi, P. S. 1999, in The Physics of Hybrid Thermal/Non-Thermal Plasmas, eds. J. Poutanen, & R. Svensson, ASP Conf. Ser., 161, 375 [Google Scholar]
- Corbel, S., Tomsick, J. A., & Kaaret, P. 2006, ApJ, 636, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Corbel, S., Coriat, M., Brocksopp, C., et al. 2013, MNRAS, 428, 2500 [NASA ADS] [CrossRef] [Google Scholar]
- Coriat, M., Corbel, S., Buxton, M. M., et al. 2009, MNRAS, 400, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Corral, A., Della Ceca, R., Caccianiga, A., et al. 2011, A&A, 530, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Agostini, G. 2005, ArXiv e-prints [arXiv:physics/0511182] [Google Scholar]
- Davis, S. W., & Hubeny, I. 2006, ApJS, 164, 530 [NASA ADS] [CrossRef] [Google Scholar]
- de Rosa, A., Panessa, F., Bassani, L., et al. 2012, MNRAS, 420, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Debnath, D., Chakrabarti, S. K., & Nandi, A. 2010, A&A, 520, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dinçer, T., Kalemci, E., Buxton, M. M., et al. 2012, ApJ, 753, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Doe, S., Nguyen, D., Stawarz, C., et al. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 543 [Google Scholar]
- Done, C., & Davis, S. W. 2008, ApJ, 683, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. J. H., Fender, R. P., Körding, E. G., Cabanac, C., & Belloni, T. 2008, MNRAS, 387, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, R. J. H., Fender, R. P., Körding, E. G., Belloni, T., & Cabanac, C. 2010, MNRAS, 403, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Falcke, H., Körding, E., & Markoff, S. 2004, A&A, 414, 895 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fender, R. P. 2001, MNRAS, 322, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Fender, R. P., Belloni, T. M., & Gallo, E. 2004, MNRAS, 355, 1105 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [CrossRef] [Google Scholar]
- Freeman, P., Doe, S., & Siemiginowska, A. 2001, in Astronomical Data Analysis, eds. J. L. Starck, & F. D. Murtagh, Proc. SPIE, 4477, 76 [Google Scholar]
- Galeev, A. A., Rosner, R., & Vaiana, G. S. 1979, ApJ, 229, 318 [NASA ADS] [CrossRef] [Google Scholar]
- García, J. A., Steiner, J. F., McClintock, J. E., et al. 2015, ApJ, 813, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, R. R., & Brandt, W. N. 2012, ApJ, 746, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Gierliński, M., Middleton, M., Ward, M., & Done, C. 2008, Nature, 455, 369 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gilfanov, M. 2010, in X-Ray Emission from Black-Hole Binaries, ed. T. Belloni, 794, 17 [Google Scholar]
- Gilli, R., Comastri, A., & Hasinger, G. 2007, A&A, 463, 79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grove, J. E., Johnson, W. N., Kroeger, R. A., et al. 1998, ApJ, 500, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Grupe, D., Komossa, S., Leighly, K. M., & Page, K. L. 2010, ApJS, 187, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Gu, M., & Cao, X. 2009, MNRAS, 399, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Hao, H., Sargent, M. T., Elvis, M., et al. 2014, ArXiv e-prints [arXiv:1408.1090] [Google Scholar]
- Heida, M., Jonker, P. G., Torres, M. A. P., & Chiavassa, A. 2017, ApJ, 846, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Heinz, S., & Sunyaev, R. A. 2003, MNRAS, 343, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Hjalmarsdotter, L., Axelsson, M., & Done, C. 2016, MNRAS, 456, 4354 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C. 2002, ApJ, 564, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Buxton, M., Markoff, S., et al. 2005, ApJ, 624, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Homan, J., Fridriksson, J. K., Jonker, P. G., et al. 2013, ApJ, 775, 9 [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hynes, R. I., Steeghs, D., Casares, J., Charles, P. A., & O’Brien, K. 2003, ApJ, 583, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Hynes, R. I., Steeghs, D., Casares, J., Charles, P. A., & O’Brien, K. 2004, ApJ, 609, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Jahoda, K., Swank, J. H., Giles, A. B., et al. 1996, in EUV, X-ray, and Gamma-ray Instrumentation for Astronomy VII, eds. O. H. W. Siegmund, & M. A. Gummin (SPIE), Int. Soc. Opt. Photon., 2808, 59 [Google Scholar]
- Kalemci, E., Dinçer, T., Tomsick, J. A., et al. 2013, ApJ, 779, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kara, E., Steiner, J. F., Fabian, A. C., et al. 2019, Nature, 565, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Kawano, T., Done, C., Yamada, S., et al. 2017, PASJ, 69, 36 [CrossRef] [Google Scholar]
- Khadka, N., & Ratra, B. 2020, MNRAS, 492, 4456 [CrossRef] [Google Scholar]
- Klindt, L., Alexander, D. M., Rosario, D. J., Lusso, E., & Fotopoulou, S. 2019, MNRAS, 488, 3109 [CrossRef] [Google Scholar]
- Kolehmainen, M., & Done, C. 2010, MNRAS, 406, 2206 [NASA ADS] [CrossRef] [Google Scholar]
- Körding, E. G., Jester, S., & Fender, R. 2006, MNRAS, 372, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., & Done, C. 2004, MNRAS, 353, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., & Done, C. 2016, MNRAS, 458, 4238 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., & Done, C. 2018, MNRAS, 480, 1247 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., & Makishima, K. 2004, ApJ, 601, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Kubota, A., Tanaka, Y., Makishima, K., et al. 1998, PASP, 50, 667 [Google Scholar]
- Kubota, A., Makishima, K., & Ebisawa, K. 2001, ApJ, 560, L147 [NASA ADS] [CrossRef] [Google Scholar]
- LaMassa, S. M., Cales, S., Moran, E. C., et al. 2015, ApJ, 800, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A. 1991, ApJ, 376, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z., Merloni, A., Georgakakis, A., et al. 2016, MNRAS, 459, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, T., Merloni, A., Wang, J.-X., et al. 2018, MNRAS, 479, 5022 [NASA ADS] [CrossRef] [Google Scholar]
- Loredo, T. J. 1992, Stat. Chall. Mod. Astron., 275 [CrossRef] [Google Scholar]
- Ludlam, R. M., Miller, J. M., & Cackett, E. M. 2015, ApJ, 806, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E. 2019, Astron. Nachr., 340, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2016, ApJ, 819, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., & Risaliti, G. 2017, A&A, 602, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lusso, E., Piedipalumbo, E., Risaliti, G., et al. 2019, A&A, 628, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maccarone, T. J. 2003, A&A, 409, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maccacaro, T., Gioia, I. M., Wolter, A., Zamorani, G., & Stocke, J. T. 1988, ApJ, 326, 680 [NASA ADS] [CrossRef] [Google Scholar]
- Maccarone, T. J., Gallo, E., & Fender, R. 2003, MNRAS, 345, L19 [NASA ADS] [CrossRef] [Google Scholar]
- MacLeod, C. L., Ross, N. P., Lawrence, A., et al. 2016, MNRAS, 457, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Marchesini, D., Celotti, A., & Ferrarese, L. 2004, MNRAS, 351, 733 [CrossRef] [Google Scholar]
- Marecki, A., & Swoboda, B. 2011, A&A, 525, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markert, T. H., Canizares, C. R., Clark, G. W., et al. 1973, ApJ, 184, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Markoff, S., Nowak, M., Corbel, S., Fender, R., & Falcke, H. 2003, A&A, 397, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martocchia, S., Piconcelli, E., Zappacosta, L., et al. 2017, A&A, 608, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateos, S., Carrera, F. J., Page, M. J., et al. 2010, A&A, 510, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McHardy, I. M., Papadakis, I. E., Uttley, P., Page, M. J., & Mason, K. O. 2004, MNRAS, 348, 783 [NASA ADS] [CrossRef] [Google Scholar]
- McHardy, I. M., Koerding, E., Knigge, C., Uttley, P., & Fender, R. P. 2006, Nature, 444, 730 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Melia, F. 2019, MNRAS, 489, 517 [CrossRef] [Google Scholar]
- Menzel, M.-L., Merloni, A., Georgakakis, A., et al. 2016, MNRAS, 457, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Heinz, S., & di Matteo, T. 2003, MNRAS, 345, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Merloni, A., Bongiorno, A., Brusa, M., et al. 2014, MNRAS, 437, 3550 [NASA ADS] [CrossRef] [Google Scholar]
- Mitsuda, K., Inoue, H., Koyama, K., et al. 1984, PASJ, 36, 741 [NASA ADS] [Google Scholar]
- Motta, S., Belloni, T., & Homan, J. 2009, MNRAS, 400, 1603 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Darias, T., Casares, J., & Martínez-Pais, I. G. 2008, MNRAS, 385, 2205 [NASA ADS] [CrossRef] [Google Scholar]
- Nandi, A., Debnath, D., Mandal, S., & Chakrabarti, S. K. 2012, A&A, 542, A56 [CrossRef] [EDP Sciences] [Google Scholar]
- Nanni, R., Vignali, C., Gilli, R., Moretti, A., & Brandt, W. N. 2017, A&A, 603, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayan, R., & Yi, I. 1994, ApJ, 428, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Nardini, E., Lusso, E., Risaliti, G., et al. 2019, A&A, 632, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niedźwiecki, A., Szanecki, M., & Zdziarski, A. A. 2019, MNRAS, 485, 2942 [NASA ADS] [CrossRef] [Google Scholar]
- Noda, H., & Done, C. 2018, MNRAS, 480, 3898 [NASA ADS] [CrossRef] [Google Scholar]
- Oda, S., Shidatsu, M., Nakahira, S., et al. 2019, PASJ, 71, 108 [CrossRef] [Google Scholar]
- Padovani, P., Alexander, D. M., Assef, R. J., et al. 2017, A&ARv, 25, 2 [Google Scholar]
- Parker, M. L., Tomsick, J. A., Kennea, J. A., et al. 2016, ApJ, 821, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Peretz, U., & Behar, E. 2018, MNRAS, 481, 3563 [NASA ADS] [CrossRef] [Google Scholar]
- Piconcelli, E., Jimenez-Bailón, E., Guainazzi, M., et al. 2005, A&A, 432, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plant, D. S., Fender, R. P., Ponti, G., Muñoz-Darias, T., & Coriat, M. 2014, MNRAS, 442, 1767 [NASA ADS] [CrossRef] [Google Scholar]
- Plotkin, R. M., Gallo, E., & Jonker, P. G. 2013, ApJ, 773, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Plotkin, R. M., Miller-Jones, J. C. A., Gallo, E., et al. 2017, ApJ, 834, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Pounds, K. A., Done, C., & Osborne, J. P. 1995, MNRAS, 277, L5 [NASA ADS] [Google Scholar]
- Poutanen, J., & Svensson, R. 1996, ApJ, 470, 249 [NASA ADS] [CrossRef] [Google Scholar]
- Pozdnyakov, L. A., Sobol, I. M., & Syunyaev, R. A. 1983, Astrophys. Space Phys. Res., 2, 189 [Google Scholar]
- Pringle, J. E. 1981, ARA&A, 19, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & McClintock, J. E. 2006, ARA&A, 44, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Reynolds, C. S. 2019, Nat. Astron., 3, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ricci, C., Trakhtenbrot, B., Koss, M. J., et al. 2017, ApJS, 233, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2015, ApJ, 815, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Lusso, E. 2019, Nat. Astron., 3, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Rothschild, R. E., Blanco, P. R., Gruber, D. E., et al. 1998, ApJ, 496, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, J. J., Anderson, S. F., Eracleous, M., et al. 2019a, ApJ, 883, 76 [CrossRef] [Google Scholar]
- Ruan, J. J., Anderson, S. F., Eracleous, M., et al. 2019b, ApJ, submitted [arXiv:1909.04676] [Google Scholar]
- Ruffini, R., & Wheeler, J. A. 1971, Phys. Today, 24, 30 [CrossRef] [Google Scholar]
- Russell, D. M., Maitra, D., Dunn, R. J. H., & Markoff, S. 2010, MNRAS, 405, 1759 [NASA ADS] [Google Scholar]
- Salvestrini, F., Risaliti, G., Bisogni, S., Lusso, E., & Vignali, C. 2020, A&A, 631, A120 [Google Scholar]
- Serafinelli, R., Vagnetti, F., & Middei, R. 2017, A&A, 600, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Shen, Y., Greene, J. E., Strauss, M. A., Richards, G. T., & Schneider, D. P. 2008, ApJ, 680, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., & Lasota, J.-P. 2007, ApJ, 658, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., & Papadakis, I. E. 2009, MNRAS, 399, 1597 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., Gierliński, M., & Siemiginowska, A. 2009, MNRAS, 394, 1640 [NASA ADS] [CrossRef] [Google Scholar]
- Sobolewska, M. A., Siemiginowska, A., & Gierliński, M. 2011, MNRAS, 413, 2259 [NASA ADS] [CrossRef] [Google Scholar]
- Sridhar, N., García, J. A., Steiner, J. F., et al. 2020, ApJ, 890, 53 [CrossRef] [Google Scholar]
- Svensson, R., & Zdziarski, A. A. 1994, ApJ, 436, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Svoboda, J., Guainazzi, M., & Merloni, A. 2017, A&A, 603, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tananbaum, H., Avni, Y., Branduardi, G., et al. 1979, ApJ, 234, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Trakhtenbrot, B., Arcavi, I., MacLeod, C. L., et al. 2019, ApJ, 883, 94 [CrossRef] [Google Scholar]
- Uttley, P., & McHardy, I. M. 2005, MNRAS, 363, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Uttley, P., McHardy, I. M., & Papadakis, I. E. 2002, MNRAS, 332, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Vagnetti, F., Antonucci, M., & Trevese, D. 2013, A&A, 550, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vahdat Motlagh, A., Kalemci, E., & Maccarone, T. J. 2019, MNRAS, 485, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- van Dyk, D. A., Connors, A., Kashyap, V. L., & Siemiginowska, A. 2001, ApJ, 548, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Vasudevan, R. V., Fabian, A. C., Reynolds, C. S., et al. 2016, MNRAS, 458, 2012 [NASA ADS] [CrossRef] [Google Scholar]
- Velten, H., & Gomes, S. 2020, Phys. Rev. D, 101, 043502 [CrossRef] [Google Scholar]
- Vincentelli, F. M., Casella, P., Maccarone, T. J., et al. 2018, MNRAS, 477, 4524 [NASA ADS] [CrossRef] [Google Scholar]
- Vito, F., Brandt, W. N., Bauer, F. E., et al. 2019, A&A, 630, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willingale, R., Starling, R. L. C., Beardmore, A. P., Tanvir, N. R., & O’Brien, P. T. 2013, MNRAS, 431, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Q., & Gu, M. 2008, ApJ, 682, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, S., Makishima, K., Done, C., et al. 2013, PASJ, 65, 80 [CrossRef] [Google Scholar]
- Yang, T., Banerjee, A., Colgáin, E., et al. 2019, ArXiv e-prints [arXiv:1911.01681] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zappacosta, L., Comastri, A., Civano, F., et al. 2018, ApJ, 854, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Johnson, W. N., & Magdziarz, P. 1996, MNRAS, 283, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Poutanen, J., Mikolajewska, J., et al. 1998, MNRAS, 301, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Poutanen, J., & Johnson, W. N. 2000, ApJ, 542, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Gierliński, M., Mikołajewska, J., et al. 2004, MNRAS, 351, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Zdziarski, A. A., Ziółkowski, J., & Mikołajewska, J. 2019, MNRAS, 488, 1026 [CrossRef] [Google Scholar]
- Zhang, W., Dovčiak, M., & Bursa, M. 2019, ApJ, 875, 148 [CrossRef] [Google Scholar]
- Zheng, X., Liao, K., Biesiada, M., et al. 2020, ApJ, 892, 103 [CrossRef] [Google Scholar]
- Życki, P. T., Done, C., & Smith, D. A. 1999, MNRAS, 309, 561 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: The robustness of spectral analysis results
In X-ray spectral analysis, the outcome of a fit should not be blindly trusted without simulations, particularly in low-count regime or when the background is at a level compatible with (part of) the source emission. Since in our science case the putative physics of the source is such that the hard component can be comparable to the RXTE background at energies above ≈10 keV, a more thorough investigation is needed to validate our spectral fit results. One should bear in mind that this does not happen necessarily only when the total flux is low, as in spectra with a strong soft component and a weak hard component the total 3 − 25 keV emission is actually around the average value of the outburst.
Two types of problems can arise in fitting the hard component that make a specific fit of a state questionable. Firstly, one may not be able to robustly fit a specific region of the source parameter space (e.g. the intrinsic photon index or hard flux) for instrumental or observational biases, for instance due to the background or to possible covariances; the fit parameters could be scattered in another region of the parameters space, physically reasonable, and the observer would have no way of knowing this from the fit alone, which can in principle appear robust. At first order, this can be tested simulating a synthetic spectrum from the best-fit parameters and fitting it again with the same model: if the input and output agree, that region of the parameters space is recoverable; if not, that spectral fit cannot be considered robust. Secondly, even if one is able to fit a specific parameters space region, one cannot be sure that biases have scattered a source, originally with other parameters, in the location of the parameter space where one has fit it. This is more subtle and would require a set of multidimensional spectral simulations, beyond the scope of this paper.
We try to address here the first problem with spectral simulations. We simulated each XRB state from the best-fit model with the pyXSPEC command fake it adding also statistical fluctuations. Then, we fit each simulated spectrum with the same model (see Sect. 3) and checked if the retrieved parameters were compatible, within errors, with the simulated spectrum (see Figs. A.1 and A.2). Simulations clearly show that for SS02, SS04 and SS07 all the spectral fits can be considered to be in reliable places of the explored parameters space. Instead, simulations of SS10 state that results from several observations are to be taken with caution (see bottom panels of Figs. A.1 and A.2): in particular, observations with relatively low count rates above ∼10 keV, namely with a factor ⪅1.5 in ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see white and grey symbols in the top panel of Figs. 3 and A.4). In most of these background-contaminated spectral states, the input and output values are compatible within their (very large) 1st−99th interquantile range, and therefore we are not overestimating our knowledge of the hard component even in these extreme cases. Nonetheless, it is evident that the median of the posterior distribution for Γ strongly departs from the simulated value. In Fig. A.3 we show all the outbursts combined, colour coding the threshold of the ratio between total (source plus background) and background-only 10 − 25 keV count rates, highlighting with white contours the sources above ∼1.3. This threshold ensures that ⪅4% of the input-output parameters are not compatible within their 16th−84th interquantile range. This represents the sub-sample selected for the comparison with AGN in Sect. 5. It is worth noting that in these background-contaminated states the presence of a disc only indirectly hampers the detectability of the hard component, as they do not host the brightest discs (see colour coding in Fig. A.4).
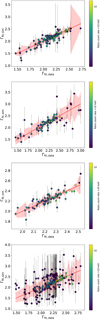 |
Fig. A.1. Comparison between the photon index obtained in the spectral fit (see Sect. 3.2; Γfit, data), which was then simulated and fit again (Γfit, simul). From top to bottom: results for SS02, SS04, SS07, and SS10 are shown. Error bars for Γfit, simul are shown (16th−84th percentiles), whereas we show uncertainties (16th−84th percentiles) in Γfit, data around the 1:1 relation. We colour coded data with the ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see white and grey symbols in the top panel of Fig. 3). |
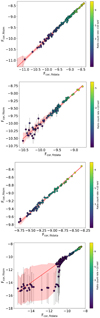 |
Fig. A.2. Same as in Fig. A.1 but with the 2 − 10 keV flux under the NTHCOMP model of the hard component. Top panel: the figure is cut around log Fcor ∼ −11 for visualisation purposes and at lower fluxes simulations and fits are compatible within their very large errors. |
 |
Fig. A.3. Same as Fig. A.1, but colour coded with the threshold on the ratio between the total (source plus background) and background-only 10 − 25 keV count rates. The one we adopted (i.e. ∼1.3) is shown with white contours on data points. |
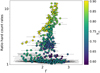 |
Fig. A.4. Ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see white and grey symbols in the top panel of Fig. 3) as a function of the fit Γ, colour coded with the fit disc temperature. |
Moreover, we show in Fig. A.4 how this count rate ratio is related to the fit Γ in our spectral analysis. As it can be noted, our cut in ratio around 1.3 also consequently narrows the Photon Index distribution, although above it one can still note the softer-when-brighter behaviour of our SSs and SIMSs. It is a typical habit to exclude extremes Γ values from AGN samples before testing for correlations and physical interpretations, with the underlying assumption that they come from low-quality spectra. This can be true in most cases, although one can see that applying a vertical selection in Fig. A.4 one could end up excluding not only the low-quality (or background-contaminated) states, but also the brightest-softest spectra and a few hard-faint (but still sufficiently-well constrained) spectra. Furthermore, excluding extremes X-ray slopes is a physical selection and applying it before looking for physical correlation and interpretations is a circular process. Conversely, a selection in count rate ratio is purely observational and for most of the sources results in an equivalent selection.
Finally, we also performed a posterior predictive check simulating 300 count rate spectra starting from the posterior distributions of the best-fit parameters. This is then visually compared with the original spectrum (examples in Fig. A.5), flagging possible energy bins in which the observed data point was not compatible within the 1st−99th interquantile range of the predicted spectra from the best-fit models. This test highlights regions of the spectrum where our model predictions of future datasets significantly depart from the observed data. In general, we observe very few of these features, meaning that the uncertainties on our model are large enough not to overestimate the information drawn from the data. In particular, this check confirmed that results for most of the SSs in SS10 can be considered reliable only within the very large uncertainties and must be taken with caution. For instance, refrain from using only median values for Γ from our SS10 results instead of considering the hard component as largely unconstrained. Alternatively, the more conservative option is to adopt the sub-sample of sources above a ratio between the total (source plus background) and background-only 10 − 25 keV count rates of ∼1.3.
 |
Fig. A.5. Two examples of the posterior predictive check performed simulating 300 count rate spectra starting from the best-fit parameters posterior distributions. Data points are the actual spectrum, with green and orange contours as 16th−84th and 1st−99th interquantile ranges representing the predictive power of the spectral model. Energy bins in which the observed data point was not compatible within the 1st−99th interquantile range of the predicted spectra from the best-fit models are shown in red. |
Appendix B: Testing different proxies for the disc and corona emission
Throughout this study, we use the 2 − 10 keV flux under the single DISKBB and NTHCOMP model as proxy for the disc and corona component, respectively. Here, we investigate whether our results change with a different proxy. For what concerns the Fdisc − Fcor in XRBs only, we tested the adoption of fluxes in the range 3 − 25 keV (the full energy range used in our spectral analysis) or a broader band: F0.001 − 100 keV, disc − F1 − 100 keV, cor (e.g. Dunn et al. 2010). As shown in Table B.1, the scatter values and slopes are compatible within errors.
Same as Table 1, but including additional columns (marked with _3−25 and _full) obtained within 3 − 25 keV and F0.001 − 100 keV, disc − F1 − 100 keV, cor, respectively.
Moreover, in Sect. 5 we changed the disc proxy using a monochromatic flux for the disc emission at 0.2 keV, which is the rough low-mass equivalent of what is 3000 Å for AGN. We then tested if in the XRBs dataset the change in disc proxy affects what is described in Sects. 3.2 and 4. As shown in Table B.2, all the scatter and most of the slope values are compatible within errors. The fact that some slopes are not validates our choice of using the scatter of the Fdisc − Fcor to test the disc-corona relation in XRBs. It also argues that uncertainties in extrapolation of the RXTE response down to 0.2 kev and in NH (which we leave free to vary within a ±15% of the tabulated value) are minimal or affect mostly the slope, if anything.
Same as Table 1, but including additional columns (marked with _0.2) obtained with F0.2 keV as a disc proxy.
Appendix C: Testing a different accretion disc model
Throughout the work, we used DISKBB as disc model for its simplicity and better coupling with the Comptonisation model NTHCOMP, with respect to more accurate disc models (e.g. BHSPEC, Davis & Hubeny 2006). DISKBB simply fits for the temperature at the inner disc radius Tin and for the normalisation, which is a function of the inner radius Rin, the distance d of the source and inclination i of the disc. Knowing Rin and its evolution is not the purpose of this work, and therefore the large uncertainties on d and i (see, e.g., Heida et al. 2017; Zdziarski et al. 2019) are not of great concern. Instead, the BHSPEC parameters are log L/LEdd, which is the luminosity of the accretion disc as a fraction of the Eddington luminosity (LEdd = 1.3 × 1038 m erg s−1), d, i, m and the spin a*. This model would in principle provide a more physical description of the accretion disc emission in terms of more useful source parameters with respect to DISKBB, although all these are very uncertain and extremely debated parameters (e.g. Hynes et al. 2003, 2004; Zdziarski et al. 2004, 2019; Muñoz-Darias et al. 2008; Kolehmainen & Done 2010; Parker et al. 2016; Ludlam et al. 2015; García et al. 2015; Heida et al. 2017). Fixing them, despite the large uncertainties, would be a much greater approximation than using DISKBB, with much less control on the many degeneracies and large dimensions involved in the problem; and the more proper approach of jointly fitting for d, i, m and a* across all the 458 states would be prohibitive.
Here, we explore the use of BHSPEC and test whether or not our data are good enough to try and directly constrain the disc parameters. We first separately fit 44 states which show a ratio between the total (source plus background) and background-only 10 − 25 keV count rates below ∼1.1, ensuring minimum contamination from non-disc components. We leave m, d, i and a* free to vary (within m = 3 − 10, d = 7 − 12 kpc, i = 5° −77° and a* = 0 − 0.9) in addition of log(L/Ledd) and the other source parameters of NTHCOMP and the Gaussian model (see Sect. 3.1). Despite the good fits, the distribution of fit BHSPEC parameters is quite diverse and unconstrained and their errors quite large. Secondly, we simultaneously fit the three states with the lowest ratio between the total (source plus background) and background-only 10 − 25 keV count rates, keeping m, d, i and a* tied together and the other source parameters free to vary. This yields a good fit with median values of m ∼ 5.8, d ∼ 7.8 kpc, i ∼ 25° and a* ∼ 0.47. However, adding one or two more states to the simultaneous fit does not reach convergence, with the sampling far from the minima found with three sources. For this reason and the fact that among the 44 states separately fit there was generally poor agreement, we refrain from using any estimate of m, d, i and a* coming from the simultaneous fit for more than just Eddington-ratio related calculations.
Now, we fit all the states in SS02 with the same configuration as in Sect. 3.1 (fixing the seed photons temperature to the value obtained with DISKBB) but with BHSPEC fixed at m ∼ 5.8, d ∼ 7.8 kpc, i ∼ 25° and a* ∼ 0.47 and free accretion rate. This allows us to estimate whether, despite the non-robust source parameters for the disc model, the impact of a different accretion disc model on our results is significant. The slope and scatter of the Fdisc − Fcor plane are 0.88 ± 0.13 and 0.34 ± 0.03 respectively, to be compared with the DISKBB run12 which yields 0.88 ± 0.17 and 0.40 ± 0.03. Both values are compatible within errors. Instead, BHSPEC yields a mean Γ ∼ 2.46 with respect to Γ ∼ 2.14 obtained with DISKBB. Hence, the Γ distribution would be even softer than in AGNs, enhancing rather than contradicting our results of Sect. 5.
Finally, we use this BHSPEC run on SS02 to compute a correction on the monochromatic Fdisc at 0.2 keV, since DISKBB is known to underestimate the very soft emission in an RXTE-like instrument, even if above ∼3 keV the two models produced the same flux (see Done & Davis 2008). DISKBB has reportedly a narrower band-pass with respect to more physical models including radiative transfer in each disc annulus, of the order of a colour correction which is however not constant in radius, and relativistic effects (e.g. Davis & Hubeny 2006). This narrower band-pass results in underestimation of soft fluxes in RXTE-like instrument or the hard-flux end of the disc emission in CCD-like instruments (see Done & Davis 2008). The offset was quantified to be a fairly narrow distribution with a median of ∼0.26 dex, for RXTE-PCA at 2 keV.
All Tables
Summary of slope and scatter of the log Fdisc − log Fcor plane computed in the 2 − 10 keV energy band across the four outbursts.
Same as Table 1, but including additional columns (marked with _3−25 and _full) obtained within 3 − 25 keV and F0.001 − 100 keV, disc − F1 − 100 keV, cor, respectively.
Same as Table 1, but including additional columns (marked with _0.2) obtained with F0.2 keV as a disc proxy.
All Figures
 |
Fig. 1. Hardness-luminosity diagram (HLD) of GX 339–4 in its four outbursts used in this analysis (i.e. 2002–2003, 2004–2005, 2006–2007 and 2010–2011). Grey circles are archival data taken from Dunn et al. (2010), over which our own data points for SS02, SS04, SS07, and SS10 are superimposed; these are colour coded following the legend in the figure. Black symbols with red contours refer to the examples in Fig. 2. |
| In the text | |
 |
Fig. 2. Three examples of source plus background spectra (black dots, error bars included), with related data–model ratios in the lower panels. The three observations were selected taking the 84th percentile, median, and 16th percentile of the total 3 − 25 keV flux distribution of the full XRB sample used in Sect. 5, shown from left to right respectively. These correspond to the three larger black symbols in Fig. 1, going downwards in the q-plot. All additive model components are shown and defined in the legend, with the total source plus background model shown in red. For each component, the solid lines represent the median of the model distribution computed from the posteriors of the fit parameters (with 16th–84th percentile coloured contours around them, in some cases smaller than the thickness of the line). |
| In the text | |
 |
Fig. 3. Evolution of the 3 − 25 keV count rate, of the fit photon index and disc temperature, and of the disc fraction DF (see Eq. (1)) is shown along the four different outbursts (same colour coding and symbols as in Fig. 1). Top panels: filled coloured symbols represent the total (source plus background) 3 − 25 keV count rates, the coloured empty symbols the total count rates in the 10 − 25 keV band, and the grey symbols the background count rates in the 10 − 25 keV band. Middle-top panel: a black dashed line at Γ = 2 is shown to guide the eye, whereas the red dot-dashed line highlights the median Γ = 2.20 of the whole XRB sample used in Sect. 5. |
| In the text | |
 |
Fig. 4. Fdisc − Fcor plane for SS02, SS04, SS07, and SS10 (from top to bottom), with fluxes scaled with their median value. As uncertainties, we report 3σ contours of the 2D distribution of fluxes from the posterior chains, shown with ellipsoids. The solid black line is the median regression line obtained with emcee, with the corresponding 16th and 84th percentiles represented with the shaded grey area. The dashed black lines show the fit scatter around the median relation. |
| In the text | |
 |
Fig. 5. Top panel: scatter of the Fdisc − Fcor relation as a function of a cut in the ratio between the total (source plus background) and background-only 10 − 25 keV count rates. Coloured points are relative to the full sample and coded with the 16th–84th interquantile range in the related Γ distributions, whereas grey points are obtained excluding SS10. Stars correspond to the starting sample with no filters. Bottom panel: scatter as a function of a cut in the fraction of time spent by GX 339–4 in a region of the outburst, including SSs and SIMSs only (see Sect. 4.2 for a detailed description). Colour coding and symbols are the same as in the top panel. |
| In the text | |
 |
Fig. 6. Hardness-intensity diagram of the four outbursts, colour coded from white to black, with MJD values, superimposed to a smoothed map showing the fraction of time spent in each region, including only SSs and SIMSs. |
| In the text | |
 |
Fig. 7. Fdisc − Fcor plane as described in Fig. 4, but shown here for all outbursts combined (top panel) and for the subset used for the comparison with AGNs (bottom panel), as described and motivated in Sect. 4.2. Bottom panel: points with a red contour highlight three states taken as examples for Fig. 8. |
| In the text | |
 |
Fig. 8. Examples of observed spectra with best-fit models (left, including background, shown with a grey-dashed line) and modelled spectral energy distributions (right, without background) of three states, selected taking the 10th, 50th, and 90th percentile of log Fcor in a narrow range of Fdisc (namely around a ±0.05 dex of the median log Fdisc). Both data and models are colour-coded with the fit Γ, highlighting a softer-when-brighter trend in log Fcor. These three states are represented by red-contour data points in the bottom panel of Fig. 7. |
| In the text | |
 |
Fig. 9. Left panels: Γ, ṁ and DF histograms of the full AGN and XRB samples (blue and red-dashed lines) with additional subsamples: “AGNc” (light blue) is obtained reshaping the original ṁ distribution to be as narrow as the one in XRBs (using its 16th and 84th percentiles), albeit keeping the same median as in the full “AGN” sample; the same reasoning is applied with the Γ distributions to select “XRBc” (orange) from “XRB”; instead, “AGNc2” (dark azure) is obtained by selecting sources with ṁ compatible within 0.4 dex with the 5th–95th interquantile of “XRB”, whereas “XRBc2” (dark orange) follows the same reasoning, selecting Γ compatible within errors with the “AGN” Γ distribution. The vertical dashed lines in the middle-left panel represent the location of the 1st and 99th percentile of multiple XRB ṁ distributions, obtained by converting the fit Tin spanning a* = 0 − 0.98 and m = 5 − 10, while we highlight with a red-dashed histogram the one obtained with a* = 0.5 and m = 5.8 (see text). Right panels: mass-normalised log Ldisc − log Lcor plane for the full AGN and XRB samples (top) and the above-mentioned “c” (middle) and “c2” (bottom) subsamples. In the latter case, the uncertainty in determining ṁ for XRBs (vertical dashed lines in the middle-left panel) reverberated in the dark-azure points spreading in the log Ldisc − log Lcor plane, covering the same dynamic range of the full AGN sample. The computed observed scatter of each relation is shown on the side, with the same colour coding as the data: 0.30 ± 0.01 dex and 0.43 ± 0.02 dex for the full samples of AGNs and XRBs, respectively; 0.30 ± 0.01 and 0.33 ± 0.02 in the respective “c” subsamples, 0.31 ± 0.01 and 0.36 ± 0.02 for the “c2”. |
| In the text | |
 |
Fig. 10. Top panel: same as the top-right panel of Fig. 9, with only the SSs and SIMSs of the 2002−2003 outburst (dark red circles, with SIMS highlighted by a thicker black contour) and its HIMSs (grey squares). Lines of approximately constant DF are shown with dashed lines, and the related values are shown in the figure. Bottom panel: same as the bottom left panel of Fig. 9, but with again the SS-SIMS (dark red dashed, with SIMS only highlighted by the dot-dashed line) and HIMS (grey) of the 2002−2003 outburst, plus the 44 radio-loud AGNs excluded from our AGN sample (black dotted line). |
| In the text | |
 |
Fig. 11. Top panel: comparison between our fit Γ (black circles) and the values obtained by Sridhar et al. (2020) for the five observations in common (squares, colour coded by the reflection strength as defined by Sridhar et al. 2020). The grey points with red contours refer to our whole sample. Bottom panel: similar comparison in the Ldisc − Lcor plane where we highlight the difference between our original Fcor, 3 − 25 keV (black circles) and the reflection-corrected |
| In the text | |
 |
Fig. A.1. Comparison between the photon index obtained in the spectral fit (see Sect. 3.2; Γfit, data), which was then simulated and fit again (Γfit, simul). From top to bottom: results for SS02, SS04, SS07, and SS10 are shown. Error bars for Γfit, simul are shown (16th−84th percentiles), whereas we show uncertainties (16th−84th percentiles) in Γfit, data around the 1:1 relation. We colour coded data with the ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see white and grey symbols in the top panel of Fig. 3). |
| In the text | |
 |
Fig. A.2. Same as in Fig. A.1 but with the 2 − 10 keV flux under the NTHCOMP model of the hard component. Top panel: the figure is cut around log Fcor ∼ −11 for visualisation purposes and at lower fluxes simulations and fits are compatible within their very large errors. |
| In the text | |
 |
Fig. A.3. Same as Fig. A.1, but colour coded with the threshold on the ratio between the total (source plus background) and background-only 10 − 25 keV count rates. The one we adopted (i.e. ∼1.3) is shown with white contours on data points. |
| In the text | |
 |
Fig. A.4. Ratio between the total (source plus background) and background-only 10 − 25 keV count rates (see white and grey symbols in the top panel of Fig. 3) as a function of the fit Γ, colour coded with the fit disc temperature. |
| In the text | |
 |
Fig. A.5. Two examples of the posterior predictive check performed simulating 300 count rate spectra starting from the best-fit parameters posterior distributions. Data points are the actual spectrum, with green and orange contours as 16th−84th and 1st−99th interquantile ranges representing the predictive power of the spectral model. Energy bins in which the observed data point was not compatible within the 1st−99th interquantile range of the predicted spectra from the best-fit models are shown in red. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.