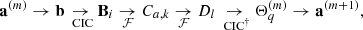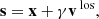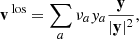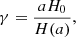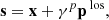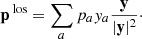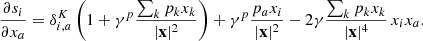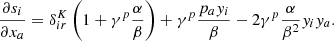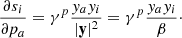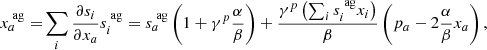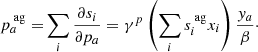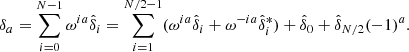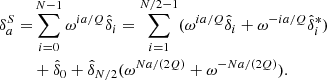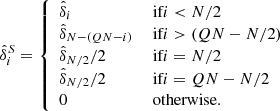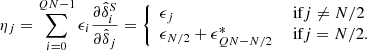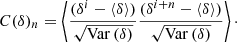| Issue |
A&A
Volume 625, May 2019
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 35 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201833710 | |
| Published online | 13 May 2019 | |
Physical Bayesian modelling of the non-linear matter distribution: New insights into the nearby universe
1
The Oskar Klein Centre, Department of Physics, Stockholm University, Albanova University Center, 106 91 Stockholm, Sweden
e-mail: j.jasche@gmx.de
2
Excellence Cluster Universe, Technische Universität München, Boltzmannstrasse 2, 85748 Garching, Germany
3
CNRS & Sorbonne Université, UMR7095, Institut d’Astrophysique de Paris, 75014 Paris, France
Received:
25
June
2018
Accepted:
18
March
2019
Accurate analyses of present and next-generation cosmological galaxy surveys require new ways to handle effects of non-linear gravitational structure formation processes in data. To address these needs we present an extension of our previously developed algorithm for Bayesian Origin Reconstruction from Galaxies (BORG) to analyse matter clustering at non-linear scales in observations. This is achieved by incorporating a numerical particle mesh model of gravitational structure formation into our Bayesian inference framework. The algorithm simultaneously infers the three-dimensional primordial matter fluctuations from which present non-linear observations formed and provides reconstructions of velocity fields and structure formation histories. The physical forward modelling approach automatically accounts for the non-Gaussian features in gravitationally evolved matter density fields and addresses the redshift space distortion problem associated with peculiar motions of observed galaxies. Our algorithm employs a hierarchical Bayes approach to jointly account for various observational effects, such as unknown galaxy biases, selection effects, and observational noise. Corresponding parameters of the data model are marginalized out via a sophisticated Markov chain Monte Carlo approach relying on a combination of a multiple block sampling framework and an efficient implementation of a Hamiltonian Monte Carlo sampler. We demonstrate the performance of the method by applying it to the 2M++ galaxy compilation, tracing the matter distribution of the nearby universe. We show accurate and detailed inferences of the three-dimensional non-linear dark matter distribution of the nearby universe. As exemplified in the case of the Coma cluster, our method provides complementary mass estimates that are compatible with those obtained from weak lensing and X-ray observations. For the first time, we also present a reconstruction of the vorticity of the non-linear velocity field from observations. In summary, our method provides plausible and very detailed inferences of the dark matter and velocity fields of our cosmic neighbourhood.
Key words: methods: data analysis / large-scale structure of Universe / methods: statistical / cosmology: observations / galaxies: statistics
© ESO 2019
1. Introduction
The goal of modern cosmology is the investigation of the dynamics of the universe and the formation of structures to determine the underlying gravitational world model. Especially observations of the cosmic microwave background (CMB), as provided by ESA’s Planck satellite mission, have contributed to firmly establishing the Λ cold dark matter (ΛCDM) framework as the standard model of cosmology (Planck Collaboration XIII 2016). This model reconciles the homogeneous expansion dynamics of the universe with the generation and evolution of cosmic structures. In particular, the present dynamical evolution of our universe is believed to be governed by dark energy and dark matter, constituting about 95% of its total energy budget. Although they are required to explain the formation of all observable structures within the standard picture of Einstein’s gravity, dark matter and dark energy so far elude direct observations and they have not yet been identified as particles or fields within more fundamental theories (see e.g., Freese 2017).
Making progress in understanding the cosmological phenomenology requires both taking ever more data and developing increasingly accurate and precise data analyses methods. This is particularly important when attempting to identify those subtle signals that could hint us towards the true nature of the physics driving the dynamical evolution of our universe.
In recent times the field of cosmology has evolved from focusing on studies of the homogeneous expansion dynamics, with supernovæ of type Ia (Perlmutter et al. 1999; Riess et al. 2016) and the observation of small density perturbations in the linear regime with CMB experiments (Mather et al. 1990; Smoot et al. 1992; Spergel et al. 2003; Planck Collaboration XIII 2016), to observations of linearly evolving structures in galaxy redshift surveys (see e.g., Tegmark et al. 2004; Percival et al. 2007; Gil-Marín et al. 2016). The natural next step consists of analysing non-linear cosmic structures in observations. In particular, most of the signal in next-generation surveys, such as will be provided by the Euclid satellite or the Large Synoptic Survey Telescope (LSST), will come from small non-linear scales. This is owed to the fact, that the amount of information grows appreciably with the number of available Fourier modes. 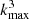 (LSST Science Collaboration 2009; Laureijs et al. 2011; Dodelson et al. 2016; Schaefer 2017). Accessing non-linear scales in observations, therefore, promises to extract additional cosmological information. As regularly mentioned in the literature (e.g., Lavaux & Wandelt 2012; Ma & Scott 2016), the number of observable modes at smaller non-linear scales is much larger than that at larger scales, which is intrinsically limited by the size of the observable Hubble volume. In addition inference of large scale fluctuations is affected most by survey geometries and selection effects which can be quite complex (see e.g., Davis et al. 1991; Peacock et al. 2001).
(LSST Science Collaboration 2009; Laureijs et al. 2011; Dodelson et al. 2016; Schaefer 2017). Accessing non-linear scales in observations, therefore, promises to extract additional cosmological information. As regularly mentioned in the literature (e.g., Lavaux & Wandelt 2012; Ma & Scott 2016), the number of observable modes at smaller non-linear scales is much larger than that at larger scales, which is intrinsically limited by the size of the observable Hubble volume. In addition inference of large scale fluctuations is affected most by survey geometries and selection effects which can be quite complex (see e.g., Davis et al. 1991; Peacock et al. 2001).
However, cosmological information at non-linear scales is locked in very complex higher order statistics and cannot be accessed entirely by only measuring simple two-point statistics (Ma & Scott 2016; Schaefer 2017). As a consequence novel data analysis methods need to study non-linearly evolving structures to make the most of coming cosmological data sets (Schaefer 2017). This requires developing novel and complex data models capable of accounting for intrinsic stochastic and systematic uncertainties of the data but also for the properties of non-linear gravitational structure formation responsible for the non-Gaussian features in observations of the non-linear cosmic large scale structure (LSS).
In many aspects, this requires to go beyond state-of-the-art in data analysis, currently relying mostly on linear data models including a linear perturbative description of observed cosmic structures (Hoffman 1994; Lahav et al. 1994; Lahav 1994; Zaroubi et al. 1995, 1999; Fisher et al. 1995; Webster et al. 1997; Erdoğdu et al. 2004; Kitaura & Enßlin 2008; Kitaura et al. 2009; Jasche et al. 2010a; Jasche & Wandelt 2013a; Elsner & Wandelt 2013; Jasche & Lavaux 2015; Granett et al. 2015). There has also been a considerable effort in going beyond linear data models to better capture the non-Gaussian nature of the observed galaxy distribution via Bayesian log-normal Poisson modelling (Kitaura et al. 2010; Jasche & Kitaura 2010; Jasche et al. 2010b).
In addition, to account for non-linear structure formation processes, we have proposed to perform Bayesian analyses of galaxy observations with full three-dimensional and physical models of gravitational structure formation (Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016). By exploiting physical models of the in-homogeneous evolution of cosmic matter, our approach allows for inferring spatially distributed density and velocity fields and quantifying corresponding uncertainties, via an efficient Markov chain Monte Carlo (MCMC) approach.
Incorporating a physical model of gravitational structure formation into the Bayesian inference approach turns the task of analysing observed non-linear cosmic structures into a statistical initial conditions problem. More specifically, we aim at inferring plausible three-dimensional initial density fields from which presently observed non-linear structures formed. In this fashion, our approach establishes an immediate link between observed present cosmic structures and their primordial initial conditions from which they formed via non-linear gravitational evolution.
It must be mentioned that naive inversion of the flow of time in corresponding physical structure formation models, to obtain initial conditions from non-linear density fields, is generally not possible due to the ill-posedness of the inverse problem (Nusser & Dekel 1992; Crocce & Scoccimarro 2006).
In this context ill-posedness is a statement on the existence of a range of feasible inference solutions that are consistent with noisy and incomplete observations, generally defying a unique model reconstruction. More specifically, in the context of the cosmic large scale structures, ill-posedness results from several instances. In particular, we usually deal with incomplete and noisy data but also dissipative processes, coarse-graining effects or incomplete access to the dark matter phase-space distribution. The combination of these effects eliminates information on the dark matter phase space distribution and prevents unique recovery of information on cosmic initial conditions via Liouville’s theorem for Hamiltonian dynamics (Liouville 1838; Gibbs 1906).
However, detailed information on the reason for ill-posedness is not required to address the problem via statistical inference. As already discussed in our previous works, we address the issue of ill-posedness by performing thorough Bayesian inference via physical forward modelling within sophisticated Hamiltonian Monte Carlo sampling approach (Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016). This MCMC approach correctly explores the space of feasible solutions for the large-scale structure inference problem, which are compatible with noisy and incomplete observations. More specifically our approach infers a set of plausible three-dimensional primordial density fields from which structures in present observations formed. Since our algorithm tries out feasible solutions purely via forward simulations, it is not affected by the problems of traditional inverse modelling, as summarized above.
Our approach also shares many beneficial properties with proposed ad-hoc BAO reconstruction methods, which have been demonstrated to increase the detectability of the BAO peaks from three to four sigma (see e.g., Noh et al. 2009; Xu et al. 2012; Schmittfull et al. 2015; Shi et al. 2018). By now several groups have proposed approaches to incorporate physical models into data analysis frameworks (Nusser & Branchini 2000; Brenier et al. 2003; Lavaux 2010; Jasche & Wandelt 2013b; Doumler et al. 2013; Wang et al. 2013, 2014; Kitaura 2013; Schmittfull et al. 2017; Seljak et al. 2017).
While previous approaches relied on perturbative descriptions of cosmic large-scale structure in this work we go beyond such limitations by incorporating fully non-linear and non-perturbative computer models of structure formation into our previously proposed algorithm for Bayesian Origin Reconstruction from Galaxies (BORG). More specifically we seek to fit a gravitational particle mesh (PM) model in its entirety to galaxy observations of the nearby universe. In contrast to contemporary analyses, limited to studying the lowest order moments of the density field (e.g., power- and bi-spectra), physical modelling of the entire three-dimensional matter distribution in observations permits us to implicitly access the entire hierarchy of higher order poly-spectra by directly fitting the filamentary three-dimensional distribution of matter in the universe.
A particularly important advantage of our approach is that it does not only provide single point estimates, such as mean or mode, but it characterizes the corresponding posterior distribution in terms of MCMC samples and thus allows for a thorough uncertainty quantification (UQ) (such as Jasche & Wandelt 2013b; Jasche et al. 2015). Previously such approaches have been considered computationally too prohibitive for numerical N-body models of structure formation. This work introduces our implementation of a non-linear large-scale structure inference framework, on the basis of the latest advances in Bayesian methodology and sampling algorithms. This permits us to apply sophisticated MCMC techniques to the title problem at scales previously inaccessible to cosmological data analysis.
Analysing cosmological surveys subject to noise and systematics is generally challenging and requiring the data model to handle a variety of nuisances. In order to address this issue we turned our BORG algorithm into a modular statistical programming engine that exploits hierarchical Bayes and block sampling techniques to flexibly build data models for different data sets. Different building blocks of the data model can be added to the Markov chain and their respective parameters will be jointly inferred within the multiple block sampling approach as visualized in Fig. 1.
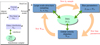 |
Fig. 1. Flow chart depicting the multi-step iterative block sampling procedure. In the first step, a three-dimensional density field will be realized conditional on the galaxy observations (top left corner). In subsequent steps observer velocity, bias parameters and the normalization parameters for the galaxy distribution are sampled conditional on respective previous samples. Iteration of this process yields samples from the full joint posterior distribution generated by the BORG algorithm. |
The present work also aims at applying our techniques to infer a coherent and consistent physical model of the three-dimensional large-scale dark matter distribution, its dynamics and formation histories in the nearby universe. This will be achieved by applying the BORG algorithm to the 2M++ galaxy sample (Lavaux & Hudson 2011).
These results will provide us with detailed and accurate maps of the expected dark matter distribution in the nearby universe and will permit us to measure the masses of prominent cosmic structures. Specifically for the case of the Coma cluster, we will demonstrate that we can obtain mass estimates that are compatible with gold-standard weak lensing measurements. We further seek to determine dynamical properties of cosmic structures and test their potential to impact cosmological measurements in the nearby universe via effects of peculiar velocities.
The manuscript is structured as follows. In Sect. 2 we describe the methodology and the modifications to the BORG algorithm. Section 3 provides a detailed overview of the data model required to compare predictions of the structure formation model with observed galaxy surveys. The main part of this work focuses on the application of our algorithm to data of the 2M++ compilation. The corresponding description of setting up these analysis run and the employed data is given in Sect. 4. Section 5 highlights some of our inference results. In particular we showcase results on galaxy biases (Sect. 5.1), the inferred three-dimensional density field at the initial conditions and in the present epoch (Sect. 5.2), the formation history of the Supergalactic plane (Sect. 5.4), the estimated mass and corresponding mass profile of the Coma cluster (Sect. 5.5), the velocity field of the Local universe (Sect. 5.6) and its possible impact on Hubble constant measurements in the nearby universe (Sect. 5.7). Finally, in Sect. 6, we conclude the paper and discuss future developments.
2. Bayesian inference with the BORG algorithm
This section provides an overview of our previously developed Bayesian inference framework including the modifications as introduced in this work.
2.1. The BORG algorithm
The presented project builds upon our previously developed algorithm for Bayesian Origin Reconstruction from Galaxies (BORG), aiming at the analysis of three-dimensional cosmic matter distribution at linear and non-linear scales of structure formation in galaxy surveys (see e.g., Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016). More explicitly the BORG algorithm fits three-dimensional models of gravitational structure formation to data.
Interestingly, introducing a physical model of gravitational structure growth immediately into the inference process turns the task of analysing the present non-linear galaxy distribution into a statistical initial conditions problem. More specifically the BORG algorithm seeks to infer the cosmic initial conditions from which present three-dimensional structures in the distribution of galaxies have formed via non-linear gravitational mass aggregation.
The BORG algorithm explores a cosmic LSS posterior distribution consisting of a Gaussian prior for the initial density field at a initial cosmic scale factor of a = 10−3 and a Poissonian model of galaxy formation at a scale factor a = 1, while initial density fields are related to the present galaxy distribution via a second order Lagrangian perturbation theory (2LPT) or a full particle mesh, as described in this work, model of gravitational structure formation (for details see Jasche & Wandelt 2013b). By exploiting non-linear structure growth models the BORG algorithm naturally accounts for the filamentary structure of the cosmic web typically associated with higher-order statistics induced by non-linear gravitational processes. As described in our previous works the posterior distribution also accounts for systematic and stochastic uncertainties, such as survey geometries, selection effects, unknown noise and galaxy biases as well as foreground contaminations (see e.g., Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016; Jasche & Lavaux 2017).
The resultant procedure is numerically highly non-trivial since it requires to explore the very high-dimensional and non-linear space of possible solutions to the initial conditions problem within a fully probabilistic approach. Typically, these spaces comprise 106–107 parameters, corresponding to amplitudes of the primordial density at different volume elements of a regular mesh in Lagrangian space for grids between 1283 and 2563 elements. Numerically efficient exploration of this highly non-Gaussian and non-linear posterior distribution is achieved via an efficient implementation of a Hamiltonian Markov chain Monte Carlo sampling algorithm (see Duane et al. 1987; Neal 2012; Jasche & Wandelt 2013b, for details).
It is important to remark that our inference process requires at no point the inversion of the flow of time in the dynamical physics model. The analysis solely depends on forward model evaluations, alleviating many of the problems encountered in previous approaches to the inference of initial conditions, such as spurious decaying mode amplification (see e.g., Nusser & Dekel 1992; Crocce & Scoccimarro 2006). Specifically (Crocce & Scoccimarro 2006) nicely demonstrate that inference of initial conditions is a fundamentally ill-posed problem. Recovering information on the initial conditions becomes harder and increasingly uncertain towards smaller scales, generally preventing unique backward in time integration of the final density field. Rather than inferring the initial conditions by backward in time integration, our approach builds a fully probabilistic non-linear filter using the dynamical forward model as a prior. This prior singles out physically reasonable LSS states from the space of all possible solutions to the statistical initial conditions problem. However, they do not strictly limit the space of initial conditions that must be searched to match observations. If for some reason unlikely events are required to explain observational data, the algorithm explores prior regions that are a priori unlikely. This allows for the potential characterization of primordial non-Gaussian signals in the recovered initial conditions for example.
Since the BORG algorithm provides an approximation to non-linear large-scale dynamics, it automatically provides information on the dynamical evolution of the large-scale matter distribution. In particular, it explores the space of plausible dynamical structure formation histories compatible with both data and model. Also note, that the BORG algorithm naturally infers initial density fields at their Lagrangian coordinates, while final density fields are recovered at corresponding final Eulerian coordinates. Therefore the algorithm accounts for the displacement of matter in the course of structure formation.
As results the algorithm provides measurements of the three dimensional density field but also performs full four-dimensional state inference and recovers the dynamic formation history and velocity fields of the cosmic LSS.
Some examples of secondary projects derived from these results aimed at studying dark matter voids in the galaxy distribution (Leclercq et al. 2015a), the phase-space distribution of matter in the SDSS survey (Leclercq et al. 2017), properties of the population of active galactic nuclei (AGN; Porqueres et al. 2018) as well as gravitational screening mechanisms (Desmond et al. 2018, 2019) and cosmic magnetic fields (Hutschenreuter et al. 2018).
2.2. Hamiltonian Monte Carlo sampling
Large-scale Bayesian inverse problems, as described in this work, belong to the most challenging tasks in the field of modern cosmological data analysis. This is mostly due to the numerical complexity of the physical model to test with data but even more so due to the high dimensional nature of the inference task itself. The combination of numerically expensive model evaluations and the curse of dimension typically renders large-scale Bayesian inverse problems numerically impractical (Bellman 1961).
A particular interesting algorithm to circumvent some of the problems associated to the curse of dimensionality is the Hamiltonian Monte Carlo (HMC) algorithm. Its numerical and statistical efficiency originates from the fact that it exploits techniques developed to follow classical dynamical particle motion in potentials. This approach provides deterministic proposals to the Metropolis-Hastings algorithm that can be accepted with very high probability (Duane et al. 1987; Neal 1993, 1996).
The HMC can be used to generate random realizations of a set of parameters {xi} of size N from any target distribution Π({xi}) by interpreting its negative logarithm as a potential for classical particle motion given as:
Introducing additional sets of auxiliary quantities, referred to as “momenta” {pi} and a “mass matrix” M, it is possible to define a Hamiltonian function analogous to classical mechanics:
It is important to remark that the joint distribution for parameters {xi} and {pi} can then be obtained via exponentiating the Hamiltonian given in Eq. (2):
As can be seen the joint distribution in Eq. (3) factorizes in a product of our target distribution Π({xi}) and a Gaussian distribution in the momenta {pi}. This demonstrates that the two sets of variables {pi} and {xi} are statistically independent and marginalization over auxiliary momenta yields the desired target distribution Π({xi}).
It is now possible to explore the joint parameter space of variables {pm} and {xm} by following persistent trajectories for some fixed amount of pseudo time τ according to Hamilton’s equations of motion:
and
In the above equation, the Hamiltonian forces are given by the gradient of the logarithmic target distribution with respect to inference parameters. Therefore, “particles” do not move freely in this high dimensional parameter space and they tend to be attracted towards regions with higher probability. New random realizations for the parameters 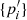 and
and 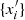 are then obtained by starting at the current position in phase space characterized by the values {pi} and {xi} and following Hamiltonian dynamics for a certain amount of pseudo time τ. The endpoint of this trajectory will then be accepted according to the standard Metropolis-Hastings acceptance rule:
are then obtained by starting at the current position in phase space characterized by the values {pi} and {xi} and following Hamiltonian dynamics for a certain amount of pseudo time τ. The endpoint of this trajectory will then be accepted according to the standard Metropolis-Hastings acceptance rule:
The particular feature that renders HMC an excellent algorithm for high dimensional parameter space exploration is precisely the conservation of the Hamiltonian by the above equation of motions. Consequently the expected acceptance rate given by Eq. (6) for the exact Hamiltonian dynamics has a value of unity.
In practice the acceptance rate may be lower due to numerical inaccuracies of the numerical integration scheme. To generate a valid Markov chain, auxiliary momenta are randomly re-drawn from a Gaussian distribution after each acceptance step and the procedure starts again. Individual momenta {pi} are not stored. Discarding auxiliary momenta simply amounts to marginalization and yields the target distribution Π({xi}).
In summary, two particular features of the HMC algorithm render it ideal for the exploration of high dimensional parameter spaces with complex physical models. First of all, it exploits conserved quantities such as the Hamiltonian to provide a high Metropolis-Hastings acceptance probability, hence reducing the amount of rejected model evaluations. More importantly, the HMC exploits gradient information of the target posterior distribution, preventing it from performing a blind random walk in high dimensions. This leads the algorithm follows targeted persistent trajectories to efficiently explore parameter spaces. For details on the numerical implementation of the HMC for cosmic large-scale structure analyses, the interested reader is also encouraged to have a look at our previous work (Jasche & Kitaura 2010; Jasche & Wandelt 2013b,a).
2.3. Modular statistical programming via Block sampling
A particular feature of the full Bayesian inference approach, as presented here, is the possibility to perform modular statistical programming. In particular, the BORG algorithm can solve any hierarchical Bayesian problem by simply adding additional components to a block sampling framework, as outlined in Fig. 1. This block sampling approach allows for straightforwardly accounting for additional observational systematics by building more complex data models and adding corresponding parameter samplers to the block sampling framework.
In this work, we use this block sampling framework to jointly account for unknown parameters of a galaxy biasing model, as described further below, and unknown noise levels for respective galaxy samples (see Fig. 1). Iterating this block sampling framework by conditionally drawing random realizations of parameters in sequence will then result in a correct Markov chain that asymptotes towards the desired joint target posterior distribution (e.g., Geman & Geman 1984).
3. A data model for non-linear LSS inference
This section describes the development and implementation of a non-perturbative data model to analyse the three-dimensional cosmic LSS at non-linear scales in data.
3.1. The general data model
The aim of the BORG algorithm is to provide a full characterization of the three-dimensional cosmic large-scale structure in observations by providing a numerical representation of the associated posterior distribution via sophisticated MCMC methods. More specifically the BORG algorithm provides data constrained realizations of a set of plausible three-dimensional matter density contrast amplitudes {δi} underlying a set of observed galaxy number counts 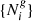 for various volume elements in the observed domain indexed by i. Using Bayes rule, the most general form of this posterior distribution can be expressed as:
for various volume elements in the observed domain indexed by i. Using Bayes rule, the most general form of this posterior distribution can be expressed as:
where the prior distribution Π({δi}) describes our a priori knowledge on the three-dimensional matter distribution in the universe, 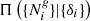 is the likelihood describing the statistical process of obtaining a set of observations
is the likelihood describing the statistical process of obtaining a set of observations 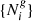 given a specific realization of the matter field {δi} and
given a specific realization of the matter field {δi} and 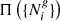 is the so-called evidence which normalizes the probability distribution. We note that Π({δi}) may depend on cosmological parameters and other auxiliary parameters, sometimes hyper-parameters, that we skip to represent for the moment in the notation.
is the so-called evidence which normalizes the probability distribution. We note that Π({δi}) may depend on cosmological parameters and other auxiliary parameters, sometimes hyper-parameters, that we skip to represent for the moment in the notation.
As already described in our previous work, a major complication arises from the fact that the prior distribution Π({δi}) for non-linear gravitationally formed density fields is not known in closed form, such as in terms of a multi-variate probability density distribution (Jasche & Wandelt 2013b). State-of-the-art approaches, therefore, assume Gaussian or log-normal distributions as approximations to the prior for the matter density contrast. However, since these distributions model only the one- and two-point statistics, they fail to capture the filamentary features of the observed cosmic web that are associated with higher order statistics (see e.g., Peebles 1980).
Additional complexity for the analysis of next-generation deep surveys arises from the fact that observed galaxy number counts are not solely determined by underlying density amplitudes but are additionally affected by dynamic effects such as redshift space distortions or light cone effects. Naive treatment of such additional dynamic structure formation processes in data would require to also self-consistently infer the three-dimensional velocity field from data. We would need to use a joint posterior distribution for density amplitudes {δi} and peculiar velocities {vi} given as:
Not only does this approach aggravate the search for a suitable prior distribution Π({δi},{vi}) but it also dramatically increases the amounts of parameters to be inferred with the three components of the spatial velocity field {vi}. We note that, generally, parameter space exploration becomes exponentially harder with the number of inference parameters. This fact is known as the curse of dimensions. Naive addition of a few million velocity amplitudes would therefore not be a wise decision when seeking to perform parameter space exploration.
While velocity fields at the present epoch are not uniquely related to the dark matter density field, the theory of gravitational structure formation and the cosmic microwave background yields indication that primordial matter fluctuations were almost at rest with respect to the Hubble flow in the early universe (Peebles 1980). In this picture, tiny fluctuations in the primordial peculiar velocity field derive uniquely from the field of initial density fluctuations by being proportional to the gradient of their gravitational potential (see e.g., Peebles 1980; Bernardeau et al. 2002).
Also, the primordial fluctuations field exhibits almost trivial statistical properties. In accordance with present theory and observations by the Planck satellite mission, the initial density field is an almost ideal Gaussian random field with zero mean and a covariance matrix corresponding to the post-recombination initial cosmological power-spectrum (see e.g., Planck Collaboration XIII 2016).
If we could, therefore, cast the problem of analysing the non-linear structures in the present universe into a problem of inferring their initial conditions, we would be able to simultaneously address the problem of finding a suitable prior distribution without the need to increase the parameter space when having to deal with the present velocity field.
The required large scale structure posterior distribution would then turn into a joint distribution of the present density field {δi} and the set of primordial density fluctuation amplitudes 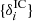 conditional on observations of galaxy number counts
conditional on observations of galaxy number counts 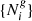 , given as:
, given as:
where 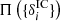 is the prior distribution of cosmic initial fluctuations and
is the prior distribution of cosmic initial fluctuations and 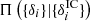 describes the process by which the present matter distribution has been obtained from their initial conditions. We further assume conditional independence
describes the process by which the present matter distribution has been obtained from their initial conditions. We further assume conditional independence 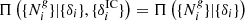 , that is, galaxy observations are conditionally independent of the primordial fluctuations once the final density field is given. This last assumption is not a fundamental limitation of the probabilistic model but it simplifies greatly the comparison to observations at the level considered in this work. The fundamental assumption is that galaxy formation is expected to depend only on the scalar fluctuations of the final conditions. Further extensions of the model, for which the galaxy formation would depend on the entire history of the dynamics, would be possible at additional computational costs.
, that is, galaxy observations are conditionally independent of the primordial fluctuations once the final density field is given. This last assumption is not a fundamental limitation of the probabilistic model but it simplifies greatly the comparison to observations at the level considered in this work. The fundamental assumption is that galaxy formation is expected to depend only on the scalar fluctuations of the final conditions. Further extensions of the model, for which the galaxy formation would depend on the entire history of the dynamics, would be possible at additional computational costs.
The distribution 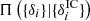 describes gravitational structure formation. It encodes the processes by which the present matter fluctuations {δi} derive from the initial conditions
describes gravitational structure formation. It encodes the processes by which the present matter fluctuations {δi} derive from the initial conditions 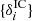 . Here we will assume that the final matter distribution derives uniquely from the initial conditions. This is, of course, the standard of cosmological modelling since cosmological simulations provide deterministic results when integrating the structure formation model. Thus we can model the final density field as a function of the initial density field:
. Here we will assume that the final matter distribution derives uniquely from the initial conditions. This is, of course, the standard of cosmological modelling since cosmological simulations provide deterministic results when integrating the structure formation model. Thus we can model the final density field as a function of the initial density field:
where 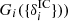 is our structure formation model that transforms initial conditions into final density fields. Since we assume this process to be deterministic we immediately obtain:
is our structure formation model that transforms initial conditions into final density fields. Since we assume this process to be deterministic we immediately obtain:
where δD(x) denotes the Dirac delta distribution. This yields the following large scale structure posterior distribution:
Marginalization over the final density fields {δi} then yields our posterior distribution:
This distribution links the present observations of the galaxy distributions 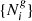 to the corresponding initial conditions
to the corresponding initial conditions 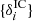 from which they originate via a gravitational structure formation model
from which they originate via a gravitational structure formation model 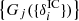 .
.
Embedding a physical structure formation model into the posterior distribution to analyse three-dimensional cosmic structures in observations thus solves many outstanding questions. Most importantly we can now address issues related to structure formation dynamics, such as redshift space distortions, light cone effects and higher order statistics associated with the filamentary structure of the cosmic web. In the following, we will discuss how to perform inferences with non-linear structure formation models.
3.2. The non-linear structure formation model
Our previous work relied on second order Lagrangian perturbation theory (LPT) to model cosmic structure formation (Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016). Even though LPT provides good approximations to the cosmic large-scale structure at the largest scales there are clear limits to its validity. Most notably the LPT approach relies on a convergence of series expansion. This expansion fails to accurately describe multi-streaming regions in high-density objects and cannot accurately capture the dynamic of gravitational evolution of dark matter at scales l ≲ 10 h−1 Mpc (see e.g., Melott et al. 1995; Tassev & Zaldarriaga 2012).
We intend to go beyond such limitations and to account for the non-linear gravitational dynamics. In this work we update the physics model of our BORG algorithm with a numerical particle mesh model (see e.g., Klypin & Shandarin 1983; Efstathiou et al. 1985; Hockney & Eastwood 1988; Klypin & Holtzman 1997).
A particle mesh code solves the gravitational N-body problem by following the dynamical trajectories of a set of simulated dark matter particles including their mutual gravitational interactions. Our implementation of this particle mesh simulator follows closely the description of Klypin & Holtzman (1997). To simulate non-linear gravitational structure formation from some predefined initial conditions to the present state of the cosmic LSS a particle mesh code solves the following equations of motion for positions x and momenta p of dark matter particles:
where a is the cosmic scale factor and 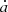 is its first time derivative. Corresponding momentum updates are given by:
is its first time derivative. Corresponding momentum updates are given by:
where 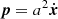 and the gravitational potential Φ is given implicitly by the Poisson equation:
and the gravitational potential Φ is given implicitly by the Poisson equation:
In the above, we have introduced the reduced gravitational potential 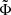 . The Poisson relation relating the density of particles to the potential
. The Poisson relation relating the density of particles to the potential 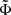 becomes:
becomes:
To estimate densities from simulated particle positions we use the cloud in cell method (see e.g., Hockney & Eastwood 1988). Then the Poisson Eq. (17) can be solved in Fourier-space by exploiting numerically efficient Fast Fourier Transforms (FFTs). Since our approach requires many model evaluations the numerical implementation of this LSS model has been parallelized via the Message Passing Interface (MPI; see e.g., Bruck et al. 1997). The detailed description of solving the model equations is provided in Appendix B.
To use the non-linear particle mesh model, within the HMC framework, we also need to derive the corresponding gradient of model predictions with respect to changes in the initial conditions. More specifically, the gradient of the particle mesh simulator provides us with the response of the simulation with respect to small changes in the initial conditions. This gradient needs to be evaluated several times within the HMC sampling steps. As discussed above, we typically deal with on the order of ten million parameters, corresponding to the density amplitudes of the primordial fluctuations field. Evaluating such a gradient via finite differencing would be numerically prohibitive. In Appendix C we, therefore, derive the tangent-adjoint model of the particle mesh simulator, which encodes the analytic derivative of the numerical forward simulation.
As demonstrated by Fig. 3, both the forward and the tangent adjoint model are fully parallel and exhibit near optimal scaling behaviour as a function of the number of tasks. Also note, that the adjoint model is only a factor two times more expensive than the forward model. Adjoint coding, therefore, provides us with an efficient means to calculate gradients of high dimensional functions.
3.3. Modelling redshift space distortions
Optical distance estimation via spectroscopic redshift measurements is subject to systematic uncertainties due to the peculiar motions of observed galaxies. Corresponding Doppler effects increase observed redshifts if peculiar velocities are pointing away from the observer and decrease the redshift if velocities are pointing towards the observer. As a consequence exact galaxy positions in three-dimensional space are subject to some uncertainty.
Since the BORG algorithm exploits a physical model for LSS formation, predicting also the motion of matter, such redshift space distortions can be taken into account naturally. In this fashion, the BORG algorithm will not only exploit positional galaxy information but well also use the dynamic information encoded in the redshift space distortion effect. In principle, there are several different possibilities of implementing a redshift space distortions treatment into the BORG algorithm. For the sake of this work we calculate the redshift distorted particle positions as follows:
with γ = a/H(a), r = x + xmin being the vector from the observer to a simulation particle and v = p/a2, where p is the momentum vector as discussed in the previous section. We include a global vector Vobs to shift particles to their redshift coordinates to account for uncertainty in the specification of the rest frame of large scale structures. This Vobs is marginalized over in the inference procedure. To generate density fields in redshift space we use the redshift space coordinates s rather than the real space coordinates x of particles within the cloud in cell approach.
3.4. Modelling observed galaxies
One of the most challenging, and yet unsolved, aspects of analysing the galaxy distribution at non-linear regimes is to account for the biased relation between observed galaxies and the underlying distribution of dark matter. For the sake of this work we follow a common approach and approximate the galaxy biasing relation by a local but non-linear bias functions Szalay (1988), Matsubara (1995, 2011), Sigad et al. (2000), Frusciante & Sheth (2012), Neyrinck et al. (2014), Ata et al. (2015), Desjacques et al. (2018). More specifically we model the expected number of galaxies ng via the following four parameter function as proposed in Neyrinck et al. (2014):
This parametrized bias function is a modification of a power-law bias model to account for suppressed clustering of galaxies in under dense regions by an additional exponential function.
Given this bias model, realizations of galaxy number counts are then assumed to follow a Poisson distribution with the Poisson intensity given as:
where Ri is the survey response operator consisting of the product of angular and radial selection function (also see Jasche & Wandelt 2013a; Jasche et al. 2015, for a discussion on the survey response operator). The logarithm of the likelihood part of the posterior distribution of Eq. (13) is then:
with the Poisson intensity field 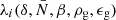 given by:
given by:
As can be seen, this is a highly non-linear data model not only due to the bias model but also due to the fact that for a Poisson distribution the noise is signal dependent and is not an additive nuisance. The four bias parameters 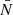 , β, ρg and ϵg are a priori unknown and have to be inferred jointly together with initial and final density fields.
, β, ρg and ϵg are a priori unknown and have to be inferred jointly together with initial and final density fields.
As discussed above, the advantage of our Bayesian approach is the possibility to add arbitrarily many parameter sampling procedures to the modular statistical programming approach via sequential block or Gibbs sampling methods. This is relevant since the biasing function as provided in Eq. (19) will not be universally valid, but will require different bias parameters for different populations of galaxies.
In particular, in this work, we will split our galaxy sample into 16 different sub-samples selected by their absolute K-band magnitude. The conditional posterior distribution for bias parameters given a sample of the three-dimensional final density field and corresponding galaxy number counts of the respective sub-samples is given by:
where the first factor on the right-hand side is the prior distribution of bias parameters and the second factor is the Poisson likelihood described in Eq. (21). We typically follow a maximum agnostic strategy by setting uniform prior distributions for the bias parameters. Since the parameters of the bias model are all required to be positive we choose the following prior distribution:
where Θ(x) is the Heaviside function. To explore the space of bias parameters we use a block sampling strategy by iteratively sampling individual parameters conditional on all other parameters. More specifically the algorithm executes the following block sampling scheme:
where the superscript n indicates the sampling step.
Iterating this procedure together with sequential density field updates will yield samples from the joint target distribution. We note, that this approach can easily be extended to account for additional survey systematics, such as foreground contaminations (see e.g., Jasche & Lavaux 2017).
A particular challenge arises from the fact, that the specific non-linear shape of the bias function in Eq. (19) does not allow us to derive a simple direct sampling approach and we have to resort to standard MCMC techniques to generate bias parameter realizations. In order to have unit acceptance rates for the MCMC bias parameter sampling, we perform a sequence of slice sampling steps (Neal 2000).
3.5. Robust inference with model errors
Most often Bayesian inference assumes that the distribution of the data agrees with the chosen class of likelihood models. More specifically it is assumed that the chosen data model is the true and correct explanation for the process that generated the actual observations. Already small deviations from these assumptions may greatly impact the Bayesian procedure.
Currently, several approaches to perform robust Bayesian inference with possible model misspecification have been proposed (see e.g., Grünwald & van Ommen 2014; Miller & Dunson 2015; Bhattacharya et al. 2016; Holmes & Walker 2017; Frazier et al. 2017). Robustness of inferences can be improved by conditioning on a neighbourhood of the empirical likelihood distribution rather than to the data directly (Miller & Dunson 2015). When defining neighbourhoods based on relative entropy estimates it can be shown, that the resulting coarser posterior distribution can be approximated by raising the likelihood to a fractional power (Miller & Dunson 2015; Bhattacharya et al. 2016; Holmes & Walker 2017). More specifically this amounts to tempering the likelihood distribution. For a Poisson distribution tempering is equivalent to using only a homogeneous subset of the data. This can be seen by raising the Poisson likelihood to some power 0 ≤ β ≤ 1:
As can be seen from Eq. (24), coarsening the posterior distribution amounts to extracting information only from a homogeneous sub-sample of galaxies 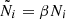 while decreasing the expected Poisson intensity
while decreasing the expected Poisson intensity 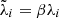 . This procedure thus is equivalent to increasing observational uncertainties resulting in conservative interpretations of the data.
. This procedure thus is equivalent to increasing observational uncertainties resulting in conservative interpretations of the data.
The procedure of coarsening the posterior distribution, therefore, does not add spurious information to the inference, quite the contrary it uses only a fraction of the available information provided by the data set. Accessing the full potential of the data would require to develop more accurate data models to compare observations of galaxies to the underlying dark matter distribution at non-linear scales. This is a currently ongoing endeavour in the scientific community. For the sake of this work we choose β = 0.3.
4. Application to observed galaxy data
This section describes the application of the BORG algorithm to galaxy observations provided by the 2M++ galaxy compilation (Lavaux & Hudson 2011). Specifically here we will follow a similar approach as previously discussed in Lavaux & Jasche (2016).
4.1. The 2M++ survey
The 2M++ (Lavaux & Hudson 2011) is a combination of the 2MASS Redshift Survey (2MRS; Huchra et al. 2012), with a greater depth and a higher sampling rate than the IRAS Point Source Catalogue Redshift Survey (PSCZ; Saunders et al. 2000). The photometry is based on the Two-Micron-All-Sky-Survey (2MASS) Extended Source Catalogue (2MASS-XSC; Skrutskie et al. 2006), an all-sky survey in the J, H and KS bands. Redshifts in the KS band of the 2MASS Redshift Survey (2MRS) are supplemented by those from the Sloan Digital Sky Survey Data Release Seven (SDSS-DR7; Abazajian et al. 2009), and the Six-Degree-Field Galaxy Redshift Survey Data Release Three (6dFGRS; Jones et al. 2009). Data from SDSS was matched to that of 2MASS-XSC using the NYU-VAGC catalogue (Blanton et al. 2005). As the 2M++ combines multiple surveys, galaxy magnitudes from all sources were first recomputed by measuring the apparent magnitude in the KS band within a circular isophote at 20 mags arcsec−2. Following a prescription described in Lavaux & Hudson (2011), magnitudes were corrected for Galactic extinction, cosmological surface brightness dimming and stellar evolution. Then the sample was limited to K2M + + ≤ 11.5 in regions not covered by the 6dFGRS or the SDSS, and limited to K2M + + ≤ 12.5 elsewhere. Incompleteness due to fibre-collisions in 6dF and SDSS was accounted for by cloning redshifts of nearby galaxies within each survey region as described in Lavaux & Hudson (2011).
The galaxy distribution on the sky and the corresponding selection at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5 are given in Fig. 2. The top row shows redshift incompleteness, i.e. the number of acquired redshifts versus the number of targets, for the two apparent magnitude bins. The lower row depicts the galaxy distribution as used in this work. We note that the galactic plane clearly stands out and that the incompleteness is evidently inhomogeneous and strongly structured.
 |
Fig. 2. 2M++ data and its selection properties. Top left panel: sky completeness at K2M + + ≤ 11.5, derived as the number of observed redshifts versus the number of targets in the 2MASS photometric sample. Top right panel: same quantity is shown but for apparent magnitudes 11.5 < K2M + + ≤ 12.5. Bottom left panel: number count of galaxies in thin radial shells for the two different magnitude cuts shown in the top row. We see that the catalogue covers a volume up to a redshift z ∼ 0.06 − 0.08. Bottom right panel: sky projection of the positions of the galaxies of the 2M++ catalogue. The local large-scale structures are clearly visible. |
 |
Fig. 3. Computational scaling properties of the code over MPI-tasks. The x-axis is the number of MPI tasks, each task being given eight cores with OpenMP parallelization. The y-axis is the wall time seconds taken by the software to execute the indicated part of the algorithm. The red lines correspond to the evaluation of one time-step of the BORG-PM forward model, that is the N-body simulation including gravity solver. The green lines correspond to the time taken to compute the adjoint gradient of that same model. We note that the cost of the adjoint gradient takes only twice as much time as the forward model itself over the entire range. Also, the scaling is strong up to ∼100 cores, the break visible at the end being because of the core saturation and the use of hyper-threading on the supercomputer. |
In addition to the target magnitude incompleteness, and the redshift angular incompleteness, one may also worry about the dependence of the completeness with redshift. This is not a problem for the lower K2M + + ≤ 11.5 which is essentially 100% complete. We do not expect much effect in the fainter magnitude bins as the spectroscopic data come from SDSS and 6dFGRS which have both a homogeneous sampling and have fainter magnitude limits as the 2M++.
We account for radial selection functions using a standard luminosity function Φ(L) proposed by Schechter (1976). Using this function we can deduce the expected number of galaxies in the absolute magnitude range, observed within the apparent magnitude range of the sample at a given redshift. The α and M* parameters are given for the KS-band in the line labelled “|b|> 10, K < 11.5” of the Table 2 of Lavaux & Hudson (2011), i.e. α = −0.94, M* = −23.28. The target selection completeness of a voxel, indexed by p, is then
where 𝒱p the co-moving coordinate set spanned by the voxel, and Vp = ∫𝒱pd3x. The full completeness of the catalogue is derived from the product of ct and the map corresponding to the considered apparent magnitude cut given in the upper panels of the Fig. 2 after its extrusion in three dimensions.
Our sampling approach accounts for luminosity dependent galaxy biases. In order to do so the galaxy sample is subdivided into eight bins of same width and without spacing in absolute K-band magnitude in the range −25 ≤ K2M + + ≤ −21. The galaxy sample is further split into two subsets depending on the apparent magnitude: if K2M + + ≤ 11.5 it belongs to the first set, otherwise, 11.5 < K2M + + ≤ 12.5 it belongs to second set. This yields a total of 16 galaxy subsets. The bias parameters of each of these subsets are inferred jointly within the multiple block sampling framework as described above. This permits to properly marginalize over these unknown bias parameters within the BORG framework. Splitting the galaxy sample permits us to treat each of these sub-samples as an individual data set, with its respective selection effects, biases and noise levels.
4.2. Non-linear analysis with the BORG algorithm
The analysis of the 2M++ galaxy sample is conducted on a cubic Cartesian domain of side length of 677.77 h−1 Mpc consisting of 2563 equidistant grid nodes. This results in a total of ∼1.6 × 107 inference parameters, corresponding to primordial density fluctuation amplitudes at respective grid nodes. The inference procedure thus yields data constrained realizations of initial conditions with a Lagrangian grid resolution of about ∼2.65 h−1 Mpc.
To integrate the effect of the growth of large scale structure, we assume a fixed standard ΛCDM cosmology with the following set of cosmological parameters (Ωm = 0.307, ΩΛ = 0.693, Ωb = 0.04825, h = 0.705, σ8 = 0.8288, ns = 0.9611). The cosmological power-spectrum of initial conditions, required by our BORG run, was evaluated via the prescription provided by Eisenstein & Hu (1998, 1999). To guarantee a sufficient resolution and smoothness of inferred final Eulerian density fields, we oversample the initial density field by a factor of eight, requiring to evaluate the particle mesh model with 5123 particles in every sampling step. To oversample we simply pad with zeros the Fourier modes of the initial conditions, which allow a clean separation of scales on a natural basis. The forward and adjoint algorithm are given in Appendix E. Additionally, we solve the Poisson equation using a grid at a resolution of 10243, corresponding to a resolution 0.66 h−1 Mpc. Experimentally, this force resolution does not lead to over-damping of the power spectrum compared to LPT models, bring much better large scale density profile of galaxy clusters, while still being tractable in an MCMC.
Running the Markov chain with a particle mesh model is numerically expensive. To save some computation time we first ran the Markov chain for 6783 transition steps using the numerically less expensive LPT model. This procedure yielded a good starting point for a Markov chain running the full particle mesh model.
4.3. Testing the sampler behaviour
To test the burn-in behaviour of the initial LPT sampling procedure we followed a similar approach as described in our previous works (see e.g., Jasche & Wandelt 2013b,a; Jasche et al. 2015; Lavaux & Jasche 2016). In particular, we initialize the Markov chain with an over-disperse random Gaussian initial density field with amplitudes a factor ten times smaller than expected in a standard ΛCDM scenario. Starting from such an over-dispersed state the Markov chain will then follow a persistent drift towards more reasonable regimes in parameter space.
To illustrate this initial automatic adjustment of the algorithm in Fig. 4, we illustrate the sequence of posterior power-spectra measured from subsequently inferred three-dimensional initial density fields during the initial burn-in phase. It can be seen that the posterior power-spectra drift towards the expected target power-spectrum. After about 4000 transition steps power-spectra oscillate around the expected values. In addition, we also trace the evolution of the one point (1-pt) distribution of inferred primordial density fluctuation during the burn-in period. As can be seen in the right panels of Fig. 4 the 1-pt distribution of successive density samples approaches the expected normal distribution within about 4000 transitions of the Markov chain. These results show no sign of any particular systematic artefact and clearly indicate a healthy burn-in behaviour of the chain.
 |
Fig. 4. Sequential posterior power-spectrum (left panel) and 1-pt distribution (right panel) of inferred primordial fluctuations measured during the burn-in of the Markov chain with an LPT model. The colour gradient indicates the step number in the chain from zero (random initial condition of small amplitude) to 6783 for which the chain is manifestly stable according to this metric. Top panels: power spectrum and 1-pt distributions measured a posteriori from the samples, while lower panels: ratio of these quantities to the expected prior values. Thick dashed lines represent the fiducial prior values. The thin (black respectively) grey dotted line indicates the Gaussian 1σ limit (2σ respectively) in the lower left panel. These results show no sign of any residual systematic artefacts, indicating a healthy burn-in behaviour of the chain. |
This initial LPT Markov run was stopped after 6783 transitions and the final result was used as the initial point to start a run with the full particle mesh model. In order to monitor the improvements that the PM model imparts on the previous LPT results, we plot the trace the negative logarithmic likelihood distribution as a function of sample number n in Fig. 5.
 |
Fig. 5. Trace plot of the negative differential logarithmic likelihood as a function of sampling steps n. The values represent logarithm of the ratios between the initial likelihood value obtained by the last sample calculated with a LPT model and subsequently evaluated particle mesh models. Right panel: trace of the total likelihood, while left panels: evolution of logarithmic likelihoods for the respective galaxy sub-catalogues as indicated in the panels. It can be seen that the Markov chain starts initially with high values for the negative logarithmic likelihood but successive sampling steps improve the consistency of inferred three-dimensional initial density fields with the observations. After 1200 steps the trace plot settles at an average value for the negative logarithmic likelihood. In terms of Bayesian odds ratios when comparing the initial guess to a sample at sampling step 2500 this is an improvement of about five orders of magnitude in logarithmic likelihood. |
As can be seen initially the Markov chain starts at high values of the negative logarithmic likelihood. These initial values correspond to the LPT results. During subsequent sampling steps the negative logarithmic likelihood values then drop by more than four orders of magnitude as the particle mesh model method successively improves the inferred non-linear density fields. Finally, it can be seen that the Markov chain settles at a constant value. At this point we start recording samples of the Markov chain.
It is very interesting to note that the initial starting point of the chain corresponds to a density field inferred with the LPT model, while subsequent samples correspond to density fields inferred with the non-linear particle mesh model. Since Fig. 5 basically shows that the logarithms of the likelihood ratios of the first LPT density fields to all subsequent PM density fields, the plot qualifies as a Bayesian model test in terms of Bayes odds ratios. Realizing this fact demonstrates that the data clearly favours density fields inferred with the PM method. On a Jeffreys scale, the statement is far more than decisive. While this statement is true for the combined logarithmic likelihood of all galaxy sub-samples, we may also look at the improvements for the individual catalogues. To show that point, we also plot in Fig. 5 the traces of the negative logarithmic likelihoods for the individual sub-catalogues. As can be seen, especially the fainter galaxies seem to live in regimes of the cosmic LSS that can be acceptably approximated by the LPT method even though PM also provides significant improvements there To quantify this effect, we present in Table 1 the actual logarithmic likelihood ratios between the initial LPT density model and the last density sample generated with the PM model. It may be interesting to investigate the details of this effect in future analyses, as it may provide a guideline to optimally select galaxies for cosmological analyses.
Logarithmic Bayes factors between a density field generated with the LPT and one with the PM model.
To conclude this first diagnostic, the Markov chain stabilizes after ∼1200 samples the moment from which on we start recording 1500 samples.
Generally, subsequent samples of a Markov chain are correlated. The sampler efficiency is therefore determined by the number of independent samples that can be drawn from a given Markov chain. As demonstrated in Appendix F, the sampler exhibits a high mixing efficiency by generating an independent sample roughly every 150th sample.
As such the presented BORG run does not qualify for a thorough Markov analysis but it provides us with sufficient information on the non-linear dynamics in the nearby universe and uncertainty quantification to warrant robust scientific analyses. The exact state of the Markov chain is stored in a restart file permitting to resume the chain at any later time if the generation of more samples will be required at any point in the future.
5. Results on cosmological inference
This section provides an overview of the inference results obtained by applying the BORG algorithm to the 2M++ galaxy compilation. In particular, the present work focusses at reconstructing the non-linear LSS and its dynamics in the nearby universe.
5.1. Inferred galaxy biases
To properly account for the unknown relationship between observed galaxies and the underlying dark matter field, the BORG algorithm jointly infers the parameters of a phenomenological, non-linear truncated power-law bias model as discussed in Sect. 3.4. In particular, the algorithm exploits an iterative block sampling framework to perform a joint Markov chain over the actual target parameters, the amplitudes of the 3D density field, and the nuisance parameters associated to the employed data model. As a consequence, the BORG algorithm also naturally provides measurements of the non-linear galaxy bias.
As described in Sect. 4.1, for the sake of this work, we have subdivided the galaxy sample of the 2M++ galaxy compilation into eight bins of same width in absolute K-band magnitude in the range −25 < K2M + + < −21 respectively for the two selections at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5. This results in a total of 16 sub-samples, for which the BORG algorithm infers the respective set of bias parameters. In this fashion, our algorithm can account for the respective systematics in the individual galaxy samples while exploiting their joint information.
Figure 6 represents our measurements of the ensemble mean bias functions and corresponding one-sigma uncertainties for the 16 galaxy sub-samples. By comparing inferred bias functions between the two selections at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5, it can be seen that within the absolute K-band magnitude in the range −23 < K2M + + < −21 the respective bias functions are in agreement. This demonstrates that the galaxies in both selections show the same clustering behaviour for the given absolute mass range. However for K-band magnitudes in the range −25 < K2M + + < −23, we observe an increasing difference between the galaxy bias functions of the two selections at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5. In particular, the brighter galaxies in the K2M + + ≤ 11.5 seem to have a steeper biasing relation as a function of the underlying density field than those in the 11.5 < K2M + + ≤ 12.5 selection. The true origin of this behaviour is not clear, but it could indicate a contamination or systematic effect of the galaxies selected at 11.5 < K2M + + ≤ 12.5. These phenomenological bias function shapes agree well with previous findings in numerical simulations (Sousbie et al. 2008).
 |
Fig. 6. Inferred non-linear bias functions for the 16 galaxy subsets of the 2M++ galaxy compilation in 8 absolute K-band magnitude bins. Blue and red lines correspond to ensemble mean bias functions, while shaded regions indicate the 1σ intervals for the two magnitude cuts as indicated in the upper left panel. Dashed lines correspond to bias functions estimated with the ensemble mean values of the bias parameters. |
In Table 2 we also report the ensemble mean values for the respective bias parameters. We note, that generally for non-linear functions, the bias function evaluated with the mean parameter values will not correspond to the ensemble mean bias function. This is a simple statement of non-Gaussian and non-linear statistics. To illustrate this fact in Fig. 6 we also plotted the bias functions evaluated at the ensemble mean parameter values.
Estimated mean parameter values for the bias functions corresponding to the respective magnitude cuts.
In Sect. 5.5 we also demonstrate that the masses estimated from our inferred dark matter density fields agree with complementary measurements via X-ray or weak lensing measurements. This is a strong indication of the fact that our inferred bias functions are a plausible description of the relationship between observed galaxies and the underlying dark matter distribution.
5.2. 3D density field in the nearby universe
The BORG algorithm aims at inferring detailed three-dimensional maps of the matter distribution in the Nearby universe constrained by data of the 2M++ galaxy compilation. In fact, our method simultaneously constrains the present non-linear matter density field and the primordial density fluctuations from which they originate.
We infer the primordial field of matter fluctuations on a Cartesian equidistant grid of resolution ∼2.65 h−1 Mpc. All primordial matter fluctuations are inferred in the initial Lagrangian space while present structures are determined at their Eulerian coordinates. Since structures collapse under their own gravity, the resolution of the initial Lagrangian grid is sufficiently high to resolve major features in the present universe, such as the Coma cluster. Corresponding non-linear density fields, as well as positions and velocities of simulation particles, are then estimated by evaluating inferred primordial initial conditions via the PM structure formation model.
The BORG algorithm not only provides simple point estimates, such as mean or maximum a posteriori value but rather provides a numerical approximation to the target posterior distribution in terms of an ensemble of Markov samples. This ensemble of data constrained realizations contains all the information on the three-dimensional density field that can be extracted from the noisy and incomplete data set and at the same time quantifies corresponding observational uncertainties that are necessary in order to not misinterpret the observations. Unlike point estimates, these posterior realizations constitute physical meaningful quantities which do not suffer from any attenuation or bias due to systematic effects in the data (also see discussions in Jasche & Wandelt 2013b; Jasche et al. 2015; Lavaux & Jasche 2016).
As an illustration of the property, we show in Fig. 7 spherical slices of thickness ∼2.6 h−1 Mpc through data constrained realizations of the three-dimensional initial and final density fields, projected onto a HEALPix map (Górski et al. 2005). The right panel depicts the non-linear density field at a distance of R = 100 h−1 Mpc from the observer overlaid by the actually observed galaxies in the 2M++ galaxy compilation. As can be seen, our algorithm recovered a highly detailed map of the filamentary cosmic web. Observed galaxies in the 2M++ survey trace the recovered spatial distribution of the underlying dark matter. Note that regions that have been traced poorly by galaxies are visually not distinct from those constrained by observations.
 |
Fig. 7. Spherical slices of thickness ∼2.6 h−1 Mpc through a data constrained realization of the three-dimensional initial (left panel) and final density field (right panel) at a distance of R = 100 h−1 Mpc from the observer. Initial density fields correspond to the epoch of a cosmic scale factor a = 0.001 while non-linear final density fields are evaluated at the present epoch (a = 1). One can see the correspondence of large scale over-densities in the initial conditions and corresponding structures in the gravitationally evolved density field. Red dots in the right panel denote the observed galaxies in the 2M++ survey. As can be seen observed galaxies trace the inferred dark matter distribution. |
This is a crucial feature of the BORG algorithm, which augments the information obtained from observations with statistically correct information on the cosmic LSS in unconstrained regions of the galaxy survey. As such, each posterior sample represents a physically meaningful and plausible realization of the actual dark matter distribution in the universe. The left panel of Fig. 7 shows the corresponding slice through a realization of the initial fluctuations field. This field represents the proto-structures from which the presently observed structures (shown in the right panel) have formed via gravitational collapse. We will further discuss the possibility to follow the structure formation history of objects below in Sect. 5.4.
To further support the qualitative statement that individual posterior realizations represent physically plausible quantities, we test the one- and two-point statistics of inferred primordial density fluctuations realizations. These results are presented in Fig. 8. As can be seen, the BORG algorithm recovers the cosmic LSS over a huge dynamic range covering more than three orders of magnitude in amplitudes of the power-spectrum. In comparison to a fiducial cosmological power-spectrum, corresponding to the set of cosmological parameters as described in Sect. 4.2, measured power-spectra do not show particular signs of bias or attenuation throughout the entire domain of Fourier modes considered in this work.
 |
Fig. 8. Posterior power-spectra measured from inferred initial density fields (left panel) and the one-point distribution of primordial density fluctuations (right panel). The plot demonstrates that individual data constrained realizations of the initial density field constitute physically valid quantities. Throughout the entire domain of Fourier modes considered in this work we do not observe any particular bias or attenuation of measured cosmic power-spectra. The measured posterior one-point distribution of primordial fluctuations is compatible with a fiducial normal one-point distribution with variance corresponding to the cosmological parameters as described in Sect. 4.2. Tests of kurtosis and skewness, as indicated in the right panel, confirm inferred initial density fluctuations to follow Gaussian statistics. |
We have also tested the one-point probability distribution of inferred primordial density fluctuations. As demonstrated by the right panel of Fig. 8, inferred primordial density amplitudes are normally distributed. In particular, the inferred one-point distribution is consistent with the expected fiducial Gaussian distribution determined by the cosmological parameters provided in Sect. 4.2. Residual uncertainties remain only in the tail of the distribution which is dominated by sample variance. To further test the normality of the inferred one-point distribution, we also test the kurtosis μ4/σ4 − 3 and skewness μ3/σ4 as indicated in the right panel of Fig. 8. Since both values agree numerically with zero, these results demonstrate that the inferred one-point distribution of matter fluctuations is compatible with Gaussian statistics.
The unbiased reconstruction of the primordial power-spectrum is also a good indicator that the BORG algorithm correctly accounted for various systematic effects. In particular improper treatment of survey geometries, foreground contamination, selection effects, and luminosity-dependent galaxy biases would typically result in excessive erroneous large-scale power (see e.g., Tegmark et al. 2004; Pullen & Hirata 2010; Jasche et al. 2010a; Leistedt & Peiris 2014; Jasche & Lavaux 2017).
As a remark, we have found that the forward modelling approach is particularly sensitive to these effects. Wrong assumptions on galaxy biasing or selection effects would not only introduce erroneous large-scale power to the density field but also affect large-scale matter flows, that are required to translate the initial matter distribution to the present non-linear density field. In particular, the non-linear and non-local nature of the employed particle mesh structure formation model enhances such effects leading to obviously erroneous results. In turn, the high sensitivity of the physical forward approach towards non-linear and luminosity-dependent galaxy biases promises to provide accurate constraints on the relation between observed galaxies and the underlying dark matter distribution, as discussed in the previous and the following sections.
The entire ensemble of physically plausible density field realizations forms a numerical approximation to the target posterior distribution. This permits us to derive any desired statistical summary and quantify corresponding uncertainties. As an example in the Fig. 9, we show the ensemble mean density fields and corresponding pixel-wise standard deviations. As can be seen, the initial and final ensemble mean density fields both approach cosmic mean density in regions which are poorly constrained by observations. This result is expected. When data does not provide any constraining information, the algorithm will return cosmic mean density on average in unobserved regions. This agrees with the prior assumption of the zero-mean Gaussian distribution of cosmic initial conditions, as described in Sect. 2.1. These results are also in agreement with our previous findings (see e.g., Jasche & Wandelt 2013b; Jasche et al. 2015, and discussions therein).
 |
Fig. 9. Spherical slices through the ensemble mean of the three-dimensional initial (left panel) and final density field (right panel) and corresponding pixel-wise variances (lower panels) at a distance of R = 100 h−1 Mpc from the observer. It is interesting to note, that the pixel-wise variance for the final density field imprints the cosmic large scale structure. Correlations between signal and noise are expected for any point process, such as the generation of galaxy observations. The BORG algorithm correctly accounts for these effects. |
Figure 9 also presents voxel-wise standard deviations of inferred density amplitudes at respective positions inside the analysis domain. It is interesting to note, that estimated standard deviations of the final density amplitudes reflect an imprint of the cosmic large-scale structure. In particular one can recognize the imprinted pattern of filaments and clusters. This is an immediate consequence of the non-linear noise properties of the galaxy point distribution. In particular, there will be a correlation between signal and noise for any inhomogeneous point process, such as the one generating the galaxy distribution. More explicitly due to the galaxy formation processes, we expect to find more galaxies in high-density regions than in low-density regions. Any such galaxy formation process will, therefore, induce correlations between the underlying dark matter distribution and the noise of the galaxy sample. As demonstrated by Fig. 9 the algorithm correctly accounts for this non-linear relation between noisy observations and the underlying density field.
In contrast, standard deviations of primordial density amplitudes are distributed more homogeneously and show no sign of correlation with the field of primordial fluctuations. This result is anticipated, due to the propagation of information from final to initial density fields as mediated by the physical forward model.
In the course of structure formation, over-densities covering a larger Lagrangian volume in the initial conditions will collapse gravitationally to form higher density objects in the final conditions, covering much smaller volumes. These clusters of matter are then traced by observed galaxies of the 2M++ survey, which provide the data constraints on inferred density fields. While this data constraining information is contained in a smaller Eulerian volume, defined by the cluster at the final conditions, it is distributed over the larger initial Lagrangian volume of the proto-cluster when propagated backward in time.
A similar argument applies to information propagation in void regions. Since voids expand over cosmic times, data constraining information, tracing the outskirts of voids at the final conditions, will be propagated back to a smaller Lagrangian volume in the initial conditions. The process of information propagation through the forward model, therefore, homogenizes the information across inferred initial conditions. This behaviour is correctly reflected by Fig. 9.
In summary, the BORG algorithm provides us with highly detailed and physically plausible representation of three-dimensional non-linear cosmic structures and their corresponding initial conditions. The BORG algorithm also provides quantification of uncertainties for all inferred quantities via a sophisticated Markov chain Monte Carlo approach.
5.3. No evidence for a local hole
The distribution of matter in our local environment has recently attracted greater interest due to the observed tension between local and CMB measurements of H0 (see e.g., Riess et al. 2016; Planck Collaboration XIII 2016). This has triggered some activity to investigate whether the local cosmic expansion rate is faster than in the remaining universe due to the existence of a local large scale under density. Indeed several works have claimed growing evidence for the existence of such a local hole. This large-scale void is believed to extend to depth of r ∼ 150 h−1 Mpc and beyond with mass deficits of about ∼4%−40% (see e.g., Frith et al. 2003; Busswell et al. 2004; Keenan et al. 2012, 2013; Whitbourn & Shanks 2014, 2016; Böhringer et al. 2015; Hoscheit & Barger 2018).
To test the existence of such a large scale under-density we inferred the averaged density contrast in radial shells around the observer. In particular we determine the ensemble mean profile and corresponding standard deviations from our Markov chain. The results are presented in Fig. 10. Averaging over the entire sky, our approach does not provide any indication for a large scale under-density. In fact, at distances of r ∼ 150 h−1 Mpc and beyond the averaged density contrast approaches cosmic mean density.
 |
Fig. 10. Radial density profiles of matter fluctuations in shells of radius r around the observer. Left panel: spherical shells covering the full sky, while middle and right panel: density fluctuations for the 6dFGS-SGC and 6dFGS-NGC region, as defined in Whitbourn & Shanks (2014), respectively. Red lines indicate our ensemble mean estimate, while dark and light grey shaded regions indicate the 2σ and 1σ limit, respectively. The black dashed line corresponds to cosmic mean density. As can be seen our inference results do not indicate striking evidence for a large scale under-dense region using the 2M++ data. |
To further compare our results to Whitbourn & Shanks (2014) we also estimate the density contrast profile in the two regions of the northern and southern galactic cap covered by the 6dFGS survey (see e.g., Jones et al. 2009). As expected the density field in the 6dFGS-SGC field shows larger voids than the corresponding more massive 6dFGS-NGC field. However, on average we do not find any significant indication for a large-scale under-density on scales of ∼150 h−1 Mpc or larger sufficiently under-dense to explain the H0 tension.
This result is in agreement with the discussion of Wu & Huterer (2017), who argue that it would be very unlikely to obtain a sufficiently under-dense large-scale void in a ΛCDM universe. Since we fitted a particle mesh model to the data, our results thus indicate that the existence and shapes of nearby cosmic large scale structures can be explained within a standard concordance model of structure formation without invoking a particular violation of the cosmological principle or the scale of homogeneity. On the contrary, in Sect. 5.7, we show that inhomogeneities of the nearby cosmic velocity field can bias local measurements of H0, when not accounted for.
5.4. The formation history of the Supergalactic plane
As mentioned above, a particularly interesting feature of the BORG algorithm is the fact that it links primordial matter fluctuations to actual non-linear structures in the nearby universe as traced by observed galaxies. Besides providing information on the state of the cosmic LSS at the initial and final conditions, the physical forward modelling approach of the BORG algorithm also traces all intermediate dynamical states. Consequently, our algorithm infers physically plausible structure formation histories of observed objects in the nearby universe, permitting to study the formation history of the cosmic web (Jasche et al. 2015; Leclercq et al. 2015b).
As an illustration, here we present the non-linear gravitational formation of cosmic structures in the Supergalactic plane. The Supergalactic plane contains local super-clusters, like the Coma and Pisces-Cetus clusters, the Shapley concentration as well as the southern and northern local super-voids. The Supergalactic plane is of particular interest to study the dynamics in our immediate cosmic neighbourhood. It has been analysed previously with various reconstruction algorithms and data sets (Bertschinger et al. 1990; Lahav et al. 2000; Romano-Diaz & van de Weygaert 2007; Lavaux et al. 2010; Lavaux & Jasche 2016). In particular the local flows in the Supergalactic plane has been studied with distance and velocity data (Dressler 1988; Zaroubi et al. 1999; Dekel et al. 1999; Courtois et al. 2012, 2013).
In Fig. 11 we show a sequence of slices showing the plausible dynamical formation history of structures in the Supergalactic plane. To demonstrate that this formation history leads to the structures as observed in the super-galactic plane, we overlaid the inferred dark matter density field in the lower right panel of Fig. 11 with the observed galaxies in the 2M++ survey. Tracing the non-linear formation of cosmic structures provides novel avenues to understand assembly histories and galaxy formation. Details of these effects will be investigated in an upcoming publication.
 |
Fig. 11. Slices through the three-dimensional density field of the Supergalactic plane at different cosmic epochs as indicated in the respective panels. The sequence of plots represents a plausible formation history of structures in the Supergalactic plane. Initially, proto-structures arise from almost homogeneous matter distributions forming, through gravitational interaction, the cosmic web of clusters and filaments. To illustrate that this formation history yields actually observed structures we overlay the density field with galaxies of the 2M++ survey in the lower right panel. It can be seen that the galaxies in the Supergalactic plane trace the recovered density field. |
5.5. Inferring the mass of the Coma cluster
In preceding sections, we demonstrated that the BORG algorithm infers detailed three-dimensional matter density fields that are in agreement with the spatial distribution of observed galaxies. We also tested posterior power-spectra to demonstrate that these density fields obey the correct statistical properties and are plausible representations for the dark matter distribution in the universe. These obtained density fields also provide a means to estimate the masses of individual large-scale structures in the nearby universe. Mass estimation is feasible, since the BORG algorithm uses a physical model to fit redshift space distortions of observed galaxies. As such the algorithm implicitly performs various dynamical mass estimation approaches that have been proposed in the literature previously (see e.g., Eisenstein et al. 1997; Rines et al. 2001; Diaferio 2009; Rines & Diaferio 2010; Serra et al. 2011; Falco et al. 2014; Ntampaka et al. 2016).
For the sake of this work, we will illustrate the feasibility if inferring masses of cosmic structures for the particular case of the Coma cluster.
Besides Virgo and Perseus, Coma is one of the best-studied galaxy clusters in the nearby universe and is frequently used as the archetype to compare with clusters at higher redshifts (Biviano 1998; Pimbblet et al. 2014). The Coma cluster is particularly appealing to observers as it is located close to the galactic pole and has almost spherical shape (Biviano 1998).
As an illustration in Fig. 12, we show the inferred ensemble mean of the projected mass density around the Coma cluster in the sky. The plot interestingly shows the two main cosmic filaments along which mass accretes onto the coma cluster. In addition one can also observe three more fainter filaments. For completeness we also present a plot of the corresponding ensemble variance field, reflecting again the expected correlation between signal and uncertainties as discussed above.
 |
Fig. 12. Projected ensemble mean mass of inferred dark matter particles around the Coma cluster (left panel) and the corresponding ensemble variance field (right panel). One can clearly see the two major filaments along which mass accretes onto the Coma cluster. Additionally one can also notice three fainter filaments. Right panel: ensemble variance estimate for the inferred mean density field. As expected, noise and signal are correlated for a galaxy clustering survey. |
First estimates of the mass of Coma date back to Zwicky (1933, 1937). Since then the mass of the Coma cluster has been estimated via various methods, such as the virial theorem, weak gravitational lensing or X-ray observations (see e.g., The & White 1986; Hughes 1989; Colless & Dunn 1996; Geller et al. 1999; Kubo et al. 2007; Gavazzi et al. 2009; Falco et al. 2014). Consequently the Coma cluster is an excellent reference to evaluate the mass estimates obtained in this work.
In particular we estimate the cumulative radial mass profile MComa(R) around the Coma cluster given as:
where R defines the comoving distance from the Coma cluster centre to be found at the coordinates: z = 0.021, RA = 195.76deg, Dec = 28.15deg.
We also determine uncertainties in our mass estimates by applying the estimator of Eq. (26) to the ensemble of inferred density fields. This permits us to estimate the ensemble mean and corresponding variance of the radial cumulative mass profile around the Coma cluster centre. In Fig. 13 we present our estimate of the mass profile around the Coma cluster. It can be seen that the algorithm provides a coherent reconstruction over large distances around the Coma cluster.
 |
Fig. 13. Coma cumulative mass profile. We show here the relation between the distance r and the mass M(< r) enclosed within that radius. The thick solid red line is the mean relation obtained through density field derived using BORG-PM, while the light grey (dark grey respectively) gives the 68% (95% respectively) limit according to that mean. The thin blue solid line indicates the profile assuming solely the mean density of the universe. We also compare our results with the findings in the literature as indicated in the plot. It can be seen that our mass estimate for Coma agrees particularly well with complementary measurements of weak gravitational lensing or X-ray observations at scales of a few h−1 Mpc. |
Literature provides several mass estimates of the Coma cluster at different radii R from its centre (The & White 1986; Hughes 1989; Colless & Dunn 1996; Geller et al. 1999; Kubo et al. 2007; Gavazzi et al. 2009; Falco et al. 2014). In Fig. 13 we also compare these literature values, as indicated in the figure, to our inferred cumulative mass profile. As demonstrated, our results are in great agreement with mass measurements provided by previous authors. Most interestingly at radii below a few h−1 Mpc we agree well with complementary mass measurements via X-ray and gold-standard gravitational weak lensing observations (see e.g., Gavazzi et al. 2009; Falco et al. 2014).
These results demonstrate that our inferred density fields provide the correct mass estimates at the correct location in three-dimensional space. Inferred density fields are therefore in agreement with the spatial distribution of observed galaxies, they show the correct physical and statistical features and they reproduce mass estimates at the right locations that agree with complementary gold standard weak lensing or X-ray measurements.
As will be demonstrated in a forthcoming publication, similar results are obtained for all major clusters in the nearby universe. In summary, our results indicate that inferred density fields represent coherent and plausible explanations for the expected dark matter distribution in our actual universe.
5.6. The velocity field in the nearby universe
The BORG algorithm provides information on the three-dimensional velocity field, by simultaneously fitting the clustering signal of galaxies and their corresponding redshift space distortions. In particular, in order to explain the three-dimensional distribution of galaxies, the dynamical structure formation model has to account correctly for the displacement of matter from its initial Lagrangian to the final Eulerian position. To fit observations, the BORG algorithm, therefore, has to reconstruct the non-linear velocity field. Also note, as discussed in Sect. 2, the velocity field derives uniquely from the initial density field. Therefore constraints on the three-dimensional primordial fluctuations will also immediately provide constraints on final non-linear velocity fields. Additional dynamical information is inferred by explicitly fitting redshift space distortions of observed galaxies by the physical forward model. This feature of the BORG algorithm permits us to access phase-space information in observations and provide detailed flow models for the nearby universe.
More specifically, we estimate that the velocity field in the nearby universe from simulated dark matter particle realizations generated by the forward PM model of the BORG algorithm. Each particle carries position and velocity information. Estimating the velocity field from simulation particles is a challenging task. Several optimal estimators have been proposed to solve this problem satisfactorily (Colombi et al. 2007; Hahn et al. 2015). In this work, we have opted the adaptive smoothing filter described in Colombi et al. (2007). This algorithm allows projecting the properties carried by particles on any desired grid. The filter is built to preserve summations over particles, notably the mass and momentum. It also guarantees that there are no empty cells by changing the smoothing radius depending on the number of the nearest neighbours, which is kept fixed except when the number of particles per cell overflow that number. This last element ensures that the entirety of the information is always used and the momentum in a cell is truly the averaged momentum of the particles in the target cell.
The procedure to generate velocity fields is the following. First, we produce both a mass and a momentum field with the adaptive smoothing filter on a regular grid of the same size as the analysis domain but on a Cartesian grid with 10243 grid nodes, corresponding to a grid resolution of 0.67 h−1 Mpc. These two fields have the same integrals as the original particle distribution over the same enclosed sub-volumes. Then for each element of the target grids, we divide the momentum components by the mass to obtain the velocity components.
Of course the first application of the obtained 3D velocity field allows for the estimation of bulk flows in the nearby universe (Hellwing et al. 2018). But we can generate at least two other interesting scientific products.
The first product is illustrated in Fig. 14. There we show a spherical slice through the three-dimensional velocity at a distance R = 60 h−1 Mpc from the observer. The plot shows the line of sight velocity component of moving cosmic structures. As can be seen, regions coloured in red correspond to structures receding from us while regions coloured in blue indicate matter approaching the observer. At the interfaces between these two regions, we can observe a zero-crossing in the line of sight component of the velocity field. Particles close to these zero-crossing regions have almost no radial peculiar velocity component and are therefore almost ideal tracers of the Hubble flow. Our results permit to identify critical points of vanishing velocity in the nearby universe, as has been proposed to provide unbiased measurements of the Hubble parameter (Liu et al. 2016).
 |
Fig. 14. Spherical slice through the inferred three dimensional ensemble mean velocity field (left panel) and corresponding variance field (right panel). Specifically the plot shows the line of sight component of the velocity field. As indicated by the colour bar, in the left panel regions indicated in red are receding from the observer while blue regions are approaching the observer. The plot also shows regions of zero velocity along the line of sight indicating that matter in these regions follows the Hubble flow. Right panel: corresponding variance field for the line of sight velocity component. |
Previous measurements relied on linear perturbation theory and accounted only for the irrotational potential flow of the dark matter (e.g., Fisher et al. 1995; Zaroubi et al. 1999; Erdoğdu et al. 2004; Lavaux et al. 2008; Carrick et al. 2015; Ata et al. 2017; Sorce et al. 2017). By exploiting the fully non-linear particle mesh model, the BORG algorithm goes beyond such limitations by also inferring the rotational component of the velocity field, which is the second product that is directly derived from our inference framework. This rotational component of the velocity field is particularly associated with non-linear structure formation. Here we use inferred velocity fields to estimate the vorticity field given via the curl of the velocity field:
We estimate the curl via finite differencing in real space.
In Fig. 15 we present the first physical inference of the vorticity field in the nearby universe. As can be seen, the absolute amplitude of the vorticity field traces the filamentary large-scale structure. These results are in agreement with the expectations that vorticity contributes to the peculiar motions of observed galaxies at scales of 3–4 h−1 Mpc (Pichon & Bernardeau 1999). Vorticity plays an important role in structure formation in the dark matter paradigm as it can explain the generation and alignment of halo angular momentum (Libeskind et al. 2013, 2014). In Fig. 15 we also show the line of sight component of the vorticity vector field. The plot shows the characteristic quadrupolar pattern of alternating directions of rotation in the plane of the sky, as expected from simulations (Laigle et al. 2015). This specific pattern guarantees the universe to be irrotational when averaged over sufficiently large scales, such that there is no large-scale net angular momentum build-up.
 |
Fig. 15. Spherical slices through the three dimensional vorticity of the velocity field at a distance R = 60 h−1 Mpc from the observer in galactic coordinates. Left panel: projection of the vorticity vector along the line of sight, while right panel: absolute amplitude of the vorticity. As can be seen the vorticity traces the high density filamentary structure of the cosmic web. The left panel also hints towards the quadrupolar structure of the vorticity as found in simulations (see e.g., Laigle et al. 2015). |
Inferred vorticity fields could also provide a new step forward in identifying rotating galaxy clusters. Due to their formation history or recent mergers clusters may have acquired angular momentum. Ignoring such rotations will result in erroneous dynamical mass estimates, affecting the cosmological constraints provided by cluster mass functions (Baldi et al. 2017; Manolopoulou & Plionis 2017). Additionally, information on the vorticity may shed new light on the alignment of galaxy angular momentum or shapes with the cosmic large-scale structure (see e.g., Lee 2013; Zhang et al. 2013; Tempel et al. 2014, 2015; Chen et al. 2019).
In summary, our results provide new promising paths forward towards studying dynamic structure formation at non-linear scales in observations. Inferred non-linear velocity fields also provide detailed dark matter flow models for the nearby universe. These flow models are of particular relevance when attempting to measure the Hubble parameter H0 from observation in the nearby universe or calibrating standard candles such as supernovæ (see e.g., Scolnic et al. 2014).
To provide the community with an accurate flow model of the nearby universe, we will make our inferred velocity fields publicly available with a forthcoming publication as well through our web platform1.
5.7. Hubble variations
As mentioned above, inferred velocity fields permit to build refined flow models for the matter distribution in the nearby universe. This may be of relevance when performing measurements of the Hubble parameter H0 in the nearby universe, where non-vanishing Doppler shifts due to peculiar motions of observed objects may bias results. To quantify this effect for our local environment we estimate fractional variations in the Hubble parameter due to peculiar velocities via:
In Fig. 16 we demonstrate the fractional Hubble uncertainty averaged over cumulative spherical shells around the observer. As indicated by the plot, local flows out to about 70 h−1 Mpc can on average bias local measurements of the Hubble parameter by about three to ten percent. Interestingly that is about the same order of magnitude required to explain the current discrepancy between measurements of the Hubble constant in the nearby universe and by measurements of the CMB via the Planck satellite mission (see e.g., Bernal et al. 2016; Addison et al. 2016; Feeney et al. 2019).
 |
Fig. 16. Possible biases arising from doing a Hubble measurement with tracers within some volume, neglecting complex cosmic flows effect. We show in red solid line the mean systematic bias for a Hubble measurement per tracer located within a sphere of radius R. The grey area corresponds to the expected 1σ fluctuation per tracer of that same measurement. We show, for reference, the measurement by Riess et al. (2016; in blue and shade of blue for the 1σ limit) of the Hubble constant relatively to the Planck one (centred on zero, and shade of green for the 1σ limit). |
In particular, we indicated the discrepancy between the measurements of the Planck collaboration (Planck Collaboration XIII 2016) and those obtained by Riess et al. (2016) in the figure. Since we have reconstructions of the three-dimensional velocity field we can also estimate the fractional Hubble uncertainty as a function of direction in the sky. These results are presented in Fig. 17. It can be seen, that there exists large coherent bulk flows in the direction towards Perseus-Pisces super-cluster, which may bias measurements of H0.
 |
Fig. 17. Prediction of the fractional Hubble uncertainty as a function of direction within 60 h−1 Mpc around the observer. As can be seen, the fractional Hubble uncertainty is highly structured on the sky, with large-scale coherent bulk flows. The dominant red central region points towards the direction of Perseus Pisces. These effects need to be accounted for when inferring the Hubble parameter from data of the nearby universe. |
It is also interesting to note, that we obtain on average a positive bias in the fractional Hubble uncertainty due to peculiar velocities. This seems to be a specific feature of the nearby matter distribution. In general, within a standard ΛCDM scenario, positive and negative bias should be equally likely on average.
Answering the question, whether or not the discrepancy in measurements of the Hubble parameters can contribute to resolving this issue needs to be investigated further in a future work. By providing new and refined flow models our work will contribute to either identifying the dynamics of the local structure as part of the systematics or ruling it out as a plausible explanation for the discrepancy of measurements of the Hubble parameter in the nearby universe.
6. Summary and conclusions
This work presents an extension of our previously developed BORG algorithm to perform analyses of observed galaxy clustering beyond the regime of linear perturbation. To achieve this goal we have implemented a numerical particle mesh algorithm into our previously developed Bayesian inference approach to account for the fully non-linear regime of gravitational structure formation.
As a result, our method fits full numerical structure formation simulations to data and infers the three-dimensional initial conditions from which present observations formed. The method is a fully Bayesian inference algorithm that jointly infers information of the three-dimensional density and velocity fields and unknown observational systematic effects, such as noise, galaxy biasing and selection effects while quantifying their respective and correlated uncertainties via a large scale Markov chain Monte Carlo framework.
Typically the algorithm explores parameter spaces consisting of the order of ten million dimensions corresponding to the amplitudes of the primordial density field at different positions in the three-dimensional volume. To perform efficient MCMC sampling with a complex physics model in such high dimensional parameter spaces we rely on a sophisticated implementation of the HMC algorithm. The HMC employs concepts of classical mechanics to reduce the random walk behaviour of standard Metropolis-Hastings algorithms by following a persistent Hamiltonian trajectory in the parameter space. In particular, the HMC exploits pseudo energy conservation to guarantee a high acceptance rate of proposed density field realizations and uses gradients of the logarithmic posterior distribution to guide the exploration in high dimensional parameter spaces. This requires providing to the algorithm derivatives of the logarithm of the likelihood distribution.
This likelihood distribution describes the statistical process by which the galaxy observations were generated given a specific realization of the non-linear density field. As described in Sect. 3, for the sake of this work, the likelihood distribution combines a non-linear galaxy biasing model and the non-linear structure formation model with a Poisson distribution to account for the noise of the observed galaxy distribution.
In order to use the HMC in this scenario, we need to provide derivatives of the logarithm of this likelihood distribution with respect to the three-dimensional field of primordial matter fluctuations, acting as the initial conditions to the employed forward physics model. Since the likelihood incorporates a non-linear numerical structure formation model there exists no analytic gradient with respect to the initial conditions. One, therefore, has to rely on numerical representations of this derivative.
We note that using finite differencing to obtain gradients will not be sufficient. First of all, gradients obtained by finite differencing are numerically too noisy to be useful. Second, evaluating gradients in this fashion would be numerically too expensive. For cases as discussed in this work, finite difference approaches would require more than 10 million model evaluations to calculate a single gradient, which is numerically prohibitive with current computing resources. To obtain gradients of the logarithmic likelihood we, therefore, need to follow a different numerical approach.
As described in Sect. 3.2, any numerical algorithm can be understood as the composition of elementary operations for which there exist analytic derivatives. As described in Appendix C, this permits us to apply the chain rule of differentiation to the physical simulation algorithm to implement an algorithmic gradient of the physics model. As demonstrated in Sect. 3.2, this algorithmic derivative comes at the cost of only two forward physics model evaluations, rendering this approach highly efficient and suitable for high dimensional problems.
To further exploit modern massive parallel computing resources we have also parallelized our algorithm via the MPI message passing systems. As demonstrated in Sect. 3.2 and by Fig. 3 the implementation of our algorithm reaches near optimal scaling as a function of the number of used cores. The numerical implementation of our algorithm, therefore, provides an efficient approach to sample the three-dimensional density and velocity fields. This constitutes the core element of our sampling scheme as outlined in Fig. 1.
Employing a forward physics model for the analysis permits us to address observational effects due to non-linear structure formation processes. First of all, our approach accounts for the higher order statistics, associated with the filamentary pattern of the cosmic web. In addition, the dynamical information provided by the physics model permits to account for redshift space distortions effects associated with the peculiar motions of observed objects. As such our method not only extracts information from the clustering signal of the galaxy number counts distribution but also extracts partial dynamic information from redshift space distortions, carrying information on the line of sight projections of peculiar velocities.
Besides accounting for structure formation effects, accessing information at non-linear regimes galaxy data is a non-trivial task. We are confronted with a variety of stochastic and systematic uncertainties, such as unknown noise levels, galaxy biases or incomplete observations. To properly account for these effects we employ a hierarchical Bayes approach in combination with a block sampling approach permitting us to flexibly construct data models to account for individual systematic uncertainties of respective datasets used for the analysis.
Specifically, in order to describe the unknown non-linear biasing relation between observed galaxies and the underlying dark matter distribution in this work, we used a phenomenological truncated power-law model as previously proposed by Neyrinck et al. (2014). This bias model has three free parameters which are inferred jointly with the three-dimensional density field via a multiple block sampling framework. Similarly, the BORG algorithm jointly infers unknown noise levels of the survey, related to the expected number of galaxies. Galaxy biasing can differ as a function of galaxy properties such as luminosity. To account for such luminosity dependent galaxy clustering we typically split our galaxy sample into different subsets according to luminosity or other parameters. The BORG algorithm then accounts for the respective uncertainties of individual subsamples while jointly inferring information from the combination of those. Joint and correlated uncertainties between all inference parameters are quantified by performing a thorough Markov chain Monte Carlo via the block sampling scheme described in Sect. 3.4 and visualized by Fig. 1.
A common issue of analysing the cosmic LSS in galaxy observations is the fact that there exists currently no accurate data model that captures all nuances of unknown galaxy formation processes at non-linear scales. Therefore a necessary requirement for the analyses of present and next-generation surveys is the construction of inference approaches that can cope with unknown systematics and misspecifications of the data model. As discussed in Sect. 3.5 we explored the possibility to perform robust inference by not conditioning directly on the likelihood but on some neighbourhood of the specified likelihood distribution. This approach amounts to tempering the likelihood distribution by raising it to some positive power, which is equivalent to using only a homogeneous subset of the data. The approach, therefore, provides conservative estimates of the cosmic large-scale structure since it effectively reduces the amount of information that can be used to reliably infer the matter distribution. Exploiting the full potential of observed data requires developing better data models, which is an ongoing activity of the cosmological community.
In Sect. 4 we perform an analysis of the cosmic LSS in the nearby universe. This is achieved by applying our BORG algorithm to the 2M++ galaxy compilation, covering about 70% of the sky. We split the 2M++ galaxy sample into a total of 16 sub-sets as a function of luminosity and the two absolute K-band magnitude cuts at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5. Splitting the galaxy sample into these subsets permits us to treat luminosity dependent galaxy biases as well as respective selection effects due to flux limitations and survey masks. The BORG algorithm infers information jointly from the combination of these galaxy subsets while accounting for their respective systematic and stochastic uncertainties.
As described in Sect. 4.2, we inferred the field of primordial matter fluctuations on a cubic equidistant Cartesian grid of side length 677.77 h−1 Mpc consisting of 2563 volume elements. This amounts to a grid resolution of ∼2.6 h−1 Mpc in initial Lagrangian space. To guarantee a sufficient resolution of the final Eulerian density field we oversample the initial density field by a factor eight, requiring to evaluate the particle mesh model with a total of 5123 simulation particles. Running the particle mesh model for every transition step in the Markov chain is numerically expensive. To efficiently pass through the initial burn-in period of the Markov chain we initialized the run with a faster but approximate Lagrangian perturbation theory model for about 6700 Markov transition steps. Then we switched to the full particle mesh model to infer the fully non-linear regime of cosmic structures in the 2M++ survey.
We tested the initial burn-in behaviour of our sampler by initializing the run with a Gaussian random guess for the initial density field and scaled the amplitudes by a factor 0.1 to start from an over-dispersed state. The initial burn-in behaviour was then tested by following the systematic drift of subsequently measured posterior power-spectra towards the preferred region in parameter space. As discussed in Sect. 4.3, this initial burn-in period is completed after about 4000 sampling steps, when inferred power-spectra start oscillating homogeneously around a fiducial cosmological power-spectrum. We note, that during the initial burn-in period our approach not only adjust the three-dimensional density field but also simultaneously explores the optimal parameter settings for the non-linear galaxy bias model and corresponding unknown noise levels.
Once we switched to running the analysis with the full particle mesh model we follow the initial burn-in behaviour of the non-linear analysis by tracing the logarithmic likelihood across subsequent sampling steps. The observed gains are considerable. With respect to the initial logarithmic likelihood value obtained from the approximate LPT run, we gain five orders of magnitude of improvement in the differential logarithmic likelihood when running the analysis with the non-linear particle mesh model. The logarithm of the ratio of the likelihood value for the LPT run and the full PM run therefore qualify for a model comparison test for the best representation of the three-dimensional density field able to explain the observations. These results are a clear demonstration that our reconstructions are clearly outperforming any previous results based on Eulerian or Lagrangian perturbation theory.
To further investigate the improvements of the PM over the LPT model, we also studied the traces of the logarithmic likelihood functions for the 16 galaxy sub-samples used for our analysis. We observed that fainter galaxy samples experience fewer improvements than brighter ones. This is expected, since fainter galaxies are believed to live in regions that can be described better by LPT rather than brighter galaxies, living in highly non-linear regimes of the cosmic LSS. It may be interesting to investigate the details of this effect in future analyses, as it may provide a guideline to optimally select galaxies for cosmological analyses.
In Sect. 5 we presented the results of our cosmological analysis of the 2M++ galaxy compilation. We first presented the inference of the 16 non-linear galaxy bias functions for the respective galaxy subsets as split by luminosity. As discussed above the galaxy biasing relation is modelled via a four parameter truncated power-law model.
It is interesting to remark that the inferred shapes of biasing functions are in agreement with the previous findings of Sousbie et al. (2008). In general we observe an agreement in the biasing functions for fainter galaxies between galaxies selected in the two K-band magnitude ranges at K2M + + ≤ 11.5 and 11.5 < K2M + + ≤ 12.5. For brighter galaxies we observe a difference in the biasing relations between the two apparent magnitude cuts. Whether this indicates a difference in clustering behaviour of galaxies in the respective samples or whether it is due to some contamination or systematic effect needs to be investigated in the future. In any case it can clearly be seen that the galaxy bias functions preferred by the data cannot be described by simple linear biasing relations.
The BORG algorithm infers the field of primordial density fluctuations with a Lagrangian resolution of ∼2.6 h−1 Mpc. This is sufficient to resolve the initial conditions of major features in the nearby universe. As demonstrated in Sect. 5.2 the BORG algorithm simultaneously infers the present non-linear matter distribution of the universe together with the three-dimensional initial conditions from which present structures formed. Our algorithm not only provides simple point estimates, such as the mean or maximum a posteriori result but provides a numerical approximation to the actual posterior distribution of the three-dimensional cosmic LSS in terms of an ensemble of density field realizations generated by the Markov chain. The ensemble of data constrained Markov samples permits us to quantify the uncertainties of inferred initial and final density fields. To illustrate this fact in Fig. 9 we show a plot of the ensemble mean density fields and corresponding standard deviations. The plot nicely demonstrates the feasibility to recover the detailed filamentary pattern of the matter distribution in our universe.
Unlike simple point estimates, respective Markov samples of the density field represent statistically and physically plausible realizations of the actual matter distribution in our universe. They are not affected by incomplete observations or selection effects and can be straightforwardly interpreted as physically reasonable quantities.
In particular, Fig. 7 demonstrates that regions which are only poorly sampled by observed galaxies are visually similar to regions with much higher signal to noise ratios. Our inferred density samples reveal a highly detailed filamentary cosmic web corresponding to the spatial distribution of actually observed galaxies in the 2M++ survey. To test whether these inferred density fields are also physically plausible representations of a dark matter density field we measured a posteriori power-spectra from inferred initial conditions. This test reveals that the BORG algorithm is able to reliably recover the dark matter distribution over a huge dynamic range covering three orders of magnitudes of the cosmological power-spectrum. As demonstrated by Fig. 8 measured power-spectra agree well with a fiducial cosmological model, demonstrating that our inference results are unbiased throughout the entire ranges of Fourier modes considered in this work. We further tested the one-point distribution of primordial density fluctuations and showed the agreement with the assumption of Gaussian statistics.
The spatial correspondence between inferred density fields and observed galaxies together with the agreement of inferred power-spectra with the fiducial cosmological model indicates that our results are physically plausible representations of the dark matter distribution in our universe.
To further investigate this fact, in Sect. 5.5 we estimated the radial mass profile around the Coma cluster. The Coma cluster is one of the best studied clusters in the nearby universe and literature provides a plenitude of measurement results for the Coma mass. In contrast to previous measurements we are able to provide the first continuous measurement of the mass profile around the Coma cluster. We also compared our estimates to previous results obtained via complementary measurements of weak lensing and X-ray observations. As demonstrated by Fig. 13 our results agree well with gold standard weak lensing mass estimates at the scales of ∼1 h−1 Mpc. These results demonstrate that our inferred dark matter density fields provide the correct amount of matter at the correct spatial locations in the nearby universe.
In summary we conclude that the obtained density fields are physically plausible representations for the matter distribution in the nearby universe. A more detailed analysis and mass estimates for various structures in our nearby neighbourhood will be presented in a coming publication.
The possibility to infer masses of respective cosmological structures is related to the fact that the BORG algorithm exploits a dynamical physical model to fit redshift space distortions of observed objects. Thus our algorithm extracts velocity information from redshift distortions and implicitly applies various dynamical mass estimation techniques that have been presented in the literature (Eisenstein et al. 1997; Rines et al. 2001; Diaferio 2009; Rines & Diaferio 2010; Serra et al. 2011; Falco et al. 2014; Ntampaka et al. 2016).
To further illustrate the feasibility to infer the dynamic state of cosmic structures from observations, in Sect. 5.6 we provide information on the inferred three-dimensional velocity field of our nearby universe.
As a complete novelty we are the first to reconstruct the rotational component of the velocity field from observations. As demonstrated by Fig. 15 this vorticity field traces the non-linear filamentary structures around the Perseus-Pisces and Virgo cluster. When studying the directional components of the vorticity vector field we find a similar quadrupolar structure has been observed in simulations previously. These results therefore provide new avenues to test the alignment of galaxy spin with the cosmic LSS and the generation of angular momentum in the course of structure formation.
Our inferred velocity fields provide a new flow model for the three-dimensional large scale motion of matter in the nearby universe. Accounting for the specific realization of the velocity field is of particular relevance to measurements of the Hubble parameter in the Nearby universe. To demonstrate this effect in Sect. 5.7 we estimated the fractional uncertainty in measurements of the Hubble parameter due to the peculiar motion of observed objects. In particular Fig. 16 indicates that there is a risk to bias estimates of the Hubble parameter when not accounting for such peculiar motions. Interestingly for tracer particles at distances between 10 and 70 h−1 Mpc our results show a fractional Hubble uncertainty due to peculiar motions that are compatible with the currently debated discrepancy in the measurements of the Hubble parameter from local and CMB observations. As demonstrated by Fig. 17, peculiar velocities introduce a highly inhomogeneous and asymmetric distribution of the fractional Hubble uncertainties at different positions in the sky. One needs to investigate further in the future whether these effects can contribute to the observed discrepancy in measurements of H0.
To further investigate the possible impact of nearby cosmic structures on local measurements of the accelerated cosmic expansion, we also investigated the possible existence of a large-scale local under density out to a depth of 150 h−1 Mpc and beyond, which could mimic the acceleration effects attributed to dark energy. Despite the claim of growing evidence for such a local hole in the literature (see e.g., Whitbourn & Shanks 2016; Hoscheit & Barger 2018), our inferred radial density profiles, shown in Fig. 10, provide no support for the existence of such a large local void. In fact, our results indicate that the existence of local cosmic structures can be explained by the concordance model of structure formation without any violation of the cosmological principle or scale of homogeneity. Our result, therefore, agrees with the discussion of Wu & Huterer (2017).
In summary, this work presents a modification of our BORG algorithm capable of exploring the non-linear regime of the observed galaxy distribution by using physical models of gravitational structure formation. The algorithm provides us with simultaneous reconstructions of present non-linear cosmic structures and the initial conditions from which they formed. We further obtain detailed measurements of the three-dimensional flow of matter and infer plausible structure formation histories for the nearby universe. Inferred density and velocity fields represent a detailed and accurate description of the actual matter distribution, resembling correctly the filamentary cosmic web and masses of individual structures in the nearby universe.
This work is a clear demonstration that complex analyses of non-linear structures in galaxy surveys subject to several systematic and stochastic uncertainties is feasible and produces significant scientific results. In consequence, the BORG algorithm provides the key technology to study the non-linear regime of three-dimensional cosmic structures in present and coming galaxy surveys.
Available at https://cosmicflows.iap.fr/
Acknowledgments
This research was supported by the DFG cluster of excellence “Origin and Structure of the Universe” (www.universe-cluster.de). This work made in the ILP LABEX (under reference ANR-10-LABX-63) was supported by French state funds managed by the ANR within the Investissements d’Avenir programme under reference ANR-11-IDEX-0004-02. The Parkes telescope is part of the Australia Telescope which is funded by the Commonwealth of Australia for operation as a National Facility managed by CSIRO. We acknowledge financial support from “Programme National de Cosmologie and Galaxies” (PNCG) of CNRS/INSU, France. This work was supported by the ANR grant ANR-16-CE23-0002. This work was granted access to the HPC resources of CINES under the allocation A0020410153 made by GENCI. We acknowledge several constructive discussions with Benjamin Wandelt, Stéphane Colombi, Franz Elsner, Florent Leclercq, Fabian Schmidt, Licia Verde, Simon White and Carlos Frenk. We also acknowledge reading of the early draft by Doogesh Kodi Ramanah. GL acknowledges the hospitality of the University of Helsinki, where part of the development of that project took place, notably Peter Johansson, Till Sawala. This work has made use of the Horizon Cluster hosted by Institut d’Astrophysique de Paris. This work has been done within the activities of the Domaine d’Intérêt Majeur (DIM) Astrophysique et Conditions d’Apparition de la Vie (ACAV), and received financial support from Région Ile-de-France.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Addison, G. E., Huang, Y., Watts, D. J., et al. 2016, ApJ, 818, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Ata, M., Kitaura, F.-S., & Müller, V. 2015, MNRAS, 446, 4250 [NASA ADS] [CrossRef] [Google Scholar]
- Ata, M., Kitaura, F.-S., Chuang, C.-H., et al. 2017, MNRAS, 467, 3993 [NASA ADS] [Google Scholar]
- Baldi, A. S., De Petris, M., Sembolini, F., et al. 2017, MNRAS, 465, 2584 [NASA ADS] [CrossRef] [Google Scholar]
- Bellman, R. 1961, Adaptive Control Processes: A Guided Tour (Princeton University Press: Princeton Legacy Library) [CrossRef] [Google Scholar]
- Bernal, J. L., Verde, L., & Riess, A. G. 2016, JCAP, 10, 019 [NASA ADS] [CrossRef] [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bertschinger, E., Dekel, A., Faber, S. M., Dressler, A., & Burstein, D. 1990, ApJ, 364, 370 [NASA ADS] [CrossRef] [Google Scholar]
- Bhattacharya, A., Pati, D., & Yang, Y. 2016, ArXiv e-prints [arXiv:1611.01125] [Google Scholar]
- Biviano, A. 1998, in Untangling Coma Berenices: A New Vision of an Old Cluster, eds. A. Mazure, F. Casoli, F. Durret, & D. Gerbal [Google Scholar]
- Blanton, M. R., Eisenstein, D., Hogg, D. W., Schlegel, D. J., & Brinkmann, J. 2005, ApJ, 629, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Chon, G., Bristow, M., & Collins, C. A. 2015, A&A, 574, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brenier, Y., Frisch, U., Hénon, M., et al. 2003, MNRAS, 346, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Bruck, J., Dolev, D., Ho, C.-T., Roşu, M.-C., & Strong, R. 1997, J. Parallel Distrib. Comput., 40, 19 [CrossRef] [Google Scholar]
- Busswell, G. S., Shanks, T., Frith, W. J., et al. 2004, MNRAS, 354, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Carrick, J., Turnbull, S. J., Lavaux, G., & Hudson, M. J. 2015, MNRAS, 450, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y. C., Ho, S., Blazek, J., et al. 2019, MNRAS, 485, 2492 [NASA ADS] [CrossRef] [Google Scholar]
- Colless, M., & Dunn, A. M. 1996, ApJ, 458, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., Chodorowski, M. J., & Teyssier, R. 2007, MNRAS, 375, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., Hoffman, Y., Tully, R. B., & Gottlöber, S. 2012, ApJ, 744, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., Pomarède, D., Tully, R. B., Hoffman, Y., & Courtois, D. 2013, AJ, 146, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Crocce, M., & Scoccimarro, R. 2006, Phys. Rev. D, 73, 063520 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Strauss, M. A., & Yahil, A. 1991, ApJ, 372, 394 [NASA ADS] [CrossRef] [Google Scholar]
- Dekel, A., Eldar, A., Kolatt, T., et al. 1999, ApJ, 522, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Desjacques, V., Jeong, D., & Schmidt, F. 2018, Phys. Rep., 733, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Desmond, H., Ferreira, P. G., Lavaux, G., & Jasche, J. 2018, MNRAS, 474, 3152 [NASA ADS] [CrossRef] [Google Scholar]
- Desmond, H., Ferreira, P. G., Lavaux, G., & Jasche, J. 2019, MNRAS, 483, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Diaferio, A. 2009, ArXiv e-prints [arXiv:0901.0868] [Google Scholar]
- Dodelson, S., Heitmann, K., Hirata, C., et al. 2016, ArXiv e-prints [arXiv:1604.07626] [Google Scholar]
- Doumler, T., Hoffman, Y., Courtois, H., & Gottlöber, S. 2013, MNRAS, 430, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A. 1988, ApJ, 329, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Duane, S., Kennedy, A. D., Pendleton, B. J., & Roweth, D. 1987, Phys. Lett. B, 195, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G., Davis, M., White, S. D. M., & Frenk, C. S. 1985, ApJS, 57, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1999, ApJ, 511, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Loeb, A., & Turner, E. L. 1997, ApJ, 475, 421 [NASA ADS] [CrossRef] [Google Scholar]
- Elsner, F., & Wandelt, B. D. 2013, A&A, 549, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Erdoğdu, P., Lahav, O., Zaroubi, S., et al. 2004, MNRAS, 352, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Eriksen, H. K., O’Dwyer, I. J., Jewell, J. B., et al. 2004, ApJS, 155, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Falco, M., Hansen, S. H., Wojtak, R., et al. 2014, MNRAS, 442, 1887 [NASA ADS] [CrossRef] [Google Scholar]
- Feeney, S. M., Peiris, H. V., Williamson, A. R., et al. 2019, Phys. Rev. Lett., 122, 061105 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, K. B., Lahav, O., Hoffman, Y., Lynden-Bell, D., & Zaroubi, S. 1995, MNRAS, 272, 885 [NASA ADS] [Google Scholar]
- Frazier, D. T., Robert, C. P., & Rousseau, J. 2017, ArXiv e-prints [arXiv:1708.01974] [Google Scholar]
- Freese, K. 2017, Int. J. Mod. Phys. D, 26, 1730012 [NASA ADS] [CrossRef] [Google Scholar]
- Frith, W. J., Busswell, G. S., Fong, R., Metcalfe, N., & Shanks, T. 2003, MNRAS, 345, 1049 [NASA ADS] [CrossRef] [Google Scholar]
- Frusciante, N., & Sheth, R. K. 2012, JCAP, 11, 016 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Adami, C., Durret, F., et al. 2009, A&A, 498, L33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geller, M. J., Diaferio, A., & Kurtz, M. J. 1999, ApJ, 517, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Geman, S., & Geman, D. 1984, IEEE Trans. Pattern Recognit., 6, 721 [Google Scholar]
- Gibbs, J. W. 1906, The Scientific Papers of J. Willard Gibbs (Longmans Green and Co.), 1 [Google Scholar]
- Gil-Marín, H., Percival, W. J., Cuesta, A. J., et al. 2016, MNRAS, 460, 4210 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Granett, B. R., Branchini, E., Guzzo, L., et al. 2015, A&A, 583, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grünwald, P., & van Ommen, T. 2014, ArXiv e-prints [arXiv:1412.3730] [Google Scholar]
- Hahn, O., Angulo, R. E., & Abel, T. 2015, MNRAS, 454, 3920 [NASA ADS] [CrossRef] [Google Scholar]
- Hellwing, W. A., Bilicki, M., & Libeskind, N. I. 2018, Phys. Rev. D, 97, 103519 [NASA ADS] [CrossRef] [Google Scholar]
- Hockney, R. W., & Eastwood, J. W. 1988, Computer Simulation using Particles (Bristol, PA, USA: Taylor & Francis, Inc.) [Google Scholar]
- Hoffman, Y. 1994, in Unveiling Large-scale Structures Behind the Milky Way, eds. C. Balkowski, & R. C. Kraan-Korteweg, ASP Conf. Ser., 67, 185 [NASA ADS] [Google Scholar]
- Holmes, C., & Walker, S. 2017, ArXiv e-prints [arXiv:1701.08515] [Google Scholar]
- Hoscheit, B. L., & Barger, A. J. 2018, ApJ, 854, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Huchra, J. P., Macri, L. M., Masters, K. L., et al. 2012, ApJS, 199, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, J. P. 1989, ApJ, 337, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Hutschenreuter, S., Dorn, S., Jasche, J., et al. 2018, Class. Quant. Grav., 35, 154001 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Kitaura, F. S. 2010, MNRAS, 407, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Lavaux, G. 2015, MNRAS, 447, 1204 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Lavaux, G. 2017, A&A, 606, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jasche, J., & Wandelt, B. D. 2013a, ApJ, 779, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., & Wandelt, B. D. 2013b, MNRAS, 432, 894 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Kitaura, F. S., Wandelt, B. D., & Enßlin, T. A. 2010a, MNRAS, 406, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Kitaura, F. S., Li, C., & Enßlin, T. A. 2010b, MNRAS, 409, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Jasche, J., Leclercq, F., & Wandelt, B. D. 2015, JCAP, 1, 36 [Google Scholar]
- Jones, D. H., Read, M. A., Saunders, W., et al. 2009, MNRAS, 399, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. C., Barger, A. J., Cowie, L. L., et al. 2012, ApJ, 754, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Keenan, R. C., Barger, A. J., & Cowie, L. L. 2013, ApJ, 775, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F.-S. 2013, MNRAS, 429, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F. S., & Enßlin, T. A. 2008, MNRAS, 389, 497 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F. S., Jasche, J., Li, C., et al. 2009, MNRAS, 400, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Kitaura, F.-S., Jasche, J., & Metcalf, R. B. 2010, MNRAS, 403, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., & Holtzman, J. 1997, ArXiv e-prints [arXiv:astro-ph/9712217] [Google Scholar]
- Klypin, A. A., & Shandarin, S. F. 1983, MNRAS, 204, 891 [NASA ADS] [Google Scholar]
- Kodi Ramanah, D., Lavaux, G., Jasche, J., & Wandelt, B. D. 2019, A&A, 621, A69 [CrossRef] [EDP Sciences] [Google Scholar]
- Kubo, J. M., Stebbins, A., Annis, J., et al. 2007, ApJ, 671, 1466 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O. 1994, in Unveiling Large-Scale Structures Behind the Milky Way, eds. C. Balkowski, & R. C. Kraan-Korteweg, ASP Conf. Ser., 67, 171 [NASA ADS] [Google Scholar]
- Lahav, O., Fisher, K. B., Hoffman, Y., Scharf, C. A., & Zaroubi, S. 1994, ApJ, 423, L93 [NASA ADS] [CrossRef] [Google Scholar]
- Lahav, O., Santiago, B. X., Webster, A. M., et al. 2000, MNRAS, 312, 166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laigle, C., Pichon, C., Codis, S., et al. 2015, MNRAS, 446, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lavaux, G. 2010, MNRAS, 406, 1007 [NASA ADS] [Google Scholar]
- Lavaux, G., & Hudson, M. J. 2011, MNRAS, 416, 2840 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., & Jasche, J. 2016, MNRAS, 455, 3169 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., & Wandelt, B. D. 2012, ApJ, 754, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., Mohayaee, R., Colombi, S., et al. 2008, MNRAS, 383, 1292 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., Tully, R. B., Mohayaee, R., & Colombi, S. 2010, ApJ, 709, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Leclercq, F., Jasche, J., Sutter, P. M., Hamaus, N., & Wandelt, B. 2015a, JCAP, 3, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Leclercq, F., Jasche, J., & Wandelt, B. 2015b, JCAP, 6, 015 [CrossRef] [Google Scholar]
- Leclercq, F., Jasche, J., Lavaux, G., Wandelt, B., & Percival, W. 2017, JCAP, 6, 049 [Google Scholar]
- Lee, J. 2013, ArXiv e-prints [arXiv:1301.0348] [Google Scholar]
- Leistedt, B., & Peiris, H. V. 2014, MNRAS, 444, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Hoffman, Y., Steinmetz, M., et al. 2013, ApJ, 766, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Hoffman, Y., & Gottlöber, S. 2014, MNRAS, 441, 1974 [NASA ADS] [CrossRef] [Google Scholar]
- Liouville, J. 1838, J. de Math., 3, 349 [Google Scholar]
- Liu, H., Mohayaee, R., & Naselsky, P. 2016, JCAP, 6, 009 [NASA ADS] [CrossRef] [Google Scholar]
- LSST Science Collaboration (Abell, P. A., et al.) 2009, ArXiv e-prints [arXiv:0912.0201] [Google Scholar]
- Ma, Y.-Z., & Scott, D. 2016, Phys. Rev. D, 93, 083510 [NASA ADS] [CrossRef] [Google Scholar]
- Manolopoulou, M., & Plionis, M. 2017, MNRAS, 465, 2616 [NASA ADS] [CrossRef] [Google Scholar]
- Mather, J. C., Cheng, E. S., Eplee, Jr., R. E., et al. 1990, ApJ, 354, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubara, T. 1995, ApJS, 101, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubara, T. 2011, Phys. Rev. D, 83, 083518 [NASA ADS] [CrossRef] [Google Scholar]
- Melott, A. L., Buchert, T., & Weiß, A. G. 1995, A&A, 294, 345 [NASA ADS] [Google Scholar]
- Miller, J. W., & Dunson, D. B. 2015, ArXiv e-prints [arXiv:1506.06101] [Google Scholar]
- Neal, R. M. 1993, Probabilistic Inference using Markov Chain Monte Carlo methods, Tech. Rep. CRG-TR-93-1 (University of Toronto) [Google Scholar]
- Neal, R. M. 1996, in Bayesian Learning for Neural Networks, 1st edn. (Springer), Lecture Notes in Statistics [CrossRef] [Google Scholar]
- Neal, R. 2000, Ann. Stat., 31, 705 [CrossRef] [Google Scholar]
- Neal, R. M. 2012, ArXiv e-prints [arXiv:1206.1901] [Google Scholar]
- Neyrinck, M. C., Aragón-Calvo, M. A., Jeong, D., & Wang, X. 2014, MNRAS, 441, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Noh, Y., White, M., & Padmanabhan, N. 2009, Phys. Rev. D, 80, 123501 [NASA ADS] [CrossRef] [Google Scholar]
- Ntampaka, M., Trac, H., Sutherland, D. J., et al. 2016, ApJ, 831, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A., & Branchini, E. 2000, MNRAS, 313, 587 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A., & Dekel, A. 1992, ApJ, 391, 443 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A., Cole, S., Norberg, P., et al. 2001, Nature, 410, 169 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton University Press) [Google Scholar]
- Percival, W. J., Cole, S., Eisenstein, D. J., et al. 2007, MNRAS, 381, 1053 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pichon, C., & Bernardeau, F. 1999, A&A, 343, 663 [NASA ADS] [Google Scholar]
- Pimbblet, K. A., Penny, S. J., & Davies, R. L. 2014, MNRAS, 438, 3049 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Porqueres, N., Jasche, J., Enßlin, T. A., & Lavaux, G. 2018, A&A, 612, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pullen, A. R., & Hirata, C. M. 2010, JCAP, 5, 027 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., & Diaferio, A. 2010, AJ, 139, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Rines, K., Geller, M. J., Kurtz, M. J., et al. 2001, ApJ, 561, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Romano-Diaz, E., & van de Weygaert, R. 2007, ArXiv e-prints [arXiv:0707.2607] [Google Scholar]
- Saunders, W., Sutherland, W. J., Maddox, S. J., et al. 2000, MNRAS, 317, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. M. 2017, ArXiv e-prints [arXiv:1701.04469] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Schmittfull, M., Feng, Y., Beutler, F., Sherwin, B., & Chu, M. Y. 2015, Phys. Rev. D, 92, 123522 [NASA ADS] [CrossRef] [Google Scholar]
- Schmittfull, M., Baldauf, T., & Zaldarriaga, M. 2017, Phys. Rev. D, 96, 023505 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D., Rest, A., Riess, A., et al. 2014, ApJ, 795, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., Aslanyan, G., Feng, Y., & Modi, C. 2017, JCAP, 2017, 009 [CrossRef] [Google Scholar]
- Serra, A. L., Diaferio, A., Murante, G., & Borgani, S. 2011, MNRAS, 412, 800 [NASA ADS] [Google Scholar]
- Shi, Y., Cautun, M., & Li, B. 2018, Phys. Rev. D, 97, 023505 [NASA ADS] [CrossRef] [Google Scholar]
- Sigad, Y., Dekel, A., & Branchini, E. 2000, in Cosmic Flows Workshop, eds. S. Courteau, & J. Willick, ASP Conf. Ser., 201, 360 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Smoot, G. F., Bennett, C. L., Kogut, A., et al. 1992, ApJ, 396, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Sorce, J. G., Hoffman, Y., & Gottlöber, S. 2017, MNRAS, 468, 1812 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., Courtois, H., Bryan, G., & Devriendt, J. 2008, ApJ, 678, 569 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Szalay, A. S. 1988, ApJ, 333, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Tassev, S., & Zaldarriaga, M. 2012, JCAP, 2012, 013 [CrossRef] [Google Scholar]
- Tegmark, M., Blanton, M. R., Strauss, M. A., et al. 2004, ApJ, 606, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Libeskind, N. I., Hoffman, Y., Liivamägi, L. J., & Tamm, A. 2014, MNRAS, 437, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Guo, Q., Kipper, R., & Libeskind, N. I. 2015, MNRAS, 450, 2727 [NASA ADS] [CrossRef] [Google Scholar]
- The, L. S., & White, S. D. M. 1986, AJ, 92, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Yang, X., & van den Bosch, F. C. 2013, ApJ, 772, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H., Mo, H. J., Yang, X., Jing, Y. P., & Lin, W. P. 2014, ApJ, 794, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Webster, M., Lahav, O., & Fisher, K. 1997, MNRAS, 287, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Whitbourn, J. R., & Shanks, T. 2014, MNRAS, 437, 2146 [NASA ADS] [CrossRef] [Google Scholar]
- Whitbourn, J. R., & Shanks, T. 2016, MNRAS, 459, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, H.-Y., & Huterer, D. 2017, MNRAS, 471, 4946 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, X., Padmanabhan, N., Eisenstein, D. J., Mehta, K. T., & Cuesta, A. J. 2012, MNRAS, 427, 2146 [NASA ADS] [CrossRef] [Google Scholar]
- Zaroubi, S., Hoffman, Y., Fisher, K. B., & Lahav, O. 1995, ApJ, 449, 446 [NASA ADS] [CrossRef] [Google Scholar]
- Zaroubi, S., Hoffman, Y., & Dekel, A. 1999, ApJ, 520, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Yang, X., Wang, H., et al. 2013, ApJ, 779, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1933, Helv. Phys. Acta, 6, 110 [NASA ADS] [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Discrete Fourier transform conventions and properties
In this appendix we summarize some conventions we use for the discrete Fourier transform and some useful properties we make use of.
A.1. Conventions
In this manuscript we use the following convention for the discrete Fourier transform ℱ. The matrix element, per dimension, of this transform is set to:
which relates the Fourier space representation 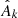 and the real space representation Ai of the same quantity sampled on a regularly spaced mono-dimensional grid of size N through:
and the real space representation Ai of the same quantity sampled on a regularly spaced mono-dimensional grid of size N through:
The discrete Fourier transform is exactly invertible, and the element of the inverse is:
also per dimension.
A.2. Translation of the discrete Fourier transform
Here we will show a lemma giving the identity between translating the matrix element of a discrete Fourier transform and the translation of the field itself. In this appendix we write i = (i0, …, id) the relation between a matrix index i and the regular grid indices (i0, …, id) in a space of dimension d. The discrete Fourier transform is a matrix linear operator ℱ given as:
with 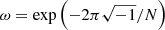 . We abuse the index notation introduced in Sect. A.1 by assimilating the scalar index i and the vector index i = (i0, …, id). Now we express the shifted discrete Fourier transform of a real vector Vi into
. We abuse the index notation introduced in Sect. A.1 by assimilating the scalar index i and the vector index i = (i0, …, id). Now we express the shifted discrete Fourier transform of a real vector Vi into 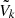 :
:
with 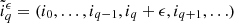 and
and 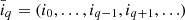 . In the above, in the transition from the second to the third line, we have exploited the periodicity of the discrete Fourier transform ωNk = ω0 = 1. The above identity stands even if the discrete Fourier transforms have different dimensions along each axis. Additionally, we have similarly:
. In the above, in the transition from the second to the third line, we have exploited the periodicity of the discrete Fourier transform ωNk = ω0 = 1. The above identity stands even if the discrete Fourier transforms have different dimensions along each axis. Additionally, we have similarly:
Appendix B: The particle mesh model
This work uses a particle mesh (PM) model to evaluate the gravitational formation of cosmic structures from their origins to the present epoch. The General relativity dynamics is approximated using linear perturbations of the background metric. In practice that means we solve for the dynamics of a set of particles interacting via a Newtonian gravitational force. In this appendix we give both a brief overview over the implementation of the particle mesh model and its corresponding derivative required for the HMC framework.
B.1. PM equation of motions
As discussed in Sect. 3.2 our implementation of the particle mesh (PM) algorithm follows closely the description in Klypin & Holtzman (1997). In particular the PM algorithm aims at solving the following set of equations of motion for comoving dark matter particle positions r and momenta p in the simulation domain:
where a is the cosmic scale factor, 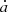 is its first time derivative and
is its first time derivative and
The corresponding momentum update is given by:
where the dimensionless gravitational potential is given through the Poisson equation
and
We will now provide details on the numerical implementation of the ordinary differential equation (ODE) solver.
B.2. Evaluation of gravitational forces
We use the standard PM approach, by first estimating the density field from particles via a CIC kernel and then solve Eq. (B.7) in Fourier space (see e.g., Hockney & Eastwood 1988; Klypin & Holtzman 1997). The Fourier kernel is computed from the 5-point stencil, approximating the Laplacian to second order. We thus obtain:
with ql ∈ {0, …, Nl − 1}3, Nl the number of grid element along the axis l, and Ll the comoving length of the simulation box along the axis l. We will also write 𝒢q for the summation over the entire three-dimensional grid of q vectors. Following Eq. (B.3), the gravitational force acting on the pth particle is given as:
with rp the position of the pth particle. Following Hockney & Eastwood (1988), to avoid self-interaction the actual value of the gradient must be derived as:
with Dr the (symmetric) finite difference operator, ℐ the CIC interpolation kernel.
B.3. Update of particle positions
To numerically integrate the equations of motion we use the leap-frog integrator (Hockney & Eastwood 1988, and also related to methods given in Sir Isaac Newton’s Dynamica). Finite differencing then yields the well known update equations for particle momenta and positions (see e.g., Klypin & Holtzman 1997):
By offsetting the initial momentum by half a time step and introducing:
and
we can write the updating scheme local in time:
Note that at the end of the updating loop one has to move the momenta further by half a time step. In the rest of this work, notably in Appendix C, we also set (yq)α = yq, α, where y can be one of p, r or 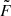 .
.
Appendix C: Tangent adjoint model of the particle mesh code
Efficient exploration of high dimensional parameter spaces is facilitated by the use of gradients. The HMC sampling framework relies on the availability of a gradient of the posterior distribution. In this appendix we derive in detail such a gradient for the PM model, which is valid for the PM algorithm as described in Appendix B. Specifically we derive expressions for the following gradient of the negative logarithmic posterior distribution 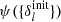 with respect to a initial density contrast amplitude
with respect to a initial density contrast amplitude 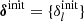 . In the following we will describe in detail how to obtain analytic gradients for numerical computer simulations of gravitational structure formation.
. In the following we will describe in detail how to obtain analytic gradients for numerical computer simulations of gravitational structure formation.
C.1. General framework to derive tangent adjoint model
Conceptually, any computer model, no matter how complex or non-linear, can be expressed as a succession of elementary algorithmic operations, such as additions and multiplications. A computer algorithm G(x) can therefore be expressed as the composition of several functions. It is simply the nested application of elementary function applications given as:
Any derivative of G(x) can then be obtained by use of the chain rule of differentiation:
As can be seen any derivative of a computer programme results just in a long sequential application of linear operations. The same approach applies to any multi-variate computer programme. In the following we will use this approach to derive the adjoint gradient of our particle mesh computer model.
C.2. The tangent adjoint model for the LSS posterior distribution
Having posited the framework, we now proceed with the first step of the derivation of ψ(δinit). The log-likelihood part of the posterior can formally be expressed as follow:
Above, L is the log-likelihood function allowing the comparison between the output of the forward model and the data (i.e. a Poisson distribution in our case as given in Sect. 3.4). Ui are the Kick-Drift element of the PM algorithm, given in Eq. (B.10). The gradient of the total log-likelihood ψ with respect to the initial parameters δinit yields:
where we made frequent use of the chain rule and u = [r, p] is a vector composed of particle positions and momenta. Also we have taken derivatives according to vector, which translates to a derivatives and implicit summations over all elements of the vectors. Equation (C.4) constitutes essentially a sequence of matrix vector applications permitting to calculate the gradient given by Eq. (C.4) via the following iterative procedure:
with 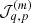 being the Jacobian matrix between successive time steps. We note that this operation is exactly an adjoint multiplication by the operator 𝒥, thus the name “tangent adjoint model” given to this whole procedure. This matrix 𝒥 is given by identification in Eq. (C.4):
being the Jacobian matrix between successive time steps. We note that this operation is exactly an adjoint multiplication by the operator 𝒥, thus the name “tangent adjoint model” given to this whole procedure. This matrix 𝒥 is given by identification in Eq. (C.4):
for l < N. We have also introduced the following notation to indicate components of vectors (Uq)α = Uq, α. For l = N, we have the special case:
and initial conditions with 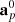 given by:
given by:
It is important to remark that at no point in the calculation of the gradient it is required to explicitly store the high dimensional matrix 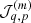 . We only need to have a procedure to evaluate exactly the sequence of matrix vector applications. In the following we will therefore derive the Jacobian
. We only need to have a procedure to evaluate exactly the sequence of matrix vector applications. In the following we will therefore derive the Jacobian 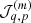 of successive time steps in standard cosmological particle mesh codes.
of successive time steps in standard cosmological particle mesh codes.
C.3. The Jacobian of particle mesh time stepping
In this work we use a different implementation of the gradient than described in Wang et al. (2013). The Jacobian between different time steps can then be obtained as:
Each element of this Jacobian matrix can be derived from the particle mesh update scheme given in Eq. (B.10). We can thus directly compute the derivatives of a particle position and velocity of a particle with respect to position and velocity of any other particle in the simulation at the previous time step:
where we have used m = N − n in the above to shorten the notation. Given these calculations 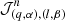 can be written as:
can be written as:
where the first term describes the Jacobian of the linear equations of motion if there were no forces and the second term accounts for the coupling of the gravitational force and again m = N − n.
A single iteration of the gradient calculation step given in (C.5) can then be calculated as:
where the vector a is made of six components decomposed into position and a velocity components as a = [a(r), a(ν)]. Each sub-vector having three dimensions indexed by q. The only challenging terms to calculate in Eq. (C.15) are the terms depending on derivatives of the gravitational force. In the next subsection we will discuss the evaluation of these terms.
C.4. Tangent adjoint gradient of the force solver
Within a standard particle mesh approach forces at particle positions are obtained via interpolation of a force field sampled at discrete positions 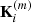 on a grid to continuous particle positions (Hockney & Eastwood 1988):
on a grid to continuous particle positions (Hockney & Eastwood 1988):
where 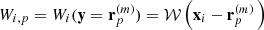 is the mass assignment kernel that interpolates between discrete grid xi and continuous particle positions
is the mass assignment kernel that interpolates between discrete grid xi and continuous particle positions 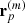 , and the discrete force
, and the discrete force 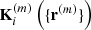 . This force array is a function of all particle positions in the simulation and denotes the force field evaluated at the grid nodes. For a particle mesh code the force calculation on the grid can be written as:
. This force array is a function of all particle positions in the simulation and denotes the force field evaluated at the grid nodes. For a particle mesh code the force calculation on the grid can be written as:
where we apply the linear operator Mi, l to the density field as inferred from the particle distribution with the appropriate gridding kernel 𝒲(y). The operator Mi, l, α is given as:
where ℱi, j and 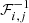 denotes the forward and backward Fast Fourier transform operators respectively, and 𝒢k is the Greens operator for the Poisson equation in Fourier space as given in Eq. (B.6). We have also introduced the notations of Appendix A.2 to grid indices i and
denotes the forward and backward Fast Fourier transform operators respectively, and 𝒢k is the Greens operator for the Poisson equation in Fourier space as given in Eq. (B.6). We have also introduced the notations of Appendix A.2 to grid indices i and  . The gradient of the force with respect to positions is:
. The gradient of the force with respect to positions is:
with the introduced kernel derivative
We derive the second term in the force derivative given in Eq. (C.19):
We now have to collapse some of these expressions to build an efficient algorithm. We first introduce the updated vector, which is a subcomponent of the vector in (C.15):
We now evaluate the force term in the adjoint update given in Eq. (C.15):
where we have introduced the vector:
which is just the vector bp interpolated to the grid with the mass assignment scheme Wi, p. We now proceed to compute the value of
To achieve this we expand further Mi, l:
with
and the notations of Appendix A.2. For the last line of Eq. (C.27), we have used the hermiticity of the  fields. We now re-express
fields. We now re-express  exploiting the periodicity of the discrete Fourier Transform ℱi, k:
exploiting the periodicity of the discrete Fourier Transform ℱi, k:
where  is simply the discrete Fourier transform of the differences in the
is simply the discrete Fourier transform of the differences in the  field along ath axis, and we have exploited the identity shown in Appendix A.2. The discrete Dl field is now obtained by applying the Greens operator 𝒢k to the components of the
field along ath axis, and we have exploited the identity shown in Appendix A.2. The discrete Dl field is now obtained by applying the Greens operator 𝒢k to the components of the  vector and performing a transposed discrete Fourier transform on the sum of the components (Eq. (C.27)).
vector and performing a transposed discrete Fourier transform on the sum of the components (Eq. (C.27)).
If we assume the mass assignment kernel Wi, p factorizes along each of the spatial coordinates, as is usually the case in particle mesh codes, then we can write (Hockney & Eastwood 1988):
This yields the gradient of the mass assignment kernel given as:
with 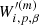 as defined in Eq. (C.20). Finally we can rewrite the Eq. (C.15), governing the update of the adjoint gradient vector from time step (m + 1) to time step (m) as follow:
as defined in Eq. (C.20). Finally we can rewrite the Eq. (C.15), governing the update of the adjoint gradient vector from time step (m + 1) to time step (m) as follow:
with
The total steps involved to compute a(m + 1) are thus:
with ℱ denoting the presence of a Fourier transform and CIC a mass assignment kernel like Cloud-In-Cell.
This demonstrates that the numerical complexity of the tangent adjoint model is the same as for the full forward model evaluation. In fact, as demonstrated by Fig. 3, the numerical costs of one tangent adjoint model evaluation is equivalent to the costs of two forward model evaluations. A single gradient evaluation requires one full forward model evaluation and a subsequent application of the tangent adjoint model. The numerical complexity of a gradient evaluation and run-times are thus about two times a single forward model evaluation. It should be remarked that the evaluation of the tangent adjoint model requires to store all particle positions and velocities at all steps of the forward model evaluation.
Appendix D: Tangent adjoint model of redshift space distortions
In Sect. 3.3, we have introduced the model we have adopted to introduce redshift space distortions in the analysis. In this appendix we detail the computation of the tangent adjoint of this model.
We introduce redshift space distortions as an additional displacement of particles compared to their final comoving positions. At first order in 1/c, we have for a single particle with position x and velocity v
where we have set
and
a being the cosmological scale factor. Internally, the particle mesh stores another variant of the velocity, the momentum, which is p = a2v. Thus we form 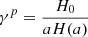 to account for the different scaling
to account for the different scaling
To follow the generic framework indicated in Appendix C, we introduce the derivative with respect to comoving coordinates xi
Let α = ∑kpkxk and β = |y|2 then:
Similarly we obtain the derivative of s with respect to velocity
Putting back together for we may derive the two adjoint gradient for the position and velocity:
The case for which no redshift space distortions is requested reduces to setting γ = 0. We indeed recover that xag = sag and vag = 0.
Appendix E: Supersampling: adjoint gradient of S
As indicated in Sect. 4.2, we over-sample the initial density fields with simulation particles to decrease particle noise in simulated density fields. Oversampling of the initial density field can be performed by extending the Fourier transform of the 3d density field with null modes beyond the Nyquist frequency. The constraint that the field remains purely real imposes some complexity to the supersampling algorithm and even more to the adjoint gradient Σ. The supersampling operation S transforms Fourier modes 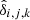 of a density field to new modes
of a density field to new modes 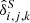 which can be used with a higher resolution Discrete Fourier transform. To simplify the presentation, we will start with the mono-dimensional case. The discrete Fourier synthesis is
which can be used with a higher resolution Discrete Fourier transform. To simplify the presentation, we will start with the mono-dimensional case. The discrete Fourier synthesis is
Artificially oversampling by a factor Q the real density field gives
The Fourier representation of this field becomes, for use in the Fast Fourier Transform:
This relation induces that, applied on vector ϵi, the adjoint gradient operator takes the following form:
Similarly as the Discrete Fourier Transform, this operator generalizes by recursion to three dimensions. Clean handling of these modes in non-shared memory environment is not entirely trivial.
Appendix F: Testing the statistical efficiency of the sampler
The statistical efficiency of a Markov chain Monte Carlo approach is determined by its ability to produce independent samples of the target distribution. Subsequent samples in a Markov chain will generally be correlated due to the finite jump size from one sample to another. The correlation between successive samples determines the number of independent samples that can be drawn from a given Markov chain. To study this effect, we follow a similar approach as described in previous works (see e.g., Eriksen et al. 2004; Jasche et al. 2010a; Jasche & Wandelt 2013b). The approach proceeds as follows. By assuming all parameters in the Markov chain to be independent, we will determine the correlation between subsequent density samples by estimating the autocorrelation function:
Here i indexes the sample number while n indicates the distance in the chain measured in terms of sampling steps (also see e.g., Eriksen et al. 2004; Jasche et al. 2010a; Jasche & Wandelt 2013b, for a similar discussion). We present the results of this test in Fig. F.1, where we show the correlation coefficients for individual density amplitudes of sampled density fields. The correlation length of the sampler can then be defined as the distance in the chain nc beyond which the correlation coefficient C(δ)n has dropped below a threshold of Cth(δ)n = 0.1. As demonstrated by Fig. F.1 the sampler exhibits an excellent mixing efficiency with a correlation length of about ∼150 samples. Despite the complexity of the data model and the high dimensionality of the inference problem considered in this work, these tests clearly demonstrate the numerical feasibility of analysing the three-dimensional cosmic large-scale structure with complex physical forward models of cosmic structure formation. To further improve statistical efficiency we are continuously developing new Markov sampling strategies. For an example in the case of sampling cosmological parameters with the BORG algorithm, the interested reader is referred to our latest work (Kodi Ramanah et al. 2019).
 |
Fig. F.1. Autocorrelation of subsequent density samples in the Markov chain as calculated by Eq. (F.1). As can be seen the correlation length of the sampler is on the order of ∼150 samples The selected voxels were selected at centred on the observer and are a contained within a ball of radius ∼13 h−1 Mpc. |
All Tables
Logarithmic Bayes factors between a density field generated with the LPT and one with the PM model.
Estimated mean parameter values for the bias functions corresponding to the respective magnitude cuts.
All Figures
 |
Fig. 1. Flow chart depicting the multi-step iterative block sampling procedure. In the first step, a three-dimensional density field will be realized conditional on the galaxy observations (top left corner). In subsequent steps observer velocity, bias parameters and the normalization parameters for the galaxy distribution are sampled conditional on respective previous samples. Iteration of this process yields samples from the full joint posterior distribution generated by the BORG algorithm. |
| In the text | |
 |
Fig. 2. 2M++ data and its selection properties. Top left panel: sky completeness at K2M + + ≤ 11.5, derived as the number of observed redshifts versus the number of targets in the 2MASS photometric sample. Top right panel: same quantity is shown but for apparent magnitudes 11.5 < K2M + + ≤ 12.5. Bottom left panel: number count of galaxies in thin radial shells for the two different magnitude cuts shown in the top row. We see that the catalogue covers a volume up to a redshift z ∼ 0.06 − 0.08. Bottom right panel: sky projection of the positions of the galaxies of the 2M++ catalogue. The local large-scale structures are clearly visible. |
| In the text | |
 |
Fig. 3. Computational scaling properties of the code over MPI-tasks. The x-axis is the number of MPI tasks, each task being given eight cores with OpenMP parallelization. The y-axis is the wall time seconds taken by the software to execute the indicated part of the algorithm. The red lines correspond to the evaluation of one time-step of the BORG-PM forward model, that is the N-body simulation including gravity solver. The green lines correspond to the time taken to compute the adjoint gradient of that same model. We note that the cost of the adjoint gradient takes only twice as much time as the forward model itself over the entire range. Also, the scaling is strong up to ∼100 cores, the break visible at the end being because of the core saturation and the use of hyper-threading on the supercomputer. |
| In the text | |
 |
Fig. 4. Sequential posterior power-spectrum (left panel) and 1-pt distribution (right panel) of inferred primordial fluctuations measured during the burn-in of the Markov chain with an LPT model. The colour gradient indicates the step number in the chain from zero (random initial condition of small amplitude) to 6783 for which the chain is manifestly stable according to this metric. Top panels: power spectrum and 1-pt distributions measured a posteriori from the samples, while lower panels: ratio of these quantities to the expected prior values. Thick dashed lines represent the fiducial prior values. The thin (black respectively) grey dotted line indicates the Gaussian 1σ limit (2σ respectively) in the lower left panel. These results show no sign of any residual systematic artefacts, indicating a healthy burn-in behaviour of the chain. |
| In the text | |
 |
Fig. 5. Trace plot of the negative differential logarithmic likelihood as a function of sampling steps n. The values represent logarithm of the ratios between the initial likelihood value obtained by the last sample calculated with a LPT model and subsequently evaluated particle mesh models. Right panel: trace of the total likelihood, while left panels: evolution of logarithmic likelihoods for the respective galaxy sub-catalogues as indicated in the panels. It can be seen that the Markov chain starts initially with high values for the negative logarithmic likelihood but successive sampling steps improve the consistency of inferred three-dimensional initial density fields with the observations. After 1200 steps the trace plot settles at an average value for the negative logarithmic likelihood. In terms of Bayesian odds ratios when comparing the initial guess to a sample at sampling step 2500 this is an improvement of about five orders of magnitude in logarithmic likelihood. |
| In the text | |
 |
Fig. 6. Inferred non-linear bias functions for the 16 galaxy subsets of the 2M++ galaxy compilation in 8 absolute K-band magnitude bins. Blue and red lines correspond to ensemble mean bias functions, while shaded regions indicate the 1σ intervals for the two magnitude cuts as indicated in the upper left panel. Dashed lines correspond to bias functions estimated with the ensemble mean values of the bias parameters. |
| In the text | |
 |
Fig. 7. Spherical slices of thickness ∼2.6 h−1 Mpc through a data constrained realization of the three-dimensional initial (left panel) and final density field (right panel) at a distance of R = 100 h−1 Mpc from the observer. Initial density fields correspond to the epoch of a cosmic scale factor a = 0.001 while non-linear final density fields are evaluated at the present epoch (a = 1). One can see the correspondence of large scale over-densities in the initial conditions and corresponding structures in the gravitationally evolved density field. Red dots in the right panel denote the observed galaxies in the 2M++ survey. As can be seen observed galaxies trace the inferred dark matter distribution. |
| In the text | |
 |
Fig. 8. Posterior power-spectra measured from inferred initial density fields (left panel) and the one-point distribution of primordial density fluctuations (right panel). The plot demonstrates that individual data constrained realizations of the initial density field constitute physically valid quantities. Throughout the entire domain of Fourier modes considered in this work we do not observe any particular bias or attenuation of measured cosmic power-spectra. The measured posterior one-point distribution of primordial fluctuations is compatible with a fiducial normal one-point distribution with variance corresponding to the cosmological parameters as described in Sect. 4.2. Tests of kurtosis and skewness, as indicated in the right panel, confirm inferred initial density fluctuations to follow Gaussian statistics. |
| In the text | |
 |
Fig. 9. Spherical slices through the ensemble mean of the three-dimensional initial (left panel) and final density field (right panel) and corresponding pixel-wise variances (lower panels) at a distance of R = 100 h−1 Mpc from the observer. It is interesting to note, that the pixel-wise variance for the final density field imprints the cosmic large scale structure. Correlations between signal and noise are expected for any point process, such as the generation of galaxy observations. The BORG algorithm correctly accounts for these effects. |
| In the text | |
 |
Fig. 10. Radial density profiles of matter fluctuations in shells of radius r around the observer. Left panel: spherical shells covering the full sky, while middle and right panel: density fluctuations for the 6dFGS-SGC and 6dFGS-NGC region, as defined in Whitbourn & Shanks (2014), respectively. Red lines indicate our ensemble mean estimate, while dark and light grey shaded regions indicate the 2σ and 1σ limit, respectively. The black dashed line corresponds to cosmic mean density. As can be seen our inference results do not indicate striking evidence for a large scale under-dense region using the 2M++ data. |
| In the text | |
 |
Fig. 11. Slices through the three-dimensional density field of the Supergalactic plane at different cosmic epochs as indicated in the respective panels. The sequence of plots represents a plausible formation history of structures in the Supergalactic plane. Initially, proto-structures arise from almost homogeneous matter distributions forming, through gravitational interaction, the cosmic web of clusters and filaments. To illustrate that this formation history yields actually observed structures we overlay the density field with galaxies of the 2M++ survey in the lower right panel. It can be seen that the galaxies in the Supergalactic plane trace the recovered density field. |
| In the text | |
 |
Fig. 12. Projected ensemble mean mass of inferred dark matter particles around the Coma cluster (left panel) and the corresponding ensemble variance field (right panel). One can clearly see the two major filaments along which mass accretes onto the Coma cluster. Additionally one can also notice three fainter filaments. Right panel: ensemble variance estimate for the inferred mean density field. As expected, noise and signal are correlated for a galaxy clustering survey. |
| In the text | |
 |
Fig. 13. Coma cumulative mass profile. We show here the relation between the distance r and the mass M(< r) enclosed within that radius. The thick solid red line is the mean relation obtained through density field derived using BORG-PM, while the light grey (dark grey respectively) gives the 68% (95% respectively) limit according to that mean. The thin blue solid line indicates the profile assuming solely the mean density of the universe. We also compare our results with the findings in the literature as indicated in the plot. It can be seen that our mass estimate for Coma agrees particularly well with complementary measurements of weak gravitational lensing or X-ray observations at scales of a few h−1 Mpc. |
| In the text | |
 |
Fig. 14. Spherical slice through the inferred three dimensional ensemble mean velocity field (left panel) and corresponding variance field (right panel). Specifically the plot shows the line of sight component of the velocity field. As indicated by the colour bar, in the left panel regions indicated in red are receding from the observer while blue regions are approaching the observer. The plot also shows regions of zero velocity along the line of sight indicating that matter in these regions follows the Hubble flow. Right panel: corresponding variance field for the line of sight velocity component. |
| In the text | |
 |
Fig. 15. Spherical slices through the three dimensional vorticity of the velocity field at a distance R = 60 h−1 Mpc from the observer in galactic coordinates. Left panel: projection of the vorticity vector along the line of sight, while right panel: absolute amplitude of the vorticity. As can be seen the vorticity traces the high density filamentary structure of the cosmic web. The left panel also hints towards the quadrupolar structure of the vorticity as found in simulations (see e.g., Laigle et al. 2015). |
| In the text | |
 |
Fig. 16. Possible biases arising from doing a Hubble measurement with tracers within some volume, neglecting complex cosmic flows effect. We show in red solid line the mean systematic bias for a Hubble measurement per tracer located within a sphere of radius R. The grey area corresponds to the expected 1σ fluctuation per tracer of that same measurement. We show, for reference, the measurement by Riess et al. (2016; in blue and shade of blue for the 1σ limit) of the Hubble constant relatively to the Planck one (centred on zero, and shade of green for the 1σ limit). |
| In the text | |
 |
Fig. 17. Prediction of the fractional Hubble uncertainty as a function of direction within 60 h−1 Mpc around the observer. As can be seen, the fractional Hubble uncertainty is highly structured on the sky, with large-scale coherent bulk flows. The dominant red central region points towards the direction of Perseus Pisces. These effects need to be accounted for when inferring the Hubble parameter from data of the nearby universe. |
| In the text | |
 |
Fig. F.1. Autocorrelation of subsequent density samples in the Markov chain as calculated by Eq. (F.1). As can be seen the correlation length of the sampler is on the order of ∼150 samples The selected voxels were selected at centred on the observer and are a contained within a ball of radius ∼13 h−1 Mpc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



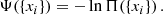
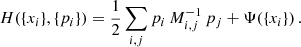
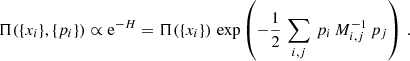
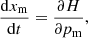
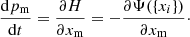
![$$ \begin{aligned} {\Pi }_A = \min \Big \{1,\exp \big [-\left(H(\{x^{\prime }_i\},\{p^{\prime }_i\})-H(\{x_i\},\{p_i\}\right)\big ]\Big \}\,. \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq9.gif)
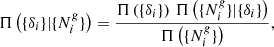
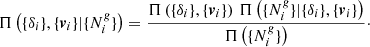
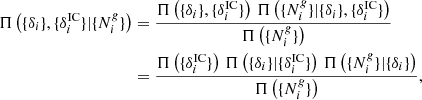
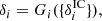
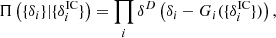
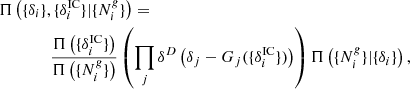
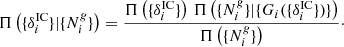
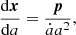
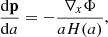
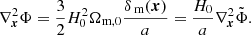
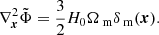
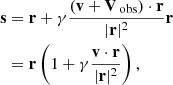
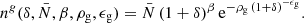
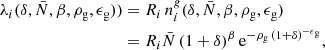
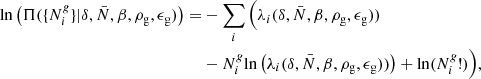
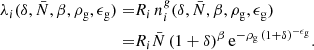
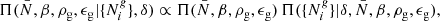
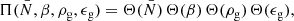
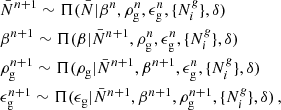
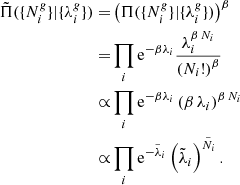
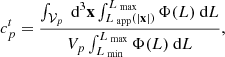
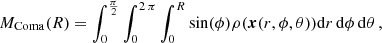
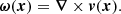
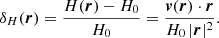
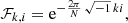
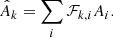
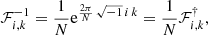
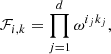
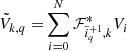
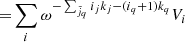
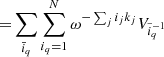
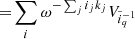
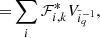
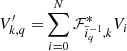
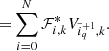
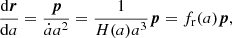
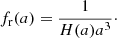
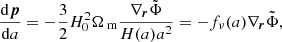
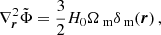
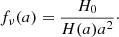
![$$ \begin{aligned} \hat{\tilde{\Phi }}(\boldsymbol{k}_{\boldsymbol{q}}) = \left\{ \sum _{l=1}^3 \left[\frac{4 N_l}{L_l} \sin \left(\frac{\pi q_l}{N_l}\right)\right]^2\right\} ^{-1} \hat{\delta }(\boldsymbol{k}_{\boldsymbol{q}}) = \mathcal{G} _{\mathbf{q}} \hat{\delta }(\mathbf{k}_{\mathbf{q}}) , \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq80.gif)
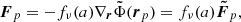
\, \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq82.gif)
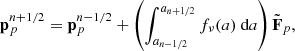
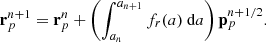
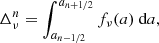
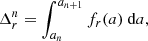
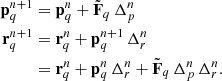
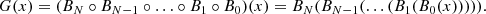
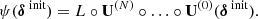
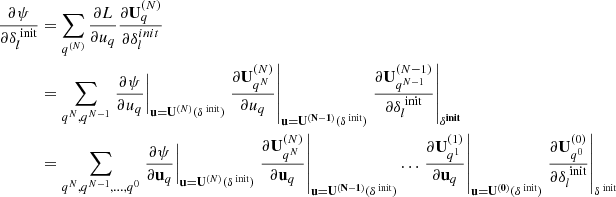
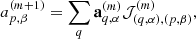
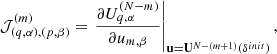
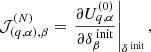
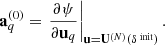
![$$ \begin{aligned} \mathcal{J} ^{(n)}_{(q,\alpha ),(l,\beta )} = \left.\frac{\partial U^{(N-n)}_{q,\alpha }}{\partial u_{l,\beta }}\right|_{\mathbf{u}=\mathbf{U}^{(N-(n+1))}(\delta _\text{ init})} = \left[ \begin{array}{ccccc} \frac{\partial r_{q,\alpha }^{(N-n)} }{ \partial r_{l,\beta }^{(N-(n+1))} }&\frac{\partial r_{q,\alpha }^{(N-n)}}{ \partial p_{l,\beta }^{(N-(n+1))} } \\ \frac{\partial p_{q,\alpha }^{(N-n)}}{ \partial r_{l,\beta }^{(N-(n+1))} }&\frac{\partial p_{q,\alpha }^{(N-n)}}{ \partial p_{l,\beta }^{(N-(n+1))}} \end{array} \right]. \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq103.gif)
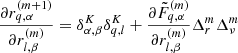
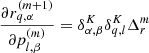
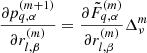
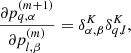
![$$ \begin{aligned} \mathcal{J} ^{(n)}_{(q,\alpha ),(l,\beta )} =&\left[ \begin{array}{ccccc} \delta ^K_{\alpha ,\beta } \delta ^K_{q,l} + \frac{\partial F^{(m)}_{q,\alpha }}{\partial r^{(m)}_{l,\beta }} \Delta ^m_r\Delta ^m_\nu&\delta ^K_{\alpha ,\beta } \delta ^K_{q,l} \Delta ^m_r \\ \frac{\partial \tilde{F}^{(m)}_{q,\alpha }}{\partial r^{(m)}_{l,\beta }} \Delta ^m_\nu&\delta ^K_{p,q} \end{array} \right] \nonumber \\=&\delta ^K_{q,l} \delta ^K_{\alpha ,\beta } \left[ \begin{array}{ccccc} 1&\Delta ^m_r \\ 0&1 \end{array} \right] + \left[ \begin{array}{ccccc} \frac{\partial \tilde{F}^{m}_{q,\alpha }}{\partial r^{m}_{l,\beta }} \Delta ^m_r \Delta ^m_\nu&0 \\ \frac{\partial \tilde{F}^{m}_{q,\alpha }}{\partial r^{m}_{l,\beta }} \Delta ^m_\nu&0 \end{array} \right], \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq109.gif)
![$$ \begin{aligned} \left[ a^{(r),(m)}_{q,\beta } \, , \, a^{(\nu ),(m)}_{q,\beta } \right] =&\left[ a^{(r),(m-1)}_{q,\beta } + \sum _{p,\alpha } \left(a^{(r),(m-1)}_{p,\alpha } \Delta ^m_r\,\Delta ^m_\nu + a^{(\nu ),(m-1)}_{q,\alpha } \Delta ^m_\nu \right) \frac{\partial \tilde{F}^{(m)}_{p,\alpha }}{\partial r^{(m)}_{q,\beta }} \right. , \nonumber \\&\left. \, a^{(\nu ),(m-1)}_{q,\beta } + a^{(r),(m-1)}_{q,\beta } \,\Delta ^{m_r} \right], \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq110.gif)
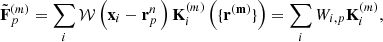
![$$ \begin{aligned} \mathbf{K}^{(m)}_i\left( \{\mathbf{r}^{(m)}\}\right) = \sum _l \mathbf{M}_{i,l} \left[ \left( \sum _q \frac{1}{\bar{N}} \mathcal{W} \left(\mathbf{x}_l - \mathbf{r}^{(n)}_q\right)\right) -1\right], \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq116.gif)
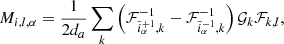
![$$ \begin{aligned} \frac{\partial \tilde{F}^{(m)}_{q,\alpha }}{\partial r^{(m)}_{l,\beta }} = \sum _i \left[ \delta ^\text{ K}_{q,l} W^{^{\prime }(m)}_{i,q} K^{(m)}_{i,\alpha } + W_{i,q} \frac{\partial K^{(m)}_{i,\alpha }}{\partial r^{(m)}_{l,\beta }} \right], \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq120.gif)
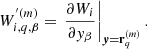
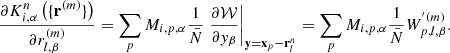
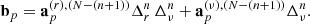
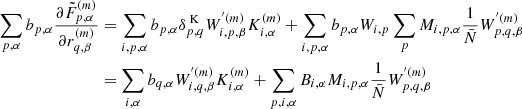
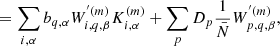
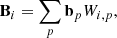
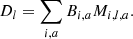
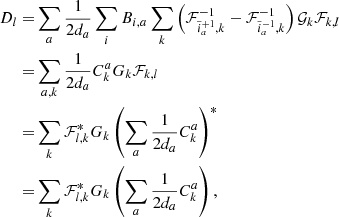
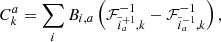
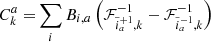
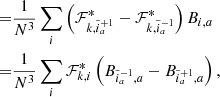
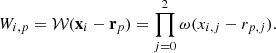
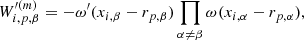
![$$ \begin{aligned} \left[ {\begin{array}{cc} \mathbf{a}_{r}^{m} \\ \mathbf{a}_{\nu }^{m} \end{array} }\right] = \left[ {\begin{array}{cc}\mathbf{a}_{r}^{(m+1)}+ \mathbf{\Theta }^{(m+1)} \\ \mathbf{a}_{\nu }^{(m+1)} +\mathbf{a}_{r}^{(m+1)} \,\Delta ^n_r \end{array} }\right]\, , \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq140.gif)
![$$ \begin{aligned} \left[\mathbf{\Theta }^{(m)}_q\right]_\beta = \Theta ^{(m)}_{q,\beta } = \sum _{p,\alpha } b_{p,\alpha } \frac{\partial \tilde{F}^{m}_{p,\alpha }}{\partial r^{m}_{q,\beta }}\cdot \end{aligned} $$](/articles/aa/full_html/2019/05/aa33710-18/aa33710-18-eq141.gif)