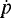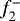| Issue |
A&A
Volume 611, March 2018
|
|
|---|---|---|
| Article Number | A85 | |
| Number of page(s) | 13 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731473 | |
| Published online | 04 April 2018 | |
The sdB pulsating star V391 Peg and its putative giant planet revisited after 13 years of time-series photometric data★,★★
1
INAF – Osservatorio Astrofisico di Torino,
strada dell’Osservatorio 20,
10025
Pino Torinese, Italy
e-mail: silvotti@oato.inaf.it
2
Max Planck Institute for Solar System Research,
Justus-von-Liebig-Weg 3,
37077
Göttingen, Germany
3
Korea Astronomy and Space Science Institute,
Daejeon
34055, South Korea
4
German Aerospace Center (DLR), Remote Sensing Technology Institute,
Münchener Str. 20,
82234
Weßling, Germany
5
Department of Physics, Astronomy and Materials Science, Missouri State University,
Springfield,
MO
65897, USA
6
INAF – Osservatorio Astronomico di Padova,
Vicolo dell’Osservatorio 5,
35122
Padova, Italy
7
Institute of Theoretical Physics and Astronomy, Vilnius University,
Gostauto 12,
Vilnius
01108, Lithuania
8
Department of Physics, University of Warwick,
Coventry
CV4 7AL, UK
9
Department of Physics and Astronomy, University of Sheffield,
Sheffield
S3 7RH, UK
10
Instituto de Astrofisica de Canarias,
Via Lactea s/n, La Laguna,
38205
Tenerife, Spain
11
Konkoly Observatory of the Hungarian Academy of Sciences,
Konkoly-Thege M. u 15-17,
1121
Budapest, Hungary
Received:
29
June
2017
Accepted:
3
November
2017
V391 Peg (alias HS 2201+2610) is a subdwarf B (sdB) pulsating star that shows both p- and g-modes. By studying the arrival times of the p-mode maxima and minima through the O–C method, in a previous article the presence of a planet was inferred with an orbital period of 3.2 years and a minimum mass of 3.2 MJup. Here we present an updated O–C analysis using a larger data set of 1066 h of photometric time series (~2.5× larger in terms of the number of data points), which covers the period between 1999 and 2012 (compared with 1999–2006 of the previous analysis). Up to the end of 2008, the new O–C diagram of the main pulsation frequency (f1) is compatible with (and improves) the previous two-component solution representing the long-term variation of the pulsation period (parabolic component) and the giant planet (sine wave component). Since 2009, the O–C trend of f1 changes, and the time derivative of the pulsation period (p.) passes from positive to negative; the reason of this change of regime is not clear and could be related to nonlinear interactions between different pulsation modes. With the new data, the O–C diagram of the secondary pulsation frequency (f2) continues to show two components (parabola and sine wave), like in the previous analysis. Various solutions are proposed to fit the O–C diagrams of f1 and f2, but in all of them, the sinusoidal components of f1 and f2 differ or at least agree less well than before. The nice agreement found previously was a coincidence due to various small effects that are carefully analyzed. Now, with a larger dataset, the presence of a planet is more uncertain and would require confirmation with an independent method. The new data allow us to improve the measurement of p. for f1 and f2: using only the data up to the end of 2008, we obtain p.1 = (1.34 ± 0.04) × 10−12 and p.2 = (1.62 ± 0.22) × 10−12. The long-term variation of the two main pulsation periods (and the change of sign of p.1) is visible also in direct measurements made over several years. The absence of peaks near f1 in the Fourier transform and the secondary peak close to f2 confirm a previous identification as l = 0 and l = 1, respectively, and suggest a stellar rotation period of about 40 days. The new data allow constraining the main g-mode pulsation periods of the star.
Key words: stars: horizontal-branch / stars: oscillations / asteroseismology / stars: individual: V391 Peg / planets and satellites: detection / planets and satellites: individual: V391 Peg b
The complete set of data shown in Fig. 1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/611/A85
© ESO 2018
1 Introduction
V391 Peg was the first case of a post-red giant branch star showing evidence of the presence of a planet (Silvotti et al. 2007 (hereafter SSJ07); Silvotti 2008), indicating that giant planets may survive the first giant expansion of a star, provided that the orbital distance is large enough. For V391 Peg b, a minimum mass of 3.2 MJup was found, with an orbital period of 3.2 years, corresponding to an orbital distance of about 1.7 AU. The presence of the planet was inferred by measuring the arrival times of the maxima and minima of the stellar light, given that V391 Peg is a pulsating subdwarf B (sdB) star with at least four p-mode pulsation periods between 344 and 354 s (Silvotti et al. 2002, 2010), and a few longer-period g-modes (Lutz et al. 2009). A recent review on hot subdwarfs of spectral type O and B is given by Heber (2016).
V391 Peg b is not the first case in which the light travel-time delay is used to detect secondary low-mass bodies. In principle, the timing technique may be used on any star or stellar system that has a sufficiently stable clock, which may be given by the oscillations of the stellar flux in pulsating stars (like in this case), but also radio signals in pulsars or eclipse timing in eclipsing binaries. Radio timing was used to detect the first planetary system around the pulsar PSR 1257+12 (Wolszczan & Frail 1992). The extremely high precision of the radio pulse made it possible to detect PSR 1257+12 b, the Moon-mass innermost planet of the system (Konacki & Wolszczan 2003). Of the planets detected through eclipse timing, the most convincing case is given by two circumbinary planets orbiting the pre-cataclysmic binary NN Ser. Eight years after the discovery paper (Qian et al. 2009; see also Beuermann et al. 2010) and 26 years after the first data, their existence remains the best explanation for the observed eclipse time variations (Bours et al. 2016). Many other detached close binaries show eclipse time variations: for some of them, the presence of planets is excluded by dynamic stability computations and the periodic O–C trends may be caused by other effects, such as Applegate-like mechanisms (Applegate 1992; Lanza 2006). However, for some others, the energy required to produce the quasi-periodic changes in the quadrupole moment of the secondary star referred to as the Applegate mechanism, is too high; and the presence of Jovian planets remains the most plausible explanation (Völschow et al. 2016).
The idea of using stellar pulsation to measure the reflex motion that is due to a companion is not new (e.g., Barnes & Moffett 1975). Recently, the high photometric accuracy achievable from space, in particular with the Kepler mission, has led to a renewed interest in this technique (Silvotti et al. 2011), and two systematic approaches based on frequency modulation (FM) and phase modulation (PM, equivalent to the O–C method) were proposed (Shibahashi & Kurtz 2012; Telting et al. 2012; Shibahashi et al. 2015; Murphy et al. 2014, 2016b).
However, to detect low-mass (substellar) companions, we need very stable pulsators. When we exclude all the solar-like oscillators, good candidates are the delta Scuti stars (Compton et al. 2016; see also recent discovery by Murphy et al. 2016a) and compact stars like white dwarfs or sdB stars. As for white dwarfs, many articles in the literature have addressed this issue (e.g., Kepler et al. 1991), but it has become increasingly evident that other effects are present that can mimic light travel time effects in the O–C diagrams of these stars (e.g., Dalessio et al. 2015). For sdB stars the situation looks more promising, perhaps because these stars have a fully radiative envelope, and there is at least one case in which the presence of a low-mass stellar companion detected from pulsation timing was confirmed by radial velocity measurements (Barlow et al. 2011b). Another recent case of a pulsation-timing detection of an F5V companion to an sdB pulsator is reported by Otani et al. (2017).
After the detection of V391 Peg b, some other planet or brown dwarf (BD) candidates orbiting sdB stars were proposed using different detection methods. From eclipse timing, about one-third of the known detached sdB/sdO + dM (dM = M-dwarf) post-common-envelope binaries (PCEB) are suspected to host planets/BDs: HW Vir (Beuermann et al. 2012 and references therein), HS 0705+6700 (alias V470 Cam, Qian et al. 2013 and references therein), HS 2231+2441 (Qian et al. 2010 and references therein; but see also Lohr et al. 2014), NSVS 14256825 (Almeida et al. 2013; Hinse et al. 2014 and references therein), NY Vir (Lee et al. 2014 and references therein), and 2M 1938+4603 (Baran et al. 2015). Interesting explorations on the origin of PCEB (and specifically sdB+MS/BD) circumbinary planets can be found in Zorotovic & Schreiber (2013), Schleicher & Dreizler (2014), Bear & Soker (2014), and Völschow et al. (2016). Very different planets or planetary remnants with terrestrial radii have been proposed from tiny reflection effects detected by the Kepler spacecraft in KIC 05807616 (Charpinet et al. 2011) and KIC 10001893 (Silvotti et al. 2014). However, none of these sdB planet/BD candidates has been confirmed with at least two independent detection methods. More robust detections of a few brown dwarfs (BDs) in eclipsing sdB binaries (also called HW Vir systems from the sdB+dM protoptype) were obtained by combining stellar radial velocities (RVs) with photometric measurements: J08205+0008, J1622+4730 and V2008-1753 have companion masses of about 71, 67, and 69 MJup, respectively (Geier et al. 2011; Schaffenroth et al. 2014a, 2015). At least two more sdB+BD eclipsing systems were recently found from the OGLE survey (Schaffenroth, in prep., priv. comm.). Finally, two more BD candidates in sdB binaries were found by combining radial velocities (RVs) with photometric reflection effects: CPD-64°6481 and PHL 457, with minimum masses of 50 and 28 MJup, respectively (Schaffenroth et al. 2014b).
In this paper we reconsider the case of V391 Peg, for which we have collected 6 years of new photometric time-series data, increasing the number of data points by a factor of about 2.5. The main stellar parameters of V391 Peg are summarized in Table 1. We note that the JHK magnitudes are compatible with a single sdB star and do not indicate any near-IR excess.
In Sect. 2 a short summary of the data acquisition and reduction is given, including the extraction of the pulsation frequencies. The analysis of the amplitude spectrum of the p-modes at different frequency resolutions is presented in Sect. 3. Section 4 is dedicated to the O–C analysis of the two main p-modes. In Sect. 5 we discuss the presence of the planet in the light of the new O–C results, including a perspective on future developments. In Sect. 6 we present an analysis of the g-mode amplitude spectrum. Finally, a summary of our results is given in Sect. 7.
 |
Fig. 1 Distribution of the 217 232 data points over 13 years. The overall duty cycle is 0.92%, and the best coverage is obtained in 2007 with a duty cycle of 5.55%. The varying relative intensity is caused by the beating between the main frequencies and also depends on the varying quality of the data. |
 |
Fig. 2 p-mode amplitude spectrum of our best-quality run of 7.9 days, with a duty cycle of 35%, obtained in October 2007 with a SLOAN g filter using two telescopes at different longitudes: the WHT 4.2m in La Palma, equipped with ULTRACAM, and the MDM 1.3m at Kitt Peak. The upper panel shows the spectral window (red), while the other panels from top to bottom show the amplitude spectra of the data and of the residuals after one, two, three, and four prewhitening steps. A plot showing the high quality of the ULTRACAM data is presented in Silvotti et al. (2010). |
Stellar parameters.
2 Time-series photometric data: extraction of the pulsation frequencies
The new time-series photometric data were obtained using different telescopes and instruments (see Table 2) with at least one and often two or more comparison stars close to the target in order to remove spurious photometric modulationsthat are due to atmospheric transparency variations. The distribution of the data during the 13 years of observation is shown in Fig. 1. Most of the data were taken using a standard Johnson B filter. Only at NOT and MERCATOR did we use a Bessell B and a Geneva B filter, respectively. Moreover, a SLOAN g filter was used in the WHT-MDMrun of October 20071. The data obtained in October 2007 at the Piszkéstető, Loiano, and Lulin Observatories were collected without any filter in order to maximize the signal-to-noise ratio (S/N) of that run. The differences introduced by the different filters in terms of amplitudes or phases of the pulsation modes were considered and found to be negligible because of the much larger volume of standard B measurements. From nonadiabatic models, these differences (in particular the phase differences) are expected to be very small for l = 0 and l = 1 modes (Randall et al. 2005; see in particular their Figs. 13 and 14). The data were reduced mainly by the observers using standard procedures for aperture differential photometry. The times of all the data (new and old) were converted into Barycentric Dynamical Times (BJDTDB) following Eastman et al. (2010).
From the reduced data we extracted accurate pulsation frequencies using a classical prewhitening technique: an iterative Fourier transform (FT) process was applied subtracting the main frequency from the data residuals at each iteration, until no frequencies with amplitudes larger than four times the FT mean noise level were present. At the end of this iterative process, the pulsation frequencies, amplitudes, and phases were optimized through a multi-sinusoidal fit, whose results are given in Table 3. Appropriate statistical weights were set and considered in the sinusoidal fits of the p-modes (Silvotti et al. 2006) in order to take the varying quality of the data into account that is due to different telescope apertures, instrument efficiencies, and weather conditions.
Time-series photometry.
Pulsation frequencies.
3 p-modes
The first problem in analyzing a data set of several years is that the pulsation frequencies are no longer constant. This was already known for V391 Peg, and a quantitative measurement of 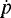 had been obtained from previous data giving
had been obtained from previous data giving 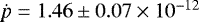 and 2.05 ± 0.26 ×10−12 for f1 and f2, respectively (SSJ07). In general, the time variation of a pulsation frequency gradually broadens the width of the peak in the Fourier transform and may split it into different close peaks if the data set is long enough. For a linear frequency variation, the time needed to split a pulsation frequency into different close peaks is given by
and 2.05 ± 0.26 ×10−12 for f1 and f2, respectively (SSJ07). In general, the time variation of a pulsation frequency gradually broadens the width of the peak in the Fourier transform and may split it into different close peaks if the data set is long enough. For a linear frequency variation, the time needed to split a pulsation frequency into different close peaks is given by
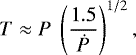 (1)
(1)
where P is the pulsation period, and the value 1.5 comes from the actual frequency resolution, given by ~1.5/T (Loumos & Deeming 1977). For V391 Peg we obtain T ≈ 10 years. However, after a few years, this effect already becomes important and makes the standard prewhitening technique (which assumes fixed frequencies and amplitudes) less efficient in returning precise frequencies. For this reason, after several tests we decided to split our analysis of the amplitude spectrum into three steps with data sets of different length and different frequency resolution.
It is useful to recall here that the two main pulsation modes of V391 Peg were identified as l = 0 and l = 1 from high-precision multi-color photometry obtained with ULTRACAM at the WHT (Silvotti et al. 2010). We show below that this identification is well supported by the current analysis.
3.1 Low-frequency resolution: main pulsation frequencies
As a first step, we consider our best-quality run of October 2007, with a length of 7.9 days and a duty cycle of 35%. At this level of frequency resolution, δf ≃ 2.2 μHz, the amplitude spectrum is very clean and shows only four pulsation modes without any trace of multiplets of close frequencies (Fig. 2).
3.2 Medium-frequency resolution: rotational splitting of f2?
As a second step, we consider a larger data set of about 220 days, collected in 2007. This data set is a compromise between best duty cycle, best data quality, and relatively long duration in order to detect possible rotational splitting of the pulsation modes with l > 0. At the same time, with 220 days, the effects of the long-term variations of the pulsation frequencies are still small, which keeps the amplitude spectrum relatively clean (Fig. 3). When we removed the four main pulsation frequencies through prewhitening, two low-amplitude peaks emerged from the noise, close to f2 and f3, while nothing appeared close to f1, which confirms that this must be an l = 0 mode. The peak close to f3 (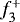 ) is only ~3.4σ above the noise, which is below our detection threshold of 4σ. Secondary peaks close to f3 are also visible when we use the whole data set (1999–2012), but with a very low S/N. The peak close to f2 (
) is only ~3.4σ above the noise, which is below our detection threshold of 4σ. Secondary peaks close to f3 are also visible when we use the whole data set (1999–2012), but with a very low S/N. The peak close to f2 (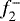 ), at about 4.3σ above the noise, differs by –0.181 μHz from f2 and is also detected in the whole data set, but at a lower S/N and smaller separation of –0.163 μHz (Fig. 4 lower right panel). Using the latter separation, which is more precise, and assuming that
), at about 4.3σ above the noise, differs by –0.181 μHz from f2 and is also detected in the whole data set, but at a lower S/N and smaller separation of –0.163 μHz (Fig. 4 lower right panel). Using the latter separation, which is more precise, and assuming that 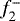 is part of an l = 1 triplet split by stellar rotation in which f2 is the central component, we obtain a stellar rotation period of about 40 days. This value is obtained in the slow rotation approximation (Ω ROT ≪ f, see Ledoux 1951),
is part of an l = 1 triplet split by stellar rotation in which f2 is the central component, we obtain a stellar rotation period of about 40 days. This value is obtained in the slow rotation approximation (Ω ROT ≪ f, see Ledoux 1951),
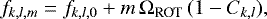 (2)
(2)
in which we have used a value of 0.43 for the Coriolis term Ck,l according to the adiabatic evolutionary models by Charpinet et al. (2002) (the model that fits best Teff, log g and P of V391 Peg is model 19 of sequence 4). The low amplitude of the secondary peak suggests a low inclination. This interpretation is consistent with the previous identification of f2 as an l = 1 mode by Silvotti et al. (2010). A rotation period of ~40 days would be compatible with the distribution of rotation periods as recently measured by the Kepler spacecraft in a sample of 18 sdB g-mode pulsators (see Zong 2017 and references therein). Thirteen of them show periods between 6 and 88 days, with a mean value of about 33 days. The other five do not show any rotational splitting of the frequencies, indicating that they may have very low inclinations and/or extremely long rotation periods.
 |
Fig. 4 Same as Figs. 2 and 3, but using the whole data set (1999–2012). Upper panels: amplitude spectrum of the data and of the residuals (on the same vertical scale) after subtracting the four main pulsation frequencies (f1 to f4). We note that the residual power is significantly higher than in Fig. 3. The small box shows the normalized spectral window (red) with the one-day aliases at ±11.57 μHz. Lower panels (from top to bottom): normalized spectral window (red) with the 1-year aliases at ±31.7 nHz, and details of the amplitude spectrum of data and residuals near f1 (left) and f2 (right). The horizontal scale in the left and right panels is the same. Two vertical dashed lines (green) highlight two components of a possible rotational splitting. See text for more details. |
 |
Fig. 3 Same as Fig. 2, but using all the data of 2007, the year with the best coverage. Thanks to the increased frequency resolution, we see that after four prewhitening steps, there is still significant power, with secondary peaks near f2 and f3 that may be due to the rotational splitting of these modes. |
3.3 High-frequency resolution: frequency and amplitude variations
When we further increase the length of the data set and consider the whole light curve in the period 1999–2012, the amplitude spectrum is much more complex because of the effects of the frequency variations, which become important (Fig. 4). When we subtract the main pulsation frequencies from the light curve through prewhitening, secondary peaks emerge very close to the main pulsation frequencies. The reason is that prewhitening subtracts from the data at each step a sine wave with constant frequency and amplitude, while on timescales of many years,pulsation frequencies and amplitudes are no longer constant. This effect, which is well visible for f1 (Fig. 4 lower left panels), adds noise to the amplitude spectrum of the residuals and may lead to incorrect determinations of the low-amplitude frequencies. In this respect, the average values of f3 and f4 might be slightly different from those reported in Table 3, with differences even larger than the errors reported there.
In order to decipher the information contained in the peaks close to f1, we conducted a small experiment with a synthetic light curve. Since the behavior of f1 is fairly regular and relatively easy to model in the period up to 2009.0, while it becomes more irregular later on (see Figs. 7–9), we considered only the period up to 2009.0. The synthetic light curve contains a single sine wave without noise with the same time distribution as the data, a frequency and amplitude equal to f1, and similar frequency and amplitude variations. In practice, we imposed a linear variation of the period with 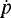 = 1.34 ×10−12 (the value found from the O–C analysis described in Sect. 4) and a sinusoidal variation of the amplitude corresponding to the sinusoidal fit shown in Fig. 7 (top right panel). The amplitude spectrum of this synthetic light curve near f1 is shown in Fig. 5 (right panels) and can be compared with the real data in the left panels. Up to the secondary peak on the right side of f1, the agreement between real and synthetic data is very good both in terms of frequency and amplitude: we obtain 2860.9418 μHz and 2.74 ppt vs. 2860.9414 μHz and 2.61 ppt, respectively (the main peak being at 2860.9382 μHz with an amplitude of 8.84 ppt). Thus we verified that a linear time variation of a pulsation period splits the frequency into three close peaks almost equally spaced in frequency. If the amplitude is constant, the two secondary peaks have the same amplitude. If the amplitude is variable as in this case, the two secondary peaks have different amplitudes.
= 1.34 ×10−12 (the value found from the O–C analysis described in Sect. 4) and a sinusoidal variation of the amplitude corresponding to the sinusoidal fit shown in Fig. 7 (top right panel). The amplitude spectrum of this synthetic light curve near f1 is shown in Fig. 5 (right panels) and can be compared with the real data in the left panels. Up to the secondary peak on the right side of f1, the agreement between real and synthetic data is very good both in terms of frequency and amplitude: we obtain 2860.9418 μHz and 2.74 ppt vs. 2860.9414 μHz and 2.61 ppt, respectively (the main peak being at 2860.9382 μHz with an amplitude of 8.84 ppt). Thus we verified that a linear time variation of a pulsation period splits the frequency into three close peaks almost equally spaced in frequency. If the amplitude is constant, the two secondary peaks have the same amplitude. If the amplitude is variable as in this case, the two secondary peaks have different amplitudes.
Before proceeding with our analysis on frequency and amplitude variations, it is important to verify that the uncertainties associated with frequencies and amplitudes such as those reported in Table 3 are correctly estimated. These uncertainties are the 1σ errors obtained from a Monte Carlo (MC) simulation on 1000 synthetic light curves in which random Gaussian noise (at the same level as the data) was added to the five p-modes listed in Table 3. In Fig. 6 the distribution of frequencies and amplitudes obtained from the MC simulations is shown for the two main pulsation modes of V391 Peg (f1 and f2).
After we verified that the error bars of our measurements were reliable, we measured the pulsation periods and amplitudes for f1 and f2 in each observing season (Fig. 7), where observing season means the period from May to December of the same year in which V391 Peg is observable. The frequencies and amplitudes shown in Fig. 7 were obtained from multi-sinusoidal fits considering only four frequencies (f1 to f4), while 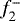 was excluded because it is not detected in most of these one-season runs. The same exercise was repeated using all five frequencies, but the results were less reliable.
was excluded because it is not detected in most of these one-season runs. The same exercise was repeated using all five frequencies, but the results were less reliable.
When we consider only the data up to 2009.0, corresponding to the green part of Fig. 7, the variation of p1 can be fit with a straight line whose slope corresponds to 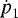 = (1.60 ± 0.20) ×10−12. In the same period, the amplitude a1 shows a fairly regular sinusoidal pattern with a period of about 3400 days (9.3 years) and an amplitude of 29%. After 2009.0, the trend of the period and amplitude variations of p1 changes and p1 starts to decrease. The reason for this behavior, which is also confirmed by the O–C analysis in Figs. 8 and 9, is not known. Although we normally attribute period and amplitude variations to nonlinear interactions between different pulsation modes, in this case, with an l = 0 mode, we cannot invoke the resonant mode coupling between the components of a multiplet of modes split by the stellar rotation, nor even the three-mode resonance, which would require that f1 corresponds to a linear combination of the other two pulsation modes that we do not see. These two mechanisms were recently invoked as a possible explanation for the frequency and amplitude variations observed in the sdB g- and p-mode pulsator KIC 10139564 (Zong et al. 2016). The lower left panel of Fig. 7 shows that when we use all the available data, the variation in p2 can be fit with a straight line whose slope corresponds to
= (1.60 ± 0.20) ×10−12. In the same period, the amplitude a1 shows a fairly regular sinusoidal pattern with a period of about 3400 days (9.3 years) and an amplitude of 29%. After 2009.0, the trend of the period and amplitude variations of p1 changes and p1 starts to decrease. The reason for this behavior, which is also confirmed by the O–C analysis in Figs. 8 and 9, is not known. Although we normally attribute period and amplitude variations to nonlinear interactions between different pulsation modes, in this case, with an l = 0 mode, we cannot invoke the resonant mode coupling between the components of a multiplet of modes split by the stellar rotation, nor even the three-mode resonance, which would require that f1 corresponds to a linear combination of the other two pulsation modes that we do not see. These two mechanisms were recently invoked as a possible explanation for the frequency and amplitude variations observed in the sdB g- and p-mode pulsator KIC 10139564 (Zong et al. 2016). The lower left panel of Fig. 7 shows that when we use all the available data, the variation in p2 can be fit with a straight line whose slope corresponds to 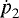 = (1.47 ± 0.41) ×10−12. In the lower right panel we see quite irregular variations of a2, but these apparent variations can be at least partially attributed to the interaction (beating) between f2 and
= (1.47 ± 0.41) ×10−12. In the lower right panel we see quite irregular variations of a2, but these apparent variations can be at least partially attributed to the interaction (beating) between f2 and 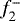 . When we also consider
. When we also consider 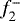 in the fit, the individual measurements of a2 may vary by several tenths of ppt, indicating that the 1σ error bars of a2 are underestimated. At shorter timescales, we did not find any periodicity in the amplitude variations of a2 that could confirm the beating effect and thus the rotation period of the star around 40 days. The mean quality of the data is not sufficient for detecting this effect. Based on our best-quality run of October 2007 at the WHT-MDM, we can only exclude short timescale variations (from night to night) for both a1 and a2 .
in the fit, the individual measurements of a2 may vary by several tenths of ppt, indicating that the 1σ error bars of a2 are underestimated. At shorter timescales, we did not find any periodicity in the amplitude variations of a2 that could confirm the beating effect and thus the rotation period of the star around 40 days. The mean quality of the data is not sufficient for detecting this effect. Based on our best-quality run of October 2007 at the WHT-MDM, we can only exclude short timescale variations (from night to night) for both a1 and a2 .
We also attempted to fit the data from 1999 to the end of 2008 with two sine waves corresponding to f1 and f2, leaving as free parameters not only the frequencies, amplitudes, and phases, but also 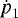 and
and 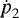 . The fit converged only when we fixed
. The fit converged only when we fixed 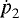 , but the value that we obtained for
, but the value that we obtained for 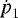 is about ten times higher than the value obtained from the direct measurements. This method is less reliable than the direct method or the O–C method described in the next section because it makes use of constant amplitudes, but we know that the amplitudes are not constant, and in particular, a1 varies significantly (Fig. 7).
is about ten times higher than the value obtained from the direct measurements. This method is less reliable than the direct method or the O–C method described in the next section because it makes use of constant amplitudes, but we know that the amplitudes are not constant, and in particular, a1 varies significantly (Fig. 7).
While amplitude variations in sdB p-mode pulsators have been known for a long time, with time scales ranging from days to years, the results reported in this section show that even the frequencies are less stable than previously believed and may suffer significant variations that are not simply due to the long-term modifications of the stellar structure. Amplitude and frequency variations have recently been detected in most of the sdB pulsators observed by the Kepler spacecraft, with complex patterns that sometimes are stochastic (Østensen et al. 2014) and sometimes more regular and periodic (e.g., Zong et al. 2016).
 |
Fig. 5 Comparison between the amplitude spectrum near f1
of the data (left) and the amplitude spectrum near f1
of a simulated data set (right) with the same time distribution. In this test we used only
the data up to 2009.0 because in this period it is easier to simulate the behavior of
f1 .
For the simulated data we used a single pure sine wave (no noise) with the same frequency and amplitude of
f1
and also with similar long-term frequency and amplitude variations (linear variation of the period with
|
 |
Fig. 6 Distribution of the frequency and amplitude deviations for the two main pulsation modes of V391 Peg. The deviations, in units of 1σ errors, are the differences between the values obtained from the original light curve and those obtained from 1000 artificial light curves created by the MC simulator of Period04 (Lenz & Breger 2005). The synthetic light curves are built using the five p-modes of Table 3 and adding Gaussian noise at the same level as the original data. The 2D distributions are also projected into 1D histograms and compared with a normal distribution (red). |
 |
Fig. 7 Period and amplitude variations of the two main pulsation modes of V391 Peg. The variation of
p1
is compatible with a linear increase up to 2009.0, when a change of regime
appears.The same change is also visible for the amplitude: up to 2009.0,
a1
shows a fairly regular sinusoidal shape with a period of about 3400 days
or 9.3 years. A linear increase of the pulsation period is visible also for
p2
when considering the whole data set, while the irregular variations of a2
can be at least partially attributed to the beating between f2
and |
4 O–C analysis
The O–C analysis (Sterken 2005; and subsequent articles in the same volume) is a powerful method for detecting tiny variations of the pulsation periods on long timescales that cannot be seen or clearly seen from direct independent measurements (like in Fig. 7). The O–C method is more sensitive than the direct method because instead of directly measuring the period change, it measures the phase variations induced by the period change. When we consider a period that changes linearly in time (a good approximation on timescales of a few years, extremely short with respect to the evolutionary timescales), the phase variations have the great advantage of being proportional to T2, where T is the duration of the observation.
In order to reduce the phase errors, the data for the O–C analysis were considered in monthly subsets. A four-sinusoid fit was applied to each subset using the best (fixed) frequencies from Table 3 (f1 to f4) and leaving amplitudes and phases as free parameters. 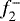 was not used because it is not detected in the monthly subsets.
was not used because it is not detected in the monthly subsets.
The difference between these monthly phases and those obtained from the whole data set are the O–C differences shown in Fig. 8, in which the phase differences have been converted into time differences. In Fig. 8 we see the same effect as was already seen in Fig. 7: since 2009, the curvature in the O–C diagram of f1 changes. We do not know the reasons for this change, it might be related to nonlinear interactions between different pulsation modes. In any case, it is clear from Fig. 8 (upper panels) that a two-component fit with a parabola plus a sinusoid (like in SSJ07) can give satisfactory results only up to ~2009. When considering only the data up to 2009.0, the long-term parabolic variation of the main pulsation period corresponds to 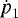 = (1.36 ± 0.06) × 10−12. In order to also fit the more recent data, we tried a different approach using two sinusoids (lower panels of Fig. 8). Even in this way, we did not obtain a reasonable fit of the whole data set, and moreover, the quality of the fit up to 2009 is lower, indicating that a sinusoidal
= (1.36 ± 0.06) × 10−12. In order to also fit the more recent data, we tried a different approach using two sinusoids (lower panels of Fig. 8). Even in this way, we did not obtain a reasonable fit of the whole data set, and moreover, the quality of the fit up to 2009 is lower, indicating that a sinusoidal 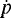 is not the solution.
is not the solution.
As a second step, the O–C analysis was repeated using larger data subsets covering a whole observing season (that is, from May to December for V391 Peg) and using the same pulsation frequencies as before. Again, 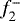 was not used because it is not detected in almost all runs. These larger subsets are particularly useful for f2 (the secondary pulsation frequency), in order to reduce the phase errors that are very large when we use the monthly subsets. The results are shown in Fig. 9. In the upper panels (from 1A to 2B), we see the O–C diagram of f1 and f2 when using only the data from 1999 to 2007.0, basically the same data as in SSJ07 (only three short runs were added), but with the new updated frequencies. These plots show that when we use better values for f3 and f4, the sinusoidal components of f1 and f2 (panels 1B and 2B) differ: even if the amplitudes and the initial phases are still in agreement (like in SSJ07), the periods are now different. In the central panels (from 3A to 4B), we see the new fits when we use the data from 1999 to 2009.0, before the change of sign of
was not used because it is not detected in almost all runs. These larger subsets are particularly useful for f2 (the secondary pulsation frequency), in order to reduce the phase errors that are very large when we use the monthly subsets. The results are shown in Fig. 9. In the upper panels (from 1A to 2B), we see the O–C diagram of f1 and f2 when using only the data from 1999 to 2007.0, basically the same data as in SSJ07 (only three short runs were added), but with the new updated frequencies. These plots show that when we use better values for f3 and f4, the sinusoidal components of f1 and f2 (panels 1B and 2B) differ: even if the amplitudes and the initial phases are still in agreement (like in SSJ07), the periods are now different. In the central panels (from 3A to 4B), we see the new fits when we use the data from 1999 to 2009.0, before the change of sign of 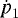 : the sinusoidal components of f1 and f2 (panels 3B and 4B) are similar to the previous ones (panels 1B and 2B), except for a larger amplitude for f2, which increases the differences between f1 and f2 . The parabolic components (panels 3A and 4A) correspond to
: the sinusoidal components of f1 and f2 (panels 3B and 4B) are similar to the previous ones (panels 1B and 2B), except for a larger amplitude for f2, which increases the differences between f1 and f2 . The parabolic components (panels 3A and 4A) correspond to 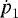 = (1.34 ± 0.04) × 10−12 and
= (1.34 ± 0.04) × 10−12 and 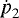 = (1.62 ± 0.22) × 10−12, in good agreement with the previous measurements of SSJ07. These numbers also agree with adiabatic theoretical expectations for the secular variation of the pulsation periods (Charpinet et al. 2002). However, the fact that
= (1.62 ± 0.22) × 10−12, in good agreement with the previous measurements of SSJ07. These numbers also agree with adiabatic theoretical expectations for the secular variation of the pulsation periods (Charpinet et al. 2002). However, the fact that 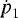 changed sign near 2009 indicates that in real stars, these processes may be more complicated. Finally, in the lower panels of Fig. 9 (from 5A to 6B), we show the best two-component fits of the whole data set using two sinusoids with different periods for f1, and a parabola plus a sinusoid for f2. Except for the last points, these fits can reproduce the general trend of the O–C data (panels 5A and 6A), but show a large dispersion, particularly for f1: the sinusoidal fits in panels 5B and 6B (chi-squared equal to 894 and 276, respectively) are only slightly better than a simple straight line (χ2 = 1075 and 322). At the same time, the two sinusoidal components have similar periods, amplitudes, and phases within 4%, 8%, and 7% respectively.
changed sign near 2009 indicates that in real stars, these processes may be more complicated. Finally, in the lower panels of Fig. 9 (from 5A to 6B), we show the best two-component fits of the whole data set using two sinusoids with different periods for f1, and a parabola plus a sinusoid for f2. Except for the last points, these fits can reproduce the general trend of the O–C data (panels 5A and 6A), but show a large dispersion, particularly for f1: the sinusoidal fits in panels 5B and 6B (chi-squared equal to 894 and 276, respectively) are only slightly better than a simple straight line (χ2 = 1075 and 322). At the same time, the two sinusoidal components have similar periods, amplitudes, and phases within 4%, 8%, and 7% respectively.
In order to explore this in more detail, we made a weighted average of the O–C data in panels 5B and 6B (which means a weighted average of the O–C data of f1 and f2 after subtracting their long-term component). The result is illustrated in Fig. 10 and shows that when we sum the information from f1 and f2, the fit of the sinusoidal component improves, and at the end, we have 9 points out of 13 that are consistent with a sine wave with a period of 1127 ± 45 days (or 3.09 ± 0.12 years) and an amplitude of 3.02 ± 0.85 light seconds. Assuming that the sine wave is caused by the planet and that the mass of the sdB star is 0.47 M⊙, these numbers correspond to an orbital distance of 1.6 AU and a minimum mass of 1.8 MJup.
Although not shown in Fig. 9, we also tried to fit the O–C plots of f1 and f2 with a parabola plus two sinusoids (corresponding to two potential planets), but we were unable to find any solution for which the six parameters of the two sinusoids were in reasonable agreement between f1 and f2 .
Several checks were made in order to ensure that the new O–C results reported in this section are correct and robust and to understand why in SSJ07 periods, amplitudes, and phases of the sinusoidal components of the O–C diagrams of f1 and f2 agreed so well. As stated previously, the current O–C results were obtained using four frequencies (f1 to f4), also including the data taken with filters different from Johnson B, and making use of statistical weights. However, we also tested different combinations without statistical weights, excluding all the data taken in filters different from Johnson B (see Sect. 2), and considering only the two main frequencies f1 and f2 . In all these tests, the results varied little2. Thus it is not easy to understand the differences between our current results and those obtained in SSJ07 (even in that analysis, similar tests with different combinations were made). We conclude that the good agreement found in SSJ07 was a coincidence due to a few small differences between the two analyses: slightly different pulsation frequencies, two NOT observing runs that were excluded in SSJ07 because they were taken with a Bessell B filter and that are now included (after careful tests of the effects on phase and amplitude), and one new standard-B-filter Monet-N observing run that was not yet available in SSJ07. Of these factors, the greatest is probably given by the different frequencies that were used. In SSJ07 we used f1 = 2860.9387, f2 = 2824.0965, f3 = 2880.6842, f4 = 2921.8463, and f5 = 2882.0039μHz. Comparing these values with those in Table 3, we see very small differences for f1 and f2, compatible with real period variations; the new value of f3 is higher by 0.4390 μHz; f5 is not confirmed and used not at all in the new analysis, but its influence must be small because of the very low amplitude. Finally and mostly important, the updated value of f4 is lower by 11.8510 μHz with respect to the old value, which means that in SSJ07, because of the poorer spectral window, we used an incorrect value corresponding to the one-day alias on the right side of the correct peak. This is probably the mean reason of the different results. An incorrect value of f4 can modify the multi-sinusoidal fits and thus slightly modify the phases of f1 and f2 as well.
 |
Fig. 8 O–C diagram of the main pulsation mode of V391 Peg when using monthly runs (each point represents the data collected within one month). Upper panels: fit of the O–C data with a parabola (long-term variation, blue continuous line) plus a sine wave (“planetary component”, red dashed line) and planetary component alone after subtracting the long-term component. This solution gives satisfactory results only up to the end of 2008, and the fit was made considering only the data up to 2009.0. Lower panels: same as upper panels, but using two sinusoids. In this case, the fit was made using all the data, but a reasonable fit is obtained only up to ~2010, indicating that two components are simply not enough to obtain a reasonable fit of all the data. When we compare the planetary component alone in the period 2000–2009.0, the fit is better when we use parabola + sine wave (χ2 = 762) with respect to the double sine wave (χ2 = 1267); for comparison, a straight line would give χ2 = 1376. |
 |
Fig. 9 Same as Fig. 8 for f1 (left) and f2 (right) for one-season runs. Panels 1A, 1B, 2A, and 2B are obtained using only the data up to 2007.0, so that we can directly compare the current results (blue and red lines) with those obtained by SSJ07 (green lines shifted by −20 and −5 s in panels 1A and 2A and 1B and 2B, respectively). The small horizontal shifts of the first and last points are due to the addition of three observing runs that were not present in SSJ07. Panels 1B and 2B show that in the current results, the period of the sinusoid is slightly shorter for f1 but longer for f2, so that at the end the agreement between f1 and f2 is worse with respect to SSJ07. The reasons of these differences are discussed in the text. When we add the new data, the longer period of the sinusoidal component of f2 with respect to f1 is confirmed (panels 3B and 4B), and moreover, we note a further difference in amplitude. Panel 3A confirms the change of regime of f1 near 2009 that was already visible in Figs. 7 and 8. This change also tends to worsen the fit of f2 (4A), and for this reason, the fits shown in panels 3A to 4B are obtained considering only the data up to 2009.0. Panels 5A and 5B show an alternative solution obtained using a low-frequency sine wave for the long-term component of f1, as in the lower panels of Fig. 8. The fits shown in panels 5A to 6B were obtained using all the available data. More comments are given in the text. |
 |
Fig. 10 O–C diagram obtained by combining the information from f1 and f2 . In practice, we have computed the weighted average of the points in panels 5B and 6B of Fig. 9 and recomputed the best fit with a sine wave. Compared with these panels, the fit is significantly improved and the residuals of 9 points out of 13 (including all those with smaller error bars) are close to zero. |
 |
Fig. 11 g-mode amplitude spectrum using our best-quality runs between 2002 and 2008 (192.8 h of observations in total). The upper right panel shows the spectral window (red), while the other panels from top to bottom show amplitude spectrum and residuals after one, two, and three prewhitening steps. We note an excess of power in two main regions near 180 and 310 μHz. After prewhitening, this excess of power is not completely removed near 180 μHz, suggesting that further low-amplitude frequencies are present in that region. |
5 V391 Peg b: real planet or false detection?
Whether V391 Peg b is a real planet or a false detection is an open question. The O–C diagrams of f1 and f2 provide arguments in favor and against the presence of V391 Peg b.
-
f1 : considering the period up to 2009.0, the O–C diagram of f1 still has a sinusoidal component that can be explained by the presence of a giant planet with a minimum mass of 3.5 MJup, orbiting V391 Peg in 3.1 years at a distance of 1.7 AU. However, the behavior of f1 after 2009.0 shows that this is more complex, and we see from Figs. 8 and 9 that a simpletwo-component fit of the O–C data is not enough to interpret the whole data set up to 2012. Using two sinusoids with different periods allows us to fit the O–C data up to 2010 or 2011, but the quality of the fit is much poorer. When we use two sinusoids, the period of the sine wave corresponding to the planet (Fig. 9/5B) is longer than the period obtained with a parabola plus a sine wave (Fig. 9/3B);
-
f2 : up to 2009.0, the O–C diagram of f2 also shows a sinusoidal component, but now, unlike SSJ07, the period and the amplitude differ from f1 by ~20% and ~36%, respectively. The new data support the previous identification of f2 as an l = 1 mode, and this implies that frequency splitting due to stellar rotation must be at work. Regardless of whether our detection of
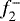 is real, these modes split by stellar rotation must be there, close to f2,
and this is a source of noise for the O–C computations of f2.
This argument makes the O–C results from f1
(which is an l = 0
mode) more reliable, and this is one of the reasons why the presence of the planet cannot be excluded.
At the same time, this argument can partially explain the discrepancies between the O–C diagrams of
f1
and f2;
is real, these modes split by stellar rotation must be there, close to f2,
and this is a source of noise for the O–C computations of f2.
This argument makes the O–C results from f1
(which is an l = 0
mode) more reliable, and this is one of the reasons why the presence of the planet cannot be excluded.
At the same time, this argument can partially explain the discrepancies between the O–C diagrams of
f1
and f2; -
f1 +f2: when we try to fit the whole set of O–C data using a sine wave plus a longer-period sinusoid for f1 and a parabola for f2 (panels 5 and 6 of Fig. 9), we see that the sine wave corresponding to the planet is very similar for f1 and f2 in terms of period, amplitude, and phase (panels 5B and 6B of Fig. 9). Although these fits are of poor quality, it is possible to obtain a substantial improvement when we use both pulsation frequencies together (Fig. 10). If we interpret this effect with the presence of the planet, we obtain a minimum mass of 1.8 MJup, while the orbital period and distance, 3.1 years and 1.65 AU, do not change much with respect to the values obtained previously.
In conclusion, while in SSJ07 the presence of a planet orbiting V391 Peg was robustly and independently suggested by the two main pulsation modes of the star, these two modes now give contradictory indications. A sinusoidal component is still visible in the O–C diagrams of both f1 and f2, but the parameters of the two sinusoids are different in general. The presence of a planet orbiting V391 Peg is clearly much less robust than before, although it cannot be entirely excluded.
The peculiar behavior of f1 with a quitesudden change of sign of its time derivative after 2008 suggests that pulsation timing is a delicate method, with aspects thatare still unclear and are likely related to nonlinear pulsation effects. As a consequence, the reliability of the O–C method to find low-mass companions should be questioned, without forgetting, however, that for sdB stars we have at least two cases in which the presence of a stellar companion was detected through pulsation timing (Barlow et al. 2011a; Otani et al. 2017), and in one case, for CS 1246, this detection was confirmed by radial velocity (RV) measurements (Barlow et al. 2011b). With respect to V391 Peg, the O–C detection was easier in both cases because of the much higher companion mass, and for CS 1246, also because of the much shorter orbital period of ~14 days, which meant no problems with the long-term variation of the pulsation period. Unlike CS 1246, which exhibits a single large-amplitude radial mode, and EC 20117-4014, which shows three low-amplitude pulsation modes with frequency separations of ~250 and ~680 μHz (Otani et al. 2017), with V391 Peg we have the additional difficulty that all four pulsation modes are concentrated within 86 μHz, which makes it more difficult to measure the phases accurately.
In orderto confirm or definitively reject the presence of V391 Peg b, an independent confirmation with another method is needed. Given that Gaia astrometry is not accurate enough at a distance of about 1400 pc, spectroscopic RVs seem the most natural way to proceed. However, the RV “noise” produced by the pulsations is a serious concern and can easily reach several hundred m/s, while the expected planetary signal is no more than 100 m/s. Given the very different time scales, it is in principle possible to remove or reduce the noise due to the pulsations, provided that we know the Fourier spectrum and the main pulsation modes in detail. This is true for the high-frequency part of the spectrum (the p-modes), which is relatively simple, with only two dominant modes that have similar periods. The noise due to the p-modes can be reduced by choosing an exposure time close to an integer multiple of ~350 s. For the g-modes, the situation is more complicated as the low-frequency part of the Fourier spectrum is not well known (see next section). The noise can be reduced by averaging the results obtained from different spectra taken in the same epoch at different pulsation phases. A great help for a precise determination of the g-modes may come from the Transiting Exoplanet Survey Satellite (TESS; Ricker et al. 2016), which can observe V391 Peg continuously for 54 days in some years from now, with a sampling time of 20 or 120 s.
6 g-modes
g-modes were detected in V391 Peg by Lutz et al. (2009). Our new larger data set has been used to confirm this detection. Given that the g-modes are particularly disturbed by the atmospheric variations that act at similar frequencies, we selected a subset of high-quality data with a length of each single run of at least a few hours. This subset, which has a total duration of 192.8 h spread over 5.8 years (between 2002 and 2008), was corrected for differential atmospheric extinction (the comparison stars are always much redder than the sdB) and analyzed. The amplitude spectrum in Fig. 11 shows two regions with an excess of power near 180 and 310 μHz and three peaks that emerge from the noise at more than 5σ. The corresponding frequencies, amplitudes, and phases are listed in Table 3. The noise threshold, which was 4σ for the p-modes, was increased to 5σ because the spectrum is much more noisy in this region. After these three peaks were subtracted from the data, the lower panel of Fig. 11 shows that some residual power is still there, suggesting that further low-amplitude frequencies are likely present below the noise threshold. As anticipated in the previous section, in 2 years from now, TESS will be able to shed light on this part of the Fourier spectrum and likely measure the rotation period of the star, confirming or refuting the tentative rotation period of ~40 days suggested by the p-mode analysis in Sect. 3.2.
7 Summary
Interpreting the new O–C results shown in Figs. 8 and 9 is more complicated than it was 10 years ago. At that time, the very good agreement between the sine-wave component of f1 and f2 strongly supported the presence of a giant planet (SSJ07). Now, with many more data, this agreement is much more uncertain and the presence of V391 Peg b is weaker and requires confirmation with an independent method. Like in SSJ07, a two-component fit (parabola + sine wave) still gives satisfactory results for both f1 and f2, at least up to 2009. The sinusoidal components of f1 and f2, however, now differ in period and amplitude by ~20% and ~36%, respectively. Starting in phase, after two cycles the O–C sine wave of f2 is antiphased with respectto f1. When we consider all the O–C data from 1999 to 2012, a two-component fit is in general not satisfactory. For f1, we tried to fit the O–C data with a double sine wave, corresponding to a sinusoidal behavior of 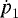 . The result is a very poor fit. However, this solution produces a certain agreement between the sinusoidal components of f1 and f2 .
. The result is a very poor fit. However, this solution produces a certain agreement between the sinusoidal components of f1 and f2 .
The change in sign of the time derivative of the main pulsation period near 2009 is an intriguing phenomenon that is difficult to explain. Nonlinear interactions between pulsation modes seem the most natural explanation, but the l = 0 identification (Silvotti et al. 2010), which is confirmed by the new data, does not help as we cannot invoke resonant mode coupling between the components of a multiplet nor resonance between modes linked by linear combinations that we do not see. The irregular behavior of f1 agrees to a certain extent with recent Kepler results, which showed that sdB pulsation frequencies are in general less stable than previously believed. The Kepler results are mostly focused on g-modes, but a similar behavior seems also relatively common for the p-modes. At least this is suggested by our results.
The l = 1 identification for f2 (Silvotti et al. 2010) is also confirmed by the new data (or at least l must be >0). A retrograde mode is detected, although at the limit of our detection threshold, and this suggests a stellar rotation period of about 40 days.
Using only the data up to 2009.0, we can improve our previous measurements of 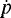 for f1 and f2 and obtain
for f1 and f2 and obtain 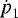 = (1.34 ± 0.04) × 10−12 and
= (1.34 ± 0.04) × 10−12 and 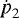 = (1.62 ± 0.22) × 10−12. The order of magnitude of these numbers is in agreement with theoretical expectations for evolved models of extreme horizontal branch stars (Charpinet et al. 2002), and their positive sign would normally be interpreted as an indicator of a stellar expansion. At least for f1, however, the change in curvature near 2009 implies that these numbers are not simply or directly related to the evolutionary timescales expected from theory, and the situation is more complicated.
= (1.62 ± 0.22) × 10−12. The order of magnitude of these numbers is in agreement with theoretical expectations for evolved models of extreme horizontal branch stars (Charpinet et al. 2002), and their positive sign would normally be interpreted as an indicator of a stellar expansion. At least for f1, however, the change in curvature near 2009 implies that these numbers are not simply or directly related to the evolutionary timescales expected from theory, and the situation is more complicated.
Finally, the new data confirm that V391 Peg is a hybrid pulsator, showing both p- and g-modes. The next opportunity for a more detailed study of this star, and in particular for the study of the low-frequency part of its Fourier spectrum, is given by the TESS mission, which may observe V391 Peg continuously for 54 days in about 2 years from now. With a better knowledge of the Fourier spectrum at low frequencies as well, it should be easier to confirm or reject the presence of a planet orbiting V391 Peg by measuring the spectroscopic radial velocities of the star.
Acknowledgements
We thank Elia Leibowitz, who made the data collected at the Wise Observatory available to us, Christopher D. J. Savoury for helping us with the ULTRACAM observations and data reduction, and Wen-Shan Hsiao for contributing the Lulin data. We also thank Patrick Lenz for providing us with a modified version of period04, which facilitated the error estimation from the MC simulations. V. S. D. and ULTRACAM are supported by STFC grant ST/J001589/1. L. M. was supported by the Hungarian National Research, Development and Innovation Office (NKFIH) grant PD-116175 and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences.
References
- Almeida, L., Jablonski, F., & Rodrigues, C. 2013, ApJ, 766, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, J. H. 1992, ApJ, 385, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Baran, A. S., Zola, S., Blokesz, A., Østensen, R. H., & Silvotti, R. 2015, A&A, 577, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barlow, B. N., Dunlap, B. H., & Clemens, J. C. 2011a, MNRAS, 414, 3434 [NASA ADS] [CrossRef] [Google Scholar]
- Barlow, B. N., Dunlap, B. H., & Clemens, J. C. 2011b, ApJ, 737, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, T. G. III, & Moffett, T. J. 1975, AJ, 80, 48 [CrossRef] [Google Scholar]
- Bear, E., & Soker N. 2014, MNRAS, 444, 1698 [NASA ADS] [CrossRef] [Google Scholar]
- Beuermann, K., Hessman, F. V., Dreizler, S., et al. 2010, A&A, 521, L60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuermann, K., Dreizler, S., Hessman, F. V., & Deller, J. 2012, A&A, 543, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bours, M. C. P., Marsh, T. R., Parsons, S. G., et al. 2016, MNRAS, 460, 3873 [NASA ADS] [CrossRef] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., & Dorman, B. 2002, ApJS 140, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charpinet, S., Fontaine, G., Brassard, P., et al. 2011, Nature, 480, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Compton, D. L., Bedding, T. R., Murphy, S. J., & Stello, D. 2016, MNRAS, 461, 1943 [CrossRef] [Google Scholar]
- Dalessio, J., Provencal, J. L., & Shipman, H. L. 2015, ASP Conf. Ser., 493, 157 [Google Scholar]
- Eastman, J., Siverd, R., & Gaudi, S. 2010, PASP, 122, 935 [NASA ADS] [CrossRef] [Google Scholar]
- Geier, S., Schaffenroth, V., Drechsel, H., et al. 2011, ApJ, 731, L22 [Google Scholar]
- Heber, U. 2016, PASP, 128, 966 [Google Scholar]
- Hinse, T., Lee, J.-W., Goździewski, K., Horner, J., & Wittenmyer, R. A. 2014, MNRAS, 438, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Hutchens, Z. L., Barlow, B. N., Vasquez Soto, A. et al. 2017, Open Astron., 26, 252 [Google Scholar]
- Kepler, S. O., Winget, D. E., Nather, R. E., et al. 1991, ApJ, 378, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Konacki, M., & Wolszczan, A. 2003, ApJ, 591, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, A. F. 2006, MNRAS, 369, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Ledoux, P. 1951, ApJ, 114, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J.-W., Hinse, T. C., Youn, J.-H., & Han, W. 2014, MNRAS, 445, 2331 [NASA ADS] [CrossRef] [Google Scholar]
- Lenz, P., & Breger, M. 2005, Commun. Asteroseismol., 146, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Lohr, M. E., Norton, A. J., Anderson, D. R., et al. 2014, A&A, 566, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Loumos, G. L., & Deeming, T. J. 1977, Ap&SS, 56, 285 [Google Scholar]
- Lutz, R., Schuh, S., & Silvotti, R. 2009, A&A, 496, 469 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murphy, S. J., Bedding, T. R., Shibahashi, H., Kurtz, D. W., & Kjeldsen, H. 2014, MNRAS 441, 2515 [Google Scholar]
- Murphy, S. J., Bedding, T. R., & Shibahashi, H. 2016a, ApJ, 827, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, S. J., Shibahashi, H., & Bedding, T. R. 2016b, MNRAS, 461, 4215 [NASA ADS] [CrossRef] [Google Scholar]
- Østensen, R., Solheim, J.-E., Heber, U., et al. 2001, A&A, 368, 175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Østensen, R. H., Reed, M. D., Baran, A. S., & Telting, J. H., 2014, A&A, 564, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Otani, T., Oswalt, T. D., Lynas-Gray, A. E., et al. 2017, ApJ, submitted, [arXiv:1708.06029] [Google Scholar]
- Qian, S.-B., Zhu, L.-Y., Zola, S., et al. 2009, ApJ, 695, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Zhu, L.-Y., Liu, L., et al. 2010, Ap&SS, 329, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Qian, S.-B., Shi, G., Zola, S., et al. 2013, MNRAS, 436, 1408 [NASA ADS] [CrossRef] [Google Scholar]
- Randall,S. K., Fontaine, G., Brassard, P., & Bergeron, P. 2005, ApJS, 161, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Ricker, G. R., Vanderspek, R., Winn, J., et al. 2016, Proc. SPIE, 9904, 99042B [Google Scholar]
- Schaffenroth, V., Geier, S., Heber, U., et al. 2014a, A&A, 564, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Classen, L., Nagel, K., et al. 2014b, A&A, 570, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schaffenroth, V., Barlow, B. N., Drechsel, H., & Dunlap, B. H. 2015, A&A, 576, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schleicher, D. R. G., & Dreizler, S. 2014, A&A 563, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shibahashi, H., & Kurtz, D. W. 2012, MNRAS, 422, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Shibahashi, H., Kurtz, D. W., & Murphy, S. J. 2015, MNRAS, 450, 3999 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R. 2008, ASP Conf. Ser., 392, 215 [Google Scholar]
- Silvotti, R., Janulis, R., Schuh, S., et al. 2002, A&A, 389, 180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silvotti, R., Bonanno, A., Bernabei, S., et al. 2006, A&A, 459, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Silvotti, R., Schuh, S., Janulis, R., et al. 2007, Nature, 449, 189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Silvotti,R., Randall, S. K., Dhillon, V. S., et al. 2010, Astron. Nachr., 331, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Silvotti, R., Szabó, R., Degroote, P., Østensen, R. H., & Schuh, S. 2011, AIP Conf. Ser., 1331, 133 [Google Scholar]
- Silvotti, R., Charpinet, S., Green, E., et al. 2014, A&A, 570, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sterken, C. 2005, ASP Conf. Ser., 335, 3 [Google Scholar]
- Telting, J. H., Østensen, R. H., Baran, A. S., et al. 2012, A&A, 544, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Völschow, M., Schleicher, D. R. G., Perdelwitz, V., & Banerjee, R. 2016, A&A, 587, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolszczan, A., & Frail, D. A. 1992, Nature, 355, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Zong, W. 2017, PhD Thesis, Univ. of Toulouse, https://tel.archives-ouvertes.fr/tel-01434986/document [Google Scholar]
- Zong, W., Charpinet, S., & Vauclair, G. 2016, A&A, 594, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zorotovic, M., & Schreiber, M. R. 2013, A&A, 549, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
The WHT data were simultaneously obtained with ULTRACAM in three photometric bands (u, g, and r) but only the g-band data are used in this article, while multi-band data were previously used to identify the main pulsation modes of V391 Peg (Silvotti et al. 2010).
When we consider only f1 and f2 in the multi-sinusoidal fits instead of four frequencies, the results are almost identical to those reported in panels 3A to 4B of Fig. 9. When we use only Johnson-B-filter data, the main difference is that the period of the sinusoidal component of f1 increases by 7%. When we do not use statistical weights, we obtain the largest difference, with the amplitude of the sinusoidal component of f2 reduced from 9.4 to 5.4 s, while all other parameters remain about the same.
All Tables
All Figures
 |
Fig. 1 Distribution of the 217 232 data points over 13 years. The overall duty cycle is 0.92%, and the best coverage is obtained in 2007 with a duty cycle of 5.55%. The varying relative intensity is caused by the beating between the main frequencies and also depends on the varying quality of the data. |
| In the text | |
 |
Fig. 2 p-mode amplitude spectrum of our best-quality run of 7.9 days, with a duty cycle of 35%, obtained in October 2007 with a SLOAN g filter using two telescopes at different longitudes: the WHT 4.2m in La Palma, equipped with ULTRACAM, and the MDM 1.3m at Kitt Peak. The upper panel shows the spectral window (red), while the other panels from top to bottom show the amplitude spectra of the data and of the residuals after one, two, three, and four prewhitening steps. A plot showing the high quality of the ULTRACAM data is presented in Silvotti et al. (2010). |
| In the text | |
 |
Fig. 4 Same as Figs. 2 and 3, but using the whole data set (1999–2012). Upper panels: amplitude spectrum of the data and of the residuals (on the same vertical scale) after subtracting the four main pulsation frequencies (f1 to f4). We note that the residual power is significantly higher than in Fig. 3. The small box shows the normalized spectral window (red) with the one-day aliases at ±11.57 μHz. Lower panels (from top to bottom): normalized spectral window (red) with the 1-year aliases at ±31.7 nHz, and details of the amplitude spectrum of data and residuals near f1 (left) and f2 (right). The horizontal scale in the left and right panels is the same. Two vertical dashed lines (green) highlight two components of a possible rotational splitting. See text for more details. |
| In the text | |
 |
Fig. 3 Same as Fig. 2, but using all the data of 2007, the year with the best coverage. Thanks to the increased frequency resolution, we see that after four prewhitening steps, there is still significant power, with secondary peaks near f2 and f3 that may be due to the rotational splitting of these modes. |
| In the text | |
 |
Fig. 5 Comparison between the amplitude spectrum near f1
of the data (left) and the amplitude spectrum near f1
of a simulated data set (right) with the same time distribution. In this test we used only
the data up to 2009.0 because in this period it is easier to simulate the behavior of
f1 .
For the simulated data we used a single pure sine wave (no noise) with the same frequency and amplitude of
f1
and also with similar long-term frequency and amplitude variations (linear variation of the period with
|
| In the text | |
 |
Fig. 6 Distribution of the frequency and amplitude deviations for the two main pulsation modes of V391 Peg. The deviations, in units of 1σ errors, are the differences between the values obtained from the original light curve and those obtained from 1000 artificial light curves created by the MC simulator of Period04 (Lenz & Breger 2005). The synthetic light curves are built using the five p-modes of Table 3 and adding Gaussian noise at the same level as the original data. The 2D distributions are also projected into 1D histograms and compared with a normal distribution (red). |
| In the text | |
 |
Fig. 7 Period and amplitude variations of the two main pulsation modes of V391 Peg. The variation of
p1
is compatible with a linear increase up to 2009.0, when a change of regime
appears.The same change is also visible for the amplitude: up to 2009.0,
a1
shows a fairly regular sinusoidal shape with a period of about 3400 days
or 9.3 years. A linear increase of the pulsation period is visible also for
p2
when considering the whole data set, while the irregular variations of a2
can be at least partially attributed to the beating between f2
and |
| In the text | |
 |
Fig. 8 O–C diagram of the main pulsation mode of V391 Peg when using monthly runs (each point represents the data collected within one month). Upper panels: fit of the O–C data with a parabola (long-term variation, blue continuous line) plus a sine wave (“planetary component”, red dashed line) and planetary component alone after subtracting the long-term component. This solution gives satisfactory results only up to the end of 2008, and the fit was made considering only the data up to 2009.0. Lower panels: same as upper panels, but using two sinusoids. In this case, the fit was made using all the data, but a reasonable fit is obtained only up to ~2010, indicating that two components are simply not enough to obtain a reasonable fit of all the data. When we compare the planetary component alone in the period 2000–2009.0, the fit is better when we use parabola + sine wave (χ2 = 762) with respect to the double sine wave (χ2 = 1267); for comparison, a straight line would give χ2 = 1376. |
| In the text | |
 |
Fig. 9 Same as Fig. 8 for f1 (left) and f2 (right) for one-season runs. Panels 1A, 1B, 2A, and 2B are obtained using only the data up to 2007.0, so that we can directly compare the current results (blue and red lines) with those obtained by SSJ07 (green lines shifted by −20 and −5 s in panels 1A and 2A and 1B and 2B, respectively). The small horizontal shifts of the first and last points are due to the addition of three observing runs that were not present in SSJ07. Panels 1B and 2B show that in the current results, the period of the sinusoid is slightly shorter for f1 but longer for f2, so that at the end the agreement between f1 and f2 is worse with respect to SSJ07. The reasons of these differences are discussed in the text. When we add the new data, the longer period of the sinusoidal component of f2 with respect to f1 is confirmed (panels 3B and 4B), and moreover, we note a further difference in amplitude. Panel 3A confirms the change of regime of f1 near 2009 that was already visible in Figs. 7 and 8. This change also tends to worsen the fit of f2 (4A), and for this reason, the fits shown in panels 3A to 4B are obtained considering only the data up to 2009.0. Panels 5A and 5B show an alternative solution obtained using a low-frequency sine wave for the long-term component of f1, as in the lower panels of Fig. 8. The fits shown in panels 5A to 6B were obtained using all the available data. More comments are given in the text. |
| In the text | |
 |
Fig. 10 O–C diagram obtained by combining the information from f1 and f2 . In practice, we have computed the weighted average of the points in panels 5B and 6B of Fig. 9 and recomputed the best fit with a sine wave. Compared with these panels, the fit is significantly improved and the residuals of 9 points out of 13 (including all those with smaller error bars) are close to zero. |
| In the text | |
 |
Fig. 11 g-mode amplitude spectrum using our best-quality runs between 2002 and 2008 (192.8 h of observations in total). The upper right panel shows the spectral window (red), while the other panels from top to bottom show amplitude spectrum and residuals after one, two, and three prewhitening steps. We note an excess of power in two main regions near 180 and 310 μHz. After prewhitening, this excess of power is not completely removed near 180 μHz, suggesting that further low-amplitude frequencies are present in that region. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.