| Issue |
A&A
Volume 606, October 2017
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 25 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201731033 | |
| Published online | 23 October 2017 | |
Eccentricity excitation and merging of planetary embryos heated by pebble accretion⋆
1 Institute of Astronomy, Charles University in Prague, V Holešovičkách 2, 18000 Prague 8, Czech Republic
e-mail: chrenko@sirrah.troja.mff.cuni.cz
2 Laboratoire Lagrange, UMR 7293, Université Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, Boulevard de l’Observatoire, 06304 Nice Cedex 4, France
Received: 24 April 2017
Accepted: 17 June 2017
Context. Planetary embryos can continue to grow by pebble accretion until they become giant planet cores. Simultaneously, these embryos mutually interact and also migrate due to torques arising from the protoplanetary disk.
Aims. Our aim is to study how pebble accretion alters the orbital evolution of embryos undergoing Type-I migration. In particular, we try to determine whether or not the embryos establish resonant chains, and if so, whether or not these chains are prone to instabilities. Further, we investigate the possibility that giant planet cores form through embryo merging which can be more rapid than pebble accretion alone.
Methods. For the first time, we perform self-consistent global-scale radiative hydrodynamic simulations of a two-fluid protoplanetary disk consisting of gas and pebbles, the latter being accreted by embedded embryos. Accretion heating, along with other radiative processes, is accounted for to correctly model the Type-I migration.
Results. We track the evolution of four super-Earth-like embryos, initially located in a region where the disk structure allows for a convergent migration. Generally, embryo merging is facilitated by rapidly increasing embryo masses and breaks the otherwise oligarchic growth. Moreover, we find that the orbital eccentricity of each embryo is considerably excited (≃0.03) due to the presence of an asymmetric under-dense lobe of gas – a so-called “hot trail” – produced by accretion heating of the embryo’s vicinity. Eccentric orbits lead the embryos to frequent close encounters and make resonant locking more difficult.
Conclusions. Embryo merging typically produces one massive core (≳10 ME) in our simulations, orbiting near 10 AU. Pebble accretion is naturally accompanied by the occurrence of eccentric orbits which should be considered in future efforts to explain the structure of exoplanetary systems.
Key words: hydrodynamics / planets and satellites: formation / planet-disk interactions / protoplanetary disks / planets and satellites: gaseous planets
The code is publicly available at http://sirrah.troja.mff.cuni.cz/~chrenko/, and also at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/606/A114
© ESO, 2017
1. Introduction
Interactions of gas and solids in protoplanetary disks are the basis for subsequent growth of all kinds of planets, whether they finally become terrestrial, super-Earths, ice giants or gas giants. These interactions have to be computed with an appropriate feedback, as there are a number of relatively complicated but inevitable phenomena. Setting the classical in-spiralling of solids due to gas drag aside, there are processes like streaming instability and local collapse (Johansen et al. 2007), pebble accretion assisted by aerodynamic drag (Lambrechts & Johansen 2012; Morbidelli & Nesvorný 2012), accretion heating of planetary embryos and surrounding gas (Benítez-Llambay et al. 2015), or embryo-disk interactions in general (e.g. Kley et al. 2009). Sufficiently complex hydrodynamic models with radiative transfer (RHD) are usually needed for realistic treatment of these processes.
The radiative properties of the protoplanetary disk are mostly determined by the opacity κ. As a flux-mean (Rosseland) value, κ is mostly caused by icy, silicate or carbonaceous dust grains (Mathis et al. 1977; Bell & Lin 1994) that have different wavelength-dependent optical constants (Jäger et al. 2003). The size-frequency distribution of dust grains is often assumed to be shallow, with a cumulative slope q = − 2.5 (Mathis et al. 1977; Birnstiel et al. 2012). Any sudden transition in the composition of the dust component (e.g. grain evaporation or “rain out”) affects local heating and cooling properties of the gas disk. Consequently, variations of the scale height H(r) might occur, and moreover, the pressure gradient might exhibit a reversal, ∇P> 0, which leads to accumulation of solids (and even planetary embryos). Typical transitions are located, for example, at the inner rim of the disk due to UV photoionisation and corotation with stellar magnetic field, at the evaporation line of silicates (Flock et al. 2016), and at the snowline corresponding to water evaporation (Morbidelli et al. 2015). Important heating sources are provided by viscous dissipation, especially in the inner disk, and stellar irradiation of the inclined/flared disk atmosphere (Bitsch et al. 2014).
While small (μm-sized) grains usually influence overall optical properties, large (mm-sized) dust particles or (cm-sized) pebbles – if already present – dominate the mass distribution. According to recent developments in the theory of planet formation, pebbles can be efficiently accreted by larger seed masses, for example planetesimals or embryos, with high enough accretion rate to finally produce giant planet cores (Lambrechts & Johansen 2012, 2014) with masses ≳10 ME, well within the protoplanetary disk lifetime, which is typically ≃10 Myr (Fedele et al. 2010). Global-scale N-body simulations demonstrated that the giant planets of the Solar System can be reproduced by pebble accretion (Levison et al. 2015), provided that dynamical stirring of orbital inclinations breaks the oligarchic growth of the seed masses (Kretke & Levison 2014).
A downside of the aforementioned global-scale simulations with pebble accretion is that they do not model the interactions between the protoplanets and the surrounding gaseous disk in a self-consistent way because no hydrodynamics is employed. However, during the evolutionary phase when multiple low-mass embryos are present, it is inevitable that these embryos interact gravitationally with the disk and undergo Type-I migration, when no gap is opened. There are many purely hydrodynamical effects contributing to the resulting torque acting on the planets: Spiral arms (launched at the Lindblad resonances and independent of viscosity ν), the corotation torque from the asymmetric gas structures formed in the corotation regions of embryos (Masset 2002) and additional forcing produced by asymmetries related to radiative effects operating in the vicinity of the embryos, for example the cold finger (Lega et al. 2014) or the heating torque (Benítez-Llambay et al. 2015).
The embryos – albeit having generally different migration rates – can accumulate near some of the pressure gradient reversals, mutually interact, and get locked in a resonant configuration and create a “convoy” (Pierens et al. 2013). Such a configuration naturally prevents any merging. It is possible that the stability of the resonant chain can be reduced by larger numbers of embryos present in the system (Pierens et al. 2013), when the disk is massive and exhibits large accretion rates, (10-7M⊙ yr-1 according to Zhang et al. 2014), or when some of the embryos enter a fast migration regime due to strong corotation torque when the initially librating gaseous material is contracted into the tadpole region (Pierens 2015). According to current understanding, it is unclear how pebble accretion and accretion heating affect the convergent migration and resonant chain stability and we address these particular issues in this paper. We aim to determine whether the migrating embryos merge or remain in the chain while they continue to grow. The resonant chain (in)stability is important also with respect to the observed exoplanetary systems because these are often non-resonant (e.g. Winn & Fabrycky 2015).
The embryo growth and/or merging closely precede an evolutionary epoch which provides important observational evidence of the planet-forming processes. Once a giant planet core is formed it can clear a gap in the disk along its orbit and its further migration is driven by the viscous evolution of the disk (the Type-II migration, e.g. Lin & Papaloizou 1986; Crida & Bitsch 2017). Such a gap may become observable and the disk is then classified as pre-transitional (according to Espaillat et al. 2010, 2014).
To summarise, the protoplanetary system within the scope of this paper is assumed to consist of a gas disk with opacities dominated by fully coupled dust, a pebble disk (strongly but not fully coupled) and already formed low-mass embryos (~1 ME) that continue to grow by pebble accretion. Our hydrodynamic simulations aim to investigate if different migration rates, evolving embryo masses, accretion heating and mutual perturbations between embryos can break the resonant chains and create a giant-planet core capable of opening a gap.
Our paper is organised as follows. In Sect. 2 we summarise all the equations and approximations of our two-dimensional (2D) RHD model. We also describe relevant initial and boundary conditions. Technical details of the model and useful explanatory derivations are given in Appendices A–C. A validation of our model is given later in Appendix D. In Sect. 3 we present results of our global-scale simulations focused on the migration of several pebble-accreting and heated embryos. Section 4 describes how the accretion heating affects the orbital eccentricities and disk torques acting on the embryos. We discuss possible future model improvements and also possibilities of relating our results with observations in Sect. 5. Section 6 is devoted to conclusions.
2. Protoplanetary system modelling
The model we present is based on the publicly available 2D hydrodynamic code fargo (Masset 2000; Baruteau & Masset 2008) which we extensively modified in order to follow the evolution and mutual interactions between three components of protoplanetary systems: a differentially rotating disk of the nebular gas, a partially coupled disk of pebbles, and several embedded planetary embryos. The fargo code is designed as an Eulerian solver on a polar staggered mesh. The numerical scheme relies on the operator-splitting technique according to Stone & Norman (1992), with a modified transport sub-step which utilises van Leer’s second-order upwind interpolation (van Leer 1977) for radial advection and the fargo algorithm (Masset 2000) in the azimuthal direction. Let us briefly summarise new physical modules that were implemented in our modified version of the code.
Considering the gaseous disk, we relax the isothermal approximation and account for the evolution of temperature within the disk. The extended set of hydrodynamic equations thus contains the energy equation with multiple relevant source terms; in particular: compressional heating, viscous heating, stellar irradiation, vertical escape of radiation, radiative diffusion in the midplane and radiative feedback to accretion heating of embryos.
Regarding the pebble disk, we assume it consists of mm- to cm-sized pebbles (Lambrechts & Johansen 2012). Pebbles orbiting within the nebular gas are subject to the aerodynamic drag which changes their angular momentum. The characteristic time scale of the angular momentum change is usually described by the stopping time ts (Adachi et al. 1976; Weidenschilling 1977). Its dimensionless form, the Stokes number, is defined as τ ≡ ΩKts, where ΩK denotes the Keplerian angular frequency. The Stokes number is an important quantity encapsulating the particle size and coupling to the nebular gas. In this study, we follow Lambrechts & Johansen (2014) and consider particles smaller than the mean free path in the nebular gas, typically with τ ≲ 0.1. The friction then arises due to anisotropic collisions between individual gas molecules and pebbles and the drag operates in the Epstein regime. Due to parametrisation by τ, we practically neglect drag regimes relative to the local Reynolds number. Because of their aerodynamic properties, pebbles are strongly coupled with the gas flow and thus we study their evolution using a two-fluid model in which the pebble disk is modelled as another Eulerian fluid which is, unlike the gas, pressureless and inviscid (e.g. Youdin & Goodman 2005).
The embedded embryos are evolved in three dimensions (3D) using a high-accuracy integration technique, accounting for close encounters, possible collisions, and merging. An artificial vertical force acting on the embryos is applied to damp their inclinations as predicted for 3D disks (Tanaka & Ward 2004). The embryos are allowed to grow by drag-assisted pebble accretion, capturing pebbles from the circumplanetary flow. We also consider that the embryos can be heated by this vigorous material deposition and consequently radiate the excessive energy into the surrounding gas.
The mutual interactions accounted for in the model are as follows. Both the gas and pebbles evolve in the gravitational potential of the protostar and embryos. The potential is computed by an averaging procedure in a direction perpendicular to the midplane to avoid unrealistic potential smoothing and spreading (Müller et al. 2012). All the embryos participate in mutual N-body interactions and they also feel the gravitational pull of the gas disk, but the gravity of the pebble disk is ignored due to its relatively low mass. The gas disk and pebbles are only coupled through the linear drag term and no self-gravity is taken into account. The detailed aspects of the model implementation into fargo are elaborated in the following individual subsections.
2.1. Two-fluid model of the gas-pebble disk
In our hydrodynamic model, we study the evolution of the gas surface density Σ, the vertically averaged gas flow velocity 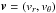 , the specific internal energy of the gas E, the surface density of the pebble disk Σp and its velocity field
, the specific internal energy of the gas E, the surface density of the pebble disk Σp and its velocity field 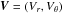 . The fundamental fluid equations to be solved can be written by means of the vertically integrated quantities as follows:
. The fundamental fluid equations to be solved can be written by means of the vertically integrated quantities as follows: 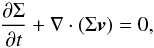 (1)
(1)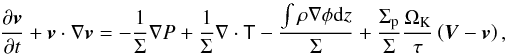 (2)
(2)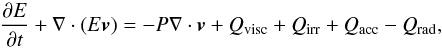 (3)
(3)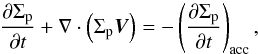 (4)
(4)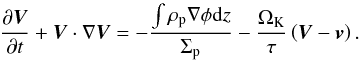 (5)Here P denotes the vertically integrated pressure, T is the viscous stress tensor (e.g. Masset 2002), φ is the gravitational potential arising from the protostar and planetary embryos, ρ and ρp are the volume densities of the gas and pebbles, respectively. The individual source terms on the right-hand side of the energy equation represent the compressional heating, the viscous heating Qvisc, the stellar irradiation Qirr, the radiative diffusion Qrad and the heating Qacc arising from pebble accretion which is symbolically considered in the pebble mass continuity equation as the − (∂Σp/∂t)acc term. We emphasise that the gradient and divergence operators are always 2D in our model.
(5)Here P denotes the vertically integrated pressure, T is the viscous stress tensor (e.g. Masset 2002), φ is the gravitational potential arising from the protostar and planetary embryos, ρ and ρp are the volume densities of the gas and pebbles, respectively. The individual source terms on the right-hand side of the energy equation represent the compressional heating, the viscous heating Qvisc, the stellar irradiation Qirr, the radiative diffusion Qrad and the heating Qacc arising from pebble accretion which is symbolically considered in the pebble mass continuity equation as the − (∂Σp/∂t)acc term. We emphasise that the gradient and divergence operators are always 2D in our model.
The following ideal gas equation of state is introduced as the thermodynamic closing relation 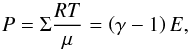 (6)with R being the universal gas constant, μ = 2.4 g mol-1 being the mean molecular weight and γ = 1.4 denoting the adiabatic index (specific heat ratio).
(6)with R being the universal gas constant, μ = 2.4 g mol-1 being the mean molecular weight and γ = 1.4 denoting the adiabatic index (specific heat ratio).
Before proceeding to the description of all the individual source terms, let us highlight that we assume a simple vertical stratification of the disk in order to approximate certain effects that are expected to operate in realistic 3D disks. The gas volume density ρ(r,θ,z) follows a Gaussian form 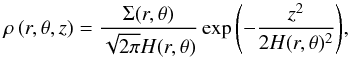 (7)where
(7)where 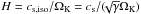 is the local pressure scale height and
is the local pressure scale height and 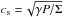 is the adiabatic sound speed which differs from the isothermal sound speed cs,iso by a factor
is the adiabatic sound speed which differs from the isothermal sound speed cs,iso by a factor 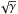 . The normalisation constant
. The normalisation constant 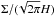 actually represents the gas volume density ρ0 in the midplane. In principle, Eq. (7) holds only for vertically isothermal disks, which is an assumption we do not impose when discussing the energy source terms in Sect. 2.2. But because recent 3D simulations demonstrated that the optically thick parts of protoplanetary disks have a flat vertical temperature distribution (Flock et al. 2013), we decided to use Eq. (7) as a viable first approximation of the vertical stratification.
actually represents the gas volume density ρ0 in the midplane. In principle, Eq. (7) holds only for vertically isothermal disks, which is an assumption we do not impose when discussing the energy source terms in Sect. 2.2. But because recent 3D simulations demonstrated that the optically thick parts of protoplanetary disks have a flat vertical temperature distribution (Flock et al. 2013), we decided to use Eq. (7) as a viable first approximation of the vertical stratification.
2.2. Energy source terms
Let us first describe how the radiation transport is treated in our model. The corresponding term Qrad is given by the vertically integrated divergence of the 3D radiative flux F3D: 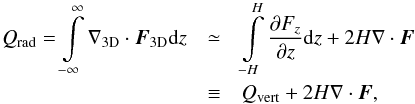 (8)where we assumed that the vertical outward radiation is liberated at H which is expected to be much smaller than the radial extent of the disk. The amount of energy transported by radiation is therefore dominant in the vertical direction (D’Angelo et al. 2003). We estimate these radiative losses caused by the vertical escape of radiation from both sides of the disk as
(8)where we assumed that the vertical outward radiation is liberated at H which is expected to be much smaller than the radial extent of the disk. The amount of energy transported by radiation is therefore dominant in the vertical direction (D’Angelo et al. 2003). We estimate these radiative losses caused by the vertical escape of radiation from both sides of the disk as 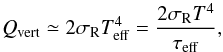 (9)where σR is the Stefan-Boltzmann constant, T stands for the midplane temperature and τeff is the effective optical depth. Hubeny (1990) generalized the gray model of stellar atmospheres in LTE for the case of accretion disks and found
(9)where σR is the Stefan-Boltzmann constant, T stands for the midplane temperature and τeff is the effective optical depth. Hubeny (1990) generalized the gray model of stellar atmospheres in LTE for the case of accretion disks and found 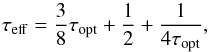 (10)where we implicitly assumed that the disk is stellar irradiated (otherwise 1 / 2 term should be replaced with
(10)where we implicitly assumed that the disk is stellar irradiated (otherwise 1 / 2 term should be replaced with 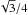 ; D’Angelo & Marzari 2012) and that the mean Rosseland opacity and the Planck opacity are identical which is a viable approximation as discussed, for example, by Bitsch et al. (2013). The relation (10) is highly convenient in the case of a protoplanetary disk because it can characterise both optically thin and thick environment.
; D’Angelo & Marzari 2012) and that the mean Rosseland opacity and the Planck opacity are identical which is a viable approximation as discussed, for example, by Bitsch et al. (2013). The relation (10) is highly convenient in the case of a protoplanetary disk because it can characterise both optically thin and thick environment.
The optical depth τopt is measured from the midplane to the disk surface and we estimate it as 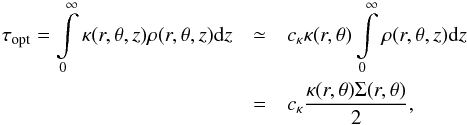 (11)where cκ = 0.6 is a correction factor that accounts for the opacity drop in the layers above the midplane (we refer to Müller & Kley 2012 for a similar approach). This parametric factor in fact sets the local efficiency of vertical cooling and can be tuned so that the resulting disk structure resembles the one obtained in 3D models.
(11)where cκ = 0.6 is a correction factor that accounts for the opacity drop in the layers above the midplane (we refer to Müller & Kley 2012 for a similar approach). This parametric factor in fact sets the local efficiency of vertical cooling and can be tuned so that the resulting disk structure resembles the one obtained in 3D models.
We adopt the power-law mean Rosseland opacity κ = κ0ρaTb with the coefficients a and b derived by Lin & Papaloizou (1985) and further refined by Bell & Lin (1994) for various temperature intervals and corresponding opacity regimes. The transitions between individual opacity regimes are smoothed out as in (Lin & Papaloizou 1985; we also refer to Keith & Wardle 2014).
Coming back to the midplane radiative flux (see Eq. (8)), we use the flux-limited diffusion approximation (Levermore & Pomraning 1981; Klahr & Kley 2006) to express 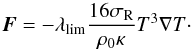 (12)In this approximation, scattering effects are neglected and λlim denotes the flux limiter, which is calculated according to Kley (1989). The radiative transport is treated by means of the one-temperature approach (Kley et al. 2009). This means that the internal energy of the gas is presumed to be dominated by the thermal energy whereas the radiative energy is relatively small. The radiation field is thermalised to the same temperature T as the gas.
(12)In this approximation, scattering effects are neglected and λlim denotes the flux limiter, which is calculated according to Kley (1989). The radiative transport is treated by means of the one-temperature approach (Kley et al. 2009). This means that the internal energy of the gas is presumed to be dominated by the thermal energy whereas the radiative energy is relatively small. The radiation field is thermalised to the same temperature T as the gas.
The stellar irradiation is governed by Qirr term which is complementary to Qvert and reads 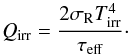 (13)The irradiation temperature Tirr can be obtained from the projection of the stellar radiation flux onto the disk surface (Chiang & Goldreich 1997; Menou & Goodman 2004; Pierens 2015)
(13)The irradiation temperature Tirr can be obtained from the projection of the stellar radiation flux onto the disk surface (Chiang & Goldreich 1997; Menou & Goodman 2004; Pierens 2015) 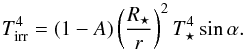 (14)Here A = 0.5 is the disk albedo, assumed to be a mean value implicitly averaged over the stellar flux, and T⋆ = 4370 K is the effective temperature of the protostar with the stellar radius R⋆ = 1.5 R⊙. Together with the stellar mass M⋆ = 1.0 M⊙, the given parameters represent a protostar similar to T Tauri type (Paxton et al. 2015). Finally, α is the grazing angle at which the starlight strikes the disk. The grazing angle can be approximated by reconstructing the disk surface from the local pressure scale height H. Adopting the geometric formulation of Baillié & Charnoz (2014), we use
(14)Here A = 0.5 is the disk albedo, assumed to be a mean value implicitly averaged over the stellar flux, and T⋆ = 4370 K is the effective temperature of the protostar with the stellar radius R⋆ = 1.5 R⊙. Together with the stellar mass M⋆ = 1.0 M⊙, the given parameters represent a protostar similar to T Tauri type (Paxton et al. 2015). Finally, α is the grazing angle at which the starlight strikes the disk. The grazing angle can be approximated by reconstructing the disk surface from the local pressure scale height H. Adopting the geometric formulation of Baillié & Charnoz (2014), we use 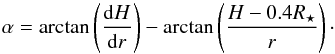 (15)If α< 0, the corresponding surface facet is not oriented towards the incident irradiating flux thus we set Qirr = 0 in this case. Unlike in an isothermal model, the aspect ratio h(r) = H(r) /r is not time independent but it evolves instead. Therefore the disk can flare in its outer parts where the stellar irradiation dominates the energy budget (D’Alessio et al. 1998; Dullemond 2002; Bitsch et al. 2013).
(15)If α< 0, the corresponding surface facet is not oriented towards the incident irradiating flux thus we set Qirr = 0 in this case. Unlike in an isothermal model, the aspect ratio h(r) = H(r) /r is not time independent but it evolves instead. Therefore the disk can flare in its outer parts where the stellar irradiation dominates the energy budget (D’Alessio et al. 1998; Dullemond 2002; Bitsch et al. 2013).
The viscous dissipation heating Qvisc is calculated according to Mihalas & Weibel Mihalas (1984)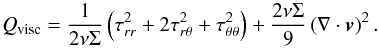 (16)Here ν = 5 × 1014 cm2 s-1 is the kinematic viscosity and τij corresponds to the individual components of the viscous stress tensor T. We emphasise that the viscosity is fixed and not solved explicitly in the model.
(16)Here ν = 5 × 1014 cm2 s-1 is the kinematic viscosity and τij corresponds to the individual components of the viscous stress tensor T. We emphasise that the viscosity is fixed and not solved explicitly in the model.
The accretion heating term Qacc is non-zero only in the nearest vicinity of embedded planetary embryos and it depends on their accretion rate. The luminosity of an accreting embryo with the mass Mem and the radius Rem is given by 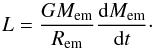 (17)The resulting heating of the surrounding gas is provided by placing an inner heat source into the grid cell which contains the respective embryo. The specific power of this source reads
(17)The resulting heating of the surrounding gas is provided by placing an inner heat source into the grid cell which contains the respective embryo. The specific power of this source reads 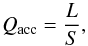 (18)where S is the cell area. In this work, we assume that the mass growth of embryos is driven solely by pebble accretion. The accretion rate dMem/ dt is computed self-consistently as described in Sect. 2.5. We emphasise that the accretion heating term Qacc is not always switched on in our simulations and we remind the reader in such cases.
(18)where S is the cell area. In this work, we assume that the mass growth of embryos is driven solely by pebble accretion. The accretion rate dMem/ dt is computed self-consistently as described in Sect. 2.5. We emphasise that the accretion heating term Qacc is not always switched on in our simulations and we remind the reader in such cases.
The numerical solution of the energy equation (Eq. (3)) is described in Appendix A.
2.3. Initial state of the gas disk
The thermal equilibrium of any gaseous disk studied in our model is achieved by a rather complicated interplay between the heating and cooling sources introduced above. Therefore it would be difficult to search for an analytic formula describing the initial state of an isolated disk in equilibrium. In order to initialise the hydrodynamic fields over the computational domain, we use either simple power-law functions or equilibrium solutions known from less sophisticated models. The resulting gas disk, which lacks the pebble component and embedded objects at this point, is then numerically relaxed towards its stationary state. This serves as a preparation stage for the following complete simulations.
The non-relaxed hydrodynamic profiles are assumed to be symmetric in θ. The surface density is described by the power-law profile Σ = 750(r/ (1 AU))-0.5 g cm-2. We start with an initially non-flaring disk, having the aspect ratio h = H/r = 0.05. In accordance with this setup, we can subsequently initialise cs, P and T. We verified that the choice of initially non-flaring disk does not prevent flaring during the relaxation. The radial velocity vr is initially set to zero, while vθ is set by imposing the equilibrium between the central gravity, pressure gradient, and centrifugal acceleration. The disk is fully extended in azimuth and radially bordered by the inner boundary rmin = 2.8 AU and the outer boundary rmax = 14 AU. The polar computational domain is divided into 1536 azimuthal sectors and 1024 evenly spaced radial rings. The grid sampling should be sufficient to reasonably resolve the corotation region of low-mass embryos and properly reproduce the related torques (e.g. Lega et al. 2014).
2.4. Initial state of the pebble disk
We use the hydrodynamic polar grid to insert a sea of pebbles within the gaseous disk which has already been relaxed towards its equilibrium state in the absence of planetary embryos. Using solely the hydrodynamic quantities together with several parameters introduced in this section, we initialise Σp, Vr and Vθ over the computational domain and evolve the fluid of pebbles over the course of the simulation.
The aerodynamic properties of pebbles which interact with the gas in the Epstein regime are characterised by the Stokes number 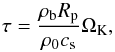 (19)where ρb = 1 g cm-3 is the pebble bulk density, Rp is the pebble size and ρ0 is the midplane volume density of the nebular gas. Then the initial velocity field can be described by an analytic estimate for a pebble drifting in a steady-state gaseous disk while neglecting the presence of any massive perturbers besides the protostar (e.g. Nakagawa et al. 1986; Guillot et al. 2014, and also Appendix B)
(19)where ρb = 1 g cm-3 is the pebble bulk density, Rp is the pebble size and ρ0 is the midplane volume density of the nebular gas. Then the initial velocity field can be described by an analytic estimate for a pebble drifting in a steady-state gaseous disk while neglecting the presence of any massive perturbers besides the protostar (e.g. Nakagawa et al. 1986; Guillot et al. 2014, and also Appendix B) 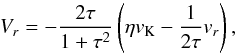 (20)
(20)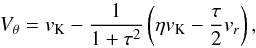 (21)where vK is the local Keplerian velocity and η measures how much the gas departs from local Keplerian rotation
(21)where vK is the local Keplerian velocity and η measures how much the gas departs from local Keplerian rotation 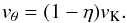 (22)In simple stationary disks, η is a monotonic function reflecting the sub-Keplerian rotation of the pressure-supported nebular gas. In realistic disks, however, the situation is more complicated; the η profile is affected, for example, by the pressure dips and bumps, which can occur at the opacity transitions (Bitsch et al. 2014), and also by viscous shear.
(22)In simple stationary disks, η is a monotonic function reflecting the sub-Keplerian rotation of the pressure-supported nebular gas. In realistic disks, however, the situation is more complicated; the η profile is affected, for example, by the pressure dips and bumps, which can occur at the opacity transitions (Bitsch et al. 2014), and also by viscous shear.
As mentioned above, we aim to describe the pebble disk by a single fluid while in reality, protoplanetary systems are certainly populated by pebbles of various sizes. Despite our simplification, we would like the material delivery towards the accreting embryos to be realistic. It is thus important to discuss the choice of the particle size and Stokes number. As argued by Birnstiel et al. (2012), most of the pebble mass is concentrated towards the upper end of the size spectrum and, at the same time, the largest pebbles are the fastest drifters. At a given radial distance, it is reasonable to assume that the pebble size distribution has a steep upper cutoff and all the particles larger than this cutoff are swiftly removed by the drift, while particles smaller than this cutoff do not significantly contribute to the total mass of solids. In this work we presume that such a dominant size is also the best choice for characterising the pebble disk by a single fluid so that its resulting hydrodynamic behaviour is the most similar to a real pebble disk, which is a mixture of many particle species. In other words, the dominant pebble size can be viewed as an effective workaround to avoid using a numerically demanding multi-fluid model and obtain a reasonably evolving disk of solids at the same time. We highlight that Rp is always understood as the dominant drift-limited size in what follows and that we also neglect other size-limiting processes such as fragmentation.
The Stokes number τd of the dominant pebble size can be found by balancing the characteristic time scale for the particle growth tgrow = Rp/Ṙp and the time scale of the particle removal by the drift tdrift = r/Vr. Following Garaud (2007) and staying within the limits of the Epstein regime, the growth time scale is 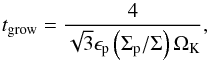 (23)and depends only on the local solid-to-gas ratio, orbital frequency and the pebble coagulation efficiency, assumed ϵp = 0.5. Because τ< 1, we approximate Vr ≈ − 2τηrΩK and, by equating the characteristic time scales, we write
(23)and depends only on the local solid-to-gas ratio, orbital frequency and the pebble coagulation efficiency, assumed ϵp = 0.5. Because τ< 1, we approximate Vr ≈ − 2τηrΩK and, by equating the characteristic time scales, we write 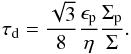 (24)Up to this point, the pebble surface density Σp was unconstrained. When studying pebble accretion, it is useful to keep track of the total radial mass flux ṀF of solids through the system. In the following, we set the initial ṀF = 2 × 10-4ME yr-1 (Lambrechts & Johansen 2014) as an input parameter and assuming an equilibrium situation, we impose the following continuity requirement (Lambrechts & Johansen 2014)
(24)Up to this point, the pebble surface density Σp was unconstrained. When studying pebble accretion, it is useful to keep track of the total radial mass flux ṀF of solids through the system. In the following, we set the initial ṀF = 2 × 10-4ME yr-1 (Lambrechts & Johansen 2014) as an input parameter and assuming an equilibrium situation, we impose the following continuity requirement (Lambrechts & Johansen 2014) 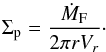 (25)Plugging Eq. (25) in (24) and using the approximate expression for Vr again, one finds
(25)Plugging Eq. (25) in (24) and using the approximate expression for Vr again, one finds 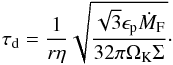 (26)The corresponding dominant particle size can be easily obtained when using the inverse of Eq. (19). In the last expression, τd depends only on two model parameters (ϵp and ṀF) and the hydrodynamic state of the gaseous background. Therefore it is a convenient starting point for the pebble disk initialisation.
(26)The corresponding dominant particle size can be easily obtained when using the inverse of Eq. (19). In the last expression, τd depends only on two model parameters (ϵp and ṀF) and the hydrodynamic state of the gaseous background. Therefore it is a convenient starting point for the pebble disk initialisation.
To summarise the initial conditions, we first use the combination of Eqs. (19) and (26) to find Rp(r). Because the relaxed gaseous disk is very close to axial symmetry (within discretisation errors and numerical artefacts) when we incorporate the pebble disk, it is reasonable to consider that the pebble size changes only radially. We further assume that once the planetary embryos are present, they do not cause global-scale changes of η, thus the initial Rp(r) profile is kept fixed during our simulations. Subsequently, we calculate the initial (Vr,Vθ) field (Eqs. (20)and (21)) which sets Σp from the mass flux conservation law (25). We emphasise that unlike Rp(r), the Stokes number τ(r,θ) is considered a cell-dependent quantity during the simulations and it is recalculated each time step to obtain proper aerodynamics for a given particle size moving in the evolving gaseous background. This is to account for situations when pebbles suddenly enter gas clumps or underdense regions.
2.5. Pebble accretion
Pebble accretion enters our model through Eq. (4) in which it acts like a mass sink. At the same time, the mass removed from the pebble component is accreted by the growing embryos. According to Lambrechts & Johansen (2012), two fundamental regimes of pebble accretion have to be considered, namely the Bondi1 and the Hill regimes, while the transition between the two occurs when the pebble accretion Bondi radius RB becomes comparable to the Hill sphere radius RH of the accreting body. The former radius corresponds to the distance whereby a pebble with impact parameter b ≤ RB will suffer a ≥1 rad deflection, while the latter radius defines the region in which the gravitational pull of the accreting body dominates over the primary field. The defining equations are 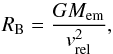 (27)and
(27)and 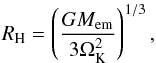 (28)where vrel denotes the relative velocity between the pebble and the accreting body with mass Mem.
(28)where vrel denotes the relative velocity between the pebble and the accreting body with mass Mem.
In the Bondi regime, if RB ≲ RH, the only pebbles that experience a significant deflection arrive through a small fraction of the Hill sphere thus they enter the encounter region with the relative velocity which is set by the local headwind experienced by the embryo, therefore vrel ≃ vhead.
On the other hand, if RB ≳ RH, the relative encounter velocity for most of the pebbles is dominated by the Keplerian shear which becomes more important than headwind on orbital separations comparable to RH. In such a case, the Hill regime is triggered. It is obvious that the equality of RB and RH is reached for a specific value of Mem called the transition mass 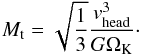 (29)Super-Earth-like embryos which we investigate in this paper usually grow in the Hill regime.
(29)Super-Earth-like embryos which we investigate in this paper usually grow in the Hill regime.
Lambrechts & Johansen (2012) also found that there is a well-defined maximum distance at which the pebbles must approach the embryo in order to be accreted. This effective accretion radius for both regimes is given by ![\begin{equation} R_{\mathrm{eff}} = \begin{cases} R_{\mathrm{B}}\sqrt{\frac{\tau}{t_{\mathrm{B}}\Omega_{\mathrm{K}}}} \,, & \text{Bondi regime } \left(M_{\mathrm{em}} < M_{\mathrm{t}}\right) \\ \min\left[R_{\mathrm{H}}\left(\frac{\tau}{0.1}\right)^{1/3}, R_{\mathrm{H}}\right] \,, & \text{Hill regime } \left(M_{\mathrm{em}}\geq M_{\mathrm{t}}\right) \end{cases} \label{eq:effective_radii} \end{equation}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq141.png) (30)where tB = RB/vrel is the crossing time of the Bondi radius.
(30)where tB = RB/vrel is the crossing time of the Bondi radius.
Because our simulations cover a relatively large portion of the protoplanetary disk, the grid resolution near embryos is not detailed enough to capture the final stage of the in-spiraling motion of pebbles. Thus the fluid model does not allow for fully self-consistent pebble accretion calculation because we are not able to resolve the flow of pebbles falling on the embryo’s surface. We instead rely on the knowledge of the effective accretion radius Reff and we employ a recipe which is somewhat similar to the usual gas accretion treatment in 2D hydrodynamic models (Kley 1999).
First, we identify all the grid cells which have a midplane distance from the embryo smaller than Reff. Second, we compute the following mass-related quantities:
-
The expected embryo mass increaseΔMexpec: here we use the analytic accretion rates derived from detailed pebble accretion models (Lambrechts & Johansen 2012). Following Morbidelli et al. (2015), we set
 (31)where vshear is the relative velocity due to Keplerian shear at the orbital separation Reff, and
(31)where vshear is the relative velocity due to Keplerian shear at the orbital separation Reff, and  (32)where the overbar indicates the mean value taken over the respective cells and Δt is the time step. Because vrel is calculated self-consistently, the pebble accretion rate is approximately corrected for eccentric orbits (vrel increases with the eccentricity, Mt increases as well and the embryo can experience a transition to the Bondi accretion regime which is less effective).
(32)where the overbar indicates the mean value taken over the respective cells and Δt is the time step. Because vrel is calculated self-consistently, the pebble accretion rate is approximately corrected for eccentric orbits (vrel increases with the eccentricity, Mt increases as well and the embryo can experience a transition to the Bondi accretion regime which is less effective). -
The total available mass ΔMavail: assuming that pebbles have non-zero scale height Hp and that their vertical z-distribution is Gaussian (like for the gas; cf. Eq. (7)), we calculate ΔMavail by numerically integrating the pebble fluid mass inside the overlap between the vertically spread disk of pebbles and the accretion sphere of radius Reff, located around the embryo which can generally be shifted in z direction. The purpose of ΔMavail is mainly to account for 3D effects, for example inclined orbits, which can lead the accreting bodies away from their feeding zones. The pebble disk scale height is (Youdin & Lithwick 2007)
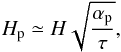 (33)where αp = 1 × 10-4 parametrises the turbulent stirring of the solids in the protoplanetary disk.
(33)where αp = 1 × 10-4 parametrises the turbulent stirring of the solids in the protoplanetary disk.
Finally, the mass transfered on the embryo in one time step is 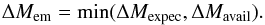 (34)The pebble surface density in the cells below Reff is reduced accordingly. This instantaneous accretion rate ΔMem/ Δt is also used to calculate the accretion heating Qacc (Eq. (18)). The change in Σp due to accretion can propagate to radial distances interior to the embryo, thus affecting the pebble mass flux.
(34)The pebble surface density in the cells below Reff is reduced accordingly. This instantaneous accretion rate ΔMem/ Δt is also used to calculate the accretion heating Qacc (Eq. (18)). The change in Σp due to accretion can propagate to radial distances interior to the embryo, thus affecting the pebble mass flux.
2.6. Numerical solution of the pebble fluid motion equation
After the accretion step, the hydrodynamic quantities describing the pebble disk are evolved as follows. First, the Stokes number τ(r,θ) is recalculated for each cell from Eq. (19) using the known dominant pebble size Rd and the quantities ρ0 and cs reflecting the state of the gaseous background. Second, the velocity field Vr, Vθ is updated under the action of the source terms standing on the right-hand side of the pebble fluid motion Eq. (5). Third, all the quantities are advected using the same transport fargo algorithm as for the gas.
Regarding the source step, it is necessary to take into consideration that pebbles are usually well coupled to the gas and they have stopping times ts much smaller than the typical time step Δt adopted for the explicit update of the gas dynamics. Applying the same explicit integration for the pebble fluid might require significant limitations of Δt. In order to avoid this, we adopt a semi-implicit solution as in (Rosotti et al. 2016; we refer to Appendix C for a brief overview of this method), also including a particle diffusion term related to turbulent mixing. This is accounted for by adding the diffusive velocity (Clarke & Pringle 1988), 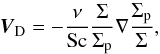 (35)to the pebble fluid velocity. The Schmidt number Sc = 1 is considered, representing the ratio of the gas diffusivity to the pebble diffusivity (e.g. Cuzzi et al. 1993; Youdin & Lithwick 2007).
(35)to the pebble fluid velocity. The Schmidt number Sc = 1 is considered, representing the ratio of the gas diffusivity to the pebble diffusivity (e.g. Cuzzi et al. 1993; Youdin & Lithwick 2007).
2.7. Boundary conditions
The radial boundaries rmin and rmax are closed for all hydrodynamic quantities. In addition, we set wave-killing zones in the annuli adjacent to the inner and outer boundary. These zones cover the intervals of r ∈ [rmin,1.2rmin] and r ∈ [0.9rmax,rmax]. Inside these zones, the following equation is solved each time the boundary condition is applied (Kley & Dirksen 2006; de Val-Borro et al. 2006) 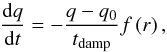 (36)where q represents any hydrodynamic quantity and q0 is its reference value that is about to be reached by the damping. The characteristic time scale is tdamp = 0.1Torb (Müller & Kley 2013) with Torb being the Keplerian orbital period at the corresponding (inner or outer) boundary. By
(36)where q represents any hydrodynamic quantity and q0 is its reference value that is about to be reached by the damping. The characteristic time scale is tdamp = 0.1Torb (Müller & Kley 2013) with Torb being the Keplerian orbital period at the corresponding (inner or outer) boundary. By 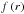 we denote a dimensionless ramp function which decreases from 1 at the boundary to 0 at the end of the wave-killing zone (de Val-Borro et al. 2006).
we denote a dimensionless ramp function which decreases from 1 at the boundary to 0 at the end of the wave-killing zone (de Val-Borro et al. 2006).
The choice of q0 for the gas disk is the following: The radial velocity vr is damped to zero at the boundaries. The remaining hydrodynamic quantities characterising the gas (Σ, E, vθ) are damped towards the values they attain at the end of the relaxation stage. Owing to these conditions, any spiral wake that is invoked by an embedded planet cannot reflect at the boundary.
The boundary conditions for pebbles are also imposed within the wave-killing zones by damping Σp, Vr and Vθ towards the initial steady-state solutions. Owing to these conditions, the outer wave-killing zone behaves like a pebble reservoir and the pebble disk does not decay in time due to its inward drift.
2.8. Embryo-disk interaction
In 2D simulations, a standard procedure when simulating the planet-disk gravitational interactions is to replace the real planetary potential with a Plummer-type smoothed potential of a point mass (Morbidelli et al. 2008) 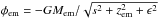 , where
, where 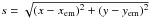 is the midplane separation between a cell center and an embryo with 3D coordinates (xem,yem,zem) and ϵ is the smoothing length, typically taken as a fraction of the pressure scale height Hem at the embryo’s orbit. The reason for the smoothing is twofold. First, it is to keep the otherwise diverging potential regular for the gas parcels located close to the planet and second, it is to mimic the interaction with columns of gas instead of razor-thin midplane distribution.
is the midplane separation between a cell center and an embryo with 3D coordinates (xem,yem,zem) and ϵ is the smoothing length, typically taken as a fraction of the pressure scale height Hem at the embryo’s orbit. The reason for the smoothing is twofold. First, it is to keep the otherwise diverging potential regular for the gas parcels located close to the planet and second, it is to mimic the interaction with columns of gas instead of razor-thin midplane distribution.
However, we decided not to use the ϵ-smoothed potential in our case because of the following inconveniences. As the embryo masses are typically Mem ≈ 1 ME, one can expect that the Hill sphere of the embryo will be smaller than the vertical extent of the disk most of the time. This means that the ϵ-smoothing based on the thickness would cause a significant underestimation of the embryo’s gravitational influence already outside the Hill sphere (Kley et al. 2009). This could have at least two negative impacts on the reliability of our model: the torques arising from the regions close to the planet would be poorly reproduced and too many pebbles might be able to cross the Hill sphere without being accreted as they would drift in a shallower potential well.
To avoid these difficulties, we follow Klahr & Kley (2006) and use the following deeper potential ![\begin{equation} \phi_{\mathrm{em}} = \begin{cases} -\frac{GM_{\mathrm{em}}}{d} , & \left(d > r_{\mathrm{sm}}\right) \\ -\frac{GM_{\mathrm{em}}}{d}\left[\left(\frac{d}{r_{\mathrm{sm}}}\right)^{4} - 2\left(\frac{d}{r_{\mathrm{sm}}}\right)^{3} + 2\frac{d}{r_{\mathrm{sm}}}\right] , & \left(d \leq r_{\mathrm{sm}}\right) \\ \end{cases} \label{eq:cubic_potential} \end{equation}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq176.png) (37)where rsm = 0.5RH is the actually used (sufficiently small) smoothing length. For the purpose of the embryo-disk interaction modelling, we assume that the gas is stratified symmetrically above and beneath the midplane, according to the distribution function (7). Hereinafter, d is the 3D separation between a point in the space (located above or below a cell center) and the embryo.
(37)where rsm = 0.5RH is the actually used (sufficiently small) smoothing length. For the purpose of the embryo-disk interaction modelling, we assume that the gas is stratified symmetrically above and beneath the midplane, according to the distribution function (7). Hereinafter, d is the 3D separation between a point in the space (located above or below a cell center) and the embryo.
Because the gas cells in our model are 2D, we employ a method to vertically average the 3D potential given by Eq. (37) in the calculations. Adopting the approach outlined by (Müller et al. 2012; we also refer to their Appendix A), the acceleration of 2D gas cells in the gravitational field of the embryo can be obtained by calculating the specific density of the force projected on the midplane 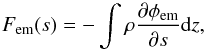 (38)where φem follows from Eq. (37) and ρ(r,θ,z) from Eq. (7). As demonstrated in Müller et al. (2012), replacing the integral with a coarse sum over at least ten vertical grid points per side of the disk leads to an accurate yet numerically feasible reproduction of the realistic 3D interaction.
(38)where φem follows from Eq. (37) and ρ(r,θ,z) from Eq. (7). As demonstrated in Müller et al. (2012), replacing the integral with a coarse sum over at least ten vertical grid points per side of the disk leads to an accurate yet numerically feasible reproduction of the realistic 3D interaction.
Equation (7) in principle neglects the influence of embryos on the vertical gas distribution in their vicinity. Although this effect can (and should) be easily incorporated in fully isothermal models (as in Müller et al. 2012), it is not straightforward in our non-isothermal disk because we only use an approximate treatment of the vertical radiation transport, the model is convection-free, and so on. Nevertheless, we found, by means of numerical experiments, that even the simple ρ(z) dependence leads to results which agree with some of the advanced 3D simulations very well (Appendix D). This justification is possible due to the local nature of the pressure scale height H in our model and also owing to the mass range of embryos which we study; they are not massive enough to perturb the disk scale height significantly, nor do they form circumplanetary disks. Absence of large gaseous structures gravitationally bound to the embryos is also a motivation for including all parts of the Hill sphere in the disk-embryo torque computation.
In general, the orbits of embryos can become inclined or eccentric during mutual close encounters, it is thus necessary to ensure the inclination damping and the circularisation of the orbit as it would operate in 3D disks. Unfortunately, our 2D disk cannot support vertical waves and moreover, Eq. (7) always leads to a symmetric density distribution with respect to the midplane which is certainly not true if inclined perturbers are present. An artificial vertical force is thus imposed on the embryos in order to damp their orbital inclinations in a fashion similar to realistic 3D disks (Tanaka & Ward 2004): 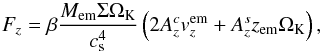 (39)where
(39)where 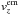 is the vertical component of the planet’s velocity,
is the vertical component of the planet’s velocity, 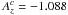 and
and 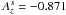 are the coefficients given by Tanaka & Ward (2004). The parameter β is problem-dependent and has to be tuned so that the eccentricity damping, provided naturally by the potential (Eq. (37)), and the inclination damping operate both on comparable time scales.
are the coefficients given by Tanaka & Ward (2004). The parameter β is problem-dependent and has to be tuned so that the eccentricity damping, provided naturally by the potential (Eq. (37)), and the inclination damping operate both on comparable time scales.
Finally, let us point out that the stellar potential is also modelled in terms of the acceleration obtained by the vertical averaging procedure. The evolution of pebbles in the gravitational field follows the same recipe as for the gas (cf. Eqs. (37)and (38)) but their scale height Hp is of course different (Eq. (33)).
2.9. Embryo-embryo interaction
The mutual gravitational interaction among the massive bodies is solved using the ias15 integrator (Rein & Spiegel 2015) from the rebound package (Rein & Liu 2012) which we interfaced with fargo. The integration follows a 15th order non-symplectic Runge-Kutta scheme improved with the Gauss-Radau quadrature (we refer also to Everhart 1985). There are several fundamental reasons for choosing this integrator over more common symplectic integrators:
-
The time step Δt in fargo is controlled by the hydrodynamic Courant-Friedrichs-Lewy (CFL) condition and the original code adopts the same time step to ensure that the planets and gas evolve synchronously. Some symplectic integration schemes can produce numerical errors if the time step is not fixed.
-
The N-body integrator must be capable of dealing with close encounters which are expected to occur in our simulations. ias15 is convenient for this purpose because of its high-order accuracy and adaptive time-step subdivision.
-
Although ias15 is not symplectic in nature, it is reported to preserve the energy error within the double floating-point machine precision (Rein & Spiegel 2015). Moreover, the energy error behaves like a random walk which we think is the best option for the rather short time spans (compared to long-term integrations in celestial mechanics) that our simulations cover.
Additionally, the rebound package contains several routines to detect and resolve collisions. In our runs, we use the direct collision search and the embryos are allowed to merge whenever they collide. Merging is treated in the most simple way, in which the mass and momentum are conserved but the released energy and possible mass loss are neglected. The embryo radii, which are used to detect collisions, are inferred from the embryo masses, assuming the spherical shape and the uniform material density 3 g cm-3.
2.10. Code performance
The performance of our new RHD code of course depends on the given machine architecture and the simulations usually require parallel computation in order to be efficient. Following the original fargo code, our version supports distributed memory parallelism using MPI-based domain decomposition, shared memory parallelism using OpenMP, or a combination of both. The simulations in this paper were performed on clusters of Intel Xeon E5-2650 CPUs (v2 and v4; with comparable core performance ≃33 according to the SPECfp2006 benchmark) using MPI exclusively. To provide a typical computation time required for our simulations, here we present values measured for a test simulation with the full two-fluid disk, four embedded embryos and all implemented radiative processes. The simulation spanned 50 kyr of evolution and required ≃5.4 d on 32 cores and ≃3 d on 96 cores.
3. Protoplanetary system simulations
3.1. Equilibrium disk structure
 |
Fig. 1 Top: radial profile of the aspect ratio h = H/r (black curve, left vertical axis) and midplane temperature T (red dashed curve, right vertical axis) in our disk model. Bottom: radial profile of the opacity κ. The plots show the state reached after a relaxation, with all the heating and cooling terms in balance. This is considered an equilibrium state prior to the follow-up simulations with embedded embryos. Vertical dotted lines indicate important changes in the disk structure, namely the snowline close to r ≃ 4 AU and the transition to the flared stellar-irradiated outer region near r ≃ 7 AU. |
In this section, we discuss global characteristics of the protoplanetary disk in thermal equilibrium, before we actually start simulations with embedded embryos. All the important hydrodynamic model parameters were introduced one by one throughout Sect. 2 and we summarise all of them in Table 1 for the reader’s convenience.
Figure 1 (top panel) shows the aspect ratio h(r) = H(r) /r and the temperature radial profile T(r) of the modelled disk. We notice that h first increases with the radius, reaches a maximum at r ≃ 4 AU, drops again when moving to r> 4 AU and has another turn-over point at r ≃ 7 AU. The temperature T on the other hand steadily decreases outwards as a sequence of power-law functions with slopes that change at radii corresponding to the inflection points in h.
We can follow the reasoning of Bitsch et al. (2013) to explain the changes in h as well as in T. Looking at the opacity profile κ(r) (bottom of Fig. 1), we notice that it has a maximum at r ≃ 4 AU. This is related to the temperature rise up to T ≈ 170 K at which ice grains sublimate (Bell & Lin 1994), a snowline is formed and silicate grains become the main source of the opacity. The opacity maximum at r ≃ 4 AU prolongs the radiative cooling time scale and viscous friction deposits more heat in the midplane and creates a thermal pressure gradient which puffs up the disk. Therefore the maximum of h corresponds to the maximum of κ.
The transition of h at r ≃ 7 AU cannot be explained in the same way because κ is steadily decreasing in this region (there is no change of the opacity regime), albeit with a shallower slope. The transition is rather caused by the change of the dominant heating source. Unlike at r< 7 AU, where the viscous shear is the main source of heating, the stellar irradiation becomes more efficient and prevails at r> 7 AU. This is possible because both Σ and κ are decreasing in the outer disk and so is the vertical optical depth τopt. Therefore starlight can penetrate deeper into the disk, counteract the radiative cooling and slow down the temperature decrease in the outer disk which becomes flared.
3.2. Dominant pebble properties
 |
Fig. 2 Radial profile of the η parameter (black curve, left vertical axis) which expresses the difference between the sub-Keplerian gas velocity and the Keplerian velocity, vθ = (1 − η)vK. Initial radial profile of the dominant Stokes number τd (blue dashed curve, right vertical axis) which characterises aerodynamic properties of pebbles prevalent in the size-frequency distribution of solid particles. |
The described transitions in the gas disk are of a great importance for the remaining components of the system – both pebbles and embryos. Let us turn our attention to pebbles first. Figure 2 shows the radial profile of the gas rotation parameter η (Eq. (22)). The profile implies that the rotation curve of the gas changes at the 4 and 7 AU transitions. For example, there is a rotation slowdown in the inner part of the disk due to stronger pressure support and viscous friction.
The rotation velocity of the gas is directly related to the headwind felt by drifting pebbles. Because the radial pebble mass flux through the disk is assumed to be at a steady state, the radial distribution of the dominant Stokes number τd (Eq. (26)) must adapt to the η profile in order to maintain the flux, as shown by the blue dashed curve in Fig. 2. We recall that in our model, the initial τd(r) profile sets the dominant pebble sizes Rp(r) throughout the system for the rest of the simulation. Going from large r inwards, Rp first grows from 7.5 to 9 cm, when crossing r ≃ 7 AU the sizes begin to decrease down to 5 cm and finally they increase at r< 4 AU up to 8 cm.
However, the described variations of particle sizes and Stokes numbers are rather small, within a factor ~2 in the region of interest. This is expected because the rotation curve transitions are smooth and the initial state of the pebble disk (Sect. 2.4) is based on the Lambrechts & Johansen (2014) model which predicts the properties of the drifting pebbles to depend weakly on η in smooth disks.
3.3. Migration map
 |
Fig. 3 Migration map based on the equilibrium state of the protoplanetary disk. The colour code shows the normalised value of the total torque γΓtot/ Γ0 acting on an embryo with the mass Mem (vertical axis) placed on a circular orbit at the radial distance r (horizontal axis) in the disk. Calculated according to Paardekooper et al. (2011), using the constant kinematic viscosity ν = 5 × 1014 cm2 s-1 and the potential smoothing parameter ϵ = 0.4Hem. |
Let us also discuss the influence of the gas disk structure on the orbital evolution of embedded planetary embryos. In particular, we can estimate the expected direction and rate of the Type-I migration of an embryo, depending on its mass and location in the disk. As in for example Kretke & Lin (2012) or Bitsch et al. (2013), we apply the analytical formulae from Paardekooper et al. (2011) on the azimuthally averaged profiles of the equilibrium disk and compute the torque acting on embryos. We do not list individual steps of the torque calculation here, as there are many, but note that the model of Paardekooper et al. (2011) is 2D and gives a prediction for low-mass planets on fixed circular orbits, while accounting for both Lindblad and corotation torques in the non-linear regime, saturated and unsaturated limits. The heating torque is not considered in their model. Moreover, they used the ϵ-smoothed Plummer-type potential for planet-disk interactions and thus their torque formulae are parametric in the smoothing length ϵ.
The resulting migration map, calculated for rather small ϵ = 0.4Hem, is shown in Fig. 3. The total torque Γtot felt by embryos of various masses Mem is normalised as γΓtot/ Γ0, where 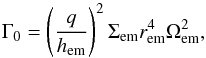 (40)q = Mem/M⋆ is the embryo-to-protostar mass ratio and all of the remaining quantities are calculated at the respective orbital radius rem. It is important to emphasise that Fig. 3 is only an auxiliary diagram which does not exactly represent the torque felt by embryos in our simulations (we refer to Appendix D for a comparison of torques with Paardekooper et al. 2011). Despite this, it is a useful tool for getting a general picture of the expected migration rates in different regions of the disk before actually performing self-consistent simulations.
(40)q = Mem/M⋆ is the embryo-to-protostar mass ratio and all of the remaining quantities are calculated at the respective orbital radius rem. It is important to emphasise that Fig. 3 is only an auxiliary diagram which does not exactly represent the torque felt by embryos in our simulations (we refer to Appendix D for a comparison of torques with Paardekooper et al. 2011). Despite this, it is a useful tool for getting a general picture of the expected migration rates in different regions of the disk before actually performing self-consistent simulations.
We notice there are two borderlines between positive and negative torques in the disk. The first is located at the snowline (r ≃ 4 AU) and the second is located at (roughly) r ≃ 7 AU, that is, the transition between the viscously heated and stellar-irradiated region. The outer borderline represents a zero-torque radius where an accumulation (convergent migration) of embryos is expected to occur because positive torques Γtot drive the embryos outwards while negative torques inwards.
In the positive torque region, the negative Lindblad torque is suppressed by the corotation torque. The corotation torque generally arises as the gas parcels performing U-turns exchange angular momentum with the embryo and it is known to be determined by the vortensity distribution which can be modified by advection along the streamlines, or additional vorticity can be produced by the temperature and entropy gradients (Baruteau & Masset 2008; Paardekooper & Papaloizou 2008). The latter is responsible for the strong positive torque between the snowline and the stellar-irradiated region because a suitable (negative) entropy gradient is present due to the aspect ratio decrease.
The positive torque region should exist only for masses 1.5 ME ≲ Mem ≲ 15 ME for which the thermodynamic conditions in the surrounding disk can sustain the corotation torque. The corotation torque can be prevented from saturation when the viscous and heat diffusion time scales are shorter than the whole libration time scale (which decreases with increasing embryo mass) but longer than the single U-turn time scale (e.g. Pierens 2015).
3.4. Case I – migration of non-accreting embryos in the gas disk only
 |
Fig. 4 Temporal evolution of semimajor axes a(t), periastron distances qp and apoastron distances Qa of four embryos with the initial mass 3 ME in three distinct simulation cases: Case I neglecting the pebble disk (top), Case II including the pebble disk but only allowing for the mass growth of embryos by pebble accretion (middle) and finally Case III, considering also the effect of accretion heating (bottom). Embryos are numbered from 1 to 4. Additional arrows and labels indicate mergers or coorbital pairs detected in the simulations, with corresponding embryo masses which can grow by pebble accretion (Cases II and III) or merging. Striking differences are observed in Case III as the migration rates are modified by the heating torque, orbits become moderately eccentric shortly after the simulation starts and the evolution is more violent compared to Cases I and II. |
Hereinafter we present and compare three different simulation cases which start from the equilibrium disk and are numerically evolved for time spans covering tspan ≈ 50 kyr. In all these simulations, we placed four embryos with equal mass Mem = 3 ME on initially circular orbits with semimajor axes equal to a1 = 5 AU, a2 = 6.7 AU, a3 = 8.4 AU and a4 = 10.1 AU; the embryos being numbered inside out. The initial inclinations were randomly chosen as small non-zero values (≲0.1°). The mass of the embryos is always introduced into the system gradually in order to avoid shocks. The same holds for the cases in which the embryos act as the heat sources – the released heat is gradually amplified from zero towards the self-consistently calculated value during several initial orbits.
The simulation cases differ in the following manner. In Case I, we completely neglect the pebble disk, thus the embryos interact only with the gaseous disk and among themselves. Their masses remain fixed and they do not release any heat into their vicinity. In Case II, the pebble disk is included and the embryos are allowed to accrete from it, but the corresponding accretion heating is still switched off. Therefore the heating torque cannot operate. Finally, Case III is the same as Case II except the accretion heating is switched on. Case I represents a relatively standard scenario (comparable e.g. with Pierens 2015) in which one can study interactions of multiple embryos with the non-isothermal radiative disk. We already made some predictions of the embryo migration rates for this case in Sect. 3.3.
Figure 4 (top panel) shows the temporal evolution of the osculating semimajor axis a, periastron distance qp = a(1 − e) and apoastron distance Qa = a(1 + e) of embryos. At the beginning, embryos 1 and 2 (purple and blue curves, respectively) migrate outwards while embryos 3 and 4 (orange and red curves) migrate inwards, in accordance with the preliminary migration map (Fig. 3). After ≃8 kyr of convergent migration towards the zero-torque radius, the outermost three embryos become locked in mutual mean-motion resonances which start to excite their orbital eccentricities. The innermost embryo catches up with the resonant chain at ≃17 kyr and shortly after its eccentricity excitation it undergoes a close encounter with the second embryo during which they switch positions in the disk. As embryo 1 is scattered outwards, it interacts with embryo 3 in a series of close encounters which, due to damping effects of the surrounding disk, end up in a formation of a coorbital pair (1:1 commensurability). The system remains stable for the rest of the simulation.
3.5. Case II – introducing pebble disk and embryo growth by pebble accretion
In Case II, the pebble disk is considered and the embryos grow by pebble accretion. The pebble accretion rate onto individual embryos, which sets their mass growth and eventually the amount of heat released to their surroundings (Sect. 3.6), is shown in Fig. 5 in terms of the filtering factor F, defined as 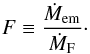 (41)We plot its temporal dependence with respect to a fixed value of the radial pebble mass flux, ṀF = 2 × 10-4ME. We compare the filtering factor measured at the beginning of Case II with the analytical formula from Lambrechts & Johansen (2014) which we applied on the equilibrium disk model. At t = 0, F is in an excellent agreement with the analytical prediction and at later times, the differences are not larger than 3%. Temporal oscillations of F are due to the nature of the accretion algorithm implementation. The expected embryo mass change ΔMexpec (Eq. (32)) depends on the instantaneous
(41)We plot its temporal dependence with respect to a fixed value of the radial pebble mass flux, ṀF = 2 × 10-4ME. We compare the filtering factor measured at the beginning of Case II with the analytical formula from Lambrechts & Johansen (2014) which we applied on the equilibrium disk model. At t = 0, F is in an excellent agreement with the analytical prediction and at later times, the differences are not larger than 3%. Temporal oscillations of F are due to the nature of the accretion algorithm implementation. The expected embryo mass change ΔMexpec (Eq. (32)) depends on the instantaneous 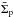 within the accretion radius. The amount of removed pebbles per Δt is not precisely balanced by the inflow of new pebbles so the removal and inflow adapt to each other. If, for example, density waves are propagating near an accreting embryo, they can temporarily increase the concentration of pebbles (
within the accretion radius. The amount of removed pebbles per Δt is not precisely balanced by the inflow of new pebbles so the removal and inflow adapt to each other. If, for example, density waves are propagating near an accreting embryo, they can temporarily increase the concentration of pebbles ( ) and we observe an increase of F. Such variations cannot be reproduced by the Lambrechts & Johansen (2014) model because it is not hydrodynamic. We verified that the filtering factors measured in Case II are in agreement with those obtained later in Case III. Finally, we notice that the outermost embryo is the fastest grower which is because F ~ 1 /η (Lambrechts & Johansen 2014) and η is smaller in the outer part of the disk (Fig. 2). However, the differences in F between individual embryos are rather marginal and the mass growth by pebble accretion initially proceeds in the oligarchic fashion, as expected (Morbidelli & Nesvorný 2012).
) and we observe an increase of F. Such variations cannot be reproduced by the Lambrechts & Johansen (2014) model because it is not hydrodynamic. We verified that the filtering factors measured in Case II are in agreement with those obtained later in Case III. Finally, we notice that the outermost embryo is the fastest grower which is because F ~ 1 /η (Lambrechts & Johansen 2014) and η is smaller in the outer part of the disk (Fig. 2). However, the differences in F between individual embryos are rather marginal and the mass growth by pebble accretion initially proceeds in the oligarchic fashion, as expected (Morbidelli & Nesvorný 2012).
 |
Fig. 5 Filtering factor F measured for the embryos at the beginning of Case II (solid curves); also applicable in Case III. As a comparison (dashed lines), we plot the filtering factors calculated at t = 0 according to formula (33) from Lambrechts & Johansen (2014). The analytical prediction is in good agreement with results of our model. |
The orbital evolution of embryos in Case II is shown in the middle panel of Fig. 4. At first, the embryos evolve similarly to Case I, but the interaction among embryos 1 and 2 results in a merger at t ≃ 16.5 kyr. The resulting mass of the merger is 6.6 ME. As the system adapts to the loss of one of its members and to the suddenly increased mass of the merger, embryo 3 is pushed slightly outwards and encounters embryo 4. One of these events scatters embryo 3 inwards where it eventually collides with the previous merger. The collision takes place at t ≃ 22.7 kyr and merges masses 3.7 ME (embryo 3) and 7 ME (previous merger). The remaining embryos are stabilised at somewhat distant orbits in comparison with Case I. The embryo masses at the end of the simulation are 12.6 ME (the inner one) and 4.9 ME (the outer one). The outer embryo 4 gained 1.9 ME by pebble accretion during the simulation time span.
Let us emphasise that as the mergers naturally occur in the system of pebble-accreting embryos, they immediately break the oligarchic growth of the embryos by pebble accretion; instead of multiple similar-sized embryos, a dominant massive core is formed within the system. In the light of this statement, models that estimate the final planetary masses by tracking a single pebble-accreting protoplanet (e.g. Bitsch et al. 2015) probably underestimate how massive the planets can actually become, at least near the zero-torque radii.
Because of possible strong sensitivity to the initial conditions, the significance of the differences that we identified between Cases I and II is debatable. To partially answer this question, we ran two more simulations for each case. In the first additional set we increased the initial inclinations to about ≃1° and in the second additional set we started from a more closely-packed system of embryos with orbital separations equal to 4.5 mutual Hill radius RmH = 0.5(a + a′) [ (q + q′) / 3 ] 1 / 3. In these additional simulations, Case I always resulted in one merger before the system became stabilised, whereas in Case II, we always detected two mergers. The larger number of mergers in Case II occurs because the resonant chains are destabilised more often. The destabilisation is provided by the mass growth which changes the strength of the resonant forcing and the streamline topology near the embryos, thus modifying the acting torques. At the same time, more massive embryos have a larger encounter cross-section. Yet our simulation statistics are too poor to estimate corresponding probabilities or merging in Cases I and II.
3.6. Case III – introducing heating by pebble accretion
We now discuss Case III, presented in the bottom panel of Fig. 4. The system evolves differently after the beginning of the simulation compared to the previous cases. First of all, the dispersion of both qp and Qa with respect to a is much larger in the presence of accretion heating. In other words, the orbits of embryos are more eccentric. We find e ≃ 0.02 for the innermost embryo 1 and e ≃ 0.04 for the outermost embryo 4 after 5 kyr of evolution, while the corresponding values in Case II were e ≃ 0.004 and e ≃ 0.01, respectively. Moreover, the increased eccentricity is not produced by the resonant forcing; it is observable already before the embryos form a closely-packed configuration. Looking at the beginning of the simulation, we see a brief period during which both the semimajor axis and orbital eccentricity swiftly increase, especially for the three outer embryos. It seems that this period of evolution must represent a transitional state of the system during which the hydrodynamic background adjusts to the presence of the new heat source and the orbits react accordingly. The ability of the gas disk to circularise the orbits is clearly reduced in this case which is a new and unexpected phenomenon, explored in detail in Sect. 4.
Modified disk torques.
Another surprising feature is that the inner embryos 1 and 2 are able to maintain outward migration despite having moderate eccentricity. We recall that the eccentricity growth leads to shrinking of the horseshoe region, and the corotation torque Γc in its unsaturated non-linear limit depends on the half-width of the horseshoe region xhs (Paardekooper & Papaloizou 2009) as 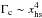 (Fendyke & Nelson 2014). The positive contribution of Γc in the region of outward migration is thus expected to vanish with increasing eccentricity (Bitsch & Kley 2010). Yet, we observe that the migration of the inner embryos 1 and 2 is still directed outwards with a rate similar to Cases I and II and the torques even allow the embryos to penetrate into the outer disk. As for the outer embryos 3 and 4, their migration first proceeds inwards (except for a short initial phase) but with significantly reduced migration rate.
(Fendyke & Nelson 2014). The positive contribution of Γc in the region of outward migration is thus expected to vanish with increasing eccentricity (Bitsch & Kley 2010). Yet, we observe that the migration of the inner embryos 1 and 2 is still directed outwards with a rate similar to Cases I and II and the torques even allow the embryos to penetrate into the outer disk. As for the outer embryos 3 and 4, their migration first proceeds inwards (except for a short initial phase) but with significantly reduced migration rate.
It is worth noting that the zero-torque radius is somewhat ignored by embryos in Case III. As a result, we do not see the embryos to become closely-packed around ≃7.5 AU like in the previous cases. Instead, embryo 2 swiftly penetrates into the outer disk and interacts with embryo 3, and shortly after that with embryo 4. Meanwhile, embryo 1 reaches the expected location of the zero-torque radius and stays there for a while, being stopped by interactions with embryo 3. But ultimately, it continues outwards, migrating along with embryo 3 almost as a pair.
Examining the excited orbital eccentricities properly, we notice that e ≃ h. Therefore one can expect significant modifications of the Lindblad torque (Papaloizou & Larwood 2000; Cresswell & Nelson 2006) as the eccentric embryos exhibit radial excursions in the disk and variations of the orbital velocity, thus periodically exciting density waves propagating inwards and outwards during the orbit. In such a case, the Lindblad torque, which is usually negative, can become reduced, or even reversed. Regarding the heating torque, its contribution is positive. But we emphasise that because of the increased eccentricity and due to narrowing of the horseshoe region, we can expect the heating torque to operate in a mode that was not described by Benítez-Llambay et al. (2015) who studied the heating torque for planets on fixed circular orbits. Here we summarise that the migration rate in Case III is driven by the modified Lindblad and heating torques acting on eccentric orbits. Detailed investigation of the torques accompanying the accretion heating is provided in Sect. 4.4.
Merging and resonant chain instabilities.
Once the embryos become closely packed, they interact violently because their eccentric orbits drive one another into frequent close encounters. At t ≃ 12 kyr, embryos 2 and 3 become temporarily locked in a coorbital resonance which is disrupted by convergent migration towards the outer embryo 4. The three outer embryos then strongly interact and swap positions several times before there is a first merger of two 4.2 ME embryos (blue and red) at ≃31 kyr. Three-body interactions of the remaining embryos produce another merger at ≃37.7 kyr when 8.7 ME embryo (blue) and 4.3 ME embryo (orange) collide. The system is stabilised by formation of a coorbital pair, having final masses of 13.8 ME and 4.3 ME.
Although the system evolves into a 1:1 orbital resonance at the end, it is not capable of establishing a global resonant chain during its evolution, apart from temporal resonant captures. This is different with respect to Cases I and II where the system becomes resonant once the embryos become closely packed and stays that way except for occasional instabilities during encounters, orbital swapping, and embryo merging. The decreased probability of resonant capture is again caused by excited eccentricities, as discussed, for example, by Batygin (2015).
Regarding the possibility of mergers, their number is the same as in Case II but they occur later during the evolution. This is slightly surprising because we already argued that close encounters are more frequent, and therefore a natural question arises – why do mergers not appear sooner? To provide a basic statistical check, as in Cases I and II, we performed two additional simulations, the first with initially smaller orbital separations (4.5 RmH) and the second with slightly larger inclinations (≃1°). The first simulation produced only one merger, the second produced none. At the same time, we confirmed the strong eccentricity increase unrelated to mutual close encounters which became frequent as a consequence of the eccentricity growth.
The reduced merging efficiency compared to Case II is probably another consequence of larger eccentricities which lead to larger relative velocities during encounters and subsequently, merging is more difficult. Regarding the second additional simulation with zero mergers, we find that orbital inclinations are not reduced enough before the close encounters start to occur. Due to larger encounter velocities, vertical stirring is observed, maintaining the inclinations above zero. Such an inclined orbital configuration is not suitable for merging.
We remark that the influence of the accretion heating on the system’s evolution and stability may be even more evident if higher numbers of embryos are considered, which is what we intend to study in the future (as proposed in Sect. 5).
In both Cases II and III, we see that mergers produce embryos massive enough to potentially become giant planet cores. However, this subsequent evolution is not covered in our simulations as the gravitational attraction and subsequent collapse of a massive gaseous envelope is a delicate and not well understood process which is beyond the scope of this paper (e.g. Ayliffe & Bate 2009; Machida et al. 2010).
Gas and pebble surface density.
To begin the investigation of the unexpected eccentricity growth related to accretion heating, we first compare snapshots of the gas and pebble surface density in Cases II and III. Figure 6 shows Σ and Σp in Case II, after 4.7 kyr of evolution. The gas disk exhibits typical features – embryos launch spiral arms and produce minor density variations in their horseshoe regions. The pebble disk is affected by the ongoing pebble accretion. Accreting embryos carve partial gaps in the pebble component along their orbits. The gap has two parts; one of them is trailing and the other one is leading the orbital motion of an embryo (which is oriented counterclockwise in all plots). The formation of these two parts can be explained simply by the trajectories of pebbles with respect to the embryo (Morbidelli & Nesvorný 2012) – those drifting from outside meet the embryo head-on, and those which have drifted across the embryo’s orbit catch up with it from behind. After a portion of the pebble flux is filtered out by the embryo, there is a paucity of pebbles behind it, slightly outside the embryo’s orbit, and another cavity is formed in the direction of orbital motion, slightly inside the embryo’s orbit.
Figure 7 shows Σ and Σp in Case III, again in simulation time 4.7 kyr. We see that the shape of spiral arms is somewhat modified, which is to be expected as the embryos already orbit with considerable eccentricities (Cresswell et al. 2007; Bitsch & Kley 2010). The gaps in the pebble disk are slightly skewed and widened because the eccentric embryos perform radial excursions while carving the gaps. But looking at Σ, there is a strange feature; underdense structures trailing the embryos, starting at their locations and stretching slightly to r>rem. An explanation of these underdensities, as well as investigation of the eccentricity growth, is given in the following section.
 |
Fig. 6 A closeup of the gas surface density Σ (top) and pebble surface density Σp (bottom) after ≃ 5 kyr of evolution in the simulation with pebble accretion but without accretion heating, i.e. Case II. The gaps in the pebble disk are opened by accreting planetary embryos. A fourth embryo is also present in the system but it is located outside the range. |
 |
Fig. 7 Same as Fig. 6 but for the simulation with accretion heating (Case III). Two embryos are located at x = 5.55,y = 4.65 AU and x = 4.35,y = 7.17 AU; two other embryos are located outside the range. The Σ distribution shows that there are trails of underdense gas stretching outwards from the embryos, trailing their orbital motion. The shape of cavities in the pebble component is affected by the eccentric orbits of embryos. Unlike in Fig. 6, the concentration peak at the embryos’ location is somewhat blurred in both gas and pebbles. |
 |
Fig. 8 Temporal evolution of the osculating eccentricity e(t) for a single 3 ME embryo in four distinct simulation setups. In the first two setups we neglect pebble accretion and the initial eccentricity is e0 = 0 (blue curve) and e0 = 0.05 (purple curve). In the other two setups, we consider pebble accretion and heating, the initial eccentricity being again e0 = 0 (red curve) and e0 = 0.05 (orange curve). Accretion heating reduces the eccentricity damping efficiency for the eccentric orbit and excites the eccentricity of the circular orbit. |
4. The “hot-trail” effect – the orbital eccentricity excitation due to accretion heating
In order to understand the process leading to the eccentricity excitation and also to the formation of underdense structures in the gas distribution adjacent to the embryos, we must first check whether we can recover these phenomena in simulations with a single embryo. This should verify whether the disk↔embryo interaction alone is sufficient to raise the eccentricity, without the help of any additional perturbers.
Starting again with the equilibrium fiducial disk, we placed a single 3 ME embryo on an orbit with semimajor axis a = 6.5 AU. The orbit was initially circular in one case, and e0 = 0.05 was assigned to the embryo in another case. Both the circular and the eccentric orbits were evolved for several hundred years; (i) in the gas disk only with fixed embryo mass, and (ii) with pebble accretion and respective heating considered. The embryo was allowed to fully interact with the disk, that is, the orbit was not held fixed.
Let us first examine the eccentricity evolution in these four simulation setups, as shown in Fig. 8. In simulations with fixed embryo mass, the initially circular orbit oscillates around small eccentricity values and the initially eccentric orbit is being damped and almost circularised (e = 0.003). On the other hand, e in simulations with accretion heating converges to moderate non-zero value (e = 0.03), even for the initially circular orbit. Therefore the eccentricity excitation and reduced eccentricity damping that we identified in Sect. 3.6 are indeed reproduced.
The simulation with e0 = 0 and heating by pebble accretion is the most interesting one because it proves that the embryo can gain and sustain eccentricity solely due to forces arising from the disk. We therefore discuss this simulation in detail for the remainder of this section. Looking at the red curve in Fig. 8, it is obvious that there are several distinct stages during which the eccentricity excitation rate changes. We pick three characteristic times t ≃ 180, 360, and 1130 yr at which we investigate the disk-embryo interaction during one orbital period. We refer to these three evolutionary stages as the onset, growth, and saturation phase for brevity.
In order to identify contributions from the disk responsible for de/ dt variations, we employ the Gauss perturbation equation for the eccentricity ![\begin{equation} \frac{\mathrm{d}e}{\mathrm{d}t} = \frac{\sqrt{1-e^{2}}}{na}[\mathcal{R}\sin{f}+\mathcal{T}(\cos{f}+\cos{E})] , \label{eq:gauss_dedt} \end{equation}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq318.png) (42)where n denotes the embryo’s mean motion, ℛ and
(42)where n denotes the embryo’s mean motion, ℛ and  are the radial and tangential components of the perturbing acceleration arising from the disk, f is the true anomaly and E is the eccentric anomaly, for which one can write cosE = (e + cosf) / (1 + ecosf). Assuming that the variation of orbital elements during one orbital period is negligible, we can limit ourselves to an analysis of the Gauss factors inside the square brackets in Eq. (42). We shall denote Gr ≡ ℛsinf and
are the radial and tangential components of the perturbing acceleration arising from the disk, f is the true anomaly and E is the eccentric anomaly, for which one can write cosE = (e + cosf) / (1 + ecosf). Assuming that the variation of orbital elements during one orbital period is negligible, we can limit ourselves to an analysis of the Gauss factors inside the square brackets in Eq. (42). We shall denote Gr ≡ ℛsinf and  .
.
 |
Fig. 9 Measures of the gravitational acceleration from the disk acting on the embryo, evolving from initially circular orbit in the presence of pebble accretion and the heating torque (i.e. red curve in Fig. 8). The values are recorded during one orbital period (represented by the true anomaly f), at around t ≃ 180, 360 and 1130 yr of the simulation, that is, during the onset, growth, and saturation phase of the eccentricity excitation. Top: evolution of the Gauss factor Gr ≡ ℛsinf (left vertical axis) and the osculating eccentricity e, which was recorded during the onset phase (right vertical axis). Middle: evolution of the Gauss factor |
4.1. Radial perturbation
Figure 9 (top panel) shows the values of Gr acting on the embryo as it travels along its orbit during the onset, growth, and saturation phases. Because ℛ itself is always negative and almost identical in all the individual phases, Gr also does not change significantly. It is a f-periodic function and we find it to be typically an order of magnitude stronger than Gθ. Thus from the dynamical point of view, it is responsible for fast variations of the orbital eccentricity which occur on the orbital time scale. The varying e(t) function corresponding to the onset phase is overplotted in Fig. 9 (dashed curve). As the embryo moves from the periastron towards the apoastron, Gr< 0 implies de/ dt< 0 which decreases e, and vice versa. Because of Gr symmetry, the respective changes of the eccentricity average out and do not lead to secular variations.
The existence of non-zero radial acceleration ℛ is due to the gas surface density profile of the surrounding disk which is in general an outward-decreasing power-law function. Consequently, within an arbitrary radius around the embryo, one can expect overabundance of gas inwards from the orbit, while the mass of the gas outwards is smaller.
4.2. Azimuthal perturbation
As argued above, Gr is related to the orbital frequency in the e-oscillations and cannot cause the runaway growth of the eccentricity. Consequently, Gθ must be responsible for the secular changes and we plot it in the middle panel of Fig. 9. In order to guide the eye, we overplot the (cosf + cosE) function for e = 0.005, scaled down to the figure range; it represents a dependence which Gθ would follow if 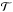 was a constant positive acceleration. Examining the Gθ profile measured in our simulation, we notice there are some asymmetries during the orbital period which can accumulate in time and cause e to grow.
was a constant positive acceleration. Examining the Gθ profile measured in our simulation, we notice there are some asymmetries during the orbital period which can accumulate in time and cause e to grow.
During the onset phase, Gθ is maximum when the embryo is at periastron and shortly afterwards. Then it decreases to zero as f → 90°, stays at low positive values through the apoastron passage and at f ≃ 290° it finally starts to increase back to the maximum value. Gθ averaged over one orbital period is positive which implies de/ dt> 0, in agreement with the onset of the eccentricity excitation in Fig. 8.
The azimuthal acceleration  related to Gθ is plotted in the bottom panel of Fig. 9. We see that the embryo undergoes strong positive acceleration in the direction of its orbital motion around the periastron, with the peak slightly shifted to f ≃ 30°. From f ≃ 110° to f ≃ 290°,
related to Gθ is plotted in the bottom panel of Fig. 9. We see that the embryo undergoes strong positive acceleration in the direction of its orbital motion around the periastron, with the peak slightly shifted to f ≃ 30°. From f ≃ 110° to f ≃ 290°,  has a flat profile and is negative. In terms of the expected gas distribution, there must be an accumulation of mass in front of the embryo around the periastron. For the rest of the orbit, this accumulation should become weaker and from f ≃ 110° to f ≃ 290°, an excess of gas behind the embryo’s orbital motion is expected.
has a flat profile and is negative. In terms of the expected gas distribution, there must be an accumulation of mass in front of the embryo around the periastron. For the rest of the orbit, this accumulation should become weaker and from f ≃ 110° to f ≃ 290°, an excess of gas behind the embryo’s orbital motion is expected.
 |
Fig. 10 Evolution of the gas surface density Σ (left column) and temperature T (right column) during one orbital period, recorded within the onset phase of the eccentricity growth. Individual snapshots are labelled with the respective simulation time t, embryo’s true anomaly f and azimuthal acceleration imposed by the disk, labelled here aazim. The figures are transformed to the corotating frame centered on the embryo. The Hill sphere and embryo’s osculating orbit are plotted and we also indicate general directions of the gas flow with respect to the embryo by arrows. The orbital direction of the embryo is directed counterclockwise and the protostar is located at (x = 0,y = 0). The top row depicts the situation in the periastron, while the third row corresponds to the apoastron. The second row is recorded approximately halfway from periastron to apoastron, and vice versa for the bottom row. |
 |
Fig. 11 Same as Fig. 10 but the hydrodynamic quantities are recorded within the saturation phase of the eccentricity excitation. |
In the growth phase, the azimuthal acceleration  remains positive for the entire orbit, having a similar orbital evolution as in the onset phase, with an enhanced peak near the periastron, followed by decrease and plateau towards the apoastron. Consequently, Gθ has an increased amplitude but it also becomes negative from f = 90° to 270°. Despite that, the averaged Gθ is again positive and so is de/ dt. The shape of
remains positive for the entire orbit, having a similar orbital evolution as in the onset phase, with an enhanced peak near the periastron, followed by decrease and plateau towards the apoastron. Consequently, Gθ has an increased amplitude but it also becomes negative from f = 90° to 270°. Despite that, the averaged Gθ is again positive and so is de/ dt. The shape of  tells us that we can expect the gas distribution around the embryo to be denser ahead of the embryo for the entire orbit.
tells us that we can expect the gas distribution around the embryo to be denser ahead of the embryo for the entire orbit.
During the saturation phase, the azimuthal acceleration  has a somewhat complex dependence on f. Its overall amplitude is smaller compared to the previous phases by an order of magnitude. The acceleration
has a somewhat complex dependence on f. Its overall amplitude is smaller compared to the previous phases by an order of magnitude. The acceleration  remains positive from periastron to apoastron and it is negative through the remaining half of the orbit, apart from a short interval at around f ≃ 275°. Looking at the respective Gθ dependence, its shape is quite similar to a π-periodic function in f, oscillating around zero, having two maxima between the periastron and f = 90° and between the apoastron and f = 270° and vice versa.
remains positive from periastron to apoastron and it is negative through the remaining half of the orbit, apart from a short interval at around f ≃ 275°. Looking at the respective Gθ dependence, its shape is quite similar to a π-periodic function in f, oscillating around zero, having two maxima between the periastron and f = 90° and between the apoastron and f = 270° and vice versa.
4.3. Hydrodynamic explanation of the eccentricity excitation
In the following, we explain the eccentricity excitation from the hydrodynamic point of view. For this purpose, we present a series of figures capturing the gas density Σ and temperature T distribution in the embryo’s vicinity, corresponding to the onset phase (Fig. 10) and the saturation phase (Fig. 11).
Let us first recall the advection-diffusion problem which causes the standard mode of the heating torque on fixed circular orbits according to Benítez-Llambay et al. (2015). The embryo heats the gas near its position and the gas becomes overheated and therefore underdense2, in order to maintain the pressure balance with the surroundings. The heated gas is being advected by the nearby flows and in the meantime, its internal energy changes by the radiative diffusion. For a circular orbit of the embryo, the gas from the outer part of the disk approaches the embryo head-on, is heated, and forms an underdense lobe behind the embryo. The gas from the inner disk, which is moving faster than the embryo, approaches from behind, forming an underdense lobe in front of the embryo. Because the gas velocity is sub-Keplerian, the corotation between the embryo and the gas is shifted slightly inwards, and therefore there is a prevalence of gas approaching as the headwind, and the underdense lobe behind the embryo is dominant.
For an embryo that is allowed to move freely in the disk, we already saw that the orbit is never perfectly circular. It periodically gains a small eccentricity (~10-3) due to the Gr forcing (Fig. 9). Thus the embryo makes small radial excursions in the disk (see the changing range of the x-axis in Fig. 10) as it performs a small epicyclic motion. The heat source located at the embryo’s position trails this epicyclic motion. In the temperature map, the epicyclic motion manifests itself as a “hot trail”, attached to the temperature maximum, which wobbles around between the individual snapshots. We thus name this new phenomenon the hot-trail effect.
Looking at the Σ profiles in Fig. 10, we see that in the periastron, there are again two underdense lobes, similar to the circular case. The deep lobe attached behind the embryo represents the dominant paucity of material. The less pronounced and more stretched lobe in front of the embryo is rather a leftover of the dominant lobe which was displaced by the epicyclic motion during the previous orbit. This is proved by the sequence of Σ profiles; as the embryo travels towards the apoastron, its radial distance increases, thus the dominant lobe is left at r<rem and subsequently moves ahead of the embryo due to the transport by the interior flows, which move faster than the embryo. In the meantime, the less dominant leftover lobe is being lost by the Keplerian shear and diffusive effects.
Near the apoastron, the embryo has the lowest orbital velocity. If we, for example, consider the eccentricity e = 0.003 (typical value due to the Gr forcing), the orbital velocity in the apoastron with respect to the Keplerian velocity is vapo = (1 − 0.003)vK. At the corresponding orbital distance r ≃ 6.5 AU, the gas orbital velocity is vθ = (1 − 0.0026)vK (cf. Fig. 2). The headwind therefore significantly vanishes and no additional lobe can be formed behind the embryo. The embryo is left with the lobe formed at the periastron which has already been transported by the flows interior to the orbit.
The position of the dominant underdense lobe is the key factor determining the resulting azimuthal acceleration  acting on the embryo. In the periastron, there is a paucity of mass behind the planet, so the acceleration is in the orbital direction. In the apoastron, the lobe is located ahead of the embryo, but it is also radially displaced (r<rem) with respect to the embryo. As a consequence,
acting on the embryo. In the periastron, there is a paucity of mass behind the planet, so the acceleration is in the orbital direction. In the apoastron, the lobe is located ahead of the embryo, but it is also radially displaced (r<rem) with respect to the embryo. As a consequence,  is negative but its magnitude is much smaller compared to that at periastron, where the underdense lobe is adjacent to the embryo. This asymmetry between the periastron and apoastron causes the eccentricity excitation.
is negative but its magnitude is much smaller compared to that at periastron, where the underdense lobe is adjacent to the embryo. This asymmetry between the periastron and apoastron causes the eccentricity excitation.
During the growth phase (not shown in figures), the situation is similar to the onset phase. But as e continuously grows, the lobe at the periastron becomes prolonged because the relative velocity of the embryo with respect to the gas increases. As a consequence, the azimuthal acceleration 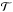 measured in the periastron of the growth phase is larger compared to the onset phase. The relative velocities become large enough for the embryo to start feeling tailwind near the apoastron, which delivers heat to the lobe positioned ahead of the embryo at that time. But because the gas is sub-Keplerian, the relative velocity is always larger in the periastron than in the apoastron thus the positive eccentricity pumping during the periastron passage still prevails and the runaway eccentricity growth continues.
measured in the periastron of the growth phase is larger compared to the onset phase. The relative velocities become large enough for the embryo to start feeling tailwind near the apoastron, which delivers heat to the lobe positioned ahead of the embryo at that time. But because the gas is sub-Keplerian, the relative velocity is always larger in the periastron than in the apoastron thus the positive eccentricity pumping during the periastron passage still prevails and the runaway eccentricity growth continues.
The eccentricity cannot grow indefinitely, however, but its excitation saturates at a certain level. The hydrodynamic state at the saturation phase is given in Fig. 11 where we see that the hot trail spans a larger portion of the embryo’s surroundings because the radial excursion (the epicycle) of the embryo has already increased significantly. As a consequence, the underdense structures are more distant from the embryo and the Hill sphere can refill with gas which is yet-to-be heated and which blurs asymmetries in the embryo’s vicinity, responsible for the eccentricity excitation. At the same time, the underdense structures are strongly affected by the Keplerian shear because their radial extension is considerable.
At the saturation phase, the eccentricity growth stops right before exceeding the local value of the aspect ratio h ≃ 0.036. For e ≳ h, the relative motions could lead to the reversal of normally negative Lindblad torque (Papaloizou & Larwood 2000). Cresswell & Nelson (2006) found that the Lindblad torque transition for e ≳ h is accompanied by very efficient eccentricity damping leading to a strong energy loss which can outweigh the angular momentum gain. This efficient damping is finally able to prevent the hot trail from exciting the eccentricity even more. But for lower e, the hot-trail effect dominates – otherwise the eccentricity would not grow in the first place.
4.4. Torque distribution
The periodic changes of Σ and of the related  are also reflected in the variations of the torque Γtot felt by the embryo during its orbit. Figure 12 shows the normalised radial torque distribution Γ(r) / Γ0 which relates to the total torque Γtot as
are also reflected in the variations of the torque Γtot felt by the embryo during its orbit. Figure 12 shows the normalised radial torque distribution Γ(r) / Γ0 which relates to the total torque Γtot as  (43)Figure 12 generally demonstrates which parts of the disk are responsible for positive and negative torques and how the magnitude of these torques changes with radial separation from the embryo.
(43)Figure 12 generally demonstrates which parts of the disk are responsible for positive and negative torques and how the magnitude of these torques changes with radial separation from the embryo.
During the onset phase (Fig. 12, top panel), the shape of Γ(r) / Γ0 is similar to the calculations of (Benítez-Llambay et al. 2015; cf. their Fig. 1). In the periastron, it exhibits a negative peak at r<rem that is smaller than a positive peak at r>rem. As the embryo travels along its orbit, the difference compared to Benítez-Llambay et al. (2015) is in the position of the profile with respect to the embryo (indicated with arrows) and in the asymmetry between the positive and negative peak. The asymmetry is pronounced in the periastron and disappears in the apoastron, in accordance with our previous findings.
During the saturation phase (Fig. 12, bottom panel), Γ(r) / Γ0 becomes wavy and complex. It corresponds to the hot trail strongly distorted by the Keplerian shear, which is produced by a large epicycle. Compared to the onset phase, the torque contribution arising from the density waves is modified. Let us focus on the situation in periastron first. Looking at Fig. 11, we notice that the gas surface density exhibits a pronounced inner density wave. The underdense structure related to the hot-trail effect is located at r>rem thus the dominant contribution to Γ(r) at r<rem must be related to the inner density wave.
 |
Fig. 12 Radial torque density Γ(r) acting on the embryo during the onset (top) and saturation (bottom) phases, normalised to Γ0. The individual curves represent measurements in the periastron (purple), apoastron (orange) and in-between. The vertical arrows indicate the instantaneous radial distance of the embryo corresponding to the individual curves. The horizontal arrows and labels approximately distinguish some of the important torque contributions discussed in the text. To avoid misinterpretation, we remark that the hot-trail torque is acting in the bottom panel as well but it spans different radial extent for each curve and thus cannot be marked unambiguously. |
The contribution from the inner density wave is labelled in Fig. 12 (bottom panel). Although the inner Lindblad torque is purely positive for circular orbits, we can see that it has both positive and negative contributions for the eccentric orbit during the saturation phase. In the apoastron, the situation is similar (but the outer density wave is more pronounced). This implies that the orbit is indeed close to the state of the Lindblad torque reversal and proves our aforementioned argument about what phenomenon finally stops the eccentricity growth.
5. Future improvements and observational signatures
Additional free parameters.
Regarding the discussion in this paper, we essentially restricted ourselves to switching pebble accretion and the accretion heating on and off, in order to understand the basic physics of the hot-trail effect and to simplify the discussion. It is clear, however, that our problem has a number of additional free parameters. In particular, the number of embryos (up to 101, for example); initial embryo masses (of the order of 100ME); initial spacing of embryos (multiples of RmH); embryo positions in the disk and with respect to the zero-torque radius; the radial pebble flux ṀF; gas surface density Σ0 and its slope; viscosity ν (or α); turbulent stirring of solids αp; or stellar luminosity L⋆; and so on. Even if we have only two values per parameter, the resulting number of models is so high that we are unable to compute a full matrix. Nevertheless, it is certainly possible to compute differences (derivatives) with respect to the fiducial model; work postponed to the following paper, in fact.
Possible model improvements.
We can outline a number of opportunities for the hydrodynamic model extensions, for example, full 3D treatment, implementation of gas accretion, deposition of pebbles in various layers of protoatmospheres, gas self-gravity, stochastic forcing by turbulent flows (Pierens et al. 2013), independently evolved dust component as the main opacity constituent, and so on.
Moreover, as we demonstrated that the hot-trail effect reduces the ability of the surrounding disk to damp the orbital eccentricity, it is also possible that the inclination damping is somehow modified if a full 3D disk is considered. In our 2D model, the inclination damping is provided by Eq. (39) which is not self-consistent but based on a model that neglects the accretion heating (Tanaka & Ward 2004). We also plan to refine this part of the model in the future.
Observational signatures.
From an observational point of view, the imprints of various migration histories and orbital excitations should be recognisable in the observed exoplanetary systems, but they can be successfully understood only when the effects described in this paper are taken into account in future works dealing with this issue.
There could be observational signatures of, for example, mergers or multiple embryos on closely-packed orbits in the datasets of the campaigns involved in the direct protoplanetary disk imaging (e.g. by ALMA). We have already started to investigate this possibility and plan to publish the study in a separate paper.
In our case, most if not all observational circumstances should be determined by 3D radiative transfer in the dust continuum. The optical thickness for the typical Bell & Lin (1994) opacity κ ≃ 100 cm2 g-1 and the surface density Σ ≃ 102 g cm-2 is τopt ≃ κΣ ≃ 102 ≫ 1. We thus definitely need a good enough description of the disk atmosphere, far from the midplane.
In order to become observable, it seems that protoplanets must open considerably large gaps in the gas disk (Rosotti et al. 2016). Partially opened gaps are probably not observable because these are still optically thick; the density contrast has to be at least 102. The close encounters between embryos in our simulations lead to an asymmetry, but are only present for a short time interval. As argued in Rosotti et al. (2016), the threshold mass for detection is about 12 ME in sub-mm. Moreover, for VLT/SPHERE or Gemini/GPI instruments, the protostar should be more massive (M⋆ ≃ 2 M⊙) to become at least a Herbig Ae star, because of current flux limitations.
6. Conclusions
In this paper, we studied the orbital evolution of four 3 ME embryos embedded in a region of a protoplanetary disk where the convergent migration is expected to occur under the influence of the standard Type-I torques. In our simulations, however, we considered that the embryos rapidly accrete mass from the pebble disk (modelled hydrodynamically). Three classes of simulations were performed: Case I as a reference scenario in which pebble accretion is completely neglected, Case II in which pebble accretion leads to the mass growth of embryos and Case III in which embryos also become heated by the deposition of pebbles. We investigated the impact of the additional processes on the migration and mutual interactions of the embryos. The simulations were performed using a new state-of-the-art and rather self-consistent hydrodynamical model, which we extensively described and verified.
We found that in both Cases I and II, the system evolves through a sequence of resonant chains, the first of which is usually established around the zero-torque radius. As the embryos gain non-zero eccentricity (typically ranging from 0.004 to 0.01) due to perturbations from the mean-motion resonances, occasional close encounters are possible, leading to mutual scattering (sometimes accompanied by a swap of orbits) or embryo merging.
We reported that merging of embryos is more probable in Case II in which the mass growth by pebble accretion is accounted for. The reason for this is that the resonant chain is destabilised more often as the masses of embryos responsible for the resonant forcing (e.g. of eccentricities) evolve. Additional forcing is provided as the streamline topology around the embryos changes with the evolving masses, thus imposing a slightly different disk torque.
In Case III, the positive heating torque changes the expected migration rates. As a result, the embryos somewhat ignore the zero-torque radius and are driven into mutual interactions preferentially in the outer part of the disk, rather than being packed in a resonant chain around the zone of convergence.
Close encounters occur frequently in Case III and cover a longer period of the evolution. We realised that the encounters are facilitated by an eccentricity increase (e ≃ h, typically ranging from 0.02 to 0.04) prior to resonant perturbations by means of a new ‘hot-trail’ effect. The effect is due to variable gravitational acceleration arising from the gas in the vicinity of each embryo, which is periodically modified by formation and advection of an overheated and thus underdense lobe trailing the epicyclic motion of the embryo. The effect was independently reported by Eklund & Masset (2017; we also refer to Masset & Velasco Romero 2017) while our research was ongoing (Chrenko & Brož 2016). The hot trail effect reduces the ability of the surrounding disk to damp the eccentricities and circularise the orbits. Despite the fact that more encounters pose more opportunities for merging, we actually found that merging is less frequent compared to Case II , probably because of larger encounter velocities on the eccentric orbits.
The eccentricity excitation by the hot-trail effect stalls when e ≃ h because the Lindblad torque acting on eccentric orbits is modified and can actually operate in a mode close to its reversal (from negative to positive, Papaloizou & Larwood 2000; Cresswell et al. 2007; Bitsch & Kley 2010). Because the transition to the reversed Lindblad torque would require the embryo to cross the orbital resonances at which it excites the density waves, strong eccentricity damping occurs and the eccentricity growth saturates. Nevertheless, the eccentricity does not decrease and is, in fact, maintained by the hot-trail effect. We note that many N-body models (e.g. Sándor et al. 2011; Izidoro et al. 2015; Coleman & Nelson 2016, and many others) usually employ a strong eccentricity damping prescription (e.g. Cresswell & Nelson 2006, 2008) derived from hydrodynamic models which neglect the accretion heating. We suggest that these analytic damping rates should be carefully refined for future applications because they could be inaccurate in cases when the protoplanets undergo any kind of strong accretion.
Orbital excitation of embryos heated by pebble accretion prevents formation of a global resonant chain, except for short transient periods. An interesting overlap of this result can be found with recent developments in the analytical theory. For example, Batygin (2015) used the Hamiltonian formalism to study the probability of the resonant capture for migrating low-mass planets and compared his predictions with the occurrence of the first-order mean-motion resonances in exoplanetary systems. He found that the probability of the resonant capture is greatly diminished (and thus the observed non-resonant systems can be explained) if a pre-encounter orbital excitation e ≳ 0.02 is considered. Our model thus provides a natural way of exciting the eccentricity enough to prevent resonant locking and may have important implications for explaining the structure of exoplanetary systems.
Mergers large enough to possibly become giant planet cores with masses ≃13 ME were found in both Cases II and III. We emphasise that merging caused by fast migration and accretion in convergence zones breaks the otherwise oligarchic nature of the embryo growth by pebble accretion.
We conclude that orbital instabilities, eccentricity excitations and (possibly) mergers naturally accompany evolution of pebble-accreting embryos and may have an important impact on shaping the final architecture of any planetary system. This is a major result compared to previous models which neglected self-consistent hydrodynamics, accretion or heating. But in order to find general implications, a larger statistical sample of simulations is required because we expect a strong dependence on the initial conditions (possibly on the initial number and masses of embryos, their position within the disk, accretion rate related to the pebble mass flux and heating efficiency influenced by the opacity).
In the original work of Lambrechts & Johansen (2012), the Bondi regime is referred to as the drift regime.
Acknowledgments
We thank Alessandro Morbidelli, Steven N. Shore and David Nesvorný for helpful discussions during this project. We are very grateful to Bertram Bitsch who kindly provided his code for calculating the migration maps. We also thank an anonymous referee for valuable comments. The work of O.C. and M.B. has been supported by Charles University in Prague (project GA UK No. 128216; project SVV-260441). The work of M.B. was supported by the Grant Agency of the Czech Republic (grant No. 13-01308S). Access to computing and storage facilities owned by parties and projects contributing to the National Grid Infrastructure MetaCentrum, provided under the program “Projects of Large Research, Development, and Innovations Infrastructures” (CESNET LM2015042), is greatly appreciated.
References
- Adachi, I., Hayashi, C., & Nakazawa, K. 1976, Prog. Theor. Phys., 56, 1756 [NASA ADS] [CrossRef] [Google Scholar]
- Ayliffe, B. A., & Bate, M. R. 2009, MNRAS, 393, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Baillié, K., & Charnoz, S. 2014, ApJ, 786, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Baruteau, C., & Masset, F. 2008, ApJ, 672, 1054 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K. 2015, MNRAS, 451, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez-Llambay, P., Masset, F., Koenigsberger, G., & Szulágyi, J. 2015, Nature, 520, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., & Kley, W. 2011, A&A, 536, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Crida, A., Morbidelli, A., Kley, W., & Dobbs-Dixon, I. 2013, A&A, 549, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Morbidelli, A., Lega, E., Kretke, K., & Crida, A. 2014, A&A, 570, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bitsch, B., Lambrechts, M., & Johansen, A. 2015, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Chrenko, O., & Brož, M. 2016, in AAS/Division for Planetary Sciences Meeting Abstracts, 48, 318.03 [Google Scholar]
- Clarke, C. J., & Pringle, J. E. 1988, MNRAS, 235, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Coleman, G. A. L., & Nelson, R. P. 2016, MNRAS, 457, 2480 [NASA ADS] [CrossRef] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2006, A&A, 450, 833 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresswell, P., Dirksen, G., Kley, W., & Nelson, R. P. 2007, A&A, 473, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crida, A., & Bitsch, B. 2017, Icarus, 285, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Cuzzi, J. N., Dobrovolskis, A. R., & Champney, J. M. 1993, Icarus, 106, 102 [NASA ADS] [CrossRef] [Google Scholar]
- D’Alessio, P., Cantö, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., & Marzari, F. 2012, ApJ, 757, 50 [NASA ADS] [CrossRef] [Google Scholar]
- D’Angelo, G., Henning, T., & Kley, W. 2003, ApJ, 599, 548 [NASA ADS] [CrossRef] [Google Scholar]
- de Val-Borro, M., Edgar, R. G., Artymowicz, P., et al. 2006, MNRAS, 370, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P. 2002, A&A, 395, 853 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eklund, H., & Masset, F. S. 2017, MNRAS, 469, 206 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., D’Alessio, P., Hernández, J., et al. 2010, ApJ, 717, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Espaillat, C., Muzerolle, J., Najita, J., et al. 2014, in Protostars and Planets VI (University of Arizona Press), 497 [Google Scholar]
- Everhart, E. 1985, in Dynamics of Comets: Their Origin and Evolution, Proceedings of IAU Colloq., 83, held in Rome, Italy, June 11–15, 1984, eds. A. Carusi, G. B. Valsecchi (Dordrecht: Reidel), Astrophys. Space Sci. Lib., 115, 185 [Google Scholar]
- Fedele, D., van den Ancker, M. E., Henning, T., Jayawardhana, R., & Oliveira, J. M. 2010, A&A, 510, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fendyke, S. M., & Nelson, R. P. 2014, MNRAS, 437, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Flock, M., Fromang, S., González, M., & Commerçon, B. 2013, A&A, 560, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Fromang, S., Turner, N. J., & Benisty, M. 2016, ApJ, 827, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Garaud, P. 2007, ApJ, 671, 2091 [NASA ADS] [CrossRef] [Google Scholar]
- Guillot, T., Ida, S., & Ormel, C. W. 2014, A&A, 572, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hubeny, I. 1990, ApJ, 351, 632 [NASA ADS] [CrossRef] [Google Scholar]
- Izidoro, A., Raymond, S. N., Morbidelli, A., Hersant, F., & Pierens, A. 2015, ApJ, 800, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Jäger, C., Dorschner, J., Mutschke, H., Posch, T., & Henning, T. 2003, A&A, 408, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansen, A., & Klahr, H. 2005, ApJ, 634, 1353 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., et al. 2007, Nature, 448, 1022 [Google Scholar]
- Keith, S. L., & Wardle, M. 2014, MNRAS, 440, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Klahr, H., & Kley, W. 2006, A&A, 445, 747 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W. 1989, A&A, 208, 98 [NASA ADS] [Google Scholar]
- Kley, W. 1999, MNRAS, 303, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Dirksen, G. 2006, A&A, 447, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kley, W., Bitsch, B., & Klahr, H. 2009, A&A, 506, 971 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kretke, K. A., & Levison, H. F. 2014, AJ, 148, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Kretke, K. A., & Lin, D. N. C. 2012, ApJ, 755, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [Google Scholar]
- Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lega, E., Crida, A., Bitsch, B., & Morbidelli, A. 2014, MNRAS, 440, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Levermore, C. D., & Pomraning, G. C. 1981, ApJ, 248, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Levison, H. F., Kretke, K. A., & Duncan, M. J. 2015, Nature, 524, 322 [CrossRef] [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1985, in Protostars and Planets II, eds. D. C. Black, & M. S. Matthews (University of Arizona Press), 981 [Google Scholar]
- Lin, D. N. C., & Papaloizou, J. 1986, ApJ, 309, 846 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Kokubo, E., Inutsuka, S.-I., & Matsumoto, T. 2010, MNRAS, 405, 1227 [NASA ADS] [Google Scholar]
- Masset, F. 2000, A&AS, 141, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S. 2002, A&A, 387, 605 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., & Velasco Romero, D. A. 2017, MNRAS, 465, 3175 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., & Goodman, J. 2004, ApJ, 606, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Mihalas, D., & Weibel Mihalas, B. 1984, Foundations of radiation hydrodynamics (New York: Oxford University Press) [Google Scholar]
- Morbidelli, A., & Nesvorný, D. 2012, A&A, 546, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Crida, A., Masset, F., & Nelson, R. P. 2008, A&A, 478, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, T. W. A., & Kley, W. 2012, A&A, 539, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. W. A., & Kley, W. 2013, A&A, 560, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, T. W. A., Kley, W., & Meru, F. 2012, A&A, 541, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2008, A&A, 485, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. C. B. 2009, MNRAS, 394, 2297 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Papaloizou, J. C. B., & Larwood, J. D. 2000, MNRAS, 315, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
- Pierens, A. 2015, MNRAS, 454, 2003 [NASA ADS] [CrossRef] [Google Scholar]
- Pierens, A., Cossou, C., & Raymond, S. N. 2013, A&A, 558, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Liu, S.-F. 2012, A&A, 537, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Rosotti, G. P., Juhasz, A., Booth, R. A., & Clarke, C. J. 2016, MNRAS, 459, 2790 [NASA ADS] [CrossRef] [Google Scholar]
- Sándor, Z., Lyra, W., & Dullemond, C. P. 2011, ApJ, 728, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Stone, J. M., & Norman, M. L. 1992, ApJS, 80, 753 [Google Scholar]
- Tanaka, H., & Ward, W. R. 2004, ApJ, 602, 388 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1977, J. Comput. Phys., 23, 276 [Google Scholar]
- Weidenschilling, S. J. 1977, MNRAS, 180, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Winn, J. N., & Fabrycky, D. C. 2015, ARA&A, 53, 409 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, X., Liu, B., Lin, D. N. C., & Li, H. 2014, ApJ, 797, 20 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Numerical scheme of the energy equation solver
This appendix summarises our approach to modelling non-isothermal disks, which undergo heating and cooling, within the framework of the original 2D fargo code. Here we elaborate the numerical update of the internal energy due to the considered source terms (Sect. 2). Following the formalism of Stone & Norman (1992), the advection term is treated separately in the transport step.
Starting with the energy equation (Eq. (3)), our aim is to derive an implicit numerical scheme. The reason for this is to avoid a possible time-step restriction which could arise in the case of an explicit solution due to the Courant-Friedrichs-Lewy condition related to the radiative transport. As discussed in Sect. 2, we assume that the specific internal energy is entirely thermal thus we can write E = ΣcVT, where cV is the specific heat at constant volume. Within the one-temperature approach, the radiation field with the energy density 4σRT4/c only contributes to the energy transport via the radiative diffusion term. In order to obtain the implicit scheme, we rewrite Eq. (3) for the temperature only and we drop the advection term, which is treated separately 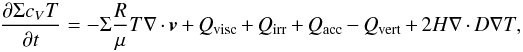 (A.1)where D = 16λσRT3/ (ρ0κ) is the diffusion coefficient.
(A.1)where D = 16λσRT3/ (ρ0κ) is the diffusion coefficient.
For simplicity, let us first discretise the diffusion term and return to the other source terms later on. Because fargo is designed as a staggered-mesh code, all scalar quantities are cell-centred whereas components of vector quantities are face-centred. In the following, the differential operators are written in polar coordinates, and integers i and j represent the indices of radial zones and azimuthal sectors, respectively: ![\appendix \setcounter{section}{1} \begin{eqnarray} && \frac{T_{i,j}^{n+1} - T_{i,j}^{n}}{\Delta t} = \left(\frac{2H}{\Sigma c_{V}}\right)_{i,j}\frac{1}{r_{i}^{\mathrm{c}}} \notag \\ & & \times \Biggl[ \frac{1}{\left(\Delta r\right)_{i}^{\mathrm{f}}} \left( r_{i+1}^{\mathrm{f}}\bar{D}^{r}_{i+1,j}\frac{T_{i+1,j}-T_{i,j}}{\left(\Delta r\right)_{i+1}^{\mathrm{c}}} - r_{i}^{\mathrm{f}}\bar{D}^{r}_{i,j}\frac{T_{i,j}-T_{i-1,j}}{\left(\Delta r\right)_{i}^{\mathrm{c}}} \right) \notag \\ && \quad+ \frac{1}{\Delta \theta} \left( \bar{D}_{i,j+1}^{\theta}\frac{T_{i,j+1}-T_{i,j}}{r_{i}^{\mathrm{c}}\Delta \theta} - \bar{D}_{i,j}^{\theta}\frac{T_{i,j}-T_{i,j-1}}{r_{i}^{\mathrm{c}}\Delta \theta} \right) \Biggl] \cdot \label{eq:discret_diffpart} \end{eqnarray}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq385.png) (A.2)Here
(A.2)Here 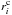 denotes the radial coordinate of a cell centre,
denotes the radial coordinate of a cell centre, 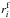 is the radius of an inner radial cell interface and Δθ denotes the angular width of sectors, which is identical for all cells. The additional quantities naturally occur because of the staggered-grid formalism:
is the radius of an inner radial cell interface and Δθ denotes the angular width of sectors, which is identical for all cells. The additional quantities naturally occur because of the staggered-grid formalism: 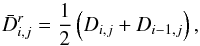 (A.3)
(A.3)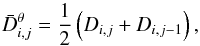 (A.4)
(A.4)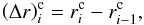 (A.5)
(A.5)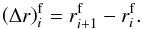 (A.6)Obviously,
(A.6)Obviously, 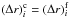 in the case of an equidistant radial spacing.
in the case of an equidistant radial spacing.
The implicit form can now be obtained by putting 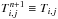 and by placing all Ti,j-dependent terms on one side of the left-hand side, while moving the remaining terms to the right-hand side. Because any non-linear terms in temperature would make the problem difficult to invert, we shall linearise the equation. To do so, the diffusion coefficients are evaluated using the hydrodynamic quantities from the beginning of the sub-step.
and by placing all Ti,j-dependent terms on one side of the left-hand side, while moving the remaining terms to the right-hand side. Because any non-linear terms in temperature would make the problem difficult to invert, we shall linearise the equation. To do so, the diffusion coefficients are evaluated using the hydrodynamic quantities from the beginning of the sub-step.
Concerning the remaining source terms and their linearity, Qvisc, Qacc and Qirr terms are temperature independent. The compressional heating term is linear in temperature and thus can be easily incorporated in the left-hand side. The vertical radiative cooling term Qvert is proportional to T4 but it can be linearised, as, for example, in Commerçon et al. (2011) or Bitsch et al. (2013). If the temperature changes over Δt are sufficiently small, we can rewrite Eq. (9)as ![\appendix \setcounter{section}{1} \begin{eqnarray} % (Q_{\mathrm{vert}})_{i,j} & =& \frac{2\sigma_{\mathrm{R}}}{(\tau_{\mathrm{eff}})_{i,j}}(T_{i,j}^{\mathrm{n}})^{4}\left(1+\frac{T-T^{\mathrm{n}}}{T^{\mathrm{n}}}\right)^{4}_{i,j} \\ & \approx &\frac{2\sigma_{\mathrm{R}}}{(\tau_{\mathrm{eff}})_{i,j}}\left[4(T^{\mathrm{n}})^{3}T - 3(T^{\mathrm{n}})^{4}\right]_{i,j} \equiv (Q'_{\mathrm{vert}}T - Q''_{\mathrm{vert}})_{i,j} . % \label{eq:qminus_linearized} \end{eqnarray}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq397.png) After some algebraic rearrangements, we can formally write
After some algebraic rearrangements, we can formally write 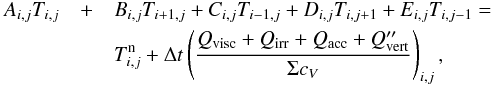 (A.9)which is a linear matrix equation. To solve this linear problem, we use the successive over-relaxation (SOR) method with odd-even ordering. Our implementation is parallelised by the domain splitting which is complementary to the radial grid decomposition of the original fargo code. The optimisation of the over-relaxation parameter is done similarly to Kley (1989).
(A.9)which is a linear matrix equation. To solve this linear problem, we use the successive over-relaxation (SOR) method with odd-even ordering. Our implementation is parallelised by the domain splitting which is complementary to the radial grid decomposition of the original fargo code. The optimisation of the over-relaxation parameter is done similarly to Kley (1989).
Appendix B: Steady-state motion equations of a pebble
Here we reproduce the derivation of Eqs. (20) and (21) which are used to initialise the velocity field of the pebble disk. The approach is well known and closely follows the derivation of Adachi et al. (1976), with one clarification.
Let us study a system consisting of a pebble with negligible mass which orbits a massive primary M⋆ and experiences the aerodynamic friction acceleration FD in the gaseous environment at the same time. We further assume that the motion is confined to one plane and no vertical perturbations are present.
The dynamical equation for the pebble takes the form 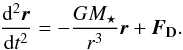 (B.1)Transforming into polar coordinates, one obtains
(B.1)Transforming into polar coordinates, one obtains 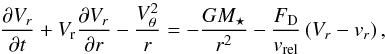 (B.2)
(B.2)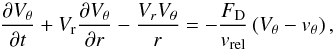 (B.3)where we utilise the fact that the friction force is directed against the relative velocity vector, having the magnitude
(B.3)where we utilise the fact that the friction force is directed against the relative velocity vector, having the magnitude 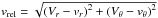 . Unlike Adachi et al. (1976), we retain the vr component of the flow and allow for the radial transport in the gaseous disk (we also refer to Guillot et al. 2014).
. Unlike Adachi et al. (1976), we retain the vr component of the flow and allow for the radial transport in the gaseous disk (we also refer to Guillot et al. 2014).
Let us simplify the equations above by assuming a steady-state situation, ∂t = 0. Furthermore, we only allow the drag force to cause small perturbations in pebbles’ azimuthal velocity, compared to the local Keplerian rotation. We thus decompose 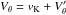 , using
, using 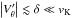 . Similarly, the radial velocity of the pebble itself is considered to be highly sub-Keplerian |Vr| ≲ δ ≪ vK. We assume that the spatial derivatives of
. Similarly, the radial velocity of the pebble itself is considered to be highly sub-Keplerian |Vr| ≲ δ ≪ vK. We assume that the spatial derivatives of  and Vr are also as small as δ.
and Vr are also as small as δ.
In Eq. (B.2), the first and the second term on the left-hand side can be neglected in our approximation, while the third term can be rearranged using the Vθ decomposition. Consequently 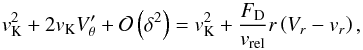 (B.4)which is obviously equivalent to
(B.4)which is obviously equivalent to 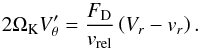 (B.5)Concerning Eq. (B.3), the first term on the left-hand side can again be discarded but the radial derivative has to be performed, leading to
(B.5)Concerning Eq. (B.3), the first term on the left-hand side can again be discarded but the radial derivative has to be performed, leading to 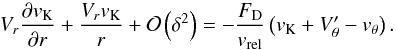 (B.6)A useful simplification of the right-hand side can be made using the η parameter, describing sub-Keplerian rotation of the gas as vθ = (1 − η)vK, yielding
(B.6)A useful simplification of the right-hand side can be made using the η parameter, describing sub-Keplerian rotation of the gas as vθ = (1 − η)vK, yielding 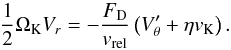 (B.7)Recalling the Stokes number definition τ = tsΩK = vrelΩK/FD, one can rewrite the set of Eqs. (B.5) and (B.7) as
(B.7)Recalling the Stokes number definition τ = tsΩK = vrelΩK/FD, one can rewrite the set of Eqs. (B.5) and (B.7) as 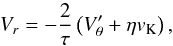 (B.8)
(B.8)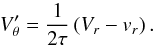 (B.9)Final arithmetic rearrangements are required to eliminate
(B.9)Final arithmetic rearrangements are required to eliminate 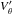 from Vr and then plug them both back into the Vθ decomposition. The resulting set of equations directly describes steady-state velocities of the drifting pebble (Guillot et al. 2014)
from Vr and then plug them both back into the Vθ decomposition. The resulting set of equations directly describes steady-state velocities of the drifting pebble (Guillot et al. 2014) 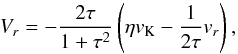 (B.10)
(B.10)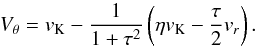 (B.11)
(B.11)
Appendix C: Semi-implicit source-term update of the pebble fluid
In order to perform the source step (Stone & Norman 1992) for the fluid of pebbles and avoid severe time-step limitations due to small friction time scales, we do not use the explicit integration scheme for pebbles and use the semi-implicit approach of Rosotti et al. (2016) instead.
Let us rewrite the fluid motion Eqs. (2) and (5) in a symbolic notation and without advection, which is solved separately. We have 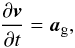 (C.1)
(C.1)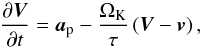 (C.2)where ap is the non-drag acceleration of the pebble fluid and ag is now understood as the total acceleration acting on the gas which is calculated explicitly at time t. We note that the drag back-reaction term is contained in ag and is also evaluated explicitly. This is justified if the solid-to-gas ratio remains low (which is what we expect in our simulations). Under these assumptions, an analytical solution for the pebble fluid velocity update can be found (Rosotti et al. 2016):
(C.2)where ap is the non-drag acceleration of the pebble fluid and ag is now understood as the total acceleration acting on the gas which is calculated explicitly at time t. We note that the drag back-reaction term is contained in ag and is also evaluated explicitly. This is justified if the solid-to-gas ratio remains low (which is what we expect in our simulations). Under these assumptions, an analytical solution for the pebble fluid velocity update can be found (Rosotti et al. 2016): ![\appendix \setcounter{section}{3} \begin{eqnarray} \vec{V}^{n+1} &=& \vec{V}^{n}\exp\left(-\Delta t\frac{\Omega_{\mathrm{K}}}{\tau}\right) + \vec{a}_{\mathrm{g}}\Delta t \notag \\ & &+ \left[\vec{v}^{n} + \left(\vec{a}_{\mathrm{p}}-\vec{a}_{\mathrm{g}}\right)\frac{\tau}{\Omega_{\mathrm{K}}}\right]\left[1-\exp\left(-\Delta t\frac{\Omega_{\mathrm{K}}}{\tau}\right)\right] \cdot \label{eq:semiimp_source_step} \end{eqnarray}](/articles/aa/full_html/2017/10/aa31033-17/aa31033-17-eq425.png) (C.3)The solution conveniently provides a smooth transition between two limiting cases: when Δt ≪ τ/ ΩK, the solution is equivalent to the explicit integration. If on the other hand Δt ≫ τ/ ΩK, the solution turns into a form known as the short friction time approximation (e.g. Johansen & Klahr 2005).
(C.3)The solution conveniently provides a smooth transition between two limiting cases: when Δt ≪ τ/ ΩK, the solution is equivalent to the explicit integration. If on the other hand Δt ≫ τ/ ΩK, the solution turns into a form known as the short friction time approximation (e.g. Johansen & Klahr 2005).
To ensure the numerical stability, a CFL condition, additional to the one that controls the gas evolution, must be imposed on the time step Δt. The condition is given by 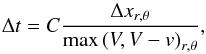 (C.4)where Δx is the cell size in the radial (index r) or azimuthal (index θ) direction and C = 0.5 is the Courant number.
(C.4)where Δx is the cell size in the radial (index r) or azimuthal (index θ) direction and C = 0.5 is the Courant number.
Appendix D: Verification of the code
Embryo-disk interaction in radiative disks.
Here we try to reproduce several recent advanced simulations of the embryo-disk interactions using our new hydrodynamic code. These test runs are compared to the original results in order to provide a verification of our code and some benchmarks. We note that most of the comparison models are 3D whereas our code is essentially 2D. The results of the verification runs therefore prove that we are indeed able to capture many aspects of 3D models if the physics is treated carefully. In the following, the stellar irradiation is always neglected as well as the pebble disk, and the opacity drop factor cκ = 0.6 is introduced into the simulation parameters. Comparison figures are always provided in the unit systems corresponding to the original works.
First, we present a reproduction of an equilibrium gas disk corresponding to the initial setup of Kley et al. (2009) who performed simulations using the 3D nirvana code. The comparison of the radial temperature profile T(r) is given in Fig. D.1. The surface density profile Σ(r) is also displayed for reference (without a comparison curve for clarity of the figure). We see that T(r) is in a good agreement with the 3D model, apart from variations in the inner disk. These are missing mostly because our 2D model does not support vertical convection.
 |
Fig. D.1 Equilibrium gas surface density Σ(r) (black curve, left vertical axis) and temperature T(r) profile (red curve, right vertical axis) in a radiative disk according to the setup from Kley et al. (2009), as it was reproduced by our code. Temperature profile obtained by the original 3D model of Kley et al. (2009) is given by the red dashed curve for comparison. The obtained disk is indeed in good agreement with the comparison simulation and serves as the hydrodynamic background for verification runs of the disk-embryo interaction. |
We use exactly this equilibrium disk to compare the embryo-disk interactions for various masses Mem. Since this work is focused on low-mass embryos, we perform tests with Mem = 2,3,5,10 and 20 ME. This range of masses was studied by Lega et al. (2014) who used the 3D fargoca code and conveniently, the same equilibrium disk model was used in their work. The embryo mass Mem = 20 ME was also studied by Kley et al. (2009). It is customary to exclude part of the gas enclosed by the Hill sphere from the torque calculation (a so-called Hill cut) if the planet is massive enough to form a distinct circumplanetary disk. However, the determination of the threshold mass is not straightforward. Thus we always perform the Hill cut for Mem = 20 ME and for Mem = 10 ME we perform two simulations with and without the Hill cut. For lower masses, no gas is excluded from calculations.
After placing the embryos on fixed circular orbits with a = aJup = 5.2 AU, we evolved the system for several tens of orbits until the torque converged to a stationary value. In Fig. D.2, we compare the measured normalised torques with results of Lega et al. (2014) as well as with the torque-mass dependence given by the formulae of Paardekooper et al. (2011), applied to the equilibrium disk. For low-mass embryos, the agreement seems good enough. The torque in our model is generally between the prediction of Paardekooper et al. (2011) and the result of the 3D model from Lega et al. (2014). The torque on the Mem = 10 ME embryo differs the most; nevertheless the result is improved when the Hill cut is applied. For the medium-mass embryo Mem = 20 ME, we see that the value is in agreement with Lega et al. (2014) which is a desirable result as 3D models generally lead to torque that is larger than the prediction by Paardekooper et al. (2011) by a factor of 3 to 4 (Bitsch & Kley 2011) for the medium-mass embryos.
Lega et al. (2014) also discovered the so-called cold finger structure near low-mass embryos. These overdensity structures are responsible for a modification of the radial torque density profile, it is thus worth checking whether or not we can find these modifications using our code as well. In Fig. D.3, we plot the normalised radial torque density Γ(r) / Γ0 (Eq. (43)) for 2 ME and 3 ME embryos, compared to corresponding results from Lega et al. (2014). It is obvious that the strong positive and negative peaks are less pronounced in our case. As the cold finger is responsible for the enhancement of these peaks, the effect is not entirely recovered by our code. We conclude that this is due to the local nature of the cold-finger effect. In our model, the gas flow around an embryo follows the velocity field affected by the vertically averaged potential and the resulting compressional heating is not strong enough for the cold-finger effect to fully develop. Nevertheless, the overall torque magnitude obtained by our model is still viable (Fig. D.2) as the asymmetry of the positive versus negative contributions is preserved to a satisfactory level.
Finally, we compare the torque for the upper end of the tested embryo mass spectrum. Figure D.4 shows the radial specific torque density (not normalised) for Mem = 20 ME compared to the result of Kley et al. (2009). The agreement is very good in this case, with slight departures from the 3D model.
 |
Fig. D.2 A comparison of the normalised total torque γΓtot/ Γ0 acting on embryos of various masses Mem, moving on fixed circular orbits in the disk shown in Fig. D.1. The results achieved with our code are shown by black circles, or open circles if the Hill cut was applied. Values obtained by 3D calculations of Lega et al. (2014) are represented by blue squares. Formula from Paardekooper et al. (2011) applied to the equilibrium disk profile (with the potential smoothing parameter ϵ = 0.4) is given by the red curve. We consider the differences between our model and the comparison simulations to be acceptable. |
 |
Fig. D.3 Normalised radial torque density Γ(r) / Γ0 acting on 2 ME and 3 ME embryos as obtained by our code (red and blue curve, respectively). Results of the original 3D experiment from Lega et al. (2014) are given for comparison (orange dashed curve for 2 ME and purple dashed curve for 3 ME). As the cold finger structure is not entirely reproduced by our code, the torque density peaks are less pronounced. However, the overall torque (i.e. the integral of Γ(r) over r) is still in very good agreement with the 3D model (cf. Fig. D.2). |
 |
Fig. D.4 Radial density of the specific torque Γ(r) acting on a 20 ME embryo as calculated by our code (black curve). The comparative profile from the original 3D experiment of Kley et al. (2009) is represented by the grey dashed line. Again, the agreement is very good. |
 |
Fig. D.5 Total torque Γtot measurement in the experiment according to Benítez-Llambay et al. (2015), reproduced using our 2D code. The 3 ME embryo is either non-accreting (black curve) or growing with the doubling time τ (we refer to the legend). The positive heating torque becomes stronger with high accretion rates corresponding to short doubling times. |
The heating torque.
In order to assess how the heating torque is recovered by our code, we repeated the numerical experiment from Benítez-Llambay et al. (2015). Their setup is different from the verification runs above; namely the surface density profile is different and the opacity is assumed constant, κ = 1 cm2 g-1. Therefore, we prevented any vertical opacity drop (cκ = 1) in our test. The stellar irradiation and pebble disk are again excluded. We use grid resolution Nr = 738 and Nθ = 1382, unlike Benítez-Llambay et al. (2015) who used 512 cells in radius and 1024 cells in azimuth but also included colatitude.
An embryo with Mem = 3 ME is embedded in the disk at aJup after the relaxation phase and the static torque is measured. The source of the mass growth and accretion heating is simply parametrised using the embryo mass doubling time τ = Mem/Ṁem. We studied cases with fixed embryo mass and with τ = 30, 55, 92 and 300 kyr. Shorter τ means higher accretion rate and should correspond to stronger heating torque.
The results of our test are shown in Fig. D.5 which can be directly compared with the original experiment in Benítez-Llambay et al. (2015); cf. their Fig. 2. First, it is important to notice that the steady-state torque on the embryo in the absence of heating is less negative in our case. This
essentially corresponds to Fig. D.2, where we found that the torque acting on the low-mass embryos in our model is always more positive than in 3D models. Another reason might be related to the midplane resolution which is slightly better in our test, thus we cover the embryo’s horseshoe region with more cells. According to Lega et al. (2014), increasing the resolution of the horseshoe region makes the torque more positive.
Because the torque in the absence of heating is less negative compared to Benítez-Llambay et al. (2015), it is easier for even the low accretion rates and respective luminosities to revert the migration because the heating torque does not have to compete with strong negative counteracting torques.
Finally, the torque scaling with increasing accretion rate is more efficient in our model than in the original 3D model. We notice that the total difference between the torque with τ = 30 kyr and the torque without accretion is ΔΓ ≈ 0.9 × 1036 g cm2 s-2, compared to ΔΓ ≈ 0.6 × 1036 g cm2 s-2 found by the 3D modelling. The slight discrepancy is again caused by the vertically averaged flow field around the planet (as already discussed for the cold-finger effect) and also due to the simplified treatment of the radiative diffusion which in our case is acting only in the midplane and is replaced by an approximation of the radiation escape in the vertical direction. Yet, we consider the heating torque to be reproduced accurately enough and we shall strive in future works to achieve an improved agreement with the 3D model.
All Tables
All Figures
 |
Fig. 1 Top: radial profile of the aspect ratio h = H/r (black curve, left vertical axis) and midplane temperature T (red dashed curve, right vertical axis) in our disk model. Bottom: radial profile of the opacity κ. The plots show the state reached after a relaxation, with all the heating and cooling terms in balance. This is considered an equilibrium state prior to the follow-up simulations with embedded embryos. Vertical dotted lines indicate important changes in the disk structure, namely the snowline close to r ≃ 4 AU and the transition to the flared stellar-irradiated outer region near r ≃ 7 AU. |
| In the text | |
 |
Fig. 2 Radial profile of the η parameter (black curve, left vertical axis) which expresses the difference between the sub-Keplerian gas velocity and the Keplerian velocity, vθ = (1 − η)vK. Initial radial profile of the dominant Stokes number τd (blue dashed curve, right vertical axis) which characterises aerodynamic properties of pebbles prevalent in the size-frequency distribution of solid particles. |
| In the text | |
 |
Fig. 3 Migration map based on the equilibrium state of the protoplanetary disk. The colour code shows the normalised value of the total torque γΓtot/ Γ0 acting on an embryo with the mass Mem (vertical axis) placed on a circular orbit at the radial distance r (horizontal axis) in the disk. Calculated according to Paardekooper et al. (2011), using the constant kinematic viscosity ν = 5 × 1014 cm2 s-1 and the potential smoothing parameter ϵ = 0.4Hem. |
| In the text | |
 |
Fig. 4 Temporal evolution of semimajor axes a(t), periastron distances qp and apoastron distances Qa of four embryos with the initial mass 3 ME in three distinct simulation cases: Case I neglecting the pebble disk (top), Case II including the pebble disk but only allowing for the mass growth of embryos by pebble accretion (middle) and finally Case III, considering also the effect of accretion heating (bottom). Embryos are numbered from 1 to 4. Additional arrows and labels indicate mergers or coorbital pairs detected in the simulations, with corresponding embryo masses which can grow by pebble accretion (Cases II and III) or merging. Striking differences are observed in Case III as the migration rates are modified by the heating torque, orbits become moderately eccentric shortly after the simulation starts and the evolution is more violent compared to Cases I and II. |
| In the text | |
 |
Fig. 5 Filtering factor F measured for the embryos at the beginning of Case II (solid curves); also applicable in Case III. As a comparison (dashed lines), we plot the filtering factors calculated at t = 0 according to formula (33) from Lambrechts & Johansen (2014). The analytical prediction is in good agreement with results of our model. |
| In the text | |
 |
Fig. 6 A closeup of the gas surface density Σ (top) and pebble surface density Σp (bottom) after ≃ 5 kyr of evolution in the simulation with pebble accretion but without accretion heating, i.e. Case II. The gaps in the pebble disk are opened by accreting planetary embryos. A fourth embryo is also present in the system but it is located outside the range. |
| In the text | |
 |
Fig. 7 Same as Fig. 6 but for the simulation with accretion heating (Case III). Two embryos are located at x = 5.55,y = 4.65 AU and x = 4.35,y = 7.17 AU; two other embryos are located outside the range. The Σ distribution shows that there are trails of underdense gas stretching outwards from the embryos, trailing their orbital motion. The shape of cavities in the pebble component is affected by the eccentric orbits of embryos. Unlike in Fig. 6, the concentration peak at the embryos’ location is somewhat blurred in both gas and pebbles. |
| In the text | |
 |
Fig. 8 Temporal evolution of the osculating eccentricity e(t) for a single 3 ME embryo in four distinct simulation setups. In the first two setups we neglect pebble accretion and the initial eccentricity is e0 = 0 (blue curve) and e0 = 0.05 (purple curve). In the other two setups, we consider pebble accretion and heating, the initial eccentricity being again e0 = 0 (red curve) and e0 = 0.05 (orange curve). Accretion heating reduces the eccentricity damping efficiency for the eccentric orbit and excites the eccentricity of the circular orbit. |
| In the text | |
 |
Fig. 9 Measures of the gravitational acceleration from the disk acting on the embryo, evolving from initially circular orbit in the presence of pebble accretion and the heating torque (i.e. red curve in Fig. 8). The values are recorded during one orbital period (represented by the true anomaly f), at around t ≃ 180, 360 and 1130 yr of the simulation, that is, during the onset, growth, and saturation phase of the eccentricity excitation. Top: evolution of the Gauss factor Gr ≡ ℛsinf (left vertical axis) and the osculating eccentricity e, which was recorded during the onset phase (right vertical axis). Middle: evolution of the Gauss factor |
| In the text | |
 |
Fig. 10 Evolution of the gas surface density Σ (left column) and temperature T (right column) during one orbital period, recorded within the onset phase of the eccentricity growth. Individual snapshots are labelled with the respective simulation time t, embryo’s true anomaly f and azimuthal acceleration imposed by the disk, labelled here aazim. The figures are transformed to the corotating frame centered on the embryo. The Hill sphere and embryo’s osculating orbit are plotted and we also indicate general directions of the gas flow with respect to the embryo by arrows. The orbital direction of the embryo is directed counterclockwise and the protostar is located at (x = 0,y = 0). The top row depicts the situation in the periastron, while the third row corresponds to the apoastron. The second row is recorded approximately halfway from periastron to apoastron, and vice versa for the bottom row. |
| In the text | |
 |
Fig. 11 Same as Fig. 10 but the hydrodynamic quantities are recorded within the saturation phase of the eccentricity excitation. |
| In the text | |
 |
Fig. 12 Radial torque density Γ(r) acting on the embryo during the onset (top) and saturation (bottom) phases, normalised to Γ0. The individual curves represent measurements in the periastron (purple), apoastron (orange) and in-between. The vertical arrows indicate the instantaneous radial distance of the embryo corresponding to the individual curves. The horizontal arrows and labels approximately distinguish some of the important torque contributions discussed in the text. To avoid misinterpretation, we remark that the hot-trail torque is acting in the bottom panel as well but it spans different radial extent for each curve and thus cannot be marked unambiguously. |
| In the text | |
 |
Fig. D.1 Equilibrium gas surface density Σ(r) (black curve, left vertical axis) and temperature T(r) profile (red curve, right vertical axis) in a radiative disk according to the setup from Kley et al. (2009), as it was reproduced by our code. Temperature profile obtained by the original 3D model of Kley et al. (2009) is given by the red dashed curve for comparison. The obtained disk is indeed in good agreement with the comparison simulation and serves as the hydrodynamic background for verification runs of the disk-embryo interaction. |
| In the text | |
 |
Fig. D.2 A comparison of the normalised total torque γΓtot/ Γ0 acting on embryos of various masses Mem, moving on fixed circular orbits in the disk shown in Fig. D.1. The results achieved with our code are shown by black circles, or open circles if the Hill cut was applied. Values obtained by 3D calculations of Lega et al. (2014) are represented by blue squares. Formula from Paardekooper et al. (2011) applied to the equilibrium disk profile (with the potential smoothing parameter ϵ = 0.4) is given by the red curve. We consider the differences between our model and the comparison simulations to be acceptable. |
| In the text | |
 |
Fig. D.3 Normalised radial torque density Γ(r) / Γ0 acting on 2 ME and 3 ME embryos as obtained by our code (red and blue curve, respectively). Results of the original 3D experiment from Lega et al. (2014) are given for comparison (orange dashed curve for 2 ME and purple dashed curve for 3 ME). As the cold finger structure is not entirely reproduced by our code, the torque density peaks are less pronounced. However, the overall torque (i.e. the integral of Γ(r) over r) is still in very good agreement with the 3D model (cf. Fig. D.2). |
| In the text | |
 |
Fig. D.4 Radial density of the specific torque Γ(r) acting on a 20 ME embryo as calculated by our code (black curve). The comparative profile from the original 3D experiment of Kley et al. (2009) is represented by the grey dashed line. Again, the agreement is very good. |
| In the text | |
 |
Fig. D.5 Total torque Γtot measurement in the experiment according to Benítez-Llambay et al. (2015), reproduced using our 2D code. The 3 ME embryo is either non-accreting (black curve) or growing with the doubling time τ (we refer to the legend). The positive heating torque becomes stronger with high accretion rates corresponding to short doubling times. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


