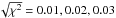| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628095 | |
| Published online | 24 May 2016 | |
The reliability of observational measurements of column density probability distribution functions
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Straße 77,
50937
Köln,
Germany
e-mail:
ossk@ph1.uni-koeln.de
2
Max-Planck Institut für Radioastronomie,
Auf dem Hügel 69, 53121
Bonn,
Germany
3
Research School of Astronomy and Astrophysics, Australian National
University, Canberra,
ACT
2611,
Australia
4
Universität Heidelberg, Zentrum für Astronomie, Institut für
Theoretische Astrophysik, 69120
Heidelberg,
Germany
Received: 8 January 2016
Accepted: 8 March 2016
Context. Probability distribution functions (PDFs) of column densities are an established tool to characterize the evolutionary state of interstellar clouds.
Aims. Using simulations, we show to what degree their determination is affected by noise, line-of-sight contamination, field selection, and the incomplete sampling in interferometric measurements.
Methods. We solve the integrals that describe the convolution of a cloud PDF with contaminating sources such as noise and line-of-sight emission, and study the impact of missing information on the measured column density PDF. In this way we can quantify the effect of the different processes and propose ways to correct for their impact to recover the intrinsic PDF of the observed cloud.
Results. The effect of observational noise can be easily estimated and corrected for if the root mean square (rms) of the noise is known. For σnoise values below 40% of the typical cloud column density, Npeak, this involves almost no degradation in the accuracy of the PDF parameters. For higher noise levels and narrow cloud PDFs the width of the PDF becomes increasingly uncertain. A contamination by turbulent foreground or background clouds can be removed as a constant shield if the peak of the contamination PDF falls at a lower column or is narrower than that of the observed cloud. Uncertainties in cloud boundary definition mainly affect the low-column density part of the PDF and the mean density. As long as more than 50% of a cloud is covered, the impact on the PDF parameters is negligible. In contrast, the incomplete sampling of the uv-plane in interferometric observations leads to uncorrectable PDF distortions in the maps produced. An extension of the capabilities of the Atacama Large Millimeter Array (ALMA) would allow us to recover the high-column density tail of the PDF, but we found no way to measure the intermediate- and low-column density part of the underlying cloud PDF in interferometric observations.
Key words: methods: data analysis / methods: statistical / ISM: structure / ISM: clouds / instrumentation: interferometers / dust, extinction
© ESO, 2016
1. Introduction
Probability distribution functions (PDFs) of column density maps of interstellar clouds have been proven to be a valuable tool to characterize the properties and evolutionary state of these clouds (see e.g., Berkhuijsen & Fletcher 2008; Kainulainen et al. 2009, 2011; Froebrich & Rowles 2010; Lombardi et al. 2011; Schneider et al. 2012, 2013, 2015a,b, 2016; Russeil et al. 2013; Kainulainen & Tan 2013; Hughes et al. 2013; Alves et al. 2014; Druard et al. 2014; Berkhuijsen & Fletcher 2015, for the observational treatment of the subject and Klessen 2000; Federrath et al. 2008, 2010; Kritsuk et al. 2011; Molina et al. 2012; Konstandin et al. 2012; Federrath & Klessen 2013; Girichidis et al. 2014 for theoretical treatment). Column density maps of dense clouds typically show a log-normal PDF at low column densities, produced by interstellar turbulence (Vazquez-Semadeni 1994; Padoan et al. 1997; Passot & Vázquez-Semadeni 1998; Federrath et al. 2008; Price et al. 2011; Federrath & Banerjee 2015; Nolan et al. 2015), and a power-law tail in the PDF at high densities due to gravitational collapse (Klessen 2000; Kritsuk et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014). The PDFs seen in 2D projections allow us to estimate the underlying 3D volume density PDFs when assuming global isotropy (Brunt et al. 2010a,b; Ginsburg et al. 2013; Kainulainen et al. 2014). The width of the log-normal part allows us to quantify the turbulent driving, that is the mechanism of the injection of turbulent energy into the interstellar medium (Nordlund & Padoan 1999; Federrath et al. 2008, 2010). If the driving is known, PDF width and Mach number can be used to constrain the magnetic pressure (Padoan & Nordlund 2011; Molina et al. 2012). The slope of the PDF power-law tail can be translated into radial profiles of collapsing clouds when assuming a spherical or cylindrical density distribution (Kritsuk et al. 2011; Federrath & Klessen 2013).
PDFs can be determined from any mapped quantity, not only column densities. For instance, Schneider et al. (2015b) combined PDFs of dust temperatures with the column-density PDFs, Burkhart et al. (2013) compared PDFs of molecular lines with different optical depths, and Miesch & Scalo (1995), Miesch et al. (1999), Hily-Blant et al. (2008), Federrath et al. (2010), Tofflemire et al. (2011) studied PDFs of centroid velocities and velocity increments. Our analysis does not make any assumptions about the quantity that is actually analyzed. As a pure statistical analysis, it can be applied to any kind of map. However, directly measured quantities have the advantage that the impact of observational noise is easier to quantify. This favors, for example, intensities over velocity centroids, or temperatures. For the sake of convenience in naming quantities and in direct comparison to the frequent computation of PDFs from column density maps, we focus on the column density as measured quantity, characterized either in terms of gas columns, visual extinction, or submm emission from dust that has a given temperature. Therefore, we use column density N and AV synonymously.
Lombardi et al. (2015) discussed the impact of statistical noise, contamination with fore- and background material, and boundary biases in the PDFs of their near-infrared extinction maps and concluded that it is impossible to reliably determine the lower-column density tail of the observed molecular cloud PDFs, leaving only the high-column density power-law tail as significant structure. For column density maps obtained from Herschel PACS and SPIRE continuum observations, Schneider et al. (2015a) showed in contrast that 1) the foreground contamination can be corrected for by assuming a constant screen of material; 2) the selection of map boundaries only affects column densities well below the column density peak; and 3) the observational noise in the Herschel maps was an order of magnitude lower allowing them to fully resolve the log-normal part of the turbulent column-density PDF.
In order to provide a general framework to assess the reliability of column density PDFs obtained in observations, here we perform a parameter study where we simulate different observational biases and limitations with a variable strength. We show under which conditions interstellar cloud PDFs can be reliably measured, when they can be recovered using parametric corrections, and when the observational limitations dominate the result.
In Sect. 2, we introduce the formalism and the simulated data used here. In Sect. 3, we study the impact of observational noise, Sect. 4 deals with line-of-sight contamination, Sect. 5 with the selection of map boundaries, and Sect. 6 with the limitations of interferometric observations. In Sect. 7 we summarize our findings.
2. Mathematical description
2.1. PDFs
PDFs of column densities p(N) are defined as the probability of the column density in a map to fall in the interval N,N + dN. As probabilities they are normalized to unity through 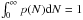 . For noisy quantities or other physical quantities that can become negative, the integral should start at −∞. Due to the huge range of densities and resulting column densities in the interstellar medium, it is more appropriate to use logarithmic bins, in other words we switch to a logarithmic scale η = ln(N/Npeak), where Npeak is the most probable column density in logarithmic bins – the peak of the distribution on a logarithmic column density scale. The translation between PDFs on linear and logarithmic scales can be easily computed by
. For noisy quantities or other physical quantities that can become negative, the integral should start at −∞. Due to the huge range of densities and resulting column densities in the interstellar medium, it is more appropriate to use logarithmic bins, in other words we switch to a logarithmic scale η = ln(N/Npeak), where Npeak is the most probable column density in logarithmic bins – the peak of the distribution on a logarithmic column density scale. The translation between PDFs on linear and logarithmic scales can be easily computed by 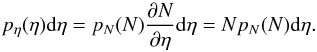 (1)Most molecular cloud observations are characterized by being log-normal at low densities, that in turn are highly probable,
(1)Most molecular cloud observations are characterized by being log-normal at low densities, that in turn are highly probable, 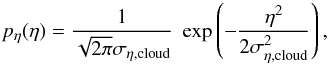 (2)having typical widths on the logarithmic scale σcloud between 0.2 and 0.5 (see e.g., Kainulainen et al. 2009; Hughes et al. 2013; Schneider et al. 2015a), and a power-law tail at higher densities
(2)having typical widths on the logarithmic scale σcloud between 0.2 and 0.5 (see e.g., Kainulainen et al. 2009; Hughes et al. 2013; Schneider et al. 2015a), and a power-law tail at higher densities 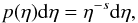 (3)where the exponent s varies in observations between about s = 1...4 (see e.g., Schneider et al. 2015b; Stutz & Kainulainen 2015). For a free-fall gravitational collapse creating the tail, we expect values s = 2...3, depending on the geometry of the collapse (Kritsuk et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014).
(3)where the exponent s varies in observations between about s = 1...4 (see e.g., Schneider et al. 2015b; Stutz & Kainulainen 2015). For a free-fall gravitational collapse creating the tail, we expect values s = 2...3, depending on the geometry of the collapse (Kritsuk et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014).
All effects of noise, contamination, and edge selection change mainly the low-density regime, so that it is sufficient to concentrate on the log-normal part here. The measurement of the power-law tail can be affected by the impact of insufficient spatial resolution and binning. This has already been studied in detail by Lombardi et al. (2010) and Schneider et al. (2015a). For our semi-analytic studies, focusing on low-density effects, we will therefore represent molecular clouds by a log-normal PDF, fully described by the two parameters Npeak and σcloud, here. A power-law tail is only added for the full cloud simulations (see Sect. 2.3).
The normalization of the density to the peak of the distribution on a logarithmic scale Npeak(η), deviates from the normalization by ⟨ N ⟩ that is often employed in the literature and that we also used in Schneider et al. (2015a). In principle, the choice of the normalization constant does not affect any of our outcomes. It is more convenient to take the logarithmic peak for log-normal distributions as it centers them at η = 0. For a log-normal distribution we find a fixed relationship between the possible normalization constants. The average column density is 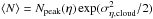 and the peak of the probability distribution in linear units falls at
and the peak of the probability distribution in linear units falls at 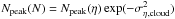 . However, we will show in Sect. 5 that a normalization by the PDF peak is much more stable against selection effects than the mean column density. Because of this, we generally recommend the choice of Npeak for the column density normalization.
. However, we will show in Sect. 5 that a normalization by the PDF peak is much more stable against selection effects than the mean column density. Because of this, we generally recommend the choice of Npeak for the column density normalization.
2.2. Contamination
All effects of contamination by observational noise or other line-of-sight material will be linear in column density N, but not in η. At every point in the map we measure a column density that is given by Ntot = Ncloud + Ncontam, meaning that on a logarithmic scale we find ηtot = ln(Ncloud + Ncontam) − ln(Npeak). The PDF of a contaminated map then results from the convolution integral of both distributions on the linear scale ![\begin{eqnarray} p_{\eta}(\eta\sub{tot}) = N\sub{tot} \int_{-\infty}^{\infty} && p_{N,{\rm contam}}(N) \label{eq_convolution} \\ && \times \frac{p_{\eta,{\rm cloud}}[\ln(N\sub{tot}-N)-\ln(N\sub{peak})]}{N} {\rm d}N . \nonumber \end{eqnarray}](/articles/aa/full_html/2016/06/aa28095-16/aa28095-16-eq26.png) (4)We can assume a normal distribution for the contamination with noise inherent in a direct measurement1
(4)We can assume a normal distribution for the contamination with noise inherent in a direct measurement1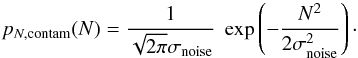 (5)For derived quantities, or measurements in particular observing modes, the errors can be either correlated or non-Gaussian, requiring convolution with a different noise distribution pN,contam(N). For the contamination by a turbulent foreground or background cloud we can use a second log-normal distribution
(5)For derived quantities, or measurements in particular observing modes, the errors can be either correlated or non-Gaussian, requiring convolution with a different noise distribution pN,contam(N). For the contamination by a turbulent foreground or background cloud we can use a second log-normal distribution 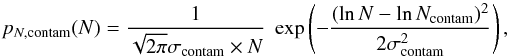 (6)where Ncontam denotes the most probable column density of the contamination on a logarithmic scale. We assume that the contaminating structures are turbulence-dominated so that they do not yet show any self-gravitating cores and can be described by a pure log-normal distribution without power-law tail. Collapsing parts that produce a power-law tail are easily identified in the maps as small structures so that they can be separated from large-scale contaminations.
(6)where Ncontam denotes the most probable column density of the contamination on a logarithmic scale. We assume that the contaminating structures are turbulence-dominated so that they do not yet show any self-gravitating cores and can be described by a pure log-normal distribution without power-law tail. Collapsing parts that produce a power-law tail are easily identified in the maps as small structures so that they can be separated from large-scale contaminations.
In principle, it is possible to compute the original cloud distribution pN,cloud(N) from the measured distribution pN(Ntot) by inverting the convolution in Fourier space if the contamination PDF, pN,contam(N), is known ![\begin{equation} p_{N, {\rm cloud}}(N)=\mathfrak{F}^{-1}\left(\frac{\mathfrak{F}[p_{N}(N)]} {\mathfrak{F}[p_{N, {\rm contam}}(N)]} \right) \label{eq_deconvolution} , \end{equation}](/articles/aa/full_html/2016/06/aa28095-16/aa28095-16-eq34.png) (7)where F and F-1 denote the normal and inverse Fourier transform. However, this operation is inherently unstable. It amplifies noise, gridding effects, and numerical uncertainties, so that it only works with very well behaving denominators. As Gaussian noise is mathematically well characterized we will test this method in Sect. 3.
(7)where F and F-1 denote the normal and inverse Fourier transform. However, this operation is inherently unstable. It amplifies noise, gridding effects, and numerical uncertainties, so that it only works with very well behaving denominators. As Gaussian noise is mathematically well characterized we will test this method in Sect. 3.
2.3. Test data
 |
Fig. 1 Test data set representing a fractal cloud with an ideal column density PDF consisting of a log-normal part and a power-law high-density tail. Coordinates are invented to allow for an easy comparison with real observations and to perform simulated ALMA observations in Sect. 6. Contours and colors visualize the same data. The contour levels are indicated in the color bar. Column densities above AV = 80 are saturated in the plot to make the turbulent cloud part better visible. The actual maximum column density is three times larger. As the peak of the log-normal PDF is located at AV = 5, the contours almost cover material in the PDF power-law tail only. Because of the low probabilities in the tail, the fraction of green pixels is already small and that of pixels with yellow and red colors is tiny. The four colored squares indicate the subregions discussed in Sect. 5. |
For a realistic data set that has all the properties of a molecular cloud column density map, but no observational limitations, we modify a fractional Brownian motion (fBm, see e.g., Stutzki et al. 1998) image to approximate the PDF seen in molecular clouds. The original fBm image is constructed with the inverse transform of a Fourier spectrum that has a given power spectral index β and random phases. For the spectral index we use a value of β = 2.8, measured in many molecular clouds (see e.g., Bensch et al. 2001; Falgarone et al. 2004) and consistent with numerical simulations (Kowal et al. 2007; Federrath et al. 2009). The fBm structure reflects the typical spatial correlations in interstellar cloud maps. The resulting image always has a Gaussian PDF (pN,fBm(N) given by Eq. (5)). To obtain the desired combination of a log-normal with a power-law column density PDF with a minimum distortion of the spatial structure we translate the fBm values into cloud column densities by ![\begin{equation} N\sub{cloud} = \Pi\sub{cloud}^{-1}\left[ \Pi\sub{fBm}(N) \right] , \end{equation}](/articles/aa/full_html/2016/06/aa28095-16/aa28095-16-eq42.png) (8)where Π denotes the integral over the normalized PDF
(8)where Π denotes the integral over the normalized PDF 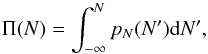 (9)varying between zero and unity. Inversion of the function Π-1 can only be computed numerically.
(9)varying between zero and unity. Inversion of the function Π-1 can only be computed numerically.
For the PDF parameters we use values measured by Schneider et al. (2015a, and 2016 in several star-forming clouds, for example, Auriga, Orion B, and Cygnus X. The peak of the PDF Npeak is located at AV = 5 and the width of the log-normal part of the PDF in units of the natural logarithm of the column density is ση,cloud = 0.45. The transition to the power-law tail occurs at AV = 11 and the tail has an exponent of s = 1.9. The PDFs in regions with somewhat lower star-forming activity are shifted towards smaller column densities. Kainulainen et al. (2009), Schneider et al. (2015a) find PDF peaks at AV ≈ 2 and deviation points for the transition to the power law tail at AV = 4...5. On the η scale, used in all simulations here, this is identical to the PDF of our test data, pη(η). Only when translating the results back to an absolute column density scale, the different PDF peak density Npeak needs to be applied. We selected a random seed for the fBm that results in a cloud well-centered in the map, similar to what an observer might choose.
The resulting map is shown in Fig. 1, where we arbitrarily placed the map on the Southern sky and assigned spatial dimensions in such a way, that it would make sense to observe the cloud with ALMA as simulated in Sect. 6. The PDF of the cloud is shown in Fig. 2.
3. Noise
3.1. Main impact
 |
Fig. 2 Impact of observational noise on the PDF measured for the cloud from Fig. 1. The red solid curve shows the analytic description of the input PDF, the blue dotted line is the measured PDF of the fractal map with a finite pixel number. The other broken lines show the column density PDF that is measured if the map is affected by different levels of observational noise, characterized by a normal distribution with a standard deviation from 10% to 100% of the peak column density. |
In a first step we study how the PDF is modified by observational noise, simulated as the superposition of normally distributed random numbers to the map. The result is shown in Fig. 2 where we varied the noise amplitude, defined as the root-mean-square (rms) of the noise distribution, between 10% and 100% of the peak density, Npeak, of the cloud PDF. We see three effects:
-
i)
An increasing noise level produces a low-density excess in the PDF. The log-normal part of the PDF is widened towards lower densities. If the low densities are completely dominated by noise, such as in the case of noise amplitudes of 50% or more of the peak column density, we find the PDF has a linear behavior at low densities p(η) ∝ η due to the factor N in Eq. (1) applied to the Gaussian noise contribution (Eq. (5)) when computing the convolution integral (Eq. (4)).
-
ii)
For high noise levels, the additional “signal” from the noise also shifts the peak of the distribution towards higher column densities which means that it may affect the measurement of Npeak.
-
iii)
For the power-law tail at high column densities, however, we find no significant impact. This confirms our earlier findings (Schneider et al. 2015a) and those of Lombardi et al. (2015) that the log-normal part of the PDF is easily affected by noise, but that the power-law tail is stable.
3.2. Parametric corrections
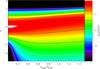 |
Fig. 3 Distributions obtained from the convolution of a log-normal cloud PDF (Eq. (2) with ση,cloud = 0.5) with a Gaussian noise PDF (Eq. (5)) as a function of the noise amplitude (σnoise) relative to the peak of the log-normal distribution (Npeak). Contours and colors visualize the same data, given on a logarithmic scale. The individual contour levels are marked in the color bar. The left edge of the figure represents the original log-normal PDF. When increasing the noise level σnoise in the right direction, we see the distortion of the PDF mainly at low column densities η. The dashed line indicates the peak of the distribution, to better follow the shift of the PDF maximum to larger column densities with increasing noise level. |
A correction of the noise effect for the log-normal part of the PDF is, however, possible if the amplitude of the noise contamination is known. To obtain such a correction, we perform a parameter study based on the analytic description of the PDFs in Eqs. (2)–(5), ignoring the power-law tail that is, in any case, not sensitive to the noise contamination. Figure 3 shows a first step in such a parameter scan for noise amplitude. Here, we display all PDFs for the different noise levels in a color-contour plot. To represent the PDFs in the two-dimensional plot equivalent to the curves in Fig. 2 we show the decadic logarithm of pη(η) in colors and contour levels. The PDFs are computed from the convolution integral (Eq. (4)) using a log-normal cloud PDF with ση,cloud = 0.5 and Gaussian noise (Eq. (5)) with a varying amplitude. The left edge of the figure represents the original log-normal PDF. With increasing noise level σnoise towards the right part of the plot, we see the increasing distortion of each part of the PDF. This allows us to quantify and correct the distortions based on noise level. Even for low noise levels there is a low-column-density excess leading to a widening of the PDF. It stays relatively constant for noise levels ση,cloud ≳ 0.5Npeak. For noise amplitudes of ≳ 0.2Npeak the PDF peak is also shifted towards higher column densities.
As the noisy PDFs are no longer log-normal they are no longer characterized by two parameters only. We have to discriminate between different methods that can be used for measuring width and peak position in PDFs. The problem is similar to that of the measurement of the position and width of individual lines in a spectroscopic observation. Use of the absolute peak for the position is sensitive to the binning details. It can be affected by fluctuations due to the low-number sampling in individual bins for a finite map size. This becomes significant in the submaps that we consider in Sect. 5. In contrast, the moments of the distribution are independent of the selected binning but strongly affected by the structure of the wings. This prevents us from applying moments computed for the contamination of a purely log-normal distribution, to a molecular cloud structure that shows an additional power-law tail. The compromise, often used in the case of spectroscopic observations, is a Gaussian fit to the distribution – a log-normal fit on our logarithmic η scale. For a log-normal distribution, all three approaches provide the same numbers, but for noise-contaminated distributions they can deviate from each other.
 |
Fig. 4 Change in the measured PDF parameters as a function of the noise amplitude. The upper plot shows the measured center position using three different measures of position. The red solid line shows the position of the maximum probability, the blue dotted line shows the first moment of the distribution, and the green dashed line gives the center of a Gaussian fit (in η). The lower plot displays the standard deviation along with the width of the Gaussian fit, also showing the higher moments. |
Figure 4 shows the PDF parameters, determined in three different ways, as a function of the amplitude of the noise contamination. The upper plot shows the center position measured by taking the maximum, represented through the first moment, and calculated as the center of a log-normal fit. They agree at zero noise contamination. The position of the peak probability gives the highest column density values for the PDF center, matching the dashed line in Fig. 3. When considering the dotted curve for the PDF centroid, we find a decrease of the center position of the distribution at low noise levels compared to the noise-free case, due to the widening of the distribution towards small column densities. The center of a log-normal fit shows an intermediate behavior.
The lower plot shows the measured widths of the distribution together with the next higher moments2. The width of a log-normal fit to the distribution is very stable. It increases by 10% only. The standard deviation σ grows much more, by a factor of almost two. With the formation of the low-density tail resulting from the noise contamination, the distribution’s skewness quickly drops to about −1.5 and the kurtosis grows. Once the linear dependence seen in Fig. 2 is reached, the skewness remains almost constant and only the increasing steepening of the high-density tail with the shift of the PDF peak further reduces the kurtosis. Because the Gaussian fit is least affected by the formation of the noise tail and is also applicable for distributions with a power-law high-density tail, we will continue with this log-normal fit characterization for more extended parameter scans.
 |
Fig. 5 Variation of the parameters of a log-normal fit to the PDFs of noise-contaminated maps as a function of noise amplitude and the width of the original cloud PDF. The upper plot shows the measured location of the PDF center, the lower plot the width of the log-normal fit. Without noise contamination ηcenter = ηpeak = 0 and the measured width matches the PDF width of the cloud, σlog − normal = σcloud. |
When assuming a log-normal cloud PDF, the noise contamination problem is fully described by two parameters, the cloud PDF width and the noise amplitude relative to the peak of the cloud PDF. Linear scaling to any cloud observation is straightforward. This allows us to provide a complete picture for the correction of noise effects. Figure 5 shows the new PDF peak position and the change of the PDF width, determined through the log-normal fit, as a function of the noise contamination amplitude and the width of the original cloud PDF. By definition the input cloud always has ηcenter = ηpeak = 0. For all cloud distributions we find an almost linear increase of the observed peak column density with noise amplitude. The highest shift of the peak position occurs in case of broad cloud distributions. The fitted PDF width reflects the properties of the underlying cloud only for noise amplitudes below about 0.4–0.5 Npeak. We find two opposite cases for the measured PDF width. For σcloud< 0.6 the broadening from the low column-density wing dominates so that the noisy PDF is broader than the underlying cloud PDF. For wider cloud distributions, the steepening at large column densities which is visible in Fig. 2, dominates so that the measured PDF width becomes narrower than the cloud PDF. At large noise amplitudes, the measured width becomes almost independent of the input cloud properties, saturating at σlog − normal = 0.5...0.7.
Figure 5 contains all the information needed to deduce the cloud properties Npeak and σcloud from a measured noisy PDF when the noise amplitude is known. For any value of σnoise/Npeak in the plot, we can transform the measured peak column density Ncenter into the corresponding logarithmic parameter ηcenter = ln(Ncenter/σnoise × σnoise/Npeak) and compare it with the values given in the upper plot in Fig. 5. The measured width σlog − normal can be looked up directly in the lower plot. Hence, we can deduce the input parameters characterizing the cloud PDF σnoise/Npeak and σcloud from a fit to the measured parameters σnoise/Ncenter and σlog − normal. The quality of the fit can be quantified in terms of the quadratic deviations of both parameters 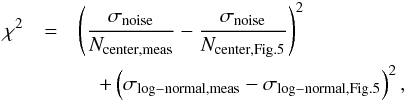 (10)where we assume the same relative accuracy for both parameters.
(10)where we assume the same relative accuracy for both parameters.
 |
Fig. 6
|
For any measured pair of σnoise/Ncenter,meas and σlog − normal,meas we obtain the cloud parameters from the location of the χ2 minimum in the σnoise/Npeak – σcloud parameter space3. This is visualized in Fig. 6. To save space, we combined the 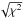 plots for four different models in a single figure. To cover a wide parameter range, we selected two log-normal cloud distributions with σcloud = 0.8 and 0.2 and contaminated the first one with noise levels of 0.2Npeak and 1.0Npeak, and the second with noise of 0.6Npeak and 1.4Npeak. Contours show levels of
plots for four different models in a single figure. To cover a wide parameter range, we selected two log-normal cloud distributions with σcloud = 0.8 and 0.2 and contaminated the first one with noise levels of 0.2Npeak and 1.0Npeak, and the second with noise of 0.6Npeak and 1.4Npeak. Contours show levels of 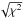 surfaces from 0.01 to 0.04.
surfaces from 0.01 to 0.04.
As we fit the observational parameters σnoise/Ncenter,meas and σlog − normal,meas in the space of the cloud parameters σnoise/Npeak and σcloud, having the same units, we can directly read the accuracy of the parameter determination from the topology of the 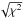 surfaces. For the example of a low noise contamination (σnoise = 0.2 Npeak) and broad cloud distributions (ση,cloud = 0.8), the contours are quite round and the
surfaces. For the example of a low noise contamination (σnoise = 0.2 Npeak) and broad cloud distributions (ση,cloud = 0.8), the contours are quite round and the 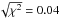 contour has a diameter of about 0.08 in terms of the cloud parameters showing that the cloud parameters are recovered with almost the same accuracy to which the observational parameters could be measured. If we increase the noise contamination instead to σnoise = 1.0 Npeak the accuracy of parameter recovery drops by a factor of three, shown by the diameter of the contours that is three times bigger. For the model with the narrow cloud distribution, ση,cloud = 0.2, parameter retrieval is limited by the degeneracy of the measured cloud width, σlog − normal, seen as extended green plateau in the lower right corner of Fig. 5. For noise amplitudes σnoise ≳ 0.4 Npeak the solution in terms of cloud widths, ση,cloud, spans a very wide range while the peak position is still well constrained. Unfortunately, this applies to many interstellar clouds which have narrow widths of 0.19 ≤ ση,cloud ≤ 0.53 (Berkhuijsen & Fletcher 2008; Hughes et al. 2013; Schneider et al. 2015a)4. In contrast, for values of ση,cloud> 0.5 we find instead a gradual decrease in the accuracy of the fit of both parameters.
contour has a diameter of about 0.08 in terms of the cloud parameters showing that the cloud parameters are recovered with almost the same accuracy to which the observational parameters could be measured. If we increase the noise contamination instead to σnoise = 1.0 Npeak the accuracy of parameter recovery drops by a factor of three, shown by the diameter of the contours that is three times bigger. For the model with the narrow cloud distribution, ση,cloud = 0.2, parameter retrieval is limited by the degeneracy of the measured cloud width, σlog − normal, seen as extended green plateau in the lower right corner of Fig. 5. For noise amplitudes σnoise ≳ 0.4 Npeak the solution in terms of cloud widths, ση,cloud, spans a very wide range while the peak position is still well constrained. Unfortunately, this applies to many interstellar clouds which have narrow widths of 0.19 ≤ ση,cloud ≤ 0.53 (Berkhuijsen & Fletcher 2008; Hughes et al. 2013; Schneider et al. 2015a)4. In contrast, for values of ση,cloud> 0.5 we find instead a gradual decrease in the accuracy of the fit of both parameters.
 |
Fig. 7
|
Figure 7 shows the result for our example cloud from Fig. 1 with ση,cloud = 0.45 and the additional power-law tail. We show again four different fits in a single figure, providing the 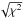 surfaces for models with a noise contamination amplitude of 0.2, 0.6, 1.0, and 1.4 Npeak. Here, we are at the edge of the parameter range dominated by the cloud width degeneracy. For a low noise contamination (σnoise< 0.3 Npeak) the input parameters are accurately recovered. At a noise level of σnoise = 0.6 Npeak the accuracy of the parameter determination drops by about a factor of two, but at higher noise levels, the cloud-width degeneracy of the observed PDF also produces an elongated parameter space for the solution, strongly reducing the accuracy of the recovery of the actual cloud PDF width, σcloud.
surfaces for models with a noise contamination amplitude of 0.2, 0.6, 1.0, and 1.4 Npeak. Here, we are at the edge of the parameter range dominated by the cloud width degeneracy. For a low noise contamination (σnoise< 0.3 Npeak) the input parameters are accurately recovered. At a noise level of σnoise = 0.6 Npeak the accuracy of the parameter determination drops by about a factor of two, but at higher noise levels, the cloud-width degeneracy of the observed PDF also produces an elongated parameter space for the solution, strongly reducing the accuracy of the recovery of the actual cloud PDF width, σcloud.
For noise contamination levels σnoise>Npeak determination of the cloud parameters becomes very uncertain. An uncertainty of 0.05 in the PDF center position of log-normal width translates into a ten times larger uncertainty of the fitted cloud parameters. Altogether, we can reliably determine Npeak from the map and a given noise amplitude if the noise rms is smaller than the PDF peak column density; for a reliable determination of the PDF width, the noise amplitude has to fall below about 0.4 × Npeak.
3.3. The zero-column-density PDF
The situation is different if the observation noise level is not known a priori, for example in continuum data with unknown receiver sensitivity. In this case, the PDF may first be used to estimate the noise in the observational data, using the probability of zero intensities or column densities, respectively. As any log-normal PDF (Eq. (2)) has a zero probability of zero column densities, due to the scaling with N (Eq. (1)), one can attribute all measured values of zero column density to the observational noise. Thus we can measure the noise amplitude through inspecting the linear-scale PDF, pN(0). Establishing the relationship between the noise amplitude σnoise/Npeak and the zero-column PDF, pN(0), is also necessary for using pN(0) in a second step to measure the line-of-sight contamination in Sect. 4.
 |
Fig. 8 Values of the linear column density PDF pN at zero column densities as a function of the observational noise level and the cloud PDF width. PDF values pN(0) are given in units of 1 /Npeak. |
Figure 8 shows the value of the linear column density PDF for N = 0 from the convolution of log-normal cloud PDFs with a normal noise PDF as a function of the noise amplitude and the cloud PDF width, ση,cloud. For very small noise amplitudes and narrow cloud PDFs, pN(0) still vanishes, but there is a systematic increase when increasing noise amplitude or cloud PDF width. For narrow cloud PDFs, the zero column density PDF peaks when the noise amplitude matches the typical cloud density; for wider cloud PDFs, the peak is shifted to lower noise amplitudes. Once the combination of noise amplitude and cloud width exceeds a particular threshold, we find only a small residual variation in the zero-column PDF between values by a factor of less than two.
Closer inspection shows that the noise dependence of pN(0) can be approximated by another log-normal function. In Appendix A we demonstrate how this approximation can be used to express the surface in Fig. 8 in terms of the ση,cloud dependence of three parameters only.
Instead of using Fig. 8 to read the zero-column PDF as a function of noise level and cloud PDF width, we can use it inversely to look up the noise level for any measured pN(0) when we know ση,cloud. From the figure it is clear that this works reliably only for low noise levels providing a steep pN(0) dependence on the noise amplitude. For large noise levels, pN(0) does not vary much, exhibiting ambiguity at the largest levels. When using the zero-column PDF to determine σnoise an iteration may be needed along with the fitting program described in the previous section to correct for the deviation of the actual cloud PDF width ση,cloud from the measured width σlog − normal.
Overall we can provide a strategy for determining the parameters of a cloud PDF from a noisy measurement. Power-law tails do not need any correction as they are unaffected by observational noise. If the noise level of the observation is known, the cloud parameters can be fitted from the measured values of σnoise/Ncenter,meas and σlog − normal,meas using the procedure described in Sect. 3.2. If the noise of the observations is unknown, it can be determined from the zero-column PDF pN(0) described by log-normal distributions with parameters given in Fig. A.2.
3.4. Deconvolution
 |
Fig. 9 Result of the numerical deconvolution of a log-normal PDF contaminated by Gaussian noise with 0.5Npeak amplitude. The red solid line shows the input PDF before the noise contamination, the blue dotted line the contaminated PDFs, and the green dashed line the result of the deconvolution. The deconvolution artifacts at large column densities can be ignored as the measured noisy PDF already reflects the cloud PDF there. |
 |
Fig. 10 Result of the numerical deconvolution of a noise-contaminated log-normal PDF for different noise levels. The red solid line shows the input PDF before the noise contamination. The contaminated PDFs are not shown here, but their shape can be taken from Fig. 3. |
As discussed in Sect. 2.2 it is, in principle, also possible to recover the full original PDF from the measured PDF if we know the noise contamination distribution. This would also allow us to recover the shape of more complex PDFs than the simple log-normal PDF (with power-law tail) used in the computations above5. Gaussian noise is the ideal case with an analytic distribution that is well confined in Fourier space allowing us to minimize the fundamental instability of the deconvolution process. Figure 9 shows one example of the numerical deconvolution of a noise-convolved PDF for a cloud with ση,cloud = 0.5 and a noise amplitude of σnoise = 0.5Npeak sampled in bins of 0.01Npeak. As discussed before, the noise contamination shifts the peak of the distribution and creates a wide low column-density tail, but leaves the high column-density part unchanged. The deconvolution through Eq. (7) perfectly recovers the central part of the PDF, but creates artifacts at low and high column densities. They result from numerical noise in sampling the wings of the Gaussian function in the denominator of Eq. (7), reflecting the fundamental instability in the division of two very small numbers. To see how the artifacts change with contamination we show the result of the numerical deconvolution of noise-convolved PDFs for three different noise amplitudes in Fig. 10 (see Fig. 3 for the noise-contaminated PDFs).
As the deconvolution has to be performed on a linear scale, the approach always suffers from a low sampling at small column densities. There the original PDF is well recovered for noise amplitudes smaller than the peak column density. We even have a dynamic range of almost two orders of magnitude over which the PDF can be reliably measured. Only when increasing the noise amplitude to the PDF peak column density, the deconvolution results in a too-broad PDF after the deconvolution. In all cases there is, however, a floor of deconvolution artifact values at high column densities. Practically, those artifacts at large column densities are not relevant as we can always return to the measured PDF where the noise contamination only changed the PDF at low column densities. At large column densities the measured PDF still reflects the true cloud PDF (see Fig. 2).
 |
Fig. 11 Result of the numerical deconvolution of the cloud PDF from Fig. 2 for a noise level of AV = 1, i.e., 0.2 Npeak. The red solid line shows the input PDF before the noise contamination. |
As a more practical example, Fig. 11 shows the result of the numerical deconvolution for the full PDF from the map in Fig. 1. The noise amplitude of AV = 1 corresponds to 0.2Npeak, the blue dotted curve in Fig. 10. We find a very similar behavior to the semi-analytic case. The dynamic range of the recovered PDF is a factor of ten smaller than in the case of the ideal log-normal cloud representation at the same noise level, but still a factor of almost 100.
The direct deconvolution needs an accurate knowledge of the noise distribution, meaning that it only works for perfectly Gaussian noise. If the noise properties are well known, the approach may allow us to recover small distortions and deviations of the PDF from the log-normal shape, but to recover the four main parameters for a log-normal PDF with power-law tail, the iterative approach described in Sect. 3.2 is sufficient and more stable.
4. Line-of-sight contamination
Schneider et al. (2015a) simulated the effect of a foreground contamination of a cloud PDF with a constant “screen”. In a more realistic scenario, however, the contaminating structure also has turbulent properties leading to a PDF similar to that of the cloud we observe. We assume that the contaminating cloud is also characterized by a log-normal distribution. This excludes star-forming clouds with a significant gravitationally dominated power-law tail but should represent the typical case where the contaminating structure is more transparent than the main cloud of interest, in other words the line-of-sight emission is dominated by the studied cloud. The resulting PDF can be computed from the same convolution integral (Eq. (4)) as used in the previous section6.
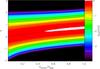 |
Fig. 12 Distributions obtained from the convolution of a log-normal cloud PDF (Eq. (2), ση,cloud = 0.5) with a second log-normal PDF (Eq. (6), σcontam = 0.5) as a function of the typical density of the contaminating structure, Ncontam, relative to the peak of the log-normal cloud distribution, Npeak. The left edge of the figure represents the original cloud PDF shown in colors of the logarithm of pη. When increasing the contamination level Ncontam in the right direction, we see the shift of the PDF towards higher logarithmic column densities, η. |
Figure 12 shows the distribution of PDFs obtained from convolution using log-normal distributions for the cloud PDF and the contamination PDF when we vary the contamination level. In this example both distributions have the same log-normal PDF width σ = 0.5. The main effect is the same as that from the contamination with a constant foreground. With increasing contamination level, the PDF peak is shifted towards higher column densities and PDF width becomes narrower. In contrast to some statements in the literature, line-of-sight contamination of multiple log-normal PDFs does not create multiple peaks, but the convolution integral simply creates a broader distribution on the linear scale. One should note that the systematic effect on the PDF peak has the same direction for noise and foreground contamination. Both artificially shift the peak towards higher column densities, but the opposite can be true for the PDF standard deviation on the logarithmic scale, where noise increases the measured standard deviation for all narrow cloud distributions, while foreground contamination tends to decrease it. The shift in the PDF peak caused by line-of-sight contamination is approximately proportional to the contamination level Ncontam.
 |
Fig. 13 PDFs of contaminated clouds, corrected for contamination by subtraction of a constant offset of the peak of the contaminating structure’s PDF. PDFs are plotted as a function of the contamination density, Ncontam, using a fixed width of the contamination PDF of σcontam = 0.5 matching the width of the main cloud PDF. Corrected distributions are represented by colors showing the logarithm of the PDF. |
This suggests that a correction by a constant offset, as applied by Schneider et al. (2015a) for their foreground “screen”, may also work for the contamination with a wider distribution. Figure 13 shows the result after subtracting the column density of the peak of the log-normal contamination. Overall we find a quite good reproduction of the central part of the original PDF even for contaminations that have the same amplitude as the cloud structure itself. The PDF peak position is recovered within Δη = 0.2. There is, however, a residual broadening of the distribution, in particular towards lower column densities, due to overcompensation of contamination contributions that have lower than typical column densities. The low column density wing of the corrected PDF appears too shallow relative to the original cloud PDF. One must take into account, however, that the plot is given in logarithmic units, meaning that the deviations occur at levels of less than 1% of the PDF peak.
 |
Fig. 14 Parameters of the PDFs of contaminated clouds corrected for the contamination through the subtraction of a constant offset given by the peak of the contaminating structure PDF. Upper plot: position of the PDF peak on the logarithmic η scale, i.e., a value of 0 represents the correct peak position and a value of 0.3 stands for a 35% overestimate of the peak density. Lower plot: width of the corrected cloud PDF relative to the original cloud PDF. In both plots we varied the amplitude of the contamination in horizontal direction and the width of the contaminating PDF in vertical direction. |
To systematically quantify the residual effects after the correction, we run a parameter scan over the full range of the two free parameters that cover the relative amplitude of the contamination relative to the cloud investigated, that is, the relative distance of the two log-normals on the η scale, and the width of the contaminating structure’s PDF relative to that of the cloud PDF studied. This produces the two-dimensional plots shown in Fig. 14. The upper plot quantifies the recovery accuracy of the PDF peak, the lower plot shows the corrected cloud PDF width relative to that of the original cloud PDF. Both quantities are computed from a Gaussian fit to the corrected PDFs. The figure shows that the cloud PDF is accurately recovered when the width of the contaminating PDF is narrow (σcontamin ≲ 0.5ση,cloud) or its column density is small (Ncontamin ≲ 0.2Npeak). Fortunately, the first condition is usually met if the contamination stems from diffuse H i clouds in the Milky Way, having typical PDF widths σcontam ≈ 0.1−0.2 (Berkhuijsen & Fletcher 2008, assuming a typical σ2D ≈ 0.2−0.4σ3D). Significant deviations occur if the properties of the contaminating structure are similar to those of the observed cloud. Then the peak column density is overestimated by 35% and the width by a factor of 1.7. If the width of the contamination PDF gets even wider, this propagates directly into the width of the corrected PDF, so that the recovered PDF can be more than twice as wide as the original PDF.
Knowing the properties of the contamination, we can use Fig. 14 to correct this effect in a parametric way as demonstrated above for the noise contamination. The typical level of contamination can usually be measured by inspecting pixels at the boundaries of the cloud that are representative of the contamination only. However, we almost never have the same statistics for the contamination as for the whole map, so that even the width of the contaminating PDF may not be known with sufficient accuracy. One last resort to infer the width is the inspection of the zero-column-density of the offset-corrected PDF, equivalent to our approach of measuring the noise in Sect. 3.3. As the two effects are usually superimposed onto one another, we must first subtract the noise contribution to the linear PDF at zero column densities using the parameters from Fig. A.2 to then derive the width of the contaminating PDF in a second step.
The procedure for this derivation is discussed in detail in Appendix B. It shows, however, that small errors in determination of the contamination amplitude lead to large errors in the measured contamination PDF width. Hence, it is very difficult in practice to use the zero-column PDF after the line-of-sight correction to estimate the width of the PDF of the contaminating structure. A direct measurement from a field tracing only the contamination seems always to be preferable if such a region can be observed.
The direct deconvolution of the contamination from the measured PDF is irrelevant in practice as we can never know the properties of the contamination accurately enough to allow for the computation of the deconvolution integral (Eq. (7)) without significant errors. Altogether, we find that the correction of line-of-sight contamination from a turbulent cloud can be easily corrected in terms of subtracting a constant screen if either the width of the PDF of the contaminating cloud is at most half the width of the cloud PDF to be investigated or if its column density is lower by a factor of 4–5. If none of the conditions is met we can still measure the PDF peak column density with an accuracy of better than 35%, but have no good handle on the PDF width of the main cloud.
5. Boundary effects
A typical limitation of interstellar cloud observations is given by the finite map size. From multi-wavelength observations it has long been known that there is no absolute definition of an interstellar cloud boundary. Depending on observational sensitivity and tracer, covering either molecular lines, extinction, or dust continuum, the extent of a cloud appears different and can just be approximated by the lowest closed contour. For convenience – and to restrict the clouds to, for example, their molecular gas content – certain extinction thresholds are proposed, such as AV = 1 or 2 (Lada et al. 2010; Heiderman et al. 2010). However, in most cases maps are centered only on prominent peaks and the total area mapped is limited due to observational constrains. These finitely sized maps obviously truncate the statistics of the cloud PDF. Schneider et al. (2015a,b) discussed the impact of incomplete PDF sampling by considering a truncation of the statistics at various contour levels. This modifies only the PDF normalization but has no effect on the measured shape. As an extreme example of this selection effect, they showed that the PDFs of Infrared Dark Clouds consist only of a power-law tail. Lombardi et al. (2015) showed that PDF width is reduced when mapping smaller areas. In real observations, however, there is often no information about the structure outside the mapped area.
In contrast, such a truncation can also be intended. Studying PDFs of selected subregions within an interstellar cloud can be a valuable tool to differentiate between the physical processes determining the column density structure. In this way Schneider et al. (2012), Russeil et al. (2013), Tremblin et al. (2014) showed that in the same cloud the PDFs of quiescent subregions have a log-normal shape, denser cloud parts exhibit a power-law tail at high column densities, and compressed shells at the interface with Hii-regions provoke a second PDF peak. Sadavoy et al. (2014) and Stutz & Kainulainen (2015) linked different PDF slopes seen in different subregions of the Perseus and Orion A clouds to the content of young stellar objects and proposed an evolutionary sequence within the cloud. Hence, it is important to quantify statistically the impact of finitely sized maps on the properties of the measured cloud PDF following the typical observer’s approaches.
 |
Fig. 15 Result of partial observations focusing on the center of the cloud. PDFs are measured for the four submaps of different sizes indicated in Fig. 1. Up to a map size of 300 × 300 pixels, all high-column-density spots are included in the map. A smaller map truncates some parts of the high-density center of the map leading to a noticeable distortion of the power-law tail. The submap sizes correspond to 69%, 44%, 25%, and 11% of the original map area. |
This is simulated in Fig. 15 where we study differently sized submaps from Fig. 1, placed around the central column density peak. In this simulation the spatial structure of the cloud starts to become relevant while in the previous sections the convolution integrals were actually independent of the cloud shape. Details of the resulting PDFs may depend on the exact shape of the mapped structure, but the general behavior is the same for all cases if we follow a typical observational approach. With our submaps, we try to mimic the observational strategy for mapping an interstellar cloud structure around the central density peaks with a finite array in a limited observing time.
If a sufficiently large part of the cloud is covered, the truncation at the boundaries removes only low column density gas from the statistics, leaving the power-law tail unchanged – except for the modified normalization. The removal of low-density pixels also shifts the peak of the log-normal part to larger column densities. The effect is small ifless than half of the pixels are removed, but even when changing from 600 × 600 pixels to 400 × 400 pixels (44% of the area) the truncation of the low-density statistics becomes significant, and we significantly overestimate the peak position. In that step we also notice a measurable reduction of the PDF width that continues at smaller submap sizes. At a submap size of 11% of the original map, we also start to loose some of the high-density structures. In this case, even the power-law tail is affected.
The impact is much stronger when considering mean quantities. This is a well known effect to most observers: increasing the mapping size around the main emission peaks tends to drastically lower the average column density since more “empty” regions are added to the statistics. For our example, in Fig. 15 we find that the measured peak of the PDF in logarithmic bins Ncenter changes by a factor of 1.6 when reducing the field size from 600 × 600 to 200 × 200 pixels (11% of the area), the same factor applies for the peak in linear units, but that the average column density increases by a factor of 2.3 when reducing the map size7.
 |
Fig. 16 Column density distribution parameters of randomly selected submaps of Fig. 1 as a function of their size. The symbols show the mean from an ensemble of 50 submaps and error bars represent the standard deviation. Red diamonds show the average map density, blue crosses give the PDF peak on the logarithmic scale, and green triangles the peak on the linear density scale. The symbols and error bars for the two PDF peaks are displaced by ±5 pixels relative to the actual submap size for a better visibility in the plot. |
To quantify this selection effect statistically, we investigate ensembles of 50 randomly selected submaps of different size and measure their average and most probable column densities. Figure 16 shows the ensemble mean and standard deviation for the average column density in the submaps and the PDF peak position Ncenter(η) on the logarithmic scale. For completeness, we also computed the center of a Gaussian PDF on the linear column density scale Ncenter(N). In contrast to the submap selection centered on the main peak in Fig. 15, the random selection provides for all three parameters a mean ensemble density that does not depend on the map size. The mean average density and PDF peak positions of the input map are recovered, but we find that the uncertainty of the parameters grows drastically towards smaller submap sizes. While the uncertainty of the PDF peak positions grows up to 25% for 200 × 200 pixel submaps, the uncertainty of the average column density grows to 45%.
This bigger uncertainty of the average density is to be expected since the average is more easily affected by low-probability outliers and they are more easily missed or hit in a random selection than values with high probabilities. This explains why the use of the PDF peaks for normalization purposes (see Sect. 2.1) always provides more stable results than the use of the average density.
6. Interferometric observations
A special source of observational uncertainty results from the incomplete sampling of the uv-plane that is unavoidable in interferometric observations. Rathborne et al. (2014) discussed the shape of the low-column density tail of a PDF obtained by combining ALMA observations with Herschel data, but they did not quantify to what degree that tail was determined by the observational limitations of the interferometric observations.
6.1. ALMA
 |
Fig. 17 Result of a simulated 2 h ALMA observation of the cloud shown in Fig. 1 where we translated the optical depth AV into an equivalent 230 GHz intensity. Upper plot: map obtained when using the 12 m array without short-spacing correction. Lower plot: map obtained after combining the 12 m array data with the data from the compact array and single-dish zero spacing. The intermediate map obtained from combining only the ALMA 12 m and ACA results is hardly distinguishable visually from the map in the lower plot, so it is not shown here. |
 |
Fig. 18 Comparison of the original cloud PDF with the PDFs of the maps obtained from the 2 h ALMA observations (Fig. 17). |
ALMA provides a better instantaneous uv-coverage than any other observatory previously available, based on the unprecedentedly large number of dishes and baselines available. However, any incomplete information in the Fourier domain may still have significant effects on the measured intensity PDF. We simulate the behavior using the ALMA simulator in CASA 4.48 with a configuration providing a resolution of 0.6′′. We used the default pipeline setup based on the standard CLEAN algorithm (Högbom 1974) that would be used by most observers. To convert our column density map into observable quantities we treated the input map as Jy/pixel units, used 230 GHz as center frequency, and a 7.5 GHz bandwidth corresponding to standard continuum observations. We used the mosaicking mode to map the total field of view of (2′)2, and combined the 12 m array and ACA observations matching what ALMA provides for continuum observations (ALMA+ACA). The choice of these parameters should not have any major impact on our results as we were not limited by sensitivity or resolution as discussed later. To obtain a complete picture for the capabilities and limitations of the approach, we also performed the step of the single-dish total power correction (ALMA+ACA+TP). Total power zero spacing is not provided for continuum observations at ALMA, only for line observations, but including this step provides us with a more complete picture in terms of the fundamental capabilities of interferometric observations. In a separate test, we added thermal noise to the simulations but found that it does not have any significant impact, indicating that the results are not limited by sensitivity but, as intended, by uv-coverage.
Figure 17 shows the maps and Fig. 18 contains the corresponding PDFs from an observation that can be executed in a 2 h observing block (2 h for 12 m array, 4 h for ACA, 8 h for TP).
The simulated observations with the 12 m array provide a reasonable reproduction only of the position and shape of the high-intensity contours, but we recover essentially no information about structures with an intensity below 20 Jy/pixel, meaning that only the high end of the PDF power-law tail (η> 3) is retained. After combining the data with the short-spacing information, some low-intensity structure is recovered appearing in spiral shapes, probably produced by the shape of the uv-tracks. But the shape of the high-intensity peaks is more heavily distorted than in the pure 12 m array data. The intermediate map obtained when combining the data from the 12 m array with the ACA data is very similar to the map obtained when including all short-spacing information. The visual impressions from the interferometric maps are confirmed by the PDFs of the maps. When sticking to the pure interferometric data, the CLEAN algorithm manages to reproduce the high-intensity peaks above η = 3 so that the high-intensity end of the PDF power-law tail is recovered. At lower intensities, however, the map PDF does not correspond at all to the underlying cloud PDF. The typical values of AV ≡ 5 Jy/pixel are strongly under-abundant and the PDF peak falls at a five times lower value. All curves show an extreme excess of low intensity contributions, similar to the observational noise effect shown in Fig. 2. When combining the interferometric data with the short-spacing information, the high-density tail is even more distorted, but the location of the PDF peak is reasonably recovered. The excess at low intensities is still high but five times lower than that of the 12 m array data.
 |
Fig. 19 Result of a simulated 8 h ALMA observation of the cloud shown in Fig. 1. The map shows the final product from combining the 12 m array data with the data from the compact array and single-dish zero spacing. |
An obvious approach to improve the mapping results is the use of longer integration times, which would automatically provide a better uv-plane coverage as a result of the earth’s rotation. Figures 19 and 20 show the results from a quadrupled observing time. Here, the simulations used a total continuous observing time of 8 h with the 12 m array. This corresponds to 40 h of total observatory time (8 h for 12 m array, 2 × 8 h for ACA, and 4 × 8 h for TP), an amount that would rarely be granted. It is, moreover, an idealized case because usually 2 h observing blocks are executed randomly by the observatory, potentially leading to overlaps in the uv-coverage.
When considering the map from the 12 m array we find no big improvement compared to the shorter integration time. Again only the high intensity end (η> 3) of the cloud PDF is recovered. More low-intensity material is detected, leading to an additional shift of the PDF maximum to even lower intensities. Adding short-spacing information no longer provides the correct PDF peak position, but by including the single-dish zero-spacing, we fully recover the high-intensity PDF power-law tail. This is also visible in the map in Fig. 19 which resembles much more closely the input map (Fig. 1), reproducing all bright structures. The combination of a very long integration time with all zero-spacing information allows us to actually recover a significant part of the underlying cloud PDF. Unfortunately, this is not currently possible for real observations as ALMA does not provide the single-dish total power information for continuum data yet. Moreover, we conclude that the need for a wide uv-coverage is not well satisfied by single observing blocks of 2 h. For the cloud statistics, it would be better to distribute the same observing time in smaller chunks over the whole visibility window of a celestial object, at least when not limited by sensitivity, as in our example.
Even in this case the PDF still does not contain any reliable information in the log-normal part. It shows the same large excess of low intensities as in the case of the shorter integration time. The excess appears very similar to the low-intensity PDF wing reported by Rathborne et al. (2014) for their interferometric data.
 |
Fig. 21 Impact of different parameters on the PDFs from the ALMA+ACA maps obtained in the simulated 8 h ALMA observations. |
Combining the data from the 12 m array and ACA, the longer integration time leads at least to an improvement in the recovery of the high-intensity tail compared to the 2 h ALMA observation, but the deviation of the measured PDF from the cloud PDF is still significant. We can only conclude that there must be a power-law tail. Measuring its parameters is still unreliable. To see whether one can better recover the cloud PDF based on the data provided by ALMA, we performed some additional tests varying the parameters of the CLEAN algorithm. The results are shown in Fig. 21. In two of the curves we modified the robustness parameter of the “Briggs” weighting (see CASA User Reference & Cookbook9). A value of −2 corresponds to uniform weighting, and cleaning with a weighting robustness of + 2 corresponds to natural weighting. The figure shows that natural weighting clearly deteriorates the recovery of the map PDF, there is no significant difference between the standard weighting (robustness of 0) and the uniform weighting. In a second test we used a mask to help the convergence of the CLEAN algorithm. This should provide a better data reduction strategy. However, we found no significant difference in outcome from using the default parameters so that the corresponding curve is not added in the plot, being almost identical to the brown curve. Finally, we tested the impact of map size by changing the pixel size of our test data set by a factor of 0.5 resulting in a map size of 1′2. In this way we should be able to quantify the pure resolution effect. The blue curve in Fig. 21 shows that this also has no significant impact on the recovery of the cloud PDF. As long as we avoid the natural “Briggs” weighting, the combined ALMA+ACA maps are equally good or bad for measuring the cloud PDF.
A reliable partial recovery of the cloud PDF is only possible when combining single dish information with integrations covering a long time span to provide a very wide uv-coverage. This requires an extension of the current capabilities of ALMA.
6.2. Fundamental limitations
To test whether the ALMA results are due to some limitation of the CLEAN algorithm combined with the continuous tracks given by the telescope baselines, or rather whether they reflect the general problem of lacking information in uv-space, we added some numerical tests with a more controlled random coverage of the uv-plane. We transformed the cloud from Fig. 1 into the Fourier domain and randomly removed a number of the points in Fourier space. The zero-spacing point, characterizing the mean intensity in the map, is always preserved.
 |
Fig. 22 Result of incomplete sampling in the uv-plane. PDFs are obtained after removing the information for half of the points randomly selected in the uv-plane. We replaced the Fourier coefficients either by zeros, by values interpolated between the retained neighboring points or by interpolated amplitudes and random phases. |
Figure 22 shows the resulting PDFs after the inverse Fourier transform when removing the information for half of the points. The brown dashed-dotted line is computed by replacing the missing information by zeros. The green dashed curve is obtained by interpolating the missing points in Fourier space, and the blue dotted curve uses interpolated amplitudes but random phases. All curves show an excess of low intensity contributions, like the ALMA maps, and a shift of the PDF peak to higher intensities compared to the input map. The highest intensity fraction is suppressed. Part of those pixels are transformed to lower values resulting in a steepening of the power-law tail. The worst reproduction of the cloud PDF is obtained when interpolating in the uv-plane. The interpolation acts like a low pass-filtering that suppresses sharp structures, therefore washing out some of the high-intensity peaks. For a fractal cloud one expects, in principle, a smooth change of the Fourier amplitudes while the phases represent the details of the realization, but the experiment with random phases does not provide any improvement from the test with the simple zero replacement. Other tests with constant phases, systematic phase changes or conjugate complex numbers also did not provide any improvement. A recovery of the underlying cloud PDF seems to be impossible. Removing half of the points in the uv-plane has a much stronger impact on the determination of the PDF than removing half the points in normal space as demonstrated in Sect. 5. As the removal of information in Fourier space affects every single pixel of a map, the impact on the real-space statistics is always worse than removing the information for the same number of pixels in the map.
 |
Fig. 23 PDFs from a variable sampling in the uv-plane. Different fractions of randomly selected points in the uv-plane were replaced by zeros. |
To get an idea about the minimum coverage of the uv-plane needed to obtain a reliable PDF measurement we repeated the test above, but removed different fractions of the points in Fourier space. Figure 23 shows the PDFs obtained when randomly replacing 1%, 10%, and 80% of the points by zeros. Even when only 10% of the uv-plane are not covered, we find a significant low intensity excess. In this case PDF peak and the high-intensity tail are still well recovered. The 80% case shows hardly any similarity with the input PDF.
 |
Fig. 24 PDFs from an incomplete sampling of the uv-plane depending on the wavenumber. The brown dashed-dotted line shows the result when randomly replacing 50% of the uv-plane by zeros, as shown already in Fig. 22. The other two PDFs are computed when removing those points only inside or outside of a circle of 20 wavenumbers. |
To better understand the reason for this effect, finally we show the dependence of the PDFs on the wavenumber coverage in Fig. 24. Again, we randomly remove 50% of the points in the uv-plane, as in Fig. 22, but also restrict the removal to the areas of small and large wavenumbers, k ≶ 20, respectively. Due to the small area of k< 20 in the uv-plane, only 0.15% of the points are removed in this case, while for k ≥ 20, 49.85% of the points are removed. We see that the main distortion of the PDF power law tail and the PDF peak stems from the missing information at small wave numbers. If we have complete coverage of the wave numbers k< 20 we recover the PDF over a dynamic range also covering a factor of 20. Lack of short-spacing information has a much worse effect on the PDF than lack of high frequency information. Any incomplete uv-coverage, however, creates a significant excess of low-intensity noise.
Combining the picture with the information from Fig. 22 suggests that it is almost impossible to obtain any reliable information on the low-intensity statistics from interferometric observations. To get a measurement of the high intensity tail and the PDF peak, a good coverage of the low wavenumbers, provided by the short-spacing range of the uv-plane, is needed. The similarity in the PDF recovery shown in Fig. 20 for the long ALMA observations and in Fig. 24 suggests that there is no fundamental difference between the map reconstruction by the CLEAN algorithm and by the direct Fourier transform. The critical point is a sufficiently dense sampling of the uv-plane, particularly for low wave numbers. Only with that dense sampling can we recover the upper part of the PDF. However, any sparse sampling of the uv-plane unavoidably leads to severe distortions of the overall PDF shape. None of our experiments simulating interferometric observations allowed us to recover the low-intensity part of the PDF including the log-normal distribution. Therefore, interpretation of PDFs from interferometric data should be done with extreme care.
7. Conclusions
When measuring interstellar cloud column density PDFs, observational effects must be carefully treated. Otherwise, all conclusions about PDF parameters can be wrong by large factors. We provide tools to derive the cloud parameters from the measured PDFs. Our focus lies on the log-normal part of the PDF because this part is most strongly affected by observational noise, contamination by fore- or background material, and the selection of the map boundaries. In single-dish observations the power-law tail in the PDF of self-gravitating clouds is typically only marginally influenced by the effects discussed here (see also Lombardi et al. 2015). This is different for interferometric observations.
Noise can be treated mathematically as a convolution integral. If the noise distribution is perfectly Gaussian the original PDF can be recovered through direct deconvolution. For general single-dish data, the PDF parameters can be computed from the measured PDF and a known noise level using the algorithm discussed in Sect. 3. This allows for an accurate measurement of all parameters of the log-normal part if the noise level falls below 40% of the typical column density in the map. This even works for noise levels up to the typical column density in the map in case of clouds with a broad PDF (ση,cloud> 0.3). For clouds with narrower PDFs and high noise contaminations, we can only retrieve the position of the PDF peak, but no longer its width. If the noise level in a map is not known a priori, it can be deduced from the zero-column PDF.
Line-of-sight contamination creates no multiple peaks in the column-density PDF, but a broader distribution on the linear scale. It can be corrected for by subtracting a constant “screen” with the typical column density of the contamination from the measurement. This works well if the contamination PDF is either a factor of two narrower or a factor of four to five weaker than that of the cloud to be characterized. If width and strength of the contamination are well known, one can also retrieve the parameters of the cloud PDF through a fit to the measured parameters, similar to the noise correction. However, in the general case of an unknown broad contamination with a column density comparable to that of the cloud studied, we find a strong ambiguity between the impacts of the two PDF widths so that it turns out to be impossible to reliably derive the cloud PDF width from the measurement. We can only recover the PDF peak position of the studied cloud with an accuracy of about 35%.
The effect of a limited field of view due to map boundaries cannot be easily corrected as we cannot invent information that was not measured. We found, however, that the effect is small if the observations cover at least 50% of the structure to be measured. Smaller maps will underestimate the PDF width and overestimate the peak position. Width is slightly more stable against selection effects than position. The sensitivity to boundary selection effects clearly discourages use of mean quantities to characterize the properties of a map. The characterization in terms of the PDF peak is more stable.
The situation is very different for interferometric observations with sparse sampling in the uv-plane. We found no way to reliably measure the statistics for the majority of the pixels in the map forming the center and low-density wing of the PDF. The removal of information in the uv-plane has a much stronger impact than the direct removal of pixels from the map. An interferometric determination of the high-density PDF tail is possible, but requires an approach that goes beyond the current capabilities of ALMA. We can, in principle, retrieve the high-density wing of a cloud PDF by combining single-dish zero spacings with 12 m array observations that densely populate the uv-plane, in particular its short-spacing area. They can be obtained through a very long integration time or with many small chunks of 12 m array observations over a long period.
An equivalent approach, defined on the linear scale, was recently introduced by Brunt (2015).
Athttp://www.astro.uni-koeln.de/ftpspace/ossk/ noisecorrectpdf we provide an Interactive Data Language (IDL)program that uses the precomputed surfaces from Fig. 5 to provide such a fit for any input map and given noise rms. There the Gaussian fit is only performed down to 1/2 of the peak to minimize the effect of distortions by PDF tails and wings.
Berkhuijsen & Fletcher (2008) provided PDFs of volume densities. The corresponding column density PDF widths can be derived following Brunt & Mac Low (2004) and Brunt et al. (2010a).
Russeil et al. (2013) and Schneider et al. (2015b) show some PDFs with small double-humps.
Correcting for the distortions introduced by material with other PDFs, for example, a constant gradient can be computed in an equivalent way. It requires convolution with a differently shaped contaminating PDF, pcontam(N), in Eq. (4), and repeating our quantitative analysis for the new convolution integral.
As our test cloud also includes a power-law tail of high densities, the average column density is not only 10% higher than Npeak as expected for a log-normal distribution (see Sect. 2.1), but 44% higher for the original map.
Acknowledgments
We thank the referee Mark Heyer for very constructive suggestions that helped to improve the paper. This work was supported by the German Deutsche Forschungsgemeinschaft, DFG via the SPP (priority programme) 1573 “Physics of the ISM”. V.O. and N.S. acknowledge support from DFG project number OS 177/2-2. C.F. acknowledges funding providedby the Australian Research Council’s Discovery Projects (grants DP130102078 and DP150104329). R.S.K. acknowledges support from the DFG via projects KL 1358/18-1 and KL 1358/19-2 and via the SFB 881 “The Milky Way System” (sub-projects B1, B2 and B8). In addition, R.S.K. is grateful for funding from the European Research Council under the European Community’s Seventh Framework Programme (FP7/2007-2013) via the ERC Advanced Grant “STARLIGHT” (project number 339177).
References
- Alves, J., Lombardi, M., & Lada, C. J. 2014, A&A, 565, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bensch, F., Stutzki, J., & Ossenkopf, V. 2001, A&A, 366, 636 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berkhuijsen, E. M., & Fletcher, A. 2008, MNRAS, 390, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Berkhuijsen, E. M., & Fletcher, A. 2015, MNRAS, 448, 2469 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M. 2015, MNRAS, 449, 4465 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M., & Mac Low, M.-M. 2004, ApJ, 604, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M., Federrath, C., & Price, D. J. 2010a, MNRAS, 403, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Brunt, C. M., Federrath, C., & Price, D. J. 2010b, MNRAS, 405, L56 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhart, B., Ossenkopf, V., Lazarian, A., & Stutzki, J. 2013, ApJ, 771, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Druard, C., Braine, J., Schuster, K. F., et al. 2014, A&A, 567, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Hily-Blant, P., & Levrier, F. 2004, Ap&SS, 292, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Banerjee, S. 2015, MNRAS, 448, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2008, ApJ, 688, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Klessen, R. S., & Schmidt, W. 2009, ApJ, 692, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Froebrich, D., & Rowles, J. 2010, MNRAS, 406, 1350 [NASA ADS] [Google Scholar]
- Ginsburg, A., Federrath, C., & Darling, J. 2013, ApJ, 779, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., Evans, II, N. J., Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hily-Blant, P., Falgarone, E., & Pety, J. 2008, A&A, 481, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Högbom, J. A. 1974, A&AS, 15, 417 [NASA ADS] [Google Scholar]
- Hughes, A., Meidt, S. E., Schinnerer, E., et al. 2013, ApJ, 779, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2014, Science, 344, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Konstandin, L., Girichidis, P., Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Kowal, G., Lazarian, A., & Beresnyak, A. 2007, ApJ, 658, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2011, A&A, 535, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miesch, M. S., & Scalo, J. M. 1995, ApJ, 450, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Miesch, M. S., Scalo, J., & Bally, J. 1999, ApJ, 524, 895 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, F. Z., Glover, S. C. O., Federrath, C., & Klessen, R. S. 2012, MNRAS, 423, 2680 [NASA ADS] [CrossRef] [Google Scholar]
- Nolan, C. A., Federrath, C., & Sutherland, R. S. 2015, MNRAS, 451, 1380 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, Å. K., & Padoan, P. 1999, in Interstellar Turbulence, eds. J. Franco, & A. Carraminana (Cambridge University Press), 218 [Google Scholar]
- Padoan, P., & Nordlund, Å. 2011, ApJ, 730, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Jones, B. J. T., & Nordlund, Å. P. 1997, ApJ, 474, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Passot, T., & Vázquez-Semadeni, E. 1998, Phys. Rev. E, 58, 4501 [NASA ADS] [CrossRef] [Google Scholar]
- Price, D. J., Federrath, C., & Brunt, C. M. 2011, ApJ, 727, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Rathborne, J. M., Longmore, S. N., Jackson, J. M., et al. 2014, ApJ, 795, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015a, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Klessen, R. S., et al. 2015b, A&A, 578, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Motte, F., et al. 2016, A&A, 587, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A. M., & Kainulainen, J. 2015, A&A, 577, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutzki, J., Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M. 1998, A&A, 336, 697 [NASA ADS] [Google Scholar]
- Tofflemire, B. M., Burkhart, B., & Lazarian, A. 2011, ApJ, 736, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Parameterization of the noisy zero-column-density PDF
Closer inspection of the linear column density PDFs at N = 0 for noise-affected cloud observations displayed in Fig. 8 shows that the noise dependence of pN(0) can also be approximated by a log-normal function. For every width of the original cloud PDF, ση,cloud, we can fit the zero column PDF as a function of the noise level by ![\appendix \setcounter{section}{1} \begin{equation} p_N(0)= \frac{a_0}{N\sub{peak}} \exp \left(-\frac{[\ln(\sigma\sub{noise}/N\sub{peak})-\ln(a_1)]^2}{2 a_2^2} \right) \label{eq_eq_zero_pdf} \end{equation}](/articles/aa/full_html/2016/06/aa28095-16/aa28095-16-eq135.png) (A.1)in the range up to σnoise/Npeak = 1. To avoid confusion with the log-normal cloud column density PDFs, we use the less intuitive parameter names, a0, a1, and a2 here10.
(A.1)in the range up to σnoise/Npeak = 1. To avoid confusion with the log-normal cloud column density PDFs, we use the less intuitive parameter names, a0, a1, and a2 here10.
The log-normal character is demonstrated in Fig. A.1 showing three cuts through Fig. 8 in the σnoise/Npeak direction and the corresponding log-normal fits using Eq. (A.1). All curves in the plot show a clear parabola shape. Except for narrow cloud widths, ση,cloud ≲ 0.2, the representation of the curves by log-normals is very good. This allows us to condense the information contained in the surface in Fig. 8 into the ση,cloud dependence of the three parameters a0, a1, and a2 only.
 |
Fig. A.1 Demonstration of the log-normal behavior of the linear zero column density PDF pN(0) as a function of the observational noise level. The three colored curves represent horizontal cuts through the surface shown in Fig. 8 for different values of the cloud PDF width. The brown dashed-dotted lines show the corresponding log-normal fits to the curves. |
Figure A.2 shows the parameters of the log-normals, a0,a1,a2, for all horizontal cuts in Fig. 8 as functions of the cloud PDF width. As is visible in Fig. A.1, the parabolas describing the zero-column density PDFs become wider with increasing cloud PDF width, the peak position moves to smaller columns, but the peak amplitude does not change significantly.
Using the three log-normal parameters, a0(ση,cloud), a1(ση,cloud), a2(ση,cloud), plotted in Fig. A.2, we produce a condensed description of the zero-column PDF as a function of noise level and cloud PDF width from Fig. 8 that can be used to look up the noise level for any measured pN(0) and ση,cloud.
 |
Fig. A.2 Parameters of the log-normal noise-amplitude dependence of the zero-column density PDF (pN(0), Eq. (A.1)) shown as a function of the cloud PDF width. The values give the center, a1, amplitude, a0, and width, a2, of the Gaussian function on a logarithmic noise-amplitude scale in units of the cloud PDF peak Npeak. |
Appendix B: Recovering the PDF width of the contaminating cloud
The typical level of the contamination can usually be measured by inspecting pixels at the boundaries of the cloud that are representative of the contamination only. However, the number of those pixels will be small when compared to those of the whole map so that higher moments and even the width of the contaminating PDF may not be known with sufficient accuracy. However, in principle, one can infer the width by inspecting the zero-column-density of the offset-corrected PDF, equivalent to our approach of measuring the noise in Sect. 3.3. The colors at the lower edge of Fig. 13 demonstrate that for high contamination levels, in other words when the reconstructed PDF is too wide compared to the cloud PDF, it extends to low column densities including pN(0). A relationship between contamination width, σcontam/ση,cloud and the zero-column PDF pN(0) could then be used to deduce the unknown contamination width.
 |
Fig. B.1 Linear column density PDF after offset correction at zero column, pN(0), as a function of the amplitude of the contamination and the width of the contaminating PDF. Colors and contours are given on a logarithmic scale. |
 |
Fig. B.2 Repeat of Fig. B.1 but using an imperfect subtraction of the typical contamination level. In the upper plot we assume that the contamination level is underestimated by 20%, in the lower plot that it is overestimated by 20%. |
In Fig. B.1 we show the linear column density pN(0) measured after the subtraction of the typical contamination level as a
function of the relative amplitude and width of the contaminating PDF. We can accurately measure the width of the contaminating PDF from the plot if it shows a steep gradient of pN(0) in the direction of the contamination width given by the vertical cut through the plot for the known contamination amplitude Ncontam. Unfortunately, we find such a steep gradient only in the case of relatively narrow PDFs of the contaminating structure of less than σcontam< 0.5ση,cloud. That is a regime where the recovery of the cloud PDF by the constant offset subtraction needs no further correction. For broader contaminations, we see a relatively shallow behavior.
Moreover, this approach depends on accurate knowledge of the contamination level, Ncontam. Any “overcorrection” of the contamination will shift the PDF towards lower densities, strongly increasing the zero column density level. A small shift can lead to a significant change of the measured probability pN(0). In Fig. B.2 we show the resulting zero-column PDF when assuming a 20% error in the amplitude of the contamination correction. When comparing the two plots in Fig. B.2 we see that the zero-column PDF can change by a factor of 100 in the sensitive range, while it still changes by a factor of five in the range of the weak dependence from the width of the contaminating PDF. Hence, it is practically very difficult to use the zero-column PDF after the line-of-sight correction to estimate the contaminating structure PDF width. A direct measurement from a field tracing only the contamination is always preferable.
All Figures
 |
Fig. 1 Test data set representing a fractal cloud with an ideal column density PDF consisting of a log-normal part and a power-law high-density tail. Coordinates are invented to allow for an easy comparison with real observations and to perform simulated ALMA observations in Sect. 6. Contours and colors visualize the same data. The contour levels are indicated in the color bar. Column densities above AV = 80 are saturated in the plot to make the turbulent cloud part better visible. The actual maximum column density is three times larger. As the peak of the log-normal PDF is located at AV = 5, the contours almost cover material in the PDF power-law tail only. Because of the low probabilities in the tail, the fraction of green pixels is already small and that of pixels with yellow and red colors is tiny. The four colored squares indicate the subregions discussed in Sect. 5. |
| In the text | |
 |
Fig. 2 Impact of observational noise on the PDF measured for the cloud from Fig. 1. The red solid curve shows the analytic description of the input PDF, the blue dotted line is the measured PDF of the fractal map with a finite pixel number. The other broken lines show the column density PDF that is measured if the map is affected by different levels of observational noise, characterized by a normal distribution with a standard deviation from 10% to 100% of the peak column density. |
| In the text | |
 |
Fig. 3 Distributions obtained from the convolution of a log-normal cloud PDF (Eq. (2) with ση,cloud = 0.5) with a Gaussian noise PDF (Eq. (5)) as a function of the noise amplitude (σnoise) relative to the peak of the log-normal distribution (Npeak). Contours and colors visualize the same data, given on a logarithmic scale. The individual contour levels are marked in the color bar. The left edge of the figure represents the original log-normal PDF. When increasing the noise level σnoise in the right direction, we see the distortion of the PDF mainly at low column densities η. The dashed line indicates the peak of the distribution, to better follow the shift of the PDF maximum to larger column densities with increasing noise level. |
| In the text | |
 |
Fig. 4 Change in the measured PDF parameters as a function of the noise amplitude. The upper plot shows the measured center position using three different measures of position. The red solid line shows the position of the maximum probability, the blue dotted line shows the first moment of the distribution, and the green dashed line gives the center of a Gaussian fit (in η). The lower plot displays the standard deviation along with the width of the Gaussian fit, also showing the higher moments. |
| In the text | |
 |
Fig. 5 Variation of the parameters of a log-normal fit to the PDFs of noise-contaminated maps as a function of noise amplitude and the width of the original cloud PDF. The upper plot shows the measured location of the PDF center, the lower plot the width of the log-normal fit. Without noise contamination ηcenter = ηpeak = 0 and the measured width matches the PDF width of the cloud, σlog − normal = σcloud. |
| In the text | |
 |
Fig. 6
|
| In the text | |
 |
Fig. 7
|
| In the text | |
 |
Fig. 8 Values of the linear column density PDF pN at zero column densities as a function of the observational noise level and the cloud PDF width. PDF values pN(0) are given in units of 1 /Npeak. |
| In the text | |
 |
Fig. 9 Result of the numerical deconvolution of a log-normal PDF contaminated by Gaussian noise with 0.5Npeak amplitude. The red solid line shows the input PDF before the noise contamination, the blue dotted line the contaminated PDFs, and the green dashed line the result of the deconvolution. The deconvolution artifacts at large column densities can be ignored as the measured noisy PDF already reflects the cloud PDF there. |
| In the text | |
 |
Fig. 10 Result of the numerical deconvolution of a noise-contaminated log-normal PDF for different noise levels. The red solid line shows the input PDF before the noise contamination. The contaminated PDFs are not shown here, but their shape can be taken from Fig. 3. |
| In the text | |
 |
Fig. 11 Result of the numerical deconvolution of the cloud PDF from Fig. 2 for a noise level of AV = 1, i.e., 0.2 Npeak. The red solid line shows the input PDF before the noise contamination. |
| In the text | |
 |
Fig. 12 Distributions obtained from the convolution of a log-normal cloud PDF (Eq. (2), ση,cloud = 0.5) with a second log-normal PDF (Eq. (6), σcontam = 0.5) as a function of the typical density of the contaminating structure, Ncontam, relative to the peak of the log-normal cloud distribution, Npeak. The left edge of the figure represents the original cloud PDF shown in colors of the logarithm of pη. When increasing the contamination level Ncontam in the right direction, we see the shift of the PDF towards higher logarithmic column densities, η. |
| In the text | |
 |
Fig. 13 PDFs of contaminated clouds, corrected for contamination by subtraction of a constant offset of the peak of the contaminating structure’s PDF. PDFs are plotted as a function of the contamination density, Ncontam, using a fixed width of the contamination PDF of σcontam = 0.5 matching the width of the main cloud PDF. Corrected distributions are represented by colors showing the logarithm of the PDF. |
| In the text | |
 |
Fig. 14 Parameters of the PDFs of contaminated clouds corrected for the contamination through the subtraction of a constant offset given by the peak of the contaminating structure PDF. Upper plot: position of the PDF peak on the logarithmic η scale, i.e., a value of 0 represents the correct peak position and a value of 0.3 stands for a 35% overestimate of the peak density. Lower plot: width of the corrected cloud PDF relative to the original cloud PDF. In both plots we varied the amplitude of the contamination in horizontal direction and the width of the contaminating PDF in vertical direction. |
| In the text | |
 |
Fig. 15 Result of partial observations focusing on the center of the cloud. PDFs are measured for the four submaps of different sizes indicated in Fig. 1. Up to a map size of 300 × 300 pixels, all high-column-density spots are included in the map. A smaller map truncates some parts of the high-density center of the map leading to a noticeable distortion of the power-law tail. The submap sizes correspond to 69%, 44%, 25%, and 11% of the original map area. |
| In the text | |
 |
Fig. 16 Column density distribution parameters of randomly selected submaps of Fig. 1 as a function of their size. The symbols show the mean from an ensemble of 50 submaps and error bars represent the standard deviation. Red diamonds show the average map density, blue crosses give the PDF peak on the logarithmic scale, and green triangles the peak on the linear density scale. The symbols and error bars for the two PDF peaks are displaced by ±5 pixels relative to the actual submap size for a better visibility in the plot. |
| In the text | |
 |
Fig. 17 Result of a simulated 2 h ALMA observation of the cloud shown in Fig. 1 where we translated the optical depth AV into an equivalent 230 GHz intensity. Upper plot: map obtained when using the 12 m array without short-spacing correction. Lower plot: map obtained after combining the 12 m array data with the data from the compact array and single-dish zero spacing. The intermediate map obtained from combining only the ALMA 12 m and ACA results is hardly distinguishable visually from the map in the lower plot, so it is not shown here. |
| In the text | |
 |
Fig. 18 Comparison of the original cloud PDF with the PDFs of the maps obtained from the 2 h ALMA observations (Fig. 17). |
| In the text | |
 |
Fig. 19 Result of a simulated 8 h ALMA observation of the cloud shown in Fig. 1. The map shows the final product from combining the 12 m array data with the data from the compact array and single-dish zero spacing. |
| In the text | |
 |
Fig. 20 PDFs of the maps obtained from the 8 h ALMA observations (Fig. 19). |
| In the text | |
 |
Fig. 21 Impact of different parameters on the PDFs from the ALMA+ACA maps obtained in the simulated 8 h ALMA observations. |
| In the text | |
 |
Fig. 22 Result of incomplete sampling in the uv-plane. PDFs are obtained after removing the information for half of the points randomly selected in the uv-plane. We replaced the Fourier coefficients either by zeros, by values interpolated between the retained neighboring points or by interpolated amplitudes and random phases. |
| In the text | |
 |
Fig. 23 PDFs from a variable sampling in the uv-plane. Different fractions of randomly selected points in the uv-plane were replaced by zeros. |
| In the text | |
 |
Fig. 24 PDFs from an incomplete sampling of the uv-plane depending on the wavenumber. The brown dashed-dotted line shows the result when randomly replacing 50% of the uv-plane by zeros, as shown already in Fig. 22. The other two PDFs are computed when removing those points only inside or outside of a circle of 20 wavenumbers. |
| In the text | |
 |
Fig. A.1 Demonstration of the log-normal behavior of the linear zero column density PDF pN(0) as a function of the observational noise level. The three colored curves represent horizontal cuts through the surface shown in Fig. 8 for different values of the cloud PDF width. The brown dashed-dotted lines show the corresponding log-normal fits to the curves. |
| In the text | |
 |
Fig. A.2 Parameters of the log-normal noise-amplitude dependence of the zero-column density PDF (pN(0), Eq. (A.1)) shown as a function of the cloud PDF width. The values give the center, a1, amplitude, a0, and width, a2, of the Gaussian function on a logarithmic noise-amplitude scale in units of the cloud PDF peak Npeak. |
| In the text | |
 |
Fig. B.1 Linear column density PDF after offset correction at zero column, pN(0), as a function of the amplitude of the contamination and the width of the contaminating PDF. Colors and contours are given on a logarithmic scale. |
| In the text | |
 |
Fig. B.2 Repeat of Fig. B.1 but using an imperfect subtraction of the typical contamination level. In the upper plot we assume that the contamination level is underestimated by 20%, in the lower plot that it is overestimated by 20%. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.