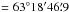| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526231 | |
| Published online | 06 August 2015 | |
Fine-structure line deficit in S 140⋆
1 I. Physikalisches Institut der Universität zu Köln, Zülpicher Straße 77, 50937 Köln, Germany
e-mail: ossk@ph1.uni-koeln.de
2 SRON Netherlands Institute for Space Research, Landleven 12, 9747 AD Groningen, The Netherlands
3 Kapteyn Institute, University of Groningen, PO Box 800, 9700 AV Groningen, The Netherlands
4 Department of Astronomy and Astrophysics, Tata Institute of Fundamental Research, Homi Bhabha Road, Colaba, 400005 Mumbai, India
5 Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
Received: 31 March 2015
Accepted: 2 June 2015
Aims. We try to understand the gas heating and cooling in the S 140 star-forming region by spatially and spectrally resolving the distribution of the main cooling lines with GREAT/SOFIA and combining our data with existing ground-based and Herschel observations that trace the energy input and the density and temperature structure of the source.
Methods. We mapped the fine-structure lines of [O i] (63 μm) and [C ii] (158 μm) and the rotational transitions of CO 13−12 and 16−15 with GREAT/SOFIA and analyzed the spatial and velocity structure to assign the emission to individual heating sources. We measure the optical depth of the [C ii] line and perform radiative transfer computations for all observed transitions. By comparing the line intensities with the far-infrared continuum we can assess the total cooling budget and measure the gas heating efficiency.
Results. The main emission of fine-structure lines in S 140 stems from a 8.3′′ region close to the infrared source IRS 2 that is not prominent at any other wavelength. It can be explained by a photon-dominated region (PDR) structure around the embedded cluster if we assume that the [O i] line intensity is reduced by a factor of seven owing to self-absorption. The external cloud interface forms a second PDR at an inclination of 80−85 degrees illuminated by a UV field of 60 times the standard interstellar radiation field. The main radiation source in the cloud, IRS 1, is not prominent at all in the fine-structure lines. We measure line-to-continuum cooling ratios below 10-4, i.e. values lower than in any other Galactic source, actually matching the far-IR line deficit seen in ULIRGs. In particular, the low intensity of the [C ii] line can only be modeled by an extreme excitation gradient in the gas around IRS 1. We found no explanation for why IRS 1 shows no associated fine-structure line peak, while IRS 2 does.
Conclusions. The inner part of S 140 mimics the far-IR line deficit in ULIRGs thereby providing a template that may lead to a future model.
Key words: ISM: individual objects: S 140 / ISM: structure / ISM: clouds / photon-dominated region (PDR) / ISM: abundances / ISM: lines and bands
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The cooling budget of the gas in galaxies is dominated by the emission in the fine-structure lines of atomic oxygen and ionized carbon (see e.g. Burton et al. 1990; Röllig et al. 2007). A large fraction of their emission stems from UV-illuminated surfaces of molecular clouds, the so-called photon-dominated regions (PDRs Tielens & Hollenbach 1985; Sternberg & Dalgarno 1995). Owing to the clumpy or fractal structure of molecular clouds, the PDR surfaces may represent a large fraction of their total volume (Ossenkopf et al. 2007). To quantify the importance of the PDRs in terms of the overall cooling balance of molecular clouds, we have to compare the fine-structure line emission with the lines of CO (and its isotopologues) that measure the emission of the molecular material and to the continuum emission from interstellar dust. The dust emission measures the combination of the total column density structure with the local heating, optically thin molecular lines provide us with a view on the spatial and velocity distribution of the molecular gas, and the fine-structure lines contain the information on the local energy input through UV radiation and the cooling balance in the gas. The German REceiver for Astronomy at Terahertz Frequencies (GREAT) on board the Stratospheric Observatory for Infrared Astronomy (SOFIA) allows for the first time velocity resolved spectra of the 63 μm line of atomic oxygen, [O i], to be obtained with a good sensitivity (Büchel et al. 2015). We used the instrument to measure the line simultaneously with the 158 μm line of ionized carbon, [C ii], in the S 140 star-forming region1.
S 140 is an H ii-region at the surface of the L 1204 molecular cloud, created by the illumination from the B0V star HD 211880, at a distance of 764 pc (Hirota et al. 2008). The external surface of the molecular cloud is exposed to a moderate UV field of 140 χ0 (Poelman & Spaans 2005) to 230 χ0 (Timmermann et al. 1996) (χ0 = standard interstellar radiation field; Draine 1978). However, ongoing star formation within the cloud already formed a cluster of deeply embedded radiation sources (Evans et al. 1989), probably creating more internal PDRs around the sources. Radio continuum observations detected ultracompact H ii regions at the strongest sources (e.g. Tofani et al. 1995; Hoare 2006). The strongest submm source, IRS 1, harbors a cluster of massive young stellar objects at a projected distance of 75′′ from the cloud interface (Minchin et al. 1993). Weigelt et al. (2002) showed the presence of an outflow cavity around IRS1. The corresponding outflow walls are illuminated by the cluster so that they form internal high-density PDRs. Dedes et al. (2010) suggested that the [C ii] emission from IRS1 measured by HIFI on board Herschel stems from these irradiated outflow walls, which are exposed to much higher radiation fields of more than 105χ0. Physical models of the structure around IRS 1 have been proposed by Harvey et al. (1978), Gürtler et al. (1991), Minchin et al. (1993), van der Tak et al. (2000), Mueller et al. (2002), de Wit et al. (2009), Maud et al. (2013). The whole cloud is fragmented and clumpy. Poelman & Spaans (2006) determined densities of nH2 ≈ 4 × 105 cm-3 for the clumps and nH2 ≈ 104 cm-3 for the interclump medium.
In Sect. 2, we present the new GREAT observations of the 63 μm [O i] and 158 μm [C ii] fine structure and the CO 16−15 and 13−12 lines towards S 140. In Sect. 3, we discuss the morphology and velocity structure of the observed emission compared to other lines, in particular low-J CO transitions, and literature data. In Sect. 4, we derive gas parameters across the map and for selected positions to understand the nature of the emitting gas. Section 5 discusses possible reasons for the association of the fine-structure emission peak with an otherwise inconspicuous source and the overall extremely low fine-structure line emission.
Parameters of the GREAT line observations.
2. GREAT observations
We used the GREAT2 (Heyminck et al. 2012) on board the Stratospheric Observatory for Infrared Astronomy (SOFIA, Young et al. 2012) to take on-the-fly maps of the central region of S 140 in [O i], 63μm, [C ii], CO 16−15, and CO 13−12.
The [O i] observations were performed on the nights of May 16 and 17, 2014. The [C ii] data were taken on May 16, 17, and 20, 2014. CO 13−12 was observed in two outer strips on May 20, 2014, and CO 16−15 was measured in the inner strip on January 13, 2015.
We mapped an area of 144 × 96′′ oriented at an angle of 37° east of north, perpendicular to the outer interface of the PDR. Because of instrument scheduling constraints, the [O i] and CO 16−15 observations were restricted to an inner strip of only 40′′ width covering the central cluster, while the observation of the CO 13−12 line avoided the central 32′′ covering only the two outer strips. In [C ii] we have a complete map covering the whole area. All observations involving [O i] were taken on a 3′′ grid to obtain full sampling; the outer strips were mapped with an 8′′ sampling, guaranteeing a nearly full sampling for the telescope beam at the [C ii] frequency. The OFF position for the observations was located southwest of the H ii region and molecular cloud at 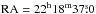 ,
, 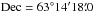 (J2000), six arcminutes away from IRS 1, our reference position in the maps at
(J2000), six arcminutes away from IRS 1, our reference position in the maps at 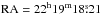 ,
, 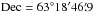 . eXtended-bandwidth Fast Fourier Transform (XFFT) spectrometers with a resolution of 44 kHz were used as backends.
. eXtended-bandwidth Fast Fourier Transform (XFFT) spectrometers with a resolution of 44 kHz were used as backends.
Atmospheric calibration was done through the standard GREAT pipeline (Guan et al. 2012). The pointing accuracy of the telescope and the alignment of the GREAT instrument relative to the telescope’s optical axis give a combined pointing error of less than 2 arcsec. The two GREAT channels operating in parallel were co-aligned to 1 arcsec accuracy. The forward efficiency is 0.97 for all observed frequencies. The other parameters of the GREAT beam at the observed frequencies are given in Table 1. All spectra were scaled to main beam Rayleigh-Jeans temperatures.
For the spectra of CO and [C ii] the default pipeline provided baselines that were quite flat. To be independent of the continuum level, a first-order baseline, measured over 100 km s-1 outside of the 15 km s-1 of the line was subtracted. As the [O i] maps suffered from some OTF-striping, these data were further processed by a secondary OFF subtraction, treating the first and last points of all OTF lines as reference allowing for the correction of gain drifts. This assumes that the map edges fall in regions free of emission, an assumption that is confirmed when inspecting the raw data. To improve the signal-to-noise ratio, the spectra were smoothed with a box-car filter to a resolution of 0.3−0.4 km s-1. Owing to the different combinations of observations, the total noise in the sum spectra taken within one beam is variable over the map. The average root mean square (rms) noise levels of the individual spectra and the beam-averaged sum spectra across the map at the smoothed resolution are given in Table 1.
Some of the [O i] spectra showed more irregular, wavy baseline structures not described by a simple linear relation. We tried to correct them by fitting various orders of polynomials to the baseline varying the order from 2 to 10. We did not find a significant global improvement of the spectra with increasing order, but an improvement of a few individual spectra. By using the criterion of the least negative values in the integrated intensity map, we selected the seventh order for all spectra, but use the outcome of the variation of the baseline orders basically as an error estimate for the baseline uncertainty. For different baseline orders, the intensities of individual bins in the line changed by up to 0.4 K and the integral over the full velocity range of the line (−15−0 km s-1) varied by up to 6 K km s-1. This uncertainty has to be added to the noise and the calibration error of the instrument of approximately 20% as the uncertainty of the data.
3. Spatial structure of the emission
 |
Fig. 1 Integrated intensity map of [C ii] overlaid on a Spitzer IRAC false-color image of the same region. The IRAC map uses the logarithmic intensities of the 3.6, 5.6, and 8μm channels. The integrated intensity contours are drawn at 50, 70, 90, 120, 150, and 180 K km s-1. The external cloud interface is visible in the southwest. The arrow shows the direction towards the illuminating source HD 211880. The red marks indicate the position of the known infrared sources: southwest is IRS 1, north is IRS 2, and southeast is IRS 3 (Evans et al. 1989), the yellow marks show the position of known submm cores (Minchin et al. 1995; Maud et al. 2013). The IRAC peak falls at the location of IRS 1. |
 |
Fig. 2 Peak intensity map of [C ii] overlaid on a IRAM 30 m map of the CO 2−1 peak intensity. The [C ii] contours are drawn at 15, 20, 25, 30, 35, 40, and 45 K. The black marks indicate the positions of IRS 1-3. |
Figure 1 shows the observed integrated intensity map of the [C ii] line superimposed on a Spitzer IRAC image of the cloud composed of the 3.6, 5.6, and 8μm channels. The IRAC image emphasizes two structures in the cloud. The peak in all bands is given by the embedded source IRS 1, relatively deep in the cloud. The embedded cluster produces about 104 solar luminosities, L⊙, heating the dust to temperatures of up to 1400 K (Koumpia et al. 2015). In the southwest we see the cloud surface illuminated by HD 211880 as a red band-like structure due to the excitation of PAHs at this external PDR. On top of these dominant features, we see some smaller spots east of IRS 1 close to IRS 3, bright in 5.6 μm emission. The [C ii] emission traces the front of the PDR in the southwest through a secondary peak, but it has a clear maximum 20′′ north of IRS 1, slightly north of IRS 2.
To compare the fine-structure lines with the molecular cloud material we use the maps of CO 1−0, 2−1, C18O 1−0, and 13CO 1−0 taken with the IRAM 30m telescope, presented and discussed by Koumpia et al. (2015). Figure 2 compares the [C ii] peak intensities with the CO 2−1 peak intensity map. The spatial distribution of the CO 2−1 line shows a behavior similar to the mid-infrared continuum. CO 2−1 peaks about 20′′ south of the [C ii] peak in a region covering IRS 1 and IRS 3. The CO 2−1 maximum falls close to IRS 3 and at the cloud surface the line is brighter than deep in the cloud. Thereis a clear layering with [C ii] peaking closer to the illuminating star and CO 2−1 deeper in the molecular cloud, as expected from standard PDR models (see e.g. Hollenbach & Tielens 1999). The location of the peak of [C ii] emission at the cloud surface therefore represents an expected morphology, but the relative shift of the emission peak to the north of IRS 1 is a striking unexpected feature in the [C ii] maps.
 |
Fig. 3 Integrated intensity map of the [O i] 63 μm line (colors) overlaid by contours of the [C ii] integrated intensity (levels as in Fig. 1). The three marks indicate the positions of IRS 1-3. All coordinates are taken relative to the position of IRS 1 at |
Figure 3 compares the [C ii] with the [O i] 63 μm line integrated intensity. The [O i] map shows a good match of the emission peak with that of [C ii]. The peak is strongly concentrated and dominates the overall map. The [O i] line also peaks slightly north of IRS 2; it may be offset from the center of the [C ii] peak by about 2′′, but this is close to our pointing accuracy. The location of the [C ii] and [O i] peaks indicates an association with IRS 2, similar to an already known small continuum feature visible at mid-infrared wavelengths (Harvey et al. 2012). The [O i] peak is slightly elongated towards the southeast in the direction towards IRS 3. IRS 1 is not prominent at all in [O i]. We also see a slightly increased [O i] intensity at the cloud interface in the region where [C ii] peaks. Unfortunately, the data quality does not allow us to determine whether there is any relative offset between the two fine-structure line peaks in that region.
 |
Fig. 4 Integrated intensity map of CO 16−15 with contours of CO 13−12 drawn at levels of 10, 20, 30, 40, 50, 60, and 70 K km s-1. Only the region around IRS 1 has been observed in CO 16−15; in CO 13−12 only two outer strips have been covered avoiding the center. The black marks indicate the positions of IRS 1-3. |
Figure 4 shows the integrated intensities of the CO 13−12 and 16−15 lines. Unfortunately, only complementary regions were mapped in the two lines with narrow overlapping strips. Therefore, the CO 13−12 observations are barely useful for understanding the nature of the peak seen in the fine-structure lines. We see, however, that both high-J CO lines show a more extended emission around the central sources compared to the fine-structure lines. The CO 16−15 peak falls between IRS 1 and IRS 2, i.e. we see a superposition of hot CO emission from both IRS 1 and from the fine-structure line peak close to IRS 2. The high-J CO lines trace both components in a similar way; they show an intermediate behavior between the fine-structure lines and the low-J CO.
3.1. Line profiles
In all the published maps of S 140 only the 13CO 1−0 line peak intensity has a global maximum close to IRS 2 like the fine-structure lines3. To understand the nature of the fine-structure line peak it is, therefore, worth comparing our observations with the 13CO 1−0 data more carefully, including the velocity structure. The 13CO 1−0 line is optically thin over most parts of the map. Koumpia et al. (2015) measured optical depth values of about 0.3 for most of the gas and a maximum value of 0.8, which is still marginally optically thin. Figure 5 compares the distribution of the peak intensity, the mean line velocity, and the line width of the 13CO 1−0 line with the corresponding parameters from the [C ii] line.
The relative proximity of the 13CO 1−0 peak and the [C ii] and [O i] peaks seem to be accidental as the overall morphology of the line maps shows no other similarities. The 13CO 1−0 emission is much more extended and has about the same level at the positions of IRS 2 and IRS 1. When inspecting the 13CO 1−0 integrated intensity, we find the same behavior as seen in the other molecular line tracers with a maximum close to IRS 1. A second similarity in the peak intensities of 13CO 1−0 and [C ii] are the relatively low values south of IRS 1. The spot matches the southern part of the molecular outflow discussed by e.g. Maud et al. (2013). The outflow is driven from IRS 1 pointing towards the northwest and southeast, leading to the velocity gradient seen, for example, in the 13CO 1−0 line position map around IRS 1. At the location of the southern outflow [C ii] is hardly present at all, but the 13CO 1−0 line is prominent, tracing the outflow through broad line wings (see Fig. 5c) that lead to a large integrated intensity there in spite of the lower peak intensity.
 |
Fig. 5 Peak intensity, first moment (centroid velocity), and second moment (translated to FWHM) of the lines of 13CO 1−0 (colors) and [C ii] contours. The black marks indicate the positions of IRS 1-3. The contour levels for the [C ii] peak intensity match those from Fig. 2; for the line position they are given at −9.5, −8.5, −7.5, and −6.5 km s-1, and for the line width at 3, 4, 5, and 6 km s-1. Velocities are given in LSR (local standard of rest) and intensities in main beam temperatures. |
The [C ii] line shows the largest line width northwest of IRS 1, in the direction of the northern outflow, but only a moderate line width at the location of the intensity peak close to IRS 2. We find a trend of anti-correlation between the [C ii] lines and the 13CO 1−0 lines. The 13CO 1−0 lines are broad in a ridge southeast and northeast of the cluster that is associated with low center velocities while [C ii] shows the broadest lines west of the cluster. Except for the southern outflow region and the northeastern boundary of the map, the [C ii] profiles are always somewhat broader than the 13CO 1−0 profiles. We interpret this as being due to optical depth broadening (see below).
When inspecting the line positions, the 13CO 1−0 profiles are dominated by the outflow pattern with slightly blueshifted velocities southeast of IRS 1 and redshifted velocities in the opposite direction4. Overall, the variations are relatively small. In contrast, [C ii] shows a clear offset in the line velocity for the bright emission component close to IRS 2. While in most of the map the [C ii] line has the same velocity (about −8 km s-1) as the bulk of the 13CO gas, the peak source has a significantly lower velocity (about −6.5 km s-1). This indicates that the bright emission source is only weakly associated with the rest of the gas and is not seen in 13CO.
 |
Fig. 6 Line profiles of the [C ii], [O i], CO 16−15, CO 2−1, C18O 1−0, and 13CO 1−0 lines at the position of the [O i] peak (0, 20 close to IRS 2), at IRS 1 (0, 0), and at the interface (−40, −54). The lines are averaged in a Gaussian beam of 17.3′′ FWHM (telescope + convolution kernel) except for the 13CO and C18O lines that can only be treated at the lower resolution of 23′′. |
Figure 6 shows the line profiles of [C ii], [O i], CO 16−15, CO 2−1, C18O 1−0, and 13CO 1−0 at the location of the fine-structure line peak close to IRS 2, at the position of the main heating source IRS 1, and at the external cloud interface. All lines trace the interface at a velocity of about −8 km s-1. The [O i] line is only marginally detected there; [C ii] and the CO lines are narrow with a width of 3−4 km s-1. The velocity of this PDR surface is slightly different from the large-scale velocity field of the thin surrounding medium which is measured through the broad H i line in the 36′ beam of the Leiden/Dwingeloo survey and peaks at −7 km s-1 (Kalberla et al. 2005).
Towards IRS 2, [C ii] peaks at −6.5 km s-1, offset in velocity from the bulk of the gas, as seen already in Fig. 5. The [O i] line shows a dip at this velocity and two peaks at the velocities of −5.5 km s-1 and −8 km s-1 coinciding with the peak velocities seen in CO 2−1 towards IRS 2 and towards the interface. However, as there is only weak [O i] emission from the interface, we think that the coincidence between [O i] and CO 2−1 is accidental and that in [O i] we see the same material that we trace in [C ii]. Consequently, [O i] exhibits a self-absorption dip at the velocity of the [C ii] peak instead of two velocity components.
CO 2−1 traces mainly other gas. We find broad outflow wings from the molecular outflow (Maud et al. 2013), only seen in the low-J CO lines. The optically thin lines of CO 16−15 and 13CO 1−0 are narrow at the peak suggesting that even the [C ii] line is broadened by a significant optical depth. The comparison of the fine-structure lines and CO 16−15 at IRS 1 shows that [C ii] only traces the velocity component matching the interface velocity there, but no emission at −6 km s-1, while CO 16−15 and [O i] show a stronger emission in the −6 km s-1 component and a weaker emission with the interface velocity there. This means that we find several gas components with different velocities and chemical properties towards IRS 1.
 |
Fig. 7 Baseline of the [C ii] profiles showing the hyperfine components of the [13C ii] transitions. The upper plot shows the sum spectrum from all spectra with integrated intensities above 100 K km s-1 from the IRS 1-3 region, the lower plot from the interface region. The blue lines represent the same spectra scaled by an abundance ratio of 1/67 and the corresponding line ratio and frequency of the three hyperfine transitions, i.e. they represent the spectrum that we expect in the case of an optically thin [C ii] line. |
To estimate the optical depth of the [C ii] line, based on the line profiles, we can use two approaches: deriving the optical-depth line broadening by comparing the line width with an optically thin tracer, and comparing the line intensity with an optically thin tracer not affected by abundance or excitation uncertainties, namely the [13C ii] transitions. In the first approach, we assume a Gaussian velocity dispersion and obtain the optical depth at the line peak from the measured line broadening 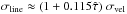 , where
, where 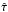 is the line-center optical depth (Phillips et al. 1979; Ossenkopf et al. 2013). Using the optically thin 13CO 1−0 to measure the true velocity dispersion, we can translate Fig. 5c into a [C ii] optical depth map, except for the region south of IRS 1 where the 13CO 1−0 line is broader than [C ii] owing to the molecular outflow. For the interface, we obtain a 13CO 1−0 line width of 3 km s-1 and a [C ii] line width of 4 km s-1; in the region between IRS 1 and IRS 2 the line widths are 5 and 6 km s-1, respectively. This translates into [C ii] peak optical depth values of 3 towards the interface and 2 towards the central cluster.
is the line-center optical depth (Phillips et al. 1979; Ossenkopf et al. 2013). Using the optically thin 13CO 1−0 to measure the true velocity dispersion, we can translate Fig. 5c into a [C ii] optical depth map, except for the region south of IRS 1 where the 13CO 1−0 line is broader than [C ii] owing to the molecular outflow. For the interface, we obtain a 13CO 1−0 line width of 3 km s-1 and a [C ii] line width of 4 km s-1; in the region between IRS 1 and IRS 2 the line widths are 5 and 6 km s-1, respectively. This translates into [C ii] peak optical depth values of 3 towards the interface and 2 towards the central cluster.
Figure 7 shows the corresponding [13C ii] spectra measured in the two regions. They are compared with a scaled version of the [C ii] line, reduced in intensity by the typical 13C/12C abundance ratio of 1/67 in the solar neighborhood (Langer & Penzias 1990, 1993) and the relative weights of the hyperfine components (0.625 at 11 km s-1, 0.25 at −65 km s-1, 0.125 at 63 km s-1 relative to [C ii], Ossenkopf et al. 2013). Towards the interface the two stronger hyperfine components are clearly detected. The peak intensity of the [13C ii] is 3.1 times higher than expected from the [C ii] line when assuming optically thin [C ii] emission. This can be translated into a line-center optical depth of about 3. Towards the embedded cluster, the strongest component appears as a shoulder of the broader [C ii] line and the two weaker components are barely visible. The factor of 2.2 difference between observed intensity and scaled optically thin [C ii] emission is also in agreement with a line-center optical depth of 2 as measured from the line broadening. Both approaches, therefore provide matching results for the [C ii] optical depth towards the two peaks of [C ii] emission.
 |
Fig. 8 Line profiles of the [C ii], [O i], CO 2−1, CO 16−15, and 13CO 1−0 lines at the position of the [O i] peak (0, 20). The lines were scaled to similar intensities at −4 km s-1. For CO 2−1, a constant emission of 20 K is subtracted to exclude the extended outflow emission. |
To resolve the intrinsic velocity profile of the main emission source at IRS 2 we compare scaled versions of the different profiles towards this source in Fig. 8. The scaling factors in the plot were adjusted for a better comparison of the red wings of the profiles at sufficiently high velocities which are not affected by self-absorption or saturation from high optical depths. For CO 2−1 we also had to subtract the very extended outflow contribution (see Fig. 6). The C18O 1−0 line is not shown here as it matches almost exactly the shape of the CO 16−15 line. A comparison of the blue wing of the profiles provides no information on the source at IRS 2 as this velocity interval is heavily affected by emission and absorption from the bulk of the gas in S 140 at −8 km s-1.
We find an almost perfect match of the red wing shape of the three (partially) optically thick lines of [C ii], [O i], and CO 2−1. In contrast, the thin lines of 13CO 1−0 and CO 16−15 are clearly narrower, not allowing a fit with the same wing. Optical depth broadening of the lines must play a significant role. The peak of the CO 16−15 line coincides with the absorption dip seen in [O i] and CO 2−1. The narrow shape of the peak of the CO 2−1 line at −4.7 km s-1 results from this absorption out of a broader emission component. The shoulder seen in the 13CO 1−0 and CO 2−1 lines at −8 km s-1 probably traces emission from IRS 1 or the extended molecular cloud material. Overall, the lines are consistent with the velocity dispersion as measured by the CO 16−15 and C18O 1−0 lines of only 2.4 km s-1 (FWHM), but an optical-depth broadening of the fine-structure lines.
For the optically thick lines, the intrinsic line intensity from the emission peak therefore should be higher than our observed integrated intensity. For [C ii], the profiles are consistent with the optical depth of about 2, leading to a 45% reduction of the integrated line intensity compared to optically thin emission. For [O i], we see, however, a clear self-absorption signature due to gas in the foreground with lower excitation temperature. That makes an estimate of the intrinsic intensity from the emission peak difficult. If we assume that the red wing is not affected by self-absorption, we can use the ratio of the integrated line intensity between [C ii] and [O i] seen in Fig. 8 as an estimate for the missing flux in the [O i] line. This indicates that the source intrinsic line flux should be higher by about 50% without foreground absorption.
From the information given in the line profiles we can already conclude that the [O i] and [C ii] emission does not seem to be related to the known outflow activity in S 140; instead it probably traces PDR interfaces. While [C ii] and [O i] are both bright at IRS 2, only [C ii] is bright at the cloud surface and [O i] is barely detected there. As the [O i] line has a critical density of 5 × 105 cm-3 (Jaquet et al. 1992, see Table 1), 100 times the critical density of the [C ii] line, this probably reflects the lower density of the interface region. In contrast, at the fine-structure line peak position, the gas must be dense and optically thick for [O i] so that the same material produces an almost Gaussian line in [C ii] and a double-peaked line in [O i]. The optically very thick CO 2−1 line only reveals a prominent redshifted wing towards IRS 2. This would be consistent with an expansion scenario of the source.
4. Properties of the gas
4.1. Gas parameters across the GREAT map
 |
Fig. 9 CO column density (upper plot: colors), gas density (lower plot: colors), and kinetic temperature (both plots: contours) derived from the RADEX fit of the integrated intensities of the observed lines of CO 1−0, 2−1, and 16−15 and the isotopologues 13CO 1−0 and C18O 1−0. |
As a first step to understanding the nature of the fine-structure lines we need to know the properties of the gas across the map. This can be done by analyzing the molecular lines of CO and its isotopologues based on our high-J CO observations and the complementary low-J CO, 13CO, and C18O IRAM data from Koumpia et al. (2015). When we know the column density, the volume density, and kinetic temperature of the gas we can compute column density maps of [C ii] and [O i] from the measured fine-structure line intensities.
We performed a fit of the CO (and isotopologues) line intensities using the non-LTE radiative transfer code RADEX (van der Tak et al. 2007) that computes the line intensities of a molecule for a set of physical parameters: kinetic temperature, H2 gas density, molecular column density, background temperature, and line width. We used the maps of CO 1−0, 2−1, 13CO 1−0, C18O 1−0, and CO 16−15 to perform a χ2 minimization fit for a range of kinetic temperatures (30−700 K), column densities (1017−4 × 1019 cm-2), and volume H2 densities (105−5 × 1010 cm-3). In the area covered by the CO 16−15 map we have enough observational constraints to determine those three free fitting parameters. For all calculations we used a fixed line width value of 3.5 km s-1. We adopted a cosmic background radiation field of 2.73 K and used the molecular data from the LAMDA database (Schöier et al. 2005).
Figure 9 shows the resulting distributions of the gas temperature, density, and column density of CO. As the CO 16−15 line has an upper level energy of 750 K and a critical density of 106 cm-3 (see Table 1), one would expect that the strong line drives the solution to high temperatures and densities on the order of the value of the critical density. However, it turns out that the low-J lines can only be fitted with lower temperatures. To excite the CO 16−15 line, RADEX then has to increase the gas density to values on the order of 108 cm-3, a value much higher than derived in all other ways. This is a strong indication that the assumption of uniform gas parameters within the individual pixels of our map is not justified in S 140. It is much more likely that the true gas composition consists of a cooler component, mainly traced by the low-J CO (and isotopologues) lines, while a second hot component is responsible for the CO 16−15 line.
As all other lines discussed here are insensitive to gas densities above 106 cm-3, the overestimate of the gas density obtained in this way should be irrelevant for the further analysis. The RADEX fit shows that the gas temperature peaks between IRS 1 and IRS 2, roughly matching the CO 16−15 intensity map. The density structure shows a density peak at the positions of IRS 1 and IRS 2. The column density mainly follows the distribution of the isotopologues which is higher towards the west region of the sources. It roughly matches the column density structure that was determined from FORCAST, PACS, and SCUBA dust observations in Koumpia et al. (2015). They also found a column density peak about 20′′ west of IRS 1 and IRS 2 and a smaller peak somewhat east of IRS 2.
The CO column densities can be translated into abundances if we know the gas column from the dust observations of the central region. To derive gas column densities from the 100μm dust opacity map, we use the dust properties of model 5 from Ossenkopf & Henning (1994) following the discussion in Koumpia et al. (2015) and the standard conversion factor of NH/AV = 1.9 × 1021 cm-2 (Bohlin et al. 1978). This provides a 100 μm optical depth of 1.30 × 10-24 cm2 × (NH + 2NH2). The resulting column density map is shown in Fig. 10.
The contours in the figure give the CO abundance computed by dividing the CO column from Fig. 9 by the dust-based gas column density. For most of the cloud we find values of X(CO)= NCO/ (NH + 2NH2) around 2−3 × 10-4. Lower values of about 1 × 10-4 are found at the submm-peak west of IRS 1. Somewhat lower values are also found towards IRS 2 and somewhat higher values occur at the positions of IRS 1 and IRS 3. A reduction of the CO abundance towards IRS 2 would be consistent with the conversion of molecular material to atomic and ionized material seen in the bright fine-structure lines. The stronger decrease towards the submm peak could indicate CO freeze-out in very cold and dense material, but overall, the abundance variations within the map are about as large as the uncertainty from the dust column5.
 |
Fig. 10 Column density map of gas derived from FORCAST, PACS, and SCUBA continuum observations in the center of the region (colors), overlaid by contours of the CO abundance, running from 1 × 10-4 to 3 × 10-4. |
A CO abundance of more than 2 × 10-4 would actually exceed the total amount of carbon available in the gas phase (see e.g. Cardelli et al. 1993). Blake et al. (1987) measured values X(CO) of only 6 × 10-5 towards the dense molecular material in the Orion molecular cloud and 2.5−3 × 10-5 in several clouds on larger scales, probably involving more atomic and ionized carbon. A higher CO abundance of 1.3 × 10-4 has been measured towards NGC 2024 by Lacy et al. (1994). Our systematically higher abundances can be explained by the uncertainty of the dust properties covering a factor of 2−3 in the 100 μm opacity (Ossenkopf & Henning 1994). When assuming a dust model with a 100 μm opacity that is two times lower, the columns in Fig. 10 increase by a factor of two, the abundance values decrease by the same factor, and we obtain values close to those from Lacy et al. (1994). Unfortunately, the resolution of the low-J CO maps is insufficient to determine the gas column density with the same resolution as the dust opacity. Hence, we can only conclude that the CO column densities are close to the upper edge of the range expected from the dust column densities. This means that most of the gas must be molecular so that we can use CO as a proxy for the total gas column in S140. This is consistent with the strong spatial confinement of the fine-structure line emission in S140 indicating that CO provides a reasonable measure for the total gas column density, even if not all gas is molecular. Assuming X(CO)= 1.3 × 10-4 we obtain hydrogen column densities NH = NH + 2NH2 between 7 × 1022 cm-2 and 1.97 × 1023 cm-2 within the map covered by the CO 16−15 observations.
 |
Fig. 11 Column density map of C+ derived from the measured [C ii] intensities using the gas parameters from the RADEX fit to the CO lines. The contours show the [C ii] line optical depth a levels of τ = 0.5,1.0,1.5,2.0. In the two pixels north of IRS 2, the optical depth is too large for a reliable column density estimate. |
 |
Fig. 12 Column density map of atomic oxygen derived from the measured [O i] intensities using the gas parameters from the RADEX fit to the CO lines. The contours show the [O i] line optical depth at levels of τ = 0.05,0.10,0.15,0.20. |
In the next step we can use the kinetic temperature and volume density from the RADEX fit of the CO lines (Fig. 9) to compute the C+ and atomic oxygen column densities from the [C ii] and [O i] observations. This allows us to compare the abundance of the different species in the gas within the telescope beam along the line of sight. Actually, we do not expect that all species are spatially co-existing − we expect instead abundance gradients along the path and within the area of the beam − but the volume-integrated abundances can be easily compared with the results from more complex models and other Galactic and extragalactic observations. The CO 16−15 line provides strong constraints on the parameters derived from the RADEX fit and it mainly stems from hot and dense gas, the same gas that should also provide the main contribution to the fine-structure line emission. Therefore, the error made in assuming the same excitation conditions as seen by CO for deriving the C+ and oxygen column densities should be smaller than the factor of two uncertainty that we already find for the gas column. To be consistent with the RADEX fit, we restrict the integration to the same velocity interval from −8.4 to −4.4 km s-1. Figures 11 and 12 show the resulting column densities and the optical depths of the lines. Although the line profiles of [O i] indicate optically thick line (Fig. 6), our resulting optical depths are τ< 1. This is probably due to the strong self-absorption in the line creating an intensity dip for the considered velocity range, leading to column densities and optical depths that are too low. The [C ii] analysis results in a column density range of 2.2 × 1017−2 × 1018 cm-3 and a range of optical depths 0.28−2.31 with the higher values closer to IRS 2 in agreement with the estimate from the line profile in Sect. 3.1.
With the hydrogen column densities from CO, the C+ column density map translates into C+/H abundances, X(C+), between 1.1 × 10-5 around the fine-structure line peak and 2−3 × 10-6 for the rest of the map. For the oxygen abundance, we find values between 4 × 10-5 around IRS 2 and 1.0−1.5 × 10-5 for the rest of the map. For both species the abundance at IRS 1 is as low as in the rest of the map outside of the fine-structure line emission peak.
These values can be compared to PDR models (Röllig et al. 2007). At a PDR surface, almost all carbon is in the form of C+. For diffuse clouds, Sofia et al. (2004) measured a C+ abundance of X(C+) = 1.6 × 10-4, but in dense regions a larger fraction of carbon is incorporated in dust and PAHs leading to a PDR surface abundance of X(C+) = 1.2 × 10-4 in dense clouds (Wakelam & Herbst 2008). Deeper in the clouds where the UV is sufficiently shielded, C+ turns into atomic carbon and subsequently into CO, so that the C+ abundance falls by three to four orders of magnitude, depending on the cosmic ray ionization rate. Even our value for IRS 2 falls far below the PDR surface limit, confirming that carbon is ionized through UV radiation only in a small gas fraction, while most of the gas is molecular. The column of molecular material should be at least ten times deeper than the C+ column produced in a PDR around IRS 2.
Depending on the local conditions the oxygen abundance in dense clouds should not vary by more than a factor of three. In the high-UV field limit, almost all gas-phase oxygen is in atomic oxygen, resulting in an abundance of X(O)= 3 × 10-4 relative to hydrogen. Deep in molecular clouds, most oxygen is incorporated in CO so that only X(O)= 1 × 10-4 is left in the gas phase. Our measured abundance still falls below this lower limit. This can be explained by the fact that most oxygen is probably at temperatures below the range of 50−70 K fitted by RADEX for a homogeneous gas. The colder oxygen does not contribute to the fitted emission, but rather creates the absorption seen in our [O i] line profiles.
4.2. The [C II] and [O I] peak
 |
Fig. 13 Intensity map of [O i] (top), [C ii] (center), and CO 16−15 (bottom) after subtracting a Gaussian intensity distribution of FWHM = 8.3′′ from the observed map. The overlaid contours show the original intensity maps at levels of 8, 24, 40, 56, and 72 K km s-1 ([O i]); 50, 70, 90, 120, 150, and 180 K km s-1 (CII); and 10, 20, 30, 40, 50, and 60 K (CO 16−15). |
To estimate the size of the region responsible for the fine-structure line emission peak, we fitted the observed [O i] integrated intensity map by a Gaussian intensity distribution peaking close to IRS 2 convolved with the telescope beam at 4.7 THz. The [O i] map provides the main constraint to the source size due to the smaller beam compared to [C ii] and the CO lines. We allowed for a 2 arcsec pointing jitter in the fit when adjusting the location of the peak. The best fit leading to a relatively smooth background after the source subtraction is obtained for a source FWHM of 8.3′′ and a peak intensity of 76 K km s-1. Figure 13 (top panel) shows the result. We see that the subtracted source covered 80 % of the intensity at the position of the peak, but that there remains a somewhat more extended emission structure north of IRS 1. IRS 1 is part of that structure, but shows no concentrated [O i] emission associated with the infrared source. In contrast, we find a secondary [O i] peak slightly north of IRS 3, the weakest infrared source in the field.
A priori, the spatial extent of the emission in [O i] and [C ii] can be different, but if we subtract a source with the same size and the peak intensity of 212 K km s-1 from the [C ii] map we also obtain a very smooth map with no further indications of the IRS 2 contribution (Fig. 13, central panel). This suggests that we see about the same gas responsible for the peak in [O i] and [C ii] spatially well confined to a region close to IRS 2. Repeating the same experiment for the CO 16−15 map, provides a peak intensity of 46 K km s-1, but a clear residual of emission from IRS 1 and IRS 3 (Fig. 13, bottom panel). This agrees with the previous analysis of Koumpia et al. (2015) finding extended hot molecular gas around IRS 1.
The identification of a spatially well-confined emission structure close to IRS 2, responsible for the observed strong fine-structure line emission allows the properties of the emitting gas to be quantified. With an FWHM of 8.3′′ we obtain a spatial angle of the emitting region of 1.8 × 10-9 sr and a diameter of 0.03 pc. This allows absolute luminosities to be computed from the integrated intensities and the source projected area of 1.0 × 1034 cm2 assuming isotropic radiation. For the [O i] line we obtain 0.28 L⊙ and for the [C ii] line 0.05 L⊙. This can be compared to the total energy input at that location. Koumpia et al. (2015) estimated a total luminosity of the source at IRS 2 of 2000 L⊙. This means that only 0.016% of the source luminosity is radiated away in the two fine-structure cooling lines. We will discuss this further in Sect. 4.4.
For the CO 16−15 line we obtain a corresponding luminosity of only 0.01 L⊙, but over the full CO ladder this will add up to a considerable net cooling. If we make the extremely conservative assumption that all CO line intensities are constant at the value of the 16−15 transition for lower J transitions and zero for higher transitions, we obtain a lower limit for the CO cooling luminosity of 0.045 L⊙ already matching the [C ii] luminosity. If we use the full SED ladder fit to the narrowest line component from Sect. 4.3, we obtain instead a cooling power of 0.096 L⊙ and if we include the emission over the total line width, the CO luminosity totals 0.13 L⊙, i.e. a value that is about half the cooling power in the [O i] line. In spite of the prominent fine-structure line peak at IRS 2, we thus find a situation where the molecular line cooling is also important besides the dominant fine-structure line cooling. This is similar to the situation found in other protostars (Karska et al. 2013). Obviously, the situation is even more extreme for IRS1, where we measure strong high-J CO emission, but basically no [C ii].
We can estimate the gas column density from the integrated [C ii] line intensity, by using the relatively constant [C ii] emissivity per column density (Eq. (2) from Ossenkopf et al. 2013). For a temperature of about 200 K we obtain 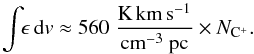 (1)As the emissivity is only weakly temperature-dependent, this value applies within a 15% error bar to all excitation temperatures between 100 K and 500 K, covering the typical range expected in PDRs. Equation (1) provides a direct translation of intensity to column density for optically thin emission. Because we know the optical depth from Sect. 3.1, the equation can also be used with the corresponding optical depth correction of 45% to compute the C+ column density for IRS 2.
(1)As the emissivity is only weakly temperature-dependent, this value applies within a 15% error bar to all excitation temperatures between 100 K and 500 K, covering the typical range expected in PDRs. Equation (1) provides a direct translation of intensity to column density for optically thin emission. Because we know the optical depth from Sect. 3.1, the equation can also be used with the corresponding optical depth correction of 45% to compute the C+ column density for IRS 2.
We obtain a C+ column density of 1.7 × 1018 cm-2. This is slightly lower than the value of 2 × 1018 cm-2 obtained for the total [C ii] emission towards IRS 2 measured in the RADEX simulation for the full map in Sect. 4.1. However, here we consider only the 73% of the [C ii] emission at that position that is attributed to the compact source. In this way we ignore a small part of the total column density. Using the carbon gas-phase abundance of 1.2 × 10-4 for dense clouds (Wakelam & Herbst 2008) (see Sect. 4.1) and assuming that all carbon is ionized, the C+ column density of 1.7 × 1018 cm-2 provides a lower limit for the total column density of the [C ii] emitting gas of 1.4 × 1022 cm-2. Higher values result for partial ionization. If we assume that the [C ii]-emitting gas fills the observed emitting volume of 1.0 × 1051 cm3, we deduce a minimum gas density of 1.4 × 105 cm-3. The derived optical depth of the clump seen in dust emission close to IRS 2 is, however, AV ≈ 100 (Koumpia et al. 2015) corresponding to gas column densities of 2 × 1023 cm-2, which means that only 7% of the gas is emitting in [C ii]. This could be explained by clumpiness of the gas within the 8.3′′ peak and high-density clumps, or more naturally by a PDR layering structure where the [C ii] emission only stems from gas with AV ≲ 2 facing the embedded sources.
Unfortunately, it is not possible to perform the same estimate for the [O i] emission. The high-temperature LTE limit of the [O i] emissivity is about three times higher than the corresponding [C ii] emissivity (Eq. (1)), but it only applies to densities above 106 cm-3 and temperatures above 200 K, and it also requires optically thin emission or an accurate estimate. The line profiles have already shown that [O i] is optically very thick and the intensity of the [O i] line is three times lower than that of [C ii]. To check the consistency of the parameters in the frame of a real radiative transfer computation we perform RADEX runs in the next section.
4.3. RADEX fit of individual sources
Line parameters of the narrow component of CO and isotopologues towards IRS 1 and IRS 2 (GREAT, IRAM, and HIFI data).
A more accurate estimate can be obtained when using the known gas parameters from a fit to the observed CO transitions and taking the line optical depth into account in the frame of a RADEX computation. As all lines are bright towards the central sources, IRS 1 (0, 0) and IRS 2 (0, 20), we can avoid the low-J CO lines there that show complex line profiles and are very optically thick and we fit only the higher transitions of CO and all available transitions of the isotopologues in RADEX. For the interface (−40, 54), the RADEX analysis was already performed in Koumpia et al. (2015) using the low-J CO lines and an additional HIFI cut measuring CO 9−8 and 13CO 10−9. As our CO 16−15 observations do not cover this region, no further constraints are provided to the fit so that we can reuse the results obtained there. The HIFI cut also covered IRS 1 so that we have the most complete data set for this source. Table 2 contains all transitions and line properties that were used for the RADEX fit and the further analysis.
 |
Fig. 14 CO ladder from the RADEX fit to the line intensities at the three prominent positions. |
Figure 14 shows the resulting CO SED from the RADEX fit for all lines up to J = 17−16 and Table 3 summarizes the resulting gas parameters. In the fourth column, we translated the CO column density into an equivalent hydrogen column density using the abundance factor of 6 × 10-5 from Sect. 4.1. The higher column density towards IRS 2 compared to that of IRS 1 is driven by the spatial distribution of the low-J CO isotopologues and the high-J CO that is stronger towards IRS 2 (see Fig. 6). The hydrogen column densities towards the two sources approximately match the visual extinction of AV ≈ 50 towards IRS 1, and AV ≈ 100 towards IRS 2 measured by Koumpia et al. (2015) when assuming a standard conversion factor of NH/AV = 1.9 × 1021 cm-2 (Bohlin et al. 1978).
The IRS 1 and IRS 2 are warmer than the interface and have a similar temperature. The absolute value of the temperature is, however, questionable as it depends on the assumption of the uniform gas parameters within the beam. As discussed already in Sect. 4.1, this leads to very high densities. The volume density estimates for IRS 1 and IRS 2 are much higher than the ones found in Koumpia et al. (2015) (~106 cm-3) owing to the inclusion of the high-J CO transitions in the fit (13−12, 16−15). We instead expect that the different transitions arise from different layers around the infrared sources. The fit produces a good match to all observed lines, so that we have an accurate estimate of the total cooling through all CO lines from the observed sources.
Physical conditions as derived with RADEX for selected positions.
We use the RADEX gas parameters again to compute the C+ and oxygen column density from the line intensities given in Table 2. For IRS 1, we get column densities for C+ and O of 7 × 1017 cm-2 and 1.8 × 1018 cm-2, respectively, for IRS 2 5 × 1018 cm-2 cm-2 and 6 × 1018 cm-2 cm-2. When comparing these values with the map analysis, we notice that the C+ column density towards IRS 2 is increased by a factor of two because we use the full line width and extract the intensity exactly at the position of the fine-structure line peak. All other values are basically unchanged. At the interface, we obtain a C+ column density of 5 × 1018 cm-2 and an oxygen column density of 3 × 1019 cm-2. We can compare these values with the column density that we obtain from the total gas column density measured by CO and the upper limits of the abundance of the two species discussed in Sect. 4.1. In this way we obtain column densities of N(C+) = 2 × 1018 cm-2 and N(O)= 5 × 1018 cm-2, i.e. much lower than computed here. The explanation must be given by the PDR nature of the cloud interface. As most CO is dissociated there, it is no longer a good measure for the total column density. The actual column density must be at least a factor of six higher when using the gas temperature obtained from CO.
4.4. Cooling balance
The ratio of the energy emitted by the interstellar gas in the two main far-infrared cooling lines ([O i] and [C ii]) relative to the integrated far-infrared continuum emitted by the dust can be used to estimate the gas-heating efficiency when assuming that the far-infrared flux reflects the total energy of the incident stellar radiation field by converting it to infrared-wavelengths through absorption and re-emission in an optically thick medium (see e.g. Okada et al. 2013). As access to the [O i] line became possible only very recently, the [C ii]/FIR intensity ratio is often used to measure the efficiency of the gas heating. This allows variations in the efficiency of the photoelectric heating from dust grains to be addressed because photoelectric heating is the most important gas heating process in PDRs (Hollenbach & Tielens 1999).
Although the definition of the far-infrared varies between different papers (e.g. as FIR integrated from 42 to 122 μm, or as TIR integrated from 3 to 1100 μm; Dale & Helou 2002), the typical range of the gas heating efficiency in Galactic PDRs, star-forming regions in LMC, and M33 is 10-3−10-2 both when being traced by [O i]+[C ii] (Okada et al. 2013; Lebouteiller et al. 2012; Mookerjea et al. 2011; Mizutani et al. 2004) and when traced only by [C ii] (Okada et al. 2015; Lebouteiller et al. 2012; Mookerjea et al. 2011). As an extreme case, Vastel et al. (2001) found an efficiency of 10-4 in W49N, which is illuminated by an intense UV field.
 |
Fig. 15 Comparison of the line cooling with the infrared continuum cooling. The background colors show the total infrared flux integrated from wavelengths starting at 11 μm (Koumpia et al. 2015). The contours give the decadic logarithm of the ratio of the integrated line flux relative to the continuum flux. In the top panel we use the sum of the [O i] and [C ii] fluxes, in the lower panel, we only show the [C ii]/TIR ratio as used in many existing investigations. |
For the region around the embedded sources, the far-infrared luminosity was derived from PACS and SOFIA-FORECAST observations by Koumpia et al. (2015). It was integrated from the observed intensities between 11 and 187 μm further extrapolated linearly to zero flux levels at longer wavelengths. Figure 15 compares the energy radiated in our fine-structure lines with the total infrared flux (λ> 11 μm) at the resolution of 13′′ from the PACS continuum data6. In the background we see the infrared flux from the three embedded sources with luminosities of 10 000 L⊙ (IRS 1), 2000 L⊙ (IRS 2), and 1300 L⊙ (IRS 3) (Koumpia et al. 2015). The contours show the ratio of the sum of the [O i] and [C ii] fluxes relative to the total infrared (upper plot) and the [C ii] line only (lower plot) in logarithmic units.
The [C ii]/TIR ratio shows an almost spherically symmetric picture around IRS 1, being dominated by the variation of the infrared continuum flux. The values of 10-3−10-2, typically observed in other Galactic PDRs, are only seen at the southwestern edge of the mapped area closest to the illumination by HD 211880. Around the embedded sources, the infrared luminosity grows without a corresponding growth of the fine-structure line luminosity resulting in [C ii]/TIR ratios below 10-5 close to IRS 1. The fine-structure peak at IRS 2 only weakens this global scenario slightly, resulting in a “dip” in the contours next to IRS 2.
When including the [O i] line in the comparison, the ratio increases by a factor of three close to the sources and the fine-structure line peak close to IRS 2 creates a plateau in the energy ratio of about 2 × 10-4 in agreement with the results obtained in Sect. 4.2. At lower densities towards the map boundaries the [O i] contribution is negligible. For IRS 1, even the cooling through the lines of the CO ladder is four times stronger than the sum of the [C ii] and [O i] cooling power (see Fig. 14), for IRS 2 CO sums up to half of the fine-structure line cooling. Including the CO rotational ladder in the gas cooling budget raises the line-to-continuum ratio to 1−3 × 10-4, i.e. values that are still extremely small in the Galactic context and that would be interpreted as FIR line deficit when observed in external galaxies (e.g. Luhman et al. 1998; Malhotra et al. 2001; Herrera-Camus et al. 2015). However, none of the proposed explanations for the FIR line deficit in external galaxies applies to our case (see Sect. 5).
 |
Fig. 16 Comparison of the total line cooling flux provided by the sum of the [O i] and [C ii] lines (colors) to the [O i]/[C ii] line flux ratio (contours from 0.4 to 2.8 in steps of 0.4). The computation is performed in a common effective beam of 15′′. |
The ratio between the [O i] and [C ii] intensities is considered as one of the main characteristics of PDRs. For high UV fields, the gas temperature is always above the upper level energy of both transitions so that the ratio between the two lines directly measures the density (Kaufman et al. 1999). However, owing to the higher energy of the [O i] transition, it falls off quite quickly at low UV fields resulting in negligible [O i] cooling for low densities and UV fields (Röllig et al. 2006).
As already seen in Fig. 15, the relative contribution of [O i] and [C ii] to the cooling changes significantly over the cloud. Figure 16 shows the total line cooling budget of the [O i] and [C ii] lines in colors and the [O i]/[C ii] line ratio in contours. We find a relatively constant ratio of 2.5−3 in the whole area of the central cluster connecting IRS 1 and IRS 2. Here, [O i] dominates the gas cooling. A value of 3 is representative of either very high UV fields and low densities or low UV fields and very high densities. For the high densities and UV fields around the central cluster, we would, however, expect much higher values as a result of the high abundance and emissivity of oxygen in that regime.
When leaving the area of the central cluster, the contribution of [O i] to the total line cooling budget quickly drops off. This should reflect a combination of a reduced density and temperature as measured by CO (Fig. 9). While the density drops more quickly south of IRS 1, the temperature drops more quickly north of IRS 2. The asymmetry of the [O i]/[C ii] ratio plot indicates that the density is the dominating factor here. In the bulk of the cloud and the interface, the cooling strength of the [O i] line can be completely neglected. [C ii] is the only relevant gas cooling line xxx there.
4.5. PDR model interpretation
To overcome the RADEX assumption of constant excitation conditions within the emitting region as an oversimplification we switch to theoretical models for PDR structures that self-consistently compute the temperature and chemical structure of PDR layers around illuminating sources, allowing us to compare the line observations with the model predictions for different densities and radiation fields.
One critical input parameter is the strength of the impinging UV radiation field. It can be computed by assuming that in an optically thick configuration all UV photons are eventually converted into observable infrared photons. Then we obtain the strength of the incident radiation field in terms of the Draine field (Draine 1978) as 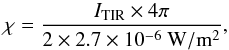 (2)where the factor of 2 in the denominator accounts for half of the heating photons at wavelengths out of the UV band (e.g. Röllig et al. 2011). Using the total infrared flux values from Sect. 4.4 results in χ = 5.6 × 104χ0 for IRS 2 and 1.2 × 105χ0 for IRS 1. For the interface, the UV field was derived previously to fall between 140 χ0 (Poelman & Spaans 2005) and 230 χ0 (Timmermann et al. 1996).
(2)where the factor of 2 in the denominator accounts for half of the heating photons at wavelengths out of the UV band (e.g. Röllig et al. 2011). Using the total infrared flux values from Sect. 4.4 results in χ = 5.6 × 104χ0 for IRS 2 and 1.2 × 105χ0 for IRS 1. For the interface, the UV field was derived previously to fall between 140 χ0 (Poelman & Spaans 2005) and 230 χ0 (Timmermann et al. 1996).
As a simple and straightforward model, we can treat the PDRs in S 140 as plane-parallel slabs simulated by Kaufman et al. (1999). In the model line and continuum, intensities are self-consistently computed for a face-on configuration taking the optical depths of the lines into account. This allows us to directly read the source parameters from the [C ii] line intensity, the [O i]/[C ii] intensity ratio, and the ([O i]+[C ii])/TIR ratio (Figs. 3−6 from Kaufman et al. 1999). As the model has only the two parameters of gas density and incident radiation field, the problem is over-determined allowing us to assess the consistency of the description. Depending on the source geometry, we may, however, introduce the inclination angle as an additional free parameter providing a line-of-sight increase in the column densities because the model is only computed for a face-on PDR.
This model is clearly appropriate for the external cloud surface representing an almost edge-on PDR illuminated by HD 211880. The main [C ii] and [O i] emission from a plane-parallel PDR stems from gas within AV ≤ 2 from the cloud surface (Röllig et al. 2007). This is also the approximate scale of chemical stratification in the PDRs (Hollenbach & Tielens 1999). In Fig. 2 we can directly measure the stratification between CO 2−1 and [C ii] as 15′′ or 0.05 pc. This allows the gas density to be estimated as nH ≈ 2 × (NH/AV)/0.05pc = 2.5 × 104 cm-3.
When reading the model predictions for the given parameter combination of density and previously fitted UV field for the interface, we obtain a [C ii] line intensity of 3 × 10-7 W sr-1 m-2, a [O i]/[C ii] energy ratio of 5, and a line-to-continuum ratio of 0.02. Unfortunately, we do not have numbers for the infrared continuum flux at the interface position as it was outside of the region observed by FORECAST and PACS. We can, however, assume that the ([O i]+[C ii])/TIR ratio falls above the value of 10-2 seen in the southwestern edge of the mapped area (Fig. 15). The measured [C ii] line intensity is, however, 10-6 W sr-1 m-2, a value that is obtained in the model only for UV fields above 2 × 104χ0 and high densities. In contrast, the measured [O i](63 μm)/[C ii] energy ratio is 0.3, a value that is found in the model only for UV fields of about 30 χ0 and below.
A solution can be achieved by introducing the inclination angle of the PDR as an additional parameter and changing the assumption on the impinging UV field. If the PDR inclination provides a geometrical magnification of the [C ii] intensity in the optically thin case and we assume that [O i] is optically thick so that it is not amplified in the same way, the observed [C ii] intensity can be corrected downwards and the [O i]/[C ii] ratio upwards. For an amplification factor of eight, we obtain a match of both quantities with the model at a UV field of 60 χ0. This is lower than obtained in the previous PDR model fits, but still six times higher than measured deeper in the S 140 region by Li et al. (2002). Because our gas density value is based on a rough estimate only, we should assume a factor of two error bar for all numbers for a conservative approach. The geometrical amplification of a factor of eight is obtained by an inclination angle of 80−85 degrees relative to the face-on orientation. The study of the [O i](145 μm)/[O i](63 μm) line ratio based on PACS data in Appendix B suggests a somewhat lower amplification factor of four.
We can try to use the same model as an approximation for the internal PDR around the cluster at IRS 2 that gives rise to the observed [C ii] and [O i] peak. Here, we assume that the PDR will form a shell around the cluster with a face-on front and back side. For the gas density, the value of 1.4 × 105 cm-3 from Sect. 4.2 provides a lower limit. Reading the observables from the model for this density and the UV field of 5.6 × 104χ0 gives a [C ii] line intensity of 1 × 10-6 W sr-1 m-2, a [O i]/[C ii] energy ratio of 40, and a ([O i]+[C ii])/TIR ratio of 3 × 10-3. Comparing this to our measured values of 1.5 × 10-6 W sr-1 m-2, 5.6, and 2 × 10-4 we find a good agreement for the [C ii] line intensity when assuming that the radiation from both surfaces adds up in the optically moderately thick line (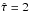 , see Sect. 3.1). However, the observed [O i] line intensity is about seven times lower than predicted resulting in a line-to-continuum ratio that is also six times lower.
, see Sect. 3.1). However, the observed [O i] line intensity is about seven times lower than predicted resulting in a line-to-continuum ratio that is also six times lower.
The much lower [O i] intensity in the observations may stem from the shell configuration where we expect a decreasing [O i] excitation temperature towards the observer in contrast to the face-on configuration of the PDR model where we directly observe the illuminated side of the PDR. For [C ii] both configurations do not make a big difference as C+ is only abundant in the narrow AV< 2 layer, but atomic oxygen is also abundant in the cool environment at the back side of the PDR, potentially absorbing a large fraction of the [O i] emission from the PDR. If we assume that this self-absorption is as strong as a factor of seven, much higher than estimated from the line profiles in Sect. 3.1, we obtain a self-consistent picture for the PDR of IRS 2 in the frame of the PDR model from Kaufman et al. (1999). This self-absorption by a factor of seven is also consistent with the [O i](145 μm)/[O i](63 μm) ratio observed by PACS (Appendix B).
By further inspecting the model output as a function of density, we can also constrain the maximum density of the PDR. When increasing the density by a factor of ten above our lower limit, the [C ii] intensity drops by a factor of two while the predicted [O i] intensity remains approximately constant. In the shell configuration this cannot be compensated by a variable inclination angle so that we can constrain the actual density range to densities below 106 cm-3. This is consistent with the central density estimate of 9 × 105 cm-3 from the dust modeling in Koumpia et al. (2015). With the assumption of a very strong [O i] self-absorption, the fine-structure line peak at IRS 2 is thus still consistent with the standard PDR picture in a UV field of 5.6 × 104χ0 and a density between 1.4 × 105 and 1 × 106 cm-3.
However, we are not able to provide a consistent PDR model explanation for the fine-structure line deficit from IRS 1. The combination of the [C ii] intensity of 4 × 10-7 W sr-1 m-2, the [O i]/[C ii] energy ratio of 1.6, the line-to-continuum ratio of 2 × 10-5, and the known UV field of 1.2 × 105χ0 provides a solution for a gas density of 50 cm-3 and a factor of 1.5 self-absorption of the [O i] 63 μm line only, but this low density is in clear contradiction to the analysis of the CO lines in Sect. 4.1 and the dust emission profile in Koumpia et al. (2015). In fact, the density around IRS 1 should be at least as high as towards IRS 2.
5. Discussion
Our observational results raise two main questions:
-
Why is the fine-structure line cooling from IRS 1so weak compared to the continuum, with[C ii]/TIR ratios as low as 10-5?
-
Why do we see significantly more fine-structure line emission from the weaker source IRS 2 than from IRS 1?
We can discard a number of easy explanations for the lack of [C ii] emission from IRS 1 and the relative weakness of the [O i] and [C ii] emission from IRS 2:
High-resolution radio continuum observations using the VLA and MERLIN (Tofani et al. 1995; Hoare 2006) showed ultracompact H ii regions at the positions of IRS 1 and IRS 2. This shows that the embedded sources produce enough UV photons with energies above 13.6 eV to ionize hydrogen. Therefore, they should also be able to ionize carbon (11.2 eV) and PAHs and dust grains leading to C+ production and a significant photoelectric heating of the gas. Similarly, Malhotra et al. (2001) proposed radiation from an older stellar population with an overall redder spectrum to explain the [C ii] deficit, but in our sources we can be sure to find a very young cluster.
PACS observations of the [N iii] 57 μm line in the frame of the Herschel key project WADI (Ossenkopf et al. 2011) did not provide any detection of the line in the 47′′ × 47′′ area centered at IRS 1. Because of the similarity of the second ionization potential of nitrogen and carbon, the lack of N++ rules out that carbon is in the form of C++ which would not contribute to the [C ii] line. Together with the non-detection of the [O iii] line, this rules out that a high ionization parameter explains the lack of [C ii] and [O i] emission. Unfortunately, the existing Spitzer IRS spectra do not allow us to constrain the abundance of other ionized species as they are saturated in most of the field owing to the large continuum flux. Future observations of infrared lines might show whether there is a general line deficit from the H ii regions that might be due to strong UV absorption by dust within the H ii regions preventing any FUV photons from arriving at the molecular gas around them.
The intensity of the far-infrared lines may be reduced by dust extinction for very large column densities (see e.g. Etxaluze et al. 2013). Mainly constrained by 450 μm SCUBA observations we derived in Koumpia et al. (2015) a total visual extinction of AV ≈ 50 towards IRS 1 and up to AV ≈ 100 towards IRS 2. The dust opacities should fall between the values for diffuse clouds (82 cm2/g at 63 μm, 12 cm2/g at 158 μm, Li & Draine 2001) and those for dense clumps (211 cm2/g at 63 μm, 41 cm2/g at 158 μm, Ossenkopf & Henning 1994, model 5) providing optical depths of τ63 μm = 0.1−0.25 and τ158 μm = 0.01−0.05 for IRS 1 and τ63 μm = 0.2−0.5 and τ158 μm = 0.03−0.2 for IRS 2 when we assume that half of the dust is located in front of the line-emitting gas. This may provide a reduction of up to 40 % for the [O i] intensity towards IRS 2, but only a negligible effect for all other cases, in particular for the [C ii] line, which does not explain the overall large deficiency.
Herrera-Camus et al. (2015) proposed a redistribution of the cooling power from [C ii] to the [O i] 63 μm line in dense material as an explanation for the [C ii] deficit, but as we observed both lines, we can be sure that this can only apply for the self-absorbed part of the [O i] line as all other photons are measured. We find, however, a redistribution of cooling power to the CO rotational lines. They can carry as much as half of the energy of the [O i] line, but clearly do not account for a factor of 100 difference.
Based on the spatial and spectral information in our data we can exclude a shock-origin of our fine-structure peak. It is about 5′′ away from the outflow knots from IRS 1 mapped by Weigelt et al. (2002) and the fine-structure lines do not show the outflow wings seen in e.g. [C i] by Minchin et al. (1994) or seen in our low-J CO data. In case of outflow-excited [O i] emission we expect a wider line width in [O i] than in CO, as observed in e.g. G5.89-0.39 by Leurini et al. (2015) and not the opposite behavior. Moreover, the [O i] line has a slightly blue-skewed profile that is representative of infall rather than outflow.
In the frame of PDRs, low line-to-continuum cooling ratios are explained by either very high or very low charging parameters χ/n (e.g. Kaufman et al. 1999). High χ/n values lead to positively charged dust grains and PAHs, lowering the photoelectric efficiency . They are obtained for very high UV fields at low densities. In the opposite case all material remains cold and no C+ is produced so that most energy is emitted in CO lines. However, our CO and dust observations exclude low densities around the infrared sources (Sect. 4.3), the measured [C ii] intensity excludes the cold-gas solution, and the UV fields are constrained by the measured infrared luminosity.
Alternatively, the photoelectric efficiency can be reduced by the destruction of PAHs since they are the dominant carrier of the photoelectric heating (Bakes & Tielens 1994). As mentioned above, the saturation of the IRS spectra around infrared sources prevent us from examining the PAH spectra directly, but when we compare the relative strength of the PAH 11.3μm feature against the underlying continuum southwest of IRS 1, we find some reduction in the area closer to IRS 1 (20−30′′ from IRS 1) compared to 30−50′′ from IRS 1. However, the spectra still show an infrared excess from very small dust grains indicating that the reduction in the PAH abundance can only weakly reduce the overall surface for the photoelectric effect.
The relative weakness of the fine-structure lines and the low [O i]/[C ii] ratio ask for an explanation by deviations of the conditions in S 140 from the “standard PDR”. For the [O i] line the low intensity can be explained by a scenario with a decreasing [O i] excitation temperature towards the observer, resulting from a decreasing gas temperature and/or density. Owing to the high column density of atomic oxygen at low temperatures, this geometry can provide a strong self-absorption, explaining the factor of seven reduction of the [O i] line intensity observed towards IRS 2. However, this mechanism can hardly be responsible for the same kind of reduction in the [C ii] line intensity towards IRS 1. As C+ quickly recombines in a dense gas at low temperatures, finally forming CO, we do not expect large quantities of cold C+ in the line of sight that can produce the same kind of self-absorption for the [C ii] fine-structure line. A very special configuration would be needed that allows for a significant amount of cold low-density C+ gas in a clumpy medium behind a layer of dense and warm gas facing the H ii region around the embedded cluster.
Beyond the relative weakness of the fine-structure lines relative to the continuum flux, we find puzzling combinations of detections:
-
1.
IRS 2, with 2000 L⊙, shows strong [O i], [C ii], and CO (and isotopologues) emission at about −6.5 km s-1 and has associated ultracompact H ii regions.
-
2.
IRS 1, with 10 000 L⊙, shows only weak [C ii] and [O i] emission at the main velocity of the cloud of −8 km s-1. The CO lines have a somewhat smaller intensity than for IRS 2 and the optically thin lines are centered at the IRS 2 velocity, showing only an emission wing at −8 km s-1 also indicating a relative lack of CO emission from IRS 1. An ultracompact H ii region and an outflow were detected.
-
3.
IRS 3, with 1300 L⊙, shows [O i] but hardly any [C ii]; CO is comparable to IRS 1, but spatially not separated in our beam. The source, however, shows no associated H ii region.
6. Summary
Our GREAT observations of S 140 showed a pronounced peak in the emission of the [O i] 63 μm and [C ii] lines 20′′ north of IRS 1, the main embedded source dominating the infrared field in the whole region. The fine-structure line peak can be associated with a weaker infrared source, IRS 2, and the GREAT observations resolve the size of the emitting region to a diameter of 0.03 pc. The velocity of the gas at that position is offset by about 1.5 km s-1 from the bulk of the molecular material in S 140. The gas density of the emitting gas must be at least 1.4 × 105 cm-3 to allow for the observed strength of the [C ii] line. In spite of its absolute strength, the [O i] 63 μm line is, however, relatively weak compared to what is expected from the [C ii] intensity and the infrared continuum. This can only be explained by a strong self-absorption in the foreground medium with a large optical depth. For [C ii] we measured an optical depth of 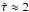 .
.
From IRS 1 we find only relatively weak [C ii] and almost no [O i] emission in spite of its high luminosity of 104L⊙ and a known ultracompact H i region. The main heating source of dust and large-scale gas in S 140 is not responsible for the [C ii] and [O i] peak, but shows an extreme fine-structure line deficit. While for IRS 2, the low value of the ([C ii]+[O i])/TIR ratio, also matching the criterion for a line deficit, can be explained by the strong [O i] self-absorption, this explanation does not work for IRS 1, and in particular not for the low [C ii] intensity observed there. Solving the puzzle of the extremely low fine-structure emission in S 140 may provide the general explanation of the fine-structure line deficit in galaxies with high infrared luminosities.
At the cloud surface of S 140 we find a classical PDR, showing the expected stratification in the line tracers and producing strong [C ii] emission. The [C ii] line is narrower there, having an optical depth of 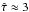 . The combination of the observed stratification and line intensities of [C ii] and [O i] can be explained by a plane-parallel PDR model with a density of 2.5 × 104 cm-3 if we assume that the surface is tilted by an inclination angle of 80−85 degrees relative to the face-on orientation and illuminated by a a UV field of 60 χ0, a value that is lower than obtained in the previous PDR model fits in the literature.
. The combination of the observed stratification and line intensities of [C ii] and [O i] can be explained by a plane-parallel PDR model with a density of 2.5 × 104 cm-3 if we assume that the surface is tilted by an inclination angle of 80−85 degrees relative to the face-on orientation and illuminated by a a UV field of 60 χ0, a value that is lower than obtained in the previous PDR model fits in the literature.
Online material
Appendix A: Comparison to Herschel data
In the frame of the WADI key project (Ossenkopf et al. 2011), S140 was observed with the HIFI and PACS instruments, also covering the [C ii] and [O i] lines7. Part of the results were also used in the papers of Dedes et al. (2010) and Koumpia et al. (2015). Due to the limited observing time in the key project only a small part of the source was covered. In the overlapping part we use the data here to check the consistency with our new, more extended observations with GREAT.
 |
Fig. A.1 Integrated map of [C ii] obtained in the GREAT observations (contours) overlaid by colors of the [C ii] line intensity from the two PACS footprints. The top image shows the intensities in the original PACS footprints. In the bottom version this is resampled to the positions of the GREAT map with an effective resolution of the 17.2′′ beam. |
Appendix A.1: PACS spectroscopy
The [O i] and [C ii] lines were observed earlier in S 140 through the PACS instrument on board Herschel in the frame of a spectral scan at two individual pointings, one centered at IRS 1 and the other close to the cloud surface towards HD 211880. The PACS footprint is not fully sampled so that it may miss part of the flux between the pixels, but if we assume a source size of 5.5′′ or above that missing flux should be small so that we can use the data to check the consistency with the GREAT observations. The spectral resolution of PACS was insufficient to resolve the line, so that we can only compare integrated intensities.
 |
Fig. A.2 Measured intensities in the different pixels from Fig. A.1b as seen by GREAT and PACS. Green asterisks represent the footprint around IRS 1, black plus signs the footprint at the outer interface. The brown line shows the identity, the blue line represents an identity with an offset of 30 K km s-1. |
Figure A.1 compares our new intensity map with the PACS data for the two footprints. We see that the spatial structure of the emission peaks around IRS 2 and the interface is consistent between PACS and GREAT data. The PACS data just miss the global emission peak, but they peak at the position closest to the true maximum and they also trace the structure of the extended emission at the outer cloud interface. When comparing absolute intensities, however, we find systematically somewhat lower intensities in the PACS data than in the GREAT data.
 |
Fig. A.3 Integrated map of [O i] obtained in the GREAT observations (contours) overlaid on the colors of the [O i] line intensity from the two PACS footprints. The top image shows the intensities in the original PACS footprints with GREAT data convolved to 10′′ resolution. In the bottom version both maps are resampled to the positions of the GREAT map for the effective resolution of a circular 12′′ beam. |
To understand whether this is a calibration problem, we computed the pixel-to-pixel statistics in the resampled map. This is shown in Fig. A.2. We find a uniform behavior between both footprints; the PACS intensity is offset from the identity by about 30 K km s-1. This means that we do not have a calibration difference, but a difference in the absolute level. This can be naturally explained if there is a 30 K km s-1 contamination of the OFF position used as the reference in the PACS observations. The GREAT observations use a well-controlled OFF position 6.5′ southwest of the molecular cloud, while the chopped PACS observations involve a reference that falls 6′ into the molecular cloud. Some [C ii] emission from that region is quite likely and would explain the constant absolute offset between the GREAT and PACS intensities.
 |
Fig. A.4 Measured intensities in the different pixels of Fig. A.3 as seen by GREAT and PACS. Green asterisks represent the footprint around IRS 1 and black plus signs the footprint at the outer interface when both data sets are resampled to a common 12′′ resolution (Fig. A.3b). Blue diamonds and orange triangles are obtained when we resample the GREAT data to the 25 pixels of the PACS array using the 9′′ PSF of PACS for the IRS 1 region and the interface, respectively (Fig. A.3a). The brown line shows the identity. |
As the [O i] emission is much less extended, we expect no OFF contamination in the PACS data for this line. Figure A.3 compares the spatial distribution of the [O i] integrated line emission measured by PACS with our GREAT observations. The spatial distributions of the emission seen through GREAT and PACS agree relatively well, having the peak again around IRS2, but for the individual intensities we find some significant deviations. Figure A.4 compares PACS and GREAT intensities from two different ways of resampling. One is shown in the lower panel of Fig. A.3, namely both maps are resampled to a common 4′′ grid with 12′′ resolution (green asterisk and black plus signs in Fig. A.4). Since the PACS map is not fully sampled, we extracted the flux based on the geometrical overlap. In the second method, we used the integrated intensity of the original 5 × 5 PACS spaxels, and resampled the GREAT data to each spaxel position (blue diamonds and orange triangles in Fig. A.3). The resulting trend is the same with both methods. There is a good match for the map around the interface and for the highest intensities close to IRS 2 at the northern boundary of the PACS field. However, across the PACS array centered at IRS 1, the intensities seem to be systematically too high. Off-contamination on the GREAT side can be excluded as it would show up as a constant offset like that seen in the [C ii] case. Moreover, we used the same reference position as for [C ii], and [O i] is rather less extended than [C ii] owing to the higher critical density. One can see in Fig. A.4 that the different ways of resampling the data do not make any significant difference. The PACS observer’s manual (v2.3) does not provide any direct
explanation. The wavelength of 63μm is not listed as a ghost from other strong emission lines and it is not in the leakage wavelength range. We can only speculate that this may be a stray-light problem where the strong [O i] emission just at the edge of the PACS footprint is partially picked up in the adjacent spaxels. Unfortunately, there are no calibration data available to verify that situation as the calibration observations were not set up to just miss the target. Hence, we cannot provide a quantitative explanation for the mismatch.
Appendix A.2: HIFI cut
 |
Fig. A.5 [C ii] spectra taken with HIFI (black) and GREAT (red) along a 37 degree cut through IRS 1 and the cloud surface. The HIFI cut extends deeper into the cloud and only every second spectrum is plotted. The corresponding GREAT spectra were averaged in a 6′′ circle around the HIFI position. |
The [C ii] line was also observed by HIFI (Dedes et al. 2010) in a single strip going through IRS 1 and the surface, oriented to the same angle of 37 degrees east of north as our GREAT map. In Fig. A.5 we compare individual HIFI spectra along that cut at a half-sampled spacing with the corresponding GREAT spectra obtained by averaging all data in a 6′′ circle around the HIFI positions.
We generally find a very good match between HIFI and GREAT spectra, in particular the line shapes agree in all details, but at some positions the GREAT peak intensities are larger by a few percent up to 15%. First of all, this confirms the good relative calibration and pointing accuracy of both instruments/telescopes. The higher intensity of GREAT at an offset of −50′′ and + 12′′ could be due to the somewhat larger telescope beam of SOFIA leading to more intensity pickup from the surface at −50′′ and from the newly detected intensity peak north of IRS 1 at + 12′′.
Appendix B: The [O II] 145 μm/63 μm ratio
 |
Fig. B.1 Observed ratio of the [O i] 145 μm to [O i] 63 μm line integrated intensity seen by PACS (colors) overlaid on the contours of the [O i] 63 μm emission measured by GREAT. |
In spite of the possible stray-light issue of the PACS [O i] map (see Appendix A.1), we can also try to use the [O i](145 μm)/ [O i](63 μm) line ratio to constrain the parameters of the PDRs in S 140, assuming that the ratio between both lines should be more robust than the simple integrated line intensity.
Because the excitation energy of the 145 μm line of 325 K lies above that of the 63 μm line (228 K) the [O i](145 μm)/ [O i](63 μm) measures temperature (or gas heating through the UV field) in the temperature range of about 300 K. In many cases, however, this ratio may be dominated by the optical depth in the 63 μm line (Kaufman et al. 1999; Malhotra et al. 2001). A low [O i](145 μm)/[O i](63 μm) compared to the PDR model
prediction is observed in many PDRs, and the foreground absorption, opacity effect of the [O i] 63 μm, and the cloud geometry are proposed as possible explanations (Liseau et al. 1999; Caux et al. 1999; Giannini et al. 2000; Okada et al. 2003). Liseau et al. (2006) provided the theoretical estimates of this ratio for different physical conditions. In the case of optically thin emission, a ratio above 0.1 can be achieved only when the gas temperature is >500 K and the collision partner is H2, which is unlikely. For the optically thick case, their calculation with the density of 3 × 104 cm-3 shows that the column density of N(H) >1024 cm-2 would be required to make the [O i](145 μm)/[O i](63 μm) ratio above 0.1.
Figure B.1 shows the integrated intensity ratio of [O i](145 μm)/[O i](63 μm) from the two PACS footprints centered at IRS 1 and at the interface observed in the frame of the Herschel key project WADI (Ossenkopf et al. 2011). For the interface parameters discussed above, the face-on PDR model produces a [O i](145 μm)/[O i](63 μm) ratio of 0.04, whereas the observed value is 0.17, i.e. about four times higher. If we interpret it through the inclination of the PDR in the same way as for the [C ii] line, the ratio asks for a geometrical amplification of the [O i] 145 μm line by a factor of four, two times lower than inferred from the [O i](63 μm)/[C ii] ratio in Sect. 4.5.
At IRS 2, [O i](145 μm)/[O i](63 μm) from the PACS observations is 0.3. For the PDR with a UV field of 5.6 × 104χ0 and a density between 1.4 × 105 and 106 cm-3 (Sect. 4.5), the predicted ratio is 0.03–0.045. Since the absorption by the cold gas at the back side of the PDR should affect only the 63μm transition, a factor of 7−10 of self-absorption is required to be consistent with the model predicted [O i](145 μm)/[O i](63 μm).
At IRS 1, the observed [O i](145 μm)/[O i](63 μm) is 0.1, which suggests PDR gas with a density of 103–104 cm-3 and a UV field of >106, but as discussed in Sect. 4.5, there is no consistent model for IRS 1.
Comparison to integrated line observations from the Herschel Space Observatory are provided in Appendix A. Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
The steep decrease in the dust column density and the corresponding virtual increase in the CO abundance at the boundaries of the map are probably due to missing flux at the edges of the PACS footprint in the analysis by Koumpia et al. (2015).
Our line cooling estimates for the 8.3′′ source at IRS 2 in Sect. 4.2 slightly deviate from the numbers given here because of the coarser resolution applied here compared to the direct fit of the emission profile.
Acknowledgments
We thank Ed Chambers, Denise Riquelme, and Christoph Buchbender for help with the data calibration and Paul Harvey for help with the continuum data and many useful discussions. This work was supported by the German Deutsche Forschungsgemeinschaft, DFG project number SFB 956, C1. The work presented here is based on observations made with the NASA/DLR Stratospheric Observatory for Infrared Astronomy. SOFIA Science Mission Operations are conducted jointly by the Universities Space Research Association, Inc., under NASA contract NAS2-97001, and the Deutsches SOFIA Institut under DLR contract 50 OK 0901. We greatfully acknowledge the support by the observatory staff. HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France and the US. Consortium members are: Canada: CSA, U.Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronómico Nacional (IGN), Centro de Astrobiologìa (CSIC-INTA). Sweden: Chalmers University of Technology − MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University − Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain).
References
- Bakes, E. L. O., & Tielens, A. G. G. M. 1994, ApJ, 427, 822 [NASA ADS] [CrossRef] [Google Scholar]
- Blake, G. A., Sutton, E. C., Masson, C. R., & Phillips, T. G. 1987, ApJ, 315, 621 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Büchel, D., Pütz, P., Jacobs, K., et al. 2015, Terahertz Science and Technology, IEEE Transactions on, 5, 207 [Google Scholar]
- Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. M. 1990, ApJ, 365, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Mathis, J. S., Ebbets, D. C., & Savage, B. D. 1993, ApJ, 402, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Caux, E., Ceccarelli, C., Castets, A., et al. 1999, A&A, 347, L1 [NASA ADS] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, W. J., Hoare, M. G., Fujiyoshi, T., et al. 2009, A&A, 494, 157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dedes, C., Röllig, M., Mookerjea, B., et al. 2010, A&A, 521, L24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Etxaluze, M., Goicoechea, J. R., Cernicharo, J., et al. 2013, A&A, 556, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Evans, II, N. J., Mundy, L. G., Kutner, M. L., & Depoy, D. L. 1989, ApJ, 346, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Giannini, T., Nisini, B., Lorenzetti, D., et al. 2000, A&A, 358, 310 [NASA ADS] [Google Scholar]
- Guan, X., Stutzki, J., Graf, U. U., et al. 2012, A&A, 542, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gürtler, J., Henning, T., Kruegel, E., & Chini, R. 1991, A&A, 252, 801 [NASA ADS] [Google Scholar]
- Harvey, P. M., Campbell, M. F., & Hoffmann, W. F. 1978, ApJ, 219, 891 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Adams, J. D., Herter, T. L., et al. 2012, ApJ, 749, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Heyminck, S., Graf, U. U., Güsten, R., et al. 2012, A&A, 542, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hirota, T., Ando, K., Bushimata, T., et al. 2008, PASJ, 60, 961 [NASA ADS] [Google Scholar]
- Hoare, M. G. 2006, ApJ, 649, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Jaquet, R., Staemmler, V., Smith, M. D., & Flower, D. R. 1992, J. Phys. B Atom. Mol. Phys., 25, 285 [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karska, A., Herczeg, G. J., van Dishoeck, E. F., et al. 2013, A&A, 552, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [NASA ADS] [CrossRef] [Google Scholar]
- Koumpia, E., Harvey, P. M., Ossenkopf, V., et al. 2015, A&A, 580, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lacy, J. H., Knacke, R., Geballe, T. R., & Tokunaga, A. T. 1994, ApJ, 428, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Penzias, A. A. 1993, ApJ, 408, 539 [NASA ADS] [CrossRef] [Google Scholar]
- Lebouteiller, V., Cormier, D., Madden, S. C., et al. 2012, A&A, 548, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leurini, S., Wyrowski, F., Wiesemeyer, H., et al. 2015, A&A, submitted [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Li, W., Evans, II, N. J., Jaffe, D. T., van Dishoeck, E. F., & Thi, W.-F. 2002, ApJ, 568, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R., White, G. J., Larsson, B., et al. 1999, A&A, 344, 342 [NASA ADS] [Google Scholar]
- Liseau, R., Justtanont, K., & Tielens, A. G. G. M. 2006, A&A, 446, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, M. L., Satyapal, S., Fischer, J., et al. 1998, ApJ, 504, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., Kaufman, M. J., Hollenbach, D., et al. 2001, ApJ, 561, 766 [Google Scholar]
- Maud, L. T., Hoare, M. G., Gibb, A. G., Shepherd, D., & Indebetouw, R. 2013, MNRAS, 428, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Minchin, N. R., White, G. J., & Padman, R. 1993, A&A, 277, 595 [NASA ADS] [Google Scholar]
- Minchin, N. R., White, G. J., Stutzki, J., & Krause, D. 1994, A&A, 291, 250 [NASA ADS] [Google Scholar]
- Minchin, N. R., Ward-Thompson, D., & White, G. J. 1995, A&A, 298, 894 [NASA ADS] [Google Scholar]
- Mizutani, M., Onaka, T., & Shibai, H. 2004, A&A, 423, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mookerjea, B., Kramer, C., Buchbender, C., et al. 2011, A&A, 532, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mueller, K. E., Shirley, Y. L., Evans, II, N. J., & Jacobson, H. R. 2002, ApJS, 143, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Okada, Y., Onaka, T., Shibai, H., & Doi, Y. 2003, A&A, 412, 199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okada, Y., Pilleri, P., Berné, O., et al. 2013, A&A, 553, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okada, Y., Requena-Torres, M. A., Güsten, R., et al. 2015, A&A, 580, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ossenkopf, V., Röllig, M., Cubick, M., & Stutzki, J. 2007, in Molecules in Space and Laboratory, eds. J. L. Lemaire, & F. Combes (S. Diana Publ.) [Google Scholar]
- Ossenkopf, V., Röllig, M., Kramer, C., et al. 2011, in EAS PS 52, eds. M. Röllig, R. Simon, V. Ossenkopf, & J. Stutzki, 181 [Google Scholar]
- Ossenkopf, V., Röllig, M., Neufeld, D. A., et al. 2013, A&A, 550, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, T. G., Huggins, P. J., Wannier, P. G., & Scoville, N. Z. 1979, ApJ, 231, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Poelman, D. R., & Spaans, M. 2005, A&A, 440, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poelman, D. R., & Spaans, M. 2006, A&A, 453, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Ossenkopf, V., Jeyakumar, S., Stutzki, J., & Sternberg, A. 2006, A&A, 451, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Abel, N. P., Bell, T., et al. 2007, A&A, 467, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röllig, M., Kramer, C., Rajbahak, C., et al. 2011, A&A, 525, A8 [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sofia, U. J., Lauroesch, J. T., Meyer, D. M., & Cartledge, S. I. B. 2004, ApJ, 605, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [NASA ADS] [CrossRef] [Google Scholar]
- Timmermann, R., Bertoldi, F., Wright, C. M., et al. 1996, A&A, 315, L281 [NASA ADS] [Google Scholar]
- Tofani, G., Felli, M., Taylor, G. B., & Hunter, T. R. 1995, A&AS, 112, 299 [NASA ADS] [Google Scholar]
- van der Tak, F. F. S., van Dishoeck, E. F., Evans, II, N. J., & Blake, G. A. 2000, ApJ, 537, 283 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vastel, C., Spaans, M., Ceccarelli, C., Tielens, A. G. G. M., & Caux, E. 2001, A&A, 376, 1064 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., & Herbst, E. 2008, ApJ, 680, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Weigelt, G., Balega, Y. Y., Preibisch, T., Schertl, D., & Smith, M. D. 2002, A&A, 381, 905 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiesenfeld, L., & Goldsmith, P. F. 2014, ApJ, 780, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Young, E. T., Becklin, E. E., Marcum, P. M., et al. 2012, ApJ, 749, L17 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Line parameters of the narrow component of CO and isotopologues towards IRS 1 and IRS 2 (GREAT, IRAM, and HIFI data).
All Figures
 |
Fig. 1 Integrated intensity map of [C ii] overlaid on a Spitzer IRAC false-color image of the same region. The IRAC map uses the logarithmic intensities of the 3.6, 5.6, and 8μm channels. The integrated intensity contours are drawn at 50, 70, 90, 120, 150, and 180 K km s-1. The external cloud interface is visible in the southwest. The arrow shows the direction towards the illuminating source HD 211880. The red marks indicate the position of the known infrared sources: southwest is IRS 1, north is IRS 2, and southeast is IRS 3 (Evans et al. 1989), the yellow marks show the position of known submm cores (Minchin et al. 1995; Maud et al. 2013). The IRAC peak falls at the location of IRS 1. |
| In the text | |
 |
Fig. 2 Peak intensity map of [C ii] overlaid on a IRAM 30 m map of the CO 2−1 peak intensity. The [C ii] contours are drawn at 15, 20, 25, 30, 35, 40, and 45 K. The black marks indicate the positions of IRS 1-3. |
| In the text | |
 |
Fig. 3 Integrated intensity map of the [O i] 63 μm line (colors) overlaid by contours of the [C ii] integrated intensity (levels as in Fig. 1). The three marks indicate the positions of IRS 1-3. All coordinates are taken relative to the position of IRS 1 at |
| In the text | |
 |
Fig. 4 Integrated intensity map of CO 16−15 with contours of CO 13−12 drawn at levels of 10, 20, 30, 40, 50, 60, and 70 K km s-1. Only the region around IRS 1 has been observed in CO 16−15; in CO 13−12 only two outer strips have been covered avoiding the center. The black marks indicate the positions of IRS 1-3. |
| In the text | |
 |
Fig. 5 Peak intensity, first moment (centroid velocity), and second moment (translated to FWHM) of the lines of 13CO 1−0 (colors) and [C ii] contours. The black marks indicate the positions of IRS 1-3. The contour levels for the [C ii] peak intensity match those from Fig. 2; for the line position they are given at −9.5, −8.5, −7.5, and −6.5 km s-1, and for the line width at 3, 4, 5, and 6 km s-1. Velocities are given in LSR (local standard of rest) and intensities in main beam temperatures. |
| In the text | |
 |
Fig. 6 Line profiles of the [C ii], [O i], CO 16−15, CO 2−1, C18O 1−0, and 13CO 1−0 lines at the position of the [O i] peak (0, 20 close to IRS 2), at IRS 1 (0, 0), and at the interface (−40, −54). The lines are averaged in a Gaussian beam of 17.3′′ FWHM (telescope + convolution kernel) except for the 13CO and C18O lines that can only be treated at the lower resolution of 23′′. |
| In the text | |
 |
Fig. 7 Baseline of the [C ii] profiles showing the hyperfine components of the [13C ii] transitions. The upper plot shows the sum spectrum from all spectra with integrated intensities above 100 K km s-1 from the IRS 1-3 region, the lower plot from the interface region. The blue lines represent the same spectra scaled by an abundance ratio of 1/67 and the corresponding line ratio and frequency of the three hyperfine transitions, i.e. they represent the spectrum that we expect in the case of an optically thin [C ii] line. |
| In the text | |
 |
Fig. 8 Line profiles of the [C ii], [O i], CO 2−1, CO 16−15, and 13CO 1−0 lines at the position of the [O i] peak (0, 20). The lines were scaled to similar intensities at −4 km s-1. For CO 2−1, a constant emission of 20 K is subtracted to exclude the extended outflow emission. |
| In the text | |
 |
Fig. 9 CO column density (upper plot: colors), gas density (lower plot: colors), and kinetic temperature (both plots: contours) derived from the RADEX fit of the integrated intensities of the observed lines of CO 1−0, 2−1, and 16−15 and the isotopologues 13CO 1−0 and C18O 1−0. |
| In the text | |
 |
Fig. 10 Column density map of gas derived from FORCAST, PACS, and SCUBA continuum observations in the center of the region (colors), overlaid by contours of the CO abundance, running from 1 × 10-4 to 3 × 10-4. |
| In the text | |
 |
Fig. 11 Column density map of C+ derived from the measured [C ii] intensities using the gas parameters from the RADEX fit to the CO lines. The contours show the [C ii] line optical depth a levels of τ = 0.5,1.0,1.5,2.0. In the two pixels north of IRS 2, the optical depth is too large for a reliable column density estimate. |
| In the text | |
 |
Fig. 12 Column density map of atomic oxygen derived from the measured [O i] intensities using the gas parameters from the RADEX fit to the CO lines. The contours show the [O i] line optical depth at levels of τ = 0.05,0.10,0.15,0.20. |
| In the text | |
 |
Fig. 13 Intensity map of [O i] (top), [C ii] (center), and CO 16−15 (bottom) after subtracting a Gaussian intensity distribution of FWHM = 8.3′′ from the observed map. The overlaid contours show the original intensity maps at levels of 8, 24, 40, 56, and 72 K km s-1 ([O i]); 50, 70, 90, 120, 150, and 180 K km s-1 (CII); and 10, 20, 30, 40, 50, and 60 K (CO 16−15). |
| In the text | |
 |
Fig. 14 CO ladder from the RADEX fit to the line intensities at the three prominent positions. |
| In the text | |
 |
Fig. 15 Comparison of the line cooling with the infrared continuum cooling. The background colors show the total infrared flux integrated from wavelengths starting at 11 μm (Koumpia et al. 2015). The contours give the decadic logarithm of the ratio of the integrated line flux relative to the continuum flux. In the top panel we use the sum of the [O i] and [C ii] fluxes, in the lower panel, we only show the [C ii]/TIR ratio as used in many existing investigations. |
| In the text | |
 |
Fig. 16 Comparison of the total line cooling flux provided by the sum of the [O i] and [C ii] lines (colors) to the [O i]/[C ii] line flux ratio (contours from 0.4 to 2.8 in steps of 0.4). The computation is performed in a common effective beam of 15′′. |
| In the text | |
 |
Fig. A.1 Integrated map of [C ii] obtained in the GREAT observations (contours) overlaid by colors of the [C ii] line intensity from the two PACS footprints. The top image shows the intensities in the original PACS footprints. In the bottom version this is resampled to the positions of the GREAT map with an effective resolution of the 17.2′′ beam. |
| In the text | |
 |
Fig. A.2 Measured intensities in the different pixels from Fig. A.1b as seen by GREAT and PACS. Green asterisks represent the footprint around IRS 1, black plus signs the footprint at the outer interface. The brown line shows the identity, the blue line represents an identity with an offset of 30 K km s-1. |
| In the text | |
 |
Fig. A.3 Integrated map of [O i] obtained in the GREAT observations (contours) overlaid on the colors of the [O i] line intensity from the two PACS footprints. The top image shows the intensities in the original PACS footprints with GREAT data convolved to 10′′ resolution. In the bottom version both maps are resampled to the positions of the GREAT map for the effective resolution of a circular 12′′ beam. |
| In the text | |
 |
Fig. A.4 Measured intensities in the different pixels of Fig. A.3 as seen by GREAT and PACS. Green asterisks represent the footprint around IRS 1 and black plus signs the footprint at the outer interface when both data sets are resampled to a common 12′′ resolution (Fig. A.3b). Blue diamonds and orange triangles are obtained when we resample the GREAT data to the 25 pixels of the PACS array using the 9′′ PSF of PACS for the IRS 1 region and the interface, respectively (Fig. A.3a). The brown line shows the identity. |
| In the text | |
 |
Fig. A.5 [C ii] spectra taken with HIFI (black) and GREAT (red) along a 37 degree cut through IRS 1 and the cloud surface. The HIFI cut extends deeper into the cloud and only every second spectrum is plotted. The corresponding GREAT spectra were averaged in a 6′′ circle around the HIFI position. |
| In the text | |
 |
Fig. B.1 Observed ratio of the [O i] 145 μm to [O i] 63 μm line integrated intensity seen by PACS (colors) overlaid on the contours of the [O i] 63 μm emission measured by GREAT. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.