| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 39 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201424188 | |
| Published online | 07 August 2015 | |
Comparison of Sunyaev-Zel’dovich measurements from Planck and from the Arcminute Microkelvin Imager for 99 galaxy clusters⋆
1
Academy of Sciences of Tatarstan, Bauman Str., 20, 420111 Kazan, Republic of Tatarstan,
Russia
2
Astrophysics Group, Cavendish Laboratory, University of
Cambridge, J J Thomson
Avenue, Cambridge
CB3 0HE,
UK
e-mail:
ycp21@mrao.cam.ac.uk
3
Atacama Large Millimeter/submillimeter Array, ALMA Santiago
Central Offices, Alonso de Cordova 3107, Vitacura, Casilla 763 0355,
Santiago,
Chile
4
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
5
CSIRO Astronomy & Space Science, Australia Telescope
National Facility, PO Box 76, Epping, NSW
1710,
Australia
6
DSM/Irfu/SPP, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
7
Department of Astronomy and Geodesy, Kazan Federal
University, Kremlevskaya Str.,
18, 420008
Kazan,
Russia
8
Dpto. Astrofísica, Universidad de La Laguna (ULL),
38206, La Laguna, Tenerife, Spain
9
European Southern Observatory, ESO Vitacura, Alonso de Cordova 3107, Vitacura, Casilla
19001, Santiago,
Chile
10
INAF − Osservatorio Astronomico di Roma, via di Frascati
33, 00040
Monte Porzio Catone,
Italy
11
Institut d’Astrophysique Spatiale, CNRS (UMR 8617) Université
Paris-Sud 11, Bâtiment
121, 91405
Orsay,
France
12
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
13
Institute of Theoretical Astrophysics, University of
Oslo, Blindern,
0371
Oslo,
Norway
14
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna,
Tenerife,
Spain
15
Jodrell Bank Centre for Astrophysics, Alan Turing Building, School
of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13
9PL, UK
16
Kavli Institute for Cosmology Cambridge,
Madingley Road, Cambridge, CB3 0HA, UK
17
Laboratoire AIM, IRFU/Service d’Astrophysique − CEA/DSM − CNRS −
Université Paris Diderot, Bât. 709, CEA-Saclay, 91191
Gif-sur-Yvette Cedex,
France
18
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de
Grenoble, 53 rue des
Martyrs, 38026
Grenoble Cedex,
France
19
Max-Planck-Institut für Extraterrestrische Physik,
Giessenbachstraße, 85748
Garching,
Germany
20
Moscow Institute of Physics and Technology, Dolgoprudny,
Institutsky per., 9, 141700
Moscow,
Russia
21
Space Research Institute (IKI), Russian Academy of
Sciences, Profsoyuznaya Str,
84/32, 117997
Moscow,
Russia
22
Tübitak National Observatory, Akdeniz University
Campus, 07058
Antalya,
Turkey
23
Universidad Andrés Bello, Dpto. de Ciencias Físicas, Facultad de
Ciencias Exactas, Astronomía,
Campus Casona de Las Condes, Fernández Concha 700, 7591538
Santiago/Las Condes,
Chile
24
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
Received: 12 May 2014
Accepted: 11 June 2015
We present observations and analysis of a sample of 123 galaxy clusters from the 2013 Planck catalogue of Sunyaev-Zel’dovich sources with the Arcminute Microkelvin Imager (AMI), a ground-based radio interferometer. AMI provides an independent measurement with higher angular resolution, 3 arcmin compared to the Planck beams of 5–10 arcmin. The AMI observations thus provide validation of the cluster detections, improved positional estimates, and a consistency check on the fitted size (θs) and flux (Ytot) parameters in the generalised Navarro, Frenk and White (GNFW) model. We detect 99 of the clusters. We use the AMI positional estimates to check the positional estimates and error-bars produced by the Planck algorithms PowellSnakes and MMF3. We find that Ytot values as measured by AMI are biased downwards with respect to the Planck constraints, especially for high Planck-S/N clusters. We perform simulations to show that this can be explained by deviation from the universal pressure profile shape used to model the clusters. We show that AMI data can constrain the α and β parameters describing the shape of the profile in the GNFW model for individual clusters provided careful attention is paid to the degeneracies between parameters, but one requires information on a wider range of angular scales than are present in AMI data alone to correctly constrain all parameters simultaneously.
Key words: cosmology: observations / galaxies: clusters: general / galaxies: clusters: intracluster medium / cosmic background radiation / X-rays: galaxies: clusters
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
The Planck satellite data-release of 2013 included a catalogue of 1227 galaxy clusters detected via the Sunyaev-Zel’dovich (SZ, Sunyaev & Zel’dovich 1972) effect (Planck Collaboration XXIX 2014). This is the deepest all-sky cluster catalogue in SZ to date, consisting of clusters spanning redshifts up to ≈1, and masses of around 1014M⊙ to 1015M⊙. SZ-selected samples have the advantage of a clean, and much less redshift-dependent (above z ≈ 0.3) selection function in mass than, for example, X-ray-selected samples (Planck Collaboration XX 2014); in addition, simulations predict that the SZ flux correlates more tightly with mass than, for example, X-ray or optical observable quantities (e.g. da Silva et al. 2004; Motl et al. 2005; Nagai 2006; Aghanim et al. 2009; Angulo et al. 2012; Kay et al. 2012). The Planck SZ catalogue is therefore a potentially very powerful tool for investigating the growth of structure in the Universe; clusters in the catalogue are being followed up with optical, radio and X-ray telescopes in order to provide multi-wavelength information to understand fully their properties.
The Arcminute Microkelvin Imager (AMI; Zwart et al. 2008) is a dual-array interferometer designed for SZ studies, which is situated near Cambridge, UK. AMI consists of two arrays: the Small Array (SA), optimised for viewing arcminute-scale features, having an angular resolution of ≈3 arcmin and sensitivity to structures up to ≈10 arcmin in scale; and the Large Array (LA), with angular resolution of ≈30 arcsec, which is insensitive to the arcminute-scale emission due to clusters and is used to characterise and subtract confusing radio sources. Both arrays operate at a central frequency of ≈15 GHz with a bandwidth of ≈4.5 GHz, divided into six channels. For further details of the instrument, see Zwart et al. (2008).
In a previous paper, (Planck and AMI Collaborations 2013, from here on AP2013) a sample of 11 clusters selected from the Planck Early Release Catalogue was followed up with AMI in order to check the consistency of the cluster parameters as measured by the two telescopes, finding the SZ signals as measured by AMI to be, on average, fainter and of smaller angular size. We have used AMI to observe all of the clusters in the Planck 2013 SZ catalogue that are at declinations easily observable with AMI (excluding those at very low redshift). This serves two purposes: (a) to investigate the discrepancies found in AP2013 further; and (b) to provide validation of, improved positional estimates for, and higher-resolution SZ maps of a large number of Planck cluster detections. We here present these observations and our analysis of them.
The paper is organised as follows. In Sect. 2 we describe the selection of the cluster sample. In Sect. 3 we describe the AMI observations and data reduction, and in Sect. 4 we outline the model used to describe the SZ signal. In Sect. 4.2 we briefly describe the Planck data analysis and describe in more detail the analysis of the AMI data in Sect. 4.3, including our detection criteria. Section 4.4 contains some representative examples of the results, and Sects. 4.4.6 and 4.4.7 compare the cluster parameter estimates produced by AMI to those produced by Planck. In Sect. 5 we use simulations to investigate the issue of variation from the universal model described in Sect. 4, and in Sect. 5.3 we present results from reanalysing the real data allowing the shape parameters in the model to vary. Finally, we conclude in Sect. 6.
2. Selection of the cluster sample
An initial selection cut of 20° ≤ δ< 87° was applied to satisfy AMI’s easy observing limits; although AMI can observe to lower declinations, increased interference due to geostationary satellites makes observing large samples below δ = 20° currently difficult. In addition, clusters with known redshifts of z ≤ 0.100 were excluded since these have large angular sizes and will be largely resolved out by AMI; although the brightest of these will still be detectable, it will be difficult to constrain their properties using AMI data. These initial cuts resulted in an initial sample size of 337 with Planck signal-to-noise (S/N) values ranging from 4.5−20. In this paper, we present results for the subset of the sample with S/N ≥ 5; this reduces the sample to 195. Results for the remaining clusters with 4.5 ≤ S/N< 5 will be released at a later date.
As in the optical, where confusion due to a bright star or a crowded field can affect the detection likelihood, a benign radio point source environment is important for AMI, but the requisite benignness is difficult to quantify. In practice, the effect of the source environment on the detection potential of a cluster depends on many factors including the number, location and orientation of the sources with respect to each other and to the sidelobes of the primary and synthesised beams. Non-trivial source environments can create complex and overlapping sidelobe patterns which can create spurious sources or reduce the flux density of real sources. In turn, the synthesised beam depends on uv-coverage, which changes for different δ and hour-angle coverage of observations of a given cluster. The primary beam is a function of frequency so the effect of a source at a given offset from the pointing centre also depends on its spectrum. These effects are almost impossible to quantify in a systematic way. In order to apply at least consistent criteria across the whole sample, the following criteria were applied based on LA observations: clusters were discarded if there were radio sources of peak flux density Speak> 5 mJy within 3 arcmin of the pointing centre, of Speak> 20 mJy within 10 arcmin of the pointing centre, or extended emission with fitted (deconvolved) major-axis size >2 arcmin and integrated flux density Sint> 2 mJy anywhere on the map; experience suggests that observation of the SZ signal in such clusters with AMI is unreliable. Clusters were discarded for source environment based either on existing observations or, for clusters that had not been previously observed with AMI, based on a short pre-screening observation carried out with the LA. It should be noted that some clusters which have been previously observed and detected by AMI are excluded by these cuts; some of the new clusters discarded by this process may also be observable.
In addition, clusters were visually inspected at various stages of the follow-up and analysis process, and some were rejected at later stages due to extra source environment problems such as extended emission not visible on the LA map, or very bright sources just outside the LA detection radius which affect the SA map due to the larger primary beam. Here we present results for the so obtained final sub-sample, which we will refer to as the SZ sample, consisting of 123 clusters. A breakdown of the numbers of clusters rejected for various reasons is shown in Table 1.
Numbers of clusters in the 20° ≤ δ< 87°, Planck S/N ≥ 5 sub-sample in various categories.
The full list of clusters within the AMI observational bounds and their reason for rejection, if not part of the SZ sample, is given in Appendix A. In addition, as a service to the community for each cluster we provide information on the 15 GHz radio point source environment1.
3. Description of AMI data
Clusters are observed using a single pointing centre on the SA, which has a primary beam of size ≈20 arcmin FWHM, to noise levels of  120 μJy beam-1. To cover the same area with the LA, which has a primary beam of size ≈6 arcmin FWHM, the cluster field is observed as a 61-point hexagonal raster. The noise level of the raster is
120 μJy beam-1. To cover the same area with the LA, which has a primary beam of size ≈6 arcmin FWHM, the cluster field is observed as a 61-point hexagonal raster. The noise level of the raster is  100 μJy beam-1 in the central 19 pointings, and slightly higher in the outer regions. Typical noise maps and uv-coverages are displayed for both arrays in Figs. 1 and 2. The average observation time for a cluster is ≈30 h on both arrays.
100 μJy beam-1 in the central 19 pointings, and slightly higher in the outer regions. Typical noise maps and uv-coverages are displayed for both arrays in Figs. 1 and 2. The average observation time for a cluster is ≈30 h on both arrays.
 |
Fig. 1 Noise maps for a typical cluster observation at δ ≈ 54° on the AMI-LA a) and SA b). The grey-scales are in μJy beam-1 and on a) the grey-scale is truncated to show the range of noise levels; b) is cut off at the 10% power point of the primary beam. |
 |
Fig. 2 uv-coverages for a typical cluster observation at δ ≈ 54°, for the AMI-LA a) and SA b). The colours indicate different channels. Note the different axis scales; the short baselines of the SA are designed for sensitivity to arcminute-scale cluster emission, while the longer baselines of the LA are insensitive to emission on this scale and are used to characterise and subtract the foreground radio sources. |
Data on both arrays are flagged for interference and calibrated using the AMI in-house software package reduce. Flux calibration is applied using contemporaneous observations of the primary calibration sources 3C 286, 3C 48, and 3C 147. The assumed flux densities for 3C 286 were converted from Very Large Array total-intensity measurements (Perley & Butler 2013), and are consistent with the Rudy et al. (1987) model of Mars transferred on to absolute scale, using results from the Wilkinson Microwave Anisotropy Probe. The assumed flux densities for 3C 48 and 3C 147 are based on long-term monitoring with the SA using 3C 286 for flux calibration (see Table 2). Phase calibration is applied using interleaved observations of a nearby bright source selected from the VLBA Calibrator survey (Petrov et al. 2008); in the case of the LA, a secondary amplitude calibration is also applied using contemporaneous observations of the phase-calibration source on the SA.
Assumed I + Q flux densities of 3C 286, 3C 48 and 3C 147.
Maps of the SA and LA data are made using aips2, cleaning in an automated manner. Source-finding is carried out at 4σ on the LA continuum map, as described in Davies et al. (2011) and Franzen et al. (2011), and sources that are detected at ≥3σ on at least three channel maps and are not extended have a spectral index α fitted across the AMI band. SA data are binned on a grid in uv-space in order to reduce the memory required for subsequent analysis.
4. Analysing the SZ signal
4.1. Cluster model
For consistency with the Planck catalogue, in this paper we assume the electron pressure profile Pe(r) of each cluster follows a generalised Navarro-Frenk-White (GNFW, Navarro et al. 1997) model, which is given by (assuming spherical geometry) ![\begin{equation} P_{\rm e}(r) = P_{0} \left ( \frac{r}{r_{\rm s}} \right )^{-\gamma} \left [ 1+\left(\frac{r}{r_{\rm s}} \right)^{\alpha} \right ]^{(\gamma - \beta)/\alpha}, \end{equation}](/articles/aa/full_html/2015/08/aa24188-14/aa24188-14-eq37.png) (1)where P0 is a normalisation coefficient, r is the physical radius, rs is a characteristic scale radius, and the parameters (γ,α,β) describe the slopes of the pressure profile at radii r ≪ rs, r ≈ rs, and r ≫ rs respectively (Nagai et al. 2007). Following Arnaud et al. (2010), we fix the slope parameters to their universal values, γ = 0.3081, α = 1.0510, β = 5.4905 derived from the REXCESS sample (Böhringer et al. 2007). They are also fixed to these values in the Planck analysis.
(1)where P0 is a normalisation coefficient, r is the physical radius, rs is a characteristic scale radius, and the parameters (γ,α,β) describe the slopes of the pressure profile at radii r ≪ rs, r ≈ rs, and r ≫ rs respectively (Nagai et al. 2007). Following Arnaud et al. (2010), we fix the slope parameters to their universal values, γ = 0.3081, α = 1.0510, β = 5.4905 derived from the REXCESS sample (Böhringer et al. 2007). They are also fixed to these values in the Planck analysis.
Given this model, the integrated SZ surface brightness, or integrated Compton-y parameter, for a cluster is given by 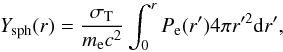 (2)where σT is the Thomson scattering cross-section, me is the electron mass, and c is the speed of light. This has an analytical solution as r → ∞, giving the total integrated Compton-y parameter Ytot,phys as
(2)where σT is the Thomson scattering cross-section, me is the electron mass, and c is the speed of light. This has an analytical solution as r → ∞, giving the total integrated Compton-y parameter Ytot,phys as 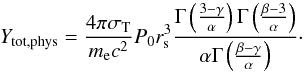 (3)With (γ,α,β) fixed, a cluster’s appearance on the sky may be described using four (observational) parameters only: (x0,y0,θs,Ytot), where x0 and y0 are the positional coordinates for the cluster, θs = rs/DA is the characteristic angular scale of the cluster on the sky (DA is the angular diameter distance to the cluster), and
(3)With (γ,α,β) fixed, a cluster’s appearance on the sky may be described using four (observational) parameters only: (x0,y0,θs,Ytot), where x0 and y0 are the positional coordinates for the cluster, θs = rs/DA is the characteristic angular scale of the cluster on the sky (DA is the angular diameter distance to the cluster), and 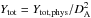 is the SZ surface brightness integrated over the cluster’s extent on the sky.
is the SZ surface brightness integrated over the cluster’s extent on the sky.
This model does not require any redshift information; physical quantities such as rs and Ytot,phys can be recovered from θs and Ytot given a redshift. Alternatively, rX and MX for some overdensity radius X can be recovered given a redshift, a concentration parameter cX ≡ rX/rs and some model or scaling relationship for translating Y into mass (e.g. Planck Collaboration XX 2014; Olamaie et al. 2012). Physical modelling will not be addressed in this paper.
Note that in the Planck analysis, in order to impose a finite integration extent, Y5R500 (the SZ surface brightness integrated to 5 × R500) is estimated rather than Ytot. For the universal GNFW parameter values, (with c500 = 1.177), the two quantities are equivalent to within 5%.
4.2. Analysis of Planck data
The Planck SZ catalogue is the union of the catalogues produced by three detection algorithms: MMF1 and MMF3, which are multi-frequency matched-filter detection methods, and PowellSnakes (PwS), which is a Bayesian detection method. Full details of these algorithms are provided in Melin et al. (2006), Carvalho et al. (2009, 2012) and Melin et al. (2012). Since the PwS analysis methodology most closely matches the Bayesian analysis procedures used to analyse AMI data, we take cluster parameters produced by PwS as our preferred Planck values, followed by MMF3, and finally MMF1 values where a particular cluster is not detected by all algorithms.
4.3. Analysis of AMI data
The model attempting to describe the AMI data is produced by a combination of the cluster model described above, the radio source environment as measured by the LA and a generalised Gaussian noise component comprising instrumental noise, confusion noise from radio sources below the detection threshold, and contamination from primordial CMB anisotropies.
Each foreground radio source is modelled by the parameters (xS,yS,S0,α). Positions (xS,yS) and initial estimates of the flux density at a central frequency (S0) are produced from the LA channel-averaged maps; for sources detected at ≥3σ on at least three of the individual channel maps, a spectral index α is also fitted to the channel flux densities. The flux density and spectral index of sources which are detected at ≥4σ on the SA map are modelled simultaneously with the cluster; this accounts for possible source variability (although we attempt to observe clusters close in time on the two arrays, this is not always possible due to different demands on the observing time of the arrays) and inter-array calibration uncertainty. Flux densities are given a Gaussian prior with σ = 40%; where α has been fitted from the LA data, a Gaussian prior with width corresponding to the fitting uncertainty is applied, otherwise a prior based on the 10C survey is applied (Davies et al. 2011). Sources detected at <4σ on the SA map are subtracted directly based on the LA values of S0 and α (or the median of the 10C prior where α has not been fitted) initially. If the cluster position output from the analysis has directly-subtracted sources within 3 arcmin, the analysis is repeated with those sources also modelled. The positions of the sources are always fixed to their LA values as the LA has higher positional precision.
In the cluster model, x0 and y0 are the offsets in RA and δ from the pointing centre of the SA observation; for previously-known clusters with existing AMI data, the pointing centre is the X-ray position of the cluster, while for new clusters it is the Planck position. Gaussian priors are used on x0 and y0, centred on the Planck position (i.e. offset from the pointing/phase reference centre, if the pointing centre is the X-ray position) and with width given by the Planck positional uncertainty up to a maximum of 5 arcmin; larger priors allow the detection algorithm to fix on noise features toward the edges of the SA primary beam, which has a FWHM of ≈20 arcmin. In practice, no PwS positional errors in the sample are greater than 5 arcmin. MMF1 does not give positional error estimates, so clusters detected only by MMF1 are given the maximum 5 arcmin error; some clusters detected by MMF3 (but not PwS) have positional errors >5 arcmin, but as will be shown in Sect. 4.4.6, MMF3 positional errors tend to be over-estimated.
Model parameter estimation is performed in a fully Bayesian manner using the AMI in-house software package McADAM, in uv-space (see, e.g. Feroz et al. 2009b for more details). Bayes’ theorem states that 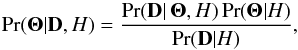 (4)where Θ is a set of parameters for a model, H, and D is the data. Thus, the posterior probability distribution, Pr(Θ | D,H), is proportional to the likelihood, Pr(D | Θ,H), multiplied by the prior, Pr(Θ | H). The normalising factor is the evidence,
(4)where Θ is a set of parameters for a model, H, and D is the data. Thus, the posterior probability distribution, Pr(Θ | D,H), is proportional to the likelihood, Pr(D | Θ,H), multiplied by the prior, Pr(Θ | H). The normalising factor is the evidence, 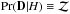 . McADAM uses the nested sampler MultiNEST (Feroz & Hobson 2008; Feroz et al. 2009a) to obtain the posterior distribution for all parameters, which can be marginalised to provide two- and one-dimensional parameter constraints.
. McADAM uses the nested sampler MultiNEST (Feroz & Hobson 2008; Feroz et al. 2009a) to obtain the posterior distribution for all parameters, which can be marginalised to provide two- and one-dimensional parameter constraints.
MultiNEST also calculates the evidence, which can be ignored for parameter estimation but is important for model selection, since it represents the probability of the data given a model and a prior, marginalised over the the model’s parameter space: 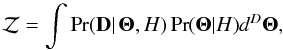 (5)where D is the dimensionality of the parameter space. The probability of two different models given the data can be compared using their evidence ratio:
(5)where D is the dimensionality of the parameter space. The probability of two different models given the data can be compared using their evidence ratio: 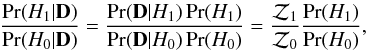 (6)where Pr(H1) / Pr(H0) is the a priori probability ratio for the two models. To assess the detection significance of a cluster, we therefore perform two parameter estimation runs – one with the full cluster + radio source environment model (H1), and one with only the radio source environment model (the null run, H0). We set Pr(H1) / Pr(H0) = 1 so that
(6)where Pr(H1) / Pr(H0) is the a priori probability ratio for the two models. To assess the detection significance of a cluster, we therefore perform two parameter estimation runs – one with the full cluster + radio source environment model (H1), and one with only the radio source environment model (the null run, H0). We set Pr(H1) / Pr(H0) = 1 so that 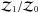 is a measure of the detection significance for the cluster. This ratio takes into account the various sources of noise as well as the goodness of fit of the radio source and cluster models.
is a measure of the detection significance for the cluster. This ratio takes into account the various sources of noise as well as the goodness of fit of the radio source and cluster models.
Figure 3 shows the distribution of 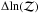 values in the SZ sample. It is also useful to define discrete detection and non-detection categories based on the continuous evidence ratio values. We follow Jeffreys (1961) in taking
values in the SZ sample. It is also useful to define discrete detection and non-detection categories based on the continuous evidence ratio values. We follow Jeffreys (1961) in taking 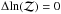 as the boundary between detections and non-detections. We also define an additional boundary
as the boundary between detections and non-detections. We also define an additional boundary 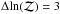 between moderate and clear detections, where moderate detections are cases where the data are more consistent with the presence of a cluster than not, but there is not enough information in the data to constrain the model parameters well. For symmetry, we also define a boundary at
between moderate and clear detections, where moderate detections are cases where the data are more consistent with the presence of a cluster than not, but there is not enough information in the data to constrain the model parameters well. For symmetry, we also define a boundary at 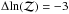 to indicate cases where the cluster model is strongly rejected by the data. These boundaries were chosen empirically, by inspecting final maps and posterior distributions. The four categories are listed in Table 3.
to indicate cases where the cluster model is strongly rejected by the data. These boundaries were chosen empirically, by inspecting final maps and posterior distributions. The four categories are listed in Table 3.
 |
Fig. 3 Distribution of evidence ratio values in the SZ sample, with the division into detection categories given in Table 3 indicated by red vertical lines. |
Evidence difference (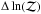 ) boundaries used for categorising clusters as clear detections, moderate detections, non-detections and clear non-detections, and the number of clusters in each category in the SZ sample.
) boundaries used for categorising clusters as clear detections, moderate detections, non-detections and clear non-detections, and the number of clusters in each category in the SZ sample.
4.3.1. Prior on Ytot and θs
The priors assigned to Ytot and θs in AP2013 and used for the Planck PwS analysis are based on marginalised distributions of Ytot and θs in a simulated population of clusters generated according to the Jenkins mass function (Jenkins et al. 2001), as described in Carvalho et al. (2012). The parameterisation functions for these priors are listed in Table 4. These priors ignore, however, the correlation between Ytot and θs; in addition, they take into account the Planck selection function only in assuming minimum and maximum cutoffs in each parameter.
To produce a better approximation to the true distribution of clusters expected to be detected by Planck, we used the results of the Planck completeness simulation (Planck Collaboration XXIX 2014, Sects. 3.1 and 3.2, Fig. 9). This simulation was produced by drawing a cluster population from the Tinker mass function (Tinker et al. 2008), and converting the redshifts and masses to Y500 and θ500 observable quantities using the scaling relations in Planck Collaboration X (2011). This cluster population was injected into the real Planck data assuming GNFW pressure profiles with the shape parameters varying according to results from Planck Collaboration Int. V (2013) and a simulated union catalogue was created by running the Planck detection pipelines on the simulated dataset in the usual manner; see Planck Collaboration XXIX (2014) for more details.
We noted that the resulting two-dimensional distribution in θs and Ytot in log-space was elliptical in shape with roughly Gaussian distribution along the principal axes and performed a two-dimensional Gaussian fit to the distribution, parameterised by width and offset in x = log 10(θs), width and offset in y = log 10(Ytot), and angle φ measured clockwise from the y-axis. The best-fit parameters are listed in Table 4, and the fit and residuals with respect to the simulated population are shown in Fig. 4. We use this fit to the simulated population as our prior on θs and Ytot.
Priors used on profile fit parameters.
 |
Fig. 4 a) Shows the sampled distribution (red histogram), and the two-dimensional elliptical Gaussian fit to the Ytot vs. θs distribution in log-space (black lines, enclosing 68% and 95% of the probability). b) Shows the residuals with respect to the simulated distribution. Note that the colour-axis scales are different. |
4.4. Results
In the SZ sample, 79 are clear detections, 20 are moderate detections, 21 are non-detections and 3 are clear non-detections. A summary of the results for each cluster in the sample is presented in Appendix A.
Some representative examples from each category are discussed in the following. In each case, two foreground-source-subtracted maps are shown; both are produced using natural weighting, and the second also has a Gaussian weighting function with the 30% point at 600 λ applied (the uv-tapered map). This taper downweights the longer baselines, which are only sensitive to small-angular-scale features, making the extended cluster more visible. The symbols × and + show the positions of subtracted sources, respectively either modelled in McAdam or directly subtracted based on LA values. Λ shows the AMI (McAdam -determined) position of the cluster, and the 1 × σPlanck positional error radius is shown as a circle. Contours are plotted at ±(2,3,4,...,10) × the rms noise level (measured using the aips task imean), and dashed contours are negative. The synthesised beam is shown in the bottom left-hand corner. We emphasise that these maps are only shown for visual inspection and to assess the residual foreground contamination; all parameter estimation is done in uv-space.
Posterior distributions for position offset, cluster model parameters and the flux densities of the closest radio sources to the cluster centre are also shown; in these plots the units are arcsec on the sky for offset in RA (x0) and δ (y0), arcmin2 for Ytot, arcmin for θs and mJy for radio source flux densities. The blue (pink) areas correspond to regions of higher (lower) probability density. The Ytot-θs posterior distribution is shown separately with solid black lines for the AMI constraints overlaid with that obtained by PwS using Planck data for the cluster in red, as well as the AMI prior (black dashed lines). The joint constraint is shown in yellow where appropriate. In all cases, the contours mark the 68% and 95% confidence limits in the posterior or prior probability distributions. Similar maps and posterior distribution plots for the entire sample are available online3.
4.4.1. Clear detections
Abell 2218 (PSZ1 G097.72+38.13)
Abell 2218 (Abell 1958) is an extremely well-known cluster and one of the earliest SZ detections (e.g. Birkinshaw et al. 1978, 1984; Jones et al. 1993). It lies at redshift z = 0.171 (Kristian et al. 1978). It has been observed by AMI previously as part of the LoCuSS sample (Rodríguez-Gonzálvez et al. 2012) and was also in AP2013. It has the highest Planck S/N in the final subsample and is also well-detected by AMI with 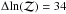 . Figure 5 shows that the cluster is resolved by AMI as the depth of the decrement increases in the uv-tapered map, and structure can be clearly seen in the naturally-weighted map. The posterior distributions (Fig. 6) show good constraints in both position and the cluster model parameters. The two-dimensional posterior distributions for the flux densities of the three most significant nearby sources are included in the plot; it can be seen that there is some correlation between the flux densities of the sources and Ytot, i.e. lower values of the flux densities allow lower values of Ytot, but this does not affect the parameter constraints significantly. There is also some correlation between the flux densities of the sources and the cluster position. The remaining two sources near the cluster centre are fainter and were not modelled in the initial analysis since they appear at <4σ on the SA map; there is no evidence for degeneracy between the flux densities of these sources and the cluster parameters. As in AP2013 (see their Fig. 5), the PwS Ytot-θs posterior overlaps with the AMI posterior, but AMI finds the cluster to be smaller and fainter than Planck (at low significance for this particular cluster).
. Figure 5 shows that the cluster is resolved by AMI as the depth of the decrement increases in the uv-tapered map, and structure can be clearly seen in the naturally-weighted map. The posterior distributions (Fig. 6) show good constraints in both position and the cluster model parameters. The two-dimensional posterior distributions for the flux densities of the three most significant nearby sources are included in the plot; it can be seen that there is some correlation between the flux densities of the sources and Ytot, i.e. lower values of the flux densities allow lower values of Ytot, but this does not affect the parameter constraints significantly. There is also some correlation between the flux densities of the sources and the cluster position. The remaining two sources near the cluster centre are fainter and were not modelled in the initial analysis since they appear at <4σ on the SA map; there is no evidence for degeneracy between the flux densities of these sources and the cluster parameters. As in AP2013 (see their Fig. 5), the PwS Ytot-θs posterior overlaps with the AMI posterior, but AMI finds the cluster to be smaller and fainter than Planck (at low significance for this particular cluster).
Ytot is the total SZ signal of the cluster and corresponds to the zero-spacing flux, which is not measured by an interferometer; the constraints produced by AMI on Ytot therefore rely on extrapolating the signal on the angular scales that AMI does measure (≈200 to 1200λ, corresponding to ≈15 to 3 arcmin) to 0λ assuming a fixed profile. Since this is a relatively nearby, large-angular-size cluster (i.e. θ500 inferred from the X-ray luminosity is 6.4 arcmin (Böhringer et al. 2000; Piffaretti et al. 2011) corresponding to θs = 5.4 arcmin for the universal value of c500 = 1.177, in agreement with the AMI constraint and slightly smaller than the preferred Planck value), much of the flux of the cluster exists on scales that are not measured by AMI. Ytot is therefore not well constrained and the Ytot-θs degeneracy is large compared to that produced by Planck, which measures Ytot directly. Nonetheless, the different degeneracy direction means that combining the two posteriors results in a tighter constraint (assuming no systematic difference between the two instruments, which will be discussed in Sect. 4.4.7).
 |
Fig. 5 SA source-subtracted map of A2218 with a) natural weighting and b) a uv-taper. The r.m.s. noise levels are 131 and 163 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 6. See Sect. 4.4 for more details on the plots. |
 |
Fig. 6 AMI posterior distributions for A2218 and the Ytot-θs posterior overlaid with that obtained by Planck in red, and the prior as a black dotted line (upper right-hand corner). The joint constraint is shown in yellow. See Sect. 4.4 for more details on the plots. |
PSZ1 G060.12+11.42
This is a new, previously unconfirmed (at the time the catalogue was published) cluster discovered by Planck at high S/N (7.2) and clearly detected by AMI with 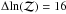 . The source-subtracted maps for the cluster are shown in Fig. 7, and the posterior distributions in Fig. 8. Again, it is clear that AMI resolves the cluster. The source flux densities of the two nearest sources are shown in the posterior distributions; there is no apparent degeneracy between the source flux densities and any of the parameters. In this case, the posterior distributions for θs and Ytot are very consistent with the PwS posteriors. The AMI and PwS degeneracies are in different directions, meaning that the joint constraints produced by combining the two are considerably tighter.
. The source-subtracted maps for the cluster are shown in Fig. 7, and the posterior distributions in Fig. 8. Again, it is clear that AMI resolves the cluster. The source flux densities of the two nearest sources are shown in the posterior distributions; there is no apparent degeneracy between the source flux densities and any of the parameters. In this case, the posterior distributions for θs and Ytot are very consistent with the PwS posteriors. The AMI and PwS degeneracies are in different directions, meaning that the joint constraints produced by combining the two are considerably tighter.
 |
Fig. 7 SA source-subtracted map of PSZ1 G060.12+11.42 with a) natural weighting and b) a uv-taper. The rms noise levels are 96 and 131 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 8. See Sect. 4.4 for more details on the plots. |
 |
Fig. 8 AMI posterior distributions for PSZ1 G060.12+11.42 and the Ytot-θs posterior overlaid with that obtained by Planck (upper right-hand corner). The joint constraint is shown in yellow. See Sect. 4.4 for more details on the plots. |
4.4.2. Moderate detections
ZW8503 (PSZ1 G072.78-18.70)
ZW8503 is a well-known cluster at z = 0.143 (Allen et al. 1992) with a large angular size (θs ≈ 8 arcmin as measured by Planck); it is therefore not too surprising that AMI does not detect it well. A decrement at the phase centre is visible in the source-subtracted maps (Fig. 9), and a model with a cluster is favoured over one without by 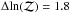 , but Fig. 10 shows that there is not enough information in the AMI data to constrain the cluster parameters well, and the Ytot–θs posterior distribution is strongly influenced by the prior (plotted as a black dotted line for comparison). There is also significant degeneracy between the cluster parameters (x0,y0,θs,Ytot) and the flux densities of the closest sources. The parameter space indicated by the Planck posterior is completely ruled out by the AMI posterior distribution. The AMI map shows a good positional coincidence with the X-ray emission (Fig. 11) and also shows some substructure within the cluster; if this is real, the spherical cluster model with the universal pressure profile (derived from fits to relaxed clusters) may not provide a good fit and the extrapolated Ytot result may be biased.
, but Fig. 10 shows that there is not enough information in the AMI data to constrain the cluster parameters well, and the Ytot–θs posterior distribution is strongly influenced by the prior (plotted as a black dotted line for comparison). There is also significant degeneracy between the cluster parameters (x0,y0,θs,Ytot) and the flux densities of the closest sources. The parameter space indicated by the Planck posterior is completely ruled out by the AMI posterior distribution. The AMI map shows a good positional coincidence with the X-ray emission (Fig. 11) and also shows some substructure within the cluster; if this is real, the spherical cluster model with the universal pressure profile (derived from fits to relaxed clusters) may not provide a good fit and the extrapolated Ytot result may be biased.
 |
Fig. 9 SA source-subtracted map of ZW8503 with a) natural weighting and b) a uv-taper. The rms noise levels are 90 and 122 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 10. See Sect. 4.4 for more details on the plots. |
 |
Fig. 10 AMI posterior distributions for ZW8503 and the Ytot-θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
 |
Fig. 11 A Chandra X-ray map of ZW85034with AMI-SA contours at ± (2,3,4) × 100 μJy overlaid to show the substructure. The grey-scale is in units of counts per pixel and is truncated at the peak value in the centre of the cluster. The AMI synthesised beam is shown in the top right-hand corner. Note that the axis scale is different to Fig. 9. |
4.4.3. Non-detections
PSZ1 G074.75-24.59
PSZ1 G074.75-24.59 is associated in the Planck catalogue with ZwCl 2143.5+2014. Despite having an S/N of 6.1 and being detected by all three of the Planck detection algorithms, it is not detected by AMI, with an evidence difference of 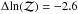 . Although there is some negative flux visible on the map, it is ruled out by the Planck positional prior (Fig. 12).
. Although there is some negative flux visible on the map, it is ruled out by the Planck positional prior (Fig. 12).
A simulated cluster using the PwS maximum a-posteriori values for θs and Ytot, observed using the same visibilities and noise levels as those in the real AMI observation, shows that this cluster should be detected at a S/N of ≈8 in the naturally-weighted map, and ≈9 in the uv-tapered map. However, the posterior distributions (Fig. 13) show that the θs/Ytot parameter space preferred by Planck cannot be ruled out by the AMI observations, so the cluster could be more extended than the Planck MAP estimate shows (although the redshift is given as 0.250 so this seems unlikely) and/or be significantly offset from its given position.
 |
Fig. 12 SA source-subtracted map of PSZ1 G074.75-24.59 with a) natural weighting and b) a uv-taper. The rms noise levels are 105 and 166 μJy beam-1 respectively. The position of ZwCl 2143.5+2014 is shown as a triangle (Zwicky & Kowal 1968). See Sect. 4.4 for more details on the plots. |
 |
Fig. 13 AMI posterior distributions for PSZ1 G074.75-24.59 and the Ytot–θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
4.4.4. Clear non-detections
PSZ1 G137.56+53.88 is a clear non-detection with evidence ratio 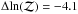 . There is no negative flux near the phase centre and no nearby point sources or positive extended emission to cause the non-detection of the cluster (Fig. 14). Simulations show the cluster should have a significance of ≈17 in both the naturally-weighted and uv-tapered maps. The posterior distribution (Fig. 15) shows that very large values of θs are required to provide any kind of consistency with the data, so that nearly all of the cluster flux would be resolved out, in disagreement with the small value for θs indicated by PwS. Noting also that although the cluster has an S/N of 5.7, it was detected by PwS only and not the other algorithms, we consider it likely to be a spurious detection.
. There is no negative flux near the phase centre and no nearby point sources or positive extended emission to cause the non-detection of the cluster (Fig. 14). Simulations show the cluster should have a significance of ≈17 in both the naturally-weighted and uv-tapered maps. The posterior distribution (Fig. 15) shows that very large values of θs are required to provide any kind of consistency with the data, so that nearly all of the cluster flux would be resolved out, in disagreement with the small value for θs indicated by PwS. Noting also that although the cluster has an S/N of 5.7, it was detected by PwS only and not the other algorithms, we consider it likely to be a spurious detection.
 |
Fig. 14 SA source-subtracted map of PSZ1 G137.56+53.88 with a) natural weighting and b) a uv-taper. The rms noise levels are 109 and 150 μJy beam-1 respectively. See Sect. 4.4 for more details on the plots. |
 |
Fig. 15 AMI posterior distributions for PSZ1 G137.56+53.88 and the Ytot–θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
 |
Fig. 16 Positional offset from AMI for the three Planck detection algorithms. The size of the points plotted increases with increasing Planck S/N; clear detections are plotted as filled circles, and moderate detections as empty circles. |
4.4.5. Validation
Detection of new clusters
Of our SZ sample, 82 clusters are previously known (the validation flag in the Planck catalogue is 20). 16 of the new clusters are already confirmed by other followup (validation =10); of these, we re-confirm 14.
We detect 14 of the remaining 25 new clusters that have not been previously confirmed by other methods, at the time of publishing of the catalogue. All of these are detected by at least two Planck pipelines, and 8 are detected by all three. For these clusters, the Planck catalogue provides a quality assessment flag between 1 and 3 (1 being the most reliable); there are 6, 4 and 4 AMI detections in the 1, 2 and 3 categories respectively.
Discussion of AMI non-detections
Across the whole sample, 75% of the AMI non- and clear non-detections have less than three Planck pipeline detections, compared to 18% for the AMI clear and moderate detections; of the previously unconfirmed clusters, none of the AMI non- and clear non-detections has a quality flag value of 1. Although it is difficult to rule out the presence of a cluster entirely using AMI data alone, these correlations indicate that an AMI non-detection is a useful indicator for a possible spurious Planck detection. Figure B.2 shows θs–Ytot posteriors for all of the non-detections; the Planck parameter space is often ruled out by the AMI posterior.
All of the three clear non-detections have <3 Planck pipeline detections. Two of these (PSZ1 G053.50+09.56 and PSZ1 G142.17+37.28) are within 5 arcmin of thermal, compact sources at 545 and/or 857 GHz, which are another indicator of a potentially spurious Planck detection caused by contamination by dust emission. The third has been addressed in Sect. 4.4.4; we consider these three likely to be spurious.
The Planck catalogue produced by the intersection of detections by the three algorithms is expected to be ≈99% pure at S/N ≥ 5 (Planck Collaboration XXIX 2014). Our SZ sample of 123 clusters contains 87 in the intersection catalogue, of which 81 are detected by AMI. This leaves six non-detections. Of these, three (PSZ1 G099.48+55.62, PSZ1 G107.32-31.51, and PSZ1 G084.84+35.04) are at known, low redshift and the posteriors in Fig. B.2 show that the region of θs–Ytot parameter space preferred by Planck cannot be ruled out by the AMI observations; i.e. these clusters are likely to be too large in angular size (and not bright enough) to be seen by AMI. Of the remaining four, PSZ1 G094.69+26.34 is predicted to have a low S/N of ≈4 in the AMI data based on the Planck maximum a-posteriori values of θs and Ytot, and could also be resolved out if the true values are toward the upper edge of the constraint. Also, although PSZ1 G050.46+67.54 should be well-detected according to its Planck size estimate of θs ≈ 3 arcmin, it is within 220 arcsec of an MCXC cluster with size θ500 = 6.89 arcmin (Piffaretti et al. 2011), corresponding to θs = 5.85 arcmin for c500 = 1.177 and may therefore also be resolved out if the Planck size is an under-estimate.
This leaves one cluster only in the intersection catalogue, PSZ1 G074.75-24.59, which simulations based on the Planck maximum a-posteriori parameter estimates predict should be well-detected by AMI; the AMI maps (Fig. 12) show no source environment problems which could explain its non-detection. More follow-up data will be required to definitively determine if this is a spurious detection, as the pressure profile of the cluster gas could deviate significantly from the universal pressure profile and/or the Planck position estimates could be offset significantly from the true position, so that the simulations do not accurately predict the AMI detection significances.
4.4.6. Positional comparison
The higher angular resolution of AMI enables a more accurate positional estimate to be produced for the clusters (although in practice this depends on a variety of factors such as signal-to-noise over the angular scales observed by both telescopes, and how successful the decoupling of the signal from the foregrounds is). This allows the accuracy of the Planck positions and error estimates to be checked. Figure 16 compares positional offsets between AMI and the three Planck detection algorithms. The offsets for MMF1 and MMF3 are very similar. The PwS offsets are slightly more clustered toward zero, and also show a greater correlation with the S/N (i.e. the highest S/N points are closer to zero than the low-S/N points).
The MMF1 algorithm does not currently output positional errors, so Fig. 17 shows the distribution of positional offsets normalised by the total error 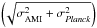 for PwS and MMF3 only. A Rayleigh distribution, (x/σ2)exp(−x2/ 2σ2) with σ = 1, is plotted for comparison – this is the expected distribution assuming the errors in RA and δ are uncorrelated and normally distributed. The PwS distribution is a reasonable match, showing that the error estimates are a good representation of the true uncertainty in the positions. In contrast, the MMF3 errors are generally overestimated in this version of the Planck catalogue.
for PwS and MMF3 only. A Rayleigh distribution, (x/σ2)exp(−x2/ 2σ2) with σ = 1, is plotted for comparison – this is the expected distribution assuming the errors in RA and δ are uncorrelated and normally distributed. The PwS distribution is a reasonable match, showing that the error estimates are a good representation of the true uncertainty in the positions. In contrast, the MMF3 errors are generally overestimated in this version of the Planck catalogue.
 |
Fig. 17 Positional offset from AMI, normalised by total error |
We estimate a rescaling factor of 0.28 for the MMF3 errors, by minimising the Kolmogorov-Smirnov test statistic between the distribution and the Rayleigh distribution. Figure 18 shows the rescaled histogram, which agrees much more closely with the Rayleigh distribution. In contrast, the same procedure gives a rescaling factor of 0.51 for the PwS errors. Figure 18 also shows a comparison between the absolute offsets between AMI and PwS and AMI and MMF3; confirming what is seen in Fig. 16, the PwS offsets are generally smaller, especially at high S/N.
The MMF3 rescaling factor is in agreement with that estimated via internal Planck quality assessment, and later versions of the catalogue have been corrected for this5.
 |
Fig. 18 a) shows the MMF3 positional offset from AMI, normalised by rescaled total error |
4.4.7. Ytot-θs comparison
A major conclusion of AP2013 was that the clusters were found overall to be smaller in angular size and fainter (lower Ytot) by AMI than by Planck. The comparison for the larger sample shows a similar trend.
To properly compare the quantities, it is necessary to look at the full, two-dimensional posteriors for Ytot and θs since the quantities are correlated. Figure B.1 shows the two-dimensional posteriors for θs and Ytot as measured by both AMI and Planck, and the joint constraints where appropriate, in descending Planck S/N order. It is clear that, especially at the high-S/N end, there are many cases where the constraints are inconsistent and in these cases the Planck posteriors usually prefer higher values of θs and Ytot.
Figure 19 shows the comparison between the AMI and PwS mean values for the entire sample of clear and moderate detections. Aside from some outliers, the θs values do not seem to be biased, but only correlate weakly, with a Pearson correlation coefficient of 0.25 (0.18) for all common AMI and PwS detections (clear AMI detections only). However, the Ytot values for the high-S/N clusters as measured by AMI are still lower overall than the Planck values; for lower S/N clusters, the bias may be obscured by the noise. Following Planck Collaboration XX (2014) for the definition of high-S/N, we make a cut at Planck S/N of 7 and fit a linear model to the Planck and AMI results for Ytot, using the SciPy orthogonal distance regression function6 to take into account errors in both the x and y direction. The best fit slope for all clusters (clear AMI detections only) above S/N of 7 is 4.2 ± 1.5 (2.45 ± 0.72); note that the slope for all clusters is driven by one very discrepant moderate detection. The slope for clear AMI detections only is consistent with the slope found in AP2013 (1.05 ± 0.05) at <2σ significance; note however that this relationship was obtained by fixing the cluster size to the θ500 inferred from the X-ray luminosity for improved consistency.
The comparison between AMI values and the values produced by the MMF algorithms is very similar.
 |
Fig. 19 Comparison between PwS and AMI mean Ytot and θs values. The size of the points plotted increases with increasing Planck S/N; clear detections are plotted as filled circles, and moderate detections as empty circles. Error bars are omitted for clarity and since the errors in Ytot and θs are correlated. The one-to-one relationship is plotted as a black dashed line. The fitted linear relationship for all clusters (clear AMI detections only) with S/N greater than 7 is plotted as a black solid (black dotted) line. |
This inconsistency could be due to the fact that AMI does not measure Ytot directly, since it is an interferometer and therefore resolves out the larger scales; as long as the cluster is resolved, the zero-spacing flux, and therefore Ytot, is never measured directly. In this case the discrepancy should be worse for larger angular-size clusters since more of an extrapolation is required to infer the zero-spacing flux. In Fig. 20a, the ratio of the Ytot values is plotted as a function of θs as measured by AMI and Planck; the discrepancy does appear worse for larger values of θs,Planck, but occurs across all values of θs,AMI. In Fig. 20b the correlation between θs and Ytot is plotted as measured by AMI and Planck, which also shows that the discrepancy occurs over the entire sample.
 |
Fig. 20 a) Shows a comparison between PwS and AMI MAP Ytot values as a function of AMI (PwS) θs values in black (red). The one-to-one relationship is plotted as a black dashed line. b) Shows Ytot as a function of θs as measured by AMI (black) and PwS (red) for all of the moderate and clear detections. In both plots, the size of the points plotted increases with increasing Planck S/N, clear detections are plotted as filled circles, and moderate detections as empty circles. Error bars are omitted for clarity and since the errors in Ytot and θs are correlated. |
Potential origins of the discrepancy
To first eliminate the possibility that the discrepancy is caused by absolute calibration problems, we obtained flux densities for two of our primary calibration sources, 3C 286 and 3C 147, at 30 and 44 GHz from the Planck Compact Source Catalogue (Planck Collaboration XXVIII 2014). These are shown in Fig. 21 with the power-law used to calculate the AMI primary calibration flux densities for comparison. All flux densities are within 3σ of the power-law, and there does not appear to be a systematic bias. We therefore discard absolute calibration as a potential cause of the discrepancy.
Several potential origins of the discrepancy were investigated in AP2013, as follows.
-
1.
The possibility that a population of faint sources existed below the LA detection threshold and acted to fill in the decrement was investigated by obtaining very deep LA observations toward the central pointing of the raster for each cluster, obtaining rms noise levels
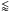 30 μ Jy beam-1, and re-extracting the cluster parameters, subtracting any extra sources detected. In one case this shifted the Ytot estimate upward by ≈1σ, but the parameters for the remaining 10 cases were not significantly changed. This is clearly not the source of the discrepancy.
30 μ Jy beam-1, and re-extracting the cluster parameters, subtracting any extra sources detected. In one case this shifted the Ytot estimate upward by ≈1σ, but the parameters for the remaining 10 cases were not significantly changed. This is clearly not the source of the discrepancy. -
2.
To eliminate any effects from differing centroid positions, the AMI and Planck data were both analysed with the position of the cluster fixed to the best-fit position obtained from an initial AMI analysis where the central position was allowed to vary. Fixing the position also had a negligible effect on the derived θs and Ytot posterior distributions.
-
3.
For five clusters with measured X-ray profiles, the cluster parameters were re-extracted using the appropriate X-ray-determined γ and α parameters rather than the universal parameters. This did not significantly improve the agreement. Note that the parameter affecting the cluster outskirts, β, was not varied since the X-ray data do not extend to this region. See AP2013 for more details.
When a point source very near the cluster centre is fitted simultaneously with the cluster model, there is often a correlation between the point source flux and the Ytot value, i.e. the data can constrain the sum of the point source flux and the cluster flux well, but not separate the two components. If this effect led to biases in the fitted Ytot values, it would worsen for smaller angular-size clusters since it becomes more difficult to distinguish between the profiles in uv-space of a marginally-resolved cluster and an unresolved point source. To test whether this could cause the discrepancy, we replotted Fig. 20 using only clusters with no fitted sources within 3 arcmin of the cluster position. This is shown in Fig. 22; although the number of clusters in the plot is much smaller, the discrepancy is clearly not resolved. In addition, we conducted tests on simulations of clusters with point sources of varying flux densities and at varying distances from the cluster centres, and found that we were able to recover Ytot values correctly.
 |
Fig. 21 Power-law relationships used to calculate primary calibration flux densities for AMI for two calibrators, 3C 286 and 3C 147, are shown with ± 5% uncertainty limits as the grey filled bands. The AMI frequency band is shown in black. Flux densities for both sources at 30 and 44 GHz taken from the Planck Compact Source Catalogue (Planck Collaboration XXVIII 2014) are shown as points with errorbars. |
 |
Fig. 22 Comparison between PwS and AMI θs and YtotMAP values, for clusters selected to have no radio point sources within 3 arcmin of the cluster position. In both plots, the black (red) points show the AMI (PwS) values, larger points have higher Planck S/N values and filled (empty) circles represent AMI clear (moderate) detections. |
Another potential problem is the mismatch between the spherical model and the real data; the higher resolution AMI data will be much more sensitive to this issue than the Planck data (in some cases, also dependent on other factors as discussed in Sect. 4.4.6). Some of the clusters have clearly non-spherical shapes in the AMI maps, but modelling with an ellipsoidal GNFW profile does not change the constraints on Ytot and θs significantly.
5. Profile investigation
The outstanding issue to be considered is the use of the universal profile shape for all clusters. AMI-SA data are not of high enough resolution to measure γ; the range of scales measured by the SA corresponds to 0.3 ≲ θ/θs ≲ 9 for clusters with angular sizes θs in the range 2 to 10 arcmin. For the smallest (largest) clusters in the sample, α (β) will be the parameter most affecting AMI data; for most clusters, both will be important.
5.1. Analysis of simulations
As a first step to understanding how variation in the shape parameters affects constraints derived from AMI data, we generated a set of simulations with realistic thermal, CMB and source confusion noise levels. We chose three representative values of θs based on the follow-up sample, and assigned realistic Ytot values to each based on clusters in the sample with a similar angular size and that were well-detected by AMI, giving (θs, Ytot) = (1.8, 0.0009), (4.5, 0.001) and (7.4, 0.007). For each (θs, Ytot), we generated simulations with α and γ set to the 31 individual fitted values from the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010), and with β drawn from a uniform distribution between 4.5 and 6.5. Figure 23a shows the result of analysing these simulations with the standard AMI analysis pipeline, assuming the universal profile parameters, whereas Fig. 23b shows the results when the simulation is both generated and analysed with the universal profile. In the former case, for the two smaller clusters, the true value is within the 68% confidence limit 29 times out of 31, but it is clear that the size and degeneracy direction of the contours varies wildly for different sets of (γ,α,β); on the whole, the mean and MAP values of θs and Ytot are biased upward slightly. For the largest cluster, the true value is within the 68% confidence limit only 2 times out of 31, and within the 95% confidence limit only 14 out of 31 times. Again, the size and degeneracy directions of the contours vary wildly; note that the very tight contours which are significantly discrepant from the rest correspond to the profile in the REXCESS sample that is most discrepant from the universal profile, with shape parameters γ = 0.065,α = 0.33. On the whole, the mean and MAP values of θs and Ytot are biased downward significantly for this cluster.
 |
Fig. 23 Posterior distribution for Ytot and θs for simulated clusters with realistic CMB and noise levels (see text for details), and a) differing GNFW shape parameter values (γ,α,β) based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010); and b) simulated with the universal values. In all cases the model used for recovering the parameters has the shape parameter values fixed to the universal values, and the joint two-dimensional prior on Ytot and θs is used. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4); the input parameter values are marked with red triangles. The contours are at the 68% and 95% confidence boundaries. |
To assess the potential for constraining α and β using AMI data, we next analysed the simulations, allowing the shape parameters to vary one at a time and using wide, uniform priors on all parameters. We found that, due to the lack of information on Ytot in the data, there are very strong degeneracies between θs and α and β, even when data with very small amounts of noise are analysed. For example, Fig. 24 shows that a profile generated with the universal value of β and a small angular size can be mimicked almost identically across a given range of angular scales using a much larger β and θs value.
In practice, these strong degeneracies were found to lead to spurious constraints in α and β in the one-dimensional marginalised posterior distribution. This is simply due to the shape of the three-dimensional posterior; more Ytot-θs space becomes available for lower values of α and β. Applying the two-dimensional prior on Ytot and θs to ensure that physically motivated parts of the Ytot–θs space are selected reduces, but does not eliminate, the problem. This is illustrated in Figs. 25 and 26 where the two- and one-dimensional posterior distributions are shown for θs, Ytot and α, with the standard two-dimensional prior on θs and Ytot and a uniform prior between 0.1 and 3.0 on α (with β fixed to the correct, input value of 5.4905). When there is little information on α in the data (particularly for the smallest cluster), the shape of the two-dimensional posteriors produces an apparent (and incorrect) constraint on α in the one-dimensional posteriors. Similar effects occur in the constraints on β, shown in Figs. 27 and 28 (in which α is fixed to the correct, input value of 1.0510).
To attempt to control these biases, we reanalysed the simulations using a Gaussian prior based on the REXCESS sample on α, namely 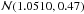 truncated at 0.3, and a tighter uniform prior on β,
truncated at 0.3, and a tighter uniform prior on β, ![\hbox{$\mathcal{U}[4.5, 6.5]$}](/articles/aa/full_html/2015/08/aa24188-14/aa24188-14-eq163.png) . Figure 29 shows the resulting posterior distributions, varying both α and β (but with γ fixed to the universal value). For the two smaller angular-size clusters, this results in correct recovery of θs and Ytot, and reduces the biassing considerably in α and β. For the largest angular-size cluster, the input values of θs and Ytot are not recovered correctly, because there is not enough information available in the angular scales measured by the SA to constrain these parameters simultaneously, so the prior on Ytot and θs biases the recovered posteriors downwards.
. Figure 29 shows the resulting posterior distributions, varying both α and β (but with γ fixed to the universal value). For the two smaller angular-size clusters, this results in correct recovery of θs and Ytot, and reduces the biassing considerably in α and β. For the largest angular-size cluster, the input values of θs and Ytot are not recovered correctly, because there is not enough information available in the angular scales measured by the SA to constrain these parameters simultaneously, so the prior on Ytot and θs biases the recovered posteriors downwards.
 |
Fig. 24 A profile generated with β = 5.4905,θs = 1.8 (the universal profile, black lines) can be mimicked for β = 8.9 using θs = 4.1 and adjusting Ytot downward (red lines). The two profiles are almost identical over the AMI-SA range of baselines, while Planck would measure the zero-spacing flux which differs by ≈7% between the two models. a) Shows the pressure profiles in radial coordinates (note that the y-axis scale is log); and b) shows the profiles in uv-space for channel 5, with the simulated AMI data shown as dots. Note that this simulation has been generated with an unrealistically small amount of thermal noise. |
 |
Fig. 25 Posterior distributions for Ytot, θs and α for simulated low-noise data, for clusters with θs = 1.8 (top), 4.5 (centre) and 7.4 (bottom) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on α between 0.1 and 3.0 (β fixed to the correct, input value). The input values are indicated by red triangles, and the posterior means with green crosses. θs is in arcmin and Ytot is in arcmin2. |
 |
Fig. 26 One-dimensional marginal constraints on Ytot, θs and α for simulated low-noise data, for clusters with θs = 1.8 (solid lines), 4.5 (dashed lines) and 7.4 (dotted lines) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on α between 0.1 and 3.0 (β fixed to the correct, input value). Input values are shown as red lines. θs is in arcmin and Ytot is in arcmin2. |
 |
Fig. 27 Posterior distributions for Ytot, θs and β for simulated low-noise data, for clusters with θs = 1.8 (top), 4.5 (centre) and 7.4 (bottom) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on β between 3.5 and 9.0 (α fixed to the correct, input value). The input values are indicated by red triangles, and the posterior means with green crosses. θs is in arcmin and Ytot is in arcmin2. |
 |
Fig. 28 One-dimensional marginal constraints on Ytot, θs and β for simulated low-noise data, for clusters with θs = 1.8 (solid lines), 4.5 (dashed lines) and 7.4 (dotted lines) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on β between 3.5 and 9.0 (α fixed to the correct, input value). Input values are shown as red lines. θs is in arcmin and Ytot is in arcmin2. |
We check for any biases due to γ being fixed (incorrectly) to the universal value by plotting the error in the recovered values of θs and Ytot as a function of the true input γ value. There is some correlation between the fractional difference in θs and γ, especially for the two smaller clusters, but mostly any correlation is beneath the level of the noise (Fig. 30).
We also add point sources of varying flux densities and at varying distances from the phase centre to test for any issues in decorrelating point source flux from cluster flux when varying the shape parameters; the parameter estimation is unaffected.
5.1.1. Adding Planck information
Although the immediate issue is to check whether we can achieve consistency between AMI and Planck results, it is also interesting to consider whether we can take advantage of the complementary nature of the two instruments to derive better constraints on the behaviour of the pressure profile over a range of radii. To this end, for each of our three simulated cluster sizes we derived a Planck-like prior on Ytot by marginalising over the θs dimension of the two-dimensional constraint produced by Planck for a cluster with similar angular size, and approximating as a Gaussian. We use this marginalised constraint as a prior rather than the full two-dimensional constraint since Planck Ytot estimation is more robust to changes in the profile shape parameters (Harrison et al. 2015). We then use our standard two-dimensional prior on θs conditioned on values drawn from the Planck-like Ytot prior; priors on α and β are as in the previous section. Figure 31 shows the resulting posterior distributions. For all three clusters, the constraints on θs and Ytot are much tighter, and for the large angular-size cluster, the true values of θs and Ytot are now recovered correctly. However, the constraints on the shape parameters are not very different.
This is a fairly crude way of including Planck information in the analysis and does not make the best use of the information available in the Planck data on the cluster shape. A full joint analysis of AMI and Planck data would fill in the gap in uv-coverage between the zero-spacing flux and the shortest AMI-SA baselines, and there would be some overlap with the shortest baselines since the resolution of Planck is ≈5 arcmin; this should produce better constraints on the profile shape parameters. This will be addressed in a future paper.
5.2. Summary of simulation results
We have shown with the simulated bank of clusters based on the REXCESS sample, that when a cluster has an angular size 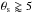 arcmin, the true input values of θs and Ytot can only be recovered correctly using AMI data when the model for the pressure profile used for parameter extraction is a good match to the actual pressure profile of the cluster. This is not surprising since, as we have mentioned, an interferometer does not measure zero-spacing flux directly and so the Ytot value measured by AMI is actually an extrapolation based on the assumed profile. This is also consistent with what we observe in the real sample; clusters with high Planck S/N (and therefore large θs) are consistently measured to be smaller and fainter by AMI.
arcmin, the true input values of θs and Ytot can only be recovered correctly using AMI data when the model for the pressure profile used for parameter extraction is a good match to the actual pressure profile of the cluster. This is not surprising since, as we have mentioned, an interferometer does not measure zero-spacing flux directly and so the Ytot value measured by AMI is actually an extrapolation based on the assumed profile. This is also consistent with what we observe in the real sample; clusters with high Planck S/N (and therefore large θs) are consistently measured to be smaller and fainter by AMI.
When attempting to vary the GNFW shape parameters, we must be careful to avoid over-interpretation of apparent constraints on parameters which are actually just caused by the shape of the two-dimensional degeneracies. Reducing the range of β and imposing a prior based on the REXCESS sample on α reduces these problems significantly. However, it is clear from Fig. 29 that in some cases these spurious constraints still do occur, particularly in α for small angular-size clusters, and β for medium angular-size clusters. Surprisingly, β is often recovered correctly for large angular-size clusters – this is due to the intersection of the physically motivated prior on θs and Ytot and the degeneracy direction between θs and β.
It is also clear from Fig. 29 that varying the shape parameters does not aid in recovering the correct θs and Ytot values for large angular-size clusters; joint analysis of Planck and AMI data is required to achieve this. As a first approximation, using a Planck-derived prior on Ytot can help, but does not improve the constraints on α and β.
It is also interesting to note that our parameter constraints are not very reliant on noise level. Our initial tests were made on simulated data with unrealistically small noise levels of 100 μJy per visibility; when we moved to simulations with more realistic noise levels (of ≈120 μJy beam-1 across the channel-averaged map), the constraints changed very little. As long as one has a good detection, it seems that the limiting factor on our parameter constraints is very much the range of angular scales present in the data with respect to the size of the cluster, rather than the detection significance.
 |
Fig. 29 Posterior distributions for simulated clusters with realistic noise levels (see text for details), and varying GNFW shape parameter values based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010). a) shows the two-dimensional θs and Ytot posterior, and b) and c) show the one-dimensional posteriors for α and β, shifted to be centred on the appropriate true value. In all cases γ is fixed to the universal value, α has a truncated Gaussian prior based on the REXCESS sample, β is varied uniformly between 4.5 and 6.5, and the joint two-dimensional prior on Ytot and θs is used. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4 arcmin); the input parameter values are marked with red triangles and lines. |
5.3. Analysis of real data
For all the clear detections in the sample, we re-extract the cluster parameters allowing α and β to vary as described in Sect. 5.1. The constraints on Ytot and θs are on the whole broader but the positions of the maxima are unchanged. The full two-dimensional constraints for the whole sample are available online7; here we present a few examples.
5.3.1. Abell 1413 (PSZ1 G226.19+76.78)
Abell 1413 is well-detected by AMI, with an evidence ratio of 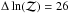 , and Planck, with a PwS S/N of 9.8 and detections by all three algorithms. It is at redshift z = 0.143 (e.g. Struble & Rood 1987) so could be expected to have a large angular size; the θ500 value inferred from the X-ray luminosity is ≈7.9 arcmin (Böhringer et al. 2000; Piffaretti et al. 2011), corresponding to θs ≈ 6.7 arcmin for c500 = 1.177. The AMI constraints on θs and Ytot could therefore be expected to be biased downward if the profile differs from the universal profile. Indeed, the Planck constraints indicate much higher values of both (see Fig. B.1 under the Planck name of PSZ1 G226.19+76.78). From the simulation results we can therefore expect to produce some constraints on α and β from the AMI data, although not to recover the correct values of θs and Ytot; the posterior distributions for the real data are shown in Fig. 32.
, and Planck, with a PwS S/N of 9.8 and detections by all three algorithms. It is at redshift z = 0.143 (e.g. Struble & Rood 1987) so could be expected to have a large angular size; the θ500 value inferred from the X-ray luminosity is ≈7.9 arcmin (Böhringer et al. 2000; Piffaretti et al. 2011), corresponding to θs ≈ 6.7 arcmin for c500 = 1.177. The AMI constraints on θs and Ytot could therefore be expected to be biased downward if the profile differs from the universal profile. Indeed, the Planck constraints indicate much higher values of both (see Fig. B.1 under the Planck name of PSZ1 G226.19+76.78). From the simulation results we can therefore expect to produce some constraints on α and β from the AMI data, although not to recover the correct values of θs and Ytot; the posterior distributions for the real data are shown in Fig. 32.
In Planck Collaboration Int. V (2013), Planck and XMM-Newton data were used to produce fitted values for α and β for a sample of high-S/N Planck clusters. The sample includes seven of the clear detections in our SZ sample (however we note that for three of these, Planck Collaboration Int. V 2013 report non-physical values for (γ,α,β) producing negative values of Ytot because of the Γ functions in Eq. (3)). Their reported values for Abell 1413 are α = 0.83 and β = 4.31 (γ fixed at 0.31), which are plotted for comparison in Fig. 32. The AMI analysis produces a somewhat higher (but consistent) value for α; although the Planck β estimate is outside our prior range for β, our analysis shows no tendency to push toward the lower limit, toward the Planck value. However, assuming the shape of the Planck α-β degeneracy for the individual clusters is similar to that for their stacked profile (reproduced in Fig. 33), the AMI and Planck constraints on β could be consistent.
5.3.2. RXC J2228.6+2036 (PSZ1 G083.30-31.01)
Similarly to Abell 1413, RXC J2228.6+2036 is well-detected by AMI (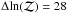 ) and Planck (S/N = 7.3, detected by all algorithms). It is at higher redshift, z = 0.412 (Böhringer et al. 2000) so the large value for θs of ≈4.5 arcmin preferred by Planck is slightly surprising. Figure 34 shows the posteriors on θs and Ytot produced by AMI and Planck, as well as the region of the space predicted by the physical model described in Olamaie et al. (2012) assuming the universal pressure profile for the gas, and the Tinker mass function (Tinker et al. 2008). The AMI posterior is much more consistent with the prediction than the Planck posterior; also our simulations have shown that if the correct value were θs ≈ 4.5, we should recover it even if the profile deviates from the universal profile. In addition, θ500 determined from the X-ray luminosity is 3.9 arcmin (Böhringer et al. 2000; Piffaretti et al. 2011), corresponding to θs = 3.3 arcmin for c500 = 1.177 is consistent with the AMI mean value of 2.3 arcmin. We therefore conclude that in this case the Planck θs estimate is likely to be an over-estimate.
) and Planck (S/N = 7.3, detected by all algorithms). It is at higher redshift, z = 0.412 (Böhringer et al. 2000) so the large value for θs of ≈4.5 arcmin preferred by Planck is slightly surprising. Figure 34 shows the posteriors on θs and Ytot produced by AMI and Planck, as well as the region of the space predicted by the physical model described in Olamaie et al. (2012) assuming the universal pressure profile for the gas, and the Tinker mass function (Tinker et al. 2008). The AMI posterior is much more consistent with the prediction than the Planck posterior; also our simulations have shown that if the correct value were θs ≈ 4.5, we should recover it even if the profile deviates from the universal profile. In addition, θ500 determined from the X-ray luminosity is 3.9 arcmin (Böhringer et al. 2000; Piffaretti et al. 2011), corresponding to θs = 3.3 arcmin for c500 = 1.177 is consistent with the AMI mean value of 2.3 arcmin. We therefore conclude that in this case the Planck θs estimate is likely to be an over-estimate.
 |
Fig. 30 Fractional difference [(MAP value − true value)/(true value)] in θsa) and Ytotb) as a function of the input value of γ. Clusters with θs = 1.8 are plotted as dots, θs = 4.5 as crosses and θs = 7.4 as open circles. |
Figure 34 also shows the posteriors on α and β resulting from the AMI analysis. Assuming the AMI value of θs is correct, we should be able to produce some constraint on β; indeed, there is a weak preference for higher values of β, while the posterior distribution for α mostly recovers the prior. The fitted α and β values from Planck Collaboration Int. V (2013) are also shown and in this case are very consistent with the AMI constraints.
 |
Fig. 31 Posterior distributions for simulated clusters with realistic noise levels (see text for details), and varying GNFW shape parameter values based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010). a) shows the two-dimensional θs and Ytot posterior, and b) and c) show the one-dimensional posteriors for α and β, shifted to be centred on the appropriate true value. In all cases γ is fixed to the universal value, α has a truncated Gaussian prior based on the REXCESS sample, β is varied uniformly between 4.5 and 6.5, a Planck-like Gaussian prior is used on Ytot and θs has the conditional prior drawn from the two-dimensional prior. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4); the input parameter values are marked with red triangles and lines. |
 |
Fig. 32 AMI posterior distributions for A1413, allowing α and β to vary. Posterior means are indicated with green lines and crosses, and the Planck + XMM-Newton estimates of α and β from Planck Collaboration Int. V (2013) are shown with red lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. |
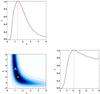 |
Fig. 33 Marginalised posterior likelihood distribution for α and β based on stacked Planck and XMM-Newton data for a sample of high-S/N Planck clusters (from Planck Collaboration Int. V 2013). The white cross marks the position of the best-fit value, and the white triangle marks the universal values. |
 |
Fig. 34 AMI posterior distributions for RXC J2228.6+2036, allowing α and β to vary. Posterior means are indicated with green lines and crosses, and the Planck values for α and β from Planck Collaboration Int. V (2013) are shown with red lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. Also shown in the upper right hand corner are the posteriors produced by AMI (black) and Planck (red) using the universal profile, and a prediction produced by the physical model described in Olamaie et al. (2012) based on a redshift of z = 0.412 (yellow). |
5.4. PSZ1 G134.31-06.57
PSZ1 G134.31-06.57 is a new Planck cluster at unknown redshift, with Planck S/N = 5.4 and AMI 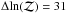 . The Planck and AMI constraints for this cluster overlap, and the different degeneracy directions result in a considerably tighter joint constraint, giving θs ≈ 4.5 arcmin (see Fig. B.1). At this angular size, AMI data should produce constraints on α. Figure 35 shows the parameter constraints – α moves away from the prior to a higher value of ≈1.5, while β also shows a weak constraint to values higher than the universal value.
. The Planck and AMI constraints for this cluster overlap, and the different degeneracy directions result in a considerably tighter joint constraint, giving θs ≈ 4.5 arcmin (see Fig. B.1). At this angular size, AMI data should produce constraints on α. Figure 35 shows the parameter constraints – α moves away from the prior to a higher value of ≈1.5, while β also shows a weak constraint to values higher than the universal value.
 |
Fig. 35 AMI posterior distributions for PSZ1 G134.31-06.57, allowing α and β to vary. Posterior means are indicated with green lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. |
5.4.1. Properties of α and β in the sample
Figure 36 shows a histogram of the recovered mean α and β values for all the clear detections in the sample.
Planck Collaboration Int. V (2013) and Sayers et al. (2013) both derive average pressure profiles for smaller samples of clusters using SZ data from Planck and BOLOCAM respectively. In both analyses, the radial profiles derived from the SZ maps are scaled by X-ray-determined r500 values and then stacked; a GNFW model is fitted to the stacked profiles (+ X-ray points for the inner part of the profile in Planck Collaboration Int. V 2013). Their final best fit parameters are given by (c500,γ,α,β) = (1.81, 0.31, 1.33, 4.1) and (1.18, 0.67, 0.86, 3.67) respectively. In contrast, the AMI analysis does not rely on X-ray estimates of r500, being based purely on the AMI SZ data. The AMI preferred values for β are on the whole centred around the universal value predicted by simulations, and do not show a trend towards the lower values derived from the Planck and BOLOCAM analyses. The AMI mean α estimates show a slight trend toward higher values, in agreement with the Planck value and in disagreement with the BOLOCAM value. However, since there are large (and different) degeneracies between the GNFW model parameters in the three analyses it is difficult to judge whether the analyses truly disagree (see Fig. 33, where it is clear that higher β values are not ruled out by the Planck likelihood).
The AMI data for these clusters therefore indicate that although individual clusters do not necessarily conform to the universal profile and it is important to take this into account when analysing AMI data, on the whole the average profile for the sample remains close to the universal profile shape even though these clusters are selected via a very different selection function compared to the REXCESS sample.
 |
Fig. 36 The distribution of mean values of α and β obtained for all the clear detections in the SZ sample. For comparison, the REXCESS-based prior on α (scaled arbitrarily) is also plotted in red, and the universal value of β predicted from numerical simulations is indicated with a red line. |
6. Conclusions
We have followed up the 195 clusters from the Planck union catalogue that are visible to AMI, lie at z> 0.100 and have Planck S/N ≥ 5. Of these, we reject 72 due to difficult radio source environment, leaving a total SZ sample of 123. We find that:
-
1.
We detect 99 of the clusters, including 79 very good detections.
-
We re-confirm 14 of 16 new clusters already confirmed by other observations, and validate 14 of 25 new clusters which were not confirmed at the time the Planck catalogue was published.
-
3.
We do not detect 24 of the clusters, which may be too extended for AMI to detect, be significantly offset from the phase centre, have a gas pressure profile deviating significantly from the universal profile, or be spurious detections by Planck. 75% of the AMI non-detections are detected by <3 Planck algorithms, as opposed to 18% of the AMI detections; none of the AMI non-detections have quality flag values of 1. These correlations indicate that an AMI non-detection is a good indicator for a spurious Planck detection.
-
4.
Comparing the AMI positional estimates to those produced by PwS and the MMF algorithms shows that PwS positional estimates are generally more accurate, a more reliable function of S/N, and have a positional error estimate consistent with the true uncertainty in the positions; in contrast, the MMF3 positional errors are over-estimated by a factor of ≈3.
-
5.
The trend seen in AP2013 where Planck consistently characterises clusters to be of larger angular size and brighter is continued in the larger sample, particularly for high Planck S/N clusters; our simulation results suggest that this may be caused by deviation from the universal profile used for parameter recovery.
-
6.
We can generalise the model used for parameter extraction from AMI data to consider variation in α and β, however the priors on the shape parameters must be considered carefully since degeneracies with θs and Ytot can produce spurious one-dimensional constraints on the shape parameters.
-
7.
AMI data alone cannot reliably constrain θs and Ytot for clusters of angular size
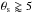 arcmin when there is uncertainty in the pressure profile of the cluster; it can however be used to constrain α and β.
arcmin when there is uncertainty in the pressure profile of the cluster; it can however be used to constrain α and β. -
8.
AMI data can be used to constrain θs, Ytot and β (α) simultaneously for clusters of angular size ≈3 arcmin (≈5 arcmin), given a careful choice of priors on α and β.
-
9.
While deviation from the universal profile has been shown to be important for analysing AMI data on a cluster-by-cluster basis, overall the β values obtained by re-analysing all of the clear detections from the Planck sample with varying α and β do not show support for deviation from the universal β value derived from numerical simulations.
Online material
Appendix A: Results table
Summary of results for all clusters between 20° ≤ δ< 87° with Planck S/N> 5.
Appendix B: Ytot–θs posterior comparison
 |
Fig. B.1 Ytot–θs posterior distributions for AMI and Planck, in descending Planck S/N order (note that this is the compatibility S/N for PwS), for all AMI detections ( |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.1 continued. |
 |
Fig. B.2 Ytot–θs posterior distributions for AMI and Planck, in descending Planck S/N order (note that this is the compatibility S/N for PwS), for all AMI non-detections ( |
 |
Fig. B.2 continued. |
Available online at http://www.astro.phy.cam.ac.uk/surveys/ami-planck/
Courtesy of the Chandra X-ray Observatory Center and the Chandra Data Archive, http://cxc.cfa.harvard.edu/cda/ (ivo://ADS/Sa.CXO#obs/13379)
See http://wiki.cosmos.esa.int/planckpla/index.php/Catalogues#The_SZ_catalogues under Caveats.
Acknowledgments
We are grateful to a substitute referee who responded rapidly, with useful comments, to our paper. The AMI telescope is supported by Cambridge University. Y.C.P. and C.R. acknowledge support from CCT/Cavendish Laboratory and STFC studentships, respectively. Y.C.P. and M.O. acknowledge support from Research Fellowships from Trinity College and Sidney Sussex College, Cambridge, respectively. This work was partially undertaken on the COSMOS Shared Memory system at DAMTP, University of Cambridge operated on behalf of the STFC DiRAC HPC Facility. This equipment is funded by BIS National E-infrastructure capital grant ST/J005673/1 and STFC grants ST/H008586/1, ST/K00333X/1. C.M. acknowledges her KICC Fellowship grant funding for the procurement of the cluster used for computational work. In addition, we would like to thank the IOA computing support team for maintaining the cluster.
References
- Abell, G. O. 1958, ApJS, 3, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Aghanim, N., da Silva, A. C., & Nunes, N. J. 2009, A&A, 496, 637 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Albert, C. E., White, R. A., & Morgan, W. W. 1977, ApJ, 211, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Allen, S. W., Edge, A. C., Fabian, A. C., et al. 1992, MNRAS, 259, 67 [NASA ADS] [Google Scholar]
- Angulo, R. E., Springel, V., White, S. D. M., et al. 2012, MNRAS, 426, 2046 [CrossRef] [Google Scholar]
- Appenzeller, I., Thiering, I., Zickgraf, F.-J., et al. 1998, ApJS, 117, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barker, R., Biddulph, P., Bly, D., et al. 2006, MNRAS, 369, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M., Gull, S. F., & Northover, K. J. E. 1978, Nature, 275, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Birkinshaw, M., Gull, S. F., & Hardebeck, H. 1984, Nature, 309, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Pratt, G. W., et al. 2007, A&A, 469, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carvalho, P., Rocha, G., & Hobson, M. P. 2009, MNRAS, 393, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Carvalho, P., Rocha, G., Hobson, M. P., & Lasenby, A. 2012, MNRAS, 427, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, A. C., Kay, S. T., Liddle, A. R., & Thomas, P. A. 2004, MNRAS, 348, 1401 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, M. L., Franzen, T. M. O., Waldram, E. M., et al. 2011, MNRAS, 415, 2708 [Google Scholar]
- Ebeling, H., Edge, A. C., & Henry, J. P. 2001, ApJ, 553, 668 [Google Scholar]
- Ebeling, H., Mullis, C. R., & Tully, R. B. 2002, ApJ, 580, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., & Hobson, M. P. 2008, MNRAS, 384, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., & Bridges, M. 2009a, MNRAS, 398, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Feroz, F., Hobson, M. P., Zwart, J. T. L., Saunders, R. D. E., & Grainge, K. J. B. 2009b, MNRAS, 398, 2049 [NASA ADS] [CrossRef] [Google Scholar]
- Fetisova, T. S. 1981, Sov. Astron., 25, 647 [Google Scholar]
- Franzen, T. M. O., Davies, M. L., Waldram, E. M., et al. 2011, MNRAS, 415, 2699 [NASA ADS] [CrossRef] [Google Scholar]
- Gower, J. F. R., Scott, P. F., & Wills, D. 1967, MmRAS, 71, 49 [NASA ADS] [Google Scholar]
- Harrison, D., Sutton, D., Carvalho, P., & Hobson, M. 2015, MNRAS, 451, 2610 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Brown, M. L., Davies, M. L., et al. 2011, MNRAS, 414, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Hurley-Walker, N., Bridle, S., Cypriano, E. S., et al. 2012, MNRAS, 419, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffreys, H. 1961, Theory of Probability, 3rd edn. (Oxford, England: Oxford) [Google Scholar]
- Jenkins, A., Frenk, C. S., White, S. D. M., et al. 2001, MNRAS, 321, 372 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jones, M., Saunders, R., Alexander, P., et al. 1993, Nature, 365, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. T., Peel, M. W., Short, C. J., et al. 2012, MNRAS, 422, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Kristian, J., Sandage, A., & Westphal, J. A. 1978, ApJ, 221, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Mehrtens, N., Romer, A. K., Hilton, M., et al. 2012, MNRAS, 423, 1024 [NASA ADS] [CrossRef] [Google Scholar]
- Melin, J., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melin, J.-B., Aghanim, N., Bartelmann, M., et al. 2012, A&A, 548, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motl, P. M., Hallman, E. J., Burns, J. O., & Norman, M. L. 2005, ApJ, 623, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D. 2006, ApJ, 650, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007, ApJ, 668, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Olamaie, M., Hobson, M. P., & Grainge, K. J. B. 2012, MNRAS, 423, 1534 [NASA ADS] [CrossRef] [Google Scholar]
- Perley, R. A., & Butler, B. J. 2013, ApJS, 204, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Petrov, L., Kovalev, Y. Y., Fomalont, E. B., & Gordon, D. 2008, AJ, 136, 580 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck and AMI Collaborations. 2013, A&A, 550, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. V. 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2011, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2011, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVIII. 2014, A&A, 571, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pravdo, S. H., & Marshall, F. E. 1984, ApJ, 281, 570 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Gonzálvez, C., Shimwell, T. W., Davies, M. L., et al. 2012, MNRAS, 425, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Rudy, D. J., Muhleman, D. O., Berge, G. L., Jakosky, B. M., & Christensen, P. R. 1987, Icarus, 71, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Sayers, J., Czakon, N. G., Mantz, A., et al. 2013, ApJ, 768, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Shimwell, T. W., Rodríguez-Gonzálvez, C., Feroz, F., et al. 2013, MNRAS, 433, 2920 [NASA ADS] [CrossRef] [Google Scholar]
- Struble, M. F., & Rood, H. J. 1987, ApJS, 63, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Comments on Astrophysics and Space Physics, 4, 173 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2009, ApJS, 183, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, Z. L., Han, J. L., & Liu, F. S. 2012, ApJS, 199, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Zwart, J. T. L., Barker, R. W., Biddulph, P., et al. 2008, MNRAS, 391, 1545 [NASA ADS] [CrossRef] [Google Scholar]
- Zwart, J. T. L., Feroz, F., Davies, M. L., et al. 2011, MNRAS, 418, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F. 1937, ApJ, 86, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Zwicky, F., & Kowal, C. T. 1968, Catalogue of Galaxies and of Clusters of Galaxies, Vol. VI [Google Scholar]
- Zwicky, F., Herzog, E., Wild, P., Karpowicz, M., & Kowal, C. T. 1961, Catalogue of galaxies and of clusters of galaxies, Vol. I [Google Scholar]
All Tables
Numbers of clusters in the 20° ≤ δ< 87°, Planck S/N ≥ 5 sub-sample in various categories.
Evidence difference (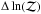 ) boundaries used for categorising clusters as clear detections, moderate detections, non-detections and clear non-detections, and the number of clusters in each category in the SZ sample.
) boundaries used for categorising clusters as clear detections, moderate detections, non-detections and clear non-detections, and the number of clusters in each category in the SZ sample.
All Figures
 |
Fig. 1 Noise maps for a typical cluster observation at δ ≈ 54° on the AMI-LA a) and SA b). The grey-scales are in μJy beam-1 and on a) the grey-scale is truncated to show the range of noise levels; b) is cut off at the 10% power point of the primary beam. |
| In the text | |
 |
Fig. 2 uv-coverages for a typical cluster observation at δ ≈ 54°, for the AMI-LA a) and SA b). The colours indicate different channels. Note the different axis scales; the short baselines of the SA are designed for sensitivity to arcminute-scale cluster emission, while the longer baselines of the LA are insensitive to emission on this scale and are used to characterise and subtract the foreground radio sources. |
| In the text | |
 |
Fig. 3 Distribution of evidence ratio values in the SZ sample, with the division into detection categories given in Table 3 indicated by red vertical lines. |
| In the text | |
 |
Fig. 4 a) Shows the sampled distribution (red histogram), and the two-dimensional elliptical Gaussian fit to the Ytot vs. θs distribution in log-space (black lines, enclosing 68% and 95% of the probability). b) Shows the residuals with respect to the simulated distribution. Note that the colour-axis scales are different. |
| In the text | |
 |
Fig. 5 SA source-subtracted map of A2218 with a) natural weighting and b) a uv-taper. The r.m.s. noise levels are 131 and 163 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 6. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 6 AMI posterior distributions for A2218 and the Ytot-θs posterior overlaid with that obtained by Planck in red, and the prior as a black dotted line (upper right-hand corner). The joint constraint is shown in yellow. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 7 SA source-subtracted map of PSZ1 G060.12+11.42 with a) natural weighting and b) a uv-taper. The rms noise levels are 96 and 131 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 8. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 8 AMI posterior distributions for PSZ1 G060.12+11.42 and the Ytot-θs posterior overlaid with that obtained by Planck (upper right-hand corner). The joint constraint is shown in yellow. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 9 SA source-subtracted map of ZW8503 with a) natural weighting and b) a uv-taper. The rms noise levels are 90 and 122 μJy beam-1 respectively. The numbered sources have posterior distributions for their flux densities plotted in Fig. 10. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 10 AMI posterior distributions for ZW8503 and the Ytot-θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 11 A Chandra X-ray map of ZW85034with AMI-SA contours at ± (2,3,4) × 100 μJy overlaid to show the substructure. The grey-scale is in units of counts per pixel and is truncated at the peak value in the centre of the cluster. The AMI synthesised beam is shown in the top right-hand corner. Note that the axis scale is different to Fig. 9. |
| In the text | |
 |
Fig. 12 SA source-subtracted map of PSZ1 G074.75-24.59 with a) natural weighting and b) a uv-taper. The rms noise levels are 105 and 166 μJy beam-1 respectively. The position of ZwCl 2143.5+2014 is shown as a triangle (Zwicky & Kowal 1968). See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 13 AMI posterior distributions for PSZ1 G074.75-24.59 and the Ytot–θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 14 SA source-subtracted map of PSZ1 G137.56+53.88 with a) natural weighting and b) a uv-taper. The rms noise levels are 109 and 150 μJy beam-1 respectively. See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 15 AMI posterior distributions for PSZ1 G137.56+53.88 and the Ytot–θs posterior overlaid with that obtained by Planck (upper right hand corner). See Sect. 4.4 for more details on the plots. |
| In the text | |
 |
Fig. 16 Positional offset from AMI for the three Planck detection algorithms. The size of the points plotted increases with increasing Planck S/N; clear detections are plotted as filled circles, and moderate detections as empty circles. |
| In the text | |
 |
Fig. 17 Positional offset from AMI, normalised by total error |
| In the text | |
 |
Fig. 18 a) shows the MMF3 positional offset from AMI, normalised by rescaled total error |
| In the text | |
 |
Fig. 19 Comparison between PwS and AMI mean Ytot and θs values. The size of the points plotted increases with increasing Planck S/N; clear detections are plotted as filled circles, and moderate detections as empty circles. Error bars are omitted for clarity and since the errors in Ytot and θs are correlated. The one-to-one relationship is plotted as a black dashed line. The fitted linear relationship for all clusters (clear AMI detections only) with S/N greater than 7 is plotted as a black solid (black dotted) line. |
| In the text | |
 |
Fig. 20 a) Shows a comparison between PwS and AMI MAP Ytot values as a function of AMI (PwS) θs values in black (red). The one-to-one relationship is plotted as a black dashed line. b) Shows Ytot as a function of θs as measured by AMI (black) and PwS (red) for all of the moderate and clear detections. In both plots, the size of the points plotted increases with increasing Planck S/N, clear detections are plotted as filled circles, and moderate detections as empty circles. Error bars are omitted for clarity and since the errors in Ytot and θs are correlated. |
| In the text | |
 |
Fig. 21 Power-law relationships used to calculate primary calibration flux densities for AMI for two calibrators, 3C 286 and 3C 147, are shown with ± 5% uncertainty limits as the grey filled bands. The AMI frequency band is shown in black. Flux densities for both sources at 30 and 44 GHz taken from the Planck Compact Source Catalogue (Planck Collaboration XXVIII 2014) are shown as points with errorbars. |
| In the text | |
 |
Fig. 22 Comparison between PwS and AMI θs and YtotMAP values, for clusters selected to have no radio point sources within 3 arcmin of the cluster position. In both plots, the black (red) points show the AMI (PwS) values, larger points have higher Planck S/N values and filled (empty) circles represent AMI clear (moderate) detections. |
| In the text | |
 |
Fig. 23 Posterior distribution for Ytot and θs for simulated clusters with realistic CMB and noise levels (see text for details), and a) differing GNFW shape parameter values (γ,α,β) based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010); and b) simulated with the universal values. In all cases the model used for recovering the parameters has the shape parameter values fixed to the universal values, and the joint two-dimensional prior on Ytot and θs is used. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4); the input parameter values are marked with red triangles. The contours are at the 68% and 95% confidence boundaries. |
| In the text | |
 |
Fig. 24 A profile generated with β = 5.4905,θs = 1.8 (the universal profile, black lines) can be mimicked for β = 8.9 using θs = 4.1 and adjusting Ytot downward (red lines). The two profiles are almost identical over the AMI-SA range of baselines, while Planck would measure the zero-spacing flux which differs by ≈7% between the two models. a) Shows the pressure profiles in radial coordinates (note that the y-axis scale is log); and b) shows the profiles in uv-space for channel 5, with the simulated AMI data shown as dots. Note that this simulation has been generated with an unrealistically small amount of thermal noise. |
| In the text | |
 |
Fig. 25 Posterior distributions for Ytot, θs and α for simulated low-noise data, for clusters with θs = 1.8 (top), 4.5 (centre) and 7.4 (bottom) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on α between 0.1 and 3.0 (β fixed to the correct, input value). The input values are indicated by red triangles, and the posterior means with green crosses. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 26 One-dimensional marginal constraints on Ytot, θs and α for simulated low-noise data, for clusters with θs = 1.8 (solid lines), 4.5 (dashed lines) and 7.4 (dotted lines) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on α between 0.1 and 3.0 (β fixed to the correct, input value). Input values are shown as red lines. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 27 Posterior distributions for Ytot, θs and β for simulated low-noise data, for clusters with θs = 1.8 (top), 4.5 (centre) and 7.4 (bottom) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on β between 3.5 and 9.0 (α fixed to the correct, input value). The input values are indicated by red triangles, and the posterior means with green crosses. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 28 One-dimensional marginal constraints on Ytot, θs and β for simulated low-noise data, for clusters with θs = 1.8 (solid lines), 4.5 (dashed lines) and 7.4 (dotted lines) arcmin and universal (γ,α,β), with the two-dimensional prior on Ytot and θs and a uniform prior on β between 3.5 and 9.0 (α fixed to the correct, input value). Input values are shown as red lines. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 29 Posterior distributions for simulated clusters with realistic noise levels (see text for details), and varying GNFW shape parameter values based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010). a) shows the two-dimensional θs and Ytot posterior, and b) and c) show the one-dimensional posteriors for α and β, shifted to be centred on the appropriate true value. In all cases γ is fixed to the universal value, α has a truncated Gaussian prior based on the REXCESS sample, β is varied uniformly between 4.5 and 6.5, and the joint two-dimensional prior on Ytot and θs is used. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4 arcmin); the input parameter values are marked with red triangles and lines. |
| In the text | |
 |
Fig. 30 Fractional difference [(MAP value − true value)/(true value)] in θsa) and Ytotb) as a function of the input value of γ. Clusters with θs = 1.8 are plotted as dots, θs = 4.5 as crosses and θs = 7.4 as open circles. |
| In the text | |
 |
Fig. 31 Posterior distributions for simulated clusters with realistic noise levels (see text for details), and varying GNFW shape parameter values based on the REXCESS sample (Böhringer et al. 2007; Arnaud et al. 2010). a) shows the two-dimensional θs and Ytot posterior, and b) and c) show the one-dimensional posteriors for α and β, shifted to be centred on the appropriate true value. In all cases γ is fixed to the universal value, α has a truncated Gaussian prior based on the REXCESS sample, β is varied uniformly between 4.5 and 6.5, a Planck-like Gaussian prior is used on Ytot and θs has the conditional prior drawn from the two-dimensional prior. Results for three different angular sizes are shown (from top to bottom, θs = 1.8,4.5 and 7.4); the input parameter values are marked with red triangles and lines. |
| In the text | |
 |
Fig. 32 AMI posterior distributions for A1413, allowing α and β to vary. Posterior means are indicated with green lines and crosses, and the Planck + XMM-Newton estimates of α and β from Planck Collaboration Int. V (2013) are shown with red lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 33 Marginalised posterior likelihood distribution for α and β based on stacked Planck and XMM-Newton data for a sample of high-S/N Planck clusters (from Planck Collaboration Int. V 2013). The white cross marks the position of the best-fit value, and the white triangle marks the universal values. |
| In the text | |
 |
Fig. 34 AMI posterior distributions for RXC J2228.6+2036, allowing α and β to vary. Posterior means are indicated with green lines and crosses, and the Planck values for α and β from Planck Collaboration Int. V (2013) are shown with red lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. Also shown in the upper right hand corner are the posteriors produced by AMI (black) and Planck (red) using the universal profile, and a prediction produced by the physical model described in Olamaie et al. (2012) based on a redshift of z = 0.412 (yellow). |
| In the text | |
 |
Fig. 35 AMI posterior distributions for PSZ1 G134.31-06.57, allowing α and β to vary. Posterior means are indicated with green lines and crosses. The priors on the parameters in the AMI analysis are shown as black dashed lines. θs is in arcmin and Ytot is in arcmin2. |
| In the text | |
 |
Fig. 36 The distribution of mean values of α and β obtained for all the clear detections in the SZ sample. For comparison, the REXCESS-based prior on α (scaled arbitrarily) is also plotted in red, and the universal value of β predicted from numerical simulations is indicated with a red line. |
| In the text | |
 |
Fig. B.1 Ytot–θs posterior distributions for AMI and Planck, in descending Planck S/N order (note that this is the compatibility S/N for PwS), for all AMI detections ( |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.1 continued. |
| In the text | |
 |
Fig. B.2 Ytot–θs posterior distributions for AMI and Planck, in descending Planck S/N order (note that this is the compatibility S/N for PwS), for all AMI non-detections ( |
| In the text | |
 |
Fig. B.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.