| Issue |
A&A
Volume 569, September 2014
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 16 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/201322902 | |
| Published online | 24 September 2014 | |
First observation of the thermal Sunyaev-Zel’dovich effect with kinetic inductance detectors
1
Laboratoire de Physique Subatomique et de Cosmologie, Université
Joseph Fourier Grenoble 1, CNRS/IN2P3, Institut Polytechnique de Grenoble ,
53 rue des Martyrs,
38026
Grenoble,
France
e-mail:
adam@lpsc.in2p3.fr
2
Institut de RadioAstronomie Millimétrique (IRAM),
38402
Grenoble,
France
3 Astronomy Instrumentation Group, University of Cardiff CF10
3XQ, UK
4
Laboratoire AIM, CEA/IRFU, CNRS/INSU, Université Paris Diderot,
CEA-Saclay, 91191
Gif-Sur-Yvette,
France
5
Institut d’Astrophysique Spatiale (IAS), CNRS and Université Paris
Sud, 91405
Orsay,
France
6
Institut d’Électronique Fondamentale (IEF), Université Paris Sud,
91405
Orsay,
France
7
Institut Néel, CNRS and Université de Grenoble,
25 rue des Martyrs,
38042
Grenoble,
France
8
Institut de RadioAstronomie Millimétrique (IRAM),
Granada,
Spain
9
Institut de Planétologie et d’Astrophysique de Grenoble (IPAG),
CNRS and Université de Grenoble, 38042
Grenoble,
France
10
Université de Toulouse, UPS-OMP, Institut de Recherche en
Astrophysique et Planétologie (IRAP), 31028
Toulouse Cedex 4,
France
11
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
12
University College London, Department of Physics and
Astronomy, Gower
Street, London
WC1E 6BT,
UK
13
School of Earth and Space Exploration and Department of Physics,
Arizona State University, Tempe, AZ
85287,
USA
14
Dipartimento di Fisica, Sapienza Università di Roma,
Piazzale Aldo Moro 5,
00185
Roma,
Italy
Received:
23
October
2013
Accepted:
1
July
2014
Context. Clusters of galaxies provide valuable information on the evolution of the Universe and large scale structures. Recent cluster observations via the thermal Sunyaev-Zel’dovich (tSZ) effect have proven to be a powerful tool to detect and study them. In this context, high resolution tSZ observations (~tens of arcsec) are of particular interest to probe intermediate and high redshift clusters.
Aims. Observations of the tSZ effect will be carried out with the millimeter dual-band NIKA2 camera, based on kinetic inductance detectors (KIDs) to be installed at the IRAM 30-m telescope in 2015. To demonstrate the potential of such an instrument, we present tSZ observations with the NIKA camera prototype, consisting of two arrays of 132 and 224 detectors that observe at 140 and 240 GHz with a 18.5 and 12.5 arcsec angular resolution, respectively.
Methods. The cluster RX J1347.5-1145 was observed simultaneously at 140 and 240 GHz. We used a spectral decorrelation technique to remove the atmospheric noise and obtain a map of the cluster at 140 GHz. The efficiency of this procedure has been characterized through realistic simulations of the observations.
Results. The observed 140 GHz map presents a decrement at the cluster position consistent with the tSZ nature of the signal. We used this map to study the pressure distribution of the cluster by fitting a gNFW model to the data. Subtracting this model from the map, we confirm that RX J1347.5-1145 is an ongoing merger, which confirms and complements previous tSZ and X-ray observations.
Conclusions. For the first time, we demonstrate the tSZ capability of KID based instruments. The NIKA2 camera with ~5000 detectors and a 6.5 arcmin field of view will be well-suited for in-depth studies of the intra cluster medium in intermediate to high redshifts, which enables the characterization of recently detected clusters by the Planck satellite.
Key words: instrumentation: detectors / techniques: high angular resolution / galaxies: clusters: individual: RX J1347.5-1145 / galaxies: clusters: intracluster medium
© ESO, 2014
1. Introduction
Galaxy clusters are the largest gravitationally bound objects in the Universe. Their formation strongly depends on the content and the history of the Universe within the framework of a bottom-up scenario (e.g., Kravtsov & Borgani 2012), where there is merging of small clusters to form larger ones. They are classically probed using X-ray produced via bremsstrahlung emission of the electrons in the intracluster medium (ICM) but are also measured in the optical and infrared wavelengths, which trace the stellar populations in the member galaxies. Their radio emission is related to the acceleration of charged particles, and the lensing of background objects provides surface mass density measurements from multi-band optical and infrared data. See Böhringer & Werner (2010); Gal (2006); Oliver et al. (2012); Feretti et al. (2012); Kneib & Natarajan (2011) for reviews on the different cluster observables.
The thermal Sunyaev-Zel’dovich (tSZ) effect (Sunyaev & Zel’dovich 1972, 1980), which consists of the inverse Compton scatter of cosmic microwave background (CMB) photons on hot electrons in the ICM, can be used as a complementary method to probe galaxy clusters (see Birkinshaw 1999; Carlstrom et al. 2002, for a detailed review on the tSZ effect). Three-dimensional information on the cluster may be inferred using the characteristic dependences of X-ray (sensitive to the line-of-sight integral of the density squared and the square root of the temperature) and tSZ (sensitive to the integrated pressure along the line-of-sight) with the properties of the ICM. This gives a more accurate picture than X-ray or tSZ alone, especially in the case of merging systems (Basu et al. 2010). In addition, unlike other observational approaches, the tSZ signal is not affected by cosmological dimming. Only the angular size of the observed cluster depends on the distance to the source. High angular resolution tSZ observations are therefore of particular interest to probe structure formation at high redshift.
The resolutions of the main current instruments measuring the tSZ effect are of the order of the arcmin. It is larger than 5 arcmin for the Planck satellite (Planck Collaboration I 2014) and about 1 arcmin for the South Pole Telescope (SPT; Carlstrom et al. 2011) and the Atacama Cosmology Telescope (ACT; Kosowsky 2003). Higher resolution instruments, such as MUSTANG (~8 arcsec resolution at 90 GHz; Mason et al. 2010; Korngut et al. 2011), may suffer from filtering of large-scale structures due to the atmospheric noise removal when observing at a single frequency band. High redshift tSZ observations, therefore, need a new generation of instruments. The New IRAM KID Arrays (NIKA) is a prototype of a high-resolution camera based on kinetic inductance detectors (KIDs; Day et al. 2003; Calvo et al. 2010) in development for millimeter wave astronomy (Monfardini et al. 2011). It consists of two arrays of 132 and 224 detectors, which observe at 140 and 240 GHz with resolutions of 18.5 and 12.5 arcsec, respectively. Due to the characteristic spectral distortion of the CMB photons induced by the tSZ effect, NIKA is an ideal instrument for high resolution tSZ observations. Indeed, the tSZ signal is strongly negative at 140 GHz and positive but close to zero at 240 GHz. The NIKA prototype has already been successfully tested during four observation campaigns (Monfardini et al. 2010, 2011) at the Institut de Radio Astronomie Millimétrique (IRAM) 30-m telescope at Pico Veleta, Granada, Spain. These observations have demonstrated performances comparable to state-of-the-art bolometer arrays operating at these wavelengths, such as GISMO (Staguhn et al. 2008). The final camera, NIKA2, will contain 1000 and 4000 detectors at 140 and 240 GHz, respectively, and should be operational in 2015.
We report the first observation of a galaxy cluster via the tSZ effect here using the NIKA prototype. It has been imaged during the fifth observation campaign of NIKA in November 2012. The targeted source is the massive intermediate redshift galaxy cluster RX J1347.5-1145 at z = 0.4516. It has been selected for both its tSZ intensity and angular size with the latter being comparable to the field of view of the NIKA prototype. Moreover, RX J1347.5-1145 is known to be a complex merging system that we aim at characterizing further with respect to previous works at scales in the range of 20 to 200 arcsec.
This paper is organized as follows. In Sect. 2, we give the status of the previous observations of RX J1347.5-1145. In Sect. 3, we provide a brief description of the NIKA camera and give an overview of the observations that is carried out during the November 2012 campaign at the IRAM 30-m telescope. Section 4 describes the tSZ dedicated data analysis and its validation on simulations is reported in Sect. 5. We present the map of RX J1347.5-1145 in Sect. 6 and the results on the pressure profile for this cluster of galaxies. These results are then compared to other experiments in Sect. 7. Throughout this paper, we assume a flat ΛCDM cosmology according to the lastest Planck results (Planck Collaboration XVI 2014) with H0 = 67.11 km s-1 Mpc-1, ΩM = 0.3175, and ΩΛ = 0.6825.
2. Previous observations of RX J1347.5-1145
The object RX J1347.5-1145 is among the clusters that have been intensively observed at several wavelengths and the most widely studied using tSZ at sub-arcmin resolution. It is a massive intermediate redshift galaxy cluster at z = 0.4516 undergoing a merging event.
This cluster is the most luminous X-ray cluster of galaxies known to date (e.g. Allen et al. 2002). It was discovered in the ROSAT X-ray all-sky survey (Voges et al. 1999) and has been the object of many studies in X-ray (Schindler et al. 1995, 1997; Allen et al. 2002; Gitti & Schindler 2004, 2005; Gitti et al. 2007b,a; Ota et al. 2008), optical (Cohen & Kneib 2002; Verdugo et al. 2012), infrared (Zemcov et al. 2007), tSZ (Pointecouteau et al. 1999; Komatsu et al. 1999, 2001; Pointecouteau et al. 2001; Kitayama et al. 2004; Mason et al. 2010; Korngut et al. 2011; Zemcov et al. 2012; Plagge et al. 2013), and multiwavelength analysis (Bradač et al. 2008; Miranda et al. 2008; Johnson et al. 2012). From ROSAT X-ray observations, this cluster was thought to be a dynamically old relaxed cool-core cluster with an extremely strong cooling flow, due to its very spherical morphology and peaked X-ray profile (ROSAT; Schindler et al. 1995, 1997). However, high angular resolution tSZ observations have proved RX J1347.5-1145 to be an ongoing merger due to the measurement of an extension toward the southeast (SE) with respect to the X-ray center (Pointecouteau et al. 1999; Komatsu et al. 2001; Kitayama et al. 2004). This illustrates how tSZ and X-ray (and other wavelengths) observations are complementary. More recent X-ray (Chandra; Allen et al. 2002) and lensing (Miranda et al. 2008) observations are consistent with this interpretation and show a clear detection of the SE extension.
High resolution tSZ maps of RX J1347.5-1145, such as the 90 GHz 8 arcsec (smoothed to 10 arcsec) resolution map of MUSTANG (Mason et al. 2010), have confirmed the presence of a strong SE extension. It is interpreted as being due to a hot gas that is heated by the merging of a subcluster crossing the main, originally relaxed, system from the south to the northeast (NE), which is perpendicular to the line-of-sight. The SE extension coincides with a radio mini-halo (Gitti et al. 2007a), which indicates the presence of non-thermal electrons, that underlies a non-thermal contribution to the total pressure. Optical observations have also confirmed this scenario with the detection of a massive elliptical galaxy, which is located 20 arcsec on the east side of the X-ray center, while the central elliptical galaxy of the main cluster remains at the X-ray peak location (Cohen & Kneib 2002).
The temperature profile of RX J1347.5-1145 varies from ~6 keV in its core to ~20 keV at 80 arcsec and decreases to ~9 keV on the outer part of the cluster (120−300 arcsec form the core). The maximum temperature is located at the SE extension, reaching kBTe ~ 25 keV (Ota et al. 2008). The Compton y parameter has been measured to be ymax ≃ 10-3 (Pointecouteau et al. 1999).
The object RX J1347.5-1145 hosts a well-known radio source within 3 arcsec of the X-ray
center in the central elliptical galaxy. Due to this contamination, the location of the tSZ
maximum is still debated. Current single dish observations are consistent with the tSZ
emission of the SE extension being stronger than that at the cluster X-ray center. However,
taking advantage of the intrinsic point source removal power of interferometric data, Plagge et al. (2013) claim that it is only a secondary
maximum. The point source has to be taken into account in the tSZ analysis. According to
Pointecouteau et al. (2001), the source follows the
spectrum 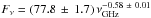 mJy. For NIKA, this corresponds to 4.4 ±
0.3 and 3.2 ±
0.2 mJy at 140 and 240 GHz, respectively.
mJy. For NIKA, this corresponds to 4.4 ±
0.3 and 3.2 ±
0.2 mJy at 140 and 240 GHz, respectively.
Finally, in addition to the central radio source, Zemcov et al. (2007) have reported the presence of two infrared galaxies. The first one (Z1 hereafter) is located at about 60 arcsec from the X-ray center in the southwest direction with a flux of 15.1 mJy (as measured with a signal to noise of 5.1) at 850 μm and 125 ± 34 mJy at 450 μm. The second source (Z2 hereafter) is located closer to the X-ray center at about 20 arcsec on the northeast side. However, it is only detected at 850 μm with a flux of 11.4 mJy (measured with a signal to noise of 4.7). The best-fit value at 450 μm is 10 ± 32 mJy. The contamination of these sources in the NIKA bands is estimated and accounted for in our analysis, as discussed in Sect. 4.2.4.
3. Observations with NIKA
3.1. Brief overview of the NIKA camera during the campaign of November 2012
Mean zenith opacity, on-source integration time, and period of the day for the three days of the campaign of November 2012.
The NIKA camera consists of two arrays of Kinetic Inductance Detectors (KIDs) with maximum transmissions at 140 and 240 GHz. Ninety percent of the total transmission of the NIKA bandpasses (see Fig. 2) is in the range 127–171 GHz for 140 GHz and 196–273 GHz for 240 GHz bands. The respective angular resolutions (FWHM) are 18.5 and 12.5 arcsec with effective fields of view of 1.8 × 1.8 and 1.0 × 1.0 arcmin. The pitch between pixels is 2.3 mm at 140 GHz and 1.6 mm at 240 GHz. This corresponds to an effective focal plane sampling of 0.77 Fλ and 0.8 Fλ at 140 and 240 GHz, respectively. In this particular campaign, the first band (140 GHz) was used with 127 detectors having a mean effective sensitivity of 29 mJy s1/2 per beam (19 mJy s1/2 per beam for the best 20% of all pixels), and the second band (240 GHz) had 91 detectors with a mean effective sensitivity of 55 mJy s1/2 per beam (37 mJy s1/2 per beam for the best 20% of all pixels). This unexpected poor sensitivity and the small number of available detectors for the 240 GHz band is due to the dysfunction of a cold amplifier during this observation campaign. Using only eight detectors of the 240 GHz array, we obtain the expected mean effective sensitivity measured to be 22 mJy s1/2 per beam. Despite the constant improvement in sensitivity over the the last campaigns (Monfardini et al. 2010, 2011; Calvo et al. 2013), the sensitivity of the instrument was limited by detector correlated noise coming from electronic and sky noise residuals. For the averaged background during observations, the expected photon noise is 5 mJy s1/2 at 140 GHz and 7 mJy s1/2 at 240 GHz.
Unlike traditional bolometric instruments, NIKA uses KIDs. The KIDs are superconducting resonators whose resonance frequency (~1−2.5 GHz) changes linearly with the absorbed optical power (see for example Swenson et al. 2010). Each resonator can be modeled by a complex transfer function in frequency with a real part I (in-phase) and imaginary part Q (quadrature; Grabovskij et al. 2008). By measuring I and Q at a constant frequency (defined for each detector by the electronics) as a function of time, we can reconstruct the shift of the resonance frequency, as described in Calvo et al. (2013). This method allows us to obtain accurate photometry to be better than 10%.
The KIDs used here are Hilbert dual-polarization designed LEKID pixels (Lumped Element KID; Doyle et al. 2008; Roesch et al. 2012), which are realized on 180 μm and 275 μm thickness silicon substrate at 240 and 140 GHz, respectively. The detector resistivity is larger than 5000 Ω cm for both wavelengths. The detectors are cooled down to about 100 mK with a 4He − 3He dilution cryostat.
More details on the NIKA prototype setup can be found in Catalano et al. (2014).
3.2. Observing strategy of the targeted galaxy clusters
Galaxy clusters are weak extended sources when seen through the tSZ effect, making their observations challenging. For this study, we have selected RX J1347.5-1145, which is an intermediate redshift cluster at z = 0.4516. The object RX J1347.5-1145 is among the most luminous tSZ sources in the sky, and it is also compact enough to have an angular size comparable to the field of view of the NIKA camera.
As shown in Fig. 1, the cluster signal is scan-modulated but there is no wobbling involved. Raster scans are made of constant elevation subscans or constant azimuth subscans. For the latter, only the low azimuth part of the field was covered due to an error in the control software. Both of them are 6 min 20s scans that are made of 19 subscans separated by 10 arcsec steps. Scans along the azimuth direction are centered at (RA, Dec) = (13h47m32s, −11°45′42′′), which sample a rectangular region of 360 × 180 arcsec (azimuth × elevation), while scans along the elevation sample a region of 180 × 180 arcsec and are centered on a point 90 arcsec away from (13h47m32s, − 11°45′42′′), which rotates with the parallactic angle. The scan velocity is about 15 arcsec s-1. The detailed integration times are given in Table 1 with the corresponding atmospheric opacities.
 |
Fig. 1 Elevation (dashed green) and azimuth (solid red) offset scans. The center is represented by a black dot and has coordinates (RA, Dec) = (13h47m32s, −11°45′42′′). The 140 GHz array is also represented by black crosses, which correspond to the position of each KID in the focal plane (gaps in the array correspond to invalid detectors). |
 |
Fig. 2 Normalized 140 GHz (solid red line) and 240 GHz (solid orange line) instrumental bandpasses. The total atmospheric transmission is also given as a solid green line for 1 mm of precipitable water vapor, according to the Pardo model (Pardo et al. 2002). The oxygen (dash-dotted light blue) and the water vapor (dashed dark blue) contributions are represented. |
3.3. Pointing, calibration, bandpasses, and beam
Uranus observations were used to reconstruct beam maps (projection of the array on the sky and measure of individual detector beams) for both wavelenghts. Nearby quasars were used for determining pointing corrections. The pointing root mean square error is estimated to be ~3 arcsec (Catalano et al. 2014). This is small compared to the beam and has a negligible impact in the case of extended sources such as RX J1347.5-1145.
We also used Uranus for absolute point source flux calibration. The flux of the planet was inferred from a frequency dependent model of the planet brightness temperature taken from Moreno (2010). The Uranus brightness temperatures are typically 113 K at 140 GHz and 94 K at 240 GHz. This model is integrated over the NIKA bandpasses for each channel, and it is assumed to be accurate at the 5% level. The final absolute calibration factor is obtained by fitting the amplitude of a Gaussian function of fixed angular size on the reconstructed maps of Uranus (representing the main beam). We neglect the angular diameter of Uranus, 3.54 arcsec at the time of the observations, when it is compared to the size of the main beam, since the convolution of the corresponding disk with a Gaussian of 12.5 and 18.5 arcsec full width at half maximum (FWHM) broadens our beam by only 0.17 arcsec at 240 GHz and 0.12 arcsec at 140 GHz.
Scales larger than 180 arcsec, which correspond to the scan size, were not measured with NIKA. By integrating the Uranus flux up to 100 arcsec, we observe that the total solid angle covered by the beam, which includes the power in the side lobes, is larger than the Gaussian best-fit of the main beam by a factor of 1.32. Scales larger than 100 arcsec are noise dominated on the Uranus map. Thus, using recent measurements of the IRAM 30-meter beam pattern with EMIR (Kramer et al. 2013), we extrapolate the angular profile of the beam from 100 arcsec to 180 arcsec, and find an overall factor equal to 1.45 (see Catalano et al. 2014, for a more detailed description). From the dispersion over different observations of Uranus, we estimate the uncertainties on the solid angle of the main beam to be about 4%. We obtain 10% uncertainties for the full beam by also considering uncertainties on the side lobes.
The sky maps (also for Uranus maps prior to calibration) are corrected for atmospheric absorption using elevation scans, or skydips (see Catalano et al. 2014, for further details). In our case, the resonance frequencies of the detectors are measured versus the optical load, which depends on the zenith opacity and the elevation. This gives the zenith opacity as a function of the resonance frequency of the detectors, which is measured for each scan. The opacity can then be corrected to good accuracy by accounting for the air mass at the elevation of the source. Furthermore, different atmospheric conditions lead to changes in the beam pattern of the instrument that also affect the absolute calibration accuracy (Catalano et al. 2014). From the dispersion of the recovered flux of Uranus, which was observed several times with different opacities during the campaign, we estimate an overall accuracy of 15% (Catalano et al. 2014) for the calibration procedure.
To summarize, the list of the main systematic uncertainties in the 140 GHz band are listed in Table 2. The total calibration uncertainty on the final data at the map level is estimated to be 16%.
Main contributions to the absolute error of the NIKA data for the 140 GHz band.
4. Thermal Sunyaev-Zel’dovich dedicated data analysis and mapmaking
4.1. Thermal Sunyaev-Zel’dovich data
In the non-relativistic limit, the tSZ effect results in a distortion of the CMB
black-body spectrum, whose intensity frequency dependence is given by (Birkinshaw 1999) 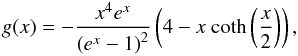 (1)where
(1)where
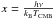 is the dimensionless frequency; h is the Planck constant, kB the Boltzmann
constant, ν
the observation frequency and TCMB the temperature of the CMB. The
induced change in intensity relative to primary CMB intensity I0 reads
is the dimensionless frequency; h is the Planck constant, kB the Boltzmann
constant, ν
the observation frequency and TCMB the temperature of the CMB. The
induced change in intensity relative to primary CMB intensity I0 reads
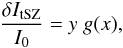 (2)where
y is the
Compton parameter. The latter measures the integrated electronic pressure Pe along the
line-of-sight
(2)where
y is the
Compton parameter. The latter measures the integrated electronic pressure Pe along the
line-of-sight 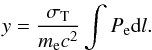 (3)The
parameter σT is the Thomson cross section,
me is the electron mass, and
c the speed
of light. The tSZ spectral distortion is null at 217 GHz, negative below this frequency,
and positive above.
(3)The
parameter σT is the Thomson cross section,
me is the electron mass, and
c the speed
of light. The tSZ spectral distortion is null at 217 GHz, negative below this frequency,
and positive above.
The unit conversion coefficients between Jy/beam and Compton parameter y are −11.8 ± 1.2 and + 2.2 ± 0.6 at 140 and 240 GHz, respectively, for the NIKA prototype. These coefficients are computed by taking the overall transmission of the instrument and the measured total beam with their respective errors into account. The Compton parameter y is first converted to Jy/sr using Eq. (2) and then converted to Jy/beam using the angular coverage of the beam. We assume a pure non-relativistic tSZ spectrum.
As the expected tSZ signal is small (up to ~10 mJy/beam), the NIKA raw data are dominated by instrumental noise
and atmospheric emission. We model the signal measured by a KID k, which operates at the
observing frequency band νb (140 GHz or 240
GHz) as 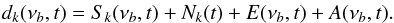 (4)The
astrophysical signal (essentially tSZ) Sk(νb,t)
is time-dependent through the scanning strategy. Furthermore, it varies with the frequency
band (Eq. (2)) and with the detector
k because
of its location in the focal plane. The variable Nk(t)
is the uncorrelated detector noise limiting the sensitivities given in Sect. 3.1. The correlated electronic noise, E(νb,t),
is well characterized by an identical common-mode for the detectors of the same band
(Bourrion et al. 2011). As we use independent
readout electronics for the two bands, the electronic noise is uncorrelated between bands.
Finally, by splitting the frequency and time dependance, the atmospheric contribution can
be modeled as
(4)The
astrophysical signal (essentially tSZ) Sk(νb,t)
is time-dependent through the scanning strategy. Furthermore, it varies with the frequency
band (Eq. (2)) and with the detector
k because
of its location in the focal plane. The variable Nk(t)
is the uncorrelated detector noise limiting the sensitivities given in Sect. 3.1. The correlated electronic noise, E(νb,t),
is well characterized by an identical common-mode for the detectors of the same band
(Bourrion et al. 2011). As we use independent
readout electronics for the two bands, the electronic noise is uncorrelated between bands.
Finally, by splitting the frequency and time dependance, the atmospheric contribution can
be modeled as 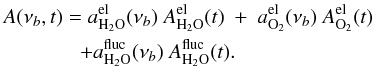 (5)The
first and the second terms give the emission change of water vapor and oxygen due to the
variation of the airmass with the elevation. The third term,
(5)The
first and the second terms give the emission change of water vapor and oxygen due to the
variation of the airmass with the elevation. The third term,
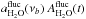 , gives the emission change due
to inhomogeneities in the water vapor distribution. We note that
, gives the emission change due
to inhomogeneities in the water vapor distribution. We note that
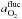 is
implicitly set to zero because of the assumption that the oxygen is locally very
homogeneous in the atmosphere. It is also important to notice that the two bands are not
sensitive to the same atmospheric components. The 140 GHz band is sensitive to the
O2 118 GHz line,
while the 240 GHz band is almost only sensitive to water vapor (Pardo et al. 2002), such that
is
implicitly set to zero because of the assumption that the oxygen is locally very
homogeneous in the atmosphere. It is also important to notice that the two bands are not
sensitive to the same atmospheric components. The 140 GHz band is sensitive to the
O2 118 GHz line,
while the 240 GHz band is almost only sensitive to water vapor (Pardo et al. 2002), such that 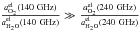 .
This can be observed in Fig. 2, where we show the
bandpasses of the NIKA prototype in red (140 GHz) and orange (240 GHz). The atmospheric
transmission is given for the oxygen (light blue dash-dotted line) and water vapor (dark
blue dashed line) contributions. The overall atmospheric transmission is given as a green
solid line, according to the Pardo model (Pardo et al.
2002). Trace constituents are neglected here (e.g., ozone).
.
This can be observed in Fig. 2, where we show the
bandpasses of the NIKA prototype in red (140 GHz) and orange (240 GHz). The atmospheric
transmission is given for the oxygen (light blue dash-dotted line) and water vapor (dark
blue dashed line) contributions. The overall atmospheric transmission is given as a green
solid line, according to the Pardo model (Pardo et al.
2002). Trace constituents are neglected here (e.g., ozone).
4.2. Time ordered data analysis
 |
Fig. 3 TOD (left) and their power spectra (right) for a given detector. The data corresponds to the calibrated TOD before (red) and after (green) the electronic and atmospheric noise decorrelation. The TOD are dominated by the atmospheric noise at low frequencies, which is responsible for the slow variations in the red TOD and the obvious rise of noise below ~1 Hz on the red power spectrum. Cosmic rays hitting the instrument can be seen as spikes in the TOD but have been removed before computing the power spectra. Pulse tube frequency lines appear in the power spectrum (e.g. the ~6 Hz line in the raw power spectrum) and are notch filtered. The electronic noise dominates at frequencies between ~1 and ~5 Hz in the power spectrum before decorrelation. |
The main steps for processing the time ordered data (TOD) are listed below.
-
Loading raw data, including the telescope parameters, the reconstruction of the projection of the array on the sky, and the atmospheric opacity.
-
Calibrating the TOD, including opacity correction.
-
Flagging invalid detectors.
-
Flagging cosmic ray impacts on the detectors.
-
Decorrelating atmospheric and electronic noise.
-
Filtering low frequencies and removing lines produced by the pulse tube of the cryostat with a notch filter.
-
Making map using inverse variance weighting.
In the following, we give details on specific points of the analysis.
4.2.1. Raw data
The raw TOD correspond to the real (Ik(t), in-phase) and imaginary (Qk(t), quadrature) parts of the transfer function of the system (array and transmission line), which are sampled on predefined frequency tones k at an acquisition rate of 23.842 Hz. We also compute the average modulation of these quantities with respect to the injected frequency (typically a few kHz), which are noted δIk(t) and δQk(t). These four quantities are used to reconstruct the shift of the resonance frequency δf0k(t), which probes the optical power absorbed by a detector (see Calvo et al. 2013, for more details). To monitor the electronic noise and possible variations of the transfer function of the transmission line, the latter is also sampled with tones that are placed off-resonance (with no correspondence to any detector), which are insensitive to optical power.
In the case of the NIKA prototype, some detectors are subject to cross talk and are not used for this analysis. Bad detectors are also flagged on the basis of the statistical properties of their noise. In particular, we use skewness and kurtosis tests, in addition to testing the stationarity of the noise. Some TODs, which are affected by baseline jumps due to the coupling with ambient magnetic fields, are also excluded. These rejected detectors are not used in the following. For the observations of RX J1347.5-1145, the number of detectors used in the analysis is 81 at 140 GHz and 45 at 240 GHz.
4.2.2. Calibration
The shift of the resonance frequency is computed for each detector. The absolute calibration from resonance frequency to flux density is applied to these TODs. The beam is measured with Uranus observations in atmospheric conditions that are similar to those for the RX J1347.5-1145 observations. The Uranus data are fitted with a Gaussian function of FWHM that is equal to 12.5 and 18.5 arcsec at 240 and 140 GHz, respectively. An opacity correction is performed by multiplying the data by exp(τνb/ sin(el)), where el is the elevation of the source. The calculation of the opacity is based on skydip measurements, as briefly described in Sect. 3.3 (for more details, see Catalano et al. 2014).
4.2.3. Glitch removal
Cosmic rays hitting the instrument induce glitches in the data. The time response of KIDs is negligible compared to the sampling frequency, such that a cosmic ray impact appears as a peak on a single data sample in the TOD. We detect about four glitches per minute. They are removed from the δf0k(t) TODs by flagging peaks that are above five times the standard deviation of the considered TOD. The TODs are flagged and interpolated at the glitch locations in order not to affect the decorrelation. These flagged data are not projected onto maps.
4.2.4. Dual-band decorrelation
As discussed above the atmospheric contribution to the NIKA data, A(νb,t), is essentially due to water vapor, to first order. Therefore, it is expected to be the same for the two frequency bands up to an amplitude factor A(240 GHz,t)/A(140 GHz,t) ≃ 5. As a consequence, we first use the 240 GHz data to build an atmospheric template and remove it from the 140 GHz data by linear fitting. The fit is performed for each subscan and for each 140 GHz detector independently. As the tSZ signal at 240 GHz is smaller by a factor of 5.5 (see unit conversion factors between Compton parameter and Jansky per beam in Sect. 4.1) with respect to the one at the 140 GHz band, the positive bias introduced in the 140 GHz data by the tSZ signal present at 240 GHz is negligible (about 27 times smaller).
As shown in the left panel of Fig. 3, where we present the raw TOI signal for a typical KID at 140 GHz in red, the atmospheric contribution is dominated by a low frequency component. These drifts correspond to the 1 /f noise-like spectrum with a knee frequency at about 1 Hz, which is presented in red on the right panel of the figure. We thus apply a low-pass filter to the atmospheric template that is deduced from the 240 GHz channel. This filter removes most of the detector correlated electronic noise in the 240 GHz band, E(240 GHz,t), which does not affect the 140 GHz data. Furthermore, it allows us to reduce the intrinsic high noise level of the 240 GHz band, which was specific to the November 2012 NIKA data due to the cold amplifier disfunction and would otherwise pollute the 140 GHz cleaned data. The low-pass filter does not affect frequencies smaller than 1.5 Hz and sets frequencies larger than 2 Hz to zero. Frequencies between 1.5 and 2 Hz are progressively attenuated using a cosine squared cutoff.
We also build a template from a high-pass filtered common-mode obtained from the TODs of the valid 140 GHz detectors. This high-pass filter is the complement to the previous low-pass filter such that their sum is equal to one for all frequencies. We linearly fit this template to each subscan of each 140 GHz detector TOD and remove it. As a consequence the correlated electronic noise, E(140 GHz,t) is removed at frequencies larger than the cutoff. We note that this does not significantly affect the tSZ signal because it is not correlated at these high frequencies between detectors as they observe different positions on the sky. Typically, 2 Hz corresponds to about 8 arcsec for the chosen scan speed (about 15 arcsec per second).
Finally, we fit and remove a template that follows the elevation of the telescope from the TODs. Indeed, as the oxygen component of the atmosphere is ignored in the dual-band decorrelation, it appears as a residual proportional to the elevation of the telescope.
The main drawback of the dual-band decorrelation technique is the possible contamination of the 140 GHz tSZ reconstructed signal by other astrophysical components present at 240 GHz. First, we consider the kinematic Sunyaev-Zel’dovich (kSZ) effect, which is due to the overall motion of a cluster (or its components) with respect to the CMB reference frame and follows a pure black-body spectrum at the CMB temperature. The kSZ signal is also reduced by a factor of ~5, such that its flux at 240 GHz should be larger than half the tSZ flux at 140 GHz to produce a non-negligible bias. This is not the case even for the most extreme clusters, such as MACS J0717.5+3745 (Mroczkowski et al. 2012; Sayers et al. 2013). Therefore, any kSZ signal present at 240 GHz is neglected in the following analysis.
We have also searched for dusty galaxies within the cluster or gravitationally lensed submilimeter high-redshift background objects that might also contaminate the signal at 140 and 240 GHz. As mentioned in Sect. 2, two of such sources are present in RX J1347.5-1145. Despite the high level of noise in the 240 GHz NIKA data for this campaign, the first source, Z1, (RA, Dec) = (13h47m27.6s, –11°45′54′′) is observed in this band with a flux of 12.7 mJy ± 6.2. The second source, Z2, (RA, Dec) = (13h47m31.3s, –11°44′57′′) is not detected in the 240 GHz NIKA band, but we obtain an upper limit of 4.4 mJy at 1σ. Using this information and the measured fluxes at 850 and 450 μm (see Sect. 2), we estimate the expected flux of the sources at 140 GHz. Assuming dust temperatures in the range of 15−20 K and dust spectral indexes βd in the range of 1.5−2, we obtain 0.85 mJy at 140 GHz for the Z1 source. For the second source, Z2, we are not able to fit a typical dust spectrum and only compute an upper limit of the flux at 140 GHz by assuming a Rayleigh-Jeans spectrum at low frequency and using the 240 GHz estimated flux. We obtain an upper limit at 140 GHz of 0.65 mJy. In the context of dual-band decorrelation, the 240 GHz fluxes are scaled down by ≃5, and they are diluted by another factor of ≃5 due the averaging over all the 240 GHz detectors, which observe the source at different time samples. As uncertainties on the estimated flux for both sources and at both wavelengths are large, we choose not to subtract them directly in the TOD but to account for them in the final analysis, as discussed in Sect. 7.5.
4.2.5. Fourier filtering
Frequency lines (e.g. at ~6 Hz) are induced by the pulse tube of the cryostat and observed in the TOD power spectra (see Fig. 3, right panel). They are flagged and set to zero. In addition, we apply a high-pass filter to remove correlated noise at frequencies lower than the subscan because no tSZ signal is present there. We also remove low frequency (below 0.05 Hz) sine and cosine from the data to further subtract correlated noise contamination.
4.3. Mapmaking
Finally, we construct surface brightness maps by projecting and averaging the signal from all KIDs on a pixelized map at 140 GHz. The projected data are weighted according to the level of noise of each detector using inverse variance weighting. To remove possible offsets in the TOD, we subtract the mean value of each TODs, and we take the zero level as the mean of the external part of the map, where no signal is detected.
4.4. Point source subtraction
The object RX J1347.51145 hosts a radio point source located within 3 arcsec of the X-ray center that has a flux of 4.4 ± 0.3 mJy and 3.2 ± 0.2 mJy at 140 and 240 GHz, respectively (Pointecouteau et al. 2001). The point source is subtracted in the TODs at both frequencies before the processing, so that it does not bias the analysis. We discuss in Sect. 7.5 how uncertainties on the point source subtraction affect the final results.
5. Validation of the analysis
We present two independent validations of the analysis pipeline. The first of them is based on a detailed simulation of the observation of a tSZ cluster with known physical parameters and typical atmospheric and electronic noise. The second one is based on the observation of a faint cluster that allow us to show that the tSZ detection is not an artifact of the data analysis and/or acquisition.
5.1. Simulation
To test the pipeline as described in Sect. 4, we simulate the NIKA observations of a cluster and construct the TODs by taking all terms of Eq. (4) into account, which includes the atmospheric contamination, the electronic noise, and the tSZ signal. The parameters used in the simulation are given in Table 3 and are representative of the weather conditions for the observations described in this paper.
Values of the parameters used in the simulation.
5.1.1. Atmospheric contribution
The atmospheric contribution A(νb,t) is simulated as described in Sect. 4.
The water vapor fluctuations (i.e., 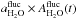 ) are obtained by simulating
a map of water vapor anisotropy that passes in front of the telescope aperture with a
speed vH2O at an altitude
hH2O above the telescope. The
power spectrum of this map is a power law with slope αH2O. The amplitudes of the
atmospheric fluctuations are then normalized to have a standard deviation over the time
of the scan equal to
) are obtained by simulating
a map of water vapor anisotropy that passes in front of the telescope aperture with a
speed vH2O at an altitude
hH2O above the telescope. The
power spectrum of this map is a power law with slope αH2O. The amplitudes of the
atmospheric fluctuations are then normalized to have a standard deviation over the time
of the scan equal to 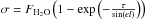 , where
τ is the
zenith opacity, el the elevation, and FH2O is the reference flux.
, where
τ is the
zenith opacity, el the elevation, and FH2O is the reference flux.
The contribution of the elevation terms, both from H2O and O2, is simulated as
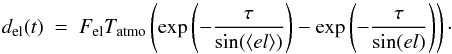 (6)The parameter
Tatmo is the temperature of the
atmosphere, and Fel is a reference flux that is
measured at both frequencies using skydips.
(6)The parameter
Tatmo is the temperature of the
atmosphere, and Fel is a reference flux that is
measured at both frequencies using skydips.
5.1.2. Electronic noise
The electronic noise E(νb,t) is simulated as a common mode with a power spectrum slope β and an amplitude E0. This common-mode is identical for all detectors in a given frequency band but differs for the two bands since the electronics is not the same. The spectrum slope is the same for the two bands, but the amplitude is higher at 240 GHz than at 140 GHz (see Table 3).
5.1.3. Uncorrelated noise
We also simulate a total uncorrelated noise term, Nk(t), independently for each detector. This term accounts for various white noise contributions, including photon noise, spontaneous Cooper pair breaking due to thermal noise fluctuations and electronic white noise. For the purpose of the simulations, we keep this noise contribution independent of the observing conditions. However, for the real observations, we find that the white noise level is coupled to the atmospheric conditions. This is mainly due to the broadening of the resonances for large optical loads, and it is not accounted for in the simulations. Similarly, we do not account for photon noise variations induced by changes in the optical load. For the sake of simplicity, the total root mean square of the uncorrelated noise is assumed to be identical for all detectors of the same array.
5.1.4. Glitches
Glitches are simulated with a rate Rg. They only affect individual samples in the TODs (i.e., the KID response is much faster than the sampling frequency) and simultaneously affect all KIDs of a given array (i.e., glitches are assumed to generate phonons that hit all the KIDs of the array). The amplitudes of the glitches are generated using a Gaussian spectrum with a standard deviation of 1.3 Jy/beam, as observed in the measured TODs.
5.1.5. Pulse tube lines
To simulate the frequency lines generated by the pulse tube, we add cosine functions to the timeline that correspond to the typical frequencies and amplitudes seen in the data (see the power spectrum of the raw data in Fig. 3).
5.1.6. The thermal Sunyaev Zel’dovich signal
We use the generalized Navarro, Frenk, and White (gNFW) pressure profile (Nagai et al. 2007b) to describe the cluster pressure
distribution out to a significant fraction of the virial radius. This profile is given
by 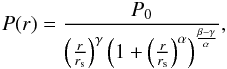 (7)where
P0 is a normalizing constant;
α,
β, and
γ set the
slope at intermediate, large, and small radii respectively, and rs is the
characteristic radius. The same profile can be written in its universal form (Arnaud et al. 2010) by relating the characteristic
radius to the concentration parameter c500, rs =
r500/c500,
with r500 the radius within which the mean
density of the cluster is equal to 500 times the critical density of the Universe at the
cluster redshift. The pressure normalization can then be written as P0 =
P500 × ℙ0, where
ℙ0 is a
normalization factor and P500 is the average pressure within
the radius r500 (related to the average mass within
the same radius, M500, by a scaling law). We finally
define θs =
rs/DA
the characteristic angular size, where DA is the angular diameter distance of
the cluster.
(7)where
P0 is a normalizing constant;
α,
β, and
γ set the
slope at intermediate, large, and small radii respectively, and rs is the
characteristic radius. The same profile can be written in its universal form (Arnaud et al. 2010) by relating the characteristic
radius to the concentration parameter c500, rs =
r500/c500,
with r500 the radius within which the mean
density of the cluster is equal to 500 times the critical density of the Universe at the
cluster redshift. The pressure normalization can then be written as P0 =
P500 × ℙ0, where
ℙ0 is a
normalization factor and P500 is the average pressure within
the radius r500 (related to the average mass within
the same radius, M500, by a scaling law). We finally
define θs =
rs/DA
the characteristic angular size, where DA is the angular diameter distance of
the cluster.
We simulate two different kinds of clusters. The first one is similar to what we observe for RX J1347.5-1145 in terms of amplitude and spatial extension (referred to as compact in the following). The second one is more diffuse, but its peak amplitude is the same as for the previous (referred to as diffuse hereafter). The corresponding parametrization can be found in Table 4. Using these sets of parameters, we compute the Compton parameter map according to Eq. (3) by integrating the pressure along the line-of-sight. The map is then convolved with the instrumental beam and converted into surface brightness. We use the same scanning strategy, as in the case of RX J1347.5-1145 observations of NIKA during the Run 5. The focal plane and the number of detectors are also the same. The clusters are centered at the tSZ signal maximum decrement that we observe on RX J1347.5-1145.
5.1.7. Validation of the pipeline on simulated data
After processing the simulated data, we recover the two cluster maps (compact is labeled C and diffuse is labeled D). Figure 4 provides the input model maps, the recovered maps after the processing, the residual between the input models and the recovered maps, and the best fit models of the recovered maps. The top line corresponds to the compact cluster and the second to the diffuse cluster. The clusters are detected with a signal-to-noise of the order of 10 and are well mapped in both cases. The signal amplitude is slightly reduced with respect to the input maps.
 |
Fig. 4 Generalized Navarro, Frenk, and White simulations of two clusters processed through the pipeline. The first one (compact cluster, as C) is similar to the NIKA map of RX J1347.5-1145 (top panels). The second (diffuse cluster, labeled D) is more extended (bottom panels). The parameters used in the cluster simulations are given in Table 4. From left to right, we show the input model maps, the recovered maps, the residual maps, and the best fit model maps of the recovered signal. They are labeled from C1 to C4 and from D1 to D4 for the compact and diffuse cluster, respectively. The maps are shown up to a noise level that is twice the minimal noise level of the map. The effective beam is shown on the bottom left corner, accounting for the instrumental beam and an extra 10 arcsec Gaussian smoothing of the maps. The contours correspond to 3, –3, –6, and –9 mJy/beam, to which we add −1 mJy/beam for the model maps. The color scales range from −13 to 13 mJy/beam, except for the residual maps for which we have −5 to 5 mJy/beam. The center of the clusters has been simulated at the tSZ peak location of the NIKA RX J1347.5-1145 map. |
Generalized Navarro, Frenk, and White parameters used to simulate the compact and diffuse clusters.
Using these maps, we compute the angular profiles of the recovered clusters by evaluating the average flux value for a set of concentric annuli. They are shown in Fig. 5, as green and red dots for the compact and diffuse clusters, respectively. Comparison with the input profiles is provided by solid lines with similar colors. We also show the profiles recovered after projection only to check zero-level effects (orange and blue diamonds for the compact and diffuse cluster, respectively), that is the input tSZ signal is simply projected without decorrelation or filtering.
 |
Fig. 5 Comparison of the profiles injected in the simulation and recovered at the end of the pipeline. The injected profiles are given as red (compact cluster) and green (diffuse cluster) solid lines. The recovered profiles are shown with dots of similar colors. We also show the recovered profiles in the case of projection only without correlated noise, glitches, or pulse tube lines included in the simulation. They are given as orange (compact cluster) and blue (diffuse cluster) diamonds. |
First of all, due to the scanning strategy, the largest angular scale that can be recovered in the map is 6 arcmin, which corresponds to the size of the observed map. In Fig. 5, we show the profile of the diffuse cluster (projection only, as blue diamonds) that reaches the zero-level at 3 arcmin, which is unlike the injected profile that extends farther. Hence, the data processing affects the map in the case of the diffuse cluster by reducing the measured flux up to 25% at a radii of ~1 arcmin. This can also be observed on the residual map of the diffuse cluster that is positive around the cluster peak. In the case of the compact cluster, the amplitude of the profile is not affected by more than 10%, and the corresponding residual map is consistent with noise. Concerning the shape of the reconstructed signal with respect to the input one, we observe a flat transfer function for angular scales between 0.4 and 4 arcmin for the compact cluster case. Finally, the remaining correlated noise can slightly contaminate the profile, but it is not significant once averaged on concentric annuli.
We use the simulated maps to fit the normalization P0 and the characteristic radius rs of the pressure profile. This is done using Markov chain Monte Carlo (MCMC) techniques that are further detailed in Sect. 6.3 (when applied on the RX J1347.5-1145 data). The recovered parameters can be compared to the input ones to estimate filtering effects and possible biases. Once marginalized, we find that the recovered parameters are within 1σ of the inputs for both P0 (10%) and rs (5%) in the case of the compact cluster. For the diffuse cluster, we find that P0 and rs are underestimated by 2.7 (17%) and 3.7 (12%) σ, respectively. The MCMC best fit maps are given in panels C4 and D4 of Fig. 4.
The effect of the radio point source subtraction (see Sect. 4.4) has also been checked via the simulations. To do so, a radio point source mimicking that, which is present in the RX J1347.5-1145 cluster has been added to the simulated data. It has then been removed during the processing by assuming a flux 3σ lower than the injected one. The results change by less than 1σ for both P0 and rs either for the diffuse or the compact cluster case.
5.2. Map of the undetected galaxy cluster IDCS J1426.5+3508
We have also observed IDCS J1426.5+3508, a faint high redshift (z = 1.75) cluster of galaxies. These observations correspond to 5 h 41 min of unflagged on-source data in atmospheric conditions, which are slightly poorer but comparable to those described in Table 1 for RX J1347.5-1145. For IDCS J1426.5+3508, the expected tSZ decrement is ~0.25 mJy/beam at 140 GHz with an angular size of ~2 arcmin (Brodwin et al. 2012). We, therefore, do not expect a detection, since its flux is below the standard deviation of the expected noise at the cluster location by a factor of ~5.
In Fig. 6, we show the map of IDCS J1426.5+3508 obtained after pipeline reduction. This map shows no evidence of tSZ signal, and it is consistent with noise as expected. This can be considered as a null test that allows us to conclude that the tSZ signal observed in the RX J1347.5-1145 data is not due to a bias in the analysis1.
 |
Fig. 6 Map at 140 GHz of the undetected galaxy cluster IDCS J1426.5+3508. |
6. Results
6.1. RX J1347.5-1145 as observed by NIKA
Figure 7 presents the RX J1347.5-1145 tSZ map obtained with the NIKA prototype. The radio source is subtracted in the right panel but not in the left panel. The associated difference map of separated equivalent subsamples (Jack-Knife), which is normalized by a factor of 2 to preserve the statistical properties of the noise in the tSZ map, is given in the left panel of Fig. 8. We also present on the middle panel of Fig. 8 the histogram of the pixel values. The outside contour of the maps shown is defined by the limit where the statistical noise level, which increases toward the edges of the full map, equals twice the minimum noise level of the inner region. The bottle-like shape of the cut-off is due to the scan strategy detailed in Sect. 3.2.
The inhomogeneity of the noise can be seen directly on the half difference map in Fig.
8. This is even more obvious on the histogram plot
that provides the noise distribution in two different regions of the half difference map
and on the standard deviation map. We observe that the standard deviation on the two
regions is significantly different, ⟨
σ ⟩ = 0.99 mJy/beam on the east side and
⟨ σ ⟩ =
1.42 mJy/beam on the west side. From the half difference map, we
estimate the overall root mean square of the noise in the cluster map to ⟨ σ ⟩ = 1.11 mJy/beam. This
is obtained by fitting the histogram of the pixel value with a Gaussian distribution. The
contours overplotted on the tSZ maps of Fig. 7
correspond to 3, −3,
−6, and −9 mJy/beam with the noise level being
1σ ≅ 1
mJy/beam at the cluster location. The beam is shown on the bottom left corner of the map,
accounting for both the 18.5 arcsec instrumental beam and the extra 10 arcsec Gaussian
smoothing of the map (i.e., 21 arcsec). In terms of the Compton parameter, the sensitivity
of the NIKA prototype camera during the campaign of November 2012 is ~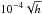 for one beam and 1σ.
for one beam and 1σ.
The maps in Fig. 7 clearly show the tSZ decrement that reaches up to ≃10σ. The signal is extended, and its maximum does not coincide with the X-ray center, (RA, Dec) = (13h47m30.59s, −11°45′10.1′′). It corresponds to the shock location, even for the radio point source subtracted map, which agrees with other single-dish observations. As mentioned in Sect. 2, these results do not agree with those from CARMA interferometric RX J1347.5-1145 observations (Plagge et al. 2013). The tSZ maximum corresponds to ≃10-3 in units of Compton parameter y, as expected for this cluster according to Pointecouteau et al. (1999). The consistency of the NIKA RX J1347.5-1145 map with previous observations is further discussed in Sect. 7.
 |
Fig. 7 NIKA map of RX J1347.5-1145 at 140 GHz. Left: original NIKA map with the radio source not subtracted. Right: same map with the radio source subtracted. The maps are given in mJy/beam. They are clipped up to a root mean square noise level that is twice the minimum of the map as detailed in the text. The contours are at 3, −3, −6 and −9 mJy/beam with 1σ ≅ 1 mJy/beam at the cluster location. The minimum value of the maps corresponds to y ≃ 10-3. The X-ray center location is represented by a white cross. The radio source location also corresponds to the white cross within 3 arcsec. The locations of the two infrared galaxies are given as red stars. |
 |
Fig. 8 RX J1347.5-1145 observations. Left: half-difference map of two equivalent subsamples mimicking the noise properties of the tSZ map. The pixels are 2 × 2 arcsec, and the map has been smoothed with a 10 arcsec Gaussian filter, which is similar to the tSZ map of Fig. 7. The noise level is not homogeneous, which is lower on the left hand side, due to the differences of acquisition time. Middle: noise distribution obtained from the half difference map. Since the noise is not homogeneous, we provide the distribution for both the eastern (left, green) and western (right, red) parts of the map. A Gaussian fit of the histograms gives the mean value of the standard deviation of the noise to be ⟨ σ ⟩ = 0.99 mJy/beam on the east side and ⟨ σ ⟩ = 1.42 mJy/beam on the west side. The minimum noise level reaches 0.8 mJy/beam. The contours of the noise map (left) correspond to the overall mean noise (i.e. ±1.11 mJy/beam). Right: standard deviation map estimated from difference maps. White regions have not been observed. Gray regions are those for which the standard deviation is higher than 6 mJy/beam. |
6.2. RX J1347.5-1145 profile
Figure 9 gives the flux profile as a function of the angular distance that is extracted from the tSZ map in Fig. 7. In the case of RX J1347.5-1145, the tSZ barycenter and the X-ray center do not coincide due to the ongoing merger. We compare the profile computed from the X-ray center, (RA, Dec) = (13h47m30.59s, −11°45′10.1′′), to the tSZ peak that is taken to be at the coordinates (RA, Dec) = (13h47m31s, −11°45′30′′) from the maximum decrement of the NIKA map. The error bars have been computed from simulated noise maps with statistical properties estimated using the half-difference map presented on the left panel of Fig. 8.
The right panel in Fig. 9 compares the profile of RX J1347.5-1145 from the X-ray center in three different areas: the northwest, the northeast, and the south. It shows the increase in thermal pressure in the southern region, where the subclump (merging) is observed in X-ray and tSZ (Sect. 2). This is due to the compression of the hot gas within the merging process, which increases the temperature and thus the pressure (deepening the tSZ decrement at 140 GHz). We note that the southern extension coincides with the presence of a radio mini-halo (see the work by Gitti et al. 2007a), which implies the presence of non-thermal electrons that could underline a non-thermal contribution to the total pressure (not seen in the tSZ signal). We also note that the radio source has been subtracted before the calculation of the profiles.
6.3. Modeling of the cluster pressure profile
The object RX J1347.5-1145 has been intensively studied in X-rays, which have revealed a fairly regular cluster at a large scale down to the center in the north direction with a low central entropy (Cavagnolo et al. 2009). The contrast with the southern part, which exhibits a tSZ and X-ray extension, suggests that RX J1347.5-1145 was a spherical, relaxed cool-core cluster that is undergoing the merging of a subcluster on its southern part. We, therefore, aim at quantifying the tSZ South East extension detected with the NIKA prototype by modeling and subtracting the signal coming from the relaxed region, which is located on the northern-west side of the X-ray center. We model the tSZ signal by considering a gNFW profile (Eq. (7)), which is centered at the X-ray position of the system, whose inner, outer, and intermediate slopes (γ, β, α) have been set equal to the cool-core best-fitting values of Arnaud et al. (2010) (γcc = 0.7736, βcc = 5.4905, αcc = 1.2223). The best-fitting values of P0 and θs are obtained using a MCMC approach. The sequence of random samples, known as the chain, has been built by implementing the Metropolis-Hasting algorithm (Chib & Greenberg 1995), which means that the parameter space is explored with a trial step drawn from a symmetric probability distribution. Convergence of the chains is checked by including the test proposed by Gelman & Rubin (1992).
The parameters P0 and θs have been
constrained by masking the southeast extension. The mask has been defined as a half ring
on the southern part of the cluster, centered on the X-ray peak with inner and outer radii
set to 10 and 80 arcsec, respectively. By masking the hottest region of the system, the
constraints obtained on the best fit parameters are mainly driven by the cool-core like
component, where the cluster temperature remains below 10 keV. Consequently, the flux
relativistic correction (Itoh et al. 1998; Nozawa et al. 1998, 2006) is estimated to be ≲7% at 140 GHz and needs to be propagated to the following results.
The best fit parameters obtained are 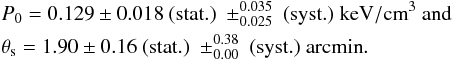 (8)The
corresponding posterior likelihood is given in Fig. 10 and accounts for statistical uncertainties only. The systematic uncertainties
have been computed by using the calibration uncertainty and considering the bias filtering
effect of the analysis that is estimated from the simulations described in Sect. 5.1.6. The pressure profile normalization parameter,
P0, is symmetrically affected by the
calibration uncertainty, while the negative bias (lowering the true value) has been
estimated to less than 20%. The parameter θs is only affected by the bias, which
is estimated to less than 20% and lowers its true value.
(8)The
corresponding posterior likelihood is given in Fig. 10 and accounts for statistical uncertainties only. The systematic uncertainties
have been computed by using the calibration uncertainty and considering the bias filtering
effect of the analysis that is estimated from the simulations described in Sect. 5.1.6. The pressure profile normalization parameter,
P0, is symmetrically affected by the
calibration uncertainty, while the negative bias (lowering the true value) has been
estimated to less than 20%. The parameter θs is only affected by the bias, which
is estimated to less than 20% and lowers its true value.
Figure 11 compares the NIKA prototype point source subtracted map with the best fit model obtained for the relaxed component, and the residual. The model represents the northern part of the tSZ map well, but the southern side cannot be explained without including an overpressure component, which is known to be due to the merging of a subcluster (see Sect. 2).
 |
Fig. 9 Radial flux profiles of RX J1347.5-1145. Left: comparison of the radial profile computed from the X-ray (red dots) and tSZ (green diamonds) centers. Right: comparison of the radial flux profile in three different regions from the X-ray center. The map is cut from the X-ray center in three equal slices: one cut is vertical coming from the north to the center, and the two others are diagonal from the southeast and the southwest to the center, respectively. The red diamonds and yellow dots profiles correspond to the northwest and northeast part of the map, respectively, where the cluster is expected to be rather relaxed. The green triangle profile corresponds to the southern part of the map, where the merging occurred. |
 |
Fig. 10 Posterior likelihood of the MCMC pressure profile fit in the plane P0 – θs. From dark to light blue, the colors correspond to 68%, 95%, and 99% confidence levels. The top and right curves show the normalized Gaussian best fit of the marginalized likelihood of P0 and θs, respectively. |
The best fit model and the residual tSZ map, as given in Fig. 11, have been used to quantify the distribution of the signal within
the region, where the intracluster gas is more relaxed toward hydrostatic equilibrium, and
the region, where it is expected to be shock heated. For this purpose, we compute the
integrated Compton parameter, as defined as 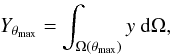 (9)over
the solid angle Ω up to the
radius θmax from the X-ray center. This is
separately done on the map and the residual (as seen in Fig. 11). Given the size of the NIKA map, we integrate up to θmax = 2 arcmin.
The total integrated Compton parameter within this radius is
(9)over
the solid angle Ω up to the
radius θmax from the X-ray center. This is
separately done on the map and the residual (as seen in Fig. 11). Given the size of the NIKA map, we integrate up to θmax = 2 arcmin.
The total integrated Compton parameter within this radius is
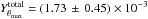 arcmin2. After
removing the best fit cool-core model and integrating the residual in the same region, we
obtain
arcmin2. After
removing the best fit cool-core model and integrating the residual in the same region, we
obtain 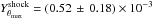 arcmin2. The
errors on the integrated fluxes account for the statistical noise only. Systematic
uncertainties are estimated to be of the order of 19%. Thus, the shock contribution is
estimated to be (30 ± 13 ± 6)%
of the total tSZ flux at these small cluster-centric distances. Considering the
Planck Y5R500
measurements (Planck Collaboration 2013), the shock
contribution corresponds to about 24% of the total tSZ flux. Previous observations by
Mason et al. (2010) and Plagge et al. (2013) are consistent with a lower relative contribution
of the shock of 9 to 10%. A direct comparison of these results with ours is difficult
because of the very different methodologies used. In particular, the angular scales probed
by the different instruments are not the same. Furthermore, Mason et al. (2010) and Plagge et al.
(2013) have used external data to compute the overall tSZ flux, while we use NIKA
data only in this paper.
arcmin2. The
errors on the integrated fluxes account for the statistical noise only. Systematic
uncertainties are estimated to be of the order of 19%. Thus, the shock contribution is
estimated to be (30 ± 13 ± 6)%
of the total tSZ flux at these small cluster-centric distances. Considering the
Planck Y5R500
measurements (Planck Collaboration 2013), the shock
contribution corresponds to about 24% of the total tSZ flux. Previous observations by
Mason et al. (2010) and Plagge et al. (2013) are consistent with a lower relative contribution
of the shock of 9 to 10%. A direct comparison of these results with ours is difficult
because of the very different methodologies used. In particular, the angular scales probed
by the different instruments are not the same. Furthermore, Mason et al. (2010) and Plagge et al.
(2013) have used external data to compute the overall tSZ flux, while we use NIKA
data only in this paper.
 |
Fig. 11 Comparison between the original point source subtracted RX J1347.5-1145 tSZ map (left panel) and the best fit model map excluding the shock area (middle panel). The residuals are given on the right panel map. The model accounts for the cluster emission well, except in the southern shocked area, as expected. |
 |
Fig. 12 Comparison of RX J1347.5-1145 tSZ maps by DIABOLO and NIKA in mJy/beam. Left: NIKA tSZ map with DIABOLO contours in red at −1, −3, −5, and −7 mJy/beam. Right: flux radial profile as measured by NIKA (purple dots) and DIABOLO (red diamonds). |
 |
Fig. 13 Left: comparison between the RX J1347.5-1145 NIKA tSZ map and the XMM X-ray data (see the work of Gitti & Schindler 2004, 2005; Gitti et al. 2007b). The XMM map has been smoothed with a 5 arcsec Gaussian filter. The red X-ray contours are in photon counts and correspond to 6, 12, 25, 50, 100, 200, and 400. Right: comparison between the best-fit radial tSZ profile of the NIKA map, excluding the shock area (see Sect. 6.3) and the profile derived from Chandra’s data by Comis et al. (2011), which is processed through the NIKA data reduction pipeline, as discussed in Sect. 4.2. The NIKA best-fit profile is given in purple with an associated 1σ statistical error range filled in blue, and the X-ray model is given in red with the 1σ statistical error limit, as two dashed lines. See text for more details on the errors limits. |
7. Comparison to other external data sets
7.1. Comparison to the Planck catalog of tSZ sources
The overall integrated Compton parameter for RX J1347.5-1145 can be compared to the Planck satellite measurement, as reported in the Planck catalog of tSZ sources (Planck Collaboration XXIX 2014). For each detection, the Planck catalog provides the two-dimensional θs – Y5r500 probability distribution. The parameter θs is again the characteristic radius of Eq. (7), and Y5r500 is the integrated Compton parameter within a radius equal to 5 × r500, therefore, assumed to be the total flux. The catalog also contains the slopes of the gNFW pressure profile used by the detection pipeline, which allows us to compute the Yθmax/Y5R500 ratio, so to extrapolate the Planck flux (Y5R500) to the integrated signal at any cluster centric distance (Yθmax). To compare our result to Planck data, we have explored two different methodologies:
-
We fixed θs to its maximum likelihood value, obtaining Y5R500 = (2.17 ± 0.36) × 10-3 arcmin2 for RX J1347.5-1145. Then, the Yθmax/Y5R500 ratio returns
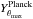 =
(1.78 ± 0.30) ×
10-3 arcmin2 for θmax = 2 arcmin, which agrees with
the NIKA value,
=
(1.78 ± 0.30) ×
10-3 arcmin2 for θmax = 2 arcmin, which agrees with
the NIKA value, 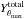 =
(1.73 ± 0.45) ×
10-3 arcmin2.
=
(1.73 ± 0.45) ×
10-3 arcmin2. -
The Planck tSZ angular size (θs) – flux (Y5r500) degeneracy can also be broken by fixing r500 to its X-ray derived value without changing the other pressure profile parameters. This includes c500 (which is kept equal to 1.1733; the value given by Arnaud et al. 2010). This is what Planck Collaboration XXIX (2014) uses, when recovering the integrated tSZ signal within the X-ray size. Following this approach, we obtain
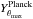 =
(1.23 ± 0.21) ×
10-3 arcmin2 for θmax = 2 arcmin. This value is
still consistent with the NIKA flux, although weaker. The latter can be understood
if we consider that the X-ray derived r500 = 1.42 Mpc ≡ θ500 =
3.94 arcmin (MCXC, Piffaretti et
al. 2011) is much larger than the reliable radial extent of the NIKA map.
The r500 that can be deduced from the
NIKA θs parameter is, by contrast,
smaller. However, we expect the two integrated Compton parameters to converge when
we move to larger θmax. Indeed, when pushing the
integration up to θmax = 2.5 arcmin (by
extrapolating the best-fit model of the relaxed region to angular distances not
directly probed through our observations and assuming that the contribution due to
the shock is negligible at scales larger than ~2 arcmin), we obtain
=
(1.23 ± 0.21) ×
10-3 arcmin2 for θmax = 2 arcmin. This value is
still consistent with the NIKA flux, although weaker. The latter can be understood
if we consider that the X-ray derived r500 = 1.42 Mpc ≡ θ500 =
3.94 arcmin (MCXC, Piffaretti et
al. 2011) is much larger than the reliable radial extent of the NIKA map.
The r500 that can be deduced from the
NIKA θs parameter is, by contrast,
smaller. However, we expect the two integrated Compton parameters to converge when
we move to larger θmax. Indeed, when pushing the
integration up to θmax = 2.5 arcmin (by
extrapolating the best-fit model of the relaxed region to angular distances not
directly probed through our observations and assuming that the contribution due to
the shock is negligible at scales larger than ~2 arcmin), we obtain
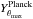 =
(1.52 ± 0.26) ×
10-3 arcmin2 versus (1.77 ± 0.45) × 10-3 arcmin2 for NIKA. Alternatively,
the larger NIKA flux can also be explained by relaxing the hypothesis of a constant
c500. The different sensitivities of
Planck+MCXC and NIKA to the signal distribution could lead to
differences in the recovered flux distribution. With r500 fixed
to its X-ray value, a larger value of c500 implies a smaller value of
θs and, therefore, that a larger
fraction of the total tSZ flux is located within the innermost regions. In this
case, we would have a better consistency between the Planck+MCXC
and the NIKA integrated Compton parameter, even at smaller cluster-centric
distances. Since the value of c500 = 1.1733 has been obtained on
an average (universal) profile (Arnaud et al.
2010) and RX J1347.5-1145 is known to have a very peaked morphology
compared to other clusters, this hypothesis is likely to be correct: the inner slope
parameter γ being fixed, c500 can
typically vary from ~0
to ~5 between clusters
(Planck Collaboration 2013).
=
(1.52 ± 0.26) ×
10-3 arcmin2 versus (1.77 ± 0.45) × 10-3 arcmin2 for NIKA. Alternatively,
the larger NIKA flux can also be explained by relaxing the hypothesis of a constant
c500. The different sensitivities of
Planck+MCXC and NIKA to the signal distribution could lead to
differences in the recovered flux distribution. With r500 fixed
to its X-ray value, a larger value of c500 implies a smaller value of
θs and, therefore, that a larger
fraction of the total tSZ flux is located within the innermost regions. In this
case, we would have a better consistency between the Planck+MCXC
and the NIKA integrated Compton parameter, even at smaller cluster-centric
distances. Since the value of c500 = 1.1733 has been obtained on
an average (universal) profile (Arnaud et al.
2010) and RX J1347.5-1145 is known to have a very peaked morphology
compared to other clusters, this hypothesis is likely to be correct: the inner slope
parameter γ being fixed, c500 can
typically vary from ~0
to ~5 between clusters
(Planck Collaboration 2013).
From the comparison to the Planck data, we can conclude that NIKA is able to recover most of the tSZ signal, despite the large angular scale cutoff (above 3 arcmin). This is consistent with what was found in the simulations in Sect. 5.1.7 and in particular for the compact cluster case, which is very similar to the NIKA RX J1347.5-1145 observations regarding the tSZ flux and angular extension. From this, we can convey that Planck and NIKA are complementary. This will be even more interesting and easily exploitable with the larger field of view (6.5 arcmin) that the NIKA2 camera will reach.
7.2. Comparison to DIABOLO tSZ observations
In Fig. 12, we present the comparison between DIABOLO and the NIKA results on RX J1347.5-1145. DIABOLO (Pointecouteau et al. 1999, 2001) was a bolometric camera that observed RX J1347.5-1145 at the IRAM 30-m telescope using a dual-band instrument at frequencies corresponding to the NIKA bands: 140 and 250 GHz. The resolution of DIABOLO was 22 arcsec at 140 GHz. The data reduction and the instrumental similarities with NIKA make it a first choice for a direct comparison.
The left panel shows the tSZ NIKA map with DIABOLO contours overplotted in red with levels of −1, −3, −5, and −7 mJy/beam (radio source not subtracted in both maps). We can see that the tSZ maxima and the external part of the cluster match within error bars. The overall amplitude of the signal is slightly higher for NIKA data than for DIABOLO. However, this difference is not significant once we account for the systematic uncertainties given in Table 2. The right panel of Fig. 12 compares the cluster pressure profile (radio source subtracted and X-rays centered) measured with both instruments. The two profiles are compatible within error bars over the whole radial range, even though NIKA seems to detect more signal in the inner part of the cluster. The reduced χ2 associated to the profile difference, which is computed up to a radius of 2.5 arcmin, is equal to 2.35. However, since this does not account for calibration uncertainties, we also give the reduced χ2 after cross calibrating the two profiles: we obtain χ2 = 1.32 with a cross-calibration factor of 1.09, which is compatible with our calibration error estimate. In both cases, the tSZ maximum is not located at the X-ray center, in contrast to interferometric CARMA measurement, but agrees with other single-dish observations.
7.3. Comparison to XMM and Chandra X-ray observations
The XMM data (Gitti & Schindler 2004) have been used to compute a photon count (exposure corrected) map of RX J1347.5-1145 that we compare to the NIKA tSZ observations. As seen in Fig. 13, the tSZ peak does not coincide with the X-ray center. The object RX J1347.5-1145 gives a striking example of the power of tSZ data and how it complements X-ray. Moreover, the mismatch between the tSZ and X-ray center gives valuable information on the gas physics at play in the ICM.
The higher resolution of the Chandra X-ray data has been used for cluster simulation purposes. In particular, the work of Comis et al. (2011) uses the publicly available, X-ray derived, pressure profiles of the ACCEPT (Archive of Chandra Cluster Entropy Profile Tables) clusters (Cavagnolo et al. 2009) to constrain the P0, rs, and γ parameters of the gNFW pressure profile (Eq. (7)). The best-fitting values for RX J1347.5-1145 (Table 5) have been used in the present work to simulate the expected tSZ signal, as explained in Sect. 5.1.6. Once processed through the pipeline, the expected profile is compared to the NIKA best-fit profile, excluding the shocked area (see Sect. 6.3) on the right panel of Fig. 13. The NIKA best-fit profile and the X-ray model are both given with the 1σ error envelope. The error on the NIKA profile only accounts for statistical uncertainties by sampling the 1σ contour of the likelihood of Fig. 10. The systematic errors (see Eq. (8)) are not shown and would result in an overall multiplicative factor on the amplitude (P0) and on the angular scale (θs). We choose to include only the error on the parameter P0 (Table 5) for the X-ray model, since it is highly degenerated with θs and γ. In addition to the X-ray systematic uncertainties, the associated systematic error, which is not included in Fig. 13, arises mainly from the unit conversion coefficient (Jansky per beam to Compton parameter: y = 10-3 ≡ 11.8 ± 1.2 mJy/beam). It has a similar effect as the error on the P0 NIKA best-fit value. The two profiles agrees within systematic and statistical uncertainties.
Modeling of the pressure profile of RX J1347.5-1145 using the fit of Chandra data (Comis et al. 2011).
7.4. Comparison to other high resolution tSZ data
We also compare the NIKA data with state-of-the-art sub-arcmin resolution data: MUSTANG (Mason et al. 2010; Korngut et al. 2011) and CARMA (Plagge et al. 2013) observations. Since these two instruments are in many ways different from NIKA, we limit ourselves to a qualitative comparison.
The instrument MUSTANG uses the single dish 100-meter Green Bank Telescope in Virginia, USA. It operates at 90 GHz with a 8 arcsec resolution. At 90 GHz, the central radio source of RX J1347.5-1145 is very bright compared to the tSZ decrement. In the case of MUSTANG, the removal of the atmospheric noise filters angular scales that are larger than about 60 arcsec. In that sense, the NIKA and MUSTANG are complementary. The instrument MUSTANG is able to measure the structural property of RX J1347.5-1145 at scales ranging from ~10−60 arcsec, while the NIKA map is reliable in the range of ~20−200 arcsec. The two instruments agree on the morphology of RX J1347.5-1145 at intermediate scales (the inner part of the −6 mJy contour on Fig. 7). The tSZ maximum coincides and the overall distribution of the tSZ signal is consistent on both observations. The excess seen in the region 2 of Fig. 5 in Mason et al. (2010) does not show up clearly in the NIKA map. However, the spatial scales of this feature are smaller than 10 arcsec, and it is likely smoothed out by the NIKA beam.
The instrument CARMA is a multifrequency interferometer (Plagge et al. 2013). For RX J1347.5-1145 observations, they were made of 23 antennae of 3.5, 6.1, and 10.4 meter operating in three configurations at 31 GHz, 86 GHz, and 90 GHz for a total of 41.7 h of unflagged on-source observation. Due to the complexity of combining the data in different configurations, the CARMA transfer function is not simple. Nevertheless, CARMA and NIKA agree well on scales greater than about 30 arcsec. At smaller scales, CARMA and NIKA disagree on the position of the tSZ peak.
7.5. Point source contamination effects
As mentioned above, the effect of point source contamination is an issue in single-dish observations. In this work, the radio source located near the X-ray center (within 3 arcsec) can affect our results. The CARMA data suggest that the flux of the source is underestimated when removed from single-dish data. Therefore, we have reprocessed the NIKA data by assuming that the source was 3σ brighter than its nominal value (i.e., 5.3 mJy instead of 4.4 mJy at 140 GHz). We obtain that the tSZ maximum is still located at the shock position. The difference in tSZ amplitude between the X-ray center and the shock is reduced but still inconsistent with CARMA, even though the discrepancy is smaller. Moving the tSZ maximum to the X-ray center would require a 5σ positive shift of the flux of the radio source. The best-fit pressure profile parameters, P0 and rs, are affected by less than 1σ (statistical only) by the point source subtraction. This is consistent with what we observed in simulations (see Sect. 5.1.7). For the infrared source Z2, 20 arcsec NE from the X-ray center, we have tested adding a 0.64 mJy source at its position, which is the upper limit that we have estimated in Sect. 4.2.4. The changes in our results are negligible for the location of the tSZ maximum and for the rs and P0 values; they change by less than 0.6σ (statistical only). The Z1 infrared source is located in the external part of the cluster and does not affect any of our results.
8. Conclusions and prospectives for NIKA2
The cluster RX J1347.5-1145 is an ongoing merger, among the most-studied galaxy clusters at arcmin angular scales, making it a good target for the first tSZ observations with the NIKA prototype camera. Using a dual-band decorrelation with a high resolution instrument, we have imaged the tSZ morphology of the cluster from the core to its outer region. The detailed data analysis is specific to KIDs and to tSZ observations and has been validated on simulations. The observation of RX J1347.5-1145 constitutes the first tSZ observations with an instrument based on KIDs.
The reconstructed tSZ map of RX J1347.5-1145 is reliable on scales going from about 20 to 200 arcsec and shows a strong southeast extension that corresponds to the merger shock, as expected from the overpressure caused by the ongoing merger. We detect the non-alignment of the tSZ maximum and the X-ray center, which agrees with other single-dish data but disagrees with CARMA interferometric data. The tSZ extension is also observed in the radial flux profile of the cluster and the residual of the map with respect to the modeling of the relaxed part of the cluster. The generalized NFW fit of the NW region enables us to constrain the cluster pressure profile parameters θs and P0. The pressure profile derived from X-ray agrees with this tSZ best-fit model.
The tSZ map and the radial profile measured with NIKA have been compared to DIABOLO observations at the same telescope with similar resolution and frequency coverage. The agreement between the two maps validates the tSZ observations presented in this work. In addition, the NIKA prototype map agrees with state-of-the-art sub-arcmin resolution tSZ observations, MUSTANG (90 GHz and 8 arcsec resolution) and CARMA (30−90 GHz and ~15 arcsec resolution) except for the tSZ peak position. The comparison shows that it is complementary to these experiments.
In this paper, KID arrays of the NIKA prototype have been proven to be competitive detectors for millimeter wave astronomy and in particular for the observation of galaxy clusters via the tSZ effect. The next generation instrument, NIKA2, consists of about 1000 detectors at 140 GHz and 4000 at 240 GHz with a field of view of ~6.5 arcmin. With these characteristics, NIKA2 is able to provide large high-resolution mapping of clusterss making it an ideal instrument for high-resolution observations of intermediate to large distance clusters of galaxies. The instrument NIKA2 will be well adapted for a follow-up of unresolved sources in the Planck cluster sample (Planck Collaboration XXIX 2014).
Acknowledgments
We would like to thank the IRAM staff for their support during the campaign. This work has been partially funded by the Foundation Nanoscience Grenoble, the ANR under the contracts “MKIDS” and “NIKA”. This work has been partially supported by the LabEx FOCUS ANR-11-LABX-0013. This work has benefited from the support of the European Research Council Advanced Grant ORISTARS under the European Union’s Seventh Framework Programme (Grant Agreement No. 291294). The NIKA dilution cryostat has been designed and built at the Institut Néel. In particular, we acknowledge the crucial contribution of the Cryogenics Group, and in particular Gregory Garde, Henri Rodenas, Jean-Paul Leggeri, Philippe Camus. R.A. would like to thank the ENIGMASS French LabEx for funding this work. B.C. acknowledges support from the CNES post-doctoral fellowship program. E.P. acknowledges the support of grant ANR-11-BS56-015. We gratefully thank the anonymous referee for useful comments that have improved not only the quality of the paper but that will also help future analysis of NIKA tSZ observations. Finally we would like to tank Céline Combet for a careful reading of the paper.
References
- Allen, S. W., Schmidt, R. W., & Fabian, A. C. 2002, MNRAS, 335, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Basu, K., Zhang, Y.-Y., Sommer, M. W., et al. 2010, A&A, 519, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birkinshaw, M. 1999, Phys. Rep., 310, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., & Werner, N. 2010, A&ARv, 18, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bourrion, O., Bideaud, A., Benoit, A., et al. 2011, JINST, 6, 06012 [Google Scholar]
- Bradač, M., Schrabback, T., Erben, T., et al. 2008, ApJ, 681, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Brodwin, M., Gonzalez, A. H., Stanford, S. A., et al. 2012, ApJ, 753, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, M., Giordano, C., Battiston, R., et al. 2010, Exp. Astron., 28, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Calvo, M., Roesch, M., Désert, F. X., et al. 2013, A&A, 551, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlstrom, J. E., Holder, G. P., & Reese, E. D. 2002, ARA&A, 40, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Catalano, A., Calvo, M., Ponthieu, N., et al. 2014 [arXiv:1402.0260] [Google Scholar]
- Cavagnolo, K. W., Donahue, M., Voit, G. M., & Sun, M. 2009, ApJS, 182, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Chib, S., & Greenberg, E. 1995, The American Statistician, 49, 327 [Google Scholar]
- Cohen, J. G., & Kneib, J.-P. 2002, ApJ, 573, 524 [NASA ADS] [CrossRef] [Google Scholar]
- Comis, B., de Petris, M., Conte, A., Lamagna, L., & de Gregori, S. 2011, MNRAS, 418, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Day, P. K., LeDuc, H. G., Mazin, B. A., Vayonakis, A., & Zmuidzinas, J. 2003, Nature, 425, 817 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Doyle, S., Mauskopf, P., & Naylon, J. 2008, J. Low Temp. Phys., 151, 530 [Google Scholar]
- Feretti, L., Giovannini, G., Govoni, F., & Murgia, M. 2012, A&ARv, 20, 54 [Google Scholar]
- Gal, R. R. 2006, [arXiv:astro-ph/0601195] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Statistical Science, 7, 457 [Google Scholar]
- Gitti, M., & Schindler, S. 2004, A&A, 427, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., & Schindler, S. 2005, Adv. Space Res., 36, 613 [NASA ADS] [CrossRef] [Google Scholar]
- Gitti, M., Ferrari, C., Domainko, W., Feretti, L., & Schindler, S. 2007a, A&A, 470, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gitti, M., Piffaretti, R., & Schindler, S. 2007b, A&A, 472, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grabovskij, G. J., Swenson, L. J., Buisson, O., et al. 2008, Appl. Phys. Lett., 93, 134102 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, N., Kohyama, Y., & Nozawa, S. 1998, ApJ, 502, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, R. E., Zuhone, J., Jones, C., Forman, W. R., & Markevitch, M. 2012, ApJ, 751, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T., Komatsu, E., Ota, N., et al. 2004, PASJ, 56, 17 [NASA ADS] [Google Scholar]
- Kneib, J.-P., & Natarajan, P. 2011, A&ARr, 19, 47 [Google Scholar]
- Komatsu, E., Kitayama, T., Suto, Y., et al. 1999, ApJ, 516, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Matsuo, H., Kitayama, T., et al. 2001, PASJ, 53, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Korngut, P. M., Dicker, S. R., Reese, E. D., et al. 2011, ApJ, 734, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Kosowsky, A. 2003, New A Rev., 47, 939 [CrossRef] [Google Scholar]
- Kramer, C., Penalver, J., & Greve, A. 2013, Improvement of the IRAM 30 m telescope pattern, Tech. Rep., IRAM [Google Scholar]
- Kravtsov, A. V., & Borgani, S. 2012, ARA&A, 50, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, B. S., Dicker, S. R., Korngut, P. M., et al. 2010, ApJ, 716, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Miranda, M., Sereno, M., de Filippis, E., & Paolillo, M. 2008, MNRAS, 385, 511 [NASA ADS] [CrossRef] [Google Scholar]
- Monfardini, A., Swenson, L. J., Bideaud, A., et al. 2010, A&A, 521, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Monfardini, A., Benoit, A., Bideaud, A., et al. 2011, ApJS, 194, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Moreno, R. 2010, Neptune and Uranus planetary brightness temperature tabulation. Tech. rep., ESA Herschel Science Center, available from ftp://ftp.sciops.esa.int/pub/hsc-calibration/PlanetaryModels/ESA2 [Google Scholar]
- Mroczkowski, T., Bonamente, M., Carlstrom, J. E., et al. 2009, ApJ, 694, 1034 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T., Dicker, S., Sayers, J., et al. 2012, ApJ, 761, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Kravtsov, A. V., & Vikhlinin, A. 2007a, ApJ, 668, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Nagai, D., Vikhlinin, A., & Kravtsov, A. V. 2007b, ApJ, 655, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, S., Itoh, N., & Kohyama, Y. 1998, ApJ, 508, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Nozawa, S., Itoh, N., Suda, Y., & Ohhata, Y. 2006, Nuovo Cimento B Serie, 121, 487 [NASA ADS] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ota, N., Murase, K., Kitayama, T., et al. 2008, A&A, 491, 363 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J., Cernicharo, J., & Serabyn, E. 2002, in Astronomical Site Evaluation in the Visible and Radio Range, eds. J. Vernin, Z. Benkhaldoun, & C. Muñoz-Tuñón, ASP Conf. Ser., 266, 188 [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plagge, T. J., Marrone, D. P., Abdulla, Z., et al. 2013, ApJ, 770, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321529 [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321591 [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, in press, DOI: 10.1051/0004-6361/201321523 [Google Scholar]
- Pointecouteau, E., Giard, M., Benoit, A., et al. 1999, ApJ, 519, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Pointecouteau, E., Giard, M., Benoit, A., et al. 2001, ApJ, 552, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Roesch, M., Benoit, A., Bideaud, A., et al. 2012, [arXiv:1212.4585] [Google Scholar]
- Sayers, J., Mroczkowski, T., Zemcov, M., et al. 2013, ApJ, 778, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Schindler, S., Guzzo, L., Ebeling, H., et al. 1995, A&A, 299, L9 [NASA ADS] [Google Scholar]
- Schindler, S., Hattori, M., Neumann, D. M., & Boehringer, H. 1997, A&A, 317, 646 [NASA ADS] [Google Scholar]
- Staguhn, J., Allen, C., Benford, D., et al. 2008, J. Low Temperature Physics, 151, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1972, Astrophys. Space Phys. Res., 4, 173 [Google Scholar]
- Sunyaev, R. A., & Zel’dovich, Y. B. 1980, ARA&A, 18, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Swenson, L. J., Cruciani, A., Benoit, A., et al. 2010, Appl. Phys. Lett., 96, 263511 [NASA ADS] [CrossRef] [Google Scholar]
- Verdugo, M., Lerchster, M., Böhringer, H., et al. 2012, MNRAS, 421, 1949 [NASA ADS] [CrossRef] [Google Scholar]
- Voges, W., Aschenbach, B., Boller, T., et al. 1999, A&A, 349, 389 [NASA ADS] [Google Scholar]
- Zemcov, M., Borys, C., Halpern, M., Mauskopf, P., & Scott, D. 2007, MNRAS, 376, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Zemcov, M., Aguirre, J., Bock, J., et al. 2012, ApJ, 749, 114 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean zenith opacity, on-source integration time, and period of the day for the three days of the campaign of November 2012.
Generalized Navarro, Frenk, and White parameters used to simulate the compact and diffuse clusters.
Modeling of the pressure profile of RX J1347.5-1145 using the fit of Chandra data (Comis et al. 2011).
All Figures
 |
Fig. 1 Elevation (dashed green) and azimuth (solid red) offset scans. The center is represented by a black dot and has coordinates (RA, Dec) = (13h47m32s, −11°45′42′′). The 140 GHz array is also represented by black crosses, which correspond to the position of each KID in the focal plane (gaps in the array correspond to invalid detectors). |
| In the text | |
 |
Fig. 2 Normalized 140 GHz (solid red line) and 240 GHz (solid orange line) instrumental bandpasses. The total atmospheric transmission is also given as a solid green line for 1 mm of precipitable water vapor, according to the Pardo model (Pardo et al. 2002). The oxygen (dash-dotted light blue) and the water vapor (dashed dark blue) contributions are represented. |
| In the text | |
 |
Fig. 3 TOD (left) and their power spectra (right) for a given detector. The data corresponds to the calibrated TOD before (red) and after (green) the electronic and atmospheric noise decorrelation. The TOD are dominated by the atmospheric noise at low frequencies, which is responsible for the slow variations in the red TOD and the obvious rise of noise below ~1 Hz on the red power spectrum. Cosmic rays hitting the instrument can be seen as spikes in the TOD but have been removed before computing the power spectra. Pulse tube frequency lines appear in the power spectrum (e.g. the ~6 Hz line in the raw power spectrum) and are notch filtered. The electronic noise dominates at frequencies between ~1 and ~5 Hz in the power spectrum before decorrelation. |
| In the text | |
 |
Fig. 4 Generalized Navarro, Frenk, and White simulations of two clusters processed through the pipeline. The first one (compact cluster, as C) is similar to the NIKA map of RX J1347.5-1145 (top panels). The second (diffuse cluster, labeled D) is more extended (bottom panels). The parameters used in the cluster simulations are given in Table 4. From left to right, we show the input model maps, the recovered maps, the residual maps, and the best fit model maps of the recovered signal. They are labeled from C1 to C4 and from D1 to D4 for the compact and diffuse cluster, respectively. The maps are shown up to a noise level that is twice the minimal noise level of the map. The effective beam is shown on the bottom left corner, accounting for the instrumental beam and an extra 10 arcsec Gaussian smoothing of the maps. The contours correspond to 3, –3, –6, and –9 mJy/beam, to which we add −1 mJy/beam for the model maps. The color scales range from −13 to 13 mJy/beam, except for the residual maps for which we have −5 to 5 mJy/beam. The center of the clusters has been simulated at the tSZ peak location of the NIKA RX J1347.5-1145 map. |
| In the text | |
 |
Fig. 5 Comparison of the profiles injected in the simulation and recovered at the end of the pipeline. The injected profiles are given as red (compact cluster) and green (diffuse cluster) solid lines. The recovered profiles are shown with dots of similar colors. We also show the recovered profiles in the case of projection only without correlated noise, glitches, or pulse tube lines included in the simulation. They are given as orange (compact cluster) and blue (diffuse cluster) diamonds. |
| In the text | |
 |
Fig. 6 Map at 140 GHz of the undetected galaxy cluster IDCS J1426.5+3508. |
| In the text | |
 |
Fig. 7 NIKA map of RX J1347.5-1145 at 140 GHz. Left: original NIKA map with the radio source not subtracted. Right: same map with the radio source subtracted. The maps are given in mJy/beam. They are clipped up to a root mean square noise level that is twice the minimum of the map as detailed in the text. The contours are at 3, −3, −6 and −9 mJy/beam with 1σ ≅ 1 mJy/beam at the cluster location. The minimum value of the maps corresponds to y ≃ 10-3. The X-ray center location is represented by a white cross. The radio source location also corresponds to the white cross within 3 arcsec. The locations of the two infrared galaxies are given as red stars. |
| In the text | |
 |
Fig. 8 RX J1347.5-1145 observations. Left: half-difference map of two equivalent subsamples mimicking the noise properties of the tSZ map. The pixels are 2 × 2 arcsec, and the map has been smoothed with a 10 arcsec Gaussian filter, which is similar to the tSZ map of Fig. 7. The noise level is not homogeneous, which is lower on the left hand side, due to the differences of acquisition time. Middle: noise distribution obtained from the half difference map. Since the noise is not homogeneous, we provide the distribution for both the eastern (left, green) and western (right, red) parts of the map. A Gaussian fit of the histograms gives the mean value of the standard deviation of the noise to be ⟨ σ ⟩ = 0.99 mJy/beam on the east side and ⟨ σ ⟩ = 1.42 mJy/beam on the west side. The minimum noise level reaches 0.8 mJy/beam. The contours of the noise map (left) correspond to the overall mean noise (i.e. ±1.11 mJy/beam). Right: standard deviation map estimated from difference maps. White regions have not been observed. Gray regions are those for which the standard deviation is higher than 6 mJy/beam. |
| In the text | |
 |
Fig. 9 Radial flux profiles of RX J1347.5-1145. Left: comparison of the radial profile computed from the X-ray (red dots) and tSZ (green diamonds) centers. Right: comparison of the radial flux profile in three different regions from the X-ray center. The map is cut from the X-ray center in three equal slices: one cut is vertical coming from the north to the center, and the two others are diagonal from the southeast and the southwest to the center, respectively. The red diamonds and yellow dots profiles correspond to the northwest and northeast part of the map, respectively, where the cluster is expected to be rather relaxed. The green triangle profile corresponds to the southern part of the map, where the merging occurred. |
| In the text | |
 |
Fig. 10 Posterior likelihood of the MCMC pressure profile fit in the plane P0 – θs. From dark to light blue, the colors correspond to 68%, 95%, and 99% confidence levels. The top and right curves show the normalized Gaussian best fit of the marginalized likelihood of P0 and θs, respectively. |
| In the text | |
 |
Fig. 11 Comparison between the original point source subtracted RX J1347.5-1145 tSZ map (left panel) and the best fit model map excluding the shock area (middle panel). The residuals are given on the right panel map. The model accounts for the cluster emission well, except in the southern shocked area, as expected. |
| In the text | |
 |
Fig. 12 Comparison of RX J1347.5-1145 tSZ maps by DIABOLO and NIKA in mJy/beam. Left: NIKA tSZ map with DIABOLO contours in red at −1, −3, −5, and −7 mJy/beam. Right: flux radial profile as measured by NIKA (purple dots) and DIABOLO (red diamonds). |
| In the text | |
 |
Fig. 13 Left: comparison between the RX J1347.5-1145 NIKA tSZ map and the XMM X-ray data (see the work of Gitti & Schindler 2004, 2005; Gitti et al. 2007b). The XMM map has been smoothed with a 5 arcsec Gaussian filter. The red X-ray contours are in photon counts and correspond to 6, 12, 25, 50, 100, 200, and 400. Right: comparison between the best-fit radial tSZ profile of the NIKA map, excluding the shock area (see Sect. 6.3) and the profile derived from Chandra’s data by Comis et al. (2011), which is processed through the NIKA data reduction pipeline, as discussed in Sect. 4.2. The NIKA best-fit profile is given in purple with an associated 1σ statistical error range filled in blue, and the X-ray model is given in red with the 1σ statistical error limit, as two dashed lines. See text for more details on the errors limits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


