| Issue |
A&A
Volume 561, January 2014
|
|
|---|---|---|
| Article Number | A97 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201321299 | |
| Published online | 13 January 2014 | |
Planck intermediate results
XIII. Constraints on peculiar velocities
1 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
2 Aalto University Metsähovi Radio Observatory, Metsähovintie 114, 02540 Kylmälä, Finland
3 Academy of Sciences of Tatarstan, Bauman Str., 20, 420111 Kazan, Republic of Tatarstan, Russia
4 African Institute for Mathematical Sciences, 6-8 Melrose Road, Muizenberg, 7950 Cape Town, South Africa
5 Agenzia Spaziale Italiana Science Data Center, c/o ESRIN, via Galileo Galilei, 00044 Frascati, Italy
6 Agenzia Spaziale Italiana, 26 Viale Liegi, Roma, Italy
7 Astrophysics Group, Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
8 CITA, University of Toronto, 60 St. George St., Toronto ON M5S 3H8, Canada
9 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
10 California Institute of Technology, Pasadena, California, USA
11 Centro de Astrofísica, Universidade do Porto, rua das Estrelas, 4150-762 Porto, Portugal
12 Centro de Estudios de Física del Cosmos de Aragón (CEFCA), Plaza San Juan, 1, planta 2, 44001 Teruel, Spain
13 Computational Cosmology Center, Lawrence Berkeley National Laboratory, Berkeley, California, USA
14 Consejo Superior de Investigaciones Científicas (CSIC), 28006 Madrid, Spain
15 DSM/Irfu/SPP, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
16 DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
17 Département de Physique Théorique, Université de Genève, 24 Quai E. Ansermet, 1211 Genève 4, Switzerland
18 Departamento de Física, Universidad de Oviedo, Avda. Calvo Sotelo s/n, 33007 Oviedo, Spain
19 Department of Astronomy and Astrophysics, University of Toronto, 50 Saint George Street, Toronto, Canada
20 Department of Astronomy and Geodesy, Kazan Federal University, Kremlevskaya Str., 18, 420008 Kazan, Russia
21 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
22 Department of Electrical Engineering and Computer Sciences, University of California, Berkeley, California, USA
23 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, Canada
24 Department of Physics and Astronomy, Dana and David Dornsife College of Letters, Arts and Sciences, University of Southern California, Los Angeles CA 90089, USA
25 Department of Physics, Gustaf Hällströmin katu 2a, University of Helsinki, 00014 Helsinki, Finland
26 Department of Physics, Princeton University, Princeton, New Jersey, USA
27 Department of Physics, University of California, Santa Barbara, California, USA
28 Dipartimento di Fisica e Astronomia G. Galilei, Università degli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
29 Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, via Saragat 1, 44122 Ferrara, Italy
30 Dipartimento di Fisica, Università La Sapienza, P. le A. Moro 2, 00185 Roma, Italy
31 Dipartimento di Fisica, Università degli Studi di Milano, via Celoria 16, 20133 Milano, Italy
32 Dipartimento di Fisica, Universitàdegli Studi di Trieste, via A. Valerio 2, 34127 Trieste, Italy
33 Dipartimento di Fisica, Università di Roma Tor Vergata, via della Ricerca Scientifica 1, 00133 Roma, Italy
34 Dipartimento di Matematica, Università di Roma Tor Vergata, via della Ricerca Scientifica 1, Roma, Italy
35 Discovery Center, Niels Bohr Institute, Blegdamsvej 17, 2100 Copenhagen, Denmark
36 Dpto. Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
37 European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo s/n, Urbanización Villafranca del Castillo, Villanueva de la Cañada, 28692 Madrid, Spain
38 European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
39 Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki, Helsinki, Finland
40 INAF−Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
41 INAF−Osservatorio Astronomico di Roma, via di Frascati 33, 00040 Monte Porzio Catone, Italy
42 INAF−Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 34143 Trieste, Italy
43 INAF/IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
44 INAF/IASF Milano, via E. Bassini 15, 20133 Milano, Italy
45 INFN, Sezione di Bologna, via Irnerio 46, 40126 Bologna, Italy
46 INFN, Sezione di Roma 1, Università di Roma Sapienza, Piazzale Aldo Moro 2, 00185 Roma, Italy
47 IUCAA, Post Bag 4, Ganeshkhind, Pune University Campus, 411 007 Pune, India
48 Imperial College London, Astrophysics group, Blackett Laboratory, Prince Consort Road, London SW7 2AZ, UK
49 Infrared Processing and Analysis Center, California Institute of Technology, Pasadena CA 91125, USA
50 Institut Universitaire de France, 103 Bd Saint-Michel, 75005 Paris, France
51 Institut d’Astrophysique Spatiale, CNRS (UMR8617) Université Paris-Sud 11, Bâtiment 121, 91405 Orsay, France
52 Institut d’Astrophysique de Paris, CNRS (UMR7095), 98 bis Boulevard Arago, 75014 Paris, France
53 Institute for Space Sciences, 077125 Bucharest-Magurale, Romania
54 Institute of Astro and Particle Physics, Technikerstrasse 25/8, University of Innsbruck, 6020 Innsbruck, Austria
55 Institute of Astronomy and Astrophysics, Academia Sinica, 96720 Taipei, Taiwan
56 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
57 Institute of Theoretical Astrophysics, University of Oslo, Blindern, 0315 Oslo, Norway
58 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
59 Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, 39005 Santander, Spain
60 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena CA 91109, USA
61 Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester M13 9PL, UK
62 Kavli Institute for Cosmology Cambridge, Madingley Road, Cambridge CB3 0HA, UK
63 LAL, Université Paris-Sud, CNRS/IN2P3, Orsay, France
64 LERMA, CNRS, Observatoire de Paris, 61 Avenue de l’Observatoire, Paris, France
65 Laboratoire AIM, IRFU/Service d’Astrophysique − CEA/DSM − CNRS − Université Paris Diderot, Bât. 709, CEA-Saclay, 91191 Gif-sur-Yvette Cedex, France
66 Laboratoire Traitement et Communication de l’Information, CNRS (UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634 Paris Cedex 13, France
67 Laboratoire de Physique Subatomique et de Cosmologie, Université Joseph Fourier Grenoble I, CNRS/IN2P3, Institut National Polytechnique de Grenoble, 53 rue des Martyrs, 38026 Grenoble Cedex, France
68 Laboratoire de Physique Théorique, Université Paris-Sud 11 & CNRS, Bâtiment 210, 91405 Orsay, France
69 Lawrence Berkeley National Laboratory, Berkeley, California, USA
70 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
71 Max-Planck-Institut für Extraterrestrische Physik, Giessenbachstraße, 85748 Garching, Germany
72 National University of Ireland, Department of Experimental Physics, Maynooth, Co. Kildare, Ireland
73 Niels Bohr Institute, Blegdamsvej 17, 2100 Copenhagen, Denmark
74 Observational Cosmology, Mail Stop 367-17, California Institute of Technology, Pasadena CA 91125, USA
75 Optical Science Laboratory, University College London, Gower Street, London, UK
76 SISSA, Astrophysics Sector, via Bonomea 265, 34136 Trieste, Italy
77 School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff CF24 3AA, UK
78 School of Physics and Astronomy, University of Nottingham, Nottingham NG7 2RD, UK
79 Space Research Institute (IKI), Russian Academy of Sciences, Profsoyuznaya Str 84/32, 117997 Moscow, Russia
80 Space Sciences Laboratory, University of California, Berkeley, California, USA
81 Stanford University,Dept of Physics, Varian Physics Bldg, 382 via Pueblo Mall, Stanford, California, USA
82 TÜBİTAK National Observatory, Akdeniz University Campus, 07058 Antalya, Turkey
83 UPMC Univ Paris 06, UMR7095, 98 bis Boulevard Arago, 75014 Paris, France
84 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
85 University Observatory, Ludwig Maximilian University of Munich, Scheinerstrasse 1, 81679 Munich, Germany
86 University of Granada, Departamento de Física Teórica y del Cosmos, Facultad de Ciencias, 18071 Granada, Spain
87 University of Miami, Knight Physics Building, 1320 Campo Sano Dr., Coral Gables, Florida, USA
Received: 15 February 2013
Accepted: 18 November 2013
Using Planck data combined with the Meta Catalogue of X-ray detected Clusters of galaxies (MCXC), we address the study of peculiar motions by searching for evidence of the kinetic Sunyaev-Zeldovich effect (kSZ). By implementing various filters designed to extract the kSZ generated at the positions of the clusters, we obtain consistent constraints on the radial peculiar velocity average, root mean square (rms), and local bulk flow amplitude at different depths. For the whole cluster sample of average redshift 0.18, the measured average radial peculiar velocity with respect to the cosmic microwave background (CMB) radiation at that redshift, i.e., the kSZ monopole, amounts to 72 ± 60 km s-1. This constitutes less than 1% of the relative Hubble velocity of the cluster sample with respect to our local CMB frame. While the linear ΛCDM prediction for the typical cluster radial velocity rms at z = 0.15 is close to 230 km s-1, the upper limit imposed by Planck data on the cluster subsample corresponds to 800 km s-1 at 95% confidence level, i.e., about three times higher. Planck data also set strong constraints on the local bulk flow in volumes centred on the Local Group. There is no detection of bulk flow as measured in any comoving sphere extending to the maximum redshift covered by the cluster sample. A blind search for bulk flows in this sample has an upper limit of 254 km s-1 (95% confidence level) dominated by CMB confusion and instrumental noise, indicating that the Universe is largely homogeneous on Gpc scales. In this context, in conjunction with supernova observations, Planck is able to rule out a large class of inhomogeneous void models as alternatives to dark energy or modified gravity. The Planck constraints on peculiar velocities and bulk flows are thus consistent with the ΛCDM scenario.
Key words: cosmology: observations / cosmic background radiation / large-scale structure of Universe / galaxies: clusters: general
© ESO, 2014
1. Introduction
Today we have a cosmological model that appears to fit all available data. Nevertheless, it is important to continue to test this picture. Peculiar velocities provide an important way to do this. According to the standard ΛCDM scenario, gravity drives the growth of inhomogeneities in the matter distribution of the Universe. After the radiation-matter equality epoch, fluctuations in the dark matter component were largely unaffected by the Thomson interaction binding the evolution of baryons and photons of the cosmic microwave background (CMB) radiation. During that epoch, the inhomogeneities in the spatial distribution of dark matter kept growing gravitationally. It was only after the epoch of hydrogen recombination that the baryons, which had just decoupled from the CMB, could freely fall into the potential wells created by the dark matter component.
Since then, the gravitational infall of matter into potential wells has been conditioned by the density field and the universal expansion rate. On large scales, where baryonic physics and non-linear evolution may be neglected safely, the continuity equation provides a simple link between the matter density field and the peculiar velocity field. In particular, in a ΛCDM scenario, this equation predicts that peculiar velocities must show typical correlation lengths between 20 and 40 h-1 Mpc, and their growth must have practically frozen since the onset of the accelerated expansion (see the review of, e.g., Strauss & Willick 1995). By averaging the peculiar velocity field on scales corresponding to galaxy groups and clusters today, it is possible to obtain linear theory predictions for the root mean square (rms) of the radial peculiar velocity of those structures. These predictions typically amount to about 230 km s-1, (see, e.g., Hernández-Monteagudo & Sunyaev 2010), with a weak dependence on the galaxy cluster/group mass. If instead one looks at the velocity amplitude for extended or correlated motion of matter on larger scales, one finds that it decreases when larger volumes are considered, but should still be at the level of 50−100 km s-1 for radii of a few hundred Mpc (see, e.g., Fig. 2 in Mak et al. 2011). The detection of these large scale, coherent flows of matter (hereafter referred to as bulk flows) has been the subject of active investigation for several decades (e.g., Tonry & Davis 1981; Aaronson et al. 1982; Dressler et al. 1987; Dekel et al. 1993; Lauer & Postman 1994; Hudson et al. 1999; Willick 1999; Riess 2000, to cite just a few). One crucial problem that most of those works encounter is related to the need to accurately determine distances to galaxies in order to subtract the Hubble flow-induced velocity.
During the nineties Lauer & Postman (1994), Willick (1999), and Hudson et al. (1999) claimed that there are large scale bulk flows with amplitudes of 350−700 km s-1 in local spheres of radii 60−150 h-1 Mpc, with somewhat discrepant directions. At the turn of the millennium, however, Riess (2000) and Courteau et al. (2000) reported the lack of any significant local bulk flow up to depths of about 150 h-1 Mpc, in apparent contradiction to the previous works. More recently, claims of the presence of a large scale, large amplitude peculiar velocity dipole have been raised again by various authors. While some works (Hudson et al. 2004; Watkins et al. 2009; Feldman et al. 2010) find evidence for a peculiar local velocity dipole of about 400 km s-1 (and in tension with ΛCDM predictions), others find lower amplitudes for the local bulk flow, (e.g., Itoh et al. 2010; Nusser & Davis 2011; Nusser et al. 2011; Ma & Scott 2013; Branchini et al. 2012; Courtois et al. 2012).
For greater depths (up to z ~ 0.2–0.3), there are also claims (Kashlinsky et al. 2008, 2010; Abate & Feldman 2012) of yet higher amplitude bulk flows (~ 1000–4000 km s-1). These cannot be accommodated within a ΛCDM context, since the theory predicts that bulk flows are negligible on the very largest scales. Moreover, these results are in contradiction with other works, (e.g., Keisler 2009; Osborne et al. 2011; Mody & Hajian 2012).
Some of the most recent results for bulk flows extending to large distances are based on the study of the kinetic Sunyaev-Zeldovich effect (hereafter kSZ; Sunyaev & Zeldovich 1980). This effect is due to the Doppler kick that CMB photons experience in Thomson scattering off free electrons moving with respect to the CMB rest frame. This process introduces intensity and polarization anisotropies in the CMB along the direction of massive clouds of ionized material, such as galaxy clusters and groups, but produces no distortion of the CMB spectrum. The kSZ effect has been theoretically exploited to characterize the growth of velocity perturbations (e.g., Ma & Fry 2002; Hernández-Monteagudo et al. 2006; Zhang et al. 2008), to search for missing baryons (DeDeo et al. 2005; Hernández-Monteagudo & Sunyaev 2008; Ho et al. 2009; Hernández-Monteagudo & Ho 2009; Shao et al. 2011) and to study bulk flows in the local Universe (Kashlinsky et al. 2008, 2010; Keisler 2009; Osborne et al. 2011; Mak et al. 2011; Mody & Hajian 2012; Lavaux et al. 2013). Very recently, Hand et al. (2012) have claimed a detection of the kSZ effect when combining spectroscopic galaxy data from the Baryonic Acoustic Oscillation Survey (BOSS) with CMB data from the Atacama Cosmology Telescope (ACT), after searching for the kSZ pairwise momentum (e.g., Groth et al. 1989; Juszkiewicz et al. 1998). On subcluster scales, as predicted by, e.g., Inogamov & Sunyaev (2003), some weak evidence of kSZ has also been reported by the Bolocam instrument (Mroczkowski et al. 2012).
In this paper we focus on the constraints that Planck1 can set on the kSZ-induced temperature anisotropies. These are given by the line-of-sight integral 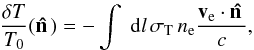 (1)where σT is the Thomson scattering cross-section, ne is the physical electron number density, ve denotes the electron peculiar velocity, c the speed of light, and
(1)where σT is the Thomson scattering cross-section, ne is the physical electron number density, ve denotes the electron peculiar velocity, c the speed of light, and 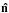 the direction of observation on the sky. We are adopting here a reference frame centred on the observer’s position, and hence infalling electrons will have negative radial velocities. Note that, unlike in other approaches based upon galaxy redshift surveys, the distance to the cluster is irrelevant to its peculiar velocity estimation. Since the expected kSZ signal coming from an individual cluster is smaller than the typical level of intrinsic CMB temperature fluctuations, we apply various filters which attempt to minimize the impact of other signals on the angular positions of a sample of galaxy clusters, and use these to extract statistical constraints on the kSZ signal in those sources. In the standard ΛCDM scenario one expects to have matter at rest with respect to the CMB on the largest scales, and hence roughly the same number of clusters with positive and negative radial velocities. This means that the mean or monopole of kSZ estimates should be consistent with zero, although there are inhomogeneous scenarios (addressed in Sect. 4.3) in which the average velocity of clusters may differ from zero. Likewise it is possible to set constraints on the kSZ-induced variance in the CMB temperature anisotropies measured along the direction of galaxy clusters. This is a direct probe of the rms peculiar velocity of those objects with respect to the CMB, and can be compared to theoretical predictions. In this context, it has been mentioned above that the motion of matter is predicted to occur in bulk flows with coherence on scales of about 30 h-1 Mpc. If these bulk flows are local and the observer is placed inside them, then they should give rise to a dipolar pattern in the kSZ measurements of individual clusters (Kashlinsky & Atrio-Barandela 2000). If they are instead distant, then the projection of the coherence length of kSZ measurements on the sky should shrink down to a few degrees (Hernández-Monteagudo et al. 2006). Therefore it is possible to use the set of individual kSZ estimates from galaxy clusters to place constraints on the monopole (mean), variance, and dipole of the peculiar velocities of the cluster population. While some of our statistical tools target the kSZ signal in each cluster separately, others are particularly designed to probe the local bulk blow and set constraints on the kSZ dipole at the positions of clusters, as shown below.
the direction of observation on the sky. We are adopting here a reference frame centred on the observer’s position, and hence infalling electrons will have negative radial velocities. Note that, unlike in other approaches based upon galaxy redshift surveys, the distance to the cluster is irrelevant to its peculiar velocity estimation. Since the expected kSZ signal coming from an individual cluster is smaller than the typical level of intrinsic CMB temperature fluctuations, we apply various filters which attempt to minimize the impact of other signals on the angular positions of a sample of galaxy clusters, and use these to extract statistical constraints on the kSZ signal in those sources. In the standard ΛCDM scenario one expects to have matter at rest with respect to the CMB on the largest scales, and hence roughly the same number of clusters with positive and negative radial velocities. This means that the mean or monopole of kSZ estimates should be consistent with zero, although there are inhomogeneous scenarios (addressed in Sect. 4.3) in which the average velocity of clusters may differ from zero. Likewise it is possible to set constraints on the kSZ-induced variance in the CMB temperature anisotropies measured along the direction of galaxy clusters. This is a direct probe of the rms peculiar velocity of those objects with respect to the CMB, and can be compared to theoretical predictions. In this context, it has been mentioned above that the motion of matter is predicted to occur in bulk flows with coherence on scales of about 30 h-1 Mpc. If these bulk flows are local and the observer is placed inside them, then they should give rise to a dipolar pattern in the kSZ measurements of individual clusters (Kashlinsky & Atrio-Barandela 2000). If they are instead distant, then the projection of the coherence length of kSZ measurements on the sky should shrink down to a few degrees (Hernández-Monteagudo et al. 2006). Therefore it is possible to use the set of individual kSZ estimates from galaxy clusters to place constraints on the monopole (mean), variance, and dipole of the peculiar velocities of the cluster population. While some of our statistical tools target the kSZ signal in each cluster separately, others are particularly designed to probe the local bulk blow and set constraints on the kSZ dipole at the positions of clusters, as shown below.
This paper is organized as follows. In Sect. 2 we describe the data used, both for the CMB and large-scale structure. The statistical tools we use for the kSZ detection are described in Sect. 3, and the results obtained from them are presented in Sect. 4. We examine the robustness of our results in Sect. 5. Finally, in Sect. 6, we discuss the cosmological implications of our findings and conclude. Throughout this paper, we use a cosmological parameter set compatible with WMAP-7 observations (Komatsu et al. 2011): density parameters ΩM = 0.272 and ΩΛ = 0.728; Hubble parameter h = 0.704; 8 h-1 Mpc normalization σ8 = 0.809; and nS = 0.96 for the spectral index of scalar perturbations.
2. Data and simulations
2.1. Planck data
Planck (Tauber et al. 2010; Planck Collaboration 2011a) is the third generation space mission to measure the anisotropy of the CMB. It observes the sky in nine frequency bands covering 30−857 GHz with high sensitivity and angular resolution from 31′ to 4.39′. The Low Frequency Instrument (LFI; Mandolesi et al. 2010; Bersanelli et al. 2010; Mennella et al. 2011) covers the 30, 44, and 70 GHz bands with amplifiers cooled to 20 K. The High Frequency Instrument (HFI; Lamarre et al. 2010; Planck HFI Core Team 2011a) covers the 100, 143, 217, 353, 545, and 857 GHz bands with bolometers cooled to 0.1 K. Polarization is measured in all but the highest two bands (Leahy et al. 2010; Rosset et al. 2010). A combination of radiative cooling and three mechanical coolers produces the temperatures needed for the detectors and optics (Planck Collaboration 2011b). Two data processing centres (DPCs) check and calibrate the data and make maps of the sky (Planck HFI Core Team 2011b; Zacchei et al. 2011). Planck’s sensitivity, angular resolution, and frequency coverage make it a powerful instrument for Galactic and extragalactic astrophysics as well as cosmology. Early astrophysics results are given in Planck Collaboration (2011c−u), based on data taken between 13 August 2009 and 7 June 2010. Intermediate astrophysics results are now being presented in a series of papers based on data taken between 13 August 2009 and 27 November 2010.
Although the 70 GHz LFI channel was included initially in the analysis, it was found that constraints were practically identical when using HFI frequency maps alone (see details in Table 1). Measuring the kSZ effect requires avoiding, in the best possible way, contamination by the much stronger thermal Sunyaev-Zeldovich effect (hereafter tSZ; Sunyaev & Zeldovich 1972). While in theory observations at 217 GHz, close to the zero of the tSZ emission, should not suffer much from tSZ contamination, it is necessary to account for the broad spectral band of each detector and each channel, (Planck HFI Core Team 2011b). In terms of the tSZ effect, the “effective” frequencies of the HFI channels (i.e., those frequencies at which the tSZ emission is equal to its integral over the frequency band) are listed in the second column of Table 1. Raw HFI frequency maps are useful for testing for systematic effects associated with foreground emission, tSZ spectral leakage, or full width at half maximum (FWHM) characterization errors. Note also that HFI frequency maps are produced in thermodynamic temperature units, so that both primary CMB and kSZ emission have constant amplitude across frequency channels. In the third column we display the corresponding tSZ Comptonization parameter (ySZ) to ΔT conversion factors. The Comptonization parameter ySZ is a dimensionless line-of-sight integral of the gas pressure, 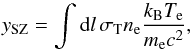 (2)with Te and me the electron temperature and rest mass, and kB the Boltzmann constant, (Sunyaev & Zeldovich 1972).
(2)with Te and me the electron temperature and rest mass, and kB the Boltzmann constant, (Sunyaev & Zeldovich 1972).
Two different strategies are used in this paper to measure the kSZ effect at the positions of the cluster catalogue. The first consists of estimating directly the kSZ signal at MCXC cluster positions from the original HFI frequency maps, using both aperture photometry and matched multi-band filtering. The second consists of first producing a map of the CMB and kSZ effect that is nearly free from tSZ contamination before estimating the kSZ emission from MCXC clusters using the aperture photometry and single frequency matched filtering. As described below, this map makes use of both HFI and LFI data.
Nominal and tSZ-effective frequencies, ΔT to ySZ conversion factors and FWHMs for each HFI channel used in this paper.
2.1.1. The two-dimensional internal linear combination map
In the absence of a fully reliable model of foreground emission (including number of foregrounds, emission laws, and coherence of their emission across Planck frequencies), a minimum variance map of CMB emission can be obtained by the so-called internal linear combination approach (hereafter ILC). The CMB map is obtained from a linear combination of input observations, subject to the constraint that the CMB is preserved. I.e., for CMB-calibrated maps (in thermodynamic units) xi, the CMB is obtained as ∑ iwixi with ∑ iwi = 1, the latter condition guaranteeing the preservation of the CMB signal. This obviously also preserves the kSZ signal, which has the same frequency dependence.
The minimum variance map, however, is not necessarily that of minimum contamination by any particular foreground. In our present analysis, the measured map of CMB+kSZ will be further processed, first being filtered on the basis of predicted kSZ cluster shapes and locations, to suppress contamination by the larger scale primary CMB, and then stacked to combine the measurements of all individual clusters. While this filtering and stacking will reduce contamination of the measurement by independent foregrounds such as Galactic dust emission, as well as by detector noise, tSZ residuals are likely to add-up coherently and contaminate the measurement significantly. The ILC must then be modified to ensure that instead of the total variance of the map being minimized, the contamination by tSZ must be minimized instead.
It is possible to extend the ILC method to add a constraint to reject the tSZ effect specifically, and thus make sure that the CMB+kSZ map is completely free from tSZ contamination. The idea is similar to that used in the unbiased multifrequency matched filter approach (Herranz et al. 2005; Mak et al. 2011), i.e., a constraint is added to null the tSZ contribution to the output map. The method is described and validated on realistic simulations in Remazeilles et al. (2011a).
Note that this method is a special case of a multi-dimensional generalization of the ILC (Remazeilles et al. 2011b), in which several components of interest with known emission laws, can be recovered simultaneously with vanishing contamination from each other. Here we consider two specific components, one with the CMB emission law, which comprises both primary CMB and kSZ, and one with the emission law of the tSZ effect (neglecting relativistic corrections). We refer to the map obtained by this method as a two-dimensional ILC (hereafter 2D-ILC).
In detail, the 2D-ILC map used in the present analysis is obtained from all LFI and HFI maps as follows. For each frequency band, point sources detected by a Mexican Hat Wavelet filter at more than 5σ at that frequency are masked. The masked region has a radius of three times the standard deviation of the Gaussian beam (i.e., 1.27 × FWHM). The masked regions are filled in by interpolation using neighbouring pixels. Maps are then analysed on a frame of spherical needlets for implementation of the ILC in needlet space, in a very similar way to what has been done on WMAP data by Delabrouille et al. (2009). However, the covariance matrices associated with the filter, instead of being computed using average covariances of needlet coefficients over HEALPix2 superpixels, are computed from products of maps of needlet coefficients, smoothed using a large Gaussian beam, similarly to what was done by Basak & Delabrouille (2012) on WMAP 7-year data. The constrained ILC filter implemented is that of Eq. (20) of Remazeilles et al. (2011a). Thus, the exact linear combination used to reconstruct the CMB+kSZ map depends both on the sky region and on the angular scale. In particular, on scales smaller than some of the Planck LFI and HFI beams, the relative weights of the corresponding lower frequency channels become negligibly small, due to their low resolution. The final CMB+kSZ map is reconstructed at 5′ resolution. In order to carry this out, at the very smallest scales the CMB+kSZ map is reconstructed mostly from observations in the frequency channels at 217 GHz and above. At intermediate scales (of order 10′), however, measurements from all HFI channels are used to reconstruct the final map.
The ILC (classical or 2D version) assumes the emission law of the component of interest to be known. This knowledge is necessary to ensure the preservation of the signal of interest (here, the kSZ effect) and, for the 2D-ILC, to reject the contaminating signal (here, the tSZ). As discussed in Dick et al. (2010), imperfect knowledge of the emission law can result in a significant loss of CMB power. In practice, the effective emission laws, as observed by the detectors, depend on the calibration of the observations in each frequency channel. For the CMB and kSZ signals, it hence depends on the absolute calibration of all the Planck channels used in the analysis (here, the HFI channels). For the tSZ, it also depends on the accuracy of the knowledge of the spectral bands, and on the validity of the non-relativistic approximation for tSZ emission.
For Planck HFI channels, the absolute calibration error is estimated (conservatively) to be less than about 0.1% in the channels calibrated on the CMB itself with the CMB dipole, and on CMB anisotropies themselves for cross-calibration, and less than a few percent on channels calibrated on the dust emission measured by FIRAS (545 and 857 GHz channels Planck HFI Core Team 2011b). Small uncertainties on the frequency dependence of the (CMB+ kSZ) signal may induce a large bias in the calibration of the output of the ILC. This effect can be strong in the high S/N regime (Dick et al. 2010), which is the case here because the strong CMB anisotropy signal itself contributes to the total signal. With CMB calibration errors of 0.1%, we check on simulated data sets generated with the Planck Sky Model (Delabrouille et al. 2013) that the corresponding error on the final map is small (less than 1%). This is also confirmed on the actual Planck data by comparing the power spectrum of the CMB+kSZ map with the current CMB best fit Cℓ, since any serious loss of power would be immediately visible in the power spectrum of the reconstructed CMB+kSZ map.
Errors in the assumed tSZ emission law (by reason of relativistic corrections, colour correction, or mis-calibration), can also potentially result in residual contamination by tSZ in the CMB+kSZ ILC map. Note, however, that the two-dimensional ILC does not amplify the contamination by a mis-calibrated tSZ component. Uncertainties of a few per cent on the tSZ frequency dependence (the typical size of relativistic corrections to the thermal SZ effect) will hence not impact the reconstruction of the CMB+kSZ signal by more than a few per cent of the original tSZ.
2.2. Tracers of moving baryons: X-ray MCXC clusters
We use the Meta Catalogue of X-ray detected Clusters of galaxies (MCXC), a compilation of all publicly available ROSAT All Sky Survey-based samples (NORAS, Böhringer et al. 2000; REFLEX, Böhringer et al. 2004; BCS, Ebeling et al. 1998, 2000; SGP, Cruddace et al. 2002; NEP, Henry et al. 2006; MACS, Ebeling et al. 2007; and CIZA, Ebeling et al. 2010; Kocevski et al. 2007), and serendipitous cluster catalogues (160SD, Mullis et al. 2003; 400SD, Burenin et al. 2007; SHARC, Romer et al. 2000; Burke et al. 2003; WARPS, Perlman et al. 2002; Horner et al. 2008; and EMSS, Gioia & Luppino 1994; Henry 2004). The information was systematically homogenized and duplicate entries were carefully handled, yielding a large catalogue of approximately 1750 clusters. The MCXC is presented in detail in Piffaretti et al. (2011), and has been used in previous Planck studies, (e.g., Planck Collaboration 2011e).
For each cluster the MCXC provides, among other quantities, the position, redshift, and mass of each cluster. The masses are estimated from the luminosities thanks to the REXCESS L500–M500 relation of Pratt et al. (2009). Hereafter, all cluster quantities with the subscript “500” are evaluated at the radius (R500) at which the average density equals 500 times the critical density at the cluster’s redshift. In this way, M500 is defined as 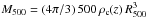 , where ρc(z) is the critical density at the cluster redshift z.
, where ρc(z) is the critical density at the cluster redshift z.
For the measurement of velocities, we also need cluster optical depths. Our approach here is based upon the study of Arnaud et al. (2010): using REXCESS data, we either use the universal pressure profile and then divide by the average temperature profile to estimate a density profile, or fit directly an average density profile. For this purpose, we make use of Y(x), the volume integral of gas pressure up to a radius given by x ≡ r/R500: 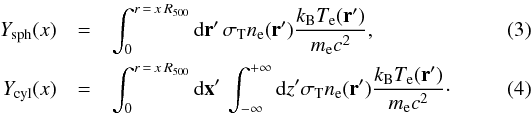 These equations describe the spherical and cylindrical integrals of pressure, respectively. The vector centred on the cluster r′ is decomposed into a vector on the plane of the sky, x′, and a vector normal to this plane (given by the component z′), r′ = (x′,z′). With this, we use the Y(x) vs. M500 relations in Arnaud et al. (2010), i.e.,
These equations describe the spherical and cylindrical integrals of pressure, respectively. The vector centred on the cluster r′ is decomposed into a vector on the plane of the sky, x′, and a vector normal to this plane (given by the component z′), r′ = (x′,z′). With this, we use the Y(x) vs. M500 relations in Arnaud et al. (2010), i.e.,  in which
in which 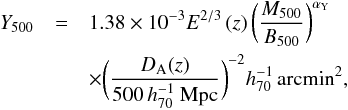 (7)and I(x) and J(x) are functions expressing the spherical/cylindrical integrals of pressure around the cluster’s centre, respectively. The factor h70 denotes the Hubble reduced parameter in units of 70 km s-1 Mpc-1. An observer’s angular aperture θ translates into an effective cluster radius r = θ DA(z), with DA(z) the angular diameter distance to redshift z. Note that, as expressed above, the cylindrical case considers a full integration along the line of sight up to a given aperture on the plane of the sky, as is the case for real observations. The spherical case, instead, integrates out to a given radius in all directions, and differs from the cylindrical case in a geometric factor. The constants in Eq. (7) are
(7)and I(x) and J(x) are functions expressing the spherical/cylindrical integrals of pressure around the cluster’s centre, respectively. The factor h70 denotes the Hubble reduced parameter in units of 70 km s-1 Mpc-1. An observer’s angular aperture θ translates into an effective cluster radius r = θ DA(z), with DA(z) the angular diameter distance to redshift z. Note that, as expressed above, the cylindrical case considers a full integration along the line of sight up to a given aperture on the plane of the sky, as is the case for real observations. The spherical case, instead, integrates out to a given radius in all directions, and differs from the cylindrical case in a geometric factor. The constants in Eq. (7) are 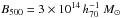 and αY = 1.78, while E(z) is the Hubble parameter normalized to its current value,
and αY = 1.78, while E(z) is the Hubble parameter normalized to its current value, 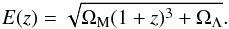 (8)The functions I(x) and J(x) depend on the particular model adopted for the pressure profile, which, in our work, is taken to follow the universal scaling provided in Eqs. (11) and (12) of Arnaud et al. (2010), for which I(x = 1) = 0.6541 and J(x = 1) = 0.7398. As addressed in Sect. 5, results do not change significantly when adopting different choices for Arnaud et al. (2010) type pressure profiles, but their uncertainty is dominated by our ignorance of the gas density profile in the clusters’ outskirts.
(8)The functions I(x) and J(x) depend on the particular model adopted for the pressure profile, which, in our work, is taken to follow the universal scaling provided in Eqs. (11) and (12) of Arnaud et al. (2010), for which I(x = 1) = 0.6541 and J(x = 1) = 0.7398. As addressed in Sect. 5, results do not change significantly when adopting different choices for Arnaud et al. (2010) type pressure profiles, but their uncertainty is dominated by our ignorance of the gas density profile in the clusters’ outskirts.
In the isothermal case, the clusters’ optical depth integrated up to xR500 is equal to the corresponding Y(x), modulo a 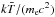 factor, where
factor, where 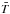 is the average spectroscopic temperature measured in a fraction of the volume enclosed by R500. To account for this, we use the
is the average spectroscopic temperature measured in a fraction of the volume enclosed by R500. To account for this, we use the 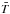 –M500 relation given in Arnaud et al. (2005):
–M500 relation given in Arnaud et al. (2005): 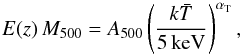 (9)with αT = 1.49 and
(9)with αT = 1.49 and 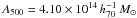 . In this simple case, it is possible to derive an expression for the optical depths τsph(x) = τ500I(x) and τcyl(x) = τ500J(x), with
. In this simple case, it is possible to derive an expression for the optical depths τsph(x) = τ500I(x) and τcyl(x) = τ500J(x), with 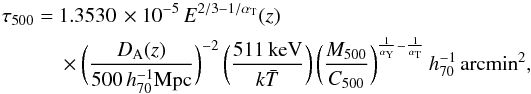 (10)and
(10)and 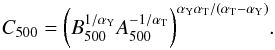 (11)For the non-isothermal case, we use the average
(11)For the non-isothermal case, we use the average 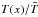 scaling obtained from the middle panel of Fig. 3 of Arnaud et al. (2010). This scaling is only applied for x < 1, and divides the pressure profile to obtain the density, which becomes the integrand in I(x) and J(x). Since the
scaling obtained from the middle panel of Fig. 3 of Arnaud et al. (2010). This scaling is only applied for x < 1, and divides the pressure profile to obtain the density, which becomes the integrand in I(x) and J(x). Since the 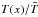 scaling has only been measured for r < R500 (x < 1), a different approach is followed for r > R500. In this radius range, we express the electron density in terms of the pressure and the entropy,
scaling has only been measured for r < R500 (x < 1), a different approach is followed for r > R500. In this radius range, we express the electron density in terms of the pressure and the entropy, 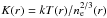 , and adopt the relation K(r) ∝ r0.5. This defines the scaling of density versus radius that enters the outer parts (r > R500) of the integrals I(x) and J(x). This constitutes our best guess of the radial dependence of density in clusters, although in Sect. 5 we discuss the motivation and limitations of this approach. Figure 1 displays a histogram of the estimated values of the cylindrical optical depth integrated out to a radius of R = 5 R500, τ5 R500, for the non-isothermal case.
, and adopt the relation K(r) ∝ r0.5. This defines the scaling of density versus radius that enters the outer parts (r > R500) of the integrals I(x) and J(x). This constitutes our best guess of the radial dependence of density in clusters, although in Sect. 5 we discuss the motivation and limitations of this approach. Figure 1 displays a histogram of the estimated values of the cylindrical optical depth integrated out to a radius of R = 5 R500, τ5 R500, for the non-isothermal case.
 |
Fig. 1 Histogram of predicted values of τ5 R500, the cylindrical optical depth times solid angle out to R = 5 R500. |
In the analyses described below, we exclude clusters located at less than 1.5 FWHM from point sources detected at more than 5σ in any of the single frequency Planck maps. This is done in order to remove any spurious signals caused by point sources associated with clusters. We also mask clusters lying in regions with high Galactic emission, and with estimated masses below 1013 M⊙. This leads to a basic mask that leaves 1405 clusters on the sky (out of the initial 1743 clusters). However, the 2D-ILC has its own (and slightly more conservative) mask, which leaves only 1321 clusters for analysis on this map.
In Fig. 2 we show the spatial distribution of the surviving clusters. The spatial distribution is quite uniform, except for some areas where deeper X-ray observations have allowed for more detections.
2.3. Simulations
In order to test and disentangle the effects of instrumental noise, CMB, Galactic and extragalactic foregrounds on our results, we make use of simulations. Specifically, we use
-
a)
simulations of clusters with similar characteristics to theMCXC sample. We simulate SZ clusters at the actual MCXCclusters’ locations, using the Arnaudet al. (2010) pressure profile, andthe cluster mass and size values obtained from X-rayobservations. Clusters are assumed to be isothermal. TheComptonization Y parameter of each cluster is then computed using the cluster mass, as outlined in Sect. 2.2. We include in the simulations a scatter in the parameters of the scaling relations with a normal distribution, which results in an averaged scatter in the Y parameter of 10%. We generate a set of 1000 such simulations at the effective frequencies in Table 1 in order to assess the effect of that scatter on our derived results.
-
b)
CMB realizations for the current WMAP-7 best-fit model (1000 of them).
-
c)
1000 noise realizations with noise variance estimated from the difference between the first and second halves of the Planck rings for a given position of the satellite and divided by Planck’s appropriate hit map (or exposure map). In doing so, we disregard noise correlations between pixels. Such simulations take into account the non-uniform sky coverage. The (non-uniform) noise level in the direction of the MCXC clusters is visible in Fig. 2.
Additionally, we make use of the simulations developed by the Planck collaboration (the Planck Sky Model, Delabrouille et al. 2013) in order to assess the Galactic contribution to the bulk flow measurement on the whole sky. These contain our current best knowledge of the diffuse Galactic component (“PSM diffuse”). Since Planck is most sensitive at frequencies above 100 GHz where the dust emission dominates, we only consider this component. We use model number 7 of Finkbeiner et al. (1999) which extrapolates the IRAS 100 μm data to lower frequency using a modified blackbody frequency dependence and a spatially varying dust grain equilibrium temperature based on the DIRBE 240/140 μm maps.
 |
Fig. 2 Locations of MCXC clusters outside the masked region. The colour scale indicates inverse noise squared at the positions of the MCXC clusters. The large coloured circles indicate directions for various dipole determinations: HFI dipole from MCXC cluster locations (green); HFI dipole from shifted positions (brown); CMB dipole (orange); Kashlinsky et al. (2010) dipole (red). The HFI dipole from MCXC cluster locations is compatible with CMB and Galactic residuals. |
3. Statistical methods
Here, we outline two different statistical approaches implemented when searching for the kSZ signal in Planck data. The first one (the aperture photometry method) is applied on a cluster by cluster basis and makes no assumption about the gas distribution within a given radius where most of the cluster signal must be generated. It nevertheless has to make assumptions about the amount of signal that is present in the outskirts. This method is quick and easy to implement, in particular when performing checks for systematic errors. The second approach (the unbiased Matched Multi-frequency Filter) makes use of information related to the expected spatial distribution of gas and the scale dependence of all sources that can be regarded as noise (including the CMB). The use of these two, different filters is motivated by the consistency requirement of having independent algorithms that should provide compatible kSZ estimates. The unbiased Multi-frequency Matched Filter was implemented independently by four different teams, two implementations being on square patches centred on clusters, and the other two on the whole celestial sphere. The first two implementations target the determination of individual cluster peculiar velocities, while the latter two are specifically developed to derive local bulk flows, since they focus on the dipole pattern of the kSZ effect in clusters on the celestial sphere. Implementations targeting clusters individually allow constraints to be placed on the mean cluster velocity (or monopole), the rms or variance of cluster peculiar velocities, and also on local bulk flows, i.e., the kSZ dipolar pattern, as shown below. Results from different codes confirm the robustness of our results.
3.1. The aperture photometry method
The aperture photometry (AP) method computes the average temperature within an input radius R, and subtracts from it the average temperature computed in a surrounding ring of inner and outer radii R and fR (f > 1), respectively (see, e.g., Hernández-Monteagudo & Rubiño-Martín 2004). In this work we use 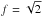 , so that the outer ring has the same area as the inner circle. This is a compromise between having too few pixels in thin rings (yielding noisy estimates of the average) and being insensitive to local background fluctuations of typical size just above R (that are washed out for choices of f which are too large). This filter constitutes a simple approach to enhance the signal coming from a region of size R against the background. In our analyses, the AP procedure was applied in the direction of each galaxy cluster, separately in each HFI frequency map. When looking at clusters, the filter scale R was taken equal to either kθ500 (k times the angle subtended by the radius at which the cluster’s density equals 500 times the critical density) or the FWHM of the beam, depending on whether the object is resolved (kθ500 > FWHM) or not. Values of k ranging from 0.25 up to 2 showed that the strongest constraints were obtained for k = 0.25. Yet smaller values of k do not yield significant differences, since for such low k practically all clusters become unresolved. We describe results with k = 0.25, unless other values are explicitly quoted.
, so that the outer ring has the same area as the inner circle. This is a compromise between having too few pixels in thin rings (yielding noisy estimates of the average) and being insensitive to local background fluctuations of typical size just above R (that are washed out for choices of f which are too large). This filter constitutes a simple approach to enhance the signal coming from a region of size R against the background. In our analyses, the AP procedure was applied in the direction of each galaxy cluster, separately in each HFI frequency map. When looking at clusters, the filter scale R was taken equal to either kθ500 (k times the angle subtended by the radius at which the cluster’s density equals 500 times the critical density) or the FWHM of the beam, depending on whether the object is resolved (kθ500 > FWHM) or not. Values of k ranging from 0.25 up to 2 showed that the strongest constraints were obtained for k = 0.25. Yet smaller values of k do not yield significant differences, since for such low k practically all clusters become unresolved. We describe results with k = 0.25, unless other values are explicitly quoted.
The subtraction of the average temperature in the outer ring from the average of the inner circle also removes some fraction of the object’s flux, which must be accounted for. This results in a correction factor of the order of 12% if clusters are smaller than the beam size (FWHM > θ500). If, instead, FWHM < θ500, this correction must make use of some model for the cluster gas density profile, as we address next.
In order to obtain velocity estimates, it is necessary to divide the filter outputs (in units of temperature) by the CMB temperature monopole and a prediction of the clusters’ optical depths integrated out to the radial aperture. This then provides an estimate of the entire cluster’s peculiar velocity. The amount of kSZ signal that is subtracted by the removal of the outer ring has to be accounted for by the same model which provides the optical depth versus aperture radius. As explained in more detail in Sect. 5, we use the REXCESS observations provided in Arnaud et al. (2010) to infer an analytic fit to the average density profile in clusters within R500, and use arguments on the behaviour of gas entropy at r > R500 to extrapolate the density profile at larger radii. The adopted model for density provides velocity amplitudes that are about 28% higher than those obtained under the assumption of isothermal clusters, although we expect clusters to be closer to our adopted profile than to an isothermal one. Nevertheless, it is our ignorance of the clusters’ density profiles which drives most of the uncertainties in the velocity constraints.
When testing for systematic effects, this same filter can easily be applied at displaced positions on the sky (that is, positions on the sky separated from the real cluster positions by a known angle). In the absence of sources and clusters, the average of the outputs of this filter at those displaced positions should be compatible with zero, and their rms provides an error estimate for the AP filter output at the real cluster’s position.
3.2. The unbiased multifrequency matched filter (uMMF) on patches
The unbiased multifrequency matched filter (uMMF; Herranz et al. 2005; Mak et al. 2011) is a linear multi-frequency filtering technique that is specifically tailored to deal with signals that have the same spatial template but different frequency dependence. A good example of this is the imprint on CMB photons caused by the tSZ and kSZ effects. The uMMF can be considered as a modification of the Multi-frequency Matched Filter (MMF, Herranz et al. 2002; Schäfer et al. 2006; Melin et al. 2006) that optimally enhances one of the two superimposed signals while cancelling out the other. As demonstrated in Herranz et al. (2005), it is possible to devise a uMMF that detects the tSZ effect and estimates its intensity without the bias produced by the kSZ effect, or a different uMMF that extracts the kSZ signal and removes the bias caused by the tSZ effect. In this paper we are interested in the latter option. In thermodynamic units, the uMMF for optimal detection and estimation of the kSZ effect is given, in Fourier space, by 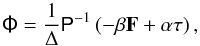 (12)where the constants α, β and Δ are given by
(12)where the constants α, β and Δ are given by 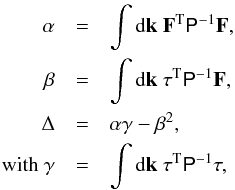 (13)and where P is the cross-power spectrum matrix of the generalized noise (CMB plus foregrounds plus instrumental noise),
(13)and where P is the cross-power spectrum matrix of the generalized noise (CMB plus foregrounds plus instrumental noise), ![\hbox{$\vec{\tau}=[\tau_{\nu}\left(\vec{k}\right)]$}](/articles/aa/full_html/2014/01/aa21299-13/aa21299-13-eq122.png) is a vector containing the spatial profile of the optical depth of the cluster (obtained from the universal profile of Arnaud et al. (2010) after dividing by the constant temperature and convolving by the beam that corresponds to each channel) and
is a vector containing the spatial profile of the optical depth of the cluster (obtained from the universal profile of Arnaud et al. (2010) after dividing by the constant temperature and convolving by the beam that corresponds to each channel) and ![\hbox{$\vec{F}=[f_{\nu} \tau_{\nu}\left(\vec{k}\right)]$}](/articles/aa/full_html/2014/01/aa21299-13/aa21299-13-eq123.png) is the vector obtained by multiplying, element by element, the profile τ by the well-known tSZ frequency dependence fν. Thus this method observes only isothermal profiles for clusters, an assumption which results in a roughly 5% low bias in the radial velocity amplitude, as shown in Sect. 5. The power spectrum matrix P is computed from real data in patches surrounding the sources. Once we have the filters (Eq. (12)), the filtered image
is the vector obtained by multiplying, element by element, the profile τ by the well-known tSZ frequency dependence fν. Thus this method observes only isothermal profiles for clusters, an assumption which results in a roughly 5% low bias in the radial velocity amplitude, as shown in Sect. 5. The power spectrum matrix P is computed from real data in patches surrounding the sources. Once we have the filters (Eq. (12)), the filtered image 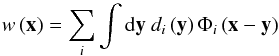 (14)is optimal for the detection of the kSZ effect and has no trace of the tSZ effect. In this equation, di represents the unfiltered map in the ith frequency channel. The filters are normalized so that w(x0), where x0 is the location of the centre of the cluster, is an unbiased estimator of the kSZ signal due to the cluster. An estimation of the error of this is given by the square root of the variance
(14)is optimal for the detection of the kSZ effect and has no trace of the tSZ effect. In this equation, di represents the unfiltered map in the ith frequency channel. The filters are normalized so that w(x0), where x0 is the location of the centre of the cluster, is an unbiased estimator of the kSZ signal due to the cluster. An estimation of the error of this is given by the square root of the variance 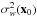 , which can be directly obtained from the filtered map or calculated through
, which can be directly obtained from the filtered map or calculated through 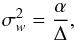 (15)where α and Δ have the same meaning as in Eq. (13).
(15)where α and Δ have the same meaning as in Eq. (13).
In this work, two different uMMF implementations on square patches were used, confirming the robustness of the results. As mentioned above, the two implementations assume that the spatial distribution of the thermal and kinetic signals follows the pressure, for which we adopt the universal pressure profile from Arnaud et al. (2010). For each cluster, the profile is scaled with R500. The two implementations mainly differ in the size of the patches used to estimate the background around each cluster and the details of the cross-power spectrum estimation on the data. In both cases, we apply the resulting uMMF to the patches and directly obtain the estimated velocity at the centre of the filtered patch. The rms of the filtered patch outside the centre region occupied by the cluster gives an estimation of the velocity error. This leads to a good statistical match between velocities measured by the two implementations, but not detailed agreement on a cluster by cluster basis. This is expected, since the peculiar velocity estimate per cluster is dominated by noise, and the actual noise component present in each estimate is dependent on the details of each specific implementation. The method provides estimates of the kSZ flux integrated over the cluster profile; these are translated into velocity estimates for each cluster after dividing by the integrated optical depth. Errors in these estimates of the optical depth will lead to errors in the velocity estimates, but, as discussed below, these should have little impact on estimates of ensemble quantities like velocity averages, dipoles, and rms estimates. More important error offsets (at the 5−25% level) are expected from inaccuracies associated with the gas density profile in clusters (see Sect. 5 for details).
The uMMF method may also be applied to a single map (as is the case for the 2D-ILC map), a situation in which the uMMF becomes a simple Matched Filter (MF).
3.3. Constraining kSZ-induced rms in AP/uMMF measurements
Since the signal-to-noise ratio (S/N) for the kSZ on a typical MCXC cluster is very small (see, e.g., (Aghanim et al. 2001) for forecasts on the analysis of bulk flows and the kSZ effect), we attempt to set constraints on the kSZ signal by performing statistical analyses on the entire MCXC cluster sample. We next describe our approach to set constraints on the kSZ contribution to the variance of a set of AP/uMMF outputs. This method relies on the fact that the kSZ contribution to our AP or uMMF measurements is uncorrelated with the dominant noise sources (CMB residuals, instrumental noise and dust emission). In practice this reduces to searching for a kSZ-induced excess variance, and this demands a good knowledge of the variance of the variance of AP/uMMF measurements, as we next describe.
In this work, we set constraints on the variance of the cluster radial peculiar velocities by looking at the variance of our filter outputs. For both AP and uMMF filters, the data consist of a radial velocity component (v| |) plus a number of noise sources (CMB anisotropies, instrumental noise, Galactic and extragalactic emissions not associated with the clusters, etc., here denoted by n): 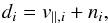 (16)where i is the index of each cluster in our sample of N = 1405 objects (N = 1321 under the strict mask). Sufficiently distant from such locations, the data d and the noise n coincide.
(16)where i is the index of each cluster in our sample of N = 1405 objects (N = 1321 under the strict mask). Sufficiently distant from such locations, the data d and the noise n coincide.
We therefore want to measure 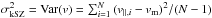 , where vm is the mean velocity. The variance of the data at cluster locations reads:
, where vm is the mean velocity. The variance of the data at cluster locations reads: 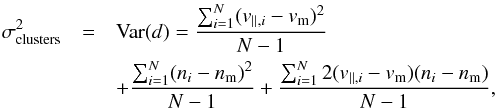 (17)where nm is the mean noise. Assuming that noise terms and cluster velocities are uncorrelated, for the large number of clusters considered here we expect the last term to be subdominant with respect to the first two. We therefore interpret the variance of the data in Eq. (17) as the sum of variances of the velocity and noise terms:
(17)where nm is the mean noise. Assuming that noise terms and cluster velocities are uncorrelated, for the large number of clusters considered here we expect the last term to be subdominant with respect to the first two. We therefore interpret the variance of the data in Eq. (17) as the sum of variances of the velocity and noise terms: 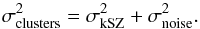 (18)We then estimate the noise variance by looking at 100 locations near to clusters where noise properties will be similar. By doing so in each of the 100 nearby locations, we can obtain 100 estimates of the noise variance and hence construct a histogram representing its probability distribution. Note that this distribution is, in general, not Gaussian. An example from the derived noise rms distributions from the AP and uMMF filters are provided in the right panels of Figs. 3 and 6, respectively.
(18)We then estimate the noise variance by looking at 100 locations near to clusters where noise properties will be similar. By doing so in each of the 100 nearby locations, we can obtain 100 estimates of the noise variance and hence construct a histogram representing its probability distribution. Note that this distribution is, in general, not Gaussian. An example from the derived noise rms distributions from the AP and uMMF filters are provided in the right panels of Figs. 3 and 6, respectively.
Given the probability distribution of the noise and our measured variance at the cluster locations, we can deduce upper limits for the clusters’ velocity variance. Because the variance velocity term is positive and added in quadrature to the noise, as in Eq. (18), we can conclude that at 95% confidence limit (C.L.) the kSZ contribution should be below the following value: 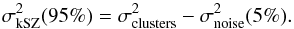 (19)Here
(19)Here 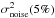 is the noise variance amplitude limiting the lowest 5% of the noise variance distribution. In practice, since our histogram is based upon 100 different variance estimates, we write:
is the noise variance amplitude limiting the lowest 5% of the noise variance distribution. In practice, since our histogram is based upon 100 different variance estimates, we write: 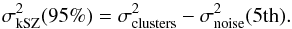 (20)In this equation,
(20)In this equation, 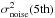 denotes the fifth lowest AP/uMMF output variance estimate picked from the 100 variance estimates making the histogram. The quantity σkSZ(95%) constitutes our limit of the peculiar radial velocity rms at the 95% confidence level. Such a constraint is, however, obtained from histograms built upon only 100 measurements. Using the histograms built upon the filter outputs in blank positions we have run Monte Carlo simulations and studied the uncertainty on the lower 5% limit on
denotes the fifth lowest AP/uMMF output variance estimate picked from the 100 variance estimates making the histogram. The quantity σkSZ(95%) constitutes our limit of the peculiar radial velocity rms at the 95% confidence level. Such a constraint is, however, obtained from histograms built upon only 100 measurements. Using the histograms built upon the filter outputs in blank positions we have run Monte Carlo simulations and studied the uncertainty on the lower 5% limit on 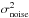 if estimated as outlined above. We find that these uncertainties lie typically below the 5% level when only a subsample of 100 clusters are used, and below 1% when using the entire cluster sample (around 1400 objects).
if estimated as outlined above. We find that these uncertainties lie typically below the 5% level when only a subsample of 100 clusters are used, and below 1% when using the entire cluster sample (around 1400 objects).
3.4. All-sky bulk flow with the unbiased multifrequency matched filter (uMMF)
In order to evaluate the bulk flow in Planck data, we adopted the procedure previously used on simulations for forecasting Planck’s performance, as detailed in Mak et al. (2011). We briefly summarize the approach here, and we refer the reader to Mak et al. (2011) for further information. In this procedure, we do not focus on the velocities of individual clusters, but rather fit for both amplitude and direction of the bulk velocity for the whole ensemble. The first step of the procedure consists of filtering the observed maps with a whole-sky version of the uMMF that adopts the universal pressure profile from Arnaud et al. (2010) convolved with the beam profile of a given frequency as in the case of uMMF on patches. For this whole-sky version, instead of designing the filters individually for each cluster (that match its size), we construct one single filter for all clusters, with a characteristic scale of θ500 = 8′. This choice is motivated by the fact that the average size of the MCXC sample is ⟨ θ500 ⟩ = 7.8′. The filtering procedure combines maps at different frequencies into a cleaned temperature map that is then used to fit for the real spherical harmonic coefficients of the dipole terms (vx, vy and vz). In doing so, we adopt the effective frequencies listed in Table 1.
We fit the dipole terms of the filtered map using a weighted least squares fit that is based on the HEALPix (Górski et al. 2005) IDL procedure remove_dipole. We weight the central pixels of the clusters that are outside the masked region with inverse noise variance weights, i.e., Wi = 1/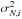 where σN,i is the ith pixel noise variance calculated from filtered CMB and noise realizations. In such realizations, the instrumental noise is white and spatially uncorrelated, with a variance estimated from the half ring maps and divided by the hit maps appropriate for Planck data in a given pixel. We convert the dipole from temperature units (δT) to velocity ones (v) by means of a conversion matrix M previously constructed using simulations of clusters with the same characteristics as the sample in hand, i.e., v = M δTT. We then evaluate the error on the bulk flow dipole coefficients by fitting dipoles to sets of simulations of CMB anisotropies, instrumental noise, and the tSZ effect. In order to do this, we assume that these sources of errors are uncorrelated, but we consider potential correlations in the errors for the dipole coefficients. The magnitude of the dipole velocity follows a χ2 probability distribution with three degrees of freedom that can be computed as follows:
where σN,i is the ith pixel noise variance calculated from filtered CMB and noise realizations. In such realizations, the instrumental noise is white and spatially uncorrelated, with a variance estimated from the half ring maps and divided by the hit maps appropriate for Planck data in a given pixel. We convert the dipole from temperature units (δT) to velocity ones (v) by means of a conversion matrix M previously constructed using simulations of clusters with the same characteristics as the sample in hand, i.e., v = M δTT. We then evaluate the error on the bulk flow dipole coefficients by fitting dipoles to sets of simulations of CMB anisotropies, instrumental noise, and the tSZ effect. In order to do this, we assume that these sources of errors are uncorrelated, but we consider potential correlations in the errors for the dipole coefficients. The magnitude of the dipole velocity follows a χ2 probability distribution with three degrees of freedom that can be computed as follows: 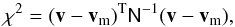 (21)where v is the variable of the distribution, vm is the mean of the velocity as estimated from simulations, and N is the noise covariance matrix under consideration. We compute the covariance matrix by passing 1000 simulations of the noise components (CMB and/or instrumental noise and/or tSZ) through our pipeline and performing the dipole fit on them. The scatter in dipole coefficients provides an estimate of the noise correlations between the dipole directions, i.e.,
(21)where v is the variable of the distribution, vm is the mean of the velocity as estimated from simulations, and N is the noise covariance matrix under consideration. We compute the covariance matrix by passing 1000 simulations of the noise components (CMB and/or instrumental noise and/or tSZ) through our pipeline and performing the dipole fit on them. The scatter in dipole coefficients provides an estimate of the noise correlations between the dipole directions, i.e., 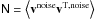 . The 95% upper limit is then determined to be the velocity at which χ2 = 7.8, which is the 95% upper limit for a χ2 distribution with three degrees of freedom. Errors on the bulk flow measurements are therefore computed on the basis of simulations, and include sources of uncertainties in the mass-observable relation as well as in the residual contamination from thermal SZ, CMB and instrumental noise.
. The 95% upper limit is then determined to be the velocity at which χ2 = 7.8, which is the 95% upper limit for a χ2 distribution with three degrees of freedom. Errors on the bulk flow measurements are therefore computed on the basis of simulations, and include sources of uncertainties in the mass-observable relation as well as in the residual contamination from thermal SZ, CMB and instrumental noise.
We verified that the most stringent constraints are obtained when only the central pixel in the direction of cluster’s location is considered after filtering the map (and since the data have already been matched filtered, applying an aperture would not be valid). For the frequency maps used, we present results based on the four lowest HFI channels, i.e., 100, 143, 217, and 353 GHz. We verified that extending the analysis to the two highest LFI channels, 44 and 70 GHz (as in Mak et al. 2011) gives consistent results, but does not significantly improve the constraints.
Finally, before we end this section we stress the difference existing between methods working on patches (such as the ones described in previous sections) and this method, which works on the entire celestial sphere. The former methods are insensitive to scales larger than the patch size, unlike all-sky methods for which filtering is implemented on all angular scales.
 |
Fig. 3 Colour coding common for all panels: black corresponds to the 100 GHz channel; red to 143 GHz; green to 217 GHz; and blue to the 2D-ILC map. Histograms are obtained from AP output at 100 displaced positions, while vertical dot-dashed lines correspond to AP outputs obtained on the clusters. The left panel refers to the AP output monopole/average, whereas the middle and right ones display histograms built upon rms estimates. |
4. Analyses and results
This section contains the entire set of results in this paper, and is divided into three sections. The first one (Sect. 4.1) addresses the constraints on the kSZ monopole and the rms of the cluster peculiar velocities, and is divided into two parts, devoted to the results obtained with the AP and uMMF filters. The second section (Sect. 4.2) studies the constraints on bulk flows, and is divided into four parts. The first three outline the constraints obtained with the three filters defined in Sect. 3. The fourth part revisits the specific filter implemented by Kashlinsky et al. (2008). Finally, the third section (Sect. 4.3) sets constraints on inhomogeneous cosmological models.
As mentioned above, the MCXC catalogue consists of a sample of massive clusters of galaxies hosting large reservoirs of hot gas, where the CMB is distorted by means of the tSZ effect (Planck Collaboration 2011e,f). We target this cluster sample in our attempt to detect or put constraints on peculiar motions in the local Universe. Provided that the expected typical correlation length for peculiar velocities is of order 20–40 h-1 Mpc, we do not expect MCXC clusters to show any significant level of coherent motion. Clusters in the MCXC catalogue cover a wide redshift range and distances between them are far larger than the velocity coherence length. However, in the last few years there have been several works (Kashlinsky et al. 2008, 2010; Abate & Feldman 2012) claiming the presence of extremely large-scale bulk flows, and such scenarios can be tested with the MCXC cluster sample.
The linear theory expectation for the line of sight peculiar velocity variance can easily be derived from the continuity equation in terms of the matter density power spectrum: ![\begin{equation} \sigma_v^2 (M)= \frac{1}{3} \int \frac{{\rm d}\vk}{(2\pi)^3} H^2(z) \biggl| \frac{{\rm d}{\cal D}_{\delta}}{{\rm d}z}\biggr|^2 \frac{P_{\rm m}(k)}{k^2} |W(kR[M])|^2. \label{eq:v2} \end{equation}](/articles/aa/full_html/2014/01/aa21299-13/aa21299-13-eq168.png) (22)This equation refers to the radial velocity rms of a cluster of mass M. The symbol W(kR [M]) corresponds to the Fourier window function associated with a top hat filter of size given by the linear scale corresponding to the cluster mass M, R = [3ρm/(4π)] 1/3, where ρm the average matter comoving density. The linear matter power spectrum is given by Pm(k),
(22)This equation refers to the radial velocity rms of a cluster of mass M. The symbol W(kR [M]) corresponds to the Fourier window function associated with a top hat filter of size given by the linear scale corresponding to the cluster mass M, R = [3ρm/(4π)] 1/3, where ρm the average matter comoving density. The linear matter power spectrum is given by Pm(k), 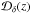 denotes the density linear growth factor, and H(z) corresponds to the Hubble parameter. The rms inferred from this expression at z = 0 is about 230 km s-1 for a 2 × 1014 h-1 M⊙ cluster. Note that the linear theory ΛCDM predictions for the peculiar velocities of the clusters are supported by the output of numerical simulations, although clusters and groups may show biases depending on their environment, with higher velocities in overdense regions, and non-Maxwellian tails (Sheth & Diaferio 2001). In any case, the velocity rms expectation, when translated into temperature fluctuations via Eq. (1), yields too small a signal to be detected on an individual basis (typical velocity estimate errors lie at the level of thousands of km s-1). This motivates a statistical approach which targets ensemble properties of the cluster peculiar velocities.
denotes the density linear growth factor, and H(z) corresponds to the Hubble parameter. The rms inferred from this expression at z = 0 is about 230 km s-1 for a 2 × 1014 h-1 M⊙ cluster. Note that the linear theory ΛCDM predictions for the peculiar velocities of the clusters are supported by the output of numerical simulations, although clusters and groups may show biases depending on their environment, with higher velocities in overdense regions, and non-Maxwellian tails (Sheth & Diaferio 2001). In any case, the velocity rms expectation, when translated into temperature fluctuations via Eq. (1), yields too small a signal to be detected on an individual basis (typical velocity estimate errors lie at the level of thousands of km s-1). This motivates a statistical approach which targets ensemble properties of the cluster peculiar velocities.
We first apply the AP filter to raw HFI frequency maps. Since this filter is applied independently on different frequency bands, it permits us to track separately the impact of other contributions like the tSZ effect or dusty point sources. When imposing constraints on the cluster peculiar velocities, we also use the cleaned 2D-ILC CMB map. Likewise, the use of the uMMF on raw HFI frequency maps allows us to test for dust contamination, tSZ spectral leakage, or errors in the cluster size determination. However, the most restrictive velocity constraints are usually obtained from the 2D-ILC map.
4.1. Constraints on kSZ monopole and rms
In this section we present the constraints that Planck sets on the amplitude of the peculiar velocity monopole (average) and rms in our cluster sample.
4.1.1. Constraints from the AP filter
For all MCXC clusters outside the joint HFI mask, an AP estimate is provided for each frequency band. In order to test for systematic errors, this filter is applied not only at the cluster positions, but also on 100 other positions displaced from the real ones in either Galactic or equatorial latitude. For each position, the amount of displacement is an integer multiple of three times the FWHM of the beam corresponding to the frequency map under study. For a fixed cluster i, the AP output rms from the displaced positions provide an estimate of the rms of the AP output at the ith cluster’s real position (σAP, i). For each displacement, we consider only positions outside the effective mask, and compute both the average (or monopole) of the AP outputs, and their rms, as we run over different clusters. The left panel of Fig. 3 displays the histograms of the AP outputs for the 100 displaced positions at 100 GHz (solid black line), 143 GHz (solid red line) and 217 GHz (solid green line). The vertical, dot-dashed lines correspond to the AP outputs at the real cluster positions (zero angular displacement).
Note that for each displacement some of the real MCXC cluster positions may fall in masked pixels. In those cases, the AP filter outputs are ignored, that is, for each set of displaced positions, the number of useful AP estimates equals the number of clusters under consideration minus the number of times that the “displaced” AP filter centres falls on a masked pixel. We hence do not consider AP outputs whenever the filter is centred on masked pixels. The left panel of Fig. 3 shows that the AP approach is sensitive to the tSZ-induced decrements at 100 and 143 GHz, since the AP output monopoles at cluster positions fall in the negative temperature range, far from the histograms coming from displaced positions (which are centred near zero). The observed monopoles in this panel are less negative (by about 20%) than predictions based upon the universal pressure profile of Arnaud et al. (2010). Given measurement errors, this low bias is marginally significant (around 3σ) and is probably due to residual point source emission and/or inaccuracies in the modelling of the beam impact on our predictions. For 217 GHz, however, the AP monopole falls on the positive part of the histogram, possibly indicating traces of tSZ-induced emission (since the effective frequency of this channel is above the tSZ null). This histogram can be converted into velocity units through dividing by each cluster’s estimated optical depth (see Sect. 2.2). After averaging over the full MCXC un-masked cluster sample one can compute the conversion factor from thermodynamic temperature fluctuations (δT) to peculiar radial velocity (v| |) for this sample, 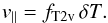 (23)This conversion factor however depends on the AP radius applied. We obtain values for fT2v of 172 km s-1 μK-1 and 203 km s-1 μK-1, for the AP radius choices of 0.25 θ500 and θ500, respectively. After weighting the AP velocity estimate of each cluster by its variance (wi = 1/
(23)This conversion factor however depends on the AP radius applied. We obtain values for fT2v of 172 km s-1 μK-1 and 203 km s-1 μK-1, for the AP radius choices of 0.25 θ500 and θ500, respectively. After weighting the AP velocity estimate of each cluster by its variance (wi = 1/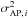 ), we obtain an estimate for the kSZ average/monopole from HFI 217 GHz data: − 212 ± 80 km s-1. If instead we use the 2D-ILC map, the constraint becomes − 1 ± 73 km s-1. The HFI data in the channel near the tSZ null seem to show some residual tSZ contamination (as expected from the effective frequency of this channel quoted in Table 1), but the 2D-ILC result is consistent with zero.
), we obtain an estimate for the kSZ average/monopole from HFI 217 GHz data: − 212 ± 80 km s-1. If instead we use the 2D-ILC map, the constraint becomes − 1 ± 73 km s-1. The HFI data in the channel near the tSZ null seem to show some residual tSZ contamination (as expected from the effective frequency of this channel quoted in Table 1), but the 2D-ILC result is consistent with zero.
The middle and right panels of Fig. 3 display the histograms of the rms values obtained from the displaced positions. As for the left panel, black and red colours refer to the 100 and 143 GHz channels, respectively. In this case, and given the measurement uncertainties, predictions from our adopted pressure profile are in good agreement with our rms-excess measurements. The AP output rms estimates determined at the positions of clusters are displayed by the vertical, dot-dashed lines: they fall clearly off the histograms obtained from displaced positions, showing an excess rms, which is however not seen at 217 GHz (green curve in the right panel). In this panel, the AP output rms estimated at the cluster positions falls in the middle of the histogram obtained from displaced positions. The same occurs for the 2D-ILC map, denoted by blue lines. This suggests that the rms excess found in the middle panel has come from tSZ, since it does not show up in the 217 GHz channel. In ideal conditions, with identical beams throughout channels and an absence of noise and foregrounds, the histograms in the middle and right panels would be identical; the differences among them are reproduced when performing the analysis on Planck simulated maps, which account for different noise levels and beam sizes.
Applying the procedure outlined in Sect. 3.3 on the AP rms distribution displayed in the right panel of Fig. 3, we set constraints on the kSZ-induced contribution to the total measured rms. We find that radial velocity rms constraints for the whole cluster sample are, at the 95% confidence level, 2017 km s-1 and 1892 km s-1, for the raw 217 GHz and 2D-ILC maps, respectively. These upper limits are about a factor of 8 above theoretical predictions, and can be only slightly improved by looking at subsets of the cluster sample. We have checked that kSZ errors decrease with cluster mass and angular distance, since the more massive clusters provide higher kSZ signals and the CMB contamination is less important on smaller angular scales. However, constraints on radial velocities do not improve significantly. By using only an un-masked cluster subsample containing the first 1000 clusters, which have larger values of mass times angular distance (M500 × DA, ⟨ M500 ⟩ subsample = 2.3 × 1014 M⊙, ⟨ z ⟩ subsample = 0.18), the 95% confidence level constraints from HFI 217 GHz and 2D-ILC data become 1806 km s-1 and 1229 km s-1, respectively. These are still a factor 5−7 above theoretical predictions for ΛCDM.
4.1.2. Constraints from the uMMF/MF filters
The uMMF approach can provide accurate kSZ amplitude estimates under the assumption that clusters, as well as being isothermal, follow the universal pressure profile of Arnaud et al. (2010). In Sect. 5 we address the bias that this assumption introduces when clusters show different density profiles, finding a roughly 5% low bias in the velocity amplitude estimates. On an individual basis, the uMMF provides velocity errors that depend on the mass and the size of each cluster on the sky, and lie at the level of a few thousand km s-1, with an average value of about 4100 km s-1 for the un-masked MCXC sample and the six HFI channels. When properly accounting for the finite bandwidth of the HFI channel spectral responses, the average peculiar radial velocity of MCXC clusters is compatible with zero (15 ± 60 km s-1). The 2D-ILC map provides 72 ± 60 km s-1.
When binning the cluster sample in redshifts, we again find no evidence for any statistically significant average peculiar velocity (see red and green symbols in Fig. 4). Estimates of the kSZ monopole for clusters belonging to different redshift bins are shown in Fig. 4.
 |
Fig. 4 Dependence of the average radial velocity of clusters for different redshift bins. Note that the “no band colour” symbols are known to give unreliable results. For clarity, symbols within the same redshift bin have been slightly shifted horizontally. |
Bear in mind that if no colour correction is taken into account, and use is made of the nominal HFI frequencies instead of the effective ones (see Table 1), then effects associated with the finite spectral response in HFI channels become of relevance. In Fig. 4 blue squares and black triangles display the average radial velocity estimates (within different redshift bins) as inferred by the uMMF when colour correction is ignored, using the three lowest frequency or six frequency channels, respectively. In those cases, average velocity estimates lie a few σ below the zero level for several redshift bins, pointing to some positive residual temperature fluctuations at the cluster positions (which is expected since the effective frequency for the third HFI channel is about 222 GHz, i.e., above the tSZ null frequency). Colour corrections must hence be made when interpreting kSZ measurements. However, the fact that velocity estimates for three and six HFI bands are compatible suggests that dust contamination is not important. We also checked that no significant differences are found when introducing changes of ±1σ in the adopted HFI Gaussian fit FWHM values.
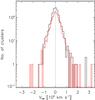 |
Fig. 5 Histogram of recovered radial peculiar velocities as estimated by the uMMF (black) and AP (red) implementations on HFI frequency maps. |
In Fig. 5 we display the histograms of radial peculiar velocities as estimated, for MCXC clusters, by the uMMF (black) and AP (red) implementations. For the uMMF case, the distribution is almost symmetric around zero and has a standard deviation of 4100 km s-1. Both histograms show non-Gaussian tails, presumably due to the presence of un-resolved point sources and other non-Gaussian signals in some galaxy clusters.
 |
Fig. 6 Left panel: estimated rms of uMMF outputs at 100 random positions within the patch surrounding each MCXC cluster versus the corresponding peculiar velocity error as predicted by the uMMF. Middle panel: histogram of mean kSZ radial velocity estimated using all un-masked MCXC clusters, for the 101 positions considered in each cluster patch. The vertical, dashed red line corresponds to the average kSZ estimate when averaging throughout the patch centres, i.e., at the real cluster positions. Right panel: uMMF velocity rms histogram obtained for the MCXC cluster set, at different positions within the patches, just as for the middle panel. Again, the vertical dashed red line corresponds to the kSZ velocity rms estimated at real cluster positions (on patch centres). |
We next conduct a spatial analysis of the Matched Filter outputs, just as done for the AP approach above, and again analysing both the set of HFI frequency maps and the 2D-ILC map. In this analysis we first apply the filter on 100 blank, random positions on the sky where no MCXC clusters are found, and compare the resulting rms of the filter velocity estimates with the rms of the estimates obtained for the real cluster positions. Contrary to the displaced positions for the AP filter, in this case the random positions on which the uMMF/MF filters are evaluated are not displaced in either equatorial or ecliptic latitude with respect to the real cluster, but simply randomly placed within a 10° × 10° patch centred on the real object. If the kSZ signal generated for those “sources” leaves a measurable effect, then the rms at the real positions of the clusters must be larger than the rms obtained at blank positions.
In each patch centred on each MCXC cluster, we record the uMMF/MF outputs for 100 random positions not coincident with the centre. This provides peculiar velocity estimates for positions where we expect the kSZ effect to be zero while, at the same time, having similar levels of instrumental noise and foreground contamination as the positions corresponding to real MCXC clusters. For each set of 100 positions, it is possible to compute the rms and compare it to the expected value predicted by the uMMF/MF method, as provided by Eq. (15). This is shown in the left panel of Fig. 6 for HFI frequency maps: the solid line displays a one to one relation, and it is roughly followed by the recovered rms from the random estimates within the patch (vertical axis) versus the predicted velocity errors (horizontal axis). Here we neglect all uMMF/MF outputs within the patch that fall in masked pixels. After fixing one of the 101 positions within each patch, we compute an average velocity by considering velocity estimates in all patches at that particular position. The histogram of these average velocities computed in the 100 displaced positions is shown in the middle panel. The vertical, red dashed line corresponds to the average velocity as computed from the velocity estimates at the patch centres, that is, at the real MCXC cluster positions. As expected, the middle panel of Fig. 6 shows that the entire ensemble of MCXC clusters exhibits average peculiar velocities that are compatible with zero. The right panel displays the histogram of the velocity rms estimates, computed exactly in the same way as for velocity averages. For each of the 101 positions within a patch, we calculate a velocity rms after considering the filter outputs for the whole set of patches at that position. We end up with 100 velocity rms estimates in displaced positions, and the resulting histogram in the right panel is compared to the velocity rms estimated at the cluster positions, again shown as a vertical, dashed red line. From this distribution, and after following Eq. (20), the uMMF/MF can set the following upper limits at 95% C.L. on the cluster radial peculiar velocity rms: 1514 km s-1 for HFI frequency maps; and 987 km s-1 for ILC data. As for the AP filter, when restricting ourselves to the cluster subsample which maximizes the product M500 × DA, we obtain improvements on these constraints: for the 1000 clusters maximizing M500 × DA, upper limits become 798 and 754 km s-1 for the raw HFI and 2D-ILC data, respectively. If we instead choose the top 100 clusters in the sorted list of the previous subsample, the constraints change, but only slightly: 794 and 614 km s-1 for raw HFI and 2D-ILC maps, respectively. These limits have systematic uncertainties at the level of a few percent, but are nevertheless a factor of about 3 above the level of ΛCDM predictions.
4.2. Constraints on bulk flows and the kSZ dipole
In this section we describe the constraints that Planck sets on the existence of bulk flows at different scales and the measurement of the kSZ dipole in our cluster sample.
4.2.1. Constraints from individual cluster velocities
Extensive efforts have been made in recent years to try to set constraints on the local bulk flow (Hudson et al. 2004; Watkins et al. 2009; Feldman et al. 2010; Nusser & Davis 2011; Ma & Scott 2013), without reaching full agreement so far. The kSZ estimates from Planck provide a different approach to the question of the local bulk flow: if clusters embedded in structure around the Local Group are comoving with it towards a nearby overdensity, then the kSZ measured for those sources should show a dipolar pattern. By looking at clusters within spheres of different radii from us it is possible to set constraints on the local bulk flow within different volumes. This provides a direct test on the studies of Kashlinsky et al. (2008, 2010, 2012), which claim that clusters extending at least up to 800 h-1 Mpc are part of a bulk flow of amplitude about 1000 km s-1.
Given any MCXC cluster subsample, we compute the amplitude of the kSZ dipole along a given direction 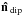 by minimizing
by minimizing 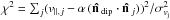 . Here, v| | ,j denotes the AP/uMMF/MF radial velocity estimate of the jth cluster (which is located in the direction
. Here, v| | ,j denotes the AP/uMMF/MF radial velocity estimate of the jth cluster (which is located in the direction 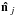 ), and σvj is its associated error. After assuming uncorrelated errors (from cluster to cluster), this minimization yields both an estimate of α and a formal associated error:
), and σvj is its associated error. After assuming uncorrelated errors (from cluster to cluster), this minimization yields both an estimate of α and a formal associated error: 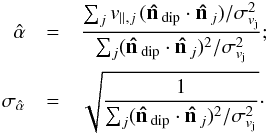 (24)We compute the kSZ dipole for cluster subsamples contained within increasing radii from the Local Group. For each cluster subsample and associated kSZ estimates, we fit a dipole along every direction in the sky, i.e., we sweep in
(24)We compute the kSZ dipole for cluster subsamples contained within increasing radii from the Local Group. For each cluster subsample and associated kSZ estimates, we fit a dipole along every direction in the sky, i.e., we sweep in 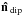 , and retain the direction which yields the highest uncertainty (i.e., highest
, and retain the direction which yields the highest uncertainty (i.e., highest 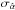 value) in order to find the corresponding upper limit. Figure 7 displays the corresponding upper limits (at the 95% confidence level, calculated as 2σ, assuming a Gaussian distribution) on the dipole values for different radii and both AP and uMMF methods on HFI frequency maps: for both methods, the 95% C.L. upper limit for radii of 90 h-1 Mpc amounts to ~ 2000 km s-1, but it decreases rapidly as the volume increases. For spheres of radius around 350 h-1 Mpc, the uMMF limits fall to about 390 km s-1, and the corresponding AP limit is just slightly higher (520 km s-1). In the largest volume probed by the MCXC clusters, the 95% C.L. upper limits become 329 and 254 km s-1 for the AP and uMMF filters, respectively. All these limits are well above the ΛCDM prediction, displayed by the red solid line. Despite being very different in their definition, the two methods give rise to a very similar pattern in the bulk flow constraints inside different volumes, and in all cases the measured dipoles are compatible with zero.
value) in order to find the corresponding upper limit. Figure 7 displays the corresponding upper limits (at the 95% confidence level, calculated as 2σ, assuming a Gaussian distribution) on the dipole values for different radii and both AP and uMMF methods on HFI frequency maps: for both methods, the 95% C.L. upper limit for radii of 90 h-1 Mpc amounts to ~ 2000 km s-1, but it decreases rapidly as the volume increases. For spheres of radius around 350 h-1 Mpc, the uMMF limits fall to about 390 km s-1, and the corresponding AP limit is just slightly higher (520 km s-1). In the largest volume probed by the MCXC clusters, the 95% C.L. upper limits become 329 and 254 km s-1 for the AP and uMMF filters, respectively. All these limits are well above the ΛCDM prediction, displayed by the red solid line. Despite being very different in their definition, the two methods give rise to a very similar pattern in the bulk flow constraints inside different volumes, and in all cases the measured dipoles are compatible with zero.
 |
Fig. 7 Upper limits at the 95% confidence level for the dipole amplitude from MCXC clusters contained in local spheres of varying radii. Blue and black arrows denote limits for AP and uMMF methods, respectively. The upper limits are indicated by the tails of the arrows. The solid red line depicts the ΛCDM prediction. |
In Fig. 8 we display the 95% upper limit on the kSZ amplitude from the uMMF filter using the whole MCXC cluster set (for which ⟨ z ⟩ = 0.18) and HFI frequency maps. In no direction does the measured dipole exceed 2σ, and the direction with the highest 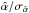 value is close to the Galactic plane. This is to be expected if the errors in the Galactic x- and y-components of the dipole are larger than the z-component, due to the lack of clusters at low Galactic latitudes. When restricting ourselves to clusters below z = 0.25, the dipole amplitude along the CMB dipole direction (l,b) = (264deg,48deg) (Hinshaw et al. 2009)3 amounts to 80 ± 150 km s-1, and limits to 50 ± 160 km s-1 along the direction of apparent motion of the Local Group with respect to the CMB, (l,b) = (276deg,30deg) (Kogut et al. 1993). This result is in clear contradiction with Kashlinsky et al. (2010), who find a bulk flow of about 1000 km s-1 amplitude within radii of 300 − 800 h-1 Mpc at ~3σ C.L. Since our error bars are a factor of about 2 smaller, this suggests that we test the outcome of the filter used by those authors on our data (see Sect. 4.2.3 below).
value is close to the Galactic plane. This is to be expected if the errors in the Galactic x- and y-components of the dipole are larger than the z-component, due to the lack of clusters at low Galactic latitudes. When restricting ourselves to clusters below z = 0.25, the dipole amplitude along the CMB dipole direction (l,b) = (264deg,48deg) (Hinshaw et al. 2009)3 amounts to 80 ± 150 km s-1, and limits to 50 ± 160 km s-1 along the direction of apparent motion of the Local Group with respect to the CMB, (l,b) = (276deg,30deg) (Kogut et al. 1993). This result is in clear contradiction with Kashlinsky et al. (2010), who find a bulk flow of about 1000 km s-1 amplitude within radii of 300 − 800 h-1 Mpc at ~3σ C.L. Since our error bars are a factor of about 2 smaller, this suggests that we test the outcome of the filter used by those authors on our data (see Sect. 4.2.3 below).
4.2.2. Constraints from all-sky method
We can also compute the bulk flow according to the procedure outlined in Sect. 3.4. We filter the observed HFI maps and fit monopole and dipole velocity coefficients to the filtered data, as well as to simulations of the data (PSM diffuse component, tSZ and CMB plus instrumental noise simulations; see Sect. 2.3). Simulations provide one way of estimating uncertainties which allow one to propagate errors on cluster-derived measurements, mainly induced by dispersion in the scaling relations, throughout the whole pipeline. An alternative procedure to derive uncertainties consists of randomizing the positions of the clusters on the sky and computing the monopole and dipole from these random directions, adopting the same procedure used on the real data. We use the latter to show the typical variations of the diffuse component’s contribution for small displacements around cluster locations. Specifically, we consider directions displaced by 30′ to 1° from the cluster nominal locations, while also avoiding mask boundaries (these are the “shifted positions” in Table 2).
Values for the resulting velocity dipole coefficients are presented in Table 2. The main result is that Planck data give dipole coefficient amplitudes consistent with those expected from the ΛCDM scenario, once one has taken into account the contamination from Galactic foregrounds and other signals. The apparent bulk flow measured is 614 km s-1. However, with this particular configuration for cluster positions, the diffuse Galactic component provides a non-negligible contribution to the dipole signal, 529 km s-1, as measured in the PSM simulations. The errors on the diffuse component, as estimated by randomizing the cluster directions on the PSM diffuse component simulations, are smaller than those induced by the thermal SZ and CMB plus instrumental noise simulations (see Table 2).
 |
Fig. 8 Mollweide projection in Galactic coordinates of the upper limit (at 95% C.L.) of the kSZ dipole amplitude from applying the uMMF approach to HFI frequency maps using the whole MCXC cluster sample. In no direction is the dipole detected at more than 2σ. |
Simulations of the tSZ component, which account for uncertainties in the SZ signal for clusters with a given temperature, induce a 1σ uncertainty on the bulk velocity of 40 km s-1, and an overall bias in the velocity estimation of the order of 400 km s-1.
Uncertainties from CMB confusion and instrumental noise (140–290 km s-1 in the different directions) are dominant over tSZ ones. The fraction of the observed bulk flow not accounted for by Galactic foregrounds (by subtracting the dipole as a vector, this amounts to 350 km s-1) is within 95% of the error on bulk flows induced by the tSZ, CMB and instrumental noise (893 km s-1) and below the 95% level of CMB plus instrumental noise alone (543 km s-1).
Estimated dipole coefficients (Cols. 2−4) and velocity magnitude (Col. 5) using the all-sky method.
By restricting the cluster sample to the objects within a specified distance from us, it is possible to constrain the bulk flow within spheres of a given comoving radius. This is what is displayed in Fig. 9, where the Galactic component has been subtracted. We notice that, for all distances, the measured bulk flow is below the 95% confidence level as measured from maps including only CMB, instrumental noise, and tSZ clusters. The upper limits reach an approximately constant value above scales around 500 h-1 Mpc, as a small fraction of the clusters in this sample are at larger distances. The 95% upper limits at 2400 h-1 Mpc are 893 km s-1 when all sources of noise are considered, reducing to 543 km s-1 when CMB plus instrumental noise are taken into account.
The results reported in Fig. 9 refer to the nominal mask, while in Table 2 we also quote results for the more restrictive mask. The two sets of results are very similar, however.
 |
Fig. 9 Bulk flow amplitude measured in Planck data with the all-sky method, after subtraction (vectorially) of the Galactic contribution (black crosses), compared with 95% upper limits derived from simulations containing CMB and instrumental noise only (blue arrows) or also including tSZ signal (black arrows). The fact that the crosses are below the arrows at all scales shows that there is no significant bulk flow detection. |
In this analysis, we also fit for the direction of the measured bulk flow. Even although the detection is not significant, it might still be instructive to compare the best fit direction to other potentially relevant directions. Results for various cluster configurations and Planck data are displayed in Fig. 2, together with the CMB dipole and the claimed dipole direction of Kashlinsky et al. (2008). We notice that the direction we determine from Planck data and MCXC clusters is quite different from both the CMB dipole and the result of Kashlinsky et al. (2008). It aligns better with the direction of the collection of clusters in the map, which happen to be in a low instrumental noise area of the sky, as one would expect from a noise–induced measurement. Indeed, simulations show that the directions of bulk flows of the magnitude seen in the data cannot be recovered with great precision. Errors are of the order of tens of degrees, depending on the bulk flow direction (Mak et al. 2011).
Finally, we notice that the upper limits to the bulk flow that we find with this method are above those found in the previous section. This is not surprising, as we are fitting here for both the velocity direction and amplitude, and we compute errors in a different way. The upper limits obtained with this approach should be considered as more conservative. Nevertheless they are about a factor of five better than what was found using WMAP data.
 |
Fig. 10 Monopole and dipole component estimates after applying the spatial filter of Kashlinsky et al. (2008) on WMAP-7 W-band data (black lines) and on Planck 2D-ILC maps (red lines). Estimates from real MCXC clusters are displayed by vertical, dot-dashed lines. Histograms are obtained after repeating the analysis on 1000 random cluster configurations, with averages indicated by the vertical, solid lines. The y-component appears discrepant here, but compare with Fig. 11. |
4.2.3. Revisiting the Kashlinsky et al. (2010) filter
The idea of constraining the local bulk flow of matter by looking at the dipolar pattern of the kSZ in the galaxy cluster population was first discussed by Haehnelt & Tegmark (1996) and further developed by Kashlinsky & Atrio-Barandela (2000). The method was applied by Kashlinsky et al. (2008, 2009) to WMAP data, analyses that have been followed by more recent studies (Kashlinsky et al. 2010, 2011). In this section, we perform a direct application of their filter to both WMAP and Planck data, and interpret it at the light of the results already outlined in this work.
We first implement the filter of Kashlinsky et al. (2010) on the MCXC cluster sample and the WMAP-7 data. After using the extended temperature KQ75 mask, we obtain filtered maps from the cleaned Q, V and W band WMAP data. Since the filtered maps for the four W-band Differencing Assemblies (DAs) used by those authors are publicly available4, a direct comparison of the filtered maps can be performed: for instance, for the filtered maps corresponding to the fourth W-band DA, the temperature rms outside the joint mask in our filtered map is 74 μK, very close to the 77 μK obtained from the map used by Kashlinsky et al. (2010). The rms of the difference map amounts to 35 μK, and a visual inspection shows the similarity between both maps. Each cluster is assigned a radius of 25′, and the remove_dipole routine from HEALPix is used when computing the monopole and dipole in the subset of pixels surrounding the clusters. The monopole and dipole components obtained for the WMAP W band are displayed by the black, vertical dot-dashed lines in Fig. 10. These are in very good agreement with the results obtained by Kashlinsky et al. (2010).
We next distribute the same number of clusters surviving the mask randomly on the unmasked sky 1000 times, assign them a circle of radius 25′ and repeat the monopole and dipole computation. For each of the 1000 cluster configurations, we separately compute the monopole and dipole for each of the DAs. This permits us to obtain the rms for each component and DA, in such a way that a combined estimate of the monopole and dipole can be extracted from all DAs by inverse-variance weighting the estimate for each DA. This is carried out for the real cluster configuration on the sky and for the 1000 mock (random) configurations. From the latter, we obtain the histograms shown in Fig. 10. The average quantities out of the 1000 simulations are displayed by the solid, vertical lines. Black lines refer to WMAP data, and our results show that the y-component of the dipole is peculiar, in the sense that it falls far in the negative tail of the distribution.
 |
Fig. 11 Histograms of the recovered cluster dipole amplitude: (a) from the 1000 Monte Carlo random cluster configurations on the sky (solid black line); (b) from rotating one random cluster configuration in Galactic latitude on the real filtered map (triple dot-dashed blue line); (c) from rotating the real MCXC cluster configuration around the Galactic z axis on the real filtered map (dashed red line); and (d) from applying the filter on the position of our MCXC cluster sample in 1000 Monte Carlo CMB simulations following the WMAP-7 best-fit model (dot-dashed green lines). The dipole amplitude recovered at the real MCXC cluster positions on the real filtered map is shown by the vertical, solid line. It is not significantly detected, provided one is careful to simulate the most important noise contributions. |
 |
Fig. 12 Same as Fig. 11, but restricting the analysis to the 200 most massive clusters outside the mask. The colour and line-style coding is identical to that figure. In this case, all histograms contain the measurement on the real positions of clusters (displayed by the vertical solid line). |
When repeating these analyses with the 2D-ILC map, we obtain the results displayed by the red lines in the same figure. In this case, the dipole components from the real data fall further outside the distribution provided by the histograms, as none of the 1000 mock cluster configurations provides a dipole of larger amplitude than the one measured from the real MCXC sample. These results suggest that the dipole measured at the MCXC cluster positions is indeed peculiar if compared to dipole estimates from randomized cluster positions.
Nevertheless, there is one aspect to be studied more closely, namely the angular distribution of clusters on the sky. In what follows, the filtered map built upon the 2D-ILC data is used. So far our Monte Carlo simulations assumed that clusters were placed randomly on the sky, i.e., the clustering of our sources has been neglected. We next perform tests in which the angular configuration of our MCXC cluster sample is preserved. The first test consists of repeating the filtering and subsequent dipole computation on 1000 CMB mock skies following the WMAP-7 best-fit model. These mock CMB maps contain no kSZ and hence should give rise to no significant kSZ dipole. Out of this ensemble of mock skies, we compute the dipole using the positions of MCXC clusters (as described above) and obtain a histogram from the recovered dipole amplitude. This permits us to judge how peculiar our measurement is with respect to the simulation outputs. In a second test, we rotate the clusters’ angular positions around the Galactic z-axis on the real filtered map obtained from the 2D-ILC data. We conduct 360 rotations of one degree step size, in Galactic longitude, while preserving Galactic latitude, and the relative angular configuration of MCXC clusters on the sky. Since the mask mostly discards pixels at low Galactic latitude (close to the Galactic plane), most clusters that are originally outside the mask remain outside the mask after rotating. For each rotation a new value of the dipole is recorded, and information on dipole statistics is then built up using outputs obtained from the real map with the real rotated cluster configuration on the sky. This rotation test, unlike the one based upon CMB mock skies, accounts for the impact of noise, foregrounds and other systematic signals that may be present in the filtered map.
The results are shown in Fig. 11. The black histogram reflects the statistics of the recovered dipole amplitudes after drawing 1000 random cluster configurations on the real filtered map, just as done for Fig. 10. The triple-dot-dashed blue histogram corresponds to the dipole outputs obtained after rotating in Galactic longitude one single random cluster configuration applied to the filtered map obtained from 2D-ILC data. Clearly, this rotation gives rise to a histogram that is very close to the one obtained from the 1000 random cluster configurations. On the other hand, the dot-dashed green histogram reflects the statistics of the recovered dipole amplitudes obtained from the 1000 Monte Carlo CMB simulations. Again, this histogram is fairly close to the one obtained after rotating the real cluster sample in Galactic longitude on the real filtered map (dashed red histogram). The recovered dipole amplitude from the real cluster positions on the real filtered map is displayed by a vertical black line.
While the measured dipole falls in the far positive tail for the simulations using random cluster configurations (black and blue histograms), it is however quite unremarkable when compared to the simulations accounting for the real configuration of clusters on the sky (red and green histograms): about 11% of cases in both CMB simulations and rotations yield dipoles larger in amplitude than the one measured on the real data. The green histogram shows that the apparent dipole can be explained by chance alignments of random, uncorrelated CMB skies. The impact of instrumental noise and other component only shifts the histogram slightly (as a comparison of the red and green histograms suggests). These results show that the dipole measured for the real MCXC cluster positions is not peculiar when compared to other dipole computations, either on mock CMB skies or on the filtered 2D-ILC map for a set of positions in which the angular clustering of the MCXC sample is preserved. When repeating this analysis on a subsample of MCXC clusters containing the 200 most massive objects, wider histograms from both rotations and CMB mock skies are obtained. The area under the histograms above the apparent dipole obtained from real data at zero-lag rotation amounts to about 56% of the total, see Fig. 12. Unlike for the entire MCXC cluster sample, the histograms obtained after randomly distributing this subsample of massive clusters on the un-masked filtered map are very similar to those obtained after running CMB mocks or rotating the clusters in Galactic longitude. This is in better agreement with Atrio-Barandela et al. (2010), who found no significant difference between the histograms obtained from CMB mocks and from randomly distributing clusters on the filtered map. This is likely due to the absence of any significant intrinsic dipole in the angular distribution of this (smaller) cluster subsample.
Finally, we perform a direct comparison of our results with Kashlinsky et al. (2011). For this purpose, we use the WMAP filtered maps and the sky mask for galaxy clusters at z < 0.25 used by Kashlinsky et al. (2008); these data are presented as supplementary materials for Kashlinsky et al. (2011). For the filtered maps corresponding to the four DAs of the WMAP W band data, we apply the rotation test in Galactic longitude. We find that, although the y-component of the dipole at no rotation is marginally peculiar (at the roughly 1−3% level), the amplitude of the dipole is not, since around 14% of the rotations yield higher amplitude dipoles. This is in good agreement with the Planck results outlined above. Hence, according to our estimations of the dipole uncertainty, we conclude that the roughly 3 μK dipole measured by Kashlinsky et al. (2008) should not be assigned to the clusters’ peculiar motion, but rather to residuals (mostly of CMB origin) in the filtered map.
4.3. Constraints on inhomogeneous cosmological models
The sensitivity of the kSZ effect to peculiar velocities and bulk flows makes it an excellent probe of nonstandard inhomogeneous cosmological models (Goodman 1995). In particular, models in which we are located near the centre of a spherically symmetric Hubble-scale void have been examined extensively in recent years as alternatives to standard accelerating models on Friedmann-Lemaître-Robertson-Walker (FLRW) backgrounds (see, e.g., Clarkson 2012, and references therein). Such void models can easily reproduce the Type Ia supernova (SN) luminosity distance-redshift data without dark energy or modified gravity. However, these models generically predict very strong outwards-directed bulk flows, due to the greater expansion rate within the void, and so are expected to produce a large kSZ monopole signal (superimposed, of course, on the usual kSZ signal from structure). Constraints on such models using kSZ upper limits from nine clusters (Holzapfel et al. 1997; Benson et al. 2003; Kitayama et al. 2004) show that the largest voids are at odds with these early data, assuming purely adiabatic initial conditions (García-Bellido & Haugbølle 2008; Yoo et al. 2010). Tight constraints have also been imposed using upper limits on the kSZ power from small-scale CMB experiments (Zhang & Stebbins 2011; Zibin & Moss 2011). However, the results based on small-scale kSZ power are uncertain, due to our inability to properly perform perturbation theory in void models and our lack of knowledge about the small-scale matter power spectrum and baryonic physics (Zibin & Moss 2011). The very tight Planck constraints on the kSZ monopole presented above are therefore expected to provide extremely stringent limits on any such large-scale features, in a manner that is free of the uncertainties due to small-scale structure.
We first briefly describe our void models and calculation methods; full details can be found in Moss et al. (2011). Growing-mode void models are characterized by a single radial function, e.g. the matter density profile. Models with significant decaying modes are ruled out by their extremely large kSZ and CMB spectral distortions (Zibin 2011; Bull et al. 2012) and so are ignored here. In this study we consider a family of smooth void profiles (taken from Moss et al. 2011) parameterized by a width, L, and a depth, δ0 < 0. Explicitly, we superpose (at early times) on a spatially flat background the total matter density contrast profile ![\begin{equation} \delta(r) = \left\{\begin{array}{ll} \displaystyle \delta_0\left[1 - 3\left(\frac{r}{L}\right)^2 + 2\left(\frac{r}{L}\right)^3\right] & \quad r \le L ,\\ \displaystyle 0 & \quad r > L , \label{eqn:polyvoid} \end{array}\right. \end{equation}](/articles/aa/full_html/2014/01/aa21299-13/aa21299-13-eq288.png) (25)for comoving radial coordinate r centred on us. In order to express our constraints in terms of more directly observable quantities, in place of L we use the corresponding redshift, zL, at which we observe an object at r = L. In place of the depth, δ0, we use the local matter density parameter at the origin today,
(25)for comoving radial coordinate r centred on us. In order to express our constraints in terms of more directly observable quantities, in place of L we use the corresponding redshift, zL, at which we observe an object at r = L. In place of the depth, δ0, we use the local matter density parameter at the origin today, 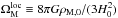 , where ρM,0 is the current total matter energy density at the centre. Thus
, where ρM,0 is the current total matter energy density at the centre. Thus 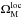 generalizes the familiar density parameter of an FLRW cosmology, and the deepest voids have the smallest values of
generalizes the familiar density parameter of an FLRW cosmology, and the deepest voids have the smallest values of 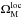 .
.
These models require a relativistic treatment at late times, since they are not well described by small perturbations from an FLRW background. We use the Lemaître-Tolman-Bondi (LTB) exact solution to Einstein’s equations to calculate the radial velocity, v∥ ,LTB(z), between a comoving scatterer (i.e., a cluster) and the local CMB frame, using the method of Moss et al. (2011).
We compare our LTB void models with the AP Planck radial velocity estimates for 1405 clusters by calculating the likelihood while varying the width and depth of the void profile. The likelihood, ℒ, is calculated using the full error distributions from the 100 displaced positions for each cluster. Importantly, for the deepest and widest void models, the typical velocities v∥ ,LTB are outside of the range of velocities for the displaced positions. This means that we cannot calculate the actual likelihoods for these models (because they are so small). Instead, we conservatively assign such models likelihoods based on the outermost sampled regions of the error distributions. This will almost certainly result in a large overestimate of the likelihood for these models, and hence we will underestimate the confidence at which they are ruled out.
In Fig. 13 we plot contours for the quantity log 10(ℒ/ℒhom) in the width-depth plane. Here ℒhom is the likelihood for the exactly homogeneous model, i.e., the model for which δ0 = 0 (which implies 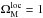 and v∥ ,LTB(z) = 0). Also shown on the plot are the confidence levels for the same void models, but using the Union2 compilation of Type Ia SNe, taken from Zibin & Moss (2011). The SN data demand deep (i.e., low
and v∥ ,LTB(z) = 0). Also shown on the plot are the confidence levels for the same void models, but using the Union2 compilation of Type Ia SNe, taken from Zibin & Moss (2011). The SN data demand deep (i.e., low 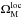 ) but wide void profiles, while the Planck kSZ data rules out all but the very shallowest (i.e.,
) but wide void profiles, while the Planck kSZ data rules out all but the very shallowest (i.e., 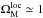 ) or narrowest (i.e., small zL) profiles. Adiabatic void models are thus ruled out at extremely high confidence. It is easy to understand the strength of this result: voids fitting the SNe have v∥ ,LTB(z) ~ 104 km s-1 at z ≃ 0.5 (Moss et al. 2011), which places them a few standard deviations into the tails of roughly 1000 cluster measurements.
) or narrowest (i.e., small zL) profiles. Adiabatic void models are thus ruled out at extremely high confidence. It is easy to understand the strength of this result: voids fitting the SNe have v∥ ,LTB(z) ~ 104 km s-1 at z ≃ 0.5 (Moss et al. 2011), which places them a few standard deviations into the tails of roughly 1000 cluster measurements.
 |
Fig. 13 Solid contours indicate log 10(ℒ/ℒhom) for the AP Planck frequency maps as a function of central matter density parameter, |
5. Robustness of the results
Returning to our main goal of determining the kSZ peculiar velocity constraints, we now address the sensitivity of our results to uncertainties in the density profile adopted for clusters and the errors in estimates of the optical depth. We also quantify the impact of non-CMB noise sources on our error bars.
5.1. Impact of changes in the density profile
As mentioned in Sect. 2.2, the adopted density profile at radii below R500 is a fit from REXCESS observations, but at larger radii (x > 1) the density is expressed in terms of the gas pressure (which follows the universal profile of Arnaud et al. 2010) and the entropy 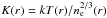 . As well as being physically motivated, the reason for this is the existence of some constraints on the scaling of the entropy for r > R500. As long as the shock front is beyond 5 × R500 (i.e., beyond our upper radial integration limit), the entropy should increase with radius with a power law of the type K(r) ∝ rγ, with γ = 1.1 for the adiabatic case, as predicted by Voit et al. (2005). Observations at r < R500 are reasonably close to this prediction, but at larger radii, the scaling should become shallower (as suggested by the observations of Walker et al. 2012). Our computations for the AP filter adopted the fixed value γ = 0.5 for r > R500, but we explored the impact of different scalings when estimating the ratio of fluxes inside the inner and outer circles of the AP filter. The solid red line in Fig. 14 displays the ratio of the kSZ flux computed in circles of radii
. As well as being physically motivated, the reason for this is the existence of some constraints on the scaling of the entropy for r > R500. As long as the shock front is beyond 5 × R500 (i.e., beyond our upper radial integration limit), the entropy should increase with radius with a power law of the type K(r) ∝ rγ, with γ = 1.1 for the adiabatic case, as predicted by Voit et al. (2005). Observations at r < R500 are reasonably close to this prediction, but at larger radii, the scaling should become shallower (as suggested by the observations of Walker et al. 2012). Our computations for the AP filter adopted the fixed value γ = 0.5 for r > R500, but we explored the impact of different scalings when estimating the ratio of fluxes inside the inner and outer circles of the AP filter. The solid red line in Fig. 14 displays the ratio of the kSZ flux computed in circles of radii 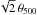 and θ500 for different scalings of the entropy, K(r) ∝ rγ. This ratio depends on the profile, but not on the cluster mass or redshift. The horizontal, dashed green line displays the isothermal case at all radii, including for x < 1. When translating these flux ratios into velocity constraints, we find that the γ = 0.5 profile introduces a boost in the peculiar velocity amplitude estimate of about 28% with respect to the case where clusters are assumed to be isothermal. For the extreme case of γ = 0 this error amounts to 36%, while for γ = 1.1 it goes down to 20%. With respect to our reference model of γ = 0.5, we expect that variations of γ in the range [− 1.1,0] will introduce changes in the velocity constraints at the level of ± 6%. If the pressure profile is changed to use the parameters that best fit the external profiles measured out to 3 × R500 (Planck Collaboration 2013), then the change in the velocity constraints are small enough to be considered negligible.
and θ500 for different scalings of the entropy, K(r) ∝ rγ. This ratio depends on the profile, but not on the cluster mass or redshift. The horizontal, dashed green line displays the isothermal case at all radii, including for x < 1. When translating these flux ratios into velocity constraints, we find that the γ = 0.5 profile introduces a boost in the peculiar velocity amplitude estimate of about 28% with respect to the case where clusters are assumed to be isothermal. For the extreme case of γ = 0 this error amounts to 36%, while for γ = 1.1 it goes down to 20%. With respect to our reference model of γ = 0.5, we expect that variations of γ in the range [− 1.1,0] will introduce changes in the velocity constraints at the level of ± 6%. If the pressure profile is changed to use the parameters that best fit the external profiles measured out to 3 × R500 (Planck Collaboration 2013), then the change in the velocity constraints are small enough to be considered negligible.
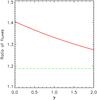 |
Fig. 14 Solid, red line: ratio of kSZ fluxes computed in circles centred on clusters with radii |
Regarding the uMMF, only the isothermal profile was implemented in the filter. In order to assess the impact of this approximation, we conduct a numerical experiment, consisting of assigning a 1000 km s-1 amplitude dipole to the cluster set of our simulations, and extracting this dipole after injecting both the isothermal and non-isothermal profiles to the clusters, but considering only the isothermal profile in the uMMF definition. We recover amplitude values of 1016 ± 106 km s-1 and 966 ± 106 km s-1 for the isothermal and non-isothermal profiles, respectively. The errors do not change, which is expected, since the profile coded in the uMMF is isothermal in both cases. The difference in the recovered values, however, suggest a potential bias in the amplitude estimate of about 50 km s-1, which amounts to around 5% of the signal amplitude. This test indicates that the uMMF is less sensitive to the assumed density profile than the AP, probably because the former assigns more weight to the central regions of the cluster where the noise (mostly induced by the CMB) is lower and where the decreasing radial pattern of temperature is less dramatic.
Hence, we conclude that uncertainties in the radial gas distribution in galaxy clusters should introduce errors in the limits imposed on peculiar velocities at the 5−30% level.
5.2. Other sources of error
Impact of uncertainties in estimates of the optical depth of clusters on the constraints imposed on the kSZ monopole, rms, and dipole from Planck data.
After repeating the analysis of the AP and MF filters on a pure CMB simulated map, we found that errors decreased to about 70% of their amplitude on HFI raw maps. This shows that the main limiting factor when estimating kSZ velocities is the intrinsic CMB component. The presence of point sources, instrumental noise and other foregrounds should be included in the remaining roughly 30%, and after properly accounting for the spectral response of HFI detectors, there seems not to be any significant tSZ leakage biasing the peculiar velocity estimates.
The AP and uMMF/MF velocity estimates, however, rely on an accurate knowledge of the cluster optical depths within a given radius. For each cluster, the integrated optical depth is estimated from the adopted radial density profile, which itself relies on the Y500–M500 and T–M500 relations. Apart from the uncertainties in the shape of the profile (addressed above), the intrinsic scatter in these scaling relations could have an impact on the peculiar velocity estimates. In order to test this we conduct a Monte Carlo analysis consisting of introducing un-correlated errors to the real estimates of the cluster optical depths. We adopt a log-normal model for the errors on the τ500, j estimate for the jth cluster: 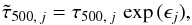 (26)with ϵj being a normally distributed variable of zero mean. The symbol
(26)with ϵj being a normally distributed variable of zero mean. The symbol  denotes the Monte Carlo estimate of the jth cluster’s optical depth obtained from the real estimate τ500, j. For each of the 100 Monte Carlo simulations, we simulate values of τ for each cluster and then repeat the full analysis, setting constraints on the kSZ monopole, kSZ-induced rms excess, and kSZ dipole, as outlined in previous sections.
denotes the Monte Carlo estimate of the jth cluster’s optical depth obtained from the real estimate τ500, j. For each of the 100 Monte Carlo simulations, we simulate values of τ for each cluster and then repeat the full analysis, setting constraints on the kSZ monopole, kSZ-induced rms excess, and kSZ dipole, as outlined in previous sections.
These analyses show that our constraints on the kSZ monopole, velocity rms, and dipole uncertainty change by less than 10% when considering errors in the optical depth estimation of the order 20–40%. Typical changes are at the level of a few percent (see Table 3); since we are constraining ensemble quantities obtained from subsamples of the cluster catalogue, errors tend to average out if they are independent from cluster to cluster (as we expect them to be). Provided that the relative uncertainty in cluster luminosities is about 40% for the L–M scaling relation (Pratt et al. 2009), and combining it with the approximate scalings L ∝ M4/3 and M ∝ R3, one deduces that the relative uncertainty in R should be at the level of about 10%. For the spherical estimates of τsph, 500 this translates into a roughly 30% uncertainty, decreasing to about 20% for the cylindrical optical depth estimate (τcyl ∝ R2). From the results of our Monte Carlo approach above, we conclude that errors in the optical depth estimates should not significantly bias our kSZ constraints.
6. Conclusions
The MCXC cluster sample has been used to search for signatures of peculiar velocities in the Planck CMB data. For this purpose, two different filters were applied: aperture photometry; and the unbiased Multi-frequency Matched Filter. The former is a simple, quick and robust tool for providing estimates of kSZ-induced temperature anisotropies, and although it detects the tSZ-induced monopole and rms excess at the cluster positions, it fails to detect the kSZ effect, setting a constraint on the kSZ-induced radial velocity rms at the level of 1200 km s-1 (95% confidence level) for a massive and distant MCXC subsample of 1000 sources. By effectively removing the tSZ signal, matched filters are able to place stronger constraints, reaching the level of 800 km s-1 (95% C.L.) for a subsample of 100 massive clusters. All these values, however, lie a factor of 3–5 above ΛCDM expectations for clusters of typical mass 2 × 1014 M⊙ at z ≃ 0.15. Thus, while our constraints are fully consistent with ΛCDM expectations, a detection of the radial velocity rms would require significant improvements over the present analysis.
Both methods also provide measurements of the clusters’ average velocity that are compatible with zero: these are at the level of 120−160 km s-1 (95% confidence level) for the uMMF and AP filters. The fact that this constraint applies to a cluster sample whose mean redshift is z ~ 0.18 provides very strong evidence that the CMB is mostly at rest with respect to those observers (as opposed to the relative motion of our local CMB to those sources, which is of the order of cz ~ 54 000 km s-1). By itself, this measurement constitutes an unprecedented and valuable confirmation of a prediction of the standard cosmological scenario, and has strong implications in discussions of the homogeneity of our Universe.
In this context, the large number and redshift distribution of the Planck cluster kSZ measurements are ideal for constraining void models, which attempt to explain the apparent acceleration without dark energy or modified gravity. Indeed, void models which fit the Union2 SN data are ruled out at extremely high confidence. In principle it may be possible to cancel the kSZ effect generated at cluster positions in these models with a large (order unity) isocurvature mode at last scattering (Yoo et al. 2010), but this would almost certainly entail substantial fine tuning of the isocurvature mode. Therefore the Planck kSZ data strongly support the conclusions of previous studies which found that void models generically predict very low H0 (e.g., Zibin et al. 2008; Bull et al. 2012) and too large kSZ power on small scales (Zhang & Stebbins 2011).
Planck’s constraints on the amplitude of the local bulk flow provide an independent view of a long ongoing debate. Unfortunately, our results are not sensitive to the local volumes where many claims for bulk flows have been raised; the limit of 390 km s-1 within spheres of 350 h-1 Mpc at 95% C.L. does not permit us to confront claims at the level of 400−700 km s-1 within radii of 50–120 h-1 Mpc, and on the convergence of the measured CMB dipole within these cosmological volumes (Hudson et al. 2004; Watkins et al. 2009; Feldman et al. 2010; Nusser & Davis 2011; Nusser et al. 2011; Branchini et al. 2012; Courtois et al. 2012; Ma & Scott 2013). The number of galaxy clusters present in those spheres is too low (78 entries in the MCXC catalogue within 80 h-1 Mpc) to decrease the statistical noise significantly. It would thus be required that future CMB experiments have sufficient angular resolution and sensitivity for galaxy groups and clusters in the neighbourhood of the Local Group in order to provide a kSZ view of the local dipole. However, on larger scales, Planck is able to set strict constraints on the amplitude of bulk flows (below 254 km s-1 at 95% C.L. for a radius of 2 h-1 Gpc), in clear contradiction with some previous claims (Kashlinsky et al. 2008, 2010; Abate & Feldman 2012). It is worth remarking that the conclusions derived from our analysis are practically insensitive to few-percent changes in the set of cosmological parameters.
The linear continuity equation states that peculiar velocity surveys are sensitive to fluctuations in the distribution of matter and energy on scales larger than density or galaxy surveys. The fact that Planck is able to set such strong constraints on peculiar velocities in a cluster population at ⟨ z ⟩ ~ 0.18 (and extending out to z ~ 1), translates into correspondingly strong constraints on the amplitude of primordial fluctuations at Gpc scales. If the Universe were inhomogeneous on scales larger than the size of the volume containing our cluster catalogue, these clusters would show a significant dipolar pattern in their kSZ velocities. We conclude that Planck constraints on peculiar velocities are compatible with ΛCDM expectations, and constitute an unprecedented piece of evidence for the local homogeneity of the Universe in the super-Gpc regime.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.
The data were downloaded from the URL site http://www.kashlinsky.info.
Acknowledgments
The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA and RES (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.rssd.esa.int/Planck. The authors from the consortia funded principally by CNES, CNRS, ASI, NASA, and Danish Natural Research Council acknowledge the use of the pipeline running infrastructures Magique3 at Institut d’Astrophysique de Paris (France), CPAC at Cambridge (UK), and USPDC at IPAC (USA). We acknowledge the use of the HEALPix package, WMAP data and the LAMBDA archive (http://lambda.gsfc.nasa.gov).
References
- Aaronson, M., Huchra, J., Mould, J., Schechter, P. L., & Tully, R. B. 1982, ApJ, 258, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Abate, A., & Feldman, H. A. 2012, MNRAS, 419, 3482 [NASA ADS] [CrossRef] [Google Scholar]
- Aghanim, N., Górski, K. M., & Puget, J.-L. 2001, A&A, 374, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pointecouteau, E., & Pratt, G. W. 2005, A&A, 441, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Atrio-Barandela, F., Kashlinsky, A., Ebeling, H., Kocevski, D., & Edge, A. 2010, ApJ, 719, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Basak, S., & Delabrouille, J. 2012, MNRAS, 419, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, B. A., Church, S. E., Ade, P. A. R., et al. 2003, ApJ, 592, 674 [NASA ADS] [CrossRef] [Google Scholar]
- Bersanelli, M., Mandolesi, N., Butler, R. C., et al. 2010, A&A, 520, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Voges, W., Huchra, J. P., et al. 2000, ApJS, 129, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Schuecker, P., Guzzo, L., et al. 2004, A&A, 425, 367 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Branchini, E., Davis, M., & Nusser, A. 2012, MNRAS, 424, 472 [NASA ADS] [CrossRef] [Google Scholar]
- Bull, P., Clifton, T., & Ferreira, P. G. 2012, Phys. Rev. D, 85, 024002 [NASA ADS] [CrossRef] [Google Scholar]
- Burenin, R. A., Vikhlinin, A., Hornstrup, A., et al. 2007, ApJS, 172, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Burke, D. J., Collins, C. A., Sharples, R. M., Romer, A. K., & Nichol, R. C. 2003, MNRAS, 341, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Clarkson, C. 2012, C. R. Phys., 13, 682 [Google Scholar]
- Courteau, S., Willick, J. A., Strauss, M. A., Schlegel, D., & Postman, M. 2000, ApJ, 544, 636 [NASA ADS] [CrossRef] [Google Scholar]
- Courtois, H. M., Hoffman, Y., Tully, R. B., & Gottlöber, S. 2012, ApJ, 744, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Cruddace, R., Voges, W., Böhringer, H., et al. 2002, ApJS, 140, 239 [NASA ADS] [CrossRef] [Google Scholar]
- DeDeo, S., Spergel, D. N., & Trac, H. 2005, unpublished [arXiv:astro-ph/0511060] [Google Scholar]
- Dekel, A., Bertschinger, E., Yahil, A., et al. 1993, ApJ, 412, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Delabrouille, J., Cardoso, J.-F., Le Jeune, M., et al. 2009, A&A, 493, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delabrouille, J., Betoule, M., Melin, J.-B., et al. 2013, A&A, 553, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dick, J., Remazeilles, M., & Delabrouille, J. 2010, MNRAS, 401, 1602 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Faber, S. M., Burstein, D., et al. 1987, ApJ, 313, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Bohringer, H., et al. 1998, MNRAS, 301, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Allen, S. W., et al. 2000, MNRAS, 318, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Barrett, E., Donovan, D., et al. 2007, ApJ, 661, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Ebeling, H., Edge, A. C., Mantz, A., et al. 2010, MNRAS, 407, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Feldman, H. A., Watkins, R., & Hudson, M. J. 2010, MNRAS, 407, 2328 [NASA ADS] [CrossRef] [Google Scholar]
- Finkbeiner, D. P., Davis, M., & Schlegel, D. J. 1999, ApJ, 524, 867 [NASA ADS] [CrossRef] [Google Scholar]
- García-Bellido, J., & Haugbølle, T. 2008, JCAP, 9, 16 [Google Scholar]
- Gioia, I. M., & Luppino, G. A. 1994, ApJS, 94, 583 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J. 1995, Phys. Rev. D, 52, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Groth, E. J., Juszkiewicz, R., & Ostriker, J. P. 1989, ApJ, 346, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Haehnelt, M. G., & Tegmark, M. 1996, MNRAS, 279, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Hand, N., Addison, G. E., Aubourg, E., et al. 2012, Phys. Rev. Lett., 109, 041101 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P. 2004, ApJ, 609, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, J. P., Mullis, C. R., Voges, W., et al. 2006, ApJS, 162, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Monteagudo, C., & Ho, S. 2009, MNRAS, 398, 790 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Monteagudo, C., & Rubiño-Martín, J. A. 2004, MNRAS, 347, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Hernández-Monteagudo, C., & Sunyaev, R. A. 2008, A&A, 490, 25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernández-Monteagudo, C., & Sunyaev, R. A. 2010, A&A, 509, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernández-Monteagudo, C., Verde, L., Jimenez, R., & Spergel, D. N. 2006, ApJ, 643, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Herranz, D., Sanz, J. L., Hobson, M. P., et al. 2002, MNRAS, 336, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Herranz, D., Sanz, J. L., Barreiro, R. B., & López-Caniego, M. 2005, MNRAS, 356, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Weiland, J. L., Hill, R. S., et al. 2009, ApJS, 180, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, S., DeDeo, S., & Spergel, D. 2009, unpublished [arXiv:astro-ph:0903.2845] [Google Scholar]
- Holzapfel, W. L., Ade, P. A. R., Church, S. E., et al. 1997, ApJ, 481, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Horner, D. J., Perlman, E. S., Ebeling, H., et al. 2008, ApJS, 176, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, M. J., Smith, R. J., Lucey, J. R., Schlegel, D. J., & Davies, R. L. 1999, ApJ, 512, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, M. J., Smith, R. J., Lucey, J. R., & Branchini, E. 2004, MNRAS, 352, 61 [Google Scholar]
- Inogamov, N. A., & Sunyaev, R. A. 2003, Astron. Lett., 29, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Itoh, Y., Yahata, K., & Takada, M. 2010, Phys. Rev. D, 82, 043530 [NASA ADS] [CrossRef] [Google Scholar]
- Juszkiewicz, R., Fisher, K. B., & Szapudi, I. 1998, ApJ, 504, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., & Atrio-Barandela, F. 2000, ApJ, 536, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Kocevski, D., & Ebeling, H. 2008, ApJ, 686, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Kocevski, D., & Ebeling, H. 2009, ApJ, 691, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., Ebeling, H., Edge, A., & Kocevski, D. 2010, ApJ, 712, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., & Ebeling, H. 2011, ApJ, 732, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kashlinsky, A., Atrio-Barandela, F., & Ebeling, H. 2012 [arXiv:1202.0717] [Google Scholar]
- Keisler, R. 2009, ApJ, 707, L42 [NASA ADS] [CrossRef] [Google Scholar]
- Kitayama, T., Komatsu, E., Ota, N., et al. 2004, PASJ, 56, 17 [NASA ADS] [Google Scholar]
- Kocevski, D. D., Ebeling, H., Mullis, C. R., & Tully, R. B. 2007, ApJ, 662, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Kogut, A., Lineweaver, C., Smoot, G. F., et al. 1993, ApJ, 419, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Lamarre, J., Puget, J., Ade, P. A. R., et al. 2010, A&A, 520, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lauer, T. R., & Postman, M. 1994, ApJ, 425, 418 [NASA ADS] [CrossRef] [Google Scholar]
- Lavaux, G., Afshordi, N., & Hudson, M. J. 2013, MNRAS, 430, 1617 [NASA ADS] [CrossRef] [Google Scholar]
- Leahy, J. P., Bersanelli, M., D’Arcangelo, O., et al. 2010, A&A, 520, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ma, C.-P., & Fry, J. N. 2002, Phys. Rev. Lett., 88, 211301 [NASA ADS] [CrossRef] [Google Scholar]
- Ma, Y.-Z., & Scott, D. 2013, MNRAS, 428, 2017 [NASA ADS] [CrossRef] [Google Scholar]
- Mak, D. S. Y., Pierpaoli, E., & Osborne, S. J. 2011, ApJ, 736, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Mandolesi, N., Bersanelli, M., Butler, R. C., et al. 2010, A&A, 520, A3 [Google Scholar]
- Melin, J.-B., Bartlett, J. G., & Delabrouille, J. 2006, A&A, 459, 341 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mennella, A., Butler, R. C., Curto, A., et al. 2011, A&A, 536, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mody, K., & Hajian, A. 2012, ApJ, 758, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Moss, A., Zibin, J. P., & Scott, D. 2011, Phys. Rev. D, 83, 103515 [NASA ADS] [CrossRef] [Google Scholar]
- Mroczkowski, T., Dicker, S., Sayers, J., et al. 2012, ApJ, 761, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Mullis, C. R., McNamara, B. R., Quintana, H., et al. 2003, ApJ, 594, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A., & Davis, M. 2011, ApJ, 736, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A., Branchini, E., & Davis, M. 2011, ApJ, 735, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, S. J., Mak, D. S. Y., Church, S. E., & Pierpaoli, E. 2011, ApJ, 737, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Perlman, E. S., Horner, D. J., Jones, L. R., et al. 2002, ApJS, 140, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Piffaretti, R., Arnaud, M., Pratt, G. W., Pointecouteau, E., & Melin, J.-B. 2011, A&A, 534, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011a, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011b, A&A, 536, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011c, A&A, 536, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011d, A&A, 536, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011e, A&A, 536, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011f, A&A, 536, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011g, A&A, 536, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011h, A&A, 536, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011i, A&A, 536, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011j, A&A, 536, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011k, A&A, 536, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011l, A&A, 536, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011m, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011n, A&A, 536, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011o, A&A, 536, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011p, A&A, 536, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011q, A&A, 536, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011r, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011s, A&A, 536, A24 [Google Scholar]
- Planck Collaboration 2011t, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2011u, A&A, 536, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration 2013, A&A, 550, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team. 2011a, A&A, 536, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck HFI Core Team. 2011b, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011a, MNRAS, 410, 2481 [NASA ADS] [CrossRef] [Google Scholar]
- Remazeilles, M., Delabrouille, J., & Cardoso, J.-F. 2011b, MNRAS, 418, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G. 2000, in Cosmic Flows Workshop, eds. S. Courteau, & J. Willick, ASP Conf. Ser., 201, 80 [Google Scholar]
- Romer, A. K., Nichol, R. C., Holden, B. P., et al. 2000, ApJS, 126, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Rosset, C., Tristram, M., Ponthieu, N., et al. 2010, A&A, 520, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schäfer, B. M., Pfrommer, C., Bartelmann, M., Springel, V., & Hernquist, L. 2006, MNRAS, 370, 1309 [NASA ADS] [CrossRef] [Google Scholar]
- Shao, J., Zhang, P., Lin, W., Jing, Y., & Pan, J. 2011, MNRAS, 413, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, R. K., & Diaferio, A. 2001, MNRAS, 322, 901 [Google Scholar]
- Strauss, M. A., & Willick, J. A. 1995, Phys. Rep., 261, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, I. B. 1980, MNRAS, 190, 413 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tonry, J. L., & Davis, M. 1981, ApJ, 246, 666 [NASA ADS] [CrossRef] [Google Scholar]
- Voit, G. M., Kay, S. T., & Bryan, G. L. 2005, MNRAS, 364, 909 [NASA ADS] [CrossRef] [Google Scholar]
- Walker, S. A., Fabian, A. C., Sanders, J. S., & George, M. R. 2012, MNRAS, 427, L45 [Google Scholar]
- Watkins, R., Feldman, H. A., & Hudson, M. J. 2009, MNRAS, 392, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Willick, J. A. 1999, ApJ, 522, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Yoo, C.-M., Nakao, K.-I., & Sasaki, M. 2010, JCAP, 10, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Zacchei, A., Maino, D., Baccigalupi, C., et al. 2011, A&A, 536, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, P., & Stebbins, A. 2011, Phys. Rev. Lett., 107, 041301 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, P., Feldman, H. A., Juszkiewicz, R., & Stebbins, A. 2008, MNRAS, 388, 884 [Google Scholar]
- Zibin, J. P. 2011, Phys. Rev. D, 84, 123508 [NASA ADS] [CrossRef] [Google Scholar]
- Zibin, J. P., & Moss, A. 2011, Class. Quant. Grav., 28, 164005 [NASA ADS] [CrossRef] [Google Scholar]
- Zibin, J. P., Moss, A., & Scott, D. 2008, Phys. Rev. Lett., 101, 251303 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Nominal and tSZ-effective frequencies, ΔT to ySZ conversion factors and FWHMs for each HFI channel used in this paper.
Estimated dipole coefficients (Cols. 2−4) and velocity magnitude (Col. 5) using the all-sky method.
Impact of uncertainties in estimates of the optical depth of clusters on the constraints imposed on the kSZ monopole, rms, and dipole from Planck data.
All Figures
 |
Fig. 1 Histogram of predicted values of τ5 R500, the cylindrical optical depth times solid angle out to R = 5 R500. |
| In the text | |
 |
Fig. 2 Locations of MCXC clusters outside the masked region. The colour scale indicates inverse noise squared at the positions of the MCXC clusters. The large coloured circles indicate directions for various dipole determinations: HFI dipole from MCXC cluster locations (green); HFI dipole from shifted positions (brown); CMB dipole (orange); Kashlinsky et al. (2010) dipole (red). The HFI dipole from MCXC cluster locations is compatible with CMB and Galactic residuals. |
| In the text | |
 |
Fig. 3 Colour coding common for all panels: black corresponds to the 100 GHz channel; red to 143 GHz; green to 217 GHz; and blue to the 2D-ILC map. Histograms are obtained from AP output at 100 displaced positions, while vertical dot-dashed lines correspond to AP outputs obtained on the clusters. The left panel refers to the AP output monopole/average, whereas the middle and right ones display histograms built upon rms estimates. |
| In the text | |
 |
Fig. 4 Dependence of the average radial velocity of clusters for different redshift bins. Note that the “no band colour” symbols are known to give unreliable results. For clarity, symbols within the same redshift bin have been slightly shifted horizontally. |
| In the text | |
 |
Fig. 5 Histogram of recovered radial peculiar velocities as estimated by the uMMF (black) and AP (red) implementations on HFI frequency maps. |
| In the text | |
 |
Fig. 6 Left panel: estimated rms of uMMF outputs at 100 random positions within the patch surrounding each MCXC cluster versus the corresponding peculiar velocity error as predicted by the uMMF. Middle panel: histogram of mean kSZ radial velocity estimated using all un-masked MCXC clusters, for the 101 positions considered in each cluster patch. The vertical, dashed red line corresponds to the average kSZ estimate when averaging throughout the patch centres, i.e., at the real cluster positions. Right panel: uMMF velocity rms histogram obtained for the MCXC cluster set, at different positions within the patches, just as for the middle panel. Again, the vertical dashed red line corresponds to the kSZ velocity rms estimated at real cluster positions (on patch centres). |
| In the text | |
 |
Fig. 7 Upper limits at the 95% confidence level for the dipole amplitude from MCXC clusters contained in local spheres of varying radii. Blue and black arrows denote limits for AP and uMMF methods, respectively. The upper limits are indicated by the tails of the arrows. The solid red line depicts the ΛCDM prediction. |
| In the text | |
 |
Fig. 8 Mollweide projection in Galactic coordinates of the upper limit (at 95% C.L.) of the kSZ dipole amplitude from applying the uMMF approach to HFI frequency maps using the whole MCXC cluster sample. In no direction is the dipole detected at more than 2σ. |
| In the text | |
 |
Fig. 9 Bulk flow amplitude measured in Planck data with the all-sky method, after subtraction (vectorially) of the Galactic contribution (black crosses), compared with 95% upper limits derived from simulations containing CMB and instrumental noise only (blue arrows) or also including tSZ signal (black arrows). The fact that the crosses are below the arrows at all scales shows that there is no significant bulk flow detection. |
| In the text | |
 |
Fig. 10 Monopole and dipole component estimates after applying the spatial filter of Kashlinsky et al. (2008) on WMAP-7 W-band data (black lines) and on Planck 2D-ILC maps (red lines). Estimates from real MCXC clusters are displayed by vertical, dot-dashed lines. Histograms are obtained after repeating the analysis on 1000 random cluster configurations, with averages indicated by the vertical, solid lines. The y-component appears discrepant here, but compare with Fig. 11. |
| In the text | |
 |
Fig. 11 Histograms of the recovered cluster dipole amplitude: (a) from the 1000 Monte Carlo random cluster configurations on the sky (solid black line); (b) from rotating one random cluster configuration in Galactic latitude on the real filtered map (triple dot-dashed blue line); (c) from rotating the real MCXC cluster configuration around the Galactic z axis on the real filtered map (dashed red line); and (d) from applying the filter on the position of our MCXC cluster sample in 1000 Monte Carlo CMB simulations following the WMAP-7 best-fit model (dot-dashed green lines). The dipole amplitude recovered at the real MCXC cluster positions on the real filtered map is shown by the vertical, solid line. It is not significantly detected, provided one is careful to simulate the most important noise contributions. |
| In the text | |
 |
Fig. 12 Same as Fig. 11, but restricting the analysis to the 200 most massive clusters outside the mask. The colour and line-style coding is identical to that figure. In this case, all histograms contain the measurement on the real positions of clusters (displayed by the vertical solid line). |
| In the text | |
 |
Fig. 13 Solid contours indicate log 10(ℒ/ℒhom) for the AP Planck frequency maps as a function of central matter density parameter, |
| In the text | |
 |
Fig. 14 Solid, red line: ratio of kSZ fluxes computed in circles centred on clusters with radii |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


