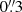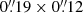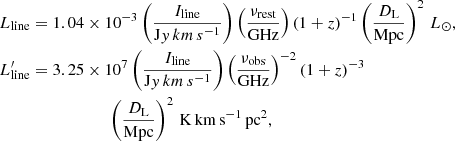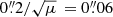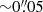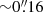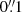| Issue |
A&A
Volume 624, April 2019
|
|
|---|---|---|
| Article Number | A138 | |
| Number of page(s) | 23 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833876 | |
| Published online | 26 April 2019 | |
CO, H2O, H2O+ line and dust emission in a z = 3.63 strongly lensed starburst merger at sub-kiloparsec scales⋆
1
European Southern Observatory, Alonso de Córdova 3107, Casilla, 19001 Vitacura, Santiago, Chile
e-mail: cyang@eso.org
2
Institut d’Astrophysique de Paris, Sorbonne Université, CNRS, UMR 7095, 98 bis bd Arago, 75014 Paris, France
3
Institut d’Astrophysique Spatiale, CNRS UMR 8617, Université Paris-Sud, Université Paris-Saclay, 91405 Orsay, France
4
Purple Mountain Observatory/Key Lab of Radio Astronomy, Chinese Academy of Sciences, Nanjing 210034, PR China
5
European Southern Observatory, Karl Schwarzschild Straße 2, 85748 Garching, Germany
6
Institute for Astronomy, University of Edinburgh, Royal Observatory, Blackford Hill, Edinburgh EH9 3HJ, UK
7
Centre for Extragalactic Astronomy, Durham University, Department of Physics, South Road, Durham, DH1 3LE, UK
8
National Radio Astronomy Observatory, 520 Edgemont Road, Charlottesville, VA 22903, USA
9
Joint ALMA Observatory, Alonso de Córdova 3107, Vitacura, Santiago, Chile
10
Institut de Radioastronomie Millimétrique (IRAM), 300 rue de la Piscine, 38406 Saint-Martin-d’Hères, France
11
Department of Physics and Astronomy, University of California, Irvine, CA 92697, USA
12
School of Physics and Astronomy, University of Nottingham, University Park, Nottingham NG7 2RD, UK
13
School of Physics and Astronomy, Cardiff University, The Parade, Cardiff CF24 3AA, UK
14
Department of Physics & Astronomy, University of Iowa, Iowa City, IA 52245, USA
15
Universidad de Alcalá, Departamento de Física y Matemáticas, Campus Universitario, 28871 Alcalá de Henares, Madrid, Spain
16
Instituto de Física y Astronomía, Universidad de Valparaíso, Avda. Gran Bretaña 1111, Valparaíso, Chile
17
Astronomical Observatory Institute, Faculty of Physics, Adam Mickiewicz University, ul. Słoneczna 36, 60-286 Poznań, Poland
18
Instituto de Astrofísica de Canarias, C/Vía Láctea, s/n, 38205 San Cristóbal de La Laguna, Tenerife, Spain
19
Universidad de La Laguna, Dpto. Astrofísica, 38206 San Cristóbal de La Laguna, Tenerife, Spain
20
Department of Astronomy, Cornell University, 220 Space Sciences Building, Ithaca, NY 14853, USA
21
Leiden Observatory, Leiden University, Post Office Box 9513, 2300 RA Leiden, The Netherlands
Received:
16
July
2018
Accepted:
28
February
2019
Using the Atacama Large Millimeter/submillimeter Array (ALMA), we report high angular-resolution observations of the redshift z = 3.63 galaxy H-ATLAS J083051.0+013224 (G09v1.97), one of the most luminous strongly lensed galaxies discovered by the Herschel-Astrophysical Terahertz Large Area Survey (H-ATLAS). We present 0.″2−0.″4 resolution images of the rest-frame 188 and 419 μm dust continuum and the CO(6–5), H2O(211−202), and Jup = 2 H2O+ line emission. We also report the detection of H2O(211−202) in this source. The dust continuum and molecular gas emission are resolved into a nearly complete ∼1.″5 diameter Einstein ring plus a weaker image in the center, which is caused by a special dual deflector lensing configuration. The observed line profiles of the CO(6–5), H2O(211−202), and Jup = 2 H2O+ lines are strikingly similar. In the source plane, we reconstruct the dust continuum images and the spectral cubes of the CO, H2O, and H2O+ line emission at sub-kiloparsec scales. The reconstructed dust emission in the source plane is dominated by a compact disk with an effective radius of 0.7 ± 0.1 kpc plus an overlapping extended disk with a radius twice as large. While the average magnification for the dust continuum is μ ∼ 10−11, the magnification of the line emission varies from 5 to 22 across different velocity components. The line emission of CO(6–5), H2O(211−202), and H2O+ have similar spatial and kinematic distributions. The molecular gas and dust content reveal that G09v1.97 is a gas-rich major merger in its pre-coalescence phase, with a total molecular gas mass of ∼1011 M⊙. Both of the merging companions are intrinsically ultra-luminous infrared galaxies (ULIRGs) with infrared luminosities LIR reaching ≳4 × 1012 L⊙, and the total LIR of G09v1.97 is (1.4 ± 0.7)×1013 L⊙. The approaching southern galaxy (dominating from V = −400 to −150 km s−1 relative to the systemic velocity) shows no obvious kinematic structure with a semi-major half-light radius of as = 0.4 kpc, while the receding galaxy (0 to 350 km s−1) resembles an as = 1.2 kpc rotating disk. The two galaxies are separated by a projected distance of 1.3 kpc, bridged by weak line emission (−150 to 0 km s−1) that is co-spatially located with the cold dust emission peak, suggesting a large amount of cold interstellar medium (ISM) in the interacting region. As one of the most luminous star-forming dusty high-redshift galaxies, G09v1.97 is an exceptional source for understanding the ISM in gas-rich starbursting major merging systems at high redshift.
Key words: galaxies: high-redshift / galaxies: ISM / gravitational lensing: strong / submillimeter: galaxies / radio lines: ISM / ISM: molecules
Reduced images and datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/624/A138
© ESO 2019
1. Introduction
Some of the most vigorous starbursts that have ever occurred are found in the high-redshift, dust-obscured submillimeter (submm) galaxies (SMGs, Smail et al. 1997; Barger et al. 1998; Hughes et al. 1998), or dusty star-forming galaxies (DSFGs, see e.g., reviews by Blain et al. 2002; Casey et al. 2014). With total infrared (IR) luminosities integrated over the rest-frame 8–1000 μm, LIR ≥ 1012 L⊙ (to even ≥1013 L⊙ for a few), SMGs reach the limit of “maximum starbursts” (Barger et al. 2014) with star formation rates (SFRs) that can exceed 1000 M⊙ yr−1 (e.g., Simpson et al. 2015a). Their extreme star formation rates indicate that these starburst galaxies are in the critical phase of rapid stellar mass growth, presumably consuming their gas reservoir on timescales ≲100 Myr. Such intense star formation seen in high-redshift SMGs is thought to be triggered by galaxy mergers or at least enhanced by interaction with neighboring galaxies (e.g., Hopkins et al. 2006; Tacconi et al. 2008; Engel et al. 2010; Ivison et al. 2000, 2012; Hayward et al. 2011, 2018; Kartaltepe et al. 2012; Hodge et al. 2012; Fu et al. 2013; Miettinen et al. 2017; Litke et al. 2019; Xue et al. 2018). This is consistent with ΛCDM (Lambda cold dark matter) simulations where merger rates are expected to increase with increasing redshift (e.g., Genel et al. 2009; Fakhouri et al. 2010; Rodriguez-Gomez et al. 2015). Nevertheless, some simulations predict that such intense star formation can also be produced through secular processes, which are driven by high gas fraction and instabilities in isolated clumpy disks at high redshift (e.g., Dekel et al. 2009; Davé et al. 2010). Such a scenario is also supported by observations (e.g., Tacconi et al. 2013; Hodge et al. 2016; Jiménez-Andrade et al. 2018).
Spectroscopic follow-up observations determined a median redshift of z ∼ 2.5 for the SMG population discovered at 870 μm (e.g., Chapman et al. 2005; Danielson et al. 2017), showing that they participate in the peak of the cosmic star formation rate density (Madau & Dickinson 2014) at z ∼ 2−3 (e.g., Chapman et al. 2005; Murphy et al. 2011a; Magnelli et al. 2013; Swinbank et al. 2014). In fact, relatively bright submm sources with S850 μm > 1 mJy contribute a significant fraction to the cosmic star formation rate at this epoch (≳10%, e.g., Le Floc’h et al. 2005; Murphy et al. 2011a; Magnelli et al. 2013; Swinbank et al. 2014; Dunlop et al. 2017; Michałowski et al. 2017). These high-redshift SMGs have many properties consistent with being progenitors of the local massive spheroidal galaxies (e.g., Lilly et al. 1999; Simpson et al. 2014; Toft et al. 2014; Gómez-Guijarro et al. 2018). They play a critical role in our understanding of the history of cosmic star formation and the physical processes underlying the most extreme phases of galaxy formation and evolution, although their nature remains hotly debated (e.g., Chakrabarti et al. 2008; Davé et al. 2010; Narayanan et al. 2015). This ongoing debate is sustained, at least in part, because the sensitivity and/or resolution of current observations are insufficient to unravel a complete picture of the complex physical conditions and spatial structure of their interstellar media (ISM) and of the processes that regulate the vigorous star formation.
Gravitational lensing provides one means to study the properties of the gas and dust at high spatial resolution and signal-to-noise ratio (S/N) in high-redshift galaxies by boosting the apparent flux and magnifying the apparent solid angle (e.g., Negrello et al. 2010; Swinbank et al. 2010; Riechers et al. 2011a; Conley et al. 2011; Dessauges-Zavadsky et al. 2015; Motta et al. 2018). At submm wavelengths, strongly lensed SMG candidates can be efficiently selected by applying a simple flux cut to survey images at far-IR, submm, and millimeter (mm) wavelengths, e.g., S500 μm > 100 mJy (Negrello et al. 2007, 2010, 2017; Wardlow et al. 2013). Although strongly lensed SMGs are rare, ≲0.3 deg−2, statistically significant samples have recently become available, thanks to extragalactic wide-area surveys such as the Herschel-Astrophysical Terahertz Large Area Survey (H-ATLAS, where sources are selected at 500 μm, Eales et al. 2010), the Herschel Multi-tiered Extragalactic Survey (HerMES, also selected at 500 μm, Oliver et al. 2012), the South Pole Telescope (SPT, 1.4 mm selected, Vieira et al. 2013), and the Planck all-sky survey (e.g., Planck Collaboration Int. XXVII 2015; Cañameras et al. 2015). These surveys have enabled the discovery and follow-up of hundreds of strongly lensed SMGs.
One of the most direct ways to understand the nature of these star-bursting dusty SMGs is by studying the raw ingredients that fuel their star formation, namely the content of their ISM. Such follow-up studies of the lensed SMGs have become routine (e.g., Cox et al. 2011; Gavazzi et al. 2011; Omont et al. 2011, 2013; Valtchanov et al. 2011; Fu et al. 2012; Lupu et al. 2012; Vieira et al. 2013; Bothwell et al. 2013; Messias et al. 2014; Dye et al. 2015; Cañameras et al. 2015, 2018; Swinbank et al. 2015; Aravena et al. 2016a; Spilker et al. 2016, 2018; Yang et al. 2016, 2017; Oteo et al. 2017; Wardlow et al. 2017; Andreani et al. 2018; Harrington et al. 2018; Zhang et al. 2018a; Marrone et al. 2018). However, most of these studies are limited in spatial resolution and only investigate their globally averaged properties. Spatially resolved observations with angular resolution approaching the characteristic scales of star-forming regions are still rare (e.g., Swinbank et al. 2015; Cañameras et al. 2017; Dye et al. 2018; Sharda et al. 2018; Massardi et al. 2018). In order to understand the detailed physical properties of high-redshift SMGs, especially their complex intrinsic structures, it is crucial to acquire high angular resolution images. From such data, fundamental information about gas and dust with different properties (e.g., density, temperature, optical depth, and mass) can be gained and related to the spatial and kinematical structures within individual sources.
However, high spatial-resolution observations of the ISM in SMGs remain a technical challenge, mostly due to their great distances. Indeed, such observations require high-sensitivity, long-baseline interferometric observations at submm/mm wavelengths. At z = 3.6, a 1″ beam translates into a physical resolution of ∼7 kpc, which is comparable to the typical total extent of cold molecular gas reservoir within SMGs (e.g., Ivison et al. 2011, 2016; Swinbank et al. 2011; Riechers et al. 2011b; Sharon et al. 2013; Thomson et al. 2015), and ≳5 times larger than the size of its star-forming dense warm gas regions (e.g., ∼1 kpc, Tacconi et al. 2008; Riechers et al. 2013; Spilker et al. 2015; Swinbank et al. 2015; Hodge et al. 2015, 2016; Simpson et al. 2015b). Reaching spatial resolutions below 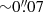 (∼500 pc physical resolution), which are needed to resolve the star-forming dense warm gas regions of high-redshift SMGs, remains challenging for current observing facilities. Nevertheless, the magnification provided by strong gravitational lensing can boost the angular spatial resolving power by typical factors of ∼2−5 (e.g., Bussmann et al. 2013, 2015; Spilker et al. 2016), enabling us, in such cases, to perform high angular resolution observations with reasonable on-source integration times.
(∼500 pc physical resolution), which are needed to resolve the star-forming dense warm gas regions of high-redshift SMGs, remains challenging for current observing facilities. Nevertheless, the magnification provided by strong gravitational lensing can boost the angular spatial resolving power by typical factors of ∼2−5 (e.g., Bussmann et al. 2013, 2015; Spilker et al. 2016), enabling us, in such cases, to perform high angular resolution observations with reasonable on-source integration times.
One of the brightest strongly lensed high-redshift SMGs in the H-ATLAS fields, J083051.0+013224 (hereafter G09v1.97), at z = 3.63 (the redshift was firstly measured from blind CO detections, Riechers et al., in prep., see Bussmann et al. 2013), is an ideal source for high spatial resolution observations. With a magnification factor of μ = 6.9 ± 0.6, estimated from 880 μm dust continuum observations with the SMA (Bussmann et al. 2013), the effective sensitivity is boosted by one order of magnitude and the angular resolution by an average factor of ∼3. Using the 1″ SMA observation (Bussmann et al. 2013) of G09v1.97, a spatial resolution of down to ∼2 kpc scales has been reached in the reconstructed source plane. G09v1.97 is intrinsically luminous in the far-infrared (far-IR) with an estimated intrinsic total IR luminosity of LIR ∼ 2.3 × 1013 L⊙ and a star formation rate surface density of ∼700 M⊙ yr−1 kpc−2 (taking the SMA-measured half-light radius size of 0.9 kpc). The total molecular gas mass is estimated to be (1.1 ± 0.5) × 1011 M⊙ (derived from 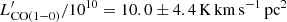 using a CO-to-gas-mass conversion factor of 0.8 M⊙(K km s−1 pc2)−1), with a gas density
using a CO-to-gas-mass conversion factor of 0.8 M⊙(K km s−1 pc2)−1), with a gas density 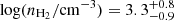 and a kinematic temperature log(Tkin/K) = 2.30 ± 0.47 (Yang et al. 2017).
and a kinematic temperature log(Tkin/K) = 2.30 ± 0.47 (Yang et al. 2017).
Here we present ALMA observations of the dust continuum, CO, H2O, and H2O+ line emission in G09v1.97 at spatial resolutions of 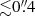 . Based on a lens model, the spatial distribution and kinematical structures of the molecular gas can be derived at angular resolutions
. Based on a lens model, the spatial distribution and kinematical structures of the molecular gas can be derived at angular resolutions 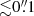 in the source plane. The physical properties traced by the molecular line and dust emission can thus be spatially resolved on sub-kiloparsec (sub-kpc) scales, helping us to gain insight of the high-redshift SMG population. The paper is organized as follows: the observations and results are reported in Sect. 2; Sect. 3 describes the properties of the continuum and emission line images and the characteristics of the molecular line spectra; the lens modeling is outlined in Sect. 4; Sect. 5 discusses the properties of the molecular gas and dust continuum in the source plane, including the gas kinematics. Finally, concluding remarks are given in Sect. 6.
in the source plane. The physical properties traced by the molecular line and dust emission can thus be spatially resolved on sub-kiloparsec (sub-kpc) scales, helping us to gain insight of the high-redshift SMG population. The paper is organized as follows: the observations and results are reported in Sect. 2; Sect. 3 describes the properties of the continuum and emission line images and the characteristics of the molecular line spectra; the lens modeling is outlined in Sect. 4; Sect. 5 discusses the properties of the molecular gas and dust continuum in the source plane, including the gas kinematics. Finally, concluding remarks are given in Sect. 6.
Throughout this work, we adopt a spatially flat ΛCDM cosmology with H0 = 67.8 ± 0.9 km s−1 Mpc−1, ΩM = 0.308 ± 0.012 (Planck Collaboration XIII 2016), with an angular-size scale of 7.4 kpc/″ at z = 3.632. Using a Chabrier (2003) initial mass function (IMF), the calibration of the far-IR star formation rate (SFR) from Kennicutt & Evans (2012) gives a relation of SFR = 1.4 × 10−10 (LIR/L⊙) M⊙ yr−1 (see also Murphy et al. 2011b).
2. Observations and data reduction
The z = 3.6321 strongly lensed SMG, G09v1.97 was observed in the 2 mm atmospheric window (Band 4) with the Atacama Large Millimeter/submillimeter Array (ALMA), in the project ADS/JAO.ALMA#2015.1.01320.S (PI: A. Omont). The observations used four spectral windows (SPW) covering two observed frequency ranges of 147.146–150.064 GHz and 159.278–162.819 GHz (see Table 1 for details). Data were acquired during two observing executions on 04-Aug-2016 and 25-Aug-2016, using 39 and 38 12 m antennas, respectively. The observations were performed with the ALMA C36-5 configuration, which provides baselines from 15 m up to about 1462 m, resulting in angular resolutions of 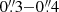 (with a Briggs robust weighting parameter of 0.5). The on-source integration time was 36.8 min for each execution, amounting to a total of 73.8 min on-source time, with a total amount of time for additional overheads of 54.8 min. The overheads include pointing, focusing, phase, flux density and bandpass calibrations. J0825+0309 was used as the phase calibrator and J0750+1231 as the bandpass calibrator. The flux calibrators were J0750+1231 and J0854+2006. A typical ALMA calibration uncertainty of 5% is adopted for the Band 4 data. J0839+0104 was also used as a check source2. The total available 7.5 GHz bandwidth of Band 4 was divided into four SPWs (i.e., SPW-0, SPW-1, SPW-2 and SPW-3, see Table 1 for details), each 1875 MHz wide, covering the major targeted lines of G09v1.97, i.e., CO(6–5) at 149.207 GHz, para-H2O(211−202)(H2O(211−202) hereafter) at 161.946 GHz and series of H2O+ lines (H2O+(202−111)(5/2−3/2) at the rest-frequency of 742.1 GHz and H2O+(211−202)(5/2−3/2) at the rest-frequency of 742.3 GHz) with a representative frequency of 160.124 GHz. In each spectral window, there are 128 frequency channels giving a resolution of 15.6 MHz (∼30 km s−1). The dust continuum in Band 4 is measured by combining all the line-free channels, resulting a representative frequency at 154.508 GHz corresponding to 1.94 mm or ∼419 μm in the rest-frame. The weather conditions were good with low water vapor and stable phase during the two observing sessions as summarized in Table 1. The root mean square (RMS) of the data reaches 0.21 mJy beam−1 in a 50 km s−1 channel width.
(with a Briggs robust weighting parameter of 0.5). The on-source integration time was 36.8 min for each execution, amounting to a total of 73.8 min on-source time, with a total amount of time for additional overheads of 54.8 min. The overheads include pointing, focusing, phase, flux density and bandpass calibrations. J0825+0309 was used as the phase calibrator and J0750+1231 as the bandpass calibrator. The flux calibrators were J0750+1231 and J0854+2006. A typical ALMA calibration uncertainty of 5% is adopted for the Band 4 data. J0839+0104 was also used as a check source2. The total available 7.5 GHz bandwidth of Band 4 was divided into four SPWs (i.e., SPW-0, SPW-1, SPW-2 and SPW-3, see Table 1 for details), each 1875 MHz wide, covering the major targeted lines of G09v1.97, i.e., CO(6–5) at 149.207 GHz, para-H2O(211−202)(H2O(211−202) hereafter) at 161.946 GHz and series of H2O+ lines (H2O+(202−111)(5/2−3/2) at the rest-frequency of 742.1 GHz and H2O+(211−202)(5/2−3/2) at the rest-frequency of 742.3 GHz) with a representative frequency of 160.124 GHz. In each spectral window, there are 128 frequency channels giving a resolution of 15.6 MHz (∼30 km s−1). The dust continuum in Band 4 is measured by combining all the line-free channels, resulting a representative frequency at 154.508 GHz corresponding to 1.94 mm or ∼419 μm in the rest-frame. The weather conditions were good with low water vapor and stable phase during the two observing sessions as summarized in Table 1. The root mean square (RMS) of the data reaches 0.21 mJy beam−1 in a 50 km s−1 channel width.
ALMA observation log of G09v1.97.
We have also included in this study ALMA Band 7 continuum archive data of G09v1.97 centered at 343.494 GHz (ADS/JAO.ALMA#2013.1.00358.S, PI: S. Eales, for further discussion of this dataset, see Amvrosiadis et al. 2018), which allow us to have a better constrain of the lens model and perform a detailed analysis of the spatial distribution and properties of dust emission. The observed frequency corresponds to a wavelength of 0.873 mm, or ∼188 μm in the rest-frame. The observations were performed on 01-Sep-2015 in good weather conditions, with 3.1 minutes on source time and a maximum baseline of 1.6 km, yielding a synthesis beam of 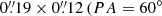 ). The bandpass, flux and phase calibrators were J0739+0137, J0510+1800, and J0839+0104, respectively. The absolute flux calibration uncertainty in Band 7 is 10%. Table 1 summarizes the details of the observations.
). The bandpass, flux and phase calibrators were J0739+0137, J0510+1800, and J0839+0104, respectively. The absolute flux calibration uncertainty in Band 7 is 10%. Table 1 summarizes the details of the observations.
Both datasets were calibrated using the ALMA calibration pipelines, with only minor flagging required. The calibrated data were then imaged and CLEANed using tclean within CASA3 version 5.1.1, with a Briggs robust weighting factor of −0.5 for the Band 4 dust continuum to generate CLEAN-component models. All the line free channels were combined by using the MS-MFS algorithm (Rau & Cornwell 2011) with multiple Taylor terms nterms=2 during the CLEAN process. We then performed several iterations of phase-only self-calibration until the S/N stopped improving. The typical phase variations are within ±50 deg and change smoothly with time. Accordingly, the corresponding gaincal solutions were applied to the entire dataset. After subtracting the dust continuum for the line emission data cube, the datasets were then CLEANed with a Briggs robust weighting factor of −0.5 for the dust continuum (using again nterms=2, combining all line-free channels), −0.2 for the CO emission, and 0.5 for the H2O and H2O+ emission, considering the optimization between the synthesized beamsize and achieved S/N level of the CLEANed images. Similar procedures of self-calibration data reduction for the Band 7 dust continuum were also performed to maximize the S/N.
3. Results
3.1. Continuum and emission line images
The ALMA images of the dust continuum and the CO(6–5), H2O(211−202), and H2O+ line emission of G09v1.97 are displayed in Fig. 1. In the upper row, the ALMA Band 4 dust continuum emission at 1.94 mm (∼419 μm in the rest-frame), at a resolution of 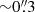 , is shown next to the Band 7 dust continuum at 0.87 mm (rest-frame ∼188 μm) at
, is shown next to the Band 7 dust continuum at 0.87 mm (rest-frame ∼188 μm) at 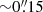 . Both the dust continuum images show a very similar structure with a nearly complete
. Both the dust continuum images show a very similar structure with a nearly complete 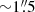 diameter Einstein ring, with three major image components. This is in agreement with the SMA 880 μm dust continuum image (Bussmann et al. 2013). In addition, there is a weaker and smaller image component at the center, which was undetected with the SMA. Among the three image components, the one to the south is by far the brightest. Finally, there is extended emission which connects the southern and northern components along the eastern side of the ring.
diameter Einstein ring, with three major image components. This is in agreement with the SMA 880 μm dust continuum image (Bussmann et al. 2013). In addition, there is a weaker and smaller image component at the center, which was undetected with the SMA. Among the three image components, the one to the south is by far the brightest. Finally, there is extended emission which connects the southern and northern components along the eastern side of the ring.
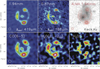 |
Fig. 1. ALMA images of the dust continuum and molecular gas emission in G09v1.97. Upper row – from left to right: 1.94 mm (rest-frame ∼419 μm) dust continuum image with |
We also show the 1.94 mm dust continuum superimposed on the Keck-II/NIRC2 Ks-band image in Fig. 1. The figure shows the two foreground deflecting galaxies, the southern galaxy at z = 0.626 (G1) and the northern one at z = 1.002 (G2), with the redshifts obtained from the William Herschel Telescope (WHT) ACAM spectroscopy through the detection of the Mg absorption and the [O II]λλ3726,3729 doublet lines, respectively. A Hubble Space Telescope (HST) image taken in the F110W band, which was obtained as part of the ID 12488 Snapshot program (PI: Negrello), also confirms such a compound lens configuration4. The unusual line-of-sight configuration, with two deflecting galaxies, complicates the model of the gravitational potential (Sect. 4). This produces a central image that is not too de-magnified which is rarely seen in lensing configurations involving a single deflector with a cuspy mass distribution.
G09v1.97 is neither detected in the Keck-II Ks-band (rest-frame 463 nm) nor in the HST F110W-band (rest-frame 221 nm) image, by checking the images after subtracting the foreground galaxies with GALFIT (Peng et al. 2002). Comparing the rest-frame 419 μm dust continuum contours with the Keck-II image, it is evident that the contribution to the dust continuum from the two foreground deflectors is negligible. Finally, the similarities of the redshift and the profiles of the molecular line emission of the central component with the components along the Einstein ring rules out that this central emission is related to the deflecting galaxies.
Figure 1 also shows the continuum-subtracted images with 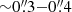 resolution of the velocity-integrated molecular line emission of CO(6–5), H2O(211−202), and H2O+ (integrated over the rest-frame 742.1 GHz H2O+(202−111)(5/2−3/2) line in SPW-1 and the 746.5 GHz H2O+(211−202)(5/2−5/2) line in SPW-0). Taking into account the range in S/N, all three molecular gas lines display a nearly complete Einstein ring morphology, akin to the one seen in the dust continuum emission, with a dominant sub-image in the south. The weak central image is detected in CO(6–5) and H2O(211−202) but not in H2O+. Nevertheless, the upper-limit from the H2O+ image is consistent with the flux ratios between the three sub-images and the central component found in the dust continuum, the CO(6–5) and H2O(211−202) line images. By comparing the detailed differences between the line emission and the dust continuum, we find that the CO(6–5) line emission has a more extended morphology and resembles a more complete ring-like structure compared to the dust emission. Comparing the ratios between the brightest southern component and the two weaker ones in the northwest and northeast, the dust continuum of the southern component is about twice as bright, while for the CO(6–5) line emission, the ratio ranges from 1.3 to 1.7 (≲20% uncertainties), and about 1.5 (with a larger uncertainty) for the H2O emission. This indicates that the rest-frame ∼200−400 μm dust emission is slightly more concentrated than the CO and H2O line emission. Finally, the H2O+ emission is detected in the brightest southern component at ∼4-σ, while it is only marginally detected in the two other components with signal-to-noise ratios of about 3 (Fig. 1).
resolution of the velocity-integrated molecular line emission of CO(6–5), H2O(211−202), and H2O+ (integrated over the rest-frame 742.1 GHz H2O+(202−111)(5/2−3/2) line in SPW-1 and the 746.5 GHz H2O+(211−202)(5/2−5/2) line in SPW-0). Taking into account the range in S/N, all three molecular gas lines display a nearly complete Einstein ring morphology, akin to the one seen in the dust continuum emission, with a dominant sub-image in the south. The weak central image is detected in CO(6–5) and H2O(211−202) but not in H2O+. Nevertheless, the upper-limit from the H2O+ image is consistent with the flux ratios between the three sub-images and the central component found in the dust continuum, the CO(6–5) and H2O(211−202) line images. By comparing the detailed differences between the line emission and the dust continuum, we find that the CO(6–5) line emission has a more extended morphology and resembles a more complete ring-like structure compared to the dust emission. Comparing the ratios between the brightest southern component and the two weaker ones in the northwest and northeast, the dust continuum of the southern component is about twice as bright, while for the CO(6–5) line emission, the ratio ranges from 1.3 to 1.7 (≲20% uncertainties), and about 1.5 (with a larger uncertainty) for the H2O emission. This indicates that the rest-frame ∼200−400 μm dust emission is slightly more concentrated than the CO and H2O line emission. Finally, the H2O+ emission is detected in the brightest southern component at ∼4-σ, while it is only marginally detected in the two other components with signal-to-noise ratios of about 3 (Fig. 1).
Our three-dimensional ALMA data cubes allow us to further study the kinematics of the CO(6–5) and H2O(211−202) emitting gas. Figure 2 shows the moment maps of the CLEANed CO(6–5) and H2O(211−202) data cubes. Both the moment maps of CO and H2O show very similar distributions in velocity and dispersion, although comparing the moments maps of H2O with the other lines is hindered by the lower S/N. The moment maps reveal noticeable velocity gradients in its major southern and northern components as shown in the 1st moment maps and are possibly arising from the same lensed structure from the source plane. The velocity dispersion distributions compared to the 1st moment maps show similar structure among the three image components (and only for two components in H2O(211−202) due to the low S/N in the central component), with the peaks in velocity dispersion being slightly spatially offset from the continuum flux peaks.
 |
Fig. 2. 1st moment (velocity, left two panels) and 2nd moment (velocity dispersion, right two panels) color maps of the CO(6–5) and H2O(211−202) line emission overlaid by the 0th moment (velocity-integrated line emission) contours. The images reveal the strongly lensed kinematic structure of G09v1.97 in the image plane in both CO(6–5) and H2O(211−202), with a significant velocity gradient seen in the northeastern and southern components. The CO and H2O lines trace similar kinematic structure as shown by the close correspondence between their first and second moment maps. |
To better compare the dust continuum and the CO(6–5) and H2O(211−202) line emission, in Fig. 3 we show the ratio of the dust continuum to the 0th moment of CO(6–5), as well as the CO(6–5)-to-H2O(211−202) ratio of the 0th and 1st moments. The map of SCOVCO/S1.94 shows clear evidence that the emission of CO(6–5) is more extended than the dust continuum at rest-frame 419 μm. And there is indeed an offset between the dust and CO/H2O emission peaks. The difference in sizes is consistent with several previous observations that the size of dust continuum is usually found smaller than the gas tracers such as the low- and mid-J CO lines (e.g., Riechers et al. 2011a; Ivison et al. 2011; Spilker et al. 2015; Chen et al. 2017; Calistro Rivera et al. 2018; Hodge et al. 2018). This could be caused by a radial dust temperature gradient (see, e.g., Miettinen et al. 2017). The 0th moment ratio of CO(6–5) to H2O(211−202) shows small variations, having flux ratios between CO(6–5) and H2O(211−202)∼1.7−2.8 with an average value of 2.4. The velocity structure of the two gas tracers are almost identical, with a ratio VCO/VH2O = 1.0 ± 0.2.
 |
Fig. 3. Top left: ratio of the 0th moment of CO(6–5) to the rest-frame 419 μm (observed wavelength of 1.94 mm) continuum. The contours are for the CO(6–5) 0th moment and are the same as in Fig. 2. Top right: 1st moment ratio map of CO(6–5) to H2O(211−202). Bottom left: 0th moment ratio map of CO(6–5) to H2O(211−202). Bottom right: histogram of the CO(6–5)-to-H2O(211−202) 0th moment ratio. The positions of the dust peak at north and south are indicated with yellow stars. The figure shows that the CO(6–5) emission is more extended than the dust continuum emission. Despite the small variation of the 0th moment ratio, CO(6–5) and H2O(211−202) show very similar velocity structure. |
3.2. Integrated spectra
The continuum-subtracted spectrum integrated over the entire source is shown in Fig. 4. The upper panel shows the combined spectra of the 2 mm windows SPW-0 and SPW-1 of the H2O and H2O+ lines, while the lower shows the CO(6–5) line covered by SPW-2. In addition to the strong CO(6–5) and H2O emission lines, there is a series of H2O+ emission lines including the dominant H2O+ feature, i.e., H2O+(211−202) (5/2−5/2) and H2O+(202−111)(5/2−3/2) (based on the analysis of the expected relative strengths of the H2O+ submm lines in Arp 220 by González-Alfonso et al. 2013). We also detect an emission line at 745 GHz, which will be discussed at the end of this section.
 |
Fig. 4. Spatially integrated, continuum-subtracted 2 mm spectra of G09v1.97 with a spectral resolution of 35 km s−1. The vertical dotted lines represent the expected central positions of the lines. As argued in the text, that the weak emission at ∼745 GHz feature is likely dominated by the H2O(211−202) line. The dot-dashed lines represent the corresponding Gaussian decompositions: blue represents the approaching gas component (marked as “B”) while orange and red represent the blue-shifted Gaussian component (marked as “Rb”) and red-shifted Gaussian component (marked as “Rr”) of the receding gas, respectively. The solid green line shows the sum. The average noise level of the spectra is ∼0.2 mJy with a spectral resolution of 50 km s−1. Top: rest-frame 738–755 GHz spectrum combining SPW-0 and SPW-1. The light-blue shaded area indicates the 746–746.5 GHz gap between SPW-0 and SPW-1. The H2O(211−202) line and the H2O+(202−111)(5/2−5/2) line are fitted with a single Gaussian profile due to limited S/N and the lack of data in the inter-band gap. Bottom: SPW-2 spectrum of CO(6–5). The dot-dashed and solid lines are the same as in the top panel. The left inset shows the fit of the spectrum using two Gaussian profiles (green lines). It is clear that a double-Gaussian profile does not fit well the total line profile of the source. It is because of this, we introduced a third Gaussian component in the fit. The right inset shows a comparison among the line profiles of CO(6–5), H2O(211−202), and H2O+(202−111)(5/2−3/2). They are found to be similar, indicating a similar spatial distribution of the line-emitting regions. |
After extracting the spectra integrated over the entire spatial region of the source, the emission lines were fitted with multiple Gaussian profiles using the Levenberg-Marquardt least-square minimization code MPFIT (Markwardt 2009). Initially, two Gaussian components were fitted. However, as indicated in Fig. 4, fitting the profile with two Gaussians results in significant residuals in the blue part of the line profiles. Therefore, we fitted the lines with three Gaussian components. The overall line profile of all the emission lines are well fitted by the three Gaussian components which we mark with “B”, “Rb”, and “Rr” in Fig. 4. Since the line profiles of the CO(6–5), H2O, and H2O+ lines agree very well with each other (Fig. 4), we fix the linewidths of the B, Rb, and Rr components to be that found for the components of the CO(6–5) line and use these line widths when fitting the profiles of the H2O and H2O+ lines. The results obtained, i.e., the velocity integrated line fluxes, linewidths (FWHM) and line centroid positions are given in (Table 2). The total integrated line fluxes for CO(6–5) and H2O(211−202) are comparable to those obtained with the IRAM 30 m telescope and NOEMA (Yang et al. 2016, 2017) indicating that there is no missing flux in the ALMA data of G09v1.97. This implies that there is no significant diffuse emission (compared with the synthesis beam size) from either the dust continuum or any of the lines studied here.
Molecular line properties derived from the integrated spectra of G09v1.97.
We note that the blue-shifted component (B) in the spectrum slightly alters the CO redshift from z = 3.634, derived from the lower S/N IRAM 30 m data (Yang et al. 2017) where only the dominant red-shifted velocity component (consisting of the components Rb and Rr) was detected, to z = 3.632. This new redshift is defined by the central line position as the center of the full width at zero intensity, representing the overall redshift of the entire system. We will consistently use z = 3.632 as the redshift for G09v1.97 in this work.
The spectra of the CO(6–5), H2O(211−202), and H2O+ lines have very similar profiles (Fig. 4), composed of three Gaussian components, “B”, “Rb”, and “Rr”. The observed velocity-integrated flux ratios between the three components are similar for the three lines within the uncertainties. The overall profiles display pronounced asymmetries with a strong red-shifted peak and a weak blue-shifted wing. The blue-shifted wing shows a single approaching gas component B centered at velocity of −240 km s−1, with a FWHM of ∼300 km s−1 and most of its fluxes resides at negative velocities. The strong (receding) red-shifted peak emission feature can be explained by the two Gaussian components Rb and Rr, dominating the fluxes in positive velocity channel bins. The linewidths for Rb and Rr are somewhat different (see Table 2), and both components are close in velocity, peaking at 100 and 237 km s−1, respectively. This suggests that Rb and Rr are likely closely related. The peak flux ratio of Rr to Rb is ∼1.3 for the lines. The possible origin of the asymmetrical line profile could be an intrinsic asymmetrical line profile or/and differential lensing. The peak of the B component is ∼4 times weaker compared to the overall receding gas (Rb+Rr), and the linewidth is 1.5 times narrower (Table 2). The fact that the velocity separation between the component B and the group Rb/Rr is much larger than the velocity separation between Rb and Rr is an indication that B is likely to be a distinct velocity component. We will further discuss the nature of these velocity components in the following sections using position-velocity (PV) diagrams in the source plane after correcting for the gravitational lensing.
The significant similarity among the gas tracers strongly suggests that the emitting regions overlap for the CO(6–5), H2O(211−202), and H2O+ lines, which is also supported by their similar moment maps (Fig. 2). All these similarities in the spatial and kinematical distributions for the lines indicate that these gas tracers and the dust continuum emission are closely related to the similar active star-forming regions (see Yang et al. 2016, 2017, who analyzed the gas excitation reaching a similar conclusion). We will further discuss the possible scenarios of the asymmetrical line profiles and compare the spatial and kinematical structure of CO(6–5) and H2O(211−202) in the source plane in Sect. 5.
We derive the apparent line luminosities, μLline and 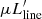 , via (see Solomon et al. 1992)
, via (see Solomon et al. 1992)
from the observed line flux densities. Iline is the velocity integrated line flux, νrest and νobs are the rest-frame and observed frequencies, and DL is the luminosity distance. The apparent CO line luminosity is around (4–10) × 108 L⊙ or (4–9) × 1010 K km s−1 pc2, which is about 7 × 10−6 weaker than the apparent LIR, while for the H2O line, the line luminosity is about 2–3 times lower than the CO line (for B, Rb, and Rr), i.e., about (2–4) × 108 L⊙ or (1–3) × 1010 K km s−1 pc2. The H2O+ lines are ∼3–4 times weaker than the H2O(211−202) line (Table 2).
At a rest-frame frequency of ∼745 GHz, we observe a 5-σ emission line with an integrated flux of 0.5 ± 0.1 Jy km s−1 and a linewidth of 250 ± 58 km s−1. A similar emission line has also been observed at ∼745.3 GHz in another H-ATLAS source, NCv1.143 (H-ATLAS J125632.7+233625), at a significance of 3-σ (Yang et al. 2016), and was tentatively identified as the H2O(211−202) line. The detected 5-σ emission at ∼745 GHz corresponds to the position of the Rb+Rr component of the rest-frame 745.320 GHz H2O(211−202) line. Therefore, the line is likely to be H2O(211−202). Strong absorption lines of 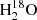 which are excited by far-IR pumping have been observed in local luminous IR galaxies (ULIRGS, defined by 1012 L⊙ < LIR < 1013 L⊙) with Herschel/PACS, indicate enhanced abundance ratios of
which are excited by far-IR pumping have been observed in local luminous IR galaxies (ULIRGS, defined by 1012 L⊙ < LIR < 1013 L⊙) with Herschel/PACS, indicate enhanced abundance ratios of 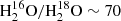 (e.g., in Arp 220, González-Alfonso et al. 2012, and, with possibly higher ratios in Mrk 231, Fischer et al. 2010; González-Alfonso et al. 2014a, 2018) suggesting that this line might be ubiquitous in starburst galaxies, and could potentially help us constrain the abundance of
(e.g., in Arp 220, González-Alfonso et al. 2012, and, with possibly higher ratios in Mrk 231, Fischer et al. 2010; González-Alfonso et al. 2014a, 2018) suggesting that this line might be ubiquitous in starburst galaxies, and could potentially help us constrain the abundance of 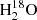 at high redshift.
at high redshift.
Another possible identification of this emission line is N2H+(8–7) at 745.210 GHz. However, we rule out this identification for the following reasons. N2H+ is known to be a tracer of the quiescent gas associated with dense, cold star-forming cores (e.g., Bachiller 1996; Caselli et al. 2002) and is therefore less likely to be detected in a intense starburst like G09v1.97. The first high-redshift detection of N2H+ was discussed in Wiklind & Combes (1996), but only absorption against the background radio source PKS 1830−211. Recently, Feruglio et al. (2017) reported an emission line at 94.83 GHz in the quasar APM 08279+5255, which they tentatively identified as N2H+(5–4) without completely ruling out other possibilities, including the detection of a low-J CO line from the foreground deflector. Aladro et al. (2015) derived a ratio of ≈2 between the ground transition lines of HCO+ and N2H+ in nearby active galaxies. If this value is also valid for higher energy levels, we would expect a similar ratio for HCO+(8–7)/N2H+(8–7). The observed integrated flux of HCO+(5–4) in G09v1.97 is about 0.5 Jy km s−1 (Yang 2017). Assuming that the flux ratio of HCO+(8–7) to HCO+(5–4) is ∼0.7 (Imanishi et al. 2017), the expected flux of N2H+(8–7) in G09v1.97 would be ∼0.2 Jy km s−1, which is less than half of the currently measured flux.
Based on the above arguments, we conclude that the emission feature detected at the rest-frame frequency of ∼745.32 GHz in G09v1.97 is most likely to be the H2O(211−202) line. This line is only seen in the red-shifted velocity component (dominated by Rr) and not in the weaker B component, which we attribute to component B having lower S/N.
4. Lens modeling
In order to derive the intrinsic properties of G09v1.97, a lens model needs to be built using both the high-resolution ALMA imaging data and the optical/near-IR images to constrain the gravitational potential of the deflectors. We stress that the main focus of this paper is to study the properties of the background lensed source, and the detailed structure of the deflecting mass distribution will be presented in a subsequent study.
Similar to the parametric lens model in Bussmann et al. (2013), the two foreground deflectors (G1 and G2, see Fig. 1) are assumed to be singular isothermal ellipsoid (SIE) mass distributions centered on the two foreground galaxies. The parameter encoding the strength of the deflector, namely the depth of the lensing potential, is represented by the velocity dispersion σv (note here σv is not the velocity dispersion of the ISM gas). The velocity dispersion of the lens model is related to the Einstein radius by REin = 4π(σv/c)2 (Dds/Dd), in which Dd and Dds are the distance between the observer and deflector, and the distance between the deflector and the lensed object, respectively. The minor-to-major axis ratio q and orientation of the major axis in the plane of the sky (position angle, PA) are left free and explored over the parameter space.
The lens model is based on the sl_fit lens inversion code, following the method described in Gavazzi et al. (2011). Here we adopted a Markov chain Monte Carlo (MCMC) method, implementing the standard Metropolis-Hastings algorithm. It explores the space of lens model parameters and builds samples of the posterior probability distribution function. The sl_fit code is mostly tailored to fit optical/near-IR data. Nevertheless, we are able to account for synthesized beam and noise correlation in the CLEANed images for our ALMA data using the methods described in Gavazzi et al. (2011). Although fitting visibilities in the uv-plane would overcome the caveats related to side-lobes and correlated noise of interferometric data (e.g., Bussmann et al. 2012, 2013; Hezaveh et al. 2013; Nightingale & Dye 2015; Spilker et al. 2016; Leung et al. 2017; Enia et al. 2018), this is not implemented yet in sl_fit. Dye et al. (2018) showed that image- and uv-plane model fitting can yield highly consistent results with ALMA data with sufficiently high uv-plane coverage and thus small dirty beam side-lobes. Since our ALMA data has such sufficiently high uv-plane coverage and S/N, we safely assume that any information loss in the source plane as a result of our image-plane analysis is negligible. We leave a thorough comparison of visibility versus image-space fitting for future studies using higher angular resolution ALMA images. However, even with higher resolution, we do not expect any significant changes.
4.1. Fitting the dust continuum emission and the mass model
Our lens model places the deflectors at their corresponding spectroscopic redshifts (z = 0.626 for G1 and z = 1.002 for G2). Following the prescription of Gavazzi et al. (2008), we allow for the slight lensing of G2 by G1 via a flat prior on the position of G2 and we check that the image-plane location of its center after modeling coincides with that observed. For G1, we apply a Gaussian prior of width 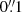 centered on its observed position to accommodate absolute astrometric uncertainties. We have also run models where both deflectors are placed at the same redshift of z = 0.626, finding very similar results apart from the central image which becomes slightly more magnified.
centered on its observed position to accommodate absolute astrometric uncertainties. We have also run models where both deflectors are placed at the same redshift of z = 0.626, finding very similar results apart from the central image which becomes slightly more magnified.
Because the dust continuum images have the best S/N values, we used the 1.94 and 0.87 mm dust continuum images (Fig. 1) to constrain simultaneously the mass distribution (SIE model) of G1 and G2 and the dust emission from the background source. The resulting best-fit mass model is then used to reconstruct, in the source plane, the line emission in each velocity channel. This approach is found to capture most of the information content of the data. Deeper and higher resolution data would enable us to perform a joint fit to the continuum and line emission, and eventually, provide the greater flexibility of creating a “pixelated source”, as was the case for the high-resolution observations of SDP 81 (e.g., Dye et al. 2015).
As discussed in Bussmann et al. (2013), a single Sérsic component of index n ≃ 1.8 was found to provide a good fit to the lower-spatial-resolution SMA data. With the improved depth and spatial resolution of our ALMA data, we can perform modeling with a more complex intrinsic light distribution. Therefore, we assume that the dust emission consists of two exponential profiles with several free parameters, e.g., positions (x, y), sizes (effective radius Reff), ellipticities (q, which equals the minor-to-major axis ratio) and orientations (PA). Those parameters can differ between each source component, although, by construction, the geometry (size, orientation, position) remains the same at 1.94 and 0.87 mm. Only the flux can differ across the two bands. In other words, each of the two background components has a constant magnification across its entire far-IR spectral energy distribution (SED). Two such sources sharing the same center would mimic a unique source with an SED gradient, should the data demand it, but these model assumptions also allow us to model two spatially distinct internally homogeneous sources. The Bayesian approach used in sl_fit requires a clear definition of modeling priors. For the lensing potential, we assume flat priors for the position of G2 and a Normal prior for the width 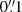 centered on the observed position of the G1 galaxy. This is to take into account the deflection of the more off-axis galaxy G2 by source G1 which lies closer to the main axis of the deflection. The orientation of the major axis has a uniform prior whereas both axis ratios have a Normal prior centered on 0.5 and of width 0.2 and set to zero outside the range [0, 1]. The prior on both Einstein radii is uniform in the range
centered on the observed position of the G1 galaxy. This is to take into account the deflection of the more off-axis galaxy G2 by source G1 which lies closer to the main axis of the deflection. The orientation of the major axis has a uniform prior whereas both axis ratios have a Normal prior centered on 0.5 and of width 0.2 and set to zero outside the range [0, 1]. The prior on both Einstein radii is uniform in the range ![$ [0{{\overset{\prime\prime}{.}}}1,1{{\overset{\prime\prime}{.}}}1] $](/articles/aa/full_html/2019/04/aa33876-18/aa33876-18-eq30.gif) . For the exponential profiles used for the morphology of the source plane dust emission, we apply a uniform prior in the range
. For the exponential profiles used for the morphology of the source plane dust emission, we apply a uniform prior in the range ![$ [-0{{\overset{\prime\prime}{.}}}2,0{{\overset{\prime\prime}{.}}}2] $](/articles/aa/full_html/2019/04/aa33876-18/aa33876-18-eq31.gif) on both coordinates of both sources5. Both axis ratios have a uniform prior distribution in the range [0.1, 0.9] and orientations are uniform on the circle. Intrinsic source plane fluxes in both frequency channels are uniformly bound between 0 and a conservative upper limit set at 1.5 times the total image plane flux in the corresponding velocity channel. Finally, we applied a Normal prior for the effective radius centered on
on both coordinates of both sources5. Both axis ratios have a uniform prior distribution in the range [0.1, 0.9] and orientations are uniform on the circle. Intrinsic source plane fluxes in both frequency channels are uniformly bound between 0 and a conservative upper limit set at 1.5 times the total image plane flux in the corresponding velocity channel. Finally, we applied a Normal prior for the effective radius centered on 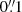 and of width
and of width 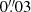 multiplied by a sharp uniform prior in the range
multiplied by a sharp uniform prior in the range ![$ [0,0{{\overset{\prime\prime}{.}}}2] $](/articles/aa/full_html/2019/04/aa33876-18/aa33876-18-eq34.gif) .
.
The results of the lens model and the reconstructed image-plane images at 1.94 and 0.87 mm are shown in panel a and b of Fig. 5. The constraints (median and 68% confidence level intervals on the marginal distributions) of the model parameters defining the mass model and the source-plane dust continuum emission are provided in Table 3. For a few relevant parameters, marginal posterior distributions and pair-wise scatter plots are shown in Fig. A.1 to illustrate possible parameters degeneracies. Despite its apparent simplicity, the model is able to reproduce most of the light distribution, leaving almost all residuals close to the noise level (<2.5σ). One can recognize a nearly fold-like configuration, with the faint parts of the source straddling the caustic. The critical lines resulting from the best fit mass distribution clearly reflect the bimodality of the foreground mass. The double nature of the deflecting system (G1 and G2) introduces a central de-magnified image that is observed and well reproduced by the model.
 |
Fig. 5. Panels a–c: image-plane lens modeling results of the 1.94 and 0.87 mm dust continuum, CO(6–5) and H2O(211−202) line emission for G09v1.97. The panels are grouped in horizontal sets of three sub-panels each showing, from left to right: i) observed image; ii) reconstructed image from the lens model; and iii) residuals from the difference between observed and model images. The red lines represent the critical curves. The central coordinates are given in Table 3. The figure clearly demonstrates that the lens model can recover the fluxes of the dust continuum and line emission accurately. The corresponding source-plane images are show in Fig. 6. All the residuals are well within ±2.5σ, showing that all the modeled images of the dust continuum and the emission lines agree very well with the overall flux distribution. |
Lens modeling results.
The two deflectors have relatively low masses with an Einstein radius of 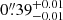 for G1 at z = 0.626 and
for G1 at z = 0.626 and 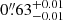 for the more distant G2 at z = 1.002, corresponding to σv= 142 ± 2 km s−1 and σv= 181 ± 2 km s−1 respectively. The two foreground galaxies have different shapes, with the ellipticity of G2 appearing to be well aligned with that of the host galaxy, and an orientation that is consistent with the shear generated by G1.
for the more distant G2 at z = 1.002, corresponding to σv= 142 ± 2 km s−1 and σv= 181 ± 2 km s−1 respectively. The two foreground galaxies have different shapes, with the ellipticity of G2 appearing to be well aligned with that of the host galaxy, and an orientation that is consistent with the shear generated by G1.
The source-plane dust continuum images at 1.94 and 0.87 mm reconstructed by the lens model are displayed in Fig. 6. The model requires two nearly concentric dust components with a very small separation, 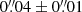 . One component is compact with a half-light radius, Reff, 1 = 0.63 ± 0.15 kpc, has a prominent north-south elongation, and contains the peak of the surface brightness distribution (the “core”). There is an additional extended envelope which is more circular and substantially larger with Reff, 2 = 1.37 ± 0.05 kpc. At 0.87 mm, the compact source is
. One component is compact with a half-light radius, Reff, 1 = 0.63 ± 0.15 kpc, has a prominent north-south elongation, and contains the peak of the surface brightness distribution (the “core”). There is an additional extended envelope which is more circular and substantially larger with Reff, 2 = 1.37 ± 0.05 kpc. At 0.87 mm, the compact source is 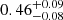 times brighter than the extended component, whereas this ratio rises to
times brighter than the extended component, whereas this ratio rises to 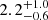 at 1.94 mm, suggesting that either the dust temperature and/or the submm optical depths might be different in the core and envelope (see Table 3). The compact core and the envelope experience a similar overall magnification. The total magnification is of order μtot = 10.3 ± 0.5, somewhat higher than the value μtot, B13 = 6.9 ± 0.6 derived by Bussmann et al. (2013).
at 1.94 mm, suggesting that either the dust temperature and/or the submm optical depths might be different in the core and envelope (see Table 3). The compact core and the envelope experience a similar overall magnification. The total magnification is of order μtot = 10.3 ± 0.5, somewhat higher than the value μtot, B13 = 6.9 ± 0.6 derived by Bussmann et al. (2013).
 |
Fig. 6. Reconstructed images of the dust continuum and line emission of G09v1.97 using the lens model, displaying: (panels a and b) the images and contours showing the source-plane 0.87 and 1.94 mm dust continuum emission, and (panels c and d) the velocity-integrated CO(6–5) and H2O(211−202) line emission with yellow contours of the 1.94 mm dust emission overlaid for comparison. The central coordinates are the same as in Fig. 5. The caustic lines are shown in red. The flux ratio of the two dust continuum disk components at 0.87 and 1.94 mm are different, indicating that the two components have either different dust temperatures and/or different submm optical depths. The average resolution indicated in panel b is derived from |
One should note that, although our double-disk model captures most of the dust continuum flux and the overall structure of the source, the 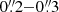 resolution ALMA continuum images could potentially even capture the flux variations at smaller scales. The average scale magnification can be inferred with
resolution ALMA continuum images could potentially even capture the flux variations at smaller scales. The average scale magnification can be inferred with 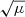 ∼ 3.2. With such a magnification, the
∼ 3.2. With such a magnification, the 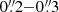 continuum image will be resolved into average scales of ∼0.4 kpc (
continuum image will be resolved into average scales of ∼0.4 kpc (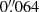 ). This has been further tested with PyAutoLens6 (Nightingale et al. 2018), which reconstructs the source-galaxy using an Adaptive Voronoi tesselation as opposed to analytic Sérsic light profiles. The analysis converges to the same lens model and reconstructs a source galaxy with the same global structure as the double-disk model, yet it reveals subtle variations on smaller scales comparable with the averaged magnified scale of angular resolution, or even slightly smaller at locations close to the caustic. Nevertheless, the discussion on such variation structures at scales <0.4 kpc are beyond the scope of this paper. This lens modeling therefore verifies our parametric lens model which we will use hereafter to determine the properties of G09v1.97.
). This has been further tested with PyAutoLens6 (Nightingale et al. 2018), which reconstructs the source-galaxy using an Adaptive Voronoi tesselation as opposed to analytic Sérsic light profiles. The analysis converges to the same lens model and reconstructs a source galaxy with the same global structure as the double-disk model, yet it reveals subtle variations on smaller scales comparable with the averaged magnified scale of angular resolution, or even slightly smaller at locations close to the caustic. Nevertheless, the discussion on such variation structures at scales <0.4 kpc are beyond the scope of this paper. This lens modeling therefore verifies our parametric lens model which we will use hereafter to determine the properties of G09v1.97.
4.2. Fitting the CO and H2O line emission
The SIE parameters of the best (lens) mass model derived from the two dust continuum images were used as input to model the data cubes of the CO(6–5) and H2O(211−202) emission lines. Due to the limited S/N at the edges of the spectra, we only performed such line-emission reconstructions in the source plane using the channel bins located in the velocity ranges within ∼±450 km s−1, which covers all the full widths at zero intensity. Performing the inversion channel per channel, we study the intrinsic source-plane line emission and, in particular, the spatial variations of the line of sight velocity distribution (LOSVD), similar to e.g., Riechers et al. 2008; Swinbank et al. 2011; Spilker et al. 2015; Leung et al. 2017. We focus on the integrated line emission map (0th moment of the LOSVD) and velocity field (1st moment of the LOSVD).
In order to perform the inversion, the data cube was binned into 10 velocity channel bins of 105 km s−1 from −478 to 467 km s−1 for the CO(6–5) and H2O(211−202) line cubes. Given the relative simplicity of the continuum emission, and in order to obtain the simplest possible source model, we assume that, up to a normalizing flux constant, the emission is identical between the CO(6–5) and H2O(211−202) lines, and each emission component is well represented by a single elliptical exponential profile whose parameters (center, ellipticity, orientation, effective radius, and fluxes) are estimated for each independent slice. This procedure is supported by the pronounced similarities in the spatial and the velocity structure of CO(6–5) and H2O(211−202) (Fig. 3). We thus fit for the 10 × 7 parameters defining the source emission while using the foreground mass distribution derived from the dust continuum modeling (Sect. 4.1). As with the modeling of this latter component, we apply the same priors on all of the source parameters. Hence, we obtain a model-predicted data cube in both the image and source planes.
As shown in panels c and d of Fig. 5, it is clear that the lens model reproduces the overall fluxes of both the CO(6–5) and H2O(211−202) line emission. Both the 0th moment maps are well reproduced with our lens models and the residual shows no significant disagreement. As shown in Fig. A.2, the model provides a good reconstruction of the line emission in each channel bin and therefore reproduces the entire velocity field. Furthermore, Fig. 7 shows that the model reproduces the observed integrated line profiles, together with the magnification factor at each channel for the lines and the two dust components.
 |
Fig. 7. Top panel: magnification factor as a function of velocity for the emission lines of CO, H2O, and H2O+, and indicated for the two dust components (the legend at the top left corner indicates the line and point style for each component of emission). Bottom panel: a comparison between the integrated spectrum of the observations and lens-model reconstructed data seen in the image plane. The filled regions show the model reconstructed using the bins in the image-plane spectra, while the histogram lines show the observed image-plane spectra (see the legend at the top left). The model overall predicts very well the spectra in the source plane. |
We also explored the nature of the H2O+ emission, which has lower S/N values than either CO(6–5) or H2O(211−202). We performed a similar analysis for the H2O+ data cube by dividing the emission into two channels, and the results are shown in Figs. 7 and A.2.
We conclude that for all the lines, the image plane reconstruction is in good agreement with the observed imaging data, suggesting that our simple modeling assumptions already capture most of the information content of the current data. Increasing the complexity of the gas distribution would require more flexible modeling techniques (and more free parameters) which are not required with these data. Based on the lens inversion results, we will describe the intrinsic physical properties of the source including its kinematics and morphology in the source plane in the following sections.
5. G09v1.97 in the source plane
5.1. Morphology of the dust continuum and line emission
As shown in Fig. 6, the molecular line maps of CO(6–5) and H2O(211−202) have an overall distribution elongated along the north-south direction. The orientation of the line emission is similar to the dust continuum at rest-frame 188 and 419 μm, albeit more complex with indications of a bimodal structure. The source-plane dust continuum image shows a predominately elongated disk-like smooth distribution along the north-south direction, and which peaks between the two gas components, albeit slightly towards the southern one.
To better demonstrate the spatial distribution of the gas emission and its velocity structure, Fig. 8 displays the gas emission per velocity channel bin as described in Sect. 4.2. As clearly seen in the figure, the two distinct components in Fig. 6 of the 0th moment map of the gas emission have significantly different velocities. The northern disk is dominated by the emission from the red-shifted gas components (corresponds to “R” in Fig. 6) while the southern component is dominated by blue-shifted gas (corresponds to “B” in Fig. 6). There is also a gas bridge peaking at ≈−59 km s−1, which is located near the peak of the dust continuum components (dashed ellipse). The reader should note that the R component in the 0th moment map corresponds to the “Rb” and “Rr” parts of the line profile observed in the image plane, while the B component is associated with the “B” part of the image-plane line profile (Fig. 4). The gas components associated with red-shifted velocities are located within the caustic pattern and hence experience a stronger magnification (μ∼ 12) than the southern blue-shifted component (μ∼ 5). This differential magnification contributes to the asymmetry of the image-plane integrated line profile, but only partially, because the intrinsic line-profile is asymmetric (Fig. 11). Most of the flux from the gas emission originates in the two blobs, i.e., R and B, with only a minor contribution from gas between the two. For the southern B component, the centroids at different velocities bins (central velocity of each bin from −478 to −163 km s−1) are varying in a very small spatial range of 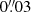 , neglecting the most blue-shifted velocity bin of −478 km s−1 which has very low flux and large uncertainties. On the other hand, the northern R component shows a clear gradual variation over
, neglecting the most blue-shifted velocity bin of −478 km s−1 which has very low flux and large uncertainties. On the other hand, the northern R component shows a clear gradual variation over 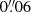 of the centroid positions from 47 to 362 km s−1 (here we also neglect the 467 km s−1 channel because of its low flux and high uncertainty). Such a difference suggests that R has a clear velocity shear, presumably rotation, while B is not kinematically resolved. We will discuss the kinematics in more detail in Sect. 5.2.
of the centroid positions from 47 to 362 km s−1 (here we also neglect the 467 km s−1 channel because of its low flux and high uncertainty). Such a difference suggests that R has a clear velocity shear, presumably rotation, while B is not kinematically resolved. We will discuss the kinematics in more detail in Sect. 5.2.
 |
Fig. 8. Ellipses showing the disk model for the CO(6–5) line emission per velocity channel bin (the central velocity of each disk is indicated by its color as indicated in the color bar). The parameters used to draw each ellipse in the diagram, i.e., half-light radius, PA, and ellipticity, are their median values. The points with error bars indicate the central positions and their uncertainties for each disk. The sizes and positions of the filled circles indicate the total flux and the center of the disk at each velocity bin (the flux scales are shown in the legend in the top left corner and the velocities are given by the color bar). The velocity bins are in steps of 105 km s−1 (see text). The figure shows clearly a concentration of fluxes with approaching velocities at radii smaller than |
Figure 8 also shows the half-light radius of the dust continuum and the line emission for each velocity channel bin, as indicated by the size of the ellipse. It shows that the overall size of gas is a bit more extended than the dust continuum emission (comparing half-light radii), with the extended part of the dust encompassing most of the line emission except for the most northern part of the R components. This is, to first order, consistent with the findings that the CO and H2O lines and submm dust continuum are presumably coming from similar active star-forming regions (Yang et al. 2016, 2017). Yet, the detailed structure of the dust and gas have two different patterns, namely a smooth single disk-like structure for the dust continuum and a bimodal-disk distribution for gas.
The northern red-shifted gas R is somewhat more diffuse than the southern blue-shifted component B. Both gas components bracket the dust continuum emission. In order to better characterize the morphology of the molecular gas traced by CO(6–5) (and H2O(211−202)), we performed a fit to the 0th moment map of CO(6–5) in the source plane with a disk model using IMFIT (Erwin 2015). The central positions, position angles, ellipticities, Sérsic indexes, and half-light radii are used as parameters to describe the disks in the model. One should note that the 0th moment image is a result of the linear sum of the disk model fitted per velocity bin (Fig. 8 as described in Sect. 4.2). The main purpose of fitting a disk model to the 0th moment map is to estimate the overall size, ellipticity, and the position of the components seen in the map. Therefore, we used three disk-components to capture the features of the R and B components, also taking into account the gas which lies between the two components. The main parameters of this fitting are the half-light radius (Reff), central position, ellipticity (e), and position angle (PA). The parameter Sérsic index used in the IMFIT is only for the propose of constraining the entire parameter set and it does not influence the final results in any significant way. We will also not discuss the gas between the two components because of its complex morphological structure and the fact that its parameters are less well constrained due to the relative low fluxes from this emission region. Using bootstrap resampling, the uncertainties from the fit are determined with uncertainties of 10%. The best fitting model determined by minimizing χ2 (best-fit χ2 = 0.1) provides a good agreement with the overall morphology of the 0th moment map, with insignificant residuals (maximum differences are less than 1% of the emission). The best fit half-light radius, Reff for R and B are 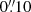 (0.8 kpc) and
(0.8 kpc) and 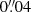 (0.3 kpc), respectively. The corresponding ellipticities e are 0.59 and 0.34, while the position angles are 4° and 97°, for R and B, respectively. The two disks, R and B with semi-major axis half-length, as (define as
(0.3 kpc), respectively. The corresponding ellipticities e are 0.59 and 0.34, while the position angles are 4° and 97°, for R and B, respectively. The two disks, R and B with semi-major axis half-length, as (define as 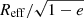 ) of 1.2 kpc and 0.4 kpc, are separated by a projected distance of
) of 1.2 kpc and 0.4 kpc, are separated by a projected distance of 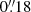 (1.3 kpc). Therefore, the overall size of the gas emission traced by CO(6–5) is ∼1.5 times larger than the dust emission size (not necessarily the size of the dust distribution), which is consistent with the estimates found in the image plane. Assuming that both R and B are thin disks, the inclination angle can be derived from the minor to major axis ratio, b/a (define as 1−e), as
(1.3 kpc). Therefore, the overall size of the gas emission traced by CO(6–5) is ∼1.5 times larger than the dust emission size (not necessarily the size of the dust distribution), which is consistent with the estimates found in the image plane. Assuming that both R and B are thin disks, the inclination angle can be derived from the minor to major axis ratio, b/a (define as 1−e), as 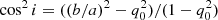 , in which the value of q0 indicates the intrinsic thickness of the disk (Hubble 1926). Choosing a typical value of q0 = 0.2 for disk galaxies (e.g., Holmberg 1946; Haynes & Giovanelli 1984), we infer inclinations for R and B of 82° and 66°, respectively.
, in which the value of q0 indicates the intrinsic thickness of the disk (Hubble 1926). Choosing a typical value of q0 = 0.2 for disk galaxies (e.g., Holmberg 1946; Haynes & Giovanelli 1984), we infer inclinations for R and B of 82° and 66°, respectively.
The projected separation between the northern and southern gas emission peaks is 1.3 kpc with a difference in velocity of order 450 km s−1 and there is a significant difference in the spatial structure between the dust continuum and the molecular gas emission (the former shows a one-fold disk-like structure while the latter shows two blobs on both sides of the dust peak). This can either be explained by two distinct galaxies separated by a projected distance of 1.3 kpc or two (very luminous) dusty star-forming clumps within a single rotating disk with a size of 0.4–1.2 kpc. Considering the first possible scenario, such a separation is consistent with the observations of local ULIRG mergers, which are in a close-to-coalesce phase or already coalescing (e.g., Rigopoulou et al. 1999; Scoville et al. 2000; Carpineti et al. 2015). Also the compact size of each merging galaxy is consistent with size estimates for other SMGs (e.g., Tacconi et al. 2008; Toft et al. 2014; Bussmann et al. 2015; Smolčić et al. 2015; Simpson et al. 2015b; Hodge et al. 2016; Spilker et al. 2016; Chen et al. 2017; Calistro Rivera et al. 2018). On the other hand, in the single-rotating-disk scenario, if the R and B components in G09v1.97 are within a single SMG, their relative large sizes compared to gas clumps (≲100–300 pc) derived from high-resolution observations in other SMGs (Swinbank et al. 2015), suggest that they are unlikely to be the resolved individual star-forming clumps, but rather two collections of clumps. Additionally, we tested this single-SMG scenario by fitting a tilted-ring model (e.g., Begeman 1987) to the source-plane CO(6–5) data cube using 3DBarolo (a 3D-Based Analysis of Rotating Objects from Line Observations, Di Teodoro & Fraternali 2015). We find that the rotating-disk model cannot explain the reconstructed source-plane data cube. The best-fitting model has a significant under-prediction for the red-shifted part of the line emission. Together with the spatial mismatch between the dust emission and the molecular line emission in the source plane (Fig. 6), the poor fit likely rules out that the source is made of several clumps in a single rotating galaxy. Therefore, we conclude that the system is made of two compact merging galaxies with a small separation.
The ratios of 1.94 and 0.87 mm dust continuum flux densities are different for the compact and extended components (Table 3). At the shorter wavelength, rest-frame 188 μm, the extended dust continuum component is brighter than the compact dust component, while at the longer wavelength, rest-frame 419 μm, the compact dust component is more luminous. This suggests that the compact dust continuum region has an intrinsic lower dust temperature than the extended dust component, and/or different submm optical depths. Such a picture is consistent with the merger scenario (but hard to be explained by dusty clumps in a single disk): the compact dust continuum component is tracing the large amount of cold dust peaking in the interacting region between R and B. This is similar to the cold dust maps seen in local mergers such as the Antennae (NGC 4038/39) (e.g., Haas et al. 2000; Wilson et al. 2000) and VV 114 (Le Floc’h et al. 2002), where the cold dust emission at relatively long wavelengths is peaking in the interacting regions between two merging galaxies, suggesting a concentration of cold dust in a pre-coalescence phase of the system. While for the extended dust component, the contribution from the warm dust emission from the nucleus of R and B, elevates the overall dust temperature compared with the interacting region (i.e., the compact dust component). Therefore, the extended dust component has a warmer dust temperature compared with the compact dust component. The line emission of CO(6–5) and H2O(211−202) is also predominantly coming from the warm dense regions (i.e., concentrated at R and B while remaining weak at the interacting region). However, the current spatial resolution limits our ability to resolve any further detailed variations in the properties of the dust emission. Higher spatial resolution and longer wavelength observations are needed to understand the distribution of the dust temperature and mass in R, B, and the interacting regions.
For the source-plane reconstruction of the H2O+ line emission, with only two velocity bins, it is difficult to infer the line’s detailed spatial structure accurately. Nevertheless, we find no evidence that the spatial distribution of the H2O+ line emission is different from those of the CO(6–5) or H2O(211−202) lines. This is consistent with the fact that the formation of H2O+ lines is associated with the strong cosmic rays from intensely star-forming regions, which are also traced by the CO(6–5) and H2O(211−202) lines (Yang et al. 2016). As in SMGs, which have very high-density star formation, we would expect to see the impact of cosmic rays on the ionization of dense molecular gas tracers as cosmic rays, rather uniquely, deposit their energy in deeply embedded dense gas (e.g., Papadopoulos 2010; Papadopoulos et al. 2011).
5.2. Kinematic structure
Figure 9 presents the source-plane reconstructed 1st moment map of the line emission and the same map in the image plane. The lens-model-reconstructed source-plane moment map shows the detailed intrinsic kinematic structure of G09v1.97. One should note that, as mentioned in Sect. 4.2, because the final source-plane cubes are reconstructed by extracting the best fitted parametric lens models from the posteriors of the MCMC realizations per velocity channel, the noise of the observed images will not be transferred into the source-plane cubes. Thus, the uncertainties could be underestimated. For the dust continuum and line emission cubes, the noise in the ALMA images is generally low. Because of this, the uncertainties of the source-plane cubes are likely to be predominately due to the goodness of the lens model, namely the posterior distribution of the parameters, which reflects how well the model fits the data. This approach is a good approximation considering the limited spatial resolution yet high sensitivity levels of the dust continuum, CO(6–5) and H2O(211−202) line images. We will omit a discussion of the image plane map of H2O(211−202) since the velocity structure is very similar to that of the CO(6–5) and we used fixed parameters when performing the lens modeling (Sect. 4.2). With these caveats in mind, we find an overall velocity gradient of the gas along the north-south direction, with the northern gas component dominating the velocity channels reward of the systemic velocity, while the southern component dominates the blue velocity channels, This is in agreement with the R and B image-components discussed in Sect. 5.1.
 |
Fig. 9. Left panels, in the image plane: PV plots in the image plane CO(6–5) data cube along the direction marked by the gray dashed lines are shown in the first column. The dark red line shows the position of the critical line. The dashed squares show the major velocity components “R” (Rb+Rr), “G”, and “B”. The second column shows the 0th & 1st moment map of CO(6–5) similar to Fig. 2. The critical line is marked by dark red line. The third column shows the slice of 1st moment CO maps according to the R, G, and B velocity ranges marked in the lower panel of the PV plot in the first column. Right panels, in the source plane: the first column shows the slice of 1st CO moment maps for R, G, and B. The second column shows a similar image of 0th & 1st moment maps of CO(6–5) in the image plane with the caustic line (dark red line) overlaid. By comparing the velocity structures of R, G, and B both in the image plane and the source plane, and also the PV plot, it is clear that the source has three major velocity structures: the approaching gas B, the bridging gas G and the receding gas component R that has a velocity-resolved structure showing a velocity gradient along the north-south direction. |
Although the 1st moment map in the source plane has a rotation-like velocity shear, it remains incompatible with a single rotating-disk model (Sect. 5.1). This demonstrates the fact that a 2D velocity map with limited spatial resolution is generally insufficient to distinguish between a system that is a merger or a clumpy rotating disk.
To further investigate the velocity structure of G09v1.97, we extract PV plots sliced from two positions in the west and south of the image-plane map (Fig. 9). The PV maps sliced from the west has a velocity range from −50 to 350 km s−1, which is mostly traces the northern disk R (which corresponds to the Rb and Rr components in the observed spectrum). It shows a typical mirrored folded structure along the two sides of the critical line (similar to e.g., the Eyelash, Swinbank et al. 2011). The continuous velocity gradient along the positional axis of the PV diagram shows the typical kinematic signature of a rotating disk, suggesting that the northern galaxy is a kinematically resolved rotating disk. However, given the limited spatial resolution, we are unable to rule out the possibility that the R component can also be a small-scale merger (see the model of e.g., Narayanan et al. 2015). We nevertheless assume R is a rotating disk in this work. The other PV plot sliced from the southern component of the image shows the full velocity range from −400 to 350 km s−1, and which consists of three major components. The R part from 0 km s−1 to 350 km s−1 is tracing the same rotating disk structure as in the first PV plot (western slice), but is less magnified and therefore shows only a marginally resolved kinematic structure. The B part in the PV plot from −400 to −150 km s−1, which is associated with the southern galaxy, is coming from the B component in the 0th moment map of the line emission. It is clear that the R and B components in the PV plot show spatially overlapping regions along the line of sight, suggesting that system cannot be a stable rotating disk. This again rules out the clumpy rotating disk interpretation. In the overlap region, there is another weak gas component from −150 to 0 km s−1, probably tracing the bridging gas in between the two merging galaxies.
To test the velocity structure of these three components found in the southern PV plot, and to check the consistency between the source- and image-plane results, we have divided both the datacube in the source and image plane into three parts: R −400 to −150 km s−1, G −150 to 0 km s−1, and B 0 to 350 km s−1. Figure 9 shows the 1st moment maps for R, G, and B in the image and source plane. The component R shows a prominent velocity gradient consistent with a rotating disk, while G and B have no clear velocity structure. The moment maps from the image and source plane match very well, suggesting that our lens model is robust. The velocity structure further suggests that the system consists of two merging galaxies – a northern rotating disk with marginally resolved kinematics and a southern compact galaxy without any clear velocity structure – during their pre-coalescence phase. These two galaxies are connected by a bridge of gas with very weak CO(6–5) emission and dominated by cold dust emission (see a sketch in Fig. 11).
5.3. The intrinsic properties of G09v1.97: ISM and star formation in the source plane
We extract the spatially integrated spectrum of the CO(6–5) and H2O(211−202) line from the reconstructed source-plane cubes, and further decompose the spectra into 3 Gaussian profiles (Fig. 11). In the fitting process, we set all the parameters free, except for the linewidth of the G component of the H2O(211−202) line (by using the value from the CO line) to achieve robust constraints on the parameters (Table 4). Both the CO(6–5) and H2O(211−202) line profiles are well-described by 3 Gaussians: a blue-shifted Gaussian profile located mainly between −400 and −150 km s−1 (in terms of FWHM), which is associated with the southern blue compact galaxy B; a red-shifted Gaussian component from 0 to 350 km s−1, originating in the northern rotating disk; and a weak Gaussian component from −150 to 0 km s−1 dominated by the gas bridge connecting the two merging galaxies. It is noticeable that due to the differential lensing, the spectrum in the source plane shows a somewhat different line profile. The R component is heavily magnified by a factor of 15–20, and has been decomposed into two Gaussian components, Rb and Rr, which are the blue-shifted side and red-shifted side of the northern rotating disk. For the G component, due to its weak flux and lower magnification (<10), it is difficult to disentangle it from components Rb and B seen in the image-plane spectrum.
Spatially integrated dust and line emission properties in the source plane.
Comparing the linewidths of the red-shifted and blue-shifted Gaussian components of the CO(6–5) line and the H2O(211−202) line, we find that the blue-shifted B has similar linewidth as the red-shifted R, despite the fact that the latter is resolved into a rotating disk while the former shows no clear velocity structure. This indicates B has a larger intrinsic velocity dispersion than R. The integrated flux ratio of R and B for the two lines are similar, IR/IB ∼ 1.5–2.1, with a peak flux ratio of about 1.6 for both. The bridging gas component contributes 20% to the total flux for both the CO(6–5) and H2O(211−202) lines. The flux ratios of CO(6–5)/H2O(211−202) for R and B are within the typical flux ratios of CO(6–5)/H2O(211−202) found in H-ATLAS SMGs (Yang et al. 2016, 2017), and is slightly higher than the value 1.4 ± 0.1 found in Arp 220 (Rangwala et al. 2011). However, this flux ratio of CO(6–5)/H2O(211−202) is a slightly lower than the value of 2.5 ± 0.7 found in the similar IR-luminous z = 5.2 SMG HLSJ0918 (Rawle et al. 2014) and 3.4 ± 1.0 in the z = 5.7 SMG ADFS-27 (Riechers et al. 2017). Since the excitation of the H2O(211−202) line is dominated by far-IR pumping, it is tracing the warm dust emission (with temperatures around 45 K, see e.g., González-Alfonso et al. 2014b), while the CO(6–5) line is tracing the warm dense gas mass. The line ratio of CO to H2O may therefore offer an estimate of the gas-to-dust mass ratio in the warm dense star-forming molecular gas. If the flux ratio of CO(6–5)/H2O(211−202) is indeed correlated with the gas-to-dust mass ratio, a similar ratio of CO(6–5)/H2O(211−202) in R and B could indicate that the dust-to-gas mass ratios of the two merging galaxies are likely to be similar. While higher flux ratios of CO(6–5)/H2O(211−202) in the z > 5 sources, such as the previously discussed HLSJ0918 and ADFS-27, suggests higher gas-to-dust mass ratios compared with the z = 2–4 H-ATLAS SMGs and local ULIRGs. Although crude, this result is consistent with the fact that the higher redshift sources tend to be gas-rich and less enriched in metals and dust (e.g., Genzel et al. 2015). More work with a larger sample is needed to test the reliability of such an assumption.
The limited spatial resolution means that we are unable to resolve the detailed structure of the dust emission and disentangle the two galaxies and their interacting regions. Nevertheless, to first order, we can assume that the total infrared luminosity is proportional to the CO(6–5) luminosity based on the tight correlation found in infrared-bright galaxies (e.g., Greve et al. 2014; Liu et al. 2015; Lu et al. 2017). Also, notice that the bridge has a lower dust temperature as indicated by its low ratio, S0.87/S1.94 = 5.4 compared to R and B (for which we assume a similar ratio, S0.87/S1.94 = 26). The fluxes of the two dust components at 0.87 and 1.94 mm, and their ratios are well constrained by our model, showing no sign of strong degeneracies between the parameters (Fig. A.1). We can decompose the total LIR into three parts using a modified black-body model (β = 2), for B, G, and R (Fig. 10). We acknowledge that there could be large uncertainties because there is no spatially resolved photometry for B, G, and R. Therefore, we introduced additional uncertainties of 50% to the resulting best-fit parameters.
The two merging galaxies are infrared luminous, with LIR, B = (4.0 ± 2.0)×1012 L⊙ and LIR, R = (6.3 ± 3.1)×1012 L⊙, and can thus be considered as ULIRGs. The dust emission between the two galaxies has a LIR, = (4.0 ± 2.0)×1011 L⊙. The merging system has a total LIR exceeding 1013 L⊙ and therefore belongs to the class of hyper-luminous infrared galaxies (HyLIRGs). The intrinsic dust temperature for the two galaxies is about 33–61 K (composite of two temperature components of 33 and 61 K), which is typical for high-redshift SMGs (e.g., Chapman et al. 2005; Magnelli et al. 2012; Shu et al. 2016). The region between the two ULIRGs has a much lower dust temperature of 17 K. This temperature is consistent with values found for the coldest dust component in a sample of high-redshift SMGs (Magnelli et al. 2012). The corresponding star formation rates for B and R are SFRB = (6 ± 3)×102 M⊙ yr−1 and SFRR = (9 ± 4)×102 M⊙ yr−1. Taking the intrinsic half-light radii of 0.4 kpc and 1.2 kpc for the two galaxies, we derive the surface star formation intensities, ΣSFR, B = (5.5 ± 2.8)×102 M⊙ yr−1 kpc−2 and ΣSFR, R = (1.2 ± 0.6)×102 kpc−2 for the B and R galaxies, respectively. Comparing these surface intensities with theoretical limits derived for an optically thick disk, where the radiation pressure on dust grains provides the pressure to support a disk against its own self-gravity (Thompson et al. 2005), the values of the star formation intensities are 2–7 times smaller and thus well below this “Eddington limit”. However, the two components of G09v1.97 are still among the strongest starbursts found in H-ATLAS sample of lensed SMGs in terms of their ΣSFR (Bussmann et al. 2013) and also comparable with SPT-selected sources (Spilker et al. 2016). Note that the ΣSFR will be further reduced by a factor of up to 5–7, if we allow for a top-heavy IMF (Zhang et al. 2018b).
Assuming similar gas excitation conditions, i.e., taking the same CO(6–5) to CO(1–0) ratio for R and B as in Yang et al. (2017), we can derive the total molecular gas mass (acknowledging the large uncertainties) for R and B of about 5 × 1010 and 4 × 1010 M⊙, respectively, suggesting the two galaxies are gas-rich. The implied gas depletion time then is 60 and 63 Myr for R and B, respectively, which are typical values found for high-redshift dusty starbursts (e.g., Aravena et al. 2016b). When comparing the luminosity ratio of CO(6–5) and infrared, we find values of LCO(6−5)/LIR, = (1.0 ± 0.5)×10−5 for the southern galaxy B and (2.1 ± 1.1)×10−5 for the northern galaxy R, which are well within the range found by statistically studying other high-redshift SMGs (Yang et al. 2017), and very close to the ratios of the local ULIRGs whose emission is dominated by star formation, not AGN (Liu et al. 2015). For the H2O(211−202) line, we derive a ratio LH2O(211−202)/LIR of (0.5 ± 0.3) × 10−5 and (0.6 ± 0.3) × 10−5 for B and R, respectively. These values are also in agreement with that of other SMGs and local star-forming dominated ULIRGs (Yang et al. 2016; Liu et al. 2017), showing that the tight correlation still holds down to sub-kpc scales in such starbursts (Fig. 12), further suggests that the submm H2O lines are robust indicators of star formation rates in these galaxies. In Fig. 12, the G component has a small positional offset, showing an excess of H2O line emission. Nevertheless, given the fact that the estimate of the SFR is very uncertain in the interaction region, it is difficult to conclude that such a deviation is significant. However, shocks over the interaction region between two merging galaxies could also enhance low-J H2O lines which may explain an excess of H2O luminosity (Flower & Pineau Des Forêts 2010; Appleton et al. 2013). Higher resolution observations are needed to further investigate such a hypothesis.
 |
Fig. 10. Dust SED of G09v1.97. The fluxes are taken from Herschel and NOEMA measurements (Yang et al. 2016), and also from this work for the 0.89 and 1.94 mm continuum fluxes (blue points). The fit also takes into account the dust continuum fluxes of the compact (the interacting region) and extended (the merging galaxies) dust component from our lens model, indicated by the open and filled circle (green and light-blue for different temperature components), respectively. The SED fit has also taken the differential magnification for the compact and extended components into account. The solid blue line shows the best fit, while other dashed/dotted lines are decompositions of different temperature components. See text for details. |
 |
Fig. 11. Left panel: spatially integrated spectra extracted from the source-plane line data-cubes constructed from the lens model. The error bars are dominated by the uncertainties in the data. The black curve shows the results of fitting 3 Gaussian line profiles: the blue line represents the B component, the green line represents the gas bridge G component, and the red line represents the receding gas R component (Rb+Rr). The line profiles of CO(6–5) and H2O(211−202) are similar, having ∼1.7 times stronger (peak flux) red-shifted emission compared to the blue-shifted emission. This indicates that there is a similar spatial distribution between the CO(6–5) and H2O(211−202) line emission. The asymmetry of the profile suggests an intrinsically complex velocity structure. Right panel: a sketch of the gas-rich major merger, G09v1.97. The source is composite of three major components, a rotating disk to the north that corresponds to the R component of the spectra shown in the left panel or the double-Gaussian component Rb+Rr seen in the image-plane spectrum, while the compact blue galaxy in the south corresponds to B part of the line profile. There is also a dust-rich gas bridge between the two over the component which has weak CO(6–5) and H2O(211−202) emission. |
 |
Fig. 12. Correlation between the star formation rate (SFR) surface density and H2O luminosity surface density in high-redshift SMGs (Yang et al. 2016) (shown in black), including HFLS3 (Riechers et al. 2013) and ADFS-27 (Riechers et al. 2017). The red, blue and green data points represent the R, B, and G components of G09v1.97 from this work. The figure shows a tight linear correlation between ΣSFR and ΣLH2O with a fitted slope of 1.0 ± 0.2, which is valid down to the sub-kpc scales. |
Our new ALMA data indicate that the ratio of the observed IH2O(211−202) to IH2O+ (the 742.1 GHz line) is about 3 for the merging galaxies (using a total averaged magnification for H2O+), which agrees with the IH2O/IH2O+ ratios reported in Yang et al. (2016) for NCv1.143, G09v1.97, and G15v2.779 based on NOEMA compact array observations. With this ratio, the model discussed in Meijerink et al. (2011), suggests a high cosmic-ray ionization rate of 10−14–10−13 s−1, with the upper limit being similar to the values derived in Arp 220 and NGC 4418 (González-Alfonso et al. 2013). Such high cosmic-ray ionization rates drive the level of the ambient ionization of the high column density clouds to ∼10−3, rather than the canonical 10−4. These cosmic rays, which are likely generated in the most intense star-forming regions, dominate the gas phase ionization and oxygen ion-neutral route of the oxygen chemistry (e.g., Meijerink et al. 2011; van der Tak et al. 2016).
In addition to the H2O+ lines, we also detected an emission line around 745.3 GHz, which we attribute to the H2O(211−202) line emission (Eup ∼ 200 K). The oxygen isotope, 18O, is predominantly made in the early stages of helium burning in massive stars (e.g., Maeder 1983). 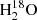 has also been detected in emission in local ULIRGs both in a local Herschel archive survey (Yang et al. 2013) and in the compact obscured nucleus of Zw 049.057 (Falstad et al. 2015). Several absorption lines of this molecule at shorter wavelengths have also been detected by Herschel/PACS in local ULIRGs (González-Alfonso et al. 2012, 2018), indicating that the excitation of
has also been detected in emission in local ULIRGs both in a local Herschel archive survey (Yang et al. 2013) and in the compact obscured nucleus of Zw 049.057 (Falstad et al. 2015). Several absorption lines of this molecule at shorter wavelengths have also been detected by Herschel/PACS in local ULIRGs (González-Alfonso et al. 2012, 2018), indicating that the excitation of 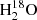 is similar to that of H2O. The integrated flux ratio of H2O(211−202) to H2O(211−202) is ∼15, while the peak flux ratio is about 8. However, with only one transition line of
is similar to that of H2O. The integrated flux ratio of H2O(211−202) to H2O(211−202) is ∼15, while the peak flux ratio is about 8. However, with only one transition line of 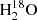 detected, it is very difficult to derive the abundance ratio of 18O/16O because of the very large optical depth of the H2O line. With better constraints on the
detected, it is very difficult to derive the abundance ratio of 18O/16O because of the very large optical depth of the H2O line. With better constraints on the 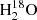 abundance (and careful astrochemical modeling), we can use this ratio to gain further insight into the IMF in high-redshift SMGs because 18O is a secondary nuclide that relies on the prior existence of the primary elements such as 12C and 16O (e.g., Clayton 1968; Danielson et al. 2013; Romano et al. 2017; Zhang et al. 2018b).
abundance (and careful astrochemical modeling), we can use this ratio to gain further insight into the IMF in high-redshift SMGs because 18O is a secondary nuclide that relies on the prior existence of the primary elements such as 12C and 16O (e.g., Clayton 1968; Danielson et al. 2013; Romano et al. 2017; Zhang et al. 2018b).
6. Summary
In this paper, we have presented high (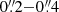 ) angular resolution ALMA observations of the lensed redshift z = 3.632 SMG, G09v1.97, in the dust continuum at the rest-frame wavelengths of 188 and 419 μm and in the molecular line emission of CO(6–5), H2O(211−202), and Jup = 2 H2O+. The 2 mm spectra provide accurate values for the apparent luminosity of the lines and detailed line profiles, as well as the first detection of a line of
) angular resolution ALMA observations of the lensed redshift z = 3.632 SMG, G09v1.97, in the dust continuum at the rest-frame wavelengths of 188 and 419 μm and in the molecular line emission of CO(6–5), H2O(211−202), and Jup = 2 H2O+. The 2 mm spectra provide accurate values for the apparent luminosity of the lines and detailed line profiles, as well as the first detection of a line of 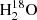 at high redshift. The images of the dust continuum and line emission show a nearly complete
at high redshift. The images of the dust continuum and line emission show a nearly complete 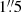 diameter Einstein ring with substructures and a weaker emission peak at the center. The central image is the result of the rare lens configuration of two compound foreground deflectors. With a magnification of μ ∼ 5–22 for the line across different velocity channels, and μ ∼ 10–11 for the continuum, the average boosted angular resolutions can reach down to scales of ∼0.4–1.3 kpc, resulting in one of the highest angular resolution images of water line emission in an extra-galactic source to date.
diameter Einstein ring with substructures and a weaker emission peak at the center. The central image is the result of the rare lens configuration of two compound foreground deflectors. With a magnification of μ ∼ 5–22 for the line across different velocity channels, and μ ∼ 10–11 for the continuum, the average boosted angular resolutions can reach down to scales of ∼0.4–1.3 kpc, resulting in one of the highest angular resolution images of water line emission in an extra-galactic source to date.
With careful lens modeling, we have reconstructed the source-plane images of G09v1.97 in the dust continuum and in the molecular emission lines of CO(6–5), H2O(211−202), and H2O+. The model reproduces, in the image plane, most of the details of the observed images of the dust continuum and the three-dimensional line emission data cubes. The dust emission appears as a compact disk surrounded by an extended overlapping disk structure. The two dust components have slightly different dust temperatures and/or submm optical depths, suggesting the dust properties in its peak region and the extended regions are different. For the molecular line emission, we find very similar kinematic structure and spatial distribution between the CO(6–5) and H2O(211−202) lines. The line emission shows a bimodal structure, with a northern disk-like gas component associated with red-shifted gas emission while the southern compact component is dominated by the blue-shifted gas. The cold dust emission peaks in between the two gas components. We argue that the two gas components in the south and north are two gas-rich galaxies, each having a total molecular gas exceeding 1010 M⊙. They are in the pre-coalescence phase, with a large amount of cold dust presented in their interacting region, and also weak bridging gas emission. The northern galaxy is kinematically resolved as a rotating disk with a semi-major half-light radius as of 1.2 kpc, while the southern galaxy, kinematically unresolved by being more turbulent, is compact with as = 0.4 kpc traced by the CO(6–5) line. The ratios of the total IR luminosities LIR to the CO(6–5) and H2O(211−202) line luminosities in the two merging galaxies are similar and consistent with the values found in other high-redshift SMGs, supporting our contention that there is a tight correlation between star formation and the H2O line luminosity. The CO(6–5)/H2O(211−202) flux ratios are found to be ≈2 (with 20% uncertainties), which is consistent with the z = 2–4 SMGs, while this flux ratio is found to be higher in z > 5 SMGs. The detection of strong H2O+ emission and its relative strength to the H2O line suggests that the cosmic ray plays an important role in the regulation of the physical and chemical processes in the ISM of high-redshift SMGs. The star formation rate surface densities of the two components are in the range of ∼120−550 M⊙ yr−1 kpc−2, being ∼2–7 times below the value set by the Eddington limit, yet they are among the strongest starbursts at high redshift.
In addition to the CO(6–5) and H2O(211−202) line, we also present the first 5-σ detection of H2O(211−202), which is about 8 times weaker than the H2O(211−202) line. This molecule may offer important information on the chemical processes of the ISM and the initial mass function in high-redshift galaxies.
Future higher angular resolution observations will be needed to explore and trace in greater detail the distribution and kinematics of the gas content in G09v1.97. With its very high luminosity, the gas-rich merger, G09v1.97, remains an exceptional target for further studies at high spatial resolution. For instance, with ALMA, a resolution of 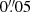 would help to further resolve the source at scales below 100 pc for G09v1.97, which is about the characteristic sizes of associations of molecular clouds. Such high spatial resolution observations will allow us to probe the properties of distinct molecular clumps in this star-bursting galaxy in the early universe.
would help to further resolve the source at scales below 100 pc for G09v1.97, which is about the characteristic sizes of associations of molecular clouds. Such high spatial resolution observations will allow us to probe the properties of distinct molecular clumps in this star-bursting galaxy in the early universe.
Common Astronomy Software Applications (McMullin et al. 2007), see https://casa.nrao.edu for more information.
Acknowledgments
We thank the anonymous referee for very helpful comments and suggestions. C.Y. was supported by an ESO Fellowship. C.Y. thanks Johan Richard and Martin Bureau for insightful discussions, and also thanks John Carpenter and Edward Fomalont for discussion on ALMA data reduction. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.01320.S and #2013.1.00358.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. C.Y. and Y.G. acknowledge support by National Key R&D Program of China (2017YFA0402700) and the CAS Key Research Program of Frontier Sciences. R.G., C.Y., and A.O. acknowledge the Programme National Cosmology and Galaxies for financial support in the early stages of this project. C.Y., A.O., and Y.G. acknowledge support from the NSFC grants 11311130491 and 11420101002. C.Y., A.O., A.B., and Y.G. acknowledge support from the Sino-French LIA-Origins joint exchange program. I.R.S. and A.M.S. acknowledge support from STFC (ST/P000541/1). S.D. is supported by the UK STFC Rutherford Fellowship scheme. E.I. acknowledges partial support from FONDECYT through grant N° 1171710. E.G.-A. is a Research Associate at the Harvard-Smithsonian Center for Astrophysics, and thanks the Spanish Ministerio de Economía y Competitividad for support under projects FIS2012-39162-C06-01 and ESP2015-65597-C4-1-R, and NASA grant ADAP NNX15AE56G. RJI acknowledges support from ERC in the form of the Advanced Investigator Programme, 321302, COSMICISM. H.F. acknowledges support from NSF grant AST-1614326. D.R. acknowledges support from the National Science Foundation under grant number AST-1614213. M.N. acknowledges financial support from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No 707601. M.J.M. acknowledges the support of the National Science Centre, Poland, through the POLONEZ grant 2015/19/P/ST9/04010; this project has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 665778. I.P.-F. acknowledges support from the Spanish grants ESP2015-65597-C4-4-R and ESP2017-86852-C4-2-R. US participants in H-ATLAS acknowledge support from NASA through a contract from JPL. Italian participants in H-ATLAS acknowledge a financial contribution from the agreement ASI-INAF I/009/10/0. SPIRE has been developed by a consortium of institutes led by Cardiff Univ. (UK) and including: Univ. Lethbridge (Canada); NAOC (China); CEA, LAM (France); IFSI, Univ. Padua (Italy); IAC (Spain); Stockholm Observatory (Sweden); Imperial College London, RAL, UCL-MSSL, UKATC, Univ. Sussex (UK); and Caltech, JPL, NHSC, Univ. Colorado (USA). This development has been supported by national funding agencies: CSA (Canada); NAOC (China); CEA, CNES, CNRS (France); ASI (Italy); MCINN (Spain); SNSB (Sweden); STFC, UKSA (UK); and NASA (USA).
References
- Aladro, R., Martín, S., Riquelme, D., et al. 2015, A&A, 579, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amvrosiadis, A., Eales, S. A., Negrello, M., et al. 2018, MNRAS, 475, 4939 [NASA ADS] [CrossRef] [Google Scholar]
- Andreani, P., Retana-Montenegro, E., Zhang, Z.-Y., et al. 2018, A&A, 615, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appleton, P. N., Guillard, P., Boulanger, F., et al. 2013, ApJ, 777, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Spilker, J. S., Bethermin, M., et al. 2016a, MNRAS, 457, 4406 [NASA ADS] [CrossRef] [Google Scholar]
- Aravena, M., Decarli, R., Walter, F., et al. 2016b, ApJ, 833, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Bachiller, R. 1996, ARA&A, 34, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., Sanders, D. B., et al. 1998, Nature, 394, 248 [NASA ADS] [CrossRef] [Google Scholar]
- Barger, A. J., Cowie, L. L., Chen, C.-C., et al. 2014, ApJ, 784, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Begeman, K. G. 1987, HI Rotation Curves of Spiral Galaxies, PhD Thesis, Kapteyn Institute [Google Scholar]
- Blain, A. W., Smail, I., Ivison, R. J., Kneib, J.-P., & Frayer, D. T. 2002, Phys. Rep., 369, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Aguirre, J. E., Chapman, S. C., et al. 2013, ApJ, 779, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Bussmann, R. S., Gurwell, M. A., Fu, H., et al. 2012, ApJ, 756, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Bussmann, R. S., Pérez-Fournon, I., Amber, S., et al. 2013, ApJ, 779, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Bussmann, R. S., Riechers, D., Fialkov, A., et al. 2015, ApJ, 812, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Cañameras, R., Nesvadba, N. P. H., Guery, D., et al. 2015, A&A, 581, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañameras, R., Nesvadba, N., Kneissl, R., et al. 2017, A&A, 604, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calistro Rivera, G., Hodge, J. A., Smail, I., et al. 2018, ApJ, 863, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Carpineti, A., Kaviraj, S., Hyde, A. K., et al. 2015, A&A, 577, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Chakrabarti, S., Fenner, Y., Cox, T. J., Hernquist, L., & Whitney, B. A. 2008, ApJ, 688, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-C., Hodge, J. A., Smail, I., et al. 2017, ApJ, 846, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Clayton, D. D. 1968, Principles of Stellar Evolution and Nucleosynthesis (New York: McGraw-Hill) [Google Scholar]
- Conley, A., Cooray, A., Vieira, J. D., et al. 2011, ApJ, 732, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, P., Krips, M., Neri, R., et al. 2011, ApJ, 740, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2013, MNRAS, 436, 2793 [NASA ADS] [CrossRef] [Google Scholar]
- Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2017, ApJ, 840, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Finlator, K., Oppenheimer, B. D., et al. 2010, MNRAS, 404, 1355 [NASA ADS] [Google Scholar]
- Dekel, A., Sari, R., & Ceverino, D. 2009, ApJ, 703, 785 [Google Scholar]
- Dessauges-Zavadsky, M., Zamojski, M., Schaerer, D., et al. 2015, A&A, 577, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., Gavazzi, R., Peirani, S., & Silk, J. 2013, MNRAS, 433, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., Furlanetto, C., Swinbank, A. M., et al. 2015, MNRAS, 452, 2258 [NASA ADS] [CrossRef] [Google Scholar]
- Dye, S., Furlanetto, C., Dunne, L., et al. 2018, MNRAS, 476, 4383 [NASA ADS] [CrossRef] [Google Scholar]
- Eales, S., Dunne, L., Clements, D., et al. 2010, PASP, 122, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Engel, H., Tacconi, L. J., Davies, R. I., et al. 2010, ApJ, 724, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Enia, A., Negrello, M., Gurwell, M., et al. 2018, MNRAS, 475, 3467 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P. 2015, ApJ, 799, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Fakhouri, O., Ma, C.-P., & Boylan-Kolchin, M. 2010, MNRAS, 406, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Falstad, N., González-Alfonso, E., Aalto, S., et al. 2015, A&A, 580, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Ferrara, A., Bischetti, M., et al. 2017, A&A, 608, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, D. R., & Pineau Des Forêts, G. 2010, MNRAS, 406, 1745 [NASA ADS] [Google Scholar]
- Fu, H., Jullo, E., Cooray, A., et al. 2012, ApJ, 753, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., Cooray, A., Feruglio, C., et al. 2013, Nature, 498, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Treu, T., Koopmans, L. V. E., et al. 2008, ApJ, 677, 1046 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, R., Cooray, A., Conley, A., et al. 2011, ApJ, 738, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Genel, S., Genzel, R., Bouché, N., Naab, T., & Sternberg, A. 2009, ApJ, 701, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Genzel, R., Tacconi, L. J., Lutz, D., et al. 2015, ApJ, 800, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez-Guijarro, C., Toft, S., Karim, A., et al. 2018, ApJ, 856, 121 [NASA ADS] [CrossRef] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2012, A&A, 541, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Bruderer, S., et al. 2013, A&A, 550, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Graciá-Carpio, J., et al. 2014a, A&A, 561, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Aalto, S., & Falstad, N. 2014b, A&A, 567, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Alfonso, E., Fischer, J., Bruderer, S., et al. 2018, ApJ, 857, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, T. R., Leonidaki, I., Xilouris, E. M., et al. 2014, ApJ, 794, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Haas, M., Klaas, U., Coulson, I., Thommes, E., & Xu, C. 2000, A&A, 356, L83 [NASA ADS] [Google Scholar]
- Harrington, K. C., Yun, M. S., Magnelli, B., et al. 2018, MNRAS, 474, 3866 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., & Giovanelli, R. 1984, AJ, 89, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Hayward, C. C., Kereš, D., Jonsson, P., et al. 2011, ApJ, 743, 159 [CrossRef] [Google Scholar]
- Hayward, C. C., Chapman, S. C., Steidel, C. C., et al. 2018, MNRAS, 476, 2278 [NASA ADS] [CrossRef] [Google Scholar]
- Hezaveh, Y. D., Marrone, D. P., Fassnacht, C. D., et al. 2013, ApJ, 767, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Hodge, J. A., Carilli, C. L., Walter, F., et al. 2012, ApJ, 760, 11 [Google Scholar]
- Hodge, J. A., Riechers, D., Decarli, R., et al. 2015, ApJ, 798, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Hodge, J. A., Swinbank, A. M., Simpson, J. M., et al. 2016, ApJ, 833, 103 [Google Scholar]
- Hodge, J. A., Smail, I. I., Walter, F., et al. 2018, ApJ, submitted [arXiv:1810.12307] [Google Scholar]
- Holmberg, E. 1946, Meddelanden fran Lunds Astronomiska Observatorium Serie II, 117, 3 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hubble, E. P. 1926, ApJ, 64, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, D. H., Serjeant, S., Dunlop, J., et al. 1998, Nature, 394, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Imanishi, M., Nakanishi, K., & Izumi, T. 2017, ApJ, 849, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Smail, I., Barger, A. J., et al. 2000, MNRAS, 315, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Papadopoulos, P. P., Smail, I., et al. 2011, MNRAS, 412, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Smail, I., Amblard, A., et al. 2012, MNRAS, 425, 1320 [NASA ADS] [CrossRef] [Google Scholar]
- Ivison, R. J., Lewis, A. J. R., Weiss, A., et al. 2016, ApJ, 832, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Jiménez-Andrade, E. F., Magnelli, B., Karim, A., et al. 2018, A&A, 615, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kartaltepe, J. S., Dickinson, M., Alexander, D. M., et al. 2012, ApJ, 757, 23 [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Koopmans, L. V. E., Bolton, A., Treu, T., et al. 2009, ApJ, 703, L51 [NASA ADS] [CrossRef] [Google Scholar]
- Le Floc’h, E., Charmandaris, V., Laurent, O., et al. 2002, A&A, 391, 417 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Floc’h, E., Papovich, C., Dole, H., et al. 2005, ApJ, 632, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Leung, T. K. D., Riechers, D. A., & Pavesi, R. 2017, ApJ, 836, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Eales, S. A., Gear, W. K. P., et al. 1999, ApJ, 518, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Litke, K. C., Marrone, D. P., Spilker, J. S., et al. 2019, ApJ, 870, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, L., Weiß, A., Perez-Beaupuits, J. P., et al. 2017, ApJ, 846, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, N., Zhao, Y., Díaz-Santos, T., et al. 2017, ApJS, 230, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lupu, R. E., Scott, K. S., Aguirre, J. E., et al. 2012, ApJ, 757, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maeder, A. 1983, A&A, 120, 113 [NASA ADS] [Google Scholar]
- Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnelli, B., Popesso, P., Berta, S., et al. 2013, A&A, 553, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- Marrone, D. P., Spilker, J. S., Hayward, C. C., et al. 2018, Nature, 553, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Massardi, M., Enia, A. F. M., Negrello, M., et al. 2018, A&A, 610, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., et al. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- Meijerink, R., Spaans, M., Loenen, A. F., & van der Werf, P. P. 2011, A&A, 525, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Messias, H., Dye, S., Nagar, N., et al. 2014, A&A, 568, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Michałowski, M. J., Dunlop, J. S., Koprowski, M. P., et al. 2017, MNRAS, 469, 492 [NASA ADS] [CrossRef] [Google Scholar]
- Miettinen, O., Novak, M., Smolčić, V., et al. 2017, A&A, 602, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motta, V., Ibar, E., Verdugo, T., et al. 2018, ApJ, 863, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Chary, R.-R., Dickinson, M., et al. 2011a, ApJ, 732, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011b, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Turk, M., Feldmann, R., et al. 2015, Nature, 525, 496 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Negrello, M., Perrotta, F., González-Nuevo, J., et al. 2007, MNRAS, 377, 1557 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Hopwood, R., De Zotti, G., et al. 2010, Science, 330, 800 [NASA ADS] [CrossRef] [Google Scholar]
- Negrello, M., Amber, S., Amvrosiadis, A., et al. 2017, MNRAS, 465, 3558 [NASA ADS] [CrossRef] [Google Scholar]
- Nightingale, J. W., & Dye, S. 2015, MNRAS, 452, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Nightingale, J. W., Dye, S., & Massey, R. J. 2018, MNRAS, 478, 4738 [NASA ADS] [CrossRef] [Google Scholar]
- Oliver, S. J., Bock, J., Altieri, B., et al. 2012, MNRAS, 424, 1614 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., Neri, R., Cox, P., et al. 2011, A&A, 530, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Omont, A., Yang, C., Cox, P., et al. 2013, A&A, 551, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oteo, I., Zhang, Z.-Y., Yang, C., et al. 2017, ApJ, 850, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P. 2010, ApJ, 720, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W.-F., Miniati, F., & Viti, S. 2011, MNRAS, 414, 1705 [NASA ADS] [CrossRef] [Google Scholar]
- Peirani, S., Dubois, Y., Volonteri, M., et al. 2017, MNRAS, 472, 2153 [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXVII. 2015, A&A, 582, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rangwala, N., Maloney, P. R., Glenn, J., et al. 2011, ApJ, 743, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, U., & Cornwell, T. J. 2011, A&A, 532, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rawle, T. D., Egami, E., Bussmann, R. S., et al. 2014, ApJ, 783, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Remus, R.-S., Dolag, K., Naab, T., et al. 2017, MNRAS, 464, 3742 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Walter, F., Brewer, B. J., et al. 2008, ApJ, 686, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Cooray, A., Omont, A., et al. 2011a, ApJ, 733, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Riechers, D. A., Carilli, L. C., Walter, F., et al. 2011b, ApJ, 733, L11 [Google Scholar]
- Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
- Riechers, D. A., Leung, T. K. D., Ivison, R. J., et al. 2017, ApJ, 850, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Rigopoulou, D., Spoon, H. W. W., Genzel, R., et al. 1999, AJ, 118, 2625 [NASA ADS] [CrossRef] [Google Scholar]
- Rodriguez-Gomez, V., Genel, S., Vogelsberger, M., et al. 2015, MNRAS, 449, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Matteucci, F., Zhang, Z.-Y., Papadopoulos, P. P., & Ivison, R. J. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Evans, A. S., Thompson, R., et al. 2000, AJ, 119, 991 [NASA ADS] [CrossRef] [Google Scholar]
- Sharda, P., Federrath, C., da Cunha, E., Swinbank, A. M., & Dye, S. 2018, MNRAS, 477, 4380 [NASA ADS] [CrossRef] [Google Scholar]
- Sharon, C. E., Baker, A. J., Harris, A. I., & Thomson, A. P. 2013, ApJ, 765, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Elbaz, D., Bourne, N., et al. 2016, ApJS, 222, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015a, ApJ, 807, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Simpson, J. M., Smail, I., Swinbank, A. M., et al. 2015b, ApJ, 799, 81 [CrossRef] [Google Scholar]
- Smail, I., Ivison, R. J., & Blain, A. W. 1997, ApJ, 490, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Smolčić, V., Karim, A., Miettinen, O., et al. 2015, A&A, 576, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solomon, P. M., Downes, D., & Radford, S. J. E. 1992, ApJ, 387, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnenfeld, A., Treu, T., Gavazzi, R., et al. 2013, ApJ, 777, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Aravena, M., Marrone, D. P., et al. 2015, ApJ, 811, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Marrone, D. P., Aravena, M., et al. 2016, ApJ, 826, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, J. S., Aravena, M., Béthermin, M., et al. 2018, Science, 361, 1016 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Smail, I., Longmore, S., et al. 2010, Nature, 464, 733 [Google Scholar]
- Swinbank, A. M., Papadopoulos, P. P., Cox, P., et al. 2011, ApJ, 742, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Simpson, J. M., Smail, I., et al. 2014, MNRAS, 438, 1267 [Google Scholar]
- Swinbank, A. M., Dye, S., Nightingale, J. W., et al. 2015, ApJ, 806, L17 [Google Scholar]
- Tacconi, L. J., Genzel, R., Smail, I., et al. 2008, ApJ, 680, 246 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tacconi, L. J., Neri, R., Genzel, R., et al. 2013, ApJ, 768, 74 [Google Scholar]
- Thompson, T. A., Quataert, E., & Murray, N. 2005, ApJ, 630, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Thomson, A. P., Ivison, R. J., Owen, F. N., et al. 2015, MNRAS, 448, 1874 [NASA ADS] [CrossRef] [Google Scholar]
- Toft, S., Smolčić, V., Magnelli, B., et al. 2014, ApJ, 782, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Valtchanov, I., Virdee, J., Ivison, R. J., et al. 2011, MNRAS, 415, 3473 [NASA ADS] [CrossRef] [Google Scholar]
- van der Tak, F. F. S., Weiß, A., Liu, L., & Güsten, R. 2016, A&A, 593, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vieira, J. D., Marrone, D. P., Chapman, S. C., et al. 2013, Nature, 495, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Wardlow, J. L., Cooray, A., De Bernardis, F., et al. 2013, ApJ, 762, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Wardlow, J. L., Cooray, A., Osage, W., et al. 2017, ApJ, 837, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Wiklind, T., & Combes, F. 1996, Nature, 379, 139 [Google Scholar]
- Wilson, C. D., Scoville, N., Madden, S. C., & Charmandaris, V. 2000, ApJ, 542, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, D., Springel, V., Sluse, D., et al. 2017, MNRAS, 469, 1824 [NASA ADS] [CrossRef] [Google Scholar]
- Xue, R., Fu, H., Isbell, J., et al. 2018, ApJ, 864, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C. 2017, Physical Conditions of the Interstellar Medium in High-redshift Submillimetre Bright Galaxies, PhD Thesis, Univ. Paris-Sud, Université Paris-Saclay [Google Scholar]
- Yang, C., Gao, Y., Omont, A., et al. 2013, ApJ, 771, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2016, A&A, 595, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, Z.-Y., Ivison, R. J., George, R. D., et al. 2018a, MNRAS, 481, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Z.-Y., Romano, D., Ivison, R. J., Papadopoulos, P. P., & Matteucci, F. 2018b, Nature, 558, 260 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Details on the lens model
In addition to the model parameters listed in Table 3, we show in Fig. A.1, the constraints (pair-wise covariance and marginal probability density functions, i.e., PDFs) we derived for some relevant parameters defining the continuum flux, size, and magnification of the two exponential profiles.
Note that the uncertainties of μ (and on the intrinsic source flux and size) do not account for the effect of mass-sheet degeneracy and do not fully explore the degeneracy of these inferred parameters with the density profile slope of the mass distribution. This fundamental limitation of lens modeling at recovering intrinsic source-plane quantities are generally overlooked. However, the assumption of isothermal mass distribution, which is able to break somewhat the degeneracy, is largely confirmed by observations (Koopmans et al. 2009; Sonnenfeld et al. 2013) and cosmological simulations (Dubois et al. 2013; Peirani et al. 2017; Xu et al. 2017; Remus et al. 2017).
 |
Fig. A.1. Constraints on some relevant model parameters characterizing the two exponential profiles used to describe the continuum emission in terms of half-light radius (Reff, 1 and Reff, 2), total magnification factor (μtot) and stellar velocity dispersion (strength of the SIS mass distribution) for the two deflectors. For each component, magnification and size are somewhat degenerate with the flux density. Contours are 1-, 2-σ, and 3-σ CL regions. Vertical lines in marginal PDF panels along the diagonal represent the mean and the ±1σ interval around the mean. |
 |
Fig. A.2. continued. For the flux densities of the compact and extended dust component at 1.94 (SC1.97, SE1.97) and 0.87 mm (SC0.87, SE0.87). The unit is mJy. And the flux ratios of the two bands for the compact (SC0.87/1.97) and extended (SE0.87/1.97) dust component are also included. |
 |
Fig. A.3. Coarse-grained channel-by-channel comparison of the reconstruction of line emissions. The content of each sub-panel is like in Fig. 5. From left to right: observed data (image plane), model-predicted image plane reconstruction, difference of these images, and right, model-predicted source plane reconstruction, successively for the CO(6–5) and H2O(211−202) lines. Sub-panels in Cols. 1,2,3,5,6,7 exhibit critical lines whereas the ones in Cols. 4,8 show caustic lines. From top to bottom: line emission channels are ordered with decreasing radial velocity, starting from −530 km s−1 (the beginning velocity of each bin), in steps of 105 km s−1. Throughout those channel maps, no residual above the ±3σ limit are found. |
 |
Fig. A.4. continued. For the H2O+ line whose cube was separated into two bins, collapsed for the entire positive and negative part of the spectrum, respectively. |
All Tables
All Figures
 |
Fig. 1. ALMA images of the dust continuum and molecular gas emission in G09v1.97. Upper row – from left to right: 1.94 mm (rest-frame ∼419 μm) dust continuum image with |
| In the text | |
 |
Fig. 2. 1st moment (velocity, left two panels) and 2nd moment (velocity dispersion, right two panels) color maps of the CO(6–5) and H2O(211−202) line emission overlaid by the 0th moment (velocity-integrated line emission) contours. The images reveal the strongly lensed kinematic structure of G09v1.97 in the image plane in both CO(6–5) and H2O(211−202), with a significant velocity gradient seen in the northeastern and southern components. The CO and H2O lines trace similar kinematic structure as shown by the close correspondence between their first and second moment maps. |
| In the text | |
 |
Fig. 3. Top left: ratio of the 0th moment of CO(6–5) to the rest-frame 419 μm (observed wavelength of 1.94 mm) continuum. The contours are for the CO(6–5) 0th moment and are the same as in Fig. 2. Top right: 1st moment ratio map of CO(6–5) to H2O(211−202). Bottom left: 0th moment ratio map of CO(6–5) to H2O(211−202). Bottom right: histogram of the CO(6–5)-to-H2O(211−202) 0th moment ratio. The positions of the dust peak at north and south are indicated with yellow stars. The figure shows that the CO(6–5) emission is more extended than the dust continuum emission. Despite the small variation of the 0th moment ratio, CO(6–5) and H2O(211−202) show very similar velocity structure. |
| In the text | |
 |
Fig. 4. Spatially integrated, continuum-subtracted 2 mm spectra of G09v1.97 with a spectral resolution of 35 km s−1. The vertical dotted lines represent the expected central positions of the lines. As argued in the text, that the weak emission at ∼745 GHz feature is likely dominated by the H2O(211−202) line. The dot-dashed lines represent the corresponding Gaussian decompositions: blue represents the approaching gas component (marked as “B”) while orange and red represent the blue-shifted Gaussian component (marked as “Rb”) and red-shifted Gaussian component (marked as “Rr”) of the receding gas, respectively. The solid green line shows the sum. The average noise level of the spectra is ∼0.2 mJy with a spectral resolution of 50 km s−1. Top: rest-frame 738–755 GHz spectrum combining SPW-0 and SPW-1. The light-blue shaded area indicates the 746–746.5 GHz gap between SPW-0 and SPW-1. The H2O(211−202) line and the H2O+(202−111)(5/2−5/2) line are fitted with a single Gaussian profile due to limited S/N and the lack of data in the inter-band gap. Bottom: SPW-2 spectrum of CO(6–5). The dot-dashed and solid lines are the same as in the top panel. The left inset shows the fit of the spectrum using two Gaussian profiles (green lines). It is clear that a double-Gaussian profile does not fit well the total line profile of the source. It is because of this, we introduced a third Gaussian component in the fit. The right inset shows a comparison among the line profiles of CO(6–5), H2O(211−202), and H2O+(202−111)(5/2−3/2). They are found to be similar, indicating a similar spatial distribution of the line-emitting regions. |
| In the text | |
 |
Fig. 5. Panels a–c: image-plane lens modeling results of the 1.94 and 0.87 mm dust continuum, CO(6–5) and H2O(211−202) line emission for G09v1.97. The panels are grouped in horizontal sets of three sub-panels each showing, from left to right: i) observed image; ii) reconstructed image from the lens model; and iii) residuals from the difference between observed and model images. The red lines represent the critical curves. The central coordinates are given in Table 3. The figure clearly demonstrates that the lens model can recover the fluxes of the dust continuum and line emission accurately. The corresponding source-plane images are show in Fig. 6. All the residuals are well within ±2.5σ, showing that all the modeled images of the dust continuum and the emission lines agree very well with the overall flux distribution. |
| In the text | |
 |
Fig. 6. Reconstructed images of the dust continuum and line emission of G09v1.97 using the lens model, displaying: (panels a and b) the images and contours showing the source-plane 0.87 and 1.94 mm dust continuum emission, and (panels c and d) the velocity-integrated CO(6–5) and H2O(211−202) line emission with yellow contours of the 1.94 mm dust emission overlaid for comparison. The central coordinates are the same as in Fig. 5. The caustic lines are shown in red. The flux ratio of the two dust continuum disk components at 0.87 and 1.94 mm are different, indicating that the two components have either different dust temperatures and/or different submm optical depths. The average resolution indicated in panel b is derived from |
| In the text | |
 |
Fig. 7. Top panel: magnification factor as a function of velocity for the emission lines of CO, H2O, and H2O+, and indicated for the two dust components (the legend at the top left corner indicates the line and point style for each component of emission). Bottom panel: a comparison between the integrated spectrum of the observations and lens-model reconstructed data seen in the image plane. The filled regions show the model reconstructed using the bins in the image-plane spectra, while the histogram lines show the observed image-plane spectra (see the legend at the top left). The model overall predicts very well the spectra in the source plane. |
| In the text | |
 |
Fig. 8. Ellipses showing the disk model for the CO(6–5) line emission per velocity channel bin (the central velocity of each disk is indicated by its color as indicated in the color bar). The parameters used to draw each ellipse in the diagram, i.e., half-light radius, PA, and ellipticity, are their median values. The points with error bars indicate the central positions and their uncertainties for each disk. The sizes and positions of the filled circles indicate the total flux and the center of the disk at each velocity bin (the flux scales are shown in the legend in the top left corner and the velocities are given by the color bar). The velocity bins are in steps of 105 km s−1 (see text). The figure shows clearly a concentration of fluxes with approaching velocities at radii smaller than |
| In the text | |
 |
Fig. 9. Left panels, in the image plane: PV plots in the image plane CO(6–5) data cube along the direction marked by the gray dashed lines are shown in the first column. The dark red line shows the position of the critical line. The dashed squares show the major velocity components “R” (Rb+Rr), “G”, and “B”. The second column shows the 0th & 1st moment map of CO(6–5) similar to Fig. 2. The critical line is marked by dark red line. The third column shows the slice of 1st moment CO maps according to the R, G, and B velocity ranges marked in the lower panel of the PV plot in the first column. Right panels, in the source plane: the first column shows the slice of 1st CO moment maps for R, G, and B. The second column shows a similar image of 0th & 1st moment maps of CO(6–5) in the image plane with the caustic line (dark red line) overlaid. By comparing the velocity structures of R, G, and B both in the image plane and the source plane, and also the PV plot, it is clear that the source has three major velocity structures: the approaching gas B, the bridging gas G and the receding gas component R that has a velocity-resolved structure showing a velocity gradient along the north-south direction. |
| In the text | |
 |
Fig. 10. Dust SED of G09v1.97. The fluxes are taken from Herschel and NOEMA measurements (Yang et al. 2016), and also from this work for the 0.89 and 1.94 mm continuum fluxes (blue points). The fit also takes into account the dust continuum fluxes of the compact (the interacting region) and extended (the merging galaxies) dust component from our lens model, indicated by the open and filled circle (green and light-blue for different temperature components), respectively. The SED fit has also taken the differential magnification for the compact and extended components into account. The solid blue line shows the best fit, while other dashed/dotted lines are decompositions of different temperature components. See text for details. |
| In the text | |
 |
Fig. 11. Left panel: spatially integrated spectra extracted from the source-plane line data-cubes constructed from the lens model. The error bars are dominated by the uncertainties in the data. The black curve shows the results of fitting 3 Gaussian line profiles: the blue line represents the B component, the green line represents the gas bridge G component, and the red line represents the receding gas R component (Rb+Rr). The line profiles of CO(6–5) and H2O(211−202) are similar, having ∼1.7 times stronger (peak flux) red-shifted emission compared to the blue-shifted emission. This indicates that there is a similar spatial distribution between the CO(6–5) and H2O(211−202) line emission. The asymmetry of the profile suggests an intrinsically complex velocity structure. Right panel: a sketch of the gas-rich major merger, G09v1.97. The source is composite of three major components, a rotating disk to the north that corresponds to the R component of the spectra shown in the left panel or the double-Gaussian component Rb+Rr seen in the image-plane spectrum, while the compact blue galaxy in the south corresponds to B part of the line profile. There is also a dust-rich gas bridge between the two over the component which has weak CO(6–5) and H2O(211−202) emission. |
| In the text | |
 |
Fig. 12. Correlation between the star formation rate (SFR) surface density and H2O luminosity surface density in high-redshift SMGs (Yang et al. 2016) (shown in black), including HFLS3 (Riechers et al. 2013) and ADFS-27 (Riechers et al. 2017). The red, blue and green data points represent the R, B, and G components of G09v1.97 from this work. The figure shows a tight linear correlation between ΣSFR and ΣLH2O with a fitted slope of 1.0 ± 0.2, which is valid down to the sub-kpc scales. |
| In the text | |
 |
Fig. A.1. Constraints on some relevant model parameters characterizing the two exponential profiles used to describe the continuum emission in terms of half-light radius (Reff, 1 and Reff, 2), total magnification factor (μtot) and stellar velocity dispersion (strength of the SIS mass distribution) for the two deflectors. For each component, magnification and size are somewhat degenerate with the flux density. Contours are 1-, 2-σ, and 3-σ CL regions. Vertical lines in marginal PDF panels along the diagonal represent the mean and the ±1σ interval around the mean. |
| In the text | |
 |
Fig. A.2. continued. For the flux densities of the compact and extended dust component at 1.94 (SC1.97, SE1.97) and 0.87 mm (SC0.87, SE0.87). The unit is mJy. And the flux ratios of the two bands for the compact (SC0.87/1.97) and extended (SE0.87/1.97) dust component are also included. |
| In the text | |
 |
Fig. A.3. Coarse-grained channel-by-channel comparison of the reconstruction of line emissions. The content of each sub-panel is like in Fig. 5. From left to right: observed data (image plane), model-predicted image plane reconstruction, difference of these images, and right, model-predicted source plane reconstruction, successively for the CO(6–5) and H2O(211−202) lines. Sub-panels in Cols. 1,2,3,5,6,7 exhibit critical lines whereas the ones in Cols. 4,8 show caustic lines. From top to bottom: line emission channels are ordered with decreasing radial velocity, starting from −530 km s−1 (the beginning velocity of each bin), in steps of 105 km s−1. Throughout those channel maps, no residual above the ±3σ limit are found. |
| In the text | |
 |
Fig. A.4. continued. For the H2O+ line whose cube was separated into two bins, collapsed for the entire positive and negative part of the spectrum, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.