| Issue |
A&A
Volume 692, December 2024
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 34 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450861 | |
| Published online | 29 November 2024 | |
Fragments of harmony amid apparent chaos: A closer look at the X-ray quasi-periodic eruptions of the galaxy RX J1301.9+2747
1
Centro de Astrobiologia (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, Campus ESAC, 28692 Villanueva de la Cañada, Madrid, Spain
2
Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology (MIT), Cambridge, MA, USA
3
International Centre for Radio Astronomy Research (ICRA), Curtin University, GPO Box U1987 Perth, WA 6845, Australia
4
Department of Astronomy/Steward Observatory, University of Arizona, 933 N Cherry Avenue, Tucson, AZ 85721-0065, USA
5
Max-Planck-Institut für extraterrestrische Physik (MPE), Giessnbachstrasse 1, 85748 Garching bei München, Germany
6
Center for Astrophysics | Harvard & Smithsonian, Cambridge, MA, USA
7
Telespazio UK for the European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
8
Dipartimento di Fisica “G. Occhialini”, Università degli Studi di Milano-Bicocca, Piazza della Scienza 3, I-20126 Milano, Italy
9
INFN, Sezione di Milano-Bicocca, Piazza della Scienza 3, I-20126 Milano, Italy
10
INAF – Osservatorio Astronomico di Brera, Via Brera 20, I-20121 Milano, Italy
11
Center for Theoretical Astrophysics and Cosmology, Institute for Computational Science, University of Zurich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland
12
Institut für Astrophysik, Universität Zürich, Winterthurerstrasse 190, CH-8057 Zürich, Switzerland
13
Max Planck Institute for Astrophysics (MPA), Karl-Schwarzschild-Strasse 1, D-85748 Garching, Germany
14
Department of Physics, Anhui Normal University, Wuhu, Anhui 241002, People’s Republic of China
15
INAF, Osservatorio Astronomico di Brera, Via E. Bianchi 46, 23807 Merate, (LC), Italy
16
IRAP, Université de Toulouse, CNRS, UPS, CNES, 9 Avenue du Colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
17
Instituto de Astrofísica de Canarias, E-38205 La Laguna, Tenerife, Spain
18
Departamento de Astrofísica, Universidad de La Laguna, E-38206 La Laguna, Tenerife, Spain
19
Serco for the European Space Agency (ESA), European Space Astronomy Centre (ESAC), Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
20
Max Planck Institute for Radio Astronomy, Auf dem Hügel 69, Bonn 53121, Germany
⋆ Corresponding author; mgiustini@cab.inta-csic.es
Received:
24
May
2024
Accepted:
2
September
2024
Quasi-periodic eruptions (QPEs) are an extreme X-ray variability phenomenon associated with low-mass (MBH < 107 M⊙) supermassive black holes (SMBHs). First discovered in the nucleus of the galaxy GSN 069, they have been so far securely detected in five other galaxies, including RX J1301.9+2747. When detected, the out-of-QPE emission (quiescence) is consistent with the high-energy tail of thermal emission from an accretion disk. In this article we present the X-ray properties of RX J1301.9+2747, both in quiescence and during QPEs, and complement this information with radio observations. We analyze X-ray data taken during five XMM-Newton observations between 2000 and 2022. The last three observations were taken in coordination with radio observations with the Karl G. Jansky Very Large Array. We also made use of EXOSAT, ROSAT, and Chandra archival observations taken between 1983 and 2009. XMM-Newton detected 34 QPEs of which eight have significantly lower amplitudes than the others. No correlated radio/X-ray variability was observed during QPEs. In terms of timing properties, the QPEs in RX J1301.9+2747 do not exhibit the striking regularity observed in the discovery source GSN 069. In fact there is no clear repetition pattern between QPEs: the average time separation between their peaks is about four hours, but it can be as short as one, and as long as six hours. The QPE spectral properties of RX J1301.9+2747 as a function of energy are, however, very similar to those of GSN 069 and of other QPE sources. During their evolution, X-ray QPEs follow a hysteresis pattern in the temperature-luminosity plane, with a hotter rise than decay. The quiescent emission of RX J1301.9+2747 is more complex than that of GSN 069, as it requires a soft X-ray excess-like component in addition to the thermal emission from the accretion disk. Its long-term X-ray quiescent flux variations are of a low amplitude and not strictly monotonic, with a general decay over the course of ∼22 years. We discuss our observational results in terms of some of the ideas and models that have been proposed so far for the physical origin of QPEs.
Key words: methods: data analysis / methods: observational / galaxies: active / galaxies: individual:: RX J1301.9+2747 / galaxies: nuclei / quasars: supermassive black holes
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
X-ray quasi-periodic eruptions (QPEs) are an extreme extragalactic variability phenomenon associated with supermassive black holes (SMBHs). They are rapid, intense, and recurrent flares of soft X-ray emission. Each QPE typically reaches a soft X-ray peak luminosity on the order of 1042 − 43 erg s−1, which is roughly one order of magnitude higher than the quiescent state. When detected, the quiescent state emission is most likely associated with thermal disk emission with a typical temperature of kT ∼ 50 − 80 eV, while QPEs have X-ray spectra consistent with blackbody-like thermal emission with a typical kT ∼ 100 − 200 eV. The typical duration of QPEs is between ≲1 h and a few hours, and their time separation is about 2.5 − 20 hours.
First discovered in the nucleus of the galaxy GSN 069 (Miniutti et al. 2019), QPEs have been so far identified in other five galaxies, along with two other promising candidates. Shortly after the very first QPE discovery, flares of a similar duration were identified in XMM-Newton archival observations of RX J1301.9+2747 (Sun et al. 2013; Middleton & Ingram 2015; Shu et al. 2017) and were confirmed to be QPEs with new observations performed in 2019 (Giustini et al. 2020). Thanks to blind searches within the all-sky SRG/eROSITA survey, X-ray QPEs have been discovered in four other galaxies: 2MASS 02314715−1020112 and 2MASX J02344872−4419325 (eRO-QPE1 and eRO-QPE2; Arcodia et al. 2021), and 2MASS 14005331−2846012 and 2MASS 04453380−1012047 (eRO-QPE3 and eRO-QPE4; Arcodia et al. 2024b). Furthermore, QPE-like soft X-ray bursts have been detected in the nuclei of the galaxies XMMSL1 J024916.6−041244 (J0249; Chakraborty et al. 2021) and 4XMM J123856.3+330957 (Tormund; Quintin et al. 2023).
Both GSN 069 and RX J1301.9+2747 were known to be active galaxies before the discovery of QPEs, albeit exhibiting only narrow optical emission lines (see respectively Miniutti et al. 2013; Dewangan et al. 2000). Also eRO-QPE1, eRO-QPE2, and J0249 were shown to host narrow emission lines in their optical spectra, indicating the presence of an ionizing photon source in excess of pure stellar light, that is, signatures of nuclear activity (Wevers et al. 2022). The eRO-QPE3 and eRO-QPE4 optical spectra taken with the Southern African Large Telescope revealed the presence of faint and narrow optical emission lines, although higher-resolution spectra are needed to confirm the exact nature of their nuclear activity (Arcodia et al. 2024b). Despite being basically unobscured in the X-rays, none of the current QPE-emitting galaxies shows signs of broad optical or UV emission lines in their spectra. This rules out the presence of a standard active galactic nucleus (AGN) in the QPE-hosting galaxies.
The QPE-hosting galaxies have black hole (BH) masses estimated through stellar velocity dispersion measurements or through continuum luminosity scaling relations on the lower end of the SMBH distribution, MBH ∼ 105 − 5 × 106 M⊙ (Shu et al. 2017; Miniutti et al. 2019; Arcodia et al. 2021; Wevers et al. 2022; Arcodia et al. 2024b). Three out of eight QPE sources (GSN 069, J0249, and Tormund) have a clear connection to tidal disruption events (TDEs; Shu et al. 2018; Sheng et al. 2021; Chakraborty et al. 2021; Quintin et al. 2023). The observation of decaying X-ray quiescent flux in eRO-QPE3 also suggests a connection to a TDE (Arcodia et al. 2024b). Optical integral field spectroscopy has revealed the presence of extended emission line regions of ionized gas in three out of five QPE host galaxies, with properties very similar to those of TDE host galaxies (Wevers et al. 2024). The accretion flow associated with TDEs is possibly too compact to support the mature broad line region typical of active galactic nuclei (AGN). The association between QPEs and TDEs thus might explain the lack of any broad emission line component in the nuclear optical spectra of QPE hosting galaxies (Wevers et al. 2022, 2024).
The signal associated with QPEs has only been observed so far in the soft X-ray band, with a maximum amplitude reached around E = 600 − 800 eV and fading away at E ≳ 1.5 keV. During the QPE evolution, the temperature smoothly rises to a peak value, and then returns to its initial level. The QPE’s properties are energy-dependent: the flares observed at higher energies have shorter durations, with high-amplitude peaks occurring at earlier times compared to lower energies (Miniutti et al. 2019; Giustini et al. 2020; Arcodia et al. 2021). Therefore, the peak temperature of QPEs is usually reached before their peak luminosity. The flares measured in the softest X-ray band begin before those measured in the hardest X-ray band in eRO-QPE1, whose longer duration QPEs allow for better energy-dependent measurements with respect to any other QPE source (Arcodia et al. 2022). Both the QPE amplitudes and the time differences between the QPE peaks (hereafter recurrence times) alternate between weak and strong, as well as short and long in GSN 069 and eRO-QPE2 (Miniutti et al. 2023a,b; Arcodia et al. 2024a, but see also Miniutti et al. 2019; Arcodia et al. 2021). The temporal behavior is more complex in eRO-QPE1, with QPEs of a different amplitude repeating with a large scatter in recurrence times (Arcodia et al. 2022; Chakraborty et al. 2024).
There are two main physical scenarios able to provide context to interpret the QPE observations: accretion flow instabilities and orbital phenomena. The former can reproduce the recurrence times and luminosities of QPEs only if strong magnetic effects are present (e.g., Pan et al. 2022; Kaur et al. 2023; Pan et al. 2023; Śniegowska et al. 2023), or in the case of instabilities leading to accretion disk tearing (Raj & Nixon 2021). However, accretion instability models generally predict a flare shape with a slow rise and a fast decay, which is opposite to what is typically observed in QPEs (e.g., Miniutti et al. 2019; Arcodia et al. 2022, 2024b). Orbital phenomena include both gravitational self-lensing of massive BH binaries of an about equal mass ratio (Ingram et al. 2021) and purely orbital motions of much smaller mass objects around a more massive BH – called extreme mass ratio inspirals (EMRI). The EMRI scenario can include single or multiple stars or stellar remnants undergoing Roche Lobe overflow or tidal stripping at each pericenter passage (e.g., King 2020; Zhao et al. 2022; Metzger et al. 2022; Wang et al. 2022; King 2022; Krolik & Linial 2022; Lu & Quataert 2023; Linial & Sari 2023; King 2023), as well as impacts between low-mass orbiting companions (stars or BHs) and an accretion flow around the primary SMBH (Suková et al. 2021; Xian et al. 2021; Linial & Metzger 2023; Franchini et al. 2023; Tagawa & Haiman 2023; Zhou et al. 2024a,b). In any case, no model so far can fully account for all the observational properties of QPEs.
In this work, we focus on RX J1301.9+2747 (RA = 13h 02m 00.138s, Dec = +27d 46m 57.855s; redshift z = 0.024). This is a young post-starburst galaxy belonging to a small group of galaxies on the outskirts of the Coma Cluster (Caldwell et al. 1999). Its optical spectrum lacks broad optical emission lines. A low BH mass has been estimated either from the width of the [O III] line (MBH = 8 × 105 M⊙, Sun et al. 2013), from spectral fitting (MBH = 1.5 − 3 × 106 M⊙, Shu et al. 2017), or from velocity dispersion measurements (MBH = 1.2 − 4.5 × 106 M⊙, Wevers et al. 2022, 2024). In the X-ray band, RX J1301.9+2747 was serendipitously discovered during an EXOSAT observation of the Coma Cluster (Branduardi-Raymont et al. 1985). It was then observed by ROSAT in 1991, by XMM-Newton in 2000, and by Chandra in 2009, in all cases showing hints of rapid variability in its light curves (Dewangan et al. 2000; Sun et al. 2013; Shu et al. 2017). More recently, the rapid X-ray variability has been observed again by Giustini et al. (2020), confirming that RX J1301.9+2747 is indeed a QPE source.
RX J1301.9+2747 is the second galaxy where X-ray QPEs have been discovered and the only one where such a phenomenon has been observed – albeit recognized a posteriori – on timescales of decades. QPEs were already present in 2000 (Sun et al. 2013), and three more QPEs were observed during a 2019 XMM-Newton observation. While the QPEs observed in RX J1301.9+2747 have amplitudes and durations comparable to those observed in GSN 069, their recurrence pattern appears to be less regular. Specifically, the time separation between the two QPEs detected in 2000 is about five hours (5h; equivalent to about 18 ks), while the time separation between the three QPEs detected in 2019 is about 5.5h (20 ks) and 3h 45m (13.5 ks) (Giustini et al. 2020).
In this article, we present X-ray data of RX J1301.9+2747 taken from 1983 until 2022. These include one EXOSAT flux measurement, ROSAT and Chandra spectra, as well as five XMM-Newton observations, of which four are pointed at the source. Each of the last three XMM-Newton observations was taken in coordination with 10 hours of exposure with the National Radio Astronomy Observatory (NRAO) Karl G. Jansky Very Large Array (VLA). We provide a detailed description of the setup for the data reduction and analysis in Sect. 2. We then present the X-ray data analysis in Sects. 3 (light curves) and 4 (spectra), and the radio data analysis in Sect. 5. We discuss our results in Sect. 6 and we conclude in Sect. 7. Details about the analysis procedures used as well as the complete set of Tables and figures can be found in Appendices A–D. Errors are quoted at the 1σ confidence level throughout the text. A flat cosmology (Λ = 0.73, q0 = 0, H0 = 70 km s−1 Mpc−1) is assumed for the computation of the intrinsic luminosities and luminosity distances.
2. Data reduction and analysis setup
There are five science observations of RX J1301.9+2747 in the XMM-Newton archive, taken between December 2000 and June 2022, for a total of ∼460 ks of exposure time. Details of the observations are reported in Table A.1. The first two short observations of this dataset have been published by Sun et al. (2013), Middleton & Ingram (2015), Shu et al. (2017), and Giustini et al. (2020), while the latest three observations contain still unpublished data. We reduce and analyze all the XMM-Newton datasets with calibration files generated in June 2023 and using homogeneous procedures. We also use archival EXOSAT, ROSAT, and Chandra data to investigate the evolution of the properties of the quiescent (non-QPE) X-ray emission of RX J1301.9+2747.
The XMM-Newton data were reduced using the Science Analysis System (SAS) v.18.0.0, following standard threads as recommended by the XMM-Newton Science Operation Centre. Strong background flares were detected at the beginning and at the end of some of the exposures and were filtered out from the event tables used in the spectral analysis. The whole event tables were instead used for the analysis of the X-ray light curves, after correcting the observed count rates for the effects of the background flares and other instrumental effects (e.g., vignetting, bad pixels, chip gaps) with the SAS task epiclccorr. The light curves times were also converted from the local satellite frame to barycentric dynamical time, whose spatial origin lies at the solar system barycenter, using the SAS task barycen with the Earth ephemeris table “DE405”. The effect of the barycentric conversion is a correction on the order of 5 − 140 s on photon arrival times, depending on the observation. The EPIC-MOS1 and MOS2 light curves were merged using the Ftool1 lcmath, while each pair of EPIC-MOS1 and MOS2 spectral products and response files were merged using the SAS task epicspeccombine. Given the instrumental calibration uncertainty, we retained events with energies greater than 300 eV for the spectral analysis, while for the timing analysis we considered events down to energies of 200 eV. The regions used to extract the source spectra were circles with radii between 20 − 32″. These were determined using the SAS task eregionanalyse, maximizing the S/N using background regions that were annuli for the EPIC-MOS (hereafter MOS) and circles for the EPIC-pn (hereafter pn) cameras. This choice was based on the strong spatial dependence of the pn instrumental background, for which we chose to extract a background as similar as possible to the source one in detector coordinates. The background regions were always larger than the source ones, and all the extraction areas were normalized using the SAS backscale task. The optical monitor data were checked for the presence of variability. We found no significant result, with light curves similar to those of GSN 069 (Extended Data Fig. 2c of Miniutti et al. 2019) and of the eRO-QPE sources (Fig. 1 and 2 of Arcodia et al. 2021 and Fig. 4 and 6 of Arcodia et al. 2024b).
3. X-ray light curve analysis
Figure 1 shows the XMM-Newton light curves of RX J1301.9+2747 with a time bin of 250 s, with light blue and dark blue symbols for the pn and MOS data. The light curves are extracted in the 0.2 − 2 keV band, as the background generally dominates the source signal at higher energies (see Fig. C.1). A total of 34 QPEs were observed between December 2000 and June 2022. Of these, three are only partially detected at the beginning of the exposures2. There are 25 QPEs with pn count rates on the order of 1 − 1.5 s−1 (hereafter strong QPEs) and eight QPEs with about half this count rate (herafter weak QPEs). The QPEs are superimposed on a much fainter emission (hereafter quiescence) with a count rate of about 0.04 s−1.
 |
Fig. 1. Background-corrected XMM-Newton light curves of RX J1301.9+2747, extracted with time bins of 250 s in the 0.2 − 2 keV band as observed by the pn in light blue and by the MOS in dark blue. The epoch of observation name used in the text as explained in Table A.1 is marked in each panel. We number QPEs from number 0 (half-detected by the MOS in 2000) to number 33 (the last detected in 2022B) and mark a few of them with gray numbers. |
We used a Bayesian statistical framework to compare the pn and MOS light curves to a model comprising a constant, representing the quiescent emission, plus Gaussians representing the QPEs. We derive posterior probability distribution functions (hereafter PDFs) and the Bayesian evidence 𝒵 with the nested sampling Monte Carlo algorithm MLFriends (Buchner 2016, 2019) using the UltraNest3 package (Buchner 2021). The quiescent level was fitted only around the QPE peak, using both pn and MOS data when available. From our fit, we estimate the most likely constant count rate (quiescent count rate), the Gaussian centroid (QPE peak arrival time), width σ, and normalization (QPE peak count rate). Details about our fitting procedure are reported in Appendix B, the individual QPE fits are shown in Fig. B.1, and the results are reported in Table B.1.
Figure 2 shows the median values of the posterior PDFs of the QPE peak count rate, the local quiescence count rate, the QPE duration, the QPE amplitude, and the time preceding each QPE, plotted against each other. The duration of each QPE was estimated as twice the FWHM of the best-fitting Gaussian, while the amplitude A is the ratio between the QPE peak count rate and the quiescent one. The small gray boxes in the lower right corner of each subplot report the correlation coefficient between pairs of parameters4. QPEs can be split into two classes depending on their amplitude: weak (A ∼ 5) and strong (A ∼ 10 − 15). They last between 2000 and 3000 s, with a tendency toward shorter durations for weak QPEs. There is a weak positive correlation between the QPE peak count rate (or amplitude) and the QPE duration, with the time preceding the QPE. In particular, whenever the recurrence time exceeds 1 h 40 m (6 ks), no weak QPEs are observed. Remarkably, there is a large scatter in recurrence times between the QPEs of RX J1301.9+2747. The most frequent recurrence time is about 5 h, while the average is 3 h 45 m (13.5 ks). The shortest recurrence time is 1 h 17 m (4.6 ks) between QPE7 and QPE8, and the largest is 6 h 05 m (21.9 ks) between QPE30 and QPE31.
 |
Fig. 2. Properties of the QPEs of RX J1301.9+2747, derived from the XMM-Newton EPIC light curves: QPE peak count rate (CR), in s−1; local quiescence count rate (CR), in s−1; QPE duration, in minutes; QPE amplitude; time between QPE number n and QPE number n − 1, in kiloseconds (ks). For each quantity, we plot the median of the posterior PDF along with its 1 standard deviation error bar. The gray boxes in the lower right corner of each subplot report the correlation coefficients between the parameters. |
The QPEs of RX J1301.9+2747 show significantly more irregular timing properties than GSN 069 and eRO-QPE2 (Miniutti et al. 2019; Arcodia et al. 2022). However, the QPEs still show an alternate long-short time separation. This is shown in Fig. 3, where we consider the three long XMM-Newton observations taken in 2020 and 2022, and plot for each QPE the time interval preceding it. The average recurrence time is 14.4 ks in 2020, 11.1 ks in 2022A, and 14.3 ks in 2022B. The light curves of 2020 and 2022B look remarkably similar. There is no clear repeating pattern, even considering even and odd (or strong and weak) QPEs separately.
 |
Fig. 3. Time (in ks) preceding each QPE of the 2020, 2022A, and 2022B XMM-Newton observations of RX J1301.9+2747. |
Despite the irregular timing properties, the QPEs in RX J1301.9+2747 are not fully chaotic either. At epochs during which weak QPEs are clearly present (roughly the first halves of observations 2020 and 2022B and almost the whole observation 2022A), QPEs clearly come in strong and weak pairs with a short time separation. On the other hand, when weak QPEs are absent (observation 2019, and roughly the second halves of observations 2020 and 2022B), the pairs are separated by significantly longer intervals. The alternation of long and short recurrence times is still present but becomes less dramatic, and the alternation of strong and weak amplitude is lost altogether. We also point out that, if the two different phases are considered separately, the repetition pattern in each phase is reminiscent of more regular QPE activity such as that observed in GSN 069 or eRO-QPE2, with averaged short and long recurrence times of 1 h 36 m (5.8 ks) and 4 h 48 m (17.3 ks) in the weak-QPE phase, and 3 h 24 m (12.2 ks) and 5 h 14 m (18.8 ks) during epochs when weak QPEs are absent.
3.1. Energy-resolved light curves
We extracted light curves in several observer frame energy bands: 0.2 − 0.4, 0.4 − 0.6, 0.6 − 0.8, 0.8 − 1.0, and 1 − 2 keV, using time bins of 200 s. The quiescent emission has a very low count rate in energy-resolved bins; hence, we compared the QPE light curves to a model comprising a Gaussian line only. We limited the energy-resolved timing analysis to the pn data.
Figure 4 shows the posterior PDF of the QPE properties measured in the five energy bands, with increasing darkness for increasing energy. From upper to lower panels, we plot the time delays of energy-resolved QPE peak times with respect to those measured in the full 0.2 − 2 keV band, the QPE duration, and the QPE peak count rate. As found already by Giustini et al. (2020) for the 2000 and 2019 datasets, and as observed in all QPE sources and QPE candidates so far, the QPEs in RX J1301.9+2747 last less and peak earlier at higher energies. The QPE peak times in the 0.4 − 0.6 keV band are comparable to those measured in the full band; those measured at lower energies arrive later by about two minutes, while those measured at higher energies arrive earlier, by up to about 10 minutes. The duration of QPEs measured between 0.2 − 0.4 keV is twice the one measured at E > 0.8 keV. There doesn’t appear to be any significant difference between strong and weak QPEs in terms of their properties as a function of energy, although the hardest energy band considered (1 − 2 keV) could not always be modeled in weak QPE data because of the very low observed count-rate. In general, as the energy increases, the QPE count rate and duration decrease, while the peak time occurs earlier. The decrease in peak count rate with energy is simply a consequence of the spectral shape of QPEs (a blackbody-like spectrum with kT ∼ 100 eV at peak, see Miniutti et al. 2019, and Sect. 4). The QPE amplitude increases with energy because the spectral decline of the quiescence is steeper than that of QPEs, as the quiescent spectrum has the signal disappearing already at ∼1 keV, while QPEs can be measured at peak up to ∼2 keV. This behavior is similar to what has been observed for other QPE sources, thus likely representing a defining property of QPE emission.
 |
Fig. 4. Properties of QPEs as a function of energy plotted as histograms of their posterior PDFs. From upper to lower panels: difference between the QPE arrival times measured in different energy bands and the QPE arrival times measured in the 0.2 − 2 keV band, QPE duration, and count rate at the QPE peak. The energies considered are 0.2 − 0.4, 0.4 − 0.6, 0.6 − 0.8, 0.8 − 1, and 1 − 2 keV from lighter to darker histograms. |
3.2. Hardness ratio
In Figure B.2 we plot in each panel the individual QPE 0.2 − 2 keV light curve and the corresponding hardness ratio (HR) computed between 0.6 − 2 keV and 0.2 − 2 keV, following Arcodia et al. (2022). One example is shown in Fig. 5 for QPE11. The QPE evolution in RX J1301.9+2747 is chromatic, as is in the other QPE sources: at a given count rate, the spectral hardness is greater during the rising phase of QPEs than during their decaying phase. The QPE peak temperature is not reached at the QPE peak count rate, but during the QPE rise. While for most of the QPEs the hysteresis cycle is clear, a subsample of them show a more complex behavior, with the HR appearing to further increase during or right after the QPE peak (e.g., QPEs numbers 3, 13, 15, 19, 20, 21, and 29). The weak QPEs numbers 8, 18, 26, and 28 also show a rather complex evolution, e.g., a decay as hard as the rise or a hardening decay. These complexities might be explained by the presence of substructures within the QPE, e.g., overlapping bursts that are not resolved by the current instruments.
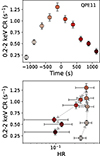 |
Fig. 5. Top panel: representative 0.2 − 2 keV background-subtracted QPE light curve, centered at the peak and binned to 250 s. Lower panel: hardness ratio (HR) between the 0.6 − 2 keV and the 0.2 − 2 keV count rates as a function of the total count rate, where each point is color-coded following the time evolution of the QPE in the panel above. The HR shows a counter-clockwise evolution, as tracked by the dashed gray arrows. The complete set of HR plots can be found in Fig. B.2. |
4. X-ray spectral analysis
The goals of the X-ray spectral analysis are twofold: (i) understanding the X-ray spectral shape and temporal evolution of the quiescent emission (i.e., QPE excluded) of RX J1301.9+2747 and comparing it with that of known accreting SMBH systems such as AGN and TDEs; and (ii) deriving the X-ray spectral and variability properties of all the QPEs detected in RX J1301.9+2747 in order to look for potential differences (e.g., between weak and strong QPEs). We thus analyze separately the quiescent (Sect. 4.1 and Appendix C) and the QPE spectra (Sect. 4.2 and Appendix D) of RX J1301.9+2747 taken by the EPIC cameras onboard XMM-Newton between 2000 and 2022. We add to our spectral analysis also archival ROSAT and Chandra data taken respectively in 1991 and 2009 (Sect. 4.1.3).
We used the software HEASoft v.6.27.2 (NASA High Energy Astrophysics Science Archive Research Center (Heasarc) 2014) with Xspec v.12.11.01 (Arnaud 1996) and the pyXspec python interface (Gordon & Arnaud 2021). For the spectral analysis, we use the Bayesian X-ray Analysis software BXA v.4.1.1 (Buchner et al. 2014) that links the Bayesian statistical framework implemented in UltraNest with Xspec. All the spectral fits assumed the photoionization cross-sections and interstellar medium abundances provided by Wilms et al. (2000) and included a minimum Galactic hydrogen-equivalent column density NH = 8.8 × 1019 cm−2 along the line of sight in the direction of RX J1301.9+2747 (HI4PI Collaboration 2016), modeled with TBabs. In all the models for the source emission, we include the zashift component for the cosmological redshift z = 0.024.
4.1. The quiescent spectra
The quiescent (source + background) and background spectra of RX J1301.9+2747 observed by XMM-Newton between 2000 and 2022 are shown in Fig. C.1, rebinned for visual purposes. The source and background spectra were obtained by excising time intervals containing QPEs, and, for each observation, we consider the average quiescent spectrum as the intra-observation variability of the quiescent count rate is minimal. The overall spectral variability between epochs is small. As in other QPE sources, the X-ray spectra of RX J1301.9+2747 are super-soft, with most of the source emission at E < 1 keV.
First, we compared the quiescent spectra to the two thermal models [bbodyrad] and [diskbb]. We found that at all epochs the [diskbb] model is preferred over the [bbodyrad] one, given the difference in logarithm of the Bayesian evidence 𝒵 always greater than 2 (the most likely model has the highest Bayesian evidence; details about our fitting procedure are reported in Appendix C). The posterior PDFs of the model [diskbb] (hereafter model 0) folded with the instrumental response are plotted in the left column of Fig. C.2 compared to the observed data for the five epochs of XMM-Newton observation and in the top panel of Fig. 6 for the 2020 epoch. It is evident that [diskbb] alone is unable to account for the data above ∼700 eV as excess emission is present, especially 2019 onwards.
 |
Fig. 6. Quiescent pn spectrum of RX J1301.9+2747 during the 2020 epoch, visually rebinned to 3σ significance and overplotted to the posterior PDF of model 0 ([diskbb], top panel), model 1 ([diskbb + bbody], middle panel), and model 4 ([diskbb + compTT], lower panel). The [diskbb] component is plotted in red, the [bbody] in orange, the [compTT] in brown, and the total model in gray. The complete set of spectra for all epochs compared to models 0 and 1 are shown in Fig. C.2. Spectra are shown up to 2 keV, as at higher energies the signal is dominated by the background, however the data were always fitted up to 10 keV. |
We then fit the five epochs with a series of multicomponent models. These are models 1: [diskbb + bbody]; 2: [diskbb + powerlaw]; 3: [diskbb + bbody + powerlaw]; and 4: [diskbb + compTT], where we use the Comptonization model by Titarchuk (1994). Results of the fit are reported in Table C.1 and Fig. 7, where we plot the histograms of the posterior PDF of various parameters for each epoch of observation for each model, using darker tones for later epochs. Models 1, 2, 3, and 4 are always strongly preferred to model 0, except for epoch 2000, when the Bayesian evidences 𝒵 are comparable. Given the likelihoods and the number of degrees of freedom (AIC, Akaike 1974), model 3 is never the most probable data representation. When using model 2, the photon index Γ > 3 is very steep. Thus the power law component of model 2 mostly accounts for the photons detected in the soft X-ray band. Indeed, for epoch 2000, when the excess of photons at E > 700 eV is the weakest, the posteriors of the bbody component of model 1 and those of the powerlaw component of model 2 are only barely constrained (Fig. 7). Model 1 is the most probable representation of the data at early epochs, while model 4 is the most probable one at late epochs; the two models are equiprobable during 2020. A visual example of the comparison between models 0, 1, and 4 is shown in Fig. 6 for the 2020 epoch. We also plot a comparison of models 0 and 1 in Fig. C.2 for all the epochs, where it is evident that the addition of the bbody component to diskbb (i.e., going from model 0 to model 1) reproduces the data very well, even if the bbody spectral parameters are largely unconstrained during 2000 (as expected, given the low Δlog𝒵 found between model 0 and model 1 for this epoch).
 |
Fig. 7. Synoptic view of the quiescent spectral properties of RX J1301.9+2747 in five epochs of XMM-Newton observation: 2000, 2019, 2020, 2022A, and 2022B (Table A.1), plotted with color tones from lighter to darker. The histograms report the posterior PDF of the parameter of interest considering five different models, 0 to 4, from the first to the fifth row. We plot in red the parameters of the diskbb component, in orange the parameters of the bbody component, in yellow the parameters of the powerlaw component, and in brown the parameters of the compTT component. |
On average, the quiescent spectra of RX J1301.9+2747 are best reproduced by the thermal emission of an accretion disk with inner temperature kT ∼ 50 − 60 eV plus a harder spectral component that can be modeled with bbody (as in model 1) or compTT (as in model 4). The median values of the posterior PDFs for the parameters of models 1 and 4 are plotted in Fig. 8, with the diskbb component in orange, the bbody component in yellow, and the compTT component in brown. From upper to lower panels, we plot the 0.3 − 2 keV luminosity L0.3 − 2 keV, the bolometric luminosity5LBOL, and the temperature kT. The main difference between model 1 and model 4 is the spectral energy distribution shape of the harder spectral component, which is broader for compTT than for bbody. As a consequence, the inferred inner temperature of the diskbb component is lower, and the estimated total bolometric luminosities are slightly higher, when using model 4 than when using model 1.
 |
Fig. 8. Evolution of the 0.3 − 2 keV luminosity (first row), bolometric luminosity (second row), and temperature (third row) of the quiescent emission of RX J1301.9+2747 in each epoch of XMM-Newton observation obtained using model 1 [diskbb + bbody] (left column) and model 4 [diskbb + compTT] (right column). Red symbols represent diskbb, orange ones bbody, and the brown ones compTT. Points represent the medians of the posterior PDFs; error bars are one standard deviation. |
The disk inner temperature is consistent with being constant, ∼60 eV, between epochs when using model 1. When using model 4, it is slightly decreasing, from 58 ± 5 eV of 2000 to 49 ± 3 eV of 2022B. The hard spectral component is barely constrained during 2000 and appears to slightly increase its temperature from 2019 to later epochs. This is independent of the underlying model adopted. The luminosity of the harder spectral component estimated using compTT is a factor of (2 − 2.4)× higher in the 0.3 − 2 keV band compared to the one estimated using bbody, while its bolometric luminosity is a factor (4 − 6)× higher, depending on the assumed plasma optical depth (the larger τ, the smaller the difference compared to bbody). This is, however, always much lower than the luminosity carried by the disk. The observed disk luminosity shows an overall decay of about 50% between 2000 and 2022, from  erg s−1 to
erg s−1 to 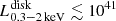 erg s−1. The 0.3 − 2 keV disk luminosity is about 2 − 4 times higher than the 0.3 − 2 keV luminosity of the harder component in all epochs except for 2000, when the luminosity of the former is > 10× the one of the latter (this component not being constrained by the data). The bolometric luminosity of the disk is instead a factor of ∼50× higher than the bolometric luminosity of the harder component when using bbody, and a factor of ∼15× higher when using compTT. When modeled with bbody, the hard spectral component has an average temperature of kT ∼ 180 eV. This temperature is typical of the soft X-ray excess observed in the spectra of most radiatively efficient AGN (Gierliński & Done 2004). When modeled with compTT, the Comptonizing plasma temperature kT is degenerate with its optical depth τ. By assuming τ = 10, the hard spectral component has an average temperature of kT ∼ 400 eV. These values are comparable to those found for the warm corona used to model the soft X-ray excess in local AGN (e.g., Mehdipour et al. 2011; Petrucci et al. 2018). We will therefore refer to this hard spectral component as the “soft X-ray excess-like” component.
erg s−1. The 0.3 − 2 keV disk luminosity is about 2 − 4 times higher than the 0.3 − 2 keV luminosity of the harder component in all epochs except for 2000, when the luminosity of the former is > 10× the one of the latter (this component not being constrained by the data). The bolometric luminosity of the disk is instead a factor of ∼50× higher than the bolometric luminosity of the harder component when using bbody, and a factor of ∼15× higher when using compTT. When modeled with bbody, the hard spectral component has an average temperature of kT ∼ 180 eV. This temperature is typical of the soft X-ray excess observed in the spectra of most radiatively efficient AGN (Gierliński & Done 2004). When modeled with compTT, the Comptonizing plasma temperature kT is degenerate with its optical depth τ. By assuming τ = 10, the hard spectral component has an average temperature of kT ∼ 400 eV. These values are comparable to those found for the warm corona used to model the soft X-ray excess in local AGN (e.g., Mehdipour et al. 2011; Petrucci et al. 2018). We will therefore refer to this hard spectral component as the “soft X-ray excess-like” component.
The total 0.3 − 2 keV quiescent luminosity of RX J1301.9+2747 is maximum during 2000 with L0.3 − 2 keV = 2.0 ± 0.5 × 1041 erg s−1 and is minimum during 2022A with L0.3 − 2 keV = 1.01 ± 0.07 × 1041 erg s−1. There are variations of quiescent luminosity between 2022A and 2022B, when L0.3 − 2 keV = 1.20 ± 0.07 × 1041 erg s−1. The estimated LBOL of each component is about one order of magnitude larger than the 0.3 − 2 keV luminosity at all epochs. The total quiescent luminosity due to the disk plus the soft X-ray excess-like component is LBOL ∼ 2 − 3 × 1042 erg s−1, depending on the epoch of observation.
We estimated the BH mass and mass accretion rate by fitting the quiescent emission to the optxagnf and tdediscspec models, which assume respectively a geometrically thin accretion disk plus a warm and hot corona and a non-stationary TDE accretion flow (see respectively Done et al. 2012; Mummery et al. 2023). By taking into account the uncertainties in the BH spin, we found a large range of admitted values for the BH mass MBH = [2 × 105 − 3 × 106] M⊙ and for the Eddington ratio ṁ = [0.03 − 0.15]. We note how the BH mass estimate from galactic bulge stars velocity dispersion is at the higher end of the estimated range from X-ray spectral fitting (Wevers et al. 2022, 2024). On the other hand, by taking the MBH optical estimate and the estimated Lbol from X-ray spectral fitting and assuming an accretion efficiency of 10%, one would obtain an ṁ < 0.02, in contrast with the thermal X-ray spectrum observed that is typical of highly-accreting BHs. We also point out that the X-ray luminosity of RX J1301.9+2747 is more than one order of magnitude lower than in GSN 069 despite very similar disk temperatures (Miniutti et al. 2019). While the velocity dispersion is very similar in the two galaxies (Wevers et al. 2024), assuming a similar mass accretion rate would lead to a significantly lighter BH in RX J1301.9+2747 than in GSN 069.
4.1.1. On the hard X-ray power law
The hard X-ray power law emission is a defining characteristic of accreting BHs. In their X-ray spectra, actively accreting SMBHs (AGN) usually show the nonthermal hard X-ray power law, a soft X-ray excess of emission compared to the power law, and, depending on the central BH mass, the accretion disk thermal emission (e.g., Done et al. 2012). The origin of the hard X-ray power law emission is commonly assumed to be due to thermal Comptonization of the accretion disk seed photons in a hot (kT ∼ 100 − 200 keV) optically thin plasma (the hot corona, Haardt & Maraschi 1991). The origin of the soft X-ray excess (Arnaud et al. 1985) is more debated and thought to be caused by either ionized reflection off the inner accretion disk (Crummy et al. 2006) or by Comptonization in a warm (kT ∼ 100 − 500 eV), optically thick plasma (the warm corona, Magdziarz et al. 1998).
The hard X-ray power law appears to be very weak or absent in QPE sources, that show instead a quiescent emission dominated by soft X-ray thermal-like spectra, most likely associated with the high-energy tail of the disk emission (Miniutti et al. 2019; Giustini et al. 2020; Arcodia et al. 2021, 2024b; Chakraborty et al. 2024). It is possible that a standard AGN corona is still present in the quiescent spectra of RX J1301.9+2747, but very weak. To test this possibility and place limits on the presence of a hard X-ray power law emission, we compared the quiescent spectra to model 3: [diskbb + bbody + powerlaw]. We assumed informed Gaussian priors for the diskbb and bbody temperatures typical of low-mass AGN, and as found for the parameters of model 1 (respectively ∼60 eV and ∼180 eV), and for the powerlaw photon index with a value typical of unabsorbed AGN (Γ ∼ 1.9). The priors for the other parameters were uninformed (see details in Appendix C).
Results for the fit to model 3 are reported in Table C.1 and are visually represented in the fourth row of Fig. 7. The posterior PDF for Γ is equal to the prior adopted, meaning that the fit is not sensitive to this parameter. The normalization is also unconstrained and consistent with the lowest values probed in our parameter investigation at all epochs. Thus the power law component of model 3 is unconstrained by the data. We conclude that a typical hard X-ray power law is not present or is very weak in the quiescent spectra of RX J1301.9+2747. An upper limit on its 2 − 10 keV luminosity can be placed by considering the highest upper limit in the power law normalization of epoch 2020, L2 − 10 keV < 4 × 1038 erg s−1. This luminosity value is extremely small and corresponds to a bolometric correction of κ2 − 10 keV > 2700. Similar conclusions were reported for the case of GSN 069, which has κ2 − 10 keV > 4000 during the highest X-ray luminosity XMM-Newton observation (Miniutti et al. 2019).
4.1.2. On the soft X-ray excess
The quiescent spectra of RX J1301.9+2747 present a soft X-ray excess-like component emerging between 2000 and 2019. Since no hard power law emission is ever detected, here the excess is defined with respect to the softer X-ray disk component rather than to the 2 − 10 keV emission as in AGN. Its characteristics are nonetheless typical of the soft X-ray excess observed in AGN: when modeled with a phenomenological blackbody, its temperature is typical of the soft X-ray excess observed in AGN (e.g., Gierliński & Done 2004); when modeled with a Comptonization model, it has properties commonly inferred for the warm coronae used to reproduce the AGN soft X-ray excess (e.g., Petrucci et al. 2020). Its temperature appears to slightly increase from 2019 to 2022, from ∼175 eV to ∼190 eV when modeled with bbody and from ∼360 eV to ∼415 eV when modeled with compTT. The soft X-ray excess-like component emits about 25% of the 0.3 − 2 keV disk luminosity in epochs from 2019 to 2022. It was much dimmer in 2000, having 10% of the disk X-ray luminosity at most. In terms of bolometric luminosity, it ranges from 1.6 − 3.3 × 1040 erg s−1 when modeled with bbody to 4.5 − 13 × 1040 erg s−1 when modeled with compTT.
The super-soft X-ray spectrum and the lack of a standard AGN-like hard X-ray continuum of RX J1301.9+2747 and all other QPE sources are highly reminiscent of the properties of most thermal X-ray TDEs. In both cases, the most likely interpretation for the super-soft component is that it represents the high-energy tail of the emission from a radiatively efficient accretion flow around a relatively low mass SMBH. As mentioned in Sect. 1, a connection between QPE sources and TDEs is emerging, based not only on the X-ray properties but also on those of their host galaxies and BH masses (Wevers et al. 2024). A fraction of thermal X-ray TDEs develop harder X-ray emission components over time. For example, AT2019azh and AT2019ehz exhibit a soft excess component with modest luminosity (compared to disk emission) as well as peculiar X-ray variability properties in analogy with RX J1301.9+2747 (Hinkle et al. 2021; Guolo et al. 2024a), and AT2020ocn developed, on timescales of hundreds of days, a high luminosity warm corona component that later appeared to make a transition to a hot corona one (Cao et al. 2024). Whether RX J1301.9+2747 is experiencing a similar evolution and will form a hot corona component in the future remains to be seen. Fast evolution of soft excess and, subsequently, power law continuum components have also been observed in the changing-look AGN/TDE 1ES 1927+654/ASASSN-18el when the Comptonized components reappeared after destruction (Masterson et al. 2022). Some of the soft excess spectral properties, in addition to the exceptional X-ray variability of 1ES 1927+654, are indeed reminiscent of RX J1301.9+2747 as well.
The physical connection between the soft X-ray excess (and, to some extent, the harder power law continuum) observed in AGN, TDEs, and QPE sources is yet to be understood. Future dense monitoring observations of fastly evolving accreting SMBH, such as TDEs and QPE sources, are likely key to make significant progress in the field.
4.1.3. Historical evolution of the RX J1301.9+2747 X-ray quiescent emission
RX J1301.9+2747 has been observed by the EXOSAT Low-Energy Imaging Telescopes (LE) in July 1983, by the ROSAT Position Sensitive Proportional Counters (PSPC) in June 1991, and by the Advanced CCD Imaging Spectrometer (ACIS) onboard Chandra in June 2009 (Table A.2).
The EXOSAT observation allowed Branduardi-Raymont et al. (1985) to estimate a 0.02 − 2.5 keV flux of ∼1.7 × 10−13 erg cm−2 s−1 assuming a powerlaw emission with Γ = 3.5 affected by Galactic absorption. We reproduced these values with the Xspec model [tbabs*powerlaw] and a dummy response file extended to low energies and estimated a 0.3 − 2 keV flux of ∼7.6 × 10−14 erg cm−2 s−1. The luminosity corrected for Galactic absorption is L0.3 − 2 keV ∼ 1.1 × 1041 erg s−1.
The ROSAT PSPC spectra were retrieved from the White-Giommi-Angelini (WGA) Catalog (White et al. 1994), which contains processed high-level products such as calibrated source and background spectra and light curves. Among the three ROSAT observations of RX J1301.9+2747 performed between 16-19 June 1991, the WGA Catalog contains the spectra extracted during the first two observations. These do not show significant variability; thus, we consider them representative of the quiescence. We fit separately the 0.1 − 1 keV spectra of the two epochs of observation using BXA. We found that model 0 [zashift*diskbb] gives a reasonable representation of the data that do not require further complexities. We computed the observed flux in the 0.3 − 2 keV band and found f0.3 − 2 keV = 1.7 ± 0.3 × 10−13 erg cm−2 s−1 for the observation of June 16, and f0.3 − 2 keV = 1.3 ± 0.4 × 10−13 erg cm−2 s−1 for the observation of June 17. These correspond to unabsorbed luminosities L0.3 − 2 keV = 2.5 ± 0.3 × 1041 erg s−1 and 1.9 ± 0.5× 1041 erg s−1.
The Chandra ACIS spectrum of RX J1301.9+2747 taken in June 2009 has an exposure of ∼5 ks, divided into a quiescent state lasting ∼4 ks and a flaring state lasting ∼0.5 ks (Sun et al. 2013). Due to the very low count statistics, we only considered the 0.4 − 1 keV quiescent spectrum. We fitted it to model 0, obtaining a 0.3 − 2 keV flux estimate of 6.7 ± 1.6 × 10−14 erg cm−2 s−1. The corresponding luminosity corrected for Galactic absorption is L0.3 − 2 keV = 1.0 ± 0.3× 1041 erg s−1.
These historical X-ray flux values for the quiescence of RX J1301.9+2747 are plotted in the top panel of Fig. 9 together with the measurements obtained from the XMM-Newton observations. The lower panel of the same figure reports the 0.3 − 2 keV disk luminosity. The long-term evolution of the quiescent emission of RX J1301.9+2747 is complex, with variations that can happen on timescales as short as two days, and that can even be non-monotonic. In particular, the observations 2022A and 2022B are separated by only about 15 hours and show a significant difference in disk luminosity, from 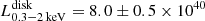 erg s−1 to
erg s−1 to 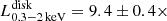 1040 erg s−1.
1040 erg s−1.
 |
Fig. 9. Top panel: 0.3 − 2 keV quiescent flux observed from RX J1301.9+2747 by various telescopes in different epochs, marked by their Modified Julian Day. For all the observations where this was possible (all except the EXOSAT one), the QPE emission was removed, leaving the quiescence only. Lower panel: 0.3 − 2 keV disk luminosity, corrected for absorption. For most of the XMM-Newton measurements, the error bars are smaller than the symbol size. Modified Julian Day. For all the observations |
By assuming a constant 0.3 − 2 keV luminosity of 1041 erg s−1, a total of 1050 erg would have been emitted by RX J1301.9+2747 in quiescence during the 40 years elapsed between the EXOSAT observation of the Coma Cluster and the latest XMM-Newton pointing at the source in 2022.
4.2. The QPE spectra
We analyzed individual QPEs one by one, dividing them in five spectral slices as done by Miniutti et al. (2019) and Miniutti et al. (2023a) for GSN 069 and by Arcodia et al. (2024b) for eRO-QPE3 and eRO-QPE4: two rises (rise-1 and rise-2), one peak, and two decays (decay-1 and decay-2). An example of the adopted spectral decomposition is illustrated in Fig. 10 for QPE2. Details about the QPE spectral fitting procedure are reported in Appendix D. In brief, after comparing the compTT, bbodyrad, and bremss components, the model [TBabs*(zashift*bbodyrad)] was compared to each QPE spectral slice, using both pn and MOS data when available. The QPEs were assumed to be an additive component with respect to the underlying quiescent emission; the quiescent spectrum of the appropriate epoch was used as the background spectrum for the QPE one6. As the neutral absorption modeled with TBabs was found to be consistent with the Galactic value for all spectral slices, we fixed its value to the 8.8 × 1019 cm−2 estimated by the HI4PI Collaboration (2016). The zashift redshift component was fixed to 0.024.
 |
Fig. 10. Example of the QPE spectral decomposition adopted: the pn data of QPE2 are plotted binned to 100 s. Rise-1 in pink, rise-2 in orange, peak in red, decay-1 in dark red, decay-2 in brown, and quiescence in gray. |
The bbodyrad component allows to recover a temperature kT and a physical size for the blackbody-emitting region, if the distance to the source is known. We adopted a luminosity distance of 100 Mpc for RX J1301.9+2747. The bolometric luminosity LBOL was estimated using a dummy spectral response matrix extended between 0.01 − 10 keV applied to the [TBabs*bbodyrad] model, setting the absorption to negligible values. The bolometric luminosity values are conservative, as the bremss and compTT models would provide a QPE bolometric luminosity estimate compared to the bbodyrad model larger by a factor of about four and two. The median values of the posterior PDFs of kT and LBOL estimated at the peak of each QPE are reported in Table B.1. The medians of the QPE temperature and bolometric luminosity posterior PDFs during each spectral slice are plotted in the top panel of Fig. 11 for the weak (open squares) and strong (filled circles) QPEs, color-coded as in Fig. 10. The lower panel of Fig. 11 reports instead the corresponding blackbody radius as a function of the spectral slice, with the profiles of the QPEs centered around their peak plotted in the background as a reference. Both the kT − LBOL and Rbb-time relations are very similar to those observed in GSN 069 and eRO-QPE1 (Miniutti et al. 2023a; Chakraborty et al. 2024). However, the decay in temperature during the QPE evolution in RX J1301.9+2747 is monotonic, while in GSN 069 and eRO-QPE1, rise-2 is generally hotter than rise-1. If interpreted as blackbody emission from a spherical surface, the Rbb evolution is consistent with an expanding emitting surface with initial/final radii on the order of 1 − 4 × 1010 cm. This is comparable to ∼0.14 − 0.6 R⊙, or to about 0.07 − 0.27(106 M⊙/MBH) Rg, where the gravitational radius Rg = GMBH/c2.
 |
Fig. 11. Top panel: average of the posterior PDFs of the temperature kT and bolometric luminosity LBOL of a redshifted blackbody model ([zashift*bbodyrad] in Xspec) compared to the five spectral slices of each QPE of RX J1301.9+2747. Weak QPEs are plotted with open squares, and strong QPEs with filled circles. The color code during the QPE evolution is the same as in Fig. 10. Lower panel: blackbody radius Rbb for each spectral slice, superimposed to the profiles of the 27 QPEs (gray thick lines) with spectral analysis available. |
Assuming a Gaussian parent distribution, we computed the stacked posterior probability density for the temperature of the accretion disk, the soft X-ray excess-like component (excluding 2000), the strong QPE peak, and the weak QPE peak. We found respectively kT = 59 ± 2 eV, 191 ± 18 eV, 132 ± 2 eV, and 119 ± 12 eV. As the peak temperatures of both weak and strong QPEs are always much lower than the temperature of the soft excess-like component measured in quiescence, it appears impossible that QPEs are associated with transient enhancements of the soft X-ray excess emission.
The general properties of the QPEs of RX J1301.9+2747 are plotted in Fig. 12. Here we plot against each other the median values of the posterior PDFs of the QPE bolometric luminosity and temperature at the peak, the QPE duration, the total QPE energy, and the time preceding each QPE. Strong QPEs are plotted with filled circles, weak QPEs with open squares. The total QPE energy was estimated as the integral of the best-fitting Gaussian emission line as 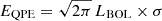 , where LBOL is estimated at the QPE peak and σ is the best-fitting Gaussian standard deviation. The LBOL and kT emitted at the QPE peak are weakly correlated, while a stronger correlation is present between the LBOL emitted by each QPE and the time preceding the QPE in question. Also, the QPE duration correlates with the time preceding each QPE, thus providing the strong observed correlation between EQPE and the time before each QPE. The temperature at the QPE peak appears to be independent of the QPE duration, energy emitted, or time preceding the QPE. In general, more powerful QPEs (i.e., with a higher amplitude, Fig. 2, or with a larger emitted energy, Fig. 12) last longer than less powerful QPEs.
, where LBOL is estimated at the QPE peak and σ is the best-fitting Gaussian standard deviation. The LBOL and kT emitted at the QPE peak are weakly correlated, while a stronger correlation is present between the LBOL emitted by each QPE and the time preceding the QPE in question. Also, the QPE duration correlates with the time preceding each QPE, thus providing the strong observed correlation between EQPE and the time before each QPE. The temperature at the QPE peak appears to be independent of the QPE duration, energy emitted, or time preceding the QPE. In general, more powerful QPEs (i.e., with a higher amplitude, Fig. 2, or with a larger emitted energy, Fig. 12) last longer than less powerful QPEs.
 |
Fig. 12. Corner plot for the medians of the posterior PDFs of various QPE parameters of RX J1301.9+2747. The quantities plotted for each QPE are: the bolometric luminosity at the QPE peak (1042 erg s−1); the temperature at the QPE peak (keV); the QPE duration (m); the QPE total emitted energy (1045 erg); and the time preceding each QPE (h). Strong QPEs are plotted with filled circles, weak QPEs with open squares. Error bars for weak QPEs have been omitted for clarity. A couple of correlation coefficients between the parameters is reported in the lower right corner of each plot: strong QPEs only on top, and both strong and weak QPEs in the gray boxes below. |
In Fig. 13, the QPE total energy radiated is plotted against the ratio between the time following and the time preceding each QPE. The time intervals that precede the most energetic QPEs happen to be longer than those that follow them. The weakest QPEs are instead preceded by much shorter time intervals compared to those that follow them. This is the opposite of what is seen in GSN 069 and eRO-QPE2 (Miniutti et al. 2023b; Arcodia et al. 2024a), where longer time intervals systematically follow stronger QPEs, although the difference between strong and weak QPEs in those two sources is much less extreme than in RX J1301.9+2747.
 |
Fig. 13. For each QPE number n of RX J1301.9+2747 with pn spectral analysis available, the total emitted energy is plotted against the ratio between the time interval between the peaks of QPE number n and QPE number n − 1 and the time interval between the peaks of QPE number n + 1 and QPE number n. |
4.2.1. Comparison with GSN 069
We perform a quantitative comparison of the QPE properties of RX J1301.9+2747 with those of GSN 069. This galaxy has QPEs qualitatively similar to those of RX J1301.9+2747 in terms of duration, amplitude, and time separations and is the best-monitored QPE source by XMM-Newton so far. For the analysis of GSN 069, we used the pn data from December 2018 until August 2022 of all the observations where QPEs are present, for a total of five XMM-Newton observations and 18 QPEs. Of these QPEs, 14 show no strong background flares, and their data were used for the spectral analysis as well: four are weak QPEs and ten are strong QPEs. For fair comparison, we consider only the pn data also for RX J1301.9+2747, i.e., we exclude QPE0 and QPE5 that are detected only by the MOS, and we discard for the spectral analysis also QPEs numbers 4, 7, and 16 that are contaminated by background flares in the pn data. We therefore consider 32 QPEs for the timing analysis7 of RX J1301.9+2747, and 24 for the spectral analysis results comparison.
The distribution of the QPE duration, computed as twice the FWHM of the best-fitting Gaussian in the 0.2 − 2 keV band, is plotted in the left panel of Fig. 14. Here we use blue histograms for the QPEs of RX J1301.9+2747 and gray histograms for the QPEs of GSN 069; in both cases, strong QPEs are plotted with thin solid lines, while weak QPEs have thicker and darker lines. The distribution of duration of QPEs in RX J1301.9+2747 peaks around 45 minutes, while the one of GSN 069’s around 70 minutes. For both sources, the weak QPEs duration appears to be lower than the strong ones.
 |
Fig. 14. Posterior PDFs of the QPE duration (left), computed as twice the FWHM of the best-fitting Gaussian to the 0.2 − 2 keV band; the QPE bolometric luminosity at the peak (center) and QPE temperature at the peak (right), computed comparing the data to a redshifted blackbody model. Data of RX J1301.9+2747 is plotted in blue, data of GSN 069 in gray; for both sources, weak QPEs are plotted with thicker and darker lines. |
Assuming that the QPEs are additive components on top of a constant quiescent emission, we compared the QPE spectral data to a redshifted blackbody model ([zashift*bbodyrad]) for both RX J1301.9+2747 and GSN 069. The posterior PDFs of the bolometric luminosity and the temperature at the QPE peak assuming such a model are reported in the central and right panels of Fig. 14. The QPEs of RX J1301.9+2747 are systematically hotter and less luminous than those of GSN 069. As is the case for the QPE duration, also the LBOL and kT of weak QPEs are systematically lower than those of strong QPEs, for both RX J1301.9+2747 and GSN 069. A more detailed analysis of the spectral properties of the QPEs during their spectral evolution is presented in Fig. 15, where we plot the posterior PDFs of strong QPEs of GSN 069 in gray, and of RX J1301.9+2747 with tones of red of increasing darkness going from rise-1 to decay-2. The difference in temperature between the strong QPEs of RX J1301.9+2747 and those of GSN 069 decreases going from the beginning of the QPE (rise-1) to the end of the QPE (decay-2), when the temperatures of the strong QPEs of the two sources converge to the same value of kT ∼ 80 eV. The average temperature during the QPE peak is ∼130 eV for RX J1301.9+2747 and ∼100 eV for GSN 069, while the average temperature during the QPE rise-1 is respectively ∼160 eV and ∼90 eV.
 |
Fig. 15. Histograms of the posterior PDFs of the temperature (left column) and of the bolometric luminosity (right column) of a blackbody model compared to each strong QPE spectral slice. From upper to lower panels: rise-1 in pink, rise-2 in orange, peak in red, decay-1 in dark red, and decay-2 in brown. The gray histograms report the GSN 069 strong QPEs data. |
4.2.2. Weak and strong QPEs
The average QPE-only spectra (that is, quiescence-subtracted spectra) for the weak and strong QPEs are shown in Fig. 16 compared to the average quiescent spectrum. Here the spectra are plotted unfolded against a power law model with Γ = 2. There appear not to be dramatic differences in the spectral properties of strong and weak QPEs. The main differences between strong and weak QPEs are the energy released and the timing properties. The peak 0.3 − 2 keV (bolometric) luminosity of strong QPEs is 1.7 ± 0.3 × 1042 erg s−1 (2.2 ± 0.3 × 1042 erg s−1). The typical luminosity of strong QPEs is a factor of ∼2.5× higher than the luminosity of weak QPEs. The duration of weak QPEs is at the lower end of the distribution (left panel of Fig. 14), thus making the total energy output of weak QPEs about 1/3 of that of strong QPEs. The temperature at peak of strong QPEs is on average kT = 130 ± 10 eV. Assuming a Gaussian parent distribution, the median temperature at the peak of weak QPEs is kT = 120 ± 20 eV, comparable to the strong QPEs one. However, looking at the right panel of Fig. 14, where the full PDFs for the QPE temperature are shown, it can be seen that the weak QPEs have systematically lower kT than the strong ones, as observed in GSN 069 (Miniutti et al. 2023b). The difference in timing properties of weak and strong QPEs is evident in Fig. 1 and Fig. 13: the recurrence time preceding weak QPEs is much shorter than the one following them. This is the opposite of what is observed in GSN 069 (Miniutti et al. 2023b), although the difference in QPE amplitude in this source is not as dramatic as in RX J1301.9+2747.
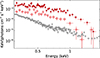 |
Fig. 16. Average 0.3 − 2 keV EF(E) quiescent spectrum of RX J1301.9+2747 (gray) plotted together with the average weak QPE (empty squares) and strong QPE (filled circles) spectra extracted during the peak. The QPE spectra are background-subtracted with the average quiescent spectrum used as background. |
5. Radio observations
The last three XMM-Newton observations of RX J1301.9+2747 were partially covered by simultaneous Karl G. Jansky VLA observations in order to check for the presence of correlated radio and X-ray variability. We observed the coordinates of RX J1301.9+2747 at 6 GHz (C-band) on 2020 July 11 and 2020 July 12 (Program ID SJ6456) and 2022 June 17 and 2022 June 19 (Program ID SL0464), where the VLA was in the extended configurations B and A, respectively. In each observation, flux and bandpass calibration was performed with 3C286 and phase calibration was performed with J1310+3220 (2020) or J1327+2210 (2022). While the 2020 radio observation had to be split in two segments due to instrumental limitations8, the 2022 light curves were continuous and allowed us to check for the presence of radio variability both before and after strong X-ray QPEs. This resulted in the two VLA observations in 2020 being 5 h long each, and the two observations in 2022 being 10 h long each.
All data were reduced in the Common Astronomy Software Package (CASA Team 2022, CASA, v5.6.3) using standard procedures, including the VLA pipeline. Images of the target field were initially made for each of the 4 observations using the CASA task tclean. An unresolved point source at the location of RX J1301.9+2747 was detected in each observation. We extracted the flux density using the CASA task imfit and by fitting an elliptical Gaussian the size of the synthesised beam. Next, 1-minute interval images of the target field were created using the CASA task tclean in order to generate a lightcurve for each of the observations. Again, the flux density of the target was extracted using the CASA task imfit and by fitting an elliptical Gaussian with the size of the synthesised beam. Additionally, we extracted the flux density of a nearby source in the field (after applying a primary beam correction), NVSS J130146+274629, in order to serve as a check source. In general, the check source appears to show some variability on the order of ∼20%, uncorrelated with any variability observed from RX J1301.9+2747. Both of the 2022 observations suffered from severe gain compression due to radio-frequency interference (RFI), particularly in the first three hours of the observations, resulting in significantly lower flux density measured for the target and check source in the field and correlated variability observed for both sources in this time. We therefore excluded these data from the analysis.
The 6 GHz flux densities measured for RX J1301.9+2747 for each of the 4 observations are reported in Table A.3. The VLA light curves of RX J1301.9+2747 for each of the 3 epochs are shown in Fig. 17. The top panel shows the 0.2 − 2 keV light curve, while the lower panel shows the 6 GHz radio flux density in ≈1-minute intervals. No evident radio variability is observed during the X-ray QPEs, except for the QPE in the 2022A observation (QPE17), where a small increase in radio flux density is seen. The flux density increases by ≈0.15 mJy during the QPE. The overall variance of the flux density during the observation is 0.09 mJy, so the small flare is detected at < 2σ significance. This increase is smaller than the variability seen earlier in the observation (and during X-ray quiescence), and we deduce it is unlikely to be associated with the X-ray QPE, especially given there is no evidence of radio variability associated with the X-ray QPEs seen in 2020 and 2022B.
 |
Fig. 17. Simultaneous X-ray and radio light curves for the 2020, 2022A, and 2022B epochs: the top panel reports the 0.2 − 2 keV light curve, and the lower panel the radio light curve at 6 GHz as measured by the VLA. In the lower panel, RX J1301.9+2747 is shown in green, and a different radio source in the field is shown in gray to serve as a check source. Each portion of the broken axes represents 0.25 d. Note that the flux density of the check source has been scaled down by a factor of 15. The gray shaded region shows the mean value for the 2020 observation plus or minus 5%, the absolute accuracy of the VLA flux density calibration. |
As a cross-check, we also used the dftphotom task within the pwkit package to fit the calibrated VLA visibilities in the uv plane directly (Williams et al. 2017). We then binned the data into ∼1 minute chunks to enable a direct comparison with the radio light curves produced by the image-based analysis. We found consistent results for all four observations, including during the time intervals most affected by RFI in the 2022 data. We therefore conclude that there is no statistically significant evidence for correlated radio and X-ray flaring activity in RX J1301.9+2747.
Whilst there does not appear to be significant radio variability associated with the X-ray QPEs in the data presented in this work, there is variability on the order of 5–10% at 6 GHz observed between epochs and within the 2022 observations over the 10 hr tracks. Additionally, Yang et al. (2022) observed RX J1301.9+2747 over 3 days in 2015 at 9 GHz and over 5 days in 2019 at 14 GHz, finding a variability on the order of 26% at 9 GHz and 12% at 14 GHz on timescales as short as a few hours. Here we assess whether the observed radio variability is consistent with interstellar scintillation (ISS) of a compact source or whether it is due to intrinsic variability of the radio source.
Using the NE2001 electron density model (Cordes & Lazio 2002), the transition frequency between strong and weak scintillation regimes occurs at ν0 = 6.4 GHz and the angular size limit of the first Fresnel zone at the transition is θF0 = 4.6 microarcsecond at the Galactic coordinates of RX J1301.9+2747. Adopting the Walker (1998) formalism for ISS as appropriate for compact extragalactic sources, RX J1301.9+2747 will therefore be in the weak scattering regime at 9 and 14 GHz and could be in the strong scattering regime at 6 GHz, but we note that it is very close to the transition frequency. The modulation expected due to ISS at the observing frequencies of 6, 9, and 14 GHz is heavily dependent on the source size. If the source is completely unresolved to scintillation (a source size ≲0.001 pc at the distance of RX J1301.9+2747), we would expect to see variation at 6 GHz of up to 69% on a timescale of 3 h, of 62% at 9 GHz on a timescale of 1.7 h, and 33% at 14 GHz on a timescale of 1.35 h. Clearly, the radio emission from RX J1301.9+2747 was not observed to vary with such high modulation amplitudes at any of the observing frequencies. However, the modulation due to ISS reduces as the source becomes resolved to ISS by a factor (θr/θs)7/6, where θr = θF0(ν/ν0)11/5 and θs is the true angular size of the source. Assuming a maximum modulation of 10% at 6 GHz was observed, this variability could be explained by ISS for a source size 0.008 pc and the timescale for this modulation would be 15 h. A modulation of 26% at 9 GHz requires a source size of 0.0011 pc with an ISS timescale of 3.5 h, and a modulation of 12% at 14 GHz requires a source size of 0.0005 pc with an ISS timescale of 3.1 h. These modulation timescales are consistent with the observed radio data.
Therefore, if the observed radio variability at 6, 9, and 14 GHz were caused by ISS, the radio-emitting region of RX J1301.9+2747 must be between 0.0005–0.008 pc, and smaller at higher frequencies. For AGN jets, the emitting region is commonly observed to be larger at lower frequencies due to the effect of core shift (e.g., Lobanov 1998). Therefore, if the radio emission from RX J1301.9+2747 is dominated by a sub-parsec jet, the emitting region would be expected to be smallest at the highest observing frequencies and larger at the lowest observing frequencies, as inferred from the scintillation analysis. Indeed, VLBA imaging of RX J1301.9+2747 at 1.6 GHz did not resolve any source structure, constraining the source size to < 0.7 pc (Yang et al. 2022). We therefore conclude that the radio variability we detect in this analysis at 6 GHz, as well as the 9 and 14 GHz variability detected by Yang et al. (2022), is not inconsistent with ISS if the radio-emitting region is < 0.008 pc. As pointed out by Yang et al. (2022), if the radio variability timescales observed are associated to a light-travel time, the inferred radio-emitting region could be as small as 0.0008 pc. This is consistent with the variability being primarily due to ISS.
6. Discussion
The two competing physical scenarios proposed so far to interpret QPEs are accretion flow instabilities and orbital phenomena. The former can have various origins: thermal, dynamical (Sect. 6.1), or magnetic (Sect. 6.2). Orbital phenomena can include both gravitational self-lensing of massive BH binaries with order unity mass ratio (Sect. 6.3) and interactions between a massive BH with mass MBH (and/or an accretion flow around it) and one or more secondary objects with much smaller mass m ≪ MBH. When the secondary object is of stellar-mass size, these systems are called extreme mass ratio inspirals (EMRIs; Sect. 6.4). We discuss the results on RX J1301.9+2737 in comparison to other QPE sources (Sect. 6.5) and to other repeating nuclear transients (Sect. 6.6).
6.1. Accretion flow instabilities
Classical radiation pressure instabilities (RPI, Lightman & Eardley 1974; Janiuk et al. 2002) of a thin accretion disk around a SMBH cannot explain the generally short timescales and high luminosities of QPEs (Arcodia et al. 2021). Magnetic or dynamical effects can shrink the disk region subject to instabilities and thus also the predicted timescales. A magnetic wind (Pan et al. 2022, 2023) or a strong disk magnetization (Kaur et al. 2023) can shorten the timescale of instability cycles enough to reproduce the timescales and spectra of QPE sources fairly well. However, the energy dependence of the QPE flare evolution (shown in the top panel of Fig. 4 for the case of RX J1301.9+2747 and observed in all the QPE sources so far) appears not to be reproduced by this class of models (e.g., Pan et al. 2022). Dynamical instabilities of the inner accretion flow have also been proposed to explain QPEs (Raj & Nixon 2021). In principle, accretion flow instabilities might explain the higher energy released by QPEs happening after longer recurrence times observed in RX J1301.9+2747 (Fig. 14). Stronger QPEs would have had more time to accumulate energy to be released in the flare compared to weak QPEs, leading to a larger energy budget that can be radiated away. However, the behavior in RX J1301.9+2747 is opposite to that observed in GSN 069 and eRO-QPE2, where longer recurrence times lead to weaker QPEs (Miniutti et al. 2023a; Arcodia et al. 2024a), thus weakening the overall argument. Furthermore, the flare shape predicted by instability models does not well describe the observed QPE shape. While QPEs generally show a faster rise and a slower decay, the opposite is predicted by RPI, independent of the existence of magnetic fields, and by dynamical instability models.
6.2. Magnetic reconnection
Magnetic instabilities (e.g., relativistic reconnection, Sironi & Spitkovsky 2014) can occur in the innermost regions around SMBHs and might be responsible for heating up the plasma generating the hard X-ray coronae (e.g., Beloborodov 2017; Sridhar et al. 2021, 2023; Masterson et al. 2023). A model for the production of episodic jets driven by magnetic reconnection around SMBHs, in analogy with the coronal mass ejections production in the Sun, was developed by Yuan et al. (2009) and expanded by Li et al. (2017, 2023). These models predict a flare shape similar to that observed in QPEs (e.g., Fig. 10 of Li et al. 2017), resulting from synchrotron emission by thermal and power-law electron distributions in an expanding hot spot close to the BH, with analogies with our findings for QPEs (see Sect. 4.2 and Fig. 11). In analogy with solar flares, the reconnection events are not completely random but are governed by self-organized criticality (Bak et al. 1987; Aschwanden et al. 2016). The resulting distribution of energy release and time of arrival of flares follows power law distributions (Lu & Hamilton 1991) and therefore could produce QPEs of different amplitudes and different recurrence times.
RX J1301.9+2747 is a known radio source, serendipitously detected at 1.4 GHz in the VLA map of the Coma Cluster (Miller et al. 2009). An extensive set of VLA observations performed between July 2015 and January 2019 has been presented by Yang et al. (2022) and showed significant variability on timescales as short as days, implying a compact size of the emission region < 10−3 pc. This scenario is compatible with our 2020–2022 VLA observations, which provided limits on the size of the radio source of < 0.008 pc, given the observed variability attributed to ISS. These results, together with VLBA imaging observations that did not resolve the source scales of < 0.7 pc and a steep radio spectrum indicating optically thin synchrotron emission (Yang et al. 2022), rule out various origins for the radio emission in RX J1301.9+2747 such as star formation or pc-scale outflows, leaving open the scenario of episodic compact jet ejections.
If X-ray QPEs were the results of episodic compact jet ejections, one might expect to observe correlated radio variability due to, for example, broadband synchrotron emission or synchrotron self-Compton. However, our simultaneous XMM-Newton/VLA observations revealed no correlated variability between the X-ray and radio bands (Fig. 17). This suggests two physical mechanisms responsible for the short-term X-ray and radio variability of RX J1301.9+2747.
The radio emission of RX J1301.9+2747 could be nonetheless connected to its quiescent X-ray emission, and in particular to the weak soft X-ray excess-like spectral component that emerges since 2019. This can be modeled with a very steep power law with Γ ≳ 3.5. One possibility is that this weak spectral component is due to magnetic reconnection in a plasma with very low magnetization. The plasma magnetization around the central BH of RX J1301.9+2747 should be very low, due to the dominant contribution in energy density of disk particles. We might thus be able to observe a few magnetic coronal loops forming. These would produce rapid radio variability, and the expected X-ray properties due to bulk Comptonization in the plasmoid chains would be consistent with those observed in RX J1301.9+2747 during quiescence: there would be a very steep X-ray power law-like emission (Sironi & Spitkovsky 2014).
As for the X-ray QPEs of RX J1301.9+2747, in principle their different amplitudes and recurrence times could be explained by magnetic reconnection. However, the regularity of appearance of weak QPEs always shortly after a strong QPE, as well as the alternate long-short separation time, are more difficult to explain in such a scenario. It is even more difficult to explain the regularity of QPE sources such as GSN 069 and eRO-QPE2 (Miniutti et al. 2019; Arcodia et al. 2021, 2022). In fact, magnetic reconnection events are expected to be, albeit not completely random, very irregularly spaced in time. A magnetic reconnection model has been invoked also to explain the flares observed from our Galactic center (e.g., Li et al. 2017; Scepi et al. 2022; Ripperda et al. 2022). However, the observed spectral properties of RX J1301.9+2747, the general self-similarity, the timescales, and the overall asymmetry of its QPE shape are in (stark) contrast with what has been observed in Sgr A* (Ponti et al. 2017; von Fellenberg et al. 2023), casting doubts on the interpretation of QPEs within the same physical context.
6.3. Gravitational self-lensing of massive black hole binary mini-disks
To the first order, models invoking massive BH binaries (MBHB) with self-lensing mini-accretion disks predict a symmetric flare shape and a wavelength-independent (achromatic) signal, which is different than the one observed in QPEs (Ingram et al. 2021). Therefore, this class of models with binaries with equal (or almost) mass ratio has received less attention so far than the high mass ratio (EMRI) scenarios. However, detailed simulations by Krauth et al. (2024) show that the expected signal can be strongly energy-dependent, with similar properties to those observed in the QPE light curves and spectra. Many deviations from a simple symmetric flare shape can occur. For example, Davelaar & Haiman (2022a,b) predict a dip near the middle of the flare. The time separations between the QPEs of RX J1301.9+2747 are however likely too short to be explained by orbital motion of a MBHB, as given the BH mass involved (∼0.4 − 4 × 106 M⊙, Wevers et al. 2022, 2024) the merger of the two BHs should have already happened (e.g., Fig. 3 of Ingram et al. 2021). Only an orbiter with significantly smaller mass than the central massive BH could be invoked, as its time-to-merger would be much longer. In any case, the requirements of a high orbital eccentricity and of having both orbiting BHs’s mini-disks lensing each other are necessary to explain the alternate long-short time separations between QPEs and the large difference between such time separations observed in RX J1301.9+2747.
6.4. Extreme mass ratio inspirals
EMRI scenarios are promising in explaining the general properties of the QPE-emitting sources (Arcodia et al. 2021). Two main classes of EMRI scenarios have been proposed for QPEs: those invoking interactions between the primary SMBH and the secondary object at the pericenter, and those invoking impacts of the secondary on the accretion flow. The first class of scenarios has been explored in a variety of configurations, including both eccentric and circular orbits of single or multiple stars or stellar remnants, experiencing Roche Lobe overflow or tidal stripping, or shocking with the stellar debris (e.g., King 2020; Zhao et al. 2022; Metzger et al. 2022; Wang et al. 2022; King 2022; Krolik & Linial 2022; Lu & Quataert 2023; Linial & Sari 2023; King 2023). The second class of scenarios has been investigated as impacts of the secondary lower-mass EMRI component on a radiatively inefficient, torus-like (Suková et al. 2021) or on a disk-like accretion flow (Xian et al. 2021; Linial & Metzger 2023; Franchini et al. 2023; Tagawa & Haiman 2023; Zhou et al. 2024a,b).
In EMRI scenarios with mass transfer at the pericenter, QPEs happen once per orbit. QPEs are then powered either by accretion of the stripped mass on the primary BH (King 2020; Zhao et al. 2022; Wang et al. 2022; Linial & Sari 2023), or by shocks between different streams of matter (Krolik & Linial 2022), or between the streams and the accretion disk around the primary BH (Lu & Quataert 2023). To the first order, the time between QPEs corresponds to the EMRI orbital period. In practice, the passages at the pericenter will occur slightly later or earlier at each orbit, due to the effects of apsidal precession of the EMRI orbit and light travel time. The QPE duration and intensity depend on the orbital eccentricity and on the relative position of the Roche lobe. The variety of stellar progenitors and orbital parameters (e.g., Lodato et al. 2009; Guillochon & Ramirez-Ruiz 2013) might explain the varieties of QPE phenomenology, with longer duration QPEs due to more gentle pericenter passages (i.e., more circular orbits) and more luminous QPEs due to a more intense mass transfer. An alternation of long-short recurrence times in these scenarios can in principle be explained by thermodynamic readjustments of the stellar structure after each mass transfer (e.g., King 2022). This seems applicable to QPE sources with more regular timing properties such as GSN 069 and eRO-QPE2, where differences between the short and long recurrence times are on the order of few % (Arcodia et al. 2022; Miniutti et al. 2023a). It is however extremely difficult to apply this class of scenarios to the cases of RX J1301.9+2747 or eRO-QPE1, where a large scatter in consecutive recurrence times is observed, as shown in this work and in Chakraborty et al. (2024).
The complexities in the light curves of RX J1301.9+2747 might be interpreted more easily in a double coplanar EMRI scenario, where perhaps weak QPEs are due to the star unable to fill much of its Roche Lobe at the pericenter passage (Metzger et al. 2022). However, in such a case, one would expect substantially different properties for weak and strong QPEs, which have not been observed.
In the case of impacts on the accretion flow, QPEs happen (at least) twice per orbit. The time separation between impacts depends on the EMRI orbital semi-major axis and eccentricity e. Unless the orbit is perfectly circular (e = 0), there is a natural expectation of alternate long-short time separation between QPEs. In general, orbits with a lower eccentricity would cause impacts (and thus QPE flares) to be more equally spaced in time, while a higher eccentricity would cause a larger difference in time preceding and following any QPE. The presence of large differences in time separation between consecutive QPEs leads to a relatively high-e scenario for the EMRI of RX J1301.9+2747, eRO-QPE1, eRO-QPE4, and to a more circular EMRI for eRO-QPE2 and GSN 069 (Franchini et al. 2023; Zhou et al. 2024a,b). In these scenarios the flare emission is likely due to an expanding bubble at the impact location, consistent with the lower panel of Fig. 11 in the case of RX J1301.9+2747, with Fig. 18 of Miniutti et al. (2023a) in the case of GSN 069, and with Fig. 2 and 3 of Chakraborty et al. (2024) in the case of eRO-QPE1. The light curve is characteristic of a mini-supernova (Linial & Metzger 2023) with a fast rise and a slower decay, as observed in QPEs.
Franchini et al. (2023) were the first to qualitatively reproduce the specific timing properties of RX J1301.9+2747 in an EMRI scenario, focusing on the 2022A light curve that is characterized by the presence of weak QPEs. In their scenario, QPEs are due to impacts between the secondary EMRI object and the precessing accretion disk surrounding the primary EMRI object. The two EMRI objects are assumed to be BHs, with the secondary having a MBH = 100M⊙. The orbit of the secondary BH is subject to apsidal and nodal precession, and this complicates the expected light curve, that can contain up to three impacts (QPEs) per orbit. By assuming a prograde and eccentric (e = 0.4) orbit of the secondary BH with a semi-major axis of 50 Rg around a SMBH with MBH = 2 × 106 M⊙ (giving an orbital period of about 6 hours, or 22 ks), the complex timing properties of RX J1301.9+2747 can be qualitatively reproduced. However, the QPE temperature expected in this scenario is kT ∼ 180 − 450 eV, a factor of about 2 − 3 above what we observe, and the relative QPE amplitudes are not always exactly matched by the model.
Zhou et al. (2024b) were the second to apply the impacts scenario to the specific case of RX J1301.9+2747. They assumed a generic stellar-mass object impacting on a TDE-disk and were able to reproduce the timing properties of the 2019 and 2020 light curves, but only when ignoring the presence of weak QPEs. In this case the orbit is still eccentric with a best-fitting e = 0.35 and an orbital period of about nine hours (32 ks). Also in this case the secondary EMRI object reaches distances very close to the central SMBH at the pericenter, and a tight constraint on its mass < 0.5 M⊙ can be placed in the case of it being a star, in order not to reach its tidal radius and thus being destroyed.
The two solutions found by Franchini et al. (2023) and Zhou et al. (2024b) reflect the difference in light curve behavior observed in 2022A compared to the one observed in 2020 as well as the fact that weak QPEs were ignored by Zhou et al. (2024b), thus selecting more regularly spaced QPEs and therefore deriving a slightly lower EMRI orbital eccentricity. The 2022B light curve is remarkably similar to the 2020 one, perhaps indicating some sort of oscillatory mechanism between the two “QPE phases” (one at higher eccentricity when weak QPEs are present, the other at lower eccentricity when weak QPEs are absent) observed in RX J1301.9+2747. We note however how a transition between the two phases appears to happen on extremely short timescales, between 2022A and 2022B. Hence, while the impacts model appears promising in RX J1301.9+2747 (and perhaps even more so in other more regular QPE sources such as GSN 069 and eRO-QPE2), a complete solution that accounts for the two different phases (with and without weak QPEs) has not been reached yet, and further work is needed (Miniutti et al., in prep.).
6.5. Comparison to other QPE sources
X-ray QPEs have been observed in six galaxies so far (GSN 069, RX J1301.9+2747, eRO-QPE1, eRO-QPE2, eRO-QPE3, and eRO-QPE4; Miniutti et al. 2019; Giustini et al. 2020; Arcodia et al. 2021, 2024b), plus two good candidates with X-ray flaring properties very similar to QPEs (J0249 and Tormund, Chakraborty et al. 2021; Quintin et al. 2023).
All these eight galaxies have an X-ray quiescent (non-QPE) emission well-represented by the high-energy tail of an accretion disk with an inner temperature of ∼40 − 100 eV. The quiescent emission of RX J1301.9+2747 appears more complex than most of the other QPE sources. In fact, it requires, in addition to the emission of an accretion disk with an inner temperature of ∼50 − 60 eV, a harder spectral component from epoch 2019 onward with properties similar to those of the AGN soft X-ray excess. It is well-reproduced by the Comptonization of the accretion disk seed photons into a plasma with optical depth τ = 10 and temperature ∼400 eV, typical of the warm coronae observed in AGN (e.g., Petrucci et al. 2020; Palit et al. 2024). A similar spectral component has been observed in eRO-QPE4 during both quiescence and the QPE emission (Arcodia et al. 2024b) and is also well-fitted by a Comptonization model in addition to disk emission.
About half of the QPE sources and candidates showed a long-term decay in their X-ray flux consistent with a TDE. The quiescent emission of GSN 069 showed a slow long-term decay (Shu et al. 2018) since the slew detection in 2010 (Miniutti et al. 2013) for about 3000 days until a sudden rebrightening (Miniutti et al. 2023a) and subsequent decline of emission were observed (Miniutti et al. 2023b). Also, the quiescent emission of eRO-QPE3 showed a decline over the ∼2.5 years probed by eROSITA observations, then completely disappeared in subsequent XMM-Newton follow-up (Arcodia et al. 2024b). J0249 and Tormund are associated with X-ray- and optically-selected TDEs, respectively, and show a decay in their quiescent X-ray flux over, respectively, about 15 years and 6 months (Chakraborty et al. 2021; Quintin et al. 2023). There is no direct evidence for a TDE in RX J1301.9+2747. However, it is a young post-starburst E+A galaxy (Caldwell et al. 1999), a kind of galactic nucleus where a high rate of TDEs is observed (Arcavi et al. 2014; Hammerstein et al. 2021) and expected (Bortolas 2022). It also likely hosts a nuclear star cluster (NSC) (Shu et al. 2017), and NSCs are also expected to enhance the TDE rate in galactic nuclei (Wang et al. 2024). The fact that there is no clear evidence of a TDE-like flare in the optical history of RX J1301.9+2747 is not surprising in the presence of a disk. In this case, the disruption of stars might not produce the typical TDE flare observed in gas-poor environments (i.e., in quiescent galaxies), but more complex light curves (Ryu et al. 2024). In particular, if the disk is dense enough, no luminous TDE flare is expected at all due to the rapid mixing of the stellar debris with the disk material. In this case, the light curve variability would reflect variations in mass accretion rate in the disk and possible changes of states or rearrangements of the inner disk, i.e., long-lived bumpy light curves. This would be compatible with the observed long-term quiescent luminosity evolution of RX J1301.9+2747.
The X-ray quiescent luminosity variability of RX J1301.9+2747 is only on the order of a factor of 2.5 over four decades, from the L0.3 − 2 keV ∼ 2.5 × 1041 erg s−1 of the first ROSAT observation to the L0.3 − 2 keV ∼ 1041 erg s−1 of the last XMM-Newton one. In comparison, the GSN 069 quiescent luminosity spans L0.3 − 2 keV ∼ 1042 − 43 erg s−1. Interestingly, the observed luminosity variations are non-monotonic. Both ROSAT observations correspond to a larger flux compared to both previous and following epochs of observations. However, they had low exposure time and moderate X-ray statistics, and the observed short-term variability is only suggestive. The non-monotonic variations during the last three XMM-Newton observations are instead significant, with the first observation of June 2022 (2022A) at a lower X-ray flux than both the previous (2020) and the following (2022B) observation. The factor of ∼15% increase in flux (and disk luminosity) between 2022A and 2022B happens in less than one day.
The quiescent emission in GSN 069 also shows the presence of a quasi-periodic oscillation (QPO) with a quasi-period similar to the recurrence time between consecutive QPEs and shifted by about 10 ks with respect to the QPE peaks in most of the observations when QPEs are present (Miniutti et al. 2023a). The quiescent emission of RX J1301.9+2747 showed hints of the presence of a QPO during a few segments of the 2020 observation (Song et al. 2020), but this has not been observed again in the 2022 data, leaving the possibility open of the presence, if any, of a weak and transient QPO in the quiescent emission of RX J1301.9+2747. However, the QPO observed in GSN 069 has a similar quasi-period as QPEs recurrence times, while the QPO in RX J1301.9+2747 is detected on much shorter timescales and appears decoupled from the QPE recurrence times; hence, they are likely not produced by the same physical phenomenon.
The QPEs in RX J1301.9+2747 have been observed persistently in all the XMM-Newton observations between 2000 and 2022. The QPEs of GSN 069 have been very regular in amplitude and recurrence time spacing until the quiescence rebrigthening, when they showed irregular behavior and the presence of weak QPEs, and then disappeared for a few months (Miniutti et al. 2023a). They then reappeared during the quiescent emission decay (Miniutti et al. 2023b). The quiescence light curve evolution suggests that GSN 069 underwent a partial TDE and that there is a quiescent luminosity threshold for the appearance of QPEs (Miniutti et al. 2023b). The QPEs of eRO-QPE2 displayed a remarkable regularity in amplitude and alternation of long/short recurrence time, similar to GSN 069, in their discovery observations (Arcodia et al. 2021). Subsequent observations have shown an evolution of the QPE properties (Arcodia et al. 2024a), which are however still much more regular in amplitude and recurrence times compared to the case of RX J1301.9+2747. This is different from what is observed in eRO-QPE1, which instead shows QPEs of different amplitudes and spacing in time (Chakraborty et al. 2024), as well as the presence of both isolated QPEs and overlapping ones (Arcodia et al. 2022). The QPE activity in eRO-QPE1 appears to have significantly weakened over the course of about four years, as shown by Chakraborty et al. (2024) (see also Pasham et al. 2024). The quiescent emission of eRO-QPE3 fell under the detection limits about one year after its first detection; however, QPEs have been observed also at later times. These have small amplitudes and irregular time separations (Arcodia et al. 2024b). The case of eRO-QPE4 appears more similar to RX J1301.9+2747 in terms of properties of QPEs: it shows in fact both weak and strong QPEs with varying time separations, although of about twice the duration and one order of magnitude higher luminosity of those of RX J1301.9+2747 (see Fig. 13 of Arcodia et al. 2024b). For Tormund and J0249, the QPE association is less secure. In the first case, a portion of a flare with spectral properties very similar to QPEs has been observed about six months after the optical TDE (Quintin et al. 2023). In the second case, one and a half QPE-like flares were observed in archival XMM-Newton observations, but no flaring emission was detected in follow-up observations with the same satellite. Interestingly, the quiescent emission of J0249 appears to have developed a harder X-ray spectral component in the 15 years elapsed between the two long XMM-Newton observations, on the last of which QPEs were not present (Chakraborty et al. 2021). It might be possible that the presence of a strong X-ray hot corona somehow inhibits the presence of QPEs. For example, in the context of stellar EMRI impact scenarios (e.g., Linial & Metzger 2023; Tagawa & Haiman 2023), the impacting star might not survive the strong ablation expected if exposed to sustained hard X-rays.
6.6. QPEs and other repeating X-ray transient phenomena
Repeating nuclear transients are not limited to QPEs; in the past few years, several extragalactic sources have been observed displaying repeating patterns of flaring emission in the X-ray band. These include ESO 243-49 HLX-1 (Farrell et al. 2009), ASASSN-14ko (Payne et al. 2021), eRASSt J0456-20 (Liu et al. 2023), and Swift J0230+28 (Evans et al. 2023; Guolo et al. 2024b). However, either the timescales between flares, the X-ray spectral properties, or the detailed spectral-timing evolution of the X-ray flares observed in the aforementioned sources differ substantially from the case of QPE sources.
The timescales between flares are much longer in HLX-1 (about one year between bursts of X-ray emission, e.g., Servillat et al. 2011; Yan et al. 2015), eRASSt J0456-20 (about 200 days, Liu et al. 2023), and ASASSN-14ko (about 100 days, e.g., Payne et al. 2021) than in QPE sources (between 2 and 20 hours). The source Swift J0230+28 has the shortest time separation among these nuclear transients (about 22 days, Evans et al. 2023; Guolo et al. 2024b), still being much longer than the typical time separation between QPEs. The X-ray spectral properties of HLX-1, ASASSN-14ko, and eRASSt J0456-20 are substantially different to those of QPE sources. In fact, they have a well-developed hard X-ray power law, which is negligible or absent in QPE sources. Swift J0230+28 is again the source most similar to QPEs, having a purely thermal X-ray spectrum with no signal above ∼2 keV. However, the detailed spectral-timing evolution of the X-ray flares observed in Swift J0230+28 is different from the one of QPEs. In Swift J0230+28, in fact, the temperature of the X-ray spectra smoothly increases during the flare evolution, until reaching a maximum at the end of the flare. This is opposite to what is observed in all the QPE sources, which show instead a decreasing temperature along the flare evolution. The detailed flare shape is also substantially different in QPE sources and in these repeating nuclear transients. In particular, eRASSt J0456-20 has a much slower rise than decay and a plateau in between them; Swift J0230+28 has a slightly slower rise than decay; and HLX-1 has fast rise, exponential decay flares with much faster rise than QPEs. ASASSN-14ko shows most of its quasi-periodic variability in the optical/UV band, with flares with varying shape in a few years, from slower rise/fast decay to more symmetric (Huang et al. 2023). Repeating nuclear transients are generally interpreted as partial TDEs. The difference in physical properties of the X-ray flares compared to QPEs might reflect a different physical configuration for the partial TDE or a different physical mechanism.
7. Conclusions
We presented the analysis of five XMM-Newton and three VLA observations of the QPE-emitting galaxy RX J1301.9+2747, complemented by archival EXOSAT, ROSAT, and Chandra X-ray observations. Based on the results of this work, any model that aims at reproducing the observed properties of RX J1301.9+2747 should take into account the following:
-
X-ray QPEs have been observed persistently in all five XMM-Newton observations between 2000 and 2022. The EPIC cameras have detected 34 QPEs. Of these, eight QPEs are weak and 26 are strong, with a difference in count rate of a factor of ∼2 (Fig. 1).
-
The time separation between the QPE peaks (recurrence time) has a large spread around an average value of 3 h 45 m (13.5 ks); the minimum is 1 h 17 m (4.6 ks), and the maximum is 6 h 05 m (21.9 ks). The X-ray QPEs of RX J1301.9+2747 are irregularly spaced in time but not fully chaotic. Strong QPEs happen after a longer recurrence time compared to weak QPEs, while no weak QPE is observed whenever the recurrence time is larger than 1 h 40 m (6 ks). Weak QPEs are not always present, as there are long phases (> 20 h) when only strong QPEs are observed, in which case QPEs appear to be more regularly spaced. The recurrence time consistently alternates between long and short; in phases where weak QPEs are not present, this alternation is less dramatic in amplitude (Fig. 3). The higher the QPE amplitude, the longer appears to be its duration.
-
The properties of QPEs as a function of energy (arrival time, duration, intensity) are similar to the properties of other QPE sources and QPE candidates. At higher energies, the QPE peaks arrive earlier (with a difference of up to ten minutes between the 0.2 − 0.4 keV and the 1 − 2 keV bands in the case of RX J1301.9+2747), last less (with a difference in duration of a factor of two between low and high energies), and have a much lower count rate (Fig. 4). This energy dependence results in a ‘hysteresis-like’ behavior: the QPE spectral evolution consists of a hard rise followed by a soft decay (because QPEs last less at higher energies), and the peak temperature is reached well before the peak luminosity (because QPEs at higher energies arrive earlier and are less energetic than QPEs at lower energies; see Fig. 5 and B.2).
-
The X-ray quiescent emission of RX J1301.9+2747 is well-detected at all epochs of observation, varying of a factor ∼2× in luminosity during 40 years. The quiescent spectra of RX J1301.9+2747 are super-soft (Fig. C.1) and well represented by the emission of a disk with inner temperature ∼50 − 60 eV and LBOL ∼ 1 − 2 × 1042 erg s−1 (L0.3 − 2 keV ∼ 0.8 − 2 × 1041 erg s−1). The inner temperature of the disk slightly decays throughout the 20 years covered by XMM-Newton observations. However, its luminosity fluctuates non-monotonically (Fig. 8). After 2019, there is the emergence of a harder spectral component in quiescence, which carries about 1/4 of the 0.3 − 2 keV disk luminosity (Fig. 6 and C.2). This component can be modeled with a thermal model with a temperature kT ∼ 180 eV, with a power law with photon index Γ ≳ 3.5, or with thermal Comptonization of the disk photons on a plasma with optical depth τ = 10 and temperature kT ∼ 400 eV. The 2 − 10 keV bolometric correction κ2 − 10 keV > 2700 is very large as the hard X-ray power law is, if present, very weak with L2 − 10 keV < 4 × 1038 erg s−1.
-
The QPE spectra are super-soft with no significant detection at E > 2 keV. They are well-represented by a blackbody or a Comptonization model; in comparison, a bremmstrahlung model is slightly less favored, and a power law model is strongly disfavored. If compared to a blackbody model, the QPE peak bolometric luminosity is ∼2 × 1042 erg s−1 and the QPE temperature at the peak luminosity is 130 eV. Weak QPEs have generally a slightly lower duration (∼35 m vs. ∼45 m), a slightly lower temperature (∼120 eV), and a lower bolometric luminosity (∼1042 erg s−1) at their peak compared to strong QPEs. The equivalent blackbody radius Rbb increases from ∼1010 cm during rise-1 to ∼4 × 1010 cm during decay-2 (Fig. 11, lower panel). Weak QPEs have systematically smaller Rbb throughout their evolution. QPEs happening after a longer recurrence time appear to last more, and there is a weak positive correlation between the energy emitted by each QPE and the time preceding it (Fig. 12).
-
Compared to the QPEs of the best-studied source, GSN 069, the QPEs of RX J1301.9+2747 last for a shorter period of time, are less luminous, and are hotter (Fig. 14). In particular, the maximum difference in QPE temperature is during the rise, while the QPE temperatures of the two sources converge during the decay (Fig. 15). In RX J1301.9+2747 the decrease in temperature appears to be monotonic from the QPE rise-1 to the QPE decay-2, from ∼160 eV to ∼80 eV (Fig. 11, top panel).
-
There is no correlated radio/X-ray variability during the QPE emission in 2020 or 2022B. Whilst there appears to be a small amount of radio variability associated with the QPE in 2022A, its significance is < 2σ. Between epochs of observations of RX J1301.9+2747, the radio source does show variability on the order of 5–10% (Fig. 17). If attributed to ISS, the observed radio variability implies a very compact size of the source emission < 0.008 pc. This is comparable to the optical and to the smallest radio-emitting regions in TDEs (∼0.003 pc). The radio emission of RX J1301.9+2747 does not look like that of TDEs, which (when detected) display consistent long-term variability attributable to outflows and may show emission at timescales > 1000 days post-disruption (e.g. Alexander et al. 2020; Goodwin et al. 2022; Cendes et al. 2024).
Given the consistent alternance of short and long recurrence times between QPEs observed throughout our campaign, EMRI scenarios appear the most favorable in explaining the complex properties of RX J1301.9+2747. Different than the cases of much more regular QPE sources such as GSN 069 or eRO-QPE2, the presence of large differences in consecutive recurrence times between the QPEs of RX J1301.9+2747 is however extremely difficult to explain in any scenario requiring a single interaction per orbit. EMRI models assuming impacts on the accretion disk appear promising but still cannot fully account for the complexities of the timing behavior in RX J1301.9+2747.
Future observations of both the quiescent emission and the QPEs of RX J1301.9+2747 are necessary to try to solve this cosmic puzzle. High-cadence monitoring of the quiescent emission on long timescales might help identify dynamical effects taking place in the nucleus of this galaxy, while long, uninterrupted light curves are necessary to try to break the enigma of the repetition pattern of its X-ray QPEs.
We also performed a fit where no such assumption has been made, applying the quiescent spectrum best-fitting model 4 [diskbb + compTT] to each QPE spectral slice with a standard background subtraction. We found that the QPE spectra are dominated by the diskbb component at any stage of their evolution, with a disk inner temperature evolution consistent with the one found when using the bbodyrad model and subtracting the quiescent spectrum. It is thus not possible to disentangle the two scenarios with the available data.
The W statistic, or wstat, is the implementation of the Cash statistic (Cash 1979) when the background is not modeled.
See the discussion in https://giacomov.github.io/Bias-in-profile-poisson-likelihood/
Acknowledgments
We thank the referee for their constructive criticism that allowed us to improve our results and their presentation. MG is supported by the “Programa de Atracción de Talento” of the Comunidad de Madrid, grant numbers 2018-T1/TIC-11733 and 2022-5A/TIC-24235. GM is supported by Grant PID2020-115325GB-C31 funded by MCIN/AEI/10.13039/501100011033. RA and PK acknowledge support from NASA through the NASA Hubble Fellowship grant HST-HF2-51534.001-A awarded by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. MB acknowledges support provided by MUR under grant “PNRR - Missione 4 Istruzione e Ricerca – Componente 2 Dalla Ricerca all’Impresa – Investimento 1.2 Finanziamento di progetti presentati da giovani ricercatori ID:SOE_0163” and by the University of Milano-Bicocca under grant “2022-NAZ-0482/B”. XS is supported by NSFC through grant No. 12192221. GP acknowledges financial support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program Hot Milk (grant agreement No. 865637), from the Bando per il Finanziamento della Ricerca Fondamentale 2022 dell’Istituto Nazionale di Astrofisica (INAF): GO Large program, and from the Framework per l’Attrazione e il Rafforzamento delle Eccellenze (FARE) per la ricerca in Italia (R20L5S39T9). We thank Chris Done for extending the optxagnf model to include negative black hole spin values. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. This work was supported by the Australian government through the Australian Research Council’s Discovery Projects funding scheme (DP200102471). This research has made use of data and/or software provided by the High Energy Astrophysics Science Archive Research Center (HEASARC), which is a service of the Astrophysics Science Division at NASA/GSFC; NASA’s Astrophysics Data System Bibliographic Services (ADS), and the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. Software used: SAS (Gabriel et al. 2004), numpy (Harris et al. 2020), Astropy (Astropy Collaboration 2013, 2018, 2022), matplotlib (Hunter 2007), Ultranest (Buchner 2021), Xspec (Arnaud 1996), pyXspec (Gordon & Arnaud 2021), BXA (Buchner et al. 2014). Based on observations obtained with XMM-Newton, an ESA science mission with instruments and contributions directly funded by ESA Member States and NASA.
References
- Akaike, H. 1974, IEEE Trans. Autom. Contr., 19, 716 [Google Scholar]
- Alexander, K. D., van Velzen, S., Horesh, A., & Zauderer, B. A. 2020, Space Sci. Rev., 216, 81 [CrossRef] [Google Scholar]
- Arcavi, I., Gal-Yam, A., Sullivan, M., et al. 2014, ApJ, 793, 38 [Google Scholar]
- Arcodia, R., Merloni, A., Nandra, K., et al. 2021, Nature, 592, 704 [NASA ADS] [CrossRef] [Google Scholar]
- Arcodia, R., Miniutti, G., Ponti, G., et al. 2022, A&A, 662, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcodia, R., Linial, I., Miniutti, G., et al. 2024a, A&A, 690, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arcodia, R., Liu, Z., Merloni, A., et al. 2024b, A&A, 684, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, ASP Conf. Ser., 101, 17 [Google Scholar]
- Arnaud, K. A., Branduardi-Raymont, G., Culhane, J. L., et al. 1985, MNRAS, 217, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Crosby, N. B., Dimitropoulou, M., et al. 2016, Space Sci. Rev., 198, 47 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Bak, P., Tang, C., & Wiesenfeld, K. 1987, Phys. Rev. Lett., 59, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Beloborodov, A. M. 2017, ApJ, 850, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Bortolas, E. 2022, MNRAS, 511, 2885 [NASA ADS] [CrossRef] [Google Scholar]
- Branduardi-Raymont, G., Mason, K. O., Murdin, P. G., & Martin, C. 1985, MNRAS, 216, 1043 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J. 2016, Stat. Comput., 26, 383 [Google Scholar]
- Buchner, J. 2019, PASP, 131, 108005 [Google Scholar]
- Buchner, J. 2021, J Open Source Softw, 6, 3001 [NASA ADS] [CrossRef] [Google Scholar]
- Buchner, J., & Boorman, P. 2023, ArXiv e-prints [arXiv:2309.05705] [Google Scholar]
- Buchner, J., Georgakakis, A., Nandra, K., et al. 2014, A&A, 564, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caldwell, N., Rose, J. A., & Dendy, K. 1999, AJ, 117, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Cao, Z., Jonker, P. G., Pasham, D. R., et al. 2024, ApJ, 970, 89 [NASA ADS] [CrossRef] [Google Scholar]
- CASA Team (Bean, B., et al.) 2022, PASP, 134, 114501 [NASA ADS] [CrossRef] [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [Google Scholar]
- Cendes, Y., Berger, E., Alexander, K. D., et al. 2024, ApJ, 971, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, J., Kara, E., Masterson, M., et al. 2021, ApJ, 921, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Chakraborty, J., Arcodia, R., Kara, E., et al. 2024, ApJ, 965, 12 [CrossRef] [Google Scholar]
- Cordes, J. M., & Lazio, T. J. W. 2002, ArXiv e-prints [arXiv: astro-ph/0207156] [Google Scholar]
- Crummy, J., Fabian, A. C., Gallo, L., & Ross, R. R. 2006, MNRAS, 365, 1067 [Google Scholar]
- Davelaar, J., & Haiman, Z. 2022a, Phys. Rev. D, 105, 103010 [NASA ADS] [CrossRef] [Google Scholar]
- Davelaar, J., & Haiman, Z. 2022b, Phys. Rev. Lett., 128, 191101 [NASA ADS] [CrossRef] [Google Scholar]
- Dewangan, G. C., Singh, K. P., Mayya, Y. D., & Anupama, G. C. 2000, MNRAS, 318, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Done, C., Davis, S. W., Jin, C., Blaes, O., & Ward, M. 2012, MNRAS, 420, 1848 [Google Scholar]
- Evans, P. A., Nixon, C. J., Campana, S., et al. 2023, Nat. Astron., 7, 1368 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, S. A., Webb, N. A., Barret, D., Godet, O., & Rodrigues, J. M. 2009, Nature, 460, 73 [Google Scholar]
- Franchini, A., Bonetti, M., Lupi, A., et al. 2023, A&A, 675, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gabriel, C., Denby, M., Fyfe, D. J., et al. 2004, ASP Conf. Ser., 314, 759 [Google Scholar]
- Gierliński, M., & Done, C. 2004, MNRAS, 349, L7 [Google Scholar]
- Giustini, M., Miniutti, G., & Saxton, R. D. 2020, A&A, 636, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goodwin, A. J., van Velzen, S., Miller-Jones, J. C. A., et al. 2022, MNRAS, 511, 5328 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, C., & Arnaud, K. 2021, Astrophysics Source Code Library [record ascl:2101.014] [Google Scholar]
- Guillochon, J., & Ramirez-Ruiz, E. 2013, ApJ, 767, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Guolo, M., Gezari, S., Yao, Y., et al. 2024a, ApJ, 966, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Guolo, M., Pasham, D. R., Zajaček, M., et al. 2024b, Nat. Astron., 8, 347 [Google Scholar]
- Haardt, F., & Maraschi, L. 1991, ApJ, 380, L51 [Google Scholar]
- Hammerstein, E., Gezari, S., van Velzen, S., et al. 2021, ApJ, 908, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- HI4PI Collaboration (Ben Bekhti, N., et al.) 2016, A&A, 594, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hinkle, J. T., Holoien, T. W. S., Auchettl, K., et al. 2021, MNRAS, 500, 1673 [Google Scholar]
- Huang, S., Jiang, N., Shen, R.-F., Wang, T., & Sheng, Z. 2023, ApJ, 956, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Ingram, A., Motta, S. E., Aigrain, S., & Karastergiou, A. 2021, MNRAS, 503, 1703 [NASA ADS] [CrossRef] [Google Scholar]
- Janiuk, A., Czerny, B., & Siemiginowska, A. 2002, ApJ, 576, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Kaur, K., Stone, N. C., & Gilbaum, S. 2023, MNRAS, 524, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2020, MNRAS, 493, L120 [Google Scholar]
- King, A. 2022, MNRAS, 515, 4344 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2023, MNRAS, 526, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Kosec, P., Kara, E., Brenneman, L., et al. 2024, ArXiv e-prints [arXiv:2406.17105] [Google Scholar]
- Krauth, L. M., Davelaar, J., Haiman, Z., et al. 2024, Phys. Rev. D, 109, 103014D [NASA ADS] [CrossRef] [Google Scholar]
- Krolik, J. H., & Linial, I. 2022, ApJ, 941, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Li, Y.-P., Yuan, F., & Wang, Q. D. 2017, MNRAS, 468, 2552 [NASA ADS] [CrossRef] [Google Scholar]
- Lightman, A. P., & Eardley, D. M. 1974, ApJ, 187, L1 [Google Scholar]
- Lin, X., Li, Y.-P., & Yuan, F. 2023, MNRAS, 520, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Linial, I., & Metzger, B. D. 2023, ApJ, 957, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Linial, I., & Sari, R. 2023, ApJ, 945, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, Z., Malyali, A., Krumpe, M., et al. 2023, A&A, 669, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Lodato, G., King, A. R., & Pringle, J. E. 2009, MNRAS, 392, 332 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, E. T., & Hamilton, R. J. 1991, ApJ, 380, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, W., & Quataert, E. 2023, MNRAS, 524, 6247 [NASA ADS] [CrossRef] [Google Scholar]
- Magdziarz, P., Blaes, O. M., Zdziarski, A. A., Johnson, W. N., & Smith, D. A. 1998, MNRAS, 301, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Masterson, M., Kara, E., Ricci, C., et al. 2022, ApJ, 934, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Masterson, M., Kara, E., Pasham, D. R., et al. 2023, ApJ, 945, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Mehdipour, M., Branduardi-Raymont, G., Kaastra, J. S., et al. 2011, A&A, 534, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metzger, B. D., Stone, N. C., & Gilbaum, S. 2022, ApJ, 926, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Middleton, M. J., & Ingram, A. R. 2015, MNRAS, 446, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, N. A., Hornschemeier, A. E., Mobasher, B., et al. 2009, AJ, 137, 4450 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., Saxton, R. D., Rodríguez-Pascual, P. M., et al. 2013, MNRAS, 433, 1764 [NASA ADS] [CrossRef] [Google Scholar]
- Miniutti, G., Saxton, R. D., Giustini, M., et al. 2019, Nature, 573, 381 [Google Scholar]
- Miniutti, G., Giustini, M., Arcodia, R., et al. 2023a, A&A, 670, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miniutti, G., Giustini, M., Arcodia, R., et al. 2023b, A&A, 674, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mummery, A., Wevers, T., Saxton, R., & Pasham, D. 2023, MNRAS, 519, 5828 [NASA ADS] [CrossRef] [Google Scholar]
- NASA High Energy Astrophysics Science Archive Research Center (Heasarc) 2014, Astrophysics Source Code Library [record ascl:1408.004] [Google Scholar]
- Palit, B., Rozanska, A., Petrucci, P. O., et al. 2024, A&A, 690, A308 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pan, X., Li, S.-L., Cao, X., Miniutti, G., & Gu, M. 2022, ApJ, 928, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, X., Li, S.-L., & Cao, X. 2023, ApJ, 952, 32 [CrossRef] [Google Scholar]
- Pasham, D. R., Coughlin, E. R., Zajaček, M., et al. 2024, ApJ, 963, L47 [CrossRef] [Google Scholar]
- Payne, A. V., Shappee, B. J., Hinkle, J. T., et al. 2021, ApJ, 910, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Ursini, F., De Rosa, A., et al. 2018, A&A, 611, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrucci, P. O., Gronkiewicz, D., Rozanska, A., et al. 2020, A&A, 634, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponti, G., George, E., Scaringi, S., et al. 2017, MNRAS, 468, 2447 [NASA ADS] [CrossRef] [Google Scholar]
- Quintin, E., Webb, N. A., Guillot, S., et al. 2023, A&A, 675, A152 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raj, A., & Nixon, C. J. 2021, ApJ, 909, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Ripperda, B., Liska, M., Chatterjee, K., et al. 2022, ApJ, 924, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, T., McKernan, B., Ford, K. E. S., et al. 2024, MNRAS, 527, 8103 [Google Scholar]
- Scepi, N., Dexter, J., & Begelman, M. C. 2022, MNRAS, 511, 3536 [NASA ADS] [CrossRef] [Google Scholar]
- Servillat, M., Farrell, S. A., Lin, D., et al. 2011, ApJ, 743, 6 [Google Scholar]
- Sheng, Z., Wang, T., Ferland, G., et al. 2021, ApJ, 920, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Wang, T. G., Jiang, N., et al. 2017, ApJ, 837, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, X. W., Wang, S. S., Dou, L. M., et al. 2018, ApJ, 857, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Sironi, L., & Spitkovsky, A. 2014, ApJ, 783, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Śniegowska, M., Grzȩdzielski, M., Czerny, B., & Janiuk, A. 2023, A&A, 672, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Song, J. R., Shu, X. W., Sun, L. M., et al. 2020, A&A, 644, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sridhar, N., Sironi, L., & Beloborodov, A. M. 2021, MNRAS, 507, 5625 [NASA ADS] [CrossRef] [Google Scholar]
- Sridhar, N., Sironi, L., & Beloborodov, A. M. 2023, MNRAS, 518, 1301 [Google Scholar]
- Suková, P., Zajaček, M., Witzany, V., & Karas, V. 2021, ApJ, 917, 43 [CrossRef] [Google Scholar]
- Sun, L., Shu, X., & Wang, T. 2013, ApJ, 768, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Tagawa, H., & Haiman, Z. 2023, MNRAS, 526, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Titarchuk, L. 1994, ApJ, 434, 570 [NASA ADS] [CrossRef] [Google Scholar]
- von Fellenberg, S. D., Witzel, G., Bauböck, M., et al. 2023, A&A, 669, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, M. A. 1998, MNRAS, 294, 307 [CrossRef] [Google Scholar]
- Wang, M., Yin, J., Ma, Y., & Wu, Q. 2022, ApJ, 933, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Lin, D. N. C., Zhang, B., & Zhu, Z. 2024, ApJ, 962, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Wevers, T., Pasham, D. R., Jalan, P., Rakshit, S., & Arcodia, R. 2022, A&A, 659, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wevers, T., French, K. D., Zabludoff, A. I., et al. 2024, ApJ, 970, L23 [NASA ADS] [CrossRef] [Google Scholar]
- White, N. E., Giommi, P., & Angelini, L. 1994, IAU Circ., 6100, 1 [NASA ADS] [Google Scholar]
- Williams, P. K. G., Clavel, M., Newton, E., & Ryzhkov, D. 2017, Astrophysics Source Code Library [record ascl:1704.001] [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [Google Scholar]
- Xian, J., Zhang, F., Dou, L., He, J., & Shu, X. 2021, ApJ, 921, L32 [NASA ADS] [CrossRef] [Google Scholar]
- Yan, Z., Zhang, W., Soria, R., Altamirano, D., & Yu, W. 2015, ApJ, 811, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, L., Shu, X., Zhang, F., et al. 2022, ApJ, 935, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, F., Lin, J., Wu, K., & Ho, L. C. 2009, MNRAS, 395, 2183 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Z. Y., Wang, Y. Y., Zou, Y. C., Wang, F. Y., & Dai, Z. G. 2022, A&A, 661, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhou, C., Huang, L., Guo, K., Li, Y.-P., & Pan, Z. 2024a, Phys. Rev. D, 109, 103031 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, C., Zhong, B., Zeng, Y., Huang, L., & Pan, Z. 2024b, Phys. Rev. D, 110, 083019 [CrossRef] [Google Scholar]
Appendix A: Observations log
Observation log for the XMM-Newton EPIC exposures on RX J1301.9+2747 between 2000 and 2022.
Log of the archival X-ray observations of RX J1301.9+2747 used in this work.
Radio flux density measurements of RX J1301.9+2747 taken with the VLA. Errors reported are the statistical error of the Gaussian point source fit combined with the image rms, but we note that the absolute flux density scale accuracy of the VLA is limited to 5%.
Appendix B: Light curve fit to individual QPEs
We fit the EPIC light curves of RX J1301.9+2747, deriving Bayesian posterior probability distributions with UltraNest. The Bayes theorem states that:
where ℒ(θ) = P(D|θ) is the likelihood that specifies the frequency of producing the dataset D given the parameters θ, P(θ) is the assumed prior, and P(θ|D) is the posterior PDF. The Bayesian evidence, or marginal likelihood 𝒵 = ∫ℒ(θ)P(θ)dθ, is the posterior normalization (e.g., Buchner & Boorman 2023).
We compared the data to the model [constant + Gaussian], comprised of a constant to represent the quiescent emission, plus Gaussian emission lines to represent the QPEs. We tried to assess if there is variability of the quiescent emission, but the results were inconclusive except for the first segment of the 2020 observation, where a clear decrease in the quiescent flux emission is observed, although of modest amplitude. We therefore assumed the quiescent count rate to be constant, although it may vary between different QPEs (i.e., the fit is performed locally around each QPE peak, with time intervals shown in the x-axis of each panel of Fig. B.1). The emission QPE profile was also fit to a profile akin to that used by Arcodia et al. (2022) to model the QPEs of eRO-QPE1, and no significant differences in terms of QPE peak position and QPE duration were found. We therefore used the simpler Gaussian to model the QPEs of RX J1301.9+2747. We used a Gaussian log-likelihood function, i.e., we assumed that the data were drawn from a Gaussian distribution, with mean equal to the model prediction and standard deviation equal to the measurement error. The prior probability distributions for the quiescence count rate CRquie, the QPE count rate CRqpe, and width σqpe were assumed to be flat and uninformed, with uniform distributions between [10−7 − 10−1] ct s−1, [0.01 − 2] ct s−1, and [100 − 1000] s, respectively. The QPE peak position tpeak was also assumed to have a flat prior probability distribution within a time interval visually centered around the peak and typically lasting between 2000 and 4000 seconds. The analysis was performed on the pn data and on the merged MOS1 and MOS2 data simultaneously, assuming that tpeak is the same for the three instruments. Results of the fit are shown in Fig. B.1, in light blue for the pn data and in dark blue for the MOS data, and reported in Table B.1.
 |
Fig. B.1. Zoom on the light curves of RX J1301.9+2747 centered on the QPEs detected by the EPIC cameras (pn in light blue, MOS in dark blue) between 2000 and 2022. The black line represents the median of the posterior PDF of the model [constant + Gaussian] used to fit the light curves, while the shaded areas represent the 1σ and 2σ equivalent percentiles. Time on the x-axis is computed from the beginning of each observation in Mission Reference Time: 92866770 s for QPE0−QPE1; 675637593 s for QPE2−QPE4; 710876963 s for QPE5−QPE14; 771890338 s for QPE15−QPE24; and 772064151 s for QPE25−QPE33. |
 |
Fig. B.1. – continued. |
QPE properties
B.1. Hardness ratios
We show in Fig. B.2 the hardness ratio plot for each QPE observed by XMM-Newton in the galaxy RX J1301.9+2747 from 2000 to 2022. The hardness ratio is computed as HR = CR(0.6 − 2)/CR(0.2 − 2), where CR(0.6 − 2) is the count rate in the 0.6 − 2 keV band and CR(0.2 − 2) is the total count rate in the 0.2 − 2 keV band.
 |
Fig. B.2. For each QPE, we plot in the top panel the 0.2 − 2 keV background-subtracted QPE light curve, centered around the QPE peak and binned to 250 s, and in the lower panel the hardness ratio HR = CR(0.6 − 2)/CR(0.2 − 2), where CR(0.6 − 2) is the count rate in the 0.6 − 2 keV band and CR(0.2 − 2) is the total count rate in the 0.2 − 2 keV band. Each point is color-coded following the time evolution of the QPE in the panel above. The HR shows a counterclockwise evolution, as highlighted by the dashed arrow. All these quantities have been computed using the pn data only. |
 |
Fig. B.2. – continued. |
 |
Fig. B.2. – continued. |
Appendix C: Fit to the quiescent spectra
The time intervals including QPEs identified with the light curve analysis were excluded in order to extract the spectra during quiescence. We used the BXA package, assuming a Poissonian likelihood function and using the W statistic9 on the unbinned 0.3 − 10 keV spectra. The background spectra were grouped to a minimum of 3 counts per energy bin in order to avoid statistical biases10. The ten EPIC quiescent spectra, one pn and one merged MOS1+MOS2 spectrum for each of the five epochs of XMM-Newton observations of RX J1301.9+2747, are shown in Fig. C.1. Each epoch of observation (2000, 2019, 2020, 2022A, and 2022B) was fit independent of the other. The pn and MOS spectra of each epoch were fit together to the same model, with a multiplicative constant factor const to take into account instrumental cross-calibration uncertainties. The priors on const were always assumed to be uniform between [0.8, 1.2]. The value of the column density was allowed to reach 1021 cm−2 during the fit, assuming uniform priors.
 |
Fig. C.1. XMM-Newton EPIC quiescent spectra (i.e., excluding time intervals when QPEs are present) of RX J3101.9+2747, rebinned for visual purposes to 3σ significance. For each epoch of observation, the pn(MOS) spectra are plotted with blue (orange) circles, while the background spectra are shaded areas of the same color. The last panel reports the five epochs together, omitting the MOS data and plotting only the highest-level (2019) and lowest-level (2022A) pn backgrounds for clarity. |
First, we compare the quiescent spectra to two soft thermal models, [zashift*bbodyrad] and [zashift*diskbb]. The [zashift] component takes into account the cosmological redshift of the emitted photons and was always fixed to z = 0.024. We assumed flat, uninformed priors on the model parameters, with normalizations spanning several orders of magnitude between [10 − 106] and the temperatures ranging between [10 − 300] eV. We found that the [zashift*diskbb] model is preferred over the [zashift*bbodyrad] one, given the Bayesian evidence found (with a difference of log𝒵 > 2 in every epoch). We call the model [zashift*diskbb] ’model 0’. Results of the fit to the five epochs of observation of the quiescent spectra of RX J1301.9+2747 to model 0 are reported in the first column of Fig. C.2, where we plot only the pn data, rebinned visually to 3σ significance, in the 0.3 − 1.5 keV band (i.e., up to where the spectra are not background-dominated, see Fig. C.1). Although the spectra are very soft and most of the flux contribution is carried by the disk component diskbb, this component alone is not able to well reproduce the data at energies E > 0.7 keV, especially from 2019 onward.
 |
Fig. C.2. The posterior probability distribution of [TBabs*zashift*diskbb] (model 0, left column) and [TBabs*zashift*(diskbb + bbodyrad)] (model 1, central column) applied to the quiescent data for the five epochs of XMM-Newton observation of RX J1301.9+2747. Data are shown for the EPIC-pn camera only and rebinned to 3σ significance. The posterior PDF unconvolved from the instrumental response is plotted for each epoch for the best-fitting model 1 in the right column. The [diskbb] posterior PDF is plotted in dark orange, the [bbodyrad] one in dark yellow, and the total model 1 in gray. |
We then compared the quiescent spectra of the five epochs to two equally complex models: [zashift*(diskbb + bbody)] (model 1) and [zashift*(diskbb + powerlaw)] (model 2). In this model scheme, diskbb represents the thermal emission from an accretion disk with inner temperature kT; bbody represents a soft X-ray excess-like warm thermal component, with temperature kT; and the powerlaw model represents the hard X-ray coronal emission with photon index Γ. The priors were all uninformed, with these ranges: [20 − 200] eV for the diskbb inner temperature and [10−4 − 108] for its normalization; [50 − 500] eV for the bbody temperature and [10−6 − 103] for its normalization; [1.5 − 4] for the powerlaw photon index, and [10−13 − 10−5] for its normalization.
Results are reported in Table C.1, where we report the median value of the posterior PDF of the model parameters along with their 1 standard deviation upper and lower credible values, the observed flux, the unabsorbed luminosity, and the logarithms of the Bayesian evidence 𝒵 and of the Akaike information criterion (AIC = C − 2 × m, where C is the likelihood and m is the number of degrees of freedom, Akaike 1974) normalized to their highest values for each epoch of observation. The model that gives the most probable representation of the data will have the highest 𝒵 and AIC.
Given the number of degrees of freedom and the Bayesian evidence 𝒵, models 1 and 2 are always strongly preferred to model 0 except for epoch 2000, when model 0 gives Δlog𝒵 = 0.9 compared to model 1, and Δlog𝒵 = −0.5 compared to model 2. Model 1 is the most probable representation of the data at all epochs except for 2022A and 2022B, when model 2 is the most probable one. The differences in log𝒵 between model 1 and model 2 are however very small, Δlog𝒵 < 1.5, except for 2019 (when Δlog𝒵 = 6.1). There are two physical reasons why model 1 can be preferred over model 2. First, the photon index Γ of the powerlaw component of model 2 is found to be very steep compared to the typical AGN values and even steeper than the most extreme observed values. Such a steep power law is likely not produced by Comptonization in a standard X-ray hot corona. On the contrary, the temperature kT of the bbody component found in model 1 is typical of the soft X-ray excess observed in AGN. Second, as the power law model diverges at low energies, the bolometric luminosity estimate in model 2 is up to one order of magnitude larger than the estimate with model 0, while it is larger by a factor of ∼4 in model 1 compared to model 0. Given that the spectra are evidently dominated by the diskbb component, we conservatively favor the model that produces a bolometric luminosity with a value more similar to this component alone. We thus adopt model 1 as our best-fitting model.
The posterior PDFs of model 0 and model 1 folded with the instrumental response are plotted in the left and central columns of Fig. C.2 compared to the observed data. The right column of the same figure reports the unconvolved posterior PDFs for the best-fitting model 1, where the accretion disk diskbb is plotted in dark orange and the soft excess bbody in light orange. We limit these plots to the 0.3 − 2 keV band, as above these energies the signal is strongly dominated by the background; however, the data were considered up to 10 keV. That the disk alone is not sufficient can be seen in the left column of Fig. C.2 and in Table C.1, where Model 0 provides the lowest 0.3 − 2 keV flux compared to all the other models, signaling that some harder-than-the-disk flux is not modeled by diskbb alone. When using model 0, the inner temperature of the accretion disk seems to increase from 2000 onward (top left panel in Fig. 7). Once the harder component is introduced, the disk inner temperature stabilizes around kT ∼ 60 eV in each epoch, and the 0.3 − 2 keV flux is recovered well (it is constant between models 1, 2, and 3). This temperature is independent of the harder component adopted, bbody or powerlaw. When using model 2, during epoch 2000 the power law is insensitive to the fit (see the third row of Fig. 7). This means that the powerlaw component is weakly required by the data during this epoch compared to the other epochs of observation. As the powerlaw model mostly models soft X-ray photons (given its very steep photon index), this result should be seen also when using model 1. Indeed, also when using model 1 the warm thermal component bbody is well constrained in each epoch of observation, except for epoch 2000 (second row of Fig. 7). This confirms that the power law component mostly models soft X-ray photons.
Finally, we compared the data of the quiescent emission of RX J1301.9+2747 to a disk plus Comptonization model, [diskbb + compTT] (model 4). We used the model developed by Titarchuk (1994) and assumed a disk geometry for the Comptonizing region, with a seed photon temperature equal to the inner temperature of the accretion disk. As there is complete degeneracy between the Comptonizing plasma temperature and optical depth, we fixed the latter to a series of values τ = 1, 5, 10, and left the former as a free parameter. We assumed uninformed priors for all parameters except for epoch 2000, when we used Gaussian priors for the temperature of the accretion disk (60 ± 10 eV) and of the Comptonizing plasma (400 ± 100 eV). The limits of the parameter values were [30 − 100] eV and [105 − 105] for the disk temperature and normalization, [0.1 − 10] keV for the Comptonizing region temperature, and [10−9 − 10−1] for its normalization. We found that a good representation of the soft X-ray excess-like spectral component is given by Comptonization of the disk seed photons on a plasma with an average temperature of 400 ± 25 eV for an optical depth τ = 10. The plasma average temperature would instead be 1.1 ± 0.1 keV for τ = 5 and 7.9 ± 0.7 keV for τ = 1. These values are typical of the warm coronae observed in AGN (e.g., Petrucci et al. 2018). The SED of compTT is broader than the one of bbody, thus when using the model [diskbb + compTT], the inferred temperature of the accretion disk is lower than when using [diskbb + bbody] (model 1). This effect is larger for lower optical depths of the Comptonizing region, going for example from 51 ± 2 eV in the case of τ = 10 to 44 ± 2 eV in the case of τ = 1.
Fit results to the XMM-Newton quiescent spectra of RX J1301.9+2747
Appendix D: Fit to the QPE spectra
The results of the Gaussian fit to the 0.2 − 2 keV light curves of Sect. 3 were used to select time intervals to extract individual QPE spectral slices. We used the median values of the posterior PDFs for the QPE arrival time tQPE and width σ, given the pn and MOS data in each epoch of XMM-Newton observation. We used a 4σ-wide time interval centered around tQPE and divided in five equally-spaced time intervals to extract the QPE spectral slices: two rises (rise-1 and rise-2), one peak, and two decays (decay-1 and decay-2). Each spectral slice has therefore a different duration, proportional to the total duration of each QPE. One example of the spectral decomposition is shown in Fig. 10 for QPE2.
For the spectral analysis, we used event tables cleaned from strong background flares. These are typically present at the beginning and at the end of XMM-Newton revolutions and affect the data of both EPIC cameras (pn and MOS) for 6 out of 34 QPEs (numbers 5, 6, 15, 25, 26, and 33), which must be discarded. The pn camera is more sensitive to background flares than the MOS and lost three further QPEs (numbers 4, 7, and 16). Due to the very low photon statistics, we discarded QPE16, which is a weak one, while retaining the MOS data of the strong QPE4 and QPE7. QPE0 was also excluded from the spectral analysis as it is only half-detected by the MOS. This gives a total of 26 QPEs (21 strong and 5 weak), for which it was possible to extract spectral information.
The QPEs were assumed to be additive components on top of a constant quiescent emission; we considered the 0.3 − 2 keV net QPE spectra by using the average quiescent spectra of each epoch as a background. The source spectra were analyzed unbinned, while the background spectra were binned to a minimum of 3 counts per bin, and the W-statistics was used. The pn and MOS data were fitted jointly for each spectral slice, using a constant factor between the two datasets.
We compared the QPE peak spectra to a blackbody ([bbodyrad]), a bremsstrahlung ([bremss]), and a Comptonization model ([compTT]). We found slightly lower Bayesian evidence for the blackbody model compared to the bremsstrahlung (Δlog𝒵 ∼ 0.5), with both models strongly favored over the Comptonization one (Δlog𝒵 ≫ 2). The model [const*TBabs*zashift*bbodyrad] was then used to extract information (LBOL, kT, Rbb) from the QPE spectral slices, with the caveat that the luminosity estimates are the lowest among the three models tested (i.e., the [bbodyrad] has the narrowest spectral energy distribution among the three).
The presence of absorption during the QPE was tested by allowing the column density of [TBabs] to be free. Uninformed priors were adopted for the cross-instrumental constant (between 0.8 and 1.2), the column density (between 1015 and 5 × 1021 cm−2), the blackbody temperature (between 30 and 300 eV), and normalization (between 10−2 and 106). The redshift was always fixed to z = 0.024. As the value of NH is consistent with the Galactic one for 132/135 of the QPE slices, we repeat the fit to the model [const*TBabs*zashift*bbodyrad] fixing the column density value to the Galactic one.
D.1. Further complexities
We tested for the presence of ionized absorption along the line of sight both during the QPE spectral evolution and during quiescence. In the former case, we compared the data of each QPE spectral slice to the [const*TBabs*zedge*zashift*bbodyrad] model, where zedge is a simple absorption edge at the redshift of the source. The absorption edge had uninformed priors for its energy (between 400 and 900 eV) and its optical depth (between 10−3 and 5). The resulting Bayesian evidences 𝒵 were compared to those obtained with the simpler const*TBabs*zashift*bbodyrad model using the Jeffrey’s scale (see Buchner et al. 2014), where a difference in log𝒵 of 2 is considered decisive, of 1.5 very strong evidence, and above 1 strong evidence that the more complex model provides a better representation of the data than the simpler model. Out of 135 QPE spectral slices, a difference in log𝒵 > 1 (strong evidence for a better data representation after the inclusion of the edge) is found in ten slices, corresponding to nine individual QPEs. These are QPEs numbers 1, 4, 10, 12, 17, 19, 21, 24, and 30. When replacing the absorption edge with a Gaussian absorption line, the statistical evidence drops in most of the QPE spectral slices; therefore, we do not interpret these results as physical, but rather as statistical fluctuations or spurious effects due to complexities in the continuum emission not taken into account. In the latter case, we applied the zedge component or a photoionized gas model generated with Xstar to both model 1 and model 4, finding no strong statistical evidence for the presence of absorption in any epoch of XMM-Newton observation.
Ionized absorption with an outflowing velocity of ∼3000 km s−1 was recently detected in the high-resolution reflection grating spectrometer (RGS) data of GSN 069, both during quiescence and during the QPEs (Kosec et al. 2024). We reduced and analyzed the RGS data of RX J1301.9+2747 by stacking all the quiescent good time intervals from 2000 to 2022B. We found that the signal to noise ratio is still completely dominated by the background, thus preventing us from searching for traces of ionized absorption in the high-resolution data. We note how even at the higher X-ray flux level of GSN 069 compared to RX J1301.9+2747, a total of about 2 Ms of exposure time had to be accumulated in order to detect the absorption lines in the high-resolution spectra. In order to better test for the presence of intrinsic ionized absorption in RX J1301.9+2747, new observations are needed: either very long ones with existing X-ray telescopes or using future detectors with a very large soft X-ray effective area.
All Tables
Observation log for the XMM-Newton EPIC exposures on RX J1301.9+2747 between 2000 and 2022.
Radio flux density measurements of RX J1301.9+2747 taken with the VLA. Errors reported are the statistical error of the Gaussian point source fit combined with the image rms, but we note that the absolute flux density scale accuracy of the VLA is limited to 5%.
All Figures
 |
Fig. 1. Background-corrected XMM-Newton light curves of RX J1301.9+2747, extracted with time bins of 250 s in the 0.2 − 2 keV band as observed by the pn in light blue and by the MOS in dark blue. The epoch of observation name used in the text as explained in Table A.1 is marked in each panel. We number QPEs from number 0 (half-detected by the MOS in 2000) to number 33 (the last detected in 2022B) and mark a few of them with gray numbers. |
| In the text | |
 |
Fig. 2. Properties of the QPEs of RX J1301.9+2747, derived from the XMM-Newton EPIC light curves: QPE peak count rate (CR), in s−1; local quiescence count rate (CR), in s−1; QPE duration, in minutes; QPE amplitude; time between QPE number n and QPE number n − 1, in kiloseconds (ks). For each quantity, we plot the median of the posterior PDF along with its 1 standard deviation error bar. The gray boxes in the lower right corner of each subplot report the correlation coefficients between the parameters. |
| In the text | |
 |
Fig. 3. Time (in ks) preceding each QPE of the 2020, 2022A, and 2022B XMM-Newton observations of RX J1301.9+2747. |
| In the text | |
 |
Fig. 4. Properties of QPEs as a function of energy plotted as histograms of their posterior PDFs. From upper to lower panels: difference between the QPE arrival times measured in different energy bands and the QPE arrival times measured in the 0.2 − 2 keV band, QPE duration, and count rate at the QPE peak. The energies considered are 0.2 − 0.4, 0.4 − 0.6, 0.6 − 0.8, 0.8 − 1, and 1 − 2 keV from lighter to darker histograms. |
| In the text | |
 |
Fig. 5. Top panel: representative 0.2 − 2 keV background-subtracted QPE light curve, centered at the peak and binned to 250 s. Lower panel: hardness ratio (HR) between the 0.6 − 2 keV and the 0.2 − 2 keV count rates as a function of the total count rate, where each point is color-coded following the time evolution of the QPE in the panel above. The HR shows a counter-clockwise evolution, as tracked by the dashed gray arrows. The complete set of HR plots can be found in Fig. B.2. |
| In the text | |
 |
Fig. 6. Quiescent pn spectrum of RX J1301.9+2747 during the 2020 epoch, visually rebinned to 3σ significance and overplotted to the posterior PDF of model 0 ([diskbb], top panel), model 1 ([diskbb + bbody], middle panel), and model 4 ([diskbb + compTT], lower panel). The [diskbb] component is plotted in red, the [bbody] in orange, the [compTT] in brown, and the total model in gray. The complete set of spectra for all epochs compared to models 0 and 1 are shown in Fig. C.2. Spectra are shown up to 2 keV, as at higher energies the signal is dominated by the background, however the data were always fitted up to 10 keV. |
| In the text | |
 |
Fig. 7. Synoptic view of the quiescent spectral properties of RX J1301.9+2747 in five epochs of XMM-Newton observation: 2000, 2019, 2020, 2022A, and 2022B (Table A.1), plotted with color tones from lighter to darker. The histograms report the posterior PDF of the parameter of interest considering five different models, 0 to 4, from the first to the fifth row. We plot in red the parameters of the diskbb component, in orange the parameters of the bbody component, in yellow the parameters of the powerlaw component, and in brown the parameters of the compTT component. |
| In the text | |
 |
Fig. 8. Evolution of the 0.3 − 2 keV luminosity (first row), bolometric luminosity (second row), and temperature (third row) of the quiescent emission of RX J1301.9+2747 in each epoch of XMM-Newton observation obtained using model 1 [diskbb + bbody] (left column) and model 4 [diskbb + compTT] (right column). Red symbols represent diskbb, orange ones bbody, and the brown ones compTT. Points represent the medians of the posterior PDFs; error bars are one standard deviation. |
| In the text | |
 |
Fig. 9. Top panel: 0.3 − 2 keV quiescent flux observed from RX J1301.9+2747 by various telescopes in different epochs, marked by their Modified Julian Day. For all the observations where this was possible (all except the EXOSAT one), the QPE emission was removed, leaving the quiescence only. Lower panel: 0.3 − 2 keV disk luminosity, corrected for absorption. For most of the XMM-Newton measurements, the error bars are smaller than the symbol size. Modified Julian Day. For all the observations |
| In the text | |
 |
Fig. 10. Example of the QPE spectral decomposition adopted: the pn data of QPE2 are plotted binned to 100 s. Rise-1 in pink, rise-2 in orange, peak in red, decay-1 in dark red, decay-2 in brown, and quiescence in gray. |
| In the text | |
 |
Fig. 11. Top panel: average of the posterior PDFs of the temperature kT and bolometric luminosity LBOL of a redshifted blackbody model ([zashift*bbodyrad] in Xspec) compared to the five spectral slices of each QPE of RX J1301.9+2747. Weak QPEs are plotted with open squares, and strong QPEs with filled circles. The color code during the QPE evolution is the same as in Fig. 10. Lower panel: blackbody radius Rbb for each spectral slice, superimposed to the profiles of the 27 QPEs (gray thick lines) with spectral analysis available. |
| In the text | |
 |
Fig. 12. Corner plot for the medians of the posterior PDFs of various QPE parameters of RX J1301.9+2747. The quantities plotted for each QPE are: the bolometric luminosity at the QPE peak (1042 erg s−1); the temperature at the QPE peak (keV); the QPE duration (m); the QPE total emitted energy (1045 erg); and the time preceding each QPE (h). Strong QPEs are plotted with filled circles, weak QPEs with open squares. Error bars for weak QPEs have been omitted for clarity. A couple of correlation coefficients between the parameters is reported in the lower right corner of each plot: strong QPEs only on top, and both strong and weak QPEs in the gray boxes below. |
| In the text | |
 |
Fig. 13. For each QPE number n of RX J1301.9+2747 with pn spectral analysis available, the total emitted energy is plotted against the ratio between the time interval between the peaks of QPE number n and QPE number n − 1 and the time interval between the peaks of QPE number n + 1 and QPE number n. |
| In the text | |
 |
Fig. 14. Posterior PDFs of the QPE duration (left), computed as twice the FWHM of the best-fitting Gaussian to the 0.2 − 2 keV band; the QPE bolometric luminosity at the peak (center) and QPE temperature at the peak (right), computed comparing the data to a redshifted blackbody model. Data of RX J1301.9+2747 is plotted in blue, data of GSN 069 in gray; for both sources, weak QPEs are plotted with thicker and darker lines. |
| In the text | |
 |
Fig. 15. Histograms of the posterior PDFs of the temperature (left column) and of the bolometric luminosity (right column) of a blackbody model compared to each strong QPE spectral slice. From upper to lower panels: rise-1 in pink, rise-2 in orange, peak in red, decay-1 in dark red, and decay-2 in brown. The gray histograms report the GSN 069 strong QPEs data. |
| In the text | |
 |
Fig. 16. Average 0.3 − 2 keV EF(E) quiescent spectrum of RX J1301.9+2747 (gray) plotted together with the average weak QPE (empty squares) and strong QPE (filled circles) spectra extracted during the peak. The QPE spectra are background-subtracted with the average quiescent spectrum used as background. |
| In the text | |
 |
Fig. 17. Simultaneous X-ray and radio light curves for the 2020, 2022A, and 2022B epochs: the top panel reports the 0.2 − 2 keV light curve, and the lower panel the radio light curve at 6 GHz as measured by the VLA. In the lower panel, RX J1301.9+2747 is shown in green, and a different radio source in the field is shown in gray to serve as a check source. Each portion of the broken axes represents 0.25 d. Note that the flux density of the check source has been scaled down by a factor of 15. The gray shaded region shows the mean value for the 2020 observation plus or minus 5%, the absolute accuracy of the VLA flux density calibration. |
| In the text | |
 |
Fig. B.1. Zoom on the light curves of RX J1301.9+2747 centered on the QPEs detected by the EPIC cameras (pn in light blue, MOS in dark blue) between 2000 and 2022. The black line represents the median of the posterior PDF of the model [constant + Gaussian] used to fit the light curves, while the shaded areas represent the 1σ and 2σ equivalent percentiles. Time on the x-axis is computed from the beginning of each observation in Mission Reference Time: 92866770 s for QPE0−QPE1; 675637593 s for QPE2−QPE4; 710876963 s for QPE5−QPE14; 771890338 s for QPE15−QPE24; and 772064151 s for QPE25−QPE33. |
| In the text | |
 |
Fig. B.1. – continued. |
| In the text | |
 |
Fig. B.2. For each QPE, we plot in the top panel the 0.2 − 2 keV background-subtracted QPE light curve, centered around the QPE peak and binned to 250 s, and in the lower panel the hardness ratio HR = CR(0.6 − 2)/CR(0.2 − 2), where CR(0.6 − 2) is the count rate in the 0.6 − 2 keV band and CR(0.2 − 2) is the total count rate in the 0.2 − 2 keV band. Each point is color-coded following the time evolution of the QPE in the panel above. The HR shows a counterclockwise evolution, as highlighted by the dashed arrow. All these quantities have been computed using the pn data only. |
| In the text | |
 |
Fig. B.2. – continued. |
| In the text | |
 |
Fig. B.2. – continued. |
| In the text | |
 |
Fig. C.1. XMM-Newton EPIC quiescent spectra (i.e., excluding time intervals when QPEs are present) of RX J3101.9+2747, rebinned for visual purposes to 3σ significance. For each epoch of observation, the pn(MOS) spectra are plotted with blue (orange) circles, while the background spectra are shaded areas of the same color. The last panel reports the five epochs together, omitting the MOS data and plotting only the highest-level (2019) and lowest-level (2022A) pn backgrounds for clarity. |
| In the text | |
 |
Fig. C.2. The posterior probability distribution of [TBabs*zashift*diskbb] (model 0, left column) and [TBabs*zashift*(diskbb + bbodyrad)] (model 1, central column) applied to the quiescent data for the five epochs of XMM-Newton observation of RX J1301.9+2747. Data are shown for the EPIC-pn camera only and rebinned to 3σ significance. The posterior PDF unconvolved from the instrumental response is plotted for each epoch for the best-fitting model 1 in the right column. The [diskbb] posterior PDF is plotted in dark orange, the [bbodyrad] one in dark yellow, and the total model 1 in gray. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



