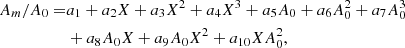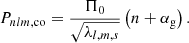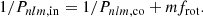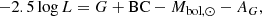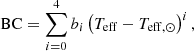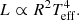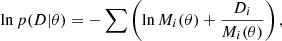Asteroseismology of the young open cluster NGC 2516

Gang Li; Conny Aerts; Timothy R. Bedding; Dario J. Fritzewski; Simon J. Murphy; Timothy Van Reeth; Benjamin T. Montet; Mingjie Jian; Joey S. G. Mombarg; Seth Gossage; Kalarickal R. Sreenivas

doi:10.1051/0004-6361/202348901

Home

All issues

Volume 686 (June 2024)

A&A, 686 (2024) A142

Full HTML

Open Access

Issue		A&A Volume 686, June 2024


Article Number		A142
Number of page(s)		23
Section		Stellar structure and evolution
DOI		https://doi.org/10.1051/0004-6361/202348901
Published online		05 June 2024

A&A, 686, A142 (2024)

I. Photometric and spectroscopic observations^⋆

Gang Li (李刚)¹, Conny Aerts¹^,2^,3, Timothy R. Bedding⁴, Dario J. Fritzewski¹, Simon J. Murphy⁵, Timothy Van Reeth¹, Benjamin T. Montet⁶^,7, Mingjie Jian (简明杰)⁸, Joey S. G. Mombarg⁹, Seth Gossage¹⁰ and Kalarickal R. Sreenivas⁴

¹ Institute of Astronomy (IvS), Department of Physics and Astronomy, KU Leuven, Celestijnenlaan 200D, 3001 Leuven, Belgium
e-mail: gang.li@kuleuven.be, conny.aerts@kuleuven.be
² Department of Astrophysics, IMAPP, Radboud University Nijmegen, PO Box 9010 6500 GL Nijmegen, The Netherlands
³ Max Planck Institut für Astronomie, Königstuhl 17, 69117 Heidelberg, Germany
⁴ Sydney Institute for Astronomy (SIfA), School of Physics, University of Sydney, Sydney, NSW 2006, Australia
⁵ Centre for Astrophysics, University of Southern Queensland, Toowoomba, QLD 4350, Australia
⁶ School of Physics, University of New South Wales, Sydney, NSW 2052, Australia
⁷ UNSW Data Science Hub, University of New South Wales, Sydney, NSW 2052, Australia
⁸ Department of Astronomy, Stockholm University, AlbaNova University Center, 106 91 Stockholm, Sweden
⁹ IRAP, Université de Toulouse, CNRS, UPS, CNES, 14 Avenue Édouard Belin, 31400 Toulouse, France
¹⁰ Center for Interdisciplinary Exploration and Research in Astrophysics (CIERA), Northwestern University, 1800 Sherman Ave, Evanston, IL 60201, USA

Received: 11 December 2023
Accepted: 13 March 2024

Abstract

Context. Asteroseismic modelling of isolated stars presents significant challenges due to the difficulty in accurately determining stellar parameters, particularly the stellar age. These challenges can be overcome by observing stars in open clusters whose coeval members share an initial chemical composition. The light curves from the all-sky survey by the Transiting Exoplanet Survey Satellite (TESS) allow us to investigate and analyse stellar variations in clusters with an unprecedented level of detail for the first time.

Aims. We aim to detect gravity-mode oscillations in the early-type main-sequence members of the young open cluster NGC 2516 to deduce their internal rotation rates.

Methods. We selected the 301 member stars with no more than mild contamination as our sample. We analysed the full-frame image light curves, which provide nearly continuous observations in the first and third years of TESS monitoring. We also collected high-resolution spectra using the Fiber-fed Extended Range Optical Spectrograph for the g-mode pulsators, with the aim of assessing the Gaia effective temperatures and gravities and preparing for future seismic modelling.

Results. By fitting the theoretical isochrones to the colour-magnitude diagram of a cluster, we determined an age of 102 ± 15 Myr and inferred that the extinction at 550 nm (A₀) is 0.53 ± 0.04 mag. We identified 147 stars with surface-brightness modulations: 24 with gravity (g-)mode pulsations (γ Doradus or slowly pulsating B-type stars) and 35 with pressure (p-)mode pulsations (δ Sct stars). When sorted by colour index, the amplitude spectra of the δ Sct stars show a distinct ordering and reveal a discernible frequency-temperature relationship. The near-core rotation rates, measured from period spacing patterns in two slowly pulsating B-type (SPB) stars and nine γ Dor stars, reach up to 3 d⁻¹. This is at the high end of the values found from Kepler data of field stars of similar variability type. The γ Dor stars of NGC 2516 have internal rotation rates as high as 50% of their critical value, whereas the SPB stars exhibit rotation rates close to their critical rate. Although the B-type stars are rotating rapidly, we did not find long-term brightness and colour variations in the mid-infrared, which suggests that there are no disc or shell formation events in our sample. We also discussed the results of our spectroscopic observations for the g-mode pulsators.

Key words: asteroseismology / stars: early-type / stars: interiors / stars: oscillations / stars: rotation / open clusters and associations: individual: NGC 2516

^⋆

All the stellar parameters of the cluster member stars, including Tables 2, 3, and A.1, are available at https://zenodo.org/records/10888387

© The Authors 2024

Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Clusters serve as excellent laboratories for stellar astrophysics due to the advantage that member stars within the same cluster typically share similar distance, age, and initial metallicity. Nevertheless, recent studies have complicated these notions: some works reveal extended coronae in nearby star clusters, where their sizes greatly exceed those of their cluster cores (Meingast & Alves 2019; Meingast et al. 2021; Bouma et al. 2021). Furthermore, both globular and open clusters have shown evidence of multiple populations, indicating complex star formation histories (Gratton et al. 2012; Li et al. 2016; Wang et al. 2022). Additionally, uncertainties arise in stellar evolutionary tracks and isochrones due to the complex input physics and poor calibration of stellar models (e.g. Martins & Palacios 2013; Johnston et al. 2019).

Rotation, a process of stellar physics that remains poorly calibrated, plays a crucial role in stellar evolution and has been recognised as such for many decades (e.g. Shajn & Struve 1929; Maeder 2009). For instance, rotation enhances element mixing and transports more fuel to the core, resulting in increased luminosity and extended lifetimes. Rapid rotation also causes a star to become oblate and generates a surface temperature gradient, affecting the observed colour and brightness (e.g. von Zeipel 1924; Zahn et al. 2010; Espinosa Lara & Rieutord 2011; Bouchaud et al. 2020; known as the gravity darkening effect). Consequently, the rotational effects strongly influence the locations of stars on the colour-magnitude diagram (CMD), leading to scatter in the observed CMD. Therefore, rotation is considered the most plausible mechanism for the extended main-sequence turn-off (eMSTO) phenomenon (e.g. Bertelli et al. 2003; Glatt et al. 2009; Bastian & de Mink 2009; Girardi et al. 2013; Correnti et al. 2015; D’Antona et al. 2015; Brandt & Huang 2015; Bastian et al. 2016, 2018; Li et al. 2019a; Gossage et al. 2019; Lim et al. 2019, among many other studies).

There is limited availability of observed rotation rates for hot eMSTO stars, but numerous surface rotation measurements are available for cool main-sequence stars (spectral class F8V or later, Kraft 1967). The rotation rates of these cool stars can be easily and accurately measured through their surface modulations. These are quasi-periodic brightness variations caused by magnetism-induced surface inhomogeneities in rotating stars (e.g. Irwin et al. 2009; McQuillan et al. 2014). These observations have paved the way for gyrochronology, a method that determines the ages of cool main-sequence stars based on their masses and rotation rates, while other physical properties remain relatively unchanged during their long main-sequence stage (Skumanich 1972; Barnes 2003, 2007). However, gyrochronology is not applicable to hot main-sequence stars since they lack thick convective envelopes, resulting in no or weak magnetic braking. Consequently, hot main-sequence stars tend to rotate rapidly, with surface rotation frequencies of the order of 1 d⁻¹ or v sin i ∼ 100 km s⁻¹ (Royer et al. 2007; Li et al. 2020a). For these stars, surface modulation is often absent or weak, but their internal rotation rates can be obtained through asteroseismology.

Asteroseismology, the field dedicated to the interpretation of stellar oscillations, has proven to be a potent tool for peering into the interior physics of stars (e.g. Aerts 2021). The fundamental concept revolves around standing waves that penetrate different layers of stars. These waves undergo modifications due to the local environment such as sound speed and density. Consequently, the eigenfrequencies carry information about the internal structure of stars (for more detailed information, we refer the reader to textbooks such as Unno et al. 1989; Aerts et al. 2010; Basu & Chaplin 2017). Notably, the temperature range at which gyrochronology loses its effectiveness aligns with the cool boundary of the classical instability strip (IS) for pulsating stars (roughly from 7000 to 10 000 K, where δ Scuti (δ Sct) stars and γ Doradus (γ Dor) stars reside Dupret et al. 2005; Bouabid et al. 2013; Xiong et al. 2016; Murphy et al. 2019). Slowly pulsating B-type (SPB) stars and β Cephei (β Cep) stars appear at higher temperature ranges (hotter than ∼10 000 K). As a result, various types of pulsating stars are being studied asteroseismically, which are hotter than solar-like excited stochastically by convection (Bedding 2014).

At the temperature range of eMSTO in young open clusters, stars more massive than the Sun are the main objects for asteroseismology. Some of these stars pulsate in pressure (p) modes, including β Cep stars (Sterken & Jerzykiewicz 1993; Aerts & De Cat 2003) and δ Sct stars (Goupil et al. 2005; Handler 2009; Bedding et al. 2020). These modes are particularly sensitive to the outer envelopes of stars. Conversely, some stars pulsate in gravity (g) modes, such as γ Dor stars (Balona et al. 1994; Kaye et al. 1999; Van Reeth et al. 2015a) and SPB stars (Waelkens 1991; De Cat & Aerts 2002; Pedersen et al. 2021), allowing us to probe deeper into the stellar structure, reaching down to the boundary of the convective core. The Gaia space mission confirmed that many pulsating stars exist between the SPB and δ Sct instability strips (Gaia Collaboration 2023a).

The excitation mechanisms behind the pulsations in this part of the Hertzsprung-Russell diagram (HRD) are numerous and quite diverse. First of all, the κ mechanism is operational in stars of spectral types O, B, A, and the hottest F stars along the main sequence (Pamyatnykh 1999). Flux blocking at the bottom of the thin convective envelope excites g modes in the γ Dor stars (Guzik et al. 2000; Dupret et al. 2005; Xiong et al. 2016). The role of turbulent pressure in the A- and F-type stars has also been investigated but is less established as a common excitation mechanism (Grassitelli et al. 2015; Houdek 2000; Antoci et al. 2014). This is also the case for the so-called edge-bump mechanism operational in chemically peculiar stars, notably in stars with strong helium depletion (Stellingwerf 1979; Murphy et al. 2020). While mode excitation is fairly well established, its interplay with damping mechanisms is less understood. Aside from radiative damping, additional physical processes affect the waves. The wave excitation, propagation, and damping are notably affected by a multitude of transport processes induced by rotation and magnetism (e.g. Mathis 2013; Aerts et al. 2019 for reviews). A main goal of asteroseismology is to better understand all these processes, starting from a well-characterised large sample of pulsators that can be accurately modelled. From an observational perspective, the ability to detect non-radial pulsators all along the main sequence significantly broadens the temperature coverage for such asteroseismic investigations (Kurtz et al. 2023).

Research on internal stellar rotation is the most attractive topic among many of those driven by asteroseismology, with significant progress in stellar physics based on rotationally induced processes (Aerts et al. 2019). Rotation lifts the degeneracy among mode frequencies, splitting modes into multiplets (Ledoux 1951). Rotational splittings have been observed in many kinds of variable stars, such as the Sun (Deubner et al. 1979), white dwarfs (Winget et al. 1991), subdwarfs (Reed et al. 2000), β Cep stars (Aerts et al. 2003), slowly-rotating γ Dor and SPB stars (Pápics et al. 2014; Kurtz et al. 2014; Saio et al. 2015; Murphy et al. 2016; Li et al. 2019b), and red giant stars (e.g. Mosser et al. 2012; Deheuvels et al. 2014; Gehan et al. 2018). The splittings observed from different p or g modes carry information on rotation rates in different stellar layers, providing the possibility to reconstruct core-to-surface differential rotation profiles (Corbard et al. 1999; Deheuvels et al. 2014, 2015, 2020; Triana et al. 2015, 2017; Di Mauro et al. 2016).

Many of the variable stars situated in hot eMSTOs rotate rapidly, notably with a rotation frequency close to the frequencies of g modes. Such modes are often in the sub-inertial regime of the frequency range (Aerts et al. 2019) and are gravito-inertial modes. The traditional approximation of rotation (TAR) offers an appropriate formalism to treat the rotational effects properly when computing such mode frequencies (Lee & Saio 1987, 1997; Townsend 2003; Mathis 2009; Van Reeth et al. 2016; Saio et al. 2018a). Under the approximation of the TAR, the mode period spacing ΔP ≡ P_{n + 1, l, m} − P_n, l, m, defined as the period difference of two modes with consecutive radial order n, but the same angular degree l and azimuthal order m, is no longer constant as predicted by asymptotic theory (Shibahashi 1979). Instead, the period spacings exhibit decreasing or increasing trends as a function of period, depending on the mode identification (Bouabid et al. 2013; Van Reeth et al. 2015b; Ouazzani et al. 2017). Prograde (m = 1) dipole (l = 1) modes are the most common in real observations and have been observed in hundreds of γ Dor or tens of SPB stars (Li et al. 2020a; Pedersen et al. 2021). They show decreasing period spacings with increasing period and allow us to measure the stars’ near-core rotation rates and calibrate internal mixing processes (Van Reeth et al. 2016; Li et al. 2020a; Szewczuk & Daszyńska-Daszkiewicz 2018; Pedersen et al. 2021; Mombarg et al. 2021). Recently discovered coupling between an inertial mode in the convective core and a gravito-inertial mode in the envelope has opened a new window for exploring the rotation and internal physics of convective cores, where g modes do not propagate (Ouazzani et al. 2020; Saio et al. 2021; Tokuno & Takata 2022; Aerts & Mathis 2023).

Our primary aim is to compile a comprehensive list of various types of pulsating stars within NGC 2516, which is a bright and young open cluster with solar metallicity. In this study, we analysed space photometry of the members of NGC 2516 from the Transiting Exoplanet Survey Satellite (TESS) mission (Ricker et al. 2015) and conducted high-resolution spectroscopic follow-up observations of the g-mode pulsators in the open cluster NGC 2516. The paper is organized as follows. Section 2 introduces the basic information concerning NGC 2516 and the sample selection criteria. Section 3 discusses the fitting of theoretical isochrones to the observed CMD. The TESS photometry and the research on variable stars are presented in Sect. 4. Spectroscopic observations and results are described in Sect. 5. Finally, conclusions are provided in Sect. 6.

2. The cluster and sample selection

2.1. Cluster information

Also known as the Southern Beehive, NGC 2516 (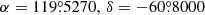 $α = 119 \overset{°}{.} 5270, δ = - 60 \overset{°}{.} 8000$ $\alpha = 119{{\overset{\circ}{.}}}5270,\,\delta = -60{{\overset{\circ}{.}}}8000$ ; Tarricq et al. 2021) is a bright, young, and solar-metallicity open cluster located in the southern hemisphere, with distance of 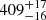$409_{- 16}^{+ 17}$ $409^{+17}_{-16}$ pc (Cantat-Gaudin et al. 2018). Its ecliptic latitude (−75° 50^m) leads this cluster to fall within the southern continuous viewing zone (CVZ) of TESS. Therefore, TESS provides one-year near-continuous light curves for NGC 2516. It is worth noting that there is another open cluster located in the northern CVZ, which is UBC1, as studied by Fritzewski et al. (2024).

Previous investigations of open clusters have typically been limited by the lack of sufficiently long light curves. These studies predominantly focused on p-mode oscillations, which exhibit relatively large frequency separations and thus require lower frequency resolution. Such analyses have been conducted for solar-like oscillators in the Kepler field (Stello et al. 2010; Basu et al. 2011; Hekker et al. 2011), as well as those in the K2 fields (Ripepi et al. 2015; Lund et al. 2016; Sandquist et al. 2020; Murphy et al. 2022), and with TESS data (Murphy et al. 2021; Bedding et al. 2023; Palakkatharappil & Creevey 2023; Pamos Ortega et al. 2023). The only research for γ Dor asteroseismology in young open clusters using TESS that we are aware of is UBC 1 by Fritzewski et al. (2024).

In the case of NGC 2516, its previous study also mainly focused on short-period oscillation signals such as Antonello & Mantegazza (1986) and Zerbi et al. (1998). Interestingly, both Antonello & Mantegazza (1986) and Zerbi et al. (1998) claimed that they found some long-period variable stars at the red edge of the instability strip, which might be the gravity-mode oscillations of γ Dor stars that were just defined in the 1990s (Balona et al. 1994; Kaye et al. 1999). The availability of one-year light curves presents an unparalleled opportunity to study gravity-mode oscillations. These oscillations are characterised by period spacings, necessitating Fourier analysis with high-frequency resolution.

The first measurements of distance, reddening, and extinction of this cluster were reported by Cox (1955) using ground-based photometry. Abundant following photometry observations were conducted, such as Feinstein et al. (1973), which reported the age of NGC 2516 of 60 Myr. After that, the age of NGC 2516 has been consistently estimated as 150 Myr via different methods (isochrone fitting: Meynet et al. 1993; Sung et al. 2002; gyrochronology and lithium depletion: Bouma et al. 2021; Fritzewski et al. 2020). It shows a very similar age to the Pleiades (whose age is estimated to be around 130 Myr with a large spread; see the introduction by Murphy et al. 2022). However, the gyrochronology of NGC 2516 shows a slower upper envelope of the rotation period distributions in Sun-like stars, implying that NGC 2516 is slightly older than the Pleiades.

Apart from their similar ages, Eggen (1964) discovered that NGC 2516, α Persei, and the Pleiades share common space motions and exhibit similar colour-magnitude diagrams (CMDs), suggesting a common origin. Abt et al. (1969) conducted spectroscopic measurements of the equatorial projected velocities (v sin i) of the 30 brightest member stars in NGC 2516 and found that the mean v sin i value is also similar to that of the Pleiades, especially after removing the numerous Ap stars (chemical peculiar stars of spectrum type A).

Metallicity is an important property in cluster age determinations since it impacts stellar evolution. NGC 2516 has near-solar metallicity; Terndrup et al. (2002) reported a metallicity difference between NGC 2516 and the Pleiades of Δ[Fe/H] = 0.04 ± 0.07 and concluded that the metallicity of NGC 2516 is [Fe/H] = 0.01 ± 0.07. Bailey et al. (2018) took multi-epoch high-dispersion optical spectra of 126 Sun-like member stars in NGC 2516 and reported a metallicity of [Fe/H] = −0.08 ± 0.01. Therefore, in our following isochrone fitting, we will use isochrones with solar metallicity based on the protosolar abundances of Asplund et al. (2009).

Ap stars have been discovered in NGC 2516 (e.g. Maitzen & Hensberge 1981), and the surface magnetic field strength has been measured in one of these stars (Bagnulo et al. 2003). Ap stars, considering their ages within the cluster, provide constraints on the evolution of fossil fields, which are typically stable over decades (Abt 1979; Thompson et al. 1987). Additionally, the discovery of white dwarfs in NGC 2516 presents an opportunity to test the high-mass end of the initial mass function (Reimers & Koester 1982; Koester & Reimers 1996).

2.2. Selection of target stars

Meingast et al. (2021) reported the membership identification of NGC 2516 and revealed that it has an extended corona spanning ∼500 pc. Bouma et al. (2021) confirmed the existence of the corona of NGC 2516 and found that the corona is coeval with its core by isochronal, rotational, and lithium dating. We therefore used the result reported by Meingast et al. (2021) as our membership input list.

Firstly, we adopted the TESS magnitude criterion of T < 13 mag for our selection. This threshold ensures the photometric quality of the TESS data because the targets are bright enough. Our scientific objective is to investigate early-type stars; therefore, we need to focus on stars with effective temperatures above ∼6000 K. In fact, the criterion of T < 13 mag is quite conservative, as subsequent research revealed that this threshold corresponds to a temperature of approximately 5230 K for main-sequence stars. We still retained those lower-temperature main-sequence stars (between 6000 K and 5230 K) because we want to observe the transition of the rotation rate at the Kraft break. Although three red giants in this cluster are brighter than T = 13 mag, their temperatures are lower than those of the early-type cluster members. The presence of these red giants offers additional constraints on the cluster’s age during the isochrone fitting process.

Secondly, we calculated the absolute magnitude of all the member stars in the sample by Meingast et al. (2021), applying a cut-off at a Gaia G-band absolute magnitude brighter than 5 mag to include supplementary stars in the sample. In this step, we found four additional stars. Finally, we obtained a sample comprising 439 stars.

In the target selection procedure, we did not implement any criteria to exclude binary stars, which can deviate from the single-star isochrone and potentially introduce systematic errors in the subsequent isochrone fitting described in Sect. 3. Previous reports have identified spectroscopic binaries (e.g. Abt & Levy 1972; Gieseking & Karimie 1982; González & Lapasset 2000), and in this work we identified five eclipsing binaries. Nevertheless, the absence of a distinct binary main sequence in the colour-magnitude diagram (CMD) suggests their limited impact on the isochrone fitting that follows.

3. Isochrone fitting

Recent studies have examined how rotation affects stellar evolution and consequently the isochrones (e.g. Paxton et al. 2019; Gossage et al. 2019). Therefore, we aim to identify the best-fitting isochrone for NGC 2516 and from it derive the age and extinction of the cluster to more effectively consider the effects of rotation. we used MIST isochrones (MESA Isochrones and Stellar Tracks, Choi et al. 2016; Dotter 2016) to fit our data. These are based on the Modules for Experiments in Stellar Astrophysics (MESA) code (version v7503, Paxton et al. 2011, 2013, 2015, 2018). The original MIST isochrones¹ only include two rotation rates – specifically v/v_crit = 0.0 and 0.4 – where v_crit represents the critical rotation at which the centrifugal force equals gravity at the equator of the isobar (Paxton et al. 2019). However, our objective is to comprehensively account for the impact of rotation. Therefore, we explored isochrones encompassing a whole range of rotation rates, ranging from 0.0 to 0.9 v/v_crit, with a step of 0.1 (Gossage et al. 2019). The physical processes related to rotation applied in the isochrone computations are done for the shellular approximation (Kippenhahn & Thomas 1970). The chemical and angular momentum transport induced by rotation is computed from the diffusion equations from (Endal & Sofia 1978). Gravity darkening was included according to Espinosa Lara & Rieutord (2011) as implemented in Paxton et al. (2019). Given that the temperature and luminosity decrease due to the gravity darkening effect depend on the inclination of the rotation axis with respect to the line-of-sight, Gossage et al. (2019) calculated the isochrones at a range of inclination angles and randomly sampled from them to create synthetic stellar populations. The isochrones used in this work represent an effect of gravity darkening averaged over inclination angles. Therefore, the scatter resulting from the gravity-darkening effect on the CMD should be distributed randomly around the best-fitting isochrone, rather than being concentrated on one side.

Due to the presence of main-sequence turn-offs and post-main-sequence stars, the shape of isochrones is rather intricate, that is, one colour index corresponds to multiple absolute magnitudes. Consequently, traditional least-squares fitting is not applicable here. Therefore, we consider an alternative fitting approach. We hypothesise that each observed data point follows a two-dimensional Gaussian distribution (without correlation) around the best-fitting point:

$\begin{matrix} P (C, G) = \frac{1}{2 π σ_{C} σ_{G}} exp (- \frac{1}{2} [{(\frac{C - C_{model}}{σ_{C}})}^{2} + {(\frac{G - G_{model}}{σ_{G}})}^{2}]), \end{matrix}$ $\begin{aligned} P(C,G) = \frac{1}{2\pi \sigma _C \sigma _G}\exp \left(-\frac{1}{2}\left[\left(\frac{C-C_{\rm model}}{\sigma _C}\right)^2+\left(\frac{G-G_{\rm model}}{\sigma _G}\right)^2\right] \right), \end{aligned}$ (1)

where C is the Gaia colour index G_BP − G_RP, and G is the absolute Gaia G-band magnitude with extinction. C_model and G_model are the colour index and absolute magnitude of the closest point in the isochrone after extinction correction, while σ_C and σ_G are the standard deviations of the colour index and of the absolute G-band magnitude. We interpolate the isochrones, inserting ten values between each pair of adjacent points, to calculate the theoretically predicted points closest to a given observed point. The observed σ_C and σ_G values obtained from Gaia are notably smaller than the scatter observed in the CMD. This discrepancy could potentially be attributed to uncertainties in input physics, including poor calibration of internal mixing, variations in inclinations, differential extinction, various initial rotation rates, and unknown physical causes of the eMSTO. Therefore, we opted to use significantly larger values for σ_C and σ_G instead of the Gaia’s observation uncertainties to represent the residual’s standard deviations. By calculating a fourth-degree polynomial fit between the absolute magnitude and the colour index, these values of the uncertainties are set to σ_C = 0.056 mag and σ_G = 0.332 mag.

The final likelihood function is the product of a series of probabilities:

$\begin{matrix} L (D | θ) = \prod_{i} P (C_{i}, G_{i}), \end{matrix}$ $\begin{aligned} L(D|\theta ) = \prod _{i} P(C_i, G_i), \end{aligned}$ (2)

where D denotes the observed data, C_i and G_i are the colour index and absolute G magnitude of the ith star, and θ = {log(age), A₀} is the vector of input parameters that contains the age and extinction at 550 nm. The input colour index and absolute magnitude derived from the MIST isochrones represent their intrinsic values, so we needed to calculate the values after extinction correction for the G, G_BP, and G_RP bands. Specifically, we applied the extinction law as described by Danielski et al. (2018), which is calculated as

$\begin{matrix} A_{m} / A_{0} = & a_{1} + a_{2} X + a_{3} X^{2} + a_{4} X^{3} + a_{5} A_{0} + a_{6} A_{0}^{2} + a_{7} A_{0}^{3} \\ + a_{8} A_{0} X + a_{9} A_{0} X^{2} + a_{10} X A_{0}^{2}, \end{matrix}$ $\begin{aligned} A_m/A_0 =&a_1+a_2X+a_3X^2+a_4X^3+a_5A_0+a_6 A_0^2+a_7A_0^3\nonumber \\&+ a_8A_0X+a_9 A_0X^2+a_{10}XA_0^2, \end{aligned}$ (3)

where A_m stands for the extinction in the G, BP, and RP bands, A₀ is the extinction at 550 nm, and X is the intrinsic colour index G_BP − G_RP. The coefficients a_i for the Gaia DR3 passband were given by Riello et al. (2021)². Considering the positions of our stars on the HRD, we used the coefficients adapted for the upper regions of the HRD, which encompass giants and the upper segment of the main sequence, up to approximately G ∼ 5 mag.

We find that the data points exhibit a large spread in the low-temperature area, where G_BP − G_RP is approximately greater than 0.65 mag (in Fig. 1). This spread is attributed to binarity, although we do not observe a clean binary sequence. This is understood by realising that binarity increases the apparent luminosity for all system configurations, while a shift to lower effective temperatures occurs for particular binaries. Since we do not have a characterisation of the multiplicity at this stage, we excluded the data points that are located above the dotted line in Fig. 1, which was manually determined to begin at (G_BP − G_RP = 0.6626, G = 3.217) and end at (G_BP − G_RP = 1.2011, G = 5.810).

Fig. 1.

Observed Gaia DR3 CMD of NGC 2516. Left panel: fits for isochrones with varying rotation rates. Isochrones with v/v_crit ≤ 0.4 effectively reproduce the observed data. Right panel: solid black isochrone represents the best-fitting result with v/v_crit = 0.3. The grey background tracks collectively represent the uncertainty, which is determined using a set of 500 isochrones randomly selected from the Monte Carlo approach explained in the main text. The dotted line marks the boundary of the binary sequence.

A pre-search of the best-fitting model was done by calculating a coarse grid, using 7 < log(age yr⁻¹) < 9 with an evolution step of 0.02 and 0 mag < A₀ < 1 mag with step of 0.025 mag. After finding the initial best-fitting values of log(age) and A₀, we estimate their uncertainties using a Monte Carlo approach. In each iteration, we added a Gaussian random noise perturbation to the original data using σ_C and σ_G and searched for the best-fitting model in a fine grid by calculating the likelihood values. The parameter spaces are ages within the first eight and last eight steps of the initial age range and extinction within a range of 0.1 mag before and after the initial extinction, with a step size of 0.01 mag. The age and A₀ corresponding to the largest likelihood in each iteration were recorded, and their uncertainties were calculated after 1000 iterations.

Figure 1 illustrates the best-fitting isochrones. In the left panel, we find that the isochrones with v/v_crit ≤ 0.4 successfully reproduce the observed CMD, while those with v/v_crit ≥ 0.5 exhibit discrepancies from the observations. Additionally, as shown in Fig. 2, isochrones within v/v_crit ≤ 0.4 yield similar maximum likelihood values, but the likelihood begins to decrease rapidly when v/v_crit ≥ 0.5. Obviously, not all stars in the cluster will have been born with the same value of v/v_crit. All the isochrones with v/v_crit ≤ 0.4 produce satisfactory results in the CMD.

Fig. 2.

Relation between log of likelihood function (Eq. (2)) of the best-fitting isochrone and rotation rates v/v_crit. Isochrones with v/v_crit > 0.5 show significantly small likelihood values, implying worse fitting compared to the observational data.

The right panel of Fig. 1 presents one of the best-fitting outcomes, featuring v/v_crit = 0.3 for all stars simultaneously. Under this premise, the grey background represents the uncertainty range obtained from 500 randomly selected isochrones from the iterations with v/v_crit ≤ 0.4. The presence of the three post-main-sequence stars imposes additional constraints on isochrone age, yet considerable spread persists in the post-main-sequence phases. Finally, under equal weighting of the isochrone fitting with v/v_crit ≤ 0.4, we derived log(age yr⁻¹) = 8.01 ± 0.06 (equivalent to 102 ± 15 Myr) and an extinction value of A₀ = 0.53 ± 0.04 mag. The posterior distributions are shown in Fig. 3. Our determined age for NGC 2516 is somewhat younger than that of the Pleiades, opposite to the prior study using gyrochronology (Fritzewski et al. 2020). The age discrepancy might arise from different approaches. Applying the same isochrone-fitting approach to both NGC 2516 and the Pleiades could still yield a similar age for both open clusters.

Fig. 3.

Posterior distributions of isochrone fitting.

Regarding the extinction, A₀ = 0.53 mag lead to a reddening of 0.25 mag given a intrinsic Gaia colour index (G_BP − G_RP)₀ = 0.2 mag. If we assume A₀ ≈ A_V and A_V = 3.1E(B − V), where A_V represents extinction at the V band, we obtained a reddening value of E(B − V)≈0.17 mag. Alternatively, using Eq. (3) and the extinction coefficients from Casagrande & VandenBerg (2018), which state that E(BP − RP) = (3.374 − 2.035)E(B − V), we obtain a similar reddening value to E(B − V)≈0.18 mag. It is worth noting that this reddening value is slightly higher than the one reported in a previous study (0.112 ± 0.024 mag) by Sung et al. (2002). Additionally, the Gaia total galactic extinction map provides an average extinction value of A₀ = 0.4358 mag within a radius of 0.25′. Even after transforming this value to E(B − V) (which is 0.14 mag), it remains slightly higher than the literature value reported by Sung et al. (2002).

We also investigated the impact of different extinction values on age determination. We find that the values suggested by Sung et al. (2002) and those from the Gaia total galactic extinction map both lead to the same age estimate of log(age yr⁻¹) = 7.99. This estimate is just one step before our best-fitting age and still falls within the uncertainty range. Therefore, it appears that extinction does not significantly change the age determination.

Figure 4 displays a zoomed-in view of the CMD, which roughly corresponds to the region of the classical instability strip. In the left panel, we can observe that Gaia’s RUWE binary indicator values (see definition in Gaia Collaboration 2023b) show little variation in this region, making it difficult to distinguish binary systems based solely on RUWE values. Only one star exhibits a significantly higher RUWE value, and, interestingly, this star happens to fall to the right of the best-fit isochrone. In the right panel, we colour-coded the points with the Gaia vbroad parameter (see definition in Frémat et al. 2023), revealing that many stars have high vbroad values (greater than 200 km s⁻¹). These stars tend to be located on the right of the best-fitting isochrone, indicating the influence of gravity darkening caused by fast rotation and the flattening it induces (Pérez Hernández et al. 1999).

Fig. 4.

Zoomed-in view of CMD of NGC 2516 showing how binarity and rotation lead a star deviating from the main sequence. The ranges of the x- and y-axes are 0.2 mag < G_BP − G_RP < 0.6 mag and 2.0 mag < M_G < 3.5 mag. The stars are colour-coded by RUWE (showing binarity) and line broadening (representing rotation rates), respectively. The small black dots are stars without broadening values in the Gaia DR3 database.

4. Light-curve reduction and variability identification

4.1. Light-curve reduction

The unique advantage of NGC 2516 is its location near the edge of the southern continuous viewing zone of the TESS satellite. Therefore, TESS offers nearly continuous observations spanning 11 sectors, for a total of approximately 297 days. Our analysis used the data from Cycle 1 and Cycle 3, encompassing sectors 1, 4, and 7 to 11, as well as sectors 27, 31, and 34 to 37. A one-year gap is seen during Cycle 2, when the TESS satellite observed the northern celestial hemisphere. In Cycle 1, observations were taken at a cadence of 30 min, whereas in Cycle 3, the cadence was reduced to ten minutes.

We used the asteroseismic reduction pipeline developed by Garcia et al. (2022a) to download and process the TESS photometric data³. The TESS Full Frame Images were obtained from the Mikulski Archive for Space Telescope (MAST) using the TESScut API (Brasseur et al. 2019). For each star, a cutout of 25 pixels × 25 pixels was applied. This size allows for the examination of neighbouring stars and the assessment of contamination, and it provides an adequate number of background pixels for subtraction.

Flux extraction using custom apertures was performed using the Python package Lightkurve (Lightkurve Collaboration 2018). While the apertures in the pipeline by Garcia et al. (2022a) were optimised to mitigate severe contamination, it is challenging to completely avoid contamination in the crowded NGC 2516 field. For stars significantly affected by contamination, we employed aperture radii smaller than those automatically determined by the code. We calculated contamination levels by fitting Gaussian profiles of the target star and nearby stars. A star was excluded from the analysis if the contaminated flux constituted more than 10% of the total flux. After excluding the contaminated stars, our sample contains 301 stars for further analysis. Subsequently, detrending was performed on a sector-by-sector basis, involving background subtraction and a principal component analysis.

After obtaining the light curves, we calculated their Fourier transform to identify their light variability. The Lomb-Scargle algorithm as implemented in ASTROPY (Astropy Collaboration 2013) was used for our stars to calculate their amplitude spectra (Lomb 1976; Scargle 1982), which is suitable for unevenly spaced data.

4.2. Variable star classification

We identified three red giant stars in the cluster, while all the other stars are main-sequence stars. Therefore, we primarily focused on the types of variables that occur among main-sequence stars, namely p-mode pulsators (mainly δ Sct stars), g-mode pulsators (γ Dor and SPB stars), stars with surface modulation, and eclipsing binaries. The g-mode and p-mode pulsators typically exhibit numerous narrow frequency peaks within their respective frequency regimes. The frequencies of p-mode pulsations are generally above ∼10 d⁻¹, while g-mode pulsations have frequencies below ∼5 d⁻¹. Eclipsing binaries often exhibit a fundamental frequency along with a series of harmonics in their power spectra. These distinct features aid us in identifying various types of variable stars. Rotational modulation occurs along the main sequence, notably in cool stars subject to magnetic braking and in hotter counterparts revealing chemical or temperature spots. Specifically, we searched for a hump in the low-frequency range caused by the rotational frequency and differing from additional narrow frequency peaks due to pulsations, and we also require the presence of harmonics of the rotational frequency.

We find 24 g-mode pulsators, 35 p-mode pulsators, five eclipsing binaries, and 147 surface modulation stars. Figure 5 illustrates the positions of these variables in the Gaia DR3 CMD of NGC 2516. For isolated stars, determining the positions of variable stars on the HRD and evolutionary stages remains challenging due to various factors, including extinction, inaccurate temperature and luminosity measurements, or large uncertainty on mass. Consequently, defining the observational instability strip (IS) of the variables in the cluster is non-trivial. The CMD of a cluster offers a better opportunity to investigate the instability strips of variable stars, as their locations and parameters are well-defined in the CMD.

Fig. 5.

Locations of variable stars on CMD of NGC 2516.

In the case of g-mode pulsators (shown in the upper left panel of Fig. 5), we observe a group of stars within a range of G_BP − G_RP values from approximately 0.4 mag to 0.6 mag, which is identified as the IS of γ Dor stars. We plotted the theoretical IS by Dupret et al. (2005) after transforming the effective temperature and luminosity to the observed Gaia colour index G_BP − G_RP and absolute G-band magnitude with extinction. We find that the theoretical IS is slightly redder than the dense area of g-mode pulsators, and many g-mode pulsators appear above the blue edge of the theoretical IS. In Fig. 6, we show the histograms as a function of colour index for the various classes of pulsators. The distribution peaks around 0.5 mag for the observed γ Dor IS. In this region, about 50% of stars show g-mode pulsations.

Fig. 6.

Histogram of numbers of p-mode pulsator, g-mode pulsator, surface modulations, and the total stars in our sample. The bin size of the colour index G_BP − G_RP is 0.05. Pulsating stars (p- and g-mode pulsators) have high fractions around G_BP − G_RP of 0.5 mag, while surface modulation stars appear with small or large G_BP − G_RP.

The upper right panel of Fig. 5 depicts the distribution of p-mode pulsators. We observe that p-mode pulsators are present within the G_BP − G_RP range of approximately 0.2 mag to 0.6 mag. These stars are classified as δ Sct stars, as their temperatures do not reach the range of β Cep stars. The observed IS of δ Sct stars in the cluster is broader than that of the γ Dor stars. We find that the observed δ Sct IS by Murphy et al. (2019) matches the observation, while the theoretical IS by Dupret et al. (2005) is still slightly redder than the observations. Examining Fig. 6, we note that δ Sct stars dominate the IS. Approximately 60% to 80% of the stars within the IS are identified as δ Sct stars. This fraction is consistent with the findings of a previous study conducted on the Pleiades cluster (Bedding et al. 2023). The fraction slightly exceeds the value found for the Kepler field (Murphy et al. 2019), which may be due to the age difference.

In the lower left panel of Fig. 5, we observe the positions of eclipsing binaries on the CMD. The majority of these binaries appear to lie near the main-sequence turn-off. This observation is consistent with the nature that high-mass stars tend to exhibit a higher binary fraction (Moe & Di Stefano 2017). In Table 1, we listed the TIC number, Gaia colour index, and the orbital period for each eclipsing binary. The orbital period was measured using the procedure described in Li et al. (2020b), which is mainly based on the O−C (O minus C) method (Sterken 2005). We find that TIC 382529041 shows a variation in eclipse depths. Its O−C diagram reveals a long-period third-component gravity perturbation with an estimated very high eccentricity.

Table 1.

Five eclipsing binaries in NGC 2516.

The stars exhibiting surface modulation are situated in the lower right panel of Fig. 5. It is evident that a distinct gap exists wherein very few stars with surface modulations are observed, ranging from G_BP − G_RP ∼ 0.2 mag to approximately 0.6 mag. This is the region predominantly occupied by δ Sct and γ Dor stars. This gap is also evident in the green histogram displayed in Fig. 6. We observe a considerably higher fraction of cool stars displaying surface modulation with G_BP − G_RP > 0.6 mag. This occurrence is attributed to low-mass stars with a convective envelope, resulting in surface activity. Furthermore, some stars located at the MSTO also show surface modulation in the presence of fast rotation close to the critical rate.

4.3. Gravity-mode pulsators

We first briefly recall the analysis procedure to detect period-spacing patterns and deduce mode identification as designed by Li et al. (2019b). After obtaining the light curves, we applied a detrending algorithm to eliminate the long-time trends. This involved calculating the median flux for each data point within a five-day moving window and normalising the flux by this median value. The window size used for TESS data is narrower than that applied to Kepler data (which is 10 days by Li et al. 2020b) because the TESS data exhibit more gaps and instrumental effects.

An iterative pre-whitening method was used to extract frequencies from the light curves. During each iteration, the frequency with the highest peak was identified and a sine function was fitted to the light curve to model this peak. This process yielded the optimised frequency, amplitude, and phase for the peak. Following each iteration, the residual from the sine function fitting was used for the subsequent iteration. The pre-whitening process was terminated once the signal-to-noise ratio (S/N) of the highest peak fell below four.

Not all of the 24 g-mode pulsators allow for mode identification, because only some of them show clear period spacing patterns. There are various period-spacing search algorithms for γ Dor stars, such as Van Reeth et al. (2015b) and Christophe et al. (2018). Here, we identified such spacing patterns following the observation-oriented method by Li et al. (2019b). This method constructed a template given the first period, the first period spacing value, and the slope (the changing rate between period spacing and period). A cross-correlation factor between the template and the real observed amplitude spectrum was calculated to reveal if a period spacing pattern is present in the data. This method yielded hundreds of γ Dor stars with identified modes in the Kepler field, including γ Dor stars in eclipsing binaries (Li et al. 2019c, 2020a,b). A similar method to search for the period spacing patterns was developed by Garcia et al. (2022a) and yielded tens of γ Dor field stars in the TESS continuous viewing zone (Garcia et al. 2022b).

We find 11 g-mode pulsators in NGC 2516 that exhibit clear period-spacing patterns. We measured their asymptotic spacings and near-core rotation rates following the framework by Van Reeth et al. (2016), which relies on the traditional approximation of rotation (TAR). In this approximation, it is assumed that only the radial component of the rotation vector matters, while the horizontal component is neglected (Townsend 2003). The TAR is an excellent approximation for γ Dor and SPB pulsators, because the displacement vectors of their g modes are dominantly horizontal (De Cat & Aerts 2002, for observed values), such that the horizontal component of the rotation vector can be ignored in the frequency regime of the gravito-inertial modes (e.g. Townsend 2003; Rui et al. 2024).

Given the influence of rotation, the period spacings for g modes are no longer constant (Bouabid et al. 2013). Rather, the g-mode periods in the co-rotating frame can be rewritten as

$\begin{matrix} P_{n l m, co} = \frac{Π_{0}}{\sqrt{λ_{l, m, s}}} (n + α_{g}) . \end{matrix}$ $\begin{aligned} P_{nlm,\mathrm{co}} = \frac{\Pi _0}{\sqrt{\lambda _{l, m, s}}}\left(n+\alpha _{\rm g}\right). \end{aligned}$ (4)

In this equation, Π₀ is the asymptotic spacing representing the travel time of the waves within their mode cavity determined by the buoyancy frequency and is hence called the buoyancy travel time (Aerts 2021), s = 2f_rot/f_co is the spin parameter as a function of the rotation frequency f_rot and pulsation frequency in the co-rotating frame f_co = 1/P_nlm, co, λ is the eigenvalue of the Laplace tidal equation, which can be computed with the GYRE code (Townsend & Teitler 2013; Townsend et al. 2018), α_g is a phase term, and n, l, m are the quantum numbers of the mode. We use the convention that positive m represents the prograde modes. The periods in the co-rotating frame can be transformed to the inertial frame P_nlm, in by

$\begin{matrix} 1 / P_{n l m, in} = 1 / P_{n l m, co} + m f_{rot} . \end{matrix}$ $\begin{aligned} 1/P_{nlm, \mathrm{in}} = 1/P_{nlm,\mathrm{co}} + m f_{\rm rot}. \end{aligned}$ (5)

Mode identification, which involves allocating l and m values, is an essential step in the TAR fitting. For γ Dor stars that rotate slowly, the l = 1 and l = 2 peaks are roughly equally spaced in period, and their period spacings exhibit a ratio of 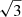$\sqrt{3}$ $\sqrt{3}$ , facilitating their identification in the period échelle diagram (e.g. Bedding et al. 2015). The prograde (m > 0) and the zonal (m = 0) modes show decreasing period spacings as a function of increasing pulsation period, while the retrograde m < 0 modes show increasing period spacings (e.g. Bouabid et al. 2013; Van Reeth et al. 2016; Ouazzani et al. 2017). For γ Dor stars that rotate rapidly, amplitude spectra often display characteristic frequency peak groups. The peak group with the highest amplitude corresponds to l = 1, m = 1 modes, namely the prograde sectoral modes, while l = 2, m = 2 modes exhibit periods that are half that of l = 1 modes (e.g. Saio et al. 2018a). It is very rare to detect non-sectoral (l ≠ m) modes in rapidly rotating γ Dor stars (Saio et al. 2018a; Li et al. 2020a). Rossby modes are seen at periods slightly lower than those twice that of l = 1 modes with increasing period spacing as a function of pulsation period, and they are often characterised by a rapidly increasing and then slowly decreasing amplitude profile for each mode as a function of increasing period (Van Reeth et al. 2016; Saio et al. 2018b; Li et al. 2019c). For Rossby modes, the quantum number l is not used; instead, the letter k is used, which falls within the range k ≤ −1 (Saio et al. 2018b). The most frequently observed Rossby modes have k = −2, m = −1 (Li et al. 2019c). Conversely, for g modes, k ≥ 0, with k = l − |m| (Saio et al. 2018b).

For our application to the NGC 2516 γ Dor stars, a Markov chain Monte Carlo (MCMC) optimisation algorithm was applied to obtain the best-fitting f_rot and Π₀ by comparing the observed and calculated period spacings (Van Reeth et al. 2016; Li et al. 2020a). All the period-spacing patterns and the TAR fitting results are shown in Appendix B.

Figure 7 displays all 11 g-mode pulsators with clear period-spacing patterns. We observe a distinct orderliness in the amplitude spectra of these stars within the same star cluster after sorting them by Gaia colour index. We find that with a colour index between 0.5 mag and 0.165 mag, those stars show similar near-core rotation rates, which is about 3 d⁻¹. The dominant mode frequencies at about 0.25 d are identified as l = 1, m = 1 g modes subject to the Coriolis acceleration and projected into the line of sight with a value of f_rot. Additionally, another group of frequencies is observed at a period of approximately 0.13 d, corresponding to l = 2, m = 2 g modes shifted by 2f_rot towards the observer’s reference frame.

Fig. 7.

Eleven g-mode pulsators with clear period spacing patterns, sorted in descending order by their Gaia colour index G_BP − G_RP from top to bottom. The red vertical lines mark their near-core rotation periods derived from the modes by adopting the TAR.

We present the results of asymptotic spacing Π₀ and near-core rotation frequency f_rot in Fig. 8 and Table 2. In the left panel of Fig. 8, we observe that the majority of our g-mode pulsators have Π₀ at ∼4900 s. This value is typical for γ Dor stars, although it is somewhat higher than the average value of the γ Dor field stars derived from Kepler and TESS data (which is 4000 s, as reported in Li et al. 2020a; Garcia et al. 2022b). The value of Π₀ is correlated with the central hydrogen abundance, along with other key quantities describing the internal mixing, as well as the initial chemical composition (Mombarg et al. 2019; Ouazzani et al. 2019). Hence, it provides an estimation of the stellar age, provided that the level of internal mixing can be deduced and that the metallicity of the star is known. Here, we assume all the cluster members were born with the same initial metallicity. Consequently, the higher value of Π₀ can be attributed to the young age of the cluster. It is worth noting that Π₀ remains relatively consistent for all pulsators within the G_BP − G_RP range of 0.2 mag to 0.6 mag, indicating a limited sensitivity to (core) mass. TIC 358466708 exhibits a value of Π₀ ≈ 7500 s, which is significantly higher than the typical value for γ Dor stars but is typical for SPB stars (Pedersen et al. 2021). Additionally, the high temperature of this star (12 070 ± 170 K) confirms its SPB nature. TIC 372913043 is also an SPB star with temperature of 11 510 ± 240 K. Their temperatures were measured using the high-resolution spectra, as discussed in Sect. 5.

Fig. 8.

Location of γ Dor stars on CMD with best-fitting isochrone. The large circles show the γ Dor stars with clear period spacings, colour-coded by their buoyancy travel time (left panel) or near-core rotation rates (right panel). The black dots are the other cluster members, and the grey solid line is the best-fitting isochrone. We also indicate the masses of the models on the right edges of each panel. In the left panel, we show the TIC numbers of the stars.

Table 2.

TAR fitting results of 11 g-mode pulsators in NGC 2516.

We show the near-core rotation rates in the right panel of Fig. 8 and find a clear correlation with colour index. The near-core rotation rates increase from about 1 d⁻¹ at G_BP − G_RP ≈ 0.6 mag to 3 d⁻¹. However, the SPB star TIC 358466708 shows a relatively slow rotation, back to 1 d⁻¹. This is in agreement with the findings for Kepler fields stars, where the SPB stars are on average slower rotators than the γ Dor stars (Aerts 2021, see their Fig. 6) The rotation rates of the γ Dor stars in NGC 2516 are significantly higher than those obtained from the Kepler and TESS data (Li et al. 2020a; Garcia et al. 2022b), where the median rotation rate is approximately 1 d⁻¹. The faster rotation that we find here for the cluster stars is due to their younger age compared to those of field stars (Mombarg et al. 2021).

Additionally, we identify two g-mode pulsators (TIC 358466708 and TIC 372913043) located at the MSTO that are categorised as SPB stars. The effective temperatures measured by the spectra in Sect. 5 further confirm the classification of SPB stars. TIC 372913043 is somewhat suspicious, as it exhibits a small asymptotic spacing value (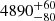 $4890_{- 80}^{+ 60}$ $4890^{+60}_{-80}$ s, Table 2), which should be within the typical range for γ Dor stars. We investigated the possibility of contamination and found the contamination level to be 1.8%, indicating that 1.8% of the flux in the aperture comes from other sources. There is only one star that could potentially contaminate the target, which is also a cluster member (TIC 372913044, with apparent Gaia G-band magnitude of 12.84 mag). As a comparison, TIC 372913043 has a magnitude of 8.74 mag, which is 4.1 mag brighter than the neighbouring star. However, given its low colour index (G_BP − G_RP = 0.92 mag, corresponding to T_eff < 5830 K), the neighbouring star TIC 372913044 is unlikely to exhibit g-mode period spacings. Therefore, we ruled out contamination as a cause. The reason for the small asymptotic spacing in this SPB star is likely due to evolution: as seen in Fig. 8, TIC 372913043 is located in the low-temperature side of the eMSTO and is departing the main sequence, which means its asymptotic spacing should be decreasing rapidly.

The mode identifications for two g-mode stars need verification. For TIC 358466708, we find that the clear modes are l = 2, m = 2 with periods around 0.28 d (see the figures in Appendix B). As illustrated in the top panel of Fig. 7, TIC 358466708 exhibits l = 1 modes at periods of approximately 0.56 d; however, the l = 1 period spacings could not be identified. Consequently, we only used the l = 2, m = 2 modes for the fitting with the TAR to determine the near-core rotation rate and the asymptotic spacing. The other star, TIC 358466729, exhibits identifiable Rossby modes around 0.55 d. Nevertheless, we were unable to identify any period spacing within its l = 1 g-mode region, which should occur at approximately 0.4 d, as shown in the third panel counting from the bottom in Fig. 7.

We also identify some g-mode pulsators situated between the SPB and γ Dor strips. This is fully in line with the findings by Gaia Collaboration (2023a) from Gaia DR3 light curves and points to fast rotators with g modes (Aerts et al. 2023).

4.4. Pressure-mode pulsators

The mode identification of δ Sct stars is a long-standing question and leads to difficulty in asteroseismic exploitation of their internal physical properties (Bedding et al. 2020). We show all the amplitude spectra of the δ Sct stars in NGC 2516, sorted by their colour index, in Fig. 9. We find that their amplitude spectra are well ordered as a function of colour index. For the low-temperature stars (G_BP − G_RP > 0.411 mag, the bottom part of Fig. 9), a series of strong frequency peaks appear near 21 d⁻¹, which is identified as the radial fundamental mode frequency (Bedding et al. 2020). In the G_BP − G_RP region from 0.5 mag to 0.4 mag (middle part of Fig. 9), we find a relation between the mean pulsation frequency and temperature. With increasing temperature, the envelope of the pulsation frequencies moves to a higher frequency (Balona & Dziembowski 2011; Barceló Forteza et al. 2018, 2020; Bowman & Kurtz 2018; Hasanzadeh et al. 2021). Finally, for the hotter stars (with G_BP − G_RP ≤ 0.396 mag), another series of strong peaks aligns at frequency around 33 d⁻¹, which we interpret as the signature of second overtone radial modes given their factor ∼0.64 shorter period than those of the fundamental modes (e.g. Netzel et al. 2022).

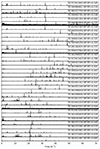Fig. 9.

Amplitude spectra of δ Sct stars in NGC 2516, sorted by colour index. The top panel has the star with the smallest colour index and hence the highest effective temperature.

We attempted to identify regular frequency separations among these δ Sct stars. In Fig. 10, the échelle diagram of TIC 308307266 displays a ridge corresponding to l = 1 modes with four distinct peaks separated by a large frequency spacing of Δν ≈ 6.21 d⁻¹, roughly in agreement with mean stellar densities of δ Sct stars if we keep in mind that Δν is affected by fast rotation. We did not observe a corresponding ridge for its l = 0 modes, but this is not so surprising given that such ridges due to radial modes tend to be strongly blended, while those of the dipole modes are not, making the latter easier to find (Bedding et al. 2020). No other δ Sct star in the cluster was found to reveal a clear large frequency separation.

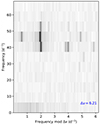Fig. 10.

Échelle diagram of δ Sct star TIC 308307266. A frequency separation is seen with Δν ≈ 6.21 d⁻¹.

4.5. Oscillations of the cluster giants

There are three red giants in NGC 2516: HR 3076 (TIC 382510863; HD 64320; G = 6.34), SAO 250043 (TIC 372913375; G = 6.30), and HD 65662 (TIC 358466601; G = 5.18). We used the SPOC two-minute light curves to search for solar-like oscillations. To measure ν_max, we used the nuSYD method described by Sreenivas et al. (2024). In HR 3076, we found a very clear detection (Fig. 11) with ν_max = 10.8 ± 0.3 μHz (measured using nuSYD) and Δν = 1.27 ± 0.02 μHz (measured by constructing an échelle diagram). In the other two stars, the oscillations were not so clear, but the likely values of ν_max are 12.5 ± 0.5 μHz for SAO 250043 and 2.6 ± 0.3 μHz for HD 65662. We were not able to identify Δν for these two stars.

Fig. 11.

Power density spectra of red giant HR 3076.

For HR 3076, we have both ν_max and Δν, and so we used the standard asteroseismic scaling relations (e.g. Jackiewicz 2021) to calculate the mass. We remind the reader that the nuSYD method has an optional correction that we did not make because it requires sufficient S/N to measure the width of the oscillation envelope reasonably accurately. Therefore, in the scaling relations we used the uncorrected solar value for ν_max of 3154 ± 30 μHz (Sreenivas et al. 2024). Using T_eff = 4704 ± 122 K from Stassun et al. (2019) gives a mass of 3.8 ± 0.5 M_⊙.

For stars without a value of Δν, we can still use ν_max to estimate a mass by using the Gaia luminosity (e.g. Miglio et al. 2012; Hon et al. 2021). We calculated the luminosities of the stars using the equation⁴

$\begin{matrix} - 2.5 log L = G + BC - M_{bol, ⊙} - A_{G}, \end{matrix}$ $\begin{aligned} -2.5\log L = G + \mathrm{BC} - M_{\rm bol,\odot } - A_G, \end{aligned}$ (6)

where G is the absolute magnitude in the Gaia G band, BC is the temperature-only-dependent bolometric correction, M_bol, ⊙ = 4.74 is the solar absolute bolometric magnitude, and A_G is the extinction in the Gaia G band given by the isochrone fitting in Sect. 3. The bolometric correction is calculated as

$\begin{matrix} BC = \sum_{i = 0}^{4} b_{i} {(T_{eff} - T_{eff, ⊙})}^{i}, \end{matrix}$ $\begin{aligned} \mathrm{BC} = \sum _{i=0}^4 b_i \left(T_{\rm eff}-T_{\rm eff,\odot }\right)^i, \end{aligned}$ (7)

with the coefficients b_i given by Andrae et al. (2018)⁵. We used the effective temperatures T_eff given by Gaia to calculate the luminosities and subsequently relied on the Stefan–Boltzmann law to estimate the radii R, namely

$\begin{matrix} L \propto R^{2} T_{eff}^{4} . \end{matrix}$ $\begin{aligned} L \propto R^2 T_{\rm eff}^4. \end{aligned}$ (8)

We obtained luminosities of 755 ± 47 L_⊙ for HR 3076, 740 ± 42 L_⊙ for SAO 250043, and 2500 ± 240 L_⊙ for HD 65662. We used effective temperatures of 4660 ± 122 K for SAO 250043 and 4281 ± 122 for HD 65662. Combining these with our ν_max measurements gave masses of 5.3 ± 0.6 for HR 3076, 6.2 ± 0.7 for SAO 250043, and 5.9 ± 1.1 for HD 65662. Meanwhile, the best-fitting isochrone gives masses of these three red giant stars around 5.1 M_⊙. The isochrone-derived masses show large spread because the isochrones at that region overlap. These values should therefore be treated with caution, pending a full seismic analysis that includes fitting of individual mode frequencies. In particular, the two mass estimates for HD 3076 differ by a few sigma.

4.6. Rotation rate as a function of colour index

In this section, we want to give the relation between stellar rotation rates and their colour index G_BP − G_RP. The peaks of the fundamental frequencies in the cluster stars with rotational modulation directly give the surface rotation rates, while the g-mode period spacings deliver the near-core rotation rates. We can compare them together because the radial differential rotations in main-sequence stars are not strong (e.g. Li et al. 2020a).

We want to measure the surface rotation of stars for two reasons: firstly, to slightly extend the samples of rotation beyond the red edge of the instability strip, and secondly, to compare with the near-core rotation measured through asteroseismology in order to determine the mild radial differential rotation of stars. We use the stars with these measurements to investigate how the rotation rates change as a function of colour index, which represents the effective temperature.

To properly determine the frequency and uncertainty of a surface modulation signal, we adopted a strategy akin to that used for solar-like oscillators. The surface activity, excited and damped over time, performs similarly to the stochastically excited oscillations observed in solar-like oscillators. Consequently, a critically sampled power spectrum of a surface modulation signal is expected to exhibit a Lorentzian profile, with the data following a χ² distribution with two degrees of freedom (Anderson et al. 1990). The likelihood function, which quantifies the probability of observed data D given a parameter θ (see Anderson et al. 1990), is given by the equation

$\begin{matrix} ln p (D | θ) = - \sum (ln M_{i} (θ) + \frac{D_{i}}{M_{i} (θ)}), \end{matrix}$ $\begin{aligned} \ln p(D|\theta ) = -\sum \left(\ln M_i(\theta ) + \frac{D_i}{M_i(\theta )}\right), \end{aligned}$ (9)

where D_i represents the ith data point, and M_i(θ) denotes the Lorentzian profile. The Lorentzian profile’s parameters, θ, include the central frequency (which is the surface rotation frequency we want to measure), amplitude, full width at half maximum (FWHM), and background noise. We used the EMCEE package (Foreman-Mackey et al. 2013) to optimise the likelihood function in Eq. (9), which is an implementation of the affine-invariant ensemble sampler of Goodman & Weare (2010). In the MCMC algorithm, we used 30 parallel chains and 5000 steps and discarded the first 1000 steps for the final posterior distributions. We visually inspected all the posterior distributions to ensure all the chains converged. The determined surface rotation frequencies and their uncertainties are listed in Table A.1, and all the surface modulation signals are illustrated in Fig. A.2. The uncertainties of these frequencies are of the order of 10⁻³ to 10⁻⁴ d⁻¹, roughly akin to the frequency resolution of the four-year light curve (∼0.0007 d⁻¹). In contrast, the uncertainties of stable oscillation signals (where amplitude, frequency, and phase remain constant) are significantly smaller. These are influenced by the S/N and are typically less than one-tenth of the frequency resolution (Montgomery & O’Donoghue 1999). Figure A.1 compares the surface modulation periods in this work and those from Fritzewski et al. (2020), Bouma et al. (2021), and Healy & McCullough (2020), and a general consistency is seen.

In Fig. 12, we present the measured rotation rates as a function of colour index. For the cool stars (with G_BP − G_RP > 0.6 mag), their rotation rates increase with increasing temperature. The rotation rate reaches approximately 1 d⁻¹ at G_BP − G_RP ≈ 0.7 mag, indicating the diminishing effect of magnetic braking. The stars with g-mode pulsations occur in the G_BP − G_RP range of 0.2 mag to 0.6 mag, where rotational modulation is less common. Given the weak radial differential rotation found in hundreds of intermediate-mass stars (Li et al. 2020a), it is reasonable to compare the rotation rates for all cluster stars having measurements for either the near-core region or the surface. The near-core rotation rates measured by g modes are approximately 3 d⁻¹, which is significantly faster than those derived for the cooler stars with magnetic braking. For stars with G_BP − G_RP < 0.2 mag, both the rotation rates measured by surface modulation and g-mode pulsations decrease dramatically, displaying a large scatter of approximately 1.5 d⁻¹, which might be suppressed by the critical rotation rates, as discussed below.

Fig. 12.

Observed rotation rates for cluster members from surface modulations or g-mode pulsations as a function of colour index. The y-axis is the rotation frequency in d⁻¹. The bottom x-axis shows the observed Gaia colour index, while the top x-axis shows both the effective temperature and the intrinsic Gaia colour index from the best-fitting isochrone. The red squares show cluster members with near-core rotation rates measured from their identified g modes, while the dark blue crosses are stars with surface rotation measurements from modulations in their light curves. Rotation uncertainties are typically smaller than the marker sizes. The grey dots are the surface rotation rates for the late-type stars used for gyrochronology in the cluster reported by Fritzewski et al. (2020). The black dotted line represents the Keplerian critical rotation rate f_rot, cri from the best-fitting isochrone model.

In addition, we calculated the critical rotation rates, which we define as the rate at which the centrifugal and gravitational accelerations at the equator on an isobar are equal (see the definition in Paxton et al. 2019). To simplify the calculation, we ignored the ellipsoidal distortion, that is

$\begin{matrix} Ω_{crit} = 2 π f_{rot, crit} = \sqrt{\frac{GM}{R^{3}}}, \end{matrix}$ $\begin{aligned} \Omega _{\rm crit} = 2\pi f_{\rm rot, crit} = \sqrt{\frac{GM}{R^3}}, \end{aligned}$ (10)

where G is the gravitational constant, M is the stellar mass, and R is the radius. We used the theoretical radii and masses obtained from the best-fitting isochrone stellar model (dotted line in Fig. 12).

The critical rotation rates obtained by best-fitting isochrones reveal three distinct regimes in Fig. 12. First, a decreasing trend is observed when G_BP − G_RP exceeds 0.6 mag, declining to approximately 6 d⁻¹, which represents the transition region from late-type to early-type stars; second, a relatively constant value is maintained between 5 and 6 d⁻¹ within the G_BP − G_RP range of 0.2 mag to 0.6 mag, where γ Dor and δ Sct stars occur; third, a rapid decline is observed for G_BP − G_RP < 0.2 mag, with the critical rotation rate dropping to approximately 2 d⁻¹, which coincides with the main-sequence turn-off of the cluster, where a few surface modulation stars and one SPB star appear.

Within the region of G_BP − G_RP between 0.2 mag and 0.6 mag, the rotation rates measured for the g-mode pulsators correspond approximately to 50% of the critical rotation rates. As pointed out by Mombarg et al. (2021) and Henneco et al. (2021), the TAR is still valid for Ω/Ω_{crit, Roche} up to 0.8, where 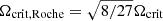$Ω_{crit, Roche} = \sqrt{8 / 27} Ω_{crit}$ $\Omega_{\mathrm{crit, Roche}} = \sqrt{8/27}\Omega_{\mathrm{crit}}$ . Mombarg (2023) found that the initial rotation frequencies of six slowly rotating field γ Dor stars near the terminal age main sequence must have originated from stars rotating below 10% of the initial critical frequency at the zero-age main sequence. Our values of Ω/Ω_crit ≈ 0.5 show that the γ Dor stars in NGC 2516 are born with a five-times-higher rotation rate. At NGC 2516’s turn-off, the rotation rates closely approach the critical rate, which is consistent with the findings of Aerts (2021) that all rotation rates, from zero to critical, are observed between stellar birth and the end of the main sequence. Our findings are also consistent with some spectropolarimetric observations of Be stars (e.g. Regulus, Achernar, and α Arae; see McAlister et al. 2005; Domiciano de Souza et al. 2003; Meilland et al. 2007).

We also calculated the observed critical rotation rates, which were calculated by the observed stellar radii and masses from the Gaia photometry. The theoretical critical rotation rates derived from isochrone models are approximately 1 d⁻¹ higher than the observed critical rotation rates, revealing a systematic deviation. This deviation is easily understood in terms of a variety of choices for the input physics of the models, notably the occurrence of major differences in internal mixing (Pedersen et al. 2021). Moreover, part of this systematic shift may arise from the neglected gravity darkening or centrifugal distortion of the fast rotation of the cluster stars, making it challenging to precisely define their T_eff, log g, and radius.

In Sect. 3, we determined that the best-fitting isochrones have v/v_crit ≤ 0.4, a finding that is incompatible with the value derived from g-mode pulsators (which is ∼0.5). This discrepancy is likely due to the inaccurate determination of v_crit. In the meantime, Brogaard et al. (2023) reported that for NGC 6866, the best-fitting isochrone indicates a lower rotation rate than the rate measured through asteroseismology. This phenomenon might suggest that the actual impact of rotation on stellar evolution is less significant than what is predicted by current 1-dimensional models.

4.7. No circumstellar disc around the fast-rotating B stars

Fast-rotating stars may experience disc formation events due to outbursts that eject surface material from their equator into a decretion disc. This phenomenon, commonly known as the Be phenomenon, has been observed for the Be star HD 49330 (Huat et al. 2009). Such decretion events can be triggered by the beating of g-mode pulsations (Kurtz et al. 2015). Notably, Neiner et al. (2020) also showed that the beating of the stochastically-excited gravito-inertial waves in HD 49330 is efficient for transporting the angular momentum from the core to the surface, causing the Be phenomenon. If similar Be phenomena are observed in the rapid rotators within our sample, the asteroseismology data might offer further insights into the mechanisms triggering these occurrences.

Outbursts akin to the one detected in the optical CoRoT light curve of HD 49330 can also be detected at mid-infrared wavelengths, such as the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010) photometry bands W1 and W2. This wavelength range notably contains the primary emissions from the decretion disc. Granada et al. (2018) found that around half of the B-type stars in four young clusters have W1 − W2 colours redder than 0.05, while the intrinsic colours of early-type stars are around −0.05. Jian et al. (2024) confirmed this conclusion, identifying 916 early-type stars that have shown outbursts associated with the Be phenomenon over the past 13 years. Given the presence of fast rotators in NGC 2516, it is plausible that some of them might experience Be phenomena, which may potentially be captured in their WISE photometry.

Following the method introduced by Jian et al. (2024), we extracted the WISE epoch photometry for all our sample stars. Figure 13 presents the colour-magnitude diagram with the median and extreme values derived from the WISE photometry for our sample of cluster members. Stars exhibiting the Be phenomena typically display a “redder and brighter” variation in their photometry. Their median (W1 − W2) will then range from 0 to 0.3 mag, and the vertical bar in Fig. 13 can extend up to 1.5 mag (see Fig. 9 in Jian et al. 2024 for comparison). Our analysis revealed that none of the stars within NGC 2516 demonstrated such behaviour. It is important to note that the larger (W1 − W2) observed at W1 > 12 mag corresponds to stars with lower effective temperatures, where their redder colours stem from the presence of molecular lines in the W1 band rather than from the Be phenomenon.

Fig. 13.

WISE colour-magnitude diagram of sample stars, with the median value of (W1 − W2) and W1 plotted as black dots, and their extreme values plotted as horizontal and vertical error bars. The red vertical-dashed line indicates the intrinsic colour (−0.05) of the stars with T_eff > 6000 K.

The reason for the absence of the Be phenomenon in NGC 2516 is still uncertain, but there are potential reasons worth considering. One possibility is the relatively old age of NGC 2516. There are 35 Be stars reported in Jian et al. (2024) that are associated with open clusters, and most of these clusters’ ages fall below 45 million years, which is less than half the age of NGC 2516. Another possible reason might be the rotation rate. The rotation rates we found for the A-type stars of NGC 2516 are at roughly 50% of the critical rate. However, as shown in Fig. 12, the B-type stars (with G_BP − G_RP < 0.2 mag) exhibit much larger v/v_crit due to the decrease in critical rotation rates at the MSTO. The critical rotation rate at the MSTO is hard to determine because of the rapid change in stellar physics. Therefore, it is still unclear if the rotation rates of our B-type stars are sufficient to induce the formation of decretion discs. It is noteworthy that some field SPB stars observed by Kepler display minor outbursts in their light curve despite the absence of discs (Van Beeck et al. 2021), indicating that additional factors beyond rotation may contribute to the occurrence or absence of the Be phenomenon (see earlier comment on Kurtz et al. 2015).

5. Spectroscopic observations

To accomplish the goal of calibrating stellar models through the detailed asteroseismic modelling of the g-mode pulsators in NGC 2516 with methods as in Aerts et al. (2018), relying solely on photometric and Gaia observations is sub-optimal. High-resolution spectroscopic observations, delivering better constraints on T_eff, log g, and metallicity, offer a powerful addition as observables. Accurate measurements of parameters such as T_eff, metallicity, and log g not only narrow down the range of possible models but also help resolve degeneracies in the high-dimensional parameter space. Additionally, measurements of surface element abundances play a crucial role in constraining the internal mixing processes within radiative envelopes, as demonstrated in previous studies (Pedersen et al. 2018, 2021; Mombarg et al. 2020, 2022; Michielsen et al. 2021).

For these reasons, we aimed to collect high-resolution spectra of the most interesting cluster members. Given their high potential for cluster modelling, we focused on the g-mode pulsators exhibiting clear period spacing patterns in this cluster and reported the data assembled so far. We conducted spectroscopic follow-up observations using the Fibre-fed Extended Range Optical Spectrograph (FEROS; Kaufer et al. 1999), which is mounted on the ESO/MPG 2.2-m telescope at La Silla, Chile. FEROS is a high-resolution spectrograph with an approximate resolution (R) of 48 000 and a wavelength coverage from 360 to 920 nm. The data reduction was performed using the publicly available pipeline Collection of Elemental Routines for Échelle Spectra (CERES; Brahm et al. 2017)⁶. All the spectra and the best-fitting results are shown in Appendix B.

We derived the global parameters, including radial velocity, T_eff, log g, projected equatorial rotation velocity (v sin i), microturbulent velocity in the atmosphere (ξ), and metallicity ([M/H]), using the spectrum analysis algorithm ZETA-PAYNE (Straumit et al. 2022). This algorithm is fully automated and machine-learning-based; specifically optimised for intermediate-to-high-mass stars with spectral types O, B, A, and F; and optimally suited to exploit FEROS spectroscopy of g-mode pulsators (Gebruers et al. 2022). The observational details and parameter results are summarised in Table 3. These observations were conducted between 12 and 16 March, 2023, with varying exposure times of 600, 900, and 1800 s, depending on the brightness of the target star. We aimed for a high S/N of 200 to ensure accurate abundance determinations. In cases where achieving S/N = 200 with a single exposure time was not feasible for faint stars, we combined multiple shorter exposures with S/N = 150 to reach the desired S/N = 200. However, it is worth noting that we still did not achieve a high S/N for some stars, such that follow-up measurements are still needed to obtain precise values of the stellar parameters.

Table 3.

Results of spectroscopic observations of g-mode pulsators in NGC 2516 (some stars were observed more than once).

As demonstrated by Gebruers et al. (2022), internal uncertainties occur in the spectrum analysis, in addition to statistical uncertainties, even when the S/N is high. Therefore, we calculated the uncertainties in surface parameters and radial velocity by quadratic summation of the observed and internal uncertainties. Figure 14 contains a comparison between the effective temperatures obtained from the FEROS spectra and those derived using the Gaia General Stellar Parametrizer from Photometry (GSP-Phot). Our analysis reveals that the temperatures derived from the spectra exhibit a smoother relation with the Gaia colour index, whereas the GSP-Phot temperatures display considerable scatter. In some cases, this scatter is as high as approximately 2000 K. Furthermore, we determined the metallicities of these stars and found them to align with solar metallicity within the uncertainties. The radial velocities (RV) of the stars also exhibit consistency, averaging ∼25 ± ∼7 km s⁻¹, which is consistent with González & Lapasset (2000). Notably, multiple observations of the same target stars do not reveal significant RV variations, excluding short-period binarity among the monitored stars.

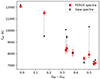Fig. 14.

Effective temperature of g-mode stars as function of their Gaia colour index. We show the effective temperatures obtained by the FEROS spectra and Gaia GSP-Phot connected by a vertical dotted line.

Figure 15 illustrates the comparison between various estimates of the projected equatorial rotation velocity (v sin i) and the true equatorial velocity for several of the cluster members. This provides a direct estimate of the inclination of the rotation axis of the stars in the line of sight. Various remarks are in order. For stars exhibiting surface modulations, we have a direct determination of the surface rotation period. We computed their equatorial velocities by multiplying with the radii as determined in Sect. 4.5. Additionally, we obtained their projected equatorial velocities using the vbroad parameter provided by the Gaia Radial Velocity Spectrometer (RVS; Frémat et al. 2023). For stars displaying period spacing patterns with identified g-mode pulsations, we have the near-core rotation rates and the v sin i values were measured from FEROS spectra. For these stars, we recalculated their radii using the more accurate effective temperatures derived from the FEROS spectra. We then determined their equatorial velocities by multiplying their radii with the near-core rotation rates, assuming these stars have rigid rotation. Figure 15 reveals that most stars with surface modulations have low v sin i values not significantly different from zero, indicative of slow rotation. When the equatorial velocity surpasses approximately 100 km s⁻¹, the stars have v sin i values significantly above zero. We find that these stars cover a range of inclinations, spanning from approximately 30° to 90°. Although it concerns relatively few cluster members, most of the stars with inclination estimates have values i ≳ 45°, resembling a distribution akin to random orientations. It is worth noting that TIC 410452218 is the only star for which the projected equatorial velocity (v sin i) is larger than the equatorial velocity. This discrepancy might be due to poor consideration of rotational distortion or gravity darkening.

Fig. 15.

Comparison between observed equatorial velocity and the observed v sin i by Gaia. For the surface modulation stars (black dot symbols), the v sin i comes from Gaia’s vbroad parameter, and the v is calculated using the rotation frequency and stellar radius. For the g-mode pulsators (red circle symbols), the v sin i are measured by the FEROS spectra, and their v is calculated by the near-core rotation rate and stellar radius. The dotted lines mark the locations with various inclinations.

We stress that the determination of the inclination angles comes with a significant degree of uncertainty. First, it is important to note that in the case of rapidly rotating stars, there are variations in both radius and temperature between the pole and equator. Therefore, the radius determined through the Stefan-Boltzmann law should be considered as an averaged value that is also influenced by the effective temperature and inclination. Secondly, differential rotation may occur while we have assumed rigid rotation for the g-mode pulsators. Observations have indicated that the difference between the near-core and surface rotation rates typically does not exceed 10% for γ Dor stars from the Kepler field (Li et al. 2020a), but these stars are much older than those in NGC 2516. However, recent two-dimensional models suggest a more complex internal rotation profile and show that the core might rotate approximately 50% faster than the envelope (Bouchaud et al. 2020; Mombarg et al. 2023). This level of differentiality in the rotation adds to the complexity and uncertainty in determining the inclination angles in these cases.

6. Conclusions

In this work, we conducted the first asteroseismic study of the young open cluster NGC 2516 from an observational perspective. Our findings reveal a variety of different types of variable stars in this cluster. These stars, along with the cluster itself, can help us calibrate the physical processes inside stars with unprecedented precision and answer long-standing questions about star clusters.

Firstly, we applied the rotating MIST isochrones to fit the CMD of the cluster. We find that isochrones with v/v_crit ≤ 0.4 closely matched the observational data and yielded consistent results for age and extinction. However, those with v/v_crit ≥ 0.5 did not provide a good fit to the data. By combining the fitting results obtained from isochrones with Ω/Ω_crit ≤ 0.4, we report an age of 102 ± 15 Myr and an extinction value at 550 nm of A₀ = 0.53 ± 0.04 mag. Our newly determined age shows that NGC 2516 is younger than the Pleiades, while we provide a slightly larger extinction and reddening than the previous study.

We used the TESS data in Cycle 1 and Cycle 3 to conduct photometry and obtained the light curves of the member stars. The almost continuous TESS light curves provided excellent data for asteroseismology. We find 24 g-mode pulsators, 35 δ Sct pulsators, 147 stars with surface modulations, five eclipsing binaries, and three post-main-sequence stars.

Among the g-mode pulsators, there are 11 with clear period spacing patterns, which allows us to determine their near-core rotation rates and asymptotic spacings. We identified most of these stars as γ Dor stars based on their asymptotic spacings (around ∼4900 s) and effective temperatures (between 7000 K and 10 000 K). Their asymptotic spacings are larger than those γ Dor stars in the Kepler field because they are young. Additionally, there are two stars with even higher effective temperatures (> 10 000 K). Considering the position of these stars at the top of the main sequence, we classified them as SPB stars. Our findings reveal that the g-mode stars in NGC 2516 exhibit rapid near-core rotation rates, some reaching values up to 3 d⁻¹. This is significantly faster than the average value for those observed for single pulsators in both the Kepler and TESS fields. The combination of a large asymptotic period spacing and high near-core rotation rates aligns with the nature that these stars are very young.

For the δ Sct stars, we observe that their amplitude spectra are well ordered when sorted by colour. In cooler stars, we find a series of frequencies at approximately 21.07 d⁻¹, while the hotter p-mode pulsators display another series of frequency peaks around 33 d⁻¹. These frequencies are identified as the fundamental frequency and second overtone, respectively. Notably, the mean pulsation frequency increases as the temperature rises, indicating a frequency-temperature relation in δ Sct stars. We cannot identify reliable frequency separations among these δ Sct stars, except for one cluster member.

For the three post-main-sequence stars, we observe a low-frequency power excess in their power density spectra in agreement with theoretical predictions for granulation resulting from magnetic activity. Based on the closest model from the best-fitting isochrone, these evolved stars have masses larger than 5 M_⊙, which is greater than the most massive star from the Kepler sample (Yu et al. 2018).

The surface modulation signals observed in 147 stars offer direct measurements of surface rotation rates. Combined with near-core rotation rates determined from g-mode pulsations, we unveil a rotation-temperature relationship among the main-sequence stars in NGC 2516. Our findings show that as temperature increases, the typical rotation rate follows a rising trend until it reaches a plateau (whose red edge is at G_BP − G_RP = 0.6 mag or T_eff = 7150 K), where it stabilises at approximately 50% of the critical rotation rates. Furthermore, we calculate the critical rotation rates using both the best-fitting stellar models and observations. We observe a rapid drop in the critical rotation rate at the main-sequence turn-off, in agreement with the observed stellar rotation rates. It is noteworthy that the rotation rate in B-type stars may approach ∼90% of the critical rotation rate. However, we did not find any evidence of circumstellar discs in these cluster stars.

Finally, we carried out high-resolution spectroscopic observations for the g-mode pulsators displaying period spacing patterns. Our spectra, with high resolution and high S/N, enabled precise measurements of the global stellar parameters and radial velocity. Our analysis confirms that the cluster has solar metallicity and exhibits a radial velocity of ∼25 km s⁻¹. These accurate spectroscopic observations will provide invaluable information for our planned detailed ensemble asteroseismic modelling of the g-mode pulsators under the constraint of equal initial chemical composition at birth, reducing computational complexity and resolving parameter degeneracies.

The NGC 2516 cluster revealed itself as optimal for combined detailed asteroseismic modelling of its g-mode pulsators. So far, such asteroseismic cluster modelling based on g-mode pulsators has not yet been done. The only young open cluster that has been scrutinised by g-mode asteroseismology so far is UBC1, which has only one g-mode pulsator with identified modes, and this cluster member has a moderate rotation (see the study by Fritzewski et al. 2024). Adopting the same methodology as that developed by these authors, we encountered the limitation of the currently available asteroseismic model grids for γ Dor stars, in the sense that none of the models predict values of Π₀ comparable to the observed ones. We ascribe this mismatch to the fast rotation of the member stars in NGC 2516, along with the use of non-rotating equilibrium models in the existing γ Dor grids. Proper asteroseismic modelling of the identified modes of the γ Dor members of NGC 2516 likely requires stellar evolution models with rotational deformation to achieve meaningful comparisons between measured and predicted asteroseismic observables. This will be addressed in a follow-up study. Since the addition of just one g-mode pulsator already implied a drastic reduction in the uncertainty of the cluster age for UBC1, our future modelling of the 11 g-mode pulsators and of the δ Sct overtone pulsators in NGC 2516 promises to be extremely rewarding and will increase our knowledge of the interior physics of intermediate-mass stars and of young open clusters, including proper age-dating.

¹

https://waps.cfa.harvard.edu/MIST/index.html

²

https://www.cosmos.esa.int/web/gaia/edr3-extinction-law

³

https://github.com/IvS-Asteroseismology/tessutils

⁴

https://gea.esac.esa.int/archive/documentation/GDR2/Data_analysis/chap_cu8par/sec_cu8par_process/ssec_cu8par_process_flame.html

⁵

The bolometric correction by Andrae et al. (2018) is valid within 4000 and 8000 K. For stars between 8000 and 12 000 K, we use the relation given by Stassun et al. (2019).

⁶

https://github.com/rabrahm/ceres

Acknowledgments

The authors are grateful to Professor Aaron Dotter for his contribution to the construction of the rotating isochrones used in this work. G.L. also thanks Doctor Sarah Gebruers for her help in the exploitation of the FEROS spectroscopy. The research leading to these results has received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE). G.L. acknowledges the Research Foundation Flanders (FWO) Grant for a long stay abroad (grant V422323N) and the Dick Hunstead Fund for Astrophysics for his 2-month stay at the University of Sydney. G.L. also acknowledges the travel support from the National Natural Science Foundation of China (NSFC) through grant 12273002. J.S.G.M. acknowledges funding the French Agence Nationale de la Recherche (ANR), under grant MASSIF (ANR-21-CE31-0018-02). C.A. acknowledges financial support from the FWO under grant K802922N (Sabbatical leave) and from the European Research Council (ERC) under the Horizon Europe programme (Synergy Grant agreement N°101071505: 4D-STAR). While partially funded by the European Union, views and opinions expressed are however those of the authors only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. This research has made use of NASA’s Astrophysics Data System Bibliographic Services and of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEOWISE are funded by the National Aeronautics and Space Administration. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. This paper includes data collected by the TESS mission, which are publicly available from the Mikulski Archive for Space Telescopes (MAST). This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013) and Lightkurve, a Python package for Kepler and TESS data analysis (Lightkurve Collaboration 2018). This research also made use of the following Python packages: astroquery (Ginsburg et al. 2019), EMCEE (Foreman-Mackey et al. 2013), corner (Foreman-Mackey 2016), MatPlotLib (Barrett et al. 2005), NumPy (Harris et al. 2020), and Pandas (The pandas development team 2020).

References

Abt, H. A. 1979, ApJ, 230, 485 [Google Scholar]
Abt, H. A., & Levy, S. G. 1972, ApJ, 172, 355 [NASA ADS] [CrossRef] [Google Scholar]
Abt, H. A., Clements, A. E., Doose, L. R., & Harris, D. H. 1969, AJ, 74, 1153 [NASA ADS] [CrossRef] [Google Scholar]
Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
Aerts, C., & De Cat, P. 2003, Space Sci. Rev., 105, 453 [CrossRef] [Google Scholar]
Aerts, C., & Mathis, S. 2023, A&A, 677, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Aerts, C., Thoul, A., Daszyńska, J., et al. 2003, Science, 300, 1926 [Google Scholar]
Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Heidelberg: Springer-Verlag) [Google Scholar]
Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [Google Scholar]
Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
Aerts, C., Molenberghs, G., & De Ridder, J. 2023, A&A, 672, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Anderson, E. R., Duvall, T. L., & Jefferies, S. M. 1990, ApJ, 364, 699 [NASA ADS] [CrossRef] [Google Scholar]
Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Antoci, V., Cunha, M., Houdek, G., et al. 2014, ApJ, 796, 118 [Google Scholar]
Antonello, E., & Mantegazza, L. 1986, A&A, 164, 40 [NASA ADS] [Google Scholar]
Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bagnulo, S., Landstreet, J. D., Lo Curto, G., Szeifert, T., & Wade, G. A. 2003, A&A, 403, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bailey, J. I., Mateo, M., White, R. J., Shectman, S. A., & Crane, J. D. 2018, MNRAS, 475, 1609 [NASA ADS] [CrossRef] [Google Scholar]
Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]
Balona, L. A., Krisciunas, K., & Cousins, A. W. J. 1994, MNRAS, 270, 905 [NASA ADS] [CrossRef] [Google Scholar]
Barceló Forteza, S., Roca Cortés, T., & García, R. A. 2018, A&A, 614, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Barceló Forteza, S., Moya, A., Barrado, D., et al. 2020, A&A, 638, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]
Barnes, S. A. 2007, ApJ, 669, 1167 [Google Scholar]
Barrett, P., Hunter, J., Miller, J. T., Hsu, J. C., & Greenfield, P. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 91 [NASA ADS] [Google Scholar]
Bastian, N., & de Mink, S. E. 2009, MNRAS, 398, L11 [NASA ADS] [CrossRef] [Google Scholar]
Bastian, N., Niederhofer, F., Kozhurina-Platais, V., et al. 2016, MNRAS, 460, L20 [NASA ADS] [CrossRef] [Google Scholar]
Bastian, N., Kamann, S., Cabrera-Ziri, I., et al. 2018, MNRAS, 480, 3739 [NASA ADS] [CrossRef] [Google Scholar]
Basu, S., & Chaplin, W. J. 2017, Asteroseismic Data Analysis: Foundations and Techniques (Princeton: Princeton University Press) [Google Scholar]
Basu, S., Grundahl, F., Stello, D., et al. 2011, ApJ, 729, L10 [Google Scholar]
Bedding, T. R. 2014, in Asteroseismology, eds. P. L. Pallé, & C. Esteban, 60 [Google Scholar]
Bedding, T. R., Murphy, S. J., Colman, I. L., & Kurtz, D. W. 2015, Eur. Phys. J. Web Conf., 101, 01005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bedding, T. R., Murphy, S. J., Hey, D. R., et al. 2020, Nature, 581, 147 [NASA ADS] [CrossRef] [Google Scholar]
Bedding, T. R., Murphy, S. J., Crawford, C., et al. 2023, ApJ, 946, L10 [NASA ADS] [CrossRef] [Google Scholar]
Bertelli, G., Nasi, E., Girardi, L., et al. 2003, AJ, 125, 770 [NASA ADS] [CrossRef] [Google Scholar]
Bouabid, M. P., Dupret, M. A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [Google Scholar]
Bouchaud, K., Domiciano de Souza, A., Rieutord, M., Reese, D. R., & Kervella, P. 2020, A&A, 633, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Bouma, L. G., Curtis, J. L., Hartman, J. D., Winn, J. N., & Bakos, G. Á. 2021, AJ, 162, 197 [NASA ADS] [CrossRef] [Google Scholar]
Bowman, D. M., & Kurtz, D. W. 2018, MNRAS, 476, 3169 [NASA ADS] [CrossRef] [Google Scholar]
Brahm, R., Jordán, A., & Espinoza, N. 2017, PASP, 129, 034002 [Google Scholar]
Brandt, T. D., & Huang, C. X. 2015, ApJ, 807, 25 [NASA ADS] [CrossRef] [Google Scholar]
Brasseur, C. E., Phillip, C., Fleming, S. W., Mullally, S. E., & White, R. L. 2019, Astrophysics Source Code Library [record ascl:1905.007] [Google Scholar]
Brogaard, K., Arentoft, T., Miglio, A., et al. 2023, A&A, 679, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]
Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
Christophe, S., Ballot, J., Ouazzani, R. M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Corbard, T., Blanc-Féraud, L., Berthomieu, G., & Provost, J. 1999, A&A, 344, 696 [NASA ADS] [Google Scholar]
Correnti, M., Goudfrooij, P., Puzia, T. H., & de Mink, S. E. 2015, MNRAS, 450, 3054 [NASA ADS] [CrossRef] [Google Scholar]
Cox, A. N. 1955, ApJ, 121, 628 [CrossRef] [Google Scholar]
Danielski, C., Babusiaux, C., Ruiz-Dern, L., Sartoretti, P., & Arenou, F. 2018, A&A, 614, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
D’Antona, F., Di Criscienzo, M., Decressin, T., et al. 2015, MNRAS, 453, 2637 [NASA ADS] [Google Scholar]
De Cat, P., & Aerts, C. 2002, A&A, 393, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Deheuvels, S., Ballot, J., Eggenberger, P., et al. 2020, A&A, 641, A117 [EDP Sciences] [Google Scholar]
Deubner, F. L., Ulrich, R. K., & Rhodes, E. J. 1979, A&A, 72, 177 [NASA ADS] [Google Scholar]
Di Mauro, M. P., Ventura, R., Cardini, D., et al. 2016, ApJ, 817, 65 [NASA ADS] [CrossRef] [Google Scholar]
Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [CrossRef] [EDP Sciences] [Google Scholar]
Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Eggen, O. J. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, 20, 10 [NASA ADS] [Google Scholar]
Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]
Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Feinstein, A., Marraco, H. G., & Mirabel, I. 1973, A&AS, 9, 233 [NASA ADS] [Google Scholar]
Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]
Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
Frémat, Y., Royer, F., Marchal, O., et al. 2023, A&A, 674, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fritzewski, D. J., Barnes, S. A., James, D. J., & Strassmeier, K. G. 2020, A&A, 641, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Fritzewski, D. J., Van Reeth, T., Aerts, C., et al. 2024, A&A, 681, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gaia Collaboration (De Ridder, J., et al.) 2023a, A&A, 674, A36 [CrossRef] [EDP Sciences] [Google Scholar]
Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Garcia, S., Van Reeth, T., De Ridder, J., et al. 2022a, A&A, 662, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Garcia, S., Van Reeth, T., De Ridder, J., & Aerts, C. 2022b, A&A, 668, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gebruers, S., Tkachenko, A., Bowman, D. M., et al. 2022, A&A, 665, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gieseking, F., & Karimie, M. T. 1982, A&AS, 49, 497 [NASA ADS] [Google Scholar]
Ginsburg, A., Sipőcz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [Google Scholar]
Girardi, L., Goudfrooij, P., Kalirai, J. S., et al. 2013, MNRAS, 431, 3501 [NASA ADS] [CrossRef] [Google Scholar]
Glatt, K., Grebel, E. K., Gallagher, J. S., et al. 2009, AJ, 138, 1403 [NASA ADS] [CrossRef] [Google Scholar]
González, J. F., & Lapasset, E. 2000, AJ, 119, 2296 [CrossRef] [Google Scholar]
Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
Gossage, S., Conroy, C., Dotter, A., et al. 2019, ApJ, 887, 199 [NASA ADS] [CrossRef] [Google Scholar]
Goupil, M. J., Dupret, M. A., Samadi, R., et al. 2005, JApA, 26, 249 [NASA ADS] [Google Scholar]
Granada, A., Jones, C. E., Sigut, T. A. A., et al. 2018, AJ, 155, 50 [NASA ADS] [CrossRef] [Google Scholar]
Grassitelli, L., Fossati, L., Langer, N., et al. 2015, A&A, 584, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]
Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [Google Scholar]
Handler, G. 2009, in Stellar Pulsation: Challenges for Theory and Observation, eds. J. A. Guzik, & P. A. Bradley, AIP Conf. Ser., 1170, 403 [NASA ADS] [CrossRef] [Google Scholar]
Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]
Hasanzadeh, A., Safari, H., & Ghasemi, H. 2021, MNRAS, 505, 1476 [NASA ADS] [CrossRef] [Google Scholar]
Healy, B. F., & McCullough, P. R. 2020, ApJ, 903, 99 [NASA ADS] [CrossRef] [Google Scholar]
Hekker, S., Basu, S., Stello, D., et al. 2011, A&A, 530, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Henneco, J., Van Reeth, T., Prat, V., et al. 2021, A&A, 648, A97 [EDP Sciences] [Google Scholar]
Hon, M., Huber, D., Kuszlewicz, J. S., et al. 2021, ApJ, 919, 131 [NASA ADS] [CrossRef] [Google Scholar]
Houdek, G. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 454 [NASA ADS] [Google Scholar]
Huat, A. L., Hubert, A. M., Baudin, F., et al. 2009, A&A, 506, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Irwin, J., Aigrain, S., Bouvier, J., et al. 2009, MNRAS, 392, 1456 [Google Scholar]
Jackiewicz, J. 2021, Front. Astron. Space Sci., 7, 102 [NASA ADS] [CrossRef] [Google Scholar]
Jian, M., Matsunaga, N., Jiang, B., Yuan, H., & Zhang, R. 2024, A&A, 682, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Johnston, C., Aerts, C., Pedersen, M. G., & Bastian, N. 2019, A&A, 632, A74 [EDP Sciences] [Google Scholar]
Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]
Kaye, A. B., Handler, G., Krisciunas, K., Poretti, E., & Zerbi, F. M. 1999, PASP, 111, 840 [Google Scholar]
Kippenhahn, R., & Thomas, H. C. 1970, in IAU Colloq. 4: Stellar Rotation, ed. A. Slettebak, 20 [CrossRef] [Google Scholar]
Koester, D., & Reimers, D. 1996, A&A, 313, 810 [NASA ADS] [Google Scholar]
Kraft, R. P. 1967, ApJ, 150, 551 [Google Scholar]
Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]
Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., & Bowman, D. M. 2015, MNRAS, 450, 3015 [NASA ADS] [CrossRef] [Google Scholar]
Kurtz, D. W., Jayaraman, R., Sowicka, P., et al. 2023, MNRAS, 521, 4765 [NASA ADS] [CrossRef] [Google Scholar]
Ledoux, P. 1951, ApJ, 114, 373 [Google Scholar]
Lee, U., & Saio, H. 1987, MNRAS, 224, 513 [Google Scholar]
Lee, U., & Saio, H. 1997, ApJ, 491, 839 [Google Scholar]
Li, C., de Grijs, R., Deng, L., et al. 2016, Nature, 529, 502 [NASA ADS] [CrossRef] [Google Scholar]
Li, C., Sun, W., de Grijs, R., et al. 2019a, ApJ, 876, 65 [Google Scholar]
Li, G., Bedding, T. R., Murphy, S. J., et al. 2019b, MNRAS, 482, 1757 [Google Scholar]
Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019c, MNRAS, 487, 782 [Google Scholar]
Li, G., Van Reeth, T., Bedding, T. R., et al. 2020a, MNRAS, 491, 3586 [Google Scholar]
Li, G., Guo, Z., Fuller, J., et al. 2020b, MNRAS, 497, 4363 [Google Scholar]
Lightkurve Collaboration (Cardoso, J. V. D. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]
Lim, B., Rauw, G., Nazé, Y., et al. 2019, Nat. Astron., 3, 76 [Google Scholar]
Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]
Lund, M. N., Basu, S., Silva Aguirre, V., et al. 2016, MNRAS, 463, 2600 [NASA ADS] [CrossRef] [Google Scholar]
Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Heidelberg: Springer-Verlag) [Google Scholar]
Maitzen, H. M., & Hensberge, H. 1981, A&A, 96, 151 [NASA ADS] [Google Scholar]
Martins, F., & Palacios, A. 2013, A&A, 560, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mathis, S. 2009, A&A, 506, 811 [CrossRef] [EDP Sciences] [Google Scholar]
Mathis, S. 2013, in Lecture Notes in Physics, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer-Verlag), 865, 23 [CrossRef] [Google Scholar]
McAlister, H. A., ten Brummelaar, T. A., Gies, D. R., et al. 2005, ApJ, 628, 439 [NASA ADS] [CrossRef] [Google Scholar]
McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]
Meilland, A., Stee, P., Vannier, M., et al. 2007, A&A, 464, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meingast, S., & Alves, J. 2019, A&A, 621, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Meingast, S., Alves, J., & Rottensteiner, A. 2021, A&A, 645, A84 [EDP Sciences] [Google Scholar]
Meynet, G., Mermilliod, J. C., & Maeder, A. 1993, A&AS, 98, 477 [Google Scholar]
Michielsen, M., Aerts, C., & Bowman, D. M. 2021, A&A, 650, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [Google Scholar]
Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
Mombarg, J. S. G. 2023, A&A, 677, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., et al. 2019, MNRAS, 485, 3248 [NASA ADS] [CrossRef] [Google Scholar]
Mombarg, J. S. G., Dotter, A., Van Reeth, T., et al. 2020, ApJ, 895, 51 [Google Scholar]
Mombarg, J. S. G., Van Reeth, T., & Aerts, C. 2021, A&A, 650, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Mombarg, J. S. G., Dotter, A., Rieutord, M., et al. 2022, ApJ, 925, 154 [NASA ADS] [CrossRef] [Google Scholar]
Mombarg, J. S. G., Rieutord, M., & Espinosa Lara, F. 2023, A&A, 677, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Montgomery, M. H., & O’Donoghue, D. 1999, Delta Scuti Star Newsletter, 13, 28 [NASA ADS] [Google Scholar]
Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [Google Scholar]
Murphy, S. J., Hey, D., Van Reeth, T., & Bedding, T. R. 2019, MNRAS, 485, 2380 [NASA ADS] [CrossRef] [Google Scholar]
Murphy, S. J., Saio, H., Takada-Hidai, M., et al. 2020, MNRAS, 498, 4272 [NASA ADS] [CrossRef] [Google Scholar]
Murphy, S. J., Joyce, M., Bedding, T. R., White, T. R., & Kama, M. 2021, MNRAS, 502, 1633 [NASA ADS] [CrossRef] [Google Scholar]
Murphy, S. J., Bedding, T. R., White, T. R., et al. 2022, MNRAS, 511, 5718 [NASA ADS] [CrossRef] [Google Scholar]
Neiner, C., Lee, U., Mathis, S., et al. 2020, A&A, 644, A9 [EDP Sciences] [Google Scholar]
Netzel, H., Pietrukowicz, P., Soszyński, I., & Wrona, M. 2022, MNRAS, 510, 1748 [Google Scholar]
Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [Google Scholar]
Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ouazzani, R. M., Lignières, F., Dupret, M. A., et al. 2020, A&A, 640, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Palakkatharappil, D. B., & Creevey, O. L. 2023, A&A, 674, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pamos Ortega, D., Mirouh, G. M., García Hernández, A., Suárez Yanes, J. C., & Barceló Forteza, S. 2023, A&A, 675, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pamyatnykh, A. A. 1999, Acta Astron., 49, 119 [Google Scholar]
The pandas development team 2020, https://doi.org/10.5281/zenodo.3509134 [Google Scholar]
Pápics, P. I., Moravveji, E., Aerts, C., et al. 2014, A&A, 570, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., 5, 715 [NASA ADS] [CrossRef] [Google Scholar]
Pérez Hernández, F., Claret, A., Hernández, M. M., & Michel, E. 1999, A&A, 346, 586 [NASA ADS] [Google Scholar]
Reed, M. D., Kilkenny, D., Kawaler, S. D., et al. 2000, Balt. Astron., 9, 183 [Google Scholar]
Reimers, D., & Koester, D. 1982, A&A, 116, 341 [NASA ADS] [Google Scholar]
Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]
Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Ripepi, V., Balona, L., Catanzaro, G., et al. 2015, MNRAS, 454, 2606 [Google Scholar]
Royer, F., Zorec, J., & Gómez, A. E. 2007, A&A, 463, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Rui, N. Z., Ong, J. M. J., & Mathis, S. 2024, MNRAS, 527, 6346 [Google Scholar]
Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]
Saio, H., Bedding, T. R., Kurtz, D. W., et al. 2018a, MNRAS, 477, 2183 [Google Scholar]
Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., & Lee, U. 2018b, MNRAS, 474, 2774 [Google Scholar]
Saio, H., Takata, M., Lee, U., Li, G., & Van Reeth, T. 2021, MNRAS, 502, 5856 [Google Scholar]
Sandquist, E. L., Stello, D., Arentoft, T., et al. 2020, AJ, 159, 96 [NASA ADS] [CrossRef] [Google Scholar]
Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]
Shajn, G., & Struve, O. 1929, MNRAS, 89, 222 [NASA ADS] [Google Scholar]
Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]
Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]
Sreenivas, K. R., Bedding, T. R., Li, Y., et al. 2024, MNRAS, 530, 3477 [NASA ADS] [CrossRef] [Google Scholar]
Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]
Stellingwerf, R. F. 1979, ApJ, 227, 935 [NASA ADS] [CrossRef] [Google Scholar]
Stello, D., Basu, S., Bruntt, H., et al. 2010, ApJ, 713, L182 [NASA ADS] [CrossRef] [Google Scholar]
Sterken, C. 2005, in The Light-time Effect in Astrophysics: Causes and Cures of the O-C Diagram, ed. C. Sterken, ASP Conf. Ser., 335, 3 [NASA ADS] [Google Scholar]
Sterken, C., & Jerzykiewicz, M. 1993, Space Sci. Rev., 62, 95 [NASA ADS] [CrossRef] [Google Scholar]
Straumit, I., Tkachenko, A., Gebruers, S., et al. 2022, AJ, 163, 236 [NASA ADS] [CrossRef] [Google Scholar]
Sung, H., Bessell, M. S., Lee, B.-W., & Lee, S.-G. 2002, AJ, 123, 290 [NASA ADS] [CrossRef] [Google Scholar]
Szewczuk, W., & Daszyńska-Daszkiewicz, J. 2018, MNRAS, 478, 2243 [Google Scholar]
Tarricq, Y., Soubiran, C., Casamiquela, L., et al. 2021, A&A, 647, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Terndrup, D. M., Pinsonneault, M., Jeffries, R. D., et al. 2002, ApJ, 576, 950 [NASA ADS] [CrossRef] [Google Scholar]
Thompson, I. B., Brown, D. N., & Landstreet, J. D. 1987, ApJS, 64, 219 [NASA ADS] [CrossRef] [Google Scholar]
Tokuno, T., & Takata, M. 2022, MNRAS, 514, 4140 [NASA ADS] [CrossRef] [Google Scholar]
Townsend, R. H. D. 2003, MNRAS, 340, 1020 [Google Scholar]
Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [Google Scholar]
Townsend, R. H. D., Goldstein, J., & Zweibel, E. G. 2018, MNRAS, 475, 879 [Google Scholar]
Triana, S. A., Moravveji, E., Pápics, P. I., et al. 2015, ApJ, 810, 16 [Google Scholar]
Triana, S. A., Corsaro, E., De Ridder, J., et al. 2017, A&A, 602, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]
Van Beeck, J., Bowman, D. M., Pedersen, M. G., et al. 2021, A&A, 655, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015a, ApJS, 218, 27 [Google Scholar]
Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015b, A&A, 574, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]
Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]
Wang, C., Langer, N., Schootemeijer, A., et al. 2022, Nat. Astron., 6, 480 [NASA ADS] [CrossRef] [Google Scholar]
Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1991, ApJ, 378, 326 [NASA ADS] [CrossRef] [Google Scholar]
Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
Xiong, D. R., Deng, L., Zhang, C., & Wang, K. 2016, MNRAS, 457, 3163 [Google Scholar]
Yu, J., Huber, D., Bedding, T. R., et al. 2018, ApJS, 236, 42 [NASA ADS] [CrossRef] [Google Scholar]
Zahn, J. P., Ranc, C., & Morel, P. 2010, A&A, 517, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Zerbi, F. M., Mantegazza, L., Campana, S., & Antonello, E. 1998, PASP, 110, 804 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Surface modulations

Figure A.1 compares the surface modulation periods by this work and by the previous studies. We collected the results by Fritzewski et al. (2020), Bouma et al. (2021), and Healy & McCullough (2020). Our results show high consistency. Table A.1 lists the periods of all the surface modulation stars. Figure A.2 depicts all the surface modulation amplitude spectra.

Fig. A.1.

Comparison of surface-modulation periods in this work and from the previous literature. We collected the results of Fritzewski et al. (2020), Bouma et al. (2021), and Healy & McCullough (2020). The grey solid, dashed, and dotted lines show the 1:1, 2:1, and 1:2 relations.

Fig. A.2.

Surface modulation signals in stars of NGC 2516 sorted by Gaia colour index. Stars with smaller colour indices are displayed at the top. Frequency (in d⁻¹) is plotted along the x-axis. The y-axis, representing amplitude, is omitted for brevity. Each panel displays the amplitude spectrum in grey, with the rotation frequency indicated by a vertical red line. The TIC number and corresponding Gaia colour index are noted in each panel.

Table A.1.

Surface modulation periods for cluster member stars in this study.

Appendix B: All the g-mode pulsators in NGC 2516

For each of the 11 g-mode pulsators, we show the amplitude spectrum with identified period spacing pattern, the best-fitting TAR results and the posterior distributions of f_rot and Π₀. We also show all the high-resolution spectra for these stars.

All Tables

Table 1.

Five eclipsing binaries in NGC 2516.

In the text

Table 2.

TAR fitting results of 11 g-mode pulsators in NGC 2516.

In the text

Table 3.

Results of spectroscopic observations of g-mode pulsators in NGC 2516 (some stars were observed more than once).

In the text

Table A.1.

Surface modulation periods for cluster member stars in this study.

In the text

All Figures

Fig. 1.

Observed Gaia DR3 CMD of NGC 2516. Left panel: fits for isochrones with varying rotation rates. Isochrones with v/v_crit ≤ 0.4 effectively reproduce the observed data. Right panel: solid black isochrone represents the best-fitting result with v/v_crit = 0.3. The grey background tracks collectively represent the uncertainty, which is determined using a set of 500 isochrones randomly selected from the Monte Carlo approach explained in the main text. The dotted line marks the boundary of the binary sequence.

In the text

	Fig. 2. Relation between log of likelihood function (Eq. (2)) of the best-fitting isochrone and rotation rates v/v_crit. Isochrones with v/v_crit > 0.5 show significantly small likelihood values, implying worse fitting compared to the observational data.
In the text

	Fig. 3. Posterior distributions of isochrone fitting.
In the text

Fig. 4.

Zoomed-in view of CMD of NGC 2516 showing how binarity and rotation lead a star deviating from the main sequence. The ranges of the x- and y-axes are 0.2 mag < G_BP − G_RP < 0.6 mag and 2.0 mag < M_G < 3.5 mag. The stars are colour-coded by RUWE (showing binarity) and line broadening (representing rotation rates), respectively. The small black dots are stars without broadening values in the Gaia DR3 database.

In the text

	Fig. 5. Locations of variable stars on CMD of NGC 2516.
In the text

	Fig. 6. Histogram of numbers of p-mode pulsator, g-mode pulsator, surface modulations, and the total stars in our sample. The bin size of the colour index G_BP − G_RP is 0.05. Pulsating stars (p- and g-mode pulsators) have high fractions around G_BP − G_RP of 0.5 mag, while surface modulation stars appear with small or large G_BP − G_RP.
In the text

	Fig. 7. Eleven g-mode pulsators with clear period spacing patterns, sorted in descending order by their Gaia colour index G_BP − G_RP from top to bottom. The red vertical lines mark their near-core rotation periods derived from the modes by adopting the TAR.
In the text

Fig. 8.

Location of γ Dor stars on CMD with best-fitting isochrone. The large circles show the γ Dor stars with clear period spacings, colour-coded by their buoyancy travel time (left panel) or near-core rotation rates (right panel). The black dots are the other cluster members, and the grey solid line is the best-fitting isochrone. We also indicate the masses of the models on the right edges of each panel. In the left panel, we show the TIC numbers of the stars.

In the text

	Fig. 9. Amplitude spectra of δ Sct stars in NGC 2516, sorted by colour index. The top panel has the star with the smallest colour index and hence the highest effective temperature.
In the text

	Fig. 10. Échelle diagram of δ Sct star TIC 308307266. A frequency separation is seen with Δν ≈ 6.21 d⁻¹.
In the text

	Fig. 11. Power density spectra of red giant HR 3076.
In the text

Fig. 12.

Observed rotation rates for cluster members from surface modulations or g-mode pulsations as a function of colour index. The y-axis is the rotation frequency in d⁻¹. The bottom x-axis shows the observed Gaia colour index, while the top x-axis shows both the effective temperature and the intrinsic Gaia colour index from the best-fitting isochrone. The red squares show cluster members with near-core rotation rates measured from their identified g modes, while the dark blue crosses are stars with surface rotation measurements from modulations in their light curves. Rotation uncertainties are typically smaller than the marker sizes. The grey dots are the surface rotation rates for the late-type stars used for gyrochronology in the cluster reported by Fritzewski et al. (2020). The black dotted line represents the Keplerian critical rotation rate f_rot, cri from the best-fitting isochrone model.

In the text

	Fig. 13. WISE colour-magnitude diagram of sample stars, with the median value of (W1 − W2) and W1 plotted as black dots, and their extreme values plotted as horizontal and vertical error bars. The red vertical-dashed line indicates the intrinsic colour (−0.05) of the stars with T_eff > 6000 K.
In the text

	Fig. 14. Effective temperature of g-mode stars as function of their Gaia colour index. We show the effective temperatures obtained by the FEROS spectra and Gaia GSP-Phot connected by a vertical dotted line.
In the text

Fig. 15.

Comparison between observed equatorial velocity and the observed v sin i by Gaia. For the surface modulation stars (black dot symbols), the v sin i comes from Gaia’s vbroad parameter, and the v is calculated using the rotation frequency and stellar radius. For the g-mode pulsators (red circle symbols), the v sin i are measured by the FEROS spectra, and their v is calculated by the near-core rotation rate and stellar radius. The dotted lines mark the locations with various inclinations.

In the text

	Fig. A.1. Comparison of surface-modulation periods in this work and from the previous literature. We collected the results of Fritzewski et al. (2020), Bouma et al. (2021), and Healy & McCullough (2020). The grey solid, dashed, and dotted lines show the 1:1, 2:1, and 1:2 relations.
In the text

Fig. A.2.

Surface modulation signals in stars of NGC 2516 sorted by Gaia colour index. Stars with smaller colour indices are displayed at the top. Frequency (in d⁻¹) is plotted along the x-axis. The y-axis, representing amplitude, is omitted for brevity. Each panel displays the amplitude spectrum in grey, with the rotation frequency indicated by a vertical red line. The TIC number and corresponding Gaia colour index are noted in each panel.

In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.

[1] Abt, H. A. 1979, ApJ, 230, 485 [Google Scholar]

[2] Abt, H. A., & Levy, S. G. 1972, ApJ, 172, 355 [NASA ADS] [CrossRef] [Google Scholar]

[3] Abt, H. A., Clements, A. E., Doose, L. R., & Harris, D. H. 1969, AJ, 74, 1153 [NASA ADS] [CrossRef] [Google Scholar]

[4] Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]

[5] Aerts, C., & De Cat, P. 2003, Space Sci. Rev., 105, 453 [CrossRef] [Google Scholar]

[6] Aerts, C., & Mathis, S. 2023, A&A, 677, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[7] Aerts, C., Thoul, A., Daszyńska, J., et al. 2003, Science, 300, 1926 [Google Scholar]

[8] Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Heidelberg: Springer-Verlag) [Google Scholar]

[9] Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [Google Scholar]

[10] Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]

[11] Aerts, C., Molenberghs, G., & De Ridder, J. 2023, A&A, 672, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[12] Anderson, E. R., Duvall, T. L., & Jefferies, S. M. 1990, ApJ, 364, 699 [NASA ADS] [CrossRef] [Google Scholar]

[13] Andrae, R., Fouesneau, M., Creevey, O., et al. 2018, A&A, 616, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[14] Antoci, V., Cunha, M., Houdek, G., et al. 2014, ApJ, 796, 118 [Google Scholar]

[15] Antonello, E., & Mantegazza, L. 1986, A&A, 164, 40 [NASA ADS] [Google Scholar]

[16] Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]

[17] Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[18] Bagnulo, S., Landstreet, J. D., Lo Curto, G., Szeifert, T., & Wade, G. A. 2003, A&A, 403, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[19] Bailey, J. I., Mateo, M., White, R. J., Shectman, S. A., & Crane, J. D. 2018, MNRAS, 475, 1609 [NASA ADS] [CrossRef] [Google Scholar]

[20] Balona, L. A., & Dziembowski, W. A. 2011, MNRAS, 417, 591 [NASA ADS] [CrossRef] [Google Scholar]

[21] Balona, L. A., Krisciunas, K., & Cousins, A. W. J. 1994, MNRAS, 270, 905 [NASA ADS] [CrossRef] [Google Scholar]

[22] Barceló Forteza, S., Roca Cortés, T., & García, R. A. 2018, A&A, 614, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[23] Barceló Forteza, S., Moya, A., Barrado, D., et al. 2020, A&A, 638, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[24] Barnes, S. A. 2003, ApJ, 586, 464 [Google Scholar]

[25] Barnes, S. A. 2007, ApJ, 669, 1167 [Google Scholar]

[26] Barrett, P., Hunter, J., Miller, J. T., Hsu, J. C., & Greenfield, P. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 91 [NASA ADS] [Google Scholar]

[27] Bastian, N., & de Mink, S. E. 2009, MNRAS, 398, L11 [NASA ADS] [CrossRef] [Google Scholar]

[28] Bastian, N., Niederhofer, F., Kozhurina-Platais, V., et al. 2016, MNRAS, 460, L20 [NASA ADS] [CrossRef] [Google Scholar]

[29] Bastian, N., Kamann, S., Cabrera-Ziri, I., et al. 2018, MNRAS, 480, 3739 [NASA ADS] [CrossRef] [Google Scholar]

[30] Basu, S., & Chaplin, W. J. 2017, Asteroseismic Data Analysis: Foundations and Techniques (Princeton: Princeton University Press) [Google Scholar]

[31] Basu, S., Grundahl, F., Stello, D., et al. 2011, ApJ, 729, L10 [Google Scholar]

[32] Bedding, T. R. 2014, in Asteroseismology, eds. P. L. Pallé, & C. Esteban, 60 [Google Scholar]

[33] Bedding, T. R., Murphy, S. J., Colman, I. L., & Kurtz, D. W. 2015, Eur. Phys. J. Web Conf., 101, 01005 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[34] Bedding, T. R., Murphy, S. J., Hey, D. R., et al. 2020, Nature, 581, 147 [NASA ADS] [CrossRef] [Google Scholar]

[35] Bedding, T. R., Murphy, S. J., Crawford, C., et al. 2023, ApJ, 946, L10 [NASA ADS] [CrossRef] [Google Scholar]

[36] Bertelli, G., Nasi, E., Girardi, L., et al. 2003, AJ, 125, 770 [NASA ADS] [CrossRef] [Google Scholar]

[37] Bouabid, M. P., Dupret, M. A., Salmon, S., et al. 2013, MNRAS, 429, 2500 [Google Scholar]

[38] Bouchaud, K., Domiciano de Souza, A., Rieutord, M., Reese, D. R., & Kervella, P. 2020, A&A, 633, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[39] Bouma, L. G., Curtis, J. L., Hartman, J. D., Winn, J. N., & Bakos, G. Á. 2021, AJ, 162, 197 [NASA ADS] [CrossRef] [Google Scholar]

[40] Bowman, D. M., & Kurtz, D. W. 2018, MNRAS, 476, 3169 [NASA ADS] [CrossRef] [Google Scholar]

[41] Brahm, R., Jordán, A., & Espinoza, N. 2017, PASP, 129, 034002 [Google Scholar]

[42] Brandt, T. D., & Huang, C. X. 2015, ApJ, 807, 25 [NASA ADS] [CrossRef] [Google Scholar]

[43] Brasseur, C. E., Phillip, C., Fleming, S. W., Mullally, S. E., & White, R. L. 2019, Astrophysics Source Code Library [record ascl:1905.007] [Google Scholar]

[44] Brogaard, K., Arentoft, T., Miglio, A., et al. 2023, A&A, 679, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[45] Cantat-Gaudin, T., Jordi, C., Vallenari, A., et al. 2018, A&A, 618, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[46] Casagrande, L., & VandenBerg, D. A. 2018, MNRAS, 479, L102 [NASA ADS] [CrossRef] [Google Scholar]

[47] Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]

[48] Christophe, S., Ballot, J., Ouazzani, R. M., Antoci, V., & Salmon, S. J. A. J. 2018, A&A, 618, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[49] Corbard, T., Blanc-Féraud, L., Berthomieu, G., & Provost, J. 1999, A&A, 344, 696 [NASA ADS] [Google Scholar]

[50] Correnti, M., Goudfrooij, P., Puzia, T. H., & de Mink, S. E. 2015, MNRAS, 450, 3054 [NASA ADS] [CrossRef] [Google Scholar]

[51] Cox, A. N. 1955, ApJ, 121, 628 [CrossRef] [Google Scholar]

[52] Danielski, C., Babusiaux, C., Ruiz-Dern, L., Sartoretti, P., & Arenou, F. 2018, A&A, 614, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[53] D’Antona, F., Di Criscienzo, M., Decressin, T., et al. 2015, MNRAS, 453, 2637 [NASA ADS] [Google Scholar]

[54] De Cat, P., & Aerts, C. 2002, A&A, 393, 965 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[55] Deheuvels, S., Doğan, G., Goupil, M. J., et al. 2014, A&A, 564, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[56] Deheuvels, S., Ballot, J., Beck, P. G., et al. 2015, A&A, 580, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[57] Deheuvels, S., Ballot, J., Eggenberger, P., et al. 2020, A&A, 641, A117 [EDP Sciences] [Google Scholar]

[58] Deubner, F. L., Ulrich, R. K., & Rhodes, E. J. 1979, A&A, 72, 177 [NASA ADS] [Google Scholar]

[59] Di Mauro, M. P., Ventura, R., Cardini, D., et al. 2016, ApJ, 817, 65 [NASA ADS] [CrossRef] [Google Scholar]

[60] Domiciano de Souza, A., Kervella, P., Jankov, S., et al. 2003, A&A, 407, L47 [CrossRef] [EDP Sciences] [Google Scholar]

[61] Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]

[62] Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[63] Eggen, O. J. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, 20, 10 [NASA ADS] [Google Scholar]

[64] Endal, A. S., & Sofia, S. 1978, ApJ, 220, 279 [NASA ADS] [CrossRef] [Google Scholar]

[65] Espinosa Lara, F., & Rieutord, M. 2011, A&A, 533, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[66] Feinstein, A., Marraco, H. G., & Mirabel, I. 1973, A&AS, 9, 233 [NASA ADS] [Google Scholar]

[67] Foreman-Mackey, D. 2016, J. Open Source Softw., 1, 24 [Google Scholar]

[68] Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]

[69] Frémat, Y., Royer, F., Marchal, O., et al. 2023, A&A, 674, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[70] Fritzewski, D. J., Barnes, S. A., James, D. J., & Strassmeier, K. G. 2020, A&A, 641, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[71] Fritzewski, D. J., Van Reeth, T., Aerts, C., et al. 2024, A&A, 681, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[72] Gaia Collaboration (De Ridder, J., et al.) 2023a, A&A, 674, A36 [CrossRef] [EDP Sciences] [Google Scholar]

[73] Gaia Collaboration (Vallenari, A., et al.) 2023b, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[74] Garcia, S., Van Reeth, T., De Ridder, J., et al. 2022a, A&A, 662, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[75] Garcia, S., Van Reeth, T., De Ridder, J., & Aerts, C. 2022b, A&A, 668, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[76] Gebruers, S., Tkachenko, A., Bowman, D. M., et al. 2022, A&A, 665, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[77] Gehan, C., Mosser, B., Michel, E., Samadi, R., & Kallinger, T. 2018, A&A, 616, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[78] Gieseking, F., & Karimie, M. T. 1982, A&AS, 49, 497 [NASA ADS] [Google Scholar]

[79] Ginsburg, A., Sipőcz, B. M., Brasseur, C. E., et al. 2019, AJ, 157, 98 [Google Scholar]

[80] Girardi, L., Goudfrooij, P., Kalirai, J. S., et al. 2013, MNRAS, 431, 3501 [NASA ADS] [CrossRef] [Google Scholar]

[81] Glatt, K., Grebel, E. K., Gallagher, J. S., et al. 2009, AJ, 138, 1403 [NASA ADS] [CrossRef] [Google Scholar]

[82] González, J. F., & Lapasset, E. 2000, AJ, 119, 2296 [CrossRef] [Google Scholar]

[83] Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]

[84] Gossage, S., Conroy, C., Dotter, A., et al. 2019, ApJ, 887, 199 [NASA ADS] [CrossRef] [Google Scholar]

[85] Goupil, M. J., Dupret, M. A., Samadi, R., et al. 2005, JApA, 26, 249 [NASA ADS] [Google Scholar]

[86] Granada, A., Jones, C. E., Sigut, T. A. A., et al. 2018, AJ, 155, 50 [NASA ADS] [CrossRef] [Google Scholar]

[87] Grassitelli, L., Fossati, L., Langer, N., et al. 2015, A&A, 584, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[88] Gratton, R. G., Carretta, E., & Bragaglia, A. 2012, A&ARv, 20, 50 [CrossRef] [Google Scholar]

[89] Guzik, J. A., Kaye, A. B., Bradley, P. A., Cox, A. N., & Neuforge, C. 2000, ApJ, 542, L57 [Google Scholar]

[90] Handler, G. 2009, in Stellar Pulsation: Challenges for Theory and Observation, eds. J. A. Guzik, & P. A. Bradley, AIP Conf. Ser., 1170, 403 [NASA ADS] [CrossRef] [Google Scholar]

[91] Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]

[92] Hasanzadeh, A., Safari, H., & Ghasemi, H. 2021, MNRAS, 505, 1476 [NASA ADS] [CrossRef] [Google Scholar]

[93] Healy, B. F., & McCullough, P. R. 2020, ApJ, 903, 99 [NASA ADS] [CrossRef] [Google Scholar]

[94] Hekker, S., Basu, S., Stello, D., et al. 2011, A&A, 530, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[95] Henneco, J., Van Reeth, T., Prat, V., et al. 2021, A&A, 648, A97 [EDP Sciences] [Google Scholar]

[96] Hon, M., Huber, D., Kuszlewicz, J. S., et al. 2021, ApJ, 919, 131 [NASA ADS] [CrossRef] [Google Scholar]

[97] Houdek, G. 2000, in Delta Scuti and Related Stars, eds. M. Breger, & M. Montgomery, ASP Conf. Ser., 210, 454 [NASA ADS] [Google Scholar]

[98] Huat, A. L., Hubert, A. M., Baudin, F., et al. 2009, A&A, 506, 95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[99] Irwin, J., Aigrain, S., Bouvier, J., et al. 2009, MNRAS, 392, 1456 [Google Scholar]

[100] Jackiewicz, J. 2021, Front. Astron. Space Sci., 7, 102 [NASA ADS] [CrossRef] [Google Scholar]

[101] Jian, M., Matsunaga, N., Jiang, B., Yuan, H., & Zhang, R. 2024, A&A, 682, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[102] Johnston, C., Aerts, C., Pedersen, M. G., & Bastian, N. 2019, A&A, 632, A74 [EDP Sciences] [Google Scholar]

[103] Kaufer, A., Stahl, O., Tubbesing, S., et al. 1999, The Messenger, 95, 8 [Google Scholar]

[104] Kaye, A. B., Handler, G., Krisciunas, K., Poretti, E., & Zerbi, F. M. 1999, PASP, 111, 840 [Google Scholar]

[105] Kippenhahn, R., & Thomas, H. C. 1970, in IAU Colloq. 4: Stellar Rotation, ed. A. Slettebak, 20 [CrossRef] [Google Scholar]

[106] Koester, D., & Reimers, D. 1996, A&A, 313, 810 [NASA ADS] [Google Scholar]

[107] Kraft, R. P. 1967, ApJ, 150, 551 [Google Scholar]

[108] Kurtz, D. W., Saio, H., Takata, M., et al. 2014, MNRAS, 444, 102 [Google Scholar]

[109] Kurtz, D. W., Shibahashi, H., Murphy, S. J., Bedding, T. R., & Bowman, D. M. 2015, MNRAS, 450, 3015 [NASA ADS] [CrossRef] [Google Scholar]

[110] Kurtz, D. W., Jayaraman, R., Sowicka, P., et al. 2023, MNRAS, 521, 4765 [NASA ADS] [CrossRef] [Google Scholar]

[111] Ledoux, P. 1951, ApJ, 114, 373 [Google Scholar]

[112] Lee, U., & Saio, H. 1987, MNRAS, 224, 513 [Google Scholar]

[113] Lee, U., & Saio, H. 1997, ApJ, 491, 839 [Google Scholar]

[114] Li, C., de Grijs, R., Deng, L., et al. 2016, Nature, 529, 502 [NASA ADS] [CrossRef] [Google Scholar]

[115] Li, C., Sun, W., de Grijs, R., et al. 2019a, ApJ, 876, 65 [Google Scholar]

[116] Li, G., Bedding, T. R., Murphy, S. J., et al. 2019b, MNRAS, 482, 1757 [Google Scholar]

[117] Li, G., Van Reeth, T., Bedding, T. R., Murphy, S. J., & Antoci, V. 2019c, MNRAS, 487, 782 [Google Scholar]

[118] Li, G., Van Reeth, T., Bedding, T. R., et al. 2020a, MNRAS, 491, 3586 [Google Scholar]

[119] Li, G., Guo, Z., Fuller, J., et al. 2020b, MNRAS, 497, 4363 [Google Scholar]

[120] Lightkurve Collaboration (Cardoso, J. V. D. M., et al.) 2018, Astrophysics Source Code Library [record ascl:1812.013] [Google Scholar]

[121] Lim, B., Rauw, G., Nazé, Y., et al. 2019, Nat. Astron., 3, 76 [Google Scholar]

[122] Lomb, N. R. 1976, Ap&SS, 39, 447 [Google Scholar]

[123] Lund, M. N., Basu, S., Silva Aguirre, V., et al. 2016, MNRAS, 463, 2600 [NASA ADS] [CrossRef] [Google Scholar]

[124] Maeder, A. 2009, Physics, Formation and Evolution of Rotating Stars (Heidelberg: Springer-Verlag) [Google Scholar]

[125] Maitzen, H. M., & Hensberge, H. 1981, A&A, 96, 151 [NASA ADS] [Google Scholar]

[126] Martins, F., & Palacios, A. 2013, A&A, 560, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[127] Mathis, S. 2009, A&A, 506, 811 [CrossRef] [EDP Sciences] [Google Scholar]

[128] Mathis, S. 2013, in Lecture Notes in Physics, eds. M. Goupil, K. Belkacem, C. Neiner, F. Lignières, & J. J. Green (Berlin: Springer-Verlag), 865, 23 [CrossRef] [Google Scholar]

[129] McAlister, H. A., ten Brummelaar, T. A., Gies, D. R., et al. 2005, ApJ, 628, 439 [NASA ADS] [CrossRef] [Google Scholar]

[130] McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [Google Scholar]

[131] Meilland, A., Stee, P., Vannier, M., et al. 2007, A&A, 464, 59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[132] Meingast, S., & Alves, J. 2019, A&A, 621, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[133] Meingast, S., Alves, J., & Rottensteiner, A. 2021, A&A, 645, A84 [EDP Sciences] [Google Scholar]

[134] Meynet, G., Mermilliod, J. C., & Maeder, A. 1993, A&AS, 98, 477 [Google Scholar]

[135] Michielsen, M., Aerts, C., & Bowman, D. M. 2021, A&A, 650, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[136] Miglio, A., Brogaard, K., Stello, D., et al. 2012, MNRAS, 419, 2077 [Google Scholar]

[137] Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]

[138] Mombarg, J. S. G. 2023, A&A, 677, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[139] Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., et al. 2019, MNRAS, 485, 3248 [NASA ADS] [CrossRef] [Google Scholar]

[140] Mombarg, J. S. G., Dotter, A., Van Reeth, T., et al. 2020, ApJ, 895, 51 [Google Scholar]

[141] Mombarg, J. S. G., Van Reeth, T., & Aerts, C. 2021, A&A, 650, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[142] Mombarg, J. S. G., Dotter, A., Rieutord, M., et al. 2022, ApJ, 925, 154 [NASA ADS] [CrossRef] [Google Scholar]

[143] Mombarg, J. S. G., Rieutord, M., & Espinosa Lara, F. 2023, A&A, 677, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[144] Montgomery, M. H., & O’Donoghue, D. 1999, Delta Scuti Star Newsletter, 13, 28 [NASA ADS] [Google Scholar]

[145] Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[146] Murphy, S. J., Fossati, L., Bedding, T. R., et al. 2016, MNRAS, 459, 1201 [Google Scholar]

[147] Murphy, S. J., Hey, D., Van Reeth, T., & Bedding, T. R. 2019, MNRAS, 485, 2380 [NASA ADS] [CrossRef] [Google Scholar]

[148] Murphy, S. J., Saio, H., Takada-Hidai, M., et al. 2020, MNRAS, 498, 4272 [NASA ADS] [CrossRef] [Google Scholar]

[149] Murphy, S. J., Joyce, M., Bedding, T. R., White, T. R., & Kama, M. 2021, MNRAS, 502, 1633 [NASA ADS] [CrossRef] [Google Scholar]

[150] Murphy, S. J., Bedding, T. R., White, T. R., et al. 2022, MNRAS, 511, 5718 [NASA ADS] [CrossRef] [Google Scholar]

[151] Neiner, C., Lee, U., Mathis, S., et al. 2020, A&A, 644, A9 [EDP Sciences] [Google Scholar]

[152] Netzel, H., Pietrukowicz, P., Soszyński, I., & Wrona, M. 2022, MNRAS, 510, 1748 [Google Scholar]

[153] Ouazzani, R.-M., Salmon, S. J. A. J., Antoci, V., et al. 2017, MNRAS, 465, 2294 [Google Scholar]

[154] Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[155] Ouazzani, R. M., Lignières, F., Dupret, M. A., et al. 2020, A&A, 640, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[156] Palakkatharappil, D. B., & Creevey, O. L. 2023, A&A, 674, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[157] Pamos Ortega, D., Mirouh, G. M., García Hernández, A., Suárez Yanes, J. C., & Barceló Forteza, S. 2023, A&A, 675, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[158] Pamyatnykh, A. A. 1999, Acta Astron., 49, 119 [Google Scholar]

[159] The pandas development team 2020, https://doi.org/10.5281/zenodo.3509134 [Google Scholar]

[160] Pápics, P. I., Moravveji, E., Aerts, C., et al. 2014, A&A, 570, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[161] Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]

[162] Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]

[163] Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]

[164] Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]

[165] Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]

[166] Pedersen, M. G., Aerts, C., Pápics, P. I., & Rogers, T. M. 2018, A&A, 614, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[167] Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., 5, 715 [NASA ADS] [CrossRef] [Google Scholar]

[168] Pérez Hernández, F., Claret, A., Hernández, M. M., & Michel, E. 1999, A&A, 346, 586 [NASA ADS] [Google Scholar]

[169] Reed, M. D., Kilkenny, D., Kawaler, S. D., et al. 2000, Balt. Astron., 9, 183 [Google Scholar]

[170] Reimers, D., & Koester, D. 1982, A&A, 116, 341 [NASA ADS] [Google Scholar]

[171] Ricker, G. R., Winn, J. N., Vanderspek, R., et al. 2015, J. Astron. Telesc. Instrum. Syst., 1, 014003 [Google Scholar]

[172] Riello, M., De Angeli, F., Evans, D. W., et al. 2021, A&A, 649, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[173] Ripepi, V., Balona, L., Catanzaro, G., et al. 2015, MNRAS, 454, 2606 [Google Scholar]

[174] Royer, F., Zorec, J., & Gómez, A. E. 2007, A&A, 463, 671 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[175] Rui, N. Z., Ong, J. M. J., & Mathis, S. 2024, MNRAS, 527, 6346 [Google Scholar]

[176] Saio, H., Kurtz, D. W., Takata, M., et al. 2015, MNRAS, 447, 3264 [Google Scholar]

[177] Saio, H., Bedding, T. R., Kurtz, D. W., et al. 2018a, MNRAS, 477, 2183 [Google Scholar]

[178] Saio, H., Kurtz, D. W., Murphy, S. J., Antoci, V. L., & Lee, U. 2018b, MNRAS, 474, 2774 [Google Scholar]

[179] Saio, H., Takata, M., Lee, U., Li, G., & Van Reeth, T. 2021, MNRAS, 502, 5856 [Google Scholar]

[180] Sandquist, E. L., Stello, D., Arentoft, T., et al. 2020, AJ, 159, 96 [NASA ADS] [CrossRef] [Google Scholar]

[181] Scargle, J. D. 1982, ApJ, 263, 835 [Google Scholar]

[182] Shajn, G., & Struve, O. 1929, MNRAS, 89, 222 [NASA ADS] [Google Scholar]

[183] Shibahashi, H. 1979, PASJ, 31, 87 [NASA ADS] [Google Scholar]

[184] Skumanich, A. 1972, ApJ, 171, 565 [Google Scholar]

[185] Sreenivas, K. R., Bedding, T. R., Li, Y., et al. 2024, MNRAS, 530, 3477 [NASA ADS] [CrossRef] [Google Scholar]

[186] Stassun, K. G., Oelkers, R. J., Paegert, M., et al. 2019, AJ, 158, 138 [Google Scholar]

[187] Stellingwerf, R. F. 1979, ApJ, 227, 935 [NASA ADS] [CrossRef] [Google Scholar]

[188] Stello, D., Basu, S., Bruntt, H., et al. 2010, ApJ, 713, L182 [NASA ADS] [CrossRef] [Google Scholar]

[189] Sterken, C. 2005, in The Light-time Effect in Astrophysics: Causes and Cures of the O-C Diagram, ed. C. Sterken, ASP Conf. Ser., 335, 3 [NASA ADS] [Google Scholar]

[190] Sterken, C., & Jerzykiewicz, M. 1993, Space Sci. Rev., 62, 95 [NASA ADS] [CrossRef] [Google Scholar]

[191] Straumit, I., Tkachenko, A., Gebruers, S., et al. 2022, AJ, 163, 236 [NASA ADS] [CrossRef] [Google Scholar]

[192] Sung, H., Bessell, M. S., Lee, B.-W., & Lee, S.-G. 2002, AJ, 123, 290 [NASA ADS] [CrossRef] [Google Scholar]

[193] Szewczuk, W., & Daszyńska-Daszkiewicz, J. 2018, MNRAS, 478, 2243 [Google Scholar]

[194] Tarricq, Y., Soubiran, C., Casamiquela, L., et al. 2021, A&A, 647, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[195] Terndrup, D. M., Pinsonneault, M., Jeffries, R. D., et al. 2002, ApJ, 576, 950 [NASA ADS] [CrossRef] [Google Scholar]

[196] Thompson, I. B., Brown, D. N., & Landstreet, J. D. 1987, ApJS, 64, 219 [NASA ADS] [CrossRef] [Google Scholar]

[197] Tokuno, T., & Takata, M. 2022, MNRAS, 514, 4140 [NASA ADS] [CrossRef] [Google Scholar]

[198] Townsend, R. H. D. 2003, MNRAS, 340, 1020 [Google Scholar]

[199] Townsend, R. H. D., & Teitler, S. A. 2013, MNRAS, 435, 3406 [Google Scholar]

[200] Townsend, R. H. D., Goldstein, J., & Zweibel, E. G. 2018, MNRAS, 475, 879 [Google Scholar]

[201] Triana, S. A., Moravveji, E., Pápics, P. I., et al. 2015, ApJ, 810, 16 [Google Scholar]

[202] Triana, S. A., Corsaro, E., De Ridder, J., et al. 2017, A&A, 602, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[203] Unno, W., Osaki, Y., Ando, H., Saio, H., & Shibahashi, H. 1989, Nonradial Oscillations of Stars (Tokyo: University of Tokyo Press) [Google Scholar]

[204] Van Beeck, J., Bowman, D. M., Pedersen, M. G., et al. 2021, A&A, 655, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[205] Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015a, ApJS, 218, 27 [Google Scholar]

[206] Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015b, A&A, 574, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[207] Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]

[208] von Zeipel, H. 1924, MNRAS, 84, 665 [NASA ADS] [CrossRef] [Google Scholar]

[209] Waelkens, C. 1991, A&A, 246, 453 [NASA ADS] [Google Scholar]

[210] Wang, C., Langer, N., Schootemeijer, A., et al. 2022, Nat. Astron., 6, 480 [NASA ADS] [CrossRef] [Google Scholar]

[211] Winget, D. E., Nather, R. E., Clemens, J. C., et al. 1991, ApJ, 378, 326 [NASA ADS] [CrossRef] [Google Scholar]

[212] Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]

[213] Xiong, D. R., Deng, L., Zhang, C., & Wang, K. 2016, MNRAS, 457, 3163 [Google Scholar]