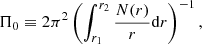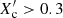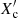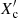EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 684 (April 2024) A&A, 684 (2024) A112 Full HTML
Open Access
Issue
A&A
Volume 684, April 2024
Article Number A112
Number of page(s) 13
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202449300
Published online 09 April 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Transport processes in stellar interiors have a significant impact on the global properties and the chemical evolution of stars across all masses (e.g. Martins & Palacios 2013; Pedersen et al. 2021; Lagarde et al. 2017, for high-, intermediate-, and low-mass stars, respectively). Asteroseismology has pinpointed two dominant, tightly connected effects of chemical mixing due to the accumulation over the core hydrogen burning main-sequence phase: a considerable increase in the main-sequence duration and a heavier helium core at the end of the main sequence (up to a factor of two more massive than without envelope mixing; see Johnston 2021; Pedersen 2022). In this work, we consider the former for intermediate-mass stars from the viewpoint of age-dating red giant stars for Galactic archaeology.

Unravelling the formation and evolutionary history of the Milky Way has many facets. One important element concerns the chemical tagging of stars dispersed throughout the galaxy (e.g. De Silva et al. 2015; Schiavon et al. 2017; Vitali et al. 2024). Other aspects involve determining the spatial structure and evolution of stellar populations, moving groups, and streams in the Milky Way’s bulge, bar, and thin and thick discs (e.g. Bovy et al. 2016; Rojas-Arriagada et al. 2017; Silva Aguirre et al. 2018; Helmi et al. 2018). Since about a decade, asteroseismology of red giants offers high-precision ages for these old bright stars across the Milky Way (see the extensive studies by Miglio et al. 2013; Chiappini et al. 2015; Montalbán et al. 2021; Hon et al. 2021; Wang et al. 2023). Age-chemo-kinematic properties of red giants indicate efficient radial migration in the thin disc, different chemo-dynamical histories of the thick and thin discs, and changes in the star formation after the formation of the thick disc (Miglio et al. 2021). The age determinations of these populations of red giants in the Galaxy are of critical importance to ensure a proper interpretation of the archaeological sites of the Milky Way. While various core boundary mixing prescriptions are nowadays being considered for the core helium burning phase of red giants (e.g. Noll et al. 2024), almost none of the constructed models take the previous long history of these stars during the core hydrogen phase into account when determining the size and mass of the helium core. Yet, the effective chemical mixing in the progenitor stars needs to be treated with great care (Montalbán et al. 2013).

In this work we focus on well-studied intermediate-mass gravity-mode pulsators on the main sequence. These γ Doradus (γ Dor) stars are the progenitors of red giants and have masses above about 1.3 M⊙. Starting from the measured internal rotation rates of a population of γ Dor stars covering the mass range 1.3 M⊙ to 2 M⊙, we aim to study the arising systematic age uncertainties of red giants, when ignoring the rotation of their progenitors in their core hydrogen burning phase.

For red giants of lower masses it is justified to ignore the mixing caused by rotation because their dwarf progenitors experience an efficient rotational slowing due to magnetic braking (Barnes 2007), as confirmed by gyrochronology studies of old open clusters based on high-precision space photometry (Meibom et al. 2011a,b, 2015; Barnes et al. 2016). Even if magnetic braking weakens during the second half of the main sequence (van Saders et al. 2016; Hall et al. 2021), stars born with a mass below 1.2 M⊙ are slow rotators from early on in their evolution, their rotation period being far longer than their critical break-up period. In addition, the rotational evolution of cool stars is only a function of mass (and metallicity), thus suppressing possible age spreads due to rotation. Hence, we only consider red giants with a mass above 1.2 M⊙ in this work and study the impact of their progenitors’ rotation on their age-dating for the evolutionary phases beyond the main sequence.

2. Sample selection and global stellar parameters

A large homogeneous sample of 611 γ Dor stars with high-precision measurements of their near-core rotation frequency, Ωrot, from Kepler space photometry (Borucki et al. 2010) was presented in Li et al. (2020). The other asteroseismic observable deduced from their detected series of identified low-degree modes of consecutive radial order is the buoyancy travel time, Π0, defined as

Π 0 ≡ 2 π 2 ( ∫ r 1 r 2 N ( r ) r d r ) − 1 , $$ \begin{aligned} \Pi _0 \equiv 2\pi ^2 \left(\int _{r_1}^{r_2} \frac{N(r)}{r} \mathrm{d}r\right)^{-1}, \end{aligned} $$(1)

where N(r) is the Brunt–Väisälä frequency and r1 and r2 are the inner and outer position of the mode propagation cavity (Aerts et al. 2010). This observable is a measure of the size and shape of the gravity-mode cavity, which changes during the evolution of the star. The chemical gradient profile notably changes as the stars’ convective cores shrink throughout the main sequence. The resulting change in the shape of N(r) has been measured from gravito-inertial asteroseismology based on 4-year Kepler light curves (e.g. Aerts et al. 2021).

We used these two powerful asteroseismic observables, Ωrot and Π0, which characterise the deep stellar interior of γ Dor stars, to estimate the stellar masses and radii from grid modelling. This type of asteroseismic modelling requires additional constraints to break degeneracies and to find unique solutions. Since we wish to apply ensemble asteroseismic grid modelling, we need to use a homogeneous set of global stellar parameters. In contrast to Li et al. (2020), who used Kepler input catalogue values, we extracted stellar parameters from Gaia Data Release 3 (DR3, Gaia Collaboration 2023a; Creevey et al. 2023), which are appropriate for F-type γ Dor pulsators as shown by Aerts et al. (2023). This yielded astrophysical parameters based on the Gaia General Stellar Parametrizer from Photometry (GSP-Phot) for 536 of the 611 stars. Six of these objects were removed as they are known binaries with pulsating components so their parameters in the Gaia data might be inaccurate.

Mombarg et al. (2021) have shown the benefit of using the Gaia stellar luminosity (L/L⊙), along with Π0, the surface gravity (log g) and the effective temperature (Teff), in asteroseismic grid modelling of identified prograde dipole modes for a sample of 37 γ Dor stars with high-resolution high signal-to-noise spectroscopy. Due to the very uncertain log g estimates, we performed grid modelling from the method by Mombarg et al. (2019) but based only on the three observables, Π0, Teff, and L/L⊙.

There are at least two ways to obtain the stellar luminosity from Gaia DR3. Firstly, the Gaia astrophysical parameter table includes the luminosity estimate from the Final Luminosity Age Mass Estimator (FLAME, Creevey et al. 2023). Secondly, we can calculate it from the observed G-band magnitude using the parallax, extinction estimate, and bolometric correction (see Creevey et al. 2023, for the Gaia bolometric correction computation). The former method relies on the same input parameters as the latter but includes a rather sophisticated scheme of placing these values on theoretical isochrones to deduce log L/L⊙. These isochrones are calibrated from slowly rotating benchmark stars, while γ Dor stars tend to be faster rotators. Hence, the FLAME luminosities, while seemingly precise, may suffer from systematic uncertainties. In order to assess this, we computed the luminosities without relying on stellar models. The downside of this method is that we need an estimate of the interstellar reddening (which we took from Gaia DR3). Yet, for most stars this reddening is small (E(GBP)−E(GRP) < 0.25 mag) as they are positioned away from the Galactic plane and typically nearby at a distance d < 1.5 kpc. Comparing the two estimates allows us to evaluate the involved uncertainties.

Figure 1 provides a comparison between both values and reveals that they are in good agreement with each other. The scatter of ±0.1 dex around the line of unity is expected because the photometric luminosities include fewer and independently treated variables whereas FLAME treats all variables in a global framework with additional model constraints. As seen in Fig. 1, we find some obvious outliers to the generally tight correlation, with the photometric luminosities maximally up to a factor of five higher than the FLAME values.

thumbnail Fig. 1.

Comparison between luminosity values obtained from the Gaia absolute G magnitude (photometric luminosity) and the model-dependent Gaia-FLAME. The dashed line is the bisector.

To further clean our sample, we investigated the correlation between the effective temperatures given by Li et al. (2020) from the Kepler Input Catalogue and those in Gaia DR3. These temperatures are mostly in agreement. However, 19 stars have an effective temperature outside the γ Dor range, indicating that they are instead early A-type or B-type pulsators (Teff > 8500 K). We used the same approach as Aerts et al. (2023) to reclassify these gravity-mode pulsators as slowly pulsating B (SPB) stars.

Even in this cleaned sample, some stars exhibit larger Π0 values than those expected for γ Dor stars (Van Reeth et al. 2016). Since we employed grid-based asteroseismic modelling, we limited the sample to stars with Π0 < 6500 s. This value might exclude some of the youngest stars, but it ensures that the modelled stars fall onto the used grid. Our final sample includes 490 stars with homogeneously deduced astrophysical parameters from Gaia DR3 and 4-year Kepler light curves.

We show the final sample in the observational Hertzsprung-Russell diagram (HRD) in Fig. 2 along with the measured Π0. Furthermore, we show the theoretical γ Dor instability strips from Dupret et al. (2005). The lower edge of the observed instability strip agrees very well with theoretical predictions (with a mixing-length parameter αMLT = 2), whereas the upper edge is at higher luminosities (cf. also Mombarg et al. 2024a). These three instability regions were calculated for only one choice of input physics and for one excitation mechanism. Many Gaia DR3 candidate γ Dor stars are observed at higher luminosities (e.g. Gaia Collaboration 2023b) as we also find here.

thumbnail Fig. 2.

Hertzsprung-Russell diagram of our final sample, which contains 490 γ Dor stars. The colour-coding gives the Π0, which is used as an input parameter in the grid modelling. The solid lines indicate the theoretical γ Dor instability strip from Dupret et al. (2005) with a mixing-length parameter αMLT = 2, while the dashed and dotted lines show the position of the instability strip for αMLT = 1.5 and αMLT = 1, respectively.

3. Asteroseismic parameter estimation

Our nominal asteroseismic modelling purpose for this work is to estimate each star’s mass (M) and evolutionary stage represented by the core hydrogen mass fraction (Xc). In order to achieve this, our approach consists of a Markov chain Monte Carlo (MCMC)-based grid search for each of the 490 stars in our final sample, which we modelled independently as it concerns field stars that do not belong to an astrophysical ensemble. We used the measured Π0 along with Gaia DR3 L/L⊙ and Teff estimates as inputs to place the stars on a stellar evolution grid.

The grid consists of quasi-randomly sampled 1D Modules for Experiment in Stellar Astrophysics (MESA r11701, Paxton et al. 2011, 2013, 2015, 2018, 2019) models computed by Mombarg et al. (2021), to which we refer for the details of the input physics. In terms of element transport, we recall here that the overall chemical mixing caused by various active physical phenomena (such as rotational mixing, internal gravity wave mixing, magnetic diffusion, etc.) is simplified in this grid of 1D models in terms of (1) instantaneous full convective mixing in the core relying on the mixing-length theory (Böhm-Vitense 1958), (2) diffusive exponentially decaying overshooting with one free parameter (fov ∈ [0.01, 0.03]) in the transition layer between the convective core and the radiative envelope, and (3) constant envelope mixing described by a free parameter. This approach allows us to assess the level of mixing in these three zones without having to rely on uncalibrated theories of element transport, because these 1D approximations of inherently 3D phenomena result in unsuitably spiky mixing profiles throughout the stellar interior, making pulsation computations unreliable (cf. Aerts 2021, for more detailed motivations of this commonly adopted approach in asteroseismic modelling of stars with a convective core). The covered mass range of the grid is [1.3, 2.0] M⊙, while the metallicity Z varies between 0.011 and 0.023 following the measured values for the sub-sample of 37 best characterised γ Dor stars with high-precision spectroscopy and its homogeneous analysis (Van Reeth et al. 2015).

For our MCMC sampling, we used flat priors in mass (M), core-hydrogen content (Xc), and core overshoot (fov); the prior in metallicity (Z) was taken from a Gaussian distribution centred on Z0 = 0.014 (σ = 0.01), given that the stars are young from a Galactic perspective and hence are expected to have near-solar metallicities. This is indeed found from various studies based on high-precision spectroscopic analyses done for various subsets of the brightest γ Dor stars in the sample, as summarised by Gebruers et al. (2021). Moreover, given its inferior effect on forward asteroseismic modelling based on the fitting of actual identified mode frequencies (Aerts et al. 2018) compared to the four unknowns (M, Z, fov, and Xc) found by Mombarg et al. (2021), and to reduce dimensionality, we fixed the envelope mixing to the lowest value of Dmix = 1 cm2 s−1 in the grid. This effectively comes down to the assumption that rotational mixing is mainly active in the shear layer above the convective core but has a negligible effect in the outer envelope of rotating F-type stars. We come back to this assumption in Sect. 6, where we assess the effect of higher levels of rotational mixing outside the core boundary layer on asteroseismic parameter determinations. The merit function for the grid evaluation is the Euclidean distance between the grid points and the measurements.

For each star the grid search results in a distribution of M, Xc, fov, and Z. The chosen prior restricted Z but it still varies across the whole range of the model grid for some stars, showing the need for these variable in the parameter estimation based on the selection of the best models. Based on the MCMC chains, we subsequently determined the best values and uncertainties for the stellar radius (R), the stellar age (t), and the mass of the convective core (Mcc) by extracting those quantities from the model grid.

Before discussing the resulting distributions, we take a look at how well the grid modelling recovers the input parameters. Similarly to the above mentioned determined properties such as the stellar radius, we determined the values and uncertainties of L/L⊙, Teff, and Π0 from the best fitting model.

Figure 3 shows the correlations between the input and recovered values. We find the majority of the recovered values to be in agreement with the input. In particular, the stellar luminosity was well retrieved. Yet, all three parameters have a varying level of outlying data points that could typically not be mapped to the grid during the modelling. However, we note that only one star is an outlier in all three parameters. In most cases a single input parameter fell outside the grid space while the others gave good constraints, indicating possibly an inaccurate measurement of the one, outlying parameter.

thumbnail Fig. 3.

Correlations between observed properties (input values) and the recovered values (model). From left to right, we show log L/L⊙, Teff, and Π0. Notably, outliers in one panel are not necessarily outliers in other panels. To show this property, we highlight the three most outlying points (the difference divided by the measurement uncertainty) in each panel with colour and indicate the same stars with coloured outlines in the other two panels. Outliers in luminosity are shown in orange, outliers in effective temperature in blue, and outliers in Π0 in green. The shift towards intermediate Π0 is discussed in the main text.

A notably exception to the random outliers is the systematic shift towards intermediate Π0 in the retrieved values. Stars for which a lower Π0 was recovered than measured (i.e. stars to the right of the line of unity) have typically measured a very high value that would indicate young stars. Their position in the HRD (Fig. 2), places them well above the zero-age main sequence (ZAMS). Hence, we can assume that these stars are either still on the pre-main sequence or well evolved with an inaccurate Π0 measurement. Our grid concerns only the main-sequence evolution, and therefore the latter assumption is incorporated into the modelling. Revisiting these stars would be of great interest to either uncover populations of young stars among the Keplerγ Dor stars or to rectify their asymptotic period-spacing. Stars to the left of the line of unity seem to be not as evolved in the HRD as indicated by their Π0, yet we find no global reasoning that could be applied to all stars to explain their data. However, we note that stars for which we could not recover the luminosity and effective temperature are typically found at the edge of the instability strip in the HRD.

Quantitatively, the luminosity shows the strongest correlation between input and recovered values with a Pearson correlation r = 0.99. The effective temperature is not that well recovered with r = 0.53. Given the often inaccurate effective temperatures from the Gaia catalogue this is not surprising. Despite the obvious horizontal band in the Π0 comparison, we find r = 0.80, due to the well recovered truly evolved stars with a low Π0.

The asteroseismic masses, normalised core hydrogen mass fraction (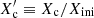 X c ′ ≡ X c / X ini $ X_{\mathrm{c}}^\prime\equiv X_{\mathrm{c}}/X_{\mathrm{ini}} $), and radii are shown in Fig. 4. We find the majority of the stars to have 1.4 ≲ M/M⊙ ≲ 1.7 (see also Mombarg et al. 2024a) and are a significant fraction into their main-sequence evolution but not near their end ( 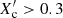X c ′ > 0.3 $ X_{\mathrm{c}}^\prime > 0.3 $). The mean age of our sample is 1.3 Gyr and we indeed find very few young stars (see the discussion above). The more massive stars in our sample tend to be most evolved. Overall, these distributions are in agreement with the position of the γ Dor instability strip (cf. Fig. 2) that is centred on these masses and narrows for evolved stars. Corresponding to the age and mass distributions, the stellar radii are distributed as expected for main-sequence γ Dor stars with the majority in the range 1.5 ≲ R/R⊙ ≲ 2.5. However, the few evolved stars near the end of their main-sequence life time have larger radii.

thumbnail Fig. 4.

Distributions of the grid modelling results. Left: asteroseismic mass against the normalised core hydrogen mass fraction, X c ′ $ X_{\mathrm{c}}^\prime $. We find the majority of stars to have masses between 1.4 and 1.7 M⊙ and to be in the first part of their main-sequence evolution with X c ′ > 0.3 $ X_{\mathrm{c}}^\prime > 0.3 $. Note that the X c ′ ′ $ X_{\mathrm{c}}^\prime $-axis is inverted to represent the time evolution from left to right. Right: radius distribution of our sample. We find only a few evolved stars, and most stars have a radius between 1.5 and 2.2 R⊙, as expected in this mass regime for main-sequence stars.

Our γ Dor sample composed in the previous section is the most homogeneous dataset of red giant progenitors with high-precision asteroseismic observables on the main sequence, covering all possible rotation rates (cf. Fig. 6 in Aerts 2021). As we are interested in the influence of rotation on stellar evolution, we next explored their second asteroseismic parameter, the near-core rotation rate Ωrot. From Fig. 5, we find a decreasing near-core rotation rate with age as previously seen in Li et al. (2020) (as a function of Π0). Asteroseismology applied to stars with a convective core across stellar evolution has shown that quasi-rigid rotation in the radiative envelope is an excellent approximation for the considered mass regime (Aerts et al. 2019; Aerts 2021), particularly for γ Dor stars (Van Reeth et al. 2018; Li et al. 2020; Saio et al. 2021) and can be modelled with an efficient angular momentum transport throughout the star (Mombarg 2023; Moyano et al. 2024).

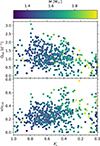thumbnail Fig. 5.

Rotational properties of the sample stars in the context of their evolutionary stage with the age represented by the normalised core hydrogen mass fraction ( X c ′ $ X_{\mathrm{c}}^\prime $). We note the inverted x-axis. Top: near-core rotation rate decreases with age as angular momentum is redistributed in the growing star. Bottom: fraction of the critical rotation rate mostly constant for the majority of stars with 0.1 < v/vcrit < 0.6.

Relying on the asteroseismic mass and radius, we estimated the current ratio between the rotational velocity and the critical velocity (v/vcrit), adopting the Keplerian approximation1 as used in the MESA Isochrones & Stellar Tracks (MIST, Dotter 2016; Choi et al. 2016) models, which rely on the MESA version published by Paxton et al. (2015). We find that very few stars in our sample exceed v/vcrit = 0.6 (Fig. 5). Indeed, the 95th percentile of the data is at v/vcrit = 0.53, while 68% of the stars are slower rotators with 0.15 < v/vcrit < 0.39. The upper boundary of v/vcrit increases with age but we observe only one γ Dor star with a near-critical rotation. In contrast to the trend of the near-core rotation, we find only a slight upward trend for the critical rotation rate with age while the majority of stars can be found at a constant rate v/vcrit ≈ 0.25. This result for field stars is in agreement with the recent findings for the young open cluster NGC 2516 (Li et al. 2024) in which the fastest γ Dor stars rotate at 0.4 v/vcrit.

The results from our grid modelling, as well as the input parameters can be found in Table A.1. Furthermore, we provide v/vcrit and the derived MIST ages at certain evolutionary points.

4. Age-dating the population of successors using MIST models

The main aim of this work is to provide age uncertainties at late stages of stellar evolution by comparing non-rotating and rotating stellar evolution tracks while keeping the other aspects of the microscopic and macroscopic input physics the same. In order to make this comparison, we relied on the often used MIST stellar evolution tracks and isochrones (Dotter 2016; Choi et al. 2016). Using precomputed grids of isochrones to age-date evolved stars is a standard approach in stellar evolution and Galactic archaeology studies.

The original database of MIST models in Choi et al. (2016) has been extended to include rotation velocities ranging from zero velocity (no rotation) to 90% of the Keplerian critical velocity (vcrit) for increasing steps of 10% in v/vcrit by Gossage et al. (2019). The entire MIST database is based on the same input physics for all aspects of the models. It thus allows us to assess the impact of rotation and its induced physical effects from grid-based modelling. The theory of shellular rotation and its accompanying rotational mixing and gravity darkening adopted in the MIST models is described extensively in Paxton et al. (2015), to which we refer for details. We used the rotating MIST models from Gossage et al. (2019) to estimate the effect of rotation on the ages of stars in the mass range M ∈ [1.3, 2.0] M⊙ for their evolved evolutionary phases lying ahead by using the population of asteroseismically studied γ Dor main-sequence stars.

Given the variation of the radius as a star evolves during the main sequence, the critical rotational velocity and hence v/vcrit change as the core hydrogen burning progresses. For each star we chose a family of tracks based on the maximum likelihood point estimator of the asteroseismic mass. Within this family, consisting of ten tracks (0.0 ≤ v/vcrit ≤ 0.9 at ZAMS), we calculated v/vcrit at the grid point closest to the current core hydrogen mass fraction. Finally, we selected the track closest to the observed v/vcrit. Figure 6 shows the distribution of the back-traced (ZAMS) v/vcrit in comparison to the observed current distribution. The current distribution (as observed from the asteroseismic modelling) is broader and shifted slightly to faster rotation as it can also be seen from Fig. 5, when interpreted as an evolutionary sequence.

thumbnail Fig. 6.

Distributions of rotation rates as a fraction of the critical rotation (v/vcrit). The black distribution shows the back-traced initial rotation (at ZAMS). It is compared to the current distribution (orange) as derived from the asteroseismic grid modelling. The stars exhibit slightly larger fractions of the critical rotation velocity with respect to their initial rotation, as expected from the population seen in Fig. 5.

Once having selected the MIST track that comes closest to the asteroseismic v/vcrit and age per star, its ages for future evolutionary stages can easily be acquired by simply considering the equivalent evolutionary point2 (EEP) on the MIST track. We considered the age effects at the terminal-age main sequence (TAMS; EEP 454), the tip of the red giant branch (TRGB; EEP 605), the zero-age helium-burning stage (ZAHeB; EEP 631), and the terminal-age helium-burning stage (TAHeB; EEP 707). For each of these evolutionary points, we also extracted the corresponding age from the non-rotating track of the same mass as the reference value to estimate the effect of internal rotation, by expressing it as a fraction of the stellar age for the non-rotating case. Since rotation introduces extra mixing in the stellar interior, we expect the ages of the stars in evolved phases resulting from the rotating MIST tracks to be above those of the non-rotating tracks.

5. Age shifts in successor populations due to main-sequence rotation

The cores of most single stars born with M ≥ 1.2 M⊙ generally rotate fast during core hydrogen burning because these stars are not slowed down by magnetic braking. As proven by asteroseismology of an ensemble of intermediate-mass field stars, their cores only slow down considerably between the TAMS and the red giant phase (Fig. 6 in Aerts 2021). While it may be justified to ignore the effects of rotation and internal mixing in stellar evolution models of intermediate-mass stars after the TAMS, this is not a good approximation during the initial 90% of their evolution (Johnston 2021). Despite this fact, age-dating of red giants from asteroseismology is usually done by ignoring the cumulative effect of the internal mixing caused by rotation in the progenitor phases (e.g. Martig et al. 2015; Ness et al. 2016; Aguirre Børsen-Koch et al. 2022). Moreover, the core overshooting description used to mimic shear mixing in the core boundary layer is often frozen to just one value in the models used to perform the age-dating of red giants, instead of allowing it to vary during the long main-sequence phase to mimic time-dependent rotational shear mixing as done in this work.

While the latest age-dating methods, such as the one developed by Aguirre Børsen-Koch et al. (2022), can accommodate rotating models, their application to populations of red giants usually ignore the progenitor’s rotational mixing, thereby underestimating the age uncertainties. Recent precision estimations for the ages of red giants with the best asteroseismology available quote ∼11% age uncertainty when ignoring the rotation as of the ZAMS (Montalbán et al. 2021). Large population studies relying on a variety of CoRoT, Kepler, K2, and Transiting Exoplanet Survey Satellite (TESS) data quote larger uncertainties, by up to 25% (Miglio et al. 2021; Stokholm et al. 2023; Willett et al. 2023).

Figure 7 shows the expected relative age differences at the TAMS and the end of the core helium-burning stage (TAHeB) from the rotating and non-rotating MIST models when we propagate the population of γ Dor stars forward towards these evolutionary phases. It can be seen that the age differences between rotating and non-rotating models reach up to 4.5% at TAMS for the fastest rotators but remain modest (below 1%) for the majority of stars for the physics of rotational mixing adopted in the MIST models.

thumbnail Fig. 7.

Relative ages between the rotating and non-rotating MIST tracks (tr/tnr) against stellar mass for two evolutionary points, TAMS (left) and TAHeB (right). The colour-coding gives the ZAMS v/vcrit value. Both distributions are qualitatively similar, although at the TAHeB the median value evolves to higher relative ages.

More specifically, we find a distinct upper envelope of the age spread with stellar mass among the successors of the lowest-mass γ Dor stars. The least massive evolved stars resulting from the main-sequence sample (M ≃ 1.3 M⊙) are hardly affected by the additional rotational mixing, given that their measured rotation rates are close to those of a non-rotating star. Starting from M = 1.4 M⊙, the progenitor stars rotate typically between 5% and 20% of the critical rotation, which adds ≤1% to the stellar age by the end of the main sequence. For more massive progenitor pulsators (M ≥ 1.5 M⊙) the age difference is purely a function of the rotation rate, that is, the distribution of age differences follows the observed distribution of the asteroseismic rotation rates and reaches ∼5%. We point out that, for M > 1.7 M⊙, the sample size of the γ Dor population is small and may not be representative of all stars of such masses.

The distribution stays very similar at later evolutionary stages, although by the end of core helium burning the overall age-spread between slowly and faster rotating γ Dor stars increases as seen from the right panel of Fig. 7. Notably the fastest rotating and most massive star exhibits a smaller relative age at TAHeB compared to the TAMS, contrary to other stars in the sample. The results for the two intermediate stages are shown in Appendix C.

The histograms in Fig. 8 shows the evolution of the relative age distributions at the four considered evolutionary stages. As discussed above, the TAMS distribution shows the smallest relative age differences with a strong peak in the smallest bin, while the distributions are somewhat wider at later stages.

thumbnail Fig. 8.

Histogram of the relative ages between rotating and non-rotating models at different evolutionary stages. The majority of red giant ages are underestimated by a few percent under the assumption of non-rotating models. The TRGB distribution is indistinguishable from the distribution at ZAHeB and hence not visible.

Our results reflect that rotational mixing is an important transport process throughout the long main-sequence evolution, which lasts about 90% of the entire lifetime of the star before it turns into a red giant and evolves further towards the white dwarf stage. Nevertheless, additional transport processes occurring specifically during the red giant phase (such as thermohaline mixing) and not considered here should also be taken into account in the determination of ages for the highest-precision Galactic archaeology based on surface abundances and asteroseismology together (Lagarde et al. 2017).

6. Additional systematic uncertainties

6.1. For the asteroseismic parameters

Recent computational work by Mombarg et al. (2024a) has shown that it is in principle possible to perform asteroseismic modelling of intermediate-mass stars from rotating stellar models. The 1D models delivered by Mombarg et al. (2022) circumvent the spiky internal mixing profiles that occur when using the 1D prescriptions from Heger et al. (2000), causing inaccuracies in the computation of oscillation modes. Mombarg et al. (2022) rely on a 1D formalism of Zahn (1992) for the implementation of rotational mixing in their models, while this is done self-consistently in 2D by Mombarg et al. (2023, 2024b). In the 1D case, the rotational profile used for computing the efficiency of rotational mixing comes from models computed with the 2D ESTER evolution code (Espinosa Lara & Rieutord 2013; Rieutord et al. 2016). The 2D-to-1D ESTER-informed mixing profile adopted in MESA evolution models brings a potential improvement of major importance in asteroseismic modelling of intermediate-mass stars with respect to the simplistic 1D treatment of chemical mixing by means of a constant and ad hoc core overshooting description as done in the literature (Aerts 2021) and adopted in Sect. 2.

Here, we provide grid-based modelling for our γ Dor sample by using a 2D-to-1D model grid from Mombarg et al. (2024a), which differs from the previously employed MESA grid by the inclusion of angular momentum transport mechanisms. This rotational mixing replaces the constant envelope mixing (Dmix) in the above used models. The angular momentum transport is implemented as diffusive processes and includes dynamical and secular shear instability, Eddington-Sweet circulation, Solberg-Høiland instability, Goldreich-Schubert-Fricke instability, and a Spruit-Tayler dynamo for angular momentum transport via magnetic torques. We refer the reader to Heger et al. (2000) and the MESA instrumentation papers (Paxton et al. 2011, 2013, 2015, 2018, 2019) for details on these processes and their implementation in MESA. Mombarg (2023) calibrated the angular momentum transport from several slowly rotating, well-studied γ Dor stars with known near-core and surface rotation rates. Their new model grid is regularly sampled with M ∈ [1.3, 2.0] (ΔM = 0.1 M⊙), fov ∈ [0.005, 0.035] (Δfov = 0.005), Ω/Ωcrit ∈ [0.05, 0.6] (ΔΩ/Ωcrit = 0.05), and fixed a metallicity Z = 0.014. The grid is more sparsely sampled than the non-rotating grid used above.

We applied these rotating models to our sample in the same way as outlined in Sects. 2–5 but included the measured asteroseismic near-core rotation rate as an additional input constraint. The stellar parameters obtained from this model are comparable to those from our previous analysis. On a star-to-star basis, shifts in the core hydrogen mass fraction are often compensated by changes in the core-overshoot and stellar mass. In combinations this results only in slight changes the evolution of the stellar properties with age as discussed in Fig. 5. Furthermore, the initial distribution of rotation rates is similar to our previous results (for a more detailed analysis of the initial rotation rates we refer the reader to Mombarg et al. 2024a).

With only minor shifts in the overall asteroseismic stellar parameters compared to our initial model, in which the mixing due to rotation was modelled with additional core overshoot, we do not find significant difference for the MIST-based ages at later evolutionary stages with respect to the analysis above. Some stars have slightly different relative ages at the four considered evolutionary points, yet the overall distribution hardly changes. This illustrates that mimicking element transport processes by a fudge factor in the overshoot zone is a valid approach, as long as the chemical mixing can be described diffusively (cf. Aerts 2021).

6.2. From evolution models with meridional circulation

In contrast to the MIST models computed with the code MESA, which adopts a diffusive approach and treats the rotationally induced mixing and angular momentum processes as described in Heger et al. (2000), other stellar evolution models rely on a diffusive-advective treatment. Such a treatment allows for the inclusion of meridional circulation, often implemented following the theory by Maeder & Zahn (1998). Here we relied on the publicly available Geneva models computed by Georgy et al. (2013) to assess the systematic age uncertainty caused by the different input physics to treat rotation.

Ouazzani et al. (2019) have shown from asteroseismology of γ Dor stars that their diffusive-advective models computed with the CESTAM code, which also relies on the theory by Maeder & Zahn (1998), need fixes in terms of angular momentum transport. Better agreement between models and asteroseismic data has been achieved by Moyano et al. (2023, 2024) from the inclusion of internal magnetism in the Geneva code, in addition to meridional circulation and shear mixing. However, neither these new Geneva models nor the CESTAM ones are publicly available. For this reason, we assessed the age uncertainty due to absence or inclusion of meridional circulation by comparing the results from the MIST models with those derived from the SCYLIST Geneva models made publicly available by Georgy et al. (2013). The use of these two sets of isochrones and stellar tracks is common to age-date stars.

It has already been shown that the inclusion of meridional circulation can result in significant differences of the evolutionary tracks of rotating models beyond the TAMS (Martins & Palacios 2013). The influence of rotation on luminosity and temperature are analysed in detail in Choi et al. (2016) and Gossage et al. (2018). We deduce from Fig. 20 of Choi et al. (2016) that the ages between rotating MIST models and Geneva models are quite different for stars with M < 3 M⊙, the mass range considered in this work.

For the models with a mass of 1.7 M⊙, which is the lowest mass in the publicly available grid of rotating Geneva models computed by Georgy et al. (2013), we find a relative age difference of 10% for v/vcrit = 0.2 at the TRGB compared to the non-rotating model, while this difference increases to 20% for v/vcrit = 0.4. These values are significantly larger than in the MIST case, for which we found 1% and 2%, respectively. When comparing ages obtained from the MIST models to these from the Geneva models, we find a very similar TRGB age in the non-rotating case, albeit a smaller TAMS age. Yet, in the Geneva case the main-sequence lifetime is extended by ∼30% for v/vcrit = 0.4, resulting in a large relative age difference at the TRGB.

We conclude that different input physics for angular momentum and/or element transport, notably the inclusion of meridional circulation due to rotation or not, may add significant systematic uncertainties in red giant ages when taking into account the rotation in their progenitor phases.

6.3. Sample selection

For this study, we employed the largest homogeneous sample of γ Dor stars with Π0 and Ωrot estimates available in the literature, in order to assess the influence of rotation on the age distribution of red giants. Despite being the largest such sample, it is still small compared to the overall stellar population and selection effects might influence our results.

The Kepler field contains mostly older field stars (Berger et al. 2020), as also seen from Fig. 4. Hence, we are missing the youngest γ Dor stars in our analysis and our sample might not represent the full variety of γ Dor stars. Future, large-scale studies similar to Li et al. (2020) with stars observed with TESS might provide insights into a younger population of γ Dor stars since the TESS continuous viewing zone contains a much younger population of stars than the Kepler field (Avallone et al. 2022).

Aerts et al. (2023) present distributions of stellar parameters for a much larger sample of 11 636 γ Dor star candidates identified from Gaia photometry (Gaia Collaboration 2023b). Our distributions of stellar parameters (Teff, log L/L⊙, R/R⊙) are in qualitative agreement with these results. The majority of these stars are currently being analysed in detail from high-cadence TESS space photometry to confirm their γ Dor nature (Hey & Aerts, in prep.) but we do not yet possess asteroseismic parameters such as Π0 and Ωrot for them. The stars from this sample (next to stars in the TESS continuous viewing zones) are prime targets for future population studies with TESS.

6.4. Insights from more massive stars

Since we focused our analysis on γ Dor stars, our sample has a very limited mass-range. The results of our grid modelling place most of the stars in the range 1.4 M⊙ ≤ M ≤ 1.7 M⊙, which coincides with the centre of the γ Dor instability strip. As seen from Fig. 5 the stars in our sample are mostly moderate rotators while higher-mass stars often rotate at higher fractions of the critical velocity. Similar to the sample of γ Dor stars, Pedersen et al. (2021) homogeneously analysed a sample of 26 slowly pulsating B (SPB) stars from the Kepler mission with asteroseismic forward modelling.

We placed the updated results for this sample from Pedersen (2022) on the MIST tracks in a similar fashion to our analysis above. Since we have only a small sample, we cannot deduce a statistically meaningful result. Yet, we find a similar relative age difference of 2 − 3% for the majority of slowly rotating stars (v/vcrit ≤ 0.5). However, near-critical rotation is a common phenomenon among B stars (Townsend et al. 2004) and some stars in the sample of Pedersen (2022) rotate with v/vcrit > 0.7. For these stars the main-sequence lifetime is extended by up to 50% at M ≈ 4 M⊙. While this is a higher mass than for most red giant stars, we have seen that the prolonged main sequence for the more massive γ Dor stars is mainly a function of the rotation rate and not so much of the mass. Hence, the distribution of the rotation rates of lower-mass SPB stars might be directly transferable to a distribution of age uncertainties for the mass regime [2, 4] M⊙.

7. Conclusions

Based on 490 γ Dor stars with homogeneously deduced astrophysical parameters from Gaia DR3 and 4-year Kepler light curves, we characterised the population of red giant progenitors with masses in the range 1.3 ≤ M/M⊙ ≤ 2.0. We employed asteroseismic grid modelling and obtained the masses, the current core hydrogen mass fractions, and the radii for these stars. Together with the asteroseismic near-core rotation rate, we adopted a common approach to age-dating stars and placed the sample stars on rotating MIST evolutionary tracks.

The current population of γ Dor stars show a moderate rotation, with 0.15 ≲ v/vcrit ≲ 0.4 for the majority of stars. When comparing the influence of this rotation to age-dating at later stages of their evolution, we find a modest increase in the age. However, the fastest rotators can be up to 5% older when leaving the main sequence. Typical fast rotation (v/vcrit ∼ 0.4) increases the main-sequence age by 2% in models that rely on the transport processes adopted in the MESA stellar evolution code, but can reach up to 20% for models that include meridional circulation.

Given the unknown rotation history of isolated red giants in the Milky Way, the age spreads caused by their rotating progenitors as presented here should always be considered in the uncertainty analysis for (asteroseismic) red giant ages. Effects of core boundary mixing during core helium burning are nowadays taken into account in the construction of red giant models calibrated by asteroseismology (Constantino et al. 2015; Bossini et al. 2017; Noll et al. 2024). Yet the rotational mixing during the long main-sequence phase is usually ignored despite it having a major impact on the size and mass of the helium core by the TAMS (Johnston 2021; Pedersen 2022). As we have shown here, the rotation during the main sequence also impacts the age by the time the star is a red giant. Our work shows the importance of taking into account transport processes in the stellar interior during the entire main sequence when age-dating red giants for high-precision Galactic archaeological studies. Asteroseismology of young and medium-aged open clusters with a variety of metallicities and both main sequence and red giant pulsators among their members offers the best way to calibrate internal mixing and angular momentum transport processes across the entire nuclear evolution phases of intermediate-mass stars (see Fritzewski et al. 2024; Li et al. 2024, for initial attempts of such modelling).

1

For this estimation, we used the mass and radius from the non-rotating asteroseismic models.

2

The EEPs describe the stellar evolution in a time-independent way to simplify the comparison between models with different physical properties (see Dotter 2016, for more details).

Acknowledgments

The authors appreciate the swift report and encouraging words from the anonymous referee. C.A. is grateful to Melissa Ness and Danny Horta for pleasant and valuable discussions on Galactic archaeology. The research leading to these results has received funding from the KU Leuven Research Council (grant C16/18/005: PARADISE). C.A. also acknowledges financial support from the European Research Council (ERC) under the Horizon Europe programme (Synergy Grant agreement N°101071505: 4D-STAR). While partially funded by the European Union, views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. J.S.G.M. acknowledges funding from the French Agence Nationale de la Recherche (ANR), under grant MASSIF (ANR-21-CE31-0018-02). This research has made use of NASA’s Astrophysics Data System Bibliographic Services and of the SIMBAD database and the VizieR catalogue access tool, operated at CDS, Strasbourg, France. This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement. Software: This work made use of Topcat (Taylor 2005). This research made use of the following Python packages: IPython (Pérez & Granger 2007); MatPlotLib (Hunter 2007); NumPy (Harris et al. 2020); Pandas (McKinney 2010); SciPy (Virtanen et al. 2020).

References

  1. Aerts, C. 2021, Rev. Mod. Phys., 93, 015001 [Google Scholar]
  2. Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Heidelberg: Springer-Verlag) [Google Scholar]
  3. Aerts, C., Molenberghs, G., Michielsen, M., et al. 2018, ApJS, 237, 15 [Google Scholar]
  4. Aerts, C., Mathis, S., & Rogers, T. M. 2019, ARA&A, 57, 35 [Google Scholar]
  5. Aerts, C., Augustson, K., Mathis, S., et al. 2021, A&A, 656, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aerts, C., Molenberghs, G., & De Ridder, J. 2023, A&A, 672, A183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Aguirre Børsen-Koch, V., Rørsted, J. L., Justesen, A. B., et al. 2022, MNRAS, 509, 4344 [Google Scholar]
  8. Avallone, E. A., Tayar, J. N., van Saders, J. L., et al. 2022, ApJ, 930, 7 [NASA ADS] [CrossRef] [Google Scholar]
  9. Barnes, S. A. 2007, ApJ, 669, 1167 [Google Scholar]
  10. Barnes, S. A., Weingrill, J., Fritzewski, D., Strassmeier, K. G., & Platais, I. 2016, ApJ, 823, 16 [Google Scholar]
  11. Berger, T. A., Huber, D., van Saders, J. L., et al. 2020, AJ, 159, 280 [Google Scholar]
  12. Böhm-Vitense, E. 1958, Z. Astrophys., 46, 108 [Google Scholar]
  13. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [Google Scholar]
  14. Bossini, D., Miglio, A., Salaris, M., et al. 2017, MNRAS, 469, 4718 [Google Scholar]
  15. Bovy, J., Rix, H.-W., Schlafly, E. F., et al. 2016, ApJ, 823, 30 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chiappini, C., Anders, F., Rodrigues, T. S., et al. 2015, A&A, 576, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102 [Google Scholar]
  18. Constantino, T., Campbell, S. W., Christensen-Dalsgaard, J., Lattanzio, J. C., & Stello, D. 2015, MNRAS, 452, 123 [Google Scholar]
  19. Creevey, O. L., Sordo, R., Pailler, F., et al. 2023, A&A, 674, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  20. De Silva, G. M., Freeman, K. C., Bland-Hawthorn, J., et al. 2015, MNRAS, 449, 2604 [NASA ADS] [CrossRef] [Google Scholar]
  21. Dotter, A. 2016, ApJS, 222, 8 [Google Scholar]
  22. Dupret, M. A., Grigahcène, A., Garrido, R., Gabriel, M., & Scuflaire, R. 2005, A&A, 435, 927 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Espinosa Lara, F., & Rieutord, M. 2013, A&A, 552, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Fritzewski, D. J., Van Reeth, T., Aerts, C., et al. 2024, A&A, 681, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Gaia Collaboration (Vallenari, A., et al.) 2023a, A&A, 674, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Gaia Collaboration (De Ridder, J., et al.) 2023b, A&A, 674, A36 [CrossRef] [EDP Sciences] [Google Scholar]
  27. Gebruers, S., Straumit, I., Tkachenko, A., et al. 2021, A&A, 650, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Georgy, C., Ekström, S., Granada, A., et al. 2013, A&A, 553, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Gossage, S., Conroy, C., Dotter, A., et al. 2018, ApJ, 863, 67 [Google Scholar]
  30. Gossage, S., Conroy, C., Dotter, A., et al. 2019, ApJ, 887, 199 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hall, O. J., Davies, G. R., van Saders, J., et al. 2021, Nat. Astron., 5, 707 [NASA ADS] [CrossRef] [Google Scholar]
  32. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [Google Scholar]
  33. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  34. Helmi, A., Babusiaux, C., Koppelman, H. H., et al. 2018, Nature, 563, 85 [Google Scholar]
  35. Hon, M., Huber, D., Kuszlewicz, J. S., et al. 2021, ApJ, 919, 131 [NASA ADS] [CrossRef] [Google Scholar]
  36. Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
  37. Johnston, C. 2021, A&A, 655, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Lagarde, N., Robin, A. C., Reylé, C., & Nasello, G. 2017, A&A, 601, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  39. Li, G., Van Reeth, T., Bedding, T. R., et al. 2020, MNRAS, 491, 3586 [Google Scholar]
  40. Li, G., Aerts, C., Bedding, T. R., et al. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202348901 [Google Scholar]
  41. Maeder, A., & Zahn, J.-P. 1998, A&A, 334, 1000 [NASA ADS] [Google Scholar]
  42. Martig, M., Rix, H.-W., Silva Aguirre, V., et al. 2015, MNRAS, 451, 2230 [NASA ADS] [CrossRef] [Google Scholar]
  43. Martins, F., & Palacios, A. 2013, A&A, 560, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
  45. Meibom, S., Barnes, S. A., Latham, D. W., et al. 2011a, ApJ, 733, L9 [Google Scholar]
  46. Meibom, S., Mathieu, R. D., Stassun, K. G., Liebesny, P., & Saar, S. H. 2011b, ApJ, 733, 115 [NASA ADS] [CrossRef] [Google Scholar]
  47. Meibom, S., Barnes, S. A., Platais, I., et al. 2015, Nature, 517, 589 [Google Scholar]
  48. Miglio, A., Chiappini, C., Morel, T., et al. 2013, MNRAS, 429, 423 [Google Scholar]
  49. Miglio, A., Girardi, L., Grundahl, F., et al. 2021, Exp. Astron., 51, 963 [NASA ADS] [CrossRef] [Google Scholar]
  50. Mombarg, J. S. G. 2023, A&A, 677, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Mombarg, J. S. G., Van Reeth, T., Pedersen, M. G., et al. 2019, MNRAS, 485, 3248 [NASA ADS] [CrossRef] [Google Scholar]
  52. Mombarg, J. S. G., Van Reeth, T., & Aerts, C. 2021, A&A, 650, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Mombarg, J. S. G., Dotter, A., Rieutord, M., et al. 2022, ApJ, 925, 154 [NASA ADS] [CrossRef] [Google Scholar]
  54. Mombarg, J. S. G., Rieutord, M., & Espinosa Lara, F. 2023, A&A, 677, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Mombarg, J. S. G., Aerts, C., & Molenberghs, G. 2024a, A&A, in press https://doi.org/10.1051/0004-6361/202449213 [Google Scholar]
  56. Mombarg, J. S. G., Rieutord, M., & Espinosa Lara, F. 2024b, A&A, 683, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Montalbán, J., Miglio, A., Noels, A., et al. 2013, ApJ, 766, 118 [Google Scholar]
  58. Montalbán, J., Mackereth, J. T., Miglio, A., et al. 2021, Nat. Astron., 5, 640 [Google Scholar]
  59. Moyano, F. D., Eggenberger, P., Salmon, S. J. A. J., Mombarg, J. S. G., & Ekström, S. 2023, A&A, 677, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Moyano, F. D., Eggenberger, P., & Salmon, S. J. A. J. 2024, A&A, 681, L16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Ness, M., Hogg, D. W., Rix, H. W., et al. 2016, ApJ, 823, 114 [NASA ADS] [CrossRef] [Google Scholar]
  62. Noll, A., Basu, S., & Hekker, S. 2024, A&A, 683, A189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Ouazzani, R. M., Marques, J. P., Goupil, M. J., et al. 2019, A&A, 626, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  64. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  65. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  66. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  67. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  68. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  69. Pedersen, M. G. 2022, ApJ, 930, 94 [NASA ADS] [CrossRef] [Google Scholar]
  70. Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., 5, 715 [NASA ADS] [CrossRef] [Google Scholar]
  71. Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
  72. Rieutord, M., Espinosa Lara, F., & Putigny, B. 2016, J. Comput. Phys., 318, 277 [NASA ADS] [CrossRef] [Google Scholar]
  73. Rojas-Arriagada, A., Recio-Blanco, A., de Laverny, P., et al. 2017, A&A, 601, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Saio, H., Takata, M., Lee, U., Li, G., & Van Reeth, T. 2021, MNRAS, 502, 5856 [Google Scholar]
  75. Schiavon, R. P., Zamora, O., Carrera, R., et al. 2017, MNRAS, 465, 501 [Google Scholar]
  76. Silva Aguirre, V., Bojsen-Hansen, M., Slumstrup, D., et al. 2018, MNRAS, 475, 5487 [NASA ADS] [Google Scholar]
  77. Stokholm, A., Aguirre Børsen-Koch, V., Stello, D., Hon, M., & Reyes, C. 2023, MNRAS, 524, 1634 [NASA ADS] [CrossRef] [Google Scholar]
  78. Taylor, M. B. 2005, in Astronomical Data Analysis Software and Systems XIV, eds. P. Shopbell, M. Britton, & R. Ebert, ASP Conf. Ser., 347, 29 [Google Scholar]
  79. Townsend, R. H. D., Owocki, S. P., & Howarth, I. D. 2004, MNRAS, 350, 189 [Google Scholar]
  80. Van Reeth, T., Tkachenko, A., Aerts, C., et al. 2015, ApJS, 218, 27 [Google Scholar]
  81. Van Reeth, T., Tkachenko, A., & Aerts, C. 2016, A&A, 593, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Van Reeth, T., Mombarg, J. S. G., Mathis, S., et al. 2018, A&A, 618, A24 [NASA ADS] [EDP Sciences] [Google Scholar]
  83. van Saders, J. L., Ceillier, T., Metcalfe, T. S., et al. 2016, Nature, 529, 181 [Google Scholar]
  84. Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
  85. Vitali, S., Slumstrup, D., Jofré, P., et al. 2024, A&A, submitted [arXiv:2401.02328] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Wang, K., Ren, A., Andersen, M. F., et al. 2023, AJ, 166, 42 [NASA ADS] [CrossRef] [Google Scholar]
  87. Willett, E., Miglio, A., Mackereth, J. T., et al. 2023, MNRAS, 526, 2141 [NASA ADS] [CrossRef] [Google Scholar]
  88. Zahn, J. P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]

Appendix A: Supplementary table

Table A.1 provides the input parameters and asteroseismically determined parameters for the 490 analysed γ Dor stars.

Table A.1.

Input parameters and asteroseismically determined parameters for the 490 analysed γ Dor stars.

Appendix B: Comparison between asteroseismically informed grid modelling and the Gaia-FLAME results

The Gaia-FLAME parameters in the astrophysical parameter tables of Gaia DR3 do not only include the above mentioned luminosity but also estimates of the stellar mass, radius, and age for most of the observed stars. In Fig. B.1, we show these three parameters in comparison to our asteroseismically inferred values. Both the masses and the radii are overall in good agreement, while the ages estimated from both methods diverge.

thumbnail Fig. B.1.

Comparison between asteroseismic parameter estimates and the Gaia-FLAME values. Left: Stellar mass estimate from our analysis. It is mostly consistent with the FLAME pipeline. However, there is a slight systematic offset to lower masses in our analysis. Centre: Most radii agree between the two methods, while some outliers with large radii from the asteroseismic analysis can be found. These stars typically have a higher asteroseismic age and are more evolved in our analysis. Right: Additional asteroseismic information from Π0 gives a good handle on the stellar age. Consequently, we observe a large scatter and a larger spread in age compared to Gaia-FLAME.

Despite being in good agreement, we find that on average the asteroseismic mass is slightly lower than the FLAME mass. This offset can mainly be attributed to the different underlying stellar models. The outliers in the left panel of Fig. B.1 are at the same level as seen in previous comparisons in the main text.

The radii are also in good agreement between the two methods. However, we find more outliers with larger asteroseismic radii. These are stars are likely more evolved in our model.

The ages are not in a good agreement between our asteroseismically informed model and FLAME. While the ages from the FLAME pipeline are mostly constrained between 0.5 and 2 Gyr, our results are between 0 and 3 Gyr. The colour gradient in right panel of Fig. B.1 shows that the additional constraint from Π0 has great probing power for stellar ages.

Appendix C: Age spread at different evolutionary points

We analysed the relative ages not only at the end of the core hydrogen and core helium burning but also at the TRGB and the beginning of the core helium burning. Fig. C.1 shows the distributions for these two evolutionary stages. As already seen from the histogram in Fig. 8 the distributions are very similar with a very slight evolution between them.

thumbnail Fig. C.1.

Relative ages at TRGB (left) and the ZAHeB (right) when comparing rotating and non-rotating models (similar to Fig. 7).

All Tables

Table A.1.

Input parameters and asteroseismically determined parameters for the 490 analysed γ Dor stars.

In the text

All Figures

thumbnail Fig. 1.

Comparison between luminosity values obtained from the Gaia absolute G magnitude (photometric luminosity) and the model-dependent Gaia-FLAME. The dashed line is the bisector.
In the text
thumbnail Fig. 2.

Hertzsprung-Russell diagram of our final sample, which contains 490 γ Dor stars. The colour-coding gives the Π0, which is used as an input parameter in the grid modelling. The solid lines indicate the theoretical γ Dor instability strip from Dupret et al. (2005) with a mixing-length parameter αMLT = 2, while the dashed and dotted lines show the position of the instability strip for αMLT = 1.5 and αMLT = 1, respectively.
In the text
thumbnail Fig. 3.

Correlations between observed properties (input values) and the recovered values (model). From left to right, we show log L/L⊙, Teff, and Π0. Notably, outliers in one panel are not necessarily outliers in other panels. To show this property, we highlight the three most outlying points (the difference divided by the measurement uncertainty) in each panel with colour and indicate the same stars with coloured outlines in the other two panels. Outliers in luminosity are shown in orange, outliers in effective temperature in blue, and outliers in Π0 in green. The shift towards intermediate Π0 is discussed in the main text.
In the text
thumbnail Fig. 4.

Distributions of the grid modelling results. Left: asteroseismic mass against the normalised core hydrogen mass fraction, X c ′ $ X_{\mathrm{c}}^\prime $. We find the majority of stars to have masses between 1.4 and 1.7 M⊙ and to be in the first part of their main-sequence evolution with X c ′ > 0.3 $ X_{\mathrm{c}}^\prime > 0.3 $. Note that the X c ′ ′ $ X_{\mathrm{c}}^\prime $-axis is inverted to represent the time evolution from left to right. Right: radius distribution of our sample. We find only a few evolved stars, and most stars have a radius between 1.5 and 2.2 R⊙, as expected in this mass regime for main-sequence stars.
In the text
thumbnail Fig. 5.

Rotational properties of the sample stars in the context of their evolutionary stage with the age represented by the normalised core hydrogen mass fraction ( X c ′ $ X_{\mathrm{c}}^\prime $). We note the inverted x-axis. Top: near-core rotation rate decreases with age as angular momentum is redistributed in the growing star. Bottom: fraction of the critical rotation rate mostly constant for the majority of stars with 0.1 < v/vcrit < 0.6.
In the text
thumbnail Fig. 6.

Distributions of rotation rates as a fraction of the critical rotation (v/vcrit). The black distribution shows the back-traced initial rotation (at ZAMS). It is compared to the current distribution (orange) as derived from the asteroseismic grid modelling. The stars exhibit slightly larger fractions of the critical rotation velocity with respect to their initial rotation, as expected from the population seen in Fig. 5.
In the text
thumbnail Fig. 7.

Relative ages between the rotating and non-rotating MIST tracks (tr/tnr) against stellar mass for two evolutionary points, TAMS (left) and TAHeB (right). The colour-coding gives the ZAMS v/vcrit value. Both distributions are qualitatively similar, although at the TAHeB the median value evolves to higher relative ages.
In the text
thumbnail Fig. 8.

Histogram of the relative ages between rotating and non-rotating models at different evolutionary stages. The majority of red giant ages are underestimated by a few percent under the assumption of non-rotating models. The TRGB distribution is indistinguishable from the distribution at ZAHeB and hence not visible.
In the text
thumbnail Fig. B.1.

Comparison between asteroseismic parameter estimates and the Gaia-FLAME values. Left: Stellar mass estimate from our analysis. It is mostly consistent with the FLAME pipeline. However, there is a slight systematic offset to lower masses in our analysis. Centre: Most radii agree between the two methods, while some outliers with large radii from the asteroseismic analysis can be found. These stars typically have a higher asteroseismic age and are more evolved in our analysis. Right: Additional asteroseismic information from Π0 gives a good handle on the stellar age. Consequently, we observe a large scatter and a larger spread in age compared to Gaia-FLAME.
In the text
thumbnail Fig. C.1.

Relative ages at TRGB (left) and the ZAHeB (right) when comparing rotating and non-rotating models (similar to Fig. 7).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.