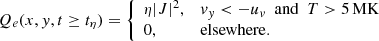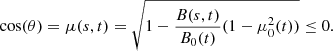| Issue |
A&A
Volume 684, April 2024
|
|
|---|---|---|
| Article Number | A171 | |
| Number of page(s) | 26 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202347600 | |
| Published online | 19 April 2024 | |
Exploring self-consistent 2.5D flare simulations with MPI-AMRVAC⋆
Centre for mathematical Plasma Astrophysics, Department of Mathematics, KU Leuven, Celestijnenlaan 200B, 3001 Leuven, Belgium
e-mail: malcolm.druett@kuleuven.be
Received:
28
July
2023
Accepted:
1
February
2024
Context. Multidimensional solar flare simulations have not yet included a detailed analysis of the lower atmospheric responses, such as downflowing chromospheric compressions and chromospheric evaporation processes.
Aims. We present an analysis of multidimensional flare simulations, including an analysis of chromospheric upflows and downflows that provides important groundwork for comparing 1D and multidimensional models.
Methods. We followed the evolution of a magnetohydrodynamic standard solar flare model that includes electron beams and in which localized anomalous resistivity initiates magnetic reconnection. We varied the background magnetic field strength to produce simulations that cover a large span of observationally reported solar flare strengths. Chromospheric energy fluxes and energy density maps were used to analyze the transport of energy from the corona to the lower atmosphere, and the resultant evolution of the flare. Quantities traced along 1D field lines allowed for detailed comparisons with 1D evaporation models.
Results. The flares produced by varying the background coronal field strength between 20 G and 65 G have GOES classifications between B1.5 and M2.3. All produce a lobster claw reconnection outflow and a fast shock in the tail of this flow with a similar maximum Alfvén Mach number of ∼10. The impact of the reconnection outflow on the lower atmosphere and the heat conduction are the key agents driving the chromospheric evaporation and “downflowing chromospheric compressions”. The peak electron beam heating flux in the lower atmospheres varies between 1.4 × 109 and 4.7 × 1010 erg cm−2 s−1 across the simulations. The downflowing chromospheric compressions have kinetic energy signatures that reach the photosphere, but at subsonic speeds they would not generate sunquakes. The weakest flare generates a relatively dense flare loop system, despite having a negative net mass flux, through the top of the chromosphere, that is to say, more mass is supplied downward than is evaporated upward. The stronger flares all produce positive mass fluxes. Plasmoids form in the current sheets of the stronger flares due to tearing, and in all experiments the loop tops contain turbulent eddies that ring via a magnetic tuning fork process.
Conclusions. The presented flares have chromospheric evaporation driven by thermal conduction and the impact and rebound of the reconnection outflow, in contrast to most 1D models where this process is driven by the beam electrons. Several multidimensional phenomena are critical in determining plasma behavior but are not generally considered in 1D flare simulations. They include loop-top turbulence, reconnection outflow jets, heat diffusion, compressive heating from the multidimensional expansion of the flux tubes due to changing pressures, and the interactions of upward and downward flows from the evaporation meeting the material squeezed downward from the loop tops.
Key words: magnetohydrodynamics (MHD) / Sun: chromosphere / Sun: corona / Sun: flares / Sun: magnetic fields / Sun: photosphere
Movies are available at https://www.aanda.org.
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
In this paper we present multidimensional simulations of solar flares, with a focus on the lower atmospheric dynamics that result from the coronal energy release.
The first solar flare models based on magnetic reconnection (Sweet 1958; Petschek 1964) were developed in the mid 1900s (Parker 1963; Carmichael 1964; Sturrock 1966) and led to the so-called standard CSHKP flare model (CSHKP being the initials of the surnames of major contributors, Sturrock 1992; Shibata 1996). These models explained generalized observed behaviors of solar flares using the release of stored magnetic energy through magnetic reconnection events (see Fig. 1). This cartoon model has been expanded upon by many works, which are summarized well in Priest & Forbes (2002). Subsequent 3D models have stressed the role of current concentrations and quasi-separatrix layers (Aulanier et al. 2012, 2013; Janvier et al. 2013, 2014).
 |
Fig. 1. Standard solar flare model. Left: Standard solar flare model in 2D, with features labeled as per the numbered points in Sect. 1, namely (1) a flux rope running normal to the plane of the cross section, (2) reconnecting field lines at an X point, (3) reconnection outflow jets, (4) reconnected hot loops that gather below the X point, (5) a termination shock, (6) field-aligned transport of energy down to the lower atmosphere (7) flare ribbons, and (8) chromospheric evaporation and downflowing chromospheric compressions. Right: Images of a solar flare over the solar limb taken with the Atmospheric Imaging Assembly (AIA) aboard the Solar Dynamics Observatory (SDO, Lemen et al. 2012) on September 10, 2017, showing the form of the standard solar flare model early in the flare (at 15:51:43 UT) in the 193 Å channel, with the loop arches at the base (green arrows) and a flux rope above it (blue arrows). Slightly later (at 15:53:20 UT) we see the flux rope erupting (moving upward). Later (at 16:18:07 UT) the flux rope has left the field of view and we see emission that is interpreted as originating from the long bright current sheet (red arrows) and dense coronal flare loops below (green arrows). These images use the short exposure AIA filters but still display significant fringe artifacts emanating outward from the bright loop arches. |
The 2.5D simulations in this work present much simpler magnetic topologies than those in 3D models but account for all the relevant thermodynamic processes and the effects of electron beams. Common features of such cross sections through solar flare models include:
-
A flux rope that runs perpendicular to the 2.5D cross section and an underlying sheared flare loop arcade with a reconnection site in between (Sturrock 1992; Shibata 1996). In eruptive flares, this flux rope is ejected outward (upward).
-
A magnetic X point below the flux rope, where successive field lines are drawn inward, reconnected, and ejected outward.
-
Fast reconnection outflow jets from the X point, in the orientation of the current sheet, one of which is directed toward the solar surface (Petschek 1964). These shocks can take a lobster claw form during the initial ejection (Zenitani & Miyoshi 2011).
-
Reconnected loops, ejected toward the surface. They group together below the X point and form hot coronal loop arcades (Sturrock 1966; Shibata 1996).
-
The outflow jets become super-Alfvénic and establish slow-mode shocks at their edges. A fast-mode termination shock forms at the interface between the core of the outflows and the hot coronal loop arcade below (Shibata 1996; Yokoyama & Shibata 2001; Ruan et al. 2020, 2023; Shen et al. 2022).
-
Energy is liberated from the magnetic field at the reconnection X point and potentially in a number of other larger volumes throughout the flare loop system, for example in slow shocks in the reconnection jets (Petschek 1964; Priest & Forbes 2002). The liberated energy is converted into many forms, including heat; models show that a significant fraction can be converted into the acceleration of high-energy nonthermal particles (Rowan et al. 2017; Werner et al. 2018; Hoshino 2023). Energy is transported from the neighborhood of the X point and the hot coronal loop tops, along magnetic field lines and toward chromospheric footpoints near the surface of the Sun. There are many proposed processes for this transport (see the review by Zharkova et al. 2011). A key process is energetic particle acceleration (electrons and ions) along the field lines (Syrovatskii & Shmeleva 1972; Emslie 1978; Holman et al. 2011; Kong et al. 2022), with the acceleration mechanism falling into three broad categories: direct current electric field acceleration by an electric field above the Dreicer limit (Dreicer 1959, 1960), shock acceleration (Ellison & Ramaty 1985), and turbulent or stochastic acceleration (Miller et al. 1996; Cargill et al. 2012; Kontar et al. 2017), including via the Kelvin Helmholtz instability in turbulent loop tops (Fang et al. 2016; Ruan et al. 2018). Other energy transport mechanisms that will be present include thermal conduction predominantly parallel to the field lines (Spitzer 1962; Spitzer & Tomasko 1968; Spitzer & Scott 1969) and Alfvén waves (Fletcher & Hudson 2008).
-
Flare ribbons are the chromospheric locations where much of the released magnetic energy is deposited. This energy heats and excites the plasma, producing increased emission. Hard X-ray (HXR) sources are generally most intense in footpoints of the flare loops. HXR sources are believed to result from the bremsstrahlung of nonthermal (high-energy) electrons that lose their energy in collisions with the ambient thermal plasma. These energetic nonthermal distributions of particles are believed to accelerate near the X point and may also be accelerated in the termination shock and the turbulent reconnection that occurs in the tops of the loop arcades or in multistage acceleration processes (Holman et al. 2011; Zharkova et al. 2011; Kong et al. 2019, 2020).
-
The energy released in the flare loop footpoints causes hot upflows (chromospheric evaporation) and cooler downflowing “chromospheric compressions” toward the solar surface. The chromospheric evaporation fills the flare loops with hot dense plasma, causing bright emission in the UV lines and soft X-ray (SXR) spectrum (Bruzek 1969; Hirayama 1974; Syrovatskii & Shmeleva 1972; Fisher et al. 1985; Polito et al. 2016, 2023; Druett et al. 2017).
In coronal physics, “condensation” refers to material that is dramatically cooling (with temperatures decreasing by an order of magnitude or so) and, typically, dropping from a higher ionization state to a lower or partially unionized state. When this occurs, the material suddenly becomes visible in chromospheric spectral lines, appearing to “condense”. “Chromospheric evaporation” refers to an upflow of chromospheric material with simultaneous heating (temperature increasing by an order of magnitude or so) and typically includes a large increase in the ionization degree of a particular state for an element. Although this “evaporation” is technically an ablation, the material appears to evaporate from chromospheric spectral lines. Therefore, we reserve the words “evaporation” and “condensation” for processes that have, at the very least, some semblance of a change in state. We note that the downflowing chromospheric compressions in flares have often been referred to in the literature as “chromospheric condensations”. However, the conditions for the “condensation” analogy do not hold true for these phenomena. Therefore, we refer to this phenomenon as a downflowing chromospheric compression in the rest of the paper.
The specialized methods of energy transport in this standard model (points 6–8) are a particularly challenging aspect for simulations. They have been investigated via 1D radiative transfer (RT) and hydrodynamic (HD) codes. These simulations generate hot upflows from the chromosphere, primarily driven by energetic electrons and protons, thermal conduction, or combinations of these processes (Fisher et al. 1985; Canfield & Gayley 1987; Allred et al. 2005, 2015; Zharkova & Zharkov 2007; Druett et al. 2017; Druett & Zharkova 2018, 2019; Unverferth & Reep 2023).
Recently, multidimensional magnetohydrodynamic (MHD) models have investigated plasma flows in flares. Cheung et al. (2019) and Rempel et al. (2023) used sub-photospheric velocity driving to build up and release energy in the corona. Kong et al. (2019, 2020, 2022), and Shen et al. (2022) reproduced and interpreted supra-arcade downflows in the corona immediately above the flare loops, with Kong et al. (2020, 2022) inspecting the energetic electron acceleration and transport without transferring energy out of or back into the MHD simulation. Kerr et al. (2020) used a set of 1D loop models to build up a 3D flaring volume. However, the main focus of multidimensional flare simulations has been on coronal dynamics. The investigation presented in this work includes a significant focus on the lower atmospheric dynamics and provides methods that, for the first time, enable clear comparisons of results from 1D and multidimensional modeling.
There have also been attempts to reproduce the standard model in multidimensional MHD models. Yokoyama & Shibata (2001) initialized their 2D model as a weak bipolar magnetic field region within a vertically stratified approximation of solar conditions. They used anomalous resistivity to trigger reconnection above the polarity inversion line, which resulted in a loop arcade forming beneath. The combination of the reconnection outflows impacting the lower atmosphere and the thermal conduction front drives chromospheric evaporation from the footpoints of the loops. The resultant dense coronal loop arcade matches the general evolution scheme of a solar flare.
Ruan et al. (2020) self-consistently built on the model of Yokoyama & Shibata (2001) in 2.5D using the message-passing-interface, adaptive mesh refinement versatile advection code MPI-AMRVAC (Keppens et al. 2012, 2023; Porth et al. 2014; Xia et al. 2018), and expanded it significantly by using the Ohmic heating term in selected regions of anomalous resistivity as an energy reservoir to accelerate nonthermal electrons along field lines. This energy is redistributed along these field lines using analytical solutions for the 1D thick-target modeling (Emslie 1978), with remotely deposited energy subsequently re-interpolated onto the automated, block-adaptive grid. However, the agents that cause chromospheric evaporation (hot upflows of plasma with chromospheric densities into the corona) in the original paper are thermal conduction and the impact of the outflows on the lower atmosphere, transported down the flare loop arcade.
A companion paper to this study presents the first self-consistent multidimensional model of this kind to reproduce chromospheric evaporation via energetic particle beams (Druett et al. 2023). Ruan et al. (2023) present a simulated flare in 3D using this modeling suite, but without including beam electrons, to study the formation of MHD turbulence in the flare loop tops.
In this paper we explore the 2.5D models that include beam electrons described in Ruan et al. (2020), in particular how variations in the coronal field strength affect the resultant coronal and lower atmospheric dynamics. This investigation provides the first solid basis for the comparison between 1D radiation HD flare simulations and multidimensional flare modeling results. Thereby, we also lay the groundwork required to assess the need for critical field-aligned 1D physics to be built into truly multidimensional flare models.
2. Model
2.1. MHD model description
The setup of the models in these experiment is comprehensively described in Ruan et al. (2020). Here we only recall the equations used, along with an overview of how this simulation reproduces features of the standard solar flare model. The MHD equations are
The equations are written in a dimensionless format. ρ, v, t, B, and e are the plasma density, velocity, time, magnetic field, and energy density. g is the gravitational acceleration, which acts vertically downward. This is calculated via the equation 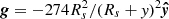 m s−2, where Rs is the solar radius. J is the current density defined by J = ∇ × B, and η is the resistivity, with anomalous forms described in Ruan et al. (2020) and Sect. 2.2.
m s−2, where Rs is the solar radius. J is the current density defined by J = ∇ × B, and η is the resistivity, with anomalous forms described in Ruan et al. (2020) and Sect. 2.2.
Equation (1) is the continuity equation, expressing the conservation of mass. Equation (2) is the equation of motion also writable as
The Lorentz force J × B has been brought to the left hand side and decomposed into the magnetic tension and pressure making the total pressure ptot = pgas + (B2/2) = pgas + pmag. The form of these equations is discussed at length in Sect. 4.3 of Goedbloed et al. (2019).
Equation (3) is the energy equation, where the total energy density is e = (ρv2)/2 + pgas/(γ − 1)+pmag with γ = 5/3. The first term on the right side of Eq. (3) represents gravitational potential energy and additional sink or source terms on the right side express heat conduction (with a thermal conductivity tensor κ), resistive effects. The term ∇ ⋅ (B × ηJ) results from the inclusion of Ohmic dissipation, but is not Ohmic heating. Instead, it shows that Ohm’s law specifies the comoving electric field to be ηJ, that total energy remains conserved in resistive MHD (see Sect. 4.4.2 of Goedbloed et al. 2019) optically thin radiative losses (Qr), and that an artificial background heating maintains the quiet-Sun coronal temperature (see Eq. (5) of Ruan et al. 2020).
In the second phase of the resistivity description, we took the Joule heating term, |ηJ2|, out of the local energy equation and used it as a reservoir of energy for the acceleration of energetic electrons (see Sect. 2.3). The term Qe represents this energy that is lost from the sites of energetic electron acceleration. The term He represents the heating of the plasma by these energetic electrons, which is nonlocal and transferred along the magnetic field lines.
Equation (4) shows the induction equation, which governs the advection of the magnetic field with the plasma. A source term on the right side describes the effects of resistive field diffusion, misaligned currents, and resistivity gradients (see Sect. 4.4.2 and Eq. (4.132) of Goedbloed et al. 2019). Coupled with the energy equation described above, this acts to convert magnetic energy into internal energy at sites of resistivity. The system of equations is closed by an ideal gas law as the equation of state.
2.2. Anomalous resistivity description
The anomalous resistivity prescription in these simulations is a two-stage model. Both are calculated as described in Ruan et al. (2020) and were based on the earlier model of Yokoyama & Shibata (2001). The first stage is used to trigger the reconnection at the X point in the corona and takes the form
η0 = 0.05 is the maximum value of the anomalous resistivity in this stage. rη = 2.4 Mm is the radius over which the anomalous resistivity drops to zero, with distance r away from the point (0, 50) Mm.
The second phase is activated at times after tη > 31.2 s, which is tη = 0.4 units of experiment time,
This generates anomalous resistivity in locations where the calculated electron drift velocity, 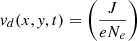 , is greater than a critical value vc = 1000uv, where uv = 128 km s−1, e is the electron charge, and α = 1 × 10−4. The resistivity produced is given a maximal value of 0.1. It is greatest at heights near the original resistivity patch, hη = 50 Mm, and decreases with a scale height of hs = 10 Mm.
, is greater than a critical value vc = 1000uv, where uv = 128 km s−1, e is the electron charge, and α = 1 × 10−4. The resistivity produced is given a maximal value of 0.1. It is greatest at heights near the original resistivity patch, hη = 50 Mm, and decreases with a scale height of hs = 10 Mm.
Ohmic heating results from the combination of the second stage anomalous resistivity description and the current in the current sheet through the domain about x = 0. This Ohmic heating term, η|J|2, is used to model unresolved microscopic instabilities and, in the second stage of our resistivity description, is the energy reservoir, Qe, used to accelerate energetic electrons:
Any number of other resistivity schemes are available. These different schemes will impact the MHD evolution of the system. Investigation of large deviations from the scheme above is outside the scope of this work. It will be investigated in other works, including Druett et al. (2023).
2.3. Beam model description
The beam electron modeling used in this work is unchanged from the description of Ruan et al. (2020), who describe the approach as a generalization of the 1D treatment provided by Emslie (1978).
Firstly, we defined the flaring region by tracing magnetic field lines forward and backward from points to the left and the right of the reconnection X point, at ( ± 2.5, 50) Mm. Within this flaring region, field lines were traced from their photospheric footpoints. A check was made that neighboring field lines did not separate from each other by more than the separation of the grid-cell centers. If they did, additional field lines were added. The points where these field lines pass closest to the line x = 0 were defined as the starting points for the subsequent 1D energy redistribution by beam electrons.
The input energy flux along each field line was calculated as the total of the Ohmic heating terms of cells that intersect with each field line, as described in Eq. (8). The energy transferred to the field lines was subtracted from the MHD energy equation as Qe. Where multiple field lines intersect a cell that produces energetic particles, the energy from that cell is shared equally between the field lines.
Our numerical treatment of purely resistive MHD is fully conservative by construction as we used a finite volume approach, but partially open boundaries can modify exact conservation. Moreover, the additional presence of electron beams implies that at any instant the beam-injected energy is stored on (evolving) field lines and given back to the plasma via interpolation from field lines to grid cells at a remote location. A consideration of how overall conservation is approximately achieved for the beam electrons at all times is given in Appendix A.
2.4. Domain and solution methods
The equations in Sect. 2.1 are solved in a spatial domain spanning −50 Mm < x < 50 Mm and 0 Mm < y < 100 Mm, using the open-source MPI-AMRVAC code (Keppens et al. 2012, 2023; Porth et al. 2014; Xia et al. 2018). The hierarchical, block-adaptive grid used has a block size of 16 by 16 cells, with a minimum of 64 cells (four by four blocks) spanning the domain in each dimension, at refinement level one. The grid is refined by splitting a block into four sub-blocks for each increase in refinement level. The maximum refinement level for the experiment is six. This means that at the lowest refinement the grid cell separation is 100/64 = 1.5625 Mm, and at maximum refinement the resolution is 100/64/25 = 48.8 km.
The refinement level is forced to be maximal below y = 3 Mm and for blocks within the box that contains the dynamically tracked magnetic field lines (with the regions as described in Appendix B of Ruan et al. 2020). Additional automatic refinement and de-refinement is switched on to ensure accurate shock capturing in locations away from the user-prescribed refinement areas. This is implemented with a weighting of 1:2:2 (as described in Keppens et al. 2012) between the conserved variables of mass density, vertical magnetic field, and internal energy density, respectively.
We employed a three-step time-stepping scheme. The flux scheme uses the Harten-Lax-van Leer (HLL) approximate Riemann solver (Harten et al. 1983) and as in Ruan et al. (2020), a mixture of high-order slope limiters is used: a third-order limiter (Čada & Torrilhon 2009) is employed in regions of low refinement (i.e., the background corona) and a second-order limiter (van Leer 1974) in the regions of high grid refinement (greater than level 3), namely the lower atmosphere, reconnection region, and flare loop. The various limiters and all solvers available are discussed in Keppens et al. (2023).
2.5. Differences to previous studies
There a few differences between the experiments presented here and that produced in Ruan et al. (2020), namely:
-
The heat saturation model parallel to the field lines has been enacted using the MPI-AMRVAC thermal conduction module Xia et al. (2018), with a monotonized central limiter as per Woodward & Colella (1984).
-
The side boundaries of the experiment (x-direction) are now treated as open, rather than the previously employed combination symmetric and asymmetric boundary conditions in the ghost zones. This avoids the reflection of shocks that emanate from the flare, and these shocks simply exit the domain from the sides of the experiment. In Ruan et al. (2020) shocks reaching the side boundaries were reflected and returned and interact with the flaring region. As a result, we now allowed (negligible) mass loss in the chromosphere and the corona via the open boundaries over the duration of the experiment. The upper and lower boundaries are unchanged from Ruan et al. (2020).
-
The magnetic field vectors are split. There is a constant background component with a distribution as in the model of Yokoyama & Shibata (2001), and we solved for a time-varying component that is zero at the start of the experiment. In Ruan et al. (2020) the background part of the field was given a magnitude of B0 = 35 G. In this investigation, four different values are used (B0 = 20 G, 35 G, 50 G, and 65 G) to explore the impact of different coronal field strength on the flare evolution.
2.6. How this experiment reproduces features of the standard solar flare model
Figure 2 shows how these experiments reproduce features of the standard solar flare model. The experiment is initialized with a low current-density vertical current sheet in the center, where the vertical background magnetic field components transition from positive (left side of the experiment) to negative values (right side). This bipolar field region undergoes magnetic reconnection due to the anomalous resistivity region inserted at a height of 50 Mm. The current sheet thins and grows stronger in the reconnecting locations (Fig. 2a).
 |
Fig. 2. Simulated analog of the standard solar flare model. Panel a shows By/B0. All the simulations presented here start from a bipolar field region with an anomalous resistivity patch at a height of y = 50 Mm over the polarity inversion line, which causes the field to reconnect and release stored magnetic energy. Panel b shows the typical vertical velocity (vy) structure at a time before the impact of the reconnection outflow on the lower atmosphere. Positive velocity (red) represents upward motion, and negative represents downward motions (blue). The reconnection outflow jets form at the X point, where reconnection occurs; one jet flows downward, and the other, upward jet leaves the domain via the top boundary. Panel c shows the vertical velocity at the time when the reconnection jet impacts the lower atmosphere. Panel d shows the typical flare loop system that is formed via this process, through a plot of absolute magnetic field strengths. Energetic electron transport is switched on after 31.2 s of the simulation. Thus, in all cases presented in this manuscript, the electrons are switched on before the impact of the reconnection jet on the lower atmosphere. In the lower panels, electron acceleration sites are shown in green and energy deposition locations in yellow. The energy deposition locations are saturated at very low values to help indicate their paths through the experiment. In fact, these beams deposit the majority of their energy in the lower atmosphere at the footpoints of the flare loops. |
The reconnection, and associated expansion of the plasma due to heating, drives outflows from the X point. One of these outflows is directed toward the surface of the Sun (see the blue patch in Fig. 2b), and the other is directed upward (the red jet in Fig. 2b). We note that there is no overhead flux rope contained in this magnetic field configuration. We replicated only the portion of the standard solar flare model below the overlaying flux rope. In these experiments the magnetic field strength was chosen to reproduce realistic values in the corona, near the reconnection site, rather than at chromospheric and photospheric heights. Indeed, our maximal field values are on the order of 2B0 in the lower corona. The chromospheric field strength values will be made more realistic in future works.
Electrons are accelerated from the reconnection site, in the outflow regions, and around magnetic islands or plasmoids (see the green regions in Figs. 2c and d). Such plasmoids are often caused by tearing events in thin current sheets in 2D simulations. The transport time for these electrons is considered to be shorter than the HD time steps of the simulation (Siversky & Zharkova 2009), and thus their energy transport is modeled as instantaneous. The energy deposition sites are shown in the lower panels using yellow coloration. This coloration is saturated at relatively low intensities to highlight the entire paths of the electrons; however, the energy deposition is actually focused in fairly concentrated kernels at the chromospheric footpoints of the flare loops. Particle trapping is possible in our beam model due to mirroring and depends on the adopted beam pitch angle (Ruan et al. 2020). In such cases the energetic electrons remain on portions of the field line in the next time step of the simulation. In practice, the (yellow) beam visualizations of the energetic electrons act as a proxy to highlight the separatrices of the reconnected field lines from those that are not currently reconnected. The inner regions of the electron energy deposition (i.e., x-locations closer to zero) are due to recently reconnected field lines still accelerating electrons in the X point outflows or in plasmoids, but also shows loops that have retained some of their energy from earlier times due to trapping of energetic electrons. We note that there are no specific mechanisms in these simulations to replicate particle acceleration in the termination shock or in turbulent flare loop tops. However, this could be enacted in the future by judiciously generalizing the current heuristic recipes for the beams.
In these models, the reconnection progresses rapidly from the start of the experiment, and thus the outflow jets impact the chromosphere more or less directly (see Fig. 2c). In a pure-MHD (no beam electrons), but 3D model, Ruan et al. (2023) first initiated a gentle reconnection phase that led to the formation of a loop arcade before the impulsive phase began. The impulsive outflow under these circumstances impacts first upon the loop tops of this arcade before reaching down the field lines to the chromosphere. For ease of comparison to the experiments of Ruan et al. (2020), we replicated their setup; this resulted in a more direct impact of the outflows on the lower atmosphere. We leave investigation of variations to a separate paper (Druett et al. 2023). The impact of the reconnection outflow on the lower atmosphere, and the heating of the lower atmosphere due to other processes such as thermal conduction, causes chromospheric evaporation. This is the heating of initially cool chromospheric material up to coronal values and its associated expansion and upflow into the coronal flare loops.
Material ejected downward from the reconnection outflows, as well as upflows from the chromospheric evaporation, increase the densities in the hot flare loops, and turbulence is also seen in the loop tops below the termination shock (Fig. 2d). Although the chromosphere is only treated in single-fluid, non-radiative MHD here, we also inspected the downward propagating shocks, which are the equivalents of downflowing chromospheric compressions in these models, and inspected the momentum they supply to the photosphere. We also calculated the SXR and HXR outputs but present only a few relevant parameters for our analysis. The X-ray periodicity, light curves, and other synthetic observables will be discussed in detail in a future work.
2.7. Free parameters
In the models presented here, there are several free parameters. The electron beams have energy profiles defined via a spectral index, lower cutoff energy, and initial mean pitch angle distribution. All of these are currently set to predetermined values as in Ruan et al. (2020; δ = 4, Ec = 20 keV, and θ = 18°, respectively) and will be updated to be based on relevant atmospheric parameters in a future work.
The evolution of the model is also controlled by the description of the anomalous resistivity involving a switch between resistivity schemes described in Ruan et al. (2020, 2023). Manipulation of resistivity parameters are presented in Druett et al. (2023), where we demonstrate how these can lead to electron beam-driven evaporation.
The geometry of the flare is determined by the strength of the background magnetic field strength (B0), the height of the resistivity patch, whether or not we insist on left-right symmetry, and thermodynamic values that initialize the atmosphere and the magnetic field structure. In this work we focus on the variations in the background magnetic field strength, B0.
3. Results
In Sect. 3.1 we discuss how the variations in the background magnetic field strength impacts the magnetic reconnection and outflows. In Sect. 3.2 we analyze the impacts on the lower solar atmosphere of the beam energetics (Sect. 3.2.1) and the reconnection outflows; they have until now been largely overlooked in multidimensional flare simulations. We analyze downflows and chromospheric compressions (Sect. 3.2.2), upflows and chromospheric evaporation (Sect. 3.2.3). In Sect. 3.3 we discuss the formation of the flare loop arcade and turbulence in the loop tops. Section 3.4 analyzes 1D cuts along field lines to investigate the evolution of the flare simulation in selected flux tubes. Much of the physics in flares is magnetic-field aligned, and there is a long history of detailed 1D flare simulations. This section establishes a basis for the comparison of results in 1D with multidimensional research. In multidimensional experiments there is a diversity of flux tube configurations. Thus, in Sects. 3.4.1–3.4.3 we present the results for three such flux tubes with footpoints at x = −10 Mm, x = −12.5 Mm, and x = −15 Mm, respectively, to provide a more complete picture of the field-aligned physics.
3.1. Reconnection and outflow
The initial atmospheres of each of the four experiments have identical thermodynamic variables. For the subsequent evolution, it is only difference in background magnetic field strengths that affects the release of magnetic energy.
The first HD sign of the reconnection in each simulation is in the conversion of magnetic energy into internal energy along the reconnecting field lines via Joule heating, which occurs before the electron acceleration process is switched on. By summing energy components over the entire domain in each simulation (not shown here for brevity) we see that the conversion of magnetic energy into internal energy continues relatively gently, while the conversion into kinetic energy accelerates with the development of the reconnection outflow. Much of this kinetic energy escapes through the top boundary of the models or is reconverted into internal energy when the reconnection outflow impacts the lower atmosphere. These downflows also transiently and locally raise the magnetic energy when the outflow compresses the magnetic loops down onto the lower atmosphere, before they rebound.
The newly reconnected magnetic configuration generates a Lorentz force. The combination of the heating and the suddenly altered pressure and Lorentz force values drives the subsequent acceleration of the plasma away from the reconnection X point. This outflow (see Fig. 3) forms a lobster claw shape for reasons discussed in Zenitani & Miyoshi (2011), namely that in the fast-mode shock the density is highest in the central location and decreases away from the center. This feature can be seen in the outflow velocity plots (top row of Fig. 3) with the velocity increasing with background field strength, due to the faster rate of energy release. The heating (second row, showing temperatures) is concentrated in the tails of these outflows (see Fig. 3 central panels, green arrows), and to a lesser extent in the outer edges of the outflows (blue arrows). The high density regions (bottom row) are concentrated in the central locations and some distance behind their leading edge. This core of high density material is more compact for simulations with stronger background magnetic field strengths (for context, see the Alfvén Mach numbers of different sections of the lobster claw outflow jets presented in Fig. 4).
 |
Fig. 3. Reconnection outflow jets of the experiments with different background magnetic field strengths. They are shown at similar morphological stages of the experiment evolution. The columns show results for different background magnetic field strengths, from B0 = 20 G on the left to B0 = 65 G on the right. The top panels show the vertical velocities of the models, and the central row shows temperatures. In the temperature panels, green arrows indicate the concentration of high temperature in the tails of the reconnection outflows, the blue arrows indicate the hotter areas at the rear of the lobster claw forms that lead the reconnection outflows. The bottom row shows plasma number density. Each panel also shows magnetic field lines in black. These are traced from footpoints at x = −2.5, −5.0, and −7.5 Mm in instances where these lines are being processed by the 1D field-line routines. In the number density panels (bottom row), beam electron acceleration sites are shown in green, and the locations where energetic electrons deposit their energy are shown in yellow. |
 |
Fig. 4. Alfvén Mach numbers of the outflow reach similar ranges and values at similar evolution epochs, independent of field strength. They are shown just prior to the impact of the outflow on the chromosphere (top row), during the compression of the flare loops by the generation of the termination shock (second row), and after the rebound of the impact once the flare loops have settled (third row). In each row a green arrow highlights the fast mode shock in the reconnection outflow. In the top row a red arrow highlights the high-density core of the lobster claw outflow formation, and a magenta arrow points to the sub-Alfvénic “claws” of this structure. In the lower panel the logarithms of the maximum downward outflow speeds are shown with dashed lines (right axis), and the maximum of the Alfvén Mach numbers in these outflows is shown with solid lines. |
Once the energetic electrons are activated in these models, the Joule heating energy term is removed from the energy equation and instead put into the acceleration of energetic particles in regions where the drift velocities of the electrons exceed a threshold value. In these locations the outflows are still generated by the Lorentz force and other heating that results from the magnetic realignment and energy release, for example, shock heating and adiabatic compression (Eq. (3): ∇ ⋅ (pgasv)) and thermal conduction (Eq. (3): ∇ ⋅ (κ∇T)).
In the bottom panels of Fig. 3 the energetic electron acceleration regions (green) and energy deposition regions (yellow) are shown using a logarithmic colorbars, so that the areas in which they are present is well highlighted. Again, these energy quantities are higher for the experiments with greater background magnetic field strengths, as the Joule heating term increases with the liberated magnetic energy. We note that we chose to visualize the four experiments in Fig. 3 at different experiment times, but at similar magnetic morphological times as seen in the selected field lines shown. Thus, the panel of this figure showing the B0 = 65 G experiment does not have energetic beam electrons because they are switched on at t = 31.2 s in all of the simulations.
The dense core of the lobster claw shock accelerates toward the local Alfvén speed (see Fig. 4, upper row, red arrows), with the claws traveling at significantly sub-Alfvénic speeds (see Fig. 4, upper row, magenta arrows). Outflows from the continuing reconnection increase in velocity to become a fast-mode shock. The fast shock forms in this tail of the outflow (see Fig. 4, green arrows). Independent of the background magnetic field strength, the outflows reach a similar Alfvén Mach number of 9–10 in each simulation (see the solid lines in Fig. 4, lower panel).
To examine whether this maximal outflow and Mach number is persistent, we also varied the free parameters that determine the anomalous resistivity values. The B0 = 35 G simulation was run two more times for 160 s of solar time, once with the anomalous resistivity a factor of two greater and another time with it a factor of two smaller. The maximum threshold values as described in Eq. (7) were also increased or decreased by the same factor. Results of these experiments are included in Fig. 4, lower panel and confirm that the limiting Alfvén Mach number of the fast shock in the outflows of the flare obtain similar maximum values independent of the resistivity or background magnetic field strength. Spiky behavior is due to the turbulent region overlapping with the diagnosed area, which was a fixed spatial box across all experiments, based on the typical region of the reconnection outflow jet. Variations in the height of the resistivity patch or asymmetries could also impact the maximum Alfvén Mach number of the outflow, which will be addressed in future work.
The timing of the outflow jet reaching this Mach number does not coincide with the timing of the maximum out-flow velocities reached in each experiment (compare the peaks in the solid and dashed lines in Fig. 4). In the stronger flare models, the current sheet thins further and plasmoids form due to tearing instability; there is also a case of plasmoid coalescence in the experiment with B0 = 65 G (see, for example, Keppens et al. 2013; Sen & Keppens 2022).
The reconnection rate in the corona can be characterized using the ideal electric field, which is given by −v × B in the reconnection region and, for the setup used here, has a magnitude |vxBy|. Ruan et al. (2020) found that the sweeping of the footpoints in their simulations, located using the peak value in the footpoint HXR signal, related to this coronal reconnection flow via the relationship presented in Isobe et al. (2002), |vxBy|CORONA = |vx(HXR)By|FOOTPOINT. Figure 5 shows the values of |vxBy| in the corona (solid lines) and |vx(HXR)By| shows values for the chromospheric footpoints (dashed lines). The units are converted into CGS ideal electric field units to aid the comparison with reconnection and acceleration studies, which often use these units. We automated the calculations, in contrast to the previous hand-made calculations of Ruan et al. (2020) seen in their Fig. 4. The reconnection inflow |vxBy|CORONA was calculated at ( − 2, 50) Mm. The values of |vxBy|FOOTPOINT were calculated from the By values at the grid cell location of the maximum HXR emission in the chromospheric footpoint on the left side of the experiment, and vx(HXR) values were taken from the apparent horizontal motion. To account for the slow movement in terms of grid cell number in the footpoints, a ten-second moving average was used for the (signed) value of vx(HXR). Once the flare loop system is stabilized a clear periodicity of the measured reconnection rates appears in the simulation with B0 = 35 G. This occurs in both the footpoints and the X point, with the footpoint reconnection measure (about 10 s) varying at half the period of the loop-top measure (about 20 s).
 |
Fig. 5. Reconnection inflow rate (solid lines) and footpoint sweeping (dashed lines) expressed as |vxBy|, in electric field units E = −v × B. The different colors show the variations in these quantities as functions of time for the experiments with different strengths of background magnetic field B0. |
The relationship |vxBy|CORONA = |vx(HXR)By|FOOTPOINT holds much more consistently at later times in the experiment, once the flare loop system is formed, as was the case in Ruan et al. (2020). It is in reasonable agreement across the range of background magnetic field strengths, B0. This is consistent with Isobe et al. (2002), who presented findings only after the initial phase of the flare, although we note numerous caveats for this comparison, including the very different timescales involved.
The spikes for the B0 = 65 G experiment at around t = 80 − 90 s are produced by a passing plasmoid, which increases the velocities and field strengths in the corona and affects the HXR footpoint locations in the chromosphere. The photospheric and chromospheric magnetic field strengths in our experiments are lower than reported solar flare field strengths by more than an order of magnitude. Typical solar magnetic field has a strong vertical gradient that is not present in our experiment. Thus, for more realistic flaring atmospheres one would expect much faster reconnection inflows in the corona than we find, if the footpoint sweeping speed was similar.
3.2. Impact on the lower atmosphere
3.2.1. Electron beam energetics
One-dimensional models of flares with energetic electron heated lower atmospheres generally do not use self-consistent energy schemes, instead injecting fluxes of high-energy electrons as functions of time at the tops of the models. The energies of these fluxes can be fixed to particular values or time profiles (Allred et al. 2005, 2015; Druett & Zharkova 2018, 2019), or can be driven by observational constraints (Druett et al. 2017; Polito et al. 2023). Figure 6 shows the chromospheric electron beam heating in our models, which can be compared with values used in 1D models such as RADYN (Allred et al. 2005, 2015), HYDRO2GEN (Druett & Zharkova 2018, 2019), and FLARIX (Varady et al. 2010; Heinzel et al. 2017). To compare a 1D beam model that uses a time-profile injected input heating with our multidimensional models, one should take a slice at a constant position (vertical slice) and read off the variations in footpoint heating flux. From the figure, one can see that our models have characteristic beam injection duration times of around 5–20 s, in line with some “elementary burst” models used in 1D simulations.
 |
Fig. 6. Electron beam heating in the chromospheric footpoints. Each panel shows results for an experiment with a different background magnetic field strength. They are shown as functions of time (y-axis) and footpoint location (x-axis). The heating at each footpoint is computed by integrating the source term for the electron beam heating rate. We integrate this quantity over a vertical distance in the spatial domain that spans from the lower boundary of the experiment up to (but not including) the grid cell where the temperature first exceeds 50 000 K. The figure then shows the electron beam flux density that is applied down through the top of the “chromospheric” material and deposited at each footpoint. The color map saturates to red at the low end. This occurs at a beam strength of F8 (F0 = 10 × 108 erg cm−2 s−1), and thus the red color indicates negligible or zero beam heating. |
It is clear that the model with B0 = 20 G represents a very weak beam injection, with “F8” energy fluxes (i.e., an input energy flux F0 on the order of 108 erg cm−2 s−1) peaking at values greater than 109 erg cm−2 s−1 at only a few locations within the domain. The B0 = 35 G experiment is a reasonable analog of a weak “F9” elementary burst model at most locations, although there is an absolute maximum flux value throughout the domain of 1.4 × 1010 erg cm−2 s−1. The stronger B0 = 50 G and B0 = 65 G models represent elementary burst models with durations of 5–20 s and moderate electron beam fluxes on the order of “F10” (i.e., with F0 ≈ 1010 erg cm−2 s−1). On the basis of 1D modeling results in the literature one would expect the stronger flare models to produce some evaporation (hot upflows) and cooler downflowing chromospheric compressions signatures as a result of the beam electrons. Figure 7 shows kinetic energy maps of the flare experiments at times after the electrons are switched on and before the impacts of the reconnection jets on the lower atmosphere. The kinetic energy signatures are shown in red with the electron energy deposition locations shown in blue. Before the impact of the reconnection outflow jets there are indeed (minor) signatures in the red kinetic energy plots of upflows and downflows in these experiments (with locations indicated by blue arrows in Fig. 7). However, the reconnection outflow jets that arrive and impact a bit later completely swamp these beam-driven evaporation signatures. The weaker flares have a much longer time window between the start of the beam heating and the impact of the reconnection jet, making it appear as if they have a greater influence on the lower atmosphere. When we instead look at similar times after the switching on of the beam, the stronger flares have stronger beams that exert a greater rate of influence, in line with what would be expected from their higher beam fluxes. In a separate paper we adapt the models presented here to investigate chromospheric evaporation driven primarily by electron beams (Druett et al. 2023).
 |
Fig. 7. Signatures of the electron beam effects on the lower atmosphere. Kinetic energy maps of the flares are shown in red, with the lobster claw reconnection outflows approaching the lower atmosphere for the experiments with B0 values of (a) 20 G at t = 73 s, (b) 35 G at t = 48 s, (c) 50 G at t = 50 s, and (d) 65 G at t = 32 s. Overlays show the electron acceleration densities in green and the energy deposition regions in blue. We note that the lower panels have energy deposition rates masked and scaled to values 100 times greater than the upper panels, in order not to completely cover the footpoint kinetic energy signatures, which are seen as small red blobs (Kinetic energy) next to the blue footpoints blobs (electron energy deposition) and highlighted with blue arrows. |
3.2.2. Chromospheric downflows
In our MHD models the lower atmosphere is highly simplified. It is treated as a fully ionized hydrogen plasma with a simple radiative loss function. The photospheric field strengths are of order 50 G, in rather stark contrast to the typical observationally derived values of a flare’s lower atmospheric field strength, which are several kilogauss. This seems to be a common situation for flare simulations derived to model coronal conditions, for example Ruan et al. (2020, 2023), and Shen et al. (2022). Simulations developed originally from photospheric models that have been extended to accurately reproduce coronal conditions do not have this proviso, for example Cheung et al. (2019) and Rempel et al. (2023). We refer to the low temperature, high density lower atmosphere region as the chromosphere despite its simplicity in our models, and to the region at the very base of our model as the photosphere, although we did not accurately reproduce this region of the Sun.
The instant the energetic electrons are switched on, they reach the lower atmosphere, as per the modeling assumptions. In all but the weakest field strength modeled, B0 = 20 G, there are electrons that reach our photosphere (i.e., the base of the model; see Figs. 8 and 9, top panels). The beam model used here, when implemented in 1D models, generally results in electrons being stopped at greater heights in the chromosphere (Emslie 1978; Allred et al. 2005, 2015). The electrons do not impart directed momentum on the plasma in these simulations, acting only through a source term in the energy Eq. (3).
 |
Fig. 8. Heating, downflows, and evaporation of chromospheric material. They are shown for simulations with increasing background magnetic field strengths in the columns from left to right, each at the same time during the simulation (t = 80 s). The top row shows the plasma density in grayscale, with electron energy deposition sites overlaid in yellow. Blue arrows indicate the locations of upflows from the chromosphere, evaporation in the case of all but the B0 = 20 G experiment. Red arrows indicate the high density impact fronts of downflowing material at the top of the chromosphere. The central panels show the temperature of the atmosphere, saturating to black at 6000 K and to white at 30 000 K. In this row green arrows indicate hot chromospheric material. The bottom rows show the kinetic energy densities with chromospheric evaporation signatures highlighted using blue arrows and significant energy transfer to photospheric levels indicated by magenta arrows. |
 |
Fig. 9. Heating, downflows, and evaporation of chromospheric material in the models. The formatting is similar to that of Fig. 8, including those features that are highlighted by arrows. This figure shows the simulations with different background magnetic field strengths, each at similar stages in the evolution of the flare, after the impact and rebound of the reconnection outflow jet. A movie is available online. |
Before the reconnection jets impact the chromosphere, the electron beams already heat the chromospheric footpoints from initial ∼6000 K temperatures up to ∼20 000 K over a range of heights that extends down to around 1.5 Mm, in the B0 = 20 G experiment (Fig. 8, left panels). For the B0 = 65 G experiment there is heating of plasma by the beam electrons to T ∼ 50 000 K just above 2 Mm, and to T ∼ 20 000 K at heights as low as 1 Mm. Moreover, for the B0 = 65 G experiment this occurs before the impact of the reconnection outflow arrives despite the only two to three second delay between the switching on of the electron beams and the arrival of the reconnection outflow jets (see B0 = 65 G experiment at t = 34 s in video form of the Fig. 9, available online.). However, the beam heating does not cause significant upflows in any of the experiments presented here. In the stronger flares there is not significant time for upflows to form before the impact of the reconnection outflow jet. In weaker flares the heating and expansion of the plasma has time to cause a gentle chromospheric upflow (with chromospheric densities), reaching up to around 3 Mm (Fig. 8, top-left panel, indicated by a blue arrow), but this does not qualify as chromospheric evaporation as it does not rise above this height.
The different stages of the downflows in the lower atmosphere can be seen for each model at t = 80 s in Fig. 8. In the left panels (weak B0), we see a lower atmosphere after the beam electrons have started heating it, but before the reconnection outflows impact it. When the outflows from the reconnection do impact the lower atmosphere they transfer downward momentum and kinetic energy, as well as increasing the pressure. There is conduction of thermal energy along field lines due to the temperature gradient. These processes heat the lower atmosphere and push it downward. Figures 8 and 9 (top panels) show dense impact fronts at the top of the hot flare chromospheres highlighted with red arrows. Above the flare chromosphere, in simulations with stronger background magnetic field, there is a stronger conversion of chromospheric material to hot plasma that upflows into the coronal loops. This will be discussed in the next section, and these upflows can be seen as gray patches of increased number density in the coronas of the top panels. They are also visible as coronal kinetic energy signatures in the lower panels, with both signatures indicated with blue arrows in the figures.
Meanwhile, below, the downflow starts to slow and cool as it travels to the photosphere (Fig. 8). Some downward traveling material is heated up to around ∼20 000 K (green arrows) and below this there is very significant kinetic energy that travels down to the photosphere (magenta arrows). The left panels (a–c) of Fig. 10 shows the downward fluxes of kinetic energy, the maximum kinetic energy density and the maximum downward velocities at different heights through the atmosphere of the simulations with B0 = 65 G. These heights were chosen at least five grid-points away from the experiment lower boundary, to avoid a significant influence from boundary effects. The peak of the downward kinetic energy flux at a height of 300 km above the photosphere across the simulations with different B0 values ranges from 2 × 1025 erg s−1 (B0 = 20 G) to 3 × 1027 erg s−1 (B0 = 65 G) with peak flux densities from 5 × 106 erg cm−2 s−1 to 4 × 108 erg cm−2 s−1. These fluxes were essentially unchanged across in simulations where we kept B0 constant and varied the initial mean pitch angles (not presented here), due to the relatively low-energy fluxes achieved via the energetic particles.
 |
Fig. 10. Impact of the flare on the dynamics of the lower atmosphere. The left column shows results for the B0 = 65 G simulation, while the right panels compare all four experiments. Shown are: (a) the total kinetic energy flux (assuming a the third-dimension depth of 100 Mm), (b) the maximum kinetic energy density directed downward, and (c) the maximum downward velocity, all shown at various heights near the photosphere. In the right column of panels we show: (d) the fraction of the lower atmospheric material that is chromospheric as functions of time for the different experiments, (e) the mass fluxes (assuming a third-dimension depth of 100 Mm), and (f) the maximum upward velocities of material, each taken at 5 Mm height. |
The downflowing chromospheric compressions travel initially as acoustic shocks (at speeds greater than the sound speed just below them, which has typical values of 8–10 km s−1). The downflowing chromospheric compression in the B0 = 20 G flare ceases to be a shock in the mid chromosphere, when its downward velocity drops below 8 km s−1. This transition occurs deeper into the model for increasing B0, but even in the strongest flare, the compression is traveling below the sound speed by the time it reaches a height of 200–300 km above the photosphere. Therefore, the downflowing chromospheric compressions in these simulations would not be expected to cause a sunquake (Kosovichev & Zharkova 2001; Macrae et al. 2018; Zharkova et al. 2020) when they move below the photosphere.
3.2.3. Evaporation
Figure 9 illustrates that the area of the chromosphere that gets heated, compressed, or evaporated due to the flare is greater with increasing field strength, both in depth (due to the higher-energy fluxes) and in lateral area (due to the faster speed of the leading edge of the flare ribbon that results from the faster reconnection rates). The fraction of the mass at heights between 300 km and 5 Mm that is at temperatures less than 20 000 K is quantified over time in Fig. 10d, alongside the chromospheric mass flux through a horizontal line at 5 Mm through the experiment (Fig. 10e). These values vary co-temporally and do not show any in-phase behaviors with periods of large photospheric mass fluxes.
Due to the mass density gradient with height that occurs between the photosphere and the chromosphere, the general plasma motions in our simulations have larger mass fluxes through the bottom boundary than through the tops of the chromosphere. These are especially larger when the front from the chromospheric compression reaches the lower boundary. These fluxes were checked and the chromospheric mass fraction in panel d of Fig. 10 showed in-phase variations with the chromospheric mass flux but no in-phase variations with these photospheric fluxes. Thus, we can be confident that the evolution of chromospheric material in panel d is due to chromospheric rather than photospheric changes.
The mass flux via evaporation (panel e) and the decrease in chromospheric material over time (panel d) both increase with background magnetic field strength between B0 = 35 G and B0 = 65 G. In the case of B0 = 20 G, we see that the net mass flux is at first consistently downward from the corona to the chromosphere, and the change in the fraction of material at chromospheric heights that has temperatures greater than 20 000 K varies relatively negligibly. Thus, it is shown to be possible for high density flare loop systems to form that are fed primarily from the coronal reconnection jets and not from the chromospheric footpoints, since dense flare loops form in all the simulations, including the B0 = 20 G experiment that shows net downward mass flux through the upper layer of the chromosphere.
There is some chromospheric evaporation in each simulation despite the net downward mass flux through the 5 Mm height plane in the simulation with B0 = 20 G. The maximum velocity of these evaporations at heights of 5 Mm are shown in Fig. 10f. These velocities scale from around 200 km s−1 to around 500 km s−1 over the simulations in reasonable agreement with typical values derived from UV line observations of chromospheric evaporations and 1D flare models (Kennedy et al. 2015; Polito et al. 2016; Druett et al. 2017). There are small peaks of high velocity that exceed the typically observed evaporation speeds in UV spectral lines, which reach up to nearly 800 km s−1 in the experiment with B0 = 65 G.
3.3. Flare loop tops
Figure 11 presents kinetic energy density maps that highlight the current sheets and flare loops. We use them to illustrate the evolution of the flare loop tops in the simulations with different magnetic field values. The top row shows the impact of the reconnection outflow jets onto the chromosphere. Strong lateral flows away from the center of the impact move along the top of the chromosphere, and a shockwave expands as a dome over the whole coronal domain outside of the flare loops, centered on those loops. This phenomenon is also present in the experiment with B0 = 20 G but with kinetic energy densities values close to the lower saturation limit that make it hard to see in the figure. The impact and rebound of the reconnection outflow on the lower atmosphere, as well as heat conduction, create strong evaporation flows up the flare loops from their footpoints. The densities and velocities of these evaporation flows scale with the density and velocity of the impacting reconnection outflow jet, and thus with the background field strength as described in Sect. 3.2.3. We note the absence of strong rebound upflows in the B0 = 20 G model, which is consistent with the lack of variation in chromospheric mass fraction and negative chromospheric mass flux for this model seen in Figs. 10d and e. Evaporation upflows do also begin for the experiment with B0 = 20 G at some time after the time shown in Fig. 11a, as can be seen in Fig. 11e.
 |
Fig. 11. Kinetic energy density color maps. Kinetic energy density is shown in red and highlights the flare loops, the current sheets, and shocks traveling through the surrounding atmosphere. Overlays show the electron acceleration energy densities in green and the energy deposition density in blue. Energy densities for all panels of this figure have a lower saturation limit of 10−1 erg cm−2 s−1 and an upper limit of 103 erg cm−2 s−1. The columns from left to right show results for the experiments with background magnetic field strengths of B0 = 20 G, 35 G, 50 G, and 65 G, respectively. The top row shows the simulations at the time after the impact of the leading edge of the reconnection outflow jet. This impact and its reflection causes hot upflows from the chromosphere. The second row shows the time at which the flare loops have rebounded after their compression during the impact. The third and fourth rows show later times, when the loop tops settle and exhibit turbulent eddies on alternating sides of the central line (that is, a magnetic tuning fork process). An animated version of the figure is provided in the online materials. |
The downflows coming from the loop tops, which are concurrent with the onset of chromospheric evaporation, are slow shocks. They are caused by a combination of the compression of the loop-top region from the impact of the reconnection outflow, and the negative pressure gradient in directions outward along the field lines from the central positions of the loop tops.
The second row of diagrams shows the flare loop arcade after the rebound of the reconnection outflow on the lower atmosphere. In each experiment, the loop tops display oblique and horizontal fast shocks and, potentially, multiple termination shocks, as described in Takasao et al. (2015) and Takasao & Shibata (2016). This pattern of shocks is a consistent feature across all the experiments. However, these typical behaviors as described in Takasao et al. (2015) and Takasao & Shibata (2016) can be disrupted by plasmoids that are ejected downward from the current sheet in the experiments with stronger background field strength (see, e.g., Fig. 11g, with B0 = 50 G).
The magnetic tuning fork process (Takasao & Shibata 2016) is a flare loop-top oscillation that is controlled by the backflow of the reconnection outflow. It is evident across all the experiments. This is shown in the lower two rows of panels, in which turbulent eddies form on each side of the termination shock, with a dominant extent that alternates between the left and right sides. These eddies are also associated with pulses of shocks that propagate out into the surrounding plasma and can be identified as sets of fringes in the kinetic energy density that move away from the loop-top locations in the lowest two rows of panels in Fig.11.
The magnetic tuning fork process and the plasmoids are both capable of sending high density flows outward around the turbulent loop tops. Sometimes these flows are dense enough to intercept a significant fraction of the energy in the energetic beams of electrons before they can reach the chromosphere. This phenomenon can be seen in the video version of Fig. 11, available online in which the beam energy deposition (blue color) increases in the coronal region of the experiment (see B0 = 65 G before and after t = 100 s, B0 = 50 G at around t = 123 − 129 s, and B0 = 35 G after t = 200 s). This interception of beam electrons is also visible in the chromospheric beam heating rates at the footpoints of the models in Fig. 6. It can be seen through the decreases in the electron beam energy reaching the chromosphere due to the deposition of a significant portion of the beam fluxes in the corona.
In the B0 = 35 G experiment we see a periodic brightening of the beam energy deposition rate in the coronal loops after t = 220 s. This appears to be associated with the magnetic tuning fork process, which periodically (around every 16 s) emits shocks into the surrounding loops. These shocks periodically increase the densities in field lines that have recently reconnected, reaching maxima around the time that the tuning fork pulse passes from one side of the loop top to the other; this occurs on both sides of the experiment. This increased density, in turn, removes energy from the beams of electrons before they reach the footpoints, with a periodicity of around 16 s. Faint traces of this process are visible in Fig.11n and the video versions of this figure. Thus, the magnetic tuning fork can directly affect the loop-top X-ray emission as described in other papers (Takasao & Shibata 2016; McLaughlin et al. 2018; Zimovets et al. 2021). For example, the waves emitted from the loop top align with the concept of a periodic fast-mode magnetoacoustic wave as per the analysis of Takasao & Shibata (2016), which used similar models to those presented here. It has been argued that such waves propagating toward reconnection X points may also generate quasi-periodic pulsations (QPPs; McLaughlin et al. 2009). Here we describe a multidimensional secondary process that can also explain simultaneous QPPs in footpoint and coronal loop HXR sources. Pure MHD models without beam electrons cannot self-consistently quantify these HXR or beam-related effects and their related to QPP variations. However, the lack of particle acceleration modeling for nonthermal electrons in the termination shock and turbulent reconnection loop-top regions means that the origins of QPPs in HXR sources cannot be definitively discerned from our models. In follow-up work we will produce a more rigorous analysis with direct synthetic images in wavebands relevant to these processes.
The experiment with B0 = 50 G also exhibits periodic pulsing of beam energy deposition in the coronal loops, but in this and the B0 = 65 G case the main factor in the disruption of the flow of electron beams from the X point to the chromosphere is plasmoids. The reduction in beam electron footpoint heating in the case of B0 = 50 G is evident at 120 s, just after a plasmoid strikes the loop tops (Fig. 6c), with the energy deposition around this time shown in Fig. 11o. For the simulations with B0 = 65 G plasmoids can be seen approaching the loop tops at around 95–100 s in Fig. 11p, and the subsequent reduction in beam heating of the chromospheric footpoints is evident for the rest of the experiment in Fig. 6d.
Within a post-processing full kinetic model that was evolved over the backdrop of a resistive MHD-simulated atmosphere, Kong et al. (2020) found that the interaction of plasmoids with the termination shock in the loop tops significantly modulated and softened (increased the negative exponent of the power law energy distribution) the electron beams accelerated. This attenuation and shift toward lower-energy electrons was related to the collisions of the plasmoids with the loop tops, because these collisions increased the number of grid cells showing compressions. Such modeling is highly valuable and may contribute to future works that include recipes for the accelerated electron spectrum in longer, larger-scale simulations at affordable computing costs. Our work does not include a detailed kinetic model for the accelerated spectrum of electrons, but the effect of the plasmoids is, rather coincidentally, similar for the thresholding of electrons reaching the chromosphere. In our experiment the collision of the plasmoid with the loop tops causes density and magnetic field variations in the corona that result in both increased beam energy deposition near the termination shock (with reductions at the footpoints) and of greater particle trapping.
We generated SXR curves for each flare model (Not shown in figures) in Watts per meter squared, in order to produce Geostationary Operational Environmental Satellite (GOES, Menzel & Purdom 1994) flare classifications. For this we used the method outlined in Ruan et al. (2018) based on the work of Del Zanna et al. (2015), Pinto et al. (2015), and Fang et al. (2016). Their formula expresses fluxes in photon cm−2 s−1. We adapted this by multiplying the integrand by the photon energy to produce a result in erg cm−2 s−1. The integral is taken between limits with energies corresponding to those of the GOES 1–8 Å band and then converted to W m−2. It is the peak of the flux in this GOES channel that defines the standard X-ray classification of a solar flare (Baker 1970). These values need to be multiplied by a representative depth in 2.5D models. For consistency with the work of Ruan et al. (2023), we chose this depth to be 100 Mm. Assuming an arcade of this depth we obtain the data seen in Table 1. The flare classifications are spread across a reasonable span of the observed range on the Sun, but do not reach the X-class flare classification.
F0 and GOES classifications of the simulated flares.
3.4. Flows along a field line
In Sect. 3.2.1, statistics for the electron beam deposition were presented at each base point of the models. Now that we have presented the multidimensional evolution of the lower and upper atmosphere we inspect the variations in 1D of parameters along individual field lines. Many of the physical processes in flare loop systems are field-aligned, and so there is significant value to inspecting the dynamics along such cuts. Moreover, this analysis provides a much greater basis than currently exists in the literature to enable the comparison of results of flare simulations in multiple dimensions with decades of research results derived from detailed 1D radiation HD modeling of flare loops.
For this investigation, we inspect the strongest (M2 class) flare with B0 = 65 G and a maximum beam electron energy flux over all space and time of 4.7 × 1010 erg cm−2 s−1. Field lines with footpoints at x = −10, −12.5 and −15 Mm are selected as representatives of the variety of locations available within this multidimensional morphology.
Plasma number densities, vertical velocities, temperatures, and kinetic energy densities are shown as functions of distance from the loop apex (y-axis) and time (x-axis) in Figs. 12–14. The electron fluxes along these field lines are shown as functions of time, over-plotted as red lines on these images. These views form the direct counterpart of restricted 1D HD models (e.g., Fig. 6 of Unverferth & Reep 2023) and can be compared readily.
 |
Fig. 12. Evolution of the atmosphere along a single field line with one footpoint at x = −10 Mm, discussed in Sect. 3.4.1 (B0 = 65 G, x = −10 Mm, F0 = 1.0F10). They are shown in plots of time on the horizontal axis and length, s, along the field line vertically, with s = 0 at x = −10 Mm, y = 0 Mm. The parameters shown are (a) plasma number density, (b) the vertical velocity, (c) the plasma temperature, (d) the kinetic energy density. The plasma number density panel show the beam electron energy flux deposited in the chromosphere above the left footpoint, over-plotted in red. This over-plot is scaled such that the maximum electron energy flux deposited throughout the entire simulation (4.7 × 1010 erg cm−2 s−1) corresponds to the peak reaching top of the panel, with zero at the bottom. The beam in this field line reaches a peak flux of 1.0 × 1010 erg cm−2 s−1. We note that the field line changes in overall length as a function of time. The extent of the experimental domain is highlighted with green lines in each panel. Before reconnection this highlights the bottom and top of the experiment, after reconnection these highlight the locations of the photospheric footpoints in each time step. Values outside of this are saturated to their photospheric values for continuity, but do not represent simulated values. |
 |
Fig. 13. Evolution of the atmosphere along a single field line with one footpoint at x = −12.5 Mm, discussed in Sect. 3.4.2 (B0 = 65 G, x = −12.5 Mm, F0 = 2.5F10). The formatting is the same as that used in Fig. 12. The beam in this field line reaches a peak flux of 2.5 × 1010 erg cm−2 s−1. |
 |
Fig. 14. Evolution of the atmosphere along a single field line with one footpoint at x = −15 Mm, discussed in Sect. 3.4.3 (B0 = 65 G, x = −15 Mm, F0 = 5.7F9). The formatting is the same as that used in Fig. 12. The beam in this field line reaches a peak flux of 5.7 × 109 erg cm−2 s−1. |
Before magnetic reconnection the tracked field lines exit the experiment at the top boundary, and after reconnection, they reach to a footpoint on the opposite side of the flare loop system. Thus, there is a sharp disconnect between the top halves of these panels at times before and after the reconnection, as this portion of the field line tracks completely different plasma. After the field lines reconnect, they rapidly retract and shorten. This can be seen by the rapidly decreasing total length of the field lines between the photospheric footpoints of the field lines. The footpoints are plotted as green lines at the tops and bottoms of the panels.
3.4.1. B0 = 65 G, x = −10 Mm, F0 = 1.0F10
From Fig. 12 one can see that this field line reconnects at t = 67 s. This is 4 s after t = 63 s, when the beam electrons switch on for this field line, accelerated in regions away from the X point. The onset of the evaporation can be seen from the lower footpoint at t = 65 s. This requires some explanation with respect to the standard flare model. Before reconnection there is significant heating (to around T = 10 MK) on this field line from energy supplied by neighboring plasma via various methods, including heat diffusion and the expansion of the neighboring flux tubes, which generates compressive heating of the flux tube we are inspecting. The heating intrudes at lengths/heights around s = −25 Mm at t = 53 s. This causes upward and downward flows to expand outward from this point. More dramatic heating occurs at t = 60 s just before the reconnection time, both at the similar heights the previous heating and near the reconnection region higher up the open field line. This heating results in heat conduction and velocity flows. This conduction front approaching the chromosphere drives evaporation up from the footpoints. The evaporated material continues to be heated and expand, driving further acceleration up to around 300 km s−1 by the time the evaporation reaches y = 20 or s = −10 Mm, at temperatures of around 2 MK.
Meanwhile, the top of the reconnected loop collapses downward at high velocity and shortens in total length. This process is visible as a dark blue horizontal stripe in vertical velocity (downflow) immediately after the reconnection event, seen in panel b. The apex of the line shortens until it is around s = 20 − 30 Mm away from the footpoints. The compression of the loop tops drives a series of hot (50–100 MK) outward (downward) flows from the apex, starting at around t = 80 s. The velocity plot, kinetic energy plot, and temperature structure of the loop tops show that the region is undergoing turbulence as well as heating events.
The downward flows driven from the loop tops meet the rising chromospheric evaporation. The evaporation and downward traveling loop-top flows shock when they meet, reducing the velocities of both streams and heating the upward moving material significantly. This can be seen in the changes of gradients of the rising and falling density fronts in Fig. 12a at around s = ±8 Mm, at t = 80 s. In the beam-driven evaporation model of Druett et al. (2023) there was no strong reconnection outflow to compress the loop tops and drive downward flow that meet the rising evaporation, in that study a significant portion of the evaporated plasma passed over the loop tops and down to the other side of the arcade. In contrast, in this study the upward evaporations do not directly pass over the loop-top region, but get caught in the turbulence until gentle downflows form at around t = 140 s. The direct passing of upflows over the loop apex and down toward the opposite footpoint can also be seen in 1D loop models, including that shown in the central and right panels of Fig. 6 of Unverferth & Reep (2023), which, due to the 1D nature of the model, shows no loop-top turbulence.
Along this field line, pulses of extra density and kinetic energy rise upward from both footpoints after around t = 85 s; they become broader, slower, and weaker over time. This occurs after the beam electron processes have ceased along the field line, possibly indicating some wave-like behavior.
3.4.2. B0 = 65 G, x = −12.5 Mm, F0 = 2.5F10
Figure 13 shows that, predictably, the field line further out reconnects later (t = 85 s). Both the beam acceleration and the evaporation processes from the footpoints start at 80 s. This is also co-temporal with the arrival of the fast downward propagating hot jet due to heating and expansion of neighboring material that heats this flux tube around s = −25 Mm beginning at around t = 75 s. The driving of the evaporation is broadly similar to that described for the footpoint at x = −10 Mm. After reconnection, the loop top collapses downward at greater velocities and halts with a wider span of s values. The simulation ends before the gentle downflows from the loop tops can reach the footpoints.
3.4.3. B0 = 65 G, x = −15 Mm, F0 = 5.7F9
Figure 14 shows that this field line experiences chromospheric evaporation (at t = 94 s) well before reconnecting (at t = 102 s) and before the beam electrons reach the chromosphere (at t = 104 s). The heat driven expansion from the nearby loops begins at positions near s = −25 Mm. Again, the hot plasma expands in upward and downward directions from s = −25 Mm. This flow reaches the chromosphere at t = 93 s and immediately drives chromospheric evaporation, which achieves similar speeds of around 300 km s−1. The evaporation collides with downflows at positions of around s = 20 Mm.
By the time this field line, which is situated in the outer region of the flare, reconnects, significant loop-top turbulence is already present. This can be seen through the high-speed, direction-varying velocities in the loop tops (panel b). Also, before the time of the reconnection of the field line there are already some slightly higher-density features in the loop tops, as well as the rising chromospheric evaporation fronts. The beam electrons deposit a significant fraction of their energy in these evaporation and loop-top features. Thus, the beam flux reaching the chromosphere is significantly reduced. A dedicated future investigation will be necessary to understand these effect in detail, including in experiments with evaporation driven by beam electrons (Druett et al. 2023).
4. Summary and discussion
In this paper we present a study of the 2.5 D MPI-AMRVAC flares that include beam electrons first reported in Ruan et al. (2020). By varying the background magnetic field strength by a factor of 3.25 in these simulations between B0 = 20 G and 65 G, the GOES classification of the simulation changes by over two orders of magnitude, between B1.5 and M2.3 (assuming a 100 Mm arcade length in the third-dimension; see Table 1).
The flux of energy supplied by energetic electrons at any given chromospheric footpoint has a characteristic duration of between five and 20 s, usually with a relatively triangular profile of flux against time, peaking earlier in the profile (see Figs. 6 and 12–14). The peak beam heating flux at a footpoint in each experiment varies between 1F9 for the case B0 = 20 G (F0 = 1 × 109 erg cm−2 s−1) and 5F10 for the case B0 = 65 G (F0 = 5 × 1010 erg cm−2 s−1), over an order of magnitude difference. This is the first paper to report the details of chromospheric beam fluxes and their evolution in multidimensional simulations.
In all simulations, bidirectional reconnection outflow jets are formed in the corona at heights of 50 Mm, where the initial reconnection X point forms. The outflows have a classic lobster claw shape (Zenitani & Miyoshi 2011). A fast shock exists in the tail of this feature and stabilizes some time after the outflow impacts the lower atmosphere. The maximum speed achieved in these flows scales by a similar amount as the background field, from around 1000 km s−1 to 3200 km s−1 across the experiments with B0 = 20 G to B0 = 65 G, respectively. As a result, after the loop system settles, the maximum outflow speed is approximately constant across the simulations when expressed as an Alfvén Mach number (see Fig. 4). It is possible that this 𝒪(10) maximum value would change based on the variation in other simulation parameters, such as the vertical position of the resistivity patch, which would provide a longer or shorter reconnection outflow jet if placed higher or lower in the atmosphere, respectively. The maximum outflow Alfvén Mach number was insensitive to changes in the maximum anomalous resistivity.
We performed the first detailed investigation of chromospheric response to the impacts of reconnection outflow jets in multidimensional models, including the changes in these responses across a variety of flare strengths. The impact of the reconnection outflow jets and the heat conduction front on the lower atmosphere heats the chromospheric material. This generates hot upflows (T ∼ 2 MK; chromospheric evaporation; see Figs. 12–14, panel c) and cooler downflows (T ∼ 20 000 K; downflowing chromospheric compressions; see Figs. 8 and 9). Chromospheric material is also heated from around 6000 K to around 20 000 K within a second of the beam electrons being switched on. Heating of the plasma to around 20 000 K extends downward from the tops of the chromosphere to depths of 1.5 Mm for the B0 = 20 G simulation and to 1.0 Mm for the B0 = 65 G case. There are noticeable kinetic energy imprints of the beam electrons at the chromospheric footpoints of the flares after the acceleration is switched on, but they are swamped by the reconnection outflow jet in the present simulation suite (see Fig. 7). This is investigated in more detail in a companion paper (Druett et al. 2023).
At heights of 300 km above the photosphere, the downward kinetic energy flux densities reach 5 × 106 erg cm−2 s−1 for the experiment with B0 = 20 G, and up to 4 × 108 erg cm−2 s−1 for B0 = 65 G. This demonstrates a significant transfer of energy and momentum to the photosphere; however, even the downflowing chromospheric compression for the strongest flare presented drops below the local sound speed at heights between 200 and 300 km above the photosphere. This implies that we would not expect these simulated flares to produce sunquakes via the downflowing chromospheric compressions. This is the first set of multidimensional flare simulations to test downflowing chromospheric compressions as potential drivers of sunquakes (see Russell et al. 2016 for an investigation in multiple dimensions that was restricted to the lower atmosphere). However, the lower atmospheres of our simulations are simplified, with field strengths and densities that are significantly lower at the base of the model than those considered to be typically “photospheric”, and this will be addressed in a future study.
Regarding the excavation of the chromosphere by evaporation processes in the flares, our 2.5D simulations (Figs. 8 and 9) bear a visual resemblance to the ribbon height substructure that can be seen in observations of the chromosphere using COCOPLOTs (Druett et al. 2022; Pietrow et al. 2024b); an example of this flare ribbon evolution is described in Pietrow et al. (2024a). In their observations, the flare ribbon emission appears to be coming from lower than the chromospheric emission, from just outside the boundaries of the flare ribbons. This can be inferred from the projection effect of the cooler chromospheric material outside the flare ribbon, which overlaps the adjacent bright flare ribbon emission in the line of sight, leading to strong absorption of the flare emission. Moreover, this effect is clearly present on the leading edge of the eastern ribbon, which, due to the viewing angle, is oriented such that if the ribbon formation is lower than the surrounding chromosphere, it is overlapping. Structures much more similar to the ribbon substructures reported by Singh et al. (priv. comm.) may relate to the periodic evaporation pulsations noted in our simulations (Figs. 12–14). Between the ribbons there appears to be a higher plateau near the polarity inversion line, which in our experiments is reproduced by the combination of the outflow impacts and the magnetic topology of the reconnected field lines. In a future work we will follow up on these MHD plus beam-driven runs with nonlocal thermodynamic equilibrium spectroscopic analysis, now possible for multidimensional setups.
The heat conduction, impact of the reconnection jets, and beam heating of the lower atmosphere (principally the impact and heat conduction) drive chromospheric evaporation, with characteristic speeds at a height of 5 Mm ranging from 200 km s−1 to 600 km s−1 across the range of the background field strengths studied; again, they scale relatively linearly with this parameter. The maximum at any time in the B0 = 65 G experiment is ∼800 km s−1, which is higher than typically observed.
Notably, there is a downward net mass flux through a height of 5 Mm in the B0 = 20 G experiment, indicating that more mass is ejected downward along the coronal loops due to the reconnection than is evaporated upward from the surface due to the energy transport. For all the other (stronger) flares, there were positive mass fluxes at this height and a clear reduction in the proportion of cool chromospheric material at low atmospheric heights due to the plasma heating and evaporation (Fig. 10).
The upward evaporation from the chromosphere meets fronts traveling in the opposite direction, down from the loop tops. These downward fronts are squeezed by the pressure gradient force along the field lines due to the impact of the reconnection outflow jet on the loop tops. These two fronts impact, and slow when they meet (Figs. 12–14). The evaporation does not directly travel from footpoint to footpoint, in contrast to a similar experiment with chromospheric evaporation driven by beam electrons (Druett et al. 2023). This difference could prove highly instructive in discerning flare evaporation mechanisms if it persists across robust variations of the simulation parameters.
The evolution of the horizontal and oblique shocks in each experiment is similar to the descriptions in Takasao et al. (2015) and Takasao & Shibata (2016) across all experiments. Also, turbulent vortices form on alternating sides of the loop tops with time. This creates the magnetic tuning fork phenomenon (Takasao & Shibata 2016), which has been suggested as a candidate process for producing flare QPPs in loop-top emissions (McLaughlin et al. 2018; Zimovets et al. 2021).
We propose a new mechanism for generating simultaneous QPPs in the footpoint and loop-top HXR sources. The magnetic tuning fork process produces pulsations in the SXR loop-top sources (Takasao & Shibata 2016). In our simulations, they have similar periods to pulsations in the loop top and in the footpoint HXR bremsstrahlung sources. This is because the magnetic tuning fork process contributes to the creation of periodic variations in the densities of material along the recently reconnected loops. This, in turn, attenuates the fluxes of electrons that reach the chromosphere from acceleration locations above the loop tops. Imaging X-ray spectra would be necessary to observe this effect in the HXR footpoint sources, which could be provided by the proposed Focusing Optics X-ray Solar Imager instrument (FOXSI, Christe et al. 2023). If, in a future study, line synthesis of the chromospheric spectral lines used in our simulations can be achieved, then we would be able to infer whether this process would also produce pulsations in visible and near-UV sources.
Our investigation of the flows along 1D field lines reveals several multidimensional effects that are not accounted for in 1D studies of solar flare loops, even those attempting to recreate multidimensional effects, such as Kerr et al. (2020) and Unverferth & Reep (2023). Firstly, the reconnection and loop-top turbulence sources are intimately linked to the multidimensional nature of the simulation. Secondly, a shock occurs when chromospheric evaporation meets downward loop-top sources that have been forced along the field lines due to the high pressure in the loop tops. Thirdly, there is chromospheric evaporation caused by heat conduction via field-aligned transport from the loop-top sources, but also from neighboring flux tubes via processes that include heat diffusion and compression. In strong flares these processes cause the leading edges of the flare ribbons to begin evaporating material via thermal conduction before the associated field lines have reconnected. These regions completely lack beam electrons and HXR sources at these times (Fig. 14). This matches the pattern of flows from UV satellite observations by the Interface Region Imaging Spectrometer (IRIS; De Pontieu et al. 2014) as reported in Polito et al. (2023), who note that the leading edges of the flare ribbons show significantly less evaporation of chromospheric material than the main bodies of the flare ribbons. Polito et al. (2023) find the beams of electrons in the leading edges of the flare ribbon to be significantly weaker (presumably associated with acceleration processes near the X point in the current sheet above the flare loops) than the beams inside the body of the flare ribbon (which may be associated with acceleration sources nearer the termination shock, the loop-top turbulence, or the flare loop tops themselves). Our models demonstrate that additional and alternative interpretations to those that can be provided by 1D analysis should be considered. However, modeling advances are required in our simulations to include particle acceleration in the termination shock and turbulent loop tops before we can provide a comprehensive answer.
Finally, we note a number of improvements that can be made to these models and the benefits they would bring. This lineage of simulations has focused on accurately reproducing coronal conditions, and future simulations should improve the modeling of lower atmosphere by increasing the magnetic field strength (eventually by several orders of magnitude at the base) and making the density profile accurately represent chromospheric and photospheric values. This would improve the accuracy and credibility of interpretations derived from spectral line synthesis regarding the motions of the downflowing chromospheric compressions, ribbon formation, and evaporation processes, thereby better constraining the energetics and fundamental flare processes responsible for visible, UV, and SXR emissions.
The beam model should be improved so that it can self-consistently be the principle agent driving evaporation. This has recently been achieved for the first time in multiple dimensions in a companion paper, Druett et al. (2023). The energy spectrum and mean pitch angles of these beams can be parameterized based on atmospheric quantities and acceleration statistics from detailed studies, including approaches by Bakke et al. (2018), Frogner et al. (2020), and Frogner & Gudiksen (2022). Effects such as self-induced electric field and return currents could also be included in the transport model (Zharkova et al. 1995). Energetic protons could be considered in the particle transport modeling as well (Zharkova & Zharkov 2015).
Detailed nonlocal thermodynamic equilibrium RT (Allred et al. 2005, 2015; Carlsson & Leenaarts 2012; Hong et al. 2022) and nonequilibrium ionization (Leenaarts et al. 2007) can be included in the lower atmosphere. This could be combined with optically thick spectral line synthesis (Osborne & Milić 2021; Jenkins et al. 2023). The combination of these advances applied to our models would provide a multidimensional context to our understanding of the inhomogeneities, flows, energy delivery, and ribbon substructures observed in a large number of currently debated flare phenomena based on observations in the visible and near-UV emissions of flares (Ichimoto & Kurokawa 1984; Osborne & Fletcher 2022; Pietrow 2022; Polito et al. 2023). Investigations could also be made regarding extremely broadened flare ribbon spectral line profiles (Zharkov et al. 2020; Druett et al. 2021; Kowalski et al. 2022; Kerr et al. 2024) and the mechanisms responsible for sunquakes (Kosovichev & Zharkova 2001; Quinn et al. 2019).
Further studies that use this model would be instructive. An investigation of the effects of varying the height of the resistivity patch and introducing asymmetries into the simulation would examine the robustness of relationships derived using our standard setup. Data-driven simulations and a systematic comparison of our multidimensional simulations with 1D simulations that include detailed physics would allow us to determine the most potent admixture of these approaches to use in future studies. Furthermore, an equivalent study for simulations with evaporation driven by beam electrons and a 3D version of the simulation would allow us to interpret observational signatures of the different evaporation mechanisms, thereby determining which processes principally drive evaporation and other fundamental flare phenomena on the Sun.
Movies
Movie 1 associated with Fig. 9 (flare_chromo_excavation) Access here
Movie 2 associated with Fig. 11 (flare_energy_densities) Access here
Acknowledgments
M.D. is supported by FWO project G0B4521N. W.R. was supported by a postdoctoral mandate (PDMT1/21/027) by KU Leuven. R.K. is supported by Internal Funds KU Leuven through the project C14/19/089 TRACESpace and an FWO project G0B4521N. M.D., W.R., and R.K. acknowledge funding from the European Research Council (ERC) under the European Union Horizon 2020 research and innovation program (grant agreement No. 833251 PROMINENT ERC-ADG 2018). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government, department EWI. M.D. acknowledges fruitful discussions with Alexander G.M. Pietrow regarding the contents of this manuscript.
References
- Allred, J. C., Hawley, S. L., Abbett, W. P., & Carlsson, M. 2005, ApJ, 630, 573 [NASA ADS] [CrossRef] [Google Scholar]
- Allred, J. C., Kowalski, A. F., & Carlsson, M. 2015, ApJ, 809, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Aulanier, G., Janvier, M., & Schmieder, B. 2012, A&A, 543, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aulanier, G., Démoulin, P., Schrijver, C. J., et al. 2013, A&A, 549, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baker, D. M. 1970, American Institute of Aeronautics and Astronautics Conference, 1370 [Google Scholar]
- Bakke, H., Frogner, L., & Gudiksen, B. V. 2018, A&A, 620, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruzek, A. 1969, Sol. Phys., 8, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Čada, M., & Torrilhon, M. 2009, J. Comput. Phys., 228, 4118 [Google Scholar]
- Canfield, R. C., & Gayley, K. G. 1987, ApJ, 322, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Cargill, P. J., Vlahos, L., Baumann, G., Drake, J. F., & Nordlund, Å. 2012, Space Sci. Rev., 173, 223 [CrossRef] [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carmichael, H. 1964, in A Process for Flares, ed. W. N. Hess (Washington, DC: National Aeronautics and Space Administration, Science and Technical Information Division), NASA SP, 50, 451 [Google Scholar]
- Cheung, M. C. M., Rempel, M., Chintzoglou, G., et al. 2019, Nat. Astron., 3, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Christe, S., Alaoui, M., Allred, J., et al. 2023, BAAS, 55, 065 [NASA ADS] [Google Scholar]
- Del Zanna, G., Dere, K. P., Young, P. R., Landi, E., & Mason, H. E. 2015, A&A, 582, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [Google Scholar]
- Dreicer, H. 1959, Phys. Rev., 115, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Dreicer, H. 1960, Phys. Rev., 117, 329 [NASA ADS] [CrossRef] [Google Scholar]
- Druett, M. K., & Zharkova, V. V. 2018, A&A, 610, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Druett, M. K., & Zharkova, V. V. 2019, A&A, 623, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Druett, M. K., Scullion, E., Zharkova, V., et al. 2017, Nat. Commun., 8, 15905 [NASA ADS] [CrossRef] [Google Scholar]
- Druett, M. K., Pietrow, A. G. M., & Vissers, G. J. M. 2021, SolFER Spring 2021 Meeting, E1 [Google Scholar]
- Druett, M. K., Pietrow, A. G. M., Vissers, G. J. M., Robustini, C., & Calvo, F. 2022, RASTI, 1, 29 [NASA ADS] [Google Scholar]
- Druett, M. K., Ruan, W., & Keppens, R. 2023, Sol. Phys., 298, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, D. C., & Ramaty, R. 1985, ApJ, 298, 400 [Google Scholar]
- Emslie, A. G. 1978, ApJ, 224, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, X., Yuan, D., Xia, C., Van Doorsselaere, T., & Keppens, R. 2016, ApJ, 833, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, G. H., Canfield, R. C., & McClymont, A. N. 1985, ApJ, 289, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, L., & Hudson, H. S. 2008, ApJ, 675, 1645 [Google Scholar]
- Frogner, L., & Gudiksen, B. V. 2022, A&A, submitted [arXiv:2210.01609] [Google Scholar]
- Frogner, L., Gudiksen, B. V., & Bakke, H. 2020, A&A, 643, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goedbloed, J. P., Keppens, R., & Poedts, S. 2019, Magnetohydrodynamics of Laboratory and Astrophysical Plasmas (Cambridge: Cambridge University Press) [Google Scholar]
- Harten, A., Lax, P. D., & van Leer, B. 1983, SIAM Rev., 25, 35 [Google Scholar]
- Heinzel, P., Kleint, L., Kašparová, J., & Krucker, S. 2017, ApJ, 847, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Hirayama, T. 1974, Sol. Phys., 34, 323 [Google Scholar]
- Holman, G. D., Aschwanden, M. J., Aurass, H., et al. 2011, Space Sci. Rev., 159, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Hong, J., Carlsson, M., & Ding, M. D. 2022, A&A, 661, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoshino, M. 2023, ApJ, 946, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Ichimoto, K., & Kurokawa, H. 1984, Sol. Phys., 93, 105 [NASA ADS] [Google Scholar]
- Isobe, H., Yokoyama, T., Shimojo, M., et al. 2002, ApJ, 566, 528 [NASA ADS] [CrossRef] [Google Scholar]
- Janvier, M., Aulanier, G., Pariat, E., & Démoulin, P. 2013, A&A, 555, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Janvier, M., Aulanier, G., Bommier, V., et al. 2014, ApJ, 788, 60 [Google Scholar]
- Jenkins, J. M., Osborne, C. M. J., & Keppens, R. 2023, A&A, 670, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennedy, M. B., Milligan, R. O., Allred, J. C., Mathioudakis, M., & Keenan, F. P. 2015, A&A, 578, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Keppens, R., Meliani, Z., van Marle, A. J., et al. 2012, J. Comput. Phys., 231, 718 [Google Scholar]
- Keppens, R., Porth, O., Galsgaard, K., et al. 2013, Phys. Plasmas, 20, 092109 [CrossRef] [Google Scholar]
- Keppens, R., Popescu Braileanu, B., Zhou, Y., et al. 2023, A&A, 673, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kerr, G. S., Allred, J. C., & Polito, V. 2020, ApJ, 900, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kerr, G. S., Kowalski, A. F., Allred, J. C., Daw, A. N., & Kane, M. R. 2024, MNRAS, 527, 2523 [Google Scholar]
- Kong, X., Guo, F., Shen, C., et al. 2019, ApJ, 887, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, X., Guo, F., Shen, C., et al. 2020, ApJ, 905, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Kong, X., Chen, B., Guo, F., et al. 2022, ApJ, 941, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Kontar, E. P., Perez, J. E., Harra, L. K., et al. 2017, Phys. Rev. Lett., 118, 155101 [NASA ADS] [CrossRef] [Google Scholar]
- Kosovichev, A. G., & Zharkova, V. V. 2001, ApJ, 550, L105 [CrossRef] [Google Scholar]
- Kowalski, A. F., Allred, J. C., Carlsson, M., et al. 2022, ApJ, 928, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., Hansteen, V., & Rutten, R. J. 2007, A&A, 473, 625 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Macrae, C., Zharkov, S., Zharkova, V., et al. 2018, A&A, 619, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., De Moortel, I., Hood, A. W., & Brady, C. S. 2009, A&A, 493, 227 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, J. A., Nakariakov, V. M., Dominique, M., Jelínek, P., & Takasao, S. 2018, Space Sci. Rev., 214, 45 [Google Scholar]
- Menzel, W. P., & Purdom, J. F. W. 1994, BAMS, 75, 757 [CrossRef] [Google Scholar]
- Miller, J. A., Larosa, T. N., & Moore, R. L. 1996, ApJ, 461, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, C. M. J., & Fletcher, L. 2022, MNRAS, 516, 6066 [NASA ADS] [CrossRef] [Google Scholar]
- Osborne, C. M. J., & Milić, I. 2021, ApJ, 917, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1963, ApJS, 8, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Petschek, H. E. 1964, in Magnetic Field Annihilation, ed. W. N. Hess (Washington, DC: National Aeronautics and Space Administration, Science and Technical Information Division), NASA SP, 50, 425 [Google Scholar]
- Pietrow, A. G. M. 2022, Ph.D. Thesis, Stockholm University, Sweden [Google Scholar]
- Pietrow, A., Cretignier, M., Druett, M. K., et al. 2024a, A&A, 682, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrow, A. G. M., Druett, M. K., & Singh, V. 2024b, A&A, in press, https://doi.org/10.1051/0004-6361/202348839 [Google Scholar]
- Pinto, R. F., Vilmer, N., & Brun, A. S. 2015, A&A, 576, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polito, V., Reep, J. W., Reeves, K. K., et al. 2016, ApJ, 816, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Polito, V., Kerr, G. S., Xu, Y., Sadykov, V. M., & Lorincik, J. 2023, ApJ, 944, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Porth, O., Xia, C., Hendrix, T., Moschou, S. P., & Keppens, R. 2014, ApJS, 214, 4 [Google Scholar]
- Priest, E. R., & Forbes, T. G. 2002, A&ARv, 10, 313 [Google Scholar]
- Quinn, S., Reid, A., Mathioudakis, M., et al. 2019, ApJ, 881, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M., Chintzoglou, G., Cheung, M. C. M., Fan, Y., & Kleint, L. 2023, ApJ, 955, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Rowan, M. E., Sironi, L., & Narayan, R. 2017, ApJ, 850, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, W., Xia, C., & Keppens, R. 2018, A&A, 618, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruan, W., Xia, C., & Keppens, R. 2020, ApJ, 896, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Ruan, W., Yan, L., & Keppens, R. 2023, ApJ, 947, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Russell, A. J. B., Mooney, M. K., Leake, J. E., & Hudson, H. S. 2016, ApJ, 831, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, S., & Keppens, R. 2022, A&A, 666, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shen, C., Chen, B., Reeves, K. K., et al. 2022, Nat. Astron., 6, 317 [NASA ADS] [CrossRef] [Google Scholar]
- Shibata, K. 1996, Adv. Space Res., 17, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Siversky, T. V., & Zharkova, V. V. 2009, A&A, 504, 1057 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1962, Physics of Fully Ionized Gases, 2nd edn. (New York: Interscience) [Google Scholar]
- Spitzer, L., Jr., & Scott, E. H. 1969, ApJ, 158, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., Jr., & Tomasko, M. G. 1968, ApJ, 152, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Sturrock, P. A. 1966, Nature, 211, 695 [Google Scholar]
- Sturrock, P. A. 1992, in IAU Colloq. 133: Eruptive Solar Flares, eds. Z. Svestka, B. V. Jackson, & M. E. Machado, 399, 397 [NASA ADS] [Google Scholar]
- Sweet, P. A. 1958, in Electromagnetic Phenomena in Cosmical Physics, ed. B. Lehnert, 6, 123 [NASA ADS] [Google Scholar]
- Syrovatskii, S. I., & Shmeleva, O. P. 1972, Soviet Ast., 16, 273 [NASA ADS] [Google Scholar]
- Takasao, S., & Shibata, K. 2016, ApJ, 823, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Takasao, S., Matsumoto, T., Nakamura, N., & Shibata, K. 2015, ApJ, 805, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Unverferth, J., & Reep, J. W. 2023, ApJ, 951, 95 [NASA ADS] [CrossRef] [Google Scholar]
- van Leer, B. 1974, J. Comput. Phys., 14, 361 [NASA ADS] [CrossRef] [Google Scholar]
- Varady, M., Kasparova, J., Moravec, Z., Heinzel, P., & Karlicky, M. 2010, IEEE Trans. Plasma Sci., 38, 2249 [CrossRef] [Google Scholar]
- Werner, G. R., Uzdensky, D. A., Begelman, M. C., Cerutti, B., & Nalewajko, K. 2018, MNRAS, 473, 4840 [Google Scholar]
- Woodward, P., & Colella, P. 1984, J. Comput. Phys., 54, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, C., Teunissen, J., El Mellah, I., Chané, E., & Keppens, R. 2018, ApJS, 234, 30 [Google Scholar]
- Yokoyama, T., & Shibata, K. 2001, ApJ, 549, 1160 [NASA ADS] [CrossRef] [Google Scholar]
- Zenitani, S., & Miyoshi, T. 2011, Phys. Plasmas, 18, 022105 [NASA ADS] [CrossRef] [Google Scholar]
- Zharkov, S., Matthews, S., Zharkova, V., et al. 2020, A&A, 639, A78 [EDP Sciences] [Google Scholar]
- Zharkova, V. V., & Zharkov, S. I. 2007, ApJ, 664, 573 [CrossRef] [Google Scholar]
- Zharkova, V., & Zharkov, S. 2015, Sol. Phys., 290, 3163 [CrossRef] [Google Scholar]
- Zharkova, V. V., Brown, J. C., & Syniavskii, D. V. 1995, A&A, 304, 284 [NASA ADS] [Google Scholar]
- Zharkova, V. V., Arzner, K., Benz, A. O., et al. 2011, Space Sci. Rev., 159, 357 [Google Scholar]
- Zharkova, V., Zharkov, S., Druett, M. K., Matthews, S., & Inoue, S. 2020, A&A, 639, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zimovets, I. V., McLaughlin, J. A., Srivastava, A. K., et al. 2021, Space Sci. Rev., 217, 66 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Beam heating and approximation of energy conservation
Once the field lines that host energetic electron beams were identified within the multidimensional simulation as described in Sect. 2.3, the 1D model of Emslie (1978) was applied to the density profiles along their paths. This created a table of energy deposition rates along each section of each field line. An interpolation routine was then used to redistribute the energy deposited from the beam back into the plasma (see Appendix D of Ruan et al. 2020).
Electrons are considered trapped on the field lines when the atmosphere through which they are traveling is such that the beam electrons gain a perpendicular pitch angle to the field line. This is modeled by consideration of the first adiabatic invariant, which produces the following relationship (Appendix A Ruan et al. 2020) between the cosine of the electron beam’s mean pitch angle, μ, at position s and its initial value at the top of the loop, μ0. This is expressed in terms of the initial field strength B0 and the field strength at position s,
Thus, in Eq. A.1, if there exists any point s along the field line where the term that is inside the square root becomes negative, the heating rate is truncated at this position and the remaining energy stored in the electrons is considered to be trapped and is carried over to the next time step. The energy and mean pitch angle of the electrons in the new time step were found by considering contributions from both the newly generated and the carried-over electron distributions. Any electrons reaching the base of the model leave the system and take with them any remaining energy.
Absolute energy conservation is not guaranteed by the interpolation of energy deposition from the 1D models back into the multidimensional domain. This applies to the beam electron energy as it deposits energy back into the MHD plasma. Energetic electrons may also exit the domain and thus make the process an overall sink of energy. A comparison was made between the energy removed from the MHD equations at the acceleration sites, Qe, and that returned to the plasma, He (Fig.A.1). The energy removed and returned track each other closely in form, and the total energy returned to the plasma never exceeds the total energy removed from the plasma. This holds true of the integrated totals at all times. Energy stored in field lines by particle trapping in previous time steps can be returned swiftly to the plasma and cause a transient excess in the heating rate, He, over Qe. This excess energy is drained from the reservoir of the energy stored in the field lines. The strong periodicity of this process shown at times after t = 150 s in the top panel of Fig.A.1 is related to the processes described in Sect. 3.3.
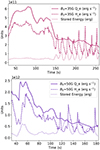 |
Fig. A.1. Approximate energy conservation of the beam processes. Results are shown for the B0 = 35 G and B0 = 50 G simulations assuming an arcade depth (third-dimension depth) of 100 Mm. The solid line shows the Ohmic heating rate Qe (integrated over the whole domain) that is subtracted from the MHD model as per Eq. 8 in units of erg s−1. The dashed line shows the beam heating rate (re-interpolated onto the adaptive mesh grid and integrated over the whole domain) that is the source term He in the MHD energy equation in units of erg s−1. The dotted line shows, at each time, the total energy stored in the field lines that is carried over from the previous time step, in units of erg. |
Appendix B: Relative importance of the beam heating in the evaporation scheme
Figure B.1 demonstrates the relatively minor contribution of the beam heating to the overall evaporation scheme by plotting the kinetic energy fluxes through a height of 5 Mm for experiments with and without the beam electron heating term, He, activated. The beam electron acceleration term, Qe, was active in all cases so that the coronal X point evolution was as near-identical as possible. These figures can be directly compared with the kinetic energy fluxes from the top panel of figure 5 in Druett et al. (2023) where the evaporation was significantly driven by the beam electrons. In the simulations presented in this work heat conduction and the impact and rebound of the reconnection outflow can be seen to be by far the greatest influences on the evaporation and downward traveling kinetic energy signatures.
 |
Fig. B.1. Kinetic energy fluxes through a height of 5 Mm in the simulations, as functions of time. They are shown for the B0 = 35 G and B0 = 50 G experiments in the top and bottom panels, respectively, assuming an arcade depth (third-dimension depth) of 100 Mm. Results are shown for the main simulation presented in this paper alongside results for a simulation with identical parameters, except for setting the beam heating term, He = 0 at all times. |
All Tables
All Figures
 |
Fig. 1. Standard solar flare model. Left: Standard solar flare model in 2D, with features labeled as per the numbered points in Sect. 1, namely (1) a flux rope running normal to the plane of the cross section, (2) reconnecting field lines at an X point, (3) reconnection outflow jets, (4) reconnected hot loops that gather below the X point, (5) a termination shock, (6) field-aligned transport of energy down to the lower atmosphere (7) flare ribbons, and (8) chromospheric evaporation and downflowing chromospheric compressions. Right: Images of a solar flare over the solar limb taken with the Atmospheric Imaging Assembly (AIA) aboard the Solar Dynamics Observatory (SDO, Lemen et al. 2012) on September 10, 2017, showing the form of the standard solar flare model early in the flare (at 15:51:43 UT) in the 193 Å channel, with the loop arches at the base (green arrows) and a flux rope above it (blue arrows). Slightly later (at 15:53:20 UT) we see the flux rope erupting (moving upward). Later (at 16:18:07 UT) the flux rope has left the field of view and we see emission that is interpreted as originating from the long bright current sheet (red arrows) and dense coronal flare loops below (green arrows). These images use the short exposure AIA filters but still display significant fringe artifacts emanating outward from the bright loop arches. |
| In the text | |
 |
Fig. 2. Simulated analog of the standard solar flare model. Panel a shows By/B0. All the simulations presented here start from a bipolar field region with an anomalous resistivity patch at a height of y = 50 Mm over the polarity inversion line, which causes the field to reconnect and release stored magnetic energy. Panel b shows the typical vertical velocity (vy) structure at a time before the impact of the reconnection outflow on the lower atmosphere. Positive velocity (red) represents upward motion, and negative represents downward motions (blue). The reconnection outflow jets form at the X point, where reconnection occurs; one jet flows downward, and the other, upward jet leaves the domain via the top boundary. Panel c shows the vertical velocity at the time when the reconnection jet impacts the lower atmosphere. Panel d shows the typical flare loop system that is formed via this process, through a plot of absolute magnetic field strengths. Energetic electron transport is switched on after 31.2 s of the simulation. Thus, in all cases presented in this manuscript, the electrons are switched on before the impact of the reconnection jet on the lower atmosphere. In the lower panels, electron acceleration sites are shown in green and energy deposition locations in yellow. The energy deposition locations are saturated at very low values to help indicate their paths through the experiment. In fact, these beams deposit the majority of their energy in the lower atmosphere at the footpoints of the flare loops. |
| In the text | |
 |
Fig. 3. Reconnection outflow jets of the experiments with different background magnetic field strengths. They are shown at similar morphological stages of the experiment evolution. The columns show results for different background magnetic field strengths, from B0 = 20 G on the left to B0 = 65 G on the right. The top panels show the vertical velocities of the models, and the central row shows temperatures. In the temperature panels, green arrows indicate the concentration of high temperature in the tails of the reconnection outflows, the blue arrows indicate the hotter areas at the rear of the lobster claw forms that lead the reconnection outflows. The bottom row shows plasma number density. Each panel also shows magnetic field lines in black. These are traced from footpoints at x = −2.5, −5.0, and −7.5 Mm in instances where these lines are being processed by the 1D field-line routines. In the number density panels (bottom row), beam electron acceleration sites are shown in green, and the locations where energetic electrons deposit their energy are shown in yellow. |
| In the text | |
 |
Fig. 4. Alfvén Mach numbers of the outflow reach similar ranges and values at similar evolution epochs, independent of field strength. They are shown just prior to the impact of the outflow on the chromosphere (top row), during the compression of the flare loops by the generation of the termination shock (second row), and after the rebound of the impact once the flare loops have settled (third row). In each row a green arrow highlights the fast mode shock in the reconnection outflow. In the top row a red arrow highlights the high-density core of the lobster claw outflow formation, and a magenta arrow points to the sub-Alfvénic “claws” of this structure. In the lower panel the logarithms of the maximum downward outflow speeds are shown with dashed lines (right axis), and the maximum of the Alfvén Mach numbers in these outflows is shown with solid lines. |
| In the text | |
 |
Fig. 5. Reconnection inflow rate (solid lines) and footpoint sweeping (dashed lines) expressed as |vxBy|, in electric field units E = −v × B. The different colors show the variations in these quantities as functions of time for the experiments with different strengths of background magnetic field B0. |
| In the text | |
 |
Fig. 6. Electron beam heating in the chromospheric footpoints. Each panel shows results for an experiment with a different background magnetic field strength. They are shown as functions of time (y-axis) and footpoint location (x-axis). The heating at each footpoint is computed by integrating the source term for the electron beam heating rate. We integrate this quantity over a vertical distance in the spatial domain that spans from the lower boundary of the experiment up to (but not including) the grid cell where the temperature first exceeds 50 000 K. The figure then shows the electron beam flux density that is applied down through the top of the “chromospheric” material and deposited at each footpoint. The color map saturates to red at the low end. This occurs at a beam strength of F8 (F0 = 10 × 108 erg cm−2 s−1), and thus the red color indicates negligible or zero beam heating. |
| In the text | |
 |
Fig. 7. Signatures of the electron beam effects on the lower atmosphere. Kinetic energy maps of the flares are shown in red, with the lobster claw reconnection outflows approaching the lower atmosphere for the experiments with B0 values of (a) 20 G at t = 73 s, (b) 35 G at t = 48 s, (c) 50 G at t = 50 s, and (d) 65 G at t = 32 s. Overlays show the electron acceleration densities in green and the energy deposition regions in blue. We note that the lower panels have energy deposition rates masked and scaled to values 100 times greater than the upper panels, in order not to completely cover the footpoint kinetic energy signatures, which are seen as small red blobs (Kinetic energy) next to the blue footpoints blobs (electron energy deposition) and highlighted with blue arrows. |
| In the text | |
 |
Fig. 8. Heating, downflows, and evaporation of chromospheric material. They are shown for simulations with increasing background magnetic field strengths in the columns from left to right, each at the same time during the simulation (t = 80 s). The top row shows the plasma density in grayscale, with electron energy deposition sites overlaid in yellow. Blue arrows indicate the locations of upflows from the chromosphere, evaporation in the case of all but the B0 = 20 G experiment. Red arrows indicate the high density impact fronts of downflowing material at the top of the chromosphere. The central panels show the temperature of the atmosphere, saturating to black at 6000 K and to white at 30 000 K. In this row green arrows indicate hot chromospheric material. The bottom rows show the kinetic energy densities with chromospheric evaporation signatures highlighted using blue arrows and significant energy transfer to photospheric levels indicated by magenta arrows. |
| In the text | |
 |
Fig. 9. Heating, downflows, and evaporation of chromospheric material in the models. The formatting is similar to that of Fig. 8, including those features that are highlighted by arrows. This figure shows the simulations with different background magnetic field strengths, each at similar stages in the evolution of the flare, after the impact and rebound of the reconnection outflow jet. A movie is available online. |
| In the text | |
 |
Fig. 10. Impact of the flare on the dynamics of the lower atmosphere. The left column shows results for the B0 = 65 G simulation, while the right panels compare all four experiments. Shown are: (a) the total kinetic energy flux (assuming a the third-dimension depth of 100 Mm), (b) the maximum kinetic energy density directed downward, and (c) the maximum downward velocity, all shown at various heights near the photosphere. In the right column of panels we show: (d) the fraction of the lower atmospheric material that is chromospheric as functions of time for the different experiments, (e) the mass fluxes (assuming a third-dimension depth of 100 Mm), and (f) the maximum upward velocities of material, each taken at 5 Mm height. |
| In the text | |
 |
Fig. 11. Kinetic energy density color maps. Kinetic energy density is shown in red and highlights the flare loops, the current sheets, and shocks traveling through the surrounding atmosphere. Overlays show the electron acceleration energy densities in green and the energy deposition density in blue. Energy densities for all panels of this figure have a lower saturation limit of 10−1 erg cm−2 s−1 and an upper limit of 103 erg cm−2 s−1. The columns from left to right show results for the experiments with background magnetic field strengths of B0 = 20 G, 35 G, 50 G, and 65 G, respectively. The top row shows the simulations at the time after the impact of the leading edge of the reconnection outflow jet. This impact and its reflection causes hot upflows from the chromosphere. The second row shows the time at which the flare loops have rebounded after their compression during the impact. The third and fourth rows show later times, when the loop tops settle and exhibit turbulent eddies on alternating sides of the central line (that is, a magnetic tuning fork process). An animated version of the figure is provided in the online materials. |
| In the text | |
 |
Fig. 12. Evolution of the atmosphere along a single field line with one footpoint at x = −10 Mm, discussed in Sect. 3.4.1 (B0 = 65 G, x = −10 Mm, F0 = 1.0F10). They are shown in plots of time on the horizontal axis and length, s, along the field line vertically, with s = 0 at x = −10 Mm, y = 0 Mm. The parameters shown are (a) plasma number density, (b) the vertical velocity, (c) the plasma temperature, (d) the kinetic energy density. The plasma number density panel show the beam electron energy flux deposited in the chromosphere above the left footpoint, over-plotted in red. This over-plot is scaled such that the maximum electron energy flux deposited throughout the entire simulation (4.7 × 1010 erg cm−2 s−1) corresponds to the peak reaching top of the panel, with zero at the bottom. The beam in this field line reaches a peak flux of 1.0 × 1010 erg cm−2 s−1. We note that the field line changes in overall length as a function of time. The extent of the experimental domain is highlighted with green lines in each panel. Before reconnection this highlights the bottom and top of the experiment, after reconnection these highlight the locations of the photospheric footpoints in each time step. Values outside of this are saturated to their photospheric values for continuity, but do not represent simulated values. |
| In the text | |
 |
Fig. 13. Evolution of the atmosphere along a single field line with one footpoint at x = −12.5 Mm, discussed in Sect. 3.4.2 (B0 = 65 G, x = −12.5 Mm, F0 = 2.5F10). The formatting is the same as that used in Fig. 12. The beam in this field line reaches a peak flux of 2.5 × 1010 erg cm−2 s−1. |
| In the text | |
 |
Fig. 14. Evolution of the atmosphere along a single field line with one footpoint at x = −15 Mm, discussed in Sect. 3.4.3 (B0 = 65 G, x = −15 Mm, F0 = 5.7F9). The formatting is the same as that used in Fig. 12. The beam in this field line reaches a peak flux of 5.7 × 109 erg cm−2 s−1. |
| In the text | |
 |
Fig. A.1. Approximate energy conservation of the beam processes. Results are shown for the B0 = 35 G and B0 = 50 G simulations assuming an arcade depth (third-dimension depth) of 100 Mm. The solid line shows the Ohmic heating rate Qe (integrated over the whole domain) that is subtracted from the MHD model as per Eq. 8 in units of erg s−1. The dashed line shows the beam heating rate (re-interpolated onto the adaptive mesh grid and integrated over the whole domain) that is the source term He in the MHD energy equation in units of erg s−1. The dotted line shows, at each time, the total energy stored in the field lines that is carried over from the previous time step, in units of erg. |
| In the text | |
 |
Fig. B.1. Kinetic energy fluxes through a height of 5 Mm in the simulations, as functions of time. They are shown for the B0 = 35 G and B0 = 50 G experiments in the top and bottom panels, respectively, assuming an arcade depth (third-dimension depth) of 100 Mm. Results are shown for the main simulation presented in this paper alongside results for a simulation with identical parameters, except for setting the beam heating term, He = 0 at all times. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



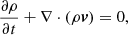
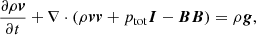
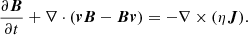
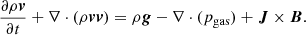
![$$ \begin{aligned} \eta (x,{ y},t < t_\eta ) = {\left\{ \begin{array}{ll} \eta _0 \left[ 2 \left( \frac{r}{r_\eta } \right)^3 - 3 \left( \frac{r}{r_\eta } \right)^2 + 1 \right] ,&r \le r_\eta \\ 0 ,&r > r_\eta . \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/04/aa47600-23/aa47600-23-eq7.gif)
![$$ \begin{aligned} \eta (x,{ y},t \ge t_\eta ) = {\left\{ \begin{array}{ll} 0,&v_d > v_c \\ \mathrm{min} \left\{ \alpha \left( \frac{v_d}{v_c} - 1 \right) \mathrm{exp} \left[ - \left( \frac{{ y}-h_\eta }{h_s} \right) ^2 \right] , 0.1 \right\} ,&v_d \ge v_c. \end{array}\right.} \end{aligned} $$](/articles/aa/full_html/2024/04/aa47600-23/aa47600-23-eq8.gif)