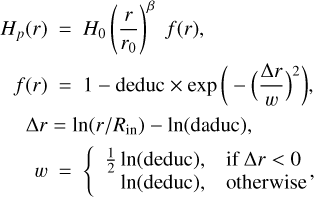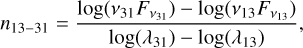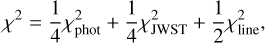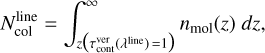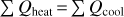| Issue |
A&A
Volume 683, March 2024
|
|
|---|---|---|
| Article Number | A219 | |
| Number of page(s) | 28 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347730 | |
| Published online | 26 March 2024 | |
2D disc modelling of the JWST line spectrum of EX Lupi
1
Space Research Institute, Austrian Academy of Sciences,
Schmiedlstr. 6,
8042
Graz, Austria
e-mail: peter.woitke@oeaw.ac.at
2
Max-Planck-Institut für extraterrestrische Physik,
Giessenbachstrasse 1,
85748
Garching, Germany
3
Kapteyn Astronomical Institute, University of Groningen,
PO Box 800,
9700 AV
Groningen, The Netherlands
4
Konkoly Observatory, HUN-REN Research Centre for Astronomy and Earth Sciences,
Konkoly-Thege Miklós út 15–17,
1121
Budapest, Hungary
5
CSFK, MTA Centre of Excellence,
Konkoly Thege Miklós út 15–17,
1121
Budapest, Hungary
6
ELTE Eötvös Loránd University, Institute of Physics,
Pázmány Péter sétány 1/A,
1117
Budapest, Hungary
7
Max Planck Institute for Astronomy,
Königstuhl 17,
69117
Heidelberg, Germany
Received:
16
August
2023
Accepted:
28
November
2023
We introduce a number of improvements to the thermo-chemical disc modelling code PRODIMO and new theoretical approaches that can be used to better predict and analyse the JWST line spectra of protoplanetary discs. We developed a new line escape probability method for disc geometries, and a new scheme for dust settling, and discuss how to apply UV molecular shielding factors to photo rates in 2D disc geometry. We show that these assumptions are crucial for the determination of gas heating and cooling rates and discuss how they affect the predicted molecular concentrations and line emissions. We apply our revised 2D models to the protoplanetary disc around the T Tauri star EX Lupi in quiescent state. We calculate infrared line emission spectra between 5 and 20 µm from CO, H2O, OH, CO2, HCN, C2H2, and H2, including lines of atoms and ions, using our full 2D predictions of molecular abundances, dust opacities, and gas and dust temperatures. We developed a disc model with a slowly increasing surface density structure around the inner rim that can simultaneously fit the spectral energy distribution, the overall shape of the JWST spectrum of EX Lupi, and the main observed molecular characteristics in terms of column densities, emitting areas, and molecular emission temperatures, which all result from one consistent disc model. The spatial structure of the line-emitting regions of the different molecules is discussed. High abundances of HCN and C2H2 are caused in the model by stellar X-ray irradiation of the gas around the inner rim.
Key words: astrochemistry / line: formation / methods: numerical / protoplanetary disks
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Medium-resolution spectroscopy of protoplanetary discs with the Spitzer Space Telescope has revealed a dense forest of H2O emission lines (Carr & Najita 2008; Salyk et al. 2008), in addition to overlapping line emission features from OH, C2H2, HCN, and CO2. From the emission temperatures of these molecules, which are of a few hundred Kelvin to about 1000 K, and the derived sizes of the line-emitting areas, it was immediately clear that these molecular spectra probe the chemistry in the terrestrial planet-forming regions; see for example the review by Pontoppidan et al. (2014). Over the past 15 yr, more than 100 Spitzer/IRS disc spectra have been analysed using simple slab-models, which has revealed certain properties of these line emissions in terms of molecular column densities, emission temperatures, and line emission areas; see Pontoppidan et al. (2010); Carr & Najita (2011); Salyk et al. (2011). Some statistics are also available, and certain trends have been identified concerning the influence of the accretion luminosity, the disc mass, the depletion of molecules in discs with large inner dust cavities, and chemical differences as a function of stellar type; see, for example, Pascucci et al. (2013); Najita et al. (2013); Walsh et al. (2015); Banzatti et al. (2017).
However, the significance of these measured molecular properties, where in the disc these molecules are present, both radially and vertically, and how this all fits together are open questions. The slab-models used for the analysis of the spectra do not provide such insights, and also have certain principle weaknesses, such as their inability to predict absorption lines, and an uncertainty as to how to include the effects of Keplerian broadening, continuous dust emission, and dust absorption under a given inclination angle.
Ultimately, we are seeking a higher level of understanding, and predictions of molecular emission features that are in accordance with the disc chemistry and the heating and cooling balance based on a model for the physical structure of the gas and dust in the disc that can predict the emission features of all molecules simultaneously. However, thermo-chemical disc models, such as those of Akimkin et al. (2013); Zhang et al. (2013); Walsh et al. (2015); Bruderer et al. (2015); Woitke et al. (2018a); Anderson et al. (2021), have yet to demonstrate that this is possible.
The puzzle of revealing the physical structure of the disc, which produces these emission lines, is complicated by the fact that we presently have little understanding of the element abundances of the gas in the inner disc. Indeed, there are very good reasons to assume that the transport of icy grains in the disc can profoundly change these element abundances during disc evolution (e.g. Ciesla & Cuzzi 2006). For example, pebble drift through the water snowline has been demonstrated in hydrodynamical disc models to increase the oxygen abundance in the inner disc (Bosman et al. 2017; Booth & Ilee 2019).
However, results from the Very Large Telescope (VLT)/MATISSE interferometer (Kokoulina et al. 2021) suggest that the dust in the inner 10 au of the disc around HD 179218 is carbon-enriched in the form of nano-carbon grains. These conclusions are based on the spectral shape of the solid opacities. Studying new VLT/MATISSE and VLT/GRAVITY data of HD 144432, Varga et al. (accepted by A&A) concluded that most of the carbon in the inner disc is in the gas phase, whereas solid iron and FeS are the main sources of dust opacity at wavelengths in the L-, M-, and N-bands. Additional clues about element transport processes have been obtained by linking the mid-infrared (MIR) line spectra to continuum images obtained with the Atacama Large Millimeter Array (ALMA). Expanding on earlier results from Najita et al. (2013), Banzatti et al. (2020) reported an anti-correlation between the infrared water line luminosity tracing the gas within a few astronomical units (au) and the distribution of solid pebbles at 10–200 au in discs. That is, radially compact discs show stronger water lines than large discs. Based on new James Webb Space Telescope (JWST) data, Banzatti et al. (2023) see more evidence for this anti-correlation. van ‘t Hoff et al. (2020) and Nazari et al. (2023) proposed that the inward transport and subsequent sublimation of carbonaceous dust grains and Polycyclic Aromatic Hydrocarbon molecules (PAHs) might enrich the inner disc with carbon.
New evidence for carbon-rich/oxygen-poor inner discs has recently been found in the first published disc spectra obtained with the James Webb Space Telescope (JWST); see Kóspál et al. (2023); Grant et al. (2023); Tabone et al. (2023); Banzatti et al. (2023); Perotti et al. (2023). A rich hydrocarbon chemistry was identified by Tabone et al. (2023) in the inner disc around the M5-star 2MASS-J16053215-1933159, with exceptionally optically thick C2H2 emission features around 7 µm and 14 µm, which are so strong that they form a wide quasi-continuum with tens of thousands of overlapping weak lines, without detecting any water lines. This is very clear evidence for a strong oxygen depletion in the inner disc of this star. Tabone et al. (2023) also mention a carbon-enrichment of the inner disc by the destruction of PAHs or carbonaceous grains as a possible cause for the large column densities of hydro-carbon molecules. However, this appears to be inconsistent with the very weak CO fundamental ro-vibrational lines as measured with JWST. To fit these lines, removal of the oxygen appears to be required, rather than enrichment of the carbon (Kanwar et al., in prep.).
In this paper, we take on the challenge of fitting the first publisheD JWST spectrum of a T Tauri star (Kóspál et al. 2023) using the 2D thermo-chemical disc model PRODIMO (Woitke et al. 2009, 2016). In Sect. 2, we report a number of important PRODIMO code changes that result in considerably improved predictions of the various MIR molecular emission features in general. In Sect. 3, we explain how we set up our disc model and how we fitted that model to the spectral energy distribution (SED) of EXLupi and its JWST/MIRI spectrum. Section 4 contains a thorough analysis of the best-fitting disc model in terms of the physical and chemical disc structure, including the calculated dust and gas temperatures. We also derive molecular column densities and emission temperatures from this model that can be compared to the values derived from slab-models, and analyse the chemical pathways in the line-forming regions of the various molecules in this section. Our conclusions are presented in Sect. 5.
2 Code improvements
Woitke et al. (2018a) demonstrated the problems faced by current standard thermo-chemical models for T Tauri discs in explaining the approximately equally strong emission features of H2O, CO2, HCN, and C2H2. First, a regular gas/dust mass ratio of 100 generally results in overly weak MIR molecular emissions. Second, while the molecular emission features of H2O and OH can be pushed to the observed flux levels using a larger gas/dust ratio of 1000 (Bruderer et al. 2015; Woitke et al. 2018a; Greenwood et al. 2019), the CO2 emission feature at 15 µm becomes too strong. Finally, the emission lines of HCN and C2H2 mostly come from a radially extended optically thin photodissociation region high above the disc in these models, but the emission lines created in these layers are generally optically thin, and their emission characteristics are in conflict with observations, in particular the molecular column densities are too low in these models; see for example Bruderer et al. (2015) for HCN. Kanwar et al. (2024) thoroughly analysed these dilute photodissociation regions using an extended hydro-carbon chemical network.
Increasing the C/O ratio can indeed boost the HCN and C2H2 line fluxes, but this leads to the loss of the CO2 emission feature (Woitke et al. 2018a), and a very fine-tuned C/O value would be required to explain the ratios of the emission line features of different molecules. In contrast, what the observations tell us is that the emission features of H2O, CO2, HCN, and C2H2 are optically thick in most cases, with column densities in excess of 1015cm−2, which causes the flux levels of these features to be on a similar level in a more robust way. We therefore carefully analysed our PRODIMO models to see how we can possibly create larger amounts of optically thick HCN and C2H2 molecules. These efforts resulted in a number of important code changes that are reported in this section. These changes are essential for fitting the first JWST spectrum, as described in Sect. 3.
2.1 A new escape probability theory for discs
Many published line fluxes from models of protoplanetary discs rely on the concept of escape probability; for example Nomura et al. (2007). Different variants of the escape probability formalism have been developed (Woods & Willacy 2009; Woitke et al. 2009; Du & Bergin 2014). In PRODIMO, while we normally perform formal solutions of the 3D line-transfer problem to calculate the line fluxes, an escape probability method is still required to compute the non-local thermodynamic equilibrium (non-LTE) populations and the heating and cooling rates. The previously used escape probability method in PRODIMO is based on Eq. (73) in Woitke et al. (2009), which is a rather crude approximation as it only considers radiative pumping by continuum photons in the radial direction and line photon escape into the upward vertical direction. In particular, the IR pumping from the disc below is incorrectly attenuated by the radial line optical depth 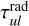 , which can be huge, which means we are likely underestimating the true IR pumping. In addition, in the outer optically thin disc regions, the escape probability is currently limited to
, which can be huge, which means we are likely underestimating the true IR pumping. In addition, in the outer optically thin disc regions, the escape probability is currently limited to 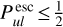 , whereas it should be
, whereas it should be 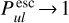 in the optically thin limit.
in the optically thin limit.
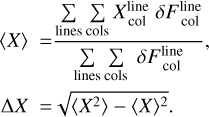
This paper introduces a new idea about how to calculate the line-averaged mean intensity 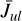 by taking into account continuum radiative transfer effects in the line resonance region:
by taking into account continuum radiative transfer effects in the line resonance region:
where ϕv is the line profile function associated with the spectral line u → 1 and Iv is the spectral intensity. Finding 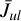 is key to formulating the effective non-LTE rates and heating and cooling functions associated with line absorption and emission; see Eqs. (80), (81), (85), and (86) in Woitke et al. (2009). Here, we show that, by making certain assumptions about disc geometry and the locality of the radiative transfer quantities explained below, it is possible to obtain a final expression that again reads
is key to formulating the effective non-LTE rates and heating and cooling functions associated with line absorption and emission; see Eqs. (80), (81), (85), and (86) in Woitke et al. (2009). Here, we show that, by making certain assumptions about disc geometry and the locality of the radiative transfer quantities explained below, it is possible to obtain a final expression that again reads
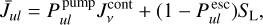 (2)
(2)
but now with new pumping and escape probabilities, 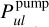 and
and 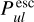 , that depend not only on line optical depths, but also on continuum optical depths, and take into account the pumping from and the escape in all directions. SL is the line source function and
, that depend not only on line optical depths, but also on continuum optical depths, and take into account the pumping from and the escape in all directions. SL is the line source function and 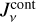 the continuous mean intensity that would result from the line having zero opacity. We write the continuum and line radiative transfer equation as
the continuous mean intensity that would result from the line having zero opacity. We write the continuum and line radiative transfer equation as
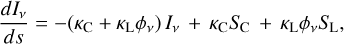 (3)
(3)
where the continuum, absorption and scattering opacities [cm−1], and the continuum source function, assuming isotropic scattering, are given by
 (4)
(4)
The line opacity [cm−1 Hz], Gaussian line profile function [Hz−1], and line source function [erg cm−2 s−1 Hz−1 sr−1] are
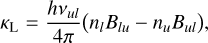 (6)
(6)
where vul is the line centre frequency, vD = vu1 Δv/c is the Doppler width, and 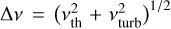 is the line width in velocity space. Introducing the optical depth and maximum optical depth as
is the line width in velocity space. Introducing the optical depth and maximum optical depth as
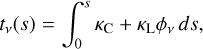 (9)
(9)
the formal solution of Eq. (3) is
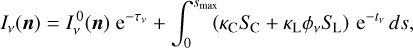 (11)
(11)
where n is the direction of the ray (unit vector) and smax is the distance backward along the ray up to the point where the ray enters the model volume. 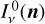 is the incident intensity at that point in direction n.
is the incident intensity at that point in direction n.
Assumption 1 (locality). We assume that all radiative transfer quantities, that is κC, κL, SL, SC, and ϕv, are independent of location and direction, and are given by their local values. Assuming SL = const is standard in escape probability theory, because the line photons typically interact only within a small ‘resonance volume’ around the point of interest. Generalising this concept to the continuum transfer properties is a new idea (however, see Hummer & Rybicki 1985).
Using the above strategy, we can capture the most relevant continuum radiative transfer effects in that resonance region, where there is competition between line and continuum absorption and emission. Constant ϕv also means that we neglect line velocity shifts; that is, we assume a static medium. The only quantities that are allowed to depend on direction are 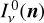 and smax (and hence τv). The formal solution of the RT Eq. (11) then simplifies to
and smax (and hence τv). The formal solution of the RT Eq. (11) then simplifies to
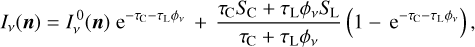 (12)
(12)
where we use the continuum and line centre optical depths τC = κCsmax and τL= κL smax.
Assumption 2 (disc geometry). We consider three major directions: radial (the rays coming from the stellar surface, which are often important for pumping), vertically upwards, and vertically downwards. At any given location in the disc, the star occupies a small solid angle Σ*. The other two principle directions each cover half of Σd = 4π − Σ*. All rays coming from the stellar surface are represented by a single radial ray. For the upward and downward directions, we approximate the disc as being plane-parallel with µ = cos(θ), where θ is the angle with the vertical. Thus, we find from Eq. (1) that
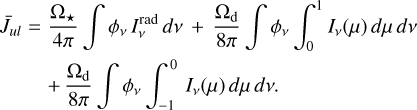 (13)
(13)
Introducing the vertically upwards and downwards (across the disc) line and continuum optical depths, 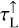 ,
, 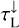 ,
, 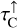 , and
, and 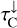 , respectively, and the radially inward line and continuum optical depths,
, respectively, and the radially inward line and continuum optical depths, 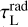 and
and 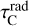 , and using plane-parallel geometry τ(µ) = τ(µ = 0)/µ, we obtain from Eqs. (12) and (13) that
, and using plane-parallel geometry τ(µ) = τ(µ = 0)/µ, we obtain from Eqs. (12) and (13) that
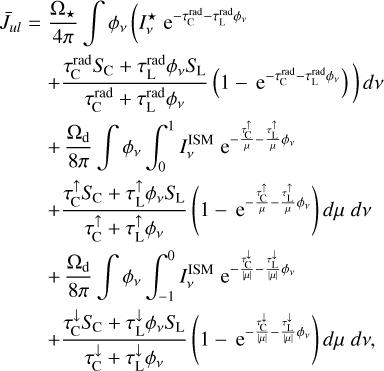 (14)
(14)
where 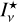 and
and 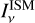 are the stellar and interstellar incident intensities, respectively. Introducing the second exponential integral function
are the stellar and interstellar incident intensities, respectively. Introducing the second exponential integral function 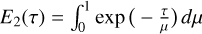 , we find
, we find
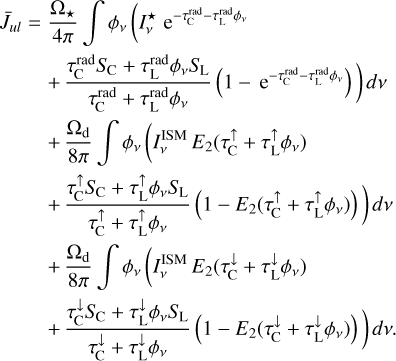 (15)
(15)
We now introduce the dimensionless profile function 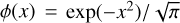 with
with 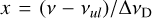 , and six basic 2D functions, which all produce values of between 0 and 1, to further simplify the result:
, and six basic 2D functions, which all produce values of between 0 and 1, to further simplify the result:
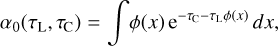 (16)
(16)
where, using the Einstein relations,
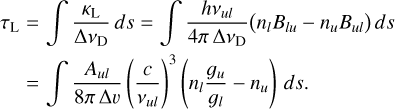 (22)
(22)
From this geometric model, we also get a prediction of the continuum; that is, the mean intensity at line centre frequency, as would be present if the line opacity was zero:
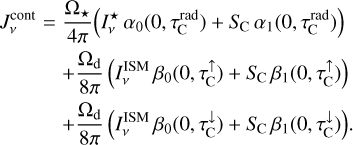 (24)
(24)
Equation (24) is used to determine SC. This means that we can calibrate SC in such a way that our simple three-way RT model with constant continuum quantities results in the correct 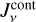 as known from the proper solution of the continuum radiative transfer problem. This confers a significant advantage as it allows us to eliminate most of the principle problems arising from the simplified three-way RT model in the continuum.
as known from the proper solution of the continuum radiative transfer problem. This confers a significant advantage as it allows us to eliminate most of the principle problems arising from the simplified three-way RT model in the continuum.
Comparing Eq. (23) to Eq. (2), we find the definitions of our new pumping and escape probabilities:
![$\matrix{ {P_{ul}^{{\rm{pump}}} = {1 \over {J_v^{{\rm{cont}}}}}\left( {{{{{\rm{\Omega }}_ \star }} \over {4\pi }}\left[ {I_v^ \star {\alpha _0}\left( {\tau _{\rm{L}}^{{\rm{rad}}},\tau _{\rm{C}}^{{\rm{rad}}}} \right) + {S_{\rm{C}}}{\alpha _1}\left( {\tau _{\rm{L}}^{{\rm{rad}}},\tau _{\rm{C}}^{{\rm{rad}}}} \right)} \right]} \right.} \hfill \cr {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {{{{\rm{\Omega }}_{\rm{d}}}} \over {8\pi }}\left[ {I_v^{{\rm{ISM}}}\left( {{\beta _0}\left( {\tau _{\rm{L}}^ \uparrow ,\tau _{\rm{C}}^ \uparrow } \right) + {\beta _0}\left( {\tau _{\rm{L}}^ \downarrow ,\tau _{\rm{C}}^ \downarrow } \right)} \right)} \right.} \hfill \cr {\left. {\left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + {S_{\rm{C}}}\left( {{\beta _1}\left( {\tau _{\rm{L}}^ \uparrow ,\tau _{\rm{C}}^ \uparrow } \right) + {\beta _1}\left( {\tau _{\rm{L}}^ \downarrow ,\tau _{\rm{C}}^ \downarrow } \right)} \right)} \right]} \right)} \hfill \cr } $](/articles/aa/full_html/2024/03/aa47730-23/aa47730-23-eq48.png) (25)
(25)
The interpretation of these results is as follows. 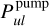 is the probability that continuum photons make it to the considered point, given the presence of line opacity. The average is taken over all continuum photons that contribute to
is the probability that continuum photons make it to the considered point, given the presence of line opacity. The average is taken over all continuum photons that contribute to 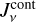 , whether they are emitted by the star or by any point in the disc, averaged over the local line profile function.
, whether they are emitted by the star or by any point in the disc, averaged over the local line profile function. 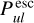 is the probability that line photons emitted anywhere in the disc – in the direction of the considered point – do not make it to the considered point, averaged over the local line profile function.
is the probability that line photons emitted anywhere in the disc – in the direction of the considered point – do not make it to the considered point, averaged over the local line profile function. 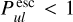 means that these line photons are either reabsorbed by line opacity, or are reabsorbed or scattered by continuum opacity along the path to the considered point.
means that these line photons are either reabsorbed by line opacity, or are reabsorbed or scattered by continuum opacity along the path to the considered point.
As the order of photon emission and reabsorption and the optical depth effects along the photon paths can be reversed, 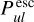 can also be interpreted as the probability that a line photon emitted from the considered point will not have another line interaction in the disc. It is important to realise the emphasis on further line interaction here.
can also be interpreted as the probability that a line photon emitted from the considered point will not have another line interaction in the disc. It is important to realise the emphasis on further line interaction here. 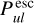 is not the probability that line photons will escape the disc. This latter interpretation is only valid when there are no continuum opacities. Continuum opacity will prevent further line interaction, and so it increases
is not the probability that line photons will escape the disc. This latter interpretation is only valid when there are no continuum opacities. Continuum opacity will prevent further line interaction, and so it increases 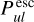 . The latter could be interpreted as ‘intrinsic escape’, meaning that, once a line photon is absorbed and re-emitted by the dust, that continuum photon will escape the disc somehow, but this is not what the equations tell us. In particular, in the optically thick limiting case with τL ≪ τC, the result is
. The latter could be interpreted as ‘intrinsic escape’, meaning that, once a line photon is absorbed and re-emitted by the dust, that continuum photon will escape the disc somehow, but this is not what the equations tell us. In particular, in the optically thick limiting case with τL ≪ τC, the result is 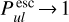 and
and 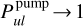 .
.
The six basic 2D functions α0(τL, τC) …β2(τL, τC) are pre-calculated in the form of 2D numerical tables. 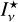 and
and 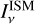 are known functions, and
are known functions, and 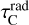 ,
, 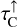 , and
, and 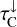 are available after initialisation of the disc structure and dust opacities in PRODIMO. As
are available after initialisation of the disc structure and dust opacities in PRODIMO. As 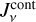 is available from the proper solution of the continuum transfer problem, we can use Eq. (24) to determine and precalculate SC for every line at any point in the disc. The centre line optical depths
is available from the proper solution of the continuum transfer problem, we can use Eq. (24) to determine and precalculate SC for every line at any point in the disc. The centre line optical depths 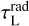 and
and 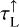 are integrated during the downward and outward sweep of the chemistry and the heating and cooling balance in PRODIMO, but we also need
are integrated during the downward and outward sweep of the chemistry and the heating and cooling balance in PRODIMO, but we also need 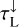 here, which requires another assumption.
here, which requires another assumption.
Assumption 3 (downward line optical depths). We calculate 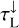 by assuming that the local line/continuum opacity ratio remains the same on the way down and across the disc:
by assuming that the local line/continuum opacity ratio remains the same on the way down and across the disc:
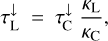 (27)
(27)
where κL and κC are the local line and continuum opacities. The old escape probability method in PRODIMO was based on
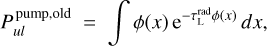 (28)
(28)
As can be easily shown, 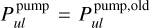 is only valid when the direct stellar illumination dominates; that is, when
is only valid when the direct stellar illumination dominates; that is, when 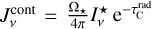 . In all other cases, the new
. In all other cases, the new 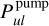 probabilities are larger.
probabilities are larger. 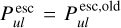 is only valid when
is only valid when 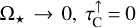 and
and 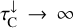 . Under any other, more realistic circumstances, the new
. Under any other, more realistic circumstances, the new 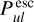 probabilities are also generally larger. Both effects are caused by the inclusion of line–continuum interactions, namely (i) locally produced continuum photons can be absorbed in the line, and (ii) line photons can be absorbed locally in the continuum. We use both limiting cases discussed above to check the numerical implementation of the new escape probability method in PRODIMO.
probabilities are also generally larger. Both effects are caused by the inclusion of line–continuum interactions, namely (i) locally produced continuum photons can be absorbed in the line, and (ii) line photons can be absorbed locally in the continuum. We use both limiting cases discussed above to check the numerical implementation of the new escape probability method in PRODIMO.
Figure 1 shows a comparison between old and new escape and pumping probabilities based on our T Tauri standard disc model. This model was introduced by Woitke et al. (2016) and has stellar, dust, and disc parameters as listed in Table A.2. The results of the new treatment show larger 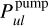 and
and 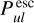 in general. The deviations are particularly obvious in the disc midplane close to the star, where trie continuum is optically thick. We see large and about equal
in general. The deviations are particularly obvious in the disc midplane close to the star, where trie continuum is optically thick. We see large and about equal 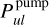 and
and 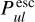 here, in contrast to the old treatment. More significant for line observations are the changes in the more transparent upper disc regions, where
here, in contrast to the old treatment. More significant for line observations are the changes in the more transparent upper disc regions, where 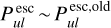 and
and 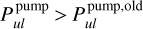 in the inner disc. However, in the outer disc, this relation is reversed and we find
in the inner disc. However, in the outer disc, this relation is reversed and we find 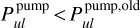 . The reasons for these changes are more complex, as
. The reasons for these changes are more complex, as 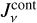 is not given by the attenuated stellar irradiation but is created mostly by continuum emission from the disc below.
is not given by the attenuated stellar irradiation but is created mostly by continuum emission from the disc below.
Figure 2 shows the resulting leading heating and cooling processes in the innermost 10 AU of the disc (T Tauri standard model). Figure A.1 shows additional vertical cuts at selected radii with more details. There are two significant changes:
- (i)
In the disc surface regions inside of 1 au, which are borderline optically thin and relevant for the IR line emission, we find increased H2O heating and cooling rates, whereas previously there was a balance between UV-driven heating by H2 formation and H2O cooling. This is due to the increased pumping and escape probabilities in these regions.
- (ii)
Thermal accommodation in the midplane is now quite unimportant for both heating and cooling, unless the midplane becomes so cold that it barely contains any molecules other than H2 due to freeze-out. In the optically thick midplane, dust and gas now exchange energy very efficiently via line photons, more efficiently than by inelastic collisions. And since the formulation of the line heating and cooling in PRODIMO is robust, including all reverse processes and stimulated emission,
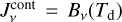 implies that a balance between line heating and cooling can only be achieved when Tg = Td.
implies that a balance between line heating and cooling can only be achieved when Tg = Td.
 |
Fig. 1 Escape probability ( |
 |
Fig. 2 Change in heating and cooling balance with the new escape probability treatment and the new 2D concept to apply UV molecular shielding factors. The plots show the leading heating process (top) and the leading cooling process (bottom) in a zoomed-in disc region responsible for the disc IR line emissions. Processes are only plotted when they fill at least 1% of the area in these plots. The dashed lines mark the visual disc surface Av,rad = 1 and the vertical optical extinction AV = 10. The model includes 103 heating and 95 cooling processes with 64910 spectral lines altogether. |
2.2 New escape probabilities for line-flux estimations
In PRODIMO, the observable line fluxes are estimated based on the escape probabilities, summing up the contributions from all spatial cells. The following expression is used to calculate the luminosity [erg s−1] of photon energy escaping in the form of line photons from a single cell in the old model:
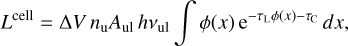 (30)
(30)
where ΔV [cm−3] is the volume of a cell k centred around point grid point (ix, iz). The line flux [erg s−1 cm−2] is then calculated as
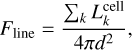 (31)
(31)
where d is the distance to the object. We consider the vertical escape here (face-on disc), and so the line and continuum optical depths are 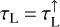 and
and 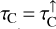 . Using the definition of the line emission coefficient, we have
. Using the definition of the line emission coefficient, we have 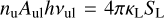 , and we can express the line luminosity of a cell, according to the old implementation, by
, and we can express the line luminosity of a cell, according to the old implementation, by
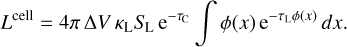 (32)
(32)
This result corresponds to the case of a cold background SC = 0, where the result is always positive; see area A in Fig. 3. However, line and continuum interfere in more complicated ways than that; there is not a simple superposition, as sketch (d) in Fig. 3 suggests, because the escaping continuum photons are partly blocked by line opacity. This effect is visualised by the lower graph in case (b).
In a more detailed model, we need to compute the upper graph in case (b) and the pure continuum, and then subtract the two to simulate the way that line fluxes are measured from observations. Without continuum, we have area A in Fig. 3:
With continuum, the (infinite) result is
Considering only the continuum, the (infinite) result is
The continuum-subtracted line flux (area O in Fig. 3) is
Equation (36) shows that there is an additional correction term with respect to the old way of calculating the escaping line luminosity from a cell (Eq. (32)), which is always negative. This new term describes the loss of continuum flux due to line absorption. The integration boundaries in these equations are −∞and +∞, and so both intermediate results (Eqs. (34) and (35)) are infinite, but the subtraction of the two (Eq. (36)) is finite. The function C1(τL) describes the probability that an outgoing line photon is not reabsorbed in the line again, and C2(τL) describes the reduction of continuum photons escaping the object due to line opacity. The two functions C1(τL) and C2(τL) are plotted in Fig. 4.
According to this new formulation of escape probability, the line flux is always smaller when continuum emission effects are included, and can become negative when the continuum source function SC is as large as the line source function SL. However, we note that the continuum and the line are usually emitted from different disc regions.
Figure 5 shows a comparison between the line-flux predictions obtained with the old and the new escape probability treatment. All results are shown with respect to the proper full PRODIMO line RT results for face-on inclination. We generally see a good agreement between the results of all three methods, with differences being of order 10–30%. The differences become more noticeable at shorter wavelengths, where the lines are mostly emitted from the inner disc. The new escape probability treatment is superior and more balanced around the y = 1 line, whereas the old escape probability treatment has the tendency to overpredict the line fluxes. Two NH3 lines at around 10.5 µm turn out to be absorption lines according to the proper line RT, and are not plotted in Fig. 5. Both escape probability methods fail to predict these lines correctly. The old escape probability method predicts (by design) emission lines. The new escape probability method does produce absorption lines as it should, but the negative fluxes are too large. We note that both escape probability methods can predict the submillimetre (submm) lines very well (e.g. low-J CO lines, CN, HCN, HCO+ in Fig. 5). The fluxes of the far-infrared (FIR) lines (e.g. Herschel/HIFI water lines, fine-structure cooling lines of oxygen) are predicted better than 10%.
 |
Fig. 3 Effect of continuum emission on line flux. Case (a) shows an emission line on a cold continuum SC = 0. Case (b) is an emission line on a warm continuum SL > SC, and case (c) is an absorption line where the continuum is hot SL < SC. The area A is the flux of photon energy [erg s−1 cm−2] carried away by line photons escaping from the object (after continuum extinction and line self-absorption) and is the same in cases (a), (b) and (c). However, the objective is to derive the area O, which is the line flux as measured by observers. For a warm continuum, clearly O < A, and for an absorption line O < 0 (although A > 0). |
2.3 Photo cross sections
PRODIMO now uses the new high-resolution photoionisation and photodissociation cross sections 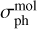 of Heays et al. (2017) obtained from the Leiden database1.
of Heays et al. (2017) obtained from the Leiden database1.
 |
Fig. 5 Line fluxes predicted by the old escape probability treatment (blue) and new escape probability treatment (orange). All line fluxes are divided by the results from the full line RT for zero inclination (face-on). |
2.4 Ultraviolet molecular shielding and self-shielding
Shielding factors are used in PRODIMO to reduce the molecular photoionisation and photodissociation rates:
where σph(v) is the photodissociation cross section and Jv is the local mean intensity. Without molecular shielding, we have 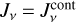 where
where 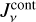 is the result from the continuum radiative transfer (RT). However, the UV molecular opacities are not included in the continuum RT; they generally cause
is the result from the continuum radiative transfer (RT). However, the UV molecular opacities are not included in the continuum RT; they generally cause 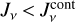 , because there is no molecular UV emission in the disc. These opacities therefore reduce the photo rates.
, because there is no molecular UV emission in the disc. These opacities therefore reduce the photo rates.
There are various molecular shielding effects included, both self-shielding i→i and shielding of a molecule j by another molecule i; see for example Bethell & Bergin (2009). Water shielding was recently discussed by Bosman et al. (2022a,b). In some cases, the shielding factors si→j are taken from published 1D semi-infinite slab-models, which resolve the UV lines and have published efficiency factors as a function of the column density of the molecular absorber ‘towards the source’ and (local) temperature:
In general, the shielding factors can be applied as a product, because 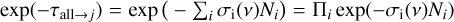 , at least approximately. Table 1 summarises the basic self-shielding functions used. In PRODIMO, all photorates are calculated by numerical integration of Eq. (37) over the frequency-dependent photo cross sections and the local UV radiation field Jv The latter is interpolated between the values known on approximately seven UV spectral gridpoints used in the continuum radiative transfer; see Woitke et al. (2009) for details. In cases where we do not have detailed photo cross sections, but only the a, β, and γ coefficients from a chemical database, we fit a generic cross-section
, at least approximately. Table 1 summarises the basic self-shielding functions used. In PRODIMO, all photorates are calculated by numerical integration of Eq. (37) over the frequency-dependent photo cross sections and the local UV radiation field Jv The latter is interpolated between the values known on approximately seven UV spectral gridpoints used in the continuum radiative transfer; see Woitke et al. (2009) for details. In cases where we do not have detailed photo cross sections, but only the a, β, and γ coefficients from a chemical database, we fit a generic cross-section 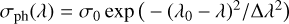 , with two free parameters σ0 and λ0, until the photorates are correct for optical extinctions AV = 0 and AV = 0.5 using standard interstellar dust extinction properties.
, with two free parameters σ0 and λ0, until the photorates are correct for optical extinctions AV = 0 and AV = 0.5 using standard interstellar dust extinction properties.
Therefore, it is relatively straightforward to use any frequency-dependent recipes to account for the effect of molecular shielding. In particular, and this is new in PRODIMO, we use the following idea to account for generic self-shielding:
Other recipes are applied to the shielding of any molecule by H2 and C; see Table 1. For example, Eq. (8) in Kamp & Bertoldi (2000) describes the T-dependent reduction of UV light by H2 lines when detected with the flat opacity of neutral C, which is assumed to provide a first approximation of the shielding effect on any molecule with uncorrected σph(λ) for wavelengths shorter than 1100 Å.
Molecular shielding and self-shielding factors in PRODIMO
2.5 New 2D treatment of molecular shielding
The question arises as to how to deal with the problem of molecular shielding in 2D, and specifically as to which column density Ni is to be considered, choosing from the radial one, the vertically upward one, a mixture, or even something else. Equation (24) holds an answer to this question. Using the explicit shapes of α0, β0 an β1 for τL → 0, and neglecting the α1 term, which is the continuum emission of the disc in the solid angle of the star, and is usually very small, this equation reads
Equation (40) states the influence of the three principle sources (the star, the ISM background, and the disc itself) on the calculated 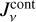 . Contrary to the IR pumping of molecules, which often comes from the warm extended dust below the point of interest, the UV radiation mainly arrives from two directions, the direct radial and the vertically downward directions. Clearly, if direct illumination from the star dominates, then
. Contrary to the IR pumping of molecules, which often comes from the warm extended dust below the point of interest, the UV radiation mainly arrives from two directions, the direct radial and the vertically downward directions. Clearly, if direct illumination from the star dominates, then 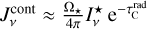 and one should use the radial column densities towards the star to compute the shielding factors. If interstellar UV irradiation dominates, one should take the vertical column densities. However, in the IR-line-emitting disc regions, neither of these two terms is usually the important one, and it is the downward scattering of star light by the small dust in the disc’s upper layers that dominates, which is represented by SC and expressed by the third term in Eq. (40).
and one should use the radial column densities towards the star to compute the shielding factors. If interstellar UV irradiation dominates, one should take the vertical column densities. However, in the IR-line-emitting disc regions, neither of these two terms is usually the important one, and it is the downward scattering of star light by the small dust in the disc’s upper layers that dominates, which is represented by SC and expressed by the third term in Eq. (40).
It is not obvious which molecular column densities should be considered for the molecular shielding factors applied to the third term in Eq. (40). The proper approach would be to consider the molecular column density along the average scattered photon path, but this information is not available. One could argue in favour of taking the radial column density at a much higher disc level up to the scattering point and then adding the downward vertical column density from that point when considering single vertical scattering events, but then the point at which that scattering event takes place needs to be determined.
Instead we follow a much more simple approach here. We assume that the second part of the molecular column density along the scattered photon path is dominant, namely the downward vertical column density from the scattering site. Since the vertical column density increases exponentially on the way down, because (a) the density increases and (b) the molecular concentration increases, it is mostly determined locally, and there is no significant difference when simply taking the full vertical column density.
According to this approach, we use the radial column densities for the first, and the vertical column densities for the second and third terms in Eq. (40), which can be reformulated as
In previous PRODIMO models, we used the stellar and interstellar irradiation terms (parts 1 and 2 in Eq. (40)) to calculate weighting factors for the application of shielding factors according to the following scheme:
where wrad and wvert are the radial and vertical weights. However, this approach involves a clearly far more questionable assumption, because the often most important term (the third term in Eq. (40)) is not even considered, and thus 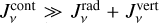 . Instead, based on the mixing ratio between
. Instead, based on the mixing ratio between 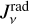 and
and 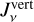 , an effective shielding factor was calculated and applied to all of
, an effective shielding factor was calculated and applied to all of 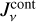 . As Eq. (48) ignores the scattering altogether, the old vertical part
. As Eq. (48) ignores the scattering altogether, the old vertical part 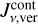 is too small, and therefore we switched from radial to vertical column densities too late. As the radial column densities are generally larger than the vertical ones, the effects of molecular shielding were overestimated in the old models.
is too small, and therefore we switched from radial to vertical column densities too late. As the radial column densities are generally larger than the vertical ones, the effects of molecular shielding were overestimated in the old models.
Figure 6 shows that, as expected, the formation of CO now happens slightly deeper in the disc. In both models, CO is found to be abundant when (i) the ionisation parameter χ/n is low enough (χ is the strength of the UV field; see Eq. (42) in Woitke et al. (2009), and n is the total hydrogen nuclei density [cm−3]) and (ii) the dust temperature is high enough Td ≳ 20 K. These two criteria are related to CO photodissociation and freeze-out. The critical value for the CO photodissociation log10(χ/n) changes from about -4.5 to -5 in the new models.
The feedback on the more complex molecules, such as HCN and C2H2, is remarkable, leading to profoundly different chemical conditions in the IR-line-emitting disc regions. In Fig. 6, we concentrate on the upper, warm line-emitting regions. There are also some regions with high concentrations of HCN and C2H2 in the midplane, but these molecules are covered by optically thick dust and play no significant role in the IR-line emission in this T Tauri standard disc setup. The formation of these IR-active molecules in the upper disc happens in slightly deeper layers according to the new models, and as the gas densities are larger there, the formation of more complex molecules is generally favoured in the new models.
In particular, the formation of C2H2 needs both H2 and neutral carbon atoms; see e.g. Agúndez et al. (2008). In the lower part of Fig. 6, we overplot H/H2 = 10 and CO/C = 100 contour lines. These two lines nicely encircle the region of high C2H2 concentrations in the model. Similar results were reported by Walsh et al. (2015) and Anderson et al. (2021). In the inner disc, these lines are crossed in our models, and so when H2 finally forms, there is no longer any neutral C, and we get no C2H2; see also Kanwar et al. (2024). In the new model, these two lines are further apart, there is a wider region to form C2H2, and that region now also extends to smaller radii.
A similar effect is found for HCN, where the changes are even more pronounced. The formation of HCN requires H2 and neutral N atoms. In the new models, both transitions H → H2 and N → N2 happen deeper in the disc, and they are vertically more separated, leading to increased HCN column densities in the upper layers of the inner disc.
2.6 Heating by photodissociation
One heating process that has so far been partly neglected in PRODIMO is the ‘direct’ heating by photodissociation:
where nmol [cm−3] is the molecular particle density, 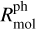 [s−1] the photodissociation rate, and ΔEmol is the mean energy liberated per photodissociation. Similar to photoionisation, the excess photon energy can create superthermal dissociation products, or can lead to vibrationally or electronically excited molecular fragments, and the key question pertains to how much of this energy is thermalised by the gas.
[s−1] the photodissociation rate, and ΔEmol is the mean energy liberated per photodissociation. Similar to photoionisation, the excess photon energy can create superthermal dissociation products, or can lead to vibrationally or electronically excited molecular fragments, and the key question pertains to how much of this energy is thermalised by the gas.
Gu et al. (2020) treated this process with 100% efficiency, assuming that the energy released as local heat is set as the incident photon energy in excess of the respective dissociation threshold:
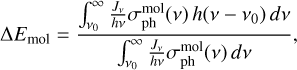 (51)
(51)
where v0 is the photodissociation threshold frequency. However, more detailed studies show that not all of this energy is thermalised; for example, excited dissociation products can decay radiatively, or can trigger follow-up chemical reactions.
Glassgold & Najita (2015) published detailed energies per photodissociation ΔE for H2 (1.2 eV), CO (1.4 eV), H2O (1.2 eV), and OH (3.6 eV), and we have now implemented these data into PRODIMO. For all other molecules, we conservatively assume ΔE ≈ 2 eV. Previously in PRODIMO, only H2, with ΔE(H2) = 0.4 eV (Black & van Dishoeck 1987), was considered for the heating by photodissociation in addition to the heating by photoionisation of H−, C, Fe, Si, and Mg. Figure 2 shows that this additional heating process can be quite relevant in the IR-active molecular layer. Interestingly, the reduced UV molecular shielding factors cause larger photorates, which lead to a more active chemistry, where the molecular fragments created by photodissociation react further exothermally, which increases the area where chemical heating is important.
 |
Fig. 6 Change of molecular concentrations caused by introducing our new 2D concept to apply molecular shielding factors. |
2.7 Chemical rate network
We used the large DIANA standard chemical network (Kamp et al. 2017) in this work, which has 235 chemical species, with reaction rates mostly taken from the UMIST 2012 database (McElroy et al. 2013), but including a simple freeze-out and desorption ice chemistry (Woitke et al. 2009), X-ray processes partly based on doubly ionised species (Aresu et al. 2011), excited molecular hydrogen (see Kamp et al. 2017), and polycyclic aromatic hydrocarbons in five different charging states (Thi et al. 2019), which is 3066 reactions altogether. H2 formation of grain surfaces is calculated according to Cazaux & Tielens (2002, 2004) with updates described in Cazaux & Spaans (2009); Cazaux & Tielens (2010). We use our standard element abundances (Table A.1), which are close to solar (C/O = 0.46) except for the depleted metals Na, Mg, Si, S, and Fe.
PAH molecules are included in the radiative transfer, with opacities calculated from their overall abundance and an assumed ratio between charged and neutral PAHs to avoid global iterations; see details in Woitke et al. (2016, 2019). PAHs are also included in the chemical network with five charging states (Thi et al. 2019), and are included in the calculation of heating and cooling rates, as the photoelectric effect on PAHs is one of the most important heating processes in the upper disc layers. The PAH heating rate is calculated from the calculated abundances of the different charging states, their individual photo-cross sections, and the calculated local radiation field.
In recent updates of our chemical network, we added a few hand-picked gas-phase reactions not included in UMIST 2012. One of these reactions turned out to be critical for the fitting of the JWST spectrum of EX Lupi (Sect. 3):
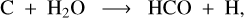 (52)
(52)
from Hickson et al. (2016), who measured surprisingly large rates for this reaction at low temperatures, enhanced by quantum mechanical tunnelling. Although the Kinetic Database For Astrochemistry (KIDA2) does not include this reaction in their standard releases, they list it with Arrhenius parameters {α = 1.07 × 10−8cm3s−1, β = −1.59 , γ = 0} with reference to Hickson et al. (2016). In our models, whenever a CO-bond is broken, for example by photodissociation or X-ray-induced reactions, this reaction would be very efficient in immediately reforming that bond, which would prohibit the subsequent formation of hydrocarbon molecules and HCN as discussed in Sect. 4.3. Tests show that if we were to include this reaction with the Arrhenius coefficients from the KIDA database, the C2H2 column density in the line emitting regions of our EX Lupi model would decrease by a factor of about 300, and peak line flux at 13.7 µm would decrease by a factor of about 5. However, closer inspection of Fig. 3 in Hickson et al. (2016) shows that the Arrhenius coefficients {α = 4.2 × 10−13cm3s−1 , β = −2.5 , γ = 0} fit the original data points at 50 K, 75 K, and 100 K much better, and are consistent with the measurements of Husain & Kirsch (1971), which show that the rate coefficient of this reaction is very small at room temperature (< 10−12 cm3s−1). We therefore decided to use our own Arrhenius fit of this reaction in this paper.
Line selection criteria for the HITRAN 2020 database.
2.8 New HITRAN line-selection rules
The expansion from the Spitzer/IRS to the JWST/MIRI wavelength range made it necessary to revise our line-selection strategy, by which we import only a limited number of molecular lines from the HITRAN database. We also updated PRODIMO to use the HITRAN 2020 catalogue (Gordon et al. 2022) instead of the HITRAN 2012 catalogue. The imported data are the upper level energies Eu, line wavelengths λul, Einstein coefficients Aul, and level degeneracies gu. The new HITRAN 2020 database has a greater number of lines, which, if we would import all lines, would vastly increase PRODIMO’s memory consumption. As explained in Woitke et al. (2018a), we therefore have to limit our line selection to lines with a minimum line strength, defined as
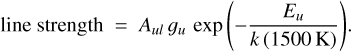 (53)
(53)
In combination with further restrictions on wavelength range and upper level energy Eu, see Table 2, we aim to select only the relevant, strong observable lines. Together with the rovibrational CO lines of the first four vibrationally excited states (Thi et al. 2013), ro-vibrational H2O lines, rotational lines of various molecules, and lines of atoms and ions (Woitke et al. 2018a), we are now tracing 64890 lines altogether in this model. All lines are automatically considered for heating and cooling.
2.9 Dust settling
Considering a turbulent one-dimensional column of gas and dust, Mulders & Dominik (2012) write down the continuity equation for passive dust particles with a size distribution function f (a, z, t) as
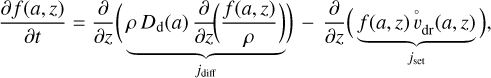 (54)
(54)
where ρ is the gas mass density, t the time, z the vertical coordinate, and a the dust particle radius. Assuming that there is no bulk gas motion, the grains are transported downwards by gravitational settling with their size-dependent equilibrium settling velocity 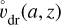 , and are transported upwards by eddy diffusion, The upward mixing is driven by vertical dust particle concentration gradients
, and are transported upwards by eddy diffusion, The upward mixing is driven by vertical dust particle concentration gradients 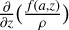 and calculated according to the local dust diffusion coefficient Dd. Assuming that the grains have relaxed towards a steady state, we have for each size ∂/∂t f(a, z) → 0 and zero net flux jdiff – jset → 0, and therefore
and calculated according to the local dust diffusion coefficient Dd. Assuming that the grains have relaxed towards a steady state, we have for each size ∂/∂t f(a, z) → 0 and zero net flux jdiff – jset → 0, and therefore
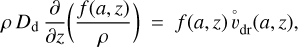 (55)
(55)
For large Knudsen numbers and subsonic particle velocities (Epstein regime), the equilibrium settling velocity, also referred to as the terminal fall speed, is given by Schaaf (1963)
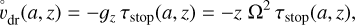 (57)
(57)
where gz is the vertical gravitational acceleration, and Ω is the Keplerian circular frequency. The stopping timescale, or frictional coupling timescale, is given by
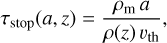 (58)
(58)
where ρm is the dust material density, and the thermal velocity is
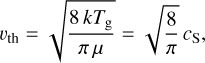 (59)
(59)
where k the Boltzmann constant, Tg the local gas temperature, µ the mean molecular weight, cS the local isothermal speed of sound, and 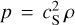 is the local gas pressure. Equation (58) appears to be widely incorrect in the literature, where cS is often erroneously used instead of the correct mean of the magnitude of the thermal velocities of gas particles υth, as required in Schaaf’s formula; see Woitke & Helling (2003).
is the local gas pressure. Equation (58) appears to be widely incorrect in the literature, where cS is often erroneously used instead of the correct mean of the magnitude of the thermal velocities of gas particles υth, as required in Schaaf’s formula; see Woitke & Helling (2003).
Eddy diffusion (‘turbulent mixing’) is assumed to be dominant over gas-kinetic diffusion. The eddy diffusion coefficient is given by a characteristic velocity multiplied by a characteristic length,
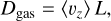 (60)
(60)
where L is the size of the largest eddies (‘mixing length’) and 〈υz〉 is the root-mean-square average of the fluctuating part of the vertical gas velocities. In a Kolmogorov-type power spectrum P(k) ∝ k−5/3, there are different turbulent modes associated with different wave-numbers k or different spatial eddy sizes l. Any given particles of size a tend to co-move with the sufficiently large and slow turbulent eddies, whereas their inertia prevents them from following the short-term, small turbulence modes. In order to arrive at an effective particle diffusion coefficient, the advective effect of all individual turbulent eddies has to be averaged, and thereby transformed into a collective particle-diffusion coefficient. This procedure has been carried out, with different methods and approximations, by Dubrulle et al. (1995), Schräpler & Henning (2004), Youdin & Lithwick (2007), and Mulders & Dominik (2012). The result of Mulders & Dominik (2012) is
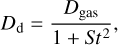 (61)
(61)
where St is the Stokes number given by
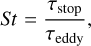 (62)
(62)
where τeddy is the eddy turnover or turbulence correlation timescale in consideration of the largest eddy, which is assumed to be equal to the mixing length L.
According to an α disc model (Shakura & Sunyaev 1973), the typical vertical length scale is 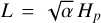 and
and 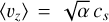 (Ormel et al. 2007), and therefore
(Ormel et al. 2007), and therefore
Our basic Eq. (56) for the balance between upward mixing and downward gravitational settling is therefore
where all quantities on the right hand side of Eq. (66), that is, Ω, α, Dgas, T, cS, µ, ρ, and ρm, can in general depend on height z. In addition, St and τstop depend on z and on grain size a.
Dubrulle et al. (1995) ignored all z-dependencies on the ride hand side of Eq. (66) and replaced all variables with their mid-plane values. These authors also dropped the (1 + St2) term. In that case, we can carry out the z-integration to find
Introducing the size-dependent dust scale height Ha via 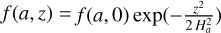 , and using
, and using 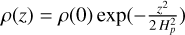 , the result is
, the result is
Riols & Lesur (2018) also drop the (1 + St2) term in Eq. (66), but take into account that τstop depends on density, and is therefore z-dependent. Furthermore, these authors explicitly assume a Gaussian for the vertical gas density distribution. In that case, the stopping timescale can be expressed as
and integration of Eq. (66), assuming that α, cS, Hp, and Ω are height-independent, yields
which reproduces Eq. (33) in Riols & Lesur (2018). The analytical solution of Eq. (69) is
The decrease in Ha with respect to Eq. (67) is remarkable; the function (2/x2)[ exp(x2/2) – 1] is 3.2 at x = 2, 20 at x = 3, and 370 at x = 4. Infrared emission lines from discs are quite typically emitted from layers located at about 3–4 scale-heights (Woitke et al. 2018b). The Riols & Lesur settling description reduces the local dust/gas ratios by orders of magnitude in these regions (see Fig. 7), and even reduces the abundance of the smallest grains at high altitudes. We suggest that Eq. (70) should become the standard in disc modelling; we have implemented it in PRODIMO, and used it in the present study.
However, in order to remain consistent with previous publications, in PRODIMO, we multiply the second terms on the right side of Eqs. (67) and (70) by a factor 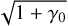 , with γ0 = 2 for compressible turbulence, and incorrectly use cS instead of υth in Eq. (57). These two changes amount to a factor of
, with γ0 = 2 for compressible turbulence, and incorrectly use cS instead of υth in Eq. (57). These two changes amount to a factor of 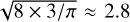 , which can be compared to the uncertainty in the settling parameter α. Equation (70) can be generalised to a numerical integration of Eq. (56) for cases where
, which can be compared to the uncertainty in the settling parameter α. Equation (70) can be generalised to a numerical integration of Eq. (56) for cases where 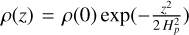 is not valid, and cS = Hp Ω is not valid, for example in hydrostatic disc models where both the gas temperature and the mean molecular weight depend on z.
is not valid, and cS = Hp Ω is not valid, for example in hydrostatic disc models where both the gas temperature and the mean molecular weight depend on z.
 |
Fig. 7 PRODIMO model for the quiescent state of EX Lupi. The top plots show the assumed gas and dust column densities (left) and scale heights (right). The second row shows the corresponding gas densities (left) and gas-to-dust mass ratio after settling (right). The third row shows the UV field strength χ (left), and the X-ray ionisation rate ζX in comparison to the cosmic-ray ionisation rate (right). The bottom row shows the resulting dust-temperature (left) and gas-temperature (right) structures. Additional contour lines show selected values for the vertical optical extinction AV and the radial optical extinction AV,rad as indicated. |
2.10 Rounded inner rims
As previous Spitzer and recent JWST observations show (Banzatti et al. 2017, 2023; Kóspál et al. 2023; Grant et al. 2023; Tabone et al. 2023), the MIR line spectroscopy of discs first and foremost probes the physics and chemistry in the innermost disc regions ≲ 1 au, close to where the dust reaches its sublimation temperature, with line-emitting radii sometimes as small as 0.1 au for T Tauri stars. Therefore, the shape of the inner rim becomes a significant factor for understanding the new JWST spectra. Our knowledge about these inner disc regions is still rather limited, because of both the difficulty in observing these regions with sufficient resolution and the complexity of the physics involved. According to radiation hydrodynamics models, the direct stellar irradiation causes the dust around the inner rim to evaporate and form a puffed-up inner rim (Natta et al. 2001; Dullemond et al. 2001; Dullemond & Monnier 2010). The radial transition in terms of gas surface density across the inner rim is not an infinitely sharp jump, but a relatively diffuse region, which means that the gas pressure stabilises the rim (Isella & Natta 2005; Kama et al. 2009; Woitke et al. 2009; Flock et al. 2017). In addition, evolutionary MHD models suggest that the switch from magnetically active inner disc to the dead zone may cause a local pressure maximum and formation of gas–dust rings (Masset et al. 2006; Dzyurkevich et al. 2010; Kadam et al. 2019, 2022), which causes a more gradual buildup of the column density towards the first pressure bump. Inspired by the inner disc structures suggested by these models, here we introduce a parametric approach, assuming
where Σ(r) is the mass column density at radius r, raduc is the radius up to which the column density initially increases, in units of the inner disc radius Rin, and reduc is the factor by which the column density is reduced in Eq. (71) at Rin. As in previous publications, Rtap is the tapering off radius, and the self-similar solution is obtained for γ = ϵ, but we rather keep ϵ and γ as independent parameters.
In hydrostatic models, where the hydrostatic equilibrium is solved in each vertical column (Natta et al. 2001; Kama et al. 2009; Dullemond & Monnier 2010), we see large scale-heights at the inner rim that is directly heated by the star, followed by a dip in Hp(r) behind the inner rim, because the inner rim casts a shadow on the subsequent disc where the temperatures are lower; see for example Fig. 9 in Woitke et al. (2009) and Fig. 6 in Woitke et al. (2016). We introduce two more parameters to describe this ubiquitous feature of hydrostatic models:
where daduc is the dip radius in units of the inner radius, and deduc is the reduction of the scale height at the dip radius. The effect of the new disc shape parameters reduc, raduc, deduc, and daduc on column density structure and scale heights is visualised in the upper panel of Fig. 7.
3 The PRODIMO disc model for EX Lupi
3.1 Stellar setup
Our photometric data collection for the quiescent state of EX Lupi is shown in Table 3, and the assumed stellar properties are listed in Table 4. Stellar luminosity, effective temperature, and optical extinction are taken from Sipos et al. (2009). Stellar mass, distance to EXLupi, and disc inclination are taken from the collection of ALMA observations by White et al. (2020). The stellar excess UV parameters are derived from XMM UV photometric observations (see Table 3). The quantity fUV = LUV/L* is the UV excess between 91.2 nm and 250 nm. pUV is a power-law index explained in Appendix A of Woitke et al. (2016). The X-ray properties are explained in Appendix A of Woitke et al. (2016) and are taken from measurements of Teets et al. (2012), which indicate a significant increase in the X-ray luminosity during burst phase, in particular for the soft X-rays. The accretion rate Ṁacc = 4 × 10−10 M⊙ yr−1 is taken from Sicilia-Aguilar et al. (2015), which is used for viscous gas heating according to Eq. (2) in D'Alessio et al. (1998); see details in Woitke et al. (2019).
Recently, Cruz-Sáenz de Miera et al. (2023) analysed an XSHOOTER spectrum of EX Lupi taken in July 2022, just one month before the JWST observations were carried out. This 0.3–2.2 µm spectrum suggests a much higher mass-accretion rate of Ṁacc ≈ (2–3) × 10−8 M⊙ yr−1. Another value was reported by Wang et al. (2023), namely Ṁacc ≈ 3 × 10−9 M⊙ yr−1. The data analysis is intertwined with the determination of the optical extinction AV of the star. Cruz-Sáenz de Miera et al. 2023 arrive at a large value of AV ≈ 1.1 using RV = 3.1. In contrast, most published works on EX Lupi have so far assumed AV ≈ 0, including Sipos et al. (2009). Varga et al. (2018) used AV = 0.2, Alcalá et al. (2017) used AV = 1.1, and Wang et al. (2023) used AV = 0.1. If AV is indeed as large as 1.1, the XMM photometric data would imply a ten times greater UV luminosity ( fUV ≈ 0.1). Extrapolating the slab-model for the continuum emission due to accretion of Cruz-Sáenz de Miera et al. 2023 to shorter wavelengths, Ábrahám (2023, priv. comm.) derive fUV ≈ 0.02, but this UV excess would not contain the strong emission lines, such as Ly-α, because of stellar activity. A discussion on how our modelling results change if larger values of fUV and Ṁacc are used can be found in Sect. 4.5.
Ansdell et al. (2018) observed EX Lupi with ALMA in band 6 continuum and 12CO 2−1, measuring a continuum disc radius of 62 ± 2 au and a CO disc radius of 178 ± 12 au. Hales et al. (2018) also imaged the disc of EX Lupi with ALMA band 6 continuum and CO isotopologues, and fitted a disc model with a tapering-off radius of Rtap ≈ 20 au. Based on SPHERE-IRDIS polarimetric observations, Rigliaco et al. (2020) favoured a scenario where the near-infrared (NIR) light is scattered by a circumstellar disc rather than an outflow, and suggest that the disc region between about 10 and 30 au might be depleted in µm-sized grains. Furlan et al. (2009) introduced an index that characterises the MIR SED slope by
where λ13 = 13 µm, λ31 = 31 µm, v13, and v31 are the corresponding frequencies, and 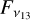 and
and 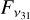 are the continuum fluxes [Jy] at λ13 and λ31, respectively. This index has been used to identify transitional discs (n13–31 > 1), disc flaring, and dust settling (Furlan et al. 2009). From the Spitzer/IRS spectrum of EX Lupi shown by Kóspál et al. (2023), with reference to Ábrahám et al. (2009), we derive a value of n13–31 ≈ −0.57, which suggests a continuous disc.
are the continuum fluxes [Jy] at λ13 and λ31, respectively. This index has been used to identify transitional discs (n13–31 > 1), disc flaring, and dust settling (Furlan et al. 2009). From the Spitzer/IRS spectrum of EX Lupi shown by Kóspál et al. (2023), with reference to Ábrahám et al. (2009), we derive a value of n13–31 ≈ −0.57, which suggests a continuous disc.
Banzatti et al. (2023) defined two classes of discs: (i) compact discs with strong low-excitation water lines and (ii) large discs, possibly with gaps and rings, with faint low-excitation water lines. Banzatti et al. (2023) associated these classes with different water-ice transport mechanisms by pebbles, favouring water enrichment in case (i), and water depletion in case (ii). Based on the published dust radii cited above, and the derived n13–31 value, EX Lupi is a relatively large but continuous disc, which does not clearly fall into either of these categories. We did not use any ALMA data in this study for the fitting, and assumed standard element abundances for our disc model; see Table A.1.
Photometric data collection for the quiescent state of EX Lupi.
Model parameters for the quiescent state of EX Lupi.
3.2 Disc shape
Finding a PRODIMO model setup that can roughly reproduce the observed JWST line and continuum data was a difficult task. Looking at Fig. 3 of Kóspál et al. (2023), the water emission lines and the peak emissions at the Q-branches of C2H2, HCN, and CO2 in the 13–17 µm spectral region all reach similar flux levels of the order of 30–60 mJy. This immediately tells us that all these spectral features must be optically thick, otherwise the certainly very different concentrations and masses of these molecules in the disc would result in very different flux levels. This conclusion is underlined by slab-model fits presented by Kóspál et al. (2023), which resulted in column densities of order 1015 – 1016 cm−2 for C2H2, HCN, and CO2, 1017 – 1018 cm−2 for H2O, and approximately 1019 cm−2 for CO.
In our standard T Tauri disc model (with parameters listed in Table A.2), the lines of C2H2 and HCN are emitted from radially extended, tenuous layers high in the disc (see Fig. 6), where UV photons dissociate CO and N2, and the resulting carbon and nitrogen atoms react further to form some C2H2 and HCN in the presence of H2. Although we can explain the overall line flux levels of H2O and CO2 from T Tauri stars this way, our standard models generally result in excessively low molecular column densities above the optically thick dust when compared to the values derived from slab-model fits to observations (e.g. Banzatti et al. 2017).
The key idea for the EX Lupi model presented in this paper was to tap into the large reservoir of C2H2 and HCN molecules that is present in our disc models in the midplane regions inside of 1 au, which are normally covered by dust opacity. To reveal these regions, we assume a slowly increasing surface density profile around the inner rim, combined with strong dust settling, which creates an almost dust-free gas around the inner dust rim; see Fig. 7. The parameters for this model are listed in Table 4. The position of the inner dust rim thereby becomes wavelength dependent. Using the radius where the vertical dust optical depth is one, the results are about 0.1 au at optical wavelengths, but about 0.4 au at λ = 15 µm in this model; see Sect. 4.2. For comparison, Sipos et al. (2009) used an inner hole of radius 0.2 au in their SED fits using RADMC to reproduce the relatively low continuum fluxes between 3 and 8 µm. This idea was later adopted by Juhász et al. (2012) and Ábrahám et al. (2019). MIDI interferometry of EX Lupi was presented by Varga et al. (2018), who measured a half-light radius of (0.77 ± 0.09) au.
3.3 Model fitting
Once an initial disc setup was found that could roughly reproduce the observed SED and JWST molecular line emission features within a factor of about 2–5, we utilised the (12, 1) genetic algorithm of Rechenberg (2000) – as explained in Woitke et al. (2019) – to optimise 17 parameters regarding disc shape, dust material and size, and PAHs. The optimised parameters are marked in Table 4. The genetic fitting algorithm seeks to minimise a total χ2,
in order to simultaneously fit the photometric data, the absolute JWST spectrum, and the continuum-subtracted JWST line spectrum. We used fast PRODIMO models with a low-resolution spatial grid 70 × 60 during the fitting phase. The models calculated the SED on 500 wavelength points between 0.1 µm and 4 mm. Based on these results, we calculated the mean quadratic deviation between model and photometric fluxes 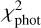 using the various filter transmission functions and the mean quadratic deviation between model and the absolute JWST spectrum
using the various filter transmission functions and the mean quadratic deviation between model and the absolute JWST spectrum 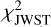 . A minimum error of 10% was assumed for all photometric and spectral data points.
. A minimum error of 10% was assumed for all photometric and spectral data points.
Each PRODIMO call was followed by two calls of the Fast Line Tracer (FLITS) developed by M. Min (Woitke et al. 2018a) in order to calculate high-resolution model spectra between 4.9 and 7.5 µm (10353 lines) and between 13 and 17.7 µm (17228 lines), respectively, both with a velocity resolution of 3 km s−1. Here we considered the atoms and ions Ne+, Ne++, Ar+, Ar++, Mg+, Fe+, Si+, S, S+, and S++, and the molecules H2O, OH, HCN, CO2, NH3, H2, C2H2, CH4, and CO. Each FLITS call calculates two spectra, a continuum model with only dust opacities and source functions, and a line and continuum model with dust and gas opacities and source functions. We then subtracted these two, and convolved the continuum-subtracted FLITS spectrum to a spectral resolution of 25003. To reduce the observational noise, we applied a box-filter of size 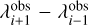 to both the observational data and the convolved model spectrum, where
to both the observational data and the convolved model spectrum, where 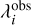 are the observational data points. Finally, we calculated the mean quadratic deviation between the continuum-subtracted FLITS model and the continuum-subtracted JWST data as
are the observational data points. Finally, we calculated the mean quadratic deviation between the continuum-subtracted FLITS model and the continuum-subtracted JWST data as 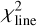 , where a 20 times higher weight was applied to the 13.5–14.1 µm and 14.8–15 µm spectral regions, which contain the crucial Q-branches of C2H2, HCN, and CO2. We assume an error of
, where a 20 times higher weight was applied to the 13.5–14.1 µm and 14.8–15 µm spectral regions, which contain the crucial Q-branches of C2H2, HCN, and CO2. We assume an error of 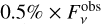 for the observed continuum-subtracted flux, where
for the observed continuum-subtracted flux, where 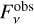 is the absolute JWST flux, to reflect the uncertainties in the continuum subtraction procedure.
is the absolute JWST flux, to reflect the uncertainties in the continuum subtraction procedure.
Each combined PRODIMO-FLITS model takes about 2 h of computational time on 16 CPUs. We ran 12 such models in parallel to complete one generation. The genetic optimisation was stopped after about 100–200 generations, which amounts to a computational cost of about 150 × 12 × 2h × 16 CPUs ≈ 60 000 CPU hours per genetic fitting run. We experimented with five such runs, using slightly different setups (total ~3 × 105 CPU hours), and selected the best one for publication.
Finally, a high-resolution 200 × 200 PRODIMO model was run for the best-fitting model to produce the results depicted in Figs. 7, 9, and 11. All PRODIMO models were performed with git version e8e68ec6 dated 2023/08/08.
4 The MIR-line-emitting regions of EX Lupi
4.1 Physico-chemical structure of the best-fitting model
Figure 7 shows the assumed gas and dust distributions in the best-fitting model. As discussed later in this section, the main line-emitting molecules observable with JWST are located at r ≈ 0.1–0.5 au around the optical disc surface marked by the AV,rad = 1 line, which corresponds to relative heights of z/r ≈ 0.05–0.3 in this model. The dust settling according to the applied recipe of Riols & Lesur (2018) with α = 5 × 10−4 is so strong that the local gas/dust ratio is about 104 along this line, and the calculated UV field strength χ is about 104–106 at densities of 1010 – 1011 cm−3, and so we need to discuss the physics and chemistry in a high-density X-ray photon-Dominated Region (XDR) with an unusually high gas/dust ratio.
We found the gas to be cooler than the dust in the line-emitting regions, but this does not lead to absorption lines in this model, because the dust is rather transparent at these radii. Therefore, the full column of gas located at these radii can contribute to the observable line spectrum in this model. Here, our working definition for molecular column densities – for the purpose to compare with the results from slab-models – is
which is the vertical integral over the molecular particle density down to the point where the dust becomes optically thick at line wavelength. In contrast, in our standard T Tauri disc model (see Fig. 6), the high gas column densities in the inner disc (> 1026 cm−2), combined with a standard gas/dust ratio of 100, ensure that the disc is optically thick up to about three scale heights. In this case, the dust covers most of the molecular gas, and the molecular column densities defined by Eq. (75) are often found to be lower than those derived from observations.
Figure 8 shows the obtained SED fit, with a magnification of the MIR spectral region in comparison to the JWST spectrum. We did not attempt any detailed dust opacity fitting in this model, and so cannot expect a much better fit than this. We achieved a reduced χphot of 1.45 and χJWST = 0.81.
Figure 9 shows some selected molecular concentrations in our best-fit model. The JWST line-emitting regions are located just below the χ/n = 10−4 line, where the major phase transitions H → H2, C → CO, and N → N2 occur. H2O extends a little higher than this, to about Tg = 2000K, and OH even higher, to about Tg = 4000 K. The CO2, HCN, and C2H2 concentrations are more difficult to understand. These molecules obtain their maximum concentrations of about 10−6 – 10−5 not far from the midplane and inside the snowline. Concerning HCN and C2H2, there are also some radially extended, high, tenuous, and spatially thin photodissociation layers with maximum concentrations of 10−9 – 10−8 just below H/H2 ≈ 1000 and 100, respectively, but the major reservoir of these molecules is the close midplane, between about 0.1 au and 0.5 au, which in this model coincides with the MIR line-emitting regions. Normally, these regions are covered by dust opacity.
Figure 10 presents the line spectrum of the best-fitting PRODIMO–FLITS model in comparison to the continuum-subtracted JWST data (Kóspál et al. 2023). The spectral contributions of H2O, CO, C2H2, HCN, CO2, OH, and H2 are indicated by different colours. Our 2D disc model can reproduce most of the observed spectral features surprisingly well. We achieve an overall fit quality with reduced χline values of 3.2 and 2.1 in the spectral regions 4.9–7.5 µm and 13–17.7 µm, respectively. The HCN fluxes are slightly weak, and some of the water line peaks are slightly too shallow; for example, the low-excitation water lines at longer wavelengths. However, some of the visible deviations are also affected by imperfect data reduction and continuum subtraction. We used the continuum-subtracted JWST data – as published in Kóspál et al. (2023; priv. comm. A. Banzatti) – reduced with JWST pipeline version 1.8.2 and continuum-subtracted at that time.
The fit is clearly not as good as what can be achieved with slab-models, where one can directly tune the molecular column densities, the sizes of the emission areas, and the emission temperatures. Nevertheless, our model is able to simultaneously explain the SED, the overall spectral shape of the JWST spectrum, and the main characteristics of the line emissions from CO, from H2O in both considered wavelength bands, and from the Q-branches of C2H2, HCN, and CO2 between 13.7 and 15 µm, and even some minor contributions of OH and H2. In our model, all column densities, dust opacities, emission temperatures, and sizes of line-emitting areas are consistent results of our 2D thermo-chemical disc structure, and we are using this complex structure under an inclination of 32° to calculate our spectra.
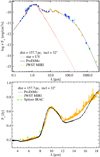 |
Fig. 8 Fit of the SED of EX Lupi in the quiescent state. The orange and green data points in the upper plot are Herschel/SPIRE and ALMA measurements. The orange spectrum is the JWST/MIRI data. The lower plot shows a magnification of the MIR spectral region. |
Total line fluxes ΣFline [W m−2], flux-mean column densities 〈Ncol〉 [cm−2], flux-mean emission temperatures 〈Tg〉 [K], and flux-mean emission radius interval 〈r1 – r2〉 of molecules, considering all lines emitted in two different spectral regions in the 2D disc model.
 |
Fig. 9 Resulting chemical concentrations ϵi = ni/n〈H〉 of selected molecules in the PRODIMO disc model for EX Lupi. Additional contour lines are plotted as boundaries, including the ionisation parameter χ/n〈H〉 (i.e. the UV field strength divided by the hydrogen nuclei particle density) and the ratios of the concentrations of the major molecules. For example, ‘H/H2=100’ means that H atoms are 100 times more abundant than H2 molecules. |
 |
Fig. 10 Continuum-subtracted JWST spectrum (black line) in comparison to the PRODIMO-FLITS disc model for EX Lupi. The coloured areas show the contributions of the different molecules to the total model line spectrum. These are therefore cumulative; i.e. the CO2-spectrum is plotted on top of the C2H2-spectrum, the HCN-spectrum on top of the (C2H2+CO2)-spectrum, and so on, such that the top of the water spectrum represents the total continuum-subtracted model spectrum. The model spectrum has been convolved to R = 2500. Furthermore, both the observational data and the model spectrum were slightly box-filtered before plotting in order to increase clarity; see main text. The broad bumps in the observational data (e.g. those around 6.3 µm and in the region 15.5 – 17.7 µm) are likely due to problems with the early data reduction and continuum subtraction. |
4.2 Deriving column densities and emission temperatures from the 2D disc model
Table 5 lists some mean quantities of the molecular emission features derived from the 2D disc structure using the line fluxes and their analysis based on escape probability in face-on geometry; see Sect.2.2. We consider the molecular column densities Ncol as defined in Eq. (75) as an integral upwards from the height z in the disc where the vertical continuum optical depth is one at line wavelength. This quantity depends on the considered line, because different lines are emitted from different radii and from different depths. We also compute mean molecular emission temperatures 〈Tg〉, where we read off the gas temperatures in the identified line-emitting regions, and the overall radial range of significant line emission. All these quantities are calculated by averaging over all lines of a selected molecule in a given spectral range and over all vertical columns in the disc model, weighted by the line flux that is generated by this column in this line, 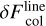 , where
, where 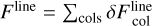 is the total line flux,
is the total line flux,
The resulting mean values and standard deviations for the molecular column densities 〈log10 Ncol〉, the emission temperatures 〈Tg〉, and the radial line emission intervals are listed in Table 5. These data roughly match the characteristics derived from slab-model fitting of the JWST EX Lupi observations as published by Kóspál et al. (2023), with CO having the largest column density of order 1019cm−2, followed by water, and then the molecules C2H2, HCN, and CO2, with column densities of 1017 – 1018 cm−2. The water emission temperature is found to be about 600–700 K depending on wavelength. The emission temperatures of C2H2 and HCN are found to be similar, 580–750 K, whereas CO2 emits at somewhat lower temperatures of ~300 K in the model. In contrast, the weak OH emission lines are emitted from much hotter gas, of namely ~1700 K. These trends are in general agreement with slab-model fits published for other TTauri stars (Salyk et al. 2011; Grant et al. 2023; Tabone et al. 2023). Interestingly, we also modelled NH3 and CH4 lines, but although the column densities of these molecules are not small in the model, these lines do not show up, or even go into absorption at shorter wavelengths.
Figure 11 visualises the line-emitting regions of the various molecules in two different spectral bands. We see a pattern that reoccurs in almost all PRODIMO models. The OH lines are emitted from the highest disc layers. Here, the OH molecule is crucial for cooling down the otherwise hot atomic gas, even before H2 becomes the dominant molecule. Below this OH-emitting layer, we find that first CO and then H2O are emitting. The lower row of plots shows the corresponding gas temperatures and shows that the carbon-to-oxygen ratio C/O in the gas phase is constant at C/O = 0.46 by assumption in the model, except in the region where water ice is found to condense, which happens in the midplane outside of about 2 au in this model.
What is special in this particular disc model for EX Lupi is that the low and increasing surface densities around the inner rim (only ~5 × 1022 cm−2 at r = 0.1 au) causes very efficient dust settling, which reveals an almost dust-free gas. Indeed, the molecular column densities above the 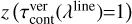 level are much larger at small radii in this model than in our standard T Tauri model (2 × 1026 cm−2 at r = 0.1 au), which uses a sharp inner rim. Therefore, line emissions by C2H2 and HCN from deep layers close to the midplane at small radii become visible. We see that the line-emitting regions of C2H2 and HCN approximately spatially coincide, whereas the line-emitting region of CO2 is located further out, which explains the somewhat lower emission temperature of CO2. All these molecules emit from significantly deeper layers compared to OH, CO, and H2O, which explains why the emission temperatures of the latter molecules are usually higher.
level are much larger at small radii in this model than in our standard T Tauri model (2 × 1026 cm−2 at r = 0.1 au), which uses a sharp inner rim. Therefore, line emissions by C2H2 and HCN from deep layers close to the midplane at small radii become visible. We see that the line-emitting regions of C2H2 and HCN approximately spatially coincide, whereas the line-emitting region of CO2 is located further out, which explains the somewhat lower emission temperature of CO2. All these molecules emit from significantly deeper layers compared to OH, CO, and H2O, which explains why the emission temperatures of the latter molecules are usually higher.
Figure 12 shows that at short wavelengths (≈ 5 µm), the lines and the continuum are coming from roughly the same disc regions, and so this is where absorption lines are more likely to occur. In contrast, at longer wavelengths (≈ 20 µm), the continuum is produced by more distant disc regions than the lines, and so a simple addition of continuum and line emission is valid, as is implicitly assumed in all slab-models.
 |
Fig. 11 Location and physical properties in the MIR line-emission regions of the EX Lupi disc model. Upper row: Line-emitting regions of different molecules in two different spectral bands in the best-fitting EX Lupi model. The left upper plot considers λ = 4-07 µm, and the right upper plot λ = 13-17 µm. The white lines at the bottom of the plots mark the location where the vertical continuum optical depth is one, considering an average of the wavelengths of all water lines in the considered wavelength region. The bottom row shows the corresponding gas temperatures (left) and the carbon-to-oxygen ratio C/O in the gas phase (right). C/O = 0.46 is constant by assumption, except for the region where water ice is found to be stable, where C/O instantly jumps to very large values of >1000. |
 |
Fig. 12 Continuum-emitting regions responsible for about 50% of the flux at different wavelengths under face-on inclination. Contour lines for the vertical optical extinction AV at 1 and 10 are added. |
4.3 Chemical pathways
For each molecule, we analysed the chemistry in the centre of the respective line-forming regions as depicted in Fig. 11. For OH, H2O, and CO2, we do not need a very sophisticated chemistry to understand their formation; a few basic photoreactions in combination with neutral-neutral reactions, and the H2-formation on grains, are sufficient. Previous work on such chemical pathways can be found for example in Thi & Bik (2005), Glassgold et al. (2009), Woitke et al. (2009), and Najita et al. (2011).
At the top of the photodissociation layer at r = 0.2 au, where AV,rad ≈ 0.07 (optically thin), the gas temperature is of the order of 3000 K, carbon is mostly ionised, oxygen is atomic, and there is almost no molecular hydrogen yet: 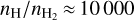 . In these circumstances, the first IR-active molecule to form is OH, with concentrations of ~10−7 via
. In these circumstances, the first IR-active molecule to form is OH, with concentrations of ~10−7 via
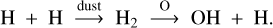 (77)
(77)
The amount of OH that can form in this way is limited by the photodissociation of OH, and by the back reaction OH + H → O + H2.
In only slightly lower layers, where AV,rad ≈ 0.3, the gas temperature is ~1500 K, carbon is still mostly ionised, oxygen is atomic, and 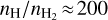 . Here, OH reacts further to form water with concentrations of ~10−7 :
. Here, OH reacts further to form water with concentrations of ~10−7 :
 (78)
(78)
limited by H2O photodissociation.
CO2 forms in similar ways to water, but only in deeper regions where H2 and CO are already abundant; see for example Thi & Bik (2005). At r = 0.5 au, at a height where Av,rad ≈ 3 and Av ≈ 0.2, we find Tg ≈ Td ≈ 360 K. Carbon is mostly present in the form of CO, oxygen is present in H2O, and hydrogen in H2. Under these circumstances, CO2 reaches concentrations of ~10−7 via
 (79)
(79)
 (80)
(80)
limited by CO2 photodissociation.
The formation of HCN and C2H2 in the close midplane is more complicated; see Fig. 11. Previous works on the chemical pathways of these species have been published; for example by Walsh et al. (2015) and Bosman et al. (2022a,b). Similar to CO2, UV-shielded conditions are required, but X-rays also play an important role here, and this is why these line-emitting regions need to be so close to the star, before the X-rays are absorbed by the gas. At r = 0.1 au, at a height where AV,rad ≈ 7 and Av ≈ 0.7, we find Tg ≈ 640 K and Td ≈ 630 K. As before, carbon is in CO, oxygen in H2O, nitrogen in N2, and hydrogen in H2. The chemical destruction timescales due to X-ray ionisations are about ζX ≈ 10−10 s−1 in this region, which means typical X-ray molecular lifetimes are a few hundred years.
Figure 13 shows the chemical pathways in this region leading to HCN and C2H2. A similar analysis was presented by Walsh et al. (2015), see their Sect. 3.2.2. The starting point is the X-ray-driven dissociation of CO, N2, and H2, which creates small amounts of C+, N, N+, and e−. By fast H2-addition reactions, C+ forms CH3+, which recombines dissociatively to CH, which is in kinetic equilibrium with CH2. These two neutral molecules react with N and C to eventually form HCN and C2H2. Another reaction chain starts with N+. By fast H2-addition reactions, N+ forms NH4+, which recombines dissociatively to NH3. NH3, NH2, and NH are in kinetic equilibrium with each other (neutral-neutral reactions vs. photodissociation), and the reaction NH + C → CN + H contributes to the production of CN, in addition to the reactions CH2 + N → CN + H2 and CH + N → CN + H from the reaction chain starting with C+. CN is in kinetic equilibrium with HCN. We find large concentrations of HCN and C2H2 this way, ~10−5 and 10−6, respectively.
Neutral carbon primarily forms via the C3 + hv → C2 + C reaction, and is mainly destroyed by the C2H2 + C → C3H + H and C2H2 + C → C3 + H2 reactions as indicated in the diagram. Concerning the C + H2O → HCO + H reaction, if we were to use reaction parameters from the KIDA database (see Sect. 2.7), the concentration of C atoms would be strongly reduced, and the formation of HCN and C2H2 strongly suppressed. In the situation shown in Fig. 13, the C + H2O → HCO + H reaction only contributes with a rate of 7 × 10−2 cm−3s−1 to the destruction of neutral carbon, that is, with less than 4%.
4.4 Chemical and cooling timescales
The chemical relaxation timescales (see Eq. (117) in Woitke et al. 2009) in the line-emitting regions are of order 0.1–10 yr.
Although this is short compared to overall disc evolutionary timescales, this could mean that the chemistry is not yet fully relaxed, because EX Lupi went through a phase of seven-times-stronger accretion about 5 months before the JWST spectrum was taken (Kóspál et al. 2023). The cooling timescales are shorter, about 10−3 − 0.1 yr, and so we do not expect any significant memory effects concerning the gas temperature in the line-emitting regions.
The most important heating and cooling processes in the inner disc of the EX Lupi model are shown in Fig. 14. In the IR line-emission regions around and below the AV,rad = 1 line, inside of about 0.5 au, there are three significant heating mechanisms: (1) viscous heating, (2) absorption of IR continuum photons – emitted from the star and from the disc – by water molecules, and (3) photodissociation heating. This heating is mostly balanced by water, CO, and OH line cooling. Below the AV,rad = 1 line, relevant for the HCN and C2H2 line emissions, there is simply a balance between water line heating and cooling. Therefore, this region has a rather specific temperature, namely the radiative equilibrium temperature in consideration of the water line opacity. As the water line opacity has a redder characteristic than the dust opacity, this region is generally found to be somewhat cooler than the local dust temperature Tg < Tđ. However, for higher mass-accretion rates, the viscous heating will eventually cause Tg > Tđ.
 |
Fig. 13 Reaction pathways to form HCN and C2H2 in the close mid-plane, where n〈H〉> = 2 × 1011 cm−3, Tg = 640 K, Td = 630 K, AV,rad = 7, and AV = 0.7. The major species are marked with thick boxes. Red species are rare and created by X-ray processes. The green numbers are the particle concentrations nmol/n〈H〉, and the blue numbers are the rates [cm−3s−1]. Wiggly arrows indicate photodissociation, and red arrows indicate X-ray processes: XPHOT is the X-ray primary ionisation of He, and XG and XI are the X-ray secondary ionisations by fast electrons. |
4.5 Dependencies on LUV, LX, and Ṁacc
The analysis of the chemical pathways in Sect. 4.3 suggests that the line fluxes of OH and H2O should depend on the UV luminosity of the star, whereas the HCN and C2H2 lines should be excited by X-rays. Table 6 shows that in our models, indeed the OH and H2O lines become stronger with increasing stellar UV luminosity. Both the sizes of the line-emitting areas and the emission temperatures become larger when LUV is increased. This trend is confirmed by observations (e.g. Fig. 3 in Banzatti et al. 2023), which show a positive correlation between the H2O line luminosity and accretion luminosity, which physically implies larger LUV. The high-UV model can be considered to represent a case in which a larger optical extinction AV was assumed for EX Lupi; see discussion in Sect. 3.1. From a theoretical point of view, the positive correlation with LUV is expected from the global energy budget of the gas in the inner disc, which is heated by stellar UV photons, and mainly cools through water emission lines. As long as the UV is mostly absorbed by the gas and not by the dust, a higher stellar UV luminosity should therefore result in stronger water emission lines. Both the OH and water line luminosities are not significantly affected by the X-ray luminosity. Concerning the increase in the mass-accretion rate, OH is not affected, but the water lines become slightly brighter. This is because the water emissions come from slightly deeper regions than OH, where viscous heating is more relevant; see Fig. 14.
The HCN and C2H2 lines behave in a different way. They actually become weaker with increasing UV, because photodissociation limits the concentrations that can build up at given X-ray-induced production rates. Table 6 shows how the column densities of HCN and C2H2 decrease when LUV is increased. However, only the C2H2 lines become clearly stronger and the C2H2 column density clearly larger when LX is increased. The HCN line fluxes and column densities remain at a similar level as LX is varied. The line-emitting areas and emission temperatures of all considered molecules do not change significantly when LX is changed; it is the column densities that are affected, which is a chemical effect.
Table 6 also shows the results for a model with a three-times-higher mass-accretion rate, a value that is close to the Ṁacc reported by Wang et al. (2023) for EX Lupi. While the H2O, OH, and CO2 line fluxes and their characteristics remain rather similar, the HCN and C2H2 lines show a strong response. Their line fluxes increase by factors of 3.0 and 2.6, respectively, while also increasing their column densities and emission temperatures. This effect is likely related to the fact that these emission lines come from relatively deep disc layers, where the viscous heating is more relevant; see Fig. 14. In addition, the line photons have to outshine the continuum photons – which come from even deeper layers – to create an emission line. The observable line fluxes therefore depend on the contrast between line and continuum emission temperatures. Although the viscous heating due to Ṁacc only slightly increases Tg locally in the deep line-emitting regions, it has a profound impact on the temperature contrast Tg − Td, creating an almost linear response to increasing Ṁacc.
5 Summary and conclusions
We implemented a number of new theories and improvements in our thermo-chemical disc modelling code PRODIMO. These improvements include a new escape probability method for spectral lines, which is relevant for the calculation of line heating and cooling rates, a new treatment of dust settling, and a new concept to apply UV molecular shielding factors to photorates within a 2D disc geometry. We show that these measures altogether result in significant changes to our predicted MIR molecular line spectra. The last column in Table 6 shows that the same disc model with the previous code version concerning escape probability, molecular shielding, and dust settling results in molecular emission features that are too strong for CO2 by a factor of 4, and too weak for HCN and C2H2 by factors of 80 and 40, respectively. The code improvements allow us to get closer to the observed JWST spectra and to the molecular properties derived from slab-model fits, such as column densities, molecular emission temperatures, and line-emitting areas.
Based on the new PRODIMO code, we developed a disc model for the quiescent state of the T Tauri star EX Lupi that can simultaneously fit the SED, the overall spectral shape of the JWST spectrum, and all important molecular emission features in the continuum-subtracted JWST spectrum between 4.9 µm and 7.5 µm, and between 13 µm and 17.7 µm, including CO, H2O, OH, C2H2, HCN, CO2, and H2. To the best of our knowledge, this is the first time that a full Spitzer or JWST line spectrum has been fitted using the complex 2D disc structure of a thermo-chemical model, with consistent dust opacities, molecular concentrations, and calculated dust and gas temperatures.
Our model uses standard element abundances with solar carbon-to-oxygen ratio (C/O = 0.46) throughout the disc. However, we do not claim that this is a unique solution. If the transport by pebble drift and subsequent sublimation of water (e.g. Booth & Ilee 2019; Banzatti et al. 2023) or carbonaceous grains and PAHs (e.g. Nazari et al. 2023; Tabone et al. 2023) can be taken into account in a quantitative way, it is very likely that other disc shapes will be able to fit the JWST data.
Our model explains the observed molecular emission features by a slowly increasing surface density profile around the inner rim in combination with strong dust settling, which creates an almost dust-free gas with large molecular column densities above the settled dust. According to this model, the observed line emissions are produced mostly by the inner disc 0.1–0.5 au, with a certain layered structure, where hot OH emits from the top, warm CO and H2O emit from the middle, and C2H2, HCN, and CO2 emit from deeper layers. The CO2-emitting region is located slightly further away from the star as compared to C2H2 and HCN, leading to lower CO2 emission temperatures. This pattern is in agreement with the general trends published for a number of T Tauri stars observed with Spitzer (e.g. Salyk et al. 2011; Najita et al. 2013; Banzatti et al. 2020) and JWST (Grant et al. 2023; Tabone et al. 2023; Banzatti et al. 2023).
At the top of the photodissociation layer, the OH molecule plays a key role in forming CO and H2O, and in cooling down the predominantly atomic gas from about 4000 K to 2000 K before the water cooling takes over, which establishes temperature conditions wherein, subsequently, other molecules can form as well. This happens at densities of about ~109−1010 cm−3 in the inner disc, where it seems critical to have a non-LTE treatment of the statistical populations of the excited ro-vibrational states of the OH molecule. The required collisional rates are available in the literature - see for example Rahmann et al. (1999); Tabone et al. (2021) – but are not yet implemented in PRODIMO. Concerning the line emissions from C2H2, HCN, and CO2, this seems less critical, because these lines are emitted from a denser gas >1011cm−3.
The existence of large amounts of HCN and C2H2 molecules in the oxygen-rich gas inside of the snowline is a consequence of an X-ray-driven chemistry in our model, where the most abundant CO and N2 molecules are partly dissociated by He+ created by the X-ray irradiation. Similar conclusions were presented by Walsh et al. (2015). These free atoms and ions quickly form C2H2 and HCN in large concentrations of about 10−6 to 10−5 in our model. But this effect is limited to the regions close to the inner rim, before the X-rays get absorbed by the gas. The chemical and cooling timescales are short in the line-emitting regions, that is, shorter than about 10 yr and 0.1 yr, respectively.
Our models show that the water and OH line luminosities increase with stellar UV luminosity, whereas the HCN and C2H2 lines show the opposite trend. We predict a positive correlation between C2H2 line luminosity and stellar X-ray luminosity. Concerning the mass-accretion rate Ṁacc, our models show an almost linear response of both the HCN and C2H2 line luminosities, whereas other molecular emissions are less affected.
 |
Fig. 14 Leading heating (left) and cooling processes (right) in the best-fitting EX Lupi model. The plots show a magnification of the inner disc relevant for the IR molecular line emissions. The dashed contour line marks the disc surface, where the radial optical extinction AV,rad = 1. |
Total line fluxes ![$\sum\nolimits_{{\rm{line}}} {F_{{\rm{mol}}}^{{\rm{line}}}} \,\left[ {{\rm{W}}{{\rm{m}}^{ - 2}}} \right]$](/articles/aa/full_html/2024/03/aa47730-23/aa47730-23-eq190.png) [W m−2], column densities 〈Ncol〉 [cm−2], emission temperatures 〈Tg〉 [K], and emitting radii 〈r1 − r2〉 [au] of selected molecules, affected by stellar UV luminosity, X-ray luminosity, and mass-accretion rate, considering all lines between 13 and 17.7 µm.
[W m−2], column densities 〈Ncol〉 [cm−2], emission temperatures 〈Tg〉 [K], and emitting radii 〈r1 − r2〉 [au] of selected molecules, affected by stellar UV luminosity, X-ray luminosity, and mass-accretion rate, considering all lines between 13 and 17.7 µm.
Acknowledgements
P.W. acknowledges funding from the European Union H2020-MSCA-ITN-2019 under Grant Agreement no. 860470 (CHAMELEON). I.K. and A.M.A. acknowledge support from grant TOP-1 614.001.751 from the Dutch Research Council (NWO).
Appendix A Additional figures and tables
Table A.1 shows the element abundances assumed throughout this paper, 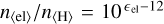 . The assumed carbon-to-oxygen ratio is 0.46. This table is a copy of Table 5 in Kamp et al. (2017). In the case of the best-fitting EX Lupi model, the PAH abundance is larger by a factor of 2.9, and so ϵPAH = 5.94.
. The assumed carbon-to-oxygen ratio is 0.46. This table is a copy of Table 5 in Kamp et al. (2017). In the case of the best-fitting EX Lupi model, the PAH abundance is larger by a factor of 2.9, and so ϵPAH = 5.94.
Figure A.1 shows vertical cuts through the disc at r = 0.1 au, 0.3 au, 1 au, 3 au, 10 au, and 30 au through our standard T Tauri disc model after the PRODIMO changes discussed in Sect. 2.1. This figure shows more details than Figure 2, but both figures show the same model.
Element abundances assumed throughout this paper.
Parameters for the PRODIMO standard T Tauri disc model.
 |
Fig. A.1 Vertical cuts at r = 0.1 au, 0.3 au, and 1 au through the standard PRODIMO T Tauri disc model after the code modifcations described in Sect. refsec:CodeChanges. The x-axis is the hydrogen nuclei column density measured from the top, relevant line formation typically happens between about 1021 cm−2 and 1024 cm−2. The left plots show the assumed hydrogen nuclei particle density n〈H〉 and the calculated gas and dust temperatures. The middle and left plots show the relevant heating and cooling rates, annotated below, where the thick grey line is the total heating and cooling rate. We note that |
 |
Fig. A.1 continued. Vertical cuts at r = 3 au, 10 au, and 30 au |
References
- Abraham, P., Juhász, A., Dullemond, C. P., et al. 2009, Nature, 459, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Abraham, P., Chen, L., Kóspál, A., et al. 2019, ApJ, 887, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Cernicharo, J., & Goicoechea, J. R. 2008, A & A, 483, 831 [Google Scholar]
- Akimkin, V., Zhukovska, S., Wiebe, D., et al. 2013, ApJ, 766, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A & A, 600, A20 [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, D. E., Blake, G. A., Cleeves, L. I., et al. 2021, ApJ, 909, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Ansdell, M., Williams, J. P., Trapman, L., et al. 2018, ApJ, 859, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Aresu, G., Kamp, I., Meijerink, R., et al. 2011, A & A, 526, A163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Banzatti, A., Pontoppidan, K. M., Salyk, C., et al. 2017, ApJ, 834, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Pascucci, I., Bosman, A. D., et al. 2020, ApJ, 903, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Banzatti, A., Pontoppidan, K. M., Carr, J. S., et al. 2023, ApJ, 957, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Bethell, T., & Bergin, E. 2009, Science, 326, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [Google Scholar]
- Booth, R. A., & Ilee, J. D. 2019, MNRAS, 487, 3998 [CrossRef] [Google Scholar]
- Bosman, A. D., Bruderer, S., & van Dishoeck, E. F. 2017, A & A, 601, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bosman, A. D., Bergin, E. A., Calahan, J., & Duval, S. E. 2022a, ApJ, 930, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Bosman, A. D., Bergin, E. A., Calahan, J. K., & Duval, S. E. 2022b, ApJ, 933, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Bruderer, S., Harsono, D., & van Dishoeck, E. F. 2015, A & A, 575, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carr, J. S., & Najita, J. R. 2008, Science, 319, 1504 [Google Scholar]
- Carr, J. S., & Najita, J. R. 2011, ApJ, 733, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2002, ApJ, 577, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2004, ApJ, 604, 222 [NASA ADS] [CrossRef] [Google Scholar]
- Cazaux, S., & Spaans, M. 2009, A & A, 496, 365 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazaux, S., & Tielens, A. G. G. M. 2010, ApJ, 715, 698 [NASA ADS] [CrossRef] [Google Scholar]
- Ciesla, F. J., & Cuzzi, J. N. 2006, Icarus, 181, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Cruz-Sáenz de Miera, F., Kóspál, A., Abraham, P., et al. 2023, A & A, 678, A88 [CrossRef] [EDP Sciences] [Google Scholar]
- D'Alessio, P., Cantö, J., Calvet, N., & Lizano, S. 1998, ApJ, 500, 411 [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [Google Scholar]
- Du, F., & Bergin, E. A. 2014, ApJ, 792, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [Google Scholar]
- Dullemond, C. P., & Monnier, J. D. 2010, ARA & A, 48, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Dullemond, C. P., Dominik, C., & Natta, A. 2001, ApJ, 560, 957 [NASA ADS] [CrossRef] [Google Scholar]
- Dzyurkevich, N., Flock, M., Turner, N. J., Klahr, H., & Henning, T. 2010, A & A, 515, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flock, M., Fromang, S., Turner, N. J., & Benisty, M. 2017, ApJ, 835, 230 [CrossRef] [Google Scholar]
- Furlan, E., Watson, D. M., McClure, M. K., et al. 2009, ApJ, 703, 1964 [Google Scholar]
- Glassgold, A. E. , & Najita, J. R. 2015, ApJ, 810, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E., Meijerink, R., & Najita, J. R. 2009, ApJ, 701, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, I. E., Rothman, L. S., Hargreaves, R. J., et al. 2022, J. Quant. Spec. Radiat. Transf., 277, 107949 [NASA ADS] [CrossRef] [Google Scholar]
- Grant, S. L., van Dishoeck, E. F., Tabone, B., et al. 2023, ApJ, 947, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Greenwood, A. J., Kamp, I., Waters, L. B. F. M., Woitke, P., & Thi, W. F. 2019, A & A, 626, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gu, H., Cui, J., Niu, D. D., et al. 2020, AJ, 159, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hales, A. S., Pérez, S., Saito, M., et al. 2018, ApJ, 859, 111 [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A & A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hickson, K. M., Loison, J.-C., Nunez-Reyes, D., & Mereau, R. 2016, arXiv e-prints [arXiv: 1608.08877] [Google Scholar]
- Hummer, D. G., & Rybicki, G. B. 1985, ApJ, 293, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Husain, D., & Kirsch, L. J. 1971, Chem. Phys. Lett., 9, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., & Natta, A. 2005, A & A, 438, 899 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juhász, A., Dullemond, C. P., van Boekel, R., et al. 2012, ApJ, 744, 118 [Google Scholar]
- Kadam, K., Vorobyov, E., Regály, Z., Kóspál, A., & Ábrahám, P. 2019, ApJ, 882, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Kadam, K., Vorobyov, E., & Basu, S. 2022, MNRAS, 516, 4448 [NASA ADS] [CrossRef] [Google Scholar]
- Kama, M., Min, M., & Dominik, C. 2009, A & A, 506, 1199 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamp, I., & Bertoldi, F. 2000, A & A, 353, 276 [NASA ADS] [Google Scholar]
- Kamp, I., Thi, W. F., Woitke, P., et al. 2017, A & A, 607, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kanwar, J., Kamp, I., Woitke, P., et al. 2024, A & A, 681, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kokoulina, E., Matter, A., Lopez, B., et al. 2021, A & A, 652, A61 [CrossRef] [EDP Sciences] [Google Scholar]
- Kóspál, Á., Ábrahám, P., Diehl, L., et al. 2023, ApJ, 945, L7 [CrossRef] [Google Scholar]
- Li, X., Heays, A. N., Visser, R., et al. 2013, A & A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lommen, D. J. P., van Dishoeck, E. F., Wright, C. M., et al. 2010, A & A, 515, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A & A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mulders, G. D., & Dominik, C. 2012, A & A, 539, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Najita, J. R., Ádámkovics, M., & Glassgold, A. E. 2011, ApJ, 743, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Najita, J. R., Carr, J. S., Pontoppidan, K. M., et al. 2013, ApJ, 766, 134 [Google Scholar]
- Natta, A., Prusti, T., Neri, R., et al. 2001, A & A, 371, 186 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nazari, P., Tabone, B., van't Hoff, M. L. R., Jørgensen, J. K., & van Dishoeck, E. F. 2023, ApJ, 951, L38 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., Aikawa, Y., Tsujimoto, M., Nakagawa, Y., & Millar, T. J. 2007, ApJ, 661, 334 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Spaans, M., & Tielens, A. G. G. M. 2007, A & A, 461, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascucci, I., Herczeg, G., Carr, J. S., & Bruderer, S. 2013, ApJ, 779, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Perotti, G., Christiaens, V., Henning, T., et al. 2023, Nature, 620, 516 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Blake, G. A., & Käufl, H. U. 2010, ApJ, 722, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Pontoppidan, K. M., Salyk, C., Bergin, E. A., et al. 2014, in Protostars and PlanetsVI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 363 [Google Scholar]
- Rahmann, U., Kreutner, W., & Kohse-Höinghaus, K. 1999, Appl. Phys. B: Lasers Opt., 69, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Rechenberg, I. 2000, Comput. Methods Appl. Mech. Eng., 186, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Rigliaco, E., Gratton, R., Kóspál, Á., et al. 2020, A & A, 641, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riols, A., & Lesur, G. 2018, A & A, 617, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., et al. 2008, ApJ, 676, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Salyk, C., Pontoppidan, K. M., Blake, G. A., Najita, J. R., & Carr, J. S. 2011, ApJ, 731, 130 [Google Scholar]
- Schaaf, S. A. 1963, Handbuch Physik, 3, 591 [NASA ADS] [Google Scholar]
- Schräpler, R., & Henning, T. 2004, ApJ, 614, 960 [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A & A, 24, 337 [NASA ADS] [Google Scholar]
- Sicilia-Aguilar, A., Fang, M., Roccatagliata, V., et al. 2015, A & A, 580, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sipos, N., Àbrahàm, P., Acosta-Pulido, J., et al. 2009, A & A, 507, 881 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabone, B., van Hemert, M. C., van Dishoeck, E. F., & Black, J. H. 2021, A & A, 650, A192 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tabone, B., Bettoni, G., van Dishoeck, E. F., et al. 2023, Nat. Astron., 7, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Teets, W. K., Weintraub, D. A., Kastner, J. H., et al. 2012, ApJ, 760, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Thi, W. F., & Bik, A. 2005, A & A, 438, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W. F., Kamp, I., Woitke, P., et al. 2013, A & A, 551, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thi, W. F., Lesur, G., Woitke, P., et al. 2019, A & A, 632, A44 [CrossRef] [EDP Sciences] [Google Scholar]
- van ’t Hoff, M. L. R., Bergin, E. A., Jørgensen, J. K., & Blake, G. A. 2020, ApJ, 897, L38 [Google Scholar]
- Varga, J., Abraham, P., Chen, L., et al. 2018, A & A, 617, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A & A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A & A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wang, M.-T., Herczeg, G. J., Liu, H.-G., et al. 2023, ApJ, 957, 113 [NASA ADS] [CrossRef] [Google Scholar]
- White, J. A., Kóspál, Á., Hughes, A. G., et al. 2020, ApJ, 904, 37 [CrossRef] [Google Scholar]
- Woitke, P., & Helling, C. 2003, A & A, 399, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W. F. 2009, A & A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Pinte, C., et al. 2016, A & A, 586, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Helling, C., Hunter, G. H., et al. 2018a, A & A, 614, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Min, M., Thi, W. F., et al. 2018b, A & A, 618, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woitke, P., Kamp, I., Antonellini, S., et al. 2019, PASP, 131, 064301 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, P. M., & Willacy, K. 2009, ApJ, 693, 1360 [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Pontoppidan, K. M., Salyk, C., & Blake, G. A. 2013, ApJ, 766, 82 [NASA ADS] [CrossRef] [Google Scholar]
The spectral resolution of the MIRI instrument depends on wavelength, see https://jwst-docs.stsci.edu/jwst-mid-infrared-instrument/miri-observing-modes/miri-medium-resolution-spectroscopy, varying between about 2000 and 3000, so our choice here is a simplification.
All Tables
Total line fluxes ΣFline [W m−2], flux-mean column densities 〈Ncol〉 [cm−2], flux-mean emission temperatures 〈Tg〉 [K], and flux-mean emission radius interval 〈r1 – r2〉 of molecules, considering all lines emitted in two different spectral regions in the 2D disc model.
Total line fluxes ![$\sum\nolimits_{{\rm{line}}} {F_{{\rm{mol}}}^{{\rm{line}}}} \,\left[ {{\rm{W}}{{\rm{m}}^{ - 2}}} \right]$](/articles/aa/full_html/2024/03/aa47730-23/aa47730-23-eq190.png) [W m−2], column densities 〈Ncol〉 [cm−2], emission temperatures 〈Tg〉 [K], and emitting radii 〈r1 − r2〉 [au] of selected molecules, affected by stellar UV luminosity, X-ray luminosity, and mass-accretion rate, considering all lines between 13 and 17.7 µm.
[W m−2], column densities 〈Ncol〉 [cm−2], emission temperatures 〈Tg〉 [K], and emitting radii 〈r1 − r2〉 [au] of selected molecules, affected by stellar UV luminosity, X-ray luminosity, and mass-accretion rate, considering all lines between 13 and 17.7 µm.
All Figures
 |
Fig. 1 Escape probability ( |
| In the text | |
 |
Fig. 2 Change in heating and cooling balance with the new escape probability treatment and the new 2D concept to apply UV molecular shielding factors. The plots show the leading heating process (top) and the leading cooling process (bottom) in a zoomed-in disc region responsible for the disc IR line emissions. Processes are only plotted when they fill at least 1% of the area in these plots. The dashed lines mark the visual disc surface Av,rad = 1 and the vertical optical extinction AV = 10. The model includes 103 heating and 95 cooling processes with 64910 spectral lines altogether. |
| In the text | |
 |
Fig. 3 Effect of continuum emission on line flux. Case (a) shows an emission line on a cold continuum SC = 0. Case (b) is an emission line on a warm continuum SL > SC, and case (c) is an absorption line where the continuum is hot SL < SC. The area A is the flux of photon energy [erg s−1 cm−2] carried away by line photons escaping from the object (after continuum extinction and line self-absorption) and is the same in cases (a), (b) and (c). However, the objective is to derive the area O, which is the line flux as measured by observers. For a warm continuum, clearly O < A, and for an absorption line O < 0 (although A > 0). |
| In the text | |
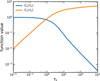 |
Fig. 4 Functions C1(τL) and C2(τL) as introduced in Eq. (36). |
| In the text | |
 |
Fig. 5 Line fluxes predicted by the old escape probability treatment (blue) and new escape probability treatment (orange). All line fluxes are divided by the results from the full line RT for zero inclination (face-on). |
| In the text | |
 |
Fig. 6 Change of molecular concentrations caused by introducing our new 2D concept to apply molecular shielding factors. |
| In the text | |
 |
Fig. 7 PRODIMO model for the quiescent state of EX Lupi. The top plots show the assumed gas and dust column densities (left) and scale heights (right). The second row shows the corresponding gas densities (left) and gas-to-dust mass ratio after settling (right). The third row shows the UV field strength χ (left), and the X-ray ionisation rate ζX in comparison to the cosmic-ray ionisation rate (right). The bottom row shows the resulting dust-temperature (left) and gas-temperature (right) structures. Additional contour lines show selected values for the vertical optical extinction AV and the radial optical extinction AV,rad as indicated. |
| In the text | |
 |
Fig. 8 Fit of the SED of EX Lupi in the quiescent state. The orange and green data points in the upper plot are Herschel/SPIRE and ALMA measurements. The orange spectrum is the JWST/MIRI data. The lower plot shows a magnification of the MIR spectral region. |
| In the text | |
 |
Fig. 9 Resulting chemical concentrations ϵi = ni/n〈H〉 of selected molecules in the PRODIMO disc model for EX Lupi. Additional contour lines are plotted as boundaries, including the ionisation parameter χ/n〈H〉 (i.e. the UV field strength divided by the hydrogen nuclei particle density) and the ratios of the concentrations of the major molecules. For example, ‘H/H2=100’ means that H atoms are 100 times more abundant than H2 molecules. |
| In the text | |
 |
Fig. 10 Continuum-subtracted JWST spectrum (black line) in comparison to the PRODIMO-FLITS disc model for EX Lupi. The coloured areas show the contributions of the different molecules to the total model line spectrum. These are therefore cumulative; i.e. the CO2-spectrum is plotted on top of the C2H2-spectrum, the HCN-spectrum on top of the (C2H2+CO2)-spectrum, and so on, such that the top of the water spectrum represents the total continuum-subtracted model spectrum. The model spectrum has been convolved to R = 2500. Furthermore, both the observational data and the model spectrum were slightly box-filtered before plotting in order to increase clarity; see main text. The broad bumps in the observational data (e.g. those around 6.3 µm and in the region 15.5 – 17.7 µm) are likely due to problems with the early data reduction and continuum subtraction. |
| In the text | |
 |
Fig. 11 Location and physical properties in the MIR line-emission regions of the EX Lupi disc model. Upper row: Line-emitting regions of different molecules in two different spectral bands in the best-fitting EX Lupi model. The left upper plot considers λ = 4-07 µm, and the right upper plot λ = 13-17 µm. The white lines at the bottom of the plots mark the location where the vertical continuum optical depth is one, considering an average of the wavelengths of all water lines in the considered wavelength region. The bottom row shows the corresponding gas temperatures (left) and the carbon-to-oxygen ratio C/O in the gas phase (right). C/O = 0.46 is constant by assumption, except for the region where water ice is found to be stable, where C/O instantly jumps to very large values of >1000. |
| In the text | |
 |
Fig. 12 Continuum-emitting regions responsible for about 50% of the flux at different wavelengths under face-on inclination. Contour lines for the vertical optical extinction AV at 1 and 10 are added. |
| In the text | |
 |
Fig. 13 Reaction pathways to form HCN and C2H2 in the close mid-plane, where n〈H〉> = 2 × 1011 cm−3, Tg = 640 K, Td = 630 K, AV,rad = 7, and AV = 0.7. The major species are marked with thick boxes. Red species are rare and created by X-ray processes. The green numbers are the particle concentrations nmol/n〈H〉, and the blue numbers are the rates [cm−3s−1]. Wiggly arrows indicate photodissociation, and red arrows indicate X-ray processes: XPHOT is the X-ray primary ionisation of He, and XG and XI are the X-ray secondary ionisations by fast electrons. |
| In the text | |
 |
Fig. 14 Leading heating (left) and cooling processes (right) in the best-fitting EX Lupi model. The plots show a magnification of the inner disc relevant for the IR molecular line emissions. The dashed contour line marks the disc surface, where the radial optical extinction AV,rad = 1. |
| In the text | |
 |
Fig. A.1 Vertical cuts at r = 0.1 au, 0.3 au, and 1 au through the standard PRODIMO T Tauri disc model after the code modifcations described in Sect. refsec:CodeChanges. The x-axis is the hydrogen nuclei column density measured from the top, relevant line formation typically happens between about 1021 cm−2 and 1024 cm−2. The left plots show the assumed hydrogen nuclei particle density n〈H〉 and the calculated gas and dust temperatures. The middle and left plots show the relevant heating and cooling rates, annotated below, where the thick grey line is the total heating and cooling rate. We note that |
| In the text | |
 |
Fig. A.1 continued. Vertical cuts at r = 3 au, 10 au, and 30 au |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



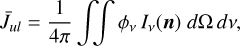
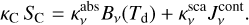
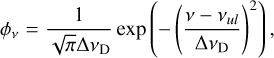
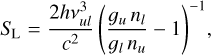
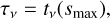
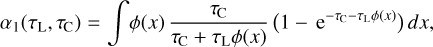
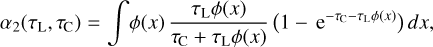
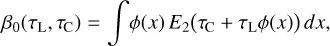
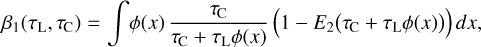
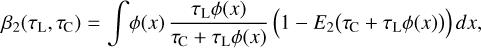
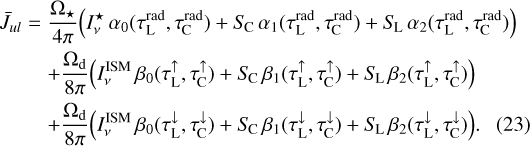
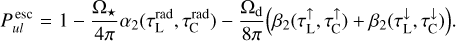
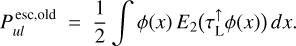
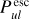
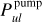
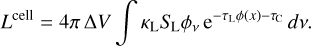
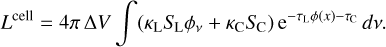
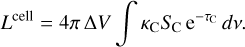
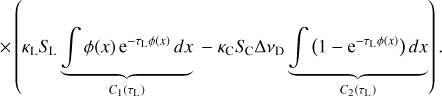
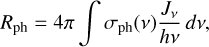
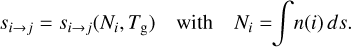
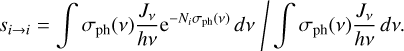
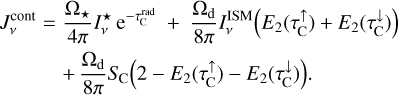
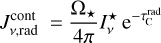
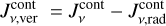
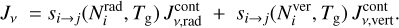
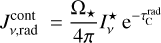
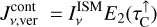
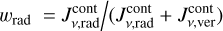
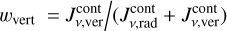
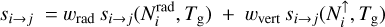
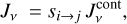
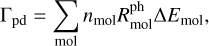
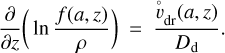
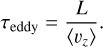
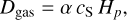
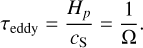
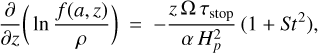
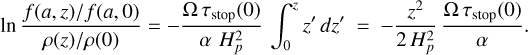
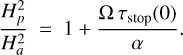
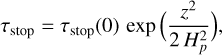
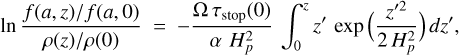
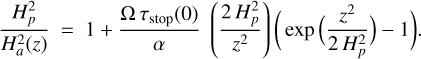
![$\matrix{ {{\rm{\Sigma }}(r) \propto \exp \,\left[ { - {{\left( {{{{R_{{\rm{soft}}}}} \over r}} \right)}^s}} \right]\,{r^{ - }}\exp \,\left[ { - {{\left( {{r \over {{R_{{\rm{tap}}}}}}} \right)}^{2 - \gamma }}} \right],} \hfill \cr {{R_{{\rm{soft}}}} = {\rm{raduc}} \times {R_{{\rm{in}}}},} \hfill \cr {\,\,\,\,\,\,\,\,s = {{\ln [\ln (1/{\rm{reduc}})]} \over {\ln ({\rm{raduc}})}},} \hfill \cr } $](/articles/aa/full_html/2024/03/aa47730-23/aa47730-23-eq165.png)