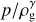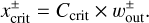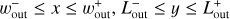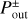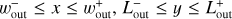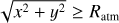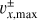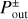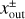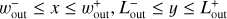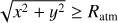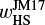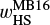| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A14 | |
| Number of page(s) | 24 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202347530 | |
| Published online | 29 January 2024 | |
Analytic description of the gas flow around planets embedded in protoplanetary disks
1
Center for Star and Planet Formation, GLOBE Institute, University of Copenhagen,
Øster Voldgade 5–7,
1350
Copenhagen,
Denmark
e-mail: ayumu.kuwahara@sund.ku.dk
2
Department of Earth and Planetary Sciences, Tokyo Institute of Technology,
2-12-1 Ookayama,
Meguro-ku,
Tokyo
152-8551,
Japan
3
Earth-Life Science Institute, Tokyo Institute of Technology,
2-12-1 Ookayama,
Meguro-ku,
Tokyo
152-8550,
Japan
4
Department of Earth Science and Astronomy, Graduate School of Arts and Sciences, The University of Tokyo,
3-8-1 Komaba,
Meguro-ku,
Tokyo
153-8902,
Japan
Received:
21
July
2023
Accepted:
3
November
2023
Context. A growing planet embedded in a protoplanetary disk induces three-dimensional gas flow, which exhibits a midplane outflow that can suppress dust accretion onto the planet and form global dust substructures (rings and gaps).
Aims. Because analytic formulae for the planet-induced outflow are useful for modeling its influences on local and global dust surface densities and planet accretion, we derived analytic formulae that describe the morphology and velocity of the planet-induced outflow.
Methods. We first performed three-dimensional, nonisothermal hydrodynamical simulations of the gas flow past a planet, which enabled us to introduce a fitting formula that describes the morphology of the outflow. We then derived an analytic formula for the outflow speed using Bernoulli’s theorem.
Results. We successfully derived a fitting formula for the midplane outflow morphology (the shape of the streamline), which is valid when the dimensionless thermal mass falls below m ≲ 0.6. The obtained analytic formulae for the outflow, such as the maximum outflow speed and the velocity distributions of the outflow in the radial and vertical directions to the disk, show good agreement with the numerical results. We find the following trends: (1) the maximum outflow speed increases with the planetary mass and has a peak of ~30–40% of the sound speed when the dimensionless thermal mass is m ~ 0.3, corresponding to a super-Earth mass planet at 1 au for the typical steady accretion disk model, and (2) the presence of the headwind (namely, the global pressure force acting in the positive radial direction of the disk) enhances (reduces) the outflow toward the outside (inside) of the planetary orbit.
Conclusions. The planet-induced outflow of the gas affects the dust motion when the dimensionless stopping time of dust falls below St ≲ min(10 m2, 0.1), which can be used to model the dust velocity influenced by the outflow.
Key words: hydrodynamics / planets and satellites: atmospheres / protoplanetary disks / planet-disk interactions
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Planets form in protoplanetary disks and interact with the surrounding gas and dust. Disk–planet interactions have been studied for a wide range of planetary masses. Planets with typically ≳15 M⊕ (Earth masses) can open a gas gap around their orbits (e.g., Duffell & MacFadyen 2013) and form substructures in the distribution of dust in disks, such as dust rings and gaps (e.g., Paardekooper & Mellema 2004).
Low-mass planets (typically ~0.1–10 M⊕) do not open a deep gas gap, but those planets embedded in protoplanetary disks also interact with surrounding disk gas and dust. When the physical radius of a planet exceeds the Bondi radius, 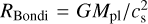 , where G is the gravitational constant, Mpl is the mass of the planet, and cs is the sound speed, the planet starts to attract a disk gas. In this study, we define the disk gas within the Bondi radius as the envelope. Recent three-dimensional hydrodynamical simulations exhibited the complex structure of the perturbed gas flow around the envelope (the planet-induced gas flow; e.g., Ormel et al. 2015b; Fung et al. 2015). Gas from the disk flows into the envelope through the poles and returns to the disk as the outflow through the midplane, which is referred to as the recycling flow (Ormel et al. 2015b). We note that though the pattern of the recycling flow was characterized in previous studies by the polar inflow and the midplane outflow (Ormel et al. 2015b; Fung et al. 2015, 2019; Lambrechts & Lega 2017; Cimerman et al. 2017; Kurokawa & Tanigawa 2018; Popovas et al. 2018; Kuwahara et al. 2019; Béthune & Rafikov 2019; Moldenhauer et al. 2021, 2022), the inflow from the midplane, sometimes accompanied by the polar outflow, has been identified in a specific situation where the planet has a high luminosity due to the accretion of solids (Chrenko & Lambrechts 2019) or experiences a strong gas headwind (Ormel et al. 2015b; Kurokawa & Tanigawa 2018; Bailey et al. 2021).
, where G is the gravitational constant, Mpl is the mass of the planet, and cs is the sound speed, the planet starts to attract a disk gas. In this study, we define the disk gas within the Bondi radius as the envelope. Recent three-dimensional hydrodynamical simulations exhibited the complex structure of the perturbed gas flow around the envelope (the planet-induced gas flow; e.g., Ormel et al. 2015b; Fung et al. 2015). Gas from the disk flows into the envelope through the poles and returns to the disk as the outflow through the midplane, which is referred to as the recycling flow (Ormel et al. 2015b). We note that though the pattern of the recycling flow was characterized in previous studies by the polar inflow and the midplane outflow (Ormel et al. 2015b; Fung et al. 2015, 2019; Lambrechts & Lega 2017; Cimerman et al. 2017; Kurokawa & Tanigawa 2018; Popovas et al. 2018; Kuwahara et al. 2019; Béthune & Rafikov 2019; Moldenhauer et al. 2021, 2022), the inflow from the midplane, sometimes accompanied by the polar outflow, has been identified in a specific situation where the planet has a high luminosity due to the accretion of solids (Chrenko & Lambrechts 2019) or experiences a strong gas headwind (Ormel et al. 2015b; Kurokawa & Tanigawa 2018; Bailey et al. 2021).
The morphology and velocity of the planet-induced outflow are crucial for investigating the hydrodynamic effects of the planet-induced outflow. In this study we use the word “morphology” to describe the shapes of the streamlines. The midplane outflow induced by an embedded planet, which occurs in the radial direction to the disk, affects the motion of approximately millimeter- to centimeter-sized dust grains. Because these small dust grains tend to follow the gas streamlines, their accretion rates onto an embedded planet with ~ 1 M⊕ are reduced by orders of magnitude due to the outflow (Popovas et al. 2018, 2019; Kuwahara & Kurokawa 2020a,b; Okamura & Kobayashi 2021). The radial drift of dust smaller than 1 cm is disturbed both inside and outside the planetary orbit by the outflow induced by the embedded planet (≳ 1 M⊕)1, which leads to the formation of the dust ring and gap, whose radial extent is ~1–10 times the gas scale height in a disk (Kuwahara et al. 2022).
Few studies have investigated the gas flow speed perturbed by an embedded planet. Ormel (2013) considered two-dimensional, isothermal, and inviscid disk gas and derived an approximate analytic solution for the gas velocity. Assuming an isothermal gas disk, Fung et al. (2015) performed three-dimensional hydrodynamical simulations and found that the outflow of the gas induced by an embedded planet at the midplane has a speed of ~20–40% of the sound speed. Kuwahara et al. (2019) assumed an isothermal, Keplerian gas disk; they performed three-dimensional hydrodynamical simulations and investigated the dependence of the outflow speed on the planetary mass, finding that the outflow speed increases with the planetary mass.
There are no comprehensive studies on the flow speed in three dimensions for a wide range of parameters, namely the planetary mass and the magnitude of the deviation of the disk gas rotation from Keplerian rotation. The sub-Keplerian motion of the gas due to the global pressure gradient in the disk alters the three-dimensional structure of the planet-induced gas flow (Ormel et al. 2015b; Kurokawa & Tanigawa 2018). Three-dimensional hydrodynamical simulations are computationally expensive, making it difficult to incorporate the hydrodynamic effects of the perturbed gas flow into models of planet formation and dust substructure formation. Thus, construction of an analytic model of the planet-induced gas flow is needed to understand gas–dust–planet interactions.
In this study, we construct an analytic model of the outflow induced by an embedded planet, guided by numerical simulations for an extensive parameter space. We first perform three-dimensional, nonisothermal hydrodynamical simulations (Sect. 2). We then derive the analytic formulae of the flow field based on the hydro-simulation results obtained in Sect. 3. In Sect. 4 we compare our analytic formula for the outflow speed with the numerical results. In Sect. 5 we discuss the implications for the dust motion influenced by the planet-induced gas flow. We conclude in Sect. 6. For readers who want to quickly see our key results, Fig. 9 in Sect. 4 shows the maximum outflow speed obtained from hydrodynamical simulations and an analytic formula for the maximum outflow speed (Eq. (27)).
2 Numerical simulations
We first performed hydrodynamical simulations for broad parameter ranges. The obtained hydro-simulations results were used to construct an analytic model of the flow field (Sect. 3). Our methods of hydrodynamical simulations are the same as described in Kuwahara & Kurokawa (2020a,b) and Kuwahara et al. (2022), but this study handles the broader parameter spaces than these previous works in terms of the planetary mass and the headwind speed caused by the global pressure gradient to derive an analytic formula for the outflow speed. Here we summarize the key points of our numerical model.
2.1 Dimensionless unit system
In this study, the length, times, velocities, and densities are normalized by the disk gas scale height, H, the reciprocal of the orbital frequency, Ω−1, the isothermal sound speed, cs, and the unperturbed gas density at the location of the planet, ρ∞, respectively. We introduced the dimensionless thermal mass of the planet as (Ormel et al. 2015a)
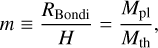 (1)
(1)
where Mth = M*h3 is the thermal mass of the planet (Goodman & Rafikov 2001), M* is the stellar mass, and h is the aspect ratio of the disk. In this study, h is used only when we convert the dimensionless quantities into dimensional ones. We describe the aspect ratio for a typical steady accretion disk model in Appendix A. The Hill radius is given by RHill = (m/3)1/3 H. We considered m = 0.03−1 in this study, which corresponds to planets with Mpl ≃ 0.2−6.6 M⊕ (Mpl ≃ 1−33 M⊕) orbiting a solar-mass star at 1 au (10 au; Fig. 1a). We considered the planet on a fixed circular orbit revolving with the Keplerian speed, υK.
The planet experiences a headwind of the gas because the disk gas rotates at a different speed from the Keplerian speed due to the global pressure gradient. The deviation of the rotation speed of the gas from Keplerian rotation can be characterized by −ηυK, where η = −1/2(cs/υK)2(d ln p/d ln a) is a dimensionless quantity characterizing the global pressure gradient of the disk gas (Nakagawa et al. 1986) and a is the orbital radius. We assumed d ln p/d ln a < 0 across the entire region of the disk. This implies that the disk gas rotates more slowly than the
Keplerian speed (sub-Keplerian motion of the gas). We defined the Mach number of the headwind as
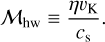 (2)
(2)
We considered ℳhw = 0−0.1 in this study. We plotted Eq. (2) for a typical steady accretion disk model in Fig. 1b.
 |
Fig. 1 Planetary mass (top) and the Mach number (bottom) as a function of the orbital radius. For the conversion, we assumed a typical steady accretion disk model with a dimensionless viscous alpha parameter (Shakura & Sunyaev 1973), αacc, including viscous heating and stellar irradiation (e.g., Ida et al. 2016). In this model, the aspect ratio is given by h = max(0.027(a/1 au)1/20, 0.024 (a/1 au)2/7), where a solar-mass star, a solar luminosity, the typical accretion rate of classical T Tauri stars, 10−8 M⊙ yr−1, and αacc = 10−3 were assumed (Appendix A). |
2.2 Methods of three-dimensional hydrodynamical simulations
Assuming a compressible, inviscid sub-Keplerian gas disk, we performed nonisothermal hydrodynamical simulations. These simulations were performed in the spherical polar coordinates, (r, θ, ϕ), co-rotating with a planet. The numerical resolution was [log r, θ, ϕ] = [128, 64, 128]. The Bondi and Hill radii are resolved by 38–88 and 69–101 cells in the radial direction in our hydrodynamical simulations. We used a free-slip condition at the inner boundary, r = rinn. Assuming the density of the planetary core to be ρpl = 5 g cm−3 and the solar-mass star, the size of the inner boundary was set to follow a mass-radius relationship of the planetary core (Kuwahara & Kurokawa 2020a):
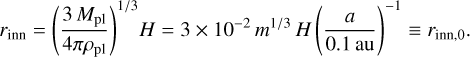 (3)
(3)
We adopted a = 0.1 in Eq. (3) in our fiducial runs. We confirmed the size of the inner boundary does not affect our results (Appendix B). Thus, when we convert the dimensionless quantity into a dimensional one, we can use an arbitrary orbital radius. As the initial state of the disk, we assumed the vertical stratification of the gas density, ρg = ρ∞ exp[−(z/2)2]. The initial gas velocity is υg = υ∞ = (−3x/2 − ℳhw)ey, where υg = (υx,g, υy,g, υz,g) is the gas velocity in the local Cartesian coordinates centered at the planet. The internal and total energies of the gas are given by U = p/(γ − 1) and 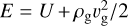 , respectively, where γ = 1.4 is the adiabatic index. At the outer boundary, r = rout, we fixed the gas density and velocity, ρg = ρ∞ and υg = υ∞. Hereafter we denote with the x-, y-, and z-directions the radially outward, azimuthal, and vertical directions to the disk, respectively.
, respectively, where γ = 1.4 is the adiabatic index. At the outer boundary, r = rout, we fixed the gas density and velocity, ρg = ρ∞ and υg = υ∞. Hereafter we denote with the x-, y-, and z-directions the radially outward, azimuthal, and vertical directions to the disk, respectively.
We solved the continuity, Euler’s, and energy conservation equations using Athena++ code2 (White et al. 2016; Stone et al. 2020). The external force in Euler’s equation includes the Coriolis force, Fcor = −2ez × υg, the tidal force, Ftid = 3xex − zez, the global pressure force due to the sub-Keplerian motion of the gas, Fhw = 2ℳhwex, and the gravitational force (e.g., Ormel et al. 2015b):
![${{\bf{F}}_{{\rm{grav}}}} = - \nabla \left( {{m \over {\sqrt {{r^2} + r_{{\rm{sm}}}^2} }}} \right)\left\{ {1 - \exp \left[ { - {1 \over 2}{{\left( {{t \over {{t_{{\rm{inj}}}}}}} \right)}^2}} \right]} \right\},$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq6.png) (4)
(4)
where 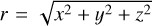 is the distance from the planet, rsm is the smoothing length, and tinj is the injection time. We set rsm = 0.1 Rgrav for our fiducial runs, where Rgrav ≡ min(RBondi, RHill) is the radius of the gravitational sphere of the planet. We investigated the effect of the smoothing length in Appendix C.
is the distance from the planet, rsm is the smoothing length, and tinj is the injection time. We set rsm = 0.1 Rgrav for our fiducial runs, where Rgrav ≡ min(RBondi, RHill) is the radius of the gravitational sphere of the planet. We investigated the effect of the smoothing length in Appendix C.
Our simulations utilized the β cooling model, where the radiative cooling occurs on a finite timescale, β (Gammie 2001). The gas is heated by adiabatic compression. Following Kurokawa & Tanigawa (2018), we assumed that the typical scale of the temperature perturbation can be estimated by the Bondi radius, RBondi = mH. The dimensionless cooling time can be described by
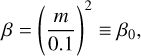 (5)
(5)
which represents the cooling time near the outer edge of the envelope, ~RBondi (Kurokawa & Tanigawa 2018). We list our parameter sets in Table 1. We set β = β0 for our fiducial runs. We investigated the effect of ßin Sect. 5.4.
2.3 Hydrodynamical simulation results
This section summarizes the hydrodynamical simulation results. Based on the numerical results, an analytic formulation of the flow field is presented in Sect. 3.
2.3.1 Summary of three-dimensional planet-induced gas flow
First, we summarize the general properties of the three-dimensional gas flow as reported in previous studies. Planets embedded in disks perturb the surrounding gas and induce the three-dimensional gas flow (Fig. 2; e.g., Ormel et al. 2015b; Fung et al. 2015). The fundamental features of the gas flow around the planet are as follows: (1) the Keplerian shear flow extends inside and outside the orbit of the planet (the green lines of Fig. 2a). (2) The horseshoe flow exists in the anterior-posterior direction of the orbital path of the planet (the orange lines of Fig. 2a). The horseshoe streamlines have a columnar structure in the vertical direction (Fung et al. 2015; Masset & Benítez-Llambay 2016). (3) An isolated inner envelope forms within the gravitational sphere of the planet, r ≲ Rgrav, due to the buoyancy barrier (Kurokawa & Tanigawa 2018). We refer to this isolated envelope as an atmosphere. (4) Gas from the disk enters the gravitational sphere of the planet (inflow) and exits (outflow; the red line of Fig. 2a). Following Ormel et al. (2015b) and Kuwahara et al. (2019), we refer to this flow as the recycling flow3. The recycling flow passes the planet, tracing the surface of the atmosphere.
The outflow of the gas occurs in the radial direction to the disk along the recycling streamlines. The following sections (Sects. 2.3.2 and 2.3.3) show the gas flow speed perturbed by the planet at the midplane. We focus especially on the gas flow in the x-direction (the radial gas flow with respect to the disk), which affects both the dust accretion onto the planet and the radial drift of dust. In the following paragraphs, we present a detailed analysis of gas flow speed at the midplane enabled by our extensive parameter studies.
2.3.2 Gas flow speed at the midplane: Dependence on planetary mass
Figure 3 shows the structure of the planet-induced gas flow at the midplane for different planetary masses, m = 0.05, 0.1, 0.5, and 0.7. We set ℳhw = 0. The outflow occurs along the inner-leading and outer-trailing recycling streamline (in the second and fourth quadrants of the x–y plane). The streamlines (the thin gray lines in Fig. 3) were plotted with the matplotlib.pyplot.streamplot library, where we used the midplane gas velocities interpolated by the bilinear interpolation method (Appendix D). We highlighted the widest horseshoe streamline and the shear streamline passing closest to the planet (the thick solid and dashed gray lines in Fig. 3; Appendix E). Since we assumed no headwind in Fig. 3, the flow morphology (the shapes of streamlines) are common in all panels. However, the gas velocity changes with the planetary mass. In particular, the x-component of the gas velocity along the inner-leading and outer-trailing recycling streamline (in other words, the outflow speed in the x-direction, υx,out, which is the main focus of this study) shows the complex dependence on the planetary mass. When m ≲ 0.5, υx,out increases with the planetary mass (Figs. 3a– c), but it seems to decrease for a higher-mass planet (Fig. 3d). From the analytic point of view, we discuss again the dependence of υx,out on the planetary mass in Sect. 4.1.1..
Hydrodynamical simulations.
2.3.3 Gas flow speed at the midplane: Dependence on headwind
Figure 4 shows the dependence of the gas flow structure on the headwind of the gas for a fixed planetary mass, m = 0.2.
The headwind of the gas breaks a rotational symmetric structure of the planet-induced gas flow (Ormel et al. 2015b; Kurokawa & Tanigawa 2010). The corotation radius for the gas, xcor,g = −2ℳhw/3, shifts in the negative direction on the x-axis as ℳhw increases, and the horseshoe region that formed around x = xcor,g also shifts in the negative x-direction. As shown in Fig. 4, the outflow speed toward the inside (outside) of the planetary orbit decreases (increases) as ℳhw increases. From the analytic point of view, we discuss again the dependence of υx,out on the Mach number of the headwind in Sect. 4.1.2.
3 Derivation of analytic formulae
Based on the numerical results obtained in Sect. 2.3, here we derive the analytic formulae describing the flow morphology, the maximum outflow speed, and the distributions of the velocity component of the outflow in the radial and vertical directions to the disk.
 |
Fig. 2 Streamlines of gas flow around the planet with m = 0.05 and ℳhw = 0.03. The arrows represent the direction of the gas flow. Panel a: perspective view of the flow field. Different colors correspond to different types of streamlines. The size of the atmosphere is 0.04 H. Panel b: same as panel a, but the color contour represents p/ρg, which is the measure of temperature (Sect. 3.3). Panel c: x-y plane viewed from the +z-direction. The critical streamline is highlighted by the color contour, which represents Bernoulli’s function, ℬ (Sects. 3.3 and 5.3). |
 |
Fig. 3 Dependence of the planet-induced gas flow on the planetary mass at the midplane. We set ℳhw = 0 in all panels. The results were obtained from m005-hw0 (panel a), m01-hw0 (panel b), m05-hw0 (panel c), and m07-hw0 (panel d). The solid thin gray lines are gas streamlines. The solid and thick dashed gray lines are the widest horseshoe streamline and the shear streamline passing closest to the planet, respectively (Appendix E). The color contour represents the flow speed in the x-direction. The dashed and dashed-dotted black circles denote the atmospheric radius (Eq. (5)) and twice the atmospheric radius, where the outflow speed is measured. The dashed blue lines are the curves representing the fitting formula for the critical recycling streamline (Eq. (11); Sect. 3.2.1). The vertical lines are the asymptotes of Eq. (11), representing the extent of the outflow region in the x-direction ((Eq. (17)); Sect. 3.2.2). The horizontal lines denote the y-coordinates of the characteristic length of the outflow region in the y-direction ((Eq. (18)); Sect. 3.2.3). |
 |
Fig. 4 Same as Fig. 3, but showing the dependence of the planet-induced gas flow on the Mach number of the headwind. We set m = 0.2 in all panels. The results were obtained from m02-hw0 (panel a), m02-hw001 (panel b), m02-hw003 (panel c), and m02-hw01 (panel d). The vertical dotted line corresponds to the corotation radius for the gas. |
3.1 Atmospheric radius
The size of an atmosphere affects gas dynamics around an embedded planet, because the recycling streamlines trace the surface of the atmosphere (Fig. 2). Hereafter, we define the size of the atmosphere as the atmospheric radius, the maximum radius where the azimuthal gas velocity is dominant in the midplane region (Moldenhauer et al. 2022):
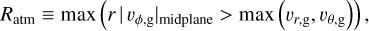 (6)
(6)
where υg = (υr,g, υθ,g, υϕ,g) is the gas velocity in the spherical polar coordinates centered at the planet. To estimate the atmospheric radius, we used the final state of the hydro-simulations data, t = tend, where the flow field seems to have reached a steady state (Appendix F).
Figure 5 shows the dependence of the atmospheric radius on the planetary mass and the Mach number of the headwind. We find that the atmospheric radius scales with the Bondi or Hill radii. The headwind of the gas reduces the atmospheric radius for a fixed planetary mass, which is consistent with previous studies (Ormel 2013; Moldenhauer et al. 2022). Assuming that the atmospheric radius decreases linearly as ℳhw increases, we introduce a fitting formula for the dimensionless atmospheric radius as
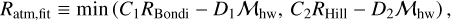 (7)
(7)
where C1, C2, D1, and D2 are the fitting coefficients. With the least-squares method, we determined the values of these coefficients: C1 = 0.84, C2 = 0.36, D1 = 0.056, and D2 = 0.22. The atmospheric radii are resolved by 28–52 cells in the radial direction in our hydrodynamical simulations.
The atmospheric radius can be constrained by the thermo-dynamical condition or the planet’s gravity, namely, the Bondi radius or the Roche lobe radius of the planet, whichever is smaller (D’Angelo & Lubow 2008; D’Angelo & Bodenheimer 2013). The Roche lobe is surrounded by the equipotential surface of the so-called Roche potential. Although the Roche lobe is not spherical, the radius of a sphere having the same volume as the Roche lobe is given by the following fitting formula (Eggleton 1983):
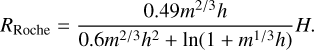 (8)
(8)
For a typical steady accretion disk model (e.g., Ida et al. 2016), the disk aspect ratio has on the order of h ~ 0.01−0.1 (Appendix A). The value of RRoche hardly changes for the range of h. We set h = h0 = 0.05 as a nominal value in Eq. (8). Since m1/3h ≪ 1 in our parameter sets, Eq. (8) can be approximated as RRoche ≃ 0.49m1/3 H ~ 2RHill/3 (Paczynski 1971), where we used ln(1 + m1/3h) ≃ m1/3h and (1 + 0.6m1/3h) ≃ 1. We plotted the following equation in Fig. 5:
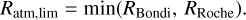 (9)
(9)
Equation (9) predicts that the scaling law changes at m ~ 0.3 and the atmospheric radius scales with ~2RHill/3 when m ≳ 0.3. These predictions are in qualitative agreement with the numerical result where the atmospheric radius scales with a fraction of the Hill radius when m ≳ 0.2.
The gas is heated by adiabatic compression and then the β cooling occurs within the gravitational sphere of the planet, leading to the formation of the low-entropy region at r ≲ Rgrav (Fig. 6a; Kurokawa & Tanigawa 2018). The buoyancy force characterized by the positive entropy gradient isolates the atmosphere from the surrounding disk gas (Kurokawa & Tanigawa 2018). We find that the temperature is nearly uniform around the atmosphere due to our choice of short cooling time when m ≲ 0.1 (β ≤ 1; Fig. 6b). The amplitude of the temperature fluctuation increases with the planetary mass, which is as high as ~75% when m = 1.
 |
Fig. 5 Atmospheric radius as a function of the planetary mass and the Mach number of the headwind of the gas. The square symbols were obtained from hydrodynamical simulations. Different colors correspond to different Mach numbers, ℳhw. The gray-shaded region is given by the fitting formula for the atmospheric radius, Ratm,fit. The dashed gray line is given by Eq. (9). |
 |
Fig. 6 Shell-averaged values of |
3.2 Morphology of the outflow region
This section introduces the fitting formulae for the morphology of the midplane outflow (the shape of the outflow streamline), describing the region where the x-component of the gas velocity, υx,g, is dominantly perturbed by the embedded planet (the deep red and black contours in Figs. 3 and 4). We refer to this region as the outflow region. The obtained formulae will be used in a future study to determine the extent of the region in which the hydrodynamic effects of the outflow on the dust motion would appear. Hereafter we restrict our attention to the limited region, |x| ≲ H and z = 0.
3.2.1 Morphology of the critical recycling streamline at the midplane
The outflow occurs along the recycling streamline, which suggests that the outflow region can be determined by the shape of the recycling streamline. The shape of the streamline is also important to estimate the outflow speed in the x-direction, υx,out, which affects the dust motion (Kuwahara & Kurokawa 2020a,b), because υx,out can be obtained by considering the angle of the flow velocity with respect to the x-axis.
Here we introduce a representative recycling streamline: a critical recycling streamline. We defined the critical recycling streamline as the separatrix streamline that divides the Keplerian shear flow and the inner-leading (outer-trailing) recycling flow at the midplane. We find that the inner-leading and outer-trailing critical recycling streamlines at the midplane can be outlined by the following fitting formulae:
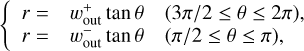 (10)
(10)
in the polar coordinates centered at the planet, where 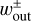 is the x-coordinate of the edge of the outflow region (described in Sect. 3.2.2). The dust motion can be disturbed by the outflow in the region where
is the x-coordinate of the edge of the outflow region (described in Sect. 3.2.2). The dust motion can be disturbed by the outflow in the region where 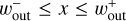 . Hereafter the plus and minus signs for an arbitrary quantity, X±, denote the quantity outside and inside the planetary orbit. Equation (10) represents the tangential curves with
. Hereafter the plus and minus signs for an arbitrary quantity, X±, denote the quantity outside and inside the planetary orbit. Equation (10) represents the tangential curves with 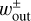 as the asymptotes. In the local Cartesian coordinates co-rotating with the planet, Eq. (10) can be written as
as the asymptotes. In the local Cartesian coordinates co-rotating with the planet, Eq. (10) can be written as
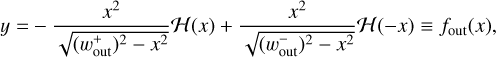 (11)
(11)
where 𝓗(x) is the Heaviside step function.
We plotted Eq. (11) in Figs. 3 and 4. Equation (11) can trace the critical recycling streamline at the midplane for a wide range of planetary mass and Mach number of the headwind. In most of the panels in Figs. 3 and 4, fout(x) is sandwiched between the widest horseshoe streamline and the shear streamline passing closest to the planet. Using Eq. (11), we estimate the outflow speed analytically near the atmospheric radius, Ratm ≲ 0.1 H, where the dominant outflow occurs (Figs. 3 and 4; described in Sect. 3.4). We use the analytically estimated outflow speed for the estimation of the outflow effect on the dust motion. Thus, the agreement between Eq. (11) and the numerically obtained critical recycling streamline in the region close to the planet (r ~ Ratm) is useful. Although Eq. (11) does not coincide with the numerically obtained critical recycling streamline in the distant region far from the planet, |y| ≳ H, the mismatch between Eq. (11) and the numerically obtained critical recycling streamline in the far region does not affect an analytic derivation of the outflow speed.
Equation (11) can be applied to trace the critical recycling streamline near the atmospheric radius for the entire range of our parameter sets (m ∈ [0.03, 1]). When m ≳ 0.6, however, we find that the dominant perturbation to υx,g occurs along the midplane horseshoe streamlines rather than the streamlines characterized by Eq. (11) (e.g., Fig. 3d; described in Sect. 4). When the planetary mass reaches the so-called pebble isolation mass, Miso = 25(h/0.05)3[0.34(3/log αacc)4 + 0.66] M⊕, a growing planet opens a shallow gas gap (Lambrechts et al. 2014; Bitsch et al. 2018; Ataiee et al. 2018). In our dimensionless unit, the pebble isolation mass can be described as
![${m_{{\rm{iso}}}} \simeq 0.6\left[ {0.34{{\left( {{3 \over {\log {\alpha _{{\rm{acc}}}}}}} \right)}^4} + 0.66} \right]{\left( {{{{M_*}} \over {{M_ \odot }}}} \right)^{ - 1}}$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq19.png) (12)
(12)
We assumed αacc = 10−3 and M* = M⊙ in Eq. (12) as nominal values. Our local simulation cannot handle the gas-gap opening in the high-mass regime (m ≳ miso). Thus, Eq. (11) is valid as a model for the outflow streamline for m ≲ miso ≃ 0.6 to investigate the hydrodynamic effect of the gas flow on the dust.
3.2.2 Width of the outflow region
In Sect. 3.2.1, we introduced a fitting formula for the critical recycling streamline, y = fout(x), which represents the edge of the outflow region whose x-coordinate approaches asymptotically to x = 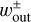 . This section describes the width of the outflow region in the x-direction (the radial direction to the disk) and introduces an analytic description for
. This section describes the width of the outflow region in the x-direction (the radial direction to the disk) and introduces an analytic description for 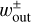 .
.
We find that the width of the outflow region is limited by the width of the subsonic region and the x-coordinate of the recycling streamline at the midplane characterized by the half-width of the horseshoe streamline. We defined the subsonic region as the region where the unperturbed gas velocity in the local frame is always subsonic, |υg,∞| ≤ cs. The x-coordinate of the edge of the subsonic region for the gas is given by
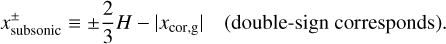 (13)
(13)
Hereafter we omit the notation of the double-sign corresponds in each equation, unless otherwise specified.
Next, we introduced the x-coordinate of a critical recycling streamline in the far field (|y| → ∞) at the midplane. We started by considering an endmember case, ℳhw = 0. The gas from the disk enters the gravitational sphere of the planet and flows back to the disk through the region between the Keplerian shear flow and the inner-leading (outer-trailing) horseshoe flow. Thus, the width of the outflow region could be constrained by the width of the horseshoe flow. When m ≲ 0.1, the half-width of the horseshoe streamline can be estimated by the linear theory, which is given by (Masset & Benítez-Llambay 2016)
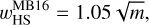 (14)
(14)
combined with the numerical factor. When m ≳ 0.1, the half-width of the horseshoe streamline is proportional to the Hill radius of the planet due to the onset of nonlinear effects in the horseshoe region, which can be fitted by wHS ≃ 2.4RHill ≃ 1.7m1/3 (Masset et al. 2006). Jiménez & Masset (2017) introduced the following fitting formula for the half-width of the horseshoe streamline, which can be applied to a wide range of planetary masses:
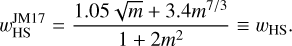 (15)
(15)
We find that Eq. (15) is a better indicator than Eq. (14) in describing the width of the outflow region for practical use, though it overestimates the widths of the outer-leading and inner-trailing parts of the horseshoe flows (Appendix G).
When the nonzero Mach number of the headwind is assumed, the horseshoe region shifts to the negative direction in the x-axis by −|xcor,g|. We find that the disk gas along the recycling streamline flows into an empty space formed by the shift of the horseshoe region (Fig. 2a). The critical recycling streamline traces this replenished flow. The x-coordinate of the critical recycling streamline at the midplane in the far field is given by
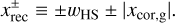 (16)
(16)
We find that the width of the outflow region in the x-direction can be characterized by xsubsonic (Eq. (13)) or xrec (Eq. (16)), whichever was smaller:
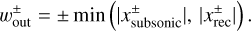 (17)
(17)
We plotted Eq. (17) in Figs. 3 and 4, which can serve as a useful guide for the extent of the region where υx,g is dominantly perturbed by the embedded planet.
Figure 7 shows the difference of the flow speed from the unperturbed sub-Keplerian speed, where m = 0.1 and 0.5, and ℳhw = 0 were assumed. When |xrec| < |xsubsonic| (m ≲ 0.3; for simplicity, we omit the plus and minus signs), the gas velocity approaches the unperturbed sub-Keplerian shear when x → xrec, leading to υx,g → 0 (Fig. 7a). When |xrec| > |xsubsonic| (m ≳ 0.3), the numerically obtained critical recycling streamline can intrude the supersonic region because its width is determined by xrec (= |wHS| > |xsubsonic|; the solid orange lines in Fig. 7b). However, υx,g along the numerically obtained critical recycling streamline approaches instantaneously to υx,g → 0 in the subsonic region (Fig. 7b). Since we defined the outflow region as the region where υx,g is dominantly perturbed by the planet, we considered that the outflow region is constrained by wout = |xsubsonic|, regardless of the x-coordinate of the numerically obtained critical recycling streamline at |y| ≳ Ly,out ≃ H. Although a mismatch between the numerically obtained critical recycling streamline and fout(x) can be seen at |y| ≳ H, again, it does not affect an analytic derivation of the outflow speed.
3.2.3 Length of the outflow region
In this section, we evaluate the characteristic length of the outflow region in the y-direction (the orbital direction of the planet). The extent of the outflow region in the y-direction can be used when we investigate the outflow effects on the dust motion during the encounter with the planet. Based on Eq. (11), we define the y-coordinate at a position close enough to the asymptotes, 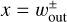 , as the characteristic length of the outflow region:
, as the characteristic length of the outflow region:
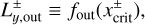 (18)
(18)
We set Ccrit = 0.95 as a fitting parameter. We plotted Eq. (18) in Figs. 3 and 4, which shows good agreement with numerical simulations.
3.3 Bernoulli’s theorem
The outflow speed can be estimated from Bernoulli’s theorem (Fung et al. 2015; Kuwahara et al. 2019). For a steady-state barotropic flow, a Bernoulli function is conserved along a streamline (Ormel 2013; Fung et al. 2015; Kuwahara et al. 2019):
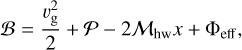 (20)
(20)
where 𝒫 = ∫ dp/ρg is the pressure function and Φeff is the effective potential. Here we assume an isothermal flow along a recycling streamline, 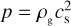 . The pressure function is described by
. The pressure function is described by 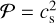 ln ρg. The effective potential is described by
ln ρg. The effective potential is described by
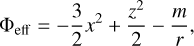 (21)
(21)
where the first and second terms in the right-hand side of Eq. (21) were originated from the tidal potential.
It should be noted that Bernoulli’s function does not strictly conserve along the streamline as shown in Fig. 2c, because the β cooling occurs on a finite timescale, β = (m/0.1)2. However, we find that Bernoulli’s theorem is still useful to estimate the outflow speed because the gas flow along a recycling streamline can be considered as an isothermal flow due to the efficient β cooling (Fig. 6b). As discussed in Sect. 3.1, when m ≲ 0.1 the temperature around the atmosphere is nearly uniform (Fig. 6b). Although the amplitude of the temperature fluctuation around the atmosphere is as high as ~40% at most when m ~ miso, we stick to an isothermal assumption regardless of the planetary mass. Again, our model for the outflow speed is not valid in the higher-mass regime (m ≳ miso; Sect. 3.2.1). We discuss the applicability of Bernoulli’s theorem in Sect. 5.3.
 |
Fig. 7 Difference of the flow speed from the unperturbed Keplerian shear. The results were obtained from m01 − hw0 (panel a) and m05 − hw0 (panel b). The dashed blue, dashed-dotted white, and dotted white lines denote the fitting formula for the critical recycling streamline, the x-coordinate of the critical recycling streamline at the midplane in the far field, and the x-coordinate of the edge of the subsonic region, respectively. As in Fig. 3, we highlight the widest horseshoe streamline and the shear streamline passing closest to the planet with the solid and dashed orange lines, respectively. |
3.4 Inflow and outflow positions
To estimate the outflow speed from Bernoulli’s theorem, following Kuwahara et al. (2019), we select a recycling streamline and set the inflow and outflow points on it, Pin and Pout, where the gas chiefly flows in and out. These points are determined by the analysis of the mass flux of the gas.
The left column of Fig. 8 shows the velocity field of the gas at the meridian plane, in which the color contour corresponds to the radial velocity in the spherical polar coordinates centered at the planet. The gas seems to be dominantly flowing in and out of the sphere of radius ≳2 Ratm. The right column of Fig. 8 shows the azimuthally averaged mass flux for a certain spherical shell of radius r, 〈ρgυr,g〉ϕ, as a function of the altitude, z. Gas flows in where 〈ρgυr,g〉ϕ < 0 and flows out where 〈ρgυr,g〉ϕ > 0. We find that gas chiefly flows in and out of twice the atmospheric radius, 2 Ratm.
Based on the above findings, we set the inflow and outflow points as Pin = (0, 0, zin) and 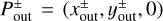 , where zin = 2 Ratm,fit and
, where zin = 2 Ratm,fit and 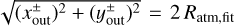 . Here we used a fitting formula for the atmospheric radius (Eq. (7)). The x- and y-coordinates of the outflow points were determined by those of the intersections of the fitting formula for the critical recycling streamline at the midplane (Eq. (11)) and the circle of twice the atmospheric radius, 2 Ratm,fit. They are given by
. Here we used a fitting formula for the atmospheric radius (Eq. (7)). The x- and y-coordinates of the outflow points were determined by those of the intersections of the fitting formula for the critical recycling streamline at the midplane (Eq. (11)) and the circle of twice the atmospheric radius, 2 Ratm,fit. They are given by
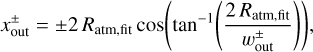 (22)
(22)
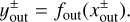 (23)
(23)
3.5 Analytic formula for the outflow speed
An analytic formula of the outflow speed was derived from Bernoulli’s theorem. We first consider the inflow point. From the analysis of the kinetic energy of gas flow in our simulations, we find that the first term in the right-hand side of Eq. (20) was negligible at the inflow point, Pin (Fung et al. 2015; Kuwahara et al. 2019). The second and fourth terms in the right-hand side of Eq. (20) are canceled with each other because the stellar gravitational potential energy balances the pressure function in hydrostatic equilibrium. Thus, Bernoulli’s function at the inflow point is described by
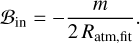 (24)
(24)
Bernoulli’s function at the outflow point is described by
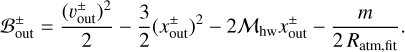 (25)
(25)
From Eqs. (24) and (25), we obtain the outflow speed at the outflow point:
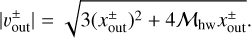 (26)
(26)
The first and second terms in the square root in the right-hand side of Eq. (26) originate from the tidal potential (Kuwahara et al. 2019) and the global pressure gradient of the disk gas, respectively.
From Eq. (26), we can estimate the flow speed in the x-direction (the radial flow speed with respect to the disk), which affects both the dust accretion onto the planet and the radial drift of dust. The x-component of the outflow speed is given by
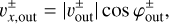 (27)
(27)
where 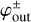 is an angle of the outflow to the x-axis at the outflow point,
is an angle of the outflow to the x-axis at the outflow point,
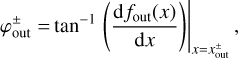 (28)
(28)
which can be described by
![$\{ \varphi _{{\rm{out}}}^ + = {\tan ^{ - 1}}\left[ { - {{x_{{\rm{out}}}^ + \left( {2{{\left( {w_{{\rm{out}}}^ + } \right)}^2} - {{\left( {x_{{\rm{out}}}^ + } \right)}^2}} \right)} \over {{{\left( {{{\left( {w_{{\rm{out}}}^ + } \right)}^2} - {{\left( {x_{{\rm{out}}}^ + } \right)}^2}} \right)}^{3/2}}}}} \right],$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq44.png) (29)
(29)
![$\{ \varphi _{{\rm{out}}}^ - = {\tan ^{ - 1}}\left[ {{{x_{{\rm{out}}}^ - \left( {2{{\left( {w_{{\rm{out}}}^ - } \right)}^2} - {{\left( {x_{{\rm{out}}}^ - } \right)}^2}} \right)} \over {{{\left( {{{\left( {w_{{\rm{out}}}^ - } \right)}^2} - {{\left( {x_{{\rm{out}}}^ - } \right)}^2}} \right)}^{3/2}}}}} \right]{\rm{.}}$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq45.png) (30)
(30)
We compare Eq. (27) with the numerical results in Sect. 4.1.
 |
Fig. 8 Gas flow structure and azimuthally averaged mass flux. The results were obtained from m02 − hw0 (panels a and b), m02 − hw01 (panels c and d), and m04 − hw0 (panels e and f). Left column: gas flow structure at the meridian plane. The color contour represents the r-component of the gas velocity in the spherical polar coordinates centered at the planet and averaged in the y-direction within the calculation domain of the hydrodynamical simulation. The dashed, dotted, and dashed-dotted circles denote the Bondi radius, the Hill radius, and twice the atmospheric radius, respectively. Right column: mass flux of the gas averaged in the azimuthal direction in the spherical polar coordinates centered at the planet, 〈ρgυr〉ϕ. Each solid line represents the changes in 〈ρgυr〉ϕ; altitude is varied along with a certain radius. We highlight the important radii with solid yellow (RBondi), blue (RHill), and red (2 Ratm) lines. |
 |
Fig. 9 Outflow speed at the midplane as a function of the dimensionless planetary mass and the Mach number of the headwind of the gas. The star symbols were obtained from hydrodynamical simulations, corresponding to the maximum flow speeds in the x-direction toward the outside (red) and inside (black) of the planetary orbit within the limited region, |
3.6 Analytic formula for the velocity distribution of the outflow
We derive analytic formulae for υx,out(x) and υx,out(z). These formulae are useful for modeling the influence of the outflow on the radial drift of dust in disks for the following reasons: (1) Dust particles drift from the outside to the inside of the planetary orbit. The radial drift of dust can be disrupted by the gas flow, leading to the formation of a dust substructure such as a dust ring and a gap (Kuwahara et al. 2022). (2) The dust is stirred up by the gas turbulence, leading to an increase in the dust scale height (e.g., Youdin & Lithwick 2007). Thus, the influence of the gas flow on the dust motion depends on the vertical structure of the planet-induced gas flow.
3.6.1 Radial direction to the disk
The outflow region has a spread in the x-direction with the width of 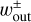 . Here we aim to model the distribution of υx,out in the x-direction at the midplane, υx,out(x). We find that υx,out(x) can be modeled by a Gaussian function with peaks at
. Here we aim to model the distribution of υx,out in the x-direction at the midplane, υx,out(x). We find that υx,out(x) can be modeled by a Gaussian function with peaks at 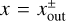 . We introduce the following formula:
. We introduce the following formula:
![${v_{x,{\rm{out}}}}(x) = v_{x,{\rm{out}}}^ + \exp \left[ { - {{{{\left( {x - x_{{\rm{out}}}^ + } \right)}^2}} \over {2{{\left( {{D^ + }} \right)}^2}}}} \right] - v_{x,{\rm{out}}}^ - \exp \left[ { - {{{{\left( {x - x_{{\rm{out}}}^ - } \right)}^2}} \over {2{{\left( {{D^ - }} \right)}^2}}}} \right],$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq50.png) (31)
(31)
where we assumed that the full width at half maximum (FWHM) corresponds to the half-width of the outflow region, 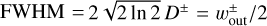 . We compare Eq. (31) with the numerical results in Sect. 4.2.
. We compare Eq. (31) with the numerical results in Sect. 4.2.
3.6.2 Vertical direction to the disk
The outflow has a vertical extent as shown in the left column of Fig. 8. The outflow speed decreases sharply at z ≳ Ratm. Assuming that υx,out(z) decreases exponentially when z > Ratm,
we introduce the following formula:
![$\eqalign{\eqalign{ & v_{x,{\rm{out}}}^ \pm (z) = {\left. {{{\left\langle {v_{x,{\rm{g}}}^ \pm } \right\rangle }_{x,y}}} \right|_{z = 0}} \times \exp \left[ { - {{\left( {{z \over {{R_{{\rm{atm}}}}}}} \right)}^2}} \right], \cr & {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} = {\left. {{{\int \int {{\rho _{\rm{g}}}} v_{x,{\rm{g}}}^ \pm {\rm{d}}x{\rm{d}}y} \over {\int \int {{\rho _{\rm{g}}}} {\rm{d}}x{\rm{d}}y}}} \right|_{{\rm{z}} = 0}} \times \exp \left[ { - {{\left( {{z \over {{R_{{\rm{atm}}}}}}} \right)}^2}} \right]. \cr} $](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq55.png) (32)
(32)
We used the numerical results to compute the integral in the right-hand side of Eq. (32). We compare Eq. (32) with the numerical results in Sect. 4.2.
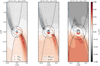 |
Fig. 10 Comparison of the point where υx,g has the maximum value at the midplane and the assumed outflow point, |
4 Comparison to numerical results
In this section, we compare our analytic formulae for the outflow speed obtained in Sect. 3 with the numerical results.
4.1 Maximum outflow speed at the midplane
Figure 9 compares our analytic formula for the x-component of the outflow speed (Eq. (27)) with the maximum flow speed in the x-direction obtained from hydrodynamical simulations, υx,max. Equation (27) reproduces the results obtained from hydrodynamical simulations for a wide range of planetary mass and Mach number of the headwind of the gas.
It should be noted that the point where |υx,g| has the maximum value, 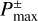 , does not necessarily coincide with the assumed outflow point,
, does not necessarily coincide with the assumed outflow point, 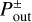 , which is determined by the analysis of the azimuthally averaged mass flux (Fig. 10). Figure 11 shows the mismatch between υx,max and υx,g at the assumed outflow point,
, which is determined by the analysis of the azimuthally averaged mass flux (Fig. 10). Figure 11 shows the mismatch between υx,max and υx,g at the assumed outflow point, 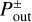 , meaning that flow speed at the exact location as the analytically-predicted outflow point does not take the maximum value. This is because the fitting formula for the critical recycling streamline, fout(x), does not trace a streamline, which gives the maximum flow speed at the midplane region. The fitting formula, ƒout(x), traces the edge of the outflow region where υx,g is dominantly perturbed (e.g., Fig. 10a). It almost coincides with the shear streamline passing closest to the planet near the atmosphere. The assumed outflow point,
, meaning that flow speed at the exact location as the analytically-predicted outflow point does not take the maximum value. This is because the fitting formula for the critical recycling streamline, fout(x), does not trace a streamline, which gives the maximum flow speed at the midplane region. The fitting formula, ƒout(x), traces the edge of the outflow region where υx,g is dominantly perturbed (e.g., Fig. 10a). It almost coincides with the shear streamline passing closest to the planet near the atmosphere. The assumed outflow point, 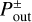 , is located at the point very close to the intersection of the shear streamline and the circle of twice the atmospheric radius, where the perturbation to υx,g along the shear streamline is small (Fig. 10). Thus, the flow speed obtained from hydrodynamical simulations at
, is located at the point very close to the intersection of the shear streamline and the circle of twice the atmospheric radius, where the perturbation to υx,g along the shear streamline is small (Fig. 10). Thus, the flow speed obtained from hydrodynamical simulations at 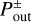 deviates from the maximum value (Fig. 11).
deviates from the maximum value (Fig. 11).
We find that 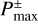 lies on a circle of radius ~1.6–4 Ratm with no clear trend in the location of
lies on a circle of radius ~1.6–4 Ratm with no clear trend in the location of 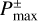 as a function of the planetary mass and the Mach number of the headwind (Fig. 10). We find that the error between the maximum value of υx,g on a circle of radius 2Ratm and υx,max is less than 30%. Thus, twice the atmospheric radius can still be considered as the radius where the dominant outflow occurs. For simplicity, we stick to setting
as a function of the planetary mass and the Mach number of the headwind (Fig. 10). We find that the error between the maximum value of υx,g on a circle of radius 2Ratm and υx,max is less than 30%. Thus, twice the atmospheric radius can still be considered as the radius where the dominant outflow occurs. For simplicity, we stick to setting 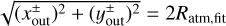 for the derivation of outflow speed.
for the derivation of outflow speed.
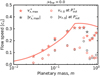 |
Fig. 11 Comparison of the maximum flow speed in the x-direction, |
 |
Fig. 12 Angle of the outflow at the outflow point, φout (Eq. (28)), cos φout, and the x-coordinate of the outflow point, |
4.1.1 Revisiting the dependence on planetary mass
Based on Fig. 9, we revisit the dependence of υx,out on the planetary mass as mentioned in Sect. 2.3.2. The outflow speed in the x-direction, υx,out, has a peak when m ~ 0.3, corresponding to a super-Earth mass planet at 1 au for a typical steady accretion disk model. From the analytic point of view, this trend can be understood by considering the dependence of the outflow angle on the planetary mass (Fig. 12). In this section, we only consider the shear only case (ℳhw = 0) for simplicity.
When m ≲ 0.3, the outflow speed is proportional to |υout| ∝ xout ∝ Ratm,fit ∝ m (Eq. (26)). We find that the cosine term in Eq. (27), cos φout, is proportional to ~m−1/3 (Fig. 12). Thus, the outflow speed in the x-direction is almost proportional to 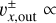 m2/3. When m ≳ 0.3, the dependence of the outflow speed on the planetary mass is slightly lower than the power of 1/3 due to the cosine term in Eq. (23),
m2/3. When m ≳ 0.3, the dependence of the outflow speed on the planetary mass is slightly lower than the power of 1/3 due to the cosine term in Eq. (23), 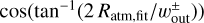 (Fig. 12). The cosine term in Eq. (27), cos φout, is proportional to ~m−1/3 (Fig. 12). Thus, υx,out decreases as the planetary mass increases.
(Fig. 12). The cosine term in Eq. (27), cos φout, is proportional to ~m−1/3 (Fig. 12). Thus, υx,out decreases as the planetary mass increases.
Our analytic formula deviates from the results obtained by hydrodynamical simulations when m ≳ 0.6 (Fig. 9). For such higher-mass planets, we find that 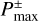 is located at the region close to the planetary orbit (Fig. 10b). In Fig. 10b, υx,g has the maximum value on the midplane horseshoe streamline, not on the critical recycling streamline. Thus, the flow speed cannot be estimated by Eq. (27). As discussed in Sect. 3.2.1, our model for the critical recycling streamline can be applied when m ≲ miso ≃ 0.6. Thus, our analytic formula for the outflow speed is also valid when m ≲ miso. We plotted miso (Eq. (12)) in Fig. 9.
is located at the region close to the planetary orbit (Fig. 10b). In Fig. 10b, υx,g has the maximum value on the midplane horseshoe streamline, not on the critical recycling streamline. Thus, the flow speed cannot be estimated by Eq. (27). As discussed in Sect. 3.2.1, our model for the critical recycling streamline can be applied when m ≲ miso ≃ 0.6. Thus, our analytic formula for the outflow speed is also valid when m ≲ miso. We plotted miso (Eq. (12)) in Fig. 9.
 |
Fig. 13 Distribution of the x-component of the gas velocity in the x-direction at the midplane, υx,max(x). The solid blue line is given by Eq. (31). The yellow dots were obtained from m02-hw0 (panel a), m02-hw001 (panel b), m02-hw003 (panel c), and m02-hw01 (panel d). We sampled the gas velocity at each radial grid of hydro-dynamical simulations where the absolute value of the gas velocity was the maximum within the limited region, |
4.1.2 Revisiting the dependence on headwind
Based on Fig. 9, we revisit the dependence of υx,out on the Mach number of the headwind, ℳhw, as mentioned in Sect. 2.3.3. The outflow speed in the x-direction toward the inside (outside) of the planetary orbit decreases (increases) as ℳhw increases. This is caused by the second term in the square root in the right-hand side of Eq. (26), which comes from the global pressure force due to the sub-Keplerian motion of the gas, Fhw = 2ℳhwex. Since the gas receives the global pressure force in the positive direction in the x-axis, the outflow toward the inside (outside) of the planetary orbit is reduced (enhanced).
When ℳhw = 0.1, the strongest Mach number considered in this study, our analytic formula deviates from the results obtained by hydrodynamical simulations inside the planetary orbit. We speculate that the deviation was caused by the changes of the actual location of the inflow point, Pin. To obtain the analytic formula for the outflow speed, we set Pin at the pole of the spherical shell of the radius 2 Ratm,fit regardless of the assumed ℳhw. In reality, Pin shifts to the negative direction in the x-axis as ℳhw increases (Fig. 8b), because the horseshoe flow shifts to the negative direction in the x-axis. However, as long as we consider the influence of the outflow on the radial drift of dust, the outflow toward the inside of the planetary orbit is less important than that toward the outside the planetary orbit.
4.2 Velocity distribution of the outflow
Figure 13 shows υx,out(x) at the midplane obtained from both our analytic formula (Eq. (31)) and hydrodynamical simulations.
We set m = 0.2 and varied the Mach number of the headwind, ℳhw = 0–0.1 in Fig. 13. We find that Eq. (31) can reproduce the trends of the hydro-simulations results: the peak speed, the FWHM, and the x-coordinate of the peak position.
Figure 14 shows υx,out(z) for different planetary masses, m = 0.2, and 0.5, and Mach numbers, ℳhw = 0, and 0.1. The left column of Fig. 14 shows the vertical structure of the gas flow field at the meridian plane obtained from hydrodynamical simulations. The gas flow velocity was averaged in the y-direction within the calculation domain of hydrodynamical simulation. The right column of Fig. 14 shows υx,out(z) obtained from both the numerical result and our analytic formula. The numerical result was obtained by averaging the simulation data as
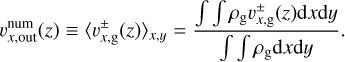 (33)
(33)
The interval of integration in the y-direction was |y| ≤ rout. In the x-direction, the interval of integration was 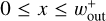 for
for 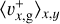 and
and 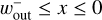 for
for 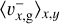 .
.
Our fitting law for υx,out(z) introduced in Eq. (32) is indeed a practical representation of 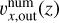 for the lower-mass planets, m ≲ 0.4 (Figs. 14b and d). For the higher-mass planets, m ≳ 0.5,
for the lower-mass planets, m ≲ 0.4 (Figs. 14b and d). For the higher-mass planets, m ≳ 0.5,
Eq. (32) reproduces a decreasing trend of 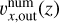 only in the range of ɀ < Ratm. For the higher-mass planets, the meridional circulation of the gas above the outflow leads to the complex behavior of the flow speed (Fig. 14e). As discussed in Sects. 3.2.1 and 4.1.1, our analytic formula for υx,out(ɀ) cannot be applied to the higher-mass regime (m ≳ miso).
only in the range of ɀ < Ratm. For the higher-mass planets, the meridional circulation of the gas above the outflow leads to the complex behavior of the flow speed (Fig. 14e). As discussed in Sects. 3.2.1 and 4.1.1, our analytic formula for υx,out(ɀ) cannot be applied to the higher-mass regime (m ≳ miso).
 |
Fig. 14 Vertical structure of the gas flow. The results were obtained from m02-hw0 (panels a and b), m02-hw01 (panels c and d), and m05-hw0 (panels e and f). Left column: same as the left column of Fig. 8, but the color contour represents υx,g averaged in the y-direction within the calculation domain of hydrodynamical simulation. Right column: the x-component of the gas flow velocity averaged in the x- and y-directions within the calculation domain of hydrodynamical simulation, |
5 Discussion
5.1 Comparison to previous studies: Atmospheric radius
An atmospheric radius is crucial to understand gas dynamics around an embedded planet. Several previous studies reported the different scaling laws for the atmospheric radius, which are summarized in Fig. 15. In this study, we estimated the atmospheric radius based on the definition given by Moldenhauer et al. (2022) and obtained a fitting formula (Eq. (7)). It should be noted that Eq. (7) differs from the scaling law obtained by Moldenhauer et al. (2022). Moldenhauer et al. (2022) performed three-dimensional radiation-hydrodynamics simulations in a local frame centered at the planet with Mpl = 1–10 M⊕ at 0.1 au (corresponding to m ~ 0.3–3 in our dimensionless unit). Based on Eq. (6), the authors estimated the atmospheric
radius and introduced the following fitting formula: 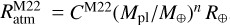 where R⊕ is the Earth radius, CM22 = 4.7 ± 0.6 and n = 0.67 ± 0.08 when the headwind is included, and CM22 = 5.7 ± 0.3 and n = 0.62 ± 0.04 without the headwind. In our dimensionless unit, this can be rewritten as
where R⊕ is the Earth radius, CM22 = 4.7 ± 0.6 and n = 0.67 ± 0.08 when the headwind is included, and CM22 = 5.7 ± 0.3 and n = 0.62 ± 0.04 without the headwind. In our dimensionless unit, this can be rewritten as
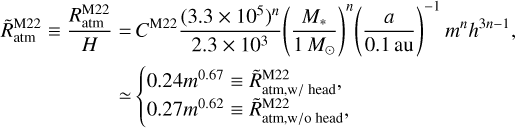 (34)
(34)
where we assumed h ≃ 0.024 for a typical steady accretion disk at 0.1 au with a solar-mass star, the typical accretion rate of classical T Tauri stars, 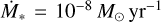 , and αacc = 10−3 (Ida et al. 2016). Moldenhauer et al. (2022) suggested that the atmospheric radius increases approximately proportional to
, and αacc = 10−3 (Ida et al. 2016). Moldenhauer et al. (2022) suggested that the atmospheric radius increases approximately proportional to 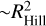 .
.
D’Angelo & Bodenheimer (2013) performed global three-dimensional radiation-hydrodynamic simulations for the embedded planets with Mpl = 5, 10, and 15 M⊕ at 5 au (corresponding to m ≃ 0.27, 0.55, and 0.82) and 10 au (m ≃ 0.15, 0.3, and 0.45 in our dimensionless unit, respectively; Fig. 1). In D’Angelo & Bodenheimer (2013), a realistic equation of state and a dust opacity were considered. Using passive tracers to determine the size of the bound atmosphere, the authors estimated the atmospheric radius as ~RHill/5–RHill/3 (see Table 3 of D’Angelo & Bodenheimer 2013, for details).
Lambrechts & Lega (2017) performed three-dimensional global radiation-hydrodynamic simulations with an embedded planet, Mpl = 5 M⊕ at 5.2 au (corresponding to m ≃ 0.26 in our dimensionless unit; Fig. 1). The authors considered the dust opacity and the luminosity from the accretion of solids. From the analysis of the mass flux within the Hill sphere of the planet, the authors estimated the atmospheric radius as ~0.3 RHill. Cimerman et al. (2017) performed three-dimensional radiation-hydrodynamic simulations in a local frame co-rotating with the planet. The authors defined the atmosphere as the region where the azimuthally averaged ratio of radial to azimuthal velocities falls below a threshold of 10%, 〈|υr/υϕ|〉ϕ ≤ 0.1. They reported that the atmospheric radii were 0.25 RBondi, 0.2 RBondi, and 0.07 RBondi for the planets with m = 0.38, 0.75, and 1.9, respectively.
Figure 15 compares the atmospheric radii obtained from above-mentioned previous studies with those obtained from our study. We emphasize that the definition of the atmospheric radius differs among previous studies. Although a direct comparison of this study with previous studies is difficult due to different simulation settings among these studies, our fiducial results agree with the results of previous studies within a factor of ~2. We note that the atmospheric radius depends on the cooling time, β The atmospheric radius changes by a factor of ~2–3 when we varied β by ~ 1–2 orders of magnitude. We discuss the dependence of the atmospheric radius on the cooling time in Sect. 5.4.
 |
Fig. 15 Comparison of the atmospheric radii obtained in our study and those in previous studies. The open and filled square symbols were obtained from our hydrodynamical simulations, ℳhw = 0 and 0.1, respectively. The gray-shaded region is given by the fitting formula for the atmospheric radius, Ratm,fit (Eq. (7)). The red dashed and dotted lines are given by Eq. (34) (Moldenhauer et al. 2022). We extrapolated Eq. (34) to the range of m ≤ 0.3. The yellow, blue, and green diamonds corresponds to the results of D’Angelo & Bodenheimer (2013), Lambrechts & Lega (2017), and Cimerman et al. (2017), respectively. To plot the results of D’Angelo & Bodenheimer (2013), the atmospheric radii were calculated by Ratm/H = CDB13a/H = CDB13/h. The values of CDB13 = 2.6 × 10−3−9.6 × 10−3 were given in Table 3 of D’Angelo & Bodenheimer (2013). We used h = max(0.027(a/1 au)1/20, 0.024 (a/1 au)2/7) (Appendix A). |
5.2 Comparison to previous studies: Outflow speed
Several previous studies have proposed analytic formulae of the outflow speed, which are plotted in Fig. 9a. Ormel (2013) considered two-dimensional, isothermal, inviscid, and compressible flow past a planet. The author derived an approximate solution of the flow pattern around the planet in the linear regime in terms of the stream function:
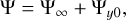 (35)
(35)
where the first and second terms in the right-hand side of Eq. (35) correspond to the unperturbed and perturbed components. Each term can be described by
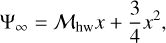 (36)
(36)
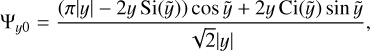 (37)
(37)
where 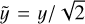 . In the right-hand side of Eq. (37), Si(y) and Ci(y) are the sine and cosine integral functions.
. In the right-hand side of Eq. (37), Si(y) and Ci(y) are the sine and cosine integral functions.
The flow speed in the x-direction (the radial direction to the disk) is given by υx,g ≈ ∂Ψy0/∂y in the linear regime. Ormel (2013) obtained the following formula:
![${\rm{\upsilon }}_{x,{\rm{ out }}}^{{\rm{O}}13} = m\left[ {{\rm{Ci}}(\tilde y)\cos \tilde y - {1 \over 2}(\pi - 2{\rm{Si}}(\tilde y))\sin \tilde y} \right]{\rm{, }}$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq89.png) (38)
(38)
where y > 0. In a procedure of the derivation of Eq. (38), the contribution of the headwind was neglected. Equation (38) gives υx,g within the horseshoe region as a function of y in the shear only case (ℳhw = 0). In the absence of the headwind, the two-dimensional flow field has a symmetric structure with respect to the x- and y-axes. Owing to the symmetry, here we can only consider x < 0 and y > 0. Assuming that the widest horseshoe streamline can be outlined by our fitting formula (Eq. (11)), we substituted
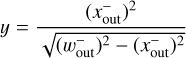 (39)
(39)
into Eq. (38). This gives us υx,g at 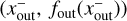 on the widest inner-leading horseshoe streamline. The result was plotted in Fig. 9a with the dashed blue line.
on the widest inner-leading horseshoe streamline. The result was plotted in Fig. 9a with the dashed blue line.
Ormel (2013) considered the two-dimensional flow, where the three-dimensional recycling streamlines do not appear. Nevertheless, Eq. (38) agrees with our results when m ≲ 0.1 (Fig. 9a). We speculate that this comes from the close relation between the outflow region and the horseshoe streamlines. Figure 16 shows isocontours of the stream function, Ψ, and the fitting formula for the outflow region, ƒout(x). In Fig. 16a, where we set m = 0.03, we find that our fitting formula is in excellent agreement with the widest horseshoe streamline characterized by 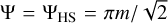 (Ormel 2013). This may lead to the agreement in the results of υx,out between our study and Ormel (2013). The linearized approximation breaks down for the higher-mass planets. In Fig. 16b, where we set m = 0.5, we find a significant mismatch between ƒout(x) and Ψ. Thus, Eq. (38) does not match with υx,out obtained in this study when m ≳ 0.3.
(Ormel 2013). This may lead to the agreement in the results of υx,out between our study and Ormel (2013). The linearized approximation breaks down for the higher-mass planets. In Fig. 16b, where we set m = 0.5, we find a significant mismatch between ƒout(x) and Ψ. Thus, Eq. (38) does not match with υx,out obtained in this study when m ≳ 0.3.
Fung et al. (2015) considered isothermal and viscous flow. The authors performed three-dimensional hydrodynamical simulation for the planet with m = 0.56 and found that the outflow speed at the midplane region was ~0.2–0.4cs. Fung et al. (2015) applied Bernoulli’s theorem along with a transient horseshoe streamline and derived the outflow speed as
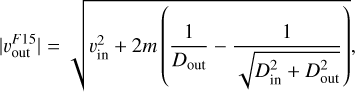 (40)
(40)
where υin is the inflow speed, Din and Dout are the distance of the inflow and outflow points from the planet. Following Fung et al. (2015), we substituted Din ≃ H and Dout ≃ wHS into Eq. (40), and neglected 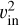 . Additionally, here we assume that the outflow occurs with an angle of ~ ± π/4 to the x-axis (e.g., Fig. 8 of Fung et al. 2015). In Fig. 9a, we plotted the following modified formula for the outflow speed in the x-direction with the dashed purple line:
. Additionally, here we assume that the outflow occurs with an angle of ~ ± π/4 to the x-axis (e.g., Fig. 8 of Fung et al. 2015). In Fig. 9a, we plotted the following modified formula for the outflow speed in the x-direction with the dashed purple line:
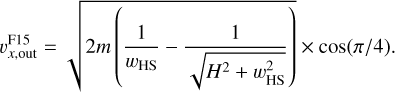 (41)
(41)
As discussed in Fung et al. (2015), Eq. (40) should be considered an upper limit because the height of the inflow point from the midplane assumed in Fung et al. (2015) was higher than ours. One can see that Eq. (41) overestimates the outflow speed compared to our results.
Kuwahara et al. (2019) considered isothermal and inviscid flow and performed three-dimensional hydrodynamical simulations for the planets with m = 0.01–2. Kuwahara et al. (2019) proposed that the outflow speed can be described by
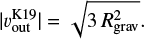 (42)
(42)
Equation (42) represents the flow speed at the intersections of a line of y = −x and a circle of radius Rgrav in the shear only case. Assuming that the critical recycling streamline at the midplane can be outlined by Eq. (11), we plotted the following modified formula for the x-component of the outflow speed in Fig. 9a with the dashed yellow line:
![$\eqalign{ & {\rm{\upsilon }}_{x,{\rm{ out }}}^{{\rm{K}}19} = \sqrt {3R_{{\rm{grav }}}^2} \cos {\varphi _{{\rm{out }}}}, \cr & \,\,\,\,\,\,\,\,\,\,\,\,\, = \sqrt {3R_{{\rm{grav}}}^2} \cos \left[ {{{\left. {{{\tan }^{ - 1}}\left( {{{{\rm{d}}{f_{{\rm{out }}}}(x)} \over {{\rm{d}}x}}} \right)} \right|}_{x = x_{{\rm{out }}}^{K19}}}} \right], \cr} $](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq97.png) (43)
(43)
where we assumed 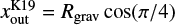 (Kuwahara et al. 2019). Equation (43) underestimates the outflow speed compared to our results for a wide range of planetary masses, m ≲ 0.3. This is caused by the following assumptions: (1) Kuwahara et al. (2019) considered an isothermal flow. (2) Kuwahara et al. (2019) set the inflow and outflow points on the sphere of radius Rgrav.
(Kuwahara et al. 2019). Equation (43) underestimates the outflow speed compared to our results for a wide range of planetary masses, m ≲ 0.3. This is caused by the following assumptions: (1) Kuwahara et al. (2019) considered an isothermal flow. (2) Kuwahara et al. (2019) set the inflow and outflow points on the sphere of radius Rgrav.
In an isothermal case, there is no clear boundary demarcating the bound atmosphere from the disk gas (Ormel et al. 2015b). The inflow of the gas intrudes deep inside the gravitational sphere of the planet. Thus, in the isothermal case, the inflow and outflow points were located at the points closer to the planetary core than in the nonisothermal case, leading to an underestimation of our results. The atmospheric radius positively correlated to the cooling timescale, β, and the atmosphere disappear in the isothermal limit, β → 0 (Kurokawa & Tanigawa 2018).
 |
Fig. 16 Isocontours of the stream function (the solid gray lines), Ψ, and the fitting formula of the critical recycling streamline at the midplane (Eq. (11); the dashed blue lines). The widest horseshoe streamlines characterized by ΨHS are highlighted with red. Isocontours of Ψ = 0.02−0.1 (panel a) and Ψ = 0.42–1.7 (panel b) are shown. |
5.3 Applicability of Bernoulli’s theorem
In Sect. 3.5, assuming an isothermal flow along a recycling streamline, we estimated the outflow speed using Bernoulli’s theorem. The applicability of Bernoulli’s theorem depends on the thermodynamics of the gas along the streamline. Our hydrodynamical simulations utilized the β cooling model in which the β cooling occurs on a finite timescale. Thus, Bernoulli’s function, ℬ, does not strictly conserve along the streamline (Fig. 2c).
We begin with a qualitative discussion. When a parcel of the gas approaches the planet and reaches the region where r ≲ Rgrav, the temperature of the parcel increases due to the adi-abatic compression. The temperature of the gas relaxes toward the background temperature with the dimensionless timescale β = (m/0.1)2 (Eq. (5)). Assuming that the gas parcel has the shear velocity, the crossing time on which the gas crosses the gravitational sphere of the planet can be estimated by the shear timescale, τcross ~ Ω−1. Thus, the isothermal assumption would be valid when β ≲ 1. We note that τcross can be longer than the shear timescale, because the gas parcel along the recycling streamline sometimes circulates the atmosphere, which leads to an increase in τcross (Fig. 2a).
Figures 17 and 18 show the quantitative description of Bernoulli’s function along a certain recycling streamline. Panels a and b in Figs. 17 and 18 represent the changes of ℬ and each term of ℬ as a function of y and r. Panel c of Figs. 17 and 18 shows a relative error between Bernoulli’s function and the unperturbed one, ℬ∞. We set 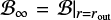 , where
, where 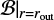 corresponds to the value of ℬ at the edge of the computational domain of hydrodynamical simulations (i.e., the starting point of the streamline).
corresponds to the value of ℬ at the edge of the computational domain of hydrodynamical simulations (i.e., the starting point of the streamline).
In Fig. 17, where we set m = 0.05 and β = 0.25, Bernoulli’s function is almost constant. The relative error between ℬ and ℬ∞ is on the order of ~10−2−10−1 and increases as the gas approaches the planet. Since the cooling time depends on the planetary mass, one would expect that the amplitude of the fluctuation of ℬ increases as the planetary mass increases. This can be seen in Fig. 18, where we set m = 0.2 and β = 4. The overall trends of Fig. 18 are similar to those of Fig. 17, but the relative error between ℬ and ℬ∞ for m = 0.2 is ~10−1−100, which is larger than that for m = 0.05. We find that the relative error between ℬ and ℬ∞ is larger for the higher-mass planets, m > 0.2 (β ≳ 10). This could lead to a mismatch between our analytic formula for the outflow speed and the numerical results in particular for a higher-mass planet (Fig. 9).
 |
Fig. 17 Quantities (panels a and b) and the relative error between ℬ and ℬ∞ (panel c) along a streamline through (x, y, z) = (0.001,0.01,0.2) (the solid colored line shown in Fig. 2c). The results were obtained from m005-hw003. Panels a and b: the solid and dotted black lines represent Bernoulli’s function, ℬ, and that in the far field, ℬ∞. The colored dashed lines correspond to the first to sixth terms in Bernoulli’s function. The dashed-dotted purple line in panel a corresponds to the x-coordinate of the streamline. The vertical solid lines in panels b and c denote twice the atmospheric radius. This figure should be compared to Fig. 2c. |
 |
Fig. 18 Same as Fig. 17, but the results were obtained from m02-003. We picked up a streamline through (x, y, z) = (0.001,0.01,0.44). |
 |
Fig. 19 Same as Fig. 9, but with the terminal velocity of dust (Eq. (45); dashed-dotted blue lines). Different colors correspond to different Stokes numbers. The vertical axis is on a log scale. |
 |
Fig. 20 Atmospheric radius as a function of the planetary mass and the cooling time, β. We set ℳhw = 0. The star symbols correspond to the results obtained from the fiducial runs (Fig. 5). |
5.4 Dependence on cooling time
So far we only showed the results obtained from the fiducial runs in which we considered a fixed cooling time, β0, for a given planetary mass (Eq. (5)). To determine the β0 value, we first considered that an inflow of a disk gas into an envelope would be heated by adiabatic compression (Sect. 2.2). We expect that the length scale of the temperature perturbation to the inflow of the disk gas can be estimated by the size of the gravitational sphere of the planet, RBondi or RHill. In this study, following Kurokawa & Tanigawa (2018), we assumed that the length scale of the temperature perturbation is equal to RBondi. The β0 value represents the cooling time near the outer edge of the atmosphere. As long as we focus on the recycling flow, we consider that β0 can be used as the typical value based on the following reasons: (1) the recycling flow traces the outer edge of the atmosphere. (2) When the dimensionless planetary mass falls below m < 0.6, which is the important mass range in this study, we always have Rgrav = RBondi.
However, the β value could vary within the atmosphere, which becomes larger in the dense region of the atmosphere. The β value also depends on the dust opacity in the atmosphere, which could be changed by orders of magnitude (Movshovitz & Podolak 2008; Ormel 2014; Mordasini 2014). In this section, we discuss the dependence of our results on the cooling time, β. An atmospheric radius, an important quantity for gas dynamics around an embedded planet, depends on β. Qualitatively, in both the isothermal (β → 0) and adiabatic (β → ∞) limits, a bound atmosphere does not appear (Kurokawa & Tanigawa 2018; Popovas et al. 2019) or is very small (<0.2 RBondi; Fung et al. 2019). Figure 20 shows the dependence of the atmospheric radius on β. We find that the atmospheric radius can be scaled with the Bondi or Hill radius of the planet even when we varied β by an order of magnitude (Fig. 20a). The atmospheric radius has a peak when β ~ 1–10 (Fig. 20b). We find that Ratm is not scaled with RBondi or RHill when β = 0.01 β0 and 100 β0. These endmember cases approach the isothermal and adiabatic conditions, where the bound atmosphere would disappear. Thus, in the limits of β → 0 and β → ∞, there is no guarantee that Ratm will scale with RBondi or RHill.
The outflow speed in the x-direction depends on β. In Fig. 21, where we set m = 0.2, ℳhw = 0, and β0 = 4, the perturbation to υx,g is the most prominent when β = 0.1 β0 = 0.4. We find that the width of the horseshoe streamline would positively correlate with the atmospheric radius. Our fitting formula for the critical recycling streamline at the midplane, ƒout(x) (Eq. (11)), cannot be applied to the endmember cases, β ≪ β0 and β ≫ β0 (Fig. 21). From a series of hydrodynamical simulations, we find that ƒout(x) and υx,out (Eq. (27)) can be used when the moderate cooling time was considered, β ~ 10−1−101. Again, the β value could be changed by orders of magnitude. Thus, further studies are needed to include the dependence of gas dynamics on the cooling time, such as the atmospheric radius, the width of the horseshoe region, and the outflow speed.
5.5 Angular momentum of the gas
Figures 17a and 18a show the changes of the x-coordinate of the gas along the recycling streamline passing outside the planetary orbit. We find that the x-coordinates of the streamline at the edges of the calculation domain of the hydrodynamical simulation do not match each other, implying that the angular momentum of the gas along the recycling streamline increases after the gravitational interaction with the planet. A detailed investigation of the net torque on the planet is beyond the scope of this study, but this result indicates that the gas flow around the planet could affect the migration rate of the planet, as suggested by Fung et al. (2015). Since our hydrodynamical simulations were performed in the local domain, our results may need to be compared with the results obtained by global hydrodynamical simulations.
 |
Fig. 21 Same as Fig. 3, but showing the dependence of the outflow speed on the cooling time. We set m = 0.2 in all panels. The results were obtained from m02-hw0-b001 (panel a), m02-hw0-b01 (panel b), m02-hw0-b10 (panel c), and m02-hw0-b100 (panel d). |
5.6 Influence of the outflow on the growth of protoplanets
Based on the analytic formula for the outflow speed (Eq. (27)), here we discuss the influence of the outflow on the growth of protoplanets. In this section, we assume that dust settle to the midplane for simplicity. More quantitatively, we assume that the vertical extent of the outflow is larger than the dust scale height. The vertical extent of the outflow can be estimated by the atmospheric radius, Ratm ≲ 0.2 H (Sect. 3.6.2). The dust scale height is given by (Youdin & Lithwick 2007)
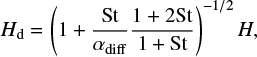 (44)
(44)
where αdiff is the dimensionless turbulent parameter. Equation (44) gives Hd ≲ 0.3 H when St ≳ 10−3 and αdiff ≲ 10−4 were assumed, which means that, under weak turbulence, the outflow has a potential to affect the dust motion.
Following Kuwahara et al. (2019), we compare υx,out (Eq. (27)) with the terminal speed of a dust particle at a distance of r = 2 Ratm,fit from the planet, where the dominant outflow of the gas occurs. Given the force balance between the gas drag and the gravity of the planet acting on the dust particle at r = 2 Ratm,fit, the terminal speed of the dust particle can be described by
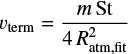 (45)
(45)
in our dimensionless unit, where St is the Stokes number (the dimensionless stopping time) of dust. We plotted Eq. (45) with different Stokes numbers, St = 10−3 10−2, and 10−1 in Fig. 19 and compared the terminal speed of the dust particle with the outflow speed. The outflow speed in the x-direction can exceed the terminal speed of the dust particle.
We derived the upper limit of the Stokes number of dust that can be affected by the outflow by the order-of-magnitude estimate. For simplicity, we neglected the effect of the headwind of the gas, ℳhw = 0, and only considered x ≥ 0. From Eqs. (27) and (45), the outflow affects the motion of dust when the Stokes number falls below the critical Stokes number:
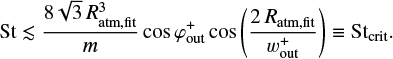 (46)
(46)
We plotted Eq. (46) in Fig. 22.
When m ≲ 0.1 (Ratm,fit = 0.84 Rвomdi), the product of the cosine terms in the right-hand side of Eq. (46) has ~0.6–1 and we obtain
![${\rm{St}} \mathbin{\lower.3ex\hbox{\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}}} 8\sqrt 3 {{\rm{m}}^2} \times [{\rm{ cos terms }}]\~10{{\rm{m}}^2}{\rm{. }}$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq104.png) (47)
(47)
When m ≳ 0.1 (Ratm,fit = 0.22 RHill), the product of the cosine terms in the right-hand side of Eq. (46) has ~0.3–0.6 and we obtain
![${\rm{St}} \mathbin{\lower.3ex\hbox{\buildrel<\over {\smash{\scriptstyle\sim}\vphantom{_x}}}} {{8\sqrt 3 } \over 3} \times {0.4^3} \times [\cos {\rm{ terms }}]\~0.1.$](/articles/aa/full_html/2024/02/aa47530-23/aa47530-23-eq105.png) (48)
(48)
In summary, the outflow could affect the dust motion and suppress the dust accretion onto the planet when St ≲ min(10m2, 0.1). This is consistent with the post-processing simulation results where the obtained hydrodynamical simulation data to calculate the dust trajectories (Kuwahara & Kurokawa 2020a,b; Okamura & Kobayashi 2021).
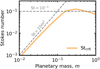 |
Fig. 22 Upper limit of the Stokes number of dust that affected by the outflow as a function of the planetary mass (Eq. (46)). |
5.7 Dust velocity influenced by the planet-induced gas flow
We expect that the analytic formulae for the distribution of the x-component of the perturbed flow velocity in the radial (υx,out(x); Eq. (31)) and vertical (υx,out(ɀ); Eq. (32)) directions to the disk can be used for modeling of the dust velocity influenced by the planet-induced gas flow. Performing hydrodynamical simulations is a direct way to investigate the influence of gas flow on dust motion, but computationally expensive. Our analytic formulae would allow us to perform an extensive parameter study of the hydrodynamic effect of the outflow on the dust motion. The above attempts at modeling dust velocity will be included in a future study.
6 Conclusions
We obtained fitting formulae that describe the morphology of gas dynamics around an embedded planet by performing three-dimensional, nonisothermal hydrodynamical simulations. We then derived an analytic formula for the planet-induced mid-plane outflow using Bernoulli’s theorem. Our main results are as follows:
- 1
A bound atmosphere forms within the gravitational sphere of the planet, whose size scales with the Bondi or Hill radius of the planet. We derived the dimensionless fitting formula for the atmospheric radius, Ratm,fit = min(0.84 RBondi – 0.056 ℳhw, 0.36 RHill – 0.22 ℳhw). Gas from the disk chiefly flows in and out of an area of twice the atmospheric radius;
- 2
The outflow of the gas occurs at the midplane. We find that the morphology of the outflow (the shape of the streamline) can be outlined by a simple tangential curve.
- 2
Based on the obtained quantitative descriptions of the outflow morphology, we derived an analytic formula for the outflow speed that is in agreement with the results of hydrodynamical simulations. The outflow speed in the radial direction to the disk has a peak speed of ~0.3–0.4 cs at m ~ 0.3, corresponding to a super-Earth mass planet at 1 au for a typical steady accretion disk model. The global pressure force of the disk gas enhances (reduces) the outflow toward the outside (inside) of the planetary orbit, causing the asymmetry of the outflow speed inside and outside the planetary orbit.
The outflow of the gas could suppress pebble accretion when St ≲ min(10m2, 0.1). Our analytic formulae can be used for modeling the hydrodynamic effects of the outflow on the dust accretion onto the planet and the radial drift of dust, which could be essential for planet formation via pebble accretion and the dust ring and gap formation in a disk.
Acknowledgements
We would like to thank the reviewer, Dr. Ondrej Chrenko for thoughtful comments that have substantially improved the quality of this manuscript. We thank Athena++ developers. Numerical computations were in part carried out on Cray XC50 at the Center for Computational Astrophysics at the National Astronomical Observatory of Japan. This work was supported by JSPS KAKENHI Grant number 20KK0080, 22H01290, 22H05150, 21H04514, and 21K13976.
Appendix A Aspect ratio of the steady accretion disk
When we convert the dimensionless quantities into dimensional ones, we considered the typical steady accretion disk model with a constant turbulence strength (Shakura & Sunyaev 1973), αacc, including viscous heating due to the accretion of the gas and irradiation heating from the central star (e.g., Ida et al. 2016). The aspect ratio of the disk is given by
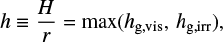 (A.1)
(A.1)
where hg,vis and hg,irr are aspect ratios given by (Ida et al. 2016)
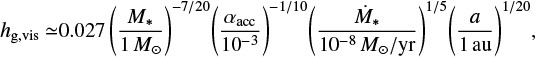 (A.2)
(A.2)
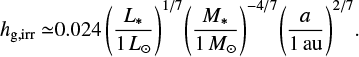 (A.3)
(A.3)
In this study, we assume a solar-mass host star, M* = 1 M⊙, the solar luminosity, L* = 1 L⊙, the typical accretion rate of classical T Tauri stars, M⊙ = 10−8 M⊙/yr, and αacc = 10−3.
Appendix B Dependence on the inner boundary
 |
Fig. B.1 Azimuthal gas velocity at the midplane averaged in the azimuthal direction in the spherical polar coordinates centered at the planet. The results were obtained from m003-hw003 and m003-hw003-01rinn. Different colors corresponds to different sizes of the inner boundary. The filled circle denotes the atmospheric radius. The dashed line shows the Keplerian speed. |
In this section we investigate the influence of the size of the inner boundary (corresponding to the planet location in this study; Eq. (3)), rinn, on the atmospheric radius. We confirmed that the size of the inner boundary does not affect our results. Previous studies reported that the azimuthal gas velocity in the spherical polar coordinates centered at the planet depends on rinn (Ormel et al. 2015b; Béthune & Rafikov 2019; Takaoka et al. 2023). We also found that the azimuthal gas velocity varies with rinn (Fig. B.1). Nevertheless, the atmospheric radius did not change significantly. When we changed rinn by an order of magnitude, the relative error between the obtained atmospheric radii with rinn = rinn,0 and 0.1 rinn,0 was small: ≲ 10% (Fig. B.2). This allows the orbital radius to be considered a free parameter regardless of a fixed rinn.
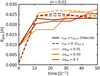 |
Fig. B.2 Time evolution of the atmospheric radius for different sizes of the inner boundary, rinn = rinn,0 (the solid lines) and rinn = 0.1 rinn,0 (the dashed lines). Different colors correspond to different Mach numbers. We set m = 0.03 and rsm = 0.1 Rgгav. |
Appendix C Dependence on the smoothing length
In this section we investigate the influence of the smoothing length on gas dynamics within the gravitational sphere of the planet, the atmospheric radius, and the outflow speed.
It is preferable to run the simulations with rsm = 0 to resolve the local gas flow around the planet. However, through the simulations with rsm = 0, we find unsteady and unphysical flow pattern within the atmosphere. The simulations were interrupted when we performed long-term simulations, t ≳ 500 Ω−1, in particular for higher-mass planets, m ≳ 0.3. To investigate this problem, we plot the shell-averaged radial velocity in Fig. C.1. This figure show that the small but nonzero inward radial gas flow occurs at the region close to the inner boundary, meaning that the hydrostatic equilibrium is not established in this region. The density of the gas increases with time due to the continuous accumulation of the gas in the inner region of the envelope, leading to the numerical errors.
There is a clear correlation between the shell-averaged radial gas flow near the inner boundary and the smoothing length. In our parameter sets, we always have the following relation: 0.1 Rgгav < 3 rinn. The larger the smoothing length, the smaller the radial gas velocity at the region close to the inner boundary. This can be seen in previous study and would disappear in a higher-resolution simulation (e.g., Fig. A.1 of Ormel et al. 2015b).
Figure C.2 shows the time evolution of the atmospheric radius for different smoothing lengths, rsm = 0, 0.1 Rgгav, and 3 rinn. In Fig. C.2a, where we set m = 0.1, we find the fluctuation of the atmospheric radius when we adopt a relatively large smoothing length, rsm = 3 rinn, corresponding to ~0.4 RBondi. The fluctuation does not occur when rsm = 0.1 Rgгav = 0.1 Rвondi. For a higher-mass planet, m = 0.5, only when we adopt the nonzero smoothing length, the results seem to reach the steady state (Fig. C.2b).
 |
Fig. C.1 Shell-averaged radial velocity of the gas in the spherical polar coordinates centered at the planet for different smoothing lengths, rsm = 0 (the dashed red line), rsm = 0.1 Rgrav (the solid blue line), and rsm = 3 rinn (the dotted yellow line). We assumed m = 0.1 in panel a and m = 0.5 in panel b. We set ℳhw = 0. |
The choice of the smoothing length does not affect significantly the outflow speed when m ≲ 0.3. Figure D.1 compares the outflow speed in the x-direction obtained from hydrodynamical simulations with different smoothing lengths, rsm = 0 and 0.1 Rgrav. When m ≲ 0.3, the obtained outflow speeds are overlapped. For higher-mass planets, m ≳ 0.3, the outflow speed obtained from hydrodynamical simulations with rsm = 0 does not match with those obtained with rsm = 0.1 Rgrav due to the unphysical flow pattern within the atmosphere.
Based on Figs. C.1–D.1, we adopt rsm = 0.1 Rgrav in our fiducial runs. It should be noted that even when we adopt the nonzero smoothing length, the inward radial gas flow does not completely disappear, indicating that the unsteady and unphysical flow pattern would eventually appear when t > 103 Ω−1.
Appendix D Interpolation of the gas velocity
We interpolated the gas velocity to plot the streamlines in the local Cartesian coordinates (e.g., the thin gray lines in Fig. 3) by using the matplotlib.pyplot.streamplot library. Our hydrodynamical simulations were performed in the spherical polar coordinates, (r, θ, ϕ), centered on the planet.
Hereafter we only consider the midplane. We set the local Cartesian coordinates, (x, y), where the following relations hold: 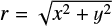 and ϕ = tan−1 (y/x). We divided the local Cartesian coordinates into N grids in the x- and y-directions with equal spacing within the view range. We set N = 50. We confirmed that the result does not change significantly when we doubled the value of N. Then, we calculated the gas velocity at each Cartesian grid point with the bilinear interpolation method. The interpolated gas velocity at an arbitrary point, (x, y), is given by
and ϕ = tan−1 (y/x). We divided the local Cartesian coordinates into N grids in the x- and y-directions with equal spacing within the view range. We set N = 50. We confirmed that the result does not change significantly when we doubled the value of N. Then, we calculated the gas velocity at each Cartesian grid point with the bilinear interpolation method. The interpolated gas velocity at an arbitrary point, (x, y), is given by
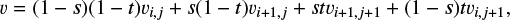 (D.1)
(D.1)
 |
Fig. C.2 Time evolution of the atmospheric radius for different smoothing lengths, rsm = 0 (the dashed red line), rsm = 0.1 Rgгav (the solid blue line), and rsm = 3 rinn (the dotted yellow line). We assumed m = 0.1 and ℳhw = 0 in panel a and m = 0.5 and ℳhw = 0 in panel b. |
where υi,j,k is the gas velocity at the center of the grid of hydrodynamical simulations, the subscripts denote the grid number, and s and t are given by
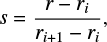 (D.2)
(D.2)
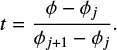 (D.3)
(D.3)
In Eqs. (D.2) and (D.3), i and j were chosen to satisfy the following relations: ri ≤ r < ri+1 and ϕj ≤ ϕ < ϕj+1.
The number of streamlines depends on the value of the "density" parameter in the matplotlib.pyplot.streamplot library. The default value is density=1. The number of streamlines increases as the value of the density parameter increases. To show the detailed structure of the gas flow, we set density=2 in Figs. 3, 4, and 21.
 |
Fig. D.1 Same as Fig. 9, but comparing the results obtained from hydrodynamical simulations with rsm = 0 (the cross symbols) and rsm = 0.1 Rgrav (the star symbols). |
Appendix E Widest horseshoe streamline and the shear streamline passing closest to the planet
We calculated the widest horseshoe streamline and the streamline of the background shearing flow passing closest to the planet with the bisection method and plotted them in Figs. 3, 4, 7, 10, and 21 without using the matplotlib.pyplot.streamplot library. The following sections describe the dedicated calculation method for these characteristic streamlines and how to determine the boundary between the widest horseshoe streamline and the shear streamline passing closest to the planet.
Appendix E.1 Dedicated calculation method for the characteristic streamlines
This section describes the dedicated calculation method for the two characteristic streamlines: the widest horseshoe streamline and the streamline of the background shearing flow passing closest to the planet. A fifth-order Runge-Kutta-Fehlberg method was used to calculate the streamlines. We set the starting point of the streamline, (x0, y0), at the edge of the calculation domain of hydrodynamical simulation. The x-coordinate of the starting point, x0, is a parameter. The y-coordinate of the starting point is given by
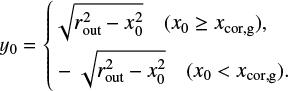 (E.1)–(E.2)
(E.1)–(E.2)
The position of the gas parcel at the i-th time step, (xi, yi), was calculated by the fifth-order Runge-Kutta-Fehlberg scheme, where the gas velocity at an arbitrary position was calculated by Eq. (D.1). Following Kuwahara & Kurokawa (2020a), the maximum relative error tolerance was set to 10−8, where the authors adopted the same scheme described in this section to compute the trajectories of dust particles influenced by the planet-induced gas flow.
We terminated the above-mentioned streamline calculation when one of the following conditions was met: (1) the gas parcel reached the edge of the computational domain of hydrodynamical simulations,  , or (2) the gas parcel reached a stagnation point. We judged that a parcel of the gas reached the stagnation point when
, or (2) the gas parcel reached a stagnation point. We judged that a parcel of the gas reached the stagnation point when
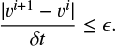 (E.3)
(E.3)
In Eq. (E.3), 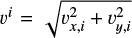 is the gas speed at (xi, yi) where the x- and y-components of the gas velocity, υx,i and υy,i are calculated by Eq. (D.1) and we set ϵ = 10−10.
is the gas speed at (xi, yi) where the x- and y-components of the gas velocity, υx,i and υy,i are calculated by Eq. (D.1) and we set ϵ = 10−10.
Appendix E.2 Determination of the boundary between the widest horseshoe streamline and the shear streamline passing closest to the planet
Based on the dedicated calculation method for the characteristic streamlines described in Appendix E.1, we determined the boundary between the widest horseshoe streamline and the shear streamline passing closest to the planet with the bisection method. We calculated the streamlines with the initial spatial intervals of δx0 = 10−2 H in the x-direction. We denote with 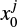 and
and 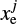 the x-coordinates of the starting and end points of the j-th streamline, respectively. We classified the obtained streamline as a horseshoe streamline when
the x-coordinates of the starting and end points of the j-th streamline, respectively. We classified the obtained streamline as a horseshoe streamline when 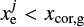 and
and 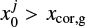 , or
, or 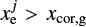 and
and 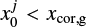 , where
, where  is the x -coordinate of the j-th streamline at the edge of the computational domain of hydrodynamical simulation; otherwise, it was classified as a shear streamline.
is the x -coordinate of the j-th streamline at the edge of the computational domain of hydrodynamical simulation; otherwise, it was classified as a shear streamline.
When the j-th and (j + 1)-th streamlines were determined to be the shear and horseshoe streamlines, respectively, we set 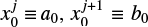 , and c0 ≡ (a0 + b0)/2. We calculated a streamline whose x-coordinate of the starting point was c0, and then set a1 ≡ c0, b1 ≡ b0 (b1 ≡ c0, a1 ≡ a0), and c1 ≡ (a1 + b1)/2 when the streamline was determined to be a shear (horseshoe) streamline. We repeated the above steps until the following condition was satisfied: |ak − bk| < 0.01 δx0 = 10−4 H (k = 0, 1,…).
, and c0 ≡ (a0 + b0)/2. We calculated a streamline whose x-coordinate of the starting point was c0, and then set a1 ≡ c0, b1 ≡ b0 (b1 ≡ c0, a1 ≡ a0), and c1 ≡ (a1 + b1)/2 when the streamline was determined to be a shear (horseshoe) streamline. We repeated the above steps until the following condition was satisfied: |ak − bk| < 0.01 δx0 = 10−4 H (k = 0, 1,…).
Appendix F Numerical convergence
To obtain the atmospheric radius, we used the final state of the hydro-simulations data (Sect. 3.1). Figure F.1 shows the time evolution of the atmospheric radius for different planetary masses, m = 0.05, 0.1, 0.2, and 0.5, and Mach numbers, ℳhw = 0−0.1. We set rsm = 0.1 Rgrav. The atmospheric radius increases in the early stage of the time evolution and reaches a steady state after t ≳ 30−100 Ω−1.
Appendix G Numerically calculated widths of the horseshoe and outflow regions
Based on the streamline calculation method described in Appendix E, we calculated numerically the x-coordinate of the critical recycling streamline at the midplane, 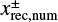 , and the half-width of the horseshoe region,
, and the half-width of the horseshoe region, 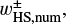 . We defined
. We defined 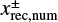 as the x-coordinate of the shear streamline passing closest to the planet at the edge of the computational domain of our hydrodynamical simulations. We defined the numerically calculated half-width of the horseshoe flow as
as the x-coordinate of the shear streamline passing closest to the planet at the edge of the computational domain of our hydrodynamical simulations. We defined the numerically calculated half-width of the horseshoe flow as
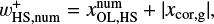 (G.1)
(G.1)
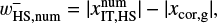 (G.2)
(G.2)
 |
Fig. F.1 Time evolution of the atmospheric radius for different planetary masses, m = 0.05 (panel a), m = 0.1 (panel b), m = 0.2 (panel c), and m = 0.5 (panel d). Different colors correspond to different Mach numbers. We set rsm = 0.1 Rgrav in this figure. |
where 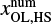 and
and 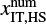 are the x-coordinates of the widest outer-leading and inner-trailing horseshoe flows at the edges of the computational domain of our hydrodynamical simulations (the starting points of the streamlines in the first and third quadrants in the x-y plane).
are the x-coordinates of the widest outer-leading and inner-trailing horseshoe flows at the edges of the computational domain of our hydrodynamical simulations (the starting points of the streamlines in the first and third quadrants in the x-y plane).
Figure G.1 compares the numerically calculated quantities, 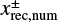 and
and 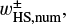 , with the analytic formulae. We find that
, with the analytic formulae. We find that 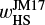 (Eq. (15)) is a better indicator than
(Eq. (15)) is a better indicator than 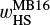 (Eq. (14)) in describing the width of the outflow region when m ≲ 0.6, though a mismatch between the numerical results and the analytic estimate is prominent when m ~ 0.2 (the circle symbols and the solid lines in Fig. G.1).
(Eq. (14)) in describing the width of the outflow region when m ≲ 0.6, though a mismatch between the numerical results and the analytic estimate is prominent when m ~ 0.2 (the circle symbols and the solid lines in Fig. G.1).
Since our analytic model for the gas flow is not valid in the higher-mass regime (m ≳ miso ≃ 0.6; see Sect. 3.2.1), here we restrict our attention to the limited range of the planetary mass, m < 0.6. We speculate that the significant deviation between 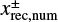 and
and 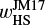 around m ~ 0.2 is related to the dependence of υx,out on the planetary mass. As shown Fig. 9, υx,out has a peak when m ~ 0.3, which means that a parcel of the gas moves significantly in the x-direction and
around m ~ 0.2 is related to the dependence of υx,out on the planetary mass. As shown Fig. 9, υx,out has a peak when m ~ 0.3, which means that a parcel of the gas moves significantly in the x-direction and 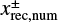 increases. The deviation between
increases. The deviation between 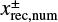 and the analytic estimate around m ~ 0.2 is likely caused by the existence of the recycling flow revealed by our local three-dimensional hydrodynamical simulations, which have a higher resolution within the gravitational sphere of the planet, Rgrav.
and the analytic estimate around m ~ 0.2 is likely caused by the existence of the recycling flow revealed by our local three-dimensional hydrodynamical simulations, which have a higher resolution within the gravitational sphere of the planet, Rgrav.
The influence of the recycling flow may not be included in both Eqs. (14) and (15). Equation (15) was based on Eq. (14), and Eq. (14) was derived by a combination of linear theory and the results of three-dimensional global hydrodynamical simulations with the moderate resolution at ≲ Rgrav (Masset & Benítez-Llambay 2016). Nevertheless, we keep ourselves conservative for the estimation of xrec and assume that Eq. (15) is valid in deriving the width of the outflow region.
While the width of the outflow region is better described by 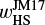 (Eq. (15)), we find that the half-width of the horseshoe flow agrees with
(Eq. (15)), we find that the half-width of the horseshoe flow agrees with 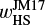 (Eq. (14)) regardless of the assumed Mach number of the headwind, except when m < 0.1 (the square symbols and the dotted lines in Fig. G.1). When m < 0.1, the horseshoe region might not be well established in our hydrodynamical simulations.
(Eq. (14)) regardless of the assumed Mach number of the headwind, except when m < 0.1 (the square symbols and the dotted lines in Fig. G.1). When m < 0.1, the horseshoe region might not be well established in our hydrodynamical simulations.
 |
Fig. G.1 Width of the horseshoe flow and the x-coordinate of the critical recycling streamline at the edge of the computational domain of hydrodynamical simulations. The solid, dotted, and dashed gray lines are given by the analytic formulae for the width of the horseshoe region (Eqs. (14) and (15)). The numerically calculated width of the outflow region (xrec,num, the circle symbols) is in better agreement with the analytic estimate based on Eq. (15) ( |
Although a discrepancy between 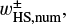 and
and 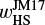 (Eq. (15)) does not affect an analytic derivation of the outflow speed, we discuss the reason of this discrepancy below. The discrepancy between
(Eq. (15)) does not affect an analytic derivation of the outflow speed, we discuss the reason of this discrepancy below. The discrepancy between 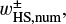 and
and 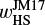 (Eq. (15)) could be caused by the limitation of our hydrodynamical simulations. Our local simulation cannot handle the gas-gap opening in the high-mass regime, m ≳ miso. Gas-gap formation reduces the Lindblad torque, leading to an extension of the horseshoe region into the Lindblad resonance region, ~H (Paardekooper & Papaloizou 2009). Then the dependence of the horseshoe width on the planetary mass deviates from
(Eq. (15)) could be caused by the limitation of our hydrodynamical simulations. Our local simulation cannot handle the gas-gap opening in the high-mass regime, m ≳ miso. Gas-gap formation reduces the Lindblad torque, leading to an extension of the horseshoe region into the Lindblad resonance region, ~H (Paardekooper & Papaloizou 2009). Then the dependence of the horseshoe width on the planetary mass deviates from 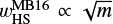 . Moreover, our local hydrodynamical simulations were performed on the spherical polar coordinates with a logarithmic grid for the radial coordinate, which has a lower resolution at the region far from the planet. We fixed the gas velocity at the outer edge of the computational domain of hydrodynamical simulations. These simulation settings could affect the width of the horseshoe flow.
. Moreover, our local hydrodynamical simulations were performed on the spherical polar coordinates with a logarithmic grid for the radial coordinate, which has a lower resolution at the region far from the planet. We fixed the gas velocity at the outer edge of the computational domain of hydrodynamical simulations. These simulation settings could affect the width of the horseshoe flow.
References
- Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailey, A., Stone, J. M., & Fung, J. 2021, ApJ, 915, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Béthune, W., & Rafikov, R. R. 2019, MNRAS, 488, 2365 [Google Scholar]
- Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chrenko, O., & Lambrechts, M. 2019, A&A, 626, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cimerman, N. P., Kuiper, R., & Ormel, C. W. 2017, MNRAS, 471, 4662 [Google Scholar]
- D’Angelo, G., & Bodenheimer, P. 2013, ApJ, 778, 77 [Google Scholar]
- D’Angelo, G., & Lubow, S. H. 2008, ApJ, 685, 560 [CrossRef] [Google Scholar]
- Duffell, P. C., & MacFadyen, A. I. 2013, ApJ, 769, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Eggleton, P. P. 1983, ApJ, 268, 368 [Google Scholar]
- Fung, J., Artymowicz, P., & Wu, Y. 2015, ApJ, 811, 101 [Google Scholar]
- Fung, J., Zhu, Z., & Chiang, E. 2019, ApJ, 887, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Gammie, C. F. 2001, ApJ, 553, 174 [Google Scholar]
- Goodman, J., & Rafikov, R. 2001, ApJ, 552, 793 [NASA ADS] [CrossRef] [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jiménez, M. A., & Masset, F. S. 2017, MNRAS, 471, 4917 [Google Scholar]
- Kurokawa, H., & Tanigawa, T. 2018, MNRAS, 479, 635 [Google Scholar]
- Kuwahara, A., & Kurokawa, H. 2020a, A&A, 633, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuwahara, A., & Kurokawa, H. 2020b, A&A, 643, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuwahara, A., Kurokawa, H., & Ida, S. 2019, A&A, 623, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuwahara, A., Kurokawa, H., Tanigawa, T., & Ida, S. 2022, A&A, 665, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., & Lega, E. 2017, A&A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Masset, F. S., & Benítez-Llambay, P. 2016, ApJ, 817, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Masset, F. S., D’Angelo, G., & Kley, W. 2006, ApJ, 652, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Moldenhauer, T., Kuiper, R., Kley, W., & Ormel, C. 2021, A&A, 646, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moldenhauer, T., Kuiper, R., Kley, W., & Ormel, C. 2022, A&A, 661, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mordasini, C. 2014, A&A, 572, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Movshovitz, N., & Podolak, M. 2008, Icarus, 194, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Nakagawa, Y., Sekiya, M., & Hayashi, C. 1986, Icarus, 67, 375 [Google Scholar]
- Okamura, T., & Kobayashi, H. 2021, ApJ, 916, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2013, MNRAS, 428, 3526 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W. 2014, ApJ, 789, L18 [Google Scholar]
- Ormel, C. W., Kuiper, R., & Shi, J.-M. 2015a, MNRAS, 446, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Ormel, C. W., Shi, J.-M., & Kuiper, R. 2015b, MNRAS, 447, 3512 [Google Scholar]
- Paardekooper, S.-J., & Mellema, G. 2004, A&A, 425, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paardekooper, S.-J., & Papaloizou, J. 2009, MNRAS, 394, 2297 [NASA ADS] [CrossRef] [Google Scholar]
- Paczynski, B. 1971, ARA&A, 9, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Popovas, A., Nordlund, Å., Ramsey, J. P., & Ormel, C. W. 2018, MNRAS, 479, 5136 [Google Scholar]
- Popovas, A., Nordlund, Å., & Ramsey, J. P. 2019, MNRAS, 482, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 24, 337 [NASA ADS] [Google Scholar]
- Stone, J. M., Tomida, K., White, C. J., & Felker, K. G. 2020, ApJS, 249, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Takaoka, K., Kuwahara, A., Ida, S., & Kurokawa, H. 2023, A&A, 674, A193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, C. J., Stone, J. M., & Gammie, C. F. 2016, ApJ, 225, 22 [NASA ADS] [Google Scholar]
- Youdin, A. N., & Lithwick, Y. 2007, Icarus, 192, 588 [NASA ADS] [CrossRef] [Google Scholar]
Precisely, the mass range is dependent on parameters such as the orbital radius; see Sect. 2.
This flow is also referred to as the transient horseshoe flow in Fung et al. (2015).
All Tables
All Figures
 |
Fig. 1 Planetary mass (top) and the Mach number (bottom) as a function of the orbital radius. For the conversion, we assumed a typical steady accretion disk model with a dimensionless viscous alpha parameter (Shakura & Sunyaev 1973), αacc, including viscous heating and stellar irradiation (e.g., Ida et al. 2016). In this model, the aspect ratio is given by h = max(0.027(a/1 au)1/20, 0.024 (a/1 au)2/7), where a solar-mass star, a solar luminosity, the typical accretion rate of classical T Tauri stars, 10−8 M⊙ yr−1, and αacc = 10−3 were assumed (Appendix A). |
| In the text | |
 |
Fig. 2 Streamlines of gas flow around the planet with m = 0.05 and ℳhw = 0.03. The arrows represent the direction of the gas flow. Panel a: perspective view of the flow field. Different colors correspond to different types of streamlines. The size of the atmosphere is 0.04 H. Panel b: same as panel a, but the color contour represents p/ρg, which is the measure of temperature (Sect. 3.3). Panel c: x-y plane viewed from the +z-direction. The critical streamline is highlighted by the color contour, which represents Bernoulli’s function, ℬ (Sects. 3.3 and 5.3). |
| In the text | |
 |
Fig. 3 Dependence of the planet-induced gas flow on the planetary mass at the midplane. We set ℳhw = 0 in all panels. The results were obtained from m005-hw0 (panel a), m01-hw0 (panel b), m05-hw0 (panel c), and m07-hw0 (panel d). The solid thin gray lines are gas streamlines. The solid and thick dashed gray lines are the widest horseshoe streamline and the shear streamline passing closest to the planet, respectively (Appendix E). The color contour represents the flow speed in the x-direction. The dashed and dashed-dotted black circles denote the atmospheric radius (Eq. (5)) and twice the atmospheric radius, where the outflow speed is measured. The dashed blue lines are the curves representing the fitting formula for the critical recycling streamline (Eq. (11); Sect. 3.2.1). The vertical lines are the asymptotes of Eq. (11), representing the extent of the outflow region in the x-direction ((Eq. (17)); Sect. 3.2.2). The horizontal lines denote the y-coordinates of the characteristic length of the outflow region in the y-direction ((Eq. (18)); Sect. 3.2.3). |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but showing the dependence of the planet-induced gas flow on the Mach number of the headwind. We set m = 0.2 in all panels. The results were obtained from m02-hw0 (panel a), m02-hw001 (panel b), m02-hw003 (panel c), and m02-hw01 (panel d). The vertical dotted line corresponds to the corotation radius for the gas. |
| In the text | |
 |
Fig. 5 Atmospheric radius as a function of the planetary mass and the Mach number of the headwind of the gas. The square symbols were obtained from hydrodynamical simulations. Different colors correspond to different Mach numbers, ℳhw. The gray-shaded region is given by the fitting formula for the atmospheric radius, Ratm,fit. The dashed gray line is given by Eq. (9). |
| In the text | |
 |
Fig. 6 Shell-averaged values of |
| In the text | |
 |
Fig. 7 Difference of the flow speed from the unperturbed Keplerian shear. The results were obtained from m01 − hw0 (panel a) and m05 − hw0 (panel b). The dashed blue, dashed-dotted white, and dotted white lines denote the fitting formula for the critical recycling streamline, the x-coordinate of the critical recycling streamline at the midplane in the far field, and the x-coordinate of the edge of the subsonic region, respectively. As in Fig. 3, we highlight the widest horseshoe streamline and the shear streamline passing closest to the planet with the solid and dashed orange lines, respectively. |
| In the text | |
 |
Fig. 8 Gas flow structure and azimuthally averaged mass flux. The results were obtained from m02 − hw0 (panels a and b), m02 − hw01 (panels c and d), and m04 − hw0 (panels e and f). Left column: gas flow structure at the meridian plane. The color contour represents the r-component of the gas velocity in the spherical polar coordinates centered at the planet and averaged in the y-direction within the calculation domain of the hydrodynamical simulation. The dashed, dotted, and dashed-dotted circles denote the Bondi radius, the Hill radius, and twice the atmospheric radius, respectively. Right column: mass flux of the gas averaged in the azimuthal direction in the spherical polar coordinates centered at the planet, 〈ρgυr〉ϕ. Each solid line represents the changes in 〈ρgυr〉ϕ; altitude is varied along with a certain radius. We highlight the important radii with solid yellow (RBondi), blue (RHill), and red (2 Ratm) lines. |
| In the text | |
 |
Fig. 9 Outflow speed at the midplane as a function of the dimensionless planetary mass and the Mach number of the headwind of the gas. The star symbols were obtained from hydrodynamical simulations, corresponding to the maximum flow speeds in the x-direction toward the outside (red) and inside (black) of the planetary orbit within the limited region, |
| In the text | |
 |
Fig. 10 Comparison of the point where υx,g has the maximum value at the midplane and the assumed outflow point, |
| In the text | |
 |
Fig. 11 Comparison of the maximum flow speed in the x-direction, |
| In the text | |
 |
Fig. 12 Angle of the outflow at the outflow point, φout (Eq. (28)), cos φout, and the x-coordinate of the outflow point, |
| In the text | |
 |
Fig. 13 Distribution of the x-component of the gas velocity in the x-direction at the midplane, υx,max(x). The solid blue line is given by Eq. (31). The yellow dots were obtained from m02-hw0 (panel a), m02-hw001 (panel b), m02-hw003 (panel c), and m02-hw01 (panel d). We sampled the gas velocity at each radial grid of hydro-dynamical simulations where the absolute value of the gas velocity was the maximum within the limited region, |
| In the text | |
 |
Fig. 14 Vertical structure of the gas flow. The results were obtained from m02-hw0 (panels a and b), m02-hw01 (panels c and d), and m05-hw0 (panels e and f). Left column: same as the left column of Fig. 8, but the color contour represents υx,g averaged in the y-direction within the calculation domain of hydrodynamical simulation. Right column: the x-component of the gas flow velocity averaged in the x- and y-directions within the calculation domain of hydrodynamical simulation, |
| In the text | |
 |
Fig. 15 Comparison of the atmospheric radii obtained in our study and those in previous studies. The open and filled square symbols were obtained from our hydrodynamical simulations, ℳhw = 0 and 0.1, respectively. The gray-shaded region is given by the fitting formula for the atmospheric radius, Ratm,fit (Eq. (7)). The red dashed and dotted lines are given by Eq. (34) (Moldenhauer et al. 2022). We extrapolated Eq. (34) to the range of m ≤ 0.3. The yellow, blue, and green diamonds corresponds to the results of D’Angelo & Bodenheimer (2013), Lambrechts & Lega (2017), and Cimerman et al. (2017), respectively. To plot the results of D’Angelo & Bodenheimer (2013), the atmospheric radii were calculated by Ratm/H = CDB13a/H = CDB13/h. The values of CDB13 = 2.6 × 10−3−9.6 × 10−3 were given in Table 3 of D’Angelo & Bodenheimer (2013). We used h = max(0.027(a/1 au)1/20, 0.024 (a/1 au)2/7) (Appendix A). |
| In the text | |
 |
Fig. 16 Isocontours of the stream function (the solid gray lines), Ψ, and the fitting formula of the critical recycling streamline at the midplane (Eq. (11); the dashed blue lines). The widest horseshoe streamlines characterized by ΨHS are highlighted with red. Isocontours of Ψ = 0.02−0.1 (panel a) and Ψ = 0.42–1.7 (panel b) are shown. |
| In the text | |
 |
Fig. 17 Quantities (panels a and b) and the relative error between ℬ and ℬ∞ (panel c) along a streamline through (x, y, z) = (0.001,0.01,0.2) (the solid colored line shown in Fig. 2c). The results were obtained from m005-hw003. Panels a and b: the solid and dotted black lines represent Bernoulli’s function, ℬ, and that in the far field, ℬ∞. The colored dashed lines correspond to the first to sixth terms in Bernoulli’s function. The dashed-dotted purple line in panel a corresponds to the x-coordinate of the streamline. The vertical solid lines in panels b and c denote twice the atmospheric radius. This figure should be compared to Fig. 2c. |
| In the text | |
 |
Fig. 18 Same as Fig. 17, but the results were obtained from m02-003. We picked up a streamline through (x, y, z) = (0.001,0.01,0.44). |
| In the text | |
 |
Fig. 19 Same as Fig. 9, but with the terminal velocity of dust (Eq. (45); dashed-dotted blue lines). Different colors correspond to different Stokes numbers. The vertical axis is on a log scale. |
| In the text | |
 |
Fig. 20 Atmospheric radius as a function of the planetary mass and the cooling time, β. We set ℳhw = 0. The star symbols correspond to the results obtained from the fiducial runs (Fig. 5). |
| In the text | |
 |
Fig. 21 Same as Fig. 3, but showing the dependence of the outflow speed on the cooling time. We set m = 0.2 in all panels. The results were obtained from m02-hw0-b001 (panel a), m02-hw0-b01 (panel b), m02-hw0-b10 (panel c), and m02-hw0-b100 (panel d). |
| In the text | |
 |
Fig. 22 Upper limit of the Stokes number of dust that affected by the outflow as a function of the planetary mass (Eq. (46)). |
| In the text | |
 |
Fig. B.1 Azimuthal gas velocity at the midplane averaged in the azimuthal direction in the spherical polar coordinates centered at the planet. The results were obtained from m003-hw003 and m003-hw003-01rinn. Different colors corresponds to different sizes of the inner boundary. The filled circle denotes the atmospheric radius. The dashed line shows the Keplerian speed. |
| In the text | |
 |
Fig. B.2 Time evolution of the atmospheric radius for different sizes of the inner boundary, rinn = rinn,0 (the solid lines) and rinn = 0.1 rinn,0 (the dashed lines). Different colors correspond to different Mach numbers. We set m = 0.03 and rsm = 0.1 Rgгav. |
| In the text | |
 |
Fig. C.1 Shell-averaged radial velocity of the gas in the spherical polar coordinates centered at the planet for different smoothing lengths, rsm = 0 (the dashed red line), rsm = 0.1 Rgrav (the solid blue line), and rsm = 3 rinn (the dotted yellow line). We assumed m = 0.1 in panel a and m = 0.5 in panel b. We set ℳhw = 0. |
| In the text | |
 |
Fig. C.2 Time evolution of the atmospheric radius for different smoothing lengths, rsm = 0 (the dashed red line), rsm = 0.1 Rgгav (the solid blue line), and rsm = 3 rinn (the dotted yellow line). We assumed m = 0.1 and ℳhw = 0 in panel a and m = 0.5 and ℳhw = 0 in panel b. |
| In the text | |
 |
Fig. D.1 Same as Fig. 9, but comparing the results obtained from hydrodynamical simulations with rsm = 0 (the cross symbols) and rsm = 0.1 Rgrav (the star symbols). |
| In the text | |
 |
Fig. F.1 Time evolution of the atmospheric radius for different planetary masses, m = 0.05 (panel a), m = 0.1 (panel b), m = 0.2 (panel c), and m = 0.5 (panel d). Different colors correspond to different Mach numbers. We set rsm = 0.1 Rgrav in this figure. |
| In the text | |
 |
Fig. G.1 Width of the horseshoe flow and the x-coordinate of the critical recycling streamline at the edge of the computational domain of hydrodynamical simulations. The solid, dotted, and dashed gray lines are given by the analytic formulae for the width of the horseshoe region (Eqs. (14) and (15)). The numerically calculated width of the outflow region (xrec,num, the circle symbols) is in better agreement with the analytic estimate based on Eq. (15) ( |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.