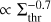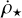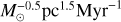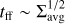| Issue |
A&A
Volume 682, February 2024
|
|
|---|---|---|
| Article Number | A76 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202347527 | |
| Published online | 05 February 2024 | |
Stellar feedback in the star formation–gas density relation: Comparison between simulations and observations
1
Aix Marseille Univ, CNRS, CNES, LAM
Marseille,
France
e-mail: paolo.suin@lam.fr
2
Institut Universitaire de France,
1 rue Descartes,
75005
Paris,
France
3
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris-Diderot Sorbonne Paris-Cité,
91191
Gif-sur-Yvette,
France
Received:
21
July
2023
Accepted:
24
November
2023
Context. The impact of stellar feedback on the Kennicutt–Schmidt (KS) law, which relates the star formation rate (SFR) to the surface gas density, is a topic of ongoing debate. The interpretation of high-resolution observations of individual clouds is challenging due to the various processes at play simultaneously and inherent biases. Therefore, a numerical investigation is necessary to understand the role of stellar feedback and identify observable signatures.
Aims. In this study we investigate the impact of stellar feedback on the KS law, aiming to identify distinct signatures that can be observed and analysed. By employing magnetohydrodynamic simulations of an isolated cloud, we specifically isolate the effects of high-mass star radiation feedback and protostellar jets. High-resolution numerical simulations are a valuable tool for isolating the impact of stellar feedback on the star formation process, while also allowing us to assess how observational biases may affect the derived relation.
Methods. We used high-resolution (<0.01 pc) magnetohydrodynamic numerical simulations of a 104 M⊙ cloud and followed its evolution under different feedback prescriptions. The set of simulations contained four types of feedback: one with only protostellar jets, one with ionising radiation from massive stars (>8 M⊙), one with the combination of the two, and one without any stellar feedback. In order to compare these simulations with the existing observational results, we analysed their evolution by adopting the same techniques applied in the observational studies. Then, we simulated how the same analyses would change if the data were affected by typical observational biases: counting young stellar objects (YSO) to estimate the SFR, the limited resolution for the column density maps, and a sensitivity threshold for detecting faint embedded YSOs.
Results. Our analysis reveals that the presence of stellar feedback strongly influences the shape of the KS relation and the star formation efficiency per free-fall time (ϵff). The impact of feedback on the relation is primarily governed by its influence on the cloud’s structure. Additionally, the evolution of ϵff throughout the star formation event suggests that variations in this quantity can mask the impact of feedback in observational studies that do not account for the evolutionary stage of the clouds. Although the ϵff measured in our clouds is higher than what is usually observed in real clouds, upon applying prescriptions to mimic observational biases we recover a good agreement with the expected values. From that, we can infer that observations tend to underestimate the total SFR. Moreover, this likely indicates that the physics included in our simulations is sufficient to reproduce the basic mechanisms that contribute to setting ϵff.
Conclusions. We demonstrate the interest of employing numerical simulations to address the impact of early feedback on star formation laws and to correctly interpret observational data. This study will be extended to other types of molecular clouds and ionising stars, sampling different feedback strengths, to fully characterise the impact of H II regions on star formation.
Key words: methods: numerical / stars: formation / ISM: clouds / HII regions / ISM: structure
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
The existence of a power-law relation between the star formation rate (SFR) per unit area and the gas surface density has long been established through observations of external galaxies (Schmidt 1959, 1963; Kennicutt 1989). The relation, known as the Kennicutt–Schmidt (KS) law, remarkably holds on scales spanning from entire galaxies to individual molecular clouds.
The dichotomy observed between starburst and non-starburst galaxies (Gao & Solomon 2004; Bigiel et al. 2008; Krumholz et al. 2012) might be a hint that stellar feedback plays a role in setting the star formation law (Ostriker & Shetty 2011), and Kennicutt & De Los Reyes (2021) suggested that this bimodal (or multi-modal) relation could originate from changes in the small-scale structure of the molecular interstellar medium. Indeed, even nearby galaxies show variations on 1.5 kpc scales when observed at higher angular resolution (Sun et al. 2023).
In effect, high-mass stars’ feedback, such as photo-ionising radiation, stellar winds, and supernova explosions, greatly impacts the surrounding environment (Chevance et al. 2022), but how it affects the star formation process is still not completely understood. For example, H II regions are capable of blowing out the molecular cloud from which they were born. Yet, their expansion locally compresses the gas, enhancing its density and directly impacting the properties of newly forming clumps (Zhang et al. 2020, 2021). These events can affect scales from tens of parsecs down to sub-parsec scales, possibly altering the local star formation properties (Palmeirim et al. 2017; Mazumdar et al. 2021), or even promoting the formation of other massive stars by inhibiting gas fragmentation (Hennebelle et al. 2022).
Recent observations from the James Webb Space Telescope of the NGC 628 galaxy (Barnes et al. 2023; Mayya et al. 2023) have shed light on the importance of understanding the role of early and smaller-scale high-mass stellar feedback for a reliable description of star formation laws. However, effects acting on such small scales are invisible when averaged on galactic scales but may be significant when considering singular molecular clouds. For this reason, observational studies have looked at the KS relation in several low- and high-mass molecular clouds (Gutermuth et al. 2011; Willis et al. 2015; Pokhrel et al. 2021; Bieging & Kong 2022), reporting a steepening of the exponent β when passing from the largest galactic scales (β ≈ 1.5; Kennicutt & Evans 2012; Kennicutt & De Los Reyes 2021) to the smallest ones (β ≈ 2; Evans et al. 2014).
Many theories attempt to explain the relation in all its shapes, but verifying or even constraining them represents a challenge for observational studies. Aside from resolution and sensitivity biases, the use of different tracers to derive the local physical conditions, and the multitude of processes ongoing simultaneously, make the comparison with the idealised cases extremely complicated. Moreover, these studies often rely on assumptions to compensate for the lack of 3D information and uncertainties in theoretical models, which hinders high-precision measurements of the real SFR–gas density relation.
For instance, one of the most popular theories is the model proposed by Krumholz & McKee (2005). Under the assumption that the main force governing the process is gravity, the model proposes a linear dependence between 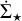 and Σgas, with the typical timescale given by the free-fall time, tff, of the region. Mathematically, this can be written as
and Σgas, with the typical timescale given by the free-fall time, tff, of the region. Mathematically, this can be written as
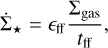 (1)
(1)
where ϵff, the star formation efficiency per free-fall time, is the only parameter required. All mechanisms other than gravity, feedback included, act to modify this coefficient. Despite its simplicity, the model yielded robust results (Krumholz et al. 2012; Usero et al. 2015; Utomo et al. 2018), opening the path to more refined theories that account for diverse local environmental properties. In particular, models incorporating the concept of multi-free-fall time are particularly promising (Hennebelle & Chabrier 2011; Padoan & Nordlund 2011; Federrath & Klessen 2012; Burkhart 2018). Unlike the original model, which relies on average density, these newer theories infer a density distribution to more accurately describe the gaseous environment. These models not only align more closely with observational data, but they also help explain the higher rates of star formation observed in starburst galaxies (Federrath 2013). Nevertheless, although elegant from an analytical perspective, using the local free-fall time represents a major challenge for astronomers. Specifically, obtaining this quantity typically requires resorting to strong assumptions to estimate the average volume density, such as the uniform-sphere approximation.
Even deriving the local SFR is complicated. In recent works conducted on nearby Galactic clouds, this is inferred by counting the number of detected young stellar objects (YSOs), but their mass and age have to be assumed (e.g. Lombardi et al. 2013; Lada et al. 2017). Additionally, in the densest regions of clouds, the count of YSOs is bound by the instruments’ sensitivity (Megeath et al. 2016). All these problems might explain why some studies claim that this parameter remains constant at all column densities (Pokhrel et al. 2021), while others suggest that the model cannot rovide a satisfactory description of the process in single molecular clouds (Evans et al. 2014; Lee et al. 2016; Bieging & Kong 2022)
Part of the problem could be that the molecular clouds used in these studies vary in mass, structure, star formation activity, and evolutionary stage. Some contain high-mass stars, while others are known to be low-mass star-forming regions. Encompassing all these effects simultaneously, the individual impacts on the star formation laws blur together. If stellar feedback actually plays a role, accurately separating the clouds according to their physical condition could solve the tension.
To overcome these challenges, we employed high-resolution numerical simulations to study the possible impact of different types of stellar feedback on the KS relation across the temporal evolution of one cloud. Using simulations allowed us to investigate the time evolution without having to deal with many of the difficulties associated with observations. Our simulation suite consisted of two runs where either protostellar jets or ionising radiation is modelled, one run in which both feedback mechanisms are included, and one simulation without any stellar feedback. In this way, we could analyse the effect of each of these feedback mechanisms separately.
The primary objectives of our work are twofold. First, we aimed to characterise the impact of stellar feedback on the star formation laws at the cloud scale and to disentangle the temporal evolution of these effects. Second, we sought to identify observational signatures associated with these phenomena. To achieve this, we analysed the simulations using observational techniques and compared our findings with recent observational results. Additionally, we considered the biases that may affect these procedures, focusing on the impact of YSO counting on the estimate of the SFR, the low resolution of column density maps, and the sensitivity limit for detecting faint and extinct stars. The purpose of our investigation is to improve our understanding of the intricate relationship between feedback, the evolutionary stage, and the observed properties of star-forming clouds.
The paper is organised as follows. In Sect. 2, we describe the simulations, and in Sect. 3 we explain the methods adopted to derive the KS relation and ϵff. Section 4 contains the results of the analysis, and in Sect. 5 we investigate the possible impact of observational biases on the observed relations. Finally, in Sect. 6 we contextualise the obtained results from a physical point of view. Conclusions are given in Sect. 7.
2 Numerical simulations
In our study, we analysed the simulations presented in Verliat et al. (2022). This set of four runs followed the evolution of the same isolated 104 M⊙ cloud under the influence of diverse feedback prescriptions: one with both ionising radiation and pro-tostellar jets, one with only ionising radiation, one with only protostellar jets, and one without any feedback. For simplicity, we refer to these runs as HIIR+PSJ, HIIR, PSJ, and NF. Thanks to the wide range of physical processes implemented and the high resolution achieved (of the order of thousands of AU), these simulations provide an ideal test-bed for investigating the effect of stellar feedback on the star formation properties and for testing the observational techniques employed in the field. Here we briefly describe the global properties and the setup of the model, referring to Verliat et al. (2022) for a complete description of how the various physical processes are implemented.
2.1 Code and numerical parameters
The magnetohydrodynamic simulations were carried out using the adaptive mesh refinement (AMR) code RAMSES (Teyssier 2002). The domain was set up as a cubic box of L = 30.4 pc, with open boundaries and an initial resolution of 1283 cells. Adopting five AMR levels, the maximum resolution achieved in each simulation is 7.4 × 10−3 pc (1.5 × 103 AU). The refinement criterion assures that the local Jeans length is always resolved with at least 40 cells. When the density of a cell at the highest AMR level exceeds 107 cm−3, a sink particle is created (Bleuler & Teyssier 2014). These sinks interact with the environment by accreting material from their surroundings and ejecting 1/3 of it under the form of protostellar jets. Each time the sinks accrete 120 M⊙ of gas overall, an ionising star is created inside one of them. The stellar mass is drawn from a Salpeter (1955) distribution between 8 and 120 M⊙. Then, the parametric mass-UV luminosity relation given in Vacca et al. (1996) sets its ionising flux. The sequence of stellar masses extracted had been preserved between simulations HIIR and HIIR+PSJ so that they formed the same stars throughout the cloud’s evolution.
2.2 Initial conditions
Initially, the cloud was modelled as an approximated 104 M⊙ Bonnor–Ebert sphere, with a diameter of 15.2 pc and a scale radius r0 = 2.5 pc. Its density was distributed according to
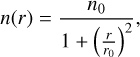 (2)
(2)
with r the distance from the box centre, and the central density n0 = 800 cm−3. The rest of the cube is filled with a uniform density of 8 cm−3 up to r = L, and the density in the remaining corner regions is set to 1 cm−3.
The gas thermal behaviour was parameterised with a cooling function that takes into account several chemical processes (see Audit & Hennebelle 2005 for a detailed description). This set the initial temperature of the medium at 10 K in the densest parts. The magnetic field was set to have a uniform mass-to-flux ratio of 8 in the x direction. Finally, the turbulence had been initialised with a velocity field normalised to have a Mach number of 6.7 in the central region, compatible with what is observed in Galactic star-forming clouds (Ma et al. 2022). A Kolmogorov power spectrum is then imposed to roughly reproduce the behaviour of the low-density gas filling the edges of the box, where the high temperatures make the flow sub/transonic and approximately incompressible (e.g. Porter et al. 1994). An alternative could have been to favour the low-temperature gas at the centre of the domain choosing a Burgers power spectrum, which better suits its high-Mach regime (Frisch & Bee 2000). In Sect. 4.2 we qualitatively discuss how this choice would not change the results of this work. However, we highlight that, given the idealised setup, the specific choice of the power spectrum has a marginal impact on the accuracy of the initial conditions. In effect, the mixture of high- and low-temperature gas is such that a simple power-law power spectrum cannot reproduce the turbulence spectrum characteristic of the medium1. Since the turbulent velocity field in our simulation is only an initial condition and not continuously driven, the velocity power spectrum will naturally evolve to adopt the energy cascade that is physically consistent with the system.
To conclude, we can summarise the initial parameters in terms of the characteristic free-fall timescales of the central region, tff ≈ 1.5 Myr2. With these initial conditions, the sound-crossing timescale of the inner region inside r0 is defined by 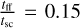 , while the Alfvén-crossing time by
, while the Alfvén-crossing time by 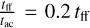 . The turbulent-crossing time was set equal to the free-fall time.
. The turbulent-crossing time was set equal to the free-fall time.
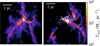 |
Fig. 1 Density projections along the z-axis for two snapshots of simulation HIIR+PSJ, at 2.3 Myr (left) and 3.15 Myr (right). White dots mark the sink particles’ positions. The left panel captures the formation of the central hub, with three filaments converging into it. In the right panel we can see how the giant H II region, originating from the lower-left filament, restructured the cloud after about 0.4 Myr. |
2.3 Evolution
Given the initial conditions, which initialised the isolated cloud with a central density enhancement, the system naturally developed a hub system within a couple of megayears, with three filaments converging onto it (cf. Fig. 1, left). The four simulations evolved identically until the formation of the first star at 1.45 Myr. Afterwards, jets started to reshape the cloud and runs PSJ and HIIR+PSJ departed from the ones without jets. Lacking any feedback initially, the HIIR and NF clouds rapidly increased the total SFR – measured as the total amount of gas converted into sinks throughout two subsequent snapshots, and divided by their temporal separation (generally ≈ 0.04 Myr). In those simulations the SFR reached its maximum at ≈ 2 Myr (Fig. 2), while in the other two, the presence of protostellar jets lowers the SFR by a factor of 4 initially3. Between 1.8 Myr and 2.15 Myr, a few ‘low’ mass ionising stars (between 8 and 18 M⊙) formed in HIIR, but their associated H II regions only mildly affected the global evolution. By 2.15 Myr, while the gravity-only run settled down to a roughly constant 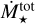 , the onset of a powerful H II region, generated by a 100 M⊙ star, caused the SFR to drop at the same level of the other two feedback simulations. In a little more than 1 Myr the cloud was wiped out and the SFR flattened at low values. In HIIR+PSJ, the same ionising stars formed at ≈ 2.75 Myr.
, the onset of a powerful H II region, generated by a 100 M⊙ star, caused the SFR to drop at the same level of the other two feedback simulations. In a little more than 1 Myr the cloud was wiped out and the SFR flattened at low values. In HIIR+PSJ, the same ionising stars formed at ≈ 2.75 Myr.
Afterwards, the behaviour mirrored that of radiation-only simulation. In the right graph of Fig. 1 we can see the H II region in the process of dispersing the gas, although some triggered over-density regions clearly arose from the shell compression. Instead, the SFR of PSJ, as that of NF, remained roughly constant up to the end of the simulation.
Therefore, it is clear that the presence of ionising stars overall reduces 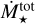 . Nevertheless, in literature, it is still greatly debated whether or not high-energy radiation can enhance the SFR and modify the star formation properties on a local scale (Pomarès et al. 2009; Elmegreen 2011; Dale et al. 2013; Roccatagliata et al. 2013; Menon et al. 2020; Wall et al. 2020). In this paper, we approached this issue from an observational perspective, investigating the underlying physical mechanisms and identifying potential biases arising from the absence of a third dimension and temporal evolution.
. Nevertheless, in literature, it is still greatly debated whether or not high-energy radiation can enhance the SFR and modify the star formation properties on a local scale (Pomarès et al. 2009; Elmegreen 2011; Dale et al. 2013; Roccatagliata et al. 2013; Menon et al. 2020; Wall et al. 2020). In this paper, we approached this issue from an observational perspective, investigating the underlying physical mechanisms and identifying potential biases arising from the absence of a third dimension and temporal evolution.
 |
Fig. 2 Temporal evolution of the SFR in the different simulations. The black line shows the simulation without any feedback. The run with only protostellar jets and the one with only ionising radiation are represented in blue and orange, respectively. Finally, the red line individuates the simulation with both feedback mechanisms active. The stars mark the formation of the giant H II region. The vertical dashed lines highlight the approximate time of the snapshots used in Figs. 4-5. |
3 Methods
3.1 Extraction of quantities
To extract the relation between the SFR and the gas density we first projected the simulation’s snapshots along the three axes at the highest resolution, giving maps of 40962 pixels. Then, we divided the column density map into a set of 500 contours, evenly log-spaced between 80 M⊙ pc−2 and Σgas = 3 × 104 M⊙ pc−2. As in some recent observational works (Pokhrel et al. 2021; Bieging & Kong 2022; Hu et al. 2022), the properties of a given contour level (the average density Σavg and its area A) were obtained integrating over all the pixels above the corresponding threshold Σthr. Figure 3 gives an idea of the contours’ shape, highlighting three levels at 500, 2500, 5000 M⊙ pc−2 in simulation HIIR+PSJ at 2.7 Myr. We did not make distinctions between detached regions that may have formed while increasing Σthr, but we averaged all the quantities on the contour total area. Following Bieging & Kong (2022), we refer to this approach as ‘cumulative’ to avoid any confusion with the ‘differential’ one, where quantities are extracted from the region included in between two subsequent contours. We retained only contours with a total surface area greater than 500 pixels, to exclude possible resolution effects on the data. As shown in Sect. 5.2 and Appendix B, this criterion was conservative in most of the cases.
Finally, we computed the SFR density 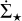 associated with each contour as
associated with each contour as
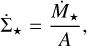 (3)
(3)
where Ṁ★ is the total mass accreted per unit time by the sinks enclosed in the contour, calculated with the same method described in the previous section. We remark that observational studies do not have direct access to such a quantity. Indeed, the limited knowledge of YSOs’ evolution leads to significant uncertainties both on their age and mass. The common approach is to assume an average mass and age for all of them, so that the SFR is proportional to the number of YSOs counted within a contour (e.g. Lombardi et al. 2014; Zari et al. 2016; Lada et al. 2017; Pokhrel et al. 2021). However, adopting this approach in our analysis would probably be affected by numerical effects. Indeed, despite the high resolution, it is not possible to carefully follow the formation of single stars and therefore to reproduce the correct initial mass function (IMF), because this would require resolution of the order of tens of AU (Lee & Hennebelle 2018). Presently, no simulation has been capable of covering such a wide range of scales while including all the physical processes treated here. We further address this issue in Sect. 5.1.
 |
Fig. 3 Zoomed-in view of the central cluster of the HIIR+PSJ simulation, at 2.7 Myr. Light green, dark green, and black lines mark the contours at 500, 2500, and 5000 M⊙ pc−2, respectively. The region covers an area of 1.8 pc × 1.1 pc. |
3.2 Free-fall timescale
The model introduced by Krumholz & McKee (2005) has the advantage of providing a physical interpretation of the law, obtaining an exponent of 1.5, similar to what is observed at galactic scales (in 2D 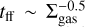 ). However, the drawback is the introduction of the new variable tff, particularly difficult to obtain from cloud-scale observations. The common approach is to evaluate tff from the projected quantities under uniform sphere approximation (Murray 2011; Pokhrel et al. 2021; Bieging & Kong 2022). Since our purpose is to supply a possible numerical counterpart to observational studies of the KS law, we employed here the same technique. In particular, for each contour, we extracted its typical free-fall timescale estimating its volume density as
). However, the drawback is the introduction of the new variable tff, particularly difficult to obtain from cloud-scale observations. The common approach is to evaluate tff from the projected quantities under uniform sphere approximation (Murray 2011; Pokhrel et al. 2021; Bieging & Kong 2022). Since our purpose is to supply a possible numerical counterpart to observational studies of the KS law, we employed here the same technique. In particular, for each contour, we extracted its typical free-fall timescale estimating its volume density as
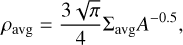 (4)
(4)
and thus computed 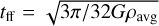 , with G the gravitational constant.
, with G the gravitational constant.
Studies conducted on galactic surveys frequently report low values of the ϵff, ranging around 0.01 (Leroy et al. 2008, 2017; Utomo et al. 2018). However, recent works dealing with Milky Way clouds, instead, report higher values, but with a significant dispersion, going from ϵff < 10−3 to ϵff > 0.1, with peaks of 0.3 (Murray 2011; Lee et al. 2016).
As mentioned in Sect. 1, more evolved models were developed in the past decade. Computing a typical timescale from the local properties of the region, theories using the multi-free-fall time proved to provide valid results on galactic and extragalactic scales. However, we highlight that our intent is to compare the star formation properties of the inner structures of molecular clouds as recovered from numerical simulations and observations. In this context, we are not aiming to utilise the most advanced model to calculate ϵff, but rather follow the very same approach used in the works based on observation we are comparing to.
 |
Fig. 4 Comparison of the star formation–gas density relation between the different simulations, shown at four different times (t = 2.1, 2.7, 3.0, and 3.5 Myr), which illustrates the evolution of the cloud. In HIIR the giant H II region develops after 2.2 Myr, while for HIIR+PSJ it starts to restructure the environment at later times (> 2.75 Myr). The colour code is the same as in Fig. 2. |
4 Resulting star formation relations
4.1 Kennicutt–Schmidt relation
We show the resulting KS relation obtained for our clouds in Fig. 4. To facilitate the comparison between simulations, we scaled the y-axis by 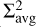 , which represents the characteristic slope observed in the radiation simulations. This is also consistent with typical values reported in observational studies conducted on cloud scales (see e.g. Gutermuth et al. 2011; Lada et al. 2013; Pokhrel et al. 2021). The plots show the projection along the z-axis, but comparisons with other lines of sight yielded similar conclusions (see our Appendix A and Khullar et al. 2019). We selected four specific snapshots to represent key stages in the simulations’ evolution:
, which represents the characteristic slope observed in the radiation simulations. This is also consistent with typical values reported in observational studies conducted on cloud scales (see e.g. Gutermuth et al. 2011; Lada et al. 2013; Pokhrel et al. 2021). The plots show the projection along the z-axis, but comparisons with other lines of sight yielded similar conclusions (see our Appendix A and Khullar et al. 2019). We selected four specific snapshots to represent key stages in the simulations’ evolution:
At 2.1 Myr: by this time the SFR of run NF has almost reached the steady state (Fig. 2), while cloud HIIR has not been affected by the eruption of the large H II region.
At 2.7 Myr: here, due to the presence of the 100 M⊙ star, the SFR of the radiation-only simulation decreased and reached the level of the runs with jets. The same star has yet to be formed in HIIR+PSJ.
At 3.0 Myr: at this time, the four clouds all present significant differences between each other, and the main H II region has started to restructure the full-feedback run (HIIR+PSJ).
Finally, we plot the situation at the very last moments of the radiation simulations, at 3.5 Myr.
The plots reveal that the different feedback prescriptions lead to significant differences in the clouds’ evolution. In the early stages, when only a few small H II regions developed, jets dominate as the primary feedback mechanism. Therefore, at 2.1 Myr, we observe strong similarities between the runs NF and HIIR (without jets) and PSJ and HIIR+PSJ (with jets). Similarly to what is displayed in Fig. 2, we see that stellar ejecta reduce the global SFR by a factor of 445, without sensibly modifying the shape of the relation.
By 2.7 Myr the situation has changed substantially. Overall, the KS relation has become an almost pure power law in all simulations. Towards the low-density edge, a clear change of slope is visible in runs with feedback, while it is almost invisible in run NF. Probably, this broken power law identifies the point at which stellar feedback counteracts the global collapse, and the cloud’s KS relation departs from that typical of a free-fall motion. Moreover, we can note HIIR+PSJ showing a slightly steeper relation compared to the jets-only simulation. Interpreting the graph, this means that the relative fraction of gas mass that is converted into stars per unit time increases at high densities when ionising radiation is included, even though at this time the total SFR is similar (Fig. 2). This behaviour is even more accentuated comparing runs HIIR and NF, where the first achieves higher values of 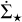 at high densities, with an exponent of its KS relation of ≈2.
at high densities, with an exponent of its KS relation of ≈2.
At 3.0 Myr, the different exponent of the HIIR+PSJ and PSJ KS relation became even more evident. Another visible feature is the departure from the power-law behaviour of run HIIR at Σavg ≈ 103 M⊙ pc−2. Given the sudden decline, we can deduce that the main H II region, dispersing the gas, sensibly lowered the column density around a sink formation site. Then, when Σthr exceeds the maximum column density of that region, the observed SFR suddenly drops. Run NF, instead, exhibited an increase in 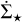 towards higher column densities. In the simulation, this increase coincides with the moment in which a clump, formed in one of the filaments, converges into the central hub.
towards higher column densities. In the simulation, this increase coincides with the moment in which a clump, formed in one of the filaments, converges into the central hub.
Finally, at 3.5 Myr, the large H II region has fully developed in the simulation HIIR+PSJ and its 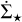 versus Σavg relation mirrors that of the radiation-only simulation. Its slope, as well as the one from HIIR, closely approaches
versus Σavg relation mirrors that of the radiation-only simulation. Its slope, as well as the one from HIIR, closely approaches 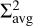 . With the system reaching a steady state, the NF run does not display significant differences compared to the previous graph, while PSJ experiences a further steepening of the relation.
. With the system reaching a steady state, the NF run does not display significant differences compared to the previous graph, while PSJ experiences a further steepening of the relation.
 |
Fig. 5 Evolution of the modified KS relation. The colour code is the same as in Fig. 2. In the graph at 3 Myr, we report the values of ϵff of the 12 Galactic clouds studied in Pokhrel et al. (2021), excluding contours with Σavg above their reliability criterion (grey lines). The grey shaded areas represent the uncertainties they gave for the ϵff measures. The axis ratios are kept the same as in Fig. to facilitate a visual comparison of slopes with the respective counterparts in the KS relation. |
4.2 Modified Kennicutt–Schmidt relation
The evolution of ϵff across time (Fig. 5), obtained inverting Eq. (1), closely reproduces that seen in Fig. 4. However, the differences in both slope and scatter between the PSJ and radiative simulations are less pronounced. In effect, one of the major strengths of the modified relation is its reduced scatter among different objects, compared to the traditional KS law (Hu et al. 2022). Observational datasets typically consist of multiple clouds at various evolutionary stages, characterised by different strengths of feedback mechanisms within the complex. Given that our simulated clouds feature different feedback prescriptions, the smaller dispersion observed in the four ϵff values aligns well with expectations based on observational results.
As in Fig. 4, the curves from radiative simulations tend to achieve higher values towards the high-density end of the graphs. Additionally, the ϵff of these simulations appears almost flat, while in runs NF and PSJ it shows a steady decline of ϵff as the density increases. Indeed, this qualitative result is confirmed when fitting a power law such as
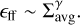 (5)
(5)
At each snapshot, we fitted6 the relation using only contours that satisfy the 500 pixels contours and have Σavg > 300 M⊙ pc−2.
This allowed us to exclude the different relation visible at lower densities (i.e. larger scales), which might be affected by the initial condition of the cloud. Indeed, the evolutionary timescales of these regions are much longer, and the system employs more time to relax from the initial conditions here. We repeated this procedure for all three projection axes and assigned to the average γ an uncertainty given by the standard deviation from the three lines of sight (the errors from the fit procedure were completely negligible).
Figure 6 shows the evolution of the exponent γ across the simulation. Again, we see that only simulations with radiation ultimately set on γ values close to zero. A ϵff independent of Σavg has also been reported in nearby Galactic cloud by Pokhrel et al. (2021), although in their dataset the value of γ scatters between −0.33 (AFGL 490) and 0.06 (Cygnus-X)7.
Nevertheless, compared to their work, we found sensibly higher values of ϵff. For comparison, we overplotted the curves they obtained for the 12 Galactic clouds in the graph at 3 Myr in Fig. 5, and we can see how the two measures differ by a factor of ≈ 5. While the influence of the SFR prescription cannot be ruled out entirely, it is improbable that such a difference is attributable entirely to the code setup8. Indeed, we expect the total simulated SFR to be reasonably accurate in runs with jets9, and the sink spatial distribution reliable at least up to Σthr > 3000 M⊙ pc−2 (roughly 3.5 in the graph, cf. with Fig. 8). Moreover, even though our simulations could not accurately follow the dynamical evolution of sinks due to the softening of gravity, Lombardi et al. (2013) and Lada et al. (2013) show that in real clouds the diffusion process due to N-body interactions does not contribute significantly to the observed 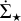 at low densities. Finally, we outline that adopting a Burgers power spectrum as initial condition for turbulence would probably not solve the tension observed with the ϵff reported in Pokhrel et al. (2021). Indeed, a steeper power spectrum means that much less kinetic energy is stored in small scales, leading to more coherent large-scale flows. Therefore, imposing a Burgers spectrum in the velocity field would have enhanced the formation of bound structures (Clark & Bonnell 2005), likely increasing the cloud’s SFR and consequently the discrepancy with the SFRs obtained from the observational data.
at low densities. Finally, we outline that adopting a Burgers power spectrum as initial condition for turbulence would probably not solve the tension observed with the ϵff reported in Pokhrel et al. (2021). Indeed, a steeper power spectrum means that much less kinetic energy is stored in small scales, leading to more coherent large-scale flows. Therefore, imposing a Burgers spectrum in the velocity field would have enhanced the formation of bound structures (Clark & Bonnell 2005), likely increasing the cloud’s SFR and consequently the discrepancy with the SFRs obtained from the observational data.
Therefore, we looked at three potential biases that may influence observational measurements. We emphasise right away that our intent is to understand how different biases could interact with the feedback mechanisms to affect the results. Although full agreement with Pokhrel et al. (2021) ϵff measures is recovered, giving a precise quantitative prediction of the impact of these biases is beyond the purpose of this paper.
 |
Fig. 6 Evolution of the slope of ϵff across the simulations. The shaded areas outline the 1σ standard deviation of the fitted exponent as obtained from the three different axes of projection. The stars mark the formation of the main H II region, as in Fig. 2 |
5 Impact of biases on the observed relation
We examined, in our simulations, the effect of three biases that affect observations: the assumption that the SFR is proportional to the number of Class 0/1 YSOs detected, the impact of resolution on column density maps, and the presence of embedded stars not visible to the telescope due to extinction. In this section we aim to understand their impact on the observed ϵff−Σavg relation. In Fig. 7, we plotted the effects of these biases separately, using the snapshot at 3 Myr as a reference (blended curves in the background). At that time, the contribution of ionising radiation in HIIR+PSJ was not as dominant as in HIIR yet. This allowed us to study how these biases intertwine with the different levels of feedback.
5.1 YSO counts
The first bias we considered is caused by the uncertainty on detected YSOs’ age and mass. Since observations cannot access the temporal evolution of the star-forming clouds, observers rely on theoretical models to constrain these properties in young stars. As mentioned in Sect. 3, the usual procedure is to assign a mean mass and age to each of them. The mass corresponds to the average mass of the IMF, which is typically around 0.5 M⊙. For Class 0/I objects, the age is commonly assumed to be 0.5 Myr Dunham et al. 2015; Megeath et al. 2022). With these values, the SFR of each contour is Ṁ★ = 1 M⊙Myr−1 × NYSO, where NYSO is the number of young stars it contains. Imitating this technique, we counted only the sinks younger than 0.5 Myr. However, we explained in Sect. 3 that the IMF in our cloud is not well sampled due to insufficient resolution. Indeed, the average stellar mass resulted to be higher than the expected 0.5 M⊙, with 〈msink〉 ≈ 0.75 M⊙ in the feedback runs and 2 M⊙ in NF at the end of the simulation. Using a coefficient of 1 M⊙ Myr−1 in the above equation would underestimate the total SFR by a factor of 〈msink〉 /0.5 M⊙. Therefore, we corrected this by assigning to each contour an internal SFR given by Ṁ★ = 〈msink〉/(0.5 Myr) × NYSO.
The first plot in Fig. 7 (upper left) demonstrates that this particular approximation well reproduces the true SFR of the cloud. Except for NF, the detected ϵff(Σavg) preserves good agreement at all contours. Minor deviations are observed at high-density contours, probably due to random fluctuations in the instantaneous SFR. In these regions, tff becomes much smaller than the assumed build-up time of 0.5 Myr, so that the integration time becomes much longer than the dynamical timescale (Pokhrel et al. 2021).
 |
Fig. 7 Effect of four different observational biases on the ϵff−Σavg relation of the clouds at 3 Myr. The blended curves are the same as in the 3 Myr panel of Fig. 5, and the grey lines are the 12 Galactic clouds studied in Pokhrel et al. (2021). |
5.2 Spatial resolution
To reproduce the second bias, we smoothed the column density maps, lowering the resolution of our ‘observation’. This bias cannot impact the measured SFR, but rather affects the ob served cloud structure10. Placing the cloud at a distance11 of 650 pc, we reproduced the physical resolution of the Herschel satellite in the 500 μm band (36 arcsec), convolving the column density maps with a Gaussian beam with a standard deviation of 0.05 pc (equivalent to a full width half maximum of 0.11 pc). We did not modify the criterion given in Sect. 3, because now the threshold does not have to define a limit for the physical reliability of the data. Moreover, in this way, we could analyse how a low spatial resolution can affect the measured ϵff if this limitation is not carefully considered.
Smoothing the maps produces what is visible in the upper right graph of Fig. 7. Except HIIR, the curves of the simulations almost overlap with the original ones below 1000 M⊙ pc−2 (presented in Fig. 5). Then, an increase is visible at the right end in HIIR+PSJ and PSJ, while this is evident at low Σavg in the radiation-only run. This behaviour can be easily explained by examining how the function A(Σavg) enters the relation.
Combining Eqs. (3), (1), and (4), we can express ϵff as12
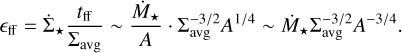 (6)
(6)
It follows that the cloud structure – A(Σavg) – plays a central role in defining the behaviour of ϵff across the column density contours. As we approach the resolution limit, the integrated probability distribution function of Σavg (usually referred to as integrated N-PDF) drops sharply, leading to an increase in the efficiency per free-fall time thanks to the negative exponent of A. This causes the knee visible at high densities.
In effect, by plotting the contour area as a function of their Σavg at high and low resolution in Fig. 8, we can identify the same feature. Moreover, we notice that the adopted threshold of 500 pixels (dashed line) effectively safeguards the data from resolution effects, as in the first graph the exponential decrease occurs beyond this point. Degrading the resolution moved this feature to lower Σavg, which caused the curves to bend towards the high-density end of Fig. 7.
However, this alone cannot explain the full picture. Indeed, we see a steepening of the power-law tail of integrated N-PDF even at low densities. Technically, such variation should not be expected, as the smoothing should not significantly affect areas much larger than the beam size13 (see e.g. Tassis et al. 2010; Schneider et al. 2015). Most probably, the pitfall lies in the integration over the whole contour. As explained in Sect. 3, the method we applied does not take into account separated structures within the same column density level. Consequently, resolution can have a much stronger impact on the observed N-PDF of a highly fragmented structure. At 3 Myr, the HIIR cloud has been significantly restructured by the H II region, resulting in the destruction of the central hub and the formation of several disconnected high-density clumps. The smoothing gives rise to a completely different γ evolution.
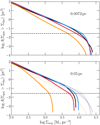 |
Fig. 8 Cumulative area of the contours as a function of their average column density at 3 Myr. The two images are obtained from the original column density map (top) and the one smoothed with a Gaussian beam with 0.05 pc standard deviation (bottom). As in Fig. 7, the blended lines in the bottom panel are the ones plotted at 0.0073 pc resolution. The dashed line marks the area corresponding to the 500 pixel criterion. |
5.3 Instrument sensitivity
Finally, we accounted for the possibility that some YSOs may be too heavily extinct to be detected in the inner regions of the cloud. We considered the observations to be taken with the Spitzer Infrared Array Camera (IRAC) 4.5 μm filter, which is extensively adopted in SFR measurements (see e.g. Evans et al. 2009; Gutermuth et al. 2011; Lombardi et al. 2013). For each sink, we evaluated its apparent magnitude as
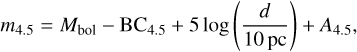 (7)
(7)
where Mbol is the bolometric luminosity of the sink, BC4.5 its bolometric correction for IRAC 4.5 μm filter, d the distance of the cloud, which we set to 650 pc, and A4.5 the extinction at 4.5 μm.
To recover the needed stellar properties such as the luminosity (L), radius (R), and bolometric correction, we compared the age and mass of each sink with the evolutionary tracks obtained from the MIST web tool14. However, considering that in Class 0/I objects the luminosity due to gas accretion, Lacc, is often a consistent fraction of their total luminosity Ltot (Antoniucci et al. 2008; Fiorellino et al. 2021), we corrected the sink’s bolometric luminosity as Ltot = L + Lacc (Fiorellino et al. 2023). Following Hartmann et al. (1998), we define Lacc as
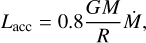 (8)
(8)
where M and Ṁ★ are the sink mass and its accretion rate averaged over ≈ 0.05 Myr. Finally, we obtained the last ingredient A4.5 evaluating the amount of gaseous material in front of the sinks, with the conversion A4.5 = 0.572 · AK provided in Ascenso etal. (2013), and adopting Σgas = 197 M⊙ pc−2 · AK (hence, Σgas = 384 M⊙ pc−2 · A4.5; Lada et al. 2013).
To be detected, we required sinks to have m4.5 < 14.5 mag, which is the sensitivity limit at 4.5 μm reported in the Spitzer/IRAC Candidate YSO (SPICY) catalogue (Kuhn et al. 2021). However, we stress once again that, with these simplified prescriptions, our goal is to understand how those biases could affect the observed ϵff–Σavg relation. Indeed, observers employ different instruments at different wavelengths to limit the impact of these biases (Harvey et al. 2007; Megeath et al. 2016). These corrections are particularly demanding to reproduce in simulations and require specific treatments that are beyond the scope of our study.
The effect of the instrument sensitivity is shown in the third graph of Fig. 7 (lower left). A notable feature is the reduction of ϵff average value. Even if caution has to be used in the interpretation, the resolution of the tension with Pokhrel et al. (2021) data could imply that the physics implemented in PSJ and HIIR+PSJ is sufficient to describe the mechanisms involved in setting the ϵff in molecular clouds. In our simulations, adding a detection threshold has a strong impact on the observed SFR, leading to an underestimation of a factor of 3 of ϵff in the full-feedback run, and ≈ 5 in the jet-only run. This difference is solely caused by the different distribution of YSOs, as supported by the fact that this bias has a softer impact on the HIIR simulation. Indeed, by 3 Myr the main H II had already significantly restructured the cloud, dispersing a consistent part of the gas, reducing the extinction experienced by stars.
Another consequence of this bias is the rapid fall of the relation at high Σavg. Being a log–log graph, the slope of ϵff is directly affected by the fractional variation of Ṁ★ at each contour. Most of the stars – and so the majority of the SFR – reside at high column densities. Therefore, all low-Σ contours have comparable Ṁ★. Similar drops are also observed in Pokhrel et al. (2021) clouds when Σthr exceeds their reliability criterion (defined by the column density at which tff > 0.5 Myr). It is important to highlight that this reduction is specific to the cumulative method. Since 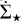 is obtained through the integration over the entire contour, missing YSO in the central regions lowers the SFR of every contour, even those with low Σavg. In contrast, a differential approach like that used in Evans et al. (2014) would not be affected, but it would require rougher assumptions for computing tff and would suffer from the lower statistics of YSOs found at low densities.
is obtained through the integration over the entire contour, missing YSO in the central regions lowers the SFR of every contour, even those with low Σavg. In contrast, a differential approach like that used in Evans et al. (2014) would not be affected, but it would require rougher assumptions for computing tff and would suffer from the lower statistics of YSOs found at low densities.
We can show this phenomenon more accurately if we extract the relation between Ṁ★ and the contour column density. In Fig. 9a, we plotted the evolution of Ṁ★ for different contour levels at the maximum resolution, as a function of the column density threshold of that contour Σthr. With this change of x-axis, we can provide a comparison with the model by Lada et al. (2013), shown in the graph as a dashed green line. According to this work, the SFR included in each contour can be described as
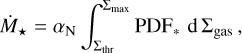 (9)
(9)
where αN is the normalisation constant and PDF* is the probability of finding a star at a given gas column density. As derived from the California Cloud in their work, we used
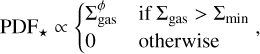 (10)
(10)
with ϕ = −0.7 and Σmin = 100 M⊙ pc−2, and integrated up to a column density Σmax = 2000 M⊙ pc−2 (AK ≈ 10 mag).
The net differences between our simulations and Eq. (10) are clear and quantitative. In fact, attempting a fit leaving Σmax and ϕ as free parameters and Σmin equal to the threshold at which the first accreting star is removed, leads to ϕ ≈ 1 in all the simulations, while for the four clouds studied Lada et al. (2017) this varies between −1 and −0.3. This picture changed after the application of all the observational biases described above (Fig. 9b). Qualitatively, the curves now resemble the model much more closely. Repeating the fit of Eq. (10), we found that only HIIR+PSJ and PSJ converged to reasonable values of ϕ (−0.32 ± 0.02 and −0.42 ± 0.02, respectively)15.
We can evaluate the derivative of Eq. (9) to understand how the sensitivity changes the contribution of Ṁ★(Σthr) ~ Ṁ★(Σavg) to the observed KS relation. Assuming that Eq. (10) holds at every density contour, with little algebra we arrive at
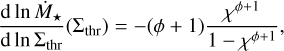 (11)
(11)
with χ = Σthr/Σmax. At lower densities, two ingredients contribute to the initial slope of Ṁ★. The first is exponent ϕ, which Lombardi et al. (2013) show to be the sum between the exponent −q of the A(Σavg) function and the exponent of the KS relation as obtained from the differential approach. The steeper this last relation, the more stars will be present at higher densities and hence the shallower the logarithmic derivative will be. The second is χ, which is the combination of the scale at which Eq. (10) ceases to be valid, and the sensitivity limit of the instrument.
 |
Fig. 9 SFR of density contours as a function of their threshold column density at 3.0 Myr. The data are normalised to the total SFR at that time. The dotted part of the lines identifies isosurfaces with an area smaller than 500 pixels. The right panel shows the same distribution, but as it appears after the application of all three biases explained in the text – YSO counting for the SFR, resolution lowered to 0.05 pc, and the masking of extinct stars. The dashed green lines reproduce the model from Lada et al. (2017), with a threshold of 2000 M⊙ pc−2 and a stellar probability distribution function of PDF* ∝ |
5.4 Biases combined
To conclude, in the last panel of Fig. 7, we plotted ϵff as seen after the application of all these biases on our column density maps. First, we masked sinks too extinct to be detected. Then, we smoothed the column density maps. Finally, we repeated the same analysis described in Sect. 3, using the new YSO count prescription to evaluate 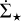 .
.
The resulting relations are similar to what we would obtain from the simple sum of all the effects, meaning that any coupling between the biases has little effect on the resulting relation. However, a notable exception arises when looking at the curve of NF. In this panel, ϵff is much higher than the one observed in the ‘Sensitivity’ graph. This cannot be due to the smoothing of the column density map, as we said that this does not affect the total SFR detected. Therefore, the YSO counting must increase the observed SFR, although the first panel clearly shows that this decreases the average ϵff when taken alone.
The answer resides in the same argument we used in Sect. 5.1. Counting YSOs accurately reproduces the SFR only when the correct average mass is used. However, if the mass distribution varies as we approach the densest regions of the cloud, then a new bias is introduced. In effect, as we increase Σthr we observe a consistent increase in the average stellar mass of the contours. In NF, the average sink mass in the hub increases significantly, and thus 〈m★〉 overestimates the mean mass of YSOs found at low densities while underestimating the ones found at the highest ones. Hence, if we remove the stars in the centre of the cloud, this approximation tends to overestimate the SFR observed.
We remark that in our cloud, this phenomenon is probably attributable to numerical effects (see Sect. 3), since in all the simulations containing feedback 〈m★〉 remains fairly constant even at high Σthr. Nevertheless, this offers insights into the interpretation of observations as well. Whether the mass function varies as a function of the local density is a subject still under debate (Raboud & Mermilliod 1998; Stolte et al. 2002; Bonnell 2008). Moreover, in young massive clusters, the mass segregation process takes place in very short timescales, possibly leading to an effect of this kind (Portegies Zwart et al. 2010; Allison et al. 2010; Suin et al. 2022).
6 The shape of the relation
6.1 Cloud structure
In the previous section, we have found clues that the function A(Σavg) plays a central role in shaping the relation. Figure 8 demonstrated that the effects produced by low resolution on the observed cloud structure directly translate into similar features in the ϵff versus Σavg graph. Simultaneously, Fig. 9 shows that the more we can access the SFR in the highest densities of the cloud, the more Ṁ★ appears flat at lower densities. This is because most of the SFR happens in the densest regions. Consequently, the shape of the relation at low-mid densities is mostly governed by the slope of the A(Σavg), while at high densities it intertwines with the loss of stars between contours. Which of the two dominates in this regime may vary from cloud to cloud (e.g. in the last panel of Fig. 7, compare HIIR with the other runs).
In Sect. 5.2, we find that the presence of ionising feedback does play a role in restructuring the cloud, changing the observed area-to-column-density relation. Even at the maximum resolution, in Fig. 8, some differences are evident between the various setups. In the radiation runs, the compression caused by the expansion of the H II region fronts is not sufficient to overcome the gas dispersion, and comprehensively the total amount of dense gas decreases, leading to a steeper relation. To measure this effect quantitatively, we fitted a power-law relation
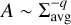 (12)
(12)
at each snapshot. We performed the fit with the Python built-in function curve_fit, using only the contours having Σavg > 400 M⊙ pc−2 (log Σavg ≈ 2.6) and an area greater than 500 pixels. The first constraint allowed us to exclude from the fit the largest scales of the simulations, which are dominated by the global collapse and thus display an exponent q similar to that of NF. In Fig. 10, we plotted the fit results, averaged over the three axes of projection. The uncertainties associated with the fit are negligible, so the shaded area represents the dispersion between the three lines of sight. Without any support from protostellar jets, the runs NF and HIIR collapsed faster and achieved lower values of q (more dense gas at high Σavg). The onset of large H II regions froze the exponent (at ≈ 2.3 Myr in HIIR and ≈ 2.8 Myr in HIIR+PSJ), which settled to a value of roughly 2 (>1.85 in HIIR+PSJ, ≈ 2.05 in HIIR).
Conversely, in NF the exponent continued to decrease down to roughly 1.6, close to what is reported and expected in gravoturbulent simulations without feedback (Burkhart et al. 2015, 2017; Chen et al. 2018). Notably, the run with only jets achieves a shallower relation than the run with only gravity, reaching values as low as 1.4. We notice that the values of q between NF and PSJ cross almost exactly at 3 Myr, so that the steeper relation is not visible in Fig. 8. However, looking at Fig. 2, we see that this excess of dense gas is not rewarded by an increase in the total SFR. This is probably because compressed material is ejected at high relative velocities relative to the surrounding gas flow.
We can compare these findings with what is usually observed in real molecular clouds16 (cf. Lombardi et al. 2015; Spilker et al. 2021). Our simulated clouds attained slopes similar to the observed ones, although it appears that values of q near or above 2 are more frequent in our Galaxy. Moreover, the fact that only clouds with radiation attained a similar exponent may represent a central result of this work. Indeed, Abreu-Vicente et al. (2015) conducted an extensive study on the N-PDF distribution in 195 Galactic molecular clouds, concluding that clouds with H II regions naturally develop a power-law tail with an index -2. The authors suggest this slope to be caused by the formation of an isothermal-sphere-like structure. Indeed, based on the work from Kritsuk et al. (2011), they show that for a spherical density distribution of the form ρgas ~ rn, with r the distance from the centre, a relation between n and q can be established, such that n = 1 + 2/q. Setting q = 2, we recovered the isothermal sphere distribution. Looking at Fig. 8, the presence of a mechanism that pushes q towards this value is also suggested by the smaller dispersion between the line of sights that characterises the radiative runs (although a larger sample of simulation would be needed to confirm this result statistically). This could potentially mean that radiation feedback plays a fundamental role in setting the density structure of clouds. This could provide valuable insights to distinguish between different classes of cloud.
Interestingly, the same study from Abreu-Vicente et al. (2015) detects that on average the star-forming clouds observed without H II regions display slopes steeper than the one reported here. This seems to contrast with our results. Nonetheless, such a steep slope is visible at the early stages of the simulations (left-hand side of Fig. 8). Thus, a possible explanation is that the clouds that have such a high q are simply younger than the others. Possibly, those clouds will proceed to evolve a shallower slope, but eventually form a massive star that interrupts the process as happened in HIIR+PSJ.
 |
Fig. 10 Temporal evolution of the fitted exponent q, averaged over the three axes, in the four simulations. The colour code is the same as in Fig. 2. The shaded areas represent the standard deviation of the sample due to the differences between the lines of sight. The uncertainties on the single fits are negligible. As in Fig. 2, the stars highlight the moment of the eruption of the main H II region. |
6.2 Impact of feedback
Figure 10 gives us the necessary instruments to interpret the behaviour of the observed KS relations in Figs. 4–5, since we found in the previous section that Ṁ★ has very little impact at low column densities. In the two figures, the radiative simulations show a slope nicely falling onto a 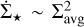 in the first and ϵff ~ const in the second. This behaviour can be perfectly explained by the reported q ≈ 2. Concerning the KS relation, combining Eq. (3) with the A(Σavg) in Eq. (12), it is clear that a nearly constant Ṁ★ leads to
in the first and ϵff ~ const in the second. This behaviour can be perfectly explained by the reported q ≈ 2. Concerning the KS relation, combining Eq. (3) with the A(Σavg) in Eq. (12), it is clear that a nearly constant Ṁ★ leads to 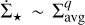 . Doing the same for Eq. (6), it is easy to find that under the same Ṁ★ ~ const approximation, a value of q ≈ 2 leads to a constant ϵff. Looking closely we can find that Figs. 6–10 closely resemble each other. At the same time, the weaker dependence on A of Eq. (6) allows the relation to be more resilient to the effect of feedback, explaining the smaller deviations between the simulations compared to the differences found in the KS relations (see Sect. 6.1).
. Doing the same for Eq. (6), it is easy to find that under the same Ṁ★ ~ const approximation, a value of q ≈ 2 leads to a constant ϵff. Looking closely we can find that Figs. 6–10 closely resemble each other. At the same time, the weaker dependence on A of Eq. (6) allows the relation to be more resilient to the effect of feedback, explaining the smaller deviations between the simulations compared to the differences found in the KS relations (see Sect. 6.1).
This also suits the shallow behaviour of HIIR and HIIR+PSJ in the 3D analysis (Fig. B.1). With little algebra, it is possible to show that if the same assumption of spherical symmetry is valid, then 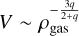 .If q ≈ 2, the influence of the volume in the tridimensional version of Eq. (6) is expected to be negligible, since
.If q ≈ 2, the influence of the volume in the tridimensional version of Eq. (6) is expected to be negligible, since
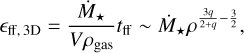 (13)
(13)
with the exponent going to zero for q = 2.
Summing up all these findings, we conclude that when ionising radiation is included in the simulation, the cloud systematically develops a KS relation more weighted towards higher column densities, as well as a higher ϵff and ϵff, 3D – although with a reduced impact. Thus, although radiation negatively impacts the SFR on the largest scale and reduces the amount of dense gas available, the remaining dense gas manifests a higher ϵff.
Unfortunately, the interpretation of the observed trend is not unique. One possible explanation is that the expansion of ionised gas promotes star formation at high densities in an active way. In this scenario, the radiation front would create favourable conditions for the development of new star formation sites, compressing the surrounding gas until it becomes gravitationally unstable (collect and collapse mechanism; Elmegreen & Lada 1977), creating converging shocks at clump surfaces capable of enhancing significantly their core density (radiation driven implosion; Sandford et al. 1982), or acting as a compressive driver for local turbulence, (as suggested by Menon et al. 2020, 2021). Alternatively, it could be suggested that massive stars wipe out only the gas that is not sufficiently gravitationally bound, leaving only the dense gas that would have formed stars regardless. This again would lead to deriving a higher star formation efficiency in the region, since the local SFR would roughly remain the same, but the observed amount of dense gas would be lower. Which of the two processes prevails is unclear and subject to intense studies in the field. Either way, the outcome of this interplay produces observable features in our cloud, which could aid in interpreting observational data. For instance, in a sample of real clouds, the differences in their evolutionary stage or variations in the feedback mechanisms’ strengths could contribute to the observed scatter in the derived KS laws.
Indeed, Figs. 4–5 show that the relations undergo significant variations over a timescale of a few million years, consistently with what is reported in Grudić et al. (2018). As time progresses, the four extracted relations intersect at different column densities. This has implications for observational studies that extract single measurements of ϵff or 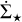 from each cloud. These analyses often adopt a common minimum Σthr to define the extent of the clouds. Our results emphasise that achieving similar values of ϵff or
from each cloud. These analyses often adopt a common minimum Σthr to define the extent of the clouds. Our results emphasise that achieving similar values of ϵff or 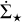 at a specific column density contour does not necessarily indicate similarities in the underlying physical conditions.
at a specific column density contour does not necessarily indicate similarities in the underlying physical conditions.
To further illustrate this point, we mimicked the analysis on an observational set of star-forming complexes, treating each snapshot as an observation of a distinct cloud. We did not apply the biases of Sect. 5, to evince conclusions that do not depend on the assumptions made in that section. For each snapshot, we extracted the value of ϵff corresponding to a given column density contour. We chose five different column densities as reference points: at 200, 500, 1000, 2000, and 5000 M⊙ pc−2. Consequently, we obtained four datasets (one for each feedback prescription) and computed the temporal average and dispersion of ϵff for each simulation. The question is whether we can distinguish the different physical conditions of the clouds when we lack information about their temporal evolution and the dependence on Σavg.
The results, presented in Fig. 11, reveal that, except for NF, the averages of the different simulations are indistinguishable because of their significant temporal variations. If these were actual observations, the impact of stellar feedback would always be secondary compared to the variation due to the cloud evolution. This does not mean that feedback has no valuable impact on the SFR, since, looking at the full picture (Fig. 5), ϵff changes substantially with Σavg when the feedback prescription is changed. Therefore, the cause is that ϵff is highly varying over time and that the different runs achieve the same ϵff during their evolution, but at different times. Only when looking at ϵff(Σavg) a clear dependence on the feedback mechanism becomes evident.
In addition, we notice that the differences just mentioned are mostly visible above the range of densities typically studied. Studies such as Lombardi et al. (2015), Pokhrel et al. (2021), or Bieging & Kong (2022) reach maximum column densities of the order of 1000 Σavg, while the high resolution of these simulations allows us to probe an order of magnitude more. This density range is mainly governed by the cloud’s structure, and observations may not be able to catch variations caused by feedback mechanisms.
Therefore, what is most interesting for observational datasets we can get with the present instrumentation are the differences in the slopes, which are detectable even at lower densities. From our study, we would expect clouds with strong radiation feedback to display the steeper slopes in the 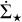 versus Σavg plot. It is extremely interesting to notice that in Pokhrel et al. (2021), clouds dominated by strong radiative feedback (Orion A, Sh2-140, Cep OB3, and Cygnus X) show on average a steeper slope than the other ones (Ophiucus, Orion B, Perseus, Aquila North, Aquila South, NGC 2264, AFGL 490, and Mon R2). In particular, the mean exponent of the KS relation found for the first clouds is 2.24 with a dispersion of 0.14, while the average for the second group is 1.87, with a dispersion of 0.24. Although the sample is limited, this supports our findings, and further studies that extend the sample could provide full confirmation of the trend.
versus Σavg plot. It is extremely interesting to notice that in Pokhrel et al. (2021), clouds dominated by strong radiative feedback (Orion A, Sh2-140, Cep OB3, and Cygnus X) show on average a steeper slope than the other ones (Ophiucus, Orion B, Perseus, Aquila North, Aquila South, NGC 2264, AFGL 490, and Mon R2). In particular, the mean exponent of the KS relation found for the first clouds is 2.24 with a dispersion of 0.14, while the average for the second group is 1.87, with a dispersion of 0.24. Although the sample is limited, this supports our findings, and further studies that extend the sample could provide full confirmation of the trend.
 |
Fig. 11 Time average of log ϵff at 250, 500, 1000, 2500, and 5000 M⊙ pc−2 in the various simulations. The data have been slightly displaced to make the comparison clearer. The different markers highlight different axes of projections, and the error bars show the dispersion of ϵff measured at a given column density due to its evolution across the simulation. The effects from the line of sight and stellar feedback are not enough to overcome this dispersion, such that in a set of clouds at different evolutionary stages they will not be visible if the dependence from Σavg is not taken into account. |
7 Conclusions
We conducted an in-depth analysis of high-resolution magnetohydrodynamic simulations to investigate the impact of stellar feedback on two different star formation models: the original KS law and the Krumholz & McKee (2005) 1ff model. Applying techniques commonly used in observational works, we reveal that substantial differences arise when stellar radiation and protostellar jets act to reshape the cloud structure. In particular, we find that the coupling between the area–column density relation and feedback mechanisms plays a major role in the observed star formation law, much more than the stellar distribution itself.
When only protostellar jets are active, they compress part of the gas such that the N-PDF becomes more weighted towards high densities. However, this does not translate directly into an increase in the SFR, instead resulting in a shallower KS law and a lower ϵff at higher column densities. On the other hand, H II regions act to disperse the gas, leading to a steeper A versus Σavg relation, with an exponent that settles around a value of q = 2. This particular value also validates the study from Abreu-Vicente et al. (2015) conducted on Galactic molecular clouds. Even though the presence of ionising stars decreases the global SFR, the steepness of the A(Σavg) function is such that the observed star formation efficiency is higher at high column densities. The result is confirmed even for ϵff, although the weaker dependence on A mitigates the differences with the jet-only run.
We also applied prescription to emulate the effect of three different biases observations have to deal with. While assigning the same mass and age to each YSO detected does not significantly alter the observed SFR, the presence of a detection threshold for embedded YSOs and the limited resolution of column density maps can modify the shape of the relation at the highest densities. In particular, we show that low-resolution column density maps can affect the A–Σavg relation when observing a highly structured cloud. In addition, we report a significant impact due to the presence of a detection threshold, which leads to both a steep drop in the observed ϵff(Σavg) relation at high densities and an underestimation of the global SFR.
When applied altogether, the effect did not couple efficiently, so the resulting relation was close to that obtained by simply summing the biases. The only exception was NF, where the mass distribution of sinks changed towards the centre of the cloud. This caused an overestimation of the SFR due to the intertwined action of the YSO counting and the lower completeness of the detected embedded sources. Although this could be attributed to numerical effects, it could play a role when observing regions where the mass segregation mechanism is ongoing (either dynamical or due to the initial cluster formation). When all the biases are applied, we recover a good agreement with the observational results from Pokhrel et al. (2021), which suggests that the physics included in our simulation is sufficient to describe the process of star formation at cloud scales.
Finally, having access to the temporal evolution of our cloud, we could show that the exponent of the KS relation and the value of ϵff can vary significantly with time. This means that in a sample of real clouds, where different evolutionary stages are present simultaneously, extracting the value of ϵff at a single column density would hide the effect of feedback. Indeed, distinct departures between the models only become evident when considering the dependence on Σavg.
We will extend the sample of numerical simulations to cover a wider range of initial conditions and feedback strengths, to parameterise the impact of ionising stars as a function of cloud and stellar properties, and to perform a direct comparison with observational data.
Acknowledgements
We thank Mark R. Krumholz for the valuable insights provided. A.Z. thanks the support of the Institut Universitaire de France (IUF). We thank the referee for his relevant and focused insights, which have helped us enhancing the contextual relevance and clarity of the developments outlined in this work. This research has received funding from the European Research Council synergy grant ECOGAL (Grant: 855130).
Appendix A Effect of projection axis
In our analysis we mainly show the results from the projection along the z-axis. However, the other axes behave similarly and no notable difference has to be reported. Figure A.l shows how the KS relation changes when averaging between the three lines of sight. The shaded areas represent the 1 σ dispersion of the three curves. It is visible that the variability decreases with time, and the results remain coherent. This could also be guessed looking at Fig. 6, where the dispersion of the fitted slope is small.
 |
Fig. A.l Same as Fig. 5, but using the average and 1 σ dispersion of ϵff obtained from the three lines of sight. Data are masked when at least one of the three contours at the same density threshold does not satisfy the 500 pixel criterion. |
Appendix B 2D versus 3D star formation relation
The non-trivial correlation between local quantities and their projected value constitutes a major challenge to the interpretation of astrophysical observations. With simulations, one can accurately preserve the evolution of physical variables for each cell, accessing the full 3D information. Therefore, it is of great interest to understand the extent to which projection effects impact the results. Hence, we extended the same cumulative method described in Sect. 3 to perform the 3D analysis. We divided the cloud into 500 volume density contours, evenly spaced in log between 103 and 107 cm−3. Converting the 500pixel criterion used for 2D contours, we require the isosurfaces to contain at least a volume greater than 5003/2 · (7.3 × 10−3pc)3 ≈ 4 × 10−3pc3. We plotted the outcome in Fig. B.1, where now we scaled the y-axis (the volume SFR density 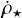 ) by
) by 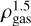 , where ρgas is the average volume density of the contour. The choice of the exponent is justified by Fig. 5. Since Eq. (1) display a constant behaviour with Σavg in the radiative simulations, we expect a similar feature when dividing by
, where ρgas is the average volume density of the contour. The choice of the exponent is justified by Fig. 5. Since Eq. (1) display a constant behaviour with Σavg in the radiative simulations, we expect a similar feature when dividing by 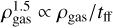 .
.
The first thing we could estimate from the plots is the limit up to which data can be considered reliable. Indeed, we expect the efficiency to increase sharply as we approach the density threshold for sink formation (Khullar et al. 2021), and we can see a steep the rise towards the very high-density edge of the graph. Keeping in mind that caution is always necessary when comparing 3D and 2D datasets, the distance between the knee of the rise and our reliability limit (beginning of the dashed line) gave us confidence that our constraint provides sufficient protection against resolution effects.
Comparing these graphs with their respective counterparts in Fig. 4, we can confirm that the features observed in the projection are supported by the 3D analysis. The plot at 2.1 Myr shows that its 3D version closely resembles the 2D version. At t = 2.7 Myr, runs with jets exhibit similar trends. At the same time, the radiation-only simulation presents a comparable 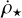 to the run with both jets and radiation at low densities, but an higher efficiency at higher densities. Graphs at 3.0 and 3.5 Myr, instead, require more attention. Indeed, the snapshot at 3.0 Myr confirms the findings of the previous section, with the relative behaviours that remain preserved, even if the differences appear to be smaller. In particular, one may notice that the departure of HIIR+PSJ from PSJ happens ‘later’. However, comparing points between the two graphs is dangerous because, without a characteristic scale, there is no exact conversion from column to volume density.
to the run with both jets and radiation at low densities, but an higher efficiency at higher densities. Graphs at 3.0 and 3.5 Myr, instead, require more attention. Indeed, the snapshot at 3.0 Myr confirms the findings of the previous section, with the relative behaviours that remain preserved, even if the differences appear to be smaller. In particular, one may notice that the departure of HIIR+PSJ from PSJ happens ‘later’. However, comparing points between the two graphs is dangerous because, without a characteristic scale, there is no exact conversion from column to volume density.
At 3.5, Myr, the slope displayed by simulations with radiation flattened out even more. However, there are some notable differences. In the HIIR run, the star formation event has nearly ceased, and the SFR density curve lies below the others. On the other hand, the HIIR+PSJ run achieves a 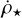 comparable to PSJ at high column densities n, although this happens just below the reliability limit. Nevertheless, this does not affect the conclusions drawn so far. Indeed, at other times in the simulations, the observed trends are consistent with the previous discussions.
comparable to PSJ at high column densities n, although this happens just below the reliability limit. Nevertheless, this does not affect the conclusions drawn so far. Indeed, at other times in the simulations, the observed trends are consistent with the previous discussions.
 |
Fig. B.1 Evolution of |
References
- Abreu-Vicente, J., Kainulainen, J., Stutz, A., Henning, T., & Beuther, H. 2015, A&A, 581, A74 [CrossRef] [EDP Sciences] [Google Scholar]
- Allison, R. J., Goodwin, S. P., Parker, R. J., Portegies Zwart, S. F., & de Grijs, R. 2010, MNRAS, 407, 1098 [NASA ADS] [CrossRef] [Google Scholar]
- Antoniucci, S., Nisini, B., Giannini, T., & Lorenzetti, D. 2008, A&A, 479, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appel, S. M., Burkhart, B., Semenov, V. A., et al. 2023, ApJ, 954, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Ascenso, J., Lada, C. J., Alves, J., Román-Zúñiga, C. G., & Lombardi, M. 2013, A&A, 549, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, A. T., Watkins, E. J., Meidt, S. E., et al. 2023, ApJ, 944, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Bieging, J. H., & Kong, S. 2022, ApJ, 938, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bleuler, A., & Teyssier, R. 2014, MNRAS, 445, 4015 [Google Scholar]
- Bonnell, I. A. 2008, in ASP Conf. Ser., 390, Pathways Through an Eclectic Universe, eds. J. H. Knapen, T. J. Mahoney, & A. Vazdekis, 26 [NASA ADS] [Google Scholar]
- Burkhart, B. 2018, ApJ, 863, 118 [CrossRef] [Google Scholar]
- Burkhart, B., Collins, D. C., & Lazarian, A. 2015, ApJ, 808, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhart, B., Stalpes, K., & Collins, D. C. 2017, ApJ, 834, L1 [Google Scholar]
- Chen, H. H.-H., Burkhart, B., Goodman, A., & Collins, D. C. 2018, ApJ, 859, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Krumholz, M. R., et al. 2022, MNRAS, 509, 272 [Google Scholar]
- Clark, P. C., & Bonnell, I. A. 2005, MNRAS, 361, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2013, MNRAS, 431, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L. 2015, MNRAS, 447, 3390 [CrossRef] [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, Neal J., I., et al. 2015, ApJS, 220, 11 [Google Scholar]
- Elmegreen, B. G. 2011, in EAS Pub. Ser., 51, Star Formation in the Local Universe, eds. C. Charbonnel, & T. Montmerle, 45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Elmegreen, B. G., & Lada, C. J. 1977, ApJ, 214, 725 [Google Scholar]
- Evans, Neal J., I., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, Neal J., I., Heiderman, A., & Vutisalchavakul, N. 2014, ApJ, 782, 114 [CrossRef] [Google Scholar]
- Federrath, C. 2013, MNRAS, 436, 3167 [CrossRef] [Google Scholar]
- Federrath, C. 2015, MNRAS, 450, 4035 [Google Scholar]
- Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 156 [Google Scholar]
- Fiorellino, E., Manara, C. F., Nisini, B., et al. 2021, A&A, 650, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiorellino, E., Tychoniec, L., Cruz-Sáenz de Miera, F., et al. 2023, ApJ, 944, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, U., & Bec, J. 2000, in New Trends in Turbulence, eds. M. Lesieur, A. Yaglom, & F. David (Springer EDP-Sciences), 341 [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Grudić, M. Y., Hopkins, P. F., Faucher-Giguère, C.-A., et al. 2018, MNRAS, 475, 3511 [CrossRef] [Google Scholar]
- Gutermuth, R. A., Pipher, J. L., Megeath, S. T., et al. 2011, ApJ, 739, 84 [Google Scholar]
- Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [Google Scholar]
- Harvey, P., Merín, B., Huard, T. L., et al. 2007, ApJ, 663, 1149 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2011, ApJ, 743, L29 [Google Scholar]
- Hennebelle, P., Lebreuilly, U., Colman, T., et al. 2022, A&A, 668, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hu, Z., Krumholz, M. R., Pokhrel, R., & Gutermuth, R. A. 2022, MNRAS, 511, 1431 [Google Scholar]
- Kennicutt, Robert C., J. 1989, ApJ, 344, 685 [CrossRef] [Google Scholar]
- Kennicutt, Robert C., J., & De Los Reyes, M. A. C. 2021, ApJ, 908, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Khullar, S., Krumholz, M. R., Federrath, C., & Cunningham, A. J. 2019, MNRAS, 488, 1407 [Google Scholar]
- Khullar, S., Federrath, C., Krumholz, M. R., & Matzner, C. D. 2021, MNRAS, 507, 4335 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Krumholz, M. R., Dekel, A., & McKee, C. F. 2012, ApJ, 745, 69 [Google Scholar]
- Kuhn, M. A., de Souza, R. S., Krone-Martins, A., et al. 2021, ApJS, 254, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., Roman-Zuniga, C., Forbrich, J., & Alves, J. F. 2013, ApJ, 778, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lewis, J. A., Lombardi, M., & Alves, J. 2017, A&A, 606, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018, A&A, 611, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, E. J., Miville-Deschênes, M.-A., & Murray, N. W. 2016, ApJ, 833, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2017, ApJ, 846, 71 [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2013, A&A, 559, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, A1 [Google Scholar]
- Ma, Y., Wang, H., Zhang, M., et al. 2022, ApJS, 262, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Mayya, Y. D., Alzate, J. A., Lomelí-Núez, L., et al. 2023, MNRAS, 521, 5492 [CrossRef] [Google Scholar]
- Mazumdar, P., Wyrowski, F., Urquhart, J. S., et al. 2021, A&A, 656, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [Google Scholar]
- Megeath, S. T., Gutermuth, R. A., & Kounkel, M. A. 2022, PASP, 134, 042001 [CrossRef] [Google Scholar]
- Menon, S. H., Federrath, C., & Kuiper, R. 2020, MNRAS, 493, 4643 [CrossRef] [Google Scholar]
- Menon, S. H., Federrath, C., Klaassen, P., Kuiper, R., & Reiter, M. 2021, MNRAS, 500, 1721 [Google Scholar]
- Murray, N. 2011, ApJ, 729, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, D., Goyal, S., & Chang, P. 2018, MNRAS, 475, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., & Shetty, R. 2011, ApJ, 731, 41 [Google Scholar]
- Padoan, P., & Nordlund, Å. 2011, ApJ, 730, 40 [Google Scholar]
- Palmeirim, P., Zavagno, A., Elia, D., et al. 2017, A&A, 605, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pokhrel, R., Gutermuth, R. A., Krumholz, M. R., et al. 2021, ApJ, 912, L19 [CrossRef] [Google Scholar]
- Pomarès, M., Zavagno, A., Deharveng, L., et al. 2009, A&A, 494, 987 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431 [NASA ADS] [CrossRef] [Google Scholar]
- Porter, D. H., Pouquet, A., & Woodward, P. R. 1994, Phys. Fluids, 6, 2133 [NASA ADS] [CrossRef] [Google Scholar]
- Raboud, D., & Mermilliod, J. C. 1998, A&A, 333, 897 [NASA ADS] [Google Scholar]
- Roccatagliata, V., Preibisch, T., Ratzka, T., & Gaczkowski, B. 2013, A&A, 554, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Sandford, M. T., I., Whitaker, R. W., & Klein, R. I. 1982, ApJ, 260, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1963, ApJ, 137, 758 [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015, A&A, 575, A79 [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., Walch, S., Girichidis, P., et al. 2017, MNRAS, 472, 4797 [NASA ADS] [CrossRef] [Google Scholar]
- Spilker, A., Kainulainen, J., & Orkisz, J. 2021, A&A, 653, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stolte, A., Grebel, E. K., Brandner, W., & Figer, D. F. 2002, A&A, 394, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suin, P., Shore, S. N., & Pavlík, V. 2022, A&A, 667, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, J., Leroy, A. K., Ostriker, E. C., et al. 2023, ApJ, 945, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Tassis, K., Christie, D. A., Urban, A., et al. 2010, MNRAS, 408, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Usero, A., Leroy, A. K., Walter, F., et al. 2015, AJ, 150, 115 [Google Scholar]
- Utomo, D., Sun, J., Leroy, A. K., et al. 2018, ApJ, 861, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Verliat, A., Hennebelle, P., González, M., Lee, Y.-N., & Geen, S. 2022, A&A, 663, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wall, J. E., Mac Low, M.-M., McMillan, S. L. W., et al. 2020, ApJ, 904, 192 [Google Scholar]
- Willis, S., Guzman, A., Marengo, M., et al. 2015, ApJ, 809, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zari, E., Lombardi, M., Alves, J., Lada, C. J., & Bouy, H. 2016, A&A, 587, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, S., Zavagno, A., Yuan, J., et al. 2020, A&A, 637, A40 [EDP Sciences] [Google Scholar]
- Zhang, S., Zavagno, A., Lopez-Sepulcre, A., et al. 2021, A&A, 646, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
It is worth noting that modern simulations can overcome this limitation by using zoom-in techniques, modelling larger galactic environments and then narrowing the focus to specific regions, using them as the initial setup for more detailed simulations (Dobbs 2015; Seifried et al. 2017). While yielding greater reliability, this approach sacrifices generalisability, as the results become are directly linked to the unique properties of the selected region.
A similar impact of jets on the total SFR has also been observed in similar studies, such as Federrath (2015) – who reports a reduction of roughly a factor of 3 – Appel et al. (2023) – roughly 2 – and Murray et al. (2018) – also slightly more than 2. Although the ratio between the SFRs in NF and PSJ simulations is initially higher, agreement with these studies is recovered once both simulations reach the steady-state.
Our findings are not the first to reveal a mismatch between the observed and simulated SFRs and ϵff. Specifically, Federrath (2015) has also highlighted that numerical simulations often result in higher SFRs than those reported in observational studies.
Resolution applied to YSOs detection constitutes instead a different issue. In high  zones, the crowding effect could lead to consistent decreases in completeness. Megeath et al. (2016, 2022) showed how accounting for this the number of YSOs could increase by 30% in the Orion complex.
zones, the crowding effect could lead to consistent decreases in completeness. Megeath et al. (2016, 2022) showed how accounting for this the number of YSOs could increase by 30% in the Orion complex.
That is the average distance of the clouds considered in Pokhrel et al. (2021) study.
With little algebra, it is possible to demonstrate that the exponent of the N-PDF computed in logscale is the same of the one obtained from the integrated N-PDF (Lada et al. 2017).
All Figures
 |
Fig. 1 Density projections along the z-axis for two snapshots of simulation HIIR+PSJ, at 2.3 Myr (left) and 3.15 Myr (right). White dots mark the sink particles’ positions. The left panel captures the formation of the central hub, with three filaments converging into it. In the right panel we can see how the giant H II region, originating from the lower-left filament, restructured the cloud after about 0.4 Myr. |
| In the text | |
 |
Fig. 2 Temporal evolution of the SFR in the different simulations. The black line shows the simulation without any feedback. The run with only protostellar jets and the one with only ionising radiation are represented in blue and orange, respectively. Finally, the red line individuates the simulation with both feedback mechanisms active. The stars mark the formation of the giant H II region. The vertical dashed lines highlight the approximate time of the snapshots used in Figs. 4-5. |
| In the text | |
 |
Fig. 3 Zoomed-in view of the central cluster of the HIIR+PSJ simulation, at 2.7 Myr. Light green, dark green, and black lines mark the contours at 500, 2500, and 5000 M⊙ pc−2, respectively. The region covers an area of 1.8 pc × 1.1 pc. |
| In the text | |
 |
Fig. 4 Comparison of the star formation–gas density relation between the different simulations, shown at four different times (t = 2.1, 2.7, 3.0, and 3.5 Myr), which illustrates the evolution of the cloud. In HIIR the giant H II region develops after 2.2 Myr, while for HIIR+PSJ it starts to restructure the environment at later times (> 2.75 Myr). The colour code is the same as in Fig. 2. |
| In the text | |
 |
Fig. 5 Evolution of the modified KS relation. The colour code is the same as in Fig. 2. In the graph at 3 Myr, we report the values of ϵff of the 12 Galactic clouds studied in Pokhrel et al. (2021), excluding contours with Σavg above their reliability criterion (grey lines). The grey shaded areas represent the uncertainties they gave for the ϵff measures. The axis ratios are kept the same as in Fig. to facilitate a visual comparison of slopes with the respective counterparts in the KS relation. |
| In the text | |
 |
Fig. 6 Evolution of the slope of ϵff across the simulations. The shaded areas outline the 1σ standard deviation of the fitted exponent as obtained from the three different axes of projection. The stars mark the formation of the main H II region, as in Fig. 2 |
| In the text | |
 |
Fig. 7 Effect of four different observational biases on the ϵff−Σavg relation of the clouds at 3 Myr. The blended curves are the same as in the 3 Myr panel of Fig. 5, and the grey lines are the 12 Galactic clouds studied in Pokhrel et al. (2021). |
| In the text | |
 |
Fig. 8 Cumulative area of the contours as a function of their average column density at 3 Myr. The two images are obtained from the original column density map (top) and the one smoothed with a Gaussian beam with 0.05 pc standard deviation (bottom). As in Fig. 7, the blended lines in the bottom panel are the ones plotted at 0.0073 pc resolution. The dashed line marks the area corresponding to the 500 pixel criterion. |
| In the text | |
 |
Fig. 9 SFR of density contours as a function of their threshold column density at 3.0 Myr. The data are normalised to the total SFR at that time. The dotted part of the lines identifies isosurfaces with an area smaller than 500 pixels. The right panel shows the same distribution, but as it appears after the application of all three biases explained in the text – YSO counting for the SFR, resolution lowered to 0.05 pc, and the masking of extinct stars. The dashed green lines reproduce the model from Lada et al. (2017), with a threshold of 2000 M⊙ pc−2 and a stellar probability distribution function of PDF* ∝ |
| In the text | |
 |
Fig. 10 Temporal evolution of the fitted exponent q, averaged over the three axes, in the four simulations. The colour code is the same as in Fig. 2. The shaded areas represent the standard deviation of the sample due to the differences between the lines of sight. The uncertainties on the single fits are negligible. As in Fig. 2, the stars highlight the moment of the eruption of the main H II region. |
| In the text | |
 |
Fig. 11 Time average of log ϵff at 250, 500, 1000, 2500, and 5000 M⊙ pc−2 in the various simulations. The data have been slightly displaced to make the comparison clearer. The different markers highlight different axes of projections, and the error bars show the dispersion of ϵff measured at a given column density due to its evolution across the simulation. The effects from the line of sight and stellar feedback are not enough to overcome this dispersion, such that in a set of clouds at different evolutionary stages they will not be visible if the dependence from Σavg is not taken into account. |
| In the text | |
 |
Fig. A.l Same as Fig. 5, but using the average and 1 σ dispersion of ϵff obtained from the three lines of sight. Data are masked when at least one of the three contours at the same density threshold does not satisfy the 500 pixel criterion. |
| In the text | |
 |
Fig. B.1 Evolution of |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.