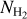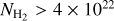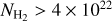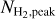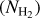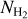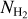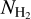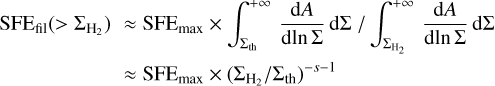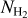| Issue |
A&A
Volume 688, August 2024
|
|
|---|---|---|
| Article Number | A163 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202449908 | |
| Published online | 20 August 2024 | |
Understanding the star formation efficiency in dense gas: Initial results from the CAFFEINE survey with ArTéMiS★
1
Laboratoire d'Astrophysique (AIM), Université Paris-Saclay, Université Paris Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
e-mail: michael.mattern@cea.fre-mail: philippe.andre@cea.fr
2
Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France
3
Institut Universitaire de France, Paris, France
4
IAP, Sorbonne Université, CNRS (UMR 7095), 75014 Paris, France
5
School of Physics and Astronomy, Cardiff University, The Parade,Cardiff CF24 3AA, UK
6
Leibniz-Institut für Astrophysik Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
7
Kyushu Kyoritsu University, 1-8, Jiyugaoka, Yahatanishi-ku, Kitakyushu-shi, Fukuoka 807-8585, Japan
8
National Research Council of Canada, Herzberg, Astronomy and Astrophysics Research Centre, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
9
Department of Physics and Astronomy, University of Victoria, Victoria, BC V8P 5C2, Canada
10
National Astronomical Observatory of Japan, Osawa 2-21-1, Mitaka, Tokyo 181-8588, Japan
11
European Southern Observatory, Karl Schwarzschild Straße 2, 85748 Garching, Germany
Received:
8
March
2024
Accepted:
18
May
2024
Context. Despite recent progress, the question of what regulates the star formation efficiency (SFE) in galaxies remains one of the most debated problems in astrophysics. According to the dominant picture, star formation (SF) is regulated by turbulence and feedback, and the SFE is ~1–2% or less per local free-fall time on all scales from Galactic clouds to high-redshift galaxies. In an alternate scenario, the star formation rate (SFR) in galactic disks is linearly proportional to the mass of dense gas above some critical density threshold ~104 cm–3.
Aims. We aim to discriminate between these two pictures thanks to high-resolution submillimeter and mid-infrared imaging observations, which trace both dense gas and young stellar objects (YSOs) for a comprehensive sample of 49 nearby massive SF complexes out to a distance of d ~ 3 kpc in the Galactic disk.
Methods. We used data from CAFFEINE, a complete 350/450 µm survey with APEX/ArTéMiS of the densest portions of all southern molecular clouds at d ≲ 3 kpc, in combination with Herschel data to produce column density maps at a factor of ~4 higher resolution (8") than standard Herschel column density maps (36″). Our maps are free of any saturation effect around luminous high-mass pro-tostellar objects and resolve the structure of dense gas and the typical ~0.1 pc width of molecular filaments out to 3 kpc, which is the most important asset of the present study and is impossible to achieve with Herschel data alone. Coupled with SFR estimates derived from Spitzer mid-infrared observations of the YSO content of the same clouds, this allowed us to study the dependence of the SFE on density in the CAFFEINE clouds. We also combine our findings with existing SF efficiency measurements in nearby clouds to extend our analysis down to lower column densities.
Results. Our results suggest that the SFE does not increase with density above the critical threshold and support a scenario in which the SFE in dense gas is approximately constant (independent of free-fall time). However, the SF efficiency measurements traced by Class I YSOs in nearby clouds are more inconclusive, since they are consistent with both the presence of a density threshold and a dependence on density above the threshold. Overall, we suggest that the SF efficiency in dense gas is primarily governed by the physics of filament fragmentation into protostellar cores.
Key words: stars: formation / ISM: clouds / clouds – ISM / ISM: structure / submillimeter: ISM
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Understanding what regulates the star formation efficiency (SFE) in the giant molecular clouds (GMCs) of galaxies is a fundamental open question in star formation (SF) research. The star formation rate (SFR) on multiple scales in galaxies is known to be strongly correlated with the mass of available molecular gas (e.g., Kennicutt 1998; Bigiel et al. 2011). Overall, SF is observed to be a very inefficient process. It has been argued that the SF per free-fall time, defined as the fraction of molecular gas that is converted into stars per free-fall time [ϵff = (SFR/Mgas) × tff], is a quasi-universal quantity with a typical value of ~1–2% on a wide range of spatial scales from local Galactic clouds to high-redshift galaxies (Krumholz & Tan 2007; Krumholz 2014), in agreement with the turbulence-regulated SF model of Krumholz & McKee (2005). If ϵff is indeed constant, this implies that the non-normalized SFE, 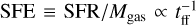 , should increase with gas density ρ, since tff ∝ ρ–1/2. In agreement with this scenario, observational evidence that ϵff may be roughly constant ~2.6% within nearby molecular clouds has been recently reported (Pokhrel et al. 2021). However, resolved observations of nearby disk galaxies indicate a roughly constant depletion time tdep = SFE–1 ~ 1–2 Gyr (Bigiel et al. 2011; Schruba et al. 2011) on kpc scales, which is at variance with a strictly constant ϵff value on all scales. Indeed, adopting an average volume density
, should increase with gas density ρ, since tff ∝ ρ–1/2. In agreement with this scenario, observational evidence that ϵff may be roughly constant ~2.6% within nearby molecular clouds has been recently reported (Pokhrel et al. 2021). However, resolved observations of nearby disk galaxies indicate a roughly constant depletion time tdep = SFE–1 ~ 1–2 Gyr (Bigiel et al. 2011; Schruba et al. 2011) on kpc scales, which is at variance with a strictly constant ϵff value on all scales. Indeed, adopting an average volume density 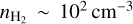 and thus an average free-fall time tff ~ 3 Myr for CO molecular clouds leads to ϵff = tff/tdep ~ 0.15–0.3% on galactic scales, which is an order of magnitude lower than the ~1–2% value quoted above. Moreover, direct observations of the connection between dense gas and SF in nearby resolved molecular clouds suggest a picture in which the SFR is directly proportional to the mass of dense molecular gas, Mdense. Here, dense gas is understood as gas with surface density
and thus an average free-fall time tff ~ 3 Myr for CO molecular clouds leads to ϵff = tff/tdep ~ 0.15–0.3% on galactic scales, which is an order of magnitude lower than the ~1–2% value quoted above. Moreover, direct observations of the connection between dense gas and SF in nearby resolved molecular clouds suggest a picture in which the SFR is directly proportional to the mass of dense molecular gas, Mdense. Here, dense gas is understood as gas with surface density 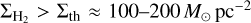 , which translates to volume densities
, which translates to volume densities 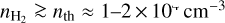 assuming clouds with a typical radial density profile
assuming clouds with a typical radial density profile  (Lada et al. 2010, 2012; Evans et al. 2014; Shimajiri et al. 2017). In this alternate picture, SF occurs mostly (if not only) in dense cloud gas above Σth in surface density or nth in volume density, and SFEdense = SFR/Mdense is roughly constant at ~5 × 10–8 yr–1, corresponding to a typical depletion time for dense gas of ~20 Myr. Accordingly, eff = SFE × tff is expected to decrease with density above ~1–2 × 104 cm–3. Such a threshold or transition picture for the SFE fits well within the filament paradigm of SF (e.g., André et al. 2014), in which prestellar cores and protostars form primarily in dense, thermally supercritical filaments with masses per unit length of > 16 M⊙ pc–1, typical widths of ~0.1 pc (e.g., Arzoumanian et al. 2019), and a typical core formation efficacy of ~15–20% (e.g., Könyves et al. 2015). The latter scenario leads to a natural transition surface density Σth ~ 160 M⊙ pc–2, equivalent to a transition volume density nth ~ 2 × 104 cm–3, set by the critical mass per unit length of molecular gas filaments.
(Lada et al. 2010, 2012; Evans et al. 2014; Shimajiri et al. 2017). In this alternate picture, SF occurs mostly (if not only) in dense cloud gas above Σth in surface density or nth in volume density, and SFEdense = SFR/Mdense is roughly constant at ~5 × 10–8 yr–1, corresponding to a typical depletion time for dense gas of ~20 Myr. Accordingly, eff = SFE × tff is expected to decrease with density above ~1–2 × 104 cm–3. Such a threshold or transition picture for the SFE fits well within the filament paradigm of SF (e.g., André et al. 2014), in which prestellar cores and protostars form primarily in dense, thermally supercritical filaments with masses per unit length of > 16 M⊙ pc–1, typical widths of ~0.1 pc (e.g., Arzoumanian et al. 2019), and a typical core formation efficacy of ~15–20% (e.g., Könyves et al. 2015). The latter scenario leads to a natural transition surface density Σth ~ 160 M⊙ pc–2, equivalent to a transition volume density nth ~ 2 × 104 cm–3, set by the critical mass per unit length of molecular gas filaments.
In this paper, we present results from CAFFEINE, a complete 350/450 µm survey with APEX/ArTéMiS of the densest portions of all molecular clouds at distances of d ≲ 3 kpc (Sect. 5.1), which help us discriminate between the scenarios described above for the SFE in dense gas. Combining the ArTéMiS observations with Herschel data, we produced column density maps with a factor of ~4 higher resolution than standard Herschel column density maps (Sect. 3). This improvement allows us to resolve the structure of dense gas and the typical ~0.1 pc width of molecular filaments/cores out to 3 kpc, which is impossible with Herschel data alone. After correcting for line-of-sight contamination (Sect. 4.1), we used our high-resolution column density maps in conjunction with SFR estimates from Spitzer young stellar object (YSO) and protostellar clump catalogs (Sect. 4.2) to study the dependence of the SFE on density in a sample of CAFFEINE clouds. We present our results and a comparison with nearby clouds in Sect. 5 and discuss their meaning in the context of two theoretical models in Sect. 6, before drawing our conclusions in Sect. 7.
2 Submillimeter and infrared data
In the present study, we introduce and focus on data from the Core And Filament Formation/Evolution In Natal Environments (CAFFEINE) survey with ArTéMiS. We complement these data with additional submillimeter dust continuum observations from the Herschel space observatory and the Planck all-sky survey, and molecular line observations of the 13CO molecule. Furthermore, to derive estimates of the SFR, we used catalogs of YSOs compiled from several infrared surveys and of protostellar clumps identified on Herschel maps.
 |
Fig. 1 Locations of the CAFFEINE targets marked as yellow circles in an artist's impression of the Milky Way by R. Hurt (NASA; JPL-Caltech). The targets selected for this study are marked by red crosses. |
2.1 The CAFFEINE imaging survey with ArTéMiS
The CAFFEINE survey was carried out between August 2018 and August 2022 as a large program of the European Southern Observatory (ESO) under projects IDs E-1102.C-0745A-2018 and 106.21MS. The data were taken with the ArTéMiS bolometer-array camera (Revéret et al. 2014; André et al. 2016; Talvard et al. 2018) at the Atacama Pathfinder Experiment (APEX) telescope (Güsten et al. 2006) in Chile. ArTéMiS produces images of the continuum emission at both 350 µm and 450 µm simultaneously. At these wavelengths, the half-power beam width (HPBW) angular resolution achieved by ArTéMiS on the 12 m APEX antenna is ~8″ and ~10″, respectively. The pointing accuracy was checked every ~1–2 h and found to be better than ≲3″. To ensure high sensitivity and data quality, observations were carried out only in submillime-ter weather conditions with a precipitable water vapor content (PWV) of <0.7 mm.
The CAFFEINE survey targets the densest (AV > 40 mag) portions of all dense star-forming complexes visible from APEX as seen by the ATLASGAL and Hi-GAl surveys (Schuller et al. 2009; Molinari et al. 2010) out to a distance d~3 kpc (Fig. 1). This distance limit allows us to achieve a physical resolution of <0.1 pc in all regions. The significance of the CAFFEINE cloud sample is that it contains two to three orders of magnitude more dense gas mass at high column density (AV > 50-200 mag) than the nearby clouds of Gould's Belt and therefore allows us to probe the high-mass SF regime and the dependence of the SFE with density.
The CAFFEINE survey encompasses observations of 80 dense molecular clouds within a distance range from ~0.6 kpc to ~3.0 kpc, following the estimates of associated Hi-GAL clumps (Russeil et al. 2011; Elia et al. 2021). In particular, we assign the average distance of the largest group of clumps with similar distances (about ±0.1 kpc) and additionally compare with the velocities of additional molecular line data (see Sect. 4.1). As the Scutum-Centaurus spiral-arm of the Milky Way is located just outside of the 3.0 kpc radius a few prominent and potentially interesting sources were also included with a strict limit at 4.0 kpc (Fig. 1).
The ArTéMiS data were processed with the dedicated ArTéMiS Pipeline using IDL and Scanamorphos (APIS)1, which takes care of converting the raw data to IDL-friendly data structures, applying flux calibration and atmospheric opacity correction, rejecting unusable pixels, removing atmospheric emission fluctuations and instrumental noise, and making maps for astro-physical use. The final intensity and weight maps were saved in FITS format. The average rms noise is 0.46 Jy/8″ beam at 350 µm and 0.37 Jy/10″ beam at 450 µm. We present in Fig. 2 (left and center) the G034 region as an example of the ArTéMiS data products created.
 |
Fig. 2 Examples of data products derived from the CAFFEINE survey. Left: dust continuum emission of the G034 region as observed at 350 µm by ArTéMiS at 8″ resolution. Center: dust continuum emission of the G034 region as observed at 450 µm by ArTéMiS at 10" resolution. Right: combined 350 µm ArTéMiS-SPIRE dust continuum emission map with 8" resolution and high dynamic range. |
Field selection
For the present analysis of the SFE at high densities, we selected a subsample of 49 clouds that have a surface area larger than 1 pc2 above a column density of 2 × 1022 cm–2. We also included the MonR2 region to compare with the results of Pokhrel et al. (2021). The selected clouds are marked in Fig. 1 and listed in Table 1 by order of right ascension. The selected fields were observed within ~215 h with ArTéMiS/APEX, which corresponds to ~75% of the total CAFFEINE observing time.
2.2 Herschel imaging data
While the ArTéMiS observations provide high angular resolution to identify small-scale structures, they are not tracing emission from scales larger than 2.5′–5′, because such extended emission is difficult to distinguish from sky noise. To recover extended emission on these scales, we utilized data from Herschel published as part of the Hi-GAL and HOBYS surveys (Molinari et al. 2010; Motte et al. 2010). In particular, we used the PACS 160 µm and SPIRE 250 µm, 350 µm and 500 µm emission data which provide FWHM resolutions of 13.5″ (Hi-GAL)/11.7″ (HOBYS), 18.2″, 24.9″, 36.3″, respectively.
For comparison with the results obtained here on the CAFFEINE sample of massive star-forming complexes, we also used column density maps of lower-mass, nearby star-forming clouds (Table 2), constructed from Herschel Gould Belt survey (HGBS) data2 at a FWHM resolution of 18.2" (André et al. 2010; Palmeirim et al. 2013).
3 Constructing column density maps
3.1 Combining ArTéMiS and Herschel data
To recover extended emission at scales larger than 2.5′, we combined the ArTéMiS maps with Herschel-SPIRE maps at similar wavelengths using the immerge task in MIRIAD (Sault et al. 1995) and the same approach as André et al. (2016) and Schuller et al. (2021a). The immerge algorithm combines the available data in the Fourier domain after determining an optimal calibration factor to align the flux scales of the input images (here from ArTéMiS and SPIRE) in a common annulus of the UV plane. Here, we adopted an annulus corresponding to the range of baselines from 0.5 m (the baseline b sensitive to angular scales λ/b ~ 2.4′ at λ = 350 µm) to 3.5 m (the diameter of the Herschel telescope) to align the flux scale of the ArTéMiS 350 µm map to the flux scale of the SPIRE 350 µm map. We used the same method to combine the ArTéMiS 450 µm data with Herschel-SPIRE maps interpolated from 350 µm and 500 µm to 450 µm, assuming a linear relation in log space.
In the combination process, we could identify several areas that suffer from saturation effects in the Herschel data. While clearly saturated pixels are masked in the published data, we found more pixels in bright areas that deviate from the typical relation between the Herschel and ArTéMiS pixel intensities. Therefore, we used this relation to correct the saturated Herschel data before performing the combination.
An example of a combined ArTéMiS-SPIRE map is shown in Fig. 2 (right) for the G034 region. The effective resolution is ~8″ and ~ 10″ (HPBW) at 350 µm and 450 µm, respectively. For the clouds GAL316, and G337.9, our method is not sufficient to recover all of the extended emission and leaves areas of "negative emission". Therefore, we used a more sophisticated method employing the Scanamorphos software for ArTéMiS (Roussel 2013, 2018), as described in Appendix B. Given the complexity of this alternative method, we applied it only in cases for which it was really necessary. All of the discussion that follows is based on these combined ArTéMiS and SPIRE maps.
CAFFEINE cloud sample analyzed in the present study.
3.2 Constructing high−resolution column density maps
We used the combined ArTéMiS−SPIRE maps at 350 µm (8″ resolution) and 450 µm (10″ resolution) to construct high− resolution column density maps, employing a pixel by pixel SED (spectral energy distribution) fitting approach. To cover a broader range of wavelengths and improve the robustness of the fitting, we also included Herschel SPIRE 250 µm (18.2″ resolution) and PACS 160 µm (13.5″ resolution) data.
To derive appropriate zero-level offsets for the ArTéMiS +Herschel maps and Herschel−only maps, we used the all−sky high sensitivity maps provided by the Planck collaboration. The Planck maps have an angular resolution of 330″ and an absolute calibration uncertainty of 7% (Planck Collaboration I. 2011). We made sufficiently large cut-outs (~1°× 1°) around the targeted clouds using the healpix library. These data were then used to derive expected intensity maps at the Herschel wavelengths. After smoothing and adapting the Herschel maps to the Planck reference the median differences at each wavelength were used as zero-level offsets (cf. Bracco et al. 2020).
Column density maps were then derived from the offset-calibrated data. To achieve the highest possible resolution (~8″), we made use of the methods described in Schuller et al. (2021a) and Appendix A of Palmeirim et al. (2013) for ArTéMiS and Herschel data, respectively. The method introduced by Schuller et al. (2021a) can be summarized in the following steps: The images in all four bands from 160 µm to 450 µm were first smoothed to the lowest resolution of 18.2″, set by the SPIRE 250 µm data. A modified blackbody function ∝Bv(Td) κv N(H2) was then fitted to the specific intensities in the four bands at every position of the field to derive a dust temperature map (and an auxiliary column density map) at 18.2″ resolution. Here, Bv(Td) denotes the Planck function at frequency v (or wavelength λ) for temperature Td and κv (or κλ) is the dust opacity at that frequency (or wavelength). The dust temperature map was subsequently used to convert the combined ArT6MiS-SPIRE map at 350 µm to a 8″-resolution column density map (Fig. 3) based on the following relation:
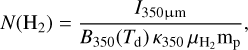 (1)
(1)
where I350µm is the specific intensity (in MJy sr−1) in the ArTéMiS–SPIRE map, µH2 = 2.8 is the mean molecular weight per H2 molecule (Kauffmann et al. 2008), mp is the proton mass, and k350 is the dust opacity at λ = 350 µm. For consistency with earlier Herschel (e.g. HGBS) work, we adopted the following simple dust opacity law at submillimeter wavelengths: κλ = 0.1 × (λ/300 µm)−β cm2 g−1 for gas + dust (Hildebrand 1983). (We note that this implicitly assumes a standard gas-to-dust mass ratio of 100.) This simple opacity law, very similar to that modeled by Preibisch et al. (1993) and Ossenkopf & Henning (1994) for dust grains with thin ice mantles but no coagulation (often referred to as OH4), has been shown to yield column density estimates agreeing within ~50% with independent dust extinction measurements for 3 × 1021 cm−2 ≲ 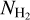 ≲ 1023 cm−2 (see Roy et al. 2014). At higher column densities,
≲ 1023 cm−2 (see Roy et al. 2014). At higher column densities, 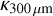 may exceed our default value of 0.1 cm2 g−1 by a factor of ~2, as in the dust model(s) with grain coagulation (OH5 or OH6) advocated by Ossenkopf & Henning (1994) for dense protostellar cores. In turn, our column density maps may overestimate actual column densities by a factor of ~2 in the densest areas, with very little influence on the discussion presented in Sect. 6.
may exceed our default value of 0.1 cm2 g−1 by a factor of ~2, as in the dust model(s) with grain coagulation (OH5 or OH6) advocated by Ossenkopf & Henning (1994) for dense protostellar cores. In turn, our column density maps may overestimate actual column densities by a factor of ~2 in the densest areas, with very little influence on the discussion presented in Sect. 6.
Following the multiscale decomposition approach introduced by Palmeirim et al. (2013), we also created column density maps at 18.2″ resolution based purely on Herschel data, which extend beyond the dense (AV > 40 mag) areas observed with good sensitivity with ArTéMiS and cover the whole extents of the target star-forming complexes. In a final step, we combined the 18.2″-resolution column density maps from Herschel with the 8″-resolution column density maps derived from ArTéMiS+Herschel data as explained above, to produce multiresolution column density maps of the target fields (Fig. 3). These multiresolution column density maps coincide with the ArTéMiS +Herschel column density maps and thus have a resolution of ~ 8″ in the dense (AV > 40 mag) inner portions of the fields and a resolution of 18.2″ in the lower-density outer parts.
The combined ArTéMiS–SPIRE maps at 350 µm and 450 µm, the ArTéMiS weight maps, and the final multiresolution column density maps, are made publicly available as data products through the ESO archive3 and the CAFFEINE web page4.
Nearby clouds considered for comparison with the CAFFEINE sample.
4 Methods and analysis
4.1 Evaluating and subtracting the line-of-sight contamination
The submillimeter dust continuum emission traced by ArTéMiS, Herschel, and Planck data covers a wide range of column densities and is therefore ideal to derive reliable cloud mass estimates. Because of the otherwise desirable sensitivity, these measurements, however, also trace emission from dust along the line-of-sight which is not associated with the targeted molecular cloud. This contribution is especially critical within the inner Galaxy where the number density of molecular clouds is high.
To address this problem, we used 13CO observations from several surveys covering the Galactic Plane. We preferably used the SEDIGISM 13CO(2–1) survey (Schuller et al. 2021b) and the catalog of identified molecular clouds (Duarte-Cabral et al. 2021). Identifying the CAFFEINE clouds within the SEDIGISM catalog ensures that the clouds are truly velocity coherent structures and that the SEDIGISM cloud masks define their spatial extents in the plane of the sky.
We found three regions where the emission detected by CAFFEINE is assigned to multiple SEDIGISM clouds. In the case of SDC338 and SDC010, the high column density areas are located within a common larger area of low column densities and the distances to the different SEDIGISM clouds are comparable within the uncertainties. Therefore, we decided to treat them as single clouds, as they were observed with CAFFEINE. In the case of I17233, three SEDIGISM clouds toward its direction exhibit large differences in distance from the Sun. We therefore separated them into two components I17233A and I17233B. The third cloud has a distance of 6.5 kpc and was thus excluded from the present analysis.
In regions for which the SEDIGISM survey is not available, we used 13CO(1–0) data from the GRS and THRUMMS surveys (Jackson et al. 2006; Barnes et al. 2015). As there are no cloud masks available for these surveys, we identified clouds directly from the corresponding data. To do so, we first selected the dominant velocity component in the line-of-sight to each region and then integrated over this component down to a signal-to-noise ratio (S/N) limit of S/N ≥ 5. The resulting integrated intensity map gave us the extent of the region similar to those of the SEDIGISM clouds.
From the molecular line data we also derived an estimate of the diffuse ISM along the line-of-sight in the Milky Way (see, e.g., Mattern et al. 2018; Peretto et al. 2023). The above-mentioned CO surveys trace any significant amount of molecular gas within the covered areas. Therefore, we derived integrated intensity maps over the full velocity range and over the velocity range of the cloud of interest, respectively. We then created a ratio map to determine the contribution of the cloud compared to the total line-of-sight. We found that all CAFFEINE clouds are the main component in their respective directions. To estimate the contribution of the diffuse gas to the total column density, we smoothed the ratio map to the resolution of the Planck column density map and subtracted this fraction. The average of the subtracted column densities over the area of each target cloud was used as an estimate of the diffuse gas column density, which we refer to as background (see N(H2)back in Table 1).
Notably, the clouds SDC340, RCW116B, SDC348, and SDC014 are located slightly off the Galactic Plane (|b| ≈ 0.5–1.0°) and are not covered by any of the above CO surveys. For these clouds the impact of diffuse line-of-sight emission is probably not negligible, but we did not find significant confusion with other clouds by comparing the distances of compact Hi-GAL sources (Elia et al. 2021) toward these clouds. We thus defined the background as a spatially constant value derived as the mean over low column density areas within each map. The clouds MonR2, R5180, and NGC2264 are even further away from the Galactic Plane or toward the outer Galaxy where the diffuse background emission is negligible.
 |
Fig. 3 Examples of high level data products from the CAFFEINE survey. Left: column density map of the G034 region at 8″ resolution derived from combined ArTéMiS and Herschel data. Right: final multiresolution column density map of the G034 region, with 8″ resolution above |
4.2 Star formation rates
4.2.1 Star formation rates from young stellar objects
To evaluate the SFRs of the CAFFEINE clouds we first need to identify the YSOs present in each. For that, we combined the YSOs catalogs from Marton et al. (2016, 2019) and Kuhn et al. (2021). Marton et al. (2016) produced a Class I/II YSO catalog from a training method analyzing the reliable 2MASS and WISE photometric data. Adding Gaia-DR2 information to the WISE data Marton et al. (2019) produced a more recent catalog that included the probability for an object to be a YSO. From this catalog, we selected objects with a probability higher than 80% of being a YSO. In addition, the YSO class (class I, II, III or flat SED) was established from the infrared spectral index αIR (calculated from the WISE magnitudes following Kang et al. 2017) using the ranges of αIR values recommended by Greene et al. (1994) for each class. An alternative YSO catalog is the Spitzer/IRAC candidate YSO (SPICY) catalog produced by Kuhn et al. (2021). This catalog is mainly based on near-IR data and is more sensitive to Class II YSOs (as illustrated by their Fig. 15). Kuhn et al. identified candidate YSOs from infrared excesses consistent with the SEDs of pre-main sequence stars with disks or envelopes. Further, they assigned a class (Class I, II, III or flat SED) to every object from the infrared spectral index (also using the αIR ranges from Greene et al. 1994). For each catalog we selected Class I, II and flat-spectrum YSOs, and then concatenated the results (taking into account duplicates) to produce a global YSO catalog. For YSO classification, these catalogs used a machine learning method which is designed to minimize contamination from galaxies and evolved stars efficiently. A fraction of 6 % of false YSO identification is estimated by Marton et al. (2019). For the MonR2 region, we adopted the publicly available YSO catalog compiled by Gutermuth et al. (in preparation) from the Spitzer Extended Solar Neighborhood Archive (SESNA).
We then selected all of the YSOs falling in the cloud mask (see Fig. 4 for the MonR2 example) and for each YSO we ran the SED fitting tool from Robitaille (2017). Following Sewiło et al. (2019) after fitting the models, we counted the number of good fits provided by each model set. Of these, the one with the largest number of good fits was selected as the best model set from which the adopted best model was that with the smallest χ2. The selected model then gave the modeled radius and temperature of the source from which we evaluated the mass using the zero-age main sequence (ZAMS) luminosity-mass relation5 as in Immer et al. (2012). We then followed the method described in Immer et al. (2012) by fitting the mass distribution histogram with a power-law curve Ψ = AM−23 (where A is the normalization factor), in accordance with the form of the Kroupa (2002) initial mass function (IMF) for M ≥ 0.5 Mθ. The fit allowed us to solve for the value of the normalization factor A. Then, assuming a continuous IMF at M = 0.5 Mθ, we deduced the normalization factors for the low-mass end of the Kroupa (2002) IMF in the range 0.01 M⊙ to 0.5 M⊙, and estimated the total mass of YSOs in the mass range 0.01 to 120 M⊙. The SFR was estimated by dividing this YSO mass by a SF timescale of 0.5 + 2 = 2.5 Myr corresponding to the estimated total duration of the Class I + Class II YSO evolutionary phases (see Evans et al. 2009). This timescale is probably uncertain by factor of ~2 on either side. On one hand, the median lifetime of Class II YSOs with significant infrared excess may be slightly longer than previously thought (i.e., ~3–4Myr, Dunham et al. 2015, and references therein). On the other hand, theoretical work on pre-main sequence (PMS) evolutionary tracks suggests that episodic accretion during the embedded protostellar phase can make a ~1 Myr old PMS star appear as old as ~ 10 Myr if standard, non-accreting isochrones are used in the Hertzsprung-Russell diagram to derive its age (Baraffe et al. 2009). In view of these uncertainties, for better consistency and easier comparison with recent literature on SFRs and SFEs, we adopted the same timescale values as Evans et al. (2009).
To evaluate the completeness of the YSO population we retrieved the WISE 4.6 µm and the IRAC 4.5 µm magnitude for PMS stars of age 0.5 Myr (typical lifetime for a Class I YSO) and 2 Myr (typical lifetime for a Class II YSO) from PARSEC6 isochrones (Bressan et al. 2012). We adopted a sensitivity limit of 15.7 mag and 14.5 mag for WISE 4.6 µm and the IRAC 4.5 µm (Koenig & Leisawitz 2014). In this way, we estimated that YSOs more massive than 3 M⊙, at 2 kpc, should be detected at least up to a column density of 1.2 × 1023cm−2. For 1 M⊙ YSOs, the detection limits are at column densities of 2 × 1022 cm−2 and 7.5 × 1022 cm−2 for Class II and Class I objects, respectively. These estimates are conservative as they do not take into account the infrared excess emission expected from accretion in Class I and Class II objects.
On the other hand, the YSOs population can be underestimated due to confusion with extended nebulosity, neighboring bright sources and/or saturation (e.g. Koenig & Leisawitz 2014). For example Megeath et al. (2016) estimated that the fraction of detected stars dropped to about 10% in the brightest parts of the Orion Nebula compared to regions with only faint nebulosity.
In practice, for the studied regions, the histograms of YSO masses suggests that good YSO completeness is reached between 2 and 4 M⊙ on average.
The uncertainty of the SFR in each cloud is given by
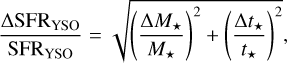 (2)
(2)
where ΔM★ and Δt★ are the stellar mass and evolutionary timescale uncertainties, respectively. We adopted a relative uncertainty of 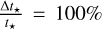 for the duration of the combined Class I plus Class II YSO evolutionary phases (cf. Evans et al. 2009). We evaluated the typical value of
for the duration of the combined Class I plus Class II YSO evolutionary phases (cf. Evans et al. 2009). We evaluated the typical value of 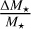 from the quadratic sum of the relative mass uncertainties coming from the SED fitting (45%), the IMF binning and fitting algorithm (40%), and the (in)completeness impact (30%).
from the quadratic sum of the relative mass uncertainties coming from the SED fitting (45%), the IMF binning and fitting algorithm (40%), and the (in)completeness impact (30%).
 |
Fig. 4 Multiresolution column density map of the MonR2 region based on ArTéMiS + Herschel data, with blue dots marking the locations of identified YSOs within the cloud area. The resolution of the map ranges from ~8″ at |
 |
Fig. 5 Multiresolution column density map of the MonR2 region based on ArTéMiS + Herschel data, with blue crosses marking the locations of identified protostellar clumps within the cloud area. The resolution of the map ranges from ~8″ at |
4.2.2 Star formation rates from protostellar clumps
We utilized the reliable catalog of compact Hi-GAL sources from Elia et al. (2021) for a second, independent estimate of SFRs. For each clump, this catalog gives the mass, distance, velocity and evolutionary status (starless, prestellar, or protostel-lar). For MonR2 (not covered by Hi-GAL), we used the clumps catalog from Rayner et al. (2017) established from the Herschel HOBYS survey. We selected the protostellar clumps (detected by Herschel/PACS at 70 µm) falling in the mask and with a velocity in the velocity range of the cloud, and then estimated an SFR using the SFR-protostellar clump mass relation given by Elia et al. (2022). As an example, we show the Hi-GAL protostellar clumps of the MonR2 region in Fig. 5. The SFR of one proto-stellar clump was calculated from the Elia et al. (2022) relation, as follows:
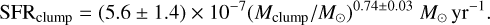 (3)
(3)
This relation is based on theoretical evolutionary tracks reported in the bolometric luminosity versus mass diagram (Molinari et al. 2008; Baldeschi et al. 2017; Elia et al. 2021). Initially developed for the formation of a single massive protostellar object, the tracks have been updated by Veneziani et al. (2017) to account for the multiplicity of sources produced during the clump collapse. Then Elia et al. (2022), following Veneziani et al. (2017), developed an algorithm which associates the final star mass to the input clump mass by interpolating the locus of final masses for known evolutionary tracks with a power law leading to Eq. (3) above. An SFRclump value was then calculated from Eq. (3) for each protostellar clump and then the SFR was estimated as the sum of the SFRclump over all clumps belonging to the region. Following Eq. (3) the uncertainty of the SFR per clump is given by
 (4)
(4)
and accordingly the uncertainty in the total SFR of the cloud was derived as  , where Nclump is the number of protostellar clumps within the region.
, where Nclump is the number of protostellar clumps within the region.
5 Results
5.1 Star formation efficiencies in CAFFEINE clouds
Given the lists of Class II YSOs and protostellar clumps for each cloud in our sample, we constructed a set of column density contours and derive the SFR and gas mass within each contour. We followed the same approach as Pokhrel et al. (2021) but used different tracers for the SFR.
To ensure a minimum level of statistical accuracy, we introduced limits for the SFR estimates. For a reliable SFR estimate derived from YSOs, we imposed a minimum number of YSOs of NYSOs > 5 within the area of a contour as the fitting of the IMF to the mass distribution would otherwise be too uncertain. We similarly imposed Nclumps > 5 as Eq. (3) (from Elia et al. 2022) refers to an average over several protostellar clumps and applying it to a region with a very small number of Hi-GAL protostellar clumps would become highly inaccurate. For a similar reason, we also excluded estimates for which the cloud mass is lower than twice the combined clump mass and imposed 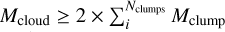 .
.
For the two different SFR estimates, the cumulative SFE within each column density contour, SFE , was then derived as:
, was then derived as:
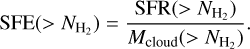 (5)
(5)
This definition is however only valid for a well-defined cloud mass. We therefore considered only SFR and SFE estimates for which the corresponding column density contour is closed within the map of the cloud (cf. Alves et al. 2017). This limiting column density can be approximated by the peak of the column density probability density function (N-PDF) in the observed region.
We derived the N-PDF 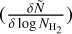 of each region from the background-corrected multiresolution column density map using a histogram of log
of each region from the background-corrected multiresolution column density map using a histogram of log 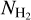 with a bin size of δ log
with a bin size of δ log 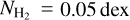 . We also translated column density to visual extinction, AV, by adopting the standard Bohlin et al. (1978) relation,
. We also translated column density to visual extinction, AV, by adopting the standard Bohlin et al. (1978) relation, ![${N_{{{\rm{H}}_2}}} = 0.94 \times {10^{21}}{\rm{c}}{{\rm{m}}^{ - 2}} \times {A_{\rm{V}}}[{\rm{mag}}]$](/articles/aa/full_html/2024/08/aa49908-24/aa49908-24-eq29.png) . The number of pixels per bin δN was then normalized to
. The number of pixels per bin δN was then normalized to 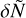 so that
so that 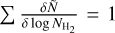 . The location of the N-PDF peak gives an indication of the lowest closed column density contour within the observed area. Furthermore, the power-law tail observed at higher column densities, described as
. The location of the N-PDF peak gives an indication of the lowest closed column density contour within the observed area. Furthermore, the power-law tail observed at higher column densities, described as 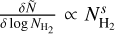 where s is the logarithmic slope of the power-law tail, is an indicator of the cloud’s overall radial density structure (e.g., see Kainulainen et al. 2009; Schneider et al. 2013). The median slope observed at high column densities in the whole CAFFEINE sample is s ≈ −2.3, which is consistent with an average radial density profile ρ(r) ∝ r−1.9 at high densities (cf. Sect. 6.1 below).
where s is the logarithmic slope of the power-law tail, is an indicator of the cloud’s overall radial density structure (e.g., see Kainulainen et al. 2009; Schneider et al. 2013). The median slope observed at high column densities in the whole CAFFEINE sample is s ≈ −2.3, which is consistent with an average radial density profile ρ(r) ∝ r−1.9 at high densities (cf. Sect. 6.1 below).
In Fig. 6, we show the N-PDFs for three example regions and the overall CAFFEINE cloud sample. The peak of the N-PDF varies from cloud to cloud and is located at about 1 × 1022 cm−2 for the combined sample. We therefore adopted this latter column density as the lower limit of reliable SFE estimates for the CAFFEINE clouds. Larger multiresolution maps would allow us to cover lower column density contours, but would increase the uncertainties due to line-of-sight confusion, in particular toward the Galactic Plane.
Over a broad range of column densities from ~1022 cm−2 to ~1023 cm−2, the standard deviation of the derived SFE values across the sample of CAFFEINE clouds is about 0.3 and 0.5 dex for the clump and YSO estimates, respectively. These values reflect the complexity of SF on cloud scales where several parameters can have an influence. As we are mostly interested in the general trend between SFE and column density, we performed a weighted geometric average (in log space) over all the CAFFEINE clouds of the form:
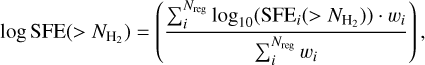 (6)
(6)
with the weight wi of a region i defined as:
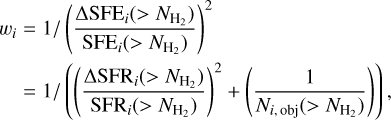 (7)
(7)
where 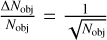 is the relative Poisson error given the num-ber of detected objects Nobj (clumps or YSOs, respectively), and
is the relative Poisson error given the num-ber of detected objects Nobj (clumps or YSOs, respectively), and 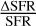 is the relative uncertainty of the SFR as given by Eqs. (2) and (4).
is the relative uncertainty of the SFR as given by Eqs. (2) and (4).
We present the average SFE estimates for column density contours of 7.1 × 1021 cm−2 to 2.2 × 1023 cm−2 with steps of 0.15 dex in Fig. 7. We chose this column density step size to ensure that typically at least one protostellar clump is located in each bin. We give the numbers of protostellar clumps and YSOs and the respective estimates of the SFR and SFE for each cloud for the contours of 1.4 × 1022 cm−2 and 7.9 × 1022 cm−2 in Table C.1 (Appendix C).
The net uncertainties in the derived average SFE values were estimated from a combination of the Poisson statistical uncertainties and the systematic uncertainties inherent to each method. The relative uncertainty in the average SFE was derived as follows:
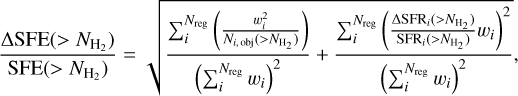 (8)
(8)
where 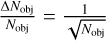 is the relative Poisson error,
is the relative Poisson error, 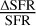 is the relative uncertainty of the SFR, and Nreg is the number of regions with a valid SFE estimate at the given column density contour. We did not include the systematic uncertainty of a factor of ~ 2 in the cloud mass as it is identical for all SFE estimates.
is the relative uncertainty of the SFR, and Nreg is the number of regions with a valid SFE estimate at the given column density contour. We did not include the systematic uncertainty of a factor of ~ 2 in the cloud mass as it is identical for all SFE estimates.
Both methods for estimating the SFE use only tracer objects to infer the full population of YSOs. This inherent limitation causes the SFR and thus the SFE to be strongly dependent on the number of identified objects. By averaging over a large number of clouds, however, the statistical uncertainties decrease, but the systematic errors remain and quickly become the dominant source of uncertainty in the weighted averages.
Despite a slight systematic disagreement between the two methods of deriving the SFR for the CAFFEINE clouds, both SFE curves presented in Fig. 7 show a consistent trend within the uncertainties. We find a relatively flat behavior around a mean of SFEclump ≈ 6.6 ± 1.2 × 10−8yr−1 for the protostellar clump SFE. The YSO fitting method generally leads to lower SFE estimates with larger variations, but is in agreement with a flat trend around a mean of SFEYS0 ≈ 3.5 ± 1.5 × 10−8 yr−1. At the highest column densities (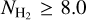 × 1022cm−2), both methods yield almost identical estimates.
× 1022cm−2), both methods yield almost identical estimates.
 |
Fig. 6 Column density probability density functions (N-PDFs) as a function of column density (top axis) and visual extinction (bottom axis) for the MonR2, G034, and OH341 regions and for all CAFFEINE regions combined in red, blue, green and black, respectively. The peaks of the distributions are indicated by dashed lines with the column density |
 |
Fig. 7 Cumulative SFE above a minimum column density |
5.2 Comparing the two types of SFE estimates for the CAFFEINE sample
As described above, both types of SFE estimates for the CAFFEINE clouds show a relatively flat behavior with increasing column density and larger variations at the highest column densities (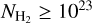 cm−2, Fig. 7). These variations arise from larger statistical uncertainties, as fewer regions are able to probe these high column densities and the impact of single clouds increases. This situation is also reflected in the lower standard deviation of the cloud SFE distributions, as indicated by the dashed-dotted lines in Fig. 7. Seeing an almost identical behavior for SFE estimates for
cm−2, Fig. 7). These variations arise from larger statistical uncertainties, as fewer regions are able to probe these high column densities and the impact of single clouds increases. This situation is also reflected in the lower standard deviation of the cloud SFE distributions, as indicated by the dashed-dotted lines in Fig. 7. Seeing an almost identical behavior for SFE estimates for 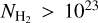 cm−2 from clumps and YSOs separately indicates that the measurements are dominated by the same clouds, which shows that estimates at high column densities are limited by the number of clouds and the amount of dense gas that can be observed.
cm−2 from clumps and YSOs separately indicates that the measurements are dominated by the same clouds, which shows that estimates at high column densities are limited by the number of clouds and the amount of dense gas that can be observed.
We also investigated the ability of the two methods to trace SF at high (column) densities. Here we looked at the number of clumps and YSOs that could be identified in each column density bin, that is, in the area between two consecutive column density contours (see Appendix A and Fig. A.1).
The number of protostellar clumps and YSOs observed between column density contours decreases at higher densities, which is predominantly an effect of the smaller enclosed area at higher column densities. The SFE estimates are also affected by the distribution of clumps and YSOs within a cloud (i.e. see Figs. 4 and 5) and their detection. To remove the area effect, we also show the surface number densities of clumps and YSOs per unit area as a function of column density in Fig. A.1.
The surface density of YSOs per unit area increases with column density (Fig. A.1), indicating a concentration of YSOs toward denser areas, with the exception of the two highest column density bins. As mentioned in Sect. 4.2.1 the WISE/Spitzer objects identified toward the CAFFEINE clouds are not a complete sample of YSOs, but only the brightest, most massive and least obscured ones. We expect a higher degree of YSO incompleteness in denser areas where extinction is higher. This effect was corrected for in our SFR estimates by fitting an IMF to the detected YSOs, but eventually leads to an underestimated SFR at very high column densities. The analysis in Appendix A suggests that our method of estimating the SFR from massive YSOs is strongly impacted by incompleteness for column densities ≳ 7.5–10 ×1022 cm−2, in agreement with the detection limit estimates made in Sect. 4.2.1.
Protostellar clumps, identified as bright peaks in far-infrared and submillimeter continuum emission, are not expected to suffer from a similar extinction limitation at high column densities. And, indeed, the surface density of Hi-GAL protostellar clumps continues to increase with column density up to the highest column density bins around ~1−2 × 1023 cm−2 (cf. Fig. A.1). The method of Elia et al. (2022) was, however, designed to derive SFRs on large scales, including many protostellar clumps. Therefore, a minimum number of clumps is necessary to get accurate SFEcıump estimates. This was ensured by imposing 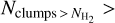 5 for a region to be considered in the calculations of the SFR in Sect. 4.2.2 and the average SFE value above a given column density
5 for a region to be considered in the calculations of the SFR in Sect. 4.2.2 and the average SFE value above a given column density 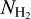 .
.
Toward lower column densities, both types of SFE estimates are limited by the spatial extent of the ArTéMiS observations and the ability to correct the data for line-of-sight confusion. We took this limitation into account by considering only measurements within closed column density contours in our analysis. As a result, the number of clouds contributing to the average SFE value in Eq. (6) is also strongly reduced for column densities ≲1022 cm−2. This column density limit is also reflected in the peak of the global column density PDF obtained when combining all CAFFEINE regions together (Fig. 6).
In summary, we conclude that the YSO SFE estimates are reliable in the range of column densities between ~ 1022 cm−2 and ≳7.5 × 1022 cm−2 and the clump SFE estimates are reliable from ~ 1022 cm−2 to ~ 1023 cm−2. Both methods indicate a similar trend between SFE and column density in this column density range. The weighted mean of the two types of SFE estimates is presented as the red line in Fig. 7. For reliable SFE estimates at column densities lower than 1022 cm−2, we analyze the results of Spitzer YSO surveys in nearby molecular clouds in the following section.
5.3 Star formation rates and efficiencies in nearby clouds
For a more complete picture of the SFE over a wide range of column densities, we also derived estimates for nearby (d < 500 pc) clouds from the Gould Belt (see Table 2). Extensive Spitzer-based catalogs of Class I and Class II YSOs are available for these clouds, which are complete down to the brown dwarf mass limit of 0.08 M⊙ out to d ≲ 500 pc (for Class Is) and d ≲ 300 pc (for Class IIs) (cf. Evans et al. 2009). Furthermore, nearby clouds can be traced down to lower column densities, but have only small amounts of gas at high column densities (i.e. see Pokhrel et al. 2021). For the analysis of these clouds, we followed a very similar approach to the method employed with CAFFEINE data (Sect. 5.1) but we concentrated on lower column densities down to 2.5 × 1021 cm−2, again with steps of 0.15 dex. We estimated the cloud masses in various column density bins using the 18.2″-resolution column density maps from the Herschel Gould Belt survey (HGBS – André et al. 2010). The SFRs were derived from the YSO catalogs of Megeath et al. (2012); Dunham et al. (2015); Lada et al. (2017). The references for the adopted maps and catalogs for each molecular cloud can be found in Table 2.
Here we also derived two independent estimates of the SFR for each region, one based on Class II YSOs and the other based on Class I YSOs. In both cases, we counted the number of YSOs belonging to the relevant class and located within a given column density contour. Especially at low AV (low 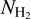 ), a fraction of the YSOs classified as Class I objects on the basis of their SEDs are known to lack a significant envelope of dense gas and are not bona fide protostars (Motte & André 2001; Heiderman & Evans 2015). As we want to focus on bona fide Class I pro-tostars, we corrected the observed numbers of Class I sources in each column density bin using the contamination curve derived by Heiderman & Evans (2015). (This contamination is very large > 90% at AV < 4 but negligible ≲10% at AV > 10.) We then multiplied the number of YSOs in each class by the same mean stellar mass of M⋆= 0.5 ± 0.1 M⊙ as adopted by Evans et al. (2009)7 and divided the result by the typical evolutionary timescale of the corresponding YSO phase, i.e., t⋆ClassII = 2.0 ± 1.0 Myr for Class II and t⋆Class I = 0.5 ± 0.2 Myr for Class I objects (Evans et al. 2009; Dunham et al. 2014, 2015).
), a fraction of the YSOs classified as Class I objects on the basis of their SEDs are known to lack a significant envelope of dense gas and are not bona fide protostars (Motte & André 2001; Heiderman & Evans 2015). As we want to focus on bona fide Class I pro-tostars, we corrected the observed numbers of Class I sources in each column density bin using the contamination curve derived by Heiderman & Evans (2015). (This contamination is very large > 90% at AV < 4 but negligible ≲10% at AV > 10.) We then multiplied the number of YSOs in each class by the same mean stellar mass of M⋆= 0.5 ± 0.1 M⊙ as adopted by Evans et al. (2009)7 and divided the result by the typical evolutionary timescale of the corresponding YSO phase, i.e., t⋆ClassII = 2.0 ± 1.0 Myr for Class II and t⋆Class I = 0.5 ± 0.2 Myr for Class I objects (Evans et al. 2009; Dunham et al. 2014, 2015).
As all of the selected Gould Belt clouds are nearby and located off the Galactic Plane, we did not subtract any background. In the cases of Lupus III, Corona Australis and Chameleon I, we used multiresolution column density maps where the HGBS maps were embedded in wider-scale column density maps from Planck data. The use of such multiresolution maps was necessary to ensure closed column density contours at 2.5 × 1021 cm−2 and 3.5 × 1021 cm−2. For Aquila and Ophiuchus, these two column density contours were ignored as YSO catalogs are only available over locations of higher column densities (Evans et al. 2003; Dunham et al. 2015).
For each cloud, the SFE within each column density contour was derived separately using either the Class II or Class I YSO SFRs following Eq. (5). For the Class II-based estimates, the cloud-to-cloud standard deviation of the SFEs is in the range of 0.15–0.25 dex below column densities of ≤ 1.4 × 1022 cm−2 but increases to ~0.3–0.6 dex at higher column densities. This latter column density is also roughly the limit above which Class II YSOs are no longer observed in all of the clouds. On the other hand, Class I-based estimates show a cloud to cloud standard deviation increasing from ~0.25 dex to 0.6 dex up to a column density of 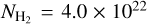 cm−2 and a standard deviation of ~0.4 dex above that.
cm−2 and a standard deviation of ~0.4 dex above that.
For the two different methods, we again averaged the results over the whole sample of clouds to identify a more general trend of the SFE with column density (see Fig. 8 below).
For each cloud, the uncertainty in the SFE estimate was derived by combining the Poisson-error associated with the number of identified YSOs within each closed contour, NYSO, the uncertainty in the average stellar mass, ∆M⋆, and the uncertainty in the evolutionary timescale, ∆t⋆. The uncertainty in the global SFE averaged over the clouds of Table 2 is thus given by
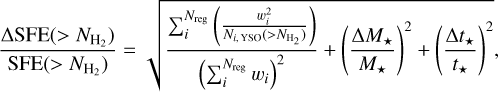 (9)
(9)
where Nreg is the number of clouds with valid SFE estimates at the given 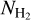 contour. As the evolutionary timescale of Class I YSOs is based on the lifetime of Class II YSOs, this dependency needs to be reflected in the uncertainties. We adopted relative uncertainties of
contour. As the evolutionary timescale of Class I YSOs is based on the lifetime of Class II YSOs, this dependency needs to be reflected in the uncertainties. We adopted relative uncertainties of 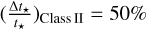 and
and 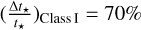 .
.
For both types of estimates, the derived 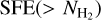 tends to increase with column density up to
tends to increase with column density up to 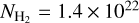 cm−2 (cf. Fig. 8). This increase is slightly more pronounced in the Class I-based estimates. Above
cm−2 (cf. Fig. 8). This increase is slightly more pronounced in the Class I-based estimates. Above 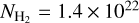 cm−2, however, the SFE estimates based on Class II YSOs start to decline, while the Class I SFEs exhibit a near power-law increase for column densities between 5.0 × 1021 cm−2 and 5.6 × 1022 cm−2 with a slope of about 0.91 ± 0.06, reaching a plateau at higher column densities. This significant difference is discussed in more detail in Sect. 6.3 below.
cm−2, however, the SFE estimates based on Class II YSOs start to decline, while the Class I SFEs exhibit a near power-law increase for column densities between 5.0 × 1021 cm−2 and 5.6 × 1022 cm−2 with a slope of about 0.91 ± 0.06, reaching a plateau at higher column densities. This significant difference is discussed in more detail in Sect. 6.3 below.
 |
Fig. 8 Cumulative SFE above a minimum column density contour as a function of column density for nearby clouds. The orange and green curves indicate the weighted averages over all significant cloud estimates with SFRs derived from Class I and Class II YSO counting, respectively. The shaded areas indicate the corresponding statistical uncertainties (cf. Eq. (9) in Sect. 5.3). The dashed-dotted lines mark the standard deviations of the sample of cloud SFE estimates above each |
6 Discussion
In Sect. 5, we used two independent methods to estimate SFRs in a wide range of column densities for a sample of 49 clouds observed as part of the CAFFEINE survey with ArTéMiS. These methods are YSO distribution fitting (Sect. 4.2.1) and Hi-GAL protostellar clump modeling (Sect. 4.2.2 Elia et al. 2022). Our SFR estimates enable us to probe the SFE at higher column densities than previous works (e.g., Evans et al. 2014; Pokhrel et al. 2021), but are limited at low column densities. Therefore, we also derived SFE estimates for a sample of nearby clouds using Class I and II YSO counting based on published Spitzer YSO catalogs and Herschel column density maps (see Sect. 5.3). Combining the results obtained for CAFFEINE clouds and nearby clouds provides a more comprehensive picture of how the SFE varies as function of gas surface density. Here, we first put our observational results in the context of two simple theoretical models for the SFE-density relation. We then compare the two models with the observations and discuss the limitations of the observational methods.
6.1 Simple models for the star formation efficiency
As briefly mentioned in Sect. 1, there are two leading simple models for the star formation efficiency SFE ≡ SFR/Mgas in molecular gas. In the first one, the SFE per free-fall time, єff ≡ (SFR/Mgas) × tff, is constant ~1–2%, independent of cloud density (Krumholz & Tan 2007; Krumholz 2014), and therefore SFE increases with gas density, since tff ∝ ρ−0.5. We refer to this first model as the єff scenario. In the second model, SFE quickly becomes negligible below some threshold or transition density 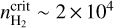 cm−3 and is roughly constant ~5 × 10−8 yr−1 above the threshold density (Lada et al. 2010; Evans et al. 2014). There is a natural interpretation of the above empirical threshold density in the context of the filament paradigm of SF supported by Herschel results in nearby molecular clouds (André et al. 2014). In this observationally-driven paradigm, the threshold density corresponds to the typical volume density of ~0.1-pc-wide trans-critical filaments with masses per unit length within a factor of 2 of the thermally critical mass per unit length
cm−3 and is roughly constant ~5 × 10−8 yr−1 above the threshold density (Lada et al. 2010; Evans et al. 2014). There is a natural interpretation of the above empirical threshold density in the context of the filament paradigm of SF supported by Herschel results in nearby molecular clouds (André et al. 2014). In this observationally-driven paradigm, the threshold density corresponds to the typical volume density of ~0.1-pc-wide trans-critical filaments with masses per unit length within a factor of 2 of the thermally critical mass per unit length 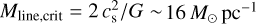 of nearly isothermal molecular gas cylinders at a temperature T ~ 10 K (i.e., a sound speed cs ~ 0.2 km s−1). In the present paper, we therefore refer to the second model as the filament or transition scenario. In the following, we derive the predictions of these two models for the dependence of the cumulative star formation efficiency
of nearly isothermal molecular gas cylinders at a temperature T ~ 10 K (i.e., a sound speed cs ~ 0.2 km s−1). In the present paper, we therefore refer to the second model as the filament or transition scenario. In the following, we derive the predictions of these two models for the dependence of the cumulative star formation efficiency 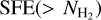 [cf. Eq. (3)] on column density
[cf. Eq. (3)] on column density  or equivalently molecular gas surface density
or equivalently molecular gas surface density 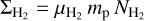 .
.
We can relate 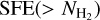 to the differential star formation efficiency,
to the differential star formation efficiency, 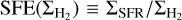 , and the column density PDF in the cloud
, and the column density PDF in the cloud  , where ΣSFR is the SFR surface density and dA is the surface area of the cloud in a logarithmic range of gas surface densities
, where ΣSFR is the SFR surface density and dA is the surface area of the cloud in a logarithmic range of gas surface densities 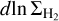 around
around 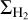 , as follows.
, as follows. 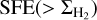 is the ratio of the cumulative star formation rate
is the ratio of the cumulative star formation rate 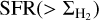 to the cumulative cloud mass
to the cumulative cloud mass 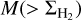 which can be expressed as
which can be expressed as
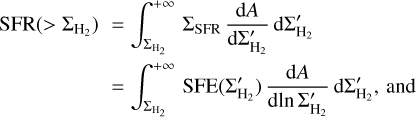 (10)
(10)
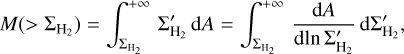 (11)
(11)
respectively. Therefore, 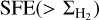 appears to be a weighted-average version of
appears to be a weighted-average version of 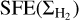 , with a weighting corresponding the column density PDF of the cloud.
, with a weighting corresponding the column density PDF of the cloud.
In the єff scenario, the differential SFE depends on the gas volume density ρ as SFE(ρ) = єff/tff(ρ), with tff(ρ) ∝ ρ−1/2. Assuming a centrally condensed, spheroidal molecular cloud with an average radial density profile ρ(r) ∝ r−α (typically 1.5 < α < 2), the gas surface density scales as 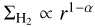 with radius and the volume density can thus be expressed in terms of surface density as
with radius and the volume density can thus be expressed in terms of surface density as 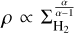 . Moreover, the index of the cloud density profile α can be conveniently related to the slope s of the column density PDF (see Sect. 5.1) as α = (s − 2)/s (see, e.g., Federrath & Klessen 2013). In the regime of column densities where the PDF is a power law, the differential SFE therefore scales as:
. Moreover, the index of the cloud density profile α can be conveniently related to the slope s of the column density PDF (see Sect. 5.1) as α = (s − 2)/s (see, e.g., Federrath & Klessen 2013). In the regime of column densities where the PDF is a power law, the differential SFE therefore scales as:
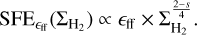 (12)
(12)
Provided that s < −2, it can also be easily shown using Eqs. (5), (10), (11), (12) that the cumulative star formation efficiency 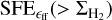 is expected to scale in the same way as the differential form
is expected to scale in the same way as the differential form 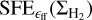 in this picture.
in this picture.
In contrast, in the filament scenario, 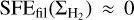 for
for 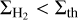 and
and 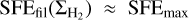 for
for 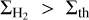 , where
, where 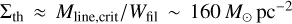 is the typical surface density of thermally transcritical filaments with width Wfil ~ 0.1 pc (André et al. 2014; Arzoumanian et al. 2011, 2019), SFEmax = CFEmax × єcore/tpre⋆ ~ 5 × 10−8 yr−1 the typical SFE expected in thermally supercritical filaments (e.g., Shimajiri et al. 2017), CFEmax ~ 20% the typical core formation efficacy in thermally supercritical filaments (e.g., Könyves et al. 2015), єcore ~ 30% the typical conversion efficacy from core mass to stellar mass (e.g., Alves et al. 2007), and tpre⋆ ~ 1.2 Myr the typical lifetime of prestellar cores (Ward-Thompson et al. 2007; Könyves et al. 2015).
is the typical surface density of thermally transcritical filaments with width Wfil ~ 0.1 pc (André et al. 2014; Arzoumanian et al. 2011, 2019), SFEmax = CFEmax × єcore/tpre⋆ ~ 5 × 10−8 yr−1 the typical SFE expected in thermally supercritical filaments (e.g., Shimajiri et al. 2017), CFEmax ~ 20% the typical core formation efficacy in thermally supercritical filaments (e.g., Könyves et al. 2015), єcore ~ 30% the typical conversion efficacy from core mass to stellar mass (e.g., Alves et al. 2007), and tpre⋆ ~ 1.2 Myr the typical lifetime of prestellar cores (Ward-Thompson et al. 2007; Könyves et al. 2015).
Using again Eqs. (5), (10), (11), we see that
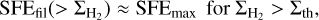 (13)
(13)
for 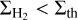 .
.
In reality, the differential star formation efficiency 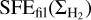 is not a true step function but a “smooth step function”, reflecting the form of the differential prestellar core formation efficacy in molecular filaments (cf. Könyves et al. 2015; André et al. 2019), which we take to be
is not a true step function but a “smooth step function”, reflecting the form of the differential prestellar core formation efficacy in molecular filaments (cf. Könyves et al. 2015; André et al. 2019), which we take to be ![${\rm{CFE}}\left( {{M_{{\rm{line}}}}} \right) = {\rm{CF}}{{\rm{E}}_{\max }} \times \left[ {1 - \exp \left( {{1 \over 2} - {{2{M_{{\rm{line}}}}} \over {3{M_{{\rm{line}}{\rm{.crit}}}}}}} \right)} \right]$](/articles/aa/full_html/2024/08/aa49908-24/aa49908-24-eq89.png) here. This leads to a smooth transition between the two regimes expressed by Eqs. (13) and (14) for
here. This leads to a smooth transition between the two regimes expressed by Eqs. (13) and (14) for 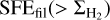 .
.
The predictions of the above two models for the SFE are compared with observations in Sect. 6.2 and Figs. 9 and 10 below. It should be noted here that, for typical N-PDF slopes such as the median slope s ≈ −2.3 observed for the CAFFEINE clouds (see Sect. 5.1), the two models behave very similarly at low column densities (below Σth) in terms of their cumulative 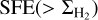 , scaling as power laws
, scaling as power laws 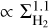 and
and 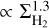 according to Eqs. (12) and (14), respectively. In the regime ofcolumn densities around Σth, the two models are thus easier to discriminate through their predictions for the differential
according to Eqs. (12) and (14), respectively. In the regime ofcolumn densities around Σth, the two models are thus easier to discriminate through their predictions for the differential 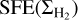 .
.
 |
Fig. 9 Average SFE above a minimum column density contour as a function of column density for the selected CAFFEINE (red) and nearby clouds (green). The shaded areas mark the corresponding uncertainties (cf. Eq. (8) in Sect. 5.1). For the CAFFEINE sample, the red line shows the weighted average of the two SFE estimates. The purple dots indicate averages offormerworks,where the bars show the interquartile range of each cloud sample. For comparison, the blue and black curves represent the two simple models for the SFE (єff and filament scenarios – see Sect. 6.1) and a factor 2 uncertainty. See Figs. 7 and 8 for more details on the observed SFEs. |
6.2 Global picture of the star formation efficiency
In Sect. 5, we derived cumulative SFE estimates as a function of column density for both the CAFFEINE clouds and nearby clouds, to cover the widest possible range of column densities.
As cumulative SFE estimates for nearby clouds based on Class I YSOs may be misleading below ~1022 cm−2 (see Sect. 6.3 below), we concentrate on Class II-based SFE estimates in this section, but discuss the differences with Class I-based SFE estimates in the next subsection. A combined plot of SFE against column density for the CAFFEINE clouds and the sample of nearby clouds in Table 2 is shown in Fig. 9, along with additional published estimates for nearby clouds at two column density levels (Ay ~ 2 mag and AV ~ 8 mag) from Lada et al. (2010) and Evans et al. (2014). The predictions of the ϵff (Krumholz 2014) and filament (André et al. 2014) scenarios described in Sect. 6.1 are also overlaid as solid and dashed lines.
The SFE estimates by Lada et al. (2010) and Evans et al. (2014) were based on SFRs derived from Class II YSO counting similar to this paper, but used cloud masses obtained from extended dust extinction maps as opposed to Herschel column density maps. Additionally, in each cloud, Lada et al. (2010) counted all YSOs within the whole cloud area, i.e., the observed area corresponding to Ay ≥ 2 mag (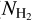 ≥ 2.0 × 1021 cm−2). This difference leads to slightly higher SFEs at high Ay than our present estimates (as we count only YSOs observed within a given Ay contour to estimate the SFE above that Ay value). The cloud-to-cloud standard deviation is, however, comparable to our findings. Evans et al. (2014) provide average SFE estimates at column densities of
≥ 2.0 × 1021 cm−2). This difference leads to slightly higher SFEs at high Ay than our present estimates (as we count only YSOs observed within a given Ay contour to estimate the SFE above that Ay value). The cloud-to-cloud standard deviation is, however, comparable to our findings. Evans et al. (2014) provide average SFE estimates at column densities of 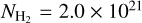 cm−2 and
cm−2 and 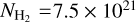 cm−2, but quote SFR estimates for each cloud only at the lower column density. At low column densities, the cloud-to-cloud dispersion of SFE values is significantly higher, as pointed out by Lada et al. (2010). This higher dispersion implies that the mean SFE value averaged over all clouds depends more strongly on the cloud sample at low column densities than at high column densities. Therefore, the slight disagreement between our SFE estimates and those of Evans et al. (2014) at Ay ~ 2 mag may be partly due to differing cloud samples.
cm−2, but quote SFR estimates for each cloud only at the lower column density. At low column densities, the cloud-to-cloud dispersion of SFE values is significantly higher, as pointed out by Lada et al. (2010). This higher dispersion implies that the mean SFE value averaged over all clouds depends more strongly on the cloud sample at low column densities than at high column densities. Therefore, the slight disagreement between our SFE estimates and those of Evans et al. (2014) at Ay ~ 2 mag may be partly due to differing cloud samples.
Comparing the CAFFEINE and nearby-cloud measurements with the two theoretical models described in Sect. 6.1, we find significantly better agreement with the filament scenario. In particular, the SFE traced by Class II YSOs in nearby clouds shows a significant increase with column density from 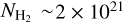 to
to 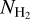 ~ 1022 cm−2 and subsequently levels off, following the predictions of the filament scenario rather closely. Class II YSOs, however, may be in the process of migrating away from their parent molecular cloud (see Sect. 6.3 below for discussion), and Class II YSO counting may thus not directly reflect the instantaneous SFR within a cloud. As it is not possible to correct for this migration effect without a detailed analysis of YSO dynamics (which is out of the scope of the present paper), Class II-based SFEs may be underestimated at the high end of the column density range presented in Fig. 9. Therefore, the turbulence-regulated ϵff scenario may also account for the measurements obtained in nearby clouds if a relatively high value of the SFE per free-fall time is adopted, ϵff ≈ 2%–4%.
~ 1022 cm−2 and subsequently levels off, following the predictions of the filament scenario rather closely. Class II YSOs, however, may be in the process of migrating away from their parent molecular cloud (see Sect. 6.3 below for discussion), and Class II YSO counting may thus not directly reflect the instantaneous SFR within a cloud. As it is not possible to correct for this migration effect without a detailed analysis of YSO dynamics (which is out of the scope of the present paper), Class II-based SFEs may be underestimated at the high end of the column density range presented in Fig. 9. Therefore, the turbulence-regulated ϵff scenario may also account for the measurements obtained in nearby clouds if a relatively high value of the SFE per free-fall time is adopted, ϵff ≈ 2%–4%.
The difference between the two models is more pronounced at higher column densities. This shows the importance of the present CAFFEINE results, which probe the behavior of the SFE in a regime of column densities that is virtually unconstrained by nearby cloud data. The relatively flat behavior of the observed cumulative SFE curve at a value of about 5.4 ± 1.5 × 10−8 yr−1 for 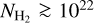 is in close agreement with the predictions of the filament scenario of SF (Fig. 9).
is in close agreement with the predictions of the filament scenario of SF (Fig. 9).
Thus, while SFE estimates in nearby clouds are not able to disprove either of the two models, the CAFFEINE data clearly favor the filament scenario. Even if observational uncertainties in SFR estimates are larger for the CAFFEINE clouds due to their larger distances, the similarity of the SFE estimates we obtained in Sect. 5 using two independent methods (Fig. 7) strengthens the result. Here, the high spatial resolution and large dynamic range of the combined ArTéMiS and Herschel data have been instrumental in allowing us to probe the SFE in molecular clouds at higher column densities than is possible in nearby clouds.
In this study, we concentrated on the SFE averaged over several molecular clouds. But we also showed in Figs. 7 and 8 that there is a significant spread of SFE values between the clouds. An obvious caveat of observational studies is the limitation to surface densities compared to volume densities that are more closely related to SF. The relation between column density and volume density is strongly dependent on the 3D geometrical structure of the clouds (Hu et al. 2022), e.g., spherical or filamentary. In the filament scenario of SF, the dense gas is assumed to be primarily structured in the form of filaments with typical half-power widths ~0.1 pc, while the low-density gas in molecular clouds may be more accurately described as spheroidal on average.
 |
Fig. 10 Differential SFE per column density bin from YSO-counting in nearby clouds vs. column density compared to both the filament or transition model (black curve) and the ϵff model (blue line). Left: comparison of both Class I-based (orange shading) and Class II-based (green shading) SFE estimates with the nominal models discussed in Sect. 6.1. Right: comparison of the Class I-based SFE estimates (orange shading) with the “best-fit” transition and ϵff models (black and blue solid lines, see text). The nominal models shown in the left panel are displayed as dashed lines. |
6.3 Caveat: Difference between Class I and Class II YSO SFE estimates in nearby clouds
The two sets of SFE estimates we derived in Sect. 5.3 for the distance-limited sample of nearby clouds in Table 2, using Class II- and Class I-YSO counting, respectively, deviate at high column densities (Fig. 8). Comparing both estimates with previous studies, we find that, taken at face value, our Class II-based estimates are consistent with the results of Lada et al. (2010) and Evans et al. (2014), while the near power-law increase of the Class I SFE estimates is reminiscent of the results presented by Pokhrel et al. (2021).
To investigate the origin of this difference between Class II-and Class I-based SFE estimates, we first look at the distributions of the numbers of Class II and Class I YSOs with increasing column density. We find that Class I YSOs are more strongly concentrated toward the dense areas than Class II YSOs (Fig. A.2). Despite the slightly different distance limits used in Sect. 5.3 for the cloud samples considered for the Class II- and Class I-based SFE estimates, the observed difference in the spatial distributions of these two classes of YSOs seems to be a robust, general trend (see, e.g., Salji et al. 2015; Gupta & Chen 2022). This is likely due to the dynamics of young stellar populations. YSOs have been observed to decouple progressively from the dense gas environment in which they were born and to migrate away from their parent molecular cloud. As a result, we expect the younger Class I YSOs to be located closer to their birth locations than the older Class II objects. In turn, the estimated SFEs per column density bin may also be expected to exhibit a significant difference depending on which class of YSOs is used to trace SF.
In Fig. 10, we show how the differential SFE varies with column density in nearby clouds based on Class II and Class I SFR estimates. Given the low number statistics per column density bin, we here treat the whole sample of nearby clouds as a single cloud, unlike the geometrical averaging we performed in Sect. 5.3 for the cumulative SFE vs. column density plots shown in Figs. 9 and 8. At low column densities, a steep rise of the differential SFE derived from Class I YSOs is observed from a value of only 3 ± 3 × 10−11 yr−1 at 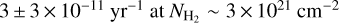 , jumping by more than two orders of magnitude to 0.5–1.5 ×10−8 yr−1 at
, jumping by more than two orders of magnitude to 0.5–1.5 ×10−8 yr−1 at 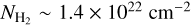 . This jump reflects the very low number of Class I YSOs found at
. This jump reflects the very low number of Class I YSOs found at 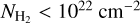 and the fact that most protostars are formed in the densest parts of the clouds. At higher column densities, a much shallower increase of the differential SFE based on Class I YSOs is seen, from 3 ± 2 × 10−8 yr−1 at
and the fact that most protostars are formed in the densest parts of the clouds. At higher column densities, a much shallower increase of the differential SFE based on Class I YSOs is seen, from 3 ± 2 × 10−8 yr−1 at 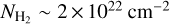 to 9 ± 7 × 10−8 yr−1 at
to 9 ± 7 × 10−8 yr−1 at 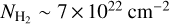 . The very low number of Class I YSOs observed below 1022 cm−2 (see Fig. A.2) implies that the near power-law increase seen in the cumulative SFE versus column density curve
. The very low number of Class I YSOs observed below 1022 cm−2 (see Fig. A.2) implies that the near power-law increase seen in the cumulative SFE versus column density curve 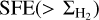 derived from Class I YSOs (Fig. 8) is primarily driven by the marked decline in cloud mass with gas density imposed by the column density PDF, e.g.,
derived from Class I YSOs (Fig. 8) is primarily driven by the marked decline in cloud mass with gas density imposed by the column density PDF, e.g., 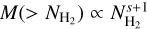 with s + 1 ≈ −1.3 (see Eq. (11) and Fig. 6), at least in the low column density regime. This conclusion is further supported by Fig. 1c of Pokhrel et al. (2021). Accordingly, as mentioned earlier, the cumulative
with s + 1 ≈ −1.3 (see Eq. (11) and Fig. 6), at least in the low column density regime. This conclusion is further supported by Fig. 1c of Pokhrel et al. (2021). Accordingly, as mentioned earlier, the cumulative 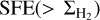 curve is not a good discriminator of the two models of Sect. 6.1 at low column densities because both models predict very similar power laws in this regime (cf. Eqs. (12) and (14)). Figure 10 also suggests that the Class I-based differential SFE levels off at column densities of ≳5 × 1022 cm−2, albeit with lower statistical significance.
curve is not a good discriminator of the two models of Sect. 6.1 at low column densities because both models predict very similar power laws in this regime (cf. Eqs. (12) and (14)). Figure 10 also suggests that the Class I-based differential SFE levels off at column densities of ≳5 × 1022 cm−2, albeit with lower statistical significance.
The average differential SFE derived from Class II-based SFR estimates is significantly higher (~1 ± 0.5 × 10−8 yr−1) than its Class I counterpart in the low column density regime 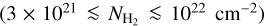 . Above
. Above 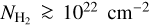 , the Class II-based differential SFE increases up to 2.3 × 10−8 yr−1 at a column density of ~2 × 1022 cm−2, but becomes less reliable at higher column densities as the total number of Class II YSOs observed in the clouds of Table 2 drops to low values (<50, see Fig. A.2).
, the Class II-based differential SFE increases up to 2.3 × 10−8 yr−1 at a column density of ~2 × 1022 cm−2, but becomes less reliable at higher column densities as the total number of Class II YSOs observed in the clouds of Table 2 drops to low values (<50, see Fig. A.2).
Above 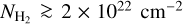 , both the differential and the cumulative SFE derived from Class I YSOs exceed their Class II counterparts by a factor ~2–3. This may be due to two effects. First, as already pointed out, Class II objects may have significantly drifted away from their dense birthplaces. Second, there is some evidence that SF has been accelerating on a typical e-folding timescale of ~ 1–3 Myr in nearby star-forming regions, possibly due to overall cloud contraction (e.g., Palla & Stahler 2000; Watkins et al. 2019). Since Class II YSOs measure SF averaged over a timescale ~2 Myr, while Class I YSOs measure SF integrated over a timescale of only ~0.5 Myr, one may expect the Class I SFRs to exceed the Class II SFRs by a significant factor in dense regions undergoing accelerated SF.
, both the differential and the cumulative SFE derived from Class I YSOs exceed their Class II counterparts by a factor ~2–3. This may be due to two effects. First, as already pointed out, Class II objects may have significantly drifted away from their dense birthplaces. Second, there is some evidence that SF has been accelerating on a typical e-folding timescale of ~ 1–3 Myr in nearby star-forming regions, possibly due to overall cloud contraction (e.g., Palla & Stahler 2000; Watkins et al. 2019). Since Class II YSOs measure SF averaged over a timescale ~2 Myr, while Class I YSOs measure SF integrated over a timescale of only ~0.5 Myr, one may expect the Class I SFRs to exceed the Class II SFRs by a significant factor in dense regions undergoing accelerated SF.
Another possible effect that can contribute to the observed difference between Class II-based and Class I-based estimates of the SFE at high column densities is extinction. The circumstel-lar envelopes of Class I YSOs causes bright far-infrared emission which is less affected by extinction. This can lead to a detection bias in favor of Class I YSOs compared to Class II YSOs in high column density regions. In summary, we consider that Class II-based SFE estimates are reliable between <3 × 1021 cm−2 and ~2 × 1022 cm−2, while our Class I-based SFE estimates seem reliable up to ~3–6 × 1022 cm−2.
Figure 11 compares the cumulative SFE traced by Class I YSOs in nearby clouds with both the CAFFEINE results and the two models introduced in Sect. 6.1. Between 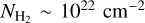 and
and 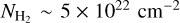 , our Class I-based SFE estimates for nearby clouds remain within the error bars of the filament-scenario predictions but are suggestive of a near power-law increase in SFE, which is consistent with the results of Pokhrel et al. (2021) and the ϵff SF model. Above ~5 × 1022 cm−2, however, the relation seems to flatten out. Again a similar behavior is found by Pokhrel et al. (2021), but in both studies the number of Class I YSOs at
, our Class I-based SFE estimates for nearby clouds remain within the error bars of the filament-scenario predictions but are suggestive of a near power-law increase in SFE, which is consistent with the results of Pokhrel et al. (2021) and the ϵff SF model. Above ~5 × 1022 cm−2, however, the relation seems to flatten out. Again a similar behavior is found by Pokhrel et al. (2021), but in both studies the number of Class I YSOs at 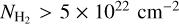 and the total gas mass available at these high column densities are insufficient for a robust conclusion.
and the total gas mass available at these high column densities are insufficient for a robust conclusion.
Overall, if we confront the two models of Sect. 6.1 with the differential form of our Class I-based SFE estimates for nearby clouds (Fig. 10), which is a better discriminator at low column densities, we find better agreement with the transition or filament scenario. The normalized chi-squared statistic  is indeed a factor of >3 lower for the nominal filament or transition model than for the ϵff=1% model. Moreover, if we relax both models somewhat and allow the threshold column density to be a free parameter of the transition scenario and the characteristic ϵff value to be a free parameter of the other model (see right panel of Fig. 10), we find that the best-fit transition model has
is indeed a factor of >3 lower for the nominal filament or transition model than for the ϵff=1% model. Moreover, if we relax both models somewhat and allow the threshold column density to be a free parameter of the transition scenario and the characteristic ϵff value to be a free parameter of the other model (see right panel of Fig. 10), we find that the best-fit transition model has 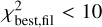 while the best-fit ϵff model has
while the best-fit ϵff model has 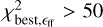 (for 10 degrees of freedom in both cases). The best-fit transition model, which has a threshold column density of ~7.5 × 1021 cm−2, is thus statistically consistent with the data to better than 1σ (p-value = 0.49). In contrast, the best-fit e¢ model, for which ϵff ≈ 0.5%, can be rejected at a >5σ confidence level (p-value << 6 X 10-6).
(for 10 degrees of freedom in both cases). The best-fit transition model, which has a threshold column density of ~7.5 × 1021 cm−2, is thus statistically consistent with the data to better than 1σ (p-value = 0.49). In contrast, the best-fit e¢ model, for which ϵff ≈ 0.5%, can be rejected at a >5σ confidence level (p-value << 6 X 10-6).
Counting Class I YSOs is probably one of the most direct methods available to estimate the SFR in nearby molecular clouds. Class I YSOs are younger and brighter than Class II sources in the mid- to far-infrared range, which render them easier to detect closer to their birthplaces. Therefore, we interpret the abrupt increase in the differential SFE (Fig. 10) and in the surface density of Class I objects (Fig. A.2) above 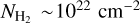 as a column density threshold for SF. This interpretation is in agreement with the findings of several earlier studies which suggested threshold values between 0.65 × 1022 cm−2 and 2.2 × 1022 cm−2 (e.g., Onishi et al. 2001; Johnstone et al. 2004; André et al. 2010; Heiderman et al. 2010; Lada et al. 2010; Heiderman & Evans 2015; Könyves et al. 2015). As already mentioned in Sect. 6.1, such a SF threshold is quite naturally accounted for in the context of the filament scenario, in which stars form primarily in dense, ~0.1-pc-wide filaments with line masses exceeding the thermally critical mass per unit length of isothermal gas cylinders (~16 M⊙/pc for gas at ~10 K) (André et al. 2014).
as a column density threshold for SF. This interpretation is in agreement with the findings of several earlier studies which suggested threshold values between 0.65 × 1022 cm−2 and 2.2 × 1022 cm−2 (e.g., Onishi et al. 2001; Johnstone et al. 2004; André et al. 2010; Heiderman et al. 2010; Lada et al. 2010; Heiderman & Evans 2015; Könyves et al. 2015). As already mentioned in Sect. 6.1, such a SF threshold is quite naturally accounted for in the context of the filament scenario, in which stars form primarily in dense, ~0.1-pc-wide filaments with line masses exceeding the thermally critical mass per unit length of isothermal gas cylinders (~16 M⊙/pc for gas at ~10 K) (André et al. 2014).
Considering all of these comparisons together, we conclude that SF traced by nearby Class I YSOs does not provide decisive evidence for one or the other of the two presented scenarios, but tends to support the transition model. The combination of our CAFFEINE findings with the results obtained for nearby clouds clearly favors the filament scenario, as can be seen in Figs. 9 and 11. In the range ofcolumn densities between ~1022 cm−2 and ~6 × 1022 cm−2 where Class I-based SFE estimates for nearby clouds overlap with CAFFEINE SFE estimates and suggest slightly different trends, we give more weight to the CAFFEINE results because the CAFFEINE cloud sample contains a factor of ~100–200 more dense gas mass in each column density bin than the nearby-cloud sample (cf. Fig. A.3). The CAFFEINE results are thus statistically more significant. Our YSO-based SFE estimates for the CAFFEINE sample use both Class II and Class I YSOs and therefore should remain reliable at high column densities, at least up to 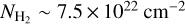 . Furthermore, we also estimate the SFEs of CAFFEINE clouds using Hi-GAL proto-stellar clumps, which are not limited by extinction and remain reliable up to
. Furthermore, we also estimate the SFEs of CAFFEINE clouds using Hi-GAL proto-stellar clumps, which are not limited by extinction and remain reliable up to 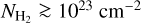 (see Sect. 5.2).
(see Sect. 5.2).
Finally, we note that the reliability of observational SFR and SFE estimates and the effect of potential observational biases has been investigated in several recent works using numerical simulations or Monte-Carlo models (Grudic et al. 2022; Suin et al. 2024; Dib et al. 2024). The most significant potential bias is that any particular SFE estimate derived from observations is an average value over a finite time span ~0.5–2 Myr8 around a specific cloud evolutionary stage and cannot take into account the time dependence of SF in a cloud. For example, over the full 9 Myr duration of the simulation discussed by Grudic et al. (2022) for a 2 × 104 M⊙ GMC, the true SFE per free-fall time ϵff exhibits very significant variations, rising from an initial value ϵff≪ 0.1% to a peak value of ~10% at 5–6 Myr, before declining to ~1% by the end of the simulation. While the observational proxy ϵff,YSO calculated by Grudic et al. (2022, see the orange curve in their Fig. 7) to mimick an observer’s Class I-based estimate fails to track the detailed variations of ϵff accurately and underestimates the peak -10% value by a factor of ≳ 3, it nevertheless follows the general evolution quite well and has an average value over the full duration of the simulation which is close to the true average value. It should also be pointed out that Grudic et al. (2022) define the “true” SFE and true в$ with respect to the total initial cloud mass and initial free-fall time in the simulation, while we are more concerned with the SFE in dense gas above a limiting column density and with the ¾ value with respect to the free-fall time of dense gas in the present work. In the context of the filament or transition scenario advocated here, the rather steep rise of both SFE and в$ seen during the first -5 Myr of the Grudic et al. (2022) simulation is easily interpreted as the direct result of a corresponding increase in the mass of dense gas (initially strictly 0) due to large-scale turbulent shock compression and gravitational collapse. In this paper, we have averaged our measurements over 49 CAFFEINE clouds, irrespective of their evolutionary state, as we are not trying to study the time evolution of the SFE. The analysis presented in Sect. 3.5 of Grudic et al. (2022) suggests that our results should describe the general trend between SFE and column density, averaged over the whole period of active SF in GMCs, to within a factor of ~2 accuracy, even if the typical values of ~1–4% we infer for ϵff in dense molecular gas may underestimate the actual peak value achieved during the entire SF history of a GMC.
 |
Fig. 11 Cumulative average SFE above a minimum column density contour as a function of column density for a selection of CAFFEINE (red) and nearby clouds (green and orange). The shaded areas mark the corresponding uncertainties. For the CAFFEINE sample, the weighted average of the two SFE estimates are shown. The purple markers indicate averages of former works, where the bars show the interquartile range of the cloud sample. For comparison, the blue and black curves show the two simple models of Sect. 6.1 for the SFE (ϵff and filament scenarios). See Figs. 7 and 8 for more details on the observed SFEs. |
 |
Fig. 12 Cumulative SFE above |
6.4 Role of stellar feedback
Given the large and diverse sample of molecular clouds, it is also possible to investigate how environmental effects and feedback from high-mass stars impact the SFR and SFE of molecular clouds. On one hand, feedback from high-mass stars can promote further SF by compressing the surrounding gas, enhancing the dense gas fraction, and weighting the associated  –PDF toward higher column densities. On the other hand, radiative feedback drives H II regions which disperse molecular gas and therefore tend to inhibit SF in their immediate vicinity. Using high-resolution MHD simulations, Suin et al. (2024) and Chevance et al. (2023) have shown that the presence of stellar feedback can indeed strongly influence the Schmidt-Kennicutt relation and the typical SFE per free-fall time, mainly through its influence on the cloud’s density structure. The role of the cloud’s column density PDF is easy to understand in the context of the two models described in Sect. 6.1 since in both models the logarithmic slope s of the PDF partly controls the expected variations of the SFE with column density (see Eqs. (12) and (14)).
–PDF toward higher column densities. On the other hand, radiative feedback drives H II regions which disperse molecular gas and therefore tend to inhibit SF in their immediate vicinity. Using high-resolution MHD simulations, Suin et al. (2024) and Chevance et al. (2023) have shown that the presence of stellar feedback can indeed strongly influence the Schmidt-Kennicutt relation and the typical SFE per free-fall time, mainly through its influence on the cloud’s density structure. The role of the cloud’s column density PDF is easy to understand in the context of the two models described in Sect. 6.1 since in both models the logarithmic slope s of the PDF partly controls the expected variations of the SFE with column density (see Eqs. (12) and (14)).
Radiative feedback in the CAFFEINE clouds is best traced by the emission of far-UV (FUV) photons, which then heat the surrounding gas. We can estimate the flux of the FUV radiation FFUV by
![${F_{{\rm{FUV}}}}\left[ {{G_0}} \right] = 4000\pi {I_{{\rm{FIR}}}}/1.6,$](/articles/aa/full_html/2024/08/aa49908-24/aa49908-24-eq123.png) (15)
(15)
where IFIR is the far infrared emission observed by Her-schel/PACS at 70 µm and 160 µm (Habing 1968; Kramer et al. 2008). As the regions imaged by CAFFEINE typically cover fields significantly larger than the area directly impacted by early feedback from high-mass stars, and over which large variations of G0 are observed, we use  , the 90th percentile of the observed G0 values in each field, as a quantitative estimate of the strength of radiative feedback on dense gas. The uncertainty in
, the 90th percentile of the observed G0 values in each field, as a quantitative estimate of the strength of radiative feedback on dense gas. The uncertainty in 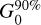 is derived from the dispersion of G0 estimates over the cloud. We plot the SFE estimated above
is derived from the dispersion of G0 estimates over the cloud. We plot the SFE estimated above 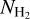 > 2.8 × 1022 cm−2 against
> 2.8 × 1022 cm−2 against 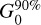 in Fig. 12.
in Fig. 12.
We find no significant correlation between our SFE and G0 estimates, which is indicated by a Pearson correlation coefficient of only r = −0.19. We also checked that this finding does not depend on the adopted minimum column density and exact per-centile in the G0 distribution per cloud: Upon varying these two parameters, the derived slope of the best-fit linear correlation (in log space) remained consistent with zero within errors, but also slightly negative. Therefore, to first order, it appears that radiative feedback has little, if any, influence on the SFE in dense gas. Its main effect may be in regulating the amount of dense gas in a given region. A more dedicated study of the role of feedback in the CAFFEINE clouds would nevertheless be needed to draw a firm conclusion on this topic. Such a study, including a comparison with numerical simulations, is currently planned and will be published in a future paper.
7 Summary and conclusions
We imaged the submillimeter dust continuum emission of 49 dense molecular clouds with APEX-ArTéMiS as part of the CAFFEINE survey. We then combined the ArTéMiS maps with Herschel data to create high-dynamic-range column density maps of the clouds, which are free of any saturation effect and have a factor of ~4 higher resolution (8″) than standard Herschel column density maps. This improved resolution is essential to resolve the regions of high column density targeted in our study.
After deriving two independent sets of SFR estimates for the CAFFEINE clouds, based on Spitzer YSO distribution fitting and Hi-GAL protostellar clump modeling, respectively, we used these high-quality maps to analyze the relation between SFE and gas (column) density. For a more complete view of the SFE at low column densities, we also used Class II- and Class I-YSO counting in combination with column density maps from the Herschel Gould Belt survey for 11 nearby clouds. Comparing the observational data with the predictions of the filament (or transition) and ϵff SF scenarios, we draw the following conclusions:
There is broad agreement between the two sets of SFRs we derive for the CAFFEINE molecular clouds (at distances 0.6 ≲ d ≲ 3 kpc), that is, between those derived from fitting a standard stellar IMF to identified Spitzer YSOs and from identified Hi-GAL protostellar clumps with the relation of Elia et al. (2022), respectively;
Star formation efficiency is found to be essentially independent of column density in the regime of column densities probed by the CAFFEINE cloud sample, namely 1022 ≲
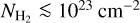 . At these column densities, the CAFFEINE clouds comprise two orders of magnitude more dense gas mass than the nearby-cloud sample (cf. Fig. A.3);
. At these column densities, the CAFFEINE clouds comprise two orders of magnitude more dense gas mass than the nearby-cloud sample (cf. Fig. A.3);In nearby molecular clouds, Class I YSOs are concentrated in areas of high column density
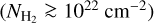 , suggesting the presence of a column density transition for SF at about
, suggesting the presence of a column density transition for SF at about 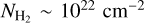 (Figs. 10 and A.2), as also pointed out by earlier studies. Above this transition column density, the SFE estimates based on nearby Class I YSOs tend to increase with column density, but become uncertain for
(Figs. 10 and A.2), as also pointed out by earlier studies. Above this transition column density, the SFE estimates based on nearby Class I YSOs tend to increase with column density, but become uncertain for 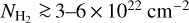 due to the small gas masses available in each cloud at these densities (cf. Fig. A.3);
due to the small gas masses available in each cloud at these densities (cf. Fig. A.3);Comparing these observational results with the two simple scenarios proposed for the SFE, we find better agreement with the transition picture and the filament scenario (Figs. 9 and 10). This conclusion is mainly based on two findings: the presence of an apparent SF threshold at
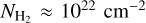 , below which the observed SFE quickly declines (cf. point 3), and the observation of a nearly constant SFE at higher column densities in the CAFFEINE sample (cf. point 2). A caveat is that available Class I-based estimates for nearby clouds are suggestive of a near power-law increase in SFE between
, below which the observed SFE quickly declines (cf. point 3), and the observation of a nearly constant SFE at higher column densities in the CAFFEINE sample (cf. point 2). A caveat is that available Class I-based estimates for nearby clouds are suggestive of a near power-law increase in SFE between 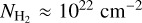 and
and 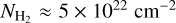 , which is reminiscent of the ϵff scenario, while remaining consistent with the transition model within error bars (see Figs. 10 and 11);
, which is reminiscent of the ϵff scenario, while remaining consistent with the transition model within error bars (see Figs. 10 and 11);We do not find any significant correlation between our measured SFEs at high column densities
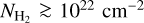 and the strength of local radiative feedback quantified by the level of FUV-radiation G0 (cf. Fig. 12). This suggests that feedback has little influence on the SFE in dense gas, even if it may control the amount of dense gas available for SF. A more dedicated study of the role of feedback in the CAFFEINE clouds is needed to confirm this preliminary conclusion.
and the strength of local radiative feedback quantified by the level of FUV-radiation G0 (cf. Fig. 12). This suggests that feedback has little influence on the SFE in dense gas, even if it may control the amount of dense gas available for SF. A more dedicated study of the role of feedback in the CAFFEINE clouds is needed to confirm this preliminary conclusion.
Acknowledgments
We thank the referee for useful comments which helped us strengthen the paper. We are very thankful for the continuous support provided by the APEX and ESO staff during ArTéMiS operations. M.M. and Ph.A. acknowledge financial support by CNES and “Ile de France” regional funding (DIM-ACAV+ Program). AZ thanks the support of the Institut Uni-versitaire de France. We also acknowledge support from the French national programs of CNRS/INSU on stellar and ISM physics (PNPS and PCMI). Software: APLpy (Robitaille 2019), astropy (Astropy Collaboration 2013), Matplotlib (Hunter 2007), NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020). This document was prepared using the Overleaf web application, which can be found at www.overleaf.com.
Appendix A Statistics of YSOs, protostellar clumps, and gas mass against column density
In Sect. 4.2.1, we derived the SFRs of CAFFEINE molecular clouds from YSOs and Hi-GAL protostellar clumps identified within the cloud boundaries. To understand the limitations of these two methods it is essential to look at the distribution of objects as a function of column density.
As most CAFFEINE clouds are quite distant (up to d ≲ 3 kpc), we expect the identified YSOs to be biased toward relatively luminous and massive objects given the resolution and sensitivity limits of the underlying infrared surveys. This limitation is accounted for by fitting an IMF to the detected YSOs and extrapolating the result to the whole stellar mass spectrum to estimate the total YSO mass and corresponding SFR, as described in Sect. 4.2.1. Additionally, the dust in the dense inner parts of the clouds will absorb the near-/mid-infrared emission from embedded YSOs and render their detection more difficult at higher column densities. The limiting column density above which YSOs can no longer be used to trace the SFR may be identified by plotting the average number and average surface density of detected YSOs per cloud and column density bin against column density, which is shown in Fig. A.1. It can be seen that the surface density of detected YSOs per unit area increases with column density up to 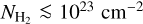 and starts dropping and fluctuating in the two highest column density bins. We thus find that our SFR estimates from massive YSOs are strongly impacted by incompleteness for column densities ≳ 1023 cm−2, which is consistent with the detection limit estimates made in Sect. 4.2.1. We do not see such an incompleteness effect for the protostel-lar clumps, as they are identified as peaks in submillimeter dust emission and not affected by dust extinction. The lower number of protostellar clumps observed at low column densities reflects the strong connection between SF and dense gas.
and starts dropping and fluctuating in the two highest column density bins. We thus find that our SFR estimates from massive YSOs are strongly impacted by incompleteness for column densities ≳ 1023 cm−2, which is consistent with the detection limit estimates made in Sect. 4.2.1. We do not see such an incompleteness effect for the protostel-lar clumps, as they are identified as peaks in submillimeter dust emission and not affected by dust extinction. The lower number of protostellar clumps observed at low column densities reflects the strong connection between SF and dense gas.
 |
Fig. A.1 Average number statistics of YSOs (olive) and Hi-GAL proto-stellar clumps (pink) in the CAFFEINE clouds of this study. The solid histograms indicate the surface number densities in each column density bin (left axis), while the dashed histograms show the absolute numbers of objects in each column density bin (right axis). |
 |
Fig. A.2 Average number statistics of Class I (orange) and Class II (green) YSOs for the nearby clouds considered in this study. The solid histograms show the surface number densities in each column density bin (left axis), while the dashed and dotted histograms give the numbers of objects ineachcolumndensitybin(rightaxis). The dashed and dotted orange histograms show the number sof Class I objects per bin before and after correction for contamination by the fraction of Class I sources with no significant protostellar envelope (cf. Sect. 5.3 and Heiderman & Evans 2015), respectively. |
Similarly, we also investigate the distribution of Class I and Class II YSOs with respect to column density in nearby clouds (Fig. A.2). We find significant differences in these distributions. While the surface density of Class I YSOs peaks at the highest density bin  the peak of Class II YSOs is at
the peak of Class II YSOs is at 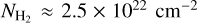 . We interpret this difference as a sign of migration of YSOs after decoupling from their parent gas structures (cf. Salji et al. 2015; Stutz 2018).
. We interpret this difference as a sign of migration of YSOs after decoupling from their parent gas structures (cf. Salji et al. 2015; Stutz 2018).
Figure A.3 shows the mean gas mass per cloud per column density bin as a function of column density, for both the CAFFEINE clouds of Table 1 and the nearby clouds of Table 2. It illustrates that the CAFFEINE clouds include one to two orders of magnitude more dense gas mass than the nearby clouds in the range of column densities of 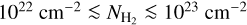 .
.
Appendix B Alternative method for combining ArTéMiS and Herschel data
In cases where the baseline method did not produce satisfactory results, the data processing of ArTéMiS data and the hybridization of SPIRE and ArTéMiS maps were performed with an extension of the Scanamorphos software for ArTéMiS (Rous-sel 2013, 2018). The first step is to compute astrometric offsets for each scan, stopping the data processing after the subtraction of the average drift and the uncorrelated drifts on the longest timescale. After projecting separately each scan, the brightest source within the corresponding field of view is fitted with a Gaussian in both the SPIRE 350 µm map and the ArTéMiS map (convolved to the angular resolution of the SPIRE 350 µm map). The data processing is then restarted with these input astromet-ric corrections. The main difference introduced with respect to the normal algorithm is that the SPIRE map (interpolated into the ArTéMiS passband at 450 µm, as described earlier) is used to ease the baseline subtraction: time series simulated from the SPIRE map are subtracted from the ArTéMiS time series (after appropriate scaling to the unit of Jy per ArTéMiS beam), baselines are subtracted from the resulting time series with the usual method, and then the simulated SPIRE time series are added back to the data. The drift subtraction on smaller spatial and temporal scales is unchanged.
 |
Fig. A.3 Mean gas mass per cloud in each column density bin against column density for the CAFFEINE sample (red) and the nearby clouds considered here (green). The shaded areas indicate the standard deviations of the sample of differential gas mass values. |
The hybridization with SPIRE and beam area recalibration are done directly in the spatial domain as described below. The hybrid map H is designed to preserve the total flux of any type of source (on any characteristic spatial scale), as measured with SPIRE. The final ArTéMiS map and the SPIRE map are first convolved to bring them to a common FWHM angular resolution (in the case of SPIRE, the FWHM increase is very modest, of 4 – 5%). Then, a filtered version of the ArTéMiS map is created, containing only pedestal emission under bright sources (to which ArTéMiS is not as sensitive as SPIRE, and that cannot be reliably recovered), and subtracted from the ArTéMiS map to create a map containing only compact sources, which we hereafter call the “compact map”, C (Cconv in its lower-resolution version). A flux calibration corrective factor is then computed as the ratio of the total emission of the SPIRE map Sconv (after subtraction of a large-scale zero-level) within a certain mask to the total emission of Cconv (with the same FWHM as Sconv) within the same mask. The brightness threshold used to define the mask selects only the brightest sources, well above the sensitivity limits of both instruments. The fiducial (Gaussian) beam area is then divided by this correctivefactor(on the order of 0.5 at both wave-lengths) to obtain the effective beam area, before converting the ArTéMiS map unit from Jy/beam to MJy/sr. A map containing only extended emission (to which SPIRE is uniquely sensitive) is then computed as E = Sconv − Cconv recal, and the hybrid map is constructed as H = Crecal + W Sconv where the weight map W multiplying the SPIRE map is W = E/Sconv. In that way, SPIRE fluxes are preserved at any location in the hybrid map.
To deal with saturation in some SPIRE fields, we modified the above process, to identify pixels affected by saturation or nonlinear response, and to set the SPIRE weight map to zero in these pixels. Care is taken to avoid discontinuities in the W map, by working temporarily with a version of Sconv where the pixels to be discarded are filled with Cconv recal, with a scalar offset.
Appendix C Detailed SFR and SFE estimates for each CAFFEINE cloud
Table C.1 provides the numbers of protostellar clumps and YSOs as well as our respective estimates of the SFR and SFE for each CAFFEINE cloud within two specific column density contours: 1.4 × 1022 cm−2 and 7.9 × 1022 cm−2.
Derived properties for the CAFFEINE clouds
References
- Alves, J., Lombardi, M., & Lada, C. J. 2007, A&A, 462, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2017, A&A, 606, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 27 [Google Scholar]
- André, P., Revéret, V., Könyves, V., et al. 2016, A&A, 592, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Arzoumanian, D., Könyves, V., Shimajiri, Y., & Palmeirim, P. 2019, A&A, 629, L4 [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, A6 [Google Scholar]
- Arzoumanian, D., André, P., Könyves, V., et al. 2019, A&A, 621, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Robitaille, T., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldeschi, A., Molinari, S., Elia, D., Pezzuto, S., & Schisano, E. 2017, MNRAS, 472, 1778 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Chabrier, G., & Gallardo, J. 2009, ApJ, 702, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, P. J., Muller, E., Indermuehle, B., et al. 2015, ApJ, 812, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Benedettini, M., Pezzuto, S., Schisano, E., et al. 2018, A&A, 619, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2011, ApJ, 730, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Bracco, A., Bresnahan, D., Palmeirim, P., et al. 2020, A&A, 644, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bresnahan, D., Ward-Thompson, D., Kirk, J. M., et al. 2018, A&A, 615, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2005, in Astrophys. Space Sci. Lib., 327, The Initial Mass Function 50 Years Later, eds. E. Corbelli, F. Palla, & H. Zinnecker, 41 [CrossRef] [Google Scholar]
- Chevance, M., Krumholz, M. R., McLeod, A. F., et al. 2023, in ASP Conf. Ser., 534, Protostars Planets VII, eds. S. Inutsuka, Y. Aikawa, T. Muto, K. Tomida, & M. Tamura, 1 [Google Scholar]
- Dib, S., Zhou, J. W., Comerón, S., et al. 2024, A&A, submitted [arXiv:2405.00095] [Google Scholar]
- Duarte-Cabral, A., Colombo, D., Urquhart, J. S., et al. 2021, MNRAS, 500, 3027 [Google Scholar]
- Dunham, M., Stutz, A., Allen, L., et al. 2014, in Protostars Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 195 [Google Scholar]
- Dunham, M. M., Allen, L. E., Evans, N. J., et al. 2015, ApJS, 220, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Merello, M., Molinari, S., et al. 2021, MNRAS, 504, 2742 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Molinari, S., Schisano, E., et al. 2022, ApJ, 941, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., Allen, L. E., Blake, G. A., et al. 2003, PASP, 115, 965 [CrossRef] [Google Scholar]
- Evans, N. J., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJ, 181, 321 [NASA ADS] [Google Scholar]
- Evans, N. J., Heiderman, A., & Vutisalchavakul, N. 2014, ApJ, 782, 114 [CrossRef] [Google Scholar]
- Fiorellino, E., Elia, D., André, P., et al. 2021, MNRAS, 500, 4257 [Google Scholar]
- Greene, T. P., Wilking, B. A., Andre, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Grudic, M. Y., Guszejnov, D., Offner, S. S. R., et al. 2022, MNRAS, 512, 216 [CrossRef] [Google Scholar]
- Gupta, A., & Chen, W.-P. 2022, AJ, 163, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Güsten, R., Nyman, L. A., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Fallscheer, C., Ginsburg, A., et al. 2013, ApJ, 764, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., & Evans, N. J. II 2015, ApJ, 806, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., Evans, N. J., Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Hu, Z., Krumholz, M. R., Pokhrel, R., & Gutermuth, R. A. 2022, MNRAS, 511, 1431 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Immer, K., Menten, K. M., Schuller, F., & Lis, D. C. 2012, A&A, 548, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jackson, J. M., Rathborne, J. M., Shah, R. Y., et al. 2006, ApJS, 163, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Johnstone, D., Di Francesco, J., & Kirk, H. 2004, ApJ, 611, L45 [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, M., Bieging, J. H., Povich, M. S., & Lee, Y. 2009, ApJ, 706, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, S.-J., Kerton, C. R., Choi, M., & Kang, M. 2017, ApJ, 845, 21 [CrossRef] [Google Scholar]
- Kauffmann, J., Bertoldi, F., Bourke, T. L., Evans, N. J., & Lee, C. W. 2008, A&A, 487, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, R. C. J. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Marocco, F., Gelino, C. R., et al. 2024, ApJS, 271, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Koenig, X., & Leisawitz, D. 2014, ApJ, 791, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [Google Scholar]
- Könyves, V., André, P., Arzoumanian, D., et al. 2020, A&A, 635, A34 [Google Scholar]
- Kramer, C., Cubick, M., Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kroupa, P. 2002, Science, 295, 82 [Google Scholar]
- Krumholz, M. R. 2014, Phys. Rep., 539, 49 [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [Google Scholar]
- Krumholz, M. R., & Tan, J. C. 2007, ApJ, 654, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Kuhn, M. A., de Souza, R. S., Krone-Martins, A., et al. 2021, ApJS, 254, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lewis, J. A., Lombardi, M., & Alves, J. 2017, A&A, 606, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ladjelate, B., André, P., Könyves, V., et al. 2020, A&A, 638, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marton, G., Tóth, L., Paladini, R., et al. 2016, MNRAS, 458, 3479 [NASA ADS] [CrossRef] [Google Scholar]
- Marton, G., Ábrahám, P., Szegedi-Elek, E., et al. 2019, MNRAS, 487, 2522 [Google Scholar]
- Mattern, M., Kauffmann, J., Csengeri, T., et al. 2018, A&A, 619, A166 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2012, AJ, 144, 27 [Google Scholar]
- Megeath, S., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5 [Google Scholar]
- Molinari, S., Pezzuto, S., Cesaroni, R., et al. 2008, A&A, 481, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molinari, S., Consortium, T. H.-G., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & André, P. 2001, A&A, 365, 440 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [CrossRef] [EDP Sciences] [Google Scholar]
- Onishi, T., Yoshikawa, N., Yamamoto, H., et al. 2001, PASJ, 53, 1017 [NASA ADS] [Google Scholar]
- Ortiz-León, G. N., Dzib, S. A., Loinard, L., et al. 2023, A&A, 673, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Palla, F., & Stahler, S. W. 2000, ApJ, 540, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peretto, N., Rigby, A. J., Louvet, F., et al. 2023, MNRAS, 525, 2935 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzuto, S., Benedettini, M., Di Francesco, J., et al. 2021, A&A, 645, A55 [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2011, A&A, 536, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pokhrel, R., Gutermuth, R. A., Krumholz, M. R., et al. 2021, ApJ, 912, L19 [CrossRef] [Google Scholar]
- Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS] [Google Scholar]
- Rayner, T. S. M., Griffin, M. J., Schneider, N., et al. 2017, A&A, 607, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Revéret, V., André, P., Le Pennec, J., et al. 2014, SPIE Conf. Ser., 9153, 915305 [Google Scholar]
- Robitaille, T. 2017, A&A, 600, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. 2019, APLpy v2.0: The Astronomical Plotting Library in Python Zenodo, https://doi.org/10.5281/zenodo.2567476 [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roussel, H. 2018, arXiv e-prints [arXiv:1803.04264] [Google Scholar]
- Roy, A., André, P., Palmeirim, P., et al. 2014, A&A, 562, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Russeil, D., Pestalozzi, M., Mottram, J. C., et al. 2011, A&A, 526, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salji, C. J., Richer, J. S., Buckle, J. V., et al. 2015, MNRAS, 449, 1769 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in ASP Conf. Ser., 77, Astron. Data Anal. Softw. Syst. IV, eds. R. A. Shaw, H. E. Payne, & J. J. E. Hayes, 433 [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2011, AJ, 142, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., André, P., Shimajiri, Y., et al. 2021a, A&A, 651, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Urquhart, J., Csengeri, T., et al. 2021b, MNRAS, 500, 3064 [Google Scholar]
- Sewiło, M., Whitney, B. A., Yung, B. H., et al. 2019, ApJS, 240, 26 [Google Scholar]
- Shimajiri, Y., André, P., Braine, J., et al. 2017, A&A, 604, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A. M. 2018, MNRAS, 473, 4890 [NASA ADS] [CrossRef] [Google Scholar]
- Suin, P., Zavagno, A., Colman, T., et al. 2024, A&A, 682, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talvard, M., Revéret, V., Le-Pennec, Y., et al. 2018, SPIE Conf. Ser., 10708, 1070838 [Google Scholar]
- Veneziani, M., Schisano, E., Elia, D., et al. 2017, A&A, 599, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Met., 17, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., Di Francesco, J., Hatchell, J., et al. 2007, PASP, 119, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Watkins, E. J., Peretto, N., Marsh, K., & Fuller, G. A. 2019, A&A, 628, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zhang, G.-Y., André, P., Men’shchikov, A., & Li, J.-Z. 2024, A&A, in press, https://doi.org/10.1051/0004-6361/202449853 [Google Scholar]
The ZAMS luminosity-mass relation is a reasonable assumption here, since most of the Spitzer/WISE YSOs selected in the CAFFEINE regions are relatively high luminosity objects (>80% are more luminous than 10 LQ, and >50% more luminous than 50 L⊙) and thus unlikely to be dominated by accretion. The detailed Spitzer study of the W51 complex by Kang et al. (2009) confirms that the ZAMS relation is generally appropriate for YSOs with Ltot > 10–50 L⊙. Moreover, the luminosity used here to derive M★ is the stellar luminosity L★ estimated from the model fitting, not the observed Ltot = L★ + Lacc.
For comparison, the mean stellar mass is ~0.4 M⊙ for the Kroupa (2002) IMF in the mass range 0.01–120 M⊙ and ~0.5 M⊙ for the Chabrier (2005) IMF in the same mass range. A recent Gaia determination of the IMF in the solar neighborhood (Kirkpatrick et al. 2024) finds a mean stellar mass of 0.41 M⊙ but is insensitive to massive stars >8 M⊙.
All Tables
All Figures
 |
Fig. 1 Locations of the CAFFEINE targets marked as yellow circles in an artist's impression of the Milky Way by R. Hurt (NASA; JPL-Caltech). The targets selected for this study are marked by red crosses. |
| In the text | |
 |
Fig. 2 Examples of data products derived from the CAFFEINE survey. Left: dust continuum emission of the G034 region as observed at 350 µm by ArTéMiS at 8″ resolution. Center: dust continuum emission of the G034 region as observed at 450 µm by ArTéMiS at 10" resolution. Right: combined 350 µm ArTéMiS-SPIRE dust continuum emission map with 8" resolution and high dynamic range. |
| In the text | |
 |
Fig. 3 Examples of high level data products from the CAFFEINE survey. Left: column density map of the G034 region at 8″ resolution derived from combined ArTéMiS and Herschel data. Right: final multiresolution column density map of the G034 region, with 8″ resolution above |
| In the text | |
 |
Fig. 4 Multiresolution column density map of the MonR2 region based on ArTéMiS + Herschel data, with blue dots marking the locations of identified YSOs within the cloud area. The resolution of the map ranges from ~8″ at |
| In the text | |
 |
Fig. 5 Multiresolution column density map of the MonR2 region based on ArTéMiS + Herschel data, with blue crosses marking the locations of identified protostellar clumps within the cloud area. The resolution of the map ranges from ~8″ at |
| In the text | |
 |
Fig. 6 Column density probability density functions (N-PDFs) as a function of column density (top axis) and visual extinction (bottom axis) for the MonR2, G034, and OH341 regions and for all CAFFEINE regions combined in red, blue, green and black, respectively. The peaks of the distributions are indicated by dashed lines with the column density |
| In the text | |
 |
Fig. 7 Cumulative SFE above a minimum column density |
| In the text | |
 |
Fig. 8 Cumulative SFE above a minimum column density contour as a function of column density for nearby clouds. The orange and green curves indicate the weighted averages over all significant cloud estimates with SFRs derived from Class I and Class II YSO counting, respectively. The shaded areas indicate the corresponding statistical uncertainties (cf. Eq. (9) in Sect. 5.3). The dashed-dotted lines mark the standard deviations of the sample of cloud SFE estimates above each |
| In the text | |
 |
Fig. 9 Average SFE above a minimum column density contour as a function of column density for the selected CAFFEINE (red) and nearby clouds (green). The shaded areas mark the corresponding uncertainties (cf. Eq. (8) in Sect. 5.1). For the CAFFEINE sample, the red line shows the weighted average of the two SFE estimates. The purple dots indicate averages offormerworks,where the bars show the interquartile range of each cloud sample. For comparison, the blue and black curves represent the two simple models for the SFE (єff and filament scenarios – see Sect. 6.1) and a factor 2 uncertainty. See Figs. 7 and 8 for more details on the observed SFEs. |
| In the text | |
 |
Fig. 10 Differential SFE per column density bin from YSO-counting in nearby clouds vs. column density compared to both the filament or transition model (black curve) and the ϵff model (blue line). Left: comparison of both Class I-based (orange shading) and Class II-based (green shading) SFE estimates with the nominal models discussed in Sect. 6.1. Right: comparison of the Class I-based SFE estimates (orange shading) with the “best-fit” transition and ϵff models (black and blue solid lines, see text). The nominal models shown in the left panel are displayed as dashed lines. |
| In the text | |
 |
Fig. 11 Cumulative average SFE above a minimum column density contour as a function of column density for a selection of CAFFEINE (red) and nearby clouds (green and orange). The shaded areas mark the corresponding uncertainties. For the CAFFEINE sample, the weighted average of the two SFE estimates are shown. The purple markers indicate averages of former works, where the bars show the interquartile range of the cloud sample. For comparison, the blue and black curves show the two simple models of Sect. 6.1 for the SFE (ϵff and filament scenarios). See Figs. 7 and 8 for more details on the observed SFEs. |
| In the text | |
 |
Fig. 12 Cumulative SFE above |
| In the text | |
 |
Fig. A.1 Average number statistics of YSOs (olive) and Hi-GAL proto-stellar clumps (pink) in the CAFFEINE clouds of this study. The solid histograms indicate the surface number densities in each column density bin (left axis), while the dashed histograms show the absolute numbers of objects in each column density bin (right axis). |
| In the text | |
 |
Fig. A.2 Average number statistics of Class I (orange) and Class II (green) YSOs for the nearby clouds considered in this study. The solid histograms show the surface number densities in each column density bin (left axis), while the dashed and dotted histograms give the numbers of objects ineachcolumndensitybin(rightaxis). The dashed and dotted orange histograms show the number sof Class I objects per bin before and after correction for contamination by the fraction of Class I sources with no significant protostellar envelope (cf. Sect. 5.3 and Heiderman & Evans 2015), respectively. |
| In the text | |
 |
Fig. A.3 Mean gas mass per cloud in each column density bin against column density for the CAFFEINE sample (red) and the nearby clouds considered here (green). The shaded areas indicate the standard deviations of the sample of differential gas mass values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.