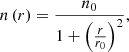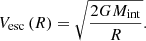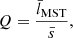| Issue |
A&A
Volume 663, July 2022
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 21 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/202141765 | |
| Published online | 01 July 2022 | |
Influence of protostellar jets and HII regions on the formation and evolution of stellar clusters
1
Laboratoire AIM, Paris-Saclay, CEA Saclay/IRFU/DAp – CNRS – Université Paris Diderot, 91191 Gif-sur-Yvette Cedex, France
e-mail: antoine.verliat@cea.fr
2
LERMA (UMR CNRS 8112), Ecole Normale Supérieure, 75231 Paris Cedex, France
3
Université Grenoble Alpes, CNRS, IPAG, 38000 Grenoble, France
4
Department of Earth Sciences, National Taiwan Normal University, 116059 Taipei, Taiwan
5
Center of Astronomy and Gravitation, National Taiwan Normal University, 116059 Taipei, Taiwan
6
Anton Pannekoek Institute for Astronomy, Universiteit van Amsterdam, Science Park 904, 1098 XH, Amsterdam, The Netherlands
Received:
11
July
2021
Accepted:
21
January
2022
Context. Understanding the conditions in which stars and stellar clusters form is of great importance. In particular, the role that stellar feedback may have is still hampered by large uncertainties.
Aims. We aim to investigate the role played by ionising radiation and protostellar outflows during the formation and evolution of a stellar cluster. To self-consistently take into account gas accretion, we start with clumps of tens of parsecs in size.
Methods. Using an adaptive mesh refinement code, we ran magneto-hydrodynamical numerical simulations aimed at describing the collapse of massive clumps with either no stellar feedback or taking into account ionising radiation and/or protostellar jets.
Results. Stellar feedback substantially modifies the protostellar cluster properties in several ways. We confirm that protostellar outflows reduce the star formation rate by a factor of a few, although the outflows do not stop accretion and, likely enough, do not modify the final cluster mass. On the other hand, once sufficiently massive stars have formed, ionising radiation efficiently expels the remaining gas and reduces the final cluster mass by a factor of several. We found that while HII radiation and jets barely change the distribution of high density gas, the latter increases the dense gas velocity dispersion again by a factor of several in a few places. As we are starting from a relatively large scale, we found that the clusters whose mass and size are, respectively, of the order of a few 1000 M⊙ and a fraction of parsec, present a significant level of rotation. Moreover, we found that the sink particles that mimic the stars themselves tend to have rotation axes aligned with the cluster’s large-scale rotation. Finally, computing the classical Q parameter used to quantify stellar cluster structure, we infer that when jets are included in the calculation, the Q values are typical of observations, while when protostellar jets are not included, the Q values tend to be significantly lower. This is due to the presence of sub-clustering that is considerably reduced by the jets.
Conclusions. Both large-scale gas accretion and stellar feedback, namely HII regions and protostellar jets, appear to significantly influence the formation and evolution of stellar clusters.
Key words: methods: numerical / stars: formation / stars: jets / ISM: jets and outflows / galaxies: star clusters: general / HII regions
© A. Verliat et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
It is largely established that a large fraction, and likely the majority, of stars form in stellar clusters (Lada & Lada 2003; Bressert et al. 2010). As such, stellar clusters are certainly amongst the most important structures to understand in galaxies. This is particularly important to know the physical conditions that prevail as a star and its surrounding planets form and evolve.
How exactly stellar clusters form remains largely unknown and has been the subject of several recent reviews (Longmore et al. 2014; Krumholz et al. 2019; Krause et al. 2020; Adamo et al. 2020). While it is well established that their births take place through the collapse of massive gas proto-clusters, which have likely been observed (Urquhart et al. 2014; Elia et al. 2017), the exact conditions under which the collapse proceeds are still a matter of debate. Not only are the initial conditions still hampered by large uncertainties, in particular because gas clouds do not seem to present gas densities sufficiently high to reproduce the ones needed to explain the stellar densities in clusters (Krumholz et al. 2019), but also the feedback effects and efficiency have still only been partially explored and quantified.
Starting from dense clumps, several authors have performed collapse calculations with various spatial resolutions ignoring stellar feedback (e.g. Bonnell et al. 2008; Bate 2012; Kuznetsova et al. 2015; Vázquez-Semadeni et al. 2017). In all these works, compact concentration of both gas and stars are naturally produced as a consequence of gravitational collapse. Lee & Hennebelle (2016a,b) closely investigated the radius of the gas proto-cluster as well as the stellar clusters and concluded that their mass-radius relations present similar scaling laws to the ones inferred from observations (e.g. Pfalzner et al. 2016). In this process, accretion-driven turbulence (Klessen & Hennebelle 2010) is playing a fundamental role. As gas falls in the gas proto-cluster, it sustains turbulent motion that get virialised and leads to the observed mass-size relation. However, it is firmly established that stellar feedback plays a fundamental role during the course of stellar cluster formation and evolution. The main stellar feedback processes believed to be significant by the time of the cluster formation are protostellar outflows, ionising radiation, and stellar winds. The supernovae themselves arrive at least 4 Myr after the formation of the most massive stars and therefore likely do not play a significant role. Numerous studies have considered one or several feedback processes. This is particularly the case for ionising feedback, which has been extensively studied (e.g. Dale et al. 2012, 2014; Walch et al. 2013; Geen et al. 2015, 2017; Gavagnin et al. 2017; Grudić & Hopkins 2019; González-Samaniego & Vazquez-Semadeni 2020). There is a general agreement that the ionising radiation can efficiently disperse molecular clouds provide they are not bound, meaning that the escape velocity should not typically be larger than the sound speed of the ionised gas that is around 5 km s−1. More precisely, for molecular clouds typical of the solar neighbourhood, it has been inferred that the typical efficiency, meaning the gas mass fraction converted into stars, is of the order of a few percent, although there are considerable variations. These variations are due on one hand to the stochastic nature of the gravo-turbulent fragmentation and on the other hand to the strong dependence of the ionising flux on the stellar mass (Geen et al. 2018).
While several studies have considered the role of jets in cores (e.g. Offner & Chaban 2017) or low-mass clusters (e.g. Cunningham et al. 2018), a somewhat more restricted number of studies have considered the role of jets at the scale of more massive clusters, that is to say, a few parsecs across. For instance, Nakamura & Li (2007) and Wang et al. (2010) considered star forming clumps of about 1000 M⊙ and showed that turbulence can be maintained through the driving of jets and that the star formation rate (SFR) can be reduced by a factor of a few compared to the case without jet driving leading to SFRs that are typical of observed values. Guszejnov et al. (2021) explored the influence of jets on a large variety of clouds and also found that they have a significant influence on their evolution, particularly on the mass spectrum of the stellar objects. Similar results regarding the star formation efficiency (SFE) have been obtained using periodic boxes, which in total also contain about 1000 M⊙ (Carroll et al. 2009; Federrath et al. 2014; Murray et al. 2018).
So far to our knowledge, no works have investigated the influence of both ionising radiation and protostellar outflows simultaneously. Moreover, most works that have included protostellar jets considered a computational domain of the order of a few parsecs, which makes the time both for accretion to proceed and for jets to reach the computational domain a little short. Both aspects, however, are essential to assess the respective roles of accretion-driven turbulence and feedback driven turbulence. Protostellar outflows from stars in HII regions have indeed been observed in our Galaxy, such as jets detected at the tip of dense gas pillars similar to the ‘Pillars of Creation’ in M16 (McLeod et al. 2016).
In the present work, we aimed to simulate the formation of a stellar cluster by describing self-consistently spatial scales from a few tens of pc down to about 1000 au. This allowed us to describe the proto-cluster environment while obtaining a reasonable description of the gaseous proto-cluster whose size ranges between 0.1 and 1 pc. We treat both ionising radiation and stellar jet feedback. By performing a series of simulations that include none, one, or both feedback processes, we can induce their respective influence, in conjunction with large-scale infall, on the gas and the stars.
The paper is organised as follows. Section 2 of the paper describes the numerical methods and the initial conditions of the runs performed. It is complemented by Appendix A that describes our jet implementation in detail. Section 3 of the paper presents the general description of the simulation results as well as a detailed analysis of the gas properties. It also discusses the star formation rate and efficiency obtained in the various simulations. Section 4 focuses on the gas properties with particular emphasis on the kinematics and the influence of the various types of feedback. Section 5 investigates the star properties reflected by the sink particle properties, namely the global rotation of the cluster, the stellar rotation axis orientation and the cluster structure, which we quantify using the Q parameter. Section 6 concludes the paper.
2. Numerical methods and initial conditions
2.1. Code and numerical parameters
To investigate the joint influences of HII regions and protostellar jets on the formation of a stellar cluster, we carried out a set of four simulations starting from 104 M⊙ of gas in a cubic box of 30.4 pc, differing only by the included type of stellar feedback. Thus, one simulation includes no feedback at all, one includes HII regions only, one includes protostellar jets only, and the last one includes both HII regions and protostellar jets.
These simulations were carried out using RAMSES (Teyssier 2002). This numerical Eulerian code uses an adaptative mesh refinement (AMR) technique to enhance resolution locally, where it is needed, on a Cartesian mesh. We used five levels of AMR, from 7 to 12. This gives a cell size of at least 0.24 pc (5 × 104 au) everywhere, and 7.4 × 10−3 pc (1.5 × 103 au) in the most refined cells. Our refinement criterion is based on Jeans length, such that each local Jeans length is described by at least 40 cells.
We used open boundary conditions for the hydro solver to allow the matter to flow out of the box, and we used periodic boundaries for gravity. The refinement is not allowed in the outer 5% of the simulation box; this is to avoid the appearance of numerical instabilities in the matter flowing out of the box.
When the density in a cell rises above 107 cm−3, we create a sink particle (Krumholz et al. 2004; Bleuler & Teyssier 2014) that interacts gravitationally with the surrounding gas and by the way of accretion and ejection processes. The radius and luminosity of the sinks are provided through evolutionary tables of Kuiper & Yorke (2013).
Our four simulations will include magnetic field. This latter is treated through the ideal magnetohydrodynamics approximation (Fromang et al. 2006). The cooling and heating processes are as described in Audit & Hennebelle (2005). It includes the most important atomic cooling and the heating photo-electric effect on polycyclic aromatic hydrocarbons (PaH) due to an external standard galactic UV field. Typically, the resulting cooling curve is almost identical to the one obtained, for instance, in Koyama & Inutsuka (2000). This is in good agreement with earlier conclusions by Levrier et al. (2012) and Glover & Clark (2012) where comparisons between atomic and molecular cooling were performed.
2.2. Stellar objects and ionising radiation
The resulting IMF in those simulations does not compare to the observed ones, partly due to a lack of numerical resolution but also to the fact that we did not treat the infrared radiation that leads to a strong heating of the high density gas (Krumholz et al. 2007; Hennebelle et al. 2020). Lee & Hennebelle (2018a) found that when using an explicit barotropic equation of state to mimic the temperature at high density, a numerical resolution typically below 10 au is needed to achieve numerical convergence on the stellar mass spectrum, in particular to describe the peak. This condition becomes even more severe (typically, at least a few au of resolution are requested) when infrared radiation is treated (Hennebelle et al. 2020). While one may argue that not properly resolving the formation of low-mass stars does not preclude to resolve the formation of high-mass stars, the issue is that too many of the latter will then be produced because the total mass of gas converted in stars does not strongly depend on resolution. This issue may be even more severe when infrared radiation is treated since the resulting gas heating may then be overestimated and the number of massive stars further amplified.
Notably, the lack of massive stars in our simulations would be problematic for studying the influence of HII regions that are mainly triggered by massive stars. More generally, the ionising flux emitted by massive stars strongly depends on their mass (e.g. Vacca et al. 1996). Even for a thousand solar masses in stars, the most massive star in our simulation hardly exceeds 10 M⊙, while observations suggest that, statistically, for a pool of 120 M⊙ of stars, one massive star typically lies in them. To overcome this issue, we proceeded as in Colling et al. (2018), where a simple sub-grid model is presented. Every time that 120 M⊙ of gas was accreted into stars, we considered that one massive star should have formed, so we created a stellar object whose mass is randomly chosen between 8 and 120 M⊙, assuming that the mass function is a power law with an index of −2.35.
We do not use the approach in, for example, He et al. (2019), where each sink particle is considered to be a core containing one massive star. This is (a) because it is still unclear how much these cores should fragment into close binaries, which would change the distribution of massive stars in the cloud; and (b) in order to allow a consistent set of stellar masses to be implemented in comparisons between simulations. The influence of the particular prescriptions made to introduce massive stars has been analysed in details by Grudić & Hopkins (2019), who concluded that it indeed results in large uncertainties, which can be as high as a factor of 3. Typically, quantifying the influence of the prescriptions such as the random choices of the massive star masses (Geen et al. 2018) would require us to perform several runs, which is outside the scope of the present work. Along the same line, a statistical sample should also be run to quantify the influence of different random seeds of the initial turbulence, although this would increase the cost of the work even further.
Each stellar object emits an ionising radiation, as given by Vacca et al. (1996). This ionises the surrounding gas, which then expands into an HII region, provided the strength of the radiative field compared to the density of the environment is sufficient, as described in Geen et al. (2015). The ionising radiation is treated using the RT method developed in Rosdahl et al. (2013), which treats the propagation of light using the reduced speed approximation (a factor of 10−4 was employed in this work as it is sufficient to capture the expansion of the ionisation front, provided it does not expand faster than 30 km s−1 – a few times the speed of sound). As in Geen et al. (2015), we used three groups of photons to describe the ionisation of hydrogen and helium.
2.3. Implementation of protostellar jets
As our maximum resolution is of the order of a thousand astronomical units, we did not resolve all the physics responsible for the ejection of matter from young accreting stars known as protostellar jets. To still be able to take into account the effect of these jets on the large-scale evolution, we implemented a sub-grid model based on the properties of the sink particles. Once a sink grows a mass higher than 0.15 M⊙, at each time step it expels 1/3 of the mass accreted during this time step in the form of a circular biconic jet. The matter is expelled with a velocity equal to 24% of the escape velocity at the surface of the star. The direction of the ejection is given by the angular momentum of the sink. Each circular cone has an opening angle of 20°. The expelled material has the same specific thermal energy as the direct surrounding of the sink particle. Technical details of the implementation and references for the values above can be found in Appendix A.
2.4. Neglect of supernovae and stellar winds
Our work omits the influence of stellar winds and supernovae from massive stars. Simulations using a similar setup have explored the interaction between photoionisation feedback and winds (Dale et al. 2014; Geen et al. 2021; Lancaster et al. 2021a,b) or supernovae (Geen et al. 2016; Kimm et al. 2022). The reason for this is both scientific and technical. Except for large, long-lived cloud complexes, supernovae either occur too late or do not have sufficient compressive power to strongly influence either their host cloud or other nearby clouds (Seifried et al. 2018), although they are thought to be a trigger for new cloud formation (Inutsuka et al. 2015; Fujii et al. 2021).
Winds are more complex, since they are produced by stars during their main sequence, similarly to ionising radiation. Stellar winds shock the cloud material to very high temperatures (> 106 K, sufficient to emit x-rays; e.g. Guedel et al. 2008), which create hot bubbles that store large quantities of energy. Their low density means the bubbles themselves do not typically radiate energy strongly Mac Low & McCray (1988). However, strong cooling channels exist either through evaporation of dense structures in the cloud overrun by the wind bubble (Arthur 2012), or by turbulent mixing with the cloud material (Rosen et al. 2014; Lancaster et al. 2021c, see also Tan et al. 2021 for an analysis of turbulent mixing on shockfronts). In this case, wind bubbles become momentum-driven rather than pressure-driven (Silich & Tenorio-Tagle 2013), and their dyanmical influence drops considerably. In this mode, winds only significantly drive the expansion of HII regions at small radii (Geen et al. 2020; Olivier et al. 2021), similarly to the influence of radiation pressure. However, they can still play a strong role in structuring the photoionised region around the star (Pellegrini et al. 2007; Rahner et al. 2017) or even trapping ionising radiation at early times (Geen & de Koter 2021). This has a non-linear influence on the evolution of HII regions that should be explored in more detail.
A more technical reason for omitting stellar winds is the relatively high computational cost in simulating them. The sound speed in photoionised gas is ∼10 km s−1, compared to speeds sometimes exceeding 3000 km s−1 for stellar winds (Vink et al. 2011; Ekström et al. 2012). The Courant condition for gas flows on the simulation grid thus requires around 100 times more time steps if winds or other sources of hot gas such as supernovae are included. We thus justify omitting them both because their influence is more subtle and requires additional research to determine when they are important, but also because to do so would drastically increase our computational costs and thus limit our ability to explore the core physics in this work.
2.5. Initial conditions
Our four simulations have the same initial conditions as they only differ by the types of stellar feedbacks included. Those initial conditions are very similar to those used by Lee & Hennebelle (2016a). To set the density, we divided the box into three concentric regions. The inner one is a Bonnor-Ebert-like spherical cloud whose diameter is 15.2 pc, that is, half of the box length. In this inner cloud, the number density n is distributed according to a top-hat function:
with r being the distance of the cell from the centre of the box, n0 = 8 × 102 cm−3, and r0 = 2.5 pc. This led to a mass of 104 M⊙ in this central region. The second region, beginning at the cloud edge, is a ring whose outer diameter is equal to the box length. The density in this ring is constant and equal to about 8 cm−3, a tenth of the cloud edge density. In the rest of the box, the eight corners are filled with a constant density of 1 cm−3.
The initial temperature set by the cooling function is about 10 K in the dense gas. We initialised the magnetic field with a uniform mass-to-flux ratio of about 8 in the x direction.
To initialise the velocity, we do not consider those three regions separately. We roughly mimicked the turbulence of the interstellar medium by constructing a velocity field according to a probability distribution of the turbulence (see, e.g. Sect. 3 of Hennebelle & Falgarone 2012, for a review on turbulence in interstellar clouds): in Fourier space, the power spectrum of the velocity field follows a Kolmogorov turbulence law1, and the phases are randomly chosen. This turbulent field is normalised to have a Mach number of 6.7.
Those initial conditions are set by specifying ratios of characteristic timescales in the inner regions of r0 in size. We then define the free-fall time to the sound-crossing time ratio 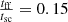 , the free-fall time to the Alfvén-crossing time ratio
, the free-fall time to the Alfvén-crossing time ratio 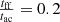 , and the free-fall time to the turbulent-crossing time
, and the free-fall time to the turbulent-crossing time 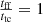 . The first two ratios show that the thermal and magnetic support against gravity are low, while the turbulent support is the dominant one.
. The first two ratios show that the thermal and magnetic support against gravity are low, while the turbulent support is the dominant one.
2.6. Runs performed
We used this numerical setup to run four simulations, which differ only by the stellar feedback that is included. The first simulation – NF – is run without feedback at all. One simulation includes only protostellar jets as stellar feedback – PSJo – and another includes only HII regions – HIIRo. The last one – PSJ-HIIR – includes both protostellar jets and HII regions. The acronyms used to refer to those simulations are summarised in Table 1.
Summary of the four runs performed.
We also ran two simulations with protostellar jets as the unique source of feedback but with different properties for the jets than in the PSJo simulation. The jets in the simulation ‘jets – wider’ exhibit a wider ejection angle of 30° while it is 20° in PSJo. The jets in the simulation ‘jets – faster’ are expelled with a velocity equal to 48% of the escape velocity of the sink, while it is 24% in PSJo.
3. General description, star formation rate, and star formation efficiency
3.1. Global appearance of the emerging structures
We first look at the appearance of the emerging star clusters and surrounding gas in Figs. 1 and 2 for the four simulations. Figure 1 shows the emerging clusters at intermediate scales, whereas Fig. 2 shows them at large scales. The first two columns show column density along two different lines of sight, and the third column shows the mean velocity norm along the second line of sight, weighted by density. The overplotted red circles represent the sink particles. The four simulations are visualised at the same time as 3.5 Myr. The first row shows the column densities of the simulation without feedback, NF; the second one those of the simulation with jets only, PSJo; the third one those of the simulation with HII regions only, HIIRo; and the last row shows the column density of the simulation with both protostellar jets and HII regions, PSJ-HIIR. The simulations that do not include HII regions are pretty similar, exhibiting a flattened cluster of stars, surrounded by spiralling gas with a disc-like shape. In the case of simulations with jets, the distribution of the gas is a bit more messy, due to the presence of jets. Those jets are visible in the third panel of the second row as high velocity components from either side of the cluster. On the other hand, the simulations that include HII regions have a qualitatively different appearance. The two simulations exhibit a distribution of the gas which is much more shredded, due to the expansion of HII regions, which is clearly visible from the velocity maps displayed in the third column of Figs. 1 and 2. The disc-like shape of the gas which was visible in the simulations without HII regions is no longer visible. However, the star cluster also seems to be a bit flattened in these simulations.
 |
Fig. 1. Global appearance of star cluster surrounded by its gas environment. Each row corresponds to a different simulation. The four simulations are visualised at the same time: 3.5 Myr. From top to bottom: are the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. Two first columns: represent column density along the y and x axis of the simulation, and the third column shows the mean of the velocity norm integrated along the line of sight, weighted by the density. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles. As the view on the two last rows, which corresponds to the simulations with HII regions, is a bit narrow, we presented the same maps with a spatial scale four times larger in Fig. 2. We also present zoomed-in views of the central star cluster in Fig. 3. |
 |
Fig. 2. Global appearance of star cluster surrounded by its gas environment, at a spatial scale four times larger than in Fig. 1. The four simulations are visualised at the same time: 3.5 Myr. Each row corresponds to a different simulation. From top to bottom: are the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. The first two columns give column density along the y and x axis of the simulation, and the third column gives the mean of the velocity norm integrated along the line of sight, weighted by the density. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles. |
In the case of the simulations without HII regions, this disc-like shape of the gas correlated to the flattened aspect of the star cluster seems to indicate that a preferred angular direction emerges as the cluster forms. This is not surprising, as Verliat et al. (2020) exposed a mechanism through which a protostellar disc naturally forms around a protostar even in the absence of initial rotation. Angular momentum with respect to the cluster centre, which is not the mass centre of the system, is produced by inertial forces. The same mechanism can be invoked here to explain the formation of this rotating structure emerging from the gravitational collapse. Moreover, Lee & Hennebelle (2016a) inferred that the clusters formed in their simulations without feedback indeed significantly rotate due to angular momentum inherited from the large-scale collapse.
An evolutionary sequence of the cluster seen at small scales is visible in Fig. 3. The arrows attached to the sink particles represent their velocities in the plane perpendicular to the line of sight. At 2 Myr, NF and HIIRo are very similar, as the expansion of HII regions has not yet occurred. At this time, the simulations with jets – PSJo and PSJ-HIIR – are already more messy and look similar. As time progresses, the cluster in NF, PSJo, and PSJ-HIIR becomes organised in the disc-like shape, which seems to rotate. In HIIRo, the cluster has been completely depleted of gas, and its rotation is less obvious.
 |
Fig. 3. Evolutionary sequence of global appearance of the star cluster. Each row corresponds to a different simulation. The four simulations are visualised at three different times: 2 Myr, 2.75 Myr, and 3.5 Myr. From top to bottom: the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions, seen from the y axis of the simulation. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles and the associated arrows represent their velocities in the plane of the visualisation. |
3.2. Star formation rate and efficiency
The first and straightforward quantity to investigate is the total mass of the sink particles as a function of time. The slope of this curve represents the rapidity at which the stars accrete and is often referred to as the SFR, while the final value of the accreted mass divided by the initial cloud mass represents the star formation efficiency (SFE).
The evolution of this total mass over time is presented in Fig. 4. The two orange curves represent the two simulations without HII regions, while the two purple ones represent the two simulations including HII regions. The two dashed lines represent the simulations without protostellar jets, while the two solid lines represent the simulations including them. The brown solid line and the yellow solid line represent the simulations with wider and faster jets, respectively.
 |
Fig. 4. Total mass of sink particles in the four simulations including (or not) different types of feedback. The two orange (respectively purple) curves stand for the simulations without (respectively with) HII regions. The dashed (respectively solid) lines represent the simulations without (respectively with) protostellar jets. |
We now compare the two orange curves, that is, the simulations without feedback at all on one hand, and with protostellar jets only on the other hand. After 2 Myr for the simulation without feedback, and 2.6 Myr for the simulations with jets, the total sink mass seems to evolve almost linearly with time. The SFR of these simulations is thus about 2 × 10#x2212;3 M⊙ yr−1 for the fisrt one, and about 8 × 10#x2212;4 M⊙ yr−1 for the second one. The difference in terms of SFR when adding protostellar jets from a situation without feedback is thus a bit more than a factor two. This is consistent with what has been inferred previously in the literature, for instance by Wang et al. (2010) and Federrath et al. (2014), as can be seen from Figs. 1 and 2 of these papers, respectively.
In Fig. 5, the orange dash-dotted curve shows the ratio of the total sink mass in the simulation with protostellar jets over the total sink mass in the simulation without feedback : Msink, PSJo/Msink, NF. This curve represents a plateau for times longer than 2.6 Myr, which corresponds to the linear regime of the orange curves in Fig. 4. The value of this plateau lies around 0.4, corresponding to the ratio 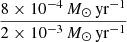 of the two SFRs. The orange dotted curve shows what this ratio would be if the difference in mass were only due to the fraction of mass ejected in protostellar jets. This difference is easy to compute as the sub-grid model used for the protostellar jets specifies that each sink particle whose mass is larger than 0.15 M⊙ expels one third of the mass it accretes. Within the limit of long times, the majority of the sink particles have a mass greatly larger than the mass threshold of 0.15 M⊙; thus, the mass expelled by each sink tends towards the limit of
of the two SFRs. The orange dotted curve shows what this ratio would be if the difference in mass were only due to the fraction of mass ejected in protostellar jets. This difference is easy to compute as the sub-grid model used for the protostellar jets specifies that each sink particle whose mass is larger than 0.15 M⊙ expels one third of the mass it accretes. Within the limit of long times, the majority of the sink particles have a mass greatly larger than the mass threshold of 0.15 M⊙; thus, the mass expelled by each sink tends towards the limit of 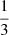 of its accreted mass, leading to a ratio of
of its accreted mass, leading to a ratio of 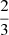 . We see that the ratio in the simulation is significantly lower than the one given by considering only ejected mass. This shows that an important effect of the protostellar jets is to diminish the accretion onto the sink particles. Thus, the difference in mass is due to both the loss of the mass directly expelled by the jets and the reduction of the accretion rate onto the sink particles due to the interaction between the jets and the environment.
. We see that the ratio in the simulation is significantly lower than the one given by considering only ejected mass. This shows that an important effect of the protostellar jets is to diminish the accretion onto the sink particles. Thus, the difference in mass is due to both the loss of the mass directly expelled by the jets and the reduction of the accretion rate onto the sink particles due to the interaction between the jets and the environment.
 |
Fig. 5. In dash-dotted lines, Msink, PSJo/Msink, NF in orange, and Msink, PSJ − HIIR/Msink, HIIRo in purple. Dotted lines represent the same ratios that would be obtained if the difference of total sink mass in those simulations were only due to the fraction of mass ejected by protostellar jets. |
The brown and yellow solid lines in Fig. 4 represent the two simulations with protostellar jets only but with different parameters for the jets than PSJo. The ‘jets – wider’ option uses wider jets, while the ‘jets – faster’ method uses faster jets. We see that the difference between these two curves and the orange solid one standing for PSJo is small compared to the influence of including or not the different types of feedback. All the analyses presented in the rest of this article were conducted for our six simulations. As the jets – wider and jets – faster simulations show similar results to PSJo for all the analysis, we then ignore these two simulations for the remaining presentation.
We now compare the four simulations: NF, PSJo, HIIRo, and PSJ-HIIR. In Fig. 4, we see that for times shorter than 2.2 Myr, the simulations without any feedback at all, and with only HII regions behave strictly the same. This reflects the late onset of HII regions. The same observation can be made comparing the simulations with protostellar jets only, and with both protostellar jets and HII regions for times lower than 2.9 Myr, with an onset of HII regions being slightly delayed due to a lower SFR in the simulations including protostellar jets. Once the HII regions begin to have an impact on its parent cloud, the behaviour of the sink’s mass starts to be different as the expansion of the HII regions becomes more and more significant with time and with the apparition of stellar objects. Thereby, the SFR in the simulations including HII regions tends to be lower and lower with time, entirely stopping star formation within a few million years, while the SFR in the simulations without HII regions is roughly constant, as the sink’s mass is nearly linear with time. Figure 6 shows the sink’s mass separately for the two simulations that include HII regions, with indicators for the moments of formation of stellar objects that give birth to HII regions. In these two panels, the mass sequence of the different stellar objects is the same as the seed chosen to initialise the random number generator is the same for all our simulations. This permits close comparison, in particular ensuring that the differences between the two simulations are not coming from the random draw on a stellar object’s mass (Geen et al. 2018). We see that the first five stellar objects to form are not so massive, and they are between 20 and 40 M⊙. As the mass of those stellar objects remains limited and since they are formed in a dense environment, the associated HII regions are not powerful enough to expand and have a significant impact on the cluster. This explains the strong similarity in the sink’s mass versus time between the corresponding simulations without HII regions, before 2.2 Myr for the ones without jets, and before 2.9 Myr for the ones with jets. This similarity is also observed qualitatively on the gas distribution. The sixth stellar object to form has a mass of 102.6 M⊙. This rather massive star is associated with a photon flux of about 1050 s−1 and is able to form a HII region powerful enough to expand in this dense medium. In fact, in the two panels of Fig. 6 we see a change in behaviour just after the formation of this massive stellar object (the vertical yellow line). Before its formation, the SFR increases over time, and just after its formation the SFR starts to decrease over time. The stellar objects that form later have less impact than the 102.6 M⊙ one, but they still contribute to the decrease in SFR.
 |
Fig. 6. Total mass of sink particles. Left: simulation including only HII regions. Right: simulation including HII regions and protostellar jets. The purple curves in the two panels thus correspond to the same ones as Fig. 4. In the two panels, the vertical lines show the moments of creation of stellar objects, with the colours of the lines coding their mass. |
In Fig. 5, the purple dash-dotted curve shows the ratio of the total sink mass in the simulation with protostellar jets and HII regions over the total sink mass in the simulation including only HII regions: Msink, PSJ − HIIR/Msink, HIIRo. Between 1.6 and 2.2 Myr, this curve is below the dotted purple curve, which represents what this ratio would be if the difference in a sink’s mass were only due to the fraction of mass ejected in protostellar jets. As stated previously for the simulations without HII regions, this shows that the difference in mass is due to both the loss of the mass directly expelled by the jets and the reduction of the accretion rate onto the sink particles due to the interaction between the jets and the environment. At 2.2 Myr, the ratio begins to increase over time. This is due to the appearance of the first HII regions, which does not occur at the same time for the two simulations. In fact, between 2.2 and 2.9 Myr, in the simulation only including HII regions, the first HII regions began to appear, while in the simulation including protostellar jets and HII regions, the HII regions have not expanded yet. Here, we thus compare simulations that present different behaviours in this time interval; therefore, this increase in the ratio is not relevant.
In Appendix B, we present the evolution of the number of sinks over time for different masses. Figure B.1 shows that for simulations with HII regions, the onset of HII regions stop most of the accretion onto the stars, while new small stars continue to form insensitively to the expansion of HII regions.
4. Gas density PDF and kinematic of the gas
In this section, we investigate the gas properties focusing on the density PDF and the Mach number density relation within the whole computational box. We complement the analysis by studying the velocity dispersion of the dense structures.
4.1. Density PDF
The density PDF is a fundamental quantity to investigate not only because it reflects the dynamical state of the gas but also because it is believed to play a fundamental role regarding the mass spectrum of stars (Padoan et al. 1997; Hennebelle & Chabrier 2008; Lee & Hennebelle 2018b).
Figure 7 displays the density PDF for the four runs NF, PSJo, HIIRo, and PSJ-HIIR for various snapshots. To make the comparison easier, we report two snapshots of run NF (dotted lines) using the colour-code to indicate what time steps would be most comparable in the top right panel (PSJo) and bottom left one (HIIRo). In the bottom right one (PSJ-HIIR), two snapshots of run HIIRo (dotted lines) are reported.
 |
Fig. 7. Density PDF for NF (top left), PSJo (top right), HIIRo (bottom left), and PSJ-HIIR (bottom right) runs for four snapshots (solid lines). The dotted lines visible in the top right and bottom left represent two snapshots of run NF, while the ones in the bottom right panel are from run HIIRo. The total accreted mass is indicated as it is more representative when comparing the runs. |
The top left panel portrays the density PDF of run NF. It is a clear power law with an index of ≃ − 1.5, which is typical of a gravitational collapse arising in turbulent flows (Kritsuk et al. 2011; Lee & Hennebelle 2018b). The power law is remarkably stable and does not evolve significantly over a period that goes from the cluster formation time up to the end of the simulation where about half of the gas has been accreted.
The top right panel reveals that the jets have no significant influence on the density PDF, while the bottom left panel shows that ionising radiation has a drastic role once massive enough stellar objects have formed. In particular, the quantity of gas at densities between 102 and 103 cm−3 is diminishing by one to two orders of magnitude compared to the case without feedback. On the contrary, the quantity of gas at densities around 10 cm−3 increases by almost one order of magnitude, which is a clear signature of the strong photo-ionisation that is induced by the massive stars. The bottom right panel shows that even in the presence of ionising radiation feedback the jets have very little influence on the density PDF. We note from both bottom panels that the high-density gas is not strongly affected by the ionising radiation, which is due to the recombination of the electron and proton being very efficient at high densities.
4.2. Mach-number-density relation
A fundamental question with the feedback processes is how exactly they operate on the surrounding gas. For instance, whether the jets increase the turbulence and by how much are crucial issues. Various teams (e.g. Carroll et al. 2009; Wang et al. 2010; Federrath et al. 2014; Offner & Chaban 2017; Murray et al. 2018) have all concluded that jets do trigger some turbulence, although the importance of the effect varies among studies. This may be a consequence of the various setups that have been employed. Figure 8 displays the mean Mach number as a function of density for the four runs using the same conventions and snapshots as in Fig. 7.
The top left panel shows that in the absence of feedback, the Mach number increases with density from about 1 to 30. It also increases with time for densities larger than ∼102 cm−3. This is obviously a consequence of gravity, which produces both infall and virial motions of the order of 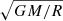 , where M is the accreted mass in the cluster and R the typical distance from the cluster centre.
, where M is the accreted mass in the cluster and R the typical distance from the cluster centre.
The top right panel reveals that the presence of jets increases the mean Mach number by tens of percents, mainly for intermediate densities of about 103 cm−3, as is visible when more than 103 M⊙ have been accreted. We therefore conclude that in the present configuration, in which the turbulence is fed by accretion and the jet directions are not widely dispersed (see Sect. 5.4), turbulence is not strongly enhanced by the presence of jets. It is therefore likely that they mainly act by repulsing some of the gas that would have otherwise been accreted as indeed envisioned by Matzner & McKee (2000).
The importance of ionising radiation is visible from bottom panels. Clearly this feedback substancially modifies the mean Mach number at almost all densities. At about 103 cm−3, it is of the order of 2, which implies a kinematic energy roughly four times larger and therefore strongly influences the gas behaviour. We note that the drop seen at 102 cm−3 is due to the increase of the gas temperature. We stress that while the ionising radiation has little effect on gas temperature for densities above 103 cm−3 and below ≃5 cm−3, it can significantly heat, typically up to T = 5000 − 8000 K, gas of intermediate densities. The presence of jets (bottom-right panel) further increases the Mach number for gas of densities 103 cm−3 (compare blue dotted line and purple solid one), which is consistent with the final SFE being a bit lower when both jets and ionising radiation are included.
4.3. Dense structure’s internal velocity dispersion
Finally, we complement the analysis presented in the previous section, which is a global estimate of all the simulations, by investigating the local velocity dispersion of dense structures. The latter were identified by running the HOP algorithm (Eisenstein & Hut 1998) on gas cells with densities larger than 104 cm−3. While the mean Mach number analysis captures the large-scale motions, which dominate in turbulent flows, the velocity dispersion of dense structures reveals the local motions in star forming clumps.
Figure 9 portrays the bi-dimensional histograms of the velocity dispersion of these structures at a time of about 3.2 Myr. The top left panel is typical of a previous analysis reported in simulations without feedback (Hennebelle 2018; Ntormousi & Hennebelle 2019). Interestingly, the top right panel shows that in the presence of jets, the histogram presents a significant population of dense structures of gaseous masses between 0.1 and 1 M⊙ that have a velocity dispersion up to five times larger than the typical velocity dispersion (∼0.3 km s−1) found in the absence of jets. This indeed confirms that, locally, jets can significantly perturb the dense structures in which they develop. We note, however, that the bulk of the dense structures, which contain most of the mass, remain very similar to the one obtained in run NF.
 |
Fig. 9. Bi-dimensional histograms showing the velocity dispersion of dense structures for the four runs NF (top-left), PSJo (top-right), HIIRo (bottom-left), and PSJ-HIIR (bottom-right) at a time of about 3.2 Myr. |
The bottom panels show that ionising radiation has a moderate impact on the velocity dispersion of dense structures. The HIIRo run presents velocity dispersion slightly larger (say ∼50%) than in run NF, while a similar, though less pronounced, trend is observed between runs PSJo and PSJ-HIIR.
We conclude that altogether stellar feedback certainly alters the velocity dispersion and motions in star forming clumps by increasing it by a factor of a few (Goldbaum et al. 2011). However the nature of these motions cannot be simply described by a mere increase of turbulence. The net effect of the jets remains modest, but they can have a very significant local impact, and this is probably why they reduce the SFR by a factor of roughly 2. On the contrary, the ionising radiation appears to have even less impact on the dense gas, but on the other hand they lead to global expansions – as visually obvious from Fig. 1 – that considerably decrease the SFE.
5. The stellar properties
We now move on to the description of the stellar properties. We then consider the sink particles as individual stars.
5.1. Bound and unbound stars
We see in Fig. 3 that a lot of stars are forming around the central, dense cluster of stars in the simulations that include HII regions. In this part, we try to distinguish between the stars bound to the cluster and the ones that are destined to leave it.
We first computed bi-dimensional histograms of the sink positions and took the bin of highest concentration as the cluster’s centre. By doing it before and after the output of interest, we are also able to estimate the velocity of the cluster centre. We then construct concentric spherical shells around the centre. For each shell, we compute the escape velocity Vesc at the shell radius R as well as the mass, Mint, obtained by summing the masses of all sinks and gas at radii lower than R:
For each sink particle in the shell, we compute its projected velocity along the unit vector from the cluster’s centre to the sink particle. This velocity is noted Vrad and is positive if the sink particle is going away from the centre and negative if going towards the centre. In Fig. 10, we plot all the sink particles in the four simulations with a colour code indicating the ratio 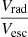 . The sink particles in blue exhibit a ratio lower than 1, indicating that they should be bound at the time of interest. On the contrary, the ones in red exhibit a ratio higher than 1. As they are moving away from the centre at a speed higher than the escape velocity, they are destined to disperse and to leave the cluster, and we can consider these stars as unbound. We see that in the two upper panels representing simulations without HII regions (NF and PSJo), all the stars in the cluster are bound. For the two bottom panels, representing simulations with HII regions (HIIRo and PSJ-HIIR), the cluster consists of a bound core, surrounded by stars that are likely to disperse over time. The existence of unbound stars is likely to be due to the star formation in the material compressed by the expansion of HII regions. The escape velocity Vesc is roughly constant over R, with a value about 2.4 km s−1. The expansion of HII regions takes place at the sound speed in the ionised gas (Geen et al. 2015), which is about ten kilometres per second. A maximum value of about 4 for the ratio
. The sink particles in blue exhibit a ratio lower than 1, indicating that they should be bound at the time of interest. On the contrary, the ones in red exhibit a ratio higher than 1. As they are moving away from the centre at a speed higher than the escape velocity, they are destined to disperse and to leave the cluster, and we can consider these stars as unbound. We see that in the two upper panels representing simulations without HII regions (NF and PSJo), all the stars in the cluster are bound. For the two bottom panels, representing simulations with HII regions (HIIRo and PSJ-HIIR), the cluster consists of a bound core, surrounded by stars that are likely to disperse over time. The existence of unbound stars is likely to be due to the star formation in the material compressed by the expansion of HII regions. The escape velocity Vesc is roughly constant over R, with a value about 2.4 km s−1. The expansion of HII regions takes place at the sound speed in the ionised gas (Geen et al. 2015), which is about ten kilometres per second. A maximum value of about 4 for the ratio 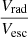 is coherent for stars that would have been formed in the expanding material of the HII regions.
is coherent for stars that would have been formed in the expanding material of the HII regions.
 |
Fig. 10. Distribution of stars in four simulations at 3.5 Myr. The ratio of the radial outward velocity of the sink particles over the escape velocity at their respective distances from the cluster’s centre is colour-coded. Particles that appear in blue are likely to be bound, whereas the ones that appear in red are likely to be unbound. |
5.2. Bound and unbound mass
We saw that in the two simulations that do not include HII regions, all the sinks are bound. This remains true for the entire temporal evolution. For the two simulations that include HII regions, namely HIIRo and PSJ-HIIR, they both exhibit unbound stars. Figure 11 shows the total amount of mass in bound and unbound stars in those two simulations. We see that in HIIRo the mass of unbound stars quickly grows to reach about a quarter of the total star mass. In PSJ-HIIR, the mass of unbound stars is three times lower, for the same mass of bound stars. As the evolution of the cluster in this simulation is slower, this indicates that the unbound stars form in the late stage, as HII regions are expanding in the outskirts of the cluster, triggering the formation of unbound stars in these regions.
 |
Fig. 11. Evolution of total mass of bound and unbound stars. The mass of unbound stars is significantly higher in the simulation HIIRo. |
5.3. Rotation of the cluster
In this section we focus on the rotation of the bound part of the cluster. As in the previous section, we identify the cluster’s centre as the place of highest concentration of stellar mass. We define the rotation axis of the cluster as the mean direction of the angular momentum of the bound sink particles. We define the equatorial plane as the plane perpendicular to the rotation axis and containing the cluster’s centre. We then construct concentric cylindrical shells around the cluster centre, which are aligned to the rotation axis. For each sink particle, we compute the azimuthal velocity. We then divide the mean of the azimuthal velocities of the sink particles by the radius of the considered shell to obtain the mean angular velocity.
The profiles of the angular velocity are presented in Fig. 12. We see that for the simulations NF, PSJo, and PSJ-HIIR, the angular velocity profiles are well defined and stable in time, except for early times (dark blue curves), when rotation seems not to be fully developed. They roughly follow a power law with an index of –1.
 |
Fig. 12. Angular velocity profiles of the bound part of the cluster in the four simulations, at several times. The legend is shared by the four panels. Some of the profiles are missing in the two left panels, since the corresponding simulations are not advanced enough. |
The bottom left panel of Fig. 12 shows the angular velocity profiles for the simulation with HII regions only: HIIRo. Its velocity profiles show different behaviours compared to the ones of the other simulations. We note that the net rotation at r ≃ 1 pc is nevertheless clear, though a factor of 2–3 lower than for the other runs. At 0.1 pc, they are lower by a factor of 10, whereas at 10 pc they show similar values. They thus exhibit a flatter power law. This behaviour could be due to the very early onset of the HII regions in this simulation, as shown by Figs. 4 and 6. This early onset could be responsible for a rapid emptying of the gas in the inner part of the cluster, disrupting the structure and preventing the stars from reaching the angular momentum corresponding to the profile observed in the other simulations. This does not happen in the simulation PSJ-HIIR, which includes both HII regions and protostellar jets. This is because the jets slow down the accretion, allowing time for gas carrying large angular momentum to reach the cluster. This effect could be enhanced by the presence of unbound stars at late stages. At 3.5 Myr, about a quarter of the mass of stars is unbound in HIIRo. These unbound stars could also play a role in perturbing the dynamics of the central bound stars.
Observationally, the situation appears to be complicated. Several authors (Hénault-Brunet et al. 2012; Kamann et al. 2018) report the presence of significant rotation on several clusters. Rotation velocities of a few km s−1 are being measured and our simulations qualitatively agrees with this. However, other observations (Kuhn et al. 2019) do not detect significant rotation in a sample of young stellar clusters. In our simulations, the presence of rotation is a clear consequence of the large-scale collapse of a gaseous turbulent clump. If confirmed, the absence of rotation in a fraction of stellar clusters will probably require alternative scenario for stellar cluster formation.
5.4. Alignment of the stars in the cluster
As the clusters are rotating, we study the alignment of the angular directions of the sink particles in our four simulations. Spin alignment in two stellar clusters has been inferred by Corsaro et al. (2017) and by Kovacs (2018) in one cluster. We investigate whether or not a privileged direction also exists in the set of sink particles. An alignment is clearly expected in the simulations without HII regions as the gas exhibits a global rotating motion at the cluster scale. Then, one may wonder what happens in the cases where HII regions are included. In particular, as the gas shows a lower global rotating motion, one may question whether the alignment still visible in the set of sink particles.
To answer these questions, we computed the mean direction of the sink particles’ angular momentum in each simulation, at each time step. The angular momentum of a sink particle is simply that of all the gas it has accreted. We then obtain the angular dispersion of the directions around this mean value by taking the standard deviation σθ of the angles between the sink directions and the mean direction previously computed. In order to be able to tell if the sinks are aligned with the mean direction, or on the contrary randomly distributed, we computed the same quantity σθ for a set with the same cardinality as the set of sink particles at each time step, exhibiting random angular orientations. The results over time for the four simulations are presented on Fig. 13. For times lower than 1.8 Myr, the curves corresponding to the simulations and the ones corresponding to sets with random orientations are not distinguishable. At those times, the sinks are not very massive, few in number, and the geometry of the gas flow is ill defined, which explains that we observe no particular alignment. However, after 1.8 Myr, the angular dispersion begins to drop, stabilising at values between 20° and 40° for the four simulations. These values are lower than the ones corresponding to the sets of random orientations, of which the values tend to be constant and equal to about 50°. This shows that in those simulations the sink particles tend to align. This is expected from the gas geometry visible in the two first panels of Fig. 1, corresponding to the simulations without HII regions. In these two simulations, the infalling gas forms a rotating disc-like structure around the star cluster, indicating a privileged direction as a global angular momentum emerges. In the two simulations that include HII regions, the sink particles also exhibit a preferred orientation. In Figs. 1 and 2, we see that the gas geometry is much more disorganised and dislocated than for the simulations without HII regions2. Nevertheless, the sink particles still exhibit a preferred orientation in these simulations, which seems to survive through time as HII regions are developing. In the bottom panels of Fig. 14, the solid lines represent the same quantity as those in Fig. 13, and we indicate the creation of the stellar objects with vertical coloured lines. In this first panel representing the simulation with HII regions only, with a solid green line, we see that after the formation of the most massive stellar object at 2.2 Myr the angular dispersion slightly increases gradually from 20° to around 33°. This increase could be due to the formation of unbound stars in the outskirts of the cluster as HII regions are expanding. Unlike central stars, unbound ones should not have a preferred direction as the dynamics of the gas is different at these places. In the second panel, representing the simulations with protostellar jets and HII regions, the solid yellow line shows that there is no clear correlation between the slight variations of the angular dispersion and the onset of HII regions. It is thus unclear whether or not the HII regions play a role in modifying the angular dispersion here. A correlation is only found in the simulation with HII regions alone. Moreover, even if the HII regions had an impact on this angular dispersion, it would be minimal as the variations in the other cases (and especially in the cases without HII regions) are of the same order of magnitude.
 |
Fig. 13. Solid lines show angular dispersion of the sink particles relatively to the mean angular direction, with each colour corresponding to a different simulation. To only consider relevant sink particles, we selected the ones with masses over 0.07 M⊙. In comparison, the dotted lines show the angular dispersion of a set with the same cardinality as the set of sink particles at each time step, exhibiting random angular orientations. For times longer than 2 Myr, the angular dispersion in the simulations is significantly lower than for a set of random orientations, implying that the sink particles have a preferred angular direction. |
The four panels of Fig. 14 represent the angular dispersion in the four simulations. The solid lines show the results for the same selection rule as that used in Fig. 13, which is that only sinks with a mass higher than 0.07 M⊙ are selected. The dashed and dotted lines show results for the sets of sink particles with a mass higher than 0.5 M⊙ and 1 M⊙, respectively. We see that for the first panel representing the NF simulation, the sets of higher masses exhibit slightly lower angular dispersion. This would mean that in this simulation the more massive stars are more aligned than the less massive ones. As the massive ones accrete more and more material from the oriented gas flow, they tend to align with time. When considering the less massive stars, as they are more sensitive to slight local variations in the gas flow, they exhibit a higher angular dispersion.
 |
Fig. 14. Angular dispersion of the sink particles distribution in each simulation. From top to bottom and from left to right: the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. The different types of lines indicate the different thresholds of sink masses used to define the sets. For the two simulations with HII regions, on the second row, we indicate the moments of creation of the stellar objects with vertical lines, the colours of which denote their masses. |
In the second and fourth panels, representing the simulation PSJo and PSJ-HIIR, respectively, the sets of higher masses show higher angular dispersion during the first hundreds of kiloyears of evolution; then, the trend reverses and the same behaviour as that seen in NF is observed. A possible explanation for this behaviour could be that at the beginning of the formation of the cluster, sinks are not particularly aligned, as shown by Fig. 13. As time goes by, sinks accrete matter. In NF, as a preferred orientation emerged from the gas flow, it is directly reflected in the sink particles’ behaviour. The massive ones accrete more matter and are then aligned more rapidly than the lower mass ones, which are more sensitive to gas properties variations. In PSJo, the presence of jets modifies the accretion onto sink particles. The sink particles with a mass higher than 0.5 M⊙ have already started to launch protostellar jets. This modifies the direct environment of these sink particles, promoting accretion in their orthogonal plane, even if a global preferred orientation of the gas flow emerges. It is thus harder to change their initial orientation when the particles are accreting this way. The higher the mass of the particles, the more powerful the jets, and therefore the more impact they have on the direct environment of the particles. It is hence more difficult for the massive particles to align when protostellar jets are included. When considering lower mass particles with a threshold of 0.07 M⊙, we take into account all the newly formed particles. These are not affected by their own protostellar jets, and thus they are more sensitive to the gas flow geometry and are directly formed with a preferred orientation on average as an orientation emerges in the flow. The angular dispersion in this set is thus lower. At 3.5 Myr for PSJo and 2.9 Myr for PSJ-HIIR, the trend reverses and the same behaviour as that of NF is observed. As the massive particles accrete more and more, they tend to align, even if the jets slow down this alignment, and we come back to a situation where the massive stars are the most aligned whereas the newly formed stars are more sensitive to variations and exhibit higher angular dispersion.
In the third panel, representing HIIRo, the three curves present similar trends. It is therefore hard to interpret the slight differences insofar as they could be due to the particular realisation. Furthermore, comparing NF and HIIRo on one hand (left panels) and PSJo and PSJ-HIIR on the other (right panels), we see that HII regions only have a minor influence on the observed behaviour, while protostellar jets seem to play a more important role in the alignment of the sink particles.
5.5. Spatial distribution of the emerging clusters
We now discuss the spatial distribution of the stars in the simulations, as traced by the sink particles. A first effect of feedback in the global cluster distribution can already be seen from visual inspection of previous figures in the text. All simulations start with a globally similar distribution of stars, as shown in the first column of Fig. 3. At later stages, however, it is clear from Fig. 2 (first column) or Fig. 10 (pay attention to spatial scales) that simulations with HII regions produce distributions with larger spatial dispersion, where the stars spread over a larger fraction of the region.
To globally characterise the distribution of stars and its evolution with time, we computed the Q parameter. This parameter, which was introduced and developed by Cartwright & Whitworth (2004, 2009), has been widely used to objectively evaluate the level of sub-clustering or concentration in stellar clusters and associations. The value of Q is given by the ratio of the mean distance of the members and the average length of their minimum spanning tree3. Cartwright & Whitworth (2004) calibrated the Q parameter in synthetic clusters and found that values of Q > 0.8 correspond to radial concentration, Q ≃ 0.8 corresponds to clusters with homogeneous distribution, and Q < 0.8 corresponds to clumpy clusters showing sub-clusterisation. To avoid over-interpretation in realistic distributions, these boundaries should not be strictly applied, and Q should be used qualitatively. In Appendix C, we explain the details on the calculations performed in this work.
The evolution of Q with time is shown in Fig. 15, where the Q parameter is plotted over time for the four simulations represented by four distinct colours. The points represent the mean value of the Q parameter, while the colour-filled areas represent the interval of the mean value ±1σ. For each simulation, we begin at a time where approximately 300 sink particles are formed in order to have enough sink particles in the sample.
 |
Fig. 15. Evolution of Q parameter with time. |
The first notable result is that two clear trends appear. On one hand, the two simulations that include jets – PSJo and PSJ-HIIR – show a similar evolution over time, while on the other hand, the two simulations that do not include jets – NF and HIIRo – also show a similar trend, which is different from the first one.
Both PSJo and PSJ-HIIR show an increase in the Q parameter between 2.1 to 2.7 Myr, followed by a significant decrease. The initial increase in the Q parameter indicates an evolution of the initial sub-structure present in PSJ-HIIR and an increase of the radial concentration in PSJo, which indeed starts with Q values of around 0.8, consistent with homogeneous distributions. In both cases, the decrease in Q around 2.7 Myr is associated with the growth of sub-structure in the outskirts of the field, far from the main cluster. These structures are small compared to the main clump of stars in the centre, but the Q parameter decreases as they become dense enough to be significant. The decrease is more abrupt in the simulation with an HII region, PSJ-HIIR, where a subsequent slow increase is also observed.
The two simulations without jets, NF and HIIRo, both show clear sub-structure at 2.1 Myr with a Q parameter of about 0.6, which slowly and steadily decreases to 0.2 at 2.8 Myr. At 3 Myr, the Q in NF slowly increases from 0.2 to 0.3 at 3.6 Myr. These values of Q ≲ 0.3 are much lower than the observed values for sub-clustered distributions and even the box-fractal models in which the method was originally calibrated. In order to understand these very low values, we computed the Q parameter of the inner part of the cluster, containing 90% of the stars’ mass. This selection thus excludes the small sub-structures that grow far away from the central cluster. The Q evolution is visible in Fig. 16 for this inner part, in the two simulations without HII regions – NF and PSJo. We see that the inner part in NF (blue dashed curve) exhibits higher and more stable values, between 0.4 and 0.7. This means that the very low values of the Q parameter for the entire cluster is largely affected by the presence of sub-clusterisation in the outskirts. We also see that in the simulation PSJo (purple dashed curve), the drop at 2.7 Myr disappears, which confirms that this drop is associated with the growth of sub-structures in the outskirts of the field. Comparing the inner parts of NF and PSJo, we find that the Q of PSJo rapidly rises over the one of NF. From 2.5 Myr, PSJo exhibits a homogeneous inner region with a Q of the order of 0.8, whereas NF still exhibits sub-clusterisation in its inner part, with a Q between 0.45 and 0.7. We conclude that the protostellar jets seem to be efficient at preventing (or at least delaying) the apparition of sub-structures in the outskirts. Broadly speaking, the Q values inferred in the presence of jets, appear in better agreement with the observations that when jets are absent.
 |
Fig. 16. Smoothed temporal evolution of Q parameter for the entire cluster and for the inner part only, in NF and PSJo. |
Our results show that protostellar jets seem to play an important role in the structuring and distribution of stars in the cluster, while HII regions, despite producing more disperse distributions, do not seem to produce statistically significant structural changes. Looking at the results presented in Sects. 4 and 5, jets and HII regions have different impacts on the gas and the star cluster. Protostellar jets only have a minor influence on the gas appearance while having a major influence on the star distribution in the cluster. Conversely, HII regions play a major role in shaping the gas, but their impact on the distribution of stars in the cluster is limited.
6. Conclusions and perspectives
6.1. Conclusions
To study the formation and evolution of stellar clusters, we performed a set a four simulations including (or not) the effects of HII regions and protostellar jets. We started from a turbulent, magnetised cloud of 104 M⊙ of gas.
The structures formed in these simulations have a very different appearance depending on whether or not HII regions are included. The expansion of the HII regions empties the central part and shreds the gas. We have shown that protostellar jets have a significant influence on the SFR. They slow down star formation, reducing the SFR by more than a factor of two, but they do not stop star formation. The onset of HII regions also reduces the SFR but quickly leads to the dispersion of the gas in the cluster, which almost completely extinguishes the accretion onto stars and then decreases the SFE.
The study of the gas reveals that the jets have almost no influence on the density distribution and a moderate influence on the Mach number. On the contrary, the HII regions strongly alter the gas at intermediate densities and strongly modify the Mach number at all densities. It is thus difficult to find evidence of the presence of jets when looking only at the kinematics of the gas. Turbulence in cluster-forming clumps is primarily due to gas accretion.
We then studied the emerging star clusters. In simulations without HII regions, all the stars formed are gravitationally bound. When HII regions are included, the cluster consists of a central core of bound stars surrounded by a number of unbound stars found on the outskirts. The clusters are rotating. We showed that the angular velocity profiles are stable in time. In the simulation with HII regions only, the early onset of HII regions could explain the low rotation of the cluster. We showed that the stars exhibit a preferred alignment of their own rotation axis. This alignment seems to persist through time, even in the simulation with only HII regions, where the global rotation of the cluster is less obvious. In order to characterise the spatial distribution of the formed stars, we calculated the Q parameter of these clusters. Protostellar jets play a major role here. They seem to prevent the formation of sub-structures in the outskirts of the cluster. The simulation including protostellar jets thus showed distribution with fewer sub-structures, and the ones that still form appear in later times.
6.2. Perspectives
It would be interesting to further investigate the Q parameter. One possibility could be to use the S2D2 algorithm developed by González et al. (2021) to detect significant small-scale sub-structures known as Nested Elementary STructures (NESTs). The study of these NESTs and their distribution could be a powerful way to interpret the Q parameter of the emerging clusters more precisely.
One of the limitations of our study is the impossibility of running simulations with a significant statistics on the initial conditions, due to the high computational cost of this type of simulation. It would be valuable to run similar simulations with different initial conditions and different seeds for the random generator of the stellar object masses. As the expansion of HII regions is known to depend on the density of the gas where it takes place, varying the initial conditions would allow us to investigate the statistics for the onset of HII regions.
One could also try to perform similar simulations with higher resolutions. It would then be possible to study the emerging initial mass function and to determine the individual and joint influences of HII regions and protostellar jets on it.
It would be interesting to investigate the mass fraction of bound and unbound stars over longer periods of time and to follow those stars in time. In fact, it is known that some of the clusters are evaporating and Gavagnin et al. (2017) showed that cluster survival depends on feedback strength. Leading this study in simulations with different initial conditions would probably shed light on the conditions and processes responsible for the evaporation of such stellar clusters.
On the last row of Fig. 1, we see that for the simulations with jets and HII regions, a small disc-like structure seems to survive at this time, while in the simulation with HII regions only, at this time the gas has been completely blown out of the cluster.
These CIC particles were originally introduced in ℛAMSES to model dark matter. In the current version of ℛAMSES, the mass of each sink particle is distributed equally onto a spherical cloud of CIC particles. The distance between each CIC particles is half the grid spacing, and the radius of the cloud of CIC particles sets the gravitational softening length. More details are given in Bleuler & Teyssier (2014).
Acknowledgments
We gratefully acknowledge the anonymous referee for their comments and suggestions that strongly improved the manuscript. SG acknowledges support from a NOVA grant for the theory of massive star formation. This work was granted access to HPC resources of CINES and CCRT under the allocation x2020047023 made by GENCI (Grand Equipement National de Calcul Intensif). This research has received funding from the European Research Council synergy grant ECOGAL (Grant: 855130).
References
- Adamo, A., Zeidler, P., Kruijssen, J. M. D., et al. 2020, Space Sci. Rev., 216, 69 [Google Scholar]
- Arthur, S. J. 2012, MNRAS, 421, 1283 [NASA ADS] [CrossRef] [Google Scholar]
- Audit, E., & Hennebelle, P. 2005, A&A, 433, 1 [CrossRef] [EDP Sciences] [Google Scholar]
- Bacciotti, F., Ray, T. P., Mundt, R., Eislöffel, J., & Solf, J. 2002, ApJ, 576, 222 [Google Scholar]
- Bacciotti, F., Whelan, E. T., Alcalá, J. M., et al. 2011, ApJ, 737, L26 [Google Scholar]
- Bate, M. R. 2012, MNRAS, 419, 3115 [NASA ADS] [CrossRef] [Google Scholar]
- Blandford, R. D., & Payne, D. G. 1982, MNRAS, 199, 883 [CrossRef] [Google Scholar]
- Bleuler, A., & Teyssier, R. 2014, MNRAS, 445, 4015 [Google Scholar]
- Bonnell, I. A., Clark, P., & Bate, M. R. 2008, MNRAS, 389, 1556 [NASA ADS] [CrossRef] [Google Scholar]
- Borůvka, O. 1926, O jistém problému minimálním [Google Scholar]
- Bressert, E., Bastian, N., Gutermuth, R., et al. 2010, MNRAS, 409, L54 [NASA ADS] [Google Scholar]
- Cabrit, S., Codella, C., Gueth, F., et al. 2007, A&A, 468, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calvet, N. 1998, in Accretion processes in Astrophysical Systems: Some like it hot! - 8th AstroPhysics Conference, eds. S. S. Holt, & T. R. Kallman, Am. Inst. Phys. Conf. Ser., 431, 495 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, J. J., Frank, A., Blackman, E. G., Cunningham, A. J., & Quillen, A. C. 2009, ApJ, 695, 1376 [NASA ADS] [CrossRef] [Google Scholar]
- Cartwright, A., & Whitworth, A. P. 2004, MNRAS, 348, 589 [Google Scholar]
- Cartwright, A., & Whitworth, A. P. 2009, MNRAS, 392, 341 [Google Scholar]
- Colling, C., Hennebelle, P., Geen, S., Iffrig, O., & Bournaud, F. 2018, A&A, 620, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corsaro, E., Lee, Y.-N., García, R. A., et al. 2017, Nat. Astron., 1, 0064 [NASA ADS] [CrossRef] [Google Scholar]
- Cunningham, A. J., Krumholz, M. R., McKee, C. F., & Klein, R. I. 2018, MNRAS, 476, 771 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ercolano, B., & Bonnell, I. A. 2012, MNRAS, 424, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, J. E., Ngoumou, J., Ercolano, B., & Bonnell, I. A. 2014, MNRAS, 442, 694 [Google Scholar]
- Eisenstein, D. J., & Hut, P. 1998, ApJ, 498, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Ekström, S., Georgy, C., Eggenberger, P., et al. 2012, A&A, 537, A146 [Google Scholar]
- Elia, D., Molinari, S., Schisano, E., et al. 2017, MNRAS, 471, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Schrön, M., Banerjee, R., & Klessen, R. S. 2014, ApJ, 790, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fujii, K., Mizuno, N., Dawson, J. R., et al. 2021, MNRAS, 505, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Gavagnin, E., Bleuler, A., Rosdahl, J., & Teyssier, R. 2017, MNRAS, 472, 4155 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., & de Koter, A. 2021, MNRAS, 509, 4498 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Hennebelle, P., Tremblin, P., & Rosdahl, J. 2015, MNRAS, 454, 4484 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Hennebelle, P., Tremblin, P., & Rosdahl, J. 2016, MNRAS, 463, 3129 [CrossRef] [Google Scholar]
- Geen, S., Soler, J. D., & Hennebelle, P. 2017, MNRAS, 471, 4844 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Watson, S. K., Rosdahl, J., et al. 2018, MNRAS, 481, 2548 [CrossRef] [Google Scholar]
- Geen, S., Pellegrini, E., Bieri, R., & Klessen, R. 2020, MNRAS, 492, 915 [NASA ADS] [CrossRef] [Google Scholar]
- Geen, S., Bieri, R., Rosdahl, J., & de Koter, A. 2021, MNRAS, 501, 1352 [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 9 [NASA ADS] [Google Scholar]
- Goldbaum, N. J., Krumholz, M. R., Matzner, C. D., & McKee, C. F. 2011, ApJ, 738, 101 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Joncour, I., Buckner, A. S. M., et al. 2021, A&A, 647, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- González-Samaniego, A., & Vazquez-Semadeni, E. 2020, MNRAS, 499, 668 [CrossRef] [Google Scholar]
- Gower, J. C., & Ross, G. J. 1969, J. R. Stat. Soc.: Ser. C (Appl. Stat.), 18, 54 [Google Scholar]
- Grudić, M. Y., & Hopkins, P. F. 2019, MNRAS, 488, 2970 [CrossRef] [Google Scholar]
- Guedel, M., Briggs, K. R., Montmerle, T., et al. 2008, Science, 319, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Guszejnov, D., Grudić, M. Y., Hopkins, P. F., Offner, S. S. R., & Faucher-Giguère, C.-A. 2021, MNRAS, 502, 3646 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., & Calvet, N. 1995, AJ, 109, 1846 [NASA ADS] [CrossRef] [Google Scholar]
- He, C.-C., Ricotti, M., & Geen, S. 2019, MNRAS, 489, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Hénault-Brunet, V., Gieles, M., Evans, C. J., et al. 2012, A&A, 545, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P. 2018, A&A, 611, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Chabrier, G. 2008, ApJ, 684, 395 [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Chabrier, G. 2020, ApJ, 904, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Inutsuka, S.-I., Inoue, T., Iwasaki, K., & Hosokawa, T. 2015, A&A, 580, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamann, S., Husser, T. O., Dreizler, S., et al. 2018, MNRAS, 473, 5591 [NASA ADS] [CrossRef] [Google Scholar]
- Kimm, T., Bieri, R., Geen, S., et al. 2022, ApJS, 259, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [Google Scholar]
- Konigl, A., & Pudritz, R. E. 2000, in Protostars and Planets IV, eds. V. Mannings, A. P. Boss, & S. S. Russell, 759 [Google Scholar]
- Kovacs, G. 2018, A&A, 612, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koyama, H., & Inutsuka, S.-I. 2000, ApJ, 532, 980 [Google Scholar]
- Krause, M. G. H., Offner, S. S. R., Charbonnel, C., et al. 2020, Space Sci. Rev., 216, 64 [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Klein, R. I. 2004, ApJ, 611, 399 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., Klein, R. I., & McKee, C. F. 2007, ApJ, 656, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kruskal, J. B. 1956, Proc. Am. Math. Soc., 7, 48 [CrossRef] [Google Scholar]
- Kuhn, M. A., Hillenbrand, L. A., Sills, A., Feigelson, E. D., & Getman, K. V. 2019, ApJ, 870, 32 [CrossRef] [Google Scholar]
- Kuiper, R., & Yorke, H. W. 2013, ApJ, 772, 61 [Google Scholar]
- Kuznetsova, A., Hartmann, L., & Ballesteros-Paredes, J. 2015, ApJ, 815, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57 [Google Scholar]
- Lancaster, L., Ostriker, E. C., Kim, J.-G., & Kim, C.-G. 2021a, ApJ, 914, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Lancaster, L., Ostriker, E. C., Kim, J.-G., & Kim, C.-G. 2021b, ApJ, 922, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Lancaster, L., Ostriker, E. C., Kim, J.-G., & Kim, C.-G. 2021c, ApJ, 914, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2016a, A&A, 591, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2016b, A&A, 591, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018a, A&A, 611, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, Y.-N., & Hennebelle, P. 2018b, A&A, 611, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Levrier, F., Le Petit, F., Hennebelle, P., et al. 2012, A&A, 544, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Longmore, S. N., Kruijssen, J. M. D., Bastian, N., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 291 [Google Scholar]
- Mac Low, M.-M., & McCray, R. 1988, ApJ, 324, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Matzner, C. D., & McKee, C. F. 2000, ApJ, 545, 364 [NASA ADS] [CrossRef] [Google Scholar]
- McLeod, A., Gritschneder, M., Dale, J., et al. 2016, MNRAS, 462, 3537 [NASA ADS] [CrossRef] [Google Scholar]
- Murray, D., Goyal, S., & Chang, P. 2018, MNRAS, 475, 1023 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, F., & Li, Z.-Y. 2007, ApJ, 662, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Ntormousi, E., & Hennebelle, P. 2019, A&A, 625, A82 [EDP Sciences] [Google Scholar]
- Offner, S. S. R., & Chaban, J. 2017, ApJ, 847, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Olivier, G. M., Lopez, L. A., Rosen, A. L., et al. 2021, ApJ, 908, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Nordlund, A., & Jones, B. J. T. 1997, MNRAS, 288, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., Brogan, C. L., et al. 2007, ApJ, 658, 1119 [NASA ADS] [CrossRef] [Google Scholar]
- Pfalzner, S., Kirk, H., Sills, A., et al. 2016, A&A, 586, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prim, R. C. 1957, Bell Syst. Techn. J., 36, 1389 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., & Norman, C. A. 1986, ApJ, 301, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Pudritz, R. E., Ouyed, R., Fendt, C., & Brandenburg, A. 2007, in Protostars and Planets V, eds. B. Reipurth, D. Jewitt, & K. Keil, 277 [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2017, MNRAS, 470, 4453 [NASA ADS] [CrossRef] [Google Scholar]
- Rosdahl, J., Blaizot, J., Aubert, D., Stranex, T., & Teyssier, R. 2013, MNRAS, 436, 2188 [Google Scholar]
- Rosen, A. L., Lopez, L. A., Krumholz, M. R., & Ramirez-Ruiz, E. 2014, MNRAS, 442, 2701 [NASA ADS] [CrossRef] [Google Scholar]
- Seifried, D., Walch, S., Haid, S., Girichidis, P., & Naab, T. 2018, ApJ, 855, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Lizano, S., Ruden, S. P., & Najita, J. 1988, ApJ, 328, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Silich, S., & Tenorio-Tagle, G. 2013, ApJ, 765, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Tan, B., Oh, S. P., & Gronke, M. 2021, MNRAS, 502, 3179 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J. S., Moore, T. J. T., Csengeri, T., et al. 2014, MNRAS, 443, 1555 [Google Scholar]
- Vacca, W. D., Garmany, C. D., & Shull, J. M. 1996, ApJ, 460, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., González-Samaniego, A., & Colín, P. 2017, MNRAS, 467, 1313 [NASA ADS] [Google Scholar]
- Verliat, A., Hennebelle, P., Maury, A. J., & Gaudel, M. 2020, A&A, 635, A130 [EDP Sciences] [Google Scholar]
- Vink, J. S., Muijres, L. E., Anthonisse, B., et al. 2011, A&A, 531, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walch, S., Whitworth, A. P., Bisbas, T. G., Wünsch, R., & Hubber, D. A. 2013, MNRAS, 435, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, P., Li, Z.-Y., Abel, T., & Nakamura, F. 2010, ApJ, 709, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Wardle, M., & Koenigl, A. 1993, ApJ, 410, 218 [Google Scholar]
Appendix A: Modelisation and implementation of protostellar jets
In our simulations, the maximum resolution associated to the finest AMR level is about 1.5 × 103 au. This prevents us from observing effects emerging from physical mechanisms happening at smaller scales. In particular, we do not resolve all the physics responsible for the emission of protostellar jets. The theories describing these ejections of matter from young accreting stars such as the centrifugal acceleration mechanism or the X-wind model (see, e.g. Federrath et al. 2014) involve physical mechanisms taking place on scales smaller than the astronomical unit. It is thus for the moment not possible to describe the emission of protostellar jets and the dynamical formation of a star cluster in a 30.4 pc simulation box consistently.
A.1. The sub-grid model
To still be able to take into account the effect of these jets on the large-scale evolution, we implement a sub-grid model based on the properties of the sinks. Once a sink grows to a mass higher than 0.15 M⊙, at each time step it expels 1/3 of the mass accreted during this time step in the form of a circular biconic jet. The matter is expelled with a velocity equal to a fraction fv of the escape velocity at the surface of the star. The direction of the ejection is given by the angular momentum of the sink. Each circular cone has an opening angle of θjet. fv and θjet are fixed and are the same for all the sink particles in the simulation. Figure A.1 shows a schematic view of the jet’s geometry around a sink particle.
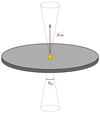 |
Fig. A.1. Illustration of geometric properties of the protostellar jets model. The central protostar schematised is yellow, surrounded by its accretion disc in grey. The third of the accreted mass at each time step is ejected in a right circular bicone of opening angle θjet and in the direction of the angular momentum of the sink particle jsink. |
A.2. Implementation in ℛAMSES
The numerical implementation of this sub-grid model of protostellar jets is made through a routine carried out just after the accretion onto the sinks. First of all, during a time step, the accretion of material onto each sink is processed. The mass accreted by each sink during this time step is stored in a variable, which is named macc, j here, with the index j referring to the sink number.
Once this accreted mass is computed, the routine setting protostellar jets is carried out. This routine contains a first loop over the CIC particles4. In doing so, it is possible to identify the gas cells around each sink particle without having to scan the entire AMR grid. During this first loop, for each sink particle, the total volume of the cells that lay in a circular bicone around the sink is computed. A second loop over the CIC particles is done to redistribute some of the accreted quantities to the gas. For each sink particle, the quantities retrieved by each gas cell are proportional to the fraction of the cell volume over the total volume of gas cells in the circular bicone. This ensures that the quantity that is redistributed in the jet launch area is homogeneous over this area.
For each sink particle j that exhibits a mass greater than 0.15 M⊙, an arbitrary fraction of 1/3 of the accreted mass macc, j is given back to the gas cells. This value of 1/3 is coherent with previous analytical, numerical, and observational studies of protostellar jets. For example, theories based on centrifugal acceleration or the X-wind model by Blandford & Payne (1982), Pudritz & Norman (1986), Shu et al. (1988), Wardle & Koenigl (1993), Konigl & Pudritz (2000), Pudritz et al. (2007) and observations by Hartmann & Calvet (1995), Calvet (1998), Bacciotti et al. (2002), Cabrit et al. (2007), Bacciotti et al. (2011) suggest a fraction of the accreted mass that is ejected in the 0.1 to 0.4 range (see page 4 of Federrath et al. 2014, for a review of these different studies and results). The arbitrary threshold of 0.15 M⊙ stands to ensure that the angular momentum of the sink particle is well defined when ejection begins. The velocity given to the ejected fraction of mass is equal to a fraction of the escape velocity at the protostar surface 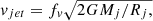 with Mj and Rj being the mass and radius of the protostar modelled by the sink particle, respectively. For fv between 0.25 and 0.5 this prescription gives jet velocities of the order of a hundred to a few hundred km.s−1. The matter deposited in the circular bicone is given a specific thermal energy that is the same as the one of the gas cell in which it is deposited.
with Mj and Rj being the mass and radius of the protostar modelled by the sink particle, respectively. For fv between 0.25 and 0.5 this prescription gives jet velocities of the order of a hundred to a few hundred km.s−1. The matter deposited in the circular bicone is given a specific thermal energy that is the same as the one of the gas cell in which it is deposited.
Once these quantities are given back to the gas, they are deduced from the sink particle’s quantity: 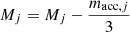 . The linear and angular momentum and the energy associated with each ejection is also calculated and subtracted from the linear and angular momentum of each sink particle.
. The linear and angular momentum and the energy associated with each ejection is also calculated and subtracted from the linear and angular momentum of each sink particle.
Appendix B: Evolution of the number of sinks
The evolution of the number of sinks with time is presented in Fig. B.1. The four panels represent the four simulations. The y-axes have the same extent, but the x-axes’ extent depends on each panel. For the two simulations including HII regions, vertical lines indicate the formation of stellar objects.
 |
Fig. B.1. Evolution of number of sinks during the temporal evolution. From top to bottom and from left to right: the NF, PSJo, HIIRo, and PSJ-HIIR simulations. For the simulations with HII regions, vertical lines indicate the formation of stellar objects, with colour-coding according to their mass. In the four panels, the solid lines indicate the total number of sinks, the other types of line (dashed, dash-dotted, and dotted, respectively) indicate the number of sinks with a mass lower than a given threshold (0.07, 0.5, and 1 M⊙, respectively). |
We see that for the simulation including HII regions – HIIRo and PSJ-HIIR – the evolution of the number of sinks without using a mass threshold or using one of 0.07 M⊙ exhibits a low influence of stellar objects formation. However, when we look at the sinks number using a mass threshold of 0.5 M⊙, we see that just after the apparition of the most massive stellar object (yellow vertical line), the increase in the number of stars shows a drastic drop. This is also the case for the stars with a mass higher than 1 M⊙ in HIIRo, but not in PSJ-HIIR, where this change in behaviour is seen at 3.3 Myr. These results show that stars continue to form in simulations with HII regions, but it essentially concerns low-mass stars. HII regions seems to be efficient at cutting accretion onto the less massive stars as they form but do not accrete enough to grow higher masses when the HII regions are developing.
Appendix C: Q parameter
In this appendix, we describe the specific calculations of Q performed in this work, along with their motivation. We refer the reader to Appendix B in González et al. (2021) for a recent review on the Q parameter method and its alternatives.
The Q parameter is defined by
where 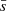 is the normalised mean distance between stars, and
is the normalised mean distance between stars, and 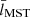 is the normalised mean edge length of the minimum spanning tree (MST) (see, e.g. Borůvka 1926; Kruskal 1956; Prim 1957; Gower & Ross 1969). A spanning tree is a set of straight lines connecting all the points of the sample without cycle. The MST is the unique spanning tree whose sum of edges is minimal. To allow for the comparison of regions of different sizes, the values of
is the normalised mean edge length of the minimum spanning tree (MST) (see, e.g. Borůvka 1926; Kruskal 1956; Prim 1957; Gower & Ross 1969). A spanning tree is a set of straight lines connecting all the points of the sample without cycle. The MST is the unique spanning tree whose sum of edges is minimal. To allow for the comparison of regions of different sizes, the values of 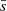 and
and 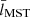 are normalised. Following Cartwright & Whitworth (2004),
are normalised. Following Cartwright & Whitworth (2004), 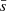 should be normalised with a radius representative of the size of the cluster, and
should be normalised with a radius representative of the size of the cluster, and 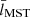 should be normalised with a factor that includes the area subtended by the MST and the minimum number of points. We use the consistent normalisation area A for the MST and the radius R for the cluster, which together follow the relationship A = πR2.
should be normalised with a factor that includes the area subtended by the MST and the minimum number of points. We use the consistent normalisation area A for the MST and the radius R for the cluster, which together follow the relationship A = πR2.
Despite giving the boundary Q = 0.8, there is some dispersion in the Q values obtained in Cartwright & Whitworth (2004) that can be associated with sampling effects and the different random realisations of each distribution. This dispersion implies that even synthetic clusters with a low degree of substructure or concentration are not statistically distinguishable from homogeneous.
As the Q parameter has been introduced to describe observed clusters, 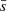 and
and 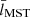 were calibrated by Cartwright & Whitworth (2004) using the projected position of the stars in the plane of the sky for a set of synthetic clusters, with radial concentration, homogeneous distribution, or fractal sub-clusterisation. Despite the fact that in our simulations we have access to the 3D positions of the stars, we performed the calculations in projection, for consistency, and to allow for comparisons with previous results. We compensate for the potential effects of projection onto a specific plane by calculating three 2D projections of each snapshot (using the x, y, and z axes of the simulation as lines of sight) and averaging the obtained value of Q of the three projections,
were calibrated by Cartwright & Whitworth (2004) using the projected position of the stars in the plane of the sky for a set of synthetic clusters, with radial concentration, homogeneous distribution, or fractal sub-clusterisation. Despite the fact that in our simulations we have access to the 3D positions of the stars, we performed the calculations in projection, for consistency, and to allow for comparisons with previous results. We compensate for the potential effects of projection onto a specific plane by calculating three 2D projections of each snapshot (using the x, y, and z axes of the simulation as lines of sight) and averaging the obtained value of Q of the three projections, 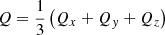 , with its corresponding standard deviation
, with its corresponding standard deviation 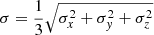 . We note that in any case, the projection effects are not severe, with globally similar results in the three projections.
. We note that in any case, the projection effects are not severe, with globally similar results in the three projections.
The values of the Q parameter can be sensitive to the presence of outliers, so we apply a resampling strategy to mitigate their effect. For each snapshot, we randomly choose a sub-sample with 90% of the stars, compute the Q parameter on this set, and repeat the process 100 times. This gives a distribution of the values of Q within the sample, with its associated mean value and standard deviation.
All Tables
All Figures
 |
Fig. 1. Global appearance of star cluster surrounded by its gas environment. Each row corresponds to a different simulation. The four simulations are visualised at the same time: 3.5 Myr. From top to bottom: are the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. Two first columns: represent column density along the y and x axis of the simulation, and the third column shows the mean of the velocity norm integrated along the line of sight, weighted by the density. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles. As the view on the two last rows, which corresponds to the simulations with HII regions, is a bit narrow, we presented the same maps with a spatial scale four times larger in Fig. 2. We also present zoomed-in views of the central star cluster in Fig. 3. |
| In the text | |
 |
Fig. 2. Global appearance of star cluster surrounded by its gas environment, at a spatial scale four times larger than in Fig. 1. The four simulations are visualised at the same time: 3.5 Myr. Each row corresponds to a different simulation. From top to bottom: are the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. The first two columns give column density along the y and x axis of the simulation, and the third column gives the mean of the velocity norm integrated along the line of sight, weighted by the density. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles. |
| In the text | |
 |
Fig. 3. Evolutionary sequence of global appearance of the star cluster. Each row corresponds to a different simulation. The four simulations are visualised at three different times: 2 Myr, 2.75 Myr, and 3.5 Myr. From top to bottom: the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions, seen from the y axis of the simulation. The colour scales are not common and depend on each map. The overplotted red circles represent the sink particles and the associated arrows represent their velocities in the plane of the visualisation. |
| In the text | |
 |
Fig. 4. Total mass of sink particles in the four simulations including (or not) different types of feedback. The two orange (respectively purple) curves stand for the simulations without (respectively with) HII regions. The dashed (respectively solid) lines represent the simulations without (respectively with) protostellar jets. |
| In the text | |
 |
Fig. 5. In dash-dotted lines, Msink, PSJo/Msink, NF in orange, and Msink, PSJ − HIIR/Msink, HIIRo in purple. Dotted lines represent the same ratios that would be obtained if the difference of total sink mass in those simulations were only due to the fraction of mass ejected by protostellar jets. |
| In the text | |
 |
Fig. 6. Total mass of sink particles. Left: simulation including only HII regions. Right: simulation including HII regions and protostellar jets. The purple curves in the two panels thus correspond to the same ones as Fig. 4. In the two panels, the vertical lines show the moments of creation of stellar objects, with the colours of the lines coding their mass. |
| In the text | |
 |
Fig. 7. Density PDF for NF (top left), PSJo (top right), HIIRo (bottom left), and PSJ-HIIR (bottom right) runs for four snapshots (solid lines). The dotted lines visible in the top right and bottom left represent two snapshots of run NF, while the ones in the bottom right panel are from run HIIRo. The total accreted mass is indicated as it is more representative when comparing the runs. |
| In the text | |
 |
Fig. 8. Same as Fig. 7, but for the Mach-density relation. |
| In the text | |
 |
Fig. 9. Bi-dimensional histograms showing the velocity dispersion of dense structures for the four runs NF (top-left), PSJo (top-right), HIIRo (bottom-left), and PSJ-HIIR (bottom-right) at a time of about 3.2 Myr. |
| In the text | |
 |
Fig. 10. Distribution of stars in four simulations at 3.5 Myr. The ratio of the radial outward velocity of the sink particles over the escape velocity at their respective distances from the cluster’s centre is colour-coded. Particles that appear in blue are likely to be bound, whereas the ones that appear in red are likely to be unbound. |
| In the text | |
 |
Fig. 11. Evolution of total mass of bound and unbound stars. The mass of unbound stars is significantly higher in the simulation HIIRo. |
| In the text | |
 |
Fig. 12. Angular velocity profiles of the bound part of the cluster in the four simulations, at several times. The legend is shared by the four panels. Some of the profiles are missing in the two left panels, since the corresponding simulations are not advanced enough. |
| In the text | |
 |
Fig. 13. Solid lines show angular dispersion of the sink particles relatively to the mean angular direction, with each colour corresponding to a different simulation. To only consider relevant sink particles, we selected the ones with masses over 0.07 M⊙. In comparison, the dotted lines show the angular dispersion of a set with the same cardinality as the set of sink particles at each time step, exhibiting random angular orientations. For times longer than 2 Myr, the angular dispersion in the simulations is significantly lower than for a set of random orientations, implying that the sink particles have a preferred angular direction. |
| In the text | |
 |
Fig. 14. Angular dispersion of the sink particles distribution in each simulation. From top to bottom and from left to right: the simulations without feedback, with protostellar jets only, with HII regions only, and with both jets and HII regions. The different types of lines indicate the different thresholds of sink masses used to define the sets. For the two simulations with HII regions, on the second row, we indicate the moments of creation of the stellar objects with vertical lines, the colours of which denote their masses. |
| In the text | |
 |
Fig. 15. Evolution of Q parameter with time. |
| In the text | |
 |
Fig. 16. Smoothed temporal evolution of Q parameter for the entire cluster and for the inner part only, in NF and PSJo. |
| In the text | |
 |
Fig. A.1. Illustration of geometric properties of the protostellar jets model. The central protostar schematised is yellow, surrounded by its accretion disc in grey. The third of the accreted mass at each time step is ejected in a right circular bicone of opening angle θjet and in the direction of the angular momentum of the sink particle jsink. |
| In the text | |
 |
Fig. B.1. Evolution of number of sinks during the temporal evolution. From top to bottom and from left to right: the NF, PSJo, HIIRo, and PSJ-HIIR simulations. For the simulations with HII regions, vertical lines indicate the formation of stellar objects, with colour-coding according to their mass. In the four panels, the solid lines indicate the total number of sinks, the other types of line (dashed, dash-dotted, and dotted, respectively) indicate the number of sinks with a mass lower than a given threshold (0.07, 0.5, and 1 M⊙, respectively). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.