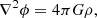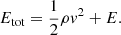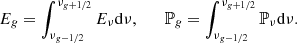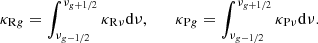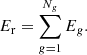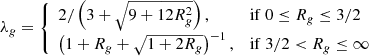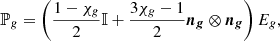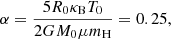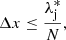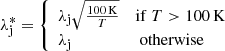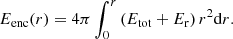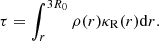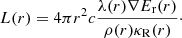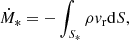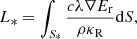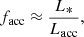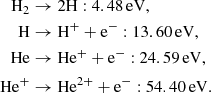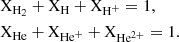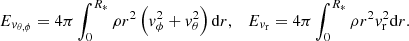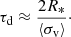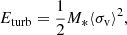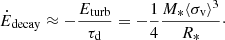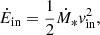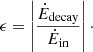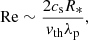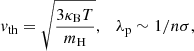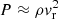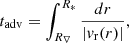| Issue |
A&A
Volume 680, December 2023
|
|
|---|---|---|
| Article Number | A23 | |
| Number of page(s) | 23 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/202346711 | |
| Published online | 05 December 2023 | |
The birth and early evolution of a low-mass protostar
1
Université Paris Cité, Université Paris-Saclay, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
e-mail: adnan.ali.ahmad1998@gmail.com
2
Université Paris-Saclay, Université Paris Cité, CEA, CNRS, AIM, 91191 Gif-sur-Yvette, France
3
Univ. Lyon, ENS de Lyon, Univ. Lyon 1, CNRS, Centre de Recherche Astrophysique de Lyon, UMR5574, 69007 Lyon, France
Received:
20
April
2023
Accepted:
2
October
2023
Context. Understanding the collapse of dense molecular cloud cores to stellar densities and the subsequent evolution of the protostar is of importance to model the feedback effects such an object has on its surrounding environment, as well as describing the conditions with which it enters the stellar evolutionary track. This process is fundamentally multi-scale, both in density and in spatial extent, and requires the inclusion of complex physical processes such as self-gravity, turbulence, radiative transfer, and magnetic fields. As such, it necessitates the use of robust numerical simulations.
Aims. We aim to model the birth and early evolution of a low-mass protostar. We also seek to describe the interior structure of the protostar and the radiative behavior of its accretion shock front.
Methods. We carried out a high resolution numerical simulation of the collapse of a gravitationally unstable 1 M⊙ dense molecular cloud core to stellar densities using 3D radiation hydrodynamics under the gray flux-limited diffusion approximation. We followed the initial isothermal phase, the first adiabatic contraction, the second gravitational collapse triggered by the dissociation of H2 molecules, and ≈247 days of the subsequent main accretion phase.
Results. We find that the subcritical radiative behavior of the protostar’s shock front causes it to swell as it accretes matter. We also find that the protostar is turbulent from the moment of its inception despite its radiative stability. This turbulence causes significant entropy mixing inside the protostar, which regulates the swelling. Furthermore, we find that the protostar is not fully ionized at birth, but the relative amount of ionized material within it increases as it accretes matter from its surroundings. Finally, we report in the appendix the results of the first 3D calculations involving a frequency-dependent treatment of radiative transfer, which has not produced any major differences with its gray counterpart.
Key words: stars: formation / stars: low-mass / stars: protostars / radiative transfer / gravitation / methods: numerical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Despite its common occurrence in the Universe, understanding the collapse of gravitationally unstable dense molecular cloud cores, mostly composed of hydrogen and helium, to stellar densities is a challenging task to overcome in stellar formation theory. This does indeed entail both complex physics and observational challenges that have so far proved extremely difficult to tackle. Newly formed protostellar cores have a typical radius of about ∼2 R⊙ and are deeply embedded in their opaque parent molecular cloud core. When coupled with the fact that most stars form in regions of our galaxy situated at ∼100 pc within relatively short timescales, observational breakthroughs have been sparse (e.g., Andre et al. 1993; Maury et al. 2019, see additionally the review by Dunham et al. 2014). From a theoretical standpoint, the challenge arises from the complex interplay between numerous physical processes: self-gravitating hydrodynamics, magnetic fields, radiative transfer, and turbulence. In addition, phase transitions such as molecular hydrogen dissociation also need to be taken into account. As a result, an analytical description of protostellar birth is virtually impossible and the field is dominated by numerical models.
The first of such works was that done by Larson (1969), who computed the collapse of a dense molecular cloud core to stellar densities in 1D spherical symmetry. In this pioneering work, Larson identified a two stage evolutionary sequence resulting in the birth of a low-mass protostar. Initially, as the cloud core collapses, any compressive heating generated by the gravitational contraction is immediately radiated away in the infrared by dust grains. This initial isothermal phase is followed by an adiabatic heating phase after the gas density reaches ∼10−13 g cm−3, where the optical depth exceeds unity and radiative cooling becomes inefficient. As a result, the central regions build enough thermal pressure support to reach a state of hydrostatic equilibrium: this is the birth of the first Larson core. It continues its contraction adiabatically with a polytropic index γeff of five-thirds, which then changes to seven-fifths once temperatures exceed 85 K and the rotational degrees of freedom of H2 are excited.
Once the temperature of the first Larson core exceeds 2000 K, the thermal dissociation of H2 is triggered, which is a highly endothermic process that consumes 4.48 eV per molecule (Stahler & Palla 2004). As a result, the energy provided by the compressive heating is mostly spent on the dissociation process instead of providing additional thermal pressure support. This breaks the state of hydrostatic equilibrium, and a violent second collapse ensues with γeff ≈ 1.1. The extreme rise in density and temperature following this event gives birth to a new protostellar object in hydrostatic equilibrium: the second Larson core1. The protostar continues accreting material from the infalling envelope, and angular momentum conservation leads to the formation of a circumstellar disk. Once core temperatures exceed 106 K, deuterium burning begins, thus ending the pre-stellar phase.
This evolutionary sequence has so far been well accepted for low-mass protostars. Since the work done by Larson (1969), the field has developed ever more robust codes to tackle the 21 orders of magnitude in density and eight in spatial extent, in fully 3D simulations in order to include the effects of magnetic fields, rotation, turbulence, as well as radiation (for a detailed summary of each milestone reached over the years, see Teyssier & Commerçon 2019). These advancements were brought about by the ever increasing amount of computing power available. However, this growing complexity of the simulations has also meant that their computational costs has increased. As a result, there is a vast parameter space to explore and determine the role different physical processes play, but this task is hindered by the technical costs of the simulations. Such technical difficulties have significantly constrained the time stepping in self-consistent 3D simulations, and current state-of-the-art papers struggle to integrate the calculations past a few years after the birth of the protostar (e.g., Vaytet et al. 2018 reached 24 days using adaptive mesh refinement, Wurster & Lewis 2020a reached 4 yr using smooth particle hydrodynamics, whereas the 1D code in Masunaga & Inutsuka 2000 reached 1.3 × 105 yr). Such constraints have forced researchers interested in larger timescales to omit the expensive calculations of the protostar by replacing it with a sink particle (Bate et al. 1995; Bleuler & Teyssier 2014), effectively reducing the feedback effects the protostar has on larger spatial scales to a sub-grid model (e.g., Vorobyov & Basu 2015; Tomida et al. 2017; Hennebelle et al. 2020a; Wurster & Lewis 2020b; Lebreuilly et al. 2021).
Despite the many advancements achieved over the years, the difficulties in integrating the simulations across large timescales has meant that the evolution of the protostar is still poorly understood. Since protostellar feedback plays a significant role in the formation and fragmentation of its surrounding disk, the temperature and structure of its envelope, as well as the overall dynamics of molecular clouds (Hennebelle et al. 2020b, 2022; Grudić et al. 2022), understanding the physics at the protostellar scale is of crucial importance. Hence, our goal is to model the birth of the protostar and study its evolution through time in a self-consistent 3D manner. We place a special focus on the interior structure of the protostar, its accretion shock, and the inner turbulent motions, in order to understand its behavior. Since previous studies in the literature involving nonideal magneto-hydrodynamics have shown that protostars are born with weak magnetic field strengths, ranging from 10−1 − 103 G (Vaytet et al. 2018; Wurster & Lewis 2020a; Wurster et al. 2022), the thermal pressure is orders of magnitude above the magnetic pressure. Hence, we have decided to omit magnetic fields from our study and have constrained ourselves to a radiation-hydrodynamics (RHD) model under the gray flux-limited diffusion (FLD) approximation. This provides the added benefit of reducing the computational cost of the simulations. Our simulations were carried out using the adaptive mesh refinement (AMR) code RAMSES (Teyssier 2002). In addition, we have for the first time carried out a 3D simulation with frequency-dependent radiative transfer leading to the formation of the protostar. Its results are in agreement with its gray counterpart, and we have reported them in the appendix.
In Sect. 2, we present the numerical methods and the initial conditions used in this work. The birth of the protostar, its evolution through time, and its chemical composition are presented in Sect. 3. Finally, the behavior of the turbulence found within the protostar is studied in Sect. 4.
2. Model
2.1. RAMSES with multigroup flux limited diffusion
Our simulations were carried out using the 3D adaptive mesh refinement and finite-volume code RAMSES (Teyssier 2002). In order to include radiative transfer, we have used the flux-limited diffusion module developed by Commerçon et al. (2011a, 2014), and its extension to a multigroup description by González et al. (2015). Since the protostar and its evolution over time are our subject of interest, we have naturally chosen the gray (single-group) approximation, which allows for better performance. However, we have also run a simulation with a multigroup description in order to compare it with its gray counterpart, the results of which are presented in Appendix C. Hence, for the sake of clarity, we present our governing equations in their general (multigroup) form, which consist of the Euler equations coupled with a radiative energy equation (González et al. 2015):
where ρ is the gas density, v its velocity vector, P its thermal pressure, T its temperature, ϕ the gravitational potential, 𝕀 the identity operator, κPg the Planck mean opacity, κRg the Rosseland mean opacity, G the gravitational constant, c the speed of light, and λg the flux limiter. We note that Ng is the total number of radiative groups whose frequency borders are νg ± 1/2. Θg is the energy carried by photons that have a Planck distribution of temperature T inside their given radiative group. Etot is the total gas energy, which includes the kinetic and internal energy E:
Eg (resp. ℙg) is the frequency-integrated radiative energy (resp. pressure tensor) inside each group:
The opacities are also computed in the same manner:
We define the total radiative energy Er as the sum of the radiative energy inside each group:
Equation (1) is the continuity equation, Eq. (2) describes the conservation of momentum, Eq. (3) the conservation of energy, Eq. (4) the conservation of radiative energy, and Eq. (5) the Poisson equation for self-gravity.
The code uses the HLL Riemann solver to solve the hydro equations, and the radiative energy equations are solved using a time implicit solver with the following flux limiter (Minerbo 1978):
with Rg = |∇Eg|/(ρκRgEg). The radiative pressure tensor is given by:
where 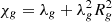 and ng = ∇Eg/|∇Eg|. Under the optically thick limit, Rg → 0 and λg → 1/3 which causes ℙg to become isotropic. In the main body of this paper, we have used the gray approximation, meaning that there is a single group of photons (i.e., Ng = 1).
and ng = ∇Eg/|∇Eg|. Under the optically thick limit, Rg → 0 and λg → 1/3 which causes ℙg to become isotropic. In the main body of this paper, we have used the gray approximation, meaning that there is a single group of photons (i.e., Ng = 1).
The equation of state used is the tabulated EOS of Saumon et al. (1995), which has been extended to lower densities by Vaytet et al. (2013). It describes the thermal properties of H2, H, H+, He, He+, and He2+. The cloud has an initial mixture of 73% H and 27% He.
The gas and dust opacities were taken from Vaytet et al. (2013), who pieced together a table of opacities in the range of 10−19 g cm−3 < ρ < 102 g cm−3 and 5 K < T < 107 K from Semenov et al. (2003), Ferguson et al. (2005) and Badnell et al. (2005; see Fig. 2 of Vaytet et al. 2013). When temperatures are below 1500 K, the dust particles (which represent 1% of the mass content of the fluid) dominate the opacities and they are in thermal equilibrium with the gas. Once temperatures exceed 1500 K, the dust sublimates and the molecular gas opacities begin to dominate. Finally, when the temperatures exceed 3200 K, all molecules are dissociated and the atomic gas opacities dominate. The Planck and Rosseland mean opacity tables are computed within each frequency group according to the Delaunay triangulation process described in Vaytet et al. (2013). In gray radiative transfer simulations, there is only a single frequency group ([105; 1019] Hz) along which the entire opacities are integrated. The resulting opacity mesh is presented in Fig. 1, and the temperature-density distribution of the cells in our computational domain at the epoch of protostellar birth is overlaid in red. At low temperatures, the dust dominates the fluid’s opacity; however, they are destroyed once temperatures exceed ≈1500 K and the subsequent drop in κR is clearly visible in the figure. Once the gas transitions toward higher densities, the atomic gas opacities begin to rise and a new opacity peak appears.
 |
Fig. 1. Opacity mesh created for our gray radiative transfer approximation. The temperature-density distribution of all cells during the epoch of protostellar birth is overlaid in red. |
Limiting ourselves to a RHD model is not without merit. Indeed, not only does this significantly reduce the computational costs of our simulations, it also has a physical justification. Current state-of-the-art papers involving nonideal MHD have consistently shown that the protostar is born with a weak magnetic field strength, thus placing the magnetic pressure orders of magnitude below the thermal pressure. One can thus omit magnetic fields when describing protostars prior to the beginning of a dynamo process.
2.2. Initial Conditions
Our initial conditions consists of a uniform density sphere of mass M0 = 1 M⊙, initial temperature T0 = 10 K, and a radius of R0 = 2.465 × 103 AU. This molecular cloud core is 100 times denser than its surrounding environment, and its ratio of thermal to gravitational energies is
where κB is Boltzmann’s constant and mH is the atomic mass constant. The mean molecular weight μ corresponds to 2.31 for our initial gas mixture.
As we have chosen to focus our attention on the formation and early evolution of the protostar, we have not included any motion in our initial conditions, be it in the form of coherent solid body rotation or any turbulent velocity vector field in the cloud core. This allows the ensuing gravitational collapse to form a spherical, central protostar in the absence of any disks. Hence, our computational resources are more devoted to the protostar, and we can integrate our simulations for longer timescales. In this respect, our study is equivalent to 1D calculations such as those of Larson (1969), Narita et al. (1970), Winkler & Newman (1980), Masunaga & Inutsuka (2000), Vaytet et al. (2013), Vaytet & Haugbølle (2017), Bhandare et al. (2018), Bhandare et al. (2020). The added benefit of carrying out these calculations in 3D is the ability to describe the turbulent motion within the second core, recently brought to light by the 2D study of Bhandare et al. (2020). As such, these initial conditions provide us with an ideal scenario to study the accretion shock and the interior structure of the protostar.
2.3. Refinement strategy
In order to resolve the interior of the protostar, an exceptionally high resolution is required. We continuously refine our AMR grid according to a modified Truelove criterion (Truelove et al. 1997):
where Δx is the cell length and N = 20. 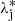 is the Jeans length computed at the cell’s given density and at a temperature of 100 K:
is the Jeans length computed at the cell’s given density and at a temperature of 100 K:
where λj is the Jean’s length. This allows the resolution to follow a length that varies in ρ−1/2 independently of temperature once T > 100 K. The coarse grid has a resolution of 643 cells (ℓmin = 6), and we allow 20 additional levels of refinement (ℓmax = 26). This results in an effective spatial resolution of Δx = 1.4 × 10−4 AU at the maximum refinement level. Although some of the protostar’s properties are not converged at this resolution (see Appendix B), we have nonetheless proceeded with it in order to circumvent the stringent time-stepping constraints.
Our refinement strategy provides us with 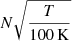 cells per actual Jeans length (until the maximum refinement level is reached), which throughout our simulation corresponds to 20 − 2 × 103 cells. In the protostar’s central region, we have ≈60 cells per jeans length. This allows us to effectively resolve turbulent motions within the protostar.
cells per actual Jeans length (until the maximum refinement level is reached), which throughout our simulation corresponds to 20 − 2 × 103 cells. In the protostar’s central region, we have ≈60 cells per jeans length. This allows us to effectively resolve turbulent motions within the protostar.
Our simulation was run on two nodes, each containing 32 CPU cores. As reported in Vaytet et al. (2018), the load balancing performs poorly in RAMSES when simulating second gravitational collapses, as the majority of the computational load is contained in a small central region. As such, a smaller CPU workforce is the optimal choice as it reduces the MPI communications load. The simulation was run for a total of 2053.75 h, which corresponds to a usage of 131 440 CPU h. By using the Berthoud et al. (2020) estimate of 4.68 g hCPU−1, the CO2 equivalent carbon footprint of our simulation is ≈615 kg.
3. Results
3.1. Genesis
We first begin by describing the system at the epoch of protostellar birth. We define this moment as the instant a second accretion shock forms (i.e., a discontinuity in the radial velocity profile). In Fig. 2, we show plots displaying various physical profiles along radius and density. Panel e shows the temperature-density distribution of our cells. Here, the previously mentioned two step evolutionary sequence is clearly visible: the collapse begins isothermally, contracts adiabatically, and once the dissociation of H2 begins, a second collapse occurs where T ∝ ρ1/10 (γeff ≈ 1.1). The supersonic free-falling gas then collides with the protostellar surface which causes the shock heating observed after ρ ∼ 10−5 g cm−3, and the gas begins a second phase of adiabatic contraction as the newly formed protostar continues accreting material. The temperatures inside the protostar reach upward of ≈8.5 × 104 K. This is a far-cry from the 106 K needed to fuse deuterium; the protostar must further contract and its core temperature needs to increase ten-fold in order to become a star and join the main sequence.
 |
Fig. 2. Various sets of 2D histograms binning the cells in our computational domain (panels a–e) at the epoch of protostellar birth. Panels a–d represent respectively radial velocity, density, entropy, and temperature as a function of radius. The solid (resp. dashed) black line in panel b displays the expected density profile for a free-falling gas (resp. for the collapse of an isothermal sphere). The solid (resp. dotted) black line in panel d represents the expected temperature profile for the collapse of an isothermal sphere with γeff = 1.1 (resp. γeff = 7/5). Panel e displays temperature as a function of density, where the overlaid solid black line displays a contraction with γeff = 1.1. Panel f represents the sum of the enclosed gas and radiative energies at radius r (solid line, see Eq. (15)), along with its constituent parts, namely internal (dashed line), kinetic (dotted line), and radiative energies (dash-dotted line). |
Panel a shows the radial velocity profile, where one can observe a prominent discontinuity at 6 × 10−3 AU (≈1.3 R⊙), which marks the protostar’s border. Another discontinuity, this time corresponding to the first Larson core border, is visible at 0.5 AU. The location of these shock fronts also correspond to steep density and temperature gradients in panels b and d. Both outside and inside the first core border, the density profile approaches ρ ∝ r−2 (dashed black line in panel b), which is characteristic of the collapse of an isothermal sphere (Larson 1969; Penston 1969). Just outside the second core border, the density profile closely approaches ρ ∝ r−1.5 (solid black line in panel b), which demonstrates that the accreted gas is free-falling into the newly formed protostar. Since T ∝ ργeff − 1, we also see two differing temperature profiles in panel d; outside the first core border, the contraction occurs with γeff = 7/5, hence T ∝ r−0.8 (dashed black line). However, inside the first core the contraction occurs with γeff ≈ 1.1. As a result, the temperature profile follows T ∝ r−0.2 (solid black line).
When the free-falling gas reaches the stellar surface, the supersonic collision heats it significantly, as it cannot dissipate its kinetic energy in the form of radiation in these extremely high optical depths (see Fig. 4b). This causes the temperature spike seen in panel d at the second core border, which exceeds the temperature in the protostar’s outer layer. This exhibits the radiative nature of the protostar at birth; it mainly radiates the accretion energy it receives at the shock front which far outweighs the cooling flux that struggles to escape the opaque interior. Once inside the protostar, there is a significant amount of spread around vr = 0, which shows that there are parcels of fluid that are both rising and falling, thus hinting at the presence of turbulent motions in the protostar’s interior. Indeed, when visualizing the velocity vector field in Fig. 3, there is a significant amount of eddies visible downstream of the accretion shock.
 |
Fig. 3. Density slices through the center of the domain at the birth of the protostar (t = 0, panel a) and roughly 2 months later (t ≈ 59 days, panel b). The swirly patterns are line integral convolution (LIC) visualizations of the velocity vector field, which display prominent eddies inside the newly formed protostar. Over the span of ≈2 months, the protostar has grown in radius by a factor ≈2.8. |
In panel c, the radial entropy2 profile is displayed. Here, we once again see two steep gradients corresponding to both core borders. Inside both cores, the entropy profile rises with the radius. This implies that the core is radiatively stable, and cannot generate any convection from its central regions3 (Stahler & Palla 2004). The nature of this turbulent motion will be studied in detail in Sect. 4.2. We subsequently also revisit the behavior of the entropy profile in Sect. 3.2.
In panel f, we display the sum of the enclosed gas and radiative energies Eenc as well as its constituent parts, namely radiative, kinetic, and internal energy, as a function of radius, and computed using
Throughout the entire volume of our computational domain, the bulk of the system’s energy resides under internal energy form, and kinetic energy is the second most prominent form. The majority of Eenc is within the protostar itself. By looking at the enclosed radiative energy curve, we can distinguish three plateaus. The first one, just outside the protostar’s border, shows that the bulk of the radiative energy at r < 0.1 AU is located inside the protostar, and is a consequence of the weak radiative energy gradient outside the second core border (see Fig. 4a). This is also suggesting that very little radiation is escaping the protostar, thus hinting at the subcritical nature of the second core accretion shock (the radiative flux escaping the shock front is inferior to the incoming energy flux). The second plateau, located outside the first core border, is in fact not a real plateau; the enclosed radiative energy is indeed increasing. However there is far too little radiative energy outside the first core to lift the curve any further. Once r > 102 AU, the enclosed radiative energy curve increases once again, as the volume integral now includes the photons emitted by the isothermal phase of the contraction. Finally, the third plateau is simply caused by the fact that we have reached the boundaries of the simulation box, and no new cells are used to compute the volume integral.
 |
Fig. 4. Radiative energy (panel a), Rosseland mean opacity (black, panel b), optical depth (red, panel b), and luminosity (panel c), averaged in radial bins and displayed as a function of radius at the epoch of the protostar’s formation. |
We now turn to studying the radiative behavior of the simulation at the birth of the protostar. Figure 4 shows the specific radiative energy (panel a), and the opacity (black curve in panel b), averaged in radial bins and displayed as a function of radius. The red curve in panel b shows the optical depth τ computed from the outer edge of the simulation box:
Panel c of this figure displays the luminosity L(r), computed as:
Panel a shows us that the radiative energy is constant at large radii (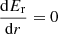 ). Since the photons being produced locally by the gas are streaming through an optically thin medium, Er remains constant during this phase of isothermal contraction. Once the gas becomes optically thick to radiation, we witness a subsequent buildup in radiative energy. A sharp gradient, corresponding to the first core accretion shock, is then seen at 0.5 AU. It should be noted however that the first core accretion shock has already radiated a substantial amount of energy, which has then propagated outward. This is made possible by the supercritical nature of the first core accretion shock (Commerçon et al. 2011b; Vaytet et al. 2018). Inside the first core, the radiative energy gradient is not as steep as that of the adiabatic gas outside of it. Since Er ∝ T4, we have Er ∝ r−3.2 outside the first core (γeff = 7/5, gray dotted line), whereas Er ∝ r−0.8 inside it (γeff = 1.1, gray dashed line). The temperatures found inside the first core exceed the dust sublimation temperature (≈1200 K), causing the drop in opacity seen in panel b. Once we reach the protostar, the high densities spike the atomic gas opacities, and the optical depth reaches a staggering 1015. This causes the steep radiative energy gradient at the protostar’s border (≈6 × 10−3 AU) and the subsequent buildup seen in its interior.
). Since the photons being produced locally by the gas are streaming through an optically thin medium, Er remains constant during this phase of isothermal contraction. Once the gas becomes optically thick to radiation, we witness a subsequent buildup in radiative energy. A sharp gradient, corresponding to the first core accretion shock, is then seen at 0.5 AU. It should be noted however that the first core accretion shock has already radiated a substantial amount of energy, which has then propagated outward. This is made possible by the supercritical nature of the first core accretion shock (Commerçon et al. 2011b; Vaytet et al. 2018). Inside the first core, the radiative energy gradient is not as steep as that of the adiabatic gas outside of it. Since Er ∝ T4, we have Er ∝ r−3.2 outside the first core (γeff = 7/5, gray dotted line), whereas Er ∝ r−0.8 inside it (γeff = 1.1, gray dashed line). The temperatures found inside the first core exceed the dust sublimation temperature (≈1200 K), causing the drop in opacity seen in panel b. Once we reach the protostar, the high densities spike the atomic gas opacities, and the optical depth reaches a staggering 1015. This causes the steep radiative energy gradient at the protostar’s border (≈6 × 10−3 AU) and the subsequent buildup seen in its interior.
In the luminosity profile shown in panel c, we see a spike at the protostar’s border. This is the second core accretion shock. Due to the temperature of the shock front, mainly Ultra-Violet photons are emitted at this radius, which are quickly reabsorbed by the optically thick gas upstream and reemitted in the infrared4. As such, the total luminosity exiting the protostellar surface should be measured just upstream of the shock front, which yields a value of ≈8 × 10−7 L⊙. Curiously, the total luminosity becomes somewhat constant with the radius starting at 20 AU, which shows that the emanating radiative flux decreases as Frad ∝ r−2. This means that the photosphere of the system is located at about this radius. The salient question one might ask here is how the system’s behavior within the photosphere impacts the amount of flux escaping it, as that would allow us to link our current theoretical understanding of newly formed protostars with photometric observations. However, we have not been able to integrate our calculations long enough to witness any noticeable change in the radiative behavior of the photosphere.
3.2. Evolution of the protostar
We now turn to studying the evolution of the protostar over time. Due to our high resolution, the time stepping is very stringent. In addition, we have ∼3 × 107 cells inside the protostar’s volume, which resulted in a very heavy computational load and our ability to integrate across long timescales was heavily impacted. Nevertheless, the results obtained provide us with valuable insights into the evolution of its physical properties and the radiative behavior of the accretion shock.
We thus begin by studying Fig. 5, which displays the evolution of various properties of the protostar. In order to compute these physical properties, we selected all cells whose thermal pressure support outweighs incoming ram pressure (see Appendix A). In addition, we leverage the complementary information available in Fig. 6, which displays various physical profiles, averaged in radial bins and displayed as a function of radius at different times.
 |
Fig. 5. Evolution of the physical properties of the protostar displayed as a function of time, where t = 0 marks the birth of the protostar. Panel a displays the protostar’s mass, panel b its radius, panel c (resp. panel d) its surface integrated luminosity (resp. mass accretion rate), panel e (resp. panel f) the average density (resp. temperature) at the shock front. The solid blue line in panel c represents the radiative efficiency of the protostar. |
 |
Fig. 6. Evolution of the density (panel a), temperature (panel b), radiative energy (panel c), radial velocity (panel d), specific entropy (panel e), and Rosseland mean opacity (panel f) profiles, averaged in radial bins and displayed as a function of radius for different times, where t = 0 marks the birth of the protostar. The last curves (dark red) on each panel correspond to t ≈ 241 days. The dashed and dotted gray lines in panels a–c are power law curves representing the expected density, temperature, and radiative energy profiles both prior to and after the accretion of the first Larson core. |
In Fig. 5, panel a displays the enclosed mass inside the protostar. The protostar is born with a mass of M* ≈ 4 × 10−3 M⊙, which steadily grows over time. The mass accretion rate, displayed in panel d, is computed by integrating the mass flux on the protostar’s surface:
where S* is the protostar’s surface. The mass accretion rate begins at a tremendous 0.2 M⊙ yr−1, and quickly declines to 5.2 × 10−3 M⊙ yr−1 by the last snapshot of our simulation. The radius of the protostar is displayed in panel b. It is formed with a radius of R* ≈ 1.3 R⊙, and it continuously increases over time. In view of the fact that it contains such a small mass, the large radii seen in panel b are intriguing. Indeed, panels a and b show that the protostar contains ≈1.7 × 10−2 M⊙ in a radius of 9.5 R⊙ by the end of the simulation. This initial bloating phase has previously been reported in the literature (Larson 1969; Narita et al. 1970; Winkler & Newman 1980; Bhandare et al. 2020), and is caused by the radiative behavior of the shock front. As can be seen in Fig. 4b, the accretion shock has a very high optical depth, and its radiation is immediately absorbed by the gas just upstream, which is also optically thick. As a result, the protostar faces immense difficulty radiating away the kinetic energy of the gas it accretes, the majority of which is dumped into the internal energy budget of the protostar. This is more readily seen in panel c of Fig. 5, which displays the surface integrated luminosity L* (measured just upstream of the accretion shock) as well as the fraction facc of the accretion luminosity Lacc radiated away (blue curve of panel c). These two quantities are computed as
where
Equation (20) is only an approximation of the radiative efficiency of the shock front because L* also contains the cooling flux emanating from the protostar’s interior, although we expect the latter to be very small due to the optical depths such radiation has to travel through. All throughout the simulation, the protostar is extremely dim and it radiates only a minute fraction of the accretion luminosity. The continuous increase in protostellar luminosity is due to two reasons; the expanding radiative surface, and the decrease in shock density (see Fig. 5e), which reduces the optical depth of the accretion shock and facilitates the escape of radiation. Although the surface temperature of the protostar also decreases, its rate of decrease is not enough to reduce its luminosity output over time.
This accumulation of energy can also be seen in Fig. 6, which displays the evolution of various radial profiles over time. In panel e of this figure, one can see that the specific entropy of the gas downstream of the shock front is continuously increasing over time: the entire profile shifts upward as accretion progresses. However as the mass accretion rate decreases, the rate of increase in specific entropy also decreases. One can also see an increase in entropy in between the first and second core borders, caused by the radiation produced at the protostar’s shock front.
Another insight provided by this plot is the fact that the entropy continuously rises with the radius inside the protostar at all times during the simulation, meaning that it remains radiatively stable. Despite this, one can see a plateau develop just downstream of the second core shock front which is induced by the transport of heat in these regions. The mechanism behind this heat transport is the turbulent motion found within the protostar, which allows for a redistribution of energy throughout the protostar, and thus causes the entire entropy profile to shift upward. This becomes prominent over time as the effects of this turbulence begin to materialize (see Sect. 4.2 and the turbulence crossing time in Fig. 15c). As a consequence, the turbulent transport of energy becomes increasingly prominent over time in the protostar’s outer layers. Having carried out our simulation in 3D, our more complete description of turbulence has allowed this plateau to develop on much smaller timescales than in Bhandare et al. (2020)’s 2D simulations (see Appendix D). One can also distinguish a second plateau develop in the innermost regions. This secondary plateau is caused by the high degree of ionization in the central regions (see Fig. 8), which causes the fluid to transition to a lower entropy regime. The turbulent transport of heat within the protostar then causes this secondary plateau to develop. The mixing of entropy plays a crucial role in regulating the protostar’s radius. Indeed, as radiative cooling struggles to evacuate the immense amount of energy being accreted by the protostar, turbulence aids this process by redistributing heat in its outer regions, thus alleviating the bloating.
Curiously, panel b of Fig. 5 displays a sudden increase in protostellar radius at t ≈ 187 days, which coincides with a sudden increase and subsequent drop in shock density and temperature. This corresponds to a free fall time of the first Larson core, and indeed the various radial profiles in Fig. 6 confirm that the first core is accreted by the protostar at this moment (see for instance the disappearance of the first core accretion shock in panel a or d). Although this causes an order of magnitude increase in protostellar luminosity, the radiative efficiency remains well below unity since the protostar is still deeply embedded in an optically thick cloud. Its radius must further increase to larger values before the accretion shock can properly evacuate its radiative energy into a less dense and optically thinner medium.
Figure 6 also informs us of the behavior of the gas upstream of the protostar’s shock front both prior to and after the accretion of the first Larson core. As mentioned previously, the density profile in the inner regions of the first Larson core follows ρ ∝ r−1.5 (gray dashed line) and ρ ∝ r−2 in its outer layers. As seen in panel a of the figure, the boundary between these two profiles expands outward over time, such that the entire density structure inside the first Larson core shifts to ρ ∝ r−1.5. This behavior has previously been reported by Larson (1972), Shu (1977). The temperature profile follows T ∝ ργeff − 1. Prior to the accretion of the first core, the H2 molecules are undergoing the dissociation process, which places γeff at ≈1.1. As a result, the temperature profile follows T ∝ r−0.15 (gray dashed line in panel b). Once the first core is accreted, the protostar directly accretes hot (and hence excited) H2 molecules, whose γeff is ≈7/5. As a result, the temperature profile now shifts to T ∝ r−0.6 (gray dotted line in panel b). We see the same behavior in the radiative energies; since Er ∝ T4, we have Er ∝ r−0.6 prior to the accretion of the first Larson core, and Er ∝ r−2.4 afterwards.
Despite the nonlinear nature of the problem, it is our hope that a sub-grid model could be developed to properly describe the radiative feedback of the protostar unto its surrounding environment. To this end, we have displayed in Fig. 7 the protostar’s surface integrated luminosity, plotted against its radius. This has demonstrated a power-law relationship between the two, where 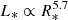 . The power-law fit was performed prior to the accretion of the first core (i.e., R* < 6 R⊙), as later times exhibit differing gas behaviors upstream of the accretion shock (Fig. 6), which in turn changes the exponent of the power-law. In addition, we do not have a sufficient number of data points to accurately describe L*(R*) after the accretion of the first core. Although this result’s robustness needs further testing and investigation, it excitingly hints at the existence of an analytical model that can be found. Such a model will need to describe the temporal evolution of the gas behavior both upstream and downstream of the shock front, whereby one estimates the amount of radiative flux escaping the protostellar surface based on the local gas structure. We plan to further explore this power-law relationship between L* and R* in the future.
. The power-law fit was performed prior to the accretion of the first core (i.e., R* < 6 R⊙), as later times exhibit differing gas behaviors upstream of the accretion shock (Fig. 6), which in turn changes the exponent of the power-law. In addition, we do not have a sufficient number of data points to accurately describe L*(R*) after the accretion of the first core. Although this result’s robustness needs further testing and investigation, it excitingly hints at the existence of an analytical model that can be found. Such a model will need to describe the temporal evolution of the gas behavior both upstream and downstream of the shock front, whereby one estimates the amount of radiative flux escaping the protostellar surface based on the local gas structure. We plan to further explore this power-law relationship between L* and R* in the future.
 |
Fig. 7. Logarithmic scatter plot showing the protostellar luminosity as a function of radius (where each scatter point is color coded with the protostellar mass). A fit (red dotted line) reveals a power law relationship between L* and R* whose exponent is ≈5.7. |
3.3. Chemical composition
An important factor to consider following our discussion in Sect. 3.2 is the dissociation of molecular hydrogen and the ionization of atomic hydrogen and helium. These processes consume energy, which is supplied by accretion and thus must be considered when attempting to determine the energy budget, and hence the radius of the protostar. The energy consumed by these processes is:
Using the equation of state table, we can directly estimate the fractions of each of these species in our computational domain by interpolating their values. As such, we do not actually model their dynamics, but simply provide the expected amount of each species for a given cell. We thus display in Fig. 8 the mass fraction of each species Xi, averaged in radial bins where
 |
Fig. 8. Fraction of H2 (red), H (blue), H+ (cyan), He (black), He+ (purple) and He2+ (pink), averaged in radial bins and displayed as a function of radius at the epoch of the protostar’s formation (panel a) and ≈2 months later (panel b). See Eq. (23). |
In panel a of this figure, we display these fractions at the epoch of the protostar’s formation. A steep gradient in the fraction of H2 (red curves) is seen, which corresponds to the protostar’s accretion shock. Here, all remaining H2 molecules are dissociated as a result of the shock heating, and only atomic hydrogen enters the protostar. The intense shock heating also begins ionizing the neutral hydrogen atoms (cyan curves), which happens in a much more gradual manner. However, the temperatures are not high enough to ionize the entirety of the atomic hydrogen reservoir, even in the central regions. We also see the onset of single (purple curves) and double (pink curves) He ionization just downstream of the accretion shock. The temperatures achieved in these regions cause a similar amount of He in first and second ionization states, although the curves begin to differ in the central regions. We see the same patterns ≈2 months later in panel b, although the accretion shock has moved outward and the total fraction of ionized H has increased, whereas the fraction of ionized He remains the same.
Using these fractions, we also compute the mass of each of these species and display them in Fig. 9 as a function of the protostar’s mass (M*, analogous to time). Since almost no hydrogen is under molecular form inside the protostar, we have omitted displaying the mass this species represents in the figure. We see an almost linear increase of all species with M*, although the slopes for each species differs. At about M* ≈ 7.5 × 10−3 M⊙, ionized Hydrogen becomes the dominant species inside the protostar in terms of mass, and by M* ≈ 1.7 × 10−2 M⊙, about ≈50% of the protostar’s mass is under ionized form. However, the estimated amount of ionized material begins to decrease shortly afterward due to the decreasing density and temperature in the central core (see Figs. 6a,b). In any case, this figure shows us that the electrical conductivity of the protostar remains high following its birth.
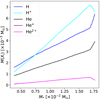 |
Fig. 9. Mass of H (blue), H+ (cyan), He (black), He+ (purple) and He2+ (pink) inside the protostar displayed as a function of protostellar mass. The purple and pink curves overlap very closely. |
By computing the total energy consumed by the dissociation and ionization processes, we find that they represent only ≈6% of the total energy injected by accretion since the protostar’s birth. As such, the rest of the accretion energy is either dumped into the internal energy budget of the protostar or used to drive turbulent motions, which are eventually converted into thermal energy. We estimate the fraction of the accretion energy used to drive turbulence in Sect. 4.2.
4. Turbulent motion within the protostar
In this section, we aim to characterize the turbulence inside the protostar shown in Fig. 3 by describing it both quantitatively and qualitatively. We subsequently study how it evolves over time in our simulation.
4.1. Onset of turbulence
As stated previously, the rising entropy profile within the protostar suggests that this turbulence is not generated by a classical convective instability as postulated by Schwarzschild’s criterion, where the protostar would exhibit a transition from a radiative zone to a convective shell. Thus, another instability seems to be at play here. Upon further investigation, we have discovered that the non-radial flow within the protostar has its origins during the hydrostatic bounce immediately following its formation.
Indeed, Fig. 10 shows the protostar at different critical moments during its birth. Panel a shows the protostar as the second core accretion shock begins to form. Here, minute deviations from a purely radial flow can be seen downstream of the shock front. These are due to our use of a Cartesian grid, which favors flow along the grid axis. Upon crossing the shock front, the upstream velocity dispersions are amplified by about an order of magnitude, which allows them to be seen in the streamlines. Nevertheless, the kinetic energy carried by the non-radial flow is well below that of the radial flow.
 |
Fig. 10. Density slices through the center of the domain showing the onset of turbulence within the protostar. Streamlines of the velocity vector field are shown in white. Each panel represents a different time, with panel a showing the protostar during the formation of the accretion shock (t = 0), panel b after the onset of a hydro-dynamical rebound from the central region (t ≈ 16.5 h), and panel c after the outgoing wave interacts with the shock front (t ≈ 21 h). The scale bar in panel b applies to the other two panels. |
Several hours later, γeff reaches 4/3 in the central regions owing to the rising density and temperature, thus forming a hydrostatic equilibrium that halts any further inward flow. This causes a hydrostatic bounce (panel b), where fluid with vr > 05 can be seen within the protostar. This bounce amplifies the non-radial flow within the protostar, although our grid geometry again seems to have an influence. Once the outgoing wave reaches the shock front, a physical instability seems to be triggered as strong vortical movement are produced within the protostar (panel c). Once the bounce has passed, these turbulent motions become sustained by accretion, as the supersonic radial flow of gas upstream of the accretion shock transfer’s some of its momentum to the downstream gas, thus sustaining or amplifying any ortho-radial components in the downstream flow. This signals the onset of strong, stochastic turbulence within the protostar, as it becomes sustained through accretion. Indeed, Fig. 11 displays the kinetic energy power spectrum Ps within the protostar throughout the simulation (panel a), which exhibits the power-law relationship governing Ps(ℓ) and ℓ, where ℓ is the inverse of the wavenumber. The exponent (n) of this power-law obtained through a numerical fit is displayed in panel b; it hovers around 2. Although n drops during the accretion of the first core when t ≈ 180 days, it returns to 2 afterwards. This implies that the turbulence within the protostar is being continuously maintained by accretion.
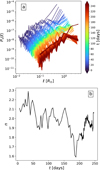 |
Fig. 11. A spectral analysis of the turbulence within the protostar. Panel a: Kinetic energy power spectrums as a function of characteristic scale ℓ of the gas within the protostar at different times, where t = 0 marks the epoch of protostellar formation. The last curve (dark red) corresponds to t ≈ 241 days. Panel b: power-law fit of the curves in panel a, where Ps(ℓ)∝ℓn. |
Another interesting observation provided by this figure is that the turbulence inside the protostar is not that expected of an incompressible fluid as postulated by Kolmogorov (1941), where Ps(ℓ)∝ℓ11/3, despite the fact that the velocity dispersions are subsonic and well below the local sound-speed (blue curve in Fig. 14). This is due to the heavily stratified nature of the protostellar interior, which hinders the inward motion of turbulent eddies.
In Fig. 12, we compare the ortho-radial kinetic energy Evθ, ϕ with its radial counterpart Evr within the protostar. These two quantities are computed as:
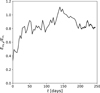 |
Fig. 12. Ratio of ortho-radial to radial kinetic energy inside the protostar (see Eq. (24)) as a function of time, where t = 0 marks the birth of the protostar. |
Where vϕ and vθ are respectively the azimuthal and meridional velocity. The curve suggests that the instability behind this turbulence causes an exponential growth of non-radial perturbations, before reaching a nonlinear phase where it stagnates. If equipartition is achieved, one would expect Evθ, ϕ/Evr ≈ 2; however, the figure shows that the ratio reaches ≈0.8 by t ≈ 30 days and hovers around this value, meaning the flow within the protostar is mainly dominated by its radial component throughout the simulation.
In addition, although the entropy profiles averaged in radial bins in Fig. 5e show that the protostar is stable against convection, Fig. 13 shows that the turbulent motions can lead to local negative entropy gradients, where lower entropy fluid lies above higher entropy fluid. This causes weak convection to occur locally across all radii, and further contributes to the stochastic nature of the turbulence within the protostar.
 |
Fig. 13. Cross-sectional view of the protostar at our final simulation snapshot, showing the interior entropy. The colorbar has been artificially anchored for visualization purposes. The gray spherical outline is an artistic choice for better visualization and serves no physical meaning. |
We have seen this same pattern in higher resolution simulations; both ℓmax = 27 and ℓmax = 28 show the exact same onset of turbulence6. Through private communications with A. Bhandare, we have learned that a similar phenomena seems to occur in Bhandare et al. (2020)’s 2D simulations run on a polar grid. Indeed, their protostar is turbulent at birth despite its radiative stability (see their Fig. C.1), and this turbulence begins following the hydrostatic bounce.
When combining all of these elements together, we can conclude that although the seed for this turbulence has its origins in our grid geometry, the hydrostatic bounce and the subsequent amplification of turbulence caused by it and its interaction with the shock front are physical. We are still unsure as to what precise instability is at play here, but we have offered some evidence that could implicate the Standing Accretion Shock Instability (SASI, Blondin et al. 2003; Scheck et al. 2004; Foglizzo et al. 2007) in Appendix E.
In real astrophysical cases, the initial cloud core possesses both turbulent and rotational motion. If minuscule disturbances in the flow such as ours can provide the seed necessary to trigger turbulence within the protostar, then we predict that all protostars will be turbulent at birth.
4.2. Accretion driven turbulence
Now that we have established that turbulent motion is created at protostellar-birth and later sustained by accretion, we proceed by providing a quantitative analysis of its behavior throughout our simulation. To this end, we begin with Fig. 14, which displays the velocity dispersions σv computed in radial bins as a function of radius (solid black line) at our last simulation snapshot. In this figure, the velocity dispersions upstream of the shock front are amplified by almost two orders of magnitude.
 |
Fig. 14. Velocity dispersion computed in radial bins (black curve) and average local sound speed (blue curve), displayed as a function of radius at our last simulation snapshot (t ≈ 241 days, where t = 0 marks the birth of the protostar). The red curve is a fit of the inertial range, whose exponent is ≈9/10. The black dotted curve represents the turbulent energy flux (displayed in units of g s−3). |
Once the matter has properly settled into the protostellar surface, the velocity dispersions scale with the radius following a power-law σv ∝ r9/10 (red fit in the figure). As the radius decreases, our ability to resolve these turbulent motions is hampered, since the number of cells in each radial bin decreases with decreasing volume. As a result, the scaling law is broken and the turbulence begins to dissipate through numerical diffusion. We would like to emphasize that the scaling law heavily depends on the internal structure of the protostar. As Fig. 6a has shown, the density profile (and hence the stratification) of the protostellar interior varies over time, which we have found is reflected in the scaling law between σv and r (the proportionality exponent between σv and r changes over time). Nevertheless, these turbulent motions carry a substantial amount of energy all throughout the protostar; the turbulent kinetic energy flux 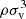 (dotted line) remains strong all throughout the interior.
(dotted line) remains strong all throughout the interior.
Since we are dealing with accretion driven turbulence, a fraction of the incoming accretion energy is used to drive turbulent motions inside the protostar. In order to determine this fraction, we base our analysis on the analytical tools provided by Klessen & Hennebelle (2010), which provides an estimate of the amount of turbulence generated by accretion and lost through decay in astrophysical bodies. Consequently, we begin by defining these tools, namely the turbulent crossing time τd, the turbulence driving scale which we assume to be 2R*, and the mean 3-dimensional velocity dispersion ⟨σv⟩ inside the protostar (Klessen & Hennebelle 2010):
One can also compute the amount of turbulent kinetic energy inside the protostar through
where M* is the protostar’s mass. Using this, we can estimate the loss of turbulent kinetic energy over time Ėdecay
Thus, in order to sustain the turbulence observed inside our protostar, it needs to be continuously driven by the incoming accretion energy Ėin
where vin is the infall velocity at the accretion shock. Finally, this allows us to compute the fraction of the accretion energy required to sustain the turbulence in the interior, which is characterized by the efficiency factor ϵ:
If ϵ < 1, then turbulence is sustained by accretion. In order to obtain ⟨σv⟩, we simply average the velocity dispersion inside the protostar by weighing it by mass. The mass weighing is done to ensure that the energy measurement is biased toward higher density gas.
In Fig. 15, we display ⟨σv⟩, Ėin, Ėdecay and ϵ as a function of time. We have also displayed in panel c the turbulent crossing time (red line), which allows us to estimate the time required for the turbulence to dissipate from large eddies down to thermal energy. As the surface integrated mass accretion rate diminishes over time (see Fig. 5d), so too does the subsonic velocity dispersion inside the protostar. As a result, the accreted kinetic energy Ėin also reduces. The turbulence decay Ėdecay also decreases over time. This is to be expected since the velocity dispersions decrease and the protostellar radius increases. Regardless, the turbulence decay Ėdecay remains well below the injected accretion energy at all times; the efficiency factor peaks at ≈31%. This shows that the injected accretion energy is abundant enough to sustain the observed turbulence inside the protostar at any point during the simulation. However, since the turbulent driving scale increases as the protostar grows, so too does the spatial extent of the turbulent cascade process. This is more readily seen in Fig. 3, where larger eddies can be seen at the accretion shock as the protostar grows. This results in an increasing turbulent timescale, where the fraction of the injected accretion energy takes a more considerable amount of time to dissipate into thermal energy.
 |
Fig. 15. Mass-weighted velocity dispersion inside the protostar (panel a), injected accretion energy alongside the turbulence decay (panel b), and efficiency factor (panel c) displayed as a function of time, where t = 0 marks the birth of the protostar. The red line in panel c corresponds to the turbulence crossing time (see Eq. (25)). |
The ubiquitous turbulence found in the protostar raises the important question of how well it is described by our simulation. It is thus helpful to estimate the Reynolds number Re found within the protostar:
where cs is the sound speed, λp the particle mean free path, and vth the thermal speed of hydrogen atoms:
where n is the number density of atoms with collision cross-section σ (≈10−16 cm2). By our simple estimates, the Reynolds number of the protostar’s fluid should be ∼1014 at the surface (cs ∼ 1 km s−1, T ∼ 103 K, n ∼ 1018 cm−3) and ∼1017 in the central regions (cs ∼ 10 km s−1, T ∼ 104 K, n ∼ 1022 cm−3). These gargantuan Reynolds numbers mean that the characteristic scales by which viscosity effectively dissipates turbulence are orders of magnitude below our maximum spatial resolution. Indeed, such dissipation scales are on the order of the particle mean free path (∼[10−6 − 10−3 cm]), whereas our maximum spatial resolution is Δx = 2.2 × 109 cm. As such, the turbulence is instead dissipated by our numerical diffusion, which means that our ability to describe this process is likely very impacted by our resolution. We have investigated the influence of our numerical resolution on the accretion driven turbulence in Appendix B and concluded that higher resolutions lead to stronger velocity dispersions in the protostar’s interior, which in turn amplifies the turbulent transport of heat. For further inquiries on turbulence in star formation related processes, we invite the reader to see McKee & Ostriker (2007), Hennebelle & Falgarone (2012).
5. Discussions
5.1. The effects of initial conditions on the first and second Larson cores
A result which initially intrigued us is the size of the first Larson core in our simulation. Indeed, Fig. 2 shows a first core radius of 0.5 AU. However, Fig. 4 shows a photosphere located at a much larger radius of 20 AU. As such, the location at which the fluid transitions from an optically thin regime to an optically thick one does not coincide with that of the first core border. This is despite the fact that isothermality is broken at the location of this transition (Fig. 2d). Hence, the radius of our first core is smaller than that which is commonly reported in the literature (e.g., Larson 1969; Vaytet et al. 2013; Vaytet & Haugbølle 2017; Bhandare et al. 2018). The small size of our first core can be attributed to our selection of the alpha value (Eq. (12)), which is smaller than those commonly adopted in the literature (> 0.5). For instance, Vaytet et al. (2013) compared the results of their simulations for different α values, and have found smaller first core radii for smaller α (see their Tables 1 and 2). This is due to the fact that smaller α values correspond to more violent gravitational collapses, where the high infall velocities and mass accretion rates lead to very strong ram pressure. As such, higher amounts of thermal pressure support are needed in order to attain a hydrostatic equilibrium in these configurations.
The value of α that we have adopted has however little bearing on the subsequent formation of the protostar. Indeed, the high mass accretion rates unto the protostar (which begin at ∼ 10−1 M⊙ yr−1 and decline to ∼ 10−3 M⊙ yr−1 by our last snapshot) have previously been reported by numerous papers independently of the initial conditions and physical model adopted (e.g., Vaytet et al. 2013; Tomida et al. 2013; Bate et al. 2014; Vaytet & Haugbølle 2017; Bhandare et al. 2020). The reason behind this is the first Larson core, which provides a momentary halt to accretion unto the central regions until temperatures can exceed ≈2000 K, by which point the second collapse ensues. Since Larson (1969) has shown that the mass accretion rate asymptotically reaches 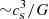 , then one can expect Ṁ∗ ∼ 10−2 M⊙ yr−1, which explains the convergence seen in the literature.
, then one can expect Ṁ∗ ∼ 10−2 M⊙ yr−1, which explains the convergence seen in the literature.
5.2. The radiative behavior of the protostar
Figure 5 has shown us that the second core accretion shock remains subcritical throughout the simulation’s duration, and as a consequence the protostar’s radius swells dramatically over time. The most similar work in the literature to our study is that of Bhandare et al. (2020), which also exhibits a substantial increase of the protostar’s radius with mass. Since their study is two dimensional, they were able to integrate for much longer timescales (hundreds of years instead of our hundreds of days), and as such they were able to witness a contraction of the protostar in some of their simulations. This is explained by a reduction of the incoming mass accretion rate (i.e., a reduction in the incoming accretion energy), and an increased protostellar luminosity. They characterize this by comparing the Kelvin–Helmholtz timescale with the accretion timescale, which we have omitted from our study since the latter remains well below the former throughout our simulation7. Once the Kelvin–Helmholtz timescale drops below the accretion timescale (i.e., facc > 1), the protostar can evacuate its energy, which causes the contraction. However, this occurs once the protostars have expanded to very large radii (on the order of a few AU, with a strong dependence on the initial cloud mass), where the accretion shock has reached first core densities. Furthermore, they do not evolve the simulations long after the contraction, meaning that it is unknown if this contraction is maintained all the way to the formation of a solar-like object. Nevertheless, the subcritical nature of the second core accretion shock has been widely reported in the literature (Larson 1969; Winkler & Newman 1980; Vaytet et al. 2013, 2018; Bate et al. 2014; Bhandare et al. 2018, 2020). It has been settled that the radiative efficiency of protostars must be high during most of its main accretion phase, as that would allow them to form with reasonably small radii (Larson 1972; Appenzeller & Tscharnuter 1975; Winkler & Newman 1980; Stahler et al. 1980). Nevertheless, providing a quantitative estimate of the radiative efficiency of the second core accretion shock and how it varies over time remains of scientific interest. Indeed, many papers in the literature that are interested in larger spatial scales omit the expensive computations that we have performed; they set aside the protostar by replacing it with a sink particle, and prescribe its feedback effects using a sub-grid model (e.g., Urban et al. 2010; Vorobyov & Basu 2015; Hennebelle et al. 2020b, 2022). Thus, the radiative feedback of the protostar in these studies is facc × Lacc, where facc is treated as a free parameter. The value of this parameter has been shown to have a significant effect on the resulting IMF (Hennebelle et al. 2020b). Our simulation shows that the radiative efficiency is extremely low immediately following its birth, and although it increases significantly over time, it remains well below the current values used in the literature. However, we expect it to reach unity once most of the envelope has been accreted, as that would significantly reduce the optical depth of the shock front. This would subsequently allow the protostar to contract by radiating away the large amount of energy it has accumulated.
5.3. The role of turbulence
Regardless of our simulation’s capacity in describing it, the existence of turbulent motion within the protostar from the moment of its inception is noteworthy, most notably for studies that aim to model the formation of stellar magnetic fields. Indeed, as stated previously, since dissipative effects such as ambipolar diffusion and ohmic dissipation considerably reduce the magnetic field strength implanted in the protostar, a dynamo process is required in order to generate the magnetic fields observed in young stellar objects (∼1 kG, Johns-Krull et al. 2009). In order to trigger such a dynamo process, convective motions are a prerequisite (e.g., Durney et al. 1993; Chabrier & Küker 2006), and it is commonly believed that such motions arise once nuclear burning begins in the stellar core. Indeed, the onset of nuclear fusion reverses the entropy profile inside the star, such that the central core will possess a higher entropy than the outer layers. This is due to the fact that the colossal amounts of energy generated by fusion can not be transported through radiation alone, and thus convective motions begin. Since our study has shown that turbulent motion emerges at protostellar birth, we reiterate Bhandare et al. (2020)’s hypothesis that a dynamo process can begin far earlier than previously thought. Since such a process draws from the kinetic energy budget of the protostar, then it can also participate in regulating its radius.
5.4. Open questions
In our opinion, our results raise important questions that we hope will be addressed in the future. Firstly, the manner in which the radiative behavior of the protostar differs when one includes more realistic initial conditions, where turbulence or solid body rotation in the initial dense molecular cloud core provide the angular momentum budget necessary to form a disk, should be thoroughly investigated. Although Bate et al. (2014), Vaytet et al. (2018) have shown that the second core accretion shock remains strongly subcritical, Vaytet et al. (2018) have shown that the poles of the protostar radiate much more efficiently.
Secondly, the extent with which turbulence helps in regulating the swelling of the protostar should be analysed in depth. Our resolution study has shown that higher resolutions lead to stronger velocity dispersions; however, since it is extremely difficult to further increase the resolution, we suggest that 1D calculations that include turbulence through mixing length theory might offer better insights in this regard (e.g., Larson 1969; Palla & Stahler 1991).
Finally, magnetic fields can help in regulating the radius of the protostar, and a quantitative study in this regard is desirable. Indeed, previous studies in the literature have shown that magnetic fields can generate outflows (e.g., Machida et al. 2006, 2007; Tomida et al. 2013; Bate et al. 2014; Tsukamoto et al. 2015; Wurster et al. 2018; Wurster & Lewis 2020a; see also Mignon-Risse et al. 2021 for the high mass case). Such outflows can extract a significant amount of energy which would have otherwise been accreted by the protostar.
6. Conclusion
We have carried out a simulation modeling the collapse of a gravitationally unstable, uniform density sphere of mass 1 M⊙ to protostellar densities, using a 3D RHD description of the gas dynamics under the FLD approximation. The calculations describe the initial isothermal phase, the first adiabatic contraction, the second gravitational collapse triggered by the dissociation of H2, and the second adiabatic contraction. We follow the evolution of the resulting protostar for ≈247 days after its formation, which is longer than the first core free fall time of ≈187 days and hence we were able to witness the latter’s accretion by the protostar. Having placed a focus on the interior structure of the protostar, the simulation was carried out with the highest ever 3D resolution, which involved the use of 26 levels of refinement and 20 − 2 × 103 cells per jeans length. Our findings can be summarized as follows:
-
(i)
Following the formation of the protostar, its radius swells dramatically over time. This is due to the subcritical radiative nature of its shock front, which struggles to evacuate the immense amount of kinetic energy injected by accretion. The radiative efficiency of the protostar remains well below unity in the time-span that we have simulated, even after the accretion of the first core. However, as the protostar swells, the density (and hence the optical depth) of the accretion shock continuously decreases, which increases its radiative efficiency. We have revealed a power-law relationship between the luminosity just upstream of the shock front and the protostellar radius, a result which could aid in inferring the radiative behavior of the protostar across larger timescales once its robustness is established.
-
(ii)
Owing to our very high resolution, we were able to reproduce the findings of Bhandare et al. (2020)’s 2D simulations, where they have discovered that the protostar is turbulent from the moment of its inception despite its radiative stability. The turbulence is created during a hydrostatic bounce immediately following the birth of the protostar; it grows exponentially before reaching its nonlinear phase, where it is then maintained by accretion. We have described this subsonic turbulence both quantitatively and qualitatively: a fraction (< 31%) of the injected accretion energy is used to drive this turbulent motion, and the velocity dispersions show a power-law scaling with the radius. Since the protostar is heavily stratified, the behavior of this turbulence differs from the classical theory of Kolmogorov (1941). Due to the very high Reynolds numbers found in the protostar, our description of this turbulence is impacted by our numerical resolution. Our grid geometry also influences the behavior of the turbulence. Nevertheless, the heat transport it provides leads to significant entropy mixing and aids in regulating the protostellar swelling.
-
(iii)
We find that the protostar is not fully ionized at birth. However, as the protostar accretes material from its surroundings, the amount of mass within it under ionized form continuously increases over time. Hence, the electrical conductivity of the protostar increases over time. Additionally, we estimate that the dissociation of H2 and the ionization of atomic hydrogen and helium represents only ≈6% of the total energy injected by accretion. As such, the energy consumption of these processes plays an insignificant role in regulating the radius of the protostar. Nevertheless, we predict that the high electrical conductivity of the protostar, when combined with the turbulence in the interior, could lead to a dynamo process prior to the onset of deuterium burning. Since generating the stellar magnetic field comes at the expense of kinetic energy, this could also aid in regulating the swelling of the protostar’s radius.
-
(iv)
For the first time, we have carried out during these calculations a frequency-dependent treatment of radiative transfer.
The results, presented in Appendix C, show no major differences to the gray approximation. This is in agreement with the 1D calculations of Vaytet et al. (2013).
Despite the short time-span of our simulation, we believe these results shed light on an otherwise poorly understood phase of the stellar formation process. We are currently investigating how this evolutionary picture changes once we include angular momentum in the system (which leads to the formation of a circumstellar disk), the results of which will be presented in a follow-up paper.
This is consistent with the 2D results of Bhandare et al. (2020).
The multigroup simulation that we have run and presented in Appendix C permits us to better distinguish what photon frequencies are produced at all radii.
We have presented the results of our ℓmax = 27 in Appendix B; however, the time-stepping after second core formation in the ℓmax = 28 was too stringent to produce any presentable results.
Our estimate of the radiative efficiency (Eq. (20)) is equivalent to the ratio of the accretion timescale to the Kelvin–Helmholtz timescale.
Acknowledgments
We thank the anonymous referee for their useful comments that have improved the quality of this paper. This work has received funding from the French Agence Nationale de la Recherche (ANR) through the projects COSMHIC (ANR-20-CE31-0009), DISKBUILD (ANR-20-CE49-0006), and PROMETHEE (ANR-22-CE31-0020). We have also received funding from the European Research Council synergy grant ECOGAL (Grant: 855130). We thank Thierry Foglizzo and Anaëlle Maury for insightful discussions during the writing of this paper. We also thank Asmita Bhandare for providing access to the data of their Bhandare et al. (2020) paper. The simulations were carried out on the Alfven super-computing cluster of the Commissariat à l’Énergie Atomique et aux énergies alternatives (CEA). Post-processing and data visualization was done using the open source https://github.com/osyris-project/osyris package.
References
- Andre, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Appenzeller, I., & Tscharnuter, W. 1975, A&A, 40, 397 [NASA ADS] [Google Scholar]
- Badnell, N. R., Bautista, M. A., Butler, K., et al. 2005, MNRAS, 360, 458 [Google Scholar]
- Bate, M. R., Bonnell, I. A., & Price, N. M. 1995, MNRAS, 277, 362 [Google Scholar]
- Bate, M. R., Tricco, T. S., & Price, D. J. 2014, MNRAS, 437, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Berthoud, F., Bzeznik, B., Gibelin, N., et al. 2020, Estimation de l’empreinte carbone d’une heure.coeur de calcul, Research report (UGA – Université Grenoble Alpes; CNRS; INP Grenoble; INRIA) [Google Scholar]
- Bhandare, A., Kuiper, R., Henning, T., et al. 2018, A&A, 618, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bhandare, A., Kuiper, R., Henning, T., et al. 2020, A&A, 638, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bleuler, A., & Teyssier, R. 2014, MNRAS, 445, 4015 [Google Scholar]
- Blondin, J. M., Mezzacappa, A., & DeMarino, C. 2003, ApJ, 584, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Küker, M. 2006, A&A, 446, 1027 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Teyssier, R., Audit, E., Hennebelle, P., & Chabrier, G. 2011a, A&A, 529, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Audit, E., Chabrier, G., & Chièze, J. P. 2011b, A&A, 530, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Commerçon, B., Debout, V., & Teyssier, R. 2014, A&A, 563, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 195 [Google Scholar]
- Durney, B. R., De Young, D. S., & Roxburgh, I. W. 1993, Sol. Phys., 145, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, J. W., Alexander, D. R., Allard, F., et al. 2005, ApJ, 623, 585 [Google Scholar]
- Foglizzo, T., Galletti, P., Scheck, L., & Janka, H. T. 2007, ApJ, 654, 1006 [NASA ADS] [CrossRef] [Google Scholar]
- González, M., Vaytet, N., Commerçon, B., & Masson, J. 2015, A&A, 578, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grudić, M. Y., Guszejnov, D., Offner, S. S. R., et al. 2022, MNRAS, 512, 216 [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Charnoz, S. 2020a, A&A, 635, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., Commerçon, B., Lee, Y.-N., & Chabrier, G. 2020b, ApJ, 904, 194 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., Lebreuilly, U., Colman, T., et al. 2022, A&A, 668, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johns-Krull, C. M., Greene, T. P., Doppmann, G. W., & Covey, K. R. 2009, ApJ, 700, 1440 [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Dokl. Akad. Nauk SSSR, 30, 301 [NASA ADS] [Google Scholar]
- Larson, R. B. 1969, MNRAS, 145, 271 [Google Scholar]
- Larson, R. B. 1972, MNRAS, 157, 121 [NASA ADS] [Google Scholar]
- Lebreuilly, U., Hennebelle, P., Colman, T., et al. 2021, ApJ, 917, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-I., & Matsumoto, T. 2006, ApJ, 647, L151 [NASA ADS] [CrossRef] [Google Scholar]
- Machida, M. N., Inutsuka, S.-I., & Matsumoto, T. 2007, ApJ, 670, 1198 [NASA ADS] [CrossRef] [Google Scholar]
- Masunaga, H., & Inutsuka, S.-I. 2000, ApJ, 531, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Maury, A. J., André, P., Testi, L., et al. 2019, A&A, 621, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [Google Scholar]
- Mignon-Risse, R., González, M., & Commerçon, B. 2021, A&A, 656, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Minerbo, G. N. 1978, J. Quant. Spectr. Rad. Transf., 20, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Narita, S., Nakano, T., & Hayashi, C. 1970, Prog. Theor. Phys., 43, 942 [CrossRef] [Google Scholar]
- Palla, F., & Stahler, S. W. 1991, ApJ, 375, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Penston, M. V. 1969, MNRAS, 144, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Saumon, D., Chabrier, G., & van Horn, H. M. 1995, ApJS, 99, 713 [NASA ADS] [CrossRef] [Google Scholar]
- Scheck, L., Plewa, T., Janka, H. T., Kifonidis, K., & Müller, E. 2004, Phys. Rev. Lett., 92, 011103 [NASA ADS] [CrossRef] [Google Scholar]
- Semenov, D., Henning, T., Helling, C., Ilgner, M., & Sedlmayr, E. 2003, A&A, 410, 611 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shu, F. H. 1977, ApJ, 214, 488 [Google Scholar]
- Stahler, S. W., & Palla, F. 2004, The Formation of Stars (Wiley-VCH) [CrossRef] [Google Scholar]
- Stahler, S. W., Shu, F. H., & Taam, R. E. 1980, ApJ, 241, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Teyssier, R., & Commerçon, B. 2019, Front. Astron. Space Sci., 6, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Tomida, K., Machida, M. N., Saigo, K., Tomisaka, K., & Matsumoto, T. 2010, ApJ, 725, L239 [NASA ADS] [CrossRef] [Google Scholar]
- Tomida, K., Tomisaka, K., Matsumoto, T., et al. 2013, ApJ, 763, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Tomida, K., Machida, M. N., Hosokawa, T., Sakurai, Y., & Lin, C. H. 2017, ApJ, 835, L11 [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1997, ApJ, 489, L179 [CrossRef] [Google Scholar]
- Tsukamoto, Y., Iwasaki, K., Okuzumi, S., Machida, M. N., & Inutsuka, S. 2015, MNRAS, 452, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Urban, A., Martel, H., & Evans, N. J. II 2010, ApJ, 710, 1343 [NASA ADS] [CrossRef] [Google Scholar]
- Vaidya, B., Mignone, A., Bodo, G., & Massaglia, S. 2015, A&A, 580, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N., & Haugbølle, T. 2017, A&A, 598, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N., Chabrier, G., Audit, E., et al. 2013, A&A, 557, A90 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaytet, N., Commerçon, B., Masson, J., González, M., & Chabrier, G. 2018, A&A, 615, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2015, ApJ, 805, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Winkler, K. H. A., & Newman, M. J. 1980, ApJ, 236, 201 [NASA ADS] [CrossRef] [Google Scholar]
- Wurster, J., & Lewis, B. T. 2020a, MNRAS, 495, 3807 [CrossRef] [Google Scholar]
- Wurster, J., & Lewis, B. T. 2020b, MNRAS, 495, 3795 [CrossRef] [Google Scholar]
- Wurster, J., Bate, M. R., & Price, D. J. 2018, MNRAS, 481, 2450 [NASA ADS] [CrossRef] [Google Scholar]
- Wurster, J., Bate, M. R., Price, D. J., & Bonnell, I. A. 2022, MNRAS, 511, 746 [CrossRef] [Google Scholar]
Appendix A: Defining the protostar in our simulation
Herein, we present our definition of the protostar, namely the criterion by which we select cells that belong to it. Ideally, one would like to select all cells at and downstream of the accretion shock. For this, we have opted to adopt the criterion of Tomida et al. (2010), which selects all cells whose thermal pressure support outweighs ram pressure (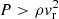 ). However, this criterion also selects cells belonging to the first core that are not currently undergoing a second gravitational collapse. As such, we have supplemented this criterion with a radius check, in which only cells at radii smaller than twice that of the 10−5g cm−3 density isocontour can be selected. In order to compute R*, we simply average the radius of the
). However, this criterion also selects cells belonging to the first core that are not currently undergoing a second gravitational collapse. As such, we have supplemented this criterion with a radius check, in which only cells at radii smaller than twice that of the 10−5g cm−3 density isocontour can be selected. In order to compute R*, we simply average the radius of the 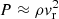 contour (i.e., the protostellar surface). The results of this criterion are presented in Fig. A.1, which displays satisfactory results as the
contour (i.e., the protostellar surface). The results of this criterion are presented in Fig. A.1, which displays satisfactory results as the 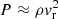 contour closely follows the accretion shock front.
contour closely follows the accretion shock front.
 |
Fig. A.1. Illustration of our protostar definition criterion in a slice through the center of the domain at the epoch of protostellar formation. The colormap represents the local radiative flux, which prominently displays the second core accretion shock. The lime contour represents our |
Appendix B: Resolution study
As mentioned previously, simulating the stellar formation process requires a robust treatment of a multitude of physical processes. As such, each physical process requires an adequate spatial sampling in order to produce physical results. The most common approach in our field is a continuous refinement of the grid based on the local Jeans length as suggested by Truelove et al. (1997). This study suggested that the Jeans length be resolved with at least four cells; however, this is inadequate to describe a second gravitational collapse, as the huge dynamical range requires a more diligent approach to spatial refinement. In addition, the inclusion of magnetic fields, be they ideal or nonideal, as well as the incorporation of radiative transfer can add further strain on simulations, as this requires additional spatial sampling to describe the full range of magnetic resistivities and the dust and gas opacities (see the discussions in Vaytet & Haugbølle 2017; Vaytet et al. 2018; Wurster et al. 2022). As such, it is important to carry out thorough examinations of the effect of resolution to test the convergence of each simulation based on the physical processes included in it, as well as the initial conditions with which it is carried out.
To this end, we have carried out two additional lower and higher resolution simulations in which we vary the maximum refinement level; however, the number of cells per  was maintained at 20 (see Eq. 13 and 14) as this has proven to be perfectly adequate. These two simulations possess a maximum refinement level ℓmax of 25 and 27, as opposed to the intermediate ℓmax = 26 of the simulation presented in the main body of this paper. This respectively offers them a spatial resolution of Δx = 2.93 × 10−4AU and Δx = 7.34 × 10−5AU at the maximal refinement level, as opposed to Δx = 1.46 × 10−4AU.
was maintained at 20 (see Eq. 13 and 14) as this has proven to be perfectly adequate. These two simulations possess a maximum refinement level ℓmax of 25 and 27, as opposed to the intermediate ℓmax = 26 of the simulation presented in the main body of this paper. This respectively offers them a spatial resolution of Δx = 2.93 × 10−4AU and Δx = 7.34 × 10−5AU at the maximal refinement level, as opposed to Δx = 1.46 × 10−4AU.
We thus show in Fig. B.1 the central temperature as a function of the central density prior to the first hydrodynamical bounce (i.e., the moment when the central density drops from one snapshot to the next). The figure shows that prior to the formation of the protostar, all three simulations have followed identical evolutionary paths. However, the maximum density reached differs; the lower resolution run with ℓmax = 25 (blue curve) has attained 3.76 × 10−2g cm−3, the intermediate ℓmax = 26 (orange curve) reached 1.05 × 10−1g cm−3, and the higher resolution ℓmax = 27 (green curve) reached 1.39 × 10−1g cm−3. Thus, the central density achieved by the second gravitational collapse is resolution dependent; however, the intermediate resolution run achieved much closer results to the higher resolution run than to its lower resolution counterpart.
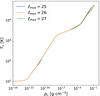 |
Fig. B.1. Central temperature plotted against central density prior to the first hydrodynamical bounce, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
We now turn to Fig. B.2, which shows density slices through the center of the domain for all three simulations with their AMR refinement level contours. These slices are shown at a moment in time where all three protostars have reached similar masses. Unsurprisingly, the spherical morphology of the protostar is better described in the intermediate (panel b) and high (panel c) resolution runs. Furthermore, the additional refinement levels allow a better resolution of the shock front, which is crucial to properly describe the sharp protostellar border. We also note that the lower resolution run displays a much larger radius than its intermediate and higher resolution counterparts.
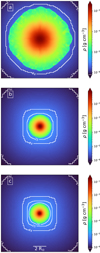 |
Fig. B.2. Density slices through the center of the domain for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, panel a), 26 (Δx = 1.46 × 10−4AU, panel b), and 27 (Δx = 7.34 × 10−5AU, panel c). The scale bar in panel (c) applies to the other two panels. These slices are shown at a moment when all three protostars have reached similar masses (5.9 × 10−3 M⊙ for panel (a), 5.75 × 10−3 M⊙ for panels (b) and (c)). |
In Fig. B.3, we display the evolution of the radius (panel a) and masses (panel b) of the protostars. We note here that the higher resolution run (green curves) forms a smaller protostar, both in radius and in mass. In addition, it consistently shows smaller radii than the ℓmax = 25 and 26 runs at similar masses. The radius of the protostar in the lower resolution simulation fluctuates wildly, as the interior is poorly resolved in this run. In addition, the protostar in this run shows a huge, spurious drop in mass by t ≈ 90 days, which demonstrates that it is inadequate to describe its evolution. Since the radiative behavior of the accretion shock front is identical in all three runs (i.e., extremely subcritical), the smaller radius in the higher resolution run is explained by the more adequate description of turbulence it provides. Indeed, we show in panel (a) of Fig. B.4 the velocity dispersions computed in radial bins inside the protostar. The higher resolution run displays stronger velocity dispersions than the other two runs, which provides a better turbulent transport of heat. As a result, the plateau in the entropy profile is better developed here than in ℓmax = 25 and 26 runs, which shows that the energy has been better redistributed. Hence, the radius of the protostar in the higher resolution run is consistently smaller.
 |
Fig. B.3. Radius (panel a) and mass (panel b) displayed as a function of time, where t = 0 marks the epoch of protostellar birth, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
 |
Fig. B.4. Velocity dispersion inside the protostar computed in radial bins (panel a) and average specific entropy (panel b), for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curves), 26 (Δx = 1.46 × 10−4AU, orange curves), and 27 (Δx = 7.34 × 10−5AU, green curves). These are shown at a moment in time where all three protostars have reached similar masses (5.9 × 10−3 M⊙ for ℓmax = 25, 5.75 × 10−3 M⊙ for ℓmax = 26 and ℓmax = 27). |
Finally, we display in Fig. B.5 the ratio of ortho-radial to radial kinetic energies (see Eq. 24) of the protostars as a function of time. The temporal evolution here is similar for the ℓmax = 26 and 27 runs, but the ℓmax = 25 once again appears to be incapable of properly describing the turbulent motions within the protostar.
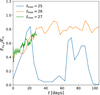 |
Fig. B.5. Kinetic energy of the ortho-radial flow compared to that of radial flow inside the protostar as a function of time, where t = 0 marks the birth of the protostar, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
In summary, although this resolution study has shown that our simulations are not converged, the differences between the ℓmax = 26 and ℓmax = 27 runs are small enough for us to conclude that our results are sufficiently realistic for physical interpretations. When taking into account the stringent time-stepping involved in the ℓmax = 27 run (which we could not integrate past a dozen days), we have concluded that ℓmax = 26 is the optimal resolution choice.
Appendix C: Collapse with multigroup radiative transfer
In order to test the robustness of our simulation’s results, which uses a gray approximation for its radiative transfer, we have conducted a second simulation with a multigroup description. It possesses the same initial conditions; however, we now split the [105; 1019Hz] frequency range into four distinctive groups. The results of the simulation are extremely similar to that of its gray counterpart, as previously reported by the 1D calculations in Vaytet et al. (2013).
Our choice of 4 groups was the result of significant memory constraints. Indeed, since our maximum refinement level is 26, this requires the allocation of around 1.5 TB of RAM memory, of which ≈ 915 GB are used by the AMR grid. Furthermore, such a memory cost meant that the 64 processing cores had to be spread across 4 times as many computing nodes, which increased the CPU communications burden. In addition to the heightened computational load, the added communications burden constrained our ability to integrate the simulation on longer timescales.
Since protostars form with temperatures > 104K, most of the radiative energy is in the ultraviolet part of the electromagnetic spectrum. This energy is later absorbed by the surrounding gas and reemitted in the infrared. We thus chose to have both an infrared and an ultraviolet-visible group, with two other radiative groups bordering these two to avoid any energy omissions. The frequency borders of each group are presented in Table C.1, and the opacity meshes created for each of them using the previously mentioned Delaunay triangulation process are presented in Fig. C.1.
 |
Fig. C.1. Rosseland mean opacity meshes created for each radiative group in our multigroup simulation (see Table C.1). The temperature-density distribution of all cells during the epoch of protostellar birth is overlaid in red. |
Frequency and corresponding wavelength borders of the 4 radiative groups used in our multigroup simulation.
These meshes are very similar to the gray mesh (see Fig. 1); the dust destruction front and the subsequent atomic opacity peak are both clearly visible except for the X-ray mesh (panel d), where the destruction of the dust particles barely has a noticeable effect. In addition, the X-ray mesh also contains a batch of triangles at log(T)∼3.5, which is due to a lack of sampling points in the Vaytet et al. (2013) dataset. However, since this radiative group is the least prominent in terms of radiative energies, this will have a minor effect on our simulation.
The results of this multigroup simulation are displayed in Figures C.2 and C.3, where we compare it with its gray counterpart. Fig. C.2 shows the luminosity of each radiative group (computed using Eq. 17). We see that the total multigroup luminosity (lime dash-dotted line) and the gray luminosity (black dotted line) are very similar, albeit the location of the first core accretion shock differs slightly (0.5 and 0.6 AU). This is due to a slightly higher amount of enclosed radiative energy inside the first core for the multigroup run (in turn due to a higher opacity for UV-Visible photons), which causes its specific entropy to increase by virtue of radiative heating from the second core accretion shock.
 |
Fig. C.2. Luminosity profiles displayed as a function of radius at the epoch of the protostar’s birth for the gray radiative transfer simulation (dotted black line) and its multigroup counterpart (colored solid lines). The lime dash-dotted line is the total luminosity in the multigroup run. |
 |
Fig. C.3. Comparison of the protostellar mass (panel a), radius (panel b), and luminosity (panel c) between our gray radiative transfer simulation (solid black lines) and its multigroup counterpart (dotted red lines). The solid (resp. dotted) blue line in panel (c) represents the protostellar radiative efficiency in the gray (resp. multigroup) simulation. |
Unsurprisingly, the UV-Visible group dominates the luminosity output of the protostar, whereas the IR group dominates everywhere else. At both first and second core shock fronts, the luminosity of each radiative group spikes, although the X-ray photons produced at these locations are quickly reprocessed by the other groups.
Finally, the evolution of the properties of the protostar formed in the multigroup run is compared to that of its gray counterpart in Fig. C.3. We find that the radii, luminosities and radiative efficiencies are extremely similar, although the mass differs slightly. As mentioned previously, the first core in the multigroup run has a slightly higher enclosed energy. This causes the mass accretion rate unto the second core to be lower. Despite the differing masses, the radii are very similar because of a similar amount of specific entropy.
This allows us to conclude that the multigroup description offers no major differences to its gray counterpart, a result which is in agreement with Vaytet et al. (2013).
Appendix D: Comparison with a 2D simulation
Herein, we compare the results of our simulation with those of the 1 M⊙ 2D collapse calculations of Bhandare et al. (2020). Since their calculations are similar to ours, this will allow us to better assess what a three dimensional description of the gas motion offers. To this end, we begin by studying Fig. D.1, which shows the protostellar radius as a function of protostellar mass. We see that protostar is consistently more compact than in the 2D calculation; it possesses a smaller radius for a given mass. Since the radiative efficiency of the protostar is extremely low in both simulations, this cannot be explained by any of the protostars radiating away more energy than the other. We explain this difference in radii by comparing their radial entropy profiles in Fig. D.2: by the time the protostar reaches a mass of ≈1.76 × 10−2 M⊙, the entropy plateau in the interior is achieved in our 3D simulation, whereas it has yet to form in the 2D counterpart. This allows us to conclude that the 3D description of the gas motion allows for more efficient entropy mixing, which regulates the radius of the protostar.
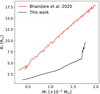 |
Fig. D.1. Radius of the protostar as a function of its mass: a comparison of the results of this paper (black curve) with those of Bhandare et al. (2020) (red curve). |
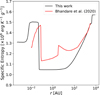 |
Fig. D.2. Comparison of the results of this paper (black curve) with those of Bhandare et al. (2020) (red curve). The curves display the specific entropy, averaged in radial bins and displayed as a function of radius, at a moment in time where both protostars have a mass of ≈1.76 × 10−2 M⊙. |
However, the entropy profile outside the second core is quite different in our two simulations. This can be explained by the different initial conditions. Indeed, Bhandare et al. (2020) have used a Bonnor-Ebert sphere as their initial conditions, whereas we have used a highly unstable uniform density sphere. This results in a shorter first core lifetime in our simulation, and it is accreted by the time our protostar has reached ≈1.76 M⊙. In addition to this, the equation of state table used in both simulations is different. This causes different behaviors in entropy, particularly inside the second Larson core since the Saumon et al. (1995) EOS takes into account the ionization of He, whereas the Vaidya et al. (2015) EOS used in Bhandare et al. (2020) does not.
Appendix E: Standing Accretion Shock Instability
Herein, we investigate wether or not the Standing Accretion Shock Instability (SASI, Blondin et al. 2003; Scheck et al. 2004; Foglizzo et al. 2007) could be the mechanism behind the onset of turbulence within our protostar. This instability is known to operate in core-collapse supernovae, where it causes them to appear aspherical. Recently, Bhandare et al. (2020) put forth the hypothesis that this instability could be at play in protostars, where it could cause oscillations of the accretion shock. SASI requires for feedback to occur between the central regions and the accretion shock. Although our physical environment heavily differs from that of a core-collapse supernova and we do not have a proto-neutron star downstream of our second core accretion shock, our protostar has a central region of highly dense, ionized gas that repulses inward flow. In this sense, the central regions of our protostar can communicate with the accretion shock through acoustic feedback. In the 2D study of Bhandare et al. (2020), the central regions (r < 10−2 AU) were a part of a reflexive inner boundary, which can naturally provide feedback to the shock front.
In order to investigate whether this mechanism is responsible for the generation of turbulence in our protostar, we study our ℓmax = 27 run presented in Appendix B due to its high spatial and temporal resolution. Indeed, this run presents oscillations of the protostellar radius possibly caused by SASI. To this end, we display in panel (a) of Fig. E.1 the amplitude of said oscillations, computed as 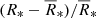 , where
, where 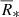 is the average radius of the protostar over a given period. Here, we can clearly see high amplitude, high frequency oscillations at protostellar birth; however, their amplitude and frequency reduces over time. This is more readily seen in the power spectrum of this curve (panel b), which shows a high energy peak corresponding to a period of ≈ 1.4 days, and a handful of lower energy low frequency peaks. These oscillation periods of the protostellar radius should be compared with the advection timescale tadv, computed as (Foglizzo et al. 2007):
is the average radius of the protostar over a given period. Here, we can clearly see high amplitude, high frequency oscillations at protostellar birth; however, their amplitude and frequency reduces over time. This is more readily seen in the power spectrum of this curve (panel b), which shows a high energy peak corresponding to a period of ≈ 1.4 days, and a handful of lower energy low frequency peaks. These oscillation periods of the protostellar radius should be compared with the advection timescale tadv, computed as (Foglizzo et al. 2007):
 |
Fig. E.1. Amplitude of oscillations of the protostellar radius in the ℓmax = 27 run (panel a), displayed as a function of time where t = 0 marks the birth of the protostar. Panel (b) displays the Fourier transform of the curve in panel (a). |
where R∇ is the radius where the gas has effectively settled following its crossing of the accretion shock (i.e., vr has reached ≈0). Our estimate of tadv has yielded ≈ 3 days, which is about twice as long as the oscillation period of the protostar. However, as the protostellar radius grows, so too does tadv, which could explain why the frequency of oscillations is reducing over time.
Although these measurements do not allow us to conclude with certainty that SASI is operating in our protostar, they do indicate that we are in the regime where it is theoretically possible.
All Tables
Frequency and corresponding wavelength borders of the 4 radiative groups used in our multigroup simulation.
All Figures
 |
Fig. 1. Opacity mesh created for our gray radiative transfer approximation. The temperature-density distribution of all cells during the epoch of protostellar birth is overlaid in red. |
| In the text | |
 |
Fig. 2. Various sets of 2D histograms binning the cells in our computational domain (panels a–e) at the epoch of protostellar birth. Panels a–d represent respectively radial velocity, density, entropy, and temperature as a function of radius. The solid (resp. dashed) black line in panel b displays the expected density profile for a free-falling gas (resp. for the collapse of an isothermal sphere). The solid (resp. dotted) black line in panel d represents the expected temperature profile for the collapse of an isothermal sphere with γeff = 1.1 (resp. γeff = 7/5). Panel e displays temperature as a function of density, where the overlaid solid black line displays a contraction with γeff = 1.1. Panel f represents the sum of the enclosed gas and radiative energies at radius r (solid line, see Eq. (15)), along with its constituent parts, namely internal (dashed line), kinetic (dotted line), and radiative energies (dash-dotted line). |
| In the text | |
 |
Fig. 3. Density slices through the center of the domain at the birth of the protostar (t = 0, panel a) and roughly 2 months later (t ≈ 59 days, panel b). The swirly patterns are line integral convolution (LIC) visualizations of the velocity vector field, which display prominent eddies inside the newly formed protostar. Over the span of ≈2 months, the protostar has grown in radius by a factor ≈2.8. |
| In the text | |
 |
Fig. 4. Radiative energy (panel a), Rosseland mean opacity (black, panel b), optical depth (red, panel b), and luminosity (panel c), averaged in radial bins and displayed as a function of radius at the epoch of the protostar’s formation. |
| In the text | |
 |
Fig. 5. Evolution of the physical properties of the protostar displayed as a function of time, where t = 0 marks the birth of the protostar. Panel a displays the protostar’s mass, panel b its radius, panel c (resp. panel d) its surface integrated luminosity (resp. mass accretion rate), panel e (resp. panel f) the average density (resp. temperature) at the shock front. The solid blue line in panel c represents the radiative efficiency of the protostar. |
| In the text | |
 |
Fig. 6. Evolution of the density (panel a), temperature (panel b), radiative energy (panel c), radial velocity (panel d), specific entropy (panel e), and Rosseland mean opacity (panel f) profiles, averaged in radial bins and displayed as a function of radius for different times, where t = 0 marks the birth of the protostar. The last curves (dark red) on each panel correspond to t ≈ 241 days. The dashed and dotted gray lines in panels a–c are power law curves representing the expected density, temperature, and radiative energy profiles both prior to and after the accretion of the first Larson core. |
| In the text | |
 |
Fig. 7. Logarithmic scatter plot showing the protostellar luminosity as a function of radius (where each scatter point is color coded with the protostellar mass). A fit (red dotted line) reveals a power law relationship between L* and R* whose exponent is ≈5.7. |
| In the text | |
 |
Fig. 8. Fraction of H2 (red), H (blue), H+ (cyan), He (black), He+ (purple) and He2+ (pink), averaged in radial bins and displayed as a function of radius at the epoch of the protostar’s formation (panel a) and ≈2 months later (panel b). See Eq. (23). |
| In the text | |
 |
Fig. 9. Mass of H (blue), H+ (cyan), He (black), He+ (purple) and He2+ (pink) inside the protostar displayed as a function of protostellar mass. The purple and pink curves overlap very closely. |
| In the text | |
 |
Fig. 10. Density slices through the center of the domain showing the onset of turbulence within the protostar. Streamlines of the velocity vector field are shown in white. Each panel represents a different time, with panel a showing the protostar during the formation of the accretion shock (t = 0), panel b after the onset of a hydro-dynamical rebound from the central region (t ≈ 16.5 h), and panel c after the outgoing wave interacts with the shock front (t ≈ 21 h). The scale bar in panel b applies to the other two panels. |
| In the text | |
 |
Fig. 11. A spectral analysis of the turbulence within the protostar. Panel a: Kinetic energy power spectrums as a function of characteristic scale ℓ of the gas within the protostar at different times, where t = 0 marks the epoch of protostellar formation. The last curve (dark red) corresponds to t ≈ 241 days. Panel b: power-law fit of the curves in panel a, where Ps(ℓ)∝ℓn. |
| In the text | |
 |
Fig. 12. Ratio of ortho-radial to radial kinetic energy inside the protostar (see Eq. (24)) as a function of time, where t = 0 marks the birth of the protostar. |
| In the text | |
 |
Fig. 13. Cross-sectional view of the protostar at our final simulation snapshot, showing the interior entropy. The colorbar has been artificially anchored for visualization purposes. The gray spherical outline is an artistic choice for better visualization and serves no physical meaning. |
| In the text | |
 |
Fig. 14. Velocity dispersion computed in radial bins (black curve) and average local sound speed (blue curve), displayed as a function of radius at our last simulation snapshot (t ≈ 241 days, where t = 0 marks the birth of the protostar). The red curve is a fit of the inertial range, whose exponent is ≈9/10. The black dotted curve represents the turbulent energy flux (displayed in units of g s−3). |
| In the text | |
 |
Fig. 15. Mass-weighted velocity dispersion inside the protostar (panel a), injected accretion energy alongside the turbulence decay (panel b), and efficiency factor (panel c) displayed as a function of time, where t = 0 marks the birth of the protostar. The red line in panel c corresponds to the turbulence crossing time (see Eq. (25)). |
| In the text | |
 |
Fig. A.1. Illustration of our protostar definition criterion in a slice through the center of the domain at the epoch of protostellar formation. The colormap represents the local radiative flux, which prominently displays the second core accretion shock. The lime contour represents our |
| In the text | |
 |
Fig. B.1. Central temperature plotted against central density prior to the first hydrodynamical bounce, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
| In the text | |
 |
Fig. B.2. Density slices through the center of the domain for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, panel a), 26 (Δx = 1.46 × 10−4AU, panel b), and 27 (Δx = 7.34 × 10−5AU, panel c). The scale bar in panel (c) applies to the other two panels. These slices are shown at a moment when all three protostars have reached similar masses (5.9 × 10−3 M⊙ for panel (a), 5.75 × 10−3 M⊙ for panels (b) and (c)). |
| In the text | |
 |
Fig. B.3. Radius (panel a) and mass (panel b) displayed as a function of time, where t = 0 marks the epoch of protostellar birth, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
| In the text | |
 |
Fig. B.4. Velocity dispersion inside the protostar computed in radial bins (panel a) and average specific entropy (panel b), for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curves), 26 (Δx = 1.46 × 10−4AU, orange curves), and 27 (Δx = 7.34 × 10−5AU, green curves). These are shown at a moment in time where all three protostars have reached similar masses (5.9 × 10−3 M⊙ for ℓmax = 25, 5.75 × 10−3 M⊙ for ℓmax = 26 and ℓmax = 27). |
| In the text | |
 |
Fig. B.5. Kinetic energy of the ortho-radial flow compared to that of radial flow inside the protostar as a function of time, where t = 0 marks the birth of the protostar, for simulations with a maximum refinement level of 25 (Δx = 2.93 × 10−4AU, blue curve), 26 (Δx = 1.46 × 10−4AU, orange curve), and 27 (Δx = 7.34 × 10−5AU, green curve). |
| In the text | |
 |
Fig. C.1. Rosseland mean opacity meshes created for each radiative group in our multigroup simulation (see Table C.1). The temperature-density distribution of all cells during the epoch of protostellar birth is overlaid in red. |
| In the text | |
 |
Fig. C.2. Luminosity profiles displayed as a function of radius at the epoch of the protostar’s birth for the gray radiative transfer simulation (dotted black line) and its multigroup counterpart (colored solid lines). The lime dash-dotted line is the total luminosity in the multigroup run. |
| In the text | |
 |
Fig. C.3. Comparison of the protostellar mass (panel a), radius (panel b), and luminosity (panel c) between our gray radiative transfer simulation (solid black lines) and its multigroup counterpart (dotted red lines). The solid (resp. dotted) blue line in panel (c) represents the protostellar radiative efficiency in the gray (resp. multigroup) simulation. |
| In the text | |
 |
Fig. D.1. Radius of the protostar as a function of its mass: a comparison of the results of this paper (black curve) with those of Bhandare et al. (2020) (red curve). |
| In the text | |
 |
Fig. D.2. Comparison of the results of this paper (black curve) with those of Bhandare et al. (2020) (red curve). The curves display the specific entropy, averaged in radial bins and displayed as a function of radius, at a moment in time where both protostars have a mass of ≈1.76 × 10−2 M⊙. |
| In the text | |
 |
Fig. E.1. Amplitude of oscillations of the protostellar radius in the ℓmax = 27 run (panel a), displayed as a function of time where t = 0 marks the birth of the protostar. Panel (b) displays the Fourier transform of the curve in panel (a). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\frac{\partial \rho }{\partial t}+\boldsymbol{\nabla }\cdot [\rho {\boldsymbol{v}}] = 0,\end{aligned} $$](/articles/aa/full_html/2023/12/aa46711-23/aa46711-23-eq1.gif)
![$$ \begin{aligned}&\frac{\partial \rho {\boldsymbol{v}}}{\partial t} + \boldsymbol{\nabla }\cdot \left[ \rho {\boldsymbol{v}} \otimes {\boldsymbol{v}} + P\mathbb{I} \right] = -\rho \boldsymbol{\nabla }\phi - \sum _{g=1}^{N_{{g}}}\lambda _{{g}}\boldsymbol{\nabla }E_{{g}},\end{aligned} $$](/articles/aa/full_html/2023/12/aa46711-23/aa46711-23-eq2.gif)
![$$ \begin{aligned}&\frac{\partial E_{\mathrm{tot}}}{\partial t} + \boldsymbol{\nabla }\cdot \left[ {\boldsymbol{v}}(E_{\mathrm{tot}} + P) \right] = -\rho {\boldsymbol{v}}\cdot \boldsymbol{\nabla }\phi \nonumber \\&\qquad \qquad - \sum _{g=1}^{N_{{g}}}\left[\kappa _{\mathrm{P}_{g}}\rho c (\Theta _{{g}}(T)-E_{{g}}) - \lambda _{g}{\boldsymbol{v}}\cdot \boldsymbol{\nabla } E_{{g}} \right],\end{aligned} $$](/articles/aa/full_html/2023/12/aa46711-23/aa46711-23-eq3.gif)
![$$ \begin{aligned}&\frac{\partial E_{{g}}}{\partial t} + \boldsymbol{\nabla }\cdot [{\boldsymbol{v}}E_{{g}}] + \mathbb{P} _{{g}} : \boldsymbol{\nabla }{\boldsymbol{v}} = \boldsymbol{\nabla } \cdot \left[ \frac{c\lambda _{g}}{\rho \kappa _{\mathrm{R}{g}}} \boldsymbol{\nabla } E_{g}\right]\nonumber \\&\qquad \qquad +\kappa _{\mathrm{P}{g}} \rho c \left(\Theta _{g}(T)-E_{g}\right) + \boldsymbol{\nabla } {\boldsymbol{v}} : \int _{\nu _{{g}-1/2}}^{\nu _{{g}+1/2}}{\partial _\nu (\nu \mathbb{P} _\nu ) \mathrm{d}\nu },\end{aligned} $$](/articles/aa/full_html/2023/12/aa46711-23/aa46711-23-eq4.gif)