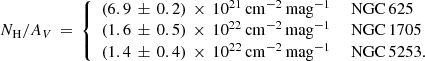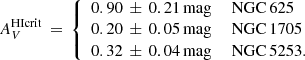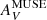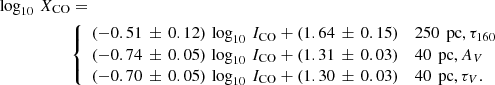| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A64 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245805 | |
| Published online | 03 July 2023 | |
Gas, dust, and the CO-to-molecular gas conversion factor in low-metallicity starbursts⋆
1
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
e-mail: leslie.hunt@inaf.it
2
Princeton University Observatory, Peyton Hall, Princeton, NJ, 08544-1001
USA
3
INAF – Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
4
Observatorio Astronómico Nacional (OAN)-Observatorio de Madrid, Alfonso XII 3, 28014 Madrid, Spain
5
Instituto de Astrofísica, Facultad de Física, Pontificia Universidad Católica de Chile, Casilla 306, Santiago 22, Chile
6
Observatoire de Paris, LERMA, Collège de France, CNRS, PSL, Sorbonne University, 75014 Paris, France
7
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121 Bonn, Germany
8
Astronomy Department, King Abdulaziz University, PO Box 80203, Jeddah, Saudia Arabia
9
INAF – Osservatorio di Astrofisica e Scienza dello Spazio, Via Piero Gobetti 93/3, 40129 Bologna, Italy
10
INAF – Istituto di Radioastronomia, Via Piero Gobetti 93/3, 40129 Bologna, Italy
11
Department of Physics – University of Pisa, Largo B. Pontecorvo 3, 56127 Pisa, Italy
12
INFN – Istituto Nazionale di Fisica Nucleare, Largo B. Pontecorvo 3, 56127 Pisa, Italy
13
INAF – Osservatorio Astronomico di Capodimonte, Via Moiariello 16, 80131 Napoli, Italy
14
Centre for Extragalactic Astronomy, Department of Physics, Durham University, South Road, Durham, DH1 3LE
UK
15
Institute for Computational Cosmology, Department of Physics, University of Durham, South Road, Durham, DH1 3LE
UK
16
European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
17
Dipartimento di Astronomia e Scienza dello Spazio, Università degli Studi di Firenze, Largo E. Fermi 2, 50125 Firenze, Italy
18
AURA for the European Space Agency, Space Telescope Science Institute, 3700 San Martin Drive, Baltimore, MD, 21218
USA
Received:
27
December
2022
Accepted:
10
May
2023
The factor relating CO emission to molecular hydrogen column density, XCO, is still subject to uncertainty, in particular at low metallicity. In this paper, to quantify XCO at two different spatial resolutions, we exploited a dust-based method together with ALMA 12-m and ACA data and H I maps of three nearby metal-poor starbursts, NGC 625, NGC 1705, and NGC 5253. Dust opacity at 250 pc resolution was derived based on dust temperatures estimated by fitting two-temperature modified blackbodies to Herschel PACS data. By using the HI maps, we were then able to estimate dust-to-gas ratios in the regions dominated by atomic gas, and, throughout the galaxy, to infer total gas column densities and H2 column densities as the difference with HI. Finally, from the ACA CO(1–0) maps, we derived XCO. We used a similar technique with 40 pc ALMA 12-m data for the three galaxies, but instead derived dust attenuation at 40 pc resolution from reddening maps based on VLT/MUSE data. At 250 pc resolution, we find XCO ∼ 1022 − 1023 cm−2/K km s−1, 5–1000 times the Milky Way value, with much larger values than would be expected from a simple metallicity dependence. Instead, at 40 pc resolution, XCO again shows large variation, but is roughly consistent with a power-law metallicity dependence, given the Z ∼ 1/3 Z⊙ metal abundances of our targets. The large scatter in both estimations could imply additional parameter dependence, which we have investigated by comparing XCO with the observed velocity-integrated brightness temperatures, ICO, as predicted by recent simulations. Indeed, larger XCO is significantly correlated with smaller ICO, but with slightly different slopes and normalizations than predicted by theory. Such behavior can be attributed to the increasing fraction of CO-faint (or dark) H2 gas with lower spatial resolution (larger beams). This confirms the idea the XCO is multivariate, depending not only on metallicity but also on the CO brightness temperature and beam size. Future work is needed to consolidate these empirical results by sampling galaxies with different metal abundances observed at varying spatial resolutions.
Key words: galaxies: starburst / galaxies: dwarf / galaxies: star formation / ISM: molecules / dust / extinction / galaxies: ISM
This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00219.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ.
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
From early cosmic times, molecular clouds are the cradles of star formation. However, molecular gas, H2, is not easily traced observationally. The rotational levels of H2 are widely separated, with negligible thermal excitation in cold clouds. In addition, H2 is a homonuclear diatomic molecule with no permanent dipole moment so that there are no rovibrational electric dipole transitions.
Luckily, molecular gas is not pure H2, but also contains heavy trace elements. The abundances of oxygen and carbon in the interstellar medium (ISM) enable the formation of carbon monoxide (CO) within dense, cold, molecular clouds. Due to its low excitation energy in the ground-state rotational transition (hν/kB ≈ 5.5 K) and its low critical density (∼1400 cm−3, for a kinetic temperature T = 25 K), CO emission can be easily excited even in cold molecular clouds1. Thus, the lowest-order CO transition J = 1 → 0 at 2.6 mm, which is fortunately located within a fairly transparent atmospheric window, has become a common tracer of H2 in the Milky Way and external galaxies.
Nevertheless, CO has its own problems. Under typical ISM conditions, CO emission is optically thick, so that even when its abundance relative to H2 is known, CO cannot be used to directly trace the molecular column density or mass along the line of sight. Thus, it is standard to connect the column (or mass) density of molecular gas NH2 to the observed 12CO(1–0) velocity-integrated brightness temperature, ICO, via a CO-to-H2 conversion factor, XCO:
where the H2 column density NH2 is in units of cm−2, and ICO is in units of K km s−1. The existence of a nearly constant XCO at solar-like metallicities where H2 and CO coexist to a large extent relies on the assumption that the optically thick CO emission comes from virialized clouds that do not overlap. Thus, XCO is essentially an empirical shortcut to count clouds along the line of sight.
Although the conversion factor XCO relating CO emission to H2 mass MH2 is relatively constant across the Galaxy (e.g., Sanders et al. 1984; Bolatto et al. 2013), at low metallicity and in starburst galaxies, its value is still uncertain. Inferring XCO in metal-poor environments has been the subject of an enormous effort, both observational and theoretical (see Bolatto et al. 2013, for an extensive review). The problem lies in the complexity of the relation between CO emission and H2. Simulations and observational work have suggested that the amount of CO and its emission depends primarily on shielding, that is the protection of CO molecules from dissociating far-ultraviolet (FUV) radiation. Self-shielding of H2 is highly efficient, meaning that the photodissociation rate of H2 is typically very small wherever there is a significant amount of H2. On the other hand, self-shielding of CO and cross-shielding of CO by H2 are inefficient processes (e.g., Gong et al. 2018). Consequently, CO needs additional protection by dust.
Photodissociation of CO tends to erode the CO-emitting regions of molecular clouds, even at solar metallicity. At subsolar abundances, stars are hotter and have higher hard photon fluxes, enhancing the effect; thus the regions where H2 resides are much larger than those where CO and H2 coexist (e.g., van Dishoeck & Black 1988). Consequently, there are extended regions of so-called “CO-faint” (or dark) gas in which the dominant forms of carbon are ionized (C+) or neutral carbon (e.g., Wolfire et al. 2010). The CO-emitting regions in low-metallicity environments are expected to be much smaller (a few parsecs) than they would be in more typical, metal-rich, conditions (e.g., Bolatto et al. 1999, 2013). Indeed, the small size of CO-emitting clouds at low metallicity has been verified observationally in the Magellanic Clouds (e.g., Pak et al. 1998; Indebetouw et al. 2013; Tokuda et al. 2021), and in nearby dwarf galaxies (e.g., Rubio et al. 2015; Schruba et al. 2017; Shi et al. 2020).
Early attempts at estimating XCO theoretically relied on models of photodissociation regions which are able to resolve the thermal and chemical structure within an individual cloud (e.g., Wolfire et al. 1993; Bell et al. 2006). Later cloud models (e.g., Glover & Mac Low 2011; Shetty et al. 2011; Glover & Clark 2016), based on hydrodynamical simulations with more complex geometries and density structure, confirmed that XCO varies with visual extinction AV, or depth within the cloud. In particular, there was evidence for an extinction threshold above which clouds become CO bright (see also Bell et al. 2006). Metallicity plays a fundamental role because lower dust abundance provides less dust shielding against CO photodissociation, resulting in more extended regions of CO-faint gas. Cosmic-ray ionization is also emerging as an important parameter (e.g., Bisbas et al. 2021).
Global models of XCO in galaxies using hydrodynamical simulations (e.g., Feldmann et al. 2012; Narayanan et al. 2012) suggest that XCO depends on metallicity, dust extinction, and H2 column density NH2; in addition, there may be a dependence on observational spatial scale (see also Rubio et al. 1993) and velocity-integrated CO brightness temperature (TB), ICO. These two latter trends reflect the fact that XCO tends to be lower when estimated from regions with higher CO surface brightness; thus from an observational perspective, smaller beams generally give lower XCO. In fact, CO observations with beam sizes of a few parsecs that resolve the central regions containing CO in low-metallicity molecular clouds tend to result in XCO values that are roughly consistent with XCO for the Milky Way (e.g., Bolatto et al. 2008).
The main problem with these global models for XCO is the determination of the physical conditions and line-emission properties on subgrid scales. More recent models overcome this limitation through a better match of large-scale simulations and the physics and chemistry of small-scale resolved cloud structure. In the solar metallicity models of Gong et al. (2017, 2018, 2020), the average XCO increases by a factor of ∼2 as the observational beam size grows from 1 to 100 pc. Moreover, the CO-dark H2 fraction ranges from ∼30 − 80%, and is anticorrelated with visual extinction. With models over a range of metallicities, Hu et al. (2022) find that the parsec-scale XCO is roughly the Galactic value, independently of metallicity once dust shielding becomes effective. Hu et al. (2022) also find that CO emission becomes more optically thin at lower metallicity (see Hunt et al. 2017, for a tentative observational verification). The Hu et al. (2022) simulations also show that although most CO emission originates from dense gas with low XCO, most of the cloud area is filled by diffuse gas with high XCO. This leads to an anticorrelation of XCO and ICO, also implying that XCO is leveraged by beam averaging, and tends to be biased toward the highest density regions of the molecular gas.
Here we attempt to test theoretical predictions of XCO at low metallicity by observationally quantifying trends of XCO with dust content and spatial resolution. Using CO maps of three iconic low-metallicity dwarf galaxies observed with the ALMA 12-m and compact (ACA, 7-m) arrays, at ∼40 pc and ∼250 pc resolutions, respectively, we first estimate dust content at ∼250 pc resolution. To do this, we calculate the dust opacity at 160 μm τ160 from Herschel observations, and compare it with HI and CO maps at the same resolution. Then, we infer dust content at ∼40 pc resolution from VLT/MUSE maps of E(B − V) and compare it with the higher resolution CO maps. Finally, we compute XCO at both resolutions, and compare the measured values with theoretical predictions. Section 2 describes the targets, and Sect. 3 the ALMA observations and our ancillary data. The determination of dust optical depth, gas content, and inference of XCO on ∼250 pc scales is given in Sect. 4, while Sect. 5 reports an analogous assessment for XCO at ∼40 pc resolution. The two sets of results are compared in Sect. 6, and Sect. 7 provides a brief discussion and our conclusions.
2. The targets
For our ALMA study, we selected three nearby (∼3–5 Mpc) metal-poor (Z/Z⊙ ∼ 0.3) dwarf starbursts having (a) HI observations necessary to quantify their total gas content (Lelli et al. 2014a; b) Hubble Space Telescope (HST) color-magnitude diagrams (CMDs) to constrain their star-formation histories (SFHs) and “burstiness” (Cannon et al. 2003; Tosi et al. 2001; Annibali et al. 2009; McQuinn et al. 2010; Cignoni et al. 2018, 2019); (c) archival MUSE data, to infer high-resolution extinction maps; and (d) archival Herschel data, to infer color temperatures for dust opacity maps. These are the only southern galaxies in the parent sample of Lelli et al. (2014a) and enable the start of a statistical approach; their properties are given in Table 1.
Parameters for observed galaxies.
− NGC 625 hosts a massive starburst with several luminous HII regions and Wolf-Rayet (W–R) spectral features (Skillman et al. 2003a,b). The current starburst is relatively long-lived (≳50 Myr Cannon et al. 2003; McQuinn et al. 2010), and the extended episode of star formation, possibly caused by an interaction or merger (Côté et al. 2000), has apparently disrupted the HI disk (Cannon et al. 2004; Lelli et al. 2014a), and caused an outflow detected in UV absorption lines (Cannon et al. 2005).
− NGC 1705 had more recent starburst episodes than NGC 625, with the older of two bursts of star formation having occurred ∼10 − 15 Myr ago, and the younger one much more recently, ∼3 Myr ago (Annibali et al. 2009; Cignoni et al. 2018). NGC 1705 is rich in star clusters (Billett et al. 2002), with the most massive one being a Super Star Cluster (SSC; O’Connell & Gallagher 1994; Vázquez et al. 2004; Martins et al. 2012), that has roughly the ∼15 Myr age of the oldest starburst event. There is evidence for a low-velocity outflow seen through UV absorption (Heckman et al. 2001), but, unlike in NGC 625, the HI is configured in a regularly rotating disk (Elson et al. 2013; Lelli et al. 2014a). With Spitzer observations of NGC 1705, Cannon et al. (2006) find that the far-infrared dust morphology differs dramatically from the optical, with two dust clouds ∼250 pc approximately east and west of the central SSC, and apparently unrelated to it. These two dust clouds also show 8 μm emission, and the central SSC is coincident with an 8 μm peak.
− NGC 5253 harbors an extremely young starburst with many massive star clusters (e.g., Calzetti et al. 1997; Cresci et al. 2005), with the majority of them in the central regions having ages of ∼1 − 10 Myr (e.g., Calzetti et al. 2015). NGC 5253 is overall more active than NGC 1705. Nevertheless, its SFH shows little evidence of a burst over the last 10–20 Myr, but this could result from the extreme crowding and incompleteness of the central region where most of the current SF is concentrated (Cignoni et al. 2019). NGC 5253’s CMD suggests that star-formation activity has been occurring for ≳450 Myr, similar to the dynamical time of the galaxy (McQuinn et al. 2010). There is also a substantial population of W–R stars (Schaerer et al. 1997; Westmoquette et al. 2013), consistent with the young age of the central clusters. The most massive cluster lies within a radio nebula (e.g., Turner et al. 2000), and is enshrouded by a dust cloud with AV ∼ 50 mag (e.g., Calzetti et al. 2015). The HI in NGC 5253 is highly perturbed (e.g., Kobulnicky & Skillman 2008; López-Sánchez et al. 2012; Lelli et al. 2014a), with infalling neutral gas that is apparently triggering the powerful current starburst (e.g., López-Sánchez et al. 2012; Turner et al. 2015). In fact, the HI kinematics is consistent with a disk-like structure dominated by a radial inflow motion of 25 km s−1 (Lelli et al. 2014a).
Although our study does not depend on specific metallicities, relative trends could be important, and affected by abundance gradients. Metallicity gradients in late-type dwarf irregulars or blue compact dwarfs tend to be generally negligible (≤0.1 dex, e.g., Croxall et al. 2009), less severe than those in more massive spirals (e.g., Pilyugin et al. 2015). Resolved abundance investigations of our targets (e.g., Westmoquette et al. 2013; Annibali et al. 2015; Monreal-Ibero et al. 2017) show this to be the case; there is no evidence for strong metallicity gradients in any of the dwarf starburst targets, although some of the O/H estimates in the literature may differ from the ones adopted here (e.g., Annibali et al. 2015).
3. The data
To perform our analysis, we have combined ALMA observations with three sets of ancillary publicly-available data as described below.
3.1. ALMA observations
We observed the 12CO(1–0) line and tried to detect the 3 mm continuum emission in the three targets, NGC 625, NGC 1705, and NGC 5253 with the ALMA 12-m and the ACA 7-m arrays during Cycle 6 using the Band 3 receivers (project-ID: #2018.1.00219.S; PI: Hunt). Other transitions including CN and SO2 were placed in different sidebands, and their analysis will be presented in future work. To cover the entire emitting regions of the galaxies, we adopted 3-point mosaics with the ALMA 12-m array and a single pointing with ACA, obtaining a field-of-view of ∼40″.
Data calibration and imaging for the 12-m and ACA data were done using the Common Astronomy Software Applications2 (CASA, McMullin et al. 2007) version 6.2.1.7. The visibility data were calibrated in the standard way. We retained the native velocity resolution of 976.6 kHz channels, corresponding to ∼2.5 km s−1. Imaging was performed with the tclean task using a Hogbom deconvolver and Briggs weighting with a robust parameter of 0.5.
For ACA, we set the pixel size of the cubes to 2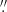 0, corresponding to ∼1/6 of the synthesized beams. The ACA cubes have typical rms noise levels σ of (6.4, 7.0, 6.4) mJy beam−1 for (NGC 625, NGC 1705, NGC 5253), respectively in velocity channels of 2.5 km s−1. The pixel size of the ALMA 12-m cubes was set to 0
0, corresponding to ∼1/6 of the synthesized beams. The ACA cubes have typical rms noise levels σ of (6.4, 7.0, 6.4) mJy beam−1 for (NGC 625, NGC 1705, NGC 5253), respectively in velocity channels of 2.5 km s−1. The pixel size of the ALMA 12-m cubes was set to 0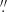 18, ∼1/11 of the synthesized beams. The final 12-m CO cubes have typical rms σ of (1.4, 1.2, 1.3) mJy beam−1 in velocity channels of 2.5 km s−1. Table 2 gives details on the CO observations for each galaxy.
18, ∼1/11 of the synthesized beams. The final 12-m CO cubes have typical rms σ of (1.4, 1.2, 1.3) mJy beam−1 in velocity channels of 2.5 km s−1. Table 2 gives details on the CO observations for each galaxy.
Observational CO parameters.
Examining the uv data showed that continuum emission is present only in NGC 5253; the continuum subtraction was performed by fitting and subtracting a first-order polynomial to line-free channels, in the uv as well as in the image planes, giving similar results. Ultimately, our final cube for NGC 5253 subtracts the continuum estimated from the image plane.
The 12-m and ACA CO data were analyzed separately, so that there are two data cubes for each galaxy. We derive total-intensity (moment-zero) maps using the task Makemask in 3DBarolo (Di Teodoro & Fraternali 2015). This task sums the signal inside a Boolean mask, which is created by smoothing the cube in space and velocity and applying specific noise thresholds (see 3DBarolo documentation for details). For this purpose, we use emission-line cubes without correction for primary beam attenuation, so the noise level is uniform and well defined across each channel map. The primary-beam correction is then applied directly to the moment-zero map. When using a Boolean mask to create a moment-zero map, the noise in the map varies from pixel to pixel because a different number of channels is summed up at each spatial position. We build a signal-to-noise (S/N) map using the relevant equation in the Appendix of Lelli et al. (2014b).
Total fluxes are estimated by summing the signal in the line-intensity (moment-zero) maps, or by summing the emission within a certain aperture in the data cubes (performed by CASA/imview). The two techniques give similar results. Figure 1 shows the ACA and 12-m spectra taken from this sum using polygonal apertures. Total fluxes for both the ACA and the 12-m array are given in Table 2. The ACA and 12-m fluxes are comparable, showing that we are not losing significant flux through interferometric filtering. For NGC 1705, the 12-m integrated flux is higher than for the ACA, by almost a factor of two, suggesting that the CO emission is intrinsically compact and the ACA data suffer from low signal-to-noise.
 |
Fig. 1. CO spectra of the target galaxies within an aperture containing the totality of CO emission regions plotted against velocity, where Vsys is given in Table 2. The full-width at zero intensity (FWZI) corresponds to the vertical dotted lines (see Table 2, Col. (2)). The 12-m spectra are shown in blue, and the ACA in red. In NGC 5253, these are both continuum-subtracted spectra. More details are given in the text. |
3.2. Ancillary data
We have used ancillary data at different resolutions to estimate dust column density and compare it to our CO maps. The VLT/MUSE E(B − V) images are compared with the 12-m ALMA CO (∼40 pc), and the Herschel/PACS and HI with the ACA CO (∼250 pc).
3.2.1. VLT/MUSE
Data from the MUSE optical integral field spectrograph at the ESO Very Large Telescope (VLT) obtained from the DWALIN (DWarf galaxies Archival Local survey for Interstellar medium investigatioN) survey database (Marasco et al. 2023). Briefly, the DWALIN sample consists of 40 nearby galaxies with archival MUSE observations selected either from (a) the Herschel Dwarf Galaxy Survey (Madden et al. 2013), or (b) the Karachentsev et al. (2013) catalog, with distance D < 11 Mpc and log(Mstar/M⊙) < 9.0.
For NGC 1705, the original data were obtained from program 094.B-0745 (PI: García-Benito). The two available MUSE pointings were stitched together to form a mosaic. For NGC 5253, original data were taken from programs 094.B-0745 (PI: García-Benito) and 095.B-0321 (PI: Vanzi). In producing the final cube some exposures were discarded due to poor seeing. For NGC 625, we used data from 094.B-0745 (PI: García-Benito) and considered only 3 of the 4 exposures due to a guiding failure during the first exposure.
The MUSE data reduction was performed using the MUSE pipeline (Weilbacher et al. 2020) v2.8.1, with the ESO Recipe flexible execution workbench (Reflex; Freudling et al. 2013), which gives a graphical and automated way to execute with EsoRex the Common Pipeline Library (CPL) reduction recipes, within the Kepler workflow engine (Altintas et al. 2006). The absolute astrometry of the final mosaics is fixed to that of archival HST imaging. In the case of NGC 625 and NGC 5253, Hα emission is saturated in the regions of brightest line emission. These regions and the surrounding area were masked by hand.
Emission line maps were derived using the PHANGS data analysis pipeline3 described in Emsellem et al. (2022). In short, the pipeline fits the stellar continuum using a set of E-MILES (Vazdekis et al. 2016) simple stellar population templates. Spectral fitting is carried out twice, first to derive the stellar kinematics, and a second time simultaneously with Gaussian templates for modeling the emission lines. Line maps are corrected for Milky Way foreground extinction.
Dust attenuation intrinsic to the galaxies is calculated using the Balmer decrement (Hα/Hβ) and assuming Case B recombination, temperature T = 104 K and density ne = 102 cm−3, leading to LHα/LHβ = 2.86. We also assume the extinction law of O’Donnell (1994) with total-to-selective extinction RV = 3.1, which is identical to the canonical Cardelli et al. (1989) parameterization. In the regions where Hα is saturated we have sufficient signal-to-noise to detect the hydrogen Paschen 10 (P10, at λ = 9017.5 Å) line, which is then used in combination with Hβ to calculate the dust attenuation using the predicted ratio from Case B LP10/LHβ = 0.0184. The CCD artifacts for the E(B − V) map of NGC 1705 do not impact our analysis. The global values of E(B − V) for our targets (Cignoni et al. 2019) are consistent with the spread of spatially resolved E(B − V) resulting from our calculations.
3.2.2. Herschel PACS
We acquired from the Herschel archive the raw scans taken with the Photodetector Array Camera and Spectrometer (PACS, Poglitsch et al. 2010) in the context of the Herschel Dwarf Galaxy Survey (Madden et al. 2013). The data available for our three targets at 70, 100, and 160 μm have full widths at half maximum (FWHM) of 5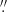 6, 6
6, 6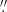 8, and 11
8, and 11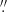 4, respectively. We reduced the raw scans using (the final) version 15.0.1 of the Herschel Interactive Processing Environment (HIPE; Ott et al. 2010) with the PACS_CAL_78_0 photometric calibration, and adopting the scanam procedure to optimize extended emission. Sky subtraction was performed within the procedure but also subsequently checked to ensure roughly zero background. The reduced, calibrated images were generated with 2
4, respectively. We reduced the raw scans using (the final) version 15.0.1 of the Herschel Interactive Processing Environment (HIPE; Ott et al. 2010) with the PACS_CAL_78_0 photometric calibration, and adopting the scanam procedure to optimize extended emission. Sky subtraction was performed within the procedure but also subsequently checked to ensure roughly zero background. The reduced, calibrated images were generated with 2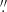 0 pixels, and to be on the same resolution scale, were then convolved to the PACS 160 μm FWHM using kernels from Aniano et al. (2011).
0 pixels, and to be on the same resolution scale, were then convolved to the PACS 160 μm FWHM using kernels from Aniano et al. (2011).
3.2.3. Atomic gas, HI
We reanalyze HI data from Lelli et al. (2014a) using HI cubes with the highest available angular resolution; beam sizes are (16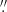 9×10
9×10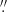 6, 8
6, 8 5×6
5×6 6, 13
6, 13 6×7
6×7 5) for (NGC 625, NGC 1705, NGC 5253), respectively. The HI data were obtained with the Very Large Array (VLA) for NGC 625 (Lelli et al. 2014a) and the Australia Telecope Compact Array (ATCA) for NGC 1705 (Elson et al. 2013) and NGC 5253 (López-Sánchez et al. 2012). We refer to those papers for details on observations and data reduction. Total-intensity (moment-zero) HI maps are derived using the same strategy as for CO maps (Sect. 3.1).
5) for (NGC 625, NGC 1705, NGC 5253), respectively. The HI data were obtained with the Very Large Array (VLA) for NGC 625 (Lelli et al. 2014a) and the Australia Telecope Compact Array (ATCA) for NGC 1705 (Elson et al. 2013) and NGC 5253 (López-Sánchez et al. 2012). We refer to those papers for details on observations and data reduction. Total-intensity (moment-zero) HI maps are derived using the same strategy as for CO maps (Sect. 3.1).
3.3. Image alignment and rebinning
The ACA CO, HI, and (convolved) PACS images have been aligned to a common center and pixel size (2″) using the routines within the GNU Astronomy Utilities (gnuastro4; Akhlaghi 2018). The 12-m and MUSE E(B − V) maps have been aligned with the same techniques, but instead with an intrinsic pixel size of 0 4. The alignment relies on the internal astrometric keywords, and thus implicitly assumes that the nominal astrometry is correct.
4. The alignment relies on the internal astrometric keywords, and thus implicitly assumes that the nominal astrometry is correct.
As mentioned above, the nominal MUSE astrometry was checked against HST and corrected as necessary. For NGC 625, there is a known discrepancy of the HST astrometry of the image used here (Cannon et al. 2003), and this was taken into account. For NGC 1705, a southward shift of of 2 5 was imposed on the nominal MUSE pipeline astrometry solution in order to align with HST and ALMA.
5 was imposed on the nominal MUSE pipeline astrometry solution in order to align with HST and ALMA.
The rebinning to large pixels was performed within the R statistical package5. For the 12-m comparison of CO with E(B − V) we used resolution elements (pixels) of 2″ on a side, and for the ACA comparison with HI and PACS, pixels of (13″, 10″, 15″) for (NGC 625, NGC 1705, and NGC 5253), respectively. The 12-m rebinning corresponds to ∼40 pc (see Table 2) and the ACA rebinning to ∼250 pc; the aim of the pixel sizes for ACA, HI, and PACS is to account approximately for the differences in distance of the targets.
Figure 2 shows the results of the small spatial scale (∼40 pc) alignments, where the 12-m CO zero-moment maps are overlaid on HST F555W images (left panel) and on the MUSE E(B − V) images (right). Also shown in Fig. 2 are specific features identified by previous work (e.g., Cannon et al. 2004, 2006; Turner et al. 2017): HII regions (NGC 625) and dust clouds (NGC 1705, NGC 5253). Interestingly, in NGC 1705, PAH emission with Spitzer/IRS is only present in the eastern dust cloud D1 (Cannon et al. 2006) which is also the only location of CO emission. In all three galaxies, CO emission is not always coincident with the stars traced by the HST images; in contrast, it almost perfectly coincides with E(B − V) from MUSE.
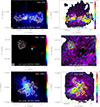 |
Fig. 2. Contours of 12CO(1–0) (12-m) overlaid on HST F555W images (left panels), and MUSE E(B − V) maps (right). The 12CO(1–0) contour levels correspond to (0.01, 0.025, 0.05, 0.1, 0.2, 0.3, 0.4, 0.450, 0.750) Jy km s−1 beam−1 for NGC 625; (0.01, 0.025, 0.05, 0.1, 0.2, 0.3) Jy km s−1 beam−1 for NGC 1705; (0.01, 0.025, 0.05, 0.1, 0.15, 0.25, 0.4, 0.5, 0.75, 1.0, 1.5) Jy km s−1 beam−1 for NGC 5253. Also marked A–D in the left panels are the HII regions identified with radio continuum maps of NGC 625 by Cannon et al. (2004); the dust clouds and SSC in NGC 1705 identified from Spitzer observations (Cannon et al. 2006); and the unusual CO+dust cloud “D1” in NGC 5253 that coincides with the brightest, highly dust embedded SSC (Turner et al. 2017). The ALMA 12-m beam is shown in the lower-left corner of the left panels. |
Figure 3 reports “false-color” RGB images at ∼250 pc resolution for the three target galaxies, using HI as blue, CO integrated intensity (zero-moment) maps as green, and PACS 160 μm as red. As in Fig. 2, the salient features identified in previous work (Cannon et al. 2004, 2006; Turner et al. 2017) are also shown. The green “spur” to the east in NGC 625 shows that CO emission is present even without significant dust emission (traced by PACS); the diffuse HI emission is not well traced by this higher-resolution HI map (see Lelli et al. 2014a). In NGC 1705, the white colors of dust cloud D1 (Cannon et al. 2006) show that CO is cospatial with HI and dust, but, as also illustrated in Fig. 2, there is no CO in the second dust cloud D2, nor at the central SSC. On the other hand, the SSC embedded within cloud D1 in NGC 5253 (Turner et al. 2017), is cospatial with CO emission, as also shown at higher resolution in Fig. 2. In all three galaxies, HI is ubiquitous, more extended than the dust and the CO emission.
 |
Fig. 3. Color RGB images for NGC 625 (left panel), NGC 1705 (middle), and NGC 5253 (right) with Herschel/PACS-R as red, ACA 12CO(1–0) as green, and HI as blue; North is up, East is to the left. The image dimensions are 130 × 105 arcsec2 for NGC 625, NGC 1705, and 120 × 105 arcsec2 for NGC 5253. All observations have roughly spatial resolutions of ∼250 pc (see text for more details). The white color indicates where HI, CO, and dust are cospatial. As in Fig. 2, also indicated are the HII regions A–D of NGC 625 (Cannon et al. 2004); the dust clouds and SSC in NGC 1705 (Cannon et al. 2006); and the unusual CO+dust cloud “D1” in NGC 5253 that coincides with the brightest, highly dust embedded SSC (Turner et al. 2017). |
3.4. Comparison with previous CO flux measurements
Although NGC 1705 was not previously observed in CO, the two other targets have prior CO observations. NGC 625 was observed in 12CO(1–0) with the MOPRA 22-m single dish by Cormier et al. (2014) and with ALMA by Imara et al. (2020). The total CO velocity-integrated TBICO given by Cormier et al. (2014) is 4.3 ± 0.6 K km s−1, or a CO(1–0) luminosity of 1.1 × 106 K km s−1 pc2. With ALMA, in a ∼1 31 ×1
31 ×1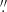 08 beam, Imara et al. (2020) find ICO = 3.0 ± 0.2 K km s−1, that over a region of 57
08 beam, Imara et al. (2020) find ICO = 3.0 ± 0.2 K km s−1, that over a region of 57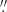 5 × 20″, gives a luminosity of 1.2 × 106 K km s−1 pc2. Since Cormier et al. (2014) and Imara et al. (2020) give total CO in units of velocity-integrated TB, as averages over regions much larger than the beams, we compare our measurements as given in Table 2 with their luminosities; 15.20 Jy km s−1 corresponds to a luminosity of 0.6 × 106 K km s−1 pc2, about half that measured by previous work. Since we find roughly the same velocity-integrated fluxes with the 12-m and ACA 7-m arrays, we would argue that the problem is not so much missing flux as possible differences in reduction and analysis procedures. The similarity of our integrated values with both arrays implies that this possible discrepancy will not significantly impact our results.
5 × 20″, gives a luminosity of 1.2 × 106 K km s−1 pc2. Since Cormier et al. (2014) and Imara et al. (2020) give total CO in units of velocity-integrated TB, as averages over regions much larger than the beams, we compare our measurements as given in Table 2 with their luminosities; 15.20 Jy km s−1 corresponds to a luminosity of 0.6 × 106 K km s−1 pc2, about half that measured by previous work. Since we find roughly the same velocity-integrated fluxes with the 12-m and ACA 7-m arrays, we would argue that the problem is not so much missing flux as possible differences in reduction and analysis procedures. The similarity of our integrated values with both arrays implies that this possible discrepancy will not significantly impact our results.
Wiklind & Henkel (1989) and Turner et al. (1997) have observed NGC 5253 with the 15 m Swedish-ESO Submillimeter Telescope (SEST, 45″ beam) and the Owens Valley Radio Observatory (OVRO), respectively. Wiklind & Henkel (1989) report a total velocity-integrated TBICO = 1.3 K km s−1, with a velocity width of 43 km s−1. With OVRO, using a 14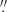 9×11
9×11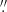 4 beam, Turner et al. (1997) find a velocity-integrated flux of 14.0 Jy km s−1, comparable to the flux recovered by our observations. NGC 5253 was also observed with ALMA in 12CO(2–1) by Miura et al. (2018), with the 12-m and 7-m arrays, and also with Total Power (TP). Within a box of 90″×84″, Miura et al. (2018) find 96.6 ± 0.2 Jy km s−1 (TP), and within a region of 22″ radius 92.6 ± 0.1 Jy km s−1 (combined TP+12m+7m). To compare their CO(2–1) observations with CO(1–0) from Wiklind & Henkel (1989), Miura et al. (2018) derive a TP velocity-integrated flux in CO(2–1) of 42.3 Jy km s−1, centered on the Wiklind et al. SEST beam with a radius of 22″. If CO is thermalized, as Miura et al. (2018) assume, this latter measurement would translate roughly into ICO ≈ 10.6 Jy km s−1 for 12CO(1–0), between 75% and 85% of our values in Table 2 over a similarly-sized area. Given the variation of the velocity-integrated fluxes found by Miura et al. (2018) in the different regions, our measurement is roughly consistent with previous work. In any case, as for NGC 625, the difference in our velocity-integrated CO flux with the 12-m and the 7-m arrays for NGC 5253 is not so large as to adversely affect our results for XCO.
4 beam, Turner et al. (1997) find a velocity-integrated flux of 14.0 Jy km s−1, comparable to the flux recovered by our observations. NGC 5253 was also observed with ALMA in 12CO(2–1) by Miura et al. (2018), with the 12-m and 7-m arrays, and also with Total Power (TP). Within a box of 90″×84″, Miura et al. (2018) find 96.6 ± 0.2 Jy km s−1 (TP), and within a region of 22″ radius 92.6 ± 0.1 Jy km s−1 (combined TP+12m+7m). To compare their CO(2–1) observations with CO(1–0) from Wiklind & Henkel (1989), Miura et al. (2018) derive a TP velocity-integrated flux in CO(2–1) of 42.3 Jy km s−1, centered on the Wiklind et al. SEST beam with a radius of 22″. If CO is thermalized, as Miura et al. (2018) assume, this latter measurement would translate roughly into ICO ≈ 10.6 Jy km s−1 for 12CO(1–0), between 75% and 85% of our values in Table 2 over a similarly-sized area. Given the variation of the velocity-integrated fluxes found by Miura et al. (2018) in the different regions, our measurement is roughly consistent with previous work. In any case, as for NGC 625, the difference in our velocity-integrated CO flux with the 12-m and the 7-m arrays for NGC 5253 is not so large as to adversely affect our results for XCO.
4. Large-scale dust opacity, gas content, and the XCO conversion factor
We trace the dust content along a line of sight at ∼250 pc resolution using the optical depth at 160 μm, τ160 (e.g., Leroy et al. 2009; Bolatto et al. 2011). We then compare the distribution of τ160 with the distributions of H I and ACA 12CO(1–0) at an angular resolution of ∼250 pc. Finally, we infer the H2 column density from the estimated dust-to-gas column density ratios, and derive the XCO conversion factor.
4.1. Infrared dust opacity from Herschel/PACS
With the exception of extreme ultra-luminous infrared galaxies (e.g., Arp 220; Wilson et al. 2014), the assumption that dust emission in galaxies is optically thin at 160 μm is well established (e.g., Misselt et al. 2001; Whelan et al. 2011). For an optically thin dust grain population with an equilibrium temperature, Tdust, τ160 is related to the measured 160 μm flux, I160, by:
where Bν corresponds to the intensity of a blackbody emitting at a temperature Tdust at wavelength λ. Thus, to compute τ160, we need to estimate the equilibrium dust temperature, Tdust.
To determine Tdust, the PACS 70, 100, and 160 μm data have been fit with two functions. One is an “MBB fit”, that is a single-temperature modified blackbody (MBB) with emissivity index β = 2.0 having two fitted parameters: τ160 and Tdust. The choice of β = 2 is consistent with current estimates for the 70 − 160 μm opacity of dust in the diffuse ISM in the solar neighborhood (Hensley & Draine 2021). The second is an “MBB-2T fit”, namely the sum of two MBBs with emissivity index β = 2.0 with dust temperatures Tcool and Twarm = 1.5 × Tcool. The two-temperature model is intended as a first approximation to the distribution of dust temperatures in a star-forming galaxy, where dust near newly-formed star clusters will be heated by more intense radiation. The choice of Twarm/Tcool = 1.5 is somewhat arbitrary, but is motivated by the factor of ∼2.3 range of wavelengths (70 μm−160 μm) used in the fit. These fits have three fitted parameters: τ160, Tcool, and γ defined as the fraction of the dust emission due to the warmer component. For these fits, there are zero degrees of freedom since the fits are limited to the three PACS cameras because we want to preserve the 250 pc resolution (and the longer Herschel/SPIRE wavelengths give, at best, a resolution 50% worse).
The MBB-2T fitting function is given by:
where τ160 is the PACS 160 μm opacity, ν0 corresponds to PACS 160 μm, γ is the fraction of the dust emission due to the warmer component, and Twarm and Tcool are the warm and cool dust temperatures defined above. The MBB model is merely Eq. (3) with γ = 0 and Tdust = Tcool. Since it is the cool dust with T = Tcool that defines τ160, the MBB-T2 model is better for our purposes. We know that there is temperature mixing along the line-of-sight, and thus almost certainly a component of warmer dust that would skew the determination of τ160. Hence, we also define an effective temperature:
The observed PACS flux ratios are shown in Fig. 4, together with individual MBB and MBB-T2 models. The comparison of IR ratios from two MBB models, with β = 1, 2 and the MBB-T2 model with γ = 0.14, the median value for NGC 1705, shows that the two-temperature MBB-T2 model with β = 2 mimics the MBB curve with lower emissivity, β = 1. This is a crude, although effective, example of temperature mixing being able to reproduce flat spectral emissivity with β ≲ 1 (e.g., Hunt et al. 2015), which however does not represent grain physical properties.
 |
Fig. 4. PACS flux ratios I100/I160 versus I70/I160. The PACS data have been rebinned to ∼250 pc resolution in order to match the HI and ACA CO maps. Heavy curves show the medians in I100/I160 bins for each galaxy, and the shaded regions indicate 1σ standard deviations. Also shown are the model MBB-T2 flux ratios with γ = 0.14 (the median value for NGC 1705), indicated by the heavy black long-dashed curve. The IR ratios from two MBB models (γ = 0) are illustrated as a long-dashed (gray) curve with β = 1 (virtually indistinguishable from the MBB-T2 curve), and a short-dashed (black) curve for β = 2. The dot-dashed curve corresponds to the best fit polynomial for the SMC by Leroy et al. (2009). The horizontal lines illustrate the I100/I160 ratios that would be expected for Tdust = 20 K, 25 K, and 30 K. The line ratios for NGC 625 and NGC 5253 are fairly well approximated by MBBs or MBB-T2 fits, while the polynomial fit by Leroy et al. (2009) is a better approximation for NGC 1705. This fit is roughly equivalent to assuming that only half of the observed 70 μm emission comes from large, “classical” grains, with the other half originating from stochastic heating of small grains. |
Figure 5 shows representative MBB-2T fits of the three targets, with nonzero γ values. The gray (solid) curve shows the best MBB-2T fits, while the long-dashed (purple) curves the single-temperature MBB fit with T = Tdust. The advantage of the two-temperature fits is evident by comparing the long-dashed MBB with Tdust to the combined MBB-2T solid curve; the single-temperature fit misses the high-frequency contribution from the warmer dust.
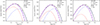 |
Fig. 5. Representative fits of Eq. (3) with significant γ values to illustrate the importance of two temperatures in the fitting function. The long-dashed red curves show the MBB with Tcool, the dot-dashed blue curves Twarm, and the gray (solid) ones the overall best fit. The (heavy) purple long-dashed curve corresponds to a single-temperature MBB with Tdust, normalized to the 160 μm data point. For γ > 0, the simple MBB is clearly missing the contribution toward higher frequencies caused by warm dust at Twarm. |
The MBB-T2 fits are numerically nontrivial. We left γ unconstrained, and in some cases, the fitted γ < 0 or γ > 1. In those cases, an MBB fit (with γ = 0, by definition) was applied with β = 2.0 as for the other MBB-T2 fits. This condition occurred for (45, 0, 33) individual resolution elements in NGC (625, 1705, 5253). Since rebinning to (13″, 10″, 15″) for NGC (625, 1705, 5253), respectively, gives (77, 33, 90) resolution elements with PACS fluxes greater than the background, there are (58%, 0, 37%) of the fitted resolution elements with single-T MBB fits.
Given that the expected uncertainty in the individual PACS photometry is ∼10%, the rms values of both MBB and MBB-2T fits are quite good, and, except for NGC 1705, well within the expected uncertainties. Moreover, as shown in Appendix A, the MBB-2T fits are overall superior to MBB, possibly due to the extra fitted parameter and the consequent zero degrees of freedom. More details of the fits to the PACS data to derive τ160 are given in Appendix A.
Figure 6 compares the best-fit Tcool with dust optical depth, τ160 (left panel), and with Tdust versus τ160 (right). We initially expected that Tcool might correlate with τ160; however as shown in the left panel of Fig. 6, it does not. The range of Tcool is relatively narrow, a standard deviation of 2–3 K, over a 3-order of magnitude range of τ160. Moreover, the median cool-dust temperatures of the three targets do not differ significantly, given the 2–3 K spread: we find Tcool = (23.0, 22.0, 24.1) K for NGC (625, 1705, 5253), respectively. These temperatures are toward the high end of the temperature range of cool dust in normal, star-forming spirals (e.g., Galametz et al. 2012).
 |
Fig. 6. Dust temperatures plotted against τ160 for the 250 pc regions within the target galaxies: in the left panel best-fit Tcool and in the right panel effective temperature Tdust. The medians binned in log10(τ160) are shown as heavy lines characterized by different colors, with the 1σ variation by shaded regions. The horizontal dashed lines correspond to the overall Tcool galaxy medians (left panel) and Tdust (right). Only in the case of NGC 5253 does the effective temperature Tdust present a trend with τ160, in the sense that more optically thick regions show higher temperatures. |
Kirkpatrick et al. (2014) found that Tcool is partly driven by star-formation activity, so that higher temperatures would be found for more intense SFRs, consistent with the starburst nature of our targets. Moreover, as shown in the right panel of Fig. 6, in NGC 5253, the effective temperature Tdust is correlated with τ160 although the other two galaxies show little trend. Thus, in extreme dusty starbursts such as NGC 5253, warmer dust is associated with higher τ160.
4.2. Infrared opacity and atomic gas surface density
Atomic gas is an important part of the overall gas budget, especially in dwarf galaxies (e.g., Hunt et al. 2020). Comparing atomic gas surface density with a measurement of dust opacity enables an estimate of the dust-to-gas ratio (DGR), as well as an assessment of the overall association of dust content with H I. Figure 7 (left panel) shows the trend of H I column density NHI with τ160 determined in the previous section; only points with signal-to-noise S/N ≥ 3 are shown. The data show a fairly tight correlation, but with an inflection or flattening at τ160 ∼ 10−4. This is due to the “saturation” of NHI at high column densities where most of the hydrogen has transitioned to molecular form, traceable by CO. Such a correlation between spatially-resolved dust content and HI is common in HI-dominated dwarf galaxies (e.g., Leroy et al. 2009), but is not generally observed in spirals (e.g., Hughes et al. 2014; Casasola et al. 2022).
 |
Fig. 7. Atomic gas column density NHI versus 160 μm optical depth τ160 (left panel) and CO ACA (velocity-integrated) TB versus τ160 (right). Only regions with S/N ≥ 3 are shown (and included in the fits). The best-fit linear relations (Eq. (6)) for τ160 as a function of NHI are shown as heavy curves (in log space), and only consider the points with 1019 ≤ NHI ≤ 1021 cm−2 because of the need to consider the regions dominated by HI. The lighter curves show the fit to Eq. (5) as described in the text, and are used to determine |
We assume that for dark clouds with large τ160 there is a finite amount of HI in the cloud “skin”, and that the cloud chemistry limits the amount of HI (see also Pineda et al. 2008). Thus, we can write:
where N0HI is the HI column density at saturation, and kHI defines the transition threshold for the dust optical depth τ160 where saturation onsets. The best fits to this function are shown as curves in the left panel of Fig. 7; only points with HI signal-to-noise (S/N) ≥ 3 are included in the fits. We will incorporate kHI to estimate XCO from AV in Sect. 5.
Following Leroy et al. (2009) and Bolatto et al. (2011), we estimate the DGR from τ160 and the total gas column density, NHI (NHI ≡ NHI + 2 NH2), by fitting a linear relation:
where δDGR is the slope of the relation, namely the DGR, and NHI is in units of column density cm−2. Here the underlying assumption is that this relation holds at all column densities. Thus, we can first calibrate it on HI, by restricting the fit to low column densities where NHI is dominated by HI, and then extrapolate it to H I+H2. The fit of Eq. (6) was applied to H I columns with 19 ≤ log(NHI/cm−2) ≤ 21; only points with signal-to-noise (S/N) ≥ 3 are included in the fit. We also performed fits with a nonzero intercept τ0, and found that it is always 0 to within the uncertainties; thus we fixed τ0 to 0 to ensure a more reliable estimation of δDGR.
As shown in Fig. 7, these linear fits well approximate the trend of τ160 and HI at low column densities where HI dominates the gas budget. The best-fit δDGR in Eq. (6) corresponds to ⟨ τ160/NHI ⟩ and differs slightly for the three galaxies, in qualitative agreement with what we would expect considering the albeit small metallicity differences (e.g., Rémy-Ruyer et al. 2014, see Table 1):
These values are 3−5 times lower than τ160/NH = 1.61 × 10−25 cm−2/H, found in the local diffuse ISM by Hensley & Draine (2021), roughly consistent with the linear trend with the 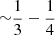 Z⊙ metallicities of our targets. The values for our dwarf starbursts are also comparable with δDGR for N 83, with O/H of
Z⊙ metallicities of our targets. The values for our dwarf starbursts are also comparable with δDGR for N 83, with O/H of 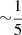 Z⊙ (e.g., Berg et al. 2012), in the Small Magellanic Cloud (SMC): τ160 = 2.3 − 4.3 × 10−26 Ngas/cm−2 (Bolatto et al. 2011), where we have reported their 36% correction for helium to our convention without the helium correction (see also Leroy et al. 2009).
Z⊙ (e.g., Berg et al. 2012), in the Small Magellanic Cloud (SMC): τ160 = 2.3 − 4.3 × 10−26 Ngas/cm−2 (Bolatto et al. 2011), where we have reported their 36% correction for helium to our convention without the helium correction (see also Leroy et al. 2009).
In the limit of the HI-dominated regime at low τ160, Eq. (5) should converge to Eq. (6) with δDGR = 1/(N0HIkHI). Thus, in principle, we could have used the fits of Eq. (5) to infer δDGR, rather than Eq. (6). However, Fig. 7 shows offsets of 30–40% between the two estimates, so it is unclear which to prefer. After error propagation, the uncertainties on δDGR from the fits of Eq. (5) are larger than those given in Eq. (7), so we prefer to adopt the results from fitting Eq. (6) with only one free parameter and over the range in column density dominated by HI.
The DGR δDGR is given in units of optical depth per H, because we want to compare dust columns with gas columns. Although it would be preferable to determine the DGR for individual regions (e.g., Bolatto et al. 2011; Sandstrom et al. 2013), this is difficult for our dwarf targets. The small number of individual resolution elements within each galaxy effectively precludes a statistically relevant spatially-resolved DGR determination. Thus, we use an average DGR determined from the data as shown in the left panel of Fig. 7. This point is further discussed in Sect. 7.
4.3. Molecular gas surface density, τ160, and XCO at 250 pc resolution
The trend of CO velocity-integrated brightness temperature observed with ACA at ∼250 pc resolution is shown in the right panel of Fig. 7. Also shown are the giant molecular clouds (GMCs) in the Milky Way (MW) studied by Lee et al. (2018), where they estimate AV from τ850. As for HI, ICO in units of K km s−1 correlates with dust opacity, although with somewhat larger scatter than for HI. At a given τ160, our low-metallicity starbursts show lower surface brightness CO emission than the MW GMCs. Part of this may be due to the much higher resolution in the MW observations (1 pc; Lee et al. 2018), relative to the 250 pc regions studied here. However, another part of this stems from the XCO factor needed to bring observed CO brightness temperatures to gas column densities.
We now have the necessary ingredients to infer NH2 from NHI and δGDR, using the following expression:
where δDGR is determined from the fit of Eq. (6). For each 250 pc resolution element, we can derive 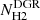 , and then use ICO to find the local XCO = ICO/
, and then use ICO to find the local XCO = ICO/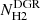 . To include a resolution element in this estimate, we require that both HI and CO binned data points have S/N ≥ 3. Thus, instead of the (70, 33, 90) 250 pc PACS resolution elements for the determination of τ160 for NGC (625, 1705, 5253), respectively, the numbers are now reduced to (26, 8, 18) usable elements for the three galaxies. However, a small fraction of these gives negative values of NH2 in Eq. (8), because the HI column density slightly exceeds what would be inferred from the ratio, τ160/δDGR. This could be a consequence of our assumption of a global DGR, as also discussed in Sect. 7. In any case, the number of regions useful for the calculation of XCO dwindles further to (20, 4, 17) for NGC (625, 1705, 5253), respectively.
. To include a resolution element in this estimate, we require that both HI and CO binned data points have S/N ≥ 3. Thus, instead of the (70, 33, 90) 250 pc PACS resolution elements for the determination of τ160 for NGC (625, 1705, 5253), respectively, the numbers are now reduced to (26, 8, 18) usable elements for the three galaxies. However, a small fraction of these gives negative values of NH2 in Eq. (8), because the HI column density slightly exceeds what would be inferred from the ratio, τ160/δDGR. This could be a consequence of our assumption of a global DGR, as also discussed in Sect. 7. In any case, the number of regions useful for the calculation of XCO dwindles further to (20, 4, 17) for NGC (625, 1705, 5253), respectively.
The results are shown in the left panel of Fig. 8, where also illustrated are the metallicity-dependent predictions for global XCO [XCO ∝ (Z/Z⊙)−1.55] according to Hunt et al. (2020). The DGR-inferred XCO values sometimes exceed the expectation from the metallicity dependence, in some cases by an order of magnitude or more. The large scatter precludes definitive statements, but the main point that emerges from Fig. 8 is that a simple metallicity dependence does not explain the XCO factors derived from the DGR on 250 pc scales.
 |
Fig. 8. Left panel: Inferred XCO conversion factor from Eq. (8) as a function of τ160. Also shown are values that would be estimated from the metallicity dependence found by Hunt et al. (2020) as XCO ∝ Z−1.55 (see also Accurso et al. 2017). Heavy curves show the medians in log10(τ160) for each galaxy (except for NGC 1705 for which there are too few points), and the shaded regions indicate 1σ standard deviations. Right panel: GDR (here we are using the inverse of δDGR) that would be inferred assuming the metallicity dependence of the XCO conversion factor found by Hunt et al. (2020). The range of GDRs estimated by different methods is shown as the hatched horizontal strips. As in the left panel, heavy curves show the medians, and shaded regions the 1σ standard deviation. |
To investigate this further, and check for consistency, the right panel of Fig. 8 shows the gas-to-dust ratios (GDRs) that would be inferred if we had assumed a metallicity-dependent XCO. The plotted GDRs are simply the inverse of δDGR that were derived in Eq. (6), and the hatched areas show the range of GDRs estimated by different methods. At τ160 ≲ 10−4, where the gas budget is dominated by HI, the inferred GDRs more or less conform to expectations. However, for higher τ160, where H2 inferred from CO starts to impact the gas content, the GDRs are lower, reaching MW values at τ160 ∼ 10−3. Such behavior is consistent with the left panel of Fig. 8 where XCO computed from the DGRs are higher than what would be expected from the global metallicity dependence found by Hunt et al. (2020). This point will be explored in Sect. 6.
5. Small-scale dust extinction, molecular gas content, and the XCO conversion factor
We now turn to the ALMA 12-m data with a higher resolution, ∼40 pc. Dust columns at this resolution are inferred from foreground visual reddening, E(B − V), estimated from the Balmer decrement from the MUSE maps. We convert E(B − V) to AV by assuming AV/E(B − V) = 3.1 (e.g., Draine 2003). The problem with tracing dust extinction through 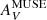 from the Balmer decrement is that AV gives attenuation rather than the true visual optical depth τV. Moreover, the attenuation
from the Balmer decrement is that AV gives attenuation rather than the true visual optical depth τV. Moreover, the attenuation 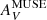 is due only to dust in front of the ionized gas, whereas τ160 measures all of the dust along the line of sight. More generally, we need to distinguish between dust attenuation from
is due only to dust in front of the ionized gas, whereas τ160 measures all of the dust along the line of sight. More generally, we need to distinguish between dust attenuation from 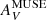 and true visual optical depth (e.g., Boquien et al. 2013). In the following, we quantify this distinction and show that
and true visual optical depth (e.g., Boquien et al. 2013). In the following, we quantify this distinction and show that 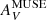 from the Balmer decrement does not always directly trace τV in these low-metallicity starbursts.
from the Balmer decrement does not always directly trace τV in these low-metallicity starbursts.
5.1. Visual attenuation versus extinction and dust optical depth
Assuming that the extinguishing dust is placed in a foreground screen, the relation between attenuation and dust optical depth is simple:
Thus, the attenuation AV is exactly proportional to the dust optical depth τV. However, assuming that the dust is uniformly mixed with the emitters gives a slightly more complicated relation:
Figure 9 illustrates these two configurations of the dust. The infrared optical depth traced by τ160 penetrates the full dust column along the line of sight, while extinction given by the Balmer decrement only probes the dust between the observer and the ionized gas. The assumption that the dust is uniformly mixed with the ionized gas is an approximation, but, as shown in the figure, has the advantage of being slightly more realistic from a physical point of view.
 |
Fig. 9. Left panel: Idealized cartoon illustrating the mixed configuration of dust, stars, and gas. Right panel: The same but with the foreground screen configuration. The amount of dust in the screen in the right panel is assumed to be roughly half of the total dust shown in the left panel. While the infrared τ160 penetrates the full dust column along the line of sight, the optical depth inferred from the Balmer decrement only captures the dust between the stars that ionize the gas and the observer. |
As described by Natta & Panagia (1984), Disney et al. (1989), and others (e.g., Witt & Gordon 1996, 2000), solutions can be obtained for even more complex assumptions on the relative geometry of the dust and the emitting regions. In any case, the problem that emerges is the derivation of τV from AV in more complex geometries of the dust relative to the emission source. Equation (10) provides a fortunate example because it is invertible using the Lambert W function as shown by Boquien et al. (2013)6:
Here we make the assumption that the dust is uniformly mixed with the ionized gas, namely that Eq. (10) is a better description of the dust column τV than Eq. (9), at least for our use of the Balmer-decrement derived 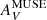 to infer dust columns. We calculate τV under this assumption and compare it with what would be inferred by simply equating τV with AV (with a small proportional factor) as in Eq. (9).
to infer dust columns. We calculate τV under this assumption and compare it with what would be inferred by simply equating τV with AV (with a small proportional factor) as in Eq. (9).
The comparison of AV and τV (Eqs. (10), (11)) under the assumption of dust uniformly mixed with the ionized gas emission is shown in Fig. 10. The dashed curve shows the analytical solution, while the solid line indicates y = log10(τV) = x − log10(1.086)+log10(2), where x = log10(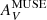 ). The factor of 2 takes into account that
). The factor of 2 takes into account that 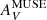 only probes the extinction along the line of sight, i.e., the front of the foreground screen (see above), and the other factor is from Eq. (9). Indeed, for small τV, Eq. (10) reduces to AV ≈ 1.086 (τV/2). The difference of the two quantities τV and y from
only probes the extinction along the line of sight, i.e., the front of the foreground screen (see above), and the other factor is from Eq. (9). Indeed, for small τV, Eq. (10) reduces to AV ≈ 1.086 (τV/2). The difference of the two quantities τV and y from 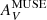 is negligible at low τV, but becomes significant (≳25%) for
is negligible at low τV, but becomes significant (≳25%) for 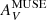 ≳ 0.3 − 0.5 mag. At AV higher than this, τV becomes clearly the better tracer of dust opacity since the assumption of a foreground screen progressively fails at high dust columns. Our preference for τV is also supported by the comparison with Galactic GMCs as discussed in the next section (see Fig. 11).
≳ 0.3 − 0.5 mag. At AV higher than this, τV becomes clearly the better tracer of dust opacity since the assumption of a foreground screen progressively fails at high dust columns. Our preference for τV is also supported by the comparison with Galactic GMCs as discussed in the next section (see Fig. 11).
 |
Fig. 10. Relations between AV and τV. Left panel: τV inferred from Eq. (11) for the targets plotted against log10( |
 |
Fig. 11. CO velocity-integrated TBICO plotted versus (logarithm) visual extinction AV (left panel) and (logarithm) visual dust optical depth τV (right). The top axes show the scale for τ160 assuming that AV/τ160 = 2180, as described in Sect. 5.3. The light curves show fits to Eq. (12). Heavy curves show the medians for each galaxy binned in log10(AV), (left), log10(τV), (right), with the shaded regions corresponding to ±1σ deviations. Also shown in both panels are the MW GMCs studied by Lee et al. (2018), with AV inferred from Planck; see Sect. 5 for more details. |
5.2. CO brightness temperature and visual extinction at 40 pc resolution
Figure 11 shows the 12-m data plotted in the left panel against 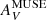 , calculated from E(B − V) and in the right against τV inferred from Eq. (11). Both data sets have been rebinned to 2″ (corresponding to ≈40 pc, see Table 1). Like the trend of ICO with τ160 at 250 pc resolution, ICO at 40 pc also varies systematically with AV and τV, albeit with significant scatter.
, calculated from E(B − V) and in the right against τV inferred from Eq. (11). Both data sets have been rebinned to 2″ (corresponding to ≈40 pc, see Table 1). Like the trend of ICO with τ160 at 250 pc resolution, ICO at 40 pc also varies systematically with AV and τV, albeit with significant scatter.
Figure 11 shows that the 40 pc CO-emitting regions have higher brightness temperatures than the ∼250 pc regions shown in (the right panel of) Fig. 7. Indeed, the surface brightness of CO in our targets at the two resolutions sampled here is very different. Comparison of Figs. 7 and 11 illustrates that ICO of the brightest CO-emitting regions that are visible at high dust columns, traced by either τ160 or τV, are a factor of ∼10 higher at 40 pc than 250 pc. This is consistent with beam dilution of a given molecular gas surface density because the ratio of the beam area is (250/40)2 ∼ 40. Such behavior is not surprising because we expect CO to be highly clumped on these scales, much more so than HI (Leroy et al. 2013). It also tells us that for probing CO emission in low-metallicity galaxies, large beams, with single-dish observations at the extreme end, are not as effective as beams on scales of (at least) a few tens of parcecs; they are unable to trace the high-density CO columns. This means that single-dish efforts to detect CO at low metallicity may be doomed to fail at the outset because of beam dilution, a point that was also made by Rubio et al. (1993) in a pioneering paper using SEST observations of the SMC. We explore this further in Sect. 6.
Also shown in Fig. 11 are the CO velocity-integrated brightness temperatures of the GMCs in our Galaxy studied at ∼1 pc resolution by Lee et al. (2018). They infer AV from E(B − V), (also using AV/E(B − V) = 3.1) derived from the dust optical depth at 850 μm τ850 as measured by Planck. (Sub)Millimeter/far-infrared optical depths such as τ850 (and even τ160) make emission at these wavelengths optically thin tracers of dust, better probing the entire line of sight through dust and gas. Comparison of the Lee et al. (2018) GMCs with our CO data is enlightening. If we assume that 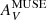 (left panel in Fig. 11) measured from the Balmer decrement is identical to AV inferred from τ850, at a given AV, we would deduce that the GMC CO 1 pc column densities are lower than those found for our low-metallicity starbursts on ∼40 pc scales. However, in the right panel where τV is plotted rather than
(left panel in Fig. 11) measured from the Balmer decrement is identical to AV inferred from τ850, at a given AV, we would deduce that the GMC CO 1 pc column densities are lower than those found for our low-metallicity starbursts on ∼40 pc scales. However, in the right panel where τV is plotted rather than 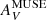 , for a given τV, the CO integrated brightness temperatures of the GMCs (with their AV taken to be equivalent to our τV) coincide very well with the CO emission observed at 40 pc resolution. This is an indication that the assumption that the obscuring dust measured by
, for a given τV, the CO integrated brightness temperatures of the GMCs (with their AV taken to be equivalent to our τV) coincide very well with the CO emission observed at 40 pc resolution. This is an indication that the assumption that the obscuring dust measured by 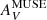 is mixed with the ionized gas, with an optical depth of τV, is better than assuming that the dust is a foreground screen. This is true for the low-metallicity starbursts studied here, but the differences would even be more profound for galaxies with larger dust content.
is mixed with the ionized gas, with an optical depth of τV, is better than assuming that the dust is a foreground screen. This is true for the low-metallicity starbursts studied here, but the differences would even be more profound for galaxies with larger dust content.
However, that the 40 pc integrated brightness temperatures of our targets are similar the GMCs in the MW observed at 1 pc resolution by Lee et al. (2018) is surprising. The GMCs would have been expected to show significantly higher surface brightness within the much smaller beam. Instead, our finding would imply that the CO clumps within the 40 pc beam are of much higher surface brightness than the GMCs measured by Lee et al. (2018), consistent with the idea that the only CO-emitting regions that remain at low metallicity are the dense cores that are sufficiently shielded to avoid photodissociation.
As discussed by Lee et al. (2018), there are at least two features in the ICO versus AV (τV) relation that would be expected from a theoretical point of view. The first is a CO-formation visual extinction threshold, below which CO emission plummets because of photodissociation of the CO molecules (e.g., van Dishoeck & Black 1988; Bell et al. 2006; Visser et al. 2009; Glover & Mac Low 2011; Shetty et al. 2011). This would be reflected in the presence of carbon emitting as C+ or CI in parts of the molecular clouds where CO is insufficiently shielded (e.g., Hollenbach & Tielens 1997; Papadopoulos et al. 2004; Wolfire et al. 2010).
Another feature expected theoretically is a flattening at high AV (τV) where CO emission saturates, becoming optically thick (e.g., Glover & Mac Low 2011; Shetty et al. 2011). Such a feature is observed in some GMC ensembles in the MW, where there is clear plateau for AV ≳ 1 mag (e.g., Lombardi et al. 2006; Pineda et al. 2008).
To test for these features in the 40 pc resolution ICO, AV (τV) relation for low-metallicity starbursts, we have fit the points in Fig. 11 with a function similar to that of Eq. (5) of the form:
where W0CO is the velocity-integrated CO brightness temperature at saturation; kCO defines the transition threshold for the dust optical depth τV where saturation sets on; and 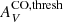 gives the onset for CO emission. As before, only points with signal-to-noise (S/N) ≥ 3 are included in the fits. The best fits to this function are shown as curves in Fig. 11; in the right panel we have substituted τV for AV in Eq. (12). The results of the fits and the visual inspection of the plots show that the saturation feature at high τV is not visible in our data; W0CO and kCO are ill-determined both for the plots using AV and those with τV. Instead, the
gives the onset for CO emission. As before, only points with signal-to-noise (S/N) ≥ 3 are included in the fits. The best fits to this function are shown as curves in Fig. 11; in the right panel we have substituted τV for AV in Eq. (12). The results of the fits and the visual inspection of the plots show that the saturation feature at high τV is not visible in our data; W0CO and kCO are ill-determined both for the plots using AV and those with τV. Instead, the 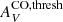 parameter is somewhat better determined with:
parameter is somewhat better determined with:
The results for 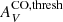 using τV, rather than AV, have somewhat higher values, although with slightly larger uncertainty. In any case, our 40 pc CO data show no evidence for a flattening at high τV, but some tentative indication of an AV CO threshold of ∼0.1 mag. This is a much lower value than given by the simulations of Glover & Clark (e.g., 2016) that predict a steep reduction for AV ≲ 1 mag; however, their simulations are at much finer (0.06 pc) resolution than our observations, so may not be directly comparable. Our value of
using τV, rather than AV, have somewhat higher values, although with slightly larger uncertainty. In any case, our 40 pc CO data show no evidence for a flattening at high τV, but some tentative indication of an AV CO threshold of ∼0.1 mag. This is a much lower value than given by the simulations of Glover & Clark (e.g., 2016) that predict a steep reduction for AV ≲ 1 mag; however, their simulations are at much finer (0.06 pc) resolution than our observations, so may not be directly comparable. Our value of 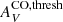 ≈ 0.1 mag is also roughly ten times lower than found by Pineda et al. (2008) with
≈ 0.1 mag is also roughly ten times lower than found by Pineda et al. (2008) with 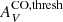 generally ≳1 mag for their sample of (solar metallicity) MW GMCs.
generally ≳1 mag for their sample of (solar metallicity) MW GMCs.
5.3. The XCO factor and visual optical depth
We can now infer the XCO conversion factor at ≈40 pc resolution from τV (or AV), similar to what we have done at lower resolution (≈250 pc) with τ160 in the previous sections. We write:
where NH/AV is the total column density of hydrogen atoms in either atomic or molecular form relative to visual extinction AV. This approach follows Lee et al. (2018), but they probed AV with dust emission, so we must make different assumptions for the dependence of NH2 on 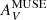 . The multiplicative factor of 2 for
. The multiplicative factor of 2 for 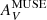 in Eq. (14) is because our estimate of
in Eq. (14) is because our estimate of 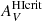 relies on τ160 which probes the entire line of sight, thus sampling the shielding layer on both the front and back sides of the medium; conversely
relies on τ160 which probes the entire line of sight, thus sampling the shielding layer on both the front and back sides of the medium; conversely 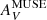 is calculated assuming a foreground screen, thus sampling only the front side (see Lee et al. 2018). The
is calculated assuming a foreground screen, thus sampling only the front side (see Lee et al. 2018). The 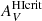 term takes into account the transition from HI to H2 at high dust and gas columns (e.g., Bigiel et al. 2008; Krumholz et al. 2009; Sternberg et al. 2014); it can be estimated from kHI in the HI formulation of radiative transfer in Eq. (5), after converting the units to AV mag−1. The analogous equation for τV would be:
term takes into account the transition from HI to H2 at high dust and gas columns (e.g., Bigiel et al. 2008; Krumholz et al. 2009; Sternberg et al. 2014); it can be estimated from kHI in the HI formulation of radiative transfer in Eq. (5), after converting the units to AV mag−1. The analogous equation for τV would be:
where 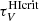 is defined as 1.086
is defined as 1.086 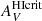 , and NH/τV is the equivalent of NH/AV but in units of τV, under the assumption that the denominator measures the extinction in the dust along the line of sight. Equation (15) could be seen as inconsistent with our conclusion that the screen geometry for dust extinction is not an accurate description; however,
, and NH/τV is the equivalent of NH/AV but in units of τV, under the assumption that the denominator measures the extinction in the dust along the line of sight. Equation (15) could be seen as inconsistent with our conclusion that the screen geometry for dust extinction is not an accurate description; however, 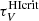 describes the impact of the conversion of H2 to HI on the extinction dependence of NH2, thus is not strictly related to the geometry of the dust relative to the ionized gas.
describes the impact of the conversion of H2 to HI on the extinction dependence of NH2, thus is not strictly related to the geometry of the dust relative to the ionized gas.
NH/AV is a critical factor in our determination of XCO from AV on ∼40 pc scales, and it relies on several assumptions. Along diffuse lines of sight in the MW, Bohlin et al. (1978) find NH/AV = 1.87 × 1021 cm−2 mag−1. Assuming AV/τ160 = 2180 (Hensley & Draine 2021), we can also estimate NH/AV from δDGR at ∼250 pc resolution (see Fig. 7, Eq. (6)) measured for our targets. We find:
As shown in the right panel of Fig. 8, there is a relatively large spread in these estimates, ranging from ∼0.2 dex to 0.5 dex. In any case, at face value, the total gas-to-extinction ratios we measure for these low-metallicity galaxies are ≈4 − 8 times higher than the MW value (e.g., Bohlin et al. 1978), qualitatively consistent with a linear metallicity scaling.
Another critical factor in our 40 pc formulation of NH2 is 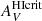 , which is directly related to kHI in Eq. (5) as is the inflection where atomic gas transitions to H2. Thus, with AV/τ160, we calculate values of
, which is directly related to kHI in Eq. (5) as is the inflection where atomic gas transitions to H2. Thus, with AV/τ160, we calculate values of 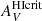 for the low-metallicity starbursts:
for the low-metallicity starbursts:
For NGC 1705 and NGC 5253, the 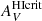 values are fairly low, as can also be seen by the curves in Fig. 7, while for NGC 625, the value is roughly 3 times higher, although also 4–5 times more uncertain. The values for NGC 1705 and NGC 5253 of 0.2–0.3 mag are consistent with
values are fairly low, as can also be seen by the curves in Fig. 7, while for NGC 625, the value is roughly 3 times higher, although also 4–5 times more uncertain. The values for NGC 1705 and NGC 5253 of 0.2–0.3 mag are consistent with 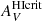 = 0.2 mag for a fixed radiation field found by Draine (1978), and by Krumholz et al. (2009), depending on dust properties.
= 0.2 mag for a fixed radiation field found by Draine (1978), and by Krumholz et al. (2009), depending on dust properties.
Finally, both Eqs. (16) and (17) rely on the conversion of AV to τ160. This conversion is uncertain, and different groups adopt a range of values. Leroy et al. (2009) use AV/mag = 1910 τ160, while Lee et al. (2015) adopt AV/mag = 2200 τ160. The higher dust temperatures and lower dust optical depth found by Planck Collaboration XI (2014) lead to AV/mag = 3246 τ160, assuming E(B − V)/AV = 3.1 as done here. Here, we adopt AV/mag = 2180 τ160 (Hensley & Draine 2021), close to the Lee et al. (2015) value, but still somewhat subject to uncertainty.
These uncertainties in the ingredients for the calculation of NH2 make our inference of XCO subject to various caveats. Nevertheless, results are encouraging. Figure 12 shows XCO computed using NH2 inferred from Eqs. (14) and (15); the left panel shows XCO versus AV and the right versus τV. Also shown in the figure are the expectations from the global metallicity dependence of XCO from Hunt et al. (2020, see also Accurso et al. 2017). There is possibly less scatter in the right panel (τV), at least for NGC 5253, but overall the two plots show mutually consistent values of XCO. While the median curve for NGC 5253 falls roughly where expected for consistency with a global metallicity dependence of XCO, NGC 625 falls fairly close to the MW. This is unexpected given that NGC 625 has the lowest O/H of our sample, although the global O/H variations among the three targets are not large. The reason why NGC 625 shows XCO at 40 pc resolution close to the Galactic value is the high value of 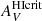 in Eq. (17). Given the relatively low signal-to-noise on the measurement of
in Eq. (17). Given the relatively low signal-to-noise on the measurement of 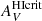 for NGC 625, we have experimented with lower values of
for NGC 625, we have experimented with lower values of 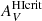 ≈ 0.2 − 0.3, and find that NGC 625 would fall closer to the global metallicity-dependent XCO expectations, consistent with the other galaxies. Nevertheless, this would be a deviation of ≳3σ, so we continue to consider the nominal
≈ 0.2 − 0.3, and find that NGC 625 would fall closer to the global metallicity-dependent XCO expectations, consistent with the other galaxies. Nevertheless, this would be a deviation of ≳3σ, so we continue to consider the nominal 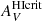 value for NGC 625.
value for NGC 625.
 |
Fig. 12. XCO estimated from Eq. (14) is plotted as a function of AV in the left panel, and of τV in the right. As in Fig. 8, we include as horizontal dashed lines, XCO that would be estimated from the metallicity dependence found by Hunt et al. (2020), as XCO ∝ Z−1.55. The MW XCO = 2.3 × 1020 cm−2/K km s−1 is also given together with the uncertainties. Heavy curves show the medians for each galaxy binned in |
6. Comparison of large- and small-scale XCO
Figures 8 and 12 present two different pictures of the behavior of XCO. At ∼250 pc resolution, conversion factors XCO show large scatter, and are generally higher than what would be predicted from a simple metallicity dependence. Instead, with 12-m data at ∼40 pc resolution, XCO values are consistent with, or even lower than, the predicted metallicity dependence, and, as at 250 pc, there is large scatter.
The large scatter and inconsistencies between the two data sets at different resolutions could also point to a dependence on additional parameters beyond metallicity. In particular, the comparison between Figs. 7 and 11 shows that the larger ACA beam, rebinned here to ∼250 pc, does not sample the brighter CO emission that emerges, instead, at ∼40 pc with the 12-m array. In the larger beam, there are more CO-faint regions than bright regions; consequently, XCO is larger.
Trends of the H2 conversion factor XCO with the observed CO velocity-integrated brightness temperature ICO are also expected theoretically. Measured ICO is mainly governed by mean density along the line-of-sight (e.g., Gong et al. 2018), since CO forms at higher volume densities (n ≳ 100 − 200 cm−3) than H2 (n ∼ 10 − 100 cm−3). This implies that, for environments with similar metallicities, ICO can be taken as a proxy of column or volume densities (e.g., Hu et al. 2022), and related to XCO, either inferred from simulations, or measured empirically, as we have done here. It is likely that the underlying reason why at 40 pc the fainter regions have larger XCO stems from the radiative transfer of CO; the faint CO emission regions are heavily subthermally excited and may even become optically thin due to the low volume and column densities with which they are associated. Subthermal excitation would make them less luminous in the CO line per hydrogen atom, compared to the higher density/column density gas with excitation temperatures approaching kinetic temperatures (e.g., Hu et al. 2022).
We have tested this hypothesis by plotting in Fig. 13XCO inferred above at the two different resolutions against ICO of the relevant data sets. An anticorrelation of XCO with ICO emerges clearly from both sets of data, with Pearson correlation coefficients of −0.65 (250 pc) and −0.7 (40 pc). This correlation is almost certainly causing at least part of the scatter in our XCO estimates shown in Figs. 8 and 12. We have performed a robust fit in logarithmic space to XCO with ICO shown as a yellow regression line in Fig. 13:
 |
Fig. 13. XCO estimated from Eq. (8) versus ICO in the top panel (250 pc resolution); XCO from Eq. (14) in the middle (40 pc resolution); and from Eq. (15) in the lower (40 pc resolution). Also shown as dark-gray dot-dashed lines are the predictions from Narayanan et al. (2012) for the different metallicities of our targets. The 1 kpc trend from Hu et al. (2022), valid for all metallicities, is shown as a light-gray solid line (labeled “1 kpc”). The brown solid (dashed) curves correspond to 0.3 Z⊙ (Z⊙) metallicities at 125 pc resolution (top panel) and at 32 pc (middle and lower ones). The 0.3 Z⊙ curves are the best approximation to the metallicities of our target starbursts. The robust fit in logarithmic space to our data is shown as a dark-yellow line with 1σ excursions by the yellow shaded area; in the lower panels, the dashed dark-yellow line reproduces the 250 pc best fit shown in the upper panel. The trends seen in our data follows the predictions of Hu et al. (2022), in terms of excursion, but we find a steeper slope and an overall higher normalization. We attribute this to the theoretical W10 not being the exact same quantity as observed ICO, so we approximate W10 as ICO, which is a better approximation at high ICO, when XCO is low, but which is far from true at low ICO, when XCO is high. See text for more details. |
The best-fit parameters for XCO estimated from the trends with AV and τV are similar, and also show a comparable mean dispersion. The slope and intercept of the 250 pc resolution data differ (at a ∼2σ level) from those of the 40 pc fits, with the larger resolution data having flatter slope and a larger intercept. We expect these relations to be accurate for galaxies of around this metallicity, 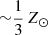 , but for higher and lower abundances, and different resolutions, more data are needed to establish similar empirical relations.
, but for higher and lower abundances, and different resolutions, more data are needed to establish similar empirical relations.
Narayanan et al. (2012) examined the dependence of XCO on metallicities, gas temperatures, and velocity dispersion of the clouds. Using post-processing of the simulated galaxies by Narayanan et al. (2011) to determine the physical and chemical state of the molecular gas, Narayanan et al. (2012) also find that XCO is well correlated with ICO, and is a function of physical conditions within the clouds. They find a simple power-law dependence of XCO on ICO and metallicity (shown as dot-dashed lines in Fig. 13), with an ICO power-law index (slope) of −0.32. Our observations are inconsistent with this slope, as it is significantly lower than the power-law index of −0.7 (40 pc) found in our data (Eq. (18)); the −0.5 slope of the 250 pc data is somewhat more consistent with the Narayanan et al. result, although still ≳2σ steeper.
To study CO emission at pc-scale resolutions, and measure XCO, Gong et al. (2018, 2020) conducted solar-metallicity magneto-hydrodynamic galactic disk simulations with post-processing that includes a chemical network and radiative transfer. Their analysis finds a slight anticorrelation between XCO and ICO, but with a very shallow power-law slope of −0.011 ± 0.005. Such a shallow slope is comparable to that of −0.05 found empirically by Remy et al. (2017) for clouds in the MW anti-center, but much flatter than the well-defined dependence for our low-metallicity starbursts.
Recent work by Hu et al. (2022), based on hydrodynamical simulations, chemistry, and radiative transfer, predict that XCO depends not only on metallicity but also on the spatial resolution of the maps and on the intensity of the emission line ICO. In Fig. 13, we have reproduced their 32 pc and 125 pc curves for Z⊙ (dashed curves) and 0.3 Z⊙ (solid ones) and their kpc-resolution trend that is valid for all metallicities. Our best-fit power-law slope of ∼ − 0.5 for 250 pc resolution is not far from their value of −0.43 (valid at 1 kpc for roughly all metallicities). At higher resolution, the individual trends found by Hu et al. (2022) for solar and 0.3 Z⊙ metallicities with region sizes from 32 pc to 125 pc (shown by brown curves in Fig. 13) show similar slopes, somewhat shallower than what we measure. Nevertheless, the agreement between our observations and the predictions of Hu et al. (2022) is reasonably good especially at high ICO.
Because of the expectation of more CO-dark gas in larger beams and at low metallicity, it is somewhat surprising that the Hu et al. simulations find that XCO is smaller with increasing beam size and decreasing metallicity. This can be understood because of the distinction between the theoretical W10 in Hu et al. (2022) and the observed quantity ICO. The cosmic microwave background (CMB) temperature, TBG, must be subtracted to calibrate observed antenna temperature, ICO; thus ICO will be identically 0 for excitation temperature Tex = 2.73 K, while W10 is only zero when NCO is zero, whatever Tex. This implies that their CO-dark gas radiates even at low H2 density, but in the observed signal ICO, it does not. Their conclusion therefore is expected to underestimate the amount of CO-dark gas.
The results of Hu et al. (2022) suggest that observed velocity-integrated TB below ∼10 K km s−1 are optically thin, and thus directly trace CO column density NCO (for NCO ≲ 1016 cm−2). This would imply that virtually all our observations are optically thin since there are very few resolution elements brighter than this limit. Most of the variation of XCO is expected to occur in the optically thin regime, as it is regulated by CO abundance and its formation by the transition from atomic carbon. Our observations are apparently consistent with these expectations, since over a roughly 3 orders of magnitude change in ICO, XCO also varies by a similar factor. Nevertheless, at the lowest ICO (lowest column densities), at both the 250 pc and 40 pc resolutions XCO exceeds by a factor of 10 or so the predictions of the Hu et al. simulations. Also, the difference we find between 250 pc and 40 pc resolution seems not to be a vertical shift, but rather a continuation to lower surface brightnesses as shown in Fig. 13. Since our targets are all at roughly the same 1/3 Z⊙ abundance, we are unable to test observational variation with metallicity. In any case, overall, our observations agree with Hu et al. (2022) that XCO is a multi-variate function of three observables, ICO, metallicity, and beam size.
7. Discussion and conclusions
Perhaps the most significant caveat in our methodology is the assumption of a single DGR across each of the galaxies, independently of spatial scale. Rigorously speaking, XCO and the DGR should be measured independently within each spatial element, as done by Sandstrom et al. (2013) on ∼kpc scales. In the study of the SMC by Bolatto et al. (2011), on ∼200 pc scales, the DGR varies by ∼0.4 dex along the SMC Bar, the Wing, and within the star-forming regions N83/N84. The assumption of a constant DGR is intimately related to our estimate of XCO, at least where CO emission dominates over HI. If we assume a constant metallicity-dependent value for XCO, as shown in the right panel of Fig. 8, we infer decreasing DGRs toward higher dust column densities. This effect may be real, but for our targets, with relatively few 250 pc resolution elements, it is impossible to assess spatial variations in the DGR, and disentangle them from variations in XCO.
7.1. Additional considerations
Putting this caveat aside, our analysis (Figs. 8 and 12) suggests that XCO is not correlated with either dust optical depth (τ160) or visual extinction/optical depth (AV, τV). This would be in disagreement with the individual cloud models by Glover & Mac Low (2011) and Shetty et al. (2011) who find a threshold effect for AV ≲1 mag. However, our observations do not resolve individual clouds, so that the discrepancy could be simply a question of spatial resolution. As pointed out by Gong et al. (2018), a resolution of ≲2 pc is necessary to resolve the average XCO within molecular clouds for conditions similar to the solar neighborhood; at lower metallicity, given the small ∼ pc scales, possibly even better resolution would be required.
Various recent simulations find that XCO is related to ICO and also to spatial scale, that is to say the region over which the parameters are averaged (e.g., Gong et al. 2018, 2020; Hu et al. 2022); observationally, spatial scale corresponds to beam size, or in our case the scale imposed by rebinning. We would argue that these parameters, ICO and spatial scale, are partially dependent, as shown in Fig. 13; relative to the 40 pc data, the data at 250 pc extend to fainter CO emission, but do not reach the brighter CO emission. It is very difficult to achieve high values of ICO with large beams as can also be appreciated by the comparison of Figs. 7 and 11.
Moreover, as might be intuitively expected, the fraction of CO-faint or dark gas is expected to increase with increasing beam size (Gong et al. 2018; Hu et al. 2022). Part of this depends on the ICO lower limit (imposed on the simulations, or observationally by signal-to-noise), and part is due to the erosion of the CO-emitting volumes by photodissociation. Photodissociation results in regions that are dominated by carbon in atomic or ionized phases, C I and CII, rather than CO, and these regions can be much more extended than the CO emission.
7.2. Summary
We have derived XCO in three low-metallicity starbursts, NGC 625, NGC 1705, and NGC 5253, using ALMA 12-m data at ∼40 pc resolution and ACA observations at ∼250 pc resolution, together with a dust-based method to infer NH2. Our work can be summarized as follows:
-
We fit the flux in Herschel PACS maps to two-temperature MBBs in order to quantify dust optical depth τ160, and compare it with HI maps and CO maps measured with ACA, all rebinned to ∼250 pc resolution.
-
By approximating the trends of HI and CO versus τ160 with linear functions and ones that reflect radiative transfer, we have quantified the DGR for each galaxy and the level at which HI is converted to H2. This makes it possible to estimate XCO at 250 pc resolution and compare it to what would be expected from global metallicity estimates for XCO. We find that the XCO values at 250 pc resolution can be as much as an order of magnitude larger than what would be expected from metallicity trends. There is also large scatter implying, possibly, spatial variation of XCO at this resolution.
-
At ∼40 pc resolution, roughly the native 12-m ALMA beam, we compare CO measured with the ALMA 12-m array and AV, estimated from the VLT/MUSE maps of the Balmer decrement. We eschew the assumption of AV as a foreground screen, and instead infer τV from AV by assuming that the extinguishing dust is well mixed with the ionized gas. Overall, this turns out to be the better assumption, as supported by the closer agreement of our data with the Galactic GMCs (see Fig. 11). By fitting the CO versus AV or τV trends, we have been able to identify in our data an AV threshold for CO emission of ∼0.1 mag for all three galaxies. This is significantly smaller than the ∼1 mag AV threshold found in simulations (e.g., Glover & Clark 2016) or observations of MW molecular clouds (e.g., Pineda et al. 2008).
-
Incorporating the DGR measured at 250 pc resolution, and the AV transition from HI to H2 at high dust optical depths
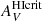 , we are able to infer XCO on 40 pc scales. Results are generally consistent with the expectations from a global metallicity-dependence of XCO, except for NGC 625 which shows values typically encountered in environments closer to solar metallicity. This almost certainly stems from the higher
, we are able to infer XCO on 40 pc scales. Results are generally consistent with the expectations from a global metallicity-dependence of XCO, except for NGC 625 which shows values typically encountered in environments closer to solar metallicity. This almost certainly stems from the higher 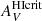 found for this galaxy (∼ 0.9 mag relative to ∼ 0.2–0.3 mag), and when we estimate XCO using these lower values also for NGC 625, XCO becomes consistent with metallicity expectations. As for the 250 pc XCO analysis, there is large scatter.
found for this galaxy (∼ 0.9 mag relative to ∼ 0.2–0.3 mag), and when we estimate XCO using these lower values also for NGC 625, XCO becomes consistent with metallicity expectations. As for the 250 pc XCO analysis, there is large scatter. -
Finally, we compare XCO to CO brightness temperature ICO, predicted by simulations to be closely related. Figure 13 shows that the two quantities are highly anticorrelated, with power-law slopes steeper than those found by the simulations of Narayanan et al. (2012) and Gong et al. (2018), although possibly consistent with the slope of ∼ − 0.4 found by Hu et al. (2022) across a range of resolutions. Relative to Narayanan et al. (2012) and Hu et al. (2022), because of the difference in power-slopes between the data and the simulations, the data show a higher normalization of the relation between XCO and ICO for faint CO emission levels. Despite these differences in details, our observations confirm that XCO depends not only on metallicity, but, also on beam size, and CO surface brightness ICO. Such behavior can be attributed to the increasing fraction of CO-dark H2 gas with lower spatial resolution (larger beams) and lower surface-brightness emission.
Our analysis is limited to three low-metallicity starbursts all of the same metallicity, ∼0.3 Z⊙. Thus, we are sampling only a narrow range of subsolar metal abundance. Future work would profit from a broader spread in metallicities and spatial resolution, and inclusion of metal-poor dwarf galaxies that are forming stars more quiescently than the starbursts studied here.
For all statistical analysis, we rely on the R statistical package: R Core Team (2018), R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria (https://www.R-project.org/).
Acknowledgments
We would like to thank the referee for thoughtful, constructive comments that greatly improved the paper. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00219.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST, and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work was partly done using GNU Astronomy Utilities (Gnuastro, http://www.ascl.net/1801.009) version 0.15. Work on Gnuastro has been funded by the Japanese Ministry of Education, Culture, Sports, Science, and Technology (MEXT) scholarship and its Grant-in-Aid for Scientific Research (21244012, 24253003), the European Research Council (ERC) advanced grant 339659-MUSICOS, European Union’s Horizon 2020 research and innovation programme under Marie Sklodowska-Curie grant agreement No 721463 to the SUNDIAL ITN, and from the Spanish Ministry of Economy and Competitiveness (MINECO) under grant number AYA2016-76219-P. SGB acknowledges support from the research project PID2019-106027GA-C44 of the Spanish Ministerio de Ciencia e Innovación, and GV acknowledges support from ANID program FONDECYT Postdoctorado 3200802.
References
- Accurso, G., Saintonge, A., Catinella, B., et al. 2017, MNRAS, 470, 4750 [NASA ADS] [Google Scholar]
- Akhlaghi, M. 2018, Astrophysics Source Code Library [record ascl:1801.009] [Google Scholar]
- Altintas, I., Barney, O., Cheng, Z., et al. 2006, J. Phys. Conf. Ser., 46, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [Google Scholar]
- Annibali, F., Tosi, M., Monelli, M., et al. 2009, AJ, 138, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Annibali, F., Tosi, M., Pasquali, A., et al. 2015, AJ, 150, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, T. A., Roueff, E., Viti, S., & Williams, D. A. 2006, MNRAS, 371, 1865 [NASA ADS] [CrossRef] [Google Scholar]
- Berg, D. A., Skillman, E. D., Marble, A. R., et al. 2012, ApJ, 754, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Billett, O. H., Hunter, D. A., & Elmegreen, B. G. 2002, AJ, 123, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Bisbas, T. G., Tan, J. C., & Tanaka, K. E. I. 2021, MNRAS, 502, 2701 [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [Google Scholar]
- Bolatto, A. D., Jackson, J. M., & Ingalls, J. G. 1999, ApJ, 513, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Rosolowsky, E., Walter, F., & Blitz, L. 2008, ApJ, 686, 948 [NASA ADS] [CrossRef] [Google Scholar]
- Bolatto, A. D., Leroy, A. K., Jameson, K., et al. 2011, ApJ, 741, 12 [CrossRef] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
- Boquien, M., Boselli, A., Buat, V., et al. 2013, A&A, 554, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Meurer, G. R., Bohlin, R. C., et al. 1997, AJ, 114, 1834 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Johnson, K. E., Adamo, A., et al. 2015, ApJ, 811, 75 [CrossRef] [Google Scholar]
- Cannon, J. M., Dohm-Palmer, R. C., Skillman, E. D., et al. 2003, AJ, 126, 2806 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., McClure-Griffiths, N. M., Skillman, E. D., & Côté, S. 2004, ApJ, 607, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., Skillman, E. D., Sembach, K. R., & Bomans, D. J. 2005, ApJ, 618, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Cannon, J. M., Smith, J.-D. T., Walter, F., et al. 2006, ApJ, 647, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Casasola, V., Bianchi, S., Magrini, L., et al. 2022, A&A, 668, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cignoni, M., Sacchi, E., Aloisi, A., et al. 2018, ApJ, 856, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Cignoni, M., Sacchi, E., Tosi, M., et al. 2019, ApJ, 887, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2014, A&A, 564, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Côté, S., Carignan, C., & Freeman, K. C. 2000, AJ, 120, 3027 [CrossRef] [Google Scholar]
- Cresci, G., Vanzi, L., & Sauvage, M. 2005, A&A, 433, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croxall, K. V., van Zee, L., Lee, H., et al. 2009, ApJ, 705, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Di Teodoro, E. M., & Fraternali, F. 2015, MNRAS, 451, 3021 [Google Scholar]
- Disney, M., Davies, J., & Phillipps, S. 1989, MNRAS, 239, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, E. C., de Blok, W. J. G., & Kraan-Korteweg, R. C. 2013, MNRAS, 429, 2550 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feldmann, R., Gnedin, N. Y., & Kravtsov, A. V. 2012, ApJ, 747, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Freudling, W., Romaniello, M., Bramich, D. M., et al. 2013, A&A, 559, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galametz, M., Kennicutt, R. C., Albrecht, M., et al. 2012, MNRAS, 425, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2016, MNRAS, 456, 3596 [Google Scholar]
- Glover, S. C. O., & Mac Low, M. M. 2011, MNRAS, 412, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, M., Ostriker, E. C., & Wolfire, M. G. 2017, ApJ, 843, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Gong, M., Ostriker, E. C., & Kim, C.-G. 2018, ApJ, 858, 16 [Google Scholar]
- Gong, M., Ostriker, E. C., Kim, C.-G., & Kim, J.-G. 2020, ApJ, 903, 142 [CrossRef] [Google Scholar]
- Heckman, T. M., Sembach, K. R., Meurer, G. R., et al. 2001, ApJ, 554, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Hensley, B. S., & Draine, B. T. 2021, ApJ, 906, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, C.-Y., Schruba, A., Sternberg, A., & van Dishoeck, E. F. 2022, ApJ, 931, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., Baes, M., Fritz, J., et al. 2014, A&A, 565, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Draine, B. T., Bianchi, S., et al. 2015, A&A, 576, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Weiß, A., Henkel, C., et al. 2017, A&A, 606, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Tortora, C., Ginolfi, M., & Schneider, R. 2020, A&A, 643, A180 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Imara, N., De Looze, I., Faesi, C. M., & Cormier, D. 2020, ApJ, 895, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Indebetouw, R., Brogan, C., Chen, C. H. R., et al. 2013, ApJ, 774, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [Google Scholar]
- Kirkpatrick, A., Calzetti, D., Kennicutt, R., et al. 2014, ApJ, 789, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Skillman, E. D. 2008, AJ, 135, 527 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., Skillman, E. D., Roy, J.-R., Walsh, J. R., & Rosa, M. R. 1997, ApJ, 477, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., McKee, C. F., & Tumlinson, J. 2009, ApJ, 693, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C., Leroy, A. K., Schnee, S., et al. 2015, MNRAS, 450, 2708 [CrossRef] [Google Scholar]
- Lee, C., Leroy, A. K., Bolatto, A. D., et al. 2018, MNRAS, 474, 4672 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014a, A&A, 566, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelli, F., Verheijen, M., & Fraternali, F. 2014b, MNRAS, 445, 1694 [Google Scholar]
- Leroy, A. K., Bolatto, A., Bot, C., et al. 2009, ApJ, 702, 352 [Google Scholar]
- Leroy, A. K., Lee, C., Schruba, A., et al. 2013, ApJ, 769, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2006, A&A, 454, 781 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- López-Sánchez, Á. R., Koribalski, B. S., van Eymeren, J., et al. 2012, MNRAS, 419, 1051 [CrossRef] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Marasco, A., Belfiore, F., Cresci, G., et al. 2023, A&A, 670, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, F., Förster Schreiber, N. M., Eisenhauer, F., & Lutz, D. 2012, A&A, 547, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2010, ApJ, 721, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Misselt, K. A., Gordon, K. D., Clayton, G. C., & Wolff, M. J. 2001, ApJ, 551, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Miura, R. E., Espada, D., Hirota, A., et al. 2018, ApJ, 864, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Monreal-Ibero, A., Walsh, J. R., Iglesias-Páramo, J., et al. 2017, A&A, 603, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Narayanan, D., Krumholz, M., Ostriker, E. C., & Hernquist, L. 2011, MNRAS, 418, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Krumholz, M. R., Ostriker, E. C., & Hernquist, L. 2012, MNRAS, 421, 3127 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., & Panagia, N. 1984, ApJ, 287, 228 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connell, R. W., Gallagher, J. S. I., & Hunter, D. A., 1994, ApJ, 433, 65 [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Ott, S. 2010, ASP Conf. Ser., 434, 139 [Google Scholar]
- Pak, S., Jaffe, D. T., van Dishoeck, E. F., Johansson, L. E. B., & Booth, R. S. 1998, ApJ, 498, 735 [NASA ADS] [CrossRef] [Google Scholar]
- Papadopoulos, P. P., Thi, W. F., & Viti, S. 2004, MNRAS, 351, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Zinchenko, I. A. 2015, MNRAS, 450, 3254 [CrossRef] [Google Scholar]
- Pineda, J. E., Caselli, P., & Goodman, A. A. 2008, ApJ, 679, 481 [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Remy, Q., Grenier, I. A., Marshall, D. J., & Casandjian, J. M. 2017, A&A, 601, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [Google Scholar]
- Rubio, M., Lequeux, J., & Boulanger, F. 1993, A&A, 271, 9 [NASA ADS] [Google Scholar]
- Rubio, M., Elmegreen, B. G., Hunter, D. A., et al. 2015, Nature, 525, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Sabbi, E., Calzetti, D., Ubeda, L., et al. 2018, ApJS, 235, 23 [Google Scholar]
- Sanders, D. B., Solomon, P. M., & Scoville, N. Z. 1984, ApJ, 276, 182 [CrossRef] [Google Scholar]
- Sandstrom, K. M., Leroy, A. K., Walter, F., et al. 2013, ApJ, 777, 5 [Google Scholar]
- Schaerer, D., Contini, T., Kunth, D., & Meynet, G. 1997, ApJ, 481, L75 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Kruijssen, J. M. D., et al. 2017, ApJ, 835, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Shetty, R., Glover, S. C., Dullemond, C. P., & Klessen, R. S. 2011, MNRAS, 412, 1686 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Wang, J., Zhang, Z.-Y., et al. 2020, ApJ, 892, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., Côté, S., & Miller, B. W. 2003a, AJ, 125, 593 [NASA ADS] [CrossRef] [Google Scholar]
- Skillman, E. D., Côté, S., & Miller, B. W. 2003b, AJ, 125, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Le Petit, F., Roueff, E., & Le Bourlot, J. 2014, ApJ, 790, 10 [CrossRef] [Google Scholar]
- Tokuda, K., Kondo, H., Ohno, T., et al. 2021, ApJ, 922, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Tosi, M., Sabbi, E., Bellazzini, M., et al. 2001, AJ, 122, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., & Hurt, R. L. 1997, ApJ, 474, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., & Ho, P. T. P. 2000, ApJ, 532, L109 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Beck, S. C., Benford, D. J., et al. 2015, Nature, 519, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, J. L., Consiglio, S. M., Beck, S. C., et al. 2017, ApJ, 846, 73 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Vázquez, G. A., Leitherer, C., Heckman, T. M., et al. 2004, ApJ, 600, 162 [CrossRef] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weilbacher, P. M., Palsa, R., Streicher, O., et al. 2020, A&A, 641, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Westmoquette, M. S., James, B., Monreal-Ibero, A., & Walsh, J. R. 2013, A&A, 550, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whelan, D. G., Johnson, K. E., Whitney, B. A., Indebetouw, R., & Wood, K. 2011, ApJ, 729, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Wiklind, T., & Henkel, C. 1989, A&A, 225, 1 [NASA ADS] [Google Scholar]
- Wilson, C. D., Rangwala, N., Glenn, J., et al. 2014, ApJ, 789, L36 [Google Scholar]
- Witt, A. N., & Gordon, K. D. 1996, ApJ, 463, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Witt, A. N., & Gordon, K. D. 2000, ApJ, 528, 799 [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & Tielens, A. G. G. M. 1993, ApJ, 402, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [Google Scholar]
Appendix A: Details of the fits to the PACS data to derive τ160
The 160 μm optical depths τ160 of the two approaches (namely modified single-temperature blackbodies, MBB, and modified two-temperature blackbodies, MBB-2T) are compared in Fig. A.1. The scatter of the comparison (with imposed γ ≥ 0) is ∼0.13 dex, with τ160(MBB-T2) larger than τ160(MBB), as shown by the nonunit power-law slope and positive intercept of the best (robust) fit.
 |
Fig. A.1. τ160 from MBB-T2 fits plotted against MBB τ160. log τ160(MBB − T2) = (1.073 ± 0.010) log τ160(MBB)+(0.46 ± 0.05) The scatter of the comparison is ∼0.13 dex; the shaded region denotes ± 1σ relative to the best fit. In general, τ160(MBB-T2) is larger than τ160(MBB), as shown by the nonunit power-law slope and positive intercept. |
The distributions of the rms (calculated as the root-mean-square difference in log10 space between the model and the data) of the two fits are reported in Fig. A.2. Given that the expected uncertainty in the individual PACS photometry is ∼10%, the rms values of both MBB and MBB-T2 fits are quite good, and, except for NGC 1705, well within the expected error. However, the MBB-T2 fits are overall superior to MBB, possibly due to the extra fitted parameter and the consequent zero degrees of freedom. Three regions in both NGC 625 and NGC 5253 are not included in Fig. A.2, because of rms > 0.5 due to the very low 70 μm fluxes and the consequent poor fits.
 |
Fig. A.2. Distributions of rms values from MBB (left) and MBB-T2 (right) fits. Median values for each galaxy are shown by vertical dashed lines. The rms values of the MBB-T2 fits is generally excellent, possibly due to the extra fitted parameter and the consequent zero degrees of freedom. There are 3 regions each in NGC 625 and NGC 5253 not included here because their rms values exceed 0.5 dex. |
The overall γ distribution (restricted to 0 ≤ γ ≤ 1) is shown in Fig. A.3. There are (45, 0, 33) fits for NGC (625, 1705, 5253), respectively, that would have preferred either γ < 0 (58%, 0, 37%). The median γ = 0.0 for NGC 625 is associated with the relatively high fraction (45/77 = 58%) of regions that would have have been best fit with these anomalous γ values.
 |
Fig. A.3. Distribution of fitted γ from MBB-T2 fits. The vertical dashed lines show the median fraction of IR emission due to the warmer component: (0.00, 0.14, 0.08) for NGC (625, 1705, 5253). |
All Tables
All Figures
 |
Fig. 1. CO spectra of the target galaxies within an aperture containing the totality of CO emission regions plotted against velocity, where Vsys is given in Table 2. The full-width at zero intensity (FWZI) corresponds to the vertical dotted lines (see Table 2, Col. (2)). The 12-m spectra are shown in blue, and the ACA in red. In NGC 5253, these are both continuum-subtracted spectra. More details are given in the text. |
| In the text | |
 |
Fig. 2. Contours of 12CO(1–0) (12-m) overlaid on HST F555W images (left panels), and MUSE E(B − V) maps (right). The 12CO(1–0) contour levels correspond to (0.01, 0.025, 0.05, 0.1, 0.2, 0.3, 0.4, 0.450, 0.750) Jy km s−1 beam−1 for NGC 625; (0.01, 0.025, 0.05, 0.1, 0.2, 0.3) Jy km s−1 beam−1 for NGC 1705; (0.01, 0.025, 0.05, 0.1, 0.15, 0.25, 0.4, 0.5, 0.75, 1.0, 1.5) Jy km s−1 beam−1 for NGC 5253. Also marked A–D in the left panels are the HII regions identified with radio continuum maps of NGC 625 by Cannon et al. (2004); the dust clouds and SSC in NGC 1705 identified from Spitzer observations (Cannon et al. 2006); and the unusual CO+dust cloud “D1” in NGC 5253 that coincides with the brightest, highly dust embedded SSC (Turner et al. 2017). The ALMA 12-m beam is shown in the lower-left corner of the left panels. |
| In the text | |
 |
Fig. 3. Color RGB images for NGC 625 (left panel), NGC 1705 (middle), and NGC 5253 (right) with Herschel/PACS-R as red, ACA 12CO(1–0) as green, and HI as blue; North is up, East is to the left. The image dimensions are 130 × 105 arcsec2 for NGC 625, NGC 1705, and 120 × 105 arcsec2 for NGC 5253. All observations have roughly spatial resolutions of ∼250 pc (see text for more details). The white color indicates where HI, CO, and dust are cospatial. As in Fig. 2, also indicated are the HII regions A–D of NGC 625 (Cannon et al. 2004); the dust clouds and SSC in NGC 1705 (Cannon et al. 2006); and the unusual CO+dust cloud “D1” in NGC 5253 that coincides with the brightest, highly dust embedded SSC (Turner et al. 2017). |
| In the text | |
 |
Fig. 4. PACS flux ratios I100/I160 versus I70/I160. The PACS data have been rebinned to ∼250 pc resolution in order to match the HI and ACA CO maps. Heavy curves show the medians in I100/I160 bins for each galaxy, and the shaded regions indicate 1σ standard deviations. Also shown are the model MBB-T2 flux ratios with γ = 0.14 (the median value for NGC 1705), indicated by the heavy black long-dashed curve. The IR ratios from two MBB models (γ = 0) are illustrated as a long-dashed (gray) curve with β = 1 (virtually indistinguishable from the MBB-T2 curve), and a short-dashed (black) curve for β = 2. The dot-dashed curve corresponds to the best fit polynomial for the SMC by Leroy et al. (2009). The horizontal lines illustrate the I100/I160 ratios that would be expected for Tdust = 20 K, 25 K, and 30 K. The line ratios for NGC 625 and NGC 5253 are fairly well approximated by MBBs or MBB-T2 fits, while the polynomial fit by Leroy et al. (2009) is a better approximation for NGC 1705. This fit is roughly equivalent to assuming that only half of the observed 70 μm emission comes from large, “classical” grains, with the other half originating from stochastic heating of small grains. |
| In the text | |
 |
Fig. 5. Representative fits of Eq. (3) with significant γ values to illustrate the importance of two temperatures in the fitting function. The long-dashed red curves show the MBB with Tcool, the dot-dashed blue curves Twarm, and the gray (solid) ones the overall best fit. The (heavy) purple long-dashed curve corresponds to a single-temperature MBB with Tdust, normalized to the 160 μm data point. For γ > 0, the simple MBB is clearly missing the contribution toward higher frequencies caused by warm dust at Twarm. |
| In the text | |
 |
Fig. 6. Dust temperatures plotted against τ160 for the 250 pc regions within the target galaxies: in the left panel best-fit Tcool and in the right panel effective temperature Tdust. The medians binned in log10(τ160) are shown as heavy lines characterized by different colors, with the 1σ variation by shaded regions. The horizontal dashed lines correspond to the overall Tcool galaxy medians (left panel) and Tdust (right). Only in the case of NGC 5253 does the effective temperature Tdust present a trend with τ160, in the sense that more optically thick regions show higher temperatures. |
| In the text | |
 |
Fig. 7. Atomic gas column density NHI versus 160 μm optical depth τ160 (left panel) and CO ACA (velocity-integrated) TB versus τ160 (right). Only regions with S/N ≥ 3 are shown (and included in the fits). The best-fit linear relations (Eq. (6)) for τ160 as a function of NHI are shown as heavy curves (in log space), and only consider the points with 1019 ≤ NHI ≤ 1021 cm−2 because of the need to consider the regions dominated by HI. The lighter curves show the fit to Eq. (5) as described in the text, and are used to determine |
| In the text | |
 |
Fig. 8. Left panel: Inferred XCO conversion factor from Eq. (8) as a function of τ160. Also shown are values that would be estimated from the metallicity dependence found by Hunt et al. (2020) as XCO ∝ Z−1.55 (see also Accurso et al. 2017). Heavy curves show the medians in log10(τ160) for each galaxy (except for NGC 1705 for which there are too few points), and the shaded regions indicate 1σ standard deviations. Right panel: GDR (here we are using the inverse of δDGR) that would be inferred assuming the metallicity dependence of the XCO conversion factor found by Hunt et al. (2020). The range of GDRs estimated by different methods is shown as the hatched horizontal strips. As in the left panel, heavy curves show the medians, and shaded regions the 1σ standard deviation. |
| In the text | |
 |
Fig. 9. Left panel: Idealized cartoon illustrating the mixed configuration of dust, stars, and gas. Right panel: The same but with the foreground screen configuration. The amount of dust in the screen in the right panel is assumed to be roughly half of the total dust shown in the left panel. While the infrared τ160 penetrates the full dust column along the line of sight, the optical depth inferred from the Balmer decrement only captures the dust between the stars that ionize the gas and the observer. |
| In the text | |
 |
Fig. 10. Relations between AV and τV. Left panel: τV inferred from Eq. (11) for the targets plotted against log10( |
| In the text | |
 |
Fig. 11. CO velocity-integrated TBICO plotted versus (logarithm) visual extinction AV (left panel) and (logarithm) visual dust optical depth τV (right). The top axes show the scale for τ160 assuming that AV/τ160 = 2180, as described in Sect. 5.3. The light curves show fits to Eq. (12). Heavy curves show the medians for each galaxy binned in log10(AV), (left), log10(τV), (right), with the shaded regions corresponding to ±1σ deviations. Also shown in both panels are the MW GMCs studied by Lee et al. (2018), with AV inferred from Planck; see Sect. 5 for more details. |
| In the text | |
 |
Fig. 12. XCO estimated from Eq. (14) is plotted as a function of AV in the left panel, and of τV in the right. As in Fig. 8, we include as horizontal dashed lines, XCO that would be estimated from the metallicity dependence found by Hunt et al. (2020), as XCO ∝ Z−1.55. The MW XCO = 2.3 × 1020 cm−2/K km s−1 is also given together with the uncertainties. Heavy curves show the medians for each galaxy binned in |
| In the text | |
 |
Fig. 13. XCO estimated from Eq. (8) versus ICO in the top panel (250 pc resolution); XCO from Eq. (14) in the middle (40 pc resolution); and from Eq. (15) in the lower (40 pc resolution). Also shown as dark-gray dot-dashed lines are the predictions from Narayanan et al. (2012) for the different metallicities of our targets. The 1 kpc trend from Hu et al. (2022), valid for all metallicities, is shown as a light-gray solid line (labeled “1 kpc”). The brown solid (dashed) curves correspond to 0.3 Z⊙ (Z⊙) metallicities at 125 pc resolution (top panel) and at 32 pc (middle and lower ones). The 0.3 Z⊙ curves are the best approximation to the metallicities of our target starbursts. The robust fit in logarithmic space to our data is shown as a dark-yellow line with 1σ excursions by the yellow shaded area; in the lower panels, the dashed dark-yellow line reproduces the 250 pc best fit shown in the upper panel. The trends seen in our data follows the predictions of Hu et al. (2022), in terms of excursion, but we find a steeper slope and an overall higher normalization. We attribute this to the theoretical W10 not being the exact same quantity as observed ICO, so we approximate W10 as ICO, which is a better approximation at high ICO, when XCO is low, but which is far from true at low ICO, when XCO is high. See text for more details. |
| In the text | |
 |
Fig. A.1. τ160 from MBB-T2 fits plotted against MBB τ160. log τ160(MBB − T2) = (1.073 ± 0.010) log τ160(MBB)+(0.46 ± 0.05) The scatter of the comparison is ∼0.13 dex; the shaded region denotes ± 1σ relative to the best fit. In general, τ160(MBB-T2) is larger than τ160(MBB), as shown by the nonunit power-law slope and positive intercept. |
| In the text | |
 |
Fig. A.2. Distributions of rms values from MBB (left) and MBB-T2 (right) fits. Median values for each galaxy are shown by vertical dashed lines. The rms values of the MBB-T2 fits is generally excellent, possibly due to the extra fitted parameter and the consequent zero degrees of freedom. There are 3 regions each in NGC 625 and NGC 5253 not included here because their rms values exceed 0.5 dex. |
| In the text | |
 |
Fig. A.3. Distribution of fitted γ from MBB-T2 fits. The vertical dashed lines show the median fraction of IR emission due to the warmer component: (0.00, 0.14, 0.08) for NGC (625, 1705, 5253). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



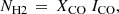
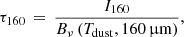
![$$ \begin{aligned} I_\nu \,=\,\tau _{\rm 160}\ \left( \frac{2\,h\,\nu ^3}{c^2} \right) \left( \frac{\nu }{\nu _0} \right)\ \left[ \frac{1\ -\ \gamma }{e^{h \nu /k T_{\rm cool}} - 1} + \frac{\gamma }{e^{h \nu /k T_{\rm warm}} - 1} \right], \end{aligned} $$](/articles/aa/full_html/2023/07/aa45805-22/aa45805-22-eq34.gif)
![$$ \begin{aligned} T_{\rm dust} = [\,(1-\gamma ) + \gamma \,(1.5)^6\,]^{1/6}\ T_{\rm cool}. \end{aligned} $$](/articles/aa/full_html/2023/07/aa45805-22/aa45805-22-eq35.gif)
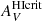
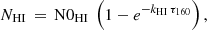
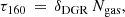
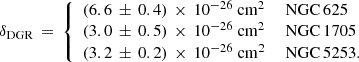
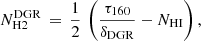
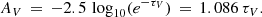
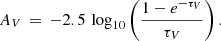
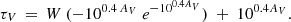
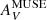
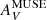
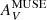
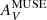
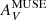
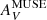
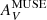
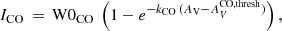
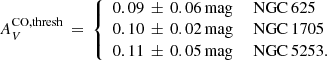
![$$ \begin{aligned} N_{\rm H2}^{\mathrm{A}_{\rm V}}\,=\,\frac{1}{2}\,\left( \frac{N_{\mathrm{H}}}{A_V} \right) \left[2\,A_V^{\mathrm{MUSE}} - A_V^{\mathrm{HIcrit}}\ \right] , \end{aligned} $$](/articles/aa/full_html/2023/07/aa45805-22/aa45805-22-eq75.gif)
![$$ \begin{aligned} N_{\rm H2}^{\tau _{\rm V}}\,=\,\frac{1}{2}\,\left( \frac{N_{\mathrm{H}}}{\tau _V} \right) \left[\tau _V - \tau _V^\mathrm{HIcrit} \ \right], \end{aligned} $$](/articles/aa/full_html/2023/07/aa45805-22/aa45805-22-eq81.gif)