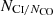EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A36 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A36
Number of page(s) 22
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202244564
Published online 27 March 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model.

Open access funding provided by Max Planck Society.

1. Introduction

Neutral atomic carbon (C0 or C I) is an important phase of carbon in the interstellar medium (ISM), alongside ionized carbon (C+ or C II) and carbon monoxide (CO). Its 3P state is split into three fine-structure levels. The 3P1 → 3P0 transition line at 492.16065 GHz, hereafter [C I](1−0), has an upper energy level of Eu = 23.620 K and a critical density of ncrit ∼ 1.0 × 103 cm−3 (at a temperature of 50 K)1, while the 3P2 → 3P1 transition line at 809.34197 GHz has Eu = 62.462 K and ncrit ∼ 3.4 × 103 cm−3. Therefore, they are easily excited in the cold ISM environment. Given the high abundance of carbon in the ISM, C I, CO, and C II are the most powerful cold ISM tracers and are the most widely used tools to probe cold ISM properties and, hence, galaxy evolution at cosmological distances.

The interstellar C I is produced from the photodissociation of CO molecules by UV photons and the recombination of C II, both taking place in photodissociation regions (PDRs; Langer 1976; de Jong et al. 1980; Tielens & Hollenbach 1985a,b; van Dishoeck & Black 1986, 1988; Sternberg & Dalgarno 1989, 1995; Hollenbach et al. 1991; Hollenbach & Tielens 1999; Kaufman et al. 1999; Wolfire et al. 2010; Madden et al. 2020; Bisbas et al. 2021; also see reviews by Genzel & Stutzki 1989; Jaffe et al. 1985; Hollenbach & Tielens 1997; Wolfire et al. 2022). In the simple plane-parallel (i.e., 1D) PDR model, C I exists in a layer where UV photons can penetrate through the molecular gas but are not able to maintain a high carbon ionizing rate. Such a layer is suggested to have an intermediate gas surface density (NH2 ∼ 1 − 4 × 1020 cm−2), fairly cold temperature (10 to a few tens K), and moderate visual extinction (AV ∼ 1 − 4). Then, CO molecules dominate the more shielded interior of this layer and C II dominates the exterior. Hydrogen molecules are gradually photodissociated to atoms across this layer (AV ∼ 0.1 − 4). This plane-parallel scenario qualitatively explains the layered structure of the Orion Bar PDR in our Galaxy on sub-pc scales (e.g., Genzel & Stutzki 1989; Tielens et al. 1993; Tauber et al. 1994; Hogerheijde et al. 1995; Hollenbach & Tielens 1999; Goicoechea et al. 2016), and the ρ Ophiuchi A PDR in a recent study with an unprecedented resolution of 360 AU (Yamagishi et al. 2021), where the interplay between individual young, massive (O, B) stars and the ISM can be directly observed.

However, such simple models cannot fully explain molecular clouds. A large number of observations in Galactic molecular clouds, H II regions, and star-forming complexes have revealed a widespread C I distribution over most areas of molecular clouds on scales of a few up to ten pc, along with a relatively high C I fractional abundance even at a large AV depth, namely, > 10 mag (Phillips et al. 1980; Phillips & Huggins 1981; Wootten et al. 1982; Keene et al. 1985, 1987; Jaffe et al. 1985; Zmuidzinas et al. 1986, 1988; Genzel et al. 1988; Frerking et al. 1989; Plume et al. 1994, 1999; Gerin et al. 1998; Tatematsu et al. 1999; Ikeda et al. 1999, 2002; Yamamoto et al. 2001; Zhang et al. 2001; Kamegai et al. 2003; Oka et al. 2004; Izumi et al. 2021).

This observational evidence requires PDRs to be clumpy, in fact (Stutzki et al. 1988; Genzel et al. 1988; Burton et al. 1990; Meixner & Tielens 1993; Spaans & van Dishoeck 1997; Kramer et al. 2004, 2008; Pineda et al. 2008; Sun et al. 2008), with a volume-filling factor that is much lower than unity (e.g., ∼0.1 − 0.3; Stutzki et al. 1988). As a result, UV photons can penetrate through most of the cloud, except for the densest clumps. Therefore, the spatial co-existence of C I and low rotational transition (low-J) CO lines can be well explained by such an inter-clump medium inside the molecular clouds. Alternatively, cosmic rays (CRs) have also been proposed to be the reason for the C I-CO association as they can penetrate much deeper than UV photons into clouds and, thus, more uniformly dissociate CO molecules into C I inside clouds (Field et al. 1969; Padovani et al. 2009; Papadopoulos 2010; Ivlev et al. 2015; Papadopoulos et al. 2018).

The spatial distributions of C I and low-J CO emission are surprisingly similar, from molecular-cloud to Galactic scales (e.g., across the Galactic plane; Wright et al. 1991; Bennett et al. 1994; Oka et al. 2005; Burton et al. 2015) as well as in external galaxies with spatially resolved observations (e.g., Schilke et al. 1993; White et al. 1994; Harrison et al. 1995; Israel et al. 1995; Israel & Baas 2001, 2003; Zhang et al. 2014; Krips et al. 2016; Cicone et al. 2018; Crocker et al. 2019; Jiao et al. 2019; Miyamoto et al. 2018, 2021; Salak et al. 2019; Izumi et al. 2020; Saito et al. 2020; Michiyama et al. 2020, 2021). However, their line intensity ratio, RC I10/CO10 = I[C I](1−0)/ICO(1−0)2, does vary according to local ISM conditions – C I and CO fractional abundance (i.e., metallicity), excitation condition (e.g., excitation temperature Tex and optical depth τ), and UV and/or the CR radiation field. At individual molecular cloud scales, RC I10/CO10 (or column density ratio) seems to vary from ≳0.5 (or ≳0.2 for column density ratio) to < 0.1 with an increasing NH2 and AV, for instance, from the cloud surface or PDR front to the interior (e.g., Frerking et al. 1982; Genzel et al. 1988; Oka et al. 2004; Kramer et al. 2004, 2008; Mookerjea et al. 2006; Sun et al. 2008; Yamagishi et al. 2021).

At sub-galactic scales, when individual clouds are smoothed out, RC I10/CO10 is found to lie in a narrower range of ∼0.1 − 0.3. For example, across the Galactic plane, the ratio is found to change only slightly within a galactocentric radius of 3−7 kpc (∼0.08 − 0.12, overall mean = 0.105 ± 0.004; Oka et al. 2005); whereas in starburst galaxies such as M 82 and NGC 253, RC I10/CO10 or the [C I]/CO abundance ratio is a factor of 3 to 5 higher than the Galactic value (Schilke et al. 1993; White et al. 1994; Krips et al. 2016). Recent high-resolution (hundred pc scales) [C I](1−0) mapping studies in the nearby spiral galaxy M 83 (Miyamoto et al. 2021) and starburst galaxy IRAS F18293−3413 (Saito et al. 2020) reported tightly correlated [C I](1−0) and CO(1 − 0) emission, with scaling relations at hundreds of parsecs, equivalent to R C I 10 / CO 10 = 0.14 × ( L CO ( 1 − 0 ) ′ / 10 6.0 [ K km s − 1 pc 2 ] ) − 0.13 $ R_{\mathrm{C}\textsc{i}10/\mathrm{CO}10} = 0.14 \times (L^\prime_{\mathrm{CO}(1{-}0)}/10^{6.0}\,[\mathrm{K\,km\,s^{-1}\,pc^{2}}])^{-0.13} $ and R C I 10 / CO 10 = 0.21 × ( L CO ( 1 − 0 ) ′ / 10 6.8 [ K km s − 1 pc 2 ] ) + 0.54 $ R_{\mathrm{C}\textsc{i}10/\mathrm{CO}10} = 0.21 \times (L^\prime_{\mathrm{CO}(1{-}0)}/10^{6.8}\,[\mathrm{K\,km\,s^{-1}\,pc^{2}}])^{+0.54} $, respectively. The discrepant power-law indices reflect different trends in individual galaxies that are not fully understood.

Meanwhile, in the central area ≲100 pc of NGC 7469, close to the X-ray-luminous active galactic nucleus (AGN), RC I/CO is found to be substantially enhanced by a factor of > 10 (reaching RC I10/CO10 ≈ 1; Izumi et al. 2020; see also the Circinus Galaxy’s AGN with RC I10/CO32 ≈ 0.9 in Izumi et al. 2018). Furthermore, in the low-metallicity Large Magellanic Cloud (LMC) and Small Magellanic Cloud (SMC) environments, a factor of 1.5 − 3× higher RC I/CO values have been found (Bolatto et al. 2000a,b; see also other low-metallicity galaxies: Bolatto et al. 2000c; Hunt et al. 2017).

These studies indicate that RC I/CO is sensitive to ISM conditions among and within galaxies. However, previous extragalactic studies are mainly focused on starburst galaxies and bright galaxy centers. The manner in which RC I/CO behaves across the disks and spiral arms of typical star-forming galaxies is much less broadly explored. The question of whether C I can trace the so-called CO-dark molecular gas at a low gas density or metallicity is also still an open question. Understanding RC I/CO variation and quantifying the C I and CO excitation in extragalactic environments is now particularly important given the rapidly growing numbers and diverse galactic environments of C I line observations at cosmological distances (e.g., Weiß et al. 2003, 2005; Pety et al. 2004; Wagg et al. 2006; Walter et al. 2011; Danielson et al. 2011; Alaghband-Zadeh et al. 2013; Gullberg et al. 2016; Bothwell et al. 2017; Popping et al. 2017; Yang et al. 2017; Emonts et al. 2018; Valentino et al. 2018, 2020; Bourne et al. 2019; Nesvadba et al. 2019; Dannerbauer et al. 2019; Jin et al. 2019; Brisbin et al. 2019; Boogaard et al. 2020; Cortzen et al. 2020; Harrington et al. 2021; Dunne et al. 2021; Lee et al. 2021).

High-resolution mappings of C I and CO from disks and spiral arms of nearby galaxies are indispensable for understanding and quantifying the ISM C I and CO physics. In particular, we consider the following questions that need such observations: (1) whether C I and low-J CO have the same spatial distributions across galaxy disks; (2) how the RC I/CO line ratio varies across galaxy disks and among different local galaxies; (3) how we may reliably convert the RC I/CO line ratio into the C I and CO column density ratio – namely, by solving their radiation transfer equations and level population statistics and obtaining optical depths and excitation temperature.

Currently, high-resolution (hundreds of parsec scale) imaging and mapping of C I in nearby galaxies relies on radio telescopes at high altitudes, such as the Atacama Large Millimeter/submillimeter Array (ALMA), Atacama Submillimeter Telescope Experiment (ASTE, 10-m single-dish), and Atacama Pathfinder Experiment (APEX, 12-m single-dish). These observations are limited to the available weather conditions, corresponding to the high frequency of C I lines. Therefore, only a handful of galaxies have been imaged or mapped thus far, including: NGC 6240 by Cicone et al. (2018), Circinus Galaxy by Izumi et al. (2018), NGC 613 by Miyamoto et al. (2018), NGC 1808 by Salak et al. (2019), NGC 7469 by Izumi et al. (2020), IRAS F18293−3413 by Saito et al. (2020), NGC 6052 by Michiyama et al. (2020, C I undetected), 36 (U)LIRGs by Michiyama et al. (2021), M 83 by Miyamoto et al. (2021, mapped the center and northern part with ASTE), Arp 220 by Ueda et al. (2022), and NGC 1068 by Saito et al. (2022a,b). Nevertheless, all of these observations, except for M 83, targeted the centers of starburst, IR-luminous and/or AGN host galaxies. M 83 is the only typical star-forming main sequence galaxy having a high-quality C I mapping. However, its map is still limited to a quarter of its inner ∼3 kpc disk.

In this work, we present two new C I mapping observations with the ALMA Atacama Compact Array (or Morita Array; 7-m dish, hereafter ACA or 7m) in nearby spiral galaxies NGC 3627 and NGC 4321. Our observations are aimed at detecting C I in the disks and are thus much larger in area and deeper than previous C I maps. By further adding a starburst and an AGN-host galaxy from the literature into our analysis, we present a comprehensive study of the RC I10/CO21 line ratio (hereafter RC I/CO; ratios of other C I/CO transitions will be explicitly written otherwise) in nearby star-forming disk, starburst, and AGN environments. In order to quantify the C I and CO abundance ratio, we have further calculated the local thermodynamic equilibrium (LTE) and non-LTE radiative transfer of C I and CO under several representative ISM conditions. The results from this study could thus be one of the most comprehensive local benchmarks for understanding the C I and CO line ratio and abundance variations.

As the first in a planned series of papers, this work is organized as follows. Section 2 describes the sample selection, observations and data reduction. Section 3 presents the spatial distribution and variation of RC I/CO. Section 4 presents the analysis of C I and CO excitation and radiative transfer and thus the abundance (species column density) ratio. In Sect. 5, we discuss various topics relating to the [C I/CO] abundance variation, CRDR, XDR, and CO-dark gas. Finally, we conclude in Sect. 6. Our companion Paper II (Liu et al., in prep.) presents the detailed radiative transfer calculation, along with the C I and CO conversion factors and is related to the abundance calculation in this paper.

2. Targets and observations

2.1. Target selection

Our targets, NGC 3627 and NGC 4321, were selected from a joint sample of the PHANGS-ALMA CO(2−1) (Leroy et al. 2021a), PHANGS-HST (Lee et al. 2022), and PHANGS-MUSE (Emsellem et al. 2022) surveys, with CO line intensities and systemic velocities that are best suitable for ALMA Band 8 C I mapping.

The PHANGS-ALMA sample consists of 90 nearby star-forming galaxies initially selected at distances of 2 ≲ d/Mpc ≲ 23, with a stellar mass log(M⋆/M⊙) > 9.75, and which are not too inclined and which are visible to ALMA. They represent the typical star-forming main sequence galaxies in the local Universe. The PHANGS-HST sample (Lee et al. 2022) is a subsample of 38 PHANGS-ALMA galaxies, providing high-resolution stellar properties. The PHANGS-MUSE large program (Emsellem et al. 2022) targeted a subsample of 19 PHANGS-ALMA galaxies suitable for VLT/MUSE optical integral field unit (IFU) observations, achieving similar spatial coverage as in PHANGS-ALMA and providing rich nebular emission lines, attenuation, stellar age and metallicity, and H II region information (e.g., Kreckel et al. 2019, 2020; Pessa et al. 2021; Santoro et al. 2022; Williams et al. 2022).

For the legacy value, we selected our sample from the joint ALMA+MUSE+HST sample pool and considered CO surface brightness, mapping area, C I line frequency, and the transmission in the ALMA Band 8. In this work, we present the new C I data of NGC 3627 and NGC 4321. Because of the ALMA Band 8 sensitivity and the expected fainter C I line intensity than CO, the C I mapping areas are smaller than their CO(2−1) maps, but they are still the largest (∼1′−2.35′) and deepest (rms ∼0.04 K per ∼5 km s−1) C I mapping with ALMA.

Furthermore, in order to study the C I and CO in different galactic environments, we selected two starbursting and/or AGN-host galaxies from the literature whose ALMA [C I](1−0) and CO(2−1) data are available in the archive: NGC 1808 (Salak et al. 2019) and NGC 7469 (Izumi et al. 2020). NGC 1808 has ALMA mosaic observations covering its ∼1 kpc starburst ring, and NGC 7469 has ALMA single-pointing observations covering its inner ∼3 kpc area.

2.2. New ALMA ACA Band 8 observations

Our C I observations for NGC 3627 were taken under the ALMA project 2018.1.01290.S (PI: D. Liu) between June 3 to September 29, 2019 with ACA-only at Band 8. The total on-source integration time was 30.8 h. A mosaic with 149 pointings was used to map an area of 94″ × 136″ at a position angle of −27°, which covers the galaxy center, bar, and the majority of the spiral arms, and is about 1/3 of the full PHANGS-ALMA CO(2−1) map area. The achieved line sensitivity per 5 km s−1 is 45−55 mK (107−130 mJy beam−1) across the [C I](1−0) line frequencies with a beam of 3.46″.

The C I mapping for NGC 4321 were taken under the ALMA project 2019.1.01635.S (PI: D. Liu; NGC 1365 is also partially observed for this project) during Dec. 3, 2019 to July 1, 2021, also with ACA-only at Band 8. The on-source integration time reached 16.1 h for the mapping of an area of 55″ × 42″ with 23 pointings using the 7 m array. The achieved line sensitivity is similar to that of NGC 3627. More detailed information is provided in Table 1.

Table 1.

Physical and data properties of the sample.

ACA (7m) was chosen to provide a matched and slightly coarser synthesized beam (∼3″ − 4″) than the PHANGS-ALMA CO(2−1) data. In comparison, the main 12m ALMA array in compact C43−1/2 configurations will result in a ∼0.4″ − 0.7″ beam and significantly miss large scale (> 4 − 6″) emission without ACA.

No total power observations were requested in our presented observation, therefore, we matched the uv ranges of the raw CO(2−1) and [C I](1−0) visibility data during our data reduction. We verified that missing flux will not substantially (∼30%) bias our analysis, using the three methods detailed in Appendix B. This includes a CASA simulation of visibilities mimicking our ACA mosaic observations in NGC 3627, from which we find a missing flux as small as 7% in C I-bright pixels and up to ∼50% in the faintest pixels (and mostly < 30%).

Our data reduction follows the PHANGS-ALMA imaging and post-processing pipeline (Leroy et al. 2021b), including imaging and deconvolution, mosaicking, broad and strict (signal) mask generation, and moment map creation. The additional steps in this study are: (a) uv-clipping in the CO(2−1) data to match the uv sampling range of [C I](1−0); and (b) making a joint mask of the individual CO(2−1) and [C I](1−0) masks then extracting the moment maps (in the joint broad mask) and line ratios maps (in the joint strict mask). More technical details are provided in Appendix A.

Our [C I](1−0) and CO(2−1) line intensity maps, the line ratio maps and HST images for the two PHANGS galaxies, NGC 3627 and NGC 4321, are presented in Figs. 1 and 2, respectively. Our data cubes and moment maps are also made publicly available at the PHANGS-ALMA CADC public repository3.

thumbnail Fig. 1.

Line intensity, ratio, and optical images of NGC 3627. Top panels: NGC 3627 [C I](1−0) (left) and CO(2−1) (right) integrated line intensity (moment-0) maps within our broad mask (representing high-completeness signals; see Appendix A). Bottom left panel: [C I](1−0)/CO(2−1) line ratio map within the combined signal mask. Bottom right panel: HST F814W − F555W − F438W RGB composite image (PHANGS-HST; Lee et al. 2022). Regions marked with the white boxes and labeled with numbers are mainly for illustration purpose and for discussion in the text. Their zoom-in images and extracted spectra are provided in our online data release. Examples for regions 1, 4, and 22 are presented in Appendix D. All images have the same field of view of 179″ × 179″ or 9.83 kpc × 9.83 kpc.

thumbnail Fig. 2.

Similar to Fig. 1, the [C I](1−0) and CO(2−1) moment-0 intensity maps and the line ratio map and the HST composite RGB image for NGC 4321. The field of view is 78″ × 78″, or 5.75 kpc × 5.75 kpc.

2.3. ALMA observations of the additional targets from the literature

The NGC 1808 ALMA [C I](1−0), CO(1−0), and CO(2−1) observations are presented in Salak et al. (2019) and all are interferometry plus total power, that is, 12 m+7 m+tp (thus, not subject to any missing flux issue). To study the C I/CO line ratio consistently with our main targets, we only used the [C I](1−0) and CO(2−1) data. We re-reduced the raw data under ALMA project 2017.1.00984.S (PI: D. Salak) with the observatory calibration pipeline. We then imaged, primary-beam-corrected, and short-spacing-corrected using the PHANGS-ALMA pipeline in the same way as for our main targets (Appendix A). We note that in this step we re-reduced and imaged the total power data with the PHANGS-ALMA singledish pipeline (Herrera et al. 2020; Leroy et al. 2021b) and carried out the short-spacing correction with the PHANGS-ALMA pipeline right after the primary beam correction. The properties of the final CO-C I beam-matched data cubes are listed in Table 1.

The NGC 7469 ALMA data are presented in Izumi et al. (2020) and we used the archival raw data of [C I](1−0) and CO(2−1) under ALMA project 2017.1.00078.S (PI: T. Izumi). These are single pointings toward the center. [C I](1−0) is observed with ACA 7 m and CO(2−1) with the 12 m array, both without total power. We re-reduced the data following the same procedure as for NGC 3627 and NGC 4321 with the PHANGS-ALMA pipeline. Our re-reduced [C I](1−0) and CO(2−1) line intensity and ratio maps for these additional galaxies are shown in Fig. 3.

thumbnail Fig. 3.

[C I](1−0) (left) and RC I/CO (right) maps of NGC 1808 in the upper panels and NGC 7469 in the lower panels. Similar to Figs. 1 and 2, the line intensity maps are defined in the broad mask and the RC I/CO maps are restricted to the combined signal mask. Boxes in the left panels indicate the manually selected central regions where the pixels are highlighted in Fig. 4. Contours in the right panels indicate the 5, 10, 20 and 50-σ levels of the left-panel C I intensity maps.

3. Results of the observed line ratios

3.1. Spatial distributions

In Figs. 1–3, we present the beam-matched [C I](1−0) and CO(2−1) integrated line intensity maps and their ratio maps. The C I/CO line ratio map is computed only for pixels within the joint strict mask area of the two lines, as described in Appendix A, representing high-confidence signals.

In NGC 3627 (Fig. 1), we visually marked 23 regions based on the C I and CO commonly-detected (S/N > 3), strict-mask areas for later analysis. Region IDs are sorted by their [C I](1−0) brightness. Region 1 corresponds to the galaxy center, regions 2 and 3 are the southern and northern bar ends, region 4 is an offset peak next to the galaxy center, and other regions mostly comprise the spiral arms. Most of these regions show a similar RC I/CO ∼ 0.1, except for, for instance, regions 20 and 22, which exhibit a somewhat higher ratio of RC I/CO ∼ 0.5. The edge of region 4 also shows an enhancement of C I, yet it is hard to tell whether this is physical or simply caused by edge effects, for instance, as seen in our simulations (Appendix C).

We also examined the integrated spectra of each region in Appendix D. The C I and CO line profiles are not always well-matched in width and shape. In the galaxy center (region 1) and at bright bar-ends (regions 2, 3, and 5), C I and CO have similar line widths, but C I has a lower intensity than CO, whereas in some fainter regions (i.e., 9, 10, 13, and 14), C I is narrower than CO and relatively weaker. In regions 4, 20, and 22 where RC I/CO is high, while C I and CO have similar line widths but the C I intensity is enhanced.

In NGC 4321 (Fig. 2), we mapped a smaller area due to its fainter CO brightness than NGC 3627. There are no regions with CO(2−1) integrated intensities > 100 K km s−1 outside our selected area in NGC 4321; whereas in comparison the NGC 3627 bar ends have CO(2−1) integrated intensities ≳300 K km s−1. The C I mapping in NGC 4321 has a similar depth to that of NGC 3627.

We marked seven regions in NGC 4321 to guide the visual inspection. A clear RC I/CO deficit can be seen in the galaxy center (region 1), with RC I/CO ∼ 0.6, nearly a factor of two smaller than its inner disk which has similar RC I/CO ∼ 0.1 as seen in the NGC 3627 disk. Some C I enhancement can be found at the edges or slightly outside these regions, where CO and C I are both faint (ICO(2 − 1) ∼ 30 − 100 K km s−1) and the edge effect of interferometric missing flux might play a role (see Appendix C).

The RC I/CO spatial distributions of the other two starburst/AGN galaxies (Fig. 3) show (in general) more enhanced RC I/CO than in the NGC 3627 and NGC 4321 disks. Large variations from the centers to outer areas can be seen, especially at the S/N threshold of ∼3 − 5 (see contours).

To quantify the spatial co-localization of the C I and CO emission, we used the JACoP tool (Bolte & Cordelières 2006)4 in the ImageJ software (Schneider et al. 2012) to measure the commonly used co-localization indicators; namely, Pearson’s coefficient (PC; equal to 0 and 1 for null and 100% localization, respectively) and Manders’ coefficients (M1 and M2; which measure the overlap between two images and are equal to one for perfect overlap). We turn on the option of using Costes’ automatic threshold (Costes et al. 2004), which automatically set a pixel value threshold for each image to minimize the contribution of noise for the comparison (Bolte & Cordelières 2006). For the C I and CO emission in our galaxies, we find PC/M1/M2 values all very close to 1, that is, nearly 100% co-localization (PC/M1/M2 = 0.934/0.985/0.990 for NGC 3627, 0.816/0.986/0.964 for NGC 4321, 0.978/0.890/0.906 for NGC 1808, and 0.935/0.999/0.998 for NGC 7469).

Overall, the spatial comparison of the C I and CO intensities demonstrates that the two species are well correlated when observed at hundred parsec scales. Meanwhile, we do see certain spectral differences in the line profiles as shown in Appendix D. This may suggest that variations exist at smaller scales than our resolution, which could be the sign of different evolutionary stages (e.g., Kruijssen & Longmore 2014) and would be interesting for higher-resolution follow-ups, for instance, with the main ALMA 12m array.

3.2. RC I/CO versus CO surface brightness and gas surface density

In Fig. 4, we show the scatter points of C I and CO line brightnesses and the RC I/CO line ratios. Systematic differences in RC I/CO can be found among these galaxies and within their galactic environments. We discuss these environments separately as follows.

thumbnail Fig. 4.

Line flux and ratio correlations. Left: I[C I](1−0) versus ICO(2 − 1) in the four galaxies we studied: NGC 3627, NGC 4321, NGC 1808 and NGC 7469. The I[C I](1−0) and ICO(2 − 1) integrated fluxes are moment-0 intensities extracted from their beam and pixel size matched data cubes. Only data points with propagated moment-0 S/N ≥ 5 are shown. The blue (with crossed hatch), green (with horizontal line hatch), gray (with dotted hatch) and light gray shadings indicate the 5σ thresholds for the four galaxies, respectively. Typical line widths of 10 km s−1 (NGC 3627 and NGC 4321) and 30 km s−1 (NGC 1808 and NGC 7469) in sigma are used to calculate the thresholds together with the channel rms in Table 1. For NGC 3627 and NGC 4321, their (uv-matched) CO(2−1) 5σ thresholds are out of the plotting range. Top axis shows the simply-converted H2 surface density using a constant αCO = 4.3 and CO excitation (i.e., CO(2−1) to CO(1−0) line ratio) R21 = 0.65. Right: same data but shown as the line ratio RC I/CO = I[C I](1−0)/ICO(2−1) versus ICO(2 − 1). The blue horizontal line indicates a star-forming (SF) disk-like RC I/CO ∼ 0.1, i.e., the spiral arms of NGC 3627 and NGC 4321. The gray horizontal line indicates a starburst (SB) disk-like RC I/CO ∼ 0.2, i.e., the ∼1 kpc SB disk/ring in NGC 1808 and NGC 7469. The red line with a slope of 0.8 in logarithm (0.035 (ICO(2 − 1)/[100 K km s−1])0.8) visually guides the trend of increasing RC I/CO in the central regions of these galaxies (see boxes in Figs. 1–3, sizes ∼300 − 500 pc).

3.2.1. Star-forming and starburst disk environments

The majority of molecular gas in the 3−7 kpc star-forming disks of NGC 3627 and NGC 4321 exhibit a tight distribution of RC I/CO around 0.1 (within about ±50%). The distribution is fairly flat over an order of magnitude in ICO(2 − 1). We denote this as the “SF disk” regime. The ratio rises to about 0.2 within a galactocentric radius of few hundred parsec to ∼1 kpc starburst areas in NGC 1808 and NGC 7469, which we define as the “SB disk” regime.

The nearly flat “SB disk” distribution is consistent with earlier studies. Salak et al. (2019) found that in NGC 1808 I[C I](1−0) is proportional to 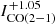I CO ( 2 − 1 ) + 1.05 $ I_{\mathrm{CO}(2{-}1)}^{+1.05} $. They also studied CO(1−0), finding that I [ C I ] ( 1 − 0 ) ∝ I CO ( 1 − 0 ) + 1.46 $ I_{[\mathrm{C}\textsc{i}](1{-}0)} \propto I_{\mathrm{CO}(1{-}0)}^{+1.46} $, that is, with a steeper slope. Saito et al. (2020) found a similar slope between I[C I](1−0) and ICO(1 − 0): I [ C I ] ( 1 − 0 ) ∝ I CO ( 1 − 0 ) + 1.54 $ I_{[\mathrm{C}\textsc{i}](1{-}0)} \propto I_{\mathrm{CO}(1{-}0)}^{+1.54} $ in IRAS F18293−3413; we note that its CO(2−1) data is insufficient for such a study (as previously mentioned). This correlation slope is likely to change with different CO transitions due to the CO excitation’s dependence on the CO luminosity or star formation rate themselves (e.g., Daddi et al. 2015; Liu et al. 2021). For higher-J CO transitions, Michiyama et al. (2021) studied C I and CO(4−3) lines in 36 (U)LIRGs, finding I [ C I ] ( 1 − 0 ) ∝ I CO ( 4 − 3 ) + 0.97 $ I_{[\mathrm{C}\textsc{i}](1{-}0)} \propto I_{\mathrm{CO}(4{-}3)}^{+0.97} $.

The upward tails seen at the CO-faint-end in the right panel of Fig. 4 are mostly due to the detection limits in each galaxy. The color shading indicates the 5-σ limit for each galaxy, assuming a typical line width of 10 km s−1. Region 22 of NGC 3627 and the outer pixels in the two starburst/AGN galaxies make the tips of the blue and gray faint-end tails, respectively. But most of these features should still be spurious. We performed CASA simulations following the real observations of NGC 3627 to verify what we would get if RC I/CO were constant across the galaxies (Appendix C) We find that noise can indeed boost a simulated RC I/CO of 0.2 to a measurement as high as 0.5 in a NGC 3627-like large mosaic, or even higher to > 1 in single-pointing ALMA data without total power or sufficient short spacing. However, the faint-end tail from the simulation is not especially similar to that of NGC 3627, raising some questions about the nature of the high-RC I/CO in region 22. Furthermore, we also carried out stacking experiments using the CO line profile as the prior to measure the C I line fluxes in bins of CO line brightnesses or galactocentric radii. We find no systematically higher RC I/CO at fainter CO pixels or at the outer radii.

3.2.2. Galaxy center environments

Most interestingly, the ≲250 pc centers of all four galaxies show dramatically different RC I/CO. It varies by a factor of ten from ∼0.05 in the center of NGC 4321 to ∼0.1 in the center of NGC 3627, then to ∼0.15 − 0.2 at the center of NGC 1808, and to ∼0.2 − 0.5 in the nucleus of NGC 7469. This “nuclei” trend has a slope of about 0.8, namely, I [ C I ] ( 1 − 0 ) ≈ 0.035 I CO ( 2 − 1 ) + 0.8 $ I_{[\mathrm{C}\textsc{i}](1{-}0)} \approx 0.035 \; I_{\mathrm{CO}(2{-}1)}^{+0.8} $, and corresponds to a Σmol range of about 103 to 104 M⊙ pc−2 if adopting an αCO = 4.3 M⊙ (K km s−1 pc2)−1 (Bolatto et al. 2013) and a CO excitation R21 = 0.65 (Leroy et al. 2022).

The reasons for the nuclei showing this trend likely include both the effect of varying [C I/CO] abundance ratio and the excitation and radiative transfer. They are determined by the actual ISM conditions in each environment, that is, the gas kinetic temperature, C I and CO column densities (NC I and NCO), line widths (Δv), and H2 volume density (nH2), and so on (analyzed in Sect. 4).

3.2.3. Histogram and curve-of-growth of the line ratio distributions

In Fig. 5, we show the histogram and cumulative distribution functions of RC I/CO (left panel) and the mean RC I/CO and the 16th to 84th percentiles in bins of CO line intensity (right panel) in our galaxies. The histogram is computed as the sum of CO line intensity in each bin of RC I/CO, representing the amount of gas at each RC I/CO. The NGC 4321 histogram is lower than others, showing that it has the least total molecular gas mass among the four galaxies within mapped areas. The NGC 3627 histogram has a peak about 0.5 dex higher than that of NGC 4321, but their peak locations are consistently at log RC I/CO ∼ −1. This is the same conclusion that can be drawn from our previous scatter plots. The two SB galaxies NGC 1808 and NGC 7469, despite having much smaller observed areas (∼1 − 2 kpc), have more than an order of magnitude higher peaks hence total molecular gas masses. The locations of their histogram peaks also shift to a systematically higher RC I/CO. It is clearly seen that both SF and SB disks lack a high-RC I/CO (log RC I/CO > −0.35) gas component which dominates the gas in the strong AGN host galaxy NGC 7469.

thumbnail Fig. 5.

Line flux ratio distributions. Left panel: histograms of the sum of CO(2−1) surface brightness over pixels in each C I/CO line ratio interval in the four galaxies. The bold curves are the cumulative distributions of the corresponding histograms. Right panel: mean C I/CO line ratio for pixels in each bin of CO(2−1) surface brightness (or molecular gas surface density as indicated by the top-axis assuming a constant αCO = 4.3 and R21 = 0.65). Shaded area enveloping each mean trend indicates the 16th to 84th percentiles in each bin, and dashed line indicates the 50th percentile. This panel thus more clearly illustrates the ridge and scatter of the trends in the right panel of Fig. 4. Detection limits are shown consistently with Fig. 4.

The curve-of-growth in the left panel of Fig. 5 further shows the cumulative CO brightness in bins of RC I/CO and also reflects the fact that the majority of gas in our galactic disks has a narrow distribution of RC I/CO (see also last few rows in Table 1). In NGC 3627, NGC 4321 and NGC 1808, the higher and lower proportion of RC I/CO gas outside ±0.1 dex around the mean RC I/CO only adds up to < 5 − 10% of their total gas masses.

In the right panel of Fig. 5, we illustrate how the mean RC I/CO changes with different gas surface density, as well as the scatter of the data point distribution. The 2D pixels are binned by CO brightness, and the mean and 16th, 50th, and 84th percentiles of the RC I/CO are computed for each bin. It sketches out the mean trends in Fig. 4 (right panel), and also reveals that (a) the scatter of RC I/CO is the largest (±0.20 dex) in the starburst disk of NGC 7469 compared to other galaxies; (b) the scatter is the smallest (±0.06 dex) in the star-forming disks of NGC 4321 and NGC 3627 where Σmol ∼ 100 − 500 M⊙ pc−2; (c) the scatters are very similar (±0.10 dex) at a relatively high Σmol ∼ 1000 M⊙ pc−2 in all our galaxies, except for NGC 4321’s center.

3.3. RC I/CO versus ISRF

Here, we study how RC I/CO correlates with the interstellar radiation field (ISRF) intensity (U; in units of Milky Way mean ISRF; Habing 1968), which is a measure of the UV radiation field strength impacting the ISM. Since C I originates from PDRs, its abundance should be highly related to the PDR properties, thus the questions of whether and/or how RC I/CO is correlated with the ISRF that illuminates the PDR is key.

The ISRF intensity U is usually measured by the re-radiated dust emission, as the original UV photons are highly attenuated by dust in the ISM. Draine & Li (2007, hereafter DL07) developed a series of dust grain models and synthesized SED templates that can describe the observed dust SEDs of nearby galaxies. A number of studies (e.g., Draine et al. 2007; Galliano et al. 2011; Dale et al. 2012; Aniano et al. 2012, 2020; Daddi et al. 2015; Chastenet et al. 2017, 2021; Liu et al. 2021) have used the DL07 models to fit the dust SEDs of galaxies near and far.

For our study, we adopted the mass-averaged ISRF ⟨U⟩ maps from an ongoing effort by Chastenet et al. (in prep.), which is a continuation of the work published for other galaxies by Chastenet et al. (2017, 2021) with the same method. In this method, the Herschel far-infrared, Spitzer and/or WISE near-infrared images5 are first PSF-matched to a common resolution ∼18″ (Herschel SPIRE 250 μm), then the SED fitting is performed using the DL07 models at each pixel. Each dust SED is fitted by two dust components: one in the ambient ISM with a constant ISRF intensity Umin and one in regions with higher U, with a power law distributed ISRF from Umin up to Umax = 107. The fitting then gives the best-fit Umin and the power-law index γ of the U distribution. The mean ISRF intensity ⟨U⟩ is calculated as the dust mass-weighted mean of the ambient and power-law ISRF intensities (in DL07, UPDR ≥ 102 is considered to be associated with the PDR) and better represents the overall ISRF than Umin.

Figure 6 presents the ⟨U⟩ maps and the RC I/CO versus ⟨U⟩ scatter plot. Since the spatial resolution of the ⟨U⟩ maps is 18″, we calculated a weighted RC I/CO in each circular aperture shown in Fig. 6, whose diameter equals the ⟨U⟩ map resolution, with weighting following the 2D Gaussian beam. In addition, we also show the central pixel value for each region in Fig. 6. We restricted the analysis to regions where both ⟨U⟩ and RC I/CO are measured.

thumbnail Fig. 6.

Line ratio versus mean ISRF intensity ⟨U⟩ measured from SED fitting to the near- to far-IR (Spitzer, Herschel) data. Left four panels: ⟨U⟩ maps of NGC 3627, NGC 4321, NGC 1808 and NGC 7469, and as described in Sect. 3.3 are obtained from the works done by Chastenet et al. (in prep.) as a continued effort of Chastenet et al. (2021). Right panel: scatter plot of RC I/CO versus ⟨U⟩ at a spatial resolution of ∼18″ in the manually-selected apertures shown in the left panels. We computed a beam-weighted mean RC I/CO and a center pixel RC I/CO for each aperture, displayed as the solid and open symbols, respectively. Error bars are the corresponding beam-weighted mean or central pixel RC I/CO uncertainties in each region. The region diameter (∼18″) corresponds to the coarsest resolution of the Herschel data used in the SED fitting. The gray dotted line shows RC I/CO = 0.07 U0.25 as a guiding line. The colored dotted contours (labeled 0.1−0.5) are the model contours of RC I/CO computed from the PDR Toolbox (using the latest wk2020 model and solar metallicity; Kaufman et al. 2006). We convert G0 from the model contour to the x-axis U by multiplying with a factor of 0.88 (Draine et al. 2007). The right y-axis indicates the PDR model’s nH2, whose range is manually adjusted so that the model contours roughly match the left x-axis. The PDR model contours show little dependence of RC I/CO on U in the horizontal direction but a strong correlation with nH2 as seen by the vertical gradient.

A weak correlation between RC I/CO and ⟨U⟩ is seen from the SF to SB disks, with a large scatter. For reference, we plot a RC I/CO = 0.07 U0.25 line to indicate this weak trend. The lowest-⟨U⟩ data point in NGC 3627 (mainly region 22) and the center of NGC 7469 do not follow this trend, possibly indicating other C I enhancement mechanisms than ⟨U⟩.

We used the popular PDR modeling software, PDR Toolbox (version 2.2.9; Kaufman et al. 2006; Pound & Wolfire 2008)6, to compute the theoretical RC I/CO in uniform grids of ISRF intensity in the Habing (1968)G0 unit and H nucleus density nH (both in log space). We adopted the latest wk2020 model set and a solar metallicity ([O/H2] = 3.2 × 10−4, [C/H2] = 1.6 × 10−4). The ISRF intensity grid can be directly scaled to U by multiplying a factor 0.88 (Draine et al. 2007), corresponding to the x-axis of Fig. 6. The nH grid is not directly linked to the left y-axis of Fig. 6, but because the model contours show fairly flat RC I/CO versus U trends, we can match the model contours and indicate the nH grid in the right y-axis of Fig. 6.

The PDR modeling predicts generally flat RC I/CO versus U trends similar to the distribution of the observed data points, although our U are diluted values at a much larger physical scale than in the PDR models. However, in PDR models, RC I/CO changes moderately with nH, and a relatively high nH ∼ 103.5 − 3.7 cm−3 is needed to reproduce an RC I/CO ∼ 0.1 − 0.2, or (equivalently) ∼1.0 − 1.9 for the ratio of [C I](1−0) and CO(2−1) fluxes in erg s−1 cm−2 sr−1 units used by the PDR Toolbox7. Furthermore, the PDR model needs a ∼0.5 dex lower nH to explain the 2× elevated RC I/CO in SB disks, which seems somewhat counterintuitive.

This apparent tension is likely caused by the observations probing a much coarser resolution that consists of a large number of PDRs with different nH and U (e.g., increasing U from 10 to 400 can increase RC I/CO from 0.2 to 0.5 based on our PDR Toolbox modeling). It may also relate to an abundance variation driven by non-PDR mechanisms, whereby the X-ray dominated region (XDR; Maloney et al. 1996; Meijerink & Spaans 2005; Meijerink et al. 2007; see also review by Wolfire et al. 2022) and cosmic ray-dominated region (CRDR; Papadopoulos 2010; Papadopoulos et al. 2011, 2018; Bisbas et al. 2015, 2017) are well-known to play an important role in AGN and starbursting environments, respectively.

As pointed out by Papadopoulos et al. (2011) and later works, ultra-luminous infrared galaxies (ULIRGs) with IR luminosities of LIR,  8 − 1000 μm ≥ 1012 L⊙ and corresponding star formation rates of SFRs > 1000 M⊙ yr−1 have cosmic-ray (CR) energy densities ∼103 − 104× higher than that of the Milky Way. In our sample, the two SB galaxies are not as intensively star-forming as ULIRGs, but their SFRs are still a factor of 2 to 20 higher than our SF galaxies. More importantly, the SB disks have considerably higher (e.g., one to two orders of magnitude) SFR surface densities than the SF disks, plausibly leading to higher CR intensities by a factor of a few tens to a few hundreds. The CRs emitted from OB star clusters and supernova remnants can penetrate deeply into the ISM and may thus nearly uniformly illuminate the ISM as well as effectively dissociate CO into C I.

A detailed simulation by Bisbas et al. (2017) showed that 10× and 100× higher CR ionization rates (ξCR) than the Milky Way level results into a factor of about 2 and 3 in mildly increased C I abundance and about 1/2 and 1/30 in strongly-decreased CO abundance, respectively (see their Fig. 3), in a 10 pc GMC with a mean gas density ⟨nH⟩ = 760 cm−3, resembling Milky Way and typical SF galaxies’ ISM conditions. Our SB galaxies probably have a ξCR around or slightly above 10, but not reaching 100 given their mild ⟨U⟩ ∼ 20 − 30 compared to the ⟨U⟩ ≳ 50 in extreme SB galaxies, for instance, local ULIRGs and high-redshift hyperluminous IR-bright (HyLIRG) as well as submm galaxies (Daddi et al. 2015; Silverman et al. 2018; Liu et al. 2021). In Sect. 4, we show that the mildly increased [C I/CO] abundance ratio from a CRDR and temperature- or density-driven excitation can lead to a factor of 2 increase in RC I/CO when going from SF to SB disks.

3.4. RC I/CO versus metallicity

Our current sample covers a relatively small range in metallicity for a metallicity–line ratio study. Given their stellar masses and metallicity maps (e.g., Kreckel et al. 2019, 2020; Williams et al. 2022), our targets probe a near-solar metallicity. NGC 3627 has a well-measured metallicity gradient of Z = 8.53 + 0.06 × [r/R25] from Kreckel et al. (2019)8, but the metallicity of individual H II regions scatter between ∼8.45 − 8.65. Williams et al. (2022) produced 2D spatial distributions of gas-phase metallicity in PHANGS-MUSE galaxies, including NGC 3627 and NGC 4321, by applying a Gaussian process regression to map the smooth, higher-order metallicity variation from the individual, sparse H II regions detected in PHANGS-MUSE (Emsellem et al. 2022; Santoro et al. 2022). This method is significantly superior to a naïve nearest neighbor interpolation method. We refer to Williams et al. (2022) for technical details and validation demonstration.

In Fig. 7, we present the trend between RC I/CO and metallicity in NGC 3627 and NGC 4321. Due to our limited metallicity range, only a very weak decreasing trend can be seen. A similar trend has been reported by Bolatto et al. (2000a), who observed CO(1−0) and [C I](1−0) in the region of N27 of the Small Magellanic Cloud and combined with literature data to present a correlation between RC I/CO and metallicity over ∼0.2 − 2 Z⊙. We overlaid the Bolatto et al. (2000a) empirical fitting9 as well as a theoretical PDR model prediction line from Bolatto et al. (1999) in Fig. 7. Although our data cover only a small metallicity range, it is encouraging to see the overall good agreement with the observationally driven trend in Bolatto et al. (2000a). A more detailed understanding of the deviation from PDR models is likely to require more C I mapping in lower metallicity galaxies.

thumbnail Fig. 7.

Line ratio versus metallicity. Left two panels: metallicity maps of NGC 3627 and NGC 4321 from Williams et al. (2022) based on PHANGS-MUSE (Emsellem et al. 2022) data. Boxes are regions as defined in Figs. 1 and 2. Right panel: RC I/CO versus metallicity scatter plot for regions in NGC 3627 and NGC 4321. The bottom axis represents the metallicity in solar units, top axis is the metallicity in 12 + log(O/H), left-axis is the line ratio of [C I](1−0) and CO(2−1) in K km s−1 units, and right-axis is the ratio of fluxes in erg s−1 cm−2 sr−1 units. The left and right axes are matched by a factor of (ν[C I]1−0/νCO1−0)3 × R21, where we adopt R21 = 0.65 (Leroy et al. 2022). Data points are the mean metallicity and RC I/CO in each region shown in left panels, with error bars indicating the typical uncertainty in RC I/CO, and vertical color shading indicating the 16th to 84th percentiles of the pixels’ RC I/CO distribution inside each region. The Bolatto et al. (2000a) empirical fitting and Bolatto et al. (1999) model prediction lines are overlaid. The three outliers in NGC 3627 with RC I/CO ∼ 0.19, 0.28, and 0.35 are regions 20, 21, and 22, respectively. The outlier point in NGC 4321 with RC I/CO ∼ 0.06 is its center is region 1.

4. Estimation of abundance ratios under representative ISM conditions

The observed RC I/CO depends on not only the C I and CO abundances ([CO/H2] and [C I/H2]), but also the ISM conditions that determine the excitation (level population) and radiative transfer of the C atoms and CO molecules – that is, the gas kinetic temperature, Tkin, volume density of H2 (nH2; as the primary collision partners of C and CO), turbulent line width Δv, and the species’ column densities, NCO and NC I. The column density divided by the line width (N/Δv) further determines the optical depth τ of each line.

In this work, having only a CO(2−1) and a [C I](1−0) line is insufficient to numerically solve all the values of Tkin, nH2, NCO/Δv, [CO/H2], and [C I/H2]. Therefore, we assume several representative ISM conditions, where Tkin, Δv and [CO/H2] are fixed to reasonable values, then we solved the NCO and NC I. We assume that C I and CO are spatially mixed at our resolution, namely, that they share the same filling factor. This is a relatively strong assumption and is likely not the real case, because although we see spatial co-localization at our ∼200 pc resolutions, the spectral profiles of CO and C I show discrepancies (Appendix D) that indicate different underlying distributions at smaller scales. With the assumption of the same filling factor (and 3D distribution), the column density ratio NC I/NCO equals the [C I/CO] abundance ratio.

We performed both LTE and non-LTE calculations, with LTE assuming that all transitions are thermalized locally and the level population follows Boltzmann statistics, so that each transition’s excitation temperature, Tex, as defined by the level population equals Tkin (e.g., Spitzer 1998; Tielens 2010; Draine 2011). The LTE assumption facilitates the computation, as we do not need to solve the level population and, thus, nH2 is not used. However, LTE is not easily reached in typical ISM conditions. Subthermalized lines need non-LTE calculations. The commonly adopted non-LTE approach is the large velocity gradient (LVG; Scoville & Solomon 1974; Goldreich & Kwan 1974), where an escape fraction is used to facilitate the local radiation intensity calculation, hence, the detailed balance of radiative and collisional (de-)excitations. We use RADEX (van der Tak et al. 2007) to compute the non-LTE C I and CO line fluxes for each fixed parameter set (Tkin, nH2, NCO, NC I, Δv), then study how [C I/CO] determines the line flux ratio RC I/CO.

We assumed the following seven representative ISM conditions: (1) inner Galactic GMCs, (2) NGC 3627/4321 disk GMCs, (3) NGC 3627 bar-end environments, (4) NGC 1808/7469 SB disk, (5) NGC 4321 center, (6) NGC 3627 center, and (7) NGC 7469 center. Conditions (1)–(3) correspond to the “SF disk” (in Fig. 4) and condition (4) represents the “SB disk”. The last three conditions are for the “nuclei”. Under each ISM condition, we set a fixed Tkin (in units of K), Δv (in units of km s−1), [CO/H2], and Σmol (in units of M⊙ pc−2). The adopted values are shown at the top of each panel in Figs. 8 and 9.

thumbnail Fig. 8.

Observed and calculated RC I/CO as a function of CO column density NCO and [C I/CO] abundance (column density) ratio NC I/NCO for seven representative ISM conditions, based on LTE calculations. Upper panels: curved lines show RC I/CO versus N C I / N CO $ N_{{\mathrm{C}\textsc{i}}/N_{\mathrm{CO}}} $ for different NCO, as indicated by the color. Dashed means CO(2−1) optically thick and [C I](1−0) optically thin, dotted means both are both optically thin, and solid line means both optically thick. Horizontal thick line is the observed RC I/CO value. Lower panels: black contours are RC I/CO = 0.05, 0.10, 0.20, and 0.50 in the CO column density versus C I/CO abundance ratio plane. Vertical color shading indicates the final NC I/NCO that can match both the observed RC I/CO and the assumed Σmol value noted at the top of each panel.

thumbnail Fig. 9.

Observed and calculated RC I/CO as a function of CO column density NCO and [C I/CO] abundance (column density) ratio NC I/NCO for seven representative ISM conditions, similar to Fig. 8 but based on non-LTE calculations. Upper panels: line ratio RC I/CO versus the abundance ratio NC I/NCO for different NCO, as indicated by the color. Dashed, dotted and solid lines are for different CO(2−1) [C I](1−0) optical depths as described in Fig. 8 caption. Horizontal thick line is the observed RC I/CO value. Lower panels: are the contours of RC I/CO = 0.05, 0.10, 0.20, and 0.50 in the CO column density versus C I/CO abundance ratio plane. Vertical color shading indicates the final abundance ratio NC I/NCO that can match both the observed RC I/CO and the assumed Σmol value noted at the top of each panel.

Our choice of Tkin considers the multi-line measurements in the literature, for instance, Heyer & Dame (2015) for the Galactic GMC ISM condition, and Teng et al. (2022) for NGC 3627 nucleus, as well as typical values in simulations (e.g., Offner et al. 2014; Glover et al. 2015; Glover & Clark 2016; Clark et al. 2019; Hu et al. 2021). Our Δv is based on the observed line width in the highest-resolution ALMA data, that is, from the original PHANGS-ALMA 1″ data (Leroy et al. 2021a) or from Salak et al. (2019) and Izumi et al. (2020) for NGC 1808 and NGC 7469, respectively. The observed line width should at least provide an upper limit, if not directly probing the turbulent Δv. The [CO/H2] is more like a fiducial value and does not obviously affect later [C I/CO] results. We also take a fiducial Σmol which matches the observed CO(1−0) line brightness temperature and a CO-to-H2 conversion factor of αCO ∼ 4 − 0.8 M⊙ (K km s−1)−1, depending on the assumed conditions (e.g., Bolatto et al. 2013; and our Paper II). This Σmol directly converts to NH2 when assuming that 36% of the mass is helium. Then NH2 and [CO/H2] together indicate NCO. It is only with these assumptions that we can unambiguously link an abundance ratio [C I/CO] (i.e., NC I/NCO) to a line flux ratio RC I/CO.

Additionally, with the same filling factor assumption, RC I/CO is also equivalent to the ratio of the CO-to-H2 and C I-to-H2 conversion factors, that is, RC I/CO = αCO/αC I, because they trace the same molecular gas at our resolution. In a companion paper (Paper II; Liu et al., in prep.), we study the behaviors of αCO and αC I in more detail, under both LTE and non-LTE conditions.

4.1. LTE results

We determine the LTE solution of [C I/CO] in Fig. 8. To illustrate the complexity of this problem and the degeneracy of the Tkin, NCO/Δv and [C I/CO] parameters, we show how RC I/CO (y-axis) varies with NC I/NCO (x-axis) and NCO (color bar) in the upper panels, as well as how RC I/CO (contour) can be pinpointed by determining the Σmol (right y-axis). At the top of each column, the key parameters of the aforementioned representative ISM conditions are shown as text. The assumed Tkin and Δv generally increase from panels (1) to (7) mimicking real conditions. Observationally driven ICO(1 − 0) ranges and the assumed Σmol for these ISM environments are also listed and can be converted one into the other via αCO. We also list the chosen [CO/H2] for clarity.

As shown in the upper panels, RC I/CO increases with both NC I/NCO and NCO under low-Tkin conditions. However, a maximum RC I/CO is reached in the high C I column density regime, where an increasing abundance ratio will no longer increase RC I/CO. The line ratio saturates at about 0.5 when Tkin ∼ 15 K, or at about 1 for Tkin ∼ 100 K. The observed line ratios (horizontal dashed lines) are all lower than the saturation limit of RC I/COmax ∼ 0.7 − 0.9, corresponding to a range of NCO or Σmol. This range is very wide in the low-Tkin conditions, with log NCO/cm−2 ∼ 17 − 19, but is very narrow at Tkin ∼ 100 K, that is, RC I/CO can be determined from [C I/CO] without much dependence on NCO.

In the lower panels, the contours of RC I/CO = 0.05, 0.1, 0.2 and 0.5 are shown in the plane of CO column density NCO versus C I/CO abundance ratio. For a fixed RC I/CO, a higher NC I/NCO corresponds to a lower NCO in the low-Tkin regime, but RC I/CO becomes insensitive to NCO at a high Tkin. In the latter case, NC I/NCO alone determines RC I/CO. By matching to the expected Σmol for each ISM condition, we can obtain an unambiguous NC I/NCO from the observed RC I/CO (as shown in Fig. 8). In this way, we determined NC I/NCO to be around 0.1−0.2 for conditions (1) and (2), and ∼0.4 for conditions (3) and (5). The SB disk (condition 4) and AGN environments (conditions 6/7) have NC I/NCO ∼ 2 and ∼1 − 10, respectively.

The strongly enhanced C I/CO abundance ratios in SB disk and AGN environments are clear signatures of CRDR and XDR, respectively. The NGC 4321 center is a low-ionization nuclear emission-line region (LINER, e.g., García-Burillo et al. 2005) and given our assumptions, it requires NC I/NCO ∼ 0.4 to explain the observed low line ratio. The gradually increasing C I/CO abundance ratios in the nuclei of NGC 4321, NGC 3627, NGC 1808, and NGC 7469 agree well with the increasing power of AGN activities, for example, their X-ray luminosities (Table 1).

Our assumptions for the Galactic cloud ISM condition are mainly based on Heyer et al. (2009), Heyer & Dame (2015) and Roman-Duval et al. (2010). The obtained [C I/CO] ∼ 0.1 also agrees well with previous studies using C I and CO isotopologues (see Sect. 1). For example, Ikeda et al. (1999) reported NC I/NCO ∼ 0.05 − 0.2 for the Orion cloud; Oka et al. (2001) found NC I/NCO = 0.064 ± 0.035 but a peak of NC I/NCO ∼ 0.15 in the DR 15 H II region and two IR dark clouds; Kramer et al. (2004) found NC I/NCO ∼ 0.11 − 0.12 in the massive SF region W3; Genzel et al. (1988) found NC I/NCO ∼ 0.2 for the massive SF region W51; Zmuidzinas et al. (1988) reported NC I/NCO ∼ 0.05 − 0.15 in several dense clouds. Recently, Izumi et al. (2021) derived an overall NC I/NCO ∼ 0.1 in the massive SF region RCW38 at AV ∼ 10 − 100, consistent with the Orion cloud, but also saw high [C I/CO] ∼ 0.2−0.6 in some even lower column density regions.

Accurate determination of all the ISM properties instead of simple assumptions as in this work requires comprehensive, multi-J CO isotopologue observations (e.g., Teng et al. 2022). Our representative ISM conditions only provide a qualitative diagnostic to understand how to infer the C I/CO abundance ratio from the observed RC I/CO quantity. Their properties may not be very accurate, and are subject to change with future multi-tracer/CO isotopologue studies.

4.2. Non-LTE results

We performed non-LTE calculations using the RADEX code (van der Tak et al. 2007) with the large velocity gradient (LVG; i.e., expanding sphere) escape probability (Scoville & Solomon 1974; Goldreich & Kwan 1974). Compared to LTE, the volume density of H2 is now an additional property that plays a role. The excitation temperature of each line no longer equals Tkin. We computed the non-LTE line ratios in a grid of (Tkin, Δv, [CO/H2], NC I/NCO, NCO, nH2) parameter sets, then studied the line and abundance ratios in a similar way as in the previous section.

In Fig. 9, we show the non-LTE version of Fig. 8. The non-LTE result does not qualitatively differ from that of LTE. The most obvious difference is that at high temperature (Tkin > 50 K, given our other assumed conditions), the required [C I/CO] is lower by ×2 for the same observed RC I/CO, whereas at low temperatures (Tkin ∼ 15 K), we expect to obtain ≲2× [C I/CO] for the observed line ratio.

As listed in the title of each panel, we assumed log nH2/cm−3 = 2.5 to 3.0 for our conditions (1) to (7). This is based on the fact that low-J CO and C I trace the bulk of molecular gas with log nH2/cm−3 ∼ 2 − 3 (e.g., Leroy et al. 2017; Liu et al. 2021), with a typical value of nH2 ∼ 300 cm−3 that is widely adopted (found) for Galactic and nearby galaxy GMCs (e.g., Koda et al. 2012; Pety et al. 2017, see also simulations of Glover & Clark 2012), whereas a smaller portion of their emission is from the dense gas with log nH2/cm−3 ∼ 4 − 6 (e.g., Gao & Solomon 2004a). The fraction of the dense gas is expected to increase in more starbursting environment (Gao & Solomon 2004b), as does the mean gas density (Liu et al. 2021). Therefore, a log nH2/cm−3 of 3.0 is perhaps a reasonable assumption – or at least a lower limit for our galaxy centers. A density value that is ten times higher does not qualitatively change the results of Fig. 9, except for shifting the expected NC I/NCO to be 50% higher in the Tkin > 50 K conditions (making Fig. 9 resemble Fig. 8).

Therefore, our non-LTE result strongly confirms the LTE result in the previous section, namely, that the intrinsic C I/CO abundance has to vary significantly from about 0.1−0.2 to about 1−3 in order to explain the observed line ratios from Galactic GMCs (hundred pc scales) and NGC 3627/4321 SF disk GMCs to NGC 1808/7469 SB disk/AGN (r ≲ 250 pc) environments.

5. Discussion

We can see from this study that the line ratio RC I/CO increases from 0.1 to 0.2 and > 0.5 from the SF disk to the SB disk and the vicinity (few hundred pc) of X-ray luminous AGN. Although we may be limited by our sample, we suggest that this trend can be extended to general cases at both local and high redshift, because the C I/CO abundance ratio enhancement is aptly predicted by the CRDR and XDR theories.

Papadopoulos (2010) and Papadopoulos et al. (2011) pointed out the key role of CRDR in local (U)LIRGs. With UV photons alone, cold gas in starbursting environments can still be well shielded, hence, as cold as ∼10 K. However, with CRs produced from O, B star clusters and supernova remnants, the gas can be uniformly illuminated and heated up. The extremely starbursty local ULIRGs have a CR density (ξCR) that is 103 − 104 times that of the Milky Way (Papadopoulos 2010) and will thus naturally dissociate more CO into C I. Bisbas et al. (2017) and Papadopoulos et al. (2018) conducted simulations of molecular gas at tens of pc scale with varying CR strength, and found that when ξCR is ∼1 − 100× the Galactic value, the gas temperature in the dense gas remains largely unaffected (∼10 K). However, when ξCR reaches ∼1000× the Galactic value as in (U)LIRGs, the gas temperature increases to 30−50 K. The Bisbas et al. (2017) simulation also shows that the C I and C II fractional abundances at log AV ∼ 0.5 increase by one and three orders of magnitude, respectively, and the CO fractional abundance decreases correspondingly by over two orders of magnitude, with an increasing ξCR from the Galactic value to 100× of that. These results are in line with our calculations in Sect. 4.1.

Meanwhile, the AGN-driven XDR chemistry and molecule or atom excitation has been firstly modeled in great detail by Maloney et al. (1996), Meijerink & Spaans (2005) and Meijerink et al. (2007). In XDRs, photo-ionization becomes the dominant heating source instead of photo-electric emission from dust grains in PDRs, thus, more molecules are dissociated and/or ionized. Meijerink & Spaans (2005)’s Model 1 shows that CO molecules are fully dissociated when NH < 1023 cm−2, then the fractional abundance is gradually increased by six orders of magnitude from NH = 1023 cm−2 to 1024 cm−2. By contrast, the C I and C II abundances are about constant until reaching the densest part (NH > 1024.5 cm−2). Unlike in PDRs, there is no clear C II/C I/CO stratification in XDRs (Meijerink et al. 2007; Wolfire et al. 2022). Their Model 2 with a 100× higher energy deposition rate shows that the CO distribution contracts to the highest gas density spots, and the total cumulative [C I/CO] is increased by about 0.2 dex, reaching NC I/NCO ∼ 1.6. This value agrees well with our calculations shown in Figs. 8 and 9 (ISM condition 7).

Therefore, both in theoretical and observational views, it is clear that the RC I/CO line ratio is a good indicator of the starburst’s CRDR and AGN’s XDR. If a RC I/CO line ratio (to be specific, I[C I](1−0)/ICO(2−1)) reaches 0.2−0.5, then the CRDR plays a crucial role and the abundance ratio [C I/CO] could be ∼1. If it exceeds 0.5−1.0, then it may only be enhanced by an XDR, for instance, caused by an X-ray luminous AGN, which boosts the abundance ratio [C I/CO] to ≳1−2.

6. Conclusion

We present new beam- and uv-coverage matched [C I](1−0) and CO(2−1) maps in the galactocentric radius r ≲ 7 kpc SF disk of NGC 3627 at ∼190 pc resolution, as well as in the r ≲ 3 kpc disk of NGC 4321 at ∼270 pc resolution. They are among the largest C I mosaic mappings available in nearby galaxies. We combined the imaging of [C I](1−0) and CO(2−1) in two nearby, more starburst- and AGN-hosting galaxies, namely, NGC 1808 central ∼1 kpc, and NGC 7469 central ∼1.5 kpc at 140−160 pc resolutions. Together, we studied the spatial distributions of C I and CO, and their line ratio RC I/CO as functions of various galaxy resolved properties, including CO brightness (Fig. 4), ISRF ⟨U⟩ (Fig. 6), and metallicity (Fig. 7).

In order to obtain the underlying intrinsic [C I/CO] abundance ratio from the observed line ratio RC I/CO, we assumed seven representative ISM conditions and did both LTE and non-LTE calculations. We summarize our findings below:

  • The majority of the molecular gas in the SF disks of NGC 3627 and NGC 4321 exhibit a uniform RC I10/CO21 = 0.10 ± 0.05. Then, [C I](1−0) and CO(2−1) exhibit very similar spatial distributions at our 140−270 pc resolution.

  • The majority of the molecular gas in the SB disk of NGC 1808 exhibit RC I10/CO21 = 0.20 ± 0.05. This elevated line ratio compared to the SF disk is likely caused by an increase of ∼3 − 5× in the [C I/CO] abundance ratio, based on our LTE and non-LTE calculations and parameter assumptions (Figs. 8 and 9).

  • The centers (r ≲ 250 pc) of NGC 4321, NGC 3627, NGC 1808, and NGC 7469 show a strongly increasing trend in RC I10/CO21, from 0.05 to 0.5, as a function of ICO(2 − 1), namely, RC I10/CO21 ≈ 0.035 (ICO(2−1)/[100 K km s−1])0.8. The inferred [C I/CO] abundance ratio from our non-LTE calculation changes from ∼0.2 to ∼3, in line with the increasing X-ray luminosity of the centers powered by AGNs.

  • The observed RC I/CO versus ISRF trend is fairly flat, that is, RC I/CO is insensitive to ISRF intensity changes, similarly to the PDR model prediction calculated with PDRToolbox (although our resolution is much coarser than the physical scale of PDR models; see Sect. 3.3).

  • We find a RC I/CO versus metallicity trend that is consistent with previous observations that covered lower-metallicity environments (∼0.2 Z⊙; Bolatto et al. 2000a), within the metallicity range (∼0.7 − 1 Z⊙) of our sample (Sect. 3.4).

  • Our inferred [C I/CO] abundance ratios are in good agreement with the CRDR and XDR theoretical studies. Given the drastically changed RC I/CO, we propose that the C I to CO line ratio can be a promising indicator of CRDR (starbursting) and XDR (AGN). For instance, an observed line flux ratio of RC I10/CO21 ∼ 0.2 − 0.5 and ≳0.5 effectively indicates CRDR and XDR, respectively.

  • We did not find ubiquitous “CO-dark”, C I-bright gas at the outer r ∼ 1 − 3 kpc disks of NGC 3627 and NGC 4321, nor any systematic enhancement in RC I/CO at CO-faintest sightlines via stacking, mainly due to the incompleteness of our data. Nevertheless, a few sightlines, for instance, region 22 in NGC 3627, show high RC I/CO ∼ 0.5, which does not fully comply with the noise behavior seen in our CASA simulations.

1

ncrit ≡ A/γ, where A is the Einstein A coefficient for the transition and γ the rate of collisional de-excitation with hydrogen molecules, with values from Schroder et al. (1991) as compiled in the Leiden Atomic and Molecular Database (Schöier et al. 2005), https://home.strw.leidenuniv.nl/~moldata/

2

The line intensity I has brightness temperature units K km s−1.

5

For the two (U)LIRGs, the WISE maps are saturated, so their inferred ISRF intensity U should be considered with a large uncertainty.

7

See https://github.com/mpound/pdrtpy-nb/blob/master/notebooks/PDRT_Example_Model_Plotting.ipynb. We scale the ratio of intensities in erg s−1 cm−2 sr−1 to the ratio of intensities in K km s−1 by a factor of (νCI10/νCO21)−3 = 9.73, where ν is the rest-frame frequency of the lines. We caution that the old version of PDRToolbox v2.1.1 does not include the CI_609/CO_21 line ratio, but has CI_609/CO_43 and CO_43/CO_21 ratios. However, we tested that the multiplication of CI_609/CO_43 and CO_43/CO_21 does not produce the same result as the direct CI_609/CO_21 ratio in the new PDRToolbox v2.2.9. We use the new version for this work.

8

Kreckel et al. (2019) used a distance of 10.6 ± 0.9 Mpc for NGC 3627. We do not directly use this metallicity gradient, but use the metallicity maps from Williams et al. (2022), where the same new distance is adopted as in the present work.

9

We adopted the equation from Bolatto et al. (2000a, Fig. 2 caption), with a typo-correction in the brackets so that the equations are: log (F[C I](11−0)/F[CO(1−0)) = − 0.47[12 + log(O/H)] + 5.0 and log(F[C I](1−0)/FCO(1−0) = − 0.82 [12 + log(O/H)] + 8.2, respectively, where F is the line flux in erg s−1 cm−2 sr−1.

Acknowledgments

We thank the anonymous referee for very helpful comments. E.S., T.S. and T.G.W. acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694343). ER acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), funding reference number RGPIN-2017-03987. The work of AKL is partially supported by the National Science Foundation under Grants No. 1615105, 1615109, and 1653300. A.U. acknowledges support from the Spanish grants PGC2018-094671-B-I00, funded by MCIN/AEI/10.13039/501100011033 and by “ERDF A way of making Europe”, and PID2019-108765GB-I00, funded by MCIN/AEI/10.13039/501100011033. R.S.K. and S.C.O.G. acknowledge financial support from the German Research Foundation (DFG) via the collaborative research center (SFB 881, Project-ID 138713538) “The Milky Way System” (subprojects A1, B1, B2, and B8). They also acknowledge funding from the Heidelberg Cluster of Excellence “STRUCTURES” in the framework of Germany’s Excellence Strategy (grant EXC-2181/1, Project-ID 390900948) and from the European Research Council via the ERC Synergy Grant “ECOGAL” (grant 855130). F.B. and I.B. acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 726384/Empire). J.C. acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme DustOrigin (ERC-2019-StG-851622). M.C. gratefully acknowledges funding from the Deutsche Forschungsgemeinschaft (DFG) in the form of an Emmy Noether Research Group (grant number CH2137/1-1). Y.G.’s work is partially supported by National Key Basic Research and Development Program of China (grant No. 2017YFA0402704), National Natural Science Foundation of China (NSFC, Nos. 12033004, and 11861131007), and Chinese Academy of Sciences Key Research Program of Frontier Sciences (grant No. QYZDJ-SSW-SLH008). A.H. was supported by the Programme National Cosmology et Galaxies (PNCG) of CNRS/INSU with INP and IN2P3, co-funded by CEA and CNES, and by the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. K.K. gratefully acknowledges funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (grant number KR4598/2-1, PI: Kreckel) J.M.D.K. and M.C. gratefully acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) in the form of an Emmy Noether Research Group (grant number KR4801/1-1) and the DFG Sachbeihilfe (grant number KR4801/2-1), and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme via the ERC Starting Grant MUSTANG (grant agreement number 714907). J.P. acknowledges support from the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES. H.A.P. acknowledges support by the Ministry of Science and Technology of Taiwan under grant 110-2112-M-032-020-MY3. The work of J.S. is partially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Canadian Institute for Theoretical Astrophysics (CITA) National Fellowship. COOL Research DAO is a Decentralized Autonomous Organisation supporting research in astrophysics aimed at uncovering our cosmic origins. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2015.1.00902.S, ADS/JAO.ALMA#2015.1.00956.S, ADS/JAO.ALMA#2015.1.01191.S, ADS/JAO.ALMA#2017.1.00078.S, ADS/JAO.ALMA#2017.1.00984.S, ADS/JAO.ALMA#2018.1.00994.S, ADS/JAO.ALMA#2018.1.01290.S, ADS/JAO.ALMA#2019.1.01635.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.

References

  1. Alaghband-Zadeh, S., Chapman, S. C., Swinbank, A. M., et al. 2013, MNRAS, 435, 1493 [Google Scholar]
  2. Aniano, G., Draine, B. T., Calzetti, D., et al. 2012, ApJ, 756, 138 [Google Scholar]
  3. Aniano, G., Draine, B. T., Hunt, L. K., et al. 2020, ApJ, 889, 150 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bennett, C. L., Fixsen, D. J., Hinshaw, G., et al. 1994, ApJ, 434, 587 [NASA ADS] [CrossRef] [Google Scholar]
  5. Bisbas, T. G., Papadopoulos, P. P., & Viti, S. 2015, ApJ, 803, 37 [NASA ADS] [CrossRef] [Google Scholar]
  6. Bisbas, T. G., van Dishoeck, E. F., Papadopoulos, P. P., et al. 2017, ApJ, 839, 90 [Google Scholar]
  7. Bisbas, T. G., Tan, J. C., & Tanaka, K. E. I. 2021, MNRAS, 502, 2701 [CrossRef] [Google Scholar]
  8. Bolatto, A. D., Jackson, J. M., & Ingalls, J. G. 1999, ApJ, 513, 275 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bolatto, A. D., Jackson, J. M., Kraemer, K. E., & Zhang, X. 2000a, ApJ, 541, L17 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bolatto, A. D., Jackson, J. M., Israel, F. P., Zhang, X., & Kim, S. 2000b, ApJ, 545, 234 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bolatto, A. D., Jackson, J. M., Wilson, C. D., & Moriarty-Schieven, G. 2000c, ApJ, 532, 909 [NASA ADS] [CrossRef] [Google Scholar]
  12. Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [CrossRef] [Google Scholar]
  13. Bolte, S., & Cordelières, F. P. 2006, J. Microsc., 224, 213 [CrossRef] [Google Scholar]
  14. Boogaard, L. A., van der Werf, P., Weiss, A., et al. 2020, ApJ, 902, 109 [NASA ADS] [CrossRef] [Google Scholar]
  15. Bothwell, M. S., Aguirre, J. E., Aravena, M., et al. 2017, MNRAS, 466, 2825 [Google Scholar]
  16. Bourne, N., Dunlop, J. S., Simpson, J. M., et al. 2019, MNRAS, 482, 3135 [Google Scholar]
  17. Brisbin, D., Aravena, M., Daddi, E., et al. 2019, A&A, 628, A104 [EDP Sciences] [Google Scholar]
  18. Burton, M. G., Hollenbach, D. J., & Tielens, A. G. G. M. 1990, ApJ, 365, 620 [NASA ADS] [CrossRef] [Google Scholar]
  19. Burton, M. G., Ashley, M. C. B., Braiding, C., et al. 2015, ApJ, 811, 13 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chastenet, J., Bot, C., Gordon, K. D., et al. 2017, A&A, 601, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Chastenet, J., Sandstrom, K., Chiang, I. D., et al. 2021, ApJ, 912, 103 [NASA ADS] [CrossRef] [Google Scholar]
  22. Cicone, C., Severgnini, P., Papadopoulos, P. P., et al. 2018, ApJ, 863, 143 [NASA ADS] [CrossRef] [Google Scholar]
  23. Clark, P. C., Glover, S. C. O., Ragan, S. E., & Duarte-Cabral, A. 2019, MNRAS, 486, 4622 [Google Scholar]
  24. Cortzen, I., Magdis, G. E., Valentino, F., et al. 2020, A&A, 634, L14 [EDP Sciences] [Google Scholar]
  25. Costes, S., Daelemans, D., Cho, E., et al. 2004, Biophys. J., 86, 3993 [NASA ADS] [CrossRef] [Google Scholar]
  26. Crocker, A. F., Pellegrini, E., Smith, J. D. T., et al. 2019, ApJ, 887, 105 [NASA ADS] [CrossRef] [Google Scholar]
  27. Daddi, E., Dannerbauer, H., Liu, D., et al. 2015, A&A, 577, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Dale, D. A., Aniano, G., Engelbracht, C. W., et al. 2012, ApJ, 745, 95 [NASA ADS] [CrossRef] [Google Scholar]
  29. Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2011, MNRAS, 410, 1687 [NASA ADS] [Google Scholar]
  30. Dannerbauer, H., Harrington, K., Díaz-Sánchez, A., et al. 2019, AJ, 158, 34 [Google Scholar]
  31. de Jong, T., Boland, W., & Dalgarno, A. 1980, A&A, 91, 68 [NASA ADS] [Google Scholar]
  32. Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton: Princeton University Press) [Google Scholar]
  33. Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [CrossRef] [Google Scholar]
  34. Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
  35. Dunne, L., Maddox, S. J., Vlahakis, C., & Gomez, H. L. 2021, MNRAS, 501, 2573 [NASA ADS] [CrossRef] [Google Scholar]
  36. Emonts, B. H. C., Lehnert, M. D., Dannerbauer, H., et al. 2018, MNRAS, 477, L60 [NASA ADS] [CrossRef] [Google Scholar]
  37. Emsellem, E., Schinnerer, E., Santoro, F., et al. 2022, A&A, 659, A191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Field, G. B., Goldsmith, D. W., & Habing, H. J. 1969, ApJ, 155, L149 [NASA ADS] [CrossRef] [Google Scholar]
  39. Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [Google Scholar]
  40. Frerking, M. A., Langer, W. D., & Wilson, R. W. 1982, ApJ, 262, 590 [Google Scholar]
  41. Frerking, M. A., Keene, J., Blake, G. A., & Phillips, T. G. 1989, ApJ, 344, 311 [Google Scholar]
  42. Galliano, F., Hony, S., Bernard, J. P., et al. 2011, A&A, 536, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Gao, Y., & Solomon, P. M. 2004a, ApJS, 152, 63 [Google Scholar]
  44. Gao, Y., & Solomon, P. M. 2004b, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
  45. García-Burillo, S., Combes, F., Schinnerer, E., Boone, F., & Hunt, L. K. 2005, A&A, 441, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Genzel, R., & Stutzki, J. 1989, ARA&A, 27, 41 [NASA ADS] [CrossRef] [Google Scholar]
  47. Genzel, R., Harris, A. I., Jaffe, D. T., & Stutzki, J. 1988, ApJ, 332, 1049 [NASA ADS] [CrossRef] [Google Scholar]
  48. Gerin, M., Phillips, T. G., Keene, J., Betz, A. L., & Boreiko, R. T. 1998, ApJ, 500, 329 [NASA ADS] [CrossRef] [Google Scholar]
  49. Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 116 [NASA ADS] [Google Scholar]
  50. Glover, S. C. O., & Clark, P. C. 2016, MNRAS, 456, 3596 [Google Scholar]
  51. Glover, S. C. O., Clark, P. C., Micic, M., & Molina, F. 2015, MNRAS, 448, 1607 [NASA ADS] [CrossRef] [Google Scholar]
  52. Goicoechea, J. R., Pety, J., Cuadrado, S., et al. 2016, Nature, 537, 207 [Google Scholar]
  53. Goldreich, P., & Kwan, J. 1974, ApJ, 189, 441 [CrossRef] [Google Scholar]
  54. Grier, C. J., Mathur, S., Ghosh, H., & Ferrarese, L. 2011, ApJ, 731, 60 [NASA ADS] [CrossRef] [Google Scholar]
  55. Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [EDP Sciences] [Google Scholar]
  56. Gullberg, B., Lehnert, M. D., De Breuck, C., et al. 2016, A&A, 591, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Habing, H. J. 1968, Bull. Astron. Inst. Neth., 19, 421 [Google Scholar]
  58. Harrington, K. C., Weiss, A., Yun, M. S., et al. 2021, ApJ, 908, 95 [NASA ADS] [CrossRef] [Google Scholar]
  59. Harrison, A., Puxley, P., Russell, A., & Brand, P. 1995, MNRAS, 277, 413 [NASA ADS] [CrossRef] [Google Scholar]
  60. Herrera, C. N., Pety, J., Hughes, A., et al. 2020, A&A, 634, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Heyer, M., & Dame, T. M. 2015, ARA&A, 53, 583 [Google Scholar]
  62. Heyer, M., Krawczyk, C., Duval, J., & Jackson, J. M. 2009, ApJ, 699, 1092 [Google Scholar]
  63. Hogerheijde, M. R., Jansen, D. J., & van Dishoeck, E. F. 1995, A&A, 294, 792 [NASA ADS] [Google Scholar]
  64. Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
  65. Hollenbach, D. J., & Tielens, A. G. G. M. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
  66. Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 [NASA ADS] [CrossRef] [Google Scholar]
  67. Hu, C.-Y., Sternberg, A., & van Dishoeck, E. F. 2021, ApJ, 920, 44 [NASA ADS] [CrossRef] [Google Scholar]
  68. Hunt, L. K., Weiß, A., Henkel, C., et al. 2017, A&A, 606, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  69. Ikeda, M., Maezawa, H., Ito, T., et al. 1999, ApJ, 527, L59 [NASA ADS] [CrossRef] [Google Scholar]
  70. Ikeda, M., Oka, T., Tatematsu, K., Sekimoto, Y., & Yamamoto, S. 2002, ApJS, 139, 467 [NASA ADS] [CrossRef] [Google Scholar]
  71. Israel, F. P., & Baas, F. 2001, A&A, 371, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Israel, F. P., & Baas, F. 2003, A&A, 404, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Israel, F. P., White, G. J., & Baas, F. 1995, A&A, 302, 343 [NASA ADS] [Google Scholar]
  74. Ivlev, A. V., Padovani, M., Galli, D., & Caselli, P. 2015, ApJ, 812, 135 [Google Scholar]
  75. Izumi, T., Wada, K., Fukushige, R., Hamamura, S., & Kohno, K. 2018, ApJ, 867, 48 [NASA ADS] [CrossRef] [Google Scholar]
  76. Izumi, T., Nguyen, D. D., Imanishi, M., et al. 2020, ApJ, 898, 75 [NASA ADS] [CrossRef] [Google Scholar]
  77. Izumi, N., Fukui, Y., Tachihara, K., et al. 2021, PASJ, 73, 174 [NASA ADS] [CrossRef] [Google Scholar]
  78. Jacobs, B. A., Rizzi, L., Tully, R. B., et al. 2009, AJ, 138, 332 [NASA ADS] [CrossRef] [Google Scholar]
  79. Jaffe, D. T., Harris, A. I., Silber, M., Genzel, R., & Betz, A. L. 1985, ApJ, 290, L59 [NASA ADS] [CrossRef] [Google Scholar]
  80. Jiao, Q., Zhao, Y., Lu, N., et al. 2019, ApJ, 880, 133 [Google Scholar]
  81. Jiménez-Bailón, E., Santos-Lleó, M., Dahlem, M., et al. 2005, A&A, 442, 861 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Jin, S., Daddi, E., Magdis, G. E., et al. 2019, ApJ, 887, 144 [Google Scholar]
  83. Kamegai, K., Ikeda, M., Maezawa, H., et al. 2003, ApJ, 589, 378 [NASA ADS] [CrossRef] [Google Scholar]
  84. Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [Google Scholar]
  85. Kaufman, M. J., Wolfire, M. G., & Hollenbach, D. J. 2006, ApJ, 644, 283 [Google Scholar]
  86. Keene, J., Blake, G. A., Phillips, T. G., Huggins, P. J., & Beichman, C. A. 1985, ApJ, 299, 967 [NASA ADS] [CrossRef] [Google Scholar]
  87. Keene, J., Blake, G. A., & Phillips, T. G. 1987, ApJ, 313, 396 [NASA ADS] [CrossRef] [Google Scholar]
  88. Koda, J., Scoville, N., Hasegawa, T., et al. 2012, ApJ, 761, 41 [NASA ADS] [CrossRef] [Google Scholar]
  89. Koribalski, B., Dahlem, M., Mebold, U., & Brinks, E. 1993, A&A, 268, 14 [NASA ADS] [Google Scholar]
  90. Kramer, C., Jakob, H., Mookerjea, B., et al. 2004, A&A, 424, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  91. Kramer, C., Cubick, M., Röllig, M., et al. 2008, A&A, 477, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
  93. Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2020, MNRAS, 499, 193 [NASA ADS] [CrossRef] [Google Scholar]
  94. Krips, M., Martín, S., Sakamoto, K., et al. 2016, A&A, 592, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  95. Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
  96. Lang, P., Meidt, S. E., Rosolowsky, E., et al. 2020, ApJ, 897, 122 [CrossRef] [Google Scholar]
  97. Langer, W. 1976, ApJ, 206, 699 [NASA ADS] [CrossRef] [Google Scholar]
  98. Lee, M. M., Tanaka, I., Iono, D., et al. 2021, ApJ, 909, 181 [NASA ADS] [CrossRef] [Google Scholar]
  99. Lee, J. C., Whitmore, B. C., Thilker, D. A., et al. 2022, ApJS, 258, 10 [NASA ADS] [CrossRef] [Google Scholar]
  100. Leroy, A. K., Usero, A., Schruba, A., et al. 2017, ApJ, 835, 217 [NASA ADS] [CrossRef] [Google Scholar]
  101. Leroy, A. K., Sandstrom, K. M., Lang, D., et al. 2019, ApJS, 244, 24 [Google Scholar]
  102. Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021a, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
  103. Leroy, A. K., Hughes, A., Liu, D., et al. 2021b, ApJS, 255, 19 [NASA ADS] [CrossRef] [Google Scholar]
  104. Leroy, A. K., Rosolowsky, E., Usero, A., et al. 2022, ApJ, 927, 149 [NASA ADS] [CrossRef] [Google Scholar]
  105. Liu, D., Gao, Y., Isaak, K., et al. 2015, ApJ, 810, L14 [NASA ADS] [CrossRef] [Google Scholar]
  106. Liu, D., Daddi, E., Schinnerer, E., et al. 2021, ApJ, 909, 56 [NASA ADS] [CrossRef] [Google Scholar]
  107. Madden, S. C., Cormier, D., Hony, S., et al. 2020, A&A, 643, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  108. Maloney, P. R., Hollenbach, D. J., & Tielens, A. G. G. M. 1996, ApJ, 466, 561 [Google Scholar]
  109. Meijerink, R., & Spaans, M. 2005, A&A, 436, 397 [CrossRef] [EDP Sciences] [Google Scholar]
  110. Meijerink, R., Spaans, M., & Israel, F. P. 2007, A&A, 461, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Meixner, M., & Tielens, A. G. G. M. 1993, ApJ, 405, 216 [NASA ADS] [CrossRef] [Google Scholar]
  112. Michiyama, T., Ueda, J., Tadaki, K.-I., et al. 2020, ApJ, 897, L19 [NASA ADS] [CrossRef] [Google Scholar]
  113. Michiyama, T., Saito, T., Tadaki, K.-I., et al. 2021, ApJS, 257, 28 [NASA ADS] [CrossRef] [Google Scholar]
  114. Miyamoto, Y., Seta, M., Nakai, N., et al. 2018, PASJ, 70, L1 [NASA ADS] [CrossRef] [Google Scholar]
  115. Miyamoto, Y., Yasuda, A., Watanabe, Y., et al. 2021, PASJ, 73, 552 [NASA ADS] [CrossRef] [Google Scholar]
  116. Mookerjea, B., Kantharia, N. G., Roshi, D. A., & Masur, M. 2006, MNRAS, 371, 761 [NASA ADS] [CrossRef] [Google Scholar]
  117. Naylor, D. A., Baluteau, J. P., Barlow, M. J., et al. 2010, in Space Telescopes and Instrumentation 2010: Optical, Infrared, and Millimeter Wave, eds. J. Oschmann, M. Jacobus, M. C. Clampin, & H. A. MacEwen, SPIE Conf. Ser., 7731, 773116 [NASA ADS] [CrossRef] [Google Scholar]
  118. Nesvadba, N. P. H., Cañameras, R., Kneissl, R., et al. 2019, A&A, 624, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Offner, S. S. R., Bisbas, T. G., Bell, T. A., & Viti, S. 2014, MNRAS, 440, L81 [NASA ADS] [CrossRef] [Google Scholar]
  120. Oka, T., Yamamoto, S., Iwata, M., et al. 2001, ApJ, 558, 176 [NASA ADS] [CrossRef] [Google Scholar]
  121. Oka, T., Iwata, M., Maezawa, H., et al. 2004, ApJ, 602, 803 [NASA ADS] [CrossRef] [Google Scholar]
  122. Oka, T., Kamegai, K., Hayashida, M., et al. 2005, ApJ, 623, 889 [NASA ADS] [CrossRef] [Google Scholar]
  123. Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  124. Papadopoulos, P. P. 2010, ApJ, 720, 226 [NASA ADS] [CrossRef] [Google Scholar]
  125. Papadopoulos, P. P., & Allen, M. L. 2000, ApJ, 537, 631 [NASA ADS] [CrossRef] [Google Scholar]
  126. Papadopoulos, P. P., Thi, W.-F., Miniati, F., & Viti, S. 2011, MNRAS, 414, 1705 [NASA ADS] [CrossRef] [Google Scholar]
  127. Papadopoulos, P. P., Bisbas, T. G., & Zhang, Z.-Y. 2018, MNRAS, 478, 1716 [NASA ADS] [CrossRef] [Google Scholar]
  128. Pessa, I., Schinnerer, E., Belfiore, F., et al. 2021, A&A, 650, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  129. Pety, J., Beelen, A., Cox, P., et al. 2004, A&A, 428, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Pety, J., Guzmán, V. V., Orkisz, J. H., et al. 2017, A&A, 599, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Phillips, T. G., & Huggins, P. J. 1981, ApJ, 251, 533 [NASA ADS] [CrossRef] [Google Scholar]
  132. Phillips, T. G., Huggins, P. J., Kuiper, T. B. H., & Miller, R. E. 1980, ApJ, 238, L103 [NASA ADS] [CrossRef] [Google Scholar]
  133. Pineda, J. L., Mizuno, N., Stutzki, J., et al. 2008, A&A, 482, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Plume, R., Jaffe, D. T., & Keene, J. 1994, ApJ, 425, L49 [NASA ADS] [CrossRef] [Google Scholar]
  135. Plume, R., Jaffe, D. T., Tatematsu, K., Evans, N. J., II, & Keene, J. 1999, ApJ, 512, 768 [NASA ADS] [CrossRef] [Google Scholar]
  136. Popping, G., Decarli, R., Man, A. W. S., et al. 2017, A&A, 602, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Pound, M. W., & Wolfire, M. G. 2008, in Astronomical Data Analysis Software and Systems XVII, eds. R. W. Argyle, P. S. Bunclark, & J. R. Lewis, ASP Conf. Ser., 394, 654 [Google Scholar]
  138. Roman-Duval, J., Jackson, J. M., Heyer, M., Rathborne, J., & Simon, R. 2010, ApJ, 723, 492 [NASA ADS] [CrossRef] [Google Scholar]
  139. Rosolowsky, E., & Leroy, A. 2006, PASP, 118, 590 [NASA ADS] [CrossRef] [Google Scholar]
  140. Rosolowsky, E., Hughes, A., Leroy, A. K., et al. 2021, MNRAS, 502, 1218 [NASA ADS] [CrossRef] [Google Scholar]
  141. Saito, T., Michiyama, T., Liu, D., et al. 2020, MNRAS, 497, 3591 [NASA ADS] [CrossRef] [Google Scholar]
  142. Saito, T., Takano, S., Harada, N., et al. 2022a, ApJ, 927, L32 [NASA ADS] [CrossRef] [Google Scholar]
  143. Saito, T., Takano, S., Harada, N., et al. 2022b, ApJ, 935, 155 [NASA ADS] [CrossRef] [Google Scholar]
  144. Salak, D., Nakai, N., Seta, M., & Miyamoto, Y. 2019, ApJ, 887, 143 [NASA ADS] [CrossRef] [Google Scholar]
  145. Sanders, D. B., Mazzarella, J. M., Kim, D. C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
  146. Santoro, F., Kreckel, K., Belfiore, F., et al. 2022, A&A, 658, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  147. Schilke, P., Carlstrom, J. E., Keene, J., & Phillips, T. G. 1993, ApJ, 417, L67 [NASA ADS] [CrossRef] [Google Scholar]
  148. Schneider, C. A., Rasband, W. S., & Eliceiri, K. W. 2012, Nat. Meth., 9, 671 [CrossRef] [Google Scholar]
  149. Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [Google Scholar]
  150. Schroder, K., Staemmler, V., Smith, M. D., Flower, D. R., & Jaquet, R. 1991, J. Phys. B: At. Mol. Opt. Phys., 24, 2487 [CrossRef] [Google Scholar]
  151. Scoville, N. Z., & Solomon, P. M. 1974, ApJ, 187, L67 [NASA ADS] [CrossRef] [Google Scholar]
  152. Silverman, J. D., Rujopakarn, W., Daddi, E., et al. 2018, ApJ, 867, 92 [NASA ADS] [CrossRef] [Google Scholar]
  153. Spaans, M., & van Dishoeck, E. F. 1997, A&A, 323, 953 [NASA ADS] [Google Scholar]
  154. Spitzer, L. 1998, Physical Processes in the Interstellar Medium (New York: Wiley-VCH) [CrossRef] [Google Scholar]
  155. Sternberg, A., & Dalgarno, A. 1989, ApJ, 338, 197 [Google Scholar]
  156. Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
  157. Stutzki, J., Stacey, G. J., Genzel, R., et al. 1988, ApJ, 332, 379 [NASA ADS] [CrossRef] [Google Scholar]
  158. Sun, K., Ossenkopf, V., Kramer, C., et al. 2008, A&A, 489, 207 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  159. Tatematsu, K., Jaffe, D. T., Plume, R., Evans, N. J., II, & Keene, J. 1999, ApJ, 526, 295 [NASA ADS] [CrossRef] [Google Scholar]
  160. Tauber, J. A., Tielens, A. G. G. M., Meixner, M., & Goldsmith, P. F. 1994, ApJ, 422, 136 [NASA ADS] [CrossRef] [Google Scholar]
  161. Teng, Y.-H., Sandstrom, K. M., Sun, J., et al. 2022, ApJ, 925, 72 [NASA ADS] [CrossRef] [Google Scholar]
  162. Tielens, A. G. G. M. 2010, The Physics and Chemistry of the Interstellar Medium (Cambridge: Cambridge University Press) [Google Scholar]
  163. Tielens, A. G. G. M., & Hollenbach, D. 1985a, ApJ, 291, 722 [Google Scholar]
  164. Tielens, A. G. G. M., & Hollenbach, D. 1985b, ApJ, 291, 747 [NASA ADS] [CrossRef] [Google Scholar]
  165. Tielens, A. G. G. M., Meixner, M. M., van der Werf, P. P., et al. 1993, Science, 262, 86 [NASA ADS] [CrossRef] [Google Scholar]
  166. Ueda, J., Michiyama, T., Iono, D., Miyamoto, Y., & Saito, T. 2022, PASJ, 74, 407 [NASA ADS] [CrossRef] [Google Scholar]
  167. Valentino, F., Magdis, G. E., Daddi, E., et al. 2018, ApJ, 869, 27 [Google Scholar]
  168. Valentino, F., Magdis, G. E., Daddi, E., et al. 2020, ApJ, 890, 24 [Google Scholar]
  169. van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  170. van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [Google Scholar]
  171. van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [Google Scholar]
  172. Wagg, J., Wilner, D. J., Neri, R., Downes, D., & Wiklind, T. 2006, ApJ, 651, 46 [NASA ADS] [CrossRef] [Google Scholar]
  173. Walter, F., Weiß, A., Downes, D., Decarli, R., & Henkel, C. 2011, ApJ, 730, 18 [Google Scholar]
  174. Weiß, A., Henkel, C., Downes, D., & Walter, F. 2003, A&A, 409, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  175. Weiß, A., Downes, D., Henkel, C., & Walter, F. 2005, A&A, 429, L25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  176. White, G. J., Ellison, B., Claude, S., Dent, W. R. F., & Matheson, D. N. 1994, A&A, 284, L23 [NASA ADS] [Google Scholar]
  177. Williams, T. G., Kreckel, K., Belfiore, F., et al. 2022, MNRAS, 509, 1303 [Google Scholar]
  178. Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [Google Scholar]
  179. Wolfire, M. G., Vallini, L., & Chevance, M. 2022, ARA&A, 60, 247 [NASA ADS] [CrossRef] [Google Scholar]
  180. Wootten, A., Phillips, T. G., Beichman, C. A., & Frerking, M. 1982, ApJ, 256, L5 [NASA ADS] [CrossRef] [Google Scholar]
  181. Wright, E. L., Mather, J. C., Bennett, C. L., et al. 1991, ApJ, 381, 200 [NASA ADS] [CrossRef] [Google Scholar]
  182. Yamagishi, M., Shimajiri, Y., Tokuda, K., et al. 2021, ApJ, 914, L9 [NASA ADS] [CrossRef] [Google Scholar]
  183. Yamamoto, S., Maezawa, H., Ikeda, M., et al. 2001, ApJ, 547, L165 [NASA ADS] [CrossRef] [Google Scholar]
  184. Yang, C., Omont, A., Beelen, A., et al. 2017, A&A, 608, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  185. Zhang, X., Lee, Y., Bolatto, A., & Stark, A. A. 2001, ApJ, 553, 274 [NASA ADS] [CrossRef] [Google Scholar]
  186. Zhang, Z.-Y., Henkel, C., Gao, Y., et al. 2014, A&A, 568, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  187. Zmuidzinas, J., Betz, A. L., & Goldhaber, D. M. 1986, ApJ, 307, L75 [NASA ADS] [CrossRef] [Google Scholar]
  188. Zmuidzinas, J., Betz, A. L., Boreiko, R. T., & Goldhaber, D. M. 1988, ApJ, 335, 774 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Data reduction, imaging, and moment map generation

After downloading the raw data, namely, 12m+7m for CO(2−1) and 7m for [C I](1−0), respectively, we ran the observatory calibration pipeline (“scriptForPI”) to reduce the data. As shown in Leroy et al. (2021b), the observatory calibration produces well-calibrated visibility data without further manual flagging. We then split out the visibility data and proceeded to the imaging step.

In order to match the spatial resolution of CO(2−1) and [C I](1−0), we carefully matched their uv ranges. We flagged the CO(2−1) visibility data outside the uv range of 19−68 m (∼15−52kλ) so as to match the uv range of the [C I](1−0) data (minimum to 80% percentile: 8.9−32 m, or ∼15−52kλ). Given that the [C I](1−0) uv plane distribution is elliptic, while the uv range selection in CASA is circular, our chosen thresholds are adjusted to make the final CO(2−1) synthesized beam similar to that of [C I](1−0). We note that in a later step, we also convolved both image cubes to the exact same rounded beam (3.46″) before generating the moment maps.

The PHANGS-ALMA imaging & post-processing pipeline10 developed by Leroy et al. (2021b) was used for creating line cubes and moment maps. The code is suitable for general nearby galaxy strong line mapping interferometric and total power mosaic data. In brief, the visibility data are carefully transformed into the user-given channel width and frequency range corresponding to the line plus line-free channels, then continuum is subtracted by fitting an order of zero polynomial. Then, two stages of imaging (“cleaning”) are performed: first a multi-scale cleaning down to ∼4σ, then a single-scale cleaning down to ∼1σ. At each stage, CASA’s tclean task is iteratively called so as to force many major cycles, which has proven to improve the accuracy of the deconvolution. Before and during the second stage cleaning, a clean mask is computed at each iteration according to the outcome of previous iteration by finding all > 2σ pixels associated with > 4σ peaks in a watershed algorithm (Rosolowsky & Leroy 2006; Rosolowsky et al. 2021). In this way, the cleaning can include as much signal as possible and ensure a signal-free residual.

Then, the image cubes were corrected for the primary beam attenuation, converted to Kelvin units, and convolved to a common beam, which is the coarser beam of CO(2−1) and [C I](1−0). Because of our uv range flagging before imaging, the directly tclean-imaged beam sizes are already close. This convolution further precisely matches CO(2−1) and [C I](1−0) image cube beams.

Next, moment maps were generated with modules in the PHANGS-ALMA pipeline, consistently for CO and C I. This process includes first constructing noise and mask cubes from the image cubes, then combining the masks (i.e., where a science signal should present), then computing moment 0 line integrated intensity, moment 1 line peak velocity, and moment 2 line width. The mask cubes are the key in producing moment maps. Here, two masks are built: a “broad mask”, which contains as much plausible science signal as possible, and a “strict mask”, which is optimized for high-confidence signal. The strict mask is made by finding peaks that have > 4σ over two consecutive channels then expanding down to 2σ also with the watershed algorithm. Then the broad mask is obtained by aggregating strict masks made from image cubes convolved to coarser resolutions (∼30″ in this work as well as in Leroy et al. 2021b). To make consistent moment maps for CO and C I, we aggregated their masks together as a joint mask, for broad and strict masks, respectively, then their final moment maps are computed within the joint mask.

The resulting CO(2−1) and [C I](1−0) line intensity maps are then used for our next line ratio analysis. The line velocity and line width maps were not further analyzed, but they are consistent with the products from the PHANGS-ALMA survey’s data release as well as those of Lang et al. (2020). Given that the PHANGS-ALMA 12m+7m+tp CO(2−1) has the full spatial information and are deeper, their line velocity and line width maps are more useful for kinematic studies than ours produced from this work.

Appendix B: Assessing the missing flux in the NGC 3627 C I data

We assess the level of missing flux in the NGC 3627 C I data in three ways: (a) comparing with the Herschel SPIRE FTS [C I](1−0) observation in this galaxy, (b) comparing the uv-trimmed CO(2-1) moment-0 map with the PHANGS-ALMA short-spacing corrected (12m+7m+tp) moment-0 map, and (c) performing CASA simulation and comparing with the “true” moment-0 from the skymodel and the derived product from the simulated visibilities.

Method (a): NGC 3627 has been observed with the Herschel SPIRE (Griffin et al. 2010) Fourier Transform Spectrometer (FTS; Naylor et al. 2010) in mapping mode with nearly Nyquist sampling. Liu et al. (2015) reduced the archival data and extracted the line fluxes for each groups of pointings. [C I](1−0) is detected with S/N ∼ 4 − 5 at three sightlines from the galaxy center to the southern bar end, with R.A. and Dec. coordinates (J2000) 170.061905, +12.991336, 170.066361 +12.987091, and 170.071243 +12.981615, respectively. The [C I](1−0) luminosities are 1.44 ± 0.31, 2.01 ± 0.48, and 1.71 ± 0.40 × 107 K km s−1 pc2, respectively, where the errors are purely from the RMS of line-free FTS spectra. By convolving our [C I](1−0) line cube to the FTS beam of ∼39″ then extracting the moment maps, we measure a [C I](1−0) line luminosity of 0.52, 0.33, and 0.29 × 107 K km s−1 pc2 at the above three positions, respectively, which means a missing flux of 36 − 75% at the galaxy center and 68 − 88% at the southern bar end (at a 95% confidence level).

Method (b): We made ratio maps of our uv-trimmed CO(2−1) moment-0 map, and that of the original PHANGS-ALMA short-spacing-corrected (12m+7m+tp) CO(2−1) data but convolved to the corresponding resolution before making the moment maps. The ratio maps are made at two resolutions: the FTS 39″ beam, and our working resolution of 3.46″. The former leads to a missing flux of 26%, 31% and 36% from the galaxy center to the southern bar end. We note that the above Herschel FTS analysis generally indicates a higher missing flux, but the FTS measurements are of low S/N and errors purely from the rms of the spectra cannot fully account for other errors such as pointing, spectral response, off-axis spaxel calibration, etc. The latter ratio map shows that the missing flux at our working resolution and within the strict mask varies from ∼60% to as low as 6% at the brightest pixels. This is consistent with our next method, which is based on simulations.

Method (c): We performed detailed simulations of 7m-only [C I](1−0) and 12m+7m CO(2−1) observations with the CASA simobserve task. We used the PHANGS-ALMA 12m+7m CO(2−1) clean model cube (one of the output products of CASA tclean runs) as the input skymodel for CO(2−1), and that scaled by a factor of 0.2 in Kelvin units for [C I](1−0), representing a constant RC I/CO = 0.2. We note that we did not use the short-spacing-corrected PHANGS-ALMA CO(2−1) cube because it has a finite beam size of ∼1″, and simulation based on that may result in more extended emissions. On the contrary, the clean model cube has an infinite resolution, and because both “multiscale” and “singlescale” cleaning are used in the PHANGS-ALMA imaging, the clean model contains point sources as well as extended sources. We also set the actual observing dates and integration times as the real observations. Then we ran CASA simobserve to simulate the visibilities of each observing block, concatenated them together, and processed them into image cubes and moment maps in the same way described in Appendix A. Meanwhile, by convolving the input skymodel with a 2D Gaussian beam corresponding to our working resolution, and integrating over the spectral axis, we obtained a “true” skymodel moment-0 map that can be directly compared to the imaged moment-0 maps from the simulation. Their ratio map shows a missing flux of ∼50% to ∼7% in the strict mask, and more specifically, 24%, 58%, 85%, and 96% pixels selected in our method as for real data have a missing flux < 20%, < 30%, < 40%, and < 50%, respectively.

Figure B.1 illustrates the results from methods (b) (upper panels) and (c) (lower panels). Left panels show the CO(2−1) moment-0 maps, analyzed at the same working resolution as our main analysis in Appendix A. The simulated data show a fainter emission because we used the clean mode cube as the skymodel, which was made by cleaning the PHANGS-ALMA 12m+7m data down to 1σ within the clean mask voxels. This will indeed lose some fluxes. However, the right panels show that the two methods lead to consistent missing flux results.

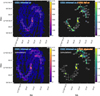thumbnail Fig. B.1.

CO(2−1) line flux and fraction of missing flux maps. Upper left panel: Short-spacing corrected (12m+7m+tp) PHANGS-ALMA CO(2-1) derived moment-0 map. Upper right panel: Ratio map of the uv-trimmed CO(2-1) moment-0 map used in this work to that in the left panel. Lower left panel: CO(2-1) moment-0 map derived from our simulation with uv trimming as for real data. Lower right panel: ratio map of the uv-trimmed CO(2-1) moment-0 map based on the simulation to the “true” skymodel moment-0 map as shown left. All moment maps are derived by first convolving cubes to our working resolution of 3.46″ then performing masking analysis as described in Appendix A, except for the “true” skymodel moment-0 map which is computed without any masking. We note that in the simulation-based analysis, some regions have too low S/N due to their faint CO brightness or insufficient cleaning, thus they are out of the mask and show blank line ratios (instead of very low missing flux) in the lower right-hand panel.

We note that in the last panel of Fig. B.1, some regions appear black in the simulation-based analysis because we require line ratios to be analyzed in the strict mask, while these regions are not in it any longer. This is because the skymodel loses some fluxes as mentioned above, thus the strict mask is smaller; in addition, this occurs because we assumed a constant RC I/CO in the simulation, which may lead to fainter C I than real data along faint sightlines, for instance, region 22, thus further shrinking the strict mask where both lines need to have sufficient S/N. Bearing these points in mind, we conclude that methods (b) and (c) have consistent results on the missing flux, while method (a) is less accurate due to the unconsidered uncertainties.

These checks show that the overall missing flux in NGC 3627 is 31% based on the full- and trimmed-uv CO(2−1) analysis, or ∼36 − 88% based on the more-uncertain Herschel data. At the pixel level, it varies from 7% to ∼50% from bright to faint sightlines at our working resolution of 3.46″. These values are as expected given our ACA-only observation setup. We emphasize again that by applying the uv-matching in our data reduction, our C I/CO line ratio study is not obviously affected by the missing flux issue, except perhaps in the faintest pixels or “cloud edges”.

Appendix C: Assessing noise-induced C I enhancement with simulation

In Appendix B we described our simulation. We also use it to assess how the noise can induce artificial [C I/CO] line ratio variation. In Fig. C.1 we show the line ratio map from the simulation with a constant RC I/CO = 0.2, and in Fig. C.1 we show the scatter plots with simulation results similar to Fig. 4. Interestingly, we see certain C I/CO variations, especially C I “enhancement” at the edge of galaxy center’s gas clump (region 1), and the edge of the northern spiral arm (region 14). Nevertheless, the trend is very different from the real data, that is, Fig. 4. First, the galaxy center has a much weaker [C I/CO] in the real data, whereas in the simulation it is inverted. Second, the scatter is much larger in real data, with a tail of C I enhanced regions which is not seen in the simulation. Third, from the bottom panels of Fig. C.1, where S/N is shown, we see that RC I/CO is biased to be lower in low-S/N situation. Thus the high C I in real data is unlikely to be a bias of low S/N.

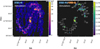thumbnail Fig. C.1.

C I line flux and RC I/CO line ratio image from the simulation mimicking real observation but with a constant input line ratio RC I/CO = 0.2.

thumbnail Fig. C.1.

Line flux, ratio and S/N correlations from our CASA simulation. Upper panels: [C I](1−0) and CO(2−1) line brightness and ratio similar to Fig. 4, but from our simulation (with a constant input RC I/CO = 0.2 as indicated by the horizontal shading in the right panels). Lower panels: Similar to the upper panels but showing line S/N instead of brightness. This illustrates how RC I/CO can be biased in low-S/N situation.

Appendix D: C I and CO spectra of selected regions in NGC 3627

We show the examples of [C I](1−0) and CO(2−1) moment-0 maps and spectra for regions 1, 4, and 22 in Fig. C.1. They represent the NGC 3627 center, the off-center location, and the location at the outer disk of the gaseous spiral arm, as discussed in Sect. 3.

thumbnail Fig. D.1.

[C I](1−0) and CO(2−1) moment-0 maps and spectra of regions 1, 4, and 22 as defined in Fig. 1. All the regions’ spectra are available in our online data release (see Sect. 2.2).

All Tables

Table 1.

Physical and data properties of the sample.

In the text

All Figures

thumbnail Fig. 1.

Line intensity, ratio, and optical images of NGC 3627. Top panels: NGC 3627 [C I](1−0) (left) and CO(2−1) (right) integrated line intensity (moment-0) maps within our broad mask (representing high-completeness signals; see Appendix A). Bottom left panel: [C I](1−0)/CO(2−1) line ratio map within the combined signal mask. Bottom right panel: HST F814W − F555W − F438W RGB composite image (PHANGS-HST; Lee et al. 2022). Regions marked with the white boxes and labeled with numbers are mainly for illustration purpose and for discussion in the text. Their zoom-in images and extracted spectra are provided in our online data release. Examples for regions 1, 4, and 22 are presented in Appendix D. All images have the same field of view of 179″ × 179″ or 9.83 kpc × 9.83 kpc.
In the text
thumbnail Fig. 2.

Similar to Fig. 1, the [C I](1−0) and CO(2−1) moment-0 intensity maps and the line ratio map and the HST composite RGB image for NGC 4321. The field of view is 78″ × 78″, or 5.75 kpc × 5.75 kpc.
In the text
thumbnail Fig. 3.

[C I](1−0) (left) and RC I/CO (right) maps of NGC 1808 in the upper panels and NGC 7469 in the lower panels. Similar to Figs. 1 and 2, the line intensity maps are defined in the broad mask and the RC I/CO maps are restricted to the combined signal mask. Boxes in the left panels indicate the manually selected central regions where the pixels are highlighted in Fig. 4. Contours in the right panels indicate the 5, 10, 20 and 50-σ levels of the left-panel C I intensity maps.
In the text
thumbnail Fig. 4.

Line flux and ratio correlations. Left: I[C I](1−0) versus ICO(2 − 1) in the four galaxies we studied: NGC 3627, NGC 4321, NGC 1808 and NGC 7469. The I[C I](1−0) and ICO(2 − 1) integrated fluxes are moment-0 intensities extracted from their beam and pixel size matched data cubes. Only data points with propagated moment-0 S/N ≥ 5 are shown. The blue (with crossed hatch), green (with horizontal line hatch), gray (with dotted hatch) and light gray shadings indicate the 5σ thresholds for the four galaxies, respectively. Typical line widths of 10 km s−1 (NGC 3627 and NGC 4321) and 30 km s−1 (NGC 1808 and NGC 7469) in sigma are used to calculate the thresholds together with the channel rms in Table 1. For NGC 3627 and NGC 4321, their (uv-matched) CO(2−1) 5σ thresholds are out of the plotting range. Top axis shows the simply-converted H2 surface density using a constant αCO = 4.3 and CO excitation (i.e., CO(2−1) to CO(1−0) line ratio) R21 = 0.65. Right: same data but shown as the line ratio RC I/CO = I[C I](1−0)/ICO(2−1) versus ICO(2 − 1). The blue horizontal line indicates a star-forming (SF) disk-like RC I/CO ∼ 0.1, i.e., the spiral arms of NGC 3627 and NGC 4321. The gray horizontal line indicates a starburst (SB) disk-like RC I/CO ∼ 0.2, i.e., the ∼1 kpc SB disk/ring in NGC 1808 and NGC 7469. The red line with a slope of 0.8 in logarithm (0.035 (ICO(2 − 1)/[100 K km s−1])0.8) visually guides the trend of increasing RC I/CO in the central regions of these galaxies (see boxes in Figs. 1–3, sizes ∼300 − 500 pc).
In the text
thumbnail Fig. 5.

Line flux ratio distributions. Left panel: histograms of the sum of CO(2−1) surface brightness over pixels in each C I/CO line ratio interval in the four galaxies. The bold curves are the cumulative distributions of the corresponding histograms. Right panel: mean C I/CO line ratio for pixels in each bin of CO(2−1) surface brightness (or molecular gas surface density as indicated by the top-axis assuming a constant αCO = 4.3 and R21 = 0.65). Shaded area enveloping each mean trend indicates the 16th to 84th percentiles in each bin, and dashed line indicates the 50th percentile. This panel thus more clearly illustrates the ridge and scatter of the trends in the right panel of Fig. 4. Detection limits are shown consistently with Fig. 4.
In the text
thumbnail Fig. 6.

Line ratio versus mean ISRF intensity ⟨U⟩ measured from SED fitting to the near- to far-IR (Spitzer, Herschel) data. Left four panels: ⟨U⟩ maps of NGC 3627, NGC 4321, NGC 1808 and NGC 7469, and as described in Sect. 3.3 are obtained from the works done by Chastenet et al. (in prep.) as a continued effort of Chastenet et al. (2021). Right panel: scatter plot of RC I/CO versus ⟨U⟩ at a spatial resolution of ∼18″ in the manually-selected apertures shown in the left panels. We computed a beam-weighted mean RC I/CO and a center pixel RC I/CO for each aperture, displayed as the solid and open symbols, respectively. Error bars are the corresponding beam-weighted mean or central pixel RC I/CO uncertainties in each region. The region diameter (∼18″) corresponds to the coarsest resolution of the Herschel data used in the SED fitting. The gray dotted line shows RC I/CO = 0.07 U0.25 as a guiding line. The colored dotted contours (labeled 0.1−0.5) are the model contours of RC I/CO computed from the PDR Toolbox (using the latest wk2020 model and solar metallicity; Kaufman et al. 2006). We convert G0 from the model contour to the x-axis U by multiplying with a factor of 0.88 (Draine et al. 2007). The right y-axis indicates the PDR model’s nH2, whose range is manually adjusted so that the model contours roughly match the left x-axis. The PDR model contours show little dependence of RC I/CO on U in the horizontal direction but a strong correlation with nH2 as seen by the vertical gradient.
In the text
thumbnail Fig. 7.

Line ratio versus metallicity. Left two panels: metallicity maps of NGC 3627 and NGC 4321 from Williams et al. (2022) based on PHANGS-MUSE (Emsellem et al. 2022) data. Boxes are regions as defined in Figs. 1 and 2. Right panel: RC I/CO versus metallicity scatter plot for regions in NGC 3627 and NGC 4321. The bottom axis represents the metallicity in solar units, top axis is the metallicity in 12 + log(O/H), left-axis is the line ratio of [C I](1−0) and CO(2−1) in K km s−1 units, and right-axis is the ratio of fluxes in erg s−1 cm−2 sr−1 units. The left and right axes are matched by a factor of (ν[C I]1−0/νCO1−0)3 × R21, where we adopt R21 = 0.65 (Leroy et al. 2022). Data points are the mean metallicity and RC I/CO in each region shown in left panels, with error bars indicating the typical uncertainty in RC I/CO, and vertical color shading indicating the 16th to 84th percentiles of the pixels’ RC I/CO distribution inside each region. The Bolatto et al. (2000a) empirical fitting and Bolatto et al. (1999) model prediction lines are overlaid. The three outliers in NGC 3627 with RC I/CO ∼ 0.19, 0.28, and 0.35 are regions 20, 21, and 22, respectively. The outlier point in NGC 4321 with RC I/CO ∼ 0.06 is its center is region 1.
In the text
thumbnail Fig. 8.

Observed and calculated RC I/CO as a function of CO column density NCO and [C I/CO] abundance (column density) ratio NC I/NCO for seven representative ISM conditions, based on LTE calculations. Upper panels: curved lines show RC I/CO versus N C I / N CO $ N_{{\mathrm{C}\textsc{i}}/N_{\mathrm{CO}}} $ for different NCO, as indicated by the color. Dashed means CO(2−1) optically thick and [C I](1−0) optically thin, dotted means both are both optically thin, and solid line means both optically thick. Horizontal thick line is the observed RC I/CO value. Lower panels: black contours are RC I/CO = 0.05, 0.10, 0.20, and 0.50 in the CO column density versus C I/CO abundance ratio plane. Vertical color shading indicates the final NC I/NCO that can match both the observed RC I/CO and the assumed Σmol value noted at the top of each panel.
In the text
thumbnail Fig. 9.

Observed and calculated RC I/CO as a function of CO column density NCO and [C I/CO] abundance (column density) ratio NC I/NCO for seven representative ISM conditions, similar to Fig. 8 but based on non-LTE calculations. Upper panels: line ratio RC I/CO versus the abundance ratio NC I/NCO for different NCO, as indicated by the color. Dashed, dotted and solid lines are for different CO(2−1) [C I](1−0) optical depths as described in Fig. 8 caption. Horizontal thick line is the observed RC I/CO value. Lower panels: are the contours of RC I/CO = 0.05, 0.10, 0.20, and 0.50 in the CO column density versus C I/CO abundance ratio plane. Vertical color shading indicates the final abundance ratio NC I/NCO that can match both the observed RC I/CO and the assumed Σmol value noted at the top of each panel.
In the text
thumbnail Fig. B.1.

CO(2−1) line flux and fraction of missing flux maps. Upper left panel: Short-spacing corrected (12m+7m+tp) PHANGS-ALMA CO(2-1) derived moment-0 map. Upper right panel: Ratio map of the uv-trimmed CO(2-1) moment-0 map used in this work to that in the left panel. Lower left panel: CO(2-1) moment-0 map derived from our simulation with uv trimming as for real data. Lower right panel: ratio map of the uv-trimmed CO(2-1) moment-0 map based on the simulation to the “true” skymodel moment-0 map as shown left. All moment maps are derived by first convolving cubes to our working resolution of 3.46″ then performing masking analysis as described in Appendix A, except for the “true” skymodel moment-0 map which is computed without any masking. We note that in the simulation-based analysis, some regions have too low S/N due to their faint CO brightness or insufficient cleaning, thus they are out of the mask and show blank line ratios (instead of very low missing flux) in the lower right-hand panel.
In the text
thumbnail Fig. C.1.

C I line flux and RC I/CO line ratio image from the simulation mimicking real observation but with a constant input line ratio RC I/CO = 0.2.
In the text
thumbnail Fig. C.1.

Line flux, ratio and S/N correlations from our CASA simulation. Upper panels: [C I](1−0) and CO(2−1) line brightness and ratio similar to Fig. 4, but from our simulation (with a constant input RC I/CO = 0.2 as indicated by the horizontal shading in the right panels). Lower panels: Similar to the upper panels but showing line S/N instead of brightness. This illustrates how RC I/CO can be biased in low-S/N situation.
In the text
thumbnail Fig. D.1.

[C I](1−0) and CO(2−1) moment-0 maps and spectra of regions 1, 4, and 22 as defined in Fig. 1. All the regions’ spectra are available in our online data release (see Sect. 2.2).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.