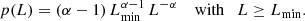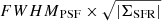| Issue |
A&A
Volume 658, February 2022
|
|
|---|---|---|
| Article Number | A188 | |
| Number of page(s) | 41 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141907 | |
| Published online | 02 March 2022 | |
PHANGS–MUSE: The H II region luminosity function of local star-forming galaxies⋆
1
Max-Planck-Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
e-mail: santoro@mpia.de
2
Astronomisches Rechen-Institut, Zentrum für Astronomie der Universität Heidelberg, Mönchhofstraße 12-14, 69120 Heidelberg, Germany
3
INAF – Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
4
Research School of Astronomy and Astrophysics, Australian National University, Canberra, ACT 2611, Australia
5
Departamento de Astronomía, Universidad de Chile, Santiago, Chile
6
Department of Physics and Astronomy, Johns Hopkins University, Baltimore, MD 21218, USA
7
Observatories of the Carnegie Institution for Science, Pasadena, CA, USA
8
Sterrenkundig Observatorium, Universiteit Gent, Krijgslaan 281 S9, 9000 Gent, Belgium
9
Universität Heidelberg, Zentrum für Astronomie, Institut für theoretische Astrophysik, Albert-Ueberle-Straße 2, 69120 Heidelberg, Germany
10
Universität Heidelberg, Interdisziplinäres Zentrum für Wissenschaftliches Rechnen, Im Neuenheimer Feld 205, 69120 Heidelberg, Germany
11
Max-Planck-Institute for extraterrestrial Physics, Giessenbachstraße 1, 85748 Garching, Germany
12
Observatorio Astronómico Nacional (IGN), C/Alfonso XII, 3, 28014 Madrid, Spain
13
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748 Garching, Germany
14
Univ Lyon, Univ Lyon1, ENS de Lyon, CNRS, Centre de Recherche Astrophysique de Lyon UMR5574, 69230 Saint-Genis-Laval, France
15
Sydney Institute for Astronomy, School of Physics, Physics Road, The University of Sydney, Darlington, 2006 NSW, Australia
16
Argelander-Institut für Astronomie, Universität Bonn, Auf dem Hügel 71, 53121 Bonn, Germany
17
Centro de Astronomía (CITEVA), Universidad de Antofagasta, Avenida Angamos 601, Antofagasta, Chile
18
Department of Physics and Astronomy, University of Wyoming, Laramie, WY 82071, USA
19
Gemini Observatory/NSF’s NOIRLab, 950 N. Cherry Avenue, Tucson, AZ 85719, USA
20
Department of Astronomy, The Ohio State University, 140 West 18th Avenue, Columbus, OH 43210, USA
21
Department of Physics, Tamkang University, No.151, Yingzhuan Rd., Tamsui Dist., New Taipei City 251301, Taiwan
22
Department of Physics, University of Alberta, Edmonton, AB T6G 2E1, Canada
23
Department of Physics, General Studies, College of Engineering, Nihon University, 1 Nakagawara, Tokusada, Tamuramachi, Koriyama, Fukushima 963-8642, Japan
24
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
25
Departamento de Física de la Tierra y Astrofísica, Universidad Complutense de Madrid, 28040 Madrid, Spain
Received:
29
July
2021
Accepted:
15
November
2021
We use an unprecedented sample of about 23 000 H II regions detected at an average physical resolution of 67 pc in the PHANGS–MUSE sample to study the extragalactic H II region Hα luminosity function (LF). Our observations probe the star-forming disk of 19 nearby spiral galaxies with low inclination and located close to the star formation main sequence at z = 0. The mean LF slope, α, in our sample is =1.73 with a σ of 0.15. We find that α decreases with the galaxy’s star formation rate surface density, ΣSFR, and argue that this is driven by an enhanced clustering of young stars at high gas surface densities. Looking at the H II regions within single galaxies, we find that no significant variations occur between the LF of the inner and outer part of the star-forming disk, whereas the LF in the spiral arm areas is shallower than in the inter-arm areas for six out of the 13 galaxies with clearly visible spiral arms. We attribute these variations to the spiral arms increasing the molecular clouds’ arm–inter-arm mass contrast and find suggestive evidence that they are more evident for galaxies with stronger spiral arms. Furthermore, we find systematic variations in α between samples of H II regions with a high and low ionization parameter, q, and argue that they are driven by the aging of H II regions.
Key words: HII regions / ISM: structure / galaxies: ISM / galaxies: star formation / galaxies: evolution / galaxies: spiral
The catalog of HII regions is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/658/A188
© F. Santoro et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1. Introduction
Hα emission is one of the most effective tracers of young stars that formed within the last 10 Myr (e.g., Kennicutt & Evans 2012a; Haydon et al. 2020). In star-forming regions, it originates from massive OB-type stars whose energetic (hard UV) radiation is able to heat and ionize the surrounding gas to form an H II region. This is why H II regions have long been considered as the optimal probes of massive star formation in galaxies (e.g., Kennicutt et al. 1989; Thilker et al. 2000; Lawton et al. 2010), though we should not forget that star formation currently ongoing within dense, dust-enshrouded cores may remain hidden for about 3 Myr (Kim et al. 2021). Since the Hα luminosity of an H II region is directly related to the amount of ionizing radiation emitted by the OB stars at its center, the H II region luminosity function (LF) allows us to constrain the mass function (MF) of young stellar regions.
Similarities between the spatial distribution of stars, stellar associations, and clusters on different physical scales indicate that star formation is a scale-free process (e.g., Efremov & Elmegreen 1998; Bastian et al. 2009; Kruijssen 2012; Hopkins 2013; Krumholz 2014, and references therein). For this reason, the mass function and the luminosity function of star-forming regions are expected to follow a power law with slope of about −2 (Elmegreen & Falgarone 1996). Studies probing the H II region LFs using different tracers largely agree with this expectation, measuring LF slopes close to −2 with minor variations of ±0.2 − 0.5 among galaxies (e.g., UV: Cook et al. 2016, Hα: Kennicutt et al. 1989, Paα: Liu et al. 2013, infrared and radio: Mascoop et al. 2021). It is worth noticing that the main physical driver behind this is hierarchical growth under the influence of gravity.
The accessibility of the Hα emission line to ground-based observations favored the study of the so-called nebular LF (i.e., built using the Hα luminosity of H II regions) in numerous extra-galactic Hα surveys (e.g., Knapen 1998; Thilker et al. 2002; Kennicutt et al. 2008). Thanks to studies in the Milky Way (MW) and the Local Group, we know that H II regions can be extremely diverse in their nature, ranging from the least bright and sub-parsec-sized regions (e.g., ultra-compact H II regions observed within the MW; see, e.g., Hoare 2005) to the most bright and ∼400 pc sized superbubbles (e.g., resembling 30 Doradus in the Large Magellanic Cloud; see Oey 1996; Pellegrini et al. 2010). Studies of nebular LFs in nearby external galaxies commonly probe H II regions ionized by star clusters and associations, but only in a few cases does the sensitivity of the observations allow probing H II regions ionized by single OB stars (e.g., Azimlu et al. 2011).
Variations in the slope of the LF can unveil whether global properties of galaxies, as well as local parameters such as chemical abundance, dust content, and gas dynamics (e.g., spiral arm perturbations), influence the star formation process. Only a handful of studies have attempted to examine the relation between the LF slope and global galaxy parameters, mostly finding weak or statistically insignificant correlations (Kennicutt et al. 1989; Elmegreen & Salzer 1999; Youngblood & Hunter 1999; van Zee 2000; Thilker et al. 2002; Liu et al. 2013; Cook et al. 2016). On the other hand, studies of individual star-forming galaxies with larger H II region samples mainly focused on variations in the LF between the inner and outer disk and between the spiral arm and inter-arm areas. These studies showed that in the inter-arm areas and in the outer disk, the H II region LF becomes steeper; however, such variations have not been found to be universal (see, e.g., Cepa & Beckman 1990; Rand 1992; Banfi et al. 1993; Knapen et al. 1993; Rozas et al. 1996; Knapen 1998; Lelièvre & Roy 2000; Thilker et al. 2000; Helmboldt et al. 2005; Gutiérrez et al. 2011; Scoville et al. 2001; Azimlu et al. 2011). Quantifying variations in the LF slope with the galaxy’s star formation rate (SFR), morphology, or local environmental properties can elucidate whether, for example, environment affects the demographics of young stellar populations and may provide new clues that help us better understand the star formation process.
New observations with integral field units (IFUs) are now allowing us to characterize the physical properties of H II regions in external galaxies in greater detail, with higher sensitivity and spatial resolution and unprecedented statistics (see, e.g., Rousseau-Nepton et al. 2018; Kreckel et al. 2019; Espinosa-Ponce et al. 2020). The PHANGS–MUSE1 data set (Emsellem et al. 2021) is now starting to unveil its full potential in resolving and studying H II region properties and connecting them to galactic structure and galaxy evolution (see, e.g., Ho et al. 2019; Kreckel et al. 2019, 2020). With its 19 nearby star-forming galaxies and the detection of tens of thousands of H II regions at a spatial resolution of about 70 pc, the PHANGS–MUSE data are ideal for studying the H II region LF, marking a turning point in terms of statistics and ability to resolve H II regions. Furthermore, the availability of PHANGS–ALMA (Leroy et al. 2021) and PHANGS–HST (Lee et al. 2022) observations opens up the possibility of comparing the H II region LFs to the MFs of giant molecular clouds (GMCs) and young stellar regions (Wei et al. 2020; Rosolowsky et al. 2021; Thilker et al. 2022; Whitmore et al. 2021) and investigating how the demographics of substructure changes over the course of the star formation and feedback process.
This work is focused on the study of nebular LFs and their variations as a function of galaxy global properties (e.g., galaxy morphology, SFR, stellar mass, and gas-phase metallicity) and galactic environment (e.g., spiral arm versus inter-arm) across the entire PHANGS–MUSE sample. The paper is structured as follows: Sect. 2 briefly describes the PHANGS–MUSE data set, the data reduction strategy, and the ancillary data that have been used. In Sect. 3 we describe the source identification technique and present our H II region catalogs. In Sect. 4 we present the nebular LF of our galaxies and the fitting technique (Sect. 4.1), and we investigate variations in the LF slope as a function of global properties across the sample (Sect. 4.2) or for different populations of H II regions within individual galaxies (Sect. 4.3). In Sect. 5 we assess the effects of completeness and crowding on our results. In Sect. 6 we discuss our results and what drives variations in the LF slope. We finally summarize our main findings in Sect. 7 and highlight future prospects in Sect. 8.
2. Observations and data
For a complete and detailed description of the PHANGS–MUSE sample and data we redirect the reader to Emsellem et al. (2021), while in this section we summarize the overall properties of the sample and provide essential details of the data reduction and analysis pipelines. In the last part of this section, we also describe the ancillary data products that we use in this work.
2.1. PHANGS–MUSE sample
The PHANGS–MUSE sample includes 19 nearby (D < 20 Mpc) star-forming galaxies (Sa–Sc Hubble morphological type) with relatively low inclination (i ≲ 55 degrees). We summarize their main properties in Table 1. The galaxies are located close to the so-called star formation main sequence and span a stellar mass range of log(M⋆/M⊙) = 9.4 − 11. The galactocentric radii used in this paper have been deprojected according to the inclinations and position angles reported in Table 1, which are taken from Lang et al. (2020) who performed modeling of the CO(2–1) kinematics using the PHANGS–ALMA data. The area covered by the MUSE observations mainly samples the star-forming disk of the galaxies. The mean maximum galactocentric radius covered across the sample is 0.86R25; the exact coverage for each galaxy is reported in Table 1.
Main properties of the galaxies in the PHANGS–MUSE sample.
2.2. PHANGS–MUSE data reduction and analysis
The PHANGS–MUSE data set (Emsellem et al. 2021) is the result of an extensive (∼170 h) observational campaign (PI E. Schinnerer) with the MUSE IFU (Bacon et al. 2010) mounted on the Unit 4 telescope (UT4) at ESO’s Very Large Telescope (VLT), with the addition of archival observations for NGC 0628 and the centers of 5 galaxies in the sample. Each galaxy has been covered by several pointings (from 3 up to 15) to obtain a contiguous mosaic of the star-forming disk. All the observations have been performed in wide-field mode (WFM; with 1′×1′ field of view), either in natural seeing (WFM-noAO, for 11 galaxies) or taking advantage of the GALACSI adaptive optics system (WFM-AO, for eight galaxies).
The data have been reduced using a version of the PYMUSEPIPE python package2, a wrapper of the ESOREX MUSE reduction recipes, tailored to the PHANGS–MUSE program (Emsellem et al. 2021). Broad-band images taken with the ESO/MPG 2.2 m Wide Field Imager and with the Du Pont Direct CCD camera (Razza et al., in prep.) were used as a reference to astrometrically align and flux calibrate the MUSE data. The complete data reduction provides a sky-subtracted, flux-calibrated, mosaicked data cube for each galaxy with a spaxel size of 0.2″. The point spread function (PSF) of the observations was determined for each pointing, and for each galaxy the largest value (reported in Table 1) was used to create PSF-homogenized data cubes. We refer to these as the “copt” data cubes to distinguish them from the “native” data cubes, maintaining the native resolution of the observations.
The data analysis of the mosaicked data cubes was performed with a data analysis pipeline (DAP) based on the GIST (Galaxy IFU Spectroscopy Tool; Bittner et al. 2019) software package and tailored to the PHANGS–MUSE program, which provides maps of stellar kinematics, stellar population properties (including stellar ages and mass surface density), and emission line fluxes and kinematics (Emsellem et al. 2021). The DAP employs the penalized pixel fitting method via the PPXF package (Cappellari 2017) to extract information on the stellar population and the ionized gas from the MUSE spectra over the wavelength range 4850 − 7000 Å taking into account the MUSE spectral resolution as parametrized in Bacon et al. (2017). First, the stellar kinematics and the stellar population information are extracted in two subsequent steps using binned spectra with a continuum S/N target of 35, and E-MILES simple stellar population models (Vazdekis et al. 2016) generated with a Chabrier (2003) initial mass function (IMF), BaSTI isochrones (Pietrinferni et al. 2004), eight ages (0.15 − 14 Gyr), and four metallicities ([Z/H] = [ − 1.5, −0.35, 0.06, 0.4]). Finally, the ionized gas analysis is performed by leveraging the previous steps and simultaneously fitting the stellar continuum and the emission lines using single spaxel spectra. Emission lines are modeled with a single Gaussian function and emission line flux maps are corrected for foreground Galactic extinction, using the O’Donnell (1994) extinction law and the E(B − V) values from Schlafly & Finkbeiner (2011). We refer the reader to the PHANGS-MUSE survey paper (Emsellem et al. 2021) for further details on the choice of models and the spectral fitting procedure. In this paper we make use of the copt Hα maps to localize H II regions and the native MUSE mosaicked data cubes to extract their integrated spectra (see Sect. 3).
2.3. Environmental and foreground stars masks
Morphological masks delimiting stellar structures by using Spitzer near-infrared (NIR) 3.6 μm imaging are available for the PHANGS–MUSE galaxies from Querejeta et al. (2021). We used these masks to define galaxy centers, bars, spiral arms, and inter-arms regions. In the work of Querejeta et al. (2021), spiral arms have been defined only when they are dominant features across the galaxy disk (omitting flocculent galaxies) by fitting a log-spiral function to bright regions in the NIR images along each spiral arm. These modeled log-spiral curves are then assigned an empirically determined width based on the overlap with CO(2–1) emission from PHANGS–ALMA data and as a last step the starting and ending azimuth of each spiral segment is adjusted to define the final spiral arm footprint. The outer edges of bars have been defined as ellipses where the bar length, ellipticity, and position angle come from a compilation of measurements from the literature based on NIR imaging (mostly from Herrera-Endoqui et al. 2015).
We make use of the Querejeta et al. (2021) environmental masks to define five environments – namely galaxy center, bar, spiral arm, inter-arm, and disk – according to the criteria described below. Our galaxy “centers” include small bulges, inner star-forming rings or nuclei. We define “bars” in the same way they are defined in the Querejeta et al. (2021) masks. For the galaxies with spiral arms, we define as “spiral arms” the regions flagged as spiral arms with the addition of the bar ends regions (when spiral arms overlap with bar ends). All remaining regions are defined as “inter-arm” for the galaxies with spiral arms and “disk” for the galaxies without spiral arms. These five environments can be visualized for NGC 4321 in Fig. 1 and for the remaining galaxies in Appendix A; in Fig. 1 we also show a sketch of the different environments to guide the reader.
 |
Fig. 1. H II regions and environments for NGC 4321. The figure shows the Hα emission in the background, color coded according to the color scheme on the right, overlaid with the borders of the H II regions in our catalog. The centers of the nebulae that have been discarded by our selection criteria are marked with crosses. Lower-left corner: the black circle indicates the PSF of the MUSE observations, and the black line marks a physical scale corresponding to 1 kpc. Both the H II regions and the discarded nebulae are color coded according to our definition of environments as outlined by the color scheme at the bottom and shown in the bottom-right sketch. |
There are a number of foreground stars across the field of view (FoV) of our observations that need to be excluded from our analysis. Masks of foreground stars for the PHANGS–MUSE galaxies are described in Emsellem et al. (2021). They have been generated by matching the positions of Gaia point sources. To avoid masking compact H II regions and galactic nuclei, which may be included as point sources in the Gaia catalog, a further check was performed to identify the rest-frame Ca II triplet absorption features at 8498, 8542, and 8662 Å in the MUSE spectra.
3. Data analysis
3.1. Ionized nebulae identification
To isolate H II regions across our sample, we make use of the PHANGS–MUSE copt Hα emission line maps provided by the DAP procedure summarized in Sect. 2.2. We chose the copt rather than the native resolution maps to mitigate the effect of PSF spatial variations across the FoV of single targets. Ionized nebulae are identified using an adaptation of the HIIPHOT software (Thilker et al. 2000) originally implemented to work with Hα narrowband images. The software first detects what are called “seed regions” and then grows them up to a given contrast (i.e., the termination gradient) that is selected by the user. We set the background level of the Hα maps to the mean Hα flux of the pixels with surface brightness below ΣHα < 1 × 10−17 erg s−1 arcsec−2 and the detection threshold to 3σ above the background, with σ being the standard deviation of the background pixels. Once the seed regions have been identified, we perform further cleaning based on visual inspection to avoid artifacts due to noise in the Hα map. We consider the total integrated flux of the seed region and impose a S/N cut of 50 (using the Hα emission line error maps to assess the noise) and a ΣHα cut above 3σ of the background. To avoid the detection of regions with unphysical sizes, we find that the best solution is to limit the spatial smoothing operated by HIIPHOT on the input maps for the iterative search of seed regions to three iterations, each time increasing the starting PSF by 10%.
Once the seed regions have been identified, HIIPHOT starts to grow them. Different methods have been used in the literature to define H II region boundaries: emission line ratios, Hα equivalent width, Hα spatial gradients, or a combination thereof (see, e.g., Blanc et al. 2009; Thilker et al. 2000; Sánchez et al. 2012; Zhang et al. 2017). In this work, we rely on HIIPHOT, which uses a user-selected termination gradient of the Hα surface brightness in units of emission measure (EM), to stop the growth of seed regions – with a lower termination gradient the seed regions are allowed to grow more and vice versa (see Thilker et al. 2000, for an example). In principle, in the classical scenario of an H II region represented as a Strömgren sphere, closer galaxies and/or better seeing conditions lead to the detection of steeper gradients and vice versa (see, e.g., Oey et al. 2007). Considering the distances of the galaxies in our sample (D < 20 Mpc) and the seeing of our observations (FWHMPSF ≤ 1.2″), after visual inspection we select a termination gradient of 2.43 × 10−16 erg s−1 arcsec−2 pc−1 (i.e., corresponding to 5 EM pc−1) to also ensure coherence with results presented in the literature (see Oey et al. 2007). In general a higher/lower termination gradient results in a steeper/shallower LF. We checked that varying the termination gradient in the interval 1.5 − 10 EM pc−1 gives LF with slopes that are, within the errors, fully compatible with what we discuss in Sect. 4.1 of this paper. Excluding the regions overlapping with foreground stars (see Sect. 2.3), we detect a total number of 31 399 ionized nebulae across the 19 galaxies of the PHANGS–MUSE sample. We use the nebulae spatial masks for each galaxy to extract the nebula integrated spectra from the MUSE native mosaicked data cubes. These spectra are then fitted using the DAP of the PHANGS–MUSE data as described in Sect. 2.2. The only difference at this level is that we fit the MUSE spectra across their entire wavelength range so to include also the modeling of the [S III]λ9069 Å emission line. It is worth noting that in this work we do not correct the emission line fluxes for the diffuse background (i.e., the emission of the diffuse ionized gas DIG component permeating star-forming disks; see Haffner et al. 2009). However, we checked that such a correction starts to be more relevant only for the Hα emission of the fainter H II regions and, therefore, does not affect the LF slopes presented in Sect. 4. Depending on the galaxy, the Hα emission outside the ionized nebulae footprints can represents 20 − 50% of the total Hα emission (see Belfiore et al. 2021).
3.2. The final H II region catalog
In order to obtain our fiducial H II regions catalog, we excluded the following five types of nebulae. The first are nebulae located in galaxy centers (as defined in Sect. 2.3); this is meant to avoid areas with a high SFR surface density (e.g., starburst rings in NGC 1300, NGC 1512, NGC 1672, NGC 3351, NGC 4303, and NGC 4321), where the deblending of H II regions is not possible at our resolution (i.e., typically a few parsec in radius; see, e.g., Barnes et al. 2020), and contamination by active galactic nuclei (AGN; i.e., NGC 1365, NGC 1512, NGC 1566, and NGC 1672 show evidence of hosting low-luminosity AGN when looking at emission line maps). This cut comprises about 1.5% of the nebulae.
Second are nebulae located outside the “H II region” area in at least one of the classical Baldwin–Phillips–Terlevich (BPT) diagrams (Baldwin et al. 1981); more specifically, these are the regions located above the Kauffmann et al. (2003) line in the [O III]/Hβ versus [N II]/Hα diagnostic, and above the Kewley et al. (2001) line in the [O III]/Hβ versus [S II]/Hα, as well as the [O III]/Hβ versus [O I]/Hα diagnostic. To build the BPT diagrams we require a S/N > 3 for the Hβ, [O III]λ5007Å, [O I]λ6300Å, Hα, [N II]λ6584Å, [S II]λ6716Å, and [S II]λ6731Å emission lines; this is meant to ensure a robust estimate of both the dust correction based on the Hα/Hβ Balmer decrement and the quantities relying on line ratios (e.g., ionization parameter and gas-phase metallicity) used in this work. This cut comprises about 23% of the nebulae.
Third are nebulae with velocity dispersion σ > 400 km s−1 for all three emission line groups (i.e., hydrogen, high ionization and low ionization lines) fitted separately by the DAP (see Emsellem et al. 2021) in order to avoid cases where the emission line fitting performs poorly and to exclude objects that are potentially supernovae remnant candidates. This cut comprises about 1% of the nebulae.
Fourth are nebulae whose geometric center matches within 0.5″ the positions of planetary nebulae identified using [O III] emission line maps (Scheuermann et al., in prep.). This cut comprises about 0.6% of the nebulae.
Fifth are nebulae where the distance of the geometric center from the edges of the MUSE mosaic FoV is less than one FWHMPSF. This cut comprises about 2% of the nebulae.
We note that the S/N of the Hα and Hβ lines is usually high, more specifically, 99% of the region spectra have a S/N ≳ 32 for the Hα line and ≳12 for the Hβ line. All together, the cuts remove about 26% of the original nebulae and leave us with a final joined catalog of 23 301 H II regions. A discussion on how selection effects may influence our results is presented in Appendix C.
In Fig. 1 we show the spatial masks of the H II regions found in NGC 4321, highlighting also the different galactic environments defined in Sect. 2.3. Analogous figures for the remaining galaxies in our sample are presented in Appendix A.
We assumed a screen geometry and used PYNEB3 (Luridiana et al. 2015) to correct line fluxes for dust extinction via the Hα/Hβ ratio, adopting the O’Donnell (1994) reddening law with RV = 3.1 and a theoretical Hα/Hβ = 2.86. The extinction-corrected emission line luminosities of the H II regions were then computed using the distances reported in Table 1. For every H II region in our catalog, we also estimated the gas-phase metallicity and the gas ionization parameter by using extinction-corrected emission line fluxes. The gas-phase metallicity O/H was calculated using the Pilyugin & Grebel (2016) S calibration (Scal hereafter). This calibration relies on three diagnostic line ratios (i.e., [N II]/Hβ, [S II]/Hβ, and [O III]/Hβ) and provides an empirical calibration against H II regions that have direct constraints on their nebular temperatures and hence their abundances. This calibration is relatively insensitive to changes in gas pressure or ionization parameter, and we adopted it as fiducial approach in this paper (see Kreckel et al. 2019, for a discussion). In addition, for each galaxy we fit the radial metallicity gradient by using an unweighted least-square linear fitting of the trend between 12 + log(O/H) and the deprojected galactocentric radius (see Fig. A.19). The gas ionization parameter represents the ratio between the ionizing photon flux density and the gas hydrogen density. In this paper, we express the ionization parameter as q = U × c = Q(H0)/4πR2n, where c is the speed of light, U is the dimensionless ionization parameter, Q(H0) is the number of hydrogen ionizing photons (E > 13.6 eV) emitted per second, R is the empty (wind-blown) radius of the H II region, and n its hydrogen density. The ionization parameter is ultimately defined by the structure of an H II region (e.g., size, gas density, filling factor) and the properties of its ionizing source. Photoionization models show that it can be extracted via different diagnostic lines (Kewley & Dopita 2002; Dors et al. 2011). In this paper we use the calibration proposed by Diaz et al. (1991) based on the [S III](9069+9532)/[S II](6717+6713) line ratio. As the [S III]λ9532 Å line falls outside the wavelength range covered by MUSE, we assumed that [S III]λ9532 Å = 2.47[S III]λ9069 Å according to default atomic data in PYNEB (Luridiana et al. 2015). It should be noted that for about 3000 H II regions we are not able to estimate the ionization parameter due to lack of detection of the [S III]λ9532 Å emission line.
The H II regions catalog containing the host galaxy name, the sky coordinates of the geometrical center, the deprojected galactocentric distance from the host galaxy center, the Hα and Hβ observed fluxes, the Hα extinction-corrected flux, the ionization parameter, and an environmental flag for all the H II regions discussed in the current paper is only available at the CDS.
4. Results
4.1. The H II region luminosity function
We make use of the extinction-corrected Hα luminosities of our H II regions to obtain the nebular LF of each galaxy in our sample. H II region LFs have long been known to be well described by a power law (Kennicutt et al. 1989). The key parameter of the LF is its slope, α. Several different methods for deriving the slope from the empirical data have been employed. Past studies have often used least-squares linear regression of binned data (i.e., histograms) in log–log space. This method, despite being widespread, can give incorrect results under relatively common conditions, as discussed in Clauset et al. (2009). In the context of LFs, this is mainly related to the fact that linear regression assumes Gaussian noise in the dependent variable, but the noise of the logarithm of a histogram is not Gaussian. Furthermore, the choice of the binning scheme (e.g., equal-luminosity bins versus equal-number bins) and the definition of the bin center can affect the LF modeling and add uncertainties to α (see, e.g., Maíz Apellániz & Úbeda 2005; Cook et al. 2016).
The slope of the LF is commonly constrained by fitting the bright end of the LF or, more specifically, H II regions with a luminosity above a given Lmin. This is the luminosity below which the LF starts to flatten – it is often referred to as the “turnover point” and, depending on the sensitivity of the observations, can arise due to incompleteness of the data. Lmin is an important parameter for determining the LF slope and in many studies it has been, quite arbitrarily, fixed to the luminosity where the histogram of the LF peaks or, alternatively, where the bin count number steadily decreases (e.g., Cook et al. 2016; Azimlu et al. 2011). As described in Clauset et al. (2009), by adopting a maximum likelihood estimation (MLE) method, in combination with the Kolmogorov–Smirnov (KS) statistic, it is possible to obtain both Lmin and α of a given LF in a statistically robust way (see Sect. 5 for further discussion).
In this paper, we adopt this method to fit an empirical LF: it does not depend on any binning scheme and, as discussed in Clauset et al. (2009), provides a statistically robust way to fit data following heavily tailed distributions. Whitmore et al. (2014) compared the performance of this method to classical ones based on histograms by fitting the LF of star clusters observed with HST and found an overall good agreement, with MLE fits giving steeper slopes for steeper LFs. To perform the LF fits, we make use of the Python package POWERLAW (Alstott et al. 2014), which follows the prescription given in Clauset et al. (2009) and models the probability distribution function (PDF) p(L) connected to the empirical LF using a power law of the form
The algorithm performs an MLE fit by recursively fixing Lmin equal to each empirical data point. For a given Lmin, the algorithm tries a range of different slopes and selects as the best fitting slope the one maximizing the likelihood estimator. At this point we have a set of models that includes the best fitting model for each fixed Lmin. The KS statistic is then used to compute the maximum distance between this set of models and the empirical cumulative distribution function. The final best fitting model is chosen as the one that minimizes the KS statistic.
We limit the search of Lmin to an interval of ±1σ around the median of the distribution (i.e., where, visually, the LFs start to flatten) and the LF slope to the interval of α = 1 − 3. The error on Lmin is taken to be the standard deviation of the Lmin values found by rerunning the fitting procedure on 1000 mock LFs extracted via bootstrapping from a given LF, after making sure that the error converges to a stable value as the number of bootstraps approaches 1000. For the error on α, we consider the trend of the likelihood estimator as a function of α for the models with the best Lmin. This trend can be well represented by a Gaussian that peaks at the best α and we compute the error on α as the standard deviation of the best fitting Gaussian function modeling the data (similar to what has been done by Whitmore et al. 2014). We do not run any test to check for the existence of an upper cutoff in the LFs.
The best fitting models of our LF are shown in Fig. 2 and reported in Table 2. The slopes we find are in the interval of α = 1.5 − 2 with a mean value of 1.73 and a σ of 0.15, in agreement with what has been discussed in the literature for Sa–Sc spiral galaxies (see, e.g., Kennicutt et al. 1989; Elmegreen & Salzer 1999; Whitmore et al. 2014). We note that for our sample, the minimum number of H II regions used to fit the LF is 300 (i.e., for NGC 7496) and that our fits can be considered robust against biases due to low-number statistics (see Sect. 5 for further discussion). In Fig. 2, we also mark the completeness limit of our LFs that will be discussed in Sect. 5. In Appendix C, we discuss how the results would change if Hα luminosities were not corrected for dust extinction (e.g., in narrowband imaging). We find that neglecting the dust extinction correction causes a slight steepening of the LFs that, within their errors, remain compatible with the slopes we report in this section.
 |
Fig. 2. Best fitting models of the H II region LF for the galaxies of our sample. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dotted black line indicates the empirical PDF, plotted as p(L) versus the logarithm of the H II regions’ Hα luminosity expressed in erg s−1. The vertical dashed line indicates the estimated completeness limit. The vertical solid black line and the shaded gray area indicate the best fitting Lmin and its uncertainty. The LF best fitting model is marked by the solid red line, while the associated slope, α, and its uncertainty are indicated in the upper-right corner of each panel. |
Properties of the H II region LF in the PHANGS–MUSE galaxies.
Before describing further the details of our data analysis, it is worth discussing the overall properties of our LFs. As can be seen in Fig. 2, our H II regions span a luminosity range of log(LHα [erg s−1]) ∼ 35 − 40. H II regions with luminosities less than a few times 1037 erg s−1 are typically ionized by single O- or B-type stars, whereas at higher luminosities and up to about 1039 erg s−1 we enter the regime where H II regions are ionized by stellar associations or clusters containing multiple OB stars. In this regime, the Hα luminosity of an H II region is expected to be roughly proportional to its number of ionizing stars. H II regions with luminosities higher than a few 1039 erg s−1 are referred to as giant or supergiant H II regions (e.g., 30 Doradus in the Large Magellanic Cloud) and are typical of late-type galaxies (Sc and Irr Hubble types; see, e.g., Kennicutt et al. 1989; Elmegreen et al. 1996).
The ionizing luminosities corresponding to Lmin in each galaxy of our sample are reported in Table 2 in terms of the number of equivalent O7 V-type stars, assuming that the number of ionizing photons per second for an O7 V star along the zero-age main sequence is ![$ \log (Q_{0}^\mathrm{O7\,V} \ [\mathrm{photons~s^{-1}}]) = 49.05 $](/articles/aa/full_html/2022/02/aa41907-21/aa41907-21-eq2.gif) following Vacca (1994). The number of equivalent O7 V stars is used here as a first order indicator of the number of ionizing stars in an H II region and at Lmin it is in the range of 0.05 − 6 in our sample. This testifies that our LF fits, extending ∼2 − 3 orders of magnitude above Lmin, are mainly probing H II regions ionized by star clusters and associations, and only for a few targets (i.e., NGC 5068, IC 3352 with smaller distances) are we probing the regime of H II regions ionized by single massive stars.
following Vacca (1994). The number of equivalent O7 V stars is used here as a first order indicator of the number of ionizing stars in an H II region and at Lmin it is in the range of 0.05 − 6 in our sample. This testifies that our LF fits, extending ∼2 − 3 orders of magnitude above Lmin, are mainly probing H II regions ionized by star clusters and associations, and only for a few targets (i.e., NGC 5068, IC 3352 with smaller distances) are we probing the regime of H II regions ionized by single massive stars.
Different studies in the literature argue that the LF steepens at luminosities higher than log(LHα [erg s−1]) = 38.6 ± 0.1 (i.e., the so-called LF cutoff or break) and is better reproduced by a double power law (i.e., type II LF, reported in individual galaxy studies; e.g., Kennicutt et al. 1989; Rand 1992; Rozas et al. 1996; Beckman et al. 2000; Thilker et al. 2000; Gutiérrez et al. 2011; Lee et al. 2011). Beckman et al. (2000) also observed a local sharp peak (adopting their nomenclature, we refer to this feature as “glitch”) in the LF of their galaxies at log(LHα [erg s−1]) = 38.6 and suggested that it marks the transition of H II regions from ionization bounding (the central star/star cluster only ionizes the gas within the H II region) at low luminosities to density bounding (a large amount of Lyman continuum photons from the central ionizing source escapes the H II region and ionizes the diffuse surrounding medium) at higher luminosities.
The number of putative density bounded H II regions in our galaxies (i.e., LHα ≥ 1038.6 erg s−1) varies from a few up to about 350 and is reported in Table 2. Neither the number of these regions nor their fraction with respect to the total number of H II regions correlates with galaxy morphological type (two targets with Sa morphology have a few tens of these regions while Sb and Sc galaxies show comparable numbers and scatter) or the physical resolution of the observations. This suggests that in our sample the detection of this kind of H II region is not purely an effect of blending due to limited spatial resolution (as suggested by the study of Lee et al. 2011).
For the nine galaxies in which we detect more than 100 density bounded H II regions, we perform an additional fit of the LF only at LHα ≥ 1038.5 erg s−1 and show the results in Fig. 3. We find that for these galaxies the slope of the upper end is indeed steeper with respect to the slope measured globally; only for two of the nine targets (i.e., NGC 1365 and NGC 4321) the variations are within the errors. However, looking at the LFs of our sample in Fig. 2, the steepening at log(LHα [erg s−1]) > 38.6 ± 0.1 and the glitch at log(LHα [erg s−1]) = 38.6 ± 0.1 are subtle features, contrary to what has been shown by Beckman et al. (2000). Assessing which LFs are better described by a double power law is behind the scope of the current paper. Overall, a single power law fit gives a good representation of the empirical data in our sample and is it thus adopted as our fiducial LF model. In the following, we take the advantage of this simpler parametrization of the LF to directly compare the LF slopes of different galaxies and of H II region subsamples within individual galaxies.
 |
Fig. 3. Best fitting model of the upper end of the H II region LF for the subsample of nine galaxies with more than 100 density bounded H II regions. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dotted black line indicates the empirical PDF, plotted as p(L), versus the logarithm of the H II regions’ Hα luminosity, expressed in erg s−1. The vertical dashed line indicates the estimated completeness limit. The vertical solid black line and the solid red line indicate the best fitting Lmin and α of the global LF as shown in Fig. 2. The solid orange line marks the best fitting model for the regions with LHα ≥ 1038.5 erg s−1. The LF slopes of the two best fitting models are indicated in the upper-right corner of each panel, following the same color coding as the models. |
4.2. LF variations among galaxies
To look at what may drive galaxy-to-galaxy variations in the LF slope in our sample, we verified that α does not have any dependence on galaxy inclination reported in Table 1 and then estimate a few global galaxy parameters, excluding the areas defined as galaxy centers (see Sect. 2.3), to be in line with the H II regions probed by our LFs. More specifically, we estimate the following four properties.
The first is the gas-phase metallicity at a representative radius, taken to be the median galactocentric radius of the H II regions detected in each galaxy. The metallicity at this radius is calculated from a linear fit to the radial metallicity gradient (shown in Fig. A.19).
The second is the total stellar mass (M*) extracted by integrating the PHANGS–MUSE stellar mass maps produced by the DAP.
The third is the total SFR extracted by integrating the PHANGS–MUSE Hα maps (not corrected for dust extinction) and applying the calibration reported in Kennicutt & Evans (2012b) taken from the work of Hao et al. (2011) and Murphy et al. (2011), who adopted a Kroupa & Weidner (2003) IMF, with a Salpeter slope (α* = −2.35) from 1 to 100 M⊙ and α* = −1.3 for 0.1 − 1 M⊙, and solar metallicity.
The fourth is the specific star formation rate (sSFR; sSFR = SFR/M*) and the SFR surface density (ΣSFR) obtained by dividing the SFR by M* and the area covered by the MUSE FoV, respectively.
Taking advantage of the study on the resolved star formation scaling relations at ∼100 pc scales carried out by Pessa et al. (2021), we also consider the offset Δ of individual galaxies with respect to the trend of the full sample for the resolved star formation main sequence (rSFMS; ΣM* versus ΣSFR), the Kennicutt–Schmidt relation (rKS; ΣH2 versus ΣSFR), and the molecular gas main sequence (rMGMS; ΣM* versus ΣH2). The offsets Δ rSFMS, Δ rKS, and Δ rMGMS have been estimated taking as a reference the modeled trends for the star formation scaling relations of the whole sample and fitting the same trends for each galaxy. The slope of the individual galaxy trends, for each scaling relation, was set to be the same as the one of the entire sample, and the offset of each galaxy from the global relation was estimated as the difference between the normalization factors of the linear fits (see Pessa et al. 2021, for additional details). It should be noted that these measurements are not available for NGC 0628 due to the quality of the MUSE data while, due the lack of significant CO(2–1) emission, IC 5332 does not have measurements of Δ rKS and Δ rMGMS. The Δ rSFMS, Δ rKS, and Δ rMGMS offsets are interesting quantities because, by construction of the star formation scaling relations, they measure the relative variations in the sSFR (ΣSFR/ΣM*), the gas depletion time (tdep= ΣH2/ΣSFR), and the molecular gas fraction (ΣH2/ΣM*) within our sample. We verified that estimating such offsets by excluding galaxy centers has no significant effect on our findings.
The trends between the LF slope α and the aforementioned parameters, with the addition of the morphological T type, are shown in Fig. 4 together with their Spearman correlation coefficient (ρ) and their p value, indicating the probability that the two sets of data are uncorrelated. We summarize the properties for which we look for a correlation in Table 4. We define a correlation to be negligible when |ρ|=[0 − 0.2], weak when |ρ|=[0.2 − 0.4], moderate when |ρ|=[0.4 − 0.6], strong when |ρ|=[0.6 − 0.8], and very strong when |ρ|=[0.8 − 1]; using the p value to evaluate the probability that, despite showing a correlation, two variables may be uncorrelated. It should be noted that only a handful of studies so far have looked at the correlation between α and global galaxy properties: Kennicutt et al. (1989), Elmegreen & Salzer (1999), Youngblood & Hunter (1999), van Zee (2000), and Thilker et al. (2002) investigated nebular LFs as in this paper, while Liu et al. (2013) identified H II regions via Paα, and Cook et al. (2016) studied the GALEX far-ultraviolet (FUV) LFs of H II regions. While the sample of Cook et al. (2016) includes a few hundred galaxies, the other studies are based on samples ranging from 10 to 35 galaxies, similar to our study. In this section and in Sect. 6.1, we compare our results to those studies that, as in our case, applied a uniform analysis methodology on galaxy samples. It should be noted that using different tracers means probing different source ages and, as reported by Oey & Clarke (1998), older H II regions tend to have steeper LF slopes, mainly due to the short main-sequence lifetimes of the more massive stars constituting the brighter H II regions. This is the reason why, for example, FUV observations, probing H II regions with ages less than 100 Myr, are expected to deliver a steeper LF compared to Hα observations, typically probing H II regions younger than 10 Myr, and our comparison remains qualitative.
 |
Fig. 4. Trends of the LF slope, α, with global galaxy properties. From top left to bottom right: we show α as a function of the galaxy morphological T class, the Scal metallicity at the median galactocentric radius covered by our observations 12 + log(O/H)⟨rgal⟩, the total stellar mass (M*), the total SFR, the sSFR, the SFR surface density (ΣSFR), the offset from the resolved star formation main sequence (Δ rSFMS), the offset from the resolved Kennicutt–Schmidt relation (Δ rKS), and the offset from the resolved molecular gas main sequence (Δ rMGMS). For each panel we report the Spearman correlation coefficient (ρ) and the p value of the plotted quantities. Middle-right panel: the solid red line shows the best fitting relation found by Cook et al. (2016), while the dashed gray and solid back horizontal lines respectively mark the α of the Cook et al. (2016) line at ΣSFR = −2.6 and the mean α of the points at ΣSFR > −2.6 (see Sect. 6.1 for further details). |
Global properties of the PHANGS–MUSE galaxies.
LF properties of H II region subsamples in the PHANGS–MUSE galaxies.
We find a weak correlation between α and the galaxy morphology (Fig. 4a), and a negligible correlation with the gas-phase metallicity (Fig. 4b) and the total stellar mass of our galaxies (Fig. 4c). Kennicutt et al. (1989) and Elmegreen & Salzer (1999) found that the LF slope flattens for later-type galaxies where the relative number of giant H II regions is noticeably higher. On the other hand, Cook et al. (2016) found no trend between α and morphology when studying a sample more representative for irregulars, arguing that the trends reported in the literature were relying on few data points in this regime. Due to the selection of the PHANGS–MUSE sample we are only probing typical star-forming galaxies with morphologies in the range Sa–Sb (corresponding roughly to T types between 1 and 6). As noted also by Kennicutt et al. (1989) the scatter between the α of spirals of the same type in their sample is comparable to the magnitude of the trend they report to exist between α and morphology. The lack of a correlation between α and morphology in our sample is thus fully compatible with the results in the literature. The lack of a correlation with the gas-phase metallicity and the total stellar mass of our galaxies, despite the differences extracting these quantities with respect to previous studies, can also be explained by sample selection effects. Our sample mainly comprises galaxies with high metallicities (i.e., 12 + log(O/H)> 8.3) and stellar masses (i.e., log M* [M⊙]> 9). Cook et al. (2016) found no trend between α and gas-phase metallicity in the range 7.2 < 12 + log(O/H)< 9.2 and only a moderate trend between α and M* in the range 6 < log M* [M⊙]< 11. The parameter space occupied by our galaxies is compatible with what has been shown by Cook et al. (2016) and we do not expect to find strong correlations.
On the other hand, SFR-related quantities show a better correlations with α (Figs. 4d–f). SFR, sSFR, and ΣSFR have a moderate, strong, and very strong correlation with α, respectively. The presence of a tighter correlation with ΣSFR is in line with the findings of Cook et al. (2016), whose best fitting relation is also shown in Fig. 4f. The negative Spearman correlation coefficient indicates that the quantities anticorrelate with α, meaning that the LF has a shallower slope (i.e., higher relative number of bright H II regions) for galaxies with higher SFR, sSFR, and ΣSFR.
Looking at where our galaxies lie in the plane of the three classical star formation scaling relations (Fig. 4g–i), we find that α anticorrelates strongly with Δ rSFMS and Δ rMGMS, and moderately with Δ rKS. The weaker correlation in the latter case can be somehow explained by the fact that, between the three, the rKS relation is the one that shows the lowest galaxy-to-galaxy scatter in our sample (Pessa et al. 2021). While the trend with Δ rSFMS confirms the trend we find with sSFR, Δ rMGMS adds information on the molecular gas fraction and indicates that galaxies with a lower fraction of molecular gas tend to have steeper LFs.
In this paper we choose to not perform any fit for the strongest correlations shown in Fig. 4 because there is no strong evidence for a particular functional form from the data (e.g., considering the scatter with respect to the errors) nor is there one expected from theoretical studies. We note that future work could explore local correlations (e.g., using H II region samples from different areas of the same galaxy), which would give more insights about this matter, but this is beyond the scope of the current paper.
4.3. LF variations within galaxies
After having investigated LF slope variations across our sample, in this section, we focus our attention on possible variations within a given galaxy by looking at the LF of H II region subsamples. In the following, we use galactic environment (spiral arm and inter-arm areas), galactocentric radius, and ionization parameter to draw, for each galaxy, H II region subsamples and fit their LFs while keeping Lmin fixed to the value found in Sect. 4.1 for each parent sample. All the details of the LFs fits performed in this section are reported in Table 4, while the actual fits are shown in Appendix B.
4.3.1. Spiral arm versus inter-arm areas
Differences in the LF slope between spiral arm and inter-arm areas have been reported in the past (Rand 1992; Banfi et al. 1993; Thilker et al. 2000), even though not always significant, with steeper LFs in inter-arm areas. However, this does not appear to be a universal property of spiral galaxies, as numerous cases are known where such variations have not been found (Knapen 1998; Rozas et al. 1996; Azimlu et al. 2011; Gutiérrez et al. 2011). This has to do with the fact that a simple spatial classification of H II regions as spiral or inter-arm regions does not guarantee to probe the conditions under which star formation happens in the two environments. Part of the H II region population in the inter-arm areas, for example, can consist of aged H II regions previously formed within spiral arms and/or as part of a recent star formation burst, depending on the star formation history (SFH) of a galaxy.
Figure 5 summarizes the result of fitting the LFs of the H II regions belonging to spiral arm and inter-arm areas (see Sect. 2.3 for our definition of the environments and Fig. B.1 for the actual LFs fits). Six of our 19 galaxies do not show evident spiral arms, for these galaxies we report the LF slope for the H II regions across the entire galaxy disk but excluding bar regions (i.e., this is the reason for slight variations with respect to the slopes reported in Table 2).
 |
Fig. 5. Slope of the LF for H II regions located in spiral arms (red points) and inter-arm areas (blue points). Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. Galaxies with no evident spiral arms are marked by black points, and their LF slope refers to the disk area (excluding bars). |
We find that the LFs in spiral arm areas are either comparable to or shallower than in inter-arm areas. We find that six out of the 13 galaxies with spiral arms, preferentially at higher stellar masses, show variations between spiral arm and inter-arm LF α that go beyond the uncertainties. By comparing the LF shapes we see that the fraction of bright to faint H II regions tends to be higher in spiral arms and lower in inter-arms areas (especially for NGC 1566 and NGC 1300); however, in general, the two LFs span quite similar ranges of luminosities and have similar turnover points. The interpretation of these results is further discussed in Sect. 6.2.
4.3.2. Inner versus outer disk
There exists evidence that the conditions under which SF happens in the outer disk of spiral galaxies are different from those of the inner disk, as suggested, for example, by an observed steepening of the GMC MF (e.g., Rosolowsky et al. 2007; Colombo et al. 2014; Rice et al. 2016; Faesi et al. 2018; Schruba et al. 2019). In line with this, radial variations in the LF are expected and have been reported in the literature suggesting that the LF is steeper in the outer disk (i.e., extending beyond R25; see, e.g., Lelièvre & Roy 2000) where H II regions tend to be smaller and fainter (see, e.g., Ferguson et al. 1998; Helmboldt et al. 2005).
To assess the presence of radial trends (which may also be connected with parameters varying radially such as the gas-phase metallicity), we study the LF at small and large galactocentric radii. To mitigate effects due to different subsample sizes, for each galaxy we select the median H II region galactocentric radius as a demarcation between the inner and the outer star-forming disk and extract two H II region subsamples of equal sizes. It should be noted that the area covered by our MUSE observations is largely contained within ∼1R25 of our targets, as can be seen looking at the rmax values reported in Table 1. What we define as the outer star-forming disk is still covering the main (i.e., molecular gas dominated) star-forming disk of our spiral galaxies and should not be confused with what is conventionally called outer (i.e., atomic gas dominated) disk in the literature (typically extending far beyond R25).
Figure 6 summarizes the results of our fits of the LF slope in the inner and outer star-forming disk (shown in Fig. B.2). The median H II region galactocentric radii, used to draw the H II region subsamples, varies between ∼0.2 R25 and 0.5 R25 across our galaxies. Most of our galaxies do not show significant variations between the LF slope of H II regions located at small and large galactocentric radii. Our results do not change if we adopt a fixed value of 0.3 R25 to draw H II region subsamples (not shown here). Only two out of 19 galaxies (i.e., NGC 1385 and NGC 1566) show a significant variation, indicating a steeper LF in the outer disk. Our results indicate that within the star-forming disk of spiral galaxies there are no significant radial trends for the LF slope. This suggests that the radial metallicity trends in our galaxies (no more than 0.2 dex variations; see Fig. A.19) do not affect the LF slope.
 |
Fig. 6. Slope of the LF for H II regions located in the inner (red points) and outer (blue points) star-forming disk. Galaxies are ordered by increasing value of their H II regions’ median galactocentric radius from left to right, and their names are indicated along the abscissa. |
4.3.3. High versus low ionization parameter
Lastly, we investigate variations in the H II region LF slope connected with the ionization parameter q of the H II regions. As for the radial bins, for each galaxy we use the median H II region q to draw two subsamples of H II regions of equal size. The median values that we find are in the range log q = 6.4 − 7. We visually inspected the spatial location of the two subsamples of H II regions for each galaxy and they both appear similarly distributed across the galaxy disks.
Figure 7 summarizes the results of the LF fit for the population of H II regions with high and low ionization parameter (shown in Fig. B.3). It is evident that for 15 out of 19 galaxies the population of H II regions with high q has, within the uncertainties, a shallower LF compared to the H II regions with low q. Also, looking at the shapes of the LFs we see that for a number of targets (e.g., IC 5332, NGC 0628, NGC 2835, NGC 3627, and NGC 5068) the H II regions with high and low q constitute, respectively, the bulk of the bright and faint H II region populations. The interpretation of these results is further discussed in Sect. 6.3.
 |
Fig. 7. Slope of the LF for H II regions with high (blue) and low (red) ionization parameters. Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. |
5. Completeness, blending, and selection effects
Observational studies of LFs suffer from two main limitations. On the one hand, faint H II regions are more difficult to detect against the diffuse Hα background. On the other hand, the brighter H II regions, often located in crowded areas such as spiral arms, are more subject to blending effects. This can artificially lower the number of detected faint regions and increase the luminosity of the brightest regions, respectively, with repercussions on the slope of the LF.
The first limitation is related to the sensitivity and the completeness limit of the observations. We estimate the completeness limit of our LFs (shown in Fig. 2) in an empirical way by looking at the distribution of the Hα flux outside the ionized nebula footprints in the Hα emission line maps, which we refer to as the Hα diffuse emission for simplicity. Given the PSF of the MUSE observations for a given galaxy, we estimate the completeness limit as the luminosity of a mock circular H II region with the size of the PSF and a uniform ΣHα equal to the 90th percentile (i.e., slightly larger than 1σ of the distribution) of the Hα diffuse emission distribution. In this way, we take into account the bright tail of the diffuse Hα background against which H II regions can remain undetected. It is worth noting that tests injecting mock H II regions are a good way forward to more robustly assess the completeness limit in the future.
As shown in Fig. 2, the completeness limit estimated in this way lies below the best fitting Lmin (i.e., the LF turnover luminosity) suggesting that the presence of a turnover point is not a completeness problem but rather an intrinsic feature of the LFs of our galaxies (see Youngblood & Hunter 1999, and references therein for a discussion). Models have shown that a turnover point is to be expected when considering a constant SFR over time, while different SFH (e.g., a star formation burst in the past) can affect the shape of the LF in a more complex way (see, e.g., M31’s double-peaked LF is attributed to a recent starburst; Azimlu et al. 2011). We note that, by taking into account the bright tail of the diffuse Hα emission, we estimate a quite conservative completeness limit especially for the targets with stronger diffuse background (i.e., the galaxies for which the completeness limit is located close to the peak of the LF in Fig. 2). However, it should be noted that higher sensitivity and resolution are expected to move the turnover point to lower luminosities and, as shown in the right panel of Fig. 8, Lmin is indeed driven by resolution of the observations in our survey. This constitutes a validation of our fitting approach and ensures that, at a given spatial resolution, the LFs α is extracted from a well-sampled luminosity regime.
 |
Fig. 8. The effect of blending and spatial resolution on α and Lmin. Left panel: LF slope plotted as a function of the |
On the other hand, the issue of blending is related to the spatial resolution of the observations and the number density (or filling factor) of star-forming regions. Intuitively, observations with coarser spatial resolution or a higher filling factor will cause nearby H II regions to blend and be detected as a single H II region, leading to a flattening of the LF. To assess the effect of blending to a first order, for each target we multiplied the FWHMPSF, which takes into account the spatial resolution of the data, by 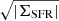 ; this gives us a handle on the mean separation between H II regions. We used this parameter as a proxy for blending and check its relation with α; as shown in the left panel of Fig. 8, we find a moderate correlation. Different studies (Kennicutt et al. 1989; Bastian et al. 2007; Cook et al. 2016) have shown that spatial resolution does not significantly change the slope of the LF at resolutions finer than few hundred parsecs, as is the case of our data (i.e., the coarser physical resolution in our sample is ∼110 pc for NGC 1512 and NGC 1365). This indicates that, although present, the effect of blending is not the main driver of the correlations we report in Sect. 4.2. It is worth noting that our checks for the blending effect are either indirect or made a posteriori. In the future, progressively degrading the MUSE data cubes at a common resolution and analyzing how the LF parameters vary will give us a more comprehensive understanding of this matter.
; this gives us a handle on the mean separation between H II regions. We used this parameter as a proxy for blending and check its relation with α; as shown in the left panel of Fig. 8, we find a moderate correlation. Different studies (Kennicutt et al. 1989; Bastian et al. 2007; Cook et al. 2016) have shown that spatial resolution does not significantly change the slope of the LF at resolutions finer than few hundred parsecs, as is the case of our data (i.e., the coarser physical resolution in our sample is ∼110 pc for NGC 1512 and NGC 1365). This indicates that, although present, the effect of blending is not the main driver of the correlations we report in Sect. 4.2. It is worth noting that our checks for the blending effect are either indirect or made a posteriori. In the future, progressively degrading the MUSE data cubes at a common resolution and analyzing how the LF parameters vary will give us a more comprehensive understanding of this matter.
In Appendix C, we also discuss how the selection criteria, we use to select our H II regions (see Sect. 3.2), have no significant effect on the measurements of the LF slope presented in Sect. 4.1.
6. Discussion: What sets the LF slope?
6.1. The SFR surface density
In Sect. 4.2 we find that in general α correlates better with the global star formation properties of our galaxies and especially with ΣSFR. We do not find any clear trends within the T-type, [O/H], and M* ranges probed by our sample. This indicates that the properties of star-forming regions are more closely connected to the global star formation properties in our sample.
One caveat to keep in mind is that the correlation between the LF and the SFR-related properties may be driven by the so-called size-of-sample effect (Larsen 2002; Weidner et al. 2004; Bastian 2008; Cook et al. 2012; Whitmore et al. 2014). This is a statistical effect (i.e., stochastic sampling) due to the fact that galaxies with higher SFRs tend to have more H II regions and, in turn, the chances of observing a higher number of bright H II regions increase in these galaxies. This is expected to drive a tight correlation between the total number of detected H II regions (and subsequently the SFR) and the luminosity of the brightest star-forming region. Intuitively, the resulting effect is a flattening of the LF for galaxies with higher SFRs. To check for this effect in our sample, in Fig. 9, we plot the number of H II regions (or similarly the number of ionized nebulae) against the maximum H II region luminosity L(Hα)max and the global SFR. We find only a weak and a moderate trend, respectively. This indicates that, thanks to the resolution of our observations and the nature of our sample, the flatter slopes we observe for the more star-forming galaxies are not simply due to a statistical effect. In addition, Cook et al. (2016) tested the size-of-sample effect using simulated LFs with α = −2 and showed that the stochastic scatter of the LF slope starts to increase symmetrically when the number of detected H II regions drops below 100. This implies that low-number statistics increases the scatter in the measured LF slope but does not drive systematic changes of α in a specific direction. Moreover, our LFs are built with H II region samples containing at least ∼500 objects, and the LF fits presented in Sect. 4.1 rely on at least 200 objects. For this reason, we expect the stochastic scatter of α to be lower in our sample compared to previous studies that often relied on smaller H II region samples.
 |
Fig. 9. Maximum luminosity among the detected H II regions (left panel) and the total SFR (right panel) as a function of the total number of detected H II regions for the galaxies of our sample. For each panel we report the Spearman correlation coefficient, ρ, between the plotted quantities. |
In agreement with Cook et al. (2016), who studied the LF in a sample of 258 nearby galaxies using GALEX FUV data, we find that the LF slope correlates best with ΣSFR. In Fig. 4f, we show the best fitting relation found by Cook et al. (2016) for a qualitative comparison. We note that our points mostly lie above this relation. A direct comparison is, however, not straightforward because of the different type of observations. In fact, FUV and Hα LFs probe different ages of H II regions, ≲100 Myr and ≲10 Myr, respectively (see, e.g., Haydon et al. 2020). Oey & Clarke (1998) predicted that older H II region populations (e.g., derived from FUV) should have steeper slopes than younger populations (e.g., derived from Hα). Overall, the average slope of the nebular LF (−2 ± 0.5; Kennicutt et al. 1989; Elmegreen & Salzer 1999), including our study (−1.73 ± 0.15), is compatible with what has been found in the FUV (−1.76 ± 0.3; Cook et al. 2016).
The observed trend indicates that a shallower LF and, thus, the formation of higher relative number of massive, luminous H II regions is connected with a higher ΣSFR. We know that the star formation process is fueled by cold gas. We thus expect the SFR-related properties we measure to be connected with the way how cold gas reservoir fuels star formation, which in turn is connected with the sSFR, the tdep, and the molecular gas fraction.
As discussed in Sect. 4.2, the offsets from the resolved star formation scaling relations can be used as a proxy for these parameters. We find that the stronger correlation is between the LF slope and Δ rSFMS (i.e., a measurement of the sSFR) indicating that, when the mass fraction between young and old stars is higher, galaxies tend to form a higher relative number of luminous H II regions, in agreement with what we find when estimating the global sSFR directly from the MUSE data (Fig. 4e). A slightly weaker but still significant trend is found between the LF slope and Δ rMGMS (i.e., a measurement of the molecular gas fraction) suggesting that, when in a galaxy the fraction of cold gas that will eventually be converted into stars is higher, the relative number of bright and massive H II regions produced by ongoing star formation is also higher.
Kruijssen (2012) formulated a theoretical framework (invoked also by Cook et al. 2016 to explain their results), in which higher SFR and cold gas densities can result in a higher parsec-scale star formation efficiency that, in turn, enhances the cluster formation efficiency, defined as the ratio between the cluster formation rate (CFR) and the SFR (Γ ≡ CFR/SFR). This means that, at higher SFR and gas densities, more stars form in (gravitationally bound) star clusters. Observational evidence has indeed been found that Γ correlates well with the SFR surface density (see, e.g., Goddard et al. 2010; Adamo et al. 2011, 2015, 2020a,b; Cook et al. 2012; Johnson et al. 2016). The trend that we find in Fig. 4e between α and ΣSFR goes in the direction predicted by this scenario. It is worth noting that, with the available PHANGS–HST data (Lee et al. 2022), it will be possible to directly measure Γ and compare it to our measured H II region LF slopes.
Quantitatively, the slope of the H II region LF might be expected to be similar to the slope of the GMC MF (historically estimated to lie between 1.6 and 2.0, e.g., Kennicutt & Evans 2012b, although more recent works find a wider range of slopes; see, e.g., Colombo et al. 2014; Rosolowsky et al. 2021). If star formation within GMCs is self-similar (Efremov & Elmegreen 1998) and the star formation efficiency is independent of the GMC mass at the observable, high-mass end of the mass range, then the slope of the H II region LF is also expected to be α = 1.6 − 2.0. Steeper slopes may then be the result of incomplete sampling of the stellar IMF, which occurs if the stellar populations born within the parent GMCs have a low mass (≲104 M⊙; Krumholz et al. 2015). Simple analytical models, in which the maximum GMC and stellar population mass scales are regulated by gravitational instability and stellar feedback, predict that the maximum mass increases approximately with the total gas surface density as 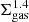 , and therefore approximately linearly with ΣSFR (Kruijssen & Longmore 2014; Reina-Campos & Kruijssen 2017). This linear relation is indeed observed by Johnson et al. (2017), who found that a maximum mass of 104 M⊙ is reached at log(ΣSFR [M⊙ yr−1 kpc−2]) ≈ −2.6. Above this SFR surface density, we expect the H II region LF to be close to the slope of the GMC MF (which in environments of high gas and SFR surface densities is about 1.6, e.g., Colombo et al. 2014; Hughes et al. 2016). Toward lower SFR surface densities, we expect the H II region LF to steepen. The same behavior, in which α declines with ΣSFR for log(ΣSFR [M⊙ yr−1 kpc−2]) ≲ −2.6 and stays approximately constant (or declines less steeply) for log(ΣSFR [M⊙ yr−1 kpc−2]) ≳ −2.6 was also found by Cook et al. (2016) and is illustrated in (Fig. 4f). Here, as a reference to illustrate this flattening, we marked with horizontal lines the α corresponding to the Cook et al. (2016) best fitting line at ΣSFR ≈ 2.6 and the mean α of our samples at ΣSFR > 2.6. Both values are remarkably close to α = 1.6, the slope of the GMC MF in the high gas and ΣSFR regime. Based on the discussion in this section, we expect this behavior to arise from a combination of increased stellar clustering at birth toward higher gas densities (and therefore pressures; Kruijssen 2012), as well as of decreased IMF sampling toward low SFR surface densities. Higher-resolution observations may be necessary to assess how blending of adjacent H II regions may affect these trends.
, and therefore approximately linearly with ΣSFR (Kruijssen & Longmore 2014; Reina-Campos & Kruijssen 2017). This linear relation is indeed observed by Johnson et al. (2017), who found that a maximum mass of 104 M⊙ is reached at log(ΣSFR [M⊙ yr−1 kpc−2]) ≈ −2.6. Above this SFR surface density, we expect the H II region LF to be close to the slope of the GMC MF (which in environments of high gas and SFR surface densities is about 1.6, e.g., Colombo et al. 2014; Hughes et al. 2016). Toward lower SFR surface densities, we expect the H II region LF to steepen. The same behavior, in which α declines with ΣSFR for log(ΣSFR [M⊙ yr−1 kpc−2]) ≲ −2.6 and stays approximately constant (or declines less steeply) for log(ΣSFR [M⊙ yr−1 kpc−2]) ≳ −2.6 was also found by Cook et al. (2016) and is illustrated in (Fig. 4f). Here, as a reference to illustrate this flattening, we marked with horizontal lines the α corresponding to the Cook et al. (2016) best fitting line at ΣSFR ≈ 2.6 and the mean α of our samples at ΣSFR > 2.6. Both values are remarkably close to α = 1.6, the slope of the GMC MF in the high gas and ΣSFR regime. Based on the discussion in this section, we expect this behavior to arise from a combination of increased stellar clustering at birth toward higher gas densities (and therefore pressures; Kruijssen 2012), as well as of decreased IMF sampling toward low SFR surface densities. Higher-resolution observations may be necessary to assess how blending of adjacent H II regions may affect these trends.
6.2. The strength of spiral arms
In Sect. 4.3.1 we showed that a flattening of the LF slope in spiral arm areas compared to inter-arm areas is evident for only about half of the galaxies with spiral arms in our sample (i.e., six out of 13 galaxies, namely NGC 1300, NGC 1365, NGC 1566, NGC 1672, NGC 3627, and NGC 4303). The Monte Carlo simulations by Oey & Clarke (1998) suggested that such variations can be expected when the H II regions populating the spiral arm areas trace a current burst of coeval star formation while the inter-arm population is an aged version thereof (i.e., aging effect). However, the same authors noted that, at any given location in a galaxy disk, the timescale between the passage of spiral density waves is on the order of 40 Myr (see, e.g., Rand 1993), much longer than the observed lifetime of H II regions (in the interval 5 − 10 Myr; Chevance et al. 2020a). This implies that H II regions detected in inter-arm areas are, potentially, tracing both a population of aging H II regions and recent star formation that is genuinely happening in inter-arm areas.
Large-scale dynamical processes shaping the distribution of cold gas that ultimately fuels the star formation can also influence the variation (or not) in the LF slopes between spiral arm and inter-arm areas. We might expect this to depend on the nature of the dynamical perturbation present in the disk (material spiral arms versus density waves) and its strength. Rand (1992), for example, found a significant difference between the LF slopes of spiral arm and inter-arm H II regions in the grand-design interacting galaxy M51 and attributed it to a shallower GMCs MF in the spiral arms. In NGC 6814, on the other hand, Knapen et al. (1993) argued that the spiral arms are not strong enough to build up the large cloud masses needed to produce the number of giant H II regions that make the spiral arm LF shallower than the inter-arm LF.
Strong spiral arms are not only capable of building high gas densities and growing high mass molecular clouds, they can also impact the likelihood of in situ inter-arm star formation, thus influencing the LFs of H II regions. Indeed, the presence of spiral arms imposes a strong organization on the gas distribution, which acts to concentrate star formation into the spiral arms. Comparing a high-resolution simulation of an M51-like galaxy with a comparable isolated galaxy, Tress et al. (2020, 2021) concluded that strong spiral arms gather molecular gas and clouds without dramatically affecting their properties, yielding similar overall SFRs.
In our case, we might thus expect that variations in cloud MFs and H II region LF slopes will be weak in systems with more uniformly distributed H II regions across the disk (weaker spirals) and stronger in systems with strong spiral arms. In line with this, we find that the galaxies that show a significant environmental change in α are those in which the distribution of the H II regions quite clearly traces the spiral arms and fewer H II regions are detected in between spiral arms (i.e., less ongoing star formation in the inter-arm areas). The galaxies with more uniformly distributed H II regions across the disk (e.g., NGC 0628, NGC 4254, and NGC 4321), on the other hand, exhibit comparable α in the two environments.
We quantify this further using the azimuthal contrast in CO brightness across our targets, which serves as a proxy for spiral arm strength (Meidt et al. 2021). For our targets, we measure the CO contrasts in a set of 150-pc wide radial bins, calculating the ratio between the brightness of the 84th percentile of the CO distribution in a given ring and a reference level defined to capture the level of low brightness inter-arm emission in Meidt et al. (2021). We then take the average of the CO contrasts measured across the full area of interest.
As shown in Fig. 10, for the six galaxies showing environmental changes of the LF slope, the magnitude of such variations appears to correlate with the spiral arm contrast. The remaining galaxies with evidently weaker spiral arms, more uniformly distributed H II regions, and no significant variation in LF slope from arm to inter-arm, do not exhibit a similar trend.
 |
Fig. 10. Change in the LF slope between inter-arm and spiral arm environments, ΔαENV (derived as αi − αa as reported in Table 4), as a function of the CO(2–1) contrast between the 84th percentile and the reference level defined in Meidt et al. (2021) for six galaxies in our sample. |
Overall, these findings suggest that environmental variations in α are sensitive to how spiral arms shape the distribution of the more massive molecular clouds that serve as the birthplace of the brightest H II regions. A study of environmental variations in GMC MFs in our sample (e.g., Rosolowsky et al. 2021; Hughes et al., in prep.) will be an important tool for recognizing how much of the change in LF slope from arm to inter-arm is due to the evolution in the distribution of progenitor clouds and how much is due to, for example, aging, as considered in the next section. The morphology of inter-arm gas (in the form of spurs/feathers and non-spiral clump features) may also yield important clues on the nature of inter-arm star formation and the change in H II region LF slope.
Given the resolution of our observations, we cannot fully exclude that H II region blending, which affects spiral arms to a greater extent, has an effect on our findings. An additional factor that we are not considering and that can play a role in this context is the SFH of the galaxies. Feinstein (1997) predicted that a past starburst can manifest as an additional peak below the LF turnover luminosity and result in a double-peaked LF as the one observed for M31 by Azimlu et al. (2011). We would need observations that are at least one order of magnitude deeper in terms of LHα to search for such features and, for this reason, we cannot deduce or fold in information on the SFH in our study of the LF.
6.3. The aging effect and the ionization parameter
According to Charlot & Longhetti (2001, Eq. (10)), by assuming that H II regions are well approximated by Strömgren spheres, the ionization parameter changes with time as U(t)∝(Q(t)nH)1/3, where Q is the rate of ionizing photons produced by the central star or cluster and nH is the hydrogen density. Considering the typical evolution of an H II region, we can expect the ionization parameter to drop as time passes: as the central ionizing star/cluster evolves its ionizing flux drops while the gas density decreases due to stellar feedback dispersing the H II region’s gas (see, e.g., Rahner et al. 2017, 2019; Pellegrini et al. 2020).
The LF slope can, in principle, be used to test this expectation by using the ionization parameter to draw subsamples of H II regions in the way we did in Sect. 4.3.3. If the ionization parameter q is related to the evolutionary stage of an H II region, it would separate less and more evolved H II regions and, ultimately, we would expect the aging effect to drive changes in the LF slope (Oey & Clarke 1998). This is the same effect discussed for environmental variations in the previous section. What we find in Sect. 4.3.3 is indeed a steeper LF for the population of H II regions with lower q that, for a number of galaxies, constitutes the bulk of the faint H II regions. This corroborates the expectations of Charlot & Longhetti (2001) from an empirical point of view, indicating that the ionization parameter can be used as a good proxy for the evolutionary stage of H II regions.
However, we know that H II regions are not always well represented by Strömgren spheres; for example, they can be asymmetric or even broken shells (see, e.g., Pellegrini et al. 2012). Also, assuming equal physical conditions for an H II region, the same ionizing flux (and thus ionization parameter) can be produced by a single very young star or a cluster of slightly older stars. Another parameter that is relevant for the interpretation of our results is the metallicity, and its long-debated degeneracy with age. In fact, an increase in stellar metallicity is also expected to lower the ionization parameter: as stellar atmospheres of O stars become cooler (Massey et al. 2005) and the mechanical energy due to photon scattering increases, dispersing gas more efficiently (Dopita et al. 2006).
Interestingly, using PHANGS–MUSE data, Kreckel et al. (2019) showed that H II regions with higher [S III]/[S II]line ratios (and thus higher ionization parameter) also tend to have higher Hα-to-FUV flux ratios, indicating younger star cluster ages. We note that the PHANGS–HST data set will be an ideal test-bed to actually connect our H II regions (and their ionization parameters) to the ages of their ionizing star(s)/cluster and shed a light on this topic. The [S III]/[S II]line ratio we use to compute the ionization parameter has been found to have only a weak dependence on the gas-phase metallicity for H II regions located in spiral galaxies. (Dors & Copetti 2005; Garnett et al. 1997; Kennicutt & Garnett 1996; Dors et al. 2011). However, the topic is still debated as other works presented contrasting results (see, e.g., Bresolin et al. 1999 for disk galaxies and Dopita et al. 2014 for Luminous Infrared Galaxies) and, above all, in our sample a clear correlation has been found between [S III]/[S II]and the gas-phase metallicity (see Fig. 4 in Kreckel et al. 2019). We confirm this by looking at the distribution of the H II region metallicities for the subsamples with high and low q. However, if the gas-phase metallicity plays a role in setting the slope of the LF, we would see it by defining H II region subsamples based on their metallicity and looking for variations in α. We conducted this test and do not find such variations. We thus conclude that the variations in the LF slope we observe in Fig. B.3 are mainly driven by aging of the H II regions rather than their metal content.
By comparing the spatial distribution of the warm ionized gas (i.e., H II regions) and the cold molecular gas (i.e., GMCs), it is now possible to infer, for example, the lifetime of GMCs tCO and the timescale over which stellar feedback acts tfb (see, e.g., Kruijssen et al. 2019; Chevance et al. 2020b; Kim et al. 2021). Assuming that the aging effect is the main driver behind the LF slope variations we observe between the H II region subsamples with high and low q, we can reasonably expect the magnitude of such variations Δαq to correlate with the timescales that regulate the star formation process (e.g., the lifetime of GMCs serving as the stellar nurseries, the timescales of stellar feedback) in a given galaxy. Following the “uncertainty principle for star formation” method of Kruijssen et al. (2018) and expanding the results of Chevance et al. (2020b), Kim et al. (in prep.) derived tCO and tfb for most of the galaxies in our sample. In that work, H II regions are traced via the Hα emission in the PHANGS–Hα data (Razza et al., in prep.), while GMCs are traced via the CO(2–1) emission in the PHANGS–ALMA data (Leroy et al. 2021). It should be noted that for IC 5332 there is no significant CO(2–1) emission detected to apply this method and the tCO and tfb measurements for NGC 0628 and NGC 3627 are taken from Chevance et al. (2020b). As shown in Fig. 11, we find a weak-to-moderate and a moderate anticorrelation between Δαq and tfb and tCO, respectively. These trends suggest that when stellar feedback occurs on shorter timescales and the GMC lifetime is shorter (i.e., they get dispersed faster due to stellar feedback) the difference between the LF slope of H II regions with high and low q increases, as it would be expected if those populations are intrinsically different in terms of their age.
 |
Fig. 11. Change in LF slope between H II regions with low and high ionization parameters (derived as αq< − αq> as reported in Table 4) as a function of the feedback timescales (upper panel) and the GMC lifetime (lower panel). For each panel we report the Spearman correlation coefficient, ρ, between the plotted quantities. |
7. Conclusions
In this paper we have studied the nebular LFs (i.e., built using the Hα luminosity of H II regions) in the star-forming disks of the 19 nearby galaxies that make up the PHANGS–MUSE sample. Thanks to the exquisite spatial resolution (mean PSFFWHM = 67 pc) and sensitivity of the data, we were able to build a catalog of about 31 400 ionized nebulae, from which we extracted an unprecedented sample of about 23 000 H II regions. With MUSE covering a large part of the optical spectrum, we were able to derive global properties (e.g., M*, SFR, sSFR) for our galaxies and characterize our H II regions in terms of their dust attenuation (via the Hα/Hβ Balmer decrement), gas-phase metallicity O/H, and ionization parameter, q. The average number of H II regions detected per galaxy is about 1200, marking a significant improvement with respect to previous spectroscopic studies at a comparable spatial resolution.
We fit the LFs via MLE (Alstott et al. 2014). This method does not require us to bin the data, is especially suited for heavily tailed distributions, and overcomes typical pitfalls of more commonly used methods (e.g., histograms combined with linear regression). We find an LF slope of α = −1.73 ± 0.15, in agreement with what has been found in the literature for Sa–Sc-type galaxies (see, e.g., Kennicutt et al. 1989; Elmegreen & Salzer 1999; Whitmore et al. 2014). Given the sensitivity of the MUSE observations, our LFs mainly probe massive star formation happening in star clusters and associations. We report evidence that the LFs of a number of galaxies steepen at luminosities above log(LHα [erg s−1]) = 38.6 (i.e., type II LF). However, this appears as a subtle feature compared to what has been shown in past studies (e.g., Beckman et al. 2000). In general, a power law with a single slope offers a good representation of the LFs and allows us to uniformly analyze the LFs across our sample.
We find that the LF slope remains largely unchanged for the inner and outer parts of the star-forming galaxy disks (Sect. 4.3.2). For the galaxies with H II regions more uniformly distributed across the star-forming disk, we do not find any significant difference between the slopes of the spiral arm and inter-arm LFs. On the other hand, we find environmental (i.e., arm versus inter-arm) LF variations for galaxies that show H II regions preferentially located along spiral arms. We attribute these variations to the spiral arms increasing the molecular clouds’ arm–inter-arm mass contrast and find suggestive evidence that they are more pronounced in galaxies with spiral arms that drive stronger dynamical perturbations.
In line with the results of Cook et al. (2016), who studied the LF of star-forming regions as traced by GALEX FUV imaging, we find that galaxies with a higher ΣSFR have a flatter LF, meaning that their relative number of bright H II regions is higher compared to galaxies with lower ΣSFR. This potentially connects to fundamental changes in the physics regulating star formation in galaxy disks. The trend we observe between α and ΣSFR is not driven by low-number statistics and provides further evidence for the prediction that the clustering of young stars is enhanced at high gas surface densities and star formation efficiencies (Kruijssen 2012). We propose that α may increase even further at log(ΣSFR [M⊙ yr−1 kpc−2]) ≲ −2.6, where observations and models find that the maximum masses of the newborn stellar populations should become so low (e.g., Johnson et al. 2017; Reina-Campos & Kruijssen 2017) that they are affected by stochastic sampling of the stellar IMF (e.g., Krumholz et al. 2015).
Finally, we find that, within each of our galaxies, H II regions with a high ionization parameter have a shallower LF compared to H II regions with a low ionization parameter. Such variations are compatible with an aging effect, suggesting that H II regions with a high q are the youngest star-forming regions, while the ones with a low q are more evolved. The lack of α trends or variations related to the H II regions’ gas-phase metallicity persuades us that the main parameter regulating changes in q is age. We also bring some tentative evidence that suggests that α variations between these H II region populations are more evident when stellar feedback acts on shorter timescales and GMC lifetimes are shorter.
8. Future prospects
We note that this work can be expanded in a number of promising directions in the near future, especially thanks to the availability of HST and ALMA data for the entire PHANGS–MUSE sample. The PHANGS–ALMA data will allow us to characterize GMCs and study their MF. Comparing GMC MF slopes with the H II regions’ LF slopes reported in this paper can bring new insights into if and how physical properties of the molecular gas influence the physics of star formation. On the other side, the PHANGS–HST data can be used to estimate the ages and metallicities of the star(s) or cluster ionizing the H II regions and help in disentangling what the main driver behind changes in the H II regions’ ionization parameter is. Furthermore, by providing a direct estimate of the clustered star formation efficiency (defined as the ratio between the CFR and the SFR; Γ ≡ CFR/SFR), it will be possible to compare Γ to the H II region LF slopes measured in this paper and test whether this is the mechanism behind the flattening of the LF that we observe with increasing ΣSFR.
Available from https://github.com/emsellem/pymusepipe
Acknowledgments
This work was carried out as part of the PHANGS collaboration. FS, ES, RME, TS, and TGW acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 694343). ATB would like to acknowledge funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No.726384/Empire). JMDK and MC gratefully acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) through an Emmy Noether Research Group (grant number KR4801/1-1), as well as from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme via the ERC Starting Grant MUSTANG (grant agreement number 714907). JMDK, MC, and JK gratefully acknowledge funding from the DFG through the DFG Sachbeihilfe (grant number KR4801/2-1). ER acknowledges the support of the Natural Sciences and Engineering Research Council of Canada (NSERC), funding reference number RGPIN-2017-03987. KK gratefully acknowledges funding from the German Research Foundation (DFG) in the form of an Emmy Noether Research Group (grant number KR4598/2-1, PI Kreckel). EJW acknowledges support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project-ID 138713538 ‘SFB 881 (‘The Milky Way System’, subproject P2). MB gratefully acknowledges support by the ANID BASAL project FB210003 and the FONDECYT regular grant 1211000. Based on observations collected at the European Southern Observatory under ESO programmes 1100.B-0651, 095.C-0473, and 094.C-0623 (PHANGS-MUSE; PI Schinnerer), as well as 094.B-0321 (MAGNUM; PI Marconi), 099.B-0242, 0100.B-0116, 098.B-0551 (MAD; PI Carollo) and 097.B-0640 (TIMER; PI Gadotti).
References
- Adamo, A., Östlin, G., & Zackrisson, E. 2011, MNRAS, 417, 1904 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Kruijssen, J. M. D., Bastian, N., Silva-Villa, E., & Ryon, J. 2015, MNRAS, 452, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Zeidler, P., Kruijssen, J. M. D., et al. 2020a, Space Sci. Rev., 216, 69 [Google Scholar]
- Adamo, A., Hollyhead, K., Messa, M., et al. 2020b, MNRAS, 499, 3267 [Google Scholar]
- Alstott, J., Bullmore, E., & Plenz, D. 2014, PLoS ONE, 9, e85777 [CrossRef] [Google Scholar]
- Anand, G. S., Lee, J. C., Van Dyk, S. D., et al. 2021, MNRAS, 501, 3621 [Google Scholar]
- Azimlu, M., Marciniak, R., & Barmby, P. 2011, AJ, 142, 139 [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, in Ground-based and Airborne Instrumentation for Astronomy III, eds. I. S. McLean, S. K. Ramsay, & H. Takami, , SPIE Conf. Ser., 7735, 773508 [Google Scholar]
- Bacon, R., Conseil, S., Mary, D., et al. 2017, A&A, 608, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Banfi, M., Rampazzo, R., Chincarini, G., & Henry, R. B. C. 1993, A&A, 280, 373 [NASA ADS] [Google Scholar]
- Barnes, A. T., Longmore, S. N., Dale, J. E., et al. 2020, MNRAS, 498, 4906 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N. 2008, MNRAS, 390, 759 [Google Scholar]
- Bastian, N., Ercolano, B., Gieles, M., et al. 2007, MNRAS, 379, 1302 [NASA ADS] [CrossRef] [Google Scholar]
- Bastian, N., Gieles, M., Ercolano, B., & Gutermuth, R. 2009, MNRAS, 392, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Beckman, J. E., Rozas, M., Zurita, A., Watson, R. A., & Knapen, J. H. 2000, AJ, 119, 2728 [NASA ADS] [CrossRef] [Google Scholar]
- Belfiore, F., Santoro, F., & Groves, B. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202141859 [Google Scholar]
- Bittner, A., Falcón-Barroso, J., Nedelchev, B., et al. 2019, A&A, 628, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanc, G. A., Heiderman, A., Gebhardt, K., Evans, N.J., & Adams, J. 2009, ApJ, 704, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kennicutt, R. C., Jr, & Garnett, D. R. 1999, ApJ, 510, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cepa, J., & Beckman, J. E. 1990, A&AS, 83, 211 [NASA ADS] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
- Charlot, S., & Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Vazquez-Semadeni, E., et al. 2020a, Space Sci. Rev., 216, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Chevance, M., Kruijssen, J. M. D., Hygate, A. P. S., et al. 2020b, MNRAS, 493, 2872 [NASA ADS] [CrossRef] [Google Scholar]
- Clauset, A., Shalizi, C. R., & Newman, M. E. J. 2009, SIAM Rev., 51, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Colombo, D., Hughes, A., Schinnerer, E., et al. 2014, ApJ, 784, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, D. O., Seth, A. C., Dale, D. A., et al. 2012, ApJ, 751, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, D. O., Dale, D. A., Lee, J. C., et al. 2016, MNRAS, 462, 3766 [NASA ADS] [CrossRef] [Google Scholar]
- Diaz, A. I., Terlevich, E., Vilchez, J. M., Pagel, B. E. J., & Edmunds, M. G. 1991, MNRAS, 253, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Fischera, J., Sutherland, R. S., et al. 2006, ApJS, 167, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Rich, J., Vogt, F. P. A., et al. 2014, Ap&SS, 350, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Dors, O. L., Jr., & Copetti, M. V. F. 2005, A&A, 437, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dors, O. L., Jr., Krabbe, A., Hägele, G. F., & Pérez-Montero, E. 2011, MNRAS, 415, 3616 [NASA ADS] [CrossRef] [Google Scholar]
- Efremov, Y. N., & Elmegreen, B. G. 1998, MNRAS, 299, 588 [Google Scholar]
- Elmegreen, B. G., & Falgarone, E. 1996, ApJ, 471, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., & Salzer, J. J. 1999, AJ, 117, 764 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Elmegreen, D. M., Salzer, J. J., & Mann, H. 1996, ApJ, 467, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Schinnerer, E., Santoro, F., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/202141727 [Google Scholar]
- Espinosa-Ponce, C., Sánchez, S. F., Morisset, C., et al. 2020, MNRAS, 494, 1622 [Google Scholar]
- Faesi, C. M., Lada, C. J., & Forbrich, J. 2018, ApJ, 857, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Feinstein, C. 1997, ApJS, 112, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., Wyse, R. F. G., Gallagher, J. S., & Hunter, D. A. 1998, ApJ, 506, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Shields, G. A., Skillman, E. D., Sagan, S. P., & Dufour, R. J. 1997, ApJ, 489, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, Q. E., Bastian, N., & Kennicutt, R. C. 2010, MNRAS, 405, 857 [NASA ADS] [Google Scholar]
- Gutiérrez, L., Beckman, J. E., & Buenrostro, V. 2011, AJ, 141, 113 [CrossRef] [Google Scholar]
- Haffner, L. M., Dettmar, R. J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [CrossRef] [Google Scholar]
- Hao, C.-N., Kennicutt, R. C., Johnson, B. D., et al. 2011, ApJ, 741, 124 [Google Scholar]
- Haydon, D. T., Kruijssen, J. M. D., Chevance, M., et al. 2020, MNRAS, 498, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Helmboldt, J. F., Walterbos, R. A. M., Bothun, G. D., & O’Neil, K. 2005, ApJ, 630, 824 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Endoqui, M., Díaz-García, S., Laurikainen, E., & Salo, H. 2015, A&A, 582, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ho, I. T., Kreckel, K., Meidt, S. E., et al. 2019, ApJ, 885, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Hoare, M. G. 2005, Ap&SS, 295, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F. 2013, MNRAS, 430, 1653 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, A., Meidt, S., Colombo, D., et al. 2016, in From Interstellar Clouds to Star-Forming Galaxies: Universal Processes?, eds. P. Jablonka, P. André, & F. van der Tak, 315, 30 [NASA ADS] [Google Scholar]
- Johnson, L. C., Seth, A. C., Dalcanton, J. J., et al. 2016, ApJ, 827, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Johnson, L. C., Seth, A. C., Dalcanton, J. J., et al. 2017, ApJ, 839, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kennicutt, R. C., Jr., & Garnett, D. R. 1996, ApJ, 456, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012a, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012b, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Edgar, B. K., & Hodge, P. W. 1989, ApJ, 337, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Lee, J. C., Funes, J. G., et al. 2008, ApJS, 178, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [Google Scholar]
- Kewley, L. J., Heisler, C. A., Dopita, M. A., & Lumsden, S. 2001, ApJS, 132, 37 [Google Scholar]
- Kim, J., Chevance, M., Kruijssen, J. M. D., et al. 2021, MNRAS, 504, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. H. 1998, MNRAS, 297, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. H., Arnth-Jensen, N., Cepa, J., & Beckman, J. E. 1993, AJ, 106, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2020, MNRAS, 499, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P., & Weidner, C. 2003, ApJ, 598, 1076 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D. 2012, MNRAS, 426, 3008 [Google Scholar]
- Kruijssen, J. M. D., & Longmore, S. N. 2014, MNRAS, 439, 3239 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Schruba, A., Hygate, A. P. S., et al. 2018, MNRAS, 479, 1866 [NASA ADS] [CrossRef] [Google Scholar]
- Kruijssen, J. M. D., Schruba, A., Chevance, M., et al. 2019, Nature, 569, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R. 2014, Phys. Rep., 539, 49 [Google Scholar]
- Krumholz, M. R., Adamo, A., Fumagalli, M., et al. 2015, ApJ, 812, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Lang, P., Meidt, S. E., Rosolowsky, E., et al. 2020, ApJ, 897, 122 [CrossRef] [Google Scholar]
- Larsen, S. S. 2002, AJ, 124, 1393 [NASA ADS] [CrossRef] [Google Scholar]
- Lawton, B., Gordon, K. D., Babler, B., et al. 2010, ApJ, 716, 453 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. H., Hwang, N., & Lee, M. G. 2011, ApJ, 735, 75 [Google Scholar]
- Lee, J. C., Whitmore, B. C., Thilker, D. A., et al. 2022, ApJS, 258, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Lelièvre, M., & Roy, J.-R. 2000, AJ, 120, 1306 [CrossRef] [Google Scholar]
- Leroy, A. K., Schinnerer, E., Hughes, A., et al. 2021, ApJS, 257, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Calzetti, D., Kennicutt, R. C., Jr., et al. 2013, ApJ, 772, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., & Úbeda, L. 2005, ApJ, 629, 873 [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mascoop, J. L., Anderson, L. D., Wenger, T. V., et al. 2021, ApJ, 910, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Massey, P., Puls, J., Pauldrach, A. W. A., et al. 2005, ApJ, 627, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Leroy, A. K., Querejeta, M., et al. 2021, ApJ, 913, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [Google Scholar]
- Oey, M. S. 1996, ApJ, 465, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., & Clarke, C. J. 1998, AJ, 115, 1543 [CrossRef] [Google Scholar]
- Oey, M. S., Meurer, G. R., Yelda, S., et al. 2007, ApJ, 661, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Baldwin, J. A., & Ferland, G. J. 2010, ApJS, 191, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Oey, M. S., Winkler, P. F., et al. 2012, ApJ, 755, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Pellegrini, E. W., Rahner, D., Reissl, S., et al. 2020, MNRAS, 496, 339 [Google Scholar]
- Pessa, I., Schinnerer, E., Belfiore, F., et al. 2021, A&A, 650, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pietrinferni, A., Cassisi, S., Salaris, M., & Castelli, F. 2004, ApJ, 612, 168 [Google Scholar]
- Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
- Querejeta, M., Schinnerer, E., Meidt, S., et al. 2021, A&A, 656, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2017, MNRAS, 470, 4453 [NASA ADS] [CrossRef] [Google Scholar]
- Rahner, D., Pellegrini, E. W., Glover, S. C. O., & Klessen, R. S. 2019, MNRAS, 483, 2547 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J. 1992, AJ, 103, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Rand, R. J. 1993, ApJ, 410, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Reina-Campos, M., & Kruijssen, J. M. D. 2017, MNRAS, 469, 1282 [CrossRef] [Google Scholar]
- Rice, T. S., Goodman, A. A., Bergin, E. A., Beaumont, C., & Dame, T. M. 2016, ApJ, 822, 52 [Google Scholar]
- Rosolowsky, E., Keto, E., Matsushita, S., & Willner, S. P. 2007, ApJ, 661, 830 [NASA ADS] [CrossRef] [Google Scholar]
- Rosolowsky, E., Hughes, A., Leroy, A. K., et al. 2021, MNRAS, 502, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Rousseau-Nepton, L., Robert, C., Martin, R. P., Drissen, L., & Martin, T. 2018, MNRAS, 477, 4152 [NASA ADS] [Google Scholar]
- Rozas, M., Beckman, J. E., & Knapen, J. H. 1996, A&A, 307, 735 [NASA ADS] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schruba, A., Kruijssen, J. M. D., & Leroy, A. K. 2019, ApJ, 883, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N. Z., Polletta, M., Ewald, S., et al. 2001, AJ, 122, 3017 [Google Scholar]
- Thilker, D. A., Braun, R., & Walterbos, R. A. M. 2000, AJ, 120, 3070 [Google Scholar]
- Thilker, D. A., Walterbos, R. A. M., Braun, R., & Hoopes, C. G. 2002, AJ, 124, 3118 [NASA ADS] [CrossRef] [Google Scholar]
- Thilker, D. A., Whitmore, B. C., Lee, J. C., et al. 2022, MNRAS, 509, 4094 [Google Scholar]
- Tress, R. G., Smith, R. J., Sormani, M. C., et al. 2020, MNRAS, 492, 2973 [Google Scholar]
- Tress, R. G., Sormani, M. C., Smith, R. J., et al. 2021, MNRAS, 505, 5438 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D. 1994, ApJ, 421, 140 [NASA ADS] [CrossRef] [Google Scholar]
- van Zee, L. 2000, AJ, 119, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Vazdekis, A., Koleva, M., Ricciardelli, E., Röck, B., & Falcón-Barroso, J. 2016, MNRAS, 463, 3409 [Google Scholar]
- Wei, P., Zou, H., Kong, X., et al. 2020, PASP, 132, 094101 [NASA ADS] [CrossRef] [Google Scholar]
- Weidner, C., Kroupa, P., & Larsen, S. S. 2004, MNRAS, 350, 1503 [CrossRef] [Google Scholar]
- Whitmore, B. C., Chandar, R., Bowers, A. S., et al. 2014, AJ, 147, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Whitmore, B. C., Lee, J. C., Chandar, R., et al. 2021, MNRAS, 502, 1366 [NASA ADS] [CrossRef] [Google Scholar]
- Youngblood, A. J., & Hunter, D. A. 1999, ApJ, 519, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Yan, R., Bundy, K., et al. 2017, MNRAS, 466, 3217 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Nebula spatial masks and metallicity gradients
In this section, we present the spatial masks of the H II regions for 18 galaxies of the PHANGS–MUSE sample (from Fig. A.1 to Fig. A.18) highlighting the H II region footprints and the different galaxy environments. At the end of this section in Fig. A.19, we also show the best fitting radial metallicity gradients for all the galaxies in our sample. They provide the measurement of the metallicity at the median galactocentric radius covered by the MUSE observations used in Sect. 4.2.
 |
Fig. A.1. H II regions and environments for IC5332. The figure shows the Hα emission in the background, color coded according to the color scheme on the right, overlaid with the borders of the H II regions in our catalog. The centers of the nebulae that have been discarded by our selection criteria are marked with crosses. In the lower-left corner, the black circle indicates the PSF of the MUSE observations, while the black line marks a physical scale corresponding to 1 kpc. Both the H II regions and the discarded nebulae are color coded according to our definition of environments as outlined by the color scheme at the bottom. |
 |
Fig. A.10. Same as Fig. A.1 but for the H II regions and environments for NGC 1672. |
 |
Fig. A.11. Same as Fig. A.1 but for the H II regions and environments for NGC 2835. |
 |
Fig. A.12. Same as Fig. A.1 but for the H II regions and environments for NGC 3351. |
 |
Fig. A.13. Same as Fig. A.1 but for the H II regions and environments for NGC 3627. |
 |
Fig. A.14. Same as Fig. A.1 but for the H II regions and environments for NGC 4254. |
 |
Fig. A.15. Same as Fig. A.1 but for the H II regions and environments for NGC 4303. |
 |
Fig. A.16. Same as Fig. A.1 but for the H II regions and environments for NGC 4535. |
 |
Fig. A.17. Same as Fig. A.1 but for the H II regions and environments for NGC 5068. |
 |
Fig. A.18. Same as Fig. A.1 but for the H II regions and environments for NGC 7496. |
 |
Fig. A.19. Fit of the radial metallicity gradients for the galaxies in the PHANGS–MUSE sample. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their name is indicated at the top right of each panel. The H II region metallicity 12 + log(O/H) is plotted against its deprojected galactocentric radius, rgal, measured in kpc (black points). The best linear unweighted least-square fit relation reported above each panel (red label) is shown using a solid red line. The dashed blue vertical and horizontal lines intercept at the metallicity given by the best fitting There seems to be a word missing here. "model"?at the mean H II region galactocentric radius, ⟨rgal⟩; this value, met⟨rgal⟩, is reported above each panel (blue label) Verify that your intended meaning has not been changed.. |
Appendix B: Variations in the LF within single galaxies
In this section we show the LFs and their fits for the H II region subsamples described in the main text in Sect. 4.3. Figure B.1 shows the LFs of the spiral arm and inter-arm areas, six of our 19 galaxies do not show evident spiral arms, for these galaxies we show the LF and best fitting models of the H II regions across the entire disk but excluding bars (i.e., this is the reason for slight variations with respect to the fits shown in Fig. 2). Figure B.2 shows the LF of the inner and outer parts of the star-forming disk while Fig. B.3 shows the LFs of H II regions with high and low ionization parameter log q.
 |
Fig. B.1. LFs for H II regions in spiral arm and inter-arm areas. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. For the 13 galaxies that show evident spiral arms, the LF and the best fitting model are shown in red and blue for H II regions located in spiral arms and inter-arms areas, respectively. For the remaining galaxies, the LF and the best fitting model refer to the H II regions located in the entire disk, excluding the areas occupied by the bars, and are drawn in black. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. |
 |
Fig. B.2. LFs for H II regions located in the inner (red colors) and outer disk (blue colors) areas. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. The median galactocentric radius, ⟨rgal⟩, of the H II region parent sample, used to separate inner and outer disks, is indicated below each galaxy name in units of R25. |
 |
Fig. B.3. Best fitting model of the H II region LF for regions with high (blue colors) and low (red colors) gas ionization parameters, q. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. The median ionization parameter, ⟨log q⟩, of the H II region parent sample, used to separate young and old H II regions, is indicated below each galaxy name in logarithmic units. |
Appendix C: The effect of dust correction and BPT cuts on the LF slopes
In this section we discuss in more detail the effect that dust extinction and selection criteria might play on the LF slopes presented in our paper. In Sect. 4.1, we discuss LFs built from extinction-corrected Hα luminosities of H II regions. The spectroscopic nature of the MUSE data allow us to perform extinction correction via the Hα/Hβ Balmer decrement; however, in some cases (i.e., when the nebular LF is obtained from narrowband Hα imaging) this is not possible. To understand the effect of dust extinction, we fit the LF built with observed Hα luminosities and in Fig. C.1 and Fig. C.2, we compare the results with what we presented in Sect. 4.1. Overall, we see only a small change in the LF slope if we do not correct for dust extinction. The variations always remain within the uncertainty estimated for the LF slope. The dust-corrected LF slopes are, as one would expect, shallower due to the presence of more luminous H II regions after the dust correction is performed. This guarantees that our results can be compared to nebular LF studies – performed with, for example, narrowband Hα observations – that do not correct for the effect of dust extinction. As can be noted in Fig. C.1 another effect of the lack of a dust correction is the lowering of Lmin due to the fact that we detect a higher number of faint H II regions.
The most significant drop in the number of ionized nebulae entering our H II region catalog is due to the cuts on the line ratios applied using semi-empirical demarcation lines in the three classical BPT diagrams (“BPT cuts” hereafter; see Sect. 3.2). It is known that, depending on their gas-phase metallicity and ionization parameter, H II regions can lie outside the boundaries that are commonly adopted to have a clean H II region sample and avoid nebulae whose gas is ionized by mechanisms other than photoionization from young OB stars (e.g., AGN photoionization/shocks). As shown by Fig. C.3 and Fig. C.4, if we drop the BPT cuts when cleaning our ionized nebula catalogs and rerun the LF fit, we find no significant variation in the measured LF slope. Remarkably, this is true also for NGC 1365 for which there is clear evidence of an AGN ionization cone extending further out the central region (Belfiore et al. 2021). As can be seen by comparing the empirical LFs, the regions that are flagged by the BPT cuts tend to populate the fainter end of the LF and thus have negligible effects on the LF shape at the bright end. In addition, we note that the LF Lmin remains substantially unchanged aside from the case of NGC 3627, the only strongly interacting galaxy in our sample.
In conclusion, we find that both the dust correction and selection effects do not have a significant impact on the slopes of the LFs that we measure in Sect. 4.
 |
Fig. C.1. Fit of the LF for H II regions obtained from the dust-corrected (same as in Fig. 2, red colors) and observed (blue colors) Hα fluxes. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. |
 |
Fig. C.2. Slope of the LF for H II regions obtained from the dust-corrected (same as in Fig. 2, red colors) and observed (blue colors) Hα fluxes. Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. |
 |
Fig. C.3. Fit of the LF for H II regions obtained applying the BPT cut (same as in Fig. 2, red colors) and not applying the BPT cut (blue colors) to our nebula catalogs. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid line respectively indicate the empirical LF and the best fitting model. The models slopes are reported in the top-right corner of each panel following the same color scheme. |
 |
Fig. C.4. Slope of the LF for H II regions obtained applying the BPT cut (same as in Fig. 2, red colors) and not applying the BPT cut (blue colors). Galaxies are ordered according to increasing stellar mass from left to right, and their names are indicated along the abscissa. |
All Tables
All Figures
 |
Fig. 1. H II regions and environments for NGC 4321. The figure shows the Hα emission in the background, color coded according to the color scheme on the right, overlaid with the borders of the H II regions in our catalog. The centers of the nebulae that have been discarded by our selection criteria are marked with crosses. Lower-left corner: the black circle indicates the PSF of the MUSE observations, and the black line marks a physical scale corresponding to 1 kpc. Both the H II regions and the discarded nebulae are color coded according to our definition of environments as outlined by the color scheme at the bottom and shown in the bottom-right sketch. |
| In the text | |
 |
Fig. 2. Best fitting models of the H II region LF for the galaxies of our sample. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dotted black line indicates the empirical PDF, plotted as p(L) versus the logarithm of the H II regions’ Hα luminosity expressed in erg s−1. The vertical dashed line indicates the estimated completeness limit. The vertical solid black line and the shaded gray area indicate the best fitting Lmin and its uncertainty. The LF best fitting model is marked by the solid red line, while the associated slope, α, and its uncertainty are indicated in the upper-right corner of each panel. |
| In the text | |
 |
Fig. 3. Best fitting model of the upper end of the H II region LF for the subsample of nine galaxies with more than 100 density bounded H II regions. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dotted black line indicates the empirical PDF, plotted as p(L), versus the logarithm of the H II regions’ Hα luminosity, expressed in erg s−1. The vertical dashed line indicates the estimated completeness limit. The vertical solid black line and the solid red line indicate the best fitting Lmin and α of the global LF as shown in Fig. 2. The solid orange line marks the best fitting model for the regions with LHα ≥ 1038.5 erg s−1. The LF slopes of the two best fitting models are indicated in the upper-right corner of each panel, following the same color coding as the models. |
| In the text | |
 |
Fig. 4. Trends of the LF slope, α, with global galaxy properties. From top left to bottom right: we show α as a function of the galaxy morphological T class, the Scal metallicity at the median galactocentric radius covered by our observations 12 + log(O/H)⟨rgal⟩, the total stellar mass (M*), the total SFR, the sSFR, the SFR surface density (ΣSFR), the offset from the resolved star formation main sequence (Δ rSFMS), the offset from the resolved Kennicutt–Schmidt relation (Δ rKS), and the offset from the resolved molecular gas main sequence (Δ rMGMS). For each panel we report the Spearman correlation coefficient (ρ) and the p value of the plotted quantities. Middle-right panel: the solid red line shows the best fitting relation found by Cook et al. (2016), while the dashed gray and solid back horizontal lines respectively mark the α of the Cook et al. (2016) line at ΣSFR = −2.6 and the mean α of the points at ΣSFR > −2.6 (see Sect. 6.1 for further details). |
| In the text | |
 |
Fig. 5. Slope of the LF for H II regions located in spiral arms (red points) and inter-arm areas (blue points). Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. Galaxies with no evident spiral arms are marked by black points, and their LF slope refers to the disk area (excluding bars). |
| In the text | |
 |
Fig. 6. Slope of the LF for H II regions located in the inner (red points) and outer (blue points) star-forming disk. Galaxies are ordered by increasing value of their H II regions’ median galactocentric radius from left to right, and their names are indicated along the abscissa. |
| In the text | |
 |
Fig. 7. Slope of the LF for H II regions with high (blue) and low (red) ionization parameters. Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. |
| In the text | |
 |
Fig. 8. The effect of blending and spatial resolution on α and Lmin. Left panel: LF slope plotted as a function of the |
| In the text | |
 |
Fig. 9. Maximum luminosity among the detected H II regions (left panel) and the total SFR (right panel) as a function of the total number of detected H II regions for the galaxies of our sample. For each panel we report the Spearman correlation coefficient, ρ, between the plotted quantities. |
| In the text | |
 |
Fig. 10. Change in the LF slope between inter-arm and spiral arm environments, ΔαENV (derived as αi − αa as reported in Table 4), as a function of the CO(2–1) contrast between the 84th percentile and the reference level defined in Meidt et al. (2021) for six galaxies in our sample. |
| In the text | |
 |
Fig. 11. Change in LF slope between H II regions with low and high ionization parameters (derived as αq< − αq> as reported in Table 4) as a function of the feedback timescales (upper panel) and the GMC lifetime (lower panel). For each panel we report the Spearman correlation coefficient, ρ, between the plotted quantities. |
| In the text | |
 |
Fig. A.1. H II regions and environments for IC5332. The figure shows the Hα emission in the background, color coded according to the color scheme on the right, overlaid with the borders of the H II regions in our catalog. The centers of the nebulae that have been discarded by our selection criteria are marked with crosses. In the lower-left corner, the black circle indicates the PSF of the MUSE observations, while the black line marks a physical scale corresponding to 1 kpc. Both the H II regions and the discarded nebulae are color coded according to our definition of environments as outlined by the color scheme at the bottom. |
| In the text | |
 |
Fig. A.2. Same as Fig. A.1 but for the H II regions and environments for NGC 0628. |
| In the text | |
 |
Fig. A.3. Same as Fig. A.1 but for the H II regions and environments for NGC 1087. |
| In the text | |
 |
Fig. A.4. Same as Fig. A.1 but for the H II regions and environments for NGC 1300. |
| In the text | |
 |
Fig. A.5. Same as Fig. A.1 but for the H II regions and environments for NGC 1365. |
| In the text | |
 |
Fig. A.6. Same as Fig. A.1 but for the H II regions and environments for NGC 1385. |
| In the text | |
 |
Fig. A.7. Same as Fig. A.1 but for the H II regions and environments for NGC 1433. |
| In the text | |
 |
Fig. A.8. Same as Fig. A.1 but for the H II regions and environments for NGC 1512. |
| In the text | |
 |
Fig. A.9. Same as Fig. A.1 but for the H II regions and environments for NGC 1566. |
| In the text | |
 |
Fig. A.10. Same as Fig. A.1 but for the H II regions and environments for NGC 1672. |
| In the text | |
 |
Fig. A.11. Same as Fig. A.1 but for the H II regions and environments for NGC 2835. |
| In the text | |
 |
Fig. A.12. Same as Fig. A.1 but for the H II regions and environments for NGC 3351. |
| In the text | |
 |
Fig. A.13. Same as Fig. A.1 but for the H II regions and environments for NGC 3627. |
| In the text | |
 |
Fig. A.14. Same as Fig. A.1 but for the H II regions and environments for NGC 4254. |
| In the text | |
 |
Fig. A.15. Same as Fig. A.1 but for the H II regions and environments for NGC 4303. |
| In the text | |
 |
Fig. A.16. Same as Fig. A.1 but for the H II regions and environments for NGC 4535. |
| In the text | |
 |
Fig. A.17. Same as Fig. A.1 but for the H II regions and environments for NGC 5068. |
| In the text | |
 |
Fig. A.18. Same as Fig. A.1 but for the H II regions and environments for NGC 7496. |
| In the text | |
 |
Fig. A.19. Fit of the radial metallicity gradients for the galaxies in the PHANGS–MUSE sample. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their name is indicated at the top right of each panel. The H II region metallicity 12 + log(O/H) is plotted against its deprojected galactocentric radius, rgal, measured in kpc (black points). The best linear unweighted least-square fit relation reported above each panel (red label) is shown using a solid red line. The dashed blue vertical and horizontal lines intercept at the metallicity given by the best fitting There seems to be a word missing here. "model"?at the mean H II region galactocentric radius, ⟨rgal⟩; this value, met⟨rgal⟩, is reported above each panel (blue label) Verify that your intended meaning has not been changed.. |
| In the text | |
 |
Fig. B.1. LFs for H II regions in spiral arm and inter-arm areas. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. For the 13 galaxies that show evident spiral arms, the LF and the best fitting model are shown in red and blue for H II regions located in spiral arms and inter-arms areas, respectively. For the remaining galaxies, the LF and the best fitting model refer to the H II regions located in the entire disk, excluding the areas occupied by the bars, and are drawn in black. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. |
| In the text | |
 |
Fig. B.2. LFs for H II regions located in the inner (red colors) and outer disk (blue colors) areas. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. The median galactocentric radius, ⟨rgal⟩, of the H II region parent sample, used to separate inner and outer disks, is indicated below each galaxy name in units of R25. |
| In the text | |
 |
Fig. B.3. Best fitting model of the H II region LF for regions with high (blue colors) and low (red colors) gas ionization parameters, q. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. The median ionization parameter, ⟨log q⟩, of the H II region parent sample, used to separate young and old H II regions, is indicated below each galaxy name in logarithmic units. |
| In the text | |
 |
Fig. C.1. Fit of the LF for H II regions obtained from the dust-corrected (same as in Fig. 2, red colors) and observed (blue colors) Hα fluxes. Galaxies are ordered by increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid lines indicate the empirical LF and the best fitting model, respectively. The LF slopes are reported in the top-right corner of each panel following the same color scheme. |
| In the text | |
 |
Fig. C.2. Slope of the LF for H II regions obtained from the dust-corrected (same as in Fig. 2, red colors) and observed (blue colors) Hα fluxes. Galaxies are ordered by increasing stellar mass from left to right, and their names are indicated along the abscissa. |
| In the text | |
 |
Fig. C.3. Fit of the LF for H II regions obtained applying the BPT cut (same as in Fig. 2, red colors) and not applying the BPT cut (blue colors) to our nebula catalogs. Galaxies are ordered according to increasing stellar mass from top left to bottom right, and their names are indicated within each panel. The dashed and solid line respectively indicate the empirical LF and the best fitting model. The models slopes are reported in the top-right corner of each panel following the same color scheme. |
| In the text | |
 |
Fig. C.4. Slope of the LF for H II regions obtained applying the BPT cut (same as in Fig. 2, red colors) and not applying the BPT cut (blue colors). Galaxies are ordered according to increasing stellar mass from left to right, and their names are indicated along the abscissa. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.