| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 32 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202142695 | |
| Published online | 17 August 2022 | |
Unexplored outflows in nearby low luminosity AGNs
The case of NGC 1052
1
IAA-CSIC – IAA – Instituto de Astrofísica de Andalucía (CSIC), Apdo. 3004, 18008 Granada, Spain
e-mail: sara@iaa.es
2
Departamento de Física de la Tierra y Astrofísica, Universidad Complutense de Madrid, 28040 Madrid, Spain
3
Instituto de Física de Partículas y del Cosmos IPARCOS, Facultad de Ciencias Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
4
Millennium Institute of Astrophysics, Nuncio Monseñor Sótero Sanz 100, Providencia, Santiago, Chile
5
Instituto de Física y Astronomía, Universidad de Valparaíso, Av. Gran Bretaña 1111, Playa Ancha, Chile
6
Dipartimento di Matematica e Fisica, Universita Roma Tre, Via della Vasca Navale 84, 00146 Roma, Italy
7
Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
8
Universidad de La Laguna, Dep. to de Astrofísica, Av. da Astrofísico F. Sánchez s/n, 38206 La Laguna, Tenerife, Spain
Received:
18
November
2021
Accepted:
4
April
2022
Context. Multi-phase outflows play a central role in galaxy evolution shaping the properties of galaxies. Understanding outflows and their effects in low luminosity active galactic nuclei (AGNs), such as low ionisation nuclear emission line regions (LINERs), is essential. LINERs bridge the gap between normal and active galaxies, being the most numerous AGN population in the local Universe.
Aims. Our goal is to analyse the kinematics and ionisation mechanisms of the multi-phase gas of NGC 1052, the prototypical LINER, in order to detect and map the ionised and neutral phases of the putative outflow.
Methods. We obtained Very Large Telescope MUSE and Gran Telescopio Canarias MEGARA optical integral field spectroscopy data for NGC 1052. In addition to stellar kinematics maps, by modelling spectral lines with multiple Gaussian components, we obtained flux, kinematic, and excitation maps of both ionised and neutral gas.
Results. The stars are distributed in a dynamically hot disc (V/σ ∼ 1.2), with a centrally peaked velocity dispersion map (σc = 201 ± 10 km s−1) and large observed velocity amplitudes (ΔV = 167 ± 19 km s−1). The ionised gas, probed by the primary component is detected up to ∼30″ (∼3.3 kpc) mostly in the polar direction with blue and red velocities (∣V∣ < 250 km s−1). The velocity dispersion map shows a notable enhancement (σ > 90 km s−1) crossing the galaxy along the major axis of rotation in the central 10″. The secondary component has a bipolar morphology, velocity dispersion larger than 150 km s−1, and velocities up to 660 km s−1. A third component is detected with MUSE (and barely with MEGARA), but it is not spatially resolved. The broad-line region (BLR) component (used to model the broad Hα emission only) has a full width at half maximum of 2427 ± 332 and 2350 ± 470 km s−1 for MUSE and MEGARA data, respectively. The maps of the NaD absorption indicate optically thick neutral gas with complex kinematics. The velocity field is consistent with a slow rotating disc (ΔV = 77 ± 12 km s−1), but the velocity dispersion map is off-centred without any counterpart in the (centrally peaked) flux map.
Conclusions. We found evidence of an ionised gas outflow (secondary component) with a mass of 1.6 ± 0.6 × 105 M⊙, and mass rate of 0.4 ± 0.2 M⊙ yr−1. The outflow is propagating in a cocoon of gas with enhanced turbulence and might be triggering the onset of kiloparsec-scale buoyant bubbles (polar emission), both probed by the primary component. Taking into account the energy and kinetic power of the outflow (1.3 ± 0.9 × 1053 erg and 8.8 ± 3.5 × 1040 erg s−1, respectively) as well as its alignment with both the jet and the cocoon, and that the gas is collisionally ionised (due to gas compression), we consider that the most likely power source of the outflow is the jet, although some contribution from the AGN is possible. The hints of the presence of a neutral gas outflow are weak.
Key words: galaxies: active / ISM: jets and outflows / ISM: kinematics and dynamics / techniques: spectroscopic / galaxies: groups: individual: NGC 1052
© S. Sawada-Satoh et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Outflows produced by active galactic nuclei (AGNs) and intense episodes of star formation are thought to play a crucial role in regulating the build up of stellar mass and black hole mass growth through negative and positive feedback (see e.g. Kormendy & Ho 2013 and references therein). Recently, it has been shown that outflows can also be driven by radio jets (e.g. Morganti et al. 2005; Harrison et al. 2014; Morganti & Oosterloo 2018; Jarvis et al. 2019; Molyneux et al. 2019; Venturi et al. 2021). The outflows might be an important source of feedback as they evolve and heat the interstellar medium (ISM) preventing the cooling of the gas possibly on large scales.
The different gas phases of outflows have been widely studied in different galaxy populations (Veilleux et al. 2005, 2020, for reviews) mostly via long-slit spectroscopy (e.g. Heckman et al. 2000; Rupke et al. 2002; Arribas et al. 2014; Villar-Martín et al. 2018; Rose et al. 2018; Hernández-García et al. 2019; Saturni et al. 2021) and integral field spectroscopy (IFS, e.g. Cazzoli et al. 2014; Cresci et al. 2015; Ramos Almeida et al. 2017; Maiolino et al. 2017; Bosch et al. 2019; Perna et al. 2020, 2021; Comerón et al. 2021) observations.
To date, the vast majority of studies of multi-phase outflows and feedback have focussed on local luminous and ultra-luminous infrared galaxies (U/LIRGs, e.g. Rupke & Veilleux 2013; Cazzoli et al. 2014, 2016; Pereira-Santaella et al. 2016, 2020; Fluetsch et al. 2021) and luminous AGNs (e.g. quasars or Seyferts galaxies; Feruglio et al. 2010; Müller-Sánchez et al. 2011; Fiore et al. 2017; Brusa et al. 2018; Venturi et al. 2018; Cazzoli et al. 2020). These works demonstrate the power of the 3D IFS in studies of this kind. For example, the wealth of optical and infrared (IR) IFS data enable the exploration of possible scaling relations between AGN properties, host galaxy properties, and outflows (e.g. Kang & Woo 2018; Fluetsch et al. 2019; Kakkad et al. 2020; Ruschel-Dutra et al. 2021; Avery et al. 2021; Luo et al. 2021; Singha et al. 2022, and references therein).
For low luminosity AGNs, such as low ionisation nuclear emission line regions (LINERs), no systematic search for outflows has been done yet. Except for individual discoveries (e.g. Dopita et al. 2015; Raimundo 2021) the only systematic studies are by Cazzoli et al. (2018) and Hermosa Muñoz et al. (2020) of ionised gas outflows in type 1 and type 2 LINERs, respectively. These two works, where 30 LINERS were studied on the basis of optical long-slit spectroscopy, indicate that multi-phase outflows are common in LINERS (detection rate: 60%, Cazzoli et al. 2018), showing an intriguing ionisation structure in which low ionisation lines (e.g. [O I]λλ6300,6364) behave differently to high ionisation lines (e.g. [O III]λλ4959,5007). Most of these spectroscopically identified outflows show in their HST-Hαλ6563 image (Pogge et al. 2000; Masegosa et al. 2011; Hermosa Muñoz et al. 2020) a large-scale biconical or bubble-like shape along with evident spatially resolved sub-structures, such as ∼20−70 pc wide gas clumps.
A 3D description of multi-phase outflows and the quantification of their feedback (mass, energy, and their rates) in low luminosity AGNs like LINERs is lacking. The exploration of outflows and feedback for this AGN family is crucial to improving our understanding of galaxy evolution as these sources are thought to bridge the gap between normal and luminous AGNs, and they belong to the most numerous AGN population in the local Universe (Ho 2008, for a review).
NGC 1052 (MCG-01-07-034, PKS 0238-084) is considered as the prototypical LINER in the local Universe (z ∼ 0.005). Table 1 summarises the basic properties of this object.
General properties of NGC 1052.
There are four previous IFS studies focussing on NGC 1052: Sugai et al. (2005), Dopita et al. (2015), and Dahmer-Hahn et al. (2019a,b). Sugai et al. (2005) probed the bulk of the outflow with channel maps of the [O III] emission line thanks to Kyoto3DII/Subaru data over the innermost 3″ × 3″. Dopita et al. (2015) (hereafter D15) analysed the stellar and gas kinematics within the inner 25″ × 38″ using WiFeS/ANU data. The authors mapped the emission line properties on scales of hundred of parsecs (spatial sampling ∼1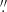 3), mainly studying shocks with no detailed information on the properties of the different kinematic components. Dahmer-Hahn et al. (2019a,b) (hereafter DH19a,b) mapped optical and near-IR lines in the inner 3
3), mainly studying shocks with no detailed information on the properties of the different kinematic components. Dahmer-Hahn et al. (2019a,b) (hereafter DH19a,b) mapped optical and near-IR lines in the inner 3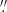 5 × 5″ (similar to the work by Sugai et al. 2005) exploiting GMOS/GEMINI data. The richness of tracers provided by the combination of multi-wavelength data offers a more detailed view than the previous works of the complex kinematics in NGC 1052. Nevertheless, the large-scale emission, on kiloparsec (kpc) scales, is not covered by the GEMINI data set. Summarising, all these IFS-based works support the presence in NGC 1052 of an emission line outflow possibly extended on kpc scales.
5 × 5″ (similar to the work by Sugai et al. 2005) exploiting GMOS/GEMINI data. The richness of tracers provided by the combination of multi-wavelength data offers a more detailed view than the previous works of the complex kinematics in NGC 1052. Nevertheless, the large-scale emission, on kiloparsec (kpc) scales, is not covered by the GEMINI data set. Summarising, all these IFS-based works support the presence in NGC 1052 of an emission line outflow possibly extended on kpc scales.
In this paper we use spectral and spatial capabilities of MUSE/VLT and MEGARA/GTC optical IFS observations to build, for the first time, a comprehensive picture of both stellar and ISM components in NGC 1052 of the outflow, at a resolution of tens of parsec (pc).
This paper is organised as follows. In Sect. 2 the data and observations are presented, as well as the data reduction. In Sect. 3 we present the spectroscopic analysis: stellar subtraction, line modelling, and map generation. Section 4 highlights the main observational results. In Sect. 5 we discuss the stellar kinematics and dynamics, and the ionised and neutral gas properties with special emphasis on outflow properties and its possible connection with the radio jet; we also estimate the black hole mass, and compare the full width at half maximum (FWHM) of the unresolved broad-line region (BLR) component with previous estimates. The main conclusions are presented in Sect. 6. In Appendix A we summarise the procedure to account for background sources. In Appendix B we present the kinematic flux-intensity maps and flux ratios from our IFS data set. Appendix C is devoted to presenting the 1D position-velocity and position-dispersion diagrams aimed at comparing gas and stellar motions along the three major axes: the major and minor axes of the host galaxy, and the radio jet.
All images and spectral maps are oriented following the standard criterion, so north is up and east to the left.
Throughout the paper, angular dimensions will be converted into physical distances using the scale distance from the Local Group of 110 pc/″ (see Table 1).
2. Observations and data reduction
In this section we describe MUSE and MEGARA data and their data reduction process (Sects. 2.1 and 2.2, respectively).
2.1. MUSE observations and data reduction
The data were gathered on September 5, 2019, with the Multi-Unit Spectroscopic Explorer (MUSE, Bacon et al. 2010, 2014), mounted at the UT4 of the Very Large Telescope at the Paranal Observatory in Chile as part of programme 0103.B-0837(B) (PI: L. Hernández-García).
They were acquired in the wide-field mode configuration with the nominal setting (i.e. no extended wavelength coverage), covering the spatial extent of 1 arcmin2 with 0.2″ pix−1 sampling. The MUSE data has a wavelength coverage of 4800−9300 Å, with a mean spectral resolution of R ∼ 3000 at 1.25 Å spectral sampling. During the observations the average DIMM seeing was 0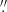 62 (varying between 0
62 (varying between 0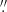 48 and 0
48 and 0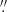 85); the mean airmass was 1.06.
85); the mean airmass was 1.06.
In total we obtained eight exposures with a total integration time of 93 min. Including the overheads the observations took two hours (i.e. two observing blocks). Each block consists of four dithered exposures of 697 s. The relative offsets in RA(Dec) were 10″, 0 5, −21
5, −21 5, and 0
5, and 0 5 (11″, 0
5 (11″, 0 5, −21
5, −21 5, and 0
5, and 0 5) with respect to the position of NGC 1052 (Table 1). The dither pattern also involves a 90° rotation for a better reconstruction of the final cube in order to have a homogeneous quality across the field of view.
5) with respect to the position of NGC 1052 (Table 1). The dither pattern also involves a 90° rotation for a better reconstruction of the final cube in order to have a homogeneous quality across the field of view.
The eight pointings constitute a mosaic covering a contiguous area of 80″ × 80″, or 8.8 kpc × 8.8 kpc at the adopted spatial scale (110 pc/″, Table 1). The radius of the covered area is about 3.5 times the effective radius of NGC 1052 (21 9, Table 1).
9, Table 1).
The data reduction was performed with the MUSE pipeline (version 2.8.1) via EsoRex (version 3.13.2). It performs the basic reduction steps (bias subtraction, flat-fielding, wavelength calibration, and illumination correction), as well as the combination of individual exposures in order to create the final mosaic. For flux calibration we used the spectrophotometric standard star Feige 110 (spectral type: DOp) observed before the science frames. Since we did not apply any telluric correction, some residuals remain in the region between 7110 and 7310 Å. In this spectral window only the He Iλ7065.3, [Ar III]λ7135.80, and [Fe II]λ7155 lines are detected, but they are not crucial for our analysis. The sky subtraction was performed in the latest step of the processing of MUSE observations using the sky background obtained from the outermost spaxels in each science exposure (no dedicated on-sky exposures were gathered). We performed the astrometry calibration using the astrometric catalogue distributed with the pipeline.
The final cube has dimensions of 418 × 422 × 3682. The total number of spectra is 176 396, of which 28 508 (16%) are not useful as they correspond to artefacts from the creation of the mosaic (i.e. empty spaxels located in the bottom left and top right corners, and at the edges of the field of view).
The radius of the point spread function (PSF) of the MUSE observations (0 4, see Fig. 1) was estimated from the FWHM of the 2D profile brightness distribution of the standard star used for flux calibration. Throughout the paper, in order to avoid any possible PSF contamination in the kinematic measurements, we conservatively consider as the ‘nuclear region’ a circular area of radius equal to the width at 5% intensity of the PSF radial profile (i.e. 0
4, see Fig. 1) was estimated from the FWHM of the 2D profile brightness distribution of the standard star used for flux calibration. Throughout the paper, in order to avoid any possible PSF contamination in the kinematic measurements, we conservatively consider as the ‘nuclear region’ a circular area of radius equal to the width at 5% intensity of the PSF radial profile (i.e. 0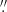 8). This area does not coincide with any peculiar feature (e.g. dust lanes) visible in the MUSE continuum image shown in the left panel of Fig. 1. The nuclear region is indicated (with a circle) in the spectral maps computed from the MUSE datacubes (see Fig. 1, but also Sect. 3 and Appendix B).
8). This area does not coincide with any peculiar feature (e.g. dust lanes) visible in the MUSE continuum image shown in the left panel of Fig. 1. The nuclear region is indicated (with a circle) in the spectral maps computed from the MUSE datacubes (see Fig. 1, but also Sect. 3 and Appendix B).
 |
Fig. 1. Optical continuum images computed from MUSE (left) and MEGARA (right) in units of erg s−1 cm−2 (logarithmic scale). To obtain these images we considered a 60 Å wide continuum band (6105 − 6165 Å). The cross is the photometric centre, and the sizes of the different PSFs for MEGARA and MUSE data are indicated in the bottom left part of the figure (see also Sect. 2). As reference we show the field of view (dashed rectangle) and average seeing (1 |
We obtained the instrumental profile by measuring the single (not blended) OHλ 7993.332 sky-line (Osterbrock et al. 1996; Bai et al. 2017). We measured it in the fully reduced datacube of the standard star Feige 110 (see above) by selecting a region of size 50 × 50 spaxels free from stellar emission. On average, the central wavelength and the width of the OH sky-line are 7993.335 ± 0.114 Å and 1.19 ± 0.13 Å, respectively. This instrumental profile correction was further checked with the 5577 Å sky-line. In this case the value of the average instrumental resolution is consistent with that from the OH line (i.e. 1.2 Å).
2.2. MEGARA observations and data reduction
The data were taken on December 28, 2019, with the MEGARA instrument (see Gil de Paz et al. 2016; Carrasco et al. 2018) located in the Cassegrain focus of GTC using the Large Compact Bundle IFU mode (GTC94-19B, PI: S. Cazzoli). The 567 fibres that constitute the MEGARA IFU (100 μm in core size) are arranged on a square microlens array that projects on the sky a field of 12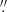 5 × 11
5 × 11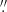 3. Each microlens is a hexagon inscribed in a circle with diameter of 0
3. Each microlens is a hexagon inscribed in a circle with diameter of 0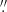 62 projected on the sky. A total of 56 ancillary fibres (organised in eight fibre bundles), located at a distance of 1.75−2.0 arcmin from the centre of the IFU field of view, deliver simultaneous sky observations.
62 projected on the sky. A total of 56 ancillary fibres (organised in eight fibre bundles), located at a distance of 1.75−2.0 arcmin from the centre of the IFU field of view, deliver simultaneous sky observations.
We made use of two low resolution volume phase holographic gratings (LR-VPHs) that provide a R ∼ 6000 in the central wavelengths of the selected bands: LR-V has a wavelength coverage 5140−6170 Å and LR-R 6100−7300 Å.
We obtained six exposures with an integration time of 900 s per VPH in two observing blocks, leading to a total observing time of four hours. The mean signal-to-noise ratio (S/N) in the spectra continuum was 25 for the LR-R and 30 for the LR-V datacube. The data reduction was done using the MEGARA Data Reduction Pipeline (Pascual et al. 2020, 2021) available as a package inside PYTHON (version 0.9.3). We performed the standard procedures: bias subtraction, flat-field correction, wavelength calibration, and flux calibration using the star HR 4963. Each fibre was traced individually at the beginning of the data reduction and, within the pipeline, we applied additional corrections for the possible differences of each fibre with respect to the whole image, including an illumination correction based on individual fibre flats. For this correction we used IRAF to smooth the sensitivity curve as (in the case of the LR-R VPH) some structure due to the lamp emission is present (see the MEGARA cookbook). The pipeline also performs the individual exposures combination to generate the final cube (one per VPH), which can be transformed into a standard IFS cube from raw stacked spectra format by means of a regularisation grid to obtain 0 4 square spaxels (see Cazzoli et al. 2020). The PSF of the MEGARA data was measured as in Sect. 2.1 with the star HR 4963, giving a FWHM of 1
4 square spaxels (see Cazzoli et al. 2020). The PSF of the MEGARA data was measured as in Sect. 2.1 with the star HR 4963, giving a FWHM of 1 2 (see Fig. 1, left).
2 (see Fig. 1, left).
Considering the wavelength ranges of the VPHs and the emission lines present in NGC 1052 spectra, we decided to combine the two cubes into a single datacube to optimise the stellar modelling and subtraction (increasing the range of line-free continuum, see Sect. 3.2). More specifically, the need to combine the two MEGARA cubes to reliably model the stellar continuum is twofold. First, the spectral range of the MEGARA LR-V cube covers only the MgI stellar feature, whereas none are present in the LR-R cube. Second, for the LR-R (red) cube, the stellar continuum emission is limited by the presence of the broad emission features and a telluric band (see Sect. 2.2). For the cube combination, we scaled the fluxes for every spaxel to have the continuum at the same level in the common wavelength range of both VPHs (6100−6170 Å). The combined datacube was used in the whole analysis.
3. Data analysis
In this section we summarise the identification and subtraction of background sources in the MUSE field of view (Sect. 3.1), and we describe the stellar continuum modelling (Sect. 3.2) and line fitting for MUSE and MEGARA cubes (Sect. 3.3).
3.1. Background sources in the MUSE field of view
We visually inspected the white light image generated in the last step of the data reduction of MUSE data: the mosaic creation (see Sect. 2) and the continuum image in Fig. 1. We note that there are a number of sources (both point-like and extended), some of which may not be part of the NGC 1052 galaxy. In Appendix A we summarise the procedure for identifying putative background sources.
We found two background galaxies at redshifts ∼0.03 and ∼0.022. Only the former is identified in NED as SDSSCGB_67616.02. Both of these galaxies were masked out from the final MUSE datacube used for the analysis.
3.2. Stellar continuum modelling
For the stellar continuum modelling we used the penalised PiXel-Fitting code (pPXF) by Cappellari & Copin (2003) (see also Cappellari 2017, and references therein) for both MEGARA and MUSE, in different coding environments. We used the pPXF code within the GIST pipeline (see below) for MUSE and within PYTHON for MEGARA.
For MUSE we used the GIST pipeline (v. 3) by Bittner et al. (2019) 1 as a comprehensive tool both to spatially bin the spectra in order to increase the S/N in the continuum and to model the stellar contribution to the observed spectra. The MUSE spectra were shifted to rest frame based on the initial guess of the systemic redshift from NED, z = 0.005 (Table 1). Then the data were spatially binned using the 2D Voronoi binning technique by Cappellari & Copin (2003) that creates bins in low S/N regions, preserving the spatial resolution of those above a minimum S/N threshold. The S/N has been calculated in the line-free wavelength band between 5350 and 5800 Å. All spaxels with a continuum S/N < 3 were discarded to avoid noisy spectra in the Voronoi bins. We found that a minimum S/N threshold of 30 results in reliable measurements of stellar kinematics in NGC 1052 as well as an optimum spatial resolution. In general, cells are not larger than 60 spaxels (2.4 arcsec2 in area), hence stellar properties are likely to be homogeneous within a Voronoi cell.
For MEGARA data the Voronoi binning was not necessary to achieve a proper stellar continuum modelling as in the spaxels with the lowest S/N (< 15), which constitute ∼12% of the total, the resulting velocity and velocity dispersion are consistent with the rest of the cube with higher S/N.
To accurately measure spectral line properties (wavelength, width, and flux), it is necessary to account for stellar absorption, which primarily affects the Balmer emission lines and the NaD absorption doublet. For MUSE we limited the wavelength range used for the fit to 4800−9000 Å, which contains spectral features from Hβ to CaT, and excluded the region of the auroral [S III]λ9069 line2. For MEGARA the total wavelength range was from 5150−7000 Å covering the main spectral features in both LR-V and LR-R bands. For both data sets we masked the spectral regions (emission lines and atmospheric and telluric absorptions) affected by emission from the interstellar medium (ISM). Additionally, we excluded the NaD absorption that is not properly matched by the stellar templates owing to the impact of interstellar absorption.
For MUSE, we used the Indo-U.S. stellar library (Valdes et al. 2004) as in Cazzoli et al. (2014, 2016, 2018). Briefly, in this library there are 885 stars selected to provide a broad coverage of the atmospheric parameters (effective temperature, surface gravity, and metallicity). The stellar spectra have a continuous spectral coverage from 3460 to 9464 Å, at a resolution of ∼1 Å FWHM (Valdes et al. 2004). For MEGARA we used the RGD synthetic stellar library (González Delgado et al. 2005; Martins et al. 2005) since it covers the whole spectral range for the combined datacubes, and the spectral resolution is consistent with that from our spectra. The library consisted on 413 stars selected with a metallicity of Z = 0.02, ranging from 4000 to 7000 Å and covering a wide range of surface gravities and temperatures (see González Delgado et al. 2005, and references therein).
Finally, we set up pPXF using four moments of the line of sight velocity distribution (LOSVD) for both MUSE and MEGARA: V, σ, h3, and h4. The additive and multiplicative polynomials were set to 4−4 (0−12) for MUSE (MEGARA) in order to, respectively, minimise template mismatch and match the overall spectral shape of the data so that the fit is insensitive to reddening by dust (see Westfall et al. 2019; Perna et al. 2020, and references therein).
An example of the pPXF modelling is shown in Fig. 2 for both MUSE (top panel) and MEGARA (bottom panel) data. The results of the pPXF fits (i.e. the stellar kinematics maps of the first two moments of the LOSVD) are shown in Fig. 3, and are discussed in Sect. 4.1. A detailed study of higher order moments of the stellar LOSVD (h3 and h4) is beyond the aim of the paper, hence the corresponding maps are not displayed.
 |
Fig. 2. Example of stellar continuum modelling and its subtraction for high S/N nuclear spectra from MUSE (top panel) and MEGARA (bottom panel) data. The red line indicates the modelled stellar spectrum that matches the observed continuum, obtained applying the pPXF (Sect. 3.2). The wavelength regions blocked for the modelling are shown in grey. Spectral features are labelled at the top, and Balmer lines, forbidden lines, and absorption lines are shown in green, blue, and pink, respectively. In case of MEGARA we combined the cubes in LR-V and LR-R bands, which have a 70 Å overlap around 6130 Å (see Sect. 2.2). |
 |
Fig. 3. NGC 1052 stellar kinematics maps from our pPXF analysis (Sect. 3.2). These maps, velocity (left) and velocity dispersion (right), are displayed in units of km s−1. In both panels the large-scale kinematics are obtained from MUSE data, whereas the insets show the smoothed pPXF-maps from MEGARA datacube. The cross indicates the photometric centre as in Fig. 1. |
Through the analysis we consider formal uncertainties provided by the pPXF tool. These are in good agreement with those from the Monte Carlo simulations performed on MUSE data. Specifically, differences are generally lower than 5 km s−1 and 7 km s−1 for velocity and velocity dispersion, respectively.
Motivated by the typical small sizes of the Voronoi cells in the MUSE data, we made the simplifying assumption that the stellar populations and kinematics do not change radically within one Voronoi bin. For each spaxel the stellar spectrum of the corresponding bin was normalised and then subtracted from the one observed to obtain a datacube consisting exclusively of ISM absorption and emission features. For the MEGARA data the stellar subtraction was performed on a spaxel-by-spaxel basis. In what follows we refer to this datacube (data–stellar model) as the ISM cube.
3.3. Line modelling
From the ISM cube we produced line maps by modelling the spectral lines with multiple Gaussian functions. To achieve this, we applied a Levenberg–Marquardt least-squares fitting routine under both interactive data analysis (IDL) and PYTHON environments, using MPFITEXPR by Markwardt (2009) and LMFIT, respectively (see Sects. 3.3.1 and 3.3.2). We imposed the intensity ratios between the [O III]λ4959,5007 (only for MUSE), [O I]λ6300,6363, and [N II]λ6548,6584 to be 2.99, 3.13, and 2.99 (Osterbrock & Ferland 2006). The ratio of the equivalent widths (EWs) of the two lines of the NaDλλ5890,5896 absorption, RNaD = EW5890/EW5896, is restricted to vary from 1 (optically thick limit) to 2 (optically thin absorbing gas), according to Spitzer (1978).
3.3.1. Emission line modelling
We derived the kinematics of the ISM properties by modelling all the spectral lines available in the cubes. To perform the fitting, and hence discriminate between line models and number of components, we followed the approach proposed by Cazzoli et al. (2018). Specifically, for the MUSE and the MEGARA data, we tested the [S II]-model and the [O I]-model, for which we first fitted in the spectrum only [S II] and [O I] lines (depending on the model) and then used them as reference to tie all the other narrow lines, so they share the same width and velocity shift. Additionally, we tested the ‘mixed’ models, using [S II] and [O I] simultaneously as reference respectively for [N II] and narrow Hα or, alternatively, using [O I] for narrow Hα and [N II], with [S II] lines behaving otherwise. For the MUSE data only (see Sect. 2.2), the best fit to the Hα ([S II]) line is applied to the Hβ ([O III]) line.
However, none of these models provided a good fit for the whole set of lines. In the MEGARA field of view the independent fitting of [O I] and [S II] lines produced differences of ∼100 km s−1 for the velocity measurements, although the line widths were similar with differences ≤50 km s−1. For the MUSE data we found that at large spatial scales (R > 10″) the kinematics of these lines are similar within 75 km s−1 (mostly) when they are fitted independently. Although large discrepancies (> 100 km s−1) arise in the central region (inside the MEGARA field of view; R < 10″ oriented E-W), with a peculiar butterfly shape (see Sect. 4). A similar behaviour was found comparing [O III] and [S II] kinematics. Moreover, the S/N of the [O I] (Hβ) drops steeply in the NW-SE direction, complicating the tying with Hα-[N II] (Hα) in both MUSE and MEGARA data. Taking all this into account, we decided to fit Hβ, [O III], [O I], and [S II] independently and use the last as a template for the Hα-[N II] blend. Finally, as NGC 1052 is a type 1.9 LINER (Table 1), we added a broad AGN component (from the unresolved BLR) with width > 600 km s−1 (1400 km s−1 in FWHM) only in Hα forcing its spatial distribution to be the same as the PSF. Figure 4 shows examples of the Gaussian fits of the whole set of emission lines for both MUSE (four upper panels) and MEGARA (two lower panels).
 |
Fig. 4. Examples of emission line spectra (black) after stellar subtraction (Sect. 3.2) and their modelling from the central region of both MUSE data (R = 0 |
The emission lines present complex profiles with broad wings and double peaks3 (Fig. 4) suggesting the presence of more than one kinematic component, especially within the innermost 10″ of radius. In order to prevent overfit, we first fitted all emission lines with one Gaussian component, and then more components were added based on the parameter εline. This parameter is defined as the standard deviation of the residuals under the emission lines, after a component is added. In the cases where εline > 2.5 × εcont (standard deviation of the line-free continuum), another Gaussian component is added. This criterion has been already successfully applied to optical spectra of active galaxies both from long-slit (Cazzoli et al. 2018; Hernández-García et al. 2019; Hermosa Muñoz et al. 2020) and IFS (Cazzoli et al. 2020).
Overall, we allowed a maximum of three Gaussians per line plus the BLR component in Hα (Fig. 4). This provides a good trade-off between a statistical good fit to the spectra (i.e. residuals are of the same order as the noise without any peculiar structures like spikes or bumps) and the number of components used having a reasonable physical explanation.
For each emission line and component found we ended up with the following information: central wavelength, width, and flux intensity along with their respective fitting uncertainties. These are the formal 1σ uncertainty weighted with the square root of χ2, as in Cazzoli et al. (2020).
Taking into account both their central velocities and line widths, we identify a primary, a secondary, and a tertiary component. More specifically, the primary component can be mapped over the whole galaxy line-emitting region (∼39″, i.e. 4.3 kpc), with clear blue and red velocities, with generally the lowest widths (it is also clearly detected by D15b). The tertiary component is not spatially resolved (it is extended within a radius of ≤2″, i.e. PSF size) being generally the broadest. The secondary component has intermediate properties; it is spatially resolved, being mapped up to R < 5″ (i.e. 550 pc), with extreme velocities (up to ∼660 km s−1). Additionally, in order to discriminate between the components (especially primary and secondary) we considered the spatial continuity of both flux and kinematic values. For the former a visual inspection was already satisfactory to prevent wild variations; for the latter we avoided sharp variations of the kinematics between adjacent spaxels. Specifically, we imposed that the values of the velocity fields vary smoothly (differences are less than 200 km s−1) and that the secondary component is broader than the primary. Differences in line widths are of ∼160−180 km s−1 on average, for the brightest lines such as [O III] and Hα-[N II]. A minor number of spaxels (< 40) constitute an exception to this general behaviour of velocity dispersion, but they are mainly located either within the PSF or at the largest radii where the secondary component is detected.
For each of these components we created velocity, velocity dispersion, and flux maps. These are shown in the figures in Appendix B (from Figs. B.1 to B.8 and from Figs. B.9 to B.11 for MUSE and MEGARA, respectively). An example of these maps is shown in Fig. 5 for the [O III] line for MUSE data. In this figure we display both the large and small scales mapped by our IFS data. As the large-scale emission is similar among emission lines, the maps in Appendix B show only the central region (R ∼ 10″) where the largest differences are observed (see Sect. 4 for details).
 |
Fig. 5. Example of emission line maps produced from the fitting of the [O III]λ5007 line using the MUSE ISM cube (Sect. 3.3.1). Shown, from left to right, are the maps for the primary component: velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (erg s−1 cm−1, log scale). The black solid line indicates the major axis of the stellar rotation (Table 4). The dot-dashed square indicates the MEGARA field of view. The contours indicate the central region at high velocity dispersion (see Sect. 4.2.3 for details). Top: maps covering a smaller field of view with respect to the original MUSE mosaic (80″ × 80″, Sect. 2.1) to highlight weak features. The dashed square indicates the selected zoomed-in view in the bottom panels of this figure and for Figs. B.1–B.13. Bottom: zoomed-in area. The dashed line indicates the orientation of the radio jet (Table 1). |
To obtain velocity dispersion for each spectrum (i.e. on a spaxel-by-spaxel basis), the effect of instrumental dispersion (i.e. σINS, see Sect. 2) was corrected for by subtracting it in quadrature from the observed line dispersion (σobs): σline = 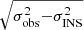 .
.
We use the [S II] ratio ([S II]λ6716/[S II]λ6731, e.g. Fig. B.4, right panel) to estimate the electron density (ne) in accordance with the relation of Sanders et al. (2016). To investigate the ionising mechanisms across the field of view for each component used to model emission features (forbidden and narrow Balmer lines), the maps of the four line ratios used in standard Baldwin, Phillips & Terlevich (BPTs) diagnostic diagrams (Baldwin et al. 1981) were also generated. The maps are presented in Appendix B (Figs. B.13–B.16) and the diagnostic diagrams in Figs. 6 and 7. For the two spatially resolved components (namely primary and secondary), the typical values of kinematics and line ratios are summarised in Tables 2 and 3.
 |
Fig. 6. Optical standard BPT diagrams for the primary component for the gas distributed in the polar direction and that in the central region at high-σ (top and bottom panels, respectively) obtained from MUSE data. The grey circles indicate the data points presented in this paper. The black lines in all diagrams represent the dividing curves between H II star-forming regions, Seyferts, and LINERs from Kewley et al. (2006) and Kauffmann et al. (2003). The pink boxes show the predictions of the photoionisation models by pAGB stars for Z = Z⊙, a burst age of 13 Gyr (Binette et al. 1994), and ionisation parameter values (log U) between −3 and −4. Log U is typically −3.5 in LINERs (Netzer 2015). The predictions of shock-ionisation models are overlaid in each diagram. Specifically, following Cazzoli et al. (2018), shock+precursor grids from Groves et al. (2004) are considered with Z = Z⊙ and for different ne. The blue and red curves correspond to models with ne = 1 cm−3 and ne = 100 cm−3, respectively (see also Sect. 4.2.1). The values plotted correspond to the minimum and maximum preshock magnetic field allowed in each model. In addition, only shock-velocities from 100 to 500 km s−1 (yellow dashed lines) are considered as larger σ are not observed for the primary component (Sect. 4.2.1). The dividing line between weak-[O I] and strong-[O I] LINERs (Filippenko & Terlevich 1992) is shown in black with a dashed line (right panels). In all diagrams, green symbols indicate the average values calculated in the polar (cross) and central (square) regions; as reference the cyan star is the typical value in the nucleus (average within the PSF region). In the top panels the pink diamond, black triangle, and black upside down triangle are the average BPT values for the faint features: the arm, the east, and south-east clumps, respectively (see Sect. 4.2.5). These features are not detected in [O I], hence no symbols are displayed in the corresponding diagnostic diagrams. |
 |
Fig. 7. Same as Fig. 6, but for the secondary component. Shock models (no precursor) are considered; the blue and red curves correspond to models with ne = 100 cm−3 and ne = 1000 cm−3, respectively (see Sect. 4.2.4). The green triangle indicates the average value of the line ratio distribution. |
Summary of measurements for the primary component from MUSE and MEGARA.
Summary of measurements for the second component from MUSE and MEGARA.
3.3.2. Sodium doublet modelling
The wavelength coverage of our MUSE and MEGARA data sets allow us to probe the NaD absorption doublet. This feature originates both in the cold-neutral ISM of galaxies and in the atmospheres of old stars (e.g. K-type giants). We modelled the doublet in the ISM cubes (after the stellar subtraction, Sect. 3.2) to obtain the neutral gas kinematics, and hence to infer whether the cold neutral gas is either participating in the ordinary disc rotation or entraining in non-rotational motions such as outflows (see e.g. Cazzoli et al. 2014, 2016).
For MUSE data the NaD is detected at S/N > 3 up to R ∼ 25 7 (2.8 kpc); however, most of the absorption (95% of the spaxels at S/N > 3) is concentrated within the inner ∼16″ (1.8 kpc). The NaD EW map is presented in Fig. 8. The values range from 0.4 to 3.3 Å (1.1 Å, on average).
7 (2.8 kpc); however, most of the absorption (95% of the spaxels at S/N > 3) is concentrated within the inner ∼16″ (1.8 kpc). The NaD EW map is presented in Fig. 8. The values range from 0.4 to 3.3 Å (1.1 Å, on average).
 |
Fig. 8. NaD EW map (in Å) from MUSE cube. The dot-dashed square indicates the MEGARA field of view. The black solid line indicates the major axis of the stellar rotation (Table 4). The contours indicate the region with enhancement velocity dispersion of emission lines (see Sect. 4.2.3 and e.g. Fig. 5). |
We prefer to model the NaD doublet on a spaxel-by-spaxel basis in the MEGARA data as it generally has a higher S/N with respect to that of the MUSE data. We considered one kinematic component (a Gaussian function for each line), and we masked the wavelength range between 5900 and 5920 Å due to some residuals from the stellar subtraction.
To infer the presence of a second component we inspected the map of the residuals (i.e. εline/εcont), as was done for the emission lines (Sect. 3.3.1). However, the values are in the range 0.7−2 (1.2, on average), hence there is not a strong indication of the need for multiple components to fit the doublet.
Figure 9 shows an example of the modelling of the NaD doublet absorption, and Fig. 10 presents the corresponding kinematic and absorbed-flux maps. The results for the NaD absorption doublet are presented in Sect. 4.6 and discussed in Sect. 5.4.
 |
Fig. 9. Example of absorption line spectra (black) after stellar subtraction (Sect. 3.2) and their modelling from the central region of MEGARA data (R = 1 |
 |
Fig. 10. Neutral gas velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (mJy) maps for the single kinematic component used to model NaD. The black lines are as in Fig. B.11. Specifically, the black solid line indicates the major axis of the stellar rotation (Table 4). The dashed lines indicate the orientation of the radio jet (Table 1). The contours indicate the region at high velocity dispersion (Sect. 5.4 for details). |
4. Main observational results
In Sect. 4.1 we present the results from the pPXF stellar kinematics analysis of both the MUSE and the MEGARA data. The emission lines detected in both MUSE and MEGARA ISM cubes are [S II], Hα-[N II], and [O I], whereas Hβ and [O III] are covered only by MUSE data (see Sect. 2). In both data sets a maximum of three kinematic components are used to model forbidden lines and narrow Hα (Sect. 3.3.1). These components have different kinematics and spatial distribution indicating that they are distinct components. In Sect. 4.2 we present the spatial distributions of kinematics and ISM properties (e.g. line ratios and electron density) measured for each of the three components in the MUSE data. The comparison between the MUSE and MEGARA results is presented in Sect. 4.4. An additional broad Hα component originating in the BLR of the AGN was used to model spectra within the nuclear region (Sect. 3.3.1). Its properties are presented in Sect. 4.5 for both data sets. Finally, Sect. 4.6 summarises the main results from the modelling of the NaD absorption (Sect. 3.3.2).
4.1. Stellar kinematics
As explained in Sect. 3.2, we used pPXF to fit the stellar continuum of the spectra for both MEGARA and MUSE datacubes. The maps of the stellar kinematics (velocity and velocity dispersion) for both data sets are shown in Fig. 3 and the main properties are summarised in Table 4.
Stellar kinematic properties of NGC 1052 from MUSE and MEGARA.
The stellar velocity field (Fig. 3, left panels) shows the typical spider-pattern consistent with a rotating disc, at both large and small spatial scales mapped by our IFS data. The peak-to-peak velocity (ΔV, Table 4) from the MUSE (MEGARA) data is 167 ± 19 km s−1 (78 ± 3 km s−1) at a galactocentric distance of 40″ (4″), which corresponds to 4.4 kpc (0.4 kpc). The ΔV from MUSE map within the MEGARA footprint, 75 ± 9 km s−1 (Table 4) is consistent with that from the MEGARA cube.
The stellar major kinematic axis estimated at the largest scales for the MUSE and MEGARA data are respectively (122 ± 10)° and (112 ± 6)° measured north-eastwards (Table 4). Both measurements indicate this axis is aligned with the photometric major axis (112.7°, Table 1).
Overall, the stellar velocity dispersion varies from 75 to 235 km s−1 for MUSE and from 100 to 250 km s−1 for MEGARA (Fig. 3, right panels). As expected in the case of a rotating disc, the stars exhibit a centrally peaked velocity dispersion map, with a maximum value of 233 ± 6 km s−1 and 241 ± 4 km s−1, as measured from the MUSE and MEGARA maps, respectively, being in positional agreement within the uncertainties with the nucleus (considered as the photometric centre, i.e. the cross in all maps).
Following Cappellari et al. (2013) for the ATLAS3D legacy project, the central velocity dispersion (σc) is calculated at a distance corresponding to Reff/8, which is R < 2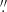 75 (303 pc) for NGC 1052. The value for the central velocity dispersion is 201 ± 10 km s−1 (215 ± 13 km s−1), whereas the extra-nuclear mean velocity dispersion is 145 ± 22 km s−1 (201 ± 16 km s−1) for MUSE (MEGARA) data (see Table 4). The mean velocity dispersion from MUSE data within the MEGARA footprint is 180 ± 6 km s−1 (Table 4), hence consistent within uncertainties with that measured directly from the MEGARA velocity dispersion map.
75 (303 pc) for NGC 1052. The value for the central velocity dispersion is 201 ± 10 km s−1 (215 ± 13 km s−1), whereas the extra-nuclear mean velocity dispersion is 145 ± 22 km s−1 (201 ± 16 km s−1) for MUSE (MEGARA) data (see Table 4). The mean velocity dispersion from MUSE data within the MEGARA footprint is 180 ± 6 km s−1 (Table 4), hence consistent within uncertainties with that measured directly from the MEGARA velocity dispersion map.
In addition to the main point-symmetric disc-like pattern, in the MUSE data towards the north-east and south-west and up to R ∼ 30″ (i.e. ∼3.3 kpc) we observe a smooth local enhancement of the velocity dispersion values. This enhancement is about 150−180 km s−1 (hence above the average, Table 4), but it does not match features in either the continuum or ISM maps (Fig. 1 and Appendix B), and it is not an artefact from cross-talk effects.
Higher velocity dispersion (∼220 km s−1) with respect to the mean values seems to be present only in MEGARA at R ∼ 5″, prominent only to the east and to the west. Given its the position, this feature it is likely caused by the lower S/N of the spaxels near the edges (see Sect. 3.2).
We obtained the position-velocity (P-V) and position-dispersion (P-σ) diagrams shown in Fig. 11 in a 1″-width pseudo-slit along the major axis of rotation listed in Table 4. In the (central) region mapped by the two data sets we checked whether the kinematics and curves are in agreement within the uncertainties (Table 4). However, as MEGARA observations cover only the innermost region (see Fig. 1 and Sect. 2), in this work we consider the kinematics from the MUSE cube as the reference for the stellar component.
 |
Fig. 11. Position-velocity (P-V, top) and position-velocity dispersion (P-σ, bottom) curves of the stellar component of NGC 1052 from MUSE data (Sect. 4.1). Both curves were obtained considering a pseudo-slit of 1″ in width aligned according to the major axis of the rotation (i.e. 112°, Table 4). Velocities are centred to the kinematic centre, and the radius is calculated as the distance from the photometric centre. In the top panel the blue and red symbols indicate the approaching (negative velocities) and receding sides (positive velocities) of the rotation, respectively. The green lines give the Reff (21 |
The large-scale rotation curve (Fig. 11, top) is characterised by two plateaus. The first flattening is at a galactocentric distance of ∼2″ (i.e. 220 pc) with velocities of ∼70 km s−1. At large distances, between 10″ and 20″, the curve rises slowly reaching values up to 140 km s−1, and then finally flattens at 30″. The velocity dispersion profile shows a sharp peak within the innermost 3″ (i.e. 330 pc) without an exponential decline up to the largest distances mapped by MUSE (Fig. 11, bottom).
4.2. Kinematics and fluxes of the different ISM components detected by MUSE
As mentioned at the end of Sect. 3.3, Tables 2 and 3 summarise the most important properties of the two spatially resolved components (primary and secondary). Figures 6 and 7 show the location of the line ratios for the narrow and secondary emission line components onto standard BPT diagrams (Baldwin et al. 1981). A direct comparison of gas and stellar motions for the primary component is presented in Fig. C.1 that includes the P-V and P-σ along the three major axes (i.e. the major and minor axes of the host galaxy, and the radio jet).
In the following we describe the overall results for each component.
4.2.1. Overall properties of the primary component
The primary component is the narrowest of the three detected (Sect. 3.3), with σ ≤ 66 km s−1 on average (except for [O I] which is 204 km s−1). Exceptions to this general behaviour are few spaxels (< 65) mostly within the PSF area (the circle in all maps in Appendix B; see also Sect. 3). The velocities are generally ∣V∣ < 350 km s−1, except for Hβ, which are up to 450 km s−1 (these extreme values are observed only towards the north-west).
The kinematic maps (both velocity and velocity dispersion) lack of any symmetry typical of a rotation dominated system (left and central panels of Fig. 5). A clear distinguishable feature in the velocity dispersion map is the σ-enhancement crossing the galaxy from east to west (along the major axis of rotation) with a butterfly-shape (contours in Figs. 5 and B.1–B.4). The gas here presents complex motions that differ markedly from gas elsewhere.
For the identification of this region with high-σ, we consider as reference the average velocity dispersion in two square regions of side 15″ (1.65 kpc) in the outer part of the maps lacking of any peculiar σ feature. Specifically, at a distance of 15″ from the photometric centre towards the north-east and south-west. In the case of [O I], the box size and distance are 5″ and 8″ (550 and 880 pc), respectively, due to the decrease in S/N already visible at a radius of 10″ (1.1 kpc).
The final threshold (i.e. 2σ above the average velocity dispersion) is 90 km s−1 for all the emission lines but [O I], for which it is 180 km s−1. Hereafter we consider as polar4 emission all the spaxels with velocity dispersion below those thresholds (Sect. 4.2.2). These are mostly distributed along the minor axis of rotation in the NE-SW direction. The properties of the intriguing feature with high-σ in the central region of NGC 1052 is described separately from that of the emitting gas organised along the polar direction (Sect. 4.2.3).
Maps of line fluxes (Figs. 5 and B.1–B.4, right panels) show a similar general morphology that is very different from the smooth continuum flux (Fig. 1). More specifically, the gas emission within the inner 3″ resembles a mini-spiral, while it appears extended along the NE-SW direction with some filaments and irregularities especially relevant up to R ∼ 10″ (mostly within the central region at high-σ). However, flux maps do not show any butterfly morphology matching that of the innermost region at high velocity dispersion. Outside the inner 10″ × 9″ (i.e. 1.1 kpc × 1.0 kpc, see Sect. 4.2.3), the flux maps do not reveal any peculiar morphology (e.g. filaments or clumps). Taking all this into account, we prefer to describe the morphology of line fluxes only in this section and not separately for the polar and central region (Sects. 4.2.2 and 4.2.3).
At all scales, line ratios from standard BPT diagnostic indicate LINER-like ionisation (see Table 2 for typical values and Fig. B.13). These line ratios are discussed in Sect. 5.2.2 together with the weak-[O I] and strong-[O I] LINER classifications by Filippenko & Terlevich (1992), as in Cazzoli et al. (2018).
The [S II] line ratio varies from 1.2 to 1.7 (Fig. B.4) excluding extreme values (i.e. the 5% at each end of the line ratio distribution). This ratio is 1.47 ± 0.2 on average, indicating a gas with relatively low density (ne < 100 cm−3).
4.2.2. Polar emission on kiloparsec scale
The velocity fields of the primary component for all the lines show a similar overall pattern (see Fig. 5 for [O III]), with well-defined blue and red sides oriented along the minor axis of rotation (polar direction, i.e. NE-SW). Even so, the velocities do not show rotating disc features (spider diagram) in any emission line (Fig. 5 and Appendix B).
The region with negative velocities extends from the photometric centre towards the north-east up to 30″ (i.e. 3.3 kpc) and 12″ for [O I] (i.e. 1.3 kpc; see Figs. 5 and B.2, left) with an opening angle of 105° as measured from the velocity maps of [O III]. The most blueshifted value of the observed velocity field is ∼250 km s−1, located at a distance of ∼11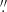 5 (i.e. 1.3 kpc) as measured from the [O III] line (Fig. 5, top left). Similar negative velocities (within the uncertainties) are seen for all the other emission lines. The unique exception is [O I], for which the maximum blueshifted velocity is of about −250 km s−1 at a radius of 7
5 (i.e. 1.3 kpc) as measured from the [O III] line (Fig. 5, top left). Similar negative velocities (within the uncertainties) are seen for all the other emission lines. The unique exception is [O I], for which the maximum blueshifted velocity is of about −250 km s−1 at a radius of 7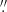 5 (825 pc) in the NE direction (Fig. 5, top left).
5 (825 pc) in the NE direction (Fig. 5, top left).
It is worth noting that these blueshifted velocities do not decrease smoothly to its minimum. Instead, the maps show three concentric arcs that do not cross each other (see Fig. 5). These arcs are not symmetric since they are absent where positive velocities are observed (see Figs. 5 and C.1) towards the south-west and up to 25″, corresponding to 2.75 kpc (15″, i.e. 1.65 kpc for [O I]). We checked the possibility that extinction due to the galaxy dusty stellar disc might have caused this asymmetry. By comparing the velocity maps of the ionised gas and that of the ratio of Hα to Hβ fluxes we did not find evident dusty structures at the location of the arcs. Hence, we excluded this possibility.
The average velocity dispersion is typically of about 50 km s−1 varying between 44 ± 21 and 54 ± 21 km s−1 for [S II] and [O III], respectively (Table 2). The [O I] emission represents the exception, with an average velocity dispersion of 115 ± 32 km s−1 (Table 2 and Fig. B.6).
The [N II]/Hα, [S II]/Hα, and [O I]/Hα line ratios for the large-scale gas distribution are homogeneous (Fig. B.13, see values in Table 2 and the discussion in Sect. 5.2.2). The typical standard deviation of the values in the maps is 0.08 in log units; the scatter for the [O III]/Hβ ratio is larger, about ∼0.2 (Fig. B.13, left). We note that low log [O III]/Hβ ratio values (< 0.1) corresponding to both log [N II]/Hα and log [S II]/Hα of about ∼−0.1−0.0, are sparsely observed at large distances from the nucleus (R > 10″) and towards the north-east and the south where faint clumpy features are detected (see Sect. 4.2.5).
4.2.3. High-σ feature in the central region of NGC 1052
For all emission lines, the region of higher velocity dispersion with σ > 90 km s−1 (σ > 180 km s−1 for [O I]; see Figs. B.1 and B.2 and Sect. 4.2.1) is located in the innermost parts of the maps, 10″ × 9″ (i.e. 1.1 kpc × 1.0 kpc, Table 2, contours in Figs. 5 and B.1–B.4). It is mostly aligned with the major axis of the stellar rotation, with a PA of ∼124° and opening angle of ∼70° measured from [O III] line (Fig. 5). This region is partially mapped also with the MEGARA data (see Sect. 4.4 and Figs. B.9 and B.10).
The line-emitting gas is spatially resolved with MUSE into streams of filamentary strands with a tail (clearly visible especially in [O III] line maps, Fig. B.1) departing from the photometric centre towards the south, with velocities up to 150 km s−1. In this central region, the velocity of the narrow component does not closely match the motion of the large-scale gas in the polar direction.
Similar patterns in kinematics maps are seen for all emission lines (Figs. B.1, B.3, B.4, and C.1) except [O I] (Figs. B.2 and C.1), for which we summarise the main results separately.
For the Balmer features and the [O III], [N II], and [S II] lines, high blueshifted (redshifted) velocities up to −290 (260) km s−1 are detected towards the east and west of the centre of the butterfly region. The southern tail generally has redshifted velocities from 100 to 180 km s−1, with a typical velocity dispersion that varies from 90 to 110 km s−1. The σ map shows non-symmetric clumpy structures in the west strands. This clumpiness is particularly evident in the Hα-[N II] velocity dispersion map (Fig. B.3, central panel).
For the [O I] line the morphology of the high-σ region is characterised by two well-defined regions with a triangular projected area (contours in Fig. B.2). The apex of the east projected triangle is at 2″ from the photometric centre, whereas that of the west one is at the photometric centre.
The velocity distribution is skewed to negative (blueshifted) velocities (60% of the spaxels in this region). The main difference of [O I] kinematics with respect to the common patterns of all other lines is seen to the east. Specifically, at this location in the velocity map two thick strands are clearly visible at negative velocities, ∼200 and ∼160 km s−1 in the northern and southern directions, respectively (Fig. B.2, left panel). For other emission lines, at the same spatial location, the velocities are negative and positive, hence partially kinematically distinct from that found for [O I].
The values of the [O I] σ-map increase gradually from the photometric centre both to the east and to the west, from ∼200 km s−1 up to ∼500 km s−1 (Fig. B.2, central panel). The highest values are seen in correspondence with the most extreme velocities (e.g. the two strands towards the east).
Apart from the flux features summarised in Sect. 4.2.1, in the innermost 10″ the maps do not reveal any peculiar morphology (e.g. clumps or filaments), but only a gradual decrease towards the external part of this region.
At the location of enhanced sigma, the line ratios indicate LINER-like emission (Fig. B.13). More specifically, the [O III]/Hβ line ratio is typically > 0.1 in log units (on average 0.46 ± 0.16, Table 2), except for an elongated region from the east to the south-west crossing the photometric centre. At this location line the log [O III]/Hβ varies between 0.005 and 0.3. This peculiar structure does not match any feature of any other map for the narrow component. However, it overlaps with the location of the secondary component. Any putative link between the properties of these two components is discussed in Sect. 5.2.3.
The main feature of the [N II]/Hα ratio map (Fig. B.13 second panel) is the presence of two clumps of similar size (diameter 1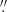 2, i.e. 130 pc). One clump is located within the PSF region (Sect. 2) with log [N II]/Hα ∼ 0.2. The other clump with log [N II]/Hα ∼ −0.3 is located 2
2, i.e. 130 pc). One clump is located within the PSF region (Sect. 2) with log [N II]/Hα ∼ 0.2. The other clump with log [N II]/Hα ∼ −0.3 is located 2 6 (290 pc) westward to the photometric centre.This clump is embedded in an area with a local enhancement of the [N II]/Hα ratio. Specifically, this region emerges from the photometric centre and extends for 8″ towards the west, and partially matches the region where the velocity dispersion is higher (about 250−350 km s−1) with respect to the butterfly average (i.e. 149 ± 52 km s−1; Table 2). Local [N II]/Hα ratios are also enhanced at a distance of 7″ to the north and to the west.
6 (290 pc) westward to the photometric centre.This clump is embedded in an area with a local enhancement of the [N II]/Hα ratio. Specifically, this region emerges from the photometric centre and extends for 8″ towards the west, and partially matches the region where the velocity dispersion is higher (about 250−350 km s−1) with respect to the butterfly average (i.e. 149 ± 52 km s−1; Table 2). Local [N II]/Hα ratios are also enhanced at a distance of 7″ to the north and to the west.
Similarly, two clumps with log [S II]/Hα ∼ 0.03 (hence lower than the average, i.e. 0.07 ± 0.06; Table 2) are detected to the north of the photometric centre at R ∼ 1 5 (Fig. B.13, right). The observed values of the log [O I]/Hα vary between −0.69 and 0.25 (−0.48 ± 0.07 on average; Table 2). The morphology of this line ratio closely matches that seen in the [O I] kinematic maps (with well-defined strands) at the same position (Fig. B.13, third panel). For a detailed discussion of ionisation mechanisms from BPTs, see Sect. 5.2.2.
5 (Fig. B.13, right). The observed values of the log [O I]/Hα vary between −0.69 and 0.25 (−0.48 ± 0.07 on average; Table 2). The morphology of this line ratio closely matches that seen in the [O I] kinematic maps (with well-defined strands) at the same position (Fig. B.13, third panel). For a detailed discussion of ionisation mechanisms from BPTs, see Sect. 5.2.2.
4.2.4. Properties of the secondary component
For the MUSE data the spatial distribution of the secondary component has a bipolar shape extended up to  , which corresponds to 790 pc (Figs. B.5–B.8); its properties are summarised in Table 3. This emission is aligned with the radio jet (PA = 70°, Table 1) with a PA of ∼75°, not centred but slightly more extended to the south of the photometric centre. The morphology is almost symmetric with respect to the photometric centre with a redshifted region towards the west of the nucleus, and a blueshifted region towards the east. Overall, the velocity distribution is large, with velocities ranging from −680 to 730 km s−1 (Table 3). The line profile is broad, generally with σ > 150 km s−1. The average values of the σ-maps are within 260 and 320 km s−1 for all emission lines, except for [O I] which is 637 ± 167 km s−1 (Table 3, Fig. B.6). Despite these high values, there is a σ-decrement (σ ∼ 80 km s−1) that mostly corresponds to the PSF region. This feature is more evident in the Hβ, [O III], and [O I] maps with respect to the same maps for [S II] and Hα-[N II]. The unique feature of the flux maps outside the PSF region is a shallow elongation towards the south-west (Figs. B.5–B.8, right panels).
, which corresponds to 790 pc (Figs. B.5–B.8); its properties are summarised in Table 3. This emission is aligned with the radio jet (PA = 70°, Table 1) with a PA of ∼75°, not centred but slightly more extended to the south of the photometric centre. The morphology is almost symmetric with respect to the photometric centre with a redshifted region towards the west of the nucleus, and a blueshifted region towards the east. Overall, the velocity distribution is large, with velocities ranging from −680 to 730 km s−1 (Table 3). The line profile is broad, generally with σ > 150 km s−1. The average values of the σ-maps are within 260 and 320 km s−1 for all emission lines, except for [O I] which is 637 ± 167 km s−1 (Table 3, Fig. B.6). Despite these high values, there is a σ-decrement (σ ∼ 80 km s−1) that mostly corresponds to the PSF region. This feature is more evident in the Hβ, [O III], and [O I] maps with respect to the same maps for [S II] and Hα-[N II]. The unique feature of the flux maps outside the PSF region is a shallow elongation towards the south-west (Figs. B.5–B.8, right panels).
The average value for the [S II] line ratio is 1.2 ± 0.5 (Fig. B.8) indicating a gas with relatively high density (100 < ne < 1000 cm−3). The values of the standard BPT line ratios (see Table 3 for average values, and Fig. B.14) indicate the LINER-like AGN photoionisation as the dominant mechanism for the gas of this component (see Fig. 7). See Sect. 5.2.2 for further discussion.
4.2.5. Faint features
All emission line maps from MUSE (e.g. [O III], Fig. 5, top panels), except [O I] due to the lower S/N (Fig. B.2), show two peculiar faint features with typical fluxes of about 3 × 10−18 erg s−1 cm−2 with kinematics (velocity and velocity dispersion) consistent with the values observed in the polar direction (Sect. 4.2.2).
On the one hand, towards the west, a stream is clearly visible in [O III] (Fig. 5, top) and Hα-[N II], whereas it is weakly or barely detected in the [S II] and Hβ maps. It extends for 18″ (2 kpc) as measured from the Hα-[N II] maps considering only the detached region to the west. The same measurement in the [O III] map (Fig. 5) is more difficult because the stream is connected to the main body of NGC 1052, and no peculiar feature in the kinematic and flux maps allows us to disentangle the stream from the body of the galaxy. This stream is found to have nearly systemic velocities (i.e. ±60 km s−1) and low velocity dispersion (< 50 km s−1, generally). A small clump of radius 0 4 (45 pc) is detected at high-σ (> 100 km s−1) in [O III] only.
4 (45 pc) is detected at high-σ (> 100 km s−1) in [O III] only.
On the other hand, towards the south and south-east, there are two detached clumps. Both clumps show redshifted velocities, but the one to the south shows the most extreme kinematics. Specifically, at this location the observed velocities vary from 80 to 150 km s−1 (130 ± 16 km s−1, on average), whereas towards the south-east the velocity maps show values between 65 and 115 km s−1 (95 ± 7 km s−1, on average). Between these two clumps the differences in velocity dispersion are mild. The average values are 45 ± 13 km s−1 and 28 ± 9 km s−1 for the south and south-east clumps, respectively.
The location of the line ratios for all these faint features on the standard BPT diagrams (Fig. 6 top panels, black and pink symbols) are generally consistent with those observed in AGNs (LINER-like) considering the dividing curves proposed by Kewley et al. (2006) and Kauffmann et al. (2003). This result excludes star formation as the dominant ionisation mechanism in these clumps.
4.3. Main kinematic properties of the third spatially unresolved component
For the MUSE data this component is generally the broadest one (σ > 400 km s−1) for Hβ and oxygen lines. For [S II] and Hα-[N II] the average line widths are 134 ± 45 and 217 ± 104 km s−1, respectively. Its velocity distribution is skewed to blueshifted velocities (typically within −600 and 200 km s−1).
In none of the earlier works but D19b, has the detection of a broad (FWHM ∼ 1380 km s−1) and blueshifted (V ∼ 490 km s−1) unresolved component in narrow lines been reported. D19b found such a broad component only in [O III], whereas with our current MUSE data we detect it in all emission lines.
The FWHM of the [O III] line is 1053 ± 84 km s−1, on average, hence lower than the measurements by D19b. Despite this discrepancy, considering such a large FWHM of the [O III] and the AGN-like BPT ratios measured for this third component, it could probe either an unresolved AGN component as proposed by DH119b or a more recent AGN-driven outflow, which is very central and therefore unresolved. However, as mentioned in Sect. 3.3.1, this component is found only in the central region affected by the PSF (Sect. 2), hence no spatially resolved analysis can be done.
4.4. Comparison between MUSE and MEGARA results
Similarly to the case of the MUSE data, with MEGARA we map three different kinematic components in narrow lines and the BLR emission in Hα. Among the detected emission lines in the MEGARA ISM cube (Sect. 4), [O I] has the lowest S/N. Hence we focus on the results from the modelling of [S II] and Hα-[N II]. These lines were tied to share the same kinematics (Sect. 3.3.1).
The field of view of MEGARA data is almost completely coincident with the region at high-σ, with a minor fraction of a few spaxels (∼14%) corresponding to the polar emission. Hence, we focus the comparison between the results from the MUSE and MEGARA ISM cubes on the butterfly region. However, we summarised the properties of the polar emission from MEGARA in Table 2 for the sake of completeness.
For the primary component, the velocity maps for the [S II] and [O I] lines from the MEGARA data set (Figs. B.9 and B.10, left panels) show a rotation pattern, with larger positive velocities in the [O I] (systematically ∼100 km s−1 higher). For both lines, there is a velocity decrement at R ∼ 5″ north-westwards from the photometric centre which continues spatially up to ∼770 pc, as seen from MUSE maps (e.g. Fig. B.1), at larger distances. This decrement is spatially coincident with the high-σ region, and divides the two strands seen in the butterfly region defined by the MUSE maps (see Sect. 4.2.3). Additionally, the velocity map of the [S II] line (Fig. B.9, left) clearly shows an arc at almost rest frame velocities at approximately 3″ northwards of the photometric centre, which is also seen in the MUSE maps (see Sect. 4.2.2; Fig. B.4).
The velocity dispersion shows an average value of the [S II] lines of 154 ± 38 km s−1, broadly consistent within the uncertainties with that of MUSE in the same innermost region (Table 2). The [S II] and [O I] lines share the same structure (Figs. B.9 and B.10), with increasing values in the western and eastern regions of the photometric centre (for MUSE, see Sect. 4.2.3). The photometric centre has lower values (∼100 km s−1) than the eastern and western parts of the map (generally > 200 km s−1), which emerge in a biconical shape (defining the wings of the butterfly) from the centre in a similar way to the MUSE maps (e.g. Figs. B.2 and B.4).
The flux maps for the narrow component of all the emission lines in the MEGARA data are not centrally peaked, but show instead a spiral-like shape with high fluxes (right panels in Figs. B.10 and B.9). It does not correspond to any peculiar feature in the kinematic maps (velocity or velocity dispersion). This structure is also present in the MUSE maps limited to the region of the MEGARA field of view, being the only noticeable feature in the maps (as mentioned in Sect. 4.2.1).
The limited spectral coverage of MEGARA data allows us to estimate the [S II]/Hα, [N II]/Hα, and [O I]/Hα line ratios (see Sect. 4). The [S II]/Hα ([N II]/Hα) ratio in log for the primary component ranges between −0.17 and 0.44 (−0.19 and 0.18), with an average value of 0.17 ± 0.06 (0.02 ± 0.04). For the [O I]/Hα ratio the values range from −1.6 to 0.3, on average −0.84 ± 0.34 in the complete MEGARA field of view (see Table 2 and Fig. B.15). In the maps of this last ratio (Fig. B.15, centre), a clump is present near the photometric centre, within the PSF, that is spatially coincident with an enhanced region of this ratio, also in the MUSE maps. Table 2 shows that the ratios are consistent within the uncertainties independently of the high-σ–polar emission splitting. We have also estimated the electronic density using the [S II] line ratio (Fig. B.9, right), which indicates a low density regime, as for MUSE data (see Sect. 4.2.1). The density maps of this component are homogeneous, with small deviations only in the outer parts of the field of view (with lower S/N).
The second component detected in the MEGARA data (Fig. B.11) has the same spatial extension as in MUSE, accounting for the differences in the spatial resolution of the two data sets. For the [S II] and [O I] velocity maps the same structure is seen, with a clear velocity distribution ranging up to an absolute value of ∼400 km s−1 for both lines. For this component the velocities of both lines are in close agreement, also with the MUSE data (see Table 3). For the velocity dispersion this component is the broadest of all the components detected in the MEGARA data (excluding the broad Hα in Sect. 4.5). The values are consistent for all lines, although the [O I] measured in MEGARA differs considerably to that from MUSE (average of 359 ± 64 vs. 627 ± 167 km s−1), probably due to the lower S/N of this line in the MEGARA data. Therefore, we cannot ensure a proper determination of the properties of the secondary component with the [O I] lines.
The flux maps of all the lines show a centrally peaked distribution, with no peculiar features. However, as in MUSE, the line ratios present elongated substructures both east and south-west from the photometric centre in both [S II]/Hα and [N II]/Hα that do not correspond to any kinematic feature (Fig. B.16). The mean values of these ratios are summarised in Table 3. For the MUSE and the MEGARA data sets the [S II] flux ratio of the second component (Fig. B.11) indicates a gas with high density, ne ∼ 1000 cm−3.
As already mentioned, MEGARA also identified a third spatially unresolved kinematic component in the emission lines. However, unlike the MUSE data, this component is detected only in [S II]. Its main kinematic properties are velocities ranging between −365 and 221 km s−1 (mean error 72 km s−1), and an average velocity dispersion of 127 ± 47 km s−1. These results are in broad agreement within the uncertainties with those obtained with the MUSE data for the [S II] lines (see Sect. 4.3).
4.5. BLR component
The broad Hα component from the spatially unresolved BLR of NGC 1052 is observed only within the PSF radius (i.e. 0 8 and 1
8 and 1 2 for MUSE and MEGARA respectively, Sect. 2) in both data sets. For this component we obtained, on average, velocities near rest frame, i.e. −38 km s−1 (−60 km s−1) as measured from MUSE (MEGARA) data. Overall, the average velocity dispersion is 1031 ± 141 km s−1 and 998 ± 200 km s−1 (2427 and 2350 km s−1 in FWHM) for the MUSE and MEGARA data, respectively.
2 for MUSE and MEGARA respectively, Sect. 2) in both data sets. For this component we obtained, on average, velocities near rest frame, i.e. −38 km s−1 (−60 km s−1) as measured from MUSE (MEGARA) data. Overall, the average velocity dispersion is 1031 ± 141 km s−1 and 998 ± 200 km s−1 (2427 and 2350 km s−1 in FWHM) for the MUSE and MEGARA data, respectively.
In the end, we note that our final modelling of the Hβ line does not require a broad component confirming the type 1.9 AGN classification of the active nucleus in NGC 1052 (see Table 1).
The FWHM of this AGN component is compared to that of previous works in Sect. 5.5.
4.6. NaD Absorption
Figure 8 shows the equivalent width map of the NaD absorption corresponding to spaxels with S/N ≥ 5 in the MUSE ISM cube. Its overall spatial distribution has an intriguing morphology similar to that of the central butterfly-like region at high-σ described in Sect. 4.2.3. It is oriented in the SE-NW direction with the north-west side more prominent (EWs generally > 1.5 Å).
Our kinematic maps obtained from the MEGARA data indicate a complex neutral gas kinematics (Fig. 10). Specifically, the velocity map shows the blue–red pattern of a rotating disc (velocities from −96 to 57 km s−1), but with a flat gradient (ΔV is 77 ± 12 km s−1, Fig. 10, left). However, the peak of the velocity dispersion map is off-centred (Fig. 10, centre). It peaks at 2 5 (277 pc) eastwards with a value of 263 ± 10 km s−1. Moreover, high velocity dispersion values (> 220 km s−1, higher than the central velocity dispersion of the stars, σc in Table 4) are observed up to 4
5 (277 pc) eastwards with a value of 263 ± 10 km s−1. Moreover, high velocity dispersion values (> 220 km s−1, higher than the central velocity dispersion of the stars, σc in Table 4) are observed up to 4 8 (530 pc) towards the north-east. These high values do not have any counterparts in either velocity or flux maps (Fig. 10, left and right).
8 (530 pc) towards the north-east. These high values do not have any counterparts in either velocity or flux maps (Fig. 10, left and right).
The maps of the ratio of the NaD fluxes indicate that the gas is optically thick (RNaD = 1.3 ± 0.1, on average) similarly to what was estimated for the nuclear spectrum analysed in Cazzoli et al. (2018) (RNaD = 1.0), so far the only study of the NaD-absorption in NGC 1052.
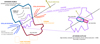 |
Fig. 12. Cartoon illustrating the proposed scenario for the stellar component and the ionised ISM for NGC 1052 (see text for details). |
5. Discussion
The results obtained with the MUSE data are in general agreement with those from the MEGARA cube at higher spectral resolution (Sects. 4.4 and 4.5). In Sect. 5.1, we discuss the stellar kinematics and dynamics using the full data set, whereas the discussion in Sect. 5.2 is mostly based on the results from the MUSE data only in order to exploit its capabilities (spectral range, spatial sampling, and field of view; Sect. 2). Sections 5.3 and 5.4 are dedicated to exploring the kinematics and energetics of the multi-phase outflow (ionised and neutral gas). Finally, in Sect. 5.5 we compare the FWHM of the unresolved BLR component with previous measurements. The estimation of the black hole mass based on the stellar kinematics and the broad Hα components is discussed in Sects. 5.1 and 5.5, respectively.
5.1. Kinematics and dynamics of the stellar disc
As mentioned in Sect. 4.1, the stellar component of NGC 1052 shows features of rotational motions on small scales (MEGARA) and on large scales (MUSE). These include a spider pattern in the velocity field and a centrally peaked velocity dispersion map (Fig. 3). In addition, the kinematic major axis coincides with the photometric major axis, which further confirms the presence of rotation-dominated kinematics.
NGC 1052 is classified as an oblate galaxy of E3-4/S0 type (Bellstedt et al. 2018, Table 1). Its stellar kinematic properties (e.g. large velocity amplitude; Table 4 and Fig. 11, bottom) suggest that NGC 1052 is more likely a lenticular-S0 galaxy (see Cappellari 2016 for a review). The motivation for this classification is twofold. First, the lack of the exponential decline in the P-σ curve (Fig. 11, bottom) indicates the presence of relevant random motions. Second, the combination of a large velocity amplitude and a symmetric velocity field (Table 4, Fig. 11, top) suggests that NGC 1052 has a prominent rotating disc.
The rotational support of the stellar disc can be drawn from the observed (i.e. no inclination corrected) velocity-to-velocity dispersion (V/σ) ratio5, calculated as the ratio of the amplitude to the mean velocity dispersion across the disc. For MUSE (MEGARA) the dynamical ratio is ∼1.2 (0.8), indicating a strong random motion component, hence a dynamical hot disc.
The results from the analysis of the stellar kinematics from present IFS data are generally in agreement with those from previous works by D15 and DH19a with optical IFS from WiFEs and GMOS/GEMINI, respectively, although these data are limited in either spectral range or in field of view, and in spatial sampling (see Sect. 1). For both these past works, the stellar velocity field shows clearly a smooth rotation. However, a 1:1 comparison is not possible as no velocity amplitude measurements are given by the authors. The velocity dispersion shows a central cusp (∼200 km s−1 and ∼250 km s−1, as measured by D15 and DH19a, respectively). This is qualitatively consistent with the shape of the P-σ curve (Fig. 11, bottom). Finally, our results are broadly consistent with those by Bellstedt et al. (2018) obtained with DEIMOS/Keck: a rotational velocity and central velocity dispersion of ∼120 km s−1 and ∼200 km s−1, respectively.
Thanks to our measurement of the stellar dynamics, we can provide an estimate of the black hole mass (MBH) based on the central velocity dispersion of stars measured in MUSE data (201 ± 10 km s−1, Table 4) and Eq. (8) by Bluck et al. (2020) (see also Saglia et al. 2016) yields MBH of 2 ± 0.5 × 108 M⊙. This value is in good agreement with the previous estimates by Beifiori et al. (2012) listed in Table 1. We note that the use of other prescriptions can return different black hole masses (see e.g. Ho 2008 and references therein), as briefly discussed in Sect. 5.5.
5.2. Multi-phase ISM properties
Early-type galaxies were traditionally thought to be uniform stellar systems with little or no gas and dust (Falcón-Barroso et al. 2006). The spatial distribution and kinematics of the ionised gas in NGC 1052 challenges this view, as ISM and stars seem completely decoupled indicating a complex interplay between the two galaxy components. The proposed scenario is summarised in the cartoon shown in Fig. 12.
In what follows we mostly focus on spatially resolved components (i.e. primary and secondary for emission lines and for the NaD absorption). We note that a third component is needed to reproduce line profiles in all forbidden lines and narrow Hα (see Sect. 3.3.1). The presence of this component is reported in Dahmer-Hahn et al. (2019b), but only in [O III] with FWHM ∼ 1380 km s−1. These authors propose that it is tracing the interaction between the jet and the ISM-environment. Even though we were able to map this component for all emission lines (from Hβ to [S II]), it is spatially unresolved (see Sect. 4.2). Due to this limitation we do not investigate this component further. However, its general properties are summarised in Sect. 4.3.
5.2.1. Intriguing ISM kinematics in NGC 1052
For NGC 1052, the presence of non-rotational motions such as an AGN-driven outflow has been suggested in many previous works on the basis of HST imaging (Pogge et al. 2000; Walsh et al. 2008) and 1D and IFS spectroscopy (Sugai et al. 2005; Dopita et al. 2015; Cazzoli et al. 2018; Dahmer-Hahn et al. 2019b), mostly in the optical band.
Generally, the detection of outflows is widely based on the comparison between the observed velocity field and line width distribution and that expected in the case of a rotating disc (see e.g. Veilleux et al. 2020 and references therein). However, for NGC 1052 the deviations from the disc-like behaviour (i.e. outflow signatures) in the kinematics maps of the two spatially resolved components are ambiguous.
On the one hand, for the primary ISM component a clear velocity gradient is observed in the perpendicular direction with respect to the stars (SE-NW direction, see Figs. 5 and C.1). This feature can be explained in terms of either large buoyant bubbles or a polar disc6. This bipolar velocity field is not perfectly symmetrical (see Sect. 4.2.2 and Figs. 5 and C.1) indicating that the putative disc could either be a perturbed rotator or a complex kinematic object according to the classification by Flores et al. (2006).
On the other hand, the velocity dispersion map is not centrally peaked as expected for rotating discs (see Figs. 5 and C.1). Instead, a σ enhancement7 > 90 km s−1 is present at a galactocentric distance smaller than 10″ with a peculiar butterfly shape (see Sect. 4.2.3 and contours in Figs. 5, B.1–B.4, and C.1). At this location the maximum velocity gradient is oriented nearly along the stellar major axis of rotation (black solid line in figures in Appendix B). The morphology and the kinematics of this butterfly feature are suggestive of the presence of two bubbles outside the plane of the galaxy similarly to the well-known superwind in NGC 3079 (an optically thin bubble with blue and red sides from the front and back volumes, e.g. Veilleux et al. 1994). Indeed, if two bubbles (or biconical outflows) are moving away in the polar direction, high velocity dispersion is expected along the major axis of rotation due to the overlap of the blue and red clouds to the line of sight. The observed butterfly feature may represent this effect.
This twofold behaviour of the ionised gas on different spatial scales might indicate that the gas probed by the primary ISM component is tracing two different substructures that are possibly related. Neither of them is likely probing a rotating disc due to the irregularities in the kinematics and the significance of shocks in ionising the gas (as discussed in Sect. 5.2.2).
For the second ISM component the blue to red velocity gradient is mostly aligned with the radio jet (70°, Table 1) with large widths (Table 3) extended mostly within 5″ from the photometric centre (see e.g. Fig. B.5).
As mentioned in Sect. 4.6 the spatial distribution of the NaD absorption has a morphology similar to that of the central region at high-σ described with a prominent north-west side (Fig. 8). However, the kinematics maps do not show clear evidence of a neutral gas outflow (Fig. 10; Sects. 4.6 and 5.4). Hence, by using the kinematics only we cannot claim the robust detection of a multi-phase outflow. In the next section we explore the ionisation structure and the possible connection with the radio jet in order to pinpoint the location of the outflow and hence study the kinematic, energetic and power source.
5.2.2. Line ratios and ionisation structure
We used the observed spatially resolved narrow emission line fluxes and line ratios to investigate the excitation mechanisms at work in NGC 1052 by means of the standard diagnostic diagrams by Baldwin et al. (1981), also known as BPT diagrams (Figs. 6 and 7).
For the MUSE data, the Hβ and [O I] lines are the weakest of those detected. Therefore, they constrain the spatial regions where the BPT analysis can be carried out (see maps in Appendix B). For the MEGARA data the main limitation is that the observed spectra lack both Hβ and [O III], preventing us from exploiting the BPT diagnostics.
In this section we mainly compare our results for ionisation mechanism with those in D15, due to the similarities in spatial and wavelength coverage. This comparison would be more difficult with the results from DH19b, as these authors present the analysis of the [N II]/Hα ratio, complemented by near-IR BPT diagrams, in the central region of NGC 1052 (i.e. 3 5 × 5
5 × 5 0). However, their general findings (i.e. LINER-like line-ratios throughout the whole GMOS/GEMINI field of view and a combination of shocks and photoionisation mechanisms in act in NGC 1052) are in broad agreement with our results (see Sect. 4 and below).
0). However, their general findings (i.e. LINER-like line-ratios throughout the whole GMOS/GEMINI field of view and a combination of shocks and photoionisation mechanisms in act in NGC 1052) are in broad agreement with our results (see Sect. 4 and below).
For the primary (narrowest) component, we exclude the pAGB or H II-ionisation scenarios in favour of a mixture of AGN photoionisation and shock excitation as the dominant mechanisms of ionisation. On the one hand, the large majority of the line ratios lie above the empirical dividing curves between H II- and AGN-like ionisation by Kewley et al. (2006) and Kauffmann et al. (2003). These line ratios are not fully reproduced by pAGBs models by Binette et al. (1994). Furthermore, the observed [O I]/Hα ratios indicate that NGC 1052 is a strong-[O I] object (i.e. genuine AGN) according to the criterion for dividing weak-[O I] and strong-[O I] LINERs, proposed by Filippenko & Terlevich (1992), that is [O I]/Hα > 0.16. Hence, these findings indicate the need of an ionisation mechanism more energetic than star formation or pAGB-stars, such as AGN photoionisation. We note that only for a small number of spaxels (50, i.e. < 1% of the map), the AGN scenario is disfavoured as the log ([O III]/Hβ) ratio is < 0.3 and log ([N II]/Hα) is < 0.2. However, these spaxels are sparsely distributed at large distances (R > 20″, i.e. 2.2 kpc), where faint gas-clumps are detected (see Sect. 4.2.5). On the other hand, shock models with a photoionising precursor (grids in Fig. 6) are able to reproduce the large majority of the observed line ratios in the [N II]/Hα and [O I]/Hα diagrams, and only partially in the [S II]/Hα diagram.
The match between data points and shock models is more accurate for the gas distributed along the polar direction (Fig. 6, top) than for that within the central region at high-σ (Fig. 6, bottom). The same two dominant sources of ionisation (AGN and shocks) acting in NGC 1052 were identified by D15. These authors propose that part of the ionised line-emitting gas is photoionised by the AGN with a central region (R < 1″) that appears shock excited. Emission lines have been modelled with a dusty plasma having a three times solar abundance and via a double-shock model. The latter combines an accretion shock with velocities of about 150 km s−1 and a cocoon shock at higher velocities of 200 − 300 km s−1. Such a model explains the high densities observed (∼104 − 106 cm−3) in the WiFes data and provides a good fit to the observed emission line spectrum. The proposed physical scenario establishes the existence of a higher ionisation cone and a large-scale bipolar outflow (energised by the jet) and a turbulent flow along the major axis of the galaxy. However, the model by D15 only marginally fits our measurements, as explained below.
On the one hand, our 2D mapping of the primary component reveals a central region at high velocity dispersion consistent with the accretion shocks proposed by D15, σ ∼ 120 − 150 km s−1, (except for [O I] for which σ ∼ 350 km s−1; Table 2). Generally, the high velocity dispersion region seen in the WiFES data match that of our IFS data. However, thanks to the high sensitivity and spatial resolution of MUSE we can map this region on a larger area and spatially resolve substructures in flux and kinematics.
On the other hand, the discrepancy is threefold. First, we do not find any indication of such extremely high density. We rather measure two regimes of gas densities, both at lower densities (i.e. ne < 104 cm−3) for the primary and second components, as mentioned in Sects. 4.2.4 and 4.2.1. Second, by using the line-flux maps from MUSE, in the central region we measured a metallicity of 8.18 ± 2.059 (the solar value is 8.69; Asplund et al. 2009) following Pérez-Díaz et al. (2021), using the HII-CHI-MISTRY tool by Pérez-Montero (2014). Hence, there are no hints of the extreme metallicities adopted by D15. Third, velocities consistent with the cocoon shock velocities (200−300 km s−1) in the model by D15 are observed for the secondary component (Table 3, except for [O I]). This is a separated component with respect to that distributed on kpc scales being extended to  , which corresponds to 790 pc (hence not only in the central R < 1″, Sect. 4.2.4) and oriented similarly to the radio jet.
, which corresponds to 790 pc (hence not only in the central R < 1″, Sect. 4.2.4) and oriented similarly to the radio jet.
For the secondary component, shock models (without a precursor) are able to reproduce satisfactorily the observed [N II]/Hα and [O I]/Hα ratios. Nearly half of the data points in the [S II]/Hα diagram are too high to be modelled either with shocks or pAGBs models (Fig. 7, grids and pink boxes, respectively).
Taking into account all this, we conclude that the emission line ionisation in NGC 1052 cannot be explained by one mechanism alone, as proposed by D15 and DH19b. The ionisation in the central region (R < 10″) is a mixture of AGN photoionisation and shock ionisation, while at larger galactocentric distances the shock mechanism is dominating. Finally, we note that we used different shocks models (with and without a precursor) to reproduce the line ratios of the two spatially resolved components. The gas probed by the primary component is self-ionising, including both shocks and a precursor. For the secondary component, the gas is collisionally ionised by the shock (i.e. no precursor) likely as a consequence of the passage of the radio jet, given the alignment between the axis of the radio jet and the secondary component.
It should be noted that although the [O I] kinematic-properties are different from those of other lines (e.g. Hα), they are consistent with the current scenario (see e.g. Fig. 12). Indeed, [O I] is highly sensitive to shocks (especially shock heating), and it is enhanced in the region where the butterfly feature is observed.
5.2.3. Connection between ISM and radio jet
NGC 1052 is a radio-loud AGN (L1−100 GHz ∼ 4.4 × 1040 erg s−1, Wrobel 1984) with a twin radio jet strongly interacting with its environment (Kadler et al. 2004a; Mukherjee et al. 2018). The jet has been detected in numerous observational studies (Falocco et al. 2020 and references therein) associated with an X-ray emitting region (spatially coincident with radio emission at 1.5 GHz, Kadler et al. 2004b).
Radio jets can produce gaseous outflows impacting the host-galaxy on sub-kpc and kpc scales (e.g. Harrison et al. 2014; Hernández-García et al. 2018; Jarvis et al. 2019; Molyneux et al. 2019; Venturi et al. 2021) with different observational features. On the one hand, powerful AGNs show high velocity dispersion along the full extent of the radio emission (e.g. Oosterloo et al. 2019). On the other hand, an enhancement of the emission-line velocity width is found to be perpendicular to the direction of the AGN ionisation cones and jets (e.g. Venturi et al. 2021).
In NGC 1052 the footprints of the interaction between the jet and the gas in the galaxy disc are probed by the primary and secondary components. Specifically, the alignment between the radio emission and ionised gas in the inner ∼1−1.2 kpc is indicative of the radio jet interacting with the ISM (PAs are about 70°, Table 1 and Sect. 4.2.4). Such an interaction can trigger an outflow and can induce large turbulence and kpc-scale bow-shocks (i.e. a jet-induced outflow acting on both sub-kpc and kpc scales). In this scenario, the outflow is probed by the second component, whereas the primary component traces both the cocoon of gas surrounding the expanding jet-induced outflow (with enhanced turbulence) and the large-scale gas (extended up to ∼2−3 kpc) expanding perpendicular to the axis of the jet. The shells seen in the blue part of the velocity field of the primary component along the polar direction could indicate shock waves propagating in a smooth medium. These could be absent on the red side of the polar emission at positive velocities, due to ISM anisotropy.
The proposed scenario for NGC 1052 is similar to that presented by Morganti et al. (2021) for PKS 0023–26 (a far-IR bright source hosting a young powerful radio source) on the basis of the results from ALMA CO (2−1) and 1.7 mm continuum data. In PKS 0023–26, the highly perturbed gas tends to follow the edge of the radio emission on sub-kpc scales, whereas the relatively mild expansion of the cocoon, created by the interaction between jet and ISM, is pushing the gas aside. For NGC 1052 the strong coupling between radio jets and the ISM is limited to the innermost 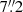 , corresponding to 790 pc (Sect. 4.2.4), with large buoyant bubbles extending up to 30″, which corresponds to 3.3 kpc (Sect. 4.2.2). As for PKS 0023–26, the cocoon does not reach extreme velocities but injects turbulence into the ISM, triggering the creation of the bubbles along the polar direction. With the present data set we cannot infer the presence of cavities devoid of dense gas at larger radii, due to the maintenance phase of outflow, nor any relation between radio lobes and the ISM, as the former are absent for the jet in NGC 1052.
, corresponding to 790 pc (Sect. 4.2.4), with large buoyant bubbles extending up to 30″, which corresponds to 3.3 kpc (Sect. 4.2.2). As for PKS 0023–26, the cocoon does not reach extreme velocities but injects turbulence into the ISM, triggering the creation of the bubbles along the polar direction. With the present data set we cannot infer the presence of cavities devoid of dense gas at larger radii, due to the maintenance phase of outflow, nor any relation between radio lobes and the ISM, as the former are absent for the jet in NGC 1052.
Although the comparison between PKS 0023–26 and our results for NGC 1052 is illustrative, it has to be taken with caution as we are tracing different gas phases within the jet–ISM interaction.
5.3. Ionised gas outflow kinematics and energetic
On the basis of the morphology and kinematics of the different components, and taking into account that shocks are a crucial mechanism of ionisation in NGC 1052, we claim the detection of an ionised gas outflow. It is probed by the secondary component, with a bipolar morphology and velocity dispersion > 150 km s−1. The outflow is strongly interacting with the surrounding ISM mapped by the primary component. Such an interplay is suggested by both the high-σ (> 90 km s−1) region with a peculiar butterfly-like morphology and the presence of two kpc scale buoyant bubbles.
In this section we summarise the main properties (kinematics and energetic) of the outflow as well as its power source (i.e. verify the jet-driven scenario proposed in Sect. 5.2.3). We assume a simple outflow model, with inclination-corrected velocities and distances, that considers the outflow oriented perpendicular to the plane of the disc.
We estimated the total mass of the emitting ionised hydrogen gas following Venturi et al. (2021) (see also Carniani et al. 2015; Cresci et al. 2017). We calculated the Hα luminosity corrected for extinction (LHα), considering the corresponding distance (i.e. 22.6 Mpc, Table 1) and using the attenuation law by Calzetti et al. (2000) for galactic diffuse ISM (RV = 3.12) and an intrinsic ratio (Hα/Hβ) = 2.86 (for an electron temperature of 104 K, Osterbrock & Ferland 2006). The intrinsic Hα luminosity is converted in mass of the ionised gas with the Eq. (1) in Venturi et al. (2021) using the median value of the electron density (i.e. 360 cm−3). We obtain a total LHα of (1.8 ± 0.7) × 1040 erg s−1 and a total mass of ionised gas in the outflow of MOF, ion = (1.6 ± 0.6) × 105 M⊙ with our data.
The mass outflow rate is ṀOF,ion = (0.4 ± 0.2) M⊙ yr−1, estimated with 3 × VOF, ion/ROF, ion × MOF, ion as in Cresci et al. (2015). We note that, in this estimation, we assumed VOF, ion to be the maximum of the velocity field from the map of the secondary component (∼655 km s−1).
We also estimated the kinetic energy and power of the outflowing ionised gas, EOF, ion = 0.5 × 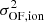 MOF, ion and ĖOF,ion = 0.5 × Ṁ × (
MOF, ion and ĖOF,ion = 0.5 × Ṁ × (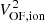 + 3
+ 3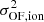 ), using an average velocity dispersion of Hα ∼ 280 km s−1. We obtained EOF, ion = (1.3 ± 0.9) × 1053 erg and ĖOF,ion = (8.8 ± 3.5) × 1040 erg s−1.
), using an average velocity dispersion of Hα ∼ 280 km s−1. We obtained EOF, ion = (1.3 ± 0.9) × 1053 erg and ĖOF,ion = (8.8 ± 3.5) × 1040 erg s−1.
An upper limit on the outflow mass and energy could be estimated by considering the whole outflow phenomenon, which is the outflow core (secondary component) plus the buoyant bubbles (primary component, excluding the faint features described in Sect. 4.2.5). Hence, the mass of the ionised gas associated with the outflow phenomenon (bubbles) is 1.8 ± 1.1 × 106 M⊙ (1.7 ± 1.1 × 106) M⊙ and the corresponding energy is 1.9 ± 1.5 × 1053 (8.1 ± 1.1 × 1052) erg.
We excluded the star formation as a power source of the outflow since the kinetic power of the starburst associated with supernovae is low (∼6.3 × 1040 erg s−1, as calculated following Veilleux et al. 2005 from the total star formation rate, SFR, i.e. 0.09 M⊙ yr−1; Table 1). In what follows we focus on distinguising between the two most likely scenarios: AGN-driven versus jet-driven outflow.
The energy rate is of the order of 0.01 of the bolometric luminosity of NGC 1052 (Lbol = 1042.91 erg s−1Onori et al. 2017a). This is in broad agreement with the results of Fiore et al. (2017) (see their Fig. 1, right) that showed that the average ratio ĖOF,ion/Lbol for AGN-driven ionised outflows is generally below 0.1. As in Venturi et al. (2021), in order to infer whether the jet is energetic enough to power the observed features, we compared the total kinetic energy of the jet (Ejet) with the kinetic energy of the outflow. By assuming the power and travelling time of the jet (1045 erg s−1 and 0.7 Myr, respectively) used in Mukherjee et al. (2018) to simulate the observed kinematics and morphology of the ionised gas in NGC 1052, we obtain a total energy of the jet of Ejet = 2.2 × 1058 erg.
The comparisons ĖOF,ion versus Lbol and Ejet versus EOF, ion indicate that both the AGN and the jet in NGC 1052 are capable of injecting the required energy into the ISM to power the outflow. However, taking into account the alignment between the radio jet, the secondary component, and the cocoon with enhanced turbulence, we consider that the most likely power source of the outflow is the jet, although some contribution from the AGN is possible.
5.4. Neutral gas outflow detection
As mentioned in Sect. 5.2.1, the mapping of the neutral gas properties does not show evident outflow features (e.g. a broad kinematic component with significant blueshifted velocities). Hence, the identification of the neutral gas outflow and the corresponding estimates provided in this section is exploratory, and hence must be taken with caution. To identify the putative neutral gas outflow we used the velocity dispersion map (Fig. 10, centre), which shows the clearest deviations from the rotating disc behaviour among those obtained from the NaD modelling (Sect. 4.6).
As a threshold to identify the outflowing neutral gas, we consider the 75th percentile of the distributions of the velocity dispersion, that is, σthr > 245 km s−1. The selected region (with σ > σthr) is marked with contours in the maps shown in Fig. 10. It is extended up to a galactocentric distance of 4 8 (530 pc), with an elongated morphology (oriented north-south), and a projected area of 3.8 arcsec2. The region is characterised by a mild kinematics with velocity and velocity dispersion of 63 ± 21 km s−1 and 251 ± 5 km s−1, respectively, on average. The EW is, on average, 1.2 ± 0.3 Å. This value is converted into column density of the wind (NH) via reddening (EB − V) following the approach by Cazzoli et al. (2014, 2016), already used for the MEGARA data by Catalán-Torrecilla et al. (2020). On average, the column density of the outflow is (2.8 ± 0.7) × 1021 cm−2. As in Catalán-Torrecilla et al. (2020) we assumed that the outflow is organised in a series of thin shells, and to obtain the deprojected velocities, distances, and solid angle we used a simple geometrical model of a conical outflow that emerges perpendicular to the disc.
8 (530 pc), with an elongated morphology (oriented north-south), and a projected area of 3.8 arcsec2. The region is characterised by a mild kinematics with velocity and velocity dispersion of 63 ± 21 km s−1 and 251 ± 5 km s−1, respectively, on average. The EW is, on average, 1.2 ± 0.3 Å. This value is converted into column density of the wind (NH) via reddening (EB − V) following the approach by Cazzoli et al. (2014, 2016), already used for the MEGARA data by Catalán-Torrecilla et al. (2020). On average, the column density of the outflow is (2.8 ± 0.7) × 1021 cm−2. As in Catalán-Torrecilla et al. (2020) we assumed that the outflow is organised in a series of thin shells, and to obtain the deprojected velocities, distances, and solid angle we used a simple geometrical model of a conical outflow that emerges perpendicular to the disc.
Following these prescriptions, the total mass of neutral gas contained in the outflowing region is (7.1 ± 2.8) × 106 M⊙ and the outflow rate is (0.86 ± 0.30) M⊙ yr−1. We also derived the total energy of the neutral outflow which is (1.1 ± 0.4) × 1055 erg.
Cold neutral gas outflows in LINERs and early-type galaxies (ETGs), probed by the NaD absorption, have been less studied compared for example to ionised and molecular outflows in Seyferts or U/LIRGs (e.g. Arribas et al. 2014; Pereira-Santaella et al. 2016, 2020; Venturi et al. 2018; Wylezalek et al. 2020; Perna et al. 2021; Comerón et al. 2021; Riffel et al. 2021). However, there are two systematic studies of neutral gas in LINERs in large samples by Lehnert et al. (2011) and Sarzi et al. (2016). Lehnert et al. (2011) detected neutral ISM gas in about one-third of their sample of 691 radio-loud ETGs on the basis of SDSS data. The detected NaD profiles suggest the presence of outflows with low velocities (∼50 km s−1) and broad profiles (∼500 km s−1). On the contrary, Sarzi et al. (2016) found that only a dozen radio AGNs (out of 103 objects) show NaD absorption from ISM, but the neutral gas never appears to be outflowing.
The unique study of the NaD absorption in NGC 1052 is by Cazzoli et al. (2018) on the basis of slit spectroscopy. In this work, the neutral gas kinematics has been interpreted as being due to rotation. However, slit observations give only a partial description of the outflow phenomenon, hence in the case of NGC 1052, IFS observations could have been the key for our (tentative) detection of the neutral gas outflow.
5.5. Comparison with current and previous Hα broad component measurements
The BLR component in NGC 1052 has been observed in polarised light (Barth et al. 1999) and at different wavelengths (Onori et al. 2017b; Cazzoli et al. 2018; Dahmer-Hahn et al. 2019a and references therein). Onori et al. (2017b) modelled the BLR component in both optical and near-IR bands with HST/FOS (R ∼ 2800) and ISAAC (R ∼ 730) spectra. The near-IR He Iλ1.083 μm line was modelled with a broad Gaussian curve with width of 2455 km s−1, a slightly smaller value (i.e. 2193 km s−1) was used for Hα. The broad Hα emission was also measured by Balmaverde & Capetti (2014) (FWHM ∼ 2240 km s−1), Constantin et al. (2015) (FWHM ∼ 2800 km s−1), and Cazzoli et al. (2018) 8 (FWHM ∼ 2915 km s−1) with HST/STIS slit spectra, all obtaining values that are in fair agreement.
There are three measurements of the width of the broad Hα component with optical IFS. Two of them are from the present MEGARA and MUSE IFS data: 2427 ± 332 and 2350 ± 470 km s−1, respectively. These values are consistent within the uncertainties, but are smaller than the value of ∼3200 km s−1 reported by DH19a from their GMOS/GEMINI cube (R ∼ 1700 and final angular resolution 0 7).
7).
We considered as the main sources of discrepancies the number of components used to model emission lines and the different spectral–spatial resolution of the different data sets (see e.g. Cazzoli et al. 2020). Another possibility for explaining the differences in the FWHM of the broad component is AGN variability (see e.g. Hernández-García et al. 2014), which is beyond the aim of the paper.
The FWHM and luminosity of the broad Hα component determined from the best-fitting model of the Hα broad component can be converted in black hole mass using the virial relation. For NGC 1052, we found that MBH is ∼3 × 105 M⊙ from Eq. (3) in Koss et al. (2017). Considering that the assumed value of luminosity is a lower limit as we did not apply any correction for reddening, the estimate of the black hole mass from Hα is in broad agreement with that by Onori et al. (2017a) using the virial relation of ∼4 × 106 M⊙ (Table 1).
However, the determination based in the broad Hα has been explored the most for luminous type 1 AGNs (see e.g. Greene & Ho 2005 for details), hence for type 1.9 LINERs like NGC 1052 (Table 1) it could be uncertain; in other words, it is challenging to isolate the AGN contribution unambiguously. Therefore, we consider the MBH from the stellar velocity dispersion to be more reliable because it is the result of coevolution between the host galaxies and the supermassive black holes.
6. Conclusions
On the basis of optical MUSE and MEGARA IFS data we have studied the properties of the stellar and ionised and neutral gas components in the LINER 1.9 NGC 1052, using as tracers both emission lines (from Hβ to [S II]) and the NaD absorption doublet.
The conclusions of this study can be summarised as follows:
-
Kinematics and dynamical support for the stellar component. The stellar velocity field is characterised by ordered large-scale rotational motions (ΔV = 167 ± 19 km s−1), although the velocity dispersion is generally high as measured from the MUSE (145 ± 22 km s−1) and MEGARA data (201 ± 16 km s−1). The rotational support is low, however. The dynamical ratio V/σ = 1.2 (0.8) from the MUSE (MEGARA) data is indicative of a dynamically hot disc with a significant random motion component. In both data sets the stellar major axis is well aligned with the photometric axis. The kinematic and dynamics of the stellar disc of NGC 1052 favour its classification as an S0-type. The black hole mass estimated from stellar dynamics is 2 ± 0.5 × 108 M⊙.
-
Ionisation mechanisms. By combining the location of line ratios onto BPTs, theoretical models of shocks and pAGBs ionisation, and the weak or strong [O I] classification, we exclude star formation and pAGB scenarios in favour of a mixture of shock excitation and AGN activity as the main mechanisms of ionisation in NGC 1052. The general behaviour is that the ionisation in the central region (R < 10″) is a mixture of AGN photoionisation and shocks, while at larger galactocentric distances the shock excitation is dominating.
-
The intriguing properties of the ionised gas probed by the primary component. The velocity field shows a large-scale structure extended in the polar direction (NE-SW direction) up to ∼30″ (∼3.3 kpc) with blue and red velocities (typically < ∣ 250 ∣ km s−1). The velocity dispersion map lacks any symmetry typical of a rotation dominated system with a notable enhancement (σ > 90 km s−1) crossing the galaxy along the major axis of rotation in the central ∼10″ (also called butterfly region within the main text). We consider that both features are likely related to the presence of an ionised gas outflow instead of, for example, a polar disc.
-
Ionised gas outflow. The outflow is probed by the secondary component with a bipolar morphology, velocity dispersions > 150 km s−1, and velocities up to 660 km s−1. The outflow (with mass of 1.6 ± 0.6 × 105 M⊙, and mass rate of 0.4 ± 0.2 M⊙ yr−1) is propagating in a cocoon of gas with enhanced turbulence (the butterfly region) and triggering the onset of kpc-scale buoyant bubbles (polar emission). Considering the energy (1.3 ± 0.9 × 1053 erg) and energy rate (8.8 ± 3.5 × 1040 erg s−1) of the outflow, both the AGN and the radio jet are able to launch the outflow. However, taking into account its alignment with the jet and with the cocoon, and that the gas is collisionally ionised, we consider that the most likely power source of the outflow is the jet, although some contribution from the AGN is possible.
-
Neutral gas content. The kinematics maps of the NaD absorption obtained with MEGARA data indicate optically thick neutral gas with complex kinematics. The velocity field is consistent with a slow rotating disc (ΔV = 77 ± 12 km s−1), but the velocity dispersion map is off-centred with a peak value of 263 ± 10 km s−1 observed at 2
 5 (277 pc) eastwards of the photometric centre without any counterpart in the (centrally peaked) flux map. The hints of the presence of the neutral gas outflow are weak, and our identification its tentative. The putative neutral gas outflow is extended to the west with a projected area of 3.8 arcsec2 with mild kinematics (i.e. with velocity and velocity dispersion of 63 ± 21 km s−1 and 251 ± 5 km s−1, respectively). The mass, the mass rate, and the energy of the neutral would be (7.1 ± 2.8) × 106 M⊙, (0.86 ± 0.30) M⊙ yr−1, and (1.1 ± 0.4) 1055 erg, respectively.
5 (277 pc) eastwards of the photometric centre without any counterpart in the (centrally peaked) flux map. The hints of the presence of the neutral gas outflow are weak, and our identification its tentative. The putative neutral gas outflow is extended to the west with a projected area of 3.8 arcsec2 with mild kinematics (i.e. with velocity and velocity dispersion of 63 ± 21 km s−1 and 251 ± 5 km s−1, respectively). The mass, the mass rate, and the energy of the neutral would be (7.1 ± 2.8) × 106 M⊙, (0.86 ± 0.30) M⊙ yr−1, and (1.1 ± 0.4) 1055 erg, respectively. -
BLR properties. In the nuclear region of NGC 1052 (≤1″) the broad Hα component that originated in the (unresolved) BLR of the AGN is modelled with a Gaussian component with FWHM of respectively 2427 ± 332 and 2350 ± 470 km s−1 for the MUSE and MEGARA data.
-
Unresolved component. This component has been detected with the MUSE data (barely with MEGARA) in all emission lines. It is observed in the central region, with a spatial extension matching that of the PSF, with an average FWHM ∼ 1380 km s−1 and line ratios indicating AGN ionisation. It could probe either an unresolved AGN component, as proposed by DH119b, or a more recent AGN-driven outflow. However, with the current data set it is not possible to distinguish between the two scenarios.
As a final remark, we highlight that studies of this kind provided valuable insight into our general understanding of multiphase outflows in low luminosity AGNs.
Double peaks were already detected by DH19a for NGC 1052 (their Fig. 3) and in other LINERs, e.g. NGC 5077 (Raimundo 2021).
Some authors (e.g. Perna et al. 2022 and references therein) use the inclination-corrected velocity to calculate the dynamical ratio. For NGC 1052 such a correction does not strongly affect the V/σ ratio; it would be 1.23 instead of 1.16, hence ∼1.2 in both cases.
We discard the scenario in which the polar gas arise from the AGN’s narrow line region (NLR). Indeed, by means of the relation between the X-ray luminosity and size of the NLR for LINERs by Masegosa et al. (2011; see their Fig. 4), for NGC 1052 the NLR physical size would be ∼600 pc. Hence, the NLR is much less extended than the polar emission detected at a distance > 3 kpc.
Acknowledgments
The authors acknowledge the anonymous referee for her/his instructive comments that helped to improve the presentation of this paper. S.C., I.M., J.M. and L.H.M. acknowledge financial support from the State Agency for Research of the Spanish MCIU through the ‘Center of Excellence Severo Ochoa’ award to the Instituto de Astrofísica de Andalucía (SEV-2017-0709). These authors are also supported by the Spanish Ministry of Economy and Competitiveness under grants no. AYA2016-76682-C3 and PID2019-106027GB-C41. L.H.M. acknowledges financial support under the FPI grant BES-2017-082471. A.G.d.P. and A.C.M. acknowledge the grant RTI-2018-096188-B-I00. L.H.G. acknowledges funds by ANID – Millennium Science Initiative Program – ICN12_009 awarded to the Millennium Institute of Astrophysics (MAS). F.L.F. acknowledges support from PRIN MIUR project ‘Black Hole winds and the Baryon Life Cycle of Galaxies: the stone-guest at the galaxy evolution supper’, contract no. 2017PH3WAT. C.R.A. acknowledges financial support from the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No 860744 (BiD4BESt) and from the State Research Agency (AEI-MCINN) and the Spanish MCINN under grant ‘Feeding and feedback in active galaxies’, with reference PID2019-106027GB-C42. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. We acknowledge the usage of the HyperLeda database (http://leda.univ-lyon1.fr). This work has made extensive use of IRAF and PYTHON, particularly with ASTROPYhttp://www.astropy.org (Astropy Collaboration 2013, 2018), MATPLOTLIB (Hunter 2007), NUMPY and LMFIT. This paper made use of the plotting package JMAPLOT, developed by Jesús Maíz-Apellániz available at: https://jmaiz.cab.inta-csic.es/software/jmaplot/current/html/jmaplot_overview.html. This research has made use of the Skycat tool that combines visualisation of images and access to catalogues and archive data for astronomy. In particular, EXTRACTOR as part of the GAIA (Graphical Astronomy and Image Analysis Tool) package. We thanks J. Perea Duarte for the technical support and B. Perez for the calculation of gas metallicity.
References
- Arribas, S., Colina, L., Bellocchi, E., Maiolino, R., & Villar-Martín, M. 2014, A&A, 568, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Avery, C. R., Wuyts, S., Förster Schreiber, N. M., et al. 2021, MNRAS, 503, 5134 [NASA ADS] [CrossRef] [Google Scholar]
- Bacon, R., Accardo, M., Adjali, L., et al. 2010, Proc. SPIE, 7735, 773508 [Google Scholar]
- Bacon, R., Vernet, J., Borisova, E., et al. 2014, The Messenger, 157, 13 [NASA ADS] [Google Scholar]
- Bai, Z.-R., Zhang, H.-T., Yuan, H.-L., et al. 2017, Res. Astron. Astrophys., 17, 091 [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Balmaverde, B., & Capetti, A. 2014, A&A, 563, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barth, A. J., Filippenko, A. V., & Moran, E. C. 1999, ApJ, 515, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Beifiori, A., Courteau, S., Corsini, E. M., & Zhu, Y. 2012, MNRAS, 419, 2497 [NASA ADS] [CrossRef] [Google Scholar]
- Bellstedt, S., Forbes, D. A., Romanowsky, A. J., et al. 2018, MNRAS, 476, 4543 [Google Scholar]
- Binette, L., Magris, C. G., Stasińska, G., & Bruzual, A. G. 1994, A&A, 292, 13 [NASA ADS] [Google Scholar]
- Bittner, A., Falcón-Barroso, J., Nedelchev, B., et al. 2019, A&A, 628, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bluck, A. F. L., Maiolino, R., Piotrowska, J. M., et al. 2020, MNRAS, 499, 230 [NASA ADS] [CrossRef] [Google Scholar]
- Bosch, G., Hägele, G. F., Amorín, R., et al. 2019, MNRAS, 489, 1787 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Cresci, G., Daddi, E., et al. 2018, A&A, 612, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2016, ARA&A, 54, 597 [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [Google Scholar]
- Cappellari, M., McDermid, R. M., Alatalo, K., et al. 2013, MNRAS, 432, 1862 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco, E., Gil de Paz, A., Gallego, J., et al. 2018, in Ground-based and Airborne Instrumentation for Astronomy VII, eds. C. J. Evans, L. Simard, & H. Takami, SPIE Conf. Ser., 10702, 1070216 [NASA ADS] [Google Scholar]
- Catalán-Torrecilla, C., Castillo-Morales, Á., Gil de Paz, A., et al. 2020, ApJ, 890, 5 [CrossRef] [Google Scholar]
- Cazzoli, S., Arribas, S., Colina, L., et al. 2014, A&A, 569, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, S., Arribas, S., Maiolino, R., & Colina, L. 2016, A&A, 590, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, S., Márquez, I., Masegosa, J., et al. 2018, MNRAS, 480, 1106 [Google Scholar]
- Cazzoli, S., Gil de Paz, A., Márquez, I., et al. 2020, MNRAS, 493, 3656 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, S., Knapen, J. H., Ramos Almeida, C., & Watkins, A. E. 2021, A&A, 645, A130 [EDP Sciences] [Google Scholar]
- Constantin, A., Shields, J. C., Ho, L. C., et al. 2015, ApJ, 814, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Marconi, A., Zibetti, S., et al. 2015, A&A, 582, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cresci, G., Vanzi, L., Telles, E., et al. 2017, A&A, 604, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Currie, M. J., Berry, D. S., Jenness, T., et al. 2014, in Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, ASP Conf. Ser., 485, 391 [NASA ADS] [Google Scholar]
- Dahmer-Hahn, L. G., Riffel, R., Ricci, T. V., et al. 2019a, MNRAS, 489, 5653 [NASA ADS] [CrossRef] [Google Scholar]
- Dahmer-Hahn, L. G., Riffel, R., Steiner, J. E., et al. 2019b, MNRAS, 482, 5211 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Ho, I.-T., Dressel, L. L., et al. 2015, ApJ, 801, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Draper, P. W., Berry, D. S., Jenness, T., & Economou, F. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 575 [NASA ADS] [Google Scholar]
- Falcón-Barroso, J., Sarzi, M., Bacon, R., et al. 2006, New Astron. Rev., 49, 515 [CrossRef] [Google Scholar]
- Falocco, S., Larsson, J., & Nandi, S. 2020, A&A, 638, A67 [EDP Sciences] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Filippenko, A. V., & Terlevich, R. 1992, ApJ, 397, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flores, H., Hammer, F., Puech, M., Amram, P., & Balkowski, C. 2006, A&A, 455, 107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2019, MNRAS, 483, 4586 [NASA ADS] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2021, MNRAS, 505, 5753 [NASA ADS] [CrossRef] [Google Scholar]
- Forbes, D. A., Sinpetru, L., Savorgnan, G., et al. 2017, MNRAS, 464, 4611 [Google Scholar]
- Gil de Paz, A., Carrasco, E., Gallego, J., et al. 2016, in Ground-based and Airborne Instrumentation for Astronomy VI, eds. C. J. Evans, L. Simard, & H. Takami, SPIE Conf. Ser., 9908, 99081K [NASA ADS] [Google Scholar]
- González Delgado, R. M., Cerviño, M., Martins, L. P., Leitherer, C., & Hauschildt, P. H. 2005, MNRAS, 357, 945 [Google Scholar]
- González-Martín, O., Masegosa, J., Márquez, I., Guainazzi, M., & Jiménez-Bailón, E. 2009, A&A, 506, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Groves, B. A., Dopita, M. A., & Sutherland, R. S. 2004, ApJS, 153, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Mullaney, J. R., & Swinbank, A. M. 2014, MNRAS, 441, 3306 [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Strickland, D. K., & Armus, L. 2000, ApJS, 129, 493 [Google Scholar]
- Hermosa Muñoz, L., Cazzoli, S., Márquez, I., & Masegosa, J. 2020, A&A, 635, A50 [EDP Sciences] [Google Scholar]
- Hernández-García, L., González-Martín, O., Masegosa, J., & Márquez, I. 2014, A&A, 569, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernández-García, L., Vietri, G., Panessa, F., et al. 2018, MNRAS, 478, 4634 [CrossRef] [Google Scholar]
- Hernández-García, L., Panessa, F., Bassani, L., et al. 2019, MNRAS, 489, 4049 [Google Scholar]
- Ho, L. C. 2008, ARA&A, 46, 475 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jarvis, M. E., Harrison, C. M., Thomson, A. P., et al. 2019, MNRAS, 485, 2710 [Google Scholar]
- Kadler, M., Kerp, J., Ros, E., et al. 2004a, A&A, 420, 467 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kadler, M., Ros, E., Lobanov, A. P., Falcke, H., & Zensus, J. A. 2004b, A&A, 426, 481 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kakkad, D., Mainieri, V., Vietri, G., et al. 2020, A&A, 642, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, D., & Woo, J.-H. 2018, ApJ, 864, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., & Makarov, D. A. 1996, AJ, 111, 794 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [Google Scholar]
- Kormendy, J., & Ho, L. C. 2013, ARA&A, 51, 511 [Google Scholar]
- Koss, M., Trakhtenbrot, B., Ricci, C., et al. 2017, ApJ, 850, 74 [Google Scholar]
- Lehnert, M. D., Tasse, C., Nesvadba, N. P. H., Best, P. N., & van Driel, W. 2011, A&A, 532, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luo, R., Woo, J.-H., Karouzos, M., et al. 2021, ApJ, 908, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Russell, H. R., Fabian, A. C., et al. 2017, Nature, 544, 202 [Google Scholar]
- Markwardt, C. B. 2009, in Astronomical Data Analysis Software and Systems XVIII, eds. D. A. Bohlender, D. Durand, & P. Dowler, ASP Conf. Ser., 411, 251 [Google Scholar]
- Márquez, I., Durret, F., González Delgado, R. M., et al. 1999, A&AS, 140, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Márquez, I., Masegosa, J., Durret, F., et al. 2003, A&A, 409, 459 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, L. P., González Delgado, R. M., Leitherer, C., Cerviño, M., & Hauschildt, P. 2005, MNRAS, 358, 49 [Google Scholar]
- Masegosa, J., Márquez, I., Ramirez, A., & González-Martín, O. 2011, A&A, 527, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Molyneux, S. J., Harrison, C. M., & Jarvis, M. E. 2019, A&A, 631, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., & Oosterloo, T. 2018, A&ARv, 26, 4 [Google Scholar]
- Morganti, R., Oosterloo, T. A., Tadhunter, C. N., van Moorsel, G., & Emonts, B. 2005, A&A, 439, 521 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Oosterloo, T., Tadhunter, C., Bernhard, E. P., & Raymond Oonk, J. B. 2021, A&A, 656, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mukherjee, D., Bicknell, G. V., Wagner, A. Y., Sutherland, R. S., & Silk, J. 2018, MNRAS, 479, 5544 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Onori, F., Ricci, F., La Franca, F., et al. 2017a, MNRAS, 468, L97 [NASA ADS] [CrossRef] [Google Scholar]
- Onori, F., La Franca, F., Ricci, F., et al. 2017b, MNRAS, 464, 1783 [NASA ADS] [CrossRef] [Google Scholar]
- Oosterloo, T., Morganti, R., Tadhunter, C., et al. 2019, A&A, 632, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of Gaseous Nebulae and Active Galactic Nuclei (Sausalito: University Science Books) [Google Scholar]
- Osterbrock, D. E., Fulbright, J. P., Martel, A. R., et al. 1996, PASP, 108, 277 [Google Scholar]
- Pascual, S., Cardiel, N., Picazo-Sanchez, P., Castillo-Morales, A., & de Paz, A. G. 2020, https://doi.org/10.5281/zenodo.3922220 [Google Scholar]
- Pascual, S., Cardiel, N., Picazo-Sanchez, P., Castillo-Morales, A., & Gil De Paz, A. 2021, https://doi.org/10.5281/zenodo.593647 [Google Scholar]
- Paturel, G., Andernach, H., Bottinelli, L., et al. 1997, A&AS, 124, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2016, A&A, 594, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2020, A&A, 643, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez-Díaz, B., Masegosa, J., Márquez, I., & Pérez-Montero, E. 2021, MNRAS, 505, 4289 [CrossRef] [Google Scholar]
- Pérez-Montero, E. 2014, MNRAS, 441, 2663 [CrossRef] [Google Scholar]
- Perna, M., Arribas, S., Catalán-Torrecilla, C., et al. 2020, A&A, 643, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Pereira Santaella, M., et al. 2021, A&A, 646, A101 [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Colina, L., et al. 2022, A&A, 662, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pogge, R. W., Maoz, D., Ho, L. C., & Eracleous, M. 2000, ApJ, 532, 323 [NASA ADS] [CrossRef] [Google Scholar]
- Raimundo, S. I. 2021, A&A, 650, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramos Almeida, C., Piqueras López, J., Villar-Martín, M., & Bessiere, P. S. 2017, MNRAS, 470, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Riffel, R. A., Storchi-Bergmann, T., Riffel, R., et al. 2021, MNRAS, 504, 3265 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, M., Tadhunter, C., Ramos Almeida, C., et al. 2018, MNRAS, 474, 128 [Google Scholar]
- Rupke, D. S. N., & Veilleux, S. 2013, ApJ, 768, 75 [Google Scholar]
- Rupke, D. S., Veilleux, S., & Sanders, D. B. 2002, ApJ, 570, 588 [NASA ADS] [CrossRef] [Google Scholar]
- Ruschel-Dutra, D., Storchi-Bergmann, T., Schnorr-Müller, A., et al. 2021, MNRAS, 507, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Saglia, R. P., Opitsch, M., Erwin, P., et al. 2016, ApJ, 818, 47 [Google Scholar]
- Sanders, R. L., Shapley, A. E., Kriek, M., et al. 2016, ApJ, 816, 23 [Google Scholar]
- Sarzi, M., Kaviraj, S., Nedelchev, B., et al. 2016, MNRAS, 456, L25 [Google Scholar]
- Saturni, F. G., Vietri, G., Piconcelli, E., et al. 2021, A&A, 654, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singha, M., Husemann, B., Urrutia, T., et al. 2022, A&A, 659, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitzer, L. 1978, Physical Processes in the Interstellar Medium (New York: Wiley) [Google Scholar]
- Sugai, H., Hattori, T., Kawai, A., et al. 2005, ApJ, 629, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [Google Scholar]
- Veilleux, S., Cecil, G., Bland-Hawthorn, J., et al. 1994, ApJ, 433, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Maiolino, R., Bolatto, A. D., & Aalto, S. 2020, A&ARv, 28, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Venturi, G., Nardini, E., Marconi, A., et al. 2018, A&A, 619, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Venturi, G., Cresci, G., Marconi, A., et al. 2021, A&A, 648, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villar-Martín, M., Cabrera-Lavers, A., Humphrey, A., et al. 2018, MNRAS, 474, 2302 [Google Scholar]
- Walsh, J. L., Barth, A. J., Ho, L. C., et al. 2008, AJ, 136, 1677 [NASA ADS] [CrossRef] [Google Scholar]
- Westfall, K. B., Cappellari, M., Bershady, M. A., et al. 2019, AJ, 158, 231 [Google Scholar]
- Wrobel, J. M. 1984, ApJ, 284, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Wylezalek, D., Flores, A. M., Zakamska, N. L., Greene, J. E., & Riffel, R. A. 2020, MNRAS, 492, 4680 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Background/foreground emission
To account for the external (background or foreground) emission from sources different from NGC 1052, from the white-light MUSE frame shown in Fig. A.1, we create a ‘sharp-divided’ image (see Márquez et al. 1999, 2003). This is obtained by dividing the original image by a filtered version of it (generated using the IRAF using the command ‘median’ with a box of 15 pixels per side). In the final sharp-divided image the identification of features departing from axisymmetry is facilitated (see e.g. Cazzoli et al. 2018; Hermosa Muñoz et al. 2020).
Then we used the sharp-divided image as input for the EXTRACTOR tool as part of the Graphical Astronomy and Image Analysis (GAIA; Draper et al. 2009) package through the STARLINK software (Currie et al. 2014) currently supported by the East Asian Observatory. We considered a 4σ threshold, a minimum area of 8 pixels (in order to avoid the inclusion of noise-spikes), and MUSE parameters from the manual (detector gain: 1.1 ADU/e−, readout noise: 2.6 e−, and saturation 65 000 e−). With these prescriptions, we generated a catalogue of putative background and foreground objects.
The catalogue is composed of 104 objects (excluding the NGC 1052 nucleus), which are shown in Fig. A.1 in different colours and listed in Table A.1 along with their positions. Of these, 18 (in red in Fig. A.1) are present in the NED database (within less than 3″ from the position measured in the MUSE field) being classified either as ‘Infrared source’, ‘Radio source’, ‘X-ray Source’, ‘UltraViolet Source’, or ‘Star Cluster’.
We visually inspected the spectra of the remaining 85 objects. For the large majority of these spectra (74 out of 85, green symbols in Fig. A.1) the Hα line is clearly visible, either in emission or in absorption, at the same redshift of NGC 1052 (see Table 1). Hence, we consider these sources as part of the galaxy. The remaining 11 of the 85 sources are mostly located at the edge of the MUSE field of view with barely detected emission or absorption lines in their (noisy) spectra. Hence these will be considered as non-detections (yellow symbols in Fig. A.1).
 |
Fig. A.1. White light image of NGC 1052 from MUSE datacube. The different symbols indicate the sources listed in Table A.1. See text for the colour-coding. |
Only in two cases do the spectra show a strong continuum and evident emission-line features, typically of emission-line galaxies. These are ID numbers 1 and 19 in Table A.1, and are marked in cyan in Fig. A.1. Source 1 has a counterpart in NED with identification SDSSCGB 67616.02, but with no redshift mentioned. In our data the Hα emission is observed at a wavelength of 6761.86 Å, resulting in a redshift measurement of 0.0303. Source 19 is not present in the NED database (within 3″ of its measured position). The Hα emission peaks at 7999.09 Å, hence the redshift is ∼0.2189. The spectra of both galaxies are shown in Fig. A.2, along with an example of the spectrum of a source having Hα in emission or absorption at the same redshift as NGC 1052, for comparison.
 |
Fig. A.2. Spectra of the objects with ID numbers 1, 19, and 4 from Table A.1 (see also Fig. A.1). The right panel shows a zoomed-in view of the spectra region around Hα. The green lines indicate the wavelength of Hα at the redshift of NGC 1052 (z = 0.005, Table 1). The magenta lines in the first and second panels indicate the wavelength of Hα at the corresponding redshift (see text for details). |
The emission from the two external galaxies was masked out from the final MUSE datacube used for the analysis, whereas that of sources at the same redshift of NGC 1052 were included.
Coordinates of the sources in Fig. A.1.
Appendix B: Spectral maps
The first part of this appendix is devoted to presenting the ionised gas velocity, velocity dispersion, and flux maps for NGC 1052 from MUSE and MEGARA data, for the two spatially resolved components detected (Sect. 4). In the second part, we show maps for the line ratios of the standard diagnostic diagrams used to pinpoint the ionisation mechanisms of the ISM gas in NGC 1052.
As for the figures in the main text, north is at the top and east to the left in all the panels. The centre (0,0) is identified with the photometric centre (see Fig. 1). The black solid line indicates the major axis of the stellar rotation (i.e. 122°, Table 4). The dot-dashed square indicates the MEGARA field of view, as in Fig. 8.
Flux intensity maps are in units of erg s−1 cm−2 and mJy for MUSE and MEGARA, respectively, and are displayed in logarithmic scale. Line fluxes are not converted to a common unit as we are mainly interested in the analysis of line ratios and we do not compare directly the line fluxes of the two data sets (e.g. due to differences in spatial resolution).
 |
Fig. B.1. [O III]λ5007 velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (erg s−1 cm−2) maps for the narrow component. The maps are as in the lower panel of Fig. 5, and are included here as reference. The black solid line indicates the major axis of the stellar rotation (Table 4). The dashed lines indicate the orientation of the radio jet (Table 1). |
 |
Fig. B.4. Maps of velocity dispersion and flux for the [S II]λ6730 line, and the [S II] flux ratio for the primary component. The lines, symbols, and contours are as in Fig. B.1. |
 |
Fig. B.5. As in Fig. B.1, but for the second component and for a smaller field of view (similar to the MEGARA footprint). |
 |
Fig. B.8. As in Fig. B.4, but for the second component and for a smaller field of view (similar to the MEGARA footprint, see Fig. B.5). |
 |
Fig. B.9. Maps of velocity, velocity dispersion, and flux maps for the narrow component from the MEGARA cube. The flux maps correspond to the lines tied together, e.g. the [S II] doublet and Hα-[N II] complex, see Sect. 3.3. The lines and symbols are as in Fig. B.1. |
 |
Fig. B.10. Same as Fig. B.9, but for [O I]. This line has been modelled separately from [S II] (see Sect. 3.3). |
 |
Fig. B.11. As in Fig. B.9, but for the second component. |
 |
Fig. B.12. As in Fig. B.11, but for the [O I] line. |
 |
Fig. B.13. Maps of the standard BPT line ratios (labelled at the top) for the narrow component (see also Fig. 6). The lines are as in Fig. B.1. |
 |
Fig. B.14. As in Fig. B.13, but for the second component and for a smaller field of view (similar to the MEGARA footprint, see e.g. Fig. B.5). |
 |
Fig. B.15. Maps of the standard BPT line ratios (labelled on the top) for the narrow component. The lines are as in Fig. B.1. |
 |
Fig. B.16. As in Fig. B.15, but for the second component. The long-dashed line gives the PA of the 20 cm emission (Table 1), as in Fig. B.5. |
Appendix C: Position-velocity and position-dispersion diagrams
This appendix is devoted to the present position-velocity (P-V, top) and position-dispersion (P-σ, bottom) for the primary component used to model the emission lines in NGC 1052 (MUSE data).
Both diagrams suggest that the kinematics of the stars is completely decoupled from that of the ionised gas. The stellar P-V and P-σ curves show a clear signature of a rotating disc, whereas this is not the case for the gas component. Specifically, along both major and minor photometric axis (left and centre panels) the ionised gas shows a very perturbed P-V curve as well as an asymmetric and not centrally peaked P-σ curve.
The curves extracted from the slit aligned according to the radio jet do not show any intriguing features.
 |
Fig. C.1. Position-velocity (P-V, top) and position-dispersion (P-σ, bottom) curves of the stellar (black) and gas component of NGC 1052 from the MUSE data. Specifically, the gas component is probed via the [O III] (magenta), [O I] (blue), and H α (green) emission lines. Similarly to Fig. 11 the curves were obtained considering a pseudo-slit 1″ in width aligned according to the major (left) and minor (centre) axis of the rotation, as well as the axis of the radio jet (right). The position angles are listed in Tables 1 and 4. Velocities are centred to the kinematic centre, and the radius is calculated as the distance from the photometric centre. The grey dashed lines show zero points for position and velocity, as reference. |
All Tables
All Figures
 |
Fig. 1. Optical continuum images computed from MUSE (left) and MEGARA (right) in units of erg s−1 cm−2 (logarithmic scale). To obtain these images we considered a 60 Å wide continuum band (6105 − 6165 Å). The cross is the photometric centre, and the sizes of the different PSFs for MEGARA and MUSE data are indicated in the bottom left part of the figure (see also Sect. 2). As reference we show the field of view (dashed rectangle) and average seeing (1 |
| In the text | |
 |
Fig. 2. Example of stellar continuum modelling and its subtraction for high S/N nuclear spectra from MUSE (top panel) and MEGARA (bottom panel) data. The red line indicates the modelled stellar spectrum that matches the observed continuum, obtained applying the pPXF (Sect. 3.2). The wavelength regions blocked for the modelling are shown in grey. Spectral features are labelled at the top, and Balmer lines, forbidden lines, and absorption lines are shown in green, blue, and pink, respectively. In case of MEGARA we combined the cubes in LR-V and LR-R bands, which have a 70 Å overlap around 6130 Å (see Sect. 2.2). |
| In the text | |
 |
Fig. 3. NGC 1052 stellar kinematics maps from our pPXF analysis (Sect. 3.2). These maps, velocity (left) and velocity dispersion (right), are displayed in units of km s−1. In both panels the large-scale kinematics are obtained from MUSE data, whereas the insets show the smoothed pPXF-maps from MEGARA datacube. The cross indicates the photometric centre as in Fig. 1. |
| In the text | |
 |
Fig. 4. Examples of emission line spectra (black) after stellar subtraction (Sect. 3.2) and their modelling from the central region of both MUSE data (R = 0 |
| In the text | |
 |
Fig. 5. Example of emission line maps produced from the fitting of the [O III]λ5007 line using the MUSE ISM cube (Sect. 3.3.1). Shown, from left to right, are the maps for the primary component: velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (erg s−1 cm−1, log scale). The black solid line indicates the major axis of the stellar rotation (Table 4). The dot-dashed square indicates the MEGARA field of view. The contours indicate the central region at high velocity dispersion (see Sect. 4.2.3 for details). Top: maps covering a smaller field of view with respect to the original MUSE mosaic (80″ × 80″, Sect. 2.1) to highlight weak features. The dashed square indicates the selected zoomed-in view in the bottom panels of this figure and for Figs. B.1–B.13. Bottom: zoomed-in area. The dashed line indicates the orientation of the radio jet (Table 1). |
| In the text | |
 |
Fig. 6. Optical standard BPT diagrams for the primary component for the gas distributed in the polar direction and that in the central region at high-σ (top and bottom panels, respectively) obtained from MUSE data. The grey circles indicate the data points presented in this paper. The black lines in all diagrams represent the dividing curves between H II star-forming regions, Seyferts, and LINERs from Kewley et al. (2006) and Kauffmann et al. (2003). The pink boxes show the predictions of the photoionisation models by pAGB stars for Z = Z⊙, a burst age of 13 Gyr (Binette et al. 1994), and ionisation parameter values (log U) between −3 and −4. Log U is typically −3.5 in LINERs (Netzer 2015). The predictions of shock-ionisation models are overlaid in each diagram. Specifically, following Cazzoli et al. (2018), shock+precursor grids from Groves et al. (2004) are considered with Z = Z⊙ and for different ne. The blue and red curves correspond to models with ne = 1 cm−3 and ne = 100 cm−3, respectively (see also Sect. 4.2.1). The values plotted correspond to the minimum and maximum preshock magnetic field allowed in each model. In addition, only shock-velocities from 100 to 500 km s−1 (yellow dashed lines) are considered as larger σ are not observed for the primary component (Sect. 4.2.1). The dividing line between weak-[O I] and strong-[O I] LINERs (Filippenko & Terlevich 1992) is shown in black with a dashed line (right panels). In all diagrams, green symbols indicate the average values calculated in the polar (cross) and central (square) regions; as reference the cyan star is the typical value in the nucleus (average within the PSF region). In the top panels the pink diamond, black triangle, and black upside down triangle are the average BPT values for the faint features: the arm, the east, and south-east clumps, respectively (see Sect. 4.2.5). These features are not detected in [O I], hence no symbols are displayed in the corresponding diagnostic diagrams. |
| In the text | |
 |
Fig. 7. Same as Fig. 6, but for the secondary component. Shock models (no precursor) are considered; the blue and red curves correspond to models with ne = 100 cm−3 and ne = 1000 cm−3, respectively (see Sect. 4.2.4). The green triangle indicates the average value of the line ratio distribution. |
| In the text | |
 |
Fig. 8. NaD EW map (in Å) from MUSE cube. The dot-dashed square indicates the MEGARA field of view. The black solid line indicates the major axis of the stellar rotation (Table 4). The contours indicate the region with enhancement velocity dispersion of emission lines (see Sect. 4.2.3 and e.g. Fig. 5). |
| In the text | |
 |
Fig. 9. Example of absorption line spectra (black) after stellar subtraction (Sect. 3.2) and their modelling from the central region of MEGARA data (R = 1 |
| In the text | |
 |
Fig. 10. Neutral gas velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (mJy) maps for the single kinematic component used to model NaD. The black lines are as in Fig. B.11. Specifically, the black solid line indicates the major axis of the stellar rotation (Table 4). The dashed lines indicate the orientation of the radio jet (Table 1). The contours indicate the region at high velocity dispersion (Sect. 5.4 for details). |
| In the text | |
 |
Fig. 11. Position-velocity (P-V, top) and position-velocity dispersion (P-σ, bottom) curves of the stellar component of NGC 1052 from MUSE data (Sect. 4.1). Both curves were obtained considering a pseudo-slit of 1″ in width aligned according to the major axis of the rotation (i.e. 112°, Table 4). Velocities are centred to the kinematic centre, and the radius is calculated as the distance from the photometric centre. In the top panel the blue and red symbols indicate the approaching (negative velocities) and receding sides (positive velocities) of the rotation, respectively. The green lines give the Reff (21 |
| In the text | |
 |
Fig. 12. Cartoon illustrating the proposed scenario for the stellar component and the ionised ISM for NGC 1052 (see text for details). |
| In the text | |
 |
Fig. A.1. White light image of NGC 1052 from MUSE datacube. The different symbols indicate the sources listed in Table A.1. See text for the colour-coding. |
| In the text | |
 |
Fig. A.2. Spectra of the objects with ID numbers 1, 19, and 4 from Table A.1 (see also Fig. A.1). The right panel shows a zoomed-in view of the spectra region around Hα. The green lines indicate the wavelength of Hα at the redshift of NGC 1052 (z = 0.005, Table 1). The magenta lines in the first and second panels indicate the wavelength of Hα at the corresponding redshift (see text for details). |
| In the text | |
 |
Fig. B.1. [O III]λ5007 velocity field (km s−1), velocity dispersion (km s−1), and flux intensity (erg s−1 cm−2) maps for the narrow component. The maps are as in the lower panel of Fig. 5, and are included here as reference. The black solid line indicates the major axis of the stellar rotation (Table 4). The dashed lines indicate the orientation of the radio jet (Table 1). |
| In the text | |
 |
Fig. B.2. As in Fig. B.1, but for [O I]λ6300. |
| In the text | |
 |
Fig. B.3. As in Fig. B.1, but for Hα. |
| In the text | |
 |
Fig. B.4. Maps of velocity dispersion and flux for the [S II]λ6730 line, and the [S II] flux ratio for the primary component. The lines, symbols, and contours are as in Fig. B.1. |
| In the text | |
 |
Fig. B.5. As in Fig. B.1, but for the second component and for a smaller field of view (similar to the MEGARA footprint). |
| In the text | |
 |
Fig. B.6. As in Fig. B.5, but for [OI]λ6300. |
| In the text | |
 |
Fig. B.7. As in Fig. B.5, but for Hα. |
| In the text | |
 |
Fig. B.8. As in Fig. B.4, but for the second component and for a smaller field of view (similar to the MEGARA footprint, see Fig. B.5). |
| In the text | |
 |
Fig. B.9. Maps of velocity, velocity dispersion, and flux maps for the narrow component from the MEGARA cube. The flux maps correspond to the lines tied together, e.g. the [S II] doublet and Hα-[N II] complex, see Sect. 3.3. The lines and symbols are as in Fig. B.1. |
| In the text | |
 |
Fig. B.10. Same as Fig. B.9, but for [O I]. This line has been modelled separately from [S II] (see Sect. 3.3). |
| In the text | |
 |
Fig. B.11. As in Fig. B.9, but for the second component. |
| In the text | |
 |
Fig. B.12. As in Fig. B.11, but for the [O I] line. |
| In the text | |
 |
Fig. B.13. Maps of the standard BPT line ratios (labelled at the top) for the narrow component (see also Fig. 6). The lines are as in Fig. B.1. |
| In the text | |
 |
Fig. B.14. As in Fig. B.13, but for the second component and for a smaller field of view (similar to the MEGARA footprint, see e.g. Fig. B.5). |
| In the text | |
 |
Fig. B.15. Maps of the standard BPT line ratios (labelled on the top) for the narrow component. The lines are as in Fig. B.1. |
| In the text | |
 |
Fig. B.16. As in Fig. B.15, but for the second component. The long-dashed line gives the PA of the 20 cm emission (Table 1), as in Fig. B.5. |
| In the text | |
 |
Fig. C.1. Position-velocity (P-V, top) and position-dispersion (P-σ, bottom) curves of the stellar (black) and gas component of NGC 1052 from the MUSE data. Specifically, the gas component is probed via the [O III] (magenta), [O I] (blue), and H α (green) emission lines. Similarly to Fig. 11 the curves were obtained considering a pseudo-slit 1″ in width aligned according to the major (left) and minor (centre) axis of the rotation, as well as the axis of the radio jet (right). The position angles are listed in Tables 1 and 4. Velocities are centred to the kinematic centre, and the radius is calculated as the distance from the photometric centre. The grey dashed lines show zero points for position and velocity, as reference. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.