EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 650 (June 2021) A&A, 650 (2021) A132 Full HTML
Open Access
Issue
A&A
Volume 650, June 2021
Article Number A132
Number of page(s) 14
Section Planets and planetary systems
DOI https://doi.org/10.1051/0004-6361/202039811
Published online 17 June 2021

© S. Savvidou and B. Bitsch 2021

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Open Access funding provided by Max Planck Society.

1 Introduction

Observational data have so far shown that planets of a few Earth masses are one of the most abundant groups of planets in the exoplanetary systems (e.g., Borucki et al. 2010; Batalha et al. 2013; Fressin et al. 2013; Petigura et al. 2013; Mulders et al. 2018). Additionally, the super-Earth planets have recently been shown to be of similar sizes within the same planetary system (Weiss et al. 2018), even though this was put into question by another analysis (Zhu et al. 2018). It is therefore of utmost interest to understand the mechanisms leading to their formation, especially given the fact that super-Earths are absent from the Solar System (Martin & Livio 2015).

The formation of planets is initiated by the coagulation (Weidenschilling 1980, 1984; Brauer et al. 2008; Zsom et al. 2011; Birnstiel et al. 2012; Testi et al. 2014) and condensation (Ros & Johansen 2013) of small dust particles, or nucleation on icy particles (Ros et al. 2019). There are several conditions that limit dust growth, such as the fragmentation barrier, the bouncing barrier, and the radial drift barrier (Brauer et al. 2007; Birnstiel et al. 2010; Zsom et al. 2010). However, these barriers help in the rapid formation of millimeter- to centimeter-sized particles or pebbles, which is an essential contributor to planet formation.

Planet formation can continue with the creation of larger bodies, for example via the streaming instability where the dust particles concentrate into filaments with sufficient densities to gravitationally collapse into planetesimals (Youdin & Goodman 2005; Johansen & Youdin 2007; Youdin & Johansen 2007; Chiang & Youdin 2010). In the classical core accretion scenario, a sufficiently large planetesimal serves as a planetary embryo, which accretes other planetesimals, and forms the planetary core (Pollack et al. 1996; Helled et al. 2014, for a review). However, this procedure has some drawbacks, among others the growth timescale, which can be even longer than the lifetime of the protoplanetary disk (Pollack et al. 1996; Rafikov 2004; Levison et al. 2010; Lambrechts & Johansen 2012; Fortier et al. 2013; Johansen & Bitsch 2019), unless the dust density is significantly enhanced (Kobayashi et al. 2011).

One of the proposed mechanisms to form super-Earths is the accretion of pebbles (millimeter- to centimeter-sized particles) onto a preexisting planetesimal or protoplanet (Johansen & Lacerda 2010; Ormel & Klahr 2010; Lambrechts & Johansen 2012; Ormel et al. 2017; Johansen & Lambrechts 2017). The accretion of solids is not limited by the available material closely around the planetary seed, but is aided by the drift of small solids or pebbles (Weidenschilling 1977). Pebble accretion thus acts on much shorter timescales compared to planetesimal accretion, especially in the outer disk regions (Lambrechts & Johansen 2014; Bitsch et al. 2015a; Lambrechts et al. 2019; Izidoro et al. 2021; Johansen & Bitsch 2019).

In this work, we focus on the accretion of the small particles by an already formed planetary seed. The planet grows until it reaches the pebble isolation mass (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014; Ataiee et al. 2018; Bitsch et al. 2018; Surville et al. 2020); it then carves a gap in the protoplanetary disk, thus trapping the pebbles in a pressure trap exterior to the planet. This critical mass depends on the disk parameters, mainly the aspect ratio, and not on the available amount of solids. Wu (2019) showed that protoplanetary cores could grow to the thermal mass in disks, which corresponds to the typical masses of planets in the mass-constrained subsample of the Kepler systems. Bitsch (2019) expanded on this, showing that the pebble isolation mass could be the main driver for this observation, with a crucial dependence on the underlying protoplanetary disk structure.

The protoplanetary disk structure thus holds most of the key parameters and conditions that define the planet formation mechanisms. On the other hand, the grain size distribution and the subsequent opacity play a very important role in the determination of the disk structure and the disk evolution (Savvidou et al. 2020). A change in opacity directly affects the cooling rate of the disk, and the new thermal structure leads to an updated grain size distribution. The opacity of the disk is then altered because the mass fractions of the grain sizes are different. This feedback loop operates until the disk reaches thermal equilibrium,which means that the resulting disk structure is heavily influenced by the grain size distribution and the opacity provided by the dust grains (Savvidou et al. 2020), and will then determine the evolution of planet formation.

In this work, we obtain disk models from hydrodynamical simulations, including self-consistent grain distribution and opacities according to the grain sizes and compositions, following our previous work (Savvidou et al. 2020). We thus have a framework that allows a self-consistent disk structure with the corresponding pebble sizes to calculate the growth rates of planetary embryos via pebble accretion. We focus on the innermost parts of a disk to study how the grain size distribution and the chemical compositions of the grains affect the formation of super-Earths.

This paper is structured as follows. In Sect. 2, we discuss the different aspects of our model, specifically the opacity prescription and the chosen chemical compositions, the grain size distribution model, the disk parameters, and the prescription for planet growth. In Sect. 3, we present the resulting disk structures from the self-consistent hydrodynamical simulations. We then discuss the pebble isolation masses of planets that could grow in the disks of our model and their growth timescales in Sect. 4. We discuss the implicationsand limitations of our model in Sect. 5, and summarize our findings in Sect. 6.

Table 1

Condensation temperatures and volume mixing ratios for the chemical species used in this work.

2 Methods

2.1 Opacities

We calculate the mean Rosseland, Planck, and stellar opacities as a function of temperature using the RADMC-3D1 code. These mean opacities are used in the energy equations of the protoplanetary disk model. In particular, the energy time evolution utilizes the Planck mean opacity, which uses as a weighting function the Planck black-body radiation energy density distribution (Bλ (λ, T)). The radiation flux is inversely proportional to the Rosseland mean opacity, which is calculated using the temperature derivative of the Planck distribution (∂Bλ(λ, T)∕∂T). Therefore, in contrast to the Planck mean opacity, the Rosseland mean opacity describes the optically thick regions well. For both of the above-mentioned opacities the temperature taken into account is the local disk temperature. However, when we want to describe the absorption of stellar photons, we use the stellar mean opacities, which are calculated in a similar manner to the Planck mean opacities, taking into account the temperature of the stellar radiation (Bλ (T⋆)), assuming isotropic radiation), which in ourmodels is T⋆ = 4370 K.

In contrast to our previous work (Savvidou et al. 2020), where only water ice and silicates were used, we include here all of the major rock- and ice-forming species. We present them in Table 1, along with their volume mixing ratios and mass fractions, following Bitsch & Battistini (2020). We discuss in detail how we obtained these opacities in Appendix A. In Fig. 1, we show the opacity as a function of temperature for six representative grain sizes. The gray vertical dashed lines correspond to the evaporation fronts for the species we include in our model. After each evaporation front, the corresponding species sublimates and no longer contributes to the overall opacity, so the mass fractions are adjusted accordingly.

2.2 Hydrodynamical simulations

The viscosity in the simulations follows an α-prescription (Shakura & Sunyaev 1973). We run simulations with three α-viscosity values, namely α = 10−3, 5 × 10−4, and 10−4, and list all parameters of the model in Table 2.

The gassurface density follows a profile 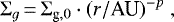Σg = Σg,0⋅(r/AU)−p ,\begin{equation*} \Sigma_{g}\,{=}\,\Sigma_{\textrm{g},0}\cdot (r/\textrm{AU})^{-p}~,\end{equation*}(1)

with p = 1∕2. For each α-viscosity we run a set of four initial gas surface densities, Σg,0 = 100, 500, 1000, and 2000 g cm−2.

In all of the simulations the stellar mass is M⋆ = 1 M⊙, the stellar temperature is T⋆ = 4370 K, and the stellar radius is R⋆ = 1.5 R⊙. The total dust-to-gas ratio is fDG = 1.5%. The disks extend from 0.1 to 4 AU, except for the simulations with Σg,0 = 2000 g/cm−2, where the inner boundary is at 0.2 or 0.3 AU. We do not include gas opacities in our model, hence this was a necessary choice to prevent the overheating of the innermost edge and a strong shadowing that would cool down the rest of the disk. The simulations run until they reach thermal equilibrium. The disk structures from the hydrodynamical simulations are used afterward todetermine the pebble isolation masses and the pebble accretion rates, which we discuss in the following sections.

thumbnail Fig. 1

Rosseland, Planck, and stellar mean opacities (from left to right) as a function of temperature for grain sizes of 0.1 μm, 1 μm, 10 μm, 100 μm, 1 mm, and 1 cm. The composition of the grain mixture is presented in Table 1. The gray dashed lines show the evaporation temperatures of the different species, which are (from lowest to the highest) CO, CH4, CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, Fe2O3, and MgSiO3. The water ice evaporation front is shown as a gray band.
Table 2

Parameters used in the simulations.

2.3 Grain size distribution

In this work, we use the Mathis et al. (1977, MRN) distribution2, where the normalized vertically integrated dust surface densities are calculated at each orbital distance as 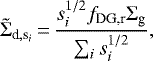Σ˜d,si = si1/2fDG,rΣg∑isi1/2,\begin{equation*}\tilde{\Sigma}_{\textrm{d},\textrm{s}_i} \,{=}\,\frac{s_i^{1/2}f_{\textrm{DG,r}}\Sigma_{\textrm{g}}}{\sum_i s_i^{1/2}},\end{equation*}(2)

with si the grain size and Σg the gas density. In order to calculate these dust surface densities, we consider the evaporation of the chemical species as we move farther-in in the disk and use fDG,r, which is the appropriate fraction of the total dust-to-gas ratio of the disk depending on how many species have evaporated at the given location (Fig. 2).

It is important to note that we do not use a constant upper boundary for the grain sizes. Instead, we use the local disk parameters to calculate the fragmentation barrier as 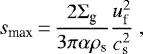smax = 2Σg3παρsuf2cs2 ,\begin{equation*}s_{\textrm{max}}\,{=}\,\frac{2\Sigma_{\textrm{g}}}{3 \pi \alpha \rho_{\textrm{s}}}\frac{u_{\textrm{f}}^2}{c_{\textrm{s}}^2}~, \end{equation*}(3)

with ρs = 1.6 g cm−3 the assumed density of each particle, uf the fragmentation threshold velocity, and cS the sound speed.

The threshold velocity uf corresponds to the threshold after which collisions between particles always lead to fragmentation (Poppe et al. 2000). For this work we test two different fragmentation velocities, uf = 1 m s−1 and uf = 10 m s−1, corresponding to the limits of laboratory experiments (Gundlach & Blum 2015; Musiolik & Wurm 2019).

2.4 Pebble accretion

We start the planetary seeds at 0.01 M⊕, assuming they have already formed. For simplicity, we only take the Hill regime into account, which should start around this planetary mass (Johansen & Lambrechts 2017), and we follow the Lambrechts & Johansen (2014) accretion recipes. This implies that the accretion radius and the accretion rates of the planet are determined by the Stokes numbers of the pebbles: 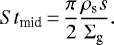Stmid = π2ρssΣg.\begin{equation*}St_{\textrm{mid}}\,{=}\,\frac{\pi}{2}\frac{\rho_{\textrm{s}} s}{\Sigma_{\textrm{g}}}.\end{equation*}(4)

For consistency, for the planet growth we only use the Stokes numbers at midplane because this is the approximation we follow in our hydrodynamical models (see a more detailed discussion on the vertical distribution of the grains in Savvidou et al. 2020). The range of grain sizes at each location of the disk is determined by the local disk properties (see maximum grain size, Eq. (3)).

To define the pebble accretion rate we need to distinguish between the 2D and the 3D regime, depending on how the pebble scale height Hd compares to the effective accretion radius of the planet 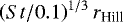(St/0.1)1/3rHill$\left(St/0.1\right)^{1/3}r_{\textrm{Hill}}$, where the Hill radius is 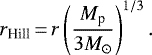rHill = r(Mp3M⊙)1/3.\begin{equation*} r_{\textrm{Hill}}\,{=}\,r\left(\frac{M_{\textrm{p}}}{3M_{\odot}}\right)^{1/3}. \end{equation*}(5)

The 2D pebble accretion rate is 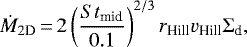M˙2D = 2(Stmid0.1)2/3rHillvHillΣd,\begin{equation*}\dot{M}_{\textrm{2D}}\,{=}\,2\left(\frac{St_{\textrm{mid}}}{0.1}\right)^{2/3}r_{\textrm{Hill}} v_{\textrm{Hill}} \Sigma_{\textrm{d}}, \end{equation*}(6)

with vHill = ΩrHill, 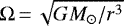Ω = GM⊙/r3$\Omega\,{=}\,\sqrt{GM_{\odot}/r^3}$, and the 3D accretion rate is M˙3D = M˙2D[π(Stmid0.1)1/3rHill22πHd].\begin{equation*}\dot{M}_{\textrm{3D}}\,{=}\, \dot{M}_{\textrm{2D}} \left[\frac{\pi\left(\frac{St_{\textrm{mid}}}{0.1}\right)^{1/3}r_{\textrm{Hill}}}{2\sqrt{2\pi}H_{\textrm{d}}}\right]. \end{equation*}(7)

The transition from the 2D to the 3D regime happens when 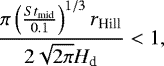π(Stmid0.1)1/3rHill22πHd<1,\begin{equation*} \frac{\pi\left(\frac{St_{\textrm{mid}}}{0.1}\right)^{1/3}r_{\textrm{Hill}}}{2\sqrt{2\pi}H_{\textrm{d}}} < 1, \end{equation*}(8)

following Morbidelli et al. (2015). The dust scale height was derived by Dubrulle et al. (1995): 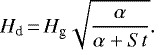Hd = Hgαα+St.\begin{equation*}H_{\textrm{d}}\,{=}\,H_{\textrm{g}}\sqrt{\frac{\alpha}{\alpha &#x002B; St}}.\end{equation*}(9)

We calculate the accretion rates in the 2D and 3D regime for each grain size of the distribution (Eq. (2)), and then add up all of the contribution to get the total accretion rate.

Within this approach we assume that the pebbles that are accreted by the planet are replenished at the planet’s location by radial drift, so that the dust surface density does not change at the planets location during pebble accretion. Future workhas to consider the grain drift and its influence on the disk’s structure with accreting planets more accurately.

thumbnail Fig. 2

Influence of the evaporation of the different chemical species on the dust-to-gas ratio in the protoplanetary disk. Left plot: dust-to-gas ratio in terms of the total dust-to-gas ratio in the disk as a function of temperature. After each species evaporates the total mass fraction decreases by the corresponding mass fraction (see Table 1) until all species evaporate beyond 1500 K. Right plot: example of the dust-to-gas ratio as a function of orbital distance for the disk with α = 10−3, Σg,0 = 2000 g cm−2, and uf = 10 m s−1, and a globaldust-to-gas ratio of 1.5%. Overplotted is the temperature of the disk where the evaporation fronts are easy to locate.

2.5 Pebble isolation mass

Planetary growth halts when the planet reaches the pebble isolation mass. At this mass the planet has accreted enough material so that it carves a gap in the gas of the protoplanetary disk and creates a pressure bump around it (Paardekooper & Mellema 2006). This bump prevents the dust from drifting onto the planet core, and growth via pebble accretion stops (Morbidelli & Nesvorny 2012; Lambrechts et al. 2014; Bitsch et al. 2018; Ataiee et al. 2018; Surville et al. 2020).

The pebble isolation mass has been approximated via hydrodynamical simulations by Bitsch et al. (2018) as 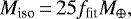Miso = 25ffitM⊕,\begin{equation*}M_{\textrm{iso}}\,{=}\,25 f_{\textrm{fit}} M_{\oplus}, \end{equation*}(10)

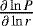with ffit = [H/r0.05]3[0.34(log(0.001)log(α))4+0.66][1−∂lnP∂lnr+2.56],\begin{equation*} f_{\textrm{fit}}\,{=}\,\left[\frac{H/r}{0.05}\right]^3 \left[0.34\left(\frac{\log(0.001)}{\log(\alpha)}\right)^4&#x002B;0.66\right]\left[1-\frac{\frac{\partial\ln P}{\partial\ln r}&#x002B;2.5}{6}\right], \end{equation*}(11)

where ∂lnP∂lnr$\frac{\partial\ln P}{\partial\ln r}$ is the radial pressure gradient. Here we let the planets grow via pebble accretion until they reach the pebble isolation mass and track the time it takes them to monitor whether the planet can reach this mass during the disk’s lifetime. However, we stop the growth at 100 Myr as this time exceeds the lifetime of protoplanetary disks quite clearly (e.g., Mamajek 2009).

2.6 Advantages and limitations of our model

Compared to 1D models, our 2D model has the advantage that the vertical structure is solved self-consistently. Furthermore, shadowing effects inside the disk caused by bumps in the disk structure that block stellar irradiation are self-consistently resolved, leading to an accurate thermal disk structure, which is not possible in 1D models. The 2D models (radial-azimuthal) of Drążkowska et al. (2019) take into account the full coagulation and drift of particles, but are limited to the isothermal approach, thus ignoring the feedback of the grain size distribution on the thermal disk structure.

One-dimensional models, on the other hand, have the possibility to be evolved over several million years (Myr), which is not possible with our 2D models. These 1D models (Birnstiel et al. 2012) can then accurately resolve the time evolution of the grain size distribution, and also investigate pileups of material in the inner disk in time, but they cannot accurately model shadowing effects. Furthermore, 1D models that self-consistently take into account grain growth, grain drift, the corresponding grain opacities, and the resulting thermal structure of the disk do not exist yet. We thus show simulations with increased dust-to-gas ratios in Sect. 4 corresponding to a pileup of grains in the inner regions caused by radial drift (Brauer et al. 2008; Birnstiel et al. 2012).

Our 2D approach allows us to explore the influence of the self-consistent disk models on pebble accretion (admittedly in a simplified way), and to emphasize that the grain size distributions, their corresponding sizes, and compositiondependent opacities affect the disk structure, and in turn the planet formation. This effect thus needs to be included in future planet formation simulations, which to date have mostly operated with disk structures independently of the pebble size distribution (e.g., Bitsch et al. 2015b, 2019; Johansen & Lambrechts 2017; Venturini et al. 2020b).

thumbnail Fig. 3

Aspect ratio (upper plot), temperature (middle plot), and gas surface density (bottom plot) asa function of orbital distance for four different initial gas surface densities, from 100 g cm−2 to 2000 g cm−2. The turbulence parameter in viscosity is α = 10−3 in the left panel, α = 5 × 10−4 in the middle panel, and α = 10−4 in the right panel. The fragmentation velocity is uf = 1 m s−1. The light blue areas in the aspect ratio and temperature plots indicate the evaporation fronts (±2 K around the evaporation temperatures of CH4, CO2 ; ±10 K for the other species). Starting from the outer boundary, for α = 10−3 the species that evaporate are CO, CH4, CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, and MgSiO3. For α = 5 × 10−4 the evaporation fronts are of CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, and MgSiO3 and for α = 10−4 they are CO2, H2O, and Fe3O4. The water ice line is shown as a dashed line.

3 Disk structure

3.1 Dependence on viscosity, gas surface density, and fragmentation velocity

We investigate the influence of different α-viscosities, initial gas surface densities, and fragmentation velocities on the grain sizes and disk structures. The specificvalues used are shown in Table 2. The influence of the different α-viscosities and surface densities Σg,0 on the resulting disk structure is discussed in detail in Savvidou et al. (2020). In a nutshell, as the α-viscosity decreases, the disk gets colder. There are two reasons for this. Since the viscous heating decreases, the disk cools down more efficiently. At the same time the dust particles face less destructive collisions, and grow to larger sizes that have lower opacities. This furtheraids the cooling of the disk.

We present the results of our simulations with different α-parameters and for different initial gas surface densities, utilizing a fragmentation velocity of 1 m s−1 in Fig. 3. Clear trends with viscosity and gas surface density are visible.

Decreasing the gas surface density scales down the total dust surface density. As a consequence, the disk is colder because the viscous heating is less efficient and radiative cooling is enhanced, given that the cooling is inversely proportional to the disk’s density. However, for very low α-viscosity values the difference between disks with different surface density diminishes (Savvidou et al. 2020). We also find that for α = 10−4 (third column in Fig. 3), the aspect ratio of the disks is very low, and is almost independent of the gas surface density. In this case the disk is mainly optically thin and the dominant heating mechanism is stellar irradiation, resulting in very similar disk structures.

The same applies to the simulations using higher fragmentation velocities. In this case larger grains are available and dominate the opacity of the disk, and hence the cooling of the disk is very efficient (Fig. 4 for α = 5 × 10−4 and 10−4). Even for the highest value, α = 10−3 (first column in Fig. 4), the difference in the aspect ratios of disks with varying surface densities is not as pronounced as in the corresponding disks with lower fragmentation velocity (Fig. 3). This shows that the larger grain sizes provide such low opacities that even an α-viscosity of 10−3 cannot heat the disk sufficiently. As a result, the water ice line is already close to 1 AU, even for the highest gas surface density.

In Figs. 3 and 4, we see some radial variations in some of the disk profiles, especially for very low surface densities. This is caused mainly by convection, created by the vertical temperature gradient which depends on the opacity gradient in the vertical direction and is present in the optically thick regions of the disk (Bitsch et al. 2013). However, in this work we have included multiple chemical species in our opacity prescription, and this creates dips in the opacity as a function of temperature at the evaporation fronts of the various species3 (see Fig. 1). Even if these dips are minimal, they can create small bumps in the aspect ratio profiles, which are amplified by the convection and lead to an enhancement of these perturbations.

The protoplanetary disks in our models, or the regions within them, that are not strongly affected by convection do not show a significant influence from the multiple evaporation fronts of the chemical species we have included because the changes in the opacity are small. The strongest effect remains with the evaporation of water ice, which causes a strong dip in the opacity and hence a more enhanced bump in the aspect ratio (Figs. 3 and 4). Nevertheless, the overall opacity is slightly different to a prescription where only water ice and silicates are used (Savvidou et al. 2020). In addition, including multiple chemical species is important because they could be used in future work to predict the possible compositions of the planets growing within the disks of our models.

In our previous work (Savvidou et al. 2020), we discuss the dependence of the water ice line position on the α-viscosity, the gas surface density, and the dust-to-gas ratio. We also find here that it moves farther in if the gas surface density or the α-viscosity decreases. Here, we also use uf = 10 m s−1, and find that the higher fragmentation velocity moves the ice line inward compared to uf = 1 m s−1. This has consequences, not only for the planet formation mechanisms, but also for the potential compositions of the created planets (Bitsch et al. 2019; Schoonenberg et al. 2019; Venturini et al. 2020b). A more detailed discussion about planet growth within the disks of our models follows in Sect. 4.

thumbnail Fig. 4

Same as Fig. 3, but using a fragmentation velocity of uf = 10 m s−1. Starting from the outer boundary, for α = 10−3 the species that evaporate are CO2, H2O, Fe3O4, C, and FeS. For α = 5 × 10−4 the ice lines are of CO2, H2O, Fe3O4, C, and FeS and for α = 10−4 they are CO2 and H2O. The water ice line is shown as a dashed line.

3.2 Disk evolution

Our 2D hydrodynamical models cannot be integrated over several Myr, due to computational limitations. Instead, the disk evolution can be mimicked by reducing the overall gas surface density, where lower disk surface densities correspond to lower stellar accretion rates, and thus to older disks (Hartmann et al. 1998). As a consequence the viscous heating is reduced and the disks become colder as they age. However, assigning an absolute age to the disk structures presented here is difficult because the exact time evolution of a disk depends on more than just the viscosity and the gas surface density, and because disk winds can drive the evolution of the disk (Bai et al. 2016; Suzuki et al. 2016).

In our model, the evaporation fronts of different solids depend on the temperature (Table 1) and consequently are also closer to the central star in disks with lower gas surface density. At the evaporation fronts, solids evaporate and the solid surface density is thus reduced (Fig. 2), leading to lower opacities and more efficient cooling, which can cause bumps in the disk structure if the solid abundances change by a large factor, for example at the water ice line. However, the maximum pebble size by fragmentation does not change because the maximum pebble size does not depend on dust surface density (Eq. (3)). As a consequence, the pebble sizes are smooth across the evaporation fronts, implying that even if disk evolution over several Myr was taken into account, it would happen smoothly and no bumps or dips will be generated at the evaporation fronts. As the disk becomes older and its surface density reduces in time, the maximum pebble size increases. We discuss the consequences of this on planet formation via pebble accretion in the next section.

4 Planet formation

An important implication that can be derived from the disk structures of the presented models is that the aspect ratio profiles, independently of the parameters used, are almost constant with orbital distance. This is expected in these inner regions where viscous heating dominates over stellar irradiation, which would flare up the disk (Chiang & Goldreich 1997; Dullemond & Dominik 2004; Bitsch et al. 2015a; Ida et al. 2016; Savvidou et al. 2020).

The implication of this observation is that the planetary systems that could potentially form in these disks would have very similar masses since the pebble isolation mass depends on the aspect ratio (see Eq. (10)). It has been recently observed among the Kepler systems that planets within the same system have similar sizes (Weiss et al. 2018). Millholland et al. (2017) suggested that the “peas-in-a-pod” trend is also true for the planetary masses within the same system.

We now compare the pebble isolation masses derived from our disk simulations with the super-Earth population, and then discuss planetary growth within these disk environments. We note here again that disks with high gas surface densities could correspond to young disks, while the disks with low gas surface densities could correspond to older disks. As the exact time evolution of disks is complicated (e.g., Bai et al. 2016; Suzuki et al. 2016) and not self-consistently included in our model, we do not link our disk structures to a time evolution, but just discuss the implications of the fixed-disk structures on planetary growth via pebble accretion under the simple assumption that the disk structure does not evolve over time.

4.1 Pebble isolation mass

We use the equilibrium disk structures from the 2D hydrodynamical simulations to study the growth of super-Earths via pebble accretion. Itis assumed that planets grow to the pebble isolation mass because then they carve a gap in the protoplanetary disk and create apressure bump exterior to their orbits which traps pebbles and prevents them from being accreted. We thus calculate the pebble isolation mass for each of our disk models to find the maximum mass that our planets could reach. The pebble isolation mass (Eq. (10)) depends on the disk structure and, specifically, its aspect ratio, α-viscosity, and the radial pressure gradient. We present the pebble isolation mass derived from our hydrodynamical simulations in Fig. 5 and Fig. 6, where we also overplot the masses of close-in super-Earths inferred, using a mass–radiusrelationship (Chen & Kipping 2017) from the Kepler observations and for planets with RV mass determinations.

The aspect ratio profiles for the disk range in our models are almost constant with orbital distance, so we expect and find a low dependence of the pebble isolation mass on the orbital distance. For α = 10−3 and uf = 1 m s−1 the pebble isolation mass reaches almost 19 M⊕ for the highest initial gas surface density, Σg,0 = 2000 g cm−2. With the same fragmentation velocity and α = 5 × 10−4 we still get high enough isolation masses that match the majority of the observed super-Earths and mini-Neptunes, mainly for the highest surface density, Σg,0 = 2000 g cm−2. However, forlower α-values or higher fragmentation velocities the pebble isolation mass hardly exceeds 3–4 M⊕. This also means that with these sets of parameters it is hard to explain the bulk of the masses of close-in super-Earths and mini-Neptunes by pure pebble accretion.

Increasing the fragmentation velocity to uf = 10 m s−1, we find that the pebble isolation masses are significantly reduced. This happens because of the larger particles (Eq. (3)), which lead to a smaller aspect ratio (see Sect. 3 and Eq. (10)). The highest mass we find is around 5 M⊕ for α = 10−3 and again the highest initial gas surface density, Σg,0 = 2000 g cm−2. For the rest of the simulations, the pebble isolation mass is so low that the masses of the inner super-Earths might not be reached without a significant number of collisions between the bodies.

Considering only the pebble isolation masses of the disks discussed here, we can conclude that in order to explain the inferred masses from Kepler detections, we would need a relatively high viscosity of α = 10−3. However, it is also important to consider whether pebble accretion can operate efficiently enough so that the planets reach these masses in a timely manner. We discuss this in the following section.

thumbnail Fig. 5

Pebble isolation mass as a function of orbital distance for disks with four different initial gas surface densities, from 100 g cm−2 to 2000 g cm−2. The turbulence parameter in viscosity is α = 10−3 in the left panel, α = 5 × 10−4 in the middle panel, and α = 10−4 in the right panel. The fragmentation velocity is uf = 1 m s−1. We also include the planetary masses of Kepler systems, with radii up to 4 R⊕, derived through the Forecaster package (Chen & Kipping 2017) (gray circles) and super-Earths detected by RV (blue circles). The dashed lines correspond to the disk regions interior to the ice line, whereas the solid lines are the regions exterior to the ice line, where the forming planets are water rich.
thumbnail Fig. 6

Same as Fig. 5, but for a fragmentation velocity of uf = 10 m s−1.

4.2 Planet growth until pebble isolation mass

To study planet growth we calculate the pebble accretion rate using Eqs. (6) and (7). The Stokes numbers are determined by the MRN distribution. For simplicity, we ignore planetary migration. We show the maximum Stokes numbers as a function of orbital distance in the upper plots of Figs. 7 and 8 for all of the parameters used. The Stokes numbers are inversely proportional to the gas density of the disk (Eq. (4)). The maximum Stokes numbers are hence an increasing function of the orbital distance. They also show some radial variations for the same reason.

We show the growth timescales for our different simulations in the bottom plots of Figs. 7 and 8. These timescales represent the time it takes for the planets to reach the pebble isolation mass at the given orbital distance (Figs. 5 and 6) accreting pebbles with a size distribution corresponding to the planets’ locations. The growth timescales are not entirely smooth. This is related, firstly, to the variations in the Stokes number (upper plots of Figs. 7 and 8 for the maximum values). Secondly, there are also some variations in the dust surface density because of the evaporation fronts (see the steps for the dust-to-gas ratio in Fig. 2).

When considering the time it takes to reach the isolation masses, it is important to compare it with the time of the gas dispersal (gray band in the bottom plots of Figs. 7 and 8). After this event, planets can continue to grow via mutual collisions; however, the formation pathway is different, and if the planets have not reached sufficient masses already, they will end up being terrestrial rather that super-Earths (Lambrechts et al. 2019).

For fragmentation velocities of 1 m s−1 and α = 10−3 pebble accretion is inefficient in the inner disk regions (with a slight dependence on the gas surface density, Fig. 7), and thus longer than the typical lifetimes of protoplanetary disks. These timescales get significantly shorter for a decrease in the α-viscosity or an increase in the fragmentation velocity to 10 m s−1 (Fig. 8), which allow larger grains to be accreted (Eq. (3)), enhancing pebble accretion (Eqs. (6) and (7)). Our simulations thus indicate that either a low α-viscosity or larger grain fragmentation velocities are needed to allow fast enough growth via pebble accretion.

In Fig. 9, we show the planetary growth of embryos located at 1 AU as a function of time for planets growing in disks with Σg,0 = 2000 g cm−2 for all α-viscosities and fragmentation velocities. The planet grows fastest in environments with low viscosities and large fragmentation velocities. However, the pebble isolation mass is small in these cases. Only for cases of high α and low fragmentation velocity is the pebble isolation mass high enough to match the observed exoplanet population.

The larger grains carry lower opacities, which enhances the cooling of the disk. The low temperature also translates to a low aspect ratio (Fig. 4), hence the isolation masses are very low (Fig. 6), and even though the timescales to reach them are very short, the planets that could potentially form cannot explain the majority of the masses of super-Earths and mini-Neptunes. The best options for sufficiently high isolation masses and short growth timescales are α = 10−3 and uf = 10 m s−1, which leads to masses from 0.4 to 5.7 M⊕, depending on the gas surface density and the orbital distance.

In the following section, we explore whether planet formation at earlier stages (high gas surface densities) and higher dust-to-gas ratios could increase the pebble isolation mass and keep the planetary growth timescales short at the same time.

thumbnail Fig. 7

Maximum Stokes number (top plot) and planetary growth timescale until the pebble isolation mass is reached (bottom plot) as a function of orbital distance, for the disks with the four different initial gas surface densities: α = 10−3 (left plot), α = 5 × 10−4 (middle plot), α = 10−4 (right plot), and uf = 1 m s−1. The gray lines show the typical lifetime range of a protoplanetary disk of 3–10 Myr.
thumbnail Fig. 8

Same as Fig. 7, but for uf = 10 m s−1.
thumbnail Fig. 9

Planetary mass as a function of time for the simulations with Σg,0 = 2000 g cm−2, all α-viscosities, and both of the fragmentation velocities at 1 AU. The dots give the final planetary mass determined by the pebble isolation mass (Figs. 5 and 6). The growth timescale is longer than 10 Myr in disks with α > 5 × 10−4 when particle collisions are limited by a fragmentation velocity of 1 m s−1.

4.3 Testing higher dust-to-gas ratio, gas surface density, and initial planetary seed mass

We have concluded that the best parameters for super-Earth formation via pebble accretion are α = 10−3 and uf = 10 m s−1. In this case, the pebble isolation mass is reached before the dispersal of the gaseous disk regardless of the surface density and the location within the disk. The isolation mass itself depends on the surface density and with the highest surface density (Σg,0 = 2000 g cm−2) planets of around 5 M⊕ could form by pure pebble accretion.

We investigate here how higher gas surface densities and higher dust-to-gas ratios influence the pebble isolation masses and the accretion times by pebble accretion. We show in Fig. 10 (top and middle panels) the pebble isolation masses and the maximum Stokes numbers from the additional simulations. We used two different total dust-to-gas ratios (fDG = 2% and fDG = 3%) with Σg,0 = 2000 g cm−2, and a higher gas surface density of Σg,0 = 5000 g cm−2 for the nominal total dust-to-gas ratio (fDG = 1.5%).

The difference between the nominal dust-to-gas ratio and the 2% value is very small, so the pebble isolation masses are very similar. We find slightly higher pebble isolation masses with a dust-to-gas ratio of 3%, but the strongest improvement comes from the simulation with Σg,0 = 5000 g cm−2. In this case, the maximum pebble isolation masses can be around 11 M⊕ near the outer boundary of the disk.

The growth timescales (bottom panel in Fig. 10) are also very similar between the simulation with the nominal total dust-to-gas ratio and the one with fDG = 2%. If we double the amount of solids (fDG = 3%), then the growth timescale is longer because of the higher isolation mass and the similar maximum Stokes numbers. If we increase the gas surface density to Σg,0 = 5000 g cm−2, there is enough material to accrete pebbles fast enough and reduce the growth timescale compared to the high dust-to-gas ratio simulations; however, it is very similar to the nominal simulation.

In Fig. 11, we show how the growth timescales change depending on the assumed initial mass of the planetary seed. We compare our nominal simulations with α = 10−3 and α = 5 × 10−4 for uf = 1 m s−1 and an initial planetary mass of Minit = 0.01 M⊕ with an increased initial mass of Minit = 0.1M⊕. We only used Σg,0 = 2000 g cm−2 because thissurface density leads to the highest pebble isolation masses. The higher initial mass reduces the growth timescale, but the difference is small and for most of the regions of the inner disks the pebble isolation mass is not reached within the lifetime of the disk.

thumbnail Fig. 10

Pebble isolation mass (top plot), maximum Stokes number (middle plot), and planetary growth timescale until the pebble isolation mass is reached (bottom plot) as a function of orbital distance, for disks with α = 10−3 and uf = 10 m s−1. Shown are disks with higher dust-to-gas ratios, fDG = 2% and fDG = 3% and higher initial surface density Σg,0 = 5000 g cm−2. For reference the nominal run with Σg,0 = 2000 g cm−2 and fDG = 1.5% is included.
thumbnail Fig. 11

Planetary growth timescale until the pebble isolation mass is reached as a function of orbital distance with initial planetary seed masses Minit = 0.1 M⊕. We tested two α-viscosities, 10−3 and 5 × 10−4 with a fragmentation velocity, uf = 1 m s−1. Overplotted are the nominal disk models with initial planetary seed masses Minit = 0.01 M⊕.

5 Discussion

5.1 Planet growth

The aspect ratios and the temperatures in our disks are relatively low, as expected for the low viscosity we used (Savvidou et al. 2020). The same is true for the disks with higher fragmentation velocities (uf = 10 m s−1 in contrast to uf = 1 m s−1) because the collisions are less destructive and the larger particles, which are allowed, carry lower opacities. In the context of pebble accretion, this means that the pebble isolation masses we calculate do not correlate sufficiently with the bulk of the planetary masses that are observations unless α = 10−3 and uf = 1 m s−1. In this specific case, we have small enough particles, so that the opacity is sufficient to prevent significant cooling and hence high enough aspect ratios.

However, in order to have fast growth of the planets, we need either α ≤ 10−4 and uf = 1 m s−1 or any α ≤ 10−3 and uf = 10 m s−1 (Figs. 7 and 8) since the maximum Stokes numbers are up to two orders of magnitude larger (Figs. 5 and 6). Therefore, there seems to be a trade-off between the possible pebble isolation mass and the timescale to reach it. The most efficient parameters that provide both high enough isolation masses and short enough timescales are α = 10−3 and uf = 10 m s−1.

Venturini et al. (2020b) find that α < 10−4 is needed to reach the pebble isolation mass in time. The maximum masses they find are around 7 M⊕ for an α = 10−5. They use slightly different parameters for their nominal runs (e.g., initial dust-to-gas ratio of 1% which can increase through radial drift in the inner disk with only a small difference if the initial dust-to-gas ratio is higher) and a different disk model where dust opacities do not contribute self-consistently to the disk model. Specifically, the dust opacities follow the Bell & Lin (1994) opacity law, which has been shown to produce misleading disk structures, especially when multiple grain sizes are included because they are based on micrometer-sized dust (Savvidou et al. 2020). Our model suggests that a higher viscosity is needed to prevent a too low pebble isolation mass. However, their conclusions remain consistent with our work: a high enough Stokes number of the particles is needed to allow fast and efficient enough growth, and that more massive ice-rich planets can emerge from the exterior to the snow line.

We do not include gas accretion into our model, because gas accretion might not be efficient for low-mass planets in the inner regions of the protoplanetary disk (Ikoma et al. 2000; Lee et al. 2014; Lambrechts & Lega 2017; Cimerman et al. 2017). Furthermore, observational constraints indicate that planets up to four Earth radii in size mostly have only a few per cent of their mass in hydrogen and helium envelopes (Zeng et al. 2019). This implies that the majority of the planetary mass for these close-in super-Earths and mini-Neptunes has to originate from solid accretion, justifying our first approach of ignoring gas accretion.

5.2 Comparison to the Kepler data

We find almost flat aspect ratios independently of the disk parameters used. This is an important observation as it could lead to planetary systems with similar masses. In Millholland et al. (2017), it is suggested that similar masses in a system would also lead to similar radii, hence the constant with orbital distance aspect ratios we note in our disks support the “peas-in-a-pod” scheme (Weiss et al. 2018). In order to reach more specific conclusions on this matter it would be important to consider multiple growing embryos at the same time.

Judgingby the almost flat, slightly flaring aspect ratios, planets allowed to migrate would be expected to migrate inward (Bitsch et al. 2015a; Savvidou et al. 2020). The pebble isolation masses have a low dependence on the orbital distance, hence the maximum mass that planets can reach would remain unchanged within our simulations, even if we were to include planet migration. Nevertheless, we expect disks to be flared (e.g., Chiang & Goldreich 1997), thus increasing the pebble isolation mass at larger distances to the star. The growth rate, though, is slower near the innermost regions of the disks, caused by the evaporation of solids, making growth to super-Earth masses even harder.

It is important to include migration in future work, not only to reach more robust conclusions on the “peas-in-a-pod” configuration, but also for the role it can play in determining the composition of the planets (Raymond et al. 2018; Bitsch et al. 2019; Izidoro et al. 2021). Even though we include several chemical species here, we do not discuss the influence they could have on the planetary compositions.

Even if we only consider the pebble isolation masses that we find here (Figs. 5 and 6), and not whether there will be time to reach them, we find that most of the observed planetary masses are above the pebble isolation masses in our simulations. This can be explained by our self-consistent disk model with the grain size distribution leading to much lower aspect ratios than used in previous models, due to the size and composition dependent opacities. The growth of the planets, though, can be aided by collisions, either before or after the dissipation of the gas disk (Kominami & Ida 2004; Ogihara & Ida 2009; Cossou et al. 2014; Izidoro et al. 2017, 2021; Ogihara et al. 2018).

The low masses that we find could also be explained if these planets are not super-Earths, but terrestrial planets. If the pebble flux is low, then we expect to have low planetary masses before the gas dissipation. Even with collisions after the gas dissipation, the masses cannot exceed a few M⊕ (Lambrechts et al. 2019), which is consistent with the mass we find in this work for α = 10−3 and uf = 10 ms−1. However, we would need to discuss the composition of the planets to define whether they are terrestrial or super-Earths. This would be important because planets formed during the gas phase could accrete small gaseous envelopes in contrast to planets that formed similarly to the terrestrial planets via collisions after the gas phase.

5.3 Disk parameters

We have explored a few pathways to either increase the pebble isolation masses or shorten the growth timescales. As a reminder, the fastest growth timescales with high enough isolation masses come from the models with α = 10−3 and uf = 10 m s−1. The nominal dust-to-gas ratio is 1.5%. As a consequence, we tested models with the above-mentioned α-viscosity and fragmentation velocity and the highest surface density with Σg,0 = 2000 g cm−2 because this density provides the highest isolation masses. We also tested the nominal dust-to-gas ratio with higher surface density, Σg,0 = 5000 g cm−2.

We find that the higher dust-to-gas ratio does indeed improve the isolation masses, mainly for the case with 3%, which is twice our nominal value. However, the masses remain just above 5 M⊕. The most significant improvement comes with the higher initial gas surface density. Especially near the outer boundary, the pebble isolation mass with Σg,0 = 5000 g cm−2 reaches approximately 10 M⊕. This implies that in order to explain the constraints of the Kepler observations (Weiss et al. 2018) we would need very high disk masses or a significant enhancement of the dust-to-gas ratio. Local enhancements could occur in the inner regions from radial drift (e.g., Birnstiel et al. 2012) or via pebble traps. These could be planet-induced pressure bumps or “traffic jams” at the evaporation fronts (Ros & Johansen 2013; Ida & Guillot 2016; Schoonenberg & Ormel 2017; Drążkowska & Alibert 2017; Ros et al. 2019).

In addition, it is worth noting the Venturini et al. (2020a) claim that the more massive inner super-Earths (the planets that would populate the second peak at larger radii in the radius distribution; e.g., Fulton et al. 2017) are actually water-rich planets originating from beyond the ice line where the pebble isolation mass is higher, which is in agreement with our model. Migration should be included in future works in order to determine the final positions and masses of the planets.

The ice line position is located around 3 AU for α = 10−3, Σg,0 = 2000 g cm−2, and uf = 1 m s−1. Lower α-viscosities, gas surface densities, or fragmentation velocities move the ice line inward (see Sect. 3 and Savvidou et al. 2020). The higher dust-to-gas ratios or gas surface densities thus also help in keeping the ice line farther out from the star. However, the position andevolution of the ice line location, along with the possibility of migration for planets defines their compositions (Bitsch et al. 2019).

6 Summary

In this work, we used the self-consistent protoplanetary disk model presented in Savvidou et al. (2020), with additional chemical species and the corresponding opacities (see Table 1 and Fig. 1), focusing on the inner parts of the disk. We used the MRN grain size distribution (Mathis et al. 1977), with a disk-dependent upper boundary for the grain sizes (Eq. (3)). We then combined the equilibrium disk structures from the hydrodynamical simulations with a framework to study planet growth via pebble accretion. The disk parameters we used are summarized in Table 2. In this work, we did not take into account planetary migration and did not discuss the planetary compositions for simplicity. Furthermore, because the growing planets are in the low-mass regime we did not model gas accretion. Additionally, we used only fixed-disk structures in time, because our 2D model cannot be evolved for several Myr.

We present the equilibrium disk structures in Figs. 3 and 4. The aspect ratio profiles are almost constant with orbital distance. This is expected because at these innermost parts of the protoplanetary disks, viscous heating dominates over stellar irradiation and the disk does not flare up (Chiang & Goldreich 1997; Dullemond & Dominik 2004; Bitsch et al. 2015a; Ida et al. 2016; Savvidou et al. 2020). This implies that the planets forming in the inner disk would have similar masses in the pebble accretion scenario because the pebble isolation mass is a strong function of the aspect ratio, supporting the “peas-in-a-pod” scheme (Millholland et al. 2017; Weiss et al. 2018).

We calculated the pebble isolation masses following the approximation by Bitsch et al. (2018) (Figs. 5 and 6) and then estimated the time it takes to reach them depending on the disk parameters (Figs. 7 and 8). Including opacities which are grain size and composition dependent means that when the disk parameters allow large particles to form, the aspect ratios will be lower. This leads to low pebble isolation masses because they directly depend on the aspect ratio of the disk (Eq. (10)). We find the highest pebble isolation masses for α = 10−3 and 5 × 10−4 when the fragmentation velocity is uf = 1 m s−1 and for α = 10−3 when uf = 10 m s−1, mainly for high gas surface densities, with Σg,0 ≥1000 g cm−2.

However, high pebble isolation masses also mean longer growth timescales because of the smaller pebbles inside the disk. Compared with the typical lifetimes of protoplanetary disks (3–10 Myr), we find that for low fragmentation velocities (uf = 1 m s−1) the timescales for planetary growth are too long (with a small dependence on the gas surface density and the orbital distance). Hence, there is a trade-off between the pebble isolation masses and the growth timescales, and we conclude that the best set of parameters is α = 10−3 and uf = 10 m s−1 within our model. With a gas surface density of Σg,0 = 2000 g cm−2 the pebble isolation masses reach almost 6 M⊕, which the planets can reach in less than 1 Myr.

The maximum mass that a planet can reach by pure pebble accretion is relatively low, and thus the masses of the majority of the observed planets can probably not be explained via pebble accretion only. We also tested higher dust-to-gas ratios and ahigher surface density (Fig. 10). Even though they do help in increasing the pebble isolation masses, they also bring longer or comparable timescales for planetary growth compared to the nominal simulations.

We also tested whether a higher planetary seed mass can shorten the growth timescales, by starting with Minit = 0.1 M⊕ instead of Minit = 0.01 M⊕. We find andshow in Fig. 11 that even though the increased initial planetary mass shortens the growth timescale, the difference is very small and growing planets still fail to reach the isolation mass within the lifetime of the disk for α = 10−3. For disks with lower alpha values, even smaller initial embryos (0.01 Earth masses) can grow fast enough to reach pebble isolation mass before the end of the disk’s lifetime.

The growth of planets via pebble accretion, can be aided by collisions either before or after the dissipation of the gas (Kominami & Ida 2004; Cossou et al. 2014; Izidoro et al. 2017, 2021). It is also possible that the low pebble isolation masses we find mean that this formation mechanism leads to planet formation after gas disk dispersal rather than to planet formation during the gas disk phase. However, even with some collisions, the expected masses are not very high (Lambrechts et al. 2019), if the initial planetary masses are small. However, in order to reach a definite conclusion on this, future simulations including N-body interactions are needed.

We have shown in this work that a self-consistent treatment between the pebble sizes and disk structures is of crucial importance for planet formation simulations. In particular, we find that disks that support a large pebble isolation mass also harbor low pebble accretion rates due to the small particle sizes, hence the growth timescales can be very long.

Acknowledgements

B.B. and S.S. thank the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support. S.S. is a Fellow of the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg (IMPRS-HD).

Appendix A Refractive indices

In Table 1, we include the sources of the refractive indices used to calculate the opacities per grain size and the composition as a function of temperature. The refractive indices are not only dependent on the wavelength of the incident

radiation, but also on the temperature of the surrounding medium. Hence, we find for some of the species used in this work different refractive indices for measurements at different temperatures.

From Henning & Mutschke (1997), we obtain refractive indices as a function of wavelength for FeS measured at T = 10 and 100 K. In our disk models we assume that the dust temperature is the same as the temperature of the surrounding gas, which is a good approximation for the optically thick parts of the disk (Kamp & Dullemond 2004). For this reason, we chose to combine the refractive indices obtained for different temperatures, so that the new refractive indices correspond to the values for T = 10 K for low temperatures, but gradually switch to the values corresponding to T = 100 K for high temperatures. In Fig. A.1, we show the Rosseland opacity as a function of temperature, calculated with the refractive indices measured atT = 10 and 100 K, and the combination of those used in the opacity module of this work.

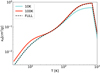thumbnail Fig. A.1

Rosseland opacity as a function of temperature for FeS calculated using refractive indices measured at two different temperatures. The black dashed line shows the opacity used here which combines the opacities derived from the two temperatures.

In Hudgins et al. (1993), the refractive indices are given for CO2 for T = 10, 30, 50, and 70 K. We plot the resulting Rosseland opacities for some of these different measurements in Fig. A.2a. We chose to use the refractive indices only for 50 K in our simulations because the differences are very small between the three different sets.

thumbnail Fig. A.2

Rosseland opacity as a function of temperature for the specified species calculated using refractive indices measured atthree different temperatures.

Similarly, for CH4 we find refractive indices for T = 10, 20, and 30 K. The resulting mean Rosseland opacities are plotted in Fig. A.2b. They are almost the same, independently of the temperature at which the measurement was made. We chose for this work to use the refractive indices at T = 20 K.

References

  1. Ataiee, S., Baruteau, C., Alibert, Y., & Benz, W. 2018, A&A, 615, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  2. Bai, X. N., Ye, J., Goodman, J., & Yuan, F. 2016, ApJ, 818, A152 [NASA ADS] [CrossRef] [Google Scholar]
  3. Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
  4. Bell, K. R., & Lin, D. N. C. 1994, ApJ, 427, 987 [NASA ADS] [CrossRef] [Google Scholar]
  5. Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Birnstiel, T., Ormel, C. W., & Dullemond, C. P. 2011, A&A, 525, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Birnstiel, T., Klahr, H., & Ercolano, B. 2012, A&A, 539, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Bitsch, B. 2019, A&A, 630, A51 [CrossRef] [EDP Sciences] [Google Scholar]
  9. Bitsch, B., & Battistini, C. 2020, A&A, 633, A10 [CrossRef] [EDP Sciences] [Google Scholar]
  10. Bitsch, B., Boley, A., & Kley, W. 2013, A&A, 550, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Bitsch, B., Johansen, A., Lambrechts, M., & Morbidelli, A. 2015a, A&A, 575, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bitsch, B., Lambrechts, M., & Johansen, A. 2015b, A&A, 582, A112 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Bitsch, B., Morbidelli, A., Johansen, A., et al. 2018, A&A, 612, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bitsch, B., Raymond, S. N., & Izidoro, A. 2019, A&A, 624, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
  16. Brauer, F., Dullemond, C. P., Johansen, A., et al. 2007, A&A, 469, 1169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Brauer, F., Dullemond, C. P., & Henning, T. 2008, A&A, 480, 859 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Chen, J., & Kipping, D. 2017, ApJ, 834, 17 [Google Scholar]
  19. Chiang, E. I., & Goldreich, P. 1997, ApJ, 490, 368 [NASA ADS] [CrossRef] [Google Scholar]
  20. Chiang, E., & Youdin, A. N. 2010, Annu. Rev. Earth Planet. Sci., 38, 493 [NASA ADS] [CrossRef] [Google Scholar]
  21. Cimerman, N. P., Kuiper, R., & Ormel, C. W. 2017, MNRAS, 471, 4662 [Google Scholar]
  22. Cossou, C., Raymond, S. N., Hersant, F., & Pierens, A. 2014, A&A, 569, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Drążkowska, J., & Alibert, Y. 2017, A&A, 608, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Drążkowska, J., Li, S., Birnstiel, T., Stammler, S. M., & Li, H. 2019, ApJ, 885, 91 [NASA ADS] [CrossRef] [Google Scholar]
  25. Dubrulle, B., Morfill, G., & Sterzik, M. 1995, Icarus, 114, 237 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dullemond, C. P., & Dominik, C. 2004, A&A, 417, 159 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Fortier, A., Alibert, Y., Carron, F., Benz, W., & Dittkrist, K. M. 2013, A&A, 549, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  28. Fressin, F., Torres, G., Charbonneau, D., et al. 2013, ApJ, 766, 81 [NASA ADS] [CrossRef] [Google Scholar]
  29. Fulton, B. J., Petigura, E. A., Howard, A. W., et al. 2017, AJ, 154, 109 [Google Scholar]
  30. Gundlach, B., & Blum, J. 2015, ApJ, 798, 34 [Google Scholar]
  31. Hartmann, L., Calvet, N., Gullbring, E., & D’Alessio, P. 1998, ApJ, 495, 385 [NASA ADS] [CrossRef] [Google Scholar]
  32. Helled, R., Bodenheimer, P., Podolak, M., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 643 [Google Scholar]
  33. Henning, T., & Mutschke, H. 1997, A&A, 327, 743 [NASA ADS] [Google Scholar]
  34. Hudgins, D. M., Sandford, S. A., Allamandola, L. J., & Tielens, A. G. G. M. 1993, ApJS, 86, 713 [NASA ADS] [CrossRef] [Google Scholar]
  35. Ida, S., & Guillot, T. 2016, A&A, 596, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  36. Ida, S., Guillot, T., & Morbidelli, A. 2016, A&A, 591, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Ikoma, M., Nakazawa, K., & Emori, H. 2000, ApJ, 537, 1013 [NASA ADS] [CrossRef] [Google Scholar]
  38. Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [Google Scholar]
  39. Izidoro, A., Bitsch, B., Raymond, S. N., et al. 2021, A&A, in press, https://doi.org/10.1051/0004-6361/201935336 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  40. Jäger, C., Dorschner, J., Mutschke, H., Posch, T., & Henning, T. 2003, A&A, 408, 193 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Johansen, A., & Bitsch, B. 2019, A&A, 631, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Johansen, A., & Lacerda, P. 2010, MNRAS, 404, 475 [NASA ADS] [Google Scholar]
  43. Johansen, A., & Lambrechts, M. 2017, Annu. Rev. Earth Planet. Sci., 45, 359 [Google Scholar]
  44. Johansen, A., & Youdin, A. 2007, ApJ, 662, 627 [Google Scholar]
  45. Kamp, I., & Dullemond, C. P. 2004, ApJ, 615, 991 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kobayashi, H., Tanaka, H., & Krivov, A. V. 2011, ApJ, 738, 35 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kominami, J., & Ida, S. 2004, Icarus, 167, 231 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lambrechts, M., & Johansen, A. 2012, A&A, 544, A32 [CrossRef] [EDP Sciences] [Google Scholar]
  49. Lambrechts, M., & Johansen, A. 2014, A&A, 572, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Lambrechts, M., & Lega, E. 2017, A&A, 606, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Lambrechts, M., Johansen, A., & Morbidelli, A. 2014, A&A, 572, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  53. Lee, E. J., Chiang, E., & Ormel, C. W. 2014, ApJ, 797, 95 [Google Scholar]
  54. Levison, H. F., Thommes, E., & Duncan, M. J. 2010, AJ, 139, 1297 [Google Scholar]
  55. Mamajek, E. E. 2009, in AIP Conf. Ser., 1158, Exoplanets and Disks: Their Formation and Diversity, eds. T. Usuda, M. Tamura, & M. Ishii, 3 [CrossRef] [Google Scholar]
  56. Martin, R. G., & Livio, M. 2015, ApJ, 810, 105 [CrossRef] [Google Scholar]
  57. Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
  58. Millholland, S., Wang, S., & Laughlin, G. 2017, ApJ, 849, L33 [NASA ADS] [CrossRef] [Google Scholar]
  59. Morbidelli, A., & Nesvorny, D. 2012, A&A, 546, A18 [CrossRef] [EDP Sciences] [Google Scholar]
  60. Morbidelli, A., Lambrechts, M., Jacobson, S., & Bitsch, B. 2015, Icarus, 258, 418 [NASA ADS] [CrossRef] [Google Scholar]
  61. Mulders, G. D., Pascucci, I., Apai, D., & Ciesla, F. J. 2018, AJ, 156, 24 [NASA ADS] [CrossRef] [Google Scholar]
  62. Musiolik, G., & Wurm, G. 2019, ApJ, 873, 58 [Google Scholar]
  63. Ogihara, M., & Ida, S. 2009, ApJ, 699, 824 [Google Scholar]
  64. Ogihara, M., Kokubo, E., Suzuki, T. K., & Morbidelli, A. 2018, A&A, 615, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Ormel, C. W., & Klahr, H. H. 2010, A&A, 520, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Ormel, C. W., Liu, B., & Schoonenberg, D. 2017, A&A, 604, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. Paardekooper, S. J., & Mellema, G. 2006, A&A, 459, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  68. Petigura, E. A., Howard, A. W., & Marcy, G. W. 2013, Proc. Natl. Acad. Sci. U.S.A., 110, 19273 [NASA ADS] [CrossRef] [Google Scholar]
  69. Pollack, J. B., Hubickyj, O., Bodenheimer, P., et al. 1996, Icarus, 124, 62 [NASA ADS] [CrossRef] [Google Scholar]
  70. Poppe, T., Blum, J., & Henning, T. 2000, ApJ, 533, 454 [NASA ADS] [CrossRef] [Google Scholar]
  71. Preibisch, T., Ossenkopf, V., Yorke, H. W., & Henning, T. 1993, A&A, 279, 577 [NASA ADS] [Google Scholar]
  72. Rafikov, R. R. 2004, AJ, 128, 1348 [NASA ADS] [CrossRef] [Google Scholar]
  73. Raymond, S. N., Boulet, T., Izidoro, A., Esteves, L., & Bitsch, B. 2018, MNRAS, 479, L81 [Google Scholar]
  74. Ros, K., & Johansen, A. 2013, A&A, 552, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  75. Ros, K., Johansen, A., Riipinen, I., & Schlesinger, D. 2019, A&A, 629, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Savvidou, S., Bitsch, B., & Lambrechts, M. 2020, A&A, 640, A63 [CrossRef] [EDP Sciences] [Google Scholar]
  77. Schoonenberg,D., & Ormel, C. W. 2017, A&A, 602, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Schoonenberg,D., Liu, B., Ormel, C. W., & Dorn, C. 2019, A&A, 627, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  79. Shakura, N. I., & Sunyaev, R. A. 1973, A&A, 500, 33 [NASA ADS] [Google Scholar]
  80. Surville, C., Mayer, L., & Alibert, Y. 2020, ApJ, submitted [arXiv:2009.04775] [Google Scholar]
  81. Suzuki, T. K., Ogihara, M., Morbidelli, A., Crida, A., & Guillot, T. 2016, A&A, 596, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  82. Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 339 [Google Scholar]
  83. Venturini, J., Guilera, O. M., Haldemann, J., Ronco, M. P., & Mordasini, C. 2020a, A&A, 643, L1 [CrossRef] [EDP Sciences] [Google Scholar]
  84. Venturini, J., Guilera, O. M., Ronco, M. P., & Mordasini, C. 2020b, A&A, 644, A174 [Google Scholar]
  85. Warren, S. G., & Brandt, R. E. 2008, J. Geophys. Res. (Atm.), 113, D14220 [NASA ADS] [CrossRef] [Google Scholar]
  86. Weidenschilling, S. J. 1977, MNRAS, 180, 57 [Google Scholar]
  87. Weidenschilling, S. J. 1980, Icarus, 44, 172 [NASA ADS] [CrossRef] [Google Scholar]
  88. Weidenschilling, S. J. 1984, Icarus, 60, 553 [NASA ADS] [CrossRef] [Google Scholar]
  89. Weiss, L. M., Isaacson, H. T., Marcy, G. W., et al. 2018, AJ, 156, 254 [Google Scholar]
  90. Wu, Y. 2019, ApJ, 874, 91 [NASA ADS] [CrossRef] [Google Scholar]
  91. Youdin, A. N., & Goodman, J. 2005, ApJ, 620, 459 [NASA ADS] [CrossRef] [Google Scholar]
  92. Youdin, A., & Johansen, A. 2007, ApJ, 662, 613 [NASA ADS] [CrossRef] [Google Scholar]
  93. Zeng, L., Jacobsen, S. B., Sasselov, D. D., et al. 2019, Proc. Natl. Acad. Sci. U.S.A., 116, 9723 [Google Scholar]
  94. Zhu, W., Petrovich, C., Wu, Y., Dong, S., & Xie, J. 2018, ApJ, 860, 101 [Google Scholar]
  95. Zsom, A., Ormel, C. W., Güttler, C., Blum, J., & Dullemond, C. P. 2010, A&A, 513, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Zsom, A., Ormel, C. W., Dullemond, C. P., & Henning, T. 2011, A&A, 534, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
2

We find that the disk structure itself is only slightly influenced if a more complex grain size distribution (Birnstiel et al. 2011) is used (Savvidou et al. 2020). For simplicity, we use the MRN distribution.

3

In contrast, our previous simulations (Savvidou et al. 2020) only included two species, resulting in fewer variations in the disk profile.

All Tables

Table 1

Condensation temperatures and volume mixing ratios for the chemical species used in this work.

In the text
Table 2

Parameters used in the simulations.

In the text

All Figures

thumbnail Fig. 1

Rosseland, Planck, and stellar mean opacities (from left to right) as a function of temperature for grain sizes of 0.1 μm, 1 μm, 10 μm, 100 μm, 1 mm, and 1 cm. The composition of the grain mixture is presented in Table 1. The gray dashed lines show the evaporation temperatures of the different species, which are (from lowest to the highest) CO, CH4, CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, Fe2O3, and MgSiO3. The water ice evaporation front is shown as a gray band.
In the text
thumbnail Fig. 2

Influence of the evaporation of the different chemical species on the dust-to-gas ratio in the protoplanetary disk. Left plot: dust-to-gas ratio in terms of the total dust-to-gas ratio in the disk as a function of temperature. After each species evaporates the total mass fraction decreases by the corresponding mass fraction (see Table 1) until all species evaporate beyond 1500 K. Right plot: example of the dust-to-gas ratio as a function of orbital distance for the disk with α = 10−3, Σg,0 = 2000 g cm−2, and uf = 10 m s−1, and a globaldust-to-gas ratio of 1.5%. Overplotted is the temperature of the disk where the evaporation fronts are easy to locate.
In the text
thumbnail Fig. 3

Aspect ratio (upper plot), temperature (middle plot), and gas surface density (bottom plot) asa function of orbital distance for four different initial gas surface densities, from 100 g cm−2 to 2000 g cm−2. The turbulence parameter in viscosity is α = 10−3 in the left panel, α = 5 × 10−4 in the middle panel, and α = 10−4 in the right panel. The fragmentation velocity is uf = 1 m s−1. The light blue areas in the aspect ratio and temperature plots indicate the evaporation fronts (±2 K around the evaporation temperatures of CH4, CO2 ; ±10 K for the other species). Starting from the outer boundary, for α = 10−3 the species that evaporate are CO, CH4, CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, and MgSiO3. For α = 5 × 10−4 the evaporation fronts are of CO2, H2O, Fe3O4, C, FeS, Mg2SiO4, and MgSiO3 and for α = 10−4 they are CO2, H2O, and Fe3O4. The water ice line is shown as a dashed line.
In the text
thumbnail Fig. 4

Same as Fig. 3, but using a fragmentation velocity of uf = 10 m s−1. Starting from the outer boundary, for α = 10−3 the species that evaporate are CO2, H2O, Fe3O4, C, and FeS. For α = 5 × 10−4 the ice lines are of CO2, H2O, Fe3O4, C, and FeS and for α = 10−4 they are CO2 and H2O. The water ice line is shown as a dashed line.
In the text
thumbnail Fig. 5

Pebble isolation mass as a function of orbital distance for disks with four different initial gas surface densities, from 100 g cm−2 to 2000 g cm−2. The turbulence parameter in viscosity is α = 10−3 in the left panel, α = 5 × 10−4 in the middle panel, and α = 10−4 in the right panel. The fragmentation velocity is uf = 1 m s−1. We also include the planetary masses of Kepler systems, with radii up to 4 R⊕, derived through the Forecaster package (Chen & Kipping 2017) (gray circles) and super-Earths detected by RV (blue circles). The dashed lines correspond to the disk regions interior to the ice line, whereas the solid lines are the regions exterior to the ice line, where the forming planets are water rich.
In the text
thumbnail Fig. 6

Same as Fig. 5, but for a fragmentation velocity of uf = 10 m s−1.
In the text
thumbnail Fig. 7

Maximum Stokes number (top plot) and planetary growth timescale until the pebble isolation mass is reached (bottom plot) as a function of orbital distance, for the disks with the four different initial gas surface densities: α = 10−3 (left plot), α = 5 × 10−4 (middle plot), α = 10−4 (right plot), and uf = 1 m s−1. The gray lines show the typical lifetime range of a protoplanetary disk of 3–10 Myr.
In the text
thumbnail Fig. 8

Same as Fig. 7, but for uf = 10 m s−1.
In the text
thumbnail Fig. 9

Planetary mass as a function of time for the simulations with Σg,0 = 2000 g cm−2, all α-viscosities, and both of the fragmentation velocities at 1 AU. The dots give the final planetary mass determined by the pebble isolation mass (Figs. 5 and 6). The growth timescale is longer than 10 Myr in disks with α > 5 × 10−4 when particle collisions are limited by a fragmentation velocity of 1 m s−1.
In the text
thumbnail Fig. 10

Pebble isolation mass (top plot), maximum Stokes number (middle plot), and planetary growth timescale until the pebble isolation mass is reached (bottom plot) as a function of orbital distance, for disks with α = 10−3 and uf = 10 m s−1. Shown are disks with higher dust-to-gas ratios, fDG = 2% and fDG = 3% and higher initial surface density Σg,0 = 5000 g cm−2. For reference the nominal run with Σg,0 = 2000 g cm−2 and fDG = 1.5% is included.
In the text
thumbnail Fig. 11

Planetary growth timescale until the pebble isolation mass is reached as a function of orbital distance with initial planetary seed masses Minit = 0.1 M⊕. We tested two α-viscosities, 10−3 and 5 × 10−4 with a fragmentation velocity, uf = 1 m s−1. Overplotted are the nominal disk models with initial planetary seed masses Minit = 0.01 M⊕.
In the text
thumbnail Fig. A.1

Rosseland opacity as a function of temperature for FeS calculated using refractive indices measured at two different temperatures. The black dashed line shows the opacity used here which combines the opacities derived from the two temperatures.
In the text
thumbnail Fig. A.2

Rosseland opacity as a function of temperature for the specified species calculated using refractive indices measured atthree different temperatures.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.