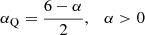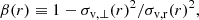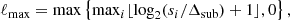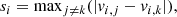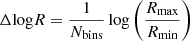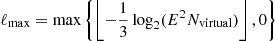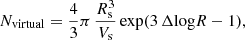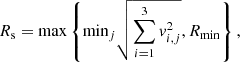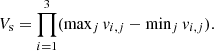| Issue |
A&A
Volume 647, March 2021
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 35 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202039719 | |
| Published online | 11 March 2021 | |
Phase-space structure of protohalos: Vlasov versus particle-mesh
Sorbonne Université, CNRS, UMR7095, Institut d’Astrophysique de Paris, 98 bis Boulevard Arago, 75014 Paris, France
e-mail: colombi@iap.fr
Received:
19
October
2020
Accepted:
8
December
2020
The phase-space structure of primordial dark matter halos is revisited using cosmological simulations with three sine waves and cold dark matter (CDM) initial conditions. The simulations are performed with the tessellation based Vlasov solver ColDICE and a particle-mesh (PM) N-body code. The analyses include projected density, phase-space diagrams, radial density ρ(r), and pseudo-phase space density: Q(r) = ρ(r)/σv(r)3 with σv the local velocity dispersion. Particular attention is paid to force and mass resolution. Because the phase-space sheet complexity, estimated in terms of total volume and simplex (tetrahedron) count, increases very quickly, ColDICE can follow only the early violent relaxation phase of halo formation. During the violent relaxation phase, agreement between ColDICE and PM simulations having one particle per cell or more is excellent and halos have a power-law density profile, ρ(r) ∝ r−α, α ∈ [1.5, 1.8]. This slope, measured prior to any merger, is slightly larger than in the literature. The phase-space diagrams evidence complex but coherent patterns with clear signatures of self-similarity in the sine wave simulations, while the CDM halos are somewhat scribbly. After additional mass resolution tests, the PM simulations are used to follow the next stages of evolution. The power law progressively breaks down with a convergence of the density profile to the well-known Navarro–Frenk–White universal attractor, irrespective of initial conditions, that is even in the three-sine-wave simulations. This demonstrates again that mergers do not represent a necessary condition for convergence to the dynamical attractor. Not surprisingly, the measured pseudo phase-space density is a power law Q(r) ∝ r−αQ, with αQ close to the prediction of secondary spherical infall model, αQ ≃ 1.875. However this property is also verified during the early relaxation phase, which is non-trivial.
Key words: gravitation / methods: numerical / Galaxy: kinematics and dynamics / dark matter
© S. Colombi 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In our current understanding of large-scale structure formation, the main matter component of the Universe is cold dark matter (CDM; e.g., Peebles 1982, 1984; Blumenthal et al. 1984), which can be modelled as a self-gravitating collisionless fluid obeying Vlasov-Poisson equations:
where f(r, u, t) is the phase-space density at physical position r and velocity u, ϕ the gravitational potential, and G the gravitational constant. In the concordance model dark matter is composed of very massive particles with very small initial velocity dispersion. This means that dark matter is, to a very good approximation, concentrated on a three-dimensional phase-space sheet folding in six-dimensional phase-space. At early times the phase-space density has the form
where the initial density ρi and velocity ui are smooth functions of position r. The scale length λ below which initial density and velocity fluctuations are smooth depends on the dark matter particle mass. In this work, following in the footsteps of previous numerical investigations (e.g., Diemand et al. 2005; Ishiyama et al. 2010; Anderhalden & Diemand 2013; Ishiyama 2014; Angulo et al. 2017), we consider a standard CDM model with neutralinos of mass 100 GeV, which implies λ of the order of a parsec.
The phase-space sheet evolves under self-gravity, and shell crossing occurs in various places of configuration space. In these regions sheets, filaments, and dark matter halos form as the result of complex processes of multi-streaming dynamics. While perturbation theory can be used to predict the early stages of clustering (e.g., Bernardeau et al. 2002), numerical simulations are required to accurately follow the dynamics of the phase-space sheet beyond shell crossing. Traditionally, dark matter is simulated with the N-body technique, in which dark matter elements are followed with a large ensemble of macroparticles interacting with each other with a softened gravitational force. There are many different N-body simulation codes, which differ mainly from each other through the way the Poisson equation is solved (e.g., Hockney & Eastwood 1988; Bertschinger 1998; Colombi 2001; Dolag et al. 2008; Dehnen & Read 2011; Vogelsberger et al. 2020, for reviews).
Even though a consensus on the robustness of the results of N-body simulations is getting close, their numerical convergence is not yet fully proven in several situations. N-body simulations are not free from biases, due to the discrete nature of the representation of the phase-space fluid with very massive macroparticles compared to the actual dark matter candidates. Discrete noise and close N-body encounters can drive the system away from the mean field limit embodied by the Vlasov equation (e.g., Aarseth et al. 1988; Goodman et al. 1993; Knebe et al. 2000; Binney 2004; Diemand et al. 2004; Joyce et al. 2009; Colombi et al. 2015; Beraldo e Silva et al. 2017, 2019; Benhaiem et al. 2018, but this list of references is far from comprehensive), and this is particularly critical in the cold case (Melott et al. 1997; Splinter et al. 1998; Melott 2007; Wang & White 2007; Angulo et al. 2013). This is why it has recently been proposed to adopt a direct approach where the phase-space sheet is described in a smooth fashion with a fine tetrahedral tessellation (Hahn et al. 2013; Sousbie & Colombi 2016; Hahn & Angulo 2016), an idea stemming directly from the waterbag approach (e.g., DePackh 1962; Janin 1971; Cuperman et al. 1971a,b; Colombi & Touma 2008, 2014)1.
In this article we compare in detail the numerical results obtained from state-of-the-art Vlasov simulations realised with the public code ColDICE (Sousbie & Colombi 2016)2 to N-body simulations realised with a standard particle-mesh (PM) code (e.g., Hockney & Eastwood 1988). Particular attention is paid to the effects of force resolution and mass resolution. We confirm again that with the proper choice of parameters, typically more than one particle per softening length of the force, the N-body approach remains perfectly reliable at the coarse level.
As the host of galaxies and clusters of galaxies, dark matter halos represent the main bricks of large-scale structure formation models and are the main focus of this numerical investigation. Following the path of many previous works, this article explores again their dynamical history, which, according to perturbation theory and cosmological simulations results, can be decomposed into the four following phases:
(i) The pre-collapse phase. At the beginning, the phase-space sheet does not self-intersect in configuration space, and its evolution can be followed analytically with a perturbative approach (e.g., Bernardeau et al. 2002). For instance, linear Lagrangian perturbation theory, the Zel’dovich approximation (Zel’dovich 1970), provides a fairly good description of the evolution of the phase-space sheet, at least from the qualitative point of view. In the Zel’dovich solution, there are locally three orthogonal directions of motion: the first non-linear structures to form are two-dimensional sheets orthogonal to one-dimensional singularities building up along the main direction of motion. Higher-order Lagrangian perturbation theory (e.g., Bouchet et al. 1992, 1995; Buchert 1993; Buchert & Ehlers 1993; Rampf 2012; Zheligovsky & Frisch 2014; Matsubara 2015) is needed for an accurate description of the pre-collapse motion (e.g., Moutarde et al. 1991). At sufficiently high order, it has been shown, using the Vlasov simulations presented in the present work, to perform very well until shell crossing (Saga et al. 2018).
(ii) The early violent relaxation phase. After shell crossing the system enters into a complex multi-stream violent relaxation phase. If collapse happens along another direction of motion, a filament forms. Then, if another shell crossing takes place along the third direction of motion, this creates the seed of a dark matter halo. The early stages of the dynamics thus build singular structures of various kinds according to the local properties of the displacement field (Arnold et al. 1982; Hidding et al. 2014; Feldbrugge et al. 2018). They correspond to foldings of the dark matter sheet in phase-space and quickly produce a very intricate spiral structure that we study in detail through phase-space slices and whose complexity is quantified in ColDICE in terms of total volume and simplex count.
This early relaxation process is of monolithic nature, that is it happens in the absence of merger. It takes place over short timescales and is very similar to the picture described in Lynden-Bell (1967), which explains the term of ‘violent relaxation’. During this phase, the dark matter protohalos build up a power-law density profile ρ(r) ∝ r−α whose logarithmic slope α ranges in the interval [1.3, 1.7] according to various results in the literature (Moutarde et al. 1991; Diemand et al. 2005; Ishiyama et al. 2010; Anderhalden & Diemand 2013; Ishiyama 2014; Angulo et al. 2017; Delos et al. 2018a,b). The exact value of the slope changes slightly according to the authors, although a consensus seems to emerge with α ≃ 1.5. We examine this in detail again by making sure that the measurements are performed during the monolithic phase of the evolution of halos extracted from CDM simulations with very small box size. Additionally, following in the footsteps of Nakamura (1985), Moutarde et al. (1991, 1995), we study highly symmetric configurations with initial conditions composed of three sine waves of various amplitudes. These investigations are conducted with ColDICE and the PM code, with thorough comparisons between both solvers.
(iii) The convergence to a universal profile. The initial power-law profile does not last long because dark matter halos are the object of perturbations, in particular successive mergers with other halos. These mergers modify the profile that converges rapidly to a dynamical attractor, the so-called Navarro–Frenk–White (NFW) profile (Navarro et al. 1996, 1997), where the radial density profile of dark matter halos has a form close to
with rs a scale radius. The shape of dark matter halos and the form given by Eq. (4) have been the object of numerous discussions and convergence analyses (e.g., Moore et al. 1998; Jing & Suto 2000; Power et al. 2003; Mansfield & Avestruz 2021). Recent investigations suggest for instance that the Einasto profile that will be used in the present work (Eq. (21); Einasto 1965) provides better fits of dark matter halo profiles (e.g., Navarro et al. 2004), but other forms have been suggested (e.g., Stadel et al. 2009).
Even though it is still debated, the nearly universal nature of the dynamical attractor seems now unquestionable and the fact that mergers contribute to its establishment has been highlighted in several works (e.g., Syer & White 1998; Ishiyama 2014; Ogiya et al. 2016; Angulo et al. 2017). However, other numerical investigations suggest that it is possible to reach the dynamical attractor even without a merger as the consequence of radial instabilities or other sources of noise (e.g., Huss et al. 1999; MacMillan et al. 2006; Ogiya & Hahn 2018). We revisit these questions in the presence and in the absence of merger by pushing further in time the simulations described in point (ii). However, due to its adaptive nature, the computational cost of ColDICE prevents it from reaching sufficiently advanced stages of this dynamical phase, which are approached solely with the PM code after careful mass resolution tests.
Another interesting property of the dynamical attractor is that the measured pseudo phase-space density,
where σv(r) is the local velocity dispersion, follows a pure power-law behaviour Q(r) ∝ r−αQ over a very large dynamical range, with a logarithmic slope very close to the prediction of the secondary spherical infall model of Bertschinger (1985), αQ = 1.875 (Taylor & Navarro 2001; Navarro et al. 2010; Ludlow et al. 2010). We show that this property stands as well during the monolithic phase (ii), for which very few studies of the pseudo phase-space density exist (but see Ishiyama et al. 2010).
(iv) The quasi-static evolution. Once the dynamical attractor is attained, the evolution of the halo becomes mainly monolithic again and its profile changes very little with time.
It should be noted that the pre-collapse phase (i) of the evolution of the phase-space sheet is well described by perturbation theory; however, the early violent relaxation phase (ii) and the convergence to the universal dynamical attractor (iii) are still poorly understood from the theoretical point of view despite numerous investigations involving maximum of entropy methods (e.g., Lynden-Bell 1967; Hjorth & Williams 2010; Pontzen & Governato 2013; Carron & Szapudi 2013), the Jeans equation (e.g., Taylor & Navarro 2001; Dehnen & McLaughlin 2005; Ogiya & Hahn 2018), post-collapse perturbation theory (e.g., Colombi 2015; Taruya & Colombi 2017; Rampf et al. 2019), as well as self-similar solutions and secondary infall models (e.g., Fillmore & Goldreich 1984; Bertschinger 1985; Henriksen & Widrow 1995; Sikivie et al. 1997; Zukin & Bertschinger 2010a,b; Alard 2013; Sugiura et al. 2020). It is not the goal in the present work to investigate in detail analytical models, but some links between our measurements and predictions from self-similarity and solutions of the Jeans equations are discussed.
This article is organised as follows. Details about ColDICE and the PM code are provided in Sect. 2, as well as the simulations suite realised for this project and other ongoing works. Sections 3 and 4 are respectively dedicated to the visual inspection of the three-dimensional projected density and phase-space diagrams. Section 5 measures the complexity in the Vlasov simulations through plots of simplex count and phase-space sheet volume. This is followed in Sect. 6 by a detailed examination of radial density profiles and of the pseudo phase-space density. Finally, Sect. 7 summarises the main results and discusses a few prospects.
2. Simulations
This section is divided into three parts. The important features of the Vlasov solver ColDICE are summarised in Sect. 2.1. The full technical details of the implementation of this massively parallel algorithm can be found in Sousbie & Colombi (2016). Then the PM code written for this project is described in Sect. 2.2. Finally, the simulation suite used in this work and other investigations (Saga et al. 2018, and in prep.; Colombi et al., in prep.) is described in Sect. 2.3. The parameters of these numerical experiments are listed in Table 1.
Details of the ensemble of simulations performed for this work.
2.1. Brief description of ColDICE
In ColDICE the phase-space sheet is tessellated with an ensemble of tetrahedra (also called simplices) whose vertices (the four corners of the tetrahedra) are initially disposed on a regular mesh of size ns corresponding to 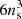 simplices. The initial comoving positions xi, j, k, i, j, k ∈ [1, …, ns] and peculiar velocities vi, j, k of the vertices are given by
simplices. The initial comoving positions xi, j, k, i, j, k ∈ [1, …, ns] and peculiar velocities vi, j, k of the vertices are given by
with L the size of simulation volume, which is a periodic cube. The unperturbed positions define the Lagrangian coordinates qi, j, k of each vertex. These phase-space coordinates are slightly perturbed according to linear Lagrangian perturbation theory (Zel’dovich 1970),
where we have dropped the subscripts (i, j, k), a, and D+ are respectively the expansion factor and the linear growing mode normalised to unity at present time, and P is the linear displacement field. Then, the tessellation evolves dynamically under self-gravity by solving standard Lagrangian equations of motion for its vertices, similarly to particles in an N-body simulation, using a simple second-order predictor corrector with slowly varying time step.
To compute the gravitational force, the tessellation is interpolated on a regular mesh of spatial resolution ng. This interpolation is performed by calculating the exact intersection between each simplex of the tessellation and each voxel cell of the mesh3. It is performed at linear order, which means that it accounts for the gradient of the volume density of the phase-space sheet inside each simplex. Once the three-dimensional projected density field is obtained, the Poisson equation is solved in Fourier space. Calculation of the force field is performed with a standard four-point finite difference stencil to compute the gradient of the gravitational potential. Finally, the force is interpolated to each vertex of the tessellation with second-order triangular shaped cloud (TSC) interpolation (Hockney & Eastwood 1988).
As a time variable, ColDICE uses the superconformal time τ given by
with H0 the Hubble constant (e.g., Doroshkevich et al. 1973; Martel & Shapiro 1998). Time step constraints combine the classical Courant–Friedrichs–Lewy (CFL) condition,
with CCFL = 0.25, and the optional additional dynamical condition,
with Cdyn = 0.01, where Ωm is the matter density parameter of the Universe and ρmax the maximum of the projected density (normalised to unity) computed in the mesh used to solve the Poisson equation. Furthermore, to avoid too large variations in the expansion factor at early times and to have the correct behaviour of the system in the (quasi-)linear regime, the additional condition Δτ ≤ 0.1a(da/dτ)−1 is enforced. For most simulations the dynamical condition (12) was ignored, except for the Vlasov runs with ng = 512 and ns = 512 in Table 1, as well as VLA-ANI2-UHR, VLA-ANI2-MRa, and VLA-SIM-MRa. It was indeed found that condition (12) did not bring significant improvements on the results during the period of time covered by the Vlasov runs.
During evolution the phase-space sheet becomes more intricate with time. In order to follow all the details of its complexity, local refinement with the bisection method is implemented in ColDICE using a local quadratic interpolation of the tessellation mesh4. This anisotropic refinement attempts to preserve in the best way possible the Hamiltonian nature of the motion by bounding local Poincare invariants,
measured over the faces of the candidate tetrahedra obtained from the refinement. Because the initial unperturbed tessellation (Eqs. (6) and (7)) has strict zero velocity, we should have at all times Ip = 0 for any closed contour inside the phase-space sheet. Refinement is locally performed so that Ip remains very small:
Various values of I used in the ColDICE simulations are listed in last column of Table 1, and range in the ensemble {10−5, 10−6, 10−7}. We note that the choice of I should somewhat relate to spatial resolution ng since the latter controls the softening of the force field, which sources the curvature of the phase-space sheet.
2.2. Brief description of the PM code
The PM code (e.g., Hockney & Eastwood 1988) written for this project is standard. Using shared memory parallelisation with OpenMP, it follows a set of 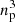 particles in a mesh of resolution ng to solve the Poisson equation. The initial conditions are the same for the PM particles as for the vertices in ColDICE: particles are set on a regular network according to Eqs. (6) and (7), with a slight perturbation on the initial positions and velocities according to Eqs. (8) and (9). The implementation of the equations of motion of the particles is also exactly analogous to what is done for the ColDICE vertices, with the same constraints on the time step, except that condition (12) was systematically enforced using Cdyn = 0.1.
particles in a mesh of resolution ng to solve the Poisson equation. The initial conditions are the same for the PM particles as for the vertices in ColDICE: particles are set on a regular network according to Eqs. (6) and (7), with a slight perturbation on the initial positions and velocities according to Eqs. (8) and (9). The implementation of the equations of motion of the particles is also exactly analogous to what is done for the ColDICE vertices, with the same constraints on the time step, except that condition (12) was systematically enforced using Cdyn = 0.1.
The main difference between the PM code and ColDICE lies in the way the Poisson equation is solved. First, the three-dimensional density is estimated on the computational mesh by projecting the particles using a TSC interpolation. Second, at variance with ColDICE, an apodisation of the Green function G(k) is performed with a Hanning filter in order to reduce small scale anisotropies,
where k is the wavenumber. Otherwise all the other steps of force field calculation are exactly the same as in ColDICE, including TSC interpolation of the force on the particles, exactly as was done in ColDICE for the vertices.
The other difference is that we do not perform local Lagrangian refinement; in other words, the number of particles does not change with time. The PM code is therefore equivalent to evolving the initial vertices of ColDICE and letting them carry the mass instead of the simplices.
The TSC interpolation used to compute the density along with Hanning filtering (15) help to reduce effects of the discrete noise of the particles, in particular local anisotropies, but add significant softening of the force field in the PM code compared to ColDICE. Calculation of the density on the computational mesh in ColDICE indeed corresponds in practice to nearest grid point (NGP) interpolation (e.g., Hockney & Eastwood 1988) in terms of convolution, so one can expect a loss of effective force resolution of the PM code compared to ColDICE when using the same value of ng, which in practice will turn out to be of about a factor 1.7 in the subsequent analyses. This approximate factor is obtained by comparing the force field generated by a particle interpolated on the grid with NGP scheme to the one obtained with TSC interpolation (which brings a factor 1.1 of effective resolution loss) combined with Hanning filtering (which brings a factor 1.5 of effective resolution loss). We note that a more complete comparison between the N-body approach and ColDICE could include PM simulations without Hanning filtering and/or with cloud-in-cell interpolation (see e.g., Hockney & Eastwood 1988) instead of TSC interpolation. We leave this for future work as we believe that these additional analyses are not necessary to prove the main points of this article.
2.3. Simulation suite
We consider two kinds of initial conditions, CDM and three sine waves, as detailed in the next two sections.
2.3.1. The ‘CDM’ simulations
For the CDM simulations, which start from fluctuations originating from a smooth random Gaussian field, the initial vertices/particle positions and velocities are computed with the public software MUSIC (Hahn & Abel 2011) used at linear order. It is important to note that, because a quadratic representation of the phase-space sheet is used, it is needed to define special tracer vertices in initial conditions. Hence, a mesh of 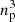 PM particles corresponds to
PM particles corresponds to 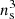 vertices of the actual tessellation, with ns = np/2, while the remaining
vertices of the actual tessellation, with ns = np/2, while the remaining 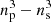 vertices are used as tracers.
vertices are used as tracers.
The assumed cosmological parameters of the CDM runs are the following (Planck Collaboration VI 2020): total matter density Ωm = 0.315, cosmological constant density parameter ΩL = 0.685, baryon density parameter Ωb = 0.0493, Hubble constant H0 ≡ 100 h = 67.4 km s−1 Mpc−1, rms density fluctuations in a 8 Mpc h−1 sphere linearly extrapolated to the present time σ8 = 0.811, and power-law index of the density perturbation spectrum after inflation nspec = 0.965. We use the extension of MUSIC of Angulo et al. (2017) to have a transfer function consistent with a neutralino of mass 100 GeV and a decoupling temperature of T = 30 MeV.
Two simulation box sizes are considered, L = 12.5 and 25 pc h−1, such that the initial density fluctuations are smooth over several spatial resolution scales L/ng and L/ns of the computational mesh and of the initial tessellation. These box sizes are obviously unrealistically small since we are not using a resimulation technique to account for tidal forces coming from scales larger than L. This is why in the figures ‘CDM’ is put in inverted commas; the halos extracted from these simulations most probably have a non-representative merger history. However, for the purpose of the present work, the random nature of the field is enough to have a qualitative idea on how the phase-space pattern changes compared to the highly symmetric case represented by the three sine waves described below.
To make sure that transients related to the fact that only linear Lagrangian theory was used to set up initial conditions do not contaminate the measurements, the simulations are started at very high redshift, ai = 10−4 for the simulations with ng = 512 and ai = 10−3 for those with lower spatial resolution.
Figure 1 shows the projected density over the whole simulation volume in the highest resolution Vlasov runs, with ng = 512 and ns = 256, and in the PM runs, with ng = 512 and np = 512. At this level of detail the differences between PM and ColDICE are nearly invisible, but it is possible to intuit a faint signature of the particle pattern in the underdense regions in the left panels.
 |
Fig. 1. Total projected density on (x, y) plane of the ‘CDM’ simulations: comparison of ColDICE to PM. The logarithmic colour table changes from dark blue to white and then to dark red when the density increases. Left and right panels: PM and ColDICE simulations, respectively, and top and bottom: box size L = 12.5 and 25 pc h−1, respectively. The simulations considered here are designated by PM-CDM12.5-HR (top left), PM-CDM25-HR (bottom left), VLA-CDM12.5-HR (top right), and VLA-CDM25-HR (bottom right) in Table 1. The expansion factor indicated in each panel corresponds to the last snapshot of the Vlasov runs. Additionally, in the right panels, circles indicate the halos selected for detailed analyses. |
Due to the smallness of the simulation volumes, only a few dark matter halos form. Five of them were selected for detailed analyses, as indicated in the right panels of Fig. 1. These halos were extracted from the simulations by simply identifying connected regions with density ρ(x) higher than 400 in the computational volume sampled with a 5123 mesh, where ρ(x) is estimated as explained in Appendix A.1. The centre of each halo was identified with the centre of mass of these regions. Projected density slices of three of these halos at the most evolved stages attained by the highest resolution ColDICE runs are shown in the right column of Fig. 2.
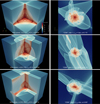 |
Fig. 2. Three-dimensional spatial density ρ(x) in typical configurations of protohalos studied in this work for the final snapshots of our highest force resolution Vlasov runs. Left panels: initial conditions given by three crossed sine waves (from top to bottom): VLA-SYM-HRS with ϵ = (1, 1), VLA-ANI2-HRS with ϵ = (3/4, 1/2), and VLA-Q1D-HR with ϵ = (1/6, 1/8). Right panels: protohalos extracted from our ‘CDM’ runs. Top two panels: halo 1 and halo 2, extracted from VLA-CDM12.5-HR, respectively and bottom panel: halo 3, extracted from VLA-CDM25-HR. The size of the subvolume on display as well as the expansion factor value are indicated in each panel. The spatial resolution scale in the left panels is εr = L/512 ≃ 0.002L, which represents about 1/51 of the subcube size; in the two upper right panels, εr = L/512 ≃ 0.025 pc h−1, which corresponds respectively to about 1/61 and 1/51 of the subcube size in the top right and middle right panels; in the bottom right panel, εr = L/512 ≃ 0.05 pc h−1, which corresponds to about 1/82 of the subcube size. |
2.3.2. Three-sine-wave simulations
In the three sine waves case, the displacement field in Eqs. (8) and (9) is given, for qx, y, z ∈ [0, L], by
where the vector A = (Ax, Ay, Az) with Ax ≥ Ay ≥ Az ≥ 0 quantifies the linear amplitudes of the waves in each direction.
This symmetrical set-up is restrictive, but remains quite generic. Near the centre of the system it indeed coincides up to quadratic order with the peak of a smooth random Gaussian field (see e.g., Bardeen et al. 1986). Following the evolution of these three-sine-wave configurations is thus expected to provide many insights into the dynamics, in particular during the early stages of the formation of dark matter halos, especially for those corresponding to high peaks of the initial field. The high level of symmetry also facilitates the calculations of analytical predictions from perturbation theory (Saga et al. 2018). The initial conditions with the three sine waves remain unrealistic, since the only contribution to the external tidal field is given by the replica of the halo due to the periodic nature of the simulated box. Additionally, the system does not experience a merger in this set-up.
Again, the three-sine-wave simulations are all started at very high redshift with ai = a(t = ti) = 0.0005 to make the contamination by transients negligible, as actually proved by the very accurate comparisons with higher order perturbation theory predictions of Saga et al. (2018). Hence, the important quantity is the relative amplitude of the waves, traced by the vector
Five different values of ϵ are considered (see Table 1), which defines three kinds of initial conditions: quasi one-dimensional (Q1D) with ϵ = (1/6, 1/8), where one amplitude dominates over the other two; anisotropic (ANI1, ANI2, ANI3), where the amplitude of each wave is different but remains of the same order; and axisymmetric (SYM) with ϵ = (1, 1). Information about the nomenclature used in the subsequent analyses is provided in Table 2, where three different regimes and the corresponding values of the expansion factor are introduced. Early time corresponds to the early violent relaxation phase (ii) described in the Introduction. Mid time corresponds to the intermediate step during which the system is progressively relaxing to the NFW dynamical attractor, point (iii) in the Introduction, attained at what we call late time.
Expansion factor values corresponding to early time, mid time, and late time for the three-sine-wave simulations.
The left panels of Fig. 2 display three-dimensional views of the projected density in the central part of the computational volume for the most evolved stages of the highest force resolution Vlasov runs with ϵ = (1, 1) (SYM), (3/4, 1/2) (ANI2), and (1/6, 1/8) (Q1D). They evidence the complex caustic pattern building up during the early violent relaxation phase, to be compared to the seemingly more intricate case of the CDM protohalos shown in the right panels.
Full details of all three-sine-wave simulations are given in Table 1. A large number of simulations was performed for extensive force resolution analyses by considering different values of ng, and for mass resolution analyses by considering different values of ns and np. In addition, as discussed in Sects. 3 and 4 below, an asymmetry can appear during runtime in ColDICE because of very small but cumulative rounding errors when projecting the tessellation on the computational mesh due to the exact superposition of the tessellation and the mesh. To try to remedy this, a shift by half a voxel size is applied to the initial conditions of the three-sine-wave simulations for some of the Vlasov runs (indicated as ‘Shift’ in the right column of Table 1), so that the vertices of the tessellation do not coincide exactly with the edges of the mesh at the centre of the system.
3. Visual inspection of the projected density
This section focuses on the visual inspection of the projected density ρ(x). Its main objectives are threefold, and set up the way it is structured. First, through force resolution analyses performed in Sect. 3.1, we show that the caustic pattern of the protohalos remains robust when sufficiently far from the centre of the system. Second, we want to confirm that the N-body approach still provides a good dynamical description of the system when particle density is high enough, despite the artificial pattern that might appear due to the discrete representation. This is supported by detailed comparisons of the PM simulations to the ColDICE simulations, along with a mass resolution analysis performed in Sect. 3.2, that includes, among other things, an analysis of the effect on the long run of changing the number of particles in the N-body simulations. Third, in order to be able to interpret the analyses performed in the next sections, Sect. 3.3 focuses on the evolution over time of the projected density for the three-sine-wave runs and for CDM halos 1 to 3.
3.1. Visual inspection: Force resolution
Figure 3 shows, at early time, the three-dimensional density ρ(x) for the three-sine-wave simulations with ϵ = (3/4, 1/2). A subcube of size L/10 is considered, where L is the simulation box size, and is sampled on 5123 voxels. Projection of the tessellation is performed in each voxel at linear order; instead of the exact but complex ray-tracing procedure used in ColDICE, we replace each tetrahedron by a dense regular network of particles, which are then assigned to the voxels using cloud-in-cell interpolation (e.g., Hockney & Eastwood 1988), as detailed in Appendix A.1. For the PM runs, a simpler NGP interpolation is performed on the voxels. Figure 4 is analogous to Fig. 3, but a zoom on halo 1 is considered. In this case the subcube considered is of size 0.12 L = 1.5 pc h−1. The colour table is almost the same for both figures, logarithmically spanning the density from blue to red in the interval log10ρ ∈ [ − 0.5, 5] and [ − 1, 4.5] respectively for the three sine waves and the CDM runs. The major differences visible in the colour pattern between the Vlasov and the PM runs are mainly due to discreteness effects; only in the high density regions, such that there is a sufficient number of particles per sampling voxel, do the PM colours become comparable to the Vlasov colours.
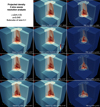 |
Fig. 3. Thorough force resolution analysis of the three-dimensional projected density ρ(x) for a three sine wave initial set-up with ϵ = (3/4, 1/2). A subcube of size L/10 is extracted from the snapshot corresponding to expansion factor a = 0.04 and sampled with 5123 voxels. The nature of the run (Vlasov or PM) and its parameters are detailed in each panel, in particular the spatial resolution ng of the grid used to solve the Poisson equation. In addition, the resolution ns of the mesh of vertices employed to construct the initial tessellation is indicated for the Vlasov runs and its analogue np for the network of |
When examining Figs. 3 and 4, the first important thing to note is that the PM simulations give very similar results to the Vlasov runs if the obvious discreteness effects related to representing the phase-space distribution function with particles are ignored. In other words, if we reconstructed a ColDICE like tessellation from the regular pattern used to build the Lagrangian initial distribution of the PM particles (as first proposed by Shandarin et al. 2012; Abel et al. 2012), we would certainly obtain results very close to the Vlasov runs, with small differences due to effective force resolution. As predicted in Sect. 2.2, because of Hanning filtering and TSC interpolation performed in the PM code, the results obtained for the N-body simulations with a given value of 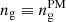 actually lie between the Vlasov runs with
actually lie between the Vlasov runs with 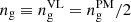 and those with
and those with 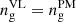 with a best match obtained for
with a best match obtained for 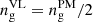 . This comparison shows that for np ≳ ng, gravitational dynamics is not significantly influenced by discrete sampling of the phase-space distribution function in the PM runs, at least during the early violent relaxation phase.
. This comparison shows that for np ≳ ng, gravitational dynamics is not significantly influenced by discrete sampling of the phase-space distribution function in the PM runs, at least during the early violent relaxation phase.
 |
Fig. 4. Example of the effects of force resolution on one of the ‘CDM’ halos. The three-dimensional projected density ρ(x) is shown for halo 1 at expansion factor a = 0.11. Top row of panels: results obtained from our high resolution Vlasov run VLA-CDM12.5-HR (left) and the PM simulation PM-CDM12.5-HR (right), both with ng = 512, that is a spatial resolution scale εr = L/ng of about 1/61 the displayed slice size. Bottom left and bottom right panels: Vlasov runs with ng = 256 (VLA-CDM12.5-MR) and ng = 128 (VLA-CDM12.5-LR), respectively, hence a spatial resolution scale of about 1/31 and 1/15 of the displayed slice size. |
Another important point concerns the caustic structure and force resolutions effects on its pattern. In Figs. 3 and 4 we see that the caustic pattern loses complexity when the force resolution is degraded, as expected, but is preserved at the coarse level. In particular, the outer caustics keep their shape and their position if sufficiently far from the centre of the system, except for the lowest force resolution runs with ng = 128. In this case the caustic structures seem slightly less extended, which we can can associate with a less evolved dynamical state as a result of excessive force softening.
The fact that the caustic structure is mainly influenced by resolution effects near the centre of the system is natural. Persistent caustics are mainly kinematic objects and local self-gravity weakly affects their dynamical evolution. The latter is mainly constrained by the global shape of the potential well in which the caustics evolve, sourced in large part by the singularity building up in the centre of the system. We note that what we call central part does not necessarily reduce to a point: it can also be a line or a surface when considering the evolution of a structure such as a filament or a pancake.
3.2. Visual inspection: Mass resolution
Examining mass resolution in the Vlasov runs consists in analysing the effects of changing the resolution ns of the mesh of vertices used to build the initial tessellation and combining it with an exploration of the space of values of the parameter I controlling deviations from local Poincaré invariants conservation (Eqs. (13) and (14)). Clearly, I is the most important parameter since it controls local mass resolution during runtime by triggering refinement when necessary. However, the choice of ns can influence dynamics in a subtle way. The scale length of fluctuations in the initial conditions needs to be captured by the tessellation, which requires a sufficiently large value of ns. At early time, when the phase-space sheet is nearly flat, tessellation resolution cannot be solely controlled by the refinement parameter I. In practice it is wise to combine the choices of I and ns in a consistent way, depending on the level of accuracy required during runtime. In particular, increasing ns should be associated with a decrease in the value of I. Similarly, taking a value of ns very different from the parameter ng controlling force resolution is possible but does not seem wise, for obvious reasons.
Comparing the first and second columns of the group of six panels on the left of Fig. 3 can give an indication of the effects of changing the mass resolution of the tessellation. We find, by comparing panels c [or a] to d and f to g, that the differences induced by changes in control parameter ns by a factor two and/or I by a factor 10 are small. This is due to the fact that all the simulations considered in this paper already follow practical accuracy constraints derived in Sousbie & Colombi (2016). However, the effects of mass resolution can be distinguished in the two bottom left panels, i and j, for which variations in the choice of ns and I are the largest. The caustics are slightly shifted away from the centre in panel j, which has a value of ns four times larger and a value of I one hundred times smaller compared to panel i. This is an effect related to curvature; as a consequence of local convexity the contours of the phase-space sheet are generally closer to the centre of the system when larger linear tetrahedra are used to sample it in order to compute projected density and solve Poisson equation. This effect can cumulate progressively with time and can have consequences on the dynamical properties of the system. We note that if we used quadratic simplices to perform the projection during runtime, the difference between panels i and j would probably become undetectable at the visual inspection level.
The effects of mass resolution on the PM runs are studied in detail in Fig. 5, again for the three-sine-wave simulations with ϵ = (3/4, 1/2). The first column of panels corresponds to early time, where data from the Vlasov runs are available, as shown in top left panel. The second and third columns of panels stand for more evolved times, designated by mid time and late time in Table 2. Mass resolution decreases from top to bottom. Only the central part of the simulation is shown, with a zoom in the interval (x, y, z) ∈ [−0.05, 0.05] for the left column of panels and (x, y, z) ∈ [−0.2, 0.2] for the two right columns. At variance with previous figures, what is displayed here is the cumulated density over the z line of sight extracted from the interval under consideration.
 |
Fig. 5. Effect of mass resolution in the PM runs: total projected density on (x, y) plane of the simulations of three crossed sine waves with ϵ = (3/4, 1/2). Except for the top panel which represents the last snapshot of the highest resolution Vlasov run, each row of panels corresponds, for various expansion factors, to a different number of particles, |
During early time all the simulations seem to match each other closely, except for the aliasing and discreteness effects due to the representation of the matter distribution with particles. We note the striking agreement between the highest resolution PM run, with ng = np = 1024, and ColDICE, with ng = 512. This agreement deteriorates slightly when decreasing spatial resolution of the PM code to ng = 512. Again, this is a consequence of force softening due to Hanning filtering and TSC interpolation, as extensively discussed in Sects. 2.2 and 3.1. Except for this there does not appear to be any artefacts in the dynamics related to N-body relaxation, at least when np ≥ 256, while it is difficult to make any definitive conclusion in the case np = 128 (bottom left panel).
Similarly, mid time stages of the evolution do not seem to be significantly affected dynamically by discreteness, at least inside the halo. In the filaments, however, the appearance of clumps for np ≤ 256 could be signatures of Jeans instability triggered by the discrete representation, although they could also be a mere signature of the pattern expected from a set of particles following regular orbits derived from the true potential. This has not been checked thoroughly and may require further investigation, yet it seems obvious that these artificial structures will grow under gravitational instability.
The last column, corresponding to late time, highlights even more visual effects due to the discrete representation. It seems unquestionable at this point that the dynamics is affected by N-body relaxation for np ≤ 256. This is also visible in the halo when examining carefully the highly concentrated cross building up during the course of dynamics. In the lower right panels, this cross presents small fluctuations that are absent from top right panels; the highly contrasted nature of these fluctuations suggests that they arise from some dynamical instability triggered by shot noise.
Figure 5 thus suggests that, at the coarse level, the overall structure of the halo remains the same whatever the value of np considered. This is confirmed by measurements of radial density profiles in Sect. 6.2. The appearance of small artificial clumps due to N-body relaxation seems unquestionable, however, and is nothing fundamentally new (see the nice illustrations of this effect in e.g., Wang & White 2007; Hahn et al. 2013). Obviously, N-body relaxation is unavoidable, but is delayed when increasing np. The practical condition np ≳ ng suggested in previous works (e.g., Melott et al. 1997; Splinter et al. 1998) agrees well at the qualitative level with visual inspection of Fig. 5.
3.3. Visual inspection: Time evolution
Figure 6 shows the evolution of the highest force resolution simulations of the three initial sine waves for three sets of values of the relative initial amplitudes. When comparing the first and second rows of panels, we observe again the excellent agreement between the PM runs with ng = 1024 and the Vlasov runs with two times lower resolution. We note, however, the small asymmetry visible in the upper left panel, which is due, as discussed at the end of Sect. 2.3.2, to very small computer rounding errors cumulating with time in ColDICE. This effect can be significantly reduced by introducing a small shift in the initial conditions, as performed in the top right panel.
 |
Fig. 6. Evolution of total projected density on (x, y) plane for different configurations of the three-sine-wave simulations. Left, middle, and right columns of panels: quasi one-dimensional set-up, ϵ = (1/6, 1/8); anisotropic set-up, ϵ = (3/4, 1/2); and axisymmetric set-up, ϵ = (1, 1), respectively. Top row of panels: results obtained at early time from high resolution Vlasov runs with ng = 512 (VLA-Q1D-HR, VLA-ANI2-FHR, and VLA-SYM-HRS in Table 1), to be compared to the second row of panels, which corresponds to the highest resolution PM runs with ng = np = 1024 (PM-Q1D-UHR, PM-ANI2-UHR, and PM-SYM-UHR). Third row of panels: same as the second row, but for a larger subcube. Last two rows of panels: results obtained from the PM runs at mid and late time. The region displayed is only a fraction of the full simulation size, namely Lsub = L/10 for the four top panels and Lsub = L/2.5 for the six bottom panels. The density contributing to the projection comes only from the cubical subvolume of size Lsub. |
A further evolution in time can be examined for the PM simulations in the last three rows of panels of Fig. 6. While the early stages of the evolution of the system clearly reflect the nature of the initial conditions (see for instance the middle left panel, which illustrates the quasi one-dimensional nature of the dynamics at large scales), in the centre of the system all the simulations build up a roughly circular halo around a three-dimensional cross, whose arms are more or less contrasted according to the strength of the initial waves. This cross is a particular feature related to the high level of symmetry of the initial conditions and is obviously not present in the CDM halos discussed below.
In the axisymmetric case, ϵ = (1, 1), the cross is perturbed, then destroyed at late time, most likely by radial orbit instabilities, but further detailed diagnostics of the dynamical properties of the flow will be needed to fully confirm this hypothesis. The high level of symmetry of the initial conditions makes the dynamics very radial and potentially prone to related instabilities especially in the axisymmetric configuration, which is analogous to the spherical case, which is known to be radially unstable when initial conditions are cold, as many works in the literature show (e.g., Vogelsberger et al. 2009; Halle et al. 2019, and references therein). This radial instability relates to force softening and particle number; for instance, in the ϵ = (1, 1) PM simulation with np = ng = 512, which is not shown here, this instability takes place later than for ng = np = 1024, with no visible symmetry breaking at mid time, unlike the right panel of the fourth row in Fig. 6.
Examining now Figs. 7–9, we turn to the CDM simulations, and inspect the evolution of halos 1, 2, and 3. A comparison of the first and second columns of panels in these figures confirms the very good, if not spectacular, agreement between the PM and Vlasov codes. Again, a careful examination of the figures shows that the best visual match is obtained between the PM runs with ng = 512 and the ColDICE runs with ng = 256.
 |
Fig. 7. Evolution of total projected density on (x, y) plane for halo 1 of the ‘CDM’ simulations with L = 12.5 Mpc h−1. First column of panels: (from top to bottom) Vlasov runs with expansion factor values a = 0.084, 0.11, 0.12, and 0.16. The two top panels were generated using the highest resolution run with ng = 512, VLA-CDM12.5-HR in Table 1, while the two bottom ones used respectively VLA-CDM12.5-MR with ng = 256 and VLA-CDM12.5-LR with ng = 128. Second column of panels: analogous to the first column, but for the PM simulation, PM-CDM12.5-HR, with ng = 512. Third column of panels: more advanced times in the PM simulation, which highlight a multiple merger (halo 1 can be seen to the right of the top panel in this column). As in Fig. 6, the mass contributing to the projection comes only from the cubical subvolume displayed on each panel. |
 |
Fig. 8. Evolution of total projected density on (x, y) plane for halo 2 of the ‘CDM’ simulations with L = 12.5 Mpc h−1. This figure is exactly analogous to Fig. 7 except that it does not have the two top panels corresponding to a = 0.084 because this halo forms later than halo 1. |
 |
Fig. 9. Evolution of total projected density on (x, y) plane for halo 3 of the ‘CDM’ simulations with L = 25 Mpc h−1. This figure is analogous to Fig. 7 except that the times considered here are slightly different and that there is one extra panel in the third column corresponding to present time, a = 1. In the third column of panels, the volume projected is larger in order to have a better view of the various structures at play. |
The three halos considered in these figures are typical of what can be expected in the CDM scenario and are similar to what is observed in other works (e.g., Ishiyama et al. 2010; Anderhalden & Diemand 2013; Angulo et al. 2017). They form at the intersection of filaments of the cosmic web. Their early evolution is monolithic and similar to the three sine waves case. At later times they are subject to successive mergers. This is illustrated by the right columns of Figs. 7 and 8, and especially by Fig. 9, which follows halo 3 until the present time, and is particularly rich in events. At the end of the simulation, halo 3 has ‘eaten’ almost all the matter available in the computing box and absorbed all the structures that formed at earlier times, in particular halos 4 and 5 (not examined in detail here). Again, we recall that these ‘CDM’ simulations are totally unrealistic because of their very small box size, so their merger history is not representative. We discuss this more in detail when analysing radial density profiles in Sect. 6.3. One obvious consequence of the simulation volume smallness is that modes aligned with the sides of the box dominate large-scale dynamics, hence the typical cross structure clearly visible in the bottom right panel of Fig. 9.
4. Phase-space sections
This section corresponds to one of the truly innovative contributions of this article. For the first time, thanks to the finesse allowed by the tessellation technique, a detailed analysis of phase-space slices is performed in the ColDICE simulations. Because the Vlasov code cannot follow the evolution of the system during many dynamical times, we consider only the early violent relaxation phase, but this will still provide us with significant insights into the dynamics.
The objectives are once more threefold, which sets up the way this section is organised. First, in Sect. 4.1 our aim is to test the robustness of the phase-space structure pattern with respect to force resolution. Second, in Sect. 4.3, through comparison of the results obtained with ColDICE to PM simulations with large number of particles, we want to validate again the N-body approach when the particle density is high enough. Third, in order to highlight specific patterns, for example related to self-similarity or to random perturbations, in Sect. 4.4 we examine how the phase-space structure evolves with time and changes according to the initial conditions.
To achieve these goals, we rely on detailed visual inspection of Figs. 10–13. To be more specific, Figs. 10–12 display phase-space slices extracted from the three-sine-wave simulations with ϵ = (3/4, 1/2). These three figures allow us to study thoroughly, at three different times, the effects of force resolution, and to compare in detail ColDICE (left panels) to the PM code (right panels). To complete the analyses, CDM halos 1, 2, and 3, already shown in Figs. 7–9, are considered for ColDICE at different force resolutions in the top three rows of panels in Fig. 13 along with the PM results in the two bottom rows. Finally, Fig. 14 examines high resolution sine wave simulations with different values of ϵ. Again, for comparison, the highest resolution PM results are shown in the last row of panels.
 |
Fig. 10. Phase-space slice. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.035. To have a better view of the fine structures of the system, the x coordinate is represented in logarithmic scale, sgn(x)log10(1 + 512 × |x|). Some values of x are indicated in blue inside each panel, while the two red vertical segments indicate the force resolution scale, L/ng, which increases from top to bottom. The Vlasov runs are considered in the left panels. In this case, the intersection of the phase-space sheet with the hyperplane y = z = 0 is calculated directly at linear order and represented in (x, vx) coordinates. The two top left panels consider Vlasov runs with ng = 512 and ns = 256. The only difference between the two simulations is the initial shift of half a voxel size imprinted in initial conditions of the simulation considered in the top left panel (VLA-ANI2-HRS in Table 1) compared to the simulation in panel just below (VLA-ANI2-HR). Our highest resolution run, VLA-ANI2-FHR (with ns = 512 instead of 256), gives nearly identical results to VLA-ANI2-HR, and is not shown here. The two bottom left panels consider lower force resolution Vlasov runs with ng = 256 (VLA-ANI2-MR) and then ng = 128 (VLA-ANI2-LR). The PM runs are examined in the right panels. In this case a very thin slice of particles is considered with (y, z) ∈ [−5 × 10−4, 5 × 10−4] as tracers of the phase-space sheet. The top right panel shows the results obtained from our highest resolution PM run, PM-ANI2-UHR, with ng = 1024 and np = 1024. The three next panels all have the same number of particles, |
 |
Fig. 11. Phase-space slice, continued. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.04. This figure is exactly the same as Fig. 10, but for a later time, a = 0.04, which is the same expansion factor as in Fig. 3. |
 |
Fig. 12. Phase-space slice, continued. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.045. This figure is exactly the same as Fig. 10, but for the most evolved time available to the high force resolution Vlasov runs. |
 |
Fig. 13. Phase-space slice of ‘CDM’ halos. Halos 1, 2, and 3 are examined in the first, second, and third column of panels, respectively. From top to bottom: Vlasov runs with increasing force resolution are considered, with ng = 128 (VLA-CDM12.5-LR in the left two panels and VLA-CDM25-LR in the right one), 256 (VLA-CDM12.5-MR and VLA-CDM25-MR), and 512 (VLA-CDM12.5-HR and VLA-CDM25-HR), then PM simulations with ng = 512 (PM-CDM12.5-HR and PM-CDM25-HR). In the last case a very thin slice of particles having (y, z) ∈ [−Δ/2, Δ/2] is represented, with Δ = 10−3L and 4 × 10−3L respectively in the fourth and fifth row of panels. |
 |
Fig. 14. Phase-space slice. Early time evolution of three-sine-wave simulations with various amplitudes. Except for the last row of panels which is dedicated to PM simulations, the Vlasov runs with ϵ = (1/6, 1/8), (3/4, 1/2), and (1, 1) are considered in the left, middle, and right columns, respectively, with time augmenting from top to bottom, starting shortly after the first shell crossing. In the two top rows of panels, the highest resolution Vlasov runs with ng = ns = 512 are under scrutiny, when available, namely VLA-ANI2-FHR and VLA-SYM-FHR in the middle and right columns, otherwise, VLA-Q1D-HR, VLA-ANI2-HRS, and VLA-SYM-HRS are considered, respectively for the left, middle, and right column, with Ng = 512 and ns = 256. To complete the figure, the last row of panels shows, at the same time as the fourth row, the results obtained from our highest resolution PM runs, with ng = np = 1024, namely (from left to right), PM-Q1D-UHR, PM-ANI2-UHR, and PM-SYM-UHR. In this case is considered, as in Figs. 10–12, a very thin slice of particles with (y, z) ∈ [−5 × 10−4, 5 × 10−4] as tracers of the phase-space sheet. |
4.1. Phase-space sections: Technical details
The phase-space slices displayed in each figure correspond, in the Vlasov code, to the intersection of the phase-space sheet with the hyperplane y = z = 0 (with the origin of coordinate system centred on the halos). We recall that the intersection of a hypersurface of dimension D = 3 with a hyperplane of dimension D′ = 4 in six-dimensional phase-space is expected to be, in the non-trivial and non-degenerate case, of dimension D + D′−6 = 1; in other words, it corresponds to a set of curves. Additionally, since the phase-space sheet is a connected periodic smooth hypersurface with no hole, this set of curves should also be fully connected, which means that in all the left panels of Figs. 10–12; in the top nine panels of Fig. 13; and in the top twelve panels of Fig. 14, there should be no loose point in the curve pattern (except the two ends on each side of each panel), which is indeed the case after a detailed visual inspection.
It should be noted that the intersection of the tessellation representing the phase-space sheet with the hyperplane y = z = 0 is calculated at linear order, which means that the curves are actually sets of segments corresponding to the intersection of each simplex with the hyperplane. One can clearly guess the segmentation pattern in the bottom left panel of Figs. 10–12. This pattern can present some small oscillations that would disappear if a second order representation of the phase-space sheet (quadratic simplices) were used, so these features are not artefacts related to dynamical instabilities. Another remark is that the figures only account for the intersections of which the count can cumulate, but no weight is given to account for volume density of the phase-space sheet, which has to be taken into account when comparing the Vlasov phase-space slices to the PM ones, which are mass weighted.
As a final remark, the top two left panels of Figs. 10–12 consider Vlasov simulations with exactly the same runtime parameters except that a small shift of half a voxel size was imprinted in the initial conditions of the simulation considered in the top left panel. As discussed at the end of Sect. 2.3.2, this procedure was introduced at some point to try to reduce the asymmetry that develops during time due to cumulative rounding errors in the Vlasov code. The effects of this asymmetry are indeed stronger without the shift. They are clearly visible in the second left panel of Figs. 11 and 12, but do not change the phase-space pattern significantly, except in the centre of the system.
4.2. Phase-space sections: force resolution
Figure 10 shows a moment at which the halo experienced only a few dynamical times, so that the phase-space structure of the system is not yet significantly intricate. As expected, this structure broadly follows a spiral pattern reminiscent of what is already well known in one dimension or in spherical symmetry (e.g., Fillmore & Goldreich 1984; Alard 2013), but is of course more complex. One can clearly guess in the top left panel the multiple crossings the system experienced along each coordinate axis. These crossings relate to duplications of portions of the phase-space spiral. Here we find that the system experienced three crossings along the x-axis, two along the y-axis, and one along the z-axis. More specifically, duplication of the external arm of the spiral pattern reflects shell crossing along the y-coordinate, while the scission in three of the central parts of the spiral corresponds to one additional shell crossing along the y-axis and one along the z-axis. Obviously, these claims cannot be derived only from the examination of the upper left panel of Fig. 10: they result from the combined analysis of the caustics pattern in Eulerian and Lagrangian spaces, which are not shown here to avoid multiplying the figures. Further discussion of the link between the Lagrangian pattern of the phase-space sheet and the internal dynamics of halos is deferred to a dedicated separate work (Colombi et al., in prep.). Interestingly enough, from a dynamical point of view, the fact that only one crossing happened along the z-axis suggests that the protohalo had just formed as a gravitationally bounded object.
When examining the two bottom left panels of Fig. 10, which correspond to lower force resolution simulations with ng = 256 and ng = 128, one can see only one duplication of each arm of the spiral, which means that collapse happened only along the x and y directions, hence that the halo is not fully formed yet. Lowering force resolution indeed delays collapse time and halo formation time. To have an accurate estimate of these times, it is required to resolve sufficiently the initial fluctuations. Softening of the force also obviously simplifies the structure of the phase-space sheet, which undergoes less folding in the centre of the system. However, the outer part of the phase-space pattern remains approximately the same at the coarse level, even at later times (left panels of Figs. 11 and 12), which confirms the conclusions from visual inspection of the projected density in Sect. 3.1 (see Fig. 3, which corresponds to the same time as Fig. 11). Naturally, these conclusions also stand when examining Fig. 13, which considers CDM halos. In this case the phase-space structure appears much less coherent than in the three-sine-wave simulations. When decreasing the force resolution this ball of yarn pattern simplifies, especially in the centre of the system, but the outer parts are mostly preserved.
4.3. Phase-space sections: Comparison with PM
Beyond the sparseness effects due to the discrete nature of the particle distribution, the match between PM and ColDICE is excellent, except that, as already extensively discussed in Sects. 2.2 and 3.1, additional softening of the force due to the TSC interpolation and Hanning filtering in the PM code makes its effective force resolution nearly two times worse than in ColDICE. This is very nicely illustrated by the phase-space diagrams, which allow us to make an accurate comparison of the morphology of the phase-space sheet obtained in the two codes, not only at the early stages of the evolution shown in Fig. 10, but also at later times, as illustrated by Figs. 11 and 12, and independently of initial conditions (Fig. 14), even in the less coherent case of the CDM halos (Fig. 13).
We repeat that if we tessellated properly the particle distribution in Lagrangian space (Shandarin et al. 2012; Abel et al. 2012) and computed the intersection of this tessellation with the hyperplane y = z = 0, the corresponding network of curves obtained from the PM particles would be very similar to that of the Vlasov code. This means that the discrete nature of the representation of the phase-space density in the PM code does not significantly affect the gravitational force field, in agreement with what we concluded from visual inspection of the density in Sect. 3.1. Again, this result is not surprising, since, as advocated by earlier works (e.g., Melott et al. 1997; Splinter et al. 1998) we consider, for the phase-space diagram analyses, only N-body simulations with at least one particle per mesh element, np ≥ ng.
It is important to note that the most evolved stages shown in Figs. 12–14 still correspond to rather early phases of the evolution of the halos. As discussed in Sect. 3.1, some instabilities due to particle shot noise in the PM code can develop at later times. Here, contrary to Sect. 3.1, more advanced times for the PM runs are not considered because the phase-space pattern becomes very intricate and indecipherable just by using directly a particle representation. A proper analysis would require the special tessellation technique on the Lagrangian particle distribution mentioned above, which has not been used here because it was deemed unnecessary to prove the important points raised in this article. Another reason is that N-body particles are unable to trace at advanced times all the complexity of the phase-space sheet, hence reconstruction of the latter with the tessellation technique is expected to become inaccurate when there are too many foldings (e.g., Hahn et al. 2013).
4.4. Phase-space sections: Pattern analysis in various cases
Figure 14 illustrates how phase space diagrams evolve with time in the high resolution sine wave simulations. Due to the highly symmetric nature of these systems, the phase-space structure remains coherent over time, taking the form of an intricate spiral. However, we only see a section of it, so calling this complex pattern a spiral is actually an abuse of language. This ‘spiral’ structure indeed experiences successive folds along the three coordinate axes, with orbital times related to the amplitude of the initial sine wave in each direction. As discussed in Sect. 4.2 for ϵ = (3/4, 1/2), shell crossings along the y- and z-axes translate into splits of the spiral arms. For instance, one can see for the quasi one-dimensional case considered in the left part of Fig. 14, a split of the central part of the spiral in second panel, which corresponds to shell crossing along the y-axis. In the right panels, since the system is axisymmetric, each shell crossing in one direction is associated with simultaneous crossings in the two orthogonal directions; hence, for each fold, each arm of the spiral is split in three parts.
Another feature of Fig. 14 is the apparent self-similar pattern of the spiral structure when it builds up complexity. Naturally, this is true only outside the central region delimited by the two red vertical segments that indicate the spatial resolution of the computational mesh used to estimate the force field. Additionally, one has to take into account in the quasi one-dimensional case (left panels) the asymmetry induced by very small but cumulative rounding errors in ColDICE. We did not apply in this case any shift to the initial conditions to remedy this defect, as discussed at the end of Sect. 2.3.2. We also note that signatures of self-similarity are less easy to decipher for this value of ϵ, due to the large difference in dynamical times associated with each axis. Self-similarity will be discussed further in Sect. 6.
Turning to more realistic configurations without imposed symmetries, an examination of Fig. 13 suggests that the phase-space structure is much less coherent in the CDM halos than in the sine wave simulations, which is not very surprising. Even so, this lack of coherence is not as strong as it seems and this is probably partly due to the choice of representation of the phase-space slices in the Vlasov simulations since the phase-space sheet was not weighted according to its local volume density. When examining the PM results, which are mass weighted, we can clearly discern a clean and rather symmetric spiral pattern at the coarse level in the two bottom left panels of Fig. 13. This is because the two halos corresponding to these plots are still in the monolithic phase, which is closely analogous to the three sine waves case. On the contrary, in the bottom right panel, which shows a composite halo (i.e. which already experienced a merger), the structure of the spiral is more intricate. Obviously, mergers contribute significantly to disorder in the phase-space structure.
5. Complexity
This section corresponds to another innovative contribution of this article. We study, for the ColDICE runs, what is referred to as complexity of the phase-space sheet through the analysis of the simplex count and of the phase-space sheet volume as functions of time. This will allow us to estimate the degree of winding of the phase-space sheet, which we try to relate to self-similarity and, if relevant, to chaotic instabilities, depending on whether it grows as a power law of time or exponentially. Confirming earlier analyses by Sousbie & Colombi (2016), we show that the phase-space sheet intricacy always increases very quickly, which unfortunately makes the adaptive tessellation method impracticable in the long run, whatever the level of optimisation.
Figures 15 and 16 respectively examine the three-sine-wave simulations and the CDM runs. The top panels of these figures show the rough simplex counts as functions of the expansion factor. As expected, during the early phases of the dynamics, the displacement field remains linear and the number of simplices Ns stays stable. At some point Ns increases very quickly until it reaches a few billion at the end of the simulations (about 10 billion in the highest resolution runs). The way this happens is related to the formation and relaxation of dark matter halos, which makes the phase-space sheet more intricate with time, as illustrated very well by the diagrams in the previous section. The phase-space sheet volume shown in the last row of panels of Figs. 15 and 16 provides a precise quantitative estimate of the actual level of complexity of the sheet. It suddenly starts to increase after the formation of the first halos5. This obviously triggers the intense refinement of the tessellation.
 |
Fig. 15. Complexity of the phase-space sheet. Simplex count and sheet volume in the simulations starting with the three crossed sine waves. Details of all the curves represented in each panel are provided in the middle panel of the second row. From left to right: different values of the initial relative amplitudes of the waves are considered, ϵ = (1/6, 1/8), (3/4, 1/2), and (1, 1), with collapse time indicated by the vertical purple segment. Top row of panels: simplex counts as functions of expansion factor for all the Vlasov runs listed in Table 1 except VLA-ANI2-LRa. Second row: simplex counts are rescaled by the factor (I/10−7)×(512/ng)α, with α = 1.6 in the two left panels and α = 2.25 in the right panel, as discussed in the main text. A fit with an ellipse portion in linear-logarithm space is also shown with red symbols (Eq. (19)). Third row: logarithmic slope of the simplex count, to be compared again to the red squares, which correspond to the logarithmic slope derived from the ellipse portion. Last row: phase-space sheet volume as a function of expansion factor. All the curves should superpose on each other; the differences relate to spatial resolution ng. The red losanges provide the prediction from the Zel’dovich approximation. |
 |
Fig. 16. Complexity of the phase-space sheet. Simplex count and sheet volume in the ‘CDM’ simulations. This figure is exactly analogous to Fig. 15, but the left and right panels correspond to all the Vlasov CDM runs with box size L = 12.5 Mpc h−1 and 25 Mpc h−1, respectively, as listed in Table 1. Details on the curves are given in second left panel. Here, comparison with the Zel’dovich approximation in the bottom panels is lacking, but would provide qualitative results similar to those in bottom panels of Fig. 15. |
The simplex count is controlled by local refinement. The pattern and finesse of the latter depend on three factors: the dynamical state of the halos, force resolution traced by ng, and the Poincaré constraint parameter I. The second row of panels of Figs. 15 and 16 combine these three elements by considering the rescaled count Ns, rescaled defined as
where the parameter α, which spans the interval [1.6, 2.25], corresponds roughly to the logarithmic slope of the radial density ρ(r) in the early relaxation phase of the halos, as measured in Sect. 6. The factor proportional to I stems from assuming that refinement is performed, in practice, in a locally isotropic fashion (Sousbie & Colombi 2016). This is not imposed by the algorithm, which allows for anisotropic refinement, but it results from the dynamics.
The factor proportional to 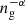 in Eq. (18) does not come from an analytic prediction. It is simply an educated guess relating to a supposed self-similar evolution of the phase-space sheet, of which we had clear hints in the previous section for the three-sine-wave simulations and which is discussed further in Sect. 6.
in Eq. (18) does not come from an analytic prediction. It is simply an educated guess relating to a supposed self-similar evolution of the phase-space sheet, of which we had clear hints in the previous section for the three-sine-wave simulations and which is discussed further in Sect. 6.
After rescaling (18), as expected, the curves in the second row of panels of Fig. 15 superpose on each other when refinement starts to dominate in terms of simplex count compared to the initial value, 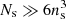 . We note, however, that the value of α was adjusted so that the superposition is visually optimal, but remains fixed in each panel of the second row of Figs. 15 and 16, as shown in the caption of the ordinates, so this result still demonstrates to a large extent the numerical consistency of ColDICE with respect to refinement in a self-similar framework.
. We note, however, that the value of α was adjusted so that the superposition is visually optimal, but remains fixed in each panel of the second row of Figs. 15 and 16, as shown in the caption of the ordinates, so this result still demonstrates to a large extent the numerical consistency of ColDICE with respect to refinement in a self-similar framework.
Turning now to the way Ns increases with time, we confirm the early findings of Sousbie & Colombi (2016), that this increase is very dramatic, which forces us to stop the runs only after a limited number of dynamical times. This highlights again the main weakness of the adaptive tessellation approach. However, in most cases the increase is not exponential. This is best illustrated by the third row of panels of Figs. 15 and 16, which display the logarithmic slope of Ns as a function of the expansion factor. For the three sine waves case, this slope suddenly grows to a peak around 10 − 30, then slowly decreases with time but still with very high values, of the order of 7 − 9 at the latest times considered in the figures. We note that the decrease is not obvious in the high resolution simulations of the axisymmetric case, but this is inconclusive due to the limited time range available.
To model the behaviour of Ns with expansion factor after the peak, an ellipse is adjusted to the black curves of the second row of panels of the figures (red squares). These curves correspond to the lowest force resolution simulations, with ng = 128, for which the available time range is the largest. The portion of the ellipse is given by the following function:
Here the four-parameter vector w = (w0, w1, w2, w3) is determined with a simplex fitting algorithm (e.g., Press et al. 1992) in the interval of values of a covered by the red squares in the figures. For completeness, the values of w are listed in Table 3.
A non-exponential behaviour of the simplex count reflects a quiescent behaviour of the dynamics or, in other words, the absence of chaos. This is what we find for the early, monolithic, violent relaxation phase of halos growing from initial conditions with three sine waves, except possibly in the axisymmetric case, but this is a very degenerate configuration. These results have to be interpreted with caution because the measurements cover a very limited time range in the highest resolution simulations. Convergence with respect to spatial resolution ng is not achieved. This is also clearly illustrated by sheet volume measurements discussed further below. This lack of convergence is even more pronounced in the CDM simulations. The blue curve in the right panel of the third row of Fig. 16 suggests an exponential behaviour of Ns at advanced times in the CDM case6. This behaviour is seen only in the highest force resolution simulation and only for a short time. This result is inconclusive, but indicates that the mergers that actually take place during this small interval of time (see Fig. 9) play an important role in introducing some chaotic signatures.
The bottom panels of Figs. 15 and 16 show the evolution of the phase-space sheet volume as a function of the expansion factor. At linear order in the geometric representation, this volume is given by the sum of the elementary volumes of each tetrahedron it is composed of. To compute the three-dimensional volume of a tetrahedron with six-dimensional coordinates, one can for instance first find the three-dimensional submanifold in which this tetrahedron lies, and then compute the volume of the tetrahedron in this submanifold. The phase-space sheet volume is therefore a difficult quantity to interpret because it overlaps the configuration and velocity spaces; it depends on the way velocities are scaled with respect to positions, that is on the choice of metric. Here, the figures assume box size and Hubble constant unity.
Even if it is difficult to interpret it in detail, the volume of the phase-space sheet remains a physical quantity, so it should not depend on any simulation parameters. This is not at all the case as soon as the first halos form. Except in the quasi-linear regime, where predictions of linear Lagrangian perturbation theory successfully reproduce simulation measurements nearly until collapse time (red losanges in the bottom panels of Fig. 15)7 the results depend strongly on spatial resolution ng (but not significantly on the other control parameters, as expected).
Halo formation marks the transition between quasi-linear and fast growth of the phase-space volume. When the value of ng is reduced, this growth is slightly delayed and becomes very significantly less prominent. This reflects the fact that during the violent relaxation phase, the phase-space sheet is subject to many foldings in the centre of the system where a power-law singularity builds up, as discussed in detail in next section. The number of these foldings and the corresponding augmentation of the volume strongly depend on force resolution. The visual inspections performed in Sects. 3.1 and 4.2 indeed show that the structure of the halos is quite insensitive to force resolution in the outer parts of the system, but it becomes more intricate in the centre with increasing ng. While the phase-space sheet volume does not seem, for this reason, to be a very useful quantity to study, it provides a robust tool to demonstrate rigorous convergence with respect to force resolution. We finally note that the exponential behaviour seen for the simplex count in the high resolution CDM simulation with L = 25 pc h−1 is not obvious in the bottom right panel of Fig. 16, but large fluctuations introduced by mergers make the results difficult to interpret.
6. Profiles
In this section we perform classic measurements of the radial density profile, ρ(r), as well as the pseudo phase-space density (Eq. (5)). Details on how the measurements are performed are provided in Appendix A.2.
The objective is to revisit phases (ii) and (iii) of the history of dark matter halos given in the Introduction. After careful tests of force and mass resolution, we examine the early violent relaxation phase of dark matter protohalos and the subsequent convergence to an universal NFW-like profile, with detailed studies of the power-law slopes of the projected and pseudo phase-space densities. One important question is whether mergers represent a sine qua non condition for the convergence to NFW. This issue will be addressed by comparing the history of CDM halos to that of idealised halos obtained from initial conditions with three sine waves and which experience a purely monolithic evolution.
This section is thus organised as follows. Exploring force resolution in Sect. 6.1 allows us to build a simple and approximate recipe for selecting the interval of scales supposedly not affected by softening of the force. Turning to mass resolution in Sect. 6.2, we show that particle number in the PM simulations does not affect the results significantly at the coarse level for all the simulations we did, except perhaps at late time, depending on the desired accuracy. Then, in Sect. 6.3 we examine the different phases of the history of density profiles for all the sine wave initial conditions as well as the five halos extracted from the two ensembles of CDM simulations. Likewise, in Sect. 6.4 we deal with the pseudo phase-space density. The measurements are put into perspective with respect to numerous and well-known results in the literature.
6.1. Force resolution
Figure 17 examines in detail the effects of changing force resolution for the three-sine-wave simulations with ϵ = (3/4, 1/2). In the left panels the quantity displayed is rαρ(r), with different values of α to emphasise the various phases of the dynamics, as discussed in detail in Sect. 6.2. To highlight the differences between the various curves, the right panels display the ratios of the measured density to that obtained from the highest available resolution run.
 |
Fig. 17. Radial density profile. Force resolution analysis of the three-sine-wave simulations with ϵ = (3/4, 1/2). Different epochs are considered following the conventions of Table 2, namely collapse time in the top panels, early time in the middle panels (for clarity, the curves corresponding to a = 0.045 are multiplied by a factor of 2) and mid to late time in the bottom panels (the curves corresponding to a = 0.185 are multiplied by a factor of 3 and 2 in the left and right panel, respectively). To have a better view of each regime, the quantity represented in the left column is the logarithm of rαρ(r), with α = 2/3, 1.6, and 2.25, respectively in the top, middle, and bottom panels (see text for details). Various simulations are considered, both in the Vlasov and PM cases, as indicated in each panel through the values of ng, ns, and np also shown in Table 1 (for the long-dashed black curve corresponding to a ColDICE run with ng = 512 and ns = 256, the simulation used is VLA-ANI2-HRS, but VLA-ANI2-HR would provide nearly identical results). In the bottom panels, the left part of the curves corresponding to the regions supposedly influenced by small-scale force softening is displayed in orange (see main text). To highlight better the differences between the various curves, the right column displays density ratios: in the top panel, the quantity displayed is ρ/ρVlasov, 1024, where ρVlasov, 1024 is the density measured in our highest resolution ColDICE run (corresponding to the dashed green curve); in the two bottom panels, the quantity displayed is ρ/ρPM, 1024, where ρPM, 1024 is the density measured in our highest resolution PM run (corresponding to the solid green curves). |
At the collapse time considered in the top panels, the structure of the local pancake singularity implies ρ(r) ∝ r−α with α = 2/3 in the centre of the halo (e.g., Arnold et al. 1982). The middle panels examine early time, during which violent relaxation takes place. In this case the radial density is close to a power law of slope α ≃ 1.6, consistent with the literature. The bottom panels show mid and late time, where the system slowly relaxes to a NFW-like profile, with a plateau consistent with secondary spherical infall prediction, α = 2.25 (Bertschinger 1985). One can also observe at mid time a regime with α = 1.2 at small radii.
As roughly demonstrated by the two top rows of panels, the mesh cell size rmin = ε ≡ L/ng seems a good estimate of the lower bound of the trustable dynamical range at collapse time and during the early relaxation phase8. This means that the effective resolution of the codes is close to optimal in this regime, as long as the quantity of interest is the radial density at the coarse level. This includes the PM simulations, despite the additional force softening introduced by Hanning filtering and TSC interpolation.
Softening of the force, however, has some non-trivial consequences at later epochs. It indeed cumulates with time by contaminating increasingly large scales. While it seems difficult to predict this effect analytically, it can be modelled in a phenomenological way by examining PM runs of various force resolutions in order to isolate the region contaminated by softening, which is represented in orange in the bottom panels of Fig. 17. This region is determined with the phenomenological formula
where aearly = 0.045 and alate = 0.19 approximately correspond to early and late time, respectively, for ϵ = (3/4, 1/2). This equation is such that rmin = L/ng for a = aearly and rmin = 2.4 L/ng for a = alate, while rmin presents a power-law behaviour as a function of expansion factor between these two values. The same formula is employed for the measurements presented in Figs. 19 and 20, but with different values of aearly and alate for the CDM halos, namely alate = 0.5 for all halos and aearly = 0.084, 0.111, 0.047, 0.067, and 0.067 for halos 1 to 5, respectively.
When looking more closely at the density profile, one can observe some fluctuations. In the top panels the density profile should be perfectly smooth, which is almost the case for the Vlasov runs9. The fluctuations in the PM simulations are simply related to discreteness effects. Their amplitude is controlled by the combination of bin width and number of particles 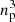 . We note that these fluctuations are much larger than the one-sigma level prediction from Poisson noise shown as very thin lines in the top panels. Indeed, at collapse time the system can still been seen as a distorted regular network of particles, which can introduce significant aliasing effects on the binned radial density.
. We note that these fluctuations are much larger than the one-sigma level prediction from Poisson noise shown as very thin lines in the top panels. Indeed, at collapse time the system can still been seen as a distorted regular network of particles, which can introduce significant aliasing effects on the binned radial density.
At later times fine variations in the density profile are mainly related to properties of the caustic pattern. Force resolution can affect this pattern, especially in the PM code, for which additional softening of the force cannot be ignored any longer. Keeping in mind the logarithmic scale used in Fig. 17, density fluctuations sufficiently far from the centre of the system still remain fairly insensitive to force resolution, consistently with the visual inspections performed in the previous sections, except at late time shown in the top curves of the bottom panels. In the latter case, force resolution seems to influence details of the radial density nearly up to the size of the system, which reflects again the cumulative nature of force softening. Hence, we finally note that using the fine instead of the coarse details of the density profile to determine the available trustable range would impose much more restrictive constraints than Eq. (20), and this even more so for the PM code.
6.2. Mass resolution
Figure 18 is analogous to Fig. 17, but studies mass resolution for the PM code. The main result of this figure is that particle count does not significantly affect the density profile at the coarse level for all the values of np considered.
 |
Fig. 18. Radial density profile. Mass resolution analysis of the three-sine-wave PM simulations with ϵ = (3/4, 1/2). This figure is analogous to Fig. 17, except that it focuses on the effect of changing the number of particles |
Turning to the finer details of the profile, we already mentioned in the previous section the aliasing effects on the measured radial density at collapse time due to the memory of the initial set-up of the particles on a regular pattern. Even with the numerous complex processes already taking place during the early part of the violent relaxation phase, this memory can persist in the multi-stream region, as long as mixing is not sufficiently rich to locally (pseudo-)randomise the particle distribution. The intrinsic softening nature of the Green function used to solve the Poisson equation can temper, at least for some time, the effects of the discrete nature of the representation of the system with particles. Hence, in the second row of the panels in Fig. 18 we can suppose that most of the additional fluctuations appearing at various radii when diluting the system are of the same nature as in the top panels, as already discussed in Sect. 3.2. At some point, however, some of these fluctuations are not transient any longer. Along with some more subtle collective effects related to shot noise (e.g., Colombi et al. 2015), they can grow through gravitational instability and introduce significant deviations from the prediction of the mean field limit. This clearly shows up at late time as noticeable differences between the top curves in the bottom panels of Fig. 18.
6.3. Time evolution: Density
Figures 19 and 20, show, for all the halos studied in this paper, the radial density profile ρ(r) and the pseudo phase-space density Q(r) (Eq. (5)).
 |
Fig. 19. Time evolution of the radial density profile (left) and of the pseudo phase-space density (right). Top two panels: results obtained for the three-sine-wave simulations for different values of ϵ. Three regimes are considered: early time, mid time (multiplied by a factor 2 for clarity on left panel), and late time (multiplied by a factor 7 in the left panel), as detailed in Table 2. The continuous curves of various colours correspond to the highest resolution PM runs, namely PM-Q1D-UHR, PM-ANI1-HR, PM-ANI2-UHR, PM-ANI3-HR, and PM-SYM-UHR in Table 1. Only the parts of the curves that are not supposed to be influenced by force softening are shown. In addition, the dashed curves of the same colour provide the measurements obtained at early time in high resolution Vlasov simulations, namely VLA-Q1D-HR, VLA-ANI1-HRS, VLA-ANI2-HR, VLA-ANI3-HRS, and VLA-SYM-HR. To emphasise the very clear power-law behaviour present at early time, the quantity actually displayed in the left panel is rαρ(r), with α = 1.6. In addition, the thin lines indicate different slopes, in particular ρ(r) ∝ r−2.25 and Q(r) ∝ r−1.875, as predicted by the secondary spherical infall model; the dashed curves show Einasto profiles with parameters given in Table 4; finally, the three close very thin lines in the top left panel also indicate small variations in the logarithmic slope: α = 1.5, 1.6, and 1.7. Next two rows of panels: as in the two top rows, but respectively for halos 1 and 2 extracted from the ‘CDM’ runs with L = 12.5 pc h−1. Several values of the expansion factor are considered to show various stages of the evolution. Again, the continuous curves of various colours correspond to the PM run PM-CDM12.5-HR. They become thinner at small scales, where force softening is thought to influence the results. The dashed curves of the same colour correspond to Vlasov simulations of the highest possible resolution available, namely VLA-CDM12.5-HR for a = 0.084 and 0.11, VLA-CDM12.5-MR for a = 0.12, and VLA-CDM12.5-LR for a = 0.16. Mergers, which induce a temporary flattening of the density profile, are emphasised by thin lines with α = 0. |
 |
Fig. 20. Time evolution of the radial density profile and the radial pseudo phase-space density: continued. Same as in Fig. 19, but for ‘CDM’ halos 3, 4, and 5, extracted from the ‘CDM’ runs with L = 25 pc h−1. Halos 4 and 5 merge with halo 3. One of these mergers is clearly captured by the orange curve corresponding to a = 0.3 in the top left panel. |
First, we focus on the left panels, which display rαρ(r) as a function of r, where α ranges in the interval [1.5, 1.8]. This value of the logarithmic slope of the density profile reflects the behaviour seen systematically in the early monolithic phase of the evolution of the protohalos, as found in many previous works, both for the three sine waves case (e.g., Nakamura 1985; Moutarde et al. 1995) and for the CDM protohalos (Diemand et al. 2005; Ishiyama et al. 2010; Anderhalden & Diemand 2013; Ishiyama 2014; Angulo et al. 2017; Delos et al. 2018a,b). What is new here is that we provide more accurate investigations of the three sine waves case with a wide variety of values of ϵ.
We find for the three sines waves that, after collapse along the three axes, the early phase of violent relaxation always builds the same kind of power-law profile, with α ≃ 1.6 ± 0.1 (the error is estimated by visual inspection), whatever ϵ = (ϵa, ϵb) with ϵa > 0 and ϵb > 010. We note a trend of the slope to increase from α ≃ 1.5 to α ≃ 1.7 − 1.8 when going from quasi one-dimensional to axisymmetric configuration, as indicated by the group of three thin lines in the top left panel of Fig. 19.
While the axisymmetric configuration is locally equivalent, at leading order, to a spherical Gaussian overdensity, ρ(r) ∝ 1 − (2πr/L)2/2, r ≪ L, the evolution of the system does not lead to the expected slope α = 2.25 predicted by the secondary spherical infall model (Gott 1975; Gunn 1977; Fillmore & Goldreich 1984; Bertschinger 1985) and measured approximately in three-dimensional N-body simulations of spherical Gaussian overdensities (e.g., Gosenca et al. 2017). One has thus to keep in mind that the axisymmetric three sine wave configuration remains, from the dynamical point of view, strongly anisotropic compared to the purely spherical case.
During the monolithic early violent relaxation phase, the ‘CDM’ experiments behave similarly to the three sine waves with a slope ranging approximately in the interval [1.5, 1.8], in agreement with the early measurements of Diemand et al. (2005), but slightly larger than the value obtained from more recent investigations, which instead suggest α ∈ [1.3, 1.5] with a preference for α ≃ 1.5 (Ishiyama et al. 2010; Anderhalden & Diemand 2013; Ishiyama 2014; Angulo et al. 2017; Delos et al. 2018a,b). These slight inconsistencies can be explained, at least partly, but in order to understand them we first need to examine the evolution with time of the various systems under consideration, which we do now.
Whatever the nature of the initial conditions, we note that the power-law behaviour seen at early time disappears at some point, and all the systems relax to a NFW-like profile (Navarro et al. 1996, 1997), or more precisely, in the analyses performed here, an Einasto-like profile (Einasto 1965),
that we abusively designate by NFW. The parameters used for the curves displayed in Figs. 19 and 20 are detailed in Table 4. The value of γ decreases with time11 down to γ = 0.15 ± 0.0312, in agreement with numerous previous works (e.g., Navarro et al. 2004, 2010; Merritt et al. 2006; Duffy et al. 2008; Gao et al. 2008; Stadel et al. 2009; Dutton & Macciò 2014; Klypin et al. 2016).
This somewhat inevitable evolution towards NFW is already well known in the literature. In the CDM case, the change in the nature of the profile is generally interpreted as the result of multiple mergers (e.g., Syer & White 1998; Ishiyama 2014; Ogiya et al. 2016; Angulo et al. 2017). However, the relaxation to a NFW-like profile is also observed in the three-sine-wave simulations (i.e. even in the absence of merger). This result is robust against particle shot noise, as illustrated by the bottom panels of Fig. 18. The fact that even in the monolithic case, the density profile and its central slope can change and also relax to NFW is not new (see e.g., Huss et al. 1999; MacMillan et al. 2006; Ogiya & Hahn 2018). Our numerical experiments confirm again the attractor nature of the NFW profile with a spectacular convergence of all the sine wave simulations at late time whatever value of ϵ we considered, as illustrated by the top curves of the upper left panel of Fig. 19.
It is important to note a potentially interesting behaviour that can be observed at mid time and at small radius for ϵ = (3/4, 1/2) and (1, 1), which seems compatible with the power law ρ(r) ∝ r−1.2. When examining close successive snapshots, it can be seen that this plateau seems to be the result of a progressive change in the slope of the power-law plateau seen at early time along with a reduction of the extension of this region. However, the simulations do not have sufficient force resolution to fully confirm this intermediary regime, especially since this α ∼ 1.2 slope can also be observed at small scales in the orange part of some of the curves in the bottom left panel of Fig. 17. In this case, it results from the softening of the force on small scales. Still, keeping this α ≃ 1.2 regime in mind, one can then isolate another scaling range with a slope compatible with the prediction α = 2.25 from secondary spherical infall, evidenced even better for ϵ = (3/4, 1/2) in the bottom left panel of Fig. 17. Finally, another regime on a larger scale compatible with the slope α = 3 can also be inferred before the cut-off limit corresponding to the halo extension. Turning to the CDM halos, the same argument may apply as long as their evolution is monolithic. They are not as well resolved as in the three-sine-wave simulations, so the examination of the left panels of Figs. 19 and 20 is inconclusive in this respect, although one might be tempted to say that halo 1 and halo 2 follow the trend discussed above for a = 0.16.
We now come back to the mild discrepancy observed between the logarithmic slope of our CDM microhalos during the early relaxation phase and the recent investigations in the literature. To suggest explanations of the differences, it can be seen that the simulations realised in the present work lack dynamical range. The periodic box size L is very small, which makes the interpretation of the results problematic because the scale corresponding to L should, in reality, become highly non-linear very quickly, which means that the tidal and merger history of the halos under consideration is unrealistic. In the real CDM scenario, one expects frequent mergers; therefore, a large fraction of protohalos could be composite and pass through the monolithic relaxation phase only shortly if at all, which implies a smaller value of α. The picture in which the first microhalos form from a single well-defined singularity might be oversimplified. It still needs to be refined, both from the theoretical point of view (following in footsteps of e.g., Arnold et al. 1982; Hidding et al. 2014; Feldbrugge et al. 2018), and the numerical point of view, by studying in detail the topology of the dynamical history of halos in the Lagrangian and Eulerian spaces. In the CDM simulations studied in the present work, all the selected halos pass through a monolithic stage, sufficiently long for the establishment of a ‘clean’ violent relaxation phase. Therefore, we might expect our CDM halos to have an initial power-law profile with α close to that of the three sine waves case, hence α ≳ 1.5, while in simulations with larger box sizes such as in Ishiyama (2014), Angulo et al. (2017), the composite yet possibly more realistic nature of the halos can lead to α ≲ 1.5.
Another limit of the simulations in the present work is their force resolution, which implies that only a restricted scale range is available to measure the slope, and this might lead to an overestimate of α. For instance, the simulation used in Ishiyama et al. (2010) has a comparable box size (30 pc) to our runs, but much higher force resolution13, which widens considerably the dynamical range for measuring radial density profiles. For the CDM halos analysed, they clearly find α ≃ 1.5. On the other hand, we have seen in the three-sine-wave simulations that the early power-law plateau seems to become less steep and less extended with time, with α ≃ 1.2 at mid time, as a result of natural evolution of the halo. In other words, the slope is time dependent, and measuring it exactly just after early relaxation is non-trivial. While resolution issues are probably real for the CDM halos analysed in the present work, this might also explain why the values of α estimated here are slightly larger than in recent analyses in the literature.
In conclusion, for halos going through a truly monolithic violent relaxation phase during their formation, it seems reasonable to think that the logarithmic slope of the power-law density profile building up during this phase can be slightly larger than 1.5. In the measurements performed for this article, α was indeed found to range in the interval [1.5, 1.8]. Then, various dynamical processes, such as evolution under slow infall as well as successive mergers decrease the effective value of α and progressively drive the system to the dynamical attractor embodied by the Einasto profile. However, we note again that it has not been proven here that all dark matter halos experience a pure monolithic phase during the early stages of their evolution, nor that a definitive answer to this question exists yet.
6.4. Time evolution: Pseudo phase-space density
The right columns of Figs. 19 and 20 plot the pseudo phase-space density Q(r) as a function of radius r14. In agreement with previous works (e.g., Taylor & Navarro 2001; Navarro et al. 2010; Ludlow et al. 2010), function Q(r) presents a power-law behaviour compatible with the prediction from secondary spherical infall model, Q(r) ∝ r−αQ with αQ = 1.875. However, the fact that this result stands irrespective of the dynamical state of the halos, even during the early violent relaxation phase and mid time (except when a merger temporarily perturbs the profile), is non-trivial and somewhat new. To our knowledge there are indeed only a few measurements in the literature of Q(r) for CDM halos during all the stages of the evolution, in particular the early violent relaxation phase. One interesting exception is the recent work of Ishiyama et al. (2010), which suggests deviations from the prediction of secondary spherical infall, with αQ ≃ 2.25 at small r. Our measurements are not sufficiently accurate to confirm this.
A power-law behaviour of function Q(r) is a clear signature of self-similarity. In the pure self-similar framework, and assuming spherical symmetry, the projected density ρ(r) and the pseudo phase-space density are both power laws, with
(e.g., Vogelsberger et al. 2011, and references therein). When the infall is purely radial, one expects α ∈ [2, 3] (Fillmore & Goldreich 1984), hence αQ ∈ [1.5, 2]. The addition of angular momentum, which provides more realistic solutions, adds spread to all the possible values of the density slope, α ∈ [0, 3] (White & Zaritsky 1992; Sikivie et al. 1997; Nusser 2001), which in turn implies αQ ∈ [1.5, 3]. In the early monolithic phase of their evolution, our halos have a clear power-law behaviour for the density with α ∈ [1.5, 1.8]. Applying naively Eq. (22) implies αQ ∈ [2.1, 2.25], which is in fact compatible with our measurements at small radii, given their level of accuracy. Along the same line of thought, the value of αQ = 2.25 measured at small radii by Ishiyama et al. (2010), whose dark matter halos have α = 1.5, is strikingly consistent with the self-similar prediction.
We recall, however, that we are far from spherical symmetry. In the triaxial case, the nature of the self-similar solutions obviously changes, and even if the expected density profile slope at small radius is analogous to that predicted in spherical symmetry with non-zero angular momentum, it may be reached only at very small radii (e.g., Lithwick & Dalal 2011). Additionally, the smooth nature of the initial overdensity deviates from the actual assumptions intrinsic to self-similar solutions, which makes the interpretation of the early monolithic phase of the evolution difficult in this framework. We recall however that in the purely spherical case, as already mentioned in the previous section, a smooth overdensity evolves to a state compatible with the secondary infall solution (Gosenca et al. 2017). Subsequent mergers add a tidal torque contribution (i.e. the generation of angular momentum from the accretion), which complicates further the interpretation of the results (although this can be also approached in spherical symmetry in a self-similar fashion; e.g., Zukin & Bertschinger 2010a,b; Lapi & Cavaliere 2011).
Even if the evolution of the phase-space density is self-similar, the finite extension of the system can imply quantities such as the projected density ρ(r) or the velocity dispersion σv(r) not to be pure power laws due to the effects of the cut-offs. But ratios such as Q(r) might just compensate for this finite size effect and evidence better the self-similar nature of the dynamics (Alard 2013). Hence, the fact that Q(r) is a pure power law is not incompatible with ρ(r) not being so, as Figs. 19 and 20 show. This is also consistent with solutions of the Jeans equation (Dehnen & McLaughlin 2005).
It is worth noting that function Q(r) tends to be more universal than the density profile. For instance, in the quantitative examples discussed above, its logarithmic slope covers a two times smaller range of values than that of density. Similarly, according to Dehnen & McLaughlin (2005), the resolution of the Jeans equation assuming a pure power law for Qr(r)≡ρ(r)/σv, r(r)3 with σv, r(r)2 the radial velocity dispersion, in practice, provides consistent solutions only if αQ, r ≡ dlnQr/dlnr = αcrit ≡ 35/18 − 2 β(r = 0)/9, where
is the velocity anisotropy parameter assumed to be linearly related to the local logarithmic density slope, with σv, ⊥(r)2 the transverse velocity dispersion. It is known that Qr(r) and Q(r) present very similar power-law behaviours, with αQ, r very slightly larger than αQ (see e.g., Ludlow et al. 2010). In other words, αQ is in practice never expected to be so different from the generic value of the secondary spherical infall model, αQ = 1.875.
In conclusion, even if it seems striking that the pseudo phase-space density is roughly compatible with the power law predicted by the standard secondary spherical infall model, αQ = 1.875, it is not surprising. It merely reflects the self-similar nature of the dynamics in phase-space (Alard 2013). Such self-similarity is also clearly suggested by the direct measurements of the history of orbits of particles in dark matter halos (Sugiura et al. 2020). While the logarithmic slope of Q(r) changes little with time, we saw in previous section that the density profile presents some striking transformations during the course of the dynamics. This is obviously related to changes in the velocity distribution, in particular to evolution of the anisotropy parameter β(r). It is indeed well known that radial instabilities play an important role in the internal dynamics of halos (e.g., Huss et al. 1999; MacMillan et al. 2006).
7. Conclusion
In this article the formation and evolution of dark matter halos have been studied in detail with the Vlasov code ColDICE and a traditional N-body particle-mesh (PM) code. Two kinds of initial conditions were considered: a highly symmetrical set-up with three sine waves, and neutralino cold dark matter (CDM) fluctuations in very small periodic boxes of size 12.5 and 25 pc h−1. In these analyses, which include projected density and phase-space diagrams, radial density profiles, and pseudo phase-space density, we paid particular attention to numerical convergence with respect to force resolution traced by the resolution ng of the mesh used to solve the Poisson equation and with respect to mass resolution traced by the initial number 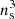 of vertices in ColDICE and the number
of vertices in ColDICE and the number 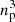 of particles in the PM simulations. The main results of this paper can be summarised as follows:
of particles in the PM simulations. The main results of this paper can be summarised as follows:
-
The N-body method is robust when there is typically more than one particle per softening length of the force, np ≳ ng. This result is well known (e.g., Melott et al. 1997), but has never been tested with comparisons of the N-body approach to a pure Vlasov code. Because of its high computational cost, ColDICE can be used to follow the evolution of halos only in the early relaxation phase. During this phase, the discrete noise of particles has little effect on the dynamical evolution of the system, and agreement between the PM code and ColDICE is excellent. Pushing the PM simulations further, the halo profiles are still not affected by N-body relaxation at the coarse level; however, some instabilities clearly develop at small scales when np < ng.
-
The early violent relaxation phase of protohalos (also called microhalos). During this phase the halos are found to display a power-law density profile, ρ(r) ∝ r−α, with α ∈ [1.5, 1.8], which agrees well with the literature, but with slightly larger values of α. Most previous investigations of CDM microhalo profiles found α ∈ [1.3, 1.5] with a preferred value α ≃ 1.5. One obvious explanation of this difference is that the CDM simulations performed in this work lack a dynamical range and that the three-sine-wave simulations are not sufficiently representative of true dark matter halos, given their very high level of symmetry. Another possible source of the difference might be related to the time at which the slope is measured. Halo profiles evolve significantly, even in the monolithic stage, which can affect measurements of the logarithmic slope. Finally, the scenario in which the halos always first form from a well-defined singularity might be oversimplified, even in the context of smooth initial conditions produced by a massive neutralino.
-
Complexity. During the early relaxation phase, it is possible to estimate the level of complexity of the ColDICE phase-space sheet by measuring its total volume Vs or the total number of simplices Ns it is composed of. While both Vs and Ns increase very quickly with time after collapse, with a growth rate ranging approximately between a7 to a30 for Ns, the increase is not exponential in most cases, which suggests the absence of chaos. Only the highest resolution CDM simulation with box size 25 Mpc h−1, which is the object of several mergers in the period covered by ColDICE, presents a clear signature of exponential growth for Ns. However, these results are inconclusive in the sense that convergence with force resolution is not demonstrated, especially when examining phase-space sheet volume.
-
Phase-space structure. During the early relaxation state, it is possible to examine in detail the structure of the phase-space sheet using phase-space diagrams. The halos originating from three sine waves display an intricate yet coherent spiral structure that is subject to multiple foldings in phase-space, which can be related to successive collapses along each axis of the dynamics. This structure also shows clear signatures of self-similarity. The random nature of CDM initial conditions makes the phase-space structure somewhat fuzzy but still coherent at the coarse level. This structure is strongly perturbed by the presence of mergers. We note that the predictions of the Vlasov code seem fairly robust with respect to force resolution when far enough from the centre of the system in terms of softening length of the force field. This is also demonstrated by the examination of the caustic pattern in the projected density.
-
Convergence to NFW-like dynamical attractor. After careful tests of convergence, the PM code was used to follow the evolution of the halos further. As already well known from many investigations in the literature, the initial power-law behaviour breaks down and the density profile converges to the dynamical NFW-like universal attractor, irrespective of the initial conditions, even in the three-sine-wave simulations. This clearly shows again that mergers do not represent a necessary condition for convergence to NFW and that radial instabilities, which change the properties of the velocity distribution, can also play a major role.
-
Pseudo phase-space density. The pseudo phase-space density Q(r) = ρ(r)/σv(r)3 measured in all the halos is compatible with the power law Q(r) ∝ r−1.875 predicted by the secondary infall model at all the times, even during the early relaxation phase. This result is well known for relaxed halos, but is non-trivial when considering the early and intermediary phases of their evolution where they display very different forms of the density profile. It represents a clear signature of self-similarity of the dynamics in phase-space.
The analyses performed in this work clearly demonstrate that it is possible to perform N-body simulations in a robust way. While the tessellation approach is free of particle shot noise, it is very costly. The extremely quick growth of the phase-space sheet complexity makes this method unaffordable beyond a limited number of dynamical times whatever its level of optimisation. To solve this problem, a hybrid implementation has been proposed, relying on tessellation in the regions where relaxation is incomplete and where the N-body technique can introduce artificial instabilities, and using particles in dense dynamically relaxed locations where the warmness of the system makes the N-body approach much more reliable (Stücker et al. 2020). However, this hybrid approach, which allows one to use the tessellation method when its cost remains affordable while, at the same time, it corrects for the main defects of the N-body approach, might seem unnecessarily complex. Instead, following a rather simple but often ignored ancient numerical strategy (e.g., Melott et al. 1997; Splinter et al. 1998), a better control of the traditional N-body approach could be achieved by making sure that there is everywhere in the computational volume at least one particle per local softening length, the main difficulty being to preserve as much as possible the Hamiltonian nature of the numerical system. This can be achieved with straightforward modifications of current N-body codes based on adaptive mesh refinement (Kravtsov et al. 1997; Teyssier 2002; Bryan et al. 2014), by improving the criteria of refinement using constraints based on estimates of local entropy production.
Another interesting result of the investigations of this article is the relaxation to a universal profile irrespective of the initial conditions, even in the absence of mergers. While this result is not fundamentally new, the detailed analyses of the three sine waves case in various configurations was never performed at the level of accuracy achieved in this work. However, the simulations, even with ng = 1024, still lack spatial resolution. It would be clearly worth reinvestigating the halos studied in the present work with high spatial resolution N-body simulations, performed in a controlled way as advocated above, to analyse in detail the evolution of the velocity field structure of the halos. In particular, it would be worth studying how the velocity anisotropy parameter β(r) (Eq. (23)) changes with time, to understand the effects of radial instabilities on the evolution of the density profile and compare them to the effects of mergers.
Neutrinos, not discussed here, compose a small fraction of dark matter. They have a large initial velocity dispersion which requires a different numerical approach from that used for cold dark matter: in this case direct Vlasov solvers rely on an Eulerian representation of the phase-space density on a six-dimensional mesh (see e.g., Yoshikawa et al. 2013, 2020).
In the bisection method, refinement is performed on the edges [a, b] of the tetrahedra, which are split into two segments [a, v] and [v, b] through the creation of a new vertex v. Then all the incident tetrahedra i, composed of vertices [a, b, ci, di], are split into two tetrahedra, composed of vertices [a, v, ci, di] and [b, v, ci, di]. To preserve the accuracy of refinement, a quadratic representation of the phase-space sheet inside each simplex is used, with the help of additional tracers corresponding to the mid-points of the edges of each tetrahedron in Lagrangian space (i.e. in the space of initial, unperturbed positions). These tracers are actually used as the candidate refinement vertices. New tracers are created each time refinement is performed by exploiting the local quadratic representation of the sheet. This refinement procedure preserves the conforming nature of the tessellation by matching up vertices, edges, and faces at the intersection between two tetrahedra, without hanging nodes, that is without an isolated vertex belonging to one tetrahedron on an edge, a face, or in the bulk of another tetrahedron.
The full formation of the halo requires, as described in the Introduction, collapses along all of the three main axes of the dynamics. In the quasi one-dimensional case, this event takes place significantly later than first shell crossing, which is shown as the vertical purple segment in each panel of Fig. 15.
To compute the prediction from linear Lagrangian perturbation theory, we create a regular network of vertices with ns = 32 following Eqs. (6) and (7), then perturb this network according to the Zel’dovich approximation up to the time of interest following Eqs. (8) and (9). These vertices are tessellated with a set of tetrahedra of which we compute the sum of the volumes, as explained in the main text.
Some small amount of noise can be discerned in the ColDICE measurements in the top right panel, but this is related to the way the density is calculated, as detailed in Appendix A.2.
However, the density ratios shown in the top right panel of Fig. 17 present small variations related to this noise.
Acknowledgments
We thank Thierry Sousbie, who wrote the source code of ColDICE, for very fruitful exchanges during several years of collaboration. We also thank Christophe Alard, Mark Neyrinck, Shohei Saga, Andrei Sobolevski and Atsushi Taruya for fruitful discussions. This work was supported by ANR grant ANR-13-MONU-0003. Numerical computation with ColDICE was carried out using the HPC resources of CINES (Occigen supercomputer) under the GENCI allocations c2016047568, 2017-A0040407568, and 2018-A0040407568. PM simulations and post-treatment of ColDICE data were performed on HORIZON cluster of Institut d’Astrophysique de Paris. Three-dimensional data visualisation (Fig. 2: left panels; and Fig. 3) was performed with ParaView (Ahrens et al. 2005) (www.paraview.org).
References
- Aarseth, S. J., Lin, D. N. C., & Papaloizou, J. C. B. 1988, ApJ, 324, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Abel, T., Hahn, O., & Kaehler, R. 2012, MNRAS, 427, 61 [CrossRef] [Google Scholar]
- Alard, C. 2013, MNRAS, 428, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Anderhalden, D., & Diemand, J. 2013, JCAP, 2013, 009 [Google Scholar]
- Angulo, R. E., Hahn, O., & Abel, T. 2013, MNRAS, 434, 3337 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, R. E., Hahn, O., Ludlow, A. D., & Bonoli, S. 2017, MNRAS, 471, 4687 [Google Scholar]
- Ahrens, J., Geveci, B., & Law, C. 2005, ParaView: An End-User Tool for Large Data Visualization, Visualization Handbook (Elsevier) [Google Scholar]
- Arnold, V. I., Shandarin, S. F., & Zel’dovich, Y. B. 1982, Geophys. Astrophys. Fluid Dyn., 20, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Bardeen, J. M., Bond, J. R., Kaiser, N., & Szalay, A. S. 1986, ApJ, 304, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Benhaiem, D., Joyce, M., Sylos Labini, F., & Worrakitpoonpon, T. 2018, MNRAS, 473, 2348 [NASA ADS] [CrossRef] [Google Scholar]
- Beraldo e Silva, L., de Siqueira Pedra, W., Sodré, L., Perico, E. L. D., & Lima, M. 2017, ApJ, 846, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Beraldo e Silva, L., de Siqueira Pedra, W., Valluri, M., Sodré, L., & Bru, J. B. 2019, ApJ, 870, 128 [Google Scholar]
- Bernardeau, F., Colombi, S., Gaztañaga, E., & Scoccimarro, R. 2002, Phys. Rep., 367, 1 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Bertschinger, E. 1985, ApJS, 58, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Bertschinger, E. 1998, ARA&A, 36, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J. 2004, MNRAS, 350, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Blumenthal, G. R., Faber, S. M., Primack, J. R., & Rees, M. J. 1984, Nature, 311, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, F. R., Juszkiewicz, R., Colombi, S., & Pellat, R. 1992, ApJ, 394, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Bouchet, F. R., Colombi, S., Hivon, E., & Juszkiewicz, R. 1995, A&A, 296, 575 [NASA ADS] [Google Scholar]
- Bryan, G. L., Norman, M. L., O’Shea, B. W., et al. 2014, ApJS, 211, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Buchert, T. 1993, A&A, 267, L51 [NASA ADS] [Google Scholar]
- Buchert, T., & Ehlers, J. 1993, MNRAS, 264, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Carron, J., & Szapudi, I. 2013, MNRAS, 432, 3161 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S. 2001, New Astron. Rev., 45, 373 [Google Scholar]
- Colombi, S. 2015, MNRAS, 446, 2902 [Google Scholar]
- Colombi, S., & Touma, J. 2008, Commun. Nonlinear Sci. Numer. Simul., 13, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., & Touma, J. 2014, MNRAS, 441, 2414 [Google Scholar]
- Colombi, S., Sousbie, T., Peirani, S., Plum, G., & Suto, Y. 2015, MNRAS, 450, 3724 [NASA ADS] [CrossRef] [Google Scholar]
- Cuperman, S., Harten, A., & Lecar, M. 1971a, Ap&SS, 13, 411 [Google Scholar]
- Cuperman, S., Harten, A., & Lecar, M. 1971b, Ap&SS, 13, 425 [Google Scholar]
- Dehnen, W., & McLaughlin, D. E. 2005, MNRAS, 363, 1057 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dehnen, W., & Read, J. I. 2011, Eur. Phys. J. Plus, 126, 55 [CrossRef] [Google Scholar]
- Delos, M. S., Erickcek, A. L., Bailey, A. P., & Alvarez, M. A. 2018a, Phys. Rev. D, 97, 041303 [Google Scholar]
- Delos, M. S., Erickcek, A. L., Bailey, A. P., & Alvarez, M. A. 2018b, Phys. Rev. D, 98, 063527 [Google Scholar]
- DePackh, D. C. 1962, J. Electr. Contrib., 13, 417 [Google Scholar]
- Diemand, J., Moore, B., Stadel, J., & Kazantzidis, S. 2004, MNRAS, 348, 977 [CrossRef] [Google Scholar]
- Diemand, J., Moore, B., & Stadel, J. 2005, Nature, 433, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Borgani, S., Schindler, S., Diaferio, A., & Bykov, A. M. 2008, Space Sci. Rev., 134, 229 [NASA ADS] [CrossRef] [Google Scholar]
- Doroshkevich, A. G., Ryaben’kii, V. S., & Shandarin, S. F. 1973, Astrophysics, 9, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [NASA ADS] [CrossRef] [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Einasto, J. 1965, Trudy Astrofizicheskogo Instituta Alma-Ata, 5, 87 [NASA ADS] [Google Scholar]
- Feldbrugge, J., van de Weygaert, R., Hidding, J., & Feldbrugge, J. 2018, JCAP, 2018, 027 [CrossRef] [Google Scholar]
- Fillmore, J. A., & Goldreich, P. 1984, ApJ, 281, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, L., Navarro, J. F., Cole, S., et al. 2008, MNRAS, 387, 536 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, J., Heggie, D. C., & Hut, P. 1993, ApJ, 415, 715 [CrossRef] [Google Scholar]
- Gosenca, M., Adamek, J., Byrnes, C. T., & Hotchkiss, S. 2017, Phys. Rev. D, 96, 123519 [Google Scholar]
- Gott, J. R. 1975, ApJ, 201, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E. 1977, ApJ, 218, 592 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, O., & Abel, T. 2011, MNRAS, 415, 2101 [NASA ADS] [CrossRef] [Google Scholar]
- Hahn, O., & Angulo, R. E. 2016, MNRAS, 455, 1115 [Google Scholar]
- Hahn, O., Abel, T., & Kaehler, R. 2013, MNRAS, 434, 1171 [Google Scholar]
- Halle, A., Colombi, S., & Peirani, S. 2019, A&A, 621, A8 [EDP Sciences] [Google Scholar]
- Henriksen, R. N., & Widrow, L. M. 1995, MNRAS, 276, 679 [NASA ADS] [CrossRef] [Google Scholar]
- Hidding, J., Shandarin, S. F., & van de Weygaert, R. 2014, MNRAS, 437, 3442 [CrossRef] [Google Scholar]
- Hjorth, J., & Williams, L. L. R. 2010, ApJ, 722, 851 [NASA ADS] [CrossRef] [Google Scholar]
- Hockney, R. W., & Eastwood, J. W. 1988, Computer Simulation Using Particles (Bristol: Hilger) [CrossRef] [Google Scholar]
- Huss, A., Jain, B., & Steinmetz, M. 1999, ApJ, 517, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ishiyama, T. 2014, ApJ, 788, 27 [Google Scholar]
- Ishiyama, T., Makino, J., & Ebisuzaki, T. 2010, ApJ, 723, L195 [Google Scholar]
- Janin, G. 1971, A&A, 11, 188 [Google Scholar]
- Jing, Y. P., & Suto, Y. 2000, ApJ, 529, L69 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Joyce, M., Marcos, B., & Sylos Labini, F. 2009, MNRAS, 397, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Klypin, A., Yepes, G., Gottlöber, S., Prada, F., & Heß, S. 2016, MNRAS, 457, 4340 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Kravtsov, A. V., Gottlöber, S., & Klypin, A. A. 2000, MNRAS, 317, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Kravtsov, A. V., Klypin, A. A., & Khokhlov, A. M. 1997, ApJS, 111, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Lapi, A., & Cavaliere, A. 2011, ApJ, 743, 127 [Google Scholar]
- Lithwick, Y., & Dalal, N. 2011, ApJ, 734, 100 [Google Scholar]
- Ludlow, A. D., Navarro, J. F., Springler, V., et al. 2010, MNRAS, 406, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D. 1967, MNRAS, 136, 101 [NASA ADS] [CrossRef] [Google Scholar]
- MacMillan, J. D., Widrow, L. M., & Henriksen, R. N. 2006, ApJ, 653, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Mansfield, P., & Avestruz, C. 2021, MNRAS, 500, 3309 [Google Scholar]
- Martel, H., & Shapiro, P. R. 1998, MNRAS, 297, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Matsubara, T. 2015, Phys. Rev. D, 92, 023534 [NASA ADS] [CrossRef] [Google Scholar]
- Melott, A. L. 2007, ArXiv e-prints [arXiv:0709.0745] [Google Scholar]
- Melott, A. L., Shandarin, S. F., Splinter, R. J., & Suto, Y. 1997, ApJ, 479, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., Graham, A. W., Moore, B., Diemand, J., & Terzić, B. 2006, AJ, 132, 2685 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Governato, F., Quinn, T., Stadel, J., & Lake, G. 1998, ApJ, 499, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Moutarde, F., Alimi, J.-M., Bouchet, F. R., Pellat, R., & Ramani, A. 1991, ApJ, 382, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Moutarde, F., Alimi, J.-M., Bouchet, F. R., & Pellat, R. 1995, ApJ, 441, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Nakamura, T. 1985, Progr. Theor. Phys., 73, 657 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Hayashi, E., Power, C., et al. 2004, MNRAS, 349, 1039 [NASA ADS] [CrossRef] [Google Scholar]
- Navarro, J. F., Ludlow, A., Springel, V., et al. 2010, MNRAS, 402, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Nusser, A. 2001, MNRAS, 325, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Ogiya, G., & Hahn, O. 2018, MNRAS, 473, 4339 [Google Scholar]
- Ogiya, G., Nagai, D., & Ishiyama, T. 2016, MNRAS, 461, 3385 [Google Scholar]
- Peebles, P. J. E. 1982, ApJ, 263, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1984, ApJ, 277, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pontzen, A., & Governato, F. 2013, MNRAS, 430, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Power, C., Navarro, J. F., Jenkins, A., et al. 2003, MNRAS, 338, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in FORTRAN. The Art of Scientific Computing (Cambridge: Cambridge University Press) [Google Scholar]
- Rampf, C. 2012, JCAP, 2012, 004 [CrossRef] [Google Scholar]
- Rampf, C., Frisch, U., & Hahn, O. 2019, ArXiv e-prints [arXiv:1912.00868] [Google Scholar]
- Saga, S., Taruya, A., & Colombi, S. 2018, Phys. Rev. Lett., 121, 241302 [Google Scholar]
- Shandarin, S., Habib, S., & Heitmann, K. 2012, Phys. Rev. D, 85, 083005 [NASA ADS] [CrossRef] [Google Scholar]
- Sikivie, P., Tkachev, I. I., & Wang, Y. 1997, Phys. Rev. D, 56, 1863 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., & Colombi, S. 2016, J. Comput. Phys., 321, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Splinter, R. J., Melott, A. L., Shandarin, S. F., & Suto, Y. 1998, ApJ, 497, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Stadel, J., Potter, D., Moore, B., et al. 2009, MNRAS, 398, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Stücker, J., Hahn, O., Angulo, R. E., & White, S. D. M. 2020, MNRAS, 495, 4943 [Google Scholar]
- Sugiura, H., Nishimichi, T., Rasera, Y., & Taruya, A. 2020, MNRAS, 493, 2765 [Google Scholar]
- Syer, D., & White, S. D. M. 1998, MNRAS, 293, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Taruya, A., & Colombi, S. 2017, MNRAS, 470, 4858 [Google Scholar]
- Taylor, J. E., & Navarro, J. F. 2001, ApJ, 563, 483 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vogelsberger, M., White, S. D. M., Mohayaee, R., & Springel, V. 2009, MNRAS, 400, 2174 [NASA ADS] [CrossRef] [Google Scholar]
- Vogelsberger, M., Mohayaee, R., & White, S. D. M. 2011, MNRAS, 414, 3044 [Google Scholar]
- Vogelsberger, M., Marinacci, F., Torrey, P., & Puchwein, E. 2020, Nat. Rev. Phys., 2, 42 [CrossRef] [Google Scholar]
- Wang, J., & White, S. D. M. 2007, MNRAS, 380, 93 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Zaritsky, D. 1992, ApJ, 394, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, K., Yoshida, N., & Umemura, M. 2013, ApJ, 762, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshikawa, K., Tanaka, S., Yoshida, N., & Saito, S. 2020, ApJ, 904, 159 [Google Scholar]
- Zel’dovich, Y. B. 1970, A&A, 500, 13 [Google Scholar]
- Zheligovsky, V., & Frisch, U. 2014, J. Fluid Mech., 749, 404 [CrossRef] [Google Scholar]
- Zukin, P., & Bertschinger, E. 2010a, Phys. Rev. D, 82, 104044 [Google Scholar]
- Zukin, P., & Bertschinger, E. 2010b, Phys. Rev. D, 82, 104045 [Google Scholar]
Appendix A: Calculation of the projected density and of radial profiles
While ColDICE uses a complex ray-tracing algorithm to compute the exact intersections between the tessellation and the mesh used to solve Poisson equation, post-treatment is performed in a less sophisticated way by replacing each simplex of the tessellation by a large number of particles. The next two sections explain how the three-dimensional projected density and the radial profiles are calculated from the tessellation structure provided by ColDICE.
A.1. Calculation of projected density
To compute the projected density used in Figs. 1–9, a three-dimensional grid of resolution nsub = 512 is defined on a cube of size Lsub that can correspond to the full simulation volume, as in Fig. 1, or a portion of it, as in Fig. 2. Then each simplex overlapping with this volume is refined recursively in an isotropic fashion ℓmax times. At the end of the process each subsimplex is replaced with a particle lying at the barycentre of the four vertices composing it. Then this particle is assigned to the computational grid with a standard cloud-in-cell interpolation (Hockney & Eastwood 1988). For each simplex, the final level of refinement ℓmax is chosen so that each subsimplex size is small enough compared to the size Δsub = Lsub/Nsub of each voxel of the mesh, namely
with
where vi, j is the ith coordinate of vertex j (j = 1, …, 4) of the simplex. With the choice of ℓmax given by Eq. (A.1), discreteness effects related to the particle representation are sufficiently small to be invisible in the figures.
A.2. Calculation of radial profiles
To compute the radial profiles the procedure is slightly different. First, considering Nbins logarithmic bins of width
in the interval [Rmin, Rmax], the simplices are refined isotropically again ℓmax times, but with a value of ℓmax defined as
with E = 0.005,
and Vs is the volume of the smallest possible parallelepiped P containing the simplex with sides aligned with the coordinates axes:
If this parallelepiped contains the origin of coordinates, Rs is also set equal to Rmin. Basically, Nvirtual represents an estimate of the number of parallelepipeds the smallest radial bin intersecting with the simplex would contain. In Eq. (A.4), E represents the order of magnitude of the maximum relative error one aims to achieve in the presence of the Poisson noise induced by the replacement of the simplices with particles.
In the last step, instead of replacing the subsimplex with a particle at the barycentre of the vertices composing it, it is replaced with a particle thrown at random inside the volume occupied by the simplex in order to reduce the aliasing effects on the binned radial profile. Then the particle is assigned to the bin directly with a weight proportional to the mass of the subsimplex. Additionally, this weight can be multiplied, depending on the quantity of interest, by the radial coordinate of the velocity, its square, or the square of the transverse velocity. The choice of E = 0.005 is such that fluctuation noise introduced by the procedure remains nearly invisible on the curves shown in Figs. 17–2015. This means that all the irregular features that can be seen in the curves shown in these figures are intrinsic and not induced by the sampling of the simplices with particles.
All Tables
Expansion factor values corresponding to early time, mid time, and late time for the three-sine-wave simulations.
All Figures
 |
Fig. 1. Total projected density on (x, y) plane of the ‘CDM’ simulations: comparison of ColDICE to PM. The logarithmic colour table changes from dark blue to white and then to dark red when the density increases. Left and right panels: PM and ColDICE simulations, respectively, and top and bottom: box size L = 12.5 and 25 pc h−1, respectively. The simulations considered here are designated by PM-CDM12.5-HR (top left), PM-CDM25-HR (bottom left), VLA-CDM12.5-HR (top right), and VLA-CDM25-HR (bottom right) in Table 1. The expansion factor indicated in each panel corresponds to the last snapshot of the Vlasov runs. Additionally, in the right panels, circles indicate the halos selected for detailed analyses. |
| In the text | |
 |
Fig. 2. Three-dimensional spatial density ρ(x) in typical configurations of protohalos studied in this work for the final snapshots of our highest force resolution Vlasov runs. Left panels: initial conditions given by three crossed sine waves (from top to bottom): VLA-SYM-HRS with ϵ = (1, 1), VLA-ANI2-HRS with ϵ = (3/4, 1/2), and VLA-Q1D-HR with ϵ = (1/6, 1/8). Right panels: protohalos extracted from our ‘CDM’ runs. Top two panels: halo 1 and halo 2, extracted from VLA-CDM12.5-HR, respectively and bottom panel: halo 3, extracted from VLA-CDM25-HR. The size of the subvolume on display as well as the expansion factor value are indicated in each panel. The spatial resolution scale in the left panels is εr = L/512 ≃ 0.002L, which represents about 1/51 of the subcube size; in the two upper right panels, εr = L/512 ≃ 0.025 pc h−1, which corresponds respectively to about 1/61 and 1/51 of the subcube size in the top right and middle right panels; in the bottom right panel, εr = L/512 ≃ 0.05 pc h−1, which corresponds to about 1/82 of the subcube size. |
| In the text | |
 |
Fig. 3. Thorough force resolution analysis of the three-dimensional projected density ρ(x) for a three sine wave initial set-up with ϵ = (3/4, 1/2). A subcube of size L/10 is extracted from the snapshot corresponding to expansion factor a = 0.04 and sampled with 5123 voxels. The nature of the run (Vlasov or PM) and its parameters are detailed in each panel, in particular the spatial resolution ng of the grid used to solve the Poisson equation. In addition, the resolution ns of the mesh of vertices employed to construct the initial tessellation is indicated for the Vlasov runs and its analogue np for the network of |
| In the text | |
 |
Fig. 4. Example of the effects of force resolution on one of the ‘CDM’ halos. The three-dimensional projected density ρ(x) is shown for halo 1 at expansion factor a = 0.11. Top row of panels: results obtained from our high resolution Vlasov run VLA-CDM12.5-HR (left) and the PM simulation PM-CDM12.5-HR (right), both with ng = 512, that is a spatial resolution scale εr = L/ng of about 1/61 the displayed slice size. Bottom left and bottom right panels: Vlasov runs with ng = 256 (VLA-CDM12.5-MR) and ng = 128 (VLA-CDM12.5-LR), respectively, hence a spatial resolution scale of about 1/31 and 1/15 of the displayed slice size. |
| In the text | |
 |
Fig. 5. Effect of mass resolution in the PM runs: total projected density on (x, y) plane of the simulations of three crossed sine waves with ϵ = (3/4, 1/2). Except for the top panel which represents the last snapshot of the highest resolution Vlasov run, each row of panels corresponds, for various expansion factors, to a different number of particles, |
| In the text | |
 |
Fig. 6. Evolution of total projected density on (x, y) plane for different configurations of the three-sine-wave simulations. Left, middle, and right columns of panels: quasi one-dimensional set-up, ϵ = (1/6, 1/8); anisotropic set-up, ϵ = (3/4, 1/2); and axisymmetric set-up, ϵ = (1, 1), respectively. Top row of panels: results obtained at early time from high resolution Vlasov runs with ng = 512 (VLA-Q1D-HR, VLA-ANI2-FHR, and VLA-SYM-HRS in Table 1), to be compared to the second row of panels, which corresponds to the highest resolution PM runs with ng = np = 1024 (PM-Q1D-UHR, PM-ANI2-UHR, and PM-SYM-UHR). Third row of panels: same as the second row, but for a larger subcube. Last two rows of panels: results obtained from the PM runs at mid and late time. The region displayed is only a fraction of the full simulation size, namely Lsub = L/10 for the four top panels and Lsub = L/2.5 for the six bottom panels. The density contributing to the projection comes only from the cubical subvolume of size Lsub. |
| In the text | |
 |
Fig. 7. Evolution of total projected density on (x, y) plane for halo 1 of the ‘CDM’ simulations with L = 12.5 Mpc h−1. First column of panels: (from top to bottom) Vlasov runs with expansion factor values a = 0.084, 0.11, 0.12, and 0.16. The two top panels were generated using the highest resolution run with ng = 512, VLA-CDM12.5-HR in Table 1, while the two bottom ones used respectively VLA-CDM12.5-MR with ng = 256 and VLA-CDM12.5-LR with ng = 128. Second column of panels: analogous to the first column, but for the PM simulation, PM-CDM12.5-HR, with ng = 512. Third column of panels: more advanced times in the PM simulation, which highlight a multiple merger (halo 1 can be seen to the right of the top panel in this column). As in Fig. 6, the mass contributing to the projection comes only from the cubical subvolume displayed on each panel. |
| In the text | |
 |
Fig. 8. Evolution of total projected density on (x, y) plane for halo 2 of the ‘CDM’ simulations with L = 12.5 Mpc h−1. This figure is exactly analogous to Fig. 7 except that it does not have the two top panels corresponding to a = 0.084 because this halo forms later than halo 1. |
| In the text | |
 |
Fig. 9. Evolution of total projected density on (x, y) plane for halo 3 of the ‘CDM’ simulations with L = 25 Mpc h−1. This figure is analogous to Fig. 7 except that the times considered here are slightly different and that there is one extra panel in the third column corresponding to present time, a = 1. In the third column of panels, the volume projected is larger in order to have a better view of the various structures at play. |
| In the text | |
 |
Fig. 10. Phase-space slice. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.035. To have a better view of the fine structures of the system, the x coordinate is represented in logarithmic scale, sgn(x)log10(1 + 512 × |x|). Some values of x are indicated in blue inside each panel, while the two red vertical segments indicate the force resolution scale, L/ng, which increases from top to bottom. The Vlasov runs are considered in the left panels. In this case, the intersection of the phase-space sheet with the hyperplane y = z = 0 is calculated directly at linear order and represented in (x, vx) coordinates. The two top left panels consider Vlasov runs with ng = 512 and ns = 256. The only difference between the two simulations is the initial shift of half a voxel size imprinted in initial conditions of the simulation considered in the top left panel (VLA-ANI2-HRS in Table 1) compared to the simulation in panel just below (VLA-ANI2-HR). Our highest resolution run, VLA-ANI2-FHR (with ns = 512 instead of 256), gives nearly identical results to VLA-ANI2-HR, and is not shown here. The two bottom left panels consider lower force resolution Vlasov runs with ng = 256 (VLA-ANI2-MR) and then ng = 128 (VLA-ANI2-LR). The PM runs are examined in the right panels. In this case a very thin slice of particles is considered with (y, z) ∈ [−5 × 10−4, 5 × 10−4] as tracers of the phase-space sheet. The top right panel shows the results obtained from our highest resolution PM run, PM-ANI2-UHR, with ng = 1024 and np = 1024. The three next panels all have the same number of particles, |
| In the text | |
 |
Fig. 11. Phase-space slice, continued. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.04. This figure is exactly the same as Fig. 10, but for a later time, a = 0.04, which is the same expansion factor as in Fig. 3. |
| In the text | |
 |
Fig. 12. Phase-space slice, continued. Force resolution analysis and comparison between Vlasov and PM for the three-sine-wave simulations with ϵ = (3/4, 1/2) and a = 0.045. This figure is exactly the same as Fig. 10, but for the most evolved time available to the high force resolution Vlasov runs. |
| In the text | |
 |
Fig. 13. Phase-space slice of ‘CDM’ halos. Halos 1, 2, and 3 are examined in the first, second, and third column of panels, respectively. From top to bottom: Vlasov runs with increasing force resolution are considered, with ng = 128 (VLA-CDM12.5-LR in the left two panels and VLA-CDM25-LR in the right one), 256 (VLA-CDM12.5-MR and VLA-CDM25-MR), and 512 (VLA-CDM12.5-HR and VLA-CDM25-HR), then PM simulations with ng = 512 (PM-CDM12.5-HR and PM-CDM25-HR). In the last case a very thin slice of particles having (y, z) ∈ [−Δ/2, Δ/2] is represented, with Δ = 10−3L and 4 × 10−3L respectively in the fourth and fifth row of panels. |
| In the text | |
 |
Fig. 14. Phase-space slice. Early time evolution of three-sine-wave simulations with various amplitudes. Except for the last row of panels which is dedicated to PM simulations, the Vlasov runs with ϵ = (1/6, 1/8), (3/4, 1/2), and (1, 1) are considered in the left, middle, and right columns, respectively, with time augmenting from top to bottom, starting shortly after the first shell crossing. In the two top rows of panels, the highest resolution Vlasov runs with ng = ns = 512 are under scrutiny, when available, namely VLA-ANI2-FHR and VLA-SYM-FHR in the middle and right columns, otherwise, VLA-Q1D-HR, VLA-ANI2-HRS, and VLA-SYM-HRS are considered, respectively for the left, middle, and right column, with Ng = 512 and ns = 256. To complete the figure, the last row of panels shows, at the same time as the fourth row, the results obtained from our highest resolution PM runs, with ng = np = 1024, namely (from left to right), PM-Q1D-UHR, PM-ANI2-UHR, and PM-SYM-UHR. In this case is considered, as in Figs. 10–12, a very thin slice of particles with (y, z) ∈ [−5 × 10−4, 5 × 10−4] as tracers of the phase-space sheet. |
| In the text | |
 |
Fig. 15. Complexity of the phase-space sheet. Simplex count and sheet volume in the simulations starting with the three crossed sine waves. Details of all the curves represented in each panel are provided in the middle panel of the second row. From left to right: different values of the initial relative amplitudes of the waves are considered, ϵ = (1/6, 1/8), (3/4, 1/2), and (1, 1), with collapse time indicated by the vertical purple segment. Top row of panels: simplex counts as functions of expansion factor for all the Vlasov runs listed in Table 1 except VLA-ANI2-LRa. Second row: simplex counts are rescaled by the factor (I/10−7)×(512/ng)α, with α = 1.6 in the two left panels and α = 2.25 in the right panel, as discussed in the main text. A fit with an ellipse portion in linear-logarithm space is also shown with red symbols (Eq. (19)). Third row: logarithmic slope of the simplex count, to be compared again to the red squares, which correspond to the logarithmic slope derived from the ellipse portion. Last row: phase-space sheet volume as a function of expansion factor. All the curves should superpose on each other; the differences relate to spatial resolution ng. The red losanges provide the prediction from the Zel’dovich approximation. |
| In the text | |
 |
Fig. 16. Complexity of the phase-space sheet. Simplex count and sheet volume in the ‘CDM’ simulations. This figure is exactly analogous to Fig. 15, but the left and right panels correspond to all the Vlasov CDM runs with box size L = 12.5 Mpc h−1 and 25 Mpc h−1, respectively, as listed in Table 1. Details on the curves are given in second left panel. Here, comparison with the Zel’dovich approximation in the bottom panels is lacking, but would provide qualitative results similar to those in bottom panels of Fig. 15. |
| In the text | |
 |
Fig. 17. Radial density profile. Force resolution analysis of the three-sine-wave simulations with ϵ = (3/4, 1/2). Different epochs are considered following the conventions of Table 2, namely collapse time in the top panels, early time in the middle panels (for clarity, the curves corresponding to a = 0.045 are multiplied by a factor of 2) and mid to late time in the bottom panels (the curves corresponding to a = 0.185 are multiplied by a factor of 3 and 2 in the left and right panel, respectively). To have a better view of each regime, the quantity represented in the left column is the logarithm of rαρ(r), with α = 2/3, 1.6, and 2.25, respectively in the top, middle, and bottom panels (see text for details). Various simulations are considered, both in the Vlasov and PM cases, as indicated in each panel through the values of ng, ns, and np also shown in Table 1 (for the long-dashed black curve corresponding to a ColDICE run with ng = 512 and ns = 256, the simulation used is VLA-ANI2-HRS, but VLA-ANI2-HR would provide nearly identical results). In the bottom panels, the left part of the curves corresponding to the regions supposedly influenced by small-scale force softening is displayed in orange (see main text). To highlight better the differences between the various curves, the right column displays density ratios: in the top panel, the quantity displayed is ρ/ρVlasov, 1024, where ρVlasov, 1024 is the density measured in our highest resolution ColDICE run (corresponding to the dashed green curve); in the two bottom panels, the quantity displayed is ρ/ρPM, 1024, where ρPM, 1024 is the density measured in our highest resolution PM run (corresponding to the solid green curves). |
| In the text | |
 |
Fig. 18. Radial density profile. Mass resolution analysis of the three-sine-wave PM simulations with ϵ = (3/4, 1/2). This figure is analogous to Fig. 17, except that it focuses on the effect of changing the number of particles |
| In the text | |
 |
Fig. 19. Time evolution of the radial density profile (left) and of the pseudo phase-space density (right). Top two panels: results obtained for the three-sine-wave simulations for different values of ϵ. Three regimes are considered: early time, mid time (multiplied by a factor 2 for clarity on left panel), and late time (multiplied by a factor 7 in the left panel), as detailed in Table 2. The continuous curves of various colours correspond to the highest resolution PM runs, namely PM-Q1D-UHR, PM-ANI1-HR, PM-ANI2-UHR, PM-ANI3-HR, and PM-SYM-UHR in Table 1. Only the parts of the curves that are not supposed to be influenced by force softening are shown. In addition, the dashed curves of the same colour provide the measurements obtained at early time in high resolution Vlasov simulations, namely VLA-Q1D-HR, VLA-ANI1-HRS, VLA-ANI2-HR, VLA-ANI3-HRS, and VLA-SYM-HR. To emphasise the very clear power-law behaviour present at early time, the quantity actually displayed in the left panel is rαρ(r), with α = 1.6. In addition, the thin lines indicate different slopes, in particular ρ(r) ∝ r−2.25 and Q(r) ∝ r−1.875, as predicted by the secondary spherical infall model; the dashed curves show Einasto profiles with parameters given in Table 4; finally, the three close very thin lines in the top left panel also indicate small variations in the logarithmic slope: α = 1.5, 1.6, and 1.7. Next two rows of panels: as in the two top rows, but respectively for halos 1 and 2 extracted from the ‘CDM’ runs with L = 12.5 pc h−1. Several values of the expansion factor are considered to show various stages of the evolution. Again, the continuous curves of various colours correspond to the PM run PM-CDM12.5-HR. They become thinner at small scales, where force softening is thought to influence the results. The dashed curves of the same colour correspond to Vlasov simulations of the highest possible resolution available, namely VLA-CDM12.5-HR for a = 0.084 and 0.11, VLA-CDM12.5-MR for a = 0.12, and VLA-CDM12.5-LR for a = 0.16. Mergers, which induce a temporary flattening of the density profile, are emphasised by thin lines with α = 0. |
| In the text | |
 |
Fig. 20. Time evolution of the radial density profile and the radial pseudo phase-space density: continued. Same as in Fig. 19, but for ‘CDM’ halos 3, 4, and 5, extracted from the ‘CDM’ runs with L = 25 pc h−1. Halos 4 and 5 merge with halo 3. One of these mergers is clearly captured by the orange curve corresponding to a = 0.3 in the top left panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



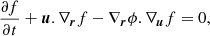
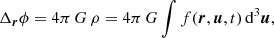
![$$ \begin{aligned} f(\boldsymbol{r},\boldsymbol{u},t=t_{\rm i})= \rho _{\rm i}(\boldsymbol{r})\,\delta _{\rm D}[\boldsymbol{u}-\boldsymbol{u}_{\rm i}(\boldsymbol{r})], \end{aligned} $$](/articles/aa/full_html/2021/03/aa39719-20/aa39719-20-eq3.gif)
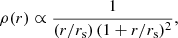
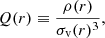
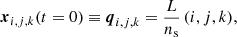
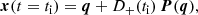
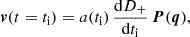
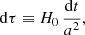
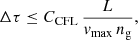
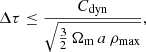
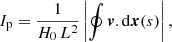
![$$ \begin{aligned} G(k)= \frac{1}{2\, k^2} \left[ 1+\cos (L\, k/n_{\rm g}) \right],\quad k \le \pi \, n_{\rm g}/L, \end{aligned} $$](/articles/aa/full_html/2021/03/aa39719-20/aa39719-20-eq18.gif)
![$$ \begin{aligned} \boldsymbol{P}=\frac{L}{2\pi } \left[ A_x \sin \left( \frac{2\pi }{L}\, q_x \right), A_y \sin \left( \frac{2\pi }{L}\, q_y \right), A_z \sin \left( \frac{2\pi }{L}\, q_z \right) \right], \end{aligned} $$](/articles/aa/full_html/2021/03/aa39719-20/aa39719-20-eq22.gif)
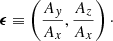
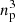
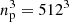
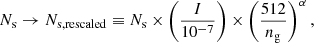
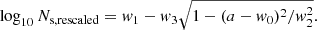
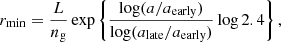
![$$ \begin{aligned} \rho (r) \propto \exp \left\{ -\frac{2}{\gamma } \left[\left( \frac{r}{r_0} \right)^\gamma - 1\right]\right\} , \end{aligned} $$](/articles/aa/full_html/2021/03/aa39719-20/aa39719-20-eq38.gif)