| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A121 | |
| Number of page(s) | 33 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201833613 | |
| Published online | 15 March 2019 | |
Density waves and the viscous overstability in Saturn’s rings
Astronomy Research Unit,
PO Box 3000,
90014
University of Oulu, Oulu,
Finland
e-mail: marius.lehmann@oulu.fi
Received:
11
June
2018
Accepted:
7
January
2019
This paper considers resonantly forced spiral density waves in a dense planetary ring that is close to the threshold for viscous overstability. We solved numerically the hydrodynamical equations for a dense thin disk in the vicinity of an inner Lindblad resonance with a perturbing satellite. Our numerical scheme is one-dimensional so that the spiral shape of a density wave is taken into account through a suitable approximation of the advective terms arising from the fluid orbital motion. This paper is a first attempt to model the co-existence of resonantly forced density waves and short-scale free overstable wavetrains as observed in Saturn’s rings, by conducting large-scale hydrodynamical integrations. These integrations reveal that the two wave types undergo complex interactions, not taken into account in existing models for the damping of density waves. In particular we found that, depending on the relative magnitude of both wave types, the presence of viscous overstability can lead to the damping of an unstable density wave and vice versa. The damping of the short-scale viscous overstability by a density wave was investigated further by employing a simplified model of an axisymmetric ring perturbed by a nearby Lindblad resonance. A linear hydrodynamic stability analysis as well as local N-body simulations of this model system were performed and support the results of our large-scale hydrodynamical integrations.
Key words: hydrodynamics / instabilities / planets and satellites: rings / waves
© ESO 2019
1 Introduction
The Cassini mission to Saturn has revealed a vast abundance of structures in the planet’s ring system, spanning a wide range of length scales. The finest of these structures have been detected by several Cassini instruments (Colwell et al. 2007; Thomson et al. 2007; Hedman et al. 2014) and are periodic and quasi-axisymmetric1 with wavelengths of some 100 m. It is generally accepted that this periodic microstructure originates from the viscous overstability mechanism, which has been studied so far only in terms of axisymmetric models (Schmit & Tscharnuter 1995, 1999; Spahn et al. 2000; Salo et al. 2001; Schmidt & Salo 2003; Latter & Ogilvie 2008, 2009, 2010; Rein & Latter 2013; Lehmann et al. 2017). On much greater scales, typically tens to hundreds of kilometers, numerous spiral density waves propagate through the rings, as these are excited at radii where the orbiting ring particles are in resonance with the gravitational perturbation of one of the moons orbiting the ring system.
The process of excitation and damping of resonantly forced density waves has been thoroughly studied, mostly in terms of hydrodynamic models (Goldreich & Tremaine 1978a,b, 1979; Shu 1984; Shu et al. 1985a,b; Borderies et al. 1985, 1986; Lehmann et al. 2016). Throughout the literature one typically distinguishes between linear and nonlinear density waves. The former are the ring’s response to a relatively small, resonantly perturbing force in the sense that the excited surface mass density perturbation is small compared to the equilibrium value. In this case the governing hydrodynamic equations can be linearized and as a consequence the density wave appears sinusoidal in shape.
The studies by Shu et al. (1985b), Borderies et al. (1986; BGT86 henceforth), and Lehmann et al. (2016; LSS2016 henceforth) considered the damping behavior of nonlinear density waves in a dense planetary ring, such as Saturn’s B ring. For a nonlinear density wave the surface density perturbation is of the same order of magnitude as the equilibrium value. Within a fluid description of the ring dynamics, the damping of a density wave is governed by different components of the pressure tensor. The model by Shu et al. (1985b) computes the pressure tensor from the kinetic second order moment equations, using a Krook-collision term. The model predicts reasonable damping lengths of a density wave for assumed ground state optical depths (or surface mass densities) that do not exceed a certain critical value (which depends on the details of the collision term). For optical depths larger than this critical value, the wave damping becomes very weak so that the resulting wavetrains propagate with ever increasing amplitude and nonlinearity. That said, the model fails to describe the damping of nonlinear waves in dense ring regions with high mutual collision frequencies of the ring particles, such as the wave excited at the 2:1 inner Lindblad resonance (ILR) with the moon Janus, propagating in Saturn’s B ring. The main reason for this behavior of the model at large collision frequencies is most likely the neglect of nonlocal contributions to the (angular) momentum transport (Shukhman 1984; Araki & Tremaine 1986) in their kinetic model. On the other hand, BGT86 compute the pressure tensor from a fluid model (Borderies et al. 1985), as well as by using empirical formulae, which yield the correct qualitative behavior of the pressure tensor in a dense ring with a large volume filling factor. The computed damping lengths for optical depths relevant to Saturn’s dense rings are fairly long and the authors suspect this to be a consequence of the fluid approximation.
Borderies et al. (1985) have shown that density waves are unstable in a sufficiently dense ring (such as Saturn’s B ring), whereas they are stable in dilute rings of small optical depth. Schmidt et al. (2016) pointed out that the instability condition of spiral density waves is identical to the criterion for spontaneous viscous overstability (Schmit & Tscharnuter 1995) in the limit of long wavelengths. In LSS2016 we derived the damping of nonlinear density waves from a different view point compared to the approaches by BGT86 and Shu et al. (1985b), which are based on the streamline formalism (see Longaretti & Borderies 1991). We considered the density wave as a pattern that forms in response to this instability, using techniques that are widely applied in the study of pattern formation in systems outside of equilibrium (Cross & Hohenberg 1993). Consequently, the wave damping is described in terms of a nonlinear amplitude equation. The resulting damping behavior is very similar to what is predicted by the BGT86 model.
While the models by BGT86 and LSS2016 can predict steady state profiles of density waves alone in an overstable ring region (see also Stewart 2016), they do not take into account the possible presence of additional wave structures that can spontaneously arise in response to the viscous overstability, independent of a perturbing satellite. A first attempt to study the presence of multiple modes in a narrow ring within the streamline formalism was made by Longaretti (1989), but further improvements are required to model the (nonlinear) interaction of different modes. The possibility of the co-existence of resonant spiral density waves and a short-scale near-axisymmetric periodic microstructure was discovered by analyzing stellar occultations of Saturn’s A ring, recorded with the Cassini Visual and Infrared Mapping Spectrometer (Hedman et al. 2014). This paper is concerned with a modeling of this co-existence and a qualitative understanding of interactions between a resonantly forced density wave and the short-scale waves generated by the viscous overstability. In our one-dimensional hydrodynamical scheme we need to assume that both the density wave and the short-scale waves are non-axisymmetric with the same azimuthal periodicity. However, since the short-scale waves resulting from spontaneous viscous overstability have wavelengths of some 100 m (implying very small cant-angles of 10−3–10−4 degrees), their dynamical evolution is expected to be very similar to that of the extensively studied axisymmetric modes (see the aforementioned papers). Hydrodynamical integrations presented in this paper confirm this expectation.
In Sect. 2 we outline the basic hydrodynamic model equations. Section 3 explains the numerical scheme applied to perform large-scale integrations of the hydrodynamical equations. Sections 4–6 discuss specific terms appearing in these equations that arise from the forcing by the satellite, the advection due to orbital motion of the ring fluid, as well as the collective self-gravity forces, respectively. Results of large-scale hydrodynamical integrations are presented in Sect. 7. Here we first describe the excitation process of a density wave as it follows from our integrations. Subsequently we test our scheme against the nonlinear models by BGT86 and LSS2016 in a marginally stable ring. In addition, we present some illustrative examples of density waves that propagate through a ring region that contains sharp radial gradients in the background surface mass density. We then consider waves that propagate in an overstable ring. In order to facilitate an interpretation of the results from our large-scale integrations, we introduce a simplified axisymmetric model to describe the perturbation of a ring due to a nearby ILR. We perform a linear hydrodynamic stability analysis of this model to compute linear growth rates of axisymmetric overstable waves in the perturbed ring. By employing the same model we then perform local N-body simulations of viscous overstability in a perturbed ring. Finally, Sect. 8 provides a discussion of the main results.
2 Hydrodynamic model
From the vertically integrated isothermal balance equations for a dense planetary ring we derive the model equations (Stewart et al. 1984; Schmidt et al. 2009
![\begin{align*}\begin{split} \partial_{t} \tau & = - \left[\Omega-\Omega_{L} \right] \, \partial_{\theta}\tau -u \partial_{r} \tau - \tau \partial_{r} u, \\ \partial_{t} u & = - \left[\Omega-\Omega_{L} \right] \, \partial_{\theta}u -u\partial_{r} u + 2\Omega v -\partial_{r}\left[\phi^{\textrm{d}} + \phi^{\textrm{s}} \right] - \frac{1}{\sigma} \partial_{r} \hat{P}_{rr} , \\ \partial_{t} v & = - \left[\Omega-\Omega_{L} \right] \, \partial_{\theta}v - u \partial_{r}v -\frac{1}{2}\Omega u -\frac{1}{r}\partial_{\theta} \phi^{\textrm{s}} - \frac{1}{\sigma} \partial_{r} \hat{P}_{r\theta}, \end{split} \end{align*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq1.png) (1)
(1)
in a cylindrical frame (r, θ, z = 0) with origin at r = rL, rotating rigidly with angular frequency ΩL = Ω(rL), where rL denotes the radial location of a specific inner Lindblad resonance (ILR) with a perturbing satellite and
![\begin{equation*} \Omega = \left[\frac{G M_{\textrm{P}}}{r^3}\right]^{1/2} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq2.png) (2)
(2)
with Saturn’s mass MP = 5.96 × 1026 kg and the gravitational constant G = 6.67 × 10−11m3 kg−1 s−2. In what follows we will also make use of the radial distance
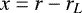 (3)
(3)
as well as its scaled version 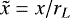 .
.
The quantity σ is the rings’ surface mass density and τ = σ∕σ0 with the ground state surface mass density σ0. The symbols u, v stand for the radial and azimuthal components of the velocity on top of the orbital velocity ![$\left[\Omega \, -\Omega_{L}\right] r$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq5.png) in the rigidly rotating frame. Furthermore,
in the rigidly rotating frame. Furthermore, 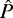 is the pressure tensor (see below). The central planet is assumed to be spherical so that Ω = κ, the latter denoting the epicyclic frequency of ring particles. The rings’ ground state, which describes the balance of central gravity and centrifugal force, is subtracted from the above equations and we neglect the large-scale viscous evolution of the rings that occurs on timescales much longer than those considered in this study.
is the pressure tensor (see below). The central planet is assumed to be spherical so that Ω = κ, the latter denoting the epicyclic frequency of ring particles. The rings’ ground state, which describes the balance of central gravity and centrifugal force, is subtracted from the above equations and we neglect the large-scale viscous evolution of the rings that occurs on timescales much longer than those considered in this study.
We neglect curvature terms containing factors 1∕r since these scale as λ∕r ~ 10−4 compared to radial derivatives. Here λ denotes the typical radial wavelength of a spiral density wave near its related Lindblad resonance where 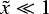 . From all terms containing derivatives with respect to θ we retain only the advective terms arising from the Keplerian motion, that is, the first terms on the right hand sides of Eqs. (1). All other θ-derivatives scale as (mλ)∕r compared to radial derivatives (m denoting the number of spiral arms of the density wave), that is, the same as curvature terms.
. From all terms containing derivatives with respect to θ we retain only the advective terms arising from the Keplerian motion, that is, the first terms on the right hand sides of Eqs. (1). All other θ-derivatives scale as (mλ)∕r compared to radial derivatives (m denoting the number of spiral arms of the density wave), that is, the same as curvature terms.
Poisson’s equation for a thin disk
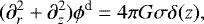 (4)
(4)
establishes a relation between the self-gravity potential ϕd and the surface density σ.
The viscous stress is assumed to be of Newtonian form such that in the cylindrical frame we can write
![\begin{equation*}\begin{split} \begin{array}{@{}*{22}{l@{}}} \hat{P} &\,=\, \begin{pmatrix} \hat{P}_{rr} \hspace{0.2 cm} & \hat{P}_{r\theta} \\[0.18cm] \hat{P}_{\theta r} \hspace{0.2 cm} & \hat{P}_{\theta\theta} \end{pmatrix}\\[0.5cm] & \,=\,\begin{pmatrix} p -\eta\left(\frac{4}{3}+\hat{\gamma}\right)\partial_{r}u \hspace{0.2 cm} & -\eta\left(-\frac{3}{2}\Omega + \partial_{r}v \right) \\[0.15 cm] -\eta\left(-\frac{3}{2}\Omega +\partial_{r}v \right) \hspace{0.2 cm} & p + \eta \left(\frac{2}{3}-\hat{\gamma}\right)\partial_{r} u \end{pmatrix} . \end{array} \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq9.png) (5)
(5)
It is thus completely described by radial gradients of the velocities u, v, the dynamic shear viscosity η, as well as the isotropic pressure p (see below). The ratio of the bulk and shear viscosity is denoted by 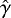 , which is assumed to be constant (Schmit & Tscharnuter 1995). The isotropic pressure and the dynamic shear viscosity take the simple forms
, which is assumed to be constant (Schmit & Tscharnuter 1995). The isotropic pressure and the dynamic shear viscosity take the simple forms
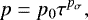 (6)
(6)
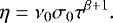 (7)
(7)
In this study we assume pσ = 1, which is theequation of state for an ideal gas. The ground state pressure can be defined in terms of an effective ground state velocity dispersion c0 such that (Schmidt et al. 2001)
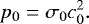 (8)
(8)
The ground state is characterized by σ0 = const., u0 = 0, v0 = 0, together with the parameters in Eqs. (6) and (7).
We neglect azimuthal contributions due to collective self-gravity forces. This neglect is adequate as long as the exerted satellite torque is much smaller than the unperturbed viscous angular momentum luminosity of the ring. That is, the (self-gravitational) angular momentum luminosity carried by the wave is negligible compared to the viscous luminosity. The linear inviscid satellite torque deposited at the resonance site reads (Goldreich & Tremaine 1979)
![\begin{equation*}T^{\textrm{s}}= -m \pi^2 \frac{ \sigma_{0}}{\mathcal{D} \, \Omega_{L}^2} \left(\epsilon \, r_{L} \Omega_{L}\right)^4 \left[ \partial_{r}\phi^{\textrm{s}} -2 m \,\phi^{\textrm{s}} \right]_{r_{L}}^2 ,\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq14.png) (9)
(9)
and (Cuzzi et al. 1984)
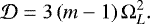 (11)
(11)
The viscous angular momentum luminosity in the unperturbed disk is given by (Lynden-Bell & Pringle 1974)
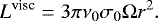
In addition it should be mentioned that we are not concerned with the long-term redistribution of ring surface mass density that occurs in response to the presence of very strong density waves (BGT86) so that we assume σ0 = const as mentioned before.
Throughout the paper we use parameters corresponding to the Prometheus 7:6 ILR, located at r ~ 126 000 km in Saturn’s A ring. We take values of the rings’ ground state shear viscosity ν0 and surface mass density σ0 (see Table 1) that can be estimated from corresponding values obtained by Tiscareno et al. (2007) for this ring region. The nominal values of β and γ correspond to values found in N-body simulations with an optical depth τdyn = 1 (see LSS2016; Sect. 3). Besides the nominal values, we use a range of values for β (Eq. (7)) and also Ts (Eq. (9)), in order to explore a variety of qualitatively different scenarios for the damping of density waves. The adopted value for the ground state velocity dispersion c0 is larger then what results from local non-gravitating N-body simulations for optical depths relevant to this study (e.g., Salo 1991) but corresponds roughly to expected values for Saturn’s A ring from self-gravitating N-body simulations exhibiting gravitational wakes and assuming meter-sized particles (Daisaka et al. 2001; Salo et al. 2018). Furthermore, the value is still small enough to ignore pressure effects on the density waves’ dispersion relation (Sect. 7.1).
Our hydrodynamic model exhibits spontaneous viscous overstability on finite wavelengths if the viscous parameter β exceeds a critical value. To see this, let us ignore the satellite forcing ϕs for the time being. We restrict ourselves to short radial length scales so that Ω = ΩL can be considered constant, except that we use
![\begin{equation*} \left[\Omega -\Omega_{L} \right]\partial_{\theta} = -\frac{3}{2} \Omega_{L} x \partial_{y} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq18.png)
in Eqs. (1). Our 1D numerical method to solve Eqs. (1) assumes that any mode that forms has m-fold azimuthal periodicity (see Sect. 5). Hence let us introduce non-axisymmetric oscillatory perturbations such that
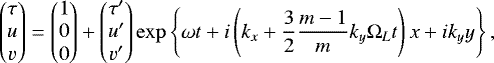 (12)
(12)
with complex oscillation frequency ω = ωR + i ωI and real-valued radial and azimuthal wavenumbers kx > 0 and 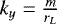 , respectively. The time-dependent contribution to the radial wavenumber in Eq. (12) stems from the winding of the perturbations due to Keplerian shear (see Meyer-Vernet & Sicardy 1987 and Eq. (47)). Since we know that the linear growth and the nonlinear saturation of spontaneous viscous overstability occurs on wavelengths of typically hundreds of meters, it turns out that we can neglect the effect of winding in Eq. (12). That is, for the relevant modes the time it takes for the winding term to become equal to kx is given by
, respectively. The time-dependent contribution to the radial wavenumber in Eq. (12) stems from the winding of the perturbations due to Keplerian shear (see Meyer-Vernet & Sicardy 1987 and Eq. (47)). Since we know that the linear growth and the nonlinear saturation of spontaneous viscous overstability occurs on wavelengths of typically hundreds of meters, it turns out that we can neglect the effect of winding in Eq. (12). That is, for the relevant modes the time it takes for the winding term to become equal to kx is given by
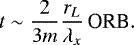
With λx = 2π∕kx ~ 100 m, this yields some 100 000 orbits, which is much longer than the timescale of the nonlinear evolution of the modes (i.e., thousands of orbits, see Latter & Ogilvie 2010; Rein & Latter 2013; LSS2017). If the effect of winding could not be neglected, the ansatz (Eq. (12)) would not be appropriate (see for instance Johnson & Gammie 2005). Furthermore, Eq. (4) yields the relationship
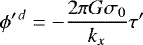 (13)
(13)
for a single wavelength mode (Shu 1984).
In the remainder of this section we apply dimensional scalings such that time is scaled with 1∕ΩL and length is scaled with c0∕ΩL. Inserting Eqs. (12) and (13) into Eq. (1) and linearizing with respect to the perturbations (the primed quantities) results in the eigenvalue problem
![\begin{align*}0 =& - \omega^3 + \omega^2 \left[- \left(\frac{7}{3} + \gamma\right) k_{x}^2 \nu_{0} + \frac{9}{2} i m \tilde{x}\right]\nonumber\\ & + \,\omega \left[-1 + 2 g k_x - k_{x}^2 - \left(\frac{4}{3} + \gamma \right) k_{x}^4 \nu_{0}^2 \right. \nonumber\\ & \left. +\, i \left(7 + 3 \gamma \right) k_{x}^2 m \tilde{x} \nu_{0} + \frac{27}{4} m^2 \tilde{x}^2 \right]\nonumber\\ & -\,k_{x}^2 \left(3 + 3 \beta - 2 g k_x + k_{x}^2\right) \nu_{0} \nonumber\\ & + \frac{1}{2} i m \tilde{x} \left(3 - 6 g k_x + 3 k_{x}^2 + \left(4 + 3 \gamma \right) k_{x}^4 \nu_{0}^2\right) \nonumber\\ & + \frac{3}{4} \left(7 + 3 \gamma \right) k_{x}^2 m^2 \tilde{x}^2 \nu_{0} - \frac{27}{8} i m^3 \tilde{x}^3 \end{align*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq23.png) (14)
(14)
for ω = ωR + iωI. The non-dimensional distance 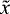 is defined as below Eq. (3). This equation can be used to obtain the growth rate ωR (kx) and oscillation frequency ωI (kx) of a given mode kx. This procedure has been carried out for axisymmetric modes (with m = 0) in several papers (see Lehmann et al. (2017), LSS2017 hereafter, and references therein for more details). It can be shown that the growth rates ωR (kx) following from Eq. (14) are independent of m (i.e., independent of ky) and agree with those of previous studies.
is defined as below Eq. (3). This equation can be used to obtain the growth rate ωR (kx) and oscillation frequency ωI (kx) of a given mode kx. This procedure has been carried out for axisymmetric modes (with m = 0) in several papers (see Lehmann et al. (2017), LSS2017 hereafter, and references therein for more details). It can be shown that the growth rates ωR (kx) following from Eq. (14) are independent of m (i.e., independent of ky) and agree with those of previous studies.
In the remainder of the paper the symbol k denotes the radial wavenumber of a given mode. The threshold for viscous oscillatory overstability, that is, a vanishing growth rate ωR (k) = 0, can be obtained by setting ω = iωI and solving the imaginary and real parts of Eq. (14) for ωI and β, respectively, for a given wavenumber k. This yields the critical frequency pair2
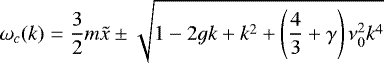 (15)
(15)
and the critical value of the viscosity parameter
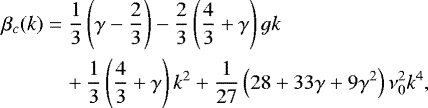 (16)
(16)
which describes the stability boundary for viscous overstability and which is also independent of m. The frequencies (Eq. (15)) are Doppler-shifted by 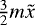 as compared to the frequencies of axisymmetric modes. We note that due to the fact that Eqs. (1) are defined in a frame rotating with ΩL, this Doppler-shift is very small as
as compared to the frequencies of axisymmetric modes. We note that due to the fact that Eqs. (1) are defined in a frame rotating with ΩL, this Doppler-shift is very small as 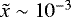 for all cases considered in this paper. The Doppler-shift can therefore be neglected. These results show that linear free non-axisymmetric short-scale modes due to spontaneous viscous overstability in our hydrodynamic model behave essentially the same as axisymmetric modes with m = 0.
for all cases considered in this paper. The Doppler-shift can therefore be neglected. These results show that linear free non-axisymmetric short-scale modes due to spontaneous viscous overstability in our hydrodynamic model behave essentially the same as axisymmetric modes with m = 0.
The curve βc(k) possesses a minimum at finite wavelength if g > 0, that is, for a non-vanishing collective self-gravity force. This wavelength is roughly two times the Jeans-wavelength 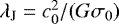 . In the above equations we define
. In the above equations we define
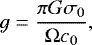 (17)
(17)
denoting the inverse of the hydrodynamic Toomre-parameter (a full list of symbols is provided in Table 2).
Hydrodynamic parameters.
3 Numerical methods
For numerical solution of Eqs. (1) we applied a finite difference flux vector splitting method employing a weighted essentially non-oscillatory (WENO) reconstruction of the flux vector components. The method is identical to that used in LSS2017, apart from the reconstruction of the flux vector.
We define the flux-conservative variables
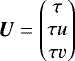
so that Eqs. (1) can be written as
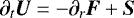 (18)
(18)
is the viscous stress tensor with Û denoting the unity tensor.
We solve Eq. (18) on a radial domain of size Lr. The domain is discretized by defining nodes rj (j = 1, 2, …, n) with constant inter-spacing h = rj+1 − rj. We adopt periodic boundary conditions in all integrations. Since a density wave is not periodic in radial direction, this requires the radial domain size Lr to be large enough so that the Lindblad resonance is located sufficiently far from the inner domain boundary and that an excited density wave is fully damped before reaching the outer domain boundary. The discretization of the flux derivative ∂r F is outlined in Appendix E. The source term (Eq. (19)) contains radial derivatives of the stress tensor that are evaluated with central discretizations of 12th order. Furthermore, the evaluation of the derivatives with respect to θ and the self-gravity force ∂rϕd appearing in Eq. (19) will be discussed in Sects. 5 and 6, respectively.
Due to the presence of the satellite forcing terms in Eq. (19) it turns out that the simple time step criterion arising from a one-dimensional advection-diffusion problem, which was used in LSS2017, is unnecessarily strict. This criterion reads
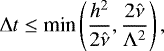 (20)
(20)
where Λ is identified with the maximal eigenvalue of the Jacobian
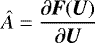 (21)
(21)
of Eqs. (18) for the whole grid and 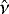 is to be identified with the maximal value of the coefficient in front of the term containing the second radial derivative
is to be identified with the maximal value of the coefficient in front of the term containing the second radial derivative 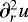 in Eqs. (1), which is
in Eqs. (1), which is
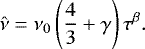
The three eigenvalues of Eq. (21) read
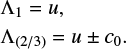
For most integrations presented in this paper the grid spacings h are large enough so that the second term in Eq. (20) is by far the smallest and can take values down to some 10−5 ORB. We find, however, that time steps in the range Δt = 1–5 × 10−4 ORB are suitable for all presented integrations, indicating that the criterion Eq. (20) cannot be appropriate. We have checked for some integrations with strong satellite forcing that reducing the time step by a factor of 0.5 does not lead to any notable changes. For later use we also define the mean kinetic energy density within the computational domain as
![\begin{equation*}e_{\textrm{kin}} = \frac{1}{L_{r}} \int\limits_{[L_{\textrm{r}}]} \mathrm{d}r \, \frac{1}{2} \sigma \left( u^2 + v^2 \right). \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq41.png) (22)
(22)
Symbols.
4 Satellite forcing
For simplicity, we restrict our study to density waves that correspond to a particular first-order inner Lindblad resonance3, so that the forcing satellite orbits exterior to the considered ring portion. The wave is excited by a particular Fourier mode of the gravitational potential due to this satellite with mass Ms and semimajor axis as and reads (cf. Sect. 5 in LSS2016)
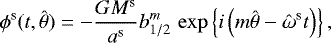
valid in an inertial frame denoted by  . The symbol
. The symbol

In the current approximation the forcing frequency reads
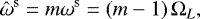 (23)
(23)
with the satellite mean motion ωs. Upon changing to the frame rotating with frequency ΩL, denoted by (r, θ), we have
![\begin{equation*} \begin{split} (m \hat{\theta} -\hat{\omega}^{\textrm{s}} t) & \rightarrow \left( m \left[\theta+\Omega_{L} t\right] -\hat{\omega}^{\textrm{s}} t\right)\\ \quad & \equiv m\theta -\omega^{\textrm{s}} t, \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq47.png)
yielding the forcing frequency in the rotating frame
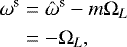 (24)
(24)
where we used Eq. (23). Therefore, the radial forcing component appearing in Eqs. (1) reads
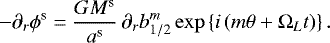 (25)
(25)
Similarly, the azimuthal component is given by
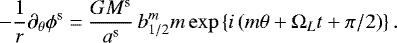 (26)
(26)
These terms are evaluated at r = rL.
5 Azimuthal derivatives
The persistent spiral shape of a (long) density wave is generated by the resonant interaction between the ring material and the perturbing satellite potential, as well as the collective self-gravity force. Since our integrations are one-dimensional, it is not possible to describe azimuthal structures directly. Therefore, we need to restrict Eqs. (1) to a radial cut that we choose to be θ = 0 without loss of generality. The information about the azimuthal structure of the density pattern (the number of spiral arms m) is then contained solely in the terms describing azimuthal advection due to orbital motion: the first terms on the right hand sides of Eqs. (1). In what follows we refer to these terms simply as “azimuthal derivatives”. Thus, the requirement is to prescribe proper values of the azimuthal derivatives at θ = 0 for each time step of the integration.
We again adopt the cylindrical coordinate frame (r, θ) of Sect. 2, which rotates with angular velocity ΩL relative to an inertial frame denoted by 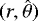 so that
so that
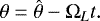
If we linearize Eqs. (1) with respect to the variables τ, u, v, and ϕd, so that we restrict these to describe linear density waves, it is possible to solve the equations in the complex plane by splitting the solution vector Ψ into its real and imaginary parts:
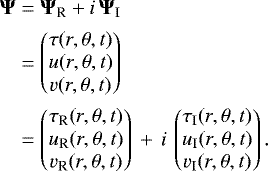 (27)
(27)
An evolving m-armed linear density wave can then be described through the complex vector of state
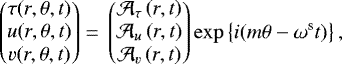 (28)
(28)
with 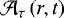 ,
, 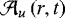 , and
, and 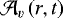 being complex amplitudes in this notation that depend on time and the radial coordinate. The time dependence of the amplitudes is generally much slower than the oscillatory terms and vanishes once the integration reaches a steady state. When inserted into the linearized Eqs. (1) we obtain two sets of three equations that are possibly coupled through the azimuthal derivatives and self-gravity, depending on the applied implementation (cf. Appendices D and F). In practice we will exclusively use the full nonlinear Eqs. (1). For sufficiently small amplitudes
being complex amplitudes in this notation that depend on time and the radial coordinate. The time dependence of the amplitudes is generally much slower than the oscillatory terms and vanishes once the integration reaches a steady state. When inserted into the linearized Eqs. (1) we obtain two sets of three equations that are possibly coupled through the azimuthal derivatives and self-gravity, depending on the applied implementation (cf. Appendices D and F). In practice we will exclusively use the full nonlinear Eqs. (1). For sufficiently small amplitudes 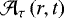 ,
, 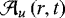 ,
, 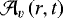 the nonlinear terms in Eqs. (1) are negligible and the equations are essentially linear.
the nonlinear terms in Eqs. (1) are negligible and the equations are essentially linear.
In orderto describe nonlinear density waves, it is necessary to make an approximation for the azimuthal dependency of the wave. To obtain such an approximation we assume that Eq. (28) holds also in the nonlinear case. We will discuss the validity of this assumption further at the end of Sect. 5. We have found two such implementations for the azimuthal derivatives (simply referred to as Methods A and B) that yield a stationary final state for Eqs. (1) in the nonlinear regime. It turns out that the application of Method A (Sect. 5) results in nonlinear wave profiles that agree better with existing nonlinear models and therefore the results presented in subsequent sections are based on integrations using this method. We additionally outline Method B (Appendix D) as we have found it to work well in the weakly nonlinear regime. For sufficiently linear waves, both methods are exact down to the numerical error.
Method A
One implementation of the azimuthal derivatives can be derived if one considers the vector of state of the weakly nonlinear model of LSS2016 in the first order approximation, where contributions from higher wave harmonics are omitted. That is, we have
![\begin{eqnarray*}\begin{pmatrix} \tilde{\phi}^{\textrm{d}}(r,\theta,t) \\ \tilde{u}(r,\theta,t) \\ \tilde{v}(r,\theta,t) \end{pmatrix} \;&{=}&\; \begin{pmatrix} -\dfrac{i 2 \tilde{\mathcal{D}} \tilde{\Omega}}{\tilde{\mathcal{D}} \tilde{x} + \left(\tilde{\omega}^{\textrm{s}} - m [\tilde{\Omega}-\tilde{\Omega}_{L}] \right)^2} \\[0.6 cm] \dfrac{i 2 \tilde{\Omega} \left( \tilde{\omega}^{\textrm{s}} - m [\tilde{\Omega}-\tilde{\Omega}_{L}] \right)}{ \tilde{\mathcal{D}} \tilde{x} + \left(\tilde{\omega}^{s} - m [\tilde{\Omega}-\tilde{\Omega}_{L}] \right)^2} \\[0.6cm] 1 \end{pmatrix}\nonumber\\ &&\times \,\mathcal{A}\left(r\right) \, \exp \left\{i \left( \, \Phi(r) + m \theta - \omega^{\textrm{s}} t \right) \right\}\hspace{0.2cm} + \textrm{c.c.}, \end{eqnarray*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq61.png) (29)
(29)
where 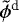 , ũ, ṽ, as well as
, ũ, ṽ, as well as  ,
, 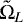 ,
, 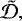 and
and 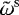 are understood to be scaled according to Table 1 in LSS2016 and
are understood to be scaled according to Table 1 in LSS2016 and 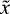 is scaled according to Table 2. We note that
is scaled according to Table 2. We note that 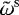 is the scaled version of Eq. (24). Equation (29) corresponds to Eqs. (35) and (45) in LSS2016, except that Eq. (29) is written in the rotating frame and is not expanded to the lowest order in
is the scaled version of Eq. (24). Equation (29) corresponds to Eqs. (35) and (45) in LSS2016, except that Eq. (29) is written in the rotating frame and is not expanded to the lowest order in 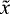 , although small corrections due to pressure and viscosity are neglected.
, although small corrections due to pressure and viscosity are neglected.
From the solution of the Poisson equation we have (Shu 1984)
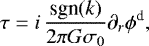 (30)
(30)
where ϕd is assumed to be given by the unscaled first component of Eq. (29) and k = ∂rΦ(r) denotes the wavenumber of the density wave. Both sides of Eq. (30) are understood to be real-valued since the sgn -function takes different signs for the two conjugate complex exponential modes in Eq. (29). The azimuthal derivative of τ is then given by
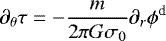 (31)
(31)
if we assume k > 0. Equation (31) shows that the azimuthal derivative of τ is directly proportional to the radial component of the self-gravity force, the computation of which we discuss in Sect. 6. The azimuthal derivatives of u and v can be directly obtained from Eq. (29) and read
![\begin{equation*} \partial_{\theta} u = -\frac{ 2 m \Omega \left( \omega^{\textrm{s}} - m [\Omega-\Omega_{L}] \right)}{ \mathcal{D} \tilde{x} + \left(\omega^{\textrm{s}} - m [\Omega-\Omega_{L}] \right)^2} v \approx 2 m v,\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq72.png) (32)
(32)
![\begin{equation*} \partial_{\theta} v = m \frac{ \mathcal{D} \tilde{x} + \left(\omega^{\textrm{s}} - m [\Omega-\Omega_{L}] \right)^2}{ 2 \Omega \left( \omega^{\textrm{s}} - m [\Omega-\Omega_{L}] \right)} u \approx -\frac{1}{2} m u .\vspace*{-3pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq73.png) (33)
(33)
The approximate expressions follow if we neglect 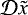 , which is fully justified since
, which is fully justified since 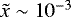 for all cases considered here.
for all cases considered here.
As mentioned before, Eq. (28) can only be used as an approximation for a nonlinear density wave. We assume that the latter is correctly described by an infinite series
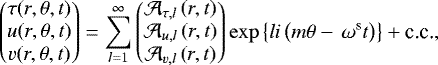 (34)
(34)
where the terms with l > 1 describe thewave’s higher harmonics. It is not straightforward to estimate the error which the use of Eq. (28) ultimately places on computed density wave profiles. We can, however, quantify further the errors of the azimuthal derivatives themselves. Let us for the time being assume that the surface density τ in a (steady state) density wave can be described through (Borderies et al. 1983, see also Sect. 7.4.3 and Appendix G)
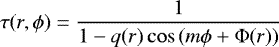 (35)
(35)
in a cylindrical frame (r, ϕ, z = 0) rotating with the satellite’s mean motion frequency 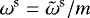 (see Eq. (23)). Furthermore, q is the nonlinearity parameter fulfilling 0 ≤ q < 1 and Φ(r) is the radial phase function of the density wave (cf. Eq. (29)). Clearly, for q not much smaller than unity, corresponding to a nonlinear wave, the variation of the surface density τ deviates significantly from a simple harmonic. Taking the azimuthal derivative of Eq. (35) yields
(see Eq. (23)). Furthermore, q is the nonlinearity parameter fulfilling 0 ≤ q < 1 and Φ(r) is the radial phase function of the density wave (cf. Eq. (29)). Clearly, for q not much smaller than unity, corresponding to a nonlinear wave, the variation of the surface density τ deviates significantly from a simple harmonic. Taking the azimuthal derivative of Eq. (35) yields
![\begin{equation*}\partial_{\phi}\tau = -m q(r) \frac{\sin \left(m \phi + \Phi(r)\right)}{\left[1-q(r) \cos \left(m \phi + \Phi(r)\right) \right]^2}. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq79.png) (36)
(36)
By expanding this expression to the first order in q, which amounts to our linear treatment of the azimuthal derivative in Eq. (31), we obtain
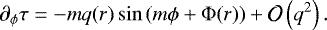 (37)
(37)
This would imply that for 0.1 < q < 0.5 the (azimuthally averaged) error made when replacing Eq. (36) with Eq. (37) (and hence also Eq. (31)) takes quite large values of ~ 10–60%.
Despite the considerable error that may be induced by the approximation Eq. (31) (and Eqs. (32) and (33)) we will see in Sect. 7.2 that the resulting error in the radial density wave profiles is actually small. As for the approximation Eq. (31) the reason is that in our integrations we evaluate this term by using an accurate (nonlinear) expression for the self-gravity force ∂rϕd (Sect. 6) so that the actual error resulting from Eq. (31) is much smaller than what would result from the linearized expression Eq. (37). This can be understood by realizing that Eq. (30) holds also for the higher harmonics (l > 1 in Eq. (34)) of τ and ϕd (see Appendix B of LSS2016 for more details), which stems from the fact that Poisson’s equation is linear. Thus, the actual error which is then made with the approximation Eq. (31) is that the contributions of the higher harmonics l > 1 in Eq. (34) are underestimated by factors of 1∕l, but not entirely neglected. On the other hand, from LSS2016 (Sect. 4.5) it follows that the approximations Eqs. (32) and (33) hold also for the second harmonics of the velocity fields up to a factor 1∕l (with l = 2) and the same is expected to apply to all higher harmonics4 l ≥ 3. Hence, the error made with Eqs. (32) and (33) is also a suppression of the higher harmonics l ≥ 2 by factors 1∕l.
Finally, we note that our approximations for the azimuthal derivatives Eqs. (31)–(33) imply that any mode which forms during an integration on top of the equilibrium state will be non-axisymmetric with azimuthal periodicity m. For this reason the short-scale overstable waves that appear in our integrations (Sect. 7.4) are non-axisymmetric with the same m as the resonantly forced density wave. As outlined in Sect. 2, it is expected that the dynamical evolution of these modes is very similar to that of axisymmetric modes. This expectation will be confirmed in Sect. 7.4.1.
6 Self-gravity
For most integrations we use the same implementation of collective radial self-gravity forces as described in detail in LSS2017. The model approximates the ring material as a collection of infinite straight wires (neglect of curvature) and predicts a self-gravity force (at grid point j)
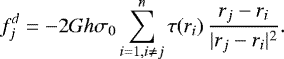 (38)
(38)
where we defined fd = −∂rϕd. This relation (Eq. (38)) does not include the force generated by mass contained in the bin j itself, which can be approximated through
![\begin{equation*} \Delta f^{d}(0) = 2 G \sigma_{0} \left[\partial_{r}\tau(0) \, h + \mathcal{O}\left(h^3\right)\right]. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq82.png)
If τ(ri) is periodic with period n the sum (Eq. (38)) can be replaced by the convolution
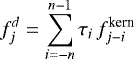 (39)
(39)
of τi = τ(ri) with the force kernel, which reads
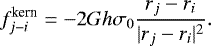
Equation (39) can then be solved with a fast Fourier transform (FFT) method. However, since the density pattern τi of a resonantly forced density wave is not periodic, we need to pad one half of the array τi with zeros in order to avoid false contributions from grid points outside the actual grid (Binney & Tremaine 1987), for example, gravitational coupling of material inside the resonance with material at far positive distances from resonance across the boundaries.
For comparison with existing models for nonlinear density waves, in Sect. 7.2 we also perform integrations which adoptthe Wentzel–Kramers–Brillouin (WKB) approximation for the radial self-gravity force. The corresponding implementation is described in Appendix F.
7 Results
7.1 Excitation of density waves
In this section we illustrate the excitation of a resonantly forced density wave as it results from our integrations. We use integrations employing the Pr76-parameters (Table 1) with different values of the forcing strength to elucidate nonlinear effects. All integrations were carried out with Lr = 450 km, Δt = 5 × 10−4 ORB, and h = 45 m. Furthermore, Method A for the azimuthal derivatives (Sect. 5) and the Straight Wire self-gravity model (Sect. 6) were employed. The initial state of each integration is the Keplerian shear flow with τ(t = 0) = 1, u(t = 0) = 0, v(t = 0) = 0 (Sect. 2) and the satellite forcing is introduced at time t = 0.
It is expected that during the excitation process the envelope of a density wave evolves in a radial direction with the local group velocity (Toomre 1969; Shu 1984). For a linear density wave described by the perturbed surface density
![\begin{equation*}\sigma = \sigma_{0} + A\left(r\right) \cdot \exp\Bigg\{i \int_{}^{r}k \left( s\right)\, \mathrm{d}s \Bigg\} \cdot \exp\left\{i\left(m\theta-\omega^{\textrm{s}} t\right) \right\}] \vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq85.png) (40)
(40)
with wavenumber k, one obtains in the frame rotating with frequency ΩL the dispersion relation (Goldreich & Tremaine 1978a; Shu 1984)
![\begin{equation*}\kappa^2 - \left(\omega^{\textrm{s}}- m [\Omega-\Omega_{L}] \right)^2 + k^2 c_{0}^2 - 2 \pi G \sigma_{0} |k| =0. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq86.png) (41)
(41)
Taking the derivative with respect to k on both sides and re-arranging terms yields the group velocity (Toomre 1969)
![\begin{equation*}v_{\textrm{g}} = \frac{\mathrm{d}\omega^{\textrm{s}}}{\mathrm{d}k} = \mathrm{sgn}(k) \frac{ \pi G \sigma_{0} - |k| c_{0}^2}{ m [\Omega-\Omega_{L}] - \omega^{\textrm{s}}}, \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq87.png) (42)
(42)
where ωs is given by Eq. (24) and sgn(k) denotes the sign of k. By defining
![\begin{equation*} D= \kappa^2 -\left(\omega^{\textrm{s}} - m \left[\Omega - \Omega_{L}\right] \right)^2 \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq88.png)
and expanding this expression about the Lindblad resonance r = rL (using the approximation κ = Ω) so that 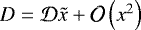 with
with 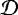 given by Eq. (11), one obtains from Eq. (41) the wavenumber dispersion for linear density waves
given by Eq. (11), one obtains from Eq. (41) the wavenumber dispersion for linear density waves
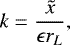 (43)
(43)
where ɛ is given by Eq. (10) and where the effects of pressure, expressed through the term quadratic in k in Eq. (41), are ignored.
The dispersion relation of nonlinear spiral density waves in the WKB-approximation reads (e.g., Eq. (87) of Shu et al. 1985a)
![\begin{equation*}\kappa^2 - \left(\omega^{\textrm{s}}- m [\Omega-\Omega_{L}] \right)^2 + I(q^2) \, k^2 \, c_{0}^2 - 2 \pi G \sigma_{0} |k| H(q^2) =0. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq92.png) (44)
(44)
In this expression the contributions due to pressure and self-gravity are modified compared to Eq. (41) and depend on the nonlinearity (or streamline-crossing) parameter q. The integral
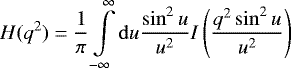
describes the nonlinear effects of self-gravity and, similarly,
![\begin{equation*} I(q^2)= \frac{2}{q^2}\left[ \left(1-q^2\right)^{-1/2} -1\right] \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq94.png)
describes nonlinear pressure effects. The functions H(q2) and I(q2) increase monotonically with q and fulfill H(q2) → 1 and I(q2) → 1 for q → 0. Furthermore, Shu et al. (1985a) have shown that in the absence of acoustic effects (i.e., for c0 = 0) the angular momentum luminosity carried by a nonlinear density wave reads
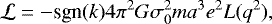
and describes the rate of angular momentum that is transported across a streamline with semimajor axis a and eccentricity e (cf. Eq. (54)). The function
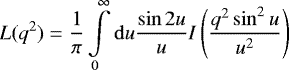
is monotonically increasing with q and possesses the limiting value L(q2) → 1∕4 for q → 0. The angular momentum (surface) density of the wave is given by (Lee & Goodman 1999; Shu 1970)
![\begin{equation*} \rho = \left(\omega^{\textrm{s}}- m \left[\Omega-\Omega_{L} \right]\right) \frac{m \sigma_{0} a^2 e^2}{2}. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq97.png)
In the linear limit q → 0 the group velocity of the wave is given by the ratio of the angular momentum flux and the angular momentum density (Dewar 1972),
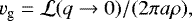 (45)
(45)
which yields Eq. (42) with c0 = 0. If one assumes Eq. (45) to hold in the nonlinear case q > 0 as well, one obtains
![\begin{equation*}v_{\textrm{g}}^{\textrm{nl}} = \mathrm{sgn}(k) \frac{ 4 \pi G \sigma_{0} L(q^2) }{ m [\Omega-\Omega_{L}] - \omega^{\textrm{s}}}. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq99.png) (46)
(46)
However, it turns out that in the nonlinear case there generally exist two characteristic velocities of a wave and these velocities do not agree with either Eq. (46) or the “nonlinear analog” of Eq. (42), which is obtained by using Eq. (44) instead of Eq. (41), except for q → 0 (Whitham 1974). Nevertheless, our results shown below indicate that these velocities must actually be close to the linear group velocity (Eq. (42)), at least for the parameter regimes considered in this paper.
Figures 1–3 show stroboscopic space–time diagrams (time-resolution of ΩL ∕(2π)) of integrations with scaled linear satellite torques of 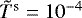 ,
,  and
and 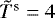 , where
, where 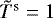 corresponds to the nominal forcing strength for the Prometheus 7:6 ILR (Table 1). In these figures the gray shading measures the value of τ so that brighter regions correspond to larger values of τ. Since at t = 0 the spatially constant satellite forcing is introduced and the disk is homogeneous, initially the hydrodynamic quantities u, v, and τ oscillate uniformly (with infinite wavelength). Due to Keplerian shear the pattern starts to wrap up at a constant rate. This transient behavior was derived by Meyer-Vernet & Sicardy (1987) who studied the interaction of a satellite with an initially homogeneous disk in the vicinity of a Lindblad resonance and in the linear limit. They showed that the wavelength of the pattern evolves as
corresponds to the nominal forcing strength for the Prometheus 7:6 ILR (Table 1). In these figures the gray shading measures the value of τ so that brighter regions correspond to larger values of τ. Since at t = 0 the spatially constant satellite forcing is introduced and the disk is homogeneous, initially the hydrodynamic quantities u, v, and τ oscillate uniformly (with infinite wavelength). Due to Keplerian shear the pattern starts to wrap up at a constant rate. This transient behavior was derived by Meyer-Vernet & Sicardy (1987) who studied the interaction of a satellite with an initially homogeneous disk in the vicinity of a Lindblad resonance and in the linear limit. They showed that the wavelength of the pattern evolves as
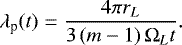 (47)
(47)
This result was obtained in the absence of collective forces. Meyer-Vernet & Sicardy (1987) argued that after a sufficiently long time the transient behavior vanishes and the system settles on a stationary solution that is governed by collective effects (self-gravity, pressure, and viscosity). They proved this for the case of a simple friction law assuming a force F =−Qu with u = (u, v) in the momentum equation. In the present situation self-gravity is the dominant collective force and the disk excites a long trailing density wave propagating outward from the ILR with group velocity approximately given by Eq. (42) (Goldreich & Tremaine 1978a; Shu 1984).
As the wavelength of the pattern decreases with time, at a certain radial location and at a certain time the wavelength will fulfill the dispersion relation Eq. (44) (and also Eq. (41) if q is sufficiently small). As soon as this is the case, the wavelength is “locked” to this value. In the Figs. 1–3, the region that becomes “locked“ is enclosed by the dashed and solid blue lines. The former marks the resonance, while the latter is the predicted path of the wavefront assuming it propagates with the linear group velocity (Eq. (42)). This path is slightly curved due to the (small) pressure contribution to the group velocity. All wave structures outside this region eventually damp as they become increasingly wound up. An exception are the short-scale waves generated by viscous overstability (Sects. 2 and 7.4). Also plotted are radial profiles of τ at four different times during the excitation process.
In Fig. 1 the blue solid line describes well the propagation of the wavefront, until a steady state is reached (around 8000 orbital periods) and the wave’s amplitude profile remains stationary. We find a number of differences when comparing the figures. First of all, with increasing torque value the wave profiles attain the typical peaky appearance of nonlinear density wavetrains in thin disks (Shu et al. 1985a; BGT86; Salo et al. 2001). Furthermore, the propagation speed of the wavefront seems to depart increasingly from the linear prediction (Eq. (42)) with increasing torque, albeit mildly. A mild increase of the propagation speed with increasing nonlinearity q of the wave would be expected if Eq. (46) correctly describes the propagation of the wavefront (neglecting the small pressure contribution). One notes that there remains a very slow phase-drift of the wave pattern towards the resonance, indicating an increasing phase velocity with decreasing distance from resonance. Theoretically, at resonance the wavenumber of the density wave (Eq. (43)) vanishes so that the wave’s phase velocity ωs ∕k diverges. It can therefore in general not be expected from a numerical method to correctly describe the wave pattern at the exact resonance location.
Figure 4 shows for the integration with 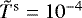 (Fig. 1) the average wavelength of the forming pattern, sampled within the radial region 50 km ≤ r–rL ≤ 150 km. The agreement with Eq. (47) is excellent for about 3000 orbital periods. After that deviations become notable as a steady state is reached where self-gravity prevents further shortening of the wavelength. The closer to the resonance r = rL, the earlier a steady state is attained as the resonant density wave pattern emerges at the resonance and propagates outward with its local group velocity.
(Fig. 1) the average wavelength of the forming pattern, sampled within the radial region 50 km ≤ r–rL ≤ 150 km. The agreement with Eq. (47) is excellent for about 3000 orbital periods. After that deviations become notable as a steady state is reached where self-gravity prevents further shortening of the wavelength. The closer to the resonance r = rL, the earlier a steady state is attained as the resonant density wave pattern emerges at the resonance and propagates outward with its local group velocity.
In Saturn’s rings an initial transient pattern as seen in our integrations might be observable for density waves driven by the co-orbital satellites Janus and Epimetheus. These satellites interchange orbits every four years so that their resonance locations in the rings shift periodically by tens of kilometers. Every time a resonance location is changed the wave excited at the preceding location continues to propagate while a new density wave is launched at the new location (Tiscareno et al. 2006).
 |
Fig. 1 Stroboscopic space–time diagram showing the evolution of the scaled surface density
τ
for an integration with the Pr76-parameters and an associated scaled torque |
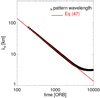 |
Fig. 4 Average wavelength of the forming pattern in the course of the integration shown in Fig. 1. The wavelength is obtained by counting the number of complete wave cycles of the (sinusoidal) surface density τ within the radial region 50 km ≤ r–rL ≤ 150 km. |
7.2 Comparison with the nonlinear models of BGT1986 and LSS2016
In this section we compare the results of hydrodynamical integrations with the nonlinear models of BGT86 and LSS2016, which we refer to as the BGT and the WNL (weakly nonlinear) model, respectively. This section is restricted to stable waves in the sense that β <βc(λ) for all wavelengths λ (cf. Eq. (16)), that is, no overstability occurs in the system. All hydrodynamical integrations presented in this section were conducted with Lr = 450 km, time steps of Δt = 5 × 10−4 ORB, and spatial resolution h = 45 m, and used the Pr76-parameters (Table 1). If not stated otherwise, all integrations employed Method A for the azimuthal derivatives (Sect. 5) and the Straight Wire self-gravity model (Sect. 6). The presented BGT model wave profiles were computed using the method of BGT86 (see their Sect. IVa), using the pressure tensor expressed in Eq. (5) with Eqs. (6) and (7). This model takes into account secular changes in the background surface mass density σ0 that accompany the steady-state density wave in order to ensure conservation of angular momentum at all radii in the steady state. These modifications are neglected in our hydrodynamical integrations as well as the WNL model. To facilitate a comparison between the three different methods, the profiles of τ resulting from the BGT model are scaled with the modified background surface mass density σ0 (r), which will not be shown.
Figure A.1 displays steady-state profiles of the hydrodynamic quantities τ, u, v as these result from integrations together with profiles obtained using the WNL model (LSS2016). The profiles in the left and right columns result from integrations that applied Method A and Method B for the azimuthal derivatives, respectively. The self-gravity is computed with the Straight Wire model. As in the previous section, the satellite forcing strengths are indicated by the fractional torque 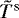 such that
such that 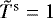 corresponds to the nominal forcing strength at the Prometheus 7:6 ILR and results in a nonlinear density wavetrain. The value
corresponds to the nominal forcing strength at the Prometheus 7:6 ILR and results in a nonlinear density wavetrain. The value 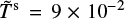 corresponds to a weakly nonlinear wave. For the latter case both Methods A and B produce very similar results in good agreement with the WNL model. Inspection of the nonlinear case
corresponds to a weakly nonlinear wave. For the latter case both Methods A and B produce very similar results in good agreement with the WNL model. Inspection of the nonlinear case 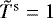 reveals significant departures at larger distances from resonance between both methods, and Method A produces a clearly better match with the WNL model. All integrations presented in the following sections were conducted with Method A.
reveals significant departures at larger distances from resonance between both methods, and Method A produces a clearly better match with the WNL model. All integrations presented in the following sections were conducted with Method A.
In Fig. A.2 we present wave profiles along with their Morlet wavelet powers (Torrence & Compo (1998)) for the case 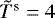 . Also, for this strongly nonlinear wave, we observe an overall good agreement for both the amplitude profiles and wavenumber dispersions. We note that the WNL model takes into account only the first two harmonics of the wave (cf. Eq. (34)), which is clearly visible in the wavelet power. This is also the reason why τ can take values below 0.5 (see LSS2016 for details).
. Also, for this strongly nonlinear wave, we observe an overall good agreement for both the amplitude profiles and wavenumber dispersions. We note that the WNL model takes into account only the first two harmonics of the wave (cf. Eq. (34)), which is clearly visible in the wavelet power. This is also the reason why τ can take values below 0.5 (see LSS2016 for details).
Finally, Fig. A.3 compares profiles obtained from integrations with the Straight Wire self-gravity (left panels) and the WKB self-gravity (Appendix F) using Eq. (F.3) (right panels) for the cases 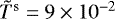 (upper panels) and
(upper panels) and 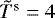 (lower panels). Comparison with corresponding BGT model wave profiles shows that the WKB approximation is fully adequate for the weakly nonlinear wave with
(lower panels). Comparison with corresponding BGT model wave profiles shows that the WKB approximation is fully adequate for the weakly nonlinear wave with 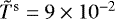 in that it yields indistinguishable results from the Straight Wire self-gravity. For the strongly nonlinear case
in that it yields indistinguishable results from the Straight Wire self-gravity. For the strongly nonlinear case 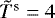 the WKB-approximation has a notable effect. As expected, its application yields overall an even better agreement with the BGT (and WNL) model. We have verified that reducing the time step or the grid spacings by factors of 1∕2 does not change the outcome of any integration presented in this section. The remaining differences between the integrated wave profiles and the model profiles are most likely due to the approximative implementation of the azimuthal derivatives. Nevertheless, the results presented here make us confident that our numerical integrations yield qualitatively correct behavior even of strongly nonlinear density waves.
the WKB-approximation has a notable effect. As expected, its application yields overall an even better agreement with the BGT (and WNL) model. We have verified that reducing the time step or the grid spacings by factors of 1∕2 does not change the outcome of any integration presented in this section. The remaining differences between the integrated wave profiles and the model profiles are most likely due to the approximative implementation of the azimuthal derivatives. Nevertheless, the results presented here make us confident that our numerical integrations yield qualitatively correct behavior even of strongly nonlinear density waves.
7.3 Wave propagation through density structures
In this section we present a few illustrative examples of hydrodynamical integrations of density waves propagating through an inhomogeneous ring. We consider only the cases of jumps in the equilibrium surface density, but in principle we could also vary other parameters with radial distance, such as the viscosity parameter β. All integrations adopted the Pr76-parameters and employed Method A for the azimuthal derivatives (Sect. 5) as well as the Straight Wire self-gravity model (Sect. 6). Figure B.1 shows space–time plots of a density wave passing a region of increased surface density (τ0 = 3, left panel) as well as a region of decreased surface density (τ0 = 0.5, right panel), in both cases of radial width 40 km. The jumps in the equilibrium surface density, whose locations are revealed in the space-time plots, act like additional sources for the density wave in the sense that the wave profile can change at these locations prior to the expected arrival time of the wavefront at these locations, the latter being indicated by the solid blue line (cf. Figs. 1–3). It is, however, not clear how this is affected by the assumption imposed by our azimuthal derivatives that the hydrodynamic quantities describe an m-armed pattern right from the start of the integration.
Figure B.2 shows steady-state profiles of τ along with corresponding wavelet-power spectra of density waves passing through regions of varying equilibrium surface density. For reference, the first row shows a density wave in a homogeneous ring. The second case, with a region of increased τ0, bears some similarities to Figs. 4 and 5 in Hedman & Nicholson (2016), showing profiles of the Mimas 5:2 density wave in Saturn’s B ring, which passes through a region of radial width ~ 60 km where the normal optical depth increases sharply from about 1.5 to values 3– 5. In the region of enhanced surface density in Fig. B.2 the wave damping is reduced due to its decreased wavenumber. Therefore, after passing the barrier the wave amplitude is enhanced as compared with the wave in the homogeneous region. The last case represents a situation with a narrow region of mildly decreased surface density τ0 = 0.5. In this region the wavenumber is enhanced, resulting in stronger wave damping.
If a density wave encounters a sharp discontinuity in the background surface density, such as a sharp ring edge, it is theoretically expected that it (partially) reflects at the boundary (see Longaretti 2018 and references therein). For the examples presented in Fig. B.2 the jumps in the background surface density are not sufficiently sharp to cause a notable reflection. However, Fig. 5 shows a space-time plot (left panel) of a wave with 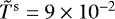 as it encounters a sharp edge near r–rL = 100 km where τ changes from 1 to 0.2. The plot clearly shows that the long trailing wave is partially reflected as a long leading wave, which rapidly damps as it propagates back towards the resonance r = rL. The remaining part of the incoming trailing wave is transmitted into the rarefied region and quickly attenuates as it propagates with strongly reduced wavelength. The long trailing wave has a negative phase velocity − ΩL∕k in our coordinate frame while its group velocity (Eq. (42)) is positive since k > 0. For the reflected leading wave, which has k < 0, the situation is exactly the opposite. Close to the edge at distances r– rL ≲ 100 km, where the reflected wave has a substantial amplitude, the resulting density pattern behaves as a left-traveling (negative phase velocity) wave, which additionally undergoes a standing-wave motion. The standing-wave motion rapidly diminishes with increasing distance from the edge due to the rapid damping of the reflected wave. The blue and red dashed curves are curves of constant phase of the incoming and reflected wave, respectively, parametrized as (cf. Eq. (40))
as it encounters a sharp edge near r–rL = 100 km where τ changes from 1 to 0.2. The plot clearly shows that the long trailing wave is partially reflected as a long leading wave, which rapidly damps as it propagates back towards the resonance r = rL. The remaining part of the incoming trailing wave is transmitted into the rarefied region and quickly attenuates as it propagates with strongly reduced wavelength. The long trailing wave has a negative phase velocity − ΩL∕k in our coordinate frame while its group velocity (Eq. (42)) is positive since k > 0. For the reflected leading wave, which has k < 0, the situation is exactly the opposite. Close to the edge at distances r– rL ≲ 100 km, where the reflected wave has a substantial amplitude, the resulting density pattern behaves as a left-traveling (negative phase velocity) wave, which additionally undergoes a standing-wave motion. The standing-wave motion rapidly diminishes with increasing distance from the edge due to the rapid damping of the reflected wave. The blue and red dashed curves are curves of constant phase of the incoming and reflected wave, respectively, parametrized as (cf. Eq. (40))
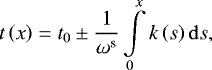 (48)
(48)
where 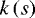 is the wavenumber of a long density wave (Eq. (43)). The initial value t0 is chosen such that the curves follow the path of a density maximum of the corresponding wave. The plot in the right panel shows the surface density τ evaluated along these lines of equal phase, represented by the solid and dashed curves. From the solid curve we can estimate the amplitude ratio of the incoming and the reflected waves by measuring the variation of τ near the edge as indicated by the arrows. That is, we have
is the wavenumber of a long density wave (Eq. (43)). The initial value t0 is chosen such that the curves follow the path of a density maximum of the corresponding wave. The plot in the right panel shows the surface density τ evaluated along these lines of equal phase, represented by the solid and dashed curves. From the solid curve we can estimate the amplitude ratio of the incoming and the reflected waves by measuring the variation of τ near the edge as indicated by the arrows. That is, we have
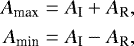
where the subscripts I and R stand for the incoming and the reflected wave, respectively. Hence,
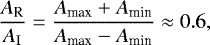 (49)
(49)
which means that the major fraction of the incoming wave is reflected. We note that it is not clear how the reflection is affected by our approximation of the azimuthal derivatives (Eq. (31)). We note also that the (viscous) timescale on which the initially imposed density jumps change in a notable manner, is much longer then the applied integration times.
 |
Fig. 5 Reflection of a (long) trailing density wave at a sharp boundary at r– rL ~ 100 km where τ0 is reduced by a factor of 1∕5. In the space–time plot (left panel) the blue (red) dashed curve traces a line of equal phase of the incoming (reflected) wave so that it follows a density maximum. Right panel: τ evaluated along these curves. As explained in the text, one can estimate the amplitude ratio of the incoming and the reflected waves from the indicated values Amax and Amin of τ (Eq. (49)). Since the considered wave is weakly nonlinear it follows H(q) ≳1 in the nonlinear dispersion relation (Eq. (44)) so that the linear limit (Eq. (43)) is not fully accurate. To compensate for this we used a slightly increased value of σ0 (by 0.25%) to compute the wavenumber k from Eq. (43), which is used in Eq. (48), to obtain a better fit to the locations of equal phase in the left panel. |
7.4 Density waves and viscous overstability
We now turn to our hydrodynamical integrations of forced spiral density waves in a model ring that is subjected to viscous overstability such that β >βc(λ) (Eq. (16)) for a non-zero range of wavelengths λ. Figure 6 displays the linear stability curve for the Pr76-parameters (Table 1) along with the different values adopted for the viscosity parameter β (Eq. (7)) in the integrations discussed in the following. These values are β =0.85, 1.10, 1.16, 1.20, 1.25, and 1.35. Viscous overstabilityis expected to develop for all but the smallest of these values, resulting in wavetrains that are believed to produce parts of the observed periodic microstructure in Saturn’s A and B rings (Thomson et al. 2007; Colwell et al. 2007; Latter & Ogilvie 2009). For the values β = 1.10, 1.16, and 1.20 linear viscous overstability is restricted to a relatively narrow band of wavelengths and the forced spiral density wave is stable.
In contrast, for the two largest values β = 1.25 and 1.35 all wavelengths larger than a critical one are unstable. For these two cases the forced spiral density wave itself is unstable and it is expected from existing models that it retains a finite amplitude (i.e., a finite nonlinearity parameter q) at large distances from resonance (see BGT86 and LSS2016 for details).
However, these models do not take into account the presence of the waves that are spontaneously generated by viscous overstability and that do not depend on the resonant forcing by an external gravitational potential. In this section we study the interplay of both types of structure in a qualitative manner. All large-scale integrations presented in this section were conducted using a grid with Lr = 450 km, h = 25 m, and applied Method A for the azimuthal derivatives (Sect. 5) as well as the Straight Wire self-gravity model (Sect. 6).
 |
Fig. 6 Linearstability curve (Eq. (16)) corresponding to the Pr76-parameters (solid curve). The dashed lines indicate the different values of the viscosity parameter
β
(Eq. (7)) that are used for the large-scale integrations of resonantly forced density waves discussed in Sect. 7.4. Viscous overstability is expected to develop for all values of
β
larger than the minimal value |
7.4.1 Hydrodynamical integrations without forcing
For reference, Figs. 7 and 8 describe an integration using β =1.25, without forcing by the satellite (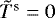 ). The seed forthis integration consists of a small amplitude superposition of linear left and right traveling overstable modes on all wavelengths down to about 200 m. We note that without any seed and in the absence of satellite forcing, no perturbations develop. Figure 7 (left panel) shows a profile of τ (top) after about 20 000 orbital periods, along with its wavelet power (bottom). The structure on wavelengths λ ~ 200–400 m represents the nonlinear saturated state of viscous overstability. This state consists of left and right traveling wave patches, separated by source and sink structures (Latter & Ogilvie 2009, 2010; LSS2017). This can also be seen in the stroboscopic space-time diagram (right panel), showing the evolution of τ over 600 orbits in the saturated state within a small portion of the computational domain near the nominal resonance location. The green dashed lines represent the expected nonlinear phase velocity vph= ωI∕k of overstable modes (Fig. 8, left panel) of wavelength λ = 300 m, with ωI and k denoting the nonlinear oscillation frequency and wavenumber of the wave. Although the modes seen in Fig. 7 are in fact non-axisymmetric with azimuthal periodicity m = 7 (see Sect. 5), their phase velocity (cf. Eq. (15)) is practically the same as for axisymmetric modes (m = 0) since we are in a frame rotating with the orbital frequency at resonance ΩL. We note that in Sect. 2 the symbol ωI was used todescribe the linear oscillation frequency of overstable waves. The sharp decay of the density pattern near the domain boundaries is due to the inclusion of buffer-regions where
). The seed forthis integration consists of a small amplitude superposition of linear left and right traveling overstable modes on all wavelengths down to about 200 m. We note that without any seed and in the absence of satellite forcing, no perturbations develop. Figure 7 (left panel) shows a profile of τ (top) after about 20 000 orbital periods, along with its wavelet power (bottom). The structure on wavelengths λ ~ 200–400 m represents the nonlinear saturated state of viscous overstability. This state consists of left and right traveling wave patches, separated by source and sink structures (Latter & Ogilvie 2009, 2010; LSS2017). This can also be seen in the stroboscopic space-time diagram (right panel), showing the evolution of τ over 600 orbits in the saturated state within a small portion of the computational domain near the nominal resonance location. The green dashed lines represent the expected nonlinear phase velocity vph= ωI∕k of overstable modes (Fig. 8, left panel) of wavelength λ = 300 m, with ωI and k denoting the nonlinear oscillation frequency and wavenumber of the wave. Although the modes seen in Fig. 7 are in fact non-axisymmetric with azimuthal periodicity m = 7 (see Sect. 5), their phase velocity (cf. Eq. (15)) is practically the same as for axisymmetric modes (m = 0) since we are in a frame rotating with the orbital frequency at resonance ΩL. We note that in Sect. 2 the symbol ωI was used todescribe the linear oscillation frequency of overstable waves. The sharp decay of the density pattern near the domain boundaries is due to the inclusion of buffer-regions where ![$\beta<\text{min}[\beta_{c}]_{\lambda}$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq121.png) , so that the condition for linear viscous overstability is not fulfilled for any wavelength within these regions. We included such buffer regions in all large-scale integrations presented in the following. Furthermore, Fig. 8 (right panel) displays for the same integration as in Fig. 7 the power spectral density of τ at two different times, as well as the evolution of the kinetic energy density (the insert). At the early time (200 ORB) the overstable waves are still in the linear growth phase and the power spectrum corresponds directly to the linear growth rates ωR (λ) (cf. Sect. 2 and the curve corresponding to β = 1.25 with q = 0 in Fig. 11). During this stage the kinetic energy density increases rapidly. At later times nonlinear effects slow down the evolution and the power spectrum at t = 20 000 ORB reflects the nonlinear saturation of the overstable waves.
, so that the condition for linear viscous overstability is not fulfilled for any wavelength within these regions. We included such buffer regions in all large-scale integrations presented in the following. Furthermore, Fig. 8 (right panel) displays for the same integration as in Fig. 7 the power spectral density of τ at two different times, as well as the evolution of the kinetic energy density (the insert). At the early time (200 ORB) the overstable waves are still in the linear growth phase and the power spectrum corresponds directly to the linear growth rates ωR (λ) (cf. Sect. 2 and the curve corresponding to β = 1.25 with q = 0 in Fig. 11). During this stage the kinetic energy density increases rapidly. At later times nonlinear effects slow down the evolution and the power spectrum at t = 20 000 ORB reflects the nonlinear saturation of the overstable waves.
In LSS2017 we have shown that axisymmetric viscous overstability in a self-gravitating disk evolves toward a state of minimal nonlinear oscillation frequency ωI (Fig. 8, left panel), or equivalently, toward a state of vanishing nonlinear group velocity d ωI ∕dk. The dashed blue lines in Figs. 7 (lower left panel) and 8 indicate the wavelength corresponding to this frequency minimum of the nonlinear dispersion relation (by margins ± 20 m). The wavelet power in Fig. 7 reveals that in the region r > rL the saturation wavelength of viscous overstability is very close to the expected value. The overstable waves in this region are responsible for the sharp peak in the power spectrum for t = 20 000 ORB at λ ≲ 300 m (Fig. 8). On the other hand, the region r < rL contains a left traveling wave with a wavelength that gradually departs from the expectation value towards the left, measuring λ ~ 400 m at the edge of the buffer region. We observe the presence of weak long-wavelength undulations on top of the overstable waves in the region r > rL. These mild, persistent undulations seem to adhere to the (long) density wave dispersion relation and result from the azimuthal derivative terms in the hydrodynamic equations (Sect. 5). They seem to prevent the saturation wavelength of overstable waves in the region r > rL from exceeding the nonlinear frequency minimum. As such, the azimuthal derivatives seem to effectively remove the artificial influence of the periodic boundary conditions on the long-term nonlinear saturation of the viscous overstability in that they sustain mild perturbations on the wave trains, at least in the region r > rL (see Latter &Ogilvie 2010 and LSS2017 for more details). This is further illustrated in Fig. C.3 where we compare these results with those of an integration without the azimuthal derivative terms. These plots confirm our finding in Sect. 2 that the linear behavior of small-scale axisymmetric and non-axisymmetric overstable modes is identical in our model. Furthermore, the nonlinear saturation behavior is very similar as well. Due to the lack of persistent perturbations in the axisymmetric (m = 0) integration, all but one of the wave defect structures will eventually merge and disappear so that the entire box will be filled out by a single wavetrain that originates from the left buffer region and whose wavelength increases with increasing distance from its origin. At the time t = 35 000 ORB its wavefront, which travels with a group velocity of several meters per orbital period, has reached a radial distance of r– rL ~ 60 km. Latter &Ogilvie (2010) have pointed out that this long-term behavior is actually an artifact of the applied periodic boundary conditions.
Due to the relatively low grid-resolution, the wave profiles are not fully developed since the higher harmonics are diminished. This, and also the effect of the azimuthal derivatives should, however, not affect our qualitative discussion of the interaction between the density wave and viscous overstability in the following.
 |
Fig. 7 Left panels: radial surface density (τ) profile and its wavelet power at t ~ 20 000 ORB of a hydrodynamical integration using the Pr76-parameters with β = 1.25 and no satellite forcing ( |
 |
Fig. 8 Left panel: linear and nonlinear frequencies of overstable waves adopting the Pr76-parameters with β = 1.25. The linear curve was obtained from numerical solution of Eq. (14). The nonlinear frequencies were obtained from small-domain hydrodynamical integrations of saturated overstable waves as described in detail in LSS2017 (see their Sect. 6.1). The minima of both curves appear at equal wavelengths, which is a consequence of the ideal gas relation Eq. (6) for the hydrostatic pressure. For more realistic equations of state the nonlinear frequency minimum occurs at larger wavelengths than the linear one (LSS2017). Right panel: power spectral density of τ from the same integration as in Fig. 7 during the linear growth phase (t = 200 ORB) and in the saturated state (t ~ 20 000 ORB) of viscous overstability. The insert displays the evolution of the kinetic energy density (Eq. (22)). The blue dashed linesin both panels indicate the expected nonlinear saturation wavelength of viscous overstability with margins ± 20 m (see the text). |
7.4.2 Co-existence of density waves and viscous overstability
In Fig. C.1 we compare integrations with a fixed forcing strength 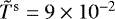 and varying value of the viscosity parameter β. The first integration shows the same case as considered in Sect. 7.2 with
and varying value of the viscosity parameter β. The first integration shows the same case as considered in Sect. 7.2 with ![$\beta<\text{min}[\beta_{c}]_{\lambda}$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq123.png) so that no viscous overstability develops. The integrations in rows 2-4 use
so that no viscous overstability develops. The integrations in rows 2-4 use ![$\text{min}[\beta_{c}]_{\lambda} < \beta < \beta_{c}(\lambda\to\infty)\equiv \beta_{c}^{\infty}$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq124.png) , while the integration shown in the bottom panel adopts
, while the integration shown in the bottom panel adopts 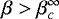 . From top to bottom the results show an increasing saturation amplitude of the viscous overstability in the evanescent region of the density wave (r < rL), as well as for large distances r ≫ rL from resonance, where the density wave is already strongly damped. Furthermore, as a reaction to the increased value of β, the amplitude of the density wave shows a mild increase as well, particularly at larger distances. These trends are expected from existing models for the nonlinear saturation of viscous overstability (Schmidt & Salo 2003; Latter & Ogilvie 2009), as well as the BGT and the WNL models for nonlinear density waves. However, the behavior seen in the integration with β = 1.35 is not correctly described by the latter models. Since in this case
. From top to bottom the results show an increasing saturation amplitude of the viscous overstability in the evanescent region of the density wave (r < rL), as well as for large distances r ≫ rL from resonance, where the density wave is already strongly damped. Furthermore, as a reaction to the increased value of β, the amplitude of the density wave shows a mild increase as well, particularly at larger distances. These trends are expected from existing models for the nonlinear saturation of viscous overstability (Schmidt & Salo 2003; Latter & Ogilvie 2009), as well as the BGT and the WNL models for nonlinear density waves. However, the behavior seen in the integration with β = 1.35 is not correctly described by the latter models. Since in this case 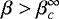 , that is, all wavelengths should be overstable, these models predict that the density wave does not damp but retains a finite (saturation) amplitude at large distances from resonance (BGT86; LSS2016). In contrast, our integration shows a damping of the wave very similar to the cases with
, that is, all wavelengths should be overstable, these models predict that the density wave does not damp but retains a finite (saturation) amplitude at large distances from resonance (BGT86; LSS2016). In contrast, our integration shows a damping of the wave very similar to the cases with 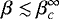 . In this case the viscous overstability possesses a sufficiently large amplitude to withstand the perturbation by the density wave at all distances r–rL, albeit with strongly diminished amplitude in the region of largest density wave amplitude. In contrast, in the first three integrations viscous overstability is fully damped for a range of distances where the density wave amplitude takes the largest values.
. In this case the viscous overstability possesses a sufficiently large amplitude to withstand the perturbation by the density wave at all distances r–rL, albeit with strongly diminished amplitude in the region of largest density wave amplitude. In contrast, in the first three integrations viscous overstability is fully damped for a range of distances where the density wave amplitude takes the largest values.
Figure C.2 shows a series of integrations with increasing forcing strength 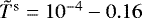 and fixed value
and fixed value 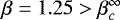 . The first wave, excited by a small torque
. The first wave, excited by a small torque 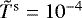 is a linear wave. The development of the viscous overstability is very similar to the case without forcing (Fig. 7). With increasing torque, the overstable waves become increasingly distorted by the density wave, showing many similarities to those in Fig. C.1. Eventually, the density wave in the bottom panel is sufficiently strong to suppress viscous overstability in the far wave zone, and the former wave attains a finite saturation amplitude at large distance from resonance until it hits the buffer zone near x = 300 km. At times t ≳ 20 000 ORB there remain small distortions in the wave profile. Furthermore, the saturation amplitude τ ~ 1.35 is slightly larger than what is predicted by the BGT and WNL models, which is τ ~ 1.15. It is possible that this is a consequence of our approximation for the azimuthal derivatives.
is a linear wave. The development of the viscous overstability is very similar to the case without forcing (Fig. 7). With increasing torque, the overstable waves become increasingly distorted by the density wave, showing many similarities to those in Fig. C.1. Eventually, the density wave in the bottom panel is sufficiently strong to suppress viscous overstability in the far wave zone, and the former wave attains a finite saturation amplitude at large distance from resonance until it hits the buffer zone near x = 300 km. At times t ≳ 20 000 ORB there remain small distortions in the wave profile. Furthermore, the saturation amplitude τ ~ 1.35 is slightly larger than what is predicted by the BGT and WNL models, which is τ ~ 1.15. It is possible that this is a consequence of our approximation for the azimuthal derivatives.
Some details of the wave patterns encountered in our integrations are illustrated in Figs. 9 and 10, which describe the integration with β = 1.20 and 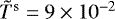 (same as in Fig. C.1, third row). Figure 9 shows a stroboscopic space-time plot of a section of the radial τ-profile for times t = 3000–5000 ORB. During this time the density wavefront traverses the considered region (indicated by the blue solid line) and clears overstable waves past a radial distance r–rL ≳ 90 km (see also Fig. C.1, fourth row). The density wave corresponds to the nearly vertical pattern with radially decreasing wavelength λ ~ 10–5 km (cf. Figs. 1–3), while (apparently right traveling) overstable waves are represented as a short-wavelength structure. The green dashed line indicates the expected (unperturbed) nonlinear phase velocity ωI ∕k of these waves, assuming a wavelength λ = 250 m (Fig. 8, left panel). We note that the frequencies drawn in Fig. 8 correspond to β =1.25, but the dependence of the overstable frequency on β is weak so that the corresponding curves for β = 1.20 are almost identical. The wavelength of overstable waves is modulated as they traverse the peaks and troughs of the density wave. That is, the green dashed line matches quite well the phase velocity of the overstable waves within the density wave peaks. In the troughs the phase velocity is notably increased, which follows fromthe decreased wavenumber of the overstable waves in these regions. Furthermore, a profile of τ at t = 1600 ORB (as marked by the arrow) is overplotted. If we assume that the density wave at a given time can be described through Eq. (35), we can estimate q ~ 0.25 in the region where overstability is damped. The red dashed lines in Fig. 9 indicate minimum and maximum values of τ resulting from Eq. (35) for q = 0.25. In a similar manner it follows that values of q ~ 0.23 and q ~ 0.20 lead to a damping of viscous overstabilityin the cases β = 1.16 and β =1.10 (Fig. C.1), respectively. The associated q-values where overstability reappears at larger distances from resonance seem to be slightly smaller in all cases. The mitigation of viscous overstability by a density wave will be discussed in more detail in the following section.
(same as in Fig. C.1, third row). Figure 9 shows a stroboscopic space-time plot of a section of the radial τ-profile for times t = 3000–5000 ORB. During this time the density wavefront traverses the considered region (indicated by the blue solid line) and clears overstable waves past a radial distance r–rL ≳ 90 km (see also Fig. C.1, fourth row). The density wave corresponds to the nearly vertical pattern with radially decreasing wavelength λ ~ 10–5 km (cf. Figs. 1–3), while (apparently right traveling) overstable waves are represented as a short-wavelength structure. The green dashed line indicates the expected (unperturbed) nonlinear phase velocity ωI ∕k of these waves, assuming a wavelength λ = 250 m (Fig. 8, left panel). We note that the frequencies drawn in Fig. 8 correspond to β =1.25, but the dependence of the overstable frequency on β is weak so that the corresponding curves for β = 1.20 are almost identical. The wavelength of overstable waves is modulated as they traverse the peaks and troughs of the density wave. That is, the green dashed line matches quite well the phase velocity of the overstable waves within the density wave peaks. In the troughs the phase velocity is notably increased, which follows fromthe decreased wavenumber of the overstable waves in these regions. Furthermore, a profile of τ at t = 1600 ORB (as marked by the arrow) is overplotted. If we assume that the density wave at a given time can be described through Eq. (35), we can estimate q ~ 0.25 in the region where overstability is damped. The red dashed lines in Fig. 9 indicate minimum and maximum values of τ resulting from Eq. (35) for q = 0.25. In a similar manner it follows that values of q ~ 0.23 and q ~ 0.20 lead to a damping of viscous overstabilityin the cases β = 1.16 and β =1.10 (Fig. C.1), respectively. The associated q-values where overstability reappears at larger distances from resonance seem to be slightly smaller in all cases. The mitigation of viscous overstability by a density wave will be discussed in more detail in the following section.
Figure 10 shows an orbit-resolved space–time plot of τ, illustrating how overstable wavetrains are distorted in direct vicinity of the Lindblad resonance in the integration displayed in Fig. C.1 corresponding to β = 1.20. In the evanescent region r < rL we recognize a right traveling overstable wave whose phase velocity undergoes periodic perturbations on the orbital timescale. These perturbations become stronger as the wave approaches the resonance r = rL. In the region r > rL the overstable waves seem to be unable to travel over any notable distance as their phase velocity rapidly changes its sign. In this region the amplitude of the overstable waves becomes strongly diminished (cf. Fig. C.1, fourth row).
 |
Fig. 9 Stroboscopic space–time diagram of a 60 km section of τ
resulting from the same hydrodynamical integration using β = 1.20 and scaled torque |
 |
Fig. 10 Orbit-resolved space–time diagram of τ for a region near the density wave resonance resulting from the integration shown in Fig. C.1 with β = 1.20 for times t ≳ 20 000 ORB. The nearly horizontal pattern that becomes increasingly pronounced with increasing r > rL represents the density wave. The smaller scale structures are overstable waves that are perturbed by the satellite resonance, causing the “wiggles” in their appearance, in contrast to the waves displayed in Fig. 7. The green dashed line is the expected phase speed ωI ∕k of (unperturbed) overstable waves with λ = 300 m obtained from Fig. 8. A profile of τ is drawn forthe time indicated by the arrow, showing how the amplitude of overstable waves is reduced in approaching the resonance from smaller radii. Visible as well are the first wave cycles of the density wave. |
7.4.3 Viscous overstability in a perturbed ring: axisymmetric approximation
The hydrodynamical integrations presented above reveal a variety of structures resulting from interactions between a spiral density wave and the free short-scale waves associated with spontaneous viscous overstability. We find that a sufficiently strong spiral density wave completely mitigates the growth of viscous overstability. In this section we will consider this aspect in a more simplified, axisymmetric model which on the one hand allows us to conduct a simple hydrodynamic stability analysis, and on the other hand can be investigated with local N-body simulations. In what follows we assume that the perturbation is due to a nearby ILR. To that end consider the axisymmetric equations
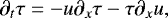 (50)
(50)
![\begin{equation*}\partial_{t} u = -u \partial_{x} u + ( \Omega_{L}^2 r + 2\Omega_{L} \, v) -\partial_{x}\left[\phi^{\textrm{d}} + \phi^{\textrm{p}}\right] - \frac{1}{\sigma} \partial_{x} \hat{P}_{xx}, \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq133.png) (51)
(51)
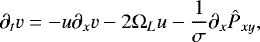 (52)
(52)
in the shearing sheet approximation (Goldreich & Lynden-Bell 1965), using a rectangular frame (x, y = 0) rotating with ΩL where x is given by Eq. (3) and where, in contrast to Eqs. (1), Ω =ΩL is now a constant. The components of the pressure tensor 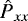 and
and 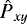 are identical to
are identical to 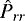 and
and 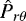 given by Eq. (5), respectively, since we had already neglected curvature terms in the latter expressions. Moreover, v denotes here the total azimuthal velocity and ϕp is the gravitational potential due to the planet. We now introduce the perturbed oscillatory ground state (Mosqueira 1996)
given by Eq. (5), respectively, since we had already neglected curvature terms in the latter expressions. Moreover, v denotes here the total azimuthal velocity and ϕp is the gravitational potential due to the planet. We now introduce the perturbed oscillatory ground state (Mosqueira 1996)
![\begin{equation*}\begin{split} \tau_{0} & = \frac{1}{1- q \cos \left(m \phi + m \Delta \right)}, \\[8pt] u_{0} & =\Omega_{L} x \, \frac{q \sin \left(m \phi + m \Delta \right)}{1-q \cos \left(m \phi + m \Delta \right)},\\[8pt] v_{0} & = -\frac{3}{2}\Omega_{L} x \, \frac{1-(4/3) q \cos \left(m \phi + m \Delta \right)}{1-q \cos \left(m \phi + m \Delta \right)}. \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq139.png) (53)
(53)
As shown in Appendix G, Eqs. (53) are valid in the vicinity of a Lindblad resonance where fluid streamlines can be described by m-lobed orbits
![\begin{equation*}r(a) = a \left[ 1- e(a) \cos \left(m \phi + m \Delta \right) \right], \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq140.png) (54)
(54)
in a cylindrical frame (r, ϕ, z = 0) rotating with the satellite’s mean motion frequency 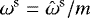 (Eq. (23)) in the present context. The quantities a and e denote a streamline’s semimajor axis and eccentricity, respectively, and Δ is a phase angle. Furthermore, q is the nonlinearity parameter (Borderies et al. 1983) fulfilling
(Eq. (23)) in the present context. The quantities a and e denote a streamline’s semimajor axis and eccentricity, respectively, and Δ is a phase angle. Furthermore, q is the nonlinearity parameter (Borderies et al. 1983) fulfilling
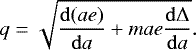 (55)
(55)
In the limit q → 0, Eqs. (53) describe the usual homogeneous unperturbed ground state as in Sect. 2. If we now adapt to the frame (r, θ, z = 0) which rotates with the local Kepler frequency ΩL at the resonance, we have
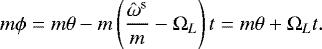 (56)
(56)
Using Eqs. (53) and (56), Eqs. (50)–(52) are identically fulfilled if one assumes a consistently expanded planetary potential
![\begin{equation*} \phi^{\textrm{p}} = -\Omega_{L}^2 \left[ r_{L}^2 - r_{L} x +x^2 \right] \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq144.png)
at y = 0 and if one neglects the radial dependencies of the phase angle Δ and the nonlinearity parameter q. We note that the terms arising from orbital advection (the azimuthal derivatives; Sect. 5) are neglected in the axisymmetric Eqs. (50)–(52). These terms would scale relative to the other terms as x∕rL ≲ 10−4 in the present situation. Since we assume that we are close to the Lindblad resonance (|x| → 0) we can ignore the radial variation of Δ in the arguments of the sine and cosine functions appearing in Eq. (53). That is, in the evanescent region close to the resonance (x ≲ 0) one can approximateq ~ ade∕da since the eccentricity increases steeply towards the resonance and the disk’s response to the perturbation is not wavelike, that is, de∕da ≫ edΔ∕da (see for instance Hahn et al. 2009). For x ≳ 0 one usually adopts the approximation that a non-vanishing q (Eq. (55)) arises only from the radial variation of the phase angle Δ. This is the tight-winding approximation for the disk’s response in the form of a long spiral density wave propagating outward with radial wavenumber md Δ∕da ≫ 1∕a. However, even in this region we can approximate Δ as a constant in Eq. (53), as long as the wavenumber of the density wave is much smaller than that of the overlying periodic microstructure that we wish to analyze. Thus, the neglect of the radial variation of Δ restricts the applicability of the above model to a small region at the resonance, since for sufficiently large x > 0 the wavelength of the density wave is not much greater than that of the overstable waves (cf. Figs. C.1 and C.2). As for the necessary approximation of a constant q we rely on previous studies that imply that for typical length scales of overstable wavetrains (several kilometers), q varies slowly (see for instance Fig. 3 of Borderies et al. 1986, Fig. 2 of Hahn et al. 2009, as well as Longaretti & Borderies 1986 and Rappaport et al. 2009 on the Mimas 5:3 wave). We note that the tight-winding approximation applied in Borderies et al. (1986) inevitably assumes q(x = 0) = 0).
Thus, in what follows we assume that the phase angle Δ is a constant and we assume (without loss of generality) that the ring is in the uncompressed state at initial time t = 0. Then Eqs. (53) together with Eq. (56) yield
![\begin{equation*}\begin{split} \tau_{0} & = \frac{1}{1- q \sin \left(\Omega_{L} t \right)}, \\[0.2cm] u_{0} & =-\Omega_{L} x \, \frac{q \cos \left( \Omega_{L} t \right)}{1-q \sin \left( \Omega_{L} t \right)}, \\[0.2cm] v_{0} & = -\frac{3}{2}\Omega_{L} x \, \frac{1-(4/3) q \sin \left( \Omega_{L} t \right)}{1-q \sin \left( \Omega_{L} t \right)}. \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq145.png) (57)
(57)
To the ground state (Eq. (57)) we now add axisymmetric perturbations
![\begin{equation*}{\bm \Psi}(x,t) = \begin{pmatrix} \tau^{\prime}(x,t) \\ u^{\prime}(x,t) \\ v^{\prime}(x,t) \end{pmatrix} = \begin{pmatrix} \hat{\tau}(x,t) \\ \hat{u}(x,t) \\ \hat{v}(x,t) \end{pmatrix} \exp\left[i k(t) x\right] \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq146.png) (58)
(58)
with time-dependent wavenumber
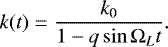 (59)
(59)
The time dependence in Eq. (59) stems from the periodic variation of the radial width of a streamline resulting from the perturbation by the density wave. This ansatz is chosen since Eqs. (57) contain only the kinematic effect of the density wave on the considered ring region. That is, Eqs. (57) describe how a single fluid streamline behaves in the presence of a density wave whose wavelength is assumed to be much larger than the extent of the streamline. For a nonlinear study of viscous overstability (implying longer timescales) in a perturbed ring region, the dynamical evolution of a streamline due to neighboring streamlines should be considered as well, which requires a more sophisticated treatment than the one adopted here. The behavior of the wavenumber according to Eq. (59) is also seen directly in N-body simulations (cf. Fig. 14).
We assume that the x-dependency of the quantities  , û (x, t), and
, û (x, t), and 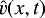 in Eq. (58) is only weak so that
in Eq. (58) is only weak so that
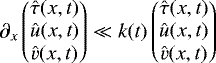 (60)
(60)
and can be ignored.
We insert the resulting expressions for τ = τ0 + τ′, u = u0 + u′, v = v0 + v′ into Eqs. (50)–(52) and linearize with respect to the perturbations τ′, u′, and v′. This procedure yields the linear system
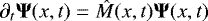 (61)
(61)
where the radial location x is a parameter and
![\begin{equation*}\begin{array}{@{}*{22}{l@{}}} \hat{M}(x,t) = \begin{pmatrix} M_{11} \hspace{0.2 cm} & M_{12} \hspace{0.2 cm} & M_{13} \hspace{0.2 cm} \\[2.5pt] M_{21} \hspace{0.2 cm} & M_{22} \hspace{0.2 cm} & M_{23} \hspace{0.2 cm} \\[2.5pt] M_{31} \hspace{0.2 cm} & M_{32} \hspace{0.2 cm} & M_{33} \hspace{0.2 cm} \\ \end{pmatrix} \end{array}\vspace*{-1pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq152.png) (62)
(62)
To arrive atEqs. (63) we also used Eqs. (13) and (17) where kx has been replaced by Eq. (59). Here we apply scalings so that time and length are scaled with 1∕ΩL and c0 ∕ΩL, respectively.We also define the dimensionless quantities
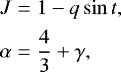 (64)
(64)
for notational brevity. To illustrate the procedure for obtaining Eq. (63) let us consider the linearization of the continuity equation, Eq. (50). The latter can be written as
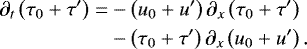
Since the ground state quantities are an exact solution in the current approximation, we end up with
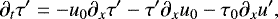
where we used ∂xτ0 = 0 (Eq. (57)). Using Eqs. (58) and (60) yields
![\begin{equation*} \partial_{t} \tau^{\prime} = -\left[ i k(t) u_{0} + \partial_{x} u_{0}\right] \, \tau^{\prime} - i k(t) \tau_{0} \,u^{\prime}.\vspace*{-3pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq157.png)
By applying Eqs. (57), (59), and (64), as well as the aforementioned scalings, we obtain M11, M12, and M13 as given in Eq. (63). All other matrix components are derived in the same fashion.
The aim is now to investigate whether a seeded overstable wavetrain (Eq. (58)) will decay or grow in amplitude by integrating Eq. (61) over a given time range. In the case q = 0 one can assume
![\begin{equation*} {\bm \Psi}(x,t)_{q=0} = \begin{pmatrix} \tau^{\prime}(x,t) \\ u^{\prime}(x,t) \\ v^{\prime}(x,t) \end{pmatrix} = \begin{pmatrix} \hat{\tau} \\ \hat{u} \\ \hat{v} \end{pmatrix} \exp\left[\omega t + i k_{0} x\right], \vspace*{-3pt}\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq158.png)
that is, the solution is a traveling wave with constant growth (or decay) rate, determined by the imaginary part of ω (Schmit & Tscharnuter 1995; Schmidt et al. 2001; Latter & Ogilvie 2009). For q > 0, the behavior is more complicated.
We integrate the complex-valued system of Eqs. (61) numerically with a fourth-order Runge-Kutta method on a grid of radial size Lx = 2 km. As initial state we use an eigenvector of Eq. (62) in the limit q → 0 at marginal stability β = βc which reads (Schmidt & Salo 2003)
![\begin{equation*}{\bm \Psi}(x,t_{0}) = \begin{pmatrix} 2 k_{0} (i k_{0}^2 \nu_{0} + s) \\[2pt] 2 s (i k_{0}^2 \nu_{0} + s) \\[2pt] - i s + k_{0}^2 (\nu_{0} + \alpha \nu_{0} s^2) + \alpha \nu_{0}^3 k_{0}^6 \end{pmatrix} \exp\left[i k_{0} \, x\right], \vspace*{-3pt}\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq159.png) (65)
(65)
is the unperturbed frequency of the overstable mode at marginal stability (cf. Eq. (15)). The initial state corresponds to a right traveling wave.
In order to obtain the growth rate of a seeded mode λn = Lx∕n where n denotes the radial mode number, we write
![\begin{equation*} {\bm \Psi}(x,t) = {\bm A}_{n}(t) \exp\left[i k_{n}(t) x\right]\vspace*{-2pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq161.png)
where kn(t) = (2π∕λn) J−1(t). The complex amplitude is then obtained by numerical solution of
![\begin{equation*}{\bm A}_{n}(t)= \frac{1}{L_{x}}\int\limits_{-L_{x}/2}^{L_{x}/2} \mathrm{d}x {\bm \Psi}(x,t) \exp\left[- i k_{n}(t) x\right]\vspace*{-2pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq162.png) (66)
(66)
for each time step. Since Eq. (65) is not an exact eigenvector of Eq. (62) for q > 0, the first orbital periods of integrations with q > 0 are excluded from the computation of the growth rates as the system is yet to settle on an exact eigensolution.
Computed growth rates of An for different radial modes n adopting the Pr76-parameters with different values of β and q are drawn in Fig. 11. These plots show a monotonic decrease of the growth rates with increasing nonlinearity parameter q on all wavelengths. At the same time the maxima of the curves shift toward larger wavelengths. From these plots we can estimate for a given β the critical values qc that yield negative growth rates on all wavelengths. In the presence of a perturbation with q ≥ qc no axisymmetric viscous overstability is expected to develop. The so-obtained values of qc seem to agree quite well with those estimated from the large-scale integrations in Sect. 7.4.2.
As an illustration, in Fig. C.4 we show space–time diagrams of the radial velocity perturbation u′ of the mode n = 10 for the case β = 1.35 with different values of q. While for q = 0 and q = 0.1 the wave amplitude grows with time, as indicated by the gradual brightening in an upward direction in the first two figures, for q = 0.4 the amplitude diminishes. Furthermore, with increasing q the overstable pattern becomes less of a uniform traveling wave. The waves seen in these space-time plots show many similarities to the overstable waves encountered in our large-scale integrations (Fig. 10).
In terms of the hydrodynamical model applied here, the mitigation of overstable oscillations by the satellite perturbation can be explained by an increasing de-synchronization of specific terms appearing in the dynamical Eq. (52). That is, the viscous overstability mechanism describes a transfer of energy from the background azimuthal shear into the epicyclic fluid motion through a coupling of the viscous stress to the Keplerian shear (Latter & Ogilvie 2006, 2009), resulting in an oscillating angular momentum flux that instigates the epicyclic oscillation if the following two conditions are met (Latter & Ogilvie 2006, 2008). On the one hand, the viscous stress needs to possess a sufficiently steep dependence on the surface mass density. This condition is expressed in terms of a critical (wavelength-dependent) viscosity parameter βc (λ) that must be exceeded for a given wavelength λ. Figure 6 shows βc(λ) for an unperturbed ring (q = 0), with minimal value ![$\text{Min}\left[\beta_{\textrm{c}}\right]_{\lambda}=1.03$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq163.png) . Figure 11 reveals that βc(λ) increases with increasing q for all λ. For instance, for q = 0.2 one finds
. Figure 11 reveals that βc(λ) increases with increasing q for all λ. For instance, for q = 0.2 one finds ![$ 1.16 > \text{Min}\left[\beta_{\textrm{c}}\right]_{\lambda} >1.1$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq164.png) . Furthermore, for q = 0.3 one can see that
. Furthermore, for q = 0.3 one can see that ![$\text{Min}\left[\beta_{\textrm{c}}\right]_{\lambda} \sim 1.25$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq165.png) .
.
The second condition that must be fulfilled for the viscous overstability to operate in a planetary ring is that the oscillation of the angular momentum flux must be sufficiently in phase with the epicyclic oscillation associated with an overstable wave. In Fig. C.5 we show snapshots of the term in the equation for the azimuthal velocity perturbation v′ that describes the coupling of the viscous stress to the Keplerian shear and which can be written M31 τ′ (cf. Eqs. (61)–(63)). The used parameters are the same as in Fig. C.4 and the snapshots cover one orbital period in equal time intervals. Over-plotted for the same instances of time is the epicyclic term M32 u′, appearing in the same equation. For q ≲ 0.3 these two terms retain a nearly constant phase shift for all times. In contrast, for larger q the phase difference of these terms drifts constantly. Therefore the energy transfer into the epicyclic oscillation is too inefficient, resulting in a damping of seeded wavetrains.
To quantify the phase relation between the angular momentum flux and the epicyclic oscillation associated with an overstable wave, we define the cross correlation of the two aforementioned relevant terms
![\begin{equation*}\mathcal{CC}(t_{s}) = \int \limits_{[l 2\pi]} \left[ M_{31}(t) \, \tau^{\prime}(t) \, M_{32}(t+t_{s}) \, u^{\prime}(t+t_{s}) \right] \mathrm{d} t, \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq166.png) (67)
(67)
where the shift parameter ts takes values between 0 and 2π and the integration is performed over l orbital periods. If the two quantities M31 τ′ and M32 u′ are periodic with a constant phase shift, their cross correlation will possess a sharp maximum for a specific value of the time shift ts. On the other hand, if their relative phase shift varies in a more or less uniform manner during one orbital period, the cross correlation will be small for all values of ts. Thus, as a measure for the synchronization of the two oscillatory quantities we take the maximum absolute value of the cross correlation  . Figure 12 displays this value for the parameters as used in Fig. 11. As anticipated, the curves show a steady decrease with increasing q and exhibit a fairly sharp drop for q = 0.3–0.4. This explains why for q ≳ 0.4 the growth rates in Fig. 11 are negative for all values of β used here. To explain the different critical values qc for which the growth rates become negative for the different β-values (e.g., qc ~ 0.2 for β =1.1), one must in addition take into account the dependence of the growth rates on β. In the unperturbed case (q = 0) the growth rates depend linearly on the factor (β − βc).
. Figure 12 displays this value for the parameters as used in Fig. 11. As anticipated, the curves show a steady decrease with increasing q and exhibit a fairly sharp drop for q = 0.3–0.4. This explains why for q ≳ 0.4 the growth rates in Fig. 11 are negative for all values of β used here. To explain the different critical values qc for which the growth rates become negative for the different β-values (e.g., qc ~ 0.2 for β =1.1), one must in addition take into account the dependence of the growth rates on β. In the unperturbed case (q = 0) the growth rates depend linearly on the factor (β − βc).
In a dilute ring, better described in terms of a kinetic model than a hydrodynamic one, the aforementioned de-synchronization can already occur in the absence of an external perturbation. In a kinetic model of a dilute ring of sufficiently low dynamical optical depth, the viscous stress tensor components are subjected to long (collisional) relaxation timescales. Therefore, these cannot follow the (fast) epicyclic oscillation of the ring flow on the orbital timescale, which also prevents viscous overstability (Latter & Ogilvie 2006).
We complement these findings with a series of local N-Body simulations of a perturbed ring that include aspects of the vertical self-gravity force in terms of an enhancement of the frequency ofvertical oscillations (Wisdom & Tremaine 1988) and also the effect of collective radial self-gravity. A detailed description of the simulation method can be found in Salo et al. (2018) and references therein. In particular, the force method for particle impacts as introduced in Salo (1995) is used and the radial self-gravity is calculated as in Salo & Schmidt (2010). The latter is parametrized through a pre-specified ground state surface mass density (see also LSS2017). Here we apply modified initial conditions and boundary conditions that account for a perturbed mean flow in the ring following the method of Mosqueira (1996). We perform simulations with meter-sized particles in a periodic box of uncompressed radial size 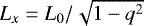 and azimuthal size Ly = 10 m. The number of particles is slightly less than 10 000 in all simulations. The quantity Lx is chosen such that the time-averaged ground state optical depth of the system is the same for different values of q, as shown below. The radial size of the simulation region changes periodically as
and azimuthal size Ly = 10 m. The number of particles is slightly less than 10 000 in all simulations. The quantity Lx is chosen such that the time-averaged ground state optical depth of the system is the same for different values of q, as shown below. The radial size of the simulation region changes periodically as
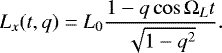 (68)
(68)
For a fixed azimuthal width and a fixed number of simulation particles, the ground state dynamical optical depth is then given by
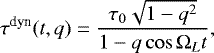 (69)
(69)
where τ0 is the time-averaged ground state optical depth over one period 2π∕ΩL, 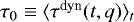 , and is independent of q. Hence, our choice of Lx removes the purely geometrical increase of the time-averaged mean optical depth with increasing q and isolates the effect of the perturbation on the evolution of viscous overstability. The quantity τ0 is not to be confused with the scaled surface density τ used elsewhere in this paper. In what follows we use τ0 = 1.5, and L0 = 2 km. The ground state surface mass density
, and is independent of q. Hence, our choice of Lx removes the purely geometrical increase of the time-averaged mean optical depth with increasing q and isolates the effect of the perturbation on the evolution of viscous overstability. The quantity τ0 is not to be confused with the scaled surface density τ used elsewhere in this paper. In what follows we use τ0 = 1.5, and L0 = 2 km. The ground state surface mass density  of the simulation region will vary in the same way as the optical depth (Eq. (69)) and we adopt a time-averaged ground state surface mass density of σ0 = 300 kg m−2. Furthermore, the simulations utilize the velocity-dependent normal coefficient of restitution by Bridges et al. (1984), while particle spins are neglected.
of the simulation region will vary in the same way as the optical depth (Eq. (69)) and we adopt a time-averaged ground state surface mass density of σ0 = 300 kg m−2. Furthermore, the simulations utilize the velocity-dependent normal coefficient of restitution by Bridges et al. (1984), while particle spins are neglected.
Figure 13 shows measurements of linear growth rates of three different seeded overstable modes in N-body simulations using different values of the nonlinearity parameter q = 0–0.6. The initial state corresponds to a standing linear overstable wave (see Eq. (37) of Schmidt et al. 2001 expanded to the lowest order of the scaled wavenumber k) in a phase where only the perturbation in the radial velocity u′ has a non-zero amplitude. When this radial perturbation velocity is seeded with small amplitude, then the simulation practically starts on an overstable eigenvector of the linear hydrodynamic model. The radial modes n =15–25 correspond to time-averaged wavelengths 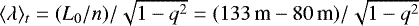 (see Eq. (68)). Figure 14 illustrates the evolution of the radial velocity perturbation for the case n = 25 with q = 0.4 during the first three orbital periods. The procedure for obtaining the growth rates is similar to that used by Schmidt et al. (2001) and LSS2017. However, in the present situation we need to take into account the varying size of the radial domain, that is, we use Eq. (66) to obtain the mode amplitude, where Ψ is replaced by the tabulated radial velocity field u′(x).
(see Eq. (68)). Figure 14 illustrates the evolution of the radial velocity perturbation for the case n = 25 with q = 0.4 during the first three orbital periods. The procedure for obtaining the growth rates is similar to that used by Schmidt et al. (2001) and LSS2017. However, in the present situation we need to take into account the varying size of the radial domain, that is, we use Eq. (66) to obtain the mode amplitude, where Ψ is replaced by the tabulated radial velocity field u′(x).
In accordance with the hydrodynamic growth rates (Fig. 11) the measured growth rates in N-body simulations (the right panels in Fig. 13) decrease with increasing magnitude of the perturbation, quantified through q. We note that the overstable modes considered here would be stable in the hydrodynamic model for all used values of β (Fig. 11). Since our N-body simulations do not include particle–particle gravitational forces (but merely the radial component of its mean-field approximation), the attained (equilibrium) velocity dispersion takes considerably smaller values than what we adopt for our hydrodynamic integrations (Table 1). This is the main reason why viscous overstabilityin the N-body simulations considered here occurs on smaller wavelengths than in our hydrodynamic model (LSS2017).
For the same parameters, Fig. 15 illustrates the nonlinear saturation of overstability in simulations that started from white noise. The left column displays curves of the kinetic energy density of perturbations that have developed on top of the ground state (Eq. (53)). The curves are sampled at quadrature (i.e., at times t where ΩL t= π∕2 + l2π with integer l) where the radially averaged (mean) optical depth takes the value 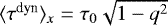 so as to mask out the orbital oscillation due to the perturbation itself. While the curves for q = 0–0.2 show a clear increase of kinetic energy with time, indicating the formation of nonlinear wavetrains, we observe a sharp drop in the kinetic energy densities for q ≥ 0.3. The right column shows snapshots of the radial particle number density profile near the end of each simulation where also
so as to mask out the orbital oscillation due to the perturbation itself. While the curves for q = 0–0.2 show a clear increase of kinetic energy with time, indicating the formation of nonlinear wavetrains, we observe a sharp drop in the kinetic energy densities for q ≥ 0.3. The right column shows snapshots of the radial particle number density profile near the end of each simulation where also 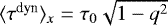 . In agreement with the energy curves we find clearly developed nonlinear overstable wavetrains for q = 0 − 0.2, while for q ≥ 0.3 the density profile develops into noise. Due to the particulate nature of the simulations, a retaining noise level induced by the (strong) perturbation is inevitable. From these results we estimate a critical value qc ~ 0.4 above which overstability is completely suppressed for the parameters used here.
. In agreement with the energy curves we find clearly developed nonlinear overstable wavetrains for q = 0 − 0.2, while for q ≥ 0.3 the density profile develops into noise. Due to the particulate nature of the simulations, a retaining noise level induced by the (strong) perturbation is inevitable. From these results we estimate a critical value qc ~ 0.4 above which overstability is completely suppressed for the parameters used here.
 |
Fig. 11 Linear hydrodynamic growth rates of overstable modes in a perturbed ring for different values of the nonlinearity parameter q describing the satellite perturbation. The wavelengths λ correspond to the uncompressed state of the model ring adopted at times t = lπ∕ΩL, with non-negative integer l (cf. Eq. (59)). The used parameters are the Pr76-parameters with varyingvalue of β and all growth rates are scaled with Ω = ΩL. In all panels the growth rates for q = 0, obtained by numerical solution of Eq. (14), are plotted additionally as black solid curves. |
 |
Fig. 12 Curves showing the maximum absolute value of the cross correlation of the quantities M31 τ′ and M32u′ (Eq. (67)) associated with an overstable mode with λ = 200 m for different values of q, and the values of β used for the plots in Fig. 11. The arrow indicates the direction of increasing β. The monotonic decrease of these curves with increasing q is the reason why the growth rates of overstable modes (Fig. 11) become smaller with increasing q. All curves have been normalized to yield unity for q = 0. |
8 Discussion
We developed a one-dimensional hydrodynamical scheme to study the excitation of a resonantly forced spiral density wave in a dense planetary ring. Due to the restriction to one space dimension, the advection caused by orbital shear needs to be approximated. We constructed corresponding azimuthal derivative terms from the weakly nonlinear model of LSS2016. Profiles of nonlinear density waves in a viscously stable ring computed with our scheme show good agreement with those resulting from the models by BGT86 and LSS2016.
We applied our scheme to investigate the damping behavior of spiral density waves in a planetary ring that is subject to viscous overstability. The results of our large-scale hydrodynamical integrations confirm the observation that resonantly forced spiral density waves can co-exist with short-scale waves generated by the viscous overstability (Hedman et al. 2014), an aspect not taken into account in existing models for the damping of density waves. Due to our approximation of the azimuthal derivative terms, the free short-scale overstable modes appearing in our hydrodynamical integrations are also non-axisymmetric with the same azimuthal periodicity m as the spiral density wave. We have shown that the nonlinear evolution of these short-scale modes is very similar to that of the strictly axisymmetric short-scale overstable modes investigated in earlier studies.
We find that the damping behavior of a spiral density wave can be very different from what is predicted by existing models, depending on its resonance strength. A sufficiently strong spiral density wave damps the short-scale viscous overstability. Furthermore, if the density wave is sufficiently strong and it is itself overstable, it behaves according to the models by BGT86 and LSS2016 in that it retains a finite saturation amplitude at large distances from resonance. If, on the other hand, the density wave is overstable and sufficiently weak, the short-scale modes dominate and damp the density wave.
It should be noted that these results are quantitatively (but most likely not qualitatively) affected by the approximation of the azimuthal derivatives in our numerical scheme. That is, although we have shown that this approximation works well if we consider a nonlinear density wave alone, or the nonlinear evolution of viscous overstability in the absence of a density wave, it cannot be ruled out that in cases where both wave types co-exist, certain nonlinear terms in the hydrodynamic Eqs. (1) would produce spurious quasi-resonant higher order coupling terms between both wave types. Such spurious terms wouldbe quasi-resonant due to the approximation that all terms in Eqs. (1) are assumed to have m-fold periodicity and the fact that the wavelength of the density wave is much greater than that of the short-scale overstable modes, at least in close vicinity of the resonance radius. It is very unlikely though that such terms would dominate the many physical coupling terms. Therefore we believe that our findings are qualitatively correct despite the approximation of the azimuthal derivatives.
We verified the damping of viscous overstability by the density wave by performing N-body simulations as well as a linear hydrodynamic stability analysis of a simplified axisymmetric model for a ring perturbed by a nearby ILR. Our N-body simulations, using modified initial and boundary conditions as introduced by Mosqueira (1996), confirm the formation of nonlinear overstable wavetrains if the perturbation by the ILR is not too strong, as well as a complete suppression of overstability if the nonlinearity parameter q associated with the perturbation exceeds a certain value. Critical values of q that result in a damping of viscous overstability obtained from our large-scale integrations compare well with those that follow from the linear stability analysis of the axisymmetric model. Based on our results, we conclude that the mitigation of viscous overstability by a density wave is due to the destruction of the phase relation of the oscillating angular momentum flux and the epicyclic oscillation associated with overstable waves. A quantitative match of q-values in the aforementioned comparison should not be expected however. That is, on the one hand the overstable waves found in our large-scale hydrodynamical integrations suffer from the relatively low spatial resolution of the computational grid, which is expected to reduce the estimates of qc from these integrations. Furthermore, the applied approximation of the azimuthal derivatives could affect these values as well. On the other hand, the neglect of the variation of the phase angle Δ due to the density wave in the linear stability analysis is most likely not justified in the far wave region of a density wave. It is not clear how this affects the computed growth rates of overstable modes and associated values of qc.
Although we understand the mitigation of viscous overstability by a density wave, an explanation for the damping of overstable density waves, such as those presented in the last panel of Fig. C.1 and the first three panels of Fig. C.2, remains to be sought for. One difficulty is that in this case the nonlinear interaction of the two different modes needs to be considered. It is noteworthy that the observed density waves in Saturn’s A ring associated with the 7:6 ILR and the 10:9 ILR with the moons Atlas and Pan, respectively, seem to correspond to this case (see Hedman et al. 2014, Fig. 5).
Furthermore, it should be noted that due to the neglect of particle–particle self-gravity in our modeling, self-gravitational wakes (Salo 1992) do not form. In principle their effect on the density wave profile may be described in terms of a gravitational viscosity (Daisaka et al. 2001). In parts of Saturn’s dense rings (particularly the A ring) it is expected that this gravitational viscosity is the dominant mode of viscosity. However, the wakes will interact with viscous overstability in a more or less complex manner (Salo et al. 2001; Ballouz et al. 2017) and as such they will indirectly affect the damping of a density wave. Moreover, in the regions of strong density waves the size of self-gravitational wakes is expected to be much increased. That is, the “straw”-like structures observed in optical Cassini images of strong density waves (e.g., Tiscareno 2017) are believed to represent self-gravity wakes of kilometer length scales. These length scales are much greater than the typical length scale of self-gravity wakes that can form in an unperturbed planetary ring (Salo 1992). An increased size of self-gravity wakes in the troughs of nonlinear density waves is also expected from N-body simulations (Salo & Schmidt 2014) and theoretical studies (Stewart 2017). Stewart (2017) has shown that the characteristic length scale of self-gravitational perturbations (the Toomre-wavelength) is greatly enhanced in the troughs of strongly nonlinear density waves. This result suggests that the gravitational viscosity, which scales with the square of the Toomre-wavelength (Daisaka et al. 2001), can be greatly enhanced in the wave region, consequently leading to a stronger damping of the density wave.
Our numerical scheme allows for, in principle, straightforward extensions, such as the inclusion of the energy equation by using the numerical method of LSS2017. Ultimately, a two-dimensional scheme should be developed to overcome the necessity of approximating the orbital advection terms.
 |
Fig. 13 Determination of linear growth rates of three different seeded overstable modes (indicated by their radial mode number n) in N-body simulations for different values of the nonlinearity parameter q, quantifying the amount of perturbation in the ground state that corresponds to a density wave. Left panels: time evolution of amplitudes An (Eq. (66)) with a sampling interval of one orbital period. Right panels: resulting growth rates obtained from linear fits as drawn in the left frames. The simulations used time-averaged values of the ground state optical depth and surface mass density of τ0 = 1.5 and σ0 = 300 kg m−2, respectively, as well as a vertical frequency enhancement of Ωz∕Ω = 2 to mimic vertical self-gravity. |
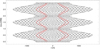 |
Fig. 14 Evolution of the radial velocity perturbation u′ during the first three orbital periods of the N-body simulation with n = 25 and q = 0.4 of Fig. 13. Clearly visible is the periodic variation of the radial size of the simulation region according to Eq. (68) which is drawn as dashed curves. Also indicated is the analogous radial variation of one wavelength of the seeded mode, represented by the two pairs of red solid curves. Since the seed is a standing wave, its amplitude undergoes an oscillation with twice the overstable wave frequency (cf. Eq. (15)). |
 |
Fig. 15 Nonlinear evolution of viscous overstability in N-body simulations of a perturbed ring.
Left panels: curves of kinetic energy density (Eq. (22)) of perturbations in units
|
Acknowledgements
We thank the reviewer Glen Stewart for helpful and constructive comments. We are grateful to Pierre-Yves Longaretti for discussions that greatly improved the manuscript. We acknowledge support from the Academy of Finland. M.L. acknowledges funding from the University of Oulu Graduate School and the University of Oulu Scholarship Foundation.
Appendix A Figures of Sect. 7.2
 |
Fig. A.1 Comparison of state variables resulting from hydrodynamical integrations and the WNL model using the
Pr76-parameters with |
 |
Fig. A.2 Comparison of profiles of τ
along with their Morlet wavelet powers resulting from a hydrodynamical integration and the WNL and BGT models using the Pr76-parameters with |
 |
Fig. A.3 Comparison of profiles of τ resulting from integrations with the Straight Wire self-gravity (left column) and the WKB self-gravity (right column) with corresponding waves of the BGT model. The WKB approximation is intrinsic to the BGT model. |
Appendix B Figures of Sect. 7.3
 |
Fig. B.1 Space–time plots of an m = 7 density wavewith scaled torque |
 |
Fig. B.2 Comparison of profiles of τ
along with their Morlet wavelet powers resulting from hydrodynamical integrations using the
Pr76-parameters and scaled torque |
Appendix C Figures of Sect. 7.4
 |
Fig. C.1 Hydrodynamical integrations using the Pr76-parameters (Table 1) with increasing value of the viscosity parameter
β = 0.85–1.35 (see Fig. 6) from top to bottom. The surface density profiles (left panels) as well as their wavelet-powers (right panels) reveal the co-existence of a resonantly forced density wave and short-scale viscous overstability for the cases
β = 1.10–1.35. All integrations use a scaled torque |
 |
Fig. C.2 Hydrodynamical integrations using the Pr76-parameters (Table 1) with increasing forcing strength from top to bottom panels
( |
 |
Fig. C.3 Comparison of the nonlinear evolution of free (Ts = 0) viscous overstability in hydrodynamical integrations with (non-axisymmetric, m = 7) and without (axisymmetric, m = 0) the azimuthal derivative terms (Sect. 5), shown as profiles of the surface density τ along with their wavelet powers for two different times (t = 500 ORB and t =35 000 ORB). The blue dashed lines indicate the expected nonlinear saturation wavelength of axisymmetric (m = 0) viscous overstability by margins ± 20 m (see Sect. 7.4.1). The red dashed curves represent the linear density wave dispersion relation (Eq. (43)). In the axisymmetric case this curve has no physical meaning. The bottom frame displays the evolution ofthe kinetic energy density for both integrations. The insert plot indicates that the linear growth phases (t ≲ 200 ORB) of non-axisymmetric and axisymmetric modes are practically identical, in agreement with our considerations in Sect. 2. The higher saturation energy of the axisymmetric integration is due to the slightly larger saturation wavelength (see Sect. 7.4.1 for explanations). |
 |
Fig. C.4 Space–time diagrams showing the linear evolution of the radial velocity field u′ of an initially seeded traveling wave in a ring with β = 1.35 perturbed by an ILR (at r = rL). The perturbation, quantified by q, increases from left to right. At initial time t = 0 the model ring is in the uncompressed state (Eq. (59)) and the initial wavelength λ = 200 m. |
 |
Fig. C.5 Snapshots of the terms M31τ′ and M32u′ that appear in the equation for the azimuthal velocity perturbation and which must be sufficiently in phase for the viscous overstability mechanism to work. The snapshots are from integrations with λ = 200 m, β = 1.35, and cover one orbital period in equal time-intervals. With increasing strength of the satellite perturbation (quantified through the nonlinearity parameter q) these terms become increasingly out of phase. For q = 0.4 almost all possible phase differences in the range 0–2π occur, which explains the negative growth rates of overstable modes on all wavelengths (Fig. 11, lower right panel).For clarity the two quantities have been rescaled so as to possess equal amplitudes in all plots. |
Appendix D Method B for the azimuthal derivatives
D.1 Linear waves
When restricting to linear density waves for the time being and adopting the notations of Eqs. (27) and (28), then the azimuthal derivative of the solution vector can be written as
![\begin{equation*}\begin{split} \partial_{\theta} {\bm \Psi}|_{\theta=0} & =\partial_{\theta} \left[ \begin{pmatrix} \mathcal{A_{\tau}}\left(r,t\right) \\ \mathcal{A}_{u}\left(r,t\right) \\ \mathcal{A}_{v}\left(r,t\right) \end{pmatrix} \exp \left\{i \left(m\theta - \omega^{\textrm{s}} t \right)\right\} \right]_{\theta=0} \\[10pt] & = -m \begin{pmatrix} \tau_{\textrm{I}}(r,t) \\ u_{\textrm{I}}(r,t) \\ v_{\textrm{I}}(r,t) \end{pmatrix} + i m \begin{pmatrix} \tau_{\textrm{R}}(r,t) \\ u_{\textrm{R}}(r,t) \\ v_{\textrm{R}}(r,t). \end{pmatrix}. \\%[0.4 cm] \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq176.png) (D.1)
(D.1)
As a result the azimuthal derivatives (Eq. (D.1)) induce a coupling between the real and imaginary parts of Eqs. (1).
D.2 Nonlinear waves
For the description of nonlinear density waves (the amplitudes 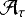 ,
, 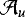 ,
, 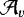 are not small) a splitting of Eqs. (1) into real and imaginary parts is not suitable. However, we can retain the description in terms of a coupled set of equations, which can be seen as follows. First we note that performing the azimuthal derivative of the vector of state (Eq. (28)) is equal to a phase shift of π∕2 and a multiplication by m, so that
are not small) a splitting of Eqs. (1) into real and imaginary parts is not suitable. However, we can retain the description in terms of a coupled set of equations, which can be seen as follows. First we note that performing the azimuthal derivative of the vector of state (Eq. (28)) is equal to a phase shift of π∕2 and a multiplication by m, so that
![\begin{equation*}\begin{split} \partial_{\theta} {\bm \Psi}(r,\theta,t) & = m {\bm \Psi}(r,\theta+ \pi/2,t)\\[0.4cm] & = m \left[{\bm \Psi}_{\textrm{R}}(r,\theta + \pi/2,t) + i\, {\bm \Psi}_{\textrm{I}}(r,\theta + \pi/2,t) +c.c. \right]\!. \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq180.png) (D.2)
(D.2)
This can also be expressed in terms of a time shift of P∕4, that is,
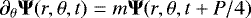
where 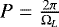 .
.
Inspection of the forcing terms Eqs. (25) and (26) show that the imaginary part of the forcing function equals the real part, but with a phase shift of − π∕2. This means that we can consider the real and imaginary parts of Eqs. (1) to describe the same forced density wave, but with a phase shift of − π∕2 so that
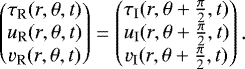 (D.3)
(D.3)
This observation is independent of whether the equations are linear ornonlinear. The idea is now to define two sets of the same nonlinear Eqs. (1), where one set is forced with the real parts of Eqs. (25) and (26) and is assumed to possess the solution vector
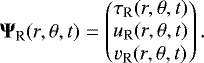
The other set is forced with the imaginary parts of Eqs. (25) and (26) and is assumed to possess the solution vector
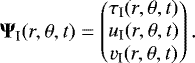
The amplitudes 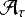 ,
, 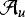 ,
, 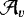 will now be affected by nonlinear terms in Eqs. (1).
will now be affected by nonlinear terms in Eqs. (1).
Combining Eqs. (D.2) and (D.3) yields
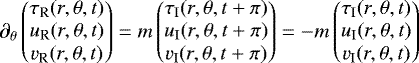
We note that although we retain the notation with subscripts R and I, the interpretation of the expressions denoting real and imaginary parts is only valid in the linear regime. In the nonlinear case the two quantities ΨR and ΨR merely describe the same density wave up to a constant relative phase shift.
Appendix E WENO reconstruction of the flux-vector
The computation of the flux derivative ∂rF in Eq. (18) includes a splitting of F according to the method of Liou & Steffen (1993), which was also used in LSS2017, and a WENO reconstruction of its individual components. In short terms the reconstruction is as follows. We have (Shu & Osher 1988)
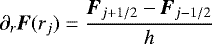 (E.1)
(E.1)
with the numerical flux F, implicitly defined through
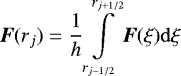 (E.2)
(E.2)
so that Eq. (E.1) is exactly fulfilled. In these expressions the subscripts j ± 1∕2 denote evaluations at radial locations 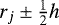 . Equation (E.2) can be used to obtain interpolating polynomials for F at a given location r, since the nodal values of the physical flux F (rj) are known for all j. We denote the so-obtained unique fifth-order accurate polynomial approximation for the numerical flux values at half nodes (see Sect. 4.1.1 of LSS2017) by
. Equation (E.2) can be used to obtain interpolating polynomials for F at a given location r, since the nodal values of the physical flux F (rj) are known for all j. We denote the so-obtained unique fifth-order accurate polynomial approximation for the numerical flux values at half nodes (see Sect. 4.1.1 of LSS2017) by 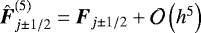 , where
, where 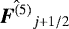 and
and 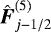 use the five-point stencils [rj−2, rj−1, …, rj+2] and [rj−3, rj−2, …, rj+1], respectively.
use the five-point stencils [rj−2, rj−1, …, rj+2] and [rj−3, rj−2, …, rj+1], respectively.
The starting point of the WENO reconstruction is the replacement of 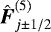 by
by
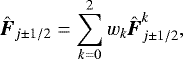 (E.3)
(E.3)
are the (unique) third-order accurate polynomial approximations for Fj+1∕2 using the three three-point stencils [rj, rj+1, rj+2], [rj−1, rj, rj+1], and [rj−2, rj−1, rj], respectively (for Fj−1∕2 these are shifted accordingly by − 1).
For a particular choice of the “weights” wk Eq. (E.3) does yield 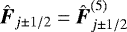 . The key point of the decomposition expressed in Eq. (E.3) is an adequate assignment of the weights wk so that these yield the standard fifth-order accurate Lagrange interpolation
. The key point of the decomposition expressed in Eq. (E.3) is an adequate assignment of the weights wk so that these yield the standard fifth-order accurate Lagrange interpolation 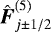 wherever F behaves smoothly across the entire five-point stencil. If, however, in some region the solution vector contains a discontinuity in one of the three sub-stencils, the corresponding weight should diminish in order to avoid spurious oscillations of the solution vector. We use the WENO-Z weights introduced by Borges et al. (2008), which yield improved accuracy near extrema, as compared with the original WENO weights (Jiang & Shu 1996). This improved accuracy is important as we are modeling wave systems that exhibit a wide range of length scales, where the shortest length scales will span only several grid points, and where the state variables can contain sharp gradients.
wherever F behaves smoothly across the entire five-point stencil. If, however, in some region the solution vector contains a discontinuity in one of the three sub-stencils, the corresponding weight should diminish in order to avoid spurious oscillations of the solution vector. We use the WENO-Z weights introduced by Borges et al. (2008), which yield improved accuracy near extrema, as compared with the original WENO weights (Jiang & Shu 1996). This improved accuracy is important as we are modeling wave systems that exhibit a wide range of length scales, where the shortest length scales will span only several grid points, and where the state variables can contain sharp gradients.
Since we apply a splitting of the flux F →F+ + F− so that ∂(F+∕−)∕∂U possess only non-negative/non-positive eigenvalues, the reconstruction outlined above applies to 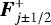 , whereas
, whereas 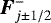 is reconstructed using stencils that are shifted by + 1 so as to ensure a correct upwinding (cf. LSS2017).
is reconstructed using stencils that are shifted by + 1 so as to ensure a correct upwinding (cf. LSS2017).
Appendix F WKB approximation for self-gravity
For integrations of linear density waves, one can implement the self-gravity terms that arise from the solution for the self-gravity potential ϕd in the WKB-approximation (cf. Eq. (30))
![\begin{equation*}\begin{split} f^{d} & = f^{d}_{\textrm{R}} +i\, f^{d}_{\textrm{I}}\\[0.1cm] & = -\partial_{r} \, \phi^{\textrm{d}}(r,t) = i \,2 \pi G \sigma_{0} \, \tau(r,t)\\[0.1cm] & = i \,2 \pi G \sigma_{0} \left[ \tau_{R}(r,t) + i \tau_{I}(r,t) \right]\\[0.1cm] & = -2 \pi G \sigma_{0}\, \tau_{I}(r,t) + i\, 2 \pi G \sigma_{0} \, \tau_{R}(r,t). \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq204.png) (F.1)
(F.1)
In this approximation, the self-gravity force at a certain grid point isgoverned by the value of the surface mass density at this particular grid point only. This implementation of the self-gravity force couples the real and imaginary parts of Eqs. (1).
An alternative way to implement the WKB self-gravity that does not induce an additional coupling between the equations and which turns out to work also in the nonlinear regime is derived from Eqs. (35), (45), (52), and (53a) in LSS2016. From these relations it follows that the disk potential 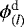 and radial velocity u(l) are related through
and radial velocity u(l) are related through
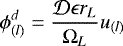
where l = 1, 2 denote the first and second harmonics of these quantities. This relation holds to the lowest order in 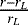 . The exact relation (in the rotating frame) is (cf. Eq. (29))
. The exact relation (in the rotating frame) is (cf. Eq. (29))
![\begin{equation*}\phi_{(l)}^{d} = - \frac{\mathcal{D} \epsilon r_{L} }{ \omega^{\textrm{s}} - m\left[\Omega-\Omega_{L} \right]} u_{(l)}. \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq208.png) (F.2)
(F.2)
If we assume this relation holds for all higher harmonics l = 3, 4, …, we can write the self-gravity force as
![\begin{equation*}\begin{split} f^{d} & = - \partial_{r} \phi^{\textrm{d}} = \frac{2 \pi G \sigma_{0}}{ \omega^{\textrm{s}} - m\left[ \Omega - \Omega_{L} \right] } \partial_{r} u. \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq209.png) (F.3)
(F.3)
For sufficiently linear waves the implementations expressed in Eqs. (F.1) and (F.3) yield identical results.
Appendix G Derivation of the perturbed ground state
We start with Eq. (54) describing an m-lobed fluid streamline and the expressions for the radial and azimuthal velocities (Borderies et al. (1983))
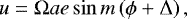 (G.1)
(G.1)
![\begin{equation*} v = r \Omega \left[ 1 + 2 e \cos m \left(\phi + \Delta \right) \right], \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq211.png) (G.2)
(G.2)
where the latter expressions are valid in an inertial frame (r, φ) with φ =ϕ + ωs(t − t0). Radial compression of the ring matter is described by
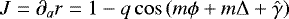 (G.3)
(G.3)
where q is the nonlinearity parameter (Eq. (55)) and ∂a denotes the derivative with respect to a. This results in the scaled surface mass density
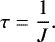 (G.6)
(G.6)
The linearized velocity fields near x = x0 are given by
![\begin{equation*} u(x) = u(x_0) + x \left[\partial_{r}u\right]_{x=x_0} , \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq216.png) (G.7)
(G.7)
![\begin{equation*} v(x) = v(x_0) + x \left[a \partial_{r} (v/r)\right]_{x=x_0} , \vspace*{-2pt} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq217.png) (G.8)
(G.8)
where ∂r = (1∕J) ∂a by Eq. (G.3). For the radial velocity u we need to compute
![\begin{equation*}\begin{split} \partial_{a} u = & \sin m \left(\phi + \Delta \right) \left[ a e \partial_{a} \Omega + \Omega e + \Omega a \partial_{a} e\right] \\ & +\Omega a e \cos m \left(\phi + \Delta \right) m \partial_{a} \Delta\\ \quad = & \sin m \left(\phi + \Delta \right) \left[ -\frac{3}{2} \Omega e + \Omega e + \Omega q \cos \hat{\gamma} \right] \\ & + \Omega q \sin \hat{\gamma} \cos m \left(\phi + \Delta \right)\\ \quad = & -\frac{\Omega e }{2} \sin m \left(\phi + \Delta \right) + \Omega q \left[\sin m \left(\phi + \Delta\right)\cos \hat{\gamma} \right. \\ \quad & \left. + \cos m \left(\phi + \Delta \right) \sin \hat{\gamma} \right]\\ \quad = & -\frac{\Omega e }{2} \sin m \left(\phi + \Delta \right) + \Omega q \sin \left[ m \left(\phi + \Delta \right) + \hat{\gamma} \right]. \end{split} \vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq218.png) (G.9)
(G.9)
For the azimuthal velocity v consider
![\begin{eqnarray*}\begin{split} \partial_{a} (v/r) = & \partial_{a} \left[ \Omega \left(1 + 2 e \cos m \left(\phi + \Delta \right) \right) \right]\\ \quad = & -\frac{3\Omega}{2 a} \left ( 1 +2 e \cos m \left(\phi + \Delta \right) \right) \\ \quad & + 2 \Omega \left[ \partial_{a} e \cos m \left(\phi + \Delta \right) -e \sin m \left(\phi + \Delta\right) m \partial_{a} \Delta \right]\\ \quad = & -\frac{3\Omega}{2 a} \left ( 1 +2 e \cos m \left(\phi + \Delta \right) \right) \\ \quad & + \frac{2 \Omega }{a} \left[ q \cos \hat{\gamma} \cos m \left(\phi + \Delta \right) - q \sin \hat{\gamma} \sin m \left(\phi + \Delta \right) \right]\\ \quad = & \frac{\Omega}{a} \left[\! {-}\frac{3}{2} -3 e \cos m \left(\phi + \Delta\right) + 2 q \cos \!\left[m \left(\phi + \Delta \right) \right]\!\right]. \end{split}\nonumber\\[-20pt] \end{eqnarray*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq220.png) (G.11)
(G.11)
Mosqueira (1996) assumes that nonlinearity (i.e., q > 0) arises solely from an eccentricity gradient, implying  (cf. Eqs. (G.4) and (G.5)), and that the eccentricity e vanishes at x = x0. These assumptions are expected to be fulfilled in the evanescent region of the density wave, close to the Lindblad resonance, that is, for x0 ≲ 0. In the frame rotating with Ω(x = x0)) we then have
(cf. Eqs. (G.4) and (G.5)), and that the eccentricity e vanishes at x = x0. These assumptions are expected to be fulfilled in the evanescent region of the density wave, close to the Lindblad resonance, that is, for x0 ≲ 0. In the frame rotating with Ω(x = x0)) we then have
![\begin{align} \tau & = \frac{1}{1 - q \cos m \left(\phi + \Delta \right) },\\[3pt] u & = \Omega q x \frac{\sin m \left(\phi + \Delta\right) }{1 - q \cos m \left(\phi + \Delta \right) },\\[3pt] v & = -\frac{3}{2} \Omega x \frac{1- \frac{4}{3} q \cos m \left(\phi + \Delta \right) }{1 - q \cos m \left(\phi + \Delta \right)}. \end{align}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq223.png)
If, on the other hand, we are in the density wave propagation region (x > 0), we can assume that nonlinearity arises solely due to the variation of the phase angle Δ, such that  . Let us rewrite Eqs. (G.10) and (G.12) using the first line of Eq. (G.9) and the second line of Eq. (G.11) such that
. Let us rewrite Eqs. (G.10) and (G.12) using the first line of Eq. (G.9) and the second line of Eq. (G.11) such that
![\begin{align} \begin{split} u = & \left[\Omega a e \sin m \left(\phi + \Delta\right) \right]_{x=x_0}\\ \quad & + \Bigg[\sin m \left(\phi + \Delta \right) \left[ \partial_{a} \Omega a e + \Omega e + \Omega a \partial_{a} e\right] \\ \quad & +\Omega a e \cos m \left(\phi + \Delta \right) m \partial_{a} \Delta \Bigg] \frac{x}{J},\\ % % v = & \left[r \Omega \left(1+ 2 e \cos m \left(\phi + \Delta\right) \right) \right]_{x=x_0}\\ \quad & + \left[ -\frac{3\Omega}{2 } \left( 1 +2 e \cos m \left(\phi + \Delta \right) \right) \right.\\ \quad & \left. + 2 \Omega a [\partial_{a} e \cos m \left(\phi + \Delta \right) -e \sin m \left(\phi + \Delta\right) m \partial_{a} \Delta \vphantom{-\frac{3\Omega}{2 }}\!]\right] \frac{x}{J}. \end{split} \end{align}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq325.png) (G.16)
(G.16)
Since we now have mae∂aΔ ≫ ∂a(ae) as well as mx∂aΔ ≫ 1 (the WKB approximation), the last term within the brackets in front of the factor 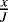 dominates for both velocities and we arrive (in the frame rotating with Ω(x = x0))) at
dominates for both velocities and we arrive (in the frame rotating with Ω(x = x0))) at
![\begin{align} \tau & = \frac{1}{1 + q \sin m \left(\phi + \Delta \right) },\\[1pt] u & = \Omega q x \frac{\cos m \left(\phi + \Delta\right) }{1 + q \sin m \left(\phi + \Delta \right) },\\[1pt] v & = -\frac{3}{2} \Omega x \frac{1 + \frac{4}{3} q \sin m \left(\phi + \Delta \right) }{1 + q \sin m \left(\phi + \Delta \right)}, \end{align}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq226.png)
which is identical to Eqs. (G.13)–(G.15), up to an irrelevant constant phase shift of π∕2.
References
- Araki, S., & Tremaine, S. 1986, Icarus, 65, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Ballouz, R. L., Richardson, D. C., & Morishima, R. 2017, AJ, 153,146 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton University Press) [Google Scholar]
- Borderies, N., Goldreich, P., & Tremaine, S. 1983 Icarus, 55, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies, N., Goldreich, P., & Tremaine, S. 1985, Icarus, 63, 406 [NASA ADS] [CrossRef] [Google Scholar]
- Borderies, N., Goldreich, P., & Tremaine, S. 1986, Icarus, 68, 522 [NASA ADS] [CrossRef] [Google Scholar]
- Borges, R., Carmona, M., Costa, B. & Don, W. S. 2008, J. Comput. Phys., 227, 3191 [Google Scholar]
- Bridges, F. G., Hatzes, A. P., & Lin, D. N. C. 1984, Nature, 309, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Colwell, J. E., Esposito, L. W., Sremčević, M., Stewart, G. R., & McClintock, W. E. 2007, Icarus, 190, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Cross, M. C., & Hohenberg, P. C. 1993, Rev. Mod. Phys., 3, 851 [Google Scholar]
- Cuzzi, J. N., Lissauer, J. J., Esposito, L. W., et al. 1984, Planetary Rings, eds. R. Greenberg & A. Brahic (Tucson, AZ: The University of Arizona Press), 73 [Google Scholar]
- Daisaka, H., Tanaka, H., & Ida. S. 2001, Icarus, 154,296 [NASA ADS] [CrossRef] [Google Scholar]
- Dewar, R. L. 1972, ApJ, 174, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Lynden-Bell, D. II. 1965, MNRAS, 130, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S., 1978a, Icarus, 34, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1978b, ApJ, 222, 850 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Tremaine, S. 1979, ApJ, 233, 857 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hahn, J. M., Spitale, J. N., & Porco, C. C., 2009, ApJ, 699, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Hedman, M. M., & Nicholson, P. D. 2016, Icarus, 279, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Hedman, M. M., Nicholson, P. D., & Salo H. 2014, AJ, 148, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, G.-S., & Shu, C.-W. 1996, J. Comput. Phys., 126, 202 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johnson, B. M., & Gammie, C. F. 2005, ApJ, 626, 978 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., & Ogilvie, G. I. 2006, Icarus, 184, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., & Ogilvie, G. I. 2008, Icarus, 195, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., & Ogilvie, G. I., 2009, Icarus, 202, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Latter, H. N., & Ogilvie, G. I. 2010, Icarus, 210, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, E., & Goodman, J. 1999, MNRAS, 308, 984 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, M., Schmidt, J., & Salo, H. 2016, ApJ, 829, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, M., Schmidt, J., & Salo H. 2017, ApJ, 851, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Liou, M. S., & Steffen, C. J. 1993, J. Comput. Phys., 107, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Longaretti, P.-Y. 1989, Icarus, 82, 281 [NASA ADS] [CrossRef] [Google Scholar]
- Longaretti, P. Y., 2018, in Planetary Ring Systems, eds. M. S. Tiscareno, & C. D. Murray (Cambridge: Cambridge University Press), 225 [CrossRef] [Google Scholar]
- Longaretti, P. Y., & Borderies, N. 1986, Icarus, 67, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Longaretti, P. Y., & Borderies, N. 1991, Icarus, 94, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Lynden-Bell, D., & Pringle, J. E. 1974, MNRAS, 168, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Meyer-Vernet, N., & Sicardy, B. 1987, Icarus, 69, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Mosqueira, I. 1996, Icarus, 122, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Rappaport, N. J., Longaretti, P.-Y., French, R. G., Marouf, E. A., & McGhee, C. A. 2009, Icarus, 199, 154 [NASA ADS] [CrossRef] [Google Scholar]
- Rein, H., & Latter, H. N. 2013, MNRAS, 431, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H. 1991, Icarus, 90, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H. 1992, Nature, 359, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H. 1995, Icarus, 117, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., & Schmidt, J. 2010, Icarus, 206, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., & Schmidt, J. 2014, European Planetary Science Congress, 9:EPSC2014–744 [Google Scholar]
- Salo, H., Schmidt, J., & Spahn, F. 2001, Icarus, 153, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., Ohtsuki, K., & Lewis, M. C. 2018, in Planetary Ring Systems, eds. M. S. Tiscareno, & C. D. Murray (Cambridge: Cambridge University Press), 434 [CrossRef] [Google Scholar]
- Schmidt, J., & Salo, H. 2003, Phys. Rev. Lett., 90, 061102 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Schmit, U., & Tscharnuter, W. M. 1995, Icarus, 115, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Schmit, U., & Tscharnuter, W. M. 1999, Icarus, 138, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, J., Salo, H., Spahn, F., & Petzschmann, O. 2001, Icarus, 153, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, J., Ohtsuki, K., Rappaport, N., Salo, H., & Spahn, F. 2009, Dynamics of Saturn’s Dense Rings (Dordrecht: Springer), 413 [Google Scholar]
- Schmidt, J., Colwell, J. E., Lehmann, M. et al. 2016, ApJ, 824, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H. 1970, AJ, 160, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H.. 1984, in Planetary Rings, eds., R. Greenberg, & A. Brahic (Tucson, AZ: University of Arizona Press), 513 [Google Scholar]
- Shu, C.-W., & Osher, S. 1988, J. Comput. Phys., 77, 439 [Google Scholar]
- Shu, F. H., Yuan, C., & J. J. Lissauer, 1985a, ApJ, 291, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Dones, L., Lissauer, J. J., Yuan, C., & Cuzzi, J. N. 1985b, ApJ, 299, 542 [NASA ADS] [CrossRef] [Google Scholar]
- Shukhman, I. G. 1984, Sov. Astron., 28, 574 [NASA ADS] [Google Scholar]
- Spahn, F., Schmidt, J., Petzschmann, O., & Salo, H. 2000, Icarus, 145, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Stewart, G. R. 2016, AAS/Division for Planetary Sciences Meeting, 48, 203.02 [NASA ADS] [Google Scholar]
- Stewart, G. R. 2017, AAS/Division of Dynamical Astronomy Meeting, 48, 400.02 [NASA ADS] [Google Scholar]
- Stewart, G. R., Lin, D. N. C., & Bodenheimer, P. 1984, in Planetary Rings, eds. R. Greenberg & A. Brahic (Tucson, AZ: University of Arizona Press), 447 [Google Scholar]
- Thomson, F. S., Marouf, E. A., Tyler, G. L., French, R. G., & Rappoport, N. J., 2007, Geophys. Res. Lett., 34, L24203.1 [CrossRef] [Google Scholar]
- Tiscareno, M. S., & Cassini Imaging Team. 2017, AAS/Division for Planetary Sciences Meeting Abstracts, 108. 02 [Google Scholar]
- Tiscareno, M.S., Nicholson, P. D., Burns, J. A., Hedman, M. M., & Porco, C. C. 2006, ApJ, 651, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Tiscareno, M. S., Burns, J. A., Nicholson, P. D., Hedman, M. M., & Porco, C. C. 2007, Icarus, 189, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Toomre, A. 1969, ApJ, 158, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Torrence, C., & Compo, G. P. 1998, Bull. Am. Meteorol. Soc., 79, 61 [Google Scholar]
- Whitham, G. 1974 Linear and Nonlinear Waves (New York: John Wiley & Sons, Inc.) [Google Scholar]
- Wisdom, J., & Tremaine, S. 1988, AJ, 95, 925 [NASA ADS] [CrossRef] [Google Scholar]
The analysis in LSS2016 is restricted to second order harmonics.
All Tables
All Figures
 |
Fig. 1 Stroboscopic space–time diagram showing the evolution of the scaled surface density
τ
for an integration with the Pr76-parameters and an associated scaled torque |
| In the text | |
 |
Fig. 2 Same as Fig. 1 except that |
| In the text | |
 |
Fig. 3 Same as Fig. 1 except that |
| In the text | |
 |
Fig. 4 Average wavelength of the forming pattern in the course of the integration shown in Fig. 1. The wavelength is obtained by counting the number of complete wave cycles of the (sinusoidal) surface density τ within the radial region 50 km ≤ r–rL ≤ 150 km. |
| In the text | |
 |
Fig. 5 Reflection of a (long) trailing density wave at a sharp boundary at r– rL ~ 100 km where τ0 is reduced by a factor of 1∕5. In the space–time plot (left panel) the blue (red) dashed curve traces a line of equal phase of the incoming (reflected) wave so that it follows a density maximum. Right panel: τ evaluated along these curves. As explained in the text, one can estimate the amplitude ratio of the incoming and the reflected waves from the indicated values Amax and Amin of τ (Eq. (49)). Since the considered wave is weakly nonlinear it follows H(q) ≳1 in the nonlinear dispersion relation (Eq. (44)) so that the linear limit (Eq. (43)) is not fully accurate. To compensate for this we used a slightly increased value of σ0 (by 0.25%) to compute the wavenumber k from Eq. (43), which is used in Eq. (48), to obtain a better fit to the locations of equal phase in the left panel. |
| In the text | |
 |
Fig. 6 Linearstability curve (Eq. (16)) corresponding to the Pr76-parameters (solid curve). The dashed lines indicate the different values of the viscosity parameter
β
(Eq. (7)) that are used for the large-scale integrations of resonantly forced density waves discussed in Sect. 7.4. Viscous overstability is expected to develop for all values of
β
larger than the minimal value |
| In the text | |
 |
Fig. 7 Left panels: radial surface density (τ) profile and its wavelet power at t ~ 20 000 ORB of a hydrodynamical integration using the Pr76-parameters with β = 1.25 and no satellite forcing ( |
| In the text | |
 |
Fig. 8 Left panel: linear and nonlinear frequencies of overstable waves adopting the Pr76-parameters with β = 1.25. The linear curve was obtained from numerical solution of Eq. (14). The nonlinear frequencies were obtained from small-domain hydrodynamical integrations of saturated overstable waves as described in detail in LSS2017 (see their Sect. 6.1). The minima of both curves appear at equal wavelengths, which is a consequence of the ideal gas relation Eq. (6) for the hydrostatic pressure. For more realistic equations of state the nonlinear frequency minimum occurs at larger wavelengths than the linear one (LSS2017). Right panel: power spectral density of τ from the same integration as in Fig. 7 during the linear growth phase (t = 200 ORB) and in the saturated state (t ~ 20 000 ORB) of viscous overstability. The insert displays the evolution of the kinetic energy density (Eq. (22)). The blue dashed linesin both panels indicate the expected nonlinear saturation wavelength of viscous overstability with margins ± 20 m (see the text). |
| In the text | |
 |
Fig. 9 Stroboscopic space–time diagram of a 60 km section of τ
resulting from the same hydrodynamical integration using β = 1.20 and scaled torque |
| In the text | |
 |
Fig. 10 Orbit-resolved space–time diagram of τ for a region near the density wave resonance resulting from the integration shown in Fig. C.1 with β = 1.20 for times t ≳ 20 000 ORB. The nearly horizontal pattern that becomes increasingly pronounced with increasing r > rL represents the density wave. The smaller scale structures are overstable waves that are perturbed by the satellite resonance, causing the “wiggles” in their appearance, in contrast to the waves displayed in Fig. 7. The green dashed line is the expected phase speed ωI ∕k of (unperturbed) overstable waves with λ = 300 m obtained from Fig. 8. A profile of τ is drawn forthe time indicated by the arrow, showing how the amplitude of overstable waves is reduced in approaching the resonance from smaller radii. Visible as well are the first wave cycles of the density wave. |
| In the text | |
 |
Fig. 11 Linear hydrodynamic growth rates of overstable modes in a perturbed ring for different values of the nonlinearity parameter q describing the satellite perturbation. The wavelengths λ correspond to the uncompressed state of the model ring adopted at times t = lπ∕ΩL, with non-negative integer l (cf. Eq. (59)). The used parameters are the Pr76-parameters with varyingvalue of β and all growth rates are scaled with Ω = ΩL. In all panels the growth rates for q = 0, obtained by numerical solution of Eq. (14), are plotted additionally as black solid curves. |
| In the text | |
 |
Fig. 12 Curves showing the maximum absolute value of the cross correlation of the quantities M31 τ′ and M32u′ (Eq. (67)) associated with an overstable mode with λ = 200 m for different values of q, and the values of β used for the plots in Fig. 11. The arrow indicates the direction of increasing β. The monotonic decrease of these curves with increasing q is the reason why the growth rates of overstable modes (Fig. 11) become smaller with increasing q. All curves have been normalized to yield unity for q = 0. |
| In the text | |
 |
Fig. 13 Determination of linear growth rates of three different seeded overstable modes (indicated by their radial mode number n) in N-body simulations for different values of the nonlinearity parameter q, quantifying the amount of perturbation in the ground state that corresponds to a density wave. Left panels: time evolution of amplitudes An (Eq. (66)) with a sampling interval of one orbital period. Right panels: resulting growth rates obtained from linear fits as drawn in the left frames. The simulations used time-averaged values of the ground state optical depth and surface mass density of τ0 = 1.5 and σ0 = 300 kg m−2, respectively, as well as a vertical frequency enhancement of Ωz∕Ω = 2 to mimic vertical self-gravity. |
| In the text | |
 |
Fig. 14 Evolution of the radial velocity perturbation u′ during the first three orbital periods of the N-body simulation with n = 25 and q = 0.4 of Fig. 13. Clearly visible is the periodic variation of the radial size of the simulation region according to Eq. (68) which is drawn as dashed curves. Also indicated is the analogous radial variation of one wavelength of the seeded mode, represented by the two pairs of red solid curves. Since the seed is a standing wave, its amplitude undergoes an oscillation with twice the overstable wave frequency (cf. Eq. (15)). |
| In the text | |
 |
Fig. 15 Nonlinear evolution of viscous overstability in N-body simulations of a perturbed ring.
Left panels: curves of kinetic energy density (Eq. (22)) of perturbations in units
|
| In the text | |
 |
Fig. A.1 Comparison of state variables resulting from hydrodynamical integrations and the WNL model using the
Pr76-parameters with |
| In the text | |
 |
Fig. A.2 Comparison of profiles of τ
along with their Morlet wavelet powers resulting from a hydrodynamical integration and the WNL and BGT models using the Pr76-parameters with |
| In the text | |
 |
Fig. A.3 Comparison of profiles of τ resulting from integrations with the Straight Wire self-gravity (left column) and the WKB self-gravity (right column) with corresponding waves of the BGT model. The WKB approximation is intrinsic to the BGT model. |
| In the text | |
 |
Fig. B.1 Space–time plots of an m = 7 density wavewith scaled torque |
| In the text | |
 |
Fig. B.2 Comparison of profiles of τ
along with their Morlet wavelet powers resulting from hydrodynamical integrations using the
Pr76-parameters and scaled torque |
| In the text | |
 |
Fig. C.1 Hydrodynamical integrations using the Pr76-parameters (Table 1) with increasing value of the viscosity parameter
β = 0.85–1.35 (see Fig. 6) from top to bottom. The surface density profiles (left panels) as well as their wavelet-powers (right panels) reveal the co-existence of a resonantly forced density wave and short-scale viscous overstability for the cases
β = 1.10–1.35. All integrations use a scaled torque |
| In the text | |
 |
Fig. C.2 Hydrodynamical integrations using the Pr76-parameters (Table 1) with increasing forcing strength from top to bottom panels
( |
| In the text | |
 |
Fig. C.3 Comparison of the nonlinear evolution of free (Ts = 0) viscous overstability in hydrodynamical integrations with (non-axisymmetric, m = 7) and without (axisymmetric, m = 0) the azimuthal derivative terms (Sect. 5), shown as profiles of the surface density τ along with their wavelet powers for two different times (t = 500 ORB and t =35 000 ORB). The blue dashed lines indicate the expected nonlinear saturation wavelength of axisymmetric (m = 0) viscous overstability by margins ± 20 m (see Sect. 7.4.1). The red dashed curves represent the linear density wave dispersion relation (Eq. (43)). In the axisymmetric case this curve has no physical meaning. The bottom frame displays the evolution ofthe kinetic energy density for both integrations. The insert plot indicates that the linear growth phases (t ≲ 200 ORB) of non-axisymmetric and axisymmetric modes are practically identical, in agreement with our considerations in Sect. 2. The higher saturation energy of the axisymmetric integration is due to the slightly larger saturation wavelength (see Sect. 7.4.1 for explanations). |
| In the text | |
 |
Fig. C.4 Space–time diagrams showing the linear evolution of the radial velocity field u′ of an initially seeded traveling wave in a ring with β = 1.35 perturbed by an ILR (at r = rL). The perturbation, quantified by q, increases from left to right. At initial time t = 0 the model ring is in the uncompressed state (Eq. (59)) and the initial wavelength λ = 200 m. |
| In the text | |
 |
Fig. C.5 Snapshots of the terms M31τ′ and M32u′ that appear in the equation for the azimuthal velocity perturbation and which must be sufficiently in phase for the viscous overstability mechanism to work. The snapshots are from integrations with λ = 200 m, β = 1.35, and cover one orbital period in equal time-intervals. With increasing strength of the satellite perturbation (quantified through the nonlinearity parameter q) these terms become increasingly out of phase. For q = 0.4 almost all possible phase differences in the range 0–2π occur, which explains the negative growth rates of overstable modes on all wavelengths (Fig. 11, lower right panel).For clarity the two quantities have been rescaled so as to possess equal amplitudes in all plots. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



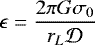
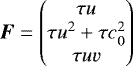
![\begin{equation*}{\bm S} = \left(\!\!\begin{array}{l} -\left[\Omega-\Omega_{L}\right] \partial_{\theta}\tau \\ -\left[\Omega-\Omega_{L}\right] \partial_{\theta}\left(u \tau\right) + 2\Omega \tau v - \tau \partial_{r} (\phi^{\textrm{d}} +\phi^{\textrm{s}}) + \frac{1}{\sigma_{0}} \partial_{r} \hat{\Pi}_{rr} \\-\left[\Omega-\Omega_{L}\right] \partial_{\theta}\left(v \tau\right) -\frac{1}{2}\Omega \tau u + \frac{1}{\sigma_{0}} \partial_{r} \hat{\Pi}_{r\theta} \end{array}\right). \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq34.png)
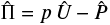
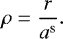
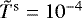
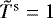
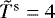
![$\text{min} [\beta_{c}]_{\lambda} = 1.03$](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq230.png)
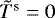
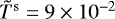
![\begin{align*}M_{11} & = q \left(1+i k(t) x\right) J^{-1} \cos t,\nonumber\\[0.5pt] M_{12} & = -ik(t) J^{-1} ,\nonumber\\[0.5pt] M_{13} & = 0 ,\nonumber\\[0.5pt] M_{21} & = i \left[2g -k(t) \left( J + \left(\beta+1\right) \alpha \nu_{0}q J^{-\beta} \cos t \right) \right], \nonumber\\[0.5pt] M_{22} & = J^{-1} q \cos t \left[ 1 + i k(t) x \right] - \alpha \nu_{0} k^2(t) J^{-\beta} , \nonumber\\[0.5pt] M_{23} & =2 ,\nonumber\\[0.5pt] M_{31} & =\frac{1}{2} i \left(\beta+1\right) k(t) \nu_{0} J^{-\beta} \left(4 q \sin t -3 \right) ,\nonumber\\[1pt] M_{32} & = -\frac{1}{2}J,\nonumber\\[1pt] M_{33} & = -k(t) \left[k(t) \nu_{0} J^{-\beta} -i q J^{-1} x \cos t \right]. \end{align*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq153.png)
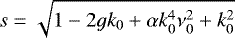
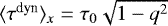
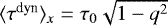
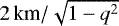
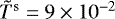
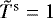
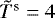
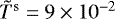
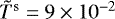
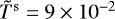
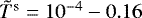
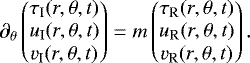
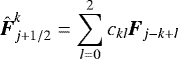
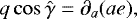
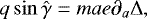
![\begin{equation*}\begin{split} u = & \left[\Omega a e \sin m \left(\phi + \Delta\right) \right]_{x=x_0}\\ \quad & +\frac{\Omega x}{J} \left[ -\frac{e}{2} \sin m \left(\phi + \Delta \right) + q \sin\left[m \left(\phi + \Delta\right) + \hat{\gamma} \right]\right]_{x=x_0}. \end{split} \vspace*{-2pt}\end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq219.png)
![\begin{equation*}\begin{split} v = & \left[r \Omega \left(1+ 2 e \cos m \left(\phi + \Delta\right) \right) \right]_{x=x_0}\\[3pt] \quad & +\frac{\Omega x}{J} \left[ - \frac{3}{2} -3 e \cos m \left(\phi + \Delta\right) + 2 q \cos \left[m \left(\phi + \Delta \right)+\hat{\gamma} \right] \right]_{x=x_0}. \end{split} \end{equation*}](/articles/aa/full_html/2019/03/aa33613-18/aa33613-18-eq221.png)