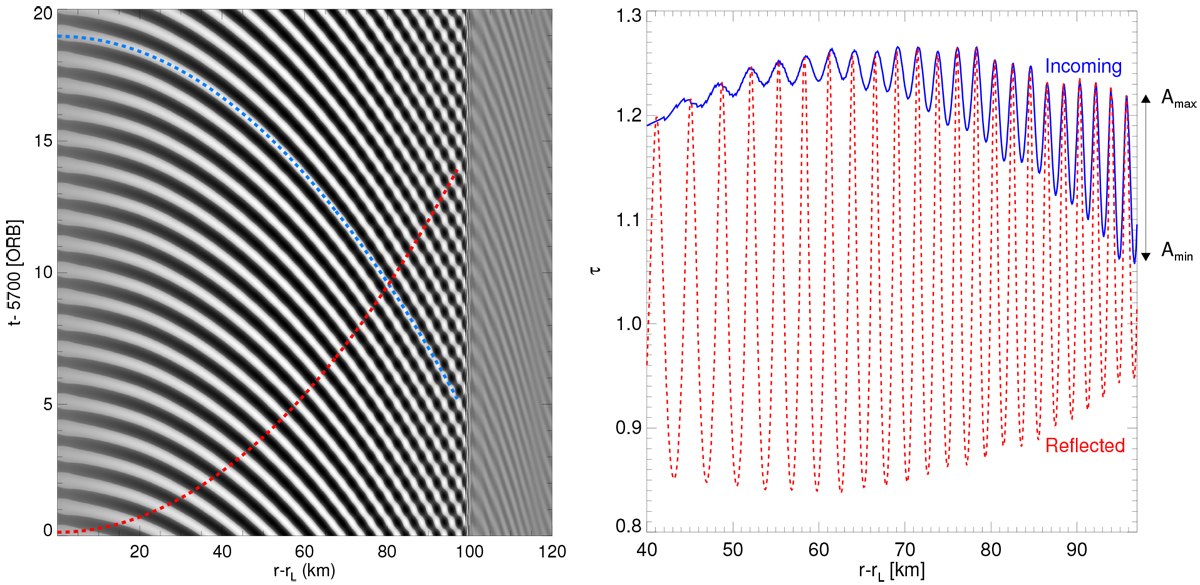
Reflection of a (long) trailing density wave at a sharp boundary at r– r_L ~ 100 km where τ₀ is reduced by a factor of 1∕5. In the space–time plot (left panel) the blue (red) dashed curve traces a line of equal phase of the incoming (reflected) wave so that it follows a density maximum. Right panel: τ evaluated along these curves. As explained in the text, one can estimate the amplitude ratio of the incoming and the reflected waves from the indicated values A_max and A_min of τ (Eq. (49)). Since the considered wave is weakly nonlinear it follows H(q) ≳1 in the nonlinear dispersion relation (Eq. (44)) so that the linear limit (Eq. (43)) is not fully accurate. To compensate for this we used a slightly increased value of σ₀ (by 0.25%) to compute the wavenumber k from Eq. (43), which is used in Eq. (48), to obtain a better fit to the locations of equal phase in the left panel.