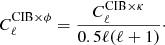| Issue |
A&A
Volume 621, January 2019
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 16 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201833765 | |
| Published online | 03 January 2019 | |
Constraining cosmology with the cosmic microwave and infrared backgrounds correlation
1
Aix Marseille Univ, CNRS, CNES, LAM, Marseille, France
e-mail: abhishek.maniyar@lam.fr
2
CEICO, Institute of Physics of the Czech Academy of Sciences, Na Slovance 2, Praha 8, Czech Republic
Received:
3
July
2018
Accepted:
12
September
2018
We explore the use of the cosmic infrared background (CIB) as a tracer of the large scale structures for cross-correlating with the cosmic microwave background (CMB) and exploit the integrated Sachs–Wolfe (ISW) effect. We used an improved linear CIB model from our previous work and derived the theoretical CIB×ISW cross-correlation for different Planck HFI frequencies (217, 353, 545 and 857 GHz) and IRAS (3000 GHz). As expected, we predict a positive cross-correlation between the CIB and the CMB whose amplitude decreases rapidly at small scales. We perform a signal-to-noise ratio (S/N) analysis of the predicted cross-correlation. In the ideal case when the cross-correlation is obtained over 70% (40%) of the sky without residual contaminants (e.g. galactic dust) in maps, the S/N ranges from 4.2 to 5.6 (3.2 to 4.3); the highest S/N comes from 857 GHz. A Fisher matrix analysis shows that an ISW signal detected with a S/N this high on the 40% sky can considerably improve the constraints on the cosmological parameters; constraints on the equation of state of the dark energy especially are improved by 80%. We then performed a more realistic analysis considering the effect of residual galactic dust contamination in CIB maps. We calculated the dust power spectra for different frequencies and sky fractions that dominate the CIB power spectra at the lower multipoles we are interested in. Considering a conservative 10% residual level of galactic dust in the CIB power spectra, we observe that the S/N drops drastically, which makes it very challenging to detect the ISW. To determine the capability of current maps to detect the ISW effect through this method, we measured the cross-correlation of the CIB and the CMB Planck maps on the so-called GASS field, which covers an area of ∼11% in the southern hemisphere. We find that with such a small sky fraction and the dust residuals in the CIB maps, we do not detect any ISW signal, and the measured cross-correlation is consistent with zero. To avoid degrading the S/N for the ISW measurement by more than 10% on the 40% sky, we find that the dust needs to be cleaned up to the 0.01% level on the power spectrum.
Key words: infrared: diffuse background / cosmic background radiation / large-scale structure of Universe / cosmological parameters / cosmology: observations / methods: statistical
© ESO 2019
1. Introduction
At the end of the last century, Riess et al. (1998) and Perlmutter et al. (1999) discovered that the expansion of the Universe is accelerating. Since then, a great wealth of theories have been put forward to explain this acceleration. The leading theory attributes it to so-called “dark energy”, an unknown component constituting around 70% of the total energy budget of the Universe according to our latest estimates (Planck Collaboration XIII 2016). The Λ cold dark matter (CDM) model, also called the concordance model, is favoured most by the data in the context of a Bayesian model comparison (Planck Collaboration XIII 2016). Currently, great effort is dedicated to constraining the parameters of our cosmological model better. Various cosmological probes of the distance scales (all the standard rulers and candles, i.e. baryonic acoustic oscillations Eisenstein & Hu 1998, supernovae Ia Betoule et al. 2014, cepheids Riess et al. 2016) and probes of the growth of structures (weak lensing Lewis & Challinor 2006, galaxy clustering Tinker et al. 2012, redshift space distortions Scoccimarro 2004) are being used to study and test cosmological models such as the ΛCDM and possible deviations from it.
One of these is the integrated Sachs–Wolfe (ISW) effect. This is another potential powerful probe of dark energy. It is the low-redshift integrated counterpart of the original Sachs–Wolfe effect (Sachs & Wolfe 1967) that occurs at the surface of the last scattering and leaves its imprints on the cosmic microwave background (CMB) anisotropies. This effect is caused by the gravitational redshifting of the photons when they exit the potential wells at the last scattering surface. The ISW effect, on the other hand, occurs in a universe that is not dominated by matter. As dark energy starts to dominate the dynamics of the Universe at late times, it causes a decay of the gravitational potential wells and hills on large scales. As a result, the CMB photons travelling across them have a net gain or loss of energy for potential wells and hills, respectively. The ISW effect is the dominant contribution to the CMB power spectrum at large angular scales and has a very small amplitude. Unfortunately, at these scales, the statistical noise that is due to cosmic variance in the CMB power spectrum is of the same order of magnitude as the signal, which makes the detection of the ISW effect in the CMB alone extremely challenging.
However, we know that the matter in the Universe shapes the underlying gravitational potentials that are responsible for the ISW effect. Therefore, a non-zero spatial correlation between the CMB anisotropies and tracers of the matter distribution is expected, and can be exploited to extract the ISW signal (e.g. Boughn et al. 1998; Boughn & Crittenden 2002). Galaxy surveys (which are proxies for large-scale structures) are an obvious choice for this purpose. Attempts to detect the ISW signal have been made with various surveys, such as Wide-field Infrared Survey Explorer (WISE; Shajib & Wright 2016; Ferraro et al. 2015), Sloan Digital Sky Survey (SDSS; Cabré et al. 2006; Giannantonio et al. 2006; Hernández-Monteagudo et al. 2014), NRAO VLA Sky Survey (NVSS; Raccanelli et al. 2008, Pietrobon et al. 2006), and Two Micron All-Sky Survey (2MASS; Francis & Peacock 2010). Joint analyses combining different data sets have also been performed (Giannantonio et al. 2008; Planck Collaboration XXI 2016; Stölzner et al. 2018). Alternative approaches have also been explored in the literature, such as stacking CMB patches at the location of superstructures that are expected to yield the strongest ISW signal (Ilić et al. 2013) and exploiting the cross-correlation between the ISW and thermal Sunyaev–Zel’dovich effects, which are both present in the CMB and take place in the same gravitational wells (Taburet et al. 2011; Creque-Sarbinowski et al. 2016). The significance of the ISW signals detected in all these studies ranges from 1σ to 5σ, and the main limiting factor is the lack of sky coverage and/or the redshift depth of the surveys. These are both crucial factors in the detection of the ISW effect because the largest structures contribute most and thus require the largest possible survey volume.
We here consider the cosmic infrared background (CIB) as a tracer of the large-scale structures to probe the ISW effect. The CIB is the weighted integral of the dust heated by the young UV-bright stars within the galaxies through cosmic time. It was first detected by Puget et al. (1996). As it traces the star formation history of the Universe, it spans a wide redshift range of 0 < z < 6. Therefore, the CIB is an exceptional tool for tracing the overall distribution of the galaxies at these high redshifts (Knox et al. 2001). Lagache & Puget (2000) and Matsuhara et al. (2000) first detected and discussed the anisotropies in the CIB that are due to unresolved extra-galactic sources. Correlated anisotropies in the CIB were discovered by Spitzer (Lagache et al. 2007) and were accurately measured by Planck and Herschel (Planck Collaboration XXX 2014; Viero et al. 2013b). These anisotropies trace the large-scale distribution of the galaxy density field and consequently, the underlying distribution of the dark matter haloes that host these galaxies, up to a bias factor. This means that the CIB can be used as a tracer of the large-scale structures (e.g. Hanson et al. 2013).
As the CIB traces the evolution of the large-scale structures over a wide range of redshifts, it is a prime choice of tracer for detecting the ISW effect. Ilić et al. (2011) showed that the CIB×ISW cross-correlation can provide us with the highest signal-to-noise ratio (S/N) for a single tracer to detect the ISW signal. Since then, our understanding and modelling of the CIB anisotropies has improved (e.g. Béthermin et al. 2013; Viero et al. 2013a; Wu et al. 2018), and we have gained new insights on their contaminants or foregrounds and thus on the intricacies of extracting the CIB signal (Planck Collaboration XXX 2014). We thus revisit the prediction for the cross-correlation between the CIB and the CMB. Maniyar et al. (2018) simultaneously considered the CIB auto- and cross-power spectra as well as the cross-correlation of the CIB×CMB lensing measurements to constrain an updated model for the CIB anisotropies. Here we use this model and predict the expected S/N for the ISW effect obtained through the CIB×CMB cross-correlation. We then perform a Fisher matrix analysis to predict the constraints on the cosmological parameters obtained from a combination of the CIB×ISW information with CMB, CIB, and CIB×CMB lensing data. Unfortunately, current CIB maps are limited by the dust contamination, especially at lower angular multipoles, where the ISW signal is expected to be strongest. Therefore we perform our analysis in two scenarios: one for the ideal situation, in which dust-free CIB spectra are extracted over the full or partial sky, and the second case for CIB maps that are contaminated by residual galactic dust emission.
This paper is structured as follows. We begin in Sect. 2 by introducing the modelling of the various cosmological probes considered in our analysis: our model for the CIB power spectrum, the CIB×CMB lensing correlation, and the CIB×ISW correlation. In Sect. 3 we provide the predictions for the ISW signal and its S/N for different cases (maps with and without residual dust contamination). In Sect. 4 we explain the Fisher matrix analysis we used to constrain the cosmological parameters and provide the results for the ΛCDM and wCDM models. Section 5 details the measurement of the cross-correlation using the available CIB and CMB Planck maps over a small portion of the sky and the corresponding results. Conclusions are provided in Sect. 6. Throughout our analysis, we use the Planck 2015 best-fit cosmology (Planck Collaboration XIII 2016) with adiabatic scalar perturbations and a nearly scale-invariant initial power spectrum.
2. Cosmological observables and their modelling
2.1. CIB power spectrum
We aim at exploiting the cross-correlation of the CIB with the CMB through the ISW effect, which is mostly significant on large angular scales. At these scales, the clustering signal is dominated by the correlation between the dark matter halos, and it is safe to ignore the non-linear effects. Thus, a linear model for calculating the CIB anisotropies is good enough for our study. The CIB power spectrum is defined as
The CIB anisotropies for a given frequency ν at redshift z and in a given direction 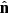 are
are
where ICIB is the CIB mean level, χ(z) is the comoving distance to redshift z and a = 1/(1 + z) is the scale factor, and j is the comoving emissivity of the CIB galaxies.
We used the CIB model presented in Maniyar et al. (2018). In order to fit for the model parameters, only CIB data in the range 145 < ℓ < 592 were used, where the linear model is a good approximation and the Limber approximation is accurate enough and simplifies the calculation. The linear CIB anisotropy power spectrum with the Limber approximation is then given as
where Plin(k, z) is the linear theory dark matter power spectrum, which has been generated using the publicly available Boltzmann code CAMB (Lewis & Bridle 2002; Lewis 2014) at the required redshifts. beff is the effective bias factor for the CIB galaxies at a given redshift. This is the mean bias of dark matter halos hosting dusty galaxies that contribute to the CIB at a given redshift weighted by their contribution to the emissivities (Planck Collaboration XXX 2014; Maniyar et al. 2018). It implies that more massive halos are more clustered and that their host galaxies emit more far-infrared emission. We used a parametric form for the evolution of the effective bias with the redshift
The bias only depends on the redshift and is scale independent. This is a good approximation at the scales where we model the CIB.
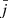 is the comoving emissivity (in Jy Mpc−1), which is derived using the star formation rate (SFR) density ρSFR (M⊙ yr−1 Mpc−3) following
is the comoving emissivity (in Jy Mpc−1), which is derived using the star formation rate (SFR) density ρSFR (M⊙ yr−1 Mpc−3) following
where K is the Kennicutt constant (Kennicutt 1998). We used a Kennicutt constant corresponding to a Chabrier initial mass function (SFR/LIR = 1.0×10−10 M⊙yr−1). Sν, eff(z) (in Jy 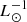 ) is the average spectral energy distribution (SED) of all the galaxies at a given redshift weighted by their contribution to the CIB. As described in Maniyar et al. (2018), they were computed using the method presented in Béthermin et al. (2013), but assuming the new updated SEDs that were calibrated with Herschel data, as presented in Béthermin et al. (2015, 2017). The parametric form of the cosmic SFR density proposed by Madau & Dickinson (2014) is used to describe ρSFR and is given by
) is the average spectral energy distribution (SED) of all the galaxies at a given redshift weighted by their contribution to the CIB. As described in Maniyar et al. (2018), they were computed using the method presented in Béthermin et al. (2013), but assuming the new updated SEDs that were calibrated with Herschel data, as presented in Béthermin et al. (2015, 2017). The parametric form of the cosmic SFR density proposed by Madau & Dickinson (2014) is used to describe ρSFR and is given by
where α, β, γ, and δ are parameters of the CIB model.
2.2. CIB×CMB lensing
As mentioned earlier, the CIB×CMB lensing cross-correlation is another ingredient of our study, which we used to further constrain the parameters of our CIB model and the cosmological parameters. The CMB photons that propagate freely from the last scattering surface towards us are gravitationally deflected by the large-scale distribution of the matter in the Universe. The gravitational lensing leaves imprints on the CMB temperature and polarisation anisotropies. A map of the lensing potential along the line of sight can be reconstructed using these imprints (Okamoto & Hu 2003). Primary sources for this CMB lensing potential are the dark matter halos that are located between us and the last scattering surface (Lewis & Challinor 2006), and a strong correlation between the CIB anisotropies and a lensing-derived projected mass map has been shown to be expected (e.g. Song et al. 2003) and indeed measured (Planck Collaboration XVIII 2014) with a high S/N.
We calculated the cross-correlation between the CIB and the CMB lensing potential, which is given by
where χ* is the comoving distance to the CMB last scattering surface, Ωm is the matter density parameter, and H0 is the value of the Hubble parameter today. From this equation, it is seen that 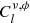 is proportional to beff, whereas
is proportional to beff, whereas 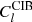 is proportional to
is proportional to 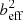 . Using the CIB×CMB lensing potential measurement in the CIB model likelihood therefore also helps us resolve the degeneracy between the evolution of beff and ρSFR to some extent.
. Using the CIB×CMB lensing potential measurement in the CIB model likelihood therefore also helps us resolve the degeneracy between the evolution of beff and ρSFR to some extent.
2.3. CIB×ISW correlation
The contribution of the ISW effect to the CMB temperature anisotropies is given by
It represents the integration of the time derivative of the Φ and Ψ Newtonian gauge gravitational potentials (with Kodama & Sasaki 1984 conventions) over the conformal time η, with ηr being the initial time deep in the radiation era, τ(η) is the optical depth, and dots denote differentiation with respect to the conformal time η.
The cross-correlation between the CIB and ISW effect for a given frequency is then
which becomes, after decomposing in the Legendre series:
where monopole and dipole are not included. The ISW effect is expected to be dominant on large angular scales (ℓ < 100). At these scales, the Limber approximation is not accurate enough. Following the calculations of Garriga et al. (2004), we obtain the CIB×ISW cross power spectrum without Limber approximation as
where 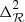 is the dimensionless primordial power spectrum related to the primordial power spectrum
is the dimensionless primordial power spectrum related to the primordial power spectrum 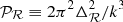 . The Ml and
. The Ml and 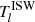 terms are
terms are
where jl are spherical Bessel functions, and 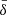 , ϕ and ψ are the time-dependent part of the dark matter density contrast δ, and the Newtonian gauge gravitational potentials Φ and Ψ, respectively. The relation between the two coefficients cΨΦ and cδΨ for the adiabatic initial conditions is given as (Ma & Bertschinger 1995)
, ϕ and ψ are the time-dependent part of the dark matter density contrast δ, and the Newtonian gauge gravitational potentials Φ and Ψ, respectively. The relation between the two coefficients cΨΦ and cδΨ for the adiabatic initial conditions is given as (Ma & Bertschinger 1995)
where Rν ≡ ρν/(ρν + ργ), with ρν and ργ being the energy densities in relativistic neutrinos and photons, respectively. Later in this work, we compute the CIB spectrum at these low multipoles in order to derive the expected covariance of the CIB×ISW power spectrum (see details in Sect. 3). In order to be as consistent and rigorous as possible, in this context we use a different expression for the CIB power spectrum compared to Eq. (3), one that does not rely on the Limber approximation:
We modified the publicly available Boltzman code CAMB to compute our observables of interest: the CIB, CIB×ISW, and CIB×CMB lensing power spectra, in addition to the standard CAMB outputs, that is, the CMB temperature and polarisation power spectra.
3. Expected CIB×ISW cross-correlation and significance
Using the formalism described in the previous section, we focus first on revisiting the predictions of Ilić et al. (2011) for the expected power spectrum and the S/N of the CIB×ISW cross-correlation, using the improved and more tightly constrained CIB model of Maniyar et al. (2018) described earlier. Before proceeding further, a fiducial set of parameter needs to be defined in order to carry out our computations. For the sake of coherence, we followed Maniyar et al. (2018): as the CIB alone cannot constrain cosmological parameters, the authors first assumed a Planck fiducial background cosmology (Planck Collaboration XIII 2016), which we chose as our fiducial cosmological parameters throughout this work. The authors then derived the best-fit parameters of their CIB model using a combination of multi-frequency measurements of the CIB and CIB×CMB lensing power spectra from Planck and IRAS, as well as SFR density measurements and mean CIB intensity levels from external surveys. We use these best-fit CIB parameters as our fiducial values throughout this work. They are given in Table 1.
Parameter values of the CIB and cosmological models.
3.1. CIB×ISW cross-correlation spectrum
We computed the CIB×ISW cross power spectra for the Planck 217, 353, 545, and 857 GHz and IRAS 3000 GHz frequency channels; these are the same frequencies as in the CIB datasets used by Maniyar et al. (2018). These power spectra are shown in Fig. 1. The amplitude of the cross-correlation is maximum around 20 < ℓ < 50 and falls off quickly at higher multipoles, as expected from the ISW effect. The amplitude of the power spectra increases with frequency. This is expected as the CIB probes galaxies at higher redshifts in low-frequency channels (and vice versa) and the main contribution to the ISW effect comes from low redshifts. This can be appreciated from the CIB anisotropy redshift distributions provided in Fig. 4 of Maniyar et al. (2018), which shows that the distribution peaks towards lower redshifts with increasingly higher frequencies. The amplitude of the signal is the highest for 857 GHz, which is slightly higher than the amplitude at 3000 GHz. The reason behind this is that the CIB has slightly more power at lower multipoles at 857 GHz than at 3000 GHz. We did not consider the signal at higher multipoles (ℓ > 100) as the non-linear counterpart to the ISW effect (the Rees–Sciama effect) starts to contribute significantly to the CMB anisotropies at these scales. The linear ISW effect still dominates near the peak of the signal, however (Seljak 1996).
 |
Fig. 1. CIB×ISW cross-correlation power spectra (in Jy sr−1) for the five frequency channels. |
3.2. Signal-to-noise ratio
After calculating the expected CIB×ISW cross-correlation signal, we determined the significance (detection level) of the signal. To do so, we performed an S/N analysis. The cumulative S/N for the ISW effect summed over all the multipoles between 2 ≤ℓ≤100 (where most of the signal resides, as shown in Fig. 1) for a given frequency ν can be written as
where the signal term Sℓ in our case is the cross-correlation power spectrum:
and the noise term Nℓ corresponds to the square root of its variance, the usual cosmic variance:
For this analysis, we considered two cases that we detail below.
Ideal case. We assumed that the CIB and the CMB maps we used to calculate the cross-correlation were extracted over the full sky and are completely free of residual contaminations (we note that instrument noise is not relevant at the angular scales of the ISW effect). The only limiting factor is the cosmic variance, and we obtain the highest S/N in this scenario. With these ideal assumptions, the CIB×ISW correlation reaches a significance level as high as ≈6.7σ. Detailed results are provided in Table 2. Cumulative S/Ns for different Planck and IRAS frequencies are shown in Fig. 2. The largest contribution to the S/N comes from l ≤ 50, after which the significance reaches a plateau. The S/N is highest for 857 GHz and reaches a value of 6.73. Although the CIB×ISW cross-correlation signal is stronger for the 3000 GHz frequency than at 217, 353, and 545 GHz at ℓ < 100, the S/N is lower than that at these frequencies. This can be explained by considering the value of the noise given by Eq. (18). The noise term for the 3000 GHz frequency is much higher at larger scales than it is for other frequencies and hence decreases the S/N. Therefore, in this ideal scenario, the optimal frequency for the ISW detection is 857 GHz. However, in reality, we have to account for sources of noise and contamination in our analysis as well as for reduced sky fractions.
Predicted S/N for the ISW signal in the ideal scenario (CIB maps free of galactic dust residuals), for 100% and 40% sky coverage.
 |
Fig. 2. Cumulative S/N for the CIB×ISW cross-correlation signal for the five frequency channels. The S/N is predicted to be highest for 857 GHz. |
Realistic case. As described earlier, in reality, we have to compromise on certain assumptions made in the previous case. In the ideal case, we assumed that the CIB×ISW cross-correlation signal can be extracted over the whole sky. In a large part of the sky, however, we have strong emissions from our own galaxy. This emission, which is due to the galactic dust, is much higher than the CIB signal. This prevents us from extracting any CIB signal in regions of the sky that are too close to the galactic plane. This directly reduces the available sky fraction for measurement by ∼30%. Even then, in the remaining part of the sky, the power spectrum measurements are contaminated by dust that needs to be removed from the maps. This removal will leave some residual noise that has to be accounted for in the analysis. In addition, at lower frequencies, the CMB starts to dominate the CIB. Therefore, the CMB contribution has also to be removed from the maps. At the scales we are interested in, the CMB is limited by cosmic variance and the instrument noise in the CMB measurements can be ignored. When we account for all these effects, the S/N becomes
where the 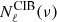 term contains the dust residuals left in the CIB maps and fsky represents the fraction of the sky where CMB and CIB are both available. The presence of dust residuals does not affect the measurement of the CIB×CMB cross-correlation as they are not correlated with the CMB.
term contains the dust residuals left in the CIB maps and fsky represents the fraction of the sky where CMB and CIB are both available. The presence of dust residuals does not affect the measurement of the CIB×CMB cross-correlation as they are not correlated with the CMB.
To quantify the dust residuals in the CIB, that is, 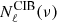 , we used the following procedure:
, we used the following procedure:
We computed the dust power spectra using the dust map provided by the PLA1 (Planck Legacy Archive) generated using the COMMANDER component separation code (Planck Collaboration X 2016). This map is provided at the reference frequency of 545 GHz. In order to account for the available sky fractions, we applied different masks to this map, also provided by PLA. We performed our analysis on 20%, 40%, 60%, 70%, and 80% of the sky. We also considered the 10% mask provided in Table 2 of Planck Collaboration XXX (2014). After applying these masks, we computed the dust power spectrum from the dust map using the Xpol software, which is an extension to the polarisation of the Xspect method (Tristram et al. 2005). The maps were analysed with the HEALPix package (Górski et al. 2005).
The power spectrum of the dust 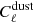 is frequency dependent. After we obtained the power spectrum of the dust at 545 GHz, we converted it into other frequencies assuming a modified black-body shape for dust emission with a given average dust temperature ⟨Td⟩ and spectral index ⟨βd⟩. The values for ⟨Td⟩ and ⟨βd⟩ were taken from Table 3 of Planck Collaboration XI (2014) for |b|> 15° and are ⟨Td⟩=20.3 K and ⟨βd⟩=1.59.
is frequency dependent. After we obtained the power spectrum of the dust at 545 GHz, we converted it into other frequencies assuming a modified black-body shape for dust emission with a given average dust temperature ⟨Td⟩ and spectral index ⟨βd⟩. The values for ⟨Td⟩ and ⟨βd⟩ were taken from Table 3 of Planck Collaboration XI (2014) for |b|> 15° and are ⟨Td⟩=20.3 K and ⟨βd⟩=1.59.
We briefly explain in Sect. 5.1 that the HI gas column density is observed to be proportional to the galactic dust emission. This relation was used to clean the CIB maps from dust contamination. Dust residuals left in the CIB maps using the HI gas as a dust tracer have been quantified by Planck Collaboration XXX (2014), as detailed in their Sects. 3.2.2 and 3.2.3. They simulated multiple maps of the dust emissivity and obtained the corresponding dust map for a given frequency by multiplying the dust emissivity maps by the GASS map of HI column densities. These dust maps were then used to create simulated maps of total sky emission at all frequencies (e.g., including CIB). Using these sky maps and performing the cleaning of the dust through the above mentioned galactic dust-HI gas column density relation, Planck Collaboration XXX (2014) found the dust residuals on the power spectrum to be of the order of 5–10% for all the frequencies (5% for 217 GHz and 10% at 857 GHz). Thus, and to be conservative, we considered here a residual dust power spectrum of 10% of 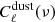 at all the frequencies. Therefore,
at all the frequencies. Therefore, 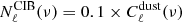 .
.
After calculating the dust power spectra and eventually 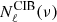 , we calculated the new S/N using Eq. (19). The results are presented in Table 3. The S/N decreases quite dramatically when the dust residuals are included in the analysis. Moreover, the S/N decreases when the available sky fraction for the analysis is inreased, which is the exact opposite to the ideal dust-free scenario, where the higher sky fraction resulted in a higher S/N. The impact of the dust on the CIB power spectra is shown in Fig. 3, where we plot the CIB and the 10% residual dust power spectra at 353 and 3000 GHz. The residual dust power spectra were calculated over 20, 40, 60, 70, and 80% of the sky. At the lower multipoles, that is, ℓ < 100 where we expect the ISW signal to be detected, the CIB spectra are completely dominated by the dust residuals. This significantly affects the S/N of the ISW signal and decreases it. The highest S/N is obtained for 353 GHz with 20% of the sky fraction available for the analysis. Equation (19) shows that a smaller sky fraction results in decreasing the S/N for the ISW detection in the case of dust-free spectra. At the same time, it is clear from Fig. 3 that the residual dust power decreases with smaller sky fractions and hence increases the S/N. This shows that there is a trade-off between the available sky fraction fsky and the S/N for all the frequencies, and in this case, a 20% sky fraction provides the best S/N for 353 GHz.
, we calculated the new S/N using Eq. (19). The results are presented in Table 3. The S/N decreases quite dramatically when the dust residuals are included in the analysis. Moreover, the S/N decreases when the available sky fraction for the analysis is inreased, which is the exact opposite to the ideal dust-free scenario, where the higher sky fraction resulted in a higher S/N. The impact of the dust on the CIB power spectra is shown in Fig. 3, where we plot the CIB and the 10% residual dust power spectra at 353 and 3000 GHz. The residual dust power spectra were calculated over 20, 40, 60, 70, and 80% of the sky. At the lower multipoles, that is, ℓ < 100 where we expect the ISW signal to be detected, the CIB spectra are completely dominated by the dust residuals. This significantly affects the S/N of the ISW signal and decreases it. The highest S/N is obtained for 353 GHz with 20% of the sky fraction available for the analysis. Equation (19) shows that a smaller sky fraction results in decreasing the S/N for the ISW detection in the case of dust-free spectra. At the same time, it is clear from Fig. 3 that the residual dust power decreases with smaller sky fractions and hence increases the S/N. This shows that there is a trade-off between the available sky fraction fsky and the S/N for all the frequencies, and in this case, a 20% sky fraction provides the best S/N for 353 GHz.
Predicted S/N for the ISW signal in the current realistic scenario, including the dust residuals in the CIB maps.
 |
Fig. 3. Power spectra of the CIB and 10% of the dust residual at 353 GHz (left panel) and 3000 GHz (right panel). The dust power spectra are computed over 20, 40, 60, 70, and 80% of the sky. The residual dust power spectra dominate the CIB at the low multipoles of interest for the ISW signal. As a consequence, the S/N decreases dramatically compared to the ideal dust-free case. |
4. Forecasting constraints on cosmological parameters
We showed in Sect. 3.2 that in the ideal scenario of the dust free CIB and CMB maps, the CIB×ISW cross-correlation can provide us with the detection of the ISW effect with the highest S/N for a single tracer. Unfortunately, we are currently limited by the dust residuals in the CIB, which reduces our ability of measuring the ISW signal with a good S/N. However, in the near future, improved cleaning techniques, additional datasets, and a better understanding of contaminants could allow us to improve the CIB maps, with much lower levels of dust residuals. In such conditions, the CIB×ISW cross-correlation would again become a very competitive probe of cosmology and dark energy in particular. Exploiting the CIB×CMB lensing cross-correlation as well could push the constraints on cosmological parameters even further. With the prospect of these future improved datasets in mind, we perform in this section a joint Fisher matrix analysis including the CMB, the CIB, the CIB×CMB lensing cross-correlation, and the ISW effect through the CIB×CMB cross-correlation and ignoring dust residuals in the CIB.
4.1. Fisher matrix formalism
We here recall briefly the principles underlying the Fisher matrix formalism. We consider a set of hypothetical N Gaussian data x with mean μ and covariance matrix Σ distributed according to the likelihood
Here both μ and Σ depend on θ = [θ1,θ2,…], the vector of parameters of the model we try to constrain. We are able to forecast the constraints on these parameters (which the hypothetical dataset would provide) in the form of a covariance matrix C, obtained by inverting the so-called Fisher matrix F. The elements of this matrix are defined as the following expectation value:
which after some work, can be rewritten as
where tr() denotes the trace of a square matrix.
In our work, we fixed the covariance matrix to its fiducial value (a common assumption in Fisher analyses) and hence the second term in the Eq. (22) vanishes as 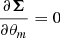 and therefore
and therefore
When needed, we computed the partial derivatives as
where for a given parameter θm, the vector θ′ represents all the other parameters that are kept constant at their fiducial value. The value of δθ is chosen small enough to stay in the Gaussian regime of the likelihood, but also large enough to not be affected by the numerical errors.
More practically, in our analysis, the parameters of the model are
where
are the seven CIB model parameters, plus five calibration factors 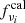 (one for each frequency), which account for relative absolute calibration uncertainties between the different frequency channels. On the other hand,
(one for each frequency), which account for relative absolute calibration uncertainties between the different frequency channels. On the other hand,
are the ΛCDM model parameters, to which we add w when we consider the wCDM model. Then, in our case, the vector μ(θ) contains the predicted values of our N observables of interest as a function of our model parameters, and Σ(θ) is their theoretical covariance matrix.
As described before, we considered the four following probes as observables: the CMB power spectra, the CIB power spectra (+ external constraints), the CIB×CMB lensing cross-spectra, and the CIB×ISW cross-spectra. Our choices for the properties of these observables allowed us to simplify the Fisher analysis. We used the CMB as a prior in our work, and thus neglected its correlation with the other three probes. We also defined our CIB and CIB×CMB lensing power spectra similarly to the actual data used in Maniyar et al. (2018), meaning that the spectra were binned in multipoles2. This allowed us firstly to ignore the correlations between bins for a given probe, and secondly to neglect correlations between the probes as their respective bins barely overlap. Finally, we can also safely ignore the correlation between the CIB×ISW spectra and the previous two, as their multipole ranges do not overlap (ℓ ∈ [2, 100]). Since we did not need to consider the correlations between our different probes, we can write our total Fisher matrix as the sum of the individual Fisher matrices of each probe:
In the following sections, we explain the construction of the Fisher matrices of the individual probes.
4.1.1. CMB Fisher matrix
Our aim is to explore the relative improvement on the constraints on the cosmological parameters set by the CMB using the ISW signal detected through the CIB×CMB cross-correlation. For this reason, we treated the CMB as prior information on all cosmological parameters and used the latest Planck data (plus some external data in the wCDM case, see Sect. 4.3) as constraints. Instead of computing the theoretical μ(θ) and Σ(θ) for the CMB power spectra, we directly derived an equivalent CMB Fisher matrix from Planck data using the official MCMC chains that are publicly available on the PLA3 by computing their covariance matrix (using the GetDist package provided by Antony Lewis) and inverting it. Since the CMB does not provide any information about the CIB model parameters, the corresponding rows and columns of the CMB Fisher matrix were set to 0.
4.1.2. CIB-related Fisher matrix
In addition to the CMB prior, we then added as much information as possible to constrain our CIB model parameters. To do so, we considered for our observable vector μ the same CIB probes as those used as data in Maniyar et al. (2018). These include the CIB auto and cross power spectra, the mean level of the CIB at different frequencies, SFR measurements, and the CIB×CMB lensing cross-correlation. The theoretical value of all these observables for any set of parameters can be computed using the models described earlier in Sects. 2.1 and 2.2. Their derivatives with respect to our model parameters were computed using Eq. (24).
For these observables, instead of computing an analytical covariance matrix Σ, which may lack subtle features that are present in the real signal (effects of the foreground removals, partial sky coverage, etc.), we used the available CIB data and directly used the estimated covariance matrix of the data from Planck Collaboration XXX (2014) as our fiducial Σ. As described at the beginning of Sect. 4.1, all CIB observables were considered independent, therefore only the diagonal blocks of the covariance matrix Σ are non-zero. This allowed us to compute their respective Fisher matrices independently (using Eq. (22)) and to sum them afterwards. We considered two hypothetical scenarios: one optimistic scenario, where we obtained a CIB map over fsky = 70% of the sky, and a more pessimistic one with fsky = 40%. We multiplied the Σ data covariance from Planck Collaboration XXX (2014), which was obtained over 10% of the sky, by a factor of 0.1/fsky to account for this hypothetical improvement of the CIB recovery.
4.1.3. CIB×ISW Fisher matrix
We considered here as observables the CIB×ISW cross-correlation power spectra for all five observed CIB frequencies of Maniyar et al. (2018) and multipoles between ℓ ∈ [2, 100]. To emulate a future analysis of actual data, and similarly to the CIB power spectra, we chose here to work with binned CIB×ISW cross-correlation power spectra, splitting the multipole range into 11 roughly equal bins. For a given [ℓ1, ℓ2] bin, we defined the binned spectrum Bℓ1, ℓ2 as a simple arithmetic mean,
where nℓ is the number of multipoles in the bin, and Cℓ in this case is the CIB×ISW power spectrum as computed using the model described in Sect. 2.3 and their derivative using Eq. (24).
We computed the covariance of the CIB×ISW power spectrum using a generalization of Eq. (18); the covariance between the cross-spectrum 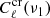 at frequency ν1 and
at frequency ν1 and 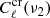 at ν2 is written as
at ν2 is written as
Similarly to the CIB observables, we considered an optimistic scenario with a dust-free CIB map available over fsky = 70% of the sky, and a more pessimistic one with fsky = 40%. Combining Eq. (30) with the definition of Eq. (29), we can derive the covariance between the binned cross-correlation 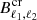 at two frequencies:
at two frequencies:
which allows us to obtain the covariance matrix Σ that is required to compute the CIB×ISW Fisher matrix, again using Eq. (22).
4.2. Forecasts for the ΛCDM model
We first present our Fisher forecasts in the context of the ΛCDM model. Table 4 shows the 1σ constraints on cosmological parameters in the various scenarios we explored, separating our results for our two choices of fsky. We show these constraints in the {CMB + CIB} case, and their relative improvements achieved by adding the CIB×CMB lensing alone, and the further improvements after adding the CIB×ISW constraints. Figure 4 shows some of these constraints. These contours have been generated using the CosmicFish software (Raveri et al. 2016). The blue ellipses represent the forecast 1σ and 2σ confidence contours obtained from the combination of CMB, CIB, and CIB×CMB lensing information. The red ellipses show the corresponding confidence regions after adding the constraints from the CIB×ISW signal.
Forecast constraints on ΛCDM cosmological parameters.
 |
Fig. 4. Fisher forecasts for the 1σ and 2σ confidence contours for the ΛCDM cosmological parameters in the fsky = 70% case. The blue contours show our results when the CMB, CIB, and CIB×CMB lensing constraints are combined. The red contours show the same results when the CIB×ISW cross-correlation constraints are added. There is a ∼17% improvement on the constraints on ΩΛ and ∼39/35% for τ/As, which are strongly correlated. |
As described before, the ISW effect is a probe of the growth of structures through time (see Eq. (8)), which itself is strongly dependent on the characteristics of the dark energy model. The cosmological constant Λ affects cosmology only at fairly late times; coupled with the fact that its energy density has remained low and constant in time, the ISW effect will not show its full potential as a probe in the flat ΛCDM model. The two main parameters governing the growth of structures in the flat ΛCDM model are the dark energy density ΩΛ (or equivalently, the matter density Ωm = 1 − ΩΛ), and the amplitude of matter fluctuations through the power spectrum amplitude As. We thus expect the constraints on these two parameters to be most improved after the ISW signal is added to the Fisher analysis (see also Coble et al. 1997). This expectation is indeed verified: using the {CMB + CIB + CIB×CMB lensing} case as a reference, we obtain an improvement of ∼17% on the error bars on ΩΛ for fsky = 70% (∼16% for fsky = 40%) and of ∼35% (∼31%) on As when the CIB×ISW information is added to the Fisher matrix (illustrated in Fig. 4). The degeneracy between τ and As is well known (e.g. Planck Collaboration XIII 2016), and it benefits from tightening the As constraints: we thus obtain a similar improvement of ∼39% (∼34%) on the τ parameter after adding the ISW information. Interestingly, Table 4 shows that the relative improvements in all constraints when adding CIB×CMB lensing and ISW information is roughly the same for both fsky (although the absolute constraints are of course better in the 70% case.)
We note that the addition of the CIB×CMB lensing cross-correlation alone also improves the constraints on some cosmological parameters. As the CMB lensing signal probes the distribution of matter while being independent of τ (Planck Collaboration I 2014), we expect it to help break the degeneracy between τ and As. This is indeed the case, as Table 4 shows that adding the CIB×CMB lensing cross-correlation mainly improves the constraints on these two parameters.
4.3. Forecasts for the wCDM model
As pointed out by various studies (e.g. Coble et al. 1997; Corasaniti et al. 2003), the ISW effect has a strong dependence on the equation of state w ≡ P/ρ of the dark energy. This is expected, as any deviation from a pure cosmological constant (i.e. w ≠ −1) has a strong influence on the growth rate of structures at all times, which in turn affect the time variation of the potential wells that the ISW effect probes directly. Combined with the fact that the CIB signal at different frequencies probes the galaxy distribution (and thus the growth of structure) at different redshifts, we thus expect that the addition of the CIB–ISW signal in our Fisher analysis will improve the constraints on wCDM parameters much more than it did for ΛCDM. We performed a Fisher analysis for the wCDM model similar to the case of the ΛCDM model. Here, along with the six cosmological parameters of the ΛCDM model, we have the additional parameter w.
The geometrical degeneracy between w and the Hubble constant H0 in the context of CMB studies is well known (e.g. Planck Collaboration XIII 2016). This degeneracy arises in order to preserve the angular size of the sound horizon at the last scattering surface. Therefore, the CMB data alone cannot constrain both H0 and w together. External cosmological datasets constraining the background evolution of the Universe, such as baryonic acoustic oscillations (BAO), supernovae type Ia (SNe Ia), and local H0 measurements, are required to break this degeneracy. In order to extract a valid covariance matrix (and thus deduce an equivalent Fisher matrix) directly from the Planck Markov chain Monte Carlo (MCMC) chains, the corresponding posterior constraints on the cosmological parameters need to follow a Gaussian distribution. This is not the case for the CMB-only chains because of the aforementioned w − H0 degeneracy. Therefore, we used the Planck chains provided on the PLA where the CMB data are combined with several BAO datasets (6dFGS, Beutler et al. 2011, SDSS MGS, Ross et al. 2015, BOSS LOWZ and CMASS, Anderson et al. 2014), the JLA supernovae dataset (Betoule et al. 2014), and the local H0 measurement from Efstathiou (2014). We refer to the sum of these constraints as CMB* in the following.
Results for the analysis of the wCDM model are presented in Fig. 5 and Table 5. Similarly to the ΛCDM analysis, the blue and red contours of Fig. 5 represent our forecasts on cosmological parameters without and with CIB–ISW constraints in the Fisher matrix, respectively. We observe a strong improvement on the equation of state w of about 80% (regardless of fsky) when the ISW signal information is added to the Fisher matrix in addition to the CMB, CIB, and CIB×CMB lensing information. As w is correlated to other cosmological parameters, improvements are partially propagated. This is especially noticeable for H0, where an improvement of ∼56% is seen for both fsky. Similarly to the ΛCDM case (cf. Sect. 4.2), the ISW signal also improves the constraints on ΩΛ (∼30%), As (∼39/33%), and thus τ (∼43/37%).
 |
Fig. 5. Fisher forecasts for the 1σ and 2σ confidence contours for the wCDM cosmological parameters in the fsky = 70% case. The blue contours show our results when the CIB, CIB×CMB lensing, and the CMB along with the external (JLA + BAO and H0 prior) constraints on the cosmological parameters are combined. The red contours show the same results when the CIB×ISW cross-correlation constraints are added. There is a ∼80% improvement on the constraints on w, ∼29% for ΩΛ, and ∼43/39% for τ/As, which are strongly correlated. |
Forecast constraints on wCDM cosmological parameters.
These results illustrate for a simple dark energy model the great potential of the CMB×CIB correlation as a probe to constrain such a model, thanks to the discriminating power of the ISW effect. We can expect it to be of similar potential when further extensions to the standard ΛCDM model are to be constrained.
5. Measurement of the ISW effect using the Planck maps
The results shown in the previous sections were obtained assuming more or less idealized scenarios. As seen in Sect. 3.2, including the effects of the dust residuals can significantly lower the S/N. In practice, the currently available CIB maps contain significant amounts of such residuals, and the error bars on the CIB×CMB signal would therefore be dominated by them, cf. Eq. (19). In this section, we present the constraints we can obtain on the cross-correlation measurement using the current CIB and CMB maps.
5.1. CIB and CMB Planck maps
Galactic dust emission is observed to be directly proportional to the HI gas column density in diffuse parts of the sky (e.g. Boulanger et al. 1996). This empirical relation is used to clean the map from dust contamination in these parts of the sky (Planck Collaboration XVIII 2011). We used the CIB maps derived in the GASS field at the Planck HFI frequencies as our CIB input maps (Planck Collaboration XXX 2014). GASS (McClure-Griffiths et al. 2009; Kalberla et al. 2010) is a 21cm line survey and is one of the most sensitive, highest angular resolution large-scale galactic HI emission surveys ever made in the southern portion of the sky. The GASS CIB maps cover almost 11% of the sky and is one of the cleanest (in terms of dust residuals) large patches of the CIB sky, as discussed in Planck Collaboration XXX (2014)4. As described earlier, we used the HEALPix package to analyse the maps. The angular resolution of the CIB maps is 16.2′ (set by the GASS survey angular resolution)5.
We used the CMB map provided by PLA generated using the SMICA component separation algorithm (Cardoso et al. 2008). The CMB map is degraded to the same angular resolution of 16.2′ as that of the GASS CIB maps. We applied the GASS field mask (Mask2 in Table 2 of Planck Collaboration XXX 2014) to both the CIB and CMB maps and cross-correlated them using Xpol at all frequencies. Masking induces correlations between different multipoles, and binning the power spectra helps to reduce these correlations. The measurements were then obtained as binned power spectra with a binning of Δℓ = 10.
Figure E.6 of Planck Collaboration IX (2016) shows that the galactic dust and the CIB residuals in the SMICA CMB maps are quite low (≤0.002%). Hence, we do not expect a cross-correlation between the SMICA CMB map and the GASS CIB maps due to residual dust or residual CIB in the CMB maps.
Figure 6 shows the observed cross-correlation compared to the theoretical prediction for the ISW signal at 217, 353, 545, and 857 GHz. The theoretical prediction for the ISW power spectrum was calculated using Eq. (11). This power spectrum was then used to create a map that was given as an input to Xpol to obtain the binned theoretical prediction for the ISW effect, which is shown as the red curve in Fig. 6. Based on the visual inspection alone, it is hard to say if the observed signal is consistent with the predictions and if so, at what level. In order to understand the observed signal, we performed some tests that are discussed below.
 |
Fig. 6. Measured CIB×CMB cross-correlation and corresponding error bars for the GASS CIB field (blue points). The predicted signal (given by Eq. (11)) is shown in red. The error bars on the predicted signal are calculated using the noise term in Eq. (39). Following Planck Collaboration XXX (2014), we assumed that the CIB power spectrum is contaminated by dust residuals at the level of 10% when the theoretical error bars were calculated. |
5.2. Significance with respect to the ΛCDM prediction
In order to calculate the significance of the measured cross-correlation 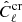 with respect to the ISW
with respect to the ISW 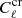 predicted by the ΛCDM model, we performed the following χ2 test. We estimated the amplitude A such that
predicted by the ΛCDM model, we performed the following χ2 test. We estimated the amplitude A such that 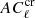 is the best-fit solution to
is the best-fit solution to 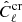 , that is, the value that minimizes the following quantity:
, that is, the value that minimizes the following quantity:
where Covcr(ν) is the expected covariance matrix on the measured signal. The same minimization also gives us the error σA on this amplitude. Such a test is convenient, as it informs us about i) whether the measured signal is compatible with our expectations, that is, A ∼ 1; and ii) whether the measured signal is significant, that is, A/σA ≫ 1.
We used a Monte Carlo approach to compute the error bars for every bin and covariance between different bins (i.e. Covcr(ν)). This approach is similar to that described by Giannantonio et al. (2008) and Serra et al. (2014), for example. We simulated 1000 pairs of CIB and CMB maps, which were correlated as expected from theory. The expected shot noise and galactic dust residual terms were added to the CIB maps. The detailed procedure is as follows:
-
A CIB map for a given frequency is created using the synfast routine from HEALPix. This map is the sum of the pure dust-free CIB term, shot noise, and the dust residual term for the given frequency. Therefore, the total input power spectra to synfast is
where
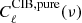 ,
, 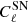 and
and 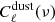 are the CIB, shot-noise, and the dust-residual power spectra for a given frequency, respectively. The CIB power spectra are obtained from CAMB. We assumed that after cleaning the GASS field using the dust to gas relation, 10% of the dust residuals are left. Hence, we took the 10% of the dust power spectra calculated as described in Sect. 3.2. The shot noise was derived from the Béthermin et al. (2013) model.
are the CIB, shot-noise, and the dust-residual power spectra for a given frequency, respectively. The CIB power spectra are obtained from CAMB. We assumed that after cleaning the GASS field using the dust to gas relation, 10% of the dust residuals are left. Hence, we took the 10% of the dust power spectra calculated as described in Sect. 3.2. The shot noise was derived from the Béthermin et al. (2013) model. -
The CMB map is created using the pure CMB term
where the
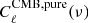 is obtained from CAMB.
is obtained from CAMB. -
The CIB and CMB maps are created and correlated using synfast. As explained before, the CIB map is created by adding the maps with the power spectra
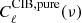 ,
, 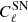 and
and 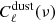 . Using the same seed as was used to create
. Using the same seed as was used to create 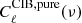 map, we created another map with the power spectra
map, we created another map with the power spectra 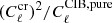 . Here,
. Here, 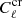 is the predicted cross-correlation between the CIB and CMB through the ISW effect given by Eq. (11) and is again obtained from CAMB. This second map is added to a third map created using a new seed and with power spectra
is the predicted cross-correlation between the CIB and CMB through the ISW effect given by Eq. (11) and is again obtained from CAMB. This second map is added to a third map created using a new seed and with power spectra 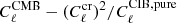 . Finally, these two maps will have amplitudes
. Finally, these two maps will have amplitudeswhere ξ is a random amplitude with zero mean and unit variance so that ⟨ξξ*⟩=1 and ⟨ξ⟩=0. This gives us
-
When these maps were obtained, the GASS field mask covering ∼11% sky was applied to both of them and their cross-power spectra were computed using Xpol. This gives us 1000 sets of cross-spectra for each frequency, which provide us with the uncertainty on our estimate. The covariance matrix for the binned power spectrum is then calculated as
where ⟨.⟩ denotes the average of the Monte Carlo samples. The error bars on every bin then become
The error bars calculated in this way can be compared with the analytical estimate:
We observe that the error bars obtained from the simulations are 22–25% higher than those obtained with Eq. (39) for different frequencies. This is expected as Eq. (39) is not very accurate for very low sky fractions, which is the case here. We calculated the correlation matrix based on the 1000 simulations for every frequency and found that the correlations between adjacent multipoles are always lower than 16% (with a binning Δℓ = 10).
After we obtained the expected covariance matrix using the above procedure, we used Eq. (32) to minimise the χ2 and fit for the amplitude A. The results are shown in Table 6. Except for 545 GHz, we see that although the amplitudes of the measured signals are roughly compatible with 1 (within the estimated error bars), the significance of these cross-correlations is quite low. At 545 GHz, A/σA is equal to 5.52 with A = 6.64. Therefore, the observed amplitude of the cross-correlation is (6.64 − 1)/1.2 = 4.7σ higher than what is expected from the ΛCDM model. Possible explanations for this high significance are explored in the next subsection.
Best-fit values and errors for the amplitude A, and significance of the signal A/σA for all the frequencies.
5.3. Null test
The previous test showed that no conclusion can be reached regarding the question whether the measured cross-correlations are consistent with a detection. Therefore, we also checked the significance of the observed signal against the null hypothesis. For this purpose, we performed a null test: for every frequency, we cross-correlated the GASS CIB field map with 1000 randomly generated CMB maps. These 1000 cross-correlations give us the covariance matrix and hence also the error bars for different bins for the null signal. Figure 7 shows the 1σ region spanned by this null signal, together with the measured CIB×CMB cross-correlation at 545 GHz.
 |
Fig. 7. Average null signal calculated using the cross-correlation of the GASS CIB field with 1000 random CMB maps shown in red. The shaded area in yellow spans the 1σ region of the null signal, which is represented by the green lines. The measured CIB×CMB cross-correlation is shown in blue. We also show the CIB×CMB cross-correlation measured using a bin size Δℓ=20 instead of 10 (black points and dashed line). |
We performed a χ2 test for the observed cross-correlation signal with the null signal such that
where 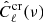 is the observed cross-correlation signal and Covcr(ν) is the covariance matrix computed from the simulations as described above for all the frequencies. We obtained a χ2 value of 6.0, 5.6, and 4.9 for 9 degrees of freedom, which corresponds to the p-value of 0.74, 0.78 and 0.84 for 217, 353, and 857 GHz, respectively, which shows that the signal is compatible with null. For 545 GHz, we obtained a χ2 of 30.7, which corresponds to a p-value of 0.0003. Such a high value of the χ2 is observed because the bump that is observed in the measured cross-correlation near ℓ ≈ 55. χ2 decreases to 16.7 with a corresponding p-value of 0.03 when this data point is not considered when χ2 is calculated.
is the observed cross-correlation signal and Covcr(ν) is the covariance matrix computed from the simulations as described above for all the frequencies. We obtained a χ2 value of 6.0, 5.6, and 4.9 for 9 degrees of freedom, which corresponds to the p-value of 0.74, 0.78 and 0.84 for 217, 353, and 857 GHz, respectively, which shows that the signal is compatible with null. For 545 GHz, we obtained a χ2 of 30.7, which corresponds to a p-value of 0.0003. Such a high value of the χ2 is observed because the bump that is observed in the measured cross-correlation near ℓ ≈ 55. χ2 decreases to 16.7 with a corresponding p-value of 0.03 when this data point is not considered when χ2 is calculated.
We investigated the source of the bump at ℓ ≈ 55. It can have three different origins: residual systematics in the data, correlated residual astrophysical signals (e.g. galactic dust), or a simple < 3σ deviation. The bump is observed at all frequencies (from 217 to 857 GHz), which tends to rule out any systematics left in the data. In the GASS field, it is also present when using the GNILC CIB map (see Appendix A) rather than the Planck 2013 CIB map, and also using different Planck CMB maps (SMICA, but also COMMANDER). In contrast, it is not visible in another field when the cross-correlation is computed using the GNILC CIB map and 11% of the sky in the northern hemisphere. This tends to show that it cannot be due to a residual astrophysical signal correlated in the CIB and CMB maps, and is thus a feature that is not statistically significant (less than 3σ) in the GASS field.
These tests show that the cross-correlation between the CIB and CMB obtained for the GASS field (with a sky fraction of 11%) is compatible with the null signal. CIB maps extracted over larger sky fractions and with lower dust residuals are required to extract the ISW signal using the CIB×CMB cross-correlation.
6. Conclusions
We used the CIB as a potential tracer of the large-scale structures to extract the ISW signal in the CMB with a high S/N. Our approach made use of the framework presented in Ilić et al. (2011). We used the improved linear CIB model of Maniyar et al. (2018), which includes the CIB×CMB lensing cross-correlation while fitting for the data, which partially breaks the degeneracy between the effective bias of the CIB galaxies and their emissivity and provides improved constraints on the CIB model parameters.
With this improved CIB model, we computed theoretical predictions for the CIB×ISW cross-correlation for different frequencies and found, as expected from the ISW effect, that it peaks at large angular scales, namely 20 < ℓ < 50 for all the frequencies considered. We showed that this cross-correlation can provide us the ISW signal with the highest S/N ever obtained for a single tracer. The optimal frequency with the highest S/N for the ISW detection in this case is 857 GHz with an S/N of 6.7σ. Using a Fisher matrix approach, we calculated the expected improvement on the constraints on the cosmological parameters as set by Planck (+SN, BAO, and H0) by adding the ISW signal obtained with the CIB×CMB cross-correlation. This analysis was done for the ΛCDM and the wCDM cosmological models, and we found as expected that the constraints on the latter are more sensitive to the addition of the ISW signal. For that model, we found that the CIB×CMB cross-correlation could potentially improve the constraints on the dark energy density parameter ΩΛ by ∼30% and the equation of state of the dark energy w by ∼80%, whether the available fraction of the sky is 70% or 40%. It also improves the constraints on the As parameter, as well as τ due to their degeneracy. The CIB×CMB lensing cross-correlation breaks the degeneracy between As and τ and improves the constraints on these parameters. The so-called stage-4 next-generation ground-based CMB experiment (CMB-S4) is expected to produce maps of unprecedented quality, improving the S/N of the reconstructed lensing map by over an order of magnitude (Abazajian et al. 2016) compared to Planck. While this will naturally improve the S/N for the CIB×CMB lensing cross-correlation, we recall that the maximum amount of cosmological information that can be extracted is ultimately limited by cosmic variance. We performed a Fisher matrix analysis to forecast the constraints on the cosmological parameters with the improved CIB×CMB lensing cross-correlation. As expected, compared to current constraints using Planck data, a small improvement (a few percent) is observed for most cosmological parameters and a significant improvement (∼30%) for τ and As.
This analysis was performed in relatively idealised scenarios with CIB maps free of any galactic dust residuals, however. To assess the effects of partial sky coverage and galactic dust residuals, we calculated the dust power spectra for all the frequencies over various sky fractions. We find that at our multipoles of interests, that is, ℓ < 100, the residual dust power spectra completely dominate the CIB power spectra. As a result, taking 10% of the dust power spectra as the possible residuals in our cleaned maps, we performed the same analysis over given portions of the sky and showed that the S/N drastically decreases with an S/N of 1.5 for 353 GHz over 20% sky fraction, for instance.
Using CIB and CMB maps obtained by Planck, we attempted to measure the CIB×CMB cross-correlation, allowing us to check the feasibility of detecting the ISW effect with the current level of dust removal and available sky fraction. This cross-correlation was computed over ∼11% of the southern sky in a field that is one of the largest and cleanest patches of the CIB to date (Planck Collaboration XXX 2014). We calculated the significance of the observed signal with respect to the ΛCDM prediction. We performed Monte Carlo simulations in order to obtain the expected covariance matrix between different bins for a given frequency for this test. We find that for all the frequencies except for 545 GHz, the signal is roughly compatible with expectations, but is detected with very low significance. At 545 GHz, the signal is detected at 5.5σ, but at the same time, its amplitude is 4.7σ higher than that predicted by the ΛCDM model. We also performed a null test to determine whether the detected signal is compatible with the null hypothesis. Again, except for 545 GHz, we find that the signal is consistent with the null hypothesis. For 545 GHz, the null hypothesis is rejected with a p-value of 0.0003, with a χ2 of 30.7 for 9 degrees of freedom. When we performed the null test by ignoring a bump observed in the cross-correlation around ℓ ∼ 55, we obtained a p-value of 0.03 with a χ2 of 16.7 for 8 degrees of freedom. These tests show that the measured CIB×CMB cross-correlation is compatible with the null hypothesis and that we do not detect any significant signal. Our analysis shows that with the current state of the maps, the ISW signal cannot be detected. A much better cleaning of galactic dust is required. If we do not wish to degrade the S/N on the measurements by more than 10% on 40% of the sky, we need to clean the dust up to the 0.01% level on the power spectrum. This is very challenging (if at all possible) to achieve, but mandatory for using the CIB as a cosmological probe either through the ISW effect but also in itself, for example, to constrain local primordial non-Gaussianity or other non-standard cosmological models. Granett et al. (2008) performed a stacking of CMB patches at the locations of a sample of 100 large voids and galaxy clusters, aiming at measuring their ISW signal. They reported a signal whose amplitude was significantly stronger than expected in the ΛCDM model. This work has later on been challenged by other groups, and was extended to larger catalogues of structures (see e.g. Kovács 2018, and references therein for a recent review), with the consensus that the stacking signal appears indeed stronger than expected. If the origin of this discrepancy were to be an excess of ISW signal, it is not straightforward to predict how (or if) it would appear in our present analysis because we work in harmonic space, whereas stacking is done directly in maps. We intend to explore this particular subject in the near future in order to determine if this potential excess ISW signal could be detected using the CIB maps along with the CMB.
We preferred using the CIB maps built as detailed in Planck Collaboration XXX (2014) rather than the CIB maps provided by the Planck Collaboration PLA and constructed with the procedure detailed in Planck Collaboration Int. XLIX (2016). This is because the Planck CIB maps, which use the GNILC technique to clean the dust, suffer from an excessive cleaning at the lower multipoles in which we are interested, and this results in CIB power removal at these scales. See the Appendix A for more details.
Acknowledgments
A.M. and G.L. warmly thank Matthieu Tristram for his invaluable help in the use of Xpol. We acknowledge financial support from the “Programme National de Cosmologie and Galaxies” (PNCG) funded by CNRS/INSU-IN2P3-INP, CEA and CNES, France, from the ANR under the contract ANR-15-CE31-0017 and from the OCEVU Labex (ANR-11-LABX-0060) and the A*MIDEX project (ANR-11-IDEX-0001-02) funded by the “Investissements d’Avenir” French government programme managed by the ANR. The research leading to these results has also received funding from the European Research Council under the European Union’s Seventh Framework Programme (FP7/2007-2013)/ERC Grant Agreement No. 617656 “Theories and Models of the Dark Sector: Dark Matter, Dark Energy and Gravity”.
References
- Abazajian, K. N., Adshead, P., Ahmed, Z., et al. 2016, ArXiv e-prints [arXiv:1610.02743] [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Wang, L., Doré, O., et al. 2013, A&A, 557, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Daddi, E., Magdis, G., et al. 2015, A&A, 573, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Béthermin, M., Wu, H.-Y., Lagache, G., et al. 2017, A&A, 607, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beutler, F., Blake, C., Colless, M., et al. 2011, MNRAS, 416, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Boughn, S. P., & Crittenden, R. G. 2002, Phys. Rev. Lett., 88, 021302 [NASA ADS] [CrossRef] [Google Scholar]
- Boughn, S. P., Crittenden, R. G., & Turok, N. G. 1998, New Astron., 3, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Cabré, A., Gaztañaga, E., Manera, M., Fosalba, P., & Castander, F. 2006, MNRAS, 372, L23 [NASA ADS] [Google Scholar]
- Cardoso, J.-F., Le Jeune, M., Delabrouille, J., Betoule, M., & Patanchon, G. 2008, IEEE J. Sel. Top. Sign. Proces., 2, 735 [CrossRef] [Google Scholar]
- Coble, K., Dodelson, S., & Frieman, J. A. 1997, Phys. Rev. D, 55, 1851 [NASA ADS] [CrossRef] [Google Scholar]
- Corasaniti, P. S., Bassett, B. A., Ungarelli, C., & Copeland, E. J. 2003, Phys. Rev. Lett., 90, 091303 [NASA ADS] [CrossRef] [Google Scholar]
- Creque-Sarbinowski, C., Bird, S., & Kamionkowski, M. 2016, Phys. Rev. D, 94, 063519 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 2014, MNRAS, 440, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., & Hu, W. 1998, ApJ, 496, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Ferraro, S., Sherwin, B. D., & Spergel, D. N. 2015, Phys. Rev. D, 91, 083533 [NASA ADS] [CrossRef] [Google Scholar]
- Francis, C. L., & Peacock, J. A. 2010, MNRAS, 406, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Garriga, J., Pogosian, L., & Vachaspati, T. 2004, Phys. Rev. D, 69, 063511 [NASA ADS] [CrossRef] [Google Scholar]
- Giannantonio, T., Crittenden, R. G., Nichol, R. C., et al. 2006, Phys. Rev. D, 74, 063520 [NASA ADS] [CrossRef] [Google Scholar]
- Giannantonio, T., Scranton, R., Crittenden, R. G., et al. 2008, Phys. Rev. D, 77, 123520 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Granett, B. R., Neyrinck, M. C., & Szapudi, I. 2008, ApJ, 683, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Hanson, D., Hoover, S., Crites, A., et al. 2013, Phys. Rev. Lett., 111, 141301 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hernández-Monteagudo, C., Ross, A. J., Cuesta, A., et al. 2014, MNRAS, 438, 1724 [NASA ADS] [CrossRef] [Google Scholar]
- Ilić, S., Douspis, M., Langer, M., Pénin, A., & Lagache, G. 2011, MNRAS, 416, 2688 [NASA ADS] [CrossRef] [Google Scholar]
- Ilić, S., Langer, M., & Douspis, M. 2013, A&A, 556, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Knox, L., Cooray, A., Eisenstein, D., & Haiman, Z. 2001, ApJ, 550, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Kodama, H., & Sasaki, M. 1984, Prog. Theor. Phys. Suppl., 78, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, A. 2018, MNRAS, 475, 1777 [NASA ADS] [CrossRef] [Google Scholar]
- Lagache, G., & Puget, J. L. 2000, A&A, 355, 17 [NASA ADS] [Google Scholar]
- Lagache, G., Bavouzet, N., Fernandez-Conde, N., et al. 2007, ApJ, 665, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A. 2014, http://cosmologist.info/notes/CAMB.pdf [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Challinor, A. 2006, Phys. Rep., 429, 1 [Google Scholar]
- Ma, C.-P., & Bertschinger, E. 1995, ApJ, 455, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Dickinson, M. 2014, ARA&A, 52, 415 [NASA ADS] [CrossRef] [Google Scholar]
- Maniyar, A. S., Béthermin, M., & Lagache, G. 2018, A&A, 614, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Matsuhara, H., Kawara, K., Sato, Y., et al. 2000, A&A, 361, 407 [NASA ADS] [Google Scholar]
- McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Okamoto, T., & Hu, W. 2003, Phys. Rev. D, 67, 083002 [NASA ADS] [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Pietrobon, D., Balbi, A., & Marinucci, D. 2006, Phys. Rev. D, 74, 043524 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XVIII. 2011, A&A, 536, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, 571, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVIII. 2014, A&A, 571, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXX. 2014, A&A, 571, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2016, A&A, 594, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXI. 2016, A&A, 594, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLIX. 2016, A&A, 596, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puget, J.-L., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 308, L5 [NASA ADS] [Google Scholar]
- Raccanelli, A., Bonaldi, A., Negrello, M., et al. 2008, MNRAS, 386, 2161 [NASA ADS] [CrossRef] [Google Scholar]
- Raveri, M., Martinelli, M., Zhao, G., & Wang, Y. 2016. ArXiv e-prints [arXiv:1606.06268] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Ross, A. J., Samushia, L., Howlett, C., et al. 2015, MNRAS, 449, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Sachs, R. K., & Wolfe, A. M. 1967, ApJ, 147, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Scoccimarro, R. 2004, Phys. Rev. D, 70, 083007 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U. 1996, ApJ, 460, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Serra, P., Lagache, G., Doré, O., Pullen, A., & White, M. 2014, A&A, 570, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shajib, A. J., & Wright, E. L. 2016, ApJ, 827, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Song, Y.-S., Cooray, A., Knox, L., & Zaldarriaga, M. 2003, ApJ, 590, 664 [NASA ADS] [CrossRef] [Google Scholar]
- Stölzner, B., Cuoco, A., Lesgourgues, J., & Bilicki, M. 2018, Phys. Rev. D, 97, 063506 [NASA ADS] [CrossRef] [Google Scholar]
- Taburet, N., Hernández-Monteagudo, C., Aghanim, N., Douspis, M., & Sunyaev, R. A. 2011, MNRAS, 418, 2207 [NASA ADS] [CrossRef] [Google Scholar]
- Tinker, J. L., Sheldon, E. S., Wechsler, R. H., et al. 2012, ApJ, 745, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Tristram, M., Macías-Pérez, J. F., Renault, C., & Santos, D. 2005, MNRAS, 358, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Moncelsi, L., Quadri, R. F., et al. 2013a, ApJ, 779, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Viero, M. P., Wang, L., Zemcov, M., et al. 2013b, ApJ, 772, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, H.-Y., Doré, O., Teyssier, R., & Serra, P. 2018, MNRAS, 475, 3974 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Choice of the CIB maps
As described in Sect. 5.1, we used the CIB maps in the GASS field built as detailed in Planck Collaboration XXX (2014), and not the GNILC CIB maps provided by the Planck Collaboration. The Planck CIB maps have been prepared by cleaning the galactic dust using the GNILC component separation method and the details are provided in Planck Collaboration Int. XLIX (2016). Figure 6 of Planck Collaboration Int. XLIX (2016) shows the power spectrum of galactic dust and galactic-dust-subtracted Planck maps (also known as the CIB), together with the best-fit model of the CIB power spectrum from Planck Collaboration XXI (2016) for different frequencies. This figure shows that there is an excessive dust cleaning at 545 and 857 GHz at low multipoles, which are of interest to us, and hence the CIB power spectra from GNILC maps is lying below the Planck Collaboration XXX (2014) best-fit model. Maniyar et al. (2018) provided an improved CIB model, using not only the CIB measurements, but also the CIB×CMB lensing cross-correlation.
To check the validity of the CIB map in the GASS field, we cross-correlated it with the lensing convergence κ map (provided by Planck6) using Xpol. For comparison, we also considered the Planck GNILC CIB map from PLA and cross-correlated it with the same lensing convergence map. The cross-correlation of CIB×CMB lensing potential ϕ is obtained as
Figure A.1 shows the 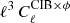 computed both for GASS CIB map and Planck GNILC CIB map for 545 GHz till ℓ = 100. The cross-correlation using the GASS CIB map falls on the Maniyar et al. (2018) model, whereas the cross-correlation with the Planck GNILC CIB map is consistently lower (by a factor of > 2 at ℓ = 50) in this range of multipoles in which we are interested in for ISW. At the same time, the error bars on the cross-correlation with the Planck GNILC CIB map are smaller than the error bars on the cross-correlation with the GASS CIB map. From Eq. (39), we can infer that the reason is the lower amount of the dust in the Planck GNILC CIB maps compared to the GASS CIB maps. These conclusions hold at 857 and 353 GHz, where the measurements are more than twice lower than what is expected from the model at ℓ = 50.
computed both for GASS CIB map and Planck GNILC CIB map for 545 GHz till ℓ = 100. The cross-correlation using the GASS CIB map falls on the Maniyar et al. (2018) model, whereas the cross-correlation with the Planck GNILC CIB map is consistently lower (by a factor of > 2 at ℓ = 50) in this range of multipoles in which we are interested in for ISW. At the same time, the error bars on the cross-correlation with the Planck GNILC CIB map are smaller than the error bars on the cross-correlation with the GASS CIB map. From Eq. (39), we can infer that the reason is the lower amount of the dust in the Planck GNILC CIB maps compared to the GASS CIB maps. These conclusions hold at 857 and 353 GHz, where the measurements are more than twice lower than what is expected from the model at ℓ = 50.
The middle panel of the Fig. 6 of Planck Collaboration Int. XLIX (2016) shows that for 545 GHz, the best-fit Planck CIB and the GNILC CIB power spectra begin to agree only after ℓ ∼ 800. Figure A.2 shows the  computed for the GASS CIB map and the Planck GNILC CIB map for 545 GHz from ℓ = 500 to ℓ = 1000. Overall, although the cross-correlation with the GASS CIB map agrees better with the Maniyar et al. (2018) model than with the Planck GNILC CIB map, the GNILC CIB maps perform better at these multipoles than at multipoles < 100 (but still systematically underestimate the cross-correlation). This shows once again an excessive cleaning of galactic dust in the Planck GNILC CIB maps, which results in partial CIB removal and hence an underestimate of the CIB power. This is the reason for our decision against this CIB map in our analysis.
computed for the GASS CIB map and the Planck GNILC CIB map for 545 GHz from ℓ = 500 to ℓ = 1000. Overall, although the cross-correlation with the GASS CIB map agrees better with the Maniyar et al. (2018) model than with the Planck GNILC CIB map, the GNILC CIB maps perform better at these multipoles than at multipoles < 100 (but still systematically underestimate the cross-correlation). This shows once again an excessive cleaning of galactic dust in the Planck GNILC CIB maps, which results in partial CIB removal and hence an underestimate of the CIB power. This is the reason for our decision against this CIB map in our analysis.
 |
Fig. A.1. CIB×CMB lensing cross-power spectra for 2 ≤ ℓ ≤ 100 at 545 GHz. The blue curve shows the CIB×CMB lensing model from Maniyar et al. (2018). The green, red, and black curves show the measured cross-correlation for GASS CIB map, GASS GNILC map, and GNILC maps on 57% of the sky, respectively. The cross-correlation is consistently below the Maniyar et al. (2018) model for the GNILC CIB map. The cross-correlation obtained with the GASS CIB map agrees better with the Maniyar et al. (2018) model. |
 |
Fig. A.2. CIB×CMB lensing cross-power spectra for 500 ≤ ℓ ≤ 1000 at 545 GHz. The blue curve shows the CIB×CMB lensing cross-correlation model by Maniyar et al. (2018). The green and red curves show the measured cross-correlation in the GASS field for the CIB maps from Planck Collaboration XXX (2014) and GNILC, respectively. The black curve is the cross-correlation using GNILC CIB map on 57% of the sky. Data points in blue show the CIB×ϕ measurements by Planck (Planck Collaboration XVIII 2014). The cross-correlation for the GASS CIB map agrees better with the Maniyar et al. (2018) model than for the Planck GNILC CIB map. |
All Tables
Predicted S/N for the ISW signal in the ideal scenario (CIB maps free of galactic dust residuals), for 100% and 40% sky coverage.
Predicted S/N for the ISW signal in the current realistic scenario, including the dust residuals in the CIB maps.
Best-fit values and errors for the amplitude A, and significance of the signal A/σA for all the frequencies.
All Figures
 |
Fig. 1. CIB×ISW cross-correlation power spectra (in Jy sr−1) for the five frequency channels. |
| In the text | |
 |
Fig. 2. Cumulative S/N for the CIB×ISW cross-correlation signal for the five frequency channels. The S/N is predicted to be highest for 857 GHz. |
| In the text | |
 |
Fig. 3. Power spectra of the CIB and 10% of the dust residual at 353 GHz (left panel) and 3000 GHz (right panel). The dust power spectra are computed over 20, 40, 60, 70, and 80% of the sky. The residual dust power spectra dominate the CIB at the low multipoles of interest for the ISW signal. As a consequence, the S/N decreases dramatically compared to the ideal dust-free case. |
| In the text | |
 |
Fig. 4. Fisher forecasts for the 1σ and 2σ confidence contours for the ΛCDM cosmological parameters in the fsky = 70% case. The blue contours show our results when the CMB, CIB, and CIB×CMB lensing constraints are combined. The red contours show the same results when the CIB×ISW cross-correlation constraints are added. There is a ∼17% improvement on the constraints on ΩΛ and ∼39/35% for τ/As, which are strongly correlated. |
| In the text | |
 |
Fig. 5. Fisher forecasts for the 1σ and 2σ confidence contours for the wCDM cosmological parameters in the fsky = 70% case. The blue contours show our results when the CIB, CIB×CMB lensing, and the CMB along with the external (JLA + BAO and H0 prior) constraints on the cosmological parameters are combined. The red contours show the same results when the CIB×ISW cross-correlation constraints are added. There is a ∼80% improvement on the constraints on w, ∼29% for ΩΛ, and ∼43/39% for τ/As, which are strongly correlated. |
| In the text | |
 |
Fig. 6. Measured CIB×CMB cross-correlation and corresponding error bars for the GASS CIB field (blue points). The predicted signal (given by Eq. (11)) is shown in red. The error bars on the predicted signal are calculated using the noise term in Eq. (39). Following Planck Collaboration XXX (2014), we assumed that the CIB power spectrum is contaminated by dust residuals at the level of 10% when the theoretical error bars were calculated. |
| In the text | |
 |
Fig. 7. Average null signal calculated using the cross-correlation of the GASS CIB field with 1000 random CMB maps shown in red. The shaded area in yellow spans the 1σ region of the null signal, which is represented by the green lines. The measured CIB×CMB cross-correlation is shown in blue. We also show the CIB×CMB cross-correlation measured using a bin size Δℓ=20 instead of 10 (black points and dashed line). |
| In the text | |
 |
Fig. A.1. CIB×CMB lensing cross-power spectra for 2 ≤ ℓ ≤ 100 at 545 GHz. The blue curve shows the CIB×CMB lensing model from Maniyar et al. (2018). The green, red, and black curves show the measured cross-correlation for GASS CIB map, GASS GNILC map, and GNILC maps on 57% of the sky, respectively. The cross-correlation is consistently below the Maniyar et al. (2018) model for the GNILC CIB map. The cross-correlation obtained with the GASS CIB map agrees better with the Maniyar et al. (2018) model. |
| In the text | |
 |
Fig. A.2. CIB×CMB lensing cross-power spectra for 500 ≤ ℓ ≤ 1000 at 545 GHz. The blue curve shows the CIB×CMB lensing cross-correlation model by Maniyar et al. (2018). The green and red curves show the measured cross-correlation in the GASS field for the CIB maps from Planck Collaboration XXX (2014) and GNILC, respectively. The black curve is the cross-correlation using GNILC CIB map on 57% of the sky. Data points in blue show the CIB×ϕ measurements by Planck (Planck Collaboration XVIII 2014). The cross-correlation for the GASS CIB map agrees better with the Maniyar et al. (2018) model than for the Planck GNILC CIB map. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



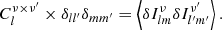
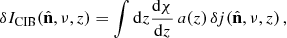
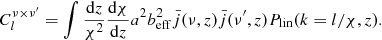
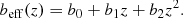
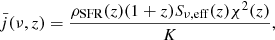
![$$ \begin{aligned} \rho _{{\mathrm{SFR}}}(z) = \alpha \dfrac{(1+z)^{\beta }}{1+ {[ (1+z)/{\gamma } ]}^{\delta }}\,{{M}}_{\odot }\,{\mathrm{yr}}^{-1}\,{\mathrm{Mpc}}^{-3}, \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq9.gif)
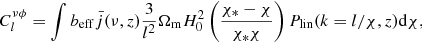
![$$ \begin{aligned} \delta T_{{\mathrm{ISW}}}({\hat{\mathbf{n }}}) = \int _{\eta _r}^{\eta _0} \mathrm{d}\eta \, \mathrm{e}^{-\tau (\eta )} ({{\dot{\Phi }}} - {{\dot{\Psi }}}) [(\eta _0 - \eta ){\hat{\mathbf{n }}}, \eta ]. \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq14.gif)
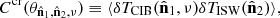
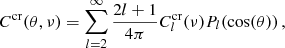
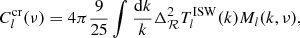
![$$ \begin{aligned} M_l(k, \nu )&= c_{{\delta \Psi }} \int _{\eta _0}^{\eta _r} \mathrm{d}\eta \, j_l(k[\eta - \eta _0]) a(\eta ) b_{\rm eff}(\nu ) \bar{j}(\nu , \eta ) \bar{\delta } (k, \eta ) \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq21.gif)
![$$ \begin{aligned} T_l^\mathrm{ISW} (k)&= \int _{\eta _0}^{\eta _r} \mathrm{d}\eta \, \mathrm{e}^{-\tau (\eta )} j_l(k[\eta - \eta _0]) (c_{{\Phi \Psi }}\, \dot{\phi } - {\dot{\psi }}), \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq22.gif)
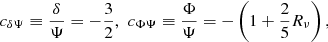
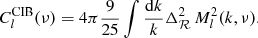
![$$ \begin{aligned} \left[\dfrac{S}{N}\right]^2(\nu ) = \sum _{\ell = 2}^{\ell _{\rm max}} \left(\frac{S_\ell (\nu )}{N_\ell (\nu )}\right)^2 , \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq26.gif)
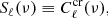
![$$ \begin{aligned} N_\ell (\nu ) \equiv \sqrt{\dfrac{\left[C_\ell ^\mathrm{cr}(\nu )\right]^2 + C_\ell ^{\mathrm{CIB} }(\nu ) C_\ell ^{\mathrm{CMB} }}{2\ell + 1}}\cdot \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq28.gif)
![$$ \begin{aligned} \left[\dfrac{S}{N}\right]^2(\nu ) = \sum _{\ell = 2}^{\ell _{\rm max}} (2\ell + 1) \dfrac{f_{\mathrm{sky} }\,\left[C_\ell ^\mathrm{cr}(\nu )\right]^2 }{\left[C_\ell ^\mathrm{cr}(\nu )\right]^2 + \left[C_\ell ^{{\mathrm{CIB} }}(\nu ) + N_\ell ^{{\mathrm{CIB} }}(\nu )\right]\, C_\ell ^{{\mathrm{CMB} }}} ,\end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq30.gif)
![$$ \begin{aligned} L = \frac{1}{(2\pi )^{n/2}\sqrt{\det \boldsymbol{\Sigma }}} \exp \left[-\frac{1}{2}(\mathbf x -\boldsymbol{\mu })^T \boldsymbol{\Sigma }^{-1} (\mathbf x -\boldsymbol{\mu }) \right]. \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq37.gif)
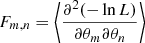
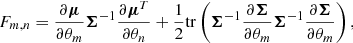
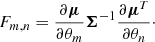
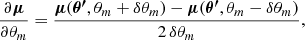
![$$ \begin{aligned} \boldsymbol{\theta } = \left[ \boldsymbol{\theta }_{\rm CIB}, \boldsymbol{\theta }_{\rm cosmo.} \right] \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq43.gif)
![$$ \begin{aligned} \boldsymbol{\theta }_{\rm CIB} = \left[ \alpha , \beta , \gamma , \delta , b_0, b_1, b_2, f_{\nu _i}^{\mathrm{cal}} \right] \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq44.gif)
![$$ \begin{aligned} \boldsymbol{\theta }_{\rm cosmo.} = \left[ H_0, \Omega _bh^2, \Omega _ch^2, \tau , n_s, A_s \right] \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq46.gif)
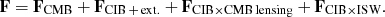
![$$ \begin{aligned} B_{\ell _1, \ell _2} = \frac{1}{n_\ell } \sum _{\ell \in [\ell _1, \ell _2]} C_\ell , \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq48.gif)
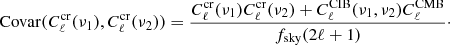
![$$ \begin{aligned} \mathrm{Covar}(B^\mathrm{cr}_{\ell _1, \ell _2}(\nu _1), B^\mathrm{cr}_{\ell _1, \ell _2}(\nu _2)) = \frac{1}{n_\ell ^2}\sum _{\ell \in [\ell _1, \ell _2]} \mathrm{Covar}(C^\mathrm{cr}_\ell (\nu _1), C^\mathrm{cr}_\ell (\nu _2)) ,\end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq53.gif)
![$$ \begin{aligned} \chi ^2(A) = {\left[\hat{C}_\ell ^\mathrm{cr}(\nu ) - AC_\ell ^\mathrm{cr}(\nu )\right]}^T {\mathrm{Cov} }_{\rm cr}^{-1}(\nu )\left[\hat{C}_\ell ^\mathrm{cr}(\nu )AC_\ell ^\mathrm{cr}(\nu )\right] , \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq58.gif)
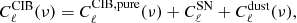
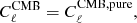
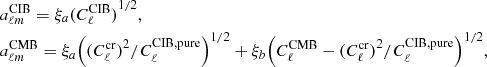
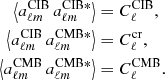
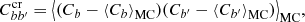
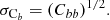
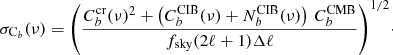
![$$ \begin{aligned} \chi ^2_{\mathrm{null} } = {\left[\hat{C}_\ell ^\mathrm{cr}(\nu )\right]}^T {\mathrm{Cov} }_{\rm cr}^{-1}(\nu )\left[\hat{C}_\ell ^\mathrm{cr}(\nu )\right] , \end{aligned} $$](/articles/aa/full_html/2019/01/aa33765-18/aa33765-18-eq77.gif)