| Issue |
A&A
Volume 614, June 2018
|
|
|---|---|---|
| Article Number | A123 | |
| Number of page(s) | 30 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201732498 | |
| Published online | 25 June 2018 | |
The physical and chemical structure of Sagittarius B2
III. Radiative transfer simulations of the hot core Sgr B2(M) for methyl cyanide
1
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77,
50937
Köln,
Germany
e-mail: pols@ph1.uni-koeln.de, schwoerer@ph1.uni-koeln.de, sanchez@ph1.uni-koeln.de
2
Max-Planck Institute for Extraterrestrial Physics,
Giessenbachstrasse 1,
85748
Garching,
Germany
Received:
19
December
2017
Accepted:
20
February
2018
Context. We model the emission of methyl cyanide (CH3CN) lines towards the massive hot molecular core Sgr B2(M).
Aims. We aim to reconstruct the CH3CN abundance field, and investigate the gas temperature distribution as well as the velocity field.
Methods. Sgr B2(M) was observed with the Atacama Large Millimeter/submillimeter Array (ALMA) in a spectral line survey from 211 to 275 GHz. This frequency range includes several transitions of CH3CN (including isotopologues and vibrationally excited states). We employed the three-dimensional radiative transfer toolbox Pandora in order to retrieve the velocity and abundance field by modeling different CH3CN lines. For this purpose, we based our model on the results of a previous study that determined the physical structure of Sgr B2(M), i.e., the distribution of dust dense cores, ionized regions, and heating sources.
Results. The morphology of the CH3CN emission can be reproduced by a molecular density field that consists of a superposition of cores with modified Plummer-like density profiles. The averaged relative abundance of CH3CN with respect to H2 ranges from 4 × 10−11 to 2 × 10−8 in the northern part of Sgr B2(M) and from 2 × 10−10 to 5 × 10−7 in the southern part. In general, we find that the relative abundance of CH3CN is lower at the center of the very dense, hot cores, causing the general morphology of the CH3CN emission to be shifted with respect to the dust continuum emission. The dust temperature calculated by the radiative transfer simulation based on the available luminosity reaches values up to 900 K. However, in some regions vibrationally excited transitions of CH3CN are underestimated by the model, indicating that the predicted gas temperature, which is assumed to be equal to the dust temperature, is partly underestimated. The determination of the velocity component along the line of sight reveals that a velocity gradient from the north to the south exists in Sgr B2(M).
Key words: radiative transfer / stars: formation / stars: massive / ISM: clouds / ISM: molecules / ISM: individual objects: SgrB2
© ESO 2018
1 Introduction
Almost all the information we have about the interstellar medium (ISM) is obtained from the analysis of electromagnetic radiation received by telescopes. Hence, in astrophysics it is crucial to predict the radiative properties of a physical model when interpreting astronomical observations. For this purpose, three-dimensional radiative transfer codes have been developed which can calculate the radiation signature associated with a three-dimensional physical model of a specific source. The results can subsequently be compared to observations to study the physical and chemical properties of astrophysical objects.
In the struggle to understand how the evolution of high-mass stars proceeds from the fragmentation of giant molecular clouds down to dense hot molecular cores (e.g., Tan et al. 2014; Schilke 2015), it is important to study the kinematics, density structure, temperature distribution, and chemical variations of the dense gas associated with these objects, as these parameters determine their dynamical evolution. The study of the emission of lines of certain molecular species can provide this crucial information as the intensity and the line profile are determined by the physical and excitation conditions of the gas.
There are several molecules in the ISM that can be used to study the dense cores where star formation takes place. However, hot molecular cores (e.g., Kurtz et al. 2000; Cesaroni 2005) associated with high temperatures (T > 100 K) and high densities (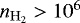 cm−3) are traced best by complex molecules (i.e., molecules with six or more atoms) that are mainly formed on dust grains and released into the gas phase during the warm-up through the heating produced by the newly born star. Among these complex molecules, CH3 CN has turned out to be an excellent tool to determine the gas temperature due to its symmetry structure (e.g., Araya et al. 2005) and due to the distribution and velocity field of the high-density gas from where high-mass stars form (see, e.g., Remijan et al. 2004; Sánchez-Monge et al. 2013; Hernández-Hernández et al. 2014).
cm−3) are traced best by complex molecules (i.e., molecules with six or more atoms) that are mainly formed on dust grains and released into the gas phase during the warm-up through the heating produced by the newly born star. Among these complex molecules, CH3 CN has turned out to be an excellent tool to determine the gas temperature due to its symmetry structure (e.g., Araya et al. 2005) and due to the distribution and velocity field of the high-density gas from where high-mass stars form (see, e.g., Remijan et al. 2004; Sánchez-Monge et al. 2013; Hernández-Hernández et al. 2014).
Sagittarius B2 (hereafter Sgr B2) is one of the most massive molecular clouds in the Galaxy. Located at a projected distance of ~100 pc from the Galactic center, which has a distance of 8.34 ± 0.16 kpc from the Sun (Reid et al. 2014), Sgr B2 is an excellent source for studying the formation of high-mass clusters and astrochemistry. It has been shown to harbor active star formation sites (Gordon et al. 1993) and contains a wide range of different molecules including complex organic species, many of which were found for the first time in space towards Sgr B2, for example acetic acid (CH3 COOH, Mehringer et al. 1997) or ethyl formate (C2 H5OCHO, Belloche et al. 2009). The Sgr B2 complex contains a total mass of ~ 107 M⊙, and a total luminosity of about 107 L⊙ (Goldsmith et al. 1990). Based on its density structure, it has been proposed that Sgr B2 is composed of three different parts (Hüttemeister et al. 1993): a low-density envelope with 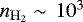 cm−3, a moderate-density region with
cm−3, a moderate-density region with  cm−3 extending around local hot molecular cores, which are the most compact and densest regions with
cm−3 extending around local hot molecular cores, which are the most compact and densest regions with 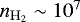 cm−3. The two main sites of star formation are the central hot molecular cores Sgr B2(N) and Sgr B2(M), which have sizes of ~0.5 pc and contain numerous ultracompact H II regions (see, e.g., Mehringer et al. 1993; Gaume et al. 1995). A more detailed description of Sgr B2 can be found in (Schmiedeke et al. 2016, hereafter Paper I) and (Sánchez-Monge et al. 2017, hereafter Paper II).
cm−3. The two main sites of star formation are the central hot molecular cores Sgr B2(N) and Sgr B2(M), which have sizes of ~0.5 pc and contain numerous ultracompact H II regions (see, e.g., Mehringer et al. 1993; Gaume et al. 1995). A more detailed description of Sgr B2 can be found in (Schmiedeke et al. 2016, hereafter Paper I) and (Sánchez-Monge et al. 2017, hereafter Paper II).
This is the third in a series of papers investigating the star-forming region Sgr B2. In this work, we model line transitions of methyl cyanide, CH3 CN, by employing radiative transfer codes. This model is based on a physical model of Sgr B2, which was developed in the first paper of this series (Paper I). The modeling of the CH3CN transitions is based on high-resolution observations of Sgr B2 obtained with the Atacama Large Millimeter/submillimeter Array (ALMA, ALMA Partnership et al. 2015). The continuum emission of these observations was presented and analyzed in the second paper of this series (Paper II). In the current paper, we focus our analysis on the hot molecular core Sgr B2(M), which exhibits a very complex and fragmented structure, and appears to be in a more evolved stage of evolution than Sgr B2(N). Earlier observations using the Submillimeter Array (SMA) by Qin et al. (2011) revealed at least 12 dense cores at a frequency of 345 GHz. Recent ALMA observations at 242 GHz (Paper II) increased this number to 27 sources including dust dense cores and some H II regions, and suggested a more complex structure with hints of the presence of filaments.
The current paper is organized as follows. In Sect. 2 we give a brief overview of the ALMA observations. In Sect. 3, we present the CH3CN data and compare the distribution of the dense gas to the continuum emission. The modeling procedure is described in Sect. 4. In Sect. 5 we describe the physical model used to model the CH3 CN emission towards Sgr B2(M). This is followed by a comparison of the simulations with the observational data in Sect. 6. Finally, Sect. 7 summarizes the main results of the paper. Appendices contain a description of the parameters of the physical model as well as several spectra comparing the observational and simulated data.
2 Observations
The observations of Sgr B2(M) were conducted using ALMA during its Cycle 2 in June 2014 and June 2015 (project number 2013.1.00332.S). The configuration used 34 and 36 antennas, with extended baselines in the range between 30 m and 650 m. At the frequency range of our observations (from 211 GHz to 275 GHz) this results in an angular resolution of 0. ′′ 4–0. ′′8. Sgr B2(M) was observed in track-sharing mode, together with Sgr B2(N), with the phase center at α(J2000) = 17h47m20s .157, δ(J2000) = −28°23′ 04. ′′ 53. The observationswere done in the spectral scan mode surveying all of ALMA band 6 from 211 to 275 GHz. The achieved spectral resolution is 0.5–0.7 km s−1 across the full frequency band. Calibration and imaging were performed in CASA1 version 4.4.0. The resulting data cubes used in this project were restored with a circular Gaussian beam of 0. ′′ 7. Further information on the calibration, observational details, and imaging can be found in Paper II.
CH3CN transitions analyzed in this paper.
3 Observational results
The frequency range of the ALMA observations covers several rotational transitions of CH3 CN in the vibrational ground state(e.g., J = 12−11 at 220.7 GHz, J = 13−12 at 239.1 GHz, and J = 14−13 at 257.5 GHz) and in the vibrationally excited state v8 = 1. An overview of the CH3CN transitions analyzed in this paper is given in Table 1.
The middle panels of Fig. 1 show the Sgr B2(M) peak intensity maps of three CH3 CN lines compared with the ALMA continuum emission (black contour; from Paper II). The image maps of the continuum emission for the frequencies of each of the selected CH3CN transitions are shown in the top panels. A first comparison of the distribution of the dense gas and the continuum emission reveals that the CH3 CN emission is much more extended than the continuum emission, especially towards the south. Moreover, the local maxima in the line emission do not necessarily coincide with the position of the peaksin the continuum maps. This is clearly seen in the northern part of Sgr B2(M) where a compact CH3CN condensation appears shifted towards the northeast with respect to the continuum. The southern region exhibits a significantly brighter and more extended CH3CN emission than towards the northern part.
In the bottom panels of Fig. 1, we present spectra extracted towards selected positions indicated with crosses in the top and middle panels of the figure. The spectra show the emission of the K lines of the ground state CH3CN transitions J = 12−11 (left panel), J = 13−12 (central panel), and J = 14−13 (right panel). The spectra show the characteristic K-ladder of a symmetric top molecule, but also the lines of other molecules that are partly blending the CH3CN lines. For a better identification of which lines actually belong to CH3CN, the reader is referred to Fig. B.1, where the observational spectra are compared to the results of our simulations. Depending on the location within Sgr B2(M), the regions show different spectral characteristics. The spectrum extracted from the northern region (Mn and red cross in Fig. 1) has clear and well-defined lines, all of them in emission. The southern position (Ms and blue cross in the figure) has slightly broader lines shifted towards lower frequencies (i.e., red-shifted velocities). Finally, the spectra extracted towards the brightest continuum source (Mm and black cross in the figure) is completely different from those obtained in the south and north. The central spectra show a complex combination of emission and absorption features belonging to CH3CN. The absorption features are related to the strong continuum emission present in the central region, which at the depicted frequency is about 180 K. The emission of a channel map of the strongest absorption feature of CH3CN (J = 12−11, K = 0) is shown in Fig. 2. The possible origin of the strong continuum emission that causes the absorption features is the presence of the numerous H II regions in Sgr B2(M). However, a comparison of the position and extent of the known H II regions with the area of absorption shows that they only partly coincide (see black circles in Fig. 2). Moreover, the absorption feature is also present at regions with no H II regions. On the contrary, the ALMA 242 GHz continuum emission (magenta contours in Fig. 2) clearly coincides with the area of absorption, indicating that bright dust continuum emission is the most probable origin of the absorption features found in the central region of Sgr B2(M). A similar absorption produced against bright dust continuum is also found in the massive hot molecular core G31.41+0.31 (Cesaroni et al. 2017).
 |
Fig. 1 Top panels: continuum maps towards Sgr B2(M) determined using STATCONT (Sánchez-Monge et al. 2018) at the frequencies of the spectral windows that cover the three CH3 CN ground state transitions: 220 GHz (left), 239 GHz (center), and 257 GHz (right). The black contour shows the 10% level of the continuum emission peak. Middle panels: intensity peak maps of different CH3 CN transitions: J = 12− 11, K = 3 (left), J = 13−12, K = 3 (center), and J = 14−13, K = 3 (right). The intensity peak maps are obtained from a narrow frequency range around the frequency indicated with a vertical dotted line in the bottom panels. The black contour depicts the 10% level of the continuum emission, as in the top panels. Bottom panels: spectra extracted at three different positions marked with crosses in the top and middle panels. The selected positions are located in the north (Mn, in red), in the center of the region associated with the brightest continuum peak (Mm, in black), and towards the south (Ms, in blue). To enhance the clarity, we shifted the red spectrum by +100 K and the blue spectrum by −200 K. The relativecontinuum levels are indicated by the dashed gray lines. |
 |
Fig. 2 Channel map at a frequency of 220.765 GHz corresponding to the line of CH3 CN (J = 12−11, K = 0). Clear absorption is observed in the center of the map. Magenta contours show the ALMA 242 GHz continuum emission from Paper II. Black circles indicate the position and extent of the H II regions (see Paper I). |
 |
Fig. 3 Combined density profile (grey area) of all the dense cores included in the model of Sgr B2(M). The average critical density of the transitions listed in Table 1 is shown as an horizontal blue line. The vertical red lines at 4.25 × 103 and 104 au indicate up to which distance from the center of the cores the LTE approximation is valid. |
4 Modeling procedure
We used the radiative transfer tool box Pandora (presented in Paper I), which in one of its implementations can use the radiative transfer code RADMC-3D to model the CH3CN line transitions in Sgr B2(M). A detailed description of the framework Pandora and the RADMC-3D code can be found in Paper I and Dullemond (2012). In this section we focus on the new routines implemented in Pandora that are necessary for the line modeling and that were therefore not described in the previous paper.
4.1 Modeling CH3CN with RADMC-3D
In order to solve the radiative transfer problem, RADMC-3D samples the density structure defined by the user by generating a grid via the method of adaptive mesh refinement. This means that parent cells are refined into children cells if the density gradient within the parent cell exceeds a certain value (details can be found in Paper I). To model the CH3CN line transitions towards Sgr B2(M), we used a cubic grid with a side length of 1 pc centered around Sgr B2(M). We set the allowed maximum density difference between the cells to 10%. This configuration results in a minimum cell size of 100 au and roughly 107 final cells. After the grid is generated the dust temperature is calculated self-consistently based on the luminosity sources by using a Monte Carlo approach (Bjorkman & Wood 2001).
In the last step of the radiative transfer simulations, we used RADMC-3D to calculate the CH3CN line emission. For this purpose, RADMC-3D first calculates the level populations for each cell in dependence of the gas temperature. We make two assumptions: first, that local thermodynamic equilibrium (LTE) conditions are present, i.e., that the energy levels are populated according to the Boltzmann distribution, and second, that the gas temperature equals the dust temperature, which is a valid assumption in high-density regions like those found towards Sgr B2(M).
Due to the high densities present in the small-scale structures of Sgr B2(M), the LTE approximation is a valid assumption. This can be seen by calculating the critical density ncrit, which is defined by the ratio of the Einstein Aul coefficient and the collisional rate coefficient Cul:
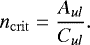 (1)
(1)
The collisional terms involve the square of the density, whereas the radiative terms only increase linearly with density. Thus, for densities much higher than ncrit, the collisional terms become dominant and the level populations are Boltzmann distributed, meaning that the LTE approximation is valid. Because Aul ∝ ν3, transitions with higher frequencies need higher densities to be thermally excited. For the transitions within one K-ladder of CH3CN this does not really matter because the transitions are closely spaced. We calculated the critical density of all J = 12−11 transitions of the main isotopologue based on the values of the Einstein Aul coefficient and the collisional rate coefficients at 100 K from the Leiden Atomic and Molecular DAtabase (LAMDA; Schöier et al. 2005) database. For all transitions the critical density is on the order of ~ 106 cm−3. Because the collisional rate coefficient depends on the temperature, the critical density also depends on the temperature. However, in the considered range of temperatures the order of magnitude remains the same. If we now compare the critical densities with the densities in Sgr B2, we find that the LTE approximation is valid within the small-scale structure of Sgr B2(M), for which the densities range from 4 × 107 to 5 × 108 cm−3. The density profiles of the cores of Sgr B2(M) are described by modified Plummer density profiles (see Paper I and Sect. 5). In Fig. 3 the modified Plummer density profiles used in the model are plotted together with the average of the critical densities. Depending on the exact parameters of the core, the LTE approximation is valid within ~ 104 au of the center of the core. We note that this is only a lower limit; the overall density is obtained as the superposition of the density profiles of all the cores, thus increasing the value of the density.
To calculate the line transitions in the LTE approximation, RADMC-3D needs information about the molecular energy levels and the transition parameters. The energy levels, transition frequencies, and Einstein Aul coefficients for the ground state transitions were taken from the CDMS (Cologne Database for Molecular Spectroscopy) catalogue (Müller et al. 2005; Endres et al. 2016), while the data of the vibrationally excited state v8 = 1 were taken from the JPL (Jet Propulsion Laboratory) database (Pickett et al. 1998). All these data are available via the Virtual Atomic and Molecular Data Centre (VAMDC).
4.2 Post-processing with CASA
The aim of the final step in the modeling procedure is to conduct a proper comparison of the radiative transfer images to the observational maps obtained with ALMA. To this end we developed a post-processing routine that uses the software package CASA2. The routine uses the uv-coverage of the ALMA observations to sample the simulated data cubes. This ensures that the post-processed files filter out and recover the same emission and spatial scales detectable in the observations. In the second step, we image the synthetic data cubes with the same imaging parameters used for the observational ALMA data. Finally, the post-processed synthetic data can be visually compared to the observational data to search for deviations that require a modification in the initial model. If a deviation is present, the physical structure of the model (i.e., molecular density, velocity field; see Sect. 5) is modified. This cycle is iterated to increase the consistency of the simulated images with the observational maps.
5 Physical model
The model used in this paper is based on the three-dimensional physical model of Sgr B2 developed in Paper I. The model was created by modeling the dust and free-free continuum emission of Sgr B2 by employing the radiative transfer toolbox Pandora. The density distribution of the cloud complex was reconstructed by comparing the emission of the model to available observational maps, including both single-dish (e.g., from Herschel/HiGAL, Molinari et al. 2010; Herschel/HIFI, Bergin et al. 2010) and high-resolution interferometric images (e.g., VLA radio-continuum maps, De Pree et al. 1998; Rolffs et al. 2011; SMA 345 GHz maps, Qin et al. 2011) covering a frequency range from 1 GHz to 4.5 THz.
The continuum maps obtained with ALMA (see Paper II) are compared with predictions from the model developed in Paper I andpresented in Fig. 12 of Paper II. We found a good correspondence between the predicted emission and the observed, with deviations of less than a factor of 2. Continuum maps at different frequencies together with spectral index3 maps were also compared to individual continuum synthetic maps at the same frequencies and to spectral index synthetic maps showing a good agreement between them (see Paper II). The main discrepancies were found to occur towards the central and brightest cores. The discrepancies can be due to different dust opacity coefficients throughout the Sgr B2(M) region. In a following paper, we will present an updated model for the continuum emission of Sgr B2, obtained by using high angular resolution ALMA observations at frequencies from 80 GHz to 275 GHz. In the current paper, we base our analysis on the physical model setup presented in Paper I, and we model several CH3CN line transitions observed with ALMA.
5.1 Physical model of Schmiedeke et al. (2016)
The physical model of Sgr B2 developed in Paper I consists of dense cores (gas and dust), stars, and H II regions. The model covers spatial scales from 45 pc down to 100 au. The density profiles of the individual cores are assumed to be modified Plummer functions given by
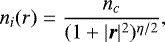 (2)
(2)
where nc is the central density given in H2 (cm−3) and |r| is the Euclidean norm including scaling factors
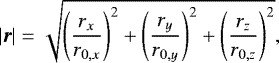 (3)
(3)
where rx,y,z are the coordinates and r0,x, r0,y and r0,z set the size of the core in the direction of each principal axis. The overall density structure is obtained by the superposition of the density profiles of all cores. The density in a cell j is then given by
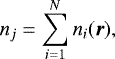 (4)
(4)
where i is the index of the dust core and N the total number of dust cores. The parameters of the cores are described in Table A.1. The left panel of Fig. 4 shows a synthetic map of the continuum emission at 242 GHz. The black numbers indicate the central position of the dust cores included in the model (see Table A.1). The model presented in Paper I, which describes all the scales from 100 au to 45 pc, also includes large-scale components to reproduce the extended envelope visible in the single-dish (and low-resolution) observations. The ALMA observations filter out the extended emission and are only sensitive to the small-scale dense cores.
All stars are assumed to be point sources, i.e., the radius is not taken into account. The model includes early-type high-mass stars and their H II regions that have been observed (e.g., De Pree et al. 1998; Rolffs et al. 2011). The stars included in the model, based on the existence of H II regions, only account for stars down to the B0 spectral type. All later spectral types with masses between 0.01 M⊙ and ~19 M⊙, i.e., stars which cannot produce H II regions detectable with current observations, were placed by an algorithm that randomly draws stars from the initial mass function (IMF) presented in Kroupa (2001) and distributes the stars randomly throughout the computational domain based on the gravitational potential. The observed H II regions created by massive stars are included in the model as Strömgen spheres, i.e., spherical structures with uniform electron density with no dust. A more detailed description of the model can be found in Paper I. In the following section we describe how the molecular density and velocity fields (necessary for line modeling) are set up in Pandora. All other constituents of the model, i.e., stars, H II regions, and dense cores that were introduced in Paper I, remain unchanged.
 |
Fig. 4 Left panel: synthetic map of the continuum emission of Sgr B2(M) at 220 GHz. The black numbers indicate the positions of the dust cores from the physical model introduced in Paper I. Right panel: integrated line intensity map of the J = 12−11, K = 3 transition predicted by the model. The black crosses indicate the positions of the dust cores as shown in the right panel. The green numbers indicate the position of the newly introduced molecular centers (see Sect. 5.3). The central region is masked out by the transparent hatched area as the CH3 CN emission in this region could not be reproduced by the model (see Sect. 6.6). |
5.2 Molecular density and velocity field
With the aim of modeling the CH3CN line emission, we implemented a molecular density and velocity field within Pandora and added them to the physical model retrieved from the continuum modeling. The molecular density is set up based on the Plummer density cores described before. Within Pandora it is possible to define a global molecular abundance factor Ω for each species. Based on this global abundance factor the molecular density in a cell j is obtained by multiplying the density in the cell nj by Ω. However, because the molecular abundance can vary significantly from position to position due to different temperatures, presence of a star, shocks, etc., it is necessary to be able to modify the molecular density on a local level. For this reason, we implemented an option to define a local abundance factor ωi for each Plummer density core. In summary, the molecular density n(CH3CN)j in a cell j is given by
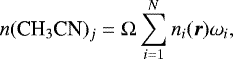 (5)
(5)
where i is the index of the dust core, N the total number of dust cores, Ω the global abundance factor, and ωi the local abundance factor of the ith dust core. The abundance for each cell is then calculated by dividing the total molecular density by the total H2 density of the cell.
In addition to the molecular density we also include a velocity field in order to describe the line profiles. This velocity field includes the velocity along the line of sight, as well as the line width due to turbulent motions of the gas. Within Pandora the velocity along the line of sight for each position is determined by defining the velocity vi for each individual Plummer core. This gives us the possibility of having different velocities at different positions. In order to ensure a smooth velocity field, the velocity of the gas vj in a cell j is determined by weighting the contribution of each core by its density at this specific cell as
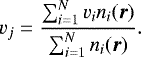 (6)
(6)
This means that the resulting velocity is dominated by the value vi of the core with the highest density at the considered cell. The turbulent line width σlinewidth is set up equivalently. The resulting line width is also determined by the thermal broadening.
 |
Fig. 5 Maps of the H2 (left panel) and CH3CN (middle panel) density and relative abundance of CH3CN with respect to H2 (right panel). The black numbers show the position of the dust cores, and the magenta crosses indicate the position of the newly introduced molecular centers, as shown in Fig. 4 (see also Table A.1). The gray circles indicate the positions and extent of H II regions, where the density of H2 and CH3CN is zero. The central region is masked out (transparent hatched area) as the CH3 CN transitions in this region cannot be reproduced well with the model (see Sect. 6.6). |
5.3 Parametrization of the molecular density field
As described in Sect. 5.2 the line transitions of CH3CN were calculated by introducing an abundance field consisting of individual cores with Plummer-like density profiles. Although we based our CH3CN abundance field on the density structure retrieved from the continuum emission by Paper I, we had to introduce modifications. These modifications are necessary because the morphology of the emission of CH3CN does not completely coincide with the continuum emission (see Fig. 1 and Sect. 3) and therefore also does not coincide with the position of the dust cores.
Moreover, the emission of CH3CN is much more extended than the continuum emission. We inspected the emission of the less abundant 13CH3CN isotopologue to determine whether the shift between line and continuum emission might be produced by opacity effects. The same morphology is retrieved for the isotopologue as for the main species. This indicates that the CH3CN abundance is in fact enhanced in the regions with local maxima, and that the morphology of the emission is not caused by opacity effects.
For this reason it is not possible to simply use the dust density structure retrieved from the continuum and to define abundance factors in order to model the CH3CN emission. Instead, we introduced new structures, which we call molecular centers (MC). These structures are located at the local maxima of the molecular line emission as seen in the CH3CN lines4. These molecular centers are diffuse in dust (H2 density) in order to make sure that the continuum remains unchanged, but they possess a high CH3CN abundance in order to reconstruct the local maxima of the line emission. The location of the molecular centers is shown in the right panel of Fig. 4. It is important to note that these newly introduced molecular centers are not necessarily real entities, but are a consequence of the current implementation of the abundance field parametrization in Pandora. By introducing these molecular centers, we are able to model the complex structure of the CH3CN emission which does not coincide with the continuum emission. Hence, only the abundance field resulting from the superposition of the cores and molecular centers as depicted in Fig. 5 should be considered as a real physical structure.
The parameters from the continuum cores and the parameters of the newly introduced molecular centers are given in Table A.1. Each core and molecular center is described by ten parameters: right ascension, declination, the displacement along the line of sight, the spatial scales as defined in Eq. (3), the exponent of the Plummer function, the central density of H2, the central density of CH3CN, and the velocity along the line of sight. For the cores located at the central region of Sgr B2(M) (M-SMA-1a, M-SMA-1b, M-SMA-1c, M-SMA-1d, M-SMA-2a, and M-SMA-2b) no central density of CH3CN is given because the line emission of this region was not modeled (see Sect. 6.6).
In Fig. 5 density maps of H2 and CH3CN as well as of the relative abundance of CH3CN with respect to H2 are depicted. The relative abundance is considerably lower at the position of the continuum cores where the H2 density is the highest. The correlation between the low abundance of CH3CN and the position of the continuum cores indicates that the chemistry at these very dense and hot regions is different and leads to the destruction of CH3CN (see Sect. 6.4).
6 Analysis of simulated and observational data
In the following sections we compare the simulated data to the observational data. For this purpose, in Sects. 6.1 and 6.2 we analyze the general morphology of the CH3CN emission by comparing integrated intensity maps, and spectra taken from the center of the cores. In Sect. 6.3 we discuss the validity of the temperature distribution determined by RADMC-3D. The abundance and velocity field are discussed in Sects. 6.4 and 6.5. Then in Sect. 6.6 we discuss the observational data from the central region, and the limitations of the current model in this region. In Sect. 6.7 we present the results from the model compared to the observations for the isotopologue 13CH3CN.
6.1 Distribution of the CH3CN emission
As already discussed in Sect. 5.2, the morphology of the CH3CN emission does not completely coincide with the continuum emission. For this reason, it was necessary to introduce molecular centers with a high CH3CN abundance in order to reconstruct the CH3CN emission from the observations. The general morphology of the CH3CN emission can be investigated by producing integrated intensity maps or zeroth-order moment maps following the expression
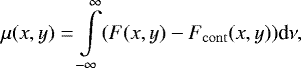 (7)
(7)
where F(x, y) is the flux at position (x, y) and Fcont the corresponding continuum flux. The zeroth-order moment maps of the J = 12−11, K = 3 transition obtained from the observations and the simulated model are shown in Fig. 6. This line was used to calculate the zeroth-order moment maps because, in most cases, it is not affected by significant line blending of other species and because it is one of the brightest lines. The comparison of the observed and simulated data shows that the emission obtained from the physical model exhibits in general the same morphology as the observed emission. It is evident that the emission indeed peaks at the position of the newly introduced molecular centers and not at the continuum cores. In the northern part we find two regions with strong emission that do not coincide with the continuum cores. For this reason it was necessary to introduce two molecular centers, MC-4 and MC-11, in order to account for the strong emission in these regions. The integrated line intensity in the northern part reaches values up to 120 K km s−1. This is significantly lower than in the southern part, where CH3CN is more abundant and the emission peaks at around 800 K km s−1. The central part of Sgr B2(M) exhibits a complex combination of CH3CN emission and absorption features (cf. Fig. 1) and only shows absorption at the considered frequency range of the depicted maps. In Sect. 6.6 we discuss in greater detail the modeling of the central region.
In the southern part four molecular centers were introduced to reconstruct the morphology of the CH3CN emission and an additional molecular center was placed near the continuum core M-SMA-10. The molecular center MC-9 was introduced in order to account for the strong emission in the most southern part, where the CH3CN emission is much more extended than the continuum. Furthermore, the molecular center MC-68 was placed between the continuum cores M-SMA-6 and M-SMA-8, and two additional molecular centers MC-7a and MC-7b were placed north and south of the continuum core M-SMA-7, respectively.
From the difference map of the observed and simulated data, we find a good agreement in regions where the CH3CN emission is strong and decreases in regions with weaker emission. This behavior can be more clearly seen by investigating radial profiles of the integrated line intensity. Radial profiles taken from the center of different molecular centers are shown in Fig. 7. The radial profiles proceed in all cases from west to east. These cuts illustrate that the morphology of the CH3CN emission can be described considerably well with modified Plummer-like functions. However, due to the modeling of the cores as spherical structures, deviations from the real structures with a certain degree of asymmetry are inevitable. Additionally, radial profiles are useful tools for identifying local maxima in the emission, e.g., the radial profile centered around molecular center MC-68 reveals that there is an additional peak in the integrated intensity farther to the east, which is associated with the molecular center MC-7b.
6.2 Spectra of the main isotopologue
In this section we compare the spectra of the observational and simulated data taken from the center of the different cores and molecular centers. On the basis of the transitions presented in this section, we reconstructed the abundance field of CH3CN (see Sect 6.4). The rotational spectrum of a symmetric-top molecule like CH3CN consists of a series of components (determined by the quantum number K) for each rotational transitions (determined by the quantum number J). This K-ladder structure results in multiple lines with different energies that are closely spaced in frequency. Several spectra taken from the center of different cores and molecular centers are shown in Fig. B.1. The intensity of the spectra is given in brightness temperatures. These spectra are only taken from cores and molecular centers located at the northern or southern regions of Sgr B2(M), as shown in Fig. 6; the spectra of the central region are discussed in Sect. 6.6.
The spectra show the frequency range from 220.55 to 220.80 GHz, which includes the first seven K-components of the J = 12−11 transition of the main isotopologue. The K = 0 and K = 1 are spaced very closely in frequency and therefore often appear as just one line. The observational data also contain higher K-components, but they are weak and sometimes blended with other species. Spectra of the J = 13−12 and J = 14−13 transitions can be found in Figs. B.2 and B.3. The K = 3 component, i.e., the linewith the fourth highest transition frequency, was used to determine the zeroth-order moment maps discussed in Sect. 6.1 and presented in Fig. 6. The intensity of this line is relatively high because the K = 3 state belongs to the ortho-configuration of CH3CN with a higher statistical weight.
The intensity of the simulated lines is in agreement with the observational spectra. The agreement is very good for the first K-components up to K = 3 and decreases for higher components. However, it is important to point out that the deviations between observational and simulated data are partly caused by line blending. Line blending describes the possibility that spectral lines undergo interference from lines of other molecular species or unidentified features and causes a major difficulty in analyzing and comparing the intensities and widths of observed spectral lines. Sgr B2 exhibits an extraordinarily rich chemistry and is composed of various kinds of molecules. As a consequence, the number of detectable species and spectral lines is large and some of the CH3CN lines are indeed blended by other lines. For example, the K = 5 component is strongly blended by two spectral features, one of them brighter than the CH3CN transition itself. For this reason the intensity of this component in the simulated data is usually smaller when compared to the observational data. The K = 4 transition is also blended with at least another strong line, but not as drastic as the K = 5 component. The significance of the line blending effects also depends on the position of the map. At locations close to the center of Sgr B2(M), e.g., the center of the molecular center MC-7a, the line blending effects are very strong due to the high line density. The spectrum of the molecular center MC-7a shows that at this position the intensity does not return to the continuum level between the individual lines. In contrast, at positions farther away from the dense center, e.g., core M-SMA-12, the individual lines are more isolated and line blending effects are less significant. Taking the blending into account would require detailed radiative transfer modeling of all species, which is beyond the scope of this paper.
Two molecules, among others, that blend with the J = 12−11 transitions are HNCO and SO2. The J = 10−9, Ka = 1, Kc = 9− 8 transition of HNCO has a rest frequency of 220.58475 GHz. This strong line is located very close to the J = 12−11, K = 6 transition with 220.593987 GHz and causes significant line blending due to its higher intensity. SO2 has two transitions at 220.59714 GHz and 220.618499 GHz. The latter could be the origin of the line detected between the K = 6 and K = 5 transitions of CH3CN. Instead, CH3NH2 has three transitions, which are detected at rest frequencies of 220.76060, 220.78077, and 220.80552 GHz. The blending lines were identified using the software package XCLASS (Möller et al. 2017), which makes use of the CDMS and JPL catalogues. A full identification of the molecular content in the Sgr B2(M) will be presented in a forthcoming paper (Möller et al. in prep).
Nonetheless, there are also K-components that are not affected significantly by line blending (e.g., K = 4), but whose line intensity is still underestimated by the model. This indicates that the gas temperature, which is assumed to be equal to the dust temperature, is too low and therefore the higher K-transitions, which exhibit higher energies, are underpopulated. A detailed discussion of the temperature distribution and the possible reasons for the discrepancy is presented in Sect. 6.3.
Moreover, the spectra emphasize that although the continuum emission is brighter at the position of the continuum cores than at the newly introduced molecular centers, the continuum-subtracted line emission is much stronger at the position of the molecular centers. This can be seen by comparing the spectra towards the molecular center MC-9 and the close dust core M-SMA-9. Also noticeable are the spectra from M-SMA-10 and MC-10, which are very close in space. These regions have relatively small line widths, but the lines exhibit extended wings, which could be related to the presence of a high-velocity outflow.
Finally, there is a qualitative difference between spectra from the northern and the southern regions of Sgr B2(M). The spectra from the southern region only show emission features, whereas the northern regions have a combination of emission and absorption features. The absorptions, which are overestimated by the model, are likely to be produced by the presence of H II regions (numerous in the northern and central regions of Sgr B2(M), see Fig. 2) that act as bright background continuum sources.
 |
Fig. 6 Integrated intensity maps (or zeroth-order moment maps) of the observational (left column) and simulated (middle column) data for the CH3CN J = 12−11, K = 3 transition. The right panels show the difference between the observational and the simulated data. The center row shows the entire Sgr B2(M) complex except for the central region, which is masked out with a transparent hatched area. The green and magenta boxes indicate the zoomed-in regions that are depicted in the top row (northern part of Sgr B2(M)) and the bottom row (southern part of Sgr B2(M)). As in previous figures, the black numbers indicate the position of the dust cores, whereas the green and magenta crosses depict the positions of the molecular centers (see Table A.1). |
 |
Fig. 7 Radial profiles of the integrated line intensity for the CH3CN J = 12−11, K = 3 transition. The radial profiles proceed from west to east and r = 0 corresponds to the center of the considered molecular centers. The first two profiles (MC-4 and MC-11) are taken from the newly introduced molecular centers in the northern region (cf. Fig. 4). The third profile (MC-68) is taken from the molecular center located between the continuum cores M-SMA-6 and M-SMA-8. The last profile (MC-9) is centered around the molecular center south to the continuum core M-SMA-9. In all panels the blue dashed line shows the observational data, whereas the red solid line corresponds to the simulated data. |
 |
Fig. 8 Temperature distribution at the z = 0 plane for SgrB2(M) as produced by the model presented in Sect. 5. The central region, which is discussed in Sect 6.6, is shown by the transparent hatched area. |
6.3 Temperature distribution
The temperature of the gas is a crucial factor that shapes the spectral features of the line emission of a molecule. In the LTE approximation the temperature alone determines the level populations and thereby affects the intensity of transitions. In our model the dust temperature is calculated self-consistently by RADMC-3D based on the available luminosity produced by the stars of the cluster. We assumed the gas temperature to be equal to the dust temperature since at these high densities we expect them to be coupled (e.g., Goldsmith 2001).
The temperature distribution determined by RADMC-3D for Sgr B2(M) at the z = 0 plane is shown in Fig. 8. The temperature ranges from around 50 to 900 K, with the hottest regions located at the position of the continuum cores. The spherical structure in the right lower corner of the southern part is associated with an H II region. A comparison of Figs. 5 and 8 shows that the hot temperature regions coincide with the continuum cores where the relative abundance of CH3CN is relatively low.
In Sect. 6.2, we compared the observational and simulated results of the J = 12−11 transition. For most of the lines there is a good agreement between simulation and observation, although the higher K-transitions are underestimated in some cases. This is partly caused by line blending, so that the line intensities appear to be stronger. However, there are also K-transitions that are apparently unaffected by line blending but nonetheless show an underestimated intensity. This may suggest that the gas temperaturein the model is too low. As described in Sect. 4, the temperature is calculated based on the stellar luminosity, and it does not include a possible contribution from accretion events. Furthermore, the gas temperature can also be increased byother heating mechanisms, for example with a mechanical origin such as turbulent dissipation or outflow shocks that are not included in the model, or local X-rays which are not considered at all. For this reason, the temperature distribution should be regarded as a lower limit for the gas temperature. Another possibility for the underestimation of the excitation is that it is affected by radiative pumping from external dust radiation, which might involve the vibrationally excited level (e.g., Hauschildt et al. 1993). This effect can produce deviations from LTE if the radiation temperature differs from the local gas kinetic temperature, even if the latter is coupled to the local dust temperature.
The states involved in the transitions considered in Sect. 6.2 have energies in the range from approximately 60 to 325 K, so that most of the states have relatively low energies. In order to investigate the validity of the temperature distribution, we have also analyzed higher energy transitions from the CH3CN vibrationally excited state v8 = 1. In particular, the transition ν8 = 1, J = 12−11, and K = 1 − (−1), with a rest frequency of 221.62582 GHz. The involved states have energies of 577 K and 588 K and hence primarily trace the hot gas. Figure 9 shows observational spectra as well as the prediction by our model for the vibrationally excited transition. Further spectra are shown in Fig. B.4. At the center of most cores and molecular centers the vibrationally excited transition is clearly detected. However, there are also regions where the transition is hardly visible, e.g., core M-SMA-12. In most cases the intensity of the transition is only slightly underestimated by our model (see, e.g., cores M-SMA-4 and M-SMA-9), indicating that the calculated temperature is consistent with the observations. However, other regions like cores M-SMA-6 and M-SMA-8 have observed lines for the vibrationally excited transition that are brighter than predicted by the model.
In order to investigate by how much the gas temperature is underestimated, we produce different models in which the gas temperature is increased compared to the dust temperature. The results of these tests are shown in Fig. 9 for cores M-SMA-6 and M-SMA-8. The figures show the spectra of the vibrationally excited transition for the temperature calculated by RADMC-3D and for two runs where the gas temperature was increased by 50 GHz and 150 K. While the simulated intensities using the dust temperature as the gas temperature are below the observed intensities, the intensity of the lines in the simulated data is in good agreement for both cores when considering an increase of 150 K in the gas temperature. This suggests that the gas temperature is not coupled to the dust temperature and should be higher in some regions, although it is not drastically underestimated.
6.4 CH3CN abundance
In this section we discuss the abundance distribution of CH3CN in Sgr B2(M). The relative abundance of CH3CN varies by three orders of magnitude within the northern and the southern regions of Sgr B2(M). A histogram of the pixel distribution of the relative abundance (CH3CN with respect to H2) can be seen in Fig. 10. For the northern region the relative abundance ranges from 4 × 10−11 to 2 × 10−8 with an average value of 1.1 × 10−9. In the southern region the relative abundance ranges from 2 × 10−10 to 5 × 10−7 with an average value of 9.0 × 10−8. The histogram illustrates that the abundance of CH3CN is significantly higher in the southern region than in the northern region. This may be related to the stronger feedback destroying CH3CN in the northern regions where more H II regions are present. A previous study of the CH3CN emission in Sgr B2 derive an average abundance for the hot cores of ~7 × 10−11 (de Vicente et al. 1997), which is much lower than our estimated value. However, the angular resolution of the observations by de Vicente et al. (1997) (~10–30′′) is coarser and most likely smears out the CH3CN emission associated with small-scale structures that are resolved in our data (with a resolution of 0. ′′ 7).
In Fig. 5 we can see an anti-correlation between the CH3CN abundance and the position of the dense cores with large H2 densities. The anti-correlation between H2 and CH3CN can be seen more clearly in Fig. 11, where we show the relation between the relative abundance of CH3CN as a function of the H2 density. The relative abundance of CH3CN decreases with increasing density according to a power law with an exponent of − 0.92. We find a similar behavior for the CH3CN abundance as a function of the temperature (see Fig. 12). In the figure we show how the relative CH3CN abundance decreases with increasing temperature. The relative CH3CN abundance is high in regions with temperatures around 150–250 K, and decreases by one or two orders of magnitude for temperatures in the range 300–500 K.
All this together suggests the existence of chemical processes in the dense regions that lead to the destruction of CH3CN. Although this needs further investigation, which will be done in forthcoming papers using chemical models, we indicate some aspects that may help to understand the anti-correlations shown in Figs. 11 and 12. First, the temperature itself has an important impact on the chemistry because it determines the efficiency of chemical reactions especially on the dust grains. Second, the radiation field of the stars, which are evolving inside the dense cores, affects the chemistry by photo-dissociation reactions and ionizations and might reduce the abundance of CH3CN at the central part of these cores. Chemical models that investigated the chemistry of nitrogen-bearing molecules including CH3CN were conducted by Rodgers & Charnley (2001). In their models they assumed a density of 107 H2 cm−3 and constant temperatures in the range of 100–300 K. Additionally, they considered different ice compositions. Depending on the time evolution, they find abundance values of CH3CN ranging from 10−9 to 10−7 for a temperature of 300 K. We find an averaged abundance of roughly 3 × 10−9 at 300 K, which in their model would correspond to a time of 2 × 104 yr. For a temperature of 100 K they find significantly lower abundance values ranging from 10−9 to only 10−8. In contrast to our results, which show a decreasing CH3CN abundance with increasing temperature, their results seem to show an opposite behavior. However, in these models they do not take into account photo-dissociation reactions. If these reactions are included, they point out that the abundance of CH3CN drops by a factor of 100after 5 × 105 yr, even if onlycosmic-ray-induced photo-dissociation is included. Their results show that CH3CN can be destroyed effectively by photo-dissociation reactions. Hence, as many continuum cores in Sgr B2(M) already contain evolving stars that have a radiation field, this could be the reason for the low abundance of CH3CN at the center of these cores. In the future it will be interesting to investigate if chemical models of hot cores with the parameters (e.g., density, radiation field) like those found towards the cores of Sgr B2(M) can reproduce the radial distribution of CH3CN.
 |
Fig. 9 Spectra of the vibrationally excited transition ν8 = 1, J = 12−11, K = 1 − (−1) taken from the center of different cores. The blue solid line shows the observational data, while the red solid lines show the simulated data when the gas temperature equals the dust temperature. The bottom panels also show the simulated spectra after modifying the gas temperature by 50 K (green) and 150 GHz (yellow), as discussed in Sect. 6.3. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
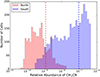 |
Fig. 10 Histogram of the distribution of the relative abundance of CH3CN for the northern (red) and southern (blue) region of Sgr B2(M). For this purpose cubes were placed around the northern and southern parts, which were composed of cells with side lengths of 695 AU. The vertical lines indicate the averaged values. |
 |
Fig. 11 Histogram of the relative abundance of CH3CN as function of the H2 density based on the developed physical model. The CH3CN abundances decrease with the H2 density with a function that can be described as a power law with an exponent of − 0.92. |
 |
Fig. 12 Histogram of the relative abundance of CH3CN as function of the temperature. |
6.5 Core velocities and turbulent line width
The analysis of spectral lines not only provides information about the temperature and the density of certain molecular species, but also provides information about the velocity structure of a cloud and its internal turbulent motion. The component of the velocity along the line of sight of individual cores can be obtained by the shift of the spectral line away from the rest frequency due to the Doppler effect. Information about the internal turbulent motion can be obtained by analyzing the line shape of spectral lines.
The spectra shown in Fig. 13 show the difference in velocity for the emission in different cores. For a northern core like N-SMA-12 (left panel) the lines are clearly shifted to high frequencies (i.e., blue-shifted) with respectto the rest frequency. On the contrary, a southern core like M-SMA-6 has the lines shifted towards lower frequencies (i.e., red-shifted). The different velocities of the cores can be seen in the values listed in Table A.1. Figure 14 shows a velocity (along the line of sight) map of the CH3CN emission in Sgr B2(M) as obtained from the model. Southern regions are clearly red-shifted with respect to the northern regions. This suggests an overall velocity gradient from north (blue-shifted velocities around 50 km s−1) to the south (red-shifted velocities around 70 km s−1).
The width of a spectral line is determined by the thermal broadening, together with non-thermal motions such as turbulence and global scale motions unresolved in our beam size. The line width σlinewidth as calculated by RADMC-3D in Pandora includes a turbulent and a thermal component as
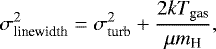 (8)
(8)
where σturb is the (micro)turbulent line width, Tgas the gas temperature, k the Boltzmann constant, μ the mean molecular weight, and mH the mass of a hydrogen atom. In our model of Sgr B2(M) we find differences in the turbulent line width between the northern and southern regions. From the depicted spectra in Fig. 13 (see also Fig. 1) the northern cores (e.g., core N-SMA-12) have a narrower line width compared to the southern cores (e.g., core N-SMA-6). All southern cores and molecular centers are modeled with a turbulent line width of 5 km s−1, except for M-SMA-10 and MC-10 for which we used 2.5 km s−1. In contrast, all the northern cores and molecular centers (MC-4, MC-11, M-SMA-4, M-SMA-11, M-SMA-12) exhibit a turbulent line width of only 2.5 km s−1. The central region exhibits broad line widths similar to the southern region. This indicates that the internal turbulent motions are larger in the southern and central regions of Sgr B2(M) compared to the northern region.
6.6 CH3CN features at the central region
So far we have only presented the simulated and observational data from the northern and southern regions of Sgr B2(M) as selected in Fig. 6, which show CH3CN spectral features in emission with the exception of only a few cases. The central region exhibits much more complex features of CH3CN. Spectra taken from the center of cores, which are located in the central region of Sgr B2(M), are presented in Fig. B.5 and exhibit a combination of emission and absorption features.
The reason for these complex spectra is that the continuum emission is very strong at the center of Sgr B2(M). As a consequence, the CH3CN between the observerand the sources leads to deep absorption features in the spectra. Because many H II regions are present in the center of Sgr B2(M), one might think that they are the reason for the deep absorption features. However, the positions of the known H II regions do not entirely coincide with the spatial extent of the observed absorption lines, indicating instead that the dust emission is the cause (see Fig. 2).
As already mentioned, the physical model presented in this paper is not able to reproduce the complex spectra at the center of Sgr B2(M). We investigated various modifications to the model in order to retrieve the behavior at the center, but could not find a model that reproduces all the features of the CH3CN transitions. Nonetheless, we give an overview of these models and briefly discuss where they failed to reproduce the observed features.
First, we tried to reproduce the absorption features by including the large-scale envelope surrounding Sgr B2(M). In addition to the small-scale structure of Sgr B2(M), the physical model developed in Paper I also includes an envelope surrounding Sgr B2(M) with an extent of ~ 104–105 au and densities of ~ 105–106 cm−3. One indication that the absorption is caused by CH3CN located in the largerscale structure (where temperatures are much lower) is that in the vibrationally excited transition (which have very high energies) we see almost no absorption features (see Fig. B.5). By defining an abundance factor of CH3CN for the envelope of 10−7 and a velocity along the line of sight of 44 km s−1, we were able to reproduce the deep absorption features at the center (see Fig. 15). However, the model with a CH3CN abundance of 10−7 in the envelope also produces absorption features in the northern and southern regions of Sgr B2(M) where no deep absorption features are observed. This is likely due to the spatial extent of the envelope, which does not cover only the central region of Sgr B2(M) but rather the entire complex. As a consequence, the CH3CN in the envelope causes absorption features towards the center and also in the northern and southern regions, even though the continuum emission in those regions is much weaker (see Fig. 15).
With the knowledge that the absorption is not caused by the gas in the small-scale structure, but by the gas located farther out, we investigate a model with a shell of enhanced CH3CN density surrounding the central part of Sgr B2(M). We consider a shell with an extent of 5000 au, which only covers the central part but not the northern and southern regions of Sgr B2(M). This prevents the model from producing absorption features at these regions. However, the spectra towards the central positions show emission and no clear sign of absorption. In order to evaluate the origin of this effect we used the software package XCLASS (Möller et al. 2017) to fit the spectrum towards the center of Sgr B2(M) and determine the temperature of the absorption layer. The best fit of the absorbing CH3CN is obtained for a temperaturein the range ~100–150 K. In XLASS a model with a Gaussian-like density distribution centered around 5000 au, a temperature between ~100 and 150 K, and a column density of 2.9 × 1014 cm−2 can reproduce the deep absorption features towards the central region (see Fig. 16). The temperature distribution calculated in our model (obtained self-consistently by RADMC-3D) along the line of sight at the center (see Fig. 17) shows that the temperature range of ~100–150 K is reached at a distance of ~20 000 au, whereas a shell at 5000 au would have a temperature of ~300–400 K, and therefore would still lead to emission features rather than absorption. For this reason the model with a shell of increased CH3CN abundance does not lead to absorption when using the temperature distribution of RADMC-3D.
All this suggests that the gas temperature distribution predicted by the model may differ in the central part of Sgr B2(M) with respectto the real distribution. In this sense, the analysis of the ALMA continuum images (see Paper II) revealed a number of continuum sources not included in the original physical model (Paper I), which might have an impact on the temperature distribution.An update of the continuum model using the ALMA data presented in Paper II and new ALMA data at lower frequencies (80–150 GHz) is planned in a forthcoming paper. Moreover, we also have to be aware that in all the described models the CH3CN density field is constructed based on spherically symmetric Plummer-like clumps. Hence, the effects of deviations from this spherical symmetry, like elongated structures along the line of sight, may help to explain the observed absorption features since higher column densities can be reached at regions where the temperature is favorable for absorption.
 |
Fig. 13 Spectra taken from a northern (M-SMA-12) and a southern (M-SMA-6) core to illustrate the shift in frequency due to the velocity component along the line of sight. The green, dashed vertical lines indicate the rest frequency of the J = 12−11, K = 0 transition. The core M-SMA-12 exhibits a blue-shifted velocity along the line of sight of 50 km s−1, while core M-SMA-6 has a red-shifted velocity of 67 km s−1. The systemic velocity of Sgr B2(M) is about 64 km s−1. |
 |
Fig. 14 Distribution of the velocity along the line of sight at the z = 0 plane, as derived from the model of Sgr B2(M). The central region is masked out by a transparent, hatched area. The black numbers and green crosses indicate the dense cores and molecular centers, respectively, as in Fig. 4. |
 |
Fig. 15 Spectra of the model after including the large-scale envelope with a CH3 CN abundance of 10−7. The left panel shows a spectrum towards the center where absorption features associated with the low-K transitions are reproduced. The right panel shows a spectrum towards the southern location MC-68. This model predicts absorptions for the low-K transitions that are not visible in the observational data. |
 |
Fig. 16 Comparison of the CH3CN J = 12−11 observational spectrum (in black) towards a central position in Sgr B2(M) and a fit (in red) obtained with the software package XCLASS. The best fit is obtained for a temperature range ~100–150 K and a column density of 2.9 × 1014 cm−2. |
 |
Fig. 17 Distribution of the dust temperature relative to the center of the model along the line of sight. The plane z = 0 has a temperature of about 700 K, while temperatures of ~100–150 K are found at a distance of ~20 000 au. |
6.7 Isotopologue 13CH3CN
The spectral line survey contains transitions of the isotoplogues of CH3CN. We consider the isotopologue in which one of the carbon atoms 12C is exchangedby the isotope 13C. Due to the increased mass of the isotopologue it also possess a larger moment of inertia, which results in a shift of the energy levels. For this reason, the isotopologues exhibit transition frequencies which are different from the main isotopologue. Because the moment of inertia also depends on the position of the 13C atom, the two isotopologues 13CH3CN and CH CN also have different transition frequencies. The isotopologue CH
CN also have different transition frequencies. The isotopologue CH CN exhibits transitions that are very close to the main isotopologue and therefore they are strongly blended, whereas the isotopologue 13CH3CN emits at frequency ranges different from the main isotopologue. For this reason, we considered 13CH3CN in order to study the isotope ratio.
CN exhibits transitions that are very close to the main isotopologue and therefore they are strongly blended, whereas the isotopologue 13CH3CN emits at frequency ranges different from the main isotopologue. For this reason, we considered 13CH3CN in order to study the isotope ratio.
Spectra of 13CH3CN taken from the center of the cores and molecular centers of Sgr B2(M) are shown in Fig. B.6. Zeroth-order moment maps comparing the observational data and simulated data of the isotopologue are shown in Fig. 18. From the observational maps it is evident that although the emission of the isotopologue does not show exactly the same morphology as the main isotopologue, the emission does coincide with the positions of the newly introduced molecular centers. This indicates that the abundance is in fact enhanced in those regions and the morphology is not caused by opacity effects.
We used an isotopologue ratio of 12CH3CN/13CH3CN = 20 in order to obtain a fit of the isotopologue transitions. The images in Fig. 18 illustrate that the model reproduces the general morphology of the emission. Nonetheless, there are some differences. In the northern region the strong emission peak in the east is underestimated by the model and it is slightly shifted to the north. In the southern part the strong emission towards MC-7a and M-SMA-7 is considerably underestimated by the model, whereas the emission at core MC-7b is overestimated. Moreover, the spectra depicted in Fig. B.6 in Appendix show that at some cores and molecular centers (e.g., MC-68, M-SMA-7, M-SMA-6, M-SMA-7a) the emission is slightly underestimated. In order to reproduce the strong emission at these regions, it is necessary to decrease the isotopologue ratio for these cores considerably. However, studies of the isotope ratio 12C/13C at the Galactic center determined values of ~20 (Wilson & Rood 1994). Furthermore, the isotopologue ratio of 20 used in the model gives good results when comparing the emission in the other regions of Sgr B2(M), and therefore it would be necessary to introduce an isotopologue ratio that varies within Sgr B2(M) in order to fit all cores and molecular centers.
 |
Fig. 18 Integrated intensity maps (or zeroth-order moment maps) of the observational (left column) and simulated (middle column) data for the CH3CN J = 13−12, K = 0, 1 transitions of the isotopologue 13CH3CN. The panels in the right column show the difference between the observational and the simulated data. The central row shows the entire Sgr B2(M) complex except for the central region, which is masked out with a transparent, hatched area. The green and magenta boxes indicate the zoomed-in regions that are depicted in the top row (northern part of Sgr B2(M)) and the bottom row (southern part of Sgr B2(M)). As in the previous figures, the black numbers indicate the position of the dust cores, whereas the green and magenta crosses depict the position of the molecular centers (see Table A.1). |
7 Summary and outlook
In this paper we present ALMA observations of different CH3CN transitions in the range 211–275 GHz (see details on the observations in Paper II) towards the hot molecular core Sgr B2(M). The achieved angular resolution of 0. ′′7 (or ~6000 au) permitted us to study the structure of the CH3CN emission at scales not previously studied before. We modeled the CH3CN emission using a three-dimensional radiative transfer model (presented in Paper I) that contains the physical structure (i.e., distribution of dense cores, H II regions, stars) of Sgr B2(M). We reconstructed the abundance field of CH3CN towards Sgr B2(M), and studied the velocity and line width variations in the region. Our main results are listed in the following:
-
We derive an average relative abundance of CH3CN (with respect to H2) of 1.1 × 10−9, covering a range from 4 × 10−11 to 2e × 10−8, towards the north of Sgr B2(M) and an abundance of 9 × 10−8, covering a range from 2 × 10−10 to 5 × 10−7, towards the south.
-
We find that the CH3CN relative abundance is lower at the center of the very dense and hot continuum cores, causing the general morphology of the CH3CN emission to not completely coincide with the dust continuum emission.
-
The spectral features of the CH3CN transitions (e.g., line intensity, line width) are reproduced well by the model; however, and especially in the southern region of Sgr B2(M), the higher K-transitions and the vibrationally excited transition are underestimated. This indicates that the gas temperature is higher than the dust temperature or that radiative pumping plays a role.
-
The velocity component along the line of sight varies from 67 km s−1 (towardsthe south) to 50 km s−1 (towardsthe north), where the systemic velocity of the cloud is about 64 km s−1.
-
The central region of Sgr B2(M) exhibits complex CH3CN spectra with a combination of absorption and emission features. We study whether the absorption features are related to the presence of H II regions, but conclude that their origin is the presence of bright dust, which at this high angular resolution reaches a high brightness temperature (about 180 K) and produces the absorption features. Despite different attempts to model this region, our current model does not produce accurate results for all the CH3CN transitions. We suggest that the calculated temperature distribution deviates from the real distribution towards the center or that the assumed spherical symmetry of the dense cores included in the model may be not accurate enough.
Modeling the emission of CH3CN for Sgr B2(M) raised some interesting questions, which deserve further investigation in the future. Some of them are listed in the following:
-
Can chemical models of hot molecular cores reproduce the low relative CH3CN abundance found towards the densest and hottest regions of the cores in Sgr B2(M)? In this sense, it is worth studying in more detail which chemical processes are crucial in the destruction of CH3CN.
-
The velocity field determined from CH3CN needs to be compared with the velocity field of other molecular tracers (e.g., SiO which traces outflow and shocked gas) and recombination lines (which trace the motions of the ionized gas) in order to study the origin of the velocity gradient from north to south observed in the dense gas.
-
Can a better determination of the continuum model or the inclusion of non-spherical symmetric structure reproduce the absorption and emission spectral line features observed towards the central region of Sgr B2(M)? Further investigations and an ongoing improvement of the model may help to better constrain the physical properties of this central region.
-
Extending the model of CH3CN to the northern hot core of Sgr B2, i.e., Sgr B2(N), will be more challenging (due to the higher density of spectral line features), but will allow us to compare the properties derived in two distinct but close high-mass star-forming sites: Sgr B2(M) being more evolved and less dense than Sgr B2(N).
Acknowledgements
This work was supported by the Deutsche Forschungsgemeinschaft (DFG) through grant SFB 956 (subproject A6) and from BMBF/Verbundforschung through the Projects ALMA-ARC 05A11PK3 and 05A14PK1. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.00332.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ.
Appendix A Parameters of the cores and molecular centers of the model of Sgr B2(M)
In Table A.1 we list the cores included in the model of Sgr B2(M). The first cores reproduce the dust continuum emission and correspond to the cores introduced in the physical model presented in Paper I. The second list of cores correspond to the molecular centers introduced to reproduce the extension of the CH3CN emission.
Parameters of the cores and molecular centers of the model of Sgr B2(M).
Appendix B Observed and simulated spectra
In Figs. B.1–B.6 we show the observed (in blue) and the simulated (in red) spectra of the different CH3CN, 13CH3CN, and vibrationally excited states towards the different dense cores and molecular centers included in the model (see Table A.1).
 |
Fig. B.1 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 12−11 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
 |
Fig. B.2 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 13−12 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
 |
Fig. B.3 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 14−13 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
 |
Fig. B.4 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the vibrationally excited transition CH3 CN ν8 = 1, J = 12−11, K = 1 − (−1). The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
 |
Fig. B.5 Observational spectra (in black) of the ground state CH3CN J = 12−11 transition towards the cores located in the central region of Sgr B2(M). The continuum level for core M-SMA-1a is about 60 K, for core M-SMA-1b about 150 K, and for the remaining cores about 100 K. A number of absorption and emission spectral linefeatures are visible in all the spectra. |
 |
Fig. B.6 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the 13CH3 CN J = 13−12 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
References
- ALMA Partnership, Fomalont, E. B., Vlahakis, C., et al. 2015, ApJ, 808, L1 [Google Scholar]
- Araya, E., Hofner, P., Kurtz, S., Bronfman, L., & DeDeo, S. 2005, ApJS, 157, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Phillips, T. G., Comito, C., et al. 2010, A&A, 521, L20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bjorkman, J. E., & Wood, K. 2001, ApJ, 554, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2006, J. Mol. Spectrosc., 240, 153 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R. 2005, in Massive Star Birth: A Crossroads of Astrophysics, eds. R. Cesaroni, M. Felli, E. Churchwell, & M. Walmsley, IAU Symp., 227, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Sánchez-Monge, Á., Beltrán, M. T., et al. 2017, A&A, 602, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Pree, C. G., Goss, W. M., & Gaume, R. A. 1998, ApJ, 500, 847 [NASA ADS] [CrossRef] [Google Scholar]
- de Vicente, P., Martin-Pintado, J., & Wilson, T. L. 1997, A&A, 320, 957 [NASA ADS] [Google Scholar]
- Dullemond, C. P. 2012, RADMC-3D: A Multi-purpose Radiative Transfer Tool, Astrophysics Source Code Library [record ascl:1202.015] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectrosc., 327, 95 [Google Scholar]
- Gadhi, J., Lahrouni, A., Legrand, J., & Demaison, J. 1995, J. Chim. Phys. Physico-chim. Biol., 92, 1984 [NASA ADS] [CrossRef] [Google Scholar]
- Gaume, R. A., Claussen, M. J., de Pree, C. G., Goss, W. M., & Mehringer, D. M. 1995, ApJ, 449, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F. 2001, ApJ, 557, 736 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Goldsmith, P. F., Lis, D. C., Hills, R., & Lasenby, J. 1990, ApJ, 350, 186 [NASA ADS] [CrossRef] [Google Scholar]
- Gordon, M. A., Berkermann, U., Mezger, P. G., et al. 1993, A&A, 280, 208 [NASA ADS] [Google Scholar]
- Hauschildt, H., Gusten, R., Phillips, T. G., et al. 1993, A&A, 273, L23 [NASA ADS] [Google Scholar]
- Hernández-Hernández, V., Zapata, L., Kurtz, S., & Garay, G. 2014, ApJ, 786, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Hüttemeister, S., Wilson, T. L., Henkel, C., & Mauersberger, R. 1993, A&A, 276, 445 [NASA ADS] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kurtz, S., Cesaroni, R., Churchwell, E., Hofner, P., & Walmsley, C. M. 2000, Protostars and Planets IV, eds. V. Mannings, A. P. Boss, S. S. Russell (Tucson: University of Arizona Press), 299 [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [NASA ADS] [Google Scholar]
- Mehringer, D. M., Palmer, P., Goss, W. M., & Yusef-Zadeh, F. 1993, ApJ, 412, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Mehringer, D. M., Snyder, L. E., Miao, Y., & Lovas, F. J. 1997, ApJ, 480, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Möller, T., Endres, C., & Schilke, P. 2017, A&A, 598, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Brown, L. R., Drouin, B. J., et al. 2015, J. Mol. Spectrosc., 312, 22 [CrossRef] [Google Scholar]
- Müller, H. S. P., Drouin, B. J., & Pearson, J. C. 2009, A&A, 506, 1487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, J. C., & Müller, H. S. P. 1996, ApJ, 471, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Qin, S.-L., Schilke, P., Rolffs, R., et al. 2011, A&A, 530, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
- Remijan, A., Sutton, E. C., Snyder, L. E., et al. 2004, ApJ, 606, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Rodgers, S. D., & Charnley, S. B. 2001, ApJ, 546, 324 [Google Scholar]
- Rolffs, R., Schilke, P., Wyrowski, F., et al. 2011, A&A, 529, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Monge, Á., Cesaroni, R., Beltrán, M. T., et al. 2013, A&A, 552, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Monge, Á., Schilke, P., Schmiedeke, A., et al. 2017, A&A, 604, A6 (Paper II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez-Monge, Á., Schilke, P., Ginsburg, A., Cesaroni, R., & Schmiedeke, A. 2018, A&A, 609, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schilke, P. 2015, EAS Pub. Ser., 75, 227 [Google Scholar]
- Schmiedeke, A., Schilke, P., Möller, T., et al. 2016, A&A, 588, A143 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tan, J. C., Beltrán, M. T., Caselli, P., et al. 2014, Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Arizona: University of Arizona Press) 149 [Google Scholar]
- Wilson, T. L.,& Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
The Common Astronomy Software Applications (CASA; McMullin et al. 2007) software can be downloaded at http://casa.nrao.edu
The spectral index α is determined as Sν ∝ να where Sν is the flux at a given frequency ν. A comparison of the observed and synthetic spectral index maps is found in Fig. 13 of Paper II.
Shifting the position of the MC by a few pixels does not significantly vary the results of the model compared to the observations. This gives us some freedom in locating the MCs, but also reveals that there is no unique set of MCs that can reproduce the observations. Follow-up papers aimed at modeling other molecular species can help to set more constraints on the location and properties (both physical and chemical) of these structures.
All Tables
All Figures
 |
Fig. 1 Top panels: continuum maps towards Sgr B2(M) determined using STATCONT (Sánchez-Monge et al. 2018) at the frequencies of the spectral windows that cover the three CH3 CN ground state transitions: 220 GHz (left), 239 GHz (center), and 257 GHz (right). The black contour shows the 10% level of the continuum emission peak. Middle panels: intensity peak maps of different CH3 CN transitions: J = 12− 11, K = 3 (left), J = 13−12, K = 3 (center), and J = 14−13, K = 3 (right). The intensity peak maps are obtained from a narrow frequency range around the frequency indicated with a vertical dotted line in the bottom panels. The black contour depicts the 10% level of the continuum emission, as in the top panels. Bottom panels: spectra extracted at three different positions marked with crosses in the top and middle panels. The selected positions are located in the north (Mn, in red), in the center of the region associated with the brightest continuum peak (Mm, in black), and towards the south (Ms, in blue). To enhance the clarity, we shifted the red spectrum by +100 K and the blue spectrum by −200 K. The relativecontinuum levels are indicated by the dashed gray lines. |
| In the text | |
 |
Fig. 2 Channel map at a frequency of 220.765 GHz corresponding to the line of CH3 CN (J = 12−11, K = 0). Clear absorption is observed in the center of the map. Magenta contours show the ALMA 242 GHz continuum emission from Paper II. Black circles indicate the position and extent of the H II regions (see Paper I). |
| In the text | |
 |
Fig. 3 Combined density profile (grey area) of all the dense cores included in the model of Sgr B2(M). The average critical density of the transitions listed in Table 1 is shown as an horizontal blue line. The vertical red lines at 4.25 × 103 and 104 au indicate up to which distance from the center of the cores the LTE approximation is valid. |
| In the text | |
 |
Fig. 4 Left panel: synthetic map of the continuum emission of Sgr B2(M) at 220 GHz. The black numbers indicate the positions of the dust cores from the physical model introduced in Paper I. Right panel: integrated line intensity map of the J = 12−11, K = 3 transition predicted by the model. The black crosses indicate the positions of the dust cores as shown in the right panel. The green numbers indicate the position of the newly introduced molecular centers (see Sect. 5.3). The central region is masked out by the transparent hatched area as the CH3 CN emission in this region could not be reproduced by the model (see Sect. 6.6). |
| In the text | |
 |
Fig. 5 Maps of the H2 (left panel) and CH3CN (middle panel) density and relative abundance of CH3CN with respect to H2 (right panel). The black numbers show the position of the dust cores, and the magenta crosses indicate the position of the newly introduced molecular centers, as shown in Fig. 4 (see also Table A.1). The gray circles indicate the positions and extent of H II regions, where the density of H2 and CH3CN is zero. The central region is masked out (transparent hatched area) as the CH3 CN transitions in this region cannot be reproduced well with the model (see Sect. 6.6). |
| In the text | |
 |
Fig. 6 Integrated intensity maps (or zeroth-order moment maps) of the observational (left column) and simulated (middle column) data for the CH3CN J = 12−11, K = 3 transition. The right panels show the difference between the observational and the simulated data. The center row shows the entire Sgr B2(M) complex except for the central region, which is masked out with a transparent hatched area. The green and magenta boxes indicate the zoomed-in regions that are depicted in the top row (northern part of Sgr B2(M)) and the bottom row (southern part of Sgr B2(M)). As in previous figures, the black numbers indicate the position of the dust cores, whereas the green and magenta crosses depict the positions of the molecular centers (see Table A.1). |
| In the text | |
 |
Fig. 7 Radial profiles of the integrated line intensity for the CH3CN J = 12−11, K = 3 transition. The radial profiles proceed from west to east and r = 0 corresponds to the center of the considered molecular centers. The first two profiles (MC-4 and MC-11) are taken from the newly introduced molecular centers in the northern region (cf. Fig. 4). The third profile (MC-68) is taken from the molecular center located between the continuum cores M-SMA-6 and M-SMA-8. The last profile (MC-9) is centered around the molecular center south to the continuum core M-SMA-9. In all panels the blue dashed line shows the observational data, whereas the red solid line corresponds to the simulated data. |
| In the text | |
 |
Fig. 8 Temperature distribution at the z = 0 plane for SgrB2(M) as produced by the model presented in Sect. 5. The central region, which is discussed in Sect 6.6, is shown by the transparent hatched area. |
| In the text | |
 |
Fig. 9 Spectra of the vibrationally excited transition ν8 = 1, J = 12−11, K = 1 − (−1) taken from the center of different cores. The blue solid line shows the observational data, while the red solid lines show the simulated data when the gas temperature equals the dust temperature. The bottom panels also show the simulated spectra after modifying the gas temperature by 50 K (green) and 150 GHz (yellow), as discussed in Sect. 6.3. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
 |
Fig. 10 Histogram of the distribution of the relative abundance of CH3CN for the northern (red) and southern (blue) region of Sgr B2(M). For this purpose cubes were placed around the northern and southern parts, which were composed of cells with side lengths of 695 AU. The vertical lines indicate the averaged values. |
| In the text | |
 |
Fig. 11 Histogram of the relative abundance of CH3CN as function of the H2 density based on the developed physical model. The CH3CN abundances decrease with the H2 density with a function that can be described as a power law with an exponent of − 0.92. |
| In the text | |
 |
Fig. 12 Histogram of the relative abundance of CH3CN as function of the temperature. |
| In the text | |
 |
Fig. 13 Spectra taken from a northern (M-SMA-12) and a southern (M-SMA-6) core to illustrate the shift in frequency due to the velocity component along the line of sight. The green, dashed vertical lines indicate the rest frequency of the J = 12−11, K = 0 transition. The core M-SMA-12 exhibits a blue-shifted velocity along the line of sight of 50 km s−1, while core M-SMA-6 has a red-shifted velocity of 67 km s−1. The systemic velocity of Sgr B2(M) is about 64 km s−1. |
| In the text | |
 |
Fig. 14 Distribution of the velocity along the line of sight at the z = 0 plane, as derived from the model of Sgr B2(M). The central region is masked out by a transparent, hatched area. The black numbers and green crosses indicate the dense cores and molecular centers, respectively, as in Fig. 4. |
| In the text | |
 |
Fig. 15 Spectra of the model after including the large-scale envelope with a CH3 CN abundance of 10−7. The left panel shows a spectrum towards the center where absorption features associated with the low-K transitions are reproduced. The right panel shows a spectrum towards the southern location MC-68. This model predicts absorptions for the low-K transitions that are not visible in the observational data. |
| In the text | |
 |
Fig. 16 Comparison of the CH3CN J = 12−11 observational spectrum (in black) towards a central position in Sgr B2(M) and a fit (in red) obtained with the software package XCLASS. The best fit is obtained for a temperature range ~100–150 K and a column density of 2.9 × 1014 cm−2. |
| In the text | |
 |
Fig. 17 Distribution of the dust temperature relative to the center of the model along the line of sight. The plane z = 0 has a temperature of about 700 K, while temperatures of ~100–150 K are found at a distance of ~20 000 au. |
| In the text | |
 |
Fig. 18 Integrated intensity maps (or zeroth-order moment maps) of the observational (left column) and simulated (middle column) data for the CH3CN J = 13−12, K = 0, 1 transitions of the isotopologue 13CH3CN. The panels in the right column show the difference between the observational and the simulated data. The central row shows the entire Sgr B2(M) complex except for the central region, which is masked out with a transparent, hatched area. The green and magenta boxes indicate the zoomed-in regions that are depicted in the top row (northern part of Sgr B2(M)) and the bottom row (southern part of Sgr B2(M)). As in the previous figures, the black numbers indicate the position of the dust cores, whereas the green and magenta crosses depict the position of the molecular centers (see Table A.1). |
| In the text | |
 |
Fig. B.1 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 12−11 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
 |
Fig. B.2 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 13−12 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
 |
Fig. B.3 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the CH3 CN J = 14−13 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
 |
Fig. B.4 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the vibrationally excited transition CH3 CN ν8 = 1, J = 12−11, K = 1 − (−1). The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
 |
Fig. B.5 Observational spectra (in black) of the ground state CH3CN J = 12−11 transition towards the cores located in the central region of Sgr B2(M). The continuum level for core M-SMA-1a is about 60 K, for core M-SMA-1b about 150 K, and for the remaining cores about 100 K. A number of absorption and emission spectral linefeatures are visible in all the spectra. |
| In the text | |
 |
Fig. B.6 Spectra of the observational (in blue) and simulated (in red) data extracted from the position of different cores and molecular centers for the 13CH3 CN J = 13−12 transition. The spectra are arranged according to the position of the corresponding cores and molecular centers along a south–north direction, starting from the most southern core. The name of the core and molecular center is shown for each panel. The continuum correction necessary to match the continuum level of the observation and simulation is indicated in the top right corner of each panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


