EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 614 (June 2018) A&A, 614 (2018) A71 Full HTML
Free Access
Issue
A&A
Volume 614, June 2018
Article Number A71
Number of page(s) 17
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/201732137
Published online 15 June 2018

© ESO 2018

1 Introduction

Type Ia supernovae (SNe Ia) are standardizable candles, and measuring their relative distances first led to the discovery of dark energy (Riess et al. 1998; Perlmutter et al. 1999). Their origin as thermonuclear explosions of carbon-oxygen white dwarfs (WDs) is well accepted, as is their importance as producers of heavy elements in the Universe (e.g., Maoz et al. 2014). It is further accepted that the light curve is powered by the decay of 56Ni, which has a half-life of ~6 days for the dominant decay channel to Co. However, the progenitor system configuration and the path to detonation is still not understood. While a small sample of nearby SNe Ia now have tight limits on companions set by the lack of interaction or non-detection of hydrogen (Leonard 2007; Bloom et al. 2012; Maguire et al. 2016), some SNe do show signs of H interaction (Hamuy et al. 2003; Aldering et al. 2006; Dilday et al. 2012) and theoretical explanations of the observed diversity prefer multiple explosion channels (Sim et al. 2013; Maeda & Terada 2016).

Current light-curve-based empirical SN Ia standardization methods yield a ~0.1 mag intrinsic dispersion (after accounting for measurement uncertainties), interpreted as a random scatter in magnitude and/or color (Betoule et al. 2014; Scolnic et al. 2014; Rubin et al. 2015). At least part of this observed scatter is due to differences in the explosion process, seen for example in a significantly reduced intrinsic dispersion when comparing spectroscopic twins (Fakhouri et al. 2015). These differences can, in turn, be expected to evolve differently with cosmic time and thus propagate into systematic limits on cosmological constraints from SNe Ia if left unresolved. Simultaneously, the origin of the peak-brightness correction for reddening is not fully understood, with lingering differences between empirical reddening curves and dust-like extinction in the U-band and between individual well-measured SNe (Guy et al. 2010; Chotard et al. 2011; Burns et al. 2014; Amanullah et al. 2015; Mandel et al. 2017; Huang et al. 2017). Evidence for an incomplete SN Ia standardization is also implied by the correlations between standardized magnitude and host-galaxy environment (Sullivan et al. 2010; Childress et al. 2013a; Rigault et al. 2013). Most recently, Rigault et al. (2017, R17) used the specific star formation rate measured at the projected SN location (local specific star formation rate, LsSFR) to statistically classify individual SNe Ia as younger or older. Younger SNe Ia are found to be 0.16 ± 0.03 mag fainter than older (after SALT2.4 standardization). The fraction of young SNe is expected to greatly increase as a function of redshift. An era where cosmology aims to be sensitive to slight deviations from the Λ cold dark matter (CDM) model requires full understanding of all such effects.

Spectral features in the rest-frame U-band region (~3200 to 4000 Å) are less well explored compared with those at redder wavelengths. Empirical studies of U-band spectroscopic variability are few, and due to the atmosphere cutoff, usually dependent on high-z or space-based data. Comparisons of samples at different redshifts have suggested an evolution of the mean U/UV properties (Ellis et al. 2008; Kessler et al. 2009; Foley et al. 2012; Milne et al. 2015). Foley et al. (2016) examined UV spectra of ten nearby SNe Ia obtained within five days of peak light, finding variations connected to optical light curve shape, and an increasing dispersion bluewards of 4000 Å (λ > 4000 Å). The Ca H&K λ 3945 “feature”, dominated by Si II λ3858, and the Ca H&K λλ 3934, 3969 doublet, are more frequently observed, but with conflicting interpretations. Maguire et al. (2012) and Foley (2013) both find differences in EW(Ca H&K λ3945) between samples divided by light curve width, but differ as to whether the Ca H&K λ 3945 velocity correlates with light curve width. Foley et al. (2011) found high-Ca II-velocity SNe to be intrinsically redder. High-velocity features (HVFs) – absorption features that are detached from a “photospheric” component – have long been observed in early SNe Ia spectra (Mazzali et al. 2005; Tanaka et al. 2006), and potentially yield insights into the outer ejecta density or ionization (Blondin et al. 2013). Several studies have tried to systematically map the presence of detached HVFs in the Ca IR and H&K regions. Fitting coupled Gaussian functions to the Ca features, Childress et al. (2014) found that neither rapidly declining SNe nor SNe with high photospheric velocity show HVFs at peak light. Silverman et al. (2015) reached similar conclusions based on a larger sample.

Individual SNe with early U-band spectroscopy include PTF13asv, showing an initially suppressed U-band flux at day − 14 that brightened significantly during the following five days (Cao et al. 2016), possibly due to an outer, thin region of radioactive material. PS1-10afx was first reported as a new transient type by Chornock et al. (2013), but was later found to be a gravitationally magnified high-z SN Ia (Quimby et al. 2013, 2014). The spectral comparison of Chornock et al. (2013, their Fig. 7) shows a brighter flux in the bluest part of the U-band, differing from comparison SNe Ia (SN2011fe, SN2011iv). The UV/U-band spectrum of SN2004dt is discussed in Wang et al. (2012), where low-resolution HST-ACS spectra show excess U-band flux close to peak. Further studies of individual SNe with U-band spectroscopic coverage have been presented for example by Patat et al. (1996); Garavini et al. (2004, 2007); Altavilla et al. (2007); Stanishev et al. (2007); Matheson et al. (2008); Wang et al. (2009, 2012); Bufano et al. (2009); Blondin et al. (2012); Silverman et al. (2012); Smitka et al. (2015). Significant variation in flux for different phases of observation and between objects can be found, but due to uneven candidate and cadence selection this variability has proven hard to quantify.

The 3000–4000 Åregion is situated at the opacity transition region, going from fully dominated by iron-group element (IGE) line absorption in the UV to electron-scattering in the B-band, with the SN spectral energy distribution (SED) shaped by a mix of IGE and intermediate-mass element (IME) features. Theoretical predictions of the U-band spectrum thus have to take both effects correctly into account (Pinto & Eastman 2000), making it hard to gauge the level of systematic uncertainties on the U-band SED predictions from current models. Simulations have found progenitor metallicity to cause significant variations bluewards of the U-band wavelength region, but with few clear predictions within this region (Timmes et al. 2003; Walker et al. 2012).

Here we attempt to gain a deeper understanding of the U-band region, bothto provide data for comparison with predictions from explosion scenarios and to improve the use of SNe Ia as standardizable candles. This will have particular implications for SNe at high-z, where restframe U-band observationsare naturally obtained by ground-based imaging surveys and important for constraining the transient type (either at initial detection to trigger follow-up, or during a final photometry-only analysis).

The initial motivation for this study and the approach of dividing the U-band spectrum into four wavelength subregions arose from the comparison of individual supernovae with similar BVR spectra and light curve properties but exhibiting spectroscopic differences in the U-band. We present the sample and introduce this subdivision in Sect. 2, and study U-band spectroscopic variability in Sect. 3. Section 4 contains a discussion of how the SN Ia explosion can be examined using U-band absorption features. In Sect. 5 we explore the consequences for SN Ia standardization. Finally, in Sect. 6 we discuss the presence of SN Ia subclasses based on U-band flux measurements, return to the question of HVFs, and provide a brief outlook. We conclude in Sect. 7.

2 Data and U-band measurables

2.1 Nearby Supernova Factory

The Nearby Supernova Factory (SNfactory) has obtained time-series spectrophotometry of a large number of SNe Ia in the Hubble flow. Observations have been performed with our SuperNova Integral Field Spectrograph (SNIFS, Aldering et al. 2002; Lantz et al. 2004). SNIFS is a fully integrated instrument optimized for automated observation of point sources on a structured background over the full ground-based optical window at moderate spectral resolution (R ~500). It consists of a high-throughput wide-band lenslet integral field spectrograph, a multi-filter photometric channel to image the field in the vicinity of the IFS for atmospheric transmission monitoring simultaneously with spectroscopy, and an acquisition/guiding channel. The IFS possesses a fully filled 6.4′′ × 6.4′′ spectroscopic field of view subdivided into a grid of 15 × 15 spatial elements, a dual-channel spectrograph covering 3200–5200 Åand 5100–10 000 Åsimultaneously, and an internal calibration unit (continuum and arc lamps). SNIFS is mounted on the south bent Cassegrain port of the University of Hawaii 2.2-m telescope onMauna Kea, and is operated remotely. Observations are reduced using a dedicated data reduction pipeline, similar to that presented in §4 of Bacon et al. (2001). Discussion of the software pipeline is given in Aldering et al. (2006) and updated in Scalzo et al. (2010). Of particular importance for this analysis is the flux calibration and Mauna Kea atmosphere model presented in Buton et al. (2013). This provides accurate flux calibration down to ~3300 Åwith a residual ~2% gray scatter.The extension to bluer wavelengths compared with most ground-based observations is a key prerequisite for this study. Host-galaxy subtraction is performed as described in Bongard et al. (2011), a methodology subsequently improved and made more flexible1. Each spectrum is corrected for Milky Way dust extinction (Schlegel et al. 1998), blue-shifted to rest-frame based on the heliocentric host-galaxy redshift (Childress et al. 2013b, R17) and the fluxes are converted to luminosity assuming distances expected forthe supernova redshifts in the cosmic microwave background frame and assuming a dark energy equation of state w = −1. For the purpose of fitting LCs with SALT2.4 and calculating Hubble residuals, magnitudes are generated through integration over the following top-hat profiles: USNf (3300–4102 Å), BSNf (4102–5100 Å), VSNf (5200–6289 Å), RSNf (6289–7607 Å) and ISNf (7607–9200 Å).

2.2 Sample

The sample is based on a slightly enlarged version of the data presented in previous SNfactory publications (Chotard et al. 2011; Rigault et al. 2013; Feindt et al. 2015; Fakhouri et al. 2015)2. We require all SNe to have an initial high signal-to-noise spectrum prior to − 2 days. We have updated SALT light curve fits to the latest version (SALT2.4, Betoule et al. 2014), and require these to provide a good fit to synthetic broadband photometry generated from the data (five failed this in a blinded inspection). USNf photometry was not included in these fits since Saunders et al. (2015) demonstrated that the UV is not well described by the SALT2.4 model. Finally, four 91bg-like SNe were removed. The final sample consists of 92 SNe Ia. Out of this set, 73 SNe are found in the 0.03 < z < 0.1 redshift range. Spectra shown below are cut redward of ~6500 Åfor display purposes only.

Host-galaxy properties were presented in Childress et al. (2013a) and R17, where z, SALT2.4 x1, c and Hubble residuals have also been tabulated. Besides the frequently used global stellar mass (Sullivan et al. 2010; Childress et al. 2013a), this includes the local specific star formation rate (LsSFR). The LsSFR combines the local Hα flux (driven by UV-emission from young stars) with the estimated local stellar mass, thus producing an estimate for the fraction of young stars at the SN location. SNe with large LsSFR values are more likely to originate from a young progenitor, while SNe in low-LsSFR environments likely originate from older systems. This provides refined information compared with earlier global measurements as star forming galaxies can have locally passive (old) regions. The light curve width, color, and host-galaxy mass distributions of this sample closely match that of the combined SNLS and SDSS data in the JLA sample (Betoule et al. 2014).

Measurements of the equivalent width (EW) and velocity of the Si II λ6355 absorption feature were made on spectra within ± 2.5 days from (B-band) maximum. These spectroscopic-indicator measurements are further described in Chotard (2011), and a spectroscopic-indicator analysis based on the full SNfactory sample will be presented in Chotard et al. (in prep.).

We focus on spectra in three restframe phase bins, pre-peak (− 8 to − 4 days with respect to B-band peak as determined by SALT2.4), peak (− 2 to 2 days) and post-peak (4 to 8 days). This selection strikes a balance between capturing how quickly SNe Ia vary while limiting the number of new parameters to inspect. Spectra are dereddened based on the optical colors so that, to first order, intrinsic spectroscopic variations can be distinguished from extinction by dust. The correct color curve to apply, which could vary from object to object, is not fully understood. We further do not want to assume that intrinsic U-band features do not correlate with reddening, as these potentially could be indirectly caused by relations between intrinsic SN-features and the progenitor environment. In order to minimize the potential impact of systematic differences due to reddening, we take two conservative steps: Remove reddened SNe with SALT2.4 color c > 0.2 from further analysis, and make an initial dereddening correction assuming the extinction curve of Fitzpatrick (1999, F99) with R = 3.1. Three SNe3 have c > 0.2 and thus will not be included in the main analysis, unless otherwise noted. The E(B − V) values used when dereddening are based on SALT2.4c measurements, derived from the BSNfVSNfRSNf bands, and converted to E(B−V) according to Eq. (6) of Guy et al. (2010). In Sect. 5.3 we will return to how this choice of method of accounting for reddening by dust influences measurements.

thumbnail Fig. 1

Comparison of the spectra of SN2011fe (SALT2.4x1 = −0.4 and c = −0.06) and SNF200805014-002 (SALT2.4x1 = −1.5 and c = −0.12) at early (left) and peak (right) phases. Small spectroscopic differences are found redwards of 4000 Å(stable Fe marked in left panel). Much larger deviation is found bluewards of this limit. The comparison at early phases differs most strongly around 3400 Åand the high velocity edge of the Ca H&K λ 3945 feature, the comparison at later phases mainly around 3550 Å. These differences led to the subdivision of the U-band into four indices, as described in the text. Vertical lines show the feature limits thus defined.

2.3 Definition of U-band indices

Here we examine SN2011fe and SNF20080514-002 as a sample pair of SNe with (relatively) similar BSNf VSNfRSNf spectra and light curve properties, but large absorption-feature differences in the U-band. Their early and peak spectra are compared in Fig. 1. Spectral differences between these objects can be localized to different behavior in four subdivisions of the U-band wavelength region: λ(uNi) (3300–3510 Å), λ(uTi) (3510–3660 Å), λ(uSi) (3660–3750 Å) and λ(uCa) (3750–3860 Å). The two redder regions, roughly covering the Ca H&K λ 3945 feature, are dominated by Si II λ3858 & Ca H&K λλ 3934, 3969 absorption. These wavelength regions are thus labeled λ(uSi) (3660–3750 Å) and λ(uCa) (3750–3860 Å). The blue half of the U-band is also divided into two parts. The left (early) panel of Fig. 1 shows differences up to ~3500 Å, a region labeled λ(uNi). The peak spectra (right panel of Fig. 1) agree in this region but differ in the subsequent ~3500 to ~3700 Åsection, here denoted λ(uTi). The ions most frequently found to dominate these regions are used as labels, but it is clear that absorbing elements will vary with phase and between SNe (see Sect. 4.1 for further discussions). In particular, HVFs dominate variations at early phases in the λ(uTi) and λ(uSi) regions, but have more limited effects at other times and regions (see Sect. 6.1.)

We use the most straightforward and simple method to quantify U-feature variations – integration of flux within each wavelength region defined above, normalized by the BSNf-band flux at the same phase. We thus determine the spectral index uNi as 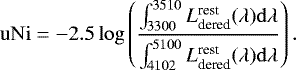(1)

The spectral indices uTi, uSi, and uCa are calculated in the same manner by simply changing the wavelength limits of the numerator. Each spectral index is thus a restframe, phase-dependent, dereddened color. For SNe with multiple spectra within a phase bin, measurements from these spectra are averaged, using the inverse variance from photon counting as weights. Within each phase bin we find weak dependencies with phase. For each feature/phase combination we fit a linear slope using the full sample and use this to correct individual measurements to the central bin phase (− 6, 0 or 6 days).

These measurements of uNi, uTi, uSi and uCa can be found in Table 1, which also identifies whether any Ca H&K λ 3945 HVF is detected based on visual inspection for each SN (see Sect. 6.1).

3 U-band variation

3.1 Meanand variation of the U-band spectrum

The mean dereddened spectrum and the 1σ sample variation for each phase bin after dereddening and normalizing to a common median BSNf-band flux can be seen in Fig. 2. The large variation in the Ca H&K+Si II feature is obvious at pre-peak phases. Also, the bluest region (λ(uNi)) shows large early variation. At roughly one week after peak, the dispersion has significantly decreased at all wavelengths. This RMS versus wavelength is directly displayed as the dashed red line in Fig. 3 with normalization to a wider wavelength range. Here, we also show the dispersion of subsets of the sample, divided according to the SALT2.4 x1 parameter and with the mean recalculated for each subset. All subsets show scatter similar to that of the full sample, with the possible exception of the post-peak λ(uTi) region. The variability in the post-peak phase bin can be described as a smooth component, only slowly declining with wavelength, with Si line variability superimposed. The λ(uNi) RMS here is 0.16 mag, comparable to that of the BSNf band (0.14 mag).

3.2 Spectroscopic variations with common SN Ia properties

Here we examine how the U-band varies with commonly used SN Ia properties by comparing composite spectra generated from subsets of the data; shown in Figs. 4 and 5. Subsets are constructed as follows: We retrieve all (restframe) spectra within a phase bin and normalize using the median flux of the BSNf band. If a SN has two spectra from different nights within this range, the closest to the center of the bin is used. If the mean phase of two (sequential) spectra is closer to the center phase, their mean spectrum is used instead. At each phase we show four composite spectra where every composite was constructed from a quarter of the SNe available. SNe are assigned to composites based on a their rank given by a secondary property. The 25% of the SNe with lowest secondary value form one subset, the next 25% another and so forth. Composites are shown, from low to high secondary value, with increasingly lighter colors (inverted for x1).

A spectral feature correlation with the secondary property, spanning the full sample and not driven by outliers, will lead to all subset composites being arranged in "color" order. Through examination of these panels we observe the following:

x1 and 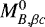(ligh curve width/luminosity). The shallow IME features of slow-declining supernovae are seen in the Ca H&K λ 3945 feature at all times (lightly shaded line). Besides this, the dominant feature is the strong correlation of the uTi-feature flux level with luminosity/light curve width. This dependence grows stronger after peak.

Color. We find no signs of persistent feature variations with SALT2.4 color after dereddening, thus visually confirming that our dereddening procedure worked as intended.

SALT2.4 standardization residuals. We identify the pre-peak uCa and uTi indices as potentially interesting for use in standardization.

EW (Si II λ6355). The width of several features vary with EW(Si II λ6355), including CaH&K+Si II, EW(Si II λ4138), and uTi at late phases. This suggests that the Branch et al. (2006) subdivision into SNe Ia with broader/narrower spectral features is present, to some extent, in the U-band.

v (Si II λ6355). As expected, SNe Ia with large Si velocities at peak also demonstrate blueshifting in the Si II λ3858 and Si II λ4138 features.

Table 1

SN U-band properties and Ca high velocity feature classification.

Table 1

continued.

thumbnail Fig. 2

Mean spectra and ± 1 standard deviation in sample at three representative phases. The four wavelength regions considered are separated by dashed lines. The interpretation of these indices will be phase dependent, as, for example, the Ti region at early phases is clearly a part of the Ca H&K λ 3945 + Si II λ3858 feature complex and Cr/Fe dominates uNi at late phases.
thumbnail Fig. 3

Intrinsic flux RMS (vs. wavelength) for SNe after division into four bins according to increasing light curve width (dark to light lines). Spectra were initially normalized to have median flux of unity over the [3300, 6900] Åwavelength region. Panels from top to bottom show the three sample phase regions (pre-peak, peak and post-peak). Vertical (dotted) lines mark boundaries of the four U-band regions. Thered dashed red line shows the RMS for the full sample.
thumbnail Fig. 4

U-band spectroscopic variation spanning the range of common SN properties: x1, dereddened MB, color (left to right). Composite spectra were calculated after dividing the sample into four quartiles based on each property, which was repeated at three representative phase ranges (− 6, 0, 6) for each subset. Subset composites were drawn such that the line color becomes darker as the parameter value decreases. Dotted lines indicate U-band spectral-index subdivision boundaries.

4 Results: Understanding the explosion

4.1 Origin of U-band index variations

We use synthetic SYNAPPS fits to determine which element changes are needed to remove the dissimilarities between the SN2011fe and SN20080514-002 spectra. SYNAPPS is a C implementation of the original Synow code (syn++) with an added optimizer, to find the best ion temperature, velocity, and optical depth combinations to fit input spectra under the Sobolev approximation for e− scattering (Thomas et al. 2011). Fits presented here include Mg II, Si II, Si III, S II, Ca II, Ti II, Fe II, Fe III, Cr II, Co II, Co III, and Ni II. We focus on the region bluewards of the Ca H&K+Si II region and thus do not attempt to reconstruct Ca H&K+Si II HVFs. No detached ions were included. The full fits including these ions capture the observed spectra well. Fits were also remade while iteratively deactivating one (or a combination) of the ions.

4.1.1 λ(uNi): 3300–3510 Å

SYNAPPS fits and their implication for the λ(uNi) spectroscopic region are shown in Fig. 6. We find that the λ(uNi) window can be tied to the presence of Ni and Co, the decay product of 56Ni at these phases. Other elements, investigated using SYNAPPS runs without Ni/Co, cannot replicate the observed spectra without distorting other parts of the spectrum. The effects of Ni and Co can be directly seen by manually decreasing the optical depths of these ions relative to the SN2011fe fit: a change of order 1 dex creates a syn++ spectrum that matches SNF20080514-002 well in the λ(uNi) region (lower panels of Fig. 6). We show contributions of all included ions to the full fit in Fig. A.1. Tanaka et al. (2008), using abundance modifications to the W7 density profile to fit SN2002bo, also found this wavelength region to be sensitive to the amount of outer Ni (see their Fig. 2). Similar results can be seen in a number of studies using different techniques: Blondin et al. (2013) presented one-dimensional delayed-detonation models that show Co II to dominate here; Hachinger et al. (2013) performed a spectral tomography analysis of SN2010jn where an early spectrum was dominated by Fe absorption at 3000 Åand the Ni /Co around 3200 Å, and a SYNAPPS study by Smitka et al. (2015) also shows strong Ni /Co absorption at ~3300 Å(although no Cr or Ti was included in these fits). Like Hachinger et al. (2013), we find that measurements of this spectral region are necessary for determining the spatial distribution of IGE elements, a key characteristic distinguishing theoretical explosion models. Cartier et al. (2017) found that V II provided improved fits to very early spectra of SN2015F, which would also impact the λ(uNi) region.

thumbnail Fig. 5

U-band spectroscopic variation spanning the range of common SN properties: Hubble residuals standardized by SALT2.4 light curve parameters, EW(Si II λ6355) and v(Si II λ6355) (left toright). Composite spectra were calculated after dividing the sample into four quartiles based on each property, which was repeated at three representative phase ranges (− 6, 0, 6) for each subset. Subset composites were drawn such that the line color becomes darker as the parameter value decreases. Dotted lines indicate U-band spectral-index subdivision boundaries.

4.1.2 uTi: 3510–3660 Å

SYNAPPS fits and their implication for the λ(uTi) region are shown in Fig. 7. Among the SYNAPPS ions included, only Ti II produces significant absorption in the 3510 to 3660 Åregion without distorting other parts of the spectrum. We display this association by manually decreasing the Ti II optical depth. We do this for SNF20080514-002 since it shows the larger absorption, and again find that a change of order − 1 dex produces a spectrum that matches the SN2011fe uTi region well. More complete radiative transfer models are needed to determine whether uTi variations are fully explained by Ti II absorption, but we note that the Ti lines at 3685, 3759 and 3761 Åwould land in the uTi wavelength region for typical SN Ia velocities. The post-peak λ(uTi) region is, ascan be seen in Figs. 4 and 5, strongly correlated with EW(Si II λ6355). As no strong Si lines are expected in this region this reflects a general connection between widths of spectroscopic features in SN Ia spectra. We show contributions of all included ions to the full fit in Fig. A.2.

4.2 Explosion models and progenitor scenarios

The single degenerate scenario – mass transfer from a red giant or main sequence star onto a carbon-oxygen white dwarf – is no longer considered as likely to explain all (or most) SNe Ia. Challenges come from the lack of companion stars close to nearby SNe (e.g., SN2011fe Li et al. 2011; Schaefer & Pagnotta 2012; Edwards et al. 2012), the statistical absence of early light curve variations due to ejecta interaction with the companion (Hayden et al. 2010), an insufficient number of such systems formed (Ruiter et al. 2011), and a large range of ejecta masses (Scalzo et al. 2014). A number of scenarios, possibly existing in parallel, are currently being investigated. These predict similar spectral energy distributions in the 4000 to 7000 Åregion around lightcurve peak and have thus proven hard to rule out using such data (Röpke et al. 2012). Bluer wavelengths, on the other hand, show significant differences between current theoretical models. We have compared output spectra from delayed detonation (model N110, Seitenzahl et al. 2014; Sim et al. 2013), violent merger (model 11+09, Pakmor et al. 2012), sub-Chandra double detonation (model 3m, Kromer et al. 2010) and sub-Chandra WD detonation (Sim et al. 2010) models. We find that none of these describe the observed U-band variations.

Miles et al. (2016) found constant Si but varying Ca abundances to be a robust consequence of changing the progenitor model metallicity. However, they do not find this to cause strong changes in the observed spectra. We nonetheless searched for uCa changes, not visible in uSi, for indications of a relationship to metallicity, but did not observe anything significant. The region identified by Miles et al. (2016) as strongly and consistently affected by metallicity was the Ti absorption at ~4300 Åat ~30 days after explosion. Similar to the uTi index, this feature is strongly correlated with peak luminosity and light curve width, making a search for a second order variation due to metallicity challenging.

A more direct way to probe Ni in the outermost layer is through observation of the very early light curve rise-time, parameterized as f ∝tn. A mixed ejecta (shallow 56Ni) will cause an immediate, gradual flux increase, while deeper 56Ni with cool outer layers experience a few days of dark time before a sharply rising light curve (Piro & Nakar 2014; Piro & Morozova 2016). In these models, the effects of outer ejecta mixing has largely disappeared approximately one week after explosion. Firth et al. (2015) examine a sample of SNe with very early observations, finding varying rise-time power-law indices n between 1.48 and 3.7, suggesting that either the outermost 56Ni layer and/orthe shock structure varies significantly between events. A sample of SNe with both early light curve data and U-band spectra would allow a direct comparison between pre-peak λ(uNi) absorption and the amount of shallow Ni predicted from the early light curve rise-time.

SN2011fe and LSQ12fxd in the Firth et al. (2015) study are included in the sample studied here and have observations at a common phase of ~10 days before peak (shown in Fig. 8). Compared with SN2011fe, LSQ12fxd has both a steeper rise-time immediately after explosion (n = 3.24 vs. n =2.15) and more Co II absorption (less λ(uNi) flux) in the line-forming region one week prior to light curve peak. A scenario explaining both observations would involve 56Ni mixed into the outermost ejecta regions in SN2011fe while being located slightly deeper and being denser in LSQ12fxd. The comparison is non-trivial as these SNe also vary significantly in light curve width and line velocities. We note, however, that neither x1 nor v(Si II λ6355) correlates strongly with early uNi and that Firth et al. (2015) find no correlation between n and light curve width.

thumbnail Fig. 6

Probing the origin of variation in the λ(uNi) region through SYNAPPS model comparisons. The top panel compares SN2011fe and SNF20080514-002 at an early phase (−10 days). The second panel repeats the early SN2011fe spectrum (blue line) together with the best SYNAPPSfit (black dashed line). The green line shows the same fit, but with the optical depth (τ) of all Ni and Co II decreased by 1 dex, effectively suppressing these ions. The third panel compares the early SNF20080514-002 spectrum with the same SN2011fe SYNAPPS fits. The SN2011fe fit with suppressed Ni; Co II optical depth matches the SNF20080514-002 λ(uNi) region well. Vertical dotted lines indicate the U-band spectral index boundaries, with λ(uNi) lightly shaded gray.
thumbnail Fig. 7

Probing the origin of uTi variation through SYNAPPS model comparisons. The top panel compares SN2011fe and SNF20080514-002 at peak light. The second panel shows SNF20080514-002 (orange line) together with the best SYNAPPS fit of this spectrum (black dashed line). The green line shows the same fit, but with the optical depth (τ) of Ti II decreased by 1 dex, effectively suppressing these ions. The third panel compares the SN2011fe spectrum with the same SNF20080514-002 SYNAPPS fits. The SNF200805014-002 fit with suppressed Ti II optical depth matches the SN2011fe λ(uTi) region well. Vertical dotted lines indicate the U-band spectral index boundaries, with λ(uTi) shaded lightgray.
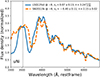thumbnail Fig. 8

Spectra of SN2011fe and LSQ12fxd at phase ~ − 8 days. LSQ12fxd has, compared with SN2011fe, both a steeper early rise-time (Firth et al. 2015) and less flux in the λ(uNi) region (i.e., stronger Co II absorption at this phase).

5 Results: Impact on standardization

Here we discuss the strong correlation between post-peak uTi and peak luminosity, and the potential impact of uCa for SN Ia standardization (Sect. 5.1). The residual magnitude correlation with host environment after standardization is explored in Sect. 5.2. In Sect. 5.3 we explore whether the systematic effects from reddening corrections could significantly affect these results.

5.1 SN Ia luminosity standardization with uTi and uCa

Many spectroscopic features show strong correlations with SN Ia luminosity. These include and , introduced by Nugent et al. (1995), and the equivalent width (or “strength”) of the Si II λ4138 feature (Arsenijevic et al. 2008; Chotard et al. 2011; Nordin et al. 2011). As discussed in Sect. 3.2, uTi displays a similarly strong sensitivity to peak luminosity, especially at post-peak phases where contamination by the blue edge of the Ca H&K λ 3945 feature is less likely. For some SNe, a direct connection to 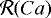, measured as the ratio between flux at the edges of the Ca H&K λ 3945 feature, could exist. We now further explore the uTi-luminosity correlation.

In Fig. 9 (mid panel) we show the uTi change with phase per SN, and with measurements color-coded by light curve width (SALT2.4 x1). From around light curve peak and later, we find a persistent and strong relation, where SNe with wider light curves have bluer uTi colors. To confirm that this correlation is not driven by the dereddening correction or changes in the BSNf band, Fig. 9 contains two modified color curves: The first (left panel) shows the observed color uTiobs,B, that is, uTi recalculated according to Eq. (1) but without dereddening spectra, and the second (right panel) shows the BSNf − VSNf color evolution (calculated based on rest-frame and dereddened spectra). We confirm that the strong x1 trend is present also without dereddening but not visible for BSNf − VSNf.

We evaluate SN Ia standardization using combinations of post-peak uTi as a replacement for x1, and pre-peak uCa as an additional standardization parameter (see Table 2). We assume a fixed Λ CDM cosmology, continue to remove red SNe (c > 0.2), and use SNein the 0.03 < z < 0.1 range to reduce scatter from peculiar velocities. We further fix the SALT2.4 β parameter (the magnitude dependence of c) to the (blinded) value determined from the full SNfactory sample (derived without cuts based on color or first phase). The two base fits include either the magnitude dependence of x1 (“α”) or the magnitude dependence of post-peak uTi. Two permutations of these are made: one (“cut”) where the sample is limited to SNe with observations at all phases (early and late), and another where pre-peak uCa is added as a second standardization parameter. To allow comparisons of χ2 between runs we add a fixed dispersion of 0.090 mag, the value required to produce χ2∕dof = 1 for the initial x1 run (first row in table). The uncertainty of each U-band index is composed of the sum of variance due to statistical uncertainties of the spectra and the propagated reddening variance, and is generally at the ~0.03 mag level (see Table 1). The measurement correlations between U-band indices and SALT2.4 fit parameters are negligible.

Our primary conclusion is that post-peak uTi standardizes SNe Ia very effectively, with an RMS of 0.116 ± 0.011 mag. A traditional x1 standardization yields a higher RMS of 0.135 ± 0.011 mag for these SNe. This is remarkable in many aspects: it is a single-color measurement made in a fairly wide phase range and using a fixed wavelength range that produces a lower χ2 fit. For the reduced sample of 57 SNe with both measurements this is an improvement over x1 with Δχ2 = 20.5, which is significant at greater than 3 σ (see also Table 3). We further investigate the potential effects of sample selection by redoing the fits based on a “cut” sample, where only SNe with both pre-peak (− 8 to − 4 days) and post-peak (4 to 8) data are included. We see no significant differences between the full and cut samples. The reduced dispersion for uTi fits is thus not due to sample selection.

The Spearman rank correlation coefficient between SALT2.4 Hubble residuals and pre-peak uCa is rs = 0.43, and the hypothesis of no correlation can be rejected at greater than 99% confidence (Fig. 10, left panel). We therefore test adding pre-peak uCa measurements as a further standardization parameter. Combining post-peak uTi and pre-peak uCa produces a Hubble diagram RMS of 0.086 ± 0.010 mag, while using only uCa and x1 reduced the RMS to 0.122 ± 0.012 mag. The driving trend of this improvement can also be seen in Fig. 10: SNe Ia with large uCa indices are too bright after SALT2.4 standardization; half of these are classified as Branch Shallow Silicon objects – this connection is further explored in Sect. 6.1.

We also note that the combined uTi + uCa fit produces a much reduced χ2 value, beyond what can beexpected just through adding another fit parameter. When rerunning the standardization without a fixed intrinsic dispersion we obtain χ2 = 38.6 for 40 degrees of freedom, thus there is no need to add any additional dispersion to reach χ2 ∕dof = 1. As the internal SALT2.4 model error propagates an effective intrinsic dispersion of 0.055 mag, other fit methods are required to investigate whether a fit without any added dispersion can be attained. For comparison, the uTi fit requires an intrinsic dispersion of σint = 0.070 ± 0.009 mag and the x1 fit requires σint = 0.090 ± 0.008 mag.

As a further test we evaluate the fit quality using the sample-size corrected Akaike Information Criteria (AICc), which penalizes models with additional fit parameters. In Table 3 each line compares uTi standardization (without any host galaxy property correction) with one other combination of standardization property and host parameter. Each comparison includes all SNe available for that combination of data, and shows both the difference in χ2 and the AICc probability ratio. Models including both uTi and uCa are strongly preferred over those using only uTi, with a P-value of < 0.001, even thoughpenalized for adding another fit parameter. Using only uTi is similarly favored compared with the x1 fit.

The significance of these improvements can also be numerically investigated by re-fitting the standardization after randomly redistributing the uCa measurements among SNe. When coupled to uTi, two out of 10000 random simulations yielded a similarly low RMS, equivalent to a P-value of <10−5; when combined with x1, zero out of 10000 did so.

Finally, the HST-STIS sample presented by Maguire et al. (2012) also included a small sample of spectra covering the λ(uTi) region and overlapping with the post-peak phase studied here (phase + 4 to + 8 days). Light curve width information (“stretch” and B − V, determined by SIFTO) exists for seven of these SNe (PTF10wof, PTF10ndc, PTF10qyx, PTF10qjl, PTF10yux, PTF09dnp, PTF10nlg). With these data we can check an external dataset for a similar correlation. We deredden the spectra as was donepreviously with the SNf data and calculate the uTi color. Figure 10 (right panel) shows a strong correlation for this small sample, compatible with the uTi trend discussed above. We find that this trend agrees well with the SNIFS measurement presented here, after converting the latter to SIFTO stretch values.

thumbnail Fig. 9

uTi vs. phase with markers colored by SALT2.4x1. The left andmid panels show the uTi color prior to and following F99 dereddening, respectively. The right panel displays the BSNf − VSNf color evolution for reference, calculated from dereddened restframe spectra. Pre-peak observations show a scatter induced by the edge of the Ca H&K λ 3945 feature. uTi colors after peak show a strong stable correlation with light curve width.
Table 2

Standardization fit results.

thumbnail Fig. 10

Left:origin of pre-peak uCa correlation with SALT2.4 Hubble residuals. The Spearman correlation coefficient of rs = 0.43 indicates a moderate correlation, with the hypothesis of no correlation at > 99% confidence. Right: comparing the post-peak uTi color integrated from HST-STIS spectra with SIFTO stretch. Spectra were dereddened according to a similar procedure as the SNfactory sample and use light curve data from Maguire et al. (2012). The SNIFS sample presented here is included for comparison, with SALT2.4 x1 values converted to SIFTO stretch using the relation provided by Guy et al. (2010). The trend with uTi agrees betwen these two data sets.
Table 3

Each line shows Hubble residual fit quality for a given standardization method, measured relative to a reference fit based on post-peak uTi data without any host property corrections (first line).

5.2 The SN progenitor environment

The R17 analysis of the local host galaxy environment found that SNe Ia in younger environments are 0.163 ± 0.029 mag (5.7σ) fainter than SNe Ia in older environments, after SALT2.4 standardization (based on a larger sample than used here). The corresponding analysis of global host galaxy mass found SNe Ia in lower mass galaxies to be 0.119 ± 0.032 mag fainter than those in more massive hosts. We recover these trends for the subset of SNe in this analysis with R17 measurements, finding a − 0.151 ± 0.028 mag step for LsSFR and 0.098 ± 0.031 mag for global host galaxy mass.

When this step analysis is performed based on the standardization residuals where uTi replaced x1 the step sizes are reduced to 0.042 ± 0.031 mag for mass and − 0.075 ± 0.031 mag for LsSFR (given in the final two columns of Table 2). uCa has less impact for environmental steps, producing modest step size reductions to 0.022 ± 0.030 mag and − 0.065 ± 0.030 mag. Δχ2 and AICc probabilities for these models, again relative to applying uTi but no host data, can also be found in Table 3. We find that the full model including uTi, uCa, and LsSFR provides the smallest χ2 ∕dof, but that the AICc find fits including uTi and uCa but no host corrections to be preferred considering the number of parameters. The fit quality of the x1 models rapidly increases as host information is included. Adding host information to the U-band parameter models is not justified as χ2 is only modestly improved.

In Fig. 11 we search for the SNe for which light curve width and uTi predict different magnitudes. As uTi and x1 are anti-correlated, we can do this by normalizing both distributions to zero mean and unity RMS and then plotting the sum of the two transformed values for each SN. Currentx1 standardization produces SN magnitudes that are too bright in passive environments (low LsSFR), that is, the x1 parameter assumes these to be intrinsically fainter than they actually are and overcorrects their magnitudes. As is visualized in Fig. 11, uTi still predicts these SNe to be intrinsically faint, but not by as much as x1, thus generating smaller magnitude corrections and avoiding overcorrection. Similarly, in actively star forming regions uTi does not predict SNe to be as intrinsically overluminous as predicted by x1. This suggests a complex relationship between progenitor age, peak magnitude and light curve width. A change in the progenitor age affects both peak energy and light curve width, but not following the familiar (and dominating) width-luminosity relation. Anexample would be a scenario in which the width-luminosity trend is mainly caused by the amount of 56Ni generated but also affected by progenitor size, for which age could be a strong driver.

The dependence on LsSFR can be visualized for this sample by comparing peak magnitude (for clarity, after color correction) versus SALT2.4 x1 (left panel of Fig. 12). For fixed x1, SNe in passive (“delayed”) environments are brighter. Performing such a comparison for uTi shows the dependence on LsSFR to be much reduced (right panel of Fig. 12).

thumbnail Fig. 11

The difference in standardization based on x1 and uTi is examined by comparing their sum (as they are anti-correlated) against local specific star formation (LsSFR). A smaller x1+uTi (y-axis) value corresponds to a SN considered fainter according to x1 relative to what uTi predicts.

5.3 U-band indices and the choice of color curve

Here we first study the potential systematic error caused by dereddening using the F99 color curve, if in fact all SNe Ia actually followed the SALT2.4 color curve. The systematic (theoretical) change in the uNi, uTi, uSi and uCa color indices between F99 and SALT2.4, as a function of the color parameter is shown in Fig. 13. We use the same conversion between E(B − V) and SALT2.4 c as previously. More than 90% of the sample has |c| < 0.15, a range where the maximum possible variation for the uTi, uSi and uCa colors is limited to less than 0.1 mag – small considering the U-band parameter value ranges found here. We therefore conclude that the standardization effects discussed above were not driven by systematic effects from the dereddening process.

An empirical SN Ia standardization model, like SALT2.4, relies on the combination of a color curve and a spectral model to predict how the intrinsic spectrum varies (for SALT the latter is parameterized by x1). Comparing the SALT2.4 spectral model with observations in the λ(uNi) region, where empirical and dust color curves start to strongly deviate, we note a clear functional difference – the uNi color decreases with wider light curve width in a way that is not captured by the SALT2.4 model (Fig. 13, right panel). Such a mismatch between the SALT2.4 template and the observed SED could, if correlated with broad-band colors, modify the derived effective color curve and potentially bias cosmological parameter constraints if the SN Ia sample distributions vary with redshift/look-back time.

6 Discussion

6.1 Literature subclasses

A potential link with Shallow Silicon SNe (Branch et al. 2006) was highlighted in connection with uCa and SN standardization (Fig. 10). In particular, SN1991T-like objects, a core group among SS SNe, have flat early U-band spectra as one of their defining features (Filippenko et al. 1992; Scalzo et al. 2012). There are eight SS SNe in this sample, out of which two are SN1991T-like. Sub-classification of the SNfactory sample will be further discussed in Chotard et al. (in prep). Here we note that the mean Hubble diagram residual bias for SS and 91T-like objects gets progressively smaller when standardizing using U-band indices, as shown in Table 4. The two 91T-like SNe have very similar uNi indices, as well as EW(Si II λ6355) and Hubble residuals, while they are separated from both other SS SNe and other SN Ia subtypes (see Fig. 14, left panel). We find no evidence of a continuous distribution connecting these to the main SN population, further suggesting that these SNe are more closely related to Super Chandrasekhar-mass SNe Ia (see discussion in Scalzo et al. 2012, 2014).

Milne et al. (2013, 2015) have suggested that SNe Ia can be divided into two subsets based on the Swift u-v color at ± 6 days from peak. In Fig. 14 we show the USNf − VSNf color as determined from a similar wide phase range. We do not find strong signs of distinct populations in the USNf − VSNf color, especially not after reddening corrections are applied. The Swift UVOT u band is bluer compared with USNf while VSNf extends slightly redder than the UVOT v band, thus filter sensitivity differences possibly cause different intrinsic SN Ia features to be probed. Cinabro et al. (2017) did not find significant signs of subsets based on modeling ground-based photometry of more distant SDSS and SNLS SNe. Milne et al. (2013) also highlighted high-velocity SNe and/or Branch Shallow Silicon SNe as having blue u-v colors, trends compatible with our data and highlighted in Fig. 14. Finally, we note that Milne et al. (2013) showed both SN2011fe and SNF20080514-002 to have similar blue UVOT u-v colors, while our analysis began with the spectroscopic differences found between these two SNe (Fig. 1). This further points to the difficulty in constraining spectroscopic variations using broadband photometry, and vice versa.

The existence of HVFs has been another approach to subclassification involving U-band data. A blinded visual search for Ca HVFs was made with the purpose of dividing the sample into SNe with and without HVFs at phase ~ −2 days. All SNfactory spectra were randomly reordered and the Ca H&K λ 3945 and Ca IR λ8579 region displayed, together with the expected photospheric line position based on the Si II λ6355 velocity at that phase. A scanner (J.N.) classified each spectrum as either having clear HVF, having good data but no HVF, or being too noisy for an accurate classification. For the small SN subset with multiple high signal-to-noise ratio (S/N) spectra prior to − 2 days, we found the visual classification to agree, showing that we consistently classified these. We show the SALT2.4x1 cumulative distributions of SNe with and without the HVF classification in Fig. 15 (listed in Table 1). As haveprevious studies (Childress et al. 2014; Silverman et al. 2015), we find narrower light curve SNe (x1 ≲−0.5) to only very rarely show HVFs at a phase, whereas a majority of the x1 > −0.5 SNe show HVFs. A KS-test rejects a common parent population at greater than 99% confidence. If the presence of HVFs were solely caused by, for example, the effective radius at a certain phase, to which x1 could be correlated through the ejecta mass, a continuously increasing probability of detecting HVFs would be expected. The data presented here are more suggestive of a rapid probability change with x1, such as would be caused if x1 ≲−0.5 originate from a distinct explosion channel. In terms of the U-band spectral indices, this difference can be seen as a consistently small RMS for uSi and uCa at early phases among the low x1 -subset in Fig. 3.

thumbnail Fig. 12

Comparing peak SN magnitude (including color correction) with SALT2.4 x1 (left panel) and uTi (right panel). Lighter shaded points were found in R17 to originate in locally passive regions, and likely from old progenitors, while dark blue points were found in regions dominated by star formation. These are separated in x1 (left), but not in uTi (right).
thumbnail Fig. 13

Left: directly comparing the difference in U-band color indices, u(Ni|Ti|Si|Ca)SALT-u(Ni|Ti|Si|Ca)F99. While systematic differences grow large for highly reddened objects, these are limited for the current sample. Short, orange vertical lines show the SALT2.4 c values of SNe in this sample. Right: SALT x1 vs. uNi at phase 4 to 8 days. The red line shows the corresponding SALT model predictions.
thumbnail Fig. 14

Left: uNi index measurements of SN1991T-like and Shallow Silicon-like SNe Ia compared with EW(Si II λ6355). The SN1991T-like SNe are disconnected from the remaining sample. Right: distribution of USNf − VSNf for spectra within 6 days of light curve peak. The figure shows data with (orange) and without (blue) reddening correction, where the linear evolution with phase was removed for each (returning distributions with zero mean). The Shallow Silicon (SS) subset of the dereddened USNf − VSNf distribution is shown by the cross-hatched histogram.
Table 4

Mean and its uncertainty of Hubble diagram residual for branch shallow silicon and SN1991T-like SNe (the latter a subset of the former), for three different standardization methods, as discussed in Sect. 5.

thumbnail Fig. 15

Cumulative x1 distributions for SNe with and without visually identified HVFs (based on spectra with phase < − 2 day).

6.2 Outlook

The wavelength limits of the U-band features used here were set based on a comparison of only two SNe, examined at two phases. These wavelength regions were then analyzed at three phase intervals chosen to roughly capture typical SN Ia spectral variations on weekly scales, but chosen prior to any knowledge regarding when certain features come to dominate. An improved future analysis will include phase-dependent wavelength regions, where observations at different phases are combined with appropriate weights. Integration of flux within fixed wavelength limits carry less stringent S/N requirements compared with measurements of individual spectroscopic features. Thus, low-resolution spectroscopy (or possibly narrow-band filters) could measure the U-band indices directly at high redshifts.

A sample of nearby SNe Ia with cadenced U-band spectroscopy starting at early phases (<−10 days) would allow novel studies of the explosion process through the temporal development of the λ(uNi) region. Simultaneously, Ca H&K λ 3945 features map IME variations and uTi provides accurate temperature estimates after peak light. Such early data are also needed to finally determine whether the lack of HVFs among narrower light curve SNe is a consequence of a less energetic explosion, or if this signals a physically different explosion mechanism and/or circumstellar material.

The limit at which HVFs disappear (x1 ~−0.5) agrees with findings by Scalzo et al. (2014), using SNfactory SNe with coverage extending to late phases, that the derived ejecta mass (Mej) points to sub-Chandrasekhar-mass explosions. The seven SNe in the sample analyzed here with derived Mej and MNi masses from Scalzo et al. (2014) are insufficient for further tests of Mej and MNi correlations, again motivating larger samples which combine several types of observations. These could also include ejecta/Ni /IGE constraints derived through nebular Co II lines (Childress et al. 2015), second maximum position (Dhawan et al. 2015), and early light curve rise-time (Firth et al. 2015), as well as measurements of ejecta asymmetry from nebular lines (Maeda et al. 2011).

We see signs that the currently most widely used SN model, SALT2.4, can be improved. Updates to the SN template in this region couldpropagate into a change in the effective color law. Creating an unbiased template for the intrinsic U-band spectrum is a requirement for current and future ground-based SN Ia analyses like DES and LSST, where the rest-frame U-band is redshifted to the wavelengths most efficiently observed from the ground.

7 Summary and conclusions

Comparing spectra of two supernovae at early and peak phases led to the subdivision of the U-band into four regions whose flux ratio relative to B-band were used to construct the uNi, uTi, uSi and uCa indices. We use a sample of 92 SNe Ia to analyze these indices at three representative phase ranges: − 8 to − 4 days (pre-peak), − 2 to 2 days (peak) and 4 to 8 days (post-peak).

SYNAPPS comparisons show that Ni/Co absorption can explain differences in the bluest feature (“uNi”) and that uNi at pre-peak phases can be used as a probe of Ni abundance, to complement constraints from the early light curve rise-time, bolometric light curves and nebular emission. In similar tests, SYNAPPS fits also show that Ti absorption differences dominate the λ(uTi) wavelength range. The uTi index is an extremely sensitive luminosity indicator. When used instead of the SALT2.4 x1 parameter the RMS scatter around the Hubble diagram falls to 0.116 ± 0.011 mag. Here we use measurements made in the post-peak phase region, but note that the uTi index at all phases after peak is strongly correlated with light curve width. Adding pre-peak uCa as a third standardization parameter further reduces the RMS around the Hubble diagram. A fit with uTi and uCa yields a 0.086 ± 0.010 mag scatter with χ2 ∕dof ~ 1 without the need to introduce intrinsic dispersion. Including U-band indices in SN Ia standardization reduces the dependence on host-galaxy environment. The difference between light curve width and uTi can be used to study SN Ia progenitor scenarios.

Shallow Silicon and 91T-like SNe have biased SALT2.4 Hubble residuals, which are substantially reduced when U-band parameters are included in the fit. The two 91T-like SNe in this sample have similar U-band properties and magnitudes, which are offset from the remaining sample. We confirm previous results that SNe Ia with narrower light curves very rarely show HVFs. We find a sharp transition in their incidence at x1 = −0.5.

Acknowledgements

We thank the technical staff of the University of Hawaii 2.2 m telescope, and Dan Birchall for observing assistance. We recognize the significant cultural role of Mauna Kea within the indigenous Hawaiian community, and we appreciate the opportunity to conduct observations from this revered site. This work was supported in part by the Director, Office of Science, Office of High Energy Physics of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Support in France was provided by CNRS/IN2P3, CNRS/INSU, and PNC; LPNHE acknowledges support from LABEX ILP, supported by French state funds managed by the ANR within the Investissements d’Avenir programme under reference ANR-11-IDEX-0004-02. Support in Germany was provided by DFG through TRR33 “The Dark Universe” and by DLR through grants FKZ 50OR1503 and FKZ 50OR1602. In China the support was provided from Tsinghua University 985 grant and NSFC grant No 11173017. Some results were obtained using resources and support from the National Energy Research Scientific Computing Center, supported by the Director, Office of Science, Office of Advanced Scientific Computing Research of the U.S. Department of Energy under Contract No. DE-AC02- 05CH11231. We thank the Gordon & Betty Moore Foundation for their continuing support. Additional support was provided by NASA under the Astrophysics Data Analysis Program grant 15-ADAP15-0256 (PI: Aldering). We also thank the High Performance Research and Education Network (HPWREN), supported by National Science Foundation Grant Nos. 0087344 & 0426879.

Appendix A Element contributions to SYNAPPS fits

We discuss in Sect. 4.1 how the observed spectral differences between SN2011fe and SNF20080514-002 can be explained by changing the early Ni/Co abundance and Ti abundance at peak. Here we show the complete set of ion contributions to the best fit SYNAPPS spectrum of SN2011fe 10 days prior to peak (Fig. A.1) and for SN200805014-002 close to peak (Fig. A.2). These fits match the observed data well.

thumbnail Fig. A.1

SYNAPPS fit to SN2011fe 10 days prior to peak. The top panel compares the observed spectrum to the full SYNAPPS fit. The lower panels show the contribution of each ion to the final spectra. These are plotted as the ratio between the spectrum with and without each ion activated. Dashed, vertical, gray lines indicate the U-band index regionboundaries, with designations given at the top.
thumbnail Fig. A.2

SYNAPPS fit to SNF20080514-002 at peak light. The top panel compares the observed spectrum to the full SYNAPPS fit. The lower panels show the contribution of each ion to the final spectra. These are plotted as the ratio between the spectrum with and without each ion activated. Dashed, vertical, gray lines indicate the U-band index regionboundaries, with designations given at the top.

References

  1. Aldering, G., Adam, G., Antilogus, P., et al. 2002, Proc. SPIE, 4836, 61 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aldering, G., Antilogus, P., Bailey, S., et al. 2006, ApJ, 650, 510 [NASA ADS] [CrossRef] [Google Scholar]
  3. Altavilla, G., Stehle, M., Ruiz-Lapuente, P., et al. 2007, A&A, 475, 585 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  4. Amanullah, R., Johansson, J., Goobar, A., et al. 2015, MNRAS, 453, 3300 [NASA ADS] [CrossRef] [Google Scholar]
  5. Arsenijevic, V., Fabbro, S., Mourão, A. M., & Rica da Silva, A. J. 2008, A&A, 492, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Bacon, R., Copin, Y., Monnet, G., et al. 2001, MNRAS, 326, 23 [NASA ADS] [CrossRef] [Google Scholar]
  7. Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Blondin, S., Matheson, T., Kirshner, R. P., et al. 2012, AJ, 143, 126 [NASA ADS] [CrossRef] [Google Scholar]
  9. Blondin, S., Dessart, L., Hillier, D. J., & Khokhlov, A. M. 2013, MNRAS, 429, 2127 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bloom, J. S., Kasen, D., Shen, K. J., et al. 2012, ApJ, 744, L17 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bongard, S., Soulez, F., Thiébaut, É., & Pecontal, É. 2011, MNRAS, 418, 258 [NASA ADS] [CrossRef] [Google Scholar]
  12. Branch, D., Dang, L. C., Hall, N., et al. 2006, PASP, 118, 560 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bufano, F., Immler, S., Turatto, M., et al. 2009, ApJ, 700, 1456 [NASA ADS] [CrossRef] [Google Scholar]
  14. Burns, C. R., Stritzinger, M., Phillips, M. M., et al. 2014, ApJ, 789, 32 [NASA ADS] [CrossRef] [Google Scholar]
  15. Buton, C., Copin, Y., Aldering, G., et al. 2013, A&A, 549, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Cao, Y., Johansson, J., Nugent, P. E., et al. 2016, ApJ, 823, 147 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cartier, R., Sullivan, M., Firth, R. E., et al. 2017, MNRAS, 464, 4476 [NASA ADS] [CrossRef] [Google Scholar]
  18. Childress, M., Aldering, G., Antilogus, P., et al. 2013a, ApJ, 770, 108 [NASA ADS] [CrossRef] [Google Scholar]
  19. Childress, M., Aldering, G., Antilogus, P., et al. 2013b, ApJ, 770, 107 [NASA ADS] [CrossRef] [Google Scholar]
  20. Childress, M. J., Filippenko, A. V., Ganeshalingam, M., & Schmidt, B. P. 2014, MNRAS, 437, 338 [NASA ADS] [CrossRef] [Google Scholar]
  21. Childress, M. J., Hillier, D. J., Seitenzahl, I., et al. 2015, MNRAS, 454, 3816 [NASA ADS] [CrossRef] [Google Scholar]
  22. Chornock, R., Berger, E., Rest, A., et al. 2013, ApJ, 767, 162 [NASA ADS] [CrossRef] [Google Scholar]
  23. Chotard, N. 2011, PhD Thesis, Lyon [Google Scholar]
  24. Chotard, N., Gangler, E., Aldering, G., et al. 2011, A&A, 529, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cinabro, D., Scolnic, D., Kessler, R., Li, A., & Miller, J. 2017, MNRAS, 466, 884 [NASA ADS] [CrossRef] [Google Scholar]
  26. Dhawan, S., Leibundgut, B., Spyromilio, J., & Maguire, K. 2015, MNRAS, 448, 1345 [NASA ADS] [CrossRef] [Google Scholar]
  27. Dilday, B., Howell, D. A., Cenko, S. B., et al. 2012, Science, 337, 942 [NASA ADS] [CrossRef] [Google Scholar]
  28. Edwards, Z. I., Pagnotta, A., & Schaefer, B. E. 2012, ApJ, 747, L19 [NASA ADS] [CrossRef] [Google Scholar]
  29. Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [NASA ADS] [CrossRef] [Google Scholar]
  30. Fakhouri, H. K., Boone, K., Aldering, G., et al. 2015, ApJ, 815, 58 [NASA ADS] [CrossRef] [Google Scholar]
  31. Feindt, U., Kerschhaggl, M., Kowalski, M., et al. 2015, A&A, 578, C1 [CrossRef] [EDP Sciences] [Google Scholar]
  32. Filippenko, A. V., Richmond, M. W., Matheson, T., et al. 1992, ApJ, 384, L15 [NASA ADS] [CrossRef] [Google Scholar]
  33. Firth, R. E., Sullivan, M., Gal-Yam, A., et al. 2015, MNRAS, 446, 3895 [NASA ADS] [CrossRef] [Google Scholar]
  34. Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
  35. Foley, R. J. 2013, MNRAS, 435, 273 [NASA ADS] [CrossRef] [Google Scholar]
  36. Foley, R. J., Sanders, N. E., & Kirshner, R. P. 2011, ApJ, 742, 89 [NASA ADS] [CrossRef] [Google Scholar]
  37. Foley, R. J., Filippenko, A. V., Kessler, R., et al. 2012, AJ, 143, 113 [NASA ADS] [CrossRef] [Google Scholar]
  38. Foley, R. J., Pan, Y.-C., Brown, P., et al. 2016, MNRAS, 461, 1308 [NASA ADS] [CrossRef] [Google Scholar]
  39. Garavini, G., Folatelli, G., Goobar, A., et al. 2004, AJ, 128, 387 [NASA ADS] [CrossRef] [Google Scholar]
  40. Garavini, G., Nobili, S., Taubenberger, S., et al. 2007, A&A, 471, 527 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Hachinger, S., Mazzali, P. A., Sullivan, M., et al. 2013, MNRAS, 429, 2228 [NASA ADS] [CrossRef] [Google Scholar]
  43. Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 2003, Nature, 424, 651 [NASA ADS] [CrossRef] [Google Scholar]
  44. Hayden, B. T., Garnavich, P. M., Kasen, D., et al. 2010, ApJ, 722, 1691 [NASA ADS] [CrossRef] [Google Scholar]
  45. Huang, X., Raha, Z., Aldering, G., et al. 2017, ApJ, 836, 157 [NASA ADS] [CrossRef] [Google Scholar]
  46. Kessler, R., Becker, A. C., Cinabro, D., et al. 2009, ApJS, 185, 32 [NASA ADS] [CrossRef] [Google Scholar]
  47. Kromer, M., Sim, S. A., Fink, M., et al. 2010, ApJ, 719, 1067 [NASA ADS] [CrossRef] [Google Scholar]
  48. Lantz, B., Aldering, G., Antilogus, P., et al. 2004, in Proc. SPIE, Optical Design and Engineering, eds. L. Mazuray, P. J. Rogers, & R. Wartmann, 5249, 146 [NASA ADS] [CrossRef] [Google Scholar]
  49. Leonard, D. C. 2007, ApJ, 670, 1275 [NASA ADS] [CrossRef] [Google Scholar]
  50. Li, W., Bloom, J. S., Podsiadlowski, P., et al. 2011, Nature, 480, 348 [NASA ADS] [CrossRef] [Google Scholar]
  51. Maeda, K., & Terada, Y. 2016, Int. J. Mod. Phys. D, 25, 1630024 [NASA ADS] [CrossRef] [Google Scholar]
  52. Maeda, K., Leloudas, G., Taubenberger, S., et al. 2011, MNRAS, 413, 3075 [NASA ADS] [CrossRef] [Google Scholar]
  53. Maguire, K., Sullivan, M., Ellis, R. S., et al. 2012, MNRAS, 426, 2359 [NASA ADS] [CrossRef] [Google Scholar]
  54. Maguire, K., Taubenberger, S., Sullivan, M., & Mazzali, P. A. 2016, MNRAS, 457, 3254 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Mandel, K. S., Scolnic, D. M., Shariff, H., Foley, R. J., & Kirshner, R. P. 2017, ApJ, 842, 93 [NASA ADS] [CrossRef] [Google Scholar]
  56. Maoz, D., Mannucci, F., & Nelemans, G. 2014, ARA&A, 52, 107 [NASA ADS] [CrossRef] [Google Scholar]
  57. Matheson, T., Kirshner, R. P., Challis, P., et al. 2008, AJ, 135, 1598 [NASA ADS] [CrossRef] [Google Scholar]
  58. Mazzali, P. A., Benetti, S., Altavilla, G., et al. 2005, ApJ, 623, L37 [NASA ADS] [CrossRef] [Google Scholar]
  59. Miles, B. J., van Rossum, D. R., Townsley, D. M., et al. 2016, ApJ, 824, 59 [NASA ADS] [CrossRef] [Google Scholar]
  60. Milne, P. A., Brown, P. J., Roming, P. W. A., Bufano, F., & Gehrels, N. 2013, ApJ, 779, 23 [NASA ADS] [CrossRef] [Google Scholar]
  61. Milne, P. A., Foley, R. J., Brown, P. J., & Narayan, G. 2015, ApJ, 803, 20 [NASA ADS] [CrossRef] [Google Scholar]
  62. Nordin, J., Östman, L., Goobar, A., et al. 2011, A&A, 526, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Nugent, P., Phillips, M., Baron, E., Branch, D., & Hauschildt, P. 1995, ApJ, 455, L147 [NASA ADS] [CrossRef] [Google Scholar]
  64. Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
  65. Patat, F., Benetti, S., Cappellaro, E., et al. 1996, MNRAS, 278, 111 [NASA ADS] [CrossRef] [Google Scholar]
  66. Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
  67. Pinto, P. A. & Eastman, R. G. 2000, ApJ, 530, 757 [NASA ADS] [CrossRef] [Google Scholar]
  68. Piro, A. L., & Nakar, E. 2014, ApJ, 784, 85 [NASA ADS] [CrossRef] [Google Scholar]
  69. Piro, A. L., & Morozova, V. S. 2016, ApJ, 826, 96 [NASA ADS] [CrossRef] [Google Scholar]
  70. Quimby, R. M., Werner, M. C., Oguri, M., et al. 2013, ApJ, 768, L20 [NASA ADS] [CrossRef] [Google Scholar]
  71. Quimby, R. M., Oguri, M., More, A., et al. 2014, Science, 344, 396 [Google Scholar]
  72. Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
  73. Rigault, M., Copin, Y., Aldering, G., et al. 2013, A&A, 560, A66 (R13) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Rigault, M., Aldering, G., Kowalski, M., et al. 2017, A&A, submitted (R17) [Google Scholar]
  75. Röpke, F. K., Kromer, M., Seitenzahl, I. R., et al. 2012, ApJ, 750, L19 [NASA ADS] [CrossRef] [Google Scholar]
  76. Rubin, D., Aldering, G., Barbary, K., et al. 2015, ApJ, 813, 137 [NASA ADS] [CrossRef] [Google Scholar]
  77. Ruiter, A. J., Belczynski, K., Sim, S. A., et al. 2011, MNRAS, 417, 408 [NASA ADS] [CrossRef] [Google Scholar]
  78. Saunders, C., Aldering, G., Antilogus, P., et al. 2015, ApJ, 800, 57 [NASA ADS] [CrossRef] [Google Scholar]
  79. Scalzo, R. A., Aldering, G., Antilogus, P., et al. 2010, ApJ, 713, 1073 [NASA ADS] [CrossRef] [Google Scholar]
  80. Scalzo, R., Aldering, G., Antilogus, P., et al. 2012, ApJ, 757, 12 [NASA ADS] [CrossRef] [Google Scholar]
  81. Scalzo, R., Aldering, G., Antilogus, P., et al. 2014, MNRAS, 440, 1498 [NASA ADS] [CrossRef] [Google Scholar]
  82. Schaefer, B. E., & Pagnotta, A. 2012, Nature, 481, 164 [NASA ADS] [CrossRef] [Google Scholar]
  83. Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
  84. Scolnic, D. M., Riess, A. G., Foley, R. J., et al. 2014, ApJ, 780, 37 [NASA ADS] [CrossRef] [Google Scholar]
  85. Seitenzahl, I. R., Ciaraldi-Schoolmann, F., Röpke, F. K., et al. 2014, MNRAS, 444, 350 [NASA ADS] [CrossRef] [Google Scholar]
  86. Silverman, J. M., Foley, R. J., Filippenko, A. V., et al. 2012, MNRAS, 425, 1789 [NASA ADS] [CrossRef] [Google Scholar]
  87. Silverman, J. M., Vinkó, J., Marion, G. H., et al. 2015, MNRAS, 451, 1973 [NASA ADS] [CrossRef] [Google Scholar]
  88. Sim, S. A., Röpke, F. K., Hillebrandt, W., et al. 2010, ApJ, 714, L52 [Google Scholar]
  89. Sim, S. A., Seitenzahl, I. R., Kromer, M., et al. 2013, MNRAS, 436, 333 [NASA ADS] [CrossRef] [Google Scholar]
  90. Smitka, M. T., Brown, P. J., Suntzeff, N. B., et al. 2015, ApJ, 813, 30 [NASA ADS] [CrossRef] [Google Scholar]
  91. Stanishev, V., Goobar, A., Benetti, S., et al. 2007, A&A, 469, 645 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Sullivan, M., Conley, A., Howell, D. A., et al. 2010, MNRAS, 406, 782 [NASA ADS] [Google Scholar]
  93. Tanaka, M., Mazzali, P. A., Maeda, K., & Nomoto, K. 2006, ApJ, 645, 470 [NASA ADS] [CrossRef] [Google Scholar]
  94. Tanaka, M., Mazzali, P. A., Benetti, S., et al. 2008, ApJ, 677, 448 [NASA ADS] [CrossRef] [Google Scholar]
  95. Thomas, R. C., Nugent, P. E., & Meza, J. C. 2011, PASP, 123, 237 [NASA ADS] [CrossRef] [Google Scholar]
  96. Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
  97. Walker, E. S., Hachinger, S., Mazzali, P. A., et al. 2012, MNRAS, 427, 103 [NASA ADS] [CrossRef] [Google Scholar]
  98. Wang, X., Li, W., Filippenko, A. V., et al. 2009, ApJ, 697, 380 [NASA ADS] [CrossRef] [Google Scholar]
  99. Wang, X., Wang, L., Filippenko, A. V., et al. 2012, ApJ, 749, 126 [NASA ADS] [CrossRef] [Google Scholar]
2

We note that Chotard et al. (2011) used slightly different filter definitions.

3

These are SN2007le, SNF20080720-001 and SN2006X.

All Tables

Table 1

SN U-band properties and Ca high velocity feature classification.

In the text
Table 1

continued.

In the text
Table 2

Standardization fit results.

In the text
Table 3

Each line shows Hubble residual fit quality for a given standardization method, measured relative to a reference fit based on post-peak uTi data without any host property corrections (first line).

In the text
Table 4

Mean and its uncertainty of Hubble diagram residual for branch shallow silicon and SN1991T-like SNe (the latter a subset of the former), for three different standardization methods, as discussed in Sect. 5.

In the text

All Figures

thumbnail Fig. 1

Comparison of the spectra of SN2011fe (SALT2.4x1 = −0.4 and c = −0.06) and SNF200805014-002 (SALT2.4x1 = −1.5 and c = −0.12) at early (left) and peak (right) phases. Small spectroscopic differences are found redwards of 4000 Å(stable Fe marked in left panel). Much larger deviation is found bluewards of this limit. The comparison at early phases differs most strongly around 3400 Åand the high velocity edge of the Ca H&K λ 3945 feature, the comparison at later phases mainly around 3550 Å. These differences led to the subdivision of the U-band into four indices, as described in the text. Vertical lines show the feature limits thus defined.
In the text
thumbnail Fig. 2

Mean spectra and ± 1 standard deviation in sample at three representative phases. The four wavelength regions considered are separated by dashed lines. The interpretation of these indices will be phase dependent, as, for example, the Ti region at early phases is clearly a part of the Ca H&K λ 3945 + Si II λ3858 feature complex and Cr/Fe dominates uNi at late phases.
In the text
thumbnail Fig. 3

Intrinsic flux RMS (vs. wavelength) for SNe after division into four bins according to increasing light curve width (dark to light lines). Spectra were initially normalized to have median flux of unity over the [3300, 6900] Åwavelength region. Panels from top to bottom show the three sample phase regions (pre-peak, peak and post-peak). Vertical (dotted) lines mark boundaries of the four U-band regions. Thered dashed red line shows the RMS for the full sample.
In the text
thumbnail Fig. 4

U-band spectroscopic variation spanning the range of common SN properties: x1, dereddened MB, color (left to right). Composite spectra were calculated after dividing the sample into four quartiles based on each property, which was repeated at three representative phase ranges (− 6, 0, 6) for each subset. Subset composites were drawn such that the line color becomes darker as the parameter value decreases. Dotted lines indicate U-band spectral-index subdivision boundaries.
In the text
thumbnail Fig. 5

U-band spectroscopic variation spanning the range of common SN properties: Hubble residuals standardized by SALT2.4 light curve parameters, EW(Si II λ6355) and v(Si II λ6355) (left toright). Composite spectra were calculated after dividing the sample into four quartiles based on each property, which was repeated at three representative phase ranges (− 6, 0, 6) for each subset. Subset composites were drawn such that the line color becomes darker as the parameter value decreases. Dotted lines indicate U-band spectral-index subdivision boundaries.
In the text
thumbnail Fig. 6

Probing the origin of variation in the λ(uNi) region through SYNAPPS model comparisons. The top panel compares SN2011fe and SNF20080514-002 at an early phase (−10 days). The second panel repeats the early SN2011fe spectrum (blue line) together with the best SYNAPPSfit (black dashed line). The green line shows the same fit, but with the optical depth (τ) of all Ni and Co II decreased by 1 dex, effectively suppressing these ions. The third panel compares the early SNF20080514-002 spectrum with the same SN2011fe SYNAPPS fits. The SN2011fe fit with suppressed Ni; Co II optical depth matches the SNF20080514-002 λ(uNi) region well. Vertical dotted lines indicate the U-band spectral index boundaries, with λ(uNi) lightly shaded gray.
In the text
thumbnail Fig. 7

Probing the origin of uTi variation through SYNAPPS model comparisons. The top panel compares SN2011fe and SNF20080514-002 at peak light. The second panel shows SNF20080514-002 (orange line) together with the best SYNAPPS fit of this spectrum (black dashed line). The green line shows the same fit, but with the optical depth (τ) of Ti II decreased by 1 dex, effectively suppressing these ions. The third panel compares the SN2011fe spectrum with the same SNF20080514-002 SYNAPPS fits. The SNF200805014-002 fit with suppressed Ti II optical depth matches the SN2011fe λ(uTi) region well. Vertical dotted lines indicate the U-band spectral index boundaries, with λ(uTi) shaded lightgray.
In the text
thumbnail Fig. 8

Spectra of SN2011fe and LSQ12fxd at phase ~ − 8 days. LSQ12fxd has, compared with SN2011fe, both a steeper early rise-time (Firth et al. 2015) and less flux in the λ(uNi) region (i.e., stronger Co II absorption at this phase).
In the text
thumbnail Fig. 9

uTi vs. phase with markers colored by SALT2.4x1. The left andmid panels show the uTi color prior to and following F99 dereddening, respectively. The right panel displays the BSNf − VSNf color evolution for reference, calculated from dereddened restframe spectra. Pre-peak observations show a scatter induced by the edge of the Ca H&K λ 3945 feature. uTi colors after peak show a strong stable correlation with light curve width.
In the text
thumbnail Fig. 10

Left:origin of pre-peak uCa correlation with SALT2.4 Hubble residuals. The Spearman correlation coefficient of rs = 0.43 indicates a moderate correlation, with the hypothesis of no correlation at > 99% confidence. Right: comparing the post-peak uTi color integrated from HST-STIS spectra with SIFTO stretch. Spectra were dereddened according to a similar procedure as the SNfactory sample and use light curve data from Maguire et al. (2012). The SNIFS sample presented here is included for comparison, with SALT2.4 x1 values converted to SIFTO stretch using the relation provided by Guy et al. (2010). The trend with uTi agrees betwen these two data sets.
In the text
thumbnail Fig. 11

The difference in standardization based on x1 and uTi is examined by comparing their sum (as they are anti-correlated) against local specific star formation (LsSFR). A smaller x1+uTi (y-axis) value corresponds to a SN considered fainter according to x1 relative to what uTi predicts.
In the text
thumbnail Fig. 12

Comparing peak SN magnitude (including color correction) with SALT2.4 x1 (left panel) and uTi (right panel). Lighter shaded points were found in R17 to originate in locally passive regions, and likely from old progenitors, while dark blue points were found in regions dominated by star formation. These are separated in x1 (left), but not in uTi (right).
In the text
thumbnail Fig. 13

Left: directly comparing the difference in U-band color indices, u(Ni|Ti|Si|Ca)SALT-u(Ni|Ti|Si|Ca)F99. While systematic differences grow large for highly reddened objects, these are limited for the current sample. Short, orange vertical lines show the SALT2.4 c values of SNe in this sample. Right: SALT x1 vs. uNi at phase 4 to 8 days. The red line shows the corresponding SALT model predictions.
In the text
thumbnail Fig. 14

Left: uNi index measurements of SN1991T-like and Shallow Silicon-like SNe Ia compared with EW(Si II λ6355). The SN1991T-like SNe are disconnected from the remaining sample. Right: distribution of USNf − VSNf for spectra within 6 days of light curve peak. The figure shows data with (orange) and without (blue) reddening correction, where the linear evolution with phase was removed for each (returning distributions with zero mean). The Shallow Silicon (SS) subset of the dereddened USNf − VSNf distribution is shown by the cross-hatched histogram.
In the text
thumbnail Fig. 15

Cumulative x1 distributions for SNe with and without visually identified HVFs (based on spectra with phase < − 2 day).
In the text
thumbnail Fig. A.1

SYNAPPS fit to SN2011fe 10 days prior to peak. The top panel compares the observed spectrum to the full SYNAPPS fit. The lower panels show the contribution of each ion to the final spectra. These are plotted as the ratio between the spectrum with and without each ion activated. Dashed, vertical, gray lines indicate the U-band index regionboundaries, with designations given at the top.
In the text
thumbnail Fig. A.2

SYNAPPS fit to SNF20080514-002 at peak light. The top panel compares the observed spectrum to the full SYNAPPS fit. The lower panels show the contribution of each ion to the final spectra. These are plotted as the ratio between the spectrum with and without each ion activated. Dashed, vertical, gray lines indicate the U-band index regionboundaries, with designations given at the top.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.