| Issue |
A&A
Volume 605, September 2017
|
|
|---|---|---|
| Article Number | A93 | |
| Number of page(s) | 19 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201630127 | |
| Published online | 18 September 2017 | |
Origin of warm and hot gas emission from low-mass protostars: Herschel-HIFI observations of CO J = 16–15⋆
I. Line profiles, physical conditions, and H2O abundance
1 Centre for Star and Planet Formation, Niels Bohr Institute and Natural History Museum of Denmark, University of Copenhagen, Øster Voldgade 5-7, 1350 Copenhagen K, Denmark
e-mail: lars.kristensen@nbi.ku.dk
2 Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
3 Max Planck Institut für Extraterrestrische Physik, Giessenbachstrasse 1, 85748 Garching, Germany
4 Max Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
5 Centre for Astronomy, Nicolaus Copernicus University, Faculty of Physics, Astronomy and Informatics, Grudziadzka 5, 87100 Torun, Poland
6 Jet Propulsion Laboratory, 4800 Oak Groave Drive, Pasadena, CA 91109, USA
7 Department of Astronomy, The University of Michigan, 500 Church Street, Ann Arbor, MI 48109-1042, USA
8 LERMA, UMR 8112 du CNRS, Observatoire de Paris, 61 Av. de l’Observatoire, 75014 Paris, France
9 Department of Physics and Astronomy, Denison University, Granville, OH 43023, USA
10 Department of Astronomy, The University of Texas at Austin, Austin, TX 78712, USA
11 LERMA, UMR 8112 du CNRS, Observatoire de Paris, École Normale Supérieure, 61 Av. de l’Observatoire, 75014 Paris, France
12 Heidelberg University, Center for Astronomy, Institute for Theoretical Astrophysics, Albert-Ueberle-Strasse 2, 69120 Heidelberg, Germany
13 Kavli Institute for Astronomy and Astrophysics, Peking University, Yi He Yuan Lu 5, Haidian Qu, 100871 Beijing, PR China
14 National Research Council Canada, Herzberg Institute of Astrophysics, 5071 West Saanich Road, Victoria, BC V9E 2E7, Canada
15 Department of Physics and Astronomy, University of Victoria, Victoria, BC V8P 1A1, Canada
16 RON Netherlands Institute for Space Research, Location Utrecht, Sorbonnelaan 2, 3584 CA Utrecht, The Netherlands
17 Department of Astronomy & Space Science, Kyung Hee University, Gyeonggi 446-701, Korea
18 Korea School of Space Research, Kyung Hee University, Yongin-shi, Kyungki-do 449-701, Korea
19 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
20 CNRS, IPAG, 38000 Grenoble, France
21 Observatorio Astronómico Nacional (IGN), Calle Alfonso XII,3. 28014 Madrid, Spain
22 European Southern Observatory, Karl-Schwarzschild-Strasse 2, 85748 Garching, Germany
23 Center for Space and Habitability, University of Bern, Sidlerstrasse 5, CH-3012 Bern, Switzerland
Received: 24 November 2016
Accepted: 23 May 2017
Context. Through spectrally unresolved observations of high-J CO transitions, Herschel Photodetector Array Camera and Spectrometer (PACS) has revealed large reservoirs of warm (300 K) and hot (700 K) molecular gas around low-mass protostars. The excitation and physical origin of this gas is still not understood.
Aims. We aim to shed light on the excitation and origin of the CO ladder observed toward protostars, and on the water abundance in different physical components within protostellar systems using spectrally resolved Herschel-HIFI data.
Methods. Observations are presented of the highly excited CO line J = 16–15 (Eup/kB = 750 K) with the Herschel Heterodyne Instrument for the Far Infrared (HIFI) toward a sample of 24 low-mass protostellar objects. The sources were selected from the Herschel “Water in Star-forming regions with Herschel” (WISH) and “Dust, Ice, and Gas in Time” (DIGIT) key programs.
Results. The spectrally resolved line profiles typically show two distinct velocity components: a broad Gaussian component with an average FWHM of 20 km s-1 containing the bulk of the flux, and a narrower Gaussian component with a FWHM of 5 km s-1 that is often offset from the source velocity. Some sources show other velocity components such as extremely-high-velocity features or “bullets”. All these velocity components were first detected in H2O line profiles. The average rotational temperature over the entire profile, as measured from comparison between CO J = 16–15 and 10–9 emission, is ~300 K. A radiative-transfer analysis shows that the average H2O/CO column-density ratio is ~0.02, suggesting a total H2O abundance of ~2 × 10-6, independent of velocity.
Conclusions. Two distinct velocity profiles observed in the HIFI line profiles suggest that the high-J CO ladder observed with PACS consists of two excitation components. The warm PACS component (300 K) is associated with the broad HIFI component, and the hot PACS component (700 K) is associated with the offset HIFI component. The former originates in either outflow cavity shocks or the disk wind, and the latter in irradiated shocks. The low water abundance can be explained by photodissociation. The ubiquity of the warm and hot CO components suggest that fundamental mechanisms govern the excitation of these components; we hypothesize that the warm component arises when H2 stops being the dominant coolant. In this scenario, the hot component arises in cooling molecular H2-poor gas just prior to the onset of H2 formation. High spectral resolution observations of highly excited CO transitions uniquely shed light on the origin of warm and hot gas in low-mass protostellar objects.
Key words: astrochemistry / ISM: jets and outflows / line: profiles / stars: formation / stars: jets / stars: winds, outflows
© ESO, 2017
1. Introduction
Characteristics of distinct kinematical and excitation components seen in high-J CO emission.
It was a surprise when the Herschel Photodetector Array Camera and Spectrometer (PACS) revealed that low- and high-mass embedded protostars host a reservoir of warm and hot material with temperatures ≳300 K, as seen in observations of highly excited CO emission (Jup> 14; Karska et al. 2013, 2014, and in prep.; Manoj et al. 2013, 2016; Green et al. 2013, 2016; Matuszak et al. 2015). The origin of this warm/hot gas is still not known partly because of uncertainty over the excitation conditions of CO (density and temperature) and because the physical processes at play on small scales (<500 AU) in low-mass protostars are still not completely understood. Few direct observations of this warm material exist because the ubiquitous tracer, H2, is not directly observable toward the deeply embedded low-mass protostars, due to the high extinction (e.g., Maret et al. 2009) often exceeding an AV of 100–1000.
Herschel-PACS observations of the CO ladder of low-mass protostars ranging from J = 14–13 to 49–48 (Eup/kB = 500–6500 K) typically show two rotational temperature components: a warm component with a rotational temperature, Trot, of ~300 K and a hot component with Trot~ 600–800 K (Manoj et al. 2013; Karska et al. 2013; Green et al. 2013). For sources with particularly bright CO emission, a third very hot component is sometimes seen with Trot> 1000 K (Manoj et al. 2013), although not always (Herczeg et al. 2012; Goicoechea et al. 2012). Clearly any successful interpretation must account for both the excitation conditions, and the universality of these components. Determining the physical origin of the CO excitation is an obvious goal, and several groups have undertaken different approaches. These approaches fall into several categories: (i) the entire CO ladder is reproduced by a single set of excitation conditions (H2 density, CO column density, and temperature), where the excitation is subthermal (Neufeld 2012; Manoj et al. 2013); (ii) the two temperature components are interpreted as two physically distinct components with different excitation conditions (Karska et al. 2013; Green et al. 2013); (iii) the entire CO ladder is reproduced by a range of temperatures, where the column density of each temperature layer follows a power-law (Neufeld 2012); or (iv) the CO ladder is modeled with a detailed physical model of the entire system (van Kempen et al. 2010; Visser et al. 2012; Lee et al. 2014). The number of possible solutions demonstrates that the integrated intensities of the CO ladder alone do not provide enough discriminating power to identify the origin of the warm and hot gas.
Sample properties.
A complementary warm gas tracer in protostellar systems is H2O (e.g., van Dishoeck et al. 2014, and references therein). Kristensen et al. (2013) and Mottram et al. (2014) recently discussed the excitation and origin of H2O emission, based on velocity-resolved H2O profiles. The H2O line profiles predominantly consist of distinct spectrally resolved components: a broad, FWHM> 20 km s-1 component centered on the source velocity, and one or more narrower components, FWHM~5–10 km s-1, offset from the source velocity by >5 km s-1 (see Table 1 for component definitions used in this paper).
Kristensen et al. (2013) and Mottram et al. (2014) proposed a scenario for interpreting the H2O profile components in which the protostellar wind is neutral and atomic (Lizano et al. 1988; Giovanardi et al. 1992; Choi et al. 1993; Lizano & Giovanardi 1995), and it drives the large-scale entrained, cold (≲100 K) outflow gas seen in low-J CO (J ≤ 6–5) emission. Where the wind is currently entraining envelope material, the conditions are conducive to efficient water formation in the gas-phase (Bergin et al. 1998), as the temperature exceeds 300 K. This shear layer or mixing layer carries the same characteristics as found in shock waves, i.e., the gas is heated collisionally, the density is high, and the gas is accelerated, giving rise to the broad outflow-like component. For these reasons, this layer was named “outflow cavity shocks” by Mottram et al. (2014). Where the wide-angle low-velocity wind directly impacts the envelope or cavity walls, discrete shocks appear as velocity-offset components in H2O and high-J CO line profiles, typically blue-shifted by ~5–10 km s-1. These are labeled spot shocks (Mottram et al. 2014) and appear with both distinct kinematical and chemical signatures (see above, Kristensen et al. 2013, 2016). In this picture, the warm (300 K) and hot (700 K) CO gas observed with PACS have two different physical origins, the outflow cavity shocks and spot shocks, respectively.
An alternative to this scenario is that the water emission directly traces the disk wind (Panoglou et al. 2012; Yvart et al. 2016). In this scenario, the dusty wind is gently accelerated over 10-AU scales, and this gentle acceleration does not lead to collisional dissociation of molecules in the wind. Furthermore, the wind is dense enough to shield molecules within the wind from the dissociating UV radiation from the accreting protostar during the most embedded stages of star formation, the so-called Class 0 stage (André et al. 1990). At later evolutionary stages, the density in the wind decreases and UV photons from the accreting protostar start to dissociate more and more wind material, thus changing the chemical make-up of this material (Nisini et al. 2015). In this scenario, the bulk of observed emission is associated with the wind.
Water suffers from the drawback that its abundance is difficult to measure because the denominator of the N(H2O)/N(H2) ratio is uncertain; H2 is not detected toward the protostellar position. Instead, CO is often used as a proxy for H2. Previous attempts at measuring the abundance with respect to low-J CO have provided values in the range of 10-8–10-4 with respect to H2, when assuming a CO/H2 abundance of 10-4 (e.g., Franklin et al. 2008; Kristensen et al. 2012). Part of the reason for this large spread is that low-J CO and H2O do not trace the same gas, as is evident when their spatial distributions are mapped out (Nisini et al. 2010; Tafalla et al. 2013). Instead, CO 16–15 and H2O seem to trace the same gas (Santangelo et al. 2013), and thus CO 16–15 provides a better reference frame for measuring the H2O abundance.
This paper addresses the physical origin of the warm and hot CO emission observed with PACS through velocity-resolved observations of CO 16–15 toward a sample of 24 low-mass embedded protostars. In particular, the question of whether or not the two rotational temperature components correspond to different physical components, as witnessed by different velocity components, will be addressed. The origin of the very hot (Trot> 1000 K) emission is not addressed here, as its contribution to the CO 16–15 line profile is too small to distinguish observationally. Finally the H2O abundance as a function of velocity will be measured using CO 16–15 as a reference frame. The mass, momentum, and energetics traced by CO 16–15 emission will be measured and compared to that measured from lower-J transitions in a subsequent paper.
The paper is organized as follows. The Herschel Heterodyne Instrument for the Far Infrared (HIFI) observations are presented in Sect. 2 along with a presentation of the source sample. The results are presented in Sect. 3 and discussed in Sect. 4. Concluding remarks are given in Sect. 5.
2. Observations
2.1. Source sample
The sources were chosen from the “Water in Star-forming regions with Herschel” (WISH, van Dishoeck et al. 2011) and “Dust, Ice, and Gas in Time” (DIGIT, Green et al. 2013) samples of nearby embedded low-mass protostars. Herschel-PACS measurements of the CO 16–15 intensity exist for all sources (Green et al. 2013; Karska et al. 2013). Specifically, the 21 brightest sources in CO 16–15 were chosen, based on whether the line profile would be detected and spectrally resolved with HIFI in less than one hour of telescope time. Furthermore the sample was augmented by WISH observations of two sources, Ser SMM1 (Kristensen et al. 2013) and DK Cha, and observations of HH46 from a Guaranteed Time program (GT1_abenz_1; PI: A.O. Benz). Thus, the total sample consists of 24 embedded sources: 13 Class 0 and 11 Class I.
The sample characteristics are provided in Table 2. HIFI H2O 110–101 spectra at 557 GHz (Kristensen et al. 2012; Green et al. 2013) exist toward all sources. HIFI observations of CO 10–9 exist toward most sources (19/24, Yıldız et al. 2013), and of H2O 212–101 at 1670 GHz toward a smaller subset (6/24, Mottram et al. 2014). This H2O line is the closest in frequency to CO 16–15 and is therefore observed in a similar beam (Mottram et al. 2014).
 |
Fig. 1 CO 16–15 spectra toward all observed sources. The source velocity is marked with a red dashed line in each panel and the baseline is shown in green. Some spectra have been magnified for clarity by a factor shown in each panel. |
2.2. HIFI data reduction
The observations consisted of single-pointing dual-beam-switched observations taken with HIFI (the Heterodyne Instrument for the Far Infrared, de Graauw et al. 2010) on Herschel (Pilbratt et al. 2010) toward the central position of each of the 24 protostars with the off-position 3′ away. The pointing accuracy is 2′′ (rms). The HIFI spectrometer was tuned to the CO 16−15 line in the upper sideband, and the OH triplet at 1834 GHz in the lower. The OH data will be presented and discussed in a forthcoming publication. The integration time varied per source and was based on the observed line intensity as reported by Green et al. (2013) and Karska et al. (2013, see Table A.1 in the appendix for details). The diffraction-limited beam size is 11.̋5 at the frequency of CO 16–15, corresponding to linear scales of 1400–5200 AU for the distances of the sources observed here.
Data were reduced using Hipe 13.0 (Ott 2010). Most spectra showed strong signs of standing waves, as expected in HIFI band 7. These waves are not perfectly sinusoidal, and so removing these features requires extra care. The removal was done through the Hipe task hebCorrection.
Furthermore, observations of the hot and cold loads can introduce standing waves with frequencies of 92 and 98 MHz (~15 km s-1 at the frequency of CO 16–15); these can be eliminated through a modified passband calibration. Additional standing waves with a frequency of ~300 MHz (~50 km s-1) were removed by using the fitHifiFringe task in Hipe. When running fitHifiFringe the central 1 GHz around the CO 6–15 line (~150 km s-1) was masked which in most cases covered the entire line. The two sources L1448 and BHR71 are known to harbor extremely high-velocity (EHV) features making the lines as broad as 200 km s-1 (full width zero intensity, e.g., Kristensen et al. 2012) and in these two cases the central 1.5 GHz (~250 km s-1) were masked out of the total bandwidth of 2.5 GHz. The amplitudes of the standing waves are typically 50 mK for the H-polarization spectra and 100 mK for the V-polarization spectra, both on the  scale. These values are comparable to the typical rms level (see below). Some spectra did not show the 300 MHz standing wave, and in these cases no fringes other than the 92/98 MHz ones were removed. Since the periods of the standing waves are similar to the expected line widths (15 and 50 km s-1), all spectra and fringe solutions were visually inspected to ensure that the line profiles were not affected.
scale. These values are comparable to the typical rms level (see below). Some spectra did not show the 300 MHz standing wave, and in these cases no fringes other than the 92/98 MHz ones were removed. Since the periods of the standing waves are similar to the expected line widths (15 and 50 km s-1), all spectra and fringe solutions were visually inspected to ensure that the line profiles were not affected.
After fitHifiFringe had been run on all spectra, they were exported to Class1 for further reduction and analysis. The reduction consisted of subtracting linear baselines from the spectra and co-adding the H- and V-polarization data after visual inspection. Typically there is a difference in rms level of up to 30% between the two polarizations. The shape of the profile qualitatively agrees for both the H- and V-polarization data, and so the spectra were averaged. The intensity was brought from the antenna temperature scale,  , to the main beam temperature scale, TMB, by using a main beam efficiency of 0.60 (Roelfsema et al. 2012). The calibration uncertainty is measured to ~10% (Roelfsema et al. 2012). The spectra were subsequently resampled to a channel width of 0.5 km s-1. The rms of each spectrum is reported in Table A.1.
, to the main beam temperature scale, TMB, by using a main beam efficiency of 0.60 (Roelfsema et al. 2012). The calibration uncertainty is measured to ~10% (Roelfsema et al. 2012). The spectra were subsequently resampled to a channel width of 0.5 km s-1. The rms of each spectrum is reported in Table A.1.
2.3. Complementary data
The CO 16–15 data presented here are complemented by observations of the H2O 110–101 and 212–101 lines at 557 and 1670 GHz, respectively, also observed with Herschel-HIFI (Kristensen et al. 2012; Green et al. 2013; Mottram et al. 2014). Furthermore, HIFI observations of the CO 10–9 line at 1153 GHz are used (Yıldız et al. 2013). These data have all been reduced in a similar manner to the CO 16–15 data and the velocity scale was subsequently interpolated to the same scale as the CO 16–15 data for easy comparison.
3. Results
As expected based on the PACS fluxes, the CO 16–15 line is detected toward every source. Furthermore, the line profiles are spectrally resolved and all spectra are displayed in Fig. 1. Typically the lines are broad (FWHM≳ 15 km s-1), and often the profiles consist of multiple dynamical components, similar to what is observed in H2O emission with HIFI (Kristensen et al. 2010, 2012, 2013; Mottram et al. 2014) and CO 10–9 (Yıldız et al. 2013; San José-García et al. 2013). Comparing the integrated fluxes to those observed with PACS shows that the two fluxes typically agree to better than 20% which is consistent with the uncertainties on the absolute flux calibration of both instruments. A few sources show larger differences, where the PACS flux is 40–50% lower than the HIFI flux. This difference may be an timescale of how the PACS emission was extracted and how well-centered the PACS pointing was on the source.
3.1. Line profiles and profile components
 |
Fig. 2 CO and H2O spectra toward Ser SMM1 and NGC1333 IRAS4A. No correction has been made for the differences in beam size of the observation. Spectra have been shifted to a velocity of 0 km s-1. The bottom panel shows all CO profiles overlaid on top of one another. |
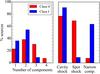 |
Fig. 3 Histograms showing the number of Gaussian components in each profile (left) and of profile components (right) toward Class 0 and I sources (red and blue, respectively). |
The maximum velocity, νmax, traced by the CO line profiles does not change with excitation (see Fig. 2 for two examples)2. Instead, CO emission at the lowest velocities decreases with excitation, until only a broad line profile is seen at J = 16–15. Toward some sources new components start appearing at higher J. This is most evident toward NGC 1333-IRAS 4A and Ser SMM1, where an offset component appears blue-shifted from the source velocity by 10 and 3–4 km s-1, respectively (Fig. 2). These offset components were first detected in H2O (Kristensen et al. 2010, 2013), and only show up in CO transitions with Jup> 10 (Yıldız et al. 2013).
The line profiles are decomposed using the minimum number of Gaussian functions required for the residual to be less than the rms, following the method of Mottram et al. (2014). Gaussian functions reproduce the different components better than, e.g., triangular or Lorentzian functions (San José-García et al. 2013). Two approaches are used: first, a fit is obtained where the Gaussian parameters are all left free; in the second approach, the best-fit parameters (ν0 and FWHM) from Mottram et al. (2014) are taken as fixed from the decomposition of H2O profiles, and a new fit is obtained. Ser-SMM4 shows a characteristic triangular profile shape, reminiscent of what is seen toward off-source outflow positions; no Gaussian functions are fitted to this profile. All results are listed in Table A.2, the spectral decompositions are shown in Fig. A.1.
Most sources show multiple components (70%). Figure 3 shows the fractional distribution of the number of Gaussian functions needed to reproduce each line profile. This distribution peaks at two components, and then falls off rapidly for higher numbers. Figure 3 also shows a histogram of the various component detections seen in CO 16–15 and their designations following Mottram et al. (2014) for H2O. They characterized each component based on its width and its offset from the source velocity and designated them either as “envelope” (narrow, centered on νsource), “cavity shocks” (broad, centered on νsource), or “spot shocks” (offset in velocity). Nearly all sources (85%) show a broad cavity shock component, irrespective of evolutionary stage, similar to H2O line profiles (Mottram et al. 2014). Primarily Class 0 sources show offset components associated with spot shocks (70% versus 10%) whereas more Class I sources show a narrow component (65% versus 10%).
The narrow component is often blue-shifted from the source velocity by 0.5–1.0 km s-1 (Fig. 4), an offset which is larger than the uncertainty on the velocity calibration (≪0.1 km s-1, Roelfsema et al. 2012). The source velocity is measured from low-J C18O emission (Yıldız et al. 2013; San José-García et al. 2013). The parts of the envelope traced by higher-J C18O 9–8 and 13CO 10–9 all move at the systemic velocity (Yıldız et al. 2013). The narrow component is in most cases (10/15) associated with H2O emission, but often blue-shifted by more than 0.5 km s-1 with respect to the H2O component (7/10 sources); sometimes the shift is larger than 1 km s-1 (5/10 sources). Of the components not seen in H2O emission, 3/5 components are shifted with respect to the source velocity as measured from low-J C18O emission.
 |
Fig. 4 Velocity of the narrow component of CO 16–15 with respect to the source velocity where the source velocity is shown in magenta (shifted to 0 km s-1), the narrow velocity component in cyan, for the nine sources where the component is offset by more than 0.5 km s-1. Source velocities are measured from low-J C18O transitions (Yıldız et al. 2013). |
 |
Fig. 5 Top: narrow emission scaled to a common distance of 200 pc versus Lbol. Class 0 sources are marked in red, Class I in blue. Upper limits (3σ) are marked with arrows. Class 0 sources are marked in red, Class I in blue. |
This narrow component is strong enough that if it were present toward all Class 0 sources, it would have been readily detected in the spectra presented here. To illustrate this, Fig. 5 shows the strength of the narrow component as a function of Lbol where all upper limits are marked. To calculate the upper limit, the average narrow component line width of 5 km s-1 is used. The limits are typically an order of magnitude lower than the detected narrow components. Applying Kendall’s τ test with the Cenken function3 from the R statistical package shows that the narrow component strength is correlated with the bolometric luminosity at the 97.1% or 2.2σ level. This test is particularly well suited to evaluate correlations where part of the data set consists of upper limits, i.e., are left-censored. When compared to other envelope parameters (envelope mass, envelope density at 1000 AU, bolometric temperature, and outflow force), there are no correlations, i.e., the significance is <1σ in all cases. Thus the narrow component does not appear to be directly connected to the envelope alone.
Finally, the fraction of emission in the broad cavity shock component compared to the total integrated intensity is shown in Fig. 6. On average, 75 ± 20% of the emission is in cavity shocks for all sources. The standard deviation refers to the spread in the percentages; the uncertainty on the decomposition is not included but is smaller. A subset of sources only show emission from the cavity shocks (IRAS 15398, Ser-SMM4, B335, TMR1, HH46, and RCrA-IRS5A). An upper limit on any narrower contribution may be estimated assuming its FWHM is 5 km s-1, the average width of this component in other sources. The 3σ limits are up to 20% for the weakest sources, i.e., consistent with a relative fraction of 75 ± 20% in the broad cavity shock component.
 |
Fig. 6 Fraction of the contribution to the total integrated CO 16–15 line intensity from the broad cavity shock component as measured from HIFI data (red). The vertical thick black line marks the division between Class 0 and I sources, where the former is to the left, the latter to the right. The blue points show the fraction of CO 16–15 emission expected to originate in the PACS warm 300 K component (Karska et al., in prep.). Both the HIFI and PACS fractions have ~10% uncertainties associated with them. The shaded red and blue regions show the spread of fractions for the HIFI and PACS components, respectively, and where there is an overlap the color is purple. Within the error bars, the fractions are the same, and the broad cavity shock component dominates emission. |
3.2. Rotational temperature
The rotational temperature as a function of velocity can be calculated from CO 16–15 and 10–9 spectra, where such data are available (Table 2). In the limit where the energy levels are thermally populated, the rotational temperature corresponds to the kinetic temperature; whether this limit applies to these data will be discussed later. To calculate the rotational temperature the spectra are rebinned to a channel size of 3 km s-1 to increase the S/N. The CO 16–16/10–9 line ratio is then calculated in channels where the S/N is >2 in both spectra and converted into a rotational temperature assuming LTE. The CO 10–9 line may be slightly optically thick at the line center (±2 km s-1; Yıldız et al. 2013) toward the brightest sources, and the line centers are ignored in the following analysis. The change in the intensity-weighted average line ratio is less than 10%, and so not significant compared to the observational uncertainties.
The CO 10–9 and 16–15 spectra are obtained in different beams, 20′′ and 11′′, respectively. Maps of CO 10–9 emission show that the emission is typically elongated along the direction of the outflow (Nisini et al. 2015). Similarly, half of the sources (9/19) where CO 10–9 data are available show extended CO 14–13 or 16–15 emission in the PACS footprints (Karska et al. 2013; Green et al. 2013). If emission from both transitions fill the larger 20′′ beam, no geometrical correction is required to the line ratio. Alternatively, if the emission follows the outflow a linear scaling with beam size is appropriate (Tafalla et al. 2010). If the emission is not extended in either of the two beams, the most appropriate geometrical scaling is a point-source scaling. In the following analysis no geometrical scaling will be applied, but the result of possible scalings will be discussed below in Sect. 3.3.
 |
Fig. 7 CO 16–15/10–9 line ratio for all 19 sources for which both data sets are available. The spectra have been rebinned to 3 km s-1 channels and only data points with S/N> 2 are included. The brightness of the color indicates the number of observations passing through a given point – brighter represents a higher number. Line ratios around ±2 km s-1 are not included. Red is for Class 0 line wings, and blue for Class I. The mean ratio is displayed with a dashed line; if a linear scaling to correct for different beam sizes is applied the mean value shifts down to the dashed line marked “linear”, and similarly for a point-source scaling. The rotational temperature corresponding to a particular line ratio is shown on the second axis. |
Figure 7 shows the average line ratio and corresponding rotational temperature for all sources where CO 10–9 data are available; similar figures for individual sources are available in the appendix (Fig. A.3). The mean ratio averaged over all sources and velocities is 0.7, corresponding to a rotational temperature of ~350 K. Most sources show a slightly lower ratio, by up to a factor of two, closer to the line center. This trend suggests that the gas at the higher velocities is warmer than at lower velocities, similar to what is seen toward outflow spots well offset from the source position (e.g., L1157-B1, Lefloch et al. 2012). If a linear scaling is applied to account for different beam sizes, the mean ratio decreases to 0.4 (240 K), and if a point-source scaling is applied the ratio decreases to 0.2 (180 K).
Herschel-SPIRE and PACS measure the integrated intensity of CO emission from J = 4–3 to 49–48, and any rotational temperature inferred from these observations are therefore intensity-weighted averages of the rotational temperatures calculated here. In order to do a direct comparison, the velocity-dependent intensities were used as weights for determining the average rotational temperatures. These intensity-weighted temperatures tend to be lower by 20 K (emission fills the beam) to 10 K (point source scaling), and the effect is therefore negligible.
3.3. H2O and CO
Herschel-PACS footprint maps of CO 16–15 and various H2O transitions show that both species follow one another spatially, as opposed to for example CO 3–2 and H2O which are spatially and kinematically distinct (e.g., Santangelo et al. 2012). This spatial correlation suggests that the best reference frame for measuring H2O abundances is a high-J CO line such as the J = 16–15 transition.
In the following analysis, the H2O abundance is measured from both the 110–101 transition at 557 GHz and the 212–101 transition at 1670 GHz (179.5 μm). The former transition is the only one observed toward all sources, but in a 38′′ beam (Kristensen et al. 2012; Green et al. 2013). The latter, on the other hand, is only observed toward six sources (Table 2) but in a 13′′ beam (Mottram et al. 2014). Thus, this line may be used to calibrate the abundance inferred from the 557 GHz transition. The ratio of these two lines is nearly constant as a function of velocity for all six sources, suggesting that both lines are equally good for calculating the water abundance, and also that most of the water emission originates from within the smaller 13′′ beam (Mottram et al. 2014), but possibly with weaker emission extending beyond the beam. This weak emission is indeed seen in Herschel-PACS footprint maps (Table 2, Karska et al. 2013; Green et al. 2013).
The H2O 212–101/CO 16–15 line ratio is shown in Fig. 8. The central ±2 km s-1 are masked out as the H2O line suffers from deep self absorption associated with cold envelope material (Fig. 2, Mottram et al. 2014). Furthermore, both spectra are rebinned to 3 km s-1 channels to increase S/N in the line wings. The line ratio shows a tendency to rise from 0.5 (low velocity) to 1.7 (high velocity) but the ratio is consistent with being constant at 1.2 ± 0.8, where the uncertainty represents the spread in values. In the following the ratio will be treated as constant.
Similarly, the H2O 110–101/CO 16–15 flux ratio is constant as a function of velocity with an average value of 0.42 ± 0.36 (Fig. 8). If a linear scaling is applied to account for the differences in beam size, the ratio increases to 1.5 ± 1.3, and it further increases to 5.3 ± 4.6 for a point-source scaling. There is no significant difference between Class 0 and I sources, although Class I sources tend to show a slightly lower line ratio. See Fig. A.4 in the appendix for individual sources.
To translate the line ratios into abundance ratios, or, more appropriately, column density ratios, a set of non-LTE 1D radiative-transfer models are run. The code Radex is used (van der Tak et al. 2007) with collisional rate coefficients from Yang et al. (2010) and Neufeld (2010) for CO, and Daniel et al. (2011) for H2O, as tabulated in LAMDA (Schöier et al. 2005). The Radex code was modified according to Mottram et al. (2014) to account for the high opacity of the H2O transitions. The excitation conditions (density and H2O column density) are taken from Mottram et al. (2014) and a temperature of 300 K is used together with ΔV = 20 km s-1. Mottram et al. (2014) found no deviation from an H2O ortho/para ratio of 3, the high-temperature statistical equilibrium value, and that is used here. Based on Radex modeling, Mottram et al. found that the best-fit solutions fell in two camps: subthermal excitation of the H2O transitions with n(H2) = 106 cm-3, N(H2O)= 4 × 1016 cm-2, and thermal excitation with n(H2) = 5 × 107 cm-3, N(H2O)= 1018 cm-2. Finally, Mottram et al. used a linear beam scaling, and that is applied here as well. The only free parameter is the CO column density which is varied until the two H2O/CO line ratios are reproduced.
Figure 9 shows the modeled intensity ratios of the H2O 212–101 and 110–101 lines to CO 16–15 versus the total H2O/CO column density ratio for both subthermal and thermal H2O excitation, together with the opacity of the CO 16–15 transition. For subthermal H2O excitation conditions, a column density ratio of H2O/CO of 0.02 best reproduces both line ratios, corresponding to a total H2O abundance of 2 × 10-6 for a CO abundance of 10-4 (Dionatos et al. 2013). For the thermal excitation conditions, a large range of H2O/CO column density ratios reproduce emission, ranging from N(H2O)/N(CO)~ 10-3 to 10-1. However, all these solutions have one thing in common: CO 16–15 must be optically thick with τ> 3 over the entire profile. Toward the source with the highest CO 16–15 flux in the sample, Ser SMM1, the observed 12CO 16–15/13CO 16–15 line ratio is 55 (Goicoechea et al. 2012), consistent with the 12CO line being optically thin. It is therefore unlikely that any other source shows optically thick emission, and the thermal H2O excitation solution can be excluded.
 |
Fig. 8 Top: H2O 212–101/CO 16–15 line ratio as a function of velocity toward the six Class 0 sources where the H2O line is observed with HIFI. The brightness of the color indicates the number of observations passing through a given poin – brighter represents a higher number. The channel size is 3 km s-1. Bottom: same as top but for the H2O 110–101/CO 16–15 line ratio where Class 0 and I sources are separated (red and blue, respectively). The total mean ratio is displayed. |
 |
Fig. 9 Modeled intensity ratio of the 557 and 1670 GHz H2O lines over CO 16–15 as a function of the H2O/CO column density ratio, where the H2O column density is both ortho- and para-H2O. The observed ratios are shown as dashed horizontal lines. The black dashed line is the CO 16–15 opacity, and is shown on the same scale as the intensity ratio. Top: subthermal excitation conditions for H2O. Bottom: thermal excitation conditions for H2O. |
4. Discussion
4.1. CO excitation
CO line profiles change gradually with excitation, ranging from the relatively narrow, centrally peaked CO 2–1 and 3–2 profiles typically observed toward outflow regions, to the broader high-J CO lines; νmax remains constant (Fig. 2). This gradual change suggests that these CO 16–15 line profiles reveal a high-temperature component not previously observed from the ground. The change in profile shape cannot be attributed to opacity effects, apart from a few km s-1 around the source velocity. The opacity will be lower for higher-excitation lines, and the emission at the lower velocities should therefore increase more compared to higher-velocity material if opacity played a major role. Yet the opposite trend is observed: emission at higher velocities increases with respect to emission at lower velocities. Opacity, therefore, plays a minor role in setting the line profile for CO 16–15.
The gradual change in CO line profile with excitation suggests that different CO transitions, up to at least J = 16–15, trace material at different temperatures, regardless of whether CO is thermally or subthermally excited. If all CO emission were to trace a single-temperature, single-density slab, the profiles should be identical as is the case for water line profiles (Mottram et al. 2014). The rotational temperature of the emitting material changes as a function of velocity (Sect. 3.2 and Fig. 7), higher temperatures at higher velocities, consistent with what is seen at outflow spots (Lefloch et al. 2012) and the protostellar position in lower-J transitions (Yıldız et al. 2013). A single isothermal slab is therefore not sufficient for reproducing the CO excitation.
When taking the most conservative estimate of the rotational temperature, 180 K obtained from the point-source scaling, the temperature is significantly higher than found for lower-J CO transitions (median Trot ~ 70 K for transitions up to 10–9; van Kempen et al. 2009; Goicoechea et al. 2012; Yıldız et al. 2013; Yang et al. 2017). The rotational temperature does approach the typical rotational temperature of ~300 K often found for this part of the CO ladder toward embedded protostars (Manoj et al. 2013; Karska et al. 2013; Green et al. 2013).
The actual kinetic temperature of the CO 16–15 emitting gas is higher than the rotational temperature measured here. The part of the CO rotation diagram going up to J ~ 14 shows positive curvature (Goicoechea et al. 2012; Yıldız et al. 2013), and from J ~ 14 to 25 the ladder shows little curvature (Manoj et al. 2013; Green et al. 2013). This curvature implies that a rotational temperature measured from, say, the J = 15–14 and 16–15 transitions will be higher than when measured from the J = 10–9 and 16–15 transitions and likely closer to that observed with PACS in the warm 300 K component. Thus, only a fraction of CO 10–9 emission traces the broad cavity shock component seen so prominently in CO 16–15 and H2O profiles.
The relative contributions to the HIFI line profiles may be compared to the warm (Trot ~ 300 K) and hot (Trot ~ 800 K) components observed with PACS (Manoj et al. 2013; Karska et al. 2013; Green et al. 2013, Karska et al., in prep.). The break between the two PACS components typically appears around J = 25–24 (Eup = 1800 K) for low-mass protostars. Given the rotational temperatures and break point, if the two rotational temperatures have different physical origins then the warm and hot PACS components contribute on average ~80% and 20% to the total CO 16–15 flux, respectively. These PACS fractions do not depend on evolutionary stage or any other source property (Karska et al., in prep.), but the fractions are constant when both components are detected. Any contribution from the very hot (Trot> 1000 K) component will not be detected in the CO 16–15 line profiles, and it is ignored in the following.
The PACS fractions depend on an extrapolation from Jup ≥ 25 (Eup/kB ~ 1800 K) down to J = 16–15 (Eup/kB ~ 750 K). Such an extrapolation carries uncertainties, especially if not all high-J CO lines are observed or detected. The extrapolation uncertainty was inferred for two representative sources, Ser-SMM1 and B335. The former is one of the sources with the highest S/N on the high-J CO transitions observed with PACS, whereas the latter was only detected in a limited number of transitions and at low S/N. For Ser-SMM1 the extrapolation uncertainty is 4%, while it is 11% for B335. Some additional uncertainty may arise from how well-centered the sources are on the central PACS spaxel, and we therefore adopt a typical extrapolation uncertainty for all sources of 10%.
If the CO ladder consists of two temperature components, and thus two physical components, then 80% of the flux originates in the warm 300 K component and 20% in the hot 750 K component. The CO 16–15 HIFI line profiles typically consist of multiple components; the dominant flux component is the broad cavity shock component, which typically contributes 75%±20% to the total flux. These relative fractions clearly overlap within the uncertainty. This overlap, and the measured rotational temperature from CO 10–9 and 16–15 (200–300 K), strongly suggests that the PACS components may be associated with corresponding HIFI components, i.e., the warm, 300 K PACS component may be associated with the broad outflow cavity shock HIFI component, and the warm 750 K PACS component to anything else contained in the HIFI line profiles. These latter components only appear in CO 16–15 profiles and not at lower J, clearly suggesting these components arise in hot gas. Furthermore, the multiple components in the HIFI line profiles implies that the PACS CO ladder consists of multiple physical components.
4.2. Physical origin of CO emission
The high-J CO emission can arise in three regions within the protostellar system: the disk; the UV-heated cavity walls; the outflow, or a combination thereof. In this context, the term outflow encompasses the wind, the envelope entrainment layers, and the jet. None of the profiles show double-peaked features as would be expected if the emission arises from the disk surface (Bruderer et al. 2012; Fedele et al. 2013; Harsono et al. 2013), and so disks are quickly ruled out as a dominant source of the observed CO emission. UV-heated outflow cavity walls are ruled out because the 300 K PACS component is ubiquitous: the protostars observed here, and in other samples, span a range of three orders of magnitude in bolometric luminosity (~0.1–100 L⊙). The UV luminosity is expected to span a similar range. For this reason, and as argued by Manoj et al. (2013), it seems unlikely that UV heating plays a dominant role in generating this emission because the UV luminosity of each source would need to be specifically tuned to reproduce a rotational temperature of 300 K everywhere. Thus, the dominant excitation mechanism must be outflow-related.
 |
Fig. 10 Schematic showing the different parts to the proposed interpretation. The top left panel shows the cooling of atomic to molecular gas, along with the dominant constituents and coolants at each stage. Top right shows a cartoon HIFI CO 16–15 profile centered at zero velocity, with the broad outflow cavity shock component shown in green, and the offset spot shock component in orange. Bottom left is a CO rotational diagram with the different temperature components highlighted. Finally, bottom right shows where these different components may be located in the protostellar system. The top part shows the scenario where the broad component is caused by outflow cavity shocks, and the lower part shows the scenario where the broad component arises in the disk wind. |
4.2.1. Origin of warm PACS emission
The bulk of the CO 16–15 emission is related to outflowing gas, both for Class 0 and I sources. Based on the association with water, it seems likely that the CO 16–15 emission primarily traces gas which is currently interacting with, or passing through, shocks, as opposed to the slower, colder entrained outflow traced by the lower-J CO emission (see also Kristensen et al. 2012; Mottram et al. 2014). The radius of the water-emitting region, and therefore also the radius of the CO 16–15 emitting region, is typically of the order of 102 AU (Mottram et al. 2014). If the emitting region is not circular but rather cylindrical, a cylinder with a diameter of 15–30 AU could account for the linear geometrical beam scaling found to be appropriate in Sect. 3.4. Such a width is consistent with both the H2O and CO cooling lengths of continuous C-type shocks with pre-shock density ≥5 × 105 cm-3, almost irrespective of shock velocity (Kristensen et al. 2007; Visser et al. 2012). In this scenario, the cavity shocks are thus located along the outflow cavity walls in a thin (≲10 AU) layer (Mottram et al. 2014).
An alternative to this scenario is that this component traces a molecular disk wind (Panoglou et al. 2012; Yvart et al. 2016). If the wind is accelerated at a steady pace, it will keep its molecular content, particularly during the deeply embedded stages where the dusty wind shields the gas from dissociating UV photons from the accreting protostar. Yvart et al. (2016) used this model to reproduce the H2O 110–101 spectra presented in Kristensen et al. (2012) and the excited line profiles in Kristensen et al. (2010), and were able to reproduce the width and intensities of the profiles with only two free parameters: the mass accretion rate and inclination angle. Clearly this model presents a very attractive alternative to the origin of water emission, and potentially also to high-J CO emission. An important test will be to see how well the model reproduces not only the H2O spectra but also the CO 16–15 spectra presented here, as well as emission from the entire CO ladder.
Irrespective of the underlying physical origin, an important question remains: why is the 300 K component ubiquitous in the PACS data with very little scatter, independent of physical conditions? What is it in these broad cavity shocks seen in the CO 16−15 line profiles that generates this temperature component? The fact that the rotational temperature is ubiquitous must imply that some fundamental aspect related to the gas cooling controls the excitation, since one would otherwise expect the excitation to depend on local parameters. Particularly, the observed dominant gas coolants (H2, CO, H2O, OH and O; Karska et al. 2013) are responsible for setting the overall temperature structure or distribution of the gas. A species may dominate the cooling over a specific range of temperatures and densities if that species is either particularly abundant, or particularly efficient at cooling the gas through excitation/deexcitation effects. If the species dominates the cooling through excitation/deexcitation effects, it will do so because the level populations react more efficiently to the change in temperature than those of other species. This information is relayed to other species through collisions. Testing this hypothesis will be done through more detailed calculations of the cooling functions of the observed dominant coolants, that includes calculating their level populations explicitly in the cooling gas (Kristensen & Harsono, in prep.).
The second part of the above question is: why always 300 K? One possibility is that the other dominant molecular coolant of warm/hot gas, H2, stops being an efficient coolant around 300 K because of the widely-spaced energy levels (the J = 2–0 transition has Eup/kB = 510 K), i.e., because other species become more efficient at cooling the gas through excitation effects. Indeed, such a scenario would explain why CO cooling always activates at this kinetic temperature, as has been shown to be the case in shocks (Neufeld & Dalgarno 1989; Flower & Pineau des Forêts 2010, 2015), see Fig. 10. Once H2 ceases to be effective, CO, as the new dominant coolant, brings the temperature gradually down to ambient temperatures.
Such a scenario can be tested by utilizing existing analytical cooling functions (Neufeld & Kaufman 1993), the results of which are shown in Fig. 11. Here, cooling rates are calculated for H2, CO, and H2O for a gas with density n = 106 cm-3, N(H2O)/N(CO)= 0.02, and starting temperature of 1000 K. In this simple calculation, CO takes over as the dominant coolant at ~500 K, i.e., somewhat higher than the observed cross-over temperature of ~300–400 K. We note that these analytical cooling functions are calculated for collisions with H2, i.e., there is no coupling to chemistry, particularly H2 formation. The more detailed calculations currently underway will provide more insight into how the level populations actually respond to the changes in the cooling gas, both physical and chemical, and over which timescales.
These analytical cooling functions generally show three regimes in which species dominate cooling: at low density (<105 cm-3), H2 dominates cooling to the lowest temperatures (<100 K) because CO is not efficiently excited. At high densities (>108 cm-3), CO is the dominant coolant throughout because the level populations are very efficiently populated all the way to very high J. In the intermediate regime, which is where H2O and CO 16–15 are excited (Mottram et al. 2014), there is a cross-over point where H2 starts as the dominant coolant, and CO then takes over.
 |
Fig. 11 Cooling curves for H2, CO, and H2O using the analytical cooling functions of Neufeld & Kaufman (1993). The colored lines are the cooling rates, and their values are shown on the left axis. The black line is for temperature (right axis). The highlighted parts on the cooling curves are for the temperature range 300–400 K. The H2 density and column densities are as shown in Fig. 9. |
4.2.2. Origin of hot PACS emission
The division between warm and hot CO emission implies that the hot 700 K PACS component is traced by anything else in the line profiles. For the Class 0 sources, this typically means spot shocks where the wind from the protostar impinges on the inner cavity wall. The pre-shock gas is likely dissociated to some degree by the UV radiation from the accreting protostar, and the shock itself is relatively slow (5–10 km s-1, Kristensen et al. 2013; Benz et al. 2016). This conclusion was reached based on detection of light ionized hydrides in this particular component, the detection of the offset spot shock component in H2O and CO 16–15 but not lower-J transitions, and the component kinematics (offset velocity and FWHM). These three observational facts (kinematics, chemistry, and excitation of the component) point to an origin in a J-type shock.
The spot shocks and narrow components typically peak at blue-shifted velocities from the source velocity. If the protostellar wind impinges on the inner envelope walls at very small radii (≲100 AU), the optically thick protostellar disk may shield the part of the wind moving away from us, i.e., the red-shifted part of the component (ALMA Partnership et al. 2015; Kristensen et al. 2013, 2016). If, on the other hand, the shocks interact with the inner envelope on scales larger than the disk, or if the disk is not optically thick at these wavelengths, both sides will be seen and the profile will appear more symmetric. Such partial continuum shielding is similar to what has been inferred from optical atomic-line observations of disk winds, where the line profiles appear skewed (e.g., Edwards et al. 1987).
The lower velocity shifts observed toward Class I sources compared to Class 0’s are consistent with the protostellar wind velocity decreasing radially away from the jet axis (Panoglou et al. 2012). As the outflow cavity opening angles increase with evolutionary stage, the part of the wind interacting with the envelope will decrease in velocity. However, only a very small velocity is required to produce the high temperature observed in the high-J part of the CO ladder. For J-type shocks, the peak temperature is 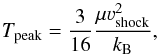 (1)where μ is the mean molecular mass, νshock the shock velocity, and kB is Boltzmann’s constant. To reach a peak temperature of 1000 K, a shock velocity of only ~5 km s-1 is required if the pre-shock gas is atomic. The above relation only applies to strong shocks where the shock speed greatly exceeds both the sound speed and the Alfvén speed, and thus may not be fully applicable to the conditions near a protostar. However, the calculation still serves to show that even shocks moving at moderate velocities are enough to heat the gas. We furthermore note that the observations likely do not probe a single shock with a single velocity, but that shocks with a range of shock velocities is contained in the beam.
(1)where μ is the mean molecular mass, νshock the shock velocity, and kB is Boltzmann’s constant. To reach a peak temperature of 1000 K, a shock velocity of only ~5 km s-1 is required if the pre-shock gas is atomic. The above relation only applies to strong shocks where the shock speed greatly exceeds both the sound speed and the Alfvén speed, and thus may not be fully applicable to the conditions near a protostar. However, the calculation still serves to show that even shocks moving at moderate velocities are enough to heat the gas. We furthermore note that the observations likely do not probe a single shock with a single velocity, but that shocks with a range of shock velocities is contained in the beam.
The scenario is as follows: close to the protostar and on the side of the outflow cavity wall facing the protostar, UV photons dissociate gas and it is either neutral atomic, or ionized. As the slow wind impinges on this gas, it heats it to temperatures >1000 K, and compresses it (Fig. 10). The compression leads to partial shielding from the UV irradiation, and the heating initiates a shock chemistry, similar to that explored by Neufeld & Dalgarno (1989) and summarized here. In this chemistry, CO and OH form first and these two species are the dominant coolants until H2 formation sets in. H2 formation becomes efficient at ~500 K, and as the H2 molecules form, the gas temperature remains constant at ~500 K, heated by the liberated binding energy. As the gas continues to compress, shield, and cool, H2O forms efficiently from the now abundant H2 and OH (plus any remaining atomic O not locked up in OH). When the temperature decreases to ~300 K, H2 stops being the dominant coolant, and CO and H2O take over, as these are the most abundant coolants. Emission in the narrow, offset shock component is thus dominated by emission from the hot pre-H2 formation zone, whereas H2O emission is dominated by the post-H2 formation zone: the H2O-emitting part is located further into the envelope where the shock velocity has already been dampened. This coherent picture provides a natural explanation for the observed characteristics of the narrow component, and the interpretation is similar to what what proposed for the spot shock identified by Kristensen et al. (2013). However, further model calculations are required to verify this picture.
The narrower components do not appear to be detected in lower-J CO emission all the way up to CO 10–9, consistent with them tracing hotter material. UV-heated cavity walls have been uniquely identified in low-J13CO emission, specifically 13CO 6–5 (Yıldız et al. 2012). The lack of any contribution to the high-J CO ladder suggests that the UV-heated material is colder, and that the temperature distribution with mass must be steeper than in shocks, i.e., there is less material at higher temperatures relative to lower temperatures than in a shock. This is consistent with the temperatures inferred by Yıldız et al. (2015), where the temperature of the UV-heated gas is of the order of ~50 K, i.e., it would not contribute strongly to the CO 16–15 emission.
The above proposed scenario depends on one factor: H2 dissociating UV photons must be present on small scales. If not, the shock speeds must be high enough that the shocks themselves are either strong enough to dissociate H2, ν≳ 30 km s-1, or strong enough to produce the H2-dissociating UV photons, ν≳ 50 km s-1 (Neufeld & Dalgarno 1989). Both these shock velocities are too high to account for the narrow emission profiles and the velocity offsets. The presence of the dissociating photons is consistent with the scenario presented by Visser et al. (2012) and Lee et al. (2014) in that H2O molecules are dissociated in the UV-heated cavity walls. To what extent UV photons aid in further heating of the cavity shocks is an open question; it is evident that the UV photons still play a crucial role in the feedback from accreting protostars (Hull et al. 2016) and in setting the chemistry (Kristensen et al. 2013; Benz et al. 2016), although not necessarily in the excitation of the 12CO ladder.
4.3. H2O abundance
The inferred H2O abundance is two orders of magnitude lower than expected if all non-refractory oxygen not locked up in CO is incorporated in water, and if all water is released from the icy grain mantles (3×10-4; van Dishoeck et al. 2014). This result applies not only to the source position, but the water abundance is generally observed to be low also toward off-source outflow positions (e.g., Bjerkeli et al. 2012; Tafalla et al. 2013; Santangelo et al. 2013). Three possible explanations exist for this lack of water: (i) water remains on the grains or quickly re-adsorbs after the passage of a shock wave; (ii) the warm gas-phase synthesis is slowed down or reversed by large amounts of atomic hydrogen; or (iii) UV photons dissociate water. These three possibilities will be discussed further below.
Icy grain mantles are sputtered through impacts with H, H2, and He in shock waves where the charged and neutral fluids are streaming past each other. Shock models demonstrate that complete removal of the icy mantles happens at ν≳ 10 km s-1 (e.g., Flower & Pineau des Forêts 2010). Another independent line of study demonstrates that in outflows, the observed column density ratio of the two grain-species water and methanol is similar to that observed in ices at the lowest outflow velocities (≲10 km s-1; Suutarinen et al. 2014), but they diverge at higher velocities where methanol is collisionally dissociated. Thus the icy grain mantles are likely completely removed in outflows. The freeze-out time estimated in Bergin et al. (1998) is typically >105 yr, i.e., significantly longer than the dynamical lifetime of the outflows; if the density is higher than 105 cm-3, the freeze-out time may be correspondingly shorter. However, it remains unlikely that of order 99% of all water hides on grains, as would be required to explain the observed line ratios.
If H2 is dissociated, either collisionally or through photodissociation, the reverse reaction (H2O + H → OH + H2) may dominate and collisionally dissociate water at high temperatures. The bond energy of the O-H bond in water is similar to the H-H bond in H2 (5.11 versus 4.52 eV) and so it is difficult to imagine a situation in which H2 is preferentially collisionally dissociated without also dissociating water, and this combination would rapidly lead to complete dissociation of all water. Photodissociation of H2 occurs at discrete wavelengths in the range 912–1050 Å, whereas H2O is photodissociated over the entire wavelength range of 912–2000 Å (Fillion et al. 2001), implying that water is more readily photodissociated. Moreover, H2 starts to self-shield even at very low AV, further lowering photodissociation of this molecule. Thus, water is more readily photodissociated than H2, and it seems unlikely that any process will enhance the H abundance without destroying water at the same time. An important test of this scenario will be to observe these systems with high sensitivity in the H I 21cm line with, e.g., the JVLA, and measure the abundance of atomic H with respect to CO and H2O, as has previously been done for a few systems (e.g., Lizano et al. 1988; Rodriguez et al. 1990; Lizano & Giovanardi 1995).
Finally, water may be photodissociated directly, even in environments where the H2 abundance is high. To estimate the required intensity of the UV field, in units of the interstellar UV field, G0, two assumptions are made: first, all water that is photodissociated immediately dissociates all the way to atomic oxygen, either directly or in two steps with OH photodissociation following H2O photodissociation; second, the only water formation route is through gas-phase synthesis with H2 at high temperature. For a water abundance of 10-6, the atomic oxygen abundance is 10-4 and the O/H2O ratio is 102. The rate of dissociation per unit volume is Rdiss = G0kdissnH2O where kdiss = 8.0 × 10-10 s-1 (van Dishoeck et al. 2006). The water formation rate is set by the two reactions O + H2→ OH + H and OH + H2→ H2O + H. The formation rate of water is: 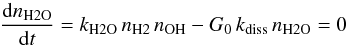 (2)assuming equilibrium. OH is assumed to be produced rapidly in reactions between O and H2 and destroyed through reactions with H2; photodissociation of OH is not considered here, i.e., nOH ≪ nH2O and nO (Wampfler et al. 2013). Thus, the formation rate is:
(2)assuming equilibrium. OH is assumed to be produced rapidly in reactions between O and H2 and destroyed through reactions with H2; photodissociation of OH is not considered here, i.e., nOH ≪ nH2O and nO (Wampfler et al. 2013). Thus, the formation rate is: 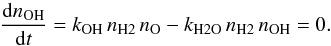 (3)Reordering these equations gives:
(3)Reordering these equations gives: 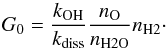 (4)For an O/H2O ratio of 102 and the kOH(T) rate coefficient from UMIST12 (McElroy et al. 2013), this expression reduces to:
(4)For an O/H2O ratio of 102 and the kOH(T) rate coefficient from UMIST12 (McElroy et al. 2013), this expression reduces to: 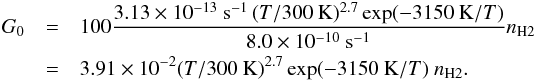 (5)The required value of G0 is shown in Fig. 12 for three different H2 densities. For a temperature of 300 K and a density of 106 cm-3, a modest value of G0 of a few is all that is required to balance the H2O production and destruction to reach an equilibrium abundance of 10-6. Naturally, these values are order-of-magnitude estimates; they may be compared to the more complete calculations of Bethell & Bergin (2009) who included OH in their simple network. The results are shown in Fig. 12 for the same initial conditions, and there is generally excellent agreement, which in this case means less than an order of magnitude difference. These simple calculations serve to illustrate that only modest values of G0 are needed to maintain low equilibrium abundances of water in low-mass protostellar sources. More sophisticated shock or wind models are required to further our understanding of water in protostars, such as those by e.g., Yvart et al. (2016) or Melnick & Kaufman (2015). Additionally, velocity-resolved observations of the [O i] transition at 63 μm with SOFIA-GREAT will further aid in constraining the water chemistry.
(5)The required value of G0 is shown in Fig. 12 for three different H2 densities. For a temperature of 300 K and a density of 106 cm-3, a modest value of G0 of a few is all that is required to balance the H2O production and destruction to reach an equilibrium abundance of 10-6. Naturally, these values are order-of-magnitude estimates; they may be compared to the more complete calculations of Bethell & Bergin (2009) who included OH in their simple network. The results are shown in Fig. 12 for the same initial conditions, and there is generally excellent agreement, which in this case means less than an order of magnitude difference. These simple calculations serve to illustrate that only modest values of G0 are needed to maintain low equilibrium abundances of water in low-mass protostellar sources. More sophisticated shock or wind models are required to further our understanding of water in protostars, such as those by e.g., Yvart et al. (2016) or Melnick & Kaufman (2015). Additionally, velocity-resolved observations of the [O i] transition at 63 μm with SOFIA-GREAT will further aid in constraining the water chemistry.
 |
Fig. 12 Required value of G0 for three different H2 densities, 105, 106, 107 cm-3 as a function of gas temperature to reach an equilibrium H2O abundance of 2 × 10-6, assuming photodissociation is the only path of destruction. The results from the network including OH from Bethell & Bergin (2009) are shown with dashed lines for the same densities. |
5. Summary and conclusions
Velocity-resolved CO 16–15 spectra of 24 embedded low-mass protostars using Herschel-HIFI have been presented. Emission is detected toward all sources, as expected from Herschel-PACS observations of the same line. The velocity-resolved line profiles are both more complex and broader than low-J CO 3–2 line profiles.
The main conclusions are the following:
-
1.
The profiles typically show multiple velocity components firstdetected in water line profiles with HIFI, in particular a broadercomponent with typical FWHM of 20 km s-1 and a narrower component with a FWHM ~ 5 km s-1 typically blue-shifted by more than 1 km s-1. Furthermore, two sources show so-called extremely-high-velocity features, or “bullets”, also seen in lower-J CO transitions and water.
-
2.
The broader component is identified as the 300 K component seen in the PACS CO data, where the rotational temperature is measured over the range Jup = 14–25. Because of its similarity to the broad H2O line profiles it is likely that H2O and CO 16–15 emission both originate in the same gas in protostellar systems. This gas is either located in shocks along the outflow cavity wall in a narrow layer (called cavity shocks) or the molecular disk wind. The water abundance, as inferred from CO 16–15, is ~2 × 10-6 with only a very small dependence on velocity. The smooth evolution of line profiles from lower-excited CO 3–2 through CO 6–5 and 10–9 to CO 16–15 illustrates that the 300 K cavity shock component traces a warmer and separate component of the classically observed molecular outflows.
-
3.
The CO excitation is thermal, up to and including CO 16–15, whereas the water excitation is modeled. The 300 K component is ubiquitous; one possible fundamental mechanism is that CO cooling turns on and becomes particularly efficient when H2 cooling ceases to be efficient. At this point CO takes over and gradually brings down the temperature to ambient. Model calculations are required, and in preparation, to test this hypothesis.
-
4.
The narrower line profile component is responsible for the hotter component seen in the CO ladder, with Trot ~ 600−800 K. This component was first identified in H2O line profiles. Based on the apparent velocity offsets and the association with H2O, a PDR origin solely in UV-heated cavity walls is ruled out; instead, an origin in dissociative shocks, where the dissociation of the pre-shock gas is provided by UV radiation from the accreting protostar, is a more likely explanation. If so, the hot part of the CO ladder traces cooling molecular gas just prior to the onset of H2 formation. Again, model calculations are under way to verify this hypothesis.
-
5.
The CO ladder from J = 1–0 to J = 49–48 thus consists of at least three distinct physical parts, all associated with the outflow. The cold <100 K component is the entrained outflow gas typically seen in low-J CO lines from the ground. The warm 300 K component is either shocks or the disk wind. Finally, the hot 600–800 K component is distinct shocks. Water is only found in the warm and hot components, not the cold outflow. Ultraviolet radiation may still play a significant role on small spatial scales in the form of dissociating envelope gas, but only on larger scales (1000 AU) is the radiation an effective heating agent, as seen in the 13CO ladder (Yıldız et al. 2012, 2015).
The observations presented here demonstrate the power of, and the necessity for, velocity resolution for interpreting emission from complex systems such as low-mass protostars. Furthermore, they open a window for characterizing the more energetic part of low-mass protostellar evolution. Several open questions still remain: if H2O is photodissociated, is the atomic oxygen abundance consistent with the inferred H2O abundance? Does H2O and high-J CO emission predominantly trace currently entrained outflow material, or does emission originate in a disk wind, or something else? The next step in understanding the energetics will be to find suitable tracers observable with facilities such as ALMA, where the enormous increase in spatial resolution will pinpoint exactly where these processes occur.
Class is part of the Gildas reduction package: http://www.iram.fr/IRAMFR/GILDAS/
The actual value of νmax is a function of integration time and S/N: when integrating deeper, νmax always tends to increase (Cernicharo et al. 1989; Rudolph 1992; Tafalla et al. 2010).
Acknowledgments
We wish to thank the entire WISH and DIGIT Herschel teams for a myriad of stimulating discussions and always entertaining team meetings.
L.E.K. and J.K.J. acknowledge support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No. 646908) through ERC Consolidator Grant “S4F”. Research at the Centre for Star and Planet Formation is funded by the Danish National Research Foundation. J.C.M. acknowledges support from the European Research Council under the European Community’s Horizon 2020 framework program (2014-2020) via the ERC Consolidator grant “From Cloud to Star Formation (CSF)” (project number 648505). A.K. acknowledges support from the Polish National Science Center grant 2013/11/N/ST9/00400.
Astrochemistry in Leiden is supported by The Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, by a Spinoza grant and grant 614.001.008 from the Netherlands Organisation for Scientific Research (NWO), and by the European Community’s Seventh Framework Programme FP7/2007-2013 under grant agreement 238258 (LASSIE).
HIFI has been designed and built by a consortium of institutes and university departments from across Europe, Canada and the United States under the leadership of SRON Netherlands Institute for Space Research, Groningen, The Netherlands and with major contributions from Germany, France and the US. Consortium members are: Canada: CSA, U. Waterloo; France: CESR, LAB, LERMA, IRAM; Germany: KOSMA, MPIfR, MPS; Ireland, NUI Maynooth; Italy: ASI, IFSI-INAF, Osservatorio Astrofisico di Arcetri-INAF; The Netherlands: SRON, TUD; Poland: CAMK, CBK; Spain: Observatorio Astronómico Nacional (IGN), Centro de Astrobiología (CSIC-INTA). Sweden: Chalmers University of Technology – MC2, RSS & GARD; Onsala Space Observatory; Swedish National Space Board, Stockholm University – Stockholm Observatory; Switzerland: ETH Zurich, FHNW; USA: Caltech, JPL, NHSC.
References
- ALMA Partnership, Brogan, C. L., Pérez, L. M., et al. 2015, ApJ, 808, L3 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Montmerle, T., Feigelson, E. D., & Steppe, H. 1990, A&A, 240, 321 [NASA ADS] [Google Scholar]
- Benz, A. O., Bruderer, S., van Dishoeck, E. F., et al. 2016, A&A, 590, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., Melnick, G. J., & Neufeld, D. A. 1998, ApJ, 499, 777 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Bethell, T., & Bergin, E. 2009, Science, 326, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Bjerkeli, P., Liseau, R., Larsson, B., et al. 2012, A&A, 546, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruderer, S., van Dishoeck, E. F., Doty, S. D., & Herczeg, G. J. 2012, A&A, 541, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cernicharo, J., Guelin, M., Penalver, J., Martin-Pintado, J., & Mauersberger, R. 1989, A&A, 222, L1 [NASA ADS] [Google Scholar]
- Choi, M., Evans, II, N. J., & Jaffe, D. T. 1993, ApJ, 417, 624 [NASA ADS] [CrossRef] [Google Scholar]
- Daniel, F., Dubernet, M.-L., & Grosjean, A. 2011, A&A, 536, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dionatos, O., Jørgensen, J. K., Green, J. D., et al. 2013, A&A, 558, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edwards, S., Cabrit, S., Strom, S. E., et al. 1987, ApJ, 321, 473 [NASA ADS] [CrossRef] [Google Scholar]
- Enoch, M. L., Evans, N. J., Sargent, A. I., & Glenn, J. 2009, ApJ, 692, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Fedele, D., Bruderer, S., van Dishoeck, E. F., et al. 2013, ApJ, 776, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Fillion, J. H., van Harrevelt, R., Ruiz, J., et al. 2001, J. Phys. Chem. A, 105, 11414 [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2010, MNRAS, 406, 1745 [NASA ADS] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 2015, A&A, 578, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Franklin, J., Snell, R. L., Kaufman, M. J., et al. 2008, ApJ, 674, 1015 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanardi, C., Lizano, S., Natta, A., Evans, II, N. J., & Heiles, C. 1992, ApJ, 397, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Goicoechea, J. R., Cernicharo, J., Karska, A., et al. 2012, A&A, 548, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Green, J. D., Evans, II, N. J., Jørgensen, J. K., et al. 2013, ApJ, 770, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Green, J. D., Yang, Y.-L., Evans, II, N. J., et al. 2016, AJ, 151, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Harsono, D., Visser, R., Bruderer, S., van Dishoeck, E. F., & Kristensen, L. E. 2013, A&A, 555, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Herczeg, G. J., Karska, A., Bruderer, S., et al. 2012, A&A, 540, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hull, C. L. H., Girart, J. M., Kristensen, L. E., et al. 2016, ApJ, 823, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Karska, A., Herczeg, G. J., van Dishoeck, E. F., et al. 2013, A&A, 552, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Karska, A., Kristensen, L. E., van Dishoeck, E. F., et al. 2014, A&A, 572, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., Ravkilde, T. L., Field, D., Lemaire, J. L., & Pineau des Forêts, G. 2007, A&A, 469, 561 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., Visser, R., van Dishoeck, E. F., et al. 2010, A&A, 521, L30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Bergin, E. A., et al. 2012, A&A, 542, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., van Dishoeck, E. F., Benz, A. O., et al. 2013, A&A, 557, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kristensen, L. E., Brown, J. M., Wilner, D., & Salyk, C. 2016, ApJ, 822, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S., Lee, J.-E., Bergin, E. A., & Park, Y.-S. 2014, ApJS, 213, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Lefloch, B., Cabrit, S., Busquet, G., et al. 2012, ApJ, 757, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Lindberg, J. E., & Jørgensen, J. K. 2012, A&A, 548, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lizano, S., & Giovanardi, C. 1995, ApJ, 447, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Lizano, S., Heiles, C., Rodriguez, L. F., et al. 1988, ApJ, 328, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Manoj, P., Watson, D. M., Neufeld, D. A., et al. 2013, ApJ, 763, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Manoj, P., Green, J. D., Megeath, S. T., et al. 2016, ApJ, 831, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Maret, S., Bergin, E. A., Neufeld, D. A., et al. 2009, ApJ, 698, 1244 [NASA ADS] [CrossRef] [Google Scholar]
- Matuszak, M., Karska, A., Kristensen, L. E., et al. 2015, A&A, 578, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Melnick, G. J., & Kaufman, M. J. 2015, ApJ, 806, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Mottram, J. C., Kristensen, L. E., van Dishoeck, E. F., et al. 2014, A&A, 572, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A. 2010, ApJ, 708, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A. 2012, ApJ, 749, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Dalgarno, A. 1989, ApJ, 340, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Kaufman, M. J. 1993, ApJ, 418, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Nisini, B., Benedettini, M., Codella, C., et al. 2010, A&A, 518, L120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisini, B., Santangelo, G., Giannini, T., et al. 2015, ApJ, 801, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Panoglou, D., Cabrit, S., Pineau des Forêts, G., et al. 2012, A&A, 538, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez, L. F., Escalante, V., Lizano, S., Canto, J., & Mirabel, I. F. 1990, ApJ, 365, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Roelfsema, P. R., Helmich, F. P., Teyssier, D., et al. 2012, A&A, 537, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rudolph, A. 1992, ApJ, 397, L111 [NASA ADS] [CrossRef] [Google Scholar]
- San José-García, I., Mottram, J. C., Kristensen, L. E., et al. 2013, A&A, 553, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santangelo, G., Nisini, B., Giannini, T., et al. 2012, A&A, 538, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santangelo, G., Nisini, B., Antoniucci, S., et al. 2013, A&A, 557, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suutarinen, A. N., Kristensen, L. E., Mottram, J. C., Fraser, H. J., & van Dishoeck, E. F. 2014, MNRAS, 440, 1844 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Santiago-García, J., Hacar, A., & Bachiller, R. 2010, A&A, 522, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Liseau, R., Nisini, B., et al. 2013, A&A, 551, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Black, J. H., Schöier, F. L., Jansen, D. J., & van Dishoeck, E. F. 2007, A&A, 468, 627 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discussions, 133, 231 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., Kristensen, L. E., Benz, A. O., et al. 2011, PASP, 123, 138 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Bergin, E. A., Lis, D. C., & Lunine, J. I. 2014, Protostars and Planets VI (University of Arizona Press), 835 [Google Scholar]
- van Kempen, T. A., van Dishoeck, E. F., Güsten, R., et al. 2009, A&A, 501, 633 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Kempen, T. A., Kristensen, L. E., Herczeg, G. J., et al. 2010, A&A, 518, L121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Visser, R., Kristensen, L. E., Bruderer, S., et al. 2012, A&A, 537, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wampfler, S. F., Bruderer, S., Karska, A., et al. 2013, A&A, 552, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, B., Stancil, P. C., Balakrishnan, N., & Forrey, R. C. 2010, ApJ, 718, 1062 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, Y.-L., Evans, II, N. J., Green, J. D., Dunham, M. M., & Jørgensen, J. K. 2017, ApJ, 835, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2012, A&A, 542, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2013, A&A, 556, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yıldız, U. A., Kristensen, L. E., van Dishoeck, E. F., et al. 2015, A&A, 576, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yvart, W., Cabrit, S., Pineau des Forêts, G., & Ferreira, J. 2016, A&A, 585, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Observational details
Observing times and Herschel obsid’s are provided in Table A.1, as are the rms values as measured in 1 km s-1 channels.
Figure A.1 shows the Gaussian fits to each line profile, where the fit parameters are listed in Table A.2. Figure A.2 shows the parameter space spanned by the different components. Figures A.3 and A.4 show the CO 16–15 CO 10–9, and H2O 110–101 line profiles overplotted on one another for each source.
 |
Fig. A.1 CO 16–15 spectra toward all observed sources. The source velocity is marked with a red dashed line in each panel and the baseline is shown in green. The best-fit Gaussian decomposition is overlaid in red, with individual Gaussian components shown in gray. The velocity scale in the L1448, BHR71, and L1157 spectra is from –100 to +100 km s-1. Ser-SMM4 is not decomposed into Gaussian functions because it appears entirely triangular. |
Observation details.
 |
Fig. A.2 Parameter space spanned by the various Gaussian components identified and labeled in Table A.2. |
 |
Fig. A.3 CO 16–15 (red) and 10–9 (blue) line spectra for all 19 sources where both data sets are available shown individually. The spectra have been rebinned to 3 km s-1 channels. The vertical dotted line is for 0 km s-1 and the horizontal dashed line is for the baseline. Both spectra have been scaled for clarity, with the scaling factor shown in each plot. |
 |
Fig. A.4 H2O 110–101 (blue) and CO 16–15 (red) line profiles for all sources shown individually. The spectra have been rebinned to 3 km s-1 channels. The central 2 km s-1 have been masked out because of self-absorption in the H2O line, and are not shown. The vertical dotted line is for 0 km s-1 and the horizontal dashed line is the baseline. Both the H2O and CO spectra have been scaled for clarity, with the scaling factor shown in each plot. |
Gaussian fits to each line profile.
All Tables
Characteristics of distinct kinematical and excitation components seen in high-J CO emission.
All Figures
 |
Fig. 1 CO 16–15 spectra toward all observed sources. The source velocity is marked with a red dashed line in each panel and the baseline is shown in green. Some spectra have been magnified for clarity by a factor shown in each panel. |
| In the text | |
 |
Fig. 2 CO and H2O spectra toward Ser SMM1 and NGC1333 IRAS4A. No correction has been made for the differences in beam size of the observation. Spectra have been shifted to a velocity of 0 km s-1. The bottom panel shows all CO profiles overlaid on top of one another. |
| In the text | |
 |
Fig. 3 Histograms showing the number of Gaussian components in each profile (left) and of profile components (right) toward Class 0 and I sources (red and blue, respectively). |
| In the text | |
 |
Fig. 4 Velocity of the narrow component of CO 16–15 with respect to the source velocity where the source velocity is shown in magenta (shifted to 0 km s-1), the narrow velocity component in cyan, for the nine sources where the component is offset by more than 0.5 km s-1. Source velocities are measured from low-J C18O transitions (Yıldız et al. 2013). |
| In the text | |
 |
Fig. 5 Top: narrow emission scaled to a common distance of 200 pc versus Lbol. Class 0 sources are marked in red, Class I in blue. Upper limits (3σ) are marked with arrows. Class 0 sources are marked in red, Class I in blue. |
| In the text | |
 |
Fig. 6 Fraction of the contribution to the total integrated CO 16–15 line intensity from the broad cavity shock component as measured from HIFI data (red). The vertical thick black line marks the division between Class 0 and I sources, where the former is to the left, the latter to the right. The blue points show the fraction of CO 16–15 emission expected to originate in the PACS warm 300 K component (Karska et al., in prep.). Both the HIFI and PACS fractions have ~10% uncertainties associated with them. The shaded red and blue regions show the spread of fractions for the HIFI and PACS components, respectively, and where there is an overlap the color is purple. Within the error bars, the fractions are the same, and the broad cavity shock component dominates emission. |
| In the text | |
 |
Fig. 7 CO 16–15/10–9 line ratio for all 19 sources for which both data sets are available. The spectra have been rebinned to 3 km s-1 channels and only data points with S/N> 2 are included. The brightness of the color indicates the number of observations passing through a given point – brighter represents a higher number. Line ratios around ±2 km s-1 are not included. Red is for Class 0 line wings, and blue for Class I. The mean ratio is displayed with a dashed line; if a linear scaling to correct for different beam sizes is applied the mean value shifts down to the dashed line marked “linear”, and similarly for a point-source scaling. The rotational temperature corresponding to a particular line ratio is shown on the second axis. |
| In the text | |
 |
Fig. 8 Top: H2O 212–101/CO 16–15 line ratio as a function of velocity toward the six Class 0 sources where the H2O line is observed with HIFI. The brightness of the color indicates the number of observations passing through a given poin – brighter represents a higher number. The channel size is 3 km s-1. Bottom: same as top but for the H2O 110–101/CO 16–15 line ratio where Class 0 and I sources are separated (red and blue, respectively). The total mean ratio is displayed. |
| In the text | |
 |
Fig. 9 Modeled intensity ratio of the 557 and 1670 GHz H2O lines over CO 16–15 as a function of the H2O/CO column density ratio, where the H2O column density is both ortho- and para-H2O. The observed ratios are shown as dashed horizontal lines. The black dashed line is the CO 16–15 opacity, and is shown on the same scale as the intensity ratio. Top: subthermal excitation conditions for H2O. Bottom: thermal excitation conditions for H2O. |
| In the text | |
 |
Fig. 10 Schematic showing the different parts to the proposed interpretation. The top left panel shows the cooling of atomic to molecular gas, along with the dominant constituents and coolants at each stage. Top right shows a cartoon HIFI CO 16–15 profile centered at zero velocity, with the broad outflow cavity shock component shown in green, and the offset spot shock component in orange. Bottom left is a CO rotational diagram with the different temperature components highlighted. Finally, bottom right shows where these different components may be located in the protostellar system. The top part shows the scenario where the broad component is caused by outflow cavity shocks, and the lower part shows the scenario where the broad component arises in the disk wind. |
| In the text | |
 |
Fig. 11 Cooling curves for H2, CO, and H2O using the analytical cooling functions of Neufeld & Kaufman (1993). The colored lines are the cooling rates, and their values are shown on the left axis. The black line is for temperature (right axis). The highlighted parts on the cooling curves are for the temperature range 300–400 K. The H2 density and column densities are as shown in Fig. 9. |
| In the text | |
 |
Fig. 12 Required value of G0 for three different H2 densities, 105, 106, 107 cm-3 as a function of gas temperature to reach an equilibrium H2O abundance of 2 × 10-6, assuming photodissociation is the only path of destruction. The results from the network including OH from Bethell & Bergin (2009) are shown with dashed lines for the same densities. |
| In the text | |
 |
Fig. A.1 CO 16–15 spectra toward all observed sources. The source velocity is marked with a red dashed line in each panel and the baseline is shown in green. The best-fit Gaussian decomposition is overlaid in red, with individual Gaussian components shown in gray. The velocity scale in the L1448, BHR71, and L1157 spectra is from –100 to +100 km s-1. Ser-SMM4 is not decomposed into Gaussian functions because it appears entirely triangular. |
| In the text | |
 |
Fig. A.2 Parameter space spanned by the various Gaussian components identified and labeled in Table A.2. |
| In the text | |
 |
Fig. A.3 CO 16–15 (red) and 10–9 (blue) line spectra for all 19 sources where both data sets are available shown individually. The spectra have been rebinned to 3 km s-1 channels. The vertical dotted line is for 0 km s-1 and the horizontal dashed line is for the baseline. Both spectra have been scaled for clarity, with the scaling factor shown in each plot. |
| In the text | |
 |
Fig. A.4 H2O 110–101 (blue) and CO 16–15 (red) line profiles for all sources shown individually. The spectra have been rebinned to 3 km s-1 channels. The central 2 km s-1 have been masked out because of self-absorption in the H2O line, and are not shown. The vertical dotted line is for 0 km s-1 and the horizontal dashed line is the baseline. Both the H2O and CO spectra have been scaled for clarity, with the scaling factor shown in each plot. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


