| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 23 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201630108 | |
| Published online | 31 May 2017 | |
X-shooter spectroscopy of young stellar objects in Lupus
Atmospheric parameters, membership, and activity diagnostics ⋆,⋆⋆
1 INAF – Osservatorio Astrofisico di Catania, via S. Sofia, 78 95123 Catania Italy
e-mail: antonio.frasca@oact.inaf.it
2 INAF – Osservatorio Astronomico di Capodimonte, via Moiariello, 16, 80131 Napoli, Italy
3 Scientific Support Office, Directorate of Science, European Space Research and Technology Centre (ESA/ESTEC), Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
4 INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
5 INAF – Osservatorio Astronomico di Roma, via Frascati 33, 00078 Monte Porzio Catone, Italy
Received: 21 November 2016
Accepted: 3 March 2017
Aims. A homogeneous determination of basic stellar parameters of young stellar object (YSO) candidates is needed to confirm their pre-main sequence evolutionary stage and membership to star forming regions (SFRs), and to get reliable values of the quantities related to chromospheric activity and accretion.
Methods. We used the code ROTFIT and synthetic BT-Settl spectra for the determination of the atmospheric parameters (Teff and log g), veiling (r), radial (RV), and projected rotational velocity (vsini) from X-shooter spectra of 102 YSO candidates (95 of infrared Class II and seven Class III) in the Lupus SFR. The spectral subtraction of inactive templates, rotationally broadened to match the vsini of the targets, enabled us to measure the line fluxes for several diagnostics of both chromospheric activity and accretion, such as Hα, Hβ, Ca ii, and Na i lines.
Results. We have shown that 13 candidates can be rejected as Lupus members based on their discrepant RV with respect to Lupus and/or the very low log g values. At least 11 of them are background giants, two of which turned out to be lithium-rich giants. Regarding the members, we found that all Class III sources have Hα fluxes that are compatible with a pure chromospheric activity, while objects with disks lie mostly above the boundary between chromospheres and accretion. Young stellar objects with transitional disks display both high and low Hα fluxes. We found that the line fluxes per unit surface are tightly correlated with the accretion luminosity (Lacc) derived from the Balmer continuum excess. This rules out that the relationships between Lacc and line luminosities found in previous works are simply due to calibration effects. We also found that the Ca ii-IRT flux ratio, FCaII8542/FCaII8498, is always small, indicating an optically thick emission source. The latter can be identified with the accretion shock near the stellar photosphere. The Balmer decrement reaches instead, for several accretors, high values typical of optically thin emission, suggesting that the Balmer emission originates in different parts of the accretion funnels with a smaller optical depth.
Key words: stars: pre-main sequence / stars: fundamental parameters / stars: chromospheres / accretion, accretion disks / open clusters and associations: individual: Lupus
Based on observations collected at the Very Large Telescope of the European Southern Observatory at Paranal, under programs 084.C-0269(A), 085.C-0238(A), 086.C-0173(A), 087.C-0244(A), 089.C-0143(A), 095.C-0134(A), 097.C-0349(A), and archive data of programmes 085.C-0764(A) and 093.C-0506(A).
Tables 1–3 are also available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/602/A33
© ESO, 2017
1. Introduction
A full characterization of members of young open clusters (OCs) and star forming regions (SFRs) is necessary to understand the mechanisms of star and planet formation, as well as the different phenomena occurring during the early phases of stellar evolution. It is therefore mandatory to derive, as homogeneously as possible, the basic physical parameters of young stellar objects (YSOs), such as effective temperature (Teff), surface gravity (log g), mass, and projected rotational velocity (vsini). These quantities are closely related to the evolutionary stage of YSOs and are also directly involved in the generation of stellar magnetic fields by dynamo processes. In the context of the magnetospheric accretion model, magnetic fields play a key role in the infall of matter from the disk onto the central star (Hartmann et al. 1994, 2016, and references therein). Magnetic fields are also responsible for the strong activity observed from the photospheres to the chromospheres and coronae of YSOs and late-type stars in general (e.g., Feigelson & Montmerle 1999; Berdyugina 2009, and references therein). Circumstellar disks, stellar rotation, magnetic activity, and accretion are all strongly involved in the process of planet formation (e.g., Hawley & Balbus 1991; Brandenburg et al. 1995; Larson 2003, and references therein).
Deriving the basic stellar parameters is particularly hard for objects belonging to very young OCs and SFRs where several phenomena, such as fast rotation, cloud extinction, and mass accretion, affect their spectra, making the analysis of their photospheres difficult. In particular, veiling of the spectra, arising from accretion shocks and, possibly, from disk gas inside the dust sublimation radius, dilutes the photospheric lines and it must be properly taken into account to derive reliable stellar parameters (see, e.g., Frasca et al. 2015, and references therein). Moreover, emission lines, which are numerous and very strong and broad in the spectra of highly accreting objects, need to be masked, leaving only limited spectral ranges suitable for the analysis of photospheric lines.
On the other hand, it is well known that the luminosity of several emission lines of the Balmer series, the He i and Ca ii lines, are well correlated with the accretion luminosity (e.g., Herczeg & Hillenbrand 2008; Alcalá et al. 2014, 2017, and references therein) and with hydrogen recombination lines in the near-infrared (Muzerolle et al. 1998; Calvet et al. 2004; Alcalá et al. 2017), highlighting the importance of these emission features as accretion diagnostics.
Spectra with both a very wide wavelength coverage and high or intermediate resolution are particularly helpful, as they offer the possibility of finding spectral intervals that are free from or little affected by these issues, where fully resolved absorption lines can be modeled to consistently derive atmospheric parameters, radial velocity, vsini, and veiling. For this reason, the VLT/X-shooter spectrograph (Vernet et al. 2011), with its wide wavelength coverage, is an ideal instrument to reach these goals.
Thanks to their relatively close distance to the Sun (150–200 pc, Comerón 2008) and the large numbers of Class II and Class III infrared sources they contain, the dark clouds in Lupus are among the best sites for which a spectroscopic determination of the atmospheric parameters for YSOs can be carried out down to the hydrogen burning mass limit. In addition, extinction to the individual YSOs is relatively low in comparison with many other SFRs.
The selection of candidates and the characterization of some of the confirmed Lupus members, both physical and kinematical, has been performed in recent years (see, e.g., Evans et al. 2009; Comerón et al. 2009, 2013; Galli et al. 2013; Herczeg & Hillenbrand 2014; Bustamante et al. 2015). However, most of these works are based on nonsimultaneous optical and IR photometry, and low-resolution spectroscopy. Moreover, the atmospheric parameters are derived mostly for the Class III sources. A homogeneous determination of the atmospheric parameters, vsini, and veiling for a large sample of Class II sources in Lupus is still lacking. In this work we aim to fill in this gap. Our study is based on X-shooter spectra of more than 100 YSO candidates in the Lupus I, II, III, and IV clouds.
The high quality and intermediate resolution of these spectra also allowed us to investigate the behavior of hydrogen, calcium, and sodium emission lines that are diagnostics of both chromospheric and accretion activity.
The paper is organized as follows. In Sect. 2 we present the data sample. The analysis of the spectra for the determination of stellar parameters and radial velocities is described in Sect. 3. The results are discussed in Sect. 4, where the properties of the targets, membership to the Lupus SFR, and line fluxes per unit surface are discussed. The main conclusions are summarized in Sect. 5.
2. Data sample
In total, we analyzed X-shooter spectra of 102 objects, 43 of which were obtained in 2010, 2011, and 2012, during National Institute of Astrophysics (INAF) guaranteed time observations (GTO; Alcalá et al. 2011a). The remaining sources were observed in the framework of the ESO-P95 proposal from March to August 2015 (48 objects) and the ESO-P97 proposal from May to June 2016 (5 objects). In addition, X-shooter spectra of six YSOs were retrieved from the ESO archive. Our sample comprises sources belonging to the infrared (IR) Class II. However, seven Class III objects were also included. Six of these objects have already been investigated by Stelzer et al. (2013) and Manara et al. (2013). The sample accounts for roughly half of the entire known population of YSOs in Lupus, but ~95% of disky YSOs. For the criteria of target selection and details about the data reduction, refer to Alcalá et al. (2014, 2017).
Stellar parameters.
Thirteen out of the 102 objects studied here were suspected to be nonmembers based on the appearance of their spectrum (Alcalá et al. 2017). The analysis we performed allowed us to definitely reject them as members.
The target list is given in Table 1 together with the heliocentric Julian Date of observation and some of the parameters derived in this work. The spectra of Sz 68, Sz 74, Sz 83, Sz 102, Sz 105, and the archive data (i.e., IM Lup, Sz 77, EX Lup, GQ Lup, Sz 76, RXJ1556.1-3655) were acquired using the 0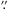 5/0
5/0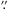 4/0
4/0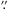 4 slits in the UVB/VIS/NIR arms, respectively. All the other targets were instead observed with the 1
4 slits in the UVB/VIS/NIR arms, respectively. All the other targets were instead observed with the 1 0/0
0/0 9/0
9/0 9 slits in the UVB/VIS/NIR arms, respectively.
9 slits in the UVB/VIS/NIR arms, respectively.
For our analysis, particularly for the vsini measurement, it is important to know the actual spectral resolution. To this purpose we used Th–Ar calibration spectra taken during our observing runs. We found that the resolving power of VIS spectra taken with the 0 9 slit was R ≃ 8400 in the spectral region used for the vsini determination (λ ~ 9700 Å), while in the highest resolution mode (0
9 slit was R ≃ 8400 in the spectral region used for the vsini determination (λ ~ 9700 Å), while in the highest resolution mode (0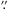 4 slit) it is about 17 000. More details can be found in Appendix A.
4 slit) it is about 17 000. More details can be found in Appendix A.
3. Atmospheric parameters, veiling, radial, and projected rotational velocities
The determination of the atmospheric parameters (Teff and log g), veiling r, projected rotational velocity (vsini), and radial velocity (RV) was accomplished through the code ROTFIT (e.g., Frasca et al. 2006, 2015).
We adopted a grid of synthetic BT-Settl spectra as templates (Allard et al. 2012) with a solar iron abundance and effective temperature in the range 2000–6000 K (in steps of 100 K) and log g from 5.5 to 0.5 dex (in steps of 0.5 dex). This grid covers the wide range in spectral type (SpT) spanned by our targets, i.e., from early-K to late-M, and also extends to lower gravities typical of giants.
The code ROTFIT was already applied to X-shooter spectra of Class III sources in Stelzer et al. (2013). However, the code was improved since then with the inclusion of further spectral segments to be analyzed both in the VIS and UVB spectra. Furthermore, in this version we implemented an accurate search for the minimum of chi-square (χ2) in the space of parameters and the evaluation of the errors based on the 1σ confidence levels. The veiling, r, was also considered a free parameter. Details concerning the application of the code to the X-shooter spectra are given in Appendix B.
3.1. Radial velocity
The RV was needed to align the synthetic template spectra with the observed spectra. The peak of the cross-correlation function (CCF) was fitted with a Gaussian for a more accurate determination of its center (see the insets in Fig. B.1). For each ith spectral segment, the error of the RVi value, σRVi, was estimated by the fitting procedure curvefit (Bevington 1969), taking into account the CCF noise, which was evaluated as the standard deviation of the CCF values outside the peak. Then, the heliocentric correction of the RV measurements was performed with the IDL procedure helcorr. The final RV for each star, reported in Table 1, is the weighted mean of the values obtained from all analyzed spectral segments using 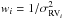 as weights. The standard error of the weighted mean was adopted as the RV uncertainty. These errors range from 0.7 to 12 km s-1 with a median value of 2.3 km s-1. As expected, the RV errors tend to be larger for stars that have higher vsini and/or low S/N spectra or for stars that are strongly affected by veiling (see Table 1).
as weights. The standard error of the weighted mean was adopted as the RV uncertainty. These errors range from 0.7 to 12 km s-1 with a median value of 2.3 km s-1. As expected, the RV errors tend to be larger for stars that have higher vsini and/or low S/N spectra or for stars that are strongly affected by veiling (see Table 1).
3.2. Accuracy of Teff and log g determinations and comparisons with the literature
The Teff errors reported in Table 1 range from about 30 to 250 K, depending on Teff (and on the S/N) with a median value of 70 K. The only exception is SSTc2dJ161045.4-385455 (σTeff = 514 K), which is a likely nonmember with a low-signal spectrum.
 |
Fig. 1 Top panel: comparison between the effective temperature determined with ROTFIT and that derived from the MK spectral classification performed for the Lupus members by Manara et al. (2013) and Alcalá et al. (2014, 2017). The continuous line represents the 1:1 relationship. The Teff differences (bottom panel) show a mean value of about −40 K (dashed line) and a standard deviation of about 100 K (dotted lines). |
To estimate the external accuracy of Teff, we compared our values with those derived from the spectral classification performed by Manara et al. (2013) for the Class III objects and by Alcalá et al. (2014, 2017) for the Class II sources, who adopted the temperature scales of Luhman et al. (2003) and Kenyon & Hartmannn (1995) for the M- and K-type stars, respectively. The comparison is shown in Fig. 1. The general agreement of the two Teff determinations is evident with a scatter of the residuals ≃100 K rms. Nevertheless, this comparison displays a systematic offset between the two Teff determinations, which is more evident in the M-type domain with the Teff values derived from SpT that are about 40 K higher, on average, than those from ROTFIT. This offset is likely due to the different Teff scales between the BT-Settl models and the empirical SpT–Teff calibration defined for M-type stars by Luhman et al. (2003). The Teff values of Luhman et al. (2003) for early M-type stars are systematically higher by ~70 K than those reported by Pecaut & Mamajek (2013) for young stars, which are based on the fitting of the optical/IR spectral energy distributions.
 |
Fig. 2 Top panel: comparison between the effective temperature determined with ROTFIT and that derived by Herczeg & Hillenbrand (2014) and Comerón et al. (2013). The solid line represents the 1:1 relationship. The Teff differences (bottom panel) show a mean value of about + 28 K (dashed line) and a standard deviation of about 100 K (dotted lines). |
As a further check on the accuracy of our determinations we searched for spectroscopic Teff measurements in the literature that are not based on X-shooter data. We compared our results with the values reported by Comerón et al. (2013) and Herczeg & Hillenbrand (2014). Both works are based on low resolution (R = 500–1000) optical spectra. We have only one star in common with Comerón et al. (2013), namely SSTc2d160836.2-392302, for which the Teff agreement is excellent (see Fig. 2). Twenty of our targets have been observed by Herczeg & Hillenbrand (2014), who list the spectral type derived from suitable spectral indices. We converted their SpT into Teff using the calibration put forward by them. The comparison is shown in Fig. 2. The agreement is evident with an average offset of +28 K and a scatter of about 100 K, as in Fig. 1. The latter can be considered the typical external accuracy of our Teff values. Despite the lower number of points, the agreement in the M-type domain looks better than that shown in Fig. 1. This is likely owing to the Teff scale, based on BT-Settl spectra, which are adopted both in the present work and in Herczeg & Hillenbrand (2014).
Concerning log g, the errors are in the range 0.1–0.5 dex with a median value of 0.21 dex. Only four objects have larger errors (up to 0.9 dex). We did not find other estimates of gravity in the literature, except for the value of log g = 4.0 reported by Comerón et al. (2013) for SSTc2d160836.2-392302, which is consistent with our estimate (4.04 ± 0.13).
3.3. Projected rotational velocity
The intermediate resolution of X-shooter allows us to measure vsini only for relatively fast rotators. To check the minimum vsini that can be measured in these spectra and to estimate the vsini errors, we ran Monte Carlo simulations on synthetic spectra with the same resolution and sampling of X-shooter, following the prescriptions given in Frasca et al. (2015). We found that the minimum detectable vsini with the 0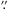 9 slit is about 8 km s-1. Therefore, we considered, as upper limits, all vsini values lower than 8 km s-1. We also evaluated the upper limit on vsini for the spectra acquired with the 0
9 slit is about 8 km s-1. Therefore, we considered, as upper limits, all vsini values lower than 8 km s-1. We also evaluated the upper limit on vsini for the spectra acquired with the 0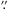 4 slit, finding a value of 6 km s-1. Details about the Monte Carlo simulations can be found in Appendix C. The errors of vsini range from 1 to 15 km s-1 (Table 1) with a median value of about 4 km s-1.
4 slit, finding a value of 6 km s-1. Details about the Monte Carlo simulations can be found in Appendix C. The errors of vsini range from 1 to 15 km s-1 (Table 1) with a median value of about 4 km s-1.
We only found determinations of vsini in the literature for a handful of the brightest sources in our sample. For Sz 68, Torres et al. (2006) report a value of vsini = 38.9 ± 0.6 km s-1, which is compatible with our determination of 39.6 ± 1.2 km s-1. Dubath et al. (1996) give only a lower limit of vsini > 60 km s-1 for Sz 121, which is one of the most rapidly rotating stars in our sample (vsini = 87 km s-1). The same authors report vsini = 10.2 ± 1.6 km s-1 for Sz 108, for which we find an upper limit of 8 km s-1. The value of 22.4 km s-1 quoted in the Catalog of Stellar Rotational Velocities (Glebocki & Gnacinski 2005) for RY Lup is marginally consistent with our value (vsini = 16.3 ± 5.3 km s-1). Finally, in the same catalog, vsini = 14.2 km s-1 is reported for Sz 98, while we find vsini < 8 km s-1.
3.4. Veiling
After several tests made with our code on Class III and X-shooter archive spectra of nonaccreting stars, we realized that values of veiling as large as 0.2 can be found, although no veiling is expected in such cases. This is probably a combined effect of the intermediate spectral resolution, small differences in the continuum setting between target and template spectra, and some trade-off between parameters. For this reason, all values r ≤ 0.2 are considered not significant and have been replaced with an upper limit of 0.2 in Table 1. We measured significant values of veiling (r> 0.2) for 12, 19, and 44 YSOs at 970 nm, 710 nm, and 620 nm, respectively. This trend is in line with the enhancement of r with decreasing wavelength (see Fig. B.4).
Herczeg & Hillenbrand (2014) report values of the veiling at 750 nm for 16 of our targets. For about a half of them we derived only upper limits, r710 ≤ 0.2, while for the remaining YSOs the veiling is always rather small. However, the comparison of these data shows that we can measure the veiling at 710 nm whenever Herczeg & Hillenbrand (2014) quote r750> 0.2.
Using the mass accretion rates derived by Alcalá et al. (2017) on the same data set, we found that high values of veiling (r620 ≥ 1.0) are only measured for the strongest accretors (Ṁacc > 10-9, see Fig. 3).
 |
Fig. 3 Veiling at 620 nm as a function of the mass accretion rate measured by Alcalá et al. (2017) on the same spectra. |
4. Results
4.1. Membership
We used the atmospheric parameters, RV, and equivalent width of the lithium line at 6707.8 Å (EWLi) to verify the membership of our targets to the Lupus SFR. Here we used the EWLi values derived by Biazzo et al. (2017).
 |
Fig. 4 Teff–log g diagram for all the objects for which a log g value was derived with ROTFIT. Gray dots represent Class II sources, red diamonds denote Class III sources, while the nonmembers are indicated by green asterisks. The full blue lines are the PMS isochrones from Baraffe et al. (2015) at 1, 3, and 10 Myr and solar metallicity. The black dashed lines are post-MS isochrones from the PARSEC database (Bressan et al. 2012) for a solar metallicity at 300 Myr and 10 Gyr. The magenta dot-dashed line is the PARSEC isochrone at 10 Gyr and Z = 0.060. |
The log g values derived with ROTFIT allow us to identify contaminants in our sample whose IR colors mimic those of cool very young stars. In Fig. 4 we show the log g–Teff diagram of our targets, where the stars suspected to be nonmembers are highlighted with green asterisks. We also plot the pre-main sequence (PMS) isochrones of Baraffe et al. (2015) and the post-main sequence isochrones from the PARSEC database (Bressan et al. 2012).
All green asterisks at Teff < 5000 K have log g< 3.0 and correspond most likely to giants. Four of these are indeed in the red giant branch (RGB) and possibly close to the red giant clump; a few others, with lower gravity, could be in the AGB phase. The star with the highest temperature, SSTc2dJ161148.7-381758, could be a MS star unrelated to the Lupus SFR, as indicated by its RV = −47.6 km s-1. The green asterisk with the largest errors located at Teff = 5114 K and log g = 3.4 corresponds to SSTc2dJ161045.4-385455. Its position on the log g–Teff plane may be compatible with the PMS locus, taking into account the errors, but the value of RV = −115.1 km s-1 strongly suggests that it is not a member of the Lupus SFR.
The other two indicators of membership, namely the RV and EWLi, are plotted in Fig. 5 with the same symbols as in Fig. 4. It is worth noting that, except for two objects (SSTc2dJ160708.6-394723 and SSTc2dJ161045.4-385455), all the stars classified as nonmembers based on the log g–Teff diagram and/or discrepant RV, have undetectable Li i lines. The nonmember with the highest EWLi (364 mÅ) is SSTc2dJ160708.6-394723. For this object we estimate Teff ≃ 4650 K and log g ≃ 2.6, thus it lies in the RGB region of the log g–Teff diagram (Fig. 4). The RV of this object is inconsistent with the Lupus SFR. Likewise, SSTc2dJ161045.4-385455 has a rather large EWLi (about 300 mÅ), but, as already mentioned, its RV = −115.1 km s-1 and the absence of emission lines rule out its membership to the Lupus SFR. Although with large errors, its atmospheric parameters suggest a G-type giant or subgiant. These two stars are most likely lithium-rich giants. More details are given in Appendix D.
Three other nonmembers based on the log g–Teff diagram (Sz 78, Sz 105, and SSTc2dJ161222.7-371328) instead have RVs that are compatible with Lupus, but have no lithium. These stars have all very low log g values of 2.04, 0.76, and 0.99, respectively, thus ruling out a PMS nature.
In conclusion, by using the three indicators, log g, RV, and EWLi, we were able to reject 13 stars as Lupus members. All the remaining 89 targets were considered members, although a few of them have a RV slightly outside the SFR average derived by us (⟨ RV ⟩ = 2.8 ± 4.2 km s-1) and external to the RV distributions for on-cloud and off-cloud sources defined by Galli et al. (2013). Nonetheless, they display a large EWLi that reinforces their membership; they could be spectroscopic binaries.
A small group of six Class II sources, namely Sz 69, Lup706, Par-Lup3-4, 2MASS J16085953-3856275, 2MASS J16085373-3914367, and SSTc2dJ154508.9-341734, instead have a RV well consistent with the Lupus SFR but a low lithium content (EWLi< 150 mÅ). Nevertheless, the spectra of these objects display other features that indicate their membership (cf. strong and wide emission lines, veiling, etc.; Alcalá et al. 2014, 2017). These cases will be discussed in more detail in Biazzo et al. (2017). Finally, the star Sz 94, classified as a Class III source with proper motions and RV compatible with Lupus, shows EWLi ≈ 0, making its membership dubious.
 |
Fig. 5 Equivalent width of the Li i λ6708 Å line from Biazzo et al. (2017) vs. radial velocity measured in the present paper. The meaning of the symbols is as in Fig. 4. The average RV of the Lupus members (2.8 km s-1) is indicated with the vertical dashed line, while the dotted lines delimit the 1σ confidence region. The blue and red histograms represent the RV distributions for the on-cloud and off-cloud Lupus stars found by Galli et al. (2013). |
4.2. Hertzsprung-Russell diagram
 |
Fig. 6 Hertzsprung-Russell diagram of the Lupus members. The evolutionary tracks of Baraffe et al. (2015) are shown as solid lines with the labels representing their masses. The isochrones at 1, 3, 10, 30, and 300 Myr by the same authors are shown with dashed lines. Big open circles denote subluminous objects. The green arrowhead indicates the position of the flat source SSTc2dJ160708.6-391408 (green filled square) when assuming the bolometric luminosity of 0.18 L⊙ (Evans et al. 2009). |
In Alcalá et al. (2017) we derived masses via four different evolutionary tracks, but only for the Class II sources. Here we derive masses and ages for both the Class III and Class II sources homogeneously via the Teff values resulting from the ROTFIT analysis.
In Fig. 6, we report the position of our targets in the Hertzsprung-Russell (HR) diagram, where we used the Teff values derived in the present work and the luminosities calculated by Manara et al. (2013) and Alcalá et al. (2014, 2017), with the same method, for the Class III and Class II sources, respectively. In the same figure we overplot the PMS evolutionary tracks and isochrones by Baraffe et al. (2015).
Most of the targets are located between the isochrones at 1 and 10 Myr, while a few of them (Lup706, Sz106, Par-Lup3-4, Sz123B, Sz133, SSTc2dJ160703.9-391112, and Sz102), shown with larger open circles in Fig. 6, appear to be subluminous. These are likely objects with rotation axes perpendicular to the line of sight where the edge-on disks reduce the stellar luminosity by extinction and light scattering (Alcalá et al. 2014, 2017). Several of these objects show an enhancement of outflow tracers, such as the low-velocity component of the [O i] λ6300 Å line, in their optical spectra (Bacciotti et al. 2011; Natta et al. 2014; Whelan et al. 2014). This line originates in a more extended volume with respect to the accretion tracers that arise from a much closer region to the stellar surface, and are suppressed by the optically thick edge-on disk. This effect is particularly important in Par-Lup3-4, Sz102 and Sz133 (Bacciotti et al. 2011; Natta et al. 2014; Nisini et al., in prep.). Another object, namely SSTc2dJ160708.6-391408, classified as a flat IR source (Merín et al. 2008) and shown with a green filled square in Fig. 6, appears subluminous because the derived stellar luminosity does not account for reprocessed stellar radiation in the infalling envelope of gas and dust (see Appendix C in Alcalá et al. 2017). This object is further discussed in Appendix D.
The evolutionary tracks and isochrones can be used to estimate the masses and ages of the targets from their location in the HR diagram by minimizing the quantity 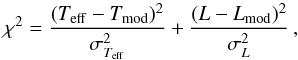 (1)where Teff and L are the stellar effective temperature and bolometric luminosity, respectively, with errors σTeff and σL, respectively. The effective temperature and stellar luminosity of the evolutionary tracks are denoted with Tmod and Lmod, respectively. We assigned the mass and age corresponding to the closest track and isochrone, which minimize χ2, to each YSO.
(1)where Teff and L are the stellar effective temperature and bolometric luminosity, respectively, with errors σTeff and σL, respectively. The effective temperature and stellar luminosity of the evolutionary tracks are denoted with Tmod and Lmod, respectively. We assigned the mass and age corresponding to the closest track and isochrone, which minimize χ2, to each YSO.
The same procedure was used for evaluating masses and ages with the Siess et al. (2000) evolutionary models that do not cover the very low-mass regime but extend to higher masses. For the stars in the mass range 0.1–1.4 M⊙ we found an excellent agreement between the masses derived with the two sets of tracks with differences within 0.05 M⊙ rms. Masses and ages, with the exception of the underluminous sources, are reported in Table 1. For the most massive star, SSTc2dJ160830.7-382827, whose position in the HR diagram is outside the mass range covered by the Baraffe et al. (2015) tracks, we adopted the Siess et al. (2000) models and we found M⋆ = 1.8M⊙ and Age = 2.9 Myr.
The mass determinations are in very close agreement with those of Alcalá et al. (2017). As stressed in previous works, the age determination suffers from uncertainties from the error on the distance of the clouds, source variability, and extinction, and depends on the adopted set of evolutionary tracks (see, e.g., Comerón 2008, and references therein). Therefore, the ages of the individual sources are affected by large uncertainties. However, the median age of the full sample analyzed in the present work is 2 Myr and the average value is 2.5 Myr, which is in good agreement with previous determinations (e.g., Alcalá et al. 2014, 2017, and references therein).
4.3. Activity and accretion diagnostics
The emission lines comprised in the X-shooter spectra have been used as diagnostics of chromospheric activity and accretion in previous works of our group (e.g., Stelzer et al. 2013; Alcalá et al. 2014). We have shown how the exceptional richness of information of these spectra allows us to probe the different layers of the atmospheres of PMS stars and to define the noise that chromospheric emission introduces into mass accretion estimates (Manara et al. 2013). These spectra allowed us to improve considerably the accuracy of the determination of mass accretion with important implications of the Ṁacc–M⋆ relationship (Alcalá et al. 2014, 2017).
We now look more closely at the Hα, Ca ii K, Ca ii infrared triplet (IRT), and at Na i D1,2. These lines, particularly Hα and Ca ii lines, have been widely used as diagnostics for both chromospheric activity (e.g., Strassmeier et al. 2000; Montes et al. 2001; Martínez-Arnáiz et al. 2011; Frasca et al. 2016, and reference therein) and accretion (e.g., Muzerolle et al. 2003; Mohanty et al. 2005; Costigan et al. 2012; Alcalá et al. 2014) because of their intensity and the high sensitivity of the CCD detectors at these wavelengths. The cores of the Na i D1,2 lines are good diagnostics of chromospheric activity (especially in late-K and M-type stars; e.g., Houdebine et al. 2009; Gomes da Silva et al. 2011), mass accretion (e.g., Rigliaco et al. 2012; Alcalá et al. 2014, 2017) and winds (e.g., Natta & Giovanardi 1990; Facchini et al. 2016).
 |
Fig. 7 Example of the spectral subtraction for the Hα line of SSTc2dJ160830.7-382827. The target spectrum normalized to the local continuum is represented by a solid black line, while the best-fitting BT-Settl spectrum is overplotted with a dotted red line. The difference spectrum is shown in the bottom of the panel, where the residual Hα emission is highlighted by the hatched green area. |
 |
Fig. 8 Example of the spectral subtraction for the Ca ii IRT lines of Sz 103. Observed spectrum and inactive template are traced with a solid black line and dotted red line, respectively. The difference between observed and template spectrum is shown in the bottom of each panel, along with the residual emission in the Ca ii IRT line cores (hatched green areas). |
We calculated the equivalent widths (EWs) and line fluxes using the spectral subtraction method (see, e.g., Frasca & Catalano 1994; Montes et al. 1995) to remove the photospheric flux and to evidence the core emission. Although this correction is negligible for objects with high accretion rates and very strong emission lines, it is absolutely needed in cases where the photospheric profile is only filled in with emission or the latter is very weak.
Figure 7 shows the result of the spectral subtraction on the Hα line of SSTc2dJ160830.7-382827, which is a weak accretor with a transitional disk (Alcalá et al. 2017). In this case, the Hα line displays an absorption profile filled-in with emission, which is only revealed by subtracting the inactive template. The latter was obtained by the interpolation of the best-fitting BT-Settl spectra at the Teff and log g of the target, which are quoted in Table 1.
The inactive templates are rotationally broadened whenever vsini is larger than the minimum detectable value (see Sect. 3.3), Doppler-shifted, and resampled on the spectral points of the target spectra before subtraction. The residual Hα profile integrated over wavelength (hatched green area in Fig. 7) provides us with the net Hα EW.
An example of the application of the spectral subtraction method to the Ca ii IRT lines is shown in Fig. 8 for the star Sz 103. The subtraction of the inactive template is necessary for a correct measurement of the Ca ii IRT EWs. In particular, the Ca ii λ 8662 line shows an emission in its core that does not reach the continuum.
The result of the spectral subtraction in the region of Na i D1,2 and He i D3 lines for Sz 97 is shown in Fig. 9. It is clear that, although the underlying photospheric spectrum barely affects the strong He i D3 line, it must be subtracted from the target spectrum to get the emission EWs in the Na i D1,2 line cores. We stress that the X-shooter spectra were also corrected for telluric absorption lines at these wavelengths, as described by Alcalá et al. (2014), and the interstellar Na i absorption only significantly affects more distant nonmembers (giants).
 |
Fig. 9 Example of the spectral subtraction for the Na i D1,2 and He i D3 lines of Sz 97. Solid and dotted red lines have the same meaning as in Fig. 7. An offset of 0.5 was applied to both the observed and synthetic spectra for visualization purposes. The hatched green areas in the “difference” spectrum represent the Na i D1,2 excess emissions, while the He i D3 residual emission is filled with violet hatching. |
We converted the observed EWs into line fluxes per unit surface by multiplying them for the continuum flux of the synthetic spectrum corresponding to the Teff and log g of the target. To get a more accurate value of the continuum flux, we interpolated in Teff and log g within the grid of BT-Settl spectra. The fluxes of Hα, Hβ, Ca ii K, Ca ii IRT, and Na i D lines are quoted in Table 2. In this table we do not report any flux value whenever the spectral subtraction does not give an emission residual profile. We treat the values for which the error is larger than the flux as upper limits.
We have already shown in Stelzer et al. (2013) the agreement between line fluxes per unit surface calculated on the basis of model spectra, as in the present paper, and those derived from the observed flux at Earth and the dilution factor, (R∗/d)2, where R∗ and d are the stellar radius and distance, respectively.
We also calculated the ratio of the line and bolometric flux, 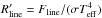 as a further chromospheric/accretion diagnostic1.
as a further chromospheric/accretion diagnostic1.
 |
Fig. 10 Left panel: Hα flux vs. Teff. Right panel: |
 |
Fig. 11 Flux-flux relations between Hα and Ca ii IRT lines (λ 8498, λ 8542, and λ 8662 Å, from the left to the right, respectively). The meaning of the symbols is as in Fig. 10. The full red lines are the least-squares regressions, whose coefficients are reported in Eq. (2). The dashed lines represent the best fits of flux-flux relations found by Stelzer et al. (2013) for Class III objects. Downward and leftward arrows indicate upper limits on Hα and Ca ii fluxes, respectively. |
For the stars with Hα line in emission above the local continuum, we also measured the full width at 10% of the line peak (10%WHα). This quantity is helpful for discriminating between accreting stars and those with pure chromospheric emission. In particular, we defined “candidate accretors” as the objects that fulfill the criterion of White & Basri (2003), which is based on both a 10%WHα ≥ 270 km s-1 and EWHα larger than given thresholds depending on spectral type; we distinguished these objects in the following plots with half-filled symbols.
In Fig. 10 we plot the Hα flux, FHα, and the ratio 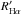 as a function of the effective temperature. In this figure, the boundary between the accreting objects and chromospherically active stars, as defined by Frasca et al. (2015) with the same criteria for the members of the Gamma Vel cluster and Cha I SFR, is also indicated. All Class III stars lie below the aforementioned boundary and all candidate accretors (half-filled symbols) are located above it, while the other Class II sources are scattered around, and mostly below, this dividing line. In particular, 17 Class II sources are located below the dividing line. However, this border cannot be considered a knife edge that separates accretors from chromospheric sources; therefore only the objects lying well below it are noteworthy. For instance, if we select only the YSOs with
as a function of the effective temperature. In this figure, the boundary between the accreting objects and chromospherically active stars, as defined by Frasca et al. (2015) with the same criteria for the members of the Gamma Vel cluster and Cha I SFR, is also indicated. All Class III stars lie below the aforementioned boundary and all candidate accretors (half-filled symbols) are located above it, while the other Class II sources are scattered around, and mostly below, this dividing line. In particular, 17 Class II sources are located below the dividing line. However, this border cannot be considered a knife edge that separates accretors from chromospheric sources; therefore only the objects lying well below it are noteworthy. For instance, if we select only the YSOs with 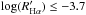 , where most of the Class III sources lie, we end up with only eight Class II sources, three of which (Lup 607, MY Lup, and SSTc2dJ160830.7-382827) are those considered “weak accretors” by Alcalá et al. (2017). The other five objects, namely SSTc2dJ160000.6-422158, SSTc2dJ155925.2-423507, Sz 95, SSTc2dJ161029.6-392215, and SSTc2dJ160703.9-391112 have rather low accretion rates according to Alcalá et al. (2017). The low Hα flux could indicate that these objects still have rather dense dusty disks that give rise to the IR excess, but these objects have low or moderate accretion rates for which the Hα fluxes are comparable with those of chromospheric sources.
, where most of the Class III sources lie, we end up with only eight Class II sources, three of which (Lup 607, MY Lup, and SSTc2dJ160830.7-382827) are those considered “weak accretors” by Alcalá et al. (2017). The other five objects, namely SSTc2dJ160000.6-422158, SSTc2dJ155925.2-423507, Sz 95, SSTc2dJ161029.6-392215, and SSTc2dJ160703.9-391112 have rather low accretion rates according to Alcalá et al. (2017). The low Hα flux could indicate that these objects still have rather dense dusty disks that give rise to the IR excess, but these objects have low or moderate accretion rates for which the Hα fluxes are comparable with those of chromospheric sources.
The presence above the dividing line of some Class II object with a substantial accretion rate (Alcalá et al. 2017) and not satisfying the White & Basri criterion shows that the latter is not 100% reliable in selecting accretors.
The objects with transitional disks (TD), shown as green open diamonds in Fig. 10, are spread all over the diagram and no clear behavior appears, in agreement with the finding by Alcalá et al. (2017) for the mass accretion rate.
The Hα and Ca ii IRT fluxes are well correlated, as apparent in Fig. 11 and suggested by the high value of Spearman’s rank correlation coefficients, which range from ρ = 0.80 to ρ = 0.83 with a significance σ in the range 10-22–10-19 (Press et al. 1992) for the three Ca ii lines. Least-squares regressions provide the following relations: 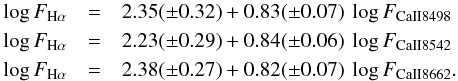 (2)It is worth noting that most of the sources display Hα fluxes in excess with respect to the mean flux-flux relations found by Stelzer et al. (2013) for Class III objects in Lupus, TWA, and σ Ori SFRs. This is particularly evident for the candidate accretors (half-filled symbols) and suggests that the accretion produces a larger Hα luminosity, compared to Ca ii IRT lines, than that originating from chromospheres. This trend can be explained by the fact that strong accretors generally also have outflows or stronger winds, which contribute to the Hα emission but do not significantly affect Ca ii lines.
(2)It is worth noting that most of the sources display Hα fluxes in excess with respect to the mean flux-flux relations found by Stelzer et al. (2013) for Class III objects in Lupus, TWA, and σ Ori SFRs. This is particularly evident for the candidate accretors (half-filled symbols) and suggests that the accretion produces a larger Hα luminosity, compared to Ca ii IRT lines, than that originating from chromospheres. This trend can be explained by the fact that strong accretors generally also have outflows or stronger winds, which contribute to the Hα emission but do not significantly affect Ca ii lines.
Hα, Hβ, Ca ii, and Na i D1,2 fluxes.
 |
Fig. 12 Flux-flux relationship between Hα and Ca ii K line (λ 3934 Å). The meaning of the symbols and lines is as in Fig. 10. |
A similar behavior is found when plotting the Hα versus the Ca ii K flux, as displayed in Fig. 12. These data can be fitted by the following linear relation: 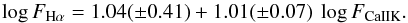 (3)The Hα and Na i D1,2 fluxes display a correlation (ρ = 0.81, σ = 7 × 10-15), as shown in Fig. 13. We remark that FNaID is the sum of the fluxes in the two sodium D lines. A least-squares regression provides the following relation:
(3)The Hα and Na i D1,2 fluxes display a correlation (ρ = 0.81, σ = 7 × 10-15), as shown in Fig. 13. We remark that FNaID is the sum of the fluxes in the two sodium D lines. A least-squares regression provides the following relation: 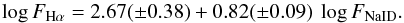 (4)We also applied the subtraction method to the strongest emission lines in the NIR spectra that are not severely affected by telluric absorption, namely the He i λ10830 Å, Paschen (Paγ and Paβ), and Brackett (Brγ) lines. The He i λ10830 Å profile often displays excess absorption components that are related to stellar and/or disk winds (e.g., Kurosawa et al. 2011). Therefore, in these cases the spectral subtraction gives rise to extra absorption. We have, therefore, discarded this line, whose study is deferred to a subsequent work.
(4)We also applied the subtraction method to the strongest emission lines in the NIR spectra that are not severely affected by telluric absorption, namely the He i λ10830 Å, Paschen (Paγ and Paβ), and Brackett (Brγ) lines. The He i λ10830 Å profile often displays excess absorption components that are related to stellar and/or disk winds (e.g., Kurosawa et al. 2011). Therefore, in these cases the spectral subtraction gives rise to extra absorption. We have, therefore, discarded this line, whose study is deferred to a subsequent work.
The fluxes of the three NIR lines, namely the Paschen β and γ lines and the Brackett γ line, were measured for most of the targets (Table 3). The fluxes of these lines are also well correlated with the Hα flux, as shown in Fig. 14. Least-squares regressions provide the following relations: 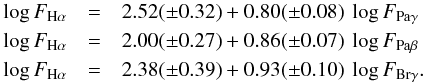 (5)
(5)
4.4. Line fluxes and accretion
Line fluxes are also very useful for evaluating the mass accretion rate and for comparing it with the rate derived from primary indicators, such as the Balmer continuum excess. Alcalá et al. (2017) calculated the accretion luminosity, Lacc, by modeling the observed flux-calibrated spectra with the sum of a nonaccreting (Class III) template and the emission from a slab of hydrogen, which accounts for Lacc. The only parameters needed to convert the flux at Earth into luminosity are the distance to the YSO and the extinction.
Mendigutía et al. (2015) have suggest that the relations between accretion and line luminosity, Lacc−Lline, may be the result of the Lacc−L∗ and Lline−L∗ correlations. Indeed, both Lacc and Lline are obtained adopting the same distance and extinction. Therefore, in their hypothesis, the observed trends may be a calibration effect rather than physical correlations.
In the present work we calculated the line fluxes per unit surface based on the continuum fluxes of the model spectra at the Teff and log g of the target. Thus, neither the distance nor the extinction enter in the determination of Fline.
We show in Fig. 15 that line fluxes are highly correlated with the accretion luminosity reported by Alcalá et al. (2017), as also witnessed by the rank-correlation coefficients ranging from 0.59 to 0.80 with significances always smaller than 10-6. This excludes a calibration effect and strengthens the validity of the emission lines as accretion diagnostics.
Paγ, Paβ, and Brγ fluxes.
4.5. Flux ratios
The ratio of fluxes in two Ca ii-IRT lines, FCaII8542/FCaII8498, is sensitive to the conditions of the emitting plasma, particularly to its optical depth. It was shown that for optically thick sources, such as dense chromospheric solar or stellar plages, the ratio is typically in the range 1–2; optically thin emission sources, such as solar prominences seen off-limb, instead have high values of this ratio, FCaII8542/FCaII8498 ≃ 4–9 (see, e.g., Herbig & Soderblom 1980; Landman 1980, and references therein). As apparent in Fig. 16, the values of this flux ratio are low for all Lupus members in our sample, both Class II and III. This suggests that the bulk of emission originates in optically thick regions, either chromospheric plages or the impact regions of accretion flows near the YSOs surface, as already suggested, e.g., by Herbig & Soderblom (1980) and Alcalá et al. (2014).
 |
Fig. 13 Flux-flux relationship between Hα and Na i D1+D2. The meaning of the symbols is as in Fig. 10. The full red line is the least-squares regression. Leftward arrows indicate upper limits on Na i fluxes. |
Another indicator of the physical conditions of the emitting matter is the Balmer decrement, which is here defined as the ratio of the Hα and Hβ fluxes. We calculated the Hβ flux at the stellar surface in the same way as the Hα flux. The Balmer decrement is shown in Fig. 17. All Class III sources have low values of FHα/FHβ, which range from about 1.5 to 3. These values are, on average, slightly higher than those typical of solar plages or pre-flare active regions (1–2), but significantly lower than in optically thin regions such as solar prominences observed off limb (e.g., Tandberg-Hanssen 1967; Landman & Mongillo 1979). This behavior was already observed in stars with a very high chromospheric activity level and explained as the result of different physical conditions in the chromospheres or a combination of plage-like and prominence-like regions in the observed flux (e.g., Hall & Ramsey 1992; Chester et al. 1994; Stelzer et al. 2013).
 |
Fig. 14 Flux-flux relations between Hα and Paγ, Paβ, and Brγ (from the left to the right, respectively). The meaning of the symbols is as in Fig. 10. The full red lines are the least-squares regressions, whose coefficients are reported in Eq. (5). Downward and leftward arrows indicate upper limits. The value of the rank-correlation coefficient ρ is also reported in each box. |
 |
Fig. 15 Line fluxes per unit surface as a function of the accretion luminosity. The meaning of the symbols is as in Fig. 10. The value of the rank-correlation coefficient ρ is also reported in each box. The subluminous objects were excluded because Lacc is underestimated (Alcalá et al. 2014, 2017), while the surface fluxes are not affected. Downward arrows indicate upper limits. |
Several accretors share the same locus of the Class III sources in this diagram, but some others (about one third) display very high values of the Balmer decrement, which indicates a prevalence of optically thin emission in their Balmer lines, similar to results from other studies of accretors (e.g., Whelan et al. 2014; Frasca et al. 2015; Antoniucci et al. 2017).
This suggests that Ca ii and Balmer lines carry information about different effects/regions of the accretion process, the former mainly originating in optically thick regions, e.g., the impact shocks produced by the accretion flows near the stellar photosphere. The Balmer lines can instead be formed in different parts of the accretion funnels with a large range of optical depth.
The subluminous YSOs, with the exception of SSTc2dJ160703.9-391112, Sz 106, and Sz 102, display high values of the Balmer decrement. This can be understood if we assume that an edge-on disk is the cause of the underluminosity. In this framework, the densest, and thus optically thickest, regions of the accretion flows are suppressed by the optically thick edge-on disk. Moreover, Antoniucci et al. (2017) report that, in most subluminous objects, the whole Balmer series decrement shows a common shape (type 1 in their classification) that is compatible with an edge-on geometry. The rather low values of Balmer decrement for SSTc2dJ160703.9-391112, Sz 106, and Sz 102 may be the result of the geometry of the star/disk system and/or of the strong mass accretion rate, which gives rise to dense flows at rather large distances from the central star.
5. Summary and conclusions
We have presented the results of the analysis of VLT/X-shooter spectra of 102 YSO candidates, mostly of infrared Class II, in the Lupus star forming region. The application of the code ROTFIT to specific spectral regions at optical and near-infrared wavelengths has allowed us to measure the effective temperature (Teff), surface gravity (log g), radial velocity (RV), and projected rotational velocity (vsini) with median errors of σTeff = 70 K, σlog g = 0.21 dex, σRV = 2.3 km s-1, and σvsini = 4 km s-1, respectively. By means of Monte Carlo simulations, we estimated the minimum detectable vsini as 8 km s-1 with the 0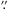 9 VIS slit and 6 km s-1 with the 0
9 VIS slit and 6 km s-1 with the 0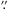 4 VIS slit, respectively. The comparison with the effective temperatures inferred from the spectral classification performed on the same spectra by Manara et al. (2013) and Alcalá et al. (2014, 2017) and with literature data stemming from low-resolution spectroscopy indicates an external accuracy of about 100 K. A similar statistical evaluation cannot be performed for the accuracy of log g and vsini because of the very few values of these parameters available in the literature, which are, however, in good agreement with our determinations. We also derived the veiling at different wavelengths and confirm previous results that the strongest accretors possess the highest veiling values.
4 VIS slit, respectively. The comparison with the effective temperatures inferred from the spectral classification performed on the same spectra by Manara et al. (2013) and Alcalá et al. (2014, 2017) and with literature data stemming from low-resolution spectroscopy indicates an external accuracy of about 100 K. A similar statistical evaluation cannot be performed for the accuracy of log g and vsini because of the very few values of these parameters available in the literature, which are, however, in good agreement with our determinations. We also derived the veiling at different wavelengths and confirm previous results that the strongest accretors possess the highest veiling values.
 |
Fig. 16 Flux ratio FCaII8542/FCaII8498 vs. FCaII8498. The range of values typical for solar plages and prominences are also shown by the shaded and hatched areas, respectively. Data for subluminous YSOs are enclosed into open violet squares. |
 |
Fig. 17 Balmer decrement (FHα/FHβ) vs. FHα. The range of values typical for solar plages and prominences are also shown by the shaded and hatched areas, respectively. Data for subluminous YSOs are enclosed in open violet squares. |
We have shown that 13 candidate members of the Lupus SFR must be definitely considered nonmembers on the basis of their discrepant RV with respect to the Lupus SFR and/or the very low log g values, which suggest that at least 11 of them are background giants in the RGB or AGB phase. Two of these objects turned out to be lithium-rich giants.
Thanks to the subtraction of inactive template spectra, we measured the line fluxes corrected for the contribution of the photospheric absorption, even in the objects with the weakest chromospheric or accretion emission. We found that all the Class III sources lie, as expected, in the locus of the Teff-FHα diagram occupied by the objects where chromospheric emission dominates over accretion as defined by Frasca et al. (2015). The Class II sources are mostly above the boundary between chromospheres and accretion, but some of them are also in the domain of the chromospheric sources. However, all the objects fulfilling the White & Basri (2003) criterion, based on the 10% width and EW of the Hα emission line, lie, correctly, above the aforementioned boundary, i.e., in the domain of accretors according to Frasca et al. (2015). We do not see any particular trend for the YSOs with transitional disks in this diagram. They display both low and high fluxes similar to the behavior of their mass accretion rate shown by Alcalá et al. (2017).
The strong correlation between our line fluxes per unit surface and the accretion luminosity (Lacc) derived by Alcalá et al. (2017) from the Balmer continuum excess has allowed us to confirm the validity of emission lines as accretion diagnostics and to exclude that the relations between Lacc and line luminosities are only the result of calibration effects.
We also investigated the relations between the Hα flux and fluxes in different emission lines (Ca ii IRT, Ca ii K, Na i D, Paγ, Paβ, and Brγ). With the exception of the Class III sources and some of the weak accretors, all the objects display an Hα flux in excess to what it is expected from the relations found by Stelzer et al. (2013) for Class III sources. This behavior is likely the result of different physical conditions in the emitting regions of the accretors with respect to chromospheric emitters, which also seem to affect the flux ratios. The latter were calculated for two Ca ii-IRT lines, FCaII8542/FCaII8498, and for the first two members of the Balmer series, FHα/FHβ, i.e., the Balmer decrement. We found that the Ca ii-IRT flux ratio always takes low values (FCaII8542/FCaII8498< 2) that indicate an optically thick emission source. This source can be identified with the accretion shock near the stellar photosphere. The Balmer decrement takes instead, for several accretors, high values that are typical of optically thin emission, suggesting that the Balmer emission originates in different parts of the accretion funnels with a smaller optical depth.
The rotational broadening kernel (see, e.g., Gray 2005) assumes a linear limb-darkened star, with the limb-darkening coefficients from Claret et al. (2012).
The final value of vsini, which is reported in Table 1, is that derived from the redder of the two spectral regions or the weighted average of the values derived in the two regions, at 9700 Å and 6200 Å, for the stars hotter than about 3500 K.
Acknowledgments
We are very grateful to the referee, Fernando Comerón, for his useful comments and suggestions. We thank the ESO staff, in particular Markus Wittkowski and Giacomo Beccari, for their excellent support during phase-2 proposal preparation, and the Paranal staff for their support during the observations. We thank G. Cupani, V. D’Odorico, P. Goldoni, and A. Modigliani for their help with the X-shooter pipeline. Financial support from INAF is also acknowledged. CMF acknowledges an ESA Research Fellowship funding. This research made use of the SIMBAD database, operated at the CDS (Strasbourg, France).
References
- Alcalá, J. M., Spezzi, L., Frasca, A., et al. 2006, A&A, 453, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Stelzer, B., Covino, E., et al. 2011a, Astron. Nachr., 332, 242 [NASA ADS] [CrossRef] [Google Scholar]
- Alcalá, J. M., Biazzo, K., Covino, E., Frasca, A., & Bedin, L. R. 2011b, A&A, 531, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Natta, A., Manara, C. F., et al. 2014, A&A, 561, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alcalá, J. M., Manara, C. F., Natta, A., et al. 2017, A&A, 600, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allard, F., Homeier, D., & Freytag, B. 2012, ASP Conf. Ser., 448, 91 [Google Scholar]
- Antoniucci, S., Nisini, B., Giannini, T., et al. 2017, A&A, 599, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacciotti, F., Whelan, E. T., Alcalá, J. M., et al. 2011, ApJ, 737, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Baraffe, I., Homeier, D., Allard, F., & Chabrier, G. 2015, A&A, 577, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V. 2009, in Cosmic Magnetic Fields: From Planets to Stars and Galaxies, eds. K. G. Strassmeier, A. G. Kosovichev, & J. E. Beckman, IAU Symp., 259, 323 [Google Scholar]
- Bevington, P. 1969, in Data Reduction and Error Analysis for the Physical Sciences (New York: Mc Graw-Hill), 237 [Google Scholar]
- Biazzo, K., Frasca, A., Alcalá, J. M., et al. 2017, A&A, submitted [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Bustamante, I., Merín, B., Ribas, Á., et al. 2015, A&A, 578, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chester, M. M., Hall, J. C., & Buzasi, D. 1994, in Eigth Cambridge Workshop on Cool Stars Slettar Systems and the Sun, ed. J.-P. Caillault, ASP Conf. Ser., 64, 1994 [Google Scholar]
- Calvet, N., & Gullbring, E. 1998, ApJ, 509, 802 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Hartmann, L., Kenyon, S. J., & Whitney, B. A. 1994, ApJ, 434, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Calvet, N., Muzerolle, J., Briceno, C., et al. 2004, AJ, 128, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- Cameron, A. G. W., & Fowler, W. A. 1971, ApJ, 164, 111 [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Casey, A. R., Ruchti, G., Masseron, T., et al. 2016, MNRAS, 461, 3336 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, L14 [Google Scholar]
- Comerón, F. 2008 in Handbook of Star Forming Regions, Vol. II: The Southern Sky ASP Monograph Publications (Bo Reipurth), 5, 295 [Google Scholar]
- Comerón, F., Spezzi, L., & López Martí, B. 2009, A&A, 500, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, F., Spezzi, L., López Martí, B., & Merín, B. 2013, A&A, 554, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Costigan, G., Scholz, A., Stelzer, B., et al. 2012, MNRAS, 427, 1344 [NASA ADS] [CrossRef] [Google Scholar]
- Dubath, P., Reipurth, B., & Mayor, M. 1996, A&A, 308, 107 [NASA ADS] [Google Scholar]
- Evans, N. J. II, Dunham, M. M., Jörgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Facchini, S., Manara, C. F., Schneider, P. C., et al. 2016, A&A, 596, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feigelson, E. D., & Montmerle, T. 1999, ARA&A, 37, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, W., Edwards, S., Hillenbrand, L., & Kwan, J. 2011, ApJ, 730, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
- Frasca, A., Guillout, P., Marilli, E., et al. 2006, A&A, 454, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., Lanzafame, A. C., et al. 2015, A&A, 575, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Molenda-Żakowicz, J., De Cat, P., et al. 2016, A&A, 594, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galli, P. A. B., Bertout, C., Teixeira, R., & Ducouran, C. 2013, A&A, 558, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glebocki, R., & Gnacinski, P. 2005, ESA SP, 560, 571 [NASA ADS] [Google Scholar]
- Gomes da Silva, J., Santos, N. C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D. F. 2005, The Observation and Analysis of Stellar Photospheres, (Cambridge: Cambridge University Press) [Google Scholar]
- Hall, J. C., & Ramsey, L. W. 1992, AJ, 104, 1942 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Kenyon, S. J., Hartmann, L., et al. 1991, ApJ, 382, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Hewett, R., & Calvet, N. 1994, ApJ, 426, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Herczeg, G., & Calvet, N. 2016, ARA&A, 54, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, J. F., & Balbus, S. A. 1991, ApJ, 376, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G. H., & Soderblom, D. R. 1980, ApJ, 242, 628 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2008, ApJ, 681, 594 [NASA ADS] [CrossRef] [Google Scholar]
- Herczeg, G. J., & Hillenbrand, L. A. 2014, ApJ, 786, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Houdebine, E. R., Junghans, K., Heanue, M. C., & Andrews, A. D. 2009, A&A, 503, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S., & Hartmann, L. 1995, ApJ, 101, 117 [Google Scholar]
- Kurosawa, R., Romanova, M. M., & Harries, T. J. 2011, MNRAS, 416, 2623 [NASA ADS] [CrossRef] [Google Scholar]
- Landman, D. A. 1980, ApJ, 237, 988 [NASA ADS] [CrossRef] [Google Scholar]
- Landman, D. A., & Mongillo, M. 1979, ApJ, 230, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 2003,Rep. Progr. Phys., 66, 1651 [Google Scholar]
- Luhman, K. L., Stauffer, J., Muench, A., et al. 2003, ApJ, 593, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Manara, C. F., Testi, L., Rigliaco, E., et al. 2013, A&A, 551, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Arnáiz, R., López-Santiago, J., Crespo-Chacón, I., & Montes, D. 2011, MNRAS, 414, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Mendigutía, I., Oudmaijer, R. D., Rigliaco, E., et al. 2015, MNRAS, 452, 2837 [NASA ADS] [CrossRef] [Google Scholar]
- Merín, B., Jørgensen, J., Spezzi, L., et al. 2008, ApJS, 177, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Modigliani, A., Goldoni, P., Royer, F., et al. 2010, in Observatory Operations: Strategies, Processes, and Systems III, eds. D. R. Silva, A. B. Peck, & B. T. Soifer, SPIE, 7737 [Google Scholar]
- Mohanty, S., Jayawardhana, R., & Basri, G. 2005,ApJ, 626, 498 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, D., de Castro, E., Fernández-Figueroa, M. J., & Cornide, M. 1995, A&AS, 114, 287 [NASA ADS] [Google Scholar]
- Montes, D., López-Santiago, J., Fernández-Figueroa, M. J., & Gálvez, M. C. 2001, A&A, 379, 976 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzerolle, J., Hartmann, L., & Calvet, N. 1998,AJ, 116, 2965 [NASA ADS] [CrossRef] [Google Scholar]
- Muzerolle, J., Hillenbrand, L., Calvet, N., Briceño, C., & Hartmann, L. 2003,ApJ, 592, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Muzic, K., Scholz, A., Geers, V. C., Jayawardhana, R., & López Martí, B. 2014, ApJ, 785, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., & Giovanardi, C. 1990, ApJ, 356, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Natta, A., Testi, L., Alcalá, J. M., et al. 2014, A&A, 569, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pecaut, M. J., & Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran, 2d edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Rigliaco, E., Natta, A., Testi, L., et al. 2012, A&A, 548, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siess, L., Dufour, E., & Forestini, M. 2000, A&A, 385, 593 [NASA ADS] [Google Scholar]
- Smiljanic, R., Franciosini, E., Randich, S., et al. 2016, A&A, 591, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stelzer, B., Frasca, A., Alcalá, et al. 2013, A&A, 558, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Strassmeier, K. G., Washuettl, A., Granzer, Th., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tandberg-Hanssen, E. 1967, Solar activity (Waltham, Mass.: Blaisdell) [Google Scholar]
- Torres, C. A. O., Quast, G. R., da Silva, L., et al. 2006, A&A, 460, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vernet, J., Dekker, H., D’Odorico, S., Kaper, L., et al. 2011, A&A, 536, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Whelan, E. T., Alcalá, J. M., Bacciotti, F., et al. 2014, A&A, 570, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- White, R. J., & Basri, G. 2003, ApJ, 582, 1109 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Resolution of X-shooter
 |
Fig. A.1 Resolution of X-shooter VIS spectra with the 0 |
To measure the resolution of X-shooter in the VIS arm, we reduced some calibration-lamp spectra following the same steps as for the science frames. We extracted the spectra from the prereduced images, summing up the same columns of the detector where the stellar spectra fall in typical seeing conditions. We chose several tens of unblended emission lines that were fitted with Gaussians to obtain the line center λi and the full width at half maximum (FWHM), Δλi. The resolution Ri = λi/ Δλi is plotted as a function of wavelength in Fig. A.1 for VIS spectra acquired with the 0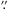 9 and 0
9 and 0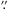 4 slits.
4 slits.
The resolution with the 0 9 slit, R ≃ 8800, is rather constant with λ and decreases only slightly toward the edges of the spectrum. Moreover, it is basically unchanged between 2011 and 2015. For our analysis we adopted the value R = 8400, which is that of the region at λ ≃ 9700 Å used for the vsini determination.
9 slit, R ≃ 8800, is rather constant with λ and decreases only slightly toward the edges of the spectrum. Moreover, it is basically unchanged between 2011 and 2015. For our analysis we adopted the value R = 8400, which is that of the region at λ ≃ 9700 Å used for the vsini determination.
The resolution with the 0 4 slit displays instead a higher variation with λ ranging from R ≃ 18 500 at the spectrum center to R ≃ 16 000 near the edges. We adopted the value R = 17 000 in our analysis.
4 slit displays instead a higher variation with λ ranging from R ≃ 18 500 at the spectrum center to R ≃ 16 000 near the edges. We adopted the value R = 17 000 in our analysis.
Appendix B: Application of ROTFIT to the X-shooter spectra
The template BT-Settl model spectra were first degraded in resolution to match that of the target spectrum and then resampled on its spectral points. Template and target spectra were then normalized to the local continuum or pseudo-continuum, paying attention to the spectral regions containing molecular bands, where the continuum level at wavelengths shorter than the band head was used as reference.
The code calculates the χ2 of the difference between observed and template spectra, where the rotational broadening was considered by convolving template spectra with a rotational profile2 of increasing vsini from 0 to 150 km s-1 in steps of 1 km s-1.
 |
Fig. B.1 Continuum-normalized VIS X-shooter spectrum of Sz 68 in the two regions selected for the measurement of vsini (black full lines) along with the best fitting template (red dotted lines). The insets in each panel show the cross-correlation function (left boxes) with the Gaussian fit overplotted in red and the χ2 as a function of vsini (right boxes). |
Spectral regions analyzed with ROTFIT.
We selected a few spectral regions that are particularly suitable for the determination of one or more stellar parameters (Table B.1). One of the main requirements is that these regions should be free, as much as possible, of strong emission lines produced by accretion or chromospheric activity. We mainly used the VIS spectra, but some portions of the UVB ones were used as well for the objects with spectra well exposed; these are mostly K-type stars and are all earlier than M4. In each spectral interval, the sensitivity to a given parameter normally changes with the characteristics of the target and mainly depends on the SpT (i.e. Teff). Therefore, we chose spectral regions that are usable in the largest possible range of SpT.
Appendix B.1: v sin i
The best intervals to perform an accurate determination of vsini with ROTFIT are those devoid of very broad lines and strong molecular bands, but encompassing several strong absorption lines. A suitable region for the GK-type stars ranges from 6050 Å to 6270 Å, where some Ca i lines and a number of unblended lines, mostly of iron-group elements, are present. These lines are also good diagnostics of temperature and gravity. However, a TiO molecular band starts to be visible for Teff≤ 4000 K and strongly affects the spectra of stars cooler than about 3500 K; for this reason we did not use that part of the spectrum for the determination of vsini for cool objects, but it is still useful to measure Teff in these cases. Another wavelength range suitable to measure vsini with X-shooter VIS spectra is between 9600 and 9800 Å3. It includes several sharp absorption lines of Ti i and Cr i that are strong enough down to Teff ≃ 2900 K. Moreover, the intensity of these lines changes mildly with the SpT, thus they can also be used as temperature indicators, although their sensitivity to Teff is not as high as that of other lines or molecular bands.
The results of the ROTFIT analysis for a rather rapid rotator (Sz 68) are illustrated in Fig. B.1. The upper and lower panels show the observed spectrum around 9700 Å and 6150 Å, respectively. The best fitting template, i.e., the synthetic BT-Settl spectrum rotationally broadened, resampled, and wavelength-shifted on the target spectrum that produces the minimum χ2, is overplotted with a red dashed line in both panels. The CCF and χ2 as a function of vsini are also shown in the insets.
Appendix B.2: Teff log g
For the determination of the atmospheric parameters, the vsini was kept fixed to the value derived through the analysis of the 9700-Å and 6150-Å spectral regions. To determine the gravity we selected two spectral regions containing the Na i doublet at λ ≈ 8190 Å and K i doublet at λ ≈ 7660–7700 Å, whose wings are very sensitive to the electronic pressure and therefore to log g. In addition, we analyzed the spectral segment from 7020 to 7150 Å, which contains three TiO molecular bands that are strongly sensitive to Teff for cool stars and substellar objects.
Figure B.2 shows an example of the results of the ROTFIT analysis for an M star (Sz 117). The left panels show the observed spectrum and the best fitting template, similar to Fig. B.1. The contour maps of the χ2 for each spectral region are shown in the right panels, where the 1σ confidence level is indicated with a thick red line. For a better determination of the Teff and log g values we performed a quadratic interpolation onto a grid finer than that of the models with 10-K and 0.1-dex steps for Teff and log g, respectively.
As mentioned above, for the hotter and best exposed sources we also analyzed three spectral segments in the UVB spectra that cover the 5300–5500 Å, 5100–5250 Å, and 4400–4600 Å ranges. The spectral features they contain carry information about Teff and log g and allow us to evaluate the veiling at these shorter wavelengths. As an example, we show the fit of the UVB spectrum of Sz 68 (K2) in Fig B.3. However, given the lower resolution of the UVB spectra, we did not use the latter to measure vsini and RV.
 |
Fig. B.2 Left panels: continuum-normalized VIS X-shooter spectrum of Sz 117 in the five regions analyzed with ROTFIT (black full lines) with the best fitting template overplotted (red dotted lines). Right panels: χ2 contour maps in the Teff–log g plane. In each panel, the blue dot indicates the best values of Teff and log g, while the 1σ confidence level is denoted by the thick red contour. The errorbars on Teff and log g are also indicated. |
 |
Fig. B.3 UVB X-shooter spectrum of Sz 68 (black lines) in the three regions that were analyzed with ROTFIT. In each box, the best fitting template is superimposed with dotted red lines. |
The adopted values of log g and Teff are the weighted averages of the results for each spectral segment according to Table B.1. These values are reported in Table 1 along with their errors and the veiling at five wavelengths.
For SSTc2dJ160034.4-422540, we failed to derive reliable atmospheric parameters because of the very low S/N of its spectrum. The VIS spectrum of this object does not display emission lines, which makes it unlikely to be a YSO. The reddest part of the VIS spectrum instead presents a number of molecular absorption bands, which are indicative of a very low Teff. We thus performed a customized analysis of the whole spectral range from 8500 to 11 000 Å, which provided us with an estimate for Teff and a value of RV. The spectral features present in this region do not provide solid constraints for log g, although this object likely has a low gravity. More details and a plot of its VIS spectrum can be found in Appendix D.
Appendix B.3: Veiling
The spectra of Class II sources, which typically undergo mass accretion from the circumstellar disk, can be affected by a different amount of veiling; this veiling normally decreases at longer wavelengths, but it can still be noticeable in the IYJ bands (e.g., Fischer et al. 2011). For this reason, we also left the veiling free to vary. This was accomplished by adding to the templates, for each iteration, a wavelength-independent veiling in each spectral segment. This assumption is justified by the limited spectral ranges that we analyzed, which are, at most, 200 Å wide. Therefore, the “veiled” template is given by  (B.1)where Fλ and FC represent the line and continuum fluxes, respectively, and the veiling r was let free to vary from 0.0 to 5.0 in 0.1 steps.
(B.1)where Fλ and FC represent the line and continuum fluxes, respectively, and the veiling r was let free to vary from 0.0 to 5.0 in 0.1 steps.
In cases of highly veiled spectra we often noticed the enhancement of r with decreasing wavelength (see Fig. B.4 for an example). This behavior is normally observed in strongly accreting objects (e.g., Hartigan et al. 1991; Fischer et al. 2011) and is interpreted as optically thick emission from the heated photosphere below the accretion shock (Calvet & Gullbring 1998). The decrease of the veiling at longer wavelengths is explained by the slow decline of the continuum accretion flux, which can be be approximated with a blackbody of T ~ 10 000 K, and the steep rise of the photospheric flux from visible to near-IR wavelengths for late-type stars.
 |
Fig. B.4 χ2 values as a function of veiling for Sz 88A in different spectral regions. We note the strong increase of the veiling at the shorter wavelengths. |
Appendix C: Monte Carlo simulations for v sin i
We run a Monte Carlo simulation to evaluate the resolution in vsini that can be reached with these data and our analysis code. To this aim, we built synthetic spectra at the same resolution and sampling as the X-shooter ones. We broadened these spectra from 0 to 24 km s-1 in steps of 1 or 2 km s-1 and made 200 simulations per each vsini, adding a random noise corresponding to signal-to-noise ratios S/N = 20, 50, and 100. These simulations were made with BT-Settl spectra corresponding to Teff = 2700, 3000, 3700, and 4800 K. We applied the code ROTFIT to each simulated spectrum, analogously to what we did with the target spectra, to determine the vsini from the spectral region centered at 9700 Å. As apparent in Fig. C.1, where only some examples are shown for the slit width 0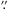 9 (R ≃ 8400), we do not resolve vsini values lower than 8 km s-1. Thereafter, the measured vsini starts to grow with the simulated vsini and smoothly follows the one-to-one line. Therefore, we adopted 8 km s-1 as the upper limit in this configuration. The vsini errors measured with ROTFIT on the target spectra were in most cases comparable with those inferred by the aforementioned Monte Carlo simulations, while for a few spectra they were larger. In these cases we adopted the error of the simulation closest in vsini, Teff and S/N to the target spectrum.
9 (R ≃ 8400), we do not resolve vsini values lower than 8 km s-1. Thereafter, the measured vsini starts to grow with the simulated vsini and smoothly follows the one-to-one line. Therefore, we adopted 8 km s-1 as the upper limit in this configuration. The vsini errors measured with ROTFIT on the target spectra were in most cases comparable with those inferred by the aforementioned Monte Carlo simulations, while for a few spectra they were larger. In these cases we adopted the error of the simulation closest in vsini, Teff and S/N to the target spectrum.
We also carried out some tests for the high-resolution X-shooter spectra (slit width 0 4, R ≃ 17 000). In this case we obtained lower vsini errors and we estimated an upper limit of 6 km s-1 (Fig. C.2).
4, R ≃ 17 000). In this case we obtained lower vsini errors and we estimated an upper limit of 6 km s-1 (Fig. C.2).
 |
Fig. C.1 Results of the Monte Carlo simulations on vsini made with synthetic spectra at three Teff for S/N = 50 and R = 8400 (slit width 0 |
 |
Fig. C.2 Results of the Monte Carlo simulations on vsini for S/N = 50 and R = 17 000 (slit width 0 |
Appendix D: Notes on individual objects
Appendix D.1: SSTc2d J160034.4-422540
SSTc2d J160034.4-422540 is a faint and very red (and/or reddened) source. The VIS spectrum does not show emission lines and has a very low signal in the spectral regions analyzed with ROTFIT, which makes the results of this code unreliable for this object. However, the reddest part of the VIS spectrum has a S/N sufficient to display the shape of the continuum and the molecular bands. We thus analyzed the flux-calibrated spectrum ranging from 8500 to 11 000 Å, with a method similar to that adopted by Alcalá et al. (2006). In particular, we scaled to unity both the target and template spectra at 9170 Å, which is the wavelength of the head of a strong TiO molecular band. We artificially reddened the template spectra with the extinction law Aλ/AV of Cardelli et al. (1989), adopting the average interstellar value for total-to-selective extinction, RV = 3.1. The extinction in the V band, AV, was let free to vary. We kept the parameters of the model spectrum and the AV value that minimize the χ2 of the fit (see Fig. D.1). As the shape of the TiO bands is not very sensitive to the gravity, log g is not well constrained by this fit, however, the atmospheric parameters found with this method (Teff = 2000 K, log g = 0) suggest a very cool giant star.
 |
Fig. D.1 VIS X-shooter spectrum of SSTc2dJ160034.4-422540 scaled to the level of the TiO molecular-band head at 9170 Å (black full line) along with the best fitting template with a Teff = 2000 K and log g = 0 (red line). An extinction AV = 7.5 mag minimizes the χ2. |
Appendix D.2: SSTc2d J160708.6-391408
This source is one of the brightest YSOs with a flat SED in Lupus (Merín et al. 2008; Evans et al. 2009). Its spectrum includes many permitted and forbidden emission lines, but the five VIS spectral segments listed in Table B.1 are free from emission lines and have a S/N sufficient to be analyzed with ROTFIT.
We found Teff = 3474 ± 206 K, which corresponds to an M2 spectral type according to the Pecaut & Mamajek (2013) calibrations. Alcalá et al. (2017) found a later spectral type (M5) but their results can also be consistent with an M3 type, for which the uncertainty results from the strong accretion and veiling of the spectrum. Our Teff determination is more consistent with the M1.75 spectral classification of Muzic et al. (2014). We also estimated Teff and extinction with the same method used for SSTc2dJ160034.4-422540. The results are shown in Fig. D.2 where the observed spectrum is best fitted with a template with Teff = 3450 K and an extinction AV = 3.5 mag.
 |
Fig. D.2 VIS X-shooter spectrum of SSTc2dJ160708.6-391408 scaled to unity at 9170 Å (black full line). The best fitting template (Teff = 3450 K) reddened to AV = 3.5 mag is overplotted with a red line. |
We dereddened the flux calibrated spectrum of SSTc2dJ160708.6-391408 (obtained merging the UVB, VIS, and NIR spectra) according to the Cardelli et al. (1989) law. Integrating the flux over all the X-shooter wavelength range and multiplying for 2πd2 (d = 200 pc), we obtain a luminosity L⋆ = 0.032 L⊙. However, it is difficult to distinguish the photospheric flux from that coming from the circumstellar matter in the SEDs of flat sources; therefore, the above measure must be considered as a rough estimate of the stellar luminosity. Nevertheless, this value makes the object rather subluminous in the HR diagram (green filled square in Fig. 6).
Since flat sources are believed to be YSOs still surrounded by an infalling envelope (Calvet et al. 1994), SSTc2d J160708.6-391408 may be in this evolutionary stage in which the energy output from the central star can heat the envelope. Therefore, the radiation emitted by the central object would be partly reprocessed by the envelope, i.e. it will emerge redistributed to longer wavelengths. In these conditions the bolometric luminosity of 0.18 L⊙, as derived by Evans et al. (2009), would be a better estimate of the total energy emitted by the central object. Adopting this value, SSTc2d J160708.6-391408 rises to the position marked by the arrowhead in Fig. 6, in good agreement with the other Lupus members. Moreover, as emphasized by Alcalá et al. (2017), the value of 0.18 L⊙would bring the ratio of accretion to bolometric luminosity in agreement with the YSOs of similar mass.
Appendix D.3: SSTc2dJ160708.6-394723 and SSTc2dJ161045.4-385455
The two nonmembers with lithium, namely SSTc2dJ160708.6-394723 and SSTc2dJ161045.4-385455, are likely lithium-rich giants. The first star has Teff ≃ 4650 K and log g ≃ 2.6 dex that locate it in the RGB region of the log g–Teff diagram close to the red clump locus (Fig. 4). For the second object we measured instead a larger gravity log g ≃ 3.4 ± 0.9 dex, which is more consistent with a subgiant or RG stage, taking into account the large error.
The origin of lithium-rich giants is still debated and different hypotheses have been put forward to explain the high lithium content in their atmospheres. The main scenarios that have been proposed are the regeneration of lithium in later evolutionary stages by the Cameron-Fowler mechanism (Cameron & Fowler 1971), the engulfment of Li-rich substellar companions (e.g., Alcalá et al. 2011b; Casey et al. 2016, and references therein) or inhibition of mixing because of fossil magnetic fields of their Ap-type progenitors (e.g., Smiljanic et al. 2016).
All Tables
All Figures
 |
Fig. 1 Top panel: comparison between the effective temperature determined with ROTFIT and that derived from the MK spectral classification performed for the Lupus members by Manara et al. (2013) and Alcalá et al. (2014, 2017). The continuous line represents the 1:1 relationship. The Teff differences (bottom panel) show a mean value of about −40 K (dashed line) and a standard deviation of about 100 K (dotted lines). |
| In the text | |
 |
Fig. 2 Top panel: comparison between the effective temperature determined with ROTFIT and that derived by Herczeg & Hillenbrand (2014) and Comerón et al. (2013). The solid line represents the 1:1 relationship. The Teff differences (bottom panel) show a mean value of about + 28 K (dashed line) and a standard deviation of about 100 K (dotted lines). |
| In the text | |
 |
Fig. 3 Veiling at 620 nm as a function of the mass accretion rate measured by Alcalá et al. (2017) on the same spectra. |
| In the text | |
 |
Fig. 4 Teff–log g diagram for all the objects for which a log g value was derived with ROTFIT. Gray dots represent Class II sources, red diamonds denote Class III sources, while the nonmembers are indicated by green asterisks. The full blue lines are the PMS isochrones from Baraffe et al. (2015) at 1, 3, and 10 Myr and solar metallicity. The black dashed lines are post-MS isochrones from the PARSEC database (Bressan et al. 2012) for a solar metallicity at 300 Myr and 10 Gyr. The magenta dot-dashed line is the PARSEC isochrone at 10 Gyr and Z = 0.060. |
| In the text | |
 |
Fig. 5 Equivalent width of the Li i λ6708 Å line from Biazzo et al. (2017) vs. radial velocity measured in the present paper. The meaning of the symbols is as in Fig. 4. The average RV of the Lupus members (2.8 km s-1) is indicated with the vertical dashed line, while the dotted lines delimit the 1σ confidence region. The blue and red histograms represent the RV distributions for the on-cloud and off-cloud Lupus stars found by Galli et al. (2013). |
| In the text | |
 |
Fig. 6 Hertzsprung-Russell diagram of the Lupus members. The evolutionary tracks of Baraffe et al. (2015) are shown as solid lines with the labels representing their masses. The isochrones at 1, 3, 10, 30, and 300 Myr by the same authors are shown with dashed lines. Big open circles denote subluminous objects. The green arrowhead indicates the position of the flat source SSTc2dJ160708.6-391408 (green filled square) when assuming the bolometric luminosity of 0.18 L⊙ (Evans et al. 2009). |
| In the text | |
 |
Fig. 7 Example of the spectral subtraction for the Hα line of SSTc2dJ160830.7-382827. The target spectrum normalized to the local continuum is represented by a solid black line, while the best-fitting BT-Settl spectrum is overplotted with a dotted red line. The difference spectrum is shown in the bottom of the panel, where the residual Hα emission is highlighted by the hatched green area. |
| In the text | |
 |
Fig. 8 Example of the spectral subtraction for the Ca ii IRT lines of Sz 103. Observed spectrum and inactive template are traced with a solid black line and dotted red line, respectively. The difference between observed and template spectrum is shown in the bottom of each panel, along with the residual emission in the Ca ii IRT line cores (hatched green areas). |
| In the text | |
 |
Fig. 9 Example of the spectral subtraction for the Na i D1,2 and He i D3 lines of Sz 97. Solid and dotted red lines have the same meaning as in Fig. 7. An offset of 0.5 was applied to both the observed and synthetic spectra for visualization purposes. The hatched green areas in the “difference” spectrum represent the Na i D1,2 excess emissions, while the He i D3 residual emission is filled with violet hatching. |
| In the text | |
 |
Fig. 10 Left panel: Hα flux vs. Teff. Right panel: |
| In the text | |
 |
Fig. 11 Flux-flux relations between Hα and Ca ii IRT lines (λ 8498, λ 8542, and λ 8662 Å, from the left to the right, respectively). The meaning of the symbols is as in Fig. 10. The full red lines are the least-squares regressions, whose coefficients are reported in Eq. (2). The dashed lines represent the best fits of flux-flux relations found by Stelzer et al. (2013) for Class III objects. Downward and leftward arrows indicate upper limits on Hα and Ca ii fluxes, respectively. |
| In the text | |
 |
Fig. 12 Flux-flux relationship between Hα and Ca ii K line (λ 3934 Å). The meaning of the symbols and lines is as in Fig. 10. |
| In the text | |
 |
Fig. 13 Flux-flux relationship between Hα and Na i D1+D2. The meaning of the symbols is as in Fig. 10. The full red line is the least-squares regression. Leftward arrows indicate upper limits on Na i fluxes. |
| In the text | |
 |
Fig. 14 Flux-flux relations between Hα and Paγ, Paβ, and Brγ (from the left to the right, respectively). The meaning of the symbols is as in Fig. 10. The full red lines are the least-squares regressions, whose coefficients are reported in Eq. (5). Downward and leftward arrows indicate upper limits. The value of the rank-correlation coefficient ρ is also reported in each box. |
| In the text | |
 |
Fig. 15 Line fluxes per unit surface as a function of the accretion luminosity. The meaning of the symbols is as in Fig. 10. The value of the rank-correlation coefficient ρ is also reported in each box. The subluminous objects were excluded because Lacc is underestimated (Alcalá et al. 2014, 2017), while the surface fluxes are not affected. Downward arrows indicate upper limits. |
| In the text | |
 |
Fig. 16 Flux ratio FCaII8542/FCaII8498 vs. FCaII8498. The range of values typical for solar plages and prominences are also shown by the shaded and hatched areas, respectively. Data for subluminous YSOs are enclosed into open violet squares. |
| In the text | |
 |
Fig. 17 Balmer decrement (FHα/FHβ) vs. FHα. The range of values typical for solar plages and prominences are also shown by the shaded and hatched areas, respectively. Data for subluminous YSOs are enclosed in open violet squares. |
| In the text | |
 |
Fig. A.1 Resolution of X-shooter VIS spectra with the 0 |
| In the text | |
 |
Fig. B.1 Continuum-normalized VIS X-shooter spectrum of Sz 68 in the two regions selected for the measurement of vsini (black full lines) along with the best fitting template (red dotted lines). The insets in each panel show the cross-correlation function (left boxes) with the Gaussian fit overplotted in red and the χ2 as a function of vsini (right boxes). |
| In the text | |
 |
Fig. B.2 Left panels: continuum-normalized VIS X-shooter spectrum of Sz 117 in the five regions analyzed with ROTFIT (black full lines) with the best fitting template overplotted (red dotted lines). Right panels: χ2 contour maps in the Teff–log g plane. In each panel, the blue dot indicates the best values of Teff and log g, while the 1σ confidence level is denoted by the thick red contour. The errorbars on Teff and log g are also indicated. |
| In the text | |
 |
Fig. B.3 UVB X-shooter spectrum of Sz 68 (black lines) in the three regions that were analyzed with ROTFIT. In each box, the best fitting template is superimposed with dotted red lines. |
| In the text | |
 |
Fig. B.4 χ2 values as a function of veiling for Sz 88A in different spectral regions. We note the strong increase of the veiling at the shorter wavelengths. |
| In the text | |
 |
Fig. C.1 Results of the Monte Carlo simulations on vsini made with synthetic spectra at three Teff for S/N = 50 and R = 8400 (slit width 0 |
| In the text | |
 |
Fig. C.2 Results of the Monte Carlo simulations on vsini for S/N = 50 and R = 17 000 (slit width 0 |
| In the text | |
 |
Fig. D.1 VIS X-shooter spectrum of SSTc2dJ160034.4-422540 scaled to the level of the TiO molecular-band head at 9170 Å (black full line) along with the best fitting template with a Teff = 2000 K and log g = 0 (red line). An extinction AV = 7.5 mag minimizes the χ2. |
| In the text | |
 |
Fig. D.2 VIS X-shooter spectrum of SSTc2dJ160708.6-391408 scaled to unity at 9170 Å (black full line). The best fitting template (Teff = 3450 K) reddened to AV = 3.5 mag is overplotted with a red line. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.