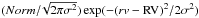| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201628169 | |
| Published online | 17 June 2016 | |
Gaia-ESO Survey: Gas dynamics in the Carina nebula through optical emission lines⋆,⋆⋆
1 INAF–Osservatorio Astronomico di Palermo G.S.Vaiana, Piazza del Parlamento 1, 90134 Palermo, Italy
e-mail: damiani@astropa.inaf.it
2 Dipartimento di Fisica e Chimica, Università di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
3 INAF–Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Firenze, Italy
4 INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
5 Armagh Observatory, College Hill, Armagh BT61 9DG, UK
6 School of Mathematics & Physics, Queen’s University Belfast, Belfast BT61 7NN, UK
7 Centro de Astrobiología (CSIC-INTA), ESAC campus, Camino bajo del castillo s/n, 28 692 Villanueva de la Cañada, Madrid, Spain
8 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
9 Instituto de Astrofísica de Andalucía-CSIC, Apdo. 3004, 18080 Granada, Spain
10 Moscow MV Lomonosov State University, Sternberg Astronomical Institute, 119992 Moscow, Russia
11 INAF–Osservatorio Astrofisico di Catania, via S. Sofia 78, 95123 Catania, Italy
12 Dipartimento di Fisica e Astronomia, Sezione Astrofisica, Università di Catania, via S. Sofia 78, 95123 Catania, Italy
13 INAF–Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
14 ASI Science Data Center, via del Politecnico SNC, 00133 Roma, Italy
15 Instituto de Física y Astronomiía, Universidad de Valparaiíso, Chile
16 European Southern Observatory, Alonso de Cordova 3107 Vitacura, Santiago de Chile, Chile
17 Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
18 Departamento de Ciencias Fisicas, Universidad Andres Bello, Republica 220, Santiago, Chile
19 INAF–Padova Observatory, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
20 Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
21 Departamento de Física, Ingeniería de Sistemas y Teoría de la Señal, Universidad de Alicante, Apdo. 99, 03080 Alicante, Spain
Received: 21 January 2016
Accepted: 1 April 2016
Aims. We present observations from the Gaia-ESO Survey in the lines of Hα, [N II], [S II], and He I of nebular emission in the central part of the Carina nebula.
Methods. We investigate the properties of the two already known kinematic components (approaching and receding), which account for the bulk of emission. Moreover, we investigate the features of the much less known low-intensity high-velocity (absolute RV >50 km s-1) gas emission.
Results. We show that gas giving rise to Hα and He I emission is dynamically well correlated with but not identical to gas seen through forbidden-line emission. Gas temperatures are derived from line-width ratios, and densities from [S II] doublet ratios. The spatial variation of N ionization is also studied, and found to differ between the approaching and receding components. The main result is that the bulk of the emission lines in the central part of Carina arise from several distinct shell-like expanding regions, the most evident found around η Car, the Trumpler 14 core, and the star WR25. These “shells” are non-spherical and show distortions probably caused by collisions with other shells or colder, higher-density gas. Some of them are also partially obscured by foreground dust lanes, while very little dust is found in their interior. Preferential directions, parallel to the dark dust lanes, are found in the shell geometries and physical properties, probably related to strong density gradients in the studied region. We also find evidence that the ionizing flux emerging from η Car and the surrounding Homunculus nebula varies with polar angle. The high-velocity components in the wings of Hα are found to arise from expanding dust reflecting the η Car spectrum.
Key words: ISM: individual objects: Carina nebula / ISM: general / HII regions
Based on observations collected with the FLAMES spectrograph at VLT/UT2 telescope (Paranal Observatory, ESO, Chile), for the Gaia-ESO Large Public Survey (program 188.B-3002).
Full Tables 1–3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/591/A74
© ESO, 2016
1. Introduction
The Carina nebula is one of the largest known star-forming complexes in the Galaxy, and has been extensively studied thanks to its relatively small distance (2.25±0.18 kpc, Davidson & Humphreys 1997; 2.35±0.05 kpc, Smith 2006), and moderate foreground reddening (E(B−V) = 0.36, Hur et al. 2012). A review of its properties is given by Smith & Brooks (2008). Several young clusters are embedded in the Nebula, most notably Trumpler 14 and 16, and Collinder 228, which all together form the Car OB1 association. This is one of the largest OB associations in the Galaxy, with more than 60 stars earlier than B0, and several Wolf-Rayet (WR) stars. The most studied member of Trumpler 16 is the luminous blue variable (LBV) η Car. About one-third of all known O3 stars in the Galaxy, and the first O2 star discovered, are found in Trumpler 14 and 16.
The age of the Carina star-forming region (SFR) and its component clusters has been estimated in the range from 1 to several Myr. Wolk et al. (2011) remarks, however, that no simple age sequence is able to explain the respective properties of clusters Trumpler 14, 15, and 16, so that other parameters come into play to define the properties of these regions. There are also hints of a past supernova explosion in the region (see Smith & Brooks 2008, Townsley et al. 2011). The region is still actively forming stars in its outer parts (Smith et al. 2000, 2004, 2005; Povich et al. 2011), and shows many dense dusty patches (“pillars”), seen against the very bright emission from the H II region. Extinction within the molecular cloud, where Carina star clusters are still partially embedded, spans a wide range (up to AV ~ 15 among X-ray detected 2MASS sources, and perhaps more, Albacete-Colombo et al. 2008), hiding most background stars from optical observations in the central parts of the clusters.
The stellar population in the Carina SFR was recently observed as part of the Gaia-ESO spectroscopic Survey, which will cover more than 105 stars belonging to all components of the Milky Way, including some very young clusters (Gilmore et al. 2012; Randich et al. 2013). More than 1000 low-mass stars and several hundred OB stars have been observed towards Carina, using the ESO VLT/FLAMES multifiber spectrograph (Pasquini et al. 2002). This allows simultaneous observations of ~130 targets (stars and sky positions) at intermediate resolution (R ~ 15 000−20 000, depending on setup) with the Giraffe spectrograph, and 7−8 positions at high resolution with the UVES spectrograph. Several fibers per Observing Block (OB; each OB comprises all spectra recorded simultaneously) were aimed at “empty” sky positions to estimate the sky contribution expected in stellar spectra. Therefore, the Survey data contain a rich dataset of pure sky spectra at positions scattered across the Nebula containing an amount of information on the ionized component of the diffuse medium towards that line of sight, which we study in this work. The spectra of low-mass stars in the field will be studied in a later work (Damiani et al., in prep.).
The diffuse medium in Carina is already known to be complex, and contains a mixture of components across a huge range of temperatures. For example, cold gas was imaged in CO lines by Yonekura et al. (2005); intermediate-temperature gas emitting in the optical lines was studied by Deharveng & Maucherat (1975), Walborn & Hesser (1975), and Meaburn et al. (1984); the whole Nebula was found to be permeated by million-degree hot gas by Seward et al. (1979) and Townsley et al. (2011). Smith & Brooks (2007) made a comparative review of large-scale observations of its diffuse medium.
In this paper, we focus on the analysis of pure sky spectra in the central part of the Carina nebula, obtained by the Gaia-ESO survey. In particular, we focus on the kinematic properties of Hα, [N II], [S II], and He I nebular emission lines. In Sect. 2 we describe the observations, while in Sect. 3 we present our results. In Sect. 4 we discuss the main implications of our work for the dynamics of gas in the Carina nebula, while Sect. 5 summarizes our conclusions.
 |
Fig. 1 DSS1 image of the central part of the Carina nebula, of size 26′ × 26′, corresponding to 17.4 pc per side at the Nebula distance of 2.3 kpc. North is up and east is to the left. Red circles indicate positions of sky fibers, using Giraffe setup HR15N. Orange circles indicate fibers on faint stars, using HR15N. Blue circles are sky fibers, using setup HR14A. Light green circles are UVES sky fibers. Big dark green circles indicate the approximate positions of clusters studied here and the Keyhole nebula. The dark green arrow indicates the star η Car. |
Double-Gaussian fitting results for Hα.
2. Observational data
The spectra used in this work were obtained mostly with the Giraffe HR15N setup (R ~ 19 000), in the wavelength range 6444−6818 Å. Thirteen OBs were executed using this setup in Carina, yielding 185 sky spectra at 137 individual sky positions (35 sky positions were observed more than once). Using Giraffe setup HR14A, 114 sky spectra are also available in the wavelength range 6301−6689 Å (R ~ 18 000), overlapping that of setup HR15N1. Moreover, 15 sky spectra were also obtained with UVES (580 nm setup, R ~ 47 000) in the ranges 4768−5802 Å (lower arm) and 5822−6831 Å (upper arm). The Survey targets are low-mass stars ranging down to magnitude V ~ 18.5: for about half of the 1085 stars observed with setup HR15N, the sky brightness at Hα (as recorded by the 1.2 arcsec Giraffe fibers) is 100−1000 times the stellar continuum, so that high-quality information on the sky emission, at least in the Hα core, was also obtained from the spectra of these faint stars2. In total, we have some information for more than 650 sky positions across the Nebula. All spectra presented here are from internal data release GESiDR4.
Figure 1 shows a DSS image of the Nebula that indicates the sky positions studied here. The bright diffuse emission is bounded towards south by a V-shaped dust obscuration. η Car is the brightest star, a few arcmin east of image center, and the cluster Trumpler 16 is found all around it, projected against the brightest part of the Nebula. The compact, massive cluster Trumpler 14 (Tr 14) is visible to the northwest. Just west of η Car, the obscured region with a peculiar shape is the Keyhole Nebula, already described by John Herschel. As the figure shows, our observations cover widely different regions of the Nebula.
 |
Fig. 2 Example of typical sky spectrum in Carina obtained with the Giraffe HR15N setup. Prominent nebular lines are labeled. |
The HR15N wavelength range contains several important nebular lines: Hα, the neighboring [N II] lines at 6548 and 6584 Å, the He I line at 6678 Å, and the two [S II] lines at 6716 and 6731 Å. The HR14A range contains the same lines except for the [S II] lines. The UVES spectra, in addition to these lines (and many others), also allow the study of Hβ.
3. Results
An example of HR15N sky spectrum is shown in Fig. 2. From a close inspection, it is seen that most line profiles show double peaks, as shown in the examples in Fig. 3. This is not a new discovery since it was already noted by several authors (Deharveng & Maucherat 1975; Walborn & Hesser 1975; Meaburn et al. 1984), but the spectral resolution and signal-to-noise ratio (S/N) offered by our new data permit a deeper study of the phenomenon. Figure 3 illustrates the wide range of emission line profiles found in the Nebula: in Hα, only panels b, c, and d show a distinct double-peak structure; panels a and f show asymmetries in the line, while a superficial look at panel e does not reveal more than a single Gaussian component. In the line profiles of panels a, f, and e, however, two components are clearly seen in the He I (magenta) and [N II] lines (blue and black). Looking at the radial velocity (RV) of the line peaks we observe an approximate correspondence between the peaks of the different lines. As panels b, c, and f show clearly, there is instead no correlation between the intensities of Hα and the corresponding peak in the [N II] line. On the contrary, the intensities of the He I peaks show a nearly perfect correspondence with those of Hα.
We have fitted all the Hα, [N II] 6584 Å, and He I line profiles using two Gaussians; we have not attempted the same fit on the [N II] 6548 Å line since this is weaker by a constant factor 2.95 (set by atomic physics) than the [N II] 6584 Å line. The best-fit functions are also shown in Fig. 3 with orange (Hα), cyan ([N II]), and purple (He I) colors: the fit to Hα is extremely good and is almost indistinguishable from the observed line profile; even in the case of distorted, single-peak profiles (e.g., panel e) two Gaussian components are actually required to yield a good fit. There are very few cases where the Hα profiles seemed to require a third component or where even a single component was sufficient: in the vast majority of cases two Gaussians are required. The [N II] and He I lines are also equally well fitted by two-Gaussian models, although in these cases the agreement is limited by the lower S/N of the lines (especially He I). We present in Tables 1–3 all the best-fit parameters of the two-Gaussian models for Hα, [N II] 6584 Å, He I, and also the [S II] 6717 and 6731 Å lines3. In Table 1, column Type/setup indicates the origin of the spectrum (sky fiber or faint star) and the Giraffe setup used; columns RV and σ are in units of km s-1.
 |
Fig. 3 Line profiles at Hα (red), [N II] 6548 (blue) and 6584 Å (black), and He I (magenta) for various positions across the Nebula. Also shown are two-Gaussian best fits for Hα (orange), [N II] 6584 Å (cyan), and He I (purple). The lines shown are scaled by the indicated factors for ease of comparison with Hα. Indicated radial velocities are heliocentric. |
Double-Gaussian fitting results for [N II] 6584 and He I 6678.
Double-Gaussian fitting results for [S II] 6717 and 6731.
There are two persistent components across the whole set of line profiles in the Nebula (analogous fits were performed on sky-dominated stellar spectra, and on HR14A spectra, with similar results), which suggests that there are two well-defined, distinct dynamical components. Since the Gaussian fits represent so faithfully the observed line profiles, we examine the properties of the two components using the best-fit parameter values. This allows the bulk of nebular emission in Carina to be studied (see Sect. 3.1.). A very careful inspection of Fig. 3, however, shows that in the far wings of Hα the two-Gaussian fit differs from the observed profiles: these residual emissions are found to possess interesting characteristics, and are studied in Sect. 3.2.
3.1. Main components
From here on, we refer to the bluer component of the lines as the “approaching” component and to the redder one as “receding”, in a relative sense since they both might have a positive (or negative) RV on the same sightline. As the sky image in Fig. 1 shows, the bright nebulosity is centered on the cluster Trumpler 16, so it can be expected that its dynamics is related to the cluster dynamics. Wilson (1953) reports for η Car a RV of − 25 km s-1. We anticipate here that bona fide low-mass members of Trumpler 16, from the same Gaia-ESO HR15N dataset studied here, have RVs in the range of − 10 to − 15 km s-1 (Damiani et al., in prep.), and the low-mass star RVs are usually more accurate than those from massive stars because these latter stars have fewer and broader lines. We assume therefore a “fiducial” RV for the Trumpler 16-14 clusters of − 12.5 km s-1; in our preliminary analysis, no difference in mean RV is found between clusters Trumpler 16 and 14.
Figure 4 shows the best-fit RVs of the receding Hα component RVred vs. that of the approaching Hα component RVblue. The datapoints refer to pure-sky HR15N data (black), sky data from faint stars (gray), and pure-sky HR14A data (blue). The orange circle describes the locus of cluster stars, i.e., the center-of-mass velocity of the cluster RVcm (Damiani et al., in prep.). It can be seen that the datapoints split naturally into two main groups (equally populated by black, gray, and blue dots): a larger group centered at (RVblue,RVred) = (−30,10) and a smaller one closer to RVcm. We have indicated these observations (at RVblue> −15 and RVred< 10) with small plus signs, and we refer to these sky locations as “zero-velocity gas” (with respect to RVcm). We note that even for zero-velocity datapoints we are still able to fit two distinct, non-degenerate Gaussian components to most lines thanks to the very high S/N of our spectra. The dashed line starting at RVcm is the expected locus for an ideal, spherical, optically thin expanding region, whatever its geometrical thickness or velocity law. The requirement of symmetry, in fact, means that for each line of sight towards it two RV values are observed, symmetrically on opposite sides of RVcm (i.e., the velocity of the center of expansion). This behavior is actually shown by planetary nebulae (Osterbrock & Ferland 2006). Figure 4 shows instead that no global spherical expansion occurs in the studied part of the Carina nebula, and there is no one-to-one correspondence between RVblue and RVred on the same line of sight. Only the average approaching and receding RVs of the main group of datapoints are found on the prolongement of the dashed segment: on average, the approaching and receding RVs are equal to RVcm−20 and RVcm + 20 km s-1, respectively, but no well-defined center of expansion is identifiable in the data.
Since the datapoints are not smoothly connected to the center-of-mass velocity, the approaching and receding components resemble two distinct layers of gas rather than a spherical distribution; alternatively, the distribution might still be spherical, but our observations only cover its central parts and omit parts where expansion is orthogonal to the line of sight, and thus at RV ~ 0. Smith & Brooks (2007) discuss the large-scale diffuse emission in Carina made of several shell-like features roughly centered on Trumpler 14-16 of sizes 20−30 pc, and suggest that the double-peaked optical lines would arise from opposite sides of those shells, along the line of sight. This hypothesis, however, fails to explain why the intensity of the Hα emission is so spatially concentrated near the central clusters, at intensities much higher than the outer border of the shells, while projection effects would cause the reverse effect (highest dilution at the center). The line-of-sight depth of the regions producing the most intense Hα emission can be expected to be on the order of its sky-projected size, or ~10 pc in diameter. This might be large enough to account for the lack of precise correspondence between RVblue and RVred along the same line of sight. We must not forget, nevertheless, the known complexity of the Carina SFR and the possibility that there are actually several distinct centers of expansion, perhaps at different RVs. The observed emission might therefore be a chaotic superposition of different expanding spheres.
 |
Fig. 4 Radial velocity of the receding component vs. RV of the approaching component. Here the black dots refer to pure-sky fibers from the HR15N setup, blue dots to pure-sky from the HR14A setup, and gray dots to sky lines from faint stars. The orange circles represent the average RV of low-mass cluster stars. The dashed line is the expected locus for purely spherical expansion. A subsample of apparently peculiar datapoints is highlighted using “+” symbols. |
 |
Fig. 5 Normalizations of best-fit Gaussians for the receding vs. approaching components. The dashed line represents identity. Other symbols as in Fig. 4. |
Figure 5 shows the intensity of Hα of the approaching component vs. that of the receding component. Only a weak correlation exists between the two, dominated by the datapoints (blue dots) from the HR14A dataset coming partly from stars outside the strong nebulosity to the southwest. The intensity pattern in the receding component is therefore sensibly different in its morphological details than that of the approaching component, a result that Hα images might have never shown. The zero-velocity gas already defined in Fig. 4 is also indicated in Fig. 5 with small plus signs. We also observe that the intensity of the Hα lines from the receding and approaching gas are, on average, similar: if they have intrinsically similar brightnesses, then the absorption towards them cannot be sensibly different (much less than one magnitude of extinction), and only a small amount of dust may exist between them, despite the great distance which is likely to separate them.
Thus far we have assumed implicitly that the receding gas is generated from expansion starting from some place inside clusters Trumpler 16 and 14 and that it is located at greater distances than the clusters themselves, while the opposite holds for the blueshifted, approaching gas. In principle, it would not be impossible to have the reversed situation where the two layers are actually moving towards one another, leading to a huge collision, which might have already generated the existing massive clusters. In order to discriminate between the two scenarios, it is necessary to determine unambiguously which layer is closer to us. We have seen that extinction differences, if they exist, are subtle and cannot be determined from the statistical arguments discussed above. However, a much more accurate way to establish the reddening suffered by optical line emission is through the Balmer decrement. For this aim we use the 15 UVES pure-sky spectra, which include both Hα and Hβ. Because it is not a spectrophotometric instrument, we cannot determine absolute reddenings for the two layers (i.e., calibrated flux ratios between Hα and Hβ); however, it is possible to find which layer has the highest reddening of the two. Figure 6 shows examples of comparison between Hα (black) and Hβ (red): in all cases the receding, redshifted layer shows slightly attenuated Hβ intensity with respect to Hα, and thus higher reddening. The reverse is never found. This may be taken as evidence that the two layers are expanding away from the central clusters and η Car, although a different temperature between the two layers might mimic the same effect (Osterbrock & Ferland 2006).
 |
Fig. 6 Examples of Hβ (red) and Hα (black) lines from pure-sky fibers using UVES. A vertical shift was applied to spectra from different sky positions. The Hβ lines were scaled up by a factor of 7. |
 |
Fig. 7 Radial velocity from the He I 6678 Å line vs. RV from Hα. Red (blue) symbols refer to the receding (approaching) component from HR15N data. Purple (pink) symbols refer to the same two components, but from HR14A pure-sky fibers. Plus symbols refer to zero-velocity gas as in previous figures. The dashed line represents identity. |
 |
Fig. 8 Fit normalization for He I vs. normalization for Hα. Symbols as in Fig. 7. The dashed line indicates a constant ratio of 1/90. |
 |
Fig. 9 Gaussian widths σ of He I lines vs. those of Hα. The three dotted lines represent loci of constant gas temperature Tgas = 5000,10 000,15 000 from top to bottom. The dashed line represents equality. Symbols as in Fig. 7. Only datapoints with the same RV from Hα and He I within 3 km s-1 are shown. |
We have compared best-fit parameters between different lines, starting from Hα and He I. The respective RVs are shown in Fig. 7, where red (blue) dots indicate the receding (approaching) components from HR15N data, and pink (purple) dots the same components from the HR14A data, respectively. The agreement is excellent, except for a few outliers, most of which are already known as the zero-velocity gas (plus signs). It should be noted that the He I line is by far the weakest line in our sample (Fig. 2), with intensity ~1/90 of Hα, so that in Fig. 7 errors in the ordinates must be much larger than errors in the abscissae; the latter are expected to be of the same size as the plotted dots. The very good coincidence in RVs strongly suggests that the same gas is emitting in these two lines. This conclusion is reinforced by the comparison of the intensities in the two lines in Fig. 8, which again shows a very tight correlation.
Since the same material emits in the Hα and He I lines, the slight difference in their line widths, already observed with reference to Fig. 3 above, must be related to microscopic properties of the gas, and can be taken as a measure of temperature. The total line width for hydrogen will be 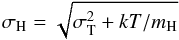 (1)and an analogous expression, with the appropriate atomic mass, for He. Here, σT is the component of the line width due to instrumental width and turbulence (and any other macroscopic velocity field, identical for hydrogen and helium, and therefore irrelevant for our derivation of temperature). Therefore, we plot in Fig. 9 the Hα and He I line widths, with three loci of constant temperature (5000, 10 000, 15 000 K). Most datapoints fall between 5000−15 000 K; strong outliers are more likely to arise from failed fits than from extremely high (low) temperatures. Datapoints for the approaching (blue) gas tend to show higher temperatures than those of receding gas, by a few thousands K. Turbulent velocities span a range of approximately 7−15 km s-1 (net of the instrumental line width), often above the sound speed for T ~ 10 000 K.
(1)and an analogous expression, with the appropriate atomic mass, for He. Here, σT is the component of the line width due to instrumental width and turbulence (and any other macroscopic velocity field, identical for hydrogen and helium, and therefore irrelevant for our derivation of temperature). Therefore, we plot in Fig. 9 the Hα and He I line widths, with three loci of constant temperature (5000, 10 000, 15 000 K). Most datapoints fall between 5000−15 000 K; strong outliers are more likely to arise from failed fits than from extremely high (low) temperatures. Datapoints for the approaching (blue) gas tend to show higher temperatures than those of receding gas, by a few thousands K. Turbulent velocities span a range of approximately 7−15 km s-1 (net of the instrumental line width), often above the sound speed for T ~ 10 000 K.
Next, we compared Hα parameters with those for [N II] 6584 Å (the strongest of the [N II] doublet). The RV comparison is shown in Fig. 10: the agreement between the respective RVs is much worse than in the case of He I of Fig. 7. The [N II] line is about 20 times stronger than the He I line, so the disagreement is certainly not due to errors, but is real and is a definite indication that the gas emitting Hα is not strictly the same as that emitting the [N II] lines. Although not the same gas, the dynamics of these two components is similar since the Hα and [N II] RVs are nevertheless well correlated (the receding gas more so than the approaching gas): they might be two adjacent layers or bubbles in the same expanding material. We note that there is no definite sense in which the respective RVs differ: if, for example, the Hα-emitting gas were moving systematically faster than the [N II]-emitting gas, one would observe a correlation with a slope different from 1 (the dashed line), still centered on RVcm. The zero-velocity outliers (plus signs) are found in [N II] sometimes at RV ~ RVcm and sometimes at definite non-zero RV. We return to this point below.
 |
Fig. 11 Fit normalization for [N II] vs. normalization for Hα. The dashed line indicates a constant ratio of 1/8. Other symbols as in Fig. 10. |
The comparison between the intensities of Hα and [N II] strengthens even more the conclusion that they arise from different material (Fig. 11); the intensity ratios between the two lines span an order of magnitude (or more). We discuss the interpretation of this result below.
The comparison between the RVs from Hα with those from the [S II] 6717 Å line is shown in Fig. 12. Here, many more datapoints are shown than in Fig. 10, from observations of sky lines from faint-star HR15N spectra. On the other hand, datapoints from HR14A observations are missing since the [S II] lines are outside their wavelength range. Figure 12 shows the same pattern as Fig. 10, with a loose correlation and a peculiar place for the zero-velocity gas. This suggests at least a similarity in the dynamics of the [S II]-emitting and [N II]-emitting gas, which is confirmed by their direct comparison shown in Fig. 13. Although both lines are stronger than He I, the latter correlation is not as tight as that between Hα and He I, so again the conclusion is that the [S II]-emitting gas is nearly coincident with but not identical to the [N II]-emitting gas. In Fig. 13 we also note that most of the zero-velocity datapoints are not outliers here, but follow the same correlation as other datapoints. Since the plotted data are statistically independent, this demonstrates that the zero-velocity points do not arise from failed fits, but have a real significance. The same considerations apply to the comparison between [S II] and [N II] intensities in Fig. 14: a good correlation, but significantly different from identity.
 |
Fig. 12 Radial velocity from the [S II] 6717 Å line vs. RV from Hα. Red (blue) symbols refer to the receding (approaching) component from HR15N data. Cyan (orange) symbols refer to the same two components, but from HR15N observations of faint stars. Other symbols as in Fig. 7. |
Following this preliminary assessment, we have examined the ratio between the two [S II] 6717/6731 Å lines, which depends only on the gas density, for densities in the range 102−105 cm-3 (Osterbrock & Ferland 2006). A plot of the ratio between the Hα and He I line widths (a proxy for temperature as discussed above) vs. the [S II] 6717/6731 Å intensity ratio is shown in Fig. 15. There is a tendency for the approaching gas to have both higher temperatures and lower densities (higher 6717/6731 Å ratio) than the receding gas; median 6717/6731 Å ratios are indicated by the vertical dashed lines, and correspond to densities of 100 (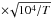 ) cm-3 and 200 (
) cm-3 and 200 (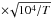 ) cm-3, respectively.
) cm-3, respectively.
A plot of the [S II] 6717/6731 Å intensity ratio vs. intensity of the [S II] 6731 Å line is instead shown in Fig. 16. The correlation, although not strict, indicates that for increasingly strong [S II] emission the density of the emitting gas also increases; the highest electron densities found are ~2 × 103 (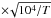 ) cm-3.
) cm-3.
 |
Fig. 15 Gaussian width ratio between Hα and He I (proxy for temperature) vs. normalization ratio between [S II] 6717/6731 Å (proxy for density). Temperature increases upwards, while density increases towards the left. Symbols are as in Fig. 7. The red (blue) vertical dashed line indicates the median [S II] 6717/6731 Å ratio for the receding (approaching) components. On average, the receding component has higher density and lower temperature than the approaching component. |
 |
Fig. 16 Intensity ratio between [S II] 6717 Å and 6731 Å lines vs. intensity of [S II] 6731 Å. Symbols as in Fig. 12. The dashed line at unity ratio corresponds to electron density Ne ~ 600 cm-3. |
 |
Fig. 17 Examples of low-intensity components in the lines, as residuals from the Gaussian best fits to the main components of Hα (orange), He I 6678 (green), [S II] 6717 Å (blue) and 6731 Å (red). The He I residuals are scaled up by a factor of 10, and those of [S II] by a factor of 3. Black vertical dashed lines indicate the RVs of the two main Gaussian components. Gray dashed lines indicate the adopted boundaries to define the wide and narrow Hα wings, all centered at RV =−12.5 km s-1. Indicated radial velocities are heliocentric. The emission features in the Hα profiles at RV ~−420 and ~ + 280 km s-1 originate from terrestrial airglow. In the plotted units, Hα peak emission before best-fit subtraction is for each panel respectively equal to 124 300 (panel a)), 27 800 b), 426 700 c), 182 600 d), 224 200 e), 50 200 f), 111 300 g), and 98 300 h). Intensity levels of ± 1% of peak emission are indicated in each panel by horizontal dashed lines. |
3.2. Low-intensity components
The two emission components nicely described by Gaussian shapes constitute the bulk of the nebular emission in the studied region. However, as expected from a close inspection of Fig. 3, there are small but significant departures from these pure Gaussian shapes in their extreme wings. We are able to study these low-intensity wings thanks to the very high S/N of our data. To this purpose we consider spectra from sky fibers alone in order to avoid any possibility of confusion with stellar features. After subtracting out the best-fit Gaussian components from the lines, residual emission can in most cases be seen, representative examples of which are shown in Fig. 17. The intensity levels of this emission are about two orders of magnitude lower than the peak Hα emission. Figure 17 shows residuals in Hα (orange), He I 6678 (green), and the [S II] lines (6717 Å in blue, and 6731 Å in red). The two black dashed lines indicate the best-fit RVs of the main Gaussian approaching/receding components. The gray dashed lines indicate RVs of RVcm ± (50,100,380) km s-1, for reference4. We demonstrate in Appendix A that the residual patterns seen in Fig. 17 are not of instrumental origin. First, we note from the figure that the residual emission in Hα shows two apparently distinct components: a lower-intensity high-velocity gas, with RV reaching (absolute) values up to 400 km s-1 or above, and a narrow component, mostly seen at lower absolute RVs between 50−100 km s-1 (relative to RVcm), i.e., between the two bands delimited by gray lines near the center. In [S II] (red/blue curves) no wide wings are seen, but the narrow components may sometimes appear at RVs close to those of Hα narrow wings. A wide variety of situations is encountered across the Nebula: the wide and narrow wings both span a wide range of intensities, and each type may be observed without the other (see, e.g., panels f and h). The wide wings present a marked symmetry between the blue and red sides, while the narrow wings much less so: the red wings may be stronger than the blue ones, or viceversa (panels b and c). When the [S II] emission is present, although it resembles the emission in the narrow Hα wings, it may be found at absolute RVs both lower (panel a) and higher (panels d, g) than the narrow Hα wings; in panel g it is very strong in relative terms. Finally, panel e shows a conspicuous case (and not the only one) of self-absorption in the inner portion of the blue wide wing at about − 100 km s-1; the width of this absorption component is considerable, ~50 km s-1. In this section we try to understand the physical meaning of all these features.
In the figure, a regular saw-tooth pattern can be seen in the residuals near RV = 0; this is not random noise, but a systematic effect. The maximum amplitude of such a residual pattern, compared to original line peaks (see figure caption), is on the order of 1−2%, in accordance with the very good appearance of fitted models in Fig. 3. From numerical experiments, it turns out that this effect occurs because no wide emission component was included in our fitting model in addition to the two Gaussian components. As a result, the widths σ of the best-fitting Gaussians are very slightly overestimated (by ~1.5%), producing exactly the same residual pattern as observed. This only affects marginally the immediate neighborhood of the main components, and therefore also the inner boundary of the narrow Hα components; farther out, however, the residual line profiles are totally unaffected. If we are able to detect systematic effects in the best-fit widths σ of such a small amplitude, random errors on σ are necessarily much smaller than 1% on average, otherwise they would mask the above effect. In general, even where wide wings are not detected, additional components of low-amplitude, compared to the main ones, will produce similar residual patterns, especially in Hα. Therefore, we consider the physical existence of gas emitting in the narrow Hα wings to be questionable. Instead, the emission features in the [S II] residuals between absolute velocities 50−100 km s-1, of amplitude much larger than the [S II] residuals in the range [RVcm−50,RVcm + 50] km s-1 can be considered a real phenomenon.
We note that Walborn et al. (2002) have found many RV components (in absorption) in the STIS UV spectra of four O stars in Carina in lines of several ionized species; for most lines, however, the STIS spectra are saturated in the RV range studied in the present paper and provide no useful information, while the many narrow absorption components at RV<−100 km s-1 found in the STIS spectra have a completely different appearance from the high-velocity components studied here, and therefore originate in different regions.
The existence of the wide Hα wings has been known for decades (Lopez & Meaburn 1984); in the direction of the Keyhole Nebula, Walborn & Liller (1977) and Boumis et al. (1998) found that they are the spectrum of η Car reflected from local dust. This explains the apparent self-absorption at RV ~−100 km s-1 seen in Fig. 17 (panel e) and in a few other places near that position. We discuss in the next section the spatial distribution of the wide-wing emission, which is strongest in coincidence with the Keyhole and along the line between it with η Car, as found by Boumis et al. (1998). This again suggests reflected emission from η Car for their origin, rather than local high-velocity gas. Our data enable us to test these two alternative hypotheses further. A detailed comparison with the actual spectra of η Car can be done using data from the ESO archive, where 16 UVES spectra are available covering the years 2002−2004; of these we only consider those without strong signs of saturation in Hα (8 spectra). A representative selection is shown in Fig. 18 in the regions around the Hα and He I lines. We looked for similarities between our residual patterns of Fig. 17 and the η Car spectra in the HR15N wavelength range. The most characteristic features seen in the η Car spectra are the wide Hα wings and a peculiarly shaped He I 6678 line (Fig. 18). Like Hα, the profile of the η Car He I 6678 line is also variable. We find a striking similarity between the latter line profiles and our He I fit residuals of Fig. 17, panels a, e, and f, and some hint of blue-wing He I residual emission also in panels b and g. This would further support the case for wide Hα wings as a reflection effect. We show below that there is no proportionality between the sky continuum intensity (from reflection nebulosity) and the wide-wing intensity. This can be reconciled with wide wings being due to reflection of η Car emission only if the sky continuum is larger than the scattered η Car continuum owing to contributions from other stellar continua as well. We find that this is indeed the case. Figure 19 shows that the η Car continuum and wide wings (downscaled by a suitable factor) describe well the lower envelope of nebular datapoints. Therefore, the missing correlation between the two quantities across the nebula is not inconsistent with the reflection hypothesis for the wide wings.
 |
Fig. 18 Selection of UVES spectra of η Car in the Hα (black) and He I 6678 lines (green) for the years 2002−2004, as indicated above each spectrum. Spectra are continuum-subtracted and shifted vertically for clarity. The He I line amplitude was enlarged 10 times to facilitate comparison with Hα. Vertical dashed gray lines indicate the same velocities as in Fig. 17. |
 |
Fig. 19 Sky continuum vs. total intensity in the wide Hα wings. Small dots refer to pure-sky fibers from setups HR15N (black) and HR14A (blue), while big red dots are the downscaled continuum and wide wings of η Car. The dashed line is a constant factor of 4 × 10-4. |
 |
Fig. 20 Intensity of red vs. blue wide Hα wings. Datapoints from pure-sky fibers of HR15N (black) and HR14A (blue) setups. The dashed line is identity. The big red dots indicate the wide wings in the η Car spectra. |
 |
Fig. 21 Ratio of red to blue wide Hα wing intensities, in the vicinity of η Car vs. radial distance. Symbols as in Fig. 20. |
 |
Fig. 22 Intensity of high-velocity components in the [S II] 6717 Å line vs. those in the [S II] 6731 Å line. The dashed line is identity. The average ratio, higher than one, indicates low densities. Symbols as in Fig. 10. |
 |
Fig. 23 Spatial map of Hα line intensity (fit normalization). The radius of each circle is proportional to intensity. Blue (cyan, purple) circles refer to the approaching component, while red (orange, pink) circles refer to the receding component. The circles are color-coded as in Figs. 7 and 12. The oblique dashed lines outline the edges of the absorption lanes visible in Fig. 1. Crosses indicate the positions of O/WR stars from Walborn (1973). The large black circles indicate the positions of Trumpler 14 (upper), η Car (middle left), and the Wolf-Rayet star WR25 (middle right). The green “+” symbols indicate the positions of zero-velocity gas (see Fig. 4). |
Figure 20 shows, as already suggested from Fig. 17, that the intensities in the blue and red parts of the wide Hα wings are very well correlated with one another. Figure 20 also shows that the intensity in the blue wide wing is systematically lower than that in the corresponding red wing. This is actually inconsistent with most of the measurements from η Car spectra (red datapoints); the signal-to-noise ratios of these spectra are so high that the errors on the η Car wing measurements are negligible (comparable to the plotted symbol size), so that the difference is highly significant. Also significantly different are the velocities of the absorption reversal in the η Car spectra (v ~ −150 km s-1) and in the nebular spectrum (v ~ −125 km s-1) of Fig. 17, panel e. Both discrepancies can be reconciled, however, by assuming that the scattering dust is not at rest. If the dust is expanding away from η Car, an observer comoving with the dust would see the η Car emission as redshifted; then, depending on the dust relative motion with respect to us, the reflected redshifted line may gain an additional redshift, a blueshift, or no shift at all. For a spherically expanding dust envelope, a total wavelength shift varying linearly with radial distance is predicted. Therefore, Fig. 21 shows the ratio between the red and blue wide Hα wings (increasing with redshift) vs. radial distance from η Car: a clear correlation is seen for most datapoints, connected smoothly with the actual η Car values at zero distance. No such correlation is instead found for distances greater than 5 arcmin from η Car. It should be noted that because of the variability found in the η Car Hα profiles (red points), some scatter in the distribution of nebular values was expected, in agreement with the handful of outliers seen in the figure. Therefore, the hypothesis of a reflection origin for the wide Hα wings is supported by our data only if the scattering dust is radially expanding away from η Car. On the other hand, we do not find any reasons why the emission from genuine high-velocity gas should show a pattern like that in Fig. 21; therefore, this hypothesis should be discarded. It should also be noted that the reflecting dust is likely to form a half shell expanding towards us, rather than away from us: in the latter case, dust observed close to η Car would move away both from this star and from us, and the corresponding redshift in the scattered emission would be larger than the redshift at the shell edge farther away where dust moves tangentially with respect to us. Therefore, a dust half-shell expanding away from us should show a negative slope in the redshift-radius diagram, whereas the positive slope seen in the diagram of Fig. 21 corresponds to a half-shell expanding towards us.
All things considered, the most reliable indicator of genuine diffuse high-velocity gas (v ~ ± 100 km s-1), found only at some places in the studied region, is the occasional emission in the [S II] wings discussed above. The doublet ratio permits the gas density of this high-velocity gas to be derived. Figure 22 shows the intensity in [S II] 6717 Å vs. [S II] 6731 Å: the former is on average higher, indicating low densities (~100 cm-3).
3.3. Spatial morphology
Important information on the emitting gas is derived from its spatial distribution. Figure 23 shows a map of the intensity of the two main components (blue/cyan/purple circles for the approaching component, red/orange/pink circles for the receding one). The circle radius is proportional to the best-fit normalization (scaled by exposure time, and thus proportional to observed flux). The dark lane position is indicated by the dashed lines. Crosses indicate O/WR stars from Walborn (1973). The large black circles indicate the positions of Trumpler 14, η Car, and the Wolf-Rayet star WR25. Finally, green plus symbols indicate the positions of zero-velocity gas identified in Fig. 4.
Figure 23 is very complex, but a few dominant features can be observed. The distribution of surface brightness is not the same for the approaching and receding components; the latter strongly dominates, especially in a region comprising η Car and towards the southwest, parallel to the southern dark lane. The approaching component dominates north of this region, and also between it and the southern dark lane with impressive regularity despite the low intensity of both approaching and receding components there. Most of the zero-velocity gas is found concentrated on two sides of Trumpler 14, again parallel to the nearest dark lane. Overall, it is evident that plane-parallel distributions prevail here over circular (or spherical) configurations for the bright material, as was already clear for the dark, obscuring material. Some sort of density stratification probably plays a very important role in shaping the entire central region of the Carina nebula. We note that the different intensity distributions for the two components could have never been discovered using narrow-band Hα images since even narrow-band filters are not wavelength-selective enough to image them one at a time.
 |
Fig. 24 Map of RV of approaching and receding gas. Symbols as in Fig. 23. Circle size is proportional to | RV−RVcm |, with the largest circle corresponding to | RV−RVcm | = 42.6 km s-1. |
The map in Fig. 24 is similar to Fig. 23, but with circle radii proportional to | RV−RVcm | for both approaching and receding components. As already suggested from the discussion of Fig. 4 there is no global velocity pattern; on smaller scales, we observe again the near-zero RVs on the two sides of Trumpler 14, and there are indications that other patterns exist on similarly sized scales. Therefore, the two main components here must be local to the inner region of the Nebula and not connected to the global expansion of the whole Carina nebula, on scales of 20−30 pc, as already discussed above.
 |
Fig. 25 Map of the distribution of intensity in the wide Hα wings (gray) and sky continuum emission (green). Circle size is proportional to intensity. Darker gray circles indicate data from pure-sky fibers using HR14A setup. Thick circles and crosses have the same meaning as in Fig. 23. The large gray circle closest to the center indicates the very intense Hα wings in the direction of the Keyhole Nebula. |
 |
Fig. 26 Map of the intensity ratio [N II] 6584 Å/Hα. Symbols as in Fig. 23, except for the cyan/orange data from faint stars, which are not used here. Circle size is proportional to ratio; the largest circle corresponds to a value of 2.4. |
Before discussing the local regions individually, we examine some other distribution maps. Figure 25 illustrates the distribution of wide Hα wings intensity (gray circles with radii proportional to intensity); it is clear that they are found all around η Car, not only in the direction of the Keyhole Nebula. The green circles instead indicate the intensity of the sky continuum, which is distinctly measurable in some of the pure-sky spectra and reveals reflection nebulosity from dust in the vicinity of bright stars. The fact that this continuum emission has no features similar to the solar spectrum and that its intensity varies among sky spectra from the same OB, ensures that it does not originate from scattered moonlight, but from dust reflection in Carina. The strongest reflection nebulosity is evidently found in Trumpler 14, but also the η Car region shows clear detections of it. As discussed in the previous section, we do not find a proportionality between the intensity of the reflected sky continuum and that of the wide Hα wings.
Figure 26 shows the spatial distribution of the intensity ratio between the [N II] 6584 Å line and Hα. However, since we found above that the respective dynamics of hydrogen and nitrogen show that the two sets of lines do not come from exactly the same gas, but merely from adjacent (or otherwise loosely connected) gaseous components, we consider their intensity ratio only in places where their RVs differ by less than 3 km s-1. For constant ionization fractions of H and N, their intensity ratio is an increasing function of gas temperature (Haffner et al. 2009). Taking it at face value, under the hypothesis of constant H and N ionization, the map would imply a wide range of temperatures for the emitting regions (about a factor of 3, with exact values depending on the assumed H and N ionization fractions). This is wider than the range derived above from the line-width ratios (outliers excluded) and, moreover, there is no correlation between the line-width ratios and the N/H intensity ratios shown in Fig. 26. Therefore, it is more likely that rather than a range in gas temperatures the N/H ratios reflect here variations in the N (or H) ionization fraction. The figure shows then that this varies strongly, and in different ways for the approaching and receding components (as found by Deharveng & Maucherat 1975); in the approaching component the N ionization increases markedly south of η Car (again, along a region parallel to the southern dark lane), while in the receding component it is more uniform with some preference for higher values in the northern parts. We discuss an interpretation of this in the next section.
 |
Fig. 27 Map of the intensity ratio between [S II] 6731/6717 Å, increasing with density. Symbols as in Fig. 23. The largest circle corresponds to a ratio of 0.65. We note the high values of this ratio near the Keyhole Nebula, ~3 arcmin NW of η Car. |
 |
Fig. 29 Position-velocity diagram for Hα in the neighborhood of Trumpler 14. Circle size is proportional to line intensity. Color codes as in Fig. 4. The distance origin is taken at the Trumpler 14 position indicated with the large black circle in the upper right of Fig. 23. Positive distances are towards the SW; the dark lane lies at position ~ + 3 arcmin. The direction of the observer is towards the bottom at negative RVs. |
Figure 27 shows the distribution of the intensity ratio between [S II] 6731/6717 Å (increasing with density), the highest values of which are most often found in the region surrounding the Keyhole Nebula. Finally, Fig. 28 shows the intensity distribution of the high-velocity [S II] emission occasionally found (see Fig. 17), which is especially frequent as a receding component north of η Car and as an approaching component next to the western lane, and may trace high-speed shocks (Hartigan et al. 1999). A closer examination of shock diagnostics will be presented in Sect. 3.5 below.
3.4. Position-velocity diagrams of shell-like structures
As discussed above with reference to Figs. 23 and 24, velocity structures seem to exist at local scales rather than on the scale of the entire studied region. It was also noted that plane-parallel geometries are dominant over circular ones, so it is natural to look for velocity structures along preferred directions rather than along the radial direction inside circular regions. The first example shown here in Fig. 29 is a position-velocity diagram in the region surrounding the northern cluster Trumpler 14, already mentioned in connection to the zero-velocity gas. In Fig. 29, the abscissa reports distance along an axis at a position angle of 110° (from north, clockwise), passing though Tr 14 center. The chosen position angle reflects the spatial alignment of zero-velocity datapoints. The circle radius is proportional to Hα intensity (fit normalization), and approaching and receding components are both shown in the same color. The pattern indicates some sort of radial expansion, approximately centered in Tr 14. The geometry is not spherical, however, but distorted, probably because the medium into which expansion is taking place has a strongly non-uniform density. Some non-spherical expansion geometry was already suggested by Deharveng & Maucherat (1975). We find an abrupt discontinuity in the RV pattern for the approaching component at projected distances between (− 2,−1) arcmin: to the left of this position the approaching gas RVs flatten out to a nearly constant value close to − 10 km s-1, as if the expanding gas had hit a much denser layer of material traveling at that speed and was basically stopped and forced to co-move with it.
Additional evidence for such an interaction having occurred between the expanding gas and another layer may come from the position-velocity diagram of Fig. 30, which differs from the previous figure in that the circle size is proportional to Hα line width σ and thus to turbulent speed (or temperature); it is clear from this diagram that the line width increases systematically and significantly in the “stopped” gas, likely as a result of a collision with a massive obstacle. Also interesting is the corresponding position-velocity diagram using [N II] instead of Hα; in this region are found many of the outliers seen in Fig. 10, where the Hα RV was near RVcm while the RV of [N II] emission was similar to the rest of the approaching gas. Analogously, Fig. 31 shows that the expansion of the Tr 14 shell seen in the [N II] line is very different than that seen in Hα; the shell morphology is barely discernable, and more importantly the [N II] emission does not indicate any slowed-down expansion where Hα does, but continues to show high approaching velocities. Obviously, the [N II] emitting gas is different, and in this particular case lying beneath the gas emitting Hα, and has yet to reach the space region where slowing down occurs.
 |
Fig. 32 Same as Fig. 29, but centered on η Car. Positive distances are in the NW direction from η Car. The Keyhole Nebula lies at position ~+3 arcmin. |
Also worth investigating is the region surrounding η Car, as noted in the discussions above on spatial distributions. Figure 32 is a velocity-position diagram like Fig. 29, but centered on η Car towards position angle 35°. Here too a sort of distorted, incomplete shell is suggested by the diagram; the incompleteness towards the south is due to the strong obscuration by the southern dust lane (left of distance of − 5 arcmin in the figure). At a projected distance of ~2.5 arcmin the shell border, converging towards RVcm, is clearly visible; the same datapoints show increased Hα line intensities (larger circles in the figure), as expected because of projection effects. This position nearly coincides with the Keyhole Nebula. To the right of this position, Hα emission is much weaker, but the RV pattern suggests another shell towards NNW, possibly centered on the O3 star HD 93250. Near a position of ~2.5 arcmin, an interaction between the two shells might be taking place and contributing to the peculiarities of the Keyhole Nebula summarized in Smith & Brooks (2008). Such an interaction might be diagnosed by an increased gas turbulence, which – as can be understood from Fig. 9 – is an important contributor to measured line widths. To investigate this possibility we show the same diagram with circle sizes proportional to Hα line widths (see Fig. 33): these are generally small (symbols adopt the same scaling factor here as in Fig. 30), but increase precisely in the group of datapoints around position ~2.5 arcmin and RV ~ −10 km s-1, i.e., the putative interaction region between the shells. This might be an indication of ongoing shell collision and merging.
 |
Fig. 34 Reconstructed geometry of the η Car shell. Bottom left axis indicates distances parallel (normal) to the plane of sky. Top and right axes indicate the original measurements, as in Fig. 32, and the symbols are also the same, except that here circle size is proportional to the Hα/[N II] intensity ratio. The brown double-lobe structure near the center represents the position and actual inclination of the Homunculus Nebula (size is not to scale). The horizontal dashed line, which defines angle θ = 0, is parallel to the sky plane; the oblique line indicates the Homunculus polar axis. |
 |
Fig. 35 Intensity ratio Hα/[N II] vs. azimuthal angle θ, defined in Fig. 34. Symbols as in Fig. 5. Vertical dashed lines indicate the projections of the Homunculus polar axis. |
The η Car shell presents a rich phenomenology that deserves a closer examination. As evident from Fig. 26, in the half-plane SE of η Car the [N II]/Hα intensity ratio is systematically higher in the blueshifted component than in the redshifted one. Moreover, under the rough zero-order assumption of spherical expansion, we can transform the line RV into a distance from the expansion center (i.e., η Car) with a best-guess conversion factor such that the shape of the shell is as round as possible. The result of this transformation is shown in Fig. 34, where axes are scaled to parsecs using the known Nebula distance; the original measurements (sky-projected distance in arcmin and RV) are shown at the top and right borders, respectively. Only components that differ in RV by less than 3 km s-1 are used to compute the [N II]/Hα ratio (proportional to symbol size in Fig. 34). We know the inclination angle to the line of sight of the Homunculus Nebula surrounding η Car (whose two lobes are indicated in Fig. 34 in brown) from the very detailed studies of Davidson et al. (2001) and Smith (2006). It turns out that the Hα/[N II] ratio varies in a systematic way with azimuthal angle θ, defined in the figure (and increasing counterclockwise), with θ = 49° corresponding to the projection of the Homunculus polar axis in the NW direction (with a component away from us), and θ = 229° corresponding to its projection towards the SE (with a component towards us). As a function of θ, the Hα/[N II] ratio is shown in Fig. 35; fairly well-defined minima are found corresponding to each of the poles. In the next section we discuss why the Hα/[N II] intensity ratio can be considered a good indicator for the ionization parameter q. Thus, the minima in Fig. 35 also correspond to minima in the ionization parameter q: gas lying along the Homunculus polar axes is therefore irradiated with much less UV flux than gas in the equatorial directions (~30 times less). This is possible if the total column density in the matter surrounding η Car is not isotropic, but much higher near the polar axes. This picture agrees very well with the findings of Smith (2006) that most of the matter forming the Homunculus was originally ejected by η Car at high latitudes and did not get its shape by the effect of a circumstellar torus. If the circumstellar torus picture were the case, we would observe a brighter UV irradiation near the poles, i.e., the opposite of what our data suggest. Our picture also implies that η Car is by far the dominant ionizing source inside its own shell, and probably throughout the entire Trumpler 16 cluster.
 |
Fig. 36 Same as Fig. 32, except that circle size is proportional to the [S II] 6731/6717 intensity ratio. |
Such directionality in the ionization pattern around η Car, and the shape itself of the Homunculus, would also suggest a polar-angle dependence for the mechanical energy output of η Car winds. If this is true, the turbulent line widths mentioned above that increase near the inter-shell boundary but not along the η Car polar axis might then suggest that winds from massive stars are a secondary contributor to turbulence in H II regions, which is in agreement with Krumholz & Burkhart (2016).
We have also examined whether a similar pattern exists for the gas density as measured from the [S II] 6731/6717 line ratio. The corresponding diagram is shown in Fig. 36, with circle sizes proportional to the [S II] 6731/6717 intensity ratio (increasing with density). Here, no dependence on closeness to the Homunculus polar axis is found; instead, the line ratio and gas density tends to increase systematically from the SE to the NW (left to right in the figure) for projected distances <3−4 arcmin, with the highest densities found near the NW shell edge, corresponding to the Keyhole nebula, as noted above.
Finally, Fig. 37 suggests the existence of a third prominent shell, centered on the Wolf-Rayet star WR25 (hereafter WR25 shell), with position angle 150°. Here too, the southern part of the shell is hidden behind the western dark dust lane, while at position ~− 2.5 arcmin the shell boundary is seen in the diagram, with enhanced Hα luminosity as above. To the left of that boundary traces of another shell can also be seen in this case (presumably the same shell north of η Car as mentioned above). Here again, we test using line widths whether interactions may be present; Fig. 38 suggests that this may indeed be the case, with increased line widths at several places near RVcm. The much increased intensity of the [S II] lines at some places in this region, shown in Fig. 39, might also be indicative of localized shocks at the interface between the two shells (Hartigan et al. 1999).
 |
Fig. 40 Intensity ratios Hα/[N II] vs. Hα/[S II]. Symbols are as in Fig. 7. Tiny dots indicate measurements where the absolute RV difference between Hα and [N II], or Hα and [S II], is larger than 3 km s-1. Black lines/polygons indicate typical loci of supernova remnants (SNR), planetary nebulae (PNe), and Galactic HII regions (H II), as labeled. The green line grid is part of the cloudy model grid shown in Viironen et al. (2007) over a range of O/H abundances and ionization parameters q, as labeled. |
All shells show a distorted shape, indicative of density gradients of the material into which they expand. For this reason it is difficult to define a typical radius for each of them. The maximum RV interval ΔRV at shell center is instead clearly defined from the position-velocity diagrams, and is found to be ΔRV ~ 35 km s-1 for the Tr 14 and WR25 shells, and a larger ΔRV ~ 45 km s-1 for the η Car shell. The approximate sizes of the shells (~5 arcmin radius) and the observed expansion speed allow a timescale estimate, which turns out to be very short (~1.5 × 105 yr for the η Car shell). Since this is much shorter than the estimated ages of the massive stars in Carina, it is likely that a much larger amount of material should be present exterior to the bright nebulosity. Detection of a complex velocity structure in the interstellar absorption Na I D lines was indeed already known towards the center of Carina (Walborn et al. 2007, and references therein), and demonstrates that substantial amounts of neutral gas are present, in addition to the predominantly ionized gas studied here. The Gaia-ESO data on the Na I interstellar lines in Carina will be studied in a future work.
3.5. Line-ratio diagrams
In this section we discuss briefly how line ratios in our dataset compare with measurements from other nebular regions, including HII regions, planetary nebulae (PNe), and supernova remnants (SNR). Line-ratio diagrams involving the lines used in this work were presented by Sabbadin et al. (1977), and then by Riesgo & López (2006) and Viironen et al. (2007). They showed that these different object classes populate different regions in the diagrams with minimal mutual overlap. We show in Fig. 40 the intensity ratios of Hα/[N II] vs. Hα/[S II]. As is clear from Figs. 10 and 12, however, some sightlines have discrepant RVs between Hα and [N II] ([S II]). Whenever the RV discrepancy is more than 3 km s-1 in absolute value, the line-ratio diagram mixes intensities of emissions from slightly different nebular layers, and must be treated with caution; therefore, the corresponding datapoints are shown with tiny dots. The black lines and polygons shown in Fig. 40 indicate typical loci of H II regions, PNe, and SNR. None of our datapoints falls in the SNR region, where heating is dominated by shocks. The bulk of the datapoints lie just above the PNe wide strip (however, the limits of these loci are only indicative; see the much wider distributions of PNe points in Riesgo & López 2006). Nearly half of our datapoints fall outside the “nominal” H II box in the figure; this same pattern has already been found for extragalactic H II regions by Viironen et al. (2007). These authors compare their datapoints with grids of nebular ionization models, and show that such a pattern is indeed expected for a fixed [O/H] abundance ratio, but a varying ionization parameter. In particular, our datapoints agree with an oxygen abundance of 8.7 < 12 + log (O/H) < 8.9, and an ionization parameter in the range 6 × 107<q< 109. Both Hα/[N II] and Hα/[S II] increase with q in the given range. Most of our datapoints fall at higher Hα/[S II] values than typical Galactic H II region, which is likely caused by the ionization parameter q in Carina exceeding typical H II values elsewhere in the Galaxy.
 |
Fig. 41 [S II] λλ 6717/6731 intensity ratio vs. Hα/[S II] ratio. Circles refer to intensity ratios in the narrow wings of [S II] and Hα, when present (violet: approaching component; purple: receding component). Other symbols are as in Fig. 12. Solid lines/polygons indicate SNR, H II, and PNe loci as in Fig. 40. Dashed horizontal lines enclose the range where the [S II] 6717/6731 ratio is a useful measure of density (increasing from top to bottom). |
Another useful diagram introduced by Sabbadin et al. (1977) is the [S II] λλ 6717/6731 intensity ratio vs. Hα/[S II] (Fig. 41). Here again loci of H II regions, PNe, and SNR are indicated. This diagram contains more datapoints than that of Fig. 40 since it is only based on three lines and does not involve [N II]. In addition, we include measurements (circles) from narrow line wings (Sect. 3.2), which are sometimes very evident in [S II]. Plus signs indicate instead zero-velocity gas, which may lie at the interface between adjacent shells. Figure 41 shows that a few datapoints from these two categories lie in the SNR region or very close to it, suggesting that shocks may indeed be present but only in very few places in the nebula including the shell boundaries.
4. Discussion
The new observations of nebular emission lines in the central regions of the Carina nebula have put into evidence a rich variety of new facts. The emitting gas is highly differentiated in its kinematic properties: in general the hydrogen-emitting and forbidden-line-emitting gas have similar motion, but may also sometimes show highly contrasting velocities, as in the case of the Tr 14 shell. The low-level high-velocity emission was studied here in greater detail than in previous studies thanks to the very high S/N of the new data.
We have presented new evidence showing that the wide Hα wings arise from a reflection of the emission of η Car off dust, which strengthens results from previous works. However, to be entirely consistent with our observations, this dust cannot be stationary, but must expand away from η Car. It should be noted that η Car is spectrally variable on timescales shorter than the light-crossing time (~11 yr) of the putative dust shell radius of ~5 arcmin. Regarding longer-term variability, we are fortunate that this 11-yr delay between the direct and reflected η Car emission coincides nearly with the time difference between our observational datasets (2002−2004 for η Car UVES spectra; April 2014 for the bulk of our HR15N nebular spectra), which means that the comparison between η Car and its reflected emission, e.g., in Fig. 21, is unaffected by long-term variations.
The narrow excess emission seen in the Hα fit residuals between absolute RVs of 50−100 km s-1 is of uncertain significance; more significant is the occasional excess emission in the [S II] lines in the same RV range. Such enhanced high-velocity [S II] emission appears at almost random places; it might have originated where the fast OB star winds encounter local overdensities in the ambient medium with the formation of shocks, as suggested by line-ratio diagrams. The reason why this phenomenon happens preferentially around | RV | ~ 100 km s-1 is also unclear; it might only be a coincidence that this is close to the sound speed in the million-degree hot plasma that is found diffusely in the same region (Townsley et al. 2011), and that is also supposed to be heated by shocks caused by the OB stars winds. A detailed theoretical investigation of the complex observed phenomena in this complex region would certainly be desirable.
The two main expanding layers at RV ~ RVcm ± 20 km s-1 were known long before this work, as mentioned in the introduction. The ~20′ × 20′ spatial region studied here in the brightest, central part of Carina is nearly the same as that studied by Deharveng & Maucherat (1975) using lower quality data, and covers about one-third of that studied by Meaburn et al. (1984), who however analyzed Fabry-Perot spectra only along two lines crossing Carina. Our findings from the previous section support a local origin for the bulk of approaching/receding line emission, from a few discrete expanding shells of gas surrounding the most massive stars. In order to place these findings in the appropriate context, we refer to the larger scale images in Smith & Brooks (2007), and their Fig. 5b in particular, showing an Hα/[O III] flux-ratio image. This figure suggests strongly that the entire Carina nebula is composed of a collection of shells and cavities, of projected sizes in the range 15−60 arcmin and therefore much larger than the shells found in this work. Both Trumpler 14 and 16 are found in the northern lobe of a bipolar cavity (see also Smith et al. 2000), apparently split in two by the dark dust lanes. The same image does not show smaller scale subshells corresponding to those we describe in the previous section (all falling in the same northern lobe of the bipolar cavity). To reconcile our results with the larger scale gas bubbles, we hypothesize that our shells have already started to merge together, producing the larger structures of the bipolar cavity. This structure, with each of its lobes having an asymmetrical shape, must also have a very complex velocity field according to Meaburn et al. (1984), who noted that a spherically expanding nebula would not fit their dynamical data. Our data do not show any velocity component clearly associated with the post-merging expansion whose velocity might be close to the dominant shell’s approaching/receding velocity or even very different but undetected because of the much lower intensity of its emission (which might have remained hidden within the complex fit residuals shown in Fig. 17).
Another important result from the data presented is the existence of significant gradients, typically with plane-parallel geometries rather than spherical geometries. In addition, the mentioned “shells” develop along preferred directions rather than along a radial direction; they should be called “cylinders”, although the physical mechanism leading to this type of expansion geometry is not easy to understand. The nitrogen ionization fraction also shows significant gradients; in the η Car shell they are explained by a polar-angle dependence of the ionizing flux incident on the Nebula. In general, two preferred directions appear to be those of the two obscuring dust lanes. In addition to this dark material, other layers of “invisible” material were also shown to exist. One example is the massive (and perhaps neutral) layer moving at RV ~ −10 km s-1 against which part of the Tr 14 shell appears to have collided; another example is the neutral material moving at RV ~ −100 to 0 km s-1, causing the known interstellar absorption lines towards Carina stars. The complexity of observed structures in the studied region is such that there are no truly representative “average” conditions that hold to a good approximation everywhere in the region. In order to put other studies (e.g. on the stellar populations of clusters Tr 14 and 16) into a proper context, a careful consideration of local conditions is essential.
5. Summary
We studied the profiles of optical emission lines of Hα, [N II], [S II], and He I on more than 650 sightlines in the central part of the Carina nebula. We recover the known double-peaked line profiles in all lines, and through Gaussian fits to the lines we also show that single-peaked lines actually arise from two distinct components, approaching and receding gas. The main properties of the gas yielding the bulk nebular emission are the following:
-
The motion of gas in the central20′ × 20′ of the Carina nebula indicates that there are several distinct expanding shells centered on η Car, Tr 14, WR25, and possibly the O3 star HD 93250.
-
The shape of these shells is non-spherical, with preferential directions for expansion that are related to the geometry of the dark obscuring dust lanes and abrupt distortions likely caused by collisions with higher-density material; traces of collisions between adjacent shells are also found.
-
Hα emitting gas is basically the same as He I emitting gas, while significant kinematical differences are found with respect to gas emitting in the forbidden lines.
-
The gas temperature is found to be ~104 K from line-width ratios of H and He, and slightly hotter in the approaching component.
-
Gas densities were derived from the [S II] doublet ratio, and found in the range 200−300 cm-3, increasing towards the inner parts of the Nebula and near inter-shell boundaries.
-
The N ionization fraction is found to increase systematically towards the south in the approaching component, with an almost opposite trend for the receding component. In the η Car shell, this varying ionization is shown to be correlated with angular distance from the Homunculus polar axis.
-
Within a small sample of sky directions, the differential Balmer decrement between approaching and receding gas indicates a very low extinction. Therefore, dust causing the occasionally high measured extinction must be located either in front of or behind the shells observed in Hα (and stars contained within them), but not inside the shells.
-
The shell sizes and expansion velocities imply short timescales of ~ 1.5 × 105 yr for the ionized gas.
We note that the observational data presented here were not originally taken with the purpose of studying the nebular emission. According to the Gaia-ESO Survey observing strategy, a number of fibers are routinely targeted at empty sky positions in order to eliminate the sky contribution from the stellar spectra. This study demonstrates the rich scientific content of the Gaia-ESO Survey data, even surpassing their intended objectives.
The typical peak Hα brightness in classical T Tauri stars rarely (if ever) exceeds 10 times the star continuum level (see, e.g., Cohen & Kuhi 1979). Moreover, most member stars in Carina are expected to be weak-line T Tauri from their weak near-IR excesses (Albacete-Colombo et al. 2008), and therefore have still weaker Hα emission.
Acknowledgments
We wish to thank an anonymous referee for the helpful suggestions. This research is based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under programme ID 188.B-3002. These data products have been processed by the Cambridge Astronomy Survey Unit (CASU) at the Institute of Astronomy, University of Cambridge, and by the FLAMES/UVES reduction team at INAF/Osservatorio Astrofisico di Arcetri. These data have been obtained from the Gaia-ESO Survey Data Archive, prepared and hosted by the Wide Field Astronomy Unit, Institute for Astronomy, University of Edinburgh, which is funded by the UK Science and Technology Facilities Council. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’Istruzione, dell’Università e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the European Science Foundation through the GREAT Research Network Programme. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Albacete-Colombo, J. F., Damiani, F., Micela, G., Sciortino, S., & Harnden, F. R., Jr. 2008, A&A, 490, 1055 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boumis, P., Meaburn, J., Bryce, M., & Lopez, J. A. 1998, MNRAS, 294, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, M., & Kuhi, L. V. 1979, ApJS, 41, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., & Humphreys, R. M. 1997, ARA&A, 35, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Davidson, K., Smith, N., Gull, T. R., Ishibashi, K., & Hillier, D. J. 2001, AJ, 121, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Deharveng, L., & Maucherat, M. 1975, A&A, 41, 27 [NASA ADS] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Haffner, L. M., Dettmar, R.-J., Beckman, J. E., et al. 2009, Rev. Mod. Phys., 81, 969 [NASA ADS] [CrossRef] [Google Scholar]
- Hartigan, P., Morse, J. A., Tumlinson, J., Raymond, J., & Heathcote, S. 1999, ApJ, 512, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & Burkhart, B. 2016, MNRAS, 458, 1671 [NASA ADS] [CrossRef] [Google Scholar]
- Lopez, J. A., & Meaburn, J. 1984, Rev. Mexicana Astron. Astrofis., 9, 119 [NASA ADS] [Google Scholar]
- Meaburn, J., Lopez, J. A., & Keir, D. 1984, MNRAS, 211, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd. edn. (Sausalito, CA: University Science Books) [Google Scholar]
- Pasquini, L., Avila, G., Blecha, A., et al. 2002, The Messenger, 110, 1 [NASA ADS] [Google Scholar]
- Povich, M. S., Smith, N., Majewski, S. R., et al. 2011, ApJS, 194, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Randich, S., Gilmore, G., & Gaia-ESO Consortium 2013, The Messenger, 154, 47 [NASA ADS] [Google Scholar]
- Riesgo, H., & López, J. A. 2006, Rev. Mexicana Astron. Astrofis., 42, 47 [Google Scholar]
- Sabbadin, F., Minello, S., & Bianchini, A. 1977, A&A, 60, 147 [NASA ADS] [Google Scholar]
- Seward, F. D., Forman, W. R., Giacconi, R., et al. 1979, ApJ, 234, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N. 2006, ApJ, 644, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., & Brooks, K. J. 2007, MNRAS, 379, 1279 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., & Brooks, K. J. 2008, Handbook of Star Forming Regions, Vol. II, 138 [Google Scholar]
- Smith, N., Egan, M. P., Carey, S., et al. 2000, ApJ, 532, L145 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Smith, N., Bally, J., & Brooks, K. J. 2004, AJ, 127, 2793 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, N., Stassun, K. G., & Bally, J. 2005, AJ, 129, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Townsley, L. K., Broos, P. S., Chu, Y.-H., et al. 2011, ApJS, 194, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Viironen, K., Delgado-Inglada, G., Mampaso, A., Magrini, L., & Corradi, R. L. M. 2007, MNRAS, 381, 1719 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1973, ApJ, 179, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., & Hesser, J. E. 1975, ApJ, 199, 535 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., & Liller, M. H. 1977, ApJ, 211, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Danks, A. C., Vieira, G., & Landsman, W. B. 2002, ApJS, 140, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R., Smith, N., Howarth, I. D., et al. 2007, PASP, 119, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1953, General Catalogue of Stellar Radial Velocities (Carnegie Institute Washington D.C. Publication) [Google Scholar]
- Wolk, S. J., Broos, P. S., Getman, K. V., et al. 2011, ApJS, 194, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Yonekura, Y., Asayama, S., Kimura, K., et al. 2005, ApJ, 634, 476 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Giraffe/HR15N instrumental line profile
In Sect. 3.2 we examined best-fit residuals with amplitudes of 1−2% with respect to peak emission. Our ability to draw meaningful conclusions from such low-level features (in relative terms) in our data requires some detailed understanding of the instrumental response. We therefore examined Th–Ar calibration lamp spectra that are nearly simultaneous to some of the data studied here. These spectra are crowded in lines, and therefore only very few lines were isolated and bright enough to study their extreme tails down to less than 1% of peak. One such example is shown in Fig. A.1, where the abscissa Δλ is transformed into a velocity scale to facilitate comparison with the results in Sect. 3.2. In the same figure we show one-Gaussian (red) and two-Gaussian (blue) best-fit models to the lamp line profile, and their residuals. The one-Gaussian model is discrepant from the observed line profile at a level of 3−4% maximum. The two-Gaussian model residuals are much smaller, slightly exceeding 1% discrepancy. The profile obtained by convolving the lamp profile with a Gaussian with σ = 10 km s-1 (e.g., a typical turbulent or thermal width), however, yields residuals of only 1% when fitted with only one Gaussian. At face value, this would suggest that by approximating the instrumental spectral response with a simple Gaussian we should expect spurious fit residuals on the order of 1% of peak emission. However, in Fig. 17 we observe that the oscillating residuals around zero velocity often exceed the 1% level (indicated by the horizontal dashed lines), and show a typical peak-to-peak RV interval of ~30−40 km s-1, while the residual oscillations in Fig. A.1 occur at the 1−2 pixel level (RV intervals ~4−8 km s-1). The latter property would especially indicate that the nebular fit residuals are unrelated to the non-Gaussianity of the instrumental line profile.
To clarify the problem more accurately, we considered the above two-Gaussian model for the lamp line profile as the basis for our nebular-line fitting procedure. The normalized lamp line profile was modeled using two Gaussians as 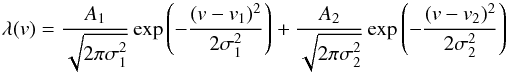 (A.1)with the best-fit parameter values v1 = −6.404371 km s-1, σ1 = 6.44256 km s-1, A1 = 0.3966431, v2 = 3.454723 km s-1, σ2 = 6.069641 km s-1, and A2 = 0.6033569.
(A.1)with the best-fit parameter values v1 = −6.404371 km s-1, σ1 = 6.44256 km s-1, A1 = 0.3966431, v2 = 3.454723 km s-1, σ2 = 6.069641 km s-1, and A2 = 0.6033569.
The convolution of λ(v) with a Gaussian was then used in place of a simple Gaussian as the basic ingredient of our two-component nebular-line fits, as in Sect. 3.1. The fit residuals were then computed as in Sect. 3.2. In this way we obtained residual patterns that are almost indistinguishable from those shown in Fig. 17. We conclude that all systematic peculiarities found in the residuals in Fig. 17, discussed in Sect. 3.2, do not arise because of instrumental effects, but reflect actual properties of the nebular lines.
 |
Fig. A.1 Giraffe HR15N Th–Ar lamp line (black), and best-fit one-Gaussian (red) and two-Gaussian (blue) models. To facilitate comparison with earlier results the abscissa is shown on a velocity scale. Best-fit residuals, scaled up three times, are shown in green and orange for the one- and two-Gaussian models, respectively. The vertical dashed gray lines correspond to those shown in Fig. 17; the horizontal dotted lines indicate amplitudes in the residuals of ± 1% of peak, like the horizontal lines in Fig. 17. |
All Tables
All Figures
 |
Fig. 1 DSS1 image of the central part of the Carina nebula, of size 26′ × 26′, corresponding to 17.4 pc per side at the Nebula distance of 2.3 kpc. North is up and east is to the left. Red circles indicate positions of sky fibers, using Giraffe setup HR15N. Orange circles indicate fibers on faint stars, using HR15N. Blue circles are sky fibers, using setup HR14A. Light green circles are UVES sky fibers. Big dark green circles indicate the approximate positions of clusters studied here and the Keyhole nebula. The dark green arrow indicates the star η Car. |
| In the text | |
 |
Fig. 2 Example of typical sky spectrum in Carina obtained with the Giraffe HR15N setup. Prominent nebular lines are labeled. |
| In the text | |
 |
Fig. 3 Line profiles at Hα (red), [N II] 6548 (blue) and 6584 Å (black), and He I (magenta) for various positions across the Nebula. Also shown are two-Gaussian best fits for Hα (orange), [N II] 6584 Å (cyan), and He I (purple). The lines shown are scaled by the indicated factors for ease of comparison with Hα. Indicated radial velocities are heliocentric. |
| In the text | |
 |
Fig. 4 Radial velocity of the receding component vs. RV of the approaching component. Here the black dots refer to pure-sky fibers from the HR15N setup, blue dots to pure-sky from the HR14A setup, and gray dots to sky lines from faint stars. The orange circles represent the average RV of low-mass cluster stars. The dashed line is the expected locus for purely spherical expansion. A subsample of apparently peculiar datapoints is highlighted using “+” symbols. |
| In the text | |
 |
Fig. 5 Normalizations of best-fit Gaussians for the receding vs. approaching components. The dashed line represents identity. Other symbols as in Fig. 4. |
| In the text | |
 |
Fig. 6 Examples of Hβ (red) and Hα (black) lines from pure-sky fibers using UVES. A vertical shift was applied to spectra from different sky positions. The Hβ lines were scaled up by a factor of 7. |
| In the text | |
 |
Fig. 7 Radial velocity from the He I 6678 Å line vs. RV from Hα. Red (blue) symbols refer to the receding (approaching) component from HR15N data. Purple (pink) symbols refer to the same two components, but from HR14A pure-sky fibers. Plus symbols refer to zero-velocity gas as in previous figures. The dashed line represents identity. |
| In the text | |
 |
Fig. 8 Fit normalization for He I vs. normalization for Hα. Symbols as in Fig. 7. The dashed line indicates a constant ratio of 1/90. |
| In the text | |
 |
Fig. 9 Gaussian widths σ of He I lines vs. those of Hα. The three dotted lines represent loci of constant gas temperature Tgas = 5000,10 000,15 000 from top to bottom. The dashed line represents equality. Symbols as in Fig. 7. Only datapoints with the same RV from Hα and He I within 3 km s-1 are shown. |
| In the text | |
 |
Fig. 10 Radial velocity from the [N II] 6584 Å line vs. RV from Hα. Symbols as in Fig. 7. |
| In the text | |
 |
Fig. 11 Fit normalization for [N II] vs. normalization for Hα. The dashed line indicates a constant ratio of 1/8. Other symbols as in Fig. 10. |
| In the text | |
 |
Fig. 12 Radial velocity from the [S II] 6717 Å line vs. RV from Hα. Red (blue) symbols refer to the receding (approaching) component from HR15N data. Cyan (orange) symbols refer to the same two components, but from HR15N observations of faint stars. Other symbols as in Fig. 7. |
| In the text | |
 |
Fig. 13 Radial velocity from the [S II] 6717 Å line vs. RV from [N II] 6584 Å. Symbols as in Fig. 7. |
| In the text | |
 |
Fig. 14 Fit normalization of [N II] 6584 Å vs. [S II] 6731 Å. Symbols as in Fig. 7. |
| In the text | |
 |
Fig. 15 Gaussian width ratio between Hα and He I (proxy for temperature) vs. normalization ratio between [S II] 6717/6731 Å (proxy for density). Temperature increases upwards, while density increases towards the left. Symbols are as in Fig. 7. The red (blue) vertical dashed line indicates the median [S II] 6717/6731 Å ratio for the receding (approaching) components. On average, the receding component has higher density and lower temperature than the approaching component. |
| In the text | |
 |
Fig. 16 Intensity ratio between [S II] 6717 Å and 6731 Å lines vs. intensity of [S II] 6731 Å. Symbols as in Fig. 12. The dashed line at unity ratio corresponds to electron density Ne ~ 600 cm-3. |
| In the text | |
 |
Fig. 17 Examples of low-intensity components in the lines, as residuals from the Gaussian best fits to the main components of Hα (orange), He I 6678 (green), [S II] 6717 Å (blue) and 6731 Å (red). The He I residuals are scaled up by a factor of 10, and those of [S II] by a factor of 3. Black vertical dashed lines indicate the RVs of the two main Gaussian components. Gray dashed lines indicate the adopted boundaries to define the wide and narrow Hα wings, all centered at RV =−12.5 km s-1. Indicated radial velocities are heliocentric. The emission features in the Hα profiles at RV ~−420 and ~ + 280 km s-1 originate from terrestrial airglow. In the plotted units, Hα peak emission before best-fit subtraction is for each panel respectively equal to 124 300 (panel a)), 27 800 b), 426 700 c), 182 600 d), 224 200 e), 50 200 f), 111 300 g), and 98 300 h). Intensity levels of ± 1% of peak emission are indicated in each panel by horizontal dashed lines. |
| In the text | |
 |
Fig. 18 Selection of UVES spectra of η Car in the Hα (black) and He I 6678 lines (green) for the years 2002−2004, as indicated above each spectrum. Spectra are continuum-subtracted and shifted vertically for clarity. The He I line amplitude was enlarged 10 times to facilitate comparison with Hα. Vertical dashed gray lines indicate the same velocities as in Fig. 17. |
| In the text | |
 |
Fig. 19 Sky continuum vs. total intensity in the wide Hα wings. Small dots refer to pure-sky fibers from setups HR15N (black) and HR14A (blue), while big red dots are the downscaled continuum and wide wings of η Car. The dashed line is a constant factor of 4 × 10-4. |
| In the text | |
 |
Fig. 20 Intensity of red vs. blue wide Hα wings. Datapoints from pure-sky fibers of HR15N (black) and HR14A (blue) setups. The dashed line is identity. The big red dots indicate the wide wings in the η Car spectra. |
| In the text | |
 |
Fig. 21 Ratio of red to blue wide Hα wing intensities, in the vicinity of η Car vs. radial distance. Symbols as in Fig. 20. |
| In the text | |
 |
Fig. 22 Intensity of high-velocity components in the [S II] 6717 Å line vs. those in the [S II] 6731 Å line. The dashed line is identity. The average ratio, higher than one, indicates low densities. Symbols as in Fig. 10. |
| In the text | |
 |
Fig. 23 Spatial map of Hα line intensity (fit normalization). The radius of each circle is proportional to intensity. Blue (cyan, purple) circles refer to the approaching component, while red (orange, pink) circles refer to the receding component. The circles are color-coded as in Figs. 7 and 12. The oblique dashed lines outline the edges of the absorption lanes visible in Fig. 1. Crosses indicate the positions of O/WR stars from Walborn (1973). The large black circles indicate the positions of Trumpler 14 (upper), η Car (middle left), and the Wolf-Rayet star WR25 (middle right). The green “+” symbols indicate the positions of zero-velocity gas (see Fig. 4). |
| In the text | |
 |
Fig. 24 Map of RV of approaching and receding gas. Symbols as in Fig. 23. Circle size is proportional to | RV−RVcm |, with the largest circle corresponding to | RV−RVcm | = 42.6 km s-1. |
| In the text | |
 |
Fig. 25 Map of the distribution of intensity in the wide Hα wings (gray) and sky continuum emission (green). Circle size is proportional to intensity. Darker gray circles indicate data from pure-sky fibers using HR14A setup. Thick circles and crosses have the same meaning as in Fig. 23. The large gray circle closest to the center indicates the very intense Hα wings in the direction of the Keyhole Nebula. |
| In the text | |
 |
Fig. 26 Map of the intensity ratio [N II] 6584 Å/Hα. Symbols as in Fig. 23, except for the cyan/orange data from faint stars, which are not used here. Circle size is proportional to ratio; the largest circle corresponds to a value of 2.4. |
| In the text | |
 |
Fig. 27 Map of the intensity ratio between [S II] 6731/6717 Å, increasing with density. Symbols as in Fig. 23. The largest circle corresponds to a ratio of 0.65. We note the high values of this ratio near the Keyhole Nebula, ~3 arcmin NW of η Car. |
| In the text | |
 |
Fig. 28 Map of intensities of emission in the far wings of [S II] 6717. Symbols as in Fig. 23. |
| In the text | |
 |
Fig. 29 Position-velocity diagram for Hα in the neighborhood of Trumpler 14. Circle size is proportional to line intensity. Color codes as in Fig. 4. The distance origin is taken at the Trumpler 14 position indicated with the large black circle in the upper right of Fig. 23. Positive distances are towards the SW; the dark lane lies at position ~ + 3 arcmin. The direction of the observer is towards the bottom at negative RVs. |
| In the text | |
 |
Fig. 30 Same as Fig. 29, except that circle size is proportional to line width σ. |
| In the text | |
 |
Fig. 31 Same as Fig. 29, but using the [N II] 6584 Å line. |
| In the text | |
 |
Fig. 32 Same as Fig. 29, but centered on η Car. Positive distances are in the NW direction from η Car. The Keyhole Nebula lies at position ~+3 arcmin. |
| In the text | |
 |
Fig. 33 Same as Fig. 32, except that circle size is proportional to line width σ. |
| In the text | |
 |
Fig. 34 Reconstructed geometry of the η Car shell. Bottom left axis indicates distances parallel (normal) to the plane of sky. Top and right axes indicate the original measurements, as in Fig. 32, and the symbols are also the same, except that here circle size is proportional to the Hα/[N II] intensity ratio. The brown double-lobe structure near the center represents the position and actual inclination of the Homunculus Nebula (size is not to scale). The horizontal dashed line, which defines angle θ = 0, is parallel to the sky plane; the oblique line indicates the Homunculus polar axis. |
| In the text | |
 |
Fig. 35 Intensity ratio Hα/[N II] vs. azimuthal angle θ, defined in Fig. 34. Symbols as in Fig. 5. Vertical dashed lines indicate the projections of the Homunculus polar axis. |
| In the text | |
 |
Fig. 36 Same as Fig. 32, except that circle size is proportional to the [S II] 6731/6717 intensity ratio. |
| In the text | |
 |
Fig. 37 Same as Fig. 29, but centered on WR25. |
| In the text | |
 |
Fig. 38 Same as Fig. 37, except that circle size is proportional to line width σ. |
| In the text | |
 |
Fig. 39 Same as Fig. 37, but now using the [S II] 6731 Å intensity. |
| In the text | |
 |
Fig. 40 Intensity ratios Hα/[N II] vs. Hα/[S II]. Symbols are as in Fig. 7. Tiny dots indicate measurements where the absolute RV difference between Hα and [N II], or Hα and [S II], is larger than 3 km s-1. Black lines/polygons indicate typical loci of supernova remnants (SNR), planetary nebulae (PNe), and Galactic HII regions (H II), as labeled. The green line grid is part of the cloudy model grid shown in Viironen et al. (2007) over a range of O/H abundances and ionization parameters q, as labeled. |
| In the text | |
 |
Fig. 41 [S II] λλ 6717/6731 intensity ratio vs. Hα/[S II] ratio. Circles refer to intensity ratios in the narrow wings of [S II] and Hα, when present (violet: approaching component; purple: receding component). Other symbols are as in Fig. 12. Solid lines/polygons indicate SNR, H II, and PNe loci as in Fig. 40. Dashed horizontal lines enclose the range where the [S II] 6717/6731 ratio is a useful measure of density (increasing from top to bottom). |
| In the text | |
 |
Fig. A.1 Giraffe HR15N Th–Ar lamp line (black), and best-fit one-Gaussian (red) and two-Gaussian (blue) models. To facilitate comparison with earlier results the abscissa is shown on a velocity scale. Best-fit residuals, scaled up three times, are shown in green and orange for the one- and two-Gaussian models, respectively. The vertical dashed gray lines correspond to those shown in Fig. 17; the horizontal dotted lines indicate amplitudes in the residuals of ± 1% of peak, like the horizontal lines in Fig. 17. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.