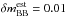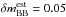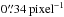| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A66 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201526378 | |
| Published online | 12 May 2016 | |
Method for improving line flux and redshift measurements with narrowband filters
1
Dark Cosmology Centre, Niels Bohr Institute, University of
Copenhagen,
Juliane Maries Vej 30,
2100
Copenhagen Ø,
Denmark
e-mail:
johannes@dark-cosmology.dk
2
European Southern Observatory, Karl-Schwarzschild-Straße 2, 85748
Garching bei München,
Germany
3
Aix-Marseille Université, CNRS, LAM (Laboratoire d’Astrophysique
de Marseille) UMR 7326, 13388
Marseille,
France
Received: 22 April 2015
Accepted: 15 February 2016
Context. High redshift star-forming galaxies are discovered routinely because of a flux excess in narrowband filters caused by an emission line. In most cases, the width of such filters is broader than typical line widths, and the throughput of the filters varies substantially within the bandpass. This leads to substantial uncertainties in redshifts and fluxes that are derived from the observations with one specific narrowband filter.
Aims. The uncertainty in measured line parameters can be sharply reduced by using repeated observations of the same target field with filters that have overlapping passbands but differ slightly in central wavelength or wavelength dependence of the effective filter curve. Such data are routinely collected with some large field imaging cameras that use multiple detectors and a separate filter for each of the detectors. An example is the European Southern Observatory’s VISTA InfraRed CAMera (VIRCAM).
Methods. We developed a method of determining more accurate redshift and line flux estimates from the ratio of apparent fluxes measured from observations in different narrowband filters and several matching broadband filters. A parameterized model of the line and continuum flux is used to predict the flux ratios as a function of redshift based on the known filter curves. These model predictions are then used to determine the most likely redshift and line flux.
Results. We tested the obtainable quality of parameter estimation for the example of Hα in the VIRCAM NB118 filters both on simulated and actual observations where the latter were based on the UltraVISTA DR2 data set. We combined the narrowband data with deep broadband data in Y, J, and H. We find that with this method, the errors in the measured lines fluxes can be reduced up to almost an order of magnitude.
Conclusions. We conclude that existing narrowband data can be used to derive accurate line fluxes if the observations include images taken with sufficiently different filter curves. For the UltraVISTA survey, the best-suited narrowband filter combinations allow an accuracy in wavelength of better than 1 nm and in flux of better than 15% at any redshift within the bandpass of the filters. In contrast, analyzing the data without exploiting the difference in filter curves leads to an uncertainty in wavelength of 10 nm and up to an order of magnitude errors in line flux estimates.
Key words: methods: observational / techniques: photometric / galaxies: photometry / galaxies: distances and redshifts / galaxies: star formation / galaxies: high-redshift
© ESO, 2016
1. Introduction
As the key signature in the spectra of star-forming galaxies, strong emission lines are important tools. The hydrogen Balmer lines are useful for determining the instantaneous star formation rate (SFR), because their strength is directly proportional to the SFR after correcting for dust (e.g., Kennicutt 1998). Other strong emission lines, like [ O ii ] λ3727, are less accurate SFR indicators owing to their metallicity dependence (Moustakas et al. 2006; Kewley et al. 2004), but certain ratios between these lines and the metallicity-independent Balmer lines can be gauged as proxies for the gas-phase metallicity (e.g., Pagel et al. 1979; Kewley & Dopita 2002).
Wide-field surveys with narrowband (NB) filters provide large line-flux-limited samples down to low equivalent widths at well-defined redshifts. The idea behind the NB selection is to identify objects through an excess of the filter-averaged NB flux density over the underlying continuum flux density, with the latter inferred from one or more suitable broadband (BB) filters (e.g., Djorgovski et al. 1985; Møller & Warren 1993; Pascual et al. 2007). When the NB observations are in a field with extensive multiwavelength data, photometric redshifts can be used to distinguish between the different lines that could be the cause of the NB excess (e.g., in the COSMOS field: Ilbert et al. 2013; Muzzin et al. 2013).
A vast number of NB surveys have been performed that target Hα, [O ii], and Lyα at different redshifts. While many studies have been using observed-frame optical NB filters (e.g., Fujita et al. 2003; Dale et al. 2010; Takahashi et al. 2007; Ly et al. 2012; Rhoads et al. 2000; Ouchi et al. 2003; Nilsson et al. 2007), currently a strong focus is put on exploiting the airglow windows in the near-infrared (NIR; e.g., Best et al. 2013; Ly et al. 2011; Kochiashvili et al. 2015). This is essential for high redshifts, since the important rest-frame optical lines shift into this wavelength regime. Among the deepest wide-field NIR surveys are the NB118 observation by Milvang-Jensen et al. (2013) and the NB118 part of UltraVISTA (Ultra Deep Survey with VISTA; McCracken et al. 2012), both of which are performed with the near-infrared camera VIRCAM (VISTA InfraRed CAMera, Dalton et al. 2006) at ESO’s 4.1 m survey telescope, VISTA (Visible and Infrared Survey Telescope for Astronomy, Emerson et al. 2006).
All these observational efforts are eventually used to estimate line fluxes from the measured NB excesses and, with the knowledge of the redshift, line luminosities. Obtaining these for large samples of galaxies at well-defined redshifts allows important insights into galaxy evolution, such as by means of determining Hα luminosity functions, which can be converted to SFR densities. Understanding can also be gained by relating other properties like galaxy mass, environment, and spatial clustering to the line luminosities (Sobral et al. 2010, 2011), and line-based SFR estimates might be compared to SFR estimates obtained by other means, allowing the galaxies’ star formation histories to be characterized (Domínguez et al. 2015).
Unfortunately, line flux measurements obtained from NB filters can have substantial uncertainties. Since the transmittance curves are often far from flat, a flux measured in the filter is consistent with a range of intrinsic line fluxes. While it is in many cases possible to overcome this problem to some extent by statistical means for sample-based statistics, other applications like identification of high redshift candidates need the best possible flux determination for individual objects.
In this paper we discuss a method that both overcomes this flux measurement problem and at the same time allows for wavelength resolution that is an order of magnitude below the NB width. This can be achieved by using slightly different filters, which allow the degeneracy between central wavelength and line flux to be broken. Hayashi et al. (2014) recently used redshift estimates from Subaru/Suprime-Cam imaging with two different NB filters. In this paper, we formalize and generalize this approach to include several NB filters in the emission line measurement and exploit information from broadband imaging to further constrain the redshift model. As strong emission lines cause a flux excess even in wide filters (e.g., Guiderdoni & Rocca-Volmerange 1987; Zackrisson et al. 2001; Schaerer & de Barros 2009; Shivaei et al. 2015), broadband photometry contains very useful additional information. In the following, we refer to our method as the throughput-variations method (TPV).
We investigate the method carefully for the VISTA NB118 filters with a special focus on Hα, both with simulations and applications to data. In VIRCAM, there is one individual copy of the NB118 filters above each of its 16 non-contiguous detectors. Although produced to be as similar as possible, the transmittance curves of the individual filters are unavoidably slightly different from each other, so are useful for the proposed TPV. The extremely deep and homogeneous BB data also available from the UltraVISTA survey are well suited to constraining the continuum and to measuring the broadband excess.
The paper is organized as follows. In Sect. 2, we explain the throughput-variations method (TPV). After describing estimation algorithm and estimation model in Sect. 3, we test usefulness and caveats of the technique based on simulations, which emulate UltraVISTA DR2 observations of Hα emitters (Sect. 4). An application of the method to actual UltraVISTA DR2 data is presented in Sect. 5. Finally, we discuss a possible modification to the UltraVISTA NB118 observing pattern for the purpose of the TPV (Sect. 5.9).
Where needed, a (flat) standard ΛCDM cosmology with H0 = 70km s-1 Mpc-1, Ωm,0 = 0.3, and ΩΛ,0 = 0.7 was assumed. Furthermore, we used AB-magnitudes throughout this paper (Oke 1974). All numbers referring to specific VISTA NB118 filters are in line with the standard VISTA detector (filter) numbering scheme (cf. Ivanov & Szeifert 2009; Milvang-Jensen et al. 2013).
All stated wavelengths are in vacuum, except when we use common identifiers like [O iii]λ5007, which are based on wavelengths in air.
All assumed VISTA/VIRCAM filter curves include quantum efficiency and mirror reflectivities, and the broadband filters curves include in addition an atmosphere with PWV = 1mm at airmass 1. For the broadband filters, Y, J, and H, we used the same filter curve for all 16 detectors, as available from the ESO webpage1. Details about the individual NB118 filter curves are given in Appendix A. Parts of the field covered by NB118 observations include data from a single filter/detector, while other parts include data from two filters (cf. Sect. 5.1). Throughout this paper we refer to “combined effective filters”, which are the effective filter responses, if data from two similar filters are combined into a single stack.
2. Method
2.1. Estimating line fluxes from NB observations
 |
Fig. 1 Illustration of how to obtain accurate line fluxes by using two NB filters. The left panel shows the throughput curves of two similar NB filters, superimposed on an emission line shifted to different wavelengths. The righthand panel shows the corresponding differences between the magnitudes measured with the two filters, Δmag, as a function of the wavelength of the emission line, λ0. Here, the green dashed lines indicate how a measurement of Δmag can be used to determine the wavelength of the line, which in turn can be used to estimate its flux using the throughput curves on the left. The shown filter combination is the filter pair 14 and 15 of the NB118 filters, where 15 is the bluer one. The meaning of the small arrows is described in Sect. 4.3.1 and the two vertical lines in Appendix B. |
Narrowband surveys, which aim at identifying emission line galaxies and measure their line fluxes, typically use one NB filter in combination with one or two broadband (BB) filters at wavelengths that are similar to the NB. In the simplest case, the NB passband is at the center of a BB passband, minimizing the impact of a sloped continuum. Then, a BB − NB> 0 indicates the presence of an emission line, because the impact of a line on the filter-averaged flux density is significantly larger in the narrower filter.
When relating the measured magnitudes to an emission line, it is useful to describe the line spectrum through the line’s flux f0, its observed-frame equivalent width EWobs, and its central wavelength λ0, or equivalently its redshift. Using these three quantities, the object’s spectrum can be written as2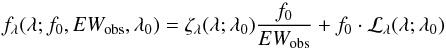 (1)where ζλ(λ) is the dimensionless spectral shape of the continuum, ℒλ(λ) the emission line spectrum in units of nm-1, ζλ(λ) is normalized at the wavelength of the relevant line, and ℒλ(λ) can include additional lines, but it is scaled so that the integral over the relevant line is one. Here, fλ is related to the observed magnitudes through (e.g., Buser 1986):
(1)where ζλ(λ) is the dimensionless spectral shape of the continuum, ℒλ(λ) the emission line spectrum in units of nm-1, ζλ(λ) is normalized at the wavelength of the relevant line, and ℒλ(λ) can include additional lines, but it is scaled so that the integral over the relevant line is one. Here, fλ is related to the observed magnitudes through (e.g., Buser 1986): 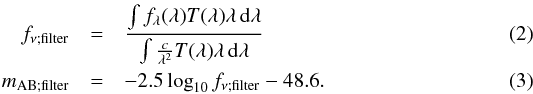 However, there is a problem when trying to estimate line fluxes from a single NB observation because the observed flux depends on the wavelength of the line. This problem can be understood from the lefthand panel of Fig. 1 for the hypothetical example of a line without continuum. It is not possible to constrain both f0 and λ0, leading to order-of-magnitude uncertainties on the flux measurement. Furthermore, the accuracy of the central wavelength estimation is limited to “somewhere within the passband”. Therefore, the redshift accuracy of typical 1% NB filters is not always much improvement over the precision of state-of-the art photometric redshifts.
However, there is a problem when trying to estimate line fluxes from a single NB observation because the observed flux depends on the wavelength of the line. This problem can be understood from the lefthand panel of Fig. 1 for the hypothetical example of a line without continuum. It is not possible to constrain both f0 and λ0, leading to order-of-magnitude uncertainties on the flux measurement. Furthermore, the accuracy of the central wavelength estimation is limited to “somewhere within the passband”. Therefore, the redshift accuracy of typical 1% NB filters is not always much improvement over the precision of state-of-the art photometric redshifts.
Only if the NB filter’s passband was top hat and if it was wider than the typical line width could the precise value of λ0 be ignored for the flux estimation. Effective top-hat filters are, however, physically impossible in the fast convergent beams of large survey telescopes, such as VISTA, CFHT, and UKIRT (cf. also Appendix A).
2.2. Observations with several NB filters
One way to solve the problem described in Sect. 2.1 is to use observations in at least two NBs that slightly differ from each other. Then, two magnitude equations (Eq. (3)) are available for determining the two unknowns, f0 and λ0. The first, f0, can be eliminated from the equation, which can subsequently be numerically solved for λ0 as a function of the measured magnitude difference between the two filters, Δmag, as illustrated in Fig. 1.
With a well-matched pair of NB filters, it is possible to determine the wavelength of a line very accurately within the range of wavelengths covered by the passband of the NB filter. Suitable filter pairs are those that result in Δmag – λ0 relations that are monotonous and steep, allowing for a good wavelength resolution, even when considering realistic uncertainties in Δmag.
By means of such Δmag – λ0 curves, we characterized the suitability of the various combinations between the 16 UltraVISTA NB118 filters for our method to determine the line fluxes from two filters. As discussed in more detail in Sect. 5.1, for 12 out of the 120 theoretically possible combinations of these 16 filters, observations become directly available as part of the standard UltraVISTA observations. One of these combinations is 14 and 15, which was used for illustration in Fig. 1.
While this specific pair is very well suited to the method, not all the possible NB118 combinations are so in the same way. In Fig. 2 four more of the 12 relevant NB118 combinations are shown, where 15 and 16 is as good, and 9 and 10 almost as good as 14 and 15. The two filters 7 and 8 are too similar to be useful for the presented method, whereas some information is still contained in the Δmag − λ0 curve of 11 and 12. A quantitative characterization of the Δmag − λ0 curves for all 120 combinations is given in Appendix B.
 |
Fig. 2 Δmag – λ0 curves for five different NB118 combinations assuming an infinite EWobs emission line. The passbands of the respective NB118 filters, for which the Δmag – λ0 are shown, are also indicated in the different panels. The axis scaling for the filter passbands is linear. |
2.3. Continuum estimation
In Sect. 2.2, we discussed the throughput variation method neglecting the continuum. But the continuum contributes significantly to the flux in NB filters for typical emission line galaxies. As a result, the magnitude differences measured for emission lines with the same f0 and λ0 also depend on the equivalent width, EWobs.
A measurement of the contribution of the continuum to the NB fluxes is required; consequently, continuum-corrected NB magnitudes can be used to estimate f0 and λ0 from the Δmag − λ0 curves for infinite EWobs. An accurate continuum estimate at the wavelength of the NB filter could be obtained from measurements in additional narrowband or mediumband filters bracketing the main NB filter. More typically, however, BB filters are used. This is mainly for reasons of time and cost efficiency. If a BB that has a passband covering the emission line is included in the estimation, f0, λ0, and EWobs need to be estimated simultaneously, and the Δmag − λ0 curves cannot be used directly. We describe a statistical approach of fitting the parameters in the next section.
3. Estimation algorithm
3.1. Concept
As explained in Sect. 2.2, Δmag – λ0 curves allow quick insight into the suitability of a specific filter combination for the throughput variation methods (TPV). In this section, we describe how to infer central wavelength λ0, line flux f0, and equivalent width EWobs simultaneously using a statistical approach.
From the observation in the different filters, which can in principle include more than two NB filters, a set M of observed magnitudes mi and estimates on their uncertainty δmi is obtained. A model relates a set of parameters p to a spectrum fλ(λ;p), from which synthetically model magnitudes in the relevant filters, mi;theo [ p ], can be calculated.
Then, the parameter set that is most probable under these data needs to be found (pest). This is to minimize the Bayesian posterior probability 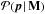 . Here,
. Here, 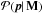 is related to the likelihood, ℒ( M ; p), and the prior on the parameters,
is related to the likelihood, ℒ( M ; p), and the prior on the parameters, 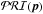 , by
, by 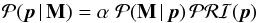 (4)where α is a normalization constant. Since we are assuming the errors in the measurements of the different magnitudes to be independent and Gaussian, the total likelihood is given by the product of the normal distributions for the individual measurements. Consequently, the negative log likelihood is one half the well known χ2:
(4)where α is a normalization constant. Since we are assuming the errors in the measurements of the different magnitudes to be independent and Gaussian, the total likelihood is given by the product of the normal distributions for the individual measurements. Consequently, the negative log likelihood is one half the well known χ2: ![\begin{equation} \chi^2 = \sum_i {\left ( \frac{m_\mathrm{i;obs} - m_\mathrm{i;theo}[{\vec{p}}]}{\delta m_\mathrm{i}} \right ) }^2\cdot \label{eq:nb118:chisquare} \end{equation}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq42.png) (5)The weight of individual filters can be artificially decreased by increasing the respective δmi in the calculation of χ2. In practice we chose a minimum δmi for the broadband filters,
(5)The weight of individual filters can be artificially decreased by increasing the respective δmi in the calculation of χ2. In practice we chose a minimum δmi for the broadband filters, 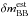 , which we default to 0.01mag. The implications from this choice are analyzed in Sect. 4.3.2.
, which we default to 0.01mag. The implications from this choice are analyzed in Sect. 4.3.2.
3.2. Choice of input model
3.2.1. Continuum shape
Both the continuum shape and the ratios between the various emission lines will differ from galaxy to galaxy, even so they are selected by the combination of NB excess and photometric redshifts to be star-forming galaxies at a well-defined redshift. If fλ(λ;p) is parametrized by Eq. (1), educated guesses need to be made for ζλ and ℒλ. Ideally, these generic choices for ζλ and ℒλ approximate the range of actual spectral energy distributions (SED) so well that the estimation of the free parameters is not affected.
While the simplest form for ζλ(λ) is a continuum flat in fν or fλ, a useful first-order correction is to add an additional parameter in the form of the power law slope β (ζλ(λ;β) ∝ λβ). This inclusion of the slope is especially relevant when the NB is off-center from the BB passband, as is the case for NB118 and J (cf. Fig. A.2).
A power law continuum will not be sufficient if the wavelength range around the considered line includes a strong spectral break, like the 4000 Å break in the case of [O ii]λ3727, but is a good assumption for Hα in the NB118 filters, as discussed in Sect. 4.2. We will address the problematic of the break on selection and measurement of [O ii] emitters in the NB118 data as part of a forthcoming publication.
3.2.2. Line shape and [N ii] contribution
When observing Hα in a NB filter, there is contamination from the collisional excited, forbidden [N ii] lines at 655.0 and 658.5 nm, which have to be included in ℒλ. In the NB118 filters, where Hα is observed at a redshift of z ~ 0.81, the lines are at a difference of 2.7 nm and 3.6 nm from Hα, respectively. While the ratio between the fluxes in the two [N ii] lines, f[ NII ] λ6583/f[ NII ] λ6548, is theoretically fixed to ~3 (Osterbrock 1989, p. 61), the flux ratio w6583 = f[ NII ] λ6583/fHα does substantially differ from galaxy to galaxy. Values vary for pure star formation depending on the metallicity and the ionization parameter between 0.0 and almost 1.0 (e.g., Kewley & Dopita 2002), with even higher ratios possible for spectra with AGN contribution (e.g., Kauffmann et al. 2003a). Based on low redshift data, a typical value has been shown to be w6583 = 0.3 (e.g., Pascual et al. 2007, and references therein). In the absence of knowledge about the metallicities, correlations between w6583 and EW, or mass can be used for a more sophisticated estimate. Using such relations in our estimation might bring some improvement, which we consider for further investigation. Throughout this work we assume a ratio of 0.3.
A wrong assumption on w6583 naturally affeccts both the f0 and λ0 estimations, where the impact on the latter can be examined by comparing Δmag – λ0 curves for different w6583. Curves for five different w6583 between 0.0 and 1.5 are shown for the example filter combination 14 and 15 in the lower panel of Fig. 3. We can conclude that, while the impact is not negligible, the resulting systematic wavelength errors are in the worst case not even larger than ~3 nm, compared to the assumption of w6583 = 0.3.
In addition to w6583, the shape of the Hα line could also differ3. Whereas line widths beyond 1000 km s-1 are not expected for solely star-forming galaxies, line widths of several 1000 km s-1 are possible when originating in a Type-I AGN. AGNs can be recognized by the use of the extensive multiwavelength data available in fields like COSMOS.
We tested the impact of the line width on the λ0 estimation by determining Δmag – λ0 curves for Gaussians with FWHM of 100, 500, 1000, and 5000 km s-1, as shown in the upper part of Fig. 3. While a line with a width of several 1000 km s-1 skews the result as expected, the difference all the way between 100 and 1000 km s-1 does not strongly impact the parameter estimation. Only if the line had broader wings than a Gaussian will the deviations be visible at lower FWHM. A 500 km s-1 boxcar line gives essentially an identical Δmag – λ0 curve as a Gaussian with the same FWHM, but a Lorentzian will cause stronger deviations from the estimated wavelength especially at low filter transmittances. In the following, we assume throughout a default FWHM of 250 km s-1. The impact of this specific choice is not expected to be large, as can be concluded from the results in this section.
 |
Fig. 3 Impact of the line shape (upper panels) and the presence of multiple lines (lower panels) on the predicted Δmag − λ0 curves. The left panels show different input spectra, and the right panels the corresponding Δmag – λ0 curves. “g”, “l”, and “b” in the legend refer to Gaussian, boxcar, and Lorentzian, respectively, with the succeeding numbers stating the line FWHM in kms-1. The presence of multiple lines is demonstrated for the relevant example of the [N ii] doublet bracketing Hα, with the values in the legend corresponding to the assumed [N ii]λ6583 to Hα ratios. All the shown results are based on the same filter combination as used for Fig. 1. |
3.3. Choice of broadband filters
To put an observational constraint on the continuum slope β, at least two flanking BBs need to be used. This is in the case of the VISTA NB118 filters in addition to J naturally Y, but also H might be included, allowing for a stronger constraint on β. For the analysis presented in the following we use all three filters.
Because Y and H alone are theoretically enough to constrain a power law continuum, and any strong emission line in the NB118 filter also contributes to the flux in J, J can in principle be used as an estimator of the emission line flux. Whether it is actually feasible to obtain an accurate estimate from the J excess depends on two main criteria. First, the contribution of the line to the filter-averaged signal needs to be significantly higher than the total noise in J. For the UltraVISTA DR2 data, the signal-to-noise ratio (S/N) for an infinite EW line is a factor 4.1 lower in J than, for example, at the peak of NB118 filter 15 (more details in Appendix D). Therefore, for the faintest lines detectable in the NB filter, the J-based estimate will not be very useful.
Second, it needs to be possible to determine the continuum contribution to J with very high precision. For example, an EWobs = 10 nm line has a J excess of only 0.06 mag, while the same object causes an excess of 0.64 mag at the peak of NB118 filter 15. As a consequence, deviations between estimation power law and actual continuum SED are for fluxes measured through the broadband excess more critical than for fluxes measured through the NB excess.
3.4. Implementation of estimation code
Range of parameters used for the pre-grid in the parameter estimation with the Nelder-Mead implementation of our code.
Finding the right global maximum in a complicated probability landscape is not always easy. We implemented two versions of a python code to determine the parameter set pest maximizing the posterior probability for a given set of measured magnitudes, M.
One version of our code makes use of the implementation of the Nelder-Mead algorithm (Nelder & Mead 1965) within python/scipy.minimize. Using the downhill simplex method, it allows to efficiently determine the maximum4. To improve the success rate of finding the global maximum, we combined it with a precalculation on a coarse-grained grid. The parameter range of this pregrid is given in Table 1. Then, we ran the Nelder-Mead algorithm three times, starting from the grid points with the three highest probabilities. After comparing the found posterior probability from each run, we assumed the found maximum with the highest probablility as the global maximum in case of differing maxima and designated the corresponding parameters as pest. If all three subruns were not converging or if λ0 for the best-fit parameter set was within 1 nm of the prior boundaries, we assumed the parameter estimation to have failed.
The Nelder-Mead implementation is relatively efficient, but it does not allow for a direct assessment of the credibility intervals. When dealing with actual observations, where the experiment cannot be repeated as in simulations, the correct way to state uncertainties is to determine the posterior probabilities, as based on a Markov chain Monte Carlo (MCMC) approach. Therefore, we also implemented a version based on the Metropolis-Hastings algorithm (Metropolis et al. 1953; Hastings 1970). The code makes use of adaptive proposal distributions based on repetitively recalculated covariance matrices, allowing for optimal efficiency (Roberts & Rosenthal 2001; Rosenthal 2014). We ran six separate chains with 100k proposal steps in each chain, where the initial proposal distribution was chosen wide enough to explore the complete parameter space.
Altogether, the set of four free-fitting parameters, p, does include the central wavelength of the main line λ0, its integrated flux f0, the observed frame equivalent width EWobs for the main line, and the slope β of the continuum. Within the prior, we constrained f0 to a physically reasonable range in order to exclude combinations of unreasonably high f0 and λ0 at low transmittances of the filters.
The range of acceptable p was set for our specific test case of Hα in the NB118 filters to 1171 nm <λ0< 1206 nm and 0.5 × 10-17 erg s-1 cm-2<f0< 100 × 10-17 erg s-1 cm-2, respectively. Moreover, we constrained 0 nm <EWobs< 300 nm.
The assumption of a flat prior for the line flux is, from a rigorous Bayesian point of view, not the right choice, because this does not reflect our complete state of prior knowledge. The line luminosities are known to be approximately distributed by a Schechter luminosity function (LF; Schechter 1976; z = 0.8Hα LFs: e.g., Villar et al. 2008; Sobral et al. 2009; Ly et al. 2011). However, for clarity of the results, we still use flat priors in this work.
4. Application to simulated observations
4.1. Mock observations
For testing the proposed TPV method systematically, we used simulated observations in this first part for a range of spectra. The input into the simulation were chosen to closely resemble the available UltraVISTA DR2 data. This means that as input we used VIRCAM filter curves, the characteristics of the VIRCAM IR-arrays (gain, zeropoint (ZP)), and realistic sky brightnesses in the NB118 and the three VIRCAM BB filters.
The sky brightnesses in the individual NB118 filters were taken from Milvang-Jensen et al. (2013) and significantly differ between the individual copies, ranging from 21.2 to 51.5 e− s-1 pixel-1. For Y, J, and H we assumed 150, 650, and 4700 e− s-1 pixel-1, respectively, which are values that are typical of the UltraVISTA observations. We set the detector gains to 4.2 e− ADU-1 and the ZPs on the AB system to 21.78, 24.12, 24.73, and 25.29 for NB118, Y, J, and H, respectively5.
Furthermore, we assumed point sources observed in 2′′ diameter circular apertures. The corresponding enclosed flux fraction within the aperture is about 75% for the UltraVISTA NB118 and J PSFs. For simplicity, the same enclosed fraction was also used for Y and H, even though the PSFs in these filters differ slightly for the actual observations.
Based on a chosen spectrum and this input, we synthetically calculated the expected aperture magnitudes, mexpect, with Eq. (3), and from the corresponding S/N, we derived the expected magnitude errors by 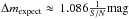 .
.
The S/N was estimated from the CCD equation (e.g., Howell 2000; Chromey 2010). Neglecting justifiable uncertainties from read-out noise, dark current, linearity corrections, flat fielding, and background subtraction, and converting electrons through the gain, g, to digital units, DN, the S/N can be calculated as 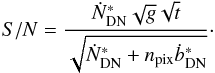 (6)Here,
(6)Here, 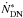 is the total number of DN per second created within the aperture due to the source, while
is the total number of DN per second created within the aperture due to the source, while 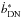 is the number of DN produced per pixel and second by the sky background. And npix is the number of pixels that constitute the aperture, and t is the exposure time.
is the number of DN produced per pixel and second by the sky background. And npix is the number of pixels that constitute the aperture, and t is the exposure time.
We assumed an observation time of 11.4 h in each of two NB118 filters through which an object is simulated to be observed, which sums to the typical per-pixel integration time available in the UltraVISTA DR2. The expected per-pixel integration time in the finished survey will be 112 h, meaning that the DR2 NB118 data includes only ~20% in time or 45% in depth of the final UltraVISTA survey goal. Similarly, for Y, J, H we assumed the 53.2, 34.9, 29.4 h available in the DR2 for the same field as the NB118 data, with the time in the finalized survey expected to be 210 h in each of the BB filters, all per pixel.
Grid of spectral energy distributions.
While we tested correctness and stability of our estimation code by using spectra as input models, which could be exactly matched by the estimation model, the mock observations used in the following were based on realistic galaxy SEDs. For the tests we used the high resolution BC03 models (Bruzual & Charlot 2003) based on the R ~ 2000 STELIB library (Le Borgne et al. 2003) assuming a Salpeter IMF (M = 0.1 − 100 M⊙, Salpeter 1955).
4.2. Quality of continuum estimation from simulations
 |
Fig. 4 Difference between the continuum of synthetic spectral energy distributions (SED) and the estimate obtained from a power law fit to these SEDs (model) using Y, J, and H filters. The magnitude difference between Jmodel and Jsed is plotted against the magnitude difference between SED and model directly at the wavelength of Hα (cf. Sect. 4.2). The range of SED parameters, for which results are shown, is summarized in Table 1. For the Z = 0.05 panel, a wider axis scale was chosen than in the other two cases. The narrower range used for Z = 0.008 and Z = 0.020 = Z⊙ is indicated as dotted box in the Z = 0.05 case. The cross in the Z = 0.020 plot represents the SED, which was used for the parameter estimation test described in Sect. 4.3. |
In the TPV estimation we use three BB filters, Y, J, H. This means that a relatively wide wavelength range is included. The range from the blue end of Y to the red end of H corresponds at z = 0.81 to a rest-frame wavelength range from 540 to 990 nm. When estimating f0 and λ0 from the throughput variations, the constraints on the continuum at the wavelength of the NB filter need to be precise. As Hα also contributes to J, an excess in J affects the estimation results with the algorithm described in Sect. 3.1. A precise measurement of the filter-averaged continuum flux density in J is required to accurately determine this excess.
Therefore, it is important to carefully assess the expected deviations between the power-law fit and the actual continua both in NB118 and J. Features in the spectral energy distributions (SEDs) could in principle result in such deviations. These do not necessarily have the same extent exactly at the wavelength of Hα in the NB118 filter and averaged over J, especially since the NB118 passband is at the blue end of the J passband.
While no strong spectral features are expected over the covered wavelength range, only a formal test can give a clear answer. Therefore, we fit power-law continua to synthetic magnitudes calculated for a grid of model SEDs without nebular emission included (Table 2). For consistency, we scaled all input model SEDs to fλ = 1 × 10-17 ergs-1cm-2nm-1 at the wavelength of Hα, before calculating input magnitudes and uncertainties as in Sect. 4.1.
In Fig. 4 the difference between the continuum magnitude at Hα from the best-fit power-law continuum, C Hαmodel and the one measured directly from the input SED, C Hαsed, is shown for a range of SEDs. The value of C Hαsed was determined by averaging the flux-densities over two 8 nm wide intervals at 1172 nm and 1205 nm, corresponding to rest-frame wavelengths of 647.5 nm and 665.7 nm, respectively. These were chosen to exclude Hα absorption. On the other axis, the differences between input and estimation are shown for J. We conclude that the deviations averaged over the J passband have a similar extent to those for the continuum magnitudes directly at Hα.
For stellar populations with both solar and subsolar (Z = 0.4 Z⊙) metallicity, these deviations are very small. Except for very young ages and for populations without ongoing star formation, the differences between fit and input magnitude are below 0.02 mag. On the other hand, strong deviations exist for super-solar metallicities, exceeding 0.1 mag for expected population ages. While this is cause for some concern, star-forming galaxies with stellar metallicity as high as Z = 2.5 Z⊙ are expected to be very rare (e.g., Gallazzi et al. 2014, at z = 0.7), even at the highest masses. Most of the NB selected galaxies will have stellar masses ≲1010M⊙ (e.g., Kochiashvili et al. 2015) and thus not be among the most metal-rich systems according to the mass-metallicity relations (e.g., Tremonti et al. 2004; at z ~ 0.7: Savaglio et al. 2005; Lamareille et al. 2009)6.
We can conclude that the continuum estimate is expected to be excellent, making both the TPV and, at least to some extent, the use of the J excess feasible.
4.3. Quality of full parameter estimation from simulations
We assessed the expected accuracy of Hα estimations at different wavelengths for different f0 and EW, different filter combinations, and different assumptions in the estimation algorithm. For this purpose we created in each considered case 500 realizations of observed magnitudes. We calculated the synthetic magnitudes and uncertainties for a given input spectrum, and randomly perturbed each of the magnitudes7.
Then, we ran our Nelder-Mead TPV code (cf. Sect. 3.4) on each of the realizations. In this way, we found the expected distribution of best-fit parameters for hypothetical repeated observations of the same object. Finally, the determined 4d distributions in the λ0–f0–EWobs–β space were reduced to 1d distributions for each of these four parameters by marginalization over the three other parameters.
In all cases we used a constantly star-forming solar metallicity SED with E(B − V) = 0.2 and an age of 3 × 108 yr as input continuum. This SED might be considered as a typical example for the Hα emitters selected in the UltraVISTA data. The expected offset between power-law continuum and this model continuum is indicated in Fig. 4 as a cross. It is important to note that this chosen continuum SED has an Hα absorption EWobs of 0.7 nm at z = 0.818. Therefore, even perfectly estimated Hα emission fluxes, f0;est, are too low by 16%, 8%, 5%, 3%, and 1% for Hα emission with EWobs of 4, 7, 10, 20, and 100nm, respectively, because the TPV code does not correct for the Hα absorption9. We added an Hα line with chosen f0 and w6583 = 0.3 to this continuum. The continuum was scaled so that the added line has a specific HαEWobs. We notice that adding Hα to a somewhat arbitrary continuum is not completely self-consistent, but using the same continuum allows for a clear comparison of the results.
In the simulation parts of this paper, line fluxes refer to total fluxes, even though all measurements and estimations are simulated to be performed within the 2′′ apertures.
4.3.1. Different line parameters
 |
Fig. 5 Distributions of the best-fit wavelength λ0;est (left panels; cumulative) and flux f0;est (right panels) for input spectra with an emission line at the effective wavelength (top panels) and at 50% transmittance (bottom panels) of the two NB118 filters’ combined passband. In each panel, distributions are shown for five different Ha fluxes. The respective values are listed in the legend in units of ergs-1cm-2. The input EWobs;in was 10 nm in all five cases. Fits were obtained at both transmittances for 500 realizations of simulated observations in NB118 14 and 15, Y, J, and H. Dashed lines indicate that the objects would not be selected as NB excess objects. |
 |
Fig. 6 Distributions of best-fit wavelength and flux similar to Fig. 5. Here, distributions for five different EWobs;in are shown. EWobs;in values stated in the legend are in units of nm. The input flux was 10 × 10-17 ergs-1cm-2 in all cases. |
Ideally, a robust parameter estimation is possible for the complete range of f0–EWobs–λ0 existing in objects selected to be Hα NB118 emitters. Therefore, we performed tests based on mock observations for a set of five input line fluxes, f0;in over the complete relevant flux range from 3.0–30.0 × 10-17ergs-1cm-2 and for five input EWobs;in over the range from 4.0–100.0 nm. In the two cases, we fixed the respective other quantity to EWobs;in = 10nm and f0;in = 10.0 × 10-17ergs-1cm-2. Throughout this section we were assuming observations in filter combination 14 and 15, which is well suited to the TPV. The resulting marginalized distributions for the best-fit f0;est and λ0;est are presented for each of the input EWobs;in–f0;in combinations at two different input wavelengths in Figs. 5 and 6. Mean and standard deviation of these distributions are stated in Table 3.
The two wavelengths correspond to the mean wavelength of the two filter’s combined effective passband and the wavelength where the transmittance of this passband is 50% of its peak value. The mean wavelength was calculated as in Eq. (6) of Milvang-Jensen et al. (2013). Table 3 includes results for two additional wavelengths. One is in the middle of the interval between mean wavelength and the 50% transmittance, and the other is at 20% transmittance. The four wavelengths are indicated as small arrows in Fig. 1.
We note that not for all EWobs–f0–λ0, combinations objects would also be selected as NB excess objects when applying selection criteria (cf. Sect. 5.3.1), either because of not having enough S/N or not a high enough NB excess. These cases are indicated both in the plots and the table.
Values for mean and standard deviation of best estimates for Hα fluxes, f0;est, and wavelengths, λ0;est, using the TPV on repeated simulations of observations of the same Hα emitters.
Several important things can be inferred from this analysis. The bias in the λ0 estimation is ≤1 nm for all those among the tested EWobs–f0 combinations, which would be selected as NB excess objects. Likewise, the spread in the estimation, σλ0;est, is in all cases with selection below 3 nm. For f0;in = 10.0 × 10-17 ergs-1cm-2, the spread is even ≤1 nm over the complete relevant EWobs range, with little dependence on the EWobs.
While the f0;est seems to significantly change with EWobs, it is important here to keep the Hα absorption in our assumed model SED in mind. At the mean wavelengths of the combined effective filter, almost all apparent bias is only for this reason, whereas at lower transmittances, there is some additional bias. This additional bias results from the mismatch in the continuum.
4.3.2. Different estimation assumptions
As discussed in Sect. 3.3, the J excess provides a flux estimate, since Y and H alone allow for a very good continuum estimate. In the case of a single NB118 filter, this would be supplemented by an additional lower limit on the flux. Therefore, one might wonder how much additional estimation power is really coming from the use of two NB filters.
To assess this, we performed the parameter estimation simulation for a galaxy with EWobs of 10nm and an Hα line with f0 of 10 × 10-17 ergs-1cm-2 using the three BB filters either combined with the pair 14 and 15 or a single NB118 filter. For the latter we assumed the combined effective filter for 14 and 15. While this does not correspond to an actual filter, it is the applicable wavelength response when analyzing a joint stack of data coming from both 14 and 15. Estimation histograms for both cases are shown in Fig. 7. Clearly, the use of the throughput variations between the two NB118 filters allows for an excellent λ0 estimation over the complete relevant wavelength range. In contrast, no robust estimation is possible when using only the single filter.
This is for two main reasons. First, while in principle a wavelength resolution is possible when combining one NB filter with the flux measured based on a BB filter, a bimodality between a blue and a red solution is unavoidable. Second, another effect is obvious at 50% transmittance. As for the specific continuum SED, the continuum magnitude is estimated slightly too bright, and the Hα flux that is estimated from the J excess alone is underestimated. Therefore, even for a line several nm away from the peak, the lower limit from the NB filter indicates a stronger flux than estimated from the excess in J. Therefore, the estimation code finds a solution at the peak of NB filter as the best possible reconciliation with the NB excess. This is why the cumulative histograms in Fig. 7 jumps at around 7nm.
The difference between using the two NB filters separately and using the single combined effective filter is not as dramatic for the flux estimate, but still results in a huge improvement. At 50% transmittance, where the line still contributes a significant signal to the NB data, the reduction of the bias due to the two NB filters corresponds for our standard 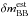 to a factor of 1.3. At higher NB transmittances the effect is even greater. Halfway between the combined filter’s mean wavelength and 50% transmittance (cf. “B” in Table 3) it is a factor of 1.6. The difference is at 20% transmittance negligible (cf. “D” in Table 3), because at the corresponding low transmittances in the NB filters the flux estimation is mainly relying on the J excess. Objects at this wavelength would not be part of our NB excess sample at the given EWobs.
to a factor of 1.3. At higher NB transmittances the effect is even greater. Halfway between the combined filter’s mean wavelength and 50% transmittance (cf. “B” in Table 3) it is a factor of 1.6. The difference is at 20% transmittance negligible (cf. “D” in Table 3), because at the corresponding low transmittances in the NB filters the flux estimation is mainly relying on the J excess. Objects at this wavelength would not be part of our NB excess sample at the given EWobs.
We also investigated the consequences of increasing 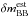 to 0.05, i.e., giving less weight to the BB filters. Clearly, the bias is significantly reduced. Even at 50% transmittance, the bias is close to zero, if keeping in mind the Hα absorption. On the other hand, the scatter is significantly increased.
to 0.05, i.e., giving less weight to the BB filters. Clearly, the bias is significantly reduced. Even at 50% transmittance, the bias is close to zero, if keeping in mind the Hα absorption. On the other hand, the scatter is significantly increased.
 |
Fig. 7 Similar to Fig. 5, but for three different assumptions in the TPV algorithm. First, results are shown both for assuming the default minimal BB estimation uncertainty (cf. Eq. (5)), |
4.3.3. Different filter combinations
 |
Fig. 8 Similar to Fig. 5, but here results are shown for different filter combinations. An EWobs;in = 10nm and a f0;in = 10 × 10-17ergs-1cm-2 were assumed. |
As a third test, we compared the estimation quality for three different filter combinations, including 14 and 15, which was used throughout Sects. 4.3.1 and 4.3.2, 7 and 8, and 11 and 12. All three combinations were discussed through Δmag – λ0 curves in Sect. 2.2. The pairs are well suited for a fair comparison, since the sky brightnesses are similar in the three pairs with 36 and 32, 38 and 30, 33 and 28 e− s-1 pixel-1, respectively.
The resulting distributions for the three different filter combinations, simulated for an EWobs;in = 10 nm line with f0;in = 10 × 10-17 ergs-1cm-2, are shown in Fig. 8. It needs to be noted that both 7 and 8 and 11 and 12 are more top-hat than 14 and 15, which means that a one-filter estimation is correct over a wider wavelength range. In Fig. 8 we show the histograms for the mean wavelength and the 50% transmittance for the respective combined effective filters.
Combination 7 and 8 behaves as expected: overall similar to a single effective filter, meaning that it is not very useful for an improved wavelength resolution. The wavelength resolution from 11 and 12 is also not as precise around the peak as for 14 and 15, since the Δmag – λ0 curve is relatively flat there. At intermediate transmittances, where the slope is similar to that of 14 and 15, the wavelength resolution is, on the other hand, similarly good.
5. Application to UltraVISTA data
5.1. UltraVISTA NB118 observing pattern
 |
Fig. 9 Diagram showing which copies of the NB118 filters contribute to the different parts of the field covered by the UltraVISTA NB118 tile. The numbers in parentheses are only relevant when using the suggested modification of the observing pattern, as discussed in Sect. 5.9. |
VISTA NB118 narrowband observations are already available from the NB118 GTO observations (Milvang-Jensen et al. 2013) and the intermediate UltraVISTA data releases (McCracken et al. 2012)10, and more data is continuing to become available within the ongoing UltraVISTA observations. Interestingly, some parts of the covered field are becoming directly applicable to our method. VIRCAM covers with a single pointing a noncontiguous area on the sky that consists of 16 separate patches, corresponding to the individual detectors. They total 0.59 deg2 (Ivanov & Szeifert 2009, p.11).
This single-pointing field coverage is referred to as a pawprint. To cover an area on the sky contiguously, a so-called tile consisting of six pawprints is required. The six contributing pawprints are three steps in one direction of the sky (y), which are performed for two steps in the perpendicular direction (x). For the NB118 part of UltraVISTA, only one of the two x-positions is observed, resulting in four stripes (cf. Fig. 9).
Each pointing in the y-direction is separated by 47.5% of a detector (or 5.́5)11. Consequently, observations of at least two pawprints contribute to the covered field with the exception of the outermost parts. The filter numbers in the different patches of the pawprint can be seen in Fig. 9. Most important for our method, in 20.5% percent of the stripes, two pawprints contribute with two different filters. In addition, for six tiny patches, which total 4.8% percent of the stripes, two pawprints contribute with one filter, while one pawprint contributes with a second filter. Owing to the random jitter within a 2′ × 2′ box, the regions are somewhat smeared out.
5.2. Data
The controlled environment of our simulations demonstrated that the TPV is expected to work. Here, we apply the method to the actual UltraVISTA DR2 data. A stack of NB118 data is available as part of this data release. In regions of overlap, this stack includes data from both contributing NB118 copies. For the purpose of the TPV, we need these data separately. Therefore, we produced 16 custom NB118 stacks, each of which including only the data from one filter or detector. Reduction, stacking, and flux calibration were basically done in the same way as for the publicly available joined NB118 DR2 stack (cf. Milvang-Jensen et al. 2013; McCracken et al. 20129), and the same observations were included.
Employing SExtractor’s (Bertin & Arnouts 1996) double-image mode, we obtained, in each of the individual NB118 filters, photometry in the same 2′′ circular apertures as in the detection image, where the latter was the joined NB118 DR2 stack including data from all 16 filters. Matching dual image photometry was also obtained for the Y, J, and H DR2 stacks. We corrected all SExtractor aperture flux and magnitude errors for correlation by means of empty aperture measurements. This was necessary because the stacks were produced on the non-native 0.̋15 pixel scale, and interpolation was required in the reduction as a consequence of the dithering strategy12. Stated observed magnitudes are aperture magnitudes in 2′′ and are written in italics, where NB118 [ x ] (x ∈ [ 1,16 ]) refers to the magnitude in an individual NB118 filter and NB118 refers to the magnitude in the joint stack.
We corrected the aperture magnitudes in Y, H, and NB118 to the J aperture based on the enclosed fractions for point sources. The NB118 per-detector aperture magnitudes were corrected taking into account that different pawprints contribute to different parts of the NB118 per-detector stacks. This means that we make certain that the remaining small seeing and ZP variations in data from different pawprints are corrected.
5.3. Sample selection
5.3.1. Selection criteria
We used the following criteria to select NB excess objects in the regions of overlapping filters.
-
Color-cut, which must be satisfied in at least one of the two contributing NB118 filters:
![\begin{equation} J_\mathrm{corr} - NB118[{i}] > 0.2 \label{eq:col_crit} , \end{equation}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq312.png) (8)where the index i refers generically to the number of this filter and the second filter in the pair is referred to as j.
(8)where the index i refers generically to the number of this filter and the second filter in the pair is referred to as j. -
Significance of NB excess at the four σ level (κ = 4) at least in one filter, which also satisfies Eq. (8)
![\begin{equation} f_{NB118[{i}]} - f_{J_{\mathrm{corr}}} > \kappa \times \delta(f_{NB118[{i}]} - f_{J_{\mathrm{corr}}}) \label{eq:colsig} . \end{equation}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq317.png) (9)This criterion corresponds to the often used Σ criterion (Bunker et al. 1995), and δ(fNB118 [ i ] − fJcorr) is the one sigma uncertainty on the flux difference. A justification of the choices in Eqs. (8) and (9) is given in Appendix F.
(9)This criterion corresponds to the often used Σ criterion (Bunker et al. 1995), and δ(fNB118 [ i ] − fJcorr) is the one sigma uncertainty on the flux difference. A justification of the choices in Eqs. (8) and (9) is given in Appendix F. -
Significance of NB118 detection in the second filter at the 2.5σ (κ = 2.5) level:
![\begin{equation} f_{NB118[{j}]} > \kappa \times \delta f_{NB118[{j}]} \label{eq:detsig} . \end{equation}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq322.png) (10)
(10) -
Mask,
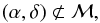 (11)where (α,δ) are the coordinates of the object, and ℳ are regions that are excluded because of bright stars, reflections (close to detector boundaries), and a defect region in detector 16. We also require that the SExtractor flags in both contributing NB118 filters and Y and J are smaller than 4.
(11)where (α,δ) are the coordinates of the object, and ℳ are regions that are excluded because of bright stars, reflections (close to detector boundaries), and a defect region in detector 16. We also require that the SExtractor flags in both contributing NB118 filters and Y and J are smaller than 4.
The flux density fJcorr is the broadband flux density corrected to the position of the NB118 filter, and Jcorr was calculated from fJcorr in the usual way by Eq. (3). We approximated fJcorr, depending on the S/N in Y, and the Y − J color, as 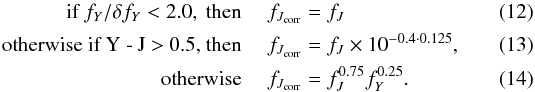 Color correction and selection criteria are based on those of Milvang-Jensen et al. (2013), but adjusted for the use of observations in two NB filters. Additional alterations include the use of flux uncertainties instead of magnitude uncertainties and a change of slope in the color correction. We justify the selection in some more detail in Appendix F.
Color correction and selection criteria are based on those of Milvang-Jensen et al. (2013), but adjusted for the use of observations in two NB filters. Additional alterations include the use of flux uncertainties instead of magnitude uncertainties and a change of slope in the color correction. We justify the selection in some more detail in Appendix F.
 |
Fig. 10 Statistical distribution of magnitude differences for objects with observations available in two different NB118 filters. Histograms are shown for the sample of 239 objects with NB excess (NBES), and for 100 comparison samples. The comparison samples have the same number of objects and distribution of stack magnitudes as the NBES in each of the 12 contributing filter combinations, but no NB excess was required. Upper: both the histogram for the NBES and the histograms obtained from the mean of the 100 comparison samples are shown. In the latter case, the standard deviation between the different samples is indicated by errorbars. Lower: cumulative distribution for the mean of the comparison samples and for the NBES sample. The maximal differences between the two samples is indicated by an arrow. In addition, for the NBES, the cumulative histograms are included for the individual filter combinations. Two subsets of the NBES are plotted. |
5.3.2. The NBES sample
Our main NB-excess sample (NBES) was selected based on the criteria in Eqs. (7)–(11), resulting in 239 objects. Matching the photo-z catalog of Ilbert et al. (2013), we can identify Hα+[N ii] or [S ii], 56 Hβ or [O iii], 28 [O ii], and six [S iii] as the cause of the NB excess in 86 cases, where the redshift cuts of 0.6 <z< 0.95, 1.25 <z< 1.55, 2.1 <z< 2.4, and 0.2 <z< 0.4 were applied, respectively. The remaining 63 objects could either not be matched to the Ilbert et al. (2013) catalog or do not have a photo-z within the four intervals. Based on a full simulation of the NB118 observing pattern, as presented in Appendix C, we expect about 100–250Hα emitters for the selection criteria, where the number depends on the chosen literature Hα luminosity function, the equivalent width distribution, and the w6583 distribution. In the final UltraVISTA data, we expect to select about twice as many Hα emitters within the same subfield.
In addition to the NBES, we picked 100 comparison samples, each of which has the same number of objects as the NBES in each of the filters with the same stack NB118 distribution. More precisely, we split the range between 19 <NB118 < 24 into 40 bins. The objects in the comparison samples (CS) were randomly drawn from a selection, where we did, by contrast to the NBES, not impose a color significance or color cut. To completely avoid NB excess objects in the comparison sample, we also created stricter versions, where we imposed Jcorr − NB118 < 0 (SCS).
5.4. Statistical analysis of throughput variations
 |
Fig. 11 Magnitude, redshift, and field distribution for our sample of NB excess objects with observations available in two different NB118 filters (NBES). Those NBES objects with their magnitudes in the two contributing NB118 filters differing by more than 2.5σ are shown in color, with the colors referring to the different filter pairs. All other NBES objects are shown in the background in gray. Upper left: the difference in magnitude between the two individual contributing filters is plotted against the magnitude in the stack. Magnitudes were measured in 2′′ diameter apertures, and errorbars are 1σ uncertainties. Upper right: the Jcorr − NB118 color excess is plotted against the magnitude difference between the individual NB118 filters. Jcorr − NB118 is corrected for the continuum slope by means of the Y − J color (see Sect. 5.3.1). Lower left: Jcorr − NB118 plotted against the photometric redshift (Ilbert et al. 2013). The three main groups are Hα (z ~ 0.8), [O iii]+ Hβ (z ~ 1.4), and [O ii] (z ~ 2.2). Different symbols refer to membership in these groups. The X (not in legend) labels objects with significant throughput variations, where no association with a specific line was possible. A histogram of the photometric redshifts is included in the upper part of this panel. The vertical lines indicate the redshift intervals that are used for the classification into [S iii] (dotted), Hα (solid), [O iii]+ Hβ (dashed), and [O ii] (dash-dotted). Lower right: position of the objects in the field of view. The DR2 NB118 stack is shown in the background. Larger symbols have a NB118 [ a ] − NB118 [ b ] > 0 and smaller symbols have NB118 [ a ] − NB118 [ b ] < 0. |
We tested whether we see NB excess objects that show throughput differences beyond the statistical fluctuations. In the upper panel of Fig. 10, the histogram of magnitude differences, Δmag = NB118 [ a ] − NB118 [ b ], is shown as a solid red curve for the NBES. All 12 filter combinations are included in the same histogram, where the identifiers a and b generically refer to the filter numbers in the pairs, with a<b. Also included in the figure is the mean histogram of the 100 CS and the corresponding standard deviation. The SCS sample is indicated as a dashed light gray line, which is hardly visible since it is basically identical with the CS histogram.
When including predominant objects without emission in the NB118 filters, the spread in the CS should be caused by noise alone. In contrast, the spread in the histogram for the NBES is expected to be caused both by noise and actual throughput variations, and indeed it clearly differs from the comparison sample. The difference can also be evaluated in the lower panel of Fig. 10, where the cumulative histograms are shown. Applying the two-sample KS test to the two histograms, we can formally rule out the null hypothesis that both samples stem from the same distribution13. The maximum difference between the two cumulative curves is marked as an arrow in the figure.
One relevant concern is that objects with unusually large random or systematic errors in one of the two filters could show the required NB excess exactly for that reason, which might lead to a misidentification of such objects as NB excess objects, hence inclusion in the NBES, biasing this sample to objects with large throughput variations. However, as discussed above and further shown in Fig. 11, photometric redshifts of 74% of the NBES objects can be identified well with actual lines, indicating a relatively clean sample. Reassuringly, the average cumulative magnitude difference curve does not change much using only this subsample (green curve in Fig. 10). For the subsample of Hα emitters the difference to the general population is slightly smaller, where it is explainable because the most extreme EWobs NB excess objects are predominately [O iii] emitters.
As a next step, we selected those objects from the main NB-excess sample (NBES). They show a flux difference between the two filters differing from zero at least at the 2.5σ level, have a Δmag> 0.05, and are fainter than NB118 = 20. The last two criteria are meant to avoid objects, where the difference might be caused by small remaining zeropoint errors or by small PSF differences, which are especially relevant for merging objects.
The resulting 55 objects, 8 of which are so close to a neighboring object that SExtractor marked them as de-blended14, are shown in four different plots in Fig. 11. While all objects of the NBES are included in the plots as gray dots, objects in the throughput difference sample are color-coded by the relevant filter pairs. Adding to the confidence that those objects with strong TPV are indeed NB excess objects caused by emission lines, a comparison of this subsample to the photometric redshifts of Ilbert et al. (2013) allowed in an even larger number than in the full NBES for an identification with one of the four main redshift solutions (85% vs. 74%)15. The eight remaining objects are classified in the Ilbert et al. (2013) catalog as either masked (2), star (1), XMM-detected (1), a photo-z not in the intervals (1), or we could not find a match within a radius of 0.̋5 (3).
While the number of objects is too small to make strong statistical conclusions for the individual filters, we find that strong throughput variations are indeed mainly found in those pairs for which they were expected (14 and 15, and also 15 and 16, and 9 and 10). However, there is one major exception. Filter pair 7 and 8 surprisingly shows (cf. Fig. 2) a relatively large number of objects with strong differences. With some of them being brighter in filter 7 and others in filter 8, an erroneous ZP can be ruled out as the reason for the behavior. A visual inspection of the objects also does not indicate obvious problems. Therefore, we need to conclude that one of the two filters seems to substantially differ from our expectations (cf. also Appendix A).
5.5. NB118 Hα measurements for individual objects
Estimates for λ0 and f0 of Hα both from our TPV method and independent methods.
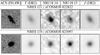 |
Fig. 12 4″ × 4″ cutouts in UltraVISTA DR2 Y and J, NB118 14 and 15, and HST/ACS/F814W for two Hα emitters with significant throughput differences between filters 14 and 15. Both objects have spectroscopic redshifts from zCOSMOS (Lilly et al. 2009) and are included in Table 4. For each object, the four UltraVISTA panels are scaled to the same surface brightness in fν. |
 |
Fig. 13 Results from the TPV parameter estimation with our MCMC code for the example object with the NBES ID 7 (zCOSMOS ID 810332). Shown are the 2D histograms, indicating the correlations between the four fitted parameters. |
5.5.1. Estimation with TPV
We applied our parameter estimation method to all those NB excess objects in our sample, which are located in one of the three filter pairs suited for our method (9 and 10, 14 and 15, and 15 and 16) and which we classify as Hα emitters based on their photo-z’s or their zCOSMOS redshifts (cf. Sect. 5.6.3) being consistent with Hα in the NB118 filter. We also verified the Hα selection through the use of a i′ − Ks versus B − r′ plot, similar to Sobral et al. (2009, 2013). For all selected objects we estimated all Hα flux (f0), central wavelength (λ0), EWobs, and continuum slope (β), and the corresponding uncertainties based on the MCMC implementation of our algorithm (cf. Sect. 3.4). Estimated λ0 and f0 for all objects are listed in Table 4. An example for the resulting credibility intervals is shown in Fig. 13 for the object with NBES ID 7, an object with high Hα flux located at the boundaries of the passband. The statistical uncertainties are very small, but as discussed above, systematic errors are at least of the same order of magnitude.
5.5.2. Estimation with generic NB118 method
For comparison, we also estimated fluxes with a conventional NB estimation method using the stack NB118 magnitudes. Here we used as estimator 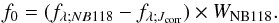 (15)The effective filter width, WNB118, was determined for the combined effective filters using the approach described by Pascual et al. (2007)16. In the WNB118 we took account of the [N ii] contribution following the approach of Pascual et al. (2007). The fλ were determined from the AB magnitudes in the normal way. The used estimator is the simplest possible form, which assumes that the impact of the emission line to the broadband magnitude can be neglected.
(15)The effective filter width, WNB118, was determined for the combined effective filters using the approach described by Pascual et al. (2007)16. In the WNB118 we took account of the [N ii] contribution following the approach of Pascual et al. (2007). The fλ were determined from the AB magnitudes in the normal way. The used estimator is the simplest possible form, which assumes that the impact of the emission line to the broadband magnitude can be neglected.
5.6. Independent Hα flux estimates
To assess the quality of our NB118 parameter estimation, we needed to compare it to estimates of λ0 and f0 from independent methods. While a direct comparison to J spectroscopy would be ideal, we had to rely on information obtained from available optical spectroscopy and multi-wavelength photometry in the absence of this data. We obtained Hα flux estimates in three ways:
-
1.
Hα fluxes obtained from SED fitting
-
2.
Conversion of the total SFR obtained from UV+IR into Hα fluxes
-
3.
Conversions between Hβ and/or [O ii] fluxes from zCOSMOS spectra into Hα fluxes
5.6.1. Estimation from SED fitting
We performed SED fitting using our own python code coniecto, which uses a common χ2 minimization to normalize a set of models with respect to mass, and consequently allows finding the model that allows for the smallest χ2. Our parameter grid was chosen fine enough to avoid biases due to degeneracies between different parameters. The full range of parameters is stated in Table 2.
As input we used the Muzzin et al. (2013) photometric catalog and included 29 filters in total in the fitting from GALEX FUV to IRAC 4. The photometry in Muzzin et al. (2013) is based on 2.̋1 diameter apertures applied to PSF homogenized images. For each of the objects, we compared our 2′′ aperture photometry for Y, J, H to that in the Muzzin et al. (2013) catalog17. On average, the difference in the magnitudes is very small at 0.018 mag. We corrected all the quantities obtained based on the Muzzin et al. (2013) photometry to match our apertures, which also crudely takes care of small differences in the centroid from our detection and the one in Muzzin et al. (2013).
In addition to stellar continua based on BC03 models (Bruzual & Charlot 2003) using a Salpeter IMF, we also added dust and nebular emission to the models, including lines and continuum. For the dust emission, we used the Dale & Helou (2002) models under the assumption of energy conservation, meaning that all radiation absorbed by dust must be emitted again. We notice that emission from dust, including PAH features, does not strongly contribute to the IRAC bands at z = 0.81.
Throughout this and the following sections, we consistently used a Calzetti et al. (2000) extinction law. The extinction of the stellar continuum, ES(B − V), was chosen to be 0.7 times the nebular extinction, EN(B − V). Calzetti et al. (2000) find a factor 0.44 between the two extinctions based on a sample of local starburst galaxies (Calzetti 1997). On the other hand, under this assumption, Erb et al. (2006) find a systematic discrepancy between Hα and UV based SFRs at z ~ 2, with equal extinction for both components giving more consistent results, in agreement with some more recent studies (e.g., Shivaei et al. 2015). Other studies argue for differential nebular and stellar extinction also at high redshifts (e.g., Förster Schreiber et al. 2009; Wuyts et al. 2011). These discrepant conclusions can be partially explained by a SFR dependence of the ratio between nebular and stellar extinction in the sense that the ratio is higher for higher SFRs (Price et al. 2014; Reddy et al. 2015). Our chosen value of 0.7 should be understood as a compromise. For Ly α, we used either the same EN(B − V) as for all other lines or, somewhat arbitrarily, a ten times higher extinction. Finally, we applied IGM absorption to the SED models using the parameterization of Inoue et al. (2014).
We interpret the calculated χ2 grid in a Bayesian way (e.g., Kauffmann et al. 2003b; Benítez 2000; da Cunha et al. 2008; Noll et al. 2009). Assuming Gaussian errors, the likelihood is given by e−1/2χ2. Since a prior is naturally imposed through the sampling of the grid, we can directly interpret the likelihoods as posterior probabilities. We determined the posterior probability distributions (PDFs) both for the input parameters and a range of derived parameters through marginalization over the other input parameters. Marginalization is realized by summing the posterior probabilities. While we determined the probabilities for the input parameters at the sampling points of these parameters, we binned for the derived parameters. Finally we determine the 68% confidence intervals by excluding the first and last 16% in the PDFs. If the point of minimum χ2 is outside the 68% interval, we extend the uncertainty interval to include the minimum χ2 value. Uncertainties derived in this way are listed for the SED based fHα estimates in Table 4 and for other SED parameters in Table E.1.
Because we are adding 5% of the flux to the formal flux-uncertainties in order to reduce artificial impacts of possible ZP uncertainties and template mismatches, the stated uncertainties should not be overinterpreted.
5.6.2. Estimation from total SFR
For those objects with a significant Spitzer/MIPS 24 μm detection in the Muzzin et al. (2013) catalog, we obtained total SFRs from the sum of UV- and IR-based SFRs. While Muzzin et al. (2013) provide these values as part of their catalog, we can assume a more precise redshift, and it is thus worth recalculating the values.
We determined total IR luminosities, LFIR, by scaling the Dale & Helou (2002) templates so that synthetic MIPS magnitudes match the measured ones, and consequently integrating the scaled templates over the range from 8–1000 μm. Following Wuyts et al. (2008) we used the mean of the Dale & Helou (2002) models for α between 1–2.5 as result, where α is the power law index, characterizing the fractional dust mass, dMd, heated by a certain interstellar radiation intensity, U, meaning dMd(U) ∝ U− αdU. The upper and lower limits of the stated uncertainties are given by the values obtained for α = 1 and α = 2.5. It is noteworthy that in the case of contribution from an AGN, the determined values will not be correct. The total infrared luminosity can be converted into a SFR by (Kennicutt 1998) ![\begin{eqnarray} {\it SFR}_\mathrm{IR}(M_\odot\;\mathrm{yr}^{-1}) = 4.5\times10^{-44} L_\mathrm{FIR} [\mathrm{erg}\;\mathrm{s}^{-1}] \label{eq:convirsfr} . \end{eqnarray}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq526.png) (16)For the unobscured UV SFR, we first determined the continuum luminosity density at a rest-frame wavelength of λ = 2800 Å from our best-fit SED model and converted this luminosity into a SFR by using (Kennicutt 1998)
(16)For the unobscured UV SFR, we first determined the continuum luminosity density at a rest-frame wavelength of λ = 2800 Å from our best-fit SED model and converted this luminosity into a SFR by using (Kennicutt 1998) ![\begin{eqnarray} {\it SFR}_\mathrm{UV}(M_\odot\;\mathrm{yr}^{-1}) = 1.4\times10^{-28} L_\nu [\mathrm{erg}\;\mathrm{s}^{-1}\;\mathrm{Hz}^{-1}] \label{eq:convluvsfr} . \end{eqnarray}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq528.png) (17)Then, we converted the determined total SFRtot, as the sum of SFRUV and SFRIR, to the Hα flux. We used the relation from Kennicutt (1998),
(17)Then, we converted the determined total SFRtot, as the sum of SFRUV and SFRIR, to the Hα flux. We used the relation from Kennicutt (1998), ![\begin{eqnarray} {\it SFR}(M_\odot\;\mathrm{yr}^{-1}) = 7.9 \times 10^{-42}\;L_{\mathrm{H}\alpha}[\mathrm{erg}\;\mathrm{s}^{-1}], \label{eq:convoiiha} \end{eqnarray}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq532.png) (18)and converted the luminosity to the observed flux by applying the generic relation between flux and luminosity for our assumed cosmology and the nebular extinction obtained from the SED fit.
(18)and converted the luminosity to the observed flux by applying the generic relation between flux and luminosity for our assumed cosmology and the nebular extinction obtained from the SED fit.
5.6.3. Estimation from zCOSMOS data
In addition, we were using redshifts and line fluxes from the zCOSMOS survey (Lilly et al. 2007; Lilly et al. 2009). Matching the coordinates of our NBES objects to the zCOSMOS-bright 20k data-set18 revealed an overlap of 35 objects with redshift information. It is reassuring that for all matched objects, the redshifts confirmed the presence of an emission line within the filter, which is for 31 objects Hα + [N ii]. The number of those Hα emitters are in the three most useful filter pairs 9 and 10, 14 and 15, and 15 and 16 are 3, 11, and 2, respectively.
The zCOSMOS VLT/VIMOS spectra cover the wavelength range from 550 to 970nm. This means that they include both [O ii]λλ3727,3729 for an object with Hα in the NB118 filter, which is unresolved in the VIMOS data, and Hβ at observed-frame wavelengths of 675 nm and 880 nm, respectively, assuming z = 0.81.
We matched the zCOSMOS spectral fluxes to our imaging apertures by multiplying the continuum flux density at the lines’ wavelength obtained from the SED fitting with the respective zCOSMOS EWobs. In this way, we avoid slit loss and flux calibration issues, with some remaining discrepancy expected from the spatial distribution of H ii regions, if objects are more extended than the PSF.
The [O ii] fluxes can be converted into SFRs, using the calibration by Kewley et al. (2004)![\begin{eqnarray} {\it SFR}(M_\odot\;\mathrm{yr}^{-1}) = (6.58\pm1.65) \times 10^{-42}\;L_\mathrm{[OII]}[\mathrm{erg}\;\mathrm{s}^{-1}] \label{eq:convoiiha2} . \end{eqnarray}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq536.png) (19)This equation is for intrinsic, meaning reddening-corrected, luminosities. Therefore, we dereddened the measured [O ii] fluxes as an intermediate step, again assuming the EN(B − V) from the best-fit SED. The obtained SFR was then converted into an Hα flux using again Eq. (18).
(19)This equation is for intrinsic, meaning reddening-corrected, luminosities. Therefore, we dereddened the measured [O ii] fluxes as an intermediate step, again assuming the EN(B − V) from the best-fit SED. The obtained SFR was then converted into an Hα flux using again Eq. (18).
The ratio between [O ii] and Hα depends to some degree on metallicity and the ionization parameter (e.g., Moustakas et al. 2006). By contrast, Hβ allows for a more direct conversion with the additional advantage of a lower difference in reddening between the wavelengths of Hβ and Hα than between [O ii] and Hα. Unfortunately, the Hβ S/N is relatively low in the zCOSMOS spectra. For those objects with Hβ detection at least at the 2σ level, we obtained an Hα estimate by converting between the reddening-corrected values. The intrinsic ratio between Hα and Hβ is 2.86 for typical conditions in H ii regions, assumed to be ne = 100cm-2 and Te = 10 000K (Osterbrock 1989, p. 84).
5.7. Comparison of TPV with other estimates
 |
Fig. 14 Comparison between Hα central wavelengths obtained from the zCOSMOS redshifts and those obtained from our TPV method. The dashed diagonal lines indicate differences of 2.5nm and 5nm from the 1:1 relation, respectively. Used symbols are explained in the legend of Fig. 15. |
Using the zCOSMOS redshifts and the line flux estimates of Sect. 5.6, we can now directly compare the TPV estimates with those from completely independent measurements and thereby measure the success of the TPV method. First, we consider the redshifts. Because of the high accuracy of the spectroscopic redshifts, the accuracy of the TPV estimates can be directly assessed with a straightforward comparison. In Fig. 14, the TPV estimates of the wavelength λ0 is plotted against the λ0 obtained from the spectroscopic zCOSMOS survey. It can be seen that the TPV wavelength estimates follow spectroscopic estimates closely, with a mean difference of −0.10 nm and a scatter of 1.9 nm. All except two objects are within 2.5 nm. Excluding these two outliers, the scatter decreases to 1.2 nm. We notice that the observed scatter is greater than the statistical error estimate from our estimation code. This indicates that the errors are dominated by systematic effects. Expected systematic uncertainties result from mismatches between true and estimation continua, discrepancies between true and assumed [N ii] ratios, and uncertainties in the available filter curves (cf. Appendix A).
Next, we consider the Hα line flux measurements. In this case, individual independent estimates are not necessarily more accurate than the TPV estimates. For that reason, we combined UV+IR, SED, [O ii], and Hβ based estimates by taking the mean of the individual values. In Fig. 15, the ratio of the NB118 line flux estimates to the combined estimates are plotted versus wavelength. The top panel shows the TPV estimates, while the bottom panel shows the generic discussed in Sect. 5.5.2. The same data is shown in a different way in Fig. 16. In this figure the ratios between the three different estimates can be directly assessed for individual objects.
 |
Fig. 15 Upper panel: ratios between the Hα fluxes estimated from a combination of different methods, which are independent of the NB118 data (ind; cf. Sects. 5.6 and 5.7), and those estimated based on the NB118 data using the TPV technique. Colors refer to the three considered filter pairs, while symbols have meanings as indicated in the legend, with combinations of the different symbols possible. Objects with strongly discrepant individual independent flux estimates are shown as faded. Lower panel: similar ratios as in the upper panel, but now using a generic NB estimation method instead of the TPV method. |
 |
Fig. 16 Ratio between the TPV and a generic NB118 flux estimate is plotted against the ratio between an independent flux estimate and the generic NB118 flux estimate. For objects on the diagonal the independent estimate and the TPV NB118 estimate are identical. The dashed lines indicate factors of 1.5 and 3 between the estimates. The symbols are explained in the legend of Fig. 15. |
For several objects the UV+IR and the SED-based estimates differ by more than a factor ten. The combined line flux for these objects is therefore uncertain, and these objects are shown as faded in the figure. Specifically marked in the figure is one of the objects, which is a broad line AGN according to the zCOSMOS flag 13.5 (cf. Lilly et al. 2009) and another object that shows [Ne v]λ3426 in its spectrum and is thus identified as hosting a type II AGN (e.g., Mignoli et al. 2013). About 80% of the field with data from the filter pairs 9 and 10, 14 and 15, and 15 and 16 are covered by Chandra data from Elvis et al. (2009), out of which ~40% have deep coverage. Matching the Chandra point source catalog, (Civano et al. 2012) revealed one further X-ray detected object. We classify it for the plot as NL AGN. Our independent flux estimates for these objects with certain AGN contribution are only of limited usefulness.
The figure demonstrates that the agreement between the TPV and combined independent line flux estimates is good. The mean of the differences is −0.06 dex with a standard deviation of 0.15 dex. In particular, there is no trend with wavelength over the complete wavelength range of the bandpass. In contrast, the generic single NB filter estimate leads to substantially biased line flux estimates, which can underestimate the flux by as much as a factor of 10 toward the edge of the filter band. Such a bias would, for example, have strong impact on the investigation of the structure at wavelengths around 1198 nm (see Sect. 5.8).
Overall, we conclude that our TPV flux estimates are robust and unbiased, and the error on the flux is smaller by as much as a factor of 20 than using generic single NB estimates to derive line fluxes.
5.8. Spatial and redshift distribution in example filter pair
 |
Fig. 17 Position and Hα wavelength obtained with the TPV method for objects in the part of UltraVISTA that is covered by the NB118 filter pair 14 and 15. Indicated as a thick cross is a BL AGN, while two NL AGNs are indicated as thin crosses. The UltraVISTA DR2 NB118 image is shown in the background. |
The use of the TPV method allows us to directly identify three-dimensional structures, such as filaments or sheets, the detection of which would otherwise require spectroscopic observations with sufficient resolution. This is demonstrated in Fig. 17, which shows the spatial distribution of Hα emitters observed with the filter pair 14 and 15, combined with the wavelength information obtained from the TPV. The size of one NB118 detector corresponds to a comoving distance of 9.7 Mpc at the redshift of Hα in the NB118 filter, while the depth of the volume covered by the wavelength range from 1180 nm to 1205 nm is much more, namely 103 Mpc comoving19. Observations with a single NB118 filter cannot resolve the depth of the field.
In contrast, the redshift resolution obtained with the TPV is sufficient to identify several objects that are at similar redshifts to the BL-AGN, revealing substantial clustering associated with the AGN. In addition, there are also several Hα emitters within the field but at the other redshift end of the volume; i.e., they are spatially well separated from the AGN cluster. Finally, there is a string of objects toward the east. This feature includes objects at various redshifts and is likely a sheet-like structure. While a deeper discussion of these structures is beyond the scope of this paper, this example demonstrates the amount of additional information that can be gained from the TPV.
5.9. Optimizing the observing pattern
 |
Fig. 18 Simulated detection completeness as a function of line flux both for the standard UltraVISTA observing pattern (without turning; solid) and a possible modification (with turning; dashed). The dot-dashed line gives the ratio between the two completeness curves. Fluxes for which twice as many objects are expected in the standard pattern as in the modified pattern are indicated by the shaded area. No objects will be detected left of this area in either of the two observing patterns. The completeness curves were calculated for point sources with a spectrum consisting of a single infinite EW emission line. The underlying detection criterion was a color-significance of the NB118 excess in the stack including data from the 16 filters jointly at least at the 5σ level (cf. Sect. 5.9 for more details). |
As discussed in Sect. 2.2, the best-suited pairs have Δ mag – λ0 curves with average slopes in Δ mag of 0.10 magnm-1 and are monotonous over the relevant wavelength range. Unfortunately, the standard UltraVISTA observing pattern leads to only three cases where the same position on the sky is observed with such ideal filter combinations, namely the filter combinations 9 and 10, 14 and 15, and 15 and 16. One reason for this is that the filter arrangement within the VISTA camera was chosen to maximize the obtainable depth, so the filters are as similar as possible within each column (Nilsson 2007; Milvang-Jensen et al. 2013). Therefore, the overlapping filters are, in most cases, more similar than the overall spread between the 16 NB118 filters suggests (cf. Fig. A.1).
To make use of the full potential of the proposed TPV method, the observing pattern should be modified to increase the number of cases where repeated observations of the same field use dissimilar filters. One strategy that is easy to implement is to turn the telescope by 180° for half of the observation time. With this strategy, each observed position is covered by at least two filters, whereas in the standard observing pattern, about 75% of all positions are covered with only one filter. Furthermore, in the other patches, where two filters already contribute in the standard observing pattern, there would be data from four filters. This increases the number of combinations, which are different enough to allow for a good parameter estimation. Out of the 44 patches, more than half (24) have an average slope of the Δmag – λ0 curve that is greater than 0.10 magnm-1 20.
While the turning pattern would be an enormous step forward for the method, it comes at the price of reduced depth. The specific positioning of similar filters is the logical step for maximizing the reachable depth. This is most crucial for one of the main science goals of the VISTA NB118 observations: the search for z = 8.8 Lyα emitters. We evaluated the impact of the turning pattern on the depth with the simulation described in Appendix C.1. This simulation takes account of the difference in filter profiles and background in the individual filters. In short, we randomly assigned positions on the sky and central wavelengths to 3 × 105 objects, simulated the observations, and determined the fraction of input objects that would be detected as a function of wavelength. Different from the selection criteria in Sect. 5.3.1, we required here a 5σ color significance in the complete stack instead of the two-filter criteria and considered the complete field. To test the effects of the finite number of simulated objects, we also tested the variance between ten subsets of 3 × 104 objects and found a negligible impact on the results.
In Fig. 18, the number of detected objects as function of the flux is shown both for the standard observing pattern and the turning modified one. There is clearly a non-negligible fraction of objects that will be missed at the very faint end when using the turning pattern. Therefore, deciding against or in favor of the turning pattern is a difficult trade-off.
6. Summary and conclusions
In this paper, we have carefully demonstrated the usefulness of the TPV method for deriving redshifts and line fluxes from wavelength-dependent throughput differences between NB filters with slightly differing, yet overlapping passbands and corresponding broadband filters. While it is possible to specifically design NB filters for this method, suitable filters and data taken with such filters already exist, such as the UltraVISTA survey taken with ESO’s VISTA/VIRCAM. For our analysis, we focused on the Hα line in the narrowband NB118 filters of that survey. About one quarter of the UltraVISTA field is covered by at least two different NB118 filters. We used simulations to assess the expected accuracy of our method given the current exposure time of the survey. We found that for the most suitable filter pair, the simulations predict that it is possible to measure wavelengths with random and systematic errors as low as 1nm for a line with f0 = 10 × 10-17ergs-1cm-2 independent of EW. The wavelength estimation results were also shown not to be strongly affected by assumptions on the line width and the required [N ii]λ6583/Hα ratio.
The accuracy in redshift compares favorably to photometric redshifts. A wavelength error of 1 nm corresponds to a 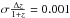 . By comparison, highest quality photometric redshifts in the COSMOS field can at best reach a resolution of about
. By comparison, highest quality photometric redshifts in the COSMOS field can at best reach a resolution of about 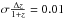 (e.g., Ilbert et al. 2013).
(e.g., Ilbert et al. 2013).
In addition to the simulations, we also applied the method to the actual UltraVISTA DR2 data. A comparison of wavelengths estimated with our method and those obtained from the spectroscopic zCOSMOS-bright 20k catalog (Lilly et al. 2009) shows excellent agreement with a measured scatter of 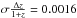 . This value is similar to the
. This value is similar to the 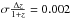 found by Hayashi et al. (2014) in their observations of a galaxy cluster with two optical NB filters in Suprime-Cam on the Subaru Telescope. Independent predictions for the Hα line flux, both based on spectroscopic [O ii] and Hβ fluxes and photometric data, also confirm that the proposed method works very well and is a significant improvement over the results from a generic line flux estimation. This improvement is shown again in Fig. 16.
found by Hayashi et al. (2014) in their observations of a galaxy cluster with two optical NB filters in Suprime-Cam on the Subaru Telescope. Independent predictions for the Hα line flux, both based on spectroscopic [O ii] and Hβ fluxes and photometric data, also confirm that the proposed method works very well and is a significant improvement over the results from a generic line flux estimation. This improvement is shown again in Fig. 16.
We therefore conclude that the TPV method is a powerful tool for deriving redshift and flux estimates from NB surveys that employ multiple versions of similar filters. One of the advantages of the method is that it exploits information that is routinely collected with some instruments. The improvement over the standard analysis is as much as an order-of-magnitude reduction in the errors.
Filter curves, detector QE and mirror reflectivities were downloaded from http://www.eso.org/sci/facilities/paranal/instruments/vircam/inst/Filters_QE_Atm_curves.tar.gz
Based on Vega ZPs from http://casu.ast.cam.ac.uk/surveys-projects/vista/technical/photometric-properties and Vega to AB corrections calculated by us for the assumed filter curves.
Typically stellar metallicities are, at least for local galaxies, 0.5 dex below the gas-phase metallicity (Gallazzi et al. 2005).
McCracken et al. (2012) are describing the UltraVISTA DR1. The current release is DR2: www.eso.org/sci/observing/phase3/data_releases/uvista_dr2.pdf
The relevant equations from Pascual et al. (2007) are especially 7 and 12.
The Y, J, H data in the Muzzin et al. (2013) catalog is based on UltraVISTA DR1 data.
The average slope was calculated as described in Appendix B. For those patches where four filters contribute, we calculated an average slope from the three largest slopes for all six possible combinations.
NDC Infrared Engineering; http://www.ndcinfrared.com
There are small differences between the Hopkins et al. (2001) and the Ly et al. (2011) versions, as mentioned in Ly et al. (2007).
Acknowledgments
We thank the anonymous referee for very constructive comments. The Dark Cosmology Centre is funded by the Danish National Research Foundation. J.Z. acknowledges support from the ERC Consolidator Grant funding scheme (project ConTExt, grant number 648179). B.M.J. and J.P.U.F. acknowledge support from the ERC-StG grant EGGS-278202. Part of this research was funded by an ESO DGDF grant to W.F. and P.M. Based on data products from observations made with ESO Telescopes at the La Silla Paranal Observatory under ESO program ID 179.A-2005 and on data products produced by TERAPIX and the Cambridge Astronomy Survey Unit on behalf of the UltraVISTA consortium. The zCOSMOS observations are based on observations made with ESO Telescopes at the La Silla or Paranal Observatories under program ID 175.A-0839. This research made use of several community-developed Python packages: Astropy (Astropy Collaboration et al. 2013), Matplotlib (Hunter 2007), SciPy and NumPy (Oliphant 2007).
References
- Atad-Ettedgui, E., & Worswick, S. P. 2003, Specialized Optical Developments in Astronomy, 4842, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Benítez, N. 2000, ApJ, 536, 571 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Best, P., Smail, I., Sobral, D., et al. 2013, in Thirty Years of Astronomical Discovery with UKIRT, Astrophysics and Space Science Proc., (Dordrecht: Springer Science+Business Media), 37, 235 [Google Scholar]
- Bland-Hawthorn, J., van Breugel, W., Gillingham, P. R., Baldry, I. K., & Jones, D. H. 2001, ApJ, 563, 611 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bunker, A. J., Warren, S. J., Hewett, P. C., & Clements, D. L. 1995, MNRAS, 273, 513 [NASA ADS] [CrossRef] [Google Scholar]
- Buser, R. 1986, in Proc. Nineteenth IAU General Assembly, Basel, Universität, Switzerland; Space Telescope Science Institute, Baltimore, MD, IN: Highlights of astronomy, 7, 799 [Google Scholar]
- Calzetti, D. 1997, AJ, 113, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Chromey, F. R. 2010, To Measure the Sky (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Civano, F., Elvis, M., Brusa, M., et al. 2012, ApJS, 201, 30 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charlot, S., & Elbaz, D. 2008, MNRAS, 388, 1595 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., & Helou, G. 2002, ApJ, 576, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Barlow, R. J., Cohen, S. A., et al. 2010, ApJ, 712, L189 [NASA ADS] [CrossRef] [Google Scholar]
- Dalton, G. B., Caldwell, M., Ward, A. K., et al. 2006, in SPIE Conf. Ser., 6269 [Google Scholar]
- Djorgovski, S., Spinrad, H., McCarthy, P., & Strauss, M. A. 1985, ApJ, 299, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, A., Siana, B., Brooks, A. M., et al. 2015, MNRAS, 451, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Elvis, M., Civano, F., Vignali, C., et al. 2009, ApJS, 184, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Emerson, J., McPherson, A., & Sutherland, W. 2006, The Messenger, 126, 41 [NASA ADS] [Google Scholar]
- Erb, D. K., Steidel, C. C., Shapley, A. E., et al. 2006, ApJ, 647, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Findlay, J. 2012, Ph.D. Thesis, Queen Mary, University of London [Google Scholar]
- Förster Schreiber, N. M., Genzel, R., Bouché, N., et al. 2009, ApJ, 706, 1364 [NASA ADS] [CrossRef] [Google Scholar]
- Fujita, S. S., Ajiki, M., Shioya, Y., et al. 2003, ApJ, 586, L115 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Bell, E. F., Zibetti, S., Brinchmann, J., & Kelson, D. D. 2014, ApJ, 788, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Ghinassi, F., Licandro, J., Oliva, E., et al. 2002, A&A, 386, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guiderdoni, B., & Rocca-Volmerange, B. 1987, A&A, 186, 1 [NASA ADS] [Google Scholar]
- Hastings, W. K. 1970, Biometrika, 57, 97 [Google Scholar]
- Hayashi, M., Kodama, T., Koyama, Y., et al. 2014, MNRAS, 439, 2571 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Irwin, M. J., & Connolly, A. J. 2001, ApJ, 558, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, S. B. 2000, Handbook of CCD Astronomy (Cambridge, New York: Cambridge University Press) [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [Google Scholar]
- Ilbert, O., McCracken, H. J., Le Fèvre, O., et al. 2013, A&A, 556, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Inoue, A. K., Shimizu, I., Iwata, I., & Tanaka, M. 2014, MNRAS, 442, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Ivanov, V. D., & Szeifert, T. 2009, VIRCAM/VISTA User Manual, 1st edn., European Southern Observatory [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Geller, M. J., & Jansen, R. A. 2004, AJ, 127, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Kochiashvili, I., Møller, P., Milvang-Jensen, B., et al. 2015, A&A, 580, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lamareille, F., Brinchmann, J., Contini, T., et al. 2009, A&A, 495, 53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Borgne, J. F., Bruzual, G., Pello, R., et al. 2003, A&A, 402, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lilly, S. J., Le Fèvre, O., Renzini, A., et al. 2007, ApJS, 172, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Le Brun, V., Maier, C., et al. 2009, ApJS, 184, 218 [Google Scholar]
- Lissberger, P. H. 1970, Rep. Prog. Phys., 33, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2007, ApJ, 657, 738 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Lee, J. C., Dale, D. A., et al. 2011, ApJ, 726, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Ly, C., Malkan, M. A., Kashikawa, N., et al. 2012, ApJ, 757, 63 [NASA ADS] [CrossRef] [Google Scholar]
- McCracken, H. J., Milvang-Jensen, B., Dunlop, J., et al. 2012, A&A, 544, A156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., & Teller, E. 1953, J. Chem. Phys., 21, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Mignoli, M., Vignali, C., Gilli, R., et al. 2013, A&A, 556, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Milvang-Jensen, B., Freudling, W., Zabl, J., et al. 2013, A&A, 560, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Møller, P., & Warren, S. J. 1993, A&A, 270, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Morelli, D. W. 1991, Interference filter handbook. A guide for specifying optimum filter performance (Santa Rosa, Ca.: Optical Coating Laboratory Inc.) (OCLI) [Google Scholar]
- Moustakas, J., Kennicutt, Jr, R. C., & Tremonti, C. A. 2006, ApJ, 642, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., Marchesini, D., Stefanon, M., et al. 2013, ApJS, 206, 8 [Google Scholar]
- Nelder, J. A., & Mead, R. 1965, Comput. J., 7, 308 [CrossRef] [Google Scholar]
- Nilsson, K. K. 2007, Ph.D. Thesis, Dark Cosmology Centre, Niels Bohr Institute Faculty of Science, University of Copenhagen [Google Scholar]
- Nilsson, K. K., Møller, P., Möller, O., et al. 2007, A&A, 471, 71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oke, J. B. 1974, ApJS, 27, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Oliphant, T. E. 2007, Comput. Sci. Eng., 9, 10 [CrossRef] [PubMed] [Google Scholar]
- Ono, Y., Ouchi, M., Shimasaku, K., et al. 2010, ApJ, 724, 1524 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, CA: University Science Books) [Google Scholar]
- Ouchi, M., Shimasaku, K., Furusawa, H., et al. 2003, ApJ, 582, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Pagel, B. E. J., Edmunds, M. G., Blackwell, D. E., Chun, M. S., & Smith, G. 1979, MNRAS, 189, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Pascual, S., Gallego, J., & Zamorano, J. 2007, PASP, 119, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Price, S. H., Kriek, M., Brammer, G. B., et al. 2014, ApJ, 788, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, N. A., Kriek, M., Shapley, A. E., et al. 2015, ApJ, 806, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Rhoads, J. E., Malhotra, S., Dey, A., et al. 2000, ApJ, 545, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, G. O., & Rosenthal, J. S. 2001, Statist. Sci., 16, 351 [CrossRef] [MathSciNet] [Google Scholar]
- Robitaille, T. P., Tollerud, E. J., et al. Astropy Collaboration 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rosenthal, J. S. 2014, in Statistics in Action: A Canadian Outlook (CRC Press), 93 [Google Scholar]
- Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
- Savaglio, S., Glazebrook, K., Le Borgne, D., et al. 2005, ApJ, 635, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., & de Barros, S. 2009, A&A, 502, 423 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechter, P. 1976, ApJ, 203, 297 [Google Scholar]
- Shivaei, I., Reddy, N. A., Steidel, C. C., & Shapley, A. E. 2015, ApJ, 804, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2009, MNRAS, 398, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Best, P. N., Geach, J. E., et al. 2010, MNRAS, 404, 1551 [NASA ADS] [Google Scholar]
- Sobral, D., Best, P. N., Smail, I., et al. 2011, MNRAS, 411, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Sobral, D., Smail, I., Best, P. N., et al. 2013, MNRAS, 428, 1128 [NASA ADS] [CrossRef] [Google Scholar]
- Takahashi, M. I., Shioya, Y., Taniguchi, Y., et al. 2007, ApJS, 172, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Vanzi, L., Gennari, S., Ciofini, M., & Testi, L. 1998, Exp. Astron., 8, 177 [Google Scholar]
- Villar, V., Gallego, J., Pérez-González, P. G., et al. 2008, ApJ, 677, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Westera, P., Lejeune, T., Buser, R., Cuisinier, F., & Bruzual, G. 2002, A&A, 381, 524 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wuyts, S., Labbé, I., Schreiber, N. M. F., et al. 2008, ApJ, 682, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Wuyts, S., Förster Schreiber, N. M., Lutz, D., et al. 2011, ApJ, 738, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., Bergvall, N., Olofsson, K., & Siebert, A. 2001, A&A, 375, 814 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: The NB118 filter curves
Throughout this paper our results were based on the set of VISTA NB118 filters. In Fig. A.1 we show all 16 filter curves used in this study and in Fig. A.2 one of the filters (filter 15) is shown in comparison to the Y and J filters.
So far, we have neglected the uncertainties in the measured filter curves. Unfortunately, there are several sources of potentially significant errors in the available filter curves. We therefore summarize the origin of the assumed filter curves and our current understanding of their accuracy in this appendix.
The VIRCAM filter curves are based on laboratory scans carried out at room temperature in the normal incidence collimated beam. These measurements have been supplied by the filter manufacturer, NDC21.
However, since the NB118 filters are multilayer dielectric interference filters, the transmittance curves depend both on the temperature and the angle of incidence of the beam. Qualitatively, both a cooling and the change from the collimated beam to larger incidence angles lead to a shift in the passband toward shorter wavelengths (Morelli 1991). This is relevant because in VIRCAM the filters are located in a fast convergent beam (e.g., Atad-Ettedgui & Worswick 2003) at cryogenic temperatures. The convergent beam can be understood as formed by rays coming from different incidence angles, each of which sees a filter curve corresponding to its incidence angle.
One way to approximate the actual filter curves within the cryogenic convergent beam is to do an entirely theoretical conversion from the collimated beam measurement. Assuming a temperature dependence of 0.0186 nm K-1 (NDC), the difference of 205 K between room temperature and filter temperature in VIRCAM (~90 K; ESO, priv. comm.), equals a blueward shift of 4.26 nm. We made the assumption that the shape of the transmittance curve is preserved under the temperature shift. The justification of this assumption was confirmed by a remeasurement of a witness sample done by NDC in 2013.
The transformation between collimated and convergent beam was based on the assumption that it is possible to approximate the filter curve in a collimated beam with non-normal incidence angle θ from that for normal incidence by 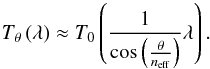 (A.1)Since the range of relevant incidence angles in the VISTA beam extends up to ~20 deg, Eq. (A.1) must be a good approximation for a wide range of angles. According to Morelli (1991), a conservation of the general filter curve shape is a good approximation up to angles of 30 deg. In the literature there are a few examples where measurements of similar NIR filters have been published for different incidence angles. For some of them, the results seem approximately consistent with Eq. (A.1) (e.g., Ghinassi et al. 2002), while there is for others a stronger discrepancy (e.g., Vanzi et al. 1998). Again based on a witness sample, NDC provided us with measurements of the material for incidence angles up to 12deg. The shape was indeed approximately conserved.
(A.1)Since the range of relevant incidence angles in the VISTA beam extends up to ~20 deg, Eq. (A.1) must be a good approximation for a wide range of angles. According to Morelli (1991), a conservation of the general filter curve shape is a good approximation up to angles of 30 deg. In the literature there are a few examples where measurements of similar NIR filters have been published for different incidence angles. For some of them, the results seem approximately consistent with Eq. (A.1) (e.g., Ghinassi et al. 2002), while there is for others a stronger discrepancy (e.g., Vanzi et al. 1998). Again based on a witness sample, NDC provided us with measurements of the material for incidence angles up to 12deg. The shape was indeed approximately conserved.
 |
Fig. A.1 Passbands of 16 NB118 filters after convergent beam transformation, with QE and mirror reflectivities applied, and artificially shifted by 3.5 nm towards the red, as motivated by the results in Milvang-Jensen et al. (2013). Filters in the four different columns of the observing pattern are marked in four different colors. Columns numbers are counted from right to left in Fig. 9. |
 |
Fig. A.2 Passbands of one of the NB118 filters (filter 15) in comparison to the VISTA/VIRCAM Y and J passbands. |
VISTA’s beam can be characterized by the radiant intensity as a function of the angle of incidence, ϵ(φ,θ). Here, φ and θ are the two-dimensional polar coordinates characterizing the latter. Neglecting all effects of wave optics, ϵ(φ,θ) can be described to first order by an annulus with constant value. The annulus’s inner radius ρin and outer radius ρout have values of 3.85deg and 8.75deg, respectively (Nilsson et al. 2007). This annulus is shifted corresponding to the object’s position in the field of view in the φ, θ plane. The angle of incidence of the annulus’s center is related to the object’s position on the sky by 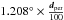 (Findlay 2012). The position dper is stated here in percentages of detectors.
(Findlay 2012). The position dper is stated here in percentages of detectors.
With this input, the effective filter curve for the complete beam can be calculated by (e.g., Lissberger 1970): 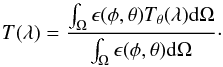 (A.2)Consequently, we can finally estimate the shape of the filter curves in VIRCAM’s convergent beam by combining Eqs. (A.1) and (A.2).
(A.2)Consequently, we can finally estimate the shape of the filter curves in VIRCAM’s convergent beam by combining Eqs. (A.1) and (A.2). 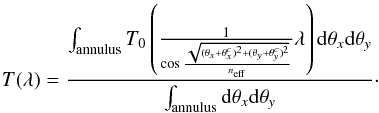 (A.3)We tested our script doing the actual convergent beam conversion based on a 1% top-hat filter and comparing the results to those presented in Bland-Hawthorn et al. (2001). Filter curves for the different steps in the conversion were shown in Fig. 4 of Milvang-Jensen et al. (2013). They found an unexpected shift in the filter curves toward the red by about 3.5 nm. While we are still investigating possible physical reasons for the shift, we assume in this work the predicted convergent beam curves shifted by 3.5 nm toward the red to account for this finding. That the presented TPV method works well for the actual data under this assumption further indicates that these filter curves are a reasonable assumption.
(A.3)We tested our script doing the actual convergent beam conversion based on a 1% top-hat filter and comparing the results to those presented in Bland-Hawthorn et al. (2001). Filter curves for the different steps in the conversion were shown in Fig. 4 of Milvang-Jensen et al. (2013). They found an unexpected shift in the filter curves toward the red by about 3.5 nm. While we are still investigating possible physical reasons for the shift, we assume in this work the predicted convergent beam curves shifted by 3.5 nm toward the red to account for this finding. That the presented TPV method works well for the actual data under this assumption further indicates that these filter curves are a reasonable assumption.
Appendix B: Quantitative assessment of throughput variation for all possible NB118 pairs
The suitability of a filter combination for the TPV can be assessed through Δmag − λ0 curves, as discussed in Sect. 2.2. We characterized the Δmag − λ0 curves for all 120 possible VIRCAM NB118 combinations by following three quantities:
-
difference between maximum and minimum Δmag;
-
percentage of the wavelength range, where the Δmag values are unique;
-
average absolute slope (| dΔmag/ dλ0 |) and its standard deviation.
For calculating these values, a relevant wavelength interval needs to be chosen. We assumed the wavelength range where the transmittance of the combined effective filter is not below 2/30 of its maximum value. This threshold is a reasonable number because it approximately corresponds to the ratio between the FWHMs of the NB118 filters and J. Consequently, an emission line causes a stronger excess in the NB118 filters than in J within the included range.
The resulting values for all 120 combinations are listed in Table B.1. For the example filter-combination 14 and 15, as shown in Fig. 1, the range in Δmag values is 3.12 with a uniqueness of 100%. The average absolute slope is 0.14 magnm-1. The assumed wavelength interval, as defined above, is indicated in the lefthand panel of Fig. 1. Assuming, for example, 5σ detections in each of the two filters, corresponding to an error of δΔmag ~ 0.3 for the magnitude difference, this would allow on average for a very good wavelength resolution of about 2 nm.
Suitability of all possible NB118 combinations for the TPV.
Appendix C: Expected number of Hα emitters in regions of filter overlap
Appendix C.1: Simulation
We estimated the number and luminosity distribution of Hα emitters that we expect to select in the area with coverage in two NB118 filters. A simulation, as described below, allowed us to obtain this estimate both for the DR2 and the finalized UltraVISTA. The simulation takes fully account for the filter curve shapes and the different background brightnesses in the individual filters. Further, the simulated observing and stacking strategy resembles that for the actual UltraVISTA observations.
As a first step, we created 300 000 simulated objects with a continuum flat in fν, a random Hα central wavelength between 1167–1209 nm, a fixed [N ii] ratio of either w6583 = 0 or w6583 = 0.3, and a fixed input Hα luminosity, ℒ0;in. The HαEW0 were drawn from a log-normal distribution with a ⟨ log 10(EW0/ nm) ⟩ = 0.35 and σ [ log 10(EW/ nm) ] = 0.4. This distribution is the best fit obtained by Ly et al. (2011) to their NEWFIRM narrowband observations. Their NB filter has a similar wavelength as the UltraVISTA NB118 filters.
After assigning to these 300 000 objects random positions within a 1.4 × 1.4 deg2 field, we checked whether an object is observed, and if so, in which filter. We determined this for a range of jitter positions for each of the three pawprints in the UltraVISTA NB118 observing pattern. For computational reasons, we simulated per pawprint only 28 random jitters drawn from a 2″ × 2″ box.
Then, we calculated synthetic flux densities, fν (Eq. (2)), and the corresponding uncertainties for each object. We separated the uncertainties into δof and δbf for object and background, respectively22. The calculations were based on the same ZPs, gains, detector-depended sky-counts, and observation times for the DR2 and final UltraVISTA as described in Sect. 4.3. Next, we combined the signal from the different jitter positions by weighting with 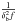 and we propagated the errors on the noise accordingly.
and we propagated the errors on the noise accordingly.
Appendix C.2: Method
The measured source flux density scales for fixed EWobs linearly with line luminosity both for the NB and the BB filter. Therefore, we can use the flux densities obtained for ℒ0;in to determine the ℒ0,req that is required to fulfill the inequality 9 for a chosen color-significance κ. This means we solve a quadratic equation 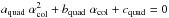 in the common way, where
in the common way, where 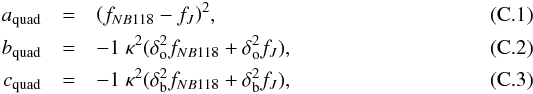 and αcol is the ratio between ℒ0,req and ℒ0;in23. Similarly, we can determine the factor αdetsig that is required to fulfill Eq. (10).
and αcol is the ratio between ℒ0,req and ℒ0;in23. Similarly, we can determine the factor αdetsig that is required to fulfill Eq. (10).
 |
Fig. C.1 Expected number of Hα emitters in the part of the UltraVISTA NB118 field with data from two different NB118 filters as a function of line luminosity. Predicted curves are included both for the UltraVISTA DR2 (blue) and the final UltraVISTA (red) for three different z = 0.8Hα LFs from the literature. Results are plotted for the assumption of w6583 = 0.3 in all three cases. In the case of the Ly et al. (2011) LF, the curve for w6583 = 0 is also shown. Small arrows indicate luminosities corresponding to line fluxes of 3.0, 5.0, 10.0, and 20.0 × 10-17 erg s-1 cm-2. The integrated numbers for objects brighter than the respective marked fluxes are stated in Table C.1. |
Integrated number of Hα emitters expected in the UltraVISTA survey above different flux thresholds.
Consequently, we found the minimum factor α, which fulfills both the color-significance combined with the color-cut (cf. Eq. (8)) in one of the two filters and the detection significance in the other filter. If any of the criteria cannot be fulfilled at any flux, we set α to ∞. In addition, we also applied the same region mask as used for the actual data (cf. Eq. (11)).
Based on the α’s obtained for the simulated objects, we determine the fraction of detections as a function of line flux. Eventually, we multiply this luminosity completeness function with luminosity functions from the literature and the volume covered by the random box. Finally, this allowed for the estimate of the number of detections as a function of line luminosity.
We used the Schechter (1976) parameterizations of the three LFs stated by Ly et al. (2011), including their own z = 0.81 LF and the two z = 0.84 LFs of Villar et al. (2008) and Sobral et al. (2009). These LFs are listed in Ly et al. (2011) with a reddening and completeness correction applied, whereas we need for the purpose of our simulation non-reddening corrected LFs. Therefore, we inverted their SFR depended reddening correction that is based on Hopkins et al. (2001)24. Assuming the underlying direct proportionality between SFR and Hα luminosity (Kennicutt 1998), the relation between intrinsic, LHα;int, and observed Hα luminosity, LH,α;int, can be written as (Ly et al. 2011): ![\appendix \setcounter{section}{3} \begin{equation} L_{\mathrm{H}\alpha;\mathrm{obs}} = L_{\mathrm{H}\alpha;\mathrm{int}}\times{\left(\frac{0.797\log (SFR_\mathrm{int}[{\rm H}\alpha]) + 3.786} {2.86}\right)}^{-2.360}\cdot \end{equation}](/articles/aa/full_html/2016/06/aa26378-15/aa26378-15-eq621.png) (C.4)
(C.4)
Appendix C.3: Results
The estimated number of galaxies per unit logarithmic luminosity interval is shown in Fig. C.1 for the three different LFs. For orientation, luminosities corresponding to fluxes of approximately253.0, 5.0, 10.0, and 20.0 × 10-17 erg s-1 cm-2 are indicated. Integrated numbers are stated down to the detection limit and to these four reference fluxes in Table C.1.
Summing it up, we estimate on the order of 200 Hα emitters at the depth of the DR2 in the part of the field with data from overlapping filters. The number for the full UltraVISTA field is expected to be about three times higher and the number for the final UltraVISTA data will almost double the number compared to the DR2.
Appendix D: Expected line S/N in NB and BB filters
Figure D.1 shows the inverse of the S/N that an emission line point source with infinite EW would reach for a given line flux in J and NB118, respectively, both for the UltraVISTA DR2 and the expected full UltraVISTA. The calculation was based on Eq. (6) and the simulation inputs described in Sect. 4.1. Assuming that the continuum flux density could be estimated without uncertainty, these would be the S/N values for the line alone, independent of the EW.
NB118 results are shown for the peak of filter 15, which has a typical sky-brightness among the 16 NB118 filters, and are plotted both for the typical per-pixel integration time and half its value. The latter is relevant when the available time is equally shared between two contributing filters.
Even so the UltraVISTA BB data is extremely deep, the line S/N in NB118 exceeds that in J by a factor 4.1 or 3.4 for the DR2 and the expected final survey, respectively. On the other hand, at low transmittance of the NB filter, the line S/N in J becomes equivalent or even higher than that in the NB filter.
 |
Fig. D.1 Inverse of the signal-to-noise as a function of line flux for an infinite EW line in J and at peak transmittance of NB118 filter 15. Curves are shown both for exposure times as in the UltraVISTA DR2 (blue) and for the final UltraVISTA survey (red). Moreover, for the NB118 filter, results are included both for the typical per pixel integration time (alone) and for half this value (overlap) (cf. Sect. 5.1). |
Appendix E: Full SED fitting results
The full SED fitting results are listed in Table E.1 for the sample of NB excess objects that have observations in either of the NB118 pairs 9 and 10, 14 and 15, or 15 and 16 (cf. Sect. 5.6.1). Additionally, the table includes the EWobs estimated through the TPV.
Properties of the best-fit SEDs from SED fitting and values for EWobs from the TPV.
Appendix F: Details about the selection of NB excess objects
Appendix F.1: Color correction for J band magnitudes
The NB118 filter is at the blue end of the J passband (Fig. A.2). Consequently, an estimate of the continuum at the wavelength of the NB118 filter needs to include more information than J alone because it is necessary to correct for the galaxies’ intrinsic colors.
Therefore, we estimated the continuum magnitude at the wavelength of the NB118 filter, Jcorr, through a linear combination of Y and J. Although this approach is identical to Milvang-Jensen et al. (2013), we adjusted the exact linear combination for two reasons. First, the zeropoints for the broadband data have been adjusted between the UltraVISTA DR1 (McCracken et al. 2012), which was used by them, and the DR210 used by us. Second, we applied in this work corrections between the Vega magnitude system and the AB system, which differ slightly from those used for both UltraVISTA data releases and the work of Milvang-Jensen et al. (2013). In the following, we justify the chosen color correction.
Under the assumption that SEDs are power laws over the wavelength range covered by the Y and J filters, the appropriate combination can be determined based on the filters’ central wavelengths. This results in 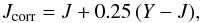 (F.1)which corresponds to Eq. (13) when using flux densities instead of magnitudes.
(F.1)which corresponds to Eq. (13) when using flux densities instead of magnitudes.
The validity of Eq. (F.1) can be verified empirically. Due to the simplicity of a one-color correction, this can be easily visualized. In Fig. F.1 we show the 2d histogram of the number of objects with J − NB118 as a function of Y − J. All sources from the NB118 detected catalog that have a NB118 detection above 5σ and Y and J detections with at least 3σ are included. The locus of the objects follows the predicted line (Eq. (F.1)) very well for Y − J< 0.5. This confirms empirically that the relation is justified.
The number of objects is small for Y − J ≳ 0.5. Nevertheless, it can be concluded that the line with a slope of −0.25 is not a good representation of their typical colors. The main reason is that this part of the color space is mainly populated by passive galaxies at z ~ 2. Their red colors are not caused by dust but by the Balmer/4000 Å break located at the interface of Y and J. Even though there might be some identifiable trend in J − NB118 as a function of Y − J also beyond Y − J> 0.5, the number of objects is small, and we decided to follow Milvang-Jensen et al. (2013) also in this part of the color space. They used for the reddest objects a constant correction to J. We determined this constant correction as minus the median J − NB118 color of all objects with Y − J> 0.5 and derived a value of 0.126. In order to have a continuous transition from F.1 into the constant part, we used: 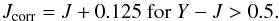 (F.2)Expressed as flux densities, this is equivalent to Eq. (12).
(F.2)Expressed as flux densities, this is equivalent to Eq. (12).
Formally, we set in absence of a Y detection (<2σ) Jcorr simply to J. However, this is not really relevant, as we do not have any NB excess objects without Y detection in the NB118 catalog created with the conservative SExtractor parameters (cf. Sect. F.2) used for this work.
Appendix F.2: Narrowband excess and detection thresholds
When selecting emission line galaxies from NB data, thresholds for the magnitude excess (cf. Eq. (8)) and its significance need to be set (cf. Eq. (9)). Good selection criteria provide a compromise between the inclusion of low EW emitters and a small contamination from objects without emission line in the NB filter.
Milvang-Jensen et al. (2013) concluded based on an analysis of stellar population models that Jcorr − NB118, which is for power law SEDs expected to be close to zero, does also for realistic stellar SEDs not exceed 0.2 by much. The largest deviations from zero are expected at redshifts where the 4000 Å/Balmer break and strong absorption lines fall into the wavelength range of the Y and J filters, especially at population ages where these features are pronounced26. A selection threshold of Jcorr − NB118 > 0.2 can be considered as a conservative choice to identify emission line galaxies. Jcorr − NB118 = 0.2 corresponds to an EWobs of 27.4 Å27.
 |
Fig. F.1 J − NB118 versus Y − J for all objects with a 5σ NB118 detection in the stack and at least a 2σ detection in the two broadband filters. Orange crosses give the median of J − NB118 for all objects within equidistant Y − J bins. The solid red line is the assumed color correction (cf. Eqs. (F.1) and (F.2)), meaning that we defined objects on this line to have a Jcorr − NB118 of zero. The J − NB118 = − 0.25(Y − J) line (Eq. (F.1)) is also shown beyond Y − J> 0.5, but there as dotted line. |
The required Jcorr − NB118 color combined with a 4σ significant color excess (Eq. (9)) is expected to result in a nearly pure sample of NB excess objects. We demonstrate this in Fig. F.2, where data for one filter from each of the 12 regions with overlapping filters is included. The plot shows 12 different lines for the color-excess criterion (Eq. (9)). The reason for this is that the depth in the 12 relevant filters strongly differs. In addition to the relevant selection curves, we also show these curves mirrored at Jcorr − NB118 = 0. This allows, at least to some extent, to judge the contamination fraction due to statistical noise. It is as expected very low.
 |
Fig. F.2 Measured NB excess as a function of the NB118 magnitude for all objects in the main NB118 detected catalog. Data is only included for the regions of overlapping filters and in each of the overlapping regions only for one of the two filters. The red-dotted horizontal line indicates the minimum required NB118 excess for objects that we classify as NB excess objects. In addition, the curves for a 4σ positive Jcorr − NB118 [ i ] are shown for each of the 12 filters. The crosses show the median of the Jcorr − NB118 in NB118 bins with a width of 0.5 mag. Finally, all mentioned lines are also plotted mirrored at Jcorr − NB118 [ i ] = 0. |
It is noteworthy that these conservative selection criteria will miss [O ii] emitters at z = 2.2 (cf. also Milvang-Jensen et al. 2013). However, this is no problem for the present work, as we are here not interested in [O ii] emitters. Refined selection criteria for these objects will be discussed in a forthcoming work.
In addition to the criteria described above, we decided to use a relatively high detection and analysis threshold of 2σ in a least four neighboring pixels for SExtractor. This detection threshold is at the limit of affecting the completeness within our selection criteria: A lower detection threshold would slightly increase the number of objects in the NBES. E.g. at a very low threshold of 0.9σ, the NBES sample would include 13 more objects (252 vs. 239). Nevertheless, we decided to use the 2σ catalog, as we aimed in this work to include only clean and well centered detections.
All Tables
Range of parameters used for the pre-grid in the parameter estimation with the Nelder-Mead implementation of our code.
Values for mean and standard deviation of best estimates for Hα fluxes, f0;est, and wavelengths, λ0;est, using the TPV on repeated simulations of observations of the same Hα emitters.
Integrated number of Hα emitters expected in the UltraVISTA survey above different flux thresholds.
Properties of the best-fit SEDs from SED fitting and values for EWobs from the TPV.
All Figures
 |
Fig. 1 Illustration of how to obtain accurate line fluxes by using two NB filters. The left panel shows the throughput curves of two similar NB filters, superimposed on an emission line shifted to different wavelengths. The righthand panel shows the corresponding differences between the magnitudes measured with the two filters, Δmag, as a function of the wavelength of the emission line, λ0. Here, the green dashed lines indicate how a measurement of Δmag can be used to determine the wavelength of the line, which in turn can be used to estimate its flux using the throughput curves on the left. The shown filter combination is the filter pair 14 and 15 of the NB118 filters, where 15 is the bluer one. The meaning of the small arrows is described in Sect. 4.3.1 and the two vertical lines in Appendix B. |
| In the text | |
 |
Fig. 2 Δmag – λ0 curves for five different NB118 combinations assuming an infinite EWobs emission line. The passbands of the respective NB118 filters, for which the Δmag – λ0 are shown, are also indicated in the different panels. The axis scaling for the filter passbands is linear. |
| In the text | |
 |
Fig. 3 Impact of the line shape (upper panels) and the presence of multiple lines (lower panels) on the predicted Δmag − λ0 curves. The left panels show different input spectra, and the right panels the corresponding Δmag – λ0 curves. “g”, “l”, and “b” in the legend refer to Gaussian, boxcar, and Lorentzian, respectively, with the succeeding numbers stating the line FWHM in kms-1. The presence of multiple lines is demonstrated for the relevant example of the [N ii] doublet bracketing Hα, with the values in the legend corresponding to the assumed [N ii]λ6583 to Hα ratios. All the shown results are based on the same filter combination as used for Fig. 1. |
| In the text | |
 |
Fig. 4 Difference between the continuum of synthetic spectral energy distributions (SED) and the estimate obtained from a power law fit to these SEDs (model) using Y, J, and H filters. The magnitude difference between Jmodel and Jsed is plotted against the magnitude difference between SED and model directly at the wavelength of Hα (cf. Sect. 4.2). The range of SED parameters, for which results are shown, is summarized in Table 1. For the Z = 0.05 panel, a wider axis scale was chosen than in the other two cases. The narrower range used for Z = 0.008 and Z = 0.020 = Z⊙ is indicated as dotted box in the Z = 0.05 case. The cross in the Z = 0.020 plot represents the SED, which was used for the parameter estimation test described in Sect. 4.3. |
| In the text | |
 |
Fig. 5 Distributions of the best-fit wavelength λ0;est (left panels; cumulative) and flux f0;est (right panels) for input spectra with an emission line at the effective wavelength (top panels) and at 50% transmittance (bottom panels) of the two NB118 filters’ combined passband. In each panel, distributions are shown for five different Ha fluxes. The respective values are listed in the legend in units of ergs-1cm-2. The input EWobs;in was 10 nm in all five cases. Fits were obtained at both transmittances for 500 realizations of simulated observations in NB118 14 and 15, Y, J, and H. Dashed lines indicate that the objects would not be selected as NB excess objects. |
| In the text | |
 |
Fig. 6 Distributions of best-fit wavelength and flux similar to Fig. 5. Here, distributions for five different EWobs;in are shown. EWobs;in values stated in the legend are in units of nm. The input flux was 10 × 10-17 ergs-1cm-2 in all cases. |
| In the text | |
 |
Fig. 7 Similar to Fig. 5, but for three different assumptions in the TPV algorithm. First, results are shown both for assuming the default minimal BB estimation uncertainty (cf. Eq. (5)), |
| In the text | |
 |
Fig. 8 Similar to Fig. 5, but here results are shown for different filter combinations. An EWobs;in = 10nm and a f0;in = 10 × 10-17ergs-1cm-2 were assumed. |
| In the text | |
 |
Fig. 9 Diagram showing which copies of the NB118 filters contribute to the different parts of the field covered by the UltraVISTA NB118 tile. The numbers in parentheses are only relevant when using the suggested modification of the observing pattern, as discussed in Sect. 5.9. |
| In the text | |
 |
Fig. 10 Statistical distribution of magnitude differences for objects with observations available in two different NB118 filters. Histograms are shown for the sample of 239 objects with NB excess (NBES), and for 100 comparison samples. The comparison samples have the same number of objects and distribution of stack magnitudes as the NBES in each of the 12 contributing filter combinations, but no NB excess was required. Upper: both the histogram for the NBES and the histograms obtained from the mean of the 100 comparison samples are shown. In the latter case, the standard deviation between the different samples is indicated by errorbars. Lower: cumulative distribution for the mean of the comparison samples and for the NBES sample. The maximal differences between the two samples is indicated by an arrow. In addition, for the NBES, the cumulative histograms are included for the individual filter combinations. Two subsets of the NBES are plotted. |
| In the text | |
 |
Fig. 11 Magnitude, redshift, and field distribution for our sample of NB excess objects with observations available in two different NB118 filters (NBES). Those NBES objects with their magnitudes in the two contributing NB118 filters differing by more than 2.5σ are shown in color, with the colors referring to the different filter pairs. All other NBES objects are shown in the background in gray. Upper left: the difference in magnitude between the two individual contributing filters is plotted against the magnitude in the stack. Magnitudes were measured in 2′′ diameter apertures, and errorbars are 1σ uncertainties. Upper right: the Jcorr − NB118 color excess is plotted against the magnitude difference between the individual NB118 filters. Jcorr − NB118 is corrected for the continuum slope by means of the Y − J color (see Sect. 5.3.1). Lower left: Jcorr − NB118 plotted against the photometric redshift (Ilbert et al. 2013). The three main groups are Hα (z ~ 0.8), [O iii]+ Hβ (z ~ 1.4), and [O ii] (z ~ 2.2). Different symbols refer to membership in these groups. The X (not in legend) labels objects with significant throughput variations, where no association with a specific line was possible. A histogram of the photometric redshifts is included in the upper part of this panel. The vertical lines indicate the redshift intervals that are used for the classification into [S iii] (dotted), Hα (solid), [O iii]+ Hβ (dashed), and [O ii] (dash-dotted). Lower right: position of the objects in the field of view. The DR2 NB118 stack is shown in the background. Larger symbols have a NB118 [ a ] − NB118 [ b ] > 0 and smaller symbols have NB118 [ a ] − NB118 [ b ] < 0. |
| In the text | |
 |
Fig. 12 4″ × 4″ cutouts in UltraVISTA DR2 Y and J, NB118 14 and 15, and HST/ACS/F814W for two Hα emitters with significant throughput differences between filters 14 and 15. Both objects have spectroscopic redshifts from zCOSMOS (Lilly et al. 2009) and are included in Table 4. For each object, the four UltraVISTA panels are scaled to the same surface brightness in fν. |
| In the text | |
 |
Fig. 13 Results from the TPV parameter estimation with our MCMC code for the example object with the NBES ID 7 (zCOSMOS ID 810332). Shown are the 2D histograms, indicating the correlations between the four fitted parameters. |
| In the text | |
 |
Fig. 14 Comparison between Hα central wavelengths obtained from the zCOSMOS redshifts and those obtained from our TPV method. The dashed diagonal lines indicate differences of 2.5nm and 5nm from the 1:1 relation, respectively. Used symbols are explained in the legend of Fig. 15. |
| In the text | |
 |
Fig. 15 Upper panel: ratios between the Hα fluxes estimated from a combination of different methods, which are independent of the NB118 data (ind; cf. Sects. 5.6 and 5.7), and those estimated based on the NB118 data using the TPV technique. Colors refer to the three considered filter pairs, while symbols have meanings as indicated in the legend, with combinations of the different symbols possible. Objects with strongly discrepant individual independent flux estimates are shown as faded. Lower panel: similar ratios as in the upper panel, but now using a generic NB estimation method instead of the TPV method. |
| In the text | |
 |
Fig. 16 Ratio between the TPV and a generic NB118 flux estimate is plotted against the ratio between an independent flux estimate and the generic NB118 flux estimate. For objects on the diagonal the independent estimate and the TPV NB118 estimate are identical. The dashed lines indicate factors of 1.5 and 3 between the estimates. The symbols are explained in the legend of Fig. 15. |
| In the text | |
 |
Fig. 17 Position and Hα wavelength obtained with the TPV method for objects in the part of UltraVISTA that is covered by the NB118 filter pair 14 and 15. Indicated as a thick cross is a BL AGN, while two NL AGNs are indicated as thin crosses. The UltraVISTA DR2 NB118 image is shown in the background. |
| In the text | |
 |
Fig. 18 Simulated detection completeness as a function of line flux both for the standard UltraVISTA observing pattern (without turning; solid) and a possible modification (with turning; dashed). The dot-dashed line gives the ratio between the two completeness curves. Fluxes for which twice as many objects are expected in the standard pattern as in the modified pattern are indicated by the shaded area. No objects will be detected left of this area in either of the two observing patterns. The completeness curves were calculated for point sources with a spectrum consisting of a single infinite EW emission line. The underlying detection criterion was a color-significance of the NB118 excess in the stack including data from the 16 filters jointly at least at the 5σ level (cf. Sect. 5.9 for more details). |
| In the text | |
 |
Fig. A.1 Passbands of 16 NB118 filters after convergent beam transformation, with QE and mirror reflectivities applied, and artificially shifted by 3.5 nm towards the red, as motivated by the results in Milvang-Jensen et al. (2013). Filters in the four different columns of the observing pattern are marked in four different colors. Columns numbers are counted from right to left in Fig. 9. |
| In the text | |
 |
Fig. A.2 Passbands of one of the NB118 filters (filter 15) in comparison to the VISTA/VIRCAM Y and J passbands. |
| In the text | |
 |
Fig. C.1 Expected number of Hα emitters in the part of the UltraVISTA NB118 field with data from two different NB118 filters as a function of line luminosity. Predicted curves are included both for the UltraVISTA DR2 (blue) and the final UltraVISTA (red) for three different z = 0.8Hα LFs from the literature. Results are plotted for the assumption of w6583 = 0.3 in all three cases. In the case of the Ly et al. (2011) LF, the curve for w6583 = 0 is also shown. Small arrows indicate luminosities corresponding to line fluxes of 3.0, 5.0, 10.0, and 20.0 × 10-17 erg s-1 cm-2. The integrated numbers for objects brighter than the respective marked fluxes are stated in Table C.1. |
| In the text | |
 |
Fig. D.1 Inverse of the signal-to-noise as a function of line flux for an infinite EW line in J and at peak transmittance of NB118 filter 15. Curves are shown both for exposure times as in the UltraVISTA DR2 (blue) and for the final UltraVISTA survey (red). Moreover, for the NB118 filter, results are included both for the typical per pixel integration time (alone) and for half this value (overlap) (cf. Sect. 5.1). |
| In the text | |
 |
Fig. F.1 J − NB118 versus Y − J for all objects with a 5σ NB118 detection in the stack and at least a 2σ detection in the two broadband filters. Orange crosses give the median of J − NB118 for all objects within equidistant Y − J bins. The solid red line is the assumed color correction (cf. Eqs. (F.1) and (F.2)), meaning that we defined objects on this line to have a Jcorr − NB118 of zero. The J − NB118 = − 0.25(Y − J) line (Eq. (F.1)) is also shown beyond Y − J> 0.5, but there as dotted line. |
| In the text | |
 |
Fig. F.2 Measured NB excess as a function of the NB118 magnitude for all objects in the main NB118 detected catalog. Data is only included for the regions of overlapping filters and in each of the overlapping regions only for one of the two filters. The red-dotted horizontal line indicates the minimum required NB118 excess for objects that we classify as NB excess objects. In addition, the curves for a 4σ positive Jcorr − NB118 [ i ] are shown for each of the 12 filters. The crosses show the median of the Jcorr − NB118 in NB118 bins with a width of 0.5 mag. Finally, all mentioned lines are also plotted mirrored at Jcorr − NB118 [ i ] = 0. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.