| Issue |
A&A
Volume 590, June 2016
|
|
|---|---|---|
| Article Number | A114 | |
| Number of page(s) | 24 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201322490 | |
| Published online | 25 May 2016 | |
Chandra X-ray spectroscopy of focused wind in the Cygnus X-1 system
II. The non-dip spectrum in the low/hard state – modulations with orbital phase
1
Dr. Karl Remeis-Sternwarte and Erlangen Centre for Astroparticle Physics,
Universität Erlangen-Nürnberg, Sternwartstr. 7, 96049
Bamberg, Germany
e-mail: joern.wilms@sternwarte.uni-erlangen.de
2
Lawrence Livermore National Laboratory,
7000 East Ave., Livermore, CA
94550,
USA
3
MIT Kavli Institute for Astrophysics and Space
Research, NE80, 77 Mass.
Ave., Cambridge,
MA
02139,
USA
4
CRESST, University of Maryland Baltimore County,
1000 Hilltop Circle,
Baltimore, MD
21250,
USA
5
NASA Goddard Space Flight Center, Astrophysics Science
Division, Code 661,
Greenbelt, MD
20771,
USA
6
AIT Austrian Institute of Technology GmbH,
Donau-City-Str. 1, 1220
Vienna,
Austria
7
Department of Astrophysics/IMAPP, Radboud University
Nijmegen, PO Box
9010, 6500 GL
Nijmegen, The
Netherlands
8
SRON Netherlands Institute for Space Research,
Sorbonnelaan 2, 3584 CA
Utrecht, The
Netherlands
9
Institute of Astronomy, University of Cambridge,
Madingley Road, Cambridge
CB3 0HA,
UK
10
Laboratoire AIM, UMR 7158, CEA/DSM-CNRS-Université Paris Diderot,
IRFU/SAp, 91191
Gif-sur-Yvette,
France
11
Max-Planck Computing and Data Facility,
Gießenbachstr. 2, 85748
Garching,
Germany
12
Department of Chemistry, Physics, and Astronomy, Georgia College
& State University, Milledgeville, GA
31061,
USA
13
Space Sciences Laboratory, 7 Gauss Way, University of
California, Berkeley,
CA
94720-7450,
USA
14
Harvard John A. Paulson School of Engineering and Applied
Sciences, and Harvard-Smithsonian Center for Astrophysics,
60 Garden Street MS-6,
Cambridge, MA
02138,
USA
Received: 14 August 2013
Accepted: 1 April 2016
Accretion onto the black hole in the system HDE 226868/Cygnus X-1 is powered by the strong line-driven stellar wind of the O-type donor star. We study the X-ray properties of the stellar wind in the hard state of Cyg X-1, as determined using data from the Chandra High Energy Transmission Gratings. Large density and temperature inhomogeneities are present in the wind, with a fraction of the wind consisting of clumps of matter with higher density and lower temperature embedded in a photoionized gas. Absorption dips observed in the light curve are believed to be caused by these clumps. This work concentrates on the non-dip spectra as a function of orbital phase. The spectra show lines of H-like and He-like ions of S, Si, Na, Mg, Al, and highly ionized Fe (Fe xvii–Fe xxiv). We measure velocity shifts, column densities, and thermal broadening of the line series. The excellent quality of these five observations allows us to investigate the orbital phase-dependence of these parameters. We show that the absorber is located close to the black hole. Doppler shifted lines point at a complex wind structure in this region, while emission lines seen in some observations are from a denser medium than the absorber. The observed line profiles are phase-dependent. Their shapes vary from pure, symmetric absorption at the superior conjunction to P Cygni profiles at the inferior conjunction of the black hole.
Key words: accretion, accretion disks / stars: individual: Cyg X-1 / stars: individual: HDE 226868 / X-rays: binaries / stars: winds, outflows
© ESO, 2016
1. Introduction
In the 50 years of persistent X-ray activity since its discovery in 1964 (Bowyer et al. 1965), the high-mass X-ray binary Cygnus X-1 (Cyg X-1) has become one of the best known X-ray
sources, but there are still many open questions, even with regard to one of its most basic
properties, the nature of the accretion process. The system consists of the supergiant O9.7
Iab-type star HDE 226868 (Walborn 1973) and a compact
object in a 5.6 d orbit (Webster & Murdin 1972;
Brocksopp et al. 1999; Gies et al. 2003) with an inclination of
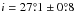 (Orosz et
al. 2011). The system has a distance
(Orosz et
al. 2011). The system has a distance 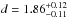 kpc (Xiang
et al. 2011; Reid et al. 2011). Based on
these measurements, masses of M2 = 19.2 ± 1.9
M⊙ for the companion star and M1 = 14.8 ± 1.0
M⊙ for the compact object have been deduced
(Orosz et al. 2011).
kpc (Xiang
et al. 2011; Reid et al. 2011). Based on
these measurements, masses of M2 = 19.2 ± 1.9
M⊙ for the companion star and M1 = 14.8 ± 1.0
M⊙ for the compact object have been deduced
(Orosz et al. 2011).
With a mass loss rate of ~10-6 M⊙ yr-1 (Herrero et al. 1995), HDE 226868 shows a strong wind. These winds are driven by radiation pressure which, owing to copious absorption lines present in the ultraviolet part of the spectrum on material in the stellar atmosphere (line-driven or Castor et al. 1975, [CAK] wind model), can reach very high velocities (v∞ ≫ 2000 km s-1; Muijres et al. 2012) and are only produced by hot, early type O or B stars. Simulations show that a steady solution of line-driven winds is not possible, i.e., perturbations are present in the wind (Feldmeier et al. 1997), causing variations of density, velocity, and temperature, which compress the gas into small, cold, and overdense structures, often referred to as clumps (Oskinova et al. 2012; Sundqvist & Owocki 2013, and references therein). The existence of clumps is supported by observations of transient X-ray absorption dips (lower flux) in the soft X-ray light curves of such systems. Sako et al. (1999) estimate that more than 90% of the total wind mass in Vela X-1 is concentrated in clumps, while the ionized gas covers more than 95% of the wind volume. Clumpiness with a filling factor of 0.09–0.10 has been confirmed in Cyg X-1 by Rahoui et al. (2011).
Strong tidal interactions between the star and the black hole and centrifugal forces make the wind distorted and asymmetric. Both the wind density and the mass loss rate are enhanced close to the binary axis, creating a so-called focused wind (Friend & Castor 1982). Evidence for the presence of such a wind around HDE 226868, which fills more than ~90% of its Roche volume (Gies & Bolton 1986), is the strong modulation of the He ii λ4686 emission line with orbital phase (Gies & Bolton 1986) and the strong phase-dependence of other optical absorption lines, which are deepest around orbital phase φorb = 0 (Gies et al. 2003), i.e., during the superior conjunction of the black hole. Further evidence comes from the modeling of the IR continuum emission (Rahoui et al. 2011). Finally, in the X-rays, the overall absorption column density and dipping vary strongly with orbital phase and are largest at φorb ~ 0.0 (e.g., Li & Clark 1974; Mason et al. 1974; Parsignault et al. 1976; Pravdo et al. 1980; Remillard & Canizares 1984; Kitamoto et al. 1984, 1989; Wen et al. 1999; Bałucińska-Church et al. 2000; Feng & Cui 2002; Lachowicz et al. 2006; Poutanen et al. 2008; Hanke et al. 2009), which is consistent with the focused wind picture (e.g., Li & Clark 1974; Remillard & Canizares 1984; Bałucińska-Church et al. 2000; Poutanen et al. 2008). Owing to the presence of the focused wind, the accretion process in Cyg X-1 is not primarily wind accretion like in other HMXBs, such as Vela X-1, SMC X-1, or 4U 1700−37 (Bondi & Hoyle 1944; Blondin & Woo 1995; Blondin 1994; Blondin et al. 1991), but a small accretion disk is present. Evidence for this disk comes from detections of the disk’s thermal spectrum (Bałucińska-Church et al. 1995; Priedhorsky et al. 1979), an X-ray disk reflection component, and a strong and broad Fe Kα line (Tomsick et al. 2014; Duro et al. 2011, and references therein).
Black hole binaries show two characteristic behaviors called the low/hard and the high/soft state. These states differ in the shape of the X-ray spectrum, the timing properties, and the radio emission (Fender et al. 1999; Belloni 2004; Wilms et al. 2006; Belloni 2010, and references therein). The spectrum of Cyg X-1 in the hard state is well described by a hard, exponentially cut-off broken power law with photon index Γ ~ 1.7 (Wilms et al. 2006). During the soft state, the power law is steeper (Γ ~ 2.5) and a luminous and less variable thermal disk component appears (Wilms et al. 2006).
Cyg X-1 is often considered to be a hard state source, since it spent most of the time in the hard state (Grinberg et al. 2013). Transitions into the soft state are observed every few years and “failed state transitions”, where the soft state is not entirely reached, are also possible (Pottschmidt et al. 2003). Since 2010 the source’s behavior has been rather unusual and it has spent significantly more time in the soft state. See Grinberg et al. (2013) for a discussion of the long-term changes in Cyg X-1 from 1996 until the end of 2012.
Since X-rays from the black hole propagate through the stellar wind, we can use these X-rays to probe its structure. For such a study it is essential that the source is in the hard state or the hard-intermediate state. The strong X-ray emission during the soft state is sufficient to completely photoionize the stellar wind. As a consequence, the wind is suppressed because the radiative driving force of the UV photons from the donor star is reduced since the ionized gas is transparent for UV radiation.
In this paper, we extend earlier work on Chandra high-resolution grating spectra from Cygnus X-1, studying the ionized material of the stellar wind of HDE 226868 during the low/hard state (Hanke et al. 2009, hereafter Paper I). We perform a detailed study of four observations at phases φorb ~ 0.05, ~0.2, ~0.5, and ~0.75, and combine it with previous results of the observation at ~0.95 (Paper I). These data provide a unique set of observations that allows us to probe all prominent parts of the wind of Cyg X-1 (Fig. 1). Our aim is to describe the complex structure and the dynamics of the stellar wind. Section 2 summarizes observations and data used in the analysis. In Sect. 3 and Sect. 4, we present the data analysis and results related to the continuum fitting and the H-like and He-like absorption lines observed in the non-dip spectra. In Sect. 5, we discuss their modulation with orbital phase. Section 6 discusses line profile variations and results from plasma density diagnostics. We summarize our conclusions in Sect. 7. Overview tables and plots of all full range spectra are given in Appendix A. Technical issues related to the analysis are discussed in Appendices B and C.
 |
Fig. 1 Orbital phase coverage of the Chandra observations of Cyg X-1 in the hard state analyzed in this work. Full arcs (dashed arcs) display TE mode (CC mode; for explanation see Sect. 2.3) observations. The labels correspond to the Chandra ObsIDs. Phase φorb = 0 corresponds to the superior conjunction of the black hole. |
Log of hard-state Chandra-HETGS observations of Cyg X-1 used in this paper.
 |
Fig. 2 1.5–12 keV RXTE-All-Sky Monitor count rate of Cyg X-1 with one day binning in the intervals of nine months during 2003, 2008, and 2010 centered at the times of Chandra observations: ObsIDs 3815 and 3814 (left), 8525 and 9847 (middle), and 11044 (right), indicated by vertical lines. The right panel also shows the MAXI light curve. |
 |
Fig. 3 Upper panel: lightcurves of all five observations as a function of orbital phase. Lower panel: variation of the hardness ratio. Except for the somewhat softer hard-intermediate state observation ObsId 3815, all observations were in the low/hard state. Dips are strongest at φorb ~ 0.0, still present at φorb ~ 0.2, and φorb ~ 0.75, and they vanish at φorb ~ 0.5. Colors indicate the parts of the observations used in the analysis (see Fig. 1), while data in black were excluded from the analysis. |
2. Observations and data reduction
2.1. Selection of observations
The main purpose of this paper is to study the variation of the X-ray spectrum with orbital phase during the hard state. Only six of the 17 available Chandra-HETG observations meet this condition: ObsIDs 2415, 3814, 3815, 8525, 9847, and 11044 (see Sect. 2.2 for a discussion of the state classification). All other Chandra observations of Cyg X-1 either caught the source in the high/soft state or were too short to obtain spectra of a sufficient S/N. ObsID 2415, taken during the intermediate state at φorb ~ 0.76 has already been analyzed by Miller et al. (2005). Table 1 gives a log of the remaining observations studied in this paper and Fig. 1 depicts their orbital coverage. Results on ObsID 3814 from Paper I will be combined with these new results in Sects. 4 and 5.
To gauge the quality of the continuum modeling, we use simultaneous pointed RXTE observations (Sect. 3.2), which were reduced using our standard procedures as described, e.g., by Wilms et al. (2006) or Grinberg et al. (2015).
2.2. Source state
Figure 2 shows the RXTE All-Sky-Monitor (ASM; Levine et al. 1996) lightcurve of Cyg X-1 around the times of the Chandra observations. The average daily ASM data point towards similar conditions during the first four observations. According to the scheme of Grinberg et al. (2013), all four observations are found in the hard state, with low count rate (14–18 cps) in ObsIDs 3814, 8525 and 9847, and a higher countrate of 26 cps in ObsID 3815.
ObsID 11044 was taken during the time when ASM was deteriorating (Vrtilek & Boroson 2013; Grinberg et al. 2013). We therefore used MAXI data (Matsuoka et al. 2009) for the assessment of this observation. Six MAXI measurements are simultaneous with ObsID 11044: they all show the source in the hard state, as defined by Grinberg et al. (2013).
2.3. Data reduction
For the spectral analysis we used the first order spectra of Chandra’s high and medium energy gratings (HEG, MEG; Canizares et al. 2005). Most HETG observations of Cyg X-1 in the analysis were performed in timed exposure (TE) mode of the advanced CCD imaging spectrometer (ACIS; Garmire et al. 2003). In this mode data are nominally accumulated for a 3.2 s frame time before being transferred into a framestore and read out, increasing the probability of pile up. In the cases of ObsIDs 3814, 8525, 9847, and 11044, the frame time was reduced to 1.7 s by using a 512 row CCD subarray readout.
In even brighter cases, as in ObsID 3815, where Cyg X-1 was in the hard-intermediate state, a continuous clocking (CC) mode was applied to avoid pile up and conserve line features. Here the CCD rows are read out continously, which reduces the exposure per row to 2.85 ms (Garmire et al. 2003) and no effects from pile up are expected. The application of CC-mode comes at the expense of one spatial dimension as the image is then reduced to 1024 × 1 pixel frames and the y-image dimension is lost. As a consequence, all image photons, including non-source dispersed photons, such as from the source scattering halo, get collapsed into the spectrum, order sorting becomes more difficult, and calibration uncertainties are higher, which leads to lesser determined continua. Some of these technical issues are discussed in detail in Appendix B.
The data were processed with the standard Chandra Interactive Analysis of Observations (CIAO) software, version 4.2. Further analysis was done with the Interactive Spectral Interpretation System (ISIS), versions 1.6.1 and 1.6.2 (Houck & Denicola 2000). Cross-sections were taken from Verner et al. (1996), abundances from Wilms et al. (2000), and atomic data from the Atomic Database, AtomDB v. 2.0.1 (Foster et al. 2012). Owing to the very low Chandra background (compared to the source), no background was subtracted from the final spectra. Data were grouped to a minimum S/N = 10. Unless noted otherwise, all uncertainties are at the 90% level for one parameter of interest (Δχ2 = 2.71; Lampton et al. 1976).
For spectra from observations performed in TE mode, the effect of pile-up has to be
considered. In the first order spectra, this causes a pure reduction of count rate. It is
stronger in the MEG spectra than in the HEG spectra owing to the lower dispersion and
higher effective area of the MEG. The apparent flux reduction is most significant near
2 keV (6–7 Å) where the spectrometer has the largest efficiency and the highest count
rates are obtained. As described in greater detail in Paper I, pile up in the gratings can
be modeled in ISIS using the nonlinear convolution model
simple_gpile2. This model describes
the reduction of the predicted source count rate, S(λ), by
pile up as 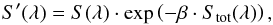 (1)where the total count rate Stot(λ) is estimated from
the effective area and the assumed (model) photon flux, and where the scale parameter
β is a fit
parameter. Stot(λ) includes the
contributions of the 1st,
2nd, and 3rd order spectra at the detector location
corresponding to λ.
(1)where the total count rate Stot(λ) is estimated from
the effective area and the assumed (model) photon flux, and where the scale parameter
β is a fit
parameter. Stot(λ) includes the
contributions of the 1st,
2nd, and 3rd order spectra at the detector location
corresponding to λ.
3. Continuum modeling
3.1. Overview
A detailed look at the light curves and spectra of the five hard state observations enables us to probe the structure of the wind and its modulation with orbital phase. As shown in Fig. 3, dipping is clearly present for most of the orbit, but the dip frequency seems to be phase dependent. Light curves around φorb ~ 0.0 are modulated by strong and complex absorption dips. Dipping already occurs at φorb ~ 0.7 and has not ceased at φorb ~ 0.2. The dip events become shorter and shallower as the black hole moves away from superior conjunction which is expected, given that the line of sight through the densest regions of the (focused) stellar wind is longest for φorb ~ 0.0. The data at φorb ~ 0.5, which probe only the outer regions of the stellar wind, do not show any dipping. This distribution of dipping is consistent with theoretical predictions and observations that see the high-density focused wind close to the binary axis at φorb = 0. A consequence is a high probability of seeing dipping events at φorb = 0 and a much smaller probability of dipping at φorb = 0.5 (Bałucińska-Church et al. 2000; Poutanen et al. 2008; Boroson & Vrtilek 2010).
The main goal of this paper is to study the effects of the stellar wind on the X-ray spectrum. The time intervals where the data are distorted by dips need to be removed from the analysis. Properties, dynamics, and origin of the dips will be discussed by Hell et al. (2013, and in prep.). Following the discussion of Hanke et al. (2008), different stages of dipping can be defined based on different count rate levels in the light curve, or on its dependence in the color-color diagram, or on the softness ratio. According to Kitamoto et al. (1984), and confirmed by the lightcurves of our observations, dips can last from several seconds to more than 10 minutes, especially around superior conjunction. We therefore extracted light curves with a 25.5 s resolution, except for ObsID 3814 where 12.25 s were used (Paper I), to be able to also identify short dipping intervals. For ObsIDs 3815, 8525, and 9847 the selection of non-dip intervals was based on the hardness ratio defined as (0.5–1.5 keV)/(3–10 keV). See Table 1 for the exact selection criteria, which vary between observations owing to differences in the continuum shape and the resulting non-dip exposure times. As shown in Fig. 3, the selection criteria work well for all observations, with only a small contribution due to residual dips with low NH remaining in the lightcurves. Choosing slightly different selection criteria shows that these residual dips do not affect our analysis. For ObsID 3814, the count-rate based selection of Paper I is used. Since no dips are present in ObsID 11044, the full ~30 ks of exposure can be used in the analysis.
Residual dipping present in the so-called non-dip spectra can influence our fitting results. To gauge the influence of dips on these spectra, we relaxed the hardness criterion and also extracted a spectrum of ObsID 8525, which includes moderate dipping and refitted the continum. The contaminated spectrum was chosen very conservatively, it corresponds to a hardness ≥0.449 in the lower panel of Fig. 3. In the combined spectrum, NH changed by 15% from 5.5 × 1021 cm-2 to 6.3 × 1021 cm-2. Because of our much more conservative selection criteria, the systematic error in our non-dip spectra is significantly smaller than that. We estimate it to be of the same order of magnitude as the statistical errors of the fits.
3.2. Continuum model
The extracted non-dip spectra are characterized by an absorbed continuum onto which a
large number of absorption lines are superimposed. As we are not focusing on a physical
interpretation of the continuum, we describe it with a simple empirical model that is
flexible enough to give an accurate representation of the proper continuum spectrum, i.e.,
an absorbed power law. Cross-checks with simultaneous broadband spectra from RXTE
performed during our Chandra observations show that our continuum
parameters are in reasonable agreement between the two satellites. We look at two extreme
observations, ObsID 3815 and 11044. In ObsID 11044 the Chandra spectrum
is neither distorted by calibration features, nor influenced by strong absorption lines.
Fitting the Chandra continuum model given in Table 2 to the simultaneous 3–6 keV PCA spectrum, leaving the normalization
value free to vary to take into account the well-known flux-cross calibration issues
between the PCA and other satellites (Nowak et al.
2011), gives a reasonable 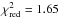 (χ2/
d.o.f. = 9.95/6)
with consistent photon indices for the two instruments. While formally not a very good
fit, the ratio between the data and the model in the PCA shows deviations of
<1% and is therefore
consistent with the calibration uncertainty of the PCA in this energy band (Jahoda et al. 2006; Shaposhnikov et al. 2012). The large χ2 is therefore due to PCA calibration
systematics. We note that the energy band chosen, 3–6 keV, represents the maximum overlap
between the PCA and the HETGS, we deliberately do not extend the PCA data to higher
energies because we are only interested in determining how well the continuum is described
by the model in the HETGS band.
(χ2/
d.o.f. = 9.95/6)
with consistent photon indices for the two instruments. While formally not a very good
fit, the ratio between the data and the model in the PCA shows deviations of
<1% and is therefore
consistent with the calibration uncertainty of the PCA in this energy band (Jahoda et al. 2006; Shaposhnikov et al. 2012). The large χ2 is therefore due to PCA calibration
systematics. We note that the energy band chosen, 3–6 keV, represents the maximum overlap
between the PCA and the HETGS, we deliberately do not extend the PCA data to higher
energies because we are only interested in determining how well the continuum is described
by the model in the HETGS band.
As a second example, we consider the continuum of Chandra ObsID 3815,
which had to be modeled using a complicated and nonphysical continuum. A direct comparison
of this model with the contemporaneous RXTE-PCA data is complicated by the fact that these
data were unfortunately taken during one of the deep dips in the lightcurve. We therefore
extracted a Chandra spectrum from the aforementioned dip and made a
comparison between only strictly simultaneous data. We modeled it with the same continuum
model that was also used for the non-dip continuum, giving APL=1.38 ± 0.04, Γ = 1.40 ± 0.03, NH = 0.33 ± 0.01 ×
1022 cm-2 and a
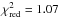 (χ2/
d.o.f. =
10550/9855). Applying the same fit to the PCA, leaving NH fixed at the
Chandra value, leaving only the normalization a parameter, gives
APL = 1.61 ±
0.01 and the
(χ2/
d.o.f. =
10550/9855). Applying the same fit to the PCA, leaving NH fixed at the
Chandra value, leaving only the normalization a parameter, gives
APL = 1.61 ±
0.01 and the 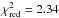 (χ2/
d.o.f. = 14.07/6).
The ratio between the data and the model again shows deviations of ≤1%, however, the residuals suggest that
adjustment of the slope of power law would improve the fit. A fit with Γ left free, APL=1.72 ± 0.06, Γ = 1.45 ± 0.02, is consistent with the
original fit to within the error bars. The data-to-model ratio deviations lie below 0.5%.
This best-fit has an unphysically good
(χ2/
d.o.f. = 14.07/6).
The ratio between the data and the model again shows deviations of ≤1%, however, the residuals suggest that
adjustment of the slope of power law would improve the fit. A fit with Γ left free, APL=1.72 ± 0.06, Γ = 1.45 ± 0.02, is consistent with the
original fit to within the error bars. The data-to-model ratio deviations lie below 0.5%.
This best-fit has an unphysically good 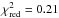 (χ2/
d.o.f. = 1.04/5),
indicating that the systematic error in the PCA has been overestimated. Fitting the PCA
data without applying a systematic error gives
(χ2/
d.o.f. = 1.04/5),
indicating that the systematic error in the PCA has been overestimated. Fitting the PCA
data without applying a systematic error gives 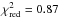 (χ2/
d.o.f. = 4.34/5).
See Nowak et al. (2011), Wilms et al. (2006), and Gierliński et
al. (1999) for physical continuum descriptions.
(χ2/
d.o.f. = 4.34/5).
See Nowak et al. (2011), Wilms et al. (2006), and Gierliński et
al. (1999) for physical continuum descriptions.
Neutral absorption is modeled with the TBnew model (Juett
et al. 2006, Paper I, and http://pulsar.sternwarte.uni-erlangen.de/~wilms/research/tbnew). Compared to
the absorption model of Wilms et al. (2000), TBnew
contains a better description of the absorption edges and allows a simple fitting of
columns of individual elements (see, e.g., Hanke et al.
2010). In gratings data this type of approach is possible when a strong
absorption edge is present in the spectrum. For the wavelength range studied here, the
most important edge is the Ne K-edge. Where indicated below, we therefore fitted the
column of neutral Ne independently of NH. Although K-edges of S, Si, Mg, and
Na are also present, they are not as clearly visible in the spectra and the abundances of
these elements were fixed to their interstellar values (Wilms et al. 2000). Taking into account pile up, the adopted continuum shape was
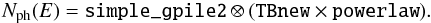 (2)In the following, we briefly discuss the
continuum properties for the four observations modeled here. We refer to Paper I for the
continuum description of the non-dip spectrum of ObsID 3814.
(2)In the following, we briefly discuss the
continuum properties for the four observations modeled here. We refer to Paper I for the
continuum description of the non-dip spectrum of ObsID 3814.
Continuum parameters of ObsID 8525, 9847, and 11044.
3.3. The continuum of ObsIDs 8525 and 9847 (φorb ~ 0.05 and φorb ~ 0.2)
After filtering for dips, only ~4.4 ks of non-dip data remain for each of the two observations. To stay above a S/N of 10, the continua of these two observations were modeled in the wavelength range 2 Å–15 Å for MEG and 2 Å–12 Å for HEG. Best-fit parameters are listed in Table 2.
Both observations show many short, but strong, dips in the light curve. It is probable that even after the exclusion of dips, the non-dip spectrum is contaminated by faint dips, which may have an influence on parameters obtained in the analysis.
3.4. The continuum of ObsID 11044 (φorb ~ 0.5)
The high S/N of this ~30 ks observation allows us to model the continuum in the range of 1.7 Å–20 Å. The continuum is well described by Eq. (2). The Ne- and also Fe-column densities were allowed to vary and are mainly constrained by the Ne K and Fe L2/L3 edges at 14.3 Å and 17.2 Å/17.5 Å, respectively, which are very prominent in the spectrum. Best-fit parameters are again shown in Table 2. As also indicated by similar behavior in RXTE-ASM (Fig. 2), ObsID 11044 was performed in a similar state as ObsID 8525 (φorb ~ 0.05) and 9847 (φorb ~ 0.2), and therefore it is not surprising that the spectral parameters are very similar.
3.5. The continuum of ObsID 3815 (φorb ~ 0.75)
The analysis of the ~45 ks non-dip spectrum of this CC-mode observation is complicated
by the lack of imaging information and by calibration issues1. Below 2 Å, both spectra show an excess of up to 50 ph cm-2
s-1 Å for HEG and up to 150 ph cm-2
s-1 Å
for HEG and up to 150 ph cm-2
s-1 Å in the MEG. This excess is probably caused
by contamination of the spectra by the dust scattering halo that surrounds the source,
which is clearly visible in the detector images of other observations (see also Xiang et al. 2011), or contamination from the wings of
0th order image. As there is no imaging information available in CC-mode, it is not
possible to correct for this contamination. Since the low S/N of the data above 15 Å does not allow
for detailed spectral modeling, only the 2–15 Å HEG and 2.5–15 Å MEG data are taken into
account in the further analysis.
in the MEG. This excess is probably caused
by contamination of the spectra by the dust scattering halo that surrounds the source,
which is clearly visible in the detector images of other observations (see also Xiang et al. 2011), or contamination from the wings of
0th order image. As there is no imaging information available in CC-mode, it is not
possible to correct for this contamination. Since the low S/N of the data above 15 Å does not allow
for detailed spectral modeling, only the 2–15 Å HEG and 2.5–15 Å MEG data are taken into
account in the further analysis.
Unlike for the TE-mode data, the continuum here cannot be described by the simple power law of Eq. (2), since non-physical curvature caused by calibration issues is present in the spectrum. We model this curvature by adding two non-physical Gaussian components, centered at ~1.12 keV and ~2.25 keV. Calibration issues causing slope differences between both instruments also necessitated separate modeling of the continua of the HEG and the MEG. The final parameters of the continuum fit are summarized in Table 3.
We note that despite the fact that the broadband CC mode calibration is suboptimal, its relative calibration over small wavelength intervals is still good. This means that parameters of absorption lines can nevertheless be measured. For example, equivalent widths of narrow absorption lines do not depend on the overall shape of the continuum and are therefore not affected by local fitting or the shape of the non-physical continuum model. Since the Ne column is, as in the other observations, obtained mainly from modeling the Ne K-edge, i.e., a local quantity, the Ne column density could be measured independently from the total column.
Continuum parameters of ObsID 3815.
4. Modeling of line features
4.1. Introduction
Visual inspection of the non-dip spectra reveals that all spectra show discrete line absorption owing to highly ionized material, mostly from H-like and He-like ions of S, Si, Al, Mg, Na, and Ne. We also observe intercombination (i) and forbidden (f) emission lines of He-like ions. Various L-shell transitions of Fe are also present. Table 4 of Paper I gives a complete list of transitions from H- and He-like ions present in the spectrum of ObsID 3814 (φorb ~ 0.95). Most of these absorption lines are also present in the spectra of ObsID 8525, 9847, and 3815 (φorb ~ 0.0–0.2 and φorb ~ 0.75). Since the wavelength range used here is smaller than in Paper I, lines from O viii, O vii, Fe xxvi, and Ni xxviii are outside of the investigated spectral range.
Low ionization Si lines in ObsIDs 8525 (φorb ~ 0.05) and 9847 (φorb ~ 0.2).
To describe the lines from the H- and He-like ions, we fit all transitions of the series from a given ion simultaneously using a curve of growth approach (see Paper I for a detailed description of this model). This approach allows us to describe weaker and often blended lines, while their description with separate Gaussian profiles would often be impossible. For each line series, the fit parameters are the column density of the ion responsible for the line, Ni, the Doppler shift, vi, and the thermal broadening parameter, ξi. All line shapes are modeled using Voigt profiles.
In addition to the lines from line series, other absorption and emission lines are also present in the spectra. Where these types of lines were identified, they were added by hand. Unless noted otherwise, line shapes were described using Voigt profiles, with fit parameters being the thermal broadening parameter, ξ, the natural line width, Γ, i.e., the full width at half maximum of the Lorentzian component of the Voigt profile, and the line flux, A. Negative fluxes denote absorption lines.
The following sections discuss the details and peculiarities of each observation.
4.2. Line spectroscopy of ObsIDs 8525 and 9847 (φorb ~ 0.05, φorb ~ 0.2)
The line identifications for these observations are shown in Figs. A.1 and A.2. While we are able to fit all line series in ObsID 9847, Ar xvii and Ca xix could not be constrained in ObsID 8525. In addition to the absorption lines from H- and He-like ions and Fe, the spectra show evidence for lower ionization absorption lines of Si xii (Li-like), Si xi (Be-like), Si x (B-like), and Si ix (C-like) in the 6.6 Å–7.0 Å band. As we will discuss in greater detail in our analysis of the dip spectrum (Hirsch et al., in prep.), these features become very strong during the deepest phases of absorption dips. Their appearance in the non-dip spectrum therefore reveals the presence of cooler dense material along the line of sight. This is not surprising given that ObsIDs 8525 and 9847 represent the densest part of the wind, φorb ~ 0.0–0.2, where most dipping is observed. The spectra taken farther away from the superior conjunction, which are far less dominated by dips, are virtually free of lower ionization Si features, with the exception of possible detections of a Si xii line in ObsID 11044 (φorb ~ 0.5) and a Si xi line in ObsID 3815 (φorb ~ 0.75). We note, however, that in all cases the optical depth of the lines is much smaller than that seen during dips and consider our results to be representative of the non-dip spectrum. Best-fit line parameters of the Si features are listed in Table 4. We also note that Si xii λ6.72 Å blends with Mg xii Lyγ and the Si xiii f emission line, while Si xi λ6.785 Å blends with a line from Fe xxiv. The parameters of these lines are therefore difficult to constrain2.
Si xiii forbidden line at 6.74 Å is a single emission feature in the spectrum
and its modeling is ambiguous owing to the possible blends described above. Fixing
Γ and fitting the feature
gives line fluxes of 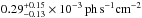 in ObsID 8525 and 0.56 ± 0.16 × 10-3 ph
s-1cm-2 in ObsID 9847, while the thermal
broadening parameter, ξ, is almost unconstrained.
in ObsID 8525 and 0.56 ± 0.16 × 10-3 ph
s-1cm-2 in ObsID 9847, while the thermal
broadening parameter, ξ, is almost unconstrained.
4.3. Line spectroscopy of ObsID 3815 (φorb ~ 0.75)
The full range spectrum is given in Fig. A.3. In this observation, the line series of Ar xvii, Ca xix, Ca xx, and Fe xvii could not be fitted. The approach of line series fitting does not allow us to describe every single line perfectly, but this is mostly only the case for weak emission lines or Fe blends. Notable is the discrepancy in the case of Ne x. If Ne x Lyα (12.13 Å) is modeled properly, then Ne x Lyβ (10.24 Å), Ne x Lyγ (9.71 Å), and Ne x Lyδ (9.48 Å) are predicted to be weaker than observed. To find the reason for this discrepancy, we excluded a very narrow region of the spectrum where the Ne x Lyα is located and fitted the spectrum without this line. All other lines of the Ne x series were described very well. There is, however, no reason to assume that the data in the region of Ne x Lyα are of low quality, especially not for non-dip spectra with their good statistics, and this discrepancy is probably due to contamination by nearby Fe lines. Ne x Lyα also appears to be asymmetric, possibly being an indication of P Cygni profiles (see Sect. 4.4). Miller et al. (2005)3 report inconsistencies in equivalent widths between individual lines in the Ne x series. Apart from (partial) saturation of the resonance line or blends of lines, the authors argue that another possible explanation could be that lines come from an inhomogeneous region, or from different regions simultaneously. Marshall et al. (2001)4 describe an opposite problem whereby, while the Lyα lines were strong, no Lyβ lines were detected, concluding that the lines were not saturated and that the absorbing gas covered more than ~50% of the source.
Emission lines are present in the spectrum, but are generally much weaker than the absorption lines. Since full width at half maximum, Γ, and the thermal broadening, ξ, of the line are correlated for Voigt profiles, it was difficult to constrain their parameters (Table 5). We therefore set Γ to a fixed value that is located at the intersection of the confidence contours for all individual emission lines from the free fits, which appeared to be split into two groups: for stronger lines, Γ was fixed to 15 eV and the thermal broadening reaches values around ~500 km s-1. The full width at half maximum of the weaker lines was fixed to 1.5 eV and ξ is mostly consistent with zero.
Intercombination (i) and forbidden (f) emission lines from He-like ions at φorb ~ 0.75 (ObsID 3815).
4.4. Line spectroscopy of ObsID 11044 (φorb ~ 0.5)
Whereas resonance transitions were always detected in absorption at early orbital phases, the spectrum at φorb ~ 0.5, taken during the inferior conjunction of the black hole, shows P Cygni profiles with an emission component at the rest wavelength and a weak blue-shifted absorption component. Owing to the complex profiles, line series fitting is not feasible in this observation. Describing the P Cygni profiles as the sum of a positive and a negative Voigt profile allows us to model the shapes of the Lyα transitions of Si xiv, Mg xii, and Ne x, Ne xβ, and δ quite well (Table A.2). In addition, the data show the Mg xi triplet, four pure emission lines, and only two pure absorption lines. See Fig. A.4 for the full spectrum.
Although the interpretation of P Cygni profiles is challenging, we attempt to determine
column densities for the absorption part of the profiles using (Mihalas 1978, see also Paper I) 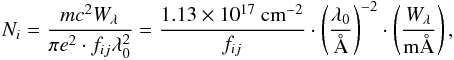 (3)assuming that the lines are not saturated
(τ(ν) ≪
1). Here, Wλ is the equivalent
width of the line, and fij is the oscillator strength of the
transition, in this case a sum of all transitions contributing to the absorption line. The
values of Ni are summarized in Table A.2. Column densities for Ne xβ and δ are outliers. Values of
~75 and ~85 × 1016 cm-2
are far too high, given the column density of Ne xα. This deviation is most
likely due to a partial filling of the absorption component by the strong emission wing,
which cannot be determined reliably owing to the low S/N of the line (Fig. A.4). Columns were also determined for the absorption line at
λ 6.705 Å,
assuming it is from Li-like Si xii, using the oscillator strength of Behar & Netzer (2002).
(3)assuming that the lines are not saturated
(τ(ν) ≪
1). Here, Wλ is the equivalent
width of the line, and fij is the oscillator strength of the
transition, in this case a sum of all transitions contributing to the absorption line. The
values of Ni are summarized in Table A.2. Column densities for Ne xβ and δ are outliers. Values of
~75 and ~85 × 1016 cm-2
are far too high, given the column density of Ne xα. This deviation is most
likely due to a partial filling of the absorption component by the strong emission wing,
which cannot be determined reliably owing to the low S/N of the line (Fig. A.4). Columns were also determined for the absorption line at
λ 6.705 Å,
assuming it is from Li-like Si xii, using the oscillator strength of Behar & Netzer (2002).
The fact that the columns of the absorption lines are much smaller in this observation compared to earlier orbital phases demonstrates that the column density of the ionized absorber is strongly modulated with orbital phase, although the blending of the absorption and the emission component strongly influences the interpretation of the columns found for this observation. A more detailed study would require fits of P Cygni profile models using line profile shapes in which the exciting source is not situated at the center of the complex, asymmetric flow. To our knowledge, such calculations are not available as yet.
Doppler shifts, vi, of the absorption and the emission components of the P Cygni profiles were determined separately (Table A.2). As the emission components are located rather close to the rest wavelength and, except for lines from Ne x, are redshifted, and the absorption tails are, in contrast, strongly blueshifted, they provide only upper/lower limits of the velocity values.
4.5. Line spectroscopy: Best-fit results
 |
Fig. 4 Fit parameters from Table A.1 for line series of H-like and He-like transitions in ObsID 3815 (squares), ObsID 8525 (circles), ObsID 9847 (stars), and also ObsID 3814 (diamonds, Paper I): top: velocity shifts, middle: column densities, bottom: thermal broadening. Colors correspond to ObsIDs as indicated. For completeness, values far above or below the displayed range are marked by triangles close to upper/lower x-axes. |
Figure 4 shows the parameters of individual line series summarized in Table A.1: Doppler velocities vi, column densities Ni and thermal broadening ξi for ObsIDs 8525, 9847, and 3815 (φorb ~ 0.0–0.2 and 0.75). Parameters obtained in Paper I from ObsID 3814, φorb ~ 0.95, are shown for comparison. Because of the different fitting approach, the parameters of ObsID 11044 (φorb ~ 0.5) are excluded from this comparison.
All series in ObsID 3815 (φorb ~ 0.75) are consistently redshifted, with values falling in the interval between 100 and 400 km s-1. The exception is the Na x line, which is Doppler shifted by ~870 km s-1. The column densities of all line series (Fig. 4) are in the interval (0–5) × 1016 cm-2 with a thermal broadening of ξ ≲ 500 km s-1, suggesting the lines originate from the same region.
Because of the short exposure of ObsIDs 8525 and 9847, many fit parameters show large uncertainties or cannot be constrained. The velocities in ObsIDs 8525 and 3814 (φorb ~ 0.0) are much lower compared to ObsID 3815, in fact, they are consistent with zero, while the ones from ObsID 9847 (φorb ~ 0.2) show mostly blueshifted values. Overall, the velocities span the range ± 500 km s-1.
The column densities of ObsIDs 8525, 9847, and 3814 are much higher than those of ObsID 3815, supporting the idea of the denser focused wind around φorb ~ 0.0. We do not see any particular trend in the thermal broadening measured in these observations, although with ≲300 km s-1 it seems to be generally lower than in ObsID 3815 (even though the broadening shows a rather large scatter). For a plasma with a temperature of T ~ 106 K, thermal velocities are on order of ~10 km s-1. The higher observed values therefore suggest that most of the broadening is due to microturbulence.
Closer investigation shows that for lines with lower S/N a higher column appears to imply smaller thermal broadening. This kind of behavior could explain the outlier lines. For example, in the case of Si xiv in ObsID 8525, assuming a typical value of ξ ~ 300 km s-1 would reduce the column density by a factor of ~10. For other lines this effect will be smaller.
5. The X-ray orbital variability of Cyg X-1
Having described the properties of the individual observations, we now turn to look at them in the context of the different lines of sight onto the black hole to better understand how the properties of the wind depend on the orbital phase. We first study the variation of the column density obtained from continuum or edge modeling with orbital phase and then investigate the variation of the ionizing absorber by looking at column densities and velocity shifts of individual line series.
 |
Fig. 5 Orbital phase variation of fitted columns, repeated twice for clarity. Gray data points show the equivalent hydrogen column density, NH, from continuum fitting the Chandra spectra (right hand y-axis). As discussed in the text, the data points are heavily influenced by systematics (the error bars shown are statistical only). The colored data points show the variation of the Ne neutral column from Ne-edge fitting (left y-axis) and corresponding NH (right y-axis) derived assuming a Ne:H abundance of 1:11481 as per Wilms et al. (2000). The phases of individual Chandra observations are denoted with colored regions. The dashed lines represent the total equivalent column density of the interstellar medium and of Ne (Xiang et al. 2011). |
5.1. Column density variation of the neutral absorber
The equivalent hydrogen column density NH found from continuum fitting is, in principle, a tracer for the material in the interstellar medium along the line of sight to the X-ray source and for the moderately ionized material in its vicinity. The reason is that 0.5–10 keV X-rays are mainly absorbed by K-shell electrons. As the cross-section of the K-shell is only mildly dependent on ionization stage, absorption in moderately ionized material can also usually be described reasonably well with cross-sections for neutral atoms, at least at the level that is usually used when modeling broadband continua. NH is thus a measure for both the ISM foreground absorption and the column of mildly ionized material in the stellar wind. Earlier monitoring, e.g., with RXTE, showed a modulation of NH with orbital phase (Grinberg et al. 2015; Hanke 2011; Wilms et al. 2006; Kitamoto et al. 2000; Holt et al. 1976), although we note that some of the modulation seen there is also caused by dips, which were not removed in these analyses.
The values obtained from the Chandra continuum fitting for the
NH (Fig. 5, gray data points) show a systematic offset compared to other determinations
of the column, with lowest values of 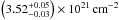 at φorb ~ 0.75
and (3.52 ± 0.04) × 1021
cm-2 (Paper I) for φorb ~
0.95. These values are smaller than the total column density of the
interstellar medium along the line of sight to Cyg X-1, which dust scattering measurements
determine to NHtot ~ 4.6 × 1021
cm-2 (Fig. 5, dashed
line; Xiang et al. 2011). This column sets the
lower limit to the total NH to Cyg X-1, which is the sum of the
intrinsic absorption in the system and the absorption in the interstellar medium. Lower
NH values, as those seen here, thus
indicate a systematic error. This is not unlikely, considering that the lowest
NH values originate from an observation
that was performed in continuous clocking mode, where the continuum has to be modeled with
additional broad Gaussians (Table 3). A further
systematic is the inability to constrain the continuum with Chandra in
these absorption line dominated data. Our experience shows that fits to simultaneous
Chandra and RXTE-PCA data do have significantly higher NH. For example,
in Paper I, we found for observation 3814 that NH increased from 3.52 ± 0.04 1021 cm-2
in the Chandra-only fits to NH = 5.4 ± 0.4 × 1021
cm-2 when including the PCA data, which was consistent with
previous measurements (Miller et al. 2002; Schulz et al. 2002) as well as with the NH obtained from
continuum fitting to observation 8525, which has a similar orbital phase. We therefore
conclude that NH values obtained from continuum modeling
the Chandra data alone suffer a large systematic uncertainty in these
line dominated data, with a clear systematic bias towards smaller NH.
at φorb ~ 0.75
and (3.52 ± 0.04) × 1021
cm-2 (Paper I) for φorb ~
0.95. These values are smaller than the total column density of the
interstellar medium along the line of sight to Cyg X-1, which dust scattering measurements
determine to NHtot ~ 4.6 × 1021
cm-2 (Fig. 5, dashed
line; Xiang et al. 2011). This column sets the
lower limit to the total NH to Cyg X-1, which is the sum of the
intrinsic absorption in the system and the absorption in the interstellar medium. Lower
NH values, as those seen here, thus
indicate a systematic error. This is not unlikely, considering that the lowest
NH values originate from an observation
that was performed in continuous clocking mode, where the continuum has to be modeled with
additional broad Gaussians (Table 3). A further
systematic is the inability to constrain the continuum with Chandra in
these absorption line dominated data. Our experience shows that fits to simultaneous
Chandra and RXTE-PCA data do have significantly higher NH. For example,
in Paper I, we found for observation 3814 that NH increased from 3.52 ± 0.04 1021 cm-2
in the Chandra-only fits to NH = 5.4 ± 0.4 × 1021
cm-2 when including the PCA data, which was consistent with
previous measurements (Miller et al. 2002; Schulz et al. 2002) as well as with the NH obtained from
continuum fitting to observation 8525, which has a similar orbital phase. We therefore
conclude that NH values obtained from continuum modeling
the Chandra data alone suffer a large systematic uncertainty in these
line dominated data, with a clear systematic bias towards smaller NH.
An independent, and likely better, measure for the absorbing column is possible by direct measurement of the optical depth at absorption edges. This approach is less dependent on systematics of the continuum modeling than fitting NH, especially considering the systematics induced by the brightness of the source. In our data, Neon is the only element for which we can measure the column density directly from the neutral edge in all of our observations (Fig. 5, colored data points). The observed variation suggests that part of the neutral NNe is intrinsic to the source and varies with orbital phase, with a minimum at φorb ~ 0.5, consistent with earlier studies of the NH variation in the system (e.g., Grinberg et al. 2015; Wen et al. 1999; Kitamoto et al. 2000). We note, however, that a potential systematic uncertainty is that only ObsID 11044 (φorb ~ 0.5) does not show any significant absorption lines in the range of the Ne edge, while for the other ObsIDs this region is populated by many strong lines from ionized Fe. It therefore cannot be excluded that some of the variation is due to a contamination of the Ne edge by these lines. A cross-check in which the continuum around the Ne edge is modeled locally reveals columns that are systematically higher by a factor of ~2, such that at least part of the modulation could be due to the Fe lines. Local and continuum modeling give similar results only for ObsID 3815 (φorb ~ 0.75). In addition to Ne, the good quality of ObsID 11044 (φorb ~ 0.5) allows us to leave the Fe column a free parameter in the continuum fitting, giving NFe = (0.15 ± 0.02) × 1018 cm-2 for this observation. This value is consistent with NFe determined from the local modeling of the edge and with the expected ISM Fe contribution using the ISM abundances of Wilms et al. (2000).
5.2. Orbital variation of the column of the ionized absorber
We now turn to the variation of the ionized absorber with phase. Figure 6 illustrates the variation of the column densities Ni of highly ionized elements with orbital phase. The parameter sample was reduced compared to the complete set of species present in the spectra by excluding all columns with uncertainties exceeding 75% of their values. For ObsIDs 3814 and 3815 (φorb ~ 0.95 and 0.76) only one Ni value per observation, from S xvi and Ar xvii, respectively, was lost. For ObsIDs 8525 and 9847 (φorb ~ 0.05 and 0.2, ~4.4 ks exposure) we discarded roughly half of the Ni values (ObsID 8525, φorb ~ 0.05: H-like series of Ne, Al, Si, S, Ar and Ca, and He-like Na; ObsID 9847, φorb ~ 0.2: both H- and He-like series of Al, Si, S, Ca, and H-like Ar). Figure 4b shows that these Ni values are, to within their uncertainties, consistent with the more tightly constrained values. Ne x and Na x of ObsID 9847 (φorb ~ 0.2) appear as outliers, although compared to other columns determined in this observation they are relatively well constrained. In ObsID 11044 (φorb ~ 0.5), where the strong lines show P Cygni profiles, the Ni shown in Fig. 6 were determined as described in Sect. 4.4 for the absorption parts of Ne xα, Mg xii, Mg xi, and Si xiv.
 |
Fig. 6 Measured column densities, Ni, of individual elements as a function of orbital phase. Left: H- and He-like line series (circles) and Fe lines (crosses). Only measurements with relative uncertainties <75% are included. Right: column densities of the four most prominent ions, Ne x (circles), Mg xii (diamonds), Mg xi (squares), and Si xiv (triangles). Filled datapoints correspond to symmetric lines (see Fig. 12 and related discussions). |
There are four ions that are strong in all five observations and so can be tracked over the whole orbit: Ne x, Mg xii, Mg xi, and Si xiv (Fig. 6, right). On closer investigation the lines appear asymmetric, even in cases where they do not show clear P Cygni profiles. As asymmetry can affect the column density measurements, we considered only those lines that do not show any asymmetry according to Sect. 6.1 (filled circles in Fig. 6). As with the cases discussed above, Ni is expected to reach its maximum at φorb ~ 0.0 and its minimum at φorb ~ 0.5. The modulation is clearly visible in Fig. 6.
5.3. The location of the absorbers
 |
Fig. 7 Stellar wind density, assuming the focused wind model of Gies & Bolton (1986) and lines of sight towards the black hole. Left: side view onto the orbital plane (dashed). Right: lines of sight projected onto the orbital plane. The black hole (cross) and its donor move clockwise around the center of mass (cross). |
The previous sections showed that both the moderately ionized material tracked by Ne-edge fitting and the highly-ionized material responsible for the H- and He-like species shows orbital modulation, i.e., the material is local to the X-ray binary. In this section, we consider the relationship between both absorbers. First, as also pointed out by Marshall et al. (2001), we note that in most observations the He-like line series show lower columns than their H-like peers, Ni,He ≤ Ni,H (Fig. 4), which indicates that most of the material traced by the H- and He-like lines is fully ionized. The best example in this respect is ObsID 3815 where, for all observed line series, the column of the H-like ions is larger than the column from the He-like ions. In this ObsID, φorb ~ 0.75, i.e., the line of sight is almost perpendicular to the binary axis. For the other observations probing the denser part of the wind, the relation between Ni,He and Ni,H is not as clear as for ObsID 3815, but Ni,He ≤ Ni,H is fulfilled for most ions.
To compare the measured variation of the columns with theoretical expectations we use the focused wind model of Gies & Bolton (1986) as a toy model. This model consists of a CAK-model with a longitudinal variation of the wind parameters in a cone ± 20° degrees from the line between the donor and the black hole. Outside of that region, we use the wind parameters at θ = 20°, where θ is the angle in the orbital plane of the binary, measured from the line between the donor and the black hole. Figure 7 shows the density structure of the focused wind, as well as the line of sight of our observations projected onto the orbital plane and in a side view. The model has been shown to be a good overall representation of the stellar wind in the HDE 226868/Cyg X-1 system, even though the detailed parameters of the wind are still debated (Gies et al. 2003, 2008; Vrtilek et al. 2008, and references therein). We emphasize that much of this discussion relates to the wind properties in the so-called shadow wind, i.e., the region of the star opposite to the black hole where X-rays are not presumed to influence the wind properties (Caballero-Nieves et al. 2009). This region is not probed by the line of sights studied here.
 |
Fig. 8 Phase variation of the column density according to the focused wind model of Gies & Bolton (1986). Shown is the column of the whole wind (solid line), and of those less ionized wind regions where the ionization parameter log ξ< 3.0 (dash dotted line) and log ξ< 2.6 (dotted line), respectively. |
Figure 8 (solid line) shows that, in the model of Gies & Bolton (1986), the total (neutral and ionized) column is around NH ~ 4 × 1022 cm-2, i.e., it is more than a factor of 10 higher than the NH measured from fitting the continuum or the NH values inferred from fitting the Ne edge. The latter vary between 6.8 × 1021 cm-2 and 1.3 × 1022 cm-2 (Fig. 5). Owing to the expected high degree of ionization caused by the black hole and the UV radiation from its donor, this difference between the measured NH and the model predicted total columns is not surprising (e.g., Holt et al. 1976; Wen et al. 1999). Figure 8 therefore also shows the expected columns from regions where the ionization parameter, log ξ, is <3 and <2.6. Following Tarter et al. (1969), we define the ionization parameter as ξ = L/ (nr2), where L is the source luminosity above the hydrogen Lyman edge, n is the absorbing particle density and r is the distance from the ionizing source. We use L = 1037 erg s-1 throughout, a typical value for our observations when taking into account the UV and >10 keV emission of the source (Table 1). Similar to Wen et al. (1999), we also ignore the contribution of the UV photons from the donor star, which systematically increases the ionization parameter. Numbers quoted in the following are therefore to be considered lower limits. We note that we use the symbol ξ for both the ionization parameter and the thermal broadening parameter in line series fitting. We do not anticipate confusion because they are used in different contexts.
Figure 8 indicates that the modulation of the absorption found in the Ne edge and in line series (Figs. 5 and 6) is in qualitative agreement with the variation expected owing to the moderately ionized region of the wind, i.e., where log ξ< 2.6. This is the outermost region of the wind (for r → ∞, log ξ → 2.5), i.e., consistent with the observational findings most of the wind is expected to be ionized. With a variation by a factor of ~2, however, the total expected variation in the model of Gies & Bolton (1986, Fig. 8 is at the lower end of what is found in the observations, where we found a variation of a factor of ~2 for tracers of the neutral column (Fig. 5, colored data points) to a factor of ~10 for the highly ionized species (Fig. 6). In addition, comparing the expected variation at low log ξ with the total column based on Fig. 8, we would expect ionized columns that are only a factor of a few larger than the neutral column, while for most ions the difference in the data is higher. It is unlikely that all of this discrepancy is due to the simplifications of the wind model of Gies & Bolton (1986) alone. We note, however, that we used the interstellar abundances to convert the overall continuum NH values to columns for the individual ions. This is probably not correct, since an evolved star such as HDE 226868 is likely to show a different abundance pattern. Assuming that the most important metals are overabundant with respect to the interstellar medium, the difference could be explained. Overabundances in Cyg X-1 were reported previously. Modeling the emission Kα line, Duro et al. (2011) and Fabian et al. (2012) determine the Fe abundance in the accretion disk to be 1.2–1.6AFe⊙. Further analysis gives much higher values of AFe ~ 3–6AFe⊙ (Duro et al. 2016). Reflection modeling also yields an iron overabundance of 1.9–2.6 (Tomsick et al. 2014). Independent of X-ray measurements, the analysis of optical and UV spectra of HDE 226868 also yields a nitrogen overabundance of five times solar (Caballero-Nieves et al. 2009). This result also suggests the possibility of the other elements being overabundant, which is not so surprising, given that the system consists of an evolved star and has experienced a supernova.
We therefore conclude that a large fraction of the observed medium is ionized and that it is very likely that the observed wind volume is enriched in metals. Since the medium is ionized, it is located fairly close to the black hole. Depending on the line of sight, the distance from the black hole within which log ξ> 2.6 is between 0.5d and 3.6d, where d is the distance between the donor and the black hole. To constrain the properties of the absorber further, we therefore need to turn to another observable, the Doppler shift of the observed lines.
 |
Fig. 9 Top: velocity shifts of individual line series (circles: H-like and He-like ions, crosses: Fe line series) and the radial velocity of the black hole (dash-dotted line, semi-amplitude of ~98 km s-1). The red sine curve shows the best fit involving all series shown (KW ~ 276 km s-1, v0 ~ −40 km s-1, and Δφ ~ 0.46), while the dashed line shows the second best fit, where the offset was fixed to the systemic velocity of the black hole (Table 6). Bottom: velocity shifts for individual ions and the radial velocity of the black hole (dash-dotted line). The sine curves represent the best fits for each of the three given line series (Table 6). Dashed lines show fits with the offset fixed to the systemic velocity of the black hole. The red sine curve is the best fit involving all three line series (Table 6). |
Sine function parameters describing the orbital modulation of the Doppler shifts.
Figure 9 shows that there is a systematic sinusoidal modulation of the velocity shifts of individual line series from the ionized absorber with orbital phase. Velocities for ObsID 11044 at φorb ~ 0.5 are systematically shifted to lower velocities because here only the absorbing part of the P Cygni profile was taken into account. We therefore ignore this observation for the remainder of our discussion.
At a first glance, the line shifts appear to be approximately in phase with the radial velocity of the black hole, which has a velocity amplitude of KBH ~ 98 km s-1 (Orosz et al. 2011) and a systemic velocity of v0 = −7.0 ± 0.5 km s-1 (Gies et al. 2003). We performed a set of fits to establish whether the wind follows the black hole, and investigated several different scenarios (Table 6): we used all line series shown in Fig. 9, including velocities from ObsID 11044, φorb ~ 0.5, the lines of Ne x, Mg xii, Si xiv together, and each of these three lines individually. Apart from a fit in which all parameters of the sine were left free, we also constrained the fits to be in phase with the black hole and to have a different amplitude to the black hole. Generally, models with varying phase shifts give better results than those with the zero phase shifts (bold rows in Table 6). The velocities of different ions are clearly not consistent with each other, indicating a complex ionization structure.
We contrast these results in Fig. 10 with the radial velocities expected from the focused wind model of Gies & Bolton (1986). A direct fit of the ion velocities to this model is not justified. Figure 10 therefore indicates the typical range for the Doppler shifts of our observations. The projected wind velocities for the range of distances in which the highly ionized lines originate according to our analysis of the columns is in agreement with the measured shifts. We note, however, that the wind model predicts a phase shift of Δφ = 0.25 between the black hole and the wind, which is different from what is seen. The measurements during phase 0 are consistent with an origin ≲0.25d from the black hole (as before, d is the distance between the donor and the black hole), while the data taken during phase 0.75 are consistent with a distance ≲0.5d. Given that this observation is the brightest of our observations, it is not unexpected that the ionized region should move away from the black hole. The overall redshift measurements therefore agree with our conclusion that the ionized absorber must originate close to the black hole, and possibly in the focused wind.
While the data from observations 3814, 3815, and 8525 could originate in the focused wind, ObsID 9847 presents an interesting outlier. During this observation the absorbing material appears to be moving towards the observer with a blueshift that is much higher than that of the black hole. As shown in Fig. 10, except for a region very close to the black hole, only positive radial velocities (=redshifts) are expected during this observation. To reconcile these data with a focused wind would require terminal velocities of >4500 km s-1. This value is much higher than the ~2500 km s-1 typically assumed for the wind at the location of the black hole (this value decreases for stream lines away from the line of symmetry of the system). As an alternative explanation, we note that during this observation we are looking through the so-called bow shock of the black hole (e.g., Manousakis 2011; Blondin & Woo 1995, and references therein), i.e., a region where the wind is strongly disturbed. It is not unlikely that, in this region, material gets so disturbed that it obtains a significant non-radial velocity which, at this phase, would show up as a high blue shift.
 |
Fig. 10 Radial velocities of the black hole (red dashed line) and of HDE 226868 (orange dashed line) and wind velocities projected onto the line of sight as a function of distance from the black hole. Distances are given in units of the distance between the black hole and its donor, a. Colored boxes indicate the range of the measured Doppler shifts from the Chandra observations, excluding ObsID 11044. |
6. Advanced line profile studies
6.1. P Cygni profiles and the stellar wind
 |
Fig. 11 Line profiles of the three most prominent absorption lines of Si xiv, Mg xii, and Ne x are shown here as they vary over the orbital phase. Lines are displayed as the ratio of data and model, offset for visual clarity. For each line, the vertical gray lines are located at rest wavelengths corresponding to zero velocity shifts. See text for explanation. |
 |
Fig. 12 The same line profiles as in Fig. 11, but this time investigating the symmetry of the profiles. The chosen absorption lines have clear P Cygni profiles at phase φorb ~ 0.5. Other lines also show, however, asymmetric profiles. The colored profiles show the original ones, while the black profiles are mirrored at the energy bin with the lowest relative flux value. |
In the previous section, we already alluded to the complexity of some line profiles. We now discuss the behavior of the absorption lines with the highest S/N, i.e., the Si xiv, Mg xii, and Ne x Ly α transitions (Fig. 11). We observe strong, pure absorption lines with small blueshift (no more than 200 km s-1, Hanke et al. 2008, and Paper I), or no shift at all between phases φorb ~ 0.0 and ~0.2. Lines at phase φorb ~ 0.5 and ~0.75 show, however, very different profiles. At phase φorb ~ 0.5, we detected clear P Cygni line profiles in the spectrum of Cyg X-1. Variable P Cygni-like line profiles have previously been seen, e.g., in Cir X-1 (Schulz & Brandt 2002; Schulz et al. 2008). In Cyg X-1, P Cygni lines have previously been suggested by Schulz et al. (2002) from data from ObsID 107. This 15 ks TE mode observation at phase φorb = 0.73–0.76 was performed during a softer, higher flux state of the source. The observed spectral features were mostly identified with Fe transitions Fe xviii–Fe xxiv, and the authors suggest that absorption and close emission lines could form P Cygni profiles in some cases. They argue, however, that the identification of the Fe lines in the range between 6 and 16 Å is difficult, as many of them are probably blended. Investigating ObsID 2415 at the same orbital phase, Miller et al. (2005) do not find convincing evidence of P Cygni features. Our spectrum of the observation at φorb ~ 0.75 (ObsID 3815) does not reveal any P Cygni line profiles, but we note that the lines appear asymmetric (see Fig. 12 and discussion below).
Given the values from Table A.2, the emission component is much stronger than the absorption. It appears slightly blueshifted, at very low velocities that are – given their uncertainty – still consistent with zero. The blueshift of the weak absorption tails is much higher. Line profiles at phase φorb ~ 0.75 are observed as pure absorption lines, but are much weaker than at φorb ~ 0.0 and redshifted by 100–400 km s-1. The high blueshift observed in the P Cygni profiles is a direct proof that a non-focused part of the wind also exists on the X-ray irradiated side of the donor star, and that it is accelerated to high velocities. If the different line profiles at φorb ~ 0.0 and ~0.5 result from the same wind structure, only seen at different viewing angles, then the weakness of the absorption lines at φorb ~ 0.5 confirms that the line of sight at this phase probes less dense regions of the wind than at φorb ~ 0.0. Since no net emission is seen at φorb ~ 0.0, any emitting gas must be at a small projected velocity, where the emission fills only part of the absorption trough in the continuum radiation created along the line of sight. As this gas is also seen at low velocity from φorb ~ 0.5, its full space velocity must be small. It could, for example, be related to the slow base of the spherical wind, or to the focused wind.
To find possible constraints on the wind in the system, Miller et al. (2005) used the observed lines (Ne ix, Ne x Si xiii, and Si xiv). Based on calculations by Kallman & McCray (1982) and using the spectral shape and luminosity appropriate for their observations, they find that these absorption features arise in a temperature region spanning over one order of magnitude as log T = 4.5–6.0. This result already implies that, even by investigating only the non-dip spectrum, we probe a multi-temperature region. Based on the ionization parameter and simplifying geometry assumptions, Miller et al. determine the distance of the absorbing region from the ionizing source to be ~3 × 1011−1012 cm.
Most of the line profiles shown in Fig. 11 give an
impression of asymmetry. To describe it quantitatively, we first mirrored the measured
line profile at the energy bin with the lowest relative flux value of the data/model ratio
(Fig. 12). The original and the flipped profiles
were then treated as “data” and “model” and a χ2-type value was calculated to describe
the “goodness” of the overlap according to 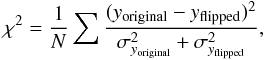 (4)where N is the total number of
bins which were taken into account to calculate the χ2. Both
profiles and obtained values of χ2 are shown in Fig. 12. The highest χ2 values were
obtained for the P Cygni profiles in ObsID 11044. Mg xii in ObsID 8525 and
Ne x in ObsID 3815 could be also described as asymmetric, but for the latter
this might also be caused by blending with Fe lines. Setting a threshold of
χ2 =
1.5, all lines in ObsID 9847, Si xiv and Ne x in
ObsID 8525, Mg xii in ObsID 3814, and Si xiv in ObsID 3815 would be
considered symmetric. For Ne x in ObsIDs 9847 and 8525, the data have, however,
high uncertainties, and are therefore not very sensitive to detecting asymmetry.
(4)where N is the total number of
bins which were taken into account to calculate the χ2. Both
profiles and obtained values of χ2 are shown in Fig. 12. The highest χ2 values were
obtained for the P Cygni profiles in ObsID 11044. Mg xii in ObsID 8525 and
Ne x in ObsID 3815 could be also described as asymmetric, but for the latter
this might also be caused by blending with Fe lines. Setting a threshold of
χ2 =
1.5, all lines in ObsID 9847, Si xiv and Ne x in
ObsID 8525, Mg xii in ObsID 3814, and Si xiv in ObsID 3815 would be
considered symmetric. For Ne x in ObsIDs 9847 and 8525, the data have, however,
high uncertainties, and are therefore not very sensitive to detecting asymmetry.
6.2. Properties of the X-ray emitting gas: density diagnostics of the Mg XI He-like triplet
Owing to the P Cygni profiles, the location of the absorber in ObsID 11044 is difficult to constrain. This observation, however, contains a strong He-like Mg triplet, i.e., the forbidden, intercombination, and recombination lines f,i, and r, between 9.1 and 9.4 Å, which is suitable for plasma diagnostics (Fig. A.4). The existence of these lines allows us to determine the physical condition of the location of the emitter, although the absorber location is indeterminable. With the triplet lines all being seen in emission, their intensity ratios G(Te) = (i + f) /r and R(ne) = f/i can be used to directly estimate electron temperature and density of the emitting plasma (Gabriel & Jordan 1969; Porquet & Dubau 2000). We note that in ObsID 3814, φorb ~ 0.0, which we studied in Paper I, only Mg xi i and f are seen in emission, while Mg xi r is in absorption, allowing only for the R-ratio to be analyzed.
In ObsID 11044, G = 1.6 ± 0.5 ≪ 4 indicates a hybrid plasma where, next to photoionization, collisional ionization plays an important role as well (Porquet & Dubau 2000). The G value corresponds to an electron temperature of roughly (3–5) × 106 K, depending on the ratio of H-like to He-like ions. Since G is a rather steep function of temperature in that range, the uncertainty of G only has very little effect on the temperature. We note that the P Cygni profile of the resonance line also adds an uncertainty to its intensity, and therefore, G.
The R-ratio of 0.6 ± 0.5 corresponds to an electron density of ~4 × 1013 cm-3. The presence of the strong UV field produced by HDE 226868 can, however, deplete the metastable upper level of the forbidden line by photoexcitation, lowering the measured R-ratio (Mewe & Schrijver 1978; Kahn et al. 2001). Thus, the derived density constitutes an upper limit.
Similar results can be obtained by directly fitting the He-like triplet using results from collisional plasma calculations by D. Huenemoerder (priv. comm., see5), which however, does not take the effects of UV radiaton into account either. This fit gives Te ~ 3 × 106 K and ne ~ 6 × 1013 cm-3.
In ObsID 3814, we could resolve two sets of Mg xii and f lines, one unshifted and the other one redshifted (Paper I). Within their uncertainties, the plasma seen in ObsID 11044 shows the same R-ratio, i.e., the same electron density, as the redshifted Mg triplet in ObsID 3814.
We note that the density determined from the emission lines is a factor of ~1000 higher than the density of the region where the absorption is thought to occur. This could mean that the emission component could originate in emitting high-density regions, such as clouds, that are mixed into the absorber. Alternatively, the high density could point to an origin not in the wind, but in the denser regions of the accretion flow within the Bondi radius.
7. Summary
Stellar winds of massive stars are highly inhomogenous phenomena: they show temperatures spanning several orders of magnitude, turbulent velocities, and highly variable densities. Gratings of the Chandra observatory provide us with the first real opportunity to investigate the narrow spectral lines of the stellar winds in great detail and so allow us to probe this variable environment. Cyg X-1, as a nearby, bright, and persistent source is an ideal target for this type of study. In this work, we presented the most extensive analysis of the Chandra-HETGS hard state spectra of Cyg X-1 so far. We investigated five spectra that cover the most important segments of orbital phase: stellar wind in its focused stream at φorb ~ 0.0, the opposite site of the focused wind at φorb ~ 0.5, as well as at parts perpendicular to the binary axis at φorb ~ 0.2 and ~0.75. This is the second paper in the series; Paper I presented analysis of one of the observations (ObsID 3814, φorb ~ 0.95), focusing only on spectra extracted at the constant flux level (dips exluded). Here, we analyzed the non-dip spectra of the remaining observations, and discussed their variation over the orbital phase.
The most important results of our analysis are:
-
1.
The intensity of dipping in light curves is phase-dependent. Strong dips are observed along the binary axis at φorb ~ 0.0, while the light curve outside the focused stellar wind at φorb ~ 0.5 is free of absorption dips in these observations.
-
2.
Non-dip spectra reveal absorption lines of H- and He-like ions of S, Si, Al, Mg, Na, and Ne, as well as L-shell Fe transitions, which correspond to highly ionized material. Spectra measured close to φorb ~ 0.0 also show lines of lower ionized stages of Si xii–Si ix. The spectrum observed outside of the wind at φorb ~ 0.5 shows clear P Cygni profiles.
-
3.
The neutral Ne K absorption edge was prominent in all investigated spectra, such that we were able to measure the neutral Ne column density independently from the total column. The values vary moderately within NNe = (0.5–1.5) × 1018 cm-2, attaining lowest values outside of the wind at φorb ~ 0.5, and highest values at φorb ~ 0.2. The Fe absorption edge was only resolved in the spectrum at φorb ~ 0.5, giving NFe = 0.15 ± 0.02 × 1018 cm-2. Deriving NH values from continuum fitting to the gratings data suffers from a large systematic error and yields values that are strongly biased towards lower columns.
-
4.
Column densities obtained from the analysis of the ionized absorption lines are phase dependent, and therefore intrinsic to the source. They are highest around φorb ~ 0.0, i.e., in the focused wind stream, and imply that the observed medium is almost fully ionized. The observed elements appear to be overabundant with respect to solar abundances.
-
5.
Doppler shifts, ± 500 km s-1, vary strongly with orbital phase. Both the column of the absorber and the Doppler shift are consistent with an absorber location that is less than 0.5d away from the black hole, where d is the distance between the donor star and the black hole. The observations suggest that we observe a complex ionization structure.
-
6.
The spectrum at φorb ~ 0.5 shows the Mg He-triplet, which is suitable for plasma diagnostics, suggesting that we also see a plasma with an electron temperature of (3–5) × 106 K, which is much denser than the locations in the wind responsible for absorption, e.g., clumps in the stellar wind.
In the next paper of this series we will study the properties of the gas responsible for the absorption dips in the light curves.
Acknowledgments
The research leading to these results was funded by the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement number ITN 215212 “Black Hole Universe” and by the Bundesministerium für Wirtschaft und Technologie under grant numbers DLR 50 OR 0701 and 50 OR 1113. This work was partially completed by Lawrence Livermore National Laboratory (LLNL) under Contract DE-AC52-07NA27344, and is supported by NASA grants to LLNL. Support for this work was also provided by NASA through the Smithsonian Astrophysical Observatory (SAO) contract SV3-73016 to MIT for Support of the Chandra X-Ray Center (CXC) and Science Instruments; CXC is operated by SAO for and on behalf of NASA under contract NAS8-03060. We acknowledge the support by the DFG Cluster of Excellence “Origin and Structure of the Universe” and are grateful for the support by MCB through the Computational Center for Particles and Astrophysics (C2PAP). We are thankful to John E. Davis for the SLXfig package that was used to create the figures throughout this paper, to David Huenemoerder for the AGLC routines that handled the grating lightcurves and routines related to plasma diagnostics, and to Thomas Dauser for parallel computing routines. This research has made use of the MAXI data provided by RIKEN, JAXA, and the MAXI team.
References
- Bałucińska-Church, M., Belloni, T., Church, M. J., & Hasinger, G. 1995, A&A, 302, L5 [NASA ADS] [Google Scholar]
- Bałucińska-Church, M., Church, M. J., Charles, P. A., et al. 2000, MNRAS, 311, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Behar, E., & Netzer, H. 2002, ApJ, 570, 165 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. 2004, Nucl. Phys. B Proc. Suppl., 132, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Belloni, T. M. 2010, in The Jet Paradigm – From Microquasars to Quasars, ed. T. M. Belloni, (Berlin: Springer), Lect. Notes Phys., 794, 53 [Google Scholar]
- Blondin, J. M. 1994, ApJ, 435, 756 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blondin, J. M., & Woo, J. W. 1995, ApJ, 445, 889 [NASA ADS] [CrossRef] [Google Scholar]
- Blondin, J. M., Stevens, I. R., & Kallman, T. R. 1991, ApJ, 371, 684 [NASA ADS] [CrossRef] [Google Scholar]
- Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, B., & Vrtilek, S. D. 2010, ApJ, 710, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Bowyer, S., Byram, E. T., Chubb, T. A., & Friedman, H. 1965, Ann. Astrophys., 28, 791 [NASA ADS] [Google Scholar]
- Brocksopp, C., Fender, R. P., Larionov, V., et al. 1999, MNRAS, 309, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero-Nieves, S. M., Gies, D. R., Bolton, C. T., et al. 2009, ApJ, 701, 1895 [NASA ADS] [CrossRef] [Google Scholar]
- Canizares, C. R., Davis, J. E., Dewey, D., et al. 2005, PASP, 117, 1144 [NASA ADS] [CrossRef] [Google Scholar]
- Castor, J. I., Abbott, D. C., & Klein, R. I. 1975, ApJ, 195, 157 [NASA ADS] [CrossRef] [Google Scholar]
- Duro, R., Dauser, T., & Grinberg, V., et al. 2016, A&A, 589, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duro, R., Dauser, T., Wilms, J., et al. 2011, A&A, 533, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fabian, A. C., Wilkins, D. R., Miller, J. M., et al. 2012, MNRAS, 424, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Feldmeier, A., Puls, J., & Pauldrach, A. W. A. 1997, A&A, 322, 878 [NASA ADS] [Google Scholar]
- Fender, R., Corbel, S., Tzioumis, T., et al. 1999, ApJ, 519, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, Y. X., & Cui, W. 2002, ApJ, 564, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Foster, A. R., Ji, L., Smith, R. K., & Brickhouse, N. S. 2012, ApJ, 756, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Friend, D. B., & Castor, J. I. 1982, ApJ, 261, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Gabriel, A. H., & Jordan, C. 1969, MNRAS, 145, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Garmire, G. P., Bautz, M. W., Ford, P. G., Nousek, J. A., & Ricker, Jr., G. R. 2003, in X-Ray and Gamma-Ray Telescopes and Instruments for Astronomy, eds. J. E. Trümper, & H. D. Tananbaum, Proc. SPIE 4851 (Bellingham, SPIE), 28 [Google Scholar]
- Gierliński, M., Zdziarski, A. A., Poutanen, J., et al. 1999, MNRAS, 309, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., & Bolton, C. T. 1986, ApJ, 304, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Bolton, C. T., Thomson, J. R., et al. 2003, ApJ, 583, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Gies, D. R., Bolton, C. T., Blake, R. M., et al. 2008, ApJ, 678, 1237 [NASA ADS] [CrossRef] [Google Scholar]
- Grinberg, V., Hell, N., Pottschmidt, K., et al. 2013, A&A, 554, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grinberg, V., Leutenegger, M. A., Hell, N., et al. 2015, A&A, 576, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanke, M. 2011, Dissertation, Friedrich-Alexander-Universität Erlangen-Nürnberg, Erlangen [Google Scholar]
- Hanke, M., Wilms, J., Nowak, M. A., et al. 2009, ApJ, 690, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Hanke, M., Wilms, J., Nowak, M. A., Barragán, L., & Schulz, N. S. 2010, A&A, 509, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanke, M., Wilms, J., Nowak, M. A., et al. 2008, PoS, Microquasar Workshop, 7, 29 [NASA ADS] [Google Scholar]
- Hell, N., Miškovičová, I., Brown, G. V., et al. 2013, Phys. Scr. T, 156, 014008 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, A., Kudritzki, R. P., Gabler, R., Vilchez, J. M., & Gabler, A. 1995, A&A, 297, 556 [NASA ADS] [Google Scholar]
- Holt, S. S., Boldt, E. A., Serlemitsos, P. J., & Kaluzienski, L. J. 1976, ApJ, 203, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Houck, J. C., & Denicola, L. A. 2000, in Astronomical Data Analysis Software and Systems IX, ed. N. Manset, C. Veillet, & D. Crabtree, ASP Conf. Ser., 216, 591 [Google Scholar]
- Jahoda, K., Markwardt, C. B., Radeva, Y., et al. 2006, ApJS, 163, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Juett, A. M., Wilms, J., Schulz, N. S., & Nowak, M. A. 2006, BA&AS, 38, 921 [Google Scholar]
- Kahn, S. M., Leutenegger, M. A., Cottam, J., et al. 2001, A&A, 365, L312 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kallman, T. R., & McCray, R. 1982, ApJS, 50, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Kitamoto, S., Miyamoto, S., Tanaka, Y., et al. 1984, PASJ, 36, 731 [NASA ADS] [Google Scholar]
- Kitamoto, S., Miyamoto, S., & Yamamoto, T. 1989, PASJ, 41, 81 [Google Scholar]
- Kitamoto, S., Egoshi, W., Miyamoto, S., et al. 2000, ApJ, 531, 546 [NASA ADS] [CrossRef] [Google Scholar]
- Lachowicz, P., Zdziarski, A. A., Schwarzenberg-Czerny, A., Pooley, G. G., & Kitamoto, S. 2006, MNRAS, 368, 1025 [NASA ADS] [CrossRef] [Google Scholar]
- Lampton, M., Margon, B., & Bowyer, S. 1976, ApJ, 208, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, A. M., Bradt, H., Cui, W., et al. 1996, ApJ, 469, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Li, F. K., & Clark, G. W. 1974, ApJ, 191, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Manousakis, A. 2011, Ph. D., Université de Genève, Geneva [Google Scholar]
- Marshall, H. L., Schulz, N. S., Fang, T., et al. 2001, in Proc. X-ray Emission from Accretion onto Black Holes, eds. T. Yaqoob, & J. H. Krolik [arXiv:astro-ph/0111464] [Google Scholar]
- Mason, K. O., Hawkins, F. J., Sanford, P. W., Murdin, P., & Savage, A. 1974, ApJ, 192, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, M., Kawasaki, K., Ueno, S., et al. 2009, PASJ, 61, 999 [NASA ADS] [CrossRef] [Google Scholar]
- Mewe, R., & Schrijver, J. 1978, A&A, 65, 99 [NASA ADS] [Google Scholar]
- Mihalas, D. 1978, Stellar Atmospheres, 2nd edn. (San Francisco: W.H. Freeman and Co.) [Google Scholar]
- Miller, J. M., Fabian, A. C., Wijnands, R., et al. 2002, ApJ, 578, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Miller, J. M., Wojdowski, P., Schulz, N. S., et al. 2005, ApJ, 620, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nowak, M. A., Hanke, M., Trowbridge, S. N., et al. 2011, ApJ, 728, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Oskinova, L. M., Feldmeier, A., & Kretschmar, P. 2012, MNRAS, 421, 2820 [NASA ADS] [CrossRef] [Google Scholar]
- Parsignault, D. R., Grindlay, J. E., Schnopper, H. W., Schreier, E. J., & Gursky, H. 1976, in X-ray binaries, eds. Y. Kondo, & E. Boldt, NASA SP–389, 429 [Google Scholar]
- Porquet, D., & Dubau, J. 2000, A&AS, 143, 495 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pottschmidt, K., Wilms, J., Nowak, M. A., et al. 2003, A&A, 407, 1039 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poutanen, J., Zdziarski, A. A., & Ibragimov, A. 2008, MNRAS, 389, 1427 [NASA ADS] [CrossRef] [Google Scholar]
- Pravdo, S. H., White, N. E., Becker, R. H., et al. 1980, ApJ, 237, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Priedhorsky, W., Garmire, G. P., Rothschild, R., et al. 1979, ApJ, 233, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Rahoui, F., Lee, J. C., Heinz, S., et al. 2011, ApJ, 736, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Reid, M. J., McClintock, J. E., Narayan, R., et al. 2011, ApJ, 742, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Remillard, R. A., & Canizares, C. R. 1984, ApJ, 278, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Sako, M., Liedahl, D. A., Kahn, S. M., & Paerels, F. 1999, ApJ, 525, 921 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, N. S., & Brandt, W. N. 2002, ApJ, 572, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, N. S., Cui, W., Canizares, C. R., et al. 2002, ApJ, 565, 1141 [NASA ADS] [CrossRef] [Google Scholar]
- Schulz, N. S., Kallman, T. E., Galloway, D. K., & Brandt, W. N. 2008, ApJ, 672, 1091 [NASA ADS] [CrossRef] [Google Scholar]
- Shaposhnikov, N., Jahoda, K., Markwardt, C., Swank, J., & Strohmayer, T. 2012, ApJ, 757, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Sundqvist, J. O., & Owocki, S. P. 2013, MNRAS, 428, 1837 [NASA ADS] [CrossRef] [Google Scholar]
- Tarter, C. B., Tucker, W. H., & Salpeter, E. E. 1969, ApJ, 156, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Tomsick, J. A., Nowak, M. A., Parker, M., et al. 2014, ApJ, 780, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Vrtilek, S. D., & Boroson, B. S. 2013, MNRAS, 428, 3693 [NASA ADS] [CrossRef] [Google Scholar]
- Vrtilek, S. D., Boroson, B. S., Hunacek, A., Gies, D., & Bolton, C. T. 2008, ApJ, 678, 1248 [NASA ADS] [CrossRef] [Google Scholar]
- Walborn, N. R. 1973, ApJ, 179, L123 [Google Scholar]
- Webster, B. L., & Murdin, P. 1972, Nature, 235, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, L., Cui, W., Levine, A. M., & Bradt, H. V. 1999, ApJ, 525, 968 [Google Scholar]
- Wilms, J., Allen, A., & McCray, R. 2000, ApJ, 542, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Wilms, J., Nowak, M. A., Pottschmidt, K., Pooley, G. G., & Fritz, S. 2006, A&A, 447, 245 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xiang, J., Lee, J. C., Nowak, M. A., & Wilms, J. 2011, ApJ, 738, 78 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Line series parameters and spectra.
H-like, He-like, and Fe absorption lines at φorb ~ 0.75, φorb ~ 0.05, and ~0.2 (ObsID 3815, 8525, and 9847).
Parameters for spectral line features for ObsID 11044.
 |
Fig. A.1 Non-dip spectrum of ObsID 8525 – displayed as the ratio between data and absorbed power-law continuum model – showing the absorption lines observed in the spectrum. Due to a relatively short exposure time of only 4.4 ks, the HEG spectra are worse than MEG at longer wavelengths. Data from HEG were therefore scaled to MEG data for visual reasons. The red line shows lines modeled with line series. Each of them is labeled at its rest wavelength. There are no significant emission lines in the spectrum, except the Si xiii forbidden line. Instead, absorption lines from Si xii (Li-like), possibly Si xi (Be-like), Si x (B-like), and Si ix (C-like), although quite weak, can be clearly identified in the “Si region” between 6.6 Å and 7 Å. |
 |
Fig. A.2 Line identifications for ObsID 9847. Non-dip data displayed as ratio between data and absorbed power-law continuum model. |
 |
Fig. A.3 Non-dip spectrum of ObsID 3815 – displayed as the ratio between data and absorbed power-law continuum model – showing the H- and He-like absorption lines, as well as the i and f emission lines of the hot gas of the stellar wind. The spectra of HEG±1 and MEG±1 were combined and binned to the same signal-to-noise ratio (S/N = 10) as for fitting. Especially notable are lines of Ne xβ at 10.24 Å, Ne xγ at 9.71 Å, and Ne xδ at 9.48 Å, because they are much stronger in the data than the profiles that are predicted by the model. We did not manage to identify the emission feature at ~7.98Å. It is also visible in ObsID 1044 (Fig. A.4), but not in ObsIDs 8525 and 9847 (Figs. A.1 and A.2). |
 |
Fig. A.4 Spectrum of ObsID 11044, displayed as the ratio between data and absorbed power-law continuum model. The most prominent absorption and emission lines have been fitted with Voigt profiles. The Lyα lines of H-like Si, Mg, and Ne show clear P Cygni profiles. The absorption line at 6.70 Å, however, cannot be related to the emission line at 6.74 Å, if the latter is due to the (dipole-) forbidden transition of Si xiii. |
Appendix B: Diffraction order determination in CIAO data reduction
 |
Fig. B.1 Banana plot – order-sorting of incoming events. Left: diffraction orders for the HEG and MEG instruments. The source itself is located at sky x-position x = 4100. The higher density of events around this region is most likely associated with a scattering halo. The different orders correspond to hyperbolas, shaped by a higher density of events. The hyperbolas with the highest event density, close to the source, represent the ± 1st order of HEG and MEG. Right: same as left figure, but showing the events assigned to the HEG and MEG in standard processing (white regions). Not all of the events are included. Changing the OSIP parameters, as described in the text, enables us to include all events belonging to each order in the analysis (black lines). |
A data processing problem that would have strongly affected any further analysis consists of the incorrect determination of the diffraction order of photons in Chandra’s standard data-reduction pipelines. Here, based on detector (ACIS) energy and position (dispersion distance or wavelength) of X-ray photons, it is possible to disentagle events into different spectral orders, as shown in so-called banana plots (Fig. B.1). Different event hyperbolas correspond to individual orders (left panel), but especially in observations of bright sources it is possible that not all events are assigned to their associated order, since the charge transfer efficiency in the detectors changes with source flux. This so-called order-sorting problem is most prominent in the first order spectra (right panel). This problem can be solved by manually changing the default values in the order sorting and integrated probability (OSIP) file used by the tg-resolve-events routine of the standard data processing, and ignoring the default values obtained from Chandra’s calibration database. This type of correction results in a much wider range of events entering the analysis (Fig. B.1).
Appendix C: Telemetry saturation
A second problem that occurs in sources with high flux is that, because of the large count rates, data are generated so fast that the telemetry stream may become saturated, causing an exposure gap in the corresponding time bin. The remaining data frame from the affected CCD chip are discarded (Fig. C.1c). Count rate light curves from observations affected by this problem – in our case ObsID 3815 – erroneously show lower fluxes because they are commonly based on the average CCD exposure instead of treating count rates for each CCD separately. This problem can be dealt with by including exposure statistics from the secondary Chandra data in the Chandra standard processing using the tool aglc (D. Huenemoerder, priv. comm.; see Fig. C.1).
 |
Fig. C.1 a) 0.5–10 keV Chandra light curve of Cyg X-1 (time resolution of 25.5 s), obtained in 2003 March (ObsID 3815). Light blue: light curve without taking telemetry drop-outs into account. Black: light curve after correcting for telemetry drop-outs. b) Ratio between the 0.5–1.5 keV and 3–10 keV energy bands, again with and without correction for the telemetry saturation. c) Fractional exposure during the observation for each CCD. Telemetry drop-outs appeared at ~20 ks and after ~40 ks (gray regions). In the latter case, 5 of 6 CCDs were affected. Since whole data frames were discarded, lower count rates were observed in the light curve in the affected time intervals before the correction was applied (panel a)). The spectrum extracted for those GTIs might be influenced as well, especially in the wavelength range of affected CCDs. These GTIs were not used in the analysis, even after correction of the count rates. |
All Tables
Intercombination (i) and forbidden (f) emission lines from He-like ions at φorb ~ 0.75 (ObsID 3815).
Sine function parameters describing the orbital modulation of the Doppler shifts.
H-like, He-like, and Fe absorption lines at φorb ~ 0.75, φorb ~ 0.05, and ~0.2 (ObsID 3815, 8525, and 9847).
All Figures
 |
Fig. 1 Orbital phase coverage of the Chandra observations of Cyg X-1 in the hard state analyzed in this work. Full arcs (dashed arcs) display TE mode (CC mode; for explanation see Sect. 2.3) observations. The labels correspond to the Chandra ObsIDs. Phase φorb = 0 corresponds to the superior conjunction of the black hole. |
| In the text | |
 |
Fig. 2 1.5–12 keV RXTE-All-Sky Monitor count rate of Cyg X-1 with one day binning in the intervals of nine months during 2003, 2008, and 2010 centered at the times of Chandra observations: ObsIDs 3815 and 3814 (left), 8525 and 9847 (middle), and 11044 (right), indicated by vertical lines. The right panel also shows the MAXI light curve. |
| In the text | |
 |
Fig. 3 Upper panel: lightcurves of all five observations as a function of orbital phase. Lower panel: variation of the hardness ratio. Except for the somewhat softer hard-intermediate state observation ObsId 3815, all observations were in the low/hard state. Dips are strongest at φorb ~ 0.0, still present at φorb ~ 0.2, and φorb ~ 0.75, and they vanish at φorb ~ 0.5. Colors indicate the parts of the observations used in the analysis (see Fig. 1), while data in black were excluded from the analysis. |
| In the text | |
 |
Fig. 4 Fit parameters from Table A.1 for line series of H-like and He-like transitions in ObsID 3815 (squares), ObsID 8525 (circles), ObsID 9847 (stars), and also ObsID 3814 (diamonds, Paper I): top: velocity shifts, middle: column densities, bottom: thermal broadening. Colors correspond to ObsIDs as indicated. For completeness, values far above or below the displayed range are marked by triangles close to upper/lower x-axes. |
| In the text | |
 |
Fig. 5 Orbital phase variation of fitted columns, repeated twice for clarity. Gray data points show the equivalent hydrogen column density, NH, from continuum fitting the Chandra spectra (right hand y-axis). As discussed in the text, the data points are heavily influenced by systematics (the error bars shown are statistical only). The colored data points show the variation of the Ne neutral column from Ne-edge fitting (left y-axis) and corresponding NH (right y-axis) derived assuming a Ne:H abundance of 1:11481 as per Wilms et al. (2000). The phases of individual Chandra observations are denoted with colored regions. The dashed lines represent the total equivalent column density of the interstellar medium and of Ne (Xiang et al. 2011). |
| In the text | |
 |
Fig. 6 Measured column densities, Ni, of individual elements as a function of orbital phase. Left: H- and He-like line series (circles) and Fe lines (crosses). Only measurements with relative uncertainties <75% are included. Right: column densities of the four most prominent ions, Ne x (circles), Mg xii (diamonds), Mg xi (squares), and Si xiv (triangles). Filled datapoints correspond to symmetric lines (see Fig. 12 and related discussions). |
| In the text | |
 |
Fig. 7 Stellar wind density, assuming the focused wind model of Gies & Bolton (1986) and lines of sight towards the black hole. Left: side view onto the orbital plane (dashed). Right: lines of sight projected onto the orbital plane. The black hole (cross) and its donor move clockwise around the center of mass (cross). |
| In the text | |
 |
Fig. 8 Phase variation of the column density according to the focused wind model of Gies & Bolton (1986). Shown is the column of the whole wind (solid line), and of those less ionized wind regions where the ionization parameter log ξ< 3.0 (dash dotted line) and log ξ< 2.6 (dotted line), respectively. |
| In the text | |
 |
Fig. 9 Top: velocity shifts of individual line series (circles: H-like and He-like ions, crosses: Fe line series) and the radial velocity of the black hole (dash-dotted line, semi-amplitude of ~98 km s-1). The red sine curve shows the best fit involving all series shown (KW ~ 276 km s-1, v0 ~ −40 km s-1, and Δφ ~ 0.46), while the dashed line shows the second best fit, where the offset was fixed to the systemic velocity of the black hole (Table 6). Bottom: velocity shifts for individual ions and the radial velocity of the black hole (dash-dotted line). The sine curves represent the best fits for each of the three given line series (Table 6). Dashed lines show fits with the offset fixed to the systemic velocity of the black hole. The red sine curve is the best fit involving all three line series (Table 6). |
| In the text | |
 |
Fig. 10 Radial velocities of the black hole (red dashed line) and of HDE 226868 (orange dashed line) and wind velocities projected onto the line of sight as a function of distance from the black hole. Distances are given in units of the distance between the black hole and its donor, a. Colored boxes indicate the range of the measured Doppler shifts from the Chandra observations, excluding ObsID 11044. |
| In the text | |
 |
Fig. 11 Line profiles of the three most prominent absorption lines of Si xiv, Mg xii, and Ne x are shown here as they vary over the orbital phase. Lines are displayed as the ratio of data and model, offset for visual clarity. For each line, the vertical gray lines are located at rest wavelengths corresponding to zero velocity shifts. See text for explanation. |
| In the text | |
 |
Fig. 12 The same line profiles as in Fig. 11, but this time investigating the symmetry of the profiles. The chosen absorption lines have clear P Cygni profiles at phase φorb ~ 0.5. Other lines also show, however, asymmetric profiles. The colored profiles show the original ones, while the black profiles are mirrored at the energy bin with the lowest relative flux value. |
| In the text | |
 |
Fig. A.1 Non-dip spectrum of ObsID 8525 – displayed as the ratio between data and absorbed power-law continuum model – showing the absorption lines observed in the spectrum. Due to a relatively short exposure time of only 4.4 ks, the HEG spectra are worse than MEG at longer wavelengths. Data from HEG were therefore scaled to MEG data for visual reasons. The red line shows lines modeled with line series. Each of them is labeled at its rest wavelength. There are no significant emission lines in the spectrum, except the Si xiii forbidden line. Instead, absorption lines from Si xii (Li-like), possibly Si xi (Be-like), Si x (B-like), and Si ix (C-like), although quite weak, can be clearly identified in the “Si region” between 6.6 Å and 7 Å. |
| In the text | |
 |
Fig. A.2 Line identifications for ObsID 9847. Non-dip data displayed as ratio between data and absorbed power-law continuum model. |
| In the text | |
 |
Fig. A.3 Non-dip spectrum of ObsID 3815 – displayed as the ratio between data and absorbed power-law continuum model – showing the H- and He-like absorption lines, as well as the i and f emission lines of the hot gas of the stellar wind. The spectra of HEG±1 and MEG±1 were combined and binned to the same signal-to-noise ratio (S/N = 10) as for fitting. Especially notable are lines of Ne xβ at 10.24 Å, Ne xγ at 9.71 Å, and Ne xδ at 9.48 Å, because they are much stronger in the data than the profiles that are predicted by the model. We did not manage to identify the emission feature at ~7.98Å. It is also visible in ObsID 1044 (Fig. A.4), but not in ObsIDs 8525 and 9847 (Figs. A.1 and A.2). |
| In the text | |
 |
Fig. A.4 Spectrum of ObsID 11044, displayed as the ratio between data and absorbed power-law continuum model. The most prominent absorption and emission lines have been fitted with Voigt profiles. The Lyα lines of H-like Si, Mg, and Ne show clear P Cygni profiles. The absorption line at 6.70 Å, however, cannot be related to the emission line at 6.74 Å, if the latter is due to the (dipole-) forbidden transition of Si xiii. |
| In the text | |
 |
Fig. B.1 Banana plot – order-sorting of incoming events. Left: diffraction orders for the HEG and MEG instruments. The source itself is located at sky x-position x = 4100. The higher density of events around this region is most likely associated with a scattering halo. The different orders correspond to hyperbolas, shaped by a higher density of events. The hyperbolas with the highest event density, close to the source, represent the ± 1st order of HEG and MEG. Right: same as left figure, but showing the events assigned to the HEG and MEG in standard processing (white regions). Not all of the events are included. Changing the OSIP parameters, as described in the text, enables us to include all events belonging to each order in the analysis (black lines). |
| In the text | |
 |
Fig. C.1 a) 0.5–10 keV Chandra light curve of Cyg X-1 (time resolution of 25.5 s), obtained in 2003 March (ObsID 3815). Light blue: light curve without taking telemetry drop-outs into account. Black: light curve after correcting for telemetry drop-outs. b) Ratio between the 0.5–1.5 keV and 3–10 keV energy bands, again with and without correction for the telemetry saturation. c) Fractional exposure during the observation for each CCD. Telemetry drop-outs appeared at ~20 ks and after ~40 ks (gray regions). In the latter case, 5 of 6 CCDs were affected. Since whole data frames were discarded, lower count rates were observed in the light curve in the affected time intervals before the correction was applied (panel a)). The spectrum extracted for those GTIs might be influenced as well, especially in the wavelength range of affected CCDs. These GTIs were not used in the analysis, even after correction of the count rates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


