| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A2 | |
| Number of page(s) | 35 | |
| Section | Numerical methods and codes | |
| DOI | https://doi.org/10.1051/0004-6361/201526758 | |
| Published online | 11 February 2016 | |
SP_Ace: a new code to derive stellar parameters and elemental abundances⋆
Astronomisches Rechen-Institut, Zentrum für Astronomie der
Universität Heidelberg, Mönchhofstr. 12–14, 69120
Heidelberg,
Germany
e-mail:
corrado@ari.uni-heidelberg.de
Received: 16 June 2015
Accepted: 18 October 2015
Context. Ongoing and future massive spectroscopic surveys will collect large numbers (106–107) of stellar spectra that need to be analyzed. Highly automated software is needed to derive stellar parameters and chemical abundances from these spectra.
Aims. We developed a new method of estimating the stellar parameters Teff, log g, [M/H], and elemental abundances. This method was implemented in a new code, SP_Ace (Stellar Parameters And Chemical abundances Estimator). This is a highly automated code suitable for analyzing the spectra of large spectroscopic surveys with low or medium spectral resolution (R = 2000–20 000).
Methods. After the astrophysical calibration of the oscillator strengths of 4643 absorption lines covering the wavelength ranges 5212–6860 Å and 8400–8924 Å, we constructed a library that contains the equivalent widths (EW) of these lines for a grid of stellar parameters. The EWs of each line are fit by a polynomial function that describes the EW of the line as a function of the stellar parameters. The coefficients of these polynomial functions are stored in a library called the “GCOG library”. SP_Ace, a code written in FORTRAN95, uses the GCOG library to compute the EWs of the lines, constructs models of spectra as a function of the stellar parameters and abundances, and searches for the model that minimizes the χ2 deviation when compared to the observed spectrum. The code has been tested on synthetic and real spectra for a wide range of signal-to-noise and spectral resolutions.
Results. SP_Ace derives stellar parameters such as Teff, log g, [M/H], and chemical abundances of up to ten elements for low to medium resolution spectra of FGK-type stars with precision comparable to the one usually obtained with spectra of higher resolution. Systematic errors in stellar parameters and chemical abundances are presented and identified with tests on synthetic and real spectra. Stochastic errors are automatically estimated by the code for all the parameters. A simple Web front end of SP_Ace can be found at http://dc.g-vo.org/SP_ACE, while the source code will be published soon.
Key words: methods: data analysis / atomic data / stars: fundamental parameters / stars: abundances / techniques: spectroscopic / surveys
Full Tables D.1–D.3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/587/A2
© ESO, 2016
1. Introduction
The physical, chemical, and kinematic information carried by the stellar spectra are fundamental for understanding how the Milky Way formed and evolved. The increasing demand for stellar spectra by astronomers engaged in Galactic archaeology led to large spectroscopic surveys that could be carried out thanks to the availability of efficient multi-object spectrographs, to the fast growth of the data storage capability, and the computational power of modern computers. Past, present, and future surveys (such as the RAdial Velocity Experiment, RAVE, Steinmetz et al. 2006; the Sloan Extension for Galactic Understanding and Exploration, SEGUE, Yanny et al. 2009; the Large Sky Area Multi-Object Fiber Spectroscopic Telescope, LAMOST, Zhao et al. 2012; The Apache Point Observatory Galactic Evolution Experiment, APOGEE, Allende Prieto et al. 2008; the Galactic Archaeology with HERMES-GALAH Survey, Zucker et al. 2012; the Gaia-ESO Public Spectroscopic Survey, Gilmore et al. 2012; the 4-Metre multi-Object Spectroscopic Telescope, 4MOST, de Jong et al. 2012; Gaia, Perryman et al. 2001; Lindegren et al. 2008) delivered and will deliver millions of stellar spectra that need to be analyzed to derive stellar parameters (effective temperatures Teff, gravity log g, metallicity [M/H]) and elemental abundances. The analysis of such an amount of data is a challenge that can be addressed by its automation. Today there is considerable effort to develop software for this purpose.
Some software packages implement the classical spectral analysis by measuring equivalent widths (EW) of isolated, well known absorption lines and by deriving stellar parameters from the excitation equilibrium and ionization balance (such as the Fast Automatic Moog Analysis, FAMA, Magrini et al. 2013; GALA, Mucciarelli et al. 2013; ARES, Sousa et al. 2007). These programs are particularly oriented to high-resolution, high signal-to-noise (S/N) spectra, for which isolated lines can be recognized, and their EW can be reliably measured thanks to a safe continuum placement. Other methods are based on grids of synthetic spectra, but they differ in the “line-fitting” or “full-spectrum-fitting” approach, i.e., by fitting isolated absorption lines one-by-one (e.g., MyGIsFOS, Sbordone et al. 2014; Stellar Parameters Determination Software, SPADES, Posbic et al. 2012), or by fitting full spectral ranges (e.g., the MATrix Inversion for Spectral SynthEsis, MATISSE, Recio-Blanco et al. 2006; neural networks, among others statnet by Bailer-Jones 1996; FERRE, Allende Prieto et al. 2006). Spectroscopy Made Easy (SME, Valenti & Piskunov 1996) distinguishes itself from the other codes since it synthesizes on-the-fly single absorption lines or parts of the spectrum to be matched with the observed ones.
The line-fitting analysis can derive stellar parameters and chemical abundances with the drawback of neglecting the significant amount of information carried by the unused part of the observed spectrum. This penalizes the line-fitting approach to low S/N, low metallicity, and low resolution spectra, in which the number of usable lines may be too small to carry out this analysis. On the other hand, the full-spectrum-fitting approach cannot deliver chemical abundances because the grid of synthetic spectra needed to cover the whole parameter and chemical space (and account for many elemental abundances) would be too big to be handled1. Other techniques can use real spectra as templates (“The Cannon”, Ness et al. 2015; ULySS, Koleva et al. 2009) with the advantage of overcoming the systematic errors that stem from the synthetic spectra (due to our incomplete knowledge of atomic parameters and stellar atmospheres) but share with the previous techniques the challenge to collect a number of templates large enough to uniformly cover the stellar parameter and chemical space.
The accuracy of the parameters derived with any of the methods proposed so far (including this work) depends on two fundamental pillars: the precision and accuracy of i) the atomic parameters of the absorption lines employed and ii) the reliability of the stellar atmosphere models. In both these areas, significant progress has been made in recent years, and because of their importance, they deserve further support. The recent praiseworthy efforts to supply laboratory oscillator strengths (Ruffoni et al. 2014, but see also other works cited later on) cover a number of lines that may meet the needs of the classical spectral analysis (i.e., the line-fitting approach), but these are too few for the needs of a full-spectrum-fitting analysis. On the other hand, the 3D stellar atmosphere modeling (Asplund 2005; Freytag et al. 2012; Magic et al. 2013) show that realistic model atmospheres can reproduce the observed spectra with great accuracy. However, the computational power required today to analyze wide spectral ranges with these tools is prohibitive.
To this lively field that is rich in new ideas, we contribute with a software called SP_Ace (Stellar Parameters And Chemical abundances Estimator) that implements a new method of performing stellar spectral analysis. SP_Ace is based on a method born from the experience of the RAVE chemical pipeline (Boeche et al. 2011) developed to derive elemental abundances from the spectra of the RAVE survey (Steinmetz et al. 2006; Kordopatis et al. 2013). The RAVE chemical pipeline relies on stellar parameters that must be provided by other sources, and it only derives chemical abundances. SP_Ace extends the RAVE chemical pipeline’s foundations and performs an independent, complete spectral analysis. Although SP_Ace employs a full-spectrum-fitting approach, it derives stellar parameters as much as chemical elemental abundances for FGK-type stars. Unlike other codes dedicated to stellar parameter estimation, SP_Ace does not rely on a library of synthetic spectra, or measure the EW of absorption lines, but it makes use of functions that describe how the EW of the lines changes in the parameter and chemical space. In the next section we explain the general concepts on which SP_Ace is based.
2. Method
The usual methods employed to estimate stellar parameters from spectra are i) to directly compare the observed spectrum with the synthetic one to find the best match and ii) to measure the EWs of the absorption lines of the observed spectrum from which the stellar parameters are inferred. In both cases the spectrum must be synthesized, and the stellar parameters of the synthetic spectrum are varied until the spectrum (first case) or the line’s EWs (second case) match the observed ones. Any spectrum synthesis depends on a stellar atmosphere model, that represents the physical conditions in the stellar atmosphere to the best of our knowledge. For this reason stellar parameters and chemical abundances obtained from spectral analysis are indirect measurements, and we say that they are derived (and not measured). Regardless of the method employed, to estimate the stellar parameters from spectra we must construct a spectrum model and compare it to the observed spectrum. SP_Ace makes no exception: it constructs a spectrum model and compares it with the observed spectrum with a simple χ2 analysis. Its peculiarity is the novel way to construct the spectrum model, which is not a direct synthesis. At first glance this method may look cumbersome, but it eventually gives consistent advantages that we describe below.
Consider a stellar spectrum of low to medium spectral resolution2 (R ~ 2000−20 000) with a known instrumental profile. An absorption line can be fit with a Voigt profile of known FWHM and strength (i.e., EW). We start from the naïve idea that a normalized spectrum can be reproduced by subtracting Voigt profiles of appropriate wavelengths, FWHMs, and EWs from a constant function equal to one (representing the normalized continuum). Under the weak line approximation the spectrum so constructed would reproduce the observed spectrum with fair precision3. To construct a full spectrum in this way we need to know the EWs of the lines at the wanted Teff, log g, and abundance [El/H]4 of the generic element “El” the lines belong to. For this purpose we synthesize the lines for a grid of stellar parameters Teff, log g, and chemical abundance [El/H]5, measure the EWs at such points, and store them into a library that we called the EW library. The EW library contains all the information that describes the strength of the lines in the stellar parameter and chemical space. So defined, the EW of an absorption line is a function of the stellar parameters that we call General Curve-Of-Growth (GCOG) to remember that it is the generalization of the well known Curve-Of-Growth (COG) function (which can be obtained from the GCOG by fixing the parameters Teff and log g, and leave the abundance [El/H] as free variable). By using the EW library we can construct spectrum models with stellar parameters and abundances corresponding to grid points of the library. To overcome the discreteness of the grid in the parameter space, we use continuous functions that fit the EWs of the lines in the parameter and chemical space. This can be done with polynomial functions that we call “polynomial GCOGs” and that we store in the “GCOG library”. The advantage of this method is that we just need to vary the parameters Teff, log g, and abundances [El/H] in the polynomial GCOGs to vary the strength of the lines and construct spectrum models for any stellar parameters and abundances until we find the one that matches the observed spectrum best6. This method is implemented in the code that we call SP_Ace.
To achieve this result, three steps are necessary: i) to build a line list of absorption lines that must be as much complete as possible (possibly all the lines visible in stellar spectra); ii) to build an EW library where the EWs of every absorption line are stored as a function of Teff, log g, and [El/H]; and iii) to use the EW library to fit the polynomial GCOGs and store their coefficients in the GCOG library that is employed by the code SP_Ace to construct the spectrum model. These steps are outlined in the next sections.
3. The line list
To build the EW library we need a list of atomic and molecular absorption lines and their physical parameters. These physical parameters are: wavelength, atom or molecule identification, oscillator strength (f, often expressed as logarithm log gf, where g is the statistical weight), excitation potential (χ), van der Waals damping constant C6, and dissociation energy D0 (only for molecules). The atomic line list was taken from the Vienna Atomic Line Database (VALD, Kupka et al. 1999), with the option that selects the lines with expected strengths larger than 1% in at least one of the normalized spectra of the Sun, Arcturus, and Procyon7. Afterwards, the EWs of these lines were re-computed with the code MOOG (Sneden 1973) and only the lines with EW> 1 mÅ in at least one of these stars were included in the line list. The molecular line list was taken from Kurucz (1995) and selected with the same procedure employed for the atomic lines. In the present work the line list covers the wavelength intervals 5212–6860 Å and 8400–8924 Å. We chose the first interval because it is commonly covered by optical spectra, while the second interval (the Ca ii triplet region) becomes particularly important because of Gaia spectral coverage. Extentions of the line list to other wavelength ranges can be done in the future.
3.1. The atomic lines
The wavelengths and excitation potentials were adopted from the VALD database. The oscillator strengths are discussed in Sect. 4. The van der Waals damping constants C6 were taken from the VALD database when such values are available. When VALD does not provide the damping constants, we adopted the Unsöld approximation (computed by MOOG) multiplied by the enhancement factor Eγ following the recipe of Edvardsson et al. (1993) and Chen et al. (2000). For the neutral iron lines Fe i, this recipe assigns Eγ = 1.2 for lines with χ ≤ 2.6 eV and Eγ = 1.4 for χ> 2.6 eV (Simmons & Blackwell 1982), whereas for the ionized Fe ii lines Eγ = 2.5 (Holweger et al. 1990). For K i, Ti i, and V iEγ = 1.5 (Chen et al. 2000), for Na iEγ = 2.1 (Holweger et al. 1971), for Ca iEγ = 1.8 (Oneill & Smith 1980), for Ba iiEγ = 3.0 (Holweger & Mueller 1974). For any other element, Eγ = 2.5 (Maeckle et al. 1975).
Precise damping constants were computed by Barklem et al. (2000) and Barklem & Aspelund-Johansson (2005). Such values are contained in the MOOG data files and, by setting the MOOG keyword “damping = 1” we imposed to use the Barklem values when they are available. There are few cases for which there are no Barklem damping constants and for which the enhancement factor Eγ does not apply. These are:
-
The strong and broad lines of H i. Our synthesis with MOOG under local thermodynamic equilibrium (LTE) assumptions and one dimensional (1D) stellar atmosphere models (see Sect. 4.1 for details) renders a too weak Hα line at the line core, whereas the synthetic Paschen H i lines in the near infrared are too strong at the tip of the line, and too weak in the wings with respect to the observed lines. For all these lines we adopted the Unsöld approximation and calibrate the log gfs by hand to improve the fit. However, the match between synthetic and observed H i lines remains unsatisfactory and the lines at 6562.797 Å, 8467.258 Å, 8502.487 Å, 8598.396 Å, 8665.022 Å, 8750.476 Å, and 8862.787 Å are neglected during the SP_Ace estimation process. The other Paschen H i lines in the interval 8400–8924 Å are so weak in our standard stars that they can be neglected in the Teff and log g range considered.
-
For Si i the damping constants reported in VALD appear always too small. In fact, the Si i lines observed in real spectra are always broader than the lines synthesized with the VALD damping constant. Also the value Eγ = 2.5 suggested by Holweger (1973) appears too small8. After some tests, we adopted Eγ = 4.5 which improves the match of the wings in many (but not all) Si i lines.
-
For the Mg i lines 8712.682 Å, 8717.815 Å, and 8736.016 Å we adopted Eγ = 6.0 in order to match better their broad wings. These lines are multiplets treated as one line (as explained in the following).
The need for the adjustments of the Eγ just reported was recognized during the firsts attempts to calibrate the log gf and applied before the final calibration procedure (described later in Sect. 4.1). In the line list there are multiplets where the lines are so close that they are physically blended. Because lines of multiplets have the same χ, these physically blended multiplets can be described (as a first approximation) as if they were one single line. For multiplets with lines closer than 0.1 Å we adopted one single line with the same χ and wavelength, which is the average of the multiplet’s wavelengths. As log gf we adopt the multiplet’s largest log gf, which is afterwards calibrated by the log gf calibration routine (described in Sect. 4).
3.2. The molecular lines
Molecular lines of several species are present in the considered wavelength ranges. While in hot stars molecules have a very low probability to form and their spectral lines have negligible strengths, in cool stars molecular lines become important. In the range 5212–6860 Å the spectra of cool stars show many absorption features that belong to the species CN, CH, MgH, and TiO. However, the very high number of molecular lines present in the range 5212–6860 Å prevents us from performing a reliable calibration of their log gfs (this is discussed in Sect. 4.7). Therefore, in this work we only treat the CN molecule in the wavelength region 8400–8924 Å where the CN lines are sparse and most of them can be identified one by one. Physical parameters such as wavelengths and excitation potential are taken from Kurucz (1995). The CN molecule dissociation energy D0 = 7.63 eV was taken from Reddy et al. (2003). Oscillator strengths for the CN were taken from Kurucz and afterwards calibrated by the log gf calibration routine (Sect. 4). Molecular multiplets are treated like the atomic multiplets (see Sect. 3.1).
4. The log gf calibration procedure
After the preparation of the line list outlined in Sect. 3 we focus on the accuracy of the gf-values.
Most of the gf-values were derived from theoretical and semi-empirical calculations (e.g., Seaton 1994; Kurucz & Peytremann 1975) which are known to have significant errors (Bigot & Thévenin 2006). Although substantial efforts have been and are currently being made to obtain precise gf-value from laboratory measurements (from Blackwell et al. 1972, 1976, 1979, 1982; to the more recent works by Ruffoni et al. 2013) the number of lines for which laboratory gf-values are available is still small with respect to the number of lines visible in a stellar spectrum. Besides, the lines targeted for gf laboratory measurements are the unblended ones, important for the classical spectral analysis. This leaves the blended lines uncovered by the laboratory measurements. To improve the quality of the numerous (but inaccurate) gf-values provided by the theoretical computations, some authors calibrate the oscillator strengths by setting the gf-values to match the strength of the synthetic line with the corresponding line in the Sun spectrum (among others Gurtovenko & Kostik 1981, 1982; Thévenin 1989, 1990; Borrero et al. 2003), in two stars like the Sun and Arcturus (Kirby et al. 2008; Boeche et al. 2011) or in three stars like the Sun, Procyon and ϵ Eri (Lobel et al. 2011). Recently, Martins et al. (2014) used the spectra of three different stars (the Sun, Arcturus, and Vega) and a statistical technique (the cross-entropy algorithm) to recover the oscillator strengths and broadening parameters that minimize the difference between the observed spectra and the synthetic ones. These works employ the idea that, by using more than one star we can disentangle lines in blends and recover their individual atomic parameters9.
For our line list we decided to calibrate the oscillator strengths of any blended or isolated line on five different stellar spectra. This is necessary because SP_Ace employs a full-spectrum-fitting analysis, and the few lines with reliable oscillator strengths available would not be sufficient. In the following we outline our calibration method. This method compares the strengths of the synthetic lines with two (or more) stellar spectra in order to correct the gf values of isolated and blended lines. The method was first proposed in Boeche et al. (2011) and we report it here.
In the framework of 1D atmosphere models and LTE assumptions, the EW of a line is a function of parameters such as Teff, log g, the abundance [El/H], the excitation potential χ, the gf-value, the damping constant, and the microturbulence ξ. Given the atomic parameters χ and damping constant C6, and assuming that we know with good accuracy the stellar parameters Teff, log g, [El/H], and ξ of the stars employed, the EW of a line can be described as a function of log gf alone 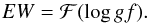 (1)Since we know the stellar parameters of the Sun, by measuring the EW of a line in the Sun spectrum we can determine its gf-value by using Eq. (1). This is the so called “astrophysical calibration” of the gf-values and it only applies to isolated lines.
(1)Since we know the stellar parameters of the Sun, by measuring the EW of a line in the Sun spectrum we can determine its gf-value by using Eq. (1). This is the so called “astrophysical calibration” of the gf-values and it only applies to isolated lines.
Now consider a blend made of two lines l1 and l2. The equivalent width of the whole blend in the solar spectrum can be written as 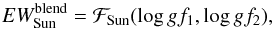 (2)and the equation is underdetermined because the two oscillator strengths are unknown. To make it determined we need to measure the EW of the blend in another star for which we know the stellar parameters and abundances. Then, we can write the equation system
(2)and the equation is underdetermined because the two oscillator strengths are unknown. To make it determined we need to measure the EW of the blend in another star for which we know the stellar parameters and abundances. Then, we can write the equation system 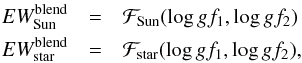 (3)and the system is determined. In the general case of a blend composed of n number of lines, the gf-values can be determined by measuring the EWs of the blends in k number of different well known stars and the equation system
(3)and the system is determined. In the general case of a blend composed of n number of lines, the gf-values can be determined by measuring the EWs of the blends in k number of different well known stars and the equation system 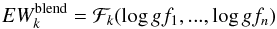 (4)is determined when k ≥ n. Degeneracy can happen when more than one line belongs to the same element and their excitation potentials χ are the same (like in multiplets). In this case the lines behave as one line. If the lines are close in wavelength we can approximate them as if they were one single line (as described in Sect. 3.1). If more than one line belongs to the same element and the χs are not the same, the degeneracy can be broken by choosing stars with different stellar parameters, so that the contribution of the lines to the total EW of the blend is different in different spectra.
(4)is determined when k ≥ n. Degeneracy can happen when more than one line belongs to the same element and their excitation potentials χ are the same (like in multiplets). In this case the lines behave as one line. If the lines are close in wavelength we can approximate them as if they were one single line (as described in Sect. 3.1). If more than one line belongs to the same element and the χs are not the same, the degeneracy can be broken by choosing stars with different stellar parameters, so that the contribution of the lines to the total EW of the blend is different in different spectra.
Ideally, equation system (4) states that for any line or blend, the log gfs can be astrophysically calibrated. In practice, this is not fully true for at least two reasons. First, we can only work with a limited number of stars, which may not be large enough to solve all the possible blends (for instance, when n>k, equation system (4) is underdetermined). Second, uncertainties in the EW measurements, in the continuum correction, or in the atmospheric parameters prevent the equality between the measured and the synthesized EWs (which can be seen as the left- and righthand side of the equation system (4)). In this realistic case (which is the case of this work) we can only minimize the residuals between the left- and the righthand side terms of the equation system. Besides, because the analytical form of the ℱ functions in the equation system are unknown, the solution of the system relies on an iterative process where the EWs of the observed spectra (lefthand terms of the system) are compared with the EWs resulting from the synthesis of the spectra (righthand terms of the system) and the variables log gfs are varied until the residuals are minimized. A further difficulty arises when some of the elemental abundances of the stars employed are unknown. If an element of unknown abundance has isolated lines in the spectra of these stars, then we can derive its abundance after the log gf of these lines have been calibrated on the Sun or on another well known star.
In the following we outline our solution, which makes use of the spectra of the Sun and other four stars.
4.1. Stellar spectra and atmosphere models
To minimize the residuals between the left- and righthand side terms of the equation system (4), we used high resolution and high S/N spectra of five stars. We chose the spectra of the Sun, Arcturus (both from Hinkle et al. 2000), Procyon, ϵ Eri, and ϵ Vir (from Blanco-Cuaresma et al. 2014). These five stars belong to the Gaia FGK benchmark stars proposed as standard stars for calibration purposes (Heiter et al. 2015; Jofré et al. 2014). The Sun and Arcturus spectra were observed with the same instrument (the Coudé feed telescope and spectrograph at Kitt Peak), while the other spectra were observed with three different spectrometers. The spectra of Procyon and ϵ Vir were observed with the NARVAL spectropolarimeter with a spectral resolution of R ~ 81 000 covering the full range of wavelengths between 3000 Å and 11 000 Å. For ϵ Eri, Blanco-Cuaresma et al. only provide spectra taken with the UVES and HARPS spectrometers, which present gaps in the wavelength coverage (at ~5304–5336 Å for HARPS and at ~5770–5840 Å and 8540–8661 Å for UVES). For this reason we employed the HARPS spectrum for the wavelength range 5712–6260 Å and the UVES spectrum everywhere else. Unfortunately, the gap at 8540–8661 Å cannot be covered, because no spectra from other instruments are available in this wavelength range. This means that for this wavelength interval, ϵ Eri does not play any role in the log gf calibration, which is only performed on the spectra of the other four stars. All the spectra were re-sampled to a dispersion of 0.01 Å/pix to match the dispersion of the synthetic spectra. In fact, the calibration routine (described in Sect. 4.2) requires that both must have the same sampling). Hinkle et al. provided the spectra free of telluric lines (they were subtracted from the observed spectra), therefore they cannot affect the strengths of the absorption lines. Conversely, the telluric lines affect the Blanco-Cuaresma spectra and, for the wavelength ranges here considered, they affect mainly the range ~6274–6320 Å. The presence of telluric lines superimposed on an absorption line can affect its log gf calibration. However, we verified that the final effect on the calibrated log gfs is in general weak or negligible because the calibration is performed simultaneously on two spectra free from telluric lines and on other three on which the telluric lines do not lie at the same wavelengths because of the different velocity correction Δv applied (the spectra exibith different radial velocities).
To synthesize the spectra we used the code MOOG (Sneden et al. 1973) and the stellar atmosphere models from the ATLAS9 grid (Castelli & Kurucz 2003) updated to the 2012 version10. For the solar spectrum we assumed an effective temperature Teff = 5777 K, gravity log g = 4.44, metallicity [M/H] = 0.00 dex. For Arcturus we assumed the stellar parameters of Ramírez & Allende Prieto (2011), while for the other stars we adopted the stellar parameters given in Jofré et al. (2014). The microturbulence ξ adopted is inferred during the calibration process as explained in Sect. 4.3. All these stellar parameters are summarized in Table 1. The elemental abundances adopted for the Sun are [El/H] = 0 dex by definition, with solar abundances adopted from Grevesse & Sauval (1998). For Arcturus we adopted the elemental abundances given by Ramírez & Allende Prieto (2011). For elements for which Ramírez & Allende Prieto gave no abundance we impose [El/H] = [M/H] at the beginning of the calibration and leave the possibility to change the abundance during the calibration process. In fact, if the element has an isolated line its log gf can be calibrated on the Sun and its abundance on Arcturus can be therefore derived. Similarly, at the beginning of the calibration process we impose [El/H] = [M/H] for the elements of the other stars and allow possible changes of [El/H] during the process.
Because the instrumental resolution varies with wavelength, and because MOOG adopts one constant FWHM per synthesized interval (used to convolve the synthetic spectrum with the adopted instrumental profile) we synthesized the spectra in four pieces covering the wavelength ranges 5212–5712 Å, 5712–6260 Å, 6260–6860 Å, and 8400–8924 Å. The line profile of the synthetic spectra was broadened with a Gaussian profile (to reproduce the instrumental profile of the spectrograph) and a macroturbulence profile, the best matching values of which were chosen via eye inspection for every wavelength range. While the macroturbulence is constant across these wavelengths, the Gaussian instrumental profile broadens with wavelength. In the last column of Table 1 we report the macroturbulence vmac adopted, while in Table 2 we summarize the best matching Gaussian FWHM chosen for the four wavelength ranges.
Effective temperature (K), gravity, metallicity (dex), micro- and macroturbulence (in km s-1) adopted to synthesize the spectra of the standard stars.
Instrumental FWHMs adopted for the synthetic spectra in the four wavelength ranges.
4.2. The log gf s calibration routine and the abundances correction
The calibration routine consists of two parts: the log gfs calibration and the abundances correction. The first part is semi-automatic, the second part is manual. The procedure begins with the first synthesis of the five spectra by using the code MOOG. At the beginning, we fix the abundances that are known and these remain unchanged through the whole process with few exceptions illustrated later on. For the Sun the abundances are fixed at [El/H] = 0 dex. For Arcturus we fix the abundances of 16 elements as given Ramírez & Allende Prieto (2011). For the other elements we set [El/H] = [M/H]. Assuming the elemental abundances of the other stars to be unknown11, we assumed at the beginning [El/H] = [M/H]. Then the first log gf calibration continues as follows:
-
1.
The 5 spectra are synthesized by using the adopted line list and atmosphere models.
-
2.
The observed spectra are re-normalized with the same routine used for the SP_Ace code (see Sect. 7.4). In this case the interval has a radius of 5 Å and only normalized fluxes larger than 0.98 are considered.
-
3.
With MOOG (driver ewfind) the equivalent widths
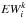 of the lines for the 5 spectra are computed. These are the expected EWs of the lines if they were isolated.
of the lines for the 5 spectra are computed. These are the expected EWs of the lines if they were isolated. -
4.
The isolation degree parameter iso for the ith line and kth star is computed as
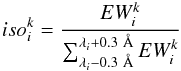 where λi is the central wavelength of the ith line. It approximates the fraction of the flux absorbed by the ith line over the total flux absorbed by any other line present in an interval 0.6 Å wide centered on the ith line.
where λi is the central wavelength of the ith line. It approximates the fraction of the flux absorbed by the ith line over the total flux absorbed by any other line present in an interval 0.6 Å wide centered on the ith line. -
5.
The Normalized Equivalent Width Residual (NEWR) for the ith line and the kth star is computed as follows
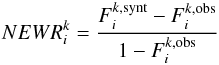 where Fi is the flux integrated over an interval centered on the ith line. The width of the interval is 0.05 Å if the EW< 70 mÅ, 0.10 Å if 70 ≤ EW< 150 mÅ, 0.15 Å if 150 ≤ EW< 200 mÅ, 0.20 Å if 200 ≤ EW< 250 mÅ, and 0.30 Å if EW ≥ 250 mÅ. The NEWR represents the residual between the strengths of the synthetic and the observed line. When the NEWR is negative this means that the synthetic line is stronger than the observed one (and vice versa).
where Fi is the flux integrated over an interval centered on the ith line. The width of the interval is 0.05 Å if the EW< 70 mÅ, 0.10 Å if 70 ≤ EW< 150 mÅ, 0.15 Å if 150 ≤ EW< 200 mÅ, 0.20 Å if 200 ≤ EW< 250 mÅ, and 0.30 Å if EW ≥ 250 mÅ. The NEWR represents the residual between the strengths of the synthetic and the observed line. When the NEWR is negative this means that the synthetic line is stronger than the observed one (and vice versa). -
6.
The log gf calibration of the ith line is performed by adding the quantity
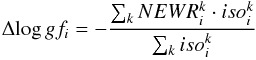 to the log gfi. If the line belongs to an atom the weighted sum considers all the five spectra, otherwise (i.e., if it belongs to a molecule) the spectrum of Procyon is neglected (because no molecular line is visible on its spectrum). If Δlog gfi> 0.05, we confine it to this value to avoid divergences. If Δlog gfi< 0.01 then we set it to zero. If log gfi< −9.99 or log gfi> 3.0 the line is removed from the line list.
to the log gfi. If the line belongs to an atom the weighted sum considers all the five spectra, otherwise (i.e., if it belongs to a molecule) the spectrum of Procyon is neglected (because no molecular line is visible on its spectrum). If Δlog gfi> 0.05, we confine it to this value to avoid divergences. If Δlog gfi< 0.01 then we set it to zero. If log gfi< −9.99 or log gfi> 3.0 the line is removed from the line list. -
7.
The EWs of the lines are computed with the driver ewfind of MOOG. The lines with EW ≤ 3 mÅ in all of the five spectra are removed from the line list.
-
8.
The routine is repeated from step 1.
This routine is always followed with three exceptions: i) for very strong lines (some tens of lines) the chosen interval (step 5 of the routine) is larger than 0.05 Å to match the full line instead of the core alone; the interval was chosen after eye inspection; ii) many intense lines on the star ϵ Eri have particularly wide wings, which cannot be well synthesized; therefore, for these lines the calibration Δlog gf was computed by neglecting the ϵ Eri spectrum; iii) for strong lines like the H i lines, the Na i doublet at 5889 and 5895 Å, the Ca ii triplet in the infrared region, and few other Fe i intense lines the log gfs were set by hand after eye inspection.
 |
Fig. 1 Distributions of the NEWRs of the elements Fe (gray points) and Ti (black points) as a function of their EW for the five stars before the beginning of the calibration routine. |
 |
Fig. 3 As in Fig. 1 but at the final stage, after many iterations of the calibration routine and properly adjusted abundances. |
At the beginning of the calibration routine the NEWRs are distributed as shown in Fig. 1 (in this and in the two following figures we only show the NEWRs of the elements Fe and Ti for the sake of clarity). After 100 iterations the NEWR distributions emerge as in Fig. 2. Note that the dispersion of the points has decreased and that the Fe lines (gray points) in Procyon, and the Ti lines (black points) in ϵ Vir have an offset. The offsets are due to the assumption of the wrong Fe and Ti abundances for these stars at the beginning of the procedure. To continue with the log gfs calibration we must apply the second part of the calibration process, i.e., the abundance correction, which is done manually. The negative offset of the Ti lines in ϵ Vir indicates that the Ti lines are too strong, therefore, to match the observed spectrum, the Ti abundance must be decreased. Similarly, when the offset is positive, the abundance must be increased. These evaluations and the consequent changes in abundance are done by observing the distribution of the NEWR for lines for which the isolation degree parameter iso is larger than 0.99 (which implies the selection of isolated lines alone) in order to guess the right abundances from isolated lines. If no isolated lines are present, the abundances remain [El/H] = [M/H]. The abundance correction is performed after the log gfs calibration and both are carried out many times until no more lines are rejected by the calibration routine and the NEWR distributions are centered on zero.
We want to spend a few more words on the abundance correction. The optimal condition for the log gfs calibration would be to have precise elemental abundances for all the stars employed (as required by Eq. (4)) so that the abundance correction would not be necessary. Because at the time of this work precise abundances of these stars were not available, in order fulfill the condition in Eq. (4) as much as possible, we adopt the known abundances, i.e., the Sun and the Arcturus abundances. For the other stars (or elements) for which we do not have chemical abundances, we adopted [El/H] = [M/H] and then followed the method described before (i.e., observing the distribution of the NEWRs of the isolated lines of an element and change its abundance to minimize the average of the absolute NEWR values) whenever the adopted initial abundance was not satisfactory for this element. In the case of the element Co on Arcturus, we decided to follow this method and we adjusted its abundance to [Co/H] = −0.23 dex because by using the value [Co/H] = −0.43 dex derived by Ramírez & Allende Prieto it was not possible to minimize the absolute average NEWR values for all the stars.
We want to stress that the solar abundances were never changed during the whole process. The Sun is synthesized with the Grevesse & Sauval (1998) solar abundances and these abundances must not be changed because this is the reference point on which the whole calibration procedure is based. Without this reference point no calibration is possible, otherwise the equation system (4) would become underdetermined.
 |
Fig. 4 Gray thick lines: observed spectra. Dotted lines: synthesized spectra with VALD log gfs but final abundances. Black lines: synthetic spectra with calibrated log gfs and final abundances. |
4.3. Setting the microturbulence
At the beginning of this work we tested several times the calibration routine in order to find the best way to follow. In some of these tests we adopted the microturbulence values reported in Jofré et al. (2014), which are 1.2, 1.3, 1.8, 1.1, and 1.1 km s-1 for the Sun, Arcturus, Procyon, ϵ Eri, and ϵ Vir, respectively. With these values we could not find satisfactory results, which means that the NEWRs of the isolated Fe lines did not align close to the NEWR = 0 line for some of the stars, no matter what Fe abundance was adopted. Therefore, we decided to change the ξ values interactively during the calibration process to minimize the absolute NEWRs values. The NEWRs values are sensitive to microturbulence and in Fig. 5 we show the difference in the NEWRs distributions observed by changing the microturbulence by 0.4 km s-1 (while all other parameters are fixed) for the Sun and Arcturus, with the best performing ξ value in the lefthand panels. Our final best ξ values are reported in Table 1.
4.4. The final line list
The whole calibration procedure described in the previous section is performed by applying alternatively the log gf routine and the abundance correction iteratively until convergence of the abundances and until no more lines are removed by the log gf routine. The process began with a line list of 8947 lines. After the convergence, the final line list counts 4643 lines. The NEWRs distribution of the final line list is shown in Fig. 3, while in Table 3 we report the abundances derived with the abundance correction procedure for the elements that we consider reliable (see Sect. 4.6 for further explanations). The final line list with the calibrated log gfs is released together with the GCOG library.
At the end of the calibration procedure we verified by eye inspection the good match between the synthetic and observed spectra over the whole wavelength range considered. In some cases there are unidentified absorption lines for which none of the lines given in the VALD database seems to match. These lines are neglected during the analysis performed by SP_Ace. We removed by hand some lines of the line list because were clearly erroneous (but not removed by the calibration routine because they lie under incorrectly fitted lines, like under the Ca triplet lines, for instance) or because their log gfs were badly affected by unidentified lines. In Fig. 4 we compare part of the synthetic and the observed spectra before and after the log gfs calibration. For this figure the synthesis was performed using the final abundances reported in Table 3, so that the differences between the spectra synthesized with the VALD log gfs and the calibrated log gfs are only due to the difference in log gfs. Figure 4 shows that the spectra synthesized with the new calibrated log gfs match the observed spectra better than the ones synthesized with the VALD log gfs.
 |
Fig. 5 NEWR distributions for the Fe lines in Arcturus (top panels) and the Sun (bottom panels) using microturbulences ξ that differ by 0.4 km s-1. Here we use Fe lines with isolation degree parameter iso> 0.99 (i.e., these Fe lines are isolated). |
4.5. Validation of the calibrated log gfs
In Fig. 6 (left panel) we compare the original log gfs of the VALD database with our final calibrated log gfs for those lines that have EW> 5 mÅ in the solar spectrum. The residuals have an average offset of ~+0.01 with a dispersion of ~0.29 (statistic computed excluding strong lines for which log gf was calibrated by hand and after rejection of outliers with a 3σ clipping). Because VALD is a database that collects data from several sources with different degrees of precision, we want to verify the robustness of our calibrated log gfs comparing them with precise values. For this purpose, we accessed the NIST database (Kramida et al. 2013) and select lines that have a gf precision better than 10% (~0.04 in log gf) and EW> 5 mÅ on the solar spectrum. With these criteria we found 328 lines in common with our line list. After removing the lines with EW< 5.0 mÅ (for which we expect the largest calibrated log gf errors) we are left with 223 lines belonging to the elemental species C i, N i, O i, Na i, Mg i, Si ii, Sc i, Sc ii, Ti i, V i, Cr i, Mn i, Fe i, and Co i. The comparison between the NIST and the calibrated log gfs is shown in right panel of Fig. 6. The comparison with high precision log gfs shows that our calibrated log gfs have an offset of ~–0.12 dex with a dispersion of ~0.1 dex. The negative offsets say that our log gfs are more negative than the corresponding NIST log gfs. This can be due to several causes, which may be i) an inappropriate line profile of the synthetic spectra (the line profiles can vary for lines with different strengths and lines broadening parameters); ii) an inappropriate continuum normalization of the observed spectra; iii) neglected Non Local Thermodynamic Equilibrium (NLTE) and 3D effects; iv) errors in the stellar parameters adopted to synthesize the spectra. As a last remark, one may regard at the solar abundances adopted (Grevesse & Sauval 1998) as the cause of the offset of our calibrated log gfs. If these abundances (and in particular the Fe abundance, which has the higher number of lines represented in Fig. 6) were too high, the calibration would render log gfs lower than expected. Some works, based on laboratory log gfs, derived a solar iron abundance12 of log [ϵ(Fe)] = 7.44 (Ruffoni et al. 2014; Bergemann et al. 2012). Since we adopted log [ϵ(Fe)] = 7.50, this would explain part of the offset observed for our log gfs.
 |
Fig. 6 Right: comparison between the VALD and our calibrated log gfs. Black and gray points represent atomic and molecular CN lines, respectively. Left: comparison between the NIST and our log gfs values for those lines with NIST log gf precision better than 10%. Only lines having EW> 5 mÅ in the solar spectrum are reported here. The offsets and standard deviations are computed as “calibrated minus reference” after rejecting the outliers (crossed points) with a 3σ clipping. |
4.6. On the accuracy of the calibrated log gfs
Although we verified by eye the good match between the spectra synthesized with our final line list and the observed spectra, this does not ensure the good accuracy of the astrophysically calibrated log gfs for all the lines of the line list. In fact, the spectra exhibit many blended features composed of many lines that cannot be fully resolved, because for such blends the equation system (4) is underdetermined. On the other hand, weak lines (EW ≲ 10 mÅ) are the ones more affected by imprecision of the continuum placement or by blends. A difference in 0.5% of the normalized flux between the synthetic and the observed spectra can look like a “good match” to an eye inspection, but it leads to a very poor accuracy of the log gf of a line having an EW of a few mÅ. Another source of uncertainty comes from the abundance correction procedure when the lines of one element are all weak in the Sun’ s spectrum. With the Sun as reference point, when the lines are weak the match with the synthetic spectrum is subject to the uncertainties discussed above, so that the reference point becomes uncertain. For this reason, the derived elemental abundances output by the code SP_Ace (in its present version), are for those species for which the number and strength of lines are big enough for a good abundance estimation of the five stars during the abundance correction process outlined in Sect. 4.2. These elemental abundances are the ones reported Table 3. The abundances of other elements are also internally derived by SP_Ace but are used as “dummy” elements and rejected at the end of the analysis.
There are further reasons why the calibrated log gfs of some lines may be not physically meaningful. We employed stellar atmosphere models that are one-dimensional and the physical processes are assumed to take place in Local Thermodynamic Equilibrium (LTE). This is an approximation that, in some cases, is too rough to describe real stellar atmospheres. Some absorption lines suffer of non-LTE effects, which can affect the observed EW. Therefore, if we perform an astrophysical calibration of the log gfs of one of these lines under LTE assumptions, the calibrated log gf value can be significantly different from the real value (which expresses the probability of the electronic transition) and the difference accounts for the neglected non-LTE effect. This is not the right way to correct for non-LTE effects and it may lead to systematic errors when stellar parameters and the chemical abundances are derived.
During the log gfs calibration and abundance correction procedure, we identified several strong lines that cannot be correctly synthesized in our five standard stars. The profiles of these synthetic lines have too strong (or too weak) wings with respect to the observed lines in the spectra of the standard stars. Some of these lines are reported in Table 4 with a qualitative goodness of fit of the wings (and strength) between the synthetic and observed lines. For some lines (such as most of the H i lines and the Na i doublet at ~5890) we changed the log gfs (and also the damping constants for the Paschen H i lines) by hand in order to match the strength of these lines in the solar spectrum. However, the match is often not satisfactory. Most of the Mn i lines show a line width too narrow in synthetic spectra with respect to the observed ones, and in the Sun synthetic spectrum these lines are too strong at the core, although their EWs seem to be close to the observed ones. The Mn i abundance is therefore rejected from the SP_Ace results. All these discrepancies can be due to non-LTE effects, 3D effects, and hyperfine splitting of the lines that we do not take into account in the present work.
Qualitative match of the wings of some intense lines between the synthetic and the observed ones.
Because these “poorly matching” lines can negatively affect the stellar parameter estimations, they are rejected from the analysis performed by SP_Ace.
However, the fact that the spectra synthesized with our line list with calibrated log gfs match reasonably well13 the great majority of the spectral range of our standard stars (which span a wide range in temperature and gravity) and that most of the abundances derived during the abundance correction process are close to the ones reported in high-resolution studies (see Table 3), suggests that our line list under LTE assumption can be employed to derive reliable stellar parameters and chemical abundances in the Teff and log g ranges covered by the five calibration stars adopted in this work.
 |
Fig. 7 Normalized spectra of the Sun (black line) and 61CygA (gray line). The “plus” symbols indicate the positions of the atomic lines. |
4.7. The molecular lines
In the previous sections we discussed mainly the atomic lines, although molecular lines of several species are present in the wavelength ranges considered. During the preparation of this work we did several tests to verify whether a log gfs calibration of atomic and molecular lines together was possible. We found that i) the calibration is not always possible; and ii) when it is possible, the calibrated log gfs are physically meaningless and can be only used as dummy values. The first point applies to the wavelength range 5212–6860 Å where the very high number of molecular lines of the species CN, CH, MgH, and TiO generate a forest of weak lines in cool star spectra that makes the identification of the lines impossible and the equation system (4) becomes underdetermined. In Fig. 7 we compare the spectrum of the Sun (normalized by Hinkle et al. 2000, Teff = 5777 K, log g = 4.44, [M/H] = 0.0 dex) and 61CygA (normalized by Blanco-Cuaresma et al. 2014, Teff = 4374 K, log g = 4.63, [M/H] = −0.33 dex). The forest of weak molecular lines in 61CygA is so dense that it creates a “pseudo-continuum” that hides the real continuum and prevents the correct estimation of the EWs of the atomic lines. This convinced us that, at present, our method cannot calibrate log gfs of molecular lines in the interval 5212–6860 Å. Besides, to calibrate log gfs of atomic lines we need spectra “free” of molecular lines. Therefore we verified that the standard stars employed for the log gf calibration are not significantly affected by molecular lines. We verified that this is true for dwarf stars having Teff≳ 5000 K and for a giant star like Arcturus.
In the interval 8400–8924 Å the second answer above applies: here we can identify the CN lines and calibrate their log gfs, but we strongly doubt the accuracy of the calibration. When the original log gf by Kurucz are applied, the synthetic CN lines of Arcturus are far too strong with respect to the observed ones. Molecular lines are known to be prone to NLTE effects (Hinkle & Lambert 1975; Schweitzer et al. 2003; Plez 2008) and 3D effects (Ivanauskas et al. 2010), and their strengths may not be correctly reproduced under 1D LTE assumption. In order to match the strenghts of the CN lines observed on the Sun and on Arcturus at the same time we needed to set the Arcturus C and N abundances to [C/H] = [N/H] = −0.34 dex, which lie between the atomic abundances by Ramírez & Allende Prieto (2011) who found [C/H] = −0.09 dex and [N/H] = −0.42 dex and the ones of Smith et al. (2013) who found [C/H] = −0.56 dex and [N/H] = −0.28 dex.
We believe that Arcturus’ low C and N abundances found by us merely counterbalance the 3D NLTE effects that we could not take in account. Thus, the CN lines in the wavelength interval 8400–8924 Å are employed by SP_Ace as “dummy” lines and the results are rejected after the estimation process.
5. The Equivalent Widths (EW) library
We built the EW library using the driver ewfind of the code MOOG, which computes the expected EW of the absorption lines for a given stellar atmosphere model. We employed the atmosphere models grid ATLAS9 by Castelli & Kurucz (2003) updated to the 2012 version. The Castelli & Kurucz grid has steps in stellar parameters (500 K in Teff, 0.5 in log g, and 0.5 in [M/H]) that are too wide for our needs. We linearly interpolated the models to obtain a finer grid with steps of 200 K in Teff, 0.4 in log g, and 0.2 dex in [M/H] and covering the ranges 3600–7400 K in Teff, 0.2 to 5.4 in log g14, and −2.4 to + 0.4 dex in [M/H]. In the following we always refers to this grid. The microturbulence ξ assigned to each atmosphere model is computed as a function of Teff and log g. This function is described in Appendix A.
Note that in Sect. 2 we defined the GCOG as a function of the three variables Teff, log g, and [El/H] (and not [M/H]). However, to construct the EW library we need the metallicity [M/H] of the atmosphere model. In fact, besides the Teff, log g, and the abundance [El/H], the EW of a line also depends on the opacity of the stellar atmosphere in which the line forms, which is driven by atmospheric metallicity [M/H]. This means that to compute the GCOG of a line we must also define the metallicity of the atmosphere model, making (in this specific case) the GCOG a function of four variables. Therefore, we define the stellar parameter grid in the three dimensions Teff, log g, and [M/H] plus a fourth dimension that accounts for the relative abundance [El/M]. To construct the EW library, for every point of the grid and every line of our line list we computed the EW of the lines at 6 different abundance enhancements with respect to the nominal metallicity of the atmosphere model, that means (for the generic element El) [El/M] = −0.4, −0.2, 0.0, + 0.2, + 0.4, and + 0.6. These 6 points belong to the COG of the lines for every grid point. The EW library so constructed contains the EWs of the lines synthesized as they were isolated. Because SP_Ace constructs the spectrum model by summing up the absorption lines with given EWs, the spectrum model is realistic if the lines are isolated or, in case of blends, if the EWs of the involved lines are small (i.e., weak line approximation). Because these conditions are not always satisfied in a real spectrum, in the following we discuss how to remove the weak line approximation.
5.1. The weak line approximation problem
Consider the case of two or more lines that are instrumentally blended but physically isolated in a spectrum. We can write 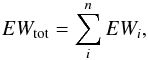 (5)where EWtot is the total EW of the blended feature, EWi are the EWs of the lines computed as isolated, and n the number of lines considered.
(5)where EWtot is the total EW of the blended feature, EWi are the EWs of the lines computed as isolated, and n the number of lines considered.
Consider now the same lines as before, but now they are physically blended. If the lines have small EWs, then Eq. (5) is still (approximately) valid because their line opacity is small and does not affect the local opacity significantly. This is what we call weak line approximation. Under these conditions we can use the EWi of the lines contained in the EW library and, assuming a line profile, subtract the lines from a normalized continuum to obtain a spectrum model which approximates the synthetic spectrum well. Unfortunately, the weak line approximation can rarely be applied because strong and broad absorption lines are common in real spectra. In case of strong lines, Eq. (5) is not true anymore, because the opacities of the lines diminish reciprocally the flux absorbed by them, and Eq. (5) becomes the inequality 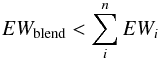 (6)where EWblend indicates the total equivalent width of the blend and EWi is as in Eq. (5). In this case, by summing up the EWi of the lines contained in the EW library would render a spectrum model where the blends are too strong with respect to the synthetic ones. This is shown in Fig. 8 where a blended feature constructed using Eq. (5) (dotted line) with EWs from the EW library turns out to be much stronger than the EWblend of the feature synthesized by MOOG (black line).
(6)where EWblend indicates the total equivalent width of the blend and EWi is as in Eq. (5). In this case, by summing up the EWi of the lines contained in the EW library would render a spectrum model where the blends are too strong with respect to the synthetic ones. This is shown in Fig. 8 where a blended feature constructed using Eq. (5) (dotted line) with EWs from the EW library turns out to be much stronger than the EWblend of the feature synthesized by MOOG (black line).
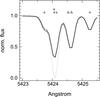 |
Fig. 8 Comparison between the synthetic spectrum with stellar parameters Teff = 4200 K, log g = 1.4, and [M/H] = 0.0 dex (the black solid line) and the corrispondent spectrum model (the gray solid line) constructed by SP_Ace using the EWs corrected for the opacity of the neighbor lines as described in Sect. 5.3. The dotted line is the spectrum model constructed using the EW of the lines computed as if they were isolated (i.e., no correction for the opacity of the neighbor lines). Plus, cross, and triangle symbols indicate the position of the Fe , V , and Ni lines, respectively. |
To correctly reproduce the blend, the EWi of the EW library must be corrected for the opacity of the neighboring lines, so that the EWs employed to construct the spectrum model are smaller than the corresponding isolated lines. These corrected quantities that we call “equivalent widths corrected for the opacity of the neigbouring lines” (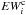 ) are smaller than EWi and satisfy the equation
) are smaller than EWi and satisfy the equation 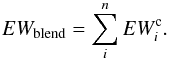 (7)The quantity
(7)The quantity 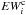 cannot be computed with MOOG. In fact, to know the quantity EWc we need to compute the fraction of the contribution function due to each absorber present in the stellar atmosphere (continuum, atoms, molecule) that form the blend. These fractions of the contribution function are not usually computed by spectral synthesis codes. This information is lost when the spectral synthesis code computes the total opacity κλ at wavelength λ by summing up the opacities of all the absorbers to obtain the optical depth τλ. The way to compute the fraction of the contribution function is discussed in Sect. 5.2 and, although a rigorous solution was found it cannot be used to correct the EWs of the library. An approximate solution must be adopted and this is outlined in Sect. 5.3.
cannot be computed with MOOG. In fact, to know the quantity EWc we need to compute the fraction of the contribution function due to each absorber present in the stellar atmosphere (continuum, atoms, molecule) that form the blend. These fractions of the contribution function are not usually computed by spectral synthesis codes. This information is lost when the spectral synthesis code computes the total opacity κλ at wavelength λ by summing up the opacities of all the absorbers to obtain the optical depth τλ. The way to compute the fraction of the contribution function is discussed in Sect. 5.2 and, although a rigorous solution was found it cannot be used to correct the EWs of the library. An approximate solution must be adopted and this is outlined in Sect. 5.3.
 |
Fig. 9 Emerging (synthetic) fluxes obtained when opacities of the continuum and the line are accounted separately. The gray solid line is the synthetic spectrum of the line Fe i at 8446.388 Å, i.e. the emerging flux when the line and continuum opacities are accounted for. The black solid line represents the emerging flux when the emissions alone are accounted for. The dotted line is the level of the continuum when the continuum opacity alone is accounted for. The dashed line is the level of the continuum across the line when both line and continuum opacities are accounted for. The y-axis is expressed as logarithm (base 10) of the normalized flux. |
5.2. Separating the contributions of each absorber
In the attempt to obtain the quantity EWc, we tackled and solved the problem to compute the fractions of the contribution function due to each absorber individually. Unfortunately, the result turned out to be inapplicable for our purpose: we can compute the flux absorbed by each absorber but this cannot be written in terms of EW. To explain this apparent paradox, we here outline the general result and point the reader to Appendix B for the full detailed solution. Although the problem concerns blends, the simple case of one isolated line is also illustrative for multiple absorbers like in blends. In fact, in the case of one line the opacity is due to two absorbers: the continuum and the line. In Fig. 9 we show an absorption line (gray solid line) and the continuum in absence of the absorption line (dotted line). The EW of this line, as commonly defined, is represented by the area between the gray and the dotted line. In this way, the EW does not represent the total flux absorbed by the line, because the continuum (dotted line) has been computed in absence of the line, i.e. the opacity of the line has been neglected. When the line opacity is taken in account, the continuum level is higher (the dashed line of Fig. 9) because it absorbs less radiation. In fact, when the line is present, its opacity diminishes the intensity of the radiation and the continuum absorber is left with less radiation to absorb. Therefore, the real flux absorbed by the line is represented by the area included between the gray and the dashed lines of Fig. 9, which is much bigger than the EW as usually defined. This proves that, although we can precisely determine the real quantity of flux absorbed by a line (in a synthetic spectrum), we still miss the solution of our problem. In fact, to reconstruct a spectrum model by summing up the absorbed fluxes we need to consider the continuum level at any wavelength. At the stage of development of our work, the variation of the continuum level as function of the strength of the lines looks too complicated to be implemented. Therefore we must follow another method to approximate the EWc quantities and apply Eq. (7) to construct the spectrum models.
5.3. Approximated correction for the opacity of the neighbor lines
The method to approximate the quantity EWc is based on the idea that when the first derivative of the COG (expressed as EW as function of abundance) inside a blend is small this means that its contribution to the absorbed flux (i.e., the EW) is small too, similarly to what happens to the isolated line. The method, outlined in the following example, makes use of EWs of synthesized isolated lines and blended features. The EWs of isolated lines are computed with the MOOG driver ewfind which numerically intergrates the depression of the synthetic line with respect to the continuum. Because this driver does not handle more than one line per time, to compute the EW of blends we need to synthesize the blend and numerically integrate the depression15.
Consider one line in a blend composed of two (or more) lines indexed with i. The lines belong to different elements Eli. By using MOOG we compute the equivalent widths EWs of the lines as isolated for 6 different abundances [Eli/M] = −0.4, −0.2, 0.0, +0.2, +0.4, +0.6 dex so that we have six points of the COG of the line (we call it COG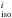 ). Similarly, for every line we synthesize the whole blend and we measure the total equivalent width of the blend
). Similarly, for every line we synthesize the whole blend and we measure the total equivalent width of the blend 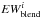 . This is done by synthesizing the blend in which all the lines have constant [Eli/M] = 0.0 but for the ith line which assumes six different abundances [Eli/M]. The six EWs of the blend so obtained represent the COG of the ith line in the blend (we call them COG
. This is done by synthesizing the blend in which all the lines have constant [Eli/M] = 0.0 but for the ith line which assumes six different abundances [Eli/M]. The six EWs of the blend so obtained represent the COG of the ith line in the blend (we call them COG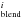 ). If the opacity of one line is not affected by the other line, then COG
). If the opacity of one line is not affected by the other line, then COG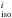 = COG
= COG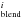 , otherwise COG
, otherwise COG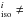 COG
COG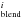 . In particular, if the first derivative of COG
. In particular, if the first derivative of COG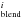 is smaller than the one of COG
is smaller than the one of COG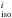 , it means that the contribution of the ith line to the absorbed flux of the blend (this is the EWc quantity we look for) is smaller than the one absorbed when the ith line is isolated. Thus, the quantity COG
, it means that the contribution of the ith line to the absorbed flux of the blend (this is the EWc quantity we look for) is smaller than the one absorbed when the ith line is isolated. Thus, the quantity COG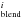 can be used to approximate EWc as follows:
can be used to approximate EWc as follows:
-
1.
Compute the first derivatives of the curves-of-growth
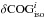 and
and
 .
. - 2.
-
3.
Under the assumption that the ratio of
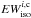 between the lines is conserved in the blend, the contribution to the absorbed flux
of the ith line in the blend is approximated as
between the lines is conserved in the blend, the contribution to the absorbed flux
of the ith line in the blend is approximated as
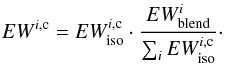
In the general case of a blend of n lines and m elements with m<n, there are two or more lines that belong to the same element El. In this case, the strengths of the El lines would change together when we change the abundance [El/M] during the synthesis of the blend, and this must be avoided in order to evaluate the COG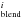 of the target line. This problem is solved by changing the log gf (and not the abundance) of the line, so that the target line is the only line the strength of which changes in the blend.
of the target line. This problem is solved by changing the log gf (and not the abundance) of the line, so that the target line is the only line the strength of which changes in the blend.
The corrected values EWi,c are computed for all the EWs contained in the EW library considering any line closer than Δλ = 0.5 Å to the target line. Figure 8 shows the improvement obtained for a blend when the corrected values EWcs are used to construct the spectrum model (gray solid line) with respect to the model constructed with EWs (dotted line).
The limit of 0.5 Å is satisfactory for most of the lines. For a few intense and broad lines (for instance, the Ti ii at 5226.538 Å), which can affect lines farther than 0.5 Å, a larger limit would be necessary. At this stage of development, SP_Ace neglects these lines during the analysis.
6. The General Curve-Of-Growth (GCOG) library
The COG of a line is a function that gives the EW of a line as a function of the abundance of the element the line belongs to. This function can be recovered from the EW library where, for each absorption line, we stored six points of the COG between the [El/M] values −0.4 and + 0.6 dex in steps of 0.2 dex. The EW library also contains the EWs that the lines assume over a grid spanning a wide range in the stellar parameters Teff, log g, and [M/H]. Because the EW of a line changes not only as a function of the abundance but also as a function of Teff and log g, we extend the concept of COG. We call General Curve-of-Growth (GCOG) the function that describes the EW of a line as function of the variables Teff, log g, and [El/H], where [El/H] represents the abundance of the generic element El the line belongs to (see Fig. 10). Unfortunately the GCOG has no analytical form, therefore, to obtain the EW of a line we must approximate the GCOG with a polynomial function in the parameter space. In principle the GCOG has a three dimensional domain (Teff, log g, [El/H]). As already reported in Sect. 5, because we rely on a grid of stellar atmosphere models the opacity of which depends on [M/H], we must construct the polynomials in a four-dimensional space (Teff, log g, [M/H], [El/M]). We refer to these functions as “polynomial GCOGs”, and they are constructed to approximate the GCOG of the lines. Thanks to the polynomial GCOGs, SP_Ace can compute the expected EW of any line at any point of the parameter space (Teff, log g, [M/H], [El/H]) removing in this way the discontinuity of the grid in the EW library.
 |
Fig. 10 Two dimensional section of the General COG of the Fe i line at 5445.042 Å as a function of Teff and log g. The [M/H] and Fe abundance has been fixed at 0.0 dex. |
 |
Fig. 11 One dimensional sections of the GCOGs of several absorption lines in the range 5212–5222 Å as a function of Teff, log g, [M/H], and abundance [El/M]. The three (out of four) fixed stellar parameters are reported in the panels. The gray points connected with gray lines represent the EWi,cs of the lines. The black lines are one dimensional sections of the polynomials GCOGs of the same absorption lines. |
6.1. The polynomial GCOGs
We fit a polynomial GCOG for every absorption line in the parameter space. Because of the difficulties in fitting a function over points covering the whole parameter space, the polynomial GCOGs fit the EWs that the line assumes over a limited stellar parameter interval surrounding the points of the grid. The width of this interval is 800 K in Teff, 1.6 in log g, 0.8 dex in [M/H], and 1.0 dex in [El/M], which includes five grid points for the first three dimensions and six for the last dimension. For instance, for the grid point Teff = 4200 K, log g = 1.4, and [M/H] = 0.0 the polynomial GCOG fits the EWs that the line has at Teff = 3800, 4000, 4200, 4400, and 4600 K, log g = 0.6, 1.0, 1.4, 1.8, and 2.2, [M/H] = −0.4, −0.2, 0.0, + 0.2, and + 0.4 dex, and the six abundance points [El/M] = −0.4, −0.2, 0.0, + 0.2, + 0.4, and + 0.6 dex (Fig. 11). In total, every polynomial GCOG fits 750 EWs. The polynomial GCOG function has the form 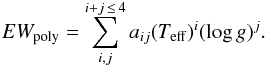 (8)So defined, the polynomial GCOG has 70 coefficients aij that are computed by using a minimization routine that minimizes the χ2 between the polynomial and the given EWs. The residuals between the EWpoly (given by the polynomial GCOG) and the EWs of the library are shown in Fig. 12. The residuals are on average 2.6% of the expected EW, which is equivalent to an error of ~0.01 dex in chemical abundance. Figure 11 shows the polynomial GCOG of 50 absorption lines compared with the expected EW plotted as a function of Teff, log g, [M/H], and abundance [El/M].
(8)So defined, the polynomial GCOG has 70 coefficients aij that are computed by using a minimization routine that minimizes the χ2 between the polynomial and the given EWs. The residuals between the EWpoly (given by the polynomial GCOG) and the EWs of the library are shown in Fig. 12. The residuals are on average 2.6% of the expected EW, which is equivalent to an error of ~0.01 dex in chemical abundance. Figure 11 shows the polynomial GCOG of 50 absorption lines compared with the expected EW plotted as a function of Teff, log g, [M/H], and abundance [El/M].
7. The SP_Ace code
In the following we outline the main structure of the code. This is not intended to be a user manual. A detailed tutorial on how to use SP_Ace and the full description of the available functionalities of the code is provided together with the code.
The SP_Ace code is written in FORTRAN95. It processes one spectrum per run. The observed spectrum must be wavelength calibrated, continuum normalized and radial velocity corrected. When launched, SP_Ace reads the parameter file that must include the name of the spectrum to process, the address of the GCOG library, a first guess of the FWHM, and other optional settings. In the following we outline the algorithm that summarized the SP_Ace analysis procedure specifying the most important routines that we explain later. This algorithm carries out the following steps:
-
1.
Upload the observed spectrum.
-
2.
Make a first rough estimation of the stellar parameters Teff, log g, and [M/H]. (This is performed by the “starting point routine”.)
-
3.
Find the closest grid point to the estimated Teff, log g, and [M/H] and upload the corresponding polynomial GCOG.
-
4.
Derive Teff, log g, and [M/H]. (This is performed by the TGM routine.)
-
5.
Find the closest grid point to the derived Teff, log g, and [M/H]. If it is different from the previous grid point, then upload the polynomial GCOG of the new grid point and go to step 4, otherwise continue.
-
6.
Re-normalize the observed spectrum. (This is performed by the re-normalization routine.)
-
7.
Derive Teff, log g, [M/H] from the re-normalized spectrum. (This is performed by the TGM routine.)
-
8.
Find the closest grid point to the estimated Teff, log g, and [M/H]. If it is different from the previous grid point, then upload the polynomial GCOG of the new grid point and go to step 6, otherwise continue.
-
9.
Derive the chemical abundances [El/M]. (This is performed by the ABD routine.)
-
10.
Go to step 6 and repeat until convergence.
-
11.
Derive the confidence limits for Teff, log g, [M/H], and [El/M] (optional).
-
12.
End the process and write out the results.
Every step is composed of routines and sub-routines. The most important ones are described in the following.
These algorithm can be executed with or without step 10. This is controlled by the keyword ABD_loop (abundance loop) that can be used by SP_Ace. When ABD_loop is switched on, step 10 is executed, otherwise it is skipped. The two settings show significant differences when run on real and synthetic spectra. This is discussed in Sect. 8.
 |
Fig. 12 Grey points: residuals between the EW given by the polynomial GCOG and the EW of the library as a function of EW for 100 absorption lines (in the range 5212–5235 Å) at the grid point Teff = 4200 K, log g = 1.4 and [M/H] = 0.0 dex. Black points: as before but for the line Fe i at 5231.395 Å alone. The residuals are normalized for the EW so that the values in the y-axis and the statistic in the panel express the errors of the polynomial GCOG normalized to the expected EW. |
7.1. The “make model” routine
To derive the stellar parameters and the chemical abundances, SP_Ace constructs several spectrum models and compares them to the observed spectrum, looking for the model that renders the minimum χ2. The routine that constructs the model (called the “make model” routine) is therefore particularly important and it follows this algorithm:
-
1.
Set the initial spectrum model with the same number of pixels and wavelengths of the observed spectrum and initial flux normalized to one. We call it the “working model”.
-
2.
Consider the stellar parameter with which the model must be constructed.
-
3.
Consider the first absorption line of the line list.
-
4.
Compute the EWc of the absorption line by using its polynomial GCOG.
-
5.
Compute the strength of the line profile at every pixel around the center of the line and subtract it from the working model. The result is the new working model.
-
6.
Consider the next line and go to step 4 until the last line has been reproduced.
The line profile adopted is a Voigt function approximated with the implementation by McLean et al. (1994). We modified this implementation so that the line profile becomes broader as a function of log g and EW with a law that can be different for some special lines (for instance, lines with large damping constants). For a detailed description of the line profile adopted we refer the reader to Appendix C.
7.2. The “starting point” routine
This routine finds the first rough estimation of the stellar parameters. It uses the “TGM routine” outlined in the next section, with the difference that the polynomial GCOG employed has been computed not over a small volume of the parameter space (as explained in Sect. 6.1) but over the whole parameter space. This polynomial GCOG has larger errors with respect to the other polynomials contained in the GCOG library, but it permits a rough and fast estimation of the parameters, which is used as starting point by the next TGM routine.
7.3. The “TGM routine”
This part of the code is responsible for deriving the stellar parameters. It employs the Levenberg-Marquadt method to minimize the χ2 between the models and the observed spectrum in the parameter space (Teff, log g, [M/H]). At the fourth step of the main algorithm, the TGM routine uses the observed spectrum as provided by the user, while at the seventh step it uses the observed spectrum after the re-normalization (explained in Sect. 7.4). Because the polynomial GCOGs were computed over an interval of stellar parameters that covers 800 K in Teff, 1.6 in log g, and 0.8 dex in [M/H] (see Sect. 6.1) centered on a grid point (we call it the “central point”), its reliability decreases with the distance from the central point. When the stellar parameters given by the TGM routine are close to a grid point that is not the central point, the TGM routine stops, uploads the polynomial GCOG for this new grid point, and repeats. In this way the routine always finds the minimum χ2 close to the central point, where the EWs provided by the polynomial GCOG are the most reliable. For some spectra (e.g., spectra with very low S/N, spectra of very cool/very hot stars, or spectra of stars with high rotational velocity Vrot) the TGM routine may try to move beyond the extension of the GCOG library. In this case SP_Ace writes a warning message and exits with no results.
Apart from the stellar parameters, the TGM routine also estimates two other parameters: the radial velocity and the FWHM of the instrumental profile. Because SP_Ace only processes radial-velocity-corrected spectra, the radial velocity estimation of SP_Ace is not a real measurement, but it is an internal setting to improve the match between the model spectrum and the observed spectrum. Usually this quantity amounts to a small fraction of FWHM. Similarly, SP_Ace searches for the FWHM that matches best the instrumental profile. The optimization of the FWHM gives to SP_Ace some flexibility in estimating the stellar parameters for stars with a rotational velocity Vrot different from zero. However, the Voigt profile adopted by SP_Ace cannot properly fit the shape of the lines of stars with high Vrot, and the Vrot limit beyond which the line profile becomes inadequate depends on the spectral resolution. This limit is higher for low-resolution spectra in which the instrumental line profile dominates over the physical profile of the line.
7.4. The re-normalization routine
As stressed before, SP_Ace can only handle flux-normalized spectra. However, it can perform a re-normalization to adjust the continuum level. This operation may be unnecessary for high-resolution and high-S/N spectra, where the continuum is clearly detectable and a normalization done with the commonly used IRAF task continuum is usually satisfactory. For low-resolution, low-S/N spectra, and in particular for spectra crowded of lines, the continuum cannot be clearly identified. At low resolution, the lines are instrumentally blended and they create a pseudo-continuum that can lie under the real continuum. In this case, the IRAF task continuum cannot correctly estimate the continuum and renders a too low continuum level, leading to an underestimation of the metallicity (as well as the other stellar parameters, since they are correlated). As an example, in Fig. 13 we show a low- and a high-resolution spectrum (synthetic) of a high-metallicity star, and the result of the continuum normalization performed with the IRAF task continuum, using a spline function and low_rej=1 and high_rej=4, settings that take the presence of absorption lines in the spectra in account.
 |
Fig. 13 Synthetic spectrum with the stellar parameters Teff = 4212 K, log g = 1.8, [M/H] = 0.0 dex, and S/N = 100 at resolution R = 20 000 (top) and R = 5000 (bottom). The black line is the correctly normalized spectrum (synthesized by MOOG and noise added), while the dashed line is the same spectrum after normalization with the task continuum of IRAF. |
 |
Fig. 14 Comparison between the IRAF and SP_Ace normalization. Top: solid and dashed black lines are as in bottom panel of Fig. 13. The gray line was obtained by processing the dashed line (IRAF normalized spectrum) with the SP_Ace re-normalization routine. Bottom: residuals between the IRAF normalized (dashed line) and SP_Ace normalized (gray line) spectra with respect to the correctly normalized spectrum. |
Because of the instrumental blend of the lines, the low-resolution spectrum suffers of a too low continuum estimation and its normalized flux is too high. When the same continuum settings are used for very low S/N spectra the normalized spectra suffer the opposite problem: the noise dominates the spectrum and the flux distribution becomes nearly symmetric with respect to the continuum. (This commonly happens in spectroscopic surveys when the number of spectra to normalize is big and the parameters of the task continuum cannot be set by hand for every spectrum.) In this case, the settings low_rej=1 and high_rej=4 are not appropriate and cause a too high estimated continuum (and an overestimation of the metallicity). To fix this problem, SP_Ace re-normalizes the observed spectrum. In the following, fobs indicates the normalized flux of the observed spectrum and fmodel indicates the normalized flux of the spectrum model. The re-normalization routine works as follows:
-
1.
Consider the ith pixel at wavelength λ(i) and the n pixels for which λ − λ(i) < 30 Å.
-
2.
Compute the average of the observed flux
 , the average of the residuals
, the average of the residuals  and their standard deviation σres of the n pixels defined before.
and their standard deviation σres of the n pixels defined before. -
3.
From the set of n pixels defined in step 1, reject the pixels with
 . The new set of pixels has now m ≤ n number of pixels.
. The new set of pixels has now m ≤ n number of pixels. -
4.
With the new set of m pixels, compute the new average of the observed flux
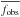 , the average of the model
, the average of the model 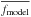 .
. - 5.
- 6.
-
7.
Move to the next ith pixel and go to step 1 until all the pixels have been processed.
In Fig. 14 we show the synthetic spectrum at R = 5000 (also seen in the bottom panel of Fig. 13) together with the IRAF normalized spectrum and the spectrum after the re-normalization. The re-normalization routine employed by SP_Ace can greatly decrease the offset caused by the IRAF normalization.
7.5. The ABD routine
The routine to derive the chemical abundances (called “the ABD routine”) works similarly as the TGM routine. The ABD routine is run after the TGM routine. The abundances [El/M] are varied by a minimization routine until the χ2 between the model and the observed spectrum is minimized.
7.6. Internal errors estimation
SP_Ace can estimate the expected errors for the parameters Teff, log g, and the chemical abundances [El/M]. The routine dedicated to this task finds the confidence limits of the stellar parameters intended as the region of the parameter space that contains a certain percentage of the probability distribution function (Press et al. 1992). If we want to determine the extension of the region that has a 68% of probability to include the resulting parameter (say 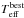 ) with the lowest χ2 (
) with the lowest χ2 (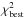 ), this region is an interval that has an upper and a lower limit
), this region is an interval that has an upper and a lower limit 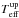 and
and 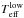 with
with 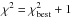 . Because the stellar parameters are correlated, the confidence limits of one parameter are a function of the others, so that the upper and lower confidence limits of Teff as a function of log g correspond to the largest and smallest values of Teff with
. Because the stellar parameters are correlated, the confidence limits of one parameter are a function of the others, so that the upper and lower confidence limits of Teff as a function of log g correspond to the largest and smallest values of Teff with 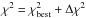 where Δχ2 depends on the number of degrees of freedom (Press et al. 1992). The higher the number of degrees of freedom, the larger the confidence limits. Because the determination of these limits is computationally expensive, we limited this determination to three variables, namely Teff, log g, and [M/H] for these three stellar parameters, and Teff, log g, and [El/M] for the chemical abundance of the generic element El. This means that we determine the upper and lower limits of any parameter at
where Δχ2 depends on the number of degrees of freedom (Press et al. 1992). The higher the number of degrees of freedom, the larger the confidence limits. Because the determination of these limits is computationally expensive, we limited this determination to three variables, namely Teff, log g, and [M/H] for these three stellar parameters, and Teff, log g, and [El/M] for the chemical abundance of the generic element El. This means that we determine the upper and lower limits of any parameter at 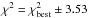 . These confidence limits must be considered as internal errors (therefore smaller than the real errors) because they do not take external errors into account like the mismatch between the atmosphere model and the real stellar atmosphere, uncertainties in the atomic transition probability, in the continuum placements and other uncertainties in the spectrum model construction.
. These confidence limits must be considered as internal errors (therefore smaller than the real errors) because they do not take external errors into account like the mismatch between the atmosphere model and the real stellar atmosphere, uncertainties in the atomic transition probability, in the continuum placements and other uncertainties in the spectrum model construction.
The error estimation is an option left to the user because it is computationally expensive: when done, it can easily double (or more) the time required to process the same spectrum without error estimation.
7.7. Output results
At the end of the process, SP_Ace writes four output files. One file called “space_TGM_ABD.dat” contains the resulting stellar parameters Teff, log g, and chemical abundances with their confidence intervals, the number of lines measured, and a few other parameters like the χ2 of the best matching spectrum model, internal RV and FWHM. The second output file called “space_model.dat” contains a table the columns of which correspond to i) the pixel wavelength of the observed spectrum; ii) the flux of the observed spectrum; iii) the flux of the observed spectrum after re-normalization; iv) the flux of the best matching model; v) the continuum level adopted for the re-normalization; and vi) the weights of the pixels (rejected pixels have weight = 0). The third output file “space_ew_meas.txt” contains the EW employed by SP_Ace to construct the model. We want to stress that these are not the EWs of the absorption lines but merely the EWc (EW corrected for the opacity of the neighboring lines) computed from the polynomial GCOG during the construction of the best matching model. The fourth output file “space_msg.txt” contains the warning messages generated when something goes wrong during the analysis.
Ages, iron abundance ranges, and coefficients m and q of the linear law [El/Fe] = m· [Fe/H] + q that expresses the chemical abundances used to synthesize the spectra of the three mock stellar populations.
8. Validation
To establish the precision and accuracy of the stellar parameters and chemical abundances derived by SP_Ace, we run the code on several sets of synthetic and real spectra with well known parameters and compare them with the parameters derived with SP_Ace. We test SP_Ace on the wavelength ranges 5212–6270 Å and 6310–6900 Å, which avoids the range 6270–6310 Å where the presence of telluric lines can affect the analysis. The tests are performed on spectra with spectral resolution between 2000 and 20 00016.
Before the presentation of these tests, we illustrate and discuss the accuracy with which SP_Ace constructs the spectrum models (i.e. how close these models match the synthetic spectra from which they are derived).
8.1. Spectrum models accuracy
In Sect. 7.1 we outlined the algorithm that constructs the spectrum model which must be compared with the observed spectrum. Our goal was to make a spectrum model that looks as close as possible to a synthetic spectrum. To evaluate the accuracy with which the spectrum models constructed by SP_Ace match the corresponding synthetic spectra, we synthesized two spectra and compared them with the corresponding spectrum models constructed with the same stellar parameters. The goodness of the match illustrates the precision with which the strength of the lines (encoded in the EW library first, and then in the GCOG library) and the line profile adopted, can reproduce a realistic spectrum model. We chose to synthesize the spectra of a dwarf star (Teff = 5800 K, log g = 4.2, [M/H] = 0.0 dex) and of a giant star (Teff = 4200 K, log g = 1.4, and [M/H] = 0.0 dex) degraded to a spectral resolution of R = 12 00017. The relatively high metallicity adopted generates spectra rich in lines, allowing us to verify how well SP_Ace can reproduce blended features (more numerous in spectra of giants) and how good it fits the profile of strong lines (usually broader in dwarf stars). In the case of blended features we test the correction for the opacity of the neighboring lines applied to the EW library (Sect. 5.3), for isolated strong and weak lines we verify the goodness of the Voigt profile adopted (described in Appendix C). In general, any line is affected by the precision with which the polynomial GCOGs represent the expected EWs. The comparison between models and synthetic spectra is shown in Fig. 15. The top panel of the figure shows that the normalized flux of the models differs by no more than 1% for most of the wavelengths, with a general standard deviation σ of 0.2% and 0.6% for the dwarf and the giant, respectively. This statistic was computed after the rejection of the gray shaded areas, which were rejected during the analysis because in the case of real spectra they are affected by unidentified lines, lines with NLTE effects, or lines for which the correction for the opacity of the neighboring lines is not satisfactory (see last paragraph of Sect. 5.3).
Although not perfect, the spectral models match the corresponding synthetic spectra with a satisfactory degree of accuracy.
 |
Fig. 15 Comparison between spectra models and the corrispondent synthetic spectra. The black lines are synthetic spectra of a cool giants stars (bottom panel) and a warm dwarf stars (middle panel) with stellar parameters as reported in the panels. The overplotted colored lines represent the spectrum models constructed by SP_Ace for the corrispondent giant (red line) and dwarf (blue line) star. The shaded areas indicate the wavelength ranges rejected during the SP_Ace analysis (see text for more details). The residuals (model minus synthetic spectra) are reported in the top panel, together with the standard deviation of the residuals for the dwarf and giants spectra (in blue and red colors, respectively) after the exclusion of the gray shaded areas. |
8.2. Tests on synthetic spectra
To verify the ability of SP_Ace to distinguish the stellar parameters and chemical abundances of different Milky Way stellar populations of different ages, metallicity, and evolutionary stages, we synthesized the spectra of three mock stellar populations with characteristics that mimic the thin disk stars, the halo/thick disk stars, and accreted stars with non-enhanced α abundances (a dwarf galaxy accreted by the Milky Way, for instance). All the synthetic spectra were synthesized with MOOG, adopting the final line list described in Sect. 4.4 and atmosphere models from the grid ATLAS9 by Castelli & Kurucz (2003) (updated to the 2012 version) linearly interpolated to the wanted stellar parameters.
8.2.1. Construction of the synthetic mock populations
We construct a mock sample for a total number of 1200 spectra for the three populations (300, 600, and 300 spectra for the thin, halo/thick, and accreted populations, respectively), randomly chosen from the PARSEC isochrones (Bressan et al. 2012 complemented by Chen et al. 2015) to cover the stellar parameter range 3600 to 7500 K in Teff, 0.2 to 5.0 in log g, and −2.0 to + 0.3 dex in [Fe/H]. In this way, the mock sample covers uniformly the chosen isochrones.
Their chemical abundances were chosen with the following characteristics:
-
mock thin disk stars: they cover the iron abundance ranges −0.8 ≤ [Fe/H] (dex) < + 0.3 and their Teff and log g were taken from isochrones with an age of 5 Gyr. Their α-elements enhancement [El/Fe] becomes progressively higher for lower [Fe/H]. (In the next plots this population is represented by blue points.)
-
mock halo/thick disk stars: they cover the iron abundance ranges −2.0 ≤ [Fe/H] (dex) < −0.2 and their Teff and log g were taken from the isochrones with an age of 10 Gyr. Their α-element enhancement [El/Fe] becomes progressively higher for lower [Fe/H] down to [Fe/H] = −1.0 dex, and stays constantly high (~+0.4) for [Fe/H] < −1.0 dex. (In the next plots this population is represented by red crosses.)
-
mock accreted stars: they cover the iron abundance ranges −2.0 ≤ [Fe/H] (dex) < −1.0 and their Teff and log g were adopted from isochrones of an age of 10 Gyr. Their α-element enhancements [El/Fe] are equal to zero. (In the next plots this population is represented by dark green triangles.)
More precisely, the abundance of the generic element El follows a linear law which can be expressed as [El/Fe] = m· [Fe/H] + q, where m and q have different values for different [Fe/H] intervals and elements. The exact m and q values for each element are listed in Table 5. The distributions of these populations in Teff and log g are shown in the left panel of Fig. 16. The samples were degraded to resolutions of R = 20 000, 12 000, 5000, and 2000 and to signal-to-noise ratios of S/N = 100, 50, 30, and 20 (by adding Poissonian noise) for a total amount of 19 200 spectra. The stellar parameters and abundances of these spectra were derived with SP_Ace and compared with the expected ones. The measurements were performed with the keyword ABD_loop on. We switched off the internal re-normalization to evaluate the goodness of the GCOG library to provide the right EW of the lines and the ability of SP_Ace to reproduce the correct line profile of the absorption lines.
 |
Fig. 16 Distribution of the three mock populations on the Teff and log g plane as synthesized (left panels) and derived by SP_Ace (right panel). The blue points, red crosses, and green triangles represent the thin, halo/thick disc, and accreted stars, respectively. The solid, dashed, and dotted black lines show isochrones at [M/H] = 0.0 dex and 5 Gyr, [M/H] = −1.0 dex and 10 Gyr, and [M/H] = −2.0 dex and 10 Gyr, respectively. The light gray errorbars represent the confidence intervals of the individual measurements. A missing errorbar indicates that the error is larger than the parameter grid. |
 |
Fig. 17 Residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). Symbols and colors are as in Fig. 16. |
 |
Fig. 18 Chemical abundances derived by SP_Ace for the three mock populations. Symbols and colors are as in Fig. 16. The reference abundances of these three populations are represented by the light blue, light red, and light green solid lines for the thin disc, the halo/thick disc, and accreted populations, respectively. |
8.2.2. Results
We run SP_Ace on the sets of synthetic spectra just outlined. For the sake of brevity, we only report here the representative case of R = 12 000 and S/N = 100. In Fig. 16 we show the distribution in Teff and log g of the synthetic spectra (left panel) in comparison with the same parameters derived by SP_Ace (right panel). The Teff and log g derived by SP_Ace follow closely the isochrones for all three synthetic populations. In Fig. 17 we show the residuals between the derived and reference values as a function of the reference stellar parameters while in Fig. 18 we report the distribution of the chemical abundances in the chemical plane for nine elements derived from the same spectra.
8.2.3. Errors estimation in synthetic spectra
In the panels of Fig. 17 we report the dispersions of the measurements around the expected values of Teff, log g, and [M/H], while the confidence interval of the single measurements (computed as explained in Sect. 7.6) are shown with the light gray errorbars. The errorbars in Fig. 17 are often smaller than the dispersion of the residuals, which suggests an underestimation of the errors. This is summarized in Fig. 19 where the overall dispersion of the residuals for the stellar parameters (derived minus reference, black symbols) are compared with the half-width of the confidence intervals (gray symbols) for different resolutions and S/Ns. The black and gray symbols are closer where the stochastic noise dominates, i.e., at low S/N, while for high S/N the confidence intervals always underestimate the stellar parameter dispersions. The reason can be guessed from Fig. 17: the overall dispersion σ is inflated by the presence of systematic errors in Teff, log g, and [Fe/H] for which the computed confidence intervals cannot account. The latter can only account for the stochastic errors. We proved the last statement by generating 100 Monte Carlo realizations of a few synthetic spectra, derived their stellar parameters and chemical abundances, and compared them with the confidence intervals computed by SP_Ace. The distributions of the parameters and the confidence intervals obtained with this test show that the confidence intervals only account for the stochastic noise and fail to recognize the systematic errors when present (the shift between the average of the black histogram and the expected value represented with a black dashed line in Fig. 20). The chemical abundances recovered by SP_Ace for the three mock samples (see Fig. 18) are accurate and follow the expected sequences traced by the colored solid lines. No particular systematic error is visible and the errorbars appear to be a good representation of the dispersion around the expected value. This is supported by the statistic obtained from the 100 Monte Carlo realizations cited before and illustrated in Fig. 21. A further discussion of the systematics errors seen in this section can be found in Sect. 8.5.
 |
Fig. 19 Black symbols: standard deviations of the residuals of the stellar parameters (expressed as estimated minus reference values) as a function of S/N for the four different resolutions considered here. Grey symbols: as the black symbols but the y-axis expresses the average semi-width of the estimated confidence interval. The black and gray symbols would match if the error distributions were Gaussian and there were no systematic errors. |
8.3. Tests on real spectra
We employed sets of publicly available spectra like the ELODIE spectral library (Prugniel et al. 2007), the spectra of the benchmark stars (Blanco-Cuaresma et al. 2014), and the spectra of the S4N catalogue (Allende Prieto et al. 2004). For the ELODIE spectra we selected those spectra for which the authors report literature stellar parameters flagged as being of good and excellent quality (quality flags “3” and “4”) to be compared with the stellar parameters derived by SP_Ace. For the benchmark and S4N stars we compare our results with the high quality stellar parameters provided by Jofré et al. and Allende Prieto et al., respectively. All these spectra have high spectral resolution (>60 000) and high S/N. To test SP_Ace on spectra of lower resolution and S/N, we degraded the spectra to resolutions of R = 20 000, 12 000, 5000, and 2000 and to S/N = 100, 50, 30, and 20 by adding artificial Poissonian noise18. Although the original spectra were already normalized, we re-normalized them after degrading them with the IRAF task continuum in order to simulate the continuum obtained when these spectra are normalized at their nominal spectral resolution. Then, the spectra were processed with SP_Ace and the derived stellar parameters compared with the reference values. For the sake of brevity, we only report here the representative case of R = 12 000 and S/N = 100. We measured the spectra with the ABD_loop keyword in the wavelength range 5212–6270 Å and 6310–6900 Å to avoid the telluric lines in the range 6270–6310 Å that may degrade the quality of the measurements. In this case we switched on the internal re-normalization as usually done for spectra for which the continuum level must be refined.
 |
Fig. 20 Distributions of the derived stellar parameters (black solid histogram), and the lower and upper limits of the confidence intervals (dotted-dashed red histogram and thick dashed green histogram, respectively) as computed in Sect. 7.6 for 100 Monte Carlo realizations of the synthetic spectrum with Teff = 4538 K, log g = 2.42, [Fe/H] = 0.30 dex, S/N = 100, and R = 12 000. The black point represents the median of the derived stellar parameters while the errorbars show the lower and upper limit of the interval that holds the 68% of the measurements. The vertical dashed lines represent the reference values. |
 |
Fig. 22 Left panel: distribution of the reference stellar parameters in the Teff and log g plane for the ELODIE library (solid points), the benchmark stars (crosses), and the S4N stars (triangles). Right panel: as before but with the stellar parameters derived by SP_Ace. The colors code the [Fe/H]. Errorbars are reported in light gray. The solid, dashed, and dotted black lines trace the isochrones for [M/H] = 0.0 dex and 5 Gyr, [M/H] = −1.0 dex and 10 Gyr, and [M/H] = −2.0 dex and 10 Gyr, respectively. |
8.3.1. Results
The distributions on the Teff and log g plane of the reference parameters and the derived parameters with SP_Ace are shown in the left and right panels of Fig.22, respectively. The derived parameters appear to follow fairly well the isochrones. In Fig. 23 the residuals between the derived and expected values as a function of the reference stellar parameters show small residuals in all the panels, except for the middle right panel, which reveals a systematically low log g with lower [Fe/H]. This feature is discussed in Sect. 8.5.1.
8.3.2. Error estimation in real spectra
Because for real spectra we do not have exact stellar parameters but estimations from high resolution spectra, our evaluation of the errors relies on the dispersion of the residuals between the parameters derived by SP_Ace and the high resolution parameters that we use as reference. This is summarized in Fig. 26 for different resolutions and S/N ratios. Because the reference parameters also suffer from errors, the dispersions reported in Fig. 26 are actually an overestimation of the SP_Ace errors because they result from the quadratic sum of the reference errors plus the SP_Ace errors19. For the individual elements, Fig. 24 shows nine relative abundances derived from the same spectra. For these quantities reference values can be only found for the S4N spectra, for which we have seven elements in common. The comparison between derived and reference abundances is reported in Fig. 25.
8.4. Measure of the whole ELODIE spectral library
We derived stellar parameters and chemical abundances for the whole ELODIE spectral library at a resolution of R = 12 000 and S/N = 100. SP_Ace provided results for 1386 spectra (out of 1959 spectra of the library) while it did not converge for those spectra which stellar parameters are beyond the stellar parameter volume covered by the GCOG library. The high number of stars provided by the full ELODIE library gives a more robust statistic with respect to the previous test. The derived parameters are reported in Appendix D, Tables D.1–D.3, and are plotted in Fig. D.4.
8.5. Discussion
Tests on synthetic and real spectra showed that the derived stellar parameters and chemical abundances are reliable and have a good precision. The accuracy suffers from systematic errors (in particular for Teff, log g, and [Fe/H]) highlighted in the test on synthetic spectra. This particularly affects spectra that have high density of strong lines, for which the correction for the opacity of the neighbor lines (seen in Sect. 5.3) applied to a wavelength interval 0.5 Å wide becomes insufficient. In this case, the expected EW of the lines stored in the EW library (and encoded in the GCOG library) is too large and leads to misestimations of the stellar parameters with the systematic errors seen in Fig. 17. However, these errors are relatively small (up to 100 K in Teff, 0.2 in log g, and 0.1 dex in [Fe/H]). While these errors affect mostly metal rich cool dwarfs (Teff < 4500 K, [Fe/H] > 0 dex) and, to some extent, cool giants (log g < 0.5) in synthetic spectra, in the test with real spectra they do not seem seem to play a significant role (Fig. 23) perhaps because they are smaller than the stochastic errors. On the other hand, the measurements done with the whole ELODIE sample (Fig. D.4) show an underestimation of the gravity for dwarfs stars cooler than Teff < 4800 K (they do not follow the isochrones, as expected) and an apparent gravity overestimation of the red clump stars of ~+0.25 in a general picture that confirms the goodness of the results in every other respect.
Another source of systematic errors is the adopted line profile (Appendix C). The SP_Ace line profile is an empirical function of the EW, broadening constants, and log g of the star, and it proved to fit reasonably well the lines for most of the stellar parameters. However, there are some discrepancies that causes the systematic deviations from the expected stellar parameters just discussed. An improved function for the line profile can reduce the systematic errors and this is one of the many possible improvements that are left for the next version of SP_Ace.
 |
Fig. 23 Residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). ELODIE, benchmark, and S4N stars are indicated with black points, red crosses, and blue triangles, respectively. Errorbars are reported in light gray. A missing errorbar indicate that the error is larger than the parameters grid. |
 |
Fig. 24 Chemical abundances derived by SP_Ace for the ELODIE, benchmark, and S4N stars. Symbols are as in Fig. 23. |
Despite the errors in stellar parameters, the resulting chemical abundances are reliable, as shown in Figs. 18 and 24 for synthetic and real spectra, respectively. For the synthetic spectra the distribution of the derived chemical abundances on the chemical plane follows closely the expected values (light colored solid lines in Fig. 18), while for real spectra the chemical abundance distributions follow fairly well the pattern expected for the Milky Way stars. A one-to-one comparison of the derived chemical abundances with the reference abundances of the S4N spectra (Fig. 25) reveals that some of the elements may suffer from systematic errors. In particular Sc and Ti seem to be underestimated by ~0.1 dex with respect to the S4N estimations. For the other elements, the abundances agree fairy well. It is not clear what may cause the underestimation of the Sc and Ti . The absorption lines of these two elements are weak in the Sun, which makes the calibration of the log gfs and the determination of the abundances of the other standard stars used for the calibration (Sect. 4) difficult. This can lead to a systematic offset of the calibrated log gfs of the lines of these elements, and therefore to an offset in the derived abundances. On the other hand, in Sect. 4.5 we showed how the calibrated log gfs seems to be smaller than the good quality log gfs we took as reference. This would lead to an overestimation of the chemical abundances, which is the opposite of the underestimation seen. Moreover, it would affect all the elements and not Sc and Ti alone.
Most of the systematic errors seen in synthetic spectra become indistinguishable in the tests with real spectra, where the stochastic errors are larger. However, there is at least one systematic error highlighted by the tests on real spectra that must be discussed. It affects the log g and it is discussed in the next section.
8.5.1. On the systematic error in log g in real spectra
The results obtained with synthetic and real spectra prove to be reliable and in fair agreement for all the stellar parameters but for log g, for which SP_Ace derives a too low gravity for metal poor spectra. The absence of this systematic error in the tests on synthetic spectra excludes that the error may originate in the way in which SP_Ace constructs the spectrum models. In the attempt to shed light on this, we tested SP_Ace with different settings, and we found that running SP_Ace with and without the keyword ABD_loop (which executes or skips the step 10 of the algorithm outlined in Sect. 7) leads to results that are in agreement for all the stellar parameters but for log g. In Fig. 27 the residuals in log g are shown as a function of [Fe/H] for both settings for comparison purposes. With ABD_loop, real spectra show the systematic error just cited, whereas this is absent in synthetic spectra. Conversely, without ABD_loop the systematic error in log g for real spectra is greatly reduced, but the same systematic with opposite sign appears in synthetic spectra for the α-enhanced stars (red crosses in Fig. 27) and not for the non-enhanced ones (green triangles). This seems to be in agreement with the real spectra, because for the stars here considered, the low metallicity stars are α-enhanced too. This suggests that the only stars affected by this systematic are the α-enhanced stars.
 |
Fig. 25 Comparison between derived and reference chemical abundances of seven elements for the S4N spectra. Points marked with crosses have been excluded by the statistic reported in the panels. |
This indicates that the discrepancy observed between synthetic and real spectra does not depend on the method employed, but that it may originate from i) incorrect microturbulence adopted for the EW library or from ii) the adopted 1D atmosphere models and LTE assumption, for which the discrepancy to the physical conditions of real stars becomes larger for lower metallicity (Asplund 2005; Bergemann et al. 2012). We are inclined to exclude that the atomic parameters like damping constants or oscillator strengths may play a significant role in this systematic error because otherwise it should equally affect metal-rich and metal-poor stars. The future development of a new GCOG library that accounts for NLTE effects and 3D atmosphere models should shed light on the origin of this systematic and, hopefully, remove it. Because this problem cannot be solved in the present work, we choose to leave the option to the user whether to use the ABD_loop keyword. In the appendix of this work, the results of the tests on real spectra run without the ABD_loop keyword are presented.
A further systematic error is the underestimation (~–0.2) of log g for dwarf (log g ≳ 4.2) stars. This effect is smaller in the test with synthetic spectra than in real spectra. The fact that for synthetic spectra this is small seems to suggest that the origin of the problem may, as before, lie in the basic assumption made, such as the LTE assumption and the stellar atmosphere models adopted.
8.6. Remark
In this paper we mostly aimed at validating the method proposed. For the sake of brevity, we do not discuss the tests done by using other functions available in SP_Ace and we just briefly mention two of them here20. SP_Ace accepts keywords like T_force and G_force that force SP_Ace to look for solutions with fixed Teff and/or log g given by the user. This is particularly useful for low S/N spectra for which SP_Ace cannot converge to precise stellar parameters. For instance, a robust photometric temperature passed to SP_Ace with the keyword T_force helps to improve the log g and chemical abundances estimations. Another useful keyword is alpha which forces SP_Ace to derive the abundance of the α-elements (Mg , Si , Ca and Ti ) as if they were one single element while any other elements (excluding C , N , and O ) are considered to be a separate single element called “metals”. As before, this is useful to get abundances from low-quality spectra that carry little information.
 |
Fig. 26 Standard deviations of the residuals of the stellar parameters derived from real spectra as a function of S/N for the fourth different resolutions considered. |
 |
Fig. 27 Residuals between derived and reference log g for real spectra (top) and synthetic spectra (bottom) when the long (left panels) and short (right panels) versions of SP_Ace are used to derive the stellar parameters. The symbols are as in Figs. 23 and 16 for real and synthetic spectra, respectively. |
9. Publication
The source code of SP_Ace will be publicly available soon together with the line list and the GCOG library. The code will be released under a GPL license. In addition, a VO-integrated service allowing operation of SP_Ace without installation is available (Boeche et al. 2015). As simple Web front end to this service can be found at http://dc.g-vo.org/SP_ACE
10. Future work
In this work we outlined the method the code SP_Ace relies upon and the solutions chosen up to now, which prove to work but are far from perfect. Many improvements and further developments are possible. Among the most important we cite the following ones:
-
Extension of the stellar parameter grid: it is possible to extend the coverage of the GCOG library to hotter temperature than the actual covered ones (Teff < 7400 K) and to higher gravities. The latter have been extended to log g = 5.4 with an extrapolation because stellar atmosphere models with log g > 5.0 are not provided by the grid ATLAS9. An extension of the stellar atmosphere grid (and subsequent extension of the GCOG library) up to log g ~ 6 is planned for the near future.
-
Extension of the line list: currently the wavelength range covered by the GCOG library is 5212–6860 Å and 8400–8920 Å. We plan to extend the wavelength range, in particular toward bluer wavelengths. With the extension of the grid to hotter stars, the line list will be augmented by ionized/high excitation potential lines only visible at high temperatures.
-
Molecular lines: at the present time the molecular lines we take in account are the CN lines in the range 8400–8920 Å. An extension to the optical region would improve the derivation of stellar parameters for cool stars. How this problem can be solved in the framework of the method used by SP_Ace is still unclear.
-
Opacity correction: an improved method to correct the EW for the opacity of the neighboring lines has to be found. A further investigation of the rigorous solution proposed in Appendix B, or new techniques of line deconvolution (like the one proposed by Sennhauser et al. 2009) may lead to a solution.
-
Improved line profile: the present line profile adopted in SP_Ace is an empirical function that represents fairly well the shape of the lines over a wide range of parameters, but still is not good enough at the borders of the parameter grid. It is possible and desirable to find a new improved line profile function that would permit the removal of some of the systematic errors seen in synthetic spectra.
-
Extension to other stellar atmosphere models: the present EW library has been constructed with the 2012 version of the ATLAS9 atmosphere grid by Castelli & Kurucz (2003), but it can be done with any other atmosphere models. The creation of EW and GCOG libraries based on MARCS (Gustafsson et al. 2008) or PHOENIX (Husser et al. 2013) models is desirable and we plan to do it in the near future.
-
Extension to 3D models and NLTE assumptions: although the construction of a whole EW library with 3D atmosphere model and NLTE assumptions seems still prohibitive in terms of computing costs, the integration of the present EW library with few important absorption lines the EWs of which have been computed under NLTE assumptions and/or a 3D atmosphere model is doable. For instance, computing the EWs of Hα, the Fe i at 5269.537 Å, and one line of the Ca ii triplet with 3D atmosphere models and/or under NLTE assumptions and integrating these EWs into the present EW library would greatly increase the ability of SP_Ace to constrain the stellar parameters, in particular for low metallicity or low S/N spectra where only strong lines can be seen.
While for some of the above points the amount of work may be considerable, for other points the necessary work is small and it would bring significant improvements in a short time.
11. Conclusions
In this work we proposed and described a new method to derive stellar parameters and chemical elemental abundances from stellar spectra. Based on calibrated oscillator strengths of a complete line list and on 1D atmosphere models and under LTE assumptions, this method relies on polynomial functions (stored in the GCOG library) that describe the EWs of the lines as a function of the stellar parameters and chemical abundance. The method is implemented in the code SP_Ace, which constructs on the fly spectral models and minimizes the χ2 computed between the models and the observed spectrum. The method has a full-spectrum-fitting approach, which means i) it assures the reliability of the spectrum models by calibrating the oscillator strengths of the line list adopted in high-resolution spectra of stars with well-known stellar parameters, and ii) it employs all the possible absorption lines (thousands) in a wide wavelength range to derive the stellar parameters and abundances, exploiting the information carried by lines that are usually rejected in the classical analysis because they are blended or have unreliable theoretical atomic parameters. This approach proved to be successful, obtaining reliable stellar parameters and chemical abundances even in spectra carrying little information, such as low-resolution or low S/N spectra, for which the classical analysis based on EW measurements cannot be applied.
The method is far from perfect, but we believe it shows considerable promise already at the present stage of development. It is highly automated, so that it is suitable for the analysis of large spectroscopic surveys. It is flexible, in the sense that its internal re-normalization and internal re-setting of the radial velocity of the spectrum make SP_Ace independent from the initial quality of the normalization and RV correction performed by previous users or reduction pipelines. It is independent from the stellar atmosphere models used to create the GCOG library on which SP_Ace relies. In fact, the GCOG library can be constructed by using any stellar atmosphere models available in the literature, or under LTE or NLTE assumptions, with no need to change the code SP_Ace.
An on-line version of the code SP_Ace is available on the German Astrophysical Virtual Observatory web server at the address http://dc.g-vo.org/SP_ACE. The source code will be made publicly available soon.
The ASPCAP pipeline can derive abundances for up to 15 elements with a technique that can be classified as a line-fitting approach. See Elia Garcia Perez et al. (2014).
We here want just outline the main idea. To generalize the method the weak line approximation must be removed, and this is discussed in Sect. 5.
The microturbulence employed is a function of Teff and log g as clarified in Appendix A.
The difference to the RAVE chemical pipeline (Boeche et al. 2011) is that this one takes Teff and log g as external input and uses polynomial COGs to only derive chemical abundances.
The VALD web interface lists the lines which strengths are larger than 1% of the normalized flux of a synthetic spectrum which stellar parameters correspond to the nearest point of the stellar parameters grid to the stellar parameters provided by the user. For instance, for the Sun the closest grid point is at Teff = 5750 K, log g = 4.5, [M/H] = 0 dex.
This is in contrast with Wedemeyer (2001) who found that the Unsöld approximation can well describe the wings of silicon lines on the Sun.
This idea was also employed by Boeche et al. (2011) for the gf calibration alone, but using a less sophisticated method.
Precise abundances of these stars have been derived by Jofré et al. (2015), whose results were not yet public at the time of this work.
The Castelli & Kurucz grid has a log g upper limit of 5.0. To explore the χ2 space around this limit (necessary for a cool dwarf stars that can have log g ~ 4.8, for instance) SP_Ace needs to construct spectral models with log g> 5.0. Thus, we extended the EW library to log g = 5.4 by computing the EW of the lines with a linear extrapolation.
At R ≲ 20 000 the line profile implemented in SP_Ace is expected to work best. See Appendix C for a short discussion on the accuracy of the line profile as a function of the spectral resolution.
Acknowledgments
B.C. thanks: H.-G. Ludwig for the numerous useful discussions on atomic parameters and stellar atmosphere models; M. Demleitner and H. Heinl for their support in preparing the web front-end of SP_Ace and useful discussions. We acknowledge advice and assistance in publishing the web service provided by the German Astrophysical Virtual Observatory (GAVO). We acknowledge funding from Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A5) of the German Research Foundation (DFG).
References
- Allen de Prieto, C., Barklem, P. S., Lambert, D. L., & Cunha, K. 2004, A&A, 420, 183 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Allen de Prieto, C., Beers, T. C., Wilhelm, R., et al. 2006, ApJ, 636, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Allen de Prieto, C., Majewski, S. R., Schiavon, R., et al. 2008, Astron. Nachr., 329, 1018 [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Bailer-Jones, C. A. L. 1996, Ph.D. Thesis, Cambridge University [Google Scholar]
- Barklem, P. S., & Aspelund-Johansson, J. 2005, A&A, 435, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barklem, P. S., Piskunov, N., & O’Mara, B. J. 2000, A&AS, 142, 467 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Bensby, T., Feltzing, S., Lundström, I., & Ilyin, I. 2005, A&A, 433, 185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergemann, M., Lind, K., Collet, R., Magic, Z., & Asplund, M. 2012, MNRAS, 427, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bigot, L., & Thévenin, F. 2006, MNRAS, 372, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco-Cuaresma, S., Soubiran, C., Jofré, P., & Heiter, U. 2014, A&A, 566, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boeche, C., Siebert, A., Williams, M., et al. 2011, AJ, 142, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Boeche, C., Demleitner, M., Heinl, H., 2015, SP_Ace spectral analysis tool, VO resource ivo://org.gavo.dc/sp_ace/q/c, http://dc.g-vo.org/browse/sp_ace/q [Google Scholar]
- Borrero, J. M., Bellot Rubio, L. R., Barklem, P. S., & del Toro Iniesta, J. C. 2003, A&A, 404, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackwell, D. E., & Collins, B. S. 1972, MNRAS, 157, 255 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Ibbetson, P. A., Petford, A. D., & Willis, R. B. 1976, MNRAS, 177, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Petford, A. D., & Shallis, M. J. 1979, MNRAS, 186, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Blackwell, D. E., Petford, A. D., & Simmons, G. J. 1982, MNRAS, 201, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Castelli, F., & Kurucz, R. L., 2003, in Modelling of Stellar Atmospheres, eds. N. Piskunov, W. W. Wiess, & D. F. Gray, IAU Symp. 210, 20 [Google Scholar]
- Chen, Y. Q., Nissen, P. E., Zhao, G., Zhang, H. W., & Benoni, T. 2000, A&AS, 141, 491 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Bellido-Tirado, O., Chiappini, C., et al. 2012, Proc. SPIE, 8446 [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 275, 101 [NASA ADS] [Google Scholar]
- Elia Garcia Perez, A., Allende-Prieto, C., Cunha, K. M., et al. 2014, Am. Astron. Soc. Meet. Abst. #223, 223, #440.07 [Google Scholar]
- Freytag, B., Steffen, M., Ludwig, H.-G., et al. 2012, J. Comput. Phys., 231, 919 [Google Scholar]
- Fuhrmann, K. 1998, A&A, 338, 161 [NASA ADS] [Google Scholar]
- Fulbright, J. P., McWilliam, A., & Rich, R. M. 2006, ApJ, 636, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Grevesse, N., Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Gurtovenko, E. A., & Kostik, R. I. 1981, A&AS, 46, 239 [NASA ADS] [Google Scholar]
- Gurtovenko, E. A., & Kostik, R. I. 1982, A&AS, 47, 193 [NASA ADS] [Google Scholar]
- Gustafsson, B., Edvardsson, B., Eriksson, K., et al. 2008, A&A, 486, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiter, U., Jofré, P., Gustafsson, B., et al. 2015, A&A, 582, A89 [Google Scholar]
- Hinkle, K. H., & Lambert, D. L. 1975, MNRAS, 170, 447 [NASA ADS] [Google Scholar]
- Hinkle, K., Wallace, L., Harmer, D., Ayres, T., & Valenti, J. 2000, IAU Joint Discussion, 1 Visible and Near Infrared Atlas of the Arcturus Spectrum 3727–9300 Å, Available at: ftp://ftp.noao.edu/catalogs/arcturusatlas/visual [Google Scholar]
- Holweger, H. 1971, A&A, 10, 128 [NASA ADS] [Google Scholar]
- Holweger, H. 1973, A&A, 26, 275 [NASA ADS] [Google Scholar]
- Holweger, H., & Mueller, E. A. 1974, Sol. Phys., 39, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Holweger, H., Heise, C., & Kock, M. 1990, A&A, 232, 510 [NASA ADS] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ivanauskas, A., Kucinskas, A., Ludwig, H. G., & Caffau, E. 2010, Nuclei in the Cosmos, 290 [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2014, A&A, 564, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jofré, P., Heiter, U., Soubiran, C., et al. 2015, A&A, 582, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Koleva, M., Prugniel, P., Bouchard, A., & Wu, Y. 2009, A&A, 501, 1269 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2013. NIST Atomic Spectra Database (ver. 5.1), available: http://physics.nist.gov/asd. National Institute of Standards and Technology, Gaithersburg, MD [Google Scholar]
- Kirby, E. N., Guhathakurta, P., & Sneden, C. 2008, ApJ, 682, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Kordopatis, G., Gilmore, G., Steinmetz, M., et al. 2013, AJ, 146, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F., Piskunov, N., Ryabchikova, T. A., Stempels, H. C., & Weiss, W. W. 1999, A&AS, 138, 119 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Kurucz, R. L. 1995, in Astrophysical Application of Powerful New Database, eds. S. J. Adelman, & W. L. Wiese (San Francisco, CA), ASP Conf. Ser., 78, 205 [Google Scholar]
- Kurucz, R. L., & Peytremann, E. 1975, SAO Spec. Rep., 362, part 1 [Google Scholar]
- Lindegren, L., Babusiaux, C., Bailer-Jones, C., et al. 2008, IAU Symp., 248, 217 [NASA ADS] [Google Scholar]
- Lobel, A. 2011, Canadian J. Phys., 89, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2006, AJ, 131, 3069 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., Kovtyukh, V. V., & Andrievsky, S. M. 2006, AJ, 132, 902 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., & Heiter, U. 2007, AJ, 133, 2464 [NASA ADS] [CrossRef] [Google Scholar]
- Luck, R. E., Andrievsky, S. M., Fokin, A., & Kovtyukh, V. V. 2008, AJ, 136, 98 [Google Scholar]
- Maeckle, R., Holweger, H., Griffin, R., & Griffin, R. 1975, A&A, 38, 239 [NASA ADS] [Google Scholar]
- Magic, Z., Collet, R., Asplund, M., et al. 2013, A&A, 557, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magrini, L., Randich, S., Friel, E., et al. 2013, A&A, 558, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martins, L. P., Coelho, P., Caproni, A., & Vitoriano, R. 2014, MNRAS, 442, 1294 [NASA ADS] [CrossRef] [Google Scholar]
- McLean, A. B., Mitchell, C. E. J., & Swanston, D. M. 1994, J. Electron Spectrosc. Relat. Phenom., 69, 125 [CrossRef] [Google Scholar]
- Mucciarelli, A., Pancino, E., Lovisi, L., Ferraro, F. R., & Lapenna, E. 2013, ApJ, 766, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Ness, M., Hogg, D. W., Rix, H.-W., Ho, A. Y. Q., & Zasowski, G. 2015, ApJ, 808, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Oneill, J. A., & Smith, G. 1980, A&A, 81, 100 [NASA ADS] [Google Scholar]
- Perryman, M. A. C., de Boer, K. S., Gilmore, G., et al. 2001, A&A, 369, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plez, B. 2008, Phys. Scr. T, 133, 014003 [Google Scholar]
- Posbic, H., Katz, D., Caffau, E., et al. 2012, A&A, 544, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prugniel, P., Soubiran, C., Koleva, M., & Le Borgne, D. 2007, VizieR Online Data Catalog: III/251 [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes: The Art of Scientific Computing, 2nd edn. (New York: Cambridge University Press) [Google Scholar]
- Ramírez, I., & Allen de Prieto, C. 2011, ApJ, 743, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Recio-Blanco, A., Bijaoui, A., & de Laverny, P. 2006, MNRAS, 370, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, R. R., Nazeer Ahammed, Y., Rama Gopal, K., & Baba Basha, D. 2003, Ap&SS, 286, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffoni, M. P., Allen de Prieto, C., Nave, G., & Pickering, J. C. 2013, ApJ, 779, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Ruffoni, M. P., Den Hartog, E. A., Lawler, J. E., et al. 2014, MNRAS, 441, 3127 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L., Caffau, E., Bonifacio, P., & Duffau, S. 2014, A&A, 564, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schweitzer, A., Hauschildt, P. H., Baron, E., & Allard, F. 2003, Stellar Atmosphere Modeling, 288, 339 [NASA ADS] [Google Scholar]
- Seaton, M. J., Yan, Y., Mihalas, D., & Pradhan, A. K. 1994, MNRAS, 266, 805 [NASA ADS] [CrossRef] [Google Scholar]
- Sennhauser, C., Berdyugina, S. V., & Fluri, D. M. 2009, A&A, 507, 1711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simmons, G. J., & Blackwell, D. E. 1982, A&A, 112, 209 [NASA ADS] [Google Scholar]
- Smith, V. V., Cunha, K., Shetrone, M. D., et al. 2013, ApJ, 765, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C., 1973, Ph.D. Thesis, Univ. Texas [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steinmetz, M., Zwitter, T., Siebert, A., et al. 2006, AJ, 132, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Thévenin, F. 1989, A&AS, 77, 137 [NASA ADS] [Google Scholar]
- Thévenin, F. 1990, A&AS, 82, 179 [NASA ADS] [Google Scholar]
- Valenti, J. A., & Piskunov, N. 1996, A&AS, 118, 595 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer, S. 2001, A&A, 373, 998 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, RA&A, 12, 723 [Google Scholar]
- Zucker, D. B., de Silva, G., Freeman, K., Bland-Hawthorn, J., & Hermes Team 2012, Galactic Archaeology: Near-Field Cosmology and the Formation of the Milky Way, 458, 421 [NASA ADS] [Google Scholar]
Appendix A: Microturbulence
Because SP_Ace cannot determine the microturbulence, the EW library must be constructed by assuming the microturbulence value ξ at each point of the grid before the EW computation. As done in a previous work (Boeche et al. 2011) we can set the microturbulence as a function of the stellar parameters (see the work done by M. Bergemann and V. Hill in the Gaia-ESO collaboration cited in Jofré et al. 2014; Allende Prieto et al. 2004). To determine such a function, we investigated how the microturbulence ξ varies on the (Teff, log g) plane for some hundreds of stars studied in high-resolution spectroscopy works found in the literature (Fuhrmann 1998; Allende Prieto et al. 2004; Bensby et al. 2005; Fulbright et al. 2006; Luck et al. 2006a,b, 2008; Luck & Heiter 2007). From such studies we used 620 derived microturbulence ξ values for dwarfs, giants, and Cepheid stars to determine a polynomial function that approximates the microturbulence on the (Teff, log g) plane21. Such stars are shown in the left panel of Fig. A.1. To fit ξ we used a fourth-degree polynomial function. Higher degrees do not improve the fit. The polynomial function is written as follows: 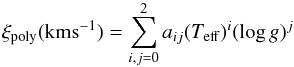 (A.1)where the coefficients aij are
(A.1)where the coefficients aij are ![\appendix \setcounter{section}{1} \begin{eqnarray} a_{00}&=&-5.11308\\[2mm]\nonumber a_{01}&=&0.58507\\[2mm]\nonumber a_{02}&=&0.471885\\[2mm]\nonumber a_{10}&=&0.00207105\\[2mm]\nonumber a_{11}&=&1.70456\times10^{-5}\\[2mm]\nonumber a_{12}&=&-0.000257162\\[2mm]\nonumber a_{20}&=&-1.0543\times10^{-7}\\[2mm]\nonumber a_{21}&=&-3.21628\times10^{-8}\\[2mm]\nonumber a_{22}&=&2.94647\times10^{-8}.\\\nonumber \end{eqnarray}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq180.png) (A.2)Because this polynomial function diverges to large positive values for high Teff and low log g and to negative values at low Teff and high log g, we imposed the following conditions: ξ = 3 km s-1 where ξ> 3 km s-1 and ξ = 0.5 km s-1 where ξ< 0.5 km s-1. The values of the polynomial function and the just cited conditions on the (Teff, log g) plane are shown in the right panel of Fig. A.1. In Fig. A.2 the residuals between the computed ξ and the literature works are shown together with the literature ξ values as a function of Teff. This polynomial function has been employed to set the microturbulence during the construction of the EW library.
(A.2)Because this polynomial function diverges to large positive values for high Teff and low log g and to negative values at low Teff and high log g, we imposed the following conditions: ξ = 3 km s-1 where ξ> 3 km s-1 and ξ = 0.5 km s-1 where ξ< 0.5 km s-1. The values of the polynomial function and the just cited conditions on the (Teff, log g) plane are shown in the right panel of Fig. A.1. In Fig. A.2 the residuals between the computed ξ and the literature works are shown together with the literature ξ values as a function of Teff. This polynomial function has been employed to set the microturbulence during the construction of the EW library.
 |
Fig. A.1 Left: distribution on the (Teff,log g) plane of the stars employed to determine the microturbulence function. Right: polynomial function adopted to represent the microturbulence ξ. For both panels the value of ξ is given by the color bar on the right. |
 |
Fig. A.2 Reference microturbulence (top) and residuals (bottom) between reference (ξ) and polynomial microturbulence (ξpoly) as a function of Teff. The colors code the gravity log g as given by the color bar on the right. |
Appendix B: Separating the contributions of different absorption lines to the total absorbed flux
In Sect. 5.2 we shortly discussed how to separate the contribution of blended lines to the total EWblend. Here we give a detailed explanation on how this can be done in the case of two blended lines. The extension to many lines is straightforward. Consider two blended absorption lines and the equation  (B.1)where
(B.1)where  and
and 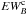 are the individual contributions to the EW of the blends of each absorption line A and B. We want to verify that Eq. (B.1) is satisfied, or, in other words, that
are the individual contributions to the EW of the blends of each absorption line A and B. We want to verify that Eq. (B.1) is satisfied, or, in other words, that 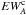 and
and 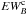 can be inferred from the radiative transfer equation.
can be inferred from the radiative transfer equation.
Because the EW of a line is the measure of the absorbed flux over the line with respect to the continuum, the previous problem is solved by verifying that the flux (intensity of radiation Iout) emerging from a layer of a stellar atmosphere over a small wavelength interval dλ can be written as 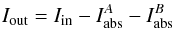 (B.2)where
(B.2)where 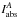 and
and 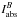 are the individual absorbed intensities due to the absorbers A and B, respectively. We are going to prove that Eq. (B.2) is true for a layer that is homogeneous in its physical conditions and chemical composition22. Then we reach the answer by extending the result to the whole atmosphere.
are the individual absorbed intensities due to the absorbers A and B, respectively. We are going to prove that Eq. (B.2) is true for a layer that is homogeneous in its physical conditions and chemical composition22. Then we reach the answer by extending the result to the whole atmosphere.
Appendix B.1: Pure absorption case
Consider one optically thick layer with two species of absorbers A and B in it, and the variation of the radiation that goes through it. The optical depth of the layer is τ = τA + τB. In the case of pure absorption the transfer equation is 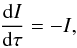 and the solution of this equation is
and the solution of this equation is 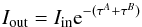 (B.3)where Iin is the intensity of the entering radiation, Iout is the intensity of the emerging radiation. We rearrange Eq. (B.2) and using Eq. (B.3) we write the absorbed intensity
(B.3)where Iin is the intensity of the entering radiation, Iout is the intensity of the emerging radiation. We rearrange Eq. (B.2) and using Eq. (B.3) we write the absorbed intensity 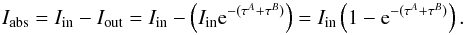 (B.4)We can ideally divide this optically thick layer (with optical deph τ) in many optically thin layers, each of them with optical depth dτi. Thus, for the ith thin layer we can write the Eq. (B.4) as follows:
(B.4)We can ideally divide this optically thick layer (with optical deph τ) in many optically thin layers, each of them with optical depth dτi. Thus, for the ith thin layer we can write the Eq. (B.4) as follows: 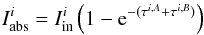 where
where  is the incoming intensity in the ith layer and τi,A and τi,B are the optical depths of the ith layer due to the A and B absorbers. By adopting the Taylor expansion of the exponential function e− (τi,A + τi,B) valid for optically thin layers, and truncating it to the first order (the residual goes to zero when τ → 0), it becomes
is the incoming intensity in the ith layer and τi,A and τi,B are the optical depths of the ith layer due to the A and B absorbers. By adopting the Taylor expansion of the exponential function e− (τi,A + τi,B) valid for optically thin layers, and truncating it to the first order (the residual goes to zero when τ → 0), it becomes 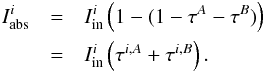 By writing
By writing 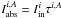 and
and 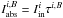 we separate the contributions of the absorbers A and B to the absorbed intensities
we separate the contributions of the absorbers A and B to the absorbed intensities 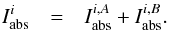 (B.5)Now we consider the ratio between the absorbed intensities
(B.5)Now we consider the ratio between the absorbed intensities 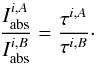 (B.6)From Eq. (B.6) we isolate the term
(B.6)From Eq. (B.6) we isolate the term 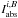 and put it in Eq. (B.5) to obtain
and put it in Eq. (B.5) to obtain 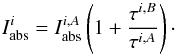 (B.7)We can write the contributions of the two absorbers A and B as follows:
(B.7)We can write the contributions of the two absorbers A and B as follows:  where
where 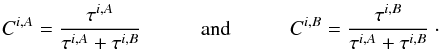 Since the thick layer is homogeneous, what holds for the ith thin layer (i.e., Eqs. (B.8) and (B.9)), must hold for the whole thick layer. (This can actually be proved by using the limit τi → 0. The residual of the Taylor expansion goes to zero faster that τi, and the Eqs. (B.8) and (B.9) are therefore valid.) Therefore, for the whole thick layer we can write
Since the thick layer is homogeneous, what holds for the ith thin layer (i.e., Eqs. (B.8) and (B.9)), must hold for the whole thick layer. (This can actually be proved by using the limit τi → 0. The residual of the Taylor expansion goes to zero faster that τi, and the Eqs. (B.8) and (B.9) are therefore valid.) Therefore, for the whole thick layer we can write 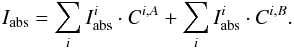 (B.10)Because Ci,A and Ci,B are constant through the whole thick layer (τi,A and τi,B do not change with i), we can write
(B.10)Because Ci,A and Ci,B are constant through the whole thick layer (τi,A and τi,B do not change with i), we can write 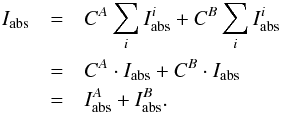 (B.11)The terms
(B.11)The terms 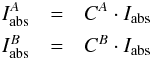 are the individual contributions to the absorbed flux of the absorbers A and B, respectively.
are the individual contributions to the absorbed flux of the absorbers A and B, respectively.
By using Eq. (B.4), 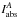 and
and 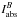 can be written as
can be written as 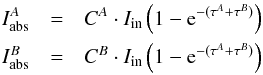 (B.12)and Eq. (B.2) is validated.
(B.12)and Eq. (B.2) is validated.
Appendix B.2: Atmosphere model case
Here we want to apply the previous result to an atmosphere model, which is composed of N number of layers (for instance, the Castelli & Kurucz atmosphere models have N = 72). Such layers have different physical conditions, but inside every layer, the physical conditions and the composition of the gas are constants and homogeneous. Under such conditions, the Eqs. (B.12) are valid for every ith layer.
Consider the transfer equation 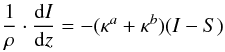 where a and b refer to two different absorbers and S is the source function. The equation can also be written as
where a and b refer to two different absorbers and S is the source function. The equation can also be written as 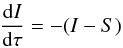 where τa = ρκadz, τb = ρκbdz and τ = τa + τb. τ grows from the bottom toward the surface of the atmosphere, so that the optical depth is 0 at the bottom and τsurf ≠ 0 at the surface. I is the monochromatic intensity of the radiation in a plane-parallel atmosphere. The solution of this equation is:
where τa = ρκadz, τb = ρκbdz and τ = τa + τb. τ grows from the bottom toward the surface of the atmosphere, so that the optical depth is 0 at the bottom and τsurf ≠ 0 at the surface. I is the monochromatic intensity of the radiation in a plane-parallel atmosphere. The solution of this equation is: 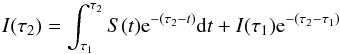 (B.13)which gives the intensity of the flux at the optical depth τ2. We can follow the intensity I(τ) as function of the optical depth τ by subdividing the atmosphere into N layers, precisely at optical depths τ1,τ2,...,τN and write
(B.13)which gives the intensity of the flux at the optical depth τ2. We can follow the intensity I(τ) as function of the optical depth τ by subdividing the atmosphere into N layers, precisely at optical depths τ1,τ2,...,τN and write 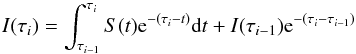 (B.14)where τi−1 and τi are the optical depths at the bottom and the top of the ith layer, respectively, and I(τi−1) is the incoming intensity at the bottom of the ith layer (and the emerging intensity from the i − 1th layer). Because every layer has constant physical conditions and constant optical thickness, we can set the optical depths τi to match the optical depths of the top of the ith layer of the atmosphere model. Because the constancy of the physical conditions in each layer, the S(t) function of the integrand in Eq. (B.14) is constant, and by solving the integral the equation becomes:
(B.14)where τi−1 and τi are the optical depths at the bottom and the top of the ith layer, respectively, and I(τi−1) is the incoming intensity at the bottom of the ith layer (and the emerging intensity from the i − 1th layer). Because every layer has constant physical conditions and constant optical thickness, we can set the optical depths τi to match the optical depths of the top of the ith layer of the atmosphere model. Because the constancy of the physical conditions in each layer, the S(t) function of the integrand in Eq. (B.14) is constant, and by solving the integral the equation becomes: 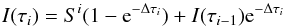 (B.15)where Δτi = τi − τi−1 is the optical thickness of the ith layer, Si is the source function and I(τi−1) the incoming intensity in the ith layer. Equation (B.15) is a recurrence relation. The line of reasoning followed for the case of pure absorption can be applied to the source function as well. In fact, the product Si(1−e− Δτi) is equivalent to the absorbed flux expressed in Eq. (B.4). Then, Eqs. (B.2) and (B.10) can be applied to the two terms of the sum in Eq. (B.15), and it becomes
(B.15)where Δτi = τi − τi−1 is the optical thickness of the ith layer, Si is the source function and I(τi−1) the incoming intensity in the ith layer. Equation (B.15) is a recurrence relation. The line of reasoning followed for the case of pure absorption can be applied to the source function as well. In fact, the product Si(1−e− Δτi) is equivalent to the absorbed flux expressed in Eq. (B.4). Then, Eqs. (B.2) and (B.10) can be applied to the two terms of the sum in Eq. (B.15), and it becomes  (B.16)where
(B.16)where ![\appendix \setcounter{section}{2} \begin{eqnarray} S^{i,A} & = & C^{i,A}\cdot S^i (1-{\rm e}^{-\Delta\tau_i})\\[2mm] S^{i,B} & = & C^{i,B}\cdot S^i (1-{\rm e}^{-\Delta\tau_i})\\[2mm] \label{frac_I_A} I_{\rm abs}^{i,A} & = & C^{i,A}\cdot I(\tau_{i-1})(1-{\rm e}^{-\Delta\tau_i})\\[2mm] \label{frac_I_B} I_{\rm abs}^{i,B} & = & C^{i,B}\cdot I(\tau_{i-1})(1-{\rm e}^{-\Delta\tau_i})\\[2mm] \label{frac_A} C^{i,A} & = & \frac{\tau_i^a}{\tau_i^a+\tau_i^b}\\[2mm] \label{frac_B} C^{i,B} & = & \frac{\tau_i^b}{\tau_i^a+\tau_i^b}\cdot \end{eqnarray}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq253.png) Rearranging the terms, Eq. (B.16) can be written as
Rearranging the terms, Eq. (B.16) can be written as  where the values in the last two terms represent the contributed intensities of the lines A and B to the intensity after the ith layer.
where the values in the last two terms represent the contributed intensities of the lines A and B to the intensity after the ith layer.
Appendix B.3: Application to two blended lines
We applied the formula to the two lines OI at 8446.359 Å (indicated with the letter a) and FeI at 8446.388 Å (indicated with letter b) and solar atmosphere model. We also need to take in account the continuum absorption as third absorber. The continuum is indicated with the letter c. For the ith layer the source function is 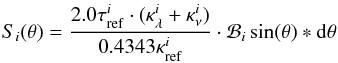 where
where 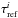 and κref are the optical depth and opacity at the reference optical depth, κλ and κν opacities of the continuum and the lines, ℬi is the Planck function, and θ the angle of view of the stellar disc, from the center (θ = 0) to the limb (θ = π/ 2). To follow how the radiation Si(θ) gets absorbed by the upper layers, we introduce a running index k which runs from i to 1 and indicates the layers crossed by the radiation along its path to the surface. We start from the layer k = i. The flux Sk(θ) generated in the kth layer gets extincted in the same layer. The corresponding outcoming flux is then
and κref are the optical depth and opacity at the reference optical depth, κλ and κν opacities of the continuum and the lines, ℬi is the Planck function, and θ the angle of view of the stellar disc, from the center (θ = 0) to the limb (θ = π/ 2). To follow how the radiation Si(θ) gets absorbed by the upper layers, we introduce a running index k which runs from i to 1 and indicates the layers crossed by the radiation along its path to the surface. We start from the layer k = i. The flux Sk(θ) generated in the kth layer gets extincted in the same layer. The corresponding outcoming flux is then  where
where  is the emerging radiation from the kth layer that was generated in the ith layer (in this case the layer is the same, k = i), and
is the emerging radiation from the kth layer that was generated in the ith layer (in this case the layer is the same, k = i), and 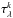 and
and 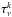 are the optical depths of the kth layer due to the continuum and the two lines, respectively. The following layer k − 1 absorbs the flux
are the optical depths of the kth layer due to the continuum and the two lines, respectively. The following layer k − 1 absorbs the flux 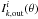 emerging from the kth layer, and the emerging flux from the k − 1th layer is
emerging from the kth layer, and the emerging flux from the k − 1th layer is 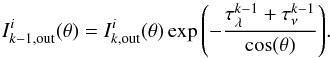 (B.23)and so on for the following layers. This is a recurrence formula, which continues until the layer k = 1 (that is at the surface) is reached. For this surface layer the emerging radiation is
(B.23)and so on for the following layers. This is a recurrence formula, which continues until the layer k = 1 (that is at the surface) is reached. For this surface layer the emerging radiation is 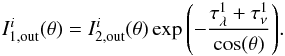 It represents the contribution function of the ith layer. At every kth layer we can compute the fraction of the radiation absorbed by the lines a and b by using the Eqs. (B.19)–(B.22). Similarly, this can be done for the continuum c. The quantity I(τk−1)(1−e− Δτk) in Eqs. (B.19) and (B.20) indicates the variation of intensity before and after the kth layer. This can be easily computed from the Eq. (B.23) by computing Ik − Ik−1.
It represents the contribution function of the ith layer. At every kth layer we can compute the fraction of the radiation absorbed by the lines a and b by using the Eqs. (B.19)–(B.22). Similarly, this can be done for the continuum c. The quantity I(τk−1)(1−e− Δτk) in Eqs. (B.19) and (B.20) indicates the variation of intensity before and after the kth layer. This can be easily computed from the Eq. (B.23) by computing Ik − Ik−1.
 |
Fig. B.1 Left panel: the black solid line represents the Fe i line at 8446.338 Å synthesized as isolated line, i.e., the emerging flux when the line and continuum absorptions are accounted for. The dashed line represent the flux in presence of the line when the continuum absorption alone is accounted for. The dotted line represent the emerging flux when the emissions alone are accounted for. The gray area represents the flux absorbed by the continuum, while the light blue area is the flux absorbed by the line. Right panel: as in the left panel, but for the two blended lines OI and FeI lines at 8446.359 Å and 8446.338 Å, respectively. The flux absorbed by the continuum and the Fe line are still represented by the gray and light blue areas, respectively, while for the OI line the absorbed flux is the red area. The y-axis represents the logarithm (base 10) of the normalized flux. |
Thus, the fractions of intensity absorbed by the two lines a, b, and the continuum c in the kth layer are ![\appendix \setcounter{section}{2} \begin{eqnarray} \label{line_a_abs} I^{i,a}_{k,{\rm abs}}(\theta) & = & \frac{\kappa^a_k}{\kappa^a_k+\kappa^b_k+\kappa^c_k}\big(I^k(\theta)-I^{k-1}(\theta)\big)\\[2mm] \label{line_b_abs} I^{i,b}_{k,{\rm abs}}(\theta) & = & \frac{\kappa^b_k}{\kappa^a_k+\kappa^c_k+\kappa^c_k}\big(I^k(\theta)-I^{k-1}(\theta)\big)\\[2mm] \label{line_c_abs} I^{i,{\rm c}}_{k,{\rm abs}}(\theta) & = & \frac{\kappa^c_k}{\kappa^a_k+\kappa^b_k+\kappa^c_k}\big(I^k(\theta)-I^{k-1}(\theta)\big).\\\nonumber \end{eqnarray}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq279.png) By summing over the index k in the Eqs. (B.24)–(B.26) we obtain the flux absorbed by the lines a, b, and c. The contribution function of the ith layer can be therefore written as
By summing over the index k in the Eqs. (B.24)–(B.26) we obtain the flux absorbed by the lines a, b, and c. The contribution function of the ith layer can be therefore written as 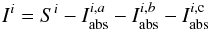 (B.27)where
(B.27)where ![\appendix \setcounter{section}{2} \begin{eqnarray} \nonumber I^{i,a}_{\rm abs} & = & \sum^{k=i}_{1} I^{i,a}_{k,{\rm abs}}(\theta)\\[2mm]\nonumber I^{i,b}_{\rm abs} & = & \sum^{k=i}_{1} I^{i,b}_{k,{\rm abs}}(\theta)\\[2mm]\nonumber I^{i,{\rm c}}_{\rm abs} & = & \sum^{k=i}_{1} I^{i,{\rm c}}_{k,{\rm abs}}(\theta).\\\nonumber \end{eqnarray}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq281.png) By summing over the i index in Eq. (B.27) we obtain the total flux at angle θ. To obtain the observed flux we must integrate from θ = 0 to θ = π/ 2.
By summing over the i index in Eq. (B.27) we obtain the total flux at angle θ. To obtain the observed flux we must integrate from θ = 0 to θ = π/ 2.
The quantities of the absorbed flux by the lines a, b, and the continuum c are illustrated in Fig. B.1, where the logarithm of the normalized flux is shown. The gray, red, and light blue areas show the flux absorbed by the continuum, the OI line, and the FeI line, respectively.
This figure shows that by using the outlined way to compute the flux we can estimate how much flux has been individually absorbed by the lines in a blend. It is now clear why this solution is not helpful in constructing the EW library we need: while the classical EW refers to the flux absorbed by a line with respect to the level of the continuum measured in absence of the line, the absorbed flux obtained in Eq. (B.27) is absolute and is much larger than the EW because the continuum level and the emitted intensity change across the line.
Appendix C: The SP_Ace line profile
The shape of an absorption line is a function of many variables (such as stellar parameters, atomic parameters, chemical abundances, radial velocity of the atmosphere layers in which the line forms) which cannot be analytically expressed but only numerically computed through spectral synthesis. However, experience says that spectral lines can be fairly well described by a Voigt function, which is the convolution of a Lorentzian function with a Gaussian function. The Lorentzian FWHM (γL) rules the width of the wings, while the Gaussian FWHM (γG) rules the width of the core of the Voigt function. Lines with larger damping constants have broader wings than the ones with smaller damping constants, and the wings’ widths also vary with the gravity log g of the star. Besides, the wings of the line profile become broader (i.e., the ratios γL/γG become bigger) for larger EW23. Thus, the profile of an absorption line can be approximated with a Voigt function in which γL and γG depend on the instrumental FWHM, EW, and log g. To allow SP_Ace to handle the shape of the absorption lines, we adopted the Voigt function implementation given in McLean et al. (1994), modified to have the γG equal to the instrumental FWHM, while γL follows the empirical law ![\appendix \setcounter{section}{3} \begin{eqnarray*} \gamma_{\rm L}={\rm d}l\cdot EW\cdot {\rm d}p\cdot \left(1.-\exp\left[-\left(\frac{EW\cdot {\rm d}p}{\sigma}\right)^2\right]\right) \end{eqnarray*}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq285.png) where EW is the equivalent width of the line, dp is the “broadening” parameter (with dp> 0), and σ and dl are functions of log g as described as follows
where EW is the equivalent width of the line, dp is the “broadening” parameter (with dp> 0), and σ and dl are functions of log g as described as follows
![\appendix \setcounter{section}{3} \begin{eqnarray*} \left\{ \begin{array}{ll} \sigma=0.14, {\rm d}l=0.8 & \text{if}\quad \log g\,>\,4.5\\[4mm] \sigma=0.16, {\rm d}l=(0.7+(\log g-3.5)\cdot0.1) & \text{if}\quad 3.5\,<\,\log g\,\leq\,4.5\\[4mm] \sigma=0.20, {\rm d}l=(0.6+(\log g-2.5)\cdot0.1) & \text{if}\quad 2.5\,<\,\log g\,\leq\,3.5\\[4mm] \sigma=0.20, {\rm d}l=0.6 & \text{if}\quad 1.5\,<\,\log g\,\leq\,2.5\\[4mm] \sigma=0.20, {\rm d}l=(0.6+(1.5-\log g)\cdot0.1) & \text{if}\quad \log g\,<\,1.5\\ \end{array} \right. . \end{eqnarray*}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq289.png) The dp parameter has been empirically derived by hand for each line with a simple manual “trial-and-error” method24: the dp parameter is varied until the matches between the line profile in the spectra models constructed by SP_Ace and the line profile in five synthetic spectra of different stellar parameters was satisfactory.
The dp parameter has been empirically derived by hand for each line with a simple manual “trial-and-error” method24: the dp parameter is varied until the matches between the line profile in the spectra models constructed by SP_Ace and the line profile in five synthetic spectra of different stellar parameters was satisfactory.
This empirical implementation of the line profile is satisfactory in most of the stellar parameters here considered. However, progressive deviation from the correct line profile is observed at Teff < 5000 K, which causes systematic errors (this is shown in tests with synthetic and real spectra in Sect. 8). The mismatch between the SP_Ace and the synthetic/real line profiles can be reduced with a new improved line profile law that will be implemented in one of the future releases of SP_Ace.
We here want to shortly discuss how the adopted line profile affects the performance of SP_Ace as a function of the spectral resolution. At low resolution the observed line profile is dominated by the instrumental profile, which is symmetric and constant for all the absorption lines. This characteristic makes the observed line profile easy to model. The higher the resolution, the more the physical profile of the lines dominates over the instrumental profile, making the observed profile difficult to model because, depending on the absorption line considered, the line can be asymmetric or deviate from the adopted Voigt function. Therefore, the line profile adopted by us matches at best the observed line profile at low resolution (where the instrumental profile dominates) and progressively loses accuracy at higher resolution. We verified that the accuracy of SP_Ace in reproducing the observed line profile is satisfactory up to R ~ 20 000. For higher resolutions the SP_Ace line profile may still be satisfactory for most of the absorption lines, but the robustness of the results has not been proved with extensive tests yet.
Appendix D: Tests on real spectra
We report here the tables and the figures of the stellar parameters and chemical abundances derived with SP_Ace of the stellar spectra ELODIE, benchmark, and S4N degraded to R = 12 000 and S/N = 100.
Stellar parameters and chemical abundances obtained with SP_Ace from the ELODIE stars.
Stellar parameters and chemical abundances obtained with SP_Ace from the benchmark stars.
Stellar parameters and chemical abundances obtained with SP_Ace from the S4N stars.
 |
Fig. D.1 Top: distribution of the reference Teff and log g of real spectra (top-left panel) and the ones derived by SP_Ace (top-right panel). Middle: residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). Bottom: chemical abundances derived by SP_Ace for the same spectra. These spectra have a resolution of R = 2000 and S/N/pixel = 100. The symbols are as in Fig. 23. |
 |
Fig. D.4 As in Fig. D.1 but for 1386 ELODIE spectra (out of the total 1959 spectra of the whole ELODIE database) measured at R = 12 000 and S/N/pixel = 100. In this case all reference parameters are considered without quality criteria selection. |
All Tables
Effective temperature (K), gravity, metallicity (dex), micro- and macroturbulence (in km s-1) adopted to synthesize the spectra of the standard stars.
Instrumental FWHMs adopted for the synthetic spectra in the four wavelength ranges.
Qualitative match of the wings of some intense lines between the synthetic and the observed ones.
Ages, iron abundance ranges, and coefficients m and q of the linear law [El/Fe] = m· [Fe/H] + q that expresses the chemical abundances used to synthesize the spectra of the three mock stellar populations.
Stellar parameters and chemical abundances obtained with SP_Ace from the ELODIE stars.
Stellar parameters and chemical abundances obtained with SP_Ace from the benchmark stars.
Stellar parameters and chemical abundances obtained with SP_Ace from the S4N stars.
All Figures
 |
Fig. 1 Distributions of the NEWRs of the elements Fe (gray points) and Ti (black points) as a function of their EW for the five stars before the beginning of the calibration routine. |
| In the text | |
 |
Fig. 2 As in Fig. 1 but after 100 iterations of the log gf calibration routine. |
| In the text | |
 |
Fig. 3 As in Fig. 1 but at the final stage, after many iterations of the calibration routine and properly adjusted abundances. |
| In the text | |
 |
Fig. 4 Gray thick lines: observed spectra. Dotted lines: synthesized spectra with VALD log gfs but final abundances. Black lines: synthetic spectra with calibrated log gfs and final abundances. |
| In the text | |
 |
Fig. 5 NEWR distributions for the Fe lines in Arcturus (top panels) and the Sun (bottom panels) using microturbulences ξ that differ by 0.4 km s-1. Here we use Fe lines with isolation degree parameter iso> 0.99 (i.e., these Fe lines are isolated). |
| In the text | |
 |
Fig. 6 Right: comparison between the VALD and our calibrated log gfs. Black and gray points represent atomic and molecular CN lines, respectively. Left: comparison between the NIST and our log gfs values for those lines with NIST log gf precision better than 10%. Only lines having EW> 5 mÅ in the solar spectrum are reported here. The offsets and standard deviations are computed as “calibrated minus reference” after rejecting the outliers (crossed points) with a 3σ clipping. |
| In the text | |
 |
Fig. 7 Normalized spectra of the Sun (black line) and 61CygA (gray line). The “plus” symbols indicate the positions of the atomic lines. |
| In the text | |
 |
Fig. 8 Comparison between the synthetic spectrum with stellar parameters Teff = 4200 K, log g = 1.4, and [M/H] = 0.0 dex (the black solid line) and the corrispondent spectrum model (the gray solid line) constructed by SP_Ace using the EWs corrected for the opacity of the neighbor lines as described in Sect. 5.3. The dotted line is the spectrum model constructed using the EW of the lines computed as if they were isolated (i.e., no correction for the opacity of the neighbor lines). Plus, cross, and triangle symbols indicate the position of the Fe , V , and Ni lines, respectively. |
| In the text | |
 |
Fig. 9 Emerging (synthetic) fluxes obtained when opacities of the continuum and the line are accounted separately. The gray solid line is the synthetic spectrum of the line Fe i at 8446.388 Å, i.e. the emerging flux when the line and continuum opacities are accounted for. The black solid line represents the emerging flux when the emissions alone are accounted for. The dotted line is the level of the continuum when the continuum opacity alone is accounted for. The dashed line is the level of the continuum across the line when both line and continuum opacities are accounted for. The y-axis is expressed as logarithm (base 10) of the normalized flux. |
| In the text | |
 |
Fig. 10 Two dimensional section of the General COG of the Fe i line at 5445.042 Å as a function of Teff and log g. The [M/H] and Fe abundance has been fixed at 0.0 dex. |
| In the text | |
 |
Fig. 11 One dimensional sections of the GCOGs of several absorption lines in the range 5212–5222 Å as a function of Teff, log g, [M/H], and abundance [El/M]. The three (out of four) fixed stellar parameters are reported in the panels. The gray points connected with gray lines represent the EWi,cs of the lines. The black lines are one dimensional sections of the polynomials GCOGs of the same absorption lines. |
| In the text | |
 |
Fig. 12 Grey points: residuals between the EW given by the polynomial GCOG and the EW of the library as a function of EW for 100 absorption lines (in the range 5212–5235 Å) at the grid point Teff = 4200 K, log g = 1.4 and [M/H] = 0.0 dex. Black points: as before but for the line Fe i at 5231.395 Å alone. The residuals are normalized for the EW so that the values in the y-axis and the statistic in the panel express the errors of the polynomial GCOG normalized to the expected EW. |
| In the text | |
 |
Fig. 13 Synthetic spectrum with the stellar parameters Teff = 4212 K, log g = 1.8, [M/H] = 0.0 dex, and S/N = 100 at resolution R = 20 000 (top) and R = 5000 (bottom). The black line is the correctly normalized spectrum (synthesized by MOOG and noise added), while the dashed line is the same spectrum after normalization with the task continuum of IRAF. |
| In the text | |
 |
Fig. 14 Comparison between the IRAF and SP_Ace normalization. Top: solid and dashed black lines are as in bottom panel of Fig. 13. The gray line was obtained by processing the dashed line (IRAF normalized spectrum) with the SP_Ace re-normalization routine. Bottom: residuals between the IRAF normalized (dashed line) and SP_Ace normalized (gray line) spectra with respect to the correctly normalized spectrum. |
| In the text | |
 |
Fig. 15 Comparison between spectra models and the corrispondent synthetic spectra. The black lines are synthetic spectra of a cool giants stars (bottom panel) and a warm dwarf stars (middle panel) with stellar parameters as reported in the panels. The overplotted colored lines represent the spectrum models constructed by SP_Ace for the corrispondent giant (red line) and dwarf (blue line) star. The shaded areas indicate the wavelength ranges rejected during the SP_Ace analysis (see text for more details). The residuals (model minus synthetic spectra) are reported in the top panel, together with the standard deviation of the residuals for the dwarf and giants spectra (in blue and red colors, respectively) after the exclusion of the gray shaded areas. |
| In the text | |
 |
Fig. 16 Distribution of the three mock populations on the Teff and log g plane as synthesized (left panels) and derived by SP_Ace (right panel). The blue points, red crosses, and green triangles represent the thin, halo/thick disc, and accreted stars, respectively. The solid, dashed, and dotted black lines show isochrones at [M/H] = 0.0 dex and 5 Gyr, [M/H] = −1.0 dex and 10 Gyr, and [M/H] = −2.0 dex and 10 Gyr, respectively. The light gray errorbars represent the confidence intervals of the individual measurements. A missing errorbar indicates that the error is larger than the parameter grid. |
| In the text | |
 |
Fig. 17 Residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). Symbols and colors are as in Fig. 16. |
| In the text | |
 |
Fig. 18 Chemical abundances derived by SP_Ace for the three mock populations. Symbols and colors are as in Fig. 16. The reference abundances of these three populations are represented by the light blue, light red, and light green solid lines for the thin disc, the halo/thick disc, and accreted populations, respectively. |
| In the text | |
 |
Fig. 19 Black symbols: standard deviations of the residuals of the stellar parameters (expressed as estimated minus reference values) as a function of S/N for the four different resolutions considered here. Grey symbols: as the black symbols but the y-axis expresses the average semi-width of the estimated confidence interval. The black and gray symbols would match if the error distributions were Gaussian and there were no systematic errors. |
| In the text | |
 |
Fig. 20 Distributions of the derived stellar parameters (black solid histogram), and the lower and upper limits of the confidence intervals (dotted-dashed red histogram and thick dashed green histogram, respectively) as computed in Sect. 7.6 for 100 Monte Carlo realizations of the synthetic spectrum with Teff = 4538 K, log g = 2.42, [Fe/H] = 0.30 dex, S/N = 100, and R = 12 000. The black point represents the median of the derived stellar parameters while the errorbars show the lower and upper limit of the interval that holds the 68% of the measurements. The vertical dashed lines represent the reference values. |
| In the text | |
 |
Fig. 21 As in Fig. 20 but for the elemental abundances of Mg , Ca , and Cr . |
| In the text | |
 |
Fig. 22 Left panel: distribution of the reference stellar parameters in the Teff and log g plane for the ELODIE library (solid points), the benchmark stars (crosses), and the S4N stars (triangles). Right panel: as before but with the stellar parameters derived by SP_Ace. The colors code the [Fe/H]. Errorbars are reported in light gray. The solid, dashed, and dotted black lines trace the isochrones for [M/H] = 0.0 dex and 5 Gyr, [M/H] = −1.0 dex and 10 Gyr, and [M/H] = −2.0 dex and 10 Gyr, respectively. |
| In the text | |
 |
Fig. 23 Residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). ELODIE, benchmark, and S4N stars are indicated with black points, red crosses, and blue triangles, respectively. Errorbars are reported in light gray. A missing errorbar indicate that the error is larger than the parameters grid. |
| In the text | |
 |
Fig. 24 Chemical abundances derived by SP_Ace for the ELODIE, benchmark, and S4N stars. Symbols are as in Fig. 23. |
| In the text | |
 |
Fig. 25 Comparison between derived and reference chemical abundances of seven elements for the S4N spectra. Points marked with crosses have been excluded by the statistic reported in the panels. |
| In the text | |
 |
Fig. 26 Standard deviations of the residuals of the stellar parameters derived from real spectra as a function of S/N for the fourth different resolutions considered. |
| In the text | |
 |
Fig. 27 Residuals between derived and reference log g for real spectra (top) and synthetic spectra (bottom) when the long (left panels) and short (right panels) versions of SP_Ace are used to derive the stellar parameters. The symbols are as in Figs. 23 and 16 for real and synthetic spectra, respectively. |
| In the text | |
 |
Fig. A.1 Left: distribution on the (Teff,log g) plane of the stars employed to determine the microturbulence function. Right: polynomial function adopted to represent the microturbulence ξ. For both panels the value of ξ is given by the color bar on the right. |
| In the text | |
 |
Fig. A.2 Reference microturbulence (top) and residuals (bottom) between reference (ξ) and polynomial microturbulence (ξpoly) as a function of Teff. The colors code the gravity log g as given by the color bar on the right. |
| In the text | |
 |
Fig. B.1 Left panel: the black solid line represents the Fe i line at 8446.338 Å synthesized as isolated line, i.e., the emerging flux when the line and continuum absorptions are accounted for. The dashed line represent the flux in presence of the line when the continuum absorption alone is accounted for. The dotted line represent the emerging flux when the emissions alone are accounted for. The gray area represents the flux absorbed by the continuum, while the light blue area is the flux absorbed by the line. Right panel: as in the left panel, but for the two blended lines OI and FeI lines at 8446.359 Å and 8446.338 Å, respectively. The flux absorbed by the continuum and the Fe line are still represented by the gray and light blue areas, respectively, while for the OI line the absorbed flux is the red area. The y-axis represents the logarithm (base 10) of the normalized flux. |
| In the text | |
 |
Fig. D.1 Top: distribution of the reference Teff and log g of real spectra (top-left panel) and the ones derived by SP_Ace (top-right panel). Middle: residuals between derived and reference parameters (y-axis) as a function of the reference parameters (x-axis). Bottom: chemical abundances derived by SP_Ace for the same spectra. These spectra have a resolution of R = 2000 and S/N/pixel = 100. The symbols are as in Fig. 23. |
| In the text | |
 |
Fig. D.2 As in Fig. D.1 but for R = 5000 and S/N/pixel = 100. |
| In the text | |
 |
Fig. D.3 As in Fig. D.1 but for R = 20 000 and S/N/pixel = 100. |
| In the text | |
 |
Fig. D.4 As in Fig. D.1 but for 1386 ELODIE spectra (out of the total 1959 spectra of the whole ELODIE database) measured at R = 12 000 and S/N/pixel = 100. In this case all reference parameters are considered without quality criteria selection. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



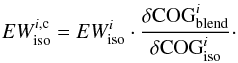
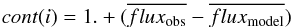
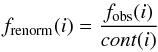
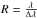
![\hbox{$\textrm{[El/H]}\,=\,\log\frac{N(\textrm{El})}{N(\textrm{H})}-\log\frac{N(\textrm{El})_{\odot}}{N(\textrm{H})_{\odot}}$}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq297.png)
![\hbox{$\log[\epsilon(\textrm{Fe})]=\log\frac{N(\textrm{Fe})}{N(\textrm{H})}+12$}](/articles/aa/full_html/2016/03/aa26758-15/aa26758-15-eq298.png)