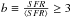| Issue |
A&A
Volume 587, March 2016
|
|
|---|---|---|
| Article Number | A72 | |
| Number of page(s) | 29 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201525692 | |
| Published online | 19 February 2016 | |
Local starburst galaxies and their descendants
Statistics from the Sloan Digital Sky Survey
1 Department of Physics and Astronomy, Uppsala University, Box 515, 751 20 Uppsala, Sweden
e-mail: nils.bergvall@astro.uu.se
2 NASA Goddard Institute for Space Studies, 2880 Broadway, New York, 10029, USA
3 Department of Astronomy, Stockholm University, 106 91 Stockholm, Sweden
Received: 20 January 2015
Accepted: 17 November 2015
Aims. Despite strong interest in the starburst phenomenon in extragalactic astronomy, the concept remains ill-defined. Here we use a strict definition of starburst to examine the statistical properties of starburst galaxies in the local universe. We also seek to establish links between starburst galaxies, post-starburst (hereafter postburst) galaxies, and active galaxies.
Methods. Data were selected from the Sloan Digital Sky Survey DR7. We applied a novel method of treating dust attenuation and derive star formation rates, ages, and stellar masses assuming a two-component stellar population model. Dynamical masses are calculated from the width of the Hα line. These masses agree excellently with the photometric masses. The mass (gas+stars) range is ~109–1011.5ℳ⊙. As a selection criterion for starburst galaxies, we use, the birthrate parameter, b = SFR/ ⟨ SFR ⟩, requiring that b ≥ 3. For postburst galaxies, we use, the equivalent width of Hδ in absorption with the criterion EWHδ,abs ≥ 6 Å.
Results. We find that only 1% of star-forming galaxies are starburst galaxies. They contribute 3−6% to the stellar production and are therefore unimportant for the local star formation activity. The median starburst age is 70 Myr roughly independent of mass, indicating that star formation is mainly regulated by local feedback processes. The b-parameter strongly depends on burst age. Values close to b = 60 are found at ages ~10 Myr, while almost no starbursts are found at ages >1 Gyr. The median baryonic burst mass fraction of sub-L∗ galaxies is 5% and decreases slowly towards high masses. The median mass fraction of the recent burst in the postburst sample is 5−10%. A smaller fraction of the postburst galaxies, however, originates in non-bursting galaxies. The age-mass distribution of the postburst progenitors (with mass fractions >3%) is bimodal with a break at logℳ(ℳ⊙) ~ 10.6, above which the ages are doubled. The starburst and postburst luminosity functions (LFs) follow each other closely until Mr ~ −21, when active galactic nuclei (AGNs) begin to dominate. The postburst LF continues to follow the AGN LF, while starbursts become less significant. This suggests that the number of luminous starbursts is underestimated by about one dex at high luminosities, because of having large amounts of dust and/or being outshone by an AGN. It also indicates that the starburst phase preceded the AGN phase. Finally, we look at the conditions for global gas outflow caused by stellar feedback and find that massive starburst galaxies are susceptible to such outflows.
Key words: galaxies: evolution / galaxies: luminosity function, mass function / galaxies: starburst / galaxies: star formation / galaxies: statistics / galaxies: stellar content
© ESO, 2016
1. Introduction
The starburst concept was established about three decades ago (Rieke et al. 1980; Weedman et al. 1981). Originally it concerned nuclear starbursts, but later, in connection to the results from objective-prism surveys, a starburst galaxy came to refer to global starbursts in sub-L∗ galaxies. Today, one paper per day or 5% of all extragalactic papers in refereed journals contain the word starburst in the abstract. However, despite this seemingly very familiar concept, we still lack a commonly accepted definition of what a starburst is. This is a bit worrisome since starbursts are associated with several important processes in the evolution of a galaxy. Among these are the ignition of activity in active galactic nuclei (AGNs) (Sanders et al. 1988; Kauffmann et al. 2003a; Knapen 2004), an intense production of super star clusters (O’Connell et al. 1994, 1995; Meurer et al. 1995; Ho & Filippenko 1996; de Grijs et al. 2003; Adamo et al. 2010) and morphological transformations due to rapid gas consumption and stellar and/or AGN driven global superwinds (Chevalier & Clegg 1985; Heckman et al. 1990; Springel et al. 2005; Scannapieco et al. 2005; Bik et al. 2015). It has been suggested that starburst galaxies are also responsible for opening channels for Lyman continuum radiation to leak out and contribute to the cosmic reionisation at redshifts below z ~ 11 (e.g. Miralda-Escude & Ostriker 1990; Songaila et al. 1990; Madau 1991; Heckman et al. 2011).
There is a problem, however, in the sense that inconsistencies in the definition of a starburst have led to considerable confusion in the field. For example, at low redshifts a high Hα emission line equivalent width, and at high redshift a high star formation rate (SFR) are often taken as evidence for starbursts, although this is not necessarily the case (see below and Noeske et al. 2007; Elbaz et al. 2007; Daddi et al. 2007, 2010). This problem can only be remedied by applying more accurate constraints on the definition of starbursts. The present investigation adds to several previous efforts by other groups (e.g. Kauffmann et al. 2003b; Brinchmann et al. 2004; Kim et al. 2006; Obrić et al. 2006; Barazza et al. 2006; Li et al. 2008; Knapen & James 2009; Lee et al. 2009b; Scudder et al. 2012) to investigate the galaxy content in the local universe and derive a more consistent view on starbursts from various aspects. Here we formulate our favoured definition of a starburst that we then apply to galaxies in the Sloan Digital Sky Survey (SDSS). Our definition is similar to that used in other studies but differs mainly in the way we apply it to the data. Throughout this paper we assume ΩΛ = 0.7,Ωm = 0.3 and h = 0.7.
The main objectives of the present investigation are to:
-
1.
identify starburst and post-starburst (hereafter called postburst) galaxies and derive their luminosity functions (LFs);
-
2.
derive lifetimes of the bursts and masses of the burst and host components;
-
3.
examine the evolutionary link between starburst and postburst galaxies;
-
4.
have a closer look at the relation between starburst galaxies and galaxies with AGNs.
2. Sample selection
Our study concerns the statistical properties of starburst and postburst galaxies selected from the SDSS data release No. 7 (DR7). Most of the galaxies are at low redshifts, z < 0.15. Below we describe the selection criteria, the spectral modelling, and its limitations, as well as potential problems with biases and aperture effects.
2.1. Defining a starburst
We begin this discussion with an effort to lay down a definition of a starburst that can be used to quantitatively investigate its impact on galaxy evolution. How to define a starburst has been widely discussed over the years (see e.g. Knapen & James 2009, and references therein). Firstly, starbursts have high star formation efficiencies and consume their fuel faster than normal galaxies (see e.g. Kennicutt 1998). Therefore, to qualify as a starburst, the global gas consumption time scale has to be significantly shorter than a Hubble time. This requirement is generally accepted by the astronomical community. The problem appears in the next step. Imagine an evolved galaxy with very low gas content. Even if this gas is consumed in star formation during a short period, we would hardly regard it as a starburst galaxy unless it was not spectacular in some sense. Therefore, in the definition of starburst galaxies, we must also raise the question of the importance of starbursts for the evolution of a galaxy. It may be a fairly simple procedure to derive the SFR and find out if it is extreme enough to qualify as a starburst, but what we also want to know from a galaxy evolutionary aspect, is how much gas is consumed during the starburst phase and if the starburst is powerful enough to produce a massive blowout of the gas in the central regions. This information cannot be obtained from one parameter, and we explain below how we chose to work on this problem.
A starburst leads to an increase in the SFR that is significantly higher than the mean past SFR. From the literature we find that there are strongly different opinions about what this means. To make our way of reasoning clear, we make an effort to classify different starburst phenomena from our point of view:
-
If star formation in a galaxy is significantly (at least a factor of three) higher than in the past, we call the phenomenon a global starburst.
-
If the increased star formation activity affects a local region of the galaxy with a size less than a few 100 pc, such as in 30 Dor of the LMC, we call it a local starburst region.
-
A special type of starburst occurs in the centres of more massive galaxies, typically with baryon masses exceeding 1010ℳ⊙. This type of starburst is called a nuclear starburst, or sometimes a circumnuclear starburst (Balzano & Weedman 1981; Balzano 1983). It is restricted to a region in the centre with a size of <1 kpc and is thought to be triggered by accretion of inflowing gas driven by bars or non-axisymmetries in the disc (Combes 2014). A prototype of such a galaxy is NGC 7714 (Weedman et al. 1981).
The character of the starburst also changes with galaxy mass. It has become evident that global starbursts in massive galaxies are rare. Starbursts in these galaxies are almost exclusively of the nuclear starburst type and involve a moderate amount of the total gas mass. Exceptions are the LIRGs and ULIRGs. The high dust obscuration of the latter makes it difficult to conclude if these galaxies are powered by starbursts or AGNs without supplementing the optical observations with observations in other wavelength bands. In some cases, however, (e.g. Downes & Solomon 1998), it can be concluded that strong starbursts are active in the central regions. As we go towards higher luminosities, the dominance of AGNs as the major power sources increases. However, we will argue below that AGNs and starbursts are always tightly connected.
The problem with applying corrections for dust obscuration in star-forming galaxies based on data from the optical region is that it increases continuously with mass, and gradually becomes severe. This is another reason why we focus our discussion on galaxies with luminosities around L∗ or fainter. We quantify the influence of dust as a function of mass below.
Here we refer to the outcome of what we call our model. This is described in more detail in Sect. 3.2. In our model we assume that there are two stellar populations – a burst population and an older host population. Among the properties we derive are the ages and masses of these two populations. The stellar population spectra used as input to the model were obtained from an in-house spectral evolutionary model (SEM) by Zackrisson et al. (2001). It has a stellar mass range of 0.08–120 ℳ⊙, adopts a Salpeter mass function and includes a nebular component based on CLOUDY (Ferland 1996; Ferland et al. 1998). Reliability issues related to the modelling are discussed in the Appendix.
To quantify the strength of the starburst we choose the often used birthrate parameter (Kennicutt 1983), 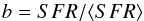 (1)i.e. the ratio between the present SFR and the mean SFR over the lifetime of the galaxy. This is our primary criterium to characterize the star formation activity. We call a galaxy with b ≥ 3 a starburst galaxy. The b-parameter should not be confused with the burst strength, b, defined by Larson & Tinsley (1978) which gives the ratio of the burst mass over the mass of the old population. This is an alternative characterization of a starburst and we discuss a similar parameter below, the burst mass fraction or burst strength, fburst = ℳburst/ ℳtot.
(1)i.e. the ratio between the present SFR and the mean SFR over the lifetime of the galaxy. This is our primary criterium to characterize the star formation activity. We call a galaxy with b ≥ 3 a starburst galaxy. The b-parameter should not be confused with the burst strength, b, defined by Larson & Tinsley (1978) which gives the ratio of the burst mass over the mass of the old population. This is an alternative characterization of a starburst and we discuss a similar parameter below, the burst mass fraction or burst strength, fburst = ℳburst/ ℳtot.
The SFR used to calculate the b-parameter is derived from the Hα flux. Using the relation obtained from Zackrisson et al. (2001), assuming a 20% solar metallicity and constant SFR, we can derive the SFR of a stellar population with a Salpeter initial mass function (IMF): 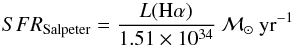 (2)where the Hα luminosity L(Hα), after correction for dust attenuation, is given in Watts. The SFR derived from this relation is 16% lower than what is obtained from Kennicutt (1998). We assume that our relation is valid for all galaxies, thereby disregarding metallicity dependence and possible fluctuations in the SFR which we consider to have marginal influence on the result.
(2)where the Hα luminosity L(Hα), after correction for dust attenuation, is given in Watts. The SFR derived from this relation is 16% lower than what is obtained from Kennicutt (1998). We assume that our relation is valid for all galaxies, thereby disregarding metallicity dependence and possible fluctuations in the SFR which we consider to have marginal influence on the result.
As was shown by Bell & de Jong (2001) and given more support by Schiminovich et al. (2007) and de Blok et al. (2008), spectrophotometric masses based on a pure Salpeter mass function results in a ℳ/L systematically higher than a ℳ/L based on maximum disc fits to galaxy rotation curves. The Kroupa IMF (Kroupa 2001) seems to give better agreement (de Blok et al. 2008). Therefore it was proposed to modify the results based on the Salpeter IMF by simply multiplying the derived masses by a factor of 0.7, corresponding to an IMF with a reduced number of stars below 0.35 ℳ⊙. As we show below in Sect. 4.2, this modification is also supported by our data. During the rest of the paper we adopt this so called diet Salpeter IMF as we calculate masses, ℳ/Lratios and SFRs: 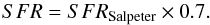 (3)The birthrate parameter is our main tool to define what a starburst galaxy is. A strong starburst in the classical sense would have
(3)The birthrate parameter is our main tool to define what a starburst galaxy is. A strong starburst in the classical sense would have 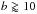 . Such cases exist in the local universe but are rare objects (see e.g. Östlin et al. 2001). Note that the more massive low-redshift starburst galaxies seem extremely rare. We only find one ULIRG within 100 Mpc–Arp 220. Within this volume we find of the order of one hundred thousand normal galaxies.
. Such cases exist in the local universe but are rare objects (see e.g. Östlin et al. 2001). Note that the more massive low-redshift starburst galaxies seem extremely rare. We only find one ULIRG within 100 Mpc–Arp 220. Within this volume we find of the order of one hundred thousand normal galaxies.
The starburst criterion we use here, b ≥ 3, was also discussed e.g. in the investigation of star-forming galaxies in the SDSS by Brinchmann et al. (2004) and also in Kauffmann et al. (2003b) in a study of descendants of starburst galaxies. A similar approach is found in the recent analysis of Herschel data (see below). We comment on their results in relation to ours below. In addition to the b-parameter we also discuss the mass fraction of the burst population, fburst. This parameter is closely related to the strength of the Hδ absorption lines in postburst galaxies which is discussed below.
2.2. Connecting starbursts with their postburst descendants
A few 107 years after a major starburst epoch has ceased, the ageing population of the starburst will produce a characteristic postburst spectral signature with strong Balmer lines in absorption. We use this signature to define our postburst sample. The only constraint we use here is that the equivalent width of Hδ in absorption is EWHδ<−6 Å, the negative sign indicating that we are dealing with an absorption line (henceforth we use this convention: negative sign means absorption line and positive sign means emission line). We want to point out however that this criterion does not guarantee that the progenitor was a starburst. A galaxy with a constant SFR and b ~ 1 lasting a few 100 Myr can also produce a postburst spectrum.
Figure 1 shows model predictions of the evolution of Hδ under two different star formation histories – an instantaneous burst (Fig. 1a) and a burst with constant SFR during 100 Myr (Fig. 1b). Here we use the models of Bruzual & Charlot (2003) that have a slightly better temporal resolution than our model. As we see in the diagram, the postburst epoch sets in quickly after the burst has ended and lasts about 1 Gyr, about 10 times as long as the typical starburst lifetime (see below).
 |
Fig. 1 EWHδ in absorption as function of burst age in two stellar populations of different star formation histories according to Bruzual & Charlot (2003). No nebular emission is included in the model. The upper diagram a) shows the evolution in a population that has experienced a short burst and in b) the SFR has been constant for 100 Myr before being abruptly shut down. The model results for three different metallicities, Z = 0.005 (dashed-dot blue), Z = 0.02 (solid green) and Z = 0.05 (dashed red) are shown. Our selection criterion for a post-starburst galaxy (EWHδ<−6 Å) is indicated with the horizontal yellow line. |
A subset of postburst galaxies are the so called E+A, k+a or a+k galaxies (Dressler & Gunn 1983; Dressler et al. 1999). These show strong Balmer lines in absorption but no [O ii]λ3727 or Hα in emission. In our postburst sample we accept the presence of [O ii] and Hα that reveal ongoing star formation, AGN activity or shock heating but with a much lower intensity than during the burst period.
In the work by Kauffmann et al. (2003b), the past star formation history of SDSS galaxies is investigated. As an indicator of the SF history, they use the strength of the 4000 Å break, D(4000), and the Hδ absorption line index. The indices are used to estimate the burst mass fraction during the last few Gyrs. Bayesian likelihood estimates are derived from Monte Carlo simulations. One of the results they obtain is that 95% of galaxies with EWHδ< ≈−6 Å should have experienced a burst of a strength fburst> 5% during the last 2 Gyr. Here we also use the Hδ criterion to select our postburst sample. However, when we look at the results from our analysis of the burst mass fraction in the postbursts, we end up with slightly different results from what Kauffmann et al. find. We find that the burst strength in more than 95% of the cases is fburst> 3% which is lower than the >5% they found in their studies. The result is displayed in Fig. 2. Two histograms are shown. One displays postburst galaxies with EWHδ<−6 Å (based on our remeasurements in Sect. 3.1) and the other is based on one additional criterion, the mean b-parameter over the burst period, ⟨ b ⟩, demanding that ⟨ b ⟩ ≥ 3. The mean b-parameter is difficult to derive for postbursts since we lack detailed information about the duration of the burst. We assume that, in the case of exponentially decaying bursts, the duration is equal to the timescale of the decay. With the b-parameter criterion active, the total number of galaxies in the diagram is reduced by about 10%. The median fburst of the postbursts is 6.6% and the histograms show a steep decline towards smaller fburst. At lower values the EWHδ criterion is invalidated. It is this limit that differs between our study and Kauffmann’s et al.. We discuss this problem in Sect. 5.
 |
Fig. 2 Mass fractions, fburst, derived for the postburst sample, both with and without the b> 3 criterion (red dashed line). The limit towards low mass fractions clearly show up as steep decline around fburst ~ 3%. About 95% of the galaxies in the larger sample have fburst ≥ 3%. |
We now look for criteria that will make it possible for us to identify the precursors of the postbursts. From our model we can obtain the equivalent width of Hα in emission (EWHα) as function of the duration of the burst. In Fig. 3 a we show how EWHα varies with the duration of the burst. It is important to be aware that the purpose of this diagram is not to show the evolution with time of EWHα but rather how the burst impacts the galaxy spectrum if we assume the same mass fraction but different durations of the burst, as given on the abscissa. Obviously the influence of the burst weakens with increasing duration and the b-parameter decreases linearly with the inverse of the duration of the burst. We look at two different burst mass fractions, fburst = 3% and fburst = 30%. In one case we assume that the burst is taking place in an old galaxy formed in a single burst (age ~14 Gyr) and in the other case we assume that the burst is taking place in a galaxy which has had a constant SFR over its lifetime. We can see from Fig. 3 that if we assume that the minimum burst mass of a postburst galaxy is 3%, the starburst cannot be older than 100 Myr. There may be younger galaxies that qualify as starbursts from the b–parameter criterion (the shaded area in the diagram), but they will not show up as postbursts since fburst< 3%.
From a semantic aspect we find it proper to say that to qualify as a burst, the duration of the SF epoch should not be longer than ~1 Gyr. From Fig. 3 we see that for a duration of 1 Gyr and b = 3, the mass fraction is 30% and EWHα is =150 Å. Thus, a minimum (but not sufficient) requirement to qualify as a starburst is that EWHα> 150 Å. A galaxy with continuous SFR over the age of the universe has EWHα~ 100 Å. In many studies of starbursts based on EWHα, the lower limit is often chosen to be 100 Å. Does this mean that a large portion of the galaxies in those studies should be disqualified as starbursts? It depends. As we argue below, the concept of age dependent dust attenuation will lead to a reduction of the observed strength of Hα but also the equivalent width. We estimate the maximum reduction to be a factor 2–3 (assuming a dust attenuation in the V band AV ≲ 1.5m for ages ≥ a few Myr). Thus in order to be on the safe side, one should examine all galaxies with EWHα above 150 Å divided by this factor. Here we have chosen our selection criterion to be EWHα> 60 Å. From this potential starburst sample we then select the final sample by applying the b> 3 criterion.
 |
Fig. 3 Upper diagrams: our model predictions of EWHα,em as function of the duration of the burst when 3 and 30% of the total mass is formed during a burst with constant SFR. Two different scenarios are displayed: 1) a burst in an old galaxy where the stars were formed in a single burst (hatched line); and 2) a burst in a galaxy which has had a constant SFR over a Hubble time (solid line). Lower diagrams: the evolution of the b-parameter. The limit of our criterion of a starburst, the soft criterion, stating that |
2.3. AGNs
As we go towards higher luminosities the importance of AGNs in combination with centrally concentrated star formation increases. Statistically (see Fig. 19), AGN dominated galaxies (with EWHα> 60 Å) occur as frequently as starbursts at Mr ~ –21. If the energy production in the central region is dominated by AGN activity it will be difficult to derive information about the possible presence of a starburst. However, if we can properly link starbursts with postbursts, we have an opportunity to statistically determine how frequently starbursts occur in active galaxies of different luminosities by using postbursts as indicators of preceding bursts.
Here we first look at the LFs of three types – starbursts, postbursts and AGNs. To identify AGNs we used two criteria – 1) the FWHM of the Hα emission line and 2) the position of a galaxy in the BPT diagram (Baldwin et al. 1981). Kauffmann et al. (2003a) derived an equation that separates star-forming galaxies from composite (thermal+non-thermal) and active galaxies in the upper part of the BPT diagram. The line ratios given in the diagram are based on line peak intensities instead of fluxes. The consequence will be that the AGNs will be shifted slightly upwards towards the right, thus increasing the separation between starbursts and AGNs. This allows us to shift the demarcation line slightly in the same direction. Thus, as the second criterion we have used a modified version of the relation given by Kauffmann et al. Figure 4 shows how our criteria separates pure starbursts from active and composite galaxies. Notice that some green dots (AGN) fall in the region below the demarcation line. These are galaxies fulfilling the second AGN criterion based on the Balmer line width.The galaxies were selected from the same sample as the starburst galaxies, i.e. all have EWHα> 60 Å. We summarize the criteria quantitatively in the next section.
2.4. Summary of selection criteria
Here we present the final selection criteria for the spectral types we wish to work with. The data were collected from SDSS DR7 (Abazajian et al. 2009). Three samples were created – a starburst sample, a postburst sample and an AGN sample. Selecting an AGN sample is motivated by the need to take into account the mixture of AGN and starbursts. In addition to the spectral criteria we also chose a redshift range of 0.02 ≤ z ≤ 0.4. The limiting magnitude of SDSS main sample spectroscopic data is Mr = 17.77 (Strauss et al. 2002) but the recommended magnitude limit for statistical studies is Mr ~ 17.51. We use the 17.5 limit when we derive the LF (see below), otherwise we use the 17.77 limit. At a redshift of z = 0.4 an apparent magnitude of 17.5 corresponds to an absolute magnitude of Mr = −24. At this luminosity it will be difficult to separate starbursts from AGNs so we chose z = 0.4 as an upper limit for our purpose. The lower limit was chosen to reduce the problems with deviations from the Hubble flow with the corresponding negative impact on the determination of absolute luminosities from the Hubble law and secondly, aperture biases, discussed in the next subsection.
Our selection criteria can be summarised as follows:
-
0.02 <z< 0.4
-
◊
Starburst candidates. All four criteria below have to be fulfilled:
-
.
EWHα≥ 60 Å
-
.
FWHMHα,em ≤ 540 km s-1
-
.
log([O iii]λ5007/Hβ) < 0.71/log([N ii]λ6584/Hα–0.25)+1.25
-
.
-
◊
Postburst candidates
-
.
EWHδ≤−6 Å
-
.
-
◊
AGNs.
-
.
EWHα≥ 60 Å and at least one of the following criteria:
-
.
FWHMHα,em > 540 km s-1
-
.
log([O iii]λ5007/Hβ) ≥ 0.71/log([N ii]λ6584/Hα–0.25)+1.25
-
.
-
◊
The total number of starburst candidates brighter than Mr = 17.77 (after correction for galactic extinction) is 9167. At a limiting magnitude of Mr = 17.5 we count 6368 galaxies. The number of starburst galaxies brighter than Mr = 17.77 with b > 3 is 1743 and the number with fburst > 3% (no restriction on b) is 3215. The number of postburst candidates is 7067. After remeasurement (cf. Sect. 3.1) of the Hδ line in absorption, the number drops to 4032. This is the sample we call postburst galaxies. Of these, 3804 galaxies have fburst > 3%. The number of AGNs is 2701.
 |
Fig. 4 BPT (Baldwin et al. 1981) diagram of the EWHα≥ 60 Å starburst galaxy candidate sample based on line peak intensity ratios. The solid red line is the empirical dividing line (a modified version of the equation given by Kauffmann et al. (2003a) shown in hatched green) between starburst galaxies (lower part, grey symbols) and galaxies containing an AGN contributing significantly to the flux in the strong emission lines (upper part, green dots). As a complementary AGN criterion we also used FWHM(Hαem) > 540 km s-1. |
 |
Fig. 5 Redshift distributions of the galaxies in the starburst and postburst samples. |
In the present investigation we only use spectral information from the central 3″ (in most cases) of the target galaxies (the diameter of the SDSS spectroscopic fiber aperture). Most of our objects are at low redshift. Figure 5 shows a histogram of the redshifts in the starburst and postburst samples. At z = 0.02 the aperture diameter will be 1.2 kpc and at the median redshift of the starburst population (b > 3), z = 0.07, the aperture is 4 kpc. At the maximum redshift we will explore (z ~ 0.3), the aperture corresponds to a size of about 13 kpc. The typical scale lengths of luminous starburst galaxies is 2–3 kpc. The effective radius is about 70% of this, i.e ≈2 kpc. As we show in Sect. 3.4, more than 50% of the light is within the aperture in about 25% of the galaxies in the starburst candidate sample, and a slightly larger fraction in the finally selected starburst sample. At higher luminosities we are more restricted to nuclear starbursts. In Sect. 3.4 we have a look at systematic trends with redshift that can be caused by aperture effects and decide whether we need to correct for such potential problems.
2.5. The data retrieval
To put these selection criteria into practice, we ran queries on the CasJobs interface of SDSS DR72, first selecting the Object-IDs and corresponding SpecObjIDs that connect the photometry tables with the spectroscopic data. In order not to skew the redshift distribution between starburst and postburst candidates, we chose only galaxies from the main galaxy sample (Strauss et al. 2002), excluding for example the Luminous Red Galaxy sample (Eisenstein et al. 2001) which would have played mainly into the postburst sample. We also set the flag to avoid blended objects and required the confidence of the redshift–determination to be >95%. Using the selected IDs, we retrieved the different photometric and spectroscopic measurements from the SDSS tables as needed and mentioned in the appropriate context below. We also downloaded the corresponding SDSS spectra as FITS files for the targets which we de-reddened and used for the model fits.
This is an example of a starburst candidate query used:
SELECT g.objID, s.specObjID FROM Galaxy g, SpecObj s, SpecLine Ha WHERE g.objID = s.bestObjID AND Ha.specObjID = s.specObjID AND Ha.LineID = 6565 AND Ha.ew>60 AND s.zConf > 0.95 AND s.z BETWEEN 0.02 AND 0.4 AND ((g.flags & 8)==0) AND (s.primtarget & 64>0)
3. Spectral analysis
3.1. Remeasuring spectral lines
When we analysed the SDSS spectra we found a problem with the SDSS derived values of the equivalent widths of Hδ in absorption. In many cases the Hδ line was misidentified or there were problems with the continuum fit. We therefore remeasured the Balmer lines listed in Table 1. We did this by defining a relatively line free region on both sides of the line. Then we calculated the mean fluxes of these regions and interpolated linearly between these across the line region to define the continuum level. In Table 1 we list the spectral windows used.
Line data.
Figure 6 shows how our measurement of EWHα in emission correlates with the data from SDSS. The agreement is good, with a trend for the SDSS values to be slightly larger (<20%). However, the correlation between EWHδ in absorption is much worse as is seen from Fig. 7. The SDSS data contains many large negative values, inconsistent with properties of a normal stellar population. In Fig. 8 we plot EWHδ versus EWHγ from our remeasured data in both cases. We see a broad distribution with a clear correlation, indicating that the data are reliable, albeit with a strong noise component, mainly from the Hγ line.
 |
Fig. 6 Hα emission line equivalent widths of our target galaxies as derived from our measurements, versus the value as obtained from the SDSS. |
 |
Fig. 7 Hδ absorption line equivalent widths of our target galaxies as derived from our measurements, versus the value as obtained from the SDSS. |
 |
Fig. 8 Hδ and Hγ absorption line equivalent widths after our remeasuring. |
3.2. Spectral modelling
In our modelling of the SDSS spectra it was assumed that the stellar population has two components – a young and an old population. The young component may have a range of ages, from 0 to 10 Gyr while the old component has a fixed age of 10 Gyr. We chose this age to agree with the cosmic lookback time at peak cosmic SFR (Hopkins & Beacom 2006). Observations of local dwarf galaxies also support the formation of most of the stars at z> 1 (Weisz et al. 2011; Zhao et al. 2011). In the first tests of the model we also had a look at cases where the old population had a declining SFR over various timescales. In the mean, however, the best fits were obtained with models assuming that the old population formed over a short period of time ≲100 Myr.
In the modelling, the programme steps through the spectral library of the young population with increasing age. At each step the young population is mixed with the old in various proportions, each time making the mix the most optimum one to agree with the observations. We have not used the nebular emission lines since the relative strengths depend strongly on the ionisation parameter, the density of the ionised gas, the filling factor and the metallicity (e.g. Osterbrock 1989; McGaugh 1991; Dopita et al. 2000; Charlot & Longhetti 2001). Therefore we have masked the strong emission lines hence the fit is more or less based on the pure stellar spectrum. Since the density of emission lines are strongest in the blue region of the spectrum we have, when we do the spectral fit, given the continuum double weight in the wavelength region 3800−4800 Å. The programme chooses the solution that gives the lowest χ2 of the different fits. We have tested various combinations of models that have different star formation histories and metallicities and decided to use the restricted number of model parameters given in Table 2. The table contains the Mode parameter. The Mode can be either a constant SFR over a time period given by τ or an exponentially declining SFR according to SFR ∝ e− t/τ, where t is the age. Our preliminary tests favour an exponentially declining SFR instead of a constant rate. An exponentially declining SFR is also supported by models (Di Matteo et al. 2007; but see also Hopkins & Hernquist 2010 who propose a power law at the end of the burst). Each track starts at an age of 0.5 Myr. The incremental time steps along each track were interpolated to a size of 0.04 dex.
Basic setup of model parameters used in the old/young mixture.
In the fit to the SDSS spectra we used two different approaches, one for the emission line galaxies and one for the postburst candidates, which we now describe.
3.2.1. Emission line galaxies
As an indicator of the amount of dust attenuation we derive the Hα/Hβ ratio from the SDSS spectrum. Then we step through the library of the model spectra from low to high ages. The library contains model spectra of ages increasing with 1 Myr between 0–20 Myr, 10 Myr between 20–150 Myr, 20 Myr between 150–250 Myr, 100 Myr between 250 Myr–1 Gyr and thereafter 1 Gyr. For each age there exists a set of reddened spectra with a range of values of the extinction coefficient. Each of these spectra is based on a sum of spectra of younger populations, assumed to have the same or higher dust opacity than the present population, as described in Sect. 3.3. For each time step we thus step through the library with increasing attenuation until we obtain a value of Hα/Hβ that corresponds to the observed value. We interpolate linearly among the spectra until we have obtained the best agreement. Once we have this value, we automatically get a value of the extinction in the old stellar component as we describe in Sect. 3.3. We then mix the reddened old and young model spectra so that EWHα agrees with the observed value. This is the final model spectrum for this particular age. We then step to the next age. When EWHα of the model spectrum is lower than the observed one, the process is stopped and the fit that gives the lowest χ2 is selected.
As an output from the model we obtain the age, relative mass and ℳ/Lof the burst population, the ℳ/Land relative mass of the old population (the age is always assumed to be 10 Gyr), the corrected Hα flux and the mean b-parameter. Having access to the distance to the galaxy we can also obtain masses and SFRs based on the corrected Hα luminosity. An example of the modelling is seen in Fig. 9.
 |
Fig. 9 An example of a model of a starburst spectrum (SDSS SpecObjId 81288133269782528). Displayed are the two model components – a young (blue line) and an old (red line) stellar population. The sum of the model spectra (dark green line) is shown on top of the observed spectrum (light green). The observed spectrum has been smoothed with a triangular filter with a width of 7 pixels. The shaded areas indicate regions we have flagged to avoid strong emission lines in the fits. Note however that EWHα,em is used as a separate criterion in the fitting. |
3.2.2. Postbursts
The postburst spectra are modelled by mixing a young and an old population in proportions that give the same EWHδ as measured in the SDSS spectra. A condition is of course that the young population has sufficiently strong Hδ in absorption to make this possible. As we describe in more detail in Sect. 3.3 we then derive the dust attenuation in each time step by gradually increasing the amount of attenuation in the model until we get the best fit to the observed spectrum. This procedure is repeated time step after time step until the postburst epoch is over. The best fit is then chosen as the solution. An example of the modelling is seen in Fig. 10. As we have limited possibilities to classify certain types of AGNs weakly present in postburst galaxies one should be aware that a substantial part of the postburst sample at higher luminosities may host AGNs. This starts to become a problem for galaxies brighter than L∗ (Mr = −20.83) (Blanton et al. 2001), corresponding to logℳbaryonic(ℳ⊙) ~ 10.6). We discuss this problem in Sect. 4.1.
 |
Fig. 10 An example of a model of a postburst spectrum (SDSS SpecObjId 85508603053604864). Displayed are the two model components – a young (blue line) and an old (red line) stellar population. The sum of the model spectra (dark green line) is shown on top of the observed spectrum (light green line). The observed spectrum has been smoothed with a triangular filter with a width of 7 pixels. The bright emission line just below 5000 Å is a remnant from the [O i]λ5577 night sky line. The emission lines in the region around Hα are the [N ii]λλ6548, 6584 lines. Since no Hα is seen (although some is probably swallowed by the stellar absorption line), most of the nitrogen lines are probably originating from a weak AGN. |
3.3. Corrections for dust attenuation
If only optical spectra are available, the corrections for dust attenuation are normally based on the Balmer emission line decrement, in particular the Hα/Hβ ratio. This is very useful if the Balmer lines are strong. But even when they are, it is not straightforward to apply the corrections since what we measure is a luminosity weighted mixture of contributions from regions of different dust content. In postburst galaxies the Balmer emission lines are practically nonexistent and we have to use another method. Below we describe how we have treated the effects of dust attenuation in the two cases.
3.3.1. Emission line galaxies
Traditionally the spectral distribution and strengths of the emission lines have been corrected for dust attenuation using the observed Hα/Hβ emission line ratio as compared to the dust free condition. A relevant extinction curve is then applied to make a correction for an interstellar medium (ISM) of this type of galaxy. For a long time it was assumed that the attenuation could be approximated by a foreground screen of dust whose column density was independent of the spatial distribution, age and metallicity variations across the main body of the galaxy. However, it has been obvious for many years that this is too crude an approximation. The optical depth in young star-forming regions is about 2 times higher than in older regions (Calzetti 1997). In the study by Charlot & Fall (2000) the effect of dust attenuation and how it changes with time during the early star-forming period when star clusters and super star clusters are formed, is discussed in detail. This model has been applied and further developed in various analyses of spectra of star-forming galaxies (e.g Brinchmann et al. 2004; Pacifici et al. 2012). In this paper we adapt a similar, but largely empirical approach to improve the correction for dust in starburst galaxies. But there are two major differences between our model and that of Charlot & Fall (2000). One is that we can correct for the influence of the temporal effect on the dust attenuation on the EWHαwhile the Charlot & Fall model does not provide this information. The second important difference is that we directly connect the age of the burst population to the Hα/Hβ ratio and the strength of the attenuation. In the work by Brinchmann et al. (2004) the correction for dust attenuation is obtained from a specific dust model while the age has to be obtained from another source. To first approximation it is our purpose to take the changes in the extinction coefficient during the early phase of star formation into account. Thus, our model adopts a correction for dust attenuation that systematically decreases with the age of the starburst population.
It is well known that a significant part of the star formation in starburst galaxies occurs in young stellar clusters. The fraction of stars formed in clusters increases with star formation density (Goddard et al. 2010) and may reach high numbers. For example, Adamo et al. (2011a) conclude that in the nearby well investigated luminous blue compact galaxies ESO 338-IG04 and Haro 11, the amount of stars formed in clusters is ~50% while the remaining stars are formed in associations and agglomerates. Here we assume that the age dependence of dust attenuation found in clusters can be applied to the young stars in the galaxy as a whole. We show below that the fits of the model spectra to the SDSS data are significantly better with this approach.
As mentioned above, it was established many years ago that the dust attenuation in star-forming galaxies is about a factor of 2 lower in the older regions than in the younger and these results have been confirmed also in studies based on SEMs (e.g. Asari et al. 2007). But there is strong support that the youngest population, i.e. stars formed during the first few Myr, is more severely affected than the young population of a normal mean age that holds for the starburst population in our study (~a few 10 Myr). The extinction is many times higher when a star formation region is only one million years old than a few millions years later when the ambient dusty clouds have been dispersed, while it appears to become constant over the rest of the time when the star-forming region is producing ionising photons.
In several papers (Goddard et al. 2010; Adamo et al. 2011b,c) the dust attenuation has been derived for star clusters of different ages. The trends found in these investigations seem to give a similar relation between the amount of attenuation and age. Following these results, we have roughly adopted a relation between age and attenuation according to Table 3 below where A0 is the attenuation during the major period of star formation. We model the Hα and Hβ line strengths as a function of age for a range of attenuation values corresponding to an attenuation in the V band of 0 ≤ A0,V ≤ 3.8 mag. As we model the SDSS spectra we step through this library with increasing age. For each age we choose the model that gives the best agreement with the measured Hα/Hβ ratio. This gives us A0. For the case of continuous star formation, each output with age ≥3 Myr contains stellar components with a range of values of the attenuation. In Fig. 11 we show the distribution of the χ2 residuals from the best fitting models of the SDSS spectra. Two cases are shown, one where we treat the dust attenuation according to Table 3 and the other where the dust attenuation in star-forming regions is twice that of non–star-forming regions. We see a clear difference between the two cases, in favour of our approach.
 |
Fig. 11 Reduced χ2 of the spectral fits adopting two different procedures for correction of dust attenuation. The hatched region shows the distribution after applying the corrections according to Table 3. The other line shows the distribution after we have applied the more classic approach with an extinction coefficient that is twice as high in star-forming regions compared to passive regions. Obviously the age dependent dust attenuation correction yields the smaller reduced χ2 values and thus gives the better fit. |
Starburst dust attenuation for a given age range.
 |
Fig. 12 a) Model of the evolution of EWHα in a star-forming galaxy under two different conditions for dust attenuation. The attenuation in the V band during the major star formation epoch is AV = 1 mag. and the SFR is constant. The full drawn line shows how the equivalent width changes with age assuming constant dust attenuation. In this case EWHα is identical to the dust free case. In the second case, shown in the dashed line, we assume an age dependency in the attenuation. b) The ratio between EWHα in the two cases. The figure shows that EWHα in the age dependent dust attenuation case drops off up to ~50%. |
The way we correct for dust attenuation has an important consequence. Since the attenuation is strongest during the epoch of highest Lyman continuum photon production, it means that EWHα will be lower than if the extinction should be assumed to be constant during the entire SF epoch. We illustrate this is Fig. 12 where we show the difference between our model and the case of constant attenuation. We see that, e.g. where A0,V = 1 mag., the case of variable attenuation will diminish EWHα up to 50%. When we discussed the selection criteria above we argued that a lower limit to EWHα of 120 Å would be a sufficient criterion to make sure that most starbursts would be captured. If we now take the effects of age dependent attenuation into account, we need to decrease the lower limit of the EWHα selection criterion. In Fig. 13 we show the distribution of the attenuation in the V-band derived for the galaxies in the starburst sample. The median attenuation is ~0.6 mag. An attenuation of AV = 1 mag. can suppress EWHα with a maximum of 50%. 94% of the sub L∗ galaxies have AV< 1.0m. At higher luminosities the dust attenuation increases to an amount that we do not properly handle here. One reason is that we will have severe problems with confusion caused by the presence of AGNs and shock heated gas caused by outflows. Another reason is that, if we wish to catch the strongly dust enshrouded starbursts (where AV ≫ 1m), we have to deal with weak emission lines (caused by dust attenuation) that would cause very unreliable results if we tried to use them for correction for dust attenuation. We show however that we still can reach interesting conclusions also in the high luminosity end by using the statistics of postbursts, being less affected by dust.
 |
Fig. 13 Luminosity weighted attenuation in the V band in the samples of starburst and postburst candidates. Notice that for clarity, the bin size differs between the two samples. |
3.3.2. Postburst galaxies
In the postburst sample we cannot use the Balmer emission lines to derive the dust attenuation. Instead we have done the following. As in the case of the starburst candidates, we step through models of increasing age and select candidates that have EWHδ≤−6 Å. At each time step we vary the attenuation in steps of AV = 0.1 mag in the range 0 ≤ AV ≤ 1.5 mag. For each value we make a fit. Finally we choose for each time step the case where the χ2 test gives the best result. We then apply the derived value of AV to the model spectra. The distribution of AV is shown in Fig. 13. It can be compared to the results of Kauffmann et al. (2003b). We conclude that the results agree in the sense that >99% of the galaxies in both cases have AV< 1.5 mag. The peak in our distribution differs by ~0.2 mag or 20% if we transform the z magnitudes (used by Kauffmann et al.) to V magnitudes but the medians are quite similar. We also find agreement between our derived distribution of AV:s and that derived for K+A galaxies by Melnick & De Propris (2013). In the Appendix we also make a successful test of the reliability of our model determination of AV. This makes us confident in our method of deriving the dust attenuation.
Here we assume that the dust is homogeneously distributed across the galaxy. This is a rough approximation and one may question if it is accurate enough to be applicable to the data in our statistical investigation. One could imagine that postburst cases where no or very weak emission lines are seen could perhaps host a starburst with high dust obscuration in the centre. But such cases appear to be quite uncommon. A look at the distribution of the young stellar population shows (Swinbank et al. 2012) that the blue population is mostly concentrated in the centre but over a larger volume than young stars in nuclear starbursts (normally constrained to the central 1 kpc). If there is a dusty starburst in the centre it should reveal itself by free–free emission in the radio domain. In a search for 20 cm emission from 36 E+A galaxies (EWHδ≤−6 Å and no [O ii]λ3727 or Hα) Goto (2004) could set upper limits that excluded strong starbursts in 34 of these galaxies and moderate starbursts in the more nearby (z ≤ 0.15) cases. This was confirmed in a similar study by Nielsen et al. (2012) of a sample of 811 K+A galaxies obtained from the FIRST survey, based on 1.4 GHz radio observations. The origin of 1.4 GHz emission is primarily thought to be synchrotron radiation from relativistic electrons, accelerated by the shocks from supernova ejecta. The signal thus can be calibrated to be used as a measure of the SFR. The results from this study are consistent with very weak or no star formation activity in general. One should also remember that a substantial part of the postburst galaxies may host AGNs which also contribute to the radio emission (Hooper et al. 2007). It thus seems we can safely assume that the dust corrections we apply are valid for most of the stars we observe in the central region.
3.3.3. General validity of the correction for dust attenuation
In Fig. 14 we show how the correction factor for dust attenuation of EWHα varies with SFR. How does this agree with other observations? Afonso et al. (2003) investigated the correlation between the SFR derived from the 1.4 GHz emission versus the Hα line – the correction factor can be estimated from their diagrams. Kennicutt et al. (2009) used Spitzer 24 μm observations to compare with the SFR determined from Hα. Although the scatter in both their data is large, we find a good (~20–30% at highest SFR) agreement between our result and theirs. At low luminosities, the SFR derived from Hα has been shown to be underestimated as compared to SFRs derived from UV fluxes (Lee et al. 2009a). One problem may be a significant UV leakage from the H ii regions (Relaño et al. 2012). Yet another problem at low luminosities is the stochasticity of the IMF. However, these problems typically emerge at a SFR below 0.01 ℳ⊙ yr-1 (da Silva et al. 2012) and thus should have a minor effect on our sample (compare the range in SFR in Fig. 14).
 |
Fig. 14 Dust correction factor of EWHα vs. dust corrected SFR for the full starburst candidate The overplotted filled circles connected with solid lines are the median values in bins along the x-axis. |
3.4. Aperture effects
Due to the small 3″ cross section of the SDSS spectrograph fibers, one has to worry about aperture losses at small redshifts. This problem has been discussed at length by Brinchmann et al. (2004) in their study of star-forming galaxies in the local universe (see also other references in the same paper). They applied corrections to their data, which they claim, nearly removed the bias. In the present investigation we wish to focus on low-to-intermediate luminosity starburst galaxies, hence we also want to push the limit as low as possible without introducing demonstrably large uncertainties in the derived data. However, we still chose a lower redshift limit (zlow = 0.02) which is 4 times higher than the zlow = 0.005 used by Brinchmann et al. (2004). Thus our data should be less affected by aperture losses than theirs for galaxies of the same physical sizes. Let us have a look at the aperture effects on the data based on our low redshift limit. In Fig. 15 we show the frequency distributions of the radii encompassing 50% (R50) and 90% (R90) of the Petrosian fluxes of our starburst galaxy candidates. The Petrosian flux is the flux within the Petrosian radius (Petrosian 1976). The Petrosian radius defines a region containing the flux of a galaxy with an exponential profile and about 80% of the flux of a galaxy with a de Vaucouleurs profile. In 25% of the cases the SDSS fiber aperture encompasses more than 50% of the Petrosian flux (R50). This indicates that aperture effects may be severe and we need to test the reliability of extrapolating the data outside the fiber aperture.
 |
Fig. 15 Radii encompassing 50% (R50) and 90% (R90) of the Petrosian flux in the r band of the starburst galaxy candidates. |
 |
Fig. 16 EWHα versus redshift in different luminosity bins after remeasurements and correction for dust attenuation. The red solid line shows the medians of log (EWHα) in bins along the x-axis. For comparison, the faint gray line shows the medians before corrections for dust attenuation. |
 |
Fig. 17 Dust attenuation in V versus redshift in different luminosity bins. The solid red line shows the medians of AV in bins along the x-axis. |
In Fig. 16 we show in grey lines how the median values of EWHα depend on redshift. We display the results in 6 boxes of increasing luminosity where the absolute magnitudes are derived as described below (see Sect. 4.1). There are significant trends with redshift at z ≤ 0.02, in particular in the −17 > Mr > −19 and −19 > Mr> −21 box. This seems to imply that we have rather significant aperture effects at low redshifts. After remeasuring EWHα and applying the corrections for dust attenuation we see from Fig. 16 that the distributions have become somewhat flatter but that the trends at low redshifts essentially persist. Given these results it would seem prudent to use data above z = 0.02, without applying other aperture corrections than a simple extrapolation from the fiber magnitudes to the total magnitudes in the r-band. Let us now examine two other parameters − the dust attenuation in V, AV, and the ℳ/LV ratio. Naively one would assume that the dust attenuation decreases with distance from the centre and thus we would expect to see AV decrease with increasing redshift for galaxies with the same luminosities. In a starburst galaxy one might also expect that the young stellar population has less and less influence at larger distances from the centre. We can see the actual situation in Figs. 17 and 18. We notice aperture effects in AV at z < 0.02 and at the highest redshifts. In the highest luminosity bin the aperture effect is severe. At these luminosities there is also a risk that the spectra are of a composite nature, containing both a starburst component, an AGN component and a shock component. We see the same problem for the ℳ/Lratios. Otherwise the distributions for the majority of the data show only weak trends of the order of 0.1 dex over the redshift interval in each luminosity bin except the −23 >Mr > −25. We therefore feel we can rely on our extrapolation from fiber data to global data for galaxies of Mr ≳ −23. We do not further discuss the properties of the brightest galaxies (Mr < −23) here.
4. Results
4.1. The luminosity function
In the derivation of the LF, Φ, we use the 1 /Vmax method (Schmidt 1968). Here we follow a procedure as described by e.g. Ellis et al. (1996). The LF can then be calculated from 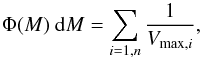 (4)where φ is the number of galaxies per volume element within a certain absolute magnitude interval dM. Vmax is the maximum volume within which the galaxy could be observed under all observational constraints, including magnitude and redshift limits and n is the number of galaxies within the absolute magnitude interval dM. Vmax is given by
(4)where φ is the number of galaxies per volume element within a certain absolute magnitude interval dM. Vmax is the maximum volume within which the galaxy could be observed under all observational constraints, including magnitude and redshift limits and n is the number of galaxies within the absolute magnitude interval dM. Vmax is given by 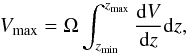 (5)where Ω is the effective area in steradians, zmin is the lower redshift limit (z = 0.02) and zmax is the upper limit, corresponding to the distance at which the apparent magnitude of the galaxy would be equal to the limiting magnitude, mr = 17.5. dV/dz is the comoving volume element per redshift interval and is given by
(5)where Ω is the effective area in steradians, zmin is the lower redshift limit (z = 0.02) and zmax is the upper limit, corresponding to the distance at which the apparent magnitude of the galaxy would be equal to the limiting magnitude, mr = 17.5. dV/dz is the comoving volume element per redshift interval and is given by 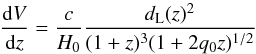 (6)over one steradian. dL is the luminosity distance given by
(6)over one steradian. dL is the luminosity distance given by 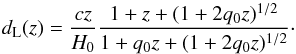 (7)The standard deviation per bin is
(7)The standard deviation per bin is 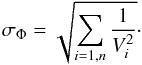 (8)The absolute magnitude of a galaxy is calculated from
(8)The absolute magnitude of a galaxy is calculated from 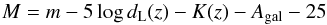 (9)where dL(z) is the luminosity distance in Mpc, K(z) is the k-correction and Agal is the galactic absorption in magnitudes.
(9)where dL(z) is the luminosity distance in Mpc, K(z) is the k-correction and Agal is the galactic absorption in magnitudes.
 |
Fig. 18 ℳ∗/LV in different luminosity bins as function of redshift, after correction for dust attenuation. The solid red line shows the medians of ℳ∗/LV in bins along the x-axis. |
 |
Fig. 19 Upper diagram: LF of 1) starburst galaxies with a birthrate parameter b > 3; 2) starburst galaxies with a mass fraction of the burst fburst > 3%; 3) postburst galaxies; 4) AGNs in the emission-line galaxy sample; 5) the full galaxy LF of the local universe as derived by Blanton et al. (2001). The sampling completeness limit based on the apparent spectroscopic limit Mr = 17.5 and the redshift limit z = 0.02 is indicated with a vertical hatched line. Lower diagram: the relative fraction of the different samples with regards to the total LF, as a function of absolute magnitude. The vertical bars are standard deviations. Please notice that we have assumed (for purely technical reasons) that the Blanton LF for normal galaxies can be extrapolated to Mr < −23. |
The LF based on the 1 /Vmax method holds true for a homogeneous distribution of sources. In shallow surveys local inhomogeneities may cause problems, in particular at low luminosities. By choosing a lower redshift limit of z = 0.02 we believe the most serious problems of this kind will be overcome except for the very faintest parts of the sample. Small number statistics also increases the uncertainty at low fluxes. At the high end one may have problems with evolutionary effects. We have very few objects above z = 0.2. Thus the upper redshift limit (z = 0.4) is sufficiently small to exclude evolutionary effects that may have an influence on the results, in particular in the low–mid range luminosity region.
In Fig. 19 we show the derived LF for 5 sets of data: 1) the full galaxy LF of the local universe as derived by Blanton et al. (2001); 2) starburst galaxies with a birthrate parameter b > 3; 3) star-forming galaxies with a mass fraction of the young population >3%; 4) postburst galaxies with EWHδ<−6 Å; 5) AGNs in the emission-line galaxy sample (EWHα,em> 60 Å). We want to point out that the starburst galaxy LF starts to become obsolete at galaxies brighter than ~L∗ (Mr-20.8; log ℳ(ℳ⊙) ~ 10.6) because of the increasing influence of AGNs and severe dust obscuration.
At this point we want to remind the reader what we mean by postburst galaxies. Strictly we would have liked to define a postburst galaxy as a galaxy that fulfills the criteria EWHδ<−6 Å and b> 3. In Sect. 2.2 we explained the problem in determining the b-parameter for postburst galaxies. 92% of the galaxies in the postburst candidate sample have ⟨ b ⟩ larger than 3, if we use the derived exponential (or constant) time scale of the burst as a rough measure of the duration of the burst. This is at least an indication that the postburst galaxies, based only on the Hδ criterion are closely linked to the starburst population. Due to the uncertainty in the determination of the b parameter however, we decided to use the term postburst for galaxies only with EWHδ,abs ≤ −6 Å, based on the remeasured values (as mentioned in Sect. 2.4).
There are a few conclusions we can immediately extract from Fig. 19. Starburst galaxies defined both from the birthrate parameter and the mass fraction criterion are less common than generally assumed. AGNs start to become significant relative to starburst galaxies at an absolute magnitude of Mr ≈ −21. At fainter luminosities we have more or less clean cut cases of starbursts. If we base our definition of starburst on the b > 3 criterion, those galaxies contribute no more than 1.0 ± 0.1% to the total LF at an absolute magnitude of Mr = −18 and 0.6 ± 0.05% at Mr = −19. According to Karachentsev et al. (2013), about 70% of the dwarf galaxies in the local universe are star-forming, i.e. are classified as Ir, Im or BCD. Comparing their fraction means that only 1% of star forming dwarfs is a starburst galaxy. The relative fraction decreases only weakly with increasing luminosity and reaches a relative fraction of 0.3−0.4% at Mr = −22.5. However, as is discussed in the next section, one has to keep in mind that a fraction of the starbursts in massive galaxies may be difficult to detect if an AGN is present at the same time.
We see from Fig. 19 that the LF of postburst galaxies tightly follows that of starburst galaxies at low-intermediate luminosities. At higher luminosities the postburst LF deviates from starbursts and joins the AGN LF. We show below that the lifetimes of the starbursts are roughly independent of mass. The lifetime of postbursts are insensitive of mass if the star formation is shut down during the postburst phase. Then the postburst criterion, EWHδ, is only a function of time. We show in Sect. 4.4 that this is probably true at high luminosities. Here, the postbursts follow the AGNs. AGNs cannot produce postburst signatures. Therefore, considering the strong correlation between starbursts and postbursts up to Mr ~ −21.5, we argue that the starburst LF follows that of the postbursts also at higher luminosities, but that the starburst galaxies for some reason are difficult to detect. One probable reason is that the AGNs are outshining the starbursts. Another reason is that starbursts in luminous galaxies are strongly dust enshrouded while the postbursts and AGNs may be less affected. We know that the dust opacity increases with mass and luminosity. At high luminosities the starburst phase is to a large extent hidden by dust while the postburst phase is less affected. This is clearly seen in Fig. 20. Notice also that the dust attenuation in posbursts reaches a maximum at Mr ~ −21.5. In Fig. 19 we see that postbursts closely follow the AGNs at high luminosities. This indicates that the AGN phase has been preceded by a dusty starburst. Shortly after the starburst, the dust opacity decreases and the postburst/AGN phase begins. We can infer from the high fraction of postbursts that the number of starbursts at high luminosities have been underestimated by about one dex. We conclude that from the fact that we find a strong link between starburst and postburst LFs, it follows that there must also be a strong link between starbursts and AGNs. The AGN phase seems to appear after the starburst has ceased, when the dust has probably been destroyed or removed by radiation pressure and/or gas outflows. This scenario is also supported from observations of luminous postburst quasars (Cales et al. 2013).
 |
Fig. 20 Dust attenuation given in AV, as function of absolute magnitude. Red dots are medians. Notice the peak in AV for the postbursts which is not seen in the starburst sample. |
An important question is how much starbursts contribute to the star formation in the local universe. Figure 21 shows how the SFR density varies with luminosity. By integrating the SFR from Mr = −17 up to −23 we find that starbursts with b > 3 have a SFR density of 4.43 ± 0.14 × 10-4ℳ⊙ yr-1 Mpc-3. The errors given are random errors, assuming a Gaussian distribution. The systematic errors dominate and mainly stem from the uncertainties in the model, the dust correction and the aperture correction. We estimate these give rise to an additional ~40% uncertainty. The given SFR density only reaches down to Mr = −17. We see from the diagram that the SFR density distribution is only slowly declining towards fainter magnitudes. We know very little about the LF of starbursts at faint absolute magnitudes. If we extrapolate down to Mr ~ −13, assuming the starburst LF to rise slowly towards fainter magnitudes as do normal SF galaxies (Moorman et al. 2015), we can obtain a rough estimate of the contribution to the SFR density from starburst galaxies at the faint end on the LF. From the diagram we estimate that this additional contribution between Mr = −17 and −13 would amount to ~3 × 10-4ℳ⊙ yr-1 Mpc-3. To this we should add the contribution hidden in AGNs. As we discussed above, the starburst LF is running in parallel to the postburst LF at intermediate to low luminosities. Postbursts are twice as common as starbursts. If we assume this to be true even at higher luminosities when starbursts are hidden by dust or outshone by bright AGNs we estimate that we miss ~1.3 × 10-4ℳ⊙ yr-1 Mpc-3. The total contribution from starbursts in the range −23 < Mr< −13 then becomes ρSFR = 8.7 × 10-4ℳ⊙ yr-1 Mpc-3 of which ~15% are lost at high masses. Brinchmann et al., display in their Fig. 16 the redshift dependence of the SFR density on redshift based on different investigations. The median redshift our starburst sample is z = 0.07. At this redshift the SFR density is ~1.7 × 10-2ℳ⊙ yr-1 Mpc-3. Their lower redshift limit restricts the sample to galaxies brighter than Mr = −14. For our starburst sample this corresponds to ρSFR = 7.7 × 10-4ℳ⊙ yr-1 Mpc-3. Thus starbursts contribute ~4.4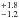 % to the total stellar production in the local (z ~ 0.07) universe.
% to the total stellar production in the local (z ~ 0.07) universe.
 |
Fig. 21 SFR density of the starburst b> 3 sample vs. absolute r-magnitude. The errors bars are standard deviations. |
It is also interesting to compare our results to results from the Herschel mission (Rodighiero et al. 2011; Sargent et al. 2012; Schreiber et al. 2015), although these investigations are based on near-IR data and do not include low mass galaxies. In these studies the starburst phenomenon is discussed in relation to the galaxy main sequence (GMS), i.e. the SFR versus the galaxy mass. One particular aspect concerns the distribution of the specific SFR (sSFR). Provided one assumes that the GMS has a Gaussian distribution in log sSFR, starbursts here appear as a separate population. Rodighiero et al. (2011) focus on the redshift interval 1.5 < z < 2.5, believed to be the epoch of peak star formation in the universe. They require a starburst galaxy to have a SFR more than 4 times the SFR on the GMS. This definition is close to the b > 3 definition in the local universe considering that the SFR has decayed since z = 2. Rodighiero et al. find that starburst galaxies represent only 2% of mass-selected SF galaxies and account for only 10% of the SFR density at z ~ 2. These results are not too different from our results. Compared to the results from Rodighiero et al., Schreiber et al. (2015) find values about 50% higher and essentially independent on redshift in the range 0.5 < z < 4.
4.2. Masses
There is an ongoing debate about the cause of the broadening of the Balmer emission lines, whether dominated by virial motions and/or regular rotation and thus potentially useful for mass determinations or by non-ordered motions caused by gas infall or supernova generated outflows. In a few papers (Terlevich & Melnick 1981; Melnick et al. 1987, 1988) it was demonstrated that the velocity dispersion of H ii regions derived from the width of the Hβ emission line, σHβ, is correlated with their luminosities, thus indicating that there should also exist a similar relation between σ and mass. Guzman et al. (1996), looking at a small number of galaxies, took the idea further and demonstrated that emission line widths can be used to derive reasonably correct masses. In two papers by Östlin et al. (1999, 2001), Fabry-Perot spectroscopy was carried out on 6 blue compact galaxies and two companions. They found a good agreement between dynamical masses and photometric masses. This is further confirmed by our recent study of a larger sample of local starburst dwarf galaxies (Marquart et al., in prep.) and other investigations (Bezanson et al. 2013).
Here we continue the comparison between dynamical and photometric masses. To derive the dynamical estimates of the masses, we use the Hα emission line widths. The velocity dispersion was derived from 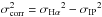 , where σHα = FWHMHα/ 2.35 and IP signifies the instrumental profile. We have assumed σIP = 70 km s-1, as obtained from the SDSS online documentation3.
, where σHα = FWHMHα/ 2.35 and IP signifies the instrumental profile. We have assumed σIP = 70 km s-1, as obtained from the SDSS online documentation3.
The dynamical masses were derived under the assumption that we are working with dynamically relaxed systems. In some starburst galaxies, in particular in mergers this is probably not a valid assumption since we expect gas infall as well as outflows caused by supernovae activity. Thus, we have poor knowledge about the kinematics of the ionised clouds in a specific galaxy, but can expect to obtain important information from a statistical sample. For simplicity we assume that the clouds move either in circular orbits in a disc like structure or in viral motions in a spherically symmetric system. A simple approximation of the relation between the dynamical mass and the width of the Hα line is give by the equation (Lequeux 1983; Östlin et al. 2001): 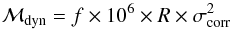 (10)f is a constant which has the value f ≈ 0.79 for a disc and f ≈ 1.1 for a spherical distribution. In the first case it is assumed that the inclinations of the disks are randomly distributed. ℳdyn is the dynamical mass in solar units, R is radius in kpc and σcorr is given in km s-1. For disks we assume that R is equal to the scale length. In the spherical case we assume that R = Reff = R50.
(10)f is a constant which has the value f ≈ 0.79 for a disc and f ≈ 1.1 for a spherical distribution. In the first case it is assumed that the inclinations of the disks are randomly distributed. ℳdyn is the dynamical mass in solar units, R is radius in kpc and σcorr is given in km s-1. For disks we assume that R is equal to the scale length. In the spherical case we assume that R = Reff = R50.
In Fig. 22 we show how our baryonic masses correlate with the dynamical masses for the two cases. To calculate the total masses we have added a crude estimate of the gas mass based on observations of star-forming galaxies of various masses. The total gas mass was estimated to be ℳgas = ℳHI + ℳHe + ℳH2. The H i relation was obtained from a linear fit to various data in the literature giving 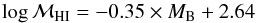 (11)(Bergvall et al., in prep.), where MB is the absolute magnitude in the Cousins B band. To this was added a helium component of 25% in mass (ℳHe). The molecular masses were obtained from Sage et al. (1992) and Georgakakis et al. (2000). We assumed a linear relation giving
(11)(Bergvall et al., in prep.), where MB is the absolute magnitude in the Cousins B band. To this was added a helium component of 25% in mass (ℳHe). The molecular masses were obtained from Sage et al. (1992) and Georgakakis et al. (2000). We assumed a linear relation giving 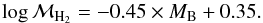 (12)Masses are in solar units. We applied these relations assuming Mg = MB where Mg is the absolute magnitude in the SDSS g band. The total baryonic mass is then ℳtot = ℳgas + ℳstars, where ℳstars includes stellar remnants.
(12)Masses are in solar units. We applied these relations assuming Mg = MB where Mg is the absolute magnitude in the SDSS g band. The total baryonic mass is then ℳtot = ℳgas + ℳstars, where ℳstars includes stellar remnants.
 |
Fig. 22 Dynamical mass, derived from the width of the Hα emission line versus the baryonic mass (stars+gas), derived from the spectral fit. The two diagrams display the results emerging from two different assumptions about the kinematics of the Hα emitting gas. In the spherical case it is assumed that virial motions take place in a spherically symmetric structure and in the disc case it is assumed that the gas clouds move in circular orbits in a disk. Overplotted circles are the median values after binning along the x-axis. The hatched line marks the 1:1 relation. |
Which of the two cases, spheroid or disk, is most probable? It depends on the mass but as has been shown from luminosity profile fitting (Micheva et al. 2013) and the central concentration index R90/R50 (Brinchmann et al. 2004), most of the star forming galaxies should be flattened systems. For a few others, e.g. mergers, the spherical case may be more appropriate. As is seen in Fig. 22, showing the fiber masses based on the velocity dispersion vs. the photometry, the disc option fits nicely to the data. The spherical case allows for a significant portion of dark matter (~60%) to be added to the baryons. Figure 23 shows the distribution of baryonic masses indicating in red the cases where σobs<σIP. About 2% of all galaxies have this problem, most of them below masses of ~109ℳ⊙.
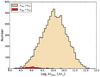 |
Fig. 23 Distribution of the baryonic (stars+gas) masses inside the fiber aperture. The small region at low masses, marked in red, corresponds to cases where σobs<σIP. |
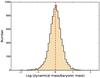 |
Fig. 24 Histogram of the ratio between the dynamical and baryonic (stars+gas) masses inside the fiber aperture. The dynamical masses are based on the disc approximation. The hatched vertical line is the median. |
From Fig. 24, we see that the distribution of the ratios between the dynamical and baryonic masses is nearly Gaussian around a value close to 1. Here the dynamical masses are based on the disc approximation. This could indicate that outflows are not prominent enough to influence the ionised gas motions in which case we would see a skewed distribution towards the positive side. The similarity between the two types of mass determinations seems to indicate that the contribution from dark matter (DM) to the the dynamical masses is insignificant within the relatively compact starburst region. There are no broad investigations of the mass distributions in starburst galaxies. If we have a look at normal galaxies it is well known that gas rich dwarf galaxies with baryonic masses below ~109ℳ⊙ are DM dominated over most of the stellar main body (e.g Oh et al. 2011). In more massive disc galaxies, ~10−50% of the mass is in baryonic form inside the peak of the rotation curve (Martinsson et al. 2013), i.e. at distances from the centre <2.2 scale lengths, which is larger than the typical spectroscopic aperture of our sample. Moreover, in starburst galaxies we expect the gaseous component to be more centrally concentrated due to angular momentum transfer from the gaseous component to the old stellar component (Papaderos et al. 1996; van Zee et al. 2001; Lelli et al. 2012, 2014). Therefore the baryonic component traced by Hα emission, tightly following the optical profile (Herrmann et al. 2013), should be more prominent than in quiescent galaxies and may account for the low influence of DM.
From the fit to the disc approximation in Fig. 22 we derive a relation between the dynamical (ℳdyn) and baryonic (ℳbary) masses based on the fiber data: 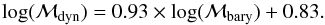 (13)The agreement at intermediate-high masses is remarkably good. A common problem with observations of starburst galaxies in the optical region is that the light from the young population completely dominates the emission and therefore makes it difficult to determine the contribution from the old stars. It seems that we have managed to take the old population into account in a way that allows us to use the masses at least for statistical purposes. The tight correlation also seems to give support to a practical use of the emission line widths at high redshifts to determine the baryonic masses inside the optical disk.
(13)The agreement at intermediate-high masses is remarkably good. A common problem with observations of starburst galaxies in the optical region is that the light from the young population completely dominates the emission and therefore makes it difficult to determine the contribution from the old stars. It seems that we have managed to take the old population into account in a way that allows us to use the masses at least for statistical purposes. The tight correlation also seems to give support to a practical use of the emission line widths at high redshifts to determine the baryonic masses inside the optical disk.
4.3. Basic properties of the candidate samples
Here we have a look at the basic characteristics of the sample constrained by EWHα≥ 60 Å for starburst candidates and EWHδ≤−6 Å for the postburst sample. Then we investigate the more constrained samples defined by the b-parameter and the fburst parameter. It is enlightening to begin by looking at where our selected galaxies end up if we would place them in the theoretical diagram seen in Fig. 3, remembering however that this diagram is based on the assumption that the SFR is constant, while we assume exponentially decaying SFR in the models. How EWHα correlates with age is seen in Fig. 25. The horizontal line corresponds to the minimum (necessary but not sufficient) value of EWHα if a star formation epoch of an age lower than 1 Gyr should be regarded as a starburst if we apply the b > 3 criterion.
 |
Fig. 25 Dust attenuation corrected EWHαversus the age of the young population in the starburst candidate sample. The sample is divided according to absolute magnitude into dwarfs and giants at Mr = −20. The solid and dashed lines are identical to those in the left part of Fig. 3 with a 3% relative mass fraction of the young population. The dotted line at EWHα = 150 Å corresponds to the minimum value (but not sufficient) of EWHα to qualify as a starburst with the b> 3 criterion and an age < 1 Gyr if the SFR is assumed to be constant during the burst. The hexagon symbols represent the surface density of the data points, where darker colours means more data. |
The situation becomes more clear if we have a look at Fig. 26 showing the b-parameter versus age, which is fairly similar to the lower part of Fig. 3. Three different subsamples of different luminosity classes, are presented. They have approximately the same number of galaxies so one can have an impression of how the distribution changes with luminosity. Not unexpectedly, the most luminous galaxies have a lack of low ages. Except for displaying the b = 3 limit (red solid horizontal line) between starbursts and non-starbursts we also show the line above which the mass of the burst is more than 3% of the total mass. We do this for three different star formation histories: constant SFR (solid blue line), an exponentially decaying SFR with times scales 10 and 100 Myr (red dashed and green dot-dashed lines). For an exponentially decaying SFR the minimum value of the b-parameter necessary to fulfil the fburst criterion at a certain burst age t∗ (in years), assuming (as we do here) that the age of the old population is 10 Gyr, can be expressed as, 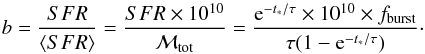 (14)If we look at the distribution of the b-parameter values in Fig. 26, in particular in the lower diagram, we notice that the maximum b-parameter decreases with age from b ~ 60 down to 3 at an age slightly below 1 Gyr. The upper envelope of the distribution in the lower diagram corresponds to fburst = 0.10–0.15. It seems that the strongest starbursts are short-lived. The reason may be that the gas is consumed in a shorter time or that the minimum mechanical energy (generated by young stars and SNe) needed to eject the fuel for the starburst is reached in a shorter time in strong starbursts. The upper limit of the ages is in reasonable agreement with the maximum gas accumulation time scale in a massive merger (Mihos & Hernquist 1996). We also note that on the righthand side of the diagram, below the b = 3 line, we find galaxies that very likely fulfil the fburst > 3% criterion but few with the b > 3 criterion. We show below that this is confirmed by the modelling. In a simple scenario, the maximum SFR allowed in a starburst is equal to the rate at which the total gas content is converted to stars over the dynamical timescale (Kennicutt 1998). For a Milky-Way type of galaxy it is convenient to express it:
(14)If we look at the distribution of the b-parameter values in Fig. 26, in particular in the lower diagram, we notice that the maximum b-parameter decreases with age from b ~ 60 down to 3 at an age slightly below 1 Gyr. The upper envelope of the distribution in the lower diagram corresponds to fburst = 0.10–0.15. It seems that the strongest starbursts are short-lived. The reason may be that the gas is consumed in a shorter time or that the minimum mechanical energy (generated by young stars and SNe) needed to eject the fuel for the starburst is reached in a shorter time in strong starbursts. The upper limit of the ages is in reasonable agreement with the maximum gas accumulation time scale in a massive merger (Mihos & Hernquist 1996). We also note that on the righthand side of the diagram, below the b = 3 line, we find galaxies that very likely fulfil the fburst > 3% criterion but few with the b > 3 criterion. We show below that this is confirmed by the modelling. In a simple scenario, the maximum SFR allowed in a starburst is equal to the rate at which the total gas content is converted to stars over the dynamical timescale (Kennicutt 1998). For a Milky-Way type of galaxy it is convenient to express it: 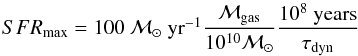 (15)where τdyn is the dynamical time scale. Consequently, the maximum b-parameter value is
(15)where τdyn is the dynamical time scale. Consequently, the maximum b-parameter value is 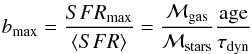 (16)where age is the age of the galaxy, assumed to be 1010 years. The total gas mass of the Milky Way is ℳgas = 7 × 109ℳ⊙. Approximately half of this is in molecular form (Combes 1991). Since stars are formed in molecular clouds this number is what we enter into the equation. Then we assume ℳstars = 6 × 1010ℳ⊙ and τ = 108 years. We then obtain bmax ~ 6, about half of the approximate upper limit in the diagram at a burst duration of 100 Myr. The content of H2 in SF galaxies is typically 5−10% of the total baryonic mass (Eqs. (11) and (12) and Leroy et al. (2005)). As we noted above, the upper limit, running parallel to the fburst = 3% line corresponds to fburst = 10–15%. In the simple scenario we have discussed, this limit therefore corresponds to an almost complete consumption of the available molecular gas available for star formation. Depending on age, is also sets the limit of the maximum value of the b-parameter. At the lowest ages, ~10 Myr, this corresponds to b ~ 60. These estimates might be too crude however. Simulations of mergers (Mihos & Hernquist 1996), taking into account orbital parameters, bulge/disk ratios and feedback processes, adds complexity to the interpretation and molecular hydrogen may be formed or destroyed (see also Bekki 2014; Hoopes et al. 2004). We return to this issue in Sect. 5.2.
(16)where age is the age of the galaxy, assumed to be 1010 years. The total gas mass of the Milky Way is ℳgas = 7 × 109ℳ⊙. Approximately half of this is in molecular form (Combes 1991). Since stars are formed in molecular clouds this number is what we enter into the equation. Then we assume ℳstars = 6 × 1010ℳ⊙ and τ = 108 years. We then obtain bmax ~ 6, about half of the approximate upper limit in the diagram at a burst duration of 100 Myr. The content of H2 in SF galaxies is typically 5−10% of the total baryonic mass (Eqs. (11) and (12) and Leroy et al. (2005)). As we noted above, the upper limit, running parallel to the fburst = 3% line corresponds to fburst = 10–15%. In the simple scenario we have discussed, this limit therefore corresponds to an almost complete consumption of the available molecular gas available for star formation. Depending on age, is also sets the limit of the maximum value of the b-parameter. At the lowest ages, ~10 Myr, this corresponds to b ~ 60. These estimates might be too crude however. Simulations of mergers (Mihos & Hernquist 1996), taking into account orbital parameters, bulge/disk ratios and feedback processes, adds complexity to the interpretation and molecular hydrogen may be formed or destroyed (see also Bekki 2014; Hoopes et al. 2004). We return to this issue in Sect. 5.2.
 |
Fig. 26 b-parameter versus age of the young population in the starburst candidate sample divided into three groups in luminosity indicated at the upper right. Each group contains about 2000 galaxies. The starburst criterion b = 3 is shown with a red horizontal line. Also displayed in three tracks are the minimum b parameter values needed to reach fburst = 3% at the age in question. In this case three alternatives of the SFH are displayed: a constant SFR (solid blue line) and exponentially decaying SFR:s on timescales of 10 and 100 Myr (red dashed line and green dash-dotted line respectively). The hexagons show the surface density of data points. Darker − more data. |
 |
Fig. 27 Ages of the starburst galaxies using the b > 3 and the fburst > 3% criteria. |
In Fig. 27 we show the age distribution of galaxies fulfilling the b > 3 and the fburst > 3% criteria. A prominent peak is seen at 50−90 Myr. The relative fraction of the decay rates chosen by the SEM as the best fit, and the median age of these subselections for the b > 3 case are as follows: τ, relative fraction, median age: 30 Myr, 53%, 57 Myr; 100 Myr, 13%, 82 Myr; 300 Myr, 19%, 213 Myr; 1 Gyr, 15%, 68 Myr. We can understand the sharpness of the peak if we consider how the visibility of the galaxy increases with age if the SFR is constant. In their simulation of gas rich mergers Mihos & Hernquist (1996) found a prominent peak in SFR at an age of 50 Myr in fair agreement with our empirical results. Another conclusion (as was also indicated by Fig. 26) is that galaxies that fulfil the mass fraction condition tend to fall below the b-parameter condition at high ages. A significant fraction, essentially the tail below b = 3 at log (age) > 8 in Fig. 27, do not have genuine starburst progenitors but are produced through a long epoch of SF at a b-parameter between 1 and 3.
 |
Fig. 28 Ages of the postburst galaxies. |
 |
Fig. 29 Difference between the luminosity at the end of the burst and the mean luminosity of the postburst phase assuming an exponentially decaying SFR on a time scale between 100 Myr and 1 Gyr. |
We may compare the age distribution of the starburst sample to the age distribution of the postburst galaxies shown in Fig. 28. A peak, corresponding to the ~100 Myr peak in the starburst sample, is seen about 300 Myrs later, more or less as we expect according to our models. Also in the Bruzual & Charlot model (Bruzual & Charlot 2003), the peak in Hδ occurs about 400 Myr after an instantaneous burst.
 |
Fig. 30 Upper part: the median b-parameter vs. the total baryonic mass (stars+gas) of the starburst (b> 3) sample. Lower part: the median of the mean value of the b-parameter during the starburst epoch, as function of the total mass. |
We can proceed a bit further with this discussion. Figure 29 shows how much fainter the postburst galaxies are expected to be if the star formation history continues with the exponential decay time scale chosen by the programme. It should be the minimum change but could be a factor of 2 higher for short bursts or rapidly quenched bursts. The change in luminosity is roughly a factor 2–3. At the same time the duration of the visible postburst phase is a few times longer than the starburst lifetime, depending on the star formation history and the starburst mass fraction. The consequence is that if we would follow the evolution of the fburst> 3% LF from the active to the passive postburst phase after the SF has ceased we would see a shift of about 1 mag towards fainter luminosities and then a shift upwards to compensate for the longer lifetimes of the postbursts. This agrees with what we observe if the lifetime of the postbursts is 3−4 times longer than the burst phase (see Fig. 19) and the dust attenuation is about the same.
4.4. Mass trends in the starburst and postburst samples
We now focus on mass trends in the two samples. We look at starbursts obeying the b-parameter criterion and the postburst sample obeying the Hδ criterion. First we look at the starburst sample.
Figure 30 shows how the b-parameter relates to the mass. In the upper part of the diagram we display the present values of the b parameter. In the lower part we show how the mean value of the b parameter, i.e. ⟨ b ⟩ = fburst × (age of galaxy)/(age of burst), varies as function of total mass. We can see that the median value of the b-parameter decreases with increasing mass, as a result either of an increasing collapse time or/and a decreasing amount of gas available to feed the burst (cf. Eq. (16)). ⟨ b ⟩ shows the same pattern but the mean ⟨ b ⟩ is about 50% higher than b. This can be understood if the SFR is decreasing with time. In the modelling of the spectra we assumed exponentially decaying SFRs. The preferred decay time scale is 100 Myr. The median age of a starburst is 68 Myr. Under the assumption of an exponentially decaying SFR and no problems with dust attenuation we would expect the ratio between ⟨ b ⟩ and b to be τ(1−e− t∗/τ) /t∗/ e− t∗/τ. Adapting t∗/τ = 68/100 we obtain ⟨ b ⟩/b = 1.4, which is close to what we observe.
 |
Fig. 31 Median burst mass fraction vs. the total baryonic mass (stars+gas) of the starburst sample with b > 3, the starburst candidate sample with fburst > 3% and the postburst sample (EWHδ < −6 Å). |
 |
Fig. 32 Total mass of stars, stellar remnants and gas versus the starburst age. Two different restrictions are applied. In the top diagram the condition is that the b parameter should be b > 3. In the lower diagram the restriction is that the burst mass fractions should be higher than 3%. The green markers are medians in log age. |
Figure 31 displays how the mass fraction relates to the total mass. As a consequence of the decrease of ⟨ b ⟩ with mass we also find a decrease of the mass fraction with mass. In the mid part of the diagram is shown the medians of the burst mass fraction. If the burst is shut down abruptly at its peak, this diagram should agree fairly well with the postburst diagram at the bottom. The agreement is fair at the mid-high mass end but deviates strongly at the low mass end. Using the same reasoning as in the preceding subsection we can estimate the maximum ratio between the total mass produced by the burst to the mass produced up to the observation of the burst (typically at an age of 68 Myr). We then obtain ℳtot/ ℳ∗ = (1−e− t∗/τ)-1 = 2.0, in strong agreement with the low mass part of the diagrams. Another reason for the difference between the mass fractions is the metallicity dependence of fburst versus the Hδ selection criterion. From Fig. 1 we see that the Hδ lines are weaker at low metallicities and that we would need more mass in the burst population to produce a 6 Å absorption line. The fact that the lower envelope of the postburst distribution in Fig. 31 is bending upwards at smaller masses indicates that the metallicity effect dominates in explaining the difference in the mass fractions. Generally speaking we can conclude that the mass fractions we derive for the postburst sample is significantly smaller than found by some other groups (Liu & Green 1996; Norton et al. 2001; Melnick & De Propris 2013) and, although still smaller, more in agreement with Swinbank et al. (2012) and Nolan et al. (2007).
Figure 32 shows how the starburst age relates to the total baryonic mass of the galaxies under two different conditions, b> 3 and fburst> 3%. In the first case the ages are almost independent of mass. This is in agreement with the analysis of ellipticals by Hopkins & Hernquist (2010). They investigate the properties of burst relic populations and try to recover the properties of the burst when it was active. They conclude that the starburst time-scale is ~100 Myr and is nearly mass-independent, in agreement with our results.
In the bottom figure we show the mass as function of age under the condition that the burst mass fraction should be larger than 3%. We can clearly define two branches in lifetimes. Part of this bimodality may be caused by the discreteness in SFR decay rates we use in the models. However, there is a prominent change in lifetime starting at a baryonic mass of log ℳ~ 10.5. The shift occurs at the same mass as the break observed by Kauffmann et al. (2003b) in the colours of SDSS galaxies. The break signals a transition from star forming dwarfish galaxies to galaxies dominated by old populations, high mass densities and a high fraction of bulges. There is also an increasing presence of bars in massive disc galaxies, starting to dominate the star-forming galaxy population at a stellar mass log ℳ~ 10.2 (Nair & Abraham 2010; Skibba et al. 2012). Bars drive inflows of gas towards the central areas (e.g Di Matteo et al. 2007). Could perhaps bars in the massive disks explain the shift at log ℳ~ 10.5? In such a scenario we can assume that the gas inflow rate 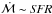 . From Fig. 32 we derive the minimum ⟨SFR⟩ for a galaxy of mass 1011ℳ⊙ to ~15 ℳ⊙ yr-1. Assuming we are dealing with inflows towards the central kpc region, our inflow rate is a magnitude higher than what models normally predict (Maciejewski 2004). However, inflow rate and burst duration are both in fair agreement with models of star formation occurring in nuclear rings formed in exponential disks with extremely high surface density (Kim et al. 2012). But according to the authors, inflows driven by the bar potential is not enough to explain the fact the star formation in nuclear rings occurs over a few Gyrs (e.g. Allard et al. 2006; Sarzi et al. 2007). Another mechanism, as for example the dynamical influence of spiral arms, seems to be needed to sustain the SF activity over a longer period of time. It thus appears that the increased lifetime of the SF regions occurring in our sample at high masses could at least partly be explained by SF in nuclear rings. However, these galaxies do not often fulfil the b> 3 criterion. An additional mechanism that may be important emerges from the simulations by Hopkins et al. (2013). They study starbursts in mergers of equal mass galaxies. In low mass mergers that burst is rapidly quenched by stellar feedback and gas is expelled to large distances. In more massive galaxies gas is expelled from feedback-driven winds in the centre but much of the material is not unbound but falls back towards the disc after a short time. This can prolong the starburst phase over a few 100 Myr.
. From Fig. 32 we derive the minimum ⟨SFR⟩ for a galaxy of mass 1011ℳ⊙ to ~15 ℳ⊙ yr-1. Assuming we are dealing with inflows towards the central kpc region, our inflow rate is a magnitude higher than what models normally predict (Maciejewski 2004). However, inflow rate and burst duration are both in fair agreement with models of star formation occurring in nuclear rings formed in exponential disks with extremely high surface density (Kim et al. 2012). But according to the authors, inflows driven by the bar potential is not enough to explain the fact the star formation in nuclear rings occurs over a few Gyrs (e.g. Allard et al. 2006; Sarzi et al. 2007). Another mechanism, as for example the dynamical influence of spiral arms, seems to be needed to sustain the SF activity over a longer period of time. It thus appears that the increased lifetime of the SF regions occurring in our sample at high masses could at least partly be explained by SF in nuclear rings. However, these galaxies do not often fulfil the b> 3 criterion. An additional mechanism that may be important emerges from the simulations by Hopkins et al. (2013). They study starbursts in mergers of equal mass galaxies. In low mass mergers that burst is rapidly quenched by stellar feedback and gas is expelled to large distances. In more massive galaxies gas is expelled from feedback-driven winds in the centre but much of the material is not unbound but falls back towards the disc after a short time. This can prolong the starburst phase over a few 100 Myr.
4.5. Cold outflows
Galactic outflows are known to be quite common in galaxies of high star formation activity (Heckman et al. 1993, 2000; Papaderos et al. 1994; Lehnert & Heckman 1996; Martin 2005; Amorín et al. 2012) and are found at all cosmic epochs (e.g Bergvall & Johansson 1985; Johansson & Bergvall 1988; Heckman 2001; Pettini et al. 2001; Frye et al. 2002; Shapley et al. 2003; Elson et al. 2013; Noterdaeme et al. 2012). As was mentioned in the introduction, under certain conditions superwinds generated by SN activity can drive cold (≲104 K) gas out to large distances from the starburst before the gas experiences instabilities and/or is heated by conduction (e.g. Chevalier & Clegg 1985). These events may have a strong influence on the global properties of starburst galaxies as well as the ambient intergalactic medium. A few observations of galaxies in the local universe show that the condition for blowout, i.e. a significant part of the cold gas being accelerated to velocities higher than the escape velocities may be fulfilled (Ott et al. 2001). Another aspect is that mass outflows may open channels for Lyα and Ly continuum radiation to leak out. The importance of starburst dwarfs as sources of the cosmic reionisation and Lyα emitting starburst galaxies as beacons in the distant universe have often been discussed (Cowie & Hu 1998; Rhoads et al. 2000).
Different methods are employed to study cold flows, e.g. broad emission lines and Hα morphologies indicating outflows in the minor axis direction (Lehnert & Heckman 1996; Bik et al. 2015) and blueshift of absorption lines in the cold gas (Heckman et al. 2000; Grimes et al. 2009; Chen et al. 2010). Next we briefly discuss the problem and see what the SDSS data can tell us.
Observations show that cold outflows occur in galaxies with a high SFR per surface area, ΣSFR. Typically, outflows are observed if ΣSFR> 0.1ℳ⊙ yr-1 kpc-2 (Heckman 2002; Chen et al. 2010). This limit is supported by theoretical modelling (Murray et al. 2011; Scannapieco 2013). We calculated ΣSFR using the area 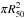 , in line with Rubin et al. (2010). Kornei et al. (2012) argue for a slightly different way of deriving the area
, in line with Rubin et al. (2010). Kornei et al. (2012) argue for a slightly different way of deriving the area 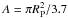 , where RP is the Petrosian radius, which will result in slightly lower values of ΣSFR.
, where RP is the Petrosian radius, which will result in slightly lower values of ΣSFR.
Figure 33 shows the ΣSFR as function of mass. The upper limit of the envelope agrees with the conclusion drawn by Lehnert & Heckman (1996), namely that no starburst seems to have a surface density of star-formation above ~20 ℳ⊙ yr-1 kpc-2. This was interpreted as an indication of self-regulation in the star-formation process. In the diagram we also see the sample divided into galaxies with high b-parameters (b > 5) superposed on galaxies with low b-parameters (b< 5). We see that there is a correlation between mass and ΣSFR. Another interesting result is that outflows in low mass galaxies often seem to be linked to strong starbursts while outflows in massive galaxies happen under more quiescent conditions.
How important are AGNs as drivers of the outflows? If they are important, one would expect to see them in action at high masses. Presumably this would lead to an anti-correlation between starburst age and galaxy mass. We find no such relation (cf. Fig. 32). Sell et al. (2014) investigate the outflows found in 12 massive galaxies, half of which contain AGNs, and conclude that the major drivers are actually starbursts. But a complete blow-out seems rare. French et al. (2015) recently discovered large amounts of molecular gas in postburst galaxies that “.. rule out complete gas consumption, expulsion, or starvation as the primary mechanism that ends the starburst in these galaxies”. We believe more information is needed in order to reach a firm conclusion.
 |
Fig. 33 SFR per area as function of baryonic mass of the galaxies in the starburst candidate sample. Galaxies with b > 5 (yellow circles) are superposed on the distribution of the remaining galaxies (blue triangles). The horizontal line marks the transition between when the energy produced by the starburst is sufficient to generate outflows, both according to models and to observations. |
5. Discussion
5.1. Comparison with other similar investigations
From the analysis above we can conclude that starburst galaxies, defined as galaxies with b > 3 or fburst > 3%, contribute marginally to the star formation history in the local universe, comprising only ~1% of the star-forming galaxies. Although we do not know of any investigation that argues for such a low frequency of starbursts as we do here, the paucity of starbursts has been confirmed by previous studies both in the local universe and at high redshifts (e.g. Kennicutt et al. 1987; Noeske 2009; Lee et al. 2009b; Rodighiero et al. 2011; Sargent et al. 2012; Karachentsev & Kaisina 2013; Schreiber et al. 2015). Rodighiero et al. were investigating the redshift interval 1.5 < z < 2.5 and found that starburst galaxies represent only 2% of star-forming galaxies and account for only 10% of the cosmic SFR density. As demonstrated by e.g. Schreiber et al. (2015) the fraction of starbursts does not change much with redshift in the range 0.5 < z < 4. To compare to our results we have to first look at the starburst selection criterion they used. The criterion they used was SFRstarburst > 4 × SFRGMS. How does this compare to the b parameter? By comparing the GMS SFR, based on the data from Elbaz et al. (2007), to our median SFR for starbursts for masses >1010ℳ⊙, we find that b > 3 corresponds to 3 < SFR/SFRGMS < 8, i.e. significantly higher than their criterion. Therefore it seems, if we take the more stringent definition we use into account, that our and the results from Rodighiero et al. agree quite well.
One may argue that using the SFR/SFRGMS to define a starburst may be a better approach than using the b parameter. We think that both methods have their pros and cons. As we mentioned above, one has to consider the fact that the relative gas content decreases with mass. We know that galaxy merging is the most probable starburst triggering mechanism in the local universe. We also know that the SFR follows the Kennicutt-Schmidt law for the H i gas (Kennicutt 1998) and similar for the H2 gas (Leroy et al. 2013). Both laws concern the relation between SFR and surface density. On the whole, the SFR is simply related to the amount of fuel available (e.g. Karachentsev & Kaisina 2013; Lelli et al. 2014). Imagine a merger between 3 normal equal-mass galaxies, after the merger resulting in an L∗ galaxy. The merged galaxy will contain about twice as much gas (both H i and H2) as an isolated galaxy of the same mass. Most probably the SFR will increase by a factor of at least ~2 without the need of referring to an increased star formation efficiency placing it above the GMS. A merger between low mass galaxies will not result in such a large increase in relative gas mass fraction. Taking this into account shows that using a constant value of the b-parameter is in fact well motivated. Although this thinking is valid in the local universe it may however fail at higher redshifts (Perret et al. 2014).
In Sect. 2.2 we examined the frequency of the past burst strength in postburst galaxies and found that 95% had fburst> 3%. We concluded that this is lower than the fburst > 5% Kauffmann et al. (2003b) found in their sample. Both were selected on the criterion EWHδ<–6 Å. In our study this conflict is of some concern since we use the postbursts to link the starburst population. In particular we use the LF of the postburst population at high luminosities to estimate the loss of starbursts due to heavy obscuration and contamination from AGNs. If the minimum burst mass fraction in postburst galaxies is in fact higher than what we found in our investigation, it means we should compare the postbursts to starbursts that are limited by fburst > 5%. Since this leads to fewer bursting galaxies, one consequence is, in order to match the relative number of the fburst> 5% sample to the postburst sample, that the duration of the postburst phase must become longer.
We now look at the possible causes of the discrepancies between our result and that of Kauffmann et al. As we show in the Appendix, the burst strength we derive is quite uncertain for spectra with low S/N (≤10). The trend at low S/N is however to overestimate the mass fraction so the difference between our result and Kauffmann et al. persists. Kauffmann et al. derive maximum-likelihood estimates of ℳ/Land mass based on two indices − the 4000 Å break and Hδ in absorption. These indices were calibrated from a Monte Carlo simulation of 32 000 spectra with different star formation histories (SFHs). In these simulations it was assumed that the starburst had a constant SFR over a distribution of timescales in the interval 3 × 107−3 × 108 years. The starburst was then mixed in various proportions with an old stellar population with decaying SFR of various timescales. The dust attenuation was determined from the amount by which the observed gri colors deviated from those predicted.
There are several details that differ between our procedure and that of Kauffmann et al.. Some may help to explain the difference between our results. While Kauffmann et al. use two parameters to determine ℳ/L-ratios and masses, we compare more or less the full optical spectra with our model predictions, all in all about 3000 model spectra corresponding to the postburst phase. The corrections for dust attenuation is another detail that differs between our procedures. The way we do it for postbursts is however not too different from theirs so this should be a minor cause of the discrepancy. But what about the SED models we use? Our model contains an integrated gaseous emission component while they subtract the nebular component before comparing to the Bruzual-Charlot stars-only model data. This difference should however play a minor role for postburst galaxies. What may be more important is the SFH adopted for the starburst population. While we assume the old component comes from a 100 Myr burst, Kauffmann et al. allow a variety of SFHs for the old component. However, this should have a minor impact. If we compare the ℳ/Ltoday between a 100 Myr burst and an exponentially decaying SFR on a timescale of 1 Gyr, the difference is ~4%. What may be more influential is the SFH of the young component. While Kauffmann et al. adopt a constant SFR of variable duration we allow for a range of both exponentially declining and constant SFHs. In the final selection of the best fits to our model we only find 11% SFHs with constant SFR. As we argue later on, and what is also stated by Kauffmann et al. as concerns the older stellar population, star formation in bursts most likely occur in a decaying mode. Yet they assume a constant SFR for their burst model. We have, among 57 models, the option to compare models based on constant SFR with those of exponentially decaying bursts to look for significant differences. Could that possibly give a hint as to why our and Kauffmann’s et al. results do not quite agree? When we do this comparison it appears the different SFHs cannot explain the disagreement. After a more detailed investigation of the error propagation generated in the processing steps of the different methods used we may possibly find an explanation but such a test is outside the scope of this paper.
Brinchmann et al. (2004) work with SDSS data and use a similar method as we do here to derive the b-parameter. Assuming a starburst to have b > 2–3 they find that starbursts contribute about 20% of the star formation in the local universe. If we apply b > 2 as a criterion, the number of starbursts increases by a factor of 2 and we arrive at a contribution of ~9%. This is significantly lower than the result by Brinchmann et al.
We conclude that, although many studies support our result regarding the paucity of starbursts, others claim a significantly higher frequency of starbursts and a higher mass fraction. What is the cause of the discrepancy? One apparent problem is how to define a starburst galaxy. In many investigations the starburst criterion is based on the EWHα. We have demonstrated that all these studies must fall short because of the lack of correction for time dependent dust attenuation. Likewise, many teams use EWHα> 100 Å as a starburst criterion. We show in Sect. 2.2 that this criterion corresponds to b ~ 1, i.e. hardly a starburst.
But now let us look more closely at the two other studies, based on SDSS data, that seem quite related to ours. We have already commented on the work by Kauffmann et al. (2003b) concerning postburst galaxies. We continue the comparison with this paper below. The second paper is the work by Brinchmann et al. (2004). They find higher values of the birthrate parameter than we do. One may suspect (cmp. Eq. (14)) that significant differences exist between the determination of the SFR and/or the masses. Alternatively the data may be plagued by selection biases at low redshifts, where low mass galaxies tend to dominate. The lower redshift limit we use is z = 0.02 while Brinchmann et al. use z = 0.005. As we demonstrated above, significant aperture problems occur below our redshift limit. Moreover, the risk of confusion between galaxies and H ii regions in nearby galaxies also increases dramatically. However, relatively few galaxies, most of them at masses lower than our low limit, should be affected. Besides, the aperture corrections applied by Brinchmann et al. seem to work fine in most cases.
For galaxies with strong emission lines, the SFR calculated by Brinchmann et al. is based on the Hα flux, corrected for dust attenuation. The method they apply for the dust correction (Charlot & Fall 2000) is different from ours. One difference that may be important here is that their model is based on the assumption that the SFR of the burst is constant. We have demonstrated in Sect. 4.4 that most galaxies have short decay rates (30 Myr in ~50% of the cases). In such cases the effect of the age dependent dust attenuation will differ from when the SFR is assumed to be constant. In order to have an idea of the effect of different SFHs on the derived present SFR we compared the best results from spectral fits based on a decay rate of 3 × 107 yr with one with a decay rate of 1 Gyr. A 1 Gyr decay rate may be regarded as a nearly constant SFR for a starburst with a duration ~100 Myr. We used our approach to correct for dust attenuation and found that in the latter case, the deduced SFR based on the Hα flux was ~10% lower than in the former. Thus, the difference between the corrections to the Hα flux because of the different assumptions as regards the SF history should not be important.
What about the derived masses? Brinchmann et al. use masses from the modelling by Kauffmann et al. (2003b). These are available from the MPA Garching homepages4 and a comparison between our masses and Kauffmann’s et al. masses indicates that the mismatch increases towards lower masses. Kauffmann et al. use two parameters − the observed 4000 Å break and Hδabs to derive ℳ/Lratios. The models include starbursts with masses 0.03−4 times the mass of the old stellar component. This definition of mass fraction is not too different from our fburst. But we show above that starbursts can have fburst< 3%. Such low-mass bursts are not modelled by Kauffmann et al. and this can lead to incorrect ℳ/Lratios as is also shown in their map of the uncertainties in derived ℳ/Lratios (see their Fig. 5). Moreover, for large fburst (and, as we have shown, fburst increases towards lower masses) it becomes difficult to derive the contribution to the light in the optical region limited to the two parameters they use. Our strategy, to base the modelling on more or less the entire optical spectrum will, in our opinion, lead to more robust results. On the other hand, our model is simpler than Kauffmann’s et al. We use only two populations, while they work with multiple component populations which is very useful when working with star-forming galaxies in general. We claim however that, using our model, we manage to derive reasonably accurate masses from spectra of starburst galaxies, using relatively few parameters.
As was described in Sect. 4.4, we found that the majority of low-mass starbursts, in contrast to the high mass starbursts, have short decay rates. The Kauffman’s et al. models are based on a constant SFR. What are the consequences of the different approaches? Most likely the age and ℳ/L of the burst population in the model with constant SFR would be highest. The burst mass would be overestimated.
Finally, we wish to mention an additional problem occurring when a fit is made to the stellar continuum at ages below a few 107 yr. If the starburst is strong, the free-free and free-bound emission from the ionised gas will make a significant contribution (e.g. Bergvall & Östlin 2002; Zackrisson et al. 2008) and cannot be neglected in the modelling. Since we include the nebular component in our model this will not be a problem for us but will have an effect in the work by Kauffmann et al. since they make a fit to the (Bruzual & Charlot 2003) SEM that contains no nebular component.
We find confidence in the fact that our mass determinations are strongly supported by the tight correlation between our photometric and dynamical mass estimates as well as the correlation between our data and model results from STARLIGHT (see Appendix).
5.2. Starbursts and galaxy evolution
In our study we have chosen to define a starburst as an event that will drastically influence the evolution of the galaxy over a short time. If we prefer to use the concept starburst as a measure of a dramatic change in the SFR compared to the present state of normal star formation activity, the b-parameter may not be the optimum parameter to use since one would have to lower the criterion with increasing mass and decreasing gas content. This motivated McQuinn et al. (2009, 2010a) to base their b-parameter on the stars formed during the latest 6 Gyr. Similarly Schreiber et al. (2015) chose to define a starburst as a 4-folded increase in SFR compared to the typical galaxy of the same mass on the GMS. This may be a valid approach but it is not possible to apply it to SDSS galaxies in general. The problem is that we have too little information about what causes the burst. As we argued above, if the starburst is caused by a merger then a large amount of gas may be transferred to the starburst host galaxy and the previous gas content becomes irrelevant.
There are many claims that starbursts are related to tidal interactions but there are also critical views of this approach. Indeed, there is statistical evidence of increased SF activity in interacting galaxies but starbursts are relatively rare (Hummel 1980, 1981; Kennicutt et al. 1987; Bushouse et al. 1988; Brosch et al. 2004; Casasola et al. 2004; Smith et al. 2007; Di Matteo et al. 2008; Knapen & James 2009). We (Bergvall et al. 2003) argued, from comparing SF properties of isolated pairs to isolated single galaxies, that interactions rarely gave rise to starbursts. We also claimed that most Arp galaxies had a modest enhancement in SFR, a result that has been confirmed in other studies (e.g. Smith et al. 2007). Many of the studies mentioned above found a weak enhancement of star-formation in disks of interacting disc galaxies but an enhanced activity in the nuclear region. We also found an increase in SFR in the very central regions of a factor of ~2. Similar results were published later, some showing a systematic increase in SFR with decreasing distance between components in pairs (e.g. Nikolic et al. 2004; Li et al. 2008; Scudder et al. 2012). In most cases however, the increase in SFR is very modest and does not influence the global SFR significantly. On the other hand, many observations (e.g. Scudder et al. 2012), including also postburst galaxies (Hiner & Canalizo 2015), indicate that the strongest starbursts were triggered by mergers and most likely the merger rate is correlated with the mean distance between galaxies. When one finds a tight pair of galaxies, there is an increased probability compared to isolated galaxies that a merger took place quite recently. One may think it is the close encounter that caused the starburst when in fact it is a recent merger and it only appears as if the neighboring galaxies caused the starburst.
Observations indicate that the merger rate increases with redshift (e.g. Conselice et al. 2003; Bell et al. 2006; Lackner et al. 2014). Does this mean that the starburst rate is also increasing with redshift? It seems not. Although the main mode of star formation in the early universe was through mergers (Overzier et al. 2008) and the general SFR increases, fluctuations from the mean seem to stay the same (Noeske et al. 2007; Sargent et al. 2012; Schreiber et al. 2015). The feedback effects nicely regulate the mean SFR.
In a study of elliptical galaxies, Hopkins & Hernquist (2010) tried to separate the burst component from the old component using the Kennicutt-Schmidt law in reverse. They came to the conclusion that single bursts typically contribute to the stellar production with about 10% of the total mass and that the star formation proceeds in cycles on a time scale of ~100 Myr. The time scale agrees nicely with what we have derived and also with Lee et al. (2009b) and determinations from CM diagrams of local galaxies (Vallenari & Bomans 1996; Dohm-Palmer et al. 1998; Weisz et al. 2008). It also agrees well with theoretical models (Mihos & Hernquist 1994; Hopkins et al. 2013) but longer than Mihos & Hernquist (1996). The burst mass fraction (cf. Fig. 31) in general is lower in our postbursts but rises towards low masses to a level close to 10%. In a simulation of the Antennae galaxy, Renaud et al. (2008) propose that the extraordinarily good conditions for star cluster formation in the system could be explained by the formation of compressive tides. Again we find the same time scale for the survival of the compressive mode, about 100 Myr. A longer duration was found by McQuinn et al. (2009, 2010b) but their definition of starburst differs from ours. Regardless, it seems obvious that starbursts occur in a breathing, episodic mode (Stinson et al. 2007) and if the bursting mode is caused by mergers, models predict a rather weak burst efficiency (Cox et al. 2008), allowing a recurrence.
An important question is what determines the duration of the starbursts. Is it the local feedback phenomena or the amount of available fuel? The gas depletion timescales of neutral hydrogen is of the order of 1 to a few Gyr (Lelli et al. 2014). But star formation is tightly coupled to the amount of H2 available. From Leroy et al. (2013) we obtain typical gas depletion time scales of molecular hydrogen for normal SF galaxies. These are remarkably independent of mass and typically ~2 Gyr. The shortest depletion timescales are ~100 Myr, close to the median lifetimes of our starbursts. A starburst with b ~ 20 could apparently consume the molecular gas over 100 Myr. As we see from Fig. 26, such cases exist but are rare. Most likely molecular clouds are dispersed by stellar feedback after a relatively small fraction of the gas has been consumed. But, since the b-parameter increases with decreasing burst age it seems that the H2 content marks the upper limit to the b-parameter at a give age.
6. Conclusions
We have used data from the SDSS DR7 release in the redshift range 0.02 ≤ z ≤ 0.4 to investigate the starburst properties of galaxies in the local universe and to establish a link between starburst and post-starburst (called postburst in our study) galaxies. We also had a first look at the role of AGNs in this context at high luminosities.
In order to select the starburst candidates we assigned a lower limit to the Hα emission line equivalent width of EWHα = 60 Å. This sample contained both starbursts and non–starburst galaxies that were later separated after proper treatment of the effects of dust attenuation. The selection criterion for the postburst galaxies was based on the Hδ line in absorption, demanding that the equivalent width should be ≤–6 Å. In our analysis, we used a spectral evolutionary model based on two stellar components – a young and an old. The young component is allowed to vary in age and mixes with the old component until we obtain a best fit that also gives an EWHα that agrees with the observations. AGNs were selected into a separate group. The AGNs start to mix with the starburst/postburst sample at Mr ≈ −21. Therefore studies of starburst properties at the bright end of the luminosity function demand special care. In this study we focus on the sub-L∗ population and do not treat the AGN problem in detail.
The corrections for dust attenuation are important and we have applied two different methods. In the emission line sample we have used the Hα/Hβ ratio and assumed that the attenuation is age dependent and dramatically changes over a few Myr during the young phase. In the postburst case we have tentatively modified the amount of dust until we get the best fit. From the model we derive SFRs, ages and masses of the young and old component.
We also derive dynamical masses from the width of the Hα emission line. These masses were compared with the photometric masses, after adding an estimate of the gas mass. We find a tight relation between the two over the entire mass range which gives us confidence that our masses are reliable to within σ = 0.35 dex.
We defined a starburst as a galaxy with a birthrate parameter 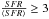 . In the lower end of the LF this population corresponds to only 0.5−1% of all galaxy types in the local universe. 1% of sub-L∗ star-forming galaxies is a starburst. We estimate that starbursts contribute only 4.4
. In the lower end of the LF this population corresponds to only 0.5−1% of all galaxy types in the local universe. 1% of sub-L∗ star-forming galaxies is a starburst. We estimate that starbursts contribute only 4.4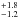 % of the total production of stars in the local universe. The median value of the birthrate parameter is b ~ 4 and decreases slowly with increasing mass. The mean birthrate parameter over the starburst epoch is higher than the present value. We interpret this as if the starbursts had a more violent past and are declining in an approximately exponential mode. The typical mass fraction of the burst population is 5% of the total mass, slowly decreasing towards higher masses.
% of the total production of stars in the local universe. The median value of the birthrate parameter is b ~ 4 and decreases slowly with increasing mass. The mean birthrate parameter over the starburst epoch is higher than the present value. We interpret this as if the starbursts had a more violent past and are declining in an approximately exponential mode. The typical mass fraction of the burst population is 5% of the total mass, slowly decreasing towards higher masses.
In the analysis of the postburst sample we find that in 95% of the sample, the decaying burst component has a mass >3% of the total mass. The median mass fraction of the postburst population is 5−10%, which is significantly smaller than what has been reported by other groups. We can select a subsample of our postburst candidate sample and derive the properties of the future generation of postburst galaxies to compare to our observed postburst sample. We then find that the observed LF of the postburst sample should run slightly above and parallel to the fburst ≥ 3% sample at low-intermediate luminosities when difference in luminosities and lifetimes between starburst and postbursts are taken into account. This is what we see in the LF we derive. We therefore think we have established a link between the active starburst and most of its descendants. Short bursts may have high birthrates but low fburst. They will not show up as postbursts. On the other hand we also find that a small part of the postburst galaxies stem from star-forming galaxies with b< 3.
The median age of the starbursts is ~70 Myr, which appears to be independent of mass. The lifetime of the burst appears to be regulated by the ratio of available gas mass and dynamical timescale. The age of the postburst population is a few 100 Myr higher as one would expect. The progenitors to the postburst galaxies, i.e. galaxies with fburst> 3% display a bimodal age distribution with a transition from ages slightly below 100 Myr to twice this value at log ℳ(ℳ⊙) = 10.5. This value is the same as found previously in the colour distribution of SDSS star-forming galaxies. We discussed possible explanations.
At high luminosities AGNs dominate the population while the starburst population diminishes. The LF of the postburst population closely follows that of the AGNs while the progenitor LF separates more and more, indicating an deficit of a factor dex at the highest luminosities. The link between the postburst LF and the AGNs tells us that starbursts are also closely linked to AGNs but are difficult to detect. There are probably two reasons for this − an increasing dust obscuration and AGN domination at high luminosities. While the starburst dust obscuration steadily increases with luminosity, the attenuation in postbursts is lower and reaches a maximum and then decreases at high luminosities. Although we have not tried to estimate the amount of obscuration in AGNs, that fact that the LF follows the postburst LF, indicates that they have similar dust properties. If so, the starburst phase would precede both the postburst and the AGN phase.
An interesting question is the ability for a starburst to create SN superwinds that can lead to the removal of a significant fraction of the gas in the system. It is a question that has an impact on our understanding of the cosmic reionisation. We used the SFR per area as a criterion for gas removal efficiency and found that massive galaxies with high b-values are the most probable drivers of mass ejection. This supports the downsizing scenario for star formation as function of redshift.
The processes that initiate starbursts, in the majority of the cases probably via mergers, seem to be balanced by feedback processes that hinder catastrophic events and ensures that the star formation efficiently has a maximum level. We find only small variations in the birthrate parameter, mass fraction and age over the entire mass range. There are reasons to believe that the situation does not dramatically change with redshift but that the change is in the mean SFR. This does not mean that starbursts are unimportant. Starburst galaxies represent the ultimate test bench on galaxy scales for the physical processes in the modern universe. By studying starbursts we learn to understand the distant universe when the occurrence of events we now call starbursts were active. The high power of starbursts makes it possible to inject lots of energy into the ISM and drastically change the conditions and properties of a galaxy. Superwinds, high neutron rate production, Lyman continuum and Lyman line leakage, AGN ignition and many other unsolved feedback processes are some of the very exotic consequences of true starbursts.
Acknowledgments
We are indebted to Dr. Polychronis Papaderos for stimulating discussions and assisting us with the use of the STARLIGHT code and CAUP computer facilities. The anonymous referee is thanked for useful comments on the draft. E.Z. acknowledges research funding from the Swedish Research Council (project 2011-5349), the Wenner-Gren Foundations and the Swedish National Space Board. This research has made use of NASA’s Astrophysics Data System Bibliographic Services. Funding for the SDSS has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. The SDSS Web site is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions. The Participating Institutions are The University of Chicago, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy, the Max-Planck-Institute for Astrophysics, New Mexico State University, University of Pittsburgh, Princeton University, the United States Naval Observatory, and the University of Washington.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Östlin, G., Zackrisson, E., et al. 2010, MNRAS, 407, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Östlin, G., & Zackrisson, E. 2011a, MNRAS, 417, 1904 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Östlin, G., Zackrisson, E., & Hayes, M. 2011b, MNRAS, 414, 1793 [NASA ADS] [CrossRef] [Google Scholar]
- Adamo, A., Östlin, G., Zackrisson, E., et al. 2011c, MNRAS, 415, 2388 [NASA ADS] [CrossRef] [Google Scholar]
- Afonso, J., Hopkins, A., Mobasher, B., & Almeida, C. 2003, ApJ, 597, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Allard, E. L., Knapen, J. H., Peletier, R. F., & Sarzi, M. 2006, MNRAS, 371, 1087 [NASA ADS] [CrossRef] [Google Scholar]
- Amorín, R., Vílchez, J. M., Hägele, G. F., et al. 2012, ApJ, 754, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Asari, N. V., Cid Fernandes, R., Stasińska, G., et al. 2007, MNRAS, 381, 263 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balzano, V. A. 1983, ApJ, 268, 602 [NASA ADS] [CrossRef] [Google Scholar]
- Balzano, V. A., & Weedman, D. W. 1981, ApJ, 243, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Barazza, F. D., Jogee, S., Rix, H.-W., et al. 2006, in New Horizons in Astronomy: Frank N. Bash Symposium, eds. S. J. Kannappan, S. Redfield, J. E. Kessler-Silacci, M. Landriau, & N. Drory, ASP Conf. Ser., 352, 225 [Google Scholar]
- Bekki, K. 2014, MNRAS, 444, 1615 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., & de Jong, R. S. 2001, ApJ, 550, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Phleps, S., Somerville, R. S., et al. 2006, ApJ, 652, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Bergvall, N., & Johansson, L. 1985, A&A, 149, 475 [NASA ADS] [Google Scholar]
- Bergvall, N., & Östlin, G. 2002, A&A, 390, 891 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergvall, N., Laurikainen, E., & Aalto, S. 2003, A&A, 405, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bezanson, R., van Dokkum, P., van de Sande, J., Franx, M., & Kriek, M. 2013, ApJ, 764, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Bik, A., Östlin, G., Hayes, M., et al. 2015, A&A, 576, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blanton, M. R., Dalcanton, J., Eisenstein, D., et al. 2001, AJ, 121, 2358 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brosch, N., Almoznino, E., & Heller, A. B. 2004, MNRAS, 349, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Bushouse, H. A., Werner, M. W., & Lamb, S. A. 1988, ApJ, 335, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Cales, S. L., Brotherton, M. S., Shang, Z., et al. 2013, ApJ, 762, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D. 1997, AJ, 113, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Casasola, V., Bettoni, D., & Galletta, G. 2004, A&A, 422, 941 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Fall, S. M. 2000, ApJ, 539, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Charlot, S., & Longhetti, M. 2001, MNRAS, 323, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-M., Tremonti, C. A., Heckman, T. M., et al. 2010, AJ, 140, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Chevalier, R. A., & Clegg, A. W. 1985, Nature, 317, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 1991, ARA&A, 29, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F. 2014, in Structure and Dynamics of Disk Galaxies, eds. M. S. Seigar, & P. Treuthardt, ASP Conf. Ser., 480, 211 [Google Scholar]
- Conselice, C. J., Bershady, M. A., Dickinson, M., & Papovich, C. 2003, AJ, 126, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Cowie, L. L., & Hu, E. M. 1998, AJ, 115, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, T. J., Jonsson, P., Somerville, R. S., Primack, J. R., & Dekel, A. 2008, MNRAS, 384, 386 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, R. L., Fumagalli, M., & Krumholz, M. 2012, ApJ, 745, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Dickinson, M., Morrison, G., et al. 2007, ApJ, 670, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- de Blok, W. J. G., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2648 [NASA ADS] [CrossRef] [Google Scholar]
- de Grijs, R., Anders, P., Bastian, N., et al. 2003, MNRAS, 343, 1285 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Bournaud, F., Martig, M., et al. 2008, A&A, 492, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dohm-Palmer, R. C., Skillman, E. D., Gallagher, J., et al. 1998, AJ, 116, 1227 [Google Scholar]
- Domínguez Sánchez, H., Pozzi, F., Gruppioni, C., et al. 2011, MNRAS, 417, 900 [NASA ADS] [CrossRef] [Google Scholar]
- Dopita, M. A., Kewley, L. J., Heisler, C. A., & Sutherland, R. S. 2000, ApJ, 542, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Downes, D., & Solomon, P. M. 1998, ApJ, 507, 615 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., & Gunn, J. E. 1983, ApJ, 270, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, A., Smail, I., Poggianti, B. M., et al. 1999, ApJS, 122, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Eisenstein, D. J., Annis, J., Gunn, J. E., et al. 2001, AJ, 122, 2267 [NASA ADS] [CrossRef] [Google Scholar]
- Elbaz, D., Daddi, E., Le Borgne, D., et al. 2007, A&A, 468, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellis, R. S., Colless, M., Broadhurst, T., Heyl, J., & Glazebrook, K. 1996, MNRAS, 280, 235 [NASA ADS] [CrossRef] [Google Scholar]
- Elson, E. C., de Blok, W. J. G., & Kraan-Korteweg, R. C. 2013, MNRAS, 429, 2550 [NASA ADS] [CrossRef] [Google Scholar]
- Fang, J. J., Faber, S. M., Koo, D. C., & Dekel, A. 2013, ApJ, 776, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J. 1996, Hazy, A Brief Introduction to Cloudy 90, University of Kentucky Internal Report [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- French, K. D., Yang, Y., Zabludoff, A., et al. 2015, ApJ, 801, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Frye, B., Broadhurst, T., & Benítez, N. 2002, ApJ, 568, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., Lo, K. Y., Lee, S.-W., & Lee, T.-H. 2001, ApJ, 548, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Forbes, D. A., & Norris, R. P. 2000, MNRAS, 318, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, Q. E., Bastian, N., & Kennicutt, R. C. 2010, MNRAS, 405, 857 [NASA ADS] [Google Scholar]
- Gómez, P. L., Nichol, R. C., Miller, C. J., et al. 2003, ApJ, 584, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, T. 2004, A&A, 427, 125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grimes, J. P., Heckman, T., Aloisi, A., et al. 2009, ApJS, 181, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Guzman, R., Koo, D. C., Faber, S. M., et al. 1996, ApJ, 460, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M. 2001, in Gas and Galaxy Evolution, eds. J. E. Hibbard, M. Rupen, & J. H. van Gorkom, ASP Conf. Ser., 240, 345 [Google Scholar]
- Heckman, T. M. 2002, in Extragalactic Gas at Low Redshift, eds. J. S. Mulchaey, & J. T. Stocke, ASP Conf. Ser., 254, 292 [Google Scholar]
- Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Lehnert, M. D., & Armus, L. 1993, in The Environment and Evolution of Galaxies, eds. J. M. Shull, & H. A. Thronson, Astrophys. Space Sci. Lib., 188, 455 [Google Scholar]
- Heckman, T. M., Lehnert, M. D., Strickland, D. K., & Armus, L. 2000, ApJS, 129, 493 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Heckman, T. M., Borthakur, S., Overzier, R., et al. 2011, ApJ, 730, 5 [Google Scholar]
- Herrmann, K. A., Hunter, D. A., & Elmegreen, B. G. 2013, AJ, 146, 104 [NASA ADS] [CrossRef] [Google Scholar]
- Hilton, M., Conselice, C. J., Roseboom, I. G., et al. 2012, MNRAS, 425, 540 [NASA ADS] [CrossRef] [Google Scholar]
- Hiner, K. D., & Canalizo, G. 2015, ApJ, 799, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, L. C., & Filippenko, A. V. 1996, ApJ, 466, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Hooper, E. J., Liu, C., van Gorkom, J., & O’Neil, K. 2007, in American Astronomical Society Meeting Abstracts, BAAS, 39, 907 [NASA ADS] [Google Scholar]
- Hoopes, C. G., Sembach, K. R., Heckman, T. M., et al. 2004, ApJ, 612, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., & Beacom, J. F. 2006, ApJ, 651, 142 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Hopkins, P. F., & Hernquist, L. 2010, MNRAS, 402, 985 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, A. M., Miller, C. J., Nichol, R. C., et al. 2003, ApJ, 599, 971 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Cox, T. J., Hernquist, L., et al. 2013, MNRAS, 430, 1901 [NASA ADS] [CrossRef] [Google Scholar]
- Hummel, E. 1980, A&A, 89, L1 [NASA ADS] [Google Scholar]
- Hummel, E. 1981, A&A, 96, 111 [NASA ADS] [Google Scholar]
- Ilbert, O., Salvato, M., Le Floc’h, E., et al. 2010, ApJ, 709, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Izotov, Y. I., Guseva, N. G., Fricke, K. J., & Henkel, C. 2014, A&A, 561, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Johansson, L., & Bergvall, N. 1988, A&A, 192, 81 [NASA ADS] [Google Scholar]
- Joseph, R. D., & Wright, G. S. 1985, MNRAS, 214, 87 [NASA ADS] [Google Scholar]
- Karachentsev, I. D., & Kaisina, E. I. 2013, AJ, 146, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Makarov, D. I., & Kaisina, E. I. 2013, AJ, 145, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Karim, A., Schinnerer, E., Martínez-Sansigre, A., et al. 2011, ApJ, 730, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003c, MNRAS, 341, 54 [Google Scholar]
- Kennicutt, Jr., R. C. 1983, ApJ, 272, 54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Kennicutt, Jr., R. C., Roettiger, K. A., Keel, W. C., van der Hulst, J. M., & Hummel, E. 1987, AJ, 93, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, M., Ho, L. C., & Im, M. 2006, ApJ, 642, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, W.-T., Seo, W.-Y., & Kim, Y. 2012, ApJ, 758, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Knapen, J. 2004, in The Neutral ISM in Starburst Galaxies, eds. S. Aalto, S. Huttemeister, & A. Pedlar, ASP Conf. Ser., 320, 205 [Google Scholar]
- Knapen, J. H., & James, P. A. 2009, ApJ, 698, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K. A., Shapley, A. E., Martin, C. L., et al. 2012, ApJ, 758, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kunth, D., & Östlin, G. 2000, A&ARv, 10, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lackner, C. N., Silverman, J. D., Salvato, M., et al. 2014, AJ, 148, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B., & Tinsley, B. M. 1978, ApJ, 219, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Tremonti, C., et al. 2009a, ApJ, 706, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Kennicutt, Jr., R. C., Funes, S. J. J. G., Sakai, S., & Akiyama, S. 2009b, ApJ, 692, 1305 [NASA ADS] [CrossRef] [Google Scholar]
- Lehnert, M. D., & Heckman, T. M. 1996, ApJ, 462, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Lelli, F., Verheijen, M., Fraternali, F., & Sancisi, R. 2012, A&A, 544, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lelli, F., Fraternali, F., & Verheijen, M. 2014, A&A, 563, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lequeux, J. 1983, A&A, 125, 394 [NASA ADS] [Google Scholar]
- Leroy, A., Bolatto, A. D., Simon, J. D., & Blitz, L. 2005, ApJ, 625, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Li, C., Kauffmann, G., Heckman, T. M., Jing, Y. P., & White, S. D. M. 2008, MNRAS, 385, 1903 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C. T., & Green, R. F. 1996, ApJ, 458, L63 [NASA ADS] [CrossRef] [Google Scholar]
- Lo Faro, B., Silva, L., Franceschini, A., Miller, N., & Efstathiou, A. 2015, MNRAS, 447, 3442 [NASA ADS] [CrossRef] [Google Scholar]
- Maciejewski, W. 2004, MNRAS, 354, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P. 1991, ApJ, 376, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, C. L. 2005, ApJ, 621, 227 [Google Scholar]
- Martinsson, T. P. K., Verheijen, M. A. W., Westfall, K. B., et al. 2013, A&A, 557, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGaugh, S. S. 1991, ApJ, 380, 140 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2009, ApJ, 695, 561 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2010a, ApJ, 721, 297 [NASA ADS] [CrossRef] [Google Scholar]
- McQuinn, K. B. W., Skillman, E. D., Cannon, J. M., et al. 2010b, ApJ, 724, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, J., & De Propris, R. 2013, MNRAS, 431, 2034 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, J., Moles, M., Terlevich, R., & Garcia-Pelayo, J.-M. 1987,MNRAS, 226, 849 [Google Scholar]
- Melnick, J., Terlevich, R., & Moles, M. 1988, MNRAS, 235, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Meurer, G. R., Heckman, T. M., Leitherer, C., et al. 1995, AJ, 110, 2665 [NASA ADS] [CrossRef] [Google Scholar]
- Michałowski, M. J., Hayward, C. C., Dunlop, J. S., et al. 2014, A&A, 571, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Micheva, G., Östlin, G., Zackrisson, E., et al. 2013, A&A, 556, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1994, ApJ, 431, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1996, ApJ, 464, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Miralda-Escude, J., & Ostriker, J. P. 1990, ApJ, 350, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Moorman, C. M., Vogeley, M. S., Hoyle, F., et al. 2015, ApJ, 810, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Moorwood, A. F. M. 1996, Space Sci. Rev., 77, 303 [Google Scholar]
- Murray, N., Ménard, B., & Thompson, T. A. 2011, ApJ, 735, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Nair, P. B., & Abraham, R. G. 2010, ApJ, 714, L260 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, D. M., Ridgway, S. E., De Propris, R., & Goto, T. 2012,ApJ, 761, L16 [Google Scholar]
- Nikola, T., Genzel, R., Herrmann, F., et al. 1998, ApJ, 504, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Nikolic, B., Cullen, H., & Alexander, P. 2004, MNRAS, 355, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G. 2009, in Galaxy Evolution: Emerging Insights and Future Challenges, eds. S. Jogee, I. Marinova, L. Hao, & G. A. Blanc, ASP Conf. Ser., 419, 298 [Google Scholar]
- Noeske, K. G., Weiner, B. J., Faber, S. M., et al. 2007, ApJ, 660, L43 [Google Scholar]
- Nolan, L. A., Raychaudhury, S., & Kabán, A. 2007, MNRAS, 375, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Norton, S. A., Gebhardt, K., Zabludoff, A. I., & Zaritsky, D. 2001, ApJ, 557, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Noterdaeme, P., Laursen, P., Petitjean, P., et al. 2012, A&A, 540, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Obrić, M., Ivezić, Ž., Best, P. N., et al. 2006, MNRAS, 370, 1677 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connell, R. W., Gallagher, III, J. S., & Hunter, D. A. 1994, ApJ, 433, 65 [NASA ADS] [CrossRef] [Google Scholar]
- O’Connell, R. W., Gallagher, III, J. S., Hunter, D. A., & Colley, W. N. 1995, ApJ, 446, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Oh, S.-H., de Blok, W. J. G., Brinks, E., Walter, F., & Kennicutt, Jr., R. C. 2011, AJ, 141, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1989, in Astrophysics of gaseous nebulae and active galactic nuclei (Mill Valley, California: University Science Book), 78 [Google Scholar]
- Östlin, G., Amram, P., Masegosa, J., Bergvall, N., & Boulesteix, J. 1999, A&AS, 137, 419 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Östlin, G., Amram, P., Bergvall, N., et al. 2001, A&A, 374, 800 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Östlin, G., Zackrisson, E., Bergvall, N., & Rönnback, J. 2003, A&A, 408, 887 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ott, J., Walter, F., Brinks, E., et al. 2001, AJ, 122, 3070 [NASA ADS] [CrossRef] [Google Scholar]
- Overzier, R. A., Heckman, T. M., Kauffmann, G., et al. 2008, ApJ, 677, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Pacifici, C., Charlot, S., Blaizot, J., & Brinchmann, J. 2012, MNRAS, 421, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Papaderos, P., Fricke, K. J., Thuan, T. X., & Loose, H.-H. 1994, A&A, 291, L13 [NASA ADS] [Google Scholar]
- Papaderos, P., Loose, H.-H., Fricke, K. J., & Thuan, T. X. 1996, A&A, 314, 59 [NASA ADS] [Google Scholar]
- Perret, V., Renaud, F., Epinat, B., et al. 2014, A&A, 562, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petrosian, V. 1976, ApJ, 209, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., Shapley, A. E., Steidel, C. C., et al. 2001, ApJ, 554, 981 [NASA ADS] [CrossRef] [Google Scholar]
- Relaño, M., Kennicutt, Jr., R. C., Eldridge, J. J., Lee, J. C., & Verley, S. 2012, MNRAS, 423, 2933 [NASA ADS] [CrossRef] [Google Scholar]
- Renaud, F., Boily, C. M., Fleck, J.-J., Naab, T., & Theis, C. 2008, MNRAS, 391, L98 [NASA ADS] [Google Scholar]
- Rhoads, J. E., Malhotra, S., Dey, A., et al. 2000, ApJ, 545, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Lebofsky, M. J., Thompson, R. I., Low, F. J., & Tokunaga, A. T. 1980, ApJ, 238, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Rodighiero, G., Daddi, E., Baronchelli, I., et al. 2011, ApJ, 739, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Rubin, K. H. R., Weiner, B. J., Koo, D. C., et al. 2010, ApJ, 719, 1503 [NASA ADS] [CrossRef] [Google Scholar]
- Sage, L. J., Salzer, J. J., Loose, H.-H., & Henkel, C. 1992, A&A, 265, 19 [NASA ADS] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salzer, J. J., MacAlpine, G. M., & Boroson, T. A. 1989, ApJS, 70, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., et al. 1988, ApJ, 325, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Sarzi, M., Allard, E. L., Knapen, J. H., & Mazzuca, L. M. 2007, MNRAS, 380, 949 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E. 2013, ApJ, 763, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Scannapieco, E., Silk, J., & Bouwens, R. 2005, ApJ, 635, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., de Barros, S., & Sklias, P. 2013, A&A, 549, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schiminovich, D., Wyder, T. K., Martin, D. C., et al. 2007, ApJS, 173, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1968, ApJ, 151, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Schreiber, C., Pannella, M., Elbaz, D., et al. 2015, A&A, 575, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scudder, J. M., Ellison, S. L., Torrey, P., Patton, D. R., & Mendel, J. T. 2012, MNRAS, 426, 549 [NASA ADS] [CrossRef] [Google Scholar]
- Sell, P. H., Tremonti, C. A., Hickox, R. C., et al. 2014, MNRAS, 441, 3417 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, A. E., Steidel, C. C., Pettini, M., & Adelberger, K. L. 2003, ApJ, 588, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Masters, K. L., Nichol, R. C., et al. 2012, MNRAS, 423, 1485 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. J., Struck, C., Hancock, M., et al. 2007, AJ, 133, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Songaila, A., Cowie, L. L., & Lilly, S. J. 1990, ApJ, 348, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., Di Matteo, T., & Hernquist, L. 2005, ApJ, 620, L79 [NASA ADS] [CrossRef] [Google Scholar]
- Stinson, G. S., Dalcanton, J. J., Quinn, T., Kaufmann, T., & Wadsley, J. 2007, ApJ, 667, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Strauss, M. A., Weinberg, D. H., Lupton, R. H., et al. 2002, AJ, 124, 1810 [NASA ADS] [CrossRef] [Google Scholar]
- Su, S., Kong, X., Li, J., & Fang, G. 2013, ApJ, 778, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Swinbank, A. M., Balogh, M. L., Bower, R. G., et al. 2012, MNRAS, 420, 672 [NASA ADS] [CrossRef] [Google Scholar]
- Terlevich, R., & Melnick, J. 1981, MNRAS, 195, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Terlevich, R., Melnick, J., Masegosa, J., Moles, M., & Copetti, M. V. F. 1991, A&AS, 91, 285 [NASA ADS] [Google Scholar]
- Torres-Papaqui, J. P., Coziol, R., Ortega-Minakata, R. A., & Neri-Larios, D. M. 2012, ApJ, 754, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Vallenari, A., & Bomans, D. J. 1996, A&A, 313, 713 [NASA ADS] [Google Scholar]
- van Zee, L., Salzer, J. J., & Skillman, E. D. 2001, AJ, 122, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Weedman, D. W., Feldman, F. R., Balzano, V. A., et al. 1981, ApJ, 248, 105 [NASA ADS] [CrossRef] [Google Scholar]
- Weisz, D. R., Skillman, E. D., Cannon, J. M., et al. 2008, ApJ, 689, 160 [NASA ADS] [CrossRef] [Google Scholar]
- Weisz, D. R., Dalcanton, J. J., Williams, B. F., et al. 2011, ApJ, 739, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Zackrisson, E., Bergvall, N., Olofsson, K., & Siebert, A. 2001, A&A, 375, 814 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zackrisson, E., Bergvall, N., & Östlin, G. 2005, A&A, 435, 29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zackrisson, E., Bergvall, N., & Leitet, E. 2008, ApJ, 676, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zhao, Y., Gu, Q., & Gao, Y. 2011, AJ, 141, 68 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Model stability
In this study our results rely heavily on the outcome of our spectral evolutionary modelling. The information contained in a low-dispersion spectrum of a young stellar population is quite limited and it is relevant to ask to what extent we can trust the results. We should also be concerned about our lack of information about what preceded a strong starburst, the metallicity of gas and stars and the stellar mass function.
Our spectral evolutionary model has previously been used in different contexts. It has been tested on super star clusters, blue compact galaxies and low surface brightness galaxies and seems to behave well in these cases (e.g. Zackrisson et al. 2001, 2005; Bergvall & Östlin 2002; Östlin et al. 2003). In the present investigation we therefore feel that we may limit ourselves to a few tests focused on the determination of the age and mass fraction of the young component.
Ideally we would like to test our model against a set of simulated galaxies with known properties of stars gas and dust, covering the range of parameters we expect in our sample. Here we do it simply (via χ2 analysis), but this is sufficient to give us the information we need. Other studies may need more advanced statistical methods. We may compare our strategy to that of the much cited work of Brinchmann et al. (2004). In our case we do not need detailed information about the likelihood distributions of the derived parameters in the manner they prefer. Instead, we obtain the information we need from the tests discussed below. The reason is that our sample of galaxies is more restricted than theirs. Brinchmann et al. work with star forming galaxies in general while we are only interested in starburst galaxies where the light in the optical region is normally completely dominated by the young stellar population. The dust attenuation can be easily controlled since the Hα and Hβ emission lines, used for deriving the extinction coefficient, are strong. Therefore, for most of the starburst galaxies the evolution of the corrected spectrum with time is close to a single parameter function: spectral slope vs time. As the starburst gets older, the extinction corrected spectrum gets redder. As we show in the diagrams below, there are therefore very few options for ambiguity and a simple χ2 test can be used to find the most adequate model of the mixed population. Similar approaches to analysing data sets by applying models with a limited number of component populations can be found elsewhere in the literature and have been demonstrated to give reasonably coherent results (e.g Ilbert et al. 2010; Domínguez Sánchez et al. 2011; Karim et al. 2011; Hilton et al. 2012; Schaerer et al. 2013; Michałowski et al. 2014; Lo Faro et al. 2015).
In order to test the reliability of our model we created a grid of simulated spectra with a mixture of an old and a young population. To this we added various amounts of random noise. We fed the resulting simulated spectrum into our SEM and compared the input spectrum with the solution proposed by the model, selecting the model with the minimum χ2 value as the best fit. In the case of the simulated spectra representing the active starburst phase, we varied the metallicity, the star formation history and the relative mass fraction to test the stability of the solutions. For example, we wanted to know if the programme could reliably distinguish between a 100 Myr starburst mixed with an old stellar population of some mass fraction from a 300 Myr starburst mixed with an old component of smaller mass. We also wanted to know when we could start to rely on the mass fractions. Starbursts with large mass fractions completely dominate the light over that from the old generation so if the spectra are noisy, to what level can we retain the initial information? We show in the following how the tests give us information about the uniqueness of the fits. Moreover, our tests not only show how unique the best fits are, but also how closely the models reproduce the input parameters. This part of the test is important, but is not often given proper emphasis in comparable investigations.
In the case of the postburst galaxies we tested the reliability of the dust attenuation correction, the derived mass fraction and the age determination. As an additional test we compared the total masses, young+old, determined by our model and the STARLIGHT spectral synthesis model (Cid Fernandes et al. 2005).
Appendix A.1: Starbursts
Appendix A.1.1: Ages
Here we have a look at the correlation between the ages of the input synthetic galaxy spectra and the ages of the best fitting models to these spectra, as suggested by our SEM. We do the same with the mass fractions. The input synthetic spectrum is a mixture of a young starburst population and a 10 Gyr old component that was formed in a burst of duration 100 Myr. The synthetic spectra were produced at a few discrete ages as seen in the figures of this appendix. The metallicity was fixed to Z = 0.008 (~40% solar). In the SEM analysis of the synthetic spectra, the metallicities of the SEM were allowed to take on the values Z = 0.004 or 0.008 and the star formation exponential timescale the values 100 Myr or 1 Gyr. The synthetic spectra were degraded with random Gaussian noise resulting in three different S/N per Å: 10, 20 and 40. This corresponds well to the range in S/N of the SDSS spectra as shown in Fig. A.1. The S/N in these were derived in the region 5400−5800 Å and the median S/N was found to be 17.6.
 |
Fig. A.1 Distribution of the S/N in the region 5400−5800 Å of the SDSS starburst candidate galaxy spectra included in this study, as measured by us. |
In Fig. A.2 we show the age we recovered from our model as a function of the age of the starburst in the synthetic spectrum. Metallicities and decay rates are the same in the model producing the synthetic spectrum as in the model recovering the age and mass fraction. The correlation is strong even in the sample with the lowest S/N, with a maximum deviation of 0.1 dex. For each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. So all in all we have 240 spectra in the diagram.
 |
Fig. A.2 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. Here the star formation history is fixed to one single model with a decay rate of 1 Gyr and a metallicity of Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
In Fig. A.3 we show a similar relation but while the metallicity is fixed to Z = 0.008, the decay rate is allowed to vary in the modelling (τ = 100 Myr or 1 Gyr). Here the fits are not as good as in the former case but large deviations only affect a few of the spectra. In about 80% of the cases the deviations are less than 0.1 dex.
 |
Fig. A.3 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. The input model has a decay rate of 1 Gyr but there are two different choices for the star formation history in the fit, either with a decay rate of 100 Myr or one with 1 Gyr. The metallicity was fixed at Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
In Fig. A.4 we fixed the metallicity and decay rate of the programme that produced the synthetic spectra (Z = 0.008, τ = 1 Gyr), but they are allowed to vary in the modelling (Z = 0.004–0.020 and τ = 100 Myr or 1 Gyr). In this case the ages agree very well even if the spectra are noisy. Note that the timescale and the metallicity of the burst that the fitting code chooses to agree almost 100% with the input data.
 |
Fig. A.4 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. The input model has a decay rate of 1 Gyr but there are two different choices for the star formation history and metallicity in the fit, either with a decay rate of 100 Myr or one with 1 Gyr and a metallicity of Z = 0.004 or Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
In Fig. A.5 we show how the mass fraction can be recovered. We see that we are quite safe with spectra of high S/N but run into problems at S/N = 20, in particular at high mass fractions and low ages. The mass fractions tend to be underestimated. We argue in our investigation that mass fractions of starbursts in general are low. Of course we cannot exclude that some of those galaxies, in case the S/N is low, in fact have a significantly higher mass fraction but continuity arguments tell us that this is very unlikely and should not affect the general results. Moreover, only 10% of the SDSS galaxies have ages below 30 Myr where the problem occurs. From the diagrams we may say that mass fractions below 50% typically agree to within 0.2 dex.
 |
Fig. A.5 Test of the reliability of the SEM mass fraction determination. Synthetic spectra were fed into our SEM model and the derived mass fraction of the burst (ordinate) versus the input mass fraction (abscissa) are displayed. The same conditions for modelling holds as in Fig. A.4. At each time step there are 8 models with different ages of the starburst: 5.5, 10, 25, 55, 95, 250, 550 and 950 Myr. Larger symbol: higher age. |
As described above, applying the model parameters given in Table 2 on each SDSS spectrum and varying the age and dust attenuation, will result in 36 (12 young × 3 old) best solutions. More information about the stability of the solutions presented here can be obtained by comparing the best fits with the worst fits among this set of 36 solutions. Figure A.6 displays histograms of the deviations between the best and worst fits. We plot the parameter Δ defined as the log of the ratio between the worst and best fits among the 36 different model results, Δ = log(worst/best) where we look at the parameters χ2, age and the mass fraction of the young component. We see from the diagram that ages (and to a lesser degree the mass fractions) can differ by a factor up to 5 but that the mass fractions are more stable and in general agree between the different solutions within a factor of 2.
 |
Fig. A.6 Illustration of how well the agreement between the best and worst spectral fits to a single SDSS spectrum agree as model metallicities, dust and star formation histories are allowed to vary. The histograms show the deviations in log of the ratio between the predicted parameter values of the worst and the best fits. |
Appendix A.2: Postbursts
Appendix A.2.1: Dust attenuation
The amount of dust attenuation in the starburst sample can be derived from the Hα/Hβ ratio. In the postburst sample we are forced to use a more unreliable method. We calculated a grid of synthetic postburst galaxies, more or less in the same spirit as with the starburst galaxies. At each time step of the modelling of a target spectrum we varied the value of the dust attenuation as we asked the code to make a new fit. That gave us the value of the amount of attenuation. How reliable is this method, considering that the shape of the spectrum is also affected by the age of the stellar population and the mass fraction? In order to test the reliability of our determination the dust attenuation expressed in magnitudes in the Johnson V band (AV) we produced a grid of 80 synthetic postburst spectra with ages 150, 250, 350, 450, 550, 750, 950 and 1500 Myr and mass fractions 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. The preceding starburst as well as the old population (age 10 Gyr) was assumed to have had a constant SFR over 100 Myr. Both have 40% solar metallicity. To these spectra we added reddening corresponding to AV = 0, 0.5 and 1 magnitudes. We then degraded the spectra with Gaussian noise corresponding to S/N perÅ = 10, 20 and 40. Finally we used our SEM to derive AV from the noisy spectra. The result is shown in Fig. A.7. The figure shows what our SEM proposes to be the most probable value of the attenuation in AV magnitudes. The S/N is varied over the range 10−40 and as we see, our SEM manages to a obtain the correct value to high degree. AV is determined to an accuracy of <0.1 dex.
 |
Fig. A.7 Test of the reliability of our determination of the dust attenuation in the V band (AV) based on a grid of 80 synthetic postburst spectra with ages 150, 250, 350, 450, 550, 750, 950 and 1500 Myr and mass fractions 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. The preceding starburst was assumed to have constant SFR over 100 Myr. The old component was assumed to have an age of 10 Gyr. Both have 40% solar metallicity. To these spectra we added reddening corresponding to AV = 0, 0.5 and 1 mag as titles in the diagrams. We then degraded the spectra with Gaussian noise corresponding to the S/N per Å = 10, 20 and 40. Finally we used our SEM to derive AV from the noisy spectra, as shown on the abscissa. The result is displayed in the histograms with the number of spectra on the ordinate. |
Appendix A.2.2: Ages
Here we carried out a test of the age determination in a similar way as with the starburst sample. We used the same spectra as were discussed in the previous section assuming AV = 0.5 for all. Figure A.8 shows the result. The correlation is fairly high with only a few outliers.
 |
Fig. A.8 Test of the reliability of our determination of the ages of the postburst galaxies. We loaded our SEM with the same set of spectra described in the previous section applying 3 different S/N reductions. Each time step contains 10 spectra with different mass fractions between 2 and 100% as previously described. Larger symbols represent larger mass fractions. |
Appendix A.2.3: Mass fractions
In a similar fashion as described above, we tested the reliability of the calculation of the mass fractions of the starburst. Fig. A.9 shows the results. We used the same synthetic spectra as described above. Clearly the determination of the mass fractions have significant problems at low S/N. We tend to overestimate the mass fractions by a factor of almost 2 at low S/N. The situation is better at higher S/N. At mass fractions below 10% the mass fractions between the input and the model results tend to agree very well.
 |
Fig. A.9 Test of the reliability of our determination of the starburst mass fractions of the postburst galaxies. The procedure used was the same as described in Fig. A.8. The size of the symbols represent different ages. Larger symbols represent larger ages. |
Appendix A.2.4: Masses
In Sect. 4.2 we demonstrated that there was a strong one-to-one correlation between dynamical mass and photometric + gas mass. We are also interested in testing our mass determinations against similar models. We have limited possibilities to do so as concerns the starburst galaxies since in almost all cases the nebular component is not included in other models. But we may compare postburst modelling. Here we have had a look at the STARLIGHT model (Cid Fernandes et al. 2005). Since our model is a bi-component model (young and old) and the STARLIGHT model is a multicomponent model, our concepts postburst component and mass fraction of the two components are non-existent in the STARLIGHT model. But we can compare the masses derived from the spectral fits, including both young and old stars. We ran about 500 galaxy spectra with STARLIGHT and then compared the derived spectro-photometric masses. Figure A.10 shows the relation between our fiber stellar masses and those derived from STARLIGHT. As mentioned above, we used the diet Salpeter IMF to derive our masses while STARLIGHT uses the Chabrier IMF (Chabrier 2003). Considering that the models have such different approaches in the derivation of the age and mass distribution of the stellar content one must say that the fit is quite satisfactory (1σ ~ 0.13 dex). The size of the symbols are roughly proportional to the inverse of the dust attenuation. Large symbols thus means the correction for dust attenuation is small. It seems that dusty galaxies with low masses systematically deviate so that our masses tend to be higher that those derived with STARLIGHT.
 |
Fig. A.10 Mass (based on fiber magnitudes) of the stellar (stars+stellar remnants) component of a set of intermediate/high-mass postburst galaxies as derived with our code (Uppsala) vs. the STARLIGHT code. The sizes of the symbols indicate the transparency of the starlight: small symbols − large dust attenuation. The hatched line marks the 1:1 relation. |
Appendix A.3: Metallicities
We have used three different metallicities in the model, 20% solar, 40% solar and 100% solar. First we wish to see if the given metallicities correspond reasonably well to the metallicities obtained from the analysis of emission lines. In Fig. A.11 we see histograms of the distribution in metallicity for three different luminosity bins. Even though we cannot really make rough determinations of metallicities from our results, it is nevertheless interesting to see it as a check of how reliable our models are. As one can see from the diagram, the model mean metallicities increase with luminosity, as expected.
 |
Fig. A.11 Metallicities of the models that gave the best fits to the observed spectra. The metallicities available in the model are given at the bottom of the figure in solar metallicity units. The sample has been divided into three bins with respect to absolute magnitude in the r band. The galaxies tend to become more metal rich with increasing luminosity. |
All Tables
All Figures
 |
Fig. 1 EWHδ in absorption as function of burst age in two stellar populations of different star formation histories according to Bruzual & Charlot (2003). No nebular emission is included in the model. The upper diagram a) shows the evolution in a population that has experienced a short burst and in b) the SFR has been constant for 100 Myr before being abruptly shut down. The model results for three different metallicities, Z = 0.005 (dashed-dot blue), Z = 0.02 (solid green) and Z = 0.05 (dashed red) are shown. Our selection criterion for a post-starburst galaxy (EWHδ<−6 Å) is indicated with the horizontal yellow line. |
| In the text | |
 |
Fig. 2 Mass fractions, fburst, derived for the postburst sample, both with and without the b> 3 criterion (red dashed line). The limit towards low mass fractions clearly show up as steep decline around fburst ~ 3%. About 95% of the galaxies in the larger sample have fburst ≥ 3%. |
| In the text | |
 |
Fig. 3 Upper diagrams: our model predictions of EWHα,em as function of the duration of the burst when 3 and 30% of the total mass is formed during a burst with constant SFR. Two different scenarios are displayed: 1) a burst in an old galaxy where the stars were formed in a single burst (hatched line); and 2) a burst in a galaxy which has had a constant SFR over a Hubble time (solid line). Lower diagrams: the evolution of the b-parameter. The limit of our criterion of a starburst, the soft criterion, stating that |
| In the text | |
 |
Fig. 4 BPT (Baldwin et al. 1981) diagram of the EWHα≥ 60 Å starburst galaxy candidate sample based on line peak intensity ratios. The solid red line is the empirical dividing line (a modified version of the equation given by Kauffmann et al. (2003a) shown in hatched green) between starburst galaxies (lower part, grey symbols) and galaxies containing an AGN contributing significantly to the flux in the strong emission lines (upper part, green dots). As a complementary AGN criterion we also used FWHM(Hαem) > 540 km s-1. |
| In the text | |
 |
Fig. 5 Redshift distributions of the galaxies in the starburst and postburst samples. |
| In the text | |
 |
Fig. 6 Hα emission line equivalent widths of our target galaxies as derived from our measurements, versus the value as obtained from the SDSS. |
| In the text | |
 |
Fig. 7 Hδ absorption line equivalent widths of our target galaxies as derived from our measurements, versus the value as obtained from the SDSS. |
| In the text | |
 |
Fig. 8 Hδ and Hγ absorption line equivalent widths after our remeasuring. |
| In the text | |
 |
Fig. 9 An example of a model of a starburst spectrum (SDSS SpecObjId 81288133269782528). Displayed are the two model components – a young (blue line) and an old (red line) stellar population. The sum of the model spectra (dark green line) is shown on top of the observed spectrum (light green). The observed spectrum has been smoothed with a triangular filter with a width of 7 pixels. The shaded areas indicate regions we have flagged to avoid strong emission lines in the fits. Note however that EWHα,em is used as a separate criterion in the fitting. |
| In the text | |
 |
Fig. 10 An example of a model of a postburst spectrum (SDSS SpecObjId 85508603053604864). Displayed are the two model components – a young (blue line) and an old (red line) stellar population. The sum of the model spectra (dark green line) is shown on top of the observed spectrum (light green line). The observed spectrum has been smoothed with a triangular filter with a width of 7 pixels. The bright emission line just below 5000 Å is a remnant from the [O i]λ5577 night sky line. The emission lines in the region around Hα are the [N ii]λλ6548, 6584 lines. Since no Hα is seen (although some is probably swallowed by the stellar absorption line), most of the nitrogen lines are probably originating from a weak AGN. |
| In the text | |
 |
Fig. 11 Reduced χ2 of the spectral fits adopting two different procedures for correction of dust attenuation. The hatched region shows the distribution after applying the corrections according to Table 3. The other line shows the distribution after we have applied the more classic approach with an extinction coefficient that is twice as high in star-forming regions compared to passive regions. Obviously the age dependent dust attenuation correction yields the smaller reduced χ2 values and thus gives the better fit. |
| In the text | |
 |
Fig. 12 a) Model of the evolution of EWHα in a star-forming galaxy under two different conditions for dust attenuation. The attenuation in the V band during the major star formation epoch is AV = 1 mag. and the SFR is constant. The full drawn line shows how the equivalent width changes with age assuming constant dust attenuation. In this case EWHα is identical to the dust free case. In the second case, shown in the dashed line, we assume an age dependency in the attenuation. b) The ratio between EWHα in the two cases. The figure shows that EWHα in the age dependent dust attenuation case drops off up to ~50%. |
| In the text | |
 |
Fig. 13 Luminosity weighted attenuation in the V band in the samples of starburst and postburst candidates. Notice that for clarity, the bin size differs between the two samples. |
| In the text | |
 |
Fig. 14 Dust correction factor of EWHα vs. dust corrected SFR for the full starburst candidate The overplotted filled circles connected with solid lines are the median values in bins along the x-axis. |
| In the text | |
 |
Fig. 15 Radii encompassing 50% (R50) and 90% (R90) of the Petrosian flux in the r band of the starburst galaxy candidates. |
| In the text | |
 |
Fig. 16 EWHα versus redshift in different luminosity bins after remeasurements and correction for dust attenuation. The red solid line shows the medians of log (EWHα) in bins along the x-axis. For comparison, the faint gray line shows the medians before corrections for dust attenuation. |
| In the text | |
 |
Fig. 17 Dust attenuation in V versus redshift in different luminosity bins. The solid red line shows the medians of AV in bins along the x-axis. |
| In the text | |
 |
Fig. 18 ℳ∗/LV in different luminosity bins as function of redshift, after correction for dust attenuation. The solid red line shows the medians of ℳ∗/LV in bins along the x-axis. |
| In the text | |
 |
Fig. 19 Upper diagram: LF of 1) starburst galaxies with a birthrate parameter b > 3; 2) starburst galaxies with a mass fraction of the burst fburst > 3%; 3) postburst galaxies; 4) AGNs in the emission-line galaxy sample; 5) the full galaxy LF of the local universe as derived by Blanton et al. (2001). The sampling completeness limit based on the apparent spectroscopic limit Mr = 17.5 and the redshift limit z = 0.02 is indicated with a vertical hatched line. Lower diagram: the relative fraction of the different samples with regards to the total LF, as a function of absolute magnitude. The vertical bars are standard deviations. Please notice that we have assumed (for purely technical reasons) that the Blanton LF for normal galaxies can be extrapolated to Mr < −23. |
| In the text | |
 |
Fig. 20 Dust attenuation given in AV, as function of absolute magnitude. Red dots are medians. Notice the peak in AV for the postbursts which is not seen in the starburst sample. |
| In the text | |
 |
Fig. 21 SFR density of the starburst b> 3 sample vs. absolute r-magnitude. The errors bars are standard deviations. |
| In the text | |
 |
Fig. 22 Dynamical mass, derived from the width of the Hα emission line versus the baryonic mass (stars+gas), derived from the spectral fit. The two diagrams display the results emerging from two different assumptions about the kinematics of the Hα emitting gas. In the spherical case it is assumed that virial motions take place in a spherically symmetric structure and in the disc case it is assumed that the gas clouds move in circular orbits in a disk. Overplotted circles are the median values after binning along the x-axis. The hatched line marks the 1:1 relation. |
| In the text | |
 |
Fig. 23 Distribution of the baryonic (stars+gas) masses inside the fiber aperture. The small region at low masses, marked in red, corresponds to cases where σobs<σIP. |
| In the text | |
 |
Fig. 24 Histogram of the ratio between the dynamical and baryonic (stars+gas) masses inside the fiber aperture. The dynamical masses are based on the disc approximation. The hatched vertical line is the median. |
| In the text | |
 |
Fig. 25 Dust attenuation corrected EWHαversus the age of the young population in the starburst candidate sample. The sample is divided according to absolute magnitude into dwarfs and giants at Mr = −20. The solid and dashed lines are identical to those in the left part of Fig. 3 with a 3% relative mass fraction of the young population. The dotted line at EWHα = 150 Å corresponds to the minimum value (but not sufficient) of EWHα to qualify as a starburst with the b> 3 criterion and an age < 1 Gyr if the SFR is assumed to be constant during the burst. The hexagon symbols represent the surface density of the data points, where darker colours means more data. |
| In the text | |
 |
Fig. 26 b-parameter versus age of the young population in the starburst candidate sample divided into three groups in luminosity indicated at the upper right. Each group contains about 2000 galaxies. The starburst criterion b = 3 is shown with a red horizontal line. Also displayed in three tracks are the minimum b parameter values needed to reach fburst = 3% at the age in question. In this case three alternatives of the SFH are displayed: a constant SFR (solid blue line) and exponentially decaying SFR:s on timescales of 10 and 100 Myr (red dashed line and green dash-dotted line respectively). The hexagons show the surface density of data points. Darker − more data. |
| In the text | |
 |
Fig. 27 Ages of the starburst galaxies using the b > 3 and the fburst > 3% criteria. |
| In the text | |
 |
Fig. 28 Ages of the postburst galaxies. |
| In the text | |
 |
Fig. 29 Difference between the luminosity at the end of the burst and the mean luminosity of the postburst phase assuming an exponentially decaying SFR on a time scale between 100 Myr and 1 Gyr. |
| In the text | |
 |
Fig. 30 Upper part: the median b-parameter vs. the total baryonic mass (stars+gas) of the starburst (b> 3) sample. Lower part: the median of the mean value of the b-parameter during the starburst epoch, as function of the total mass. |
| In the text | |
 |
Fig. 31 Median burst mass fraction vs. the total baryonic mass (stars+gas) of the starburst sample with b > 3, the starburst candidate sample with fburst > 3% and the postburst sample (EWHδ < −6 Å). |
| In the text | |
 |
Fig. 32 Total mass of stars, stellar remnants and gas versus the starburst age. Two different restrictions are applied. In the top diagram the condition is that the b parameter should be b > 3. In the lower diagram the restriction is that the burst mass fractions should be higher than 3%. The green markers are medians in log age. |
| In the text | |
 |
Fig. 33 SFR per area as function of baryonic mass of the galaxies in the starburst candidate sample. Galaxies with b > 5 (yellow circles) are superposed on the distribution of the remaining galaxies (blue triangles). The horizontal line marks the transition between when the energy produced by the starburst is sufficient to generate outflows, both according to models and to observations. |
| In the text | |
 |
Fig. A.1 Distribution of the S/N in the region 5400−5800 Å of the SDSS starburst candidate galaxy spectra included in this study, as measured by us. |
| In the text | |
 |
Fig. A.2 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. Here the star formation history is fixed to one single model with a decay rate of 1 Gyr and a metallicity of Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
| In the text | |
 |
Fig. A.3 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. The input model has a decay rate of 1 Gyr but there are two different choices for the star formation history in the fit, either with a decay rate of 100 Myr or one with 1 Gyr. The metallicity was fixed at Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
| In the text | |
 |
Fig. A.4 Test of the reliability of the SEM age determination. Synthetic spectra were fed into our SEM model and the derived age of the burst (ordinate) versus the input age (abscissa) are displayed. The input model has a decay rate of 1 Gyr but there are two different choices for the star formation history and metallicity in the fit, either with a decay rate of 100 Myr or one with 1 Gyr and a metallicity of Z = 0.004 or Z = 0.008. At each time step there are 10 models with different mass fractions: 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. Larger symbol: larger mass fraction. |
| In the text | |
 |
Fig. A.5 Test of the reliability of the SEM mass fraction determination. Synthetic spectra were fed into our SEM model and the derived mass fraction of the burst (ordinate) versus the input mass fraction (abscissa) are displayed. The same conditions for modelling holds as in Fig. A.4. At each time step there are 8 models with different ages of the starburst: 5.5, 10, 25, 55, 95, 250, 550 and 950 Myr. Larger symbol: higher age. |
| In the text | |
 |
Fig. A.6 Illustration of how well the agreement between the best and worst spectral fits to a single SDSS spectrum agree as model metallicities, dust and star formation histories are allowed to vary. The histograms show the deviations in log of the ratio between the predicted parameter values of the worst and the best fits. |
| In the text | |
 |
Fig. A.7 Test of the reliability of our determination of the dust attenuation in the V band (AV) based on a grid of 80 synthetic postburst spectra with ages 150, 250, 350, 450, 550, 750, 950 and 1500 Myr and mass fractions 2, 4, 6, 8, 10, 20, 40, 60, 80 and 100%. The preceding starburst was assumed to have constant SFR over 100 Myr. The old component was assumed to have an age of 10 Gyr. Both have 40% solar metallicity. To these spectra we added reddening corresponding to AV = 0, 0.5 and 1 mag as titles in the diagrams. We then degraded the spectra with Gaussian noise corresponding to the S/N per Å = 10, 20 and 40. Finally we used our SEM to derive AV from the noisy spectra, as shown on the abscissa. The result is displayed in the histograms with the number of spectra on the ordinate. |
| In the text | |
 |
Fig. A.8 Test of the reliability of our determination of the ages of the postburst galaxies. We loaded our SEM with the same set of spectra described in the previous section applying 3 different S/N reductions. Each time step contains 10 spectra with different mass fractions between 2 and 100% as previously described. Larger symbols represent larger mass fractions. |
| In the text | |
 |
Fig. A.9 Test of the reliability of our determination of the starburst mass fractions of the postburst galaxies. The procedure used was the same as described in Fig. A.8. The size of the symbols represent different ages. Larger symbols represent larger ages. |
| In the text | |
 |
Fig. A.10 Mass (based on fiber magnitudes) of the stellar (stars+stellar remnants) component of a set of intermediate/high-mass postburst galaxies as derived with our code (Uppsala) vs. the STARLIGHT code. The sizes of the symbols indicate the transparency of the starlight: small symbols − large dust attenuation. The hatched line marks the 1:1 relation. |
| In the text | |
 |
Fig. A.11 Metallicities of the models that gave the best fits to the observed spectra. The metallicities available in the model are given at the bottom of the figure in solar metallicity units. The sample has been divided into three bins with respect to absolute magnitude in the r band. The galaxies tend to become more metal rich with increasing luminosity. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.