EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 571 (November 2014) A&A, 571 (2014) A27 Full HTML
Planck 2013 results
Free Access
Issue
A&A
Volume 571, November 2014
Planck 2013 results
Article Number A27
Number of page(s) 11
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/201321556
Published online 29 October 2014

© ESO, 2014

1. Introduction

This paper, one of a set associated with the 2013 release of data from the Planck1 mission (Planck Collaboration I 2014), presents a study of Doppler boosting effects using the small-scale temperature fluctuations of the Planck cosmic microwave background (CMB) maps.

Observations of the relatively large amplitude CMB temperature dipole are usually taken to indicate that our Solar System barycentre is in motion with respect to the CMB frame (defined precisely below). Assuming that the observed temperature dipole is due entirely to Doppler boosting of the CMB monopole, one infers a velocity v = (369 ± 0.9) km s-1 in the direction 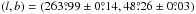, on the boundary of the constellations of Crater and Leo (Kogut et al. 1993; Fixsen et al. 1996; Hinshaw et al. 2009).

In addition to Doppler boosting of the CMB monopole, velocity effects also boost the order 10-5 primordial temperature fluctuations. There are two observable effects here, both at a level of β ≡ v/c = 1.23 × 10-3. First, there is a Doppler “modulation” effect, which amplifies the apparent temperature fluctuations in the velocity direction, and reduces them in the opposite direction. This is the same effect which converts a portion of the CMB monopole into the observed dipole. The effect on the CMB fluctuations is to increase the amplitude of the power spectrum by approximately 0.25% in the velocity direction, and decrease it correspondingly in the anti-direction. Second, there is an “aberration” effect, in which the apparent arrival direction of CMB photons is pushed towards the velocity direction. This effect is small, but non-negligible. The expected velocity induces a peak deflection of 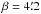and a root-mean-squared (rms) deflection over the sky of 3′, comparable to the effects of gravitational lensing by large-scale structure, which are discussed in Planck Collaboration XVII (2014). The aberration effect squashes the anisotropy pattern on one side of the sky and stretches it on the other, effectively changing the angular scale. Close to the velocity direction we expect that the power spectrum of the temperature anisotropies, Cℓ, will be shifted so that, e.g., ℓ = 1000 → ℓ = 1001, while ℓ = 1000 → ℓ = 999 in the anti-direction. In Fig. 1 we plot an exaggerated illustration of the aberration and modulation effects. For completeness we should point out that there is a third effect, a quadrupole of amplitude β2 induced by the dipole (see Kamionkowski & Knox 2003). However, extracting this signal would require extreme levels of precision for foreground modelling at the quadrupole scale, and we do not discuss it further.

thumbnail Fig. 1

Exaggerated illustration of the aberration and Doppler modulation effects, in orthographic projection, for a velocity v = 260 000 km s-1 = 0.85c (approximately 700 times larger than the expected magnitude) towards the northern pole (indicated by meridians in the upper half of each image on the left). The aberration component of the effect shifts the apparent position of fluctuations towards the velocity direction, while the modulation component enhances the fluctuations in the velocity direction and suppresses them in the anti-velocity direction.

Open with DEXTER

In this paper, we will present a measurement of β, exploiting the distinctive statistical signatures of the aberration and modulation effects on the high-ℓ CMB temperature anisotropies. In addition to our interest in making an independent measurement of the velocity signature, the effects which velocity generates on the CMB fluctuations provide a source of potential bias or confusion for several aspects of the Planck data. In particular, velocity effects couple to measurements of: primordial “τNL”-type non-Gaussianity, as discussed in Planck Collaboration XXIV (2014); statistical anisotropy of the primordial CMB fluctuations, as discussed in Planck Collaboration XXIII (2014); and gravitational lensing, as discussed in Planck Collaboration XVII (2014). There are also aspects of the Planck analysis for which velocity effects are believed to be negligible, but only if they are present at the expected level. One example is measurement of fNL-type non-Gaussianity, as discussed in Catena et al. (2013). Another example is power spectrum estimation – as discussed above, velocity effects change the angular scale of the acoustic peaks in the CMB power spectrum. Averaged over the full sky this effect is strongly suppressed, as the expansion and contraction of scales on opposing hemispheres cancel out. However the application of a sky mask breaks this cancellation to some extent, and can potentially be important for parameter estimation (Pereira et al. 2010; Catena & Notari 2013). For the 143 and 217 GHz analysis mask used in the fiducial Planck CMB likelihood (Planck Collaboration XV 2014), the average lensing convergence field associated with the aberration effect (on the portion of the sky which is unmasked) has a value which is 13% of its peak value, corresponding to an expected average lensing convergence of β × 0.13 = 1.5 × 10-4. This will shift the angular scale of the acoustic peaks by the same fraction, which is degenerate with a change in the angular size of the sound horizon at last scattering, θ∗ (Burles & Rappaport 2006). A 1.5 × 10-4 shift in θ∗ is just under 25% of the Planck uncertainty on this parameter, as reported in Planck Collaboration XVI (2014) – small enough to be neglected, though not dramatically so. This therefore motivates us to test that the observed aberration signal is not significantly larger than expected. With such a confirmation in hand, a logical next step is to correct for these effects by a process of de-boosting the observed temperature (Notari & Quartin 2012; Yoho et al. 2012). Indeed, an analysis of maps corrected for the modulation effect described here is performed in Planck Collaboration XXIII (2014).

Before proceeding to discuss the aberration and modulation effects in more detail, we note that in addition to the overall peculiar velocity of our Solar System with respect to the CMB, there is an additional time-dependent velocity effect from the orbit of Planck (at L2, along with the Earth) about the Sun. This velocity has an average amplitude of approximately 30 km s-1, less than one-tenth the size of the primary velocity effect. The aberration component of the orbital velocity (more commonly referred to in astronomy as “stellar aberration”) has a maximum amplitude of 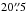and is corrected for in the satellite pointing. The modulation effect for the orbital velocity switches signs between each 6-month survey, and so is suppressed when using multiple surveys to make maps (as we do here, with the nominal Planck maps, based on a little more than two surveys), and so we will not consider it further2.

2. Aberration and modulation

Here we will present a more quantitative description of the aberration and modulation effects described above. To begin, note that, by construction, the peculiar velocity, β, measures the velocity of our Solar System barycentre relative to a frame, called the CMB frame, in which the temperature dipole, a1m, vanishes. However, in completely subtracting the dipole, this frame would not coincide with a suitably-defined average CMB frame, in which an observer would expect to see a dipole C1 ~ 10-10, given by the Sachs-Wolfe and integrated Sachs-Wolfe effects (see Zibin & Scott 2008 for discussion of cosmic variance in the CMB monopole and dipole). The velocity difference between these two frames is, however, small, at the level of 1% of our observed v.

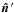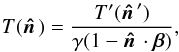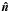If T′ and are the CMB temperature and direction as viewed in the CMB frame, then the temperature in the observed frame is given by the Lorentz transformation (see, e.g., Challinor & van Leeuwen 2002; Sollom 2010), (1)where the observed direction is given by (2)and γ ≡ (1 − β2)− 1 / 2. Expanding to linear order in β gives 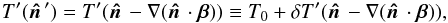(3)so that we can write the observed temperature fluctuations as 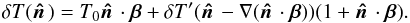(4)Here T0 = (2.7255 ± 0.0006) K is the CMB mean temperature (Fixsen 2009). The first term on the right-hand side of Eq. (4)is the temperature dipole. The remaining term represents the fluctuations, aberrated by deflection 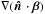and modulated by the factor .

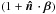The Planck detectors can be modelled as measuring differential changes in the CMB intensity at frequency ν given by (5)We can expand the measured intensity difference according to 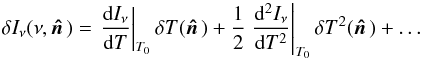(6)Substituting Eq. (4)and dropping terms of order β2 and (δT′)2, we find (7)where the frequency dependent boost factor bν is given by 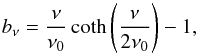(8)with ν0 ≡ kBT0/h ≃ 57 GHz. Integrated over the Planck bandpasses for the 143 and 217 GHz channels, these effective boost factors are given by b143 = 1.961 ± 0.015, and b217 = 3.071 ± 0.018, where the uncertainties represent the scatter between the individual detector bandpasses at each frequency. We will approximate these boost factors simply as b143 = 2 and b217 = 3, which is sufficiently accurate for the precision of our measurement.

In the mapmaking process, the fluctuations are assumed to satisfy only the linear term in Eq. (6). Therefore, the inferred temperature fluctuations will be 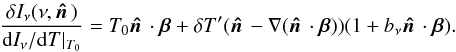(9)Notice that, compared with the actual fluctuations in Eq. (4), the modulation term in Eq. (9)has taken on a peculiar frequency dependence, represented by bν. This has arisen due to the coupling between the fluctuations and the dipole, 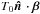, which leads to a second-order term in the expansion of Eq. (6). Intuitively, the CMB temperature varies from one side of the sky to the other at the 3 mK level. Therefore so does the calibration factor dIν/ dT, as represented by the second derivative d2Iν/ dT2. We note that such a frequency-dependent modulation is not uniquely a velocity effect, but would have arisen in the presence of any sufficiently large temperature fluctuation. Of course if we measured 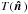directly (for example by measuring 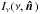at a large number of frequencies), we would measure the true fluctuations, Eq. (4), i.e., we would have a boost factor of bν = 1. However, this is not what happens in practice, and hence the velocity-driven modulation has a spectrum which mixes in a d2Iν/ dT2 dependence.

3. Methodology

The statistical properties of the aberration-induced stretching and compression of the CMB anisotropies are manifest in “statistically anisotropic” contributions to the covariance matrix of the CMB, which we can use to reconstruct the velocity vector (Burles & Rappaport 2006; Kosowsky & Kahniashvili 2011; Amendola et al. 2011). To discuss these it will be useful to introduce the harmonic transform of the peculiar velocity vector, given by 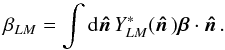(10)Here βLM is only non-zero for dipole modes (with L = 1). Although most of our equations will be written in terms of βLM, for simplicity of interpretation we will present results in a specific choice of basis for the three dipole modes of orthonormal unit vectors, labelled β∥ (along the expected velocity direction), β× (perpendicular to β∥ and parallel to the Galactic plane, near its centre), and the remaining perpendicular mode β⊥. The directions associated with these modes are plotted in Fig. 2.

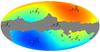thumbnail Fig. 2

Specific choice for the decomposition of the dipole vector β in Galactic coordinates. The CMB dipole direction is given as β∥, while two directions orthogonal to it (and each other) are denoted as β⊥ and β×. The vector β× lies within the Galactic plane.

Open with DEXTER

In the statistics of the CMB fluctuations, peculiar velocity effects manifest themselves as a set of off-diagonal contributions to the CMB covariance matrix: 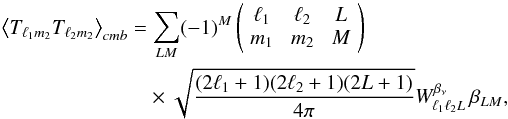(11)where the weight function Wβν is composed of two parts, related to the aberration and modulation effects, respectively, 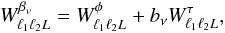(12)and the term in large parentheses is a Wigner 3-j symbol. It should be understood that in all of the expressions in this section, we take L = 1 for our calculations. We have written the expressions in more general form to allow easier connection to more general estimators in the literature. The aberration term, for example, is identical to that found when considering gravitational lensing of the CMB by large-scale structure (Lewis & Challinor 2006; Planck Collaboration XVII 2014), (13)while the modulation term is identical to that produced by an inhomogeneous optical depth to the last scattering surface (Dvorkin & Smith 2009), 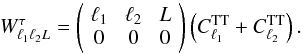(14)Note that one might, in principle, be concerned about order β2 corrections to the covariance matrix, particularly at high ℓ (see, e.g., Notari & Quartin 2012). However, these are small, provided that the spectra are relatively smooth. Although the order β (≃10-3) deflections give large changes to the aℓms for ℓ > 103, the changes to the overall covariance are small (Chluba 2011), since the deflection effect is coherent over very large scales.

The basic effect of these boosting-induced correlations is to couple ℓ modes with ℓ ± 1 modes. They therefore share this property with pure dipolar amplitude modulations studied in the context of primordial statistical anisotropy (see, e.g., Prunet et al. 2005), as well as with dipolar modulations in more general physical parameters (Moss et al. 2011). However, these other cases do not share the frequency dependence of the boosting modulation effect, since they are not accompanied by a temperature dipole.

We measure the peculiar velocity dipole using quadratic estimators, essentially summing over the covariance matrix of the observed CMB fluctuations, with weights designed to optimally extract β. A general quadratic estimator 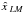for βLM is given by (Hanson & Lewis 2009) (15)where 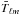are a set of inverse-variance filtered temperature multipoles, 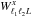is a weight function and 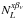is a normalization. To study the total boosting effect we use Eq. (12)for the weight function, but we will also use weight functions designed to extract specifically the aberration and modulation components of the effect. The ensemble average term ⟨⟩ is taken over signal+noise realizations of the CMB in the absence of velocity effects. It corrects for the statistical anisotropy induced by effects like beam asymmetry, masking, and noise inhomogeneity. We evaluate this term using Monte Carlo simulations of the data, as discussed in Sect. 4.

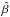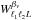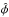We use three different quadratic estimators to measure the effects of boosting. The first, , simply adopts the weight function , and provides a minimum-variance estimator of the total peculiar velocity effect. The two additional estimators, and 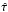, isolate the aberration and modulation aspects of the peculiar velocity effect, respectively. This can be useful, as they are qualitatively quite distinct effects, and suffer from different potential contaminants. The modulation effect, for example, is degenerate with a dipolar pattern of calibration errors on the sky, while the aberration effect is indistinguishable from a dipolar pattern of pointing errors.

There is a subtlety in the construction of these estimators, due to the fact that the covariances, described by Wφ and Wτ, are not orthogonal. To truly isolate the aberration and modulation effects, we form orthogonalized weight matrices as 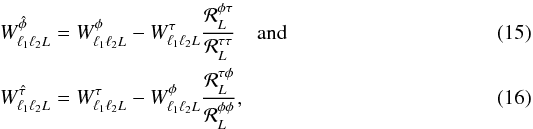where the response function ℛ is given by 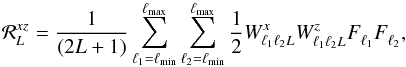(18)with x,z = βν,φ,τ. The construction of these estimators is analogous to the construction of “bias-hardened” estimators for CMB lensing (Namikawa et al. 2013). The spectra Fℓ are diagonal approximations to the inverse variance filter, which takes the sky map . We use the same inverse variance filter as that used for the baseline results in Planck Collaboration XVII (2014), and the approximate filter functions are also specified there. 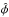Note that our estimator is slightly different from that used in Planck Collaboration XVII (2014), due to the fact that we have orthogonalized it with respect to τ.

The normalization 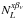can be approximated analytically as (19)This approximation does not account for masking. On a masked sky, with this normalization, we expect to find that 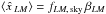, where 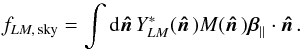(20)Here 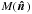is the sky mask used in our analysis. For the fiducial sky mask we use (plotted in Fig. 2, and which leaves approximately 70% of the sky unmasked), taking the dot product of f1M, sky with our three basis vectors we find that f∥ , sky = 0.82, f⊥ , sky = 0.17, and f× , sky = − 0.04. The large effective sky fraction for the β∥ direction reflects the fact that the peaks of the expected velocity dipole are untouched by the mask, while the small values of fsky for the other components reflects that fact that the masking procedure does not leak a large amount of the dipole signal in the β∥ direction into other modes.

thumbnail Fig. 3

Measured dipole direction in Galactic coordinates as a function of the maximum temperature multipole used in the analysis, ℓmax. We plot the results for the four data combinations discussed in Sect. 4: 143 × 143 (▾ symbol); 217 × 217 (▴ symbol); 143 × 217 (× symbol); and 143 + 217 (+ symbol). The CMB dipole direction β∥ has been highlighted with 14° and 26° radius circles, which correspond roughly to our expected uncertainty on the dipole direction. The black cross in the lower hemisphere is the modulation dipole anomaly direction found for WMAP at ℓmax = 64 in Hoftuft et al. (2009), and which is discussed further in Planck Collaboration XXIII (2014). Note that all four estimators are significantly correlated with one another, even the 143 × 143 and 217 × 217 results, which are based on maps with independent noise realizations. This is because a significant portion of the dipole measurement uncertainty is from sample variance of the CMB fluctuations, which is common between channels.

Open with DEXTER

4. Data and simulations

Given the frequency-dependent nature of the velocity effects we are searching for (at least for the τ component), we will focus for the most part on estimates of β obtained from individual frequency maps, although in Sect. 6 we will also discuss the analysis of component-separated maps obtained from combinations of the entire Planck frequency range. Our analysis procedure is essentially identical to that of Planck Collaboration XVII (2014), and so we only provide a brief review of it here. We use the 143 and 217 GHz Planck maps, which contain the majority of the available CMB signal probed by Planck at the high multipoles required to observe the velocity effects. The 143 GHz map has a noise level that is reasonably well approximated by 45 μK arcmin white noise, while the 217 GHz map has approximately twice as much noise power, with a level of 60 μK arcmin. The beam at 143 GHz is approximately 7′ FWHM, while the 217 GHz beam is 5′ FWHM. This increased angular resolution, as well as the larger size of the τ-type velocity signal at higher frequency, makes 217 GHz slightly more powerful than 143 GHz for detecting velocity effects (the HFI 100 GHz and LFI 70 GHz channels would offer very little additional constraining power). At these noise levels, for 70% sky coverage we Fisher-forecast a 20% measurement of the component β∥ at 217 GHz (or, alternatively, a 5σ detection) or a 25% measurement of β∥ at 143 GHz, consistent with the estimates of Kosowsky & Kahniashvili (2011) and Amendola et al. (2011). As we will see, our actual statistical error bars determined from simulations agree well with these expectations.

The Planck maps are generated at HEALPix (Górski et al. 2005)3Nside = 2048. In the process of mapmaking, time-domain observations are binned into pixels. This effectively generates a pointing error, given by the distance between the pixel centre to which each observation is assigned and the true pointing direction at that time. The pixels at Nside = 2048 have a typical dimension of 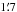. As this is comparable to the size of the aberration effect we are looking for, this is a potential source of concern. However, as discussed in Planck Collaboration XVII (2014), the beam-convolved CMB is sufficiently smooth on these scales that it is well approximated as a gradient across each pixel, and the errors accordingly average down with the distribution of hits in each pixel. For the frequency maps that we use, the rms pixelization error is on the order of 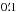, and not coherent over the large dipole scales which we are interested in, and so we neglect pixelization effects in our measurement.

We will use several data combinations to measure β. The quadratic estimator of Eq. (15)has two input “legs”, i.e., the ℓ1m1 and ℓ2m2 terms. Starting from the 143 and 217 GHz maps, there are three distinct ways we may source these legs: (1) both legs use either the individually filtered 143 GHz or 217 GHz maps, which we refer to as 143 × 143 and 217 × 217, respectively; (2) we can use 143 GHz for one leg, and 217 GHz for the other, referred to as 143 × 217; and (3) we can combine both 143 and 217 GHz data in our inverse-variance filtering procedure into a single minimum-variance map, which is then fed into both legs of the quadratic estimator. We refer to this final combination schematically as “143+217”. Combinations (2) and (3) mix 143 and 217 GHz data. When constructing the weight function of Eq. (12)for these combinations we use an effective bν = 2.5. Note that this effective bν is only used to determine the weight function of the quadratic estimator; errors in the approximation will make our estimator suboptimal, but will not bias our results. To construct the 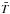, which are the inputs for these quadratic estimators, we use the filtering described in Appendix A of Planck Collaboration XVII (2014), which optimally accounts for the Galactic and point source masking (although not for the inhomogeneity of the instrumental noise level). This filter inverse-variance weights the CMB fluctuations, and also projects out the 857 GHz Planck map as a dust template.

To characterize our estimator and to compute the mean-field term of Eq. (15), we use a large set of Monte Carlo simulations. These are generated following the same procedure as those described in Planck Collaboration XVII (2014); they incorporate the asymmetry of the instrumental beam, gravitational lensing effects, and realistic noise realizations from the FFP6 simulation set described in Planck Collaboration I (2014) and Planck Collaboration (2013). There is one missing aspect of these simulations which we discuss briefly here: due to an oversight in their preparation, the gravitational lensing component of our simulations only included lensing power for lensing modes on scales L ≥ 2, which leads to a slight underestimation of our simulation-based error bars for the φ component of the velocity estimator. The lensing dipole power in the fiducial ΛCDM model is 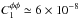, which represents an additional source of noise for each mode of β, given by σφ,lens = 1.2 × 10-4, or about one tenth the size of the expected signal. The φ part of the estimator contributes approximately 46% of the total β estimator weight at 143 GHz, and 35% at 217 GHz. Our measurement errors without this lensing noise on an individual mode of β are σβ ≃ 2.5 × 10-4, while with lensing noise included we would expect this to increase to 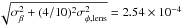. This is small enough that we have neglected it for these results (rather than include it by hand).

We generate simulations both with and without peculiar velocity effects, to determine the normalization of our estimator, which, as we will see, is reasonably consistent with the analytical expectation discussed around Eq. (20). All of our main results with frequency maps use 1000 simulations to determine the estimator mean field and variance, while the component separation tests in Sect. 6 use 300 simulations.

5. Results

We present our results visually in Fig. 3, where we plot the total measured dipole direction 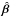as a function of the maximum temperature multipole ℓmax used as input to our quadratic estimators. We can see that all four of our 143/217 GHz based estimators converge towards the expected dipole direction at high ℓmax. At ℓmax< 100, we recover the significantly preferred direction of Hoftuft et al. (2009), which is identified when searching for a dipolar modulation of the CMB fluctuations (see Planck Collaboration XXIII 2014). The τ component of the velocity effect is degenerate with such a modulation (at least at fixed frequency), and φ gets little weight from ℓ < 100, so this is an expected result. The significance of this preferred direction varies as a function of smoothing scale (Hanson & Lewis 2009; Bennett et al. 2011; Planck Collaboration XXIII 2014). To minimize possible contamination of our results by this potential anomaly, from here onward we restrict the temperature multipoles used in our β estimation to ℓmin = 500. This cut removes only about 10% of the total number of modes measured by Planck, and so does not significantly increase our error bars. Note also that we have verified that our error bars do not shrink significantly for ℓmax> 2000, since almost all of the modes measured by Planck are at ℓ < 2000.

There is a clear tendency in Fig. 3 for the measured velocity to point towards the expected direction β∥. At Planck noise levels, we expect a 1σ uncertainty on each component of β of better than 25%. A 25% uncertainty corresponds to an arctan(1 / 4) = 14° constraint on the direction of β. We plot this contour, as well as the corresponding 2σ contour arctan(2 / 4) = 26°. It is apparent that the measured velocity directions are in reasonable agreement with the CMB dipole.

thumbnail Fig. 4

Measurements of β using combinations of the 143 and 217 GHz Planck maps, normalized using Eq. (19)and then divided by the fiducial amplitude of β = 1.23 × 10-3. These estimates use ℓmin = 500 and ℓmax = 2000. In addition to the total minimum variance estimate , the measurement is also broken down into its aberration-type part, , and modulation-type part, . Vertical lines give the Planck measurement for the four estimates described in the text. Grey histograms give the distribution of estimates for simulations of the 143 × 217 estimator, which do not contain peculiar velocity effects (the other estimators are very similar). The red histograms give the distribution for simulations which do contain peculiar velocity effects, simulated with the fiducial direction (along β∥) and amplitude. Black triangles on the x-axis indicate the relevant component of fsky given by Eq. (20), which agrees well with the peak of the velocity simulations.

Open with DEXTER

We now proceed to break the measurement of Fig. 3 into its constituent parts for ℓmax = 2000 (and truncating now at ℓmin = 500). In Fig. 4 we plot our quadratic estimates of the three components of β, as well as the decomposition into aberration and modulation components, for each of our four frequency combinations. The vertical lines in Fig. 4 give the amplitude estimates for each component measured from the data, while the coloured and grey histograms give the distribution of these quantities for the 143 × 217 estimator, for simulations with and without velocity effects, respectively (the other estimators are similar). As expected, the velocity effects show up primarily in β∥; there is little leakage into other components with our sky mask. For all four estimators, we see that the presence of velocity along β∥ is strongly preferred over the null hypothesis. At 143 GHz this signal comes from both 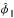and 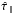. At 217 GHz it comes primarily from 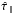. Additionally, there is a somewhat unexpected signal at 217 GHz in the β× direction, again driven by the τ component. Given the apparent frequency dependence, foreground contamination seems a possible candidate for this anomalous signal. We will discuss this possibility further in the next section.

Table 1

Significance measures for the β estimates of Fig. 4.

Table 2

Measured velocity amplitudes along the β∥ direction, in units of 369, using combinations of the 143 and 217 GHz data, as discussed in Sect. 4.

In Table 1 we present χ2 values for the β measurements of Fig. 4 under both the null hypothesis of no velocity effects, and assuming the expected velocity direction and amplitude. We can see that all of our measurements are in significant disagreement with the “no velocity” hypothesis. The probability-to-exceed (PTE) values for the “with velocity” case are much more reasonable. Under the velocity hypothesis, 217 × 217 has the lowest PTE, of 11%, driven by the large .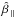

In Table 2 we focus on our measurements of the velocity amplitude along the expected direction β∥, as well as performing null tests among our collection of estimates. For this table, we have normalized the estimators, such that the average of 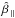on boosted simulations is equal to the input value of 369. For all four of our estimators, we find that this normalization factor is within 0.5% of that given by Nxβνf∥ ,sky, as is already apparent from the triangles along the horizontal axis of Fig. 4. We can see here, as expected, that our estimators have a statistical uncertainty on β∥ of between 20% and 25%. However, several of our null tests, obtained by taking the differences of pairs of β∥ estimates, fail at the level of 2−3σ. We take the 143 × 217 GHz estimator as our fiducial measurement; because it involves the cross-correlation of two maps with independent noise realizations it should be robust to noise modelling. Null tests against the individual 143 and 217 GHz estimates are in tension at a level of 2σ for this estimator. We take this tension as a measure of the systematic differences between these two channels, and conservatively choose the largest discrepancy with the 143 × 217 GHz estimate, namely 0.31, as our systematic error. We therefore report a measurement of 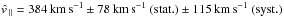, a significant confirmation of the expected velocity amplitude.

thumbnail Fig. 5

Plot of velocity amplitude estimates, similar to Fig. 4, but using an array of component-separated maps, rather than specific combinations of frequency maps. The production and characterization of these component-separated maps is presented in Planck Collaboration XII (2014). Histograms of simulation results without velocity effects are overplotted in grey for each method; they are all very similar. Vertical coloured bars correspond to the maps indicated in the legend, using the combination of our fiducial galaxy mask (which removes approximately 30% of the sky), as well as the specific mask produced for each component separation method. We see significant departures from the null-hypothesis simulations only in the β∥ direction, as expected. Vertical black lines show the 143 × 217 measurement of Fig. 4. Note the discussion about the subtleties in the normalization of these estimates in Sect. 6.

Open with DEXTER

6. Potential contaminants

There are several potential sources of contamination for our estimates above which we discuss briefly here, although we have not attempted an exhaustive study of potential contaminants for our estimator.

Galactic Foregrounds: given the simplicity of the foreground correction we have used (consisting only of masking the sky and projecting out the Planck 857 GHz map as a crude dust template), foreground contamination is a clear source of concern. The frequency dependence of the large β× signal seen at 217 GHz, but not at 143 GHz, seems potentially indicative of foreground contamination, as the Galactic dust power is approximately 10 times larger at 217 than at 143 GHz. To test the possible magnitude of residual foregrounds, we apply our velocity estimators to the four component-separated CMB maps of Planck Collaboration XII (2014), i.e., NILC, SMICA, SEVEM, and COMMANDER-RULER. Each of these methods combines the full set of nine Planck frequency maps from 30 to 857 GHz to obtain a best-estimate CMB map. To characterize the scatter and mean field of each method’s map we use the set of common simulations which each method has been applied to. These simulations include the effect of the aberration part of the velocity dipole, although not the frequency-dependent modulation part. For this reason, it is difficult to accurately assess the normalization of our estimators when applied to these maps, particularly as they can mix 143 and 217 GHz as a function of scale, and the modulation part is frequency dependent. We can, however, study them at a qualitative level. The results of this analysis are shown in Fig. 5. To construct our β estimator for the component-separated maps we have used bν = 2.5, assuming that they contain roughly equal contributions from 143 and 217 GHz. Note that, because the simulations used to determine the mean fields of the component-separated map included the aberration part of the velocity effect, it will be absorbed into the mean field if uncorrected. Because the aberration contribution is frequency independent (so there are no issues with how the different CMB channels are mixed), and given the good agreement between our analytical normalization and that measured using simulations for the frequency maps, when generating Fig. 5 we have subtracted the expected velocity contribution from the mean field analytically. We see generally good agreement with the 143 × 217 estimate on which we have based our measurement of the previous section; there are no obvious discrepancies with our measurements in the β∥ direction, although there is a somewhat large scatter between methods for 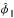. In the β× direction the component-separated map estimates agree well with the 143 × 217 estimator, and do not show the significant power seen for 217 × 217, suggesting that the large power that we see there may indeed be foreground in origin.

Calibration errors: position-dependent calibration errors in our sky maps are completely degenerate with modulation-type effects (at fixed frequency), and so are very worrisome as a potential systematic effect. We note that the Planck scan strategy strongly suppresses map calibration errors with large-scale structure (such as a dipole, see Planck Collaboration VIII 2014). As the satellite spins, the detectors mounted in the focal plane inscribe circles on the sky, with opening angles of between 83° and 85° (for the 143 and 217 GHz detectors we use). For a time-dependent calibration error to project cleanly into a dipolar structure on the sky, it would need to have a periodicity comparable to the spin frequency of the satellite (1 min-1). Slower fluctuations in the calibration should be strongly suppressed in the maps. There are calibration errors which are not suppressed by the scan strategy, however. For example, a nonlinear detector response could couple directly to the large CMB dipole temperature. Ultimately, because position-dependent calibration errors are completely degenerate with the τ component of the velocity effect, the only handle which we have on them for this study is the consistency between 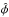and 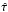. From another viewpoint, the consistency of our measurement with the expected velocity modulation provides an upper bound on dipolar calibration errors.

Pointing errors: in principle, errors in the pointing are perfectly degenerate with the aberration-type velocity effect in the observed CMB. However the Planck pointing solution has an uncertainty of a few arcseconds rms in both the co- and cross-scan directions (Planck Collaboration VI 2014). The 3′ rms aberrations induced by velocity effects are simply too large to be contaminated by any reasonable pointing errors.

7. Conclusions

From Fig. 3 it is clear that small-scale CMB fluctuations observed in the Planck data provide evidence for velocity effects in the expected direction. This is put on more quantitative footing in Fig. 4 and Table 2, where we see that all four of the 143 and 217 GHz velocity estimators which we have considered show evidence for velocity effects along β∥ at above the 4σ level. Detailed comparison of 143 and 217 GHz data shows some discrepancies, which we have taken as part of a systematic error budget; however, tests with component-separated maps shown in Fig. 5 provide a strong indication that our 217 GHz map has slight residual foreground contamination. The component-separated results are completely consistent with the 143 × 217 estimator which we quote for our fiducial result.

Beyond our peculiar velocity’s impact on the CMB, there have been many studies of related effects at other wavelengths (e.g., Blake & Wall 2002; Titov et al. 2011; Gibelyou & Huterer 2012). Closely connected are observational studies which examine the convergence of the clustering dipole (e.g., Itoh et al. 2010; Bilicki et al. 2011). Indications of non-convergence might be evidence for a super-Hubble isocurvature mode, which can generate a “tilt” between matter and radiation (Turner 1991), leading to an extremely large-scale bulk flow. Such a long-wavelength isocurvature mode could also contribute a significant “intrinsic” component to our observed temperature dipole (Langlois & Piran 1996). However, a peculiar velocity dipole is expected at the level of 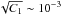due to structure in standard ΛCDM (see, e.g., Zibin & Scott 2008), which suggests that an intrinsic component, if it exists at all, is subdominant. In addition, such a bulk flow has been significantly constrained by Planck studies of the kinetic Sunyaev-Zeldovich effect (Planck Collaboration Int. XIII 2014). In this light, the observation of aberration at the expected level reported in this paper is fully consistent with the standard, adiabatic picture of the Universe.

The Copernican revolution taught us to see the Earth as orbiting a stationary Sun. That picture was eventually refined to include Galactic and cosmological motions of the Solar System. Because of the technical challenges, one may have thought it very unlikely to be able to measure (or perhaps even to define) the cosmological motion of the Solar System ... and yet it moves.

1

Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states (in particular the lead countries France and Italy), with contributions from NASA (USA) and telescope reflectors provided by a collaboration between ESA and a scientific consortium led and funded by Denmark.

2

Note that in both stellar and cosmological cases, the aberration is the result of local velocity differences (Eisner 1967; Phipps 1989): in the former case, between Earth’s velocity at different times of the year, and in the latter between the actual and CMB frames.

Acknowledgments

The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN, JA, and RES (Spain); Tekes, AoF, and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). A description of the Planck Collaboration and a list of its members, including the technical or scientific activities in which they have been involved, can be found at http://www.sciops.esa.int/index.php?project=planck&page=Planck_Collaboration. Some of the results in this paper have been derived using the HEALPix package. This research used resources of the National Energy Research Scientific Computing Center, which is supported by the Office of Science of the US Department of Energy under Contract No. DE-AC02-05CH11231. We acknowledge support from the Science and Technology Facilities Council [grant number ST/I000976/1].

References

All Tables

Table 1

Significance measures for the β estimates of Fig. 4.

In the text
Table 2

Measured velocity amplitudes along the β∥ direction, in units of 369, using combinations of the 143 and 217 GHz data, as discussed in Sect. 4.

In the text

All Figures

thumbnail Fig. 1

Exaggerated illustration of the aberration and Doppler modulation effects, in orthographic projection, for a velocity v = 260 000 km s-1 = 0.85c (approximately 700 times larger than the expected magnitude) towards the northern pole (indicated by meridians in the upper half of each image on the left). The aberration component of the effect shifts the apparent position of fluctuations towards the velocity direction, while the modulation component enhances the fluctuations in the velocity direction and suppresses them in the anti-velocity direction.

Open with DEXTER
In the text
thumbnail Fig. 2

Specific choice for the decomposition of the dipole vector β in Galactic coordinates. The CMB dipole direction is given as β∥, while two directions orthogonal to it (and each other) are denoted as β⊥ and β×. The vector β× lies within the Galactic plane.

Open with DEXTER
In the text
thumbnail Fig. 3

Measured dipole direction in Galactic coordinates as a function of the maximum temperature multipole used in the analysis, ℓmax. We plot the results for the four data combinations discussed in Sect. 4: 143 × 143 (▾ symbol); 217 × 217 (▴ symbol); 143 × 217 (× symbol); and 143 + 217 (+ symbol). The CMB dipole direction β∥ has been highlighted with 14° and 26° radius circles, which correspond roughly to our expected uncertainty on the dipole direction. The black cross in the lower hemisphere is the modulation dipole anomaly direction found for WMAP at ℓmax = 64 in Hoftuft et al. (2009), and which is discussed further in Planck Collaboration XXIII (2014). Note that all four estimators are significantly correlated with one another, even the 143 × 143 and 217 × 217 results, which are based on maps with independent noise realizations. This is because a significant portion of the dipole measurement uncertainty is from sample variance of the CMB fluctuations, which is common between channels.

Open with DEXTER
In the text
thumbnail Fig. 4

Measurements of β using combinations of the 143 and 217 GHz Planck maps, normalized using Eq. (19)and then divided by the fiducial amplitude of β = 1.23 × 10-3. These estimates use ℓmin = 500 and ℓmax = 2000. In addition to the total minimum variance estimate , the measurement is also broken down into its aberration-type part, , and modulation-type part, . Vertical lines give the Planck measurement for the four estimates described in the text. Grey histograms give the distribution of estimates for simulations of the 143 × 217 estimator, which do not contain peculiar velocity effects (the other estimators are very similar). The red histograms give the distribution for simulations which do contain peculiar velocity effects, simulated with the fiducial direction (along β∥) and amplitude. Black triangles on the x-axis indicate the relevant component of fsky given by Eq. (20), which agrees well with the peak of the velocity simulations.

Open with DEXTER
In the text
thumbnail Fig. 5

Plot of velocity amplitude estimates, similar to Fig. 4, but using an array of component-separated maps, rather than specific combinations of frequency maps. The production and characterization of these component-separated maps is presented in Planck Collaboration XII (2014). Histograms of simulation results without velocity effects are overplotted in grey for each method; they are all very similar. Vertical coloured bars correspond to the maps indicated in the legend, using the combination of our fiducial galaxy mask (which removes approximately 30% of the sky), as well as the specific mask produced for each component separation method. We see significant departures from the null-hypothesis simulations only in the β∥ direction, as expected. Vertical black lines show the 143 × 217 measurement of Fig. 4. Note the discussion about the subtleties in the normalization of these estimates in Sect. 6.

Open with DEXTER
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.