| Issue |
A&A
Volume 566, June 2014
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 24 | |
| Section | Galactic structure, stellar clusters and populations | |
| DOI | https://doi.org/10.1051/0004-6361/201322183 | |
| Published online | 11 June 2014 | |
The central dynamics of M3, M13, and M92: stringent limits on the masses of intermediate-mass black holes⋆,⋆⋆,⋆⋆⋆
1
Leibniz-Institut für Astrophysik Potsdam (AIP),
An der Sternwarte 16,
14482
Potsdam,
Germany
2
Institut für Astrophysik, Universität Göttingen,
Friedrich-Hund-Platz
1, 37077
Göttingen,
Germany
e-mail:
skamann@astro.physik.uni-goettingen.de
Received:
1
July
2013
Accepted:
7
April
2014
We used the PMAS integral field spectrograph to obtain large sets of radial velocities in the central regions of three northern Galactic globular clusters: M3, M13, and M92. By applying the novel technique of crowded field 3D spectroscopy, we measured radial velocities for about 80 stars within the central ~10″ of each cluster. These are by far the largest spectroscopic datasets obtained in the innermost parts of these clusters up to now. To obtain kinematical data across the whole extent of the clusters, we complement our data with measurements available in the literature. We combine our velocity measurements with surface brightness profiles to analyse the internal dynamics of each cluster using spherical Jeans models, and investigate whether our data provide evidence for an intermediate-mass black hole in any of the clusters. The surface brightness profiles reveal that all three clusters are consistent with a core profile, although shallow cusps cannot be excluded. We find that spherical Jeans models with a constant mass-to-light ratio provide a good overall representation of the kinematical data. A massive black hole is required in none of the three clusters to explain the observed kinematics. Our 1σ (3σ) upper limits are 5300 M⊙ (12 000 M⊙) for M3, 8600 M⊙ (13 000 M⊙) for M13, and 980 M⊙ (2700 M⊙) for M92. A puzzling circumstance is the existence of several potential high velocity stars in M3 and M13, as their presence can account for the majority of the discrepancies that we find in our mass limits compared to M92.
Key words: stars: kinematics and dynamics / globular clusters: individual: M3 / globular clusters: individual: M13 / globular clusters: individual: M92 / black hole physics
Based on observations collected at the Centro Astronómico Hispano-Alemán (CAHA) at Calar Alto, operated jointly by the Max-Planck Institut für Astronomie and the Instituto de Astrofísica de Andalucía (CSIC).
Appendices are available in electronic form at http://www.aanda.org
Tables D.1 to D.6 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/566/A58
© ESO, 2014
1. Introduction
Over the past years, the search for intermediate-mass black holes (IMBHs) has attracted remarkable attention. With ~102–104 solar masses, they would bridge the gap from stellar-mass black holes to supermassive ones (SMBHs). Constraining their population statistics might answer the question how SMBHs assemble their masses. The scaling relations observed between SMBHs and fundamental properties of their host bulges, such as luminosities (Kormendy & Richstone 1995), stellar masses (Magorrian et al. 1998; Marconi & Hunt 2003; Häring & Rix 2004) or stellar velocity dispersions (Ferrarese & Merritt 2000; Gebhardt et al. 2000; Gültekin et al. 2009) suggest that their growth is closely linked to the evolution of the host galaxy (Silk & Rees 1998; but see also Jahnke & Macciò 2011). The progenitors of SMBHs are likely to be found in the building blocks of present-day galaxies. The close connection of Galactic globular clusters to the build-up of the Milky Way was proposed already by Searle & Zinn (1978) and is supported by cosmological simulations (e.g., Moore et al. 2006). Globular clusters can therefore be considered as promising candidates to host IMBHs. Interestingly, a straightforward extrapolation of the SMBH scaling relations to the properties of globular clusters also yields black hole masses in the range 102−105 solar masses. Clearly, such an extrapolation is a huge simplification, and there may be evidence that the common relations disagree with the observations already in the regime of low-mass galaxies (Greene et al. 2010).
The runaway merging of massive stars in the early phases of cluster evolution has been suggested as a formation channel for IMBHs in dense star clusters (Portegies Zwart & McMillan 2002). However, it has been argued (e.g. Glebbeek et al. 2009) that strong stellar winds restrict the resulting black holes to stellar masses (≳10 M⊙). An alternative formation scenario involves the collapse of massive population III stars (e.g. Madau & Rees 2001).
Observational evidence for (but also against) the existence of IMBHs is still extremely scant. Gas accretion onto such a black hole would allow for its detection using radio or X-ray observations, such as in the case of the IMBH candidate HLX-1 in the galaxy ESO 243-49 (Farrell et al. 2009). G1 in M31, the most massive known globular cluster in the local group, was detected in both radio (Ulvestad et al. 2007) and X-ray observations (Trudolyubov & Priedhorsky 2004; Kong et al. 2010), although Miller-Jones et al. (2012) could not confirm the radio detection. Recent observations by Strader et al. (2012b) place stringent upper limits on the amount of radio emission coming from Galactic globular clusters. Translating those into mass limits, however, requires making assumptions about the accretion physics that are not well understood.
Several authors investigated the possibility that IMBHs imprint their presence onto photometrically observable properties of a globular cluster. Baumgardt et al. (2005) and Noyola & Baumgardt (2011) found that a massive black hole should produce a shallow cusp in the central surface brightness profile of the surrounding cluster. A large ratio of core to half-mass radius was suggested as indirect evidence for the presence of an IMBH by Trenti et al. (2007). Furthermore, the existence of extreme horizontal branch stars has been proposed as a tracer for IMBHs by Miocchi (2007). Gill et al. (2008) investigated the influence of black holes on mass segregation among the cluster stars.
Arguably, the most direct way to not only find massive black holes but also obtain their masses is the detection of their kinematic fingerprints. The best SMBH mass estimates were obtained from stellar kinematics in our own galaxy (Gillessen et al. 2009) or gas kinematics in NGC 4258 (Herrnstein et al. 2005). However, obtaining meaningful kinematic measurements in the central regions of globular clusters is a challenging task: while the measurement of individual stellar velocities is hampered by crowding, integrated-light analyses can be significantly affected by shot noise from the few brightest giants (Dubath et al. 1997). Kinematic studies of the centres of globular clusters remained ambiguous so far, in some cases even contradictory conclusions were reached for the same clusters. A prominent example is ω Centauri, for which Anderson & van der Marel (2010) and van der Marel & Anderson (2010) find no evidence for an IMBH while Noyola et al. (2010) and Jalali et al. (2012) claim the detection of one, with a mass of 4 × 104 M⊙. Similarly, the detection of an IMBH with 17 000 solar masses in NGC 6388 by Lützgendorf et al. (2011) was not confirmed by Lanzoni et al. (2013), who obtain an upper limit of 2000 M⊙ instead. Further detections of IMBHs have been reported in a small number of massive clusters, G1 (Gebhardt et al. 2005) among them. In a sample recently studied by Lützgendorf et al. (2012b, 2013), the kinematics in 2 out of 7 clusters suggested the presence of an IMBH, while for the remaining clusters upper limits of typically >1000 solar masses were derived. Similar mass limits were also reported in other studies, carried out for M15 by Gerssen et al. (2002) and van den Bosch et al. (2006), for 47 Tuc by McLaughlin et al. (2006) or for NGC 6266 by McNamara et al. (2012).
Clearly, a conclusive picture of which globular clusters host IMBHs is not established yet. Consequently, the question whether the scaling relations established for SMBHs can be extrapolated into the regime of globular clusters is also unanswered. Alternatively, IMBHs might follow different scaling relations, as suggested by Miocchi (2007). More observations are the only way to make progress here.
So far, all claimed IMBH detections come from integrated light spectroscopy, whereas studies based on the kinematics of resolved stars derived upper limits which in some cases are in conflict with the detections from the former approach. This may suggest that the influence of the few brightest stars still hampers the integrated light measurements. In any case, resolving this situation requires new techniques for spectroscopy in crowded stellar fields and a better understanding of its capabilities and limitations. In Kamann et al. (2013, hereafter Paper I, we recently presented a new method for analysing integral field spectroscopy (IFS) data of such fields. It extends the established analysis techniques for crowded field photometry into the domain of three-dimensional datacubes by fitting a wavelength dependent point spread function (PSF) to deblend stellar spectra. In this paper, we apply this technique to IFS data of three Galactic globular clusters, M3, M13, and M92, with the aim of constraining the presence of IMBHs in the objects. The paper is organized as follows. After laying out the target selection, the observations, and their reduction in Sects. 2 to 4, we describe the analysis of the photometric (Sect. 5) and the kinematic data (Sect. 6). In Sect. 7, the cluster dynamics are analysed and the search for IMBHs in the clusters via Jeans modelling is performed. Our findings are discussed in Sect. 8, and we provide our conclusions in Sect. 9.
 |
Fig. 1 Central surface number densities of sources brighter than a given magnitude for the three clusters of our sample, colour-coded as indicated in the upper left corner of the plot. Magnitudes are given relative to the main sequence turn-off (MSTO) in each cluster. The solid horizontal line corresponds to the source density where we expect to hit the confusion limit. Below the density indicated by a dashed line the deblended spectra will likely have a sufficient signal-to-noise ratio for radial velocity (RV) determination. |
Fundamental properties of the observed clusters.
2. Target selection
We searched the catalogue of Harris (1996) for globular clusters visible from Calar Alto Observatory and selected the objects that were best suited for an analysis. This was done based on the following criteria. As we showed in Paper I, the confusion limit below which individual stellar spectra cannot be resolved any more is about 0.4 stars per resolution element. Assuming a typical seeing of 1.0″, this implies that we can resolve stars down to a density of 0.3 arcsec-2. Using the V- and I-band photometry obtained in the ACS Survey of Galactic globular clusters (Sarajedini et al. 2007; Anderson et al. 2008), we determined the I-band magnitudes where the confusion limit is reached by counting the stars in the central 20″ of each cluster. Only clusters where spectroscopic observations down to this limit are feasible with a 3.5 m telescope were considered. Additionally, we restricted ourselves to clusters with a confusion limit in the central region close to the main sequence turn-off (MSTO). The motivation for this selection criterion was that the number of stars per magnitude bin increases strongly below this point and we planned to analyse not only the resolved stars but also the unresolved stellar component after we subtracted the bright stars. Now, if we can resolve nearly all stars on the red giant branch of the cluster, we ensure that within the unresolved stellar component many stars have similar brightnesses and that the integrated light of that component is not dominated by few bright stars. To illustrate this second criterion, we show in Fig. 1 the source density as a function of I-band magnitude for the three clusters that best fulfilled our selection criteria, M3 (NGC 5272), M13 (NGC 6205), and M92 (NGC 6341). The expected confusion limit in each cluster is indicated. We also provide the “usefulness” limit, motivated by the fact found in Paper I that roughly half of the deblended spectra allow for a measurement of the radial velocity (RV) of the star. The analysis of the unresolved stellar component will be presented in a later publication and is not discussed in this study. Table 1 summarizes some fundamental properties of our sample clusters. The three targets are among the most massive clusters visible in the northern sky and are also located at relatively small distances from the sun.
We did not perform a preselection based on photometric properties, such as the central slopes of the surface brightness profiles of the clusters. Baumgardt et al. (2005) suggested that the central slopes might be used as an indicator for the presence of IMBHs in the sense that clusters harbouring one should have a shallow cusp in their surface brightness profiles. However, we wanted to avoid biases for selecting “favourable” objects.
Dynamical studies have been previously performed for each of the three clusters. The kinematics in M3 were investigated already by Gunn & Griffin (1979) who found that King-Mitchie models provided a valid framework for the kinematical data available back then. The authors suggested a transition from an isotropic core to an anisotropic outer region occurring at ~15 core radii (~5′). This finding was confirmed by Cudworth (1979) from proper motions. In a similar fashion to Gunn & Griffin (1979), Lupton et al. (1987) studied the cluster M13 and found a transition to anisotropy occurring at ~5 core radii. Furthermore, the collected RV data showed evidence for rotation at larger radii. Leonard et al. (1992) combined the kinematical data of Lupton et al. (1987) with proper motions collected by Cudworth & Monet (1979) to infer the mass and stellar content of M13, by analytically solving the spherical Jeans equation under the assumption of a Plummer density profile.
More recently, McLaughlin & van der Marel (2005) performed dynamical modelling on a large sample of 57 clusters, including M3, M13, and M92. To infer structural parameters, three different models were used that mainly varied in their behaviour at large radii, thus corresponded to different strengths of a tidal cut-off. For the three targets investigated in this study, models with a moderate truncation (Wilson models) turned out to be a valid choice and we will refer to those when comparing our results with those of McLaughlin & van der Marel. M92 was also included in the sample studied by Zocchi et al. (2012) who found it to be a relaxed cluster well described by an isotropic King model.
We note that M13 was identified by Miocchi (2007) as a possible candidate to host an IMBH according to its central surface brightness profile and extended horizontal branch.
Summary of the PMAS observations.
3. Observations
We observed the three clusters using the PMAS instrument (Roth et al. 2005) mounted on the Calar Alto 3.5 m telescope. PMAS is an optical
integral field spectrograph without adaptive optics. The data were obtained in 4 different
observing runs in 2010 and 2011. In Table 2 we give a
summary of the different observing runs. All observations were carried out using a spatial
pixel (“spaxel”) scale of 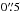 on the sky and the R1200 grating in first
order mounted backwards. With this configuration, we covered the wavelength range from
7300 Å to 8900 Å and achieved a spectral resolution of
R =
λ/ Δλ ~ 7 000 around
the infrared Ca ii-triplet. The precise value of R varied with wavelength and
fibre. For M13 and M92 some observations were repeated in a later observing run, which enabled us
to search for stars with variable RV.
on the sky and the R1200 grating in first
order mounted backwards. With this configuration, we covered the wavelength range from
7300 Å to 8900 Å and achieved a spectral resolution of
R =
λ/ Δλ ~ 7 000 around
the infrared Ca ii-triplet. The precise value of R varied with wavelength and
fibre. For M13 and M92 some observations were repeated in a later observing run, which enabled us
to search for stars with variable RV.
PMAS covers a contiguous area of 8″ × 8″ in the sky in the selected mode. For each of the observed targets, the aim was to completely cover the central region of the cluster, out to a radius of about 15″. Due to weather losses, however, some fields could not be observed and the achieved coverage varied from cluster to cluster. Additionally, the final acquisition of the PMAS IFS had to be performed manually. In a crowded stellar field like a globular cluster, this procedure has an error of at least 1″−2″ which constrained our final pointing accuracy.
Except for the first run (ID 173), science observations were alternated with shorter observations of blank sky fields to allow for a better subtraction of sky lines during the data reduction.
4. Data reduction
The bulk part of the data reduction was performed using p3d1, a dedicated software package to reduce fibre-fed integral field observations (Sandin et al. 2010). We carried out the basic parts of the reduction cascade, such as bias subtraction, tracing, and extraction of the spectra, wavelength calibration, and rebinning the data onto a regular grid. Recently, the dedicated cosmic-ray-rejection routine pyCosmic (Husemann et al. 2012) has been implemented into p3d and we followed the suggestions by Husemann et al. to detect cosmic ray hits in the raw data.
We used an optimal extraction method to obtain the individual spectra. Although optimal extraction is not strictly necessary for data observed with the PMAS lens array (the gaps between individual fibres are sufficiently large that crosstalk is a negligible issue), it has the big advantage over the simpler boxcar extraction that pixels affected by cosmic rays can be masked out, so we did not rely on any interpolation scheme to assign values to those pixels.
All of our data were observed using the new PMAS CCD (Roth et al. 2010), which exhibits some features that required special treatment during the reduction. Some steps of the data reduction were therefore performed outside of p3d and are outlined in Appendix A.
5. Photometry
5.1. Generating a complete source list
Our analysis depends crucially on the availability of high quality photometric data, in particular near the cluster centres, for two reasons. First, our analysis of the IFS data relies on a reference catalogue containing locations and magnitudes of the stars. Second, the Jeans modelling approach used in Sect. 7 below uses the surface brightness profile of the clusters as input.
To obtain a high quality reference catalogue around the centres of the clusters, we started again from the photometry obtained in the ACS Survey of Galactic globular clusters, certainly the most comprehensive photometric dataset available for our clusters. In Fig. B.2 we show a colour−magnitude diagram of the three clusters based on this data. One common issue of ACS observations is that the brightest stars are often heavily saturated and cause strong bleeding artefacts. Although the ACS survey included an observing strategy to overcome this effect as much as possible and saturated stars were treated separately in the analysis by Anderson et al. (2008), we decided to cross-check with a second dataset. In fact, a single PMAS datacube only contains 256 spaxels, so even a single star that is significantly detectable yet missing in the reference catalogue would have a strong effect on the analysis. We performed a search and correction for such stars using WFPC2 data as outlined in Appendix B.
5.2. Determination of the cluster centres
For the later analysis, a proper determination of the central coordinates of each cluster was important. Measured cluster properties such as the surface brightness profile or the velocity dispersion profile can deviate significantly from the intrinsic ones if the true centre is offset from the assumed one. Several methods were proposed in the literature to determine the (photometric) centre of a globular cluster, such as fitting ellipses to the number density contours of the cluster and determining the centre by averaging the centres of the different ellipses. Other methods exploit the symmetry of the density around putative centres. For the clusters in the ACS survey, these methods were applied by Goldsbury et al. (2010). Since our photometry is based on more or less the same data (the few missing stars have marginal influence) we adopted the centres reported by Goldsbury et al. They are also provided in Table 1.
The central coordinates deviate slightly from those measured by Noyola & Gebhardt (2006). The offsets are
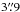 for M3,
for M3, 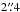 for M13, and
for M13, and 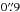 for M92. A reason for this might be that all targets have rather large cores
(>10″, Harris 1996) so that
measurements of the centres are not well constrained. The measurements performed by Noyola & Gebhardt were based on WFPC2 data that
cover a smaller fraction of the central region than ACS does. Therefore, we relied on the
Goldsbury et al. centres.
for M92. A reason for this might be that all targets have rather large cores
(>10″, Harris 1996) so that
measurements of the centres are not well constrained. The measurements performed by Noyola & Gebhardt were based on WFPC2 data that
cover a smaller fraction of the central region than ACS does. Therefore, we relied on the
Goldsbury et al. centres.
5.3. Surface brightness profiles
 |
Fig. 2 Left-hand side: surface brightness profiles of the clusters M3, M13, and M92 over the entire extent of each cluster. Right-hand side: zoom into the central region of each cluster. Measurements based on star counts in the HST data are shown using green squares while blue diamonds represent the data of Trager et al. (1995). A solid red line shows the best-fit extended Nuker profile. For M3 and M13, we also show a Nuker profile with a core (i.e. γ = 0) as a dashed cyan line. The surface brightness profiles have been corrected for extinction. |
To generate surface brightness profiles from the photometric catalogues, we proceeded as follows. We counted the stars in concentric annuli around the cluster centre. The size of each annulus was chosen so that it contained 100 stars brighter than a magnitude V = 19 in order to have the same number statistics in each bin. Note that except for the cut in magnitude, each star was weighted equally, so this method is robust against shot noise from a few bright giant stars. To translate the measured projected number density into a surface brightness, we assumed a constant conversion factor with radius. By doing so we neglected any mass segregation among our sample stars. However, as the stars that we probe fall in a narrow range in mass, mass segregation is not a major concern.
Our approach allowed us to constrain the central profile for approximately the same subsets of stars for which we expected to obtain kinematic measurements. The adapted magnitude cut of V = 19 is slightly fainter than the assumed limit of our spectroscopic observations but this should have no effect. When we used a brighter magnitude cut the shape of the profile did not change significantly, only the number statistics got poorer. This also shows that the catalogue is quite complete at this brightness levels.
Our catalogues only cover the central regions of the clusters. To obtain profiles across the whole extent of each object, we complemented them with the data of Trager et al. (1995). No uncertainties are provided with the data, only a relative weight is assigned to each datapoint. McLaughlin & van der Marel (2005) proposed a way to obtain meaningful uncertainties by scaling the weights with a constant factor until the measurements are consistent with a smooth function. We followed that approach and used the same scaling factors as McLaughlin & van der Marel and also omitted datapoints that were assigned a weight <0.15. To merge the two catalogues, the number density profiles from the HST data were shifted vertically to match the surface brightness profiles of Trager et al. in the region where the two overlap.
The resulting profiles were corrected for interstellar extinction and fitted with an
extended Nuker profile, the functional form of which is given by ![\begin{equation} \label{eq:ext_nuker} I(r) = I_\mathrm{b}\,2^{\left(\frac{\beta-\gamma}{\alpha}\right)}\,\left(\frac{r}{r_\mathrm{b}}\right)^{-\gamma}\,\left[1 + \left(\frac{r}{r_\mathrm{b}}\right)^\alpha\right]^{-\left(\frac{\beta-\gamma}{\alpha}\right)}\,\left[1 + \left(\frac{r}{r_\mathrm{c}}\right)^{\delta}\right]^{-\left(\frac{\epsilon-\beta}{\delta}\right)}. \end{equation}](/articles/aa/full_html/2014/06/aa22183-13/aa22183-13-eq49.png) (1)The “original” Nuker
profile (omitting the second term in square brackets) was initially proposed by Lauer et al. (1995) to describe the surface brightness
profiles of galaxies that showed a power-law cusp I ∝ r−γ towards the centre and a logarithmic
decline ∝β for radii
>rb. The generalized version given in Eq.
(1) was used by van der Marel & Anderson (2010) to describe the surface
brightness profile of ω Centauri. It
has an additional break radius rc where the logarithmic slope changes
from β to
ϵ. The
physical justification for this second break is that many clusters have rather
well-defined truncation radii.
(1)The “original” Nuker
profile (omitting the second term in square brackets) was initially proposed by Lauer et al. (1995) to describe the surface brightness
profiles of galaxies that showed a power-law cusp I ∝ r−γ towards the centre and a logarithmic
decline ∝β for radii
>rb. The generalized version given in Eq.
(1) was used by van der Marel & Anderson (2010) to describe the surface
brightness profile of ω Centauri. It
has an additional break radius rc where the logarithmic slope changes
from β to
ϵ. The
physical justification for this second break is that many clusters have rather
well-defined truncation radii.
In Fig. 2 we show the results from fitting Eq. (1) to the surface brightness profiles. The parameters of each best-fit Nuker profile are given in Table 3. The fits provide a good global representation of the measured profiles. In all three cases we obtain χ2 values indicating that the fitted profile is fully consistent with the data (cf. Table 3).
Parameters of the best-fit Nuker profiles.
 |
Fig. 3 Colour–magnitude diagrams of the areas covered by our PMAS observations, coding source categories by different colours and symbols: individually deblended sources (green diamonds), sources deblended together with a brighter neighbour (red open triangles), sources contributing to the grainy stellar background (black squares), and unused sources (grey circles). |
An important parameter regarding the presence of IMBHs is the central slope of the profile, γ. Our fits result in low γ values, in fact M92 is best fit by a core (i.e. γ = 0) profile, and for the other two clusters, the deviation from core profiles is only mild (cf. Fig. 2, right). However, as pointed out by van der Marel & Anderson (2010), γ is not very well constrained in a fit of the whole surface brightness profile because its influence is limited to the innermost few datapoints. To obtain realistic confidence intervals on γ, we fitted the data within a distance of 0.5rb to the centre with a simple power-law and obtained the range of slopes consistent with the data. We only allowed for γ values that still provided a reasonable fit to the overall profile within 90% confidence. This calculation yields γ < 0.54 in M3, γ < 0.34 in M13 and γ < 0.43 in M92.
In summary, none of our clusters shows significant evidence for a central cusp in its surface brightness profile. This result is in agreement with other studies. The central slopes reported by Noyola & Gebhardt (2006) for the three targets are smaller than their respective uncertainties. More recently, Miocchi et al. (2013) found that King and Wilson profiles provide an adequate representation of the clusters and detected no evidence of any central cusp.
A comparison of the core radii obtained by us with those listed in the catalogue of Harris (1996, M3:
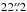 , M13:
, M13: 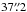 , M92:
, M92: 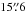 shows remarkable agreement for
M13 and M92, only the value we get for M3
is about twice as large. Our measurements correspond to physical sizes of 2.1 pc (M3), 1.4 pc
(M13), and 0.6 pc (M92).
shows remarkable agreement for
M13 and M92, only the value we get for M3
is about twice as large. Our measurements correspond to physical sizes of 2.1 pc (M3), 1.4 pc
(M13), and 0.6 pc (M92).
We performed another consistency check by calculating the integrated magnitude of each target, either by numerical integration of the data or Eq. (1). Again, the different values, included in Table 3, are largely consistent with one another.
The combination of a large core radius and a shallow surface brightness cusp led Miocchi (2007) to the conclusion that M13 is a good candidate to host an IMBH. Our photometric analysis confirms the large core. Also, the confidence interval for the central slope that we obtain is consistent with the value γ ≲ 0.25 suggested by Miocchi and others (Baumgardt et al. 2005; Noyola & Baumgardt 2011). Our analysis further suggests that the photometric properties of M3 are not so different from those of M13, in particular with respect to the large core radius.
6. Kinematic data
6.1. Deblending spectra in the PMAS data
In Paper I, we presented an algorithm to deblend stellar spectra from IFS datacubes via PSF fitting. Starting from an inventory of the stars in the field (hereafter called “reference catalogue”), we locate the sources in the datacube and determine the subset of sources for which spectra can be deblended at the (typically lower) spatial resolution of the IFS data. Using an iterative approach, we then determine the wavelength dependent PSF as well as the precise coordinate transformation from the reference catalogue to the datacube. In the final step, all the spectra of the resolved sources are simultaneously deblended using a linear least-squares fit. More details are given in Paper I.
6.1.1. Source selection
First, we determined the expected confusion limit in each datacube, i.e., the magnitude below which no individual sources can be deblended any more. It is roughly equal to the magnitude when the density of brighter sources approaches 0.4 stars per resolution element. Due to the variable seeing conditions, this limit varied from frame to frame. We then determined the expected signal-to-noise ratio (S/N) of each target above the confusion limit and only accepted stars above a S/N threshold of 5. Note that the S/N is an estimate purely based on the brightness of the star, its location in- or outside the PMAS field of view, and the presence of bright neighbours. The actual S/N of each extracted spectrum was determined afterwards as outlined below.
Each spaxel will not only contain contributions from the resolved stars, but also from the unresolved ones and the night sky. We assume that the night sky brightness is constant across the small PMAS field of view and account for it by including an additional component in the analysis of each data cube that is spatially flat. To account for the contribution of the unresolved stars, we considered the following. Stars just below the confusion limit still cause a grainy structure across the field of view, similar to the surface brightness fluctuations observed in nearby galaxies. Therefore, we used an additional component in the deblending process, containing all stars within 2 mag below the confusion limit. The flux ratios of the individual stars in that component were fixed to their relative I-band brightnesses. The range of 2 mag was chosen because stars inside this range account for the vast majority of the graininess and the contribution of even fainter stars is essentially flat across the field of view, so that is is indistinguishable from the contribution of the night sky.
 |
Fig. 4 Comparison of derived PSF parameters. Each panel shows the FWHM: as a function of the airmass of the observation (left), and as a function of β (right). Each plotted point corresponds to the mean value obtained in a datacube. Different symbols indicate different clusters as indicated in the legend. The error bars represent the standard deviations over the cubes, including variations with wavelength. |
Note that the inclusion of these unresolved components in combination with the PSF-based extraction of the spectra of the resolved stars accurately cleans the extracted spectra from any (stellar or telluric) background. This is the big advantage of our approach with respect to simpler analysis methods such as aperture extraction, where such a decomposition is not possible.
To visualize the results of the source selection process, we show a colour−magnitude diagram of the covered area in each cluster in Fig. 3 and highlight the sources that passed the various selection criteria. In all three clusters, our data allowed us to deblend spectra almost all the way down the red giant branch. Note that the few bright sources marked by red triangles in Fig. 3 fell below the S/N threshold because of their small distances (≤0.3 × the seeing FWHM) to a brighter neighbour. For those sources we did not try to deblend individual spectra but accounted for their contributions by modifying the PSF of the neighbour as outlined in Paper I. The transitions between the individual selection categories in Fig. 3 are not sharp because the confusion limit varied with the observing conditions.
6.1.2. PSF
Owing to the small field of view of PMAS, the data cubes generally did not contain any bright and isolated stars useful for determining the PSF. Therefore, we determined the PSF using all the resolved stars instead. For each such star, a PSF model was centred on the location of the star in the data cube and the model was optimized via a least squares fit to all resolved sources. We modelled the PSF as a Moffat function with up to 4 free parameters: the full width at half maximum (FWHM), the β parameter controlling the kurtosis of the profile, the position angle, and the ellipticity. For each observed datacube, the FWHM was a free parameter in the initial fit, using a prior guess matched to the seeing of the observation. In the majority of the cases, we also allowed β to vary. Exceptions were made for some observations where either no reasonably bright star was in the observed field or the seeing was rather poor (≳2″). In those cases, the contrast was not high enough to yield useful constraints on the value of β and we fixed it to a typical value for the observations taken during the same night. Figure 4 shows a summary of all the values we obtained for FWHM and β. The wide distribution of FWHM values gives a good impression of the different seeing conditions (and thus spatial resolutions) in our data. As a side note, no correlation is observed between the FWHM and the airmass in the observation although one would expect the seeing to increase with airmass. Also, we observe no correlation between the FWHM and β and in most cases, the values of the latter scatter around β ~ 3. The rather low values of β indicate that the PMAS PSF has extended wings and that a Gaussian profile would not be a valid description of the PSF. There are two notable exceptions with values of β ~ 6. These two datacubes of M92 were observed within the same night in the October 2011 run. During this run we observed only one additional datacube, also of M92, where we find a rather normal β value. So it remains unclear what caused the high values in the two mentioned cases. Using an elliptical PSF did not significantly improve the results, so we always assumed a circular PSF.
6.1.3. Source coordinates
We always modelled the coordinate transformation using four free parameters, two to
define the scaling and rotation of the reference coordinates into a PMAS field of view,
and another two to describe shifts along the x- and y-axes. PMAS has a nominal spaxel scale of
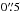 and a fixed rotation angle of zero
degrees. The reference coordinates have a pixel scale of
and a fixed rotation angle of zero
degrees. The reference coordinates have a pixel scale of
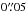 with the y-axis pointing north
(Anderson et al. 2008), which is why we expect a
scaling factor of ξ =
0.1 and zero rotation angle. As can be seen from Fig. 5, where we show the scaling factors and rotation
angles for all datacubes, this is not the case: on average, we obtain ξ <
0.1, indicating a slightly bigger size of the PMAS spaxels. Simply
taking the mean and standard deviation of all measurements gives ξ = 0.0997 ± 0.0002. If
we assume that the coordinates are correct in the centre of the PMAS field of view, this
corresponds to an uncertainty near the edges of the field of view of ~3% per spaxel, similar to what we found
in our analysis of simulated PMAS data in Paper
I.
with the y-axis pointing north
(Anderson et al. 2008), which is why we expect a
scaling factor of ξ =
0.1 and zero rotation angle. As can be seen from Fig. 5, where we show the scaling factors and rotation
angles for all datacubes, this is not the case: on average, we obtain ξ <
0.1, indicating a slightly bigger size of the PMAS spaxels. Simply
taking the mean and standard deviation of all measurements gives ξ = 0.0997 ± 0.0002. If
we assume that the coordinates are correct in the centre of the PMAS field of view, this
corresponds to an uncertainty near the edges of the field of view of ~3% per spaxel, similar to what we found
in our analysis of simulated PMAS data in Paper
I.
We note that for the simulated PMAS data we also found a mild tendency that the recovered scaling factors came out too large. Compared to the nominal spaxel scale of PMAS, the observed data show the opposite trend. However, differences in the scaling of this order can also occur within the instrument, e.g., caused by a temperature dependent focus. In our dataset, we do not find a significant correlation between the recovered scaling factor and the ambient temperature during the observation. Given the small spread in ξ, this is not surprising.
The rotation angle shows significant offsets from zero, up to a few degrees. We observe a bimodal distribution, with the values for the M3 data being consistent with an angle of θ = −3°, while for M13 and M92, the values cluster around θ = +0.5°. An explanation for this behaviour is that the M3 data were all obtained in 2010, before the telescope experienced a significant downtime and refurbishment, while the other two targets were observed after that period. As the Cassegrain flange has an adjustable rotation mechanism, the most likely explanation is that during this period of time, when the instrument was dismounted from the telescope, the previous angle setting was lost.
6.1.4. Extraction of spectra
Using the wavelength dependent PSF parameters and coordinate transformations, we deblended the spectra for the sources identified in the reference catalogue. In Fig. 6 we present the results of this process for the three clusters. Together with an HST image and a white light mosaic of the integral field data, we also show the residuals after subtraction of the modelled sources. Note that the non-trivial mosaic patterns that we covered with the PMAS observations have two reasons. We already mentioned the pointing inaccuracy of 1−2″ that was a consequence of the telescope acquisition procedure. Additionally, some fields were observed because they contained several bright stars and thus allowed for a good PSF reconstruction. One example of such a field is the isolated one to the south west in M13. The reason that in M3 our pointings are asymmetric with respect to the cluster centre is that the centre we assumed during the observations was offset from the one we used in the analysis. One field in M3 is not shown because it is located at a larger distance (~30″) to the cluster centre.
In each panel in Fig. 6, coloured crosses indicate the positions where stellar spectra were extracted, with the colour coding matched to the S/N of the spectrum. The S/N values were determined following the prescription of Stoehr et al. (2007). The number of stellar spectra that we deblended in such a small region of the sky is quite remarkable. As expected, the spectra cover a broad range in S/N, with the brightest stars having values of S/N > 100. Some example spectra, extracted from the central pointing in M13, are shown in Fig. 7 together with their positions in the cluster. For the brightest giant near the centre of the field of view we obtain a spectrum with a very high S/N as expected. The spectrum of the star uncovered from under the PSF wings of the bright star has a substantially lower S/N. Note that PSF fitting is the only technique that allows one to obtain an uncontaminated spectrum for this star at all. The same is true for stars of similar brightnesses close to each other. This is illustrated by the two stars towards the upper left corner of the field of view. As can be seen from the right panel of Fig. 7, one of them is a horizontal branch star that has a spectrum that is different from the one of its neighbour, with no mutual contamination visible in the spectrum of either star. This highlights the power of our approach. In a few cases (marked by open triangles in Fig. 3) the distance between two stars is so small that even with PSF fitting techniques they cannot be accurately deblended because their PSF images become indistinguishable. In such cases we obtained a single spectrum for the two stars that was accordingly flagged during the further analysis. In total, we extracted spectra for 102 stars in M3, 141 in M13, and 98 in M92. The subsequent analysis of these extracted spectra will be discussed below.
 |
Fig. 5 Average spatial scaling factors (top) and rotation angles (bottom) of all PMAS datacubes with respect to the reference catalogue. As in Fig. 4, the error bars represent the standard deviations over the cubes, including variations with wavelength. Dashed lines in both panels show the values expected for the nominal characteristics of PMAS in the instrument setup that was used. |
When comparing the results for M92 with those obtained for M13 in Fig. 6 it becomes clear how strongly the seeing influences the quality of the data. Relative to the number of pointings, we can extract significantly more stars in the M92 data than in the M13 data. On average, the stars in M92 also have a higher S/N than those in M13. The observations of M3 were carried out under similar conditions to those of M13, but the average S/N of the stars is higher. The reason for this can be seen in Fig. 1, where we plot the stellar density as a function of magnitude. The density of M13 increases much steeper towards the confusion limit compared to M3 or M92. This implies that in M13 we select many stars of almost equal brightness right above the confusion limit.
 |
Fig. 6 Results of the deblending of the stellar spectra. For each cluster the panels show, from left to right: an HST image of the central region with the PMAS pointings overplotted, a white light image of the combined PMAS data, and the residuals from the PMAS data after the sources were subtracted. In each HST panel, a green circle marks the cluster centre. We highlight the positions of the extracted spectra by coloured crosses, with the colour coding of the crosses matched to the S/N of the respective spectrum as indicated by the colour bar below the panels. |
 |
Fig. 7 Example spectra deblended from the central PMAS pointing in M13. The left panel shows an HST image of the region, a white light image of our PMAS data is shown in the central panel. In both panels, black crosses indicate the positions where single stellar spectra were extracted. The spectra of the four sources marked by coloured crosses are depicted in the right panel, the calculated S/N is given below each spectrum. The colour coding used to plot the spectra and to indicate their positions is the same in all three panels. |
6.2. Radial velocities
6.2.1. Cross-correlation of PMAS spectra
The determination of radial velocities via cross-correlation requires an accurate determination and subtraction of the continuum of each spectrum. To do so, we followed Siebert et al. (2011): each spectrum was initially fitted with a polynomial, then κ-σ-clipping was performed on the residuals, using asymmetric κ-values for the upper and the lower threshold. While the upper threshold remained fixed at κup = 3, the lower threshold κlow was adjusted based on the S/N of the spectrum, with higher values being used for lower S/N values and vice versa. This was necessary because spectral lines in high-S/N spectra must be clipped, whereas noise spikes in low-S/N spectra should not be spuriously identified as spectral lines.
We cross-correlated the extracted spectra against synthetic templates, taken from the library of Munari et al. (2005), to determine absolute velocities. A potential source of error when using synthetic spectra is that their line profiles do not match the line spread function (LSF) of the observations. The PMAS LSF, as measured from the emission lines of the arc lamp calibration data, showed strong wavelength-depended asymmetries. To account for those, we fitted each emission line with a Gauss-Hermite function and modelled the change of the shape parameters with wavelength as a low order polynomial. This resulted in a wavelength-dependent model of the LSF that each template was convolved with before the cross-correlation. The correction for the shape of the LSF was small (≲1 km s-1) in M13 and M92, yet significant (~4 km s-1) for the M3 data, observed in a single run in 2010.
Our samples not only include red giants, but also stars on the horizontal branch. As visible from Fig. 7, these stars have broad Paschen absorption lines in the covered spectral range. To obtain a matching template for each extracted star, we constructed an isochrone for each cluster using the tool of Marigo et al. (2008) and inferred effective temperatures Teff and surface gravities log g for the cluster stars. Each spectrum was then cross-correlated against the library template that best matched the star in terms of Teff, log g, and [Fe/H].
To assess the quality of a cross-correlation result, we used the rcc statistic
for a cross correlation peak (Tonry & Davis
1979), 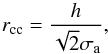 (2)where σa is the
normalized standard deviation of the antisymmetric component of the cross correlation
spectrum. Tonry & Davis showed that the
uncertainty tailored to a measured RV is proportional to (1 +
rcc)-1. A common method to
determine the proportionality factor C is to via the repeated observations of the same
stars (e.g. Pryor et al. 1988; Drukier et al. 2007), as the quantity
(2)where σa is the
normalized standard deviation of the antisymmetric component of the cross correlation
spectrum. Tonry & Davis showed that the
uncertainty tailored to a measured RV is proportional to (1 +
rcc)-1. A common method to
determine the proportionality factor C is to via the repeated observations of the same
stars (e.g. Pryor et al. 1988; Drukier et al. 2007), as the quantity
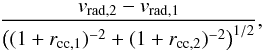 (3)should be distributed
normally with a standard deviation of C. However, as Kurtz & Mink (1998) showed the uncertainty should also be proportional
to the width w of the correlation peak. As a consequence of the
different line widths in our observed spectra (cf. Fig. 7), we obtained a large range in w values. For this reason, we investigated the
scatter of the quantity
(3)should be distributed
normally with a standard deviation of C. However, as Kurtz & Mink (1998) showed the uncertainty should also be proportional
to the width w of the correlation peak. As a consequence of the
different line widths in our observed spectra (cf. Fig. 7), we obtained a large range in w values. For this reason, we investigated the
scatter of the quantity 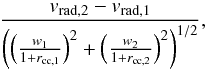 (4)and found it to be
normally distributed with standard deviation of
(4)and found it to be
normally distributed with standard deviation of 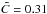 , so our final equation
for obtaining uncertainties was
, so our final equation
for obtaining uncertainties was 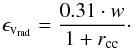 (5)In Fig. 8 we plot the distribution of our measured radial
velocities for the three clusters in the rcc − vrad
plane. Kurtz & Mink (1998) called it the
“blunder diagram” and proposed to use it in order to set a reliability threshold on
rcc in the sense that for lower values
of rcc, the measured radial velocities can
be arbitrarily high. Gerssen et al. (2002) showed
that a threshold in rcc in combination with a cut in the
S/N of the sources is an efficient way to clean a RV sample from unreliable
measurements. In our case, a combination of rcc,min = 4 and
S/Nmin =
7 proved to be a good choice. After applying these selection
criteria, we were left with 137 reliable velocity measurements of 56 stars in M3, 262 measurements of 86 stars in M13, and 165 measurements of 83 stars in M92. They are summarized in Tables D.1 (M3), D.2 (M13), and D.3 (M92), available at
the CDS.
(5)In Fig. 8 we plot the distribution of our measured radial
velocities for the three clusters in the rcc − vrad
plane. Kurtz & Mink (1998) called it the
“blunder diagram” and proposed to use it in order to set a reliability threshold on
rcc in the sense that for lower values
of rcc, the measured radial velocities can
be arbitrarily high. Gerssen et al. (2002) showed
that a threshold in rcc in combination with a cut in the
S/N of the sources is an efficient way to clean a RV sample from unreliable
measurements. In our case, a combination of rcc,min = 4 and
S/Nmin =
7 proved to be a good choice. After applying these selection
criteria, we were left with 137 reliable velocity measurements of 56 stars in M3, 262 measurements of 86 stars in M13, and 165 measurements of 83 stars in M92. They are summarized in Tables D.1 (M3), D.2 (M13), and D.3 (M92), available at
the CDS.
 |
Fig. 8 Offsets between the measured radial velocities and the systemic velocity of each cluster as a function of the cross correlation statistic rcc. The offsets are normalized using the measurement uncertainties and the central velocity dispersion of each cluster (cf. Table 1). Data are colour-coded according to the S/N of the individual spectra as indicated by the colour bar to the right-hand side of the plot. To highlight differences at low S/N values, the colour-coding is truncated at S/N = 50. Spectra below the cut value of S/N = 7 are plotted with small squares, those above with larger circles. The vertical lines denote the selected cut in rcc. |
6.2.2. Literature data
Literature data used to complement our radial velocities.
Our data cover the very central region of each cluster. Clearly, this is where our crowded field IFS approach is most efficient. To probe the kinematics over the full radial extent of our targets we searched the literature for additional radial velocity data. At larger distances to the centres the source densities become significantly lower so that these regions become more accessible also for traditional spectroscopy. When collecting these complementary data from the literature we concentrated on studies that involved more than a minimum of about 50 stars. We only selected data where meaningful uncertainties were provided with the measured RVs. A summary of the catalogues that we included is provided in Table 4. All literature studies that we used provide radial velocities with typical uncertainties ≤1 km s-1.
To obtain the final set of radial velocities, we combined the results from the individual studies of each cluster. In this process that is described in detail in Appendix C, we checked the consistency of the velocities reported by the individual studies and flagged stars that showed evidence for RV variations. We summarize the results of our literature search in Tables D.4 (M3), D.5 (M13), and D.6 (M92), available at the CDS.
6.2.3. Comparison between PMAS and literature data
 |
Fig. 9 Radial velocities of all stars in the three clusters as a function of distance to the cluster centre. Radial velocity measurements from our PMAS data are plotted using green diamonds, black squares refer to literature data. Open symbols are used to indicate stars that show variability, either photometrically or kinematically. Horizontal lines indicate mean velocities of the samples. Note that for clarity, 2 stars in M3 and in M13 with large uncertainties (>20 km s-1) are not shown. |
In Fig. 9 we plot the radial velocities we obtained from our PMAS data and from the literature as a function of the distance to the centre of each of the three clusters. The complementarity is obvious: traditional spectroscopy is nearly “blind” in the central regions of the clusters, where instruments such as PMAS provide the highest gain, limited only by their small field of view.
When comparing the mean velocities of the subsamples, we obtain good agreement for M13 (PMAS: −246.7 ± 1.2 km s-1, literature: −246.4 ± 0.4 km s-1) and M92 (PMAS: −120.7 ± 1.0 km s-1, literature: −121.1 ± 0.3 km s-1). Only in the case of M3, a larger discrepancy of 2.8 km s-1 between the mean velocities is observed (PMAS: −244.2 ± 1.2 km s-1, literature: −247.0 ± 0.4 km s-1). Note that this discrepancy increases if the LSF of PMAS is not accounted for.
For further investigation we matched the literature data to our reference catalogue to check whether some stars were covered by our PMAS footprint. This was done by overlaying both the sources and our reference catalogue objects on an HST footprint and visually identifying the counterparts. In the process of doing this we found that some stars have very inaccurate positional data in the literature, especially in M3, where we observed an average offset of ~1″. The scatter in M13 is only ~0.2″, but some outliers with offsets around 2″ were observed. The positions in M92 are the most accurate ones, showing a scatter of ~0.1″ and only some outliers with offsets ~1″. A likely explanation for the inaccuracies is that the input catalogues used in the literature studies reach back to, e.g., Ludendorff (1905). Such offsets render the measured radial velocities less reliable. In a crowded stellar field such as a globular cluster, an observation will yield a spectrum even if the target star is (partly) missed. However, this spectrum may not only contain light coming from the target star but also a contribution from the numerous fainter stars in its vicinity. Nearby (≲1″) bright stars can cause a similar effect and are therefore equally undesirable. We flagged all stars that (i) had bright neighbours that likely influenced the measurement of the radial velocity or (ii) were significantly offset from a bright HST counterpart or even had no obvious counterpart on the HST footprint at all. These stars were excluded from further analysis. The flags are also included in Tables D.4−D.6.
In M3 and M13, a few of the stars with RV measurements available in the literature are located within our PMAS pointings: four in M13 and five in M3. When comparing our RV measurements with those in the literature, we find an excellent agreement for the sources in M13, the rms deviation of 0.7 km s-1 is the same as the typical measurement uncertainties. However, in M3 the situation is more complex: the rms deviation of 2.6 km s-1 exceeds the typical measurement uncertainties by a factor of 4. Intrinsic RV variability is unlikely to be the reason for this, as none of the stars shows signs of variability, neither in the literature data nor in our dataset. Also, accounting for the measured offset in the mean velocities of the samples does not improve the agreement. We rather suspect that the literature measurements suffer from inaccuracies in the assumed positions of the stars. All stars where we observed a significant discrepancy between our data and the literature were also flagged when checking their positions in the HST image. They were therefore not included in the further analysis.
Inspection of the radial velocities shown in Fig. 9 reveals that some stars have high relative velocities compared to the cluster means. The presence of such high-velocity stars in M3 was already noted by Gunn & Griffin (1979), who detected two stars (those with the highest relative velocities in the literature sample of M3) that showed velocities that could not be explained by the (Gaussian) velocity distribution of the cluster members. Gunn & Griffin (1979) speculated on their origin and considered it unlikely that they were formed either via binary disruption or strong two-star encounters, suggesting that they might be remainders from the formation of the cluster (although the slowing down time due to dynamical friction is quite short). More recently, Lützgendorf et al. (2012a) suggested that such a star can be formed in a single encounter between a main sequence binary star and a stellar-mass black hole.
When identifying high-velocity stars, one has to keep in mind that measurement
uncertainties will on average push the velocity away from the cluster mean. So the
important quantity is not the absolute velocity offset but the offset relative to the
corresponding measurement uncertainty. For this reason, we determined for each star an
effective velocity dispersion as 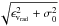 ,
where ϵvrad is the measurement
uncertainty of the star and the central velocity dispersion of the cluster is taken from
Table 1. We identified as a potential outlier
each star with a relative velocity larger than 3 × the effective dispersion. In the
literature data, except for the stars in M3
already identified by Gunn & Griffin
(1979), only the sample of M92
contains some candidates, yet all three of them show evidence for RV variability.
However, our PMAS data contain four suspicious stars for which no RV variability is
observed, one in M3, another two in M13, and a horizontal branch star with poorly
determined RV in M92. While it seems reasonable
to attribute their presence to the mechanisms that we mentioned earlier, we did not want
to exclude the possibility that these stars simply represent the tail of the velocity
distribution. We will discuss their influence when we calculate dynamical models for the
clusters.
,
where ϵvrad is the measurement
uncertainty of the star and the central velocity dispersion of the cluster is taken from
Table 1. We identified as a potential outlier
each star with a relative velocity larger than 3 × the effective dispersion. In the
literature data, except for the stars in M3
already identified by Gunn & Griffin
(1979), only the sample of M92
contains some candidates, yet all three of them show evidence for RV variability.
However, our PMAS data contain four suspicious stars for which no RV variability is
observed, one in M3, another two in M13, and a horizontal branch star with poorly
determined RV in M92. While it seems reasonable
to attribute their presence to the mechanisms that we mentioned earlier, we did not want
to exclude the possibility that these stars simply represent the tail of the velocity
distribution. We will discuss their influence when we calculate dynamical models for the
clusters.
We also investigated the possibility that the high velocity stars are not members of the clusters. However, V- and I-band colours place them nicely on the red giants branches of the respective clusters (and on the horizontal branch of M92). Further, we determined the strengths of the calcium triplet lines. For red giant stars, the equivalent widths of these lines can be approximated as a linear function of V-magnitude and are commonly used as a measure for metallicity (e.g. Armandroff & Da Costa 1991). For two out of the three candidates for which we have spectra available, the measured equivalent widths agree well with those of other red giants with comparable magnitudes. One candidate in M13 (the star with ID 56100 in Table D.2) shows an offset of ~20% to lower equivalent widths.
6.3. Variable stars
As mentioned above, stars with variable radial velocities are flagged in order to exclude them from the analysis of the cluster kinematics. Since RV variations either originate from intrinsic variability or the presence of binary stars, the measured velocities do not necessarily trace the cluster gravitational potential. Intrinsic variability can easily cause variations of the order of the velocity dispersion of the cluster. For example, an RR Lyrae star with a period of 0.5 days will show variations by ±20 km s-1, assuming a change in radius by 0.5 solar radii (Kolenberg et al. 2010).
The importance of binary stars is expected to decrease with the density and the mass of the cluster. Kouwenhoven & de Grijs (2008) predicted the impact of binaries on the estimate of the dynamical mass of a cluster depending on its mass and half-mass radius. They found that the influence of binaries can be neglected if the central velocity dispersion is ≳10 km s-1 while they dominate the dynamics in the regime ≲1 km s-1. This puts our clusters right on the edge of where binaries become negligible. Observational determinations of the binary fraction in the three clusters were carried out, e.g., by Milone et al. (2012) using HST photometry. They determined low binary fractions of about 1−2%. The determination of binary fractions based on spectroscopy is challenging and so far limited to less dense clusters (e.g., M4, Sommariva et al. 2009).
We searched for stars with variable radial velocities in our PMAS data by comparing the radial velocities obtained for the same stars from different exposures. Observations during two epochs only exist for part of the covered fields (5/6 observed fields in M13; 1/3 fields in M92), yet pulsating stars or close binaries can show strong velocity variations during a single night. Therefore we plot in Fig. 10 the maximum measured differences in the radial velocities for all observed stars where at least two reliable measurements are available. We used a probability <1% that the offset is consistent with the measurement uncertainties as a criterion for a variable star. This results in 1 RV variable out of 40 stars in M3, 7 out of 61 in M13, and 5 out of 62 in M92.
It is quite remarkable that the two stars with the highest measured S/N in M13 (with ID 58408 and 55692, respectively, in our reference catalogue) are both flagged as possible RV variable stars. They are also the brightest stars in the entire stellar sample of our PMAS data of M13, both lying at the tip of the red giant branch. Gunn & Griffin (1979) already noticed that such stars often show stronger variability than expected based on the measurement uncertainties. They concluded that likely the stars experience a low magnitude pulsation and added an additional uncertainty of 0.8 km s-1 to account for this “jitter”. The fainter of the two stars is also included in the compilation of variable stars in globular clusters by Clement et al. (2001) as a pulsating star.
 |
Fig. 10 Time variability in the radial velocities measured in our PMAS data for all stars where multiple radial velocity measurements are available. We show, as a function of the S/N of a star, the probability that the maximum velocity difference is consistent with the measurement uncertainties. A horizontal line indicates the thresholds used to identify variable stars. Stars represented by open symbols are known photometric variables. |
Two other stars identified in the catalogue of Clement et al. (2001) as RR Lyrae stars were covered by our PMAS data, one in M92 and one in M3. For the star in M92 we observe a change in the radial velocity of ~10 km s-1 during a single night, while the object in M3 does not show significant variations in our observations. However, we flagged the two stars accordingly in Tables D.1 and D.3 and excluded them from further analysis.
In the literature data we find evidence for variable radial velocities in 16 out of 142 stars with multi-epoch data in M3, 4 of which are known photometric variables. In M13, the numbers are 31 out of 200 with 11 photometric variables and in M92, 20 out of 250 with 2 photometric variables included. Combined with our PMAS data, the fraction of RV variable stars we detect is 9.3% in M3, 14.5% in M13, and 8.0% in M92. These are higher than the photometric binary fractions determined by Milone et al. (2012) in the core of each cluster (~1%). While these fractions were obtained using main sequence stars, we targeted giant stars were pulsating stars are more common. We can conclude that, although some RV variable stars in our samples may remain undetected because of our sparse sampling of the temporal domain, both, our integral field data and the literature data are consistent with low binary fractions.
7. Cluster dynamics
The radial velocities measured from the PMAS data have uncertainties ranging from ≲1 km s-1, well below the expected velocity dispersions of the clusters, to ≳10 km s-1, comparable to the expected dispersions. Large uncertainties, however, do not imply that the measurements are useless in the determination of the velocity dispersion. An efficient way to handle the uncertainties in the analysis of the cluster dynamics was summarized by Pryor & Meylan (1993) who used a maximum likelihood approach for this task. The relevant formulae to obtain vsys and σlos – the mean velocity and the velocity dispersion along the line of sight from a sample of velocity measurements are provided in Pryor & Meylan (1993) and not repeated here.
To obtain uncertainties for the maximum likelihood estimates, we used Monte Carlo
simulations: 1000 realizations were created for each stellar sample by assigning each star
in the sample a new velocity drawn from from a velocity distribution with effective
dispersion 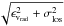 ,
where again ϵvrad is the velocity
measurement uncertainty of the star, and re-calculating σlos. A convenient
side effect of these simulations was that they also allowed us to check for any bias in the
maximum likelihood estimators which are known to become increasingly biased when the number
of stars decreases or the measurement uncertainties grow relative to σlos. We found
that in general the velocity dispersions are slightly underestimated, but the offsets were
always below 1 km s-1
and well within the respective error bars. Not surprisingly, the bias was stronger for our
PMAS data (~0.5 km s-1) than for the literature
data (~0.2 km s-1). This is a consequence
of the wide range of velocity uncertainties in our data.
,
where again ϵvrad is the velocity
measurement uncertainty of the star, and re-calculating σlos. A convenient
side effect of these simulations was that they also allowed us to check for any bias in the
maximum likelihood estimators which are known to become increasingly biased when the number
of stars decreases or the measurement uncertainties grow relative to σlos. We found
that in general the velocity dispersions are slightly underestimated, but the offsets were
always below 1 km s-1
and well within the respective error bars. Not surprisingly, the bias was stronger for our
PMAS data (~0.5 km s-1) than for the literature
data (~0.2 km s-1). This is a consequence
of the wide range of velocity uncertainties in our data.
Another way to obtain the uncertainties would be via a jackknife technique (Lupton 1993), where the velocity dispersion is re-calculated leaving out one star at a time. The agreement with our simulations is in most cases better than 0.2 km s-1. However, the jackknife technique is only valid if the data points have comparable uncertainty variances (e.g. Hogg et al. 2010) which is not strictly the case for our data set. Therefore we stick to the results from the Monte Carlo simulation.
7.1. Rotation in the clusters
 |
Fig. 11 Search for internal rotation of the clusters M3 (top), M13 (centre), and M92 (bottom). For each cluster, 4 radial annuli around the cluster centre are shown, with radius increasing from left to right. The stars in each bin were divided into two subsamples under the assumption of different rotation axes and the difference in mean velocity was calculated. The position angle is zero when aligned in east-west direction, and increases anticlockwise. The extent of the radial bins is indicated in each panel. |
We first checked if any of the clusters in our sample shows signs of rotation. To this aim we separated our data into 4 radial bins per cluster. In each bin the measured radial velocities were further divided into two halves with respect to an assumed rotation axis. We determined the mean velocity and its uncertainty in each half-bin using the maximum likelihood approach and determined the difference in mean velocity to the whole sample. This step was repeated assuming different rotation angles. In case of a non-zero rotational component, one expects a sinusoidal variation of the mean velocity difference with axis angle. The relation between the two quantities in the three clusters is shown in Fig. 11.
In M3, only a weak rotation signal with projected amplitude ≲1 km s-1 is observed. For M13, Lupton et al. (1987) already reported that this cluster shows rotation. While no clear rotational signal is detected in the central bin, the three outer bins suggest rotation with a projected amplitude ~2 km s-1, in reasonable agreement with the measurements of Lupton et al. The rotation axis is tilted ~45° with respect to the east-west direction. Finally, in M92 all four radial bins suggest a small rotational component, with a projected amplitude ~1–2 km s-1. Yet, when comparing the curves depicted in the different panels shown for M92 in Fig. 11, the axis angle suggested by the data seems to be quite variable.
In summary, all clusters display signs of internal rotation. However, unless very unfortunate projection effects are at work, its amplitudes are much lower than the expected velocity dispersion. This is important because the Jeans models we discuss below assume spherical symmetry which would be broken in strongly rotating stellar systems. The generalisation to such systems can be done via axis-symmetric models that we do not consider here.
A word of caution is in order regarding M3. As discussed in Sect. 6.1, our PMAS pointings only cover the region west of the cluster centre, so in the unfortunate case that the cluster rotates around the north-south axis, we would not detect the rotation signal. Such rotation might serve as an explanation for the larger discrepancy in the mean velocities of our PMAS data and the literature sample (cf. Sect. 6.2). However, the offset is still significantly smaller than the velocity dispersion expected in the centre.
7.2. Velocity dispersion profiles
 |
Fig. 12 Velocity dispersion as a function of projected distance to the cluster centre for M3, M13, and M92. The PMAS data and the literature data were analysed separately in the sense that no bin included data from both sets. Note that the horizontal bars do not represent error bars but indicate the range in radii covered by the individual bins. |
A disadvantage of the maximum likelihood approach is that it is prone to outliers. In Sect. 6.2 we identified several stars in the central cluster regions as potential high-velocity stars, deviating from the mean cluster velocity by more than 3σ0, where a literature value for the central dispersion was used. As our PMAS data significantly enhances the kinematic information available near the centres, we re-evaluated the significance of the outliers by using a local estimate of the velocity dispersion, obtained from the 25 nearest stars in distance to the cluster centre. Only for the candidate in M92 the offset to the mean velocity was larger than 3 × this value, while it was smaller for the other candidates. For this reason, we decided to include these stars in the analysis and will discuss their influence separately when comparing them to models in Sect. 7.3.
We obtained a velocity dispersion profile by binning the data radially, where the bin sizes were chosen so that each bin again contained at least 25 stars. Figure 12 gives an overview of the profiles obtained this way. Note that the bins were created separately for the PMAS data and the literature data to facilitate a comparison between the two. In general, the agreement is good. Only in M3, the outer PMAS bin seems to be indicate a significantly higher dispersion than the innermost literature bin.
None of the profiles in Fig. 12 shows a central cusp that could be interpreted as evidence for an IMBH. Instead, the velocity dispersion seems to decrease towards the centres of M3 and M92. To check whether this decrease is significant, we modelled the dispersion within the core radius determined in Sect. 5.3 (cf. Table 3) as a simple power-law and found the range of exponents consistent with the data (using the approach outlined in Appendix D). We found the trend to be significant in both clusters.
The rise in the velocity dispersion profile that is visible in the very outskirts of M92 was interpreted by Drukier et al. (2007) as a consequence of stars escaping from the cluster. No such rise is observed for the other two clusters. McLaughlin & van der Marel (2005) derive tidal radii of rt = 178 pc (M3), 74 pc (M13), and 59 pc (M92), respectively. For the distances of the clusters, those values correspond to projected radii of 60′, 36′ and 23′. A comparison with Fig. 12 shows that in M92, the rise in the velocity dispersion is observed at radii ≳1/3rt. Neither in M3 nor M13 do we have sufficient kinematical data at such large radii to look for a similar effect.
7.3. Jeans modelling
Jeans modelling is a widely used technique to investigate the dynamics of gravitationally
bound stellar systems. It is discussed in detail in Binney
& Tremaine (2008). A good overview is also given in van der Marel & Anderson (2010). The idea behind Jeans
modelling is to estimate the stellar gravitational potential of a cluster from the
measured surface brightness profile via an assumption on the mass-to-light ratio
Υ. The gravitational
potential of a putative IMBH might be added. For a given potential that is spherically
symmetric, the Jeans equations yields a prediction of the second order velocity moments of
the distribution function of the stars inside the cluster,
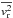 ,
,
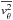 ,
and
,
and 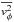 .
For a comparison with our observations, these moments must be projected into the line of
sight. We further require an estimate of the anisotropy in the system to obtain the second
order velocity moment along the line of sight,
.
For a comparison with our observations, these moments must be projected into the line of
sight. We further require an estimate of the anisotropy in the system to obtain the second
order velocity moment along the line of sight, 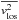 .
The anisotropy is often parametrized via
.
The anisotropy is often parametrized via 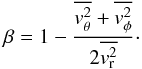 (6)A system with
preferentially tangential orbits has β < 0, a system with
β >
0 has preferentially radial orbits. For an isotropic system,
(6)A system with
preferentially tangential orbits has β < 0, a system with
β >
0 has preferentially radial orbits. For an isotropic system,
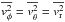 .
.
The second order velocity central moment is the squared sum of the line of sight components of the velocity dispersion and the rotational velocity. The analysis in Sect. 7.1 showed that the rotational component in the clusters is small. For simplicity, we will therefore refer to the projected second order velocity moment as the velocity dispersion and denote it by σlos in the remainder of the paper.
We calculated dynamical models for each of the clusters in our sample. The procedure we followed for every cluster can be summarized as follows. The surface brightness profile of the cluster was parametrized as an extended Nuker profile, cf. Sect. 5.3. Furthermore, we made an assumption about the anisotropy profile β(r) in the cluster, starting from an isotropic profile, i.e. β = 0, and considering anisotropy only in M92 where the comparison between the isotropic profile and the data suggested it. For a given mass-to-light ratio Υ and a given black hole mass MBH we then determined the RV dispersion profile σlos(r) as a function of projected distance to the cluster centre and projected into the line of sight. This profile was finally compared to our kinematical data. The code to perform the Jeans modelling was kindly provided by R. van der Marel (priv. comm.). We discuss our results for each cluster in the following.
It should be highlighted that the comparison of our data to the models does not involve binning. When combining the data into radial bins, one has to select a useful bin size. Using too few bins might wash out some characteristics of the data. For example, the upturn in the velocity dispersion at the largest radii in M92 disappears when a size of 50 stars per bin is chosen. On the other hand, too many bins might introduce spurious features in the radial profile due to shot noise resulting from a low number of stars per bin. Therefore we decided to follow the approach by Gerssen et al. (2002) that does not rely on binning and is outlined in Appendix D. The velocity dispersion profiles shown in Fig. 12 will only be used for illustration purposes.
7.3.1. M3
 |
Fig. 13 Results of the Jeans modelling of M3. Models were calculated over a grid of constant mass-to-light ratios Υ and black-hole masses MBH. Left: distribution of likelihoods in the MBH − Υ plane. Contours trace the 1, 2 and 3σ confidence intervals. Centre: one-dimensional likelihoods as a function of MBH (solid line) and Υ (dashed line), respectively, obtained by marginalizing the two-dimensional distribution over the other parameter. Horizontal dotted lines indicate the 1 and 3σ confidence limits. Right: comparison between the data and the velocity dispersion profiles predicted by the models with the most likely mass-to-light ratio and a range of black-hole masses, as indicated in the plot. |
As input for the Jeans models we used constant mass-to-light ratios in the range Υ = (MM3/M⊙) / (LV,t/LV, ⊙) = 0.8–1.8 and included contributions of a central black hole in the mass range 0–20 000 M⊙ in the gravitational potential. For each model curve of σlos(r) we calculated the likelihood according to Eq. (D.2). Estimates and confidence intervals for MBH and Υ were obtained by marginalizing the likelihoods over the other quantity. The likelihoods of the individual models on the MBH − Υ grid and the marginalized likelihoods of MBH and Υ are shown in Fig. 13. The most likely model has no black hole and a mass to light ratio of Υ = 1.30.
Marginalizing over models with identical mass-to-light ratio yields
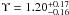 ,
corresponding to a cluster mass of MM3 = (2.68 ± 0.38) ×
105M⊙. The mass-to-light
ratio we measure is higher than the value reported by McLaughlin & van der Marel (2005) for the same cluster
(
,
corresponding to a cluster mass of MM3 = (2.68 ± 0.38) ×
105M⊙. The mass-to-light
ratio we measure is higher than the value reported by McLaughlin & van der Marel (2005) for the same cluster
(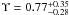 ).
The offset is explainable, however, as McLaughlin
& van der Marel obtained a dynamical mass-to-light ratio by scaling the
velocity dispersion profile predicted by the Wilson model to a central value of
5.6 km s-1,
which is smaller than the value predicted by the model that best fits our data. Our
model with Υ = 0.8 and no
black hole predicts a central dispersion of 5.5 km s-1, fully consistent with the one used by McLaughlin & van der Marel.
).
The offset is explainable, however, as McLaughlin
& van der Marel obtained a dynamical mass-to-light ratio by scaling the
velocity dispersion profile predicted by the Wilson model to a central value of
5.6 km s-1,
which is smaller than the value predicted by the model that best fits our data. Our
model with Υ = 0.8 and no
black hole predicts a central dispersion of 5.5 km s-1, fully consistent with the one used by McLaughlin & van der Marel.
Our models do not suggest the presence of an intermediate-mass black hole in the cluster centre. We obtain a 1σ upper limit of MBH < 5300 M⊙ when marginalizing over the models with identical black hole mass. Using a more conservative 3σ limit increases the black hole mass limit to 12 000 M⊙. In the right panel of Fig. 13 we show a comparison between the velocity dispersion derived from our data and the predictions of the various models with Υ = 1.20. The distinction between the models with different black hole masses is almost exclusively based on the velocities of the stars in the innermost data bin. The velocity dispersion that we measure in the centre is in good agreement with the model without IMBH. However, none of the model predictions seems to agree with the measured velocity dispersion at distances ~20″ to the centre. A possible explanation for this are the potential high-velocity stars, as exclusion of the star with the highest relative velocity brings the data in agreement with the model curves and the 1σ limit on the black hole mass decreases to 2200 M⊙. On the other hand, the discrepancy may indicate that some of the assumptions in the analysis are not fulfilled, e.g. that the true (kinematic) centre of the cluster is offset from the one we assumed. Unfortunately, our kinematical data in this cluster is limited and also asymmetric with respect to the cluster centre, so we cannot check for this.
We also investigated how the central slope of the surface brightness profile influences our limits on the black hole mass. The profile that provided the best fit to the photometric data was basically a core profile (γ = 0.03), yet shallow cusps could not be excluded in the analysis of Sect. 5.3. We ran the same grid of models as before, but used the maximum cuspy model (γ = 0.54) that is still consistent with the photometric data of M3. Again no evidence for a black hole was found, instead we obtained a lower 1σ-limit of 1700 M⊙.
7.3.2. M13
The likelihood distribution of the different models calculated for M13 is shown in the left panels of Fig. 14. The most likely model is obtained for a black hole with MBH = 2000 M⊙ and a mass-to-light ratio of Υ = 2.20.
The marginalized mass-to-light ratio estimate of
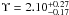 that we find is again higher than the value determined by McLaughlin & van der Marel (2005) for the same cluster
(
that we find is again higher than the value determined by McLaughlin & van der Marel (2005) for the same cluster
(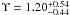 ).
The explanation for this discrepancy is the same as for M3, as McLaughlin & van der
Marel scaled their profile to a central velocity dispersion of 7.1 km s-1 that is below our
measurements. Using our estimate of the mass-to-light ratio, we obtain a cluster mass of
MM13 = (4.02 ±
0.42) × 105 M⊙.
).
The explanation for this discrepancy is the same as for M3, as McLaughlin & van der
Marel scaled their profile to a central velocity dispersion of 7.1 km s-1 that is below our
measurements. Using our estimate of the mass-to-light ratio, we obtain a cluster mass of
MM13 = (4.02 ±
0.42) × 105 M⊙.
The central panel of Fig. 14 shows that the difference in likelihoods between including or excluding an IMBH of 2000 M⊙ is not significant. After marginalizing over Υ, we obtain an upper limit (1σ) of 8100 M⊙. A comparison between the velocity dispersion data and the model predictions for different black hole masses in M13 is shown in the right panel of Fig. 14. The measured profile is well described by models with low black hole masses.
We found in Sect. 5.3 that the surface brightness
profile allows for a range in central slopes, with γ <
0.34. We investigated the influence of the uncertainty in the
measured surface brightness profile on our IMBH constraint in the same manner as for
M3. For a model with a core we got only
marginal changes in the deduced mass-to-light ratio and upper mass limit for an IMBH.
However, if we use the maximum cuspy profile as input to the modelling we find that an
IMBH of 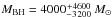 yields a
better representation of the data at the 2σ level, compared to the model without a black
hole. As a conservative value we therefore adopt an upper mass limit in M13 of MBH < 8600
M⊙ (1σ) or MBH < 13
000 M⊙ (3σ).
yields a
better representation of the data at the 2σ level, compared to the model without a black
hole. As a conservative value we therefore adopt an upper mass limit in M13 of MBH < 8600
M⊙ (1σ) or MBH < 13
000 M⊙ (3σ).
However, we find that the mass range that a putative IMBH can occupy is significantly narrowed if the two potential high velocity stars in this cluster are excluded from the comparison. In that case we find that irrespectively of the assumed central slope of the surface brightness profile, the model that maximizes the likelihood has no black hole, and that every black hole with a mass >2000 M⊙ is excluded at the 1σ level.
7.3.3. M92
When calculating Jeans models for this cluster we excluded stars with projected distances >400″ to the cluster centre. The reason for this is the observed rise in the velocity dispersion at the largest projected radii (cf. Fig. 12), probably due to stars escaping from the cluster. The velocities of these stars apparently do not trace the gravitational potential of the cluster any more, but this is the quantity we want to constrain by our models.
We proceeded in analogy to the other two clusters. The distribution of likelihood values is depicted in the left panel of Fig. 15. The model that maximizes the likelihood has no central black hole and a mass-to-light ratio of Υ = 1.60.
A dynamical mass-to-light ratio of 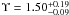 (cf. Fig. 15, centre) is obtained by marginalizing
over the black-hole mass. The value is again higher than the value obtained by McLaughlin & van der Marel (2005) for the
same cluster,
(cf. Fig. 15, centre) is obtained by marginalizing
over the black-hole mass. The value is again higher than the value obtained by McLaughlin & van der Marel (2005) for the
same cluster, 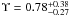 (for the same reason mentioned for M3 and
M13), while it is slightly below the one
obtained by Zocchi et al. (2012) for a King
model, Υ = 1.83. For our
measurement we obtain a cluster mass of MM92 = (2.30 ± 0.29) ×
105 M⊙.
(for the same reason mentioned for M3 and
M13), while it is slightly below the one
obtained by Zocchi et al. (2012) for a King
model, Υ = 1.83. For our
measurement we obtain a cluster mass of MM92 = (2.30 ± 0.29) ×
105 M⊙.
In the right panel of Fig. 15 we show the velocity dispersion profiles predicted for models with Υ = 1.50 and for a range in MBH and compare them to the data. As can be seen from the central panel of Fig. 15, our modelling does not favour a massive black hole in the cluster centre, yielding a 1σ upper mass limit of 980 M⊙. The 3σ limit is 2700 M⊙. Our PMAS dataset contains ~50 stars in the region where the models for different black hole masses diverge. Thanks to the more favourable seeing conditions the average S/N of the deblended spectra is also higher than in the other two clusters. This allows us to put a more stringent constraint to the mass of a possible IMBH in the cluster. The overall velocity dispersion profile is well reproduced by the model without a central black hole. There is a slight tendency that even that model overpredicts the central velocity dispersion.
In Sect. 5.3 we found that the measured surface
brightness profile was best represented using a core profile but that a profile with a
central surface brightness cusp γ < 0.43 was also
consistent with the data. By computing the same suite of models, but using a cuspy
profile with γ =
0.43 as input, we obtained a consistent estimate of the mass-to-light
ratio, 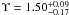 and our 1σ
limit for the mass of a black hole decreased only slightly (820 M⊙).
and our 1σ
limit for the mass of a black hole decreased only slightly (820 M⊙).
Intermediate-mass black holes in globular clusters. Constraints from kinematical studies.
For this cluster, we also compared our data to the self-consistent models calculated by Miocchi (2007). These are based on King profiles with different black hole masses added. We obtained model predictions for a central potential of W0 = 7.7 (as determined by Miocchi et al. 2013) and mass ratios of black hole to cluster mass ranging from 0 to 0.9%. For each profile, we determined the scale radius by fitting the predicted surface brightness profile to the data within the half-light radius obtained by Miocchi et al. (2013). Then, we compared the predicted velocity dispersion profiles to our data via the same maximum likelihood approach used for the Jeans models. We find that models with IMBH masses <0.6% of the cluster mass provide an acceptable fit to our data. Using our estimate of the cluster mass, this limit corresponds to ~1400 M⊙, in good agreement with our limit obtained from the Jeans models.
8. Discussion
We do not find strong evidence for the presence of intermediate-mass black holes in the clusters. M13 seems to be the most ambiguous case, as our upper limit is least stringent in this cluster and the presence of an IMBH could even be preferred if we adopt a surface brightness profile with the steepest cusp consistent with the photometric data. However, the ambiguity can largely be attributed to the presence of two potential high velocity stars, as excluding them results in an upper limit ~2000 M⊙ regardless of the assumed surface brightness profile. However, our current dataset does not allow us to exclude these stars on firm statistical grounds. M13 may be considered the best candidate to search for such a black hole, using data with a higher resolution compared our PMAS cubes.
We now compare our measurements in Table 5 to other searches for IMBHs in globular clusters. Only studies based on the internal cluster dynamics are considered. It should also be mentioned that Table 5 includes clusters for which conflicting results were obtained. Therefore care must be taken when interpreting the data. The majority of the work done so far focussed on the most massive clusters in the Milky Way (or M31 in the case of G1). While M3, M13, and M92 still belong to the more massive part of the overall globular cluster population in the Milky Way, they cover the lower end of the mass range studied so far. Compared to the limits on black hole masses found for more massive clusters, the upper limit we find for M92 is very stringent. To our knowledge, it is the lowest one determined so far for a massive globular cluster from the kinematics of resolved stars. This is quite remarkable given that our observations were carried out from the ground under modest seeing conditions with a 4 m-class telescope. It shows the power of our crowded field 3D spectroscopy approach.
The spherical Jeans modelling approach employed by us to interpret the kinematics of our sample clusters does involve some simplifications. We now discuss the most important of those and check whether they are likely to affect our results significantly.
A constant mass-to-light ratio Υ was assumed throughout our dynamical modelling. This is a simplification because the dynamical evolution of the cluster will lead to mass segregation. A rise of Υ in the outskirts is expected because of the increased abundance of low-mass stars. At the smallest radii, the situation might be more complex. The accumulation of heavy stellar remnants has been predicted to cause a central spike in the Υ profile. Gebhardt & Fischer (1995) found such a behaviour only in very concentrated clusters, where the mass-to-light ratio had a minimum at distances around 1′ towards the centre. In less concentrated clusters, Υ decreased monotonically with radius. A central increase in Υ would also increase the central velocity dispersion predicted by the model. In the cases of M3 and M92, such an increase would reduce the agreement with our measurements. So our data do not suggest that Υ increases towards the centre of either M3 or M92.
It is not fully understood how the inclusion of a dedicated mass-to-light ratio profile influences the search for an IMBH. While Gerssen et al. (2002, 2003) found that in M15 the need for an IMBH is diminished when including a model-predicted profile, Lützgendorf et al. (2012b) observed the opposite trend in NGC 2808. Note that in the latter case the largest changes occurred at radii ≳10″ where the predicted velocity dispersion profile underestimated their data. So their higher IMBH mass limit could also be a consequence of this mismatch.
We do not expect that the assumption of a constant mass-to-light ratio profile has led us to significantly underestimate the upper limits on the black hole masses that are large determined by the innermost datapoints. Minor discrepancies between the data and our models at larger radii, such as observed in M92 at distances ~10″−100″, might be hinting towards a more complex M/L profile. It is possible to obtain such a profile for example via Fokker-Planck models (e.g. Dull et al. 1997, 2003, for M15) or by N-body simulations. However, this is beyond the scope of this work. On the other hand, if all three components of the velocity dispersion are known, it is also possible to constrain the profile of the mass-to-light ratio directly from observations. Such has been done by van den Bosch et al. (2006) for M15 or by van de Ven et al. (2006) for ω Centauri. The combination of our data with proper motions could be very promising in this respect.
We observed only one component of the velocity dispersion, namely the one along the line of
sight. For this reason we cannot infer whether the velocity distribution is anisotropic in
any of our target clusters. Anisotropy has been identified as a significant nuisance in the
search for massive black holes. For example, a radially biased velocity distribution can
mimic the presence of a black hole (Binney & Tremaine
2008). On the other hand, any initial anisotropy in a stellar system will decrease
with time due to relaxation processes. The high stellar densities in the cluster centres
imply relaxation timescales that are only a small fraction of the lifetime of a cluster
(e.g. Meylan 1988). While evidence for anisotropy has
been detected in M3 and M13, it is restricted to larger radii, so we do not expect
this to strongly affect our analysis of the central kinematics. However, the presence of a
massive black hole can lead to a tangential bias because stars on high-eccentricity orbits
are ejected by the black hole (Gebhardt et al. 2003).
In M92 there is a tendency that the model
prediction overestimates the velocity dispersion in the central region. Such a trend might
be caused by tangential anisotropy in the centre. To test whether our data supports such a
scenario, we ran anisotropic Jeans models for M92
with β(r) parametrized as 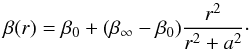 (7)The anisotropy radius
a was fixed
to the core radius (~10′′, cf. Table 3) and
β∞
was set to zero because the cluster is known to be isotropic at larger radii (Cudworth 1976). No black hole was included, the
mass-to-light ratio was fixed to the value that maximized the likelihood in the isotropic
case, and β0 was varied between −3 and 0. We find a confidence interval of
(7)The anisotropy radius
a was fixed
to the core radius (~10′′, cf. Table 3) and
β∞
was set to zero because the cluster is known to be isotropic at larger radii (Cudworth 1976). No black hole was included, the
mass-to-light ratio was fixed to the value that maximized the likelihood in the isotropic
case, and β0 was varied between −3 and 0. We find a confidence interval of
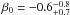 .
Thus, while our data may suggest tangential anisotropy in the core, we do not detect it
significantly.
.
Thus, while our data may suggest tangential anisotropy in the core, we do not detect it
significantly.
A valid dynamical modelling of the central regions depends critically on an accurate
determination of the centre of the cluster. As mentioned earlier, we adopted the photometric
cluster centres determined by Goldsbury et al. (2010)
using two different methods. A correct localization of the centre is more difficult in
clusters with a shallow central density gradient. In this respect, the large core radii
found in M3 and M13 might be problematic. Yet Goldsbury et
al. give small uncertainties for all clusters that we studied
(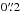 for M3,
for M3, 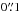 for M13 and
for M13 and 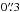 for M92). Our analysis is based on the assumption that the photometric centre of
each cluster coincides with the kinematic centre. The peculiarity of distinct kinematical
and photometric centres has been discussed for ω Centauri (Noyola et
al. 2010) which seems far more complex than our clusters. It might be an
explanation for the deviation we observe between our data and the models in M3. However, our data do not cover a large enough region of
the central region to test this.
for M92). Our analysis is based on the assumption that the photometric centre of
each cluster coincides with the kinematic centre. The peculiarity of distinct kinematical
and photometric centres has been discussed for ω Centauri (Noyola et
al. 2010) which seems far more complex than our clusters. It might be an
explanation for the deviation we observe between our data and the models in M3. However, our data do not cover a large enough region of
the central region to test this.
9. Conclusions
We introduce crowded field 3D spectroscopy as a powerful tool to study the central kinematics of Galactic globular clusters. The combination of PMAS integral field data with PSF fitting techniques allows us to gather large samples of stellar spectra in the highly crowded centres of the three clusters M3, M13, and M92. In our seeing limited datasets, individual stars are resolvable down to the main sequence turn-off of each cluster. As expected, the S/N of the deblended spectra decreases as the stars get fainter, yet reliable RV measurements are still possible for stars below the horizontal branch. The combination of our new measurements with literature data allows us to gather kinematic information at all cluster radii. All our catalogues of RV measurements are made available in the online version of this paper.
Our PMAS stars constitute by far the largest spectroscopic samples obtained in the central 10−20″ of any of the three clusters to date. They allow us for the first time to put meaningful constraints on the presence of IMBHs in these clusters. Using spherical Jeans models, we find that a massive black hole is required in none of them to reach agreement between the Jeans models and our data. Our analysis thus puts stringent upper limits on the mass of any such object in the investigated clusters. In M92 we can rule out an IMBH more massive than 2700 M⊙ at the 3σ level.
Our 3σ upper limits for M3 (12 000 M⊙) and M13 (13 000 M⊙) are more relaxed. M13 remains the least conclusive object we investigated. In contrast to the other two clusters, the most likely model for this cluster does contain a black hole (of 2000 M⊙). However, the improvement over the model without a black hole is insignificant. In this respect, it is unfortunate that the kinematical data in the centre of M13 suffered from non-optimal observing conditions. In summary, we consider M13 the most promising candidate to potentially host an IMBH, still below our sensitivity limit but possibly detectable with better data.
The analysis of the central kinematics in the two clusters M3 and M13 is complicated by the presence of a few potential high velocity stars. Excluding these stars from the analysis would strongly narrow the range of black hole masses allowed by our modelling. Our current dataset is insufficient to discriminate whether these stars represent the wings of the internal velocity dispersion or have been accelerated by other means. Acceleration by an undetected IMBH is unlikely in view of the relatively large distances to the centres and the sizes of the stellar samples (Drukier & Bailyn 2003). As mentioned earlier, another possible scenario involves the acceleration by stellar mass black holes. Heating by stellar mass black holes has also been suggested as an explanation for large core radii (Mackey et al. 2008; Strader et al. 2012a). In this respect, the large core radii of M3 (1.1 pc, McLaughlin & van der Marel 2005) and M13 (1.2 pc) are intriguing, they may suggest a wealthy black hole population in the centres of the clusters and larger kinematic samples will be able to investigate this.
The search for IMBHs in globular clusters has gained a lot of attention over the past years. Many of the recent studies rely on observations at the highest possible spatial resolutions. In the future such observations may be used to address the questions beyond the sensitivity of our dataset. However, the requirement for adaptive optics or multi-epoch HST observations makes them rather expensive in terms of observing time. We demonstrated in this work that meaningful results can be obtained based on less demanding observations. It is also clear that significant further improvements can be expected from applying the technique of crowded field 3D spectroscopy to higher quality data.
Online material
Appendix A: Data reduction
Appendix A.1: Scattered light subtraction
Besides the traces of the individual science fibres and the bias level, we found an additional light component in each of our exposures, scattered all over the CCD. The origin of this straylight component is unknown. It may be light scattered in the spectrograph or result from problems with the CCD controller (Husemann et al. 2013). However, it varies in strength and can reach intensities comparable to the science signal. Therefore we had to develop a method to subtract it. Using the trace mask, i.e. the position of each fibre in cross-dispersion direction as a function of wavelength, we first masked out all pixels around the traces. The remaining pixels should then contain only the scattered light. For each column of the CCD, we modelled the scattered light along the cross-dispersion direction by fitting a low order polynomial to the unmasked pixels. To obtain a smooth representation of the scattered light also as a function of wavelength, the sequence of one-dimensional fits was finally smoothed with a Gaussian kernel. This procedure has meanwhile also been implemented into p3d (Sandin et al. 2012).
In Fig. A.1 we show the drastic improvement in data quality that we achieved when we accounted for scattered light. The difference image shows that the scattered light was not just a spatially flat component in the reduced datacubes, but strongly influenced the relative amount of light that was extracted for individual fibres. Remember that our analysis relies on determining the PSF in an observation from the datacube and using this information to deblend stellar spectra. Any artefact in the data that changes the relative intensities of spaxels would have a severe influence on the determination of the PSF because the intensities of the individual spaxels are no more governed by the shape of the PSF. Therefore, it is no surprise that the scattered
light strongly biases the spectra that are extracted for the individual stars. This can be verified from the two spectra that are shown in the rightmost panel of Fig. A.1 that were extracted for the same star, before and after the scattered light subtraction.
 |
Fig. A.1 Effect of scattered light in our PMAS data. For a reduced data cube of our central PMAS pointing in M3 the first three panels show, from left to right, a white light image with the scattered light still included, a white light image with the scattered light subtracted, and the difference in flux between the two. All images are displayed on the same intensity scale indicated by the colour bar on the right-hand side of the plot. The rightmost panel compares the spectra extracted for the star marked by a white cross in the PMAS data before and after the scattered light subtraction. |
Appendix A.2: Flat fielding
In order to obtain correct relative spaxel intensities, a high quality fibre-to-fibre flat fielding of the data is essential. A problem of PMAS is that calibration data obtained during the night cannot be used to correct for the different efficiencies of the individual fibres because the calibration lamps do not illuminate the lens array homogeneously. Therefore one has to rely on twilight flats. However, PMAS is mounted on the Cassegrain focus of the telescope, thereby it is strongly affected by flexure. As a consequence, the twilight flats cannot be used to correct the data for the fringing of the CCD because the fringing pattern is time-dependent.
We applied the following flat fielding procedure: starting from the reduced twilight flat, we divided each fibre signal by the mean of all fibres and fitted the resulting curves with Chebyshev polynomials of order around 10. Each science datacube was then flat fielded using the polynomial fits. This step corrects for the different (wavelength-dependent) transmissivities of the fibres, but it does not correct for the fringing. The fringing pattern was removed using the night-time calibration data: each spectrum in the continuum flat, originally used to trace the spectra across the CCD, was also fitted with a Chebyshev polynomial and afterwards divided by the fit. As a result, we obtained a normalized spectrum for each fibre that still included the fringes. Division of the science data by these spectra finally removed the fringes.
Appendix B: Checking the completeness of the ACS data
To cross-check the photometry we searched for data obtained with WFPC2. While probably being less accurate compared to ACS, WFPC2 data do not suffer as strongly from bleeding artefacts. For M13, we used the available photometry from Piotto et al. (2002). Unfortunately, neither M3 nor M92 were observed during this campaign. For those two clusters, however, we obtained raw V- and I-band photometry from the HST archive and analysed them using dolphot (Dolphin 2000). The available photometry for M13 covers the B- and V-bands, but our spectra are in the near infrared and I-band magnitudes were used in the source selection process for the deblending. To get I-band magnitudes for the M13 stars, we used the isochrones of Marigo et al. (2008), available for a wide range of magnitudes in the HST photometric system. We compared the magnitudes in B and V for every star in the HST photometry to those in the isochrone and then assigned it the I-band magnitude of the best match in the isochrone.
As expected, the ACS catalogue is quite complete at the magnitude levels that we are most interested in. However, we find that occasionally giant stars are missing. The reason for this becomes clear in Fig. B.1, where we illustrate the result of our cross checking procedure for M3. The image shown in Fig. B.1 is a combination of all data used to create the ACS catalogue. If bright stars were located directly on the bleeding artefacts caused by even brighter ones, they might have been missed. To avoid this, a single short exposure was taken as part of the ACS survey for every cluster observed. However, ACS has a gap of some arcseconds width in between the two chips and no short exposure data exist in that area. The stars we additionally detect using the second catalogue lie preferentially in the same area and are highlighted in the colour−magnitude diagrams in Fig. B.2. We note that some of the added stars are offset from the cluster population, especially for M92. We verified that those are not spurious detections. However, their measurements might have been affected by the presence of nearby stars that are significantly brighter.
 |
Fig. B.1 Illustration of incompleteness in the ACS input catalogue, using the central region of M3. Green crosses indicate sources included in the ACS catalogue, sources marked by red circles were added after a comparison with archival WFPC2 photometry. For clarity, only stars with I-band magnitudes brighter than 17 are highlighted. The cluster centre is located directly on the central bright star. |
 |
Fig. B.2 Colour−magnitude diagrams of M3 (left), M13 (centre), and M92 (right). The photometry obtained in the ACS survey of Galactic globular clusters is shown as a blue density plot. Red crosses mark the individual stars we added based on the analysis of archival HST WFPC2 data. |
Appendix C: Processing of literature data
 |
Fig. C.1 Comparison of the different literature datasets in M3 (top), M13 (centre), and M92 (bottom). The different panels show the offsets in the measured radial velocities between the various studies and the reference study for stars present in both samples. The probability that the scatter of the individual offsets is consistent with the provided uncertainties is given in the upper right corner of each panel. The abbreviations used to denote the individual studies are given in Table 4. |
For each star in each catalogue listed in Table 4, we determined the weighted mean velocity and its uncertainty from the available data. This combination process also offers a convenient way to detect stars with variable radial velocities. For the scatter of the individual measurements to be consistent with the uncertainties, their χ2 value should be comparable to the number of degrees of freedom Ndof, i.e., the number of measurements minus one. For any combination of χ2 and Ndof, the probability of consistency can be calculated from the probability density function of the χ2 distribution. We identified as “RV variable” all stars with probabilities less than 1% and absolute offsets ≥2 km s-1.
Any meaningful combination of the velocities relies on the assumption that the individual studies yield consistent results. We checked that this is the case by defining a reference dataset for each cluster and identifying the subset of stars that was also observed by one or more of the other studies. For this subset, which contained ≳20 stars for any given combination of two studies, we computed the differences in the measured radial velocities. In the case of consistent results, the differences should scatter around zero. If the mean of the distribution deviates from zero, this indicates different assumed systemic cluster velocities, a minor inconsistency that can be easily corrected for. We show the results of this comparison in Fig. C.1. In most of the cases, the measured offsets were small (≲1 km s-1) and no systematic trends were observed. A notable exception are the data of Soderberg et al. (1999) in M92. As already mentioned by Drukier et al. (2007), the velocities measured are biased towards the cluster mean, a trend likely caused by the presence of interstellar absorption lines in the spectra. We observed the same trend with respect to both comparison catalogues and therefore decided to omit this dataset. However, neither in M13 nor in M3 did we observe a similar trend, likely because the spectra covered a different wavelength range. Therefore, we kept the data of Soderberg et al. for those two clusters.
After checking the measured velocities for their reliability, we used the comparison shown in Fig. C.1 to further check whether the uncertainties provided in the different studies are reliable. In that case, the scatter of the individual offsets should again be consistent with the measurement errors, i.e., the χ2 value should be of the order of the number of degrees of freedom, in this case the number of stellar pairs minus one. Radial velocity variables will bias this comparison. Therefore we iteratively cleaned the comparison samples from such stars. For each combination plotted in Fig. C.1 the probability that the scatter is consistent with the uncertainties is provided. The probabilities are sometimes quite small, indicating that the uncertainties may be underestimated. In such cases we applied a constant correction factor to the uncertainties that yielded a χ2 equal to the number of degrees of freedom. In doing so, we started from the data of Drukier et al. (2007) in M92 as it contains by far the largest sample of stars and uncertainties were determined very carefully. We then determined the correction factors successively for all other studies. The factors that we obtained were small (~1.2−1.5).
In the final step, we combined the results of the individual samples and again flagged all stars that showed evidence for RV variations, using the same criteria as before. This yielded the final set of stellar velocities that we used in our subsequent analysis.
Appendix D: Comparing data to models
When a model prediction of (vsys, σlos) is
available as a function of radius, as we obtain from our Jeans models, it is possible to
investigate the agreement between the model and the kinematical data without binning the
latter. To do so, the likelihood of each model given the data is computed under the
assumption that each measurement is drawn from the probability distribution
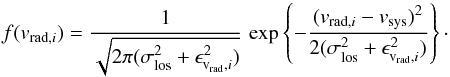 (D.1)Recall that
vrad,i is the
measured velocity of star i (i ∈ [1,N ]) and ϵvrad,i
its uncertainty. The likelihood ℒ of the model parameters is the product of the individual
probabilities. Following Gerssen et al. (2002),
we calculate the quantity λ
≡ −2lnℒ and obtain
(D.1)Recall that
vrad,i is the
measured velocity of star i (i ∈ [1,N ]) and ϵvrad,i
its uncertainty. The likelihood ℒ of the model parameters is the product of the individual
probabilities. Following Gerssen et al. (2002),
we calculate the quantity λ
≡ −2lnℒ and obtain ![\appendix \setcounter{section}{4} \begin{equation} \label{eq:lambda_stat} \lambda = \sum_{i=1}^N \ln \left[ 2\pi(\sigma_\mathrm{los}^2+\epsilon_{\mathrm{v_{rad}},i}^2) \right] + \sum_{i=1}^N \frac{(v_{\mathrm{rad,}i}-v_\mathrm{sys})^2}{\sigma_\mathrm{los}^2+\epsilon_{\mathrm{v_{rad}},i}^2}\cdot \end{equation}](/articles/aa/full_html/2014/06/aa22183-13/aa22183-13-eq339.png) (D.2)
(D.2)
It can be shown that λ follows a χ2
distribution with N degrees of freedom around the expectation value,
![\appendix \setcounter{section}{4} \begin{equation} \label{eq:lambda_expval} \langle\lambda\rangle = \sum_{i=1}^N \ln \left[ 2\pi(\sigma_\mathrm{los}^2+\epsilon_{\mathrm{v_{rad}},i}^2) \right] + N\cdot \end{equation}](/articles/aa/full_html/2014/06/aa22183-13/aa22183-13-eq341.png) (D.3)Whether or not
a model is statistically acceptable can thus be verified using the well known
characteristics of the
(D.3)Whether or not
a model is statistically acceptable can thus be verified using the well known
characteristics of the 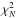 -distribution.
-distribution.
Furthermore, likelihood ratio tests can be applied to discriminate between individual
models in a statistical manner. We assume that the likelihood of models has been
calculated on an m-dimensional grid and that the model that
maximizes the likelihood has λmin. If the range of models is
restricted to an 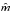 -dimensional
subspace, the quantity λ −
λmin will be ≥0 for each model in
-dimensional
subspace, the quantity λ −
λmin will be ≥0 for each model in
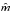 .
A well-known theorem from statistical theory (Wilks
1938) states that for large sample sizes N, the difference
λ −
λmin is distributed according to a
χ2-distribution with
.
A well-known theorem from statistical theory (Wilks
1938) states that for large sample sizes N, the difference
λ −
λmin is distributed according to a
χ2-distribution with
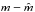 degrees of freedom. Therefore, confidence intervals can also be obtained using
χ2 statistics. This approach was also
followed, e.g., by Merritt & Saha (1993)
or Gerssen et al. (2002).
degrees of freedom. Therefore, confidence intervals can also be obtained using
χ2 statistics. This approach was also
followed, e.g., by Merritt & Saha (1993)
or Gerssen et al. (2002).
Acknowledgments
The authors are grateful to Roeland van der Marel for sharing his Jeans modelling code. S.K. acknowledges support from the ERASMUS-F project through funding from PT-DESY, grant No. 05A09BAA, and from DFG via SFB 963/1 “Astrophysical flow instabilities and turbulence” (project A12). C.S. was supported by funds of DFG and Land Brandenburg (SAW funds from WGL), and also by funds of PTDESY-0512BA1. Part of this work is based on observations made with the NASA/ESA Hubble Space Telescope, and obtained from the Hubble Legacy Archive, which is a collaboration between the Space Telescope Science Institute (STScI/NASA), the Space Telescope European Coordinating Facility (ST-ECF/ESA) and the Canadian Astronomy Data Centre (CADC/NRC/CSA). Some of the data presented in this paper were obtained from the Mikulski Archive for Space Telescopes (MAST). STScI is operated by the Association of Universities for Research in Astronomy, Inc., under NASA contract NAS5-26555. Support for MAST for non-HST data is provided by the NASA Office of Space Science via grant NNX09AF08G and by other grants and contracts. This research has made use of the products of the Cosmic-Lab project funded by the European Research Council.
References
- Anderson, J., & van der Marel, R. P. 2010, ApJ, 710, 1032 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, J., Sarajedini, A., Bedin, L. R., et al. 2008, AJ, 135, 2055 [NASA ADS] [CrossRef] [Google Scholar]
- Armandroff, T. E., & Da Costa, G. S. 1991, AJ, 101, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgardt, H., Makino, J., & Hut, P. 2005, ApJ, 620, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 2008, Galactic Dynamics, 2nd edn. (Princeton University Press) [Google Scholar]
- Clement, C. M., Muzzin, A., Dufton, Q., et al. 2001, AJ, 122, 2587 [NASA ADS] [CrossRef] [Google Scholar]
- Cudworth, K. M. 1976, AJ, 81, 975 [NASA ADS] [CrossRef] [Google Scholar]
- Cudworth, K. M. 1979, AJ, 84, 1312 [NASA ADS] [CrossRef] [Google Scholar]
- Cudworth, K. M., & Monet, D. G. 1979, AJ, 84, 774 [NASA ADS] [CrossRef] [Google Scholar]
- Dolphin, A. E. 2000, PASP, 112, 1383 [NASA ADS] [CrossRef] [Google Scholar]
- Drukier, G. A., & Bailyn, C. D. 2003, ApJ, 597, L125 [NASA ADS] [CrossRef] [Google Scholar]
- Drukier, G. A., Cohn, H. N., Lugger, P. M., et al. 2007, AJ, 133, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Dubath, P., Meylan, G., & Mayor, M. 1997, A&A, 324, 505 [NASA ADS] [Google Scholar]
- Dull, J. D., Cohn, H. N., Lugger, P. M., et al. 1997, ApJ, 481, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Dull, J. D., Cohn, H. N., Lugger, P. M., et al. 2003, ApJ, 585, 598 [NASA ADS] [CrossRef] [Google Scholar]
- Farrell, S. A., Webb, N. A., Barret, D., Godet, O., & Rodrigues, J. M. 2009, Nature, 460, 73 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Feldmeier, A., Lützgendorf, N., Neumayer, N., et al. 2013, A&A, 554, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., & Fischer, P. 1995, AJ, 109, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Richstone, D., Tremaine, S., et al. 2003, ApJ, 583, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Gebhardt, K., Rich, R. M., & Ho, L. C. 2005, ApJ, 634, 1093 [NASA ADS] [CrossRef] [Google Scholar]
- Gerssen, J., van der Marel, R. P., Gebhardt, K., et al. 2002, AJ, 124, 3270 [NASA ADS] [CrossRef] [Google Scholar]
- Gerssen, J., van der Marel, R. P., Gebhardt, K., et al. 2003, AJ, 125, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Gill, M., Trenti, M., Miller, M. C., et al. 2008, ApJ, 686, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Gillessen, S., Eisenhauer, F., Trippe, S., et al. 2009, ApJ, 692, 1075 [NASA ADS] [CrossRef] [Google Scholar]
- Glebbeek, E., Gaburov, E., de Mink, S. E., Pols, O. R., & Portegies Zwart, S. F. 2009, A&A, 497, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsbury, R., Richer, H. B., Anderson, J., et al. 2010, AJ, 140, 1830 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Peng, C. Y., Kim, M., et al. 2010, ApJ, 721, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Gültekin, K., Richstone, D. O., Gebhardt, K., et al. 2009, ApJ, 698, 198 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., & Griffin, R. F. 1979, AJ, 84, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Häring, N., & Rix, H.-W. 2004, ApJ, 604, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, W. E. 1996, AJ, 112, 1487 [NASA ADS] [CrossRef] [Google Scholar]
- Herrnstein, J. R., Moran, J. M., Greenhill, L. J., & Trotter, A. S. 2005, ApJ, 629, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Hogg, D. W., Bovy, J., & Lang, D. 2010, unpublished [arXiv:1008.4686] [Google Scholar]
- Husemann, B., Kamann, S., Sandin, C., et al. 2012, A&A, 545, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jahnke, K., & Macciò, A. V. 2011, ApJ, 734, 92 [NASA ADS] [CrossRef] [Google Scholar]
- Jalali, B., Baumgardt, H., Kissler-Patig, M., et al. 2012, A&A, 538, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kamann, S., Wisotzki, L., & Roth, M. M. 2013, A&A, 549, A71 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolenberg, K., Fossati, L., Shulyak, D., et al. 2010, A&A, 519, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kong, A. K. H., Heinke, C. O., di Stefano, R., et al. 2010, MNRAS, 407, L84 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J., & Richstone, D. 1995, ARA&A, 33, 581 [NASA ADS] [CrossRef] [Google Scholar]
- Kouwenhoven, M. B. N., & de Grijs, R. 2008, A&A, 480, 103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kurtz, M. J., & Mink, D. J. 1998, PASP, 110, 934 [NASA ADS] [CrossRef] [Google Scholar]
- Lanzoni, B., Mucciarelli, A., Origlia, L., et al. 2013, ApJ, 769, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Lauer, T. R., Ajhar, E. A., Byun, Y.-I., et al. 1995, AJ, 110, 2622 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leonard, P. J. T., Richer, H. B., & Fahlman, G. G. 1992, AJ, 104, 2104 [NASA ADS] [CrossRef] [Google Scholar]
- Ludendorff, H. 1905, Publikationen des Astrophysikalischen Observatoriums zu Potsdam, 50, 1 [NASA ADS] [Google Scholar]
- Lupton, R. 1993, Statistics in theory and practice (Princeton: University Press) [Google Scholar]
- Lupton, R. H., Gunn, J. E., & Griffin, R. F. 1987, AJ, 93, 1114 [NASA ADS] [CrossRef] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Noyola, E., et al. 2011, A&A, 533, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Gualandris, A., Kissler-Patig, M., et al. 2012a, A&A, 543, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Gebhardt, K., et al. 2012b, A&A, 542, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lützgendorf, N., Kissler-Patig, M., Gebhardt, K., et al. 2013, A&A, 552, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mackey, A. D., Wilkinson, M. I., Davies, M. B., & Gilmore, G. F. 2008, MNRAS, 386, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Madau, P., & Rees, M. J. 2001, ApJ, 551, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Magorrian, J., Tremaine, S., Richstone, D., et al. 1998, AJ, 115, 2285 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., & Hunt, L. K. 2003, ApJ, 589, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McLaughlin, D. E., & van der Marel, R. P. 2005, ApJS, 161, 304 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, D. E., Anderson, J., Meylan, G., et al. 2006, ApJS, 166, 249 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. J., Harrison, T. E., Baumgardt, H., & Khalaj, P. 2012, ApJ, 745, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Merritt, D., & Saha, P. 1993, ApJ, 409, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Mészáros, S., Dupree, A. K., & Szalai, T. 2009, AJ, 137, 4282 [NASA ADS] [CrossRef] [Google Scholar]
- Meylan, G. 1988, A&A, 191, 215 [NASA ADS] [Google Scholar]
- Miller-Jones, J. C. A., Wrobel, J. M., Sivakoff, G. R., et al. 2012, ApJ, 755, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Milone, A. P., Piotto, G., Bedin, L. R., et al. 2012, A&A, 540, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miocchi, P. 2007, MNRAS, 381, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Miocchi, P., Lanzoni, B., Ferraro, F. R., et al. 2013, ApJ, 774, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, B., Diemand, J., Madau, P., Zemp, M., & Stadel, J. 2006, MNRAS, 368, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Sordo, R., Castelli, F., & Zwitter, T. 2005, A&A, 442, 1127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyola, E., & Baumgardt, H. 2011, ApJ, 743, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., & Gebhardt, K. 2006, AJ, 132, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Noyola, E., Gebhardt, K., Kissler-Patig, M., et al. 2010, ApJ, 719, L60 [NASA ADS] [CrossRef] [Google Scholar]
- Pilachowski, C. A., Sneden, C., Kraft, R. P., Harmer, D., & Willmarth, D. 2000, AJ, 119, 2895 [NASA ADS] [CrossRef] [Google Scholar]
- Piotto, G., King, I. R., Djorgovski, S. G., et al. 2002, A&A, 391, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Portegies Zwart, S. F., & McMillan, S. L. W. 2002, ApJ, 576, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Pryor, C., & Meylan, G. 1993, in Structure and Dynamics of Globular Clusters, eds. S. G. Djorgovski & G. Meylan, ASP Conf. Ser., 50, 357 [Google Scholar]
- Pryor, C. P., Latham, D. W., & Hazen, M. L. 1988, AJ, 96, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Fechner, T., Wolter, D., et al. 2010, in Proc. SPIE, 7742, 12 [Google Scholar]
- Sandin, C., Becker, T., Roth, M. M., et al. 2010, A&A, 515, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandin, C., Weilbacher, P., Tabataba-Vakili, F., Kamann, S., & Streicher, O. 2012, in Proc. SPIE, 8451, 0F [Google Scholar]
- Sarajedini, A., Bedin, L. R., Chaboyer, B., et al. 2007, AJ, 133, 1658 [NASA ADS] [CrossRef] [Google Scholar]
- Searle, L., & Zinn, R. 1978, ApJ, 225, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Siebert, A., Williams, M. E. K., Siviero, A., et al. 2011, AJ, 141, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Soderberg, A. M., Pilachowski, C. A., Barden, S. C., Willmarth, D., & Sneden, C. 1999, PASP, 111, 1233 [NASA ADS] [CrossRef] [Google Scholar]
- Sommariva, V., Piotto, G., Rejkuba, M., et al. 2009, A&A, 493, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stoehr, F., Fraquelli, D., Kamp, I., et al. 2007, Space Telescope European Coordinating Facility Newsletter, 42, 4 [NASA ADS] [Google Scholar]
- Strader, J., Chomiuk, L., Maccarone, T. J., Miller-Jones, J. C. A., & Seth, A. C. 2012a, Nature, 490, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Strader, J., Chomiuk, L., Maccarone, T. J., et al. 2012b, ApJ, 750, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Tonry, J., & Davis, M. 1979, AJ, 84, 1511 [NASA ADS] [CrossRef] [Google Scholar]
- Trager, S. C., King, I. R., & Djorgovski, S. 1995, AJ, 109, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Trenti, M., Ardi, E., Mineshige, S., & Hut, P. 2007, MNRAS, 374, 857 [NASA ADS] [Google Scholar]
- Trudolyubov, S., & Priedhorsky, W. 2004, ApJ, 616, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., Greene, J. E., & Ho, L. C. 2007, ApJ, 661, L151 [NASA ADS] [CrossRef] [Google Scholar]
- van de Ven, G., van den Bosch, R. C. E., Verolme, E. K., & de Zeeuw, P. T. 2006, A&A, 445, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van den Bosch, R., de Zeeuw, T., Gebhardt, K., Noyola, E., & van de Ven, G. 2006, ApJ, 641, 852 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Anderson, J. 2010, ApJ, 710, 1063 [NASA ADS] [CrossRef] [Google Scholar]
- Wilks, S. 1938, Annals of Mathematical Statistics, 9, 60 [Google Scholar]
- Zocchi, A., Bertin, G., & Varri, A. L. 2012, A&A, 539, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Intermediate-mass black holes in globular clusters. Constraints from kinematical studies.
All Figures
 |
Fig. 1 Central surface number densities of sources brighter than a given magnitude for the three clusters of our sample, colour-coded as indicated in the upper left corner of the plot. Magnitudes are given relative to the main sequence turn-off (MSTO) in each cluster. The solid horizontal line corresponds to the source density where we expect to hit the confusion limit. Below the density indicated by a dashed line the deblended spectra will likely have a sufficient signal-to-noise ratio for radial velocity (RV) determination. |
| In the text | |
 |
Fig. 2 Left-hand side: surface brightness profiles of the clusters M3, M13, and M92 over the entire extent of each cluster. Right-hand side: zoom into the central region of each cluster. Measurements based on star counts in the HST data are shown using green squares while blue diamonds represent the data of Trager et al. (1995). A solid red line shows the best-fit extended Nuker profile. For M3 and M13, we also show a Nuker profile with a core (i.e. γ = 0) as a dashed cyan line. The surface brightness profiles have been corrected for extinction. |
| In the text | |
 |
Fig. 3 Colour–magnitude diagrams of the areas covered by our PMAS observations, coding source categories by different colours and symbols: individually deblended sources (green diamonds), sources deblended together with a brighter neighbour (red open triangles), sources contributing to the grainy stellar background (black squares), and unused sources (grey circles). |
| In the text | |
 |
Fig. 4 Comparison of derived PSF parameters. Each panel shows the FWHM: as a function of the airmass of the observation (left), and as a function of β (right). Each plotted point corresponds to the mean value obtained in a datacube. Different symbols indicate different clusters as indicated in the legend. The error bars represent the standard deviations over the cubes, including variations with wavelength. |
| In the text | |
 |
Fig. 5 Average spatial scaling factors (top) and rotation angles (bottom) of all PMAS datacubes with respect to the reference catalogue. As in Fig. 4, the error bars represent the standard deviations over the cubes, including variations with wavelength. Dashed lines in both panels show the values expected for the nominal characteristics of PMAS in the instrument setup that was used. |
| In the text | |
 |
Fig. 6 Results of the deblending of the stellar spectra. For each cluster the panels show, from left to right: an HST image of the central region with the PMAS pointings overplotted, a white light image of the combined PMAS data, and the residuals from the PMAS data after the sources were subtracted. In each HST panel, a green circle marks the cluster centre. We highlight the positions of the extracted spectra by coloured crosses, with the colour coding of the crosses matched to the S/N of the respective spectrum as indicated by the colour bar below the panels. |
| In the text | |
 |
Fig. 7 Example spectra deblended from the central PMAS pointing in M13. The left panel shows an HST image of the region, a white light image of our PMAS data is shown in the central panel. In both panels, black crosses indicate the positions where single stellar spectra were extracted. The spectra of the four sources marked by coloured crosses are depicted in the right panel, the calculated S/N is given below each spectrum. The colour coding used to plot the spectra and to indicate their positions is the same in all three panels. |
| In the text | |
 |
Fig. 8 Offsets between the measured radial velocities and the systemic velocity of each cluster as a function of the cross correlation statistic rcc. The offsets are normalized using the measurement uncertainties and the central velocity dispersion of each cluster (cf. Table 1). Data are colour-coded according to the S/N of the individual spectra as indicated by the colour bar to the right-hand side of the plot. To highlight differences at low S/N values, the colour-coding is truncated at S/N = 50. Spectra below the cut value of S/N = 7 are plotted with small squares, those above with larger circles. The vertical lines denote the selected cut in rcc. |
| In the text | |
 |
Fig. 9 Radial velocities of all stars in the three clusters as a function of distance to the cluster centre. Radial velocity measurements from our PMAS data are plotted using green diamonds, black squares refer to literature data. Open symbols are used to indicate stars that show variability, either photometrically or kinematically. Horizontal lines indicate mean velocities of the samples. Note that for clarity, 2 stars in M3 and in M13 with large uncertainties (>20 km s-1) are not shown. |
| In the text | |
 |
Fig. 10 Time variability in the radial velocities measured in our PMAS data for all stars where multiple radial velocity measurements are available. We show, as a function of the S/N of a star, the probability that the maximum velocity difference is consistent with the measurement uncertainties. A horizontal line indicates the thresholds used to identify variable stars. Stars represented by open symbols are known photometric variables. |
| In the text | |
 |
Fig. 11 Search for internal rotation of the clusters M3 (top), M13 (centre), and M92 (bottom). For each cluster, 4 radial annuli around the cluster centre are shown, with radius increasing from left to right. The stars in each bin were divided into two subsamples under the assumption of different rotation axes and the difference in mean velocity was calculated. The position angle is zero when aligned in east-west direction, and increases anticlockwise. The extent of the radial bins is indicated in each panel. |
| In the text | |
 |
Fig. 12 Velocity dispersion as a function of projected distance to the cluster centre for M3, M13, and M92. The PMAS data and the literature data were analysed separately in the sense that no bin included data from both sets. Note that the horizontal bars do not represent error bars but indicate the range in radii covered by the individual bins. |
| In the text | |
 |
Fig. 13 Results of the Jeans modelling of M3. Models were calculated over a grid of constant mass-to-light ratios Υ and black-hole masses MBH. Left: distribution of likelihoods in the MBH − Υ plane. Contours trace the 1, 2 and 3σ confidence intervals. Centre: one-dimensional likelihoods as a function of MBH (solid line) and Υ (dashed line), respectively, obtained by marginalizing the two-dimensional distribution over the other parameter. Horizontal dotted lines indicate the 1 and 3σ confidence limits. Right: comparison between the data and the velocity dispersion profiles predicted by the models with the most likely mass-to-light ratio and a range of black-hole masses, as indicated in the plot. |
| In the text | |
 |
Fig. A.1 Effect of scattered light in our PMAS data. For a reduced data cube of our central PMAS pointing in M3 the first three panels show, from left to right, a white light image with the scattered light still included, a white light image with the scattered light subtracted, and the difference in flux between the two. All images are displayed on the same intensity scale indicated by the colour bar on the right-hand side of the plot. The rightmost panel compares the spectra extracted for the star marked by a white cross in the PMAS data before and after the scattered light subtraction. |
| In the text | |
 |
Fig. B.1 Illustration of incompleteness in the ACS input catalogue, using the central region of M3. Green crosses indicate sources included in the ACS catalogue, sources marked by red circles were added after a comparison with archival WFPC2 photometry. For clarity, only stars with I-band magnitudes brighter than 17 are highlighted. The cluster centre is located directly on the central bright star. |
| In the text | |
 |
Fig. B.2 Colour−magnitude diagrams of M3 (left), M13 (centre), and M92 (right). The photometry obtained in the ACS survey of Galactic globular clusters is shown as a blue density plot. Red crosses mark the individual stars we added based on the analysis of archival HST WFPC2 data. |
| In the text | |
 |
Fig. C.1 Comparison of the different literature datasets in M3 (top), M13 (centre), and M92 (bottom). The different panels show the offsets in the measured radial velocities between the various studies and the reference study for stars present in both samples. The probability that the scatter of the individual offsets is consistent with the provided uncertainties is given in the upper right corner of each panel. The abbreviations used to denote the individual studies are given in Table 4. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




