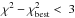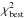| Issue |
A&A
Volume 563, March 2014
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 21 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201323026 | |
| Published online | 20 March 2014 | |
Multiwavelength study of the high-latitude cloud L1642: chain of star formation⋆,⋆⋆,⋆⋆⋆
1
Department of PhysicsUniversity of Helsinki,
PO Box 64,
00014
Helsinki,
Finland
e-mail:
johanna.malinen@helsinki.fi
2
Eötvös Loránd University, Department of Astronomy,
Pázmány P. s. 1/A, 1117
Budapest,
Hungary
3
Université de Toulouse, UPS-OMP, IRAP, 31028
Toulouse Cedex 4,
France
4
CNRS, IRAP, 9
Av. colonel Roche, BP
44346, 31028
Toulouse Cedex 4,
France
5
Institute of Space and Aeronautical Science, Japan Aerospace Exploration Agency,
229-8510
Kanagawa,
Japan
6
Department of Astronomy, Graduate School of Science, The
University of Tokyo, 113-0033
Tokyo,
Japan
7
Department of Earth Science and Astronomy, College of Arts and
Sciences, the University of Tokyo, Tokyo
153-8902,
Japan
8
Finnish Centre for Astronomy with ESO (FINCA), University of
Turku, Väisäläntie
20, 21500
Piikkiö,
Finland
9
National Astronomical Observatory of Japan,
2-21-1 Osawa, Mitaka,
181-8588
Tokyo,
Japan
10
Joint ALMA Observatory, Alonso de Cordova 3107 Vitacura, 763 0355
Santiago,
Chile
11
Nobeyama Radio Observatory, NAOJ, 462-2, Nobeyama, Minamisaku,
Nagano,
Japan
12
Department of Astronomy, Graduate School of Science, the Univ. of Tokyo,
7-3-1 Hongo,
Bunkyo-ku, Tokyo,
Japan
13
Konkoly Observatory, Research Center for Astronomy and Earth
Sciences, Hungarian Academy of Sciences ; Konkoly Thege 15-17,
1121
Budapest,
Hungary
14
Infrared Processing and Analysis Center, MS 220-6, California
Institute of Technology, Pasadena
CA
91125,
USA
15
Laboratoire AIM, CEA/DSM-CNRS-Université Paris Diderot,
IRFU/Service d’Astrophysique, CEA Saclay, 91191
Gif-sur-Yvette,
France
16
College of Science, Ibaraki University,
Bunkyo 2-1-1,
310-8512
Mito,
Japan
17
IAS, CNRS (UMR8617), Université Paris-Sud,
Bât. 121,
91400
Orsay,
France
Received:
11
November
2013
Accepted:
13
January
2014
Context. L1642 is one of the two high galactic latitude (|b| > 30°) clouds confirmed to have active star formation.
Aims. We examine the properties of this cloud, especially the large-scale structure, dust properties, and compact sources at different stages of star formation.
Methods. We present high-resolution far-infrared and submillimetre observations with the Herschel and AKARI satellites and millimetre observations with the AzTEC/ASTE telescope, which we combined with archive data from near- and mid-infrared (2MASS, WISE) to millimetre wavelength observations (Planck).
Results. The Herschel observations, combined with other data, show a sequence of objects from a cold clump to young stellar objects (YSOs) at different evolutionary stages. Source B-3 (2MASS J04351455-1414468) appears to be a YSO forming inside the L1642 cloud, instead of a foreground brown dwarf, as previously classified. Herschel data reveal striation in the diffuse dust emission around the cloud L1642. The western region shows striation towards the NE and has a steeper column density gradient on its southern side. The densest central region has a bow-shock like structure showing compression from the west and has a filamentary tail extending towards the east. The differences suggest that these may be spatially distinct structures, aligned only in projection. We derive values of the dust emission cross-section per H nucleon of σe(250 μm) = 0.5−1.5 × 10-25 cm2/H for different regions of the cloud. Modified black-body fits to the spectral energy distribution of Herschel and Planck data give emissivity spectral index β values 1.8–2.0 for the different regions. The compact sources have lower β values and show an anticorrelation between T and β.
Conclusions. Markov chain Monte Carlo calculations demonstrate the strong anticorrelation between β and T errors and the importance of millimetre wavelength Planck data in constraining the estimates. L1642 reveals a more complex structure and sequence of star formation than previously known.
Key words: ISM: structure / ISM: clouds / stars: formation / submillimeter: ISM / ISM: individual objects: L1642
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
The reduced PACS and SPIRE data, including T and beta maps (in FITS format) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/563/A125
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
High galactic latitude (|b| > 30°) molecular clouds have low background and foreground emission, and are usually quite nearby. They are mostly diffuse or translucent clouds with a low density and typically no signs of star-formation, see McGehee (2008) for a review. These features make them ideal for studying the interstellar medium and interstellar radiation field, as well as low-mass objects in selected regions. LDN 16421 (Lynds 1962) (often also called L1642) is one of the two clouds at high galactic latitudes confirmed to have active star-formation, the other one is MBM 12 (Luhman 2001). Studying this cloud might give constraints of the mechanisms that affect cloud evolution and trigger low-mass star formation. In this article, we use the abbreviation L1642. The cloud is also called MBM 20 (Magnani et al. 1985) and G210.90-36.55 (Juvela et al. 2012).
L1642 is one of the Orion outlying clouds, see Alcalá et al. (2008) for a review of the area and earlier studies. It forms a blob in the head of a HI cloud with cometary structure, the tail of which extends over 5° in the north-east direction in equatorial coordinates, directly towards the Galactic plane. The cloud is projected on the edge of the Orion-Eridanus Bubble (Brown et al. 1995). On the sky, L1642 is ~10° from the filamentary reflection nebula IC 2118, or Witch Head nebula, which also contains the molecular clouds MBM 21 and 22 (Kun et al. 2001, 2004; Alcalá et al. 2008). The different clouds are marked in Fig. 1.
 |
Fig. 1 Surrounding region of L1642. Planck 857 GHz intensity map (left) and close-ups of Planck 857 GHz (middle) and AKARI 140 μm (right) intensity maps. L1642 and other nearby clouds are marked in the maps. The 1 pc scale is marked assuming a distance of 140 pc. |
The Galactic coordinates of L1642 are l = 210.9° and b = −36.55°, and the equatorial coordinates are α2000 = 4h35m and δ2000 = −14°15′ (~68.75° and −14.25°, respectively). Hearty et al. (2000) determined the distance of L1642 to be 112–160 pc. The X-ray observations of Kuntz et al. (1997) suggested that the cloud is close to the edge of the Local Bubble, and not necessarily inside the Orion-Eridanus Bubble, indicating a distance of approximately 140 pc according to Sfeir et al. (1999). See Welsh & Shelton (2009) for a description of the Local Bubble. We adopted the distance of 140 pc similarly to Russeil et al. (2003) and Lehtinen et al. (2004).
L1642 has been studied using several molecules, see Liljestrom (1991) for a review of the early studies. Liljestrom (1991) studied L1642 in CO, HCO+ and NH3 and concluded that the cloud is in virial equilibrium and older than 106 years. More recently, Russeil et al. (2003) studied the morphology and kinematics of L1642 using CO observations obtained with the SEST radio telescope. Their results showed that the cloud consists of a main structure at radial velocity 0.2 km s-1 with higher velocity components forming an incomplete ring around it, suggesting an expanding shell. Based on 13CO data, the peak column density is N(H2) ~ 6 × 1021 cm-2 and the cloud mass ~59 M⊙.
L1642 has also been widely studied using other methods such as dust emission in mid- and far-infrared (Laureijs et al. 1987; Reach et al. 1998; Verter & Rickard 1998; Verter et al. 2000; Lehtinen et al. 2004, 2007) and optical (360–600 nm) surface brightness (Laureijs et al. 1987; Mattila et al. 2012). Mattila et al. (2007) studied scattered Hα light in L1642. The shadowing provided by L1642 has also been used in studies of Galactic diffuse X-ray radiation (e.g., Galeazzi et al. 2007; Gupta et al. 2009).
The small distance, high galactic latitude with little foreground contamination, and the modest column density make L1642 a good target for studying low-mass star formation and the effect of potential external triggering. Sandell et al. (1987) identified two IRAS sources, IRAS 04327-1419 = L1642-1 (V* EW Eri, HBC 413) and IRAS 04325-1419 = L1642-2 (HBC 410), found within L1642, to be faint nebulous binary stars with very active secondaries. The primary of L1642-1 was spectroscopically classified to be a K7IV T Tauri star. Liljestrom et al. (1989) found a weak, bipolar outflow around the binary L1642-2. Reipurth & Heathcote (1990) discovered a Herbig-Haro object, HH123, also originating from L1642-2. They also concluded that the primary object of L1642-2 is a low-luminosity M0 Hα-emission star, and the secondary component is an Hα-emission star as well. Correia et al. (2006) observed L1642-1 in search of high-order multiplicity, but did not find a third component. Lehtinen et al. (2004) concluded that none of the other four IRAS sources projected within L1642 are likely to be young stellar objects (YSOs) inside the cloud.
The 2MASS point source catalogue object 2MASS J04351455-1414468 is situated towards the densest part of L1642 on the sky. Cruz et al. (2003) classified it as a young (~10 Myr) object. They estimated the distance to be probably within 30 pc, meaning that the object would be clearly outside the L1642 star-forming region. Later, several studies have made the assumption or conclusion that the object is a brown dwarf located in front of the L1642 cloud, at a distance of 14–30 pc (Faherty et al. 2009; Antonova et al. 2013). In this article, we re-evaluate the classification and distance estimate of this object.
The early low-resolution studies treated the L1642 cloud as a single entity. Lehtinen et al. (2004) presented ISOPHOT far-infrared (FIR) data of L1642 and studied the cloud structure in separate components (named A1, A2, B, and C). Neither of the IRAS point sources nor new YSO candidates were seen in their 200 μm maps. Lehtinen et al. (2007) compared far-IR data with visual extinction and studied the dust grain emissivity properties in L1642. They found that FIR dust emissivity increases by a factor of two between regions with colour temperatures 19 K and 14 K. This might be caused by grain growth in the dense and cold areas.
L1642 was recently observed as part of the Herschel open time key programme Galactic Cold Cores (Juvela et al. 2010) with unprecedented spatial resolution and sensitivity at 100, 160, 250, 350 and 500 μm. Juvela et al. (2012) presented these observations and studied the properties of the cloud on large-scale images, without separating the distinct objects. In Rivera-Ingraham et al. (in prep.) we will be carrying out a detailed Herschel-based compact source and environmental study of all high-latitude fields (including L1642) from our programme. Furthermore, we have carried out 1.1 mm dust-continuum observations toward L1642 with the AzTEC/ASTE instrument. In this paper, we use these new data, along with other, already published data, to complete the spectral energy distribution of L1642 in the long-wavelength region and advance with this (i) the study of the large-scale structure of the cloud; (ii) the investigation of general dust properties; and (iii) the characterisation of point and compact sources related to the cloud.
The contents of the article are the following: we present the observations and data processing in Sect. 2 and methods in Sect. 3. The results based on the observations are shown in Sect. 4. We present a radiative transfer model of L1642 in Appendix D. We discuss the results in Sect. 5 and present our conclusions in Sect. 6.
2. Observations and data processing
2.1. Herschel
L1642 (G210.90-36.55) was observed by the Herschel satellite (Pilbratt et al. 2010) instruments SPIRE (Griffin et al. 2010) in March 2011 and PACS (Poglitsch et al. 2010) in July 2011 in photometric mode, using wavelengths 100 and 160 μm for PACS and 250, 350, and 500 μm for SPIRE. The observations covered a rectangular area of approximately 50′ × 50′. The SPIRE observations were reduced with the Herschel Interactive Processing Environment HIPE v.10.0.0 using the official pipeline2 with the iterative destriper and the extended emission calibration options. The SPIRE maps3 were then produced using the HIPE naive map-making routine, which projects the data onto the sky and then averages the time-ordered data. The PACS data were processed up to Level 1 within HIPE v10.0.0, after which Scanamorphos v20 (Roussel 2013) was used to create the map products3. The original resolution of the maps, in order of increasing wavelength, is 7″, 12″, 18″, 25″, and 36″.
We made zero-point and colour corrections to the Herschel data and corrected the effect of very small grain emission in the 100 μm data as in Juvela et al. (2011). In the zero-point correction, we used Planck (Tauber et al. 2010) data and the IRIS (Miville-Deschênes & Lagache 2005) version of IRAS data as reference. For the 100 μm map, we compared the mean of the Herschel map with the mean of the IRIS data. For the longer wavelengths, we made a linear fit between Herschel data and the values that were interpolated from Planck and IRIS maps using a modified black-body curve. These linear relations were extrapolated to zero Planck and IRIS values to obtain the offsets for the Herschel data. The second method requires a clear correlation between the Herschel and Planck+IRIS data. In the case of L1642, 160 μm and the SPIRE channels still give quite good correlations, and the second method can be used. An advantage of the second method is that it does not require the calibrations to be the same. Moreover, because it is insensitive to multiplicative errors, it is more reliable with respect to the uncertainties of colour corrections and interpolation of Planck and IRIS data.
The data were initially colour corrected assuming modified black-body emission with T = 15 K and a spectral index of β = 1.8. The zero-point correction and colour temperature calculations were iterated, and the final colour-correction corresponds to the temperature calculated from the final SPIRE maps. The fit used in the zero-point correction is an unweighted robust least-squares fit. The error estimates used in this procedure and later in the calculations of temperature and optical depth are 15% and 7% for PACS and SPIRE, respectively.
2.2. Planck
We used archived Planck4 data (Planck Collaboration I. 2014) of the L1642 area. The data, corresponding to the first 15.5 months of Planck observations, are available through the Planck Legacy Archive5. We used maps at 217, 353, 545, and 857 GHz, corresponding to the wavelengths at 1380, 850, 550, and 350 μm. The angular resolutions (full width at half maximum (FWHM) beam size) of the maps are 5.01′, 4.86′, 4.84′, and 4.63′, respectively. We converted the 217 and 353 GHz maps from KCMB units to MJy/sr units using the coefficients given in Table 6 of Planck Collaboration IX. (2014) (483.690 and 287.450 MJy/sr/KCMB). Rotational transition lines of CO can significantly affect the signal of Planck channels 100 GHz (CO J = 1−0), 217 GHz (CO J = 2−1), and 353 GHz (CO J = 3−2). We performed a CO correction for the 217 GHz and 353 GHz maps using the SEST CO data described in Sect. 2.5. The CO correction coefficients and the process are described in Sect. 3.2 of Planck Collaboration XIII. (2014). We compare the SEST CO maps to the CO maps available from the Planck Archive in Appendix C. We colour-corrected all the Planck maps with the method described in Planck Collaboration IX. (2014) and the Planck Explanatory Supplement, using the colour-temperature map derived from Herschel observations.
The calibration accuracy of the Planck HFI early maps is estimated to be ~7% for the two highest frequencies and ≤2% for the lower frequencies (Planck HFI Core Team VI. 2011). We used 7% as an error estimate for all the four Planck maps to cover also the uncertainties in the CO correction of the 217 GHz and 353 GHz maps.
2.3. Other infrared data
We used the FIR AKARI survey (Murakami et al. 2007) observations of L1642 obtained with the FIS instrument in the narrow-band filters N60 and N160 (central wavelengths 65 and 160 μm) and in the wide-band filters WideS and WideL (central wavelengths 90 and 140 μm). The spatial resolutions of the AKARI maps are 37″, 39″, 58″, and 61″ for the N60, WideS, WideL, and N160 filters, respectively. We used the AKARI/IRC Point Source Catalogue6 9 and 18 μm data and AKARI/FIS Bright Source Catalogue7 (Yamamura et al. 2010) 65, 90, 140, and 160 μm data for the point sources.
We used the archived WISE satellite (Wright et al. 2010) mid-infrared (MIR) 3.4, 4.6, 12.0, and 22.2 μm maps and WISE All-Sky Source Catalog data for the point sources. The beam sizes are 6.1″, 6.4″, 6.5″, and 12.0″, in order of increasing wavelength.
We used the archived Two Micron All Sky Survey (2MASS) (Skrutskie et al. 2006) near-infrared (NIR) J, H, and KS band data to produce an extinction map of the L1642 field and to examine the point sources that are believed to be associated with the cloud L1642 itself. The limiting magnitudes of 2MASS are J = 15.8m, H = 15.1m, and KS = 14.3m.
We used the IRAS point source catalogue data (MIR-FIR 12, 25, 60, and 100 μm) and IRIS (the reprocessed IRAS) maps (Miville-Deschênes & Lagache 2005). The spatial resolutions of the IRIS maps at 12, 25, 60, and 100 μm are 3.8′, 3.8′, 4.0′, and 4.3′, respectively.
We compared our results with the 200 μm observations at 90″ resolution (Lehtinen et al. 2004), obtained with the ISOPHOT instrument of the ISO satellite (Kessler et al. 1996).
2.4. AzTEC/ASTE
From 2008 October to November, we carried out 1.1 mm dust-continuum observations towards L1642 with the AzTEC camera (Wilson et al. 2008) on the ASTE 10 m telescope (Ezawa et al. 2004; Kohno et al. 2004) located at Pampa la Bola, Chile, at an altitude of 4800 m. The AzTEC camera temporarily mounted on the ASTE telescope is a 144-element bolometric camera tuned to operate in the 1.1 mm atmospheric window, which provides a FWHM resolution of 28″ (Wilson et al. 2008). Observations were performed in raster-scan mode. The pointing uncertainty of the AzTEC map is estimated to be better than 2″. We observed Uranus as a flux calibrator twice per night. We measured the flux conversion factor (FCF) from the optical loading value (in watts) to the source flux (in Jy beam-1) for each detector element. The principal component analysis (PCA) (Scott et al. 2008) cleaning method was applied to remove atmospheric noise. Details of the flux calibration are described by Wilson et al. (2008) and Scott et al. (2008). Since the PCA method does not preserve the extended components reliably, we applied the iterative mapping method FRUIT (Liu et al. 2010; Shimajiri et al. 2011) to recover the extended components. The noise level is 4.5 mJy beam-1 in the central region, and the effective beam size is 35″ after FRUIT imaging.
2.5. CO
We compared our observations with the CO observations described in Russeil et al. (2003), where the cloud L1642 was mapped in the J = 1−0 and J = 2−1 transitions of 12CO, 13CO and C18O with the SEST radio telescope. The half-power beam widths are 45″ (J = 1−0) and 23″ (J = 2−1), and the grid spacing is 3′. Typical noise levels in the data were ΔTrms = 0.06 K (C18O(2–1)) and ~0.15 K (other transitions).
3. Methods
3.1. Source extraction
We extracted sub-millimetre clumps and calculated their fluxes from Herschel 160–500 μm maps using Getsources (Men’shchikov et al. 2012), a source-extraction method developed for the Herschel Gould Belt survey (André et al. 2010) and Herschel HOBYS survey (Motte et al. 2010). The source extraction (Montillaud et al., in prep.) was made as part of the effort to catalogue the cold clumps detected in the fields observed in the Galactic Cold Cores project (Juvela et al. 2010). The method proceeds in several steps, first extracting sources independently in each band, then combining all the data. In the extraction, we used 160, 250, 350, and 500 μm intensity maps and the optical depth at 250 μm, τ250, obtained from Markov chain Monte Carlo calculations (see Sect. 4.2). The optical depth τ250 was used in the source extraction to ensure that the extracted sources correspond to dense clumps. All the maps were convolved to a resolution of ~40″.
We calculated the flux of the point sources in Herschel 100 μm and ASTE 1.1 mm (and also in other Herschel bands for comparison) using aperture photometry with a circular aperture. The same aperture sizes were used for all clumps and maps. The aperture radius is 40″ and the annulus radii 55″ and 85″. We subtracted the mean value of the annulus from the aperture values. Differences in background subtraction and in the size of the aperture can cause significant bias in the derived fluxes in the FIR regime, and it is therefore important to use the same method when comparing and fitting the values based on different data sets.
3.2. Mass calculation
We calculated the masses of a chosen region by summing the pixel values of the region
using equation 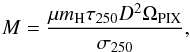 (1)where
μ is the
mean weight per H atom (1.4), mH the mass of a hydrogen atom,
τ250 the optical depth at 250
μm,
D the
distance, ΩPIX the
solid angle of a pixel, and σ250 the absorption cross-section per H
atom at 250 μm.
(1)where
μ is the
mean weight per H atom (1.4), mH the mass of a hydrogen atom,
τ250 the optical depth at 250
μm,
D the
distance, ΩPIX the
solid angle of a pixel, and σ250 the absorption cross-section per H
atom at 250 μm.
The virial mass can be derived using equation 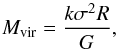 (2)where
G is the
gravitational constant, R the cloud radius, k a factor depending on the
radial density distribution, and σ the three-dimensional velocity dispersion (MacLaren et al. 1988). σ is given by the equation
(2)where
G is the
gravitational constant, R the cloud radius, k a factor depending on the
radial density distribution, and σ the three-dimensional velocity dispersion (MacLaren et al. 1988). σ is given by the equation
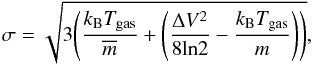 (3)where kB is the
Boltzmann constant, Tgas the kinetic gas temperature,
(3)where kB is the
Boltzmann constant, Tgas the kinetic gas temperature,
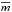 the mean
molecular mass (μmH, where
μ = 2.33
is the mean molecular weight per free particle), m the mass of the molecule
used for observations (13CO or C18O), and ΔV the observed line width (FWHM) corrected for
opacity line-broadening. Lehtinen et al. (2004)
derived virial masses using these equations, and assuming that k = 1.25, a value between
the density distributions ρ(r) = r-1
and ρ(r) = r-2.
To compare our results with this, we used the same value for k.
the mean
molecular mass (μmH, where
μ = 2.33
is the mean molecular weight per free particle), m the mass of the molecule
used for observations (13CO or C18O), and ΔV the observed line width (FWHM) corrected for
opacity line-broadening. Lehtinen et al. (2004)
derived virial masses using these equations, and assuming that k = 1.25, a value between
the density distributions ρ(r) = r-1
and ρ(r) = r-2.
To compare our results with this, we used the same value for k.
 |
Fig. 2 Herschel intensity maps showing the areas used in the analysis. The maps show the total intensity after zero-point correction. (Top left) 350 μm (26.8″ resolution) showing the larger regions (A1, A2, B and C) and the background area (BG) used in the analysis. (Top right) 250 μm (18.3″ resolution) map showing the striation in L1642. (Bottom left) 160 μm (18.3″ resolution) showing the most prominent clumps identified by Getsources. FWHM ellipses of the clumps are drawn in the figure. (Bottom right) 100 μm (18.3″ resolution) showing the circular apertures (with 80″ diameter) used in the aperture photometry of the point sources marked in the figure. |
3.3. Classifying sources
Young stellar objects can be classified into five classes, based on the slope of the
NIR–MIR (~2–24 μm) spectral energy
distribution (SED) or spectral index 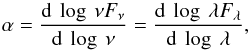 (4)where Fν is the flux as a
function of frequency, ν, and Fλ the flux as a
function of wavelength, λ, (combining the work of Lada 1987; Greene et al. 1994;
and André et al. 1993). Class 0 objects are
undetectable at λ < 20 μm.
The spectral index limits are α > 0.3, 0.3 > α > −0.3,
−0.3 > α > −1.6,
and −1.6 > α, for Class I,
Flat spectrum, Class II, and Class III sources, respectively. The classes are assumed to
describe the evolutionary sequence from deeply embedded Class 0 objects through Classes
I–II with NIR and MIR excess to Class III, where most of the surrounding disk has
disappeared, and only little NIR excess is seen.
(4)where Fν is the flux as a
function of frequency, ν, and Fλ the flux as a
function of wavelength, λ, (combining the work of Lada 1987; Greene et al. 1994;
and André et al. 1993). Class 0 objects are
undetectable at λ < 20 μm.
The spectral index limits are α > 0.3, 0.3 > α > −0.3,
−0.3 > α > −1.6,
and −1.6 > α, for Class I,
Flat spectrum, Class II, and Class III sources, respectively. The classes are assumed to
describe the evolutionary sequence from deeply embedded Class 0 objects through Classes
I–II with NIR and MIR excess to Class III, where most of the surrounding disk has
disappeared, and only little NIR excess is seen.
Robitaille et al. (2006) presented a grid of 20 000 radiation transfer models of YSOs in different evolutionary stages and from ten different viewing angles, resulting in 200 000 SEDs. These models used multiwavelength information to classify the potential YSOs, instead of just NIR–MIR fluxes used in the traditional classification system. Longer wavelengths can be useful in identifying the properties of the surrounding envelope and disk, and not just the central source. However, there are two main shortcomings in the models concerning our data. Firstly, the models cut the envelope when the dust temperature falls below 30 K. This means that the FIR spectrum maximum has to be below 100 μm. If there is a significant amount of surrounding cold dust within the aperture, the models cannot fit the Herschel bands. Secondly, all the models are based on single objects. In our case, the two young stars in L1642 are known binary stars. However, the models allow large inner envelope and disk holes, which can correspond to the effects of binary systems. Close-by binary objects do not necessarily change the SED notably. Moreover, Robitaille et al. (2007) showed (in their Fig. 1) the SEDs of two binary stars, where the models fit the data quite well.
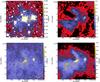 |
Fig. 3 WISE 3.4 μm and AzTEC/ASTE 1.1 mm intensity maps (top row). Herschel 100 and 160 μm intensity maps (without zero-point correction) at the original resolution (7″ and 12″, respectively, bottom row). The sources B-1, B-2, B-3, and G (see text) are marked on the Herschel and WISE maps, using their 2MASS coordinates. The marker circles show the beam FWHM. |
4. Data analysis and results
4.1. Surface brightness maps and the general structure of L1642
We present surface brightness maps of L1642 using Herschel, Planck, AKARI, and AzTEC/ASTE data. The Planck 857 GHz map of L1642 and the surrounding area is shown in Fig. 1 (left). We show a close-up of the same area in Fig. 1 with Planck and AKARI data. Straight lines following the pillars from L1642, IC 2118 (Witch Head nebula) and LBN 991 are drawn to the figures, leading to the centre at α2000 = 4h56m, δ2000 = −12°10′.
L1642 consists of dense regions, surrounded by more diffuse material. Lehtinen et al. (2004) named the dense regions A1, A2, B, and C. We adopt this naming convention and show the regions in Fig. 2 (top left panel). The high-resolution Herschel data show considerably more details than the earlier ISO observations at 90″ resolution, especially in the densest region B. In the eastern part of region B, there is an intensity maximum separated from the main clump, justifying the division of region B into areas B1 and B2, similarly to region A. Two filaments lead from these two B region maxima southwards to the C clump. The Herschel data also show striation in the diffuse dust emission around the cloud L1642, especially at the northern part. This is a real structure and not an observational artefact. The striation is mainly towards north-east direction from the cloud, especially near region A, and does not follow the scanning direction. At the northern side of the B clump there is one denser elongated structure, marked N in Fig. 2 (bottom-left panel). This structure, like the fainter striations, was not resolved in the earlier studies (Russeil et al. 2003; Lehtinen et al. 2004). The structure can be seen in all the Herschel maps and the ASTE 1.1 mm map and to some extent also in the AKARI 140 and 160 μm maps.
The point sources inside the cloud were not detected in the ISO data (Lehtinen et al. 2004). In the Herschel data, however, point sources can be seen even at longer wavelengths in all bands 100–500 μm. Figure 2 (bottom-left panel) shows the most prominent clumps obtained with Getsources (Men’shchikov et al. 2012) from the Herschel data (see Sect. 3.1). We also studied sources marked B-1, B-2, B-3, and B-4 with aperture photometry. The apertures with 80″ diameter are marked in Fig. 2 (bottom-right panel). We present region B and the point sources inside it in more detail in Fig. 3 with WISE, ASTE and Herschel data. Point sources B-1, B-2, and B-3 can be seen in WISE 3.4–12.0 μm maps and in the Herschel data. Sources B-1 and B-2 can also be seen even in the ASTE data at 1.1 mm. B-3 and B-4 are not as prominent in ASTE data, but they are situated near local intensity maxima. The beam FWHM is drawn on the sources in the Herschel maps, indicating that the point sources are extended structures in FIR wavelengths. However, in 100 μm, the FWHM of source B-3 is very close to the beam FWHM.
The object marked E in Fig. 2 (bottom-left panel) can be clearly seen in the Herschel 100–350 μm maps. This is the object IRAS 04336-1412 (or L 1642-3) that was mentioned, but not studied in more detail, in Sandell et al. (1987) and Lehtinen et al. (2004). NED8 identifies this object as a galaxy 2MASX J04355560-1405542. There is a suitable counterpart in the WISE catalogue, WISE J043555.67-140554.1, within 2″.
At the northern end of the elongated structure N, a compact point source can be seen in the 100 μm map at 7″ resolution in Fig. 3 (bottom-left panel), marked G, at coordinates 4h35m05.157s−14°10′01.85″. 2MASS 04350296-1410159 and WISE J043504.98–141002.4 (within 2.7″) are the closest counterparts, and the object is clearly seen in the WISE maps. There are no NED objects within 1′, and the nature of this object is unclear. The object cannot be seen in the convolved Herschel maps, even at 100 μm. There are several similar objects within the Herschel map area, which are probably galaxies.
 |
Fig. 4 Maps derived by MCMC fitting with a constant β = 1.8, using Herschel 250–500 μm maps at 40″ resolution. Background is not subtracted from the maps. (Left) Optical depth τ250 with contours of column density NH2 derived from 13CO observations of Russeil et al. (2003) drawn at levels 4, 3, 2, and 1 × 1021 cm-2. (Right) Colour temperature T with contours of the τ250 map drawn at levels 0.0035, 0.0029, and 0.0017. Sources B-1, B-2, B-3, and B-4 are marked with crosses (Getsources coordinates) and circles (WISE coordinates). |
4.2. Colour temperature, optical depth, and spectral index maps
Colour temperature, optical depth, and spectral index maps can be derived by fitting the
observed FIR intensity maps with the modified black-body (MBB) law 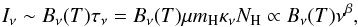 (5)where
Iν is the observed
intensity, Bν(T)
is the Planck radiation law for temperature T and frequency ν, τν is the optical depth
at frequency ν, μ is the mean weight per H atom (1.4),
mH is the mass of H atom, κν is the mass absorption
(or emission) coefficient (cm2/g) relative to gas mass (often called opacity),
NH is the column density of H atoms
(1/cm2), and
β is the
dust emissivity spectral index. T and β can be kept as constants or free parameters in
the fitting. The equation assumes optically thin emission. We use wavelength instead of
frequency in the notation throughout the article, e.g., τ250 = τ250 μm.
(5)where
Iν is the observed
intensity, Bν(T)
is the Planck radiation law for temperature T and frequency ν, τν is the optical depth
at frequency ν, μ is the mean weight per H atom (1.4),
mH is the mass of H atom, κν is the mass absorption
(or emission) coefficient (cm2/g) relative to gas mass (often called opacity),
NH is the column density of H atoms
(1/cm2), and
β is the
dust emissivity spectral index. T and β can be kept as constants or free parameters in
the fitting. The equation assumes optically thin emission. We use wavelength instead of
frequency in the notation throughout the article, e.g., τ250 = τ250 μm.
We used Markov chain Monte Carlo (MCMC) fitting (Veneziani et al. 2010; Juvela et al. 2013) to derive colour temperature T, optical depth at 250 μm τ250, and spectral index β maps from the Herschel 160–500 μm intensity maps. The data used in the fitting and the resulting maps are all at 40″ resolution. The calculations employed flat priors where the allowed parameter ranges were 5 K < T < 35 K and 0.3 < β < 4.0. The derived β and T maps are shown in Fig. A.1. Within region B, β values are mostly between 1.7 and 1.9. However, outside the densest region, noise dominates the derived β map.
The calculations were also performed using the fixed spectral index value of β = 1.8, in which case only wavelengths 250–500 μm were used. 160 μm was omitted, as the PACS channels have a smaller area, leaving the eastern tail of the cloud out of the map. PACS maps also have a lower S/N than SPIRE maps, and the shorter wavelengths might introduce more bias, which might lead to an underestimation of the optical depth (e.g., Shetty et al. 2009; Malinen et al. 2011). This can be more important than the increase in the statistical noise. Including 160 μm in the derivation of τ250 would lead to masses smaller by <2% for most of the regions in the analysis of Sect. 4.4.
Fitted optical depth and colour temperature maps, using β = 1.8, are shown in Fig. 4. The contours of the column density map derived from the 13CO data of Russeil et al. (2003) are drawn in the optical depth map in Fig. 4 (left). The CO-based column density map has a lower resolution because the line observations were obtained with a 3′ step. In both cases, the local diffuse background was not subtracted and the total intensities (with the intensity zero-points derived from comparison with Planck data) were used when deriving the τ250, β, and T maps.
For the analysis of regions A1, A2, B, and C, we derived the τ250 and T maps with a constant value β = 1.8, using background-subtracted intensity maps. The areas used in the analysis and the reference area used for the local diffuse background subtraction are marked in the derived τ250 and T maps in Fig. A.2.
4.3. Dust opacity
We studied the dust properties in different areas of the cloud by deriving the dust
opacity, the ratio of FIR optical depth to column density, ![\begin{equation} \sigma_{\rm e}(\nu) = \tau_{\nu}/N_{\rm H} = \mu m_{\rm H} \kappa_{\nu} [{\rm cm}^2/{\rm H}]. \label{eq:sigma} \end{equation}](/articles/aa/full_html/2014/03/aa23026-13/aa23026-13-eq95.png) (6)We used τJ obtained from the NIR
extinction map as an independent tracer of column density. We derived an extinction map of
L1642 using 2MASS stars (excluding the YSOs) and the NICER method (Lombardi & Alves 2001) and converted the map to optical depth
at J band,
τJ, shown in Fig. A.3 (left panel). We used the extinction curves of Cardelli et al. (1989), with, for instance,
AJ/E(J − K) = 1.67.
The original pixel size of the extinction map is 30″. We compared the τJ map based on
extinction with the optical depth map at 250 μm, τ250, derived from Herschel
data (pixel size 12″). A τ250/τJ
map at 180″ resolution is
shown in Fig. A.3 (right panel). The reference area
used in the background subtraction of both optical depth maps is marked in the figure. The
map shows that at low resolution, the densest areas A, B, and C have a considerably higher
emissivity than the surrounding diffuse areas.
(6)We used τJ obtained from the NIR
extinction map as an independent tracer of column density. We derived an extinction map of
L1642 using 2MASS stars (excluding the YSOs) and the NICER method (Lombardi & Alves 2001) and converted the map to optical depth
at J band,
τJ, shown in Fig. A.3 (left panel). We used the extinction curves of Cardelli et al. (1989), with, for instance,
AJ/E(J − K) = 1.67.
The original pixel size of the extinction map is 30″. We compared the τJ map based on
extinction with the optical depth map at 250 μm, τ250, derived from Herschel
data (pixel size 12″). A τ250/τJ
map at 180″ resolution is
shown in Fig. A.3 (right panel). The reference area
used in the background subtraction of both optical depth maps is marked in the figure. The
map shows that at low resolution, the densest areas A, B, and C have a considerably higher
emissivity than the surrounding diffuse areas.
 |
Fig. 5 (Top) Relation between τ250 and τJ. The line length shows the τJ range used in the total least squares fitting. The slopes (k) of the fits are indicated on the plot with the same colour as the fitted line. The ranges used are 0–2.5 (black), 0.25–2.5 (red), 0.5–2.5 (blue), 0.5–1 (green), and 1–2.5 (cyan). (Middle) Relation between τ250 (with resolution 40″) and τJ of individual stars, using a limit ΔτJ < 0.95. (Bottom) Relation between τ250 and τJ. The data of each region are fitted separately. The slope k and the mean error bars are indicated on the plots. The colour scales in the top and bottom panels correspond to the logarithmic density of points. |
The relation between τ250 and τJ is shown in Fig. 5 (top panel). We made linear fits of τ250 vs. τJ using the total least-squares method, which takes into account the error estimates in both variables. For τJ the error estimates were calculated by the NICER method. The uncertainties of τ250 were estimated as part of the MCMC calculations. Taking into account the spatial averaging to 180″ resolution, the average formal uncertainty becomes ~0.15 × 10-4. The estimates are probably very optimistic because imperfections in map making result in surface brightness errors that are correlated at scales larger than the beam size. To take this partly into account, we increased the τ250 error estimates ad hoc by 50%. The larger error estimates also have a systematic effect of lowering the slope values by ~10%, the effect rising to ~20% for regions A and C. This shows that in these regions the results are quite sensitive also to the accuracy of error estimates. Line-of-sight (LOS) temperature variations might also cause bias and lead to an underestimation of the optical depth and of the dust opacity (e.g., Shetty et al. 2009; Malinen et al. 2011). The samples were taken in 1/3 beam steps.
In Fig. 5 (top panel), we show the slopes that were obtained in different τJ ranges. If the data are cut simply at fixed values of τJ, one can bias the slope estimates. Therefore, we first scaled the τ250 values so that the median uncertainties were equal along both axes, which causes the confidence regions of typical measurement points to become spherical. The data selection was then made using two delimiting lines that are perpendicular to the line fitted to all data points; these lines cross the fitted line at the selected τJ positions. Because the error distributions at this point are roughly spherical (on average, although not for every measurement point) and because the cut is made perpendicular to the expected direction of the fitted line, the selection procedure probably does not bias the slope of the linear fit to the selected data significantly. The fitted slope values and their error estimates are marked in the figure. The slopes differ between values (11.2−13.0) × 10-4 when using different τJ ranges.
Obtained values describing the regions A1, A2, B, C, and the whole cloud L1642.
The correlation between τ250 (with resolution 40″) and τJ of individual stars is shown in Fig. 5 (middle panel). The scatter of the points below τ250 = 0.005 shows the large errors in the τJ values. The τJ values of individual stars are very noisy, but they correspond to extremely narrow beams through the cloud. The spatial averaging of τJ values might bias the τJ map because fewer stars are visible through regions with higher column densities. If this were a strong effect, the τ250/τJ slope would be fainter when using τJ of individual stars than when using a τJ map at 180″ resolution. Figure 5 (middle panel) shows no sign of such a bias. In the following analysis, we use τ250/τJ data at 180″ resolution.
To compare with the earlier results of Lehtinen et al. (2007, Fig. 3), we derived total least-squares fits of τ250 vs. τJ also separately for different regions. These are shown in Fig. 5 (bottom panel), with the fitted slope values and their error estimates. The slope values show much more variation, (3.5−10.9) × 10-4, than when simply cutting the data based on the τJ range.
The τ250/τJ slopes can be converted into opacity or dust emission cross-section per H nucleon, σe(250) using the relation σe(250) = 1.33 × 10-22τ250/τJ cm2/H (see the derivation in Malinen et al. 2013). This relation assumes the ratio of hydrogen column density and NIR colour excess N(HI + H2)/E(B − V) = 5.8 × 1021 cm-2/mag appropriate for diffuse medium (Bohlin et al. 1978). E(B − V) is converted to τJ using the Cardelli et al. (1989) extinction curve. The relation is derived assuming RV = 3.1. With the assumption RV = 4.0, the derived value would be ~40% higher. As the density within the cloud varies, the choice of RV is not obvious, and the value might be even higher in the densest B region.
For τ250/τJ = 10.0 × 10-4, the previous relation (assuming RV = 3.1) leads to a value σe(250) = 1.33 × 10-25 cm2/H. The obtained σe(250) values for regions A1, A2, B, and C are 0.56, 0.47, 1.45, and 1.04 × 10-25 cm2/H.
Lehtinen et al. (2007, Table 1) showed their results as σe(200). These can be converted into σe(250) with the equation σe(250) = σe(200) × (200.0/250.0)β. We used value β = 1.8. Using this conversion, the σe(250) values of Lehtinen et al. (2007) are 0.27−0.47 × 10-25, 0.67−0.80 × 10-25, 0.40 × 10-25, and 0.80−0.87 × 10-25 cm2/H for A (A1+A2), B, C, and L1642 interclump dust, respectively. We derived up to 2–3 times higher values than Lehtinen et al. (2007). This difference is mainly due to the intensity in the ISO maps, which is lower by a factor of 2–3, see also Sect. 4.4. In Lehtinen et al. (2007), the change in σe is ~2–3 between different regions. In our data, the relative change between regions is of the same order.
4.4. Properties of large regions
We calculated the average properties of regions A1, A2, B, and C using the elliptical regions shown in Figs. 2 (top left) and A.2. Background was subtracted from the intensity maps before deriving the optical depth and T maps, using the area marked in the figures. All the maps used are at 40″ resolution. We used the method described in Sect. 3.2 to calculate the masses of the regions.
Lehtinen et al. (2004) used the value σ200 = 1.5 × 10-25 cm2/H for the absorption cross-section, corresponding to σ250 ~ 1.0 × 10-25 cm2/H. In Sect. 4.3 we derived the σ250 values for different regions. As there are significant uncertainties in the derivation of the σ250 values, and the values change between regions, we calculated masses using two different constant values, σ250 = 1.5 × 10-25 cm2/H and 1.0 × 10-25 cm2/H, in addition to the individual values for each region.
The derived properties are shown in Table 1, using σ250 = 1.5 × 10-25 cm2/H. For comparison, we derived the masses also from the data of Lehtinen et al. (2004) (ISO data convolved to IRAS resolution 4.5′) using the same method and regions. These are also shown in Table 1. Using Herschel data, we obtain ~3–6% lower temperatures and ~2–3 times higher masses than from the earlier ISO+IRAS data. The difference in the masses is mainly caused by differences in the intensity maps, because the Herschel map (after converting 250 μm to 200 μm) gives intensities higher by 2–3 times than the ISO map.
With σ250 = 1.0 × 10-25 cm2/H, the masses are 4.4, 4.5, 28.2, and 11.5 M⊙ (using Herschel data) or 1.5, 1.7, 10.9, and 5.4 M⊙ (using ISO+IRAS data) for the regions A1, A2, B, and C, respectively. Lehtinen et al. (2004) derived masses 0.8, 0.8, 13, and 2.9 M⊙ and mean colour temperatures 16.1, 16.3, 14.2, and 16.1 K for the regions A1, A2, B, and C, respectively. The differences in the estimates based on ISO+IRAS data are mainly due to different methods of background subtraction, different β (they had 2.0, we used 1.8) and opacity. They calculated the background separately for each clump in the vicinity of the clump, which led to lower mass estimates. We used a common background area for the whole map.
Using the individual opacities for each region, shown in Fig. 5 (bottom panel), we derive masses 7.8, 9.6, 19.6, and 11.1 M⊙ for A1, A2, B, and C, respectively. Lehtinen et al. (2004) derived virial masses for the regions using the method described in Sect. 3.2. They used values for gas temperature Tgas (10 K) and ΔV derived from the CO observations of Russeil et al. (2003). They derived virial masses 10, 12, 15, and 33 M⊙, for regions A1, A2, B, and C, respectively, concluding that only region B is close to the virial mass and therefore potentially gravitationally bound. Our data give further evidence that region B is more massive than the approximated virial mass and confirm that it is gravitationally bound. The other regions A1, A2, and C seem to be below their virial masses, even though we derive higher masses than previous studies did.
4.5. Properties of compact sources within the main cloud of L1642
We study the character and properties of the compact sources B-1, B-2, B-3, and B-4 found within the cloud L1642 and marked in Fig. 2. B-1 and B-2 are well-known binary stars, also known as L1642-1 and L1642-2 (Sandell et al. 1987), respectively. B-3 has been classified as a dwarf at a distance of ~30 pc (Cruz et al. 2003), but we study the possibility, that it is instead a YSO inside the L1642 cloud. B-4 is a cold clump seen as a temperature minimum and optical depth maximum. The secondary component of B-2, L1642-2B, appears as a separate object in the 2MASS catalogue. There is no counterpart for this in the WISE catalogue. The secondary of B-1, L1642-1B, does not have a separate entry in the catalogues. B-4 does not appear in any of the point source catalogues.
We calculated the Herschel 160–500 μm fluxes for the sources using Getsources (Men’shchikov et al. 2012), as described in Sect. 3.1. All the maps were convolved to ~ 40″ resolution. The most prominent clumps obtained with Getsources are marked in Fig. 2 (bottom left panel). We calculated the flux of the sources in Herschel 100 μm and ASTE 1.1 mm maps (and also in other Herschel bands for comparison) using aperture photometry with a circular aperture, with 40″ aperture radius and 55″ and 85″ annulus radii, as described in Sect. 3.1. These data are all convolved to ~40″ resolution. The aperture size was chosen to be small, to avoid flux coming from the surroundings of the central source. However, also part of the flux coming from the source can therefore be lost. We use these fluxes only to make a comparison between the Herschel and ASTE data levels, and do not use these in the other fits. The circular apertures are shown in Fig. 2 (bottom right panel). The sources are also marked on the column density N(H2) map of Russeil et al. (2003) in Fig. 6.
SEDs of these sources are shown in Fig. 7, using values from 2MASS, WISE, IRAS and AKARI catalogs. We also show Herschel data obtained with Getsources and by aperture photometry, and ASTE data obtained by aperture photometry, both convolved to ~40″ resolution. For B-1 and B-2 ,we get rather similar values for the fluxes using these two methods. However, for B-3 and B-4, the aperture photometry gives notably smaller values, indicating the differences in the size and shape of the used area to measure flux. We tested the consistency of the ASTE fluxes by fitting a MBB model, with β = 1.8, to the 160–500 μm Herschel fluxes obtained with aperture photometry, and compared the fit to the ASTE flux. Figure 7 shows that the ASTE fluxes are within ~40% of the values predicted by the MBB fit, and notably closer to the line in the case of source B-1.
We used the YSO classification system based on the slope of the NIR–MIR SEDs or spectral index α, as described in Sect. 3.3. Using the slope between wavelengths 3.4 and 22 μm (WISE channels 1 and 4), we derived α values −0.89, 0.23, and −2.34, leading to Class II, Flat spectrum, and Class III, for B-1, B-2, and B-3, respectively. Using the slope between 3.4 and 12 μm would lead to the same classes. This implies that the sources are in the order of the age, starting from the youngest, B-2, on the west side, and going towards the oldest, B-3, to east.
 |
Fig. 6 H2 column density map derived from 13CO, reproduced from the data of Russeil et al. (2003). Contours start from 1.0 × 1020 cm-2 and grow by 5.0 × 1020 cm-2 up till 6.1 × 1021 cm-2 . The positions of the four targets are marked. The starless core, target B-4, remains invisible in the data. |
 |
Fig. 7 SEDs of the sources B-1 (red circle), B-2 (blue square), B-3 (black triangle), and B-4 (green diamond). 2MASS (J, H, Ks), WISE (3.4, 4.6, 12.0, 22.2 μm), Herschel (Getsources: 160, 250, 350, 500 μm) marked with solid line, AKARI (9 and 18 μm and 65, 90, 140, and 160 μm) marked with dotted line and IRAS (12, 25, 60, and 100 μm) marked with dashed line. Also fluxes obtained with aperture photometry (with 40″ aperture radius and 55″ and 85″ annulus radii) are shown for Herschel 100, 160, 250, 350, 500 μm data (dashed line) and AzTEC/ASTE 1.1 mm data. Herschel and ASTE data are based on maps at 40″ resolution, the others are catalogue values. Solid gray lines show a MBB fit, with β = 1.8, to the 160–500 μm Herschel aperture photometry fluxes. |
We fitted the SEDs of the sources B-1, B-2, and B-3 with the online SED fitting tool of Robitaille et al. (2007)9. We used 2MASS, WISE, AKARI (only for B-1 and B-2), and Herschel (Getsources) fluxes in the SEDs. The photometric data and aperture sizes used in the fitting are shown in Table 2. Using the different catalogue values at their original resolution should be reliable in the NIR–MIR range, and the SED fitter takes into account the different aperture sizes. We used a free AV range, 0.01–20 mag, in the fitting. For all the sources, we fitted the data both with a strict distance limit, with ~10% error of the assumed 140 pc distance, leading to the range 126–154 pc, and a free distance range 20–800 pc. When the distance was free, the ten best fits to both B-1 and B-2 showed much variation of the distance estimates and often very low values (~40–70 pc), therefore we do not show these results. The ten best fits of B-3 with a free distance range gave distance estimates 145–209 pc. B-2 is well fitted, except for the NIR part. Both B-1 and B-3 show a double peak in the SED, with a well-fitting NIR–MIR part and a FIR peak above 100 μm. Because the Robitaille models cannot handle FIR peaks above 100 μm (see Sect. 3.3), the FIR points are poorly fitted. However, one might fit the SEDs with a model with a colder component in the envelope. We also fitted the B-3 data using only NIR–MIR points. In that case, the ten best fits with a free distance range gave very well limited distance estimates of 174–182 pc. The best obtained fits are shown in Fig. 8. The parameter limits for stellar mass M, stellar temperature T, and luminosity L from the ten best-fitting models are shown in Table 3. The highest obtained value for stellar T and L are very high compared with the best-fit values, and probably reflect the uncertainties in the fitting. B-1 and B-2 are known binary stars, and the NIR fluxes only contain the primary star, whereas the longer-wavelength fluxes with larger apertures contain both objects.
Photometric data (flux F and flux error ΔF) from source catalogues and using Getsources for Herschel data, and aperture sizes for the Robitaille fits of sources B-1, B-2, and B-3.
 |
Fig. 8 SEDs of the sources B-1, B-2, and B-3, fitted with the YSO models of Robitaille et al. (2007). Filled circles show the
fitted 2MASS (J, H, Ks), WISE (3.4, 4.6, 12.0, 22.2
μm),
AKARI (only for B-1 and B-2) and Herschel (Getsources: 160, 250,
350, 500 μm) fluxes shown in Table 2. Error bars are shown, but they are often
smaller than the data points. The solid black line shows the best-fitting model, and
the possible grey lines show the models that fit the criteria
|
Parameter limits from the ten best Robitaille fits for sources B-1, B-2, and B-3.
We calculated a virial mass for source B-4 using Eqs. (2) and (3) and a value of Tgas = 10 K. Lehtinen et al. (2004) stated, based on the data of Russeil et al. (2003), that in region B, the mean value for the observed line width from the C18O line is ΔV(C18O) = 0.52 km s-1. Using this value, we derived the value 1.93 M⊙ for the virial mass of B-4, with a 40″ radius. We calculated the mass of B-4 as in the previous section, and obtained values of 0.83 M⊙ with σ250 = 1.0 × 10-25 cm2/H and 0.57 M⊙ with σ250 = 1.5 × 10-25 cm2/H. We also tested the effect of changing the central coordinates from the coordinates given by Getsources to the T minimum and to the τ250 maximum, which are both close by, but not exactly at the same point. These changes did not significantly affect the derived masses. The derived masses of B-4 are clearly below the derived virial mass, indicating that the object is not gravitationally bound.
In the appendix, we study the other potential YSOs located within L1642 or nearby.
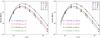 |
Fig. 9 MBB fits to the SEDs of regions A1, A2, B, and C. The values are based on background-subtracted Herschel 100–500 μm and Planck 350–1382 μm intensity maps. 100 μm data are not included in the fitting. The fitted values of colour temperature T and spectral index β are marked in the figure. (Left) Fixed β = 1.8. (Right) β as a free parameter. |
 |
Fig. 10 MBB fits to the SEDs of sources B-1, B-2, B-3 and B-4, with 80″ aperture. The values are based on background-subtracted Herschel 100–500 μm and ASTE 1.1 mm maps. 100 μm and ASTE data are not included in the fitting. The fitted values of colour temperature T and spectral index β are marked in the figure. The fits were performed both with a fixed value of β = 1.8 (left) and with free β (right). |
4.6. Dust emissivity spectral index
We studied the dust emission in the submillimetre spectral range, especially the dust emissivity spectral index β, both in the large-scale regions as defined in Sect. 4.4 and in the compact sources studied in Sect. 4.5.
We calculated the mean intensity of the regions marked in Fig. 2 (top left panel) using background-subtracted Herschel 100–500 μm and Planck 350–1382 μm intensity maps. All data were convolved to the lowest resolution of the Planck maps, 5.01′. We fitted the SED with an MBB model, Eq. (5), shown in Fig. 9. Here, we used a direct least-squares fit with χ2 estimates. The flux at 100 μm can contain emission from small, transiently heated dust particles, and it is sensitive to warmer dust. The assumed effect of the small grains was corrected for in the data processing, but the data might still be biased. Therefore, the 100 μm data were not included in the fitting, but the value is shown in the figure for reference. The MBB model fits the data well, both with a fixed value of β = 1.8 and with a free β. When β is kept as a free parameter, the obtained β values are ~1.8 for both A1 and A2, ~1.9 for C and ~2.0 for the densest area, B. Temperature estimates for region B are 13.6 K with free β and 14.9 K with a fixed value β = 1.8.
Similar to the larger regions, we calculated the mean intensity in circular 80″ point-source apertures marked in Fig. 2 (bottom-right panel) using background-subtracted Herschel 100–500 μm and ASTE 1.1 mm intensity maps. All data were convolved to 40″. We fitted the obtained SED with the MBB function shown in Fig. 10. Extended structures are filtered in the AzTEC/ASTE data reduction, and therefore we considered the ASTE intensity only as a lower limit for 1.1 mm. Herschel 100 μm and ASTE data were not included in the fitting, but the values are shown in the figure for reference. Here, the MBB model also fits the Herschel data remarkably well, except for the 100 μm data in B-2, both with fixed and free β. The ASTE data are, however, significantly lower than those of the MBB model. The filtering of the extended emission appears to also have affected the scale of the compact sources, 80″. The free β fit gives value β = 1.75 for sources B-1, B-3 and B-4. For B-2, the obtained value is much lower, β = 1.25. Here, the 100 μm values are mostly close to the line, except for B-1, in which the value is higher than the line.
The colour temperature T and emissivity spectral index β were also estimated with MCMC calculations, using the same intensity values and uncertainties as in the least-squares fit and using flat priors for the T and β parameters. Compared with the χ2 estimates, the main advantage of the MCMC method is that it maps the full probability distribution of the parameters (Veneziani et al. 2010; Juvela et al. 2013). This provides a much better picture of the actual uncertainties than the mere 1σ error estimates.
The obtained probability distributions are shown in Figs. 11 and 12 as a function of T and β. These are based on several million MCMC steps that were registered after an initial burn-in phase, in which the initial samples were discarded. For regions A1, A2, B, and C, the results are shown separately for the Herschel data in the wavelength intervals 100–500 μm and 160–500 μm and for the combination of the Herschel and Planck data 160–1380 μm. Figure 12 shows the results for the compact sources B-1, B-2, B-3, and B-4 in the wavelength ranges 100–500 μm and 160–500 μm.
The figures show the strong anticorrelation between the T and β errors. The results obtained with different wavelength combinations are consistent. Including 100 μm in these fits does not produce noticeable bias, but can instead be used to constrain the values. Figure 11 also demonstrates the importance of the Planck data in constraining β and, consequently, also the temperature estimates. The temperatures in the larger regions differ slightly, and especially region B is much colder than the others. The β values are similar in all regions, and the data do not show a clear correlation or anticorrelation between T and β. Source B-2 is warmer than the other sources and has a smaller β. Using the wavelength range 100–500 μm, the sources show a clear T–β anticorrelation. However, with the range 160–500 μm, the difference between the sources is only marginal.
5. Discussion
We have used a wide range of data from NIR to mm to study the high-latitude cloud L1642 in more detail, especially the large-scale structure, the general dust properties, and the star formation within the cloud. We discuss these main points in the following subsections.
 |
Fig. 11 (T,β) probability distributions calculated for areas A1, A2, B, and C with the MCMC method. Each column corresponds to one of the areas and the rows to different wavelength ranges used in the MBB fits. The contours correspond to the 90% confidence regions. The maximum-likelihood solutions obtained by combining Herschel and Planck observations are shown as black circles. The 90% contours for all cases in the same column or row are shown in the last column or row, respectively. The contour colours are red, green, blue, and black, from left to right or from top to bottom. |
 |
Fig. 12 The (T, β) probability distributions calculated for sources B-1, B-2, B-3, and B-4 using the MCMC method. The contours correspond to 90% confidence regions. The black circles indicate the maximum-likelihood solutions that were obtained with Herschel data in the range 160–500 μm. The contours of all cases are shown in the rightmost column and bottom row, similarly as in Fig. 11. |
5.1. Structure and evolution of L1642
L1642 forms the head of a large cometary structure whose tail extends across 5° towards the Galactic plane. Figure 1 shows that the clouds L1642, IC 2118, and LBN 991 can be connected with straight lines following the pillars leading from the clouds to the centre at approximately α2000 = 4h56m, δ2000 = −12°10′. The Planck 817 GHz map shows the pillar to LBN 991 more clearly, but the AKARI 140 μm map reveals the warmer material and shows that the different clouds appear to be connected. L1642 is estimated to be closer than IC 2118, which is situated at ~210 pc (Kun et al. 2001), and it is possible that the pillar of L1642 is directed towards the viewer. These pillars can be seen already in the earlier IRAS data. These clouds have typically been studied separately, and especially LBN 991 has not been much investigated (see Alcalá et al. 2008). Studying the possible connection between these clouds might help to constrain the distance estimates and birth mechanisms of the clouds.
High-resolution Herschel data reveal new details in the structure of L1642, including small-scale elongated structures around the main cloud and striations in the diffuse dust, especially in the northern part. Whether star formation in L1642 is triggered, and if so, by which source, is still an open question. In Rivera-Ingraham et al. (in prep.) we study the properties and relevance of this type of structures, the local environment, and possible triggering effects at high-latitude fields, including L1642.
We investigated the velocity structure of L1642 and its surroundings using HI data from the LAB survey (Kalberla et al. 2005). The HI spectrum towards L1642 shows three radial velocity components, broad features at ~−13 km s-1 and ~+14 km s-1, and a narrow feature around 0 km s-1 that corresponds to the radial velocity of the CO lines. A detailed study of the kinematics of the larger environment of L1642 is not possible because we lack molecular line observations. The filament that connects L1642 to the clouds closer to the Galactic plane does not appear to have a clear continuous velocity gradient in HI data, although the analysis is complicated by the presence of several velocity components. However, even the radial velocity of IC 2118 is only +4 km s-1 and thus the structures that appear to be connected in the projection may be continuous structures also in real space, in spite of the wide range of estimated distances, 140 pc for L1642 and 210 pc for IC 2118 at the other end of the filamentary structures. IC 2118 is likely to be inside the Orion-Eridanus bubble and is directly affected by the massive star towards equatorial east (Kun et al. 2001). In contrast, L1642 appears to be beyond the influence of the Orion region and is mainly affected by a flow from the west or is itself travelling west through the ambient medium.
The velocity field within a few degrees of L1642 was analysed by Taylor et al. (1982) using HI observations made with the Parkes radio telescope (~15′ beam width). The narrow HI line component associated with the cloud has a peak in declination one degree south of the molecular cloud. The HI velocity is lowest on the eastern side of the molecular cloud but increases in all directions. Especially towards SE both the radial velocity and the line width increase. This is interpreted as a shearing flow that is caused by material flowing around the cloud. The velocity gradient 5 km s-1 per degree corresponds to a radial velocity gradient of ~2 km s-1 pc-1. The overall kinematics is explained by a cometary structure where the low-velocity gradients on the western side may be a result of a geometry, where on that side of the cloud the gas is flowing mainly in the plane of the sky. Taylor et al. (1982) predicted that the shearing flow will enhance the density towards the head of the cometary cloud, increase turbulence in the outer parts, and can lead to the formation of hydrodynamical instabilities.
This can be contrasted with the new data on the dense molecular part of L1642. There is some compression from the west that is reflected in the general structure of the cloud (consistent with the interpretation of the HI data; see Fig. B.1), in the striation associated especially with region A, and in the bow-shock-like structure on the western border of region B, close to source B-2 (see Fig. 2). However, in the dense regions of the molecular cloud the effect of a possible slow shock remains weak. With a steeper column density gradient on its southern edge and with striation extending towards NE, region A has the appearance of being compressed by a force from SW. In region B, the morphology suggests a force acting more directly from the west. Region B is also associated with a filamentary structure, a possible tail, that extends directly eastward, up to the edge of the Herschel map, and then curves north. The CO data indicate only a moderate level of turbulence, and there are no signs of instabilities (e.g., classical Kelvin-Helmholtz) within the area mapped by Herschel. The difference in morphology suggests that regions A and B may be physically separate structures, aligned only in projection. One can also conjecture that the striation may be linked to a magnetic field geometry that is moderating the effects of the shearing flow in the low-density envelope. The striations look very similar to the findings of Goldsmith et al. (2008) and Palmeirim et al. (2013) in Taurus. These authors concluded that striations in the diffuse regions tend to follow the magnetic field direction. This question will be clarified when Planck measurements of dust polarisation become available and the main direction of the magnetic field can be measured.
5.2. Dust properties
We derived values of the dust emission cross-section per H nucleon of σe(250) = 0.56, 0.47, 1.45, and 1.04 × 10-25 cm2/H for regions A1, A2, B, and C with the assumption that RV = 3.1 (diffuse cloud). In high-latitude, diffuse areas, the dust opacity is estimated to be σe(250 μm) ~ 1.0 × 10-25 cm2/H (see, e.g., Boulanger et al. 1996; Planck Collaboration XXV. 2011). In dense areas, the opacity can be 2–4 times higher (see, e.g., Juvela et al. 2011; Planck Collaboration XXV. 2011; Martin et al. 2012; Roy et al. 2013). Malinen et al. (2013) derived σe(250 μm) values ~1.7–2.4 × 10-25 cm2/H for a filament in Taurus at a similar distance of ~140 pc. The newly derived opacities for the different regions of L1642 correspond to the opacities found in diffuse areas, except for region B, where the opacity is higher, at the lower limit of denser areas.
The WISE 3.4 μm map in Fig. 3 shows some extended emission from the densest part of L1642. This could be caused by scattered MIR light (the core-shine phenomenon) that is associated with grain growth (Steinacker et al. 2010). However, this can also be explained by the PSF tails of the bright point sources and by the additional scattering (and potential dust emission) associated with the embedded sources.
MBB fits to the SED of Herschel and Planck data give β values 1.8–2.0 for the different regions of L1642. MCMC fits of the SEDs show a strong anticorrelation between β and T errors and the importance of Planck data in constraining β and T estimates. For all the regions, the recovered values of the emissivity spectral index are consistent with those found in molecular clouds at large scales (Planck Collaboration XXV. 2011), but are somewhat lower than the values reported by Paradis et al. (2010) and Planck Collaboration XXIII. (2011) for regions of similarly low temperature. We find no clear correlation or anticorrelation between T and β in the different regions. However, the compact sources show a T-β anticorrelation when all Herschel wavelengths 100–500 μm are used. This corresponds to the results of Malinen et al. (2011), showing that internal heating sources produce an anticorrelation between T and β.
The fits to the SED of compact sources B-1, B-3, and B-4, using only Herschel data, give slightly lower values, β ~ 1.75. For source B-2, we obtain a much lower value, β = 1.25. Radiative transfer modelling (in Appendix D) suggests that low β values towards the sources can be caused by the LOS temperature variations, similarly to the results of, e.g., Malinen et al. (2011). On the other hand, away from the sources, the optical depth estimates are probably not affected by the LOS temperature variations by more than ~10%.
5.3. Star formation in L1642
The view of L1642 has changed from a “small, somewhat insignificant cloud” (Taylor et al. 1982) to an interesting object in several aspects, as shown by the various studies already mentioned. So far, B-1 and B-2 are the only known stars associated to L1642. We have questioned this view and studied the possibility of other signs of star formation within L1642.
5.3.1. Source B-3: YSO in L1642 or a foreground dwarf
Cruz et al. (2003) classified 2MASS J04351455-1414468 to be a young (~10 Myr) object. They estimated the distance to be probably within 30 pc, meaning that the object would be clearly in front of the L1642 star-forming region. Their Fig. 9 shows no clear sign of lithium (Li I) absorption at 6708 Å, which would be a sign of a probable brown dwarf (although see the caution of Kirkpatrick et al. (2006) of the usability of this test). Faherty et al. (2009) marked the object as a red photometric outlier, based on the red NIR colour. They also gave a very low tangential velocity for the object, vtan = 1 ± 1 km s-1. They classified the object as a low surface gravity dwarf with spectral class M8.
Chauvin et al. (2012) used deep NIR Ks observations to search for companions around this object. No companions were detected. They used the distance estimate of Cruz et al. (2003), but stated that the object is close to the cloud L1642 and that the red colour is probably due to extinction caused by surrounding material and not to the chemical properties of the object itself. Based on the spectra, they assigned a tentative spectral type M 6δ ± 1, where δ means a very young (Taurus-like) object, following the spectral classification system of Kirkpatrick (2005) and Kirkpatrick et al. (2006). Also, Antonova et al. (2013) treated B-3 as a low-mass dwarf in front of the L1642 cloud. Caballero (2007) used the brown dwarf list of Cruz et al. (2003) to study the proper motions of low-mass objects. The low proper motion of B-3 obtained is consistent with the one expected for the L1642 cloud.
The Herschel data show that the point source B-3 (using 2MASS or WISE coordinates) precisely coincides with an intensity maximum in the centre of a local clump projected on L1642 on the sky, visible at all wavelengths 100–500 μm. The MBB fits to this source are very similar to the other sources known to reside in the cloud. Moreover, the models of Robitaille et al. (2007) support the longer distance, and give a relatively good, even though not perfect, fit to the data. Furthermore, CO data show no other kinematic components that would suggest the presence of a second cloud on this line-of-sight.
We studied the possibility of classifying B-3 as a dwarf using WISE and 2MASS data and the method shown in Kirkpatrick et al. (2011). WISE (Vega) magnitudes from PSF fitting are 9.711, 9.268, 9.136, and 8.514. The derived colours are W1 − W2 = 0.443, W2 − W3 = 0.132, and W3 − W4 = 0.623. 2MASS J, H, and Ks magnitudes are 11.879, 10.622, and 9.951, respectively. These values correspond to basically stellar colours with some IR excess, meaning that they are consistent with a YSO. The colours are, however, not inconsistent with a mid-L dwarf. We tested this object with the brown dwarf search criteria of Kirkpatrick et al. (2011). B-3 would fail the first criteria for the coldest brown dwarfs with type T5 or bigger (W1 − W2 > 1.5). It would pass the colour criteria for bright, nearby L and T dwarfs (W1 − W2 > 0.4). However, as the object is clearly seen in 2MASS (and also faintly in DSS optical data), it would be dropped from the brown dwarf list. We also compared the colours of B-3 to the colour–colour and colour vs. spectral type plots of Kirkpatrick et al. (2011, Figs. 1–10). Based on these comparisons, we conclude that B-3 colours are marginally too red in W1-W2 and clearly too red in J − H to match Faherty et al. (2009) spectroscopic classification of M8. However, the colours of B-3 fit the colours of a mid-L type dwarf quite well, except in W2 − W3, where it is slightly too blue.
Koenig et al. (2012) have adapted the photometric YSO classification method designed for Spitzer (e.g., Gutermuth et al. 2008, 2009) to WISE bands. Their method is designed to classify only YSOs with excess emission at NIR–MIR wavelengths, that is, Class I–II objects. This system cannot classify diskless Class III objects. However, Koenig et al. (2012) also show the previously found diskless YSOs in their colour–colour plots. We compared the WISE colours of B-3 with these plots (their Figs. A.7–11) and conclude that B-3 fits the group of diskless YSOs well.
The perfect positional coincidence of the NIR/MIR and FIR source positions strongly suggests that the point source in B-3 is located within the cloud L1642. The fact that the object can be clearly seen in the 100 μm map, showing mainly dust emission, similarly to only YSOs inside the cloud and a single galaxy, suggests that the object is surrounded by dust. The 160 μm map already shows a clearly extended object, with an internal, warming source. These data support the view that B-3 is a YSO situated within the cloud L1642.
5.3.2. Chain of star formation
The point sources B-1 and B-2 are well known binary T Tauri stars. We discussed the characteristics of B-3 in more detail in Sect. 5.3.1. Our results show that B-3 is more likely to be a YSO within the cloud L1642 than a dwarf in front of the cloud, contrary to previous studies. The SEDs clearly show the difference between the evolutionary stages of these objects. Using the NIR–MIR slope, we derived YSO Classes II, a flat spectrum, and III for B-1, B-2, and B-3, respectively. This indicates that the objects are situated in the age order from the youngest B-1 in west to the oldest B-3 in the east.
B-4 can be seen as a clear temperature minimum and optical depth maximum in the maps, south of the chain of the other sources. However, we derived a mass for this object using an 80″ aperture, and concluded that the obtained mass is smaller than the virial mass. It appears that B-4 is a cold clump, with some substructure visible, for example, in the PACS data. Based on the estimated virial masses, the clump is not gravitationally bound, at least within the used aperture. However, the potential pre-stellar nature of this object needs to be investigated in more detail.
The mass estimates from the Robitaille models for sources B-1, B-2, and B-3 (1.71, 3.07, and 0.13 M⊙, respectively, see Table 3) divided by the cloud mass of 72.1 M⊙ (see Table 1) gives a star formation efficiency of ~7% for L1642.
6. Conclusions
We have studied the properties of L1642, one of the two high galactic latitude (|b| > 30°) clouds with active star-formation. The high latitude (−36.4°), indicating no foreground contamination, the small distance (~140 pc), the modest column density (AV < 12m), and the spatially distinct sequence of star-forming cores make L1642 one of the best targets for studying the initial stages of low-mass star formation. We presented in detail high-resolution far-infrared and submillimetre observations with Herschel and AKARI satellites and millimetre observations with AzTEC/ASTE telescope and combined them with archive data from NIR (2MASS) and MIR (WISE) to millimetre (Planck). We studied both larger regions (A1, A2, B, C) and compact sources (both previously known binary T Tauri stars and potential new objects) within the main cloud. Our main conclusions are the following:
-
The high-resolution Herschel observations, combined withother data, show an evolutionary sequence from a cold clump(B-4) to young stellar objects of different spectralclasses: B-1 (L1642-1,Class II), B-2 (L1642-2, Flatspectrum), and B-3 (Class III).
-
Based on Herschel FIR–submm data, the point source B-3 (2MASS J04351455-1414468) appears to be a YSO forming inside the L1642 cloud, instead of a foreground brown dwarf, contrary to previous classification.
-
Herschel data reveal striation in the diffuse dust around the cloud L1642, especially in the northern part. Region A shows striation extending towards the NE and has a correspondingly steeper column density gradient on its southern side. Region B has the appearance of being compressed from the west and has a filamentary tail extending eastward. The differences suggest that these may be spatially distinct structures, aligned only in projection.
-
Both Herschel FIR–submm and AzTEC/ASTE mm data show an elongated structure north-east of the binary star B-2 (L1642-2), which was not visible in earlier observations. The structure is aligned with the general striation pattern, but it has a significantly higher column density.
-
We derived values of the dust emission cross-section per H nucleon of σe(250) = 0.56, 0.47, 1.45, and 1.04 × 10-25 cm2/H for the different regions.
-
Modified black-body fits to the SED of Herschel and Planck data give emissivity spectral index β values 1.8–2.0 for the different regions of L1642.
-
Markov chain Monte Carlo fits of the SEDs show a strong anticorrelation between β and T errors and the importance of Planck data in constraining β and T estimates.
-
The compact sources show a T-β anticorrelation, but on larger scale the data show no clear correlation or anticorrelation.
-
Radiative transfer modelling suggests that low beta values towards the sources might be caused to a large extent by the LOS temperature variations. On the other hand, the optical depth estimates are expected to be quite accurate (to within ~10%) away from the sources.
Online material
Appendix A: Additional maps of L1642
MCMC fitting with free β (see Sect. 4.2) produces the β and T maps shown in Fig. A.1. MCMC fitting with a constant value β = 1.8, using background-subtracted intensity maps, produces the τ250 and T maps in Fig. A.2. These maps were used in the analysis of the different regions marked in the figures. An extinction map and a τ250/τJ map (described in Sect. 4.3) are shown in Fig. A.3.
 |
Fig. A.1 Maps of β (left) and T (right) derived by MCMC fitting with free β, using Herschel 160–500 μm maps. Background is not subtracted. Contours of the τ250 map are drawn on both maps at levels 0.0035, 0.0029, and 0.0019. |
 |
Fig. A.2 Maps derived by MCMC fitting with a constant β = 1.8, using Herschel 250–500 μm maps at 40″ resolution. The maps are based on background-subtracted intensity maps, using the area marked BG as background. Areas of the clumps A1, A2, B, and C, and the main part of cloud (marked L1642) used in the analysis. The maps are τ250 (left) and T (right). |
 |
Fig. A.3 (Left) Optical depth τJ map derived from 2MASS data. The resolution of the map is 180″. (Right) τ250/τJ map with resolution 180″. The black contours are drawn on τ250 levels 0.0016, 0.0008, and 0.0004. The green contours are drawn on τJ levels 2, 1, and 0.5. Areas where τJ < 0.0001 or τ250 < 0.00004 are masked. The area marked with a yellow rectangle was used as a background when subtracting the background from the two optical depth maps. |
Appendix B: Other possible YSOs
We used a subset of the WISE catalogue to search for other YSO candidates. This subset contained sources with A photometric quality (S/N > 10) in at least three of the four bands and at least B quality (S/N > 3) in one of the bands. We searched previously classified sources in the SIMBAD and VizieR catalogues with a radius of 5″. We used the quadratic discriminant analysis (QDA, McLachlan 1992) to separate the sources with known object types (galaxies, evolved stars, single stars, ISM-related objects, and YSOs) and to determine the boundaries in the multidimensional parameter space. These boundaries were then applied to the sources with unknown object types. The sources that were similar to the known YSOs were selected as YSO candidates. The multidimensional parameter space included the following colours: J−H, H−K, K−W1, W1−W2, W2−W3, W3−W4, and also the W1 brightness. J, H, and K data are from 2MASS catalogue.
This method for YSO selection has been previously used in several studies (Tóth et al. 2013; Marton et al. 2013; Cambrésy et al. 2013) and will be discussed in more detail in a forthcoming paper (Marton et al., in prep.). Tóth et al. (2013) found that the reliability of the classification is higher than 90% compared with known YSOs. Marton et al. (in prep.) have found a quite good reliability using the current WISE catalogue. In their study, only 0.33% of all the other known sources (including galaxies, stars, etc.), 0.77% of galaxies and 73.5% of the known YSOs were classified as YSO candidates. Based on the classification in the SDSS catalogue, 6.79% of the sources classified as YSO candidates are galaxies. However, biases in the WISE catalogue might affect these results.
We located six other YSO candidates in addition to B-1, B-2, and B-3 within a 1° radius of the centre of L1642, based on WISE data. These objects are shown in Fig. B.1. Two of the
objects are within or at the edge of the densest part of the cloud on the sky, in region C. These two are plotted in our Herschel maps and can be seen in the 100 μm map as faint objects. The other four are projected on a more diffuse area, but still within the larger structure of L1642 cloud. We fitted these objects with the SED models of Robitaille et al. (2007) using optical, NIR (2MASS), and MIR (WISE) data. The most probable distances provided by the SED model fits for the objects are mostly between 350 pc and 800 pc, clearly farther away than the estimated distance of L1642. There is no evidence that any of these sources are inside the L1642 cloud, but confirming this would require more study.
 |
Fig. B.1 Point sources B-1, B-2, and B-3 (diamonds) and other YSO candidates (crosses) marked on the Planck 857 GHz intensity map. |
 |
Fig. C.1 Relation between the Planck Legacy Archive CO maps and the SEST CO data of Russeil et al. (2003) using Planck Type 3 J = 1–0 data (left, 6′ resolution) and using Type 2 data (15′ resolution) for J = 1–0 (middle) and J = 2–1 (right). The blue crosses show the relation between Planck CO and the SEST 12CO line area, the red crosses the relation between Planck CO and the sum of SEST 12CO and 13CO line areas. |
Appendix C: Comparing SEST and Planck CO maps
We used the SEST CO data of Russeil et al. (2003) to correct the Planck 217 and 353 GHz maps for the contribution of CO line emission. We compared the SEST data with the maps of integrated CO line area that have been derived from Planck data and are available in the Planck Legacy Archive10. The Planck archive includes three separate estimates of the CO emission. Type 1 products are based on the bandpass measurements of individual Planck channels, include separate estimates of the J = 1–0, J = 2–1, and J = 3–2 line intensities, but have relatively low SN. Type 2 maps include estimates of the CO J = 1–0 and J = 2–1 emission that were obtained by a joint analysis of multiple Planck frequency channels and have a higher S/N. Type 3 maps additionally use prior information of the CO line ratios resulting in a combined CO emission map with a good S/N.
The comparison between SEST and the Type 2 and Type 3 data is shown in Fig. C.1. The correlation is very good between Type III J = 1–0 line areas and the sum of SEST 12CO(1–0) and 13CO(1–0) data (left panel). Type 2 (1–0) maps give slightly higher line areas than Type 3 maps, and Type 2 (2–1) maps give lower values than SEST. However, because the calibration errors of the SEST data can be ~10% , the correlations are still quite good. Note that the SEST values are antenna temperatures corrected using the Moon efficiency.
Appendix D: Radiative transfer model of L1642
We carried out radiative transfer modelling of L1642 to qualitatively estimate the effects that LOS temperature variations have on estimates of the optical depth and the emissivity spectral index. The initial model is based on the column density map derived from observations, the Mathis et al. (1983) model of the interstellar radiation field (ISRF), and the dust properties corresponding to observations of diffuse interstellar medium (Draine 2003). However, to be consistent with the previous analysis, the dust model was adjusted so that the spectral index was exactly β = 1.8 for all wavelengths λ > 100 μm.
The density distribution was defined using a 1323 Cartesian grid with a cell size corresponding to 6″. Thus the model covers an area of 13.2′× 13.2′ that includes the sources B-1, B-2, B-3, and B-4. The initial column density distribution was obtained from the analysis of Herschel observations. The LOS density distribution was assumed to be Gaussian with a FWHM corresponding to the value of ~6′ visible in the plane of the sky. The external radiation field was assumed to be isotropic. Corresponding to the sources B-1, B-2, and B-3, we added three radiation sources inside the cloud. In the plane of the sky these are the positions of the local peaks measured in the 250 μm surface brightness maps, and along the LOS they are in the middle of the cloud. We treated B-4 as a clump heated from the outside, and did not add an internal source there. A non-LTE radiative transfer program was used to estimate the dust temperature distributions and to calculate synthetic surface brightness maps at the Herschel wavelengths (Juvela & Padoan 2003).
The initial model was optimised by comparing the observed and modelled surface brightness maps. We used observations that were background subtracted using a reference area around the position RA = 4h34m52s, Dec = −14°25′15″ (J2000.0). For each LOS, the densities of the model cloud were scaled so that one reproduces the observed 250 μm surface brightness data at the observed resolution. The ISRF was scaled to reproduce the observed surface brightness ratio 160 μm/500 μm that was estimated from the central area of 4.4′ × 4.4′. The embedded sources B-1, B-2, and B-3 were assumed to be black-bodies at a temperature of 8000 K. Their luminosities were adjusted so that the surface brightness ratios between 160 μm and 250 μm bands had the observed values when measured towards the sources, using the resolution of the observed maps (12.0″ and 18.3″ for 160 μm and 250 μm, respectively). The calculations were iterated until the 250 μm surface brightness, the average colour of the central regions, and the colours towards the three sources all matched to a few per cent. This is only a crude model and, in particular, the effect of the sources depends sensitively on their position along the LOS, their temperature, and the density structures in their immediate vicinity.
 |
Fig. D.1 Analysis of model surface brightness and optical depth. Panel a) shows the 250 μm surface brightness and the apertures used for flux measurements of sources B-1, B-2, B-3, and B-4. Panel b) shows the ratio of optical depths that are estimated from synthetic surface brightness data and the actual 250 μm optical depth of the model cloud. Panels c) and d) show the residuals between the actual Herschel observations and the model predictions at 160 μm and 350 μm, respectively. Panel e) shows the SEDs derived for the sources using the model-predicted intensities and quotes the results of the MBB fits. |
Figure D.1 shows the final 250 μm surface brightness map (within ~1% of the observed values) as well as the residuals of the 160 μm and 350 μm surface brightness data. The residuals are low at the very positions of the three sources. However, the heating effect of source B-2 is too extended. Because of the constraint on the average colour, the model is correspondingly too cold around the sources B-1 and B-3, leaving positive residuals in the 160 μm map. In the immediate vicinity of B-2 the high residuals are caused by the fact that the source is associated with some extended emission and the peak position changes with wavelength. At 160 μm the relative error is up to ~20% around B-2 and rises to ~30% around the sources B-1 and B-3. Compared with 160 μm, the relative errors are of similar magnitude at 350 μm and 500 μm, but are, of course, in the opposite direction. Because of these inaccuracies, we used the model mainly for qualitative analysis.
Figure D.1e shows the spectra calculated for the four sources using 80″ apertures. Because the effect of point sources appears to be more extended than in Herschel data, we used flux densities in the apertures without further subtracting the surrounding annulus. Thus, the values do not exactly correspond to those derived from Herschel data. The most noticeable fact is that the estimated spectral indices are lower than the opacity spectral index β = 1.8 of the dust grains. The strongest source B-2 has a value of β = 1.63 that is 0.17 units lower than the intrinsic beta value. In the observations, the value was even lower, β = 1.25 (see the right panel of Fig. 10). Nevertheless, the model suggests
that most if not all of the difference to diffuse regions might be caused by temperature variations within the beam.
Figure D.1b compares the optical depth map obtained directly from the model density cube with the optical depth τ(250 μm) derived from the synthetic surface brightness maps at a resolution of 40″. The optical depth was estimated as described in Sect. 4.2, using a fixed value of β = 1.8 when performing least-squares fits of MBB spectra. Because the result depends on the assumed dust opacity, we normalised the results so that the mean optical depth ratio is one in the area where the Herschel column density is between 1 × 1021 cm-2 and 2 × 1021 cm-2. The result shows that at the moderate column densities of L1642, the temperature variations (colour temperature exceeding the mass-averaged temperature) generally leads to no more than an underestimation of ~10% in optical depth. However, the errors increase to ~30% towards the sources B-1 and B-3 and the largest error towards B-2 is larger by a factor of ~3.
The reduced data will become available through the ESA web site http://herschel.esac.esa.int/UserReducedData.shtml. Further information is available on the homepage of the Cold Cores project https://wiki.helsinki.fi/display/PlanckHerschel/The+Cold+Cores
Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada.
Acknowledgments
We thank the anonymous referee for detailed comments which improved the paper. We thank Kimmo Lehtinen and Delphine Russeil for providing us data from their earlier studies. J.Ma and M.J. acknowledge the support of the Academy of Finland Grants No. 250741 and 127015. The development of Planck has been supported by: ESA; CNES and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MICINN and JA (Spain); Tekes, AoF and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); and PRACE (EU). This research is based on observations with AKARI, a JAXA project with the participation of ESA. We also acknowledge the ASTE staff both for operating ASTE and for helping us with the data reduction. Observations with ASTE were (in part) carried out remotely from Japan by using NTT’s GEMnet2 and its partner R&E (Research and Education) networks, which are based on the AccessNova collaboration of the University of Chile, NTT Laboratories, and the National Astronomical Observatory of Japan. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration. This research has made use of the NASA/IPAC Infrared Science Archive, which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.
References
- Alcalá, J. M., Covino, E., & Leccia, S. 2008, in Handbook of Star Forming Regions, Vol. I, ed. B. Reipurth, 801 [Google Scholar]
- André, P., Ward-Thompson, D., & Barsony, M. 1993, ApJ, 406, 122 [NASA ADS] [CrossRef] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Antonova, A., Hallinan, G., Doyle, J. G., et al. 2013, A&A, 549, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Boulanger, F., Abergel, A., Bernard, J.-P., et al. 1996, A&A, 312, 256 [NASA ADS] [Google Scholar]
- Brown, A. G. A., Hartmann, D., & Burton, W. B. 1995, A&A, 300, 903 [NASA ADS] [Google Scholar]
- Caballero, J. A. 2007, ApJ, 667, 520 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L., Marton, G., Feher, O., Tóth, L. V., & Schneider, N. 2013, A&A, 557, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Chauvin, G., Faherty, J., Boccaletti, A., et al. 2012, A&A, 548, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Correia, S., Zinnecker, H., Ratzka, T., & Sterzik, M. F. 2006, A&A, 459, 909 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cruz, K. L., Reid, I. N., Liebert, J., Kirkpatrick, J. D., & Lowrance, P. J. 2003, AJ, 126, 2421 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Ezawa, H., Kawabe, R., Kohno, K., & Yamamoto, S. 2004, in Proc. SPIE, 5489, ed. J. M. Oschmann, Jr., 763 [Google Scholar]
- Faherty, J. K., Burgasser, A. J., Cruz, K. L., et al. 2009, AJ, 137, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Galeazzi, M., Gupta, A., Covey, K., & Ursino, E. 2007, ApJ, 658, 1081 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, T. P., Wilking, B. A., André, P., Young, E. T., & Lada, C. J. 1994, ApJ, 434, 614 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gupta, A., Galeazzi, M., Koutroumpa, D., Smith, R., & Lallement, R. 2009, ApJ, 707, 644 [NASA ADS] [CrossRef] [Google Scholar]
- Gutermuth, R. A., Myers, P. C., Megeath, S. T., et al. 2008, ApJ, 674, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Gutermuth, R. A., Megeath, S. T., Myers, P. C., et al. 2009, ApJS, 184, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Hearty, T., Fernández, M., Alcalá, J. M., Covino, E., & Neuhäuser, R. 2000, A&A, 357, 681 [NASA ADS] [Google Scholar]
- Juvela, M., & Padoan, P. 2003, A&A, 397, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Montier, L. A., et al. 2010, A&A, 518, L93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pelkonen, V.-M., et al. 2011, A&A, 527, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pagani, L., et al. 2012, A&A, 541, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juvela, M., Montillaud, J., Ysard, N., & Lunttila, T. 2013, A&A, 556, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Kirkpatrick, J. D. 2005, ARA&A, 43, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Barman, T. S., Burgasser, A. J., et al. 2006, ApJ, 639, 1120 [NASA ADS] [CrossRef] [Google Scholar]
- Kirkpatrick, J. D., Cushing, M. C., Gelino, C. R., et al. 2011, ApJS, 197, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Koenig, X. P., Leisawitz, D. T., Benford, D. J., et al. 2012, ApJ, 744, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Kohno, K., Yamamoto, S., Kawabe, R., et al. 2004, in Proc. The Dense Interstellar Medium in Galaxies, eds. S. Pfalzner, C. Kramer, C. Staubmeier, & A. Heithausen (Berlin, Heidelberg: Springer), 91, 349 [Google Scholar]
- Kun, M., Aoyama, H., Yoshikawa, N., et al. 2001, PASJ, 53, 1063 [NASA ADS] [Google Scholar]
- Kun, M., Prusti, T., Nikolić, S., Johansson, L. E. B., & Walton, N. A. 2004, A&A, 418, 89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kuntz, K. D., Snowden, S. L., & Verter, F. 1997, ApJ, 484, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J. 1987, in Star Forming Regions, eds. M. Peimbert, & J. Jugaku, IAU Symp., 115, 1 [Google Scholar]
- Laureijs, R. J., Mattila, K., & Schnur, G. 1987, A&A, 184, 269 [NASA ADS] [Google Scholar]
- Lehtinen, K., Russeil, D., Juvela, M., Mattila, K., & Lemke, D. 2004, A&A, 423, 975 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lehtinen, K., Juvela, M., Mattila, K., Lemke, D., & Russeil, D. 2007, A&A, 466, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liljestrom, T. 1991, A&A, 244, 483 [NASA ADS] [Google Scholar]
- Liljestrom, T., Mattila, K., & Friberg, P. 1989, A&A, 210, 337 [NASA ADS] [Google Scholar]
- Liu, G., Calzetti, D., Yun, M. S., et al. 2010, AJ, 139, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L. 2001, ApJ, 560, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Lynds, B. T. 1962, ApJS, 7, 1 [NASA ADS] [CrossRef] [Google Scholar]
- MacLaren, I., Richardson, K. M., & Wolfendale, A. W. 1988, ApJ, 333, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., Blitz, L., & Mundy, L. 1985, ApJ, 295, 402 [NASA ADS] [CrossRef] [Google Scholar]
- Malinen, J., Juvela, M., Collins, D. C., Lunttila, T., & Padoan, P. 2011, A&A, 530, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malinen, J., Juvela, M., Pelkonen, V.-M., & Rawlings, M. G. 2013, A&A, 558, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, P. G., Roy, A., Bontemps, S., et al. 2012, ApJ, 751, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Marton, G., Verebélyi, E., Kiss, C., & Smidla, J. 2013, Astron. Nachr., 334, 924 [NASA ADS] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Mattila, K., Juvela, M., & Lehtinen, K. 2007, ApJ, 654, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Mattila, K., Lehtinen, K., Väisänen, P., von Appen-Schnur, G., & Leinert, C. 2012, in IAU Symp. 284, eds. R. J. Tuffs, & C. C. Popescu, 429 [Google Scholar]
- McGehee, P. M. 2008, in Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, 813 [Google Scholar]
- McLachlan, G. J. 1992, Discriminant analysis and statistical pattern recognition (New York: Wiley) [Google Scholar]
- Men’shchikov, A., André, P., Didelon, P., et al. 2012, A&A, 542, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., & Lagache, G. 2005, ApJS, 157, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., Zavagno, A., Bontemps, S., et al. 2010, A&A, 518, L77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Murakami, H., Baba, H., Barthel, P., et al. 2007, PASJ, 59, 369 [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paradis, D., Veneziani, M., Noriega-Crespo, A., et al. 2010, A&A, 520, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIII. 2011, A&A, 536, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2014, A&A, submitted [arXiv:1303.5062] [Google Scholar]
- Planck Collaboration IX. 2014, A&A, in press, DOI. 10.1051/0004-6361/20132153 [Google Scholar]
- Planck Collaboration XIII. 2014, A&A, submitted [arXiv:1303.5073] [Google Scholar]
- Planck HFI Core Team VI. 2011, A&A, 536, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reach, W. T., Wall, W. F., & Odegard, N. 1998, ApJ, 507, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Reipurth, B., & Heathcote, S. 1990, A&A, 229, 527 [NASA ADS] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., Wood, K., & Denzmore, P. 2006, ApJS, 167, 256 [NASA ADS] [CrossRef] [Google Scholar]
- Robitaille, T. P., Whitney, B. A., Indebetouw, R., & Wood, K. 2007, ApJS, 169, 328 [NASA ADS] [CrossRef] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Roy, A., Martin, P. G., Polychroni, D., et al. 2013, ApJ, 763, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Juvela, M., Lehtinen, K., Mattila, K., & Paatero, P. 2003, A&A, 409, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandell, G., Reipurth, B., & Gahm, G. 1987, A&A, 181, 283 [NASA ADS] [Google Scholar]
- Scott, K. S., Austermann, J. E., Perera, T. A., et al. 2008, MNRAS, 385, 2225 [NASA ADS] [CrossRef] [Google Scholar]
- Sfeir, D. M., Lallement, R., Crifo, F., & Welsh, B. Y. 1999, A&A, 346, 785 [NASA ADS] [Google Scholar]
- Shetty, R., Kauffmann, J., Schnee, S., Goodman, A. A., & Ercolano, B. 2009, ApJ, 696, 2234 [NASA ADS] [CrossRef] [Google Scholar]
- Shimajiri, Y., Kawabe, R., Takakuwa, S., et al. 2011, PASJ, 63, 105 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Steinacker, J., Pagani, L., Bacmann, A., & Guieu, S. 2010, A&A, 511, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tauber, J. A., Mandolesi, N., Puget, J.-L., et al. 2010, A&A, 520, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Taylor, M. I., Taylor, K. N. R., & Vaile, R. A. 1982, PASA, 4, 440 [NASA ADS] [Google Scholar]
- Tóth, L. V., Marton, G., Zahorecz, S., et al. 2013 [arXiv:1309.6258] [Google Scholar]
- Veneziani, M., Ade, P. A. R., Bock, J. J., et al. 2010, ApJ, 713, 959 [NASA ADS] [CrossRef] [Google Scholar]
- Verter, F., & Rickard, L. J. 1998, AJ, 115, 745 [NASA ADS] [CrossRef] [Google Scholar]
- Verter, F., Magnani, L., Dwek, E., & Rickard, L. J. 2000, ApJ, 536, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Welsh, B. Y., & Shelton, R. L. 2009, Ap&SS, 323, 1 [Google Scholar]
- Wilson, G. W., Austermann, J. E., Perera, T. A., et al. 2008, MNRAS, 386, 807 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamura, I., Makiuti, S., Ikeda, N., et al. 2010, VizieR Online Data Catalog: II/298 [Google Scholar]
All Tables
Photometric data (flux F and flux error ΔF) from source catalogues and using Getsources for Herschel data, and aperture sizes for the Robitaille fits of sources B-1, B-2, and B-3.
Parameter limits from the ten best Robitaille fits for sources B-1, B-2, and B-3.
All Figures
 |
Fig. 1 Surrounding region of L1642. Planck 857 GHz intensity map (left) and close-ups of Planck 857 GHz (middle) and AKARI 140 μm (right) intensity maps. L1642 and other nearby clouds are marked in the maps. The 1 pc scale is marked assuming a distance of 140 pc. |
| In the text | |
 |
Fig. 2 Herschel intensity maps showing the areas used in the analysis. The maps show the total intensity after zero-point correction. (Top left) 350 μm (26.8″ resolution) showing the larger regions (A1, A2, B and C) and the background area (BG) used in the analysis. (Top right) 250 μm (18.3″ resolution) map showing the striation in L1642. (Bottom left) 160 μm (18.3″ resolution) showing the most prominent clumps identified by Getsources. FWHM ellipses of the clumps are drawn in the figure. (Bottom right) 100 μm (18.3″ resolution) showing the circular apertures (with 80″ diameter) used in the aperture photometry of the point sources marked in the figure. |
| In the text | |
 |
Fig. 3 WISE 3.4 μm and AzTEC/ASTE 1.1 mm intensity maps (top row). Herschel 100 and 160 μm intensity maps (without zero-point correction) at the original resolution (7″ and 12″, respectively, bottom row). The sources B-1, B-2, B-3, and G (see text) are marked on the Herschel and WISE maps, using their 2MASS coordinates. The marker circles show the beam FWHM. |
| In the text | |
 |
Fig. 4 Maps derived by MCMC fitting with a constant β = 1.8, using Herschel 250–500 μm maps at 40″ resolution. Background is not subtracted from the maps. (Left) Optical depth τ250 with contours of column density NH2 derived from 13CO observations of Russeil et al. (2003) drawn at levels 4, 3, 2, and 1 × 1021 cm-2. (Right) Colour temperature T with contours of the τ250 map drawn at levels 0.0035, 0.0029, and 0.0017. Sources B-1, B-2, B-3, and B-4 are marked with crosses (Getsources coordinates) and circles (WISE coordinates). |
| In the text | |
 |
Fig. 5 (Top) Relation between τ250 and τJ. The line length shows the τJ range used in the total least squares fitting. The slopes (k) of the fits are indicated on the plot with the same colour as the fitted line. The ranges used are 0–2.5 (black), 0.25–2.5 (red), 0.5–2.5 (blue), 0.5–1 (green), and 1–2.5 (cyan). (Middle) Relation between τ250 (with resolution 40″) and τJ of individual stars, using a limit ΔτJ < 0.95. (Bottom) Relation between τ250 and τJ. The data of each region are fitted separately. The slope k and the mean error bars are indicated on the plots. The colour scales in the top and bottom panels correspond to the logarithmic density of points. |
| In the text | |
 |
Fig. 6 H2 column density map derived from 13CO, reproduced from the data of Russeil et al. (2003). Contours start from 1.0 × 1020 cm-2 and grow by 5.0 × 1020 cm-2 up till 6.1 × 1021 cm-2 . The positions of the four targets are marked. The starless core, target B-4, remains invisible in the data. |
| In the text | |
 |
Fig. 7 SEDs of the sources B-1 (red circle), B-2 (blue square), B-3 (black triangle), and B-4 (green diamond). 2MASS (J, H, Ks), WISE (3.4, 4.6, 12.0, 22.2 μm), Herschel (Getsources: 160, 250, 350, 500 μm) marked with solid line, AKARI (9 and 18 μm and 65, 90, 140, and 160 μm) marked with dotted line and IRAS (12, 25, 60, and 100 μm) marked with dashed line. Also fluxes obtained with aperture photometry (with 40″ aperture radius and 55″ and 85″ annulus radii) are shown for Herschel 100, 160, 250, 350, 500 μm data (dashed line) and AzTEC/ASTE 1.1 mm data. Herschel and ASTE data are based on maps at 40″ resolution, the others are catalogue values. Solid gray lines show a MBB fit, with β = 1.8, to the 160–500 μm Herschel aperture photometry fluxes. |
| In the text | |
 |
Fig. 8 SEDs of the sources B-1, B-2, and B-3, fitted with the YSO models of Robitaille et al. (2007). Filled circles show the
fitted 2MASS (J, H, Ks), WISE (3.4, 4.6, 12.0, 22.2
μm),
AKARI (only for B-1 and B-2) and Herschel (Getsources: 160, 250,
350, 500 μm) fluxes shown in Table 2. Error bars are shown, but they are often
smaller than the data points. The solid black line shows the best-fitting model, and
the possible grey lines show the models that fit the criteria
|
| In the text | |
 |
Fig. 9 MBB fits to the SEDs of regions A1, A2, B, and C. The values are based on background-subtracted Herschel 100–500 μm and Planck 350–1382 μm intensity maps. 100 μm data are not included in the fitting. The fitted values of colour temperature T and spectral index β are marked in the figure. (Left) Fixed β = 1.8. (Right) β as a free parameter. |
| In the text | |
 |
Fig. 10 MBB fits to the SEDs of sources B-1, B-2, B-3 and B-4, with 80″ aperture. The values are based on background-subtracted Herschel 100–500 μm and ASTE 1.1 mm maps. 100 μm and ASTE data are not included in the fitting. The fitted values of colour temperature T and spectral index β are marked in the figure. The fits were performed both with a fixed value of β = 1.8 (left) and with free β (right). |
| In the text | |
 |
Fig. 11 (T,β) probability distributions calculated for areas A1, A2, B, and C with the MCMC method. Each column corresponds to one of the areas and the rows to different wavelength ranges used in the MBB fits. The contours correspond to the 90% confidence regions. The maximum-likelihood solutions obtained by combining Herschel and Planck observations are shown as black circles. The 90% contours for all cases in the same column or row are shown in the last column or row, respectively. The contour colours are red, green, blue, and black, from left to right or from top to bottom. |
| In the text | |
 |
Fig. 12 The (T, β) probability distributions calculated for sources B-1, B-2, B-3, and B-4 using the MCMC method. The contours correspond to 90% confidence regions. The black circles indicate the maximum-likelihood solutions that were obtained with Herschel data in the range 160–500 μm. The contours of all cases are shown in the rightmost column and bottom row, similarly as in Fig. 11. |
| In the text | |
 |
Fig. A.1 Maps of β (left) and T (right) derived by MCMC fitting with free β, using Herschel 160–500 μm maps. Background is not subtracted. Contours of the τ250 map are drawn on both maps at levels 0.0035, 0.0029, and 0.0019. |
| In the text | |
 |
Fig. A.2 Maps derived by MCMC fitting with a constant β = 1.8, using Herschel 250–500 μm maps at 40″ resolution. The maps are based on background-subtracted intensity maps, using the area marked BG as background. Areas of the clumps A1, A2, B, and C, and the main part of cloud (marked L1642) used in the analysis. The maps are τ250 (left) and T (right). |
| In the text | |
 |
Fig. A.3 (Left) Optical depth τJ map derived from 2MASS data. The resolution of the map is 180″. (Right) τ250/τJ map with resolution 180″. The black contours are drawn on τ250 levels 0.0016, 0.0008, and 0.0004. The green contours are drawn on τJ levels 2, 1, and 0.5. Areas where τJ < 0.0001 or τ250 < 0.00004 are masked. The area marked with a yellow rectangle was used as a background when subtracting the background from the two optical depth maps. |
| In the text | |
 |
Fig. B.1 Point sources B-1, B-2, and B-3 (diamonds) and other YSO candidates (crosses) marked on the Planck 857 GHz intensity map. |
| In the text | |
 |
Fig. C.1 Relation between the Planck Legacy Archive CO maps and the SEST CO data of Russeil et al. (2003) using Planck Type 3 J = 1–0 data (left, 6′ resolution) and using Type 2 data (15′ resolution) for J = 1–0 (middle) and J = 2–1 (right). The blue crosses show the relation between Planck CO and the SEST 12CO line area, the red crosses the relation between Planck CO and the sum of SEST 12CO and 13CO line areas. |
| In the text | |
 |
Fig. D.1 Analysis of model surface brightness and optical depth. Panel a) shows the 250 μm surface brightness and the apertures used for flux measurements of sources B-1, B-2, B-3, and B-4. Panel b) shows the ratio of optical depths that are estimated from synthetic surface brightness data and the actual 250 μm optical depth of the model cloud. Panels c) and d) show the residuals between the actual Herschel observations and the model predictions at 160 μm and 350 μm, respectively. Panel e) shows the SEDs derived for the sources using the model-predicted intensities and quotes the results of the MBB fits. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.