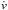| Issue |
A&A
Volume 554, June 2013
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 22 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201221008 | |
| Published online | 04 June 2013 | |
Spectrophotometric time series of SN 2011fe from the Nearby Supernova Factory⋆,⋆⋆
1
Université de Lyon 1, France, CNRS/IN2P3, Institut de Physique Nucléaire de
Lyon,
69622
Villeurbanne Cedex,
France
e-mail:
rui.pereira@in2p3.fr
2
Computational Cosmology Center, Computational Research Division,
Lawrence Berkeley National Laboratory, 1 Cyclotron Road MS 50B-4206, Berkeley, CA, 94611,
USA
3
Physics Division, Lawrence Berkeley National
Laboratory, 1 Cyclotron
Road, Berkeley,
CA
94720,
USA
4
Laboratoire de Physique Nucléaire et des Hautes Énergies,
Université Pierre et Marie Curie Paris 6, Université Paris Diderot Paris 7,
CNRS-IN2P3, 4 place
Jussieu, 75252
Paris Cedex 05,
France
5
Department of Physics, Yale University,
New Haven, CT
06520-8121,
USA
6
Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741
Garching bei München,
Germany
7
Physikalisches Institut, Universität Bonn,
Nußallee 12, 53115
Bonn,
Germany
8
Tsinghua Center for Astrophysics, Tsinghua
University, Beijing
100084, PR
China
9
Department of Physics, University of California
Berkeley, 366 LeConte Hall MC
7300, Berkeley,
CA, 94720-7300, USA
10
National Astronomical Observatories, Chinese Academy of
Sciences, Beijing
100012, PR
China
11
Centre de Physique des Particules de Marseille, Aix-Marseille
Université, CNRS/IN2P3, 163, avenue
de Luminy, Case 902, 13288
Marseille Cedex 09,
France
12
Space Sciences Laboratory, University of California
Berkeley, 7 Gauss
Way, Berkeley,
CA
94720,
USA
13
Centre de Recherche Astronomique de Lyon, Université Lyon
1, 9 avenue Charles
André, 69561
Saint Genis Laval Cedex,
France
Received: 26 December 2012
Accepted: 21 January 2013
We present 32 epochs of optical (3300−9700 Å) spectrophotometric observations of the nearby quintessential “normal” type Ia supernova (SN Ia) SN 2011fe in the galaxy M101, extending from −15 to +97 d with respect to B-band maximum, obtained by the Nearby Supernova Factory collaboration. SN 2011fe is the closest (μ = 29.04) and brightest (Bmax = 9.94 mag) SN Ia observed since the advent of modern large scale programs for the intensive periodic followup of supernovae. Both synthetic light curve measurements and spectral feature analysis attest to the normality of SN 2011fe. There is very little evidence for reddening in its host galaxy. The homogeneous calibration, intensive time sampling, and high signal-to-noise ratio of the data set make it unique. Thus it is ideal for studying the physics of SN Ia explosions in detail, and for furthering the use of SNe Ia as standardizable candles for cosmology. Several such applications are shown, from the creation of a bolometric light curve and measurement of the 56Ni mass, to the simulation ofdetection thresholds for unburned carbon, direct comparisons with other SNe Ia, and existing spectral templates.
Key words: supernovae: individual: SN 2011fe
A movie is available in electronic form at http://www.aanda.org
All the reduced spectra are available as FITS files in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/554/A27
© ESO, 2013
1. Introduction
Having exploded in the Pinwheel galaxy just 6.4 Mpc distant (z = 0.00080 ± 0.00001; μ = 29.04 ± 0.19, Paturel et al. 2003; Shappee & Stanek 2011), the Type Ia supernova SN 2011fe represents a rare opportunity for intensive study. Its discovery (Nugent et al. 2011a) by the Palomar Transient Factory (PTF; Law et al. 2009; Rau et al. 2009) less than 12 h after outburst (Nugent et al. 2011b) precipitated a number of diverse ground-based and space-based follow-up campaigns. Promptly initiated, high-cadence observations from a number of these have been published already. Brown et al. (2012) presented two months of nearly continuous Swift/UVOT follow-up in ultraviolet uvw2, uvm2, and uvw1 filters. BVRI photometry obtained over six months appeared in Richmond & Smith (2012), Vinkó et al. (2012) and Munari et al. (2013). Tammann & Reindl (2011) used extensive optical photometry of SN 2011fe obtained by the American Association of Variable Star Observers (AAVSO) and the tip of the red-giant branch distance to its host (M101) to measure H0. Covering the near-infrared, Matheson et al. (2012) presented high-cadence JHK photometry from the Wisconsin Indiana Yale NOAO (WIYN) telescope with WHIRC. The apparent brightness (V ~ 10 at peak) of SN 2011fe made multi-epoch spectropolarimetry much more accessible than usual (Smith et al. 2011). Finally, Parrent et al. (2012) have published 18 optical spectra from multiple telescopes, starting 1.2 days after explosion with a 1.8 day average cadence, along with a spectroscopic analysis including constraints on unburned carbon.
These data sets and others can address numerous long-standing questions about the nature of the Type Ia supernova (SN Ia) progenitor systems, environs, and explosion mechanisms. It has generally been thought that SNe Ia arise from the thermonuclear disruption of white dwarf stars accreting material from a companion donor star (for an overview, see e.g. Branch et al. 1995). Using images obtained just hours after outburst, pre-explosion X-ray limits, and the inferred 56Ni yield, Bloom et al. (2012) constrain the progenitor primary of SN 2011fe to be a white dwarf or neutron star − the first direct imaging evidence for a compact primary. Pre-explosion multi-wavelength archival images of the SN 2011fe stellar neighborhood require the mass-donating secondary to be another white dwarf, subgiant, or main-sequence star; red giants and helium stars are excluded with the companion restricted to M < 3.5 M⊙ (Li et al. 2011). Radio and x-ray observations probing the circumstellar environment of SN 2011fe imply a progenitor system with a mass loss rate as low as 6 × 10-10 M⊙ yr-1, severely constraining models where the secondary is not a white dwarf (Chomiuk et al. 2012; Horesh et al. 2012; Margutti et al. 2012). A case study in attempting to constrain explosion models from spectrophotometric observations slightly favors a white dwarf companion (Röpke et al. 2012) but further detailed modeling is needed to be more conclusive. The future emergence (or absence) of a surviving non-compact secondary, brightened as a consequence of its interaction with the SN ejecta, may be decisive in identifying the progenitor system (Shappee et al. 2013).
Such progress is exciting for several reasons; chief among these is the potential ability for such results to reduce uncertainty about the reliability of SNe Ia as tools for observational cosmology. The use of SNe Ia as standardizable candles (Phillips 1993) brought about the discovery of the accelerating expansion of the Universe just over a decade ago (Riess et al. 1998; Perlmutter et al. 1999). SNe Ia have since become a key means for constraining the unknown physics of cosmic acceleration, called “Dark Energy” (e.g., Guy et al. 2010; Howell 2011; Suzuki et al. 2012). A fundamental physics result is thus inextricably linked to the details of binary stellar evolution and stellar death, details which SN 2011fe may help sort out. It is thus fortuitous that SN 2011fe is also a normal SN Ia, and is highly representative of the typical SN Ia sought for placement on a Hubble diagram.
In this article, the Nearby Supernova Factory (SNfactory, Aldering et al. 2002) presents an atlas of 32 spectrophotometric observations of SN 2011fe extending from −15 to +97 d with respect to the time of maximum light. Some of these spectra have appeared in the Röpke et al. (2012) study and a quick-pipeline reduction of the first spectrum presented here has appeared in Parrent et al. (2012). This atlas should become a useful resource in studying SN Ia physics, in exploring systematics in the analysis of SN Ia spectra and spectral indicators, and in constructing spectral templates for SN cosmology applications.
The remainder of this article is organized as follows. In Sect. 2 we describe the observations and data reduction procedure, present the reduced spectrophotometric time series, synthesize photometry from it, and analyze the synthetic light curves using a standard SN Ia light curve fitter. Analyses of light curve residuals, possible extinction in the host galaxy, and the bolometric light curve appear in Sect. 3. This section also covers spectral feature measurements, sub-classification within existing schemes, parameterized spectral fitting, and examination of unburned carbon signatures. In Sect. 4, we place our data and analysis in context but primarily seek to demonstrate some useful features and applications of the data set. Conclusions appear in Sect. 5. The spectrophotometry of SN 2011fe is available for download in electronic form at the SNfactory project website1.
2. Spectrophotometric observations
2.1. Data acquisition
The data were obtained using the SuperNova Integral Field Spectrograph (SNIFS, Lantz et al. 2004). SNIFS is a fully integrated instrument optimized for automated observation of point sources on a structured background over the full ground-based optical window at moderate spectral resolution. It consists of a high-throughput wide-band pure-lenslet integral field spectrograph (IFS, “à la TIGER”; Bacon et al. 1995, 2001), a multi-filter photometric channel to image the stars in the vicinity of the IFS field-of-view (FOV) to monitor atmospheric transmission during spectroscopic exposures, and an acquisition/guiding channel. The IFS possesses a fully-filled 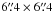 spectroscopic field of view subdivided into a grid of 15 × 15 spatial elements, a dual-channel spectrograph covering 3200−5200 Å and 5100−10 000 Å simultaneously with FWHM resolutions of 5.65 Å and 7.54 Å respectively, and an internal calibration unit (continuum and arc lamps). SNIFS is continuously mounted on the south bent Cassegrain port of the University of Hawaii 2.2 m telescope (UH 2.2 m) on Mauna Kea. The telescope and instrument, under script control, are supervised remotely.
spectroscopic field of view subdivided into a grid of 15 × 15 spatial elements, a dual-channel spectrograph covering 3200−5200 Å and 5100−10 000 Å simultaneously with FWHM resolutions of 5.65 Å and 7.54 Å respectively, and an internal calibration unit (continuum and arc lamps). SNIFS is continuously mounted on the south bent Cassegrain port of the University of Hawaii 2.2 m telescope (UH 2.2 m) on Mauna Kea. The telescope and instrument, under script control, are supervised remotely.
PTF discovered SN 2011fe (PTF11kly) in images obtained on 2011 Aug. 24.2 (UTC, used throughout). Nugent et al. (2011b) derive an explosion date of Aug. 23.7. SNfactory follow-up observations commenced on Aug. 26.3, an estimated 2.6 days after the explosion, and encompass 32 nights with two consecutive spectrophotometric exposures on most of the nights. The observing log is shown in Table 1. Daily observational cadence was maintained until 12.5 days after explosion. Lack of telescope access then forced a four day gap, but the daily cadence was re-established for days 16.5 to 21.5 after explosion. The cadence was relaxed to every 2−3 days until SN 2011fe was no longer observable from Hawaii, 41.5 days after explosion. Follow-up resumed a month and a half later, when observations were made over 7 nights spanning 20 days. The last spectra reported here were obtained Dec. 16.6, about 115 days after explosion. The position of SN 2011fe on the sky during the follow-up campaign forced observations at low altitude. The mean airmass was 2.1 and most of the early observations were taken during astronomical twilight.
Observing log for SNIFS spectra of SN 2011fe.
2.2. Data calibration
All spectra were reduced using SNfactory’s dedicated data reduction pipeline, similar to that presented in Sect. 4 of Bacon et al. (2001). A brief discussion of the software pipeline is presented in Aldering et al. (2006) and is updated in Sect. 2.1 of Scalzo et al. (2010). SN 2011fe is an unusual target for SNIFS and its associated data reduction software pipeline. The brightness of the SN itself and the small amount of time that the target was above the horizon imposed constraints on integration time. This affects our ability to use our standard multi-filter photometric channel for flux calibration on non-photometric nights. Also, some observations were obtained using interrupt time limited to ~1 h which did not allow for execution of more than one standard star observation needed for optimal calibration. Together, these factors limit the accuracy of our flux calibration of SN 2011fe, despite the brightness of the target. We will thus elaborate on the data reduction discussion given in Scalzo et al. (2010) and on modifications needed in order to flux calibrate the observations presented here.
Following standard low-level processing, CCD frames from both SNIFS channels are mapped into (x,y,λ) datacubes. Spectra are extracted from these using a chromatic spatial point-spread function (PSF) assuming spatially flat background, thus removing most of the host galaxy light as part of the sky. Host galaxy light contamination was evaluated using a background-subtracted stack of 5 × 60 s CFH12k R-band exposures of the host galaxy of SN 2011fe (M101), which was photometrically calibrated using SDSS r-band observations of the same region. Several SNIFS acquisition images were stacked and astrometrically aligned to the CFH12k stack in order to determine the location of SN 2011fe within the CFHT image. The mean r-band host galaxy surface brightness, inside the SNIFS FOV centered around the SN, equals 22.15 mag arcsec-2 and is almost flat, with structured residuals in the order of r ~ 23 mag inside 1′′ diameter apertures. The remaining background structural effects are thus considered negligible with respect to the brightness of SN 2011fe, so the detailed host galaxy subtraction method described by Bongard et al. (2011) was not necessary.
The extracted spectra are next merged and truncated to the final wavelength range of 3300−9700 Å. Flux calibration is performed using an instrumental flux solution derived from all spectrophotometric standard stars observed during the same night, and a mean atmospheric extinction computed from 6 years of SNIFS data (Buton et al. 2013). Observations of multiple standard stars were not always possible, particularly on interrupt nights. This limits a proper nightly extinction computation, so for the sake of consistency we use the mean extinction law on all nights. In this particular framework, the precision of the flux calibration depends on the number of standard stars observed per night, but not on their airmass distribution.
During non-photometric nights, any achromatic (grey) differential atmospheric attenuation between the observations of SN 2011fe and the standard stars is accounted for using simultaneous observations of field stars, through the SNIFS multi-filter photometric channel. Because SN 2011fe was very bright, relatively short exposure times were used to avoid saturation of the spectrograph, so the number of field stars visible at all epochs under very different attenuation conditions is small. After detection of the objects in the multi-filter field, the object catalogs were manually inspected to insure proper star selection and to prevent inaccurate inter-epoch astrometric and photometric alignments, which are performed using a modified version of the SuperNova Legacy Survey photometry code (poloka, Astier et al. 2006). The flux ratio between each exposure and a reference exposure (with the best seeing) equals the integral of the convolution kernel needed to degrade the reference image PSF into the “photometric frame” of the other image. This night-to-night variation in the brightness of the field stars, normalized by observations on photometric nights, provides the photometric scaling between fields and is used as a per-exposure grey flux correction to the mean atmospheric extinction, thus allowing absolute flux calibration. Seeing and night photometricity were assessed using quantitative analyses of SNIFS guider video frames acquired during our exposures, along with deglitched CFHT Skyprobe data (Cuillandre et al. 2002), attenuation estimates from the instrumental flux solution and photometric ratio computations (cf. Sect. 5 of Buton et al. 2013), and infrared satellite imagery.
The flux-calibrated spectra were corrected for telluric absorption using a nightly average spectrum determined using standard star observations. While consistent with the errors, this correction is nevertheless imperfect, and some (very small) glitches are visible in the spectra, especially for later phases at λ > 9000 Å. Milky Way dust extinction along the line of sight is corrected assuming E(B − V) = 0.0088 mag (Schlegel et al. 1998) and an extinction law with RV = 3.1 (Cardelli et al. 1989; O’Donnell 1994). No extinction correction for dust in the host galaxy is applied (see Sect. 3.2). Multiple spectra obtained the same night were merged using a variance-weighted mean.
2.3. Spectral time series and synthesized photometry
 |
Fig. 1 SNIFS spectrophotometric time series of SN 2011fe from −15 to 100 days relative to B-band maximum light. Breaks in the axis on the right indicate gaps and changes to the observing cadence. The first break corresponds to a four-day gap in daily cadence before maximum. The second marks the change from daily to alternating two/three day cadence. The final break is a 50 day hiatus imposed by lack of accessibility to the target from Mauna Kea. |
The final spectrophotometric time series of SN 2011fe is depicted in Fig. 1. The time series possesses a number of outstanding qualities, beyond the extremely high signal-to-noise ratio (S/N), despite the calibration challenges. Each spectrum spans the entire ground-based optical wavelength window. Excluding an inconvenient four day gap, daily sampling is achieved on the rising side of the light curve. Even though SN 2011fe observations were performed on non-standard conditions when compared to the typical SNIFS target, our observing strategy and calibration procedure do an excellent job of removing atmospheric artifacts. These features, combined with the cosmological utility of SN 2011fe as a “normal” SN Ia, should make these data a highly useful resource.
Synthetic light curves were generated by integrating the product of each spectrum with a set of non-overlapping top-hat filters with perfect photon transmission in the following wavelength ranges: 3300−4102 Å, 4102−5100 Å, 5200−6289 Å, 6289−7607 Å, and 7607−9200 Å, respectively UBVRISNf. This filter set avoids the split between both SNIFS spectrograph channels but is contiguous otherwise. For convenience these measurements are given in the Vega magnitude system by applying zero-points computed from the latest Hubble Space Telescope (HST) spectral observation of Vega (Bohlin 2007), available from the CALSPEC database2. The synthesized photometry is listed in Table 2, along with the integrated flux over the whole SNIFS optical window. For ease of comparison with other SNe, we also present synthetic light curves created using the latest photonic responses and zero-points given by Bessell & Murphy (2012, BM12), which are denoted as BVRIBM12 in Table 2. After interpolation of those filter responses into 10 Å steps using cubic splines, our integrator agrees at the 0.001 mag level with the colors measured by Bessell & Murphy (2012) using the aforementioned Vega spectrum and the zero-points derived by these authors.
The achromatic absolute flux calibration accuracy for each night as estimated by the calibration pipeline is shown in the σ column of Table 2. This value takes into account the errors of the spectral extraction using the chromatic spatial PSF, estimated from the mean scatter of flux calibrated standard star observations during all the photometric nights of the SNfactory data set, as well as the errors of the instrumental flux solution, the mean atmospheric extinction and the photometric ratio computations. The main contributions are the achromatic extraction uncertainty of 0.03 mag and 0.02 mag empirically found for bright and faint standard stars (Buton 2009), and a 0.03 mag additional uncertainty on non-photometric nights due to the photometric ratios usage (Pereira 2008). The chromatic spatial PSF flux extraction efficiency was evaluated on residual spectra, extracted from the PSF-subtracted datacubes by performing aperture photometry centered at the position of the SN and within a radius of 3σ seeing. The median missing flux for all exposures, on the 5 broad-band filters of the SNfactory filter set, was found to be below the half-percent level for all bands except for USNf, where it is ~0.7%. A ≲1% residual color effect is also discernible, when comparing BSNf with the other bands at high airmasses (>2.7), and is due to the fact that at such atypically large airmass, the atmospheric differential refraction (ADR) is so large that too much light is projected out of the SNIFS FOV. The contribution to the total error from both residual chromatic effects is much smaller than that from the absolute flux calibration.
2.4. SALT2 fit
 |
Fig. 2 SN 2011fe synthesized light curves using the UBVRISNf filter set. Filled and open symbols stand for photometric and non-photometric nights respectively. The results of a SALT2 simultaneous fit of UBVRSNf in the phase range −16 < t < +25 d are shown as solid lines, along with the corresponding residuals (SALT2 – SNIFS) on the lower panel. The shaded areas represent the SALT2 model error. The residuals for the first points of USNf and BSNf fall outside the panel, and the rms on the residuals for each band ignores the first 2 points. The break in the time axis corresponds to the ~50 day gap in follow-up during which SN 2011fe was not visible during the night from Hawaii. Note the change of scale of the extended time axis covering the late observations. |
The UBVRSNf light curves were simultaneously fitted using SALT2.2 (Guy et al. 2010, SALT2 henceforth), for estimation of the date of maximum light and assigning phases to the observations (relative to maximum light). The publicly available SALT2 spectral model3 seems to attain the (synthesized) B peak slightly before phase 0, which is a nuisance when we use it for a precise determination of the date of maximum light of our light curve. The shift needed to be applied to the fitted date of maximum, in order for it to match with phase 0 in B, was determined empirically to be ΔDayMaxB ≈ −0.7 d. The SALT2 code used here was modified to take this shift into account.
For a coherent treatment of the SNfactory filter set by SALT2, which uses a BD+174708 based magnitude system, the following zero-points are added to the BD17-snls3.dat magnitude system configuration file: 9.787, 9.791, 9.353, 9.011, and 8.768; which represent BD+174708’s synthetic magnitudes with relation to the Vega spectrum, in UBVRISNf respectively. Equivalently, if we intend to use SALT2 to fit light curves synthesized using the UBVRIBM12 photonic responses, the zero-points to be added to the configuration file are 9.709, 9.902, 9.469, 9.163, and 8.843. It should be stressed that every SALT2 fit result presented here is in the “standard” SALT2 UBVRI magnitude system, allowing direct comparison with the literature. This magnitude system is based on the Bessell (1990) filter transmissions, shifted to match Landolt (1992) observations. If we use instead the magnitude system based on the BM12 transmissions, the effect on the fitted parameters is very small, and completely within the quoted uncertainties.
The fit was performed using all available observations within four weeks of maximum light, including the very first one, which falls just outside the default SALT2 phase range of −15 < t < +45 d. Early observations are deweighted by the SALT2 error model. Simply omitting the first four observations (phases <-12 d) results in a shift in the date of maximum of −0.018 d, well inside the quoted error.
The light curves, fits and corresponding residuals can be seen in Fig. 2 (for a comparison with light curve results already published on the literature see Sect. 3.1). The fitted B maximum of 9.94 ± 0.01 mag was reached on 2011 September 10.5. The best-fit SALT2 parameters are x1 = −0.206 ± 0.071,c = −0.066 ± 0.021 (see Table 3 for a full summary of extracted photometric and spectroscopic parameters). Excluding USNf-band data from the fit, we obtain a negligible shift for the date and magnitude at maximum, and x1 = −0.149 ± 0.096, c = −0.061 ± 0.027. The light curve shape parameters are typical of a “normal” (if slightly blue) SN Ia: the median values for the x1 and c distributions of the nearby (z ≤ 0.1) SNe Ia used by Conley et al. (2011) are respectively −0.249 and −0.026 (J. Guy, priv. comm.). The V-band absolute magnitude (assuming μ = 29.04 ± 0.19, Shappee & Stanek 2011) at B peak, MmaxBV = −19.05 ± 0.19 mag matches perfectly the average found by Riess et al. (2009, −19.06 ± 0.05.
The rms of the residuals of the four fitted filters, ignoring the first two exposures due to the large discrepancies with the SALT2 model (cf. Sect. 4.2), are respectively 0.06, 0.03, 0.04 and 0.04 mag. The points that deviate the most from the fit are those for phases t < −10 d, showing the inadequacy of the SALT2 model for such early phases. Nevertheless, the exposure of night MJD 55 805 (t ~ −9 d, cf. Fig. 2) seems to present a systematic error in its flux calibration of ~0.1 mag, since it is brighter than we would expect based on observations on neighboring nights.
Synthetic light curves of SN 2011fe.
3. Analysis
3.1. Light curve comparison
The optical light curves of SN 2011fe published by different authors allow us to assess the reciprocal precision of multiple independent observations of this SN, and ultimately the benefits of using SNe Ia spectrophotometry for synthetic light curve creation. We use for these comparisons the first set of SNfactory observations, up to MJD 55 840. For every comparison light curve provided by other followup campaigns, the approach used to compute the residuals with respect to the reference SNIFS is the same: a light curve is synthesized from our spectrophotometric time series in the same passband as the comparison light curve, and then fit using Gaussian processes (as implemented by scikit-learn; Pedregosa et al. 2011) employing a squared euclidean correlation model weighted by measurement errors. The fitted model is then used to evaluate the synthesized SNIFS light curve at the same observation dates of the comparison light curves. The magnitude residuals are always reference (SNIFS) minus comparison. Positive or negative residuals thus mean that the comparison observation is respectively brighter or fainter than the reference.
We start with a brief comparison with the space-based Swift/UVOT observations by Brown et al. (2012, B12), before performing an extensive comparison with the three ground-based photometric followup compaigns who published observations of SN 2011fe: Richmond & Smith (2012, RS12), Vinkó et al. (2012, V12) and Munari et al. (2013, M13). This trio of light curves and residuals with relation to synthesized SNIFS photometry using BM12 passbands and zero points, are shown in the two upper panels of Fig. 3. While a quick look at the superposed light curves may give the impression of a good agreement between all experiments, a careful study of the residuals shows that this is not always the case. The median and normalized median absolute deviation (nMAD) of the residuals between all the experiments are summarized in the matrices shown in the lower two panels of Fig. 3. These matrices relate the statistics of the residuals (observational bias and scatter) between a specific data set and all the other ones, where each row uses a common reference and each column represents a different comparison data set. The bias and scatter matrices are not perfectly (anti-)symmetric since that the interpolation of the light curve depends on the time sampling and measurement errors of the reference data set, allied to the fact that the nMAD is less dependent on outliers. The statistics of the residuals with relation to SNIFS, plotted on the second panel of Fig. 3, can be read from the topmost row of each matrix.
 |
Fig. 3 First panel: comparison of synthesized BVRI SNIFS light curves of SN 2011fe, using BM12 passbands and zero points, with published photometry from Richmond & Smith (2012, RS12), Vinkó et al. (2012, V12) and Munari et al. (2013, M13). Second panel: residuals between all light curves and the SNIFS interpolated light curve, whose uncertainty is represented as the gray shaded region. Third & forth panel: median and normalized median absolute deviation of the residuals for each combination of reference (row) and comparison (column) light curves. The statistics of the residuals shown in the second panel, with SNIFS as reference, are on the topmost row of each matrix. The RCIC filters used by M13 are not directly comparable to RI from RS12 and V12. |
3.1.1. Brown et al. (2012)
B12 present measurements in several UVOT filters, of which only b and v (Poole et al. 2008) fully overlap with the SNIFS wavelength range. Unfortunately both filters saturated before maximum light, and as such our comparison is limited to phases t < −8 d and +18 < t < +25 d. We use the most recent UVOT effective area curves and zero points (Breeveld et al. 2011) and integrate our spectra in Fν. This approach was validated using a Vega spectrum, from which we found exactly the same zero points as reported by Breeveld et al. (2011). We found a clear bias on the residuals, whose median values are −0.14 and −0.20 mag respectively for b (with comparison dates only at t < −8 d) and v, with no evident correlation with magnitude. This bias also seems to be present for the bluer filters (cf. Sect. 3.3). The cause for this effect is not clear. The photometric calibration of UVOT is a notoriously difficult endeavor (Poole et al. 2008), and the fact that the instrument nears the saturation limit for SN 2011fe could point to problems in the coincidence loss or aperture corrections. S-corrections (Suntzeff 2000) may also play a role, since Brown et al. (2012) use the Hsiao et al. (2007) template to convert the observed count rates into flux, while these template spectra do not exactly match the observed ones at early phases (cf. Sect. 4.2).
3.1.2. Richmond & Smith (2012)
RS12 present BVRI observations coming primarily from the Rochester Institute of Technology (RIT) observatory. These observations are the most extensive and consistently calibrated from the full AAVSO followup sample used by Tammann & Reindl (2011). The biases for VRI are small and within the quoted errors of the synthetic photometry presented in this work, while the scatters are smaller or similar to the ones found for the SALT2 fit. The B-band however shows a large bias with relation to SNIFS observations (~0.1 mag), due to an S-correction problem with the calibration of RS12. That is evidenced by the unusually large color coefficient derived by the authors for this filter (0.24 ± 0.04), and by the fact that when using the RS12 B-band light curve as reference (second row of the first matrix), we find large biases with relation to every other data set. The CCD used in the RIT observatory has a very pronounced quantum efficiency (QE) drop in the B-band wavelength range, which explains this effect. Using CALSPEC spectra for stars with similar colors to the ones from the PG1633+099 standard field used by RS12 for their calibration, the BM12 passbands convolved by the KAF−1600 CCD QE curve, and an atmospheric extinction model (pyExtinction; Buton et al. 2013) based on typical atmospheric values for the RIT site, we obtain a b − v color coefficient of 0.31 ± 0.10, while that ignoring the QE effect gives −0.07 ± 0.08. The QE convolved passbands also improve the correlation of the B-band synthetic photometry with the instrumental bSN − bVega, after inversion of the color correction performed by RS12. Differential ADR between a blue SN Ia and red reference stars will also affect filter photometry at some level, especially at the high airmasses of SN 2011fe observations. The authors’ derived values for the B-band date of maximum, peak magnitude and decline rate are then naturally different from ours, being greater by approximately 1 day, 0.05 mag and 0.14 respectively. We point out that the same values derived by Tammann & Reindl (2011) using the full AAVSO sample are perfecly compatible with those found in the present work.
3.1.3. Vinkó et al. (2012)
V12 published BVRI photometry obtained at the Konkoly Observatory. The BI bands are more compatible with SNIFS observations than their RS12 counterparts, but this is not the case for VR. The CCD that was used has a less steep QE curve in the bluer wavelengths, and is thus less prone to S-correction problems as shown by the smaller bias for the B-band, still ~0.04 mag fainter than the SNIFS photometry. This bias does not seem to be present if we use M13 (cf. 3.1.4) instead as the reference light curve, which leads us to think that the bias is affected by the quality of the interpolated light curve, and its dependence on individual point measurement errors. Globally, V12 data shows some tension when used as reference, especially with SNIFS for BVR. The scatter of the residuals with relation to SNIFS is of the order of 0.05 mag for all bands, which is higher than RS12, especially for the redder filters. The B-band date of maximum and decline rate obtained by V12 using MLCS2K2 are in accord with our own.
3.1.4. Munari et al. (2013)
Finally, M13 published BVRCIC photometry obtained using several telescopes of the Asiago Novae and Symbiotic stars collaboration (ANS; Munari et al. 2012). They acknowledge the importance of S-corrections when doing SNe Ia photometry with multiple instrumental setups: in addition to accurate photometric calibration sequences (Henden et al. 2012), M13 implement a light curve merging method that uses phase-dependent zero points for each telescope, found via a global χ2 minimization per band. For the comparisons with the RCIC photometry, which is different from that synthesized using BM12’s RI, we used the Landolt (1992) passbands adjusted to photon count transmission, in accord with the standard star catalogs used for calibration by Henden et al. (2012). M13 do not publish individual measurement errors, but present instead the calibration error for each band. This error is smaller than the merged light curve individual night scatter, when multiple observations are available. We thus average all same night observations, and use as a conservative error the error on the mean of those same observations added quadratically to the corresponding band calibration error. The error for single observation nights is set to the average of the errors of all multiple observation nights. The B-band bias and scatter with relation to SNIFS are the lowest of the three photometric data sets considered, attesting to the quality of their calibration procedure: M13 is a very good reference for all the B data sets not affected by S-correction problems. The biases in the other bands are comparable and do not exceed ~0.02 mag. The observational scatters are slightly larger for VI probably due to outliers in one of the 3 merged telescope data sets. The B-band date of maximum and peak magnitude found by M13, for which they do not quote any error estimate, are very close to our own (within 0.2 d and 0.02 mag), while the decline rate is perfectly compatible within our estimated error.
The synthetic light curves derived from the spectrophotometric time series presented in this paper were compared with those in the literature. Most of the data sets have the smallest residual biases in V, and show an intrinsic scatter of 0.02−0.03 mag for all bands. The typical scatter between data sets comes mostly from calibration issues, and is of the order of 0.03−0.06 mag, similar to the SALT2 fit residuals and with no difference when the comparison is made between purely photometric data sets or with SNIFS. This highlights a major benefit of the SNfactory data, which is at the same time impervious to S-correction problems due to its spectophotometric nature, and of photometric quality comparable to traditional photometric followup data sets, even under the extreme observational conditions pertaining to SN 2011fe.
3.2. Interstellar absorption in M101
Estimates of reddening by the host galaxy may be obtained from either photometric or spectral data. We consider our photometric data first. Folatelli et al. (2010) reapplied the procedure used by Lira (1996) and Phillips et al. (1999) and derived an intrinsic color law for the “tail” of SN Ia light curves, and for maximum light using pseudocolors (the difference between the magnitudes of two bands at each band’s date of maximum). Their color law uses measurements on the CSP photometric system, which we synthesize from our spectra using the filters and zero-points given by Stritzinger et al. (2011). The light curves obtained are interpolated using SALT2 and two independent fits on BVCSP. We measure Δm15(BCSP) = 1.056 ± 0.035 and obtain E(B − V)max = 0.002 ± 0.062 mag, by applying Eq. (3) of Folatelli et al. (2010). We added 0.060 mag in quadrature to the error, to account for the dispersion of the fit by Folatelli et al. (2010). Applying their Eq. (2) to the three spectra whose phase is +30 < t < +80 d with respect to VCSP maximum, we find a weighted mean and standard deviation of E(B − V)tail = 0.038 ± 0.045 mag. Each individual measurement error was increased in quadrature by the dispersion of the corresponding fit, 0.077 mag. Both values are compatible and agree with the trend found by Folatelli et al. (2010) between the difference of both measurements and E(B − V)max (upper-left panel of their Fig. 12). Using a weighted mean of these estimates, and assuming they are independent, we find ⟨E(B − V)host⟩ = 0.026 ± 0.036 mag for the reddening due to dust on the line of sight to SN 2011fe in M101. This is compatible with the value (0.03 ± 0.06 mag) found by Tammann & Reindl (2011) using SN Ia intrinsic colors derived empirically by Reindl et al. (2005).
Spectroscopically, we measured simultaneously the equivalent width of Na i D for the Milky Way (MW) and M101 using fixed Gaussian profiles with a doublet ratio of 2:1. We obtain respectively EW(Na i D)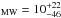 mÅ and EW(Na i D)
mÅ and EW(Na i D)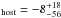 mÅ, with a 95% confidence limit at 162 mÅ. The latter is consistent with the value found by Nugent et al. (2011b) using HiRES (45 ± 9 mÅ) and both results are also compatible with high resolution measurements by Patat et al. (2013), who find 38 ± 5 mÅ and 47 ± 2 mÅ respectively. Using the empirical relation proposed by Poznanski et al. (2012) to derive the dust extinction from the D1 + D2 Na i D lines, we obtain E(B − V)host = 0.014 ± 0.003 mag, in accord with our photometrically derived value. Here we find only a statistical uncertainty, as the systematic errors are difficult to quantify.
mÅ, with a 95% confidence limit at 162 mÅ. The latter is consistent with the value found by Nugent et al. (2011b) using HiRES (45 ± 9 mÅ) and both results are also compatible with high resolution measurements by Patat et al. (2013), who find 38 ± 5 mÅ and 47 ± 2 mÅ respectively. Using the empirical relation proposed by Poznanski et al. (2012) to derive the dust extinction from the D1 + D2 Na i D lines, we obtain E(B − V)host = 0.014 ± 0.003 mag, in accord with our photometrically derived value. Here we find only a statistical uncertainty, as the systematic errors are difficult to quantify.
In conclusion, we confirm there is little evidence for significant extinction of SN 2011fe by dust in its host galaxy. Therefore, no reddening corrections are performed on the SNIFS spectra, other than for MW extinction.
3.3. Bolometric light curve and 56Ni mass
To construct a bolometric light curve of SN 2011fe, we combine SNIFS optical spectrophotometry with ultraviolet (UV) and near-infrared (NIR) SN Ia spectral templates.
The UV template (1600−3400 Å) was constructed from 25 HST STIS spectroscopic observations of SN 2011fe, encompassing phases −15 ≤ t < +24 d. All observations are part of the proposal GO-12298 (Ellis 2009) and are publicly available from the HST archive. All spectra were taken using the 52 × 0.2″ long-slit aperture and one of the UV (G230L or G230LB) or the G430L gratings, together covering ~1600−5700 Å. Same-night observations were averaged, and spectra from different gratings merged together by averaging over their common wavelength range. The ensemble was cut between 1700−3400 Å and set to decrease linearly to zero flux at 1600 Å. Reduction artifacts identified as big isolated “spikes” in the spectra were removed. A multi-phase SN 2011fe UV template was then created, by linear extrapolation of the time evolution of the flux per wavelength bin, for the original 25 phases plus a null spectrum at −20 d, to represent the pre-explosion phase. For each phase of SN 2011fe we intend to reproduce, the template is (achromatically) flux normalized with respect to the SNIFS spectrum at their common wavelength range (3300−3400 Å), in order to account for miscalibrations of the HST data. The median of the residuals of synthetic photometry performed on the final template, with respect to the measurements reported by Brown et al. (2012) for Swift/UVOT uvw2, uvm2 and uvw1, are respectively: −0.22, −0.21 and −0.20 mag. These values are similar to what was found in 3.1.1, once again implying that the UVOT SN 2011fe measurements suffer from large biases. These residuals should be taken with caution however, since they are very dependent on the blueward flux distribution of the HST spectra, where the noise is high and our template is therefore less accurate. Nevertheless, since the UV flux of a normal SNe Ia represents only a small fraction of the total flux (cf. Fig. 4), the impact of using a crude UV template for the bolometric flux will be modest. The variance of the template is constructed so that we have a 0.03 mag error on the full integrated UV flux.
 |
Fig. 4 Phase evolution of the ratio of flux in the ultraviolet (1600−3400 Å) and near-infrared (9700−24 000 Å) to total bolometric flux for SN 2011fe. The dashed lines represent cubic spline fits. |
For the NIR (9700−24 000 Å), the Hsiao et al. (2007) SN Ia spectral template was used as a starting point. After extrapolation to each phase, the template is chromatically warped in order to match the SN 2011fe JHK observations of Matheson et al. (2012) from WIYN/WHIRC. A quadratic spline, constructed from the ratio of observed over synthetic photometry for each of the effective wavelengths of the three WHIRC filters, is used. The variance is constructed from a flat error estimation and warped chromatically in a similar way, in order to match the Matheson et al. (2012) measurement errors. The median residuals and scatter of the final NIR template with relation to observations are at or below the half percent level.
The bolometric flux is obtained by integrating the full wavelength range 1600−24 000 Å of the UV + SNIFS + NIR spectra. The evolution of the ratio of UV and NIR flux to total flux is shown in Fig. 4. The UV flux accounts for a few percent of the total flux with a maximum contribution of about 13% attained five days before B-band maximum. It then decreases steadily to reach about 2% at t > +20 d. The NIR contribution starts at about 15% at very early phases and declines to 5% around 10 days after B maximum, increasing once again to reach 15−20% at the time of the secondary maximum in the NIR (t ~ 30 d), that our data did not sample.
In order to study the time evolution of integrated filter photometry relative to the bolometric flux, we simulated the ratio to total flux of individual or combined optical passbands, using the BM12 throughputs. For the full phase range considered here, the individual band with the least scatter on the ratio of bolometric flux is I, even if the mean ratio to total flux is small (7.3% ± 2%). The mean flux ratio on V is higher while keeping a relatively small scatter (15.7% ± 3.1%), similar to what was seen by Wang et al. (2009) for SN 2005cf. If we sum fluxes of multiple bands, the most promising combinations are those including bands from both extremes of the optical window, namely UVI (36.7% ± 1.3%) and URI (38.0% ± 1.5%). The scatter of the URI combination decreases below the percent level if one limits phases to t < 15 d. The best non-U combination is BI, with mean ratio and scatter of 32.1% ± 1.9%. Assuming the relative normality of SN 2011fe, these ratios can thus be used to compute estimates of total bolometric flux from near maximum optical measurements of a typical SN Ia.
 |
Fig. 5 Bolometric light curve for SN 2011fe (filled red circles). The open circles represent the integrated flux over the full SNIFS wavelength range and the dashed line is a cubic spline fit for determination of the date of maximum. The inset is a zoom of the area marked by a dashed box, where a quadratic rise is fit to the first 3 nights of SNIFS observations. The vertical dotted lines mark the time of observations presented by Nugent et al. (2011b). |
The distance-corrected (Shappee & Stanek 2011) bolometric luminosity is presented in the last column of Table 2, and the bolometric flux is plotted in Fig. 5, along with the integrated flux over the full SNIFS optical window. A t2 power law was fitted to our first three observations (inset of Fig. 5), under the assumption that the luminosity dependence is dominated by the evolution of the photosphere surface area (Riess et al. 1999; Goldhaber et al. 2001; González-Gaitán et al. 2012; Piro 2012) until about five days after the explosion. We find an explosion date (MJD) t0 = 55 796.81 ± 0.13, where the ~3 h precision is due to the lack of earlier SNIFS observations. The value is compatible with the one found by Nugent et al. (2011b) (55 796.696 ± 0.003) using g-band observations which start two days before the SNfactory ones. The goodness of the fit decreases if we include the fourth night of SNIFS observations, supporting the hypothesis that the t2 model is only valid until ~5 d after the explosion. By letting the exponent of the power law float we find a best-fit exponent of 2.21 ± 0.51 and t0 = 55 796.47 ± 0.83. This is a fully constrained fit with 3 parameters on 3 points, and earlier observations would be needed for better precision. The former (t2) analysis made using the VBM12 band yields t0 = 55 796.68 ± 0.12, in closer accordance with the PTF value, the one found by Brown et al. (2012) when using the v band of UVOT (55 796.62 ± 0.03), and by Vinkó et al. (2012) (55 796.70 ± 0.16) using R-band observations. The derived data of explosion thus seems to be dependent on the wavelengths that are included in the bolometric flux.
By fitting a cubic spline to the bolometric light curve in the phase range −9 < t < +15 d, we find the date of maximum bolometric luminosity and derive a bolometric rise time τr, bol = tmax, bol − t0 = 16.58 ± 0.14 d, where we use the explosion date found with the bolometric flux and the t2 power law, and assume an error on the determination of the date of maximum of 0.06 d, as with the SALT2 fits. Using the date of B-band maximum from Sect. 2.4, we obtain τr, B = 17.70 ± 0.14 d, 1.1 d more than the bolometric rise time and compatible with the SN Ia sample of Contardo et al. (2000), who found both rise-times to be within 2 days. One should notice that those authors used pseudo-bolometric light curves from integrated UBVRI, most closely matched by our SNIFS integrated flux, from which we find a date of maximum 0.5 d later than τr, bol and hence closer to τr, B. Employing similarly integrated SNIFS data, Scalzo et al. (2012) found a difference of ~1 d for a sample of overluminous SNe Ia. Our stretch-corrected 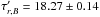 d is in agreement with the median value found by González-Gaitán et al. (2012) for the SNLS sample when using SALT2 (18.16 ± 0.44 d).
d is in agreement with the median value found by González-Gaitán et al. (2012) for the SNLS sample when using SALT2 (18.16 ± 0.44 d).
The maximum bolometric luminosity of SN 2011fe obtained from the spline fit is Lmax,bol = (1.17 ± 0.04) × 1043 erg s-1. This can be used along with the light curve rise-time to compute the 56Ni mass synthesized in the explosion. Different authors used different rise-time estimates, either from (pseudo) bolometric or integrated band light curves. As already shown, these estimates will differ slightly, thus impacting the computed 56Ni mass. We chose to use our bolometric rise time τr, bol. Using Eqs. (3) and (4) of González-Gaitán et al. (2012), which reproduce Howell et al. (2009) and use γ ≡ α = 1.2 ± 0.2, we find M56Ni = (0.44 ± 0.08) × (1.2/α) M⊙. The α dependency is stated explicitly due to its large influence on the final 56Ni mass (Scalzo et al. 2010), and its uncertainty was propagated in the calculations. If one assumes α = 1.0 ± 0.2 (Arnett’s rule) as in Stritzinger et al. (2006), Wang et al. (2009) and Hayden et al. (2010), we obtain M56Ni = 0.53 ± 0.11 M⊙. This value is compatible with the amount of 56Ni mass that the explosion models used by Röpke et al. (2012) were set up to produce (~0.6 M⊙).
3.4. Spectral indicators
Several spectral indicators defined using maximum light spectral features were measured for the SN 2011fe spectrum closest to B maximum light: the ℛSi depth ratio and the ℛCa and ℛSiS flux ratios (Nugent et al. 1995; Bongard et al. 2006); the ℛ642/443 flux ratio (Bailey et al. 2009); the Ca ii H&K (Walker et al. 2010), Si iiλ4131 (Bronder et al. 2008; Arsenijevic et al. 2008; Chotard et al. 2011), Si iiλ5972 & λ6355 (Hachinger et al. 2006; Branch et al. 2006, 2009) and C iiλ6580 (cf. Sect. 3.6) equivalent widths. The S iiλ5640, Si iiλ6355 (Benetti et al. 2004, 2005; Hachinger et al. 2006) and C iiλ6580 feature velocities were also measured for all of the spectra for which the features were detectable. For most of these spectral indicators (all except ℛSiS and ℛ642/443), a precise estimate of the extrema wavelength and flux positions enclosing the feature or defining the velocity is needed in order to make a proper measurement. This was done by automatically measuring the maximum/minimum flux of the smoothed spectra in a given wavelength range, and confirming each measurement visually. The uncertainties on each of these values were derived using a Monte Carlo procedure that takes into account the impact of the method used to select the feature boundaries, the extrema wavelength and flux positions, as well as the small contribution of the photon noise. A detailed description of the measurement method with the corresponding results on a large part of the SNfactory data set will be presented by Chotard et al. (in prep.).
 |
Fig. 6 Phase evolution of the expansion velocities of S iiλ5640, Si iiλ6355, C iiλ6580 (top) and the pseudo-equivalent width of C iiλ6580 (bottom). A linear fit for the post-maximum velocity gradient of Si iiλ6355 is overplotted as a red line. |
The values of these measurements made on the spectrum closest to maximum light appear in Table 3, while the phase evolution of the expansion velocity of S ii, Si ii, C ii and the pseudo-equivalent width of C iiλ6580 are plotted in Fig. 6. The velocity gradient of Si iiλ6355, as defined by Benetti et al. (2005), was computed using a linear least squares fit for −2 < t < +25 d overplotted on Fig. 6, and we find 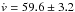 km s-1 d-1. The velocity evolution of S iiλ5640, which Benetti et al. (2004) suggests is an effective probe of the true photospheric velocity, is similar to that observed by those authors for SNe 1998bu, 1994D and 1990N. It decreases from ~12 000 km s-1 at −15 d to approximately 8000 km s-1 at +10 d, passing through ~9500 km s-1 at maximum.
km s-1 d-1. The velocity evolution of S iiλ5640, which Benetti et al. (2004) suggests is an effective probe of the true photospheric velocity, is similar to that observed by those authors for SNe 1998bu, 1994D and 1990N. It decreases from ~12 000 km s-1 at −15 d to approximately 8000 km s-1 at +10 d, passing through ~9500 km s-1 at maximum.
Using these spectral indicators and the light curve decline rate (cf. Table 3) we place SN 2011fe within the SN Ia classification schemes proposed by Benetti et al. (2005) and Branch et al. (2006), as seen in Fig. 7. From this comparison, SN 2011fe seems to be a spectroscopically “core normal” SN Ia whose expansion velocity rate of change lies close to the separation between the “low” and “high” velocity gradient groups as defined by Benetti et al. (2005, 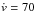 km s-1 d-1. It is also a “normal” SN Ia according to the Wang et al. (2009) definition, based on the Si iiλ6533 expansion velocity at maximum (cf. top panel of Fig. 6).
km s-1 d-1. It is also a “normal” SN Ia according to the Wang et al. (2009) definition, based on the Si iiλ6533 expansion velocity at maximum (cf. top panel of Fig. 6).
3.5. SYNAPPS fitting
We analyze the spectral time series of SN 2011fe with the help of the highly parameterized SYNAPPS fitting code (Thomas et al. 2011b). The objective is to identify ions by their spectroscopic signatures taking line-blending into account. The main radiative transfer assumptions underlying SYNAPPS are: spherical symmetry, a sharply-defined blackbody-emitting pseudo-photosphere, pure-resonance line transfer under the Sobolev approximation, with line opacity parameterized radially according an exponential functional form and per line assuming Boltzmann excitation. SYNAPPS combines this parameterized spectrum synthesis calculation with a parallel non-linear optimization framework to reduce the need for tedious interactive adjustment of fit parameters and to assure more systematic sampling of the parameter space. The assumptions are simple but sufficient for our immediate purpose; a detailed abundance tomography analysis with more sophisticated tools will be the subject of future work.
 |
Fig. 7 Top: ℛ(Si ii) and |
Early, at-peak, and two weeks post-peak fits to SNIFS data appear in Fig. 8. Extreme late-time data (after +70 d) are arguably more difficult to analyze with SYNAPPS as its physical assumptions are less applicable then. The evolution of the spectral features follows the usual pattern of normal SNe Ia. Early on, strong contributions from O i, Mg ii, Si ii, S ii, and Ca ii are detected. C iiλ6580 and C iiλ7234 are detected with high confidence. High velocity components for Si ii and Ca ii features are needed to achieve a good fit in the first spectrum. By maximum light the high velocity features have weakened and only photospheric-velocity opacity components are needed. The C iiλ6580 feature is reproduced by SYNAPPS to some extent at maximum, but the fit is not perfect. At about two weeks after maximum, the spectrum is dominated by lines from Fe ii. We find evidence that some Cr ii and/or Co ii may be present in the spectrum at this point, though Parrent et al. (2012) did not invoke it in their analysis. In all other respects we confirm the analysis presented by Parrent et al. (2012).
3.6. Carbon signatures
 |
Fig. 8 SYNAPPS fits to selected SNIFS spectrophotometry of SN 2011fe. Major ion signatures in the first two spectra are shown. The identified species are typical of a normal SN Ia early on and near maximum light. Two weeks after maximum, the spectrum is dominated by numerous blends from iron-peak elements (Cr ii, Fe ii, Co ii) blueward of about 5000 Å. |
The spectra of SN 2011fe contain signatures of unburned carbon from the earliest observations through maximum (Cenko et al. 2011; Parrent et al. 2012). Carbon in SN Ia ejecta is most robustly detected using C iiλ6580 absorption signatures in pre-maximum spectra (Thomas et al. 2007; Parrent et al. 2011; Thomas et al. 2011a; Folatelli et al. 2012; Silverman & Filippenko 2012; Blondin et al. 2012). High S/N, mostly nightly cadence, and proper treatment of telluric absorptions allow us to trace the detailed evolution of relatively weak C iiλ6580 and also λ7234 in the SNIFS time series (Fig. 9). Both signatures manifest quite clearly in the earliest spectrum, and gradually fade away. C iiλ6580 is just barely detectable in the +3.7 d spectrum, and absent afterward. After −5.3 d, it becomes harder to clearly identify the absorption associated with C iiλ7234.
 |
Fig. 9 Evolution of C iiλ6580 and λ7234 features in the spectral time series of SN 2011fe. Two axes depicting blueshift with respect to 6580 Å and 7234 Å are overlaid, with velocities given in units of 103 km s-1. C iiλ6580 begins as a notch which gradually recedes in velocity and weakens progressively until it is difficult or impossible to reliably identify at +6.7 d. C iiλ7234 follows a similar evolution, but disappears by −1.3 d. |
Relevant parameters for SN 2011fe derived from this work.
In Fig. 6, the blueshift at absorption minimum is plotted. The velocity measurements are compared to the ones extracted from Si iiλ6355 and S iiλ5640. At all phases, the measured C ii velocity is smaller than that measured from the Si ii feature, and tracks that of the S ii line more closely. This offset could be sensitive to how strong the Si ii line is relative to the other two − increasing line opacity in expanding atmospheres (leaving other variables fixed) tends to blue-shift absorption minima (e.g. Jeffery & Branch 1990). The plot suggests that unburned material is present at roughly the same velocities as freshly synthesized intermediate mass element ejecta. The carbon appears to extend from 15 000 km s-1 (blue absorption edge in the first spectrum) down to 8000 or 9000 km s-1.
We extract a pseudo-equivalent width for the C iiλ6580 absorption feature and plot it in Fig. 6 as well. Folatelli et al. (2012) suggest that the pseudo-equivalent width of this feature may increase and then decrease with time. This behavior was detected by Silverman & Filippenko (2012) in SN 1994D, but the peak was not well-sampled. The daily follow-up cadence allows us to explore the evolution of this quantity in detail in SN 2011fe. The equivalent width at first decreases for two days, increases back to roughly the same value, and then decreases again. This behavior was strongly correlated with the velocity evolution in SN 1994D (Silverman & Filippenko 2012) but here no such correlation is detected.
4. Discussion
The analysis of the SNIFS spectrophotometric time series confirms that SN 2011fe is a “textbook case” SN Ia. The light curve shape and color parameters are close to those of a fiducial SALT2 SN Ia (Table 3 summarizes these and other pertinent parameters derived for SN 2011fe in the previous sections). The early and near-maximum spectra exhibit typical strong low-to-intermediate-mass ion signatures (O i, Mg ii, Si ii, S ii, Ca ii) at typical SN Ia ejection velocities. Neither the presence of C ii nor high-velocity Ca ii absorption (Mazzali et al. 2005) are considered particularly unusual. As expected, iron-peak element signatures dominate at late times as the photosphere recedes deeper into the ejecta. Furthermore, there is little evidence for substantial extinction due to dust in M101 along the line of sight.
The high cadence of observation, broad wavelength range, high S/N, and good calibration make the data set presented here not only an asset for studying SN Ia physics in detail, but also for simulations and SN cosmology systematic error analysis. In this section, we use our observations of SN 2011fe to consider a few fundamental questions about the conventional analysis of SNe Ia in those areas. This gives us an opportunity to demonstrate some generically useful features of the data.
4.1. Comparisons with other SNe Ia
Figure 10 compares selected SNIFS observations of SN 2011fe with some of SNF20080514-002 (Aldering et al. 2008) and SN 2009ig (Kleiser et al. 2009). Here we normalize the mean flux between 3500 and 7500 Å in each spectrum involved, and overlay matched phases. The relative flux as a function of phase is not preserved, but this allows us to compare spectral features. These two SNe Ia are selected for comparison because they have been identified previously as basically “normal” SNe Ia (Thomas et al. 2011a; Foley et al. 2012a).
SNF20080514-002 and SN 2011fe are a good match at all phases compared, but they are not identical twins (Fig. 10a). The agreement is best redward of 4000 Å, in terms of what features are present and their morphologies. For example, both objects have strong C iiλ6580 absorption notches early on (see inset, near 6300 Å). The double notch S ii features near 4700 Å and other small-scale features are also matched well. In contrast, however, the −10.2 d spectrum of SN 2011fe exhibits a very slight high-velocity Ca ii infrared triplet absorption that is weaker or absent from the corresponding SNF20080514-002 spectrum. This is mirrored in the near-UV where the Ca ii H&K absorption feature extends to higher velocity in SN 2011fe than in SNF20080514-002. In fact, at this phase the spectra blueward of 3800 Å are markedly dissimilar. Five days later, the morphologies of the near-UV spectra appear to have converged together. About three weeks past maximum, some overall color difference is apparent between the two SNe, but again the spectral features are quite similar.
There is substantial evidence in the literature for greater diversity in the near-UV properties of SNe Ia than in the optical (Ellis et al. 2008; Brown et al. 2010; Milne et al. 2010; Cooke et al. 2011; Wang et al. 2012; Foley et al. 2012b). The near-UV behavior depicted in Fig. 10a supports the idea that this extends to the time domain as well. Increased diversity in the near-UV at early times relative to later phases seems plausible from a physical standpoint. This region of the spectrum is particularly sensitive to the composition, density, and temperature of the outer layers of the ejecta, and at early times the spectrum forms in these layers.
SN 2009ig (Fig. 10b) provides an excellent foil for SN 2011fe. Foley et al. (2012a) noted the relatively high blueshifts of absorption features in its spectra, and here we can see the contrast with the more typical blueshifts exhibited by SN 2011fe. In the earliest spectrum we clearly see the systematically higher velocity absorptions of Ca ii H&K and infrared triplet and Si iiλ6355 in SN 2009ig. The blue edges of these features weaken with time, but overall the absorption lines remain faster in SN 2009ig than in SN 2011fe. An inset compares the region of the spectrum around the C iiλ6580 notch in the first spectrum of either SN. A robust notch is seen in SN 2011fe, but any C ii absorption in SN 2009ig at the same phase is much weaker (Parrent et al. 2011; Foley et al. 2012a).
The above meta-comparison demonstrates a key benefit of the dense temporal sampling of our SN 2011fe spectrophotometry, that it is a trivial matter to find SN 2011fe spectra to compare to spectra of other SNe at practically exactly the same phase. This should be a highly useful feature of the data set for other researchers who wish to contrast their observations with a classic, normal SN Ia in a systematic way.
4.2. Comparisons with spectral surface templates
Here we examine how well the color and detailed spectral evolution of SN 2011fe are described by spectral surface (λ,t) templates used for conventional light curve fitting and K- and S-corrections. Such templates should do well at describing “archetypical” SNe Ia. Our default expectation is that the template spectra should have high fidelity to the “ground truth” time series, that of SN 2011fe. The comparison allows us to gauge the level of that fidelity, and identify transient or systematic deficiencies in the templates themselves. We begin by examining the agreement between true and template-synthesized color curves and then take a closer look at the agreement at the fine spectral level.
 |
Fig. 10 Comparison of selected epochs of SN 2011fe with SNF20080514-002 (left, panel a)) and SN 2009ig (right, panel b)). All observations were obtained with SNIFS. Insets in each panel show the region around the C iiλ6580 absorption notch (5800−6800 Å rest-frame) in the earliest pair of spectra compared. |
B − V, V − R, and V − I color curves of SN 2011fe, synthesized from SNIFS spectrophotometry (Sect. 2.3) up to 40 days past explosion, using BM12 passbands and zero points, appear in Fig. 11. Color curves synthesized from standard templates (Nugent et al. 2002; Hsiao et al. 2007), corrected to the stretch and observed colors at peak luminosity, are shown for comparison.
The observed B − V color curve closely follows the Hsiao template starting at about −10 d, while the match with the Nugent template is only good after about −5 d and diverges slightly starting at +5 d. For very early epochs (before −10 d) neither template seems to be a good match.
In the case of the V − R color evolution, SN 2011fe matches reasonably well with the Hsiao template after maximum light, while earlier phases differ significantly. Interestingly, the Nugent template shows a large deviation from the Hsiao template at the same phases that the Hsiao template differs from the SN 2011fe observations; notably the “bumps” at −10 d and (to a lesser extent) + 5 d. While this difference is not as pronounced as the one between both templates, one could argue that in the small sample of SNe Ia used to construct the Nugent et al. (2002) template, there are spectra whose time evolution is closer to that of SN 2011fe than the average SN Ia spectral time series represented by the Hsiao et al. (2007) template. This appears to be confirmed by the fact that the two SNe Ia that SN 2011fe is most similar to spectroscopically (SN 1992A and SN 1994D, according to Nugent et al. 2011b) are those contributing the most spectra to the Nugent template, along with SN 1989B.
 |
Fig. 11 Synthetic color curves of SN 2011fe from SNIFS spectrophotometry. Both spectral templates from Nugent et al. (2002); Hsiao et al. (2007) are corrected to the observed stretch and peak colors. The SALT2 curves are derived from the fitted light curves on the different bands. The error bars on the SN 2011fe values are smaller than the plot symbols. |
The evolution of V − I is similar to that of V − R. After maximum light, the data agree rather well with the Hsiao template, with the Nugent template being a better match from +15 d onwards. At earlier phases the observations display a significant systematic departure from any of the templates, being closer to the Nugent template at about −10 d. From both this color curve and the previous, it is apparent that the second SNIFS spectrum (MJD 55 800) has a problem at redder wavelengths, being fainter than we would expect it to be. This systematic error (~−0.03 and ~−0.04 mag for RI respectively) is close to the statistical uncertainty for the flux calibration of that night and seems to be due to extraction problems, not with the SN itself but rather with the sole standard star used for calibration.
The “fitted” SALT2 color curves and error bands are also plotted in Fig. 11. For these, we can see that the fitted colors are accurate throughout all of the phases after −5 d, but start to break away from the observations at phases ≲−10 d for B − V and before −5 d for both color curves using the redder parts of the spectra. For the latter, the fits are systematically too red, though the observations are within the quoted model errors. This is not unexpected since the SALT2 model is trained on both nearby and high-z SNe Ia observations, with the former often lacking observations at very early phases, and the latter being affected by low S/N for the redder bands due to quantum efficiency drops and atmospheric extinction effects.
 |
Fig. 12 Comparison of six different phases of SN 2011fe (black line) with the Hsiao et al. (2007) (black dashed lines) and SALT2 (red line with grey error model) SNe Ia spectral surface templates. The Hsiao et al. (2007) spectra are warped to match the observed broad-band colors of SN 2011fe. SALT2 spectra are created directly from the template using the light curve fit parameters. The lower panels plot the percent residuals of each template with relation to the observed SN 2011fe spectra. |
Next we consider agreement at the fine spectral level. Figure 12 is a comparison of six representative SNIFS observations of SN 2011fe with two SN Ia spectral surface templates available in the literature, that from Hsiao et al. (2007) and SALT2. The rapidly changing spectral features during the rise in luminosity to peak are the most interesting to consider, so four spectra leading up to maximum are shown. Observations after peak brightness are represented by the spectra at +11.7 and +23.7 d.
The Hsiao template spectra were warped as in Foley et al. (2012a), in order to emulate their usage in K- or S-correction computations. For each phase the template spectrum is normalized by a cubic spline fitted to the five ratios of synthetic UBVRISNf fluxes between the template and our spectrum for that same phase. In this way the template is forced to match the observed broad-band colors of SN 2011fe.
The SALT2 spectra, on the other hand, are created directly from the template using the light curve fit parameters (x0, x1 and c) found in Sect. 2.4, without any additional warping over wavelength or time. Thus, the projected spectrum from SALT2 is what it predicts the underlying SN spectrum looks like without modification. No scaling in flux is added to improve the agreement, even cosmetically. The SALT2 model 1σ error is depicted as the gray shaded region in each panel of Fig. 12. The lower plot in each panel shows the percent residual differences between each template and the observations.
Though there are both transient and persistent artifacts in the residuals, a general trend is also evident. The agreement between the templates and SN 2011fe improves as maximum light is approached. Near maximum, where the population of SNe Ia available for constructing either template is very well sampled, the discrepancies are relatively smaller. After this point, glitches in the residuals become larger again. We note that the residuals are decidedly not the result of a bias induced by comparing the spectra to templates scaled by synthetic photometry, the high S/N of the observations limits this effect to less than 1%.
We start by examining the agreement between SN 2011fe and both templates at phases t < −10 d. The disagreement between the projected SALT2 spectrum in Fig. 12 and SN 2011fe at −15.2 d is at first striking. The SALT2 error model strongly deweights this observation (and others at the earliest phases, see Sect. 2.4), so the mismatch is not ultimately catastrophic. To an extent, this suggests that these early epochs are underutilized in modeling SNe Ia for cosmological applications today. By −12.2 d, the template shows signs of converging toward SN 2011fe but both the estimated errors and residuals remain large. The Hsiao template is not a particularly good match to SN 2011fe at these phases either. In particular, it seems to systematically underestimate the depths and widths of the stronger absorption features. The template is based on a comparatively small number of spectra at early phases: 13 spectra with phases between −15 and −10 d, compared to 50 spectra or more in each 5-day bin from −10 to +15 d. The template is obviously much more susceptible to biases in the input sample before −10 d.
SALT2 systematically under-estimates the flux at wavelengths redward of about 7500 Å, at all phases. Setting aside the case of −15.2 d, the SALT2-predicted flux at these wavelengths always appears to be smaller than the true value, and the shape of the broad Ca ii infrared triplet feature is poorly reconstructed. The warped Hsiao template seems to have higher fidelity to SN 2011fe at these wavelengths than SALT2 in all but the first two spectra shown. While there are similarly sized offsets at the bluest wavelengths, they are not either systematically low or high as at the red end.
Interestingly, at all phases where the bellwether Si iiλ6355 absorption is unblended and easily discernable in the observed spectrum, it corresponds to a prominent, isolated, coherent feature of the residuals. The same applies to the Ca ii H&K feature. Discrepancies in feature strength, width, and blueshift are all to blame. Even at maximum light, the residuals relative to SALT2 are larger than the model error in certain places (by factors of several at some wavelengths) while the integral of those residuals in the photometric band considered remains small. This emphasizes the difficulty in extracting accurate spectral templates by combining spectra with photometry, and the usefulness of spectrophotometric SN follow-up for this purpose. In the last spectrum, we see that most of the features are reconstructed at the right wavelength, but the emission profiles in either template are too low or too high.
Considering the SALT2 residuals, it at first seems plausible that discrepancies such as those noted here are symptoms of incompleteness in the sample used to create the template. Merely expanding the sample would then ameliorate any resulting errors. This suggestion is certainly applicable to the earliest observations, but seems less reasonable closer to maximum light. The fact that the SALT2 template spectrum at −0.3 d very closely resembles that of a normal SN Ia suggests that quantity and quality of the underlying sample are not the only issues. Rather, it seems plausible that additional information in the form of one or more model parameters (beyond light curve shape and color) are needed to null out coherent residuals associated with major spectral features, in particular those originating in the Ca ii H&K and Si iiλ6355 features (see also Chotard et al. 2011). It seems quite plausible that in these features the residuals arise from velocity mismatch, and that if spectra were used to constrain the template fit, the contribution to the photometric correction error could be reduced. Of course, spectrophotometric measurements eliminate the problem entirely.
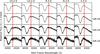 |
Fig. 13 Effect of noise at various phases on the C iiλ6580 absorption notch. The top row depicts the neighborhood of the feature as observed by SNIFS. Each successive row simulates progressively noisier observations, with the S/N per Å labeled at right. The red vertical line depicts the center of the C ii notch to guide the eye. Early observations are no guarantee of a C ii detection even if it is there at lower S/N but generally the feature becomes harder to discern with time as the notch amplitude decreases. Wavelength and flux scales depicted are the same in each panel. |
It is important to acknowledge that comparing templates designed to stand in for archetypical SNe Ia to SN 2011fe may suggest an optimistic outlook in the context of light curve fit systematics. On the other hand, it provides a near best-case or at least typical scenario. To contrast, we refer the reader to a similar comparison of SN 2009ig and the Hsiao et al. (2007) template by Foley et al. (2012a). In that particular case, the discrepancies in spectral evolution presented were portrayed as severe. We note that we performed the same projected SALT2 residuals analysis as depicted in Fig. 12 for SN 2009ig, and find the same kinds of residual structures with often larger but at times smaller magnitude than is seen in SN 2011fe. A more systematic analysis of spectral surface templates is underway and will be presented elsewhere (Saunders et al., in prep.).
4.3. Detecting C ii in SN Ia spectra
Since SNe Ia are likely the thermonuclear incineration of carbon-oxygen white dwarfs, estimates of the total mass and spatial distribution of unprocessed carbon in SN ejecta provide a way to constrain the explosion mechanism. Pure turbulent deflagration models predict that a large amount of unprocessed carbon may remain after explosion (e.g., Gamezo et al. 2003; Röpke & Hillebrandt 2005; Röpke et al. 2007). Models where this deflagration is followed by a detonation phase consume much of the remaining carbon (e.g., Höflich et al. 2002; Kasen et al. 2009). Oxygen signatures in the photospheric phase are less useful, because oxygen is both a fuel and product in the explosion.
The high quality of the SNIFS time series and the clear presence of C iiλ6580 provide us with the opportunity to explore some questions about the efficiency of carbon detection in SN Ia spectra. SN 2011fe gives us a “ground truth” C iiλ6580 detection at high S/N needed to simulate the impact of noise and spectrograph resolution on this principal carbon indicator. The feature manifests as a small notch or small-amplitude depression in flux, so both noise and resolution are important factors in its (positive) detection. Parrent et al. (2011) briefly explore the effect of noise, but only on a single illustrative example spectrum. Here we perform simulations at several phases, especially later than −15 d which is more typical for initial SN Ia follow-up. Specifically, we are interested in simulating quick analyses done by observers attempting to assess whether C iiλ6580 is present in freshly obtained spectra, as is commonly described in astronomical circulars.
 |
Fig. 14 Same as Fig. 13 but rebinned by a factor of eight (bin size ~19 Å). Rebinning noisy data may improve confidence in C iiλ6580 detection in some cases. |
 |
Fig. 15 Same as Fig. 13 but with the spectral resolution degraded to R ~ 100. The top row depicts the smoothed input to the simulation, which nearly completely destroys the C ii signature at all epochs. At the earliest phase a “break” in the shape of the Si iiλ6355 feature can be seen near 6250 Å. The break signature may be a way to detect C ii at lower spectral resolutions and binning than our observations here, but only at the earliest phases. |
Figure 13 demonstrates the effect of lowering the S/N in five pre-maximum spectra of SN 2011fe where C iiλ6580 is clearly evident in the SNIFS data. The real observations of the C iiλ6580 region, adopted as effectively perfect, appear in the top row of panels in the figure. The same spectrum is shown on each subsequent row with gradually decreasing S/N (given as S/N per rest-frame Å in the neighborhood of the carbon notch). At a S/N of 10 per rest-frame Å (bottom row), the C ii notch is completely obscured at the native SNIFS extraction binning (2.38 Å). Overall, the figure suggests that relatively low S/N may be tolerable at early times for making a correct carbon detection, because the feature’s signal is strongest then. Positive identification becomes more difficult as the feature fades away. Indeed, it is hard to make a case that the C iiλ6580 notch is clearly present at −1.3 d at any simulated S/N.
Binning the data can recover the feature, but at the cost of effectively smoothing the data, as shown in Fig. 14. Simulations generated as in Fig. 13 are binned by a factor of eight. This is particularly detrimental at the earliest phases and, somewhat surprisingly, at the lowest S/N. The small wavelength scale of the feature means that it is susceptible to contrast losses if the data are simply binned by too large a factor. We suggest that binning may help improve confidence in more marginal C ii detections at low S/N, but not always. Also, systematic spectral feature modeling (e.g., Thomas et al. 2011a) may eventually provide a quantitative approach.
Finally, Fig. 15 depicts simulated data as before, but with the resolution degraded to R ~ 100. The top row again shows the SNIFS spectra without any noise added, but with a Gaussian filter applied. Only a single noisy realization is plotted here, since it is clear from the top row of the figure that at this resolution the C iiλ6580 feature is obliterated nearly completely at all phases. Unless careful modeling is used, it is doubtful that a positive carbon detection would be made at any phase. A characteristic “break” at about 6250 Å at the earliest phase in the simulated spectrum may be a useful signature, but could be indistinguishable from normal variation in the morphology of Si iiλ6355 features.
The above reinforces the somewhat obvious fact that constructing an accurate descriptive census of carbon in SN Ia ejecta requires both high S/N and moderately high resolution. Earlier is better than later, but blue-shifted C iiλ6580 notches “blend” more readily with the Si iiλ6355 absorption at lower S/N. Lower resolution robotic integral field spectrographs, such as the SED Machine (Ben-Ami et al. 2012), are an excellent way to provide prompt broad classifications and phase estimates for SNe, but are unlikely to directly contribute to a carbon census in SNe Ia. This will fall to higher resolution spectrographs with larger apertures that can trigger on early SN Ia alerts from first-response screening that such instruments as the SED Machine provide. Real-time forward modeling of features that includes instrumental effects may be critical to make the most of such data.
Given the difficulties inherent in translating early discovery into early spectroscopic follow-up of SNe Ia, it seems quite possible that photospheric-velocity carbon signatures at the earliest phases may be anything from common to ubiquitous. Considering also that C ii line strengths vary from object to object and as a function of phase (e.g., Parrent et al. 2011; Thomas et al. 2011a), the clearest route to a proper census is also the most challenging: orchestrating discovery and follow-up on the same or next night for day-old SNe Ia. This remains far from routine for wide-field surveys (such as PTF). High-cadence surveys targeting nearby galaxies (e.g., the Lick Observatory Supernova Search, Filippenko et al. 2001) may slowly build up a sample of bright objects. For now, it seems wise to consider the current rate estimates from the literature (Parrent et al. 2011; Thomas et al. 2011a; Folatelli et al. 2012; Silverman & Filippenko 2012; Blondin et al. 2012) to be lower limits.
The qualitative study presented here highlights the usefulness of high S/N, flux calibrated time series to study detection systematics of narrow and weak spectral features. Our data are a natural input for systematics study simulations where the accurate shape of the SN pseudo-continuum is important. Using any of the current templates for the same purpose will yield biased results, since they are by nature capturing an average behavior, tuned to be useful in a different context.
5. Conclusion
We have presented a new atlas of spectrophotometry of SN 2011fe, a photometrically and spectroscopically normal SN Ia. SN 2011fe is not the typical SNfactory target, and hence its calibration route is not the standard one used for the bulk of the SNfactory data set. Difficulties encountered were the result of short exposure times and very high airmass. Still, the attained level of calibration, high S/N, and observing cadence make this data set extremely useful for a variety of science applications.
The SALT2 fit performed on synthesized light curves shows SN 2011fe to have attained a B-band maximum of 9.94 ± 0.01 mag on MJD 55814.51 ± 0.06, with “standard” lightcurve shape parameters (x1 = −0.206 ± 0.071,c = −0.066 ± 0.021). The residual scatter when compared with published SN 2011fe photometry is comparable to the errors estimated for the flux calibration, and of the same order as the SALT2 fit residuals and the scatter between independent photometric followup campaigns. Reddening due to dust in the host galaxy is found to be very moderate and in accordance with independent spectroscopic determinations. An ultraviolet + optical + near-infrared template was built from SNIFS data and public UV spectroscopy and NIR photometry, to construct a bolometric light curve. From it we derive a date of explosion t0 = 55 796.62 ± 0.13 in the assumption of a t2 luminosity evolution for the very early phases, with a rise-time τr = 16.58 ± 0.14 d and an inferred 56Ni mass of (0.44 ± 0.08) × (1.2/α) M⊙.
The analysis of spectral indicators shows SN 2011fe to be a spectroscopically core-normal SN Ia, on the lower side of the separation between the HVG and LVG groups as defined by the rate of change of the expansion velocity of Si iiλ6355 (59.6 ± 3.2 km s-1 d-1). The evolution of spectral features is typical of a normal SN Ia, with low to intermediate-mass elements dominating the early spectra, and iron-peak signatures strengthening after maximum light. High-velocity Ca ii and Si ii are needed to explain the early spectra, but these weaken by maximum light. C iiλ6580 and C iiλ7234 are detected in pre-maximum spectra, and our high S/N observations and daily cadence allow us to follow the evolution of these features very closely as they fade: apparently unburned carbon extends as deep as 8000 km s-1 in some normal SNe Ia.
The SNIFS time series possesses a number of features that should make it highly useful for interpreting other SNe Ia, investigating systematic errors in traditional light curve analysis, and making forecasts for new instruments’ sensitivities to detecting physically important features.
Online material
Animation of the spectral evolution of SN 2011fe for phases −15 < t < +45 d. The SNIFS spectrophotometric data was interpolated linearly per wavelength bin between each observation date. The inset shows the light curves synthesized using the UBVRISNf filter set, represented as colored shaded regions.
MP4 Animation (2.972 MB) Access here
Vinkó et al. (2012) attribute this difference to a probable misprint, and find Δm15(B) = 1.12 ± 0.05 using RS12 data. Fitting the same data with SALT2 we find 1.17 ± 0.04.
Acknowledgments
We thank the following University of Hawaii astronomers, who graciously granted us interrupt time so that we could observe SN 2011fe during its earliest phases: Colin Aspin, Eric Gaidos, Andrew Mann, Marco Micheli, Timm Riesen, Sarah Sonnett, and David Tholen. The engineering and technical staff of the University of Hawaii 2.2 m telescope helped make this work possible. We recognize the significant cultural role of Mauna Kea within the indigenous Hawaiian community, and we appreciate the opportunity to conduct observations from this revered site. We thank Peter Brown and Ulisse Munari for providing early access to the full tables of Swift/UVOT and ANS measurements, Xiaofeng Wang for providing the HST spectra of SN 2005cf, and Dan Birchall for his assistance in collecting data with SNIFS. This work was supported by the Director, Office of Science, Office of High Energy Physics, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231; by a grant from the Gordon & Betty Moore Foundation; in France by support from CNRS/IN2P3, CNRS/INSU, and PNCG; and in Germany by the DFG through TRR33 “The Dark Universe.” Some results were obtained using resources and support from the National Energy Research Scientific Computing Center, supported by the Director, Office of Science, Office of Advanced Scientific Computing Research, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. Some results were obtained within the framework of the Lyon Institute of Origins under grant ANR-10-LABX-66.
References
- Aldering, G., Adam, G., Antilogus, P., et al. 2002, in SPIE Conf. Ser. 4836, eds. J. A. Tyson, & S. Wolff, 61 [Google Scholar]
- Aldering, G., Antilogus, P., Bailey, S., et al. 2006, ApJ, 650, 510 [NASA ADS] [CrossRef] [Google Scholar]
- Aldering, G., Bongard, S., Childress, M., et al. 2008, ATel, 1532, 1 [NASA ADS] [Google Scholar]
- Arsenijevic, V., Fabbro, S., Mourão, A. M., & Rica da Silva, A. J. 2008, A&A, 492, 535 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bacon, R., Adam, G., Baranne, A., et al. 1995, A&AS, 113, 347 [NASA ADS] [Google Scholar]
- Bacon, R., Copin, Y., Monnet, G., et al. 2001, MNRAS, 326, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Bailey, S., Aldering, G., Antilogus, P., et al. 2009, A&A, 500, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ben-Ami, S., Konidaris, N., Quimby, R., et al. 2012, in SPIE Conf. Ser., 8446 [Google Scholar]
- Benetti, S., Meikle, P., Stehle, M., et al. 2004, MNRAS, 348, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Benetti, S., Cappellaro, E., Mazzali, P. A., et al. 2005, ApJ, 623, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M. S. 1990, PASP, 102, 1181 [NASA ADS] [CrossRef] [Google Scholar]
- Bessell, M., & Murphy, S. 2012, PASP, 124, 140 [Google Scholar]
- Blondin, S., Matheson, T., Kirshner, R. P., et al. 2012, AJ, 143, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Bloom, J. S., Kasen, D., Shen, K. J., et al. 2012, ApJ, 744, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C. 2007, in The Future of Photometric, Spectrophotometric and Polarimetric Standardization, ed. C. Sterken, ASP Conf. Ser., 364, 315 [Google Scholar]
- Bongard, S., Baron, E., Smadja, G., Branch, D., & Hauschildt, P. H. 2006, ApJ, 647, 513 [Google Scholar]
- Bongard, S., Soulez, F., Thiébaut, É., & Pecontal, É. 2011, MNRAS, 418, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Livio, M., Yungelson, L. R., Boffi, F. R., & Baron, E. 1995, PASP, 107, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Dang, L. C., Hall, N., et al. 2006, PASP, 118, 560 [NASA ADS] [CrossRef] [Google Scholar]
- Branch, D., Dang, L. C., & Baron, E. 2009, PASP, 121, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Breeveld, A. A., Landsman, W., Holland, S. T., et al. 2011, in AIP Conf. Ser. 1358, eds. J. E. McEnery, J. L. Racusin, & N. Gehrels, 373 [Google Scholar]
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brown, P. J., Roming, P. W. A., Milne, P., et al. 2010, ApJ, 721, 1608 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, P. J., Dawson, K. S., de Pasquale, M., et al. 2012, ApJ, 753, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Buton, C. 2009, Ph.D. Thesis, Université Claude Bernard − Lyon I [Google Scholar]
- Buton, C., Copin, Y., Aldering, G., et al. 2013, A&A, 549, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Cenko, S. B., Thomas, R. C., Nugent, P. E., et al. 2011, ATel, 3583, 1 [NASA ADS] [Google Scholar]
- Chomiuk, L., Soderberg, A. M., Moe, M., et al. 2012, ApJ, 750, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Chotard, N., Gangler, E., Aldering, G., et al. 2011, A&A, 529, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contardo, G., Leibundgut, B., & Vacca, W. D. 2000, A&A, 359, 876 [NASA ADS] [Google Scholar]
- Cooke, J., Ellis, R. S., Sullivan, M., et al. 2011, ApJ, 727, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Cuillandre, J., Magnier, E. A., Isani, S., et al. 2002, in SPIE Conf. Ser. 4844, ed. P. J. Quinn, 501 [Google Scholar]
- Ellis, R. 2009, in HST Proposal, 12298 [Google Scholar]
- Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Filippenko, A. V., Li, W. D., Treffers, R. R., & Modjaz, M. 2001, in Small Telescope Astronomy on Global Scales, eds. B. Paczynski, W.-P. Chen, & C. Lemme, IAU Colloq. 183, ASP Conf. Ser., 246, 121 [Google Scholar]
- Folatelli, G., Phillips, M. M., Burns, C. R., et al. 2010, AJ, 139, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Folatelli, G., Phillips, M. M., Morrell, N., et al. 2012, ApJ, 745, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Challis, P. J., Filippenko, A. V., et al. 2012a, ApJ, 744, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Foley, R. J., Kromer, M., Howie Marion, G., et al. 2012b, ApJ, 753, L5 [Google Scholar]
- Gamezo, V. N., Khokhlov, A. M., Oran, E. S., Chtchelkanova, A. Y., & Rosenberg, R. O. 2003, Science, 299, 77 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Goldhaber, G., Groom, D. E., Kim, A., et al. 2001, ApJ, 558, 359 [NASA ADS] [CrossRef] [Google Scholar]
- González-Gaitán, S., Conley, A., Bianco, F. B., et al. 2012, ApJ, 745, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hachinger, S., Mazzali, P. A., & Benetti, S. 2006, MNRAS, 370, 299 [NASA ADS] [Google Scholar]
- Hayden, B. T., Garnavich, P. M., Kessler, R., et al. 2010, ApJ, 712, 350 [NASA ADS] [CrossRef] [Google Scholar]
- Henden, A., Krajci, T., & Munari, U. 2012, IBVS, 6024, 1 [NASA ADS] [Google Scholar]
- Höflich, P., Gerardy, C. L., Fesen, R. A., & Sakai, S. 2002, ApJ, 568, 791 [NASA ADS] [CrossRef] [Google Scholar]
- Horesh, A., Kulkarni, S. R., Fox, D. B., et al. 2012, ApJ, 746, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A. 2011, Nature Communications, 2 [Google Scholar]
- Howell, D. A., Sullivan, M., Brown, E. F., et al. 2009, ApJ, 691, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Hsiao, E. Y., Conley, A., Howell, D. A., et al. 2007, ApJ, 663, 1187 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffery, D. J., & Branch, D. 1990, in Supernovae, Jerusalem Winter School for Theoretical Physics, eds. J. C. Wheeler, T. Piran, & S. Weinberg, 149 [Google Scholar]
- Kasen, D., Röpke, F. K., & Woosley, S. E. 2009, Nature, 460, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kleiser, I., Cenko, S. B., Li, W., & Filippenko, A. V. 2009, CBET, 1918, 1 [NASA ADS] [Google Scholar]
- Landolt, A. U. 1992, AJ, 104, 340 [NASA ADS] [CrossRef] [Google Scholar]
- Lantz, B., Aldering, G., Antilogus, P., et al. 2004, in SPIE Conf. Ser. 5249, eds. L. Mazuray, P. J. Rogers, & R. Wartmann, 146 [Google Scholar]
- Law, N. M., Kulkarni, S. R., Dekany, R. G., et al. 2009, PASP, 121, 1395 [NASA ADS] [CrossRef] [Google Scholar]
- Li, W., Bloom, J. S., Podsiadlowski, P., et al. 2011, Nature, 480, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P. 1996, Master’s Thesis, MS Thesis. Univ. Chile (1996) [Google Scholar]
- Margutti, R., Soderberg, A. M., Chomiuk, L., et al. 2012, ApJ, 751, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Matheson, T., Joyce, R. R., Allen, L. E., et al. 2012, ApJ, 754, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzali, P. A., Benetti, S., Altavilla, G., et al. 2005, ApJ, 623, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Milne, P. A., Brown, P. J., Roming, P. W. A., et al. 2010, ApJ, 721, 1627 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, U., Bacci, S., Baldinelli, L., et al. 2012, BaltA, 21, 13 [Google Scholar]
- Munari, U., Henden, A., Belligoli, R., et al. 2013, New A, 20, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Phillips, M., Baron, E., Branch, D., & Hauschildt, P. 1995, ApJ, 455, L147 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Kim, A., & Perlmutter, S. 2002, PASP, 114, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P., Sullivan, M., Bersier, D., et al. 2011a, ATel, 3581, 1 [NASA ADS] [Google Scholar]
- Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011b, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- O’Donnell, J. E. 1994, ApJ, 422, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Parrent, J. T., Thomas, R. C., Fesen, R. A., et al. 2011, ApJ, 732, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Parrent, J. T., Howell, D. A., Friesen, B., et al. 2012, ApJ, 752, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Patat, F., Cordiner, M. A., Cox, N. L. J., et al. 2013, A&A, 549, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Paturel, G., Theureau, G., Bottinelli, L., et al. 2003, A&A, 412, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Machine Learning Res., 12, 2825 [Google Scholar]
- Pereira, R. 2008, Ph.D. Thesis, Université Paris 7 [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M., Lira, P., Suntzeff, N. B., et al. 1999, AJ, 118, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Piro, A. L. 2012, ApJ, 759, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Poole, T. S., Breeveld, A. A., Page, M. J., et al. 2008, MNRAS, 383, 627 [NASA ADS] [CrossRef] [Google Scholar]
- Poznanski, D., Prochaska, J. X., & Bloom, J. S. 2012, MNRAS, 426, 1465 [NASA ADS] [CrossRef] [Google Scholar]
- Rau, A., Kulkarni, S. R., Law, N. M., et al. 2009, PASP, 121, 1334 [NASA ADS] [CrossRef] [Google Scholar]
- Reindl, B., Tammann, G. A., Sandage, A., & Saha, A. 2005, ApJ, 624, 532 [NASA ADS] [CrossRef] [Google Scholar]
- Richmond, M. W., & Smith, H. A. 2012, J. American Association of Variable Star Observers (JAAVSO), 216 [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Filippenko, A. V., Li, W., et al. 1999, AJ, 118, 2675 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Macri, L., Li, W., et al. 2009, ApJS, 183, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., & Hillebrandt, W. 2005, A&A, 431, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Röpke, F. K., Hillebrandt, W., Schmidt, W., et al. 2007, ApJ, 668, 1132 [NASA ADS] [CrossRef] [Google Scholar]
- Röpke, F. K., Kromer, M., Seitenzahl, I. R., et al. 2012, ApJ, 750, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Scalzo, R. A., Aldering, G., Antilogus, P., et al. 2010, ApJ, 713, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Scalzo, R., Aldering, G., Antilogus, P., et al. 2012, ApJ, 757, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Schlegel, D. J., Finkbeiner, D. P., & Davis, M. 1998, ApJ, 500, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., & Stanek, K. Z. 2011, ApJ, 733, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Shappee, B. J., Kochanek, C. S., & Stanek, K. Z. 2013, ApJ, 765, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Silverman, J. M., & Filippenko, A. V. 2012, MNRAS, 425, 1917 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. S., Williams, G. G., Smith, N., et al. 2011, ApJ, submitted [arXiv:1111.6626] [Google Scholar]
- Stritzinger, M., Mazzali, P. A., Sollerman, J., & Benetti, S. 2006, A&A, 460, 793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stritzinger, M. D., Phillips, M. M., Boldt, L. N., et al. 2011, AJ, 142, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Suntzeff, N. B. 2000, in AIP Conf. Ser. 522, eds. S. S. Holt, & W. W. Zhang, 65 [Google Scholar]
- Suzuki, N., Rubin, D., Lidman, C., et al. 2012, ApJ, 746, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Tammann, G. A., & Reindl, B. 2011, ApJ, submitted [arXiv:1112.0439] [Google Scholar]
- Taubenberger, S., Hachinger, S., Pignata, G., et al. 2008, MNRAS, 385, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, R. C., Aldering, G., Antilogus, P., et al. 2007, ApJ, 654, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, R. C., Aldering, G., Antilogus, P., et al. 2011a, ApJ, 743, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, R. C., Nugent, P. E., & Meza, J. C. 2011b, PASP, 123, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Vinkó, J., Sárneczky, K., Takáts, K., et al. 2012, A&A, 546, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walker, E. S., Hook, I. M., Sullivan, M., et al. 2010, MNRAS, 1811 [Google Scholar]
- Wang, X., Li, W., Filippenko, A. V., et al. 2009, ApJ, 697, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, X., Wang, L., Filippenko, A. V., et al. 2012, ApJ, 749, 126 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 SNIFS spectrophotometric time series of SN 2011fe from −15 to 100 days relative to B-band maximum light. Breaks in the axis on the right indicate gaps and changes to the observing cadence. The first break corresponds to a four-day gap in daily cadence before maximum. The second marks the change from daily to alternating two/three day cadence. The final break is a 50 day hiatus imposed by lack of accessibility to the target from Mauna Kea. |
| In the text | |
 |
Fig. 2 SN 2011fe synthesized light curves using the UBVRISNf filter set. Filled and open symbols stand for photometric and non-photometric nights respectively. The results of a SALT2 simultaneous fit of UBVRSNf in the phase range −16 < t < +25 d are shown as solid lines, along with the corresponding residuals (SALT2 – SNIFS) on the lower panel. The shaded areas represent the SALT2 model error. The residuals for the first points of USNf and BSNf fall outside the panel, and the rms on the residuals for each band ignores the first 2 points. The break in the time axis corresponds to the ~50 day gap in follow-up during which SN 2011fe was not visible during the night from Hawaii. Note the change of scale of the extended time axis covering the late observations. |
| In the text | |
 |
Fig. 3 First panel: comparison of synthesized BVRI SNIFS light curves of SN 2011fe, using BM12 passbands and zero points, with published photometry from Richmond & Smith (2012, RS12), Vinkó et al. (2012, V12) and Munari et al. (2013, M13). Second panel: residuals between all light curves and the SNIFS interpolated light curve, whose uncertainty is represented as the gray shaded region. Third & forth panel: median and normalized median absolute deviation of the residuals for each combination of reference (row) and comparison (column) light curves. The statistics of the residuals shown in the second panel, with SNIFS as reference, are on the topmost row of each matrix. The RCIC filters used by M13 are not directly comparable to RI from RS12 and V12. |
| In the text | |
 |
Fig. 4 Phase evolution of the ratio of flux in the ultraviolet (1600−3400 Å) and near-infrared (9700−24 000 Å) to total bolometric flux for SN 2011fe. The dashed lines represent cubic spline fits. |
| In the text | |
 |
Fig. 5 Bolometric light curve for SN 2011fe (filled red circles). The open circles represent the integrated flux over the full SNIFS wavelength range and the dashed line is a cubic spline fit for determination of the date of maximum. The inset is a zoom of the area marked by a dashed box, where a quadratic rise is fit to the first 3 nights of SNIFS observations. The vertical dotted lines mark the time of observations presented by Nugent et al. (2011b). |
| In the text | |
 |
Fig. 6 Phase evolution of the expansion velocities of S iiλ5640, Si iiλ6355, C iiλ6580 (top) and the pseudo-equivalent width of C iiλ6580 (bottom). A linear fit for the post-maximum velocity gradient of Si iiλ6355 is overplotted as a red line. |
| In the text | |
 |
Fig. 7 Top: ℛ(Si ii) and |
| In the text | |
 |
Fig. 8 SYNAPPS fits to selected SNIFS spectrophotometry of SN 2011fe. Major ion signatures in the first two spectra are shown. The identified species are typical of a normal SN Ia early on and near maximum light. Two weeks after maximum, the spectrum is dominated by numerous blends from iron-peak elements (Cr ii, Fe ii, Co ii) blueward of about 5000 Å. |
| In the text | |
 |
Fig. 9 Evolution of C iiλ6580 and λ7234 features in the spectral time series of SN 2011fe. Two axes depicting blueshift with respect to 6580 Å and 7234 Å are overlaid, with velocities given in units of 103 km s-1. C iiλ6580 begins as a notch which gradually recedes in velocity and weakens progressively until it is difficult or impossible to reliably identify at +6.7 d. C iiλ7234 follows a similar evolution, but disappears by −1.3 d. |
| In the text | |
 |
Fig. 10 Comparison of selected epochs of SN 2011fe with SNF20080514-002 (left, panel a)) and SN 2009ig (right, panel b)). All observations were obtained with SNIFS. Insets in each panel show the region around the C iiλ6580 absorption notch (5800−6800 Å rest-frame) in the earliest pair of spectra compared. |
| In the text | |
 |
Fig. 11 Synthetic color curves of SN 2011fe from SNIFS spectrophotometry. Both spectral templates from Nugent et al. (2002); Hsiao et al. (2007) are corrected to the observed stretch and peak colors. The SALT2 curves are derived from the fitted light curves on the different bands. The error bars on the SN 2011fe values are smaller than the plot symbols. |
| In the text | |
 |
Fig. 12 Comparison of six different phases of SN 2011fe (black line) with the Hsiao et al. (2007) (black dashed lines) and SALT2 (red line with grey error model) SNe Ia spectral surface templates. The Hsiao et al. (2007) spectra are warped to match the observed broad-band colors of SN 2011fe. SALT2 spectra are created directly from the template using the light curve fit parameters. The lower panels plot the percent residuals of each template with relation to the observed SN 2011fe spectra. |
| In the text | |
 |
Fig. 13 Effect of noise at various phases on the C iiλ6580 absorption notch. The top row depicts the neighborhood of the feature as observed by SNIFS. Each successive row simulates progressively noisier observations, with the S/N per Å labeled at right. The red vertical line depicts the center of the C ii notch to guide the eye. Early observations are no guarantee of a C ii detection even if it is there at lower S/N but generally the feature becomes harder to discern with time as the notch amplitude decreases. Wavelength and flux scales depicted are the same in each panel. |
| In the text | |
 |
Fig. 14 Same as Fig. 13 but rebinned by a factor of eight (bin size ~19 Å). Rebinning noisy data may improve confidence in C iiλ6580 detection in some cases. |
| In the text | |
 |
Fig. 15 Same as Fig. 13 but with the spectral resolution degraded to R ~ 100. The top row depicts the smoothed input to the simulation, which nearly completely destroys the C ii signature at all epochs. At the earliest phase a “break” in the shape of the Si iiλ6355 feature can be seen near 6250 Å. The break signature may be a way to detect C ii at lower spectral resolutions and binning than our observations here, but only at the earliest phases. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.