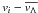| Issue |
A&A
Volume 544, August 2012
|
|
|---|---|---|
| Article Number | A103 | |
| Number of page(s) | 17 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201118688 | |
| Published online | 07 August 2012 | |
Turbulence in the ICM from mergers, cool-core sloshing, and jets: results from a new multi-scale filtering approach
1 Jacobs University Bremen, Campus Ring 1, 28759 Bremen, Germany
e-mail: f.vazza@jacobs-university.de
2 INAF/Istituto di Radioastronomia, via Gobetti 101, 40129 Bologna, Italy
Received: 20 December 2011
Accepted: 15 March 2012
We have designed a simple multi-scale method that identifies turbulent motions in hydrodynamical grid simulations. The method does not assume any a priori coherence scale to distinguish laminar and turbulent flows. Instead, the local mean velocity field around each cell is reconstructed with a multi-scale filtering technique, yielding the maximum scale of turbulent eddies by means of iterations. The method is robust, fast, and easily applicable to any grid simulation. We present here the application of this technique to the study of spatial and spectral properties of turbulence in the intra-cluster medium, measuring turbulent diffusion and anisotropy of the turbulent velocity field for a variety of driving mechanisms: a) accretion of matter in galaxy clusters (simulated with ENZO); b) sloshing motions around cool-cores (simulated with FLASH); c) jet outflows from active galactic nuclei (AGN, simulated with FLASH). The turbulent velocities driven by matter accretion in galaxy clusters are mostly tangential in the inner regions (inside the cluster virial radius) and isotropic in regions close to the virial radius. The same is found for turbulence excited by cool-core sloshing, while the jet outflowing from AGN drives mostly radial turbulence motions near its sonic point and beyond. Turbulence leads to a diffusivity in the range Dturb ~ 1029−1030 cm2 s-1 in the intra-cluster medium. On average, the energetically dominant mechanism of turbulence driving in the intra cluster medium is represented by accretion of matter and major mergers during cluster evolution.
Key words: hydrodynamics / methods: numerical / large-scale structure of Universe / turbulence / galaxies: jets
© ESO, 2012
1. Introduction
On many scales, astrophysical fluids show signs of turbulence whose dynamical contribution may range from significant, as in the case of the intra cluster medium (ICM) (e.g. Norman & Bryan 1999; Dolag et al. 2005; Subramanian et al. 2006) to dominant, as in the case of the interstellar medium (ISM) (e.g. Larson 1981; Goldreich & Sridhar 1995; Padoan & Nordlund 2002; Mac Low & Klessen 2004). Turbulence is a fundamental phenomenon that provides viscosity in accretion disks (e.g. Brandenburg et al. 1995; Balbus & Hawley 1998), that transports matter in stellar atmospheres (e.g. Canuto & Mazzitelli 1991) and mixes high- and low-metallicity ICM in cluster cores (e.g. Rebusco et al. 2006).
The direct numerical simulations of turbulence need to follow the turbulent cascade over a wide range of length scales. Recently, this has become feasible, as hydrodynamical simulations can reach fairly wide dynamic ranges (of ~2−3 orders of magnitude in scales, e.g. Jones et al. 2011, and references therein). However, these high-resolution simulations do not resolve the length scale of physical turbulent dissipation, and subgrid turbulent closures that incorporate the evolution and effect of turbulence on unresolved scales have been developed (e.g. Schmidt et al. 2006; Scannapieco & Brüggen 2008; Maier et al. 2009).
The analysis of turbulence simulations of realistic systems (e.g. galaxy clusters) requires the separation of bulk and turbulent flows, and a number of strategies have been proposed in the recent past. A simple method would be that of computing the turbulent velocity field as the residual respect to the ICM velocity field, averaged over spherical shells from the cluster centre (Norman & Bryan 1999; Iapichino & Niemeyer 2008; Lau et al. 2009). Alternatively, on can compute the average velocity field of the ICM via 3D interpolation, and consider as turbulent the velocity structure below the interpolation scale (Dolag et al. 2005; Vazza et al. 2006, 2009, 2011a; Valdarnini 2011). Alternative approaches focus on the decomposition of solenoidal and rotational components of the velocity field (Ryu et al. 2008; Zhu et al. 2010), or employ sub-grid modelling (Maier et al. 2009; Iapichino et al. 2011). These methods a priori assume limiting length scales of turbulence, possibly leading to inconsistent results. For instance, for a similar cluster mass the estimated amount of turbulent pressure in the cluster core may range from ~0.2 percent of the total gas pressure using sub-grid modelling estimates (Maier et al. 2009) to ~2 percent of the total gas pressure by filtering the velocity field with a radial average (Iapichino & Niemeyer 2008), to ~2−5 percent by using a filtering scale of ≈300 kpc (Vazza et al. 2009).
In this article, we propose a method that locally determines the velocity coherent scale and uses this to distinguish the laminar and the turbulent components of the velocity field. Thus, the method needs no a priori assumptions of the typical scales of the flow in the simulated volume (Sect. 2). The performances of our method are tested with an idealised setup in Sect. 2.1. We present the first results on the properties of turbulence stirred by major mergers and accretions (Sect. 3.1), gas sloshing in cool cores (Sect. 3.2), and active galactic nuclei (AGN) outbursts (Sect. 3.3). Our conclusions are given in Sect. 4; in the Appendix we give an example of our algorithm in IDL 7.0 syntax.
2. Multi-scale filtering
Turbulent fluids are characterised by a hierarchy of scales, ranging from the injection or driving scale, Lo, down to the physical dissipation scale, λdiss, which sets the minimum scale available to the motion (e.g. Landau & Lifshitz 1966; Shore 2007). In incompressible turbulence, the flux of kinetic energy across spatial scales is constant and, if the flow is stationary and uniform, the spectral energy distribution for scales smaller than Lo is described by E(k)dk ∝ k−5/3dk (Kolmogorov 1941).
This power-law translates into a simple relation between the physical size of turbulent eddies, l, and their internal velocity dispersion, σv: 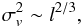 (1)(e.g. Landau & Lifshitz 1966). In most available numerical schemes, however, the smallest scale available to the fluid motions is much larger than the physical dissipation one, thus breaking the power-law behaviour at some numerical scale (~4−8 cells in most grid codes, Porter & Woodward e.g. 1994).
(1)(e.g. Landau & Lifshitz 1966). In most available numerical schemes, however, the smallest scale available to the fluid motions is much larger than the physical dissipation one, thus breaking the power-law behaviour at some numerical scale (~4−8 cells in most grid codes, Porter & Woodward e.g. 1994).
The scale that contains the maximum kinetic energy is the “integral scale” (e.g. Shore 2007), and for homogeneous isotropic turbulence it is given by 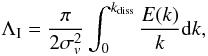 (2)while the largest correlation scale in the fluid, Λ, is defined by the maximum of k·E(k).
(2)while the largest correlation scale in the fluid, Λ, is defined by the maximum of k·E(k).
According to this picture, the flow structure is uncorrelated for scales ≫ Λ, and the average velocity within this scale tends to the average fluid velocity. Based on that, we designed a recursive method to compute the average value of velocity around a cell for increasingly larger scales, until numerical convergence is achieved. The local mean field computed in this way (averaging for ≤ Λ) can be used to compute the turbulent velocity fluctuations inside this scale.
In detail, our algorithm works as follows:
-
at a given nth iteration, the components of the local mean velocity field around each cell are calculated as
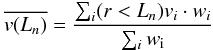 (3)where wi
is a weighting function (e.g. gas density or gas mass);
(3)where wi
is a weighting function (e.g. gas density or gas mass); -
we compute the local “turbulent” velocity field at each nth iteration:
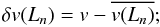 (4)
(4) -
the local and the turbulent velocity field are computed at each nth iteration for increasing values of Ln until the relative variation of turbulent local velocity between two iterations is below the given tolerance parameter, ϵ:
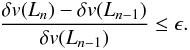 (5)In our case,
ΔL = Ln − Ln − 1
is bound to be the minimum available cell size. The parameter ϵ is a
small tolerance parameter, whose value is tuned by testing (we usually adopt
ϵ ≤ 0.1, see below);
(5)In our case,
ΔL = Ln − Ln − 1
is bound to be the minimum available cell size. The parameter ϵ is a
small tolerance parameter, whose value is tuned by testing (we usually adopt
ϵ ≤ 0.1, see below); -
once convergence of Eq. (5) is reached, we fix Λ = Ln and
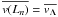 , and we compute the local turbulent velocity field
of the cell as
, and we compute the local turbulent velocity field
of the cell as 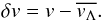 (6)
(6)
Note that if we choose the gas density as the weighting function, wi, in Eq. (3) the numerical noise potentially arising by having gas cells at lower resolution far away from the cell location is minimised. This makes the scheme also readily applicable to SPH, after interpolation onto a regular mesh.
The numerical noise produced near strong shocks in the simulated volume affects the correct measurement of Λ and 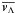 . In this case, the convergence of Eq. (5) is made slower because two different pre-shock and post-shock velocities are averaged across the shock. Strong shocks are characterised by a highly skewed distribution of velocities across the shock, and therefore monitoring the skewness of each velocity component in the volume around each cell is an efficient way of identifying the contribution from shocks to the local estimate of
. In this case, the convergence of Eq. (5) is made slower because two different pre-shock and post-shock velocities are averaged across the shock. Strong shocks are characterised by a highly skewed distribution of velocities across the shock, and therefore monitoring the skewness of each velocity component in the volume around each cell is an efficient way of identifying the contribution from shocks to the local estimate of 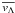 . In detail, prior to our analysis we measure the “bulk” skewness (hereafter simply “skewness”) of the velocity field (separately for each component) in volumes of NS = 83 cells around each cell in the domain
. In detail, prior to our analysis we measure the “bulk” skewness (hereafter simply “skewness”) of the velocity field (separately for each component) in volumes of NS = 83 cells around each cell in the domain 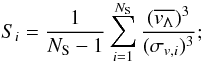 (7)where σv,i is the variance of the velocity component inside the NS volume around each cell1. At each iteration of Eq. (5), we measure an average skewness inside the radius of integration by volume-averaging the previously measured values of Si,
(7)where σv,i is the variance of the velocity component inside the NS volume around each cell1. At each iteration of Eq. (5), we measure an average skewness inside the radius of integration by volume-averaging the previously measured values of Si, 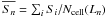 , where Ncell(Ln) is the number of cells within the integration radius, Ln. If a shock enters the integration volume, the average skewness around the cell becomes rapidly very large, and the iterations are stopped to avoid strong contaminations from velocity jumps at shocks. We found that stopping the iterations when
, where Ncell(Ln) is the number of cells within the integration radius, Ln. If a shock enters the integration volume, the average skewness around the cell becomes rapidly very large, and the iterations are stopped to avoid strong contaminations from velocity jumps at shocks. We found that stopping the iterations when 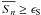 , with ϵS = 1 provides reliable results for our simulated ICM with PPM methods. Using as a reference the realistic case of high-resolution ENZO simulated galaxy clusters (as in Sect. 3.1), we verified that slighly different choices in the range ϵS = 0.5−3, or in the number of cells used for the local estimate of skewness, NS = 53−153, yield very similar results (with differences at the ~percent level on the values of turbulent energy) in the final 3D distributions of turbulent velocity field with this method.
, with ϵS = 1 provides reliable results for our simulated ICM with PPM methods. Using as a reference the realistic case of high-resolution ENZO simulated galaxy clusters (as in Sect. 3.1), we verified that slighly different choices in the range ϵS = 0.5−3, or in the number of cells used for the local estimate of skewness, NS = 53−153, yield very similar results (with differences at the ~percent level on the values of turbulent energy) in the final 3D distributions of turbulent velocity field with this method.
 |
Fig. 1 Maps of absolute value of the total velocity field (left, in arbitrary code units), of the turbulent velocity field reconstructed with our method (centre) and of the input turbulent velocity field (right) for two tests with a different slope for the background velocity profile (α) and for the number of injected turbulent patches, N (see Sect. 2.1 for details). In the top row we assumed α = −0.5, N = 10 and σv/vtot = 0.3, while in the bottom row we assumed α = −0.5, N = 40 and σv/vtot = 3. |
In principle, more complex and accurate shock-detecting schemes can be used (e.g. Vazza et al. 2011b, and references therein), usually employing other physical quantities, e.g. gas temperature, pressure, sound speed. However, in our algorithm we ideally aim at reconstructing the turbulent field using only the geometrical information on the velocity field. This makes the application of our method to a variety of simulations straightforward, without requiring fine tuning of parameters. The only internal parameters needed to stop the iterations of our algorithm are set after our preliminary testing: one for the convergence of the mean local velocity field (ϵ = 0.1) and a second one to remove the spurious contribution of shock waves (ϵk = 1). In a nearly homogeneous gas density distribution, the weighting function in Eq. (3) can also be omitted, and therefore the only physical field needed is the velocity field.
Since our algorithm tries to reconstruct the typical scale of the signal in each point in space, this method is conceptually similar to the wavelet decomposition analysis used in turbulence studies (e.g. Muzy et al. 1991). However, in our approach we do not aim at decomposing the 3D flows in its spatial components, as in the multi-resolution analysis (e.g. Mallat 1989), but uniquely to constrain the largest outer scale of turbulence around each cell.
In the Appendix, we reproduce the source code of the basic version of the multi-scale filtering technique, written in IDL syntax for 3D distributions.
 |
Fig. 2 Trend with number of iterations of the mean local velocity field and turbulent velocity field reconstructed by our method for eight random points extracted in the first test of Fig. 1. The top panel shows how the mean velocity and the turbulent velocity of each points change as the number of iterations is increased (the iterations are stopped when ϵ ≤ 10-3; the lower panel shows the trend of the fractional increase of the turbulent velocity field with the number of iterations (Eq. (5)) for the same points. Our fiducial threshold value to stop the iterations, ϵ = 0.1, as well as ϵ = 0.05 and ϵ = 0.01 is shown for comparison. |
2.1. Tests in two dimensions
We tested our procedure and our choice of convergence parameters against idealized 2D setups, in which we constructed combinations of average background velocity field and patches of chaotic turbulent velocity fields for a 2002 grid. For the regular large-scale velocity field, we set up a simple radial inflow, according to vR(r) = A + B·rα, where we set A = B = 1 (in arbitrary code units). We tested α = −0.1, α = −0.5 and α = −1. These profiles represent a very generalised version of the profiles of radial velocity found in simulations of the ICM (Norman & Bryan 1999; Faltenbacher et al. 2005). We added patches of chaotic velocity field by generating an additional 2D velocity field, vinput, with a random extraction from an energy spectrum obeying the E(k) ∝ k − 5/3 law. In our fiducial model, we imposed a minimum wavenumber kin = 10 for the turbulent velocity; we also tested the cases kin = 1 and kin = 5. Then we randomly selected N circular regions with random centres and radii. For the areas inside the extracted circular regions, we added the turbulent field to the background field, vtot = vo + vinput.
As an example, we show in Fig. 1 the maps of the total velocity field created in this way (left), of the turbulent velocity field reconstructed with our algorithm (centre) and of the input turbulent of velocity field (right) for two of our tests. Figure 2 shows the convergence of the local mean velocity and the turbulent velocity with iteration time steps for a random cells extracted in the first test of Fig. 1. Our algorithm on average requires 5 − 10 iterations to converge on δv for each cell, within the ϵ = 0.1 tolerance. The second panel of Fig. 2 shows the behaviour of the fractional change of the turbulent velocity fluctuation (Eq. (5)) as a function of the number of iterations. In the vast majority of cases, stopping the iterations when this fractional change is below ϵ = 0.1 represents a very good approximation to constrain the turbulent field around the cell location. If we let the iterations proceed until a fractional variation less than ϵ = 0.01 is reached, the number of iterations increases but the final improvement on the turbulent velocity field is not substantial. Also based on our tests in the more realistic case presented in Sect. 3.1, we suggest that our fiducial choice of ϵ = 0.1 is the best compromise between a robust reconstruction of the turbulent field and the speed of the algorithm.
In Fig. 3 we show the distribution of velocities for several tests, comparing the results of our algorithm to the input laminar and turbulent velocity fields.
Our method performs well in reconstructing the original distribution of turbulent velocities in most cases, with no strong dependence on the background radial profiles (tests a)–c)). Misidentification can happen when the turbulent patches are so numerous that they frequently “merge” into a larger pattern, as in test d). In this case, the algorithm requires more iterations and a larger scan region to converge, and the estimated local mean field can be biased in this case. The best morphological reconstruction of turbulent patches is obtained when the turbulent structures are well separated, and their typical internal velocity is significantly different from the local mean velocity.
Sharp cusps in steep velocity profiles can be misidentified as a turbulent fluctuation, as shown in test e), where no additional turbulent field, vinput, is added to the regular radial profile. However, such sharp peaks are unlikely in realistic simulations of the ICM. Our tests show that the use of ϵ = 0.1 is generally the best compromise between the need of a fast convergence of Eq. (5) outside of turbulent structures, and the necessity that the algorithm must not misidentify regular large-scale gradients as turbulent fluctuations.
A second limitation of our method is that it relies on the assumption that the typical scale length of the laminar flow is larger than the maximum size of turbulent “eddies” in the simulated volume. When the two scales are comparable there is an excess of correlation within Λ, due to purely bulk motions, which could bias high the estimated turbulent velocity. Indeed, when we impose kin = 5 or kin = 1 (tests g), h)) as an outer scale to add turbulent motions in our tests, differences are found between the distribution of velocity reconstructed by our method and the correct one.
 |
Fig. 3 Distribution of the velocity modulus for the numerical tests described in Sect. 2.1. From top left to bottom right: a) background velocity profile with α = −1 and N = 10 additional patches of turbulent field with σv/vo = 0.3; b) same as a), but with α = −0.5; c) same as a), but with α = −0.1; d) same as b), but with N = 50; e) only background velocity field with α = −0.5, no turbulent patches; f) as in b), but with turbulent patches everywhere; g) as in b), but assuming an outer scale of turbulent motions kin = 5; h) as in b), but assuming an outer scale of turbulent motions kin = 1. In each panel, the black lines show the total input velocity field, the blue lines the input turbulent field, and the red lines the field reconstructed with our algorithm. |
 |
Fig. 4 Power spectra of velocity field for tests b), d) e) and f), g) and h) of Fig. 3. The black lines show the total input velocity field, the blue lines the input turbulent field, and the red lines the field reconstructed with our algorithm. Note that the low k cut-off in the turbulent spectra of test h) is caused by our procedure of extracting small patches of turbulent motions in the simulated volume, while the original turbulent velocity field has by construction an unbroken power-law spectrum from k = 1 on. |
In Fig. 4 we compare the power spectra of the input velocity field and the result of our algorithm for the few representative cases of tests b), d)–h). In intermittent as well as uniform turbulence cases (b) and f)) the input and measured spectra of turbulence are very similar for all scales, and they perfectly match the spectral shape of the input turbulence at the smallest scale. For the case without input turbulent field (test e)), as discussed above there is some residual pattern of misidentified turbulence. However, these patterns contain very low kinetic energy (~10-3−10-4 of the total energy), and they can be regarded as the unavoidable level of “noise” in our method. As mentioned above, for turbulent modes with a scale similar to the large-scale correlation of the profile of laminar motions (tests g), h)) our method faces a limitation, and at turbulent power spectra at the smallest k are not fully captured.
We conclude that the method is accurate enough to separate laminar and turbulent pattern of motions in configurations similar to the simulated ICM. In realistic situations, the major caveat to the use of our procedure is that it is difficult to fully detect the largest-scale turbulent modes if they have a size similar to the largest scale in the computational domain. In this case an accurate measure of the outer injection scales of turbulent modes is only approximate, and the power spectra measured are in general an underestimate at low k. This problem arises only when the physical injection scale and the physical scale of the ordered field are of the same order of magnitude. We will show that this unfortunate condition does not occur in the interesting cases of cluster mergers, cool-core sloshing and AGN-jets, which will be explored in the remainder of the paper.
 |
Fig. 5 Two-dimensional maps of total gas velocity fields through a cosmological AMR simulation at z = 0.6. Top left: total gas velocity (in [km s-1]); top right: turbulent velocity field captured by our new multi-scale filter; bottom left: turbulent velocity field after the removal of L ≥ 300 kpc scales; bottom right: turbulent velocity field after the removal of L ≥ 1000 kpc scales. The side of each panel is 8 Mpc h-1. |
3. Applications
We applied the multi-scale filter method to three important dynamical processes in galaxy clusters: turbulent motions in cosmological simulation of galaxy clusters, excited by mergers and accretion (Sect. 3.1); turbulence in sloshing cool cores (Sect. 3.2); turbulence injected by AGN outflows (Sect. 3.3). In each case, we derived the turbulent power spectra, the anisotropy of the turbulent velocity and the resulting turbulent diffusion.
3.1. Turbulence from mergers in galaxy clusters
The presence of turbulent motions on scales ≫ kpc in the ICM is inferred from several observations. Measures of Faraday rotation suggest the presence of chaotic super-Alfvénic motions in the ICM, possibly excited by merger events (e.g. Enßlin & Vogt 2003; Murgia et al. 2004; Guidetti et al. 2008; Bonafede et al. 2010; Vacca et al. 2010). Moreover, pseudo-pressure maps of cluster cores derived from X-ray observations and the lack of resonant scattering effects in the X-ray spectra provide hints of turbulence in the ICM (Schuecker et al. 2004; Churazov et al. 2004; Sanders & Fabian 2012). Important constraints on the fraction of turbulent and thermal energy in the cores of clusters are also based on the broadening of the lines in the emitted X-ray spectra of cool-core clusters (Sanders et al. 2010). In the next few years the satellite Astro-H with its high spectral resolution will provide an important tool to observationally constrain the energy ratio of turbulence in the ICM of real galaxy clusters (e.g. Zhuravleva et al. 2011).
Present-day cosmological numerical simulations routinely find that a significant amount of pressure support (i.e. ~10−30 percent of the total pressure inside 0.5Rvir) in the ICM is caused by chaotic motions, continuously excited by major and minor mergers (e.g. Iapichino 2011; Vazza 2011; Jones et al. 2011, for recent reviews).
Here we study turbulence in the ICM of relaxed, merging and post-merger galaxy clusters at high resolution, with the set of simulations presented in Vazza et al. (2010a, 2011a). These runs were produced with the cosmological adaptive mesh refinement code ENZO 1.5 (e.g. Norman et al. 2007; Collins et al. 2010). ENZO is currently developed by the Laboratory for Computational Astrophysics at the University of California in San Diego (http://lca.ucsd.edu).
In Fig. 5 we show the massive galaxy cluster, E1, during a major merger event (z ≈ 0.6). We show the total velocity field in the centre of mass frame, the turbulent field after applying our multi-scale filter and the turbulent field below the fixed filtering length of 300 kpc or 1000 kpc.
Inside the cluster atmosphere, chaotic motions are well developed and significantly volume filling, and similar patterns of turbulence are detected regardless of the adopted scale for the filtering (as long as the filtering scales is a few ~100 kpc). This follows from the fact that, usually, the velocity field of the ICM in clusters is tangled for scales ≤ 1 Mpc. However, the agreement between methods using a fixed filtering scale and our method becomes less satisfactory approaching the outer cluster regions, because towards Rvir large-scale infall motions become more frequent, and large patches of laminar infalling gas are found in correlations with large-scale filaments. In these cases, equally strong smooth and chaotic flows can be found at roughly the same distance from the cluster centre, and distinguishing among them is quite difficult if using a fixed scale.
We compare in Fig. 6 the mass-weighted radial profiles of total velocity and several estimates of turbulence in the same volume: by assuming fixed filtering scales (300 kpc and 1000 kpc) and with our multi-scale filtering algorithm. In the same figure, we additionally show the results of slightly different choices of ϵ to stop the iterations in Eq. (5) (ϵ = 0.3, = 0.05 and = 0.01). Both fixed filtering scales yield in general a slightly higher turbulent velocity at all radii compared to our method; the differences with respect to the filter = 300 kpc are on average very small. On the other hand, the turbulent velocity estimated with our method is lower by a factor ~2−5, with respect to the total velocity field of this cluster, for R > 500 kpc h-1. The choice of different values of ϵ to stop the iterations of our algorithm does not have dramatic consequences in the reconstructed velocity field. However, differently from the our tests in Sect. 2.1, in this more realistic situation the choice of very low values of ϵ may also cause problems, because to pin down the fractional change of the turbulent velocity field around the cell, very a large volume is scanned in the iterations, which can be as large as the cluster itself. Our fiducial choice of ϵ = 0.1 ensures a reasonable compromise between accuracy in the iterations, and the need of avoiding contamination from well-separated regions (and shocks) in simulated galaxy clusters.
For completeness, we also show in Fig. 7 a map of the scale Λ of the velocity field inside the same scale as for the same region of Fig. 5. The value of Λ shown is the average between the three velocity components. Across most of the cluster volume, Λ fluctuates in the range ~100−300 kpc. This suggests that, on average, the use of a simple fixed filtering scale in this range (as performed in the past by Dolag et al. 2005; Vazza et al. 2006, 2009) is still a good approximation to study turbulent motions in the ICM, and that the energy profiles obtained with this technique in the past are fairly consistent with these new and more elaborated ones.
3.1.1. Turbulent energy budget in clusters
We applied our filtering procedure to four additional galaxy clusters of total final virial mass Mtot ~ 3 × 1014 M⊙ h-1, which we already studied in previous works (Vazza et al. 2010b). These systems have different dynamical states: we have two “post-merger” objects (H5 and H6, with a merger with a mass ratio higher than 1/3 for z ≤ 0.5), one merging cluster (H3) and one relaxed system (H1, without evidence of past or ongoing major merger for z < 0.5). Figure 8 shows the average radial profiles of turbulent and total kinetic energy within shells for these clusters, normalised to the thermal energy within the same volume, similar to Fig. 6. The turbulent energy of cells is computed as 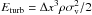 , where σv is the modulus of the 3D velocity field below the assumed spatial scale, computed in Eq. (6), and Δx is the resolution of the cell. Using the total velocity field would overestimate the turbulent budget by a factor ~3−10 at all radii for all objects. The ratio between turbulent and thermal energy flattens with radius in the range ~0.5−2Rvir, with Eturb/Etherm ~ 0.1, while the kinetic energy increases continuously with radius and approaches the thermal energy budget at Rv. The trend of Eturb/Etherm with the dynamical state of host clusters is quite regular inside ~Rvir (post-merger systems present a higher content of turbulent energy compared to relaxed systems, while merging systems stay in between), whereas for ≤ 0.5Rvir the trend becomes sensitive to the timing of the merger event, and to shock heating episodes (which affect the thermal energy of the ICM).
, where σv is the modulus of the 3D velocity field below the assumed spatial scale, computed in Eq. (6), and Δx is the resolution of the cell. Using the total velocity field would overestimate the turbulent budget by a factor ~3−10 at all radii for all objects. The ratio between turbulent and thermal energy flattens with radius in the range ~0.5−2Rvir, with Eturb/Etherm ~ 0.1, while the kinetic energy increases continuously with radius and approaches the thermal energy budget at Rv. The trend of Eturb/Etherm with the dynamical state of host clusters is quite regular inside ~Rvir (post-merger systems present a higher content of turbulent energy compared to relaxed systems, while merging systems stay in between), whereas for ≤ 0.5Rvir the trend becomes sensitive to the timing of the merger event, and to shock heating episodes (which affect the thermal energy of the ICM).
The radial turbulent energy weighted profiles of the maximum coherence scale, Λ(r), for these same clusters are shown in Fig. 9. The trend of this scale with cluster dynamical states suggest that on average the most perturbed systems host the largest turbulent patterns, with Λ ~ 250 kpc, while the average values are almost half of that are found for the relaxed system H1. The differences tend to be smaller at Rvir, where on average all systems present correlation scales of Λ(r) ~100−150 kpc.
These results cast doubts on the usual assumption of an injection scale of turbulence at shocks of the order of the curvature radius of accretion shocks, ~0.5−1 Rv (e.g. Cavaliere et al. 2011). For our clusters this would indeed imply values of ~1−2 Mpc h-1 for the outer scale of turbulent motions, Λ, one order of magnitude larger than what we measure here. Also, the energy budget at ~Rvir would be overestimated by a factor ~5−10 by assuming such a high value of Λ. The reason for this significant difference is likely that, in the outskirts of simulated galaxy clusters, turbulence is mostly injected at the scale ~100−300 kpc, typical of the density/pressure inhomogeneities of the ICM, downstream of accretion shocks.
 |
Fig. 6 Mass-weighted profiles of velocity from the centre of the cluster in Fig. 5. The different lines show the total velocity (solid black), velocity field below the fixed scale of 1000 kpc (blue) and 300 kpc (light blue), turbulent velocity field reconstructed by our algorithm with fiducial parameters (ϵ = 0.1, in red). We additionally show in grey the results of our algorithm for different choices of ϵ to stop the iterations in Eq. (5): ϵ = 0.3 (dashed), ϵ = 0.05 (dot-dashed) and ϵ = 0.01 (long-dashed). |
 |
Fig. 7 Two-dimensional slice showing the distribution of coherence scales (in kpc) for a velocity field of the same region as in Fig. 5. |
 |
Fig. 8 Average radial profile for kinetic to thermal energy inside radial shells for four simulated clusters, for the total velocity field (dotted lines) and for the turbulent velocity field reconstructed with our method (solid lines). |
 |
Fig. 9 Average radial profile of the outer scale for turbulence, Λ(r), for four simulated galaxy clusters. |
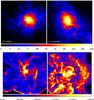 |
Fig. 10 Top panel: map of gas density for a slice of 100 kpc h-1 through the centre of the major merger cluster H5 (right column) and of the merging cluster H3 (left column). The top row shows the projected average gas density (in [ρ/ρcr,b], where ρcr,b is the critical baryon density), the bottom row shows the projected map of the turbulent diffusion for the same regions (in units of [cm2 s-1]). |
 |
Fig. 11 Average radial profile of the anisotropy parameter (for the total velocity field, in dashed, or for the turbulent velocity field, in solid) for four simulated galaxy clusters. |
 |
Fig. 12 Energy spectra of the 3D velocity field for three galaxy clusters (E1, H1 and H5). The dotted lines show the spectra of the total velocity field, the solid lines show the spectra of the turbulent velocity field. The gray lines shows the slope of α = 1 and α = 2/3 to guide the eye. |
3.1.2. Turbulent diffusion in clusters
Our algorithm offers a straightforward estimate of turbulent diffusion in the simulated ICM, that is of the order of:
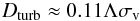 (8)(e.g. Dennis & Chandran 2005). Together with other mechanisms in the ICM, such as stellar feedback or galactic winds, turbulent diffusion may have an important role in transporting metals from active galaxies to the ICM. For instance, Rebusco et al. (2006) analysed the diffusion coefficient needed to model the metallicity observed around several central galaxies in nearby clusters, and found most likely values of the turbulent diffusion in the range Dturb ~ 1028−1029 cm2 s-1.
(8)(e.g. Dennis & Chandran 2005). Together with other mechanisms in the ICM, such as stellar feedback or galactic winds, turbulent diffusion may have an important role in transporting metals from active galaxies to the ICM. For instance, Rebusco et al. (2006) analysed the diffusion coefficient needed to model the metallicity observed around several central galaxies in nearby clusters, and found most likely values of the turbulent diffusion in the range Dturb ~ 1028−1029 cm2 s-1.
We show in Fig. 10 the projected map of volume-weighted turbulent diffusion for the post-merger system H5 and for the merging cluster H3 along with their projected density for a slice of depth 200 kpc. In the major merger cluster H5 the ICM is characterised by volume-filling turbulent motions, which attain a maximum of Dturb ~ 0.5−1 × 1030 cm2 s-1 in localised patches of a few ~100 kpc in size, and ~1029 cm2 s-1 elsewhere. In the pre-merger system H3 most of the cluster volume is characterised by lower values of turbulent diffusion, Dturb < 5 × 1028 cm2 s-1, but a few localised patches attaining higher diffusion are found related to minor mergers along the direction of the large-scale infall of matter (E-W direction in the image). Values in the same range are measured in the virial volume of the other two clusters.
These results agree with the estimates of turbulent diffusion of previous studies of the simulated ICM using tracers (Vazza et al. 2010b) and imply that the efficiency of particle transport in these simulated clusters is much higher than that caused by thermal diffusion (e.g. Shtykovskiy & Gilfanov 2010).
In the following sections we compare the distribution of turbulent diffusion in these runs with that of cool-core sloshing in the Virgo cluster (3.2) and with that of AGN outflows (3.3).
3.1.3. Anisotropy of turbulence in clusters
Our method also offers a way to monitor the anisotropy of the turbulent velocity field within the cluster volume, as a function of radius, 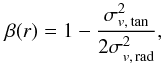 (9)where the turbulent field is decomposed into its tangential and radial component from the cluster centre. Knowing the anisotropy of the velocity field of galaxy clusters simulated in “simple physics” cosmological simulations is important to pinpoint the additional effects of MHD instabilities, which can potentially lead to a radial alignment of B and of the velocity field in the cluster outskirts (e.g. Quataert 2008; Ruszkowski et al. 2011; Parrish et al. 2011). Without a reliable method of detecting turbulent motions, laminar contributions of large-scale bulk flows can significantly bias the estimate of radial turbulent motions in the ICM.
(9)where the turbulent field is decomposed into its tangential and radial component from the cluster centre. Knowing the anisotropy of the velocity field of galaxy clusters simulated in “simple physics” cosmological simulations is important to pinpoint the additional effects of MHD instabilities, which can potentially lead to a radial alignment of B and of the velocity field in the cluster outskirts (e.g. Quataert 2008; Ruszkowski et al. 2011; Parrish et al. 2011). Without a reliable method of detecting turbulent motions, laminar contributions of large-scale bulk flows can significantly bias the estimate of radial turbulent motions in the ICM.
Figure 11 shows the average profiles of β(r) for the four clusters; as a comparison we also overplot the corresponding profiles of the anisotropy parameter that we would obtain from the total unfiltered velocity field. Close to Rvir, we note the striking feature that while the total velocity field is preferentially radial (β ~ 0.5−1), the turbulent velocity field is close to isotropic (β ~ 0). Inside the virial radius, both velocity fields become preferentially tangential. Also in this case, the turbulent velocity field of all clusters is in general closer to isotropic than the total velocity field. These trends follow from the fact that while the bulk motions of satellites are characterised by strong radial motions towards the cluster centre, ram pressure stripping and the hydro-dynamical interaction with the ICM inject chaotic motions in a more isotropic way inside ~Rvir.
3.1.4. Power spectra of turbulence in clusters
Finally, we compute the power spectra of the turbulent velocity field and compare them with the power spectrum of the unfiltered velocity field studied in our previous works (Vazza et al. 2010b, 2011a). In Fig. 12 we show the spectra for three clusters (E1 at z = 0.6, H1 and H5 at z = 0) with a zero-padding technique and employing an apodisation function to avoid spurious effects at the edges of the domain (Vazza et al. 2010b; Valdarnini 2011). The wavenumbers are normalised to the virial radius of each cluster, k0 = 2π/Rvir. To determine the injection scale, for each cluster we plot the spectral energy per mode, k·E(k) (a Kolmogorov spectrum would have a ∝ k−2/3 scaling here, see the dotted gray lines in the figure). Unfiltered spectra (dotted lines) present power law spectra for k > 1−2 k0, with slopes in the range of α ~ 2/3−1. For the post-merger cluster H3, there is some flattening on scales of the virial radius. These results qualitatively agree with power spectra reported in the literature, based on different numerical methods (Dolag et al. 2005; Ryu et al. 2008; Xu et al. 2009).
The turbulent velocity spectra of all clusters show a peak at k/k0 ~ 10−30, corresponding to spatial scales ~0.1−0.3Rvir (~150−500 kpc h-1 for the range of masses we consider here). We cannot detect a single sharp scale responsible of the injection of turbulent energy in the cluster volume, but a quite broad range of scales, consistent with the patchy distribution of scales shown in Figs. 7 and 9. For the post-merger system H5, the turbulent energy peaks at a larger spatial scale compared to the relaxed cluster of equal mass, H1, implying the presence of strong turbulent motions caused by the most recent merger event. At smaller spatial scales, k/k0 > 50 ( ≤ 300 kpc-1), all clusters show a power-law spectrum with a slope slightly steeper than the Kolmogorov one.
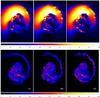 |
Fig. 13 Gas sloshing in the VIRGO cluster, triggered by a minor merger (Roediger et al. 2011). The images are slices through the centre of the simulation box, showing the absolute value of the total (top panels) and turbulent (lower panels) velocity for the three different resolutions: 2 kpc (LR), 1 kpc (MR) and 0.5 kpc (HR). The colour coding is in [km s-1], each image has sides ~250 × 300 kpc. |
Our findings suggest that, despite the clear power-law behaviour of the spectral energy distribution of the ICM velocity field (which runs for almost 2 orders of magnitude in spatial scales), turbulent motions indeed dominate the cascade of energy only for k/k0 > 30 (corresponding to ~0.3Rvir, or ~0.5−1 Mpc h-1 for these masses). The spectral behaviour of the 3D velocity field of the ICM for scales ≥ 0.3−0.5Rvir is on the other hand dominated by the pattern of velocities driven by large-scale infall, whose kinetic energy is mostly characterised by a laminar pattern.
3.2. Cool core sloshing
Our next example concerns ICM sloshing and the resulting formation of cold fronts (CFs). These are discontinuities in X-ray brightness and temperature, where the brighter side is also the cooler one. They come in two varieties (see also review by Markevitch & Vikhlinin 2007): merger CFs with stronger temperature contrasts across the fronts are the contact discontinuities between the intra-cluster media of two merging clusters, and sloshing CFs (Markevitch et al. 2001) are named after their most likely origin. For the latter, the idea is that a gas-free subcluster moved through a galaxy cluster and its ICM. During the pericentre passage, the combined gravitational and hydrodynamical interaction slightly offsets the ICM in the cluster core without disrupting it. After the subcluster has passed the central region and moves away, the offset ICM falls back towards the main cluster DM peak and starts to slosh inside the main potential well (Ascasibar & Markevitch 2006). Thus, sloshing CFs are contact discontinuities between gases of different entropy, originating from different cluster radii. Usually, the subcluster passes the main cluster core at some distance, it transfers angular momentum to the ICM, and the sloshing takes on a spiral-like appearance, and so do the resulting CFs, which are wrapped around the cluster core2. Measuring the amount of small-scale turbulent motions in these simulations is important because the excitation of turbulence around sloshing cool cores has recently been proposed as a mechanism to power radio mini-halos via turbulent re-acceleration of γ ~ 103 electrons in the magnetised ICM (e.g. Mazzotta & Giacintucci 2008; ZuHone et al. 2011a).
Roediger et al. (2011) simulated ICM sloshing specifically in the Virgo cluster, using the AMR code FLASH (version 3.2 Dubey et al. 2009). The simulations were performed in 3D in a simulation box of size of 3 × 3.5 × 3 Mpc3.
Besides the superimposed sloshing and rotational large-scale motions, hydrodynamical instabilities at the CFs introduce a certain amount of turbulence, which we analyse here for the fiducial case with a subcluster of mass 2 × 1013 M⊙, scale radius 100 kpc, and pericentre distance of 100 kpc. To check the dependence of the turbulent velocity field on the numerical resolution, we compared three re-simulations of the Virgo cluster with increasing maximum resolution: Δx ≈ 0.5 kpc (HR run), ≈ 1 kpc (MR) and ≈ 2 kpc (LR).
Figure 13 shows the trend with resolution of the total velocity field (top panels) and turbulence (bottom panels) for thin cuts through the middle of runs LR, MR, and HR at the same time step. To run our algorithm over the same number of cells, we sampled all outputs at the resolution of the LR run (2 kpc).
The increase of resolution enables us to capture the formation of Kelvin-Helmholtz (KH) instabilities along the spiral arms in detail, and to separate them more efficiently from the large scale rotation. The coherent rotation is characterised by values of ~ 300 − 500 km s-1 at large scale in all runs. At low resolution (2 kpc) no KH rolls are observed along the spiral arms of the sloshing core, while at intermediate (1 kpc) and high resolution (0.5 kpc) the KH instabilities can form, and develop patches of turbulent velocities of up to ~ 100 − 200 km s-1.
3.2.1. Power spectra of turbulence in sloshing cool cores
In Fig. 14 we present the 3D power spectrum of the total and of the turbulent velocity field for a region of (500 kpc)3 in the three runs. A large-scale correlation in the total velocity is found at all resolutions, with an overall slope steeper than the Kolmogorov spectrum. This correlation is mostly due to the correlation imposed by the large-scale pattern of rotation after the crossing of the cluster satellite.
The increase of resolution creates a bump in the turbulent velocity spectrum for k > 30 (corresponding to scales < 20 kpc); this bump exactly corresponds to the peak of turbulent energy reconstructed by our algorithm, suggesting that the increase of resolution causes a real development of turbulent motions in this range of scales.
3.2.2. Anisotropy of turbulence in sloshing cool cores
Furthermore, we computed the average radial profiles of the anisotropy parameter for the total and the turbulent velocity field in these three runs (Fig. 15). However, in contrast to our previous results on clusters, the tangential motions of the sloshing core strongly dominate the total velocity field inside 100 kpc, and become more isotropic approaching the innermost cluster core. The convergence on β(r) is very good at all radii > 20 kpc. The turbulent field is also preferentially tangential inside 100 kpc, but no clear convergence with resolution is observed within the cluster core, likely in response to the growth of KH instabilities at small scales as resolution is increased. In the top panels of Fig. 16 we show the components of the turbulent velocity field for a slice of 1 kpc in run HR. The turbulent motions are well-confined within the innermost 100 kpc of the cluster, also when seen in projection, as shown in the bottom left panel.
 |
Fig. 14 Power spectra for the total velocity field (dot-dashed lines) and for the turbulent velocity field (solid lines) for the Virgo simulation at the three resolutions. The spectra are computed for a cubic region with the side of 250 kpc. The x-axis is in unit of 2π/L, where L is the size of the box. The features at k ≥ 50 only present in run LR are an artifact of coarse resolution. |
 |
Fig. 15 Radial average profiles of the anisotropy parameter, β(r), for the Virgo simulation at three resolutions. The dashed lines are for the total velocity field, the solid lines are for the turbulent velocity field. |
3.2.3. Turbulent diffusion in sloshing cool cores
As for the case of clusters, we computed the turbulent diffusion reconstructed with our method (bottom right panel of Fig. 16). Values of Dturb ~ 1 − 2 × 1028 cm2 s-1 are found in a thin stripe along the spiral arm of the sloshing, and in the innermost 100 kpc around the cluster centre. It is intriguing that despite the differences in resolution and driving mechanism in the simulations, this range of values is very similar to what we obtained for the case of galaxy clusters simulated with ENZO (Sect. 3.1).
3.3. AGN outflows in cluster cores
Powerful outflows from AGN are a viable mechanism to induce significant turbulent motions in the innermost region of galaxy clusters, contributing to the mixing of metals in the ICM, and to the lifting of cold and low-entropy materials to the outer cluster volume, thus reducing or quenching cluster cooling flows (e.g. Ciotti & Ostriker 1997; Churazov et al. 2001; Brüggen et al. 2005; Rebusco et al. 2006). Only recently fully cosmological grid simulations have reached a sufficient dynamical range to model the evolution and feedback of AGN outflows in detail, studying the interplay between AGNs and the ICM (e.g. Xu et al. 2009; Teyssier et al. 2011; Dubois et al. 2011; Kim et al. 2011).
Recently, the outflows from AGNs in the multiphase ICM has been simulated in detail with FLASH simulations by Gaspari et al. (2012a,b). These authors reported typical values of ~100−300 km s-1 for the turbulent velocity injected by the AGN, ruling the onset of non-linear instabilities and leading to the condensation of cold gas filaments.
We analysed the output of the simulated AGN-driven outflow in the Hydra A cluster, simulated with FLASH 3.2. The volume around the jet injection has a side length of 1 Mpc and employs AMR to reach the maximum spatial resolution of 0.5 kpc per cell. The AGN jet is reconstructed by two circular back-to-back inflow boundaries 12 resolution elements in diameter (2 kpc). The jet material is injected in opposite directions (at a velocity of vjet = 3 × 104 km s-1), with a total power of Wjet = 3 × 1045 erg s-1. At the epoch analysed here, the bulk velocity along the jet is ~1500−1800 km s-1, and a powerful M ~ 1.3 shock has been driven into the surrounding ICM. To mimic the observed offset between the shock centre and the AGN, a smooth velocity field of ~670 km s-1 has also been imposed to the simulation, as a potential flow around a sphere of 100 kpc radius directed towards ( − 1,1,0). For more details of the simulation setup, we refer the reader to Brüggen et al. (2007) and Simionescu et al. (2009).
In Fig. 17 we show maps of the module of the turbulent velocity field for a slice of depth 1 kpc (left) and for the volume-weighted projection along 500 kpc (right) for a region around the cluster centre.
As in the Virgo runs, our method is very efficient in removing the large-scale (>50 kpc) laminar component of the velocity field, and highlights the complex pattern of turbulent structures associated to the interaction of the jet with the ICM atmosphere. Even if the bulk velocity along the jet axis can be as high as ~2000 km s-1, turbulence is on average injected by rolls of size ~10−20 kpc, via hydrodynamical instabilities, at the low velocity of ~200−300 km s-1. Weaker motions (~10−100 km s-1) are also injected in the innermost 100 kpc, perpendicular to the jet axis, following lateral expanding weak shock waves. These findings are consistent with the recent ones of Gaspari et al. (2012a,b). Some of the turbulent features of the outer jet structure may be detected in nearby AGN inside the galaxy by Astro-H or Athena (e.g. Heinz et al. 2010; Mendygral et al. 2011).
3.3.1. Anisotropy of turbulence in AGN outflows
Figure 18 shows the average radial trend of β(r) for the total (solid line) and for the turbulent velocity field reconstructed with our filter (dot-dashed). The large-scale velocity field is dominated by radial motions outside of 100 kpc (associated with the expansion of the jet and of the running shock at the boundaries of the domain), with strong features of radial motions inside 100 kpc, connected to high-velocity “knots” along the jet. The turbulent motions are close to isotropic along the whole jet structure, suggesting that instabilities are very efficient in distributing the driving kinetic power of the jet in 3D.
This implies that the dissipation of kinetic energy in the surrounding ICM is very isotropic, which aids the AGN’s capability of heating the cool core of the cluster. However, the presence of an even weak magnetic field carried with the jet is expected to have a sizable effect, for instance affecting the exchange of heat between the jet region and the surrounding ICM due to the local magnetic pressure gradient (e.g. O’Neill & Jones 2010).
3.4. Power spectra of turbulence in AGN outflows
As before, we used the power spectrum of the turbulent velocity field to investigate the important physical scales of the turbulence in the simulation volume (Fig. 19). We also decomposed the spectra showing the contribution from the three velocity components separately. While at very large scales there is some small excess of power along the initial injection axis of the jet (Y), as well as the lack of large-scale motions along the Z-axis (owing the large-scale velocity field along (−1,1,0) imposed by construction), for most of the scales in the spectrum the power of the three components is very similar. Turbulence peaks at very small scales (k ~ 50−100, corresponding to ~ 5−10 kpc), but the resolution of this run appears to be insufficient to measure the spectral shape of the turbulent cascade in a clear way.
3.5. Turbulent diffusion for AGN outflows
Figure 20 shows the projected map of average turbulent diffusion across 500 kpc in the Hydra A run, measured as in the previous sections. The highest values of turbulent diffusion on large scales are associated with the most prominent turbulent rolls in the range ~50−100 kpc from the centre, with Dturb ~ 1.5−2 × 1028 cm2 s-1, while much lower values (~1027 cm2 s-1) are found in the inner 50 − 100 kpc around the cluster core. Extended patterns of efficient diffusion are also associated to the motions perpendicular to the jet axis in the downstream region of laterally expanding shock waves excited in the AGN outflows. The values we measure for the Hydra A run are compatible with the turbulent diffusion necessary to explain the gradient of metallicity in the innermost cluster regions (Rebusco et al. 2006; Roediger et al. 2007), provided that what we measure here is turbulent diffusion ~160 Myr after the initial jet was launched in the simulation box.
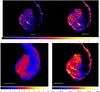 |
Fig. 16 Top panels: slices of 1 kpc through the centre of the Virgo run HR, showing the radial component of the turbulent velocity field (left, in [km s-1]) and the tangential one (right, in [km s-1]). Bottom panels: volume-averaged maps of turbulent velocity field (im [km s-1]) for a line of sight of 200 kpc in run HR (left panel) and maps of turbulent diffusion for a slab of 20 kpc (right, in units of [cm2 s-1]). Each image has sides 400 × 500 kpc. |
 |
Fig. 17 Maps of turbulent velocity module (in units of [km s-1]) for the a slice of 1 kpc centred on the Hydra run (left) and for the volume-weighted projection across 500 kpc (right). Each image has sides 300 × 500 kpc. |
 |
Fig. 18 Average radial profile of the anisotropy parameters of turbulent motions in the Hydra A simulation. We show as a dashed line the profile of the total velocity field, and as a solid line the profile of the turbulent velocity field. |
 |
Fig. 19 Power spectra for the total velocity field (thin upper lines) and for the turbulent velocity field (lower thick lines) for the same region as in Fig. 17. The different colour-coding shows the spectra for the component of velocities along the three axes of the simulation (direction “Y” is the propagation axis of the jet). |
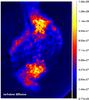 |
Fig. 20 Map of average turbulent diffusion (in [cm2 s-1]) for the projection along 500 kpc in the Hydra A run. The size of the image is the same as in Fig. 17. |
4. Conclusion
We have presented and tested a simple and robust algorithm for extracting the turbulent velocity field from a generic 3D velocity field in grid simulations. The algorithm is based on an iterative geometrical analysis of the velocity field, and makes no a priori assumption on a physical scale when filtering out laminar motions. It iteratively calculates the local mean velocity and the turbulent velocity for increasing volumes around each cell of the simulation, until convergence is reached, taking into account spurious steep gradients related to shock waves.
Our tests in Sect. 2.1 show that our method performs well in reconstructing the morphology and spectral features of intermittent patterns of subsonic and transonic turbulent motions embedded in a large-scale background field. The main limitations of the algorithm emerge in the presence of cuspy background velocity profiles (where the change of slope in the profile may be filtered as a small-scale turbulent fluctuations, if the variations occur on ~few cells), and if the outer scale of turbulence is very close to the typical scale of the laminar flow.
We applied our method to cosmological simulations of galaxy clusters with ENZO 1.5 (Sect. 3.1), to sloshing cool-core clusters (Sect. 3.2 and to AGN outflows (Sect. 3.3) simulated with FLASH 3.2.
In cosmological simulations, we find that turbulent velocities are slightly tangential in the inner regions and isotropic in regions close to the virial radius. The same is found for turbulence excited by cool-core sloshing, while a jet produces slightly radial turbulence and isotropic turbulence near its sonic point and beyond.
Our method naturally provides a way to estimate the turbulent diffusion in simulations, Dturb ∝ Λ·σv. We show in Fig. 21 the direct comparison of the volume and mass distribution of turbulent diffusion in the three cases. Each mechanism presents a particular shape of the distribution. Turbulent diffusion from cluster mergers in general has a “simple” distribution with a maximum at Dturb ~ 1029 cm2 s-1 (volume-weighted distribution), with the tendency of post-merger systems to present tails of enhanced diffusion, up to several ~1030 cm2 s-1. In the sloshing cool core, we observe two maxima in the distribution: one at ~1029 cm2 s-1 and associated with the innermost turbulent region close to the cluster centre, and one with less efficient diffusion, ~1026 − 1027 cm2 s-1, associated with the KH rolls along the spiral arms of the sloshing ICM. While the first feature is very stable against the change in resolution, the second one evolves with the increase of resolution because of the effect of a more efficient separation of differential rotation and turbulent KH rolls in our algorithm, and also because of the real onset of KH instabilities at smaller scales in the simulation. The turbulent diffusion in the Hydra A jet is expected to be more time-dependent compared to the other two. The distribution ~160 Myr after the jet launching presents a more complex distribution, owing to different patches of fast diffusion in the jet-ICM regions of interactions.
 |
Fig. 21 Volume (left) and mass (right) distribution of turbulent diffusion for all runs studied in this paper. We show in red the turbulent diffusion from the AGN-jet of Hydra, in blue the distributions of turbulent diffusion from the sloshing core in Virgo (we plot with different line-styles the distributions at different resolution, as in Sect. 3.2), and in black the turbulent diffusion from cosmological clusters (the different line-styles are for each different object studied in Sect. 3.1, while the shadowed region shows the uncertainty in the overall cluster sample). |
Overall, the maximum values of turbulent diffusion attained by these mechanisms in the simulated ICM fall in the range Dturb ~ 1029 − 1030 cm2 s-1. Merger and accretion episodes in the ICM provide a more volume-filling mechanism of turbulent diffusion, and turbulent diffusion about one order of magnitude faster than jets and cool-core sloshing. We note that the average values we measure are of the order of the upper limits derived with XMM-Newton observations of pseudo-pressure fluctuations in Coma (Dturb ≤ 3 × 1029 cm2 s-1, Schuecker et al. 2004), provided that our 3D distributions of turbulent diffusion are usually patchy, and make a direct comparison non-trivial.
 |
Fig. 22 Combined 3D power spectra from three clusters simulated with ENZO (Sect. 3.1), for the FLASH simulations of the sloshing cool-core in the Virgo cluster (Sect. 3.2) and of the AGN-jet in the Hydra cluster (Sect. 3.3). All spectra were normalised to have to obtain the same power at 200 kpc, while the wave numbers k are the physical ones of each simulation. |
A physical ingredient that can alter some of our findings is the magnetic field. While its inclusion is not expected to change the dynamics of turbulent motions driven by large-scale mergers and accretion on ≫ kpc scales (e.g. Xu et al. 2009; Ruszkowski et al. 2011; Bonafede et al. 2011), local amplification of B in shear flows can suppress the growth of instabilities and mixing motions along the spiral arms of sloshing structures (ZuHone et al. 2011b) and along AGN-jets (O’Neill & Jones 2010).
We end by noting that to resolve the turbulence excited by cluster mergers, sloshing and AGN-jets in the same simulation and keeping the hydro-dynamic details presented in these runs, one would need to cover scales ranging from Rvir ~ 3 Mpc down to the presumed scale of physical dissipation at ~0.1 kpc. As an illustration of that, we show in Fig. 22 a composite power-spectrum of the simulated ICM, obtained by stacking the power spectra of total velocity and of turbulence for the simulations analysed in this work. Since the masses of the clusters as well as the kinetic energy input differ, we rescaled the turbulent energy to the turbulent energy contained within ~(200 kpc)3 (which is well-captured in all runs) in the relaxed cluster H1. This plot illustrates what might be the power spectrum for a cluster of total mass ≈3 × 1014 M⊙ and radius ≈ 1900 kpc, subject to sloshing event and a low-power jet of Wjet ~ 1044 erg s-1 in the last ~100 Myr (the power of the jet is estimated from the amount of the rescaling needed to match the spectrum of the Hydra run to that of the simulated cluster H1 at 200 kpc).
The obvious caveat is that because the different turbulent motions come from independent volumes, the interaction of turbulent modes along the turbulent cascade cannot be captured in this way. However, it is interesting that when rescaled in this way, the total velocity field from all simulations sits on a large-scale power-law, with k·E(k) ∝ k−4/3 (equivalent to E(k) ~ k − 7/3), from ~3−5 Mpc to ~0.5−1 kpc. Because in all simulations the background density profile is close to a beta-model, we propose that this broad-spectrum unveils the typical structure of correlated velocity field imposed in the stratified ICM, mainly because of geometrical reasons. When turbulent motions are intermittently injected into the ICM, they would add their spectral power to this pre-existing power law, causing bumps in the spectrum. They would also cause a flattening in the “background” velocity spectrum along their turbulent cascade, producing a spectral slope close to E(k) ~ k − 5/3 − k-2. In the near future, the efficient design of filtering methods to analyse this wide range of dynamical scales will be an important challenge for the theoretical understanding of turbulent motions in cosmological simulations of large-scale structures.
This type of CF is reported to be ubiquitous (Markevitch & Vikhlinin 2007), and high-resolution observations are available for several clusters (see Roediger et al. 2011, and references therein).
Acknowledgments
F.V. and M.B. acknowledge support from the grant FOR1254 from the Deutsche Forschungsgemeinschaft (DFG). E.R. acknowledges the support of the Priority Programme Witnesses of Cosmic History of the DFG, the supercomputing grants NIC 2877, 3229 and 3711 at the John-Neumann-Institut at the Forschungszentrum Jülich. F.V. acknowledges using computational resources under the CINECA-INAF-2008/2010 agreement. Some of the results presented were produced using the FLASH code, a product of the DOE ASC/Alliances-funded Center for Astrophysical Thermonuclear Flashes at the University of Chicago. We acknowledge K. Dolag, I. Zhuravleva, J. Niemeyer, and W. Schmidt for fruitful technical discussions. We thank G. Brunetti, C. Gheller, and R. Brunino for their collaboration in producing the ENZO simulations analysed in this work. We thank M. Gaspari for his carefully reading of the text, and his very helpful feedback on the filtering method.
References
- Ascasibar, Y., & Markevitch, M. 2006, ApJ, 650, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1998, Rev. Mod. Phys., 70, 1 [Google Scholar]
- Bonafede, A., Feretti, L., Murgia, M., et al. 2010, A&A, 513, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonafede, A., Govoni, F., Feretti, L., et al. 2011, A&A, 530, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brandenburg, A., Nordlund, A., Stein, R. F., & Torkelsson, U. 1995, ApJ, 446, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., Ruszkowski, M., & Hallman, E. 2005, ApJ, 630, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Brüggen, M., Heinz, S., Roediger, E., Ruszkowski, M., & Simionescu, A. 2007, MNRAS, 380, L67 [NASA ADS] [CrossRef] [Google Scholar]
- Canuto, V. M., & Mazzitelli, I. 1991, ApJ, 370, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., Lapi, A., & Fusco-Femiano, R. 2011, A&A, 525, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churazov, E., Brüggen, M., Kaiser, C. R., Böhringer, H., & Forman, W. 2001, ApJ, 554, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Churazov, E., Forman, W., Jones, C., Sunyaev, R., & Böhringer, H. 2004, MNRAS, 347, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Ciotti, L., & Ostriker, J. P. 1997, ApJ, 487, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Collins, D. C., Xu, H., Norman, M. L., Li, H., & Li, S. 2010, ApJS, 186, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Dennis, T. J., & Chandran, B. D. G. 2005, ApJ, 622, 205 [NASA ADS] [CrossRef] [Google Scholar]
- Dolag, K., Vazza, F., Brunetti, G., & Tormen, G. 2005, MNRAS, 364, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Dubey, A., Reid, L. B., Weide, K., et al. 2009, Parallel Computing, 35, 512 [CrossRef] [Google Scholar]
- Dubois, Y., Devriendt, J., Teyssier, R., & Slyz, A. 2011, MNRAS, 417, 1853 [NASA ADS] [CrossRef] [Google Scholar]
- Enßlin, T. A., & Vogt, C. 2003, A&A, 401, 835 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Faltenbacher, A., Kravtsov, A. V., Nagai, D., & Gottlöber, S. 2005, MNRAS, 358, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Brighenti, F., & Temi, P. 2012a, MNRAS, 424, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Gaspari, M., Ruszkowski, M., & Sharma, P. 2012b, ApJ, 746, 94 [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Guidetti, D., Murgia, M., Govoni, F., et al. 2008, A&A, 483, 699 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heinz, S., Brüggen, M., & Morsony, B. 2010, ApJ, 708, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Iapichino, L. 2011, Mem. Soc. Astron. It., 82, 605 [NASA ADS] [Google Scholar]
- Iapichino, L., & Niemeyer, J. C. 2008, MNRAS, 388, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Iapichino, L., Schmidt, W., Niemeyer, J. C., & Merklein, J. 2011, MNRAS, 414, 2297 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, T. W., Porter, D. H., Ryu, D., & Cho, J. 2011, Mem. Soc. Astron. It., 82, 588 [NASA ADS] [Google Scholar]
- Kim, J.-H., Wise, J. H., Alvarez, M. A., & Abel, T. 2011, ApJ, 738, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Kolmogorov, A. 1941, Akademiia Nauk SSSR Doklady, 30, 301 [Google Scholar]
- Landau, L. D., & Lifshitz, E. M. 1966, Hydrodynamik (Pergamon) [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Lau, E. T., Kravtsov, A. V., & Nagai, D. 2009, ApJ, 705, 1129 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, A., Iapichino, L., Schmidt, W., & Niemeyer, J. C. 2009, ApJ, 707, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Mallat, S. G. 1989, IEEE Trans. Patt. Anal. Mach. Intell., 11, 674 [Google Scholar]
- Markevitch, M., & Vikhlinin, A. 2007, Phys. Rep., 443, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markevitch, M., Vikhlinin, A., & Mazzotta, P. 2001, ApJ, 562, L153 [NASA ADS] [CrossRef] [Google Scholar]
- Mazzotta, P., & Giacintucci, S. 2008, ApJ, 675, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Mendygral, P. J., O’Neill, S. M., & Jones, T. W. 2011, ApJ, 730, 100 [NASA ADS] [CrossRef] [Google Scholar]
- Murgia, M., Govoni, F., Feretti, L., et al. 2004, A&A, 424, 429 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muzy, J. F., Bacry, E., & Arneodo, A. 1991, Phys. Rev. Lett., 67, 3515 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Norman, M. L., & Bryan, G. L. 1999, in The Radio Galaxy Messier 87, eds. H.-J. Röser, & K. Meisenheimer, Lecture Notes in Physics (Berlin: Springer Verlag), 530, 106 [Google Scholar]
- Norman, M. L., Bryan, G. L., Harkness, R., et al. 2007 [arXiv:0705.1556] [Google Scholar]
- O’Neill, S. M., & Jones, T. W. 2010, ApJ, 710, 180 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Parrish, I. J., McCourt, M., Quataert, E., & Sharma, P. 2011, MNRAS, L356 [Google Scholar]
- Porter, D. H., & Woodward, P. R. 1994, ApJS, 93, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Quataert, E. 2008, ApJ, 673, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Rebusco, P., Churazov, E., Böhringer, H., & Forman, W. 2006, MNRAS, 372, 1840 [Google Scholar]
- Roediger, E., Brüggen, M., Rebusco, P., Böhringer, H., & Churazov, E. 2007, MNRAS, 375, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Roediger, E., Brüggen, M., Simionescu, A., et al. 2011, MNRAS, 413, 2057 [NASA ADS] [CrossRef] [Google Scholar]
- Ruszkowski, M., Lee, D., Brüggen, M., Parrish, I., & Oh, S. P. 2011, ApJ, 740, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Ryu, D., Kang, H., Cho, J., & Das, S. 2008, Science, 320, 909 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Sanders, J. S., & Fabian, A. C. 2012, MNRAS, 421, 726 [NASA ADS] [Google Scholar]
- Sanders, J. S., Fabian, A. C., & Smith, R. K. 2010, MNRAS, 1534 [Google Scholar]
- Scannapieco, E., & Brüggen, M. 2008, ApJ, 686, 927 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, W., Niemeyer, J. C., & Hillebrandt, W. 2006, A&A, 450, 265 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuecker, P., Finoguenov, A., Miniati, F., Boehringer, H., & Briel, U. G. 2004, A&A, 426, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shore, S. N. 2007, Astrophysical Hydrodynamics: An Introduction (Weinheim: WILEY-VCH Verlag GmbH & Co KGaA) [Google Scholar]
- Shtykovskiy, P., & Gilfanov, M. 2010, MNRAS, 401, 1360 [NASA ADS] [CrossRef] [Google Scholar]
- Simionescu, A., Roediger, E., Nulsen, P. E. J., et al. 2009, A&A, 495, 721 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Subramanian, K., Shukurov, A., & Haugen, N. E. L. 2006, MNRAS, 366, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R., Moore, B., Martizzi, D., Dubois, Y., & Mayer, L. 2011, MNRAS, 414, 195 [CrossRef] [Google Scholar]
- Vacca, V., Murgia, M., Govoni, F., et al. 2010, A&A, 514, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valdarnini, R. 2011, A&A, 526, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F. 2011, Mem. Soc. Astron. It., 82, 609 [NASA ADS] [Google Scholar]
- Vazza, F., Tormen, G., Cassano, R., Brunetti, G., & Dolag, K. 2006, MNRAS, 369, L14 [NASA ADS] [Google Scholar]
- Vazza, F., Brunetti, G., Kritsuk, A., et al. 2009, A&A, 504, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., Gheller, C., & Brunino, R. 2010a, New A, 15, 695 [Google Scholar]
- Vazza, F., Gheller, C., & Brunetti, G. 2010b, A&A, 513, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Brunetti, G., Gheller, C., Brunino, R., & Brüggen, M. 2011a, A&A, 529, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazza, F., Dolag, K., Ryu, D., et al. 2011b, MNRAS, 418, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., Li, H., Collins, D. C., Li, S., & Norman, M. L. 2009, ApJ, 698, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, W., Feng, L.-L., & Fang, L.-Z. 2010, ApJ, 712, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zhuravleva, I. V., Churazov, E. M., Sazonov, S. Y., Sunyaev, R. A., & Dolag, K. 2011, Astron. Lett., 37, 141 [NASA ADS] [CrossRef] [Google Scholar]
- ZuHone, J., Markevitch, M., & Brunetti, G. 2011a, Mem. Soc. Astron. It., 82, 632 [NASA ADS] [Google Scholar]
- ZuHone, J. A., Markevitch, M., & Lee, D. 2011b, ApJ, 743, 16 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Appendix
Below we give an example of our multi-scale algorithm written in IDL 7.0, designed to recursively analyse one velocity component of a 3D field.
The program takes as input a 3D velocity field, vel (we assume here it is written in binary format), as a regular grid of linear dimension of n cells. The fiducial tolerance parameters eps=0.1 and epssk=1 are used in the computation, and a kernel scale of nk=8 is preliminarly used to compute the average skewness of the velocity field around each cell.
The final output of the code are 3D distributions of the turbulent field (turb), of the outer scale (scale), and of the skewness of the velocity field (sk).
This code makes intensive use of the intrinsic IDL functions smooth, convol, and where to reduce the usage of 3D loops. We verified that this greatly speeds up the execution.
In Fig. A.1 we show the benchmark tests of the code applied to HR runs of the Virgo cluster (Sect. 3.2) and interpolated to four different grid resolutions of 643, 1283, 2563 and 5123. For a sufficiently high resolution, the scaling of our algorithm is very close to linear with respect to the number of cells analysed. The execution time to perform the multi-scale filter analysis of one component of velocity in a 5123 grid is ~45 min, and ~3 min for a 2563 grid. However, the details of the performance and scaling may change from problem to problem, depending on the intermittency of the 3D velocity field under analysis.
The source code for our algorithm can also be downloaded at this URL: http://www.ira.inaf.it/~vazza/papers/turbofilter.pro.
Also, a sample 3D file of velocity extracted from a cluster simulation is given as an example, at this URL: http://www.ira.inaf.it/~vazza/papers/sample_velocity.dat.
 |
Fig. A.1 Scaling between the CPU time employed by our algorithm and the total number of cells in the computational volume for four different resolution of the Virgo HR run (Sect. 3.2). Tests run on an Intel Quad-Core Xeon E5345 Linux Cluster. |
pro turbofilter
n=256 ;...linear size of the grid
vel=fltarr(n,n,n) ;...3D array of velocity
openr,3,’vel.dat’ ;...the grid is read
readu,3,vel
close,3
;...needed parameters and thresholds
r2=uint(n*0.5-1.) ;...upper limit for L
r1=4 ;....lower limit
turbo=fltarr(n,n,n) ;....turbulent field
scale=fltarr(n,n,n) ;....scale of the flow
sk=fltarr(n,n,n) ;....skewness
scale(*,*,*)= 0. ;...initialization
turbo(*,*,*)=0. ;...
eps=0.1 ;...tolerance in Eq.5
nk=8 ;...number of cells to compute skewness
epssk=1. ;...tolerance for the skewness
drr=1. ;...radial step for Eq.5
;... preliminary computation of the skewness
meanv = smooth(vel,nk,/EDGE_TRUNCATE)
sc = abs((vx-meanv)/vel)
kernel=MAKE_ARRAY(nk,nk,nk, /float, value = 1.)
kernel(0,*,*) = 0.
kernel(*,0,*) = 0.
kernel(*,*,0) = 0.
kernel(nk-1,*,*) = 0.
kernel(*,nk-1,*) = 0.
kernel(*,*nk-1) = 0.
sk=convol((vel-meanv)^2,kernel,/edge_truncate)
sk=meanv^3/float(sk^1.5) ; skewness, Eq.7
sc1 = 0 ;.....
;....iterations to constrain turbulence
for r=r1,r2,drr do begin
width = 2.*r+1 ; width of box
meanv = smooth(vel,width,/EDGE_TRUNCATE) ;...mean local velocity at each scale
sc = abs((vel-meanv)/vel) ;...differential change in vel, Eq.5
skm=smooth(sk,width,/EDGE_TRUNCATE) ;average skewness within L
;...check of which cells are converged
ibox=where((abs(sc-sc1)/float(sc1) lt eps or abs(skm) gt epssk) and scalex eq 0.,nn)
if nn gt 0 then begin
turbo(ibox)=vel(ibox)-meanv(ibox) ;...turbulent velocity in the cell
scale(ibox) = float(r+0.01) ;...outer scale L
endif
sc1=sc
;..zc=n*0.5
;tvscl,[vel(*,*,zc),meanv(*,*,zc),
turbo(*,*,zc)]
endfor
;....saves our final results
;...final turbulent field
openw,3,"turb.dat"
writeu,3,turb
close,3
;...outer scale
openw,3,"scale.dat"
writeu,3,scale
close,3
;...skewness
openw,3,"skewness.dat"
writeu,3,sk
close,3
end
All Figures
 |
Fig. 1 Maps of absolute value of the total velocity field (left, in arbitrary code units), of the turbulent velocity field reconstructed with our method (centre) and of the input turbulent velocity field (right) for two tests with a different slope for the background velocity profile (α) and for the number of injected turbulent patches, N (see Sect. 2.1 for details). In the top row we assumed α = −0.5, N = 10 and σv/vtot = 0.3, while in the bottom row we assumed α = −0.5, N = 40 and σv/vtot = 3. |
| In the text | |
 |
Fig. 2 Trend with number of iterations of the mean local velocity field and turbulent velocity field reconstructed by our method for eight random points extracted in the first test of Fig. 1. The top panel shows how the mean velocity and the turbulent velocity of each points change as the number of iterations is increased (the iterations are stopped when ϵ ≤ 10-3; the lower panel shows the trend of the fractional increase of the turbulent velocity field with the number of iterations (Eq. (5)) for the same points. Our fiducial threshold value to stop the iterations, ϵ = 0.1, as well as ϵ = 0.05 and ϵ = 0.01 is shown for comparison. |
| In the text | |
 |
Fig. 3 Distribution of the velocity modulus for the numerical tests described in Sect. 2.1. From top left to bottom right: a) background velocity profile with α = −1 and N = 10 additional patches of turbulent field with σv/vo = 0.3; b) same as a), but with α = −0.5; c) same as a), but with α = −0.1; d) same as b), but with N = 50; e) only background velocity field with α = −0.5, no turbulent patches; f) as in b), but with turbulent patches everywhere; g) as in b), but assuming an outer scale of turbulent motions kin = 5; h) as in b), but assuming an outer scale of turbulent motions kin = 1. In each panel, the black lines show the total input velocity field, the blue lines the input turbulent field, and the red lines the field reconstructed with our algorithm. |
| In the text | |
 |
Fig. 4 Power spectra of velocity field for tests b), d) e) and f), g) and h) of Fig. 3. The black lines show the total input velocity field, the blue lines the input turbulent field, and the red lines the field reconstructed with our algorithm. Note that the low k cut-off in the turbulent spectra of test h) is caused by our procedure of extracting small patches of turbulent motions in the simulated volume, while the original turbulent velocity field has by construction an unbroken power-law spectrum from k = 1 on. |
| In the text | |
 |
Fig. 5 Two-dimensional maps of total gas velocity fields through a cosmological AMR simulation at z = 0.6. Top left: total gas velocity (in [km s-1]); top right: turbulent velocity field captured by our new multi-scale filter; bottom left: turbulent velocity field after the removal of L ≥ 300 kpc scales; bottom right: turbulent velocity field after the removal of L ≥ 1000 kpc scales. The side of each panel is 8 Mpc h-1. |
| In the text | |
 |
Fig. 6 Mass-weighted profiles of velocity from the centre of the cluster in Fig. 5. The different lines show the total velocity (solid black), velocity field below the fixed scale of 1000 kpc (blue) and 300 kpc (light blue), turbulent velocity field reconstructed by our algorithm with fiducial parameters (ϵ = 0.1, in red). We additionally show in grey the results of our algorithm for different choices of ϵ to stop the iterations in Eq. (5): ϵ = 0.3 (dashed), ϵ = 0.05 (dot-dashed) and ϵ = 0.01 (long-dashed). |
| In the text | |
 |
Fig. 7 Two-dimensional slice showing the distribution of coherence scales (in kpc) for a velocity field of the same region as in Fig. 5. |
| In the text | |
 |
Fig. 8 Average radial profile for kinetic to thermal energy inside radial shells for four simulated clusters, for the total velocity field (dotted lines) and for the turbulent velocity field reconstructed with our method (solid lines). |
| In the text | |
 |
Fig. 9 Average radial profile of the outer scale for turbulence, Λ(r), for four simulated galaxy clusters. |
| In the text | |
 |
Fig. 10 Top panel: map of gas density for a slice of 100 kpc h-1 through the centre of the major merger cluster H5 (right column) and of the merging cluster H3 (left column). The top row shows the projected average gas density (in [ρ/ρcr,b], where ρcr,b is the critical baryon density), the bottom row shows the projected map of the turbulent diffusion for the same regions (in units of [cm2 s-1]). |
| In the text | |
 |
Fig. 11 Average radial profile of the anisotropy parameter (for the total velocity field, in dashed, or for the turbulent velocity field, in solid) for four simulated galaxy clusters. |
| In the text | |
 |
Fig. 12 Energy spectra of the 3D velocity field for three galaxy clusters (E1, H1 and H5). The dotted lines show the spectra of the total velocity field, the solid lines show the spectra of the turbulent velocity field. The gray lines shows the slope of α = 1 and α = 2/3 to guide the eye. |
| In the text | |
 |
Fig. 13 Gas sloshing in the VIRGO cluster, triggered by a minor merger (Roediger et al. 2011). The images are slices through the centre of the simulation box, showing the absolute value of the total (top panels) and turbulent (lower panels) velocity for the three different resolutions: 2 kpc (LR), 1 kpc (MR) and 0.5 kpc (HR). The colour coding is in [km s-1], each image has sides ~250 × 300 kpc. |
| In the text | |
 |
Fig. 14 Power spectra for the total velocity field (dot-dashed lines) and for the turbulent velocity field (solid lines) for the Virgo simulation at the three resolutions. The spectra are computed for a cubic region with the side of 250 kpc. The x-axis is in unit of 2π/L, where L is the size of the box. The features at k ≥ 50 only present in run LR are an artifact of coarse resolution. |
| In the text | |
 |
Fig. 15 Radial average profiles of the anisotropy parameter, β(r), for the Virgo simulation at three resolutions. The dashed lines are for the total velocity field, the solid lines are for the turbulent velocity field. |
| In the text | |
 |
Fig. 16 Top panels: slices of 1 kpc through the centre of the Virgo run HR, showing the radial component of the turbulent velocity field (left, in [km s-1]) and the tangential one (right, in [km s-1]). Bottom panels: volume-averaged maps of turbulent velocity field (im [km s-1]) for a line of sight of 200 kpc in run HR (left panel) and maps of turbulent diffusion for a slab of 20 kpc (right, in units of [cm2 s-1]). Each image has sides 400 × 500 kpc. |
| In the text | |
 |
Fig. 17 Maps of turbulent velocity module (in units of [km s-1]) for the a slice of 1 kpc centred on the Hydra run (left) and for the volume-weighted projection across 500 kpc (right). Each image has sides 300 × 500 kpc. |
| In the text | |
 |
Fig. 18 Average radial profile of the anisotropy parameters of turbulent motions in the Hydra A simulation. We show as a dashed line the profile of the total velocity field, and as a solid line the profile of the turbulent velocity field. |
| In the text | |
 |
Fig. 19 Power spectra for the total velocity field (thin upper lines) and for the turbulent velocity field (lower thick lines) for the same region as in Fig. 17. The different colour-coding shows the spectra for the component of velocities along the three axes of the simulation (direction “Y” is the propagation axis of the jet). |
| In the text | |
 |
Fig. 20 Map of average turbulent diffusion (in [cm2 s-1]) for the projection along 500 kpc in the Hydra A run. The size of the image is the same as in Fig. 17. |
| In the text | |
 |
Fig. 21 Volume (left) and mass (right) distribution of turbulent diffusion for all runs studied in this paper. We show in red the turbulent diffusion from the AGN-jet of Hydra, in blue the distributions of turbulent diffusion from the sloshing core in Virgo (we plot with different line-styles the distributions at different resolution, as in Sect. 3.2), and in black the turbulent diffusion from cosmological clusters (the different line-styles are for each different object studied in Sect. 3.1, while the shadowed region shows the uncertainty in the overall cluster sample). |
| In the text | |
 |
Fig. 22 Combined 3D power spectra from three clusters simulated with ENZO (Sect. 3.1), for the FLASH simulations of the sloshing cool-core in the Virgo cluster (Sect. 3.2) and of the AGN-jet in the Hydra cluster (Sect. 3.3). All spectra were normalised to have to obtain the same power at 200 kpc, while the wave numbers k are the physical ones of each simulation. |
| In the text | |
 |
Fig. A.1 Scaling between the CPU time employed by our algorithm and the total number of cells in the computational volume for four different resolution of the Virgo HR run (Sect. 3.2). Tests run on an Intel Quad-Core Xeon E5345 Linux Cluster. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.