| Issue |
A&A
Volume 533, September 2011
|
|
|---|---|---|
| Article Number | A73 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201117206 | |
| Published online | 30 August 2011 | |
Dissecting a hot molecular core: the case of G31.41+0.31⋆
1
Osservatorio Astrofisico di Arcetri, INAF,
Largo E. Fermi 5, 50125
Firenze,
Italy
e-mail: cesa@arcetri.astro.it
2
Harvard-Smithsonian Center for Astrophysics,
Cambridge, MA
02138,
USA
e-mail: qzhang@cfa.harvard.edu
3
Max-Planck-Institut für Astronomie, Königstuhl 17, 69117
Heidelberg,
Germany
e-mail: beuther@mpia-hd.mpg.de
4
Department of Physics and Astronomy, University of
Victoria, 3800 Finnerty Road,
Victoria, BC
V8P 5C2,
Canada
e-mail: cassandra.fallscheer@nrc-cnrc.gc.ca
Received:
6
May
2011
Accepted:
26
June
2011
Context. The role of disks in the formation of high-mass stars is still a matter of debate but the detection of circumstellar disks around O-type stars would have a profound impact on high-mass star formation theories.
Aims. We made a detailed observational analysis of a well known hot molecular core lying in the high-mass star-forming region G31.41+0.31. This core is believed to contain deeply embedded massive stars and presents a velocity gradient that has been interpreted either as rotation or as expansion, depending on the authors. Our aim was to shed light on this question and possibly prepare the ground for higher resolution ALMA observations, which could directly detect circumstellar disks around the embedded massive stars.
Methods. Observations at sub-arcsecond resolution were performed with the Submillimeter Array in methyl cyanide, a typical hot molecular core tracer, and 12CO and 13CO, well known outflow tracers. We also obtained sensitive continuum maps at 1.3 mm.
Results. Our findings confirm the existence of a sharp velocity gradient across the core, but cannot confirm the existence of a bipolar outflow perpendicular to it. The improved angular resolution and sampling of the uv plane allow us to attain higher quality channel maps of the CH3CN lines with respect to previous studies and thus significantly improve our knowledge of the structure and kinematics of the hot molecular core.
Conclusions. While no conclusive argument can rule out any of the two interpretations (rotation or expansion) proposed to explain the velocity gradient observed in the core, in our opinion the observational evidence collected so far indicates the rotating toroid as the most likely scenario. The outflow hypothesis appears less plausible, because the dynamical time scale is too short compared to that needed to form species such as CH3CN, and the mass loss and momentum rates estimated from our measurements appear too high.
Key words: stars: formation / ISM: individual objects: G31.41+0.31 / ISM: molecules / ISM: jets and outflows / accretion, accretion disks
© ESO, 2011
1. Introduction
High-mass stars are usually defined as those exceeding ~8 M⊙, based on the fact that stars above this mass limit do not have a pre-main sequence phase (Palla & Stahler 1993). This means that accretion is ongoing until the star ignites hydrogen burning and reaches the zero-age main sequence (ZAMS). At this point the strong radiation pressure may halt and even reverse infall and thus stop further growth of the stellar mass. This led to the so-called “radiation pressure problem”. Recent studies have demonstrated that this limitation holds only in spherical symmetry. As first envisioned by Nakano (1987) and recently demonstrated by Krumholz et al. (2009) and Kuiper et al. (2010), accretion through a circumstellar disk can explain the formation of stars up to the upper limit of the initial mass function, by allowing part of the photons to escape along the disk axis and boosting the ram pressure of the accreting gas through the small disk solid angle. It also appears that the powerful ionizing fluxes from these OB-type stars are not sufficient to destroy the disk, which eventually turns into an ionized, rotating accretion flow close to the star (Sollins et al. 2005; Keto 2007).
For these reasons it seems established that circumstellar accretion disks play a crucial role in the formation of all stars and not only solar-type stars. This theoretical result contrasts with the limited observational evidence of disks in high-mass (proto)stars. Only in recent years the number of disk candidates associated with luminous young stellar objects (YSOs) has significantly increased, mostly owing to the improvement of (sub)millimeter interferometers in terms of angular resolution and sensitivity. The main problems that one has to face in this type of search are the large distances to the sources (typically a few kpc) and the confusion caused by stellar crowding (OB-type stars form in clusters). These factors may explain the failure to detect disks in O-type stars, as opposed to the number of detections obtained for B-type stars (Cesaroni et al. 2007). In association with the most luminous YSOs one finds only huge (≲0.1 pc), massive (a few 100 M⊙) cores, with velocity gradients suggesting rotation. These objects, named “toroids”, are likely non-equilibrium structures, because the ratio between the accretion time scale and the rotation period is shorter than for disks: this implies that the toroid does not have enough time to adjust its structure to the new fresh material falling onto it (Cesaroni et al. 2007; Beltrán et al. 2011).
With this in mind, one can see that understanding the formation of the most massive stars (>20 M⊙) may benefit from a detailed investigation of toroids, also because these objects might be hosting true circumstellar disks in their interiors. Moreover, their mere existence may set tighter constraints on theoretical models. Despite the number of candidates, the existence of rotating toroids is still a matter of debate. What is questioned is the nature of the velocity gradient, which is sometimes interpreted as expansion instead of rotation (see e.g. Gibb et al. 2004; Araya et al. 2008, and references therein), thus suggesting that one might be seeing a compact bipolar outflow rather than a rotating core. In an attempt to distinguish between these two possibilities and more in general to shed light on these intriguing objects, we have focused our attention on one of the best examples: the hot molecular core (HMC) G31.41+0.31 (hereafter G31.41).
This prototypical HMC is located at a kinematic distance of 7.9 kpc and was originally imaged in the high-excitation (4, 4) inversion transition of ammonia (Cesaroni et al. 1994a) and in the (6–5) rotational transitions of methyl cyanide (CH3CN; Cesaroni et al. 1994b). The latter showed the existence of a striking velocity gradient (centered at an LSR velocity of ~96.5 km s-1) across the core in the NE–SW direction, already suggested by the distribution and velocities of OH masers (Gaume & Mutel 1987). Follow-up interferometric observations with better angular resolution and in high-energy tracers have confirmed this result and revealed the presence of deeply embedded YSOs, which in all likelihood explains the temperature increase toward the core center (Beltrán et al. 2004, 2005, hereafter BEL04 and BEL05; Cesaroni et al. 2010). The G31.41 HMC is separated by ~5″ from an ultracompact (UC) Hii region, and overlaps in projection on a diffuse halo of free-free emission, possibly associated with the UC Hii region itself (see e.g. Fig. 2c of Cesaroni et al. 1998). The SPITZER/GLIMPSE images (Benjamin et al. 2003) show that the HMC lies in a complex pc-scale region where both extended emission and multiple stellar sources are detected. All these facts complicate the interpretation of the HMC structure and its relationship with the molecular surroundings and call for additional high-quality observations.
An important aspect of a proper interpretation of the velocity gradient observed in the HMC is the existence of an associated molecular outflow. A reasonable assumption, suggested by the analogy with low-mass YSOs, is that a disk actively undergoing accretion must be associated with a bipolar jet/outflow expanding along the disk rotation axis. Therefore, a way to distinguish between the two interpretations of the HMC velocity gradient (expansion vs rotation) is to search for a molecular outflow perpendicular to the gradient. Previous interferometric observations in the 13CO(1–0) line have suggested the presence of a collimated outflow directed SE–NW (Olmi et al. 1996), but the poor uv coverage, especially on the shortest baselines, makes this result questionable. We have therefore conducted new interferometric observations at 1.3 mm with the Submillimeter Array (SMA) in the typical HMC tracer CH3CN and in standard outflow tracers such as 12CO and 13CO. In order to be sensitive to extended structures filtered out by the interferometer, we have also mapped the region over ~2′ with the IRAM 30-m telescope. The observational details are given in Sect. 2, while the results are illustrated in Sect. 3 and discussed in Sect. 4. Finally, the conclusions are drawn in Sect. 5.
2. Observations and data reduction
Our observations have been performed with the SMA interferometer and IRAM 30-m telescope. The former was used with the aim to image the 12CO and 13CO (2–1) lines and the CH3CN(12–11) transitions, but the 2 GHz bandwidth in both the LSB and USB allowed us to cover a much larger number of lines from a plethora of different molecules. Despite the richness of the spectrum, in this article we will present only the results obtained for the above mentioned lines, which are the best tracers for our purposes. The 30-m telescope was used to fill the zero-spacing of the SMA maps in the 12CO and 13CO lines and thus help establishing the morphology of the emission at all velocities and on all scales. Technical details of the observations are given in the next two sections.
Parameters of SMA images.
2.1. SMA interferometer
Observations of G31.41 were carried out with the SMA1 (Ho et al. 1996) in the 230 GHz band in
the compact and extended configurations. The correlator was configured to a uniform
spectral resolution of 0.41 MHz (0.6 km s-1) over the entire 4 GHz spectral
window. With IF frequencies of 4 to 6 GHz, the observations covered the rest frequencies
from 219.3–221.3 GHz in the lower side band (LSB), and 229.3–231.3 GHz in the upper side
band (USB). The compact configuration data were obtained on 2007 July 09 with eight
antennas. With 225 GHz zenith opacity of 0.05 to 0.1, the typical double side-band system
temperatures were around 200 K. The very extended data were obtained on 2007 May 21 with
seven antennas. At 225 GHz the zenith opacity was about 0.2 and the double side-band
system temperatures were around 400 K. For both tracks, we used Vesta and 3C 273 for flux
and bandpass calibrations. The time-dependent gains were calibrated using 1751 + 096 and
1830 + 063. The phase center of the observations was
α(J2000) = 18h47m34 315,
δ(J2000) = –01°12′45
315,
δ(J2000) = –01°12′45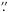 9.
The primary beam of the 6-m antennas is about 55″ at the operating frequencies.
9.
The primary beam of the 6-m antennas is about 55″ at the operating frequencies.
The visibility data were calibrated in the IDL superset MIR2 and MIRIAD (Sault et al. 2004), and were exported to MIRIAD format for imaging. The projected baselines of the combined visibilities from both configurations range from 12 m to 500 m. The continuum data were constructed from line free channels and the continuum was subtracted from the line uv data.
Continuum and channel maps of the CH3CN and
CH313CN lines were created and cleaned in MIRIAD by weighting the
data with “robust = 0” to find a compromise between angular resolution and sensitivity to
extended structures. The resulting synthesized beam is approximately
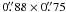 ,
with PA 53°. The 1σ rms is 5.8 mJy/beam in the continuum, and 89 mJy/beam
in the line images with 0.6 km s-1 spectral resolution. The 12CO and
13CO (2–1) line data were imaged in a similar fashion, but using natural
weighting to enhance extended emission. The resulting synthesized beam is
,
with PA 53°. The 1σ rms is 5.8 mJy/beam in the continuum, and 89 mJy/beam
in the line images with 0.6 km s-1 spectral resolution. The 12CO and
13CO (2–1) line data were imaged in a similar fashion, but using natural
weighting to enhance extended emission. The resulting synthesized beam is
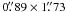 with PA 53°. The 1σ rms in the 1 km s-1 channel maps is
50 mJy/beam.
with PA 53°. The 1σ rms in the 1 km s-1 channel maps is
50 mJy/beam.
The 12CO and 13CO data were also combined with the 30-m data (see
Sect. 2.2) to recover extended structure resolved
out by the interferometer. The single-dish maps were Fourier-transformed and then suitably
sampled in the uv domain, then merged with the SMA data. Finally natural weighted maps
were created using the same procedure as for the non-merged data. The resulting
synthesized beam is 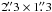 with PA 63° and the 1σ rms in the 1 km s-1 channel maps is
66 mJy/beam.
with PA 63° and the 1σ rms in the 1 km s-1 channel maps is
66 mJy/beam.
2.2. IRAM 30-m telescope
Maps of G31.41 with the 30-m telescope were made on November 4th, 2007. The HERA
multi-beam receiver was used to cover a region of 2′ × 2′ centered on
α(J2000) = 18h47m34 3
and δ(J2000) = –01°12′45
3
and δ(J2000) = –01°12′45 9,
using the on-the-fly-mode. To prevent systematic effects, the region was scanned
alternatively along right ascension and declination, and all the data were eventually
averaged to obtain the final map. The receiver was tuned to the frequencies of the
12CO(2–1) (HERA1) and 13CO(2–1) (HERA2) lines, which were hence
observed simultaneously. Both lines were covered with the VESPA autocorrelator, with
0.4 km s-1 spectral resolution. The reference position used for all maps was
α(J2000) = 18h45m15
9,
using the on-the-fly-mode. To prevent systematic effects, the region was scanned
alternatively along right ascension and declination, and all the data were eventually
averaged to obtain the final map. The receiver was tuned to the frequencies of the
12CO(2–1) (HERA1) and 13CO(2–1) (HERA2) lines, which were hence
observed simultaneously. Both lines were covered with the VESPA autocorrelator, with
0.4 km s-1 spectral resolution. The reference position used for all maps was
α(J2000) = 18h45m15 24
and δ(J2000) = –00°55′56
24
and δ(J2000) = –00°55′56 09.
This was carefully chosen from CO surveys such as that by Sanders et al. (1986), and checked to be free of emission in the
observed lines. Data were reduced with the program CLASS of the GILDAS package3 and channel maps with 1 km s-1 resolution
were created.
09.
This was carefully chosen from CO surveys such as that by Sanders et al. (1986), and checked to be free of emission in the
observed lines. Data were reduced with the program CLASS of the GILDAS package3 and channel maps with 1 km s-1 resolution
were created.
3. Results
In the following we illustrate the results obtained, first for the typical hot core tracers (continuum, CH3CN, and CH313CN lines4) and then for the outflow tracers (12CO and isotopomers).
3.1. Core tracers
Compared to previous Plateau de Bure interferometer (PdBI) observations in the same lines
(BEL04, BEL05), our SMA observations benefit from a better uv coverage and more circular
beam, thus allowing us to attain sub-arcsec resolution in all directions (see Table 1; for comparison, the synthesized beam of the
PdBI images was 1 1 × 0
1 × 0 5
with PA = 189°).
5
with PA = 189°).
 |
Fig. 1 Spectra obtained by integrating the line emission over the whole core. Top: ground-state K-components of the J = 12 → 11 transition of CH3CN (numbers above the spectrum) and of the CH313CN isotopomer (numbers below the spectrum). Note how most K-lines are blended with each other and/or with lines of other molecules. Middle: vibrationally excited (v8 = 1) lines of CH3CN. The K, l quantum numbers of the transitions are indicated above the spectrum. Bottom: ground state K = 3 component. The dotted lines mark the velocity ranges used to produce the maps in Figs. 2 and 3. |
To give an idea of the complexity of the line emission from the G31.41 HMC, in Fig. 1 we show a spectrum covering all CH3CN(12–11) transitions with K ≤ 10, obtained by integrating the emission over the whole core. For an estimate of the CH3CN and CH313CN line parameters we refer to the study of BEL05 (see their Table 4). We did not attempt the identification of all lines detected, because this goes beyond the purposes of the present study. However, we note that a number of CH3CN and CH313CN transitions are heavily blended with each other and/or with other lines. Only the CH3CN K = 2, 3, 4, 8 and the CH313CN K = 2, 6 components appear free enough of contamination to be used for a detailed investigation. A similar consideration holds for the vibrationally excited (v8 = 1) lines, shown in the same figure. Here, only the (K = 3, l = −1) and (K = 6l = 1) transitions are clearly detected and sufficiently separated from other lines to be considered for our study. Note that our bandwidth covers all v8 = 1 lines down to the (11, –1) at 220788.016 MHz, but the lines below 221.19 GHz are too weak or too blended: this is the reason why the CH3CN(12–11) v8 = 1 spectrum in Fig. 1 is displayed only above this frequency.
 |
Fig. 2 Maps of the line and continuum emission toward the G31.41 HMC. The line maps have
been obtained by averaging the emission under the whole line profile, namely from
88.9 km s-1 to 103.9 km s-1 (see Fig. 1, bottom). The tracer used is indicated in the
top right of each panel. The two white points mark the positions of the
free-free-continuum sources detected by Cesaroni et al. (2010). The contour levels start from 0.072 Jy/beam and increase
in steps of 0.12 Jy/beam for all line maps, and range from 0.035 Jy/beam to
1.785 Jy/beam in steps of 0.175 Jy/beam for the continuum map. Offsets are measured
with respect to the phase center
α(J2000) = 18h47m34 |
Continuum parameters.
 |
Fig. 3 Same as Fig. 2, with the line maps obtained by averaging the emission from 95.5 km s-1 to 97.3 km s-1 (see Fig. 1, bottom). Contour levels start from 0.15 Jy/beam and increase in steps of 0.2 Jy/beam for all line maps, and range from 0.035 Jy/beam to 1.785 Jy/beam in steps of 0.175 Jy/beam for the continuum map. |
Figure 2 shows continuum and line emission maps obtained by averaging the emission under the line and Table 2 lists the main parameters of the continuum emission. The most obvious feature is that the maps of all tracers are slightly elongated in the NE–SW direction, suggesting that the distribution of the molecular gas is flattened approximately in the direction defined by the two free-free continuum sources detected by Cesaroni et al. (2010).
From the same figure one can also note that the high-energy transitions and the isotopomer emission peak approximately at the same position as the continuum, whereas the maximum of the low-energy K = 2 component appears to be slightly offset from it. Such an offset is evident for all components with K ≤ 6, while the K = 7 and 8 line maps look more circular and peak at the core center. Nothing can be said about the K = 9 transition, which is heavily blended with the 13CO(2–1) line. A plausible interpretation is that the opacity decreases with increasing excitation energy. In confirmation of that, one can see that this effect is even more prominent in the maps obtained by integrating the line emission over a narrow velocity range around the systemic LSR velocity, i.e. from 95.5 to 97.3 km s-1(see Fig. 3). Now, the K = 2 emission clearly splits into two peaks located on opposite sides with respect to the continuum and also the corresponding CH313CN line map shows a similar pattern. We conclude that opacity plays a crucial role in the CH3CN emission of this HMC and cannot be neglected in the analysis of the line emission.
A qualitative impression of the CH3CN emission can be obtained from visual inspection of the channel maps shown in Fig. 4. In order to improve the signal-to-noise, such maps have been obtained by averaging the emission in the K = 2, 3, and 4 components. These transitions have been chosen because they do not seem to be affected by significant contamination by other lines and have comparable excitation energies, which suggests that they are likely tracing the same gas.
 |
Fig. 4 Channel maps of the CH3CN(12–11) emission obtained by averaging the K = 2, 3, and 4 components. The number in the top left of each panel gives the corresponding LSR velocity. The values of the contour levels are indicated by the tick marks in the intensity scale to the right. The cross denotes the phase center. The ellipse in the bottom right of the last panel is the full-width-at-half power of the synthesized beam. |
Clearly, the emission gradually drifts from SW to NE with increasing velocity and outlines an “8-shaped” pattern close to the systemic velocity of ~96.5 km s-1. These characteristics resemble those observed in rotating circumstellar disks around low-mass stars (see e.g. Fig. 1 of Simon et al. 2001). We will discuss this problem in Sect. 4.3. A more quantitative analysis of the velocity field traced by the CH3CN emission is attained – in analogy with the previous study by BEL04 – by fitting the K = 0 to 4 components simultaneously, after fixing their separations in frequency to the laboratory values and forcing the line widths to be equal5. This procedure improves the quality of the fit with respect to fitting a single K line, but we stress that a similar result is obtained by fitting a single Gaussian to any of the unblended K components. A map of the LSR velocity is presented in Fig. 5, which confirms the existence of a clear velocity gradient directed approximately NE–SW (PA ≃ 68°) and roughly centered on the peak of the continuum emission. A different and more detailed representation of the same velocity gradient is presented in Fig. 6, where the position-velocity plots along the velocity gradient (PA = 68°) and perpendicular to it (PA = –22°) are shown for three different lines of CH3CN and CH313CN. Note that to enhance the signal-to-noise ratio in the plots, we have averaged the emission along the direction perpendicular to the cut along which the position–velocity plot is calculated. As expected, no velocity trend is seen in the plots along PA = –22°.
 |
Fig. 5 Overlay of the map of the 1.3 mm continuum emission (contours) on that of the CH3CN(12–11) line velocity (color scale). Contour levels range from 0.1 to 2 in steps of 0.2 Jy/beam. Offsets are measured with respect to the phase center. The two white dots denote the free-free continuum sources detected by Cesaroni et al. (2010). The synthesized beam is shown in the bottom left. |
 |
Fig. 6 Position-velocity plots of along PA = 68° (left panels) and –22° (right panels) for three different lines (indicated in each panel). Offsets are measured with respect to the phase center. Contour levels start from 0.12 Jy/beam and increase in steps of 0.12 Jy/beam. The cross in the bottom left of each box denotes the angular and spectral resolutions. |
It is worth comparing our results to those of BEL04. With respect to their Fig. 2e, our Fig. 5 presents a slightly broader velocity range (~5.5 km s-1 instead of ~4 km s-1), over a larger region (~3″ instead of ~2″). These differences are probably caused by the different angular resolutions and sensitivities. A more evident discrepancy appears in the map of the CH3CN(12–11) emission, i.e. our Fig. 3 and their Fig. 1. In the former, the K = 2 emission appears to outline two peaks located approximately to the NW and SE with respect to the core center, whereas in Fig. 1 of BEL04 the peaks lie to the E and W. However, one should keep in mind that this map was obtained integrating the emission under the K = 0, 1, and 2 components. Moreover, we have averaged the emission over a narrow interval around the peak, whereas BEL04 integrated under the whole line profile. Finally, the angular resolution is different for the two data sets. In order to attain a more consistent comparison, we have reconstructed our maps using the same clean beam as BEL04 and integrating over the same frequency interval. The new map (shown in Fig. 7) is now much more similar to that of BEL04, demonstrating how the apparent morphology of the emission may depend significantly on the resolution. Given the larger number of antennas and more circular beam, we believe that our SMA images reproduce the structure of the emission more faithfully than the old maps by BEL04 and BEL05.
 |
Fig. 7 Map of the CH3CN(12–11) emission obtained by averaging the emission
under the K = 0 and 1 components. The image has been reconstructed
with a clean beam (ellipse in the bottom right) equal to that of the images of
BEL04, i.e. 1 |
3.2. Outflow tracers
One of the purposes of the present study was to compare the structure and kinematics of the HMC with those of a possible bipolar outflow associated with it. The existence of such an outflow had been suggested by Olmi et al. (1996), whose Plateau de Bure images in the 13CO(1–0) line seem to reveal two narrow lobes oriented SE–NW (see their Fig. 5). With this in mind, we have imaged G31.41 in the 12CO and 13CO J = 2–1 rotational transitions with both the SMA and 30-m IRAM telescope, to recover also the emission filtered out by the interferometer. Figure 8 shows channel maps in the 12CO(2–1) line and effectively demonstrates the complexity of the region. Only at high velocities the emission appears quite compact, whereas close to the systemic velocity the structure presents a complicated pattern. In particular, from 95 to 100 km s-1 the emission is uniformly distributed over an extended region: this means that the line opacity is sufficiently high that one can see only the surface of the cloud at these velocities, consistent with the relatively low values of the brightness temperature (10–15 K).
 |
Fig. 8 Channel maps in the 12CO(2–1) line obtained by combining single-dish (IRAM 30-m) and interferometric (SMA) data. The number in the top left of each panel gives the corresponding LSR velocity. The values of the contour levels are indicated by the tick marks in the intensity scale to the right. The ellipse in the bottom right of the last panel is the full-width-at-half power of the resulting instrumental beam. |
One arrives at the same conclusion by looking at Fig. 9, where a comparison is shown of the single-dish spectra obtained by averaging the emission of three different CO isotopomers over a square region, 30″ in size, centered at the HMC position. While the 12CO and 13CO profiles are double-peaked with a dip at ~97 km s-1, the optically thin(ner) C17O(2–1) line (Cesaroni, unpublished data) is Gaussian and peaks right at the velocity of the dip in the other two lines. This is an indication of self-absorption and thus of high optical depth in the 12CO and 13CO transitions.
An apparent feature of the 12CO(2–1) profile is the presence of broad wings. From Fig. 8 one sees that this high-velocity emission originates from 2–3 compact structures located roughly to the E (red-shifted) and W (blue-shifted) of the HMC. Whether this morphology is consistent with that of a bipolar outflow cannot be trivially decided on the basis of the evidence presented so far and requires a detailed analysis and discussion that we postpone to Sect. 4.2.
4. Discussion
The main purpose of the present study is to shed light on the nature of the velocity gradient observed in this HMC (e.g. Fig. 5). As already mentioned, BEL04 and BEL05 favored the rotating toroid scenario. In contrast, other authors (Gibb et al. 2004; Araya et al. 2008) preferred the outflow interpretation, thus posing a problem that we wish to address with our new SMA data.
Besides the (possible) existence of rotation and/or outflow, the situation in G31.41 is complicated by the existence of infall, detected by Girart et al. (2009) as an inverse P-Cygni profile of the C34S(7–6) line observed with the SMA. Therefore, before making a comparative discussion of the different models for the velocity gradient, we need to verify to what extent our CH3CN measurements may be affected by infall.
4.1. Evidence for infall
As already discussed in Sect. 3.2, Fig. 9 clearly reveals that the 12CO and 13CO (2–1) lines are affected by self-absorption. However, only a weak asymmetry is seen in the line profile, with the red-shifted peak being slightly more prominent than the blue-shifted one. If such an asymmetry were caused by infalling gas, the blue-shifted peak should be stronger; hence we can conclude that no obvious evidence of infall is present on the large scale (30″ or 1.1 pc) over which the spectra in Fig. 9 have been calculated. It thus seems that the infall detected by Girart et al. (2009) occurs close to the HMC. Do we see any evidence of this in the HMC tracers that we observed? All CH3CN and CH313CN (12–11) lines shown in Fig. 1 have Gaussian profiles with no hint of (self-)absorption, unlike the C34S(7–6) line observed by Girart and collaborators. However, this is not surprising, because both the excitation energy and critical density of the latter (49 K and ~ 107 cm-3) are less than those of the former transitions (58–926 K and ≳ 108 cm-3). This implies that the C34S(7–6) line traces large radii of the HMC that are characterized by a relatively low temperature, and thus absorb the hot continuum photons emitted from the central region of the core. This effect does not apply to the CH3CN(12–11) transitions, because these arise from a smaller hot shell, whose excitation temperature is much more similar to the brightness temperature of the dust continuum.
Despite the apparent lack of evidence for infall in the CH3CN transitions, we have attempted a more detailed analysis to see whether some hint of asymmetry was present in the line profiles. The idea is that if the line shape is skewed toward the blue (although very weakly), a Gaussian fit should give a peak velocity less than the systemic velocity. With this in mind, in Fig. 10 we plot the line first moment (solid curves) as a function of distance from the HMC center along an axis with PA = –22°, i.e. perpendicular to the direction of the velocity gradient. For the sake of completeness, also the line zero moment (integrated intensity) along the same direction is shown (dashed curves). This is done for the K = 2, 3, 4, and 8 components of the ground-state transition and the (3,–1) line of CH3CN v8 = 1. Evidently, up to K = 8 the line velocity attains a minimum value close to the HMC center, whereas this minimum is not seen in the v8 = 1 line. This proves that the lower energy lines are slightly skewed to the blue toward the bright continuum peak, as expected for weak red-shifted absorption caused by infall. This effect is not seen in the highest energy line, coming from the innermost, hottest layers of the core.
 |
Fig. 9 Spectra of the 12CO( (solid histogram), 13CO (dashed), and C17O (dotted; Cesaroni, unpublished data) (2–1) lines obtained by averaging the emission over a square region 30″ in size, centered on the HMC. The data have been taken with the IRAM 30-m telescope. |
 |
Fig. 10 Solid curves represent the first moments of several CH3CN(12–11)
components (indicated in the top left of each panel) estimated along a cut through
the continuum peak
(α(J2000) = 18h47m34 |
We conclude that some of the CH3CN(12–11) lines are affected by red-shifted absorption, although in a much less prominent way than the C34S(7–6) line measured by Girart et al. (2009). Note that this absorption causes only a marginal shift in the line velocity, of ~0.5 km s-1, and is going to have only negligible effects on our study of the velocity shift of ~5 km s-1 observed across the HMC.
4.2. The NE–SW velocity gradient
The existence of a velocity gradient in the CH3CN lines is proved beyond any doubt by Figs. 4–6. The high angular resolution allows us to establish that the velocity is shifting smoothly across the core, and one can reasonably exclude that this shift is caused by two unresolved velocity components (sub-cores) with different velocities. The question we intend to address here is whether this velocity gradient is caused by rotation of the HMC about a SE–NW axis, as hypothesized by BEL04, or to expansion in a bipolar outflow oriented NE–SW, as proposed by Gibb et al. (2004) and Araya et al. (2008). How can one distinguish between these two scenarios? As explained in Sect. 1, it is common belief that disks and outflows are tightly associated, with the latter being ejected along the rotation axis of the former. Therefore, if the velocity gradient in the G31.41 HMC is caused by rotation, one would expect to detect a bipolar outflow perpendicular to it, on a larger scale. In contrast, if the velocity gradient is tracing the “root” of a bipolar outflow, on a larger scale this outflow should become clearly visible along the same direction defined by the (small-scale) velocity gradient. Our combined single dish and interferometric observations in typical outflow tracers such as 12CO and 13CO should hence be well suited for our purposes, given the sensitivity to both small (a few arcsec) and large (a couple of arcmin) scales.
The results reported in Sect. 3.2 are quite ambiguous. The blue- and red-shifted 12CO and 13CO gas is oriented like the CH3CN velocity gradient, suggesting that the two are manifestations of the same phenomenon. The existence of a NE–SW bipolarity in the 12CO emission can be appreciated in Fig. 11, where we show the blue- and red-shifted 12CO(2–1) emission in pairs of channels equally offset from the systemic velocity. One is tempted to conclude that 12CO is indeed associated with a bipolar outflow, whose densest component is traced by the CH3CN emission. However, this bipolarity in the CO maps is seen only on a small scale, because no evidence of high-velocity CO emission is found beyond ~5″ (i.e. 0.2 pc) from the HMC, implying an unusually small size for a typical outflow associated with a high-mass star-forming region. This casts some doubt on the outflow interpretation. Below we discuss the two hypotheses (outflow and toroid) in detail.
4.2.1. Bipolar outflow
The outflow hypothesis is supported by a couple of facts. First of all, if the CH3CN gradient is caused by a rotating toroid, one expects to find a bipolar outflow perpendicular to it, but this is not seen in our maps. Second, the position velocity plot of the 12CO emission in the direction of the CH3CN velocity gradient suggests that the gas velocity is proportional to the distance from the star (as discussed later in Sect. 4.2.2), consistent with the Hubble-law expansion observed in molecular outflows from YSOs.
 |
Fig. 11 Channel maps of the 12CO(2–1) line emission observed with the SMA. Each box contains pairs of maps corresponding to the blue- (solid contours) and red-shifted (dashed) emission at the same velocity offset (in absolute value) from the the systemic velocity (~96.5 km s-1). The corresponding LSR velocities are indicated in the top right of the box. Contour levels increase from 0.5 Jy/beam in steps of 0.5 Jy/beam. Also shown is a map of the CH3CN(12–11) K = 4 line emission averaged over the range 95.2–96.7 km s-1. The ellipse in the bottom left denotes the synthesized beam of the observations. |
In order to check the plausibility of the outflow scenario, we have calculated the
outflow parameters from the CH3CN, CH313CN,
12CO, and 13CO lines, in the latter two cases using the combined
30-m and SMA data. These are given in Table 3,
where we report the mass of the outflow, M, the momentum,
P, the energy, E, and the corresponding rates
obtained by dividing the previous quantities by the dynamical time scale (see below). In
practice,
M = ∑ imi,
P = ∑ imiVi,
and 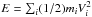 , where the sums
are extended over only those channels, i, falling in the velocity
ranges given in the footnotes of Table 3, and
mi is the mass moving with velocity
Vi relative to the systemic velocity.
This mass is computed by integrating the line emission inside the regions corresponding
to the 5σ level of the blue- and red-shifted emission. Note that the
velocity intervals were chosen by inspecting the channel maps and selecting only those
channels where the emission was sufficiently strong and at the same time not affected by
the missing flux problem close to the systemic velocity. In our calculations we assume a
temperature of ~100 K for both molecules, intermediate between the peak
brightness temperature (77 K) of the 12CO(2–1) line and the rotational
temperature (164 K) estimated by BEL05 from the CH313CN(6–5),
CH313CN(12–11), and
CH3CN(6–5) v8 = 1 lines (see their Fig. 6).
While this temperature may seem too high for the outflow component traced by the CO
isotopomers, assuming 50 K instead of 100 K would reduce the outflow parameters by only
a factor 0.6. The abundance of CH3CN and 12CO relative to
H2 are assumed equal to 10-8 and 10-4 respectively
(see e.g. Van Dishoek et al. 1993), while the
isotopic ratios 12CO/13CO and
CH3CN/CH313CN are taken equal to 50 after Wilson
& Rood (1994), for a galactocentric
distance of 4.5 kpc. The dynamical time scale of the outflow,
tdyn ≃ 4 × 103 yr, is calculated from the
maximum size (~0.12 pc) and velocity (~30 km s-1) of the
12CO lobes. Note that the (unknown) inclination of the outflow with respect
to the line of sight has not been taken into account in our estimates.
, where the sums
are extended over only those channels, i, falling in the velocity
ranges given in the footnotes of Table 3, and
mi is the mass moving with velocity
Vi relative to the systemic velocity.
This mass is computed by integrating the line emission inside the regions corresponding
to the 5σ level of the blue- and red-shifted emission. Note that the
velocity intervals were chosen by inspecting the channel maps and selecting only those
channels where the emission was sufficiently strong and at the same time not affected by
the missing flux problem close to the systemic velocity. In our calculations we assume a
temperature of ~100 K for both molecules, intermediate between the peak
brightness temperature (77 K) of the 12CO(2–1) line and the rotational
temperature (164 K) estimated by BEL05 from the CH313CN(6–5),
CH313CN(12–11), and
CH3CN(6–5) v8 = 1 lines (see their Fig. 6).
While this temperature may seem too high for the outflow component traced by the CO
isotopomers, assuming 50 K instead of 100 K would reduce the outflow parameters by only
a factor 0.6. The abundance of CH3CN and 12CO relative to
H2 are assumed equal to 10-8 and 10-4 respectively
(see e.g. Van Dishoek et al. 1993), while the
isotopic ratios 12CO/13CO and
CH3CN/CH313CN are taken equal to 50 after Wilson
& Rood (1994), for a galactocentric
distance of 4.5 kpc. The dynamical time scale of the outflow,
tdyn ≃ 4 × 103 yr, is calculated from the
maximum size (~0.12 pc) and velocity (~30 km s-1) of the
12CO lobes. Note that the (unknown) inclination of the outflow with respect
to the line of sight has not been taken into account in our estimates.
Outflow parameters calculated from different lines.
From Table 3 one notes that the values increase with decreasing abundance of the molecule. This can be explained in terms of decreasing optical depth, because higher opacities lead to an underestimate of the column density and hence of the mass. Indeed, from the ratio between the 12CO and 13CO emission in the line wings one derives opacities as high as ~30 for 12CO. Therefore, the most reliable estimates should be those obtained from CH313CN. These depend significantly on the CH3CN abundance, which is known to present considerable variations in molecular clouds. However, the value assumed in our calculations is one of the highest found in the literature and we therefore believe that our estimates are likely to be lower limits. This leads us to another consideration. Our estimates are very close to the largest outflow parameters ever measured (see e.g. López-Sepulcre et al. 2009; Wu et al. 2004), corresponding to a YSO powering the outflow of at least ~105 L⊙. More precisely, using Wu et al. (2004) relationship between bolometric luminosity (Lbol) of the powering source and outflow momentum rate, from the value in Table 3 one obtains Lbol = 6 × 106 L⊙. This is much higher than the luminosity estimated for the HMC (~105 L⊙) by Osorio et al. (2009) and that obtained from the corresponding IRAS fluxes (2.6 × 105 L⊙; see Cesaroni et al. 1994a). Moreover, the momentum rate of 0.3 M⊙ km s-1 yr-1 is an order of magnitude higher than that estimated by Cesaroni et al. (2010) from VLA observations of the free-free continuum emission (~0.03–0.06 M⊙ km s-1 yr-1).
It is also worth noting that the velocity gradient in G31.41 seems to involve the whole core and not only the gas emitting in the line wings. Usually, in outflow sources the emission close to the systemic velocity – i.e. that inside the FWHM of the line – traces the molecular core; in contrast, in G31.41 most of the CH3CN emission is affected by the velocity gradient, as one can see from the channel maps in Fig. 4, where only emission over a limited velocity range (~2–3 km s-1) appears to arise from the central region. As discussed below in Sect. 4.3, this situation is reminiscent of that observed in circumstellar disks around lower-mass YSOs. Our estimates of the outflow parameters based only on the line-wing emission are likely lower limits, which makes the case of G31.41 even more extreme compared to typical outflows.
In conclusion, the outflow hypothesis seems to yield values for the outflow parameters that are too high. In addition, one should note that the typical parameters given in studies such as those quoted above refer to single-dish observations of pc-scale flows, an order of magnitude higher than that observed in G31.41. Although we cannot exclude that in G31.41 one is observing the earliest stages of the expansion, it is questionable that the parameters of a young, compact outflow are greater than those typical of much older, extended outflows.
Finally, we note that the dynamical time scale of the putative outflow is an order of magnitude shorter than the time needed to form typical hot core species – such as methyl cyanide – according to theoretical models (see e.g. Charnley et al. 1992). Our estimate of tdyn is affected by large uncertainties, owing to the unknown inclination angle and the difficulty in tracing the whole extent of the lobes. However, to increase tdyn by a factor ≳ 10 one has to assume that the outflow lies very close ( ≲ 6°) to the line of sight and/or that we detect only the most compact part of lobes extending over a region 10 times larger than that imaged in our CH3CN and CO maps. The latter explanation is ruled out by our SMA+30m combined maps that do not reveal any large-scale bipolar outflow. The former would imply a significant overlap between the blue- and red-shifted lobes in the plane of the sky, which is not seen in Fig. 14. Indeed, from the observed separation between the peaks of the red- and blue-shifted emission (~1″), assuming that the intrinsic length of the CH3CN lobes is comparable to the radius of the CH3CN core measured in the plane of the sky (~1″), one can obtain a rough estimate of the inclination angle of arcsin(0.5) = 30°. Correspondingly, tdyn would increase by only a factor 1.7.
 |
Fig. 12 Position-velocity plots along the direction with PA = 68° passing through the HMC. The offset is measured from the phase center, positive toward NE. Contours correspond the CH3CN(12–11) K = 4 component emission, while gray scales indicate the 12CO(2–1) and 13CO(2–1) line emission, as indicated in each box. Contour levels increase from 0.2 in steps of 0.2 Jy/beam for CH3CN, from 0.24 in steps of 0.24 Jy/beam for 12CO SMA, from 0.6 in steps of 1 Jy/beam for 12CO SMA+30 m, from 0.12 in steps of 0.175 Jy/beam for 13CO SMA, and from 0.15 in steps of 0.5 Jy/beam for 13CO SMA+30 m. The cross in the bottom left of each box denotes the angular and spectral resolutions. |
Given the number of problems encountered in the outflow scenario, we investigate also a second possibility, namely that the velocity gradient of the HMC is due to a rotating toroid.
4.2.2. Rotating toroid
In an attempt to shed light on the velocity field in the HMC and its molecular surroundings, we overlay in Fig. 12 the position-velocity plots along the velocity gradient in high- and low-density tracers. For the sake of completeness we show both the SMA and the combined 30 m+SMA data in the 12CO and 13CO (2–1) transitions. Note that the cut was made along PA = 68° and all plots were obtained after averaging the emission along the direction perpendicular to the cut. This has the twofold purpose of increasing the S/N of the plots and taking into account emission at all offsets along the (putative) rotation axis.
As already explained, the 12CO and 13CO emission close to the systemic velocity is highly opaque and does not convey any information on the HMC, but is instructive to study the high-velocity and/or low-density gas around it. Vice versa, the CH3CN emission is an excellent HMC tracer, but is not detected at high velocities and/or beyond ~2″ from the center. Combining all these tracers is the only way to perform a detailed and complete analysis of the velocity field in this core. Indeed, Fig. 12 is very instructive. It shows that the velocity trend observed in CH3CN is complementary to that seen in the CO isotopomers and fills the gap caused by the interferometer resolving out the extended, bulk CO emission.
A more thorough inspection of this figure reveals that, despite the similarity, the 12CO and 13CO plots are significantly different. While the 13CO and CH3CN patterns match very well in the overlapping regions (i.e. between 89 and 94 km s-1 and between 102 and 105 km s-1), the 12CO emission is offset by ~1″ from the CH3CN and 13CO patterns, to the SW in the blue-shifted part, and to the NE in the red-shifted part. An interesting difference between CH3CN and 13CO, on the one hand, and 12CO, on the other, is that the high-velocity emission is found at relatively large offsets in 12CO, whereas in 13CO it appears to peak close to the HMC center.
Is it possible to find a coherent interpretation of all these facts in the rotating toroid scenario? A possible explanation is that of a self-gravitating structure with a heavy, compact stellar cluster at the center. In the outer regions (traced by 12CO), the gravitational field is determined by the gas mass and the rotation curve flattens, whereas close to the center (where 13CO and CH3CN are detected) the velocity field resembles Keplerian rotation, because the gas mass becomes comparable to the stellar mass. This scenario is analogous to that studied by Bertin & Lodato (1999), who determined the rotation curve of a self-gravitating disk with a central star.
In order to check the viability of this interpretation, below we first estimate the mass of the HMC and then verify whether this suffices to support rotational equilibrium.
From the continuum flux (see Table 2), we derive a mass of 1700 M⊙ for the HMC, assuming a dust temperature of 100 K and a dust absorption coefficient at 1.3 mm of 0.005 cm2 g-1 (Kramer et al. 2003). The temperature of 100 K is a lower limit, because the real temperature must be higher than or equal to the maximum brightness temperature of the CH3CN lines measured in the synthesized beam (~95 K). The latter corresponds to the surface temperature of the HMC, because the ground state CH3CN lines are optically thick and, as discussed by BEL05, the temperature inside the HMC is likely increasing. The mass obtained is affected by a large uncertainty mostly because of the poorly known dust properties: for example, BEL04 adopted an absorption coefficient of 0.02 cm2 g-1, which would imply a HMC mass of only 420 M⊙.
In Fig. 13 we show the same position-velocity
plot of the CH3CN and 13CO lines as in Fig. 12, this time overlaying the pattern outlining the region inside
which emission is expected for a Keplerian rotating and free-falling disk. The latter
does not take into account the line-width nor the spectral and angular resolutions and
has been obtained assuming that the gas velocity is the vector sum of a tangential
component due to Keplerian rotation about a central mass, M, plus a
radial component due to free-fall onto the same mass. Under these assumptions the
velocity component along the line of sight can be expressed as
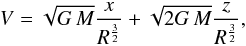 (1)where
x and z are the coordinates, respectively, along the
disk plane and the line of sight, and
(1)where
x and z are the coordinates, respectively, along the
disk plane and the line of sight, and 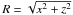 is the distance from the center of the disk. We also assume that R lies
between the disk radius, Ro, and a minimum inner radius,
Ri. The first term on the right hand side of the equation
is the component due to Keplerian rotation, the second that due to free fall. The dashed
pattern in Fig. 12 has been obtained by plotting
the maximum and minimum velocities V for z varying
across the disk, i.e. from
is the distance from the center of the disk. We also assume that R lies
between the disk radius, Ro, and a minimum inner radius,
Ri. The first term on the right hand side of the equation
is the component due to Keplerian rotation, the second that due to free fall. The dashed
pattern in Fig. 12 has been obtained by plotting
the maximum and minimum velocities V for z varying
across the disk, i.e. from 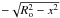 and
and 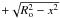 ,
taking into account that the region
R < Ri is forbidden. In our case,
a satisfactory fit is obtained for
M = 330 M⊙,
Ro = 3″ (or 0.11 pc), and
,
taking into account that the region
R < Ri is forbidden. In our case,
a satisfactory fit is obtained for
M = 330 M⊙,
Ro = 3″ (or 0.11 pc), and
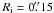 (or 0.0055 pc). Note that the signature of (pseudo-)Keplerian rotation is the
“butterfly” shape of the plot, determined by the two “spurs” of emission at about ± 3″
and ± 4 km s-1 relative to the systemic velocity
(~96.5 km s-1), plus the presence of high-velocity emission at
zero offset6. It is worth stressing that the
contribution of the 13CO(2–1) line is crucial to outline such a pattern,
which cannot be recognized from the sole CH3CN emission. This explains why
BEL05 managed to fit their CH3CN data assuming a flat or solid-body rotation
curve, and Girart et al. (2009), from a number of
CH3OH lines, found that the rotation velocity increases with radius.
(or 0.0055 pc). Note that the signature of (pseudo-)Keplerian rotation is the
“butterfly” shape of the plot, determined by the two “spurs” of emission at about ± 3″
and ± 4 km s-1 relative to the systemic velocity
(~96.5 km s-1), plus the presence of high-velocity emission at
zero offset6. It is worth stressing that the
contribution of the 13CO(2–1) line is crucial to outline such a pattern,
which cannot be recognized from the sole CH3CN emission. This explains why
BEL05 managed to fit their CH3CN data assuming a flat or solid-body rotation
curve, and Girart et al. (2009), from a number of
CH3OH lines, found that the rotation velocity increases with radius.
One may wonder whether a HMC as massive as several 100 M⊙ may be undergoing Keplerian rotation. As suggested by Cesaroni et al. (2007) and demonstrated by Beltrán et al. (2011), these massive, large rotating cores are to be considered transient toroidal structures feeding a cluster of YSOs rather than stable circumstellar accretion disks. In fact, the latter are stabilized by the central star(s), whose mass is greater than that of the disk, whereas the former are dynamically dominated by the gas mass and hence are short-lived. Although this scenario may be true in most cases, G31.41 might represent an exception. We speculate that this HMC could contain a large number of stars tightly packed in the central region. In this case the stars could have a stabilizing effect analogous to that of a single point-like object located at the HMC center, similar to the previously mentioned model by Bertin & Lodato (1999).
 |
Fig. 13 Overlay of the 13CO(2–1) (only SMA data; contours) and CH3CN(12–11) K = 4 position-velocity plots along the direction with PA = 68° passing through the HMC. The offset is measured from the phase center, positive toward NE. Contour levels increase from 0.2 in steps of 0.2 Jy/beam for CH3CN and from 0.1 in steps of 0.1 Jy/beam for 12CO. The vertical and horizontal solid lines denote the position of the continuum peak and the systemic velocity, respectively. The thick dashed pattern encompasses the region inside which emission is expected from a disk with radius of 3″ (or 0.11 pc) undergoing free-fall and Keplerian rotation about 330 M⊙. The cross in the bottom left denotes the angular and spectral resolutions. |
With all this in mind, the pseudo-Keplerian pattern recognized in Fig. 13 suggests that the HMC mass should be comparable to
the total mass of the embedded stars that are tightly packed at the center. Is this
scenario plausible? Indeed, in the case of G10.62–0.38, a massive star forming region
with a luminosity of 9.2 × 105 L⊙, Sollins
et al. (2005) suggest that within a radius of
0.03 pc, several O stars with a total mass of 175 M⊙ have
formed at the center of a flattened disk. In our case, the existence of (at least) two
high-mass YSOs close to the HMC center and separated (in projection) by only
0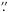 19
or 1480 AU has been proved by Cesaroni et al. (2010), who detected the free-free continuum emission. In terms of mass, these
two YSOs represent only the tip of the iceberg, because the total mass of the associated
cluster is dominated by (undetected) low-mass stars. Assuming e.g. a Miller &
Scalo (1979) mass function, one can estimate the
cluster mass from that of the most massive star. For this we can use the value of
20–25 M⊙ computed by Osorio et al. (2009) from their model fit and obtain a total mass of the cluster of
~103 M⊙. The same result is obtained
by fixing the total luminosity of the cluster to the value of
2 × 105 L⊙ quoted by Osorio et al. (2009). In all likelihood
~103 M⊙ is an upper limit to the real
stellar mass, because the cluster mass function may be highly incomplete in such a small
region. However, this estimate indicates that the dynamical mass of
~330 M⊙, obtained from the fit in Fig. 13, is probably dominated by the stellar mass, which
would lend support to the application of Bertin & Lodato (1999) model to the case of G31.41.
19
or 1480 AU has been proved by Cesaroni et al. (2010), who detected the free-free continuum emission. In terms of mass, these
two YSOs represent only the tip of the iceberg, because the total mass of the associated
cluster is dominated by (undetected) low-mass stars. Assuming e.g. a Miller &
Scalo (1979) mass function, one can estimate the
cluster mass from that of the most massive star. For this we can use the value of
20–25 M⊙ computed by Osorio et al. (2009) from their model fit and obtain a total mass of the cluster of
~103 M⊙. The same result is obtained
by fixing the total luminosity of the cluster to the value of
2 × 105 L⊙ quoted by Osorio et al. (2009). In all likelihood
~103 M⊙ is an upper limit to the real
stellar mass, because the cluster mass function may be highly incomplete in such a small
region. However, this estimate indicates that the dynamical mass of
~330 M⊙, obtained from the fit in Fig. 13, is probably dominated by the stellar mass, which
would lend support to the application of Bertin & Lodato (1999) model to the case of G31.41.
Finally, we note that the toroid interpretation is compatible with the hourglass-shaped
morphology of the magnetic field (see Girart et al. 2009), whose symmetry axis is directed SE–NW, because the latter coincides
with the rotation axis of the toroid. However, a caveat is in order. Girart et al.
(2009) find a significant correlation between
rotation velocity and radius in the core, using different tracers. In particular, they
conclude that in the region sampled by their observations (lying between
~0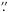 5
and 1
5
and 1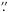 6),
velocity increases with distance from the HMC center (see their Fig. 4). This result
seems inconsistent with our hypothesis that the core is undergoing pseudo-Keplerian
rotation, because in this case the rotation velocity should decrease with radius.
Perhaps this discrepancy can be explained by the presence of the magnetic field. Higher
angular resolution observations are needed to sample the velocity field inside the core
and thus obtain a reliable, direct measurement of the rotation curve.
6),
velocity increases with distance from the HMC center (see their Fig. 4). This result
seems inconsistent with our hypothesis that the core is undergoing pseudo-Keplerian
rotation, because in this case the rotation velocity should decrease with radius.
Perhaps this discrepancy can be explained by the presence of the magnetic field. Higher
angular resolution observations are needed to sample the velocity field inside the core
and thus obtain a reliable, direct measurement of the rotation curve.
4.3. The CH3CN “8-shaped” structure
The last aspect we will discuss in the context of the outflow/toroid controversy, is the double-peaked, “8-shaped” structure observed in the CH3CN K = 2 map at the systemic velocity (see Fig. 3). The same morphology is seen in all components up to K = 6, i.e. up to excitation energies of ~300 K, whereas the K = 8 map (energy of 513 K) presents a single peak at the HMC center (Fig. 3). In Sect. 3.1 we interpreted these facts in terms of opacity and temperature gradients. Indeed, BEL05 found that the CH3CN rotational temperature peaks toward the HMC center and from the ratio between our CH3CN and CH313CN (12–11) K = 2 data we calculate an optical depth at the peak of the line in the range 8–77 across the HMC. The interplay between opacity and temperature can explain the existence of a dip at the HMC center, but does not justify the lack of circular symmetry in the low-K maps. Here, we wish to find an explanation for the “8-shaped” feature and check whether this can better fit into the outflow or toroid model.
As a basis for our discussion, in Fig. 14 we present an overlay of the blue- and red-shifted CH3CN K = 4 emission on the bulk emission in the same line. In this way, one is comparing the high- with the low-velocity emission.
In the outflow scenario, a naïve interpretation of this figure is that the high-velocity gas is leaking from the HMC through the axis of a “donut-like” structure seen edge-on, corresponding to the “8-shaped” feature in the map. In this case, the two peaks would coincide with the maxima of column density across the “donut”. Albeit plausible, this interpretation has a problem. The large CH3CN opacity should prevent the detection of two distinct peaks, because the line brightness is independent of column density. Therefore, instead of the 8-shaped feature, one should see an elongated structure perpendicular to the bipolar outflow and peaking at the center of it (i.e. at the HMC center).
 |
Fig. 14 Maps of the blue- (solid contours) and red-shifted (dashed) emission in the CH3CN(12–11) K = 4 line overlayed on the bulk emission (gray scale) in the same line. The integration was performed over the velocity ranges 88.9–91.3 km s-1, 100.9–103.3 km s-1, and 95.2–96.7 km s-1, respectively. Contour levels increase from 0.15 in steps of 0.27 Jy/beam for the blue- and red-shifted gas, and from 0.2 in steps of 0.2 Jy/beam for the bulk emission. The synthesized beam of the images is drawn in the bottom left. The two white points mark the positions of the two compact free-free sources detected by Cesaroni et al. (2010). |
Explaining the presence of the 8-shaped structure appears to be a problem also in the toroid scenario. In fact, if the toroid is seen edge-on, the emission at the systemic velocity should peak in between the blue- and red-shifted emission. However, if the toroid is inclined with respect to the line of sight, the nearest and farthest sides of it are seen displaced from one another on the plane of the sky, symmetrically displaced with respect to the center. This is indeed what we see in Fig. 14, where the two peaks lie along the (projection of the) rotation axis and are equally offset from the center. The situation depicted in this figure resembles that of the ring undergoing Keplerian rotation about the low-mass system GG Tau (see Fig. 6a of Guilloteau et al. 1999). Clearly, this comparison is inappropriate, because the scales of the two objects differ by more than an order of magnitude. Moreover, G31.41 is probably more similar to a “puffy pancake” rather than a “donut” or ring, because gas and dust are present at all radii, as demonstrated by the continuum and high-energy line emission peaking at the center of the HMC (see Figs. 2 and 3). Note, however, that the emission from the lower energy lines may be arising mostly from the colder outer region and hence be confined in a ring. Finally, G31.41, unlike GG Tau, is embedded in a dense pc-scale envelope, which complicates the line and continuum radiative transfer. Despite all these differences, the comparison between the two objects is intriguing and may qualitatively explain the features observed in G31.41.
Further support for this interpretation is obtained by comparing the case of G31.41 to that of a source closer in mass than GG Tau. This is the Herbig Ae star MWC 758, which is surrounded by a circumstellar disk, as demonstrated by the model fit of Isella et al. (2010). A comparison between the channel maps presented by these authors (see their Fig. 2) with those in Fig. 4 reveals a surprising similarity: in both cases the shape of the emission is circular and peaks at opposite positions with respect to the center in the blue- and red-shifted channels, but turns into an 8-shaped structure close to the systemic velocity. This fact may be the fingerprint of a rotating disk in G31.41, as well as in MWC 758.
5. Summary and conclusions
With the present study we have performed a deep analysis of the geometrical structure and kinematics of the HMC in the high-mass star-forming region G31.41. Thanks to new high angular resolution SMA images and complementary IRAM 30-m maps, we have investigated both the HMC, through the CH3CN(12–11) transition, and the lower density surroundings, through 12CO and 13CO. We could thus search for a possible outflow powered by the star(s) embedded in the HMC. In particular, our main goal was to shed light on the nature of the NE–SW velocity gradient, previously detected in the HMC by various authors, and possibly distinguish between rotation and expansion.
Our new data confirm the presence of the velocity gradient basically in all HMC tracers observed, and indicate that a red–blue symmetry along the same axis is seen also in the CO isotpomers. We were unable to detect any bipolar outflow along the SE–NW direction, in contrast with the findings of Olmi et al. (1996). The latter was probably an artifact caused by very limited uv sampling and lack of zero-spacing information.
We find a hint of infall in the HMC, consistent with the results of Girart et al. (2009). A comparison between the CH3CN and CO maps suggests that these species are tracing the same phenomenon. Especially the 13CO(2–1) line emission appears to be the obvious prosecution of the CH3CN(12–11) emission on a larger scale.
We have discussed whether the velocity gradient observed in G31.41 is a compact bipolar outflow or a rotating, geometrically thick, toroidal structure. The former hypothesis implies outflow parameters typical of high-mass stars with luminosities in excess of 105 L⊙, whereas previous estimates by Osorio et al. (2009) and Cesaroni et al. (1994a; 2010) indicate a significantly lower luminosity for G31.41. Moreover, such an outflow would be much more compact than typical bipolar outflows detected in high-mass star-forming regions and the dynamical time scale would be an order of magnitude shorter than that needed to form HMC spacies such as CH3CN. It is also worth noting that a core undergoing expansion seems difficult to reconcile with the detection of infall.
The composite CH3CN and 13CO position-velocity plot can be explained if the gas is undergoing both (pseudo-)Keplerian rotation and infall, suggesting that this massive object could be dynamically stabilized by a compact cluster of YSOs tightly packed inside a few 1000 AU from the center. In this scenario the 12CO emission could be tracing the outer regions, where the gravitational field is dominated by the gas and the rotation velocity tends to a constant value. Albeit intriguing, this interpretation remains speculative and could be proved only by producing synthetic CH3CN and CO maps and position-velocity plots to be compared with the data. This numerical effort goes beyond the purposes of the present study.
We conclude that the case of G31.41 could be a scaled-up version of lower-mass YSOs, such as GG Tau and MWC 758, where circumstellar disks have been detected and successfully modeled. We stress that whatever the interpretation, the observations of this object have produced an important finding for the study of high-mass star formation. We obtained iron-clad evidence for the existence of a velocity gradient across the HMC and demonstrated that this gradient is not due to multiple cores unresolved in the beam and moving at different velocities, but to the gas undergoing a smooth drift in (line-of-sight) velocity from the one end to the other of the core. If, as we believe, one is dealing with a rotating toroid, then this indicates that star formation in this HMC may proceed in a similar way to low-mass stars, namely through circumstellar, centrifugally supported disks “hidden” inside the densest interiors of the toroid itself. If, instead, the outflow interpretation were correct, such a sharp, neat velocity gradient would strongly suggest the existence of a very effective focusing mechanism for the outflow and the best candidate as a collimating agent would be a (yet undetected) circumstellar disk. Therefore, regardless of whether the G31.41 HMC is undergoing expansion or rotation, the role of disks in the mechanism of high-mass star formation seems to be strengthened by our findings. The advent of ALMA will be crucial to detect deeply embedded disks in HMCs.
The MIR cookbook can be found at https://www.cfa.harvard.edu/~cqi/mircook.html
The GILDAS software is available at http://www.iram.fr/IRAMFR/GILDAS
Parameters of the CH3CN and CH313CN transitions can be found, e.g., in the “splatalogue” database: http://www.splatalogue.net/
Acknowledgments
We thank the SMA staff for their help during the observations. The GILDAS team is also acknowledged for the excellent software that we used to analyze our data.
References
- Araya, E., Hofner, P., Kurtz, S., Olmi, L., & Linz, H. 2008, ApJ, 675, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Neri, R., et al. 2004, ApJ, 601, L187 (BEL04) [NASA ADS] [CrossRef] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Neri, R., et al. 2005, A&A, 435, 901 (BEL05) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beltrán, M. T., Cesaroni, R., Neri, R., & Codella, C. 2011, A&A, 525, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benjamin, R. A., Churchwell, E., Babler, B. L., et al. 2003, PASP, 115, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, G., & Lodato, G. 1999, A&A, 350, 694 [NASA ADS] [Google Scholar]
- Cesaroni, R., Churchwell, E., Hofner, P., Walmsley, C. M., & Kurtz, S. 1994a, A&A, 288, 903 [NASA ADS] [Google Scholar]
- Cesaroni, R., Olmi, L., Walmsley, C. M., Churchwell, E., & Hofner, P. 1994b, ApJ, 435, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Cesaroni, R., Hofner, P., Walmsley, C. M., & Churchwell, E. 1998, A&A, 331, 709 [NASA ADS] [Google Scholar]
- Cesaroni, R., Galli, D., Lodato, G., Walmsley, C. M., & Zhang, Q. 2007, in Protostars and Planets V, ed. B. Reipurth, D. Jewitt, & K. Keil (Tucson: Univ. of Arizona Press), 197 [Google Scholar]
- Cesaroni, R., Hofner, P., Araya, E., & Kurtz, S. 2010, A&A, 509, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Charnley, S. B., Tielens, A. G. G. M., & Millar, T. J. 1992, ApJ, 399, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Gaume, R. A., & Mutel, R. L. 1987, ApJS, 65, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Gibb, A. G., Wyrowski, F., & Mundy, L. G. 2004, ApJ, 616, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Girart, J. M., Beltrán, M. T., Zhang, Q., Rao, R., & Estalella, R. 2009, Science, 324, 1408 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Guilloteau, S., Dutrey, A., & Simon, M. 1999, A&A, 348, 570 [NASA ADS] [Google Scholar]
- Ho, P. T. P., Moran, J. M., & Lo, K. Y. 2004, ApJ, 616, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Isella, A., Natta, A., Wilner, D., Carpenter, J. M., & Testi, L. 2010, ApJ, 725, 1735 [NASA ADS] [CrossRef] [Google Scholar]
- Keto, E. H. 2007, ApJ, 666, 976 [NASA ADS] [CrossRef] [Google Scholar]
- Kramer, C., Richer, J., Mookerjea, B., Alves, J., Lada, C. 2003, A&A 399, 1073 [Google Scholar]
- Krumholz, M. R., Klein, R. I., McKee, C. F., Offner, S. S. R., & Cunningham, A. J. 2009, Science, 323, 754 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kuiper, R., Klahr, H., Beuther, H., & Henning, Th. 2010, ApJ, 722, 1556 [CrossRef] [Google Scholar]
- López-Sepulcre, A., Codella, C., Cesaroni, R., Marcelino, N., & Walmsley, C. M. 2009, A&A, 499, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miller, G. E., & Scalo, J. M. 1979, ApJ, 41, 513 [Google Scholar]
- Nakano, T. 1987, MNRAS, 224, 107 [NASA ADS] [Google Scholar]
- Olmi, L., Cesaroni, R., Neri, R., & Walmsley, C. M. 1996, A&A, 315, 565 [NASA ADS] [Google Scholar]
- Osorio, M., Anglada, G., Lizano, S., & D’Alessio, P. 2009, ApJ 694, 29 [Google Scholar]
- Palla, F., & Stahler, S. W. 1993, ApJ, 418, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Clemens, D. P., Scoville, N. Z., & Solomon, P. M. 1986, ApJS, 60, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sault, R. J., Teuben, P. J., & Wright, M. C. H. 1995, in Astronomical Data Analysis Software and Systems IV, ASP Conf. Ser. 77, 433 [Google Scholar]
- Simon, M., Guilloteau, S., & Dutrey, A. 2001, ApJ, 545, 1034 [Google Scholar]
- Sollins, P. K., Zhang, Q., Keto, E., & Ho, P. T. P. 2005, ApJ, 624, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Van Dishoeck, E. F., Blake, G. A., Draine, B. T., & Lunine, J. I. 1993, Protostars and Planets III, ed. E. H. Levy, & J. I. Lunine, (Tucson: Univ. of Arizona Press), 163 [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y., Wei, Y., & Zhao, M. 2004, A&A, 426, 503 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Spectra obtained by integrating the line emission over the whole core. Top: ground-state K-components of the J = 12 → 11 transition of CH3CN (numbers above the spectrum) and of the CH313CN isotopomer (numbers below the spectrum). Note how most K-lines are blended with each other and/or with lines of other molecules. Middle: vibrationally excited (v8 = 1) lines of CH3CN. The K, l quantum numbers of the transitions are indicated above the spectrum. Bottom: ground state K = 3 component. The dotted lines mark the velocity ranges used to produce the maps in Figs. 2 and 3. |
| In the text | |
 |
Fig. 2 Maps of the line and continuum emission toward the G31.41 HMC. The line maps have
been obtained by averaging the emission under the whole line profile, namely from
88.9 km s-1 to 103.9 km s-1 (see Fig. 1, bottom). The tracer used is indicated in the
top right of each panel. The two white points mark the positions of the
free-free-continuum sources detected by Cesaroni et al. (2010). The contour levels start from 0.072 Jy/beam and increase
in steps of 0.12 Jy/beam for all line maps, and range from 0.035 Jy/beam to
1.785 Jy/beam in steps of 0.175 Jy/beam for the continuum map. Offsets are measured
with respect to the phase center
α(J2000) = 18h47m34 |
| In the text | |
 |
Fig. 3 Same as Fig. 2, with the line maps obtained by averaging the emission from 95.5 km s-1 to 97.3 km s-1 (see Fig. 1, bottom). Contour levels start from 0.15 Jy/beam and increase in steps of 0.2 Jy/beam for all line maps, and range from 0.035 Jy/beam to 1.785 Jy/beam in steps of 0.175 Jy/beam for the continuum map. |
| In the text | |
 |
Fig. 4 Channel maps of the CH3CN(12–11) emission obtained by averaging the K = 2, 3, and 4 components. The number in the top left of each panel gives the corresponding LSR velocity. The values of the contour levels are indicated by the tick marks in the intensity scale to the right. The cross denotes the phase center. The ellipse in the bottom right of the last panel is the full-width-at-half power of the synthesized beam. |
| In the text | |
 |
Fig. 5 Overlay of the map of the 1.3 mm continuum emission (contours) on that of the CH3CN(12–11) line velocity (color scale). Contour levels range from 0.1 to 2 in steps of 0.2 Jy/beam. Offsets are measured with respect to the phase center. The two white dots denote the free-free continuum sources detected by Cesaroni et al. (2010). The synthesized beam is shown in the bottom left. |
| In the text | |
 |
Fig. 6 Position-velocity plots of along PA = 68° (left panels) and –22° (right panels) for three different lines (indicated in each panel). Offsets are measured with respect to the phase center. Contour levels start from 0.12 Jy/beam and increase in steps of 0.12 Jy/beam. The cross in the bottom left of each box denotes the angular and spectral resolutions. |
| In the text | |
 |
Fig. 7 Map of the CH3CN(12–11) emission obtained by averaging the emission
under the K = 0 and 1 components. The image has been reconstructed
with a clean beam (ellipse in the bottom right) equal to that of the images of
BEL04, i.e. 1 |
| In the text | |
 |
Fig. 8 Channel maps in the 12CO(2–1) line obtained by combining single-dish (IRAM 30-m) and interferometric (SMA) data. The number in the top left of each panel gives the corresponding LSR velocity. The values of the contour levels are indicated by the tick marks in the intensity scale to the right. The ellipse in the bottom right of the last panel is the full-width-at-half power of the resulting instrumental beam. |
| In the text | |
 |
Fig. 9 Spectra of the 12CO( (solid histogram), 13CO (dashed), and C17O (dotted; Cesaroni, unpublished data) (2–1) lines obtained by averaging the emission over a square region 30″ in size, centered on the HMC. The data have been taken with the IRAM 30-m telescope. |
| In the text | |
 |
Fig. 10 Solid curves represent the first moments of several CH3CN(12–11)
components (indicated in the top left of each panel) estimated along a cut through
the continuum peak
(α(J2000) = 18h47m34 |
| In the text | |
 |
Fig. 11 Channel maps of the 12CO(2–1) line emission observed with the SMA. Each box contains pairs of maps corresponding to the blue- (solid contours) and red-shifted (dashed) emission at the same velocity offset (in absolute value) from the the systemic velocity (~96.5 km s-1). The corresponding LSR velocities are indicated in the top right of the box. Contour levels increase from 0.5 Jy/beam in steps of 0.5 Jy/beam. Also shown is a map of the CH3CN(12–11) K = 4 line emission averaged over the range 95.2–96.7 km s-1. The ellipse in the bottom left denotes the synthesized beam of the observations. |
| In the text | |
 |
Fig. 12 Position-velocity plots along the direction with PA = 68° passing through the HMC. The offset is measured from the phase center, positive toward NE. Contours correspond the CH3CN(12–11) K = 4 component emission, while gray scales indicate the 12CO(2–1) and 13CO(2–1) line emission, as indicated in each box. Contour levels increase from 0.2 in steps of 0.2 Jy/beam for CH3CN, from 0.24 in steps of 0.24 Jy/beam for 12CO SMA, from 0.6 in steps of 1 Jy/beam for 12CO SMA+30 m, from 0.12 in steps of 0.175 Jy/beam for 13CO SMA, and from 0.15 in steps of 0.5 Jy/beam for 13CO SMA+30 m. The cross in the bottom left of each box denotes the angular and spectral resolutions. |
| In the text | |
 |
Fig. 13 Overlay of the 13CO(2–1) (only SMA data; contours) and CH3CN(12–11) K = 4 position-velocity plots along the direction with PA = 68° passing through the HMC. The offset is measured from the phase center, positive toward NE. Contour levels increase from 0.2 in steps of 0.2 Jy/beam for CH3CN and from 0.1 in steps of 0.1 Jy/beam for 12CO. The vertical and horizontal solid lines denote the position of the continuum peak and the systemic velocity, respectively. The thick dashed pattern encompasses the region inside which emission is expected from a disk with radius of 3″ (or 0.11 pc) undergoing free-fall and Keplerian rotation about 330 M⊙. The cross in the bottom left denotes the angular and spectral resolutions. |
| In the text | |
 |
Fig. 14 Maps of the blue- (solid contours) and red-shifted (dashed) emission in the CH3CN(12–11) K = 4 line overlayed on the bulk emission (gray scale) in the same line. The integration was performed over the velocity ranges 88.9–91.3 km s-1, 100.9–103.3 km s-1, and 95.2–96.7 km s-1, respectively. Contour levels increase from 0.15 in steps of 0.27 Jy/beam for the blue- and red-shifted gas, and from 0.2 in steps of 0.2 Jy/beam for the bulk emission. The synthesized beam of the images is drawn in the bottom left. The two white points mark the positions of the two compact free-free sources detected by Cesaroni et al. (2010). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


