| Issue |
A&A
Volume 525, January 2011
|
|
|---|---|---|
| Article Number | A77 | |
| Number of page(s) | 15 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201014363 | |
| Published online | 02 December 2010 | |
Submillimeter absorption from SH+, a new widespread interstellar radical, 13CH+ and HCl⋆
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
e-mail: kmenten;wyrowski@mpifr-bonn.mpg.de; belloche@mpifr-bonn.mpg.de; rguesten@mpifr-bonn.mpg.de; ldedes@mpifr-bonn.mpg.de
2
I. Physikalisches Institut, Universität zu Köln,
Zülpicher Str. 77, 50937
Köln,
Germany
hspm@ph1.uni-koeln.de
Received: 5 March 2010
Accepted: 10 September 2010
We have used the Atacama Pathfinder Experiment 12 m telescope (APEX) to carry out an absorption study of submillimeter wavelength rotational ground-state lines of H35Cl, H37Cl, 13CH+, and, for the first time, of the SH+ radical (sulfoniumylidene or sulfanylium). We detected the quartet of ground-state hyperfine structure lines of SH+ near 683 GHz with the CHAMP+ array receiver against the strong continuum source Sagittarius B2, which is located close to the center of our Galaxy. In addition to absorption from various kinematic components of Galactic center gas, we also see absorption at the radial velocities belonging to intervening spiral arms. This demonstrates that SH+ is a ubiquitous component of the diffuse interstellar medium. We do not find clear evidence for other SH+ lines we searched for, which is partially due to blending with lines from other molecules. In addition to SH+, we observed absorption from H35Cl, H37Cl, and 13CH+. The observed submillimeter absorption is compared in detail with absorption in 3 mm transitions of H13CO+ and c-C3H2 and the CO J = 1−0 and 3−2 transitions.
Key words: astrochemistry / ISM: abundances / ISM: molecules
© ESO, 2010
1. Introduction
1.1. (Sub)millimeter spectroscopy of diffuse interstellar clouds
Starting in the late 1930s, studies of molecular absorption toward diffuse and translucent clouds have traditionally been in the realm of optical and, later, ultraviolet (UV) and infrared (IR) spectroscopy. Over the last 15 years, observations at radio and (sub)mm wavelengths have greatly added to our knowledge of the chemistry of the diffuse interstellar medium (ISM) (see, e.g., the review of Snow & McCall 2006). Measurements toward strong continuum sources are a powerful means to detect spectral lines that have their lower level in (or near) the rotational ground state of a molecule and may be the only way to detect a number of species in low density environments or even at all. In particular, the large rotational constants of light hydrides, resulting in a rotational spectrum starting at submillimeter or far-infrared wavelengths, together with substantial electric dipole moments, make collisional excitation negligible compared to radiative decay. This leaves substantial population only in the lowest energy level, which can be split in the case of fine structure (fs) or hyperfine structure (hfs).
Two particularly fruitful avenues of research have emerged; first, choosing extragalactic sources with strong mm- and cm-wavelength continuum emission as background objects, Liszt and Lucas have studied the abundances of a variety of di-, tri-, and even polyatomic molecules toward up to 20 lines of sight with often surprising results (see, e.g., Liszt & Lucas 2002, and references therein). A second possibility is using as a background the thermal continuum from star-forming regions, (mostly) free-free emission at cm- and longer mm-wavelengths and dust emission at shorter wavelengths. Particularly interesting lines of sights are those toward regions M and N in the Sagittarius B2 Giant Molecular Cloud (GMC), which allow sensitive absorption spectroscopy of the ISM surrounding the Galactic center (GC) near which they are located at a distance of ~8 kpc (Reid et al. 2009) as well as of intervening GMCs. For a long time, absorption between –120 kms -1 and Sgr B2’s local velocity range (>+50 kms -1) has been observed in the HI 21 cm line (see Garwood & Dickey 1989, and references therein) as well as in (mostly) mm-wavelength lines from quite a number of molecules (see Linke et al. 1981; Nyman 1983; Greaves & Williams 1994, and references therein). Intervening spiral arm absorption toward other bright inner Galaxy (sub)mm continuum sources has been found as well, most prominently toward the central radio/(sub)mm source Sgr A⋆ and W49N (see, e.g., Liszt et al. 1977; Linke et al. 1981; Cox et al. 1988; Greaves & Williams 1994; Plume et al. 2004; Polehampton et al. 2005b).
At submillimeter wavelengths, numerous molecules have been detected in
absorption via their ground-state transitions (until recently mostly) toward Sgr B2 (for
summaries see Menten 2004; Lis et al. 2009). In particular, the 110−101
transition of ortho- and
-
and
- was detected with the Submillimeter Wave
Astronomy Satellite (Neufeld et al. 2000); this
was detected with the Submillimeter Wave
Astronomy Satellite (Neufeld et al. 2000); this
 line, near 557 GHz, is responsible for
much of the Earth atmosphere’s shorter-wavelength submillimeter opacity.
line, near 557 GHz, is responsible for
much of the Earth atmosphere’s shorter-wavelength submillimeter opacity.
In fact, atmospheric absorption by the rotational spectrum of H2O (and to a lesser extent of O2) makes the ground-state lines of many light hydride species unaccessible from the ground. Using the Long Wavelength Spectrometer (LWS) aboard the Infrared Space Observatory (ISO), which covered frequencies >1.5 THz (wavelengths <200 μm), several hydroxyl isotopologues (Polehampton et al. 2003, 2005a) were detected, as well as CH2 (Polehampton et al. 2005b), and para-H2D+ (Cernicharo et al. 2007). From the excellent high altitude site in the Atacama desert, recently OH+ was found with the APEX telescope by Wyrowski et al. (2010a).
Very recently, a new era in submillimeter absorption spectroscopy started with operation of the High Frequency Instrument for the Far Infrared (HIFI, see de Graauw et al. 2010) aboard Herschel (Pilbratt et al. 2010). Utilizing the superb sensitivity of Herschel’s 3.5 m aperture combined with HIFI’s high spectral resolution heterodyne receivers operating in a low thermal background space environment, revolutionized observations of light hydrides. (Mainly) in the framework of the guaranteed time key projects Herschel observations of EXtra-Ordinary Sources (HEXOS) (PI: Bergin) and PRobing InterStellar Molecules with Absorption line Studies (PRISMAS, PI: Gerin) observations were made of H2O+, H3O+, H2O and its isotopologues, H2Cl+, C3, CH, and CH+, as well as NH and NH2, while NH+ has so far remained undetected (Ossenkopf et al. 2010; Schilke et al. 2010; Gerin et al. 2010; Wyrowski et al. 2010b; Neufeld et al. 2010a; Lis et al. 2010b; Melnick et al. 2010; Comito et al. 2010; Lis et al. 2010a; Phillips et al. 2010; Neufeld et al. 2010b; Sonnentrucker et al. 2010; Mookerjea et al. 2010; Qin et al. 2010; Falgarone et al. 2010; Persson et al. 2010).
High quality optical/UV observations, needed, e.g., for meaningful abundance
determinations, mostly sample relatively nearby clouds since they require optically bright
background stars, typically members of OB associations (with HD catalogue numbers) within
a few kpc (see, e.g. Gredel 1997; Stahl et al. 2008, and references therein). In
contrast, being much less affected by interstellar extinction, radio/submm and near
infrared absorption observations, e.g. of the key 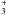 molecular ion (Geballe & Oka 1996), are capable of probing diffuse clouds
throughout the Milky Way.
molecular ion (Geballe & Oka 1996), are capable of probing diffuse clouds
throughout the Milky Way.
1.2. Interstellar SH+
The ionized hydride SH+ (sulfoniumylidene or sulfanylium) potentially is a probe of comets, photon-dominated regions (PDRs), shocked interstellar gas and diffuse molecular clouds (Horani et al. 1985) . Toward the latter, optical absorption measurements have shown for a very long time large abundances of another ionized molecule, methylidynium, CH+, the first interstellar molecule, detected by Dunham (1937) and identified by Douglas & Herzberg (1941). CH+’s abundance is orders of magnitude higher than predicted by otherwise successful models (see, e.g., van Dishoeck & Black 1986). This has been a long-standing puzzle to astrochemists, who invoked shock wave scenarios to overcome the formation reaction’s endothermicity (Federman 1982).
Millar et al. (1986) and also Pineau des Forêts et al. (1986) have extended chemical models by including sulfur chemistry and predicted efficient SH+ formation to occur in shocked diffuse clouds and that the abundance of SH+ can approach that of CH+ in moderate velocity magnetic shocks, but is negligible for a non-magnetic shock. This, in principle, could make the CH+/SH+ abundance ratio a good shock indicator.
Spectroscopic data and beam-averaged continuum brightness temperature assumed for the LTE modeling of the absorption lines toward Sgr B2(M).
Millar & Hobbs (1988) made sensitive searches of an optical wavelength electronic transition of SH+ from the A3Π − X3Σ(0,0) band at 3363.49 Å toward the well-studied diffuse cloud in the direction of ζ Oph, which shows significant CH+ absorption. They were only able to put an upper limit on the SH+ column density of 1 × 1013 cm-2, which is a factor of 3 lower than the measured CH+ column density. Magnani & Salzer (1991) searched for this line and another one at 3366.08 Å toward a sample of 13 stars with known diffuse molecular clouds in front of them and were only able to determine comparable 3σ upper limits on the SH+ column density between 0.4 and 1 × 1013 cm-2 and upper limits on the [SH+/CH+] abundance ratio between 0.12 and 2. An earlier search by Magnani & Salzer (1989) toward a sample of diffuse and high-latitude clouds resulted in a factor of a few coarser limits on the SH+ abundance. High (Galactic) latitude clouds belong to the so-called translucent clouds.
Translucent clouds, which were recognized as a class by van Dishoeck & Black (1986) have physical properties in between those of diffuse and dense dark clouds. In particular, they have higher visual extinctions, AV , (1–a few mag) than diffuse clouds (<1 mag) and, consequently, a higher ratio of molecular to atomic gas.
Other astrochemical interest in SH+ derives from the fact that, given a possible formation route via doubly ionized sulfur (S+2), it is predicted to be a diagnostic of X-ray dominated regions (XDRs) (Abel et al. 2008). Stäuber et al. (2007) report an observation of the SH+N = 1−0, J = 0−1, F = 0.5−1.5 line near 346 GHz toward the high-mass young stellar object (YSO) AFGL 2591, which is surrounded by an XDR. Since this line is blended with a 34SO2 line, they were only able to quote an upper limit to the SH+ line’s intensity. Again very recently, Herschel/HIFI observations led to the discovery of emission in the 526 GHz 12−01 transition of SH+ toward the high-mass protostar W3 IRS 5 (Benz et al. 2010).
In Sect. 2 of this paper we review the laboratory spectroscopy picture for both SH+ and 13CH+. In Sect. 3 we describe our submillimeter observations. Our results and the analysis procedure used to determine primary parameters of the observed lines are presented in Sect. 4. In Sect. 5 we discuss the derived information in an astrochemical context.
2. Rest frequencies
2.1. Accurate SH+ frequencies
Savage et al. (2004) performed the only
measurements of SH+ with microwave accuracy. They obtained rest frequencies for
four hfs lines from the X 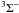 N = 1−0 state, one near
346 and three near 526 GHz. A previous study by Hovde
& Saykally (1987) employed laser magnetic resonance to record rotational
spectra. Recently, Brown & Müller (2009) used
these and further rovibrational (infrared) data on energy levels of SH+ in and
between the 3 = 0 and 1 vibrational states of the
X3Σ− electronic ground state to perform a single,
weighted least-squares fit in order to determine an improved set of molecular parameters
for this molecule. They used their results to calculate the rotational spectrum of
SH+ in these vibrational levels up to the N = 4−3
transition. The predictions presented in the catalog section1 of the Cologne Database for Molecular Spectroscopy, CDMS, (Müller et al. 2001, 2005) are based on the data from Savage et al.
(2004), on weighted averages of the experimental data from Hovde & Saykally (1987) extrapolated to zero field taken from the
fit of Brown & Müller (2009) and all available
infrared data (up to 3 = 4−3). These predictions are essentially identical to those in
Brown & Müller (2009), in particular when the
uncertainties are taken into account. The dipole moment of 1.285 D in the ground
vibrational state has been taken from an ab initio calculation by Senekowitsch et al. (1985). The rest frequencies from the CDMS catalog
are given in Table 1. Fig. 1 presents the lower part of the rotational energy level diagram of
SH+.
N = 1−0 state, one near
346 and three near 526 GHz. A previous study by Hovde
& Saykally (1987) employed laser magnetic resonance to record rotational
spectra. Recently, Brown & Müller (2009) used
these and further rovibrational (infrared) data on energy levels of SH+ in and
between the 3 = 0 and 1 vibrational states of the
X3Σ− electronic ground state to perform a single,
weighted least-squares fit in order to determine an improved set of molecular parameters
for this molecule. They used their results to calculate the rotational spectrum of
SH+ in these vibrational levels up to the N = 4−3
transition. The predictions presented in the catalog section1 of the Cologne Database for Molecular Spectroscopy, CDMS, (Müller et al. 2001, 2005) are based on the data from Savage et al.
(2004), on weighted averages of the experimental data from Hovde & Saykally (1987) extrapolated to zero field taken from the
fit of Brown & Müller (2009) and all available
infrared data (up to 3 = 4−3). These predictions are essentially identical to those in
Brown & Müller (2009), in particular when the
uncertainties are taken into account. The dipole moment of 1.285 D in the ground
vibrational state has been taken from an ab initio calculation by Senekowitsch et al. (1985). The rest frequencies from the CDMS catalog
are given in Table 1. Fig. 1 presents the lower part of the rotational energy level diagram of
SH+.
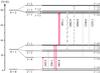 |
Fig. 1 Detail of the energy level diagram of SH+. The solid arrows mark transitions observed in the course of this work. The thickness of the arrows indicates the relative strengths of the transitions. The hyperfine splitting has been exaggerated slightly for clarity reasons. |
2.2. The J = 1−0 transition of 13CH+
The X 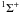 J = 1−0 rotational
ground-state transition of the main isotopologue of methylidynium,
12CH+, near 835.2 GHz, cannot be observed from the ground for
objects with Galactic radial velocities because of a strong telluric O2 line
approximately 1.1 GHz lower (Golubiatnikov & Krupnov
2003; Drouin et al. 2010). Observations of
the J = 1−0 line of 13CH+ at an ~5 GHz lower
frequency are however possible.
J = 1−0 rotational
ground-state transition of the main isotopologue of methylidynium,
12CH+, near 835.2 GHz, cannot be observed from the ground for
objects with Galactic radial velocities because of a strong telluric O2 line
approximately 1.1 GHz lower (Golubiatnikov & Krupnov
2003; Drouin et al. 2010). Observations of
the J = 1−0 line of 13CH+ at an ~5 GHz lower
frequency are however possible.
Falgarone et al. (2005) reported its detection toward the bright star-forming region G10.6−0.4 and evaluated from their observation the rest frequency as 830 132 ± 3 MHz. Two alternative values for the rest frequency, 830 107 ± 1 or 830 193 ± 4 MHz, remained viable due to ambiguities in ascribing the observed feature to LSR velocity components possibly associated with this source. These were discarded on the basis of the poor agreement with the prediction of Pearson & Drouin (2006) who had reported a transition frequency for J = 1−0 of 12CH+ and predicted the corresponding 13CH+ rest frequency as 830 134.3 MHz. This value was based on a combined analysis of their frequency and of optical CH+ data of four isotopologues employing an isotopically scaled Dunham analysis.
Our observations of 13CH+, however (see Sect. 3) indicate a rest frequency of around 830.2 GHz if we assume that this cation has an absorption profile similar to SH+, HCl, H13CO+, or c-C3H2.
Müller (2010) performed an analysis similar to the one published by Pearson & Drouin (2006) in order to evaluate rotational data for isotopologues of CH+ independently. Applying appropriate parameters which describe the breakdown of the Born-Oppenheimer approximation, he obtained a rest frequency for 13CH+J = 1−0 compatible with the present observations. The reviewer of Müller (2010) pointed out new laboratory measurements of the J = 1−0 transitions of 12CH+, 13CH+, and 12CD+ which were submitted subsequently by Amano (2010). Not only was the value for 13CH+ in quite good agreement with the estimate from our observations, but it was also shown that the previously reported value for 12CH+ was incorrect by several tens of megahertz. Including the data from Amano (2010) in his analysis, Müller (2010) calculated transition frequencies for several isotopologues of CH+ which now should be quite reliable and which are in the CDMS catalog. The 13CH+J = 1−0 value is again given in Table 1.
The dipole moment of 1.683 D for CH+ in the ground vibrational state has been taken from an ab initio calculation by Cheng et al. (2007); the change in dipole moment upon substitution of 12C with 13C is assumed to be small. A value of 1.7 D was used in the CDMS catalog (Müller et al. 2001, 2005).
2.3. HCl, c-C3H2, H13CO+, and CO
The rest frequencies for the J = 1−0 transitions of both H35Cl and H37Cl, which have hfs, were taken from the JPL catalog 2 (Pickett et al. 1998). These frequencies were published by De Lucia et al. (1971). The dipole moment of H35Cl for 3 = 0, J = 1 has been determined as 1.1086 (3) D by de Leluw & Dymanus (1973); the dipole moment of H37Cl is expected to be only marginally different. See Table 1 for the frequencies of HCl and the other species considered.
The estimated accuracy for each of the three hyperfine components is 100 kHz, sufficient for the present analysis. It should be mentioned in this context that improved rest frequencies have been published by Klaus et al. (1998) and Cazzoli & Puzzarini (2004) employing Lamb-dip spectroscopy.
The c-C3H2 frequency data were also taken from the JPL catalog. The 212−101 transition was measured by Vrtilek et al. (1987); the reported uncertainty is smaller than the value used in the JPL catalog.
The H13CO+ and CO rest frequencies were taken from the CDMS catalog (Müller et al. 2001, 2005). The rest frequency of the J = 1−0 transition of H13CO+ is from an astronomical observation by Schmid-Burgk et al. (2004); values for both CO transitions result from Lamb-dip measurements by Winnewisser et al. (1997).
3. Observations and data reduction
3.1. Overview
We have used the Atacama Pathfinder Experiment (APEX) 12 m telescope for observations of several sources in a number of submillimeter wavelength transitions of SH+ whose accurate frequencies have recently been determined (see Sect. 2); these included the quartet of ground-state hfs lines near 683 GHz. Our observations, described in Sect. 3.2, led to the detection of these lines in absorption against Sgr B2(M) and (N). In addition to absorption from gas associated with the GC, we also find absorption at the radial velocities belonging to intervening spiral arms, which demonstrates that this species is widespread in the Galactic ISM.
For diverse reasons, our results for other SH+ lines were not as clear as those obtained for the 683 GHz line, namely the N = 1−0,J = 0−1 lines near 346 GHz, which are completely blended with the CO J = 3−2 line and our observations of the N = 2−1,J = 1−1 lines were inconclusive. We made, however, an unambiguous detection of absorption in the J = 1−0 transition of the 13CH+ radical near 830 GHz, again from gas in the Sgr B2 region and from spiral arm clouds. Absorption in that line has previously been reported by Falgarone et al. (2005) toward G10.6+0.4, leading to an estimate of its rest frequency that is discussed in Sect. 2.2.
Finally, we took a wide bandwidth spectrum that covers the J = 1−0 transitions of both the H35Cl and H37Cl isotopologues of hydrochloric acid. The former had been observed by Zmuidzinas et al. (1995) toward a position midway between Sgr B2(M) and (N). Since their spectrum only covered the LSR velocity range between −10 and +140 km s-1 it does not contain information for the spiral arm feature velocities. While we confirm the Sgr B2 velocity absorption, no clear absorption is found toward the latter in our more sensitive and wider bandwidth spectra. In Sect. 4.1.4, our upper limits for these diffuse lines of sight are compared with the tentative ultraviolet detection of HCl absorption toward ζ Oph by Federman et al. (1995).
3.2. APEX observations and data reduction
Our SH+ observations were made on 2008 September 19 and 25 under good to very good weather conditions with the 12-m Atacama Pathfinder Experiment telescope, APEX3 (Güsten et al. 2006). The precipitable water vapor (PWV) content was between 0.3 and 0.7 mm throughout the observations.
The 683 and 893 GHz lines were measured in the lower sideband (LSB) with the MPIfR-built CHAMP+ receiver array (Kasemann et al. 2006). CHAMP+ consists of two modules of 7 pixels each with one central pixel and the others forming a hexagon around it. The one module covers the 350 μm atmospheric window and the other the 450 μm window. Calibration was obtained using the chopper wheel technique, considering the different atmospheric opacities in the signal and image sidebands of the employed double sideband receivers. The image sideband was rejected to the 10 dB level. During the observations the single sideband system temperatures at 683 GHz were between 1700 and 2600 K. To ensure flat spectral baselines, the wobbling secondary was chopped with a frequency of 1.5 Hz and a throw of 240′′ about the cross elevation axis. The wobbler was operated in symmetric mode, which means that the on source and off positions are interchanged between subsequent subscans, which cancels any asymmetries in the optical paths. Such observations deliver a reliable estimate of the continuum level. We found, however, that the quality of the baseline deteriorated with increasing continuum flux density.
The radiation was analyzed with a new incarnation of the MPIfR Fast Fourier Transform spectrometer (FFTS)(Klein et al. 2006), which provided two 1.5 GHz wide modules set to 1024 frequency channels each. The resultant channel spacing was 1.46 MHz, corresponding to 0.49 and 0.70 km s-1 at the highest and lowest frequency we observed (893 and 625 GHz, respectively). The FFTS modules were operated in series with an overlap of 300 MHz to provide a total coverage of 2.4 GHz bandwidth. To check the telescope pointing, drift scans were made across the continuum of Sgr B2(N). Pointing corrections were derived from these measurements. The pointing was found to be accurate to within ≈3′′, acceptable given the FWHM beam size, θB, which is 9′′FWHM at 683 GHz.
The SH+ line near 346 GHz was observed with the 345 GHz atmospheric window module of the Swedish heterodyne facility instrument for the APEX telescope (Vassilev et al. 2008) with system temperatures between 320 and 370 K. Two facility FFTS backends with 1 GHz bandwidth and 8192 channels each were connected to the receiver with a slight overlap to reach a total bandwidth of 1.8 GHz. The beam width at the observing frequency is about 18′′. Pointing was again checked with continuum scans on Sgr B2(N).
Observations of the  J = 1−0 lines near 830 GHz
were performed using the CHAMP+ array on 2009, August 11 under extremely good weather
conditions with a PWV content of 0.14 to 0.2 mm. Two 1.5 GHz FFTS modules were used with
overlap to reach a total bandwidth of 2.4 GHz. Prior to the integration on Sgr B2, the
telescope was pointed on the continuum of Sgr B2(N) and G10.62−0.38. For the line
observations again the wobbler was used with a throw of 240′′ and a chopping frequency of
1.5 Hz.
J = 1−0 lines near 830 GHz
were performed using the CHAMP+ array on 2009, August 11 under extremely good weather
conditions with a PWV content of 0.14 to 0.2 mm. Two 1.5 GHz FFTS modules were used with
overlap to reach a total bandwidth of 2.4 GHz. Prior to the integration on Sgr B2, the
telescope was pointed on the continuum of Sgr B2(N) and G10.62−0.38. For the line
observations again the wobbler was used with a throw of 240′′ and a chopping frequency of
1.5 Hz.
Finally, observations of the H35Cl and H37Cl J = 1−0 transitions were made with CHAMP+’s lower frequency module in 2009 June under superb weather conditions.
4. Results and data analysis
During our three observing campaigns, we have gathered data that allow unambiguous identification of the SH+ and 13CH+ molecules toward Sgr B2. In addition, we have made observations of the J = 1−0 ground-state transition of both the H35Cl and H37Cl isotopologues of hydrogen chloride.
In absorption spectroscopy, the column density in a transition’s lower energy level,
Nl, can be calculated from its observed optical depth,
τ and line width Δv if its excitation temperature,
Tex, is known:
![\begin{equation} N_{\rm l} = {{h}\over{8\pi^2}}{{g_{\rm l}}\over{S\mu^2}}\big[1-{\rm e}^{-h\nu/kT_{\rm ex}} \big]^{-1}\tau \Delta v, \end{equation}](/articles/aa/full_html/2011/01/aa14363-10/aa14363-10-eq104.png) (1)where Aul is the
Einstein A coefficient; h and k are the Planck and
Boltzmann constants, respectively, and
ν = Eu−El
the transition’s rest frequency; Eu and
El are its upper and lower energy levels, respectively.
(1)where Aul is the
Einstein A coefficient; h and k are the Planck and
Boltzmann constants, respectively, and
ν = Eu−El
the transition’s rest frequency; Eu and
El are its upper and lower energy levels, respectively.
The total column density, Ntot, is given by 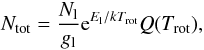 (2)where Q is the partition
function for the rotation temperature, Trot.
(2)where Q is the partition
function for the rotation temperature, Trot.
In the case of a line with a single absorption component, the optical depth and line width
are usually determined by a Gaussian fit to the line profile and τ is
calculated from the line to continuum intensity ratio:
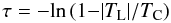 (3)where TL and
TC are the observed line and continuum brightness temperature,
respectively.
(3)where TL and
TC are the observed line and continuum brightness temperature,
respectively.
Things are generally not so simple for the immensely line-rich Sgr B2 sources, for which practically the whole (sub)mm range contains a large number of lines from different species in each chosen frequency interval, many of them blended. To make things even more complex, many of the simpler species show multiple absorption components originating from various spiral arms along the line of sight that are blended with each other and with spectral components from lines of other species at GC velocities. Lines showing hfs, such as SH+ are yet more difficult to analyze. To deal with this, we employ, as described by Belloche et al. (2008), the XCLASS4 program created and developed by Peter Schilke. XCLASS is an extension of the CLASS spectral line data reduction program that is part of the GILDAS5 software package developed by the Institute for Radio Astronomy at Millimeter Wavelengths (IRAM). Using XCLASS one may fit all lines in a spectrum simultaneously as described in Sect. 4.1.
For each species, XCLASS assumes that the level populations are described by a single excitation temperature, which we refer to as the rotation temperature, Trot. Different species can have different rotation temperatures. Here we divide between two cases: First, the critical densities of all the lines in the frequency range of interest are lower than the density in the modeled emission region. Then we are dealing with local thermodynamic equilibrium (LTE), which applies, e.g., for the extremely line rich hot cores associated with Sgr B2(M) and (N). In particular in the latter, the complex molecules NH2CH2CN, C2H5OCHO, and C3H7CN along with the 13C isotopologues of vinyl cyanide have recently been identified using XCLASS with model temperatures of ≈100–150 K (Belloche et al. 2008, 2009; Müller et al. 2008). In the second, very low density case, which applies for the absorption lines discussed in this paper, Trot equals the temperature of the cosmic microwave background radiation, TCMB, i.e. 2.728 K. While this might be a good assumption for clouds far from the strong Sgr B2 continuum sources, e.g., in the spiral arms, assuming Trot = TCMB will underestimate column densities for molecules in the vicinity of Sgr B2(M) and (N).
4.1. Modeling of the absorption lines toward Sgr B2(M)
4.1.1. The model for the spiral arm and galactic center LSR velocity features
The SH+(11–01) spectra obtained with the CHAMP+ array consist of the superposition of a number of absorption components associated with the dense core Sgr B2(M) and several molecular clouds distributed along the line of sight with different systemic velocities (see, e.g., Greaves & Williams 1994).
The association of the absorption components’ LSR velocities with Galactic spiral arms or kinematic features associated with the GC located along the line of sight is presented in Table 2. It is essentially based on the velocity interpretation of H2CO and CS absorption by Whiteoak & Gardner (1979) and Greaves & Williams (1994), respectively, as well as the analyses of Sofue (2006) and Vallée (2008). Although in the GC direction absorption close to Vlsr = 0 could in principle come from any location on the line of sight, we favor a physical association with the GC since Gardner & Whiteoak (1981) found low values of the 12C/13C ratio (20–30) for this velocity range, consistent with a Galactic center origin.
The blending of these absorption components is further complicated by the hyperfine structure of the SH+ transition. To allow meaningful fitting, we used information derived from the absorption spectra of other molecules obtained as part of a complete line survey done with the IRAM 30 m telescope in the 3 mm atmospheric window toward both hot cores Sgr B2(M) and Sgr B2(N) (see Belloche et al. 2008, 2009).
The line survey was analysed with the XCLASS software (see Sect. 4)6 . Each molecule identified in the survey was modeled with the following free parameters: source size, temperature, column density, linewidth, and velocity offset with respect to the systemic velocity of the source, 62 km s-1 for Sgr B2(M). When several components were needed to reproduce the observed spectrum of a molecule, we fitted a set of parameters for each component. The combination of the predicted spectra of all identified molecules was done assuming that the emission adds up linearly (for more details, see Belloche et al. 2008).
To model the absorption lines observed toward Sgr B2(M), we assumed a beam-averaged
continuum brightness temperature Tcont of 5.9 K in the 3 mm
window, as derived from the saturated absorption spectra of HCN and CN (see Table 1). The modeling of the absorption components was
done in the Trot = TCMB
approximation with a flag indicating that the absorption spectrum has to be computed
against a background emission consisting of both the continuum emission and the
contribution of the other molecules seen in emission, i.e. for each absorption component
with the equation 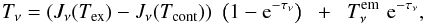 (4)with Tex the
excitation temperature, Tcont the background brightness
temperature,
(4)with Tex the
excitation temperature, Tcont the background brightness
temperature, 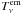 the emission line spectrum, and
τν the opacity of the line at
frequency ν, for a beam filling factor of 1.
the emission line spectrum, and
τν the opacity of the line at
frequency ν, for a beam filling factor of 1.
Velocity ranges and 12C/13C isotopic ratios of the Galactic absorption components along the line of sight of Sgr B2(M).
Table 2 also lists the 12C/13C isotopic ratios we assumed. The 12C/13C isotopic ratio of the Galactic Center components was fixed to 20 (Müller et al. 2008). This value is compatible with the Galactic gradient derived by Milam et al. (2005, Eq. (5)). Their equation was additionally employed to fix the ratio to 40 for the Scutum and Norma arm components, and 60 for the Sagittarius arm components, with the galactocentric distances of Vallée (2008). The 16O/18O isotopic ratio was taken from Wilson & Rood (1994): 250 for the GC components, 327 for the Scutum and Norma arm components, and 560 for the Sagittarius arm components.
 |
Fig. 2 From bottom to top, panels a) to c) show absorption spectra taken with the APEX telescope with the CHAMP+ receiver array. Spectra a) and b) were taken with the central pixel of CHAMP+ toward Sgr B2(M) (see Fig. 5). Spectrum b) was obtained toward a position (− 20.4″,1.4″) offset from Sgr B2(M) with the CHAMP+ pixel 2. a): H35Cl 1−0 absorption spectrum. b): SH+ 11–01 absorption spectrum. c): 13CH+ 1–0 absorption spectrum. In panels a)–c), the red curve is the synthetic spectrum described in Sect. 4.1 and the horizontal dotted line shows the continuum level. d) and e): same as b for the c-C3H2 212–101 and H13CO+ 1–0 transitions observed toward Sgr B2(M) with the IRAM 30 m telescope, respectively. Panel f) shows the optical depth of the 21 cm HI line vs. LSR velocity as derived by the procedure described in Sect. 5.1.2. In panels d) and e), the red curve is the synthetic spectrum of the molecule, the green curve is the predicted spectrum including in addition all molecules identified in our complete 3 mm line survey so far, and the horizontal dotted line indicates the zero level (after baseline removal because the observations were performed in position-switching mode with a far OFF position, which yields a very uncertain baseline level). In all panels, the spectra are plotted in main-beam brightness temperature scale, the vertical dotted line marks the systemic velocity of the source (62 km s-1). |
Parameters of the best-fit LTE models of SH+, 13CH+, and c-C3H2, as well as the alternative LTE model of H13CO+ fitted with the same velocity components as c-C3H2.
We present, in Fig. 2d and e, the results of our modeling for c-C3H2(212–101) and H13CO+(1–0), respectively. The model for H13CO+(1–0) was obtained by fitting HCO+, H13CO+, and HC18O+ simultaneously. The fit to the observed H13CO+(1–0) spectrum consists of four components in emission (one for the main emission peak and three to reproduce the wings), one absorption component to mimic the self-absorption in Sgr B2(M)7 and 34 absorption components associated with the diffuse clouds along the line of sight, with linewidths varying between 3 and 8 km s-1 and an excitation temperature arbitrarily fixed to 2.7 K. The parameters of the fit to H13CO+ are listed in Table 4. The model predicts too strong absorption for the H13CO+(1–0) components with v < −50 km s-1, while the corresponding HCO+(1–0) components are well fitted (not shown here). The disagreement must result either from an underestimate of the 12C/13C isotopic ratio or from contamination by emission lines that are not yet included in our complete model. It could in principle also result from larger excitation temperatures for HCO+ compared to H13CO+.
The fit to c-C3H2 was done with velocity and linewidth parameters slightly different from HCO+, although we tried to stay as close as possible to the components identified in HCO+. The parameters of the fit to c-C3H2 are listed in Table 3. The model consists of one component in emission (we did not attempt to model the possible wing emission in this case), one absorption component to mimic the self-absorption, and 30 absorption components associated with the diffuse clouds, with an excitation temperature of 2.7 K and linewidths varying between 3 and 6 km s-1.
 |
Fig. 3 a)–d) Column density profiles computed by adding the Gaussian velocity absorption components listed in Table 3. The components with upper limit were not included. e)–g) Abundance profiles relative to H2. The H2 column density was computed from the HCO+ column density assuming an HCO+ abundance of 5 × 10-9. h)–j) Abundance profiles relative to H i. k) The H i column density was computed from comparing an H i absorption with an H i emission profile (see text). |
4.1.2. Modeling the SH+ absorption
Since we considered c-C3H2 a priori to be a better diffuse gas tracer than 13HCO+ (but see Sect. 5) and because of the added uncertainty of assigning a 12C/13C ratio to each absorption components, we decided to model the SH+ absorption spectrum based on the parameters derived for c-C3H2, i.e. we used the same number of absorption components with the same velocities and line widths, except for the component physically associated with Sgr B2(M) itself. Again, we fixed the excitation temperature of each component to 2.7 K. Since the observations were done in wobbler mode, we trusted the baseline level and derived the level of continuum emission directly from the observed spectra shown in Fig. 5. To compute the synthetic spectra, we assumed that the physical parameters of the absorbing components are uniform across the CHAMP+ field of view and therefore we used the same set of parameters for all pixels. The resulting synthetic spectra are overlaid on the observed spectra in Fig. 5. The agreement is quite good in general, which gives us some more confidence in the way we estimated the continuum level. However, significant deviations are seen for pixels 1, 3, and 4. As mentioned in Sect. 3, the baseline quality of the CHAMP+ array drops with increasing level of continuum emission and line contamination from the hot molecular core associated with Sgr B2(M). Pixel 4 is the most affected, and we believe that the poor quality of the fit is mainly due to this problem. As far as the northern pixels 1 and 3 are concerned, the main absorption component is much stronger than the one predicted by our simple model. This may be due to spatial variations of the SH+ column density across the Sgr B2 molecular cloud since the cloud is far from being uniform (in particular, the hot, dense core Sgr B2(N) is located ~50″ to the north of Sgr B2(M)). If the variations from pixel to pixel can be trusted, then we can estimate the variations of the SH+ column densities in the spiral arm diffuse clouds over the footprint of CHAMP+ by modeling each pixel separately. This exercise yields column density variations typically on the order of a factor 2, but in some cases up to a factor 5. However, given the low signal-to-noise ratio, the unknown baseline quality, and the line blending, these numbers are very uncertain and it is unlikely that they really reflect the spatial variations of the SH+ column density.
The parameters used to fit the SH+ 11–01 absorption spectrum are listed in Table 3 and the fit to the spectrum obtained with pixel 2 is plotted again in Fig. 2b for a direct comparison with HCl, 13CH+, c-C3H2, and H13CO+. Although the decision to fix the linewidths and velocities to those derived from c-C3H2 helps a lot to constrain the SH+ model, the hyperfine structure of SH+ and the limited signal-to-noise ratio of the observed spectra do not allow to find a unique solution. Using the somewhat different set of velocity and linewidth parameters derived from HCO+, we were able to find a synthetic spectrum for SH+ as good as the SH+ model derived from c-C3H2 (the parameters of this alternative model are listed in Table 4). Therefore, the SH+ model described in Table 3 should be considered as a possible model rather than the best-fit model. Nevertheless, if we assume that c-C3H2 and SH+ trace the same diffuse clouds, then it makes sense to compare the column densities listed in Table 3. Column 10 lists the column density ratio SH+/c-C3H2. It varies by nearly two orders of magnitude, from <0.6 to ~33. As a caveat, we remind that the SH+ model assumes no contamination from emission lines of other molecules. If there are contaminating emission lines, then the column densities derived for the SH+ components contaminated by these emission lines are lower limits.
Unfortunately, the SH+ 10–01 line at 345.9 GHz is heavily blended with the spiral arm components of the CO 3–2 line seen in absorption (see Fig. 6a). The Trot = TCMB model derived for the 11–01 line predicts 10–01 spiral arm components in absorption that are relatively consistent with the observed spectrum dominated by the CO 3–2 features, except around 62 km s-1, the systemic velocity of Sgr B2(M). At 893 GHz, there is no clear evidence for the SH+ 21–11 line (see Fig. 7). Our Trot = TCMB model predicts no significant absorption for this higher energy transition (see red spectrum in Fig. 7). On the other hand, this transition could partly contribute to the broad feature detected in emission between 58 and 125 km s-1 (although the higher velocity half of that feature is uncertain due to the limited baseline quality). An additional model component in emission is indeed permitted by the 893 GHz spectrum and can even solve the disagreement at 62 km s-1 between the synthetic and observed spectra of the 10–01 transition. If this emission component has a size smaller than ~20″, then the Trot = TCMB synthetic spectrum of the (− 20.4′′, +1.4′′) CHAMP+ pixel at 683 GHz (shown in Fig. 2) will be unaffected and still provide a good fit to the observations. However, the fit to the spectrum of the central pixel at 683 GHz (see Fig. 5) will be worse, and a more elaborate radiative transfer modeling would be needed to find a consistent fit for this potential emission component.
4.1.3. The 13CH+ absorption
The 13CH+ 1–0 transition detected in absorption toward Sgr B2(M) was also modeled in the Trot = TCMB approximation (see Fig. 2c). We used the SH+ model as a reference, keeping the velocity offsets and linewidths unchanged. The resulting fit, shown in red in this figure, is in good agreement with the observed spectrum, although it could certainly be somewhat better if the line widths were taken as free parameters for the fitting.
The column densities resulting from this fit are listed in Table 3, as well as the SH+/13CH+ and the SH+/12CH+ column density ratio. The latter varies significantly from component to component, from 0.07 to 1.2, if we exclude components 31 and 32 in Table 3 at whose velocity the signal-to-noise ratio in the SH+ spectrum is very low and which are not detected in the 13CH+ absorption at all.
The 13CH+ 1−0 spectrum shows an absorption feature at +172.6 km s-1. Although absorption in CO is detected at this velocity in our 3 mm line survey in the CO 1–0 and 13CO 1–0 lines (see Fig. 6), this component is neither detected in H13CO+ 1–0, c-C3H2 212–101, nor in SH+ 11–01 (see Fig. 2). Features at this velocity are usually attributed to the Expanding Molecular Ring (EMR, e.g. Morris & Serabyn 1996) but +172.6 km s-1 would refer to the far side of the ring, hence no absorption is expected and it is possibly more likely that this feature is an as yet unidentified (U) absorption line.
We also list in Table 3 the parameters of an alternative H13CO+Trot = TCMB model fitted with the same velocity components as c-C3H2 (i.e. same linewidths and LSR velocities). This model is less good than the one that we described above and that we showed in Fig. 2e, but it can be used to roughly estimate the SH+/HCO+ column density ratio (Col. 12 of Table 3). This ratio varies by about one order of magnitude, from 0.07 to 2.38.
4.1.4. Modeling the HCl absorption only from the Sgr B2 region
The HCl and H37Cl transitions detected in absorption toward Sgr B2(M) were also modeled in the Trot = TCMB approximation (see Fig. 8). We used the SH+ model as a reference, keeping the velocity offsets and linewidths unchanged, except for the main absorption component associated with Sgr B2(M) itself. The resulting fit is shown in red in Fig. 8 and the fit parameters are listed in Table 5. Only the main absorption component is clearly detected for both isotopologues. For all other velocity components but one, we used a column density of 2.8 × 1012 cm-2, represented by the red line in Fig. 8, to get a rough estimate of the column density upper limits. Only one additional velocity component (nc = 6; ~17 km s-1) marginally shows absorption in the main isotopologue HCl at 2.8 times this value. Due to the compact hyperfine structure, the line width of the main absorption component (8 km s-1) is somewhat uncertain, but our modeling suggests that it is significantly smaller than for the other species. Finally, for Sgr B2(M) we derive an isotopic [H35Cl/H37Cl] ratio of ~4, consistent with the terrestrial value.
 |
Fig. 5 SH+ absorption spectra obtained toward Sgr B2(M) with the 7-pixel array CHAMP+ at the APEX telescope. The equatorial offset position of each pixel relative to Sgr B2(M) is given in the bottom left corner of each panel. In each panel, the dotted line shows the continuum level as measured over the emission/absorption-free channels, and the red curve is the spectrum predicted by the Trot = TCMB model described in Sect. 4.1. All spectra are plotted in main-beam brightness temperature scale. |
Parameters of the best-fit LTE model of H13CO+ and the LTE model of SH+ fitted with the same velocity components as H13CO+.
4.2. Summary of modeling
To visualize the results of our modeling presented in Tables 3 and 4, we show, in Fig. 3, the column densities and abundances that we derived for the species considered as functions of LSR velocity. Figure 4 presents the CH+ to SH+ abundance ratio vs. LSR velocity.
5. Discussion
5.1. Column densities and abundances
5.1.1. Caveats
We would like to precede our discussion of the SH+, 13CH+, and HCl abundances in the spiral arm clouds with some cautionary notes. First, the assignment of velocity features to Galactocentric distance is by no means clear-cut. For example, Sofue (2006), from a careful analysis of the longitude-velocity diagram of the GC region, assigns certain velocity features to peculiar components of the complex Galactic center velocity field, namely the GC molecular ring and the GC expanding ring, both within a Galactocentric radius, R, of 600 pc of the GC. In addition to several spiral arms, he invokes expanding rings at R = 3 and 4 kpc. Some of Sofue’s conclusions are at variance from the LSR velocity-location assignment we present in Sect. 4.1. Second, SH+ and 13CH+ may in principle be associated with predominantly atomic or molecular diffuse clouds. For meaningful abundance calculations, it is thus necessary to have values for both the atomic hydrogen column density, N(HI), and the molecular hydrogen column density, N(H2). Actually, the clouds from which we see absorption may have complex structure, e.g., a Giant Molecular Cloud region and a diffuse atomic envelope (see Sect. 5.2) and/or we may be dealing with more than one cloud along each line of sight. Certainly, the HI spin temperatures are in the range of values found for diffuse clouds and significantly higher than the canonical GMC temperatures values of 20–30 K.
 |
Fig. 6 a) Spectrum obtained toward Sgr B2(M) at the frequency of the SH+ 10–01 line with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, the horizontal dotted line shows the continuum level, and the vertical dotted line marks the systemic velocity of the source (62 km s-1). The strong absorption lines are spiral arm components of CO 3–2. The lower axis gives the LSR velocity for SH+, while the upper axis refers to CO, with the same labeling as in panel b). b) CO(1–0) spectrum obtained toward Sgr B2 as part of our line survey with the IRAM 30 m telescope. The horizontal dotted line indicates the zero level (after baseline removal because the observations were performed in position-switching mode with a far OFF position, which yields a very uncertain baseline level). In both panels, the dashed line marks the systemic velocity of the source in CO 3–2 and the dot-dashed line indicates the CO velocity +172.6 km s-1 at which an extra absorption component appears in the 13CH+ spectrum (see discussion in Sect. 4.1.3.) |
 |
Fig. 7 Spectrum obtained toward Sgr B2(M) at the frequency of SH+ 21–11 with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, i.e., showing no detectable emission, the horizontal dotted line shows the continuum level, and the vertical dotted line marks the systemic velocity of the source (62 km s-1). The absorption line appearing at ~− 105 km s-1 is the JKaKc = 111−000 ground-state line of HDO at 893 638.7 MHz (Comito et al. 2003). |
 |
Fig. 8 Spectrum obtained toward Sgr B2(M) around 625 GHz with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, the horizontal dotted line shows the continuum level, and the left and right vertical dotted lines mark the systemic velocity of the source (62 km s-1) for HCl and H37Cl, respectively. The strong emission close to the HCl line is likely due to a SO2 line at 626 087.3 MHz. |
Two final, more technical caveats relate to the way we derive column densities. For the 3 mm Sgr B2(M) spectra for H13CO+ and c-C3H2 we have constructed full XCLASS models considering all the absorption from these molecules plus emission from them and all other molecules. In contrast, for the submillimeter spectra, we have not done this. While even the 3 mm spectra may be contaminated by emission features inadequately treated by the model, for the submm absorption spectra this is a much greater source of uncertainty for line assignments and intensity predictions, making, strictly speaking all the column densities we determine lower limits. We do at present not feel confident to construct a comprehensive model for the submm spectra. Similarly, if, as discussed in Sect. 4, excitation by the ambient radiation field is non-negligible, then Trot > TCMB, which would make our column densities underestimates.
Finally, our XCLASS-based method makes it difficult to derive statistical errors and, thus, upper limits rigorously in a χ2 sense. Rather, upper limits are determined by assuming a column density, calculating a model spectrum and then “eye-balling” whether it is consistent with the data.
5.1.2. Atomic and molecular hydrogen column densities
The column density of atomic hydrogen, N(HI), can be calculated from measurements of the 21 cm HI line’s optical depth, τ(HI), at the intervening clouds’ velocities (e.g., Garwood & Dickey 1989) and a determination of their spin temperatures, Ts, as described by Lazareff (1975). The method invokes a combination of interferometric observations to, first, directly determine the optical depths of the absorption components and, second, single dish observations to measure the (optically thick) line’s brightness temperature. As described in a forthcoming paper, we have performed the necessary single dish observations with the Effelsberg 100 m telescope and obtained an optical depth spectrum (τ(HI) vs. Vlsr) measured toward Sgr B2(M) with the NRAO Very Large Array from Lang (pers. comm.). We note our values for N(HI) are generally lower than those derived by Vastel et al. (2002). This is partially due to their assumption of Ts = 150 K for all velocity components.
A determination of N(H2) is more difficult, as selection of a “universal” trace molecule for molecular hydrogen is not straightforward. For meaningful modeling, such a molecule’s lines would be required to be subthermally excited, meaning that their relative level populations be determined by TCMB. This means, for example that, due to their small dipole moments and resulting low critical densities, isotopologues of CO are not suited. A possible choice for an H2 tracer, which we adopt here, might be HCO+. Lucas & Liszt (1996) from their study of this molecule’s 89 GHz J = 1−0 ground-state transition, conclude its abundance (relative to H2) to be “ ~3–6 × 10-9 across a very broad range of extinction”, meaning between hydrogen column densities ~0.1 and 4 × 1020 cm-2. These authors base this finding, first, on the very tight correlation between the HCO+ and the OH column densites and, second, on the fact that OH has the same abundance (10-7) in diffuse as in dense dark clouds. While their own absorption data only sample hydrogen column densities within the range quoted above, they find that the correlation holds at >10 times higher values than its upper boundary. Here we adopt 5 × 10-9 for the HCO+/H2 abundance ratio. This value is of the same magnitude as that listed by van Dishoeck et al. (1993) for (high column density) regions of low and high mass star formation.
Since HCO+ absorption toward Sgr B2 is optically thick even for the non-Sgr B2 region velocity features, we use, as described in Sect. 4.1, H13CO+ spectra and obtain the main-isotope’s column density by scaling with the appropriate 12C/13C ratios given in Col. 4 of Table 3.
Our estimates for N(HI) and N(H2) for the absorption components are listed in Table 6. For simplicity’s sake and motivated by our optical depth fitting of the HI data and also to allow comparison with other studies, we have grouped the velocity components into seven intervals. The HI and H2 column densities and HI spin temperatures were derived as described above from HI and H13CO+ data fixed to values compatible with the values given in the table. The column densities of SH+ and CH+, presented in Table 7, were obtained by summing over the individual velocity components in Table 3 and multiplying the CH+ column densities by the 12C/13C ratios given for each component in that table.
5.2. The origin of the 13CH+ and SH+ absorption
Since it is a priori not clear whether the observed SH+, CH+ and HCl molecules are only associated with either atomic or molecular gas or both, when calculating abundance ratios, we might want to refer to the total column density of hydrogen nuclei, N(H) ≡ N(HI) + 2 N(H2). Inspecting Table 6, we find that over all velocity ranges showing absorption, N(H2) greatly exceeds N(HI), by factors between 13 and 133, approaching the value for Sgr B2 (138). This means that the absorbing medium is dominated by GMC gas. This is reinforced by the densities derived by Greaves et al. (1992) from LVG modeling of the two lowest rotational lines of CS, which, between 0.4 and 2 × 104 cm-3, are actually even higher than values in most of a GMC’s volume.
Both the total hydrogen nuclei column density, N(H), and the H2/HI ratio are much larger than the values found in translucent and diffuse clouds. Gredel et al. (1992) in their study of the archetypical translucent cloud toward HD 210121 find N(H2) = 8 × 1020 cm-2 and N(HI) = 1−5 × 1020 cm-2 for the molecular and atomic hydrogen absorption column densities, respectively. In comparison, the classic diffuse cloud line of sight toward ζ Oph has comparable HI and H2 column densities of ≈5 × 1020 cm-2 or a column density of hydrogen nuclei of N(H) = 1.5 × 1021 cm-2 (van Dishoeck & Black 1986).
Parameters of the best-fit LTE model of HCl and H37Cl.
As discussed above, the absorbing material is dominated by GMCs. There is, however, nothing that does imply that the observed quantities of CH+ and SH+ are associated with gas within a GMC, although little is known about the abundance of both species in such objects. Model calculations predict significant column densities in lower-AV portions of dense (>105 cm-3) PDRs illuminated by intense ultraviolet fields (Sternberg & Dalgarno 1995). Even more extreme conditions (XDRs) are required to produce significant amounts of SH+ in dense regions (Abel et al. 2008). However, both dense P and XDRs have small volume filling factors, making them unlikely absorbers. These findings point to an (at least) two component picture for most of the absorption components, i.e., a diffuse envelope traced by HI, CH+ and SH+ absorption plus a denser core region, a view that is also invoked by Vastel et al. (2002) to explain the absorption they observed with ISO in the C+ and O0 fine structure transitions.
H i and H2 column densities of the absorption components.
In Fig. 9 we plot CH+ column density vs. hydrogen column density, N(HI) as defined above, for the seven velocity ranges in Table 6 (coded A–G). For each CH+ column density entry two data points are plotted, both taken from the table. The left one (open squares) assumes that the CH+ is only associated with atomic hydrogen, whereas the right one (filled squares) assumes it is only associated with molecular hydrogen or, essentially, all the hydrogen since N(H2) ≫ N(HI) for all velocities. We also plot (as circles) data for the two classic diffuse clouds against ζ Oph and ζ Per. For these, N(H2) ≈ N(HI) ≈ 5 × 1020 cm-2. In addition, we present data for the translucent cloud toward HD 210121 where, again, two points assuming that the CH+ is only associated with atomic (left) or molecular gas (right) are plotted. All values for the latter three sources, N(H2), N(HI), and N(CH+), are taken from de Vries & van Dishoeck (1988). The circles represent the absorption data Gredel (1997) determined toward a sample of southern OB associations. For these lines of sight, which have higher extinctions, between 0.36 and 4.2 mag, (mostly) corresponding to translucent clouds, we cannot discriminate between atomic and molecular hydrogen columns as Gredel lists N(CH)+ vs. AV, which contains contributions from both. To convert his AV values to hydrogen column densities we use the results of the classic study of Bohlin et al. (1978), who found for low values of visual extinction (0.02 < AV < 0.6) a linear relation between AV and hydrogen column density, which as first argued by Dickman (1978), also holds for significantly higher AV values. It is consistent with a relation derived from modeling of x-ray data (Güver & Özel 2009): N(H(cm-2)) ≈ 2 × 1021 AV(mag).
5.2.1. Comparison with individual diffuse clouds
While we advocate above a diffuse cloud origin of the CH+ absorption, we note that, apart from one velocity range (B, 12.9–23.2 km s-1), our CH+ column densities are much higher than found in diffuse clouds and mostly higher than in the translucent cloud sample. However, the velocity ranges over which the values were determined, are mostly much larger than the line widths found in diffuse or translucent clouds (and even GMCs). For this reason, we plot in the lower panel of Fig. 9 the average column densities that a cloud with “typical” line width ΔVtyp would have. This means we have divided for each of the velocity intervals A–G, both, CH+ and hydrogen column densities by the ratio of the width of the velocity interval and ΔVtyp. We chose ΔVtyp to be 4.3 km s-1 FWHM, which is the mean of the sample of diffuse lines of sight for which Crane et al. (1995) present high spectral resolution CH+ data8. This value is consistent with that discussed by Gredel (1997) for his translucent cloud sample. The thus calculated values correspond to a “typical” cloud with averaged properties.
 |
Fig. 9 CH+ column density versus hydrogen column density. The ordinate gives the CH+ column density for the seven different velocity intervals listed in Table 7. The capital letters designate the entries in table (top to bottom). The open circles represent data taken from the diffuse/translucent cloud sample of Gredel (1997). The squares connected by lines mark the CH+ column densities determined in this work. For the open squares it is assumed that all the absorption is from atomic gas; the abscissa corresponds to the HI column density (Table 6), whereas for the filled squares it is assumed that all the absorption is from molecular gas; the abscissa corresponds to the H2 column density (Table 6). For the upper panel, column densities were calculated from the absorption over the whole velocity range of each interval, whereas in the lower panel average column densities normalized to a typical line width of 4.3 km s-1 were used (see text). |
Inspecting the CH+ column densities for these typical clouds we find values very similar to those found in diffuse and translucent clouds. We note that the ratio of molecular to atomic hydrogen column densities is in most cases higher than that found in translucent and much higher than in diffuse molecular clouds. The reason for this is almost certainly sight line superposition of the CH+-containing diffuse/translucent and denser molecular clouds, as discussed above.
5.3. Comparison – SH+ and other S-bearing species and the CH+/SH+ ratio
The values we derive for the SH+ column density, N(SH+), for the non-Sgr B2 region velocity ranges go up to 7 × 1013 cm-2 (see Table 7). Considering again the differences in line widths, these values are comparable with the upper limits found for optical SH+ absorption from diffuse and translucent clouds (i.e. 1 × 1013 cm-2; see Sect. 1.2).
Column densities of the absorption components and abundances relative to H.
The column densities of other sulfur bearing species in the velocity ranges of Table 7 have been determined by Greaves et al. (1992), who studied CS, and Tieftrunk et al. (1994) (SO, H2S, and SO2). Comparing with our values for SH+ (Table 6), we find [SH+/CS] abundance ratios between 0.5 and 3, [SH+/SO] between 1.6 and >55, and [SH+/SO2] >2. For the [SH+/H2S] ratio we find values >2, except for the −33.2 to −50.1 km s-1 velocity range, for which we find the low ratio of 0.3. We note that the velocity of this absorption places it in the Norma spiral arm. From Table 6 we see that this range has the highest H2 column density and the highest H2/HI ratio of all the (non-Sgr B2 region) absorption components and resembles most closely a GMC or GMC core. This reinforces SH+’s nature as a tracer of more diffuse gas whose abundance drops in denser environments.
As discussed by Tieftrunk et al. (1994),
SH+ and H2S are chemically related, as H3S+,
from which the latter forms via dissociative recombination is formed by the reaction
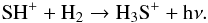 With respect to chemical models (Millar et al. 1986; Pineau des Forêts et al. 1986), it is also worth noting that, as can be seen
from Table 7, the SH+/CH+
ratio, [SH+/CH+], which is 0.56 for Sgr B2(M) only varies between
0.11 and 0.26 for all but one of the non-Sgr B2 absorption features. These values are
consistent with the upper limits on this ratio (0.12–2) for diffuse and translucent lines
of sight (see Sect. 1.2). The component with the
higher ratio, ≈0.9 is in the −90.2 to −123.7 km s-1 range, which corresponds
to peculiar velocity gas associated with the GC. Interestingly, this velocity range has
also by far the highest SiO column density measured for the various velocity components by
Greaves et al. (1996). These two findings may
have a common (shock-wave) origin as an increased SiO abundance is commonly ascribed to
shock chemistry (Schilke et al. 1997).
With respect to chemical models (Millar et al. 1986; Pineau des Forêts et al. 1986), it is also worth noting that, as can be seen
from Table 7, the SH+/CH+
ratio, [SH+/CH+], which is 0.56 for Sgr B2(M) only varies between
0.11 and 0.26 for all but one of the non-Sgr B2 absorption features. These values are
consistent with the upper limits on this ratio (0.12–2) for diffuse and translucent lines
of sight (see Sect. 1.2). The component with the
higher ratio, ≈0.9 is in the −90.2 to −123.7 km s-1 range, which corresponds
to peculiar velocity gas associated with the GC. Interestingly, this velocity range has
also by far the highest SiO column density measured for the various velocity components by
Greaves et al. (1996). These two findings may
have a common (shock-wave) origin as an increased SiO abundance is commonly ascribed to
shock chemistry (Schilke et al. 1997).
5.4. Limits on HCl absorption in the diffuse material
The HCl column density, N(HCl), we derive for the gas associated with Sgr B2(M) (see Table 5) is in good agreement, i.e. 16% higher, with the value derived by Zmuidzinas et al. (1995).
For the velocity components corresponding to the diffuse lines of sight we derive an upper limit on the HCl column density, N(HCl), of 8.4 × 1012 cm-2 (see Table 5 and Fig. 8 in Sect. 4.1.4). Since N(H) ranges from 0.5–2.4 × 1022 cm-2 we calculate an HCl to hydrogen nuclei abundance ratio [HCl/H] of 0.6−3 × 10-10. Our upper limit is much coarser than the (2.7 ± 1.0) × 1011 cm-2Federman et al. (1995) determine for N(HCl) from an UV absorption line toward ζ Oph.
6. Conclusions
We have reported submillimeter wavelength absorption from rotational ground-state transitions of 13CH+, H35Cl, H37Cl, and, for the first time, of the SH+ molecule toward the strong Galactic center continuum source Sgr B2(M). From 13CH+ and SH+ we detect absorption at the systemic LSR velocity of Sgr B2(M) and in addition over a wide range of lower velocities belonging to intervening material. For the intervening clouds we have derived molecular hydrogen column densities from optically thin H13CO emission and atomic column densities from HI 21 cm line data. For all the clouds we find that the former is larger than the latter by factors between 15 and 130. If we “scale” the observed velocity ranges of the individual clouds to the line widths of single diffuse and translucent molecular clouds in the Solar neighborhood, we find similar 13CH+ column densities in both types of clouds. Most likely the reason for this is that the observed 13CH+ is indeed mostly associated with atomic material surrounding molecular material. The [SH+/CH+] ratio is consistent with upper limits from optical data. Our upper limits on the HCl column density in the absorption components not associated with Sgr B2 are consistent with but coarser than measurements of UV absorption from this molecule.
Website: http://spec.jpl.nasa.gov/ftp/pub/catalog/catdir.html, see also http://spec.jpl.nasa.gov/
Although the fits to the self-absorption features in Fig. 2d and e look relatively good, we emphasize that a uniform Trot = TCMB model is not complex enough to provide reliable physical parameters to describe the self-absorption. The parameters listed for the self-absorption components in the following tables should therefore be viewed with caution.
Acknowledgments
We would like to thank the referee for a very thorough reading of the manuscript and comments that led to significant improvements. We thank Cornelia Lang for providing an electronic version of her HI spectrum. H.S.P.M. is grateful to the Bundesministerium für Bildung und Forschung (BMBF) for financial support which was administered by the Deutsches Zentrum für Luft- und Raumfahrt (DLR).
References
- Abel, N. P., Federman, S. R., & Stancil, P. C. 2008, ApJ, 675, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Amano, T. 2010, ApJ, 716, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Belloche, A., Menten, K. M., Comito, C., et al. 2008, A&A, 492, 769 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Garrod, R. T., Müller, H. S. P., et al. 2009, A&A, 499, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benz, A. O., Bruderer, S., van Dishoeck, E. F., et al. 2010, A&A, 521, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, J. M., & Müller, H. S. P. 2009, J. Mol. Spectrosc., 255, 68 [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2004, J. Mol. Spectrosc., 226, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Polehampton, E., & Goicoechea, J. R. 2007, ApJ, 657, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, M., Brown, J. M., Rosmus, P., et al. 2007, Phys. Rev. A, 75, 012502 [NASA ADS] [CrossRef] [Google Scholar]
- Comito, C., Schilke, P., Gerin, M., et al. 2003, A&A, 402, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comito, C., Schilke, P., Rolffs, R., et al. 2010, A&A, 521, L38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, P., Guesten, R., & Henkel, C. 1988, A&A, 206, 108 [NASA ADS] [Google Scholar]
- Crane, P., Lambert, D. L., & Sheffer, Y. 1995, ApJS, 99, 107 [NASA ADS] [CrossRef] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [Google Scholar]
- de Leluw, F. H., & Dymanus, A. 1973, J. Mol. Spectrosc., 48, 427 [NASA ADS] [CrossRef] [Google Scholar]
- De Lucia, F. C., Helminger, P., & Gordy, W. 1971, Phys. Rev. A, 3, 1849 [NASA ADS] [CrossRef] [Google Scholar]
- de Vries, C. P., & van Dishoeck, E. F. 1988, A&A, 203, L23 [NASA ADS] [Google Scholar]
- Dickman, R. L. 1978, ApJS, 37, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, A. E., & Herzberg, G. 1941, ApJ, 94, 381 [Google Scholar]
- Drouin, B. J., Yu, S., Miller, C. E., et al. 2010, J. Quant. Spectrosc. Radiat. Transfer, 111, 1167 [Google Scholar]
- Dunham, T. 1937, PASP, 49, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Phillips, T. G., & Pearson, J. C. 2005, ApJ, 634, L149 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Ossenkopf, V., Gerin, M., et al. 2010, A&A, 518, L118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Federman, S. R. 1982, ApJ, 257, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Federman, S. R., Cardelli, J. A., van Dishoeck, E. F., Lambert, D. L., & Black, J. H. 1995, ApJ, 445, 325 [NASA ADS] [CrossRef] [Google Scholar]
- Gardner, F. F., & Whiteoak, J. B. 1981, MNRAS, 194, 37P [NASA ADS] [Google Scholar]
- Garwood, R. W., & Dickey, J. M. 1989, ApJ, 338, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Geballe, T. R., & Oka, T. 1996, Nature, 384, 334 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gerin, M., de Luca, M., Black, J., et al. 2010, A&A, 518, L110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Golubiatnikov, G. Y., & Krupnov, A. F. 2003, J. Mol. Spectrosc., 217, 282 [NASA ADS] [CrossRef] [Google Scholar]
- Greaves, J. S., & Williams, P. G. 1994, A&A, 290, 259 [NASA ADS] [Google Scholar]
- Greaves, J. S., White, G. J., Ohishi, M., Hasegawa, T., & Sunada, K. 1992, A&A, 260, 381 [NASA ADS] [Google Scholar]
- Greaves, J. S., Ohishi, M., & Nyman, L. 1996, A&A, 307, 898 [NASA ADS] [Google Scholar]
- Gredel, R. 1997, A&A, 320, 929 [NASA ADS] [Google Scholar]
- Gredel, R., van Dishoeck, E. F., de Vries, C. P., & Black, J. H. 1992, A&A, 257, 245 [NASA ADS] [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Güver, T., & Özel, F. 2009, MNRAS, 400, 2050 [NASA ADS] [CrossRef] [Google Scholar]
- Horani, M., Rostas, J., & Roueff, E. 1985, A&A, 142, 346 [NASA ADS] [Google Scholar]
- Hovde, D. C., & Saykally, R. J. 1987, J. Chem. Phys., 87, 4332 [NASA ADS] [CrossRef] [Google Scholar]
- Kasemann, C., Güsten, R., Heyminck, S., et al. 2006, in SPIE Conf. Ser., 6275 [Google Scholar]
- Klaus, T., Belov, S. P., & Winnewisser, G. 1998, J. Mol. Spectrosc., 187, 109 [Google Scholar]
- Klein, B., Philipp, S. D., Krämer, I., et al. 2006, A&A, 454, L29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lazareff, B. 1975, A&A, 42, 25 [NASA ADS] [Google Scholar]
- Linke, R. A., Stark, A. A., & Frerking, M. A. 1981, ApJ, 243, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Lis, D. C., Goldsmith, P. F., Bergin, E. A., et al. 2009, in ed. D. C. Lis, J. E. Vaillancourt, P. F. Goldsmith, T. A. Bell, N. Z. Scoville, & J. Zmuidzinas, ASP Conf. Ser., 417, 23 [Google Scholar]
- Lis, D. C., Pearson, J. C., Neufeld, D. A., et al. 2010a, A&A, 521, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lis, D. C., Phillips, T. G., Goldsmith, P. F., et al. 2010b, A&A, 521, L26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H., & Lucas, R. 2002, A&A, 391, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liszt, H. S., Burton, W. B., Sanders, R. H., & Scoville, N. Z. 1977, ApJ, 213, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
- Magnani, L., & Salzer, J. J. 1989, AJ, 98, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., & Salzer, J. J. 1991, AJ, 101, 1429 [NASA ADS] [CrossRef] [Google Scholar]
- Melnick, G. J., Tolls, V., Neufeld, D. A., et al. 2010, A&A, 521, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Menten, K. M. 2004, in The Dense Interstellar Medium in Galaxies, ed. S. Pfalzner, C. Kramer, C. Staubmeier, & A. Heithausen, 69–82 [Google Scholar]
- Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [NASA ADS] [CrossRef] [Google Scholar]
- Millar, T. J., Adams, N. G., Smith, D., Lindinger, W., & Villinger, H. 1986, MNRAS, 221, 673 [Google Scholar]
- Millar, T. J., & Hobbs, L. M. 1988, MNRAS, 231, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Mookerjea, B., Giesen, T., Stutzki, J., et al. 2010, A&A, 521, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, M., & Serabyn, E. 1996, ARA&A, 34, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P. 2010, A&A, 514, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Belloche, A., Menten, K. M., Comito, C., & Schilke, P. 2008, J. Mol. Spectrosc., 251, 319 [CrossRef] [Google Scholar]
- Neufeld, D. A., Ashby, M. L. N., Bergin, E. A., et al. 2000, ApJ, 539, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Goicoechea, J. R., Sonnentrucker, P., et al. 2010a, A&A, 521, L10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neufeld, D. A., Sonnentrucker, P., Phillips, T. G., et al. 2010b, A&A, 518, L108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nyman, L. 1983, A&A, 120, 307 [NASA ADS] [Google Scholar]
- Ossenkopf, V., Müller, H. S. P., Lis, D. C., et al. 2010, A&A, 518, L111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, J. C., & Drouin, B. J. 2006, ApJ, 647, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Persson, C. M., Black, J. H., Cernicharo, J., et al. 2010, A&A, 521, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Phillips, T. G., Bergin, E. A., Lis, D. C., et al. 2010, A&A, 518, L109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pickett, H. M., Poynter, I. R. L., Cohen, E. A., et al. 1998, J. Quant. Spectrosc. Radiat. Transfer, 60, 883 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Pineau des Forêts, G., Roueff, E., & Flower, D. R. 1986, MNRAS, 223, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Plume, R., Kaufman, M. J., Neufeld, D. A., et al. 2004, ApJ, 605, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Polehampton, E. T., Brown, J. M., Swinyard, B. M., & Baluteau, J. 2003, A&A, 406, L47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polehampton, E. T., Baluteau, J.-P., & Swinyard, B. M. 2005a, A&A, 437, 957 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polehampton, E. T., Menten, K. M., Brünken, S., Winnewisser, G., & Baluteau, J.-P. 2005b, A&A, 431, 203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qin, S., Schilke, P., Comito, C., et al. 2010, A&A, 521, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Reid, M. J., Menten, K. M., Zheng, X. W., Brunthaler, A., & Xu, Y. 2009, ApJ, 705, 1548 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, C., Apponi, A. J., & Ziurys, L. M. 2004, ApJ, 608, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Schilke, P., Walmsley, C. M., Pineau des Forêts, G., & Flower, D. R. 1997, A&A, 321, 293 [NASA ADS] [Google Scholar]
- Schilke, P., Comito, C., Mueller, H. S. P., et al. 2010, A&A, 521, L11 [Google Scholar]
- Schmid-Burgk, J., Muders, D., Müller, H. S. P., & Brupbacher-Gatehouse, B. 2004, A&A, 419, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Senekowitsch, J., Werne, H., Rosmus, P., Reinsch, A., & Oneil, S. V. 1985, J. Chem. Phys., 83, 4661 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Sofue, Y. 2006, PASJ, 58, 335 [NASA ADS] [Google Scholar]
- Sonnentrucker, P., Neufeld, D. A., Phillips, T. G., et al. 2010, A&A, 521, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stahl, O., Casassus, S., & Wilson, T. 2008, A&A, 477, 865 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stäuber, P., Benz, A. O., Jørgensen, J. K., et al. 2007, A&A, 466, 977 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Tieftrunk, A., Pineau des Forêts, G., Schilke, P., & Walmsley, C. M. 1994, A&A, 289, 579 [NASA ADS] [Google Scholar]
- Vallée, J. P. 2008, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Blake, G. A., Draine, B. T., & Lunine, J. I. 1993, in Protostars and Planets III, ed. E. H. Levy & J. I. Lunine, 163–241 [Google Scholar]
- Vastel, C., Polehampton, E. T., Baluteau, J., et al. 2002, ApJ, 581, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Vrtilek, J. M., Gottlieb, C. A., & Thaddeus, P. 1987, ApJ, 314, 716 [NASA ADS] [CrossRef] [Google Scholar]
- Whiteoak, J. B., & Gardner, F. F. 1979, MNRAS, 188, 445 [NASA ADS] [Google Scholar]
- Wilson, T. L., & Rood, R. 1994, ARA&A, 32, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Winnewisser, G., Belov, S. P., Klaus, T., & Schieder, R. 1997, J. Mol. Spectrosc., 184, 468 [NASA ADS] [CrossRef] [Google Scholar]
- Wyrowski, F., Menten, K. M., Güsten, R., & Belloche, A. 2010a, A&A, 518, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wyrowski, F., van der Tak, F., Herpin, F., et al. 2010b, A&A, 521, L34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zmuidzinas, J., Blake, G. A., Carlstrom, J., Keene, J., & Miller, D. 1995, ApJ, 447, L125 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
All Tables
Spectroscopic data and beam-averaged continuum brightness temperature assumed for the LTE modeling of the absorption lines toward Sgr B2(M).
Velocity ranges and 12C/13C isotopic ratios of the Galactic absorption components along the line of sight of Sgr B2(M).
Parameters of the best-fit LTE models of SH+, 13CH+, and c-C3H2, as well as the alternative LTE model of H13CO+ fitted with the same velocity components as c-C3H2.
Parameters of the best-fit LTE model of H13CO+ and the LTE model of SH+ fitted with the same velocity components as H13CO+.
All Figures
 |
Fig. 1 Detail of the energy level diagram of SH+. The solid arrows mark transitions observed in the course of this work. The thickness of the arrows indicates the relative strengths of the transitions. The hyperfine splitting has been exaggerated slightly for clarity reasons. |
| In the text | |
 |
Fig. 2 From bottom to top, panels a) to c) show absorption spectra taken with the APEX telescope with the CHAMP+ receiver array. Spectra a) and b) were taken with the central pixel of CHAMP+ toward Sgr B2(M) (see Fig. 5). Spectrum b) was obtained toward a position (− 20.4″,1.4″) offset from Sgr B2(M) with the CHAMP+ pixel 2. a): H35Cl 1−0 absorption spectrum. b): SH+ 11–01 absorption spectrum. c): 13CH+ 1–0 absorption spectrum. In panels a)–c), the red curve is the synthetic spectrum described in Sect. 4.1 and the horizontal dotted line shows the continuum level. d) and e): same as b for the c-C3H2 212–101 and H13CO+ 1–0 transitions observed toward Sgr B2(M) with the IRAM 30 m telescope, respectively. Panel f) shows the optical depth of the 21 cm HI line vs. LSR velocity as derived by the procedure described in Sect. 5.1.2. In panels d) and e), the red curve is the synthetic spectrum of the molecule, the green curve is the predicted spectrum including in addition all molecules identified in our complete 3 mm line survey so far, and the horizontal dotted line indicates the zero level (after baseline removal because the observations were performed in position-switching mode with a far OFF position, which yields a very uncertain baseline level). In all panels, the spectra are plotted in main-beam brightness temperature scale, the vertical dotted line marks the systemic velocity of the source (62 km s-1). |
| In the text | |
 |
Fig. 3 a)–d) Column density profiles computed by adding the Gaussian velocity absorption components listed in Table 3. The components with upper limit were not included. e)–g) Abundance profiles relative to H2. The H2 column density was computed from the HCO+ column density assuming an HCO+ abundance of 5 × 10-9. h)–j) Abundance profiles relative to H i. k) The H i column density was computed from comparing an H i absorption with an H i emission profile (see text). |
| In the text | |
 |
Fig. 4 Ratio of the column density profiles of CH+ and SH+ shown in Fig. 3. |
| In the text | |
 |
Fig. 5 SH+ absorption spectra obtained toward Sgr B2(M) with the 7-pixel array CHAMP+ at the APEX telescope. The equatorial offset position of each pixel relative to Sgr B2(M) is given in the bottom left corner of each panel. In each panel, the dotted line shows the continuum level as measured over the emission/absorption-free channels, and the red curve is the spectrum predicted by the Trot = TCMB model described in Sect. 4.1. All spectra are plotted in main-beam brightness temperature scale. |
| In the text | |
 |
Fig. 6 a) Spectrum obtained toward Sgr B2(M) at the frequency of the SH+ 10–01 line with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, the horizontal dotted line shows the continuum level, and the vertical dotted line marks the systemic velocity of the source (62 km s-1). The strong absorption lines are spiral arm components of CO 3–2. The lower axis gives the LSR velocity for SH+, while the upper axis refers to CO, with the same labeling as in panel b). b) CO(1–0) spectrum obtained toward Sgr B2 as part of our line survey with the IRAM 30 m telescope. The horizontal dotted line indicates the zero level (after baseline removal because the observations were performed in position-switching mode with a far OFF position, which yields a very uncertain baseline level). In both panels, the dashed line marks the systemic velocity of the source in CO 3–2 and the dot-dashed line indicates the CO velocity +172.6 km s-1 at which an extra absorption component appears in the 13CH+ spectrum (see discussion in Sect. 4.1.3.) |
| In the text | |
 |
Fig. 7 Spectrum obtained toward Sgr B2(M) at the frequency of SH+ 21–11 with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, i.e., showing no detectable emission, the horizontal dotted line shows the continuum level, and the vertical dotted line marks the systemic velocity of the source (62 km s-1). The absorption line appearing at ~− 105 km s-1 is the JKaKc = 111−000 ground-state line of HDO at 893 638.7 MHz (Comito et al. 2003). |
| In the text | |
 |
Fig. 8 Spectrum obtained toward Sgr B2(M) around 625 GHz with the APEX telescope in main beam brightness temperature. The red curve is the synthetic spectrum described in Sect. 4.1, the horizontal dotted line shows the continuum level, and the left and right vertical dotted lines mark the systemic velocity of the source (62 km s-1) for HCl and H37Cl, respectively. The strong emission close to the HCl line is likely due to a SO2 line at 626 087.3 MHz. |
| In the text | |
 |
Fig. 9 CH+ column density versus hydrogen column density. The ordinate gives the CH+ column density for the seven different velocity intervals listed in Table 7. The capital letters designate the entries in table (top to bottom). The open circles represent data taken from the diffuse/translucent cloud sample of Gredel (1997). The squares connected by lines mark the CH+ column densities determined in this work. For the open squares it is assumed that all the absorption is from atomic gas; the abscissa corresponds to the HI column density (Table 6), whereas for the filled squares it is assumed that all the absorption is from molecular gas; the abscissa corresponds to the H2 column density (Table 6). For the upper panel, column densities were calculated from the absorption over the whole velocity range of each interval, whereas in the lower panel average column densities normalized to a typical line width of 4.3 km s-1 were used (see text). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.