EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 690 (October 2024) A&A, 690 (2024) A372 Full HTML
Open Access
Issue
A&A
Volume 690, October 2024
Article Number A372
Number of page(s) 11
Section Interstellar and circumstellar matter
DOI https://doi.org/10.1051/0004-6361/202451412
Published online 29 October 2024

© The Authors 2024

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1 Introduction

The measurements of isotopic ratios in the interstellar medium (ISM) are important for understanding Galactic chemical evolution (GCE) due to different stellar yields with different masses (Guesten & Mezger 1982; Maeder 1983; Iben & Renzini 1983; Clayton 2003; Kobayashi et al. 2011, 2020; Romano et al. 2017). One of the few isotopic ratios that can be easily measured is 12C/13C. Notably, 12C is mainly produced through He-burning as the primary element (e.g., core-collapse supernovae and He-burning shells in low-mass stars), while 13C is an intermediate product of CNO cycling in intermediate-mass asymptotic giant branch (AGB) stars (Kobayashi et al. 2011; Romano et al. 2017). Since the timescale in which massive stars release the elements into the ISM is much shorter than for low-to-intermediate mass stars, the 12C/13C ratios predicted from GCE models would decrease as a function of time with a given initial mass function (IMF). In the Milky Way, a radial gradient in the 12C/13C ratio inferred from 12C18O and 13C18O rises from approximately 24 at a galactocentric distance (RGC) of ~0.5 kiloparsec (kpc) to roughly 70 at RGC ~ 12 kpc (Langer & Penzias 1990, 1993).

While various methodologies and tracers have been employed in recent years to constrain the Galactic 12C/13C gradient (Halfen et al. 2017; Yan et al. 2019; Jacob et al. 2020; Sun et al. 2024), the different methods have yielded inconsistent results, especially for the Galactic center (GC) regions. Measuring the 12C/13C isotopic ratio with molecular lines faces challenges from both observational factors (e.g., opacity, beam dilution) and chemical effects (e.g., selective photodissociation and fractionation). The most abundant carbon-bearing isotopologs (e.g., 12CO, H12CO+, H12CN) can easily become optically thick in dense clouds, making precise estimation of column densities difficult. In diffuse and translucent clouds, the main isotopologs may not pose challenges for optical depths, but the rare isotopologs are often difficult to detect due to their low abundance and sub-thermally excitation of even the ground state transition (Godard et al. 2010; Luo et al. 2020). Additionally, distant clouds have smaller beam-filling factors, which reduces the reliability of the measurements observed with a single dish.

Isotope-selective photodissociation and isotopic exchange reactions can strongly alter the 12C/13C isotopic ratios in molecules from the original element ratios. For abundant species such as CO, the self-shielding of 12CO is significantly stronger than less abundant isotopologs (e.g., 13CO and C18O). Thus, the 12C/13C ratio in CO would be higher under the existence of external UV radiation (Bally & Langer 1982; Chu & Watson 1983; Liszt 2007). Additionally, due to the differences in zero-point energy between different isotopologs, isotopic exchange reactions can further alter 12C/13C ratios in various molecules. For instance, the isotopic exchange reaction between 13C+ and CO is exothermic, leading to an enrichment of 13C in CO and other molecules primarily formed through CO in cold environments (Watson et al. 1976; Langer et al. 1984; Roueff et al. 2015; Colzi et al. 2020; Sipilä et al. 2023).

Absorption lines against strong continuum sources can overcome such difficulties. The advantage of using absorption lines is to measure the optical depth as well as the column density precisely even if the transition is sub-thermally excited. Such a methodology has been widely used to quantify the physical properties of low-density gas (Lucas & Liszt 1996, 1998; Luo et al. 2020, 2023b; Rybarczyk et al. 2022b; Liszt & Gerin 2023; Gerin et al. 2024). Lucas & Liszt (1998) is one of the first works that measured the isotopic ratios in the solar neighborhood through millimeter molecular absorption lines. Liszt & Gerin (2018) measured the H12CO+/H13CO+ ratios in four directions toward the Galactic bulge, and they inferred a much higher value (~60) than the other tracers (~20). Inspired by these pioneering works, systematic measurements at different RGC with such a methodology could be useful to constrain the 12C/13C gradient.

In this work, we present a new measurement of the Galactic 12C/13C gradient by using absorption lines of H12CO+ and H13CO+ with high-angular observations of the Atacama Large Millimeter/submillimeter Array (ALMA) and the Northern Extended Millimeter Array (NOEMA). We emphasize that such a methodology to constrain the isotopic gradient of the Milky Way with a large sample, especially for future searches in the anti-center direction (though rare and challenging), could provide valuable constraints for GCE models.

thumbnail Fig. 1

Distribution of the observed quasar sight lines (yellow lines) and ultra-compact H II region (red crosses) projected onto a top-down schematic view of the Milky Way (artist’s concept, R. Hurt: NASA/JPLCaltech/SSC).

2 Observations

2.1 Quasar sight lines

We carried out H12CO+ and H13CO+ J=1–0 observations toward six quasars (Fig. 1). Five were observed with ALMA (2022.1.01438.S, PI: Thomas G. Bisbas) during March 20–30, 2023, and one source (3C 111) was observed with NOEMA (W20BB, PI: Gan Luo) in December 2020 and January 2021. The angular resolution of ALMA is ~0.6″ at 89 GHz. The spectral resolution of ALMA is 122 kHz, corresponding to a velocity resolution of ~0.4 km s−1 at 89 GHz. The raw data was calibrated using the standard pipeline with the Common Astronomy Software Applications (CASA, version 6.4.1; CASA Team 2022). The imaging of the calibrated visibilities was performed using the tclean algorithm with Briggs weighting (robust = 0.5). The NOEMA observations have an angular resolution of ~2.1″ at 89 GHz and a velocity resolution of ~0.21 km s−1. The PolyFiX backend of NOEMA covers H12CN, H13CN, HN12C, and HN13C J=1–0 transitions simultaneously. The calibration of the raw data was performed using CLIC software in the GILDAS.1 The typical optical depth noise levels are 3~7×10−3 per 0.4 km s−1 velocity channel for ALMA observations and 2×10−3 per 0.21 km s−1 velocity channel for NOEMA observations.

2.2 UCH II sight lines

The ALMA observations toward ten UCH II regions (red crosses in Fig. 1), which were selected from the ALMA Three-millimeter Observations of Massive Star-forming regions (ATOMS) survey (2019.1.00685.S, PI: Tie Liu), were observed from September to November 2019 with both 12-m and 7-m arrays at band 3. The baselines of ATOMS range from 15 to 783.5m, corresponding to an angular resolution of ~1.2″ at 89 GHz. The spectral resolution of H12CO+ and H13CO+ J=1–0 transitions are 0.2 km s−1 and 0.422 km s−1, respectively. The raw data were calibrated using CASA version 5.6, and the combination and imaging of 12-m and 7-m data were performed with CASA version 6.4.1. The sensitivity of the resultant spectra depends on the properties of each source, a detailed description of observations can be found in Liu et al. (2020).

3 Results

3.1 Absorption spectra and integrated optical depth

The absorption spectra of HCO+ (hereafter, HCO+ refers to H12CO+) and H13CO+2 were extracted from the continuum peak of each source. Figure 2 shows an example of normalized spectra of HCO+ and H13CO+ toward J1851+0035. Spectra toward all other sources can be found in Appendix A.

Since most of the sources are located in the Galactic plane (|b| < 2°), the foreground absorption components are mixed, and it is difficult to decompose individual Gaussian components (except for the high-latitude source 3C111; see Appendix B). To obtain the column density ratios, we integrated the optical depths (∫ τvdυ) of HCO+ and H13CO+ in the same velocity range (shadowed region in Figs. 2 and A.1). We set four criteria when identifying the integrated range: (1) H13CO+ absorption should not be contaminated with absorption features of other molecules (e.g., −25 km s−1 component of H13CO+ in Fig. 2); (2) each of the integrated ranges of H13CO+ should be distinguished from the others (no overlap); (3) the absorption profile of HCO+ should not be saturated (e−τ > rms); and (4) absorption spectra toward UCH II regions should not be contaminated with emission features from the compact foreground envelopes. The uncertainty of ∫ τvdυ (σI) through an error propagation formula is thus defined by σI=dv2∑i=1N−1(στi2+στi+12),$\[\sigma_{\mathrm{I}}=\frac{\mathrm{d} v}{2} \sqrt{\sum_{i=1}^{N-1}\left(\sigma_{\tau_i}^2+\sigma_{\tau_{i+1}}^2\right)},\]$(1)

where dυ is the channel width, N is the length of the data array in the velocity range over which the opacity profile is integrated, and στi=RMS/e−τi$\[\sigma_{\tau_{\mathrm{i}}}=\mathrm{RMS} / \mathrm{e}^{-\tau_{\mathrm{i}}}\]$ is the uncertainty of τ at the ith channel. The integrated optical depths of HCO+ and H13CO+ toward all sources are listed in Table C.1.

The molecular column density can be written as a function of ∫ τvdυ (Mangum & Shirley 2015): Ntot=3h8π3|μlu|2QrotgueEukTexehνkTex−1∫τνdv,$\[N_{\mathrm{tot}}=\frac{3 h}{8 \pi^3\left|\mu_{\mathrm{lu}}\right|^2} \frac{Q_{\mathrm{rot}}}{g_{\mathrm{u}}} \frac{e^{\frac{E_{\mathrm{u}}}{k {T}_{\mathrm{ex}}}}}{e^{\frac{h \nu}{k {T}_{\mathrm{ex}}}}-1} \int \tau_\nu d v,\]$(2)

where h is the Planck constant, k is the Boltzman constant, |μlu|2 is the dipole matrix element, Qrot is the rotational partition function, gu is the degeneracy of the upper energy level, Eu is the upper energy level, and Tex is the excitation temperature. For each transition, |μlu|2, Eu, and the rest frequency ν were taken from the Cologne Database for Molecular Spectroscopy (CDMS; Müller et al. 2001, 2005), and they are listed in Table D.1. For linear molecules, the simplified partition function is given by McDowell (1987) Qtot =kThB0ehB03kT,$\[Q_{\text {tot }}=\frac{k T}{h B_0} e^{\frac{h B_0}{3 k T}},\]$(3)

where B0 is the rigid rotor rotation constant.

The excitation temperature of HCO+ in diffuse molecular clouds is usually close to the cosmic microwave background temperature (TCMB = 2.73 K) (Godard et al. 2010; Luo et al. 2020). If we fill in all the constants in Eq. (2) and take Tex = 2.73 K for both HCO+ and H13CO+, the column density ratios can be simplified as NHCO+NH13CO+=0.974∫τHCO+dv∫τH13CO+dv.$\[\frac{N_{\mathrm{HCO}^{+}}}{N_{\mathrm{H}^{13} \mathrm{CO}^{+}}}=0.974 \frac{\int \tau_{\mathrm{HCO}^{+}} d v}{\int \tau_{\mathrm{H}^{13} \mathrm{CO}^{+}} d v}.\]$(4)

Though Tex of HCO+ can rise above 2.73 K when the gas density is higher than 300 cm−3 (Rybarczyk et al. 2022a), a variance of Tex from 2.73 to 5 K only results in a variance of the column density ratio of less than 1%. The calculated ratios in our samples range from 12.7±0.23 to 139.4±38.0 (Table B.1).

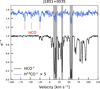thumbnail Fig. 2

Normalized absorption spectra of HCO+ (black curve) and H13CO+ (blue curve) toward J1851+0035. The spectrum of H13CO+ has been scaled by a factor of five and shifted upward by 0.5 for better display. The gray shaded regions denote the velocity ranges used to calculate the column density ratios. The red vertical lines represent HCO absorption, where the −25km s−1 component of H13CO+ absorption is contaminated with HCO J=1/2–1/2, F=1–1. Thus, these components were discarded since they can only obtain lower limits of 12C/13C.

3.2 The 12C/13 C gradient

Obtaining an accurate distance of a distant molecular cloud is difficult, especially without parallax measurements from maser emissions. The most common estimation of such a distance is based on kinematic distance. We calculated the RGC for each velocity component with the Monte Carlo kinematic distance method, using the latest rotational curve and updated solar motion parameters (Wenger et al. 2018). This model is obtained through the trigonometric parallax results from the high-mass star-forming regions (HMSFRs) in the BeSSeL Survey (Reid et al. 2014, 2019). This method samples the local standard of rest velocity (Vlsr) and Galactic rotational curve parameters for HMSFRs and derives the probability density distribution (PDF) of kinematic distance, resulting in a median uncertainty of 13% to the parallax distances. A detailed description of this method can be found in Wenger et al. (2018).

The optical depth-weighted Vlsr in our samples is calculated by Vlsr=∫vτHCO+dv∫τHCO+dv.$\[V_{\mathrm{lsr}}=\frac{\int v \tau_{\mathrm{HCO}^{+}} d v}{\int \tau_{\mathrm{HCO}^{+}} d v}.\]$(5)

The calculated Vlsr and RGC as well as the uncertainties are listed in Table B.1. We note that such an estimation with pure circular motions may fail to predict the RGC near the GC (e.g., the highly negative Vlsr toward J1720–3552), in which non-circular motions should be taken into account (Liszt & Gerin 2018). Therefore, we used the tilted-disk model presented by Burton & Liszt (1978) to estimate the velocity components of Vlsr < −140 km s−1 toward J1720–3552, resulting in an RGC between 1.24 to 1.5 kpc. Thus, we adopted a value of 1.37±0.04 kpc for this component.

Figure 3 shows the measured HCO+/H13CO+ ratios as a function of RGC. The weighted-mean 12C/13C ratios increase from 42±1 toward the GC to 66±5 in the solar neighborhood. To avoid an underestimation of the HCO+ optical depth when τ is large, we set stricter constraints (τ < 3) when fitting a gradient. We used the Markov chain Monte Carlo (MCMC) method within the emcee code (Foreman-Mackey et al. 2013) to sample the free parameters and the posterior probability distribution. The maximum likelihood fit of the data is shown with a red solid curve in Fig. 3, which gives a H12CO+/H13CO+ gradient as a function of RGC: H12CO+H13CO+=(6.4±1.9)RGCkpc+(25.9±10.5).$\[\frac{\mathrm{H}^{12} \mathrm{CO}^{+}}{\mathrm{H}^{13} \mathrm{CO}^{+}}=(6.4 \pm 1.9) \frac{R_{\mathrm{GC}}}{\mathrm{kpc}}+(25.9 \pm 10.5).\]$(6)

4 Analysis and discussion

4.1 The 12C/13 C ratios in the solar neighborhood

While the 12C/13C ratios in the nearby molecular clouds have been derived extensively with various molecules, the most reliable tracer thought to represent the true element 12C/13C ratios is CH+ (Ritchey et al. 2011). The measured 12C/13 ratios from our HCO+ samples range from 62.0±4.4 to 139.4±38.0 within 500 pc of the solar circle (7.6 ≤ RGC ≤ 8.6 kpc), with a weighted mean value of 66±5. This value is in good agreement with the mean value obtained through optical 12CH+/13CH+ measurements toward diffuse sight lines (74.4±7.6, Ritchey et al. 2011) and the −0.9 km s−1 component of 3C 111 (Appendix B).

thumbnail Fig. 3

Measurements of H12CO+/H13CO+ as a function of RGC and comparison of the derived gradients between different works. Blue dots represent τHCO+ < 3, and black dots represent τHCO+ > 3. The two lower limits are shifted to RGC = 0.5 kpc for better visualization. The red curve denotes the maximum likelihood fit of the blue points only; orange curves denote the 3σ deviation from the MCMC sampling.

4.2 The 12C/13 C ratios in the Galactic center

The measurements of the 12C/13C ratio within ~2 kpc of the GC are rare. This is mainly due to the high gas column density (e.g., NH2$\[N_{\mathrm{H}_2}\]$ ≳ 1024 cm−2), which makes the molecular transitions optically thick, even for the rare isotopologs (e.g., C18O). Halfen et al. (2017) measured the isotopic ratios using complex organic molecules (COMs) toward Sgr B2(N) and found an average value of 24±7, which is similar to the value obtained from dense gas tracers (e.g., C34S, Humire et al. 2020). The measurements from absorption lines of CH toward Sgr B2(M) and H2CO toward Sgr B2 result in 12C/13C ratios of 15.8±2.4 (Jacob et al. 2020) and 11.48±0.03 (Yan et al. 2019), respectively.

Previous absorption observations toward the Galactic bulge have revealed a significantly high 12C/13C ratio (~60, Liszt & Gerin 2018). However, since these observations integrated the full velocity range, which has HCO+ absorptions (the H13CO+ absorptions are much narrower), the absorption of HCO+ could be contaminated with foreground diffuse gas, leading to a high value. Since the HCO+ absorptions toward the dense regions (e.g., Sgr B2(N)) are completely saturated, the measured values at RGC < 2 kpc in our work are in fact the diffuse molecular components (a few hundred cm−3, Gerin & Liszt 2017; Liszt & Gerin 2018).

The two measurements at RGC < 2 kpc from our observations have 12C/13C ratios of 42.2± 1.7 and 37.5±6.5, values which are consistent with absorption measurements of c-C3H2 (~40 at RGC < 1 kpc, Corby et al. 2018) but still larger than the other tracers in high-density (nH2$\[n_{\mathrm{H}_2}\]$ > 105 cm−3) regions. Furthermore, the two lower limits of 12C/13C at −181 and −162 km s−1 of J1720–3552 are > 19 and > 31. These results are consistent with previous observations of CH+ toward Sgr A* and Sgr B2(N) (e.g., 12CH/13CH >30 at −168 ~ −150 km s−1 of Sgr A*, Godard et al. 2012), which is again distinct from the previously reported low values toward Sgr B2 but supports our results. Thus, either opacity effects or fractionation may have an impact on the measured isotopic ratios in the high-density tracers (e.g., CN, and COMs), while our measurements at low density are less influenced.

4.3 The 12C/13 C gradient and comparison with GCE models

Different tracers have been used to calculate the Galactic 12C/13C gradient. This gradient is mostly constrained by results from 12C18O/13C18O (e.g., Langer & Penzias 1990, 1993; Wouterloot & Brand 1996; Giannetti et al. 2014); 12CN/13CN (e.g., Savage et al. 2002; Milam et al. 2005; Sun et al. 2024); H212CO/H213CO$\[\mathrm{H}_2^{12} \mathrm{CO} / \mathrm{H}_2^{13} \mathrm{CO}\]$ (Henkel et al. 1982; Yan et al. 2019); C34S (Yan et al. 2023); and a combined analysis from various tracers (e.g., COMs, CH; Halfen et al. 2017; Jacob et al. 2020). The gradients from different methodologies are shown with different curves in Fig. 34.

By comparing the gradients using different tracers, we found that the measurements in the low-density molecular clouds (HCO+, nH2$\[n_{\mathrm{H}_2}\]$ ~ a few 102 cm−3) are higher than those from higher density environments (nH2$\[n_{\mathrm{H}_2}\]$ ≥ a few 104 cm−3), such as C18O, H2CO, CS, and CN (Giannetti et al. 2014; Yan et al. 2019, 2023; Sun et al. 2024). The systematically increasing trend of the 12C/13C gradient from high-density to low-density gas may again suggest that fractionation plays a crucial role in the measured 12C/13C ratios in molecules. Predictions from the chemical models by Colzi et al. (2020) are in agreement with this observational trend, finding that 12C/13C ratios of HCN, HNC, and HCO+ tend to increase from the higher (106 cm−3) to the lower (103 cm−3) densities.

The comparison between the derived 12C/13C gradient and the GCE models presented in Colzi et al. (2022) is shown in Fig. 4, in which the models consider different mass ranges for white dwarf progenitors and average ejected masses of 13C and 15N per nova outburst (Romano et al. 2019, 2021). Our result is reasonably consistent with the GCE models with a mass range of white dwarf progenitors 1–8 M⊙ and higher average ejected masses of 13C (models 3 and 4). Given the limited range of RGC in the current samples, future observations at RGC > 10 kpc would be exceptionally useful to constrain GCE models.

However, one should always keep in mind that the formula of the isotopic gradient strongly depends on the accuracy of the RGC, which is mostly based on the kinematic distance estimation. For instance, the estimated RGC before and after the model by Reid et al. (2019) could differ by several kpc (Sun et al. 2024). The large scatter of 12C/13C at RGC between 4 kpc to 8 kpc in both our work and the literature may suggest that our understanding of the Milky Way rotational model or inhomogeneous mixing of the elements may also contribute to the scatter.

4.4 Chemical effects on the measured 12C/13 C ratios

The isotopic exchange reactions could be one of the main processes that lead to different isotopic ratios in HCO+. In this section, we consider the isotopic exchange reaction that produces H13CO+ (Langer et al. 1978; Roueff et al. 2015; Colzi et al. 2020)5: 13C++CO⇌13CO+C,$\[{ }^{13} \mathrm{C}^{+}+\mathrm{CO} \rightleftharpoons{ }^{13} \mathrm{CO}+\mathrm{C},\]$(R1) 13CO+HCO+⇌H13CO++CO.$\[{ }^{13} \mathrm{CO}+\mathrm{HCO}^{+} \rightleftharpoons \mathrm{H}^{13} \mathrm{CO}^{+}+\mathrm{CO}.\]$(R2)

We considered the main formation pathways of H13CO+ in low-to-intermediate density gas (van Dishoeck & Black 1988; Luo et al. 2023b): 13CO++H2→H13CO++H,$\[{ }^{13} \mathrm{CO}^{+}+\mathrm{H}_2 \rightarrow \mathrm{H}^{13} \mathrm{CO}^{+}+\mathrm{H},\]$(R3) 13C++H2O→H13CO++H,$\[{ }^{13} \mathrm{C}^{+}+\mathrm{H}_2 \mathrm{O} \rightarrow \mathrm{H}^{13} \mathrm{CO}^{+}+\mathrm{H},\]$(R4) 13CH+O→H13CO++e.$\[{ }^{13} \mathrm{CH}+\mathrm{O} \rightarrow \mathrm{H}^{13} \mathrm{CO}^{+}+\mathrm{e}.\]$(R5)

The destruction of HCO+ (and H13CO+) is dominated by electrons: HCO++e−→CO+H.$\[\mathrm{HCO}^{+}+\mathrm{e}^{-} \rightarrow \mathrm{CO}+\mathrm{H}.\]$(R6)

Thus, the isotopic exchange reaction would influence the HCO+/H13CO+ ratio only if the right side reaction R2 is comparable to reactions (R3)–(R5). The reaction rate of the above reaction is 2.6 × 10−10 × (T/300)−0.4 cm3 s−1 (Roueff et al. 2015). The typical abundance of CO+ is 10−10 ~ 10−9 (Stäuber & Bruderer 2009; Treviño-Morales et al. 2016), the abundance of HCO+ is a few 10−9 (Lucas & Liszt 1996; Gerin et al. 2019; Luo et al. 2020), and the abundance of CH is 3 × 10−8 (Liszt & Lucas 2002; Sheffer et al. 2008; Tang et al. 2021; Luo et al. 2023a). Even if we only consider reaction (R3) (the reaction rate k = 7.5 × 10−10 cm3 s−1; McElroy et al. (2013)) and scale the above abundance with 12C/13C = 70, the formation of H13CO+ through reaction (R3) would overwhelm reaction (R2) by over four orders of magnitude at the typical gas temperature of ~50 K (Snow & McCall 2006). Therefore, fractionation would have little impact on the measured HCO+/H13CO+ ratios in low-density gas. This is also consistent with various chemical modelings of carbon fractionation, in which HCO+/H13CO+ can overall best represent the original 12C/13C element ratio in low-to-intermediate density gas (Szűcs et al. 2014; Roueff et al. 2015; Colzi et al. 2020; Sipilä et al. 2023).

In dense regions, CO becomes the precursor of HCO+ (Dalgarno 2006; Indriolo & McCall 2012; Bisbas et al. 2015): CO+H3+→HCO++H2.$\[\mathrm{CO}+\mathrm{H}_3^{+} \rightarrow \mathrm{HCO}^{+}+\mathrm{H}_2.\]$(R7)

Since reaction (R6) is still the dominant formation channel of CO even in high-density clouds (Luo et al. 2023a), the fractionation of CO in the dense cloud could greatly impact the isotopic ratio in HCO+ only if reaction (R7) is comparable to reaction (R6). However, the gas density that will significantly alter the 12C/13C ratio measured in HCO+ would be above 104 cm−3 (Sipilä et al. 2023). The highest column density of HCO+ in Table B.1 is ~3.4 × 1013 cm−2, corresponding to an H2 column density of 1022 cm−2, assuming a constant HCO+ abundance (3 × 10−9, Lucas & Liszt 1996; Liszt & Gerin 2016)6 Therefore, most components are not expected to trace such a high-density regime and will be less influenced by the fractionation effect. Nevertheless, both detailed chemical modeling (Colzi et al., in prep.) and the constraints of gas volume density and temperature through multiple lines in the future are necessary to determine where and how fractionation impacts the isotopic ratios.

thumbnail Fig. 4

Comparison between observations and GCE models, in which the models are taken from Table 2 in Colzi et al. (2022) with the same numbers.

5 Conclusion

In this work, we have performed high sensitivity absorption line observations toward strong continuum sources (including quasars and UCH II regions). We derived 12C/13C ratios from HCO+ absorption and RGC according to the latest parallax-based distance calculation. Our main conclusions are as follows:

  1. The derived 12C/13C gradient from HCO+ absorption measurements is (6.4±1.9)RGC/kpc+(25.9±10.5), which is reasonably consistent with current GCE models;

  2. The derived weighted mean 12C/13C ratio in the solar neighborhood is 66±5, which is consistent with those measured from CH+ (74.4±7.6);

  3. Our measurements toward the GC are two to three times higher than those measured with dense gas tracers toward Sgr B2 (11~24). Nevertheless, our results are supported by the CH+ observations toward Sgr A* and Sgr B2(N) (>30) as well as absorption measurements of c-C3H2 (~40);

  4. The discrepancy between our method and those from dense gas tracers suggests that opacity effects and fractionation may have a larger impact on the dense gas tracers in high-density regions.

We highlight the use of absorption lines to measure the isotopic ratios with interferometry observations, which are less affected by optical depth, beam dilution, and chemical fractionation. Future large samples toward the GC and the anti-center directions may provide more constraints on the Galactic 12C/13C gradient as well as the GCE models.

Acknowledgements

We are grateful to the anonymous referee for the thoughtful comments and suggestions that greatly improved the clarity of our work, especially the suggestion of including the non-circular motion to estimate the distance near the GC. We thank Zhiyu Zhang, Jérôme Pety, and Michel Guélin for their useful comments, Donatella Romano for providing the GCE models, and the staffs at IRAM for carrying out the NOEMA observations and reducing the data. L. C acknowledges support from the grant No. PID2022-136814NB-I00 by the Spanish Ministry of Science, Innovation and Universities/State Agency of Research MICIU/AEI/10.13039/501100011033 and by ERDF, UE. Tie Liu acknowledges the supports by the National Key R&D Program of China (No. 2022YFA1603100), National Natural Science Foundation of China (NSFC) through grants No.12073061 and No.12122307, and the Tianchi Talent Program of Xinjiang Uygur Autonomous Region. D. L. is a New Cornerstone investigator. N.-Y. Tang is sponsored by the University Annual Scientific Research Plan of Anhui Province (No. 2023AH030052, No. 2022AH010013), the China Manned Space Program through its Space Application System, Zhejiang Lab Open Research Project (No. K2022PE0AB01). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2022.1.01438.S and ADS/JAO.ALMA#2019.1.00685.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. This work is based on observations carried out under project number W20BB with the IRAM NOEMA Interferometer. IRAM is supported by INSU/CNRS (France), MPG (Germany) and IGN (Spain).

Appendix A Absorption spectra toward all sources

The normalized absorption profiles of 14 sources are shown in Fig. A.1. Note that for the UCH II sight lines, the H40α emissions are usually associated with UCH II regions (Liu et al. 2020) (e.g., −150 ~ −80 km s−1 toward I15254+5621), this is not the bad baseline. Furthermore, since the emission from the compact structures around UCH II regions could have a high excitation temperature, the spectra may still show emission in conjunction with absorption. We avoid these velocity ranges in our calculation. Future high angular resolution and high sensitivity observations may help reconstruct both the emission and absorption profiles around UCH II regions.

thumbnail Fig. A.1

Same as Fig. 2 but for other sources. Red vertical lines denote HCO absorption.

Appendix B Gaussian decomposition of absorption profiles toward 3C 111

Absorption profiles and Gaussian decomposition of H12CN, H13CN, HN12C, and HN13C J=1–0 transitions toward 3C 111 are shown in Fig. B.1, in which the spectra of H12CN and H13CN are hyperfine transitions. The Gaussian decomposition is performed with curve_fit package in scipy using the Levenberg-Marquardt algorithm, and the resultant optical depths and linewidth (ΔV) are shown in Table B.1. We set constraints when fitting hyperfine transitions that all hyperfine lines have 1) the same linewidth (ΔV) and 2) the same velocity offset with respect to Vlsr.

thumbnail Fig. B.1

Gaussian decomposition of normalized absorption profiles of HCN, H13CN, HNC, and H13NC toward 3C 111. Red dashed curves denote the fitting results, and green dotted lines denote each Gaussian component.
Table B.1

Optical depths and line widths toward 3C 111.

There are two velocity components (−0.9 km s−1 and −2.5 km s−1) in front of 3C 111, the 3D extinction indicates that the cloud is within 300 pc from the Sun (Lucas & Liszt 1998). The gas volume density at −0.9 km s−1 is nH2$\[n_{\mathrm{H}_2}\]$ = 398 ± 22 cm−3 (Luo et al. in prep), and nH2$\[n_{\mathrm{H}_2}\]$ is supposed to be much lower at −2.5 km s−1 than at −0.9 km s−1 (Lucas & Liszt 1998). However, the HCO+ absorption profile is almost saturated toward 3C 111 and we cannot get a good Gaussian decomposition. Thus, we use HCN and HNC to derive the 12C/13C ratio. The optical depth ratios of the H12CN hyperfine transitions are 1:2.3:3.5 and 1:2.9:4.6 at −0.9 km s−1 and −2.5 km s−1, respectively. While the latter represents the intrinsic line ratio (1:3:5), the former deviates from it by 30%, indicating that the optical depths of the H12CN (F=1–1 and 2–1) at −0.9 km s−1 are underestimated. As an alternative, we can fix the optical depth ratios at 1:3:5 instead of treating them as free parameters to obtain a more accurate value of the column density.

The 12C/13C ratio at −0.9 km s−1 derived from H12CN/H13CN is 74±3, which is 30% higher than that previously obtained by Lucas & Liszt (1998). Measurement from HN12C/HN13C (62±6) also show similar result. The 12C/13C ratio at −2.5 km s−1 component derived from H12CN/H13CN is 138±28, which is ~2 times higher than that at −0.9 km s−1. As suggested by Lucas & Liszt (1998), this could be a particular case, where the 13CO has been enriched and fractionation leads to a deficit of 13C in less abundant carbon carriers. Chemical models that consider the isotopic fractionation also predict a higher isotopic ratio of H12CN/H13CN than that from CO or HCO+ (Roueff et al. 2015; Colzi et al. 2020). Our detection of HN13C at −2.5 kms s−1 (S/N of ∫ τdυ ~ 4) is consistent with the hypothesis (HN12C/HN13C = 95 ± 39).

Appendix C The source properties

The derived source properties from Sec. 3 are shown in Table C.1.

Table C.1

Source name, velocity, galactocentric distance, integrated optical depths, isotopic ratios, and RMS of the absorption spectra.

Appendix D The Molecular transitions

The molecular transitions mentioned in this work are taken from the CDMS database (Müller et al. 2001, 2005), which are listed in Table D.1.

Table D.1

Molecular transitions mentioned in this work.

Appendix E The unusual low H12CO+/H13CO+ toward J1720-3552

The −22 km s−1 velocity component was recognized as an independent component in the H13CO+ line profiles when we calculated the H12CO+/H13CO+ ratios. The derived isotopic ratio is more than three times lower than the components toward the GC; however, the reason is still unclear. If this low value is caused by chemical fractionation, the gas component at −22 km s−1 must have a high density and compact size (≤0.01 pc at a distance of ~ 3 kpc; otherwise, we would see emission lines around the continuum source). It should be surrounded by low-density envelopes since the H12CO+/H13CO+ ratios toward the neighboring velocity components are much higher. Future high-J molecular line observations may help reveal the nature of this low value.

References

  1. Bally, J., & Langer, W. D. 1982, ApJ, 255, 143 [NASA ADS] [CrossRef] [Google Scholar]
  2. Bisbas, T. G., Papadopoulos, P. P., & Viti, S. 2015, ApJ, 803, 37 [NASA ADS] [CrossRef] [Google Scholar]
  3. Burton, W. B., & Liszt, H. S. 1978, ApJ, 225, 815 [NASA ADS] [CrossRef] [Google Scholar]
  4. CASA Team (Bean, B., et al.) 2022, PASP, 134, 114501 [NASA ADS] [CrossRef] [Google Scholar]
  5. Chu, Y. H., & Watson, W. D. 1983, ApJ, 267, 151 [NASA ADS] [CrossRef] [Google Scholar]
  6. Clayton, D. 2003, Handbook of Isotopes in the Cosmos (Cambridge, UK: Cambridge University Press) [Google Scholar]
  7. Colzi, L., Sipilä, O., Roueff, E., Caselli, P., & Fontani, F. 2020, A&A, 640, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Colzi, L., Romano, D., Fontani, F., et al. 2022, A&A, 667, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  9. Corby, J. F., McGuire, B. A., Herbst, E., & Remijan, A. J. 2018, A&A, 610, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  10. Dalgarno, A. 2006, PNAS, 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
  11. Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
  12. Gerin, M., & Liszt, H. 2017, A&A, 600, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Gerin, M., Liszt, H., Neufeld, D., et al. 2019, A&A, 622, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Gerin, M., Liszt, H., Pety, J., & Faure, A. 2024, A&A, 686, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  15. Giannetti, A., Wyrowski, F., Brand, J., et al. 2014, A&A, 570, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Godard, B., Falgarone, E., Gerin, M., Hily-Blant, P., & de Luca, M. 2010, A&A, 520, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Godard, B., Falgarone, E., Gerin, M., et al. 2012, A&A, 540, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Guesten, R., & Mezger, P. G. 1982, Vistas Astron., 26, 159 [Google Scholar]
  19. Halfen, D. T., Woolf, N. J., & Ziurys, L. M. 2017, ApJ, 845, 158 [Google Scholar]
  20. Henkel, C., Wilson, T. L., & Bieging, J. 1982, A&A, 109, 344 [NASA ADS] [Google Scholar]
  21. Humire, P. K., Thiel, V., Henkel, C., et al. 2020, A&A, 642, A222 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Iben, I. J., & Renzini, A. 1983, ARA&A, 21, 271 [NASA ADS] [CrossRef] [Google Scholar]
  23. Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
  24. Jacob, A. M., Menten, K. M., Wiesemeyer, H., et al. 2020, A&A, 640, A125 [EDP Sciences] [Google Scholar]
  25. Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [Google Scholar]
  26. Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
  27. Langer, W. D., & Penzias, A. A. 1990, ApJ, 357, 477 [Google Scholar]
  28. Langer, W. D., & Penzias, A. A. 1993, ApJ, 408, 539 [NASA ADS] [CrossRef] [Google Scholar]
  29. Langer, W. D., Wilson, R. W., Henry, P. S., & Guelin, M. 1978, ApJ, 225, L139 [NASA ADS] [CrossRef] [Google Scholar]
  30. Langer, W. D., Graedel, T. E., Frerking, M. A., & Armentrout, P. B. 1984, ApJ, 277, 581 [Google Scholar]
  31. Liszt, H. S. 2007, A&A, 476, 291 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Liszt, H., & Lucas, R. 2002, A&A, 391, 693 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Liszt, H. S., & Gerin, M. 2016, A&A, 585, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  34. Liszt, H., & Gerin, M. 2018, A&A, 610, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Liszt, H., & Gerin, M. 2023, ApJ, 943, 172 [NASA ADS] [CrossRef] [Google Scholar]
  36. Liu, T., Evans, N. J., Kim, K.-T., et al. 2020, MNRAS, 496, 2790 [Google Scholar]
  37. Lucas, R., & Liszt, H. 1996, A&A, 307, 237 [NASA ADS] [Google Scholar]
  38. Lucas, R., & Liszt, H. 1998, A&A, 337, 246 [NASA ADS] [Google Scholar]
  39. Luo, G., Li, D., Tang, N., et al. 2020, ApJ, 889, L4 [NASA ADS] [CrossRef] [Google Scholar]
  40. Luo, G., Zhang, Z.-Y., Bisbas, T. G., et al. 2023a, ApJ, 942, 101 [NASA ADS] [CrossRef] [Google Scholar]
  41. Luo, G., Zhang, Z.-Y., Bisbas, T. G., et al. 2023b, ApJ, 946, 91 [NASA ADS] [CrossRef] [Google Scholar]
  42. Maeder, A. 1983, A&A, 120, 113 [NASA ADS] [Google Scholar]
  43. Mangum, J. G., & Shirley, Y. L. 2015, PASP, 127, 266 [Google Scholar]
  44. McDowell, R. S. 1987, J. Quant. Spec. Radiat. Transf., 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
  45. McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Milam, S. N., Savage, C., Brewster, M. A., Ziurys, L. M., & Wyckoff, S. 2005, ApJ, 634, 1126 [Google Scholar]
  47. Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
  48. Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
  49. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2014, ApJ, 783, 130 [Google Scholar]
  50. Reid, M. J., Menten, K. M., Brunthaler, A., et al. 2019, ApJ, 885, 131 [Google Scholar]
  51. Ritchey, A. M., Federman, S. R., & Lambert, D. L. 2011, ApJ, 728, 36 [NASA ADS] [CrossRef] [Google Scholar]
  52. Romano, D., Matteucci, F., Zhang, Z. Y., Papadopoulos, P. P., & Ivison, R. J. 2017, MNRAS, 470, 401 [NASA ADS] [CrossRef] [Google Scholar]
  53. Romano, D., Matteucci, F., Zhang, Z.-Y., Ivison, R. J., & Ventura, P. 2019, MNRAS, 490, 2838 [NASA ADS] [CrossRef] [Google Scholar]
  54. Romano, D., Magrini, L., Randich, S., et al. 2021, A&A, 653, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  55. Roueff, E., Loison, J. C., & Hickson, K. M. 2015, A&A, 576, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Rybarczyk, D. R., Gong, M., Stanimirović, S., et al. 2022a, ApJ, 926, 190 [NASA ADS] [CrossRef] [Google Scholar]
  57. Rybarczyk, D. R., Stanimirović, S., Gong, M., et al. 2022b, ApJ, 928, 79 [NASA ADS] [CrossRef] [Google Scholar]
  58. Savage, C., Apponi, A. J., Ziurys, L. M., & Wyckoff, S. 2002, ApJ, 578, 211 [NASA ADS] [CrossRef] [Google Scholar]
  59. Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [Google Scholar]
  60. Sipilä, O., Colzi, L., Roueff, E., et al. 2023, A&A, 678, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Snow, T. P., & McCall, B. J. 2006, ARA&A, 44, 367 [Google Scholar]
  62. Stäuber, P., & Bruderer, S. 2009, A&A, 505, 195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Sun, Y., Zhang, Z.-Y., Wang, J., et al. 2024, MNRAS, 527, 8151 [Google Scholar]
  64. Szűcs, L., Glover, S. C. O., & Klessen, R. S. 2014, MNRAS, 445, 4055 [CrossRef] [Google Scholar]
  65. Tang, N., Li, D., Luo, G., et al. 2021, ApJS, 257, 47 [NASA ADS] [CrossRef] [Google Scholar]
  66. Treviño-Morales, S. P., Fuente, A., Sánchez-Monge, Á., et al. 2016, A&A, 593, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  67. van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [Google Scholar]
  68. Watson, W. D., Anicich, V. G., & Huntress, W. T. J., 1976, ApJ, 205, L165 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wenger, T. V., Balser, D. S., Anderson, L. D., & Bania, T. M. 2018, ApJ, 856, 52 [Google Scholar]
  70. Wouterloot, J. G. A., & Brand, J. 1996, A&AS, 119, 439 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Yan, Y. T., Zhang, J. S., Henkel, C., et al. 2019, ApJ, 877, 154 [Google Scholar]
  72. Yan, Y. T., Henkel, C., Kobayashi, C., et al. 2023, A&A, 670, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
2

All transitions refers to J=1–0 rotational transition unless otherwise noted.

3

However, this low value (<30) is only derived at Vlsr = −22 km s−1 toward 11720–3552; see Appendix E for more detail.

4

For different works using the same tracer, we adopted the latest gradient.

5

The forward reaction only has high efficiency (≥50%) in cold environments (e.g., Tk < 30 K).

6

However, since the integrated velocity range is over 20 km s−1 and contains a few velocity components, the actual column density of each component should be a few fractions of the total.

All Tables

Table B.1

Optical depths and line widths toward 3C 111.

In the text
Table C.1

Source name, velocity, galactocentric distance, integrated optical depths, isotopic ratios, and RMS of the absorption spectra.

In the text
Table D.1

Molecular transitions mentioned in this work.

In the text

All Figures

thumbnail Fig. 1

Distribution of the observed quasar sight lines (yellow lines) and ultra-compact H II region (red crosses) projected onto a top-down schematic view of the Milky Way (artist’s concept, R. Hurt: NASA/JPLCaltech/SSC).
In the text
thumbnail Fig. 2

Normalized absorption spectra of HCO+ (black curve) and H13CO+ (blue curve) toward J1851+0035. The spectrum of H13CO+ has been scaled by a factor of five and shifted upward by 0.5 for better display. The gray shaded regions denote the velocity ranges used to calculate the column density ratios. The red vertical lines represent HCO absorption, where the −25km s−1 component of H13CO+ absorption is contaminated with HCO J=1/2–1/2, F=1–1. Thus, these components were discarded since they can only obtain lower limits of 12C/13C.
In the text
thumbnail Fig. 3

Measurements of H12CO+/H13CO+ as a function of RGC and comparison of the derived gradients between different works. Blue dots represent τHCO+ < 3, and black dots represent τHCO+ > 3. The two lower limits are shifted to RGC = 0.5 kpc for better visualization. The red curve denotes the maximum likelihood fit of the blue points only; orange curves denote the 3σ deviation from the MCMC sampling.
In the text
thumbnail Fig. 4

Comparison between observations and GCE models, in which the models are taken from Table 2 in Colzi et al. (2022) with the same numbers.
In the text
thumbnail Fig. A.1

Same as Fig. 2 but for other sources. Red vertical lines denote HCO absorption.
In the text
thumbnail Fig. B.1

Gaussian decomposition of normalized absorption profiles of HCN, H13CN, HNC, and H13NC toward 3C 111. Red dashed curves denote the fitting results, and green dotted lines denote each Gaussian component.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.