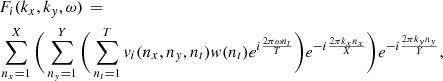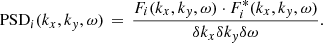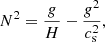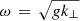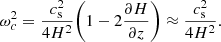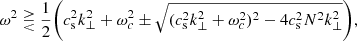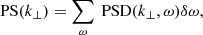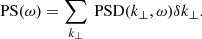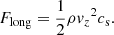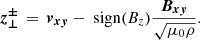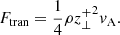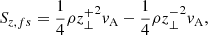| Issue |
A&A
Volume 665, September 2022
|
|
|---|---|---|
| Article Number | A118 | |
| Number of page(s) | 29 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202243947 | |
| Published online | 16 September 2022 | |
Stirring the base of the solar wind: On heat transfer and vortex formation
1
Department of Astrophysics-AIM, University of Paris-Saclay and University of Paris, CEA, CNRS, Gif-sur-Yvette Cedex 91191, France
e-mail: adam.finley@cea.fr
2
Rosseland Centre for Solar Physics, University of Oslo, PO Box 1029 Blindern 0315 Oslo, Norway
3
Institute of Theoretical Astrophysics, University of Oslo, PO Box 1029, Blindern 0315 Oslo, Norway
4
Bay Area Environmental Research Institute, Moffett Field, CA 94035, USA
5
Lockheed Martin Solar and Astrophysics Laboratory, Palo Alto, CA 94304, USA
6
National Astronomical Observatory of Japan, National Institutes of Natural Sciences, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
Received:
4
May
2022
Accepted:
5
July
2022
Context. Current models of the solar wind must approximate (or ignore) the small-scale dynamics within the solar atmosphere; however, these are likely important in shaping the emerging wave-turbulence spectrum that ultimately heats and accelerates the coronal plasma.
Aims. This study strives to make connections between small-scale vortex motions at the base of the solar wind and the resulting heating and acceleration of the coronal plasma.
Methods. The Bifrost code produces realistic simulations of the solar atmosphere which facilitate the analysis of spatial and temporal scales which are currently at, or beyond, the limit of modern solar telescopes. For this study, the Bifrost simulation is configured to represent the solar atmosphere in a coronal hole region, from which the fast solar wind emerges. The simulation extends from the upper-convection zone (2.5 Mm below the photosphere) to the low corona (14.5 Mm above the photosphere), with a horizontal extent of 24 Mm × 24 Mm. The network of magnetic funnels in the computational domain influence the movement of plasma, as well as the propagation of magnetohydrodynamic waves into the low corona.
Results. The twisting of the coronal magnetic field by photospheric flows efficiently injects energy into the low corona. Poynting fluxes of up to 2 − 4 kWm−2 are commonly observed inside twisted magnetic structures with diameters in the low corona of 1–5 Mm. Torsional Alfvén waves are favourably transmitted along these structures, and subsequently escape into the solar wind. However, reflections of these waves from the upper boundary condition make it difficult to unambiguously quantify the emerging Alfvén wave-energy flux.
Conclusions. This study represents a first step in quantifying the conditions at the base of the solar wind using Bifrost simulations. It is shown that the coronal magnetic field is readily braided and twisted by photospheric flows. Temperature and density contrasts form between regions with active stirring motions and those without. Stronger whirlpool-like flows in the convection, concurrent with magnetic concentrations, launch torsional Alfvén waves up through the magnetic funnel network, which are expected to enhance the turbulent generation of magnetic switchbacks in the solar wind.
Key words: Sun: atmosphere / solar wind
© A. J. Finley et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
The term solar wind describes the mixture of charged particles and magnetic flux that is constantly emerging from the Sun and filling the heliosphere (Parker 1958). Studies of the heating and acceleration of the solar wind have gained momentum during the past several decades (Marsch 2018; Verscharen et al. 2019, and references therein), motivated (in part) by technological advances that heavily rely on space-based infrastructure1 (assets that need to be protected from extreme space weather; Varela et al. 2022). There are many physical processes that could explain the heating and acceleration of the solar wind (see reviews by Parnell & De Moortel 2012; Hansteen & Velli 2012), most of them have been studied theoretically, observed remotely, and/or measured in situ. Yet it appears that no single mechanism alone can explain the heating of the corona (see discussion in Klimchuk 2015). Instead, a number of different processes are likely occurring simultaneously, and with varying degrees of significance, under the different conditions found in the solar atmosphere, from coronal holes to active regions (Cranmer & Winebarger 2019).
Despite significant advances, the solar wind remains challenging to model (and importantly forecast) due to the large range of scales that need to be incorporated. It is well known that energy is injected into the corona at all scales, from magnetohydrodynamic (MHD) waves (Nutto et al. 2012; Van Doorsselaere et al. 2020) to flares and coronal mass ejections with global extent (Aschwanden et al. 2017; Green et al. 2018; Wyper et al. 2018). In addition to the range of spatial scales, heating events take place on a variety of timescales (Hollweg 1973; Viall & Klimchuk 2017). Putting aside large-scale eruptions so as to focus on the quasi-steady input of energy into the corona, it is possible to distinguish three broad magnetic configurations of the solar atmosphere for modelling purposes. These are the quiet Sun (Danilovic et al. 2010; Rempel 2014), active or enhanced regions (Carlsson et al. 2016; Chen et al. 2021), and coronal holes (Wójcik et al. 2019). In each of these configurations, energy is channelled from the convection into the low corona. Coronal holes are the dominant source of the solar wind in the heliosphere (Cranmer et al. 2017; Stansby et al. 2021), typically producing the fast solar wind (McComas et al. 2008; Ebert et al. 2009; Macneil et al. 2020a; Wang 2020). The magnetic field configuration of a coronal hole is relatively simple, compared with the quiet Sun and active regions, given that the field is principally open to the solar wind (Lowder et al. 2017; Hofmeister et al. 2019). However, there are still a range of dynamic processes taking place, such as the braiding of magnetic field lines (Wedemeyer-Böhm et al. 2012; Wedemeyer et al. 2013; Huang et al. 2018) and the emergence of new magnetic flux (Murray et al. 2009). These can trigger the formation of jets (Shen et al. 2017; Yang et al. 2017) and other phenomena, which are then observed as spicules (Martínez-Sykora et al. 2017; Bose et al. 2021) or fibrils (Hansteen et al. 2006; Leenaarts et al. 2015).
Vortical flows (so-called solar tornadoes) have garnered significant interest in recent years as they can efficiently channel mass and energy from the photosphere, through the chromosphere, and into the low corona. These tornado-like events have been observed across the solar surface (e.g. Wedemeyer-Böhm & Rouppe van der Voort 2009). Starting in the photosphere, whirlpool-like flows form in down-flow lanes of the granulation, where strong magnetic elements can accumulate and suppress the magnetoconvection. The photospheric plasma twists the magnetic field, and in turn this acts on the material above, forcing a swirling and rotation of the chromospheric plasma (Bonet et al. 2010; Park et al. 2016; Tziotziou et al. 2018) and coronal plasma in some cases (Wedemeyer-Böhm et al. 2012). Typically, these flows are observed to have a diameter of 0.5 − 2 Mm in the photosphere (see Murabito et al. 2020, and references therein), though numerical models suggest the average size to be smaller (less than 0.1 Mm across; Liu et al. 2019). These flows are expected to expand in the chromosphere to around 1.5–5 Mm (Battaglia et al. 2021), and they may continue higher in the low corona. In addition to vortical flows, there exist a range of linear (horizontal and vertical) drivers in the photosphere (typically identified by the motion of magnetic bright points, e.g. Bodnárová et al. 2014). These linear motions were more readily identified at first (Nisenson et al. 2003); however, magnetohydrodynamic modelling typically shows that the emerging linear wave-energy flux is not as efficiently transmitted into the low corona (Vigeesh et al. 2012), when compared with the torsional wave-energy flux.
Along with low-frequency Alfvén waves, a range of MHD waves are generated in the photosphere and travel out along the coronal magnetic field lines (see review of Srivastava et al. 2021), including acoustic-gravity waves (Vigeesh et al. 2017; Fleck et al. 2021), magnetosonic waves (Yadav et al. 2021), kink waves (Tiwari et al. 2019; Morton et al. 2021), and other Alfvénic fluctuations (Jess et al. 2009; Wang & Yokoyama 2020; Pelekhata et al. 2021). The propagation and characteristics of these waves are likely modified by the configuration of the overlying magnetic field (Bogdan et al. 2003; Snow et al. 2018). Subsequently, these waves may generate magnetosonic shocks (Wang et al. 2021), or otherwise undergo mode conversion (Schunker & Cally 2006; Shoda & Yokoyama 2018a) and/or phase mixing (Pagano & De Moortel 2017; Shoda & Yokoyama 2018a; Boocock & Tsiklauri 2021), before finally escaping into the solar wind, where they may be further subject to the parametric decay instability (Réville et al. 2018). In most current models of the solar wind, Alfvén waves, generated by the shaking of the magnetic field in the photosphere, are responsible for the heating and acceleration of the solar wind when they undergo dissipation with counter-propagating (reflected) waves in the corona (Cranmer & Van Ballegooijen 2005; Van Ballegooijen et al. 2011).
Heliospheric models tend to account for the turbulent process of Alfvén wave dissipation either on a sub-grid scale (Usmanov et al. 2011; Chhiber et al. 2021), or with a simplified physical Wentzel-Kramer-Brillouin (WKB) description (van der Holst et al. 2014). In the simplest case, one additional equation that describes the wave-energy conservation can be added to the set of standard MHD equations (see Réville et al. 2020). In this case, three values must be specified a priori: (1) input wave amplitude (or equivalently the input Alfvén wave energy), (2) the length scale of dissipation, and (3) the degree to which waves are reflected as they propagate into the heliosphere. Fully resolving the Alfvén wave turbulence requires a model with an increased spatial and temporal resolution. Therefore models of this kind have a smaller physical extent (1D, or wedge configuration) in order to balance the increased computational cost (Suzuki 2011; Shoda et al. 2019, 2020). These models reproduce many of the properties of the solar wind observed in situ, but they still rely on an injected spectrum of Alfvénic fluctuations. Generally, this spectrum is prescribed based on current knowledge of the smallest scales on the Sun (see review of Jess et al. 2015). However current observations (from the Swedish 1-m Solar Telescope, Hinode, etc.) are unlikely to capture all the spatial scales and frequencies at which energy is being transported into the low corona (though the Daniel K. Inouye Solar Telescope (DKIST) will soon be fully operational; Rimmele et al. 2020). As some small scales remain out of reach of current instruments, it is reasonable to turn towards advanced numerical simulations to derive the conditions at the base of the solar wind.
In this study, we examine the small-scale dynamics found inside a realistic 3D model of a coronal hole, in connection with how they may relate to the heating and acceleration of the solar wind. Section 2 presents the Bifrost code (Gudiksen et al. 2011) and the computational setup that is used. Section 3 discusses the dynamical processes observed within the simulated coronal hole, including the braiding of magnetic flux and the formation of vortex-like flows and structures. In Sect. 4, we evaluate a number of quantities which are of interest to the solar wind modelling community, such as the amplitude of horizontal fluctuations and the strength of the vertical Poynting flux. Finally, we conclude by summarising how these results could be used to improve future solar wind modelling.
2. Numerical simulation
2.1. The Bifrost code
The simulation analysed in this study was performed with the 3D radiation magnetohydrodynamics (RMHD) code Bifrost (described fully within Gudiksen et al. 2011). Bifrost solves the MHD equations on a staggered Cartesian grid and includes (in this case) the influence of; thermal conduction along magnetic field lines (Spitzer & Cook 1957), ohmic heating, viscous dissipation, and a range of radiative heating/cooling processes. The Bifrost code utilises a split-diffusive operator such that diffusive terms are separated into a small globally applicable term and a local term (often referred to as ‘hyper diffusion’). This allows the code to remain highly stable and compute parameter regimes which would not be possible using a single value. This means, however, that the values of magnetic diffusivity and viscosity vary in time and space during the computation.
To account for the radiative processes, Bifrost solves for the radiation field within the domain in parallel with solving the MHD equations. The radiative transfer is performed in two manners, (1) optically thin radiative transfer for the coronal/chromospheric plasma with T > 2 × 104 K, which utilises a pre-computed transfer function f(T), derived from tabulated atomic data in CHIANTI (Dere et al. 1997; Landi et al. 2006). This is supplemented with empirical fits from Carlsson & Leenaarts (2012), which describe; the losses form the chromosphere due to strong lines, the heating from the Lyα line of Hydrogen, and the heating of EUV photons (thin losses from the transition region and corona). Furthermore, (2) full radiative transfer for the optically thick regions (typically in the photosphere and low chromosphere). The second method is computationally costly and so some approximations are made, that is to say a static medium, and local thermodynamic equilibrium (LTE) for the gas opacity (thus the opacity σ(ρ, T) can be pre-computed). Scattering is also included (Skartlien 2000), though this means that the radiative transfer equation must be solved iteratively to produce a consistent radiation field. To simplify the number of spectral lines, Bifrost implements an approximate opacity spectrum by replacing monochromatic opacities with mean opacities and solving the wavelength-integrated radiative transfer in four opacity bins instead (Nordlund 1982; Hayek et al. 2010).
To close the MHD equations an Equation of State (EoS) is needed. The code has a variety of EoS implementations. For this study the EoS includes ionisation and excitation calculated in LTE from 16 elements (H, He, C, N, O, Ne, Na, Mg, Al, Si, S, K, Ca, Cr, Fe and Ni) with abundances from Gustafsson et al. (1975). This (old) set of abundances was chosen in order to have the same EoS as in the relaxed simulations of solar convection by Stein & Nordlund (e.g. Stein & Nordlund 2000) used as a starting point for the simulations, see below.
2.2. The coronal hole patch
We examine the simulation ‘ch024031_by200bz005’, which was originally produced as part of a set of simulations for the Hinode Science Data Centre2, intended for comparison with high resolution observations of the solar atmosphere (see discussion in Carlsson et al. 2016). The computational domain has a horizontal extent of 24 × 24 Mm2 with a resolution of dx = dy = 31 km, and spans from 2.5 Mm below the photosphere to 14.5 Mm above with a varying vertical resolution of dz = 12–82 km (in total 768 × 768 × 768 grid points).
The horizontal boundary conditions are periodic, the lower and the top boundaries are open. The entropy of the incoming fluid at the bottom boundary is set with the aim of giving the solar effective temperature of 5780 K. The effective temperature is not quite 5780 K. It varies in time between 5720 and 5774 K. To get it closer to 5780 K would mean changing the value of the incoming entropy and waiting for the atmosphere to relax – a very time-consuming process.
The simulation started from a simulation cube from Stein & Nordlund (2000) with a horizontal extent of 6 × 6 Mm2 spanning from 2.5 Mm below the photosphere to 0.5 Mm above. This was duplicated first to a 12 × 12 Mm2 box and then to a 24 × 24 Mm2 box and run until the periodicities disappeared. This photospheric box (768 × 768 × 192 grid points) was run until well relaxed (14 hours of solar time). The magnetic field in the simulation box is the result of the field in the initial simulation cube, a small scale dynamo and the insertion of a horizontal field with a strength of 45 G in the inflow regions. The vertical field is balanced with zero average signed vertical field. A plane-parallel chromosphere and corona was added to this relaxed photospheric simulation. The density and temperature structure was taken from another simulation and the magnetic field was taken from a potential field extrapolation from the photospheric simulation. This was run for 900 s after which a unipolar vertical field of 5 G was added in order to mimic the mean signed field of coronal holes (Zwaan 1987). The initial chromosphere and corona cools down because there is no heating in the plane-parallel atmosphere with a potential magnetic field to balance the optically thin radiative cooling and the energy transport to the lower atmosphere through conduction. At the time of the addition of the vertical field, the upper atmosphere has cooled down to about 200 kK. More and more waves and currents provide heating and the corona slowly heats up to reach a quasi-steady temperature structure after about 8000 s with a coronal temperature of 0.8–1 MK.
Figure 1 shows a 3D visualisation of the magnetic field in the simulation domain. The simulation contains no large-scale bipoles in the magnetic field. The majority of the magnetic flux has been swept into the intergranular lanes (see Fig. 2) with an average unsigned field of 40 G. A quasi-steady temperature structure has developed inside the simulation domain, depicted in Fig. 2, with a photospheric temperature around 5780 K, cool chromosphere, and hot corona. The publicly available dataset spans approximately two hours of solar time, with snapshots available at a cadence of 10 s. We have continued this computation for an additional hour and a half of solar time, which allows more structure to develop in the computational domain via the convective braiding of magnetic field lines. A comparison of the magnetic field and temperature structure with the publicly available dataset is available in Appendix A. For this study, we consider the final hour of the simulation (t = 9580 − 13 180 s) and utilise a snapshot cadence of 10 s.
 |
Fig. 1. 3D visualisation of ch024031_by200bz005 at t = 40 min. The computational domain spans 24 Mm × 24 Mm × 17 Mm. Left: magnetic field lines are coloured by temperature from blue in the upper-convection zone (≈5800 K), to light blue in the temperature minimum region (≈3200 K), and finally yellow in the low corona (≈1 MK). Right: vertical magnetic field strength at the photosphere (Z = 0 Mm). |
 |
Fig. 2. Snapshot of ch024031_by200bz005 at t = 40 min. Top: temperature structure in a vertical cut through the computational domain at Y = 19 Mm (indicated with a dashed line in the lower panel). The plasma β equal to one surface is highlighted with a thin dashed line. Bottom: vertical velocity at the photosphere (Z = 0 Mm). The strongest magnetic field enhancements are highlighted by polarity (purple = negative and green = positive). The field at the photosphere is mostly negative and contained in the intergranular lanes. Data are shown from the same snapshot as Fig. 2. |
3. Simulation results
3.1. Overview
Bifrost simulations are rich in dynamical phenomena, with this case being no different. During the hour of data selected for analysis, the magnetic field continually evolves due to the presence of convective motions at the photosphere. This triggers sporadic mass transfer into the corona, as well as braiding of the coronal magnetic field, and the modification of MHD wave propagation through the simulation domain. Despite the large number of time-varying processes, the average density and temperature profiles versus height remain roughly constant; shown in Fig. 3. For this study, our interest is focussed on the dynamics of the simulation and so we do not discuss, in detail, the various physical processes that heat and cool the plasma during the computation.
 |
Fig. 3. Average density (top), temperature (middle), plasma beta, and the sound/Alfvén speeds (bottom) profiles in the simulation domain for each 10 s snapshot during the hour under investigation. Variations in the density above the chromosphere occur due to the launching of jets. Variation in the maximum temperature results from the varying degrees of twisted magnetic structures that facilitate vertical energy transport. |
In Fig. 4, a range of quantities taken from a vertical pencil at X = 12 Mm and Y = 12 Mm (i.e. the centre of the box) are plotted during the entire hour of data. We note that structures can move in and out of the selected column as the simulation is 3D. Figure 4 illustrates the vertical structuring of the domain, and the degree to which this evolves with time. The vertical movement vz of plasma in the corona shows plasma rising and falling at speeds of around 30 km s−1, in contrast to speeds of a few km/s in the upper-convection zone. Large upflows can supply significant amounts of material into the chromosphere (and to a lesser degree the low corona), as indicated by the increased density contrast δρ/⟨ρ⟩xy (where ⟨ρ⟩xy is the horizontally averaged density ρ). As the field in the low corona is unipolar and negative, the vertical extent of the closed magnetic field can be inspected from the ratio of the vertical magnetic field strength Bz and the magnitude of the magnetic field vector |B|, that is Bz/|B| (indicating the degree to which the field is vertical). The closed field is generally contained below Z = 2.5 Mm (identifiable by Bz/|B|≥0). This coincides with the top of the chromosphere, which is visible in the plasma temperature T.
 |
Fig. 4. Time-distance plots of a vertical pencil in the simulation domain at X = 12 Mm and Y = 12 Mm. Quantities shown are; the vertical flow velocity vz, the normalised vertical magnetic field Bz/|B|, the ratio of the Alfvén speed to the sound speed vA/cs, the plasma temperature T, the density fluctation with respect to the average of the horizontal domain δρ/⟨ρ⟩xy, and the vertical Poynting flux Sz. |
The sound and Alfvén wave speeds are a crucial diagnostic of the state of the atmosphere, these are given by,
and
respectively, where P is the gas pressure, γ is the adiabatic index, and μ0 is the vacuum permeability. The average profiles of these wave speeds versus altitude in the simulation domain are shown in Fig. 3. The surface where the ratio of the Alfvén speed to the sound speed vA/cs is equal to one, is approximately the plasma beta β equals one surface and is highlighted with a black line in the time-distance plot of vA/cs (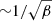 ) in Fig. 4. The plasma beta is given by,
) in Fig. 4. The plasma beta is given by,
Below the β = 1 surface, the plasma pressure dominates the magnetic pressure, and vice versa above. This surface is located around 1–1.5 Mm above the photosphere. Thus the convection efficiently influences the magnetic field at the photosphere, whereas the magnetic field (relaxation) dominates the dynamics in the low corona (discussed in Sect. 3.2). As well as indicating the changing pressure regime, the vA/cs = 1 surface is also a location of significant interest for mode conversion (discussed in Sect. 3.3).
3.2. Twisting and braiding the coronal magnetic field
There are many routes to forming twisted structures in the solar atmosphere. It is known that convective motions can generate vorticity in-between neighbouring convective granules (Giagkiozis et al. 2018), and that this can twist-up the magnetic field rooted in the intergranular lanes (when β ≫ 1). Similarly, Fischer et al. (2020) found evidence for the generation of twisted horizontal structures, by shallow recirculation near the photosphere. In addition to braiding at the solar surface, the emerging flux may already have become twisted as it rose through the upper-convective zone (Pinto & Brun 2013; MacTaggart & Prior 2021; MacTaggart et al. 2021). In the ch024031_by200bz005 simulation, the braiding of field lines and generation of structure in the low corona is principally driven by the convective motions dragging the footpoints of the magnetic field around the photosphere. The coronal magnetic field in the simulation is structured into many distinct magnetic funnels. These funnels originate from magnetic concentrations (MCs) in the photosphere that expand with height into the low corona where they jostle with other funnels to fill the available volume. This configuration has been well documented (Hofmeister et al. 2019) and discussed in the literature (see Tu et al. 2005, and references therein).
These funnel networks are thought to evolve slowly, with theoretical studies often examining the dynamics of simplified (often 2D) funnel configurations (Pascoe et al. 2014; Wójcik et al. 2019). In the Bifrost simulation, the MCs (which are the sources of the funnels in the photosphere) move around the domain relatively slowly (up to ∼5 Mm h−1), matching the average horizontal flow velocity at the photosphere of ∼2 km s−1. For reference, the average Alfvén and sound speeds at the photosphere are ∼0.5 km s−1 and ∼8 km s−1, respectively. The MCs migrate around the intergranular lane network, where the magnetic flux of each MC can be broken apart and shuffled around. There are around 50 distinct MCs at any time in the simulation, that contain an average unsigned magnetic flux of 1.5 × 1016 Mx, and area of 4 × 10−2 Mm2 (a cross-section of ∼0.11 Mm). These MCs are associated with an average kinetic helicity v ⋅ (∇×v) of 50 m s−2 (with current helicity B/(μ0ρ)⋅(∇ × B) of 4 m s−2). The shuffling of MCs slowly adds complexity to the coronal magnetic field by braiding together different magnetic field lines from various locations across the photosphere. Figure 5 shows the locations of MCs in the photosphere, coloured by simulation time (beginning blue and finishing red), which shows their confinement in the intergranular lanes. During extreme events, localised vortex-flows in the photosphere can rapidly twist the magnetic field, on timescales of 30 s to a few minutes (seen also in observations Bonet et al. 2010).
 |
Fig. 5. Time-evolution of Magnetic Concentrations (MCs) and strong vertical Poynting fluxes. Left: location of MCs at the photosphere (Z = 0 Mm) during the hour of simulation time. Right: location of strong vertical Poynting fluxes in the low corona (Z = 12 Mm), associated with the braiding and twisting of the magnetic field by convective motions, and the release of energy in Swirling Events (SEs). The spatial distribution of the MCs and Swirls at t = 40 min are highlighted in black. |
Figure 6 shows the magnitude of vorticity at the photosphere (Z = 0 Mm) and the low corona (Z = 12 Mm). At the photosphere, hot material rises up inside the granular convection after which it cools and is displaced towards the intergranular lanes. These flow merge in the intergranular lanes where the density becomes enhanced and vortical flows are generated (an initial source of vorticity is required to generate a true whirlpool down-flow, see Simon & Weiss 1997). Large values of the kinetic helicity are highlighted with red contours, and follow the structure of the intergranular lanes. The current helicity is also enhanced at the base of the magnetic funnel structures, where the field strengths are largest. Areas with high current helicity, blue contours in Fig. 6, are more susceptible to forming the strong whirlpool-like down-flows. The flow vorticity is largest in the chromosphere above, as the density decreases and so the flow speeds can be consequently larger for the same amount of energy. The MCs, which expand with height to form the magnetic funnel network, are regularly buffeted by the convective/vortical motions. This launches torsional Alfvén waves up and along the funnels, which results in the vorticity of the low corona being highly structured and complex (see Fig. 6). The propagation of these fluctuations will be discussed in Sect. 3.3.
 |
Fig. 6. Horizontal cuts of the vorticity magnitude |∇×v|z at Z = 0 Mm and Z = 12 Mm, for t = 40 min. Contours of the kinetic helicity v ⋅ (∇×v) (red) and current helicity B/(μ0ρ)⋅(∇ × B) (blue) at a value of 100 m s−2 are plotted with the vorticity in the Z = 0 Mm panel. The zoomed inset within the first column (Z = 0 Mm) is 4 Mm × 4 Mm, centred on X = 7 Mm and Y = 19 Mm. The same patch of the domain is discussed again in Fig. 7. |
Twisting motions in the magnetic field, driven by the photospheric convection, transfer magnetic energy into the low corona as a Poynting flux (see discussion of Hansteen et al. 2015). The vertical Poynting flux is given by
where E is the electric field given by E = − v × B + ηJ. The current density is given by J = 1/μ0∇×B. The vertical Poynting flux Sz can be broken down into three terms, the first being the emerging Poynting flux,
the second being the field shaking/shearing Poynting flux,
and the third resulting from the finite magnetic diffusivity η,
The sum of these terms equals the total vertical Poynting flux, that is Sz = Sz, fe + Sz, fs + Sz, η. The term Sz, fe is associated with the advection of horizontal magnetic field by a vertical flow, and the term Sz, fs is linked with the horizontal motion (shaking/shearing) of vertically aligned field (this is how energy is transported by Alfvén waves, further discussed in Sect. 4.6). The term Sz, η relates to the dissipation of currents and is negligible (|Sz, η|≪10−10 W m−2) such that Sz ≈ Sz, fe + Sz, fs. In general, the emergence term dominates the average Poynting flux in the convective zone (as vertical fluid motions control the motion of the field) and is typically negative due to the subduction of magnetic field in intergranular lanes. Above the photosphere the shaking/shearing term dominates and is on average positive (though its strength diminishes with altitude). The location of Poynting flux enhancements at Z = 12 Mm are shown in Fig. 5, in comparison to the driving MCs in the photosphere. Upon visual inspection, the locations of Poynting flux enhancements and the movements of MCs across the photosphere are related. However the low corona magnetic field is deformed from purely vertical, due to its expansion, so magnetic energy is not always deposited directly above the driving MCs. The largest and most complex network of MCs, with braided coronal field, almost continuously heat the low corona above them during the hour of simulation time. This has interesting implications for the solar wind above, that are discussed in Sect. 4.2.
For the majority of interactions between the convection and the photospheric magnetic field, a moderate twist is applied to the field and this magnetic energy can be transmitted into the low corona by a steady Poynting flux. The unravelling of these twisted structures is often resisted/delayed by the accumulation of chromospheric plasma that feels a reduced ‘effective’ gravitational force due to the increased horizontal component of the magnetic field. Thus the chromosphere can sometimes thicken inside these twisted structures. However, when the convective motions drive MCs into complex intersections between multiple granules, they can remain in place long enough to influence the magnetoconvection. Often this creates a whirlpool-like down-flow, as material sinks towards the centre of the depression whilst conserving angular momentum (Kitiashvili et al. 2012; Moll et al. 2012; Silva et al. 2020). Whirlpool-like photospheric flows twist the magnetic field too quickly for it to remain in equilibrium with its surroundings. This causes the field to dramatically rotate/swirl which we refer to as a swirling event (SE).
Figure 7 follows the merging of MCs at an intersection of granulation, and the subsequent generation of a SE in the low corona, during a 30 min interval. At t1, two neighbouring flux bundles, that are embedded along the same intergranular lane, are forced to merge due to random convective motions. The movement of the magnetic funnels generates a vortical flow around the flux bundle in the chromosphere. At t2, the flows around each funnel merge and cancel out some of the vorticity associated with one of the flux bundles. The remaining flow encircles the recently merged flux, allowing the bundles to merge. During t3, the newly formed MC is compacted by the converging granulation flows and placed in the intersection of granulation, which produces a localised depression in the photosphere. A whirlpool-like flow begins to form in the depression. At t4, the field starts to be twisted by the photospheric flow. The coronal field begins to slowly twist (transferring a steady Poynting flux into the low corona) which (in this case) reverses the pre-existing circulation of the chromospheric flow to match that of the photosphere. The magnetic field generates a horizontal component due to the twisting which can support additional chromospheric plasma, and so the chromosphere thickens with the additional material resisting the twisting of the field (storing magnetic energy). At t5, the whirlpool-like flow in the photosphere has strengthened and rapidly twists the MC. The field above is stressed too quickly to remain stable (typically the low corona magnetic field rotates violently one to two minutes after the whirlpool formation). The magnetic tension force dominates in the chromosphere, and the entire magnetic funnel structure begins to rotate, launching an Alfvénic pulse from the release of the stored magnetic energy. This disturbance propagates up along the magnetic field lines (ejecting chromospheric plasma into the low corona) followed by a swirling motion, driven directly by the convection. At t6 the MC leaves the intersection, and becomes less concentrated. The overlying field can now relax, returning to a single magnetic funnel anchored to a MC. As the chromospheric plasma has been largely ejected, the plasma pressure within the funnel is low, in addition to the β = 1 surface being depressed due to the suppression of magnetoconvection (see Fig. 2). Finally, at t7 the magnetic funnel is slowly split apart by the convective motions, breaking apart the MC. Additional energetic events are driven by the merging and splitting of the magnetic funnels, though here only the dominant swirling event has been discussed. Despite the event lasting around 30 min from start to finish, the SE (the release of built-up magnetic energy) lasted around 10 min, beginning shortly after t4 and reaching a relaxed state at t6.
 |
Fig. 7. Snapshots during a ∼30 min period that display the merging of two MCs within the intersection of multiple granules, and the subsequent excitation of a SE. A subsection of the computational domain is shown that extends from the bottom boundary up to 6 Mm above the photosphere, with a horizontal extent of 4 Mm × 4 Mm (centred on X = 7 Mm and Y = 19 Mm). A top-down view of the domain is shown above each snapshot. The same cut in the domain is highlighted in Fig. 6. The upper-convection zone is coloured by vertical velocity (red is rising, blue is falling material). Selected magnetic field lines are coloured by temperature as in Fig. 1. The flow velocity in the chromosphere is indicated with arrows, the size and colour of which depend on the magnitude of the local flow speed. Cartoon annotations indicate the direction of advection for the MCs (green) and the important/prevailing flow patterns in the photosphere (magenta), chromosphere (white), and low corona (red). |
As twisted/braided magnetic field lines carry significant Poynting fluxes into the low corona, this is used as a criterion to highlight these structures inside the computational domain. Figure 8 shows a snapshot of all the magnetic field lines which have |Sz|> 2 kWm−2 at a height of 6 Mm. This criterion is chosen as it highlights the majority of twisted structures in the computational domain. The photospheric footpoints of the field lines identified by this criterion are indicated with green markers. From this visualisation, it is clear that there are a range of stressed-structures in the domain, with a variety of sizes and shapes. Each magnetic funnel that has been twisted or braided together has varying degrees of stressed field lines inside, thus the structure in the Poynting flux is often of a finer-scale than the overall funnel-size. The fine-structure in the Poynting flux is observed in Fig. 4 from t = 35 min to t = 55 min (circled with a dashed magenta line), when a twisted funnel structure enters the vertical cut (the signature of this is the ratio of Bz/|Bz| decreasing). In Fig. 8, the Poynting flux enhancements are not always positive (both blue and yellow tones are visible). This is largely due to two factors. Firstly the sinking of coronal plasma back to the photosphere, and secondly the unwinding of the magnetic field in the direction of the photosphere (often observed as a collapse in the centre of large structures). A clear trend emerges when viewing a timeseries of visualisations like Fig. 8, the more magnetic field is braided together from different MCs (i.e. increasing the complexity of the structure), the more time it will take to dissipate/unwind. The smallest stressed bundles of field lines, which do not have a particular shape, come and go from the detection criterion of |Sz|> 2 kWm−2, in around 20 s to a few minutes. Whereas small vortex-like structures above isolated MCs (2–5 Mm in diameter in the low corona) can remain visible for around 5–10 min. The most complex structures (∼10 Mm in diameter), resembling multiple structures braided together, can remain for up to 30–40 min at a time.
 |
Fig. 8. 3D rendering of the twisted magnetic field structures in the simulation domain at t = 40 min, identified with large values of Poynting flux (|Sz|> 2 kWm−2) at Z = 6 Mm. Top left: as viewed from above. Bottom left: The location of the magnetic field footpoints at the photosphere (Z = 0 Mm) are highlighted with green markers. |
The field lines highlighted by this criterion have photospheric footpoints in the intergranular lanes with MCs, as expected. The largest structures, are composed of tangled magnetic field from a variety of photospheric sources. To show this, Fig. 9 displays another visualisation of the same snapshot, now focussing on the largest twisted structure in the domain. Field lines from four photospheric sources are drawn, each with a different colour. Due to the shuffling of MCs around the intergranular lanes, the magnetic field from the four sources is tangled together into a large-scale braided field. Field lines in magenta depict a relaxed magnetic funnel, this is the typical configuration of the magnetic field emerging from MCs. The green field lines highlight a magnetic funnel that has whirlpool-like motions currently at its base, and so is being actively stressed (see Fig. 8, where this structure is also annotated). Streamlines inside the green funnel show the plasma inside the funnel is swirling around, and that material is sinking into the whirlpool at the photosphere. The magnetic field highlighted in red corresponds to a patch of network field, that is the field not originating exactly from the MCs and instead having a more diffuse origin (centred on the given coordinates). It is thought that the presence of this network field may be responsible for the formation of the large-scale braiding here. This field acts like an anchor, allowing the other elements to be wrapped around it by the shuffling of MCs in the intergranular lanes.
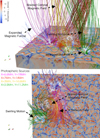 |
Fig. 9. 3D visualisation of a subset of the braided coronal magnetic field, at t = 40 min. Magnetic field lines are traced from four photospheric sources (seed points are initiated within 0.25 Mm of the given coordinates). Field lines are coloured by their source location. Streamlines of the velocity field are initiated at the photospheric sources, and are coloured by vertical flow velocity vz. The lower panel shows the same visualisation, now viewed from above. |
Given the orientation of the magnetic field, the twisting and un-twisting of funnel structures (and the larger braided structures) appears as a flux emergence in the low corona. So the stirring of the low corona by convective motions is examined further by evaluating the significance of the emerging Poynting flux term to shaking/shearing term in the Poynting flux. The horizontally averaged values of the Poynting flux terms are shown in Fig. 10 for a single snapshot, along with the ratio |Sz, fe|/(|Sz, fe|+|Sz, fs|), which weighs the relative strength of the two terms. The vertically averaged value of this quantity in the low corona (above 6 Mm) is plotted to the right. As previously discussed, the shaking/shearing term dominates the quasi-steady background of fluctuations and so the average at the top of the simulation domain is largely grey/white. However the unwinding of the magnetic field is highlighted with darker tones (including its fine-structure). Using this criterion, the stirring of the low corona is far more continuous than indicated by examining the extreme values of Sz. These un-winding motions are prevalent throughout the entire low corona. The overall pattern changes very slowly during the hour under investigation, as this relates to the buffeting of the magnetic funnel network by convective motions at its base. Thus the pattern evolves on the timescale of the convection, and only when MCs are able to generate whirlpool-like flows in the photosphere, are the strongest Poynting flux enhancements triggered (the darkest, time-dependent features). In the low corona, the dissipation of these stirring motions by Ohmic and viscous dissipation is low. Dissipation is largest at the boundaries of the twisted magnetic funnels, however these values are orders of magnitude smaller than the Poynting flux contained inside the twisted magnetic fields.
 |
Fig. 10. Comparison of the field shaking Sz, fs and flux emergence Sz, fe terms of the vertical Poynting flux in the simulation domain, at t = 40 min. Left: average total Poynting flux versus height in black, with the field shaking and flux emergence terms in red and blue respectively. Due to the range of scale, the y-axis is limited to a few kW/m2. The floating values indicate the approximate value of each term in the upper-convection zone. The average contribution of the flux emergence term to the vertical Poynting flux versus height is also shown. Right: this ratio is instead vertically averaged above 6 Mm (i.e. at the top of the simulation domain), again for t = 40 min. This highlights the network of magnetic swirls/funnels that exist throughout the domain. |
The magnetic energy released from a SE is primarily converted into the kinetic energy of the ejected chromospheric plasma, and the heating of that plasma to coronal temperatures. The kinetic energy density of chromospheric plasma inside a funnel structure with an active SE is enhanced by a factor of ∼5 compared to the background chromospheric plasma. In the low corona, the average plasma temperature inside a magnetic funnel connected to a SE is ∼0.2 MK larger than the average background temperature (of 0.9 − 1.0 MK). The twisted structures in the chromosphere and the low corona have typical diameters of 2–5 Mm and 4–11 Mm, respectively (as the funnel expands into the low corona). However, the enhancements in Sz are generally limited to an area of ∼2 Mm2 inside these structures.
It is difficult to truly distinguish between the SEs and the more gradual twisting of the field, as they form a continuous spectrum of events with a variety of energies and sizes. The physical size of an individual SE is connected to the amount of flux inside the MC at its base, and the expansion of the magnetic funnel above. The rate at which they occur is related to how frequently the random convective motions force MCs into the intersections of granulation, where whirlpool-like flows are more readily formed. If for example, the background magnetic field in the simulation domain were stronger, we may expect the movement of the MCs through the intergranular lanes to be slower (as the dynamics would be dominated more by the magnetic field), and thus find a reduced global braiding to the coronal magnetic field. However, slightly stronger magnetic fields may increase the likelihood of generating depressions in the convection around MCs, and subsequently produce more whirpool-like flows which locally twist the coronal magnetic field. Clearly, the properties of the structures formed in the simulation domain, from the global braiding to the SEs, are linked to magnetic field structure in the low corona, and the convection set-up, and so care must be taken in their interpretation.
3.3. Tracing wave injection into the low corona
As the coronal magnetic field is highly twisted, and dynamically evolving, the vertical propagation of MHD waves should be affected. Previous works, that experimented with a range of photospheric drivers at the base of simplified magnetic funnels (Bogdan et al. 2003; Mumford et al. 2015), have shown that torisional oscillations preferentially produce Alfvénic wave modes (as observed during the SEs), whereas vertical perturbations excite magnetosonic waves, and horizontal driving favours kink modes. A preliminary assessment of the wave-action in the domain is made by performing Fourier Transforms3 on the spatial and temporal evolution of vertical velocity vz and horizontal velocity 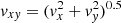 in horizontal cuts through the simulation at varying heights. The components of velocity, initially described as vi(x, y, t), are transformed into their resulting Power Spectral Density (PSD) by the discrete Fourier transform,
in horizontal cuts through the simulation at varying heights. The components of velocity, initially described as vi(x, y, t), are transformed into their resulting Power Spectral Density (PSD) by the discrete Fourier transform,
where w(nt) is a Hanning window function (Blackman & Tukey 1958) of duration 30 min, nx, ny, and nt represent the indices of the spatial and temporal directions which have lengths X, Y, and T respectively. Thus the wavenumbers and frequencies (f = ω/2π) sampled are in steps of δkx = 2π/(Xdx), δky = 2π/(Ydy), and δω = 2π/(Tδt). The smallest wavenumber sampled is 0.08 cycles Mm−1 and the smallest frequencies are 0.3 mHz. The discrete Fourier transform Fi can then be multiplied by its conjugate 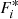 to recover the PSD as,
to recover the PSD as,
The kx and ky directions are further quadratically summed to produce k⊥. The PSD for the two components of velocity (vz and vxy), at four different heights in the domain (−2 Mm, 0 Mm, 4 Mm, and 12 Mm), are depicted in Figs. 11 and 12. In the upper-convection zone and at the photosphere, the high plasma β enables the convective motions to generate acoustic waves. These waves are associated with two characteristic frequencies, the Brunt-Vaisala (or buoyancy) frequency N, and the acoustic cutoff frequency ωc. The Brunt-Vaisala frequency and acoustic cutoff frequency are related to the gravitational acceleration g, the density scale height H = −(∂lnρ/∂lnz)−1, and the sound speed cs by,
 |
Fig. 11. Power Spectral Density (PSD) in wavenumber-frequency space for the vertical flow speed vz, taken at various heights in the computational domain; Z = −2 Mm (upper-convection zone), Z = 0 Mm (photosphere), Z = 4 Mm (above the chromosphere), and Z = 12 Mm (low corona). For the photospheric slice, the typical acoustic-gravity wave cut-off frequencies are indicated, given the average pressure, density, and magnetic field strength. Classically, waves in the shaded region are evanescent (under the assumption of a stably stratified atmosphere). For completeness the lamb-mode (ω = csk⊥) and f-mode ( |
 |
Fig. 12. Same as Fig. 11, but now for the horizontal flow speed vxy. Enhancements in the horizontal velocity PSD at the box-mode frequencies/wavenumbers are highlighted. |
and
The linear wave equation, when applied to a non-magnetic plane-stratified atmosphere, produces a simple dispersion relation (dependant on these two frequencies) which identifies regions of f − k⊥ space where acoustic waves can propagate, acoustic-gravity waves can propagate, and where the waves are evanescent (see Srivastava et al. 2021, and references therein). Summarised as,
where the acoustic wave frequencies are > with the + sign, and the gravity wave frequencies are < with the − sign. In a more realistic atmosphere, this picture is complicated by structuring in density, and the presence of the magnetic field. The presence of strong magnetic fields can provide pathways for acoustic waves to propagate up into the chromosphere and corona (magnetic ‘pinholes’ or ‘windows’; Spruit 1981; Jefferies et al. 2006). However to first order, the simplified picture holds and is a useful tool. By averaging the properties of the Z = 0 Mm layer, the cut-off frequencies are estimated and the evanescent region is over-plotted in Fig. 11. In the solar atmosphere, the acoustic cut-off frequency is estimated to be around 5mHz (Vigeesh et al. 2017), which effectively traps the acoustic waves excited by the convective motions below the photosphere. These waves reflect and resonate inside the solar convection zone, forming the well known p-mode oscillations (Ulrich 1970).
Our simulation does not encompass enough of the convection zone for the classical 5-min p-mode oscillations to develop. However, as the computational domain is small, and a pressure node is set at the lower boundary, the acoustic waves generated by the convection can create quasi-standing modes with large amplitudes in the upper-convection zone. These pressure-modes (discussed in Fleck et al. 2021), are clearly distinguishable in Fig. 11. Due to the finite depth of the upper-convection zone (∼2 Mm), and the travel time of acoustic waves (∼10 km s−1), positive interference is created at similar frequencies to the classical p-modes observed on the Sun (∼300 s). Along with the pressure-modes (henceforth referred to as “box-modes”; to indicate their origin), the convective flows shape the velocity PSDs, primarily at low frequencies. The dominant frequencies in the low corona for both the velocity components correspond to the vertical convective motions, and the box-modes. Comparing the PSD at 4 Mm and 12 Mm in Fig. 11, there is little change in the low corona for vertical fluctuations. In contrast, Fig. 12 shows the horizontal fluctuations generally decrease in amplitude with increasing height in the domain, except for the highest frequencies.
To illustrate further the evolution of the velocity components with altitude, we calculate the Power Spectrum (PS) from the PSD, at various wavenumbers (given in units of cycles/Mm) and frequencies (given in units of mHz), that is to say
and
Figures 13 and 14 show the resulting PS versus height in the simulation domain. The horizontally averaged amplitude of the velocity components vz and vxy, versus height in the domain, are over-plotted with solid white lines. The average sound and Alfvén speeds are shown for comparison with magneta dotted and dashed lines, respectively. To make clear any frequency/wavenumber-dependent changes in the velocity amplitudes, the horizontally averaged velocities of three wavenumber ranges: less than 0.5 cycles Mm−1 (solid red), 0.5–3 cycles Mm−1 (dashed orange) and greater than 3 cycles Mm−1 (dotted blue), along with four frequency ranges: less than 2.5 mHz (solid red), 2.5–5 mHz (dashed orange), 5–10 mHz (dash-dot green), and greater than 10 mHz (dotted blue), are also displayed in Figs. 13 and 14. The wavenumber ranges are an arbitrary choice, unlike the frequency ranges which are chosen to match those used in Shoda & Yokoyama (2018a). The spatially reconstructed velocity components, from which the horizontal averages were calculated are discussed in Appendix B. Horizontal cuts of the frequency-filtered velocities vz and vxy are shown at the same four heights used in Figs. 11 and 12, at t = 40 min in Figs. B.1–B.4.
 |
Fig. 13. Wavenumber power spectrum of the vertical (left) and horizontal (right) components of velocity, versus height (in both cases normalised by the maximum horizontal PS at each height). The PS of the vertical and horizontal flows become almost identical around Z = 1–1.5 Mm likely as a result of mode-conversion and/or magnetosonic shocks at the vA/cs = 1 surface, which allows for wave-energy to pass between longitudinal and transverse oscillations. The horizontally averaged velocity amplitude in overploted with a solid white line for each component. The amplitudes of the filtered velocity components from three wavenumber ranges, are similarly over-plotted with coloured lines. The time-averaged sound and Alfvén speeds versus height are also shown with magenta dotted and dashed lines, respectively. |
 |
Fig. 14. Same as Fig. 13, but now showing the frequency power spectrum versus height. Peaks in the PS can be found at 5–10 mHz which correspond to the box-modes frequencies (see Fig. 11). In the vertical flow speed, the box-modes are able to survive into the low corona by travelling along the network of magnetic funnel structures. A similar, but less pronounced, enhancement in the PS is visible in the horizontal flow speed, which moves to progressively higher frequencies with height. |
As plasma rises to the top of the upper-convection zone, there is a progression of energy from large to small scales in both velocity components. Near the photosphere, the large-scale convective motions breakdown into the smaller granulation flows. In Fig. 13, a shift in the amplitude of the vertical flow towards wavenumbers at the scale of the granulation is observed (see the k⊥ = 0.5–3 cycles Mm−1 range). The recirculating plasma at the photosphere also generates increased power in the horizontal flow. Just above the photosphere, there is a decrease in the strength of the PS, as the movement of chromospheric plasma is restricted inside small regions of closed network field. The subsequent increase in strength of the PS towards the top of the chromosphere/low corona results from three main factors; (1) the decreasing density allows for larger velocities with the same kinetic energy, (2) the motion of the magnetic field is transferred to the plasma as the plasma-β regime has reversed, and (3) the geometrical expansion of the magnetic funnels in regions of the chromosphere where the Mach number of the flow is greater than one enhances existing motions.
In Fig. 14, there is a clear enhancement of the vertical flows in the low corona around 4–6 mHz. This corresponds to the range of box-mode frequencies at the photosphere, that appear to resonate in the atmosphere above. A smaller enhancement in this frequency range is visible in the horizontal flow. Unlike the vertical fluctuations, which remain in the same range throughout the low corona, the horizontal fluctuations undergo dissipation and spread to higher frequencies with altitude. This is likely due to the dissipation of the torsional oscillations in the magnetic funnels. The high frequency horizontal fluctuations continue to gain amplitude until around Z = 10 Mm. The lower frequency modes, show a corresponding decrease as energy is being dissipated into the higher frequencies. These fluctuations have the largest amplitude of the four reconstructed frequency ranges at Z = 8–12 Mm, after which they are influenced by the upper boundary condition. In fact, the upper boundary conditions influence all of the flow components (most significantly high frequencies and wavenumbers), though in most cases this is limited to above Z = 14 Mm.
Fluctuations travelling from the photosphere into the chromosphere should be significantly suppressed/damped by the evanescence of the acoustic modes. Yet the amplitude of the velocity fluctuations increases above the chromosphere. Using a simplified MHD model, Snow et al. (2018) showed that vortex/funnel structures can act as wave-guides, and that the interaction of twisted funnels can lead to an enhanced energy transfer from the photosphere. In our simulation, the transmission/reflection of waves through the chromosphere, transition region, and into the corona is difficult to follow due to the many geometrical and dissipative processes that influence their propagation. However, the typical amplitudes of the longitudinal (assumed acoustic) and transverse (assumed Alfvén) waves in the computational domain can be readily computed. Their wave-energy fluxes Fwave are given by the product of the energy in a given wave mode Ewave and its corresponding wave speed vwave. This methodology follows closely that used in Shoda & Yokoyama (2018a). It is important to note that Fwave is not a conserved quantity here, as there are significant vertical flows in the domain, in addition to the wave-energy flux being time-dependent. Regardless, a Fourier analysis is performed, as done previously for the velocity components, now with the following wave-energy fluxes. For longitudinal acoustic waves travelling vertically through the domain, their wave-energy flux is defined as,
For the transverse waves, Alfvénic fluctuations are considered, and so the Elsasser variables are defined as
It is important to note that the Elsasser variables are not characteristic variables in a compressible plasma (discussed in Sect. 4.5), as they are defined for an incompressible plasma (Marsch & Mangeney 1987). However, they are expected to produce a reasonable assessment of the amplitude of transverse Alfvénic fluctuations (Magyar et al. 2019). Similarly to Flong, the transverse wave-energy flux is defined as
It can be shown that Ftran directly relates to the field shaking/shearing Poynting flux Sz, fs by
where the two terms correspond to the upward and downward propagating Alfvénic waves, respectively.
Figures 15 and 16, present vertical and horizonatal cuts of the wave-energy fluxes in the computation domain. The upper-convective zone is a reservoir of acoustic wave-energy however, as previously discussed, the acoustic waves are significantly damped due to the evanescent regions of the atmosphere. Acoustic waves with frequencies above the acoustic cut-off frequency, could propagate into the low corona, however the convective motions produce predominantly low frequency waves. Magnetosonic waves that succeed to enter the chromosphere typically produce shocks, which are also highlighted in Figs. 15 and 16 (discussed in Sect. 3.4). The location of the vertical cut in Figs. 15 and 16 is chosen so that it passes through a magnetic funnel (shown in detail in Fig. 7). This magnetic funnel can be seen to act as a gateway to the low corona for transverse waves, which are driven by photospheric motions. From the Fourier transforms of Flong and Ftran, the spatial variation of each wave-energy flux is reconstructed in four different frequency ranges. A 3D visualisation of the wave-energy fluxes is shown in Fig. 17. The limited vertical extent of the longitudinal wave-energy is again easily observed, along with the enhanced transverse wave-energy flux inside the magnetic funnels (in areas without twisted magnetic funnels, the transverse wave-energy is typically confined below the plasma β = 1 surface).
 |
Fig. 15. Longitudinal (acoustic) wave-energy flux at t = 40 min for a vertical cut through the domain at Y = 19 Mm, and horizontal cut at Z = 2 Mm. Fast and slow magnetosonic shocks, which are identified through a threshold on ∇ ⋅ v, are indicated in red and green colours, respectively. For the horizontal slice, shocks are highlighted at a range of heights throughout the chromosphere (not just from Z = 2 Mm). The plasma β equal to one surface is highlighted with a thin dashed black line. |
 |
Fig. 17. 3D visualisation of the Flong and Ftran wave-energy fluxes at t = 40 min. The magnetic field structure previously presented in Fig. 1, is now shown in grey. Semi-opaque isosurfaces highlight the wave-energy fluxes at 3 kWm−2 in each reconstructed frequency range; less than 2.5 mHz (red), between 2.5 mHz and 5 mHz (orange), between 5 mHz and 10 mHz (green), and greater than 10 mHz (cyan). The white opaque surface represents plasma β equal to one. |
The transverse wave-energy flux is most often in the form of torsional oscillations in the braided magnetic funnel structure. At higher frequencies these oscillations are limited to the outer edges of the funnels, and are subsequently smaller-scale. The lowest frequencies recover the twisting/undulating motion of the entire low corona, driven by the persistent buffeting/shuffling of MCs around the intergranular lanes (where most of the open magnetic field is rooted). The majority of transverse wave-energy reaches the top of the domain in the low frequency oscillations. The lowest frequencies (f < 2.5 mHz) have Ftran around a factor of ten larger than the higher frequency ranges at Z = 14Mm.
Figure 18 shows the PS of the wave-energy fluxes in frequency space versus height in the domain. The average amplitude of the wave-energy fluxes versus height are over-plotted along with the averages of four reconstructed frequency ranges. As observed in Fig. 15, there is a large amount of energy in the acoustic waves/convective motions in the upper-convection zone. However, this wave-energy is largely confined below the photosphere, such that the average energy flux versus height decays rapidly. The Alfvénic waves have far less energy in the upper-convection zone, but are enhanced at two altitudes: the photosphere (Z = 0 Mm) and the cs = vA surface (Z ≈ 1.5 Mm). At the photosphere, the plasma and magnetic field strongly coupled, with MCs being directly driven by convective motions. Power in the Alfvén waves therefore rises through the photosphere, approaching equivalence with the power in the acoustic waves. This effect is seen in all of the frequency ranges (coloured lines). After this, the transverse fluctuations are similarly damped like the acoustic waves in the chromosphere. However, around Z = 1.5 Mm the transverse wave-energy flux is once again enhanced. At this height the sound speed and Alfvén speeds are equivalent, so mode-conversion (Schunker & Cally 2006; Cally & Goossens 2007) may take place (we note that the decay of the acoustic wave-energy flux becomes stronger here). Magnetosonic shocks also form at this height, driven by both upward propagating waves and previously ejected plasma falling back down to the chromosphere. These shocks may dissipate energy into Alfvén waves as they shake the surrounding field lines. In addition to these enhancements, the funnel network helps to reduce the dissipation/reflection of the transverse wave-energy as inside the gradients in density and local Alfvén speed are smaller. Frequently, Alfvénic fluctuations have their amplitudes increased by the expansion of the funnels with Mach number greater than one flows. Once above the chromosphere, Alfvénic waves propagate with little dissipation in the magnetically dominated low corona. The amplitude of wave-energy flux that propagates up into the low corona, and would subsequently enter the solar wind, is quantitatively discussed in Sect. 4.
 |
Fig. 18. Frequency power spectrum of the longitudinal (acoustic) wave-energy flux Flong (left) and the transverse (Alfvén) wave-energy flux Ftran (right), versus height (in both cases normalised by the maximum transverse PS at each height). Coloured lines are over-plotted showing the average energy flux versus height for four frequency ranges and their total. Grey lines show the other wave flux averages for comparison. The upper-convection zone is a source of both longitudinal and transverse waves, with the longitudinal waves having an energy flux that is 2–3 orders of magnitude larger than the transverse waves. However, the longitudinal wave-energy flux decays exponentially with height. Such that in the low corona, the relative balance of energies is reversed. |
3.4. Magnetosonic shocks
Due to the sharp density gradients in the solar atmosphere, MHD waves can transform into magnetosonic shocks (Delmont & Keppens 2011). The location of magnetosonic shocks inside the ch024031_by200bz005 simulation are identified by a criterion on the extreme negative values of ∇ ⋅ v, as done previously by (Wang & Yokoyama 2020, and reference therein). The frequency distribution of ∇ ⋅ v around zero is symmetric for linearly propagating waves in the domain. The presence of shocks creates an asymmetry in the distribution by increasing the frequency of extreme negative values. Thus, by selecting the grid cells responsible for the asymmetric tail of the ∇ ⋅ v distribution, the location of shocks in the domain can be found. However, there will be some contamination via linear waves with large amplitudes. The criterion for shock selection is given,
where ξ is a free parameter that is used to set the threshold for identification, based on the sound speed and the numerical grid spacing. The vertical grid spacing dz is used here for two reasons, (1) the shocks are typically orientated towards the vertical, and (2) the vertical grid spacing changes with altitude so this effectively accounts for that in the selection criterion. As done in the appendix of Wang & Yokoyama (2020), we manually select a value of ξ = 0.1 which avoids the majority of the linear compressions (based on the extent of the positive distribution).
Once the shocks are identified, the shock direction is derived based on the local pressure gradient. To identify the type of shock, the magnetic pressure gradient is compared to the plasma pressure gradient over the shock. If the two pressure gradients are aligned, the shock is labelled as a fast-magnetosonic shock. If the two pressure gradients are oppositely directed, the shock is labelled as a slow-magnetosonic shock. The location of detected shocks are displayed in Figs. 15 and 16. It is well known that shocks play a vital role in heating the chromosphere (Carlsson & Stein 1992, 1997). Thus it may be possible to constrain their heating rates with the ch024031_by200bz005 simulation, however a quantitative analysis is left for future work.
Shocks are produced throughout the chromosphere in the simulation, as waves encounter the rapidly decreasing density gradient and shock. Longitudinal waves can avoid this fate by undergoing mode-conversion into a transverse wave mode, which can propagate more freely in the low corona. The shocks detected inside the chromosphere of the simulation are more typically fast-magnetosonic shocks, at an altitude of around 1.5–2 Mm. The formation of shocks appears to be suppressed inside the twisted magnetic funnels structures (see arrows in horizontal cut of Fig. 16). This may arise from the locally enhanced wave transmission, reducing the likelihood of wave-energy dissipation into shocks. At times when the funnel structures undergo SEs, chromospheric plasma is typically launched into the low corona. This can create a small number of slow-magnetosonic shocks higher up in the solar atmosphere (around 3–6 Mm above the photosphere). This is unlikely to represent a large amount of energy (especially compared with the Poynting flux enhancements), but illustrates that SEs may trigger further mechanisms of energy dissipation higher up in the solar atmosphere.
4. Implications for the solar wind
This study aims to establish connections between the small-scale dynamics observed in the realistic solar atmosphere produced by Bifrost, and the heating/acceleration of the solar wind. In this Section, the simulation results are discussed in the context of recent observations by Parker Solar Probe (PSP), which is currently measuring the solar wind closer to the solar surface than ever before (Kasper et al. 2021). Following this, we argue that high-resolution imaging of the solar chromosphere (see review of Carlsson et al. 2019, and reference therein) may be able to validate some of our conclusions.
4.1. Generation of flux ropes
The nature of the Sun’s magnetic field, and subsequently that of the interplanetary magnetic field, has been shown to be comprised of smaller twisted strands (this is visibly apparent in the context of coronal loops Williams et al. 2020). The term flux rope (or flux tube) is used throughout the heliophysics literature to describe these smaller structures. Our simulation results show that the magnetic field of the low corona can be readily braided into flux rope-like strands by the motion of MCs along the intergranular lanes. The magnetic field is braided in such a way that there are naturally differing degrees of twist between strands in the flux rope, which is necessary for their stability (Wilson 1977). Assuming that the simulation captures the smallest meaningful scales of this braiding, then the diameter of flux robes should depend on the scale of the granulation pattern (more specifically the spatial distribution of intergranular lanes in which the magnetic flux is transported) and the strength of any dissipative processes that can untangle the field.
Ohmic heating and viscous dissipation are largest at the borders of the twisted magnetic funnels, however their absolute strengths are relatively small in our simulation (< 3 mW m−2) when compared with the average kinetic, and magnetic energy fluxes (∼5 W m−2, and ∼0.6 kWm−2, respectively) above 6 Mm in altitude. Therefore, the twisted structures are subject to negligible dissipation in the low corona after their formation, and are stable. In reality, these dissipative terms may differ in strength to those used in our simulation (perhaps due to non-ideal processes). By increasing the dissipation, we might expect to generate smaller flux ropes, as the field can more easily untwist. We remind the reader that the Bifrost simulations operate with a split-diffusive operator for the diffusive terms in the MHD equations. Further studies that can effectively control these parameters may be needed to quantify exactly how large these braided structures can become. According to our computation, the average flux rope weaves together around 2–3 photospheric sources (MCs) such that in the low corona, they have a combined diameter of 5–15 Mm. Isolated magnetic funnels that are stressed into twisted configurations (without the addition of neighbouring flux) have most-often diameters of 4–6 Mm. These isolated magnetic funnels are often subject to SEs, and so this sets the diameter of Poynting flux enhancements. However, it is difficult to quantify how much these sizes are influenced by the size of the computational domain.
4.2. Structured outflow
PSP is now routinely sampling the solar wind below 0.25 au, with the ultimate goal of making in-situ measurements as close as 10 R⊙ (Fox et al. 2016). Such unprecedented access to the emerging solar wind has given authors the opportunity to make connections between the structure at the base of the wind and the structure observed in-situ. This is especially true for the origins of reversals in the polarity of the solar wind magnetic field, referred to as switchbacks (Owens et al. 2018; Kasper et al. 2019; Mozer et al. 2020; McManus et al. 2020; Macneil et al. 2020b). Switchbacks are frequently observed in patches (de Wit et al. 2020), that have been inferred to correspond to the scales of super granulation at the solar surface (see Fargette et al. 2021, and references therein). Bale et al. (2021) suggest that the spatial variation of switchback patches corresponds to how the solar wind magnetic field emerges from the network of magnetic funnels rooted in the photosphere. Thus the results from the ch024031_by200bz005 simulation may directly support or invalidate this hypothesis.
As discussed throughout this study, in our simulation, the outflowing material is structured by the underlying network of magnetic funnels. The left panels of Fig. 19 present a snapshot of the footpoints of the open magnetic field in the photosphere (on top of the convection pattern), along with the variation of the footpoint field strength in the open magnetic field (when traced down from Z = 12 Mm). The variation in plasma density and temperature are also depicted at an altitude of Z = 12 Mm. Along with the mass flux and transverse wave-energy flux at Z = 12 Mm. Bale et al. (2021) report that the solar wind inside the switchback patches is faster, and hotter than the background solar wind. Our simulation does indeed produce a temperature contrast between elements of the funnel network however, instead of a variation between the centre of the funnels and their edges (as suggested by Bale et al. 2021), this corresponds to the inhomogeneous braiding of the coronal field (and the subsequent releases of energy in SEs). There is a large variation in the photospheric magnetic field strength of neighbouring funnels in the low corona, with SEs typically occurring in those with the strongest magnetic fields (identified by MCs). An intermittent mass-flux is driven into the low corona above these MCs, which is accompanied by an enhanced Poynting flux (due to the SEs). Therefore, the low corona above MCs has an increased temperature, and density (both ∼25% larger at Z = 12 Mm) with respect to the average coronal plasma. The enhanced Poynting flux also indicates a more effective transmission of Alfvén wave-energy, which may ultimately feed the turbulent-formation of switchbacks in the solar wind.
 |
Fig. 19. Resulting conditions near the top of the simulation domain (i.e. at the base of the solar wind). Top left: location of the open magnetic field lines at the photosphere (traced down from Z = 12 Mm), with the convection pattern shown bellow. Bottom left: open magnetic field at Z = 12 Mm coloured by their photospheric field strength. Top middle and right: density and temperature variation with respect to the horizontal average at Z = 12 Mm. Bottom middle: mass flux at Z = 12 Mm. Bottom right: transverse wave-energy-flux at Z = 12 Mm. Each panel is taken at t = 40 min. The contrast in density, temperature and upward wave-energy is evident, resulting from the different MC field strengths at the base of the braided magnetic field structures. |
Given the limited vertical extent of our simulation, it is difficult to say how the patchy heating of the coronal funnel network by ohmic heating and SEs will influence the formation of the solar wind above, or if this contrast in properties at the base of the solar wind is enough to drive the variations observed in-situ. It is unclear whether or not these variations will be able to survive out to large distances, without being disrupted by turbulent mixing or dissipative processes. Work from Borovsky (2021) appears to suggest that various kinds of structures embedded in the solar wind can remain coherent from 1au out to larger distances (despite the turbulent nature of the solar wind), thus the same may be true for variations in the near-Sun environment (though this is purely speculative). The ch024031_by200bz005 simulation also has a relatively small horizontal scale, in the context of the PSP observations (more consistent with the scales sizes proposed by Fargette et al. 2021), thus it is possible that the variations in the solar wind are organised on a larger-scale than is available to us here.
4.3. Enhancing the turbulence generation of switchbacks
The exact mechanism(s) that generates switchbacks in the solar wind remains unknown, though there are many theoretical models (Squire et al. 2020; Fisk & Kasper 2020; Zank et al. 2020; Mallet et al. 2021; Schwadron & McComas 2021; Drake et al. 2021; Magyar et al. 2021). Some models favour the formation of switchbacks close to the solar surface as Alfvénic fluctuations (often as a result of interchange reconnection), whilst others argue that switchbacks are generated as the solar wind expands into the Heliosphere (via turbulence, shears in velocity, etc.). Shoda et al. (2021) find that switchbacks are naturally generated through the non-linear evolution of Alfvénic fluctuations with turbulence, which directly links this phenomena to the fundamental heating/acceleration of the wind. However the frequency of occurrence of switchbacks generated through this turbulent process in the model of Shoda et al. (2021) is far lower than measured in-situ by PSP. Shoda et al. (in prep.) further develop this idea, and show that the occurrence rate of switchbacks can be dramatically increased (without significantly increasing the input Poynting flux) by including a coherent torsional driving at the base of the wind (i.e. stirring the field lines in the low corona). Figures 8 and 10 show the structure of the Poynting flux in our simulation, which contains a quasi-steady background of torsional Alfvén waves along with the stronger SEs. Both of which, given the results from Shoda et al. (in prep.), are expected to increase the rate of turbulent switchback formation. As well as providing a clear example of the torsional driving required to better reconcile the turbulent generation of switchbacks with observations, our simulation also provides a mechanism for clustering the switchbacks into patches due to the varying conditions between neighbouring flux tubes.
4.4. Chromospheric swirls
Simulations using similar numerical methods and physics to Bifrost (notably the MURaM code; Vögler et al. 2005) have commonly found the formation of vortex flows, and/or vortex-like structures in the chromospheric magnetic field (Kitiashvili et al. 2012; Moll et al. 2012; Amari et al. 2015; Kato & Wedemeyer 2017; Rappazzo et al. 2019; Yadav et al. 2020; Silva et al. 2020), supporting the existence of these structures in the solar atmosphere. However, in general, these studies have been focussed on the chromospheric dynamics, which can produce an observational signature (Wedemeyer-Böhm & Rouppe van der Voort 2009; Battaglia et al. 2021). Such signatures have been observed in high-resolution solar imagery (in observations these structures are often referred to as swirls), generally centred over enhancements in the photospheric magnetic field (i.e. MCs), which are embedded in the narrow intergranular lanes. Wedemeyer-Böhm et al. (2012) were able to show correlated signatures of these swirls at various heights in the solar atmosphere (see also Tziotziou et al. 2018), reinforcing again the connection with the stirring motions in this study. Chromospheric swirls have typical diameters of ∼2 Mm and lifetimes of around 9–10 min, in quiet-Sun regions (Shetye et al. 2019). The average diameters of SEs in our simulation, and there durations, are comparable to the observations of chromospheric swirls by Shetye et al. (2019) and with some observations of solar tornadoes (discussed in; Wedemeyer & Steiner 2014). We propose that some of these chromospheric swirls could be explained by the SEs captured in our simulation, with MCs at their base. This assumes that the Poynting flux carried by the SE is able to heat the chromospheric plasma sufficiently to reproduce the observations, which is left for future works to investigate.
Our simulated swirls undergo phases of activity with loading and unloading of the magnetic field lines, during which time the chromospheric plasma is heated. This timescale is governed by a number of factors, though the most significant appear to be: (1) the size of the intergranular network, (2) the speed of MCs travelling through the network, and (3) the disspative processes that prevent energy being built up in the twist of the magnetic funnels. Therefore, if chromospheric swirls could be observed in a coronal hole region, the statistics of their sizes, and occurrence frequency, may be used to constrain the injection of heating (and torsional driving) through SEs into the solar wind.
At present, the authors are not aware of any high-resolution observations of chromospheric swirls (or the lack there of) in coronal hole regions. As coronal holes are often located at the poles of the Sun, this may result from observational bias. The observations of Shetye et al. (2019) are taken from quiet-Sun regions, and may not be directly comparable to our simulation results. However, the configuration of the solar atmosphere in areas of quiet-Sun can be very similar to that in areas of coronal holes (just with a closed network of magnetic field that extends higher in altitude). So it may be reasonable to infer that, the presence of chromospheric swirls in the quiet-Sun regions indicates that there is similar braiding of the vertical/open magnetic field by the convective motions below. Thus the observations of chromospheric swirls by Shetye et al. (2019) could be an indirect observation of slow solar wind emerging from quiet-Sun regions (slow solar wind sources are discussed in Abbo et al. 2016).
4.5. Implications for Alfvén wave-driven wind models
The Alfvén wave-turbulence paradigm for heating and accelerating the solar wind has been generally successful at reproducing in-situ observations of the solar wind (see comparison with PSP observations by Réville et al. 2020). However, models that self-consistently capture the propagation and dissipation of the Alfvén waves are often limited to 1D (Suzuki 2011), or a 2D/3D wedge configuration (Matsumoto & Suzuki 2012; Shoda et al. 2019; Magyar & Nakariakov 2021). In such models, the input wave-energy spectrum is based on the spectrum of observed convective motions and/or the movements of photospheric bright points (see Cranmer & Van Ballegooijen 2005, and reference therein), which are assumed to shake the footpoints of the solar wind magnetic field lines. Global models of the solar wind typically favour a parameterised description of this phenomena, which by-passes the need to resolve the scales of the wave propagation and dissipation. This simplified description has a few control parameters, one relating to the input wave-energy flux (discussed in Sect. 4.6), and two-three other parameters describing how the waves dissipate their energy and momentum.
Simulations performed by the Bifrost code are able to follow waves/fluctuations from the upper-convection zone into the low corona. Understanding how the wave spectrum at the base of the solar wind differs from current models of the solar wind, and in future from different configurations of the Bifrost code, is crucial to better constraining models of the solar wind. In Fig. 20, the PS taken from the ch024031_by200bz005 simulation at various altitudes in the domain, are compared with the corresponding PS obtained from the simulation of Shoda et al. (2021) at a height of 35 Mm (the lowest height with data available). The simulation of Shoda et al. (2021) is performed in a 3D wedge configuration that extends from 1.02 solar radii to 40 solar radii. The horizontal extent of the domain at Z = 35 Mm is 31.5 × 31.5 Mm2 (comparable with the 24 × 24 Mm2 of our simulation domain). The magnetic field in the simulation of Shoda et al. (2021) has a strength of 1.1 G at the bottom boundary of Z = 14 Mm, which is far weaker than the ∼5 G coronal field in our simulation domain. PS of the horizontal flow, the horizontal magnetic field, the positive (outward) Elsasser variable and the negative (inward) Elsasser variable, are displayed in Fig. 20. Our computational domain does not extend as high as Z = 35 Mm, however the PS evolves slowly with altitude in the low corona so direct comparison can be justified.
 |
Fig. 20. Power spectra versus wavevector and frequency at various heights in the computational domain for the horizontal flow speed, magnetic field strength, and Elsasser variables. The power spectra from the simulation of Shoda et al. (2021) at a height of Z = 35 Mm are over-plotted for comparison with dashed blue lines. |
The amplitude of the horizontal flow at low frequencies and wavenumbers in the Bifrost simulation is remarkably similar to that in the model of Shoda et al. (2021). In our simulation, the horizontal flow amplitude is maximised around Z = 5 Mm. At f = 1 mHz, both simulations produce a vxy amplitude in the low corona of ∼10 km s−1. The two PS depart at higher frequencies, around a few mHz, where our simulation has larger amplitudes. This is likely a result of the box-modes in the simulation domain which have already been shown to impact the PSD of the velocity components in the low corona. Higher frequencies are energised by these modes through dissipation. Differences in the amplitude Bxy can in-part be explained by the higher coronal density in the Bifrost simulation. The influence of a higher density on Alfvénic fluctuations is estimated using 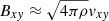 , and also the larger vertical field strength Bz in the domain. Using f = 1 mHz, the field strength amplitude in our simulation is ∼3 G, compared with ∼0.1 G at the same frequency in the model of Shoda et al. (2021). As the Alfvénic relation includes density, and ρ ≈ 5 × 10−12 kg cm−3 in the low corona (see Fig. 3) which is a factor of ten larger here than in the model of Shoda et al. (2021). It is expected that for the same value of vxy, our Bxy should be a factor of
, and also the larger vertical field strength Bz in the domain. Using f = 1 mHz, the field strength amplitude in our simulation is ∼3 G, compared with ∼0.1 G at the same frequency in the model of Shoda et al. (2021). As the Alfvénic relation includes density, and ρ ≈ 5 × 10−12 kg cm−3 in the low corona (see Fig. 3) which is a factor of ten larger here than in the model of Shoda et al. (2021). It is expected that for the same value of vxy, our Bxy should be a factor of  larger. The actual factor is around 30, which is significantly larger than predicted by the Alfvénic relation alone. The remaining discrepancy is due to the stronger coronal magnetic field strengths in our simulation, compared with that of Shoda et al. (2021), which are significantly twisted into the horizontal direction. The larger field strengths in our simulation may be explained by the artificial configuration of the simulation domain. As we use a Cartesian box geometry and conserve magnetic flux, the field strength does not decay with altitude. Ultimately, this results in the
larger. The actual factor is around 30, which is significantly larger than predicted by the Alfvénic relation alone. The remaining discrepancy is due to the stronger coronal magnetic field strengths in our simulation, compared with that of Shoda et al. (2021), which are significantly twisted into the horizontal direction. The larger field strengths in our simulation may be explained by the artificial configuration of the simulation domain. As we use a Cartesian box geometry and conserve magnetic flux, the field strength does not decay with altitude. Ultimately, this results in the 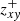 Elssasser amplitude at the top of the domain being much larger that the values from Shoda et al. (2021).
Elssasser amplitude at the top of the domain being much larger that the values from Shoda et al. (2021).
In Fig. 20 the negative Elsasser variable, which in ideal non-compressible MHD describes the inward propagating Alfvén waves, is larger than might be expected (in the simulated low corona 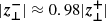 ). As the Bifrost code is compressible, the separation of the inward and outward propagating waves into the Elsasser variables is imperfect. In compressible MHD, the outward propagating Alfvén waves can appear in the inward variable and vice versa. However this is expected to be a smaller effect than observed here (see discussion of Magyar et al. 2019, and references therein). Therefore it is likely that the open boundary condition at the top of the simulation domain is not perfectly transmitting the Alfvén waves out of the domain. This limitation will be discussed further in Sect. 5. Fundamentally, this means that the inward Elsasser variable from the ch024031_by200bz005 simulation should be interpreted with caution, but the outward Elsasser variable should still be representative of the upward Alfvénic fluctuations.
). As the Bifrost code is compressible, the separation of the inward and outward propagating waves into the Elsasser variables is imperfect. In compressible MHD, the outward propagating Alfvén waves can appear in the inward variable and vice versa. However this is expected to be a smaller effect than observed here (see discussion of Magyar et al. 2019, and references therein). Therefore it is likely that the open boundary condition at the top of the simulation domain is not perfectly transmitting the Alfvén waves out of the domain. This limitation will be discussed further in Sect. 5. Fundamentally, this means that the inward Elsasser variable from the ch024031_by200bz005 simulation should be interpreted with caution, but the outward Elsasser variable should still be representative of the upward Alfvénic fluctuations.
4.6. Estimating the Alfvén wave energy input
As previously discussed, a parameterised version of Alfvén wave-turbulence is used in many global solar wind models (most notably the AWSoM and wind_predict models; van der Holst et al. 2014; Hazra et al. 2021). In this description, there are some free parameters that are naturally tuned to get the best results. As the solar wind can be measured in-situ, the optimisation of these parameters is feasible and can provide insight into how much energy is deposited by Alfvén waves into the solar wind. However, when the same parameterisations (and even codes) are used in an astrophysical context (e.g. for solar-like stars), the input Alfvén wave-energy flux is no longer constrained (see discussion in Saikia et al. 2020). It is not obvious how the input Alfvén wave flux (often denoted SA in the literature) should change for a young solar-analogue (e.g. Evensberget et al. 2021), when compared to the current Sun. To increase the predictive power of these global solar/stellar wind models, it is necessary to understand how changing the magnetic field configuration (and atmospheric structuring) will influence the input Alfvén wave-energy into the wind. This requires a better understanding of the progression of energy through the chromosphere and into the corona, under arbitrary conditions, than is currently available from models within the literature.
The Alfvén wave-energy flux SA = Ftran in the low corona of the ch024031_by200bz005 simulation is estimated in Sect. 3.3 via Eq. (18). Typically the input energy flux to the wind is expected to be proportional to the field strength itself, and so the input parameter to the solar wind models is typically SA/B (i.e. the energy flux normalised by the photospheric field strength). Figure 18 shows the average Alfvén wave-energy flux in the low corona is around 1.5 kWm−2 which, when normalised by the average photospheric field strength of 40 G (4 mT), gives a value of SA/B = 3.8 × 105 Wm−2 T−1. This is around a factor of three smaller than the typical input to solar wind models, for example Sokolov et al. (2013) estimate a value of SA/B = 1.1 × 106 Wm−2 T−1. Future work could explore the dependence of the Alfvén wave-energy versus photospheric magnetic field strength, for a range of Bifrost simulations. However, performing 3D realistic simulations currently remains very challenging and computationally costly. Similar studies have been performed with 1D models (see Sakaue & Shibata 2021).
To reduce the need for expensive computations, previous works have used analytical models, that attempt to follow Alfvénic fluctuations from the solar/stellar convection zone to their dissipation in the wind (Suzuki 2011; Cranmer & Saar 2011; Arber et al. 2016). However with the current advances in both, in-situ measurements of the solar wind, and remote-sensing observations from both the ground (Rimmele et al. 2020) and the network of Heliospheric observers (Auchère et al. 2020), these analytic models are limited by the temporal scales and degree of non-linearity that they can capture. Thus codes like Bifrost, which are well suited to study small-scale dynamics, may be needed to feed back into the global wind models and analytic scaling relations.
4.7. Limitations of the simulated coronal hole patch
The solar wind is accelerated over a large domain, essentially from the solar surface (or coronal base) to a few solar radii, or some ten coronal scale heights above the photosphere, where the wind becomes supersonic. The solar wind is primarily driven by the pressure gradient; as long as the corona is sufficiently hot and the magnetic field is open to interplanetary space, a supersonic wind ensues (see e.g. Hansteen & Velli 2012). This heating can take the form of a Poynting flux carried by Alfvén waves, braiding of field lines, or some other mechanism. In addition, in order to ensure a fast wind, energy must be added beyond the critical point as pointed out by Leer & Holzer (1980); this additional push is often assumed to be caused by Alfvén waves. Thus an interpretation of our simulation results, in the context of the solafr wind, must acknowledge that our domain only spans a third of a coronal scale height, and that it has a horizontal size that is only slightly larger than a supergranule.
As stated in the preceding sections, a major stumbling block has been achieving a good understanding of how Alfvénic waves are generated and carry a sufficient Poynting flux to push the wind and potentially heat the corona. The simulations presented here show that photospheric motions and their work on the magnetic field can drive the generation of Alfvén waves of a sufficient strength to be of interest to solar wind acceleration. This conclusion can potentially reduce the number of free parameters that go into (global) solar and stellar wind models. That said, it would of course be of interest to extend the 3D simulations to greater heights, at least one coronal scale height, and horizontally so that several supergranular cells can be accommodated. The latter would also require that the simulation extends a further distance below the photosphere, to at least of the order of 10 Mm.
Furthermore, it is important to note that the upper boundary in the simulations presented here are not perfectly transmissible to Alfvén waves, and that reflections off the top boundary give rise to an inwardly propagating wave flux. Such an inwardly propagating flux is expected (see Verdini & Velli 2007) from models of Alfvén wave dissipation in the solar wind where the outwardly propagating wave flux is reflected off perturbations in the solar wind’s atmosphere, but perhaps not with the amplitude due to our imperfect open boundary. We therefore have not discussed the inwardly directed Alfvén wave flux in any detail.
Running full 3D simulations spanning the upper convection zone through the photosphere and chromosophere to the first coronal scale height is a challenge; the scales are relatively large compared to the resolution required to accurately model the generation of Alfvénic waves by photospheric convection or chromospheric dynamics and only a small sub-set of the configurations desired are possible to do in a finite time. This last point should be alleviated by the enormous technical progress seen in high performance computers in the last decades which should allow us to run a sufficient number of scenarios to complete parameter studies, both for solar and stellar configurations.
5. Conclusions
In this study, the Bifrost RMHD code is used to produce a realistic simulation of the solar atmosphere. The simulation is configured to emulate a coronal hole region, with a uni-polar magnetic field in the low corona that would later open into the solar wind. The photospheric magnetic field of the coronal hole is driven into MCs by the granulation pattern. The movement of photospheric flux around the network of intergranular lanes then effectively braids together the coronal magnetic field to form flux rope-like structures. If a MC enters the intersection of multiple granules, the accumulating magnetic flux can suppress the local magnetoconvection and trigger the formation of a whirlpool-like flow which can drive the magnetic field to rotate and effectively stir the low corona.
Stirring motions are associated with an enhanced Poynting flux, which heats the plasma and drives material up into the low corona. Vertical Poynting fluxes as large as 2 − 4 kWm−2 can persist for minutes at a time inside twisted magnetic funnel structures. The spatial distribution of heating in the low corona is established by the underlying braided magnetic field. The patchy-nature of this heating leads to a structure at the base of the solar wind that is of the order of super-granulation. This is a similar scale to what is inferred for the modulation of velocity, temperature and density, and switchback occurrence in the recent observations from PSP (Fargette et al. 2021; Bale et al. 2021).
The observational phenomena of chromospheric swirls (in quiet-Sun regions) may be an indicator of the same kind of stirring motions (e.g. Shetye et al. 2019). The detection of chromospheric swirls in a coronal hole region would therefore be a useful diagnostic of the energy input to the solar wind. Stirring motions are a natural consequence of the interplay of convection and the network of magnetic funnels in coronal holes. Their potential ubiquity at the base of the solar wind may increase the frequency of switchback generation by Alfvénic turbulence in the solar wind (Shoda et al., in prep.). At present, the turbulent generation of switchbacks is unable to explain the occurrence rate of switchbacks observed by PSP (Shoda et al. 2020). The strength of the Alfvén wave-energy flux (SA/B = 3.8 × 105 Wm−2 T−1) at the top of our simulation domain is weaker than required by current models of the solar wind that are driven by Alfvén wave turbulence (e.g. Shoda et al. 2019). However, due to the braiding of the coronal magnetic field, energy can be channelled into the low corona more rapidly. This may offset the decreased amplitude of fluctuations in the overall energy budget of the solar wind.
Parallels can be drawn with the 19th century, which saw many advances in meteorology due to the increasing demand for safe travel and transportation via the oceans (Hearn 2002).
The Hinode Science Data Centre Europe (http://sdc.uio.no/search/simulations).
Acknowledgments
This research has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 810218 WHOLESUN) and by the Research Council of Norway through its Centres of Excellence scheme, project number 262622, and through grants of computing time from the Programme for Supercomputing. Some of the work was also performed with support from NASA’s HTMS grant 80NSSC20K1272 ‘Flux emergence and the structure, dynamics, and energetics of the solar atmosphere’. We acknowledge funding support from INSU/PNST and CNES Solar Orbiter and Space Weather programs. Data manipulation and Fourier Transforms were performed using the numpy (Harris et al. 2020) and scipy (Virtanen et al. 2020) python packages. Figures in this work are produced using the python package matplotlib (Hunter 2007).
References
- Abbo, L., Ofman, L., Antiochos, S., et al. 2016, Space Sci. Rev., 201, 55 [Google Scholar]
- Amari, T., Luciani, J.-F., & Aly, J.-J. 2015, Nature, 522, 188 [NASA ADS] [CrossRef] [Google Scholar]
- Arber, T., Brady, C. S., & Shelyag, S. 2016, ApJ, 817, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Aschwanden, M. J., Caspi, A., Cohen, C. M., et al. 2017, ApJ, 836, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Auchère, F., Andretta, V., Antonucci, E., et al. 2020, A&A, 642, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bale, S. D., Horbury, T. S., Velli, M., et al. 2021, ApJ, 923, 174 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, A. F., Canivete, C., José, R., et al. 2021, A&A, 649, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blackman, R. B., & Tukey, J. W. 1958, Bell Sys. Tech. J., 37, 185 [CrossRef] [Google Scholar]
- Bodnárová, M., Utz, D., & Rybák, J. 2014, Sol. Phys., 289, 1543 [CrossRef] [Google Scholar]
- Bogdan, T., Carlsson, M., Hansteen, V., et al. 2003, ApJ, 599, 626 [NASA ADS] [CrossRef] [Google Scholar]
- Bonet, J., Márquez, I., Almeida, J. S., et al. 2010, ApJ, 723, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Boocock, C., & Tsiklauri, D. 2021, MNRAS, 510, 2618 [Google Scholar]
- Borovsky, J. E. 2021, Front. Astron. Space Sci., 8, 131 [NASA ADS] [Google Scholar]
- Bose, S., Joshi, J., Henriques, V. M., & van der Voort, L. R. 2021, A&A, 647, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cally, P. S., & Goossens, M. 2007, in Helioseismology, Asteroseismology, and MHD Connections (Springer), 251 [Google Scholar]
- Carlsson, M., & Leenaarts, J. 2012, A&A, 539, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., & Stein, R. F. 1992, ApJ, 397, L59 [Google Scholar]
- Carlsson, M., & Stein, R. F. 1997, ApJ, 481, 500 [Google Scholar]
- Carlsson, M., Hansteen, V. H., Gudiksen, B. V., Leenaarts, J., & De Pontieu, B. 2016, A&A, 585, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carlsson, M., De Pontieu, B., & Hansteen, V. H. 2019, ARA&A, 57, 189 [Google Scholar]
- Chen, F., Rempel, M., & Fan, Y. 2021, ApJ, submitted [arXiv:2106.14055] [Google Scholar]
- Chhiber, R., Usmanov, A. V., Matthaeus, W. H., & Goldstein, M. L. 2021, ApJ, 923, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Saar, S. H. 2011, ApJ, 741, 54 [Google Scholar]
- Cranmer, S., & Van Ballegooijen, A. 2005, ApJS, 156, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Cranmer, S. R., & Winebarger, A. R. 2019, ARA&A, 57, 157 [Google Scholar]
- Cranmer, S. R., Gibson, S. E., & Riley, P. 2017, Space Sci. Rev., 212, 1345 [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. 2010, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delmont, P., & Keppens, R. 2011, J. Plasma Phys., 77, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Dere, K., Landi, E., Mason, H., Fossi, B. M., & Young, P. 1997, A&AS, 125, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Wit, T. D., Krasnoselskikh, V. V., Bale, S. D., et al. 2020, ApJS, 246, 39 [Google Scholar]
- Drake, J., Agapitov, O., Swisdak, M., et al. 2021, A&A, 650, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ebert, R., McComas, D., Elliott, H., Forsyth, R., & Gosling, J. 2009, J. Geophys. Res. Space Phys., 114, A01109 [Google Scholar]
- Evensberget, D., Carter, B. D., Marsden, S. C., Brookshaw, L., & Folsom, C. P. 2021, MNRAS, 506, 2309 [NASA ADS] [CrossRef] [Google Scholar]
- Fargette, N., Lavraud, B., Rouillard, A., et al. 2021, ApJ, 919, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, C., Vigeesh, G., Lindner, P., et al. 2020, ApJ, 903, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Fisk, L., & Kasper, J. 2020, ApJ, 894, L4 [Google Scholar]
- Fleck, B., Carlsson, M., Khomenko, E., et al. 2021, Philos. Trans. R. Soc. A, 379, 20200170 [NASA ADS] [CrossRef] [Google Scholar]
- Fox, N., Velli, M., Bale, S., et al. 2016, Space Sci. Rev., 204, 7 [Google Scholar]
- Giagkiozis, I., Fedun, V., Scullion, E., Jess, D. B., & Verth, G. 2018, ApJ, 869, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Green, L. M., Török, T., Vršnak, B., Manchester, W., & Veronig, A. 2018, Space Sci. Rev., 214, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Gudiksen, B. V., Carlsson, M., Hansteen, V. H., et al. 2011, A&A, 531, A154 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gustafsson, B., Bell, R. A., Eriksson, K., & Nordlund, A. 1975, A&A, 42, 407 [NASA ADS] [Google Scholar]
- Hansteen, V. H., & Velli, M. 2012, Space Sci. Rev., 172, 89 [Google Scholar]
- Hansteen, V. H., De Pontieu, B., van der Voort, L. R., Van Noort, M., & Carlsson, M. 2006, ApJ, 647, L73 [NASA ADS] [CrossRef] [Google Scholar]
- Hansteen, V., Guerreiro, N., De Pontieu, B., & Carlsson, M. 2015, ApJ, 811, 106 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hayek, W., Asplund, M., Carlsson, M., et al. 2010, A&A, 517, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hazra, S., Réville, V., Perri, B., et al. 2021, ApJ, 910, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Hearn, C. G. 2002, in Tracks in the Sea: Matthew Fontaine Maury and the Mapping of the Oceans (International Marine Publishing Company) [Google Scholar]
- Hofmeister, S. J., Utz, D., Heinemann, S. G., Veronig, A., & Temmer, M. 2019, A&A, 629, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hollweg, J. V. 1973, ApJ, 181, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, Z., Xia, L., Nelson, C. J., et al. 2018, ApJ, 854, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jefferies, S. M., McIntosh, S. W., Armstrong, J. D., et al. 2006, ApJ, 648, L151 [Google Scholar]
- Jess, D. B., Mathioudakis, M., Erdélyi, R., et al. 2009, Science, 323, 1582 [Google Scholar]
- Jess, D., Morton, R., Verth, G., et al. 2015, Space Sci. Rev., 190, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Kasper, J. C., Bale, S. D., Belcher, J. W., et al. 2019, Nature, 576, 228 [Google Scholar]
- Kasper, J. C., Klein, K. G., Lichko, E., et al. 2021, Phys. Rev. Lett., 127, 255101 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, Y., & Wedemeyer, S. 2017, A&A, 601, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kitiashvili, I., Kosovichev, A., Mansour, N., & Wray, A. 2012, ApJ, 751, L21 [NASA ADS] [CrossRef] [Google Scholar]
- Klimchuk, J. A. 2015, Philos. Trans. R. Soc. A: Math. Phys. Eng. Sc., 373, 20140256 [NASA ADS] [CrossRef] [Google Scholar]
- Landi, E., Del Zanna, G., Young, P., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Leenaarts, J., Carlsson, M., & van der Voort, L. R. 2015, ApJ, 802, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Leer, E., & Holzer, T. E. 1980, J. Geophys. Res., 85, 4681 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, J., Carlsson, M., Nelson, C. J., & Erdélyi, R. 2019, A&A, 632, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lowder, C., Qiu, J., & Leamon, R. 2017, Sol. Phys., 292, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Macneil, A. R., Owens, M. J., Berčič, L., & Finley, A. J. 2020a, MNRAS, 498, 5273 [Google Scholar]
- Macneil, A. R., Owens, M. J., Wicks, R. T., et al. 2020b, MNRAS, 494, 3642 [Google Scholar]
- MacTaggart, D., & Prior, C. 2021, Geophys. Astrophys. Fluid Dyn., 115, 85 [NASA ADS] [CrossRef] [Google Scholar]
- MacTaggart, D., Prior, C., Raphaldini, B., Romano, P., & Guglielmino, S. 2021, Nat. commun., 12, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Magyar, N., & Nakariakov, V. 2021, ApJ, 907, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Magyar, N., Van Doorsselaere, T., & Goossens, M. 2019, ApJ, 873, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Magyar, N., Utz, D., Erdélyi, R., & Nakariakov, V. M. 2021, ApJ, 911, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Mallet, A., Squire, J., Chandran, B. D., Bowen, T., & Bale, S. D. 2021, ApJ, 918, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Marsch, E. 2018, Ann. Geophys., 36, 1607 [CrossRef] [Google Scholar]
- Marsch, E., & Mangeney, A. 1987, J. Geophys. Res. Space Phys., 92, 7363 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Sykora, J., De Pontieu, B., Hansteen, V. H., et al. 2017, Science, 356, 1269 [Google Scholar]
- Matsumoto, T., & Suzuki, T. K. 2012, ApJ, 749, 8 [Google Scholar]
- McComas, D., Ebert, R., Elliott, H., et al. 2008, Geophys. Res. Lett., 35, 18 [NASA ADS] [CrossRef] [Google Scholar]
- McManus, M. D., Bowen, T. A., Mallet, A., et al. 2020, ApJS, 246, 67 [Google Scholar]
- Moll, R., Cameron, R., & Schüssler, M. 2012, A&A, 541, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morton, R. J., Tiwari, A. K., Van Doorsselaere, T., & McLaughlin, J. A. 2021, ApJ, 923, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Mozer, F., Agapitov, O., Bale, S., et al. 2020, ApJS, 246, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Mumford, S., Fedun, V., & Erdélyi, R. 2015, ApJ, 799, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Murabito, M., Shetye, J., Stangalini, M., et al. 2020, A&A, 639, A59 [EDP Sciences] [Google Scholar]
- Murray, M. J., van Driel-Gesztelyi, L., & Baker, D. 2009, A&A, 494, 329 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nisenson, P., Van Ballegooijen, A., De Wijn, A., & Sütterlin, P. 2003, ApJ, 587, 458 [NASA ADS] [CrossRef] [Google Scholar]
- Nordlund, A. 1982, A&A, 107, 1 [Google Scholar]
- Nutto, C., Steiner, O., Schaffenberger, W., & Roth, M. 2012, A&A, 538, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owens, M. J., Lockwood, M., Barnard, L. A., & MacNeil, A. R. 2018, ApJ, 868, L14 [Google Scholar]
- Pagano, P., & De Moortel, I. 2017, A&A, 601, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Park, S.-H., Tsiropoula, G., Kontogiannis, I., et al. 2016, A&A, 586, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Parker, E. N. 1958, ApJ, 128, 664 [Google Scholar]
- Parnell, C. E., & De Moortel, I. 2012, Philos. Trans. R. Soc. A Math. Phys. Eng. Sci., 370, 3217 [NASA ADS] [CrossRef] [Google Scholar]
- Pascoe, D., Nakariakov, V., & Kupriyanova, E. 2014, A&A, 568, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pelekhata, M., Murawski, K., & Poedts, S. 2021, A&A, 652, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinto, R., & Brun, A. 2013, ApJ, 772, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Rappazzo, A., Velli, M., Dahlburg, R., & Einaudi, G. 2019, ApJ, 883, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Rempel, M. 2014, ApJ, 789, 132 [Google Scholar]
- Réville, V., Tenerani, A., & Velli, M. 2018, ApJ, 866, 38 [CrossRef] [Google Scholar]
- Réville, V., Velli, M., Panasenco, O., et al. 2020, ApJS, 246, 24 [Google Scholar]
- Rimmele, T. R., Warner, M., Keil, S. L., et al. 2020, Sol. Phys., 295, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Saikia, S. B., Jin, M., Johnstone, C., et al. 2020, A&A, 635, A178 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sakaue, T., & Shibata, K. 2021, ApJ, 919, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Schunker, H., & Cally, P. S. 2006, MNRAS, 372, 551 [Google Scholar]
- Schwadron, N., & McComas, D. 2021, ApJ, 909, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Liu, Y. D., Su, J., Qu, Z., & Tian, Z. 2017, ApJ, 851, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Shetye, J., Verwichte, E., Stangalini, M., et al. 2019, ApJ, 881, 83 [Google Scholar]
- Shoda, M., & Yokoyama, T. 2018a, ApJ, 854, 9 [CrossRef] [Google Scholar]
- Shoda, M., & Yokoyama, T. 2018a, ApJ, 859, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Shoda, M., Suzuki, T. K., Asgari-Targhi, M., & Yokoyama, T. 2019, ApJ, 880, L2 [Google Scholar]
- Shoda, M., Suzuki, T. K., Matt, S. P., et al. 2020, ApJ, 896, 123 [Google Scholar]
- Shoda, M., Chandran, B. D., & Cranmer, S. R. 2021, ApJ, 915, 52 [CrossRef] [Google Scholar]
- Silva, S. S., Fedun, V., Verth, G., Rempel, E. L., & Shelyag, S. 2020, ApJ, 898, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Silva, S. S., Murabito, M., Jafarzadeh, S., et al. 2022, ApJ, 927, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Simon, G., & Weiss, N. 1997, ApJ, 489, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Skartlien, R. 2000, ApJ, 536, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Snow, B., Fedun, V., Gent, F., Verth, G., & Erdélyi, R. 2018, ApJ, 857, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Sokolov, I. V., Van der Holst, B., Oran, R., et al. 2013, ApJ, 764, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., & Cook, C. J. 1957, Phys. Today, 10, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1981, A&A, 98, 155 [NASA ADS] [Google Scholar]
- Squire, J., Chandran, B. D., & Meyrand, R. 2020, ApJ, 891, L2 [NASA ADS] [CrossRef] [Google Scholar]
- Srivastava, A. K., Ballester, J. L., Cally, P. S., et al. 2021, J. Geophys. Res. Space Phys., 126, e2020JA029097 [Google Scholar]
- Stansby, D., Green, L. M., van Driel-Gesztelyi, L., & Horbury, T. S. 2021, Sol. Phys., 296, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Stein, R. F., & Nordlund, Å. 2000, Sol. Phys., 192, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Suzuki, T. K. 2011, Space Sci. Rev., 158, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Tiwari, A. K., Morton, R. J., Régnier, S., & McLaughlin, J. A. 2019, ApJ, 876, 106 [Google Scholar]
- Tu, C.-Y., Zhou, C., Marsch, E., et al. 2005, Science, 308, 519 [Google Scholar]
- Tziotziou, K., Tsiropoula, G., Kontogiannis, I., Scullion, E., & Doyle, J. 2018, A&A, 618, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ulrich, R. K. 1970, ApJ, 162, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Usmanov, A. V., Matthaeus, W. H., Breech, B. A., & Goldstein, M. L. 2011, ApJ, 727, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Van Ballegooijen, A., Asgari-Targhi, M., Cranmer, S., & DeLuca, E. 2011, ApJ, 736, 3 [NASA ADS] [CrossRef] [Google Scholar]
- van der Holst, B., Sokolov, I. V., Meng, X., et al. 2014, ApJ, 782, 81 [Google Scholar]
- Van Doorsselaere, T., Nakariakov, V. M., Li, B., & Antolin, P. 2020, Front. Astron. Space Sci., 6, 79 [CrossRef] [Google Scholar]
- Varela, J., Brun, A. S., Strugarek, A., et al. 2022, A&A, 659, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verdini, A., & Velli, M. 2007, ApJ, 662, 669 [Google Scholar]
- Verscharen, D., Klein, K. G., & Maruca, B. A. 2019, Liv. Rev. Sol. Phys., 16, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Viall, N. M., & Klimchuk, J. A. 2017, ApJ, 842, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Vigeesh, G., Fedun, V., Hasan, S., & Erdélyi, R. 2012, ApJ, 755, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Vigeesh, G., Jackiewicz, J., & Steiner, O. 2017, ApJ, 835, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [Google Scholar]
- Wang, Y.-M. 2020, ApJ, 904, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., & Yokoyama, T. 2020, ApJ, 891, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Yokoyama, T., & Iijima, H. 2021, ApJ, 916, L10 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer, S., & Steiner, O. 2014, PASJ, 66, 1088 [Google Scholar]
- Wedemeyer, S., Scullion, E., Steiner, O., de la Cruz Rodriguez, J., & van der Voort, L. H. M. R. 2013, J. Phys. Conf. Ser., 440 [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 507, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., Scullion, E., Steiner, O., et al. 2012, Nature, 486, 505 [Google Scholar]
- Williams, T., Walsh, R. W., Winebarger, A. R., et al. 2020, ApJ, 892, 134 [Google Scholar]
- Wilson, P. 1977, ApJ, 214, 917 [NASA ADS] [CrossRef] [Google Scholar]
- Wójcik, D., Kuźma, B., Murawski, K., & Srivastava, A. 2019, ApJ, 884, 127 [CrossRef] [Google Scholar]
- Wyper, P., DeVore, C., & Antiochos, S. 2018, ApJ, 852, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, N., Cameron, R. H., & Solanki, S. K. 2020, ApJ, 894, L17 [Google Scholar]
- Yadav, N., Cameron, R. H., & Solanki, S. K. 2021, A&A, 652, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Yang, L., Peter, H., He, J., et al. 2017, ApJ, 852, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Zank, G., Nakanotani, M., Zhao, L.-L., Adhikari, L., & Kasper, J. 2020, ApJ, 903, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zwaan, C. 1987, ARA&A, 25, 83 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Developing complexity from the public snapshots
In this work, the ch024031_by200bz005 simulation is continued from a publicly available snapshot in order to allow magnetic complexity to further develop in the low corona. As twisted coronal structures are primarily generated by the advection of MCs around the intergranular lanes, they take time to form in the domain. Firstly, the convection must expel the photospheric field into the intergranular lanes, forming concentrations in the magnetic field of sufficient strength to be braided together and produce long-lasting structure in the low corona. Secondly, as the MCs are shuffled around the intergranular lanes at a speed of ∼5 Mm/hour, this sets a characteristic timescale for this kind of structure to develop. As such, a few hours are required for the 24 × 24 Mm2 domain to be sufficiently traversed by MCs, and reach a quasi-steady state. This is reflected in the temperature structure in the simulated atmosphere.
Figure A.1 shows four snapshots from the ch024031_by200bz005 simulation, each taken one hour apart. These snapshots span from the start of the publicly available dataset, to the end of the dataset used in the study. During the course of the public dataset the temperature of the low corona is observed to warm substantially from around 0.5 Mk to a more reasonable 0.9-1 Mk. The coronal temperature evolves slowly during this period as larger and larger Poynting fluxes are transmitted through the domain by braided magnetic field lines. The coronal magnetic field at the start of the computation strongly resembles the initial vertical magnetic field added to the Bifrost simulation. After an hour of computation, the simulation domain contains many twisted/braided magnetic field structures, and the magnetic field in the photosphere is more spatially concentrated. The onset of widespread SEs in the simulation domain starts around t = 4, 000 s. As noted by Silva et al. (2022), who analysed a snapshot of ch024031_by200bz005 at t = 4, 610 s. During the hour of simulation time investigated in this work (t = 9, 580 − 13, 180 s), the temperature structure in the domain remains quasi-stationary (as shown in Figure 3). However some relaxation of the simulation is still expected, given the thermal relaxation timescale of the plasma in the computational domain.
 |
Fig. A.1. Comparison of the 3D magnetic field and temperature structure in the ch024031_by200bz005 simulation domain in the publicly available dataset (t = 2, 490 − 8, 670 s) and that used in this study (t = 9, 580 − 13, 180 s). The four snapshots are each taken one hour apart (times are given with respect to the start of the hour used in this study). The magnetic field lines are coloured by plasma temperature. The photosphere is indicated in each case, and coloured by the vertical flow speed. |
Appendix B: Reconstructed frequency-filtered velocity components
From the Fourier transformations Fi of the velocity components vz and vxy in Section 3.3, it is possible to reconstruct the strength of each component in selected wavenumber/frequency ranges by performing the inverse Fourier transform and using only the Fourier coefficients from those chosen frequencies. For the same four heights shown in Figures 11 and 12, the flow speeds in three wavenumber ranges: less than 0.5 cycles/Mm, 0.5 - 3 cycles/Mm and greater than 3 cycles/Mm, along with four frequency ranges: less than 2.5 mHz, 2.5 - 5 mHz, 5 - 10 mHz, and greater than 10 mHz, are recovered. The reconstructed velocity components at t = 40 min are displayed in Figures B.1, B.2, B.3 and B.4. For the horizontal velocity, the colour displays the magnitude of the flow speed and the arrows indicate the flow direction. In the upper-convection zone, the flow is dominated by the slowly evolving convective motions (as shown in Figures 11 and 12). At the photosphere, these slow vertical convective motions become the recognisable granulation pattern in the lowest frequency range, and the Mm-scale wavelength range. The circulation of plasma from the up-welling of hot material in the centre of the granule to the cooler down-flow lanes generates a low frequency horizontal flow (including vortical flows around complex intersections). The forcing from convective granules in the photosphere generates wave-trains, that are visible in the two middle frequency ranges of vz in Fig. B.2 at Z = 0 Mm. These waves experience less resistance to their propagation in the intergranular lanes. They may also gain energy from the box-modes that resonate inside the convection zone. As the highest frequency waves are mostly confined to the intergranular lanes at the photosphere. High frequency fluctuations can influence the plasma above by interacting with the MCs that also reside in the intergranular lanes, and extend up into the low corona.
 |
Fig. B.1. Vertical velocity reconstructed at t = 40 min by filtering the wavenumbers used in the inverse Fourier transform (the panels on the left show a slice through the simulation domain without any filtering). |
 |
Fig. B.2. Vertical velocity reconstructed at t = 40 min by filtering the frequencies used in the inverse Fourier transform. |
 |
Fig. B.3. Same as Figure B.1, but now for the magnitude of the horizontal flow speed |vxy|. Arrows indicate the direction of the flow in the x-y plane. |
In the low corona, the low frequency/wavenumber motions are dominated by stirring from the magnetic funnels and SEs. The vertical components shows the hot rising material associated with the heating from twisted magnetic field structures, and cool sinking material elsewhere. The horizontal flow is organised into clear swirls which follow the twisted magnetic field structures. The higher frequency components have increased in amplitude through the chromosphere/transition region. Theses frequencies are dominated by torsional oscillations inside the twisted magnetic field structures. Towards the top of the domain, the strength of the horizontal component in the two middle frequency ranges begins to dissipate (also visible in Fig. 12), which is not observed for the highest frequencies. Comparing the PSD at 4 Mm and 12 Mm in Figures 11 and 12, there appears to be little change in the low corona for vertical fluctuations. Waves mostly propagate towards the top of the domain and escape through the open boundary condition. The dominant frequencies in the low corona for both the velocity components correspond to the vertical convective motions, and the box-modes.
All Figures
 |
Fig. 1. 3D visualisation of ch024031_by200bz005 at t = 40 min. The computational domain spans 24 Mm × 24 Mm × 17 Mm. Left: magnetic field lines are coloured by temperature from blue in the upper-convection zone (≈5800 K), to light blue in the temperature minimum region (≈3200 K), and finally yellow in the low corona (≈1 MK). Right: vertical magnetic field strength at the photosphere (Z = 0 Mm). |
| In the text | |
 |
Fig. 2. Snapshot of ch024031_by200bz005 at t = 40 min. Top: temperature structure in a vertical cut through the computational domain at Y = 19 Mm (indicated with a dashed line in the lower panel). The plasma β equal to one surface is highlighted with a thin dashed line. Bottom: vertical velocity at the photosphere (Z = 0 Mm). The strongest magnetic field enhancements are highlighted by polarity (purple = negative and green = positive). The field at the photosphere is mostly negative and contained in the intergranular lanes. Data are shown from the same snapshot as Fig. 2. |
| In the text | |
 |
Fig. 3. Average density (top), temperature (middle), plasma beta, and the sound/Alfvén speeds (bottom) profiles in the simulation domain for each 10 s snapshot during the hour under investigation. Variations in the density above the chromosphere occur due to the launching of jets. Variation in the maximum temperature results from the varying degrees of twisted magnetic structures that facilitate vertical energy transport. |
| In the text | |
 |
Fig. 4. Time-distance plots of a vertical pencil in the simulation domain at X = 12 Mm and Y = 12 Mm. Quantities shown are; the vertical flow velocity vz, the normalised vertical magnetic field Bz/|B|, the ratio of the Alfvén speed to the sound speed vA/cs, the plasma temperature T, the density fluctation with respect to the average of the horizontal domain δρ/⟨ρ⟩xy, and the vertical Poynting flux Sz. |
| In the text | |
 |
Fig. 5. Time-evolution of Magnetic Concentrations (MCs) and strong vertical Poynting fluxes. Left: location of MCs at the photosphere (Z = 0 Mm) during the hour of simulation time. Right: location of strong vertical Poynting fluxes in the low corona (Z = 12 Mm), associated with the braiding and twisting of the magnetic field by convective motions, and the release of energy in Swirling Events (SEs). The spatial distribution of the MCs and Swirls at t = 40 min are highlighted in black. |
| In the text | |
 |
Fig. 6. Horizontal cuts of the vorticity magnitude |∇×v|z at Z = 0 Mm and Z = 12 Mm, for t = 40 min. Contours of the kinetic helicity v ⋅ (∇×v) (red) and current helicity B/(μ0ρ)⋅(∇ × B) (blue) at a value of 100 m s−2 are plotted with the vorticity in the Z = 0 Mm panel. The zoomed inset within the first column (Z = 0 Mm) is 4 Mm × 4 Mm, centred on X = 7 Mm and Y = 19 Mm. The same patch of the domain is discussed again in Fig. 7. |
| In the text | |
 |
Fig. 7. Snapshots during a ∼30 min period that display the merging of two MCs within the intersection of multiple granules, and the subsequent excitation of a SE. A subsection of the computational domain is shown that extends from the bottom boundary up to 6 Mm above the photosphere, with a horizontal extent of 4 Mm × 4 Mm (centred on X = 7 Mm and Y = 19 Mm). A top-down view of the domain is shown above each snapshot. The same cut in the domain is highlighted in Fig. 6. The upper-convection zone is coloured by vertical velocity (red is rising, blue is falling material). Selected magnetic field lines are coloured by temperature as in Fig. 1. The flow velocity in the chromosphere is indicated with arrows, the size and colour of which depend on the magnitude of the local flow speed. Cartoon annotations indicate the direction of advection for the MCs (green) and the important/prevailing flow patterns in the photosphere (magenta), chromosphere (white), and low corona (red). |
| In the text | |
 |
Fig. 8. 3D rendering of the twisted magnetic field structures in the simulation domain at t = 40 min, identified with large values of Poynting flux (|Sz|> 2 kWm−2) at Z = 6 Mm. Top left: as viewed from above. Bottom left: The location of the magnetic field footpoints at the photosphere (Z = 0 Mm) are highlighted with green markers. |
| In the text | |
 |
Fig. 9. 3D visualisation of a subset of the braided coronal magnetic field, at t = 40 min. Magnetic field lines are traced from four photospheric sources (seed points are initiated within 0.25 Mm of the given coordinates). Field lines are coloured by their source location. Streamlines of the velocity field are initiated at the photospheric sources, and are coloured by vertical flow velocity vz. The lower panel shows the same visualisation, now viewed from above. |
| In the text | |
 |
Fig. 10. Comparison of the field shaking Sz, fs and flux emergence Sz, fe terms of the vertical Poynting flux in the simulation domain, at t = 40 min. Left: average total Poynting flux versus height in black, with the field shaking and flux emergence terms in red and blue respectively. Due to the range of scale, the y-axis is limited to a few kW/m2. The floating values indicate the approximate value of each term in the upper-convection zone. The average contribution of the flux emergence term to the vertical Poynting flux versus height is also shown. Right: this ratio is instead vertically averaged above 6 Mm (i.e. at the top of the simulation domain), again for t = 40 min. This highlights the network of magnetic swirls/funnels that exist throughout the domain. |
| In the text | |
 |
Fig. 11. Power Spectral Density (PSD) in wavenumber-frequency space for the vertical flow speed vz, taken at various heights in the computational domain; Z = −2 Mm (upper-convection zone), Z = 0 Mm (photosphere), Z = 4 Mm (above the chromosphere), and Z = 12 Mm (low corona). For the photospheric slice, the typical acoustic-gravity wave cut-off frequencies are indicated, given the average pressure, density, and magnetic field strength. Classically, waves in the shaded region are evanescent (under the assumption of a stably stratified atmosphere). For completeness the lamb-mode (ω = csk⊥) and f-mode ( |
| In the text | |
 |
Fig. 12. Same as Fig. 11, but now for the horizontal flow speed vxy. Enhancements in the horizontal velocity PSD at the box-mode frequencies/wavenumbers are highlighted. |
| In the text | |
 |
Fig. 13. Wavenumber power spectrum of the vertical (left) and horizontal (right) components of velocity, versus height (in both cases normalised by the maximum horizontal PS at each height). The PS of the vertical and horizontal flows become almost identical around Z = 1–1.5 Mm likely as a result of mode-conversion and/or magnetosonic shocks at the vA/cs = 1 surface, which allows for wave-energy to pass between longitudinal and transverse oscillations. The horizontally averaged velocity amplitude in overploted with a solid white line for each component. The amplitudes of the filtered velocity components from three wavenumber ranges, are similarly over-plotted with coloured lines. The time-averaged sound and Alfvén speeds versus height are also shown with magenta dotted and dashed lines, respectively. |
| In the text | |
 |
Fig. 14. Same as Fig. 13, but now showing the frequency power spectrum versus height. Peaks in the PS can be found at 5–10 mHz which correspond to the box-modes frequencies (see Fig. 11). In the vertical flow speed, the box-modes are able to survive into the low corona by travelling along the network of magnetic funnel structures. A similar, but less pronounced, enhancement in the PS is visible in the horizontal flow speed, which moves to progressively higher frequencies with height. |
| In the text | |
 |
Fig. 15. Longitudinal (acoustic) wave-energy flux at t = 40 min for a vertical cut through the domain at Y = 19 Mm, and horizontal cut at Z = 2 Mm. Fast and slow magnetosonic shocks, which are identified through a threshold on ∇ ⋅ v, are indicated in red and green colours, respectively. For the horizontal slice, shocks are highlighted at a range of heights throughout the chromosphere (not just from Z = 2 Mm). The plasma β equal to one surface is highlighted with a thin dashed black line. |
| In the text | |
 |
Fig. 16. Same as Fig. 15, but now for the transverse (Alfvén) waves. |
| In the text | |
 |
Fig. 17. 3D visualisation of the Flong and Ftran wave-energy fluxes at t = 40 min. The magnetic field structure previously presented in Fig. 1, is now shown in grey. Semi-opaque isosurfaces highlight the wave-energy fluxes at 3 kWm−2 in each reconstructed frequency range; less than 2.5 mHz (red), between 2.5 mHz and 5 mHz (orange), between 5 mHz and 10 mHz (green), and greater than 10 mHz (cyan). The white opaque surface represents plasma β equal to one. |
| In the text | |
 |
Fig. 18. Frequency power spectrum of the longitudinal (acoustic) wave-energy flux Flong (left) and the transverse (Alfvén) wave-energy flux Ftran (right), versus height (in both cases normalised by the maximum transverse PS at each height). Coloured lines are over-plotted showing the average energy flux versus height for four frequency ranges and their total. Grey lines show the other wave flux averages for comparison. The upper-convection zone is a source of both longitudinal and transverse waves, with the longitudinal waves having an energy flux that is 2–3 orders of magnitude larger than the transverse waves. However, the longitudinal wave-energy flux decays exponentially with height. Such that in the low corona, the relative balance of energies is reversed. |
| In the text | |
 |
Fig. 19. Resulting conditions near the top of the simulation domain (i.e. at the base of the solar wind). Top left: location of the open magnetic field lines at the photosphere (traced down from Z = 12 Mm), with the convection pattern shown bellow. Bottom left: open magnetic field at Z = 12 Mm coloured by their photospheric field strength. Top middle and right: density and temperature variation with respect to the horizontal average at Z = 12 Mm. Bottom middle: mass flux at Z = 12 Mm. Bottom right: transverse wave-energy-flux at Z = 12 Mm. Each panel is taken at t = 40 min. The contrast in density, temperature and upward wave-energy is evident, resulting from the different MC field strengths at the base of the braided magnetic field structures. |
| In the text | |
 |
Fig. 20. Power spectra versus wavevector and frequency at various heights in the computational domain for the horizontal flow speed, magnetic field strength, and Elsasser variables. The power spectra from the simulation of Shoda et al. (2021) at a height of Z = 35 Mm are over-plotted for comparison with dashed blue lines. |
| In the text | |
 |
Fig. A.1. Comparison of the 3D magnetic field and temperature structure in the ch024031_by200bz005 simulation domain in the publicly available dataset (t = 2, 490 − 8, 670 s) and that used in this study (t = 9, 580 − 13, 180 s). The four snapshots are each taken one hour apart (times are given with respect to the start of the hour used in this study). The magnetic field lines are coloured by plasma temperature. The photosphere is indicated in each case, and coloured by the vertical flow speed. |
| In the text | |
 |
Fig. B.1. Vertical velocity reconstructed at t = 40 min by filtering the wavenumbers used in the inverse Fourier transform (the panels on the left show a slice through the simulation domain without any filtering). |
| In the text | |
 |
Fig. B.2. Vertical velocity reconstructed at t = 40 min by filtering the frequencies used in the inverse Fourier transform. |
| In the text | |
 |
Fig. B.3. Same as Figure B.1, but now for the magnitude of the horizontal flow speed |vxy|. Arrows indicate the direction of the flow in the x-y plane. |
| In the text | |
 |
Fig. B.4. Same as Figure B.2, but now for the magnitude of the horizontal flow speed |vxy|. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



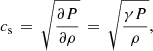
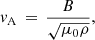
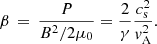
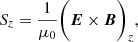
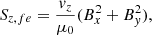
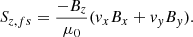
![$$ \begin{aligned} S_{z,\eta }= \frac{\eta }{\mu _0^2}\bigg [\bigg (\frac{\partial B_z}{\partial { y}}-\frac{\partial B_{ y}}{\partial z}\bigg )B_x+\bigg (\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\bigg )B_{ y}\bigg ]. \end{aligned} $$](/articles/aa/full_html/2022/09/aa43947-22/aa43947-22-eq8.gif)